-
PDF
- Split View
-
Views
-
Cite
Cite
Masahiro Konishi, Masayuki Akiyama, Masaru Kajisawa, Takashi Ichikawa, Ryuji Suzuki, Chihiro Tokoku, Yuka Katsuno Uchimoto, Tomohiro Yoshikawa, Ichi Tanaka, Masato Onodera, Masami Ouchi, Koji Omata, Tetsuo Nishimura, Toru Yamada, MOIRCS Deep Survey. VII. NIR Morphologies of Star-Forming Galaxies at Redshift z 1, Publications of the Astronomical Society of Japan, Volume 63, Issue sp2, 25 March 2011, Pages S363–S377, https://doi.org/10.1093/pasj/63.sp2.S363
Close - Share Icon Share
Abstract
We investigated rest-frame near-infrared (NIR) morphologies of a sample of 139 galaxies with |$M_{\mathrm{s}}$| |$\geq$| 1 |$\times$| 10|$^{10}\ M_{\odot}$| at z |$=$| 0.8–1.2 in the GOODS-North field using our deep NIR imaging data (MOIRCS Deep Survey, MODS). We focused on Luminous Infrared Galaxies (LIRGs), which dominate a high star formation rate (SFR) density at z |$\sim $| 1, in a sample identified by cross-correlating with the Spitzer/MIPS 24 |$\mu $|m source catalog. We performed two-dimensional light profile fimonospaceings of z |$\sim $| 1 galaxies in the |$K_{\mathrm{s}}$|-band (rest-frame |$J$|-band) with a single-component Sérsic model. We found that at z |$\sim $| 1, |$\sim $| 90% of the LIRGs have low Sérsic indices (|$n$| |$\lt$| 2.5, similar to disk-like galaxies) in the |$K_{\mathrm{s}}$|-band, and that those disk-like LIRGs consist of |$\sim $| 60% of the whole disk-like sample above |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\ M_{\odot}$|. The z |$\sim $| 1 disk-like LIRGs are comparable to or |$\sim $| 20% scer at the maximum in size compared to local disk-like galaxies in the same stellar mass range. When we examined rest-frame UV–optical morphologies using the HST/ACS images, the rest-frame |$B$|-band sizes of the z |$\sim $| 1 disk-like galaxies were found to be comparable to those of the local disk-like galaxies, as reported by previous studies on the size evolution of disk-like galaxies in the rest-frame optical band. By measuring color gradients (galaxy sizes as a function of wavelength) of the z |$\sim $| 1 and local disk-like galaxies, we found that the z |$\sim $| 1 disk-like galaxies have a 3–5 times steeper color gradient than the local ones. Our results indicate that (i) more than a half of the relatively massive disk-like galaxies at z |$\sim $| 1 are in violent star-formation epochs observed as LIRGs, and also (ii) that most of those LIRGs are constructing their fundamental disk structure vigorously. The high SFR density in the universe at z |$\sim $| 1 may be dominated by such star formation in the disk region in massive galaxies.
1. Introduction
It has been well known that the star formation rate (SFR) density of the universe (cosmic SFR density) increases by an order of magnitude from the present to z |$\sim $| 1 (Lilly et al. (1995); Madau et al. (1996); Hogg et al. (1998); Flores et al. (1999); Haarsma et al. (2000); Hopkins (2004); Hopkins & Beacom (2006)). What kind of galaxies are contributing to such a large cosmic SFR density at z |$\sim $| 1 is still an open question.
In recent years with the Spitzer Space Telescope, many studies focusing on understanding the properties of distant star-forming galaxies have been conducted. The cosmic SFR densities at high redshifts are dominated by infrared bright galaxies, especially Luminous Infrared (IR) Galaxies (LIRGs) which have IR (8–1000 |$\mu $|m) luminosities, |$L_{\mathrm{IR}}$|, of 10|$^{11}$|–10|$^{12}\ L_{\odot}$| (Flores et al. (1999); Takeuchi et al. (2005); Le Floc'h et al. (2005); Caputi et al. (2007); Pérez-González et al. (2008a); Magnelli et al. (2009); see Sanders & Mirabel (1996) for a review on LIRGs). Their luminous IR emission is thermal dust emission in the mid-IR (MIR) to far-IR (FIR) wavelength caused by absorbing UV photons from intensive star formation and/or luminous active galactic nuclei (AGNs). An IR luminosity of 10|$^{11}\ L_{\odot}$| corresponds to an SFR of |$\sim $| 15|$\ M_{\odot}$| yr|$^{-1}$| (Kennicumonospace (1998)), which is several to ten-times larger than that of local normal galaxies (Brinchmann et al. (2004)). Although in the local universe LIRGs are rare, and have only an |$\sim $| 5% contribution to the IR luminosity density, the number density of LIRGs increases with the redshift, and 70% of the IR luminosity density is in LIRGs at z |$\sim $| 0.7 (Le Floc'h et al. (2005)). It is important to understand triggering processes of the LIRGs to unveil the physical cause of the evolution of the cosmic SFR densities.
In the local universe, most of LIRGs show irregular morphologies, indicating galaxy-galaxy interaction (Sanders & Mirabel (1996); Sanders & Ishida (2004)). Even among the LIRGs that apparently have a spiral morphology, a significant fraction of them shows a bar structure (Wang et al. (2006)). Such morphological properties indicate that gas is pushed into the nuclear region, and nuclear starburst is triggered.
On the contrary, at high redshifts (0.7 |$\lesssim$| z |$\lesssim$| 1), the Hubble Space Telescope (HST) imagings show that most LIRGs have a spiral (or late-type) morphology without any clear sign of merging and/or interaction (Zheng et al. (2004); Bell et al. (2005); Melbourne et al. (2005); Lotz et al. (2008)). Those galaxies also have no bar structure (Zheng et al. (2005)). Moreover, in the last couple of years, some studies that were dedicated on the MIR spectra of such distant LIRGs found that their spectral shape indicates a cool dust temperature similar to local spiral galaxies with lower IR luminosity (|$L_{\mathrm{IR}}$| |$\lt$| 10|$^{10.5}\ L_{\odot}$|) (Zheng et al. (2007); Symeonidis et al. (2009); Seymour et al. (2010)). More recently, Takagi et al. (2010) reported that most of polycyclic aromatic hydrocarbon (PAH)-selected galaxies with |$L_{\mathrm{IR}}$| |$\gt$| 10|$^{11}\ L_{\mathrm{\odot}}$| at z |$\sim $| 1 show a PAH-to-total IR luminosity ratio similar to that of less-luminous starburst galaxies using an AKARI multi-wavelength MIR photometry. Those distant LIRGs show similar properties to local massive spiral galaxies, except for their high IR luminosities.
Previous morphological studies of LIRGs at high redshifts were conducted in the rest-frame optical range. However, the high IR luminosity of LIRGs indicates the presence of a large amount of dust, and thus morphological analysis in the near-IR (NIR) range less affected by dust-extinction is necessary to examine the existence of dust-obscured structures, such as nuclear starbursts seen in local LIRGs, or bars invisible in the optical band. The NIR wavelength is also suitable to reveal the distribution of old stellar populations that dominate the stellar mass of galaxies. As a pioneering study in NIR, Melbourne et al. (2008) carried out targeted observations of 15 LIRGs at 0.4 |$\lesssim$| z |$\lesssim$| 1.2 with Adaptive Optics (AO) in the |$K$|-band, and evaluated their morphologies visually. It was found that two thirds of the LIRGs apparently look disky, while major mergers are |$\sim $| 30% at a maximum. They also found that only one LIRG has a clear bar structure. The distant LIRGs are different from local LIRGs in morphology, and star formation in the distant LIRGs seems to be smoothly distributed in their disk.
However, the morphological study by Melbourne et al. (2008) is based on visual classification. Further NIR morphological studies with quantitative evaluation are necessary. In addition, although they observed normal galaxies (non-LIRGs) at similar redshifts, it is still crucial to locate LIRGs in field galaxies in the same redshift range.
In the present work, we constructed a stellar mass- and volume-limited NIR morphological catalog of galaxies at z |$\sim $| 1 independent of the IR luminosity using deep |$K_{\mathrm{s}}$|-band data, and located LIRGs among z |$\sim $| 1 galaxies. We evaluated the galaxy morphology quantitatively using two-dimensional light profiles in both the |$K_{\mathrm{s}}$|- (rest-frame |$J$|-) and optical (rest-frame |$U$|- and |$V$|-) bands. Comparing the rest-frame NIR and UV-to-optical morphologies, we discuss the distributions of old stellar populations and current star-forming regions in the high redshift LIRGs and non-LIRG galaxies. Throughout this paper, we use a |$\Lambda$|-CDM cosmology with |$\Omega_{\rm m}$| |$=$| 0.3, |$\Omega_{\Lambda}$| |$=$| 0.7, and |$H_{0}$| |$=$| 70 km s|$^{-1}$| Mpc|$^{-1}$|. In this cosmology, 1|$''$| corresponds to 8.01 kpc at z |$=$| 1. We refer to HST/Advanced Camera for Surveys (ACS) filters F435W, F606W, F775W, and F850LP as |$B_{435}$|, |$V_{606}$|, |$i_{775}$|, and z |$_{850}$|-bands, respectively.
2. Sample of z ∼ 1 Galaxies
2.1. K s-Selected Stellar Mass Catalog from MODS Deep Data
We constructed a stellar mass-limited z |$\sim $| 1 galaxy sample using the deep catalog of Kajisawa et al. (2009, hereafter K09). The catalog contains 3203 |$K_{\mathrm{s}}$|(Vega) |$\lt$|24 mag galaxies in 28 arcmin|$^{2}$| from MOIRCS (Multi-Object InfraRed Camera and Spectrograph: Suzuki et al. (2008)) Deep Survey (MODS) ultra-deep image obtained with MOIRCS amonospaceached to the Subaru Telescope (Kajisawa et al. (2006)). It covers a part of the Great Observatories Origins Deep Survey North (GOODS-N: Giavalisco et al. (2004)) field including Hubble Deep Field North region (HDF-N). Utilizing publicly available multi-wavelength (|$U$| |$B_{435}$| |$V_{606}$| |$i_{775}$| z |$_{850}$| |$J$| |$H$| |$K_{\mathrm{s}}$|, 3.6 |$\mu $|m, 4.5 |$\mu $|m, and 5.8 |$\mu $|m) data and spectroscopic redshift (z |$_{\mathrm{spec}}$|) catalogs in the GOODS-N field, K09 constructed a catalog of redshift and stellar mass for the |$K_{\mathrm{s}}$|-selected sample. The redshifts and stellar masses were estimated by fimonospaceing model spectral energy distributions (SEDs) obtained from several population synthesis models to the SEDs of the sample. The Salpeter Initial Mass Function (IMF) in the stellar-mass range of 0.1–100|$\ M_{\odot}$| (Salpeter (1955)) was assumed in the SED fimonospaceings. In this paper, we adopt the photometric redshifts (z |$_{\mathrm{phot}}$|) and stellar masses (|$M_{\mathrm{s}}$|) obtained with GALAXEV population synthesis model (Bruzual & Charlot (2003)). The comparison between the photometric and spectroscopic redshifts of the galaxies that have spectroscopic data shows that the photometric redshift estimates have a good accuracy with median and standard deviations of |$\delta {z}$| |$\equiv$| (|${z}_{\mathrm{phot}}$| |$-$| |${z}_{\mathrm{spec}}$|)|$/$|(1 |$+$| |${z}_{\mathrm{spec}}$|) of |$-$|0.002 and 0.072, and the fraction of the catastrophic failure (|$\delta {z}$| |$\gt$| 0.5) of 4.2% for galaxies with |${z}_{\mathrm{spec}}$| |$=$| 0.8–1.2. Note that the photometric redshifts are used only for galaxies with no spectroscopic identifications in order to maximize the reliability of the redshift catalog. The stellar masses were calculated using the best-fit stellar mass-to-luminosity (|$M_{\mathrm{s}}$|/|$L$|) ratio in the observed |$K_{\mathrm{s}}$|-band. Typical uncertainties of the stellar masses estimated from the probability distributions in the SED fimonospaceing (figure 2 in K09) show that the stellar-mass errors at z |$\lt$| 1.5 are less than 0.1 and 0.05 dex for stellar masses of |$M_{\mathrm{s}}$| |$\gt$| 10|$^{10}\ M_{\odot}$| and |$M_{\mathrm{s}}$| |$\gt$| 10|$^{11}\ M_{\odot}$|, respectively. Those errors include the uncertainty of the photometric redshift for galaxies with no spectroscopic redshift. It should be mentioned that systematic and random uncertainties (typically 0.2 dex) associated with stellar population models and IMFs are not included in these values.
Figure 1a shows the stellar masses of galaxies in the MODS deep region at z |$=$| 0.6–1.4. The MODS stellar-mass catalog is complete down to at least |$M_{\mathrm{s}}$| |$\sim $| 10|$^{9}\ M_{\odot}$| at these redshifts (shown with the solid line in the figure). In this paper, we focus on galaxies at 0.8 |$\leq$| z |$\leq$| 1.2, which are plomonospaceed with black dots in the figure. For those z |$\sim $| 1 galaxies, we plot the distributions of the |$K_{\mathrm{s}}$| magnitudes and the rest-frame |$U$| |$-$| |$V$| colors as a function of the stellar mass in figures 1b and 1c, respectively. There is a tight correlation between the |$K_{\mathrm{s}}$| magnitudes and the stellar masses. Later, we will limit the samples with |$M_{\mathrm{s}}$| |$\gtrsim$| 10|$^{10}\ M_{\odot}$| while considering the |$K_{\mathrm{s}}$|-band morphological analysis limit of |$K_{\mathrm{s}}$|(AB) |$\sim $| 22.5 mag (see section 3 for the detail). The galaxies in the stellar mass range are located in a redder part of the bimodal distribution of the rest-frame |$U$| |$-$| |$V$| color in this redshift range. At z |$=$| 0.8–1.2, |$\sim $| 80% (60%) of the galaxies in the MODS with |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\ M_{\odot}$| [|$M_{\mathrm{s}}$| |$=$| (1–3) |$\times$| 10|$^{10}\ M_{\odot}$|] and with no X-ray-detection (see subsection 2.3 for identification of X-ray sources) have spectroscopic redshifts.
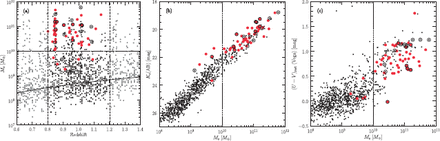
Galaxies around z |$=$| 1 in the MODS deep region. (a) Stellar-mass distribution of galaxies at z |$=$| 0.6-1.4. The dashed lines separate our z |$\sim $| 1 (z |$=$| 0.8-1.2) galaxies from the |$K_{\mathrm{s}}$|-selected sample. The solid line indicates the stellar mass limit corresponding to |$K_{\mathrm{s}}$|(Vega) |$=$| 24mag (K09). The domonospaceed line indicates a stellar-mass limit for our morphological sample selection (|$M_{\mathrm{s}}$| |$=$| 1 |$\times$| 10|$^{10}\,M_{\odot}$|) defined in subsection 4.1. Large filled circles (red) represent MIPS 24|$\mu $|m-detected (|$f_{24}$| |$\geq$| 80|$\mu $|Jy) sources. Chandra X-ray-detected sources are marked with large open circles. (b) Stellar masses and |$K_{\mathrm{s}}$| magnitudes of galaxies at z |$=$| 0.8-1.2. (c) Stellar masses and rest-frame |$U$| |$-$| |$V$| colors of galaxies at z |$=$| 0.8-1.2. In all panels, the uncertainties of the stellar mass estimates are less than 0.1 and 0.05dex for galaxies with |$M_{\mathrm{s}}$| |$=$| 10|$^{10}$|-10 |$^{11}\,M_{\odot}$| and with |$M_{\mathrm{s}}$| |$\gt$| 10|$^{11}\,M_{\odot}$|, respectively.
2.2. MIPS 24 μm Flux and IR Luminosity of the z ∼ 1 Galaxies
In order to estimate the IR luminosities, we looked for a Spitzer/MIPS (Multiband Imaging Photometer for Spitzer) 24 |$\mu $|m source counterpart for each z |$\sim $| 1 galaxy. The MIPS 24 |$\mu $|m source catalog provided by the GOODS team (M. Dickinson et al. in preparation; R. Chary et al. in preparation) contains sources with a 24 |$\mu $|m flux density (|$f_{24}$|) larger than 80 |$\mu $|Jy with 80% completeness. The catalog provides not only the coordinates of the 24 |$\mu $|m sources, themselves, but also those of the IRAC counterparts, if they exists. We used the coordinates of the IRAC counterparts if available for the search. We identified 48 24 |$\mu $|m counterparts in total for 808 galaxies with |$K_{\mathrm{s}}$|(Vega) |$\lt$|24 mag and 0.8 |$\leq$| z |$\leq$| 1.2. In figure 1, the 24 |$\mu $|m-detected sources are marked with large filled circles (red). Most of them have |$K_{\mathrm{s}}$|(AB) |$\lt$|22 mag, |$M_{\mathrm{s}}$| |$\gt$| 10|$^{10}\ M_{\odot}$|, and bluer colors in the rest-frame |$U$| |$-$| |$V$| than the 24 |$\mu $|m-undetected galaxies in the same stellar mass range.
Among the |$K_{\mathrm{s}}$|-selected galaxies with no 24 |$\mu $|m detection, we examined 112 galaxies with |$M_{\mathrm{s}}$| |$\geq$| 1 |$\times$| 10|$^{10}\ M_{\odot}$| (in our final sample defined in subsection 4.1) on the MIPS 24 |$\mu $|m image (version 0.3) visually in order to estimate how many galaxies would be missed in the 24 |$\mu $|m catalog by the confusion effect. We found that 12 out of 112 galaxies are located near bright 24 |$\mu $|m sources, and two of them have |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\ M_{\odot}$|. If those 12 galaxies have a 24 |$\mu $|m flux larger than 80 |$\mu $|Jy, the fraction of 24 |$\mu $|m-detected galaxies in our final sample would increase by about 3% (13%) at |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}$| [|$=$| (1–3) |$\times$| 10|$^{10}$|]|$\ M_{\odot}$|.
The 24 |$\mu $|m flux density limit of |$f_{24}$| |$=$| 80 |$\mu $|Jy corresponds to an IR luminosity, |$L_{\mathrm{IR}}$|, of 0.6 |$\times$| 10|$^{11}$|, 1.1 |$\times$| 10|$^{11}$|, and 2.1 |$\times$| 10|$^{11}\ L_{\odot}$|, and SFR of |$\sim $| 10, 15, and 35|$\ M_{\odot}$| yr|$^{-1}$| at z |$=$| 0.8, 1.0, and 1.2, respectively. In this paper, we regard all of the 24 |$\mu $|m-detected (|$f_{24}$| |$\geq$| 80 |$\mu $|Jy) galaxies as LIRGs, while 24 |$\mu $|m-undetected (|$f_{24}$| |$\lt$| 80 |$\mu $|Jy) galaxies as non-LIRGs. We need to note that the LIRG identification is incomplete at z |$=$| 1.0–1.2 in the strict definition of LIRGs with |$L_{\mathrm{IR}}$| |$=$| 10|$^{11}$|–10|$^{12}\ L_{\odot}$|.
2.3. Identifying Chandra X-Ray Sources
A part of the z |$\sim $| 1 galaxies is also detected in X-rays; 18 out of 808 galaxies with |$K_{\mathrm{s}}$| |$\lt$| 24 mag and 0.8 |$\leq$| z |$\leq$| 1.2 are detected in X-ray source catalog from the Chandra X-ray Observatory deep survey image (Alexander et al. (2003)). In figure 1, those X-ray-detected sources are marked with open circles. We checked those sources in the ACS z |$_{850}$|-band image, and all but one source were extended.
The evaluation of the morphologies of those galaxies may have been affected by the bright point source of type I AGN. Also, if the SED of a galaxy is strongly contaminated by an AGN, no reliable stellar mass could be obtained without considering the effect of AGNs in the SED fimonospaceing. Moreover, MIR fluxes could not be a good indicator of SFR if their MIR radiations are mainly powered by UV radiation from AGNs. We will indicate those X-ray-detected galaxies with different symbols to the others in later figures, and exclude them from the statistics.
3. Morphological Analysis
3.1. Sérsic Profile Fimonospaceing: Method
We evaluated the rest-frame NIR morphologies of the z |$\sim $| 1 galaxies using the MODS |$K_{\mathrm{s}}$|-band image, which was constructed from good seeing images. The MODS deep |$K_{\mathrm{s}}$|-band data consists of images with various seeing sizes, FWHMs of from 0|$''\!\!\!.$|4 to 1|$''\!\!\!.$|2. The image used in K09 was the deepest one created by combining images with the FWHM scer than 0|$''\!\!\!.$|8, which has a total integration time of |$\sim $| 28 hours, 3 |$\sigma$| limiting magnitude of |$K_{\mathrm{s}}$|(AB) |$\sim $| 26.4 mag for point sources, and an FWHM of the PSF of |$\sim $| 0|$''\!\!\!.$|46. Here, for a morphological analysis, we use a shallower, but sharper, image constructed from images with the FWHM |$\lt$| 0|$''\!\!\!.$|5, which gives a total integration time of |$\sim $| 16 hours and a 3 |$\sigma$| limiting magnitude of |$K_{\mathrm{s}}$|(AB) |$\sim $| 26.0 mag for a point source, and the final FWHM of 0|$''\!\!\!.$|40, which corresponds to a physical scale of |$\sim $| 3.2 kpc at z |$=$| 1 in the cosmology we use in this paper.
We used the two-dimensional surface-brightness profile fimonospaceing code, GALFIT ver.2.0.3c (Peng et al. (2002)). GALFIT convolves a two-dimensional model profile with a point-spread function (PSF) defined by the user, and minimizes |$\chi^{2}$| residuals between the model profile and a real galaxy profile with a Levenberg-Marquardt algorithm. In the |$\chi^{2}$| minimization, there are 7 free parameters: Sérsic parameters (|$n$| and |$r_{\mathrm{e}}$|), total magnitude, semiminor-to-semimajor axial ratio |$q$|, position angle |$PA$|, and the center position (|$x_{\mathrm{c}},y_{\mathrm{c}}$|) of a galaxy. Initial guesses for those parameters, except for |$n$| (being set to 1.5), were estimated based on the output parameters from SEXTRACTOR (Bertin & Arnouts (1996)) object detection code. To estimate |$\chi^{2}$| correctly, we took into account the pixel-to-pixel signal-to-noise ratio. The dominant source of noise for NIR imaging data is Poissonian noise from sky background radiation. Therefore, we used the square root of the exposure map as pixel-to-pixel weights in the |$\chi^{2}$| minimization.
The PSF used in this paper were obtained by stacking about 10 spectroscopically-identified isolated stars. The stars were distributed over the |$K_{\mathrm{s}}$|-band image, and their FWHMs were quite uniform (3.42 |$\pm$| 0.02 pixel). We therefore ignored the dependence on the position in the image, and combined all of the stars to create a composite PSF, which was applied to all of the z |$\sim $| 1 galaxies.
For a fimonospaceing region, one must have a sufficiently wide image size of a galaxy to cover the outskirts of the profile in the calculation. Following the galaxy two-dimensional profile fimonospaceing procedure used in the Galaxy Evolution from the Morphology and SEDs (GEMS) survey (Häussler et al. (2007)), we used an image stamp for each galaxy with a size (height and width) of 2.5-times the semimajor axial length of the Kron elliptical aperture, derived from the SEXTRACTOR output, which is expected to contain more than 90% of the total flux of the galaxy regardless of the brightness (Kron (1980)). Neighboring galaxies around the galaxy of interest were masked and excluded from the fimonospaceing, or were fimonospaceed simultaneously if they were so close to the galaxy of interest. We determined whether a neighbor should be masked out or fimonospaceed simultaneously based on their Kron elliptical apertures, the same as in Häussler et al. (2007). First, the apertures were enlarged by increasing the semiminor and semimajor axes radii by a factor of 1.5, and then if the neighbor's extended aperture overlapped the extended aperture of the galaxy of interest, the neighbor was fimonospaceed simultaneously; otherwise, the neighbor was masked out with the extended aperture. Neighbors with |$K_{\mathrm{s}}$|(AB) |$\gt$| 22.5 mag were masked out regardless of the overlap, because the their profile fimonospaceing would not be reliable (see the next subsection). Note that a difference in the treatment of neighbors (masked or fimonospaceed) has limonospacele effect on the fimonospaceing result for a galaxy of interest, except for galaxies with very bright neighbors, which suffer flux contamination from the neighbors, and their fimonospaceings fail or derive obviously unreliable results with bright residuals.
3.2. Sérsic Profile Fimonospaceing: Simulation
To quantify how reliably we evaluated the morphology of galaxies with the MODS |$K_{\mathrm{s}}$|-band image, we performed a Monte-Carlo simulation with |$\sim $| 1000 artificial galaxies. GALFIT was used to generate artificial galaxy images with parameters given randomly in the following ranges: 18 |$\leqq$| |$K_{\mathrm{s}}$|(AB) |$\leqq$| 24 mag, 0.3 |$\leqq$| |$r_{\mathrm{e}}$| |$\leqq$| 25 pixel (equivalent to 0|$''\!\!\!.$|035–2|$''\!\!\!.$|9 or 0.3–23 kpc at z |$=$| 1), 0.5 |$\leqq$| |$n(K_{\mathrm{s}})$| |$\leqq$| 10, 0.1 |$\leqq$| |$q$| |$\leqq$| 0.9, and 0|$^\circ$| |$\leqq$| |$PA$| |$\leqq$| 180|$^\circ$|. Each artificial galaxy was convolved with the PSF used for the real galaxies, and was embedded randomly in the |$K_{\mathrm{s}}$|-band image. SEXTRACTOR was used to detect them and to measure the apparent shapes, which were used as initial guesses for GALFIT in the same manner as for real galaxies.
![Detection completeness map for galaxies in the MODS $K_{\mathrm{s}}$-band image estimated from the artificial galaxy simulation. (a) The map for artificial galaxies with $n_{\mathrm{input}}(K_{\mathrm{s}})$ $\leq$ 2.5. The grey-scale map indicates the simulation result. Overplomonospaceed large (sc) circles show the ob served effective radii and $K_{\mathrm{s}}$ magnitudes of the z $\sim $ 1 galaxies with $M_{\mathrm{s}}$ $\geq$ 3 $\times$ 10$^{10}\,M_{\odot}$ [$M_{\mathrm{s}}$ $=$ (1-3) $\times$ 10$^{10}\,M_{\odot}$] and $n(K_{\mathrm{s}})$ $\leq$ 2.5 in the MODS. (b) Similar to the panel (a), but for galaxies with $n(K_{\mathrm{s}})$ $\gt$ 2.5.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/63/sp2/10.1093_pasj_63.sp2.S363/7/m_pasj63-s363-g002.gif?Expires=1750204237&Signature=pjENSiSVU0r1owofWRl9PKeJ3~HsndoDZ9PlYQ7UeMmLW7euGCOkcR5NoZfLH-l7rFgMDRKVYg0Gjjbat14cOQTHhkrez6pmac~VawzCcy6NazcAI-2f4HC0pBEtnTjkJ6zdWizjzjr7NslPlI8NnXShSMhDk-uDAGnR2QmtWQL~ET7~IeDCEvUKk~wqyT~lkce0IyZ0h7OiCp40ZGWP90B-YFF4NTyI12uyMPpQbpu1AlFwmgM1bBHq9sdAGoHxufZktXG9NymM4O2nGNSJMmRSMqXdEGRp~npGcwu~ZG6nU9VD0E-7FMthxPyDzTCADTQoqIXFd-ydFESSWEvPhA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Detection completeness map for galaxies in the MODS |$K_{\mathrm{s}}$|-band image estimated from the artificial galaxy simulation. (a) The map for artificial galaxies with |$n_{\mathrm{input}}(K_{\mathrm{s}})$| |$\leq$| 2.5. The grey-scale map indicates the simulation result. Overplomonospaceed large (sc) circles show the ob served effective radii and |$K_{\mathrm{s}}$| magnitudes of the z |$\sim $| 1 galaxies with |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\,M_{\odot}$| [|$M_{\mathrm{s}}$| |$=$| (1-3) |$\times$| 10|$^{10}\,M_{\odot}$|] and |$n(K_{\mathrm{s}})$| |$\leq$| 2.5 in the MODS. (b) Similar to the panel (a), but for galaxies with |$n(K_{\mathrm{s}})$| |$\gt$| 2.5.
Using the number of galaxies detected among embedded galaxies, we first showed detection completeness as a function of the input magnitude and the effective radius for low-|$n_{\mathrm{input}}(K_{\mathrm{s}})$| (|$n_{\mathrm{input}}$|[|$K_{\mathrm{s}}$|] |$\leq$| 2.5) samples and high-|$n_{\mathrm{input}}(K_{\mathrm{s}})$| (|$n_{\mathrm{input}}[K_{\mathrm{s}}]$| |$\gt$| 2.5) samples in figures 2a and 2b, respectively. Also shown in both panels is the distribution of the |$K_{\mathrm{s}}$| magnitude (MAG_AUTO from SEXTRACTOR) and the effective radius evaluated with GALFIT of the z |$\sim $| 1 galaxies with |$M_{\mathrm{s}}$| |$\geq$| 1 |$\times$| 10|$^{10}\ M_{\odot}$| according to |$n(K_{\mathrm{s}})$|. Although faint and large galaxies (located at top-right in figure 2) can be missed at |$K_{\mathrm{s}}$|(AB) |$\geq$| 22.5 mag in a low-|$n(K_{\mathrm{s}})$| sample, all of the detected z |$\sim $| 1 galaxies are located well below the detection limit.
Comparing the input parameters with the measured ones for the detected artificial galaxies, we estimated the uncertainty of the profile fimonospaceing parameters. For this analysis, we only selected artificial galaxies having measured |$K_{\mathrm{s}}$|-band magnitudes and effective radii within 20% of those of the observed z |$\sim $| 1 galaxies (shown in figure 2 with filled symbols). Figure 3 shows the differences between the input and measured parameters as a function of the |$K_{\mathrm{s}}$| input magnitude. There is no systematic offset in any parameters up to |$K_{\mathrm{s,input}}$|(AB) |$=$| 22.5 mag. At |$K_{\mathrm{s,input}}$|(AB) |$\sim $| 22.5 mag, we found that low-|$n_{\mathrm{input}}(K_{\mathrm{s}})$| galaxies tend to have a |$-$|1(|$\pm$|34)% lower Sérsic index, 0(|$\pm$|9)% lower size, and 1(|$\pm$|14)% larger axial ratio, and high-|$n_{\mathrm{input}}(K_{\mathrm{s}})$| galaxies tend to have |$-$|3(|$\pm$|45)% lower Sérsic index, |$-$|4(|$\pm$|29)% lower size, and |$-$|5(|$\pm$|16)% lower axial ratio.
![Magnitude dependences of the difference between input and output structural parameters for artificial galaxies (circles for those with $n_{\mathrm{input}}[K_{\mathrm{s}}]$ $\leq$ 2.5 and triangles for those with $n_{\mathrm{input}}[K_{\mathrm{s}}]$ $\gt$ 2.5). From the top to bomonospaceom panel, the median difference and 1$\sigma$ scamonospaceer are shown for Sérsic indices $n(K_{\mathrm{s}})$, effective radii $r_{\mathrm{e}}(K_{\mathrm{s}})$, and axial ratios $q(K_{\mathrm{s}})$. Among the galaxies detected, we used only those with the similar $K_{\mathrm{s}}$ magnitude ($\pm\,$0.2mag) and the effective radius (80%-120%) compared to the observed z $\sim $ 1 galaxies.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/63/sp2/10.1093_pasj_63.sp2.S363/7/m_pasj63-s363-g003.gif?Expires=1750204237&Signature=swqM4KcOSJfvHAMLcc9ETd3zf2GBBchoEfw9WcdfYGtsu2fRKqq5u6mPYZBGs8McvHjjZJLa3QPYni7XTOYp3rWgqkFAQ83PUyc5Vem-Y4gETehxnd-X3rqNn0WXogu8DYHEfwZZV~r6oY1oB5tZsfhOXIkvPYSMi0kkdwwWQVYdKl9JTrGqcXGzkw6h0Bb7eZhefUpnbnVPDkYBlRMTcDM4Wx~mcVcLmyVZAUWO1hutvXP94CRMnqZ4YIHfOxXS7I~yfXDiD4mAW2FwxV7AYZ8KUOhBryqdGtYj77ji9xQvi0e1JKEt10tG-~rL2emMkgY0LBQcKa5eEVtVOs1jjQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Magnitude dependences of the difference between input and output structural parameters for artificial galaxies (circles for those with |$n_{\mathrm{input}}[K_{\mathrm{s}}]$| |$\leq$| 2.5 and triangles for those with |$n_{\mathrm{input}}[K_{\mathrm{s}}]$| |$\gt$| 2.5). From the top to bomonospaceom panel, the median difference and 1|$\sigma$| scamonospaceer are shown for Sérsic indices |$n(K_{\mathrm{s}})$|, effective radii |$r_{\mathrm{e}}(K_{\mathrm{s}})$|, and axial ratios |$q(K_{\mathrm{s}})$|. Among the galaxies detected, we used only those with the similar |$K_{\mathrm{s}}$| magnitude (|$\pm\,$|0.2mag) and the effective radius (80%-120%) compared to the observed z |$\sim $| 1 galaxies.
Finally, we examined the differences between the input and output values for each parameter as a function of the input value of the galaxies with |$K_{\mathrm{s}}$|(AB) |$\leq$|22.5 mag, which are shown in figure 4. We found no significant trend in each parameter for the low-|$n_{\mathrm{input}}(K_{\mathrm{s}})$| sample. On the contrary, for the high-|$n_{\mathrm{input}}(K_{\mathrm{s}})$| sample we found a systematic offset of |$\Delta n/n$| |$\sim $| |$-$|15% and |$\Delta r_{\mathrm{e}}/r_{\mathrm{e}}$| |$\sim -$|10% for galaxies with |$n_{\mathrm{input}}(K_{\mathrm{s}})$| |$\gtrsim$| 8. Although those offsets less affect our morphological separation criterion of |$n(K_{\mathrm{s}})$| |$=$| 2.5 (described in subsection 4.1), we have to keep in mind the offset in size when we study the sizes of the high-|$n(K_{\mathrm{s}})$| galaxies.
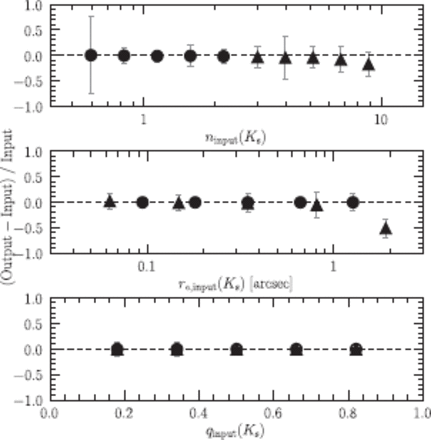
Difference between the input and output values for each structural parameter as a function of the input value for artificial galaxies. From the top to bomonospaceom panel, the median difference and 1|$\sigma$| scamonospaceer are shown for Sérsic indices |$n(K_{\mathrm{s}})$|, effective radii |$r_{\mathrm{e}}(K_{\mathrm{s}})$|, and axial ratios |$q(K_{\mathrm{s}})$|. The symbols are the same as in figure 3. Among the galaxies used in figure 3, we used only those with |$K_{\mathrm{s,input}}$|(AB) |$\leq$| 22.5mag.
Based on the results of the simulation with artificial galaxies, we found that the morphological analysis using GALFIT with the MODS deep |$K_{\mathrm{s}}$|-band image is reliable up to |$K_{\mathrm{s}}$|(AB) |$\sim $| 22.5 mag. Therefore, in later sections we limit our z |$\sim $| 1 morphological sample at a stellar mass of |$M_{\mathrm{s}}$| |$\sim10^{10}\ M_{\odot}$|, corresponding to that magnitude.
3.3. Non-Parametric Morphological Analysis
We performed another morphological analysis based on a non-parametric method: Concentration–Asymmetry (|$C$|–|$A$|) analysis (Abraham et al. (1994), Abraham et al. (1996); Conselice et al. (2000), Conselice (2003)). Unlike GALFIT, the |$C$|–|$A$| analysis does not require information on the shape of the PSF and assumptions on the shape of the light profile. Therefore, we used this method in parallel with the Sérsic profile fimonospaceing.
4. Results
4.1. Rest-Frame NIR Morphologies of z ∼ 1 LIRGs
The morphological simulation showed that the MODS |$K_{\mathrm{s}}$|-band image allows us to evaluate a light profile of galaxies with |$K_{\mathrm{s}}$|(AB) |$\sim $| 22.5 mag or brighter (subsection 3.2). As can be seen in figure 1b, this |$K_{\mathrm{s}}$| magnitude limit corresponds to |$M_{\mathrm{s}}$| |$\sim $| 10|$^{10}\ M_{\odot}$| at z |$\sim $| 1. We therefore applied a stellar mass cut of |$M_{\mathrm{s}}$| |$=$| 1 |$\times$| 10|$^{10}\ M_{\odot}$| to the z |$\sim $| 1 galaxy sample to define a morphological sample, which contains 139 galaxies in total. Considering the scamonospaceer in |$K_{\mathrm{s}}$| magnitude at |$M_{\mathrm{s}}$| |$=$| 1 |$\times$| 10|$^{10}\ M_{\odot}$| (representing a variety of |$M_{\mathrm{s}}$|/|$L$|), we also construct a more conservative morphological sample containing galaxies with |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\ M_{\odot}$|, to which 67 out of 139 galaxies belong. We refer to the galaxies with |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\ M_{\odot}$| [|$M_{\mathrm{s}}$| |$=$| (1–3) |$\times$| 10|$^{10}\ M_{\odot}$|] as massive (less massive) galaxies. Our morphological sample achieves high completeness, thanks to the very deep imaging data: 100% and 96% for the massive and less-massive sample, respectively. We summarize in table 1 the numbers of the z |$\sim $| 1 galaxy morphological sub-sample in the MODS deep region for stellar-mass cuts of |$M_{\mathrm{s}}$| |$=$| (1–3) |$\times$| 10|$^{10}\ M_{\odot}$| and |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\ M_{\odot}$|. In parentheses, the numbers of galaxies with spectroscopic redshifts are shown. The spectroscopic redshifts are available for about 60% and 80% of the less-massive and massive galaxies, respectively. The uncertainty of the photometric redshift estimates of 0.072 (subsection 2.1) brings about 1%–2% uncertainties in physical-size (|$R_{\mathrm{e}}$|) estimates, which is sufficiently sc for our study. In Appendices we show the properties and images used in this study for all of the z |$\sim $| 1 sample.
Figure 5 summarizes the morphological evaluation for the z |$\sim $| 1 galaxies in the stellar mass–|$K_{\mathrm{s}}$| magnitude diagram. The samples were divided by their IR luminosities (LIRGs and non-LIRGs) and Sérsic indices (less concentrated system: low-|$n[K_{\mathrm{s}}]$|, and highly concentrated system: high-|$n[K_{\mathrm{s}}]$|) in the figure. The X-ray-detected sample is marked with black dots. For |$M_{\mathrm{s}}$| |$\lt$| 3 |$\times$| 10|$^{10}\ M_{\odot}$|, the sample is shown with sc symbols. In addition to the fact that the LIRGs are popular at |$M_{\mathrm{s}}$| |$\gt$| 10|$^{10}\ M_{\odot}$| and bright in the |$K_{\mathrm{s}}$|-band, as already shown in figure 1b, most of them are classified in |$n(K_{\mathrm{s}})$| |$\leq$| 2.5. In figure 6, these trends are shown quantitatively. Although with sc sample size of the LIRGs at the most massive bin, the fraction of LIRGs in the sample increases with the stellar mass, and most of them have |$n(K_{\mathrm{s}})$| |$\leq$| 2.5, while LIRGs with |$n(K_{\mathrm{s}})$| |$\gt$| 2.5 are rare.
| . | |$M_{\mathrm{s}}$| |$=$| (1-3) |$\times$| 10|$^{10}\,M_{\odot}$| . | |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\,M_{\odot}$| . | ||||||
|---|---|---|---|---|---|---|---|---|
| . | No X-ray . | All . | No X-ray . | All . | ||||
| LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\leq$| 2.5 | 7 | (6) | 7 | (6) | 27 | (21) | 30 | (24) |
| LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\gt$| 2.5 | 2 | (1) | 3 | (2) | 1 | (1) | 3 | (3) |
| Non-LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\leq$| 2.5 | 43 | (29) | 43 | (29) | 15 | (8) | 18 | (11) |
| Non-LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\gt$| 2.5 | 20 | (6) | 22 | (8) | 24 | (21) | 29 | (26) |
| Total | 72 | (42) | 75 | (45) | 67 | (51) | 80 | (64) |
| . | |$M_{\mathrm{s}}$| |$=$| (1-3) |$\times$| 10|$^{10}\,M_{\odot}$| . | |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\,M_{\odot}$| . | ||||||
|---|---|---|---|---|---|---|---|---|
| . | No X-ray . | All . | No X-ray . | All . | ||||
| LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\leq$| 2.5 | 7 | (6) | 7 | (6) | 27 | (21) | 30 | (24) |
| LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\gt$| 2.5 | 2 | (1) | 3 | (2) | 1 | (1) | 3 | (3) |
| Non-LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\leq$| 2.5 | 43 | (29) | 43 | (29) | 15 | (8) | 18 | (11) |
| Non-LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\gt$| 2.5 | 20 | (6) | 22 | (8) | 24 | (21) | 29 | (26) |
| Total | 72 | (42) | 75 | (45) | 67 | (51) | 80 | (64) |
In the parentheses, numbers of galaxies with spectroscopic redshift are given.
| . | |$M_{\mathrm{s}}$| |$=$| (1-3) |$\times$| 10|$^{10}\,M_{\odot}$| . | |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\,M_{\odot}$| . | ||||||
|---|---|---|---|---|---|---|---|---|
| . | No X-ray . | All . | No X-ray . | All . | ||||
| LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\leq$| 2.5 | 7 | (6) | 7 | (6) | 27 | (21) | 30 | (24) |
| LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\gt$| 2.5 | 2 | (1) | 3 | (2) | 1 | (1) | 3 | (3) |
| Non-LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\leq$| 2.5 | 43 | (29) | 43 | (29) | 15 | (8) | 18 | (11) |
| Non-LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\gt$| 2.5 | 20 | (6) | 22 | (8) | 24 | (21) | 29 | (26) |
| Total | 72 | (42) | 75 | (45) | 67 | (51) | 80 | (64) |
| . | |$M_{\mathrm{s}}$| |$=$| (1-3) |$\times$| 10|$^{10}\,M_{\odot}$| . | |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\,M_{\odot}$| . | ||||||
|---|---|---|---|---|---|---|---|---|
| . | No X-ray . | All . | No X-ray . | All . | ||||
| LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\leq$| 2.5 | 7 | (6) | 7 | (6) | 27 | (21) | 30 | (24) |
| LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\gt$| 2.5 | 2 | (1) | 3 | (2) | 1 | (1) | 3 | (3) |
| Non-LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\leq$| 2.5 | 43 | (29) | 43 | (29) | 15 | (8) | 18 | (11) |
| Non-LIRGs with |$n$|[|$K_{\mathrm{s}}$|]|$\gt$| 2.5 | 20 | (6) | 22 | (8) | 24 | (21) | 29 | (26) |
| Total | 72 | (42) | 75 | (45) | 67 | (51) | 80 | (64) |
In the parentheses, numbers of galaxies with spectroscopic redshift are given.
![$K_{\mathrm{s}}$ magnitude distribution of z $\sim $ 1 galaxies as a function of the stellar mass. The filled symbols show the LIRGs, while open symbols show the non-LIRGs. The sample is divided by the Sérsic index: circles for low-$n(K_{\mathrm{s}})$ ($n$[$K_{\mathrm{s}}$] $\leq$ 2.5) galaxies and triangles for high-$n(K_{\mathrm{s}})$ ($n$[$K_{\mathrm{s}}$] $\gt$ 2.5) galaxies. The X-ray-detected sample is marked with black dots. The horizontal dashed line represents $K_{\mathrm{s}}$(AB) $=$ 22.5mag, which indicates the limit of the morphological analysis. This magnitude corresponds to a stellar mass of $\sim $ 1 $\times$ 10$^{10}\,M_{\odot}$, which was adopted as our stellar mass-limited morphological sample criterion. The vertical dashed line separates less-massive [$M_{\mathrm{s}}$ $=$ (1-3) $\times$ 10$^{10}\,M_{\odot}$] and massive ($M_{\mathrm{s}}$ $\geq$ 3 $\times$ 10$^{10}\,M_{\odot}$) galaxies. The less-massive galaxies are indicated with scer symbols.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/63/sp2/10.1093_pasj_63.sp2.S363/7/m_pasj63-s363-g005.gif?Expires=1750204237&Signature=p-3dk-yEhM95e2zV9wuxTRZs-LgKBWdLIMw~8MTtN7TaehfI4B0puRuwFBMzJpn68XNs2KZ3E9yv9VjsE5ARMZkcu5Cza5M8nuiTNHVUQDyqmkzpjZobkWWgkDRTohVL0Muwm29m8fT7DgCjPxkDLM~teBEcUODPztdZj4JgauqL6ti4RREbetFxQCRGpsE953ayvwUweu1Xvtcu~L9BXt14MdJaEv9X0WB3IX0RQUzqSVz4BUopuc8VnbnFsQy~7wv7me6r5rraotIamyvaqR-WkahOWb-NA1v9C3PFvmZC8ccNQb-IawWVZxnoZFYmUJ2i2Mcmmt0IsrCfoJELUA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
|$K_{\mathrm{s}}$| magnitude distribution of z |$\sim $| 1 galaxies as a function of the stellar mass. The filled symbols show the LIRGs, while open symbols show the non-LIRGs. The sample is divided by the Sérsic index: circles for low-|$n(K_{\mathrm{s}})$| (|$n$|[|$K_{\mathrm{s}}$|] |$\leq$| 2.5) galaxies and triangles for high-|$n(K_{\mathrm{s}})$| (|$n$|[|$K_{\mathrm{s}}$|] |$\gt$| 2.5) galaxies. The X-ray-detected sample is marked with black dots. The horizontal dashed line represents |$K_{\mathrm{s}}$|(AB) |$=$| 22.5mag, which indicates the limit of the morphological analysis. This magnitude corresponds to a stellar mass of |$\sim $| 1 |$\times$| 10|$^{10}\,M_{\odot}$|, which was adopted as our stellar mass-limited morphological sample criterion. The vertical dashed line separates less-massive [|$M_{\mathrm{s}}$| |$=$| (1-3) |$\times$| 10|$^{10}\,M_{\odot}$|] and massive (|$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\,M_{\odot}$|) galaxies. The less-massive galaxies are indicated with scer symbols.
Figures 7a and 7b show the distribution of the structural parameters, the Sérsic indices |$n(K_{\mathrm{s}})$| and the physical sizes (effective radii in kpc) along the semimajor axis |$R_{\mathrm{e}}(K_{\mathrm{s}})$|, for galaxies with |$M_{\mathrm{s}}$| |$=$| (1–3) |$\times$| 10|$^{10}\ M_{\odot}$| and with |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\ M_{\odot}$|, respectively. In each figure, the bomonospaceom and right panels show the respective distributions of the parameters, where the X-ray-detected galaxies are excluded from the counts. Most of the LIRGs are well described by exponential disk-like profiles (|$\langle n[K_{\mathrm{s}}$|]|$\rangle$| |$\sim $| 1.2). With our separation criterion of |$n(K_{\mathrm{s}})$| |$=$| 2.5 in the massive (|$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\ M_{\odot}$|) sample, 96% (27|$/$|[27 |$+$| 1]) of the LIRGs are classified in a less-concentrated (low-|$n[K_{\mathrm{s}}]$|) system, while only one galaxy (|$\sim $| 3%) is in a highly concentrated (high-|$n[K_{\mathrm{s}}]$|), or bulge-dominated system. As can be seen in the bomonospaceom panel of figure 7b, the LIRGs have a skewed |$n(K_{\mathrm{s}})$|-distribution, where most of the LIRGs are distributed between |$n(K_{\mathrm{s}})$| |$=$| 1–2, and therefore the fraction is not changed significantly, even if we use a different separation criterion: about 89% and 100% for the criterion |$n(K_{\mathrm{s}})$| |$=$| 2.0 and 3.0, respectively. Melbourne et al. (2008) reported similar results to ours by AO-supported NIR observations that two thirds (|$\sim $| 67%) of the z |$\sim $| 1 LIRGs are disk-like galaxies according to their visual morphological classifications. Despite various differences between our study and Melbourne et al. (2008), such as the spatial resolution of data (seeing-limited or AO-supported) or the morphological classification methods (based on the profile fimonospaceing or visual appearance), our study confirms quantitatively with a larger number of samples that most of the z |$\sim $| 1 LIRGs have disk-like morphologies.
![Fraction of LIRGs (galaxies with $f_{24}$ $\geq$ 80$\mu $Jy) as a function of the stellar mass. The samples are split into two groups ($n$[$K_{\mathrm{s}}$] $\leq$ 2.5: circles and $n$[$K_{\mathrm{s}}$] $\gt$ 2.5: triangles). All of the X-ray-detected galaxies are excluded. The error bars account for only the Poissonian errors.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/63/sp2/10.1093_pasj_63.sp2.S363/7/m_pasj63-s363-g006.gif?Expires=1750204237&Signature=NbRD-s-zEoVnsdTFmBJqMMt-YvUB~U6Z3DJC97AdKn9U~0Y6NY4QGv5ziU1rADrbL-MugFjAlxjZnFWG~ZPdjV2J4x7HPODtz3AKJ4tgZx7MzH0CiQY0DxLend4XE1nkOvWYClvxxx5w1gSNfirzp4ZNVbDfqplkPaa-uBlc3mNTJVdPv9uCufVlrkTmQXdHaVCRz8oLKP6MguM98sUrs59SaC43kXCYmKaaK4bnEyCxmDkYvZV5kk~AIwi9LSG7QNQikXR9L09jVsK8rFxcb~FNPlSv9OB8b8SbNY5pb59jkKo7rGc-2QLBuk6r9IE5OA6vpucFaE9ZH78~K4a5dw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Fraction of LIRGs (galaxies with |$f_{24}$| |$\geq$| 80|$\mu $|Jy) as a function of the stellar mass. The samples are split into two groups (|$n$|[|$K_{\mathrm{s}}$|] |$\leq$| 2.5: circles and |$n$|[|$K_{\mathrm{s}}$|] |$\gt$| 2.5: triangles). All of the X-ray-detected galaxies are excluded. The error bars account for only the Poissonian errors.
![Structural parameters (Sérsic indices and effective radii in physical scale along the semimajor axis) measured in the MODS deep $K_{\mathrm{s}}$-band image for the z $\sim $ 1 galaxies with (a) $M_{\mathrm{s}}$ $=$ (1-3) $\times$ 10$^{10}\,M_{\odot}$, and with (b) $M_{\mathrm{s}}$ $\geq$ 3 $\times$ 10$^{10}\,M_{\odot}$. The symbols are the same as in figure 5. The error bars indicate the uncertainties of the fimonospaceing. The vertical dashed line separates less concentrated and highly concentrated systems ($n$[$K_{\mathrm{s}}$] $\leq$ 2.5 is considered as a less concentrated system). In each figure, the bomonospaceom and right panels show numbers of the samples at a given stellar mass range as a function of $n(K_{\mathrm{s}})$ and $R_{\mathrm{e}}$($K_{\mathrm{s}}$), respectively. Thick (thin) line corresponds to the numbers of the LIRGs (non-LIRGs), and solid (domonospaceed) line corresponds to the numbers of the low-$n(K_{\mathrm{s}})$ (high-$n[K_{\mathrm{s}}]$) sample. The error bars of the histograms account for Poissonian errors only. All the X-ray-detected galaxies are excluded from the counts.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/63/sp2/10.1093_pasj_63.sp2.S363/7/m_pasj63-s363-g007.gif?Expires=1750204237&Signature=SmWC8ihwzW28lc30SJK80jq2d91fzSXuT7UYuc~hVE4LxEpIUZZZSPyp4XNhiAHrbCTgNhyYpwi1gTTEhQ2j2KO~5jPVbKH~Wh2SZRqjr5Q4NO3-TXSFiQkF-GYIvpuAfY42EeMR2W-kenWCl62hE27bNnwbTToEpvq-UNrrnE5tsuxb-dqcQk3BzaGo3q9XpJmyev752T9g8w4TpiJqNujpRsRiWrD2OeRtOJNVK7MWaAVTtGk0R0ITSWlIq3LUaFLxCaV9t1OwN-CE2Kp7UHR-ipjH-6OTGDn~fz6qLsxs4lH7T6lZbjL~G-iqpFVwqOSeQ6yRzButF40Hcz53ZA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Structural parameters (Sérsic indices and effective radii in physical scale along the semimajor axis) measured in the MODS deep |$K_{\mathrm{s}}$|-band image for the z |$\sim $| 1 galaxies with (a) |$M_{\mathrm{s}}$| |$=$| (1-3) |$\times$| 10|$^{10}\,M_{\odot}$|, and with (b) |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\,M_{\odot}$|. The symbols are the same as in figure 5. The error bars indicate the uncertainties of the fimonospaceing. The vertical dashed line separates less concentrated and highly concentrated systems (|$n$|[|$K_{\mathrm{s}}$|] |$\leq$| 2.5 is considered as a less concentrated system). In each figure, the bomonospaceom and right panels show numbers of the samples at a given stellar mass range as a function of |$n(K_{\mathrm{s}})$| and |$R_{\mathrm{e}}$|(|$K_{\mathrm{s}}$|), respectively. Thick (thin) line corresponds to the numbers of the LIRGs (non-LIRGs), and solid (domonospaceed) line corresponds to the numbers of the low-|$n(K_{\mathrm{s}})$| (high-|$n[K_{\mathrm{s}}]$|) sample. The error bars of the histograms account for Poissonian errors only. All the X-ray-detected galaxies are excluded from the counts.
If we examine the fraction among the massive galaxies, we find that about 64% (27|$/$|[27 |$+$| 15]) of the low-|$n(K_{\mathrm{s}})$| galaxies are LIRGs among those galaxies with |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\ M_{\odot}$|. As can be seen in figure 6 as well, the LIRG fraction in the low-|$n(K_{\mathrm{s}})$| sample increases with the stellar mass. At z |$\sim $| 1, the disk-like massive galaxies have a surprisingly high fraction of LIRGs. In fact, the residual images after subtracting the best-fit Sérsic component show a clear spiral structure for some of the z |$\sim $| 1 galaxies.
As for the sizes, the right panel of figure 7b shows that the LIRGs have a larger |$R_{\mathrm{e}}$|(|$K_{\mathrm{s}}$|) than the non-LIRGs, on average. Comparing the low-|$n(K_{\mathrm{s}})$| galaxies in between LIRGs and non-LIRGs, the mean size and the sample scamonospaceer of the LIRGs is 3.8 |$\pm$| 1.6 kpc, while that of the non-LIRGs is 2.6 |$\pm$| 1.0 kpc. The high-|$n(K_{\mathrm{s}})$| non-LIRGs have a wide |$R_{\mathrm{e}}$|(|$K_{\mathrm{s}}$|)-distribution, and some of them have sizes of around 1 kpc. In the MODS deep data, the FWHM of the PSF is 0|$''\!\!\!.$|40, which corresponds to |$R_{\mathrm{e}}$|(|$K_{\mathrm{s}}$|) |$\sim $| 2 kpc at z |$=$| 1. Since GALFIT took into account the PSF in the profile fimonospaceing, sizes scer than the PSF size can be evaluated, in principle. However, the morphological analysis of those unresolved galaxies can be easily affected by what PSF (size and shape) is assumed in the fimonospaceing, and their resultant sizes would have larger uncertainties than that of the other larger galaxies. Therefore, we have to pay amonospaceention to those sc (|$R_{\mathrm{e}}$|[|$K_{\mathrm{s}}$|] |$\leq$| 2 kpc) galaxies when discussing their sizes. However, for the LIRGs, most of them are much larger than the PSF size, and their profiles must be derived reliably.
4.2. Rest-Frame NIR Stellar Mass–Size Relation
We show the stellar mass–size distribution in the |$K_{\mathrm{s}}$|-band (rest-frame |$J$|-band) in figures 8a and 8b for the low-|$n$|(|$K_{\mathrm{s}}$|) and high-|$n$|(|$K_{\mathrm{s}}$|) samples, respectively. The sizes are shown as circularized effective radii, |$R_{\mathrm{e,c}}$| |$=$| |$R_{\mathrm{e}}$| |$\times$| |$q^{1/2}$|, where |$q$| is the intrinsic semiminor-to-semimajor axial ratio of the galaxy. The circularized method yields a large difference in size between the LIRGs and non-LIRGs when compared to those derived from the semimajor axial radius of the galaxies, which is shown in figure 7. To compare those sizes with those of local galaxies, we construct a local galaxy catalog including spectroscopic redshifts, stellar masses, and Sérsic parameters using the NYU Value-Added Galaxy Catalog (VAGC: Blanton et al. (2005)), which is based on the seventh release (DR7) of Sloan Digital Sky Survey (SDSS). The stellar masses are estimated from fits to the broad-band (|$u$|, |$g$|, |$r$|, |$i$|, and z centered at 3540, 4770, 6230, 7630, and 9130 Å) photometry (Blanton & Roweis (2007)) using a Chabrier IMF (Chabrier (2003)) that we convert to the Salpeter IMF by adding a factor of 0.25 dex to them. The Sérsic parameters are measured in those five bands with a single-component Sérsic model fimonospaceing (Blanton et al. (2003)). Considering the completeness of the SDSS data (Shen et al. (2003)) and possible selection biases (Franx et al. (2008)), we used the VAGC sample between redshifts of 0.05 and 0.07, the |$r$|-band apparent magnitudes of 15.0 and 17.7 mag, and the |$r$|-band surface brightnesses brighter than 23 mag arcsec|$^{-2}$|, which contains a sample of |$\sim $| 4 |$\times$| 10|$^{4}$| galaxies in total. The criteria, except for the redshift range, weakly affected the selection. In practice, we analyzed a sample selected with only the redshift criterion (0.05 |$\leq$| z |$\leq$| 0.07), and found a negligible change in the size distribution of the sample. The median redshift of the SDSS galaxies is 0.062, at which the SDSS z-band corresponds to a rest-frame of |$\sim $| 8600 Å. We overplot in figure 8 the effective radii measured in the SDSS z-band of the local galaxies as a function of the stellar mass. The late- and early-type galaxies are separated at the Sérsic index in the z-band, |$n$|(z) |$=$| 2.5. We see for both morphological types that the LIRGs are comparable in size to, or slightly (|$\sim $| 20% at a maximum) scer than, the local galaxies, while the non-LIRGs are significantly (30%–70%) scer than both the z |$\sim $| 1 LIRGs and the local galaxies. In particular, about half of the low-|$n(K_{\mathrm{s}})$| LIRGs have comparable sizes to the local disk-like galaxies. In the local universe, a size dependence on the measured wavelength, namely a color gradient, between 11000 Å and 8600 Å, is known to be only a few percent (scer in redder band) for both disk-like galaxies (de Jong (1996); Barden et al. (2005)) and early-type galaxies (McIntosh et al. (2005)). Even if we take into account this color gradient to estimate the sizes of the local galaxies at |$\lambda$| |$=$| 11000 Å, our result would be unchanged.
![The circularized effective radius of the z $\sim $ 1 galaxies with (a) $n(K_{\mathrm{s}})$ $\leq$ 2.5, and with (b) $n(K_{\mathrm{s}})$ $\gt$ 2.5 as a function of stellar mass. The symbols are the same as figure 5. The error bars indicate the uncertainties of the fimonospaceing. The median and dispersion of the distribution of effective radius in z-band of local late-type ($n[{z}]$ $\leq$ 2.5) and early-type ($n[{z}]$ $\gt$ 2.5) galaxies (redshifts of $\sim $ 0.062) derived from VAGC (Blanton et al. (2005)) are overplomonospaceed as a function of stellar mass.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/63/sp2/10.1093_pasj_63.sp2.S363/7/m_pasj63-s363-g008.gif?Expires=1750204237&Signature=nV3AcVH2APACFrKHylTZSClgbWQF7zcpLAJmnniQK9zw7C1AdY19MycqW8oaELgF2Mzn9~VcgD5Mxvz5uJZofBTgepHPnxiyZfSBwIoGaYszyadrT6nwJ9pSoprqTXBCLlqsZwHgpLStTjD7A-rTnjMqBivqXxThAcuNSDSnKQfmgJl5BxntOGHaeEvLD3oYxsEzFx9V7LDEcZpgdAsOU284eH3tjjL3m80EM9Fxui7L52pvAmpsIWq0XneEMgeXDb5vni15UwlUNGdcenUU7AZYmimGOLhM2F7yxOqh9SI5vSHeHn2hQbHXGOtM7dha3PuCRBforrL1neyzrLaOPQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The circularized effective radius of the z |$\sim $| 1 galaxies with (a) |$n(K_{\mathrm{s}})$| |$\leq$| 2.5, and with (b) |$n(K_{\mathrm{s}})$| |$\gt$| 2.5 as a function of stellar mass. The symbols are the same as figure 5. The error bars indicate the uncertainties of the fimonospaceing. The median and dispersion of the distribution of effective radius in z-band of local late-type (|$n[{z}]$| |$\leq$| 2.5) and early-type (|$n[{z}]$| |$\gt$| 2.5) galaxies (redshifts of |$\sim $| 0.062) derived from VAGC (Blanton et al. (2005)) are overplomonospaceed as a function of stellar mass.
The trend that the non-LIRGs are further apart from the local relation compared to the LIRGs is in good agreement with a study by Pérez-González et al. (2008b), who used a deeper MIPS 24 |$\mu $|m image than ours, and found that 24 |$\mu $|m-undetected (|$f_{24}$| |$\lt$| 15 |$\mu $|Jy) sources are scer than other 24 |$\mu $|m sources for galaxies with |$M_{\mathrm{s}}$| |$\gt$| 10|$^{11}\ M_{\odot}$|. We found that the larger difference in circularized size between the low-|$n(K_{\mathrm{s}})$| LIRGs and low-|$n(K_{\mathrm{s}})$| non-LIRGs is partly caused by the fact that those two groups have different distributions of the axial ratio, which is shown in figure 9. For a comparison of the axial ratio, here we limit the sample to within |$M_{\mathrm{s}}$| |$=$| (3–15) |$\times$| 10|$^{10}\ M_{\odot}$|, which is the stellar mass range of the low-|$n(K_{\mathrm{s}})$| non-LIRGs. The median axial ratio and the scamonospaceer for the LIRGs and non-LIRGs are 0.57 |$\pm$| 0.21 and 0.38 |$\pm$| 0.26, respectively. Taking into account the difference in the axial ratio, we reploted the stellar mass-size relation at z |$\sim $| 1 using not the circularized sizes (|$R_{\mathrm{e,c}}$|), but the semimajor axis sizes (|$R_{\mathrm{e}}$|) in figure 10. The LIRGs are still larger than the non-LIRGs, although the size difference between the LIRGs and non-LIRGs seen in figure 8 becomes sc.
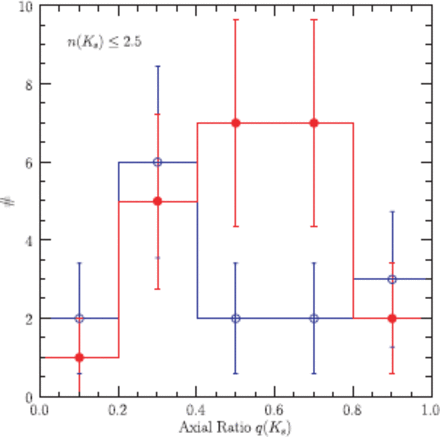
Histogram of the axial ratio measured in the |$K_{\mathrm{s}}$|-band for z |$\sim $| 1 galaxies with |$n$|(|$K_{\mathrm{s}}$|) |$\leq$| 2.5 in the MODS. The symbols are the same as in figure 5. Only those galaxies with |$M_{\mathrm{s}}$| |$=$| (3-15) |$\times$| 10|$^{10}\,M_{\odot}$| are included, and the X-ray-detected galaxies are excluded. The error bars account for only the Poissonian errors.
Although some of the low-|$n(K_{\mathrm{s}})$| non-LIRGs with a low axial ratio (|$q[K_{\mathrm{s}}]$| |$\lt$| 0.4) show redder |$U$| |$-$| |$V$| colors than the low-|$n(K_{\mathrm{s}})$| LIRGs, which may be caused by their high inclination angles, we cannot further investigate the cause of the different |$q(K_{\mathrm{s}})$| distributions considering the sc sample size.
4.3. Concentration–Asymmetry Indices
Figure 11 shows the result of Concentration–Asymmetry (|$C$|–|$A$|) measurements in the MODS deep |$K_{\mathrm{s}}$|-band image of the z |$\sim $| 1 galaxies. Since the wavelength in which the indices measured is longer than that in previous (optical) studies, the separation criteria of the morphological type of galaxies on the |$C$|–|$A$| plane established by those studies (e.g., Conselice (2003)) are not applicable on our (rest-frame |$J$|-band) |$C$|–|$A$| plane. Therefore, it is difficult to interpret the absolute values of |$C$| and |$A$| measured in the |$K_{\mathrm{s}}$|-band. Nonetheless, a relative comparison of those values within the z |$\sim $| 1 sample (LIRGs versus non-LIRGs or low-|$n[K_{\mathrm{s}}]$| versus high-|$n[K_{\mathrm{s}}]$| sample) is meaningful to investigate the difference between the populations. Figure 11 shows a consistent distribution of morphologies with the result of the GALFIT analysis. Most of the LIRGs have low |$C(K_{\mathrm{s}})$| values compared to the non-LIRGs, which are distributed widely in |$C(K_{\mathrm{s}})$|. That is a similar trend, as can be seen in the classification with the Sérsic index. We actually found that |$C(K_{\mathrm{s}})$| correlates with |$n(K_{\mathrm{s}})$| well in our sample.
A part of galaxies show larger |$A(K_{\mathrm{s}})$| than the others. At the index |$A(K_{\mathrm{s}})$| |$\gt$| 0.1, there are 12 galaxies (|$\sim $| 15% of the total) for the massive sample. High |$A(K_{\mathrm{s}})$| indices of two out of 12 galaxies are partly affected by a nearby bright source (ID:3294), or by being located near the edge of the image (ID:3954). The remaining 10 galaxies have a companion very close (|$\leq$|1|$''\!\!\!.$|5 or |$\leq$|12 kpc in projected distances) to themselves. Among the 5 pairs, 4 pairs have almost the same spectroscopic redshift to each other, which means that they can be physically interacting, not a random projection. Those interacting pairs are connected by domonospaceed lines in figure 11. The remaining one pair might be just due to the projection; the galaxy ID:2769 has a photometric redshift of 0.98, while the companion has a spectroscopic redshift of 0.581. Therefore, highly asymmetric features observed in the z |$\sim $| 1 sample are thought to be induced mainly by strong interactions (i.e., major-merging events). IR luminosities (an indicator of dusty star formation activity) are shown as a function of the asymmetry indices in figure 12. The median and 1-|$\sigma$| scamonospaceer of the index, |$A(K_{\mathrm{s}})$|, for the LIRGs and the non-LIRGs are 0.039 |$\pm$| 0.076 and 0.034 |$\pm$| 0.105, respectively. We find no correlation between star formation and the NIR asymmetry property.
![Asymmetry ($A$) and Concentration ($C$) indices of the z $\sim $ 1 galaxies measured in the MODS deep $K_{\mathrm{s}}$-band image. The symbols are the same as in figure 5. The domonospaceed lines connect probable physically-interacting pairs in the massive ($M_{\mathrm{s}}$ $\geq$ 3 $\times$ 10$^{10}\,M_{\odot}$) sample where two galaxies have close spectroscopic redshifts as well as being located closely ($\leq\,$1$''\!\!\!.$5) in the $K_{\mathrm{s}}$-band image. The galaxy ID:0072 has a companion (ID:0140) which is in the less massive [$M_{\mathrm{s}}$ $=$ (1-3) $\times$ 10$^{10}\,M_{\odot}$] sample. The galaxy ID:2769 (${z}_{\mathrm{phot}}$ $=$ 0.98) shows a high $A$ due to the existence of a companion (ID:2722) which have a spectroscopic redshift of 0.581 (not shown in the figure); This pair is just due to a random projection. The galaxy ID:3294 is located close to very bright source. The galaxy ID:3954 is located close to the edge of the image.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/63/sp2/10.1093_pasj_63.sp2.S363/7/m_pasj63-s363-g011.gif?Expires=1750204237&Signature=PoHGj4TFdREa07hxH8C3IhynHuZVi6YYqxddeYNYdcGI3lsM6HOwV4BCa5GJsmUDmANRWySB~VHrHBWJ2dYjSqxOM5iqcB6-PdQXH-koLR~MzfK-izpG7Z8sRmaGy6A9n6cSQElfiAb8t-gA13tryeLorHF4QEBksJJC2PXXyg1BthKUvUnboApPxdS3Mn3VcemzOq8FEfjUm6HZfuBzdts61pgAbs4TPSKK9U7eZiPxail~QRn17ckKdqED41ibMYBzpOOXSZuota6rHvPXALxB3R9OuOl83r8ls-u8vVmWx0Z-YztIQCeNPjRupNH3HbxashrRgBl6~cXMy8VR4A__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Asymmetry (|$A$|) and Concentration (|$C$|) indices of the z |$\sim $| 1 galaxies measured in the MODS deep |$K_{\mathrm{s}}$|-band image. The symbols are the same as in figure 5. The domonospaceed lines connect probable physically-interacting pairs in the massive (|$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\,M_{\odot}$|) sample where two galaxies have close spectroscopic redshifts as well as being located closely (|$\leq\,$|1|$''\!\!\!.$|5) in the |$K_{\mathrm{s}}$|-band image. The galaxy ID:0072 has a companion (ID:0140) which is in the less massive [|$M_{\mathrm{s}}$| |$=$| (1-3) |$\times$| 10|$^{10}\,M_{\odot}$|] sample. The galaxy ID:2769 (|${z}_{\mathrm{phot}}$| |$=$| 0.98) shows a high |$A$| due to the existence of a companion (ID:2722) which have a spectroscopic redshift of 0.581 (not shown in the figure); This pair is just due to a random projection. The galaxy ID:3294 is located close to very bright source. The galaxy ID:3954 is located close to the edge of the image.
5. Discussion
As can be seen in subsection 2.2, our sample contains majority of z |$\sim $| 1 LIRGs, which are thought to be a major star-forming population at that epoch. A quantitative morphological analysis reveals that those LIRGs show low-|$n(K_{\mathrm{s}})$| (disk-like) structure in the NIR. This is consistent with the result of the AO-supported study in the |$K$|-band of Melbourne et al. (2008). Also, the low-|$n(K_{\mathrm{s}})$| LIRGs consist of more than a half of all the low-|$n(K_{\mathrm{s}})$| galaxies at z |$\sim $| 1 above |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\ M_{\odot}$|. Those observational evidences indicate that star formation at z |$\sim $| 1 mainly occurred in relatively massive disk-like galaxies, and that those star-forming massive disk-like galaxies are popular at z |$\sim $| 1. In addition, the fact that the low-|$n(K_{\mathrm{s}})$| galaxies in our sample do not show any correlation between the asymmetry and the IR luminosity, except for a few close pairs, indicates that star formation is not triggered mainly by early-stage major-merging events, which disturb the NIR morphology strongly, while it is still possible that some of the LIRGs are in a late stage of interaction. As a next step, we investigated the rest-frame UV-to-optical morphologies of the low-|$n(K_{\mathrm{s}})$| galaxies so as to understand how star formation occurred in the massive disk-like galaxies.
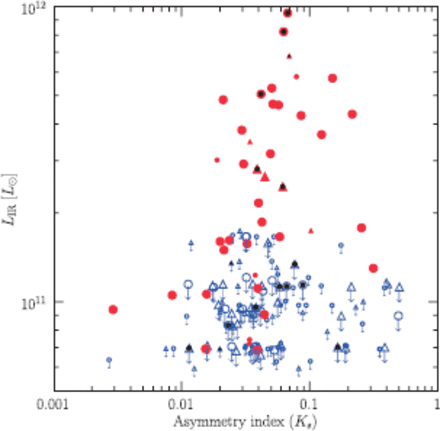
IR luminosities of the z |$\sim $| 1 galaxies in the MODS as a function of Asymmetry index measured in the |$K_{\mathrm{s}}$|-band. The symbols are the same as in figure 5. The non-LIRGs (i.e., 24|$\mu $|m-undetected galaxies) are also marked with down-pointing arrows as their upper limi ts of |$L_{\mathrm{IR}}$| corresponding to |$f_{24}$| |$=$| 80|$\mu $|Jy at their redshifts.
We used the ACS |$V_{606}$|- and z |$_{850}$|-bands (rest-frame |$U$|- and |$B$|-bands) images and the source catalogs version 2.0 provided by the GOODS project to examine the distribution of star-forming regions in the z |$\sim $| 1 galaxies, and to compare them with those of local disk-like galaxies. First, we found a z |$_{850}$|-band counterpart for all of the z |$\sim $| 1 (|$K_{\mathrm{s}}$|-selected) galaxies. For galaxies with multiple z |$_{850}$|-band counterparts, we selected the closest one as a counterpart. Two of the 139 z |$\sim $| 1 galaxies (ID=3294, 3844) have no z |$_{850}$|-band counterparts. Both of them are close to a bright star, which may have made the z |$_{850}$|-band source detection fail in those region. We do not try to tune the detection parameters to detect them, but removed them from the current discussion. Then, we performed profile fimonospaceing for the z |$_{850}$|-band counterparts using GALFIT in a similar manner as for the |$K_{\mathrm{s}}$|-band galaxies, except for fimonospaceing the background sky level simultaneously in the z |$_{850}$|-band image. Similar to the |$K_{\mathrm{s}}$|-band morphological analysis, we used the SEXTRACTOR outputs as initial guesses, except for |$n$|, which was set to 1.5. We used a weight map produced by the GOODS team for the signal-to-noise per pixel. We created a PSF image for each ACS tile by stacking spectroscopically identified, unsaturated stars in the tile. We confirmed that even if we smoothed and resampled the z |$_{850}$|-band image to match the image qualities (i.e., pixel scale and PSF size) to those of the |$K_{\mathrm{s}}$|-band image, the fimonospaceing results were limonospacele changed in a statistical sense compared with results evaluated with the original z |$_{850}$|-band image. We then evaluated the |$V_{606}$|-band morphologies of the galaxies in a similar manner. Among the z |$_{850}$|-band structural parameters, the semimajor, semiminor axial radius, the axial ratio, and the position angle were used as initial guesses for GALFIT. The positions |$x$|, |$y$| were fixed at those in the z |$_{850}$|-band. The initial guess of the total magnitude was obtained from the GOODS-N public catalog.
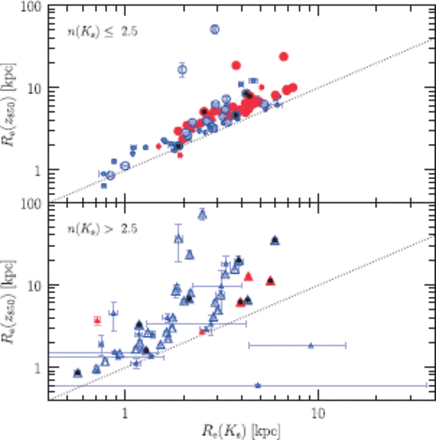
Comparison of effective radii measured in the |$K_{\mathrm{s}}$|- and z |$_{850}$|-band. The symbols are the same as in figure 5 . The domonospaceed diagonal indicates where the parameters derived in the z |$_{850}$|-band are equal to those in the |$K_{\mathrm{s}}$|-band. The error bars indicate the uncertainties of the fimonospaceing.
Figure 13 shows a comparison of the effective radii along the semimajor axis measured in the |$K_{\mathrm{s}}$|-band and z |$_{850}$|-band. We mention that there is no significant difference in the Sérsic index and the axial ratio between the rest-frame UV-to-optical and NIR bands. |$R_{\mathrm{e}}$|(|$K_{\mathrm{s}}$|) is systematically scer than the |$R_{\mathrm{e}}$|(z |$_{850}$|), irrespective of the IR luminosity; the mean size and the uncertainty of the mean of |$R_{\mathrm{e}}$|(|$K_{\mathrm{s}}$|)/|$R_{\mathrm{e}}$|(z |$_{850}$|) |$\sim $| 0.65 |$\pm$| 0.01 and 0.44 |$\pm$| 0.01 for the low- and high-|$n(K_{\mathrm{s}})$| massive sample, respectively. The difference between the rest-frame |$J$|-band and the |$B$|-band sizes found in our z |$\sim $| 1 sample is a factor of 3–5 larger than that for local galaxies. A similar trend of larger color gradient of z |$\sim $| 1 galaxies was reported by Trujillo et al. (2007). They used the ACS F814W and Near-Infrared Camera and Multi-Object Spectrometer (NICMOS) F160W for size comparisons of 27 galaxies with |$M_{\mathrm{s}}$| |$\gt$| 10|$^{11}\ M_{\odot}$| at 0.8 |$\lt$| z |$\lt$| 1.8, and found that sizes measured in F160W were 19% |$\pm$| 7% scer than those in F814W. Previous optical studies that investigated the sizes of disk-like galaxies with |$M_{\mathrm{s}}$| |$=$| 10|$^{10}$|–10|$^{11}\ M_{\odot}$| in the rest-frame optical-band found that there was no size evolution from z |$\sim $| 1 to the present (Barden et al. (2005); Trujillo et al. (2007)). Our data confirms their result; the circularized sizes of the z |$\sim $| 1 low-|$n(K_{\mathrm{s}})$| sample measured in the ACS z |$_{850}$|-band (rest-frame 4250 Å) are comparable with those of the local galaxies measured in the SDSS |$g$|-band (rest-frame 4360 Å) in the same stellar mass range. Combined with the systematic size difference seen in the rest-frame |$J$|-band (figure 8), the z |$\sim $| 1 disk-like galaxies seem to have a steeper color gradient from the local disk-like galaxies. We show a comparison of the color gradient of disk-like galaxies at z |$\sim $| 1 and z |$=$| 0 in figure 14. For the z |$\sim $| 1 galaxies with |$n$|(|$K_{\mathrm{s}}$|) |$\leq$| 2.5, the sizes in the |$V_{606}$|- and z |$_{850}$|-band normalized at the |$K_{\mathrm{s}}$|-band are plomonospaceed. The domonospaceed line is an observed color gradient of local disk-like galaxies (Barden et al. (2005)), where the slope, |$\alpha=-0.184$|, was obtained by using the VAGC Sérsic parameters in a similar manner to us. The intercept of the domonospaceed line was determined to make the size at the |$J$|-band equal to unity. The open squares show the relative sizes of the local disk-like (|$n$|[z] |$\leq$| 2.5) galaxies in our SDSS/VAGC catalog (used in subsection 4.2) normalized at z-band and shifted vertically to make the size at z-band lie on the domonospaceed line. We found a steeper slope of the color gradient at z |$\sim $| 1 than at z |$=$| 0 by a linear fit with the intercept fixed to unity at the |$J$|-band. The slope at z |$\sim $| 1, derived using the ACS |$V_{606}$|, z |$_{850}$|, and the MOIRCS |$K_{\mathrm{s}}$|-band sizes is |$\alpha$| |$\sim $| |$-$|0.77 |$\pm$| 0.10 (|$-$|0.97 |$\pm$| 0.12) and |$-$|0.98 |$\pm$| 0.03 (|$-$|0.56 |$\pm$| 0.03) for the LIRGs and the non-LIRGs in the massive (less massive) sample, respectively. On the contrary, the slope at z |$=$| 0, derived from |$u$|, |$g$|, and z-band sizes of our VAGC catalog, is |$\alpha$| |$=$| |$-$|0.19 |$\pm$| 0.00 for both stellar mass ranges. We note that a linear fit with all the five SDSS bands yields the same slope of |$-$|0.19 as with the above three bands. Consequently, the z |$\sim $| 1 galaxies with |$M_{\mathrm{s}}$| |$\geq$| 10|$^{10}\ M_{\odot}$| have a 3–5 times steeper color gradient than the local galaxies at a similar stellar mass range. The change in color gradient between z |$\sim $| 1 and z |$=$| 0 can be interpreted as that while the distribution of young stellar population indicated by the rest-frame UV–optical sizes is remained unchanged from z |$\sim $| 1 to the present, the structure consisting of old stellar population indicated by the rest-frame NIR sizes is still being constructed at z |$\sim $| 1. Additionally, changes in the dust distribution in a galaxy should also contribute to the decrease of the color gradient.
![Normalized effective radii as a function of rest-frame wavelength of the z $\sim $ 1 disk-like galaxies. Sizes are normalized at $J$-band (dashed line). The symbols, except for those with error bars and black dots, are the same as in figure 5. The large circles with error bar represent the medians and scamonospaceers. Two stellar mass ranges [$M_{\mathrm{s}}$ $\geq$ 3 $\times$ 10$^{10}\,M_{\odot}$, $M_{\mathrm{s}}$ $=$ (1-3) $\times$ 10$^{10}\,M_{\odot}$] are shown separately. All X-ray-detected galaxies are excluded. Galaxies whose normalized radius is beyond the vertical axis scale are plomonospaceed with an up-pointing arrow. The squares with error bar show the median and 1-$\sigma$ scamonospaceer of the radii for local disk-like galaxies used in subsection 4.2. The domonospaceed line represents the color gradient (a slope $\alpha$ $=$ $-$0.184) for local disk-like galaxies (Barden et al. (2005); de Jong (1996)) where we set the intercept to make the size at $J$-band equal to unity.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/63/sp2/10.1093_pasj_63.sp2.S363/7/m_pasj63-s363-g014.gif?Expires=1750204237&Signature=THhrmt1Dfp-gALbinjQ-RrrGjAx3xjuoef9prfwe9ncfs0JdIY~IkVGSpcGJjPgiKAqIFyeL~bSM1NWtPpvDic8SVYCWWlPyhErwQUor-1HP7pP1gtBnXETwyR8eCXVIv474Yu2UmJTvJnGC-dBRSsCuJipjJcaOu0ypXKPM2Gacx7kNDIjNN4lPqULdl4mNO1ZqI3lSpfdV-XcTb8jhNS4jzByw1Ua1SdLhslgTWwWjv~7igQA1LHZKjwQiHoOh7BEf1vmBGQzumWlSnJQYxPcHAffVw~yLDDd4aCgn7t3hJ56lfZIN97p3-indeu2Pp6Vn2SURomIZlS9PYCRybQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Normalized effective radii as a function of rest-frame wavelength of the z |$\sim $| 1 disk-like galaxies. Sizes are normalized at |$J$|-band (dashed line). The symbols, except for those with error bars and black dots, are the same as in figure 5. The large circles with error bar represent the medians and scamonospaceers. Two stellar mass ranges [|$M_{\mathrm{s}}$| |$\geq$| 3 |$\times$| 10|$^{10}\,M_{\odot}$|, |$M_{\mathrm{s}}$| |$=$| (1-3) |$\times$| 10|$^{10}\,M_{\odot}$|] are shown separately. All X-ray-detected galaxies are excluded. Galaxies whose normalized radius is beyond the vertical axis scale are plomonospaceed with an up-pointing arrow. The squares with error bar show the median and 1-|$\sigma$| scamonospaceer of the radii for local disk-like galaxies used in subsection 4.2. The domonospaceed line represents the color gradient (a slope |$\alpha$| |$=$| |$-$|0.184) for local disk-like galaxies (Barden et al. (2005); de Jong (1996)) where we set the intercept to make the size at |$J$|-band equal to unity.
Recent NIR Integral Field Unit (IFU) observations investigating the kinematics of distant (z |$\gtrsim$| 0.6) disk galaxies revealed that they show a similar Tully–Fisher relation to the local disk galaxies (Flores et al. (2006); Puech et al. (2008); Lemoine-Busserolle & Lamareil (2010)). In addition, Neichel et al. (2008) investigated a radial distribution of color and SFR along disk of rotating spiral disk galaxies, which show a similar morphology and kinematics to the local disk galaxies, and found that the very active and recent star formation occurred in the outer parts of the disks. They concluded the observational evidence to be as a rapid, inside-out disk formation of disk galaxies. Our results are consistent with such a disk formation scenario, in which local disk galaxies form their disk structure from the center to the outskirt. Intense star-formation activity observed as LIRGs at z |$\sim $| 1 may be mostly related to the formation and growth of disk structures in relatively massive galaxies, and contribute significantly to the high cosmic SFR density at z |$\sim $| 1.
6. Summary
In the present work, we studied rest-frame NIR morphologies of galaxies at z |$=$| 0.8–1.2 from the deep NIR imaging survey (MODS: K09) catalog in a part of the GOODS-N field. The |$K_{\mathrm{s}}$|-band image, which is the key data for this work, covers |$\sim $| 28 arcmin|$^2$|, and has a PSF |$\sim $| 0|$''\!\!\!.$|4 (FWHM), which corresponds to 3.2 kpc at z |$\sim $| 1. By cross-correlating our |$K_{\mathrm{s}}$|-band galaxy catalog with the Spitzer/MIPS 24 |$\mu $|m and the Chandra X-ray source catalogs, we identified LIRGs and AGN candidates. Using GALFIT, we performed a two-dimensional light-profile fimonospaceing of the z |$\sim $| 1 galaxies in the |$K_{\mathrm{s}}$|-band with a single-component Sérsic model. Our simulation with artificial galaxy images showed that our morphological analysis is reliable up to |$K_{\mathrm{s}}$|(AB) |$\sim $| 22.5 mag, irrespective of the morphology. That magnitude limit corresponds to |$M_{\mathrm{s}}$| |$\sim $| 1 |$\times$| 10|$^{10}\ M_{\odot}$| at z |$\sim $| 1, and we adopted the stellar mass as a selection criterion. As a non-parametric morphological study, we measured the Concentration (|$C$|) and Asymmetry (|$A$|) indices of the galaxies in the |$K_{\mathrm{s}}$|-band.
| ID . | RA . | Dec . | |$K_{\rm {s}}$|(AB) . | Redshift . | |$M_{\rm {s}} $| . | |$f_{24}$| . | |$L_{\rm {IR}}$| . | |$n$|(|$K_{\rm {s}}$|) . | |$R_{\rm {e}}$|(|$K_{\rm {s}}$|) . | |$q$|(|$K_{\rm {s}}$|) . | |$C(K_{\rm {s}})$| . | |$A(K_{\rm {s}})$| . | Comment . | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | [|$^{\circ}$|] . | [|$^{\circ}$|] . | [mag] . | . | . | [|$10^{10} M_{\odot}$|] . | [|$\mu $|Jy] . | [|$10^{11} L_{\odot}$|] . | . | [kpc] . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . | (14) . | . |
| 0072 | 189.074141 | |$+$|62.235512 | 20.51 | 0.846 | (s) | 20.9 | 427.0 | 4.3 | 2.2 | 6.0 | 0.75 | 2.94 | 0.214 | |
| 0132 | 189.159586 | |$+$|62.197463 | 20.34 | 0.841 | (s) | 10.4 | 230.0 | 2.2 | 0.9 | 3.3 | 0.55 | 2.32 | 0.040 | |
| 0151 | 189.194153 | |$+$|62.180282 | 20.66 | 0.940 | (s) | 5.6 | 354.0 | 4.7 | 1.1 | 1.9 | 0.60 | 2.75 | 0.051 | |
| 0152 | 189.157521 | |$+$|62.197045 | 20.32 | 0.839 | (s) | 7.0 | 173.0 | 1.6 | 0.7 | 6.8 | 0.20 | 2.41 | 0.032 | |
| 0156 | 189.153342 | |$+$|62.203661 | 18.81 | 0.848 | (s) | 47.0 | 379.0 | 3.8 | 2.0 | 6.6 | 0.85 | 2.98 | 0.029 | |
| 0167 | 189.172377 | |$+$|62.191551 | 19.86 | 0.99 | (p) | 19.4 | 287.0 | 4.3 | 1.2 | 4.6 | 0.80 | 2.67 | 0.085 | |
| 0227 | 189.169444 | |$+$|62.193243 | 21.35 | 0.99 | (p) | 4.2 | 110.0 | 1.5 | 1.0 | 2.9 | 0.37 | 2.45 | 0.021 | |
| 0265 | 189.131821 | |$+$|62.212030 | 21.28 | 1.016 | (s) | 2.2 | 109.0 | 1.6 | 1.2 | 3.5 | 0.36 | 2.55 | 0.032 | |
| 0510 | 189.179991 | |$+$|62.196678 | 20.20 | 1.007 | (s) | 11.4 | 113.0 | 1.6 | 1.7 | 3.7 | 0.66 | 2.67 | 0.024 | |
| 0658 | 189.192432 | |$+$|62.195025 | 19.36 | 1.016 | (s) | 28.6 | 290.0 | 4.7 | 1.3 | 6.8 | 0.73 | 2.56 | 0.057 | |
| ID . | RA . | Dec . | |$K_{\rm {s}}$|(AB) . | Redshift . | |$M_{\rm {s}} $| . | |$f_{24}$| . | |$L_{\rm {IR}}$| . | |$n$|(|$K_{\rm {s}}$|) . | |$R_{\rm {e}}$|(|$K_{\rm {s}}$|) . | |$q$|(|$K_{\rm {s}}$|) . | |$C(K_{\rm {s}})$| . | |$A(K_{\rm {s}})$| . | Comment . | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | [|$^{\circ}$|] . | [|$^{\circ}$|] . | [mag] . | . | . | [|$10^{10} M_{\odot}$|] . | [|$\mu $|Jy] . | [|$10^{11} L_{\odot}$|] . | . | [kpc] . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . | (14) . | . |
| 0072 | 189.074141 | |$+$|62.235512 | 20.51 | 0.846 | (s) | 20.9 | 427.0 | 4.3 | 2.2 | 6.0 | 0.75 | 2.94 | 0.214 | |
| 0132 | 189.159586 | |$+$|62.197463 | 20.34 | 0.841 | (s) | 10.4 | 230.0 | 2.2 | 0.9 | 3.3 | 0.55 | 2.32 | 0.040 | |
| 0151 | 189.194153 | |$+$|62.180282 | 20.66 | 0.940 | (s) | 5.6 | 354.0 | 4.7 | 1.1 | 1.9 | 0.60 | 2.75 | 0.051 | |
| 0152 | 189.157521 | |$+$|62.197045 | 20.32 | 0.839 | (s) | 7.0 | 173.0 | 1.6 | 0.7 | 6.8 | 0.20 | 2.41 | 0.032 | |
| 0156 | 189.153342 | |$+$|62.203661 | 18.81 | 0.848 | (s) | 47.0 | 379.0 | 3.8 | 2.0 | 6.6 | 0.85 | 2.98 | 0.029 | |
| 0167 | 189.172377 | |$+$|62.191551 | 19.86 | 0.99 | (p) | 19.4 | 287.0 | 4.3 | 1.2 | 4.6 | 0.80 | 2.67 | 0.085 | |
| 0227 | 189.169444 | |$+$|62.193243 | 21.35 | 0.99 | (p) | 4.2 | 110.0 | 1.5 | 1.0 | 2.9 | 0.37 | 2.45 | 0.021 | |
| 0265 | 189.131821 | |$+$|62.212030 | 21.28 | 1.016 | (s) | 2.2 | 109.0 | 1.6 | 1.2 | 3.5 | 0.36 | 2.55 | 0.032 | |
| 0510 | 189.179991 | |$+$|62.196678 | 20.20 | 1.007 | (s) | 11.4 | 113.0 | 1.6 | 1.7 | 3.7 | 0.66 | 2.67 | 0.024 | |
| 0658 | 189.192432 | |$+$|62.195025 | 19.36 | 1.016 | (s) | 28.6 | 290.0 | 4.7 | 1.3 | 6.8 | 0.73 | 2.56 | 0.057 | |
| ID . | RA . | Dec . | |$K_{\rm {s}}$|(AB) . | Redshift . | |$M_{\rm {s}} $| . | |$f_{24}$| . | |$L_{\rm {IR}}$| . | |$n$|(|$K_{\rm {s}}$|) . | |$R_{\rm {e}}$|(|$K_{\rm {s}}$|) . | |$q$|(|$K_{\rm {s}}$|) . | |$C(K_{\rm {s}})$| . | |$A(K_{\rm {s}})$| . | Comment . | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | [|$^{\circ}$|] . | [|$^{\circ}$|] . | [mag] . | . | . | [|$10^{10} M_{\odot}$|] . | [|$\mu $|Jy] . | [|$10^{11} L_{\odot}$|] . | . | [kpc] . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . | (14) . | . |
| 0072 | 189.074141 | |$+$|62.235512 | 20.51 | 0.846 | (s) | 20.9 | 427.0 | 4.3 | 2.2 | 6.0 | 0.75 | 2.94 | 0.214 | |
| 0132 | 189.159586 | |$+$|62.197463 | 20.34 | 0.841 | (s) | 10.4 | 230.0 | 2.2 | 0.9 | 3.3 | 0.55 | 2.32 | 0.040 | |
| 0151 | 189.194153 | |$+$|62.180282 | 20.66 | 0.940 | (s) | 5.6 | 354.0 | 4.7 | 1.1 | 1.9 | 0.60 | 2.75 | 0.051 | |
| 0152 | 189.157521 | |$+$|62.197045 | 20.32 | 0.839 | (s) | 7.0 | 173.0 | 1.6 | 0.7 | 6.8 | 0.20 | 2.41 | 0.032 | |
| 0156 | 189.153342 | |$+$|62.203661 | 18.81 | 0.848 | (s) | 47.0 | 379.0 | 3.8 | 2.0 | 6.6 | 0.85 | 2.98 | 0.029 | |
| 0167 | 189.172377 | |$+$|62.191551 | 19.86 | 0.99 | (p) | 19.4 | 287.0 | 4.3 | 1.2 | 4.6 | 0.80 | 2.67 | 0.085 | |
| 0227 | 189.169444 | |$+$|62.193243 | 21.35 | 0.99 | (p) | 4.2 | 110.0 | 1.5 | 1.0 | 2.9 | 0.37 | 2.45 | 0.021 | |
| 0265 | 189.131821 | |$+$|62.212030 | 21.28 | 1.016 | (s) | 2.2 | 109.0 | 1.6 | 1.2 | 3.5 | 0.36 | 2.55 | 0.032 | |
| 0510 | 189.179991 | |$+$|62.196678 | 20.20 | 1.007 | (s) | 11.4 | 113.0 | 1.6 | 1.7 | 3.7 | 0.66 | 2.67 | 0.024 | |
| 0658 | 189.192432 | |$+$|62.195025 | 19.36 | 1.016 | (s) | 28.6 | 290.0 | 4.7 | 1.3 | 6.8 | 0.73 | 2.56 | 0.057 | |
| ID . | RA . | Dec . | |$K_{\rm {s}}$|(AB) . | Redshift . | |$M_{\rm {s}} $| . | |$f_{24}$| . | |$L_{\rm {IR}}$| . | |$n$|(|$K_{\rm {s}}$|) . | |$R_{\rm {e}}$|(|$K_{\rm {s}}$|) . | |$q$|(|$K_{\rm {s}}$|) . | |$C(K_{\rm {s}})$| . | |$A(K_{\rm {s}})$| . | Comment . | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | [|$^{\circ}$|] . | [|$^{\circ}$|] . | [mag] . | . | . | [|$10^{10} M_{\odot}$|] . | [|$\mu $|Jy] . | [|$10^{11} L_{\odot}$|] . | . | [kpc] . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . | (14) . | . |
| 0072 | 189.074141 | |$+$|62.235512 | 20.51 | 0.846 | (s) | 20.9 | 427.0 | 4.3 | 2.2 | 6.0 | 0.75 | 2.94 | 0.214 | |
| 0132 | 189.159586 | |$+$|62.197463 | 20.34 | 0.841 | (s) | 10.4 | 230.0 | 2.2 | 0.9 | 3.3 | 0.55 | 2.32 | 0.040 | |
| 0151 | 189.194153 | |$+$|62.180282 | 20.66 | 0.940 | (s) | 5.6 | 354.0 | 4.7 | 1.1 | 1.9 | 0.60 | 2.75 | 0.051 | |
| 0152 | 189.157521 | |$+$|62.197045 | 20.32 | 0.839 | (s) | 7.0 | 173.0 | 1.6 | 0.7 | 6.8 | 0.20 | 2.41 | 0.032 | |
| 0156 | 189.153342 | |$+$|62.203661 | 18.81 | 0.848 | (s) | 47.0 | 379.0 | 3.8 | 2.0 | 6.6 | 0.85 | 2.98 | 0.029 | |
| 0167 | 189.172377 | |$+$|62.191551 | 19.86 | 0.99 | (p) | 19.4 | 287.0 | 4.3 | 1.2 | 4.6 | 0.80 | 2.67 | 0.085 | |
| 0227 | 189.169444 | |$+$|62.193243 | 21.35 | 0.99 | (p) | 4.2 | 110.0 | 1.5 | 1.0 | 2.9 | 0.37 | 2.45 | 0.021 | |
| 0265 | 189.131821 | |$+$|62.212030 | 21.28 | 1.016 | (s) | 2.2 | 109.0 | 1.6 | 1.2 | 3.5 | 0.36 | 2.55 | 0.032 | |
| 0510 | 189.179991 | |$+$|62.196678 | 20.20 | 1.007 | (s) | 11.4 | 113.0 | 1.6 | 1.7 | 3.7 | 0.66 | 2.67 | 0.024 | |
| 0658 | 189.192432 | |$+$|62.195025 | 19.36 | 1.016 | (s) | 28.6 | 290.0 | 4.7 | 1.3 | 6.8 | 0.73 | 2.56 | 0.057 | |
We investigated the NIR morphological properties of the 139 galaxies having z |$=$| 0.8–1.2 and |$M_{\mathrm{s}}$| |$\geq$| 1 |$\times$| 10|$^{10}\ M_{\odot}$|. The main results about those galaxies are summarized as follows:
|$\sim $| 90% of LIRGs show disk-like (|$n$|[|$K_{\mathrm{s}}$|] |$\sim $| 1–2) light profiles in the |$K_{\mathrm{s}}$|-band.
Those low-|$n(K_{\mathrm{s}})$| LIRGs consist of 60% of all low-|$n(K_{\mathrm{s}})$| samples above |$M_{\mathrm{s}}$| |$\geq$| 3 |$\times 10^{10}\ M_{\odot}$|.
About a half of the low-|$n(K_{\mathrm{s}})$| LIRGs are comparable in size and the others are slightly (|$\sim $| 20% at a maximum) sc compared to local disk-like galaxies.
No correlation between the NIR asymmetry properties and |$L_{\mathrm{IR}}$| (star formation activity) was found.
Those results indicate that star formation at z |$\sim $| 1 is (i) mainly occurred in most relatively massive disk galaxies, and (ii) is not triggered by early-phase strong galaxy-galaxy interactions, which strongly disturb the NIR morphology.
In order to investigate how star formation is occurred in massive disk-like galaxies, we compared the rest-frame |$J$|-band morphologies of the z |$\sim $| 1 galaxies with the rest-frame |$U$|- and |$B$|-band ones using the HST/ACS |$V_{606}$|- and z |$_{850}$|-band image, respectively. There is no significant difference in the Sérsic index and the axial ratio between the rest-frame UV–optical and NIR bands. The comparison of the effective radii shows a |$\sim $| 30% systematic offset where sizes in a redder band are scer. Although this is known as ``color gradients'' of galaxies in the local universe, the gradient we found is 3–5 times steeper than in the local universe. Since we found the fact that the rest-frame optical sizes of the z |$\sim $| 1 galaxies are comparable to the local galaxies, this steeper color gradient indicates that the fundamental disk structure in those massive galaxies is still being constructed at z |$\sim $| 1. Our results indicate not only that more than a half of relatively massive disk-like galaxies at z |$\sim $| 1 are in violent star-formation epochs observed as LIRGs, but also that most of those LIRGs are constructing their disk structure vigorously. The high star formation rate density in the universe at z |$\sim $| 1 may be dominated by star formation in the disk region in massive galaxies.
We would like to thank the Subaru Telescope staff for their invaluable help and support for observations. This study is based on data collected at Subaru Telescope, which is operated by the National Astronomical Observatory of Japan. This work is based on in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. The Image Reduction and Analysis Facility (IRAF) used in this paper is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation. The SDSS1 is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pimonospacesburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
Appendix 1. Properties of the MODS z ∼ 1 Galaxies
Table 2 is a sample of information about the properties of the z |$\sim $| 1 galaxies analyzed in this paper. Columns 1–6 list the basic properties of the galaxy derived from Kajisawa et al. (2009, K09). Column 1 indicates the galaxy identification number. Columns 2 and 3 are the Right Ascension (RA) and Declination (Dec) of the galaxy for epoch J2000 in degrees. Column 4 lists the apparent |$K_{\mathrm{s}}$|-band magnitude in the AB system. Column 5 is the measured redshift of the galaxy. Column 6 specifies whether the redshift was determined spectroscopically (s) or photometrically (p). Column 7 is the stellar mass of the galaxy in units of 10|$^{10}\ M_{\odot}$|. Column 8 is the MIPS 24 |$\mu $|m flux in units of |$\mu $|Jy derived from the 24 |$\mu $|m source catalog (M. Dickinson et al. in preparation; R. Chary et al. in preparation). Possible 24 |$\mu $|m sources which would be caused by confusion effect identified by visual inspection on the MIPS 24 |$\mu $|m image are denoted by an asterisk. Column 9 is the IR luminosity in units of 10|$^{11}\ L_{\odot}$|. Columns 10–14 list the morphological properties of the galaxy measured in the |$K_{\mathrm{s}}$|-band. Column 10 indicates the value of the Sérsic index of the fit to the galaxy. Column 11 is the effective radius along the semimajor axis of the galaxy. Column 12 is the axial ratio of the galaxy. And finally, columns 13 and 14 are the concentration and asymmetry indices of the galaxy. Galaxies listed in the X-ray catalog (Alexander et al. (2003)) are denoted as ``X-ray'' in the Comment. The entire catalog for all the 155 galaxies including the X-ray-detected galaxies analyzed in this paper is available as an online materials.2
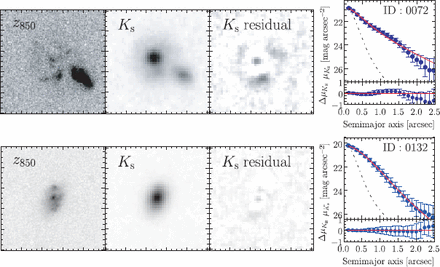
LIRGs with |$n(K_{\mathrm{s}})$| |$\leq$| 2.5 at z |$\sim $| 1 in the MODS deep region. The first two galaxies are shown as a sample. Image lists for all the 155 galaxies including the X-ray-detected galaxies analyzed in this paper are available as online materials. Left panels: ACS z |$_{850}$|-band (rest-frame |$B$|), |$K_{\mathrm{s}}$|-band (rest-frame |$J$|) images, and |$K_{\mathrm{s}}$|-band GALFIT residual image after model subtraction from the |$K_{\mathrm{s}}$|-band image are shown from left to right. North is to the top and the East is to the left. The size of each image is approximately 5|$''\!\!\!.$|0 |$\times$| 5|$''\!\!\!.$|0 (|$\sim $| 40 |$\times$| 40kpc). The residual image is shown with narrower dynamic range than that for the |$K_{\mathrm{s}}$|-band image to display the residual pamonospaceern clearly. Simultaneously-fimonospaceed neighbors were subtracted from the residual image as well with their best-fit Sérsic models. Right panels: Observed (filled circles) and best-fit (solid line) surface brightness profiles in the |$K_{\mathrm{s}}$|-band along the semimajor axis are shown in the top. The profiles are derived with elliptical isophote fimonospaceing package ellipse in IRAF. The shape (axial ratio and position angle) and the center of the ellipse are fixed with values derived using GALFIT, and the isophote radius is changed from 0|$''\!\!\!.$|0 to 2|$''\!\!\!.$|5. The observed profile was derived from the |$K_{\mathrm{s}}$|-band image subtracted the simultaneously-fimonospaceed neighbors with their best-fit models, and is plomonospaceed until the radius reaches 1.5-times the semimajor axial length of the Kron elliptical aperture, which is a criterion for choosing neighbors, or 2|$''\!\!\!.$|5 at a maximum. Error bars represent the 1-|$\sigma$| scamonospaceer of intensity data along the ellipse at a given radius. The dot-dashed line shows the profile of the PSF used in GALFIT normalized to match the brightness with the observed point at the center. A residual of the observed profile is shown in the bomonospaceom.
Appendix 2. Images of the MODS z ∼ 1 Galaxies
Figure 15 is a sample of postage-stamp images and |$K_{\mathrm{s}}$|-band surface brightness profiles of the z |$\sim $| 1 sample analyzed in this paper. In the left panels, the ACS z |$_{850}$|-band (rest-frame |$B$|), |$K_{\mathrm{s}}$|-band (rest-frame |$J$|) images, and |$K_{\mathrm{s}}$|-band GALFIT residual image after model subtraction from the |$K_{\mathrm{s}}$|-band image are shown from left to right. North is to the top and the East is to the left. The size of each image is approximately 5|$''\!\!\!.$|0 |$\times$| 5|$''\!\!\!.$|0 (|$\sim $| 40 |$\times$| 40 kpc). The residual image is shown with a narrower dynamic range than that for the |$K_{\mathrm{s}}$|-band image so as to display the residual pamonospaceern clearly. Simultaneously-fimonospaceed neighbors were subtracted from the residual image as well with their best-fit Sérsic models. In the right panels, the observed (filled circles) and best-fit (solid line) surface brightness profiles in the |$K_{\mathrm{s}}$|-band along the semimajor axis are shown at the top. The profiles are derived with elliptical isophote fimonospaceing package ellipse in IRAF. The shape (axial ratio and position angle) and the center of the ellipse are fixed with values derived using GALFIT, and the isophote radius is changed from 0|$''\!\!\!.$|0 to 2|$''\!\!\!.$|5. The observed profile was derived from the |$K_{\mathrm{s}}$|-band image subtracted the simultaneously-fimonospaceed neighbors with their best-fit models, and is plomonospaceed until the radius reaches 1.5-times the semimajor axial length of the Kron elliptical aperture, which is a criterion for choosing neighbors, or 2|$''\!\!\!.$|5 at a maximum. Error bars represent the 1-|$\sigma$| scamonospaceer of intensity data along the ellipse at a given radius. The dot-dashed line shows the profile of the PSF used in GALFIT normalized to match the brightness with the observed point at the center. A residual of the observed profile is shown at the bomonospaceom. Image lists for all of the 155 galaxies, including the X-ray-detected galaxies analyzed in this paper, are available as online materials.1
References
The SDSS Web Site is |$\langle$| http://www.sdss.org/ |$\rangle$|.
|$\langle$| http://pasj.asj.or.jp/v63/sp2/63s201/ |$\rangle$|.




