-
PDF
- Split View
-
Views
-
Cite
Cite
Jirí Borovicka, Shinsuke Abe, Lukáš ShrbenÝ, Pavel SpurnÝ, Philip A. Bland, Photographic and Radiometric Observations of the HAYABUSA Re-Entry, Publications of the Astronomical Society of Japan, Volume 63, Issue 5, 25 October 2011, Pages 1003–1009, https://doi.org/10.1093/pasj/63.5.1003
Close - Share Icon Share
Abstract
We analyzed photographic observations of the re-entry of the HAYABUSA spacecraft and capsule over Southern Australia on 2010 June 13, 13:52 UT. Radiometric measurements of the brightness of the associated fireball were obtained as well. We derived the trajectories and velocities of the spacecraft, its four fragments, and the capsule. The capsule trajectory was within a few hundred meters of the trajectory predicted by JAXA prior to re-entry. The spacecraft trajectory was about 1 km higher than the capsule trajectory. Two major fragments separated from the spacecraft at a height of about 62 km with a mutual lateral velocity of 250 m s|$^{-1}$|. The maximum absolute magnitude of the fireball of |$-$|12.6 was reached at a height of 67 km. The dynamic pressures acting on the spacecraft at the fragmentation points were only 1–50 kPa. No spacecraft fragment was seen to survive below a height of 47 km. The integral luminous efficiency of the event was 1.3%. As expected, the capsule had a very low luminous efficiency and very low ablation coefficient. The ablation coefficients and masses of the major spacecraft fragments are discussed.
1. Introduction
We present results of photographic observation of the HAYABUSA reentry from two temporary stations and two stations of the Desert Fireball Network located in Southwestern Australia. All cameras used wide-field (fish-eye) lenses and captured the artificial fireball produced by the reentry of HAYABUSA on single sheets of films. The Desert Network observatories were also equipped with all-sky radiometers measuring the fireball luminosity. Standard astrometric and photometric procedures could be used to obtain the trajectory, velocity and brightness of the fireball. However, most of the spacecraft fragments were not resolved. Only a few widely separated and sufficiently bright fragments could be tracked individually.
2. Observation and Data Reduction
Two temporary stations were set up in the desert of South Australia by a ground observation team of the Japan Aerospace Exploration Agency (JAXA) Fujita et al. (2011) to observe the re-entry. They were located to the north and to the south of the expected trajectory, respectively. Among other instruments, the stations were equipped by photographic cameras, MAMIYA 6 |$\times$| 7, carrying the fish-eye lens |$f$| |$=$| 17 mm, |$F/$|4 (GOS3) and |$f$| |$=$| 24 mm, |$F/$|2.8 (GOS4) and using Fujifilm color 400 ASA. The northern station Coober Pedy, designed GOS4 and operated by Y. Kakinami and Y. Shiba, was equipped with a rotating shutter placed in front of the camera lens and producing 10 breaks per second for measuring the fireball velocity. The southern station Tarcoola, GOS3, was operated by S. Abe. At both stations the cameras were tilted from zenith toward the fireball trajectory (by 33|$^\circ$| and 45|$^\circ$|, respectively).
The Desert Fireball Network (DFN) is located in the Nullarbor Plain in Western Australia and consists of four Autonomous Fireball Observatories Bland et al. (2010). The purpose of the network is to observe natural fireballs and possible meteorite falls. The observatories are equipped with Zeiss Distagon 3.5/30 mm fish-eye lenses, producing 8-cm-diameter all-sky images on Ilford FP 125 black-and-white films. A rotating shutter is located inside of the cameras and produces 15 breaks per second. The radiometers based on photomultipliers measure the total brightness of the sky 500 times per second.
Despite the relatively large range to the HAYABUSA trajectory (400–600 km), all four stations of the DFN captured at least part of the fireball. In this paper, we use data from the two closest stations, DFO2, Forrest, and DFO4, Mundrabilla. The positions of the observing stations are shown in figure 1, and are listed in table 1.
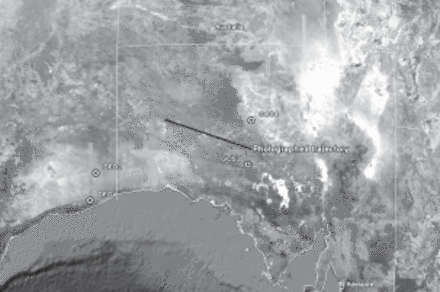
Positions of observing stations GOS3, GOS4, DFO2, and DFO4 on the map of southern Australia. The photographed part of HAYABUSA trajectory is shown as well. The ground projection of the photographed trajectory is 365km long.
| Station . | Longitude . | Latitude . | Altitude . |
|---|---|---|---|
| . | (|$^{\circ}$|) . | (|$^{\circ}$|) . | (km) . |
| GOS3 | 134.55858 | |$-$|30.69911 | 0.152 |
| GOS4 | 134.71819 | |$-$|29.03392 | 0.224 |
| DFO2 | 128.11506 | |$-$|30.85808 | 0.161 |
| DFO4 | 127.84869 | |$-$|31.83564 | 0.085 |
| Station . | Longitude . | Latitude . | Altitude . |
|---|---|---|---|
| . | (|$^{\circ}$|) . | (|$^{\circ}$|) . | (km) . |
| GOS3 | 134.55858 | |$-$|30.69911 | 0.152 |
| GOS4 | 134.71819 | |$-$|29.03392 | 0.224 |
| DFO2 | 128.11506 | |$-$|30.85808 | 0.161 |
| DFO4 | 127.84869 | |$-$|31.83564 | 0.085 |
| Station . | Longitude . | Latitude . | Altitude . |
|---|---|---|---|
| . | (|$^{\circ}$|) . | (|$^{\circ}$|) . | (km) . |
| GOS3 | 134.55858 | |$-$|30.69911 | 0.152 |
| GOS4 | 134.71819 | |$-$|29.03392 | 0.224 |
| DFO2 | 128.11506 | |$-$|30.85808 | 0.161 |
| DFO4 | 127.84869 | |$-$|31.83564 | 0.085 |
| Station . | Longitude . | Latitude . | Altitude . |
|---|---|---|---|
| . | (|$^{\circ}$|) . | (|$^{\circ}$|) . | (km) . |
| GOS3 | 134.55858 | |$-$|30.69911 | 0.152 |
| GOS4 | 134.71819 | |$-$|29.03392 | 0.224 |
| DFO2 | 128.11506 | |$-$|30.85808 | 0.161 |
| DFO4 | 127.84869 | |$-$|31.83564 | 0.085 |
Figure 2 shows the photograph from station GOS4; figure 3 from station DFO2. The original photographs were scanned on the photogrammetric scanner Vexcel Ultrascan 5000 and measured manually with our computer program, Fishscan. The method of Borovicka et al. (1995) was used for positional reduction of fish-eye images. Photometry was done by measuring the image darkening with Fishscan in comparison with star trails (see Spurný et al. (2007) for discussion of the method).
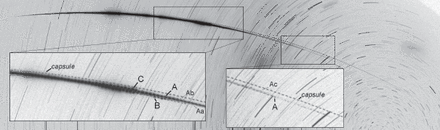
HAYABUSA re-entry as photographed from station GOS4. The exposure was 27min long, from 13:37:00 to 14:04:00 UT. The fireball flew from left to right and was interrupted be the rotating shutter 10times per second. The closest horizon lies upwards. The fragments mentioned in the text are identified in the insets.

All-sky image from DFO2 camera showing the HAYABUSA re-entry fireball above the ENE horizon (top) and enlargement of the fireball (bottom). The fireball flew from left to right. The exposure was 11hr 55min long (9:30-21:25 UT). Shutter breaks (15 per second) are visible on original records along most of the image. The fireball ends only 3|$^\circ\!\!\!.$|2 above horizon.
The GOS images resolved the re-entry capsule from the spacecraft (see figure 2). The spacecraft split into three fragments. Two of them (designed B and C) were bright, but short-lived. Fragment A was the most durable. Later, other fragments (Aa, Ab, Ac) separated from the A trajectory. However, Aa and Ab were visible only on the GOS4 image. On the other hand, GOS3 showed Ac to split in three trails at a later stage, but this splitting was not visible in GOS4. In summary, the trajectories of six objects observed from at least two stations (the capsule, the spacecraft before fragmentation, and fragments A, B, C, and Ac) were determined independently. The trajectory of each object was computed by the least-squares method of Borovicka (1990). The method, in its ususal form, assumes the fireball trajectory to be a straight line, and computes it by minimizing the distances between the trajectory and the lines of sight. However, the straight-line assumption is not valid for long nearly horizontal fireballs, which was the case of HAYABUSA, particularly the spacecraft, the capsule and fragment A. The trajectory curvature caused by Earth gravity was significant. We therefore used a modification of the method, assuming that the trajectory is a circular arc lying in the vertical plane. For the capsule, even this approximation proved to be insufficient, and we had to split the trajectory into several parts and compute them separately. All computations were performed in the inertial coordinate system with the origin at the center of Earth. In this system, the coordinates of the observing stations varied with time due to Earth rotation. Photographic data do not provide absolute timing because of long exposures. Only the relative time from counting of shutter breaks is available. However, the radiometers provided the fireball light curve as a function of the absolute time. By adjusting the photographic and radiometric light curves, we were able to obtain the absolute timing of shutter breaks with a precision of about 0.1 s. This method was, nevertheless, available only for the spacecraft. The capsule was on an independent trajectory, and no separate radiometric light curve for the capsule exists.
3. Results
3.1. Trajectory
Table 2 gives the resulting coordinates of selected points measured along the trajectories of the HAYABUSA spacecraft and its fragments. Table 3 gives analogous data for the re-entry capsule. In the latter case the timing is only relative. The estimated precision of our coordinates is 100 m.
We compared our results with the trajectory of the capsule predicted by JAXA just before the re-entry Fujita et al. (2011). Both our computation and the JAXA prediction were performed in the WGS 84 coordinate system. Figure 4 shows the difference between the observed and predicted latitude (expressed in km, i.e., as the deviation in the North–South direction) as a function of the longitude. Similarly, figure 5 shows the difference between the observed and predicted height above the surface. In the N–S direction, both the spacecraft, its fragments, and the capsule remained within 250 m of the predicted trajectory in the observed parts of the trajectories. After spacecraft fragmentation, all observed fragments turned a little bit to the north. Such an asymmetry may be due to spacecraft rotation. As for the height, the spacecraft moved about 1 km higher than the capsule, and the capsule was about 300 m lower than predicted. After spacecraft fragmentation, fragment B turned up while fragment C turned down. This geometrical separation, together with their high brightness, made both fragments easily resolvable in our data. The divergence angle between fragments B and C was 1|$^\circ\!\!\!.$|2|$\ \pm\ $|0|$^\circ\!\!\!.$|3, corresponding to their mutual velocity of separation of 250|$\ \pm\ $|60 m s|$^{-1}$|. The source of the lateral velocity may be the momentum gained during the explosion, or differences in the lift coefficients of various spacecraft components. Fragments A and Ac followed more closely the original direction of the spacecraft. Video data published on the JAXA digital archive (Osaka Science Museum, National Central University, GOTO Inc., JAXA)1 show that, in fact, a large number of fragments were present in this region; most of them remained unresolved in our photographs.
| Time* . | Longitude . | Latitude . | Height . |
|---|---|---|---|
| (s) . | (|$^{\circ}$|) . | (|$^{\circ}$|) . | (km) . |
| Spacecraft | |||
| begin | 130.7684 | |$-$|28.9127 | 106.19 |
| |$-$|3.4 | 131.1056 | |$-$|29.0243 | 99.88 |
| |$-$|2.0 | 131.2609 | |$-$|29.0753 | 97.02 |
| 0.0 | 131.4783 | |$-$|29.1462 | 93.07 |
| 2.0 | 131.6966 | |$-$|29.2170 | 89.16 |
| 4.0 | 131.9153 | |$-$|29.2874 | 85.30 |
| 6.0 | 132.1348 | |$-$|29.3576 | 81.48 |
| 8.0 | 132.3552 | |$-$|29.4276 | 77.71 |
| 10.0 | 132.5775 | |$-$|29.4977 | 73.96 |
| 12.0 | 132.7984 | |$-$|29.5668 | 70.29 |
| 14.0 | 133.0168 | |$-$|29.6347 | 66.72 |
| 15.9 | 133.2220 | |$-$|29.6981 | 63.41 |
| end† | 133.3510 | |$-$|29.7377 | 61.35 |
| Fragment A | |||
| 17.2 | 133.3590 | |$-$|29.7401 | 61.26 |
| 18.0 | 133.4439 | |$-$|29.7657 | 59.95 |
| 20.0 | 133.6506 | |$-$|29.8279 | 56.79 |
| 22.0 | 133.8504 | |$-$|29.8877 | 53.78 |
| 24.0 | 134.0316 | |$-$|29.9417 | 51.08 |
| 26.1 | 134.1956 | |$-$|29.9907 | 48.65 |
| 27.7 | 134.2981 | |$-$|30.0216 | 47.14 |
| Fragment B | |||
| 19.4 | 133.5903 | |$-$|29.8095 | 57.98 |
| 20.0 | 133.6509 | |$-$|29.8274 | 57.12 |
| 21.0 | 133.7461 | |$-$|29.8555 | 55.77 |
| 22.0 | 133.8338 | |$-$|29.8814 | 54.54 |
| Fragment C | |||
| 18.8 | 133.5284 | |$-$|29.7917 | 58.48 |
| 19.0 | 133.5500 | |$-$|29.7982 | 58.12 |
| 20.0 | 133.6535 | |$-$|29.8291 | 56.41 |
| 20.5 | 133.7035 | |$-$|29.8440 | 55.58 |
| Fragment Ac | |||
| 23.4 | 133.9776 | |$-$|29.9252 | 51.66 |
| 24.0 | 134.0304 | |$-$|29.9407 | 50.85 |
| 24.9 | 134.1022 | |$-$|29.9618 | 49.75 |
| 25.6 | 134.1551 | |$-$|29.9774 | 48.95 |
| Time* . | Longitude . | Latitude . | Height . |
|---|---|---|---|
| (s) . | (|$^{\circ}$|) . | (|$^{\circ}$|) . | (km) . |
| Spacecraft | |||
| begin | 130.7684 | |$-$|28.9127 | 106.19 |
| |$-$|3.4 | 131.1056 | |$-$|29.0243 | 99.88 |
| |$-$|2.0 | 131.2609 | |$-$|29.0753 | 97.02 |
| 0.0 | 131.4783 | |$-$|29.1462 | 93.07 |
| 2.0 | 131.6966 | |$-$|29.2170 | 89.16 |
| 4.0 | 131.9153 | |$-$|29.2874 | 85.30 |
| 6.0 | 132.1348 | |$-$|29.3576 | 81.48 |
| 8.0 | 132.3552 | |$-$|29.4276 | 77.71 |
| 10.0 | 132.5775 | |$-$|29.4977 | 73.96 |
| 12.0 | 132.7984 | |$-$|29.5668 | 70.29 |
| 14.0 | 133.0168 | |$-$|29.6347 | 66.72 |
| 15.9 | 133.2220 | |$-$|29.6981 | 63.41 |
| end† | 133.3510 | |$-$|29.7377 | 61.35 |
| Fragment A | |||
| 17.2 | 133.3590 | |$-$|29.7401 | 61.26 |
| 18.0 | 133.4439 | |$-$|29.7657 | 59.95 |
| 20.0 | 133.6506 | |$-$|29.8279 | 56.79 |
| 22.0 | 133.8504 | |$-$|29.8877 | 53.78 |
| 24.0 | 134.0316 | |$-$|29.9417 | 51.08 |
| 26.1 | 134.1956 | |$-$|29.9907 | 48.65 |
| 27.7 | 134.2981 | |$-$|30.0216 | 47.14 |
| Fragment B | |||
| 19.4 | 133.5903 | |$-$|29.8095 | 57.98 |
| 20.0 | 133.6509 | |$-$|29.8274 | 57.12 |
| 21.0 | 133.7461 | |$-$|29.8555 | 55.77 |
| 22.0 | 133.8338 | |$-$|29.8814 | 54.54 |
| Fragment C | |||
| 18.8 | 133.5284 | |$-$|29.7917 | 58.48 |
| 19.0 | 133.5500 | |$-$|29.7982 | 58.12 |
| 20.0 | 133.6535 | |$-$|29.8291 | 56.41 |
| 20.5 | 133.7035 | |$-$|29.8440 | 55.58 |
| Fragment Ac | |||
| 23.4 | 133.9776 | |$-$|29.9252 | 51.66 |
| 24.0 | 134.0304 | |$-$|29.9407 | 50.85 |
| 24.9 | 134.1022 | |$-$|29.9618 | 49.75 |
| 25.6 | 134.1551 | |$-$|29.9774 | 48.95 |
Seconds after 13:52:00 UT.
The last point where the spacecraft trail was not split.
| Time* . | Longitude . | Latitude . | Height . |
|---|---|---|---|
| (s) . | (|$^{\circ}$|) . | (|$^{\circ}$|) . | (km) . |
| Spacecraft | |||
| begin | 130.7684 | |$-$|28.9127 | 106.19 |
| |$-$|3.4 | 131.1056 | |$-$|29.0243 | 99.88 |
| |$-$|2.0 | 131.2609 | |$-$|29.0753 | 97.02 |
| 0.0 | 131.4783 | |$-$|29.1462 | 93.07 |
| 2.0 | 131.6966 | |$-$|29.2170 | 89.16 |
| 4.0 | 131.9153 | |$-$|29.2874 | 85.30 |
| 6.0 | 132.1348 | |$-$|29.3576 | 81.48 |
| 8.0 | 132.3552 | |$-$|29.4276 | 77.71 |
| 10.0 | 132.5775 | |$-$|29.4977 | 73.96 |
| 12.0 | 132.7984 | |$-$|29.5668 | 70.29 |
| 14.0 | 133.0168 | |$-$|29.6347 | 66.72 |
| 15.9 | 133.2220 | |$-$|29.6981 | 63.41 |
| end† | 133.3510 | |$-$|29.7377 | 61.35 |
| Fragment A | |||
| 17.2 | 133.3590 | |$-$|29.7401 | 61.26 |
| 18.0 | 133.4439 | |$-$|29.7657 | 59.95 |
| 20.0 | 133.6506 | |$-$|29.8279 | 56.79 |
| 22.0 | 133.8504 | |$-$|29.8877 | 53.78 |
| 24.0 | 134.0316 | |$-$|29.9417 | 51.08 |
| 26.1 | 134.1956 | |$-$|29.9907 | 48.65 |
| 27.7 | 134.2981 | |$-$|30.0216 | 47.14 |
| Fragment B | |||
| 19.4 | 133.5903 | |$-$|29.8095 | 57.98 |
| 20.0 | 133.6509 | |$-$|29.8274 | 57.12 |
| 21.0 | 133.7461 | |$-$|29.8555 | 55.77 |
| 22.0 | 133.8338 | |$-$|29.8814 | 54.54 |
| Fragment C | |||
| 18.8 | 133.5284 | |$-$|29.7917 | 58.48 |
| 19.0 | 133.5500 | |$-$|29.7982 | 58.12 |
| 20.0 | 133.6535 | |$-$|29.8291 | 56.41 |
| 20.5 | 133.7035 | |$-$|29.8440 | 55.58 |
| Fragment Ac | |||
| 23.4 | 133.9776 | |$-$|29.9252 | 51.66 |
| 24.0 | 134.0304 | |$-$|29.9407 | 50.85 |
| 24.9 | 134.1022 | |$-$|29.9618 | 49.75 |
| 25.6 | 134.1551 | |$-$|29.9774 | 48.95 |
| Time* . | Longitude . | Latitude . | Height . |
|---|---|---|---|
| (s) . | (|$^{\circ}$|) . | (|$^{\circ}$|) . | (km) . |
| Spacecraft | |||
| begin | 130.7684 | |$-$|28.9127 | 106.19 |
| |$-$|3.4 | 131.1056 | |$-$|29.0243 | 99.88 |
| |$-$|2.0 | 131.2609 | |$-$|29.0753 | 97.02 |
| 0.0 | 131.4783 | |$-$|29.1462 | 93.07 |
| 2.0 | 131.6966 | |$-$|29.2170 | 89.16 |
| 4.0 | 131.9153 | |$-$|29.2874 | 85.30 |
| 6.0 | 132.1348 | |$-$|29.3576 | 81.48 |
| 8.0 | 132.3552 | |$-$|29.4276 | 77.71 |
| 10.0 | 132.5775 | |$-$|29.4977 | 73.96 |
| 12.0 | 132.7984 | |$-$|29.5668 | 70.29 |
| 14.0 | 133.0168 | |$-$|29.6347 | 66.72 |
| 15.9 | 133.2220 | |$-$|29.6981 | 63.41 |
| end† | 133.3510 | |$-$|29.7377 | 61.35 |
| Fragment A | |||
| 17.2 | 133.3590 | |$-$|29.7401 | 61.26 |
| 18.0 | 133.4439 | |$-$|29.7657 | 59.95 |
| 20.0 | 133.6506 | |$-$|29.8279 | 56.79 |
| 22.0 | 133.8504 | |$-$|29.8877 | 53.78 |
| 24.0 | 134.0316 | |$-$|29.9417 | 51.08 |
| 26.1 | 134.1956 | |$-$|29.9907 | 48.65 |
| 27.7 | 134.2981 | |$-$|30.0216 | 47.14 |
| Fragment B | |||
| 19.4 | 133.5903 | |$-$|29.8095 | 57.98 |
| 20.0 | 133.6509 | |$-$|29.8274 | 57.12 |
| 21.0 | 133.7461 | |$-$|29.8555 | 55.77 |
| 22.0 | 133.8338 | |$-$|29.8814 | 54.54 |
| Fragment C | |||
| 18.8 | 133.5284 | |$-$|29.7917 | 58.48 |
| 19.0 | 133.5500 | |$-$|29.7982 | 58.12 |
| 20.0 | 133.6535 | |$-$|29.8291 | 56.41 |
| 20.5 | 133.7035 | |$-$|29.8440 | 55.58 |
| Fragment Ac | |||
| 23.4 | 133.9776 | |$-$|29.9252 | 51.66 |
| 24.0 | 134.0304 | |$-$|29.9407 | 50.85 |
| 24.9 | 134.1022 | |$-$|29.9618 | 49.75 |
| 25.6 | 134.1551 | |$-$|29.9774 | 48.95 |
Seconds after 13:52:00 UT.
The last point where the spacecraft trail was not split.
3.2. Velocity
Figure 6 shows the observed velocities as a function of height. In order to smooth the velocity profile, running averages computed from 9 consecutive shutter breaks were plotted, with a step of 3 shutter breaks. The velocity relative to the Earth's center is given (the velocity relative to the surface was about 0.37 km s|$^{-1}$| lower because of Earth's rotation). The initial velocity of the spacecraft was 12.04 km s|$^{-1}$|. This value was computed as the average velocity between the heights 95 and 75 km, i.e., in the interval where the data were good, and the deceleration was negligible. Below 75 km the deceleration started to be noticeable.
| Time (s)* . | Longitude (|$^{\circ}$|) . | Latitude (|$^{\circ}$|) . | Height (km) . |
|---|---|---|---|
| begin | 132.9673 | |$-$|29.6209 | 66.47 |
| 16.0 | 133.0768 | |$-$|29.6545 | 64.71 |
| 19.0 | 133.4016 | |$-$|29.7532 | 59.60 |
| 22.0 | 133.7122 | |$-$|29.8466 | 54.81 |
| 25.0 | 134.0014 | |$-$|29.9328 | 50.43 |
| 28.0 | 134.2593 | |$-$|30.0092 | 46.58 |
| 32.0 | 134.5429 | |$-$|30.0921 | 42.39 |
| 34.8 | 134.6962 | |$-$|30.1367 | 40.09 |
| end† | (134.7368) | (|$-$|30.1486) | (39.47) |
| Time (s)* . | Longitude (|$^{\circ}$|) . | Latitude (|$^{\circ}$|) . | Height (km) . |
|---|---|---|---|
| begin | 132.9673 | |$-$|29.6209 | 66.47 |
| 16.0 | 133.0768 | |$-$|29.6545 | 64.71 |
| 19.0 | 133.4016 | |$-$|29.7532 | 59.60 |
| 22.0 | 133.7122 | |$-$|29.8466 | 54.81 |
| 25.0 | 134.0014 | |$-$|29.9328 | 50.43 |
| 28.0 | 134.2593 | |$-$|30.0092 | 46.58 |
| 32.0 | 134.5429 | |$-$|30.0921 | 42.39 |
| 34.8 | 134.6962 | |$-$|30.1367 | 40.09 |
| end† | (134.7368) | (|$-$|30.1486) | (39.47) |
Relative time.
Coordinates are less relaible because of uncertain timing.
| Time (s)* . | Longitude (|$^{\circ}$|) . | Latitude (|$^{\circ}$|) . | Height (km) . |
|---|---|---|---|
| begin | 132.9673 | |$-$|29.6209 | 66.47 |
| 16.0 | 133.0768 | |$-$|29.6545 | 64.71 |
| 19.0 | 133.4016 | |$-$|29.7532 | 59.60 |
| 22.0 | 133.7122 | |$-$|29.8466 | 54.81 |
| 25.0 | 134.0014 | |$-$|29.9328 | 50.43 |
| 28.0 | 134.2593 | |$-$|30.0092 | 46.58 |
| 32.0 | 134.5429 | |$-$|30.0921 | 42.39 |
| 34.8 | 134.6962 | |$-$|30.1367 | 40.09 |
| end† | (134.7368) | (|$-$|30.1486) | (39.47) |
| Time (s)* . | Longitude (|$^{\circ}$|) . | Latitude (|$^{\circ}$|) . | Height (km) . |
|---|---|---|---|
| begin | 132.9673 | |$-$|29.6209 | 66.47 |
| 16.0 | 133.0768 | |$-$|29.6545 | 64.71 |
| 19.0 | 133.4016 | |$-$|29.7532 | 59.60 |
| 22.0 | 133.7122 | |$-$|29.8466 | 54.81 |
| 25.0 | 134.0014 | |$-$|29.9328 | 50.43 |
| 28.0 | 134.2593 | |$-$|30.0092 | 46.58 |
| 32.0 | 134.5429 | |$-$|30.0921 | 42.39 |
| 34.8 | 134.6962 | |$-$|30.1367 | 40.09 |
| end† | (134.7368) | (|$-$|30.1486) | (39.47) |
Relative time.
Coordinates are less relaible because of uncertain timing.
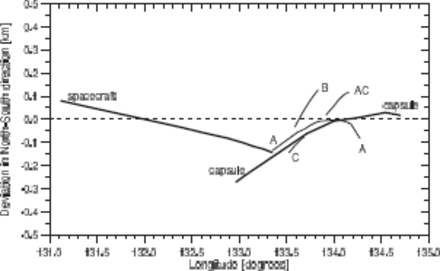
Deviation of the observed latitude of the spacecraft, its fragments and the capsule from the JAXA prediction for the capsule as a function of the observed longitude. The error of trajectory determination is about 0.1km. Note that fragment A was in fact a whole swarm of fragments not resolved in photographic data.
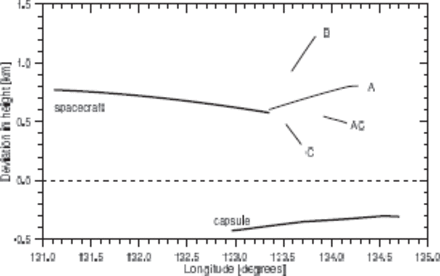
Deviation of the observed height of the spacecraft, its fragments and the capsule from the JAXA prediction for the capsule as a function of observed longitude. The error of the trajectory determination is about 0.1km.
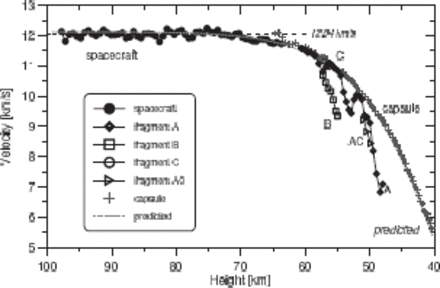
Measured velocity (relative to the Earth center) of the spacecraft, its fragments, and the capsule as a function of height above the surface compared to the JAXA prediction for the capsule. Each velocity point was computed from 9 consecutive time marks on the GOS4 image. The points are given in an interval of 3 time marks, i.e., 0.3s. The DFO2 and DFO4 images gave similar results for the spacecraft, but with a larger scatter.
The capsule was a much fainter object, and started to be visible on the photographs at a height of 66.5 km, when the deceleration was already in progress. The velocity data at the beginning are rather uncertain. The first good data point is at a height of 63 km, where the velocity was 11.75 km s|$^{-1}$|. The deceleration was then smooth, and closely followed the JAXA prediction, although the velocity was systematically higher by about 0.1 km s|$^{-1}$| than predicted over the whole observed arc down to a height of 40 km. The last measured velocity was 5.63 km s|$^{-1}$| at a height of 40.4 km.
The last piece of fragment A ceased to be visible on our photographs at a height of 47 km; its velocity at that time was about 7 km s|$^{-1}$|. The bright fragments B and C disappeared at heights of around 55 km. Fragment B decelerated much more than fragment C.
The trajectory and initial velocity of the spacecraft were used for computing the geocentric and heliocentric orbits of HAYABUSA at the moment of re-entry. The data are given in table 4.
3.3. Brightness
We performed photometric measurements at stations DFO2 and DFO4, where the individual fragments, and the capsule were not resolved and the total brightness of the fireball was therefore measured, and at station GOS3, where the fragments were measured individually. The fragment measurement was, however, possible only after the fragments became well separated from other fragments, i.e., not at all points where the positions and velocities were measured. More importantly, the fireball in its bright part was saturated in the GOS3 image, and the resulting brightness was underestimated. At DFO2 and DFO4, on the other hand, the calibration was a problem in the second part of the trajectory because of the proximity of the fireball to the horizon. The brightness seems to be overestimated here. The photometry of the whole fireball was therefore best obtained from radiometric data. Figure 7 shows the radiometric light curves in linear scale relative units as a function of time. Although there is some noise in the data, the similarity of the DFO2 and DFO4 curves demonstrates that many features seen on the light curves are real. The conversion of the radiometric signal to absolute magnitude was done using the known response of radiometers as a function of the zenith distance of the object and the known range to the fireball. The scale was then adjusted using photographic photometry at GOS3 and DFO2 for fireball heights of around 80 km, where both photographic records were obtained without calibration problems and in good mutual agreement.
Geocentric and heliocentric orbits of the spacecraft at the beginning of re-entry.
| Geocentric orbit | |
| Eccentricity | 1.32 |
| Inclination | 34|$^\circ\!\!\!.$|52 |
| Right ascension of the ascending node | 7|$^\circ\!\!\!.$|58 |
| Pericenter distance | 6310 km |
| Longitude of pericenter | 255|$^\circ\!\!\!.$|58 |
| Heliocentric orbit (J2000.0) | |
| Semimajor axis | 1.278 AU |
| Perihelion distance | 0.9824 AU |
| Eccentricity | 0.231 |
| Inclination | 1|$^\circ\!\!\!.$|59 |
| Argument of perihelion | 145|$^\circ\!\!\!.$|63 |
| Longitude of the ascending node | 82|$^\circ\!\!\!.$|360 |
| Geocentric orbit | |
| Eccentricity | 1.32 |
| Inclination | 34|$^\circ\!\!\!.$|52 |
| Right ascension of the ascending node | 7|$^\circ\!\!\!.$|58 |
| Pericenter distance | 6310 km |
| Longitude of pericenter | 255|$^\circ\!\!\!.$|58 |
| Heliocentric orbit (J2000.0) | |
| Semimajor axis | 1.278 AU |
| Perihelion distance | 0.9824 AU |
| Eccentricity | 0.231 |
| Inclination | 1|$^\circ\!\!\!.$|59 |
| Argument of perihelion | 145|$^\circ\!\!\!.$|63 |
| Longitude of the ascending node | 82|$^\circ\!\!\!.$|360 |
Geocentric and heliocentric orbits of the spacecraft at the beginning of re-entry.
| Geocentric orbit | |
| Eccentricity | 1.32 |
| Inclination | 34|$^\circ\!\!\!.$|52 |
| Right ascension of the ascending node | 7|$^\circ\!\!\!.$|58 |
| Pericenter distance | 6310 km |
| Longitude of pericenter | 255|$^\circ\!\!\!.$|58 |
| Heliocentric orbit (J2000.0) | |
| Semimajor axis | 1.278 AU |
| Perihelion distance | 0.9824 AU |
| Eccentricity | 0.231 |
| Inclination | 1|$^\circ\!\!\!.$|59 |
| Argument of perihelion | 145|$^\circ\!\!\!.$|63 |
| Longitude of the ascending node | 82|$^\circ\!\!\!.$|360 |
| Geocentric orbit | |
| Eccentricity | 1.32 |
| Inclination | 34|$^\circ\!\!\!.$|52 |
| Right ascension of the ascending node | 7|$^\circ\!\!\!.$|58 |
| Pericenter distance | 6310 km |
| Longitude of pericenter | 255|$^\circ\!\!\!.$|58 |
| Heliocentric orbit (J2000.0) | |
| Semimajor axis | 1.278 AU |
| Perihelion distance | 0.9824 AU |
| Eccentricity | 0.231 |
| Inclination | 1|$^\circ\!\!\!.$|59 |
| Argument of perihelion | 145|$^\circ\!\!\!.$|63 |
| Longitude of the ascending node | 82|$^\circ\!\!\!.$|360 |
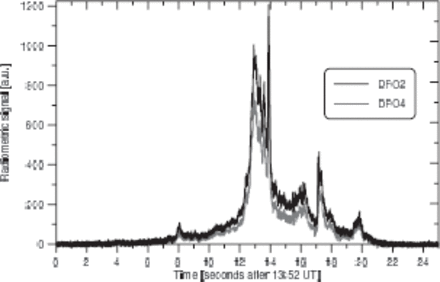
Radiometric light curves of the HAYABUSA fireball recorded on the DFO2 (upper black curve) and DFO4 (lower gray curve) stations.
The measured absolute magnitude as a function of height is given in figure 8. The spacecraft was first observed at a height of about 100 km, where it was of magnitude |$-$|2. The brightness then gradually increased, with two minor peaks at 85.1 and 77.5 km, until the broad maximum, which started at 68.5 km. The maximal magnitude of |$-$|12.6 was reached at a height of 66.9 km. The fireball brightness then fluctuated, but remained high until the final peak at 56.7 km. During this period, the spacecraft disintegrated. After that, the brightness rapidly decreased.
| Time (s) . | Height (km) . | Mag . | Velocity (km s|$^{-1}$|) . | Dyn. pressure (kPa) . |
|---|---|---|---|---|
| 4.1 | 85.1 | |$-$|6.6 | 12.05 | 1.1 |
| 8.1 | 77.5 | |$-$|9.3 | 12.05 | 3.6 |
| 12.9 | 68.5 | |$-$|12.3 | 11.9 | 13 |
| 13.9 | 66.9 | |$-$|12.6 | 11.85 | 16 |
| 16.2 | 62.8 | |$-$|11.3 | 11.65 | 27 |
| 17.1 | 61.3 | |$-$|11.8 | 11.6 | 32 |
| 19.8 | 56.7 | |$-$|10.8 | 11.1 | 54 |
| Time (s) . | Height (km) . | Mag . | Velocity (km s|$^{-1}$|) . | Dyn. pressure (kPa) . |
|---|---|---|---|---|
| 4.1 | 85.1 | |$-$|6.6 | 12.05 | 1.1 |
| 8.1 | 77.5 | |$-$|9.3 | 12.05 | 3.6 |
| 12.9 | 68.5 | |$-$|12.3 | 11.9 | 13 |
| 13.9 | 66.9 | |$-$|12.6 | 11.85 | 16 |
| 16.2 | 62.8 | |$-$|11.3 | 11.65 | 27 |
| 17.1 | 61.3 | |$-$|11.8 | 11.6 | 32 |
| 19.8 | 56.7 | |$-$|10.8 | 11.1 | 54 |
| Time (s) . | Height (km) . | Mag . | Velocity (km s|$^{-1}$|) . | Dyn. pressure (kPa) . |
|---|---|---|---|---|
| 4.1 | 85.1 | |$-$|6.6 | 12.05 | 1.1 |
| 8.1 | 77.5 | |$-$|9.3 | 12.05 | 3.6 |
| 12.9 | 68.5 | |$-$|12.3 | 11.9 | 13 |
| 13.9 | 66.9 | |$-$|12.6 | 11.85 | 16 |
| 16.2 | 62.8 | |$-$|11.3 | 11.65 | 27 |
| 17.1 | 61.3 | |$-$|11.8 | 11.6 | 32 |
| 19.8 | 56.7 | |$-$|10.8 | 11.1 | 54 |
| Time (s) . | Height (km) . | Mag . | Velocity (km s|$^{-1}$|) . | Dyn. pressure (kPa) . |
|---|---|---|---|---|
| 4.1 | 85.1 | |$-$|6.6 | 12.05 | 1.1 |
| 8.1 | 77.5 | |$-$|9.3 | 12.05 | 3.6 |
| 12.9 | 68.5 | |$-$|12.3 | 11.9 | 13 |
| 13.9 | 66.9 | |$-$|12.6 | 11.85 | 16 |
| 16.2 | 62.8 | |$-$|11.3 | 11.65 | 27 |
| 17.1 | 61.3 | |$-$|11.8 | 11.6 | 32 |
| 19.8 | 56.7 | |$-$|10.8 | 11.1 | 54 |
Table 5 lists the positions of the most pronounced peaks on the light curve. Each peak likely corresponds to a fragmentation event. Our photographs do not show geometrically separated fragments above a height of 61.5 km but the major release of small fragments must have occurred at the main flare at 66.9 km. The trajectories (see figure 5) suggest that the major fragments A and B separated most likely at the flare at 62.8 km. The brightness of fragments B and C could be first measured at heights of around 57 km, where both of them were of magnitude about |$-$|9. Fragment B then weakened while fragment C remained bright until its end.
The brightness of the capsule was measured on the GOS3 image. The light curve was smooth with a broad maximum of |$-$|3.5 mag between heights of 55–50 km. The measurements at larger heights are sparse, and have large errors because of the proximity of the capsule trail to the bright spacecraft.
From the predicted apparent magnitudes of the capsule at different stations Fujita et al. (2011), it can be inferred that the predicted absolute (100 km distance) brightness of the capsule was |$-$|5.5 mag at a height of 50 km. The actual brightness was by 2 magnitudes (factor of 6) lower. The expected brightness of the spacecraft was not published.
4. Discussion
Our data confirm that the capsule re-entry trajectory predicted by JAXA was correct within few hundreds of meters. This is in agreement with the expected accuracy of the prediction, which was estimated to be 500 |$\times$| 200 m (2|$\ \sigma$|) at a height of 50 km. The expected error in velocity, 30 m s|$^{-1}$| (3|$\ \sigma$|), seems to have been underestimated, since the observed deviation was 100 m s|$^{-1}$|. The spacecraft followed almost the same trajectory as the capsule, the most significant difference being that the spacecraft was about one kilometer higher at a given longitude.
To our knowledge, our observation provided the first wide-field, multi-station photographic data for a re-entering object with good independent telemetry available. Similar observations of the Stardust re-entry used different techniques Desai & Qualls (2010). Our work provided an excellent validation of the astrometric and reduction procedures used in fireball networks for the determination of trajectories and velocities of natural fireballs.
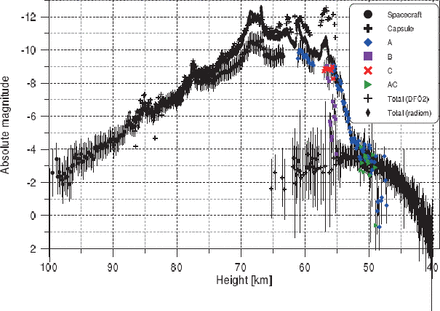
Absolute magnitude of the spacecraft, its fragments and the capsule as measured on the GOS3 photograph as a function of height and the total brightness of the fireball as measured on DFO2 photograph and DFO2 radiometer. Formal error bars are given for GOS3. Note that the brightness near the maximum is underestimated on the GOS3 image because of saturation, and the brightness toward the fireball end is overestimated on the DFO2 image because of uncertain calibration corrections near the horizon.
The HAYABUSA re-entry can be compared with the entries of natural meteoroids in several aspects: luminous efficiency, dynamic pressure acting at the moment of fragmentation, and apparent ablation coefficient.
The integral luminous efficiency is defined as the ratio of the total radiated energy to the initial kinetic energy of the object. Using the radiometric light curve (figure 8) and taking into account that a zero-magnitude meteor radiates about 1500 W at all wavelengths to all directions Ceplecha et al. (1998), the total radiative output of the HAYABUSA fireball was determined to 3.6 |$\times$| 10|$^{8}\ $|J. Using the mass of the spacecraft of about 400 kg and the velocity, relative to the atmosphere, of 11.7 km s|$^{-1}$|, the luminous efficiency was found to be 1.3%. Note that the used conversion from magnitudes to watts is valid for a plasma temperature of 4500 K. The actual temperatures inferred from HAYABUSA spectroscopy were in the range of 4500–6000 K Abe et al. (2011). For 6000 K the radiative output and the luminous efficiency would be about 25% lower.
For natural fireballs, the luminous efficiency is a poorly known parameter, which depends on the meteoroid velocity, mass, and structure. The empirical formula of Brown et al. (2002), based on more energetic events, predicts 4% for the HAYABUSA energy. On the other hand, the formula of Pecina and Ceplecha (1983), valid for relatively small meteoroids, gives only 0.5%. ReVelle and Ceplecha (2001) gave the average luminous efficiency for type I fireballs as 5.57% and for more fragile type II fireballs as 1.35%. We can therefore say that the luminous efficiency of HAYABUSA was in the range expected for natural fireballs of similar parameters.
The total radiative output of the capsule was only 2.8 |$\times$| 10|$^{5}\ $|J. The capsule lost only a small part from its initial mass of about 20 kg during re-entry, but it decelerated from 11.7 km s|$^{-1}$| to just few km s|$^{-1}$| during the ablation phase, so it deposited about 10|$^{9}\ $|J into the atmosphere. Only about 0.03% of this energy was radiated out. The low luminous efficiency was due to the special material used for the ablation shield. Spectroscopy revealed that the capsule spectrum was dominated at visible wavelengths by black-body radiation of the capsule surface Abe et al. (2011). Without ablation products, no large radiating plasma envelope, which normally provides most luminosity of fireballs, developed around the capsule.
The dynamic pressure, |$p$| |$=$| |$\rho v^2$|, where |$\rho$| is the atmospheric density and |$v$| is the velocity, acts on objects moving in the atmosphere. If the dynamic pressure exceeds the material strength, fragmentation occurs. Fragmentation is often accompanied by a flare on the light curve. The last column of table 5 lists the dynamic pressures at the flares during the HAYABUSA re-entry. The pressures are quite low and comparable only to the most fragile natural meteoroids of cometary origin Borovicka (2006). This is not surprising because the spacecraft was not a compact solid body, but in fact a quite porous object. Nevertheless, it may be surprising that no piece survived below 47 km.
Finally, the dynamics (deceleration) of fireballs can be fitted using the classical meteor equations Ceplecha et al. (1998). The most interesting parameters of the fit are the ablation coefficient, |$\ \sigma$|, and the combination |$Km^{-1/3}$| |$=$| |$\Gamma A \delta^{-2/3}\ m^{-1/3}$|; here, |$\Gamma$| is the drag coefficient and |$A$|, |$\delta$|, and |$m$| are the meteoroid shape coefficient, bulk density, and mass, respectively. The dynamic mass of the meteoroid can therefore be determined if we know or assume |$\Gamma$|, |$A$|, and |$\delta$|.
The typical ablation coefficient of natural fireballs varies from 0.014 s|$^{2}$| km|$^{-2}$| for not-so-much fragmenting type I fireballs to about 0.2 s|$^{2}$| km|$^{-2}$| for the most fragile type IIIB fireballs Ceplecha et al. (1998). We fitted the dynamics of the capsule and spacecraft fragments B and C. For the capsule, we obtained |$\ \sigma$| |$=$| 0.0014|$\ \pm\ $|0.001 s|$^{2}$| km|$^{-2}$|, a very low value, which is, nevertheless, understandable for a specially designed re-entry object. For fragment B, we obtained |$\ \sigma$| |$=$| 0.07|$\ \pm\ $|0.02 s|$^{2}$| km|$^{-2}$| and for fragment C an extremely high |$\ \sigma$| |$=$| 1.1|$\ \pm\ $|0.1 s|$^{2}$| km|$^{-2}$|.
The resulting |$Km^{-1/3}$| for the capsule can be separated, for example, into the following reasonable values: |$\Gamma A$| |$=$| 0.7, |$\delta$| |$=$| 0.63 g cm|$^{-3}$| and |$m$| |$=$| 21 kg (almost constant mass). For fragments B and C we have no idea about their shape and density. They may in fact represent clouds of small fragments. Formally, we assumed |$\Gamma A$| |$=$| 1.0 and |$\delta$| |$=$| 2 g cm|$^{-3}$| for both B and C. Then, the mass of B was 0.12 kg at a height of 58 km. Such mass, however, cannot explain the observed high luminosity. Either there were more fragments, or the density was about 10-times lower and the mass 100-times higher. For C, we obtained 12 kg at 58.5 km, which can provide the observed luminosity at that point. However, the computed mass was rapidly decreasing toward lower heights while the luminosity remained high. This discrepancy can be explained if the object was continuously flattened by ablation, i.e. the shape coefficient was changing.
We thank the JAXA team members who organized and participated in the recovery operations, especially Kazuhisa Fujita (JAXA), who is the chief coordinator of the ground-based observation, Yoshihiro Kakinami (Hokkaido University), Yasuo Shiba (Nippon Meteor Society), Masaharu Suzuki (GOTO Inc.), and other members who assisted in observing at GOS3 and GOS4 stations. The work on the Czech side was supported by GACR grants No. 205/08/0411 and P209/11/1382. SA was supported by the JAXA and the National Science Council of Taiwan (NSC 97-2112-M-008-014-MY3). PAB would like to thank the Science and Technology Facilities Council. This work was supported under grants ST/F003072/1 and ST/H002464/1. We thank the referee, P. Brown, for useful comments, which helped us to improve the paper.
References
|$\langle$| http://jda.jaxa.jp |$\rangle$|.



