https://orcid.org/0000-0002-4470-1277
ABSTRACT
We study the impact of a small-scale dynamo in core-collapse supernovae using a 3D neutrino magnetohydrodynamics (MHD) simulation of a 15 M⊙ progenitor. The weak seed field is amplified exponentially in the gain region once neutrino-driven convection develops, and remains dominated by small-scale structures. About |$250\, \mathrm{ms}$| after bounce, the field energy in the gain region reaches |${\sim } 50{{\ \rm per\ cent}}$| of kinetic equipartition. This supports the development of a neutrino-driven explosion with modest global anisotropy, which does not occur in a corresponding model without magnetic fields. Our results suggest that magnetic fields may play a beneficial subsidiary role in neutrino-driven supernovae even without rapid progenitor rotation. Further investigation into the nature of MHD turbulence in the supernova core is required.
1 INTRODUCTION
Magnetic field effects pervade many astrophysical fluid dynamics problems such as stellar surface convection, stellar winds, and star formation. It has long been speculated that magnetic fields also play a critical role in some core-collapse supernova explosions of massive stars. The idea of tapping the rotational energy stored in the supernova core using strong magnetic fields has a long history (e.g. Bisnovatyi-Kogan, Popov & Samokhin 1976; Meier et al. 1976; Akiyama et al. 2003; Burrows et al. 2007). In recent years, models of such magnetorotational explosions have matured considerably, and 3D simulations based on rapidly rotating stellar progenitor models are now available (Winteler et al. 2012; Mösta et al. 2014; Obergaulinger & Aloy 2017; Kuroda et al. 2020). Since strong magnetic fields in the progenitor star would lead to effective core spin-down, magnetorotational explosions require some amplification mechanism to generate strong large-scale magnetic fields on short time-scales after core collapse, such as the magnetorotational instability (Balbus & Hawley 1991; Akiyama et al. 2003) or an α–Ω dynamo in the proto-neutron star (PNS) convection zone (Raynaud et al. 2020). Despite progress in understanding these amplification processes by means of idealized local and global simulations and analytical theory (Obergaulinger et al. 2009; Masada et al. 2012; Sawai et al. 2013; Guilet, Müller & Janka 2015; Mösta et al. 2015; Masada, Takiwaki & Kotake 2020; Raynaud et al. 2020), the stellar pre-collapse rotation rate remains a major unknown for this supernova mechanism. Current stellar evolution models including magnetic torques (Heger, Woosley & Spruit 2005) predict core spin rates that are too low for magnetorotational explosions, and still underestimate core spin-down in the case of low-mass red giants (Cantiello et al. 2014) for which asteroseismic measurements are available. Thus, magnetorotational explosions are likely rare and probably only explain ‘hypernovae’ with unusually high explosion energies. For the majority of massive stars with moderate or slow core rotation, the neutrino-driven mechanism (Müller 2016) remains the favoured scenario.
Magnetohydrodynamic (MHD) effects in non-rotating or slowly rotating progenitors have received less attention, though a few studies have explored the amplification and dynamical role of Alfvén waves (Suzuki, Sumiyoshi & Yamada 2008; Guilet, Foglizzo & Fromang 2011) and field amplification by the standing accretion shock instability (Endeve et al. 2010, 2012). Supernova simulations of non-rotating progenitors with MHD and neutrino transport have so far been conducted in axisymmetry (2D) only (Obergaulinger, Janka & Aloy 2014). These models have indicated that for strong fields of |${\sim }10^{12}\, \mathrm{G}$|, MHD effects could play an auxiliary role in neutrino-driven explosions by facilitating the formation of large high-entropy bubbles.
However, MHD effects could play a more important and more generic role in neutrino-driven supernovae than these 2D simulations suggested, since dynamo field amplification cannot operate in 2D (Cowling 1933). More efficient field amplification might occur in 3D by a small-scale turbulent dynamo. A small-scale dynamo was in fact seen in idealized 3D simulations of the standing accretion shock instability by Endeve et al. (2012), though the fields did not become dynamically significant in their study. Moreover, conventional estimates for the field strengths in the cores and inner shells of massive stars could be too pessimistic. The magnetic field strengths of |$10^3{-}10^9\, \mathrm{G}$| in white dwarfs (Ferrario, de Martino & Gänsicke 2015) may not be indicative of the conditions in massive stars at the pre-collapse stage, where convective burning could generate strong small-scale fields via a turbulent dynamo. Considering ubiquitous observations of magnetic field strengths close to kinetic equipartition in similar settings (Christensen, Holzwarth & Reiners 2009; Brun & Browning 2017), one should expect fields of the order of |$10^{10}{-}10^{11}\, \mathrm{G}$| in the innermost active burning shells at collapse. Here, we explore the amplification of such seed fields by a small-scale dynamo and their interplay with neutrino heating and the hydrodynamic instabilities in a progenitor with a moderate rotation rate for the first time in a 3D MHD simulation with neutrino transport.
2 PROGENITOR MODEL AND INITIAL CONDITIONS
We simulate the collapse of the 15 M⊙ model m15b6 from Heger et al. (2005), whose evolution up to collapse has been calculated assuming magnetic torques. The progenitor has a central rotation rate of |$0.05\, \mathrm{rad}\, \mathrm{s}^{-1}$|, which translates into a neutron star birth spin period of |$11 \, \mathrm{ms}$| assuming that the collapsing core does not exchange angular momentum with the ejecta during the explosion. The neutron star’s rotational energy of |${\sim } 2 \times 10^{50}\, \mathrm{erg}$| would thus be too small to power a supernova with normal energy by MHD effects alone.
3 NUMERICAL METHODS
4 SIMULATION RESULTS
The maximum, minimum, and average shock radii evolve very similarly in the MHD model and the hydro model up to |$250 \, \mathrm{ms}$| after bounce (Fig. 1a). Small differences arise because of stochastic variations during prompt convection, which affect the entropy profiles of the PNS mantle and translate into a slightly smaller PNS radius and gain radius in the MHD model. These differences are also reflected in the critical ratio between the advection time-scale τadv and the heating time-scale τheat that quantifies the proximity to runaway shock expansion (Buras et al. 2006); τadv/τheat is initially smaller in the MHD model.
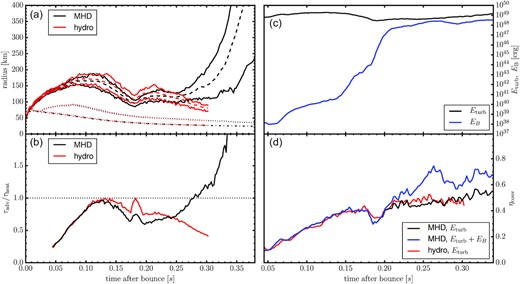
Evolution of the MHD model (black/blue curves) and the hydro model (red). (a) Maximum, minimum (solid), and average shock radius (dashed), gain radius (dotted), and PNS radius (dash–dotted). (b) Critical time-scale ratio τadv/τheat. (c) Turbulent kinetic energy Eturb (black) and magnetic energy in the gain region (blue) in the MHD model. (d) Efficiency ηconv for the conversion of neutrino heating into turbulent energy kinetic energy (black/red) or total turbulent energy including magnetic fields (blue).
Around |$250 \, \mathrm{ms}$|, however, the critical ratio τadv/τheat and the shock radius in the MHD model overtake the hydro model. At |$275 \, \mathrm{ms}$| the runaway condition τadv/τheat > 1 is met, and steady shock expansion commences with the maximum shock radius reaching |$1160\, \mathrm{km}$| by the end of the simulation. The diagnostic explosion energy (Buras et al. 2006) has only reached |$2.3 \times 10^{49}\, \mathrm{erg}$| at this stage, but is growing at a rate of |$4 \times 10^{50}\, \mathrm{erg}\, \mathrm{s}^{-1}$|. No explosion develops in the hydro simulation in agreement with results obtained with more sophisticated neutrino transport for the same progenitor (Summa et al. 2018).
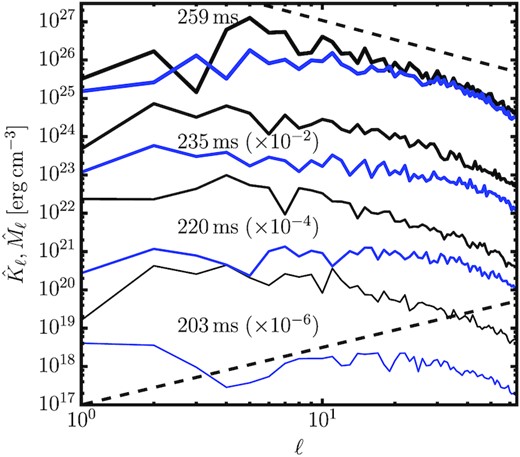
Angular power spectra |$\hat{K}_\ell$| and |$\hat{M}_\ell$| of the energy contained in radial turbulent motions (black) and the radial component of the magnetic field (blue) for the MHD model at different post-bounce times, measured in the lower half of the gain region. Dashed lines indicate slopes of −5/3 and 3/2 for Kolmogorov and Kazantsev spectra.
Volume rendering of the entropy in kb/nucleon (top) and the inverse of the plasma-β (bottom) for the MHD model at a time of |$260 \, \mathrm{ms}$|. Neutrino-heated bubbles are visible in red and the shock and PNS surface in light green in the top panel. The magnetic field is dominated by small-scale structures. It is distributed relatively homogeneously across the gain region, though it tends to be expelled from bigger convective bubbles.
Although the behaviour of the MHD model is compatible with the gross features of a small-scale dynamo, there are subtle differences to field amplification by isotropic and homogeneous turbulence. Amplification is driven mostly by shear motions around the gain radius, and the lowest values of the plasma-β are reached in this layer in line with the notion of flux expulsion from convective regions (Weiss 1966). However, the fields approach or even exceed equipartition with the thermal energy in strongly magnetized filaments (Fig. 3) whose volume fraction increases with time.
It remains to be discussed why magnetic field amplification close to kinetic equipartition results in more favourable conditions for shock revival. Supernova theory has established that the beneficial role of hydrodynamic ‘turbulence’ (in the broad sense of deviations of the flow from spherical symmetry) is through Reynolds stresses and turbulent heat transfer between the gain radius and the shock, and that the size of these beneficial effects depends on the turbulent kinetic energy (Couch & Ott 2015; Müller & Janka 2015; Müller 2020). Similarly, beneficial effects of magnetic fields, e.g. an extra contribution of magnetic pressure and a reduction of the binding energy of the gain region, should scale with the magnetic energy. Although it is by no means clear that adding the same turbulent kinetic or magnetic energy has the same impact on the explosion conditions, it is therefore instructive to compare the total turbulent kinetic and magnetic energy in and immediately below the gain region in the MHD model and the hydro model. Since the turbulent motions are driven by neutrino heating, we consider the dimensionless efficiency parameter |$\eta _\mathrm{conv}=E_\mathrm{turb}/(\dot{Q}_\nu \Delta R)^{2/3}$| (Müller & Janka 2015), where |$\dot{Q}_\nu$| is the volume-integrated heating rate in the gain region and ΔR is the width of the gain region. Fig. 1(d) shows that, when taking only the turbulent kinetic energy into account, ηconv is very similar in the magnetic and non-magnetic case, reaching a plateau at ηconv ≈ 0.5 once convection has fully developed. If the magnetic energy is included, |$\eta _\mathrm{conv}=(E_\mathrm{turb}+E_\mathrm{ B})/(\dot{Q}_\nu \Delta R)^{2/3}$| reaches significantly higher values. In other words, a larger amount of total turbulent energy can be stored in the gain region for the same neutrino heating rate if magnetic fields are present; it is not that the same amount of energy needs to be shared between turbulent motions and the additional degrees of freedom in the system. This is in line with the finding that the magnetic contributions to the turbulent energy flux in the gain region almost vanishes. Maintaining balance between neutrino heating and the turbulent energy flux in a quasi-steady state therefore requires similar convective velocities in the magnetic and non-magnetic case, and the turbulent magnetic energy will be added on top on a level set by the balance between field amplification and the backreaction of the fields on the flow.
5 CONCLUSIONS
Our simulations suggest that magnetic fields can have a substantial and beneficial impact on neutrino-driven shock revival even in slowly rotating progenitors with weak seed fields. Field amplification by a small-scale dynamo in the gain region is sufficient to amplify fields almost to kinetic equipartition within the first hundreds of milliseconds after bounce. Judging by the turbulent magnetic energy that can be reached, adding magnetic fields does, however, have a smaller impact than going from spherically symmetric models to multidimensional hydrodynamic models. The effect size of magnetic fields on the explosion conditions will need to be compared to other factors that influence the heating conditions, such as general relativity and the treatment of neutrino transport and neutrino interactions. Considering their impact on τadv/τheat, magnetic fields are likely one among many factors that can contribute to a similar degree to successful explosions in generic, slowly rotating supernova progenitors without qualitatively changing the picture of neutrino-driven explosions.
Our MHD simulation prompts a number of questions for future research. To avoid an overproduction of magnetars, one important constraint is that the neutron star magnetic fields created during a typical explosion must not be too strong. In our MHD model, the dipole field strength on a density isosurface at |${\sim } 10^{10}\, \mathrm{g}\, \mathrm{cm}^{-3}$| is several |$10^{13}\, \mathrm{G}$| and hence somewhat on the high side for typical pulsars. However, the final dipole field strength of the neutron star cannot be confidently predicted from our short simulation. Turbulent reconnection and field burial (Torres-Forné et al. 2016) may yet bring the dipole field strength down to lower values. Nor can we exclude that the relatively strong dipole has arisen by chance, due to limitations in numerical resolution, or due to the choice of the initial field. Clearly, more simulations are needed to determine the robustness of our results; unfortunately the closest analogue to our models – the idealized 3D simulations of Endeve et al. (2012) – are far too different in design to offer a meaningful point of comparison.
Further work is also required to investigate whether our results are sensitive to non-ideal effects. Conservative estimates of the physical viscosity and resistivity based on Spitzer (1965) place the magnetic Prandtl number in the gain region on the order of Pm > 103. While our ideal MHD simulation comports with the expectations for Pm > 1, the numerical Prandtl number is likely no more than a few (Federrath et al. 2011). The numerical Reynolds number is also bound to be well below the physical value of Re ∼ 1015 (Abdikamalov et al. 2015). Since the growth rate of the small-scale dynamo for Pm ≫ 1 scales with Re1/2 during the kinematic phase (Schober et al. 2012), saturation on the resistive scale should be reached almost instantly in nature, but the question becomes whether the growth of the field on larger scales during the subsequent dynamic phase is slow and whether saturation may happen well below kinetic equipartition under certain conditions (Schekochihin et al. 2002). Simulations (Haugen, Brandenburg & Dobler 2004) and more recent analytic models (e.g. Stepanov & Plunian 2008; Schober et al. 2015) do not support such adverse effects on the growth and saturation of the small-scale dynamo for Pr > 1. However, any extrapolation to the physical regime is still far from certain, and substantial neutrino drag (Melson, Kresse & Janka 2020) in the shear layer at the bottom of the gain region further complicates the picture. Much remains to be done to substantiate the interesting prospect that magnetic fields may play a beneficial subsidiary role in shock revival next to neutrino heating and hydrodynamical turbulence.
ACKNOWLEDGEMENTS
BM was supported by ARC Future Fellowship FT160100035. This research was undertaken with the assistance of resources and services from the National Computational Infrastructure (NCI) and the Pawsey Supercomputing Centre.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
REFERENCES
