Tidal disruption event rates in galaxy merger remnants Free

ABSTRACT

1 INTRODUCTION

When a star passes sufficiently close to a massive black holes (BHs), it can get accreted. For solar-type stars and BHs with mass up to ∼|$10^8 \, \mathrm{ M}_{\odot }$|⁠, the star is not swallowed whole, but it is tidally perturbed and destroyed, with a fraction of its mass falling back on to the BHs causing a bright flare, known as a tidal disruption event (TDE; Hills 1975; Rees 1988).

A growing body of evidence suggests that TDEs are more likely to occur in host galaxies associated with recent starbursts (Arcavi et al. 2014; French, Arcavi & Zabludoff 2016; Stone & Metzger 2016; Stone & van Velzen 2016; French, Arcavi & Zabludoff 2017; Law-Smith et al. 2017; Graur et al. 2018): the TDEs rate in these galaxies can be 30–200 times higher than in main-sequence galaxies, with galaxy mergers a possible cause for the starburst (Zabludoff et al. 1996; Yang et al. 2004, 2008; Wild et al. 2009). Stone & van Velzen (2016) advanced the hypothesis that this increase could be due to an anomalously high central stellar density, from which most TDEs are sourced, caused by the starburst. To test this hypothesis, we set ourselves in a case including a strong nuclear starburst: a galaxy merger, when gas inflows due to tidal forces and ram-pressure shocks can trigger nuclear starbursts that form a dense stellar cusp and temporarily increase the central density (Mihos & Hernquist 1996; Van Wassenhove et al. 2014; Capelo & Dotti 2017; Stone et al. 2018). Van Wassenhove et al. (2014) find an enhancement of almost two orders of magnitude of the density within 10 pc around the secondary BH of a 1:4 merger, during the 150 Myr following the starburst. This suggests that, during the merger, the TDEs rate can increase by a few orders of magnitude.

2 A LOWER LIMIT FOR THE TIDAL DISRUPTION EVENT RATE

In this section, we perform an approximate calculation to understand what are the physical parameters affecting the TDE rate Γ, defined as the number of disruptions per galaxy per unit time. In practice, for the rest of this work, we estimate the TDE rate with a more elaborated method detailed in Section 3.3.

Stars of mass m_⋆ and radius R_⋆ are disrupted if the pericentre distance to the BHs, of mass M_•, is smaller than the tidal disruption radius r_t ∼ (M_•/m_⋆)^1/3R_⋆. This defines a ‘loss cone’ (Lightman & Shapiro 1977) in angular momentum of size |$L_{\mathrm{lc}}^2/L_{\mathrm{c}}^2(E)$|⁠, where |$L_{\mathrm{lc}}=\sqrt{2 G M_{\bullet }r_{\mathrm{t}}}$| is the maximal angular momentum per unit mass for disruption, G the gravitational constant, L_c(E) is the circular (maximal) angular momentum per unit mass of an orbit, with energy per unit mass E = v²/2 + Φ(r), Φ(r) is the gravitational potential, and r and v are, respectively, the distance to the BHs and relative speed.

It is customary to define two regions, whose contributions to the flux of stars match at the critical radius r_c, with the corresponding specific energy E_c = Φ(r_c) (Syer & Ulmer 1999). The first is a region close to the BHs (E < E_c, r < r_c), where the time to diffuse across the loss cone is longer than the orbital period. All stars inside the loss cone will be disrupted at periapsis and the loss cone is empty. Farther away from the BHs (E > E_c, r > r_c), the time to diffuse across the loss cone is shorter than the orbital period. Stars will scatter in and out of the loss cone during the orbital motion and the loss cone is full.

During a galaxy merger, ρ(r_c) can change by orders of magnitude (Van Wassenhove et al. 2014), while there is only moderate change in M_• and σ (and, consequently, r_c). Therefore, our limit to the TDEs rate depends, almost exclusively, on the density at the radius r_c, which depends only on the BH mass, for stars with similar mass and radius. This calculation is presented to understand the physical parameters impacting the TDE rate. We describe the method we use to estimate Γ in Section 3.3.

3 SIMULATIONS

Similarly to Pfister et al. (2017), we perform a zoom re-simulation of the 1:4 coplanar, prograde–prograde galaxy merger from Capelo et al. (2015), which was shown to have a strong burst of nuclear star formation (see also Van Wassenhove et al. 2014), and is adopted here as a reference merger to highlight the various physical processes responsible for the evolution of the nucleus. Similar bursts were also observed in mergers with mass ratio 1:2 (coplanar and inclined orbital configurations), whereas lower mass-ratio mergers had weaker (1:6 case) or negligible (1:10) nuclear starbursts. Initially BH1, with a mass of |$3.53\times 10^6 \, \mathrm{ M}_{\odot }$|⁠, is in the main galaxy, whereas BH2, with a mass of |$0.88\times 10^6 \, \mathrm{ M}_{\odot }$|⁠, is in the secondary galaxy.

We re-simulate the merger phase (see Capelo et al. 2015), which begins at the second pericentre, at |${t\sim 1\, \mathrm{ Gyr }}$|⁠, and lasts until the binary BHs has formed, 300 Myr later. It is during this phase that the starburst occurs and we expect variations in the density and, consequently, in the TDEs rate.

This re-simulation (Resim0) is performed with the public code ramses (Teyssier 2002). ramses is an adaptive mesh refinement code in which the evolution of the gas is followed using a second-order unsplit Godunov scheme for the Euler equation. The approximate Harten–Lax–Van Leer Contact (Toro 1997) Riemann solver with a MinMod total variation diminishing scheme to reconstruct the interpolated variables from their cell-centred values is used to compute fluxes at cell interfaces. Collisionless particles, dark matter (DM), stellar, and BHs particles, are evolved using a particle-mesh solver with a cloud-in-cell (CIC) interpolation. The mass of DM particles (⁠|$m_\mathrm{DM} = 1.1\times 10^5\, \mathrm{ M}_{\odot }$|⁠) and stellar particles (⁠|$3.3\times 10^3\, \mathrm{ M}_{\odot }$|⁠) is kept similar to that in Capelo et al. (2015) but we allow for better spatial resolution (down to |$\Delta x=0.76 \, \mathrm{ pc }$|⁠), refining the mesh where |$M_\mathrm{DM}^\mathrm{cell}+ 10 M_{\rm b}^\mathrm{cell} \ge 8 m_\mathrm{DM}$|⁠, where M_DM and |$M_{\rm b}^\mathrm{cell}$| are, respectively, the mass of DM and baryons in the cell. Maximum refinement is enforced within 4Δx around the BHs.

3.1 Physics of galaxies

Gas is allowed to cool with the contribution of hydrogen, helium, and metals using tabulated cooling rates from Sutherland & Dopita (1993) above |$10^4\, \mathrm{ K }$|⁠, and rates from Rosen & Bregman (1995) below |$10^4\, \mathrm{ K }$| and down to |$10 \, \mathrm{ K }$|⁠.

Star formation, occurring at gas densities above |$1\, \rm H\, cm^{-3}$|⁠, is stochastically sampled from a random Poisson distribution (see Rasera & Teyssier 2006 for details) following a Schmidt law for the local star formation rate |$\dot{\rho }= \epsilon \rho _{\rm gas}/t_{\rm ff}$|⁠, where ρ and ρ_gas are the stellar and gas density, respectively, t_ff is the local gas free-fall time, and ϵ depends on the local gravoturbulent properties of the gas, as detailed in Trebitsch et al. (2018).

For the feedback from supernovae (SNe), we use the Sedov/snowplough-aware method described in Kimm & Cen (2014), in which stars release |$2\times 10^{49}\, \mathrm{ erg }\, \, \mathrm{ M}_{\odot } ^{-1}$| after |$5\, \mathrm{ Myr }$| (assuming 20 per cent of the mass of star particles contributes to Type II SNe).

3.2 Physics of black holes

We use the model of BHs described in Dubois et al. (2012), where accretion is computed using the Bondi–Hoyle–Lyttleton formalism capped at the Eddington luminosity. BH feedback consists of a dual-mode approach, wherein thermal energy, corresponding to 15 per cent of the bolometric luminosity (with radiative efficiency ϵ_r = 0.1), is injected at high accretion rates (luminosity above 0.01 the Eddington luminosity); otherwise, feedback is modelled with a bipolar jet with a velocity of 10⁴ km s⁻¹ and an efficiency of 100 per cent.

We modify the implementation of BHs dynamics. In Dubois et al. (2012), the mass of the BHs is spread in a sphere of 4Δx radius around the BHs in order to smooth the gravitational potential it generates. However, when two BHs approach each other, the formation of the binary is delayed. Here, we deposit all the mass of each individual BHs on the particle before performing the CIC interpolation, to obtain more accurate dynamics.

3.3 TDEs rate in the simulation

In Section 2, we derived equation (5) to get a physical insight of the relevant parameters affecting the TDEs rate. In practice, however, we measure the stellar density profiles around BHs for each snapshot in our simulation and fit them with a double power-law profile ρ(r) = ρ₀r^γ(1 + r/r₀)^{β − γ}. We then pass these density profiles to the phaseflow code (included in Agama; Vasiliev 2017, 2019) which Eddington inverses them to obtain the density function f(E), and compute the loss-cone filling factor |$q(E) = \mu P(E) L_{\mathrm{c}}^2/L_{\mathrm{lc}}^2 = \mathcal {F}_\mathrm{empty} / \mathcal {F}_\mathrm{full} \ln (L_{\mathrm{c}}/L_{\mathrm{lc}})$|⁠. The phaseflow code is conceived to solve the time-dependent Fokker–Planck equation, but we only use it to estimate f and q at each time-step corresponding to a snapshot of the simulation.

4 RESULTS

4.1 Nuclear starburst

In Fig. 1, we show stellar density maps of our simulation. In Fig. 2, we show the enclosed stellar mass around each BHs as a function of time, for different radii in the re-simulation. It is clear from Fig. 2 that the primary galaxy is not affected by the merger: during the |${300 \, \mathrm{ Myr }}$| of the simulation, very few stars form around the primary BH, in agreement with the lower resolution run (Capelo et al. 2015). Therefore, the TDEs rate should remain roughly constant.

Figure 1.

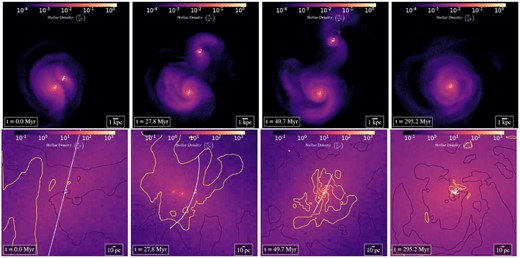
Stellar density maps of the two galaxies (top row) and centred on the secondary BHs (bottom row). Initially, the BHs proceeds on a smooth trajectory (first column); then, the starburst occurs and some newly formed stellar clumps deviate the BHs from its smooth trajectory (second column); at some point, those clumps merge and the BHs gets trapped (third column); finally, the BHs binary forms in the remnant galaxy (fourth column). The white line in the bottom images represents the position of the BHs within |$\pm 1\, \mathrm{ Myr }$|⁠. In order to show how irregular is the gas density compared with the stellar one, we indicate the iso-ρ_gas contours of 1 (10) amu cm⁻³ with purple (yellow) lines.

Open in new tabDownload slide

Figure 2.

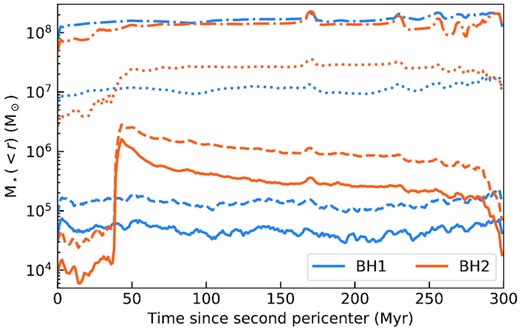
Enclosed stellar mass within 3 (solid), 5 (dashed), 30 (dotted), and 100 (dash–dotted) pc around each BHs, as a function of time elapsed since the second pericentre.

Open in new tabDownload slide

The secondary galaxy, instead, undergoes a major starburst just after the second pericentre, lasting |${50\, \mathrm{ Myr }}$|⁠. As the gas is perturbed by tidal torques and ram-pressure shocks, it loses angular momentum and falls towards the centre, triggering nuclear star formation. In the original simulation from Capelo et al. (2015), this first burst is followed by other bursts similar in magnitude (see the left-hand panel of fig. 1 in Capelo et al. 2015) that we do not see in the re-simulation. The main reason is the increase of resolution, which results in higher gas density, causing initially elevated levels of nuclear star formation, with respect to the lower resolution run, which consume a fraction of the accumulating gas. Another difference with the original simulation from Capelo et al. (2015) is that we use a more physically motivated model for star formation, with a variable star formation efficiency: the star formation rate, therefore, is not directly proportional to the gas density. Furthermore, our much higher resolution results in clumpy star formation, as shown in the second column of Fig. 1. These clumps are fairly small (few pc size) but can be very massive, up to a few |$10^6 \, \mathrm{ M}_{\odot }$|⁠, similar to the mass of BH2 (⁠|${\sim } 1.4\times 10^6 \, \mathrm{ M}_{\odot }$|⁠). This leads to interactions that scatter the BHs. Consequently, the density ‘seen’ by the BHs is highly dependent on local stochastic processes. The enclosed mass within |${5\, \mathrm{ pc }}$| from BH2 (orange dashed line in Fig. 2) is almost constant, until it increases abruptly as the clumps merge and capture the BHs at about 50 Myr. This is clear both from the third column of Fig. 1 and from Fig. 2. After this rise in density, the enclosed mass within 5 pc does not vary until the binary forms, whereas the enclosed mass within 3 pc decreases. This is contrary to the expectations of the evolution of a mass distribution around a BH, which normally contracts (Bahcall & Wolf 1976; Quinlan, Hernquist & Sigurdsson 1995). However, at difference with the assumptions in classic approaches, which look at equilibrium, steady-state solutions or BHs growing slowly within the stellar distribution, the BH enters rapidly the stellar clump, and the mass of the clump and the BH are similar. The effect we observe can be explained assuming that the system BH-clumps suffers a series of high-speed encounters (Binney & Tremaine 1987), bringing enough energy to start the disruption of the clump, although we cannot rule out that the effect is numerical. When the binary forms, i.e. the BHs are separated by about 1 pc, the enclosed mass decreases again. This might be due to heating: when the binary shrinks, it releases energy in the nucleus. Since the simulation cannot resolve scatterings between stars and the binary, we are unable to rigorously confirm if this effect is physical or a numerical artefact, although detailed N-body simulations show similar results (e.g. Milosavljević & Merritt 2001).

In summary, the amount of stars around BH2 changes significantly during the merger, and thus we expect large variations of its TDEs rate. However, the exact enhancement may depend on the position of the BHs, which can be chaotic due to three-body interactions with stellar clumps. The amount of stars around BH1 remains fairly constant and we do not expect much change in the TDEs rate until it binds with BH2 and it is embedded in the same stellar environment.

4.2 TDE rate

Using the techniques described in Section 3.3, we estimate the TDEs rate as a function of time in the simulations. Note that here we have taken the conservative assumption of not including an inner cusp around the BHs (Bahcall & Wolf 1976), hence the estimated TDEs rate is a lower bound.

We show in Fig. 3, as a function of time, the TDEs rate around each BHs (solid line) and the density at the critical radius (dashed line), as defined in equation (7). Note the remarkable agreement between the TDEs rate measured with the phaseflow code and the stellar density at r_c.

Figure 3.

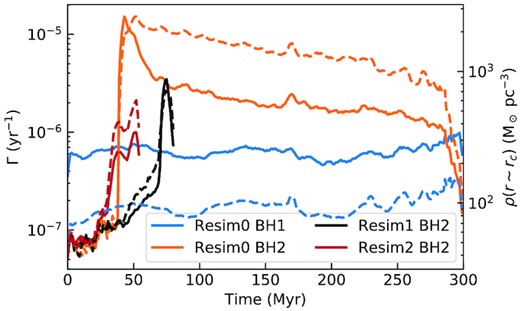
TDE rate around each BHs (solid line) and stellar density at the critical radius (dashed line). r_c is estimated from equation (7): as the masses of BH1 and BH2 are, respectively, 4.4 × 10⁶ and |$1.4\times 10^6 \, \mathrm{ M}_{\odot }$|⁠, their respective r_c are |$22$| and |$5 \, \mathrm{ pc }$|⁠. We show the same quantities for BH2 in the other re-simulations (see Section 4.3), which are run for a shorter time as we are only interested in the enhancement of the stellar density following the first starburst. All quantities are shown as a function of time.

Open in new tabDownload slide

The initial TDEs rate is very small (∼|$10^{-7}\, \mathrm{ yr }^{-1}$| for both BHs), because the density around each BHs is very low: we find, for the two BHs, a stellar density of ∼|$10^2\, \mathrm{ M}_{\odot } \, \, \mathrm{ pc }^{-3}$|⁠, which is one to two orders of magnitude lower than in local galaxies (Faber et al. 1997). The reason is that the analytical initial conditions of the merging galaxies (Capelo et al. 2015) assume that the stellar bulge is described by a spherical Hernquist profile (Hernquist 1990) with inner logarithmic slope γ = −1, whereas local galaxies exhibit a range of inner density slopes going from γ ∼ 0 to γ = −2 (Faber et al. 1997; Lauer et al. 2007), up to γ = −4 in the presence of nuclear star clusters, common in low-mass galaxies (Glass et al. 2011). In addition, before the beginning of the merger simulation, galaxies are relaxed for |${100\, \mathrm{ Myr }}$| and, during this time, the velocity distribution near the resolution limit (⁠|${10 \, \mathrm{ pc }}$|⁠) is not well sampled because of the limited number of stars, leading to an even shallower profile than the initial Hernquist profile.

The TDEs rate around BH1 is fairly constant, irrespective of the dynamical phase of the merger: since the stellar density profile around BH1 is not affected by the merger, the amount of stars available to be disrupted is constant and so is the TDEs rate. The TDEs rate around BH2 is instead increased by a factor of about 30 during the |$250\, \mathrm{ Myr }$| following the burst, with a short peak of more than two orders of magnitude enhancement. During the first 200 Myr of this enhancement, the two galaxies can be separated by more than 1 kpc, up to 10 kpc. While the maximum value of ∼|$10^{-5} \, \mathrm{ yr }^{-1}$| may seem surprisingly low, we recall that the initial density profile, after relaxing the initial conditions, was shallow and we do not include the possibility of a stellar cusp due to unresolved stellar dynamics, which would increase the initial TDE rate and, perhaps, decrease the relative enhancement caused by merger-driven nuclear star formation.

As discussed in Section 4.1, the central density and the TDEs rate drop once the binary is formed. However, to calculate the TDE rate we assumed a single BHs surrounded by a spherical density distribution, which is not valid any longer after formation of the binary. More sophisticated techniques, beyond the scope of this paper, can be used for binary BHs (e.g. Lezhnin & Vasiliev 2019), which often result in an increased rate, at least for a short time (e.g. Chen et al. 2009, 2011; Li et al. 2017).

4.3 Effect of stochasticity

We rerun the exact same simulation, but changing the random seed used in the stochastic sampling of star formation (Resim1 and Resim2), and perform the same analysis. This test is done for three main reasons: first, reproducibility of our results; secondly, the small number of particles around the BH in the early phase before the starburst (about |$10^4 \, \mathrm{ M}_{\odot }$| within 3 pc, corresponding to 10 stellar particles; see Fig. 2) might affects our results; thirdly, because reaching pc-resolution is a double-edged sword. On the one hand, we resolve the gas flows and star formation very close to the BHs. On the other hand, the stochasticity of very local processes becomes important. The exact position and mass of the forming stellar clumps have strong effects on both the orbits of BHs and on the density around them.

We show in Fig. 3 the TDEs rate and density at the critical radius around BH2. In all cases, the same common trends appear: there is a starburst, which results in an enhancement of the density at the critical radius, causing an increase of the TDEs rate around BH2, followed by a decay on Myr scales. However, the exact moment when the density increases, and its exact peak value, depend on the simulation, showing how small changes (the random seed and therefore the exact location of star formation) in this chaotic system can affect the TDEs rate in galaxies. We note that, since the galaxy hosting BH1 is not experiencing strong star formation, the results for BH1 are the same in all three re-simulations. Overall, the mean maximal enhancement of the TDE around BH2 in the three simulations is about 140.

5 CONCLUSIONS

We assess the TDEs rate around BHs using high-resolution hydrodynamical simulations of galaxies during and after a merger with mass ratio 1:4 coupled to the analytical formalism detailed in Section 2. This allows us to track the evolution of the central stellar mass during and after the merger-induced starburst, but also to measure the TDEs rate in a realistic, although still idealized environment.

We summarize our findings below:

• After the first passage below |$10 \, \mathrm{ kpc }$|⁠, a nuclear starburst promotes an enhancement of the stellar density around the BHs in the least massive galaxy. As a consequence, the TDEs rate also increases by up to two orders of magnitude for a short duration, and more than one order of magnitude on average.

• The nuclear starburst produces stellar clumps that scatter the BHs and modulate the stellar density in its vicinity. The enhancement of the TDEs rate and its duration can therefore vary significantly in different realizations of the same process.

• The environment and TDEs rate around the BHs in the most massive galaxy are rather unaffected by the merger.

This confirms that the TDEs rate should be larger in galaxies in the final phases of mergers or the immediate post-merger phase, lasting a few hundreds of Myr, than in galaxies in isolation. However, large column densities of gas and dust concurrent with the early starburst phases (Capelo et al. 2017; Blecha et al. 2018) can hinder detection of TDEs; whereas the column density decreases in the post-merger phase allowing for easier TDE detection. This picture is independent of the stochastic behaviour of the star formation process in such a clumpy and turbulent interstellar medium. However, the exact details of the TDEs enhancement, and the moment it happens, change due to the small-scale turbulent dynamics (here mimicked by our perturbed resampling of our stochastic model for star formation), the exact set-up of the initial conditions, and additional parameters, e.g. the existence of a pre-existing cusp, or a different initial gas distribution may modulate the results. This is the first study of TDEs rates using hydrodynamical simulations to track how the stellar profile is modified by star formation and external processes. We stress that this is a proof-of-concept experiment, since we have only explored one particular merger. Future work will expand to cosmological simulations.

ACKNOWLEDGEMENTS

MV, YD, and HP acknowledge support from the European Research Council (Project no. 614199, ‘BLACK’). BB is supported by membership from Martin A. and Helen Chooljian at the Institute for Advanced Study. We also thank the anonymous referee for the time taken to carefully read and improve our manuscript. This work was granted access to the HPC resources under the allocations A0020406955 and A0040406955 made by GENCI. This work has made use of the Horizon Cluster hosted by the Institut d’Astrophysique de Paris; we thank Stephane Rouberol for running smoothly this cluster for us.

REFERENCES