-
PDF
- Split View
-
Views
-
Cite
Cite
Philip G Breen, Light element variations in globular clusters via nucleosynthesis in black hole accretion discs, Monthly Notices of the Royal Astronomical Society: Letters, Volume 481, Issue 1, November 2018, Pages L110–L114, https://doi.org/10.1093/mnrasl/sly169
Close - Share Icon Share
ABSTRACT
Ancient globular clusters contain multiple stellar populations identified by variations in light elements (e.g. C, N, O, Na). Although many scenarios have been suggested to explain this phenomenon, all are faced with challenges when compared with all the observational evidence. In this Letter, we propose a new scenario in which light element variations originate from nucleosynthesis in accretion discs around black holes. Since the black holes form after a few Myrs, the cluster is expected to still be embedded in a gas-rich environment. Through a simplified accretion model, we show that the correct light element anticorrelations can be produced. Assuming a Kroupa stellar initial mass function, each black hole would only have to process ≈300 M⊙ of material in order to explain multiple populations; over a period of 3 Myr this corresponds to ∼10−4 M⊙ yr−1 (similar to the estimated accretion rate for the X-ray binary SS 433).
1 INTRODUCTION
Ancient globular clusters have been found to exhibit light element variations in the form of anticorrelation in Na−O and N−C, where some stars show enrichment in Na (N) and depletion in O (C) relative to field stars with the same metallicity (see Gratton, Carretta & Bragaglia 2012; Bastian & Lardo 2017, for a review). Evidence has also been found of multiple populations in young massive clusters (YMC), with ages in the range 2–8 Gyr, see Krause et al. (2016) for a review. So far no evidence of multiple populations have been found in massive clusters younger than ∼2 Gyr (e.g. Mucciarelli et al. 2008, 2014; Martocchia et al. 2017).
A number of scenarios have been put forward to explain this phenomenon, usually involving pollution by a first generation of stars. The most studied scenario involves pollution by slow moving winds from AGB stars (see e.g. Cottrell & Da Costa 1981; D’Ercole et al. 2008; Bekki 2017), which cools and collects in the centre of the cluster to form the polluted stars. However, this scenario requires clusters to have an initial mass, several times the present value, the so-called mass budget problem (D’Ercole et al. 2008; Conroy 2012).
Other possible sources of pollution include fast rotating massive stars (Decressin et al. 2007), interacting binaries (de Mink et al. 2009), stripped envelopes of high mass stars (Prantzos & Charbonnel 2006; Elmegreen 2017) and a single very massive star (Denissenkov & Hartwick 2014; Gieles et al. 2018). It has also been suggested by Marcolini et al. (2009) that the order in which the populations form may be reversed; this scenario involves a pre-enrichment phase with Type II supernovae as well as local enrichment by a single Type Ia SN and AGB stars. Another possibility is that the enriched stars are not the result of multiple epochs of star formation but the result of the pollution of protoplanetary discs of low-mass stars (Bastian et al. 2013).
All current scenarios face challenges when compared to all the observational constraints (e.g. see fig. 6 in Bastian & Lardo 2017). One challenge for all models is the ability to create discrete sub-populations (e.g. Milone et al. 2015); there is also a need for stochasticity in the pollution process in order to explain the high degree of cluster-to-cluster variations (Bastian, Cabrera-Ziri & Salaris 2015; Milone et al. 2015). Another constraint is that properties of the pollution mechanism seem to be correlated to the cluster mass; for example both the fraction of polluted stars and the size of the abundance spread is correlated with the mass of the cluster (Milone et al. 2017). Evidence that YMC have been found to be gas free at ∼7 Myr or earlier, appears to indicate that multiple populations are at least approximately coeval (see Bastian & Lardo 2017, and references therein), if clusters are required to retain pristine gas in order to produce multiple populations.
Here, we propose that light element variations can be generated in accretion discs around stellar-mass black holes.
2 BLACK HOLE ACCRETION SCENARIO
2.1 Stellar mass black holes in globular clusters
Assuming a Kroupa (2001) initial mass function (IMF), the total number of black holes (Nbh) expected to form is Nbh ≈ 2.2 × 10−3N*, where N* is the total number of stars in the cluster (assuming a mass range of 0.1−100.0 M⊙ and that all stars over 25 M⊙ become black holes). Some black holes might escape the cluster shortly after formation due to a ‘natal kick’ resulting from asymmetries in the supernova; however, if the most massive black holes (with progenitor mass ≳40 M⊙) form via direct collapse then there is no supernova and no ‘natal kick’ (e.g. see Fryer 1999; Fryer & Kalogera 2001; Heger et al. 2003; Fryer et al. 2012), therefore these objects would be retained in the cluster. The fraction among black holes with progenitors in the mass range 40−100 M⊙ is approximately 0.45. Arca Sedda Askar & Giersz (2018) preformed Monte Carlo simulations of globular clusters using a natal kick prescription from Belczynski (2002) and found at 20–30 Myr the black hole retention fraction (fr,bh) is in the range 0.15–0.55.
The present day black hole population of globular clusters is poorly constrained; a number of black hole candidates (in binaries with luminous stars) have been identified in globular clusters (Maccarone et al. 2007; Strader et al. 2012; Chomiuk et al. 2013; Giesers et al. 2018). Arca Sedda, Askar & Giersz (2018b) proposed a novel way to identify the size of the black hole population, using a concept similar to ‘influence radius’ and found that many of the Milky Way’s globular clusters likely host as many as several hundreds of black holes, at the present time. Note that it is the initial population that is important here and not the present-day one, as over time the black hole population decreases due to dynamical ejection (see e.g. Breen & Heggie 2013).
2.2 Total amount of enriched gas
2.3 Accretion, outflows, and feedback
Since the black holes are formed after a few Myr, we assume that the conditions are similar to when star formation began, i.e. the environment is gas rich, consisting of a hierarchical structure with many dense clumps (McKee & Ostriker 2007; Tan et al. 2014). As in the Competitive Accretion model of massive star formation (Bonnel et al. 2001), we argue that the potential of the clusters acts to funnel gas down to the centre of the cluster creating a gas reservoir which can be replenished by gas inflow. If we assume that the black holes are in clumps of total mass 103 M⊙ and radius 0.1pc than the typical velocity would be |$v \sim \sqrt{GM/r} \sim 7$| km s−1, using MBH = 10 M⊙ and ρg = 10−16 g cm−3 then the resulting accretion rate is |$\dot{M}_{\mathrm{ ac}} = 4\pi \rho _\mathrm{ g} (GM_{\mathrm{ BH}})^2/v^3 \sim 10^{-4}\,{\rm M}_{\odot }{\rm yr}^{-1}$|, at these rates the enriched gas could be produced in ≈3 Myr. Our crude estimate places the model just within the constraints from YMC being gas free by ∼7 Myr and shorter for a lower fraction of enriched stars. Note the accretion rates based on Bondi–Hoyle formalism can be very sensitive to small changes in the physical parameters (Bonnel & Bate 2006), and therefore the accretion rate is highly uncertain.
For a 10 M⊙ black hole, the Eddington luminosity (Led) is reached at an mass accretion rate of ≈10−8 M⊙ yr−1, assuming a radiative efficiency of 0.1, i.e. |$\dot{M}_{\mathrm{ ed}}=L_{\mathrm{ ed}}/(0.1c^2)$|. The accretion rates considered above are orders of magnitude above Eddington, so it is expected that most of the accredited mass escapes in outflows (e.g. see King & Pounds 2003). Our model requires that enough of the gas is exposed to high temperatures before escaping. Shakura & Sunyaev (1973) suggested that most of the mass would be lost from the radius at which Led is first reached. A simple model for the outflow assumes |$\dot{M} \propto r^s$|, where s is in the range 0 < s < 1 (Blandford & Begelman 1999). Using s = 1 (Begelman 2012), the outflow from the region where our simple model predicts the light element enrichment are generated (see Sections 2.4 and 2.5) is approximately |$70{{\ \rm per\ cent}}$| of the inflow.
Using ultra-luminosity X-ray sources (ULXs) as a guide (e.g. see Kaaret, Feng & Roberts 2017) the outflows could have speeds of ∼100 to |${\sim } 1000\, {\rm km\, s}^{-1}$|. These would be in excess of the escape velocity. However, as long as the cluster is embedded the outflows will lose kinetic energy when they sweep up pristine gas. Wünsch et al. (2017) considered fast-moving winds with radiative cooling of gas and found a significant fraction of fast winds (|${\gtrsim } 1000\, {\rm km\, s}^{-1}$|) could be retained within the cluster. Even if the bulk of the black holes form without supernova (via direct collapse), there may still be some pair instability supernovae and supernova from stars with ≤40 M⊙, however, as winds from supernova travel an order of magnitude faster (∼104 km s−1) they may preferentially escape with little effect on the gas.
If the black holes were all radiating at the Eddington Luminosity, since the mass budget in the central region will be dominated by gas, the overall gravitational attraction will far exceed the radiation pressure. Over time the radiation and winds from the black holes will heat the gas and eventually deplete it, estimates from Leigh et al. (2013) require ≳10 Myr for gas expulsion which will allow sufficient time for the enriched stars to form.
2.4 Conditions in the accretion disc
The topic of accretion discs around black holes is a rich and interesting subject; see Abramowic & Fragile (2013) for a review on the subject. One of the most studied accretion disc models is the thin disc model of Shakura & Sunyaev (1973), where the model is geometrically thin, optically thick, radiatively efficient, and uses a dimensionless constant, α, to parametrize uncertainty over the viscosity mechanism. The model also admits analytic solutions under assumptions of the pressure and opacity (for the general relativistic versions see Novikov & Thorne 1973). However, as we are concerned with high accretion rates the thin disc model, is unsuitable because the assumption that the disc is radiatively efficient breaks downs as cooling by advection becomes more important (e.g. see Abramowic & Fragile 2013).
In advection-dominated accretion flows (ADAF) temperatures can reach almost virial values (Rees et al. 1982; Narayan & Yi 1994; Narayan & McClintock 2008), though they are usually studied in the optically thin regime where flow is radiatively inefficient due to low densities. At the high accretion rates considered in Section 2.3 the disc would be both geometrically thick and optically thick. If the optical depth is large enough the radiative cooling becomes inefficient and more of the energy generated by viscous heating would be retained and advected in the flow. Note that in a radiatively inefficient flow the gravitational potential energy cannot be radiated away. Once advection becomes important, the accretion flow will increase in temperature reaching approximately virial values (assuming cooling mechanisms are inefficient). Since the conditions may become similar to stellar interiors, the term ‘Quasi-Stellar Flow’ seems appropriate. A schematic representation is given in Fig. 1.
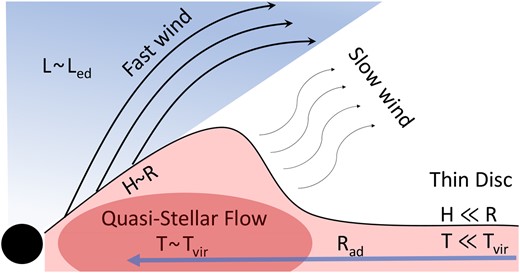
Schematic of accretion flow around the black hole. The blue arrows gives the direction of the flow. Far from the black hole, where advection is unimportant and radiative cooling is efficient the conditions are similar to that of a thin disc. Here, the height of the disc (H) is small compared to the radius (R), and the temperature (T) is low compared to the virial temperature. At the radius at which advection becomes important (Rad), radiative cooling becomes inefficient and heat generated by viscosity is advected with the flow, causing the flow to heat and expand. This results in the flow becoming quasi-spherical (i.e. H ∼ R) and temperatures becoming approximately virial (assuming cooling is inefficient). This region has been labelled ‘Quasi-Stellar Flow’, as we assume that conditions here are similar to stellar interiors. The flow is constantly losing mass in the form of winds which increase in speed with decreasing R, resulting in the accretion rate dropping to |$\dot{M}_{ed}$| closer to the black hole.
2.5 Nucleosynthesis in accretion discs
Nucleosynthesis usually is not included in models of accretion discs, though there has been some work on the topic. Mukhopadhyay & Chakrabarti (2000) showed that significant nucleosynthesis could take place around a 10 M⊙ and a 106 M⊙ black hole if the viscosity is low enough (also see Arai & Hashimoto 1992; Hu & Peng 2008).
The Na−O and N−C anticorrelations are produced at roughly 5 × 107 K, which under the assumption of a virial temperature profile (see Section 2.4), corresponds to a radius of ≈5.4 × 1010 cm (≈2 × 104Rs). We will consider a shell from T = 2.5 × 107 − 7.5 × 107 K and assume that yields will be similar to that of the composition being evolved at fixed ρ and T = 5 × 107 K. The yields were calculated using the publicly available nuclear reaction network Torch by Timmes (1999)1 and the initial composition used is the same as that given in Decressin et al. (2007; their table 3) corresponding to a metallicity of [Fe/H] = −1.5. The initial and final mass fractions of C, N, O, and Na are given in Table 1. Radial velocities (|$v$|r) are calculated by dividing the width of a shell by time spent at the temperature.
α element symbol, Mfr,i initial mass fraction, Mfr,f final mass fraction, and log10(Mfr,f/Mfr,i) enrichment factor.
| α . | M fr,i . | M fr,f . | log10(Mfr,f/Mfr,i) . |
|---|---|---|---|
| C | 3.50 × 10−5 | 3.39 × 10−6 | −1.01 |
| N | 1.03 × 10−5 | 3.13 × 10−4 | 1.48 |
| O | 3.00 × 10−4 | 3.02 × 10−6 | −2.00 |
| Na | 3.30 × 10−7 | 1.94 × 10−5 | 1.76 |
| α . | M fr,i . | M fr,f . | log10(Mfr,f/Mfr,i) . |
|---|---|---|---|
| C | 3.50 × 10−5 | 3.39 × 10−6 | −1.01 |
| N | 1.03 × 10−5 | 3.13 × 10−4 | 1.48 |
| O | 3.00 × 10−4 | 3.02 × 10−6 | −2.00 |
| Na | 3.30 × 10−7 | 1.94 × 10−5 | 1.76 |
α element symbol, Mfr,i initial mass fraction, Mfr,f final mass fraction, and log10(Mfr,f/Mfr,i) enrichment factor.
| α . | M fr,i . | M fr,f . | log10(Mfr,f/Mfr,i) . |
|---|---|---|---|
| C | 3.50 × 10−5 | 3.39 × 10−6 | −1.01 |
| N | 1.03 × 10−5 | 3.13 × 10−4 | 1.48 |
| O | 3.00 × 10−4 | 3.02 × 10−6 | −2.00 |
| Na | 3.30 × 10−7 | 1.94 × 10−5 | 1.76 |
| α . | M fr,i . | M fr,f . | log10(Mfr,f/Mfr,i) . |
|---|---|---|---|
| C | 3.50 × 10−5 | 3.39 × 10−6 | −1.01 |
| N | 1.03 × 10−5 | 3.13 × 10−4 | 1.48 |
| O | 3.00 × 10−4 | 3.02 × 10−6 | −2.00 |
| Na | 3.30 × 10−7 | 1.94 × 10−5 | 1.76 |
The results for Na enrichment are shown in Fig. 2. As long as the flow is slow enough, for a given mean density, Na is significantly enriched by a factor 58 (and similarly N by 30). Assuming a dilution factor of fd = 0.5 (see Section 2.2), this will produce a spread of 1.5 dexs in Na (1.1 for N) between enriched and pristine stars. Similarly O and C are reduced by factors 0.01 and 0.1, since these values are small, the spreads in O and C result from the dilution of pristine gas and will be approximately log10(1 − fd).
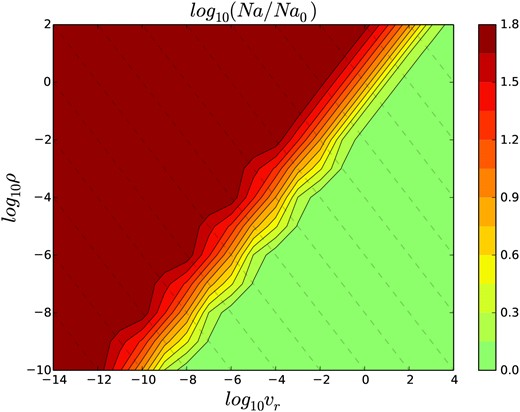
Ratio of initial to final Na as a function of mean ρ and |$v$|r. For reference the free fall velocity in this region is |$v$|ff ∼ 108cm s−1. The dashed lines correspond to fixed accretion rates assuming quasi-spherical accretion i.e. |$\rho \approx \dot{M}/(4\pi r^2 v_r)$|. For a range of values Na is enriched by 101.8, so long as |$v$|r is sufficiently low or the ρ is sufficiently high, see text for details.
3 DISCUSSION
We have argued that the light element variations observed in globular clusters could be generated in accretion discs around stellar-mass black holes. In this scenario, the black holes form from the earliest massive stars after a few megayears and are born into a gas-rich environment. The black holes are expected to experience similar accretion rates as those estimated for the formation of a massive star. The accreted gas is then subjected to high temperatures in the inner part of the disc after which it escapes in outflows. If temperatures in the accretion disc are high enough significant nucleosynthesis will occur and the required light element variations can be generated. The polluted material escapes from the disc in outflows which mix with pristine gas, from which the enriched stars are formed.
Using a highly simplified model we have shown that a population of stellar-mass black holes could produce sufficient material to produce a polluted population of stars with Na−O and N−C anticorrelation, which is the main signature of multiple populations. These results need to be compared with more detailed models and numerical simulations of accretion flow, but the aim of this Letter is to show that such a model is plausible and warrants further study.
The model presented in this Letter has many promising features. First, since pollution takes place over a short time scale ≲10 Myr the populations are co-evolved. Secondly, since the black holes process the pristine gas, there is no mass budget problem and there is also a natural dilution mechanism as outflows from the accretion disc sweep up pristine gas. Thirdly, since accretion rates and times depend on the properties of the host system, the fraction of enriched stars and abundances are expected to correlate with the cluster mass. Fourthly, it has been recently suggested by Carretta, Bragaglia & Lucatello (2018) that simple dilution models cannot explain the light element variations observed in NGC 2808 and that polluters of different masses are required. This might not be an issue for the model proposed because the black holes will have a range of masses and even for a single accretion disc the composition of the wind (and wind speed) will likely vary with radius in the accretion disc. Fifthly, since higher temperatures than those considered in Section 2.5 are expected at smaller radii, the scenario could potentially explain small Fe spreads measured in some globular clusters (e.g. M22 Da Costa et al. 2009; Marino et al. 2009, 2011) without the need to retain supernova ejecta. Interestingly, if the enriched stars are formed in the vicinity of accreting black holes then their stellar masses may be limited by competitive accretion (Bonnel et al. 2001). If the maximum mass is limited to below the main sequence turn-off for a cluster of ∼2Gyr, then this would explain why multiple populations have not been observed in YMC below this age (e.g. see Bastian & Lardo 2017).
In this Letter, we have made the assumption that cooling is inefficient in the accretion flow. If the optical depth is large it is reasonable to assume that radiative cooling is inefficient, however, it is possible the flow may cool by another mechanism e.g. energy loss through outflows. A key next step to develop the scenario is to construct a more detailed model of the accretion flow. This will help constrain the conditions required to reach the temperatures needed for nucleosynthesis to occur. We have also made the assumption that the black holes will experience similar accretion rates as for massive star formation. However, the feedback from black holes will be different which may affect the accretion rates. Also feedback from the black holes may affect the star formation rates. Hydrodynamic models are required to further explore these issues and will be one of the next steps in developing the model.
The greatest uncertainty in the scenario is whether nucleosynthesis does actually occur in accretion flows around black holes. A good candidate to test the possibility of nucleosynthesis in accretion flows is SS 433 (for review see Fabrika 2004), which is believed to be accreting at similar rates as considered in the Letter. There is already evidence of an overabundance of elements (Ni, Si, and S, see Brinkmann, Kotani & Kawai 2005) in the jets of SS 433. These elements have heavier atomic numbers than Na, in the scenario only a small percentage (|${\sim } 0.01$| per cent) of the overall accretion flow makes it to the jet and this material would be exposed to higher temperatures than the bulk of the inflow. A prediction of the model presented in this Letter, is that the outflows of SS 433 will be enriched in light elements.
If we consider a cluster of N* = 106 stars and if all the black holes are radiating at the Eddington luminosity, then the luminosity would be ∼1042 erg s−1, i.e. at the top end of the range for an ULX source or the lower end of an active galactic nucleus (AGN). However, embedded clusters are likely Compton thick and obscured in X-ray (also see Krause et al. 2012), except during the brief period when most of the cluster gas has been expelled and before the accretion discs have been exhausted. If a black hole is dynamically ejected with its accretion disc intact, then it will become visible once free of the cluster and may appear as an ULX, if the emission of radiation is anisotropic (King et al. 2001). Indeed a physical association between the ULXs and super star clusters in large starburst galaxies has been suggested (e.g. see Kaaret, Ward & Zezsa 2004; Poutanen et al. 2013). However, the nature of ULXs is still an open question and most probably consists of a class of objects (for a review see Kaaret et al. 2017).
In the scenario, we have only considered stellar mass black holes. Though it is possible that some enrichment could have been produced by an intermediate mass black hole or even a supermassive black hole. In this context, the origin of the large population of N-rich stars in the bulge\inner halo (Schiavon et al. 2017) would have originated from pollution by our galaxies supermassive black hole.
ACKNOWLEDGEMENTS
The author is grateful to Anna Lisa Varri, Douglas Heggie, Glenn van de Ven, and Enrico Vesperini for many helpful comments on a draft version of the manuscript. The author would also like to thank Maximilian Ruffert and Ken Rice for interesting scientific discussions, and the anonymous referees for their many helpful comments. The author is very grateful to Frank Timmes for his publicly available nuclear reaction network codes. The author acknowledges support from the Leverhulme Trust (Research Project Grant RPG-2015-408)
Footnotes
REFERENCES



