Gas response in chaotic bars Free

Abstract

1 Introduction

The standard picture of shocks encountered in the gas flow in the bar region of rotating barred potentials is based on the presence of a stable x1 family of periodic orbits in the underlying stellar component (Athanassoula 1992a,b). These shocks resemble the observed dust lanes in the optical images of the bars of barred galaxies and so they are frequently called ‘dust lane shocks’. In the case of strong barred perturbations, the morphology of the dust lanes is that of straight line segments. An observational assessment of how the dust lane shape correlates with the bar strength has been recently presented by Comerón et al. (2009). The presence of a stable x1 family (Contopoulos 1981) guarantees the flow of the gas in elliptical motion around the centre of the galaxy. The ‘dust lanes’ are formed as the gas reaches the potential minima, shocks, loses angular momentum and moves to smaller radii, continuing its journey towards the centre of the galaxy (Engelmaier & Gerhard 1997).

In a recent paper, Patsis, Kalapotharakos & Grosbøl (2010) studied the dynamics of a stellar response model that formed a bar of ansae type (Danby 1965; Martinez-Valpuesta, Shlosman & Heller 2006; Martinez-Valpuesta, Knapen & Buta 2007; Martinez-Valpuesta 2009) by particles being practically completely in chaotic motion. This is the response model ‘Model 1’ of that paper and corresponds to a 2D potential Φ(R, θ) with planar geometry, which was investigated as a possible candidate for describing the dynamics of the galaxy NGC 1300. Potential estimations have been based on the K-band photometry of the galaxy obtained with the SOFI instrument of the NTT/ESO telescope at La Silla. In polar coordinates (R, θ), the potential is of the general form

(1)

Both even and odd Fourier terms are taken into account up to k_max= 6. The potential is presented in detail as ‘Model A’ in section 4.1 in Kalapotharakos, Patsis & Grosbøl (2010a).

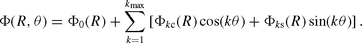
Bars supported by particles in chaotic motion, that is by particles following orbits in chaotic seas on the corresponding surfaces of section, have been found in the responses of a set of potentials of this type (2D case in Kalapotharakos et al. 2010a; Kalapotharakos, Patsis & Grosbøl 2010b) that rotate with pattern speeds in the range 19 < Ω_p < 24 km s⁻¹ kpc⁻¹. The stellar response of the model with Ω_p= 22 km s⁻¹ kpc⁻¹ is given in Fig. 1.

Figure 1

The stellar response of the barred galaxy model we study in this Letter. Isocontours indicate an ansae-type morphology. Arrows point to the ‘bottlenecks’ that give the bar its characteristic shape. For details, see Patsis et al. (2010).

Open in new tabDownload slide

Details about the stellar orbital dynamics, the morphology of the chaotic orbits that support the bar and the dynamical mechanisms behind the structure of the bar we present in Fig. 1 are given in Patsis et al. (2010).

In this Letter, we present the gas response in the same potential. In Section 2, we describe our hydrodynamical simulation, in Section 3, we present the flow that leads to this structure and finally in Section 4, we enumerate our conclusions.

2 Gas Simulations

We follow the gas response of ‘Model 1’ in Patsis et al. (2010) by means of the smoothed particle hydrodynamics (SPH) method (Gingold & Monaghan 1977; Lucy 1977). The particular code we use has been applied in the past to follow the gas response of models for normal spiral galaxies (Patsis et al. 1994) as well as for barred galaxies (Patsis & Athanassoula 2000) and has been successfully compared with other SPH schemes like the one by Bate, Bonnell & Price (1995). The gas is assumed isothermal with a constant sound speed c_s and we use the standard form of the SPH artificial viscosity (Lattanzio et al. 1986). The self-gravity of the gas is not taken into account. For more code-related details, the reader should refer to Patsis et al. (1994).

We have run a number of simulations, where we varied various hydrodynamical parameters, like the sound speed c_s, the artificial viscosity parameters (α, β) and the time T_f within which the barred-spiral perturbation is introduced in the response model. In most cases, we used 3 × 10⁴ gaseous particles, initially distributed randomly in a gaseous disc of 15 kpc radius. The particles have been put initially on circular motion in the axisymmetric part of the potential (Patsis et al. 2010).

In these simulations, we found that the most important factor for the response of the gas is T_f. Straight line ‘dust lane shocks’ are clearly formed in the snapshots with an orientation as the one we observe in Fig. 2(a), after one pattern rotation, when the perturbation is introduced relatively abruptly, that is, with T_f < 0.25T_p, where T_p is the time during which the system completes one pattern rotation. The system is rotating counterclockwise. The panels of Fig. 2 are density maps created by means of the ESO-MIDAS system. They are in logarithmic scale for panels (a) and (b), and linear for panel (c); the colour bars below them indicate denser regions from the left-hand to right-hand side. In the particular model presented in Fig. 2(a), we have c_s= 10 km s⁻¹ and artificial viscosity parameters (α, β) = (1, 1). The basic response was the same for c_s= 20 or 30 km s⁻¹. Differences have been mainly observed in the thickness of the ‘dust lanes’, as well as in secondary features and in the shocks outside the bar. However, the flow of the gas on the discs of our models, which is the subject of this Letter, was similar in all studied cases with the same T_f.

Figure 2

The gas response of ‘Model 1’ of Patsis et al. (2010). The bar is rotating counterclockwise. The colour bars below each panel indicate increasing surface densities from the left-hand side to right-hand side [logarithmic scale for panels (a) and (b), and linear scale for panel (c)]. In panels (a) and (b), the total perturbation is introduced within a quarter of a system's period, while in panel (c) within two pattern periods. In the case where the perturbation is introduced abruptly in the system [panels (a) and (b)], straight line shocks appear in the bar region immediately. In panel (a), we are at t≈ 1 T_p and in panel (b) at t≈ 3T_p. When the perturbation is introduced gradually, ‘dust lane’ shocks appear in the response only after several pattern periods, while the response of the model, at least during the growing amplitude phase, is like in panel (c).

Open in new tabDownload slide

The gas inflow in the cases with small T_f was very strong. Fig. 2(b) is a snapshot after almost three pattern rotations. About 50 per cent of the particles, initially randomly distributed on the disc, are located now at radii r < 2 kpc. If we want to keep the simulation running, we have to apply a replenishment scheme. Since the response in the central region of the model is not changing conspicuously during our runs and since we are interested in the shocks in the area of the main bar, we can remove particles from the innermost r < 1 kpc region when they exceed a critical number n_c we define arbitrarily. By applying this replenishment scheme, we consider the snapshots every 0.25T_p and as soon as we find n > n_c at r < 1 kpc, we remove the surplus SPH particles and redistribute them at random positions on the disc. In different models, either we have put the redistributed particles on circular motion like in our initial setup or we have given them random velocities. In the latter case, the measure of the maximum velocity allowed is taken as large as the maximum velocity of the rotation curve of the model. The responses we find in the next snapshots are similar, whether we apply the first or the second scheme. Particle replenishment retains a morphology like Fig. 2(a) for as long as we continue our simulation. A larger initial number of particles, n, provide the model with particles needed in later-time snapshots. However, models with large n do not provide more information about the flow and require larger computational times.

In models where we introduce the barred spiral perturbation gradually, we observe differences in the response. Fig. 2(c) shows the response of a model with c_s= 30 km s⁻¹, (α, β) = (1, 1), for which the perturbation gets its maximum strength at T_f= 2T_p. The snapshot given here is for t≈ 3T_p. However, a similar response morphology is already observed during the growing amplitude phase of the simulation and also until time t≈ 4T_p. The patchy density maxima of the gas in the bar region that are formed during the two first periods of the system are dissolved very slowly. In this ‘long T_f’ simulation, ‘dust lane shocks’ are observed for t > 4T_p, but not from the beginning of their formation, at the leading sides of the bar. We find them initially at the trailing sides. In later snapshots, they fade and finally the ‘dust lanes’ appear at the leading sides of the bar. In the snapshot of Fig. 2(c), we observe that there are density enhancements in the trailing sides of the dense regions of the gas in the bar, inclined roughly 60° with respect to its minor axis. However, we can also observe density enhancements being formed at the leading edges of the bar. In later snapshots, they will be part of ‘dust lanes’ with orientations similar to those in Figs 2(a) and (b).

3 The Flow

The purpose of this Letter is to present a kind of gas response that gives the ‘dust lanes’ in the absence of a regular ‘x1 flow’. The paradigm is given in the snapshot of Fig. 2(a) and is a typical case for the whole class of our models with a chaotic ansae-type stellar bar. The velocity field of the gas for this snapshot is given in Fig. 3(a), while in Figs 3(b) and (c), we give enlarged views of the regions close to the upper and lower ‘dust lane’. We observe that gaseous particles are streaming towards the straight line segments from both sides (leading and trailing) of the bar. The overall flow in the model is characterized by two large anticyclones centred at the Lagrangian points L₄ and L₅ at the sides of the bar. The minimization of the sizes of the velocity's arrows in Fig. 3 indicates the presence of Lagrangian points at the corresponding regions of the disc. In Patsis et al. (2010), we have shown that there are multiple Lagrangian points in the effective potential of ‘Model 1’ (cf. fig. 2 in Patsis et al. 2010). We denote on Fig. 3(a) only four Lagrangian points (L₁, L₂, L₄ and L₅). The first two are close to the major-axis, but at different radii (), while the latter two are close to the minor-axis of the bar. However, the presence of the additional Lagrangian points, and mainly of the additional unstable one, at (x, y) ≈ (0.38 kpc, 4 kpc), as well as the presence of the spiral part in the imposed potential, makes the anticyclonic structures complicated. The flow is deformed at the spiral arm regions and density enhancements are formed outside the bar at its upper left-hand and lower right-hand regions, that is, at its leading sides. Nevertheless, the main spiral structure that appears in the model emerges from the regions close to the points L₁ and L₂. The gas flow in these spiral arms is along them in agreement with the corresponding flows we found in other potentials (Tsigaridi & Patsis 2010).

Figure 3

Panel (a): the velocity field in the snapshot of the model of Fig. 2(a). In panels (b) and (c), we give enlarged views of the regions close to the ‘dust lanes’. We observe the flow of gaseous particles along the straight lines that have been formed.

Open in new tabDownload slide

The gas response in the bar region is characterized by the two straight line segments, the ‘dust lanes’. At the ‘dust lanes’, we observe that the velocity arrows are oriented along the shocks, so that the straight lines, which are formed, work like funnels that bring the gaseous particles towards the centre of the system. Gaseous particles are coming on the ‘dust lanes’ from both sides of them, but they are mainly sliding along the bar from the L₁ and L₂ regions following the ‘dust lanes’.

In order to clearly show the differences between the flow we find in this Letter and the standard x1 flow, which leads to the appearance of the dust lanes in the bar region, we give in Fig. 4 the gas response when we impose a non-homogeneous Ferrers bar perturbation. The potential is the one used in Patsis & Athanassoula (2000) and has its L₁ and L₂ points at r= 6 kpc along the major-axis of the bar. This imposed potential has a typical stable x1 family. The bar is populated by regular orbits trapped around the stable periodic orbits. In Fig. 4(a), we see the straight ‘dust lane’ shocks formed in an SPH model, similar to the one in our previous example, with c_s= 20 km s⁻¹ and (α, β) = (1, 2). In Fig. 4(b), we give the flow, which is characterized by motion around the centre of the system in the bar region. By comparing Fig. 4 with Fig. 3, the differences between the two flows become evident. Contrary to the flow around the centre of the galaxy in elliptical motion across the ‘dust lanes’ in Fig. 4, the flow in Fig. 3 is along the ‘dust lanes’, as described above.

Figure 4

The x1 flow that leads to the formation of ‘dust lane’ shocks in the bar region of a Ferrers bar model (see text). (a) The morphology of the shocks in the bar and (b) the associated flow. The L₁, L₂ points are at r= 6 kpc along the y-axis.

Open in new tabDownload slide

A detailed comparison of the stellar and gaseous flows depends on the hydrodynamical parameters of each SPH model and will be presented in a forthcoming paper. Here, in Fig. 5, we just present the gaseous response of our example of Figs 2(a) and (b) (black points) on top of the stellar response of the model given in Fig. 1. We show that the straight line segments have an orientation typical of the dust lanes observed inside strong bars. In models where the perturbation is introduced abruptly, we have a displacement between the stellar and gaseous spiral arms that emerge close to the L₁ and L₂ points, by the time the straight line segments appear in the model. There is much better agreement between these stellar and gaseous spiral arms, when in models, we introduce our perturbation slowly (compare Fig. 5 with Fig. 2c). However, the flow along the spirals in both cases is similar.

Figure 5

The gas response in our example of Fig. 2(a) (black points) overplotted on the stellar response given in Fig. 1 (red points). The orientation of the straight line segment ‘dust lanes’ is typical for the dust lanes observed in the optical images of strong bars.

Open in new tabDownload slide

4 Discussion and Conclusions

In this Letter, we present an alternative mechanism for the formation of ‘dust lane’ shocks in the bars of barred galaxies, other than the standard x1 flow of the gas around the centre of the system (see e.g. fig. 13b in Contopoulos & Patsis 2006).

The main conclusions of our study are as follows:

• (i)

  We find ‘dust lane shocks’ in the bar region of a gas response model that lacks the backbone of stable x1 orbits in its stellar counterpart. The stellar bar in this case is of ansae type and is built out of particles in chaotic motion. Our mechanism is facilitated by the presence of five Lagrangian points roughly along the major-axis of the bar, three of which are unstable and two stable (fig. 2 in Patsis et al. 2010).

• (ii)

  Abrupt introduction of the perturbation in the system favours the formation of straight ‘dust lane shocks’.

• (iii)

  The overall flow on the disc is dominated by the formation of two distorted anticyclonic structures centred at the Lagrangian points L₄ and L₅. This gas flow forms dense regions outside the bar that correspond to spiral arms or segments of spiral arms. The flow at the spiral arms of the model that emerge close to the Lagrangian points L₁ and L₂ is along the arms.

• (iv)

  The streaming of the particles along the two straight line segments (‘dust lanes’) in the bar region results from particles that enter the bar both from its leading and from its trailing sides. The two main anticyclonic structures meet close to the L₁ and L₂ points and particles slide from these two regions towards the centre of the system along the ‘dust lanes’, which act like a funnel.

Acknowledgments

We thank Prof. G. Contopoulos for fruitful discussions. We also thank an anonymous referee for constructive comments. All image processing was done with the ESO-MIDAS system. This work has been partially supported by the Research Committee of the Academy of Athens through the project 200/739.

References