-
PDF
- Split View
-
Views
-
Cite
Cite
Magdalena Siwek, Luke Zoltan Kelley, Lars Hernquist, Signatures of circumbinary disc dynamics in multimessenger population studies of massive black hole binaries, Monthly Notices of the Royal Astronomical Society, Volume 534, Issue 3, November 2024, Pages 2609–2620, https://doi.org/10.1093/mnras/stae2251
Close - Share Icon Share
ABSTRACT
We investigate the effect of the cutting-edge circumbinary disc (CBD) evolution models on massive black hole binary (MBHB) populations and the gravitational wave background (GWB). We show that CBD-driven evolution leaves a tell-tale signature in MBHB populations, by driving binaries towards an equilibrium eccentricity that depends on the binary mass ratio. We find high orbital eccentricities (|$e_{\rm b} \sim 0.5$|) as MBHBs enter multimessenger observable frequency bands. The CBD-induced eccentricity distribution of MBHB populations in observable bands is independent of the initial eccentricity distribution at binary formation, erasing any memory of eccentricities induced in the large-scale dynamics of merging galaxies. Our results suggest that eccentric MBHBs are the rule rather than the exception in upcoming transient surveys, provided that CBDs regularly form in MBHB systems. We show that the GWB amplitude is sensitive to CBD-driven preferential accretion onto the secondary, resulting in an increase in GWB amplitude |$A_{\rm yr^{-1}}$| by over 100 per cent with just 10 per cent Eddington accretion. As we self-consistently allow for binary hardening and softening, we show that CBD-driven orbital expansion does not diminish the GWB amplitude, and instead increases the amplitude by a small amount. We further present detection rates and population statistics of MBHBs with |$M_{\rm b} \gtrsim 10^6 \, {\rm M}_{\odot }$| in Laser Interferometer Space Antenna, showing that most binaries have equal mass ratios and can retain residual eccentricities up to |$e_{\rm b} \sim 10^{-3}$| due to CBD-driven evolution.
1 INTRODUCTION
Pulsar Timing Arrays (PTAs; Foster & Backer 1990) have found strong evidence for a gravitational wave background (GWB; Agazie et al. 2023a; EPTA Collaboration 2023; Reardon et al. 2023; Xu et al. 2023), likely originating from the inspiral of massive black hole binaries (MBHBs; Agazie et al. 2023c). Concurrently, the most comprehensive study of optical transients with the Legacy Survey of Space and Time (LSST; Ivezić et al. 2019) at the Rubin Observatory is approaching. If electromagnetic (EM) signatures of MBHBs are found, the synergy of these detection methods will enable the multimessenger study of MBHBs using transient surveys and low-frequency gravitational waves (GWs), and elucidate the evolution and fate of MBHBs across cosmic time.
MBHBs form as a result of galaxy mergers. The massive black holes (MBHs) contained in the merger remnant initially evolve through dynamical friction, followed by stellar scattering (e.g. Begelman, Blandford & Rees 1980; Quinlan & Hernquist 1997; Sesana, Haardt & Madau 2006), which is likely efficient at hardening binaries to parsec separations (e.g. Yu 2002; Khan, Just & Merritt 2011; Gualandris et al. 2017). At parsec scales, the formation of a circumbinary disc (CBD) is likely in the gas-rich environment of a post-merger galaxy (e.g. Barnes & Hernquist 1991, 1996). In such cases, the orbital evolution of sub-parsec MBHBs may be dominated by CBD physics until the GW-driven evolution takes over. Partially as a result of their significance in MBHB evolution and the multimessenger signatures expected from accreting MBHBs, CBD-driven orbital evolution has gained significant attention in the literature. Accretion from a CBD has three main effects on the binary evolution:
Preferential accretion onto the secondary will increase the mass ratio (|$q_{\rm b}$|) of the binary (e.g. Farris et al. 2014; Duffell et al. 2020), even in eccentric binaries (Siwek et al. 2023a), potentially leading to significant increases in the GWB amplitude (Siwek, Kelley & Hernquist 2020).
The semimajor axis (|$a_{\rm b}$|) of the binary evolves. The binary can undergo orbital decay (‘hardening’; Haiman, Kocsis & Menou 2009) or orbital expansion (‘softening’; Miranda, Muñoz & Lai 2017), depending on numerous factors, including (but likely not limited to) binary mass ratio and eccentricity (Siwek, Weinberger & Hernquist 2023b), as well as accretion disc hydrodynamics.
Dynamical interaction between the binary and the CBD leads to a stabilizing effect on the orbital eccentricity (|$e_{\rm b}$|), and the emergence of an ‘equilibrium eccentricity’ (e.g. Roedig et al. 2011; D’Orazio & Duffell 2021; Zrake et al. 2021), which depends on binary mass ratio (Siwek et al. 2023b).
CBD-driven orbital hardening is likely a less important mechanism in determining the merger time-scales of MBHBs than, for instance, dynamical friction and stellar scattering (e.g. Kelley et al. 2017b; Bortolas et al. 2021). However, the effect of accretion and orbital eccentricity induced by the CBD could imprint itself on the population statistics of MBHBs observed in EM and GW observatories. Identifying signatures of CBD physics requires population synthesis modelling of MBHB populations, and assumptions about their initial mass ratio and eccentricity distributions.
The initial mass ratio distribution of MBHBs is set by the MBH pairs that co-evolve during galaxy mergers. The pairings of MBHs depend on cosmological factors such as hierarchical structure formation and the large-scale dynamics of MBHs during galaxy mergers, which determines what pairs form bona fide MBHBs. While the initial mass ratios can be estimated from cosmological simulations, accretion episodes following a galaxy merger are expected to modify this distribution (e.g. Siwek et al. 2020). Since cosmological simulations have insufficient resolution to track the accretion and evolution of MBHBs at sub-kpc scales, these populations must be modelled through semi-analytic methods.
MBH pairs may accrete independently from one another at kpc scales, and their mass ratios at binary formation will depend on how much gas has been stripped from or retained in the vicinity of the respective MBHs following a galaxy merger. Due to the resolution limitations discussed above, it is currently unclear how accretion prior to binary formation affects the mass ratio distribution. At sub-parsec separations, however, CBD-driven accretion models can be used to model the mass ratio evolution. The processes determining gas inflow rates to the galactic nucleus are determined on larger scales than the binary separation, such that only the total binary mass is relevant, and a total accretion rate onto the binary is estimated. CBD simulations can then be utilized to divide the accretion rate between the two black holes, evolving the mass ratio of the system.
Siwek et al. (2020) showed that preferential accretion onto the secondary MBH shifts the mass ratio distribution towards unity, and depletes the number of lower mass ratio systems. This has significant consequences for multimessenger studies of MBHBs, modifying the population statistics of transients, their merger rates, and the GW signatures emitted during inspiral. In this work, we verify these results with updated CBD accretion models (Siwek et al. 2023a) that account for the effect of orbital eccentricity on the binary mass ratio evolution, and in turn the effect of the evolving mass ratio on the semimajor axis and eccentricity evolution rates (Siwek et al. 2023b), which in turn determines the abundance of sub-parsec systems per mass ratio bin.
While initial mass ratio distributions can be constrained by cosmological simulations and semi-analytic population studies (e.g. Siwek et al. 2020), the evolution of orbital eccentricity of MBHs prior to binary formation is highly uncertain. At kpc scales, recent simulations have found that MBHs may be on highly eccentric orbits around the post-merger Galactic Centre (|$e_{\rm b} \sim 0.7$|; e.g. Chen et al. 2022). Gualandris et al. (2022) analysed massive gas-free galaxy mergers from the early stages of a merger to the hardening phase, and similarly found the orbital eccentricity of the MBHB at formation to be highly eccentric, in the range |$0.5 \lesssim e_{\rm b} \lesssim 0.9$|. The eccentricity of MBHBs also depends on their orbital motion in the core of their host galaxies. In particular, the eccentricity evolution is sensitive to the binary motion relative to the corotating or counterrotating stellar background. Generally, corotation results in low orbital eccentricities (e.g. Dotti et al. 2007), while high eccentricities have been seen in counterrotating models (e.g. Sesana, Gualandris & Dotti 2011; Madigan & Levin 2012; Mirza et al. 2017). However, small perturbations in the galaxy merger orbit can lead to large variations in the MBHB eccentricity at formation (Rawlings et al. 2023), highlighting that the initial eccentricity distribution of MBHBs at formation is still highly uncertain.
As the two MBHs become gravitationally bound, their orbital evolution is governed by angular momentum exchange with individual stars. While ejecting stars from the galactic centre, the semimajor axis decreases and the orbital eccentricity increases (Quinlan & Hernquist 1997; Sesana et al. 2006). Sesana (2010) found that residual eccentricities from stellar scattering may be detectable in the Laser Interferometer Space Antenna (LISA) and PTA bands, ranging from |$10^{-3} \ \mathrm{ to} \ 0.2$| and |$0.03 \ \mathrm{ to} \ 0.3$|, respectively (see also Porter & Sesana 2010 who find even higher eccentricities as binaries enter the LISA band). However, the effect of stellar scattering on orbital eccentricity is mild, dependent on the uncertain initial eccentricity distribution set at large scales.
The initial eccentricity and mass ratio distributions of MBHBs at formation are therefore highly uncertain. In this paper, we apply the most recent CBD-driven evolution models of binaries from Siwek et al. (2023a, b) to a sample of MBHBs from the Illustris simulation. By analysing the MBHB population in the observable multimessenger bands, we show that:
the CBD erases the initial conditions of the highly uncertain binary eccentricity distribution by quickly and efficiently evolving the eccentricity to an equilibrium value;
unless all binaries form on extremely eccentric orbits (|$e_{\rm b, 0} \gtrsim 0.9$|), eccentricities in CBD-driven systems are up to two orders of magnitude higher than in gas-poor systems;
mass ratio distributions are shifted towards unity in CBD-driven evolution models; and
the GWB amplitude resulting from the MBHB population is boosted by 100 per cent when binaries accrete at just 10 per cent their Eddington limit.
2 METHODS
We generate a sample of MBHBs from the Illustris simulation (Genel et al. 2014; Vogelsberger et al. 2014a, b) and semi-analytically evolve the population over several evolution (‘hardening’) regimes using the MBHB population synthesis code holodeck (Kelley, Blecha & Hernquist 2017a; Kelley et al., in preparation).
The MBHB population is obtained by tracking the galaxy mergers in the Illustris simulation, and noting the black hole masses, separation, and redshift. Following selection cuts, primarily on lower mass MBHs, this method yields a sample of 2749 MBH pairs. The properties of the two MBHs in their post-merger host galaxy are taken as the initial condition for each MBH pair in holodeck, and are then evolved using the semi-analytic model described below. The MBHB population in our sample has a mass range |$10^6 \lesssim M_{\rm b} \lesssim 10^{10}\, \mathrm{ M}_{\rm \odot }$|, and peaks at |${\sim} 10^7 \, {\rm M}_{\odot }$|. The formation redshift of the MBH pair, defined as the redshift at which the two MBHs are numerically merged in Illustris, peaks near |$z \sim 2$|, though MBH pairs continue to form until |$z \gtrsim 10^{-2}$|. Finally, the mass ratio distribution peaks at |$q_{\rm b} \lesssim 1$|. Further details on the MBHB population obtained from Illustris can be found in fig. 2 of Kelley et al. (2017a). As the eccentricities of MBHBs at formation are highly uncertain (see Section 1), we impose a variety of initial eccentricity distributions on the MBHB population.
Similar to previous work in Kelley et al. (2017a, b) and Siwek et al. (2020), binaries are evolved with several hardening mechanisms (Begelman et al. 1980):
Dynamical friction (DF) prescription (Begelman et al. 1980);
Stellar scattering (SS; Quinlan & Hernquist 1997; Sesana et al. 2006);
GW emission (Peters 1964).
The addition of CBD torques and accretion is the main focus of this work. We implement the cutting-edge binary evolution models from Siwek et al. (2023a, b) and apply these to MBHBs that have reached the final parsec within a Hubble time.
We note that the binary separation at which CBD formation maybe feasible is highly uncertain, and possibly depends on the binary mass, which we neglect here. If stable CBDs form only at separations |${\ll} \mathrm{ pc}$|, the impact of the CBD accretion and dynamical evolution may be diminished, especially if GW emission already dominates the binary evolution. However, if CBDs can form at |${\gg} \mathrm{ pc}$| scales, MBHBs would evolve towards high eccentricities and mass ratios earlier, albeit at scales where they cannot be identified by GW or EM observatories. Our model includes evolution rates for the binary mass ratio |$\dot{q}_{\rm b}(q_{\rm b}, e_{\rm b})$|, semimajor axis |$\dot{a}_{\rm b}(q_{\rm b}, e_{\rm b})$|, and orbital eccentricity |$\dot{e}_{\rm b}(q_{\rm b}, e_{\rm b})$|. The evolution rates are obtained from the simulations presented in Siwek et al. (2023a, b), who established that
binaries of all mass ratios and eccentricities preferentially accrete onto the secondary, thereby increasing the mass ratio of the system;
the orbital eccentricity of binaries at all mass ratios evolves towards a steady-state value, which itself is a function of mass ratio. Siwek et al. (2023b) established that the steady-state eccentricity increases with mass ratio; and
the evolution rate and direction of the semimajor axis depend on mass ratio and eccentricity, with both inspiral and outspiral occurring. While circular binaries tend to outspiral, binaries at their steady-state eccentricities with mass ratios |$q_{\rm b} \gtrsim 0.3$| always inspiral due to CBD dynamics. Therefore, binaries remain in the GW-dominated regime slightly longer, as these binaries will have circularized due to GW emission, while CBD torques marginally increase their lifetimes.
The CBD simulation suite presented in Siwek et al. (2023a, b) explores the mass ratio and eccentricity parameter space in detail, yielding enough values of |$\dot{q}_{\rm b}(q_{\rm b}, e_{\rm b})$|, |$\dot{a}_{\rm b}(q_{\rm b}, e_{\rm b})$|, and |$\dot{e}_{\rm b}(q_{\rm b}, e_{\rm b})$| to allow for interpolation for arbitrary combinations of |$e_{\rm b}$| and |$q_{\rm b}$|. By performing 2D interpolation for each evolution rate in |$e_{\rm b}$| and |$q_{\rm b}$| on the fly, we derive ad hoc values for |$\dot{q}_{\rm b}$|, |$\dot{a}_{\rm b}$|, and |$\dot{e}_{\rm b}$| for each binary at each point in time, allowing us to update all binary parameters following each time-step. CBD-driven evolution furthermore depends on the accretion rate of the binary system, which we parametrize by the Eddington fraction |$f_{\rm Edd}$|. In this work, we fiducially assume a constant accretion rate at 10 per cent of the Eddington limit for each binary system, |$f_{\rm Edd} = 0.1$|. We assume that CBDs form around binaries upon reaching parsec separation, as active galactic nucleus (AGN) discs at larger than parsec scales maybe susceptible to disc fragmentation (Goodman 2003). The CBD-driven accretion and orbital evolution models are therefore applied in each binary system from parsec scales until merger. To motivate this assumption, we refer to the AGN disc lifetime, which is expected to persist for around |${\sim} 10^8$| yr (e.g. Yu & Tremaine 2002), and up to |$10^9$| yr for some models (Marconi et al. 2004). As these time-scales are comparable to the binary hardening time-scale at parsec separation (Kelley et al. 2017b), we assume that the CBD is long-lived and remains around the binary throughout its evolution.
We investigate two fiducial scenarios. Initially, each MBHB forms on an almost circular orbit with a small initial eccentricity |$e_{\rm b,0} = 0.01$|, and is then evolved with or without CBD-driven orbital evolution and accretion. We choose initially nearly circular orbits in order to compare our results with previous studies, where circular MBHBs are typically assumed (e.g. Katz et al. 2020; Bortolas et al. 2021).
nCBD_eb0 = 1.e-2: Binaries form with an initial eccentricity |$e_{\rm b, 0} = 10^{-2}$| and experience DF, SS, and GW evolution. We apply no accretion, i.e. |$\dot{M}_{\rm b} = 0$|, and, as a result, CBD-driven evolution rates are also zero, |$\dot{a}_{\rm b,CBD} = 0$| and |$\dot{e}_{\rm b,CBD} = 0$|.
yCBD_eb0 = 1.e-2: Binaries form with an initial eccentricity |$e_{\rm b, 0} = 10^{-2}$|, and subsequently experience DF, SS, CBD, and GW evolution. Our fiducial accretion rate is set to 10 per cent Eddington, and as a result, accretion and CBD-driven evolution rates are non-zero, i.e. we apply |$\dot{M}_{\rm b} = 0.1\, \dot{M}_{\rm b,Edd}$|, |$\dot{a}_{\rm b,CBD}(q_{\rm b}, e_{\rm b})$|, and |$\dot{e}_{\rm b,CBD}(q_{\rm b}, e_{\rm b})$|.
|$\dot{M}_{\rm b,Edd}$| is the Eddington accretion rate for an object with mass |$M_{\rm b}$|, defined as |${L_{\rm Edd}}/{\epsilon c^2}$| with a radiative efficiency |$\epsilon = 0.1$|. To account for uncertainties in the initial eccentricity of binary systems at formation, we investigate two additional scenarios where binaries form with a random initial eccentricity:
nCBD_eb0 = rand: Binaries form with a random initial eccentricity between |$0 \ \mathrm{ and} \ 0.999$|, and subsequently experience DF, SS, and GW evolution. We apply no accretion, i.e. |$\dot{M}_{\rm b} = 0$|, and, as a result, CBD-driven evolution rates are also zero, |$\dot{a}_{\rm b,CBD} = 0$| and |$\dot{e}_{\rm b,CBD} = 0$|.
yCBD_eb0 = rand: Binaries form with a random initial eccentricity between |$0 \ \mathrm{ and} \ 0.999$|, and subsequently experience DF, SS, CBD, and GW evolution. Our fiducial accretion rate is set to 10 per cent Eddington, i.e. we apply |$\dot{M}_{\rm b} = 0.1\, \dot{M}_{\rm b,Edd}$|, |$\dot{a}_{\rm b,CBD}(q_{\rm b}, e_{\rm b})$|, and |$\dot{e}_{\rm b,CBD}(q_{\rm b}, e_{\rm b})$|.
Additionally, we investigate the effect of accretion rates on the population by probing regimes where binaries accrete at Eddington fractions |$f_{\rm Edd} = [0.01, \ 0.10, \ 1.00]$|. For each population, we report eccentricity and mass ratio distributions in the LSST and PTA bands, GWB amplitudes, and detection rates in the LISA band. In the following, we analyse the results and report the effect of CBD-driven evolution on properties of the MBHB population.
3 RESULTS
3.1 Eccentricity evolution in MBHB populations
In Fig. 1, we show the median binary eccentricity as a function of GW frequency (top panel) and binary separation (bottom panel) for all binaries in our sample. The shaded regions around each line correspond to the 32nd and 68th percentiles. The shaded regions in the upper panel refer to the LSST and North American Nanohertz Observatory for Gravitational Waves (NANOGrav) bands, which are |$6\times 10^{-9} \lesssim {\nu }_{\rm LSST} \lesssim 10^{-6} \, {\rm Hz}$| and |$10^{-9} \lesssim {\nu }_{\rm PTA} \lesssim 5 \times 10^{-8} \, {\rm Hz}$|, respectively. For more details on the LSST band limits, see Section 3.3.
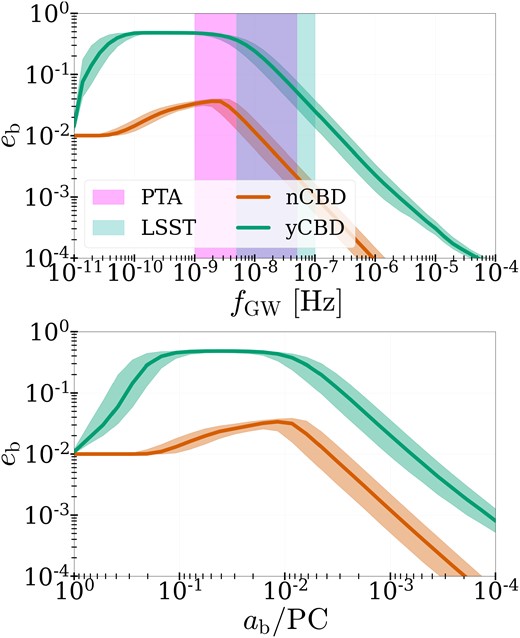
Median, 32nd and 68th percentile of binary eccentricity as a function of frequency (top panel) and semimajor axis (bottom panel), showing fiducial runs yCBD_eb0 = 1.e-2 and nCBD_eb0 = 1.e-2 (green and orange lines, respectively). CBD torques boost the median eccentricities of close binaries by one to two orders of magnitude. Significant eccentricities are expected in sub-parsec MBHBs, as they enter the PTA band. Large orbital eccentricities are still present in the LSST band, where GW-driven circularization begins to take over.
We compare our two fiducial models: binaries initialized at a low eccentricity |$e_{\rm b,0} = 0.01$|, and evolved either without CBD torques and accretion (orange line), or with both CBD torques and preferential accretion models (green line; Siwek et al. 2023a, b). While both models start out at the same initial eccentricity |$e_{\rm b,0} = 0.01$| at |$a_{\rm b} = 1\, \rm {pc}$|, CBD torques lead to a sharp increase in binary eccentricity, up to a median peak eccentricity capped at |${\sim} 0.5$|. This is in line with the CBD-induced equilibrium binary eccentricity recently reported in D’Orazio & Duffell (2021), Zrake et al. (2021), and Siwek et al. (2023b). As GW emission becomes the dominant evolution process, MBHBs begin to circularize at |$a_{\rm b} \sim 10^{-2} \, \rm {pc}$|, or |$f_{\rm GW} \sim 10^{-8}\, \rm {Hz}$|. However, since the GW circularization rate is the same for both populations, a one to two order of magnitude gap remains that distinguishes the CBD-driven model from the model that excluded CBD torques.
In Fig. 2, we show the median, 32nd and 68th percentile of CBD-driven binary eccentricity as a function of GW frequency (top panel) and binary separation (bottom panel) for a range of mass bins: |$10^6 \lesssim M_{\rm b} \lesssim 10^7 \, {\rm M}_{\odot }$|, |$10^7 \lesssim M_{\rm b} \lesssim 10^8 \, {\rm M}_{\odot }$|, |$10^8 \lesssim M_{\rm b} \lesssim 10^9 \, {\rm M}_{\odot }$|, and |$10^9 \lesssim M_{\rm b} \lesssim 10^{10} \, {\rm M}_{\odot }$|, indicated by colours ranging from light to dark blue. Similar to the green line in Fig. 1, eccentricity increases as a result of CBD-driven orbital evolution before circularization due to GWs taking over. The transition frequency/separation depends on total binary mass: at higher binary masses, GW-dominated evolution takes over earlier than it does in lower mass binaries. We attribute this to the scale-free nature of the hydrodynamic simulations that our CBD-driven evolution models are based on. While |$\dot{e}_{\rm b}$| and |$\dot{a}_{\rm b}$| are independent of binary mass, the GW-driven orbital evolution rates do depend on binary mass. As a result, the transition from CBD-driven to GW-driven evolution occurs earlier for higher mass binaries and later for lower mass binaries. This leads binaries with lower masses to retain higher eccentricities than higher mass binaries, when compared at the same separation.
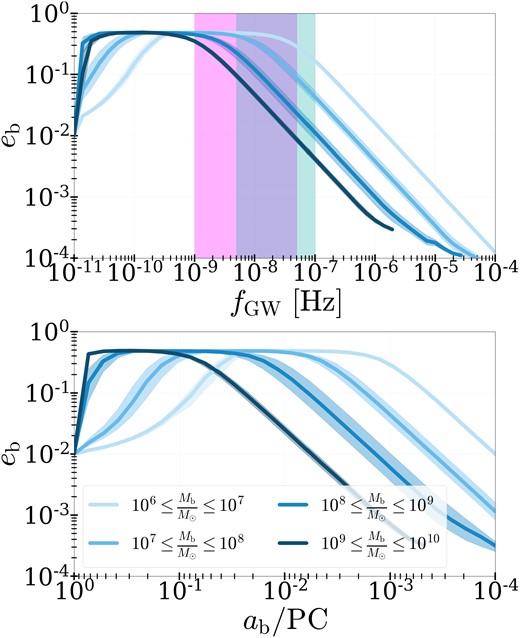
MBHB orbital eccentricity evolution in our fiducial yCBD_eb0 = 1.e-2 simulation. Median binary eccentricity along with 32nd and 68th percentiles is shown as a function of GW frequency (top panel), again showing the PTA and LSST regimes in pink and teal, respectively. The bottom panel shows the orbital eccentricity as a function of the semimajor axis. Here, the MBHB population is separated into mass bins to analyse the mass dependence of the eccentricity evolution at a given frequency/separation.
In Fig. 3, we show MBHB populations in the LSST and PTA bands, plotting the median binary eccentricity as a function of binary mass. We contrast populations evolved without CBD physics (orange line), and with CBD physics applied at increasing accretion rates. The light green line indicates that all binaries accrete at 1 per cent of their Eddington limit, medium green corresponds to 10 per cent Eddington, and dark green to 100 per cent. In all cases, the median orbital eccentricity is inversely related to binary mass. The slopes in all cases are approximately similar, while the accretion rate increases the amplitude of the |$e_{\rm b}$| versus |$M_{\rm b}$| relation.
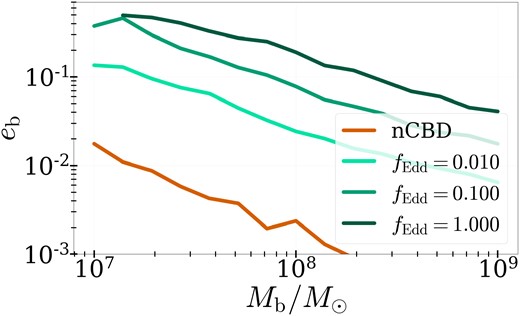
Orbital eccentricity versus combined mass in binary systems within the LSST and PTA frequency bands. The orange line represents a population of MBHBs not evolved with CBD physics, while light, medium, and dark greens refer to MBHB populations evolved with CBD physics and increasing accretion rates. In all cases, binary mass is associated inversely with orbital eccentricity.
3.2 Dependence on initial conditions
The initial eccentricity of MBHBs is intrinsically uncertain, since even small perturbations in the galaxy merger orbit can lead to large variations in the final MBHB eccentricity (e.g. Rawlings et al. 2023). To check the dependence of a potentially observable eccentricity distribution on the initial binary eccentricity, we run several realizations of our binary evolution with a range of initial eccentricities: |$e_{\rm b, 0} = [0.0001, 0.01, 0.1, 0.9]$|, and compare the eccentricity evolution as a function of binary separation in each case. The results are shown in Fig. 4. In the case of binaries evolved without CBD torques (dashed lines), the initial eccentricity of the binary strongly influences the population going forward. However, when we apply CBD torques (solid lines), the initial conditions are erased: all binaries end up at the same eccentricity-separation track. The CBD-evolved population maintains a higher orbital eccentricity at sub-parsec separations than any other realization without CBD effects, unless all binaries are initialized with a very high initial eccentricity (|$e_{\rm b,0} \sim 0.9$|). Our results therefore indicate that, unless binaries form at extremely high initial eccentricities, CBD-evolved populations will achieve the highest median orbital eccentricities at sub-parsec separations, and the value of this eccentricity is always the same, irrespective of the initial conditions. Unless other eccentricity pumping mechanisms are invoked (e.g. three-body interactions, Kozai–Lidov), CBD torques are the only mechanism leading to the MBHB eccentricity distributions we report here.
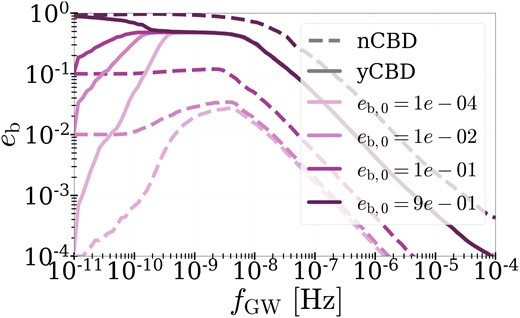
Median eccentricities of MBHBs as a function of GW frequency, comparing a range of initial eccentricities. The solid and dashed lines show populations evolved with and without CBD physics, respectively, while colours indicate the orbital eccentricity at which the binary systems were initialized. The convergence of the solid lines indicates that CBD physics erases the initial conditions and dominates the eccentricity evolution of sub-parsec MBHBs, despite initial eccentricities varying by several orders of magnitude.
3.3 CBD signatures in MBHB populations
PTAs have recently found strong evidence for a GWB emitted by MBHBs (e.g. Agazie et al. 2023a, c) during their long-term inspiral. Such a measurement probes the net MBHB population, and can constrain their number densities and masses. Additionally, PTAs are expected to detect individual MBHBs as ‘continuous wave’ sources (Kelley et al. 2018), which would allow for a detailed study of sub-parsec MBHB dynamics without the degeneracies of modelling large populations. A recent analysis of the NANOGrav 15-yr data set yielded only upper limits, but some tantalizing hints of excess power at |${\sim} 4 $| and |${\sim} 170 \, \rm {nHz}$| (Agazie et al. 2023b).
A much larger sample of MBHB candidates is likely to be detected (Kelley et al. 2019) by the LSST (Ivezić et al. 2019) at the Rubin Observatory (Ivezić et al. 2019). In addition to PTAs probing the MBHB population via GW detection, LSST will reveal the EM counterparts of such systems in the optical band. This will enable a multimessenger view of the evolution and fate of MBHBs across cosmic time. LSST is expected to detect up to |$10^8$| MBHBs (Xin & Haiman 2021), providing a detailed population overview up to redshift |$z \sim 6$|.
For the purposes of this analysis, we consider MBHBs in the PTA range emitting at frequencies between |$10^{-9}$| and |$10^{-8}\, \rm Hz$|. We sample the MBHB population generated as stated in Section 2 in this frequency range to obtain characteristics of this population, including their masses, mass ratios, and eccentricities. LSST will nominally observe for 10 yr (Ivezić et al. 2019). Similar to Charisi et al. (2016), who search for binary AGN in PTF data requiring at least 1.5 cycles, we select only binaries in our sample that can complete at least two orbital cycles over LSST mission time (note that more cycles may be needed to confidently detect periodicities; Vaughan et al. 2016), and fall below the higher frequency cadence of |${\sim} 1$| week. With those parameters, we define the LSST frequency band |$6 \times 10^{-9} \!-\! 10^{-6} \, \rm Hz$|, where the lower limit represents a binary with a period of 5 yr (two cycles in the 10 yr LSST baseline), and the upper limit is set by the estimated maximum cadence of 1 week at which a source may be observed. The orbital frequencies corresponding to the PTA band overlap significantly with the range of orbital frequencies detectable with LSST (see also the shaded regions in Fig. 1). As a result, the population statistics are similar, and we show the combined PTA and LSST detectable populations in our results.
In the following, we present the characteristics of the MBHB populations in our sample that fall into the PTAs and LSST frequency bands. We show all the binaries in our sample that fall into the frequency range of PTAs and LSST. We do not take any luminosity cuts to account for LSST sensitivity. This is because luminosity cuts turn out to be irrelevant for binaries accreting at 10 per cent Eddington, as most of these systems are luminous enough to be detected, and because we aim to study the underlying MBHB population, without considering detection bias. We note, however, that MBHB systems have to be luminous enough to be above LSST’s single-exposure limit, potentially posing challenges for the less massive MBHBs in our sample. We reserve further study of this caveat for future studies on CBD-induced variability detection in MBHBs. In Fig. 5, we show the expected number of MBHBs at any given time (per logarithmic bin width) as a function of binary eccentricity (|$e_{\rm b}$|; left) and mass ratio (|$q_{\rm b}$|; right). We contrast distributions from populations evolved without CBD models (orange lines) and with CBD accretion and orbital evolution models from Siwek et al. (2023a, b) (green lines). Most populations start with the fiducial initial binary eccentricity |$e_{\rm b,0} = 0.01$|, aside from the light orange line that is evolved without CBD physics but initialized with a random eccentricity distribution. As before, the shade of the green line refers to the accretion rate parametrized by the Eddington accretion rate fraction. MBHBs evolved with CBD models enter the PTA/LSST frequency range with significantly higher eccentricities. The median eccentricity in the case without CBDs, initialized at |$e_{\rm b,0} = 0.01$|, is at |$e_{\rm b,med} \sim 4\times 10^{-2}$|, just above the initial eccentricity |$e_{\rm b,0} = 0.01$| (dark orange line). In the case of the nCBD population evolved with random initial eccentricity (light orange), the median eccentricity in the PTA/LSST band is higher, at |$e_{\rm b,med} \sim 2\times 10^{-1}$|, but still lower than the median eccentricities reached by any of the yCBD cases. The populations evolved with CBD torques measure median eccentricities up to |$e_{\rm b,m} \sim 0.5$|, and sharply decrease in number density below the peak at|$e_{\rm b,m} \sim 0.5$|.
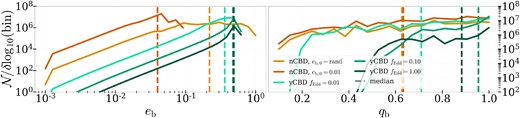
Number of MBHBs in an observer’s light-cone as a function of binary eccentricity (left) and mass ratio (right), including binaries in the PTA and LSST frequency bands. The dark and light orange lines show models evolved without CBD torques, with either |$e_{\rm b,0} = 0.01$| or random initial eccentricities, respectively. The green lines show populations evolved with CBD models from Siwek et al. (2023a, b). The shade of green refers to the Eddington fraction at which binaries accrete, with the lightest green representing 1 per cent Eddington and the dark green representing 100 per cent Eddington. In all cases, CBD-evolved populations have higher median eccentricities and mass ratios than populations evolved without CBD torques.
In the right panel, we show the mass ratio distributions for all our models using the same colours as before. We find that the mass ratio distribution in the populations evolved without CBD accretion or with very low accretion rate is flat, with a median |$q_{\rm b,m} \sim 0.6$|. In the yCBD cases, the mass ratio distribution is sharply peaked towards unity, and median mass ratios are |$q_{\rm b,m} \gtrsim 0.9$|.
In Fig. 6, we show the PTA/LSST MBHB population across the mass ratio versus eccentricity parameter space. We contrast simulations with various initial conditions, evolution models, and accretion parameters: in the first column, separated from the rest of the panels, we show the populations evolved without CBD torques. We test three different initial eccentricity distributions: |$e_{\rm b,0} = 0.01$| (top panel), randomly drawn values of |$e_{\rm b,0}$| in the range [0, 1.0) (middle panel), and |$e_{\rm b,0} = 0.9$| (bottom panel). We find that significant memory of the initial eccentricity distribution is retained in the populations when no CBD torques are included.
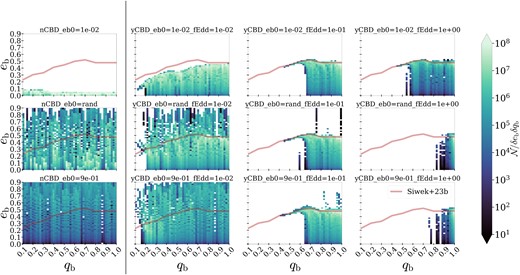
Eccentricities of MBHBs as a function of binary mass ratio, corresponding to binaries in the PTA and LSST frequency ranges. The red line shows binary equilibrium eccentricities as a function of mass ratio, as found in Siwek et al. (2023b). The first column shows MBHBs evolved without CBDs. The following columns going from left to right show MBHBs evolved with CBDs, with increasing accretion rates from 1 per cent Eddington (first column after vertical line) up to 100 per cent Eddington in the rightmost column. The rows indicate the initial eccentricity distribution of MBHBs at formation, with the top row showing our fiducial value |$e_{\rm b,0} = 0.01$|, the middle row uses a randomly drawn initial eccentricity distribution, and the bottom row sets |$e_{\rm b,0} = 0.9$| uniformly.
The remainder of the panels on the right-hand side of the black bar show MBHB populations evolved with CBD physics. The columns increase from left to right in their accretion rates. The first column shows binary systems with |$e_{\rm b,0} = 0.01$| (top), |$e_{\rm b,0} = \rm {rand}$| (middle), and |$e_{\rm b,0} = 0.9$| (bottom), all evolved with CBD physics but at low accretion rates |$f_{\rm Edd} = 0.01$|. While the initial eccentricity distribution affects the population statistics, the systems have evolved towards the equilibrium eccentricity |$e_{\rm b,eq}$| versus |$q_{\rm b}$| relation, overplotted in the red line. The second column shows populations again with |$e_{\rm b,0} = 0.01$| (top), |$e_{\rm b,0} = \rm {rand}$| (middle), and |$e_{\rm b,0} = 0.9$| (bottom), but evolved at the fiducial accretion rate |$f_{\rm Edd} = 0.10$|. In this case, the population statistics are nearly identical, and closely trace the |$e_{\rm b,eq}$| versus |$q_{\rm b}$| relation. Any initial conditions appear to have been erased by the CBD-driven evolution. In the right column, the accretion rate is set to |$f_{\rm Edd} = 1$|. In this case, most binaries have evolved towards |$q_{\rm b} = 1$|, except in the case where |$e_{\rm b,0} = 0.01$|, where a low mass ratio tail remains. This is due to an increased number of low mass ratio binaries reaching the PTA/LSST bands, likely as a result of stronger CBD-driven inspiral in near-circular systems (see fig. 2 in Siwek et al. 2023b). In the middle and bottom panels, where |$e_{\rm b,0} = \rm {rand}$| (middle) and |$e_{\rm b,0} = 0.9$| (bottom), most binaries have equal mass ratios and eccentricities|$e_{\rm b} \lesssim 0.5$|.
3.4 The effect of CBD accretion on the GWB spectrum
In Fig. 7, we show the GWB spectrum emitted by four MBHB populations evolved with distinct CBD accretion and orbital evolution: the orange line refers to our fiducial nCBD_eb0 = 1.e-2 model, while the green lines refer to yCBD_eb0 = 1.e-2, each evolved with a different accretion rate. As before, the shade of green saturates with increasing Eddington fraction. Each binary in our sample begins accreting once it reaches sub-parsec separation, and subsequently accretes at a constant Eddington fraction. Higher accretion rates evolve MBHBs to overall higher masses, but more importantly also increase the mass ratios. The chirp mass |$\mathcal {M}$| of a binary depends sensitively on its mass ratio |$q_{\rm b}$| and total mass |$M_{\rm b} = M_1 + M_2$|,
The GW spectrum depends on the chirp mass, and its amplitude |$h_{\rm c}$| scales as follows with chirp mass and frequency (Enoki & Nagashima 2007),
A modest increase in the mass ratio distribution of MBHBs can thus result in a significant increase in the overall GWB amplitude. We find that even models with just 1 per cent Eddington accretion throughout the sub-parsec evolution of the binary show a small increase in the GWB amplitude at |$f_{\rm GW} = 1\, \rm {yr}^{-1}$|. At 10 per cent Eddington, the GWB amplitude has increased by a factor of |$2\!-\!3$|, while at 100 per cent Eddington the amplitude is over five times higher when compared with the nCBD_eb0 = 1.e-2 model. Our result suggests that CBD accretion can boost the GWB amplitude measurably, and may account for the higher than expected amplitude recently inferred by PTAs (Agazie et al. 2023a; EPTA Collaboration 2023; Reardon et al. 2023; Xu et al. 2023). We note that the difference in amplitude between our models and the NANOGrav measurement is likely due to an incomplete sample of MBHBs in our simulations. We infer binaries from galaxy mergers in the Illustris simulations, but the volume limit may lead to a dearth in the highest mass MBHs, simply because these systems are already scarce. In future studies, we plan to repeat our population studies with the IllustrisTNG (Marinacci et al. 2018; Naiman et al. 2018; Nelson et al. 2018; Pillepich et al. 2018; Springel et al. 2018) and MillenniumTNG (e.g. Delgado et al. 2023) simulations, which cover larger volumes.
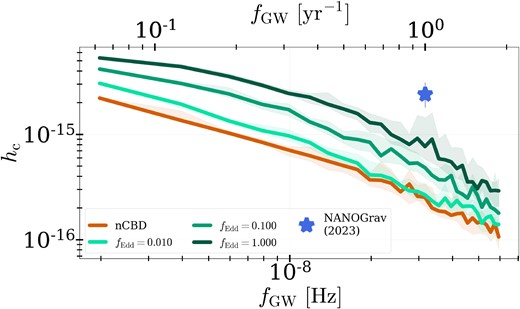
GWB spectrum calculated for models evolved with CBDs, but with different accretion rates. We compare spectra resulting from MBHB populations evolved without CBD physics (orange line) to those with CBD physics at Eddington accretion rates |$f_{\rm Edd} = 0.01$| (light green line), |$f_{\rm Edd} = 0.10$| (medium green line), and |$f_{\rm Edd} = 1.00$| (dark green line).
We also note that the highest accretion rate models exhibit some indication of a turnover at the lowest frequencies shown here. Current evidence for the GWB suggests that the spectral slope may be flatter than |${\propto} f^{-2/3}$| as is expected for binaries hardening through GW emission only. The slope carries information about environmental effects and their impact on MBHB dynamics. A flattening of the slope indicates that binaries move through frequency bins faster than through GW emission only, indicating that environmental effects such as gas (e.g. Kocsis & Sesana 2011) dominates their evolution (see e.g. Sesana 2013, for a review on GWB physics). Our models provide one possible explanation for this, as higher accretion rates seem to flatten the spectrum out to higher frequencies close to |$1\, \rm {yr}^{-1}$|.
3.4.1 CBD softening: a positive effect on the GWB
Recent simulations indicate that the net torque acting between a binary and CBD can cause orbital expansion (‘softening’; Miranda et al. 2017; Moody, Shi & Stone 2019; Muñoz, Miranda & Lai 2019; Duffell et al. 2020; Muñoz et al. 2020; D’Orazio & Duffell 2021; Siwek et al. 2023b). Siwek et al. (2023b) showed that whether a binary softens or hardens in the presence of a CBD depends on both binary mass ratio and eccentricity. This effect is self-consistently included in our population modelling, by interpolating the hardening/softening rates depending on the orbital parameters of each binary at a given time-step. In Fig. 8, we show the effect of CBD-driven semimajor axis evolution on the GWB spectrum. We plot the GWB spectrum in a population that includes CBD physics, but allows only for orbital hardening (i.e. |$\dot{M}_{\rm b} \gt 0$| and |$\dot{a}_{\rm b} \le 0$|; pink line) while neglecting any instances of CBD-induced orbital softening, alongside a full CBD model including softening (light blue line). We find that CBD softening results in a slight increase in the GWB amplitude. This effect can be attributed to prolonged time periods of accretion. Orbital softening allows binaries to accrete over a longer time periods ahead of reaching the PTA frequency range. This allows them to grow to larger masses compared with binaries that do not experience CBD softening. Any softening-induced increase in time spent in the PTA band is not significant in increasing the amplitude, instead, it is the increase in total mass and chirp mass that boosts the GWB amplitude. However, this is a minor effect, and only noticeable if the accretion rates are sufficiently high, here at 100 per cent Eddington. Other than small increases in total mass, we find no noticeable differences in MBHB population statistics due to CBD softening. We note that Bortolas et al. (2021) previously found that orbital stalling due to a CBD can cause significant mass growth, also enhancing the GWB. They further argued in such cases, MBHBs may grow massive enough for GW-driven inspiral to exceed CBD-driven stalling, causing them to eventually merge within a Hubble time.
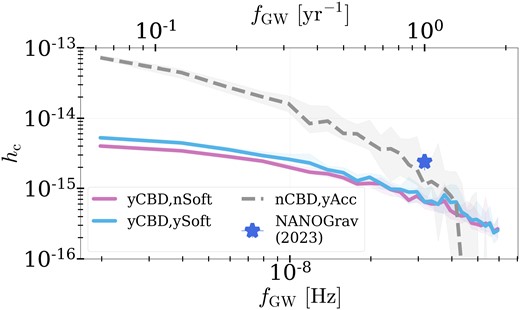
GWB spectrum from MBHB populations evolved with CBD physics, allowing both softening and hardening (blue line) and hardening only (pink line). We also show a model that includes CBD accretion at the same rate as the other two models (100 per cent Eddington), but does not apply any orbital evolution rates (grey dashed line). This leads to a dramatic increase in the GWB amplitude, as binaries get to grow through accretion without experiencing the hardening effects of the CBD.
We also investigate a model where binaries accrete gas without any hardening or softening torques from the CBD (grey dashed line in Fig. 8). This leads to a dramatic increase in the GWB amplitude, as no hardening effects are applied, and the binaries grow in mass over longer time-scales. This limit test serves to account for potentially large uncertainties in CBD evolution models. Current CBD simulations are typically in 2D, with pure hydrodynamics and an |$\alpha$|-disc model. However, the semimajor axis hardening rate is quite sensitive to the gas distribution in the CBD cavity, which itself is governed by hydrodynamics in the disc (e.g. Tiede et al. 2020). As current models neglect significant physical processes in the disc (such as radiative transport, magnetic fields, jets and winds, and self-consistent viscous transport through magnetorotational instabilities), the hardening rates from the current 2D hydrodynamic models are highly uncertain, and could be much smaller than expected. In such a case, the effect on the GWB would again be positive: while binaries take longer to merge, they also have longer time-scales to accrete gas from their CBDs and thus boost the GWB amplitude.
3.5 MBHBs in LISA
The LISA (Amaro-Seoane et al. 2017) will detect the mergers of MBHBs with total masses ranging |$10^3 \lesssim M_{\rm b} \lesssim 10^9\, {\rm M}_{\odot }$| (Amaro-Seoane et al. 2017; Katz & Larson 2019). However, population synthesis models that analyse the detectability of MBHBs typically assume circular orbits (e.g. Katz et al. 2020). Here we analyse the effect of CBD-driven evolution on the detectability of MBHBs in the LISA frequency range.
Fig. 9 shows the characteristics of the MBHBs in our simulations that could be detected with LISA. To determine whether a source is detectable, we compare its GW strain to the LISA sensitivity at that frequency. We contrast populations evolved without any CBD physics (orange lines) to those evolved with CBD physics, at a range of accretion rates. The leftmost panel shows the distribution of total binary masses, with the majority of binaries detectable near |$M_{\rm b} \sim 10^8 \, {\rm M}_{\odot }$|. We note that the accretion of gas onto the binary produces only a moderate shift in the total mass distribution, even when binaries accrete at 100 per cent Eddington throughout their final parsec evolution. In the middle panel of Fig. 9, we show the mass ratio distribution in the contrasting populations. Since CBD accretion favours the secondary, we see the expected shift towards |$q_{\rm b} = 1$| in the CBD-evolved populations, most notably in those with higher accretion rates. Despite the minor shift in total mass, the mass ratio increase can lead to a significant increase in chirp masses, allowing more MBHBs to be detectable in LISA. In the rightmost panel, we show the orbital eccentricity distributions. As all populations are initialized at a low orbital eccentricity |$e_{\rm b,0} = 0.01$|, the nCBD binaries enter the LISA band with undetectable residual eccentricities. However, even at low accretion rates, CBD-driven eccentricity evolution is efficient enough to shift the distribution by over an order of magnitude. At 100 per cent Eddington, the residual eccentricities in the LISA band are near |$10^{-3}$|, close to the regime where detection of orbital eccentricity is expected (e.g. Garg et al. 2024). Consistent with Zrake et al. (2021), we find that residual eccentricities are higher in lower mass binary systems (see Fig. 2), and plan to investigate the impact of CBD physics on intermediate-mass black holes in future studies.
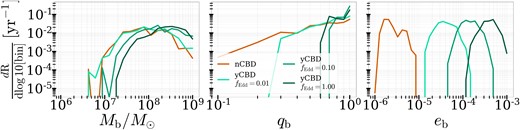
Population statistics of detectable binaries in the LISA band, with rates in each logarithmic bin shown per year. Since our binary sample has a lower mass limit of |${\sim} 10^6\, {\rm M}_{\odot }$| at formation, the rates of detections in the LISA band are low.
In Fig. 10, we show the rate of mergers detected in our binary sample per harmonic in which they were detected. The distribution of GW power emitted across the harmonics is computed based on the formalism in Enoki & Nagashima (2007), specifically equations (2.3)–(2.6). The GW strain at each harmonic is then calculated, and compared with the LISA sensitivity curve at the frequency associated with the harmonic. This yields estimates for the number of MBHBs detectable per harmonic in the observer’s light-cone. When comparing the yCBD/nCBD (green and orange, respectively), we find that the presence of a CBD is associated with a higher rate of detected n = 3 harmonics. We find that CBD-driven evolution causes detection of the n = 3 harmonic for a few per cent of the detected n = 2 binaries, especially if CBD accretion rates are high. We note that all binaries that were detected in the n = 3 harmonic were also detected in the n = 2 harmonic, i.e. there are no MBHBs in our sample that are only detectable in LISA due to the excitation of an eccentric harmonic. However, this may change in lower mass binaries, where higher residual eccentricities may be expected (see Fig. 3).
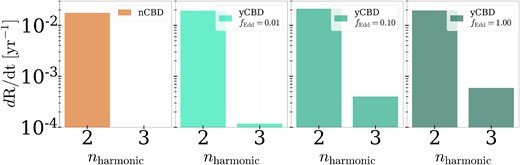
The rate of detected harmonics per year in the LISA band. We show models without CBDs (left) and with CBDs and increasing accretion rates (1, 10, and 100 per cent Eddington going left to right). The detection rate of n = 3 harmonics increases with the total binary accretion rate.
We note that our analysis serves to demonstrate that many binaries that co-evolve with CBDs emit enough GW power in their higher harmonics to be detectable. This is also a very conservative demonstration as a templated search will be much more sensitive to detecting eccentricity than simply searching for particular |$n\gt 2$| harmonics.
4 SUMMARY AND DISCUSSION
We have examined the impact of CBD-driven evolution and preferential accretion on the population statistics of potentially observable MBHBs, the GWB, and LISA binaries. Our analysis is based on a sample of MBHBs derived from galaxy mergers in the Illustris simulation, and semi-analytically evolved using holodeck (Kelley et al. 2017a). We have performed parameter studies testing several initial conditions, with initial eccentricities |$e_{\rm b,0}$| either randomly drawn or uniformly set to the following values: |$e_{\rm b,0} = [0.0001, 0.001, 0.01, 0.9]$| (see Figs 4 and 6). Our fiducial case forms MBHBs at near circular binaries with |$e_{\rm b,0} = 0.01$|. As the impact of CBD-driven orbital evolution is scaled by the total binary accretion rate (for further details we refer to the orbital evolution models presented in Siwek et al. 2023a, b), we tested various levels Eddington rates at |$f_{\rm Edd} = [0.01, 0.10, 1.0]$| (see Figs 5, 6, and 7). Our fiducial case is |$f_{\rm Edd} = 0.10$|. Finally, the orbital evolution models our population study is based on containing semimajor axis evolution rates of binaries with a range of mass ratios and eccentricities. We, therefore, self-consistently allow for binary hardening and softening, and present the results of self-consistent binary softening on the GWB (see Fig. 8). Our analysis compares MBHBs evolved semi-analytically with large-scale galactic processes, CBDs, and GWs to a population of MBHBs evolved without any CBD contribution. Using this parameter study, we have identified signatures of CBD-driven binary evolution for upcoming multimessenger observations of MBHBs. Our key results are as follows.
CBD dynamics dominate the eccentricity evolution of sub-parsec MBHBs, which evolve up to orbital eccentricities |$e_{\rm b} \sim 0.5$| as they enter the PTA band.
When CBD physics is applied, the eccentricities of MBHBs in the observable bands are independent of their highly uncertain initial eccentricity distribution at formation, erasing any memory of it.
CBD-driven semimajor axis evolution has a minor effect on the GWB, counterintuitively leading to a small boost in the GWB amplitude due to prolonged accretion.
The recently discovered |$e_{\rm b}$| versus |$q_{\rm b}$| relationship induced by CBD dynamics (Siwek et al. 2023b) leaves an unambiguous signature in detectable MBHB populations.
MBHBs in the LISA band retain eccentricity from the CBD-driven evolution, boosting the median eccentricity of the population by up to two orders of magnitude.
Increased orbital eccentricities enhance the likelihood that eccentricities are detected in the LISA band.
In the following, we put our findings in the context of the relevant literature. We outline any caveats the reader may wish to consider when interpreting our results.
4.1 Comparison with the literature
We have shown that CBD dynamics is a non-negligible contributor to MBHB eccentricity evolution. Our results are based on the first comprehensive MBHB population synthesis model that uses numerically derived CBD-driven orbital evolution rates of binaries with arbitrary mass ratios and eccentricities (Siwek et al. 2023a, b). Prior studies have investigated the eccentricity evolution of LISA and PTA binaries without generalized CBD-driven evolution (e.g. Sesana 2010; Sayeb et al. 2021; however, see Zrake et al. 2021, who studied the CBD and GW-driven orbital evolution of binaries), and we outline the main differences and agreements with this work.
Sesana (2010) has conducted a detailed population analysis of MBHBs with varying mass ratios and eccentricities, evolved semi-analytically with stellar scattering models (Sesana, Vecchio & Colacino 2008) and GW emission (Peters & Mathews 1963). Similar to our work, Sesana (2010) finds that low-mass binaries retain the highest eccentricities at observable frequencies (see Fig. 3). Conversely, they find that low mass ratio binaries enter observable bands at higher eccentricities, while we find the opposite (Fig. 6). Our results include the influence of CBD-driven evolution on the orbital eccentricity, and thus deviate from their results. While we use the same stellar scattering models that favour eccentricity pumping in low mass ratio systems, we find that CBD-driven evolution is more significant. CBDs evolve binaries towards eccentricities that increase with mass ratio, and we find that this signature mechanism of CBD physics remains visible in PTA and LSST bands (see Fig. 6). We further find that very few low mass ratio systems with |$q_{\rm b} \lesssim 0.6$| remain by the time binaries have evolved towards the detectable bands. We explain that this is due to CBD-driven preferential accretion on the secondary. Sesana (2010), on the other hand, does not include CBD-driven accretion to evolve binary mass ratios. They also cover a larger parameter space with mass ratios as low as |$q_{\rm b} = 1/729$|, and as a result their sample contains a larger number of very low mass ratio binary systems. As low mass ratio binaries evolve towards the highest eccentricities due to stellar scattering, they predict higher residual eccentricities in the LISA band than our simulations (see Fig. 9).
Commenting on the dearth of low mass ratio systems in our sample compared to Sesana (2010), we point out that CBD accretion may not always lead to an increase in mass ratio. Instead, a turnover in the preferential accretion ratio (Farris et al. 2014) could lead to a bimodal mass ratio distribution in MBHBs (as seen in Siwek et al. 2020). Further numerical studies are needed to investigate this turnover, as preferential accretion models have only been tested numerically down to |$q_{\rm b} \sim 0.01$| (e.g. Farris et al. 2014; Duffell et al. 2020). While these simulations hint at a potential turnover in the preferential accretion ratios, and could thus lead to a bimodal mass ratio distribution, further studies with a focus on low mass ratio binaries are needed to confirm this.
Sesana (2010) finds that the properties of MBHBs in observable frequency bands depend on the initial orbital eccentricities in their population. However, a main result of our work is that the observed eccentricities in MBHB populations do not depend on initial conditions, as a result of CBDs. CBD-driven evolution erases the initial eccentricity distribution in MBHBs, and thus the initial eccentricity distribution is irrelevant to the properties of observable MBHB populations. This disagrees with Sesana (2010), and vastly simplifies parameter studies of MBHB populations, if CBD-driven evolution is indeed a common pathway in sub-parsec MBHBs.
Roedig et al. (2011) conducted a numerical study that suggested a steady-state or ‘limiting’ eccentricity in MBHBs due to CBD-driven evolution in the range |$0.6\!-\!0.8$|. This limiting eccentricity was obtained for a binary with |$q_{\rm b} = 1/3$|, and therefore in tension with the results in Siwek et al. (2023b). Possible reasons for the discrepancy include numerical resolution of gas in the inner region of the CBD, as well as effects from self-gravity in the CBD modelled by Roedig et al. (2011).
They evolved binaries from the limiting eccentricity with GW-driven orbital evolution rates, and as a result estimates the eccentricity of post-CBD binaries in the LISA band to be |$10^{-3}\!-\!10^{-2}$| in low-mass binaries with |$M_{\rm b} \lesssim 10^{6}\, {\rm M}_{\odot }$|. Given the slightly higher steady-state eccentricity and low binary mass, their results appear to be in line with our estimates (see Fig. 3).
Bortolas et al. (2021) investigated the effect of stars and CBD-driven orbital evolution on the GW detection prospects of circular, equal-mass MBHBs. Although they do not account for binary eccentricities, we can draw some parallels to our work. Similar to our findings, they find that CBD-induced orbital expansion only temporarily stalls binaries, while other effects (such as mass growth and stellar interactions) eventually bring the binary to the merger. This is also reflected in the GWB calculation shown in our Fig. 8, where CBD-induced softening has allowed binaries to grow in mass by a small amount, rather than stalling the population and preventing GW emission.
Bortolas et al. (2021) further predict that high accretion rates may lead to a larger number of low-mass MBHBs detectable in the LISA band. They attribute this to the overall mass growth, while our analysis predicts an increase in eccentric merger detections due to accretion (see Figs 10 and 11).
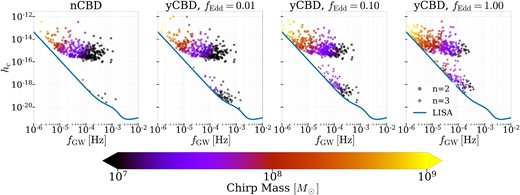
Detectable binaries in the LISA band, showing colour-coded masses of binaries detected in n = 2 (circles) and n = 3 (stars) harmonics. The higher the accretion rate, the more binaries are detected in eccentric harmonics.
4.2 Caveats
We have made several simplifications and assumptions in our simulations, which should be taken into account when interpreting our results.
Our models assume that the CBD is aligned with the binary angular momentum vector, leading to prograde rotation. However, gas inflow can occur from arbitrary angles (chaotic accretion), and may thus result in inclined or retrograde accretion flows. Recently, Tiede & D’Orazio (2024) showed that equal mass ratio binaries in retrograde CBDs can evolve to much higher eccentricities than binaries evolving in prograde discs. This may lead to much higher MBHB eccentricities, and residual eccentricities in the PTA, LSST, and LISA bands may increase accordingly.
Our models do not currently account for the case of MBH triples forming as a result of repeated galaxy mergers (e.g. Bonetti et al. 2018a, b; Ryu et al. 2018; Sayeb, Blecha & Kelley 2024). If triples form frequently, the merger time-scales as well as eccentricity evolution of the inner binary can be affected significantly. Such binary systems may show up as outliers in population studies, with above-average residual eccentricities close to merger, but further numerical studies are needed to better understand the interplay between CBD dynamics and three-body interactions.
We do not currently account for luminosities or AGN fuelling times of MBHBs in our population simulations to calculate the rates at which these systems may be detectable with LSST. Optical luminosities from CBDs are uncertain, and depend on the radiative processes in the inner and outer discs, which are poorly understood and depend on hydrodynamic modelling of the accretion disc (e.g. Krauth et al. 2023). Generally, however, higher mass binaries may be more luminous and potentially more easily detected. In future surveys, this could lead to a systematic shift in the eccentricity distribution of MBHBs as high-mass MBHBs are expected to be on less eccentric orbits (see Fig. 3). Related to this, our MBHB sample is based on the Illustris simulation, and as a result has a cut on low-mass MBHs. Including more low-mass MBHs in population studies would likely increase the median eccentricities of MBHBs in observable bands significantly, and lead to more stringent constraints of CBD-driven residual eccentricities in LISA mergers.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.



