-
PDF
- Split View
-
Views
-
Cite
Cite
Lucie Scharré, Daniele Sorini, Romeel Davé, The effects of stellar and AGN feedback on the cosmic star formation history in the simba simulations, Monthly Notices of the Royal Astronomical Society, Volume 534, Issue 1, October 2024, Pages 361–383, https://doi.org/10.1093/mnras/stae2098
Close - Share Icon Share
ABSTRACT
Using several variants of the cosmological simba simulations, we investigate the impact of different feedback prescriptions on the cosmic star formation history. Adopting a global-to-local approach, we link signatures seen in global observables, such as the star formation rate density (SFRD) and the galaxy stellar mass function (GSMF), to feedback effects in individual galaxies. We find a consistent picture: stellar feedback mainly suppresses star formation below halo masses of |$M_{\rm H} = 10^{12} \rm \, {\rm M}_{\odot }$| and before |$z = 2$|, whereas AGN feedback quenches the more massive systems after |$z = 2$|. Among simba’s AGN feedback modes, AGN jets are the dominant quenching mechanism and set the shape of the SFRD and the GSMF at late times. AGN-powered winds only suppress the star formation rate in intermediate-mass galaxies (|$M_{\rm \star } = 10^{9.5 - 10} \rm \, {\rm M}_{\odot }$|), without affecting the overall stellar mass-assembly significantly. At late times, the AGN X-ray feedback mode mainly quenches residual star formation in massive galaxies. Our analysis reveals that this mode is also necessary to produce the first fully quenched galaxies before |$z=2$|, where the jets alone are inefficient. These initially highly star-forming galaxies contain relatively large black holes, likely strengthening the X-ray-powered heating and ejection of gas from the dense, central region of galaxies. Such extra heating source quenches the local star formation and produces a more variable accretion rate. More generally, this effect also causes the break down of correlations between the specific star formation rate, the accretion rate and the black hole mass.
1 INTRODUCTION
Understanding the physical processes that shape the cosmic star formation history, and thus the stellar mass assembly in dark matter haloes, is essential to develop a comprehensive model of galaxy evolution. While the hierarchical formation of dark matter structures is well established through the convergence of efficient gravity-only N-body simulations (Frenk et al. 1988; Primack 2005; Springel 2005; Diemand, Kuhlen & Madau 2007; Klypin, Trujillo-Gomez & Primack 2011; Angulo et al. 2012; Frenk & White 2012), the hydrodynamical interactions governing baryonic components are complex and costly to model computationally.
Early attempts to model the formation of stars from the cold halo gas either utilized fully analytic approaches (White & Rees 1978; Dekel & Silk 1986), or semi-analytic models (earliest attempts by White & Frenk 1991; Kauffmann, White & Guiderdoni 1993; Cole et al. 1994), in which the evolution of baryons is modelled on to dark matter haloes extracted from N-body simulations. These works showed that assuming the cooling time as the bottleneck for star formation leads to an overproduction of stars with respect to observations. This is known as the ‘overcooling problem’, which was subsequently confirmed by early hydrodynamical simulations (Balogh et al. 2001; Dave et al. 2001).
The solution to the overcooling problem lies in the inclusion of so-called ‘feedback processes’, an umbrella term for self-regulating mechanisms arising from star formation and the supermassive black holes accreting in the centre of massive galaxies (active galactic nuclei, AGNs). Pioneering works by Larson (1974) and Dekel & Silk (1986) showed that the momentum output from supernovae (SNe) can cause significant gas-loss and thus deplete the reservoir for star formation. Silk & Rees (1998) similarly argued that the release of gravitational potential energy from a fast-accreting AGN becomes comparable to the binding energy of the host galaxy, which may contribute to quenching. Modern analytic (Hernquist & Springel 2003; Rasera & Teyssier 2006; Davé, Finlator & Oppenheimer 2012; Salcido, Bower & Theuns 2020; Sharma & Theuns 2020; Sorini & Peacock 2021; Fukugita & Kawasaki 2022) and semi-analytic (Henriques et al. 2015; Hirschmann, De Lucia & Fontanot 2016; Lacey et al. 2016) models include at least some of these feedback processes and generally predict a more realistic star formation history.
Nevertheless, the exact quenching mechanisms, their relative importance, and the coupling of the released energy to the interstellar gas, remain unclear (see reviews by Somerville & Davé 2015; Naab & Ostriker 2016). A range of physical processes acting on different temporal and spatial scales may contribute to the overall quenching of galaxies. Full hydrodynamic cosmological simulations are thus a valuable testing ground for different theories, as increased computational power and refined hydrodynamics code solvers (Hernquist et al. 1989; Teyssier 2002; Springel et al. 2005, 2021; Schaller et al. 2024) have enabled the modelling of all galactic components across cosmic time. Despite this progress, numerical constraints often require a trade-off between resolution and simulated volume, hence making it unfeasible to describe sub-galactic feedback process within cosmological simulations from first principles. Instead, their presumed macroscopic effects are modelled via so-called sub-grid prescriptions (see e.g. Crain & van de Voort 2023, for a recent review).
The general consensus is that stellar feedback is primarily efficient at quenching low-mass systems, due to their relatively low gravitational potential, and at early times, where AGNs have not yet grown and matured enough to affect the galaxy. Associated processes such as SNe and stellar winds are largely understood to cause outflows, in line with observations of high mass-loss rates in star-forming galaxies (Heckman et al. 1990; Veilleux, Cecil & Bland-Hawthorn 2005; Rubin et al. 2014). High cooling rates in the dense environments at high-redshift mean that most thermal energy input cools away too quickly to have a lasting effect on the interstellar medium (ISM; Somerville & Davé 2015).
At late times, AGNs are thought to deposit significant amounts of thermal and kinetic energy into the gas reservoirs of massive galaxies. Observational studies have broadly identified two main regimes. At accretion rates close to the Eddington limit, AGN feedback is radiatively efficient. Gravitational potential energy from the infalling matter is released as radiation, triggering winds capable of driving cool ISM gas out of the galaxy at non-relativistic speeds (e.g. Simionescu et al. 2008; Rupke & Veilleux 2011; Fabian 2012; Cicone et al. 2014; Harrison et al. 2014; King & Pounds 2015; Concas et al. 2022; Kubo et al. 2022). This is often called ‘quasar’ or ‘wind’ mode. The radiatively inefficient regime at low accretion rates is referred to as ‘jet’ or ‘radio’ mode, as these AGNs can launch bipolar radio jets at relativistic speeds, carrying large amounts of kinetic and thermal energy (Fabian 2012; Heckman & Best 2014; Blandford, Meier & Readhead 2019). Galaxies with observed AGN jets are characterized by low star formation rates (SFRs), hinting at efficient quenching mechanisms.
Some studies suggest that jets deposit their thermal energy into the circumgalactic medium (CGM) and intracluster medium (ICM). For example jets often coincide with bubbles of hot gas visible in X-ray, which regularly penetrate as far as hundreds of kpc into the ICM and have likely been heated by shocks (Suresh et al. 2015; Turner et al. 2017; Mukherjee et al. 2018; Christiansen et al. 2020; Fielding et al. 2020). This could be enough to offset cooling flows, i.e. the accretion of cooled CGM gas on to the galaxy, and thus starve active star formation (Croton et al. 2006; Gabor & Davé 2015; Peng, Maiolino & Cochrane 2015). In some instances, jet-driven outflows have been found to be significantly mass-loaded to limit star formation via direct removal of gas from the central regions (Morganti et al. 2013; Jarvis et al. 2019). Jets could also heat and accelerate existing wind-driven outflows (Dasyra et al. 2014; Tadhunter et al. 2014), potentially boosting their efficiency in quenching star formation. In addition to AGN-driven winds and jets, X-ray radiation from the accretion disc is thought to heat and exert pressure on the gas surrounding the black hole (Sazonov, Ostriker & Sunyaev 2004; Hambrick et al. 2011; Choi et al. 2012).
State-of-the-art cosmological simulations typically incorporate both stellar and AGN feedback mechanisms. Some simulations adopt a single AGN feedback prescription (e.g. Schaye et al. 2015, 2023; Davé, Thompson & Hopkins 2016; McCarthy et al. 2017), while others distinguish between a radiative wind mode at high accretion rates and a jet mode at low accretion rates (e.g. Vogelsberger et al. 2013, 2014; Dubois et al. 2014; Pillepich et al. 2018; Davé et al. 2019; Pakmor et al. 2023). Thus, the exact implementations of feedback processes differ substantially between simulations and rely on distinct physical assumptions. Nevertheless, they all broadly succeed at reproducing several observational benchmarks, such as the galaxy stellar mass function (e.g. Baldry, Glazebrook & Driver 2008; Baldry et al. 2012; Bernardi et al. 2013; D’Souza, Vegetti & Kauffmann 2015), the star formation efficiency (e.g. Guo et al. 2011; Behroozi, Wechsler & Conroy 2013; Moster, Naab & White 2013), the galaxy black hole–stellar mass relationship (e.g. Kormendy & Ho 2013; McConnell & Ma 2013), or the gas fraction within haloes (e.g. Giodini et al. 2009; Lovisari, Reiprich & Schellenberger 2015), although in some cases free parameters were tuned to obtain this agreement.
While encouraging, the broad agreement between observations and different simulations makes it harder to discern the validity and limitations of different models of galaxy formation. However, activating only specific feedback modes across different variants of otherwise identical simulations can reveal the exact effect of each prescription on the star formation history. Applying this strategy to the owls project (Schaye et al. 2010; van de Voort et al. 2011) showed that AGN feedback is a major cause for the decline of the cosmic SFR density after |$z=2$|. Qualitatively similar conclusions were reached by Weinberger et al. (2017) and Salcido et al. (2018) using different variants of the illustrisTNG (Pillepich et al. 2018) and eagle (Schaye et al. 2015) simulations, respectively.
A rigorous study seeking to isolate the effect of every feedback prescription on star formation history has not yet been undertaken for the simba simulation (Davé et al. 2019), which encompasses key novelties in the modelling of AGN feedback and black hole accretion with respect to previous state-of-the-art cosmological simulations. On top of implementing both jet and radiative wind feedback kinetically, simba is the first cosmological-scale simulation to also explicitly model thermal energy input from X-ray heating processes, and to adopt a dual gas accretion mechanism on to black holes depending on the gas temperature. The simulation suite contains five variants of a |$50 \, h^{-1} \,\mathrm{cMpc}$| cosmological box, which isolate simba’s four different feedback prescriptions. These have already been used to constrain the effects of different feedback modes on the global statistics of galaxy properties (Davé et al. 2019), the distribution and thermal state of baryons within haloes and in the intergalactic medium (Borrow, Anglés-Alcázar & Davé 2020; Christiansen et al. 2020; Bradley et al. 2022; Sorini et al. 2022; Yang et al. 2022; Khrykin et al. 2024), the CGM (Appleby et al. 2019; Sorini, Davé & Anglés-Alcázar 2020; Yang et al. 2024), and galaxy profiles (Appleby et al. 2021).
In this work, we provide a comprehensive theoretical study on how simba’s stellar and AGN feedback modes shape the cosmic star formation history. First, we investigate the signature of each feedback mode on global observables, such as the cosmic SFR density, on different halo populations, and even individual galaxies. We then connect our results with key properties of the simulated galaxies and their central black holes.
The paper is organized as follows. In Section 2, we describe the simba runs considered. We then present our analysis, following a global-to-local approach. In Section 3.1, we assess the overall evolution of cosmic star formation by examining global star formation and stellar mass statistics in the five simulation runs. In Section 3.2, we examine the star formation history within halo populations of different mass. In Section 3.3, we focus on the contribution to quenching from different AGN feedback modes on individual galaxies after |$z \sim 2$|, while Section 3.4 specifically focuses on effects caused by the X-ray heating mode on highly star-forming galaxies and black hole growth. In Section 4, we coalesce our results into a cohesive picture of how the different feedback prescriptions shape the cosmic star formation history and further compare our results with previous works on simba as well as other simulations. Finally, Section 5 summarizes our results.
2 SIMULATIONS
2.1 SIMBA
simba (described in detail in Davé et al. 2019) is a suite of cosmological simulations built upon the gizmo gravity plus hydrodynamics solver (Hopkins 2015). gizmo is composed of the gadget-3 tree–particle–mesh gravity solver (Springel 2005) for dark matter particles and a meshless finite mass approach for the hydrodynamic evolution of gas particles. The simulations assume a cosmological model according to the Planck Collaboration XIII (2016) specifications, with the following parameters: |$\Omega _\mathrm{ M}=0.3, \Omega _{\Lambda }=0.7, \Omega _b=0.048, H_0=68 \mathrm{~km} \mathrm{~s}^{-1} \mathrm{Mpc}\, {h}^{-1} \sigma _8=0.82, n_s=0.97$|. Cosmological initial conditions are created using music (Hahn & Abel 2011).
Star formation in simba is modelled according to a sub-grid implementation by Krumholz & Gnedin (2011) of an |$H_{2}$|-based Schmidt (1959) law, where the |$H_{2}$| fraction is estimated using the local metallicity and column density of the gas. The SFR is then computed using the ratio of the molecular gas density and dynamical time, with a star-forming efficiency of 0.02, inspired by Kennicutt (1998). If the hydrogen number density |$n_{\mathrm{H}}$| is above the threshold |$n_{\mathrm{th}} = 0.13 \mathrm{~cm}^{-3}$|, and the temperature is at most 0.5 dex above
a gas element is defined as ISM gas and can spontaneously turn into a stellar particle, conserving mass and momentum.
Type II SNe, Type Ia SNe, and asymptotic giant branch (AGB) stars will release metals into the surrounding gas, according to the chemical enrichment model by Oppenheimer & Davé (2006), which tracks the evolution of eleven different elements (H, He, C, N, O, Ne, Mg, Si, S, Ca, Fe). Within simba’s dust cycle module metals from the SNe and AGB ejecta will partially condense into dust, which can then grow further via gas-phase metal accretion. Dust is destroyed via thermal sputtering, SNe shocks, and in processes involving heated gas, such as hot winds, star formation and AGN X-ray, and jet mechanisms. Radiative cooling and photoionization heating processes are incorporated into the simulation via the grackle-3.1 library (Smith et al. 2017). simba also employs a uniform ionizing background as detailed in Haardt & Madau (2012), with modifications made by Rahmati et al. (2013) to incorporate self-shielding on the fly.
Feedback from star formation is modelled as a kinetic ejection of metal-enriched wind particles, representing the aggregate effect of Type II SNe, stellar winds, and radiation pressure. Gas elements in proximity to star-forming regions are decoupled from the bulk flow and expelled with a new velocity perpendicular to their prior velocity and acceleration vectors. Winds are two-phase, meaning 30 per cent of the wind particles are ejected in a ‘hot’ state, with a temperature based on the supernova energy and the kinetic wind energy, while the remaining 70 per cent are ejected at |$10^3\rm K$|. The mass-loading factor of the wind is scaled with the galaxy’s stellar mass according to a broken power-law, a fit to mass outflow rates in the FIRE zoom-in simulations (Anglés-Alcázar et al. 2017b):
where |$\mathrm{M_{0}=5.2 \times 10^{9} \, {\rm M}_{\odot }}$|.
simba’s wind speed scaling is based on the rates predicted by Muratov et al. (2015), also using the FIRE simulations. In order to represent enrichment due to Type II SNe, wind metallicities are determined by the Type II SNe yield and the mass-loading factor. Eventually, ejected particles will recouple, based on the surrounding gas conditions and the elapsed time since decoupling. Feedback from SNe Type Ia are modelled separately, via a prompt and a delayed component as described in (Davé et al. 2016). However, since these are rare events and deposit negligible amounts of energy into the gas, we do not consider this feedback type further in this work.
simba’s black hole particles are seeded into galaxies with stellar mass |$\mathrm{M_{\star }} \gtrsim 10^{9.5}\mathrm{\, {\rm M}_{\odot }}$|, with initial seed masses of |$10^4 \, \mathrm{M}_{\odot }h^{-1}$|. Growth occurs via two accretion modes, which are implemented as sub-grid models. They distinguish between a spherical Bondi accretion from hot non-ISM gas (Bondi 1952) and a disc-like torque-limited accretion mode from cold ISM gas. This mode is driven by gravitational instabilities and is able to recover the relation between black holes and their host galaxy masses without self-regulation (Hopkins & Quataert 2011; Anglés-Alcázar, Özel & Davé 2013; Anglés-Alcázar et al. 2015, 2017a).
simba further employs three AGN feedback modes, which aim to model quenching mechanisms driven by the release of gravitational potential energy in the accretion process. These modes are active depending on the mass of the black hole, its accretion rate, and the gas fraction of the host galaxy. At high accretion rates with Eddington ratio |$f_\mathrm{edd} \gt 0.2$|, defined relative to the Eddington rate of the black hole particle, the radiative AGN wind mode produces bipolar outflows, which are modelled as a momentum injection in the direction parallel to the disc’s angular momentum. Gas particles are randomly selected within the black hole kernel, decoupled and ejected at a new speed, given by:
where |$\mathrm{M_{\mathrm{BH}}}$| is the black hole mass in solar masses |$\mathrm{{\rm M}_{\odot }}$|. At top speed, the gas particles are ejected at 1200|$\mathrm{~km} \mathrm{~s}^{-1}$|.
Below 0.2 |$f_\mathrm{edd}$|, AGN transition into jet mode, given their black hole mass |$\mathrm{M_{\mathrm{BH}}}$| exceeds |$10^{7.5}\mathrm{\, {\rm M}_{\odot }}$|. Similarly to the winds mode, this mechanism is modelled kinetically. Gas particles are ejected in the same fashion as before, but with a boosted velocity. This boost is inversely dependent on |$f_\mathrm{edd}$|:
The velocity increase due to jets is capped at 7000|$\mathrm{~km} \mathrm{~s}^{-1}$|. The fastest particles accelerated by AGN winds and jets can thus reach up to 8200 |$\mathrm{~kms}^{-1}$|, an order-of-magnitude faster than in the pure radiative winds mode. While gas particles are ejected at the original temperature in the wind mode, jet mode outflows are heated to the virial temperature of the halo, |$\mathrm{T_{vir}=10^{7}(M_{\text{H}}/10^{15} \, {\rm M}_{\odot })^{1/3} \mathrm{~K}}$| (Voit 2005), motivated by observations of hot gas carried in jets (Fabian 2012). The gas is recoupled after |$10^{-4}$| of the Hubble time has passed.
Lastly, simba accounts for X-ray radiation emitted by the accretion disc, which heats the surrounding gas and imparts radial momentum via radiation pressure. The energy input is quantified according to equation 12 of Choi et al. (2012). simba’s X-ray mode operates on galaxies with active jets, if the galaxy’s gas fraction |$f_\mathrm{gas} = \frac{M_\mathrm{gas}}{M_{\star }}$| is also below 0.2. In gas-rich galaxies, which typically exhibit lower velocity winds and no jets, much of this energy input would be absorbed and re-radiated, making this feedback inefficient. In contrast to the wind and jet modes, the energy input is spherical and impacts gas particles according to their proximity to the black hole. Non-ISM gas experiences an increase in temperature, while for ISM gas, half of the X-ray energy is converted into heat, and the other half is injected as radial outward momentum, computed by treating the remaining energy as kinetic. This was done in order to ensure that the energy deposit into simba’s low-resolution, pressurized ISM does not dissipate too quickly through cooling.
2.2 Runs
The simba simulation suite comprises a range of simulation runs with different volumes and input physics. Unless otherwise specified, co-moving units are indicated with a ‘c’ prefix. In this work, we make use of five simulation variants, which each span a volume of |$50 \, h^{-1} \mathrm{cMpc}$| and are populated by |$512^{3}$| dark matter and |$512^{3}$| gas elements. They were performed from |$z=249$| to |$z=0$| with the same initial conditions, but sequentially deactivated feedback prescriptions, as outlined in Table 1. simba-50, the fiducial run, contains all four prescriptions, for a full physics simulation. No-X-ray excludes only the X-ray mode, whereas the No-jet run excludes both jets and X-ray heating. In the No-AGN run, the winds mode is deactivated as well, such that only the stellar feedback prescription remains. The No-feedback run straightforwardly contains no feedback processes. Contrasting results from these different runs will allow us to isolate the effects of each of the four different sub-grid prescriptions in the following analysis. We note, that the No-feedback and No-AGN run still include black hole seeds and the dual accretion mode. Due to the self-regulation of the torque-limited accretion mode (see Anglés-Alcázar et al. 2017a; Davé et al. 2019), black hole–galaxy scaling relations are conserved, even when compounded with Bondi accretion and in the absence of feedback. We demonstrate this for the |$M_\mathrm{BH}$|–|$M_{\star }$| relation in Appendix A. Thus, any difference in star formation history between the simulation variants will be a direct consequence of the respective feedback modes, rather than an indirect consequence of a potentially overactive accretion history that has diminished the gas reservoir.
| Simulation . | Box size (|$h^{-1}$| cMpc) . | Minimum gravitational softening length (|$h^{-1}$| kpc) . | DM mass resolution (|${\rm M}_{\odot }$|) . | Gas mass resolution (|${\rm M}_{\odot }$|) . | No. of particles . | Stellar feedback . | Radiative winds . | Jets . | X-ray heating . |
|---|---|---|---|---|---|---|---|---|---|
| simba-100 | 100 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 1024^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-50 | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-25 | 25 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 256^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-25 High-res. | 25 | 0.25 | |$1.2 \times 10^{7}$| | |$2.28 \times 10^{6}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| No-X-ray | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |
| No-jet | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | ||
| No-AGN | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |||
| No-feedback | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| |
| Simulation . | Box size (|$h^{-1}$| cMpc) . | Minimum gravitational softening length (|$h^{-1}$| kpc) . | DM mass resolution (|${\rm M}_{\odot }$|) . | Gas mass resolution (|${\rm M}_{\odot }$|) . | No. of particles . | Stellar feedback . | Radiative winds . | Jets . | X-ray heating . |
|---|---|---|---|---|---|---|---|---|---|
| simba-100 | 100 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 1024^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-50 | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-25 | 25 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 256^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-25 High-res. | 25 | 0.25 | |$1.2 \times 10^{7}$| | |$2.28 \times 10^{6}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| No-X-ray | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |
| No-jet | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | ||
| No-AGN | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |||
| No-feedback | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| |
| Simulation . | Box size (|$h^{-1}$| cMpc) . | Minimum gravitational softening length (|$h^{-1}$| kpc) . | DM mass resolution (|${\rm M}_{\odot }$|) . | Gas mass resolution (|${\rm M}_{\odot }$|) . | No. of particles . | Stellar feedback . | Radiative winds . | Jets . | X-ray heating . |
|---|---|---|---|---|---|---|---|---|---|
| simba-100 | 100 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 1024^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-50 | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-25 | 25 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 256^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-25 High-res. | 25 | 0.25 | |$1.2 \times 10^{7}$| | |$2.28 \times 10^{6}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| No-X-ray | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |
| No-jet | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | ||
| No-AGN | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |||
| No-feedback | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| |
| Simulation . | Box size (|$h^{-1}$| cMpc) . | Minimum gravitational softening length (|$h^{-1}$| kpc) . | DM mass resolution (|${\rm M}_{\odot }$|) . | Gas mass resolution (|${\rm M}_{\odot }$|) . | No. of particles . | Stellar feedback . | Radiative winds . | Jets . | X-ray heating . |
|---|---|---|---|---|---|---|---|---|---|
| simba-100 | 100 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 1024^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-50 | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-25 | 25 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 256^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| simba-25 High-res. | 25 | 0.25 | |$1.2 \times 10^{7}$| | |$2.28 \times 10^{6}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |$\surd$| |
| No-X-ray | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | |$\surd$| | |
| No-jet | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |$\surd$| | ||
| No-AGN | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| | |$\surd$| | |||
| No-feedback | 50 | 0.5 | |$9.6 \times 10^{7}$| | |$1.82 \times 10^{7}$| | |$2 \times 512^{3}$| |
We further considered three additional runs of different volumes and resolution in order to test convergence. However, for these runs only the full fiducial set-up is available and, consequently, we can only assess volume and resolution convergence for the simba-50 run. simba-25 and simba-100 were performed at the same resolution as simba-50, containing |$2 \times 256^{3}$| and |$2 \times 1024^{3}$| particles in volumes |$25\, h^{-1}\mathrm{cMpc}$| and |$100\, h^{-1}\mathrm{cMpc}$|, respectively. simba-25 High-res. contains |$2 \times 512^{3}$| particles in its |$25\, h^{-1}\mathrm{cMpc}$| volume. We note that in this run, the particle masses have been reduced by a factor of 8, to compensate for the increase in number of particles. The minimum gravitational softening length and mass resolutions for all runs are listed in Table 1. A convergence test can be found in the Appendix B.
Haloes were identified on the fly within simba, using gizmo’s three-dimensional friends-of-friends (FOF) and a linking length of 0.2 times the mean interparticle distance. FOF haloes were then cross-matched with haloes and galaxies found using the python package caesar (Davé et al. 2019). caesar also generates catalogues containing all identified haloes and galaxies, along with key properties such as their masses and SFR’s, which form the basis of the following analysis. The majority of these files are publicly available in the simba Project Repository.1
3 RESULTS
In the following analysis, we contrast key observables across the five |$50 \, h^{-1} \mathrm{cMpc}$| simulation variants in order to isolate the global effects of simba’s stellar and AGN feedback modes on the cosmic star formation history. We subsequently connect them to the evolution of star formation and stellar mass in halo populations of different mass, as well as individual galaxies.
Davé et al. (2019) used some of the observables presented in this paper to test simba’s ability to reproduce key galaxy properties. However, thus far there has not been an analysis contrasting all five |$50 h^{-1} \mathrm{cMpc}$| runs with different feedback prescriptions for a unified picture of how they affect simba’s cosmic star formation history. Where appropriate, we provide a summary of these prior assessments in the context of our results and refer the reader to the relevant publication for more detailed comparisons with observational results.
3.1 The evolution of the global star formation history
We begin with an assessment of how simba’s feedback modes affect the overall cosmic star formation and the resulting stellar mass growth.
3.1.1 Cosmic star formation rate density
The cosmic star formation rate density (SFRD) tracks the overall SFR of the simulation volume and is thus a good starting point for our analysis. In Fig. 1, we compare the temporal evolution of the SFRD across the five |$50 \, h^{-1} \mathrm{cMpc}$| simulation variants. In order to compute the SFRD, we extract and sum up the SFRs for all FOF haloes at distinct snapshots between |$z = 0-9$| and then divide each value by the comoving volume of the simulation box. We repeat this computation for the simba-50 (green), No-X-ray (blue), No-jet (blue), No-AGN (purple), and No-feedback (orange) runs. A collection of survey results by Madau & Dickinson (2014; black data points, hereafter MD14) is shown for comparison.
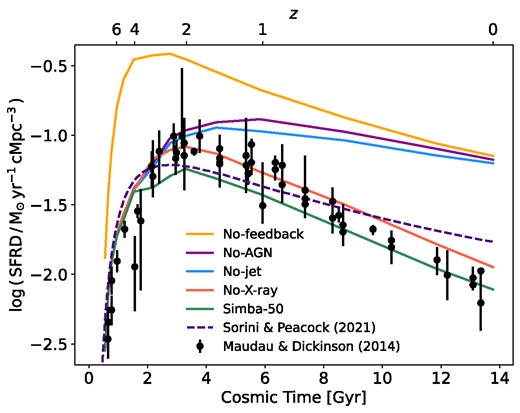
Cosmic star formation rate density for decreasing redshift, in |$50 \, h^{-1} \mathrm{cMpc}$|simba simulation variants with different feedback prescriptions (solid lines): No-feedback (yellow), No-AGN (purple), No-jet (red), No-X-ray (blue), and the full physics simba-50 (green) run. Additionally shown are a collection of survey results (Madau & Dickinson 2014; data points) and an analytical model from Sorini & Peacock (2021; indigo dashed line). While stellar feedback is responsible for quenching the SFRD before |$z \sim 2$|, AGN feedback, specifically the jets, takes over as the dominant quenching mode thereafter. Including X-ray heating already produces a minor suppression from |$z \sim 4$|.
The No-feedback run exhibits a sharp increase in SFRD before |$z \sim 4$|, culminating in a peak around |$z \sim 3$| and a gradual decline at low redshifts. This conflicts with the observations from MD14, who find a later peak at |$z \sim 2$|, with its maximum value 0.7 dex below the No-feedback curve. The discrepancy between the predicted and observed SFRD grows up to |$1\, \rm dex$| by |$z=0$|. The excess production of stars at all cosmic times in the No-feedback variant of simba is an unsurprising manifestation of the aforementioned overcooling problem. However, within a hierarchical structure formation scenario, and in the absence of any feedback mechanism, the SFRD is expected to form more stars even earlier than in the No-feedback model considered here, due to its limited resolution, and therefore worsen the overcooling problem (Dave et al. 2001). The high-redshift growth of the SFRD in the No-feedback run is thus partly a numerical artefact. At higher redshift, massive haloes become increasingly rare due to the evolution of the halo mass function, hence a progressively larger fraction of haloes falls below the mass resolution limit of the simulation. Clearly, such haloes cannot contribute to the production of stars.
simba runs with feedback modes are increasingly successful at reproducing the MD14 results. Including stellar feedback in the No-AGN run appears to efficiently quench the SFRD at high-redshift. The slowed increase up to the peak at |$z \sim 2$| is well represented, but it fails to reproduce the declining SFRD of the MD14 results thereafter. Including AGN radiative winds in the No-jet run, in addition to stellar feedback, suppresses the SFRD by less than 0.1 dex at |$z \lt 2$| and has no discernible effect before. Only when including AGN jets, in the No-X-ray run, the SFRD starts showing a slight downturn just before |$z=2$| and is strongly suppressed thereafter. The slope of the SFRD after cosmic noon becomes steeper, closely resembling the shape traced by the data. By redshift |$z \sim 0$|, the jets have produced a cumulative suppression of almost 1 dex.
Interestingly, the impact of different feedback prescriptions on the SFRD that we just described is in broad agreement with the predictions of recent analytical models of cosmic star formation. We report in Fig. 1 the SFRD given by the Sorini & Peacock (2021) model (purple dashed line) as an example. Such model constitutes a generalization of the formalism introduced by Hernquist & Springel (2003) and calculates the SFRD by integrating the SFR within haloes of a given total mass, weighted by the halo mass function. For a given population of haloes of fixed mass, the SFR is determined by whichever time-scale is the shortest: the cooling time at low-redshift, and an average gas consumption time-scale (based on the reasoning in Springel & Hernquist 2003) at high-redshift. Additionally, Sorini & Peacock (2021) introduced a simple constant stellar wind model to mimic the effect of stellar feedback in reducing the gas reservoir available for the production of stars at any given time.
It is noteworthy that the Sorini & Peacock (2021) model agrees with the fiducial simba run not only |$z\gtrsim 3$|, where stellar feedback appears to be the dominant driver of quenching, but also around cosmic noon. The increasing discrepancy in the slope of the SFRD at later times is due to the absence of an explicit AGN feedback mechanism in the Sorini & Peacock (2021) model. This also explains why the slope given by the analytical model matches the one found in the No-AGN simba run. However, analytical SFRD at |$z\lt 2$| exhibits a lower normalization, yielding a better match with data. This happens because, although Sorini & Peacock (2021) do not model AGN feedback, the underlying parameters of their formalism are still calibrated to reproduce observations of the Kennicutt–Schmidt (Kennicutt 1998) and baryonic Tully–Fisher (McGaugh et al. 2000) relationships (Genzel et al. 2010 and Lelli, McGaugh & Schombert 2016, respectively). On the contrary, no parameter is recalibrated within the simba suite of simulations once a specific feedback module is deactivated. It is therefore expected that, for the same set of feedback mechanisms, the simba results lie farther away from the data. Similar considerations can be made when comparing the analytical SFRD at low-redshift with the results of the No-jet run, which do not significantly deviate from those of the No-AGN run.
We therefore suggest that the inclusion of some form of AGN-jet mechanical feedback in analytical models along the lines of Sorini & Peacock (2021) can improve the match with observations. However, this might not be the case for other analytical models that rely on a different formalism. For instance, a smaller impact of AGN versus stellar feedback on the late-time SFRD has been highlighted also by the Salcido et al. (2020) analytical model, which, unlike Sorini & Peacock (2021), includes a phenomenological implementation of feedback from radiative AGN winds (following Benson & Bower 2010; Benson 2012). If the Salcido et al. (2020) AGN prescriptions are turned off, the slope of the late-time SFRD remains essentially unchanged, while it is still in agreement with observations. However, a comprehensive comparison of the numerical predictions of the different simba variants against analytical models of star formation goes beyond the scope of this manuscript, and we leave it for future work.
Another result emerging from Fig. 1 is that X-ray heating may play a relatively important role in shaping the SFRD both at high- and low-redshift. Such feedback mechanism is included in the fiducial simba-50 run and the resulting SFRD displays a further suppression of around 0.2 dex, in excellent agreement with MD14 at late times. However, it appears that before |$z \sim 1$|, the data are better reproduced by the No-X-ray run than the full-physics simba-50 run. Nevertheless, the predictions of both the No-X-ray and simba-50 runs agree with most data points within the error bars, hence current SFRD observations cannot definitively discriminate between these models. Furthermore, some data may be affected by systematic errors, since parametric models estimating the SFRD from the spectral energy distributions of observed galaxies may impose strong priors on the underlying physical parameters, hence biasing the results (Carnall et al. 2019). Thus, the imperfect match between the No-X-ray or simba-50 runs and the Madau, Shen & Governato (2014) compilation in certain redshift ranges should not be concerning.
We further note that while quenching of the SFRD in the No-X-ray and No-jet runs set in just before |$z \sim 2$|, the suppression in the simba-50 run begins already at |$z \sim 4$|. We discuss the origin of this feature further in Section 3.4.1. Lastly, we note that our curve for the simba-50 run is consistent with Davé et al. (2019), who in their fig. 7 compare the SFRD in the full physics simba-100 run to the MD14 results. This means that the predictions of the simba variants displayed in Fig. 1 are well converged with respect to the box size (see also Fig. B1 and the discussion in Appendix B).
In summary, we conclude that simba’s stellar feedback mode is responsible for quenching the SFRD before |$z \sim 2$|. Simulation variants including AGN feedback prescriptions do not exhibit a significant difference to the No-AGN run before |$z \sim 2$|, with the exception of a drop in SFRD of around 0.2 dex after |$z \sim 4$| in the fiducial simba-50 run. This indicates that, overall, AGN feedback is only able to efficiently quench cosmic star formation activity after |$z \sim 2$|, while the inclusion of X-ray heating creates a minor suppression already at |$z \gt 2$|. After |$z \sim 2$|, the AGN jet mode appears to be by far the most efficient at suppressing the SFRD, while the inclusion of X-ray heating only provides a minor contribution to quenching. Radiative AGN winds have almost no effect on the overall evolution of the SFRD.
3.1.2 Galaxy stellar mass function
The effects described in Section 3.1.1 represent the ‘macroscopic’ impact of different feedback mechanisms on the star formation history, as the cosmic SFRD is a global quantity that incorporates the contributions from all galaxies. In this section, we will investigate how the different feedback prescriptions affect the growth of galaxies of different stellar masses. This can be done by studying the GSMF, which characterizes the number density of galaxies per co-moving volume and logarithmic stellar mass bin. In Fig. 2, we present the GSMF (here denoted as |$\Phi$|) at |$z = 4, 2, 1$|, and 0. In the same colour-code as in Fig. 1, we show the |$50 h^{-1} \mathrm{cMpc}$| simulation variants, as well as the full-physics simba-100 run (grey). Errors due to cosmic variance (shaded areas) have been estimated by jackknife re-sampling over the eight sub-octants of the simulation volume.
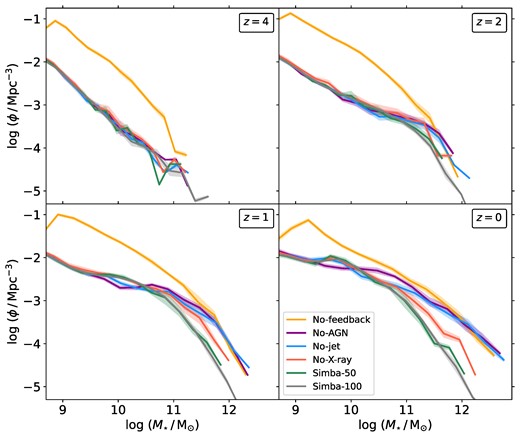
Galaxy stellar mass function (GSMF, here |$\Phi$|) in five simulation variants, shown in the same colours as in Fig. 1. Additionally shown is the simba-100 run (grey). Errors (shaded areas) are computed by jackknife re-sampling. Overall, the GSMF is lowered by stellar feedback up to |$z = 2$|. Thereafter, AGN feedback suppresses the GSMF at stellar masses above |$10^{10.5}\mathrm{\, {\rm M}_{\odot }}$|. Jets and X-ray heating also truncate the GSMF at the high-mass end at |$z = 1$| and 0.
At |$z=4$|, all |$50 \, h^{-1} \mathrm{cMpc}$| simulation runs are populated with galaxies containing stellar masses lower than |$10^{11.25}\mathrm{\, {\rm M}_{\odot }}$|, and considerably more low-mass galaxies of around |$10^{9}\mathrm{\, {\rm M}_{\odot }}$| than higher mass galaxies. Across all mass bins, the No-feedback GSMF is around 1 dex higher than in all other runs. The runs with at least stellar feedback appear almost identical, consistent with the result from Section 3.1.1 that stellar feedback is primarily responsible for quenching galaxies at early times, where AGN feedback effects are not yet significant.
At |$z = 2$|, the GSMF flattens above |$10^{11}\mathrm{\, {\rm M}_{\odot }}$| for all runs containing feedback. They only diverge around |$10^{11.5-11.7} \mathrm{\, {\rm M}_{\odot }}$|, where the No-X-ray and simba-50 runs show a slight trend toward fewer high-mass galaxies. However, at this epoch, all runs contain few massive galaxies, meaning the high-mass end of the GSMF is affected by small number statistics. There appears to be no significant difference between the No-X-ray and simba-50 runs, indicating that the gap between the SFRD given by these runs at |$z \sim 2-4$| (see Fig. 1) does not seem to translate into significant differences in the GSMF. This suggests that the early quenching due to the activation of the X-ray mode is not enough to slow the overall stellar mass growth.
If the stellar feedback mode is active, the low-mass end of the GSMF flattens out even more at |$z = 1$| and 0, with a drop-off of varying steepness above |$10^{10.5}\mathrm{\, {\rm M}_{\odot }}$|. We note that above this threshold the GSMF seems to converge across the No-feedback, No-AGN, and No-jet runs. Both stellar feedback and AGN winds do not appear to be effective at suppressing the formation of galaxies with high stellar mass content. In contrast, the No-X-ray run and simba-50 runs, show a decreased GSMF at these masses, indicating a suppression due to the AGN jets and the X-ray mode. Galaxies with stellar mass above |$10^{12.25}\mathrm{\, {\rm M}_{\odot }}$| and |$10^{12}\mathrm{\, {\rm M}_{\odot }}$| do not form in the No-X-ray and simba-50 run, respectively.
A minor peak emerges around |$10^{9.5}\mathrm{\, {\rm M}_{\odot }}$| for all runs containing AGN feedback, which coincides with the stellar mass necessary to seed a black hole particle into the galaxy (see Section 2). This peak reflects an accumulation of galaxies reaching this stellar mass and immediately being affected by their new black hole, which slows the growth of additional stellar mass. Except for this peak, the AGN feedback runs show no significant difference to the No-AGN run below |$10^{10.5}\mathrm{\, {\rm M}_{\odot }}$|, indicating that the upper threshold of the GSMF is set by the stellar feedback mode in this mass regime. Lastly, we note that with decreasing redshift the low-mass end of the No-feedback GSMF shrinks at the expense of a growing high-mass tail. Thus, this run assembles most of its mass earlier than the other runs and primarily grows low-mass galaxies to higher masses at late times.
In conclusion, we find that before |$z\sim 2$|, the overall stellar mass growth in simba is regulated by stellar feedback. After |$z\sim 2$| the AGN jet mode, and to a lesser extent the X-ray mode, suppress the formation of galaxies with high stellar masses. Below |$10^{10.5}\, \mathrm{{\rm M}_{\odot }}$|, the shape of the GSMF continues to be largely set by stellar feedback.
Across the redshift range considered in Fig. 2, the GSMF from the fiducial simba-50 and simba-100 runs are consistent with each other, indicating that our results are converged volume wise. A comparison of the GSMF against observations was already undertaken for the simba-100 simulation across the redshift range |$0\lt z\lt 6$| by Davé et al. (2019). The simba-100 simulation was found to yield good agreement with data below |$10^{11}\mathrm{\, {\rm M}_{\odot }}$|. However, similarly to other cosmological simulations (e.g. eagle; Schaye et al. 2015), Davé et al. (2019) identified an excess of galaxies at |$10^{11}\mathrm{\, {\rm M}_{\odot }}$|. They attributed this to both numerical uncertainties and observational difficulties in quantifying massive systems, as well as dust-obscuration potentially causing rest-frame optical surveys to miss massive galaxies. We refer the interested reader to Davé et al. (2019) for further details.
3.2 Stellar- and halo-mass dependence of stellar and AGN feedback effects
In Section 3.1, a consistent picture emerged for the global evolution of the cosmic star formation activity and the resulting stellar mass build-up in simba: stellar feedback is responsible for quenching the overall star formation before |$z \sim 2$|, whereas AGN feedback is the dominant mechanism at lower redshift. The evolution of the GSMF indicates that this transition is mass-dependent, where stellar feedback slows the stellar mass assembly in low-mass systems, but does not affect the formation of high-mass galaxies significantly. The number density of these galaxies is instead set by AGN feedback, in particular the jet feedback mode. In this section, we split simba’s halo population according to mass to further examine how their SFRs and relative stellar content are affected by each of the implemented feedback models.
3.2.1 Evolution of the star formation rate in low- and high-mass haloes
We first consider how the instantaneous SFR evolves in haloes of different total mass. At snapshots between |$z=6$| and 0 in each of the |$50 \, h^{-1} \mathrm{cMpc}$| simulations, we categorize all FOF haloes with at least one galaxy into four logarithmic mass bins. These bins are symmetric and centred on |$M_\mathrm{H} = 10^{11}, 10^{12}, 10^{13}$|, and |$10^{14}\mathrm{\, {\rm M}_{\odot }}$|. For all haloes in the simulation variants, we find the normalized SFR (|$\rm nSFR \equiv SFR/\mathit {M}_\mathrm{H}$|), which provides a relative measure of the star-forming activity for each halo. In Fig. 3, we then compare the temporal evolution of the median nSFR in each of the mass bins across the simulation variants, colour-coded as in Figs 1 and 2. The shaded area represents the 16th to 84th percentile spread.
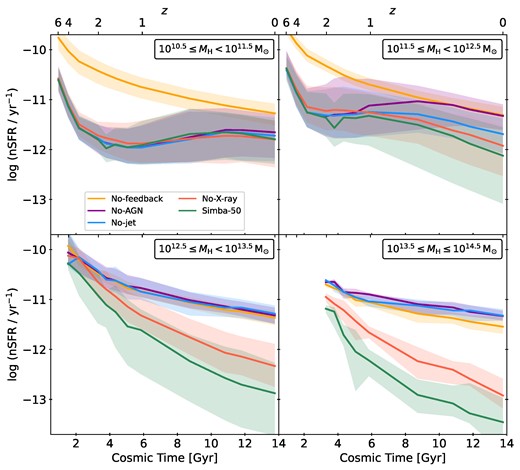
Median of normalized star formation rate (|$\rm nSFR \equiv SFR/\mathit {M}_\mathrm{H}$|) with 16th–84th percentile spread in four halo mass bins centred on |$M_\mathrm{H} = 10^{11}$|, |$10^{12}$|, |$10^{13}$|, and |$10^{14}\mathrm{\, {\rm M}_{\odot }}$|, shown for simulation runs with different feedback implementations. Lower halo masses |$\lesssim 10^{12}\mathrm{\, {\rm M}_{\odot }}$| are mainly affected by stellar feedback, while AGN feedback quenches the nSFR at higher masses |$\gtrsim 10^{13}\mathrm{\, {\rm M}_{\odot }}$|. The AGN jets emerge again as the most powerful mode.
For haloes in the |$10^{11}\mathrm{\, {\rm M}_{\odot }}$| bin, only the No-feedback run differs from the other four simulation variants. The nSFR is up to 1.5 dex greater and exhibits a gradual decrease from |$10^{-10} \, \mathrm{yr}^{-1}$| to just below |$10^{-11} \, \mathrm{yr}^{-1}$|. This evolution is similar at all halo masses, as the star formation limit is only set by the cooling time and the availability of cold and dense ISM gas. Except for a very slight divergence close to |$z\sim 0$|, the nSFRs in the other simulation variants appear almost identical to the No-AGN feedback run, regardless of the modes activated. The median nSFR exhibits an initial quenching between redshifts 6 and 2 and subsequently continues at a roughly constant rate between |$10^{-11.5} \, \mathrm{yr}^{-1}$| and |$10^{-12} \, \mathrm{yr}^{-1}$|. At these low masses, either black holes have not been seeded due to similarly low stellar masses, or if they have, they are in early evolutionary stages. This would mean that either the more powerful AGN jets and X-ray heating modes have not been active or their effect on the surrounding gas has not accumulated enough to exhibit a significant impact on the nSFR evolution.
At |$M_{\rm H} \sim 10^{12}\mathrm{\, {\rm M}_{\odot }}$|, the four simulations with feedback show differences after |$z\sim 1$|, where potential black hole particles in the more massive haloes within this bin have had time to be seeded and evolve. At this epoch, as well as across the entire evolution in all higher mass bins, the No-AGN run converges with the No-feedback run, while the runs with AGN feedback show a continued suppression.
simba’s stellar feedback thus shapes the nSFR evolution in lower mass haloes, but is not effective at higher masses. Above |$M_{\rm H} \sim 10^{12.5}\mathrm{\, {\rm M}_{\odot }}$|, the stronger gravitational potential likely keeps accelerated gas elements from escaping the galaxy through outflows. Additionally, the mass loading of stellar winds follows a broken power-law (see equation 2). Haloes containing more stellar mass than the threshold value of |$\mathrm{M_{0}=5.2 \times 10^{9} \, {\rm M}_{\odot }}$|, are assigned a mass-loading factor that declines much more steeply with stellar mass. This reduced mass-loading factor results in fewer ejected gas particles. As larger haloes typically contain more stellar mass, this further diminishes the impact of stellar feedback in these larger systems.
As for the effects of AGN feedback after |$z\sim 1$| in the |$M_{\rm H} = 10^{12}\mathrm{\, {\rm M}_{\odot }}$| bin, we note that each feedback mode contributes to the overall quenching of the median nSFR. This is the only mass range, where the No-jet run shows a visible difference from the No-AGN run, meaning that radiative AGN winds have quenched the nSFR by around |$0.5 \, \rm dex$| at |$z = 0$|. Similarly as for the stellar feedback, the gravitational potential of more massive haloes is likely too strong for wind-ejected particles to escape. Even for the largest black holes, the maximum speed a gas particle can reach in wind mode is around 1200 |$\rm km\, {s}^{-1}$|, while the escape velocity for massive haloes is approximately an order-of-magnitude greater. Therefore, simba’s AGN-driven winds are only able to quench the star formation in haloes of around |$10^{11.5}$| to |$10^{12.5}\mathrm{\, {\rm M}_{\odot }}$|.
As a result, the influence from stellar and radiative wind feedback modes is negligible in the |$10^{13}$| and |$10^{14}\mathrm{\, {\rm M}_{\odot }}$| mass bins. Instead, the AGN jets and X-ray heating modes are the dominant quenching mechanisms. At |$z \sim 0$|, the No-X-ray run shows a significant suppression of the median nSFR by approximately 1 dex in the |$10^{13}\mathrm{\, {\rm M}_{\odot }}$| bin and 1.5 dex in the |$10^{14}\mathrm{\, {\rm M}_{\odot }}$| bin. This confirms that simba’s AGN jets are in large part responsible for the overall quenching of star formation in high-mass haloes. In the simba-50 run, the additional X-ray heating causes a further reduction of the median nSFR by |$\sim 0.5 \, \rm dex$| in both high-mass bins. In the |$10^{13}\mathrm{\, {\rm M}_{\odot }}$| bin, the divergence from the No-X-ray run, appears as early as |$z \sim 4$|, consistent with the early quenching of the SFR density in the simba-50 run seen in Fig. 1. In the |$10^{14}\mathrm{\, {\rm M}_{\odot }}$| bin, all nSFR curves begin at |$z \sim 2$|, meaning that such massive haloes have not formed before this epoch. The particular influence of the jet and X-ray feedback modes at these high halo masses is likely a consequence of larger mass haloes housing black holes that are not only more massive and have a larger sphere of influence, but are also further along in their evolutionary trajectory. Older black holes tend to reach lower accretion rates, which will allow the activation the jet mode and, if the gas fraction is low, the X-ray mode. The jet mode, in particular, will significantly increase the ejection speeds and thermal energy of the wind particles.
In summary, we find a clear mass dependence in how simba’s feedback modes affect the evolution of the normalized SFR in different halo populations. Stellar feedback sets the star formation activity for haloes smaller than |$10^{12.5}\mathrm{\, {\rm M}_{\odot }}$|. After |$z \sim 1$|, haloes between |$10^{11.5}$| and |$10^{12.5}\mathrm{\, {\rm M}_{\odot }}$| are also affected by radiative winds, jets, and X-ray heating. Above this threshold, stellar and AGN winds cease to be effective and instead the jets and X-ray heating modes become the significant quenching mechanisms in haloes above |$10^{12.5} \mathrm{\, {\rm M}_{\odot }}$|. This mass dependence arises due to the competing factors from each system’s gravitational potential, the evolutionary state of the AGN, as well as the mass-dependent parameter scaling of the stellar mode efficiency.
3.2.2 The stellar mass–halo mass ratio at |$z \le$| 2
The previous section has shown that the AGN-jet and X-ray feedback modes in simba are efficient at suppressing the median nSFR of haloes with |$M\gt 10^{12.5}\mathrm{\, {\rm M}_{\odot }}$| and contribute to quenching haloes between |$10^{11.5}$| and |$10^{12.5}\mathrm{\, {\rm M}_{\odot }}$| after |$z \sim 1$|. However, this broad statistic does not demonstrate how each mode shapes the stellar content of haloes as a result. To disentangle the impact of each of the three AGN feedback mechanisms, we thus examine the stellar mass–halo mass (SMHM) ratio, revealing the efficiency with which haloes of different mass turn their gas into stellar mass.
We calculate the SMHM ratios of all haloes at |$z = 2$| and |$z = 0$| by dividing the stellar mass within the central galaxy of each halo by the total halo mass. This calculation eliminates any contribution from small satellite galaxies, which might otherwise obscure the trends observed in the massive central galaxies that are most impacted by the growth and feedback of their central black holes. Figs 4 and 5 then show two-dimensional histograms of the SMHM ratio against halo mass for the runs containing at least stellar feedback, respectively at |$z = 2$| and |$z=0$|. In order to directly connect the relative stellar content to the star-forming activity, the bins are coloured by the specific SFR |$(\rm sSFR \equiv SFR/\mathit {M}_{\star }$|) of the central galaxy. We additionally show the median SMHM ratio (red line in Fig. 4, blue line in Fig. 5) and 16th–84th percentile spread (black lines). At the low-halo mass ends, the median relations are biased by the diagonal resolution cut-off, which enforces a minimum number of stellar particles for a halo to be considered well-resolved, corresponding to a stellar mass of |$\sim 10^{8.5} \mathrm{\, {\rm M}_{\odot }}$|. This starts affecting the median relations below halo masses of approximately |$10^{11.2} \mathrm{\, {\rm M}_{\odot }}$| at |$z=2$| and |$\sim 10^{11.7} \mathrm{\, {\rm M}_{\odot }}$| at |$z=0$| (relations shown in dashed instead of solid lines). Above the resolution cut, we compare to the median from the universemachine abundance matching (Behroozi et al. 2019, purple), which assumes a one-to-one correspondence between galaxies and dark matter haloes by comparing observed galaxy properties to the properties of simulated haloes.
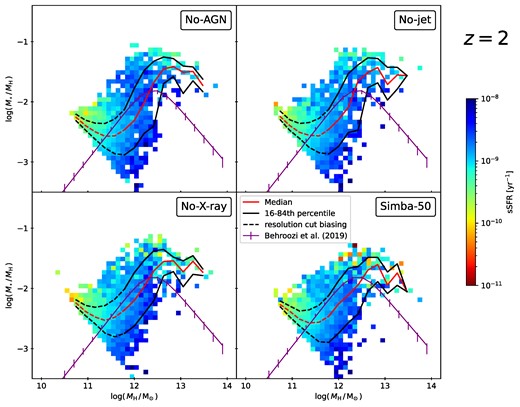
Two-dimensional histograms of the SMHM ratio for |$z = 2$| in the four simulation variants containing feedback. Bins are coloured by the sSFR. Additionally shown are the median relation (red lines) with the 16th to 84th percentile (black lines), as well as the universemachine median (Behroozi et al. 2019; purple). Below halo masses of |$\sim 10^{11.7}\mathrm{\, {\rm M}_{\odot }}$| we expect the resolution cut to affect the median relation significantly (change from solid to dashed lines). At this epoch, star formation rates are generally high and all feedback runs exhibit remarkably similar features, except for a few quenched bins in the simba-50 run due to X-ray feedback. This means, stellar feedback is the dominant mechanism shaping stellar mass assembly and AGN feedback is not yet efficient.
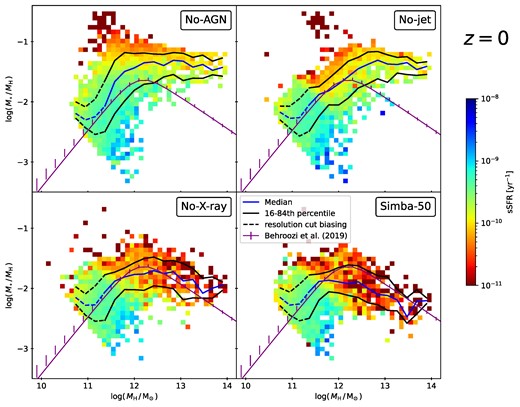
Two-dimensional histograms of the SMHM ratio for |$z = 0$|, in a configuration otherwise identical to Fig. 4. The resolution cut biasing affects halo masses below |$\sim 10^{11.2}\mathrm{\, {\rm M}_{\odot }}$|. For readability purposes, the median relation is shown in blue instead of red here. Jets introduce the sharp turnover in the No-X-ray run at |$10^{12}\mathrm{\, {\rm M}_{\odot }}$|, showing a continuous suppression of stellar mass assembly in large haloes. AGN winds from newly seeded black holes suppress the sSFR at intermediate masses, while X-ray feedback contributes to the quenching of galaxies in massive haloes.
At |$z = 2$|, the histograms exhibit a largely similar pattern across the shown runs, in agreement with the findings that simba’s AGN feedback is largely active after |$z=2$|. Most bins show a high sSFR ranging from approximately |$10^{-9}$| to |$10^{-8} \, \mathrm{yr}^{-1}$|. The lower end of the halo mass spectrum, below |$10^{11}\mathrm{\, {\rm M}_{\odot }}$|, displays a moderate reduction in sSFR, likely due to the highly effective stellar feedback in small systems. In the full simba-50 run, a few high-mass bins appear quenched, with specific SFRs as low as |$10^{-10}$| to |$10^{-11} \, \mathrm{yr}^{-1}$|. Moreover, the histogram in the simba-50 run is slightly truncated, with the highest ratios reaching only up to |$\sim 10^{-1.25}$| rather than extending to |$\sim 10^{-1.10}$| as seen in the other runs. These haloes thus contain a relatively smaller fraction of stellar mass compared to haloes of the same mass in the other runs. This indicates that a minor suppression of stellar mass growth has taken place before |$z = 2$|, and is likely correlated with the early quenching of the SFR density in the simba-50 run (see Section 3.1.1). We further find excellent agreement of the median relation with Behroozi et al. (2019) in all feedback simulation runs, until the turnover at around |$M_\mathrm{H}=10^{12.5}\mathrm{\, {\rm M}_{\odot }}$|. As shown in Fig. 3, within this mass range the nSFR is governed by the stellar feedback mode at |$z\gt 1$|, explaining the lack of differences between them. At the high-mass end, the simba simulations generally predict SMHM ratios that are larger than the median relation reported in Behroozi et al. (2019). None of the runs fully captures the turnover point in the relation, with the simba-50 run showing the closest approximation. This means that even with all AGN feedback modes, simba could overestimate the amount of stellar mass contained in high-mass haloes at |$z=2$|. As referenced in Section 3.1.2, this excess of high-mass galaxies is discussed in Davé et al. (2019). For Fig. 4 in particular, we also note that the universemachine median is itself derived from significantly processed data and thus subject to additional assumptions. As a result, the mismatch with the simba-50 run is not overly concerning.
At |$z = 0$| the histograms of the SMHM ratio exhibit stark differences. sSFR’s in the No-AGN run are most quenched at high stellar mass fractions, likely because large amounts of the gas have already been turned into stars. AGN winds have additionally quenched the sSFR in the No-jet run for halo masses between |$10^{11}$| and |$10^{12}\mathrm{\, {\rm M}_{\odot }}$|, which has largely prevented stellar mass fractions of |$10^{-1.5}$| and above. These represent haloes with stellar masses larger than the seeding threshold |$\mathrm{M_{\star ,BH}} = 10^{9.5}\mathrm{\, {\rm M}_{\odot }}$|, which are impacted by their new black hole. While radiative winds have shown only a minimal ability to quench star formation in prior figures, we show here that this is sufficient to affect stellar mass growth in intermediate mass haloes. We further note that the No-AGN and No-jet runs include a population of highly quenched haloes with stellar mass fractions exceeding |$10^{-1}$|. This is an artefact of the FOF halo finder, where small galaxies in their own subhalo, but in close proximity to a large halo, are interpreted as central galaxies instead of satellite galaxies. These populations only occur in the No-AGN and No-jet run, as the inclusion of jets prevents these galaxies from forming in the first place. We do not consider these populations true quenched central galaxies and thus exclude them from our further discussion.
In the No-X-ray run, the jets introduce the expected turnover at |$10^{12}\mathrm{\, {\rm M}_{\odot }}$| into the median SMHM ratio. Histogram bins reveal a continued quenching of the sSFR above this threshold, which has led to lower stellar mass fractions in high-mass haloes. This is consistent with the turnover seen in Behroozi et al. (2019). Nevertheless, beyond |$\sim 10^{13.4}\mathrm{\, {\rm M}_{\odot }}$|, the No-X-ray run still slightly overpredicts the relation. In contrast, the Behroozi et al. (2019) median remains within the 16th to 84th percentile range in the full simba-50 run up to the highest halo masses. The activation of X-ray feedback further enhances the dampening of the sSFR for massive haloes, with an increased number of bins exhibiting a sSFR values as low as |$10^{-11}\, \mathrm{yr}^{-1}$|.
In summary, we find that the inclusion of simba’s X-ray mode has slightly reduced the SMHM ratio in massive haloes before |$z=2$|, while the AGN winds and the jets alone have not altered the histograms significantly compared to the No-AGN run. At |$z=0$|, the suppression of star formation due to simba’s radiative AGN winds has limited stellar mass growth in haloes ranging from |$\sim 10^{11}$| to |$10^{12}\mathrm{\, {\rm M}_{\odot }}$|. At higher halo masses, AGN jets produce the turnover of the SMHM ratios at around |$10^{12}\mathrm{\, {\rm M}_{\odot }}$|. Adding the X-ray heating mode sees a further quenching of the sSFR at high halo masses and slightly decreased SMHM ratios with respect to the No-X-ray run.
3.3 AGN feedback effects in individual galaxies at |$z \le$| 2
Thus far, we have examined the mass- and redshift-dependence of stellar and AGN feedback-induced quenching in both global statistics, as well as at fixed halo mass. In this section, we will further trace the efficiency of simba’s AGN feedback modes to the properties of individual galaxies and their black holes.
3.3.1 sSFR–|$M_{\star }$| relation
In Figs 6 (|$z=2$|) and 7 (|$z=0$|), we consider the scatter of the sSFR–|$M_{\star }$| relation for all central galaxies with a black hole particle in the No-AGN, No-jet, No-X-ray, and simba-50 runs. Galaxies have been categorized according to their eligibility for each of the three AGN feedback modes. In the following, ‘eligibility’ means fulfilling the criteria related to |$M_{\rm BH}$|, |$f_{\rm edd}$|, and |$f_{\rm gas}$| outlined in Section 2. Thus, all galaxies with either |$f_{\rm edd}\gt 0.2$| or |$\mathrm{log}(M_{\rm BH})\lt 7.5$| are eligible for wind mode only (circular markers). At |$f_{\rm edd}\lt 0.2$| and |$\mathrm{log}(M_{\rm BH})\gt 7.5$| galaxies are also eligible for jets, which act in addition to the wind mode (square markers). When, additionally to |$f_{\rm edd}\lt 0.2$| and |$\mathrm{log}(M_{\rm BH})\gt 7.5$|, the gas fraction |$f_{\rm gas}$| is below 0.2, galaxies are eligible for X-ray mode, in addition to winds and jets (triangular markers). We stress that if a galaxy is eligible for a certain feedback mode, that does not necessarily imply that said mode is active. For example galaxies that are marked as eligible for AGN-jet feedback according to the aforementioned criteria, will clearly not undergo this feedback mode in the No-jet run. As we consider only galaxies with a central black hole, Figs 6–7 exclude the smallest galaxies below |$10^{9.5}\mathrm{\, {\rm M}_{\odot }}$|.
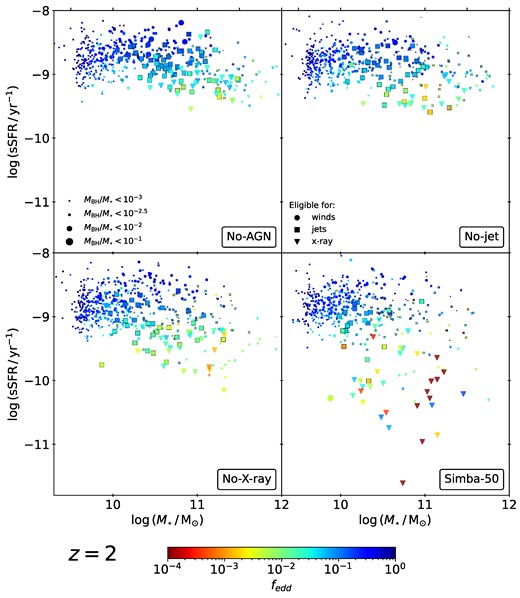
Scatter plots of the sSFR–|$M_{\star }$| relation for all central galaxies at |$z=2$| in the four runs containing feedback, coloured by Eddington ratio of the AGN. Galaxies eligible for AGN winds are shown in circles, jets in squares (with a black outline as a visual aid), and X-ray feedback in triangles. The marker size indicates the mass of the black hole relative to the galaxy’s stellar mass, as indicated in the legend. While some galaxies in the No-X-ray run show slightly reduced sSFR’s, only the simba-50 run contains quenched galaxies at this epoch.
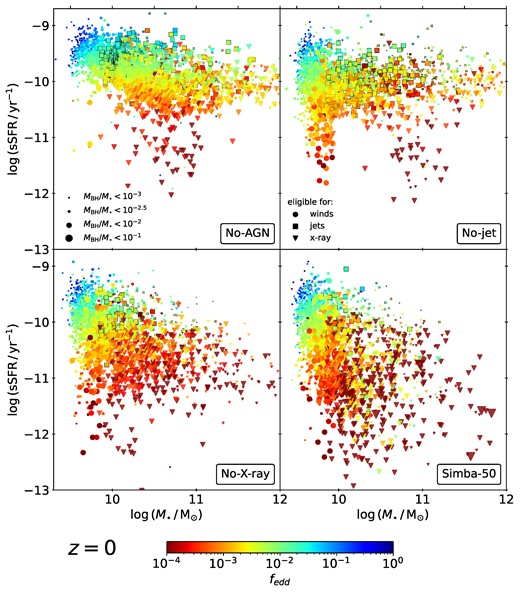
Same layout as Fig. 6, except at |$z=0$|. Including AGN winds reduces sSFR’s for intermediate-mass galaxies below |$10^{10.5} \, \rm {\rm M}_{\odot }$|. Jets quench galaxies above |$10^{10} \, \rm {\rm M}_{\odot }$| and introduce a correlation between the sSFR and the accretion rate. This correlation is broken by the X-ray mode in the simba-50 run, where although high-mass galaxies are further quenched, Eddington ratios are more variable.
As the mass of the black hole directly scales the strength of the AGN wind mode, as well as determines the sphere of influence of the black hole, we further indicate the ratio of the black hole-to-stellar mass ratio in the marker size. We distinguish between |$M_\mathrm{BH}/M_{\star } \lt 10^{-3}$|, |$10^{-3} \lt M_\mathrm{BH}/M_{\star } \lt 10^{-2.5}$|, |$10^{-2.5} \lt M_\mathrm{BH}/M_{\star } \lt 10^{-2}$|, and |$10^{-2} \lt M_\mathrm{BH}/M_{\star } \lt 10^{-1}$|. Lastly, we colour-code markers by the Eddington ratio of the black hole. We note, that all square markers, signifying eligibility for jet feedback (but not X-ray feedback), have been given a black outline as a visual aid.
At |$z=2$|, galaxies in the No-AGN run exhibit sSFR’s between |$10^{-9.5}$| and |$10^{-8}\, \mathrm{yr}^{-1}$|, with no clear trend across all stellar masses. This finding aligns with our results from earlier sections, where we established that simba’s stellar feedback has minimal impact on high-mass galaxies. Broadly, the type of feedback a galaxy is eligible for depends on stellar mass. Galaxies that would be eligible solely for radiative winds, are concentrated among lower stellar masses, typically between |$10^{9.5}$| and |$10^{10}\mathrm{\, {\rm M}_{\odot }}$|. Between roughly |$10^{10}$| and |$10^{11}\mathrm{\, {\rm M}_{\odot }}$|, most galaxies are eligible for jet feedback. At even higher stellar masses, an increasing number of galaxies would qualify for X-ray feedback as well. This division remains in subsequent plots and is a consequence of the co-evolution of galaxies and black holes. As none of these prescriptions are included in the No-AGN run, we do not expect any effect due to AGN feedback. However, while the accretion rate is high for most AGNs in this run, a few galaxies at the higher mass end exhibit lowered values for |$f_\mathrm{edd}$|. These coincide with slightly lower sSFR’s, which illustrates that since both accretion and star formation draws from the gas reservoir of the host galaxy, these processes are intimately connected, even in the absence of AGN feedback prescriptions.
The No-jet run follows a similar pattern to the No-AGN run, in agreement with our findings from previous sections that at |$z=2$|, radiative winds have not yet significantly affected galaxies. A few galaxies exhibit low accretion rates, with slightly lowered sSFR’s, but they generally remain in the |$10^{-9.5}-10^{-8}\, \mathrm{yr}^{-1}$| range, with no qualitative difference from the No-AGN run. In the No-X-ray run, this trend of decreased sSFR’s with lower accretion rates becomes more pronounced, as the sSFR in some galaxies with jet and X-ray eligibility is suppressed to around |$10^{-10}\, \mathrm{yr}^{-1}$|, a commonly used threshold for a galaxy to still be classified as star-forming. These galaxies with sSFR’s around |$10^{-10}\, \mathrm{yr}^{-1}$| also exhibit relatively large |$M_\mathrm{BH}/M_{\star }$| and Eddington fractions below |$10^{-1}$|.
In the simba-50 run, the majority of galaxies with |$f_\mathrm{edd}\lt 10^{-1}$| show quenched sSFR’s between |$10^{-10}$| and |$10^{-11}\, \mathrm{yr}^{-1}$|. Almost all of these affected galaxies are eligible for X-ray feedback, explaining why this feature is only seen in this full physics run, when X-ray feedback is actually activated. These galaxies are the origin of the gap between the SFRD evolution, in the No-X-ray and simba-50 runs, shown in Fig. 1. However, it is surprising that only a few tens of quenched galaxies in this run make up the difference of 0.2 dex in the overall star formation at |$z \sim 2$|. We investigate this feature further in the following section.
In addition to the X-ray-affected galaxies, there are two galaxies with sSFR’s below |$10^{-10} \, \mathrm{yr}^{-1}$| and accretion rates below |$10^{-2}$|, which are in wind-only mode (overlapping circular markers of slightly different green tones). Their black hole masses are just below |$10^{7.5}\mathrm{\, {\rm M}_{\odot }}$| and thus the jet mode is not yet active. However, compared to their stellar mass, these black holes are relatively massive (|$M_\mathrm{BH}/M_{\star } \gt 10^{-2.5}$|), which is likely the cause of their low sSFR’s compared to their other wind-only counterparts at this stellar mass. Their wind velocities must be close to |$750\, \rm km \, s^{-1}$|, which is significant compared to escape velocities of |$10^{10}\mathrm{\, {\rm M}_{\odot }}$| galaxies.
At |$z=0$|, the sSFR in the entire galaxy population in the No-AGN run is at least 1 dex lower relative to the |$z=2$| snapshot. We note that the quenched galaxies with sSFR between |$10^{-11}$| and |$10^{-12} \mathrm{yr^{-1}}$| and stellar masses between |$10^{10}$| and |$10^{11}\mathrm{\, {\rm M}_{\odot }}$|, match the population with high stellar mass fractions in Fig. 5, which we identified as probable halo finder artefacts. We thus exclude these galaxies, and the analogous population in the No-jet plot, from further analysis.
In the No-jet run, the AGN winds quench the sSFR in galaxies with a relatively large black hole and stellar masses between |$10^{9.5}$| and |$10^{10.5}\mathrm{\, {\rm M}_{\odot }}$|. Additionally, there is a trend toward generally lower stellar masses, while in the No-AGN run, most galaxies accumulate at intermediate stellar masses. This suggests that feedback from AGN winds has slowed the growth of stellar masses for smaller galaxies. Larger galaxies appear unaffected by the inclusion of AGN winds, in agreement with our earlier findings.
Activating the jets in the No-X-ray run results in the quenching of most galaxies with stellar mass |$\gt 10^{10}\mathrm{\, {\rm M}_{\odot }}$|, which again demonstrates the powerful impact of jet feedback. This creates a clear downward slope, where above |$10^{11}\mathrm{\, {\rm M}_{\odot }}$|, there are almost no galaxies with |$\rm sSFR \gt 10^{-10}\, \mathrm{yr^{-1}}$|, which dominate the No-jet run. Below stellar masses of |$10^{10}\mathrm{\, {\rm M}_{\odot }}$|, most black hole particles have masses below |$10^{7.5}\mathrm{\, {\rm M}_{\odot }}$| (see also Fig. A1), thus preventing the activation of jet feedback until the black hole has grown to this threshold. These low-mass galaxies continue to exhibit a wide range of sSFR’s between |$10^{-9}$| and |$10^{-12}\mathrm{yr^{-1}}$|. We further note a clear correlation between |$f_\mathrm{edd}$| and the sSFR, where the most severely quenched galaxies also exhibit the lowest accretion rates. Most of these quenched galaxies would also be eligible for X-ray feedback, if it was included in this run, meaning these galaxies exhibit low gas fractions. This is in contrast with the No-jet run, which showed much more galaxies above |$10^{10}\mathrm{\, {\rm M}_{\odot }}$| as eligible for jets, meaning higher gas fractions. With the inclusion of the X-ray feedback mode in the simba-50 run, the sSFR’s are further suppressed in many galaxies, with a significant number of them exhibiting values below |$10^{-11.5}\mathrm{yr^{-1}}$|. There is a larger fraction of galaxies in the |$10^{9.5}-10^{10}\mathrm{\, {\rm M}_{\odot }}$| range, indicating that the impact of X-ray heating has been sufficient to slow down the growth of stellar mass in individual galaxies. While the No-X-ray run showed a clear correlation between the Eddington ratio and the sSFR across all galaxies, we find that in the full physics run, galaxies affected by X-ray feedback exhibit a much larger scatter in |$f_\mathrm{edd}$|. Two galaxies of similar stellar mass and similarly quenched sSFR’s, might differ up to 2 dex in their Eddington fraction. This is surprising, since both accretion and star formation draw from the gas reservoir of the galaxy. It is likely a consequence of the central energy input from the X-ray mode, which increases the relative contribution of Bondi accretion from hot gas to the overall accretion rate and suppresses local star formation. We explore this connection further in Section 3.4.2. Lastly, we note that more galaxies in this run contain galaxies with particularly large black holes for their stellar masses, suggesting that the activation of the X-ray mode in some cases allows for more efficient black hole growth. This occurs because once a black hole is growing via Bondi accretion, its accretion rate scales as |$M_\mathrm{BH}^2$|, which for massive black holes can result in rapid growth.
3.4 Impact of X-ray feedback on highly star-forming galaxies and black hole growth
3.4.1 Cosmic star formation rate density in star-forming and quiescent galaxies
In prior sections, we have shown repeatedly that the X-ray heating mode in simba has a non-negligible effect on star formation even before |$z = 2$|. The SFR density in Fig. 1 showed a discrepancy of around 0.2 dex between the curves for the No-X-ray and simba-50 runs. The SMHM ratio at |$z=2$| (Fig. 4) exhibited lower stellar mass fractions at high halo masses, as well as some bins with suppressed specific SFRs for the simba-50 run, suggesting that this early quenching of a few galaxies is enough to alter the overall distribution of stellar mass in the simulation. In Section 3.3.1, we identified a small number of individual galaxies which presented suppressed sSFR’s at |$z=2$|. In this last section, we investigate why these galaxies are sufficient to lower the overall SFRD before |$z=2$|.
The quenching of these galaxies would be fractionally substantial if the X-ray mode primarily suppressed star formation in previously highly star-forming galaxies. To assess the overall contribution to the SFRD from galaxies at different SFR, we bin all galaxies into five equally spaced logarithmic bins, which are centred on |$\mathrm{10^{-1}}, 1, 10, 10^{2}$|, and |$\mathrm{10^{3} \, M}_{\odot } \, \mathrm{yr}^{-1}$| and extend 0.5 dex above and below these values. In Fig. 8, we display the SFRD computed for galaxies in each of these bins (see colour-code in legend), alongside the total SFRD (black dashed line) in the No-jet, No-X-ray, and simba-50 runs (top panels and bottom left panel). To guide the comparison, we further include the total SFRD from the runs in preceding panels (grey dashed lines).
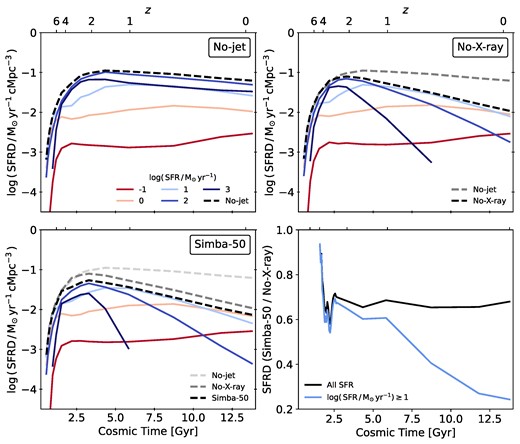
Top panels and bottom left panel: SFRD in galaxies in bins of SFR between |$\rm log(SFR/{\rm M}_{\odot } yr^{-1})$| = −1 and 3 (see legend). Different panels show the No-jet, No-X-ray, and simba-50 run, with the total SFRD from all galaxies in the indicated run (black dashed line). As a visual reference, we further include the total SFRD from the previous panel (grey dashed lines). The highest SFR bins suffer the most quenching by jets and X-ray heating. For X-ray feedback, this suppression of the SFRD sets in before |$z=2$|, while the jets are only efficient after |$z=2$|. Bottom right panel: Ratio between the SFRD in the No-X-ray and the simba-50 run from galaxies with |$\mathrm{SFR \gt 10 \, M}_{\odot } \, \mathrm{yr}^{-1}$| (blue) and all galaxies (black). Before |$z=2$|, the ratio between the SFRD from highly star-forming galaxies in the No-X-ray and simba-50 runs closely traces the ratio of the SFRD from all galaxies. This indicates that the quenching of these galaxies due to X-ray heating is responsible for the early discrepancy between these runs.
In the No-jet run, the SFRD contribution from all SFR bins remains relatively constant, with particularly high contributions from the highest SFR bins, specifically |$10$| to |$\mathrm{10^{3} \, {\rm M}_{\odot } yr^{-1}}$| (blue lines). However, upon activating jets in the No-X-ray run, there is already a noticeable decrease in the SFRD contributions from galaxies in these SFR bins when compared to the No-jet run. As a result, the |$\mathrm{10 \, M}_{\odot } \mathrm{yr}^{-1}$| bin begins to set the shape of the SFRD after |$z \sim 1$|. While the suppression of the |$10^{2}$| and |$\mathrm{10^{3} \, {\rm M}_{\odot }} \mathrm{yr}^{-1}$| bins begins just before |$z\sim 2$|, the overall SFRD is not lowered significantly until after |$z \sim 2$|. Instead, an increased SFRD contribution from the |$\mathrm{10 \, M}_{\odot } \mathrm{yr}^{-1}$| bin before |$z\sim 2$| compensates for the early suppression.
In contrast, the simba-50 run shows that the 102 and |$\mathrm{10^{3} \, M}_{\odot } \mathrm{yr}^{-1}$| bins are quenched by 0.2–0.3 dex from |$z \sim 4$|, and to a lesser extent, so is the |$\mathrm{10 \, M}_{\odot } \mathrm{yr}^{-1}$| bin. Lower SFR bins appear largely unchanged. This suggests that the quenching of the overall SFRD before |$z=2$| is indeed primarily due to the reduced contribution from highly star-forming galaxies under X-ray heating.
We further verify that the quenching of formerly highly star-forming galaxies is quantitatively responsible for the difference in SFRD at |$z\sim 2-4$| between the No-X-ray and simba-50 runs. In the bottom right panel of Fig. 8, we show the ratio of the SFRD from all galaxies (black) in both runs and the SFRD ratio of the galaxies with |$\mathrm{SFR \gt 10 \, M}_{\odot } \mathrm{yr}^{-1}$| (blue). Up to just before |$z=2$|, the ratio of the SFRD from all galaxies in the entire simba-50 run with respect to the No-X-ray run is mirrored by the SFRD ratio computed from only the highly star-forming galaxies. After |$z=2$|, the SFRD ratio from these galaxies decreases to 0.2–0.3, meaning residual quenching of lower-SFR galaxies due to X-ray heating only contributes significantly to the gap between the No-X-ray and simba-50 SFRD’s at late times. Thus, we conclude that the gap between |$z=2-4$| across the No-X-ray and simba-50 runs in Fig. 1 can be fully explained by the quenching of a small number of galaxies that were initially highly star-forming.
3.4.2 Distribution of sSFR for galaxies on the |$f_{\rm edd}$|–|$M_{\rm BH}$| relation
In this section, we aim to explain why the |$f_\mathrm{edd}$|–sSFR correlation breaks down upon the activation of the X-ray mode, as seen in Fig. 7. Additionally, we further examine the relationship of the galaxy sSFR’s to the accretion rate and the black hole mass. In Fig. 9, we show scatter plots of the |$f_{\rm edd}$|–|$M_{\rm BH}$| relation for all central galaxies in the No-X-ray and simba-50 runs at |$z=4$|, 2, 1, and 0. Markers are coloured by the galaxy’s sSFR. Similar to Fig. 6, we represent galaxies eligible for AGN winds with circular markers, those eligible for jets with square markers (outlined in black as a visual aid), and galaxies eligible for X-ray feedback with triangular markers. The size of each marker corresponds to the ratio of black hole mass to stellar mass of the host galaxy.
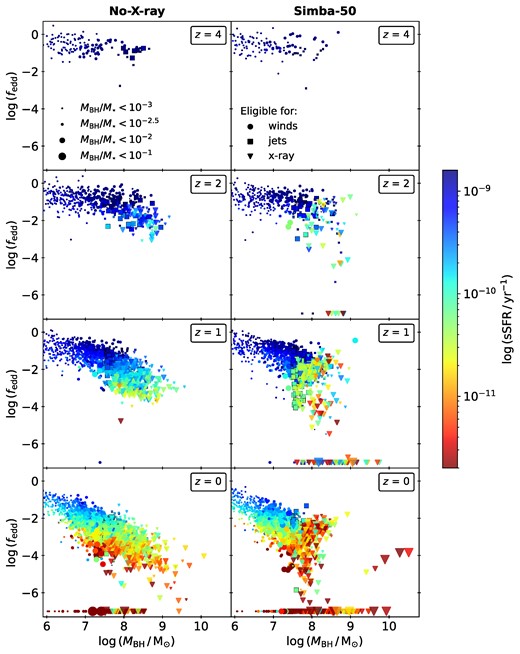
Scatter plots of the |$f_{\rm edd}$|–|$M_{\rm BH}$| relation for all central galaxies in the No-X-ray and simba-50 runs between |$z=4-0$|, coloured by sSFR. As in Fig. 6, galaxies eligible for AGN winds are shown in circles, jets in squares (with a black outline as a visual aid) and X-ray feedback in triangles, with the marker size indicating the size of the black hole. While the No-X-ray run shows a clear anticorrelation between the |$f_{\rm edd}$| and |$M_{\rm BH}$|, the inclusion of X-ray feedback in the simba-50 run introduces a break above |$M_\mathrm{BH} = 10^{7.5}\, \rm {\rm M}_{\odot }$|.
At |$z=4$|, all galaxies within both runs exhibit high sSFR’s with no discernible signs of quenching. The majority of these galaxies are primarily influenced by AGN winds, given that most of their black holes are still below the |$M_\mathrm{BH} = 10^{7.5}\, \rm {\rm M}_{\odot }$| threshold. However, a few larger galaxies beyond this threshold feature sufficiently low accretion rates to be eligible for jet feedback. We note a slight tendency toward higher |$M_{\rm BH}/M_{\star }$| ratios in the No-X-ray run. In the simba-50 run, temporary activity of the X-ray mode may have caused slightly lower stellar masses within these galaxies.
At |$z=2$|, the runs show more pronounced differences. Both runs now include galaxies eligible for X-ray feedback, which contributes to the emergence of quenched galaxies in the simba-50 run, consistent with Fig. 6. These galaxies further exhibit accretion rates below |$\rm log (\mathit {f}_{edd}) = -3.5$|, which similarly do not occur in the No-X-ray run. Some galaxies with low Eddington fractions are only eligible for jets. They are characterized by relatively small black hole masses and exhibit high sSFR’s, indicating that they are not quenched. These low accretion rates are likely a result of the small spheres of influence of the black holes and the reduced gas concentrations in the galactic centre due to temporary X-ray feedback.
At |$z=1$|, quenched galaxies are also observed in the No-X-ray run. Galaxies display a positive correlation between the sSFR and the |$f_{\rm edd}$|, which in turn shows a clear anticorrelation with |$M_{\rm BH}$|. In contrast, galaxies eligible for X-ray feedback in the simba-50 run show more variable accretion rates and sSFR’s. Black holes with zero accretion rates have been assigned |$\rm log (\mathit {f}_{edd}) = -6.5$|. Additionally, a population of galaxies with |$M_{\rm BH} \sim 7.5$|, which are only eligible for jets, not X-ray, exhibits significantly decreased accretion rates below |$\rm log (\mathit {f}_{edd}) = -2$|. This population is notably absent in the No-X-ray run. It is likely that these galaxies were affected by X-ray feedback, causing rapid quenching of their accretion rates, and a subsequent re-accretion of some gas led to higher gas fractions, deactivating the X-ray mode. A further investigation showed that gas fractions in these galaxies indeed hover around 0.2, the threshold for X-ray feedback activation.
At |$z=0$|, the anticorrelation between |$f_{\rm edd}$| and |$M_{\rm BH}$|, along with a correlation with sSFR, persists in the No-X-ray run. In the simba-50 run, the anticorrelation holds until |$M_\mathrm{BH} = 10^{7.5}\, \rm {\rm M}_{\odot }$|, above which the X-ray mode causes considerable variations in Eddington ratios and sSFR’s of up to 2.5 and 1.5 dex, respectively.
Thomas et al. (2019) found the same break in the |$f_{\rm edd}$|–|$M_{\rm BH}$| anticorrelation in the simba-100 run. They ascribe this to variable accretion rates due to the Bondi accretion mode for hot gas, which is inherently less stable than the tidal accretion mode for cold gas. The sudden input of thermal energy close to the black hole could transform a significant amount of ISM-gas into non-ISM gas, which would both quench the SFR and increase the contribution from Bondi accretion. We explain this reasoning in more detail in Section 4.1.4.
4 DISCUSSION
4.1 Feedback effects on the cosmic star formation history in simba: a cohesive picture
In previous sections, we examined various observables related to star formation and stellar masses and subsequently contrasted their evolution in different simba simulation variants with isolated feedback prescriptions. In this section, we unify these results into a cohesive picture of how the cosmic star formation history is affected by stellar and AGN feedback in the full-physics simba simulations. We proceed by explaining how each feedback mode acting in individual galaxies at specific redshifts gives rise to key features in global observables, such as the SFRD and the GSMF.
4.1.1 Stellar feedback
From the beginning of star formation at early epochs, galaxies are subject to the effects of simba’s stellar feedback mode. This mainly affects further star formation due the ejection of particles from mass-loaded two-phase winds, resulting in galaxy outflows, which significantly reduce the availability of cold gas for star formation and thus curtail the star-forming activity in these galaxies. Due to the inverse scaling of the mass-loading factor with stellar mass, according to a power-law with break at |$\mathrm{M_{0}=5.2 \times 10^{9}\, {\rm M}_{\odot }}$| (see equation 2), as well as the mass scaling of the counteracting gravitational potential, stellar feedback is more effective in low-mass haloes, which are more prevalent at high-redshifts.
As a result of stellar feedback, the median nSFR in halo populations with low total masses (|$M_\mathrm{H}\lt 10^{12.5}\rm \, {\rm M}_{\odot }$|) is lowered in all runs relative to the No-feedback run (see Fig. 3). This is entirely responsible for the high-redshift suppression of the SFRD by 0.8 dex until |$z\approx 4$|, after which AGN feedback starts suppressing and even quenching star formation in more massive haloes (see Fig. 1). After |$z=4$|, stellar feedback contributes a continued, albeit decreasing, suppression of the SFRD until |$z=0$|. This slows stellar mass growth in low-mass systems and, consequently, the GSMF (Fig. 2) is reduced by 1 dex at all masses for |$z = 4$| and below |$M_\mathrm{\star } \sim 10^{10}\rm \, {\rm M}_{\odot }$| at |$z=1$| and 0.
4.1.2 AGN winds
As stellar masses gradually increase, albeit at a slowed pace due to the influence of stellar feedback, galaxies eventually reach stellar masses of |$M_{\star } \gtrsim 10^{9.5}\mathrm{\, {\rm M}_{\odot }}$|. At this point the first black holes are seeded, with seed masses of |$10^{4}\mathrm{\, {\rm M}_{\odot }}h^{-1}$|. These newly formed black holes exhibit high accretion rates, and AGN winds are active immediately. However, the wind velocities scale with the black hole mass and are thus low initially. For |$M_\mathrm{BH} = 10^{4}\mathrm{\, {\rm M}_{\odot }}h^{-1}$|, the wind velocity is approximately |$\approx 170 \rm \, km \, s^{-1}$| (see equation 3). This may be insufficient to exert significant influence on the star-forming activity. During this early phase, galaxies remain gas-rich, fuelling high accretion and SFRs. At around |$z \sim 2$|, Fig. 6 shows only a few instances of slightly lowered accretion rates due to the influence of AGN winds.
At later cosmic epochs, black holes have grown more massive and accelerated AGN wind particles can achieve velocities of up to |$\sim 1200\, \rm km \, s^{-1}$| for black hole masses of |$10^{10}\mathrm{\, {\rm M}_{\odot }}$|. This mode is relevant for quenching intermediate-mass systems, where black hole masses are not yet large enough for jets to have taken over as the dominant quenching mode. As shown in Fig. 7, galaxies at |$z = 0$| with |$M_{\star } \sim 10^{9.5}-10^{10}\mathrm{\, {\rm M}_{\odot }}$| and relatively large black holes at low accretion rates (|$f_\mathrm{edd} \lt 0.01$|) exhibit sSFR’s below |$10^{-11} \mathrm{yr^{-1}}$|. As a result of the slowed stellar mass growth, galaxies accumulate at this mass range at the expense of more massive systems. This translates into the minor peak in the GSMF for galaxies with stellar masses around |$10^{9.5}-10^{10}\mathrm{\, {\rm M}_{\odot }}$| observed in Fig. 2.
The quenching of intermediate-mass galaxies further manifests in the SMHM ratio at |$z=0$|, as shown in Fig. 5. In this case, stellar mass fractions are reduced within haloes in the mass range of |$M_\mathrm{H} \sim 10^{11}-10^{12}\mathrm{\, {\rm M}_{\odot }}$|. The suppression of the sSFR in individual galaxies has a cumulative effect on the median nSFR after |$z \sim 1$| in Fig. 3, where haloes with |$M_\mathrm{H} \sim 10^{12}\rm \, {\rm M}_{\odot }$| exhibit a noticeable drop of 0.5 dex in the No-jet run. At higher masses, the escape velocity exceeds the maximum achievable wind speed (1200|$\mathrm{~km} \mathrm{~s}^{-1}$|), which renders the wind mode insufficient to quench the nSFR.
4.1.3 Jet feedback
The first galaxies eligible for the jet mode appear around |$z=4$|, as shown in Fig. 9. However, their sSFR’s remain relatively high, at around |$10^{-9} \mathrm{yr^{-1}}$|. Fig. 6 shows that upon reaching |$z = 2$| in the No-X-ray run, individual high-mass galaxies with jets and low accretion rates (|$f_\mathrm{edd} \lt 10^{-2.2}$|) exhibit sSFR’s below |$10^{-9.5}\mathrm{yr^{-1}}$|, which are not present in the No-jet run. This trend can also be seen in the SFRD (Figs 1 and 8). It coincides with a reduced number of galaxies at high stellar masses with respect to the No-jet run (see Figs 6 and 2). However, jets are in general not efficient at fully quenching galaxies at these epochs, except in special cases that have specific environmental conditions (Szpila et al. 2024).
After |$z=2$|, however, jets become the dominant quenching mechanism in simba. By |$z=0$|, they have significantly altered the slope of the sSFR–|$M_{\star }$| relation in the No-X-ray run, particularly impacting galaxies with |$M_{\star } \gtrsim 10^{10} \, \mathrm{M}_{\odot }$| (Fig. 7). This translates into a reduction of the median nSFR by |$1-1.5\,$|dex for halo populations with masses greater than |$10^{12.5} \, \mathrm{M}_{\odot }$|, as well as a decrease of the overall SFRD by 1 dex. Stellar mass growth is slowed drastically, as a result, and the jets crucially introduce a downward bend into SMHM ratio at |$M_\mathrm{H} \sim 10^{12} \, \mathrm{M}_{\odot }$| and reduce the GSMF by up to 1 dex at |$M_{\star } \gtrsim 10^{11} \, \mathrm{M}_{\odot }$|.
We further find a clear correlation of |$f_\mathrm{edd}$| and sSFR in the No-X-ray run. Both star formation and accretion processes draw from the galaxy’s gas reservoir and they thus correlate with the amount of available gas. Gas is more easily heated and expelled from the galaxy for higher outflow velocities. Since the speed of AGN jets scales inversely with the logarithmic accretion rate down to |$f_\mathrm{edd} = 0.02$| (equation 4), then a lower accretion rate is associated with lower sSFR.
The efficiency of the jet mode at late times is connected to the detailed mechanism powering this AGN feedback mode, and the redshift evolution of the properties of the CGM. The particles that are ejected by the AGN jets are heated to the virial temperature of the halo and subsequently deposited in the CGM outside the galaxy, at distances of around |$50 \, \rm kpc$|. Ejected particles are initially decoupled, meaning that they undergo no hydrodynamic interactions with the surrounding gas. After |$10^{-4}$| Hubble times, particles recouple and deposit their high thermal energy in the CGM. Before |$z \sim 2$|, the CGM is characterized by high densities. The heating introduced by AGN feedback thus tends to dissipate quickly due to elevated cooling rates. As a result, AGN jets are not effective in high-redshift environments. At lower redshifts, the CGM is more diffuse and retains most of the deposited heat. Appleby et al. (2021) showed that at low redshifts, the CGM of No-X-ray and simba-50 galaxies with |$M_{\star } \gtrsim 10^{10} \, \mathrm{M}_{\odot }$| is primarily composed of hot gas, with temperatures |$\gt 0.5\, T_{\rm vir}$|. This restricts the (re-)accretion of CGM gas on to the galaxy, creating a scenario where galaxies effectively starve due to low gas availability, resulting in a slow quenching of the SFR and the accretion rate over dynamical time-scales (see slow quenching described in Montero et al. 2019). Importantly, this form of AGN feedback is mostly preventative, and does not significantly affect the local ISM within galaxies. Instead, only a small fraction of the ejected particles, approximately a |$1/50$| of the gas mass, is carried out by the feedback process.
Jets affect particularly high-mass haloes, as they typically contain larger and more mature black holes with low accretion rates, which are required for the jets to initially activate and then reach velocities high enough for heated gas particles to leave the galaxy. Additionally, the virial temperature scales with halo mass, resulting in larger amounts of thermal energy being carried by the jets. The vast majority of jet energy is kinetic, however, as the virial velocity of massive haloes is |$\sim 10^3$| K while the jet velocity is |$\sim 10^4$| K.
We note that previous work with the simba suite of simulations has also identified |$z=2$| as a critical epoch. Sorini et al. (2022) showed that before this redshift, stellar feedback is the dominant mechanism shaping the distribution of baryons in the IGM, and within low-mass haloes and their CGM. After |$z=2$|, the AGN-jet feedback mode exhibits the strongest impact on the baryonic content of high-mass haloes and their CGM, as well as the content and thermal state of the IGM (see also Christiansen et al. 2020; Khrykin et al. 2024). Our work therefore shows that the relative importance of different feedback modes on star formation and baryon distribution are closely related. The underlying reason is most likely connected to the smaller number of galaxies eligible for AGN-jet feedback before |$z=2$| (Fig. 9).
4.1.4 X-ray heating
The inclusion of X-ray heating is crucial for producing quenched galaxies before |$z = 2$|. This is evident in Fig. 6, where a few tens of galaxies in the full simba-50 run exhibit sSFR’s below |$10^{-10}\mathrm{yr^{-1}}$|, which are notably absent in the No-X-ray run. These galaxies also contain relatively large black holes for their stellar masses. Fig. 8 has confirmed that the quenching of this small number of formerly highly star-forming galaxies (SFR |$\gt 10 \, \mathrm{{\rm M}_{\odot } \, yr^{-1}}$|) is responsible for the diverging SFRD at |$z\sim 4$| in the full simba-50 run in Fig. 1. Signs of early quenching resulting from the activation of the X-ray mode also manifest in the median nSFR for haloes around |$10^{13} \rm \, {\rm M}_{\odot }$| and a few bins with low sSFR’s in the SMHM ratio histogram in Fig. 4. Notably, since these effects are limited to only a handful of galaxies, they have exerted a relatively minor influence on the overall stellar mass distribution at |$z=2$|. Consequently, no significant differences in the GSMF and only a slight trend toward lower SMHM ratios are evident at this epoch.
After |$z = 2$|, when the jets can efficiently quench galaxies, simba’s X-ray heating mode plays a minor role. It remains responsible for suppressing residual star formation in high-mass galaxies, as seen in the sSFR’s of individual galaxies with stellar masses exceeding |$10^{10} \mathrm{\, {\rm M}_{\odot }}$| in Fig. 7 and the quenching |$\rm \sim 0.5~dex$| of the median nSFR of haloes with |$M_\mathrm{H}\gt 10^{12.5} \mathrm{\, {\rm M}_{\odot }}$|. This further results in a continued 0.2 dex suppression of the overall SFRD after |$z\sim 2$|. The resulting stellar mass growth is only affected at the highest masses, as X-ray feedback reduces the number of galaxies with |$M_{\star } = 10^{11}-10^{12} \mathrm{\, {\rm M}_{\odot }}$| in the GSMF and results in a decline in SMHM ratios for haloes with masses exceeding |$10^{13} \mathrm{\, {\rm M}_{\odot }}$|. Lastly, we note that the X-ray mode breaks the anticorrelation between black hole mass and accretion rate (Fig. 9), as well as the correlation of sSFR and accretion rate (Fig. 7), which were both present in the No-X-ray run.
In summary, we explain the diverse effects of the X-ray mode on galaxies at different epochs as follows: already before |$z=2$| both the No-X-ray and the simba-50 contain some galaxies with unusually massive and mature black holes for their galaxies. These galaxies likely contained large amounts of gas initially, which resulted in significant black hole growth and high SFRs. Eventually the accretion rate drops below |$f_\mathrm{edd} =0.2$|, which activates the jet mode. These are not efficient at quenching star formation by themselves at this point, but eventually gas fractions are low enough for the X-ray mode to turn on, which quenches star formation activity in the central regions. This is seen in the central suppression of the sSFR in simba-50 galaxies compared to galaxies in the No-X-ray run (Appleby et al. 2019). While the radiative wind and jet modes act in the purely bipolar fashion and do not affect the local ISM significantly, the energy input of the X-ray mode is spherical and directly affects the central gas. All ISM and non-ISM gas particles within the black hole kernel receive a temperature increase, as well as a radial outward momentum kick for just the ISM gas. In addition to dispelling the ISM gas from the central regions, the thermal input may be significant enough to surpass the ISM temperature floor defined in equation (1) and the affected gas is thus no longer eligible for star formation. The resulting quenching of the central star formation is rapid (Montero et al. 2019) and independent of the current accretion rate. Residual star formation outside of the central region will vary among different galaxies, thus explaining the break of the correlation between |$f_\mathrm{edd}$| and the overall sSFR’s upon the activation of X-ray feedback. Early quenched galaxies with formerly high star formation rates were likely particularly affected due to their large black hole masses, whose increased sphere of influence was able to quench most of the star formation.
The black hole accretion rate itself is similarly affected by the central thermal energy input. For cold gas, torque-limited accretion is the dominant accretion mode, since it accretes gas below |$T \lt 10^{5} \rm K$|, which is primarily in the ISM phase. If gas in the black hole kernel is suddenly heated to higher temperatures, it is accreted via spherical Bondi accretion. This mode is much less stable, resulting in a significantly more variable accretion rate. As a result, the anticorrelation between the Eddington ratio and the black hole mass also breaks down. Thomas et al. (2019) follow a similar reasoning related to the prevalence of hot gas at the expense of cold gas in quenched systems to explain the same feature found in the simba-100 run. They ascribed the origin of the imperfect anticorrelation between black hole accretion rate and mass to the action of AGN jets. However, as we showed in this manuscript, only upon contrasting different simba runs isolating the AGN feedback prescriptions, it becomes clear that only the inclusion of the X-ray feedback produces this feature. Similarly, Szpila et al. (2024) examined early (|$z\ge 2$|) quenched galaxies in simba-100, and by tracking individual systems showed that each early quenching event was preceded by going into jet mode. Our analysis using the simba variants suggests that it is primarily the influence of the X-ray feedback accompanying AGN jets that drives early quenching.
4.2 Comparisons to other cosmological simulations
Most modern cosmological simulations and galaxy evolution models contain prescriptions for stellar feedback and AGN feedback. Despite some similarities in the modelling approach, each of them differs in the exact parametrization and underlying assumptions. In this section, we compare our results with previous similar attempts at disentangling the effects of different feedback prescriptions on the star formation history predicted by other cosmological simulations.
Vogelsberger et al. (2013) analyse several variants of a |$25 h^{-1}\mathrm{cMpc}$| cosmological box with the galaxy formation model that forms the basis of the illustris simulations (Vogelsberger et al. 2014). Similar to simba, stellar feedback is implemented kinetically and three distinct prescriptions are used to model AGN feedback. illustris uses a thermal ‘quasar mode’ at high accretion rates and a kinetic ‘radio mode’ at low accretion rates. Additionally, ‘electromagnetic’ feedback from the excess UV photoionizing and photoheating radiation in the proximity of AGN is included in the fiducial run. However, since the strength of this mode depends on the luminosity output of the AGN, its effects are only significant in the radiatively efficient quasar mode. Vogelsberger et al. (2013) then compare the evolution of key galaxy properties across runs with successive inclusions of the feedback modes. Similar to our results from simba, they find that stellar feedback shapes the cosmic SFR density at early times, whereas specifically the low-accretion radio mode takes over at late times. This transition begins around |$z=4$|, earlier than simba’s jet mode is able to quench galaxies. However, the inclusion of the X-ray mode in simba decreases the SFRD to a similar degree after |$z=4$|, thus the fiducial simba and illustris show a similar evolution overall. Vogelsberger et al. (2013) further find that the GSMF at |$z=0$| is shaped by stellar feedback in galaxies below |$M_{\star } \sim 10^{11}\mathrm{\, {\rm M}_{\odot }}$|, above which the radio mode takes over. This is again in agreement with the effects of simba’s stellar and jet modes. The quasar and electromagnetic AGN mode in illustris have almost no effect on both the SFRD and GSMF.
illustrisTNG (Weinberger et al. 2017; Pillepich et al. 2018) is the successor to the illustris simulations. Among other modelling improvements, it contains a more sophisticated stellar feedback model (see Pillepich et al. 2018) and a kinetic radio feedback mode (see Weinberger et al. 2017). The kinetic radio mode generates bipolar jets, but unlike the AGN-jet mode in simba, their direction is randomized, thus not generally aligned with the rotation axis of the inner galactic disc. The original thermal quasar and the radiative electromagnetic prescriptions remain the same as in illustris. Pillepich et al. (2018) compare the galaxy populations in several |$25 h^{-1} \mathrm{cMpc}$| runs with isolated mechanisms for stellar and AGN feedback. As in simba and illustris, the SFRD evolution is shaped exclusively by stellar feedback before |$z=4$|, after which AGN feedback becomes relevant and creates a peak at |$z=2-3$|. illustrisTNG’s stellar feedback similarly sets the GSMF at |$z=0$| below |$M_{\star } \sim 10^{11}\mathrm{\, {\rm M}_{\odot }}$|, while AGN feedback regulates the GSMF at higher masses. For the SFRD and GSMF, effects from the quasar and thermal kinetic mode are not considered separately. However, the SMHM ratio shows that quasar mode is at least partially responsible for suppressing stellar mass growth in haloes between |$10^{11}$| and |$10^{12}\mathrm{\, {\rm M}_{\odot }}$|, whereas the radio mode is needed to create the peak at |$10^{12}\mathrm{\, {\rm M}_{\odot }}$|.
The horizon-AGN (Dubois et al. 2014) simulations models stellar feedback kinetically for the first |$50 \, \rm Myr$| and thermally thereafter. As in illustrisTNG, AGN feedback is once again split into an isotropic thermal ‘quasar’ mode at high-accretion rates and a kinetic jet-producing ‘radio’ mode at low-accretion rates. We note however, that the transition between these modes, as well as the exact implementation differs from that of illustrisTNG. Kaviraj et al. (2017) compare the evolution of the GSMF in the fiducial horizon-AGN run to the horizon-NoAGN run, where all AGN feedback is disabled. They find that AGN feedback is crucial to reproduce observed number densities of high-mass galaxies (|$M_{\star } \gt 10^{11}\mathrm{\, {\rm M}_{\odot }}$|) below redshifts |$z \sim 2$|.
eagle (Schaye et al. 2015) is unique among modern cosmological simulations, as both its stellar and its sole AGN feedback mode are modelled as an input of thermal energy. Among a comparison of |$50 h^{-1}\mathrm{cMpc}$|eagle variants based on different cosmologies, Salcido et al. (2018) show the SFRD evolution in a fiducial and a No-AGN version of the |$\Lambda$| cold dark matter (CDM) Universe.In the absence of AGN feedback, they find an increased normalization of around 0.25 dex after |$z=4$| and no change in slope. While the time where AGN feedback becomes relevant is in agreement with other simulations, this is a much weaker effect than in simba, illustris, and illustrisTNG. In those simulations, the continued quenching due to AGN feedback produces a suppression of at least 0.5 dex at |$z=0$| and is needed to move the peak of the SFRD between |$z=2$| and 3, as well as steepen its late-time slope. Salcido et al. (2018) only show the GSMF at |$z=0.1$|, but they find the same mass cut-off at |$M_{\star } = 10^{11}\mathrm{\, {\rm M}_{\odot }}$|, above which AGN feedback suppresses the number density of galaxies.
Overall, the cosmological simulations illustris, illustrisTNG, horizon-AGN, eagle, and simba largely find that their stellar and AGN feedback modes affect global galaxy statistics in a similar way, despite differing implementations and underlying assumptions. This converges to a unified picture where the SFRD is shaped by stellar feedback at early times, while AGN feedback starts showing effects after |$z=4$| and becomes the dominant quenching mechanism after |$z=2$|. AGN feedback produces a sharp turnover at |$M_{\star } = 10^{11}\mathrm{\, {\rm M}_{\odot }}$| in the GSMF, while below this threshold stellar feedback suppresses the number density of galaxies. A feature that is introduced with kinetic AGN feedback modes is a steeper decrease of the SFRD at late times. However, it does not appear to be crucial in order to reproduce the observed SFRD. Indeed, eagle yields a good match with the observed SFRD by using a single, purely radiative, AGN feedback prescription.
The overall similarity of the conclusions that can be drawn from different models suggests that the emerging picture of star formation history in a cosmological context is robust. However, this makes it harder to discriminate amongst different feedback prescriptions with observations of global properties such as the SFRD or GSMF. A more promising strategy would be focussing on potentially more sensitive observables. A good example is the evolution of the |$f_{\rm edd}-M_{\rm BH}$| relationship, which we showed to be highly sensitive to X-ray feedback. A complementary approach would be to track the evolution of the star formation history of individual galaxies in key mass ranges, and especially across |$z=2$|, which acts as a watershed between a stellar-feedback and AGN-feedback-dominated eras for high-mass haloes. Indeed, even if different models broadly agree on the global star formation history, they may still differ in their predictions for restricted populations of galaxies. We will address these questions in future work.
5 CONCLUSIONS
In this work, we investigated the impact of stellar and AGN feedback on the cosmic star formation history using the cosmological simba simulation suite. By comparing the redshift evolution of key observables across different runs of the 50 |$h^{-1} \mathrm{cMpc}$| run with isolated feedback variants, we have successfully connected the overall quenching seen in global statistics to feedback mechanisms acting in individual haloes and galaxies. This enabled us to form a cohesive picture of how simba’s feedback modes have shaped the cosmic star formation history:
While AGN feedback starts quenching star formation in individual haloes after |$z=4$|, |$z=2$| emerges as a key redshift transition, after which AGN feedback modes take over as the dominant quenching mechanisms. Before |$z=2$|, the shape of global statistics like the SFRD (Fig. 1) and the GSMF (Fig. 2) is set by stellar feedback. This conclusion is analogous to the findings by Sorini et al. (2022) on the impact of feedback modes on the distribution of gas within haloes, in the CGM, and in the IGM, hence underscoring the tight correlation between the effect of feedback on the gaseous and stellar components.
The extent to which different haloes are affected by each feedback mode strongly depends on their mass. Stellar feedback shapes both the evolution of the instantaneous SFR (see Fig. 3), as well as the associated stellar mass growth (Figs 4 and 5), in low-mass haloes of |$\lesssim 10^{12} \rm \, {\rm M}_{\odot }$|, which are also more common at |$z\gt 2$|. In these haloes, the gravitational potential is too low to compete with the speeds of mass-loaded stellar winds, leading to outflows large enough to quench the star formation rate. In larger haloes, above |$10^{12} \rm \, {\rm M}_{\odot }$|, stellar feedback becomes less effective due to an increased gravitational potential and a decreased mass-loading factor in simba. These haloes tend to contain massive black holes, which have matured to low accretion rates, thus enabling efficient quenching due to AGN feedback.
Among the three AGN feedback modes in simba, jet feedback at low accretion rates is by far the most effective at quenching star formation. This is largely a slow quenching mechanism, where the jets heat the surrounding CGM to high temperatures, which prevents further gas accretion. The radiative AGN winds alone at high accretion rates are only relevant for quenching intermediate-mass galaxies between |$M_{\star } \sim 10^{9.5}$| and |$10^{10}\mathrm{\, {\rm M}_{\odot }}$|. X-ray heating mainly quenches residual star formation in the central regions, which at late times mainly affects the number of massive galaxies between |$10^{11}$| and |$10^{12}\mathrm{\, {\rm M}_{\odot }}$|, as well as their SFRs, which have already been quenched by jets.
We further found new that the X-ray heating mode, in particular, is necessary to produce the first fully quenched massive galaxies before |$z=2$|, where jets alone are not yet efficient (Figs 6 and 7). As soon as galaxies become eligible for X-ray feedback, the gas temperature around the black hole is increased and/or the gas is pushed outwards spherically. For a few galaxies with a particularly massive black hole and a centrally concentrated star formation, this produces the earliest galaxies with quenched sSFR’s below |$10^{-10}\mathrm{yr^{-1}}$|. As both black hole growth and star formation draw from the same gas reservoir, this small number of galaxies initially showed the highest SFRs prior to quenching. Their quenching is significant enough to manifest in a suppression of the overall SFRD already after |$z=4$| (Fig. 8).
The X-ray mode is also responsible for breaking the anticorrelation between the Eddington ratio and the black hole mass (Fig. 9), which had been identified in the fiducial simba-100 run by (Thomas et al. 2019). The heating of the central gas likely leads to a preferential accretion via the spherical Bondi mode, which is much less stable than the torque-limited accretion from cold gas. As a result, the accretion rates are more variable for any given black hole mass and no longer correlated with the specific SFR’s.
Comparing our results with previous similar works utilizing other cosmological simulations (e.g. Vogelsberger et al. 2013, 2014; Weinberger et al. 2017; Pillepich et al. 2018; Salcido et al. 2018), we find broad agreement on the effect of different feedback modes on global observables of the star formation history, such as the SFRD and GSMF. However, the inclusion of a kinetic AGN feedback mechanism at low-accretion rates in simulations that adopt multiple feedback modes appears to be necessary in order to match the late-time slope of the observed SFRD. The eagle simulation represents an exception, as it reproduces the data with a single radiative AGN feedback mode only.
Despite the agreement on global observables, different models may still predict different evolutions of the properties of individual galaxies. For instance, the aforementioned models produce significantly different cool gas contents within galaxies (Davé et al. 2020) and predictions for sub-millimetre galaxies (Lovell et al. 2021). We wish to explore more such discriminating scenarios in future work. We further want to assess the feasibility of observationally confirming or rejecting the characteristic predictions of simba for the effect of X-ray feedback in the accretion rate–mass relationship of supermassive black holes.
ACKNOWLEDGEMENTS
We are grateful to Nicole Thomas and the members of the simba collaboration for helpful discussions. We acknowledge the yt team for development and support of yt. RD and DS were supported by the Science and Technology Facilities Council (STFC) consolidated grant no. RA5496. This work used the Distributed Research Utilising Advanced Computing (DiRAC)@Durham facility managed by the Institute for Computational Cosmology on behalf of the STFC DiRAC High Performance Computing (HPC) Facility. The equipment was funded by Business, Energy and Industrial Strategy (BEIS) capital funding via STFC capital grants ST/P002293/1, ST/R002371/1, and ST/S002502/1, Durham University and STFC operations grant ST/R000832/1. DiRAC is part of the National e-Infrastructure. This work made extensive use of the National Aeronautics and Space Administration (NASA) Astrophysics Data System and of the astro-ph preprint archive at arXiv.org. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.
DATA AVAILABILITY
The simulation data underlying this article are publicly available.2 The derived data will be shared upon reasonable request to the corresponding author.
Footnotes
REFERENCES
APPENDIX A: |$M_\mathrm{BH}$|–|$M_{\star }$| relation
Fig. A1 shows the median |$M_\mathrm{BH}$|–|$M_{\star }$| relation at |$z=0$| for all five simulation variants. We compare the No-feedback (yellow), No-AGN (purple), No-jet (red), No-X-ray (blue), and the full physics simba-50 (green) run, with 16th–84th percentile spreads (shaded areas). With the exception of the simba-50 run above |$M_{\star }$| = |$10^{11.6}\, \rm {\rm M}_{\odot }$|, all lines lie within the overlapping percentile ranges. While stellar and black hole masses generally reach higher values in the No-feedback, No-jet, and No-AGN runs, they follow the same |$M_\mathrm{BH}$|–|$M_{\star }$| relation as the other runs. This indicates that the exclusion of AGN feedback modes does not fundamentally change the relationship between black holes and stellar growth in simba. Fig. A1 thus mirrors the results from Anglés-Alcázar et al. (2017a, particularly fig. 4), who found that when incorporating the same torque-limited accretion as simba, black hole–galaxy scaling relations arise self-consistently and are relatively insensitive to the black hole feedback model.

Median |$M_\mathrm{BH}$|–|$M_{\star }$| relation at |$z=0$| for the No-feedback (yellow), No-AGN (purple), No-jet (red), No-X-ray (blue), and the full physics simba-50 (green) run, with 16th–84th percentile spreads (shaded areas). Except for the high-mass end of the simba-50 run, all runs follow a similar |$M_\mathrm{BH}$|–|$M_{\star }$| relationship.
Only the simba-50 run lies above the other relations at |$M_{\star } \gt 10^{11.6}\, \rm {\rm M}_{\odot }$| and |$M_\mathrm{BH} \gt 10^{9}\, \rm {\rm M}_{\odot }$|. As described in 3.3.1, these particularly massive black holes are likely a result of the central heating from the X-ray mode, which increases the relative contribution of Bondi accretion from hot gas to the overall accretion rate. As the black holes are generally massive by the time X-ray feedback turns on, and the Bondi accretion rate scales as |$M_\mathrm{BH}^2$|, these black holes have likely been able to grow efficiently. The initial temperature increase due to the X-ray mode also pushes the gas above the ISM temperature threshold set in equation (1), meaning that the gas consumed in Bondi accretion is defined as non-ISM gas and thus unable to form stars. The quenching of local star formation in simba-50 (see Section 4.1.4) is therefore a direct consequence of the X-ray heating, rather than the removal of gas in an overactive accretion.
Overall, we thus do not expect black hole accretion alone to impact star formation significantly in any of the simba runs. We come to the same conclusion when comparing the |$M_\mathrm{BH}$|–|$\sigma$| relations. As a result, all differences in the cosmic star formation history across the five simulation variants can be attributed to the respective feedback modes.
APPENDIX B: NUMERICAL CONVERGENCE
Fig. B1 shows a volume and resolution convergence test for the SFRD using the different simulations with full physics simba models. We contrast simba-100 (blue), s imba-50 (black), simba-25 (green), and simba-25 High-res runs (red). We refer to Table 1 for the specifications of each run.
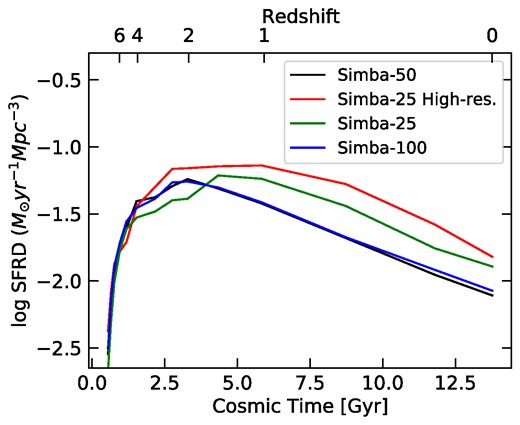
Convergence test for the SFRD. We compare the simba-50 fiducial run (black) to the simba-100 (blue), simba-25 (green), and the simba-25 High res run (red). While volume-wise convergence between simba-50 and simba-100 is excellent, the simba-25 versions produce slightly increased SFRD’s.
Comparing runs with the same resolution, we note excellent volume-wise convergence between the simba-100 model and simba-50. simba-25 exhibits a higher SFRD by around 0.2 dex, which is likely because the small volume produces fewer massive haloes. As a result, the AGN jet feedback is not well-sampled, which produces the most significant suppression in the SFRD. The resolution-wise convergence between the simba-25 and the simba-25 High-res run is not as close. The SFRD in the High-res run is increased by 0.1–0.25 dex with respect to the simba-25 run, as small haloes, in particular, are better resolved.
We note, however, that the purpose of this work is to isolate the relative strength of simba’s feedback modes, rather than qualifying results from the fiducial model. Since the runs with different feedback variants are only available for simba-50, we unfortunately cannot test the volume and resolution dependence of the effects due to each feedback mode.



