-
PDF
- Split View
-
Views
-
Cite
Cite
J -F Donati, P I Cristofari, A Carmona, K Grankin, SPIRou monitoring of the protostar V347 Aur: binarity, magnetic fields, pulsed dynamo, and accretion, Monthly Notices of the Royal Astronomical Society, Volume 534, Issue 1, October 2024, Pages 231–250, https://doi.org/10.1093/mnras/stae2076
Close - Share Icon Share
ABSTRACT
We present in this paper an analysis of near-infrared observations of the 0.3-|${\rm M}_{\odot }$| protostar V347 Aurigae (V347 Aur) collected with the SPIRou high-resolution spectropolarimeter and velocimeter at the 3.6-m Canada-France-Hawaii Telescope from 2019 October to 2023 April. From a set of 79 unpolarized and circularly polarized spectra of V347 Aur to which we applied Least-Squares Deconvolution (LSD), we derived radial velocities and longitudinal fields, along with their temporal variations over our monitoring campaign of 1258 d. Our data show that V347 Aur is an eccentric binary system with an orbital period of |$154.6\pm 0.7$| d, experiencing strong-to-extreme accretion events near periastron. The companion is a |$29.0\pm 1.6$||${\rm M}_{{2\!\!_{\mathbf +}}}$| brown dwarf, a rare member of the brown dwarf desert of close companions around M dwarfs. We detect weak longitudinal fields (|$\lt $|100 G) at the surface of V347 Aur, significantly weaker than those of more evolved prototypical T Tauri stars. These fields show small-amplitude rotational modulation, indicating a mainly axisymmetric parent large-scale magnetic topology, and larger fluctuations at half the orbital period, suggesting that what we dub a ‘pulsed dynamo’ triggered by orbital motion and pulsed accretion operates in V347 Aur. Applying Zeeman–Doppler imaging to our circularly polarized LSD profiles, we find that the large-scale field of V347 Aur is mainly toroidal for most of our observations, with the toroidal component switching sign near periastron and apoastron. The weak large-scale dipole (|$\simeq 30$| G) is not able to disrupt the disc beyond 1.3 |$R_{\star }$| even at the lowest accretion rates, implying longitudinally distributed (rather than localized) accretion at the surface of the protostar.
1 INTRODUCTION
Stars are born from giant filamentary molecular clouds locally collapsing under the effect of gravitation and turbulence, forming protostellar embryos feeding from their accretion discs and known as Class-0 then Class-I objects, with the youngest (Class-0) ones having yet accreted no more than a small fraction of their final mass. Embedded within dusty envelopes, protostars are opaque at optical wavelengths, with Class-0 ones mostly detectable at millimetre and radio wavelengths, sometimes in the near-infrared (nIR; e.g. Greene, Gully-Santiago & Barsony 2018; Le Gouellec et al. 2024), while the more evolved Class-I objects are visible at nIR wavelengths and redwards (e.g. André, Basu & Inutsuka 2009). Class-I objects subsequently evolve into pre-main sequence (PMS) stars (T Tauri stars for low-mass objects), lacking a dense circumstellar envelope and thereby observable at optical wavelengths. They are called Class-II objects when they still accrete from their discs and Class-III objects once accretion no longer occurs at the surface of the star. Planetary systems are presumably born simultaneously with the central star, from the accretion discs formed during the cloud collapse (e.g. Hennebelle et al. 2020).
Magnetic fields play a key role at all stages and scales in this process, within dense cores, accretion discs, and associated outflows in the earliest phases, and within protostars and PMS stars once these gathered most of the surrounding mass and become the main driver of the formation process. In particular, magnetic fields are likely responsible for reducing the rate of star formation, for causing magnetic braking that impacts the outcome of the star formation process, for generating outflows and jets evacuating most of the initial angular momentum, for regulating the rotation rates of protostars and PMS stars by coupling them to the inner regions of their accretion discs, and for affecting planetary formation and migration within protoplanetary discs (e.g. Romanova et al. 2002; Bouvier et al. 2007, 2014; Hennebelle & Fromang 2008; Hennebelle & Teyssier 2008; Zanni & Ferreira 2013; Blinova, Romanova & Lovelace 2016; Hennebelle & Inutsuka 2019).
Whereas magnetic fields of star-forming cores and protostellar discs of Class-0 and Class-I objects are being extensively characterized at millimetre wavelengths (e.g. Maury, Hennebelle & Girart 2022), those of accreting and non-accreting T Tauri stars are scrutinized in the optical and nIR domains using high-resolution spectroscopy and spectropolarimetry (e.g. Johns-Krull 2007; Donati et al. 2020a, 2024a; Finociety et al. 2021, 2023; López-Valdivia et al. 2021), focussing in particular on the dynamo processes amplifying such fields and on the magnetospheric accretion processes taking place between the stars and their inner discs. However, very few studies exist regarding magnetic fields of Class-I protostars and the way they accrete mass from their accretion discs (Johns-Krull et al. 2009; Flores et al. 2019, 2024). Yet this is a critical piece of the puzzle for us to bridge the gap between both sets of studies, and ultimately merge all observational constraints about the role of magnetic fields at all temporal stages and spatial scales of the star and planet formation process.
In this aim, the young protostar V347 Aurigae (V347 Aur) is a particularly interesting object. With a spectral index |$\alpha$| (describing the slope of the spectral energy distribution between nIR and mid-infrared wavelengths) close to 0 (Connelley & Greene 2010), V347 Aur is classified as a flat-spectrum source, in transition between Class-I and Class-II formation stages (Greene et al. 1994). Relatively bright in the nIR, V347 Aur was recently characterized through high-resolution spectroscopy (Flores et al. 2019, 2024), showing in particular that it hosts kG small-scale magnetic fields at its surface (from the broadening and intensification of spectral features sensitive to magnetic fields). V347 Aur is also known to undergo frequent and regular accretion outbursts (Dahm & Hillenbrand 2020) possibly caused by the presence of an unseen companion, making it even more suited for an in-depth monitoring study of its spectral properties.
We thus embarked on a multiseason programme using SPIRou, the nIR high-resolution cryogenic spectropolarimeter/velocimeter at the Canada-France-Hawaii Telescope (CFHT), an ideal instrument to monitor the spectral properties of V347 Aur, and in particular its large- and small-scale magnetic field and its velocimetric behaviour. This paper describes a monitoring effort of V347 Aur carried out over 3.5 yr, from late 2019 to early 2023. We start by summarizing the main properties of V347 Aur in Section 2, then present our SPIRou observations of V347 Aur in Section 3, outline our spectropolarimetric and velocimetric results in Sections 4 and 5, and describe our magnetic modelling of V347 Aur using Zeeman–Doppler imaging (ZDI) in Section 6. We finally describe in Section 7 the accretion properties of V347 Aur as derived from the variability of photospheric and accretion lines, before summarizing and discussing our results in Section 8.
2 THE PROTOSTAR V347 AUR
V347 Aur (HBC 428, IRAS 04530+5126, 2MASS J04565702+5130509) is a highly variable young star located |$206.6\pm 2.3$| pc away from the Sun (Gaia Collaboration 2023) in the Taurus–Auriga complex, relatively isolated from known star-forming regions. Being still embedded within its natal molecular cloud L1438, V347 Aur interacts with the surrounding nebular material and is associated with a small reflection nebula. With an emission line spectrum and a location in a colour–magnitude diagram that are characteristic of an extremely young object, it was first classified as a Class-I protostar of spectral type M2 suffering significant extinction (Cohen 1978), then shown to be a flat spectrum source in transition towards a Class-II T Tauri star (Connelley & Greene 2010).
From low- and high-resolution nIR spectra, V347 Aur was confirmed to be an M2 star (with spectral type varying from M1 to M3, Connelley & Greene 2010; Dahm & Hillenbrand 2020), corresponding to an average effective temperature |${T_{\rm eff}}\simeq 3500$| K (Pecaut & Mamajek 2013). By fitting recent high-resolution nIR spectra of V347 Aur, Flores et al. (2019) finds a lower |$T_{\rm eff}$| of |$3230\pm 100$| K and a logarithmic gravity of |${{\rm log}\,\, g}=3.25\pm 0.15$| (in cgs units), and reports the presence of a small-scale magnetic field of average strength |$1.36\pm 0.06$| kG at the surface of the star, broadening and intensifying the profiles of atomic lines (with all measurements confirmed within error bars in their new study; Flores et al. 2024). Our own measurements from SPIRou spectra, yielding similar results (|${T_{\rm eff}}=3340\pm 50$| K and |${{\rm log}\,\, g}=3.30\pm 0.10$|; see Section 3), further confirm those of Flores et al. (2019). We use a combination of both, i.e. |${T_{\rm eff}}=3300\pm 50$| K and |${{\rm log}\,\, g}=3.30\pm 0.10$|, in the following sections.
Adjusting both |$T_{\rm eff}$| and |$\log g$| to the evolutionary tracks of Baraffe et al. (2015) for low-mass stars yields a mass of |${M_{\star }}=0.25\pm 0.03$||${\rm M}_{\odot }$|, a radius of |${R_{\star }}=1.9\pm 0.3$||${\rm R}_{\odot }$|, and an age of |$\simeq$|0.8 Myr, with similar results when using the non-magnetic tracks of Feiden (2016), both sets of models being known to underestimate masses by |$\simeq$|10 per cent for stars with |${M_{\star }}\ \lt\ 0.6$||${\rm M}_{\odot }$| (Braun et al. 2021). Comparing now with the magnetic tracks of Feiden (2016) yields |${M_{\star }}=0.45\pm 0.06$||${\rm M}_{\odot }$|, |${R_{\star }}=2.4\pm 0.3$||${\rm R}_{\odot }$|, and an age of |$\simeq$|0.8 Myr. Although presumably more adapted to a magnetic star like V347 Aur, these models are however reported to overestimate masses by |$\simeq$|30 per cent for the same mass range (Braun et al. 2021). Correcting for these under and overestimates, and taking the average of the corrected values yields |${M_{\star }}=0.33\pm 0.05$||${\rm M}_{\odot }$|, |${R_{\star }}=2.2\pm 0.3$||${\rm R}_{\odot }$| (hence a logarithmic bolometric luminosity relative to the Sun |$\log ({L_{\star }}/{{\rm L}_{\odot }})=-0.3\pm 0.2$|), and an age of |$\simeq$|0.8 Myr for V347 Aur, a set of parameters roughly consistent with that of Dahm & Hillenbrand (2020) and which we use in the rest of our study.
Our measurements of the rotation period (|${P_{\rm rot}}=4.12\pm 0.03$| d; see Section 4) and of the line-of-sight projected equatorial rotation velocity (|${v \sin i}=12.0\pm 0.5$| km s|$^{-1}$|; see Section 6, in good agreement with Flores et al. 2019) of V347 Aur independently yield |${R_{\star }}\sin i=0.98\pm 0.05$||${\rm R}_{\odot }$|, implying an inclination angle i of the rotation axis of V347 Aur to the line of sight of |$i=26\pm 5{^\circ }$|. Assuming an accretion disc whose rotation axis is aligned with that of the star, it implies a system geometrical orientation that is only |$\simeq$|26|$^\circ$| away from being face-on. Little is known about the disc itself beyond an old radio measurement of the 1.3 mm dust continuum with the 30-m IRAM interferometer, which derived a small disc mass of only 0.0014 |${\rm M}_{\odot }$| (Osterloh & Beckwith 1995). We list the main stellar parameters of V347 Aur in Table 1 and adopt values of |$i=26$||$^\circ$|, |${M_{\star }}=0.33~{{\rm M}_{\odot }}$|, and |${R_{\star }}=2.2~{{\rm R}_{\odot }}$| in the following.
| Distance (pc) | |$206.6\pm 2.3$| | Gaia Collaboration (2023) |
| |$\log ({L_{\star }}/{{\rm L}_{\odot }})$| | |$-0.3\pm 0.2$| | |
| |$T_{\rm eff}$| (K) | |$3300\pm 50$| | |
| |$\log g$| (dex) | |$3.30\pm 0.10$| | |
| |$M_{\star }$| (|${\rm M}_{\odot }$|) | |$0.33\pm 0.05$| | Baraffe et al. (2015); Feiden (2016) |
| |$R_{\star }$| (|${\rm R}_{\odot }$|) | |$2.2\pm 0.3$| | Baraffe et al. (2015); Feiden (2016) |
| Age (Myr) | |$\simeq$|0.8 | Baraffe et al. (2015); Feiden (2016) |
| |$P_{\rm rot}$| (d) | 4.12 | Period used to phase data |
| |$P_{\rm rot}$| (d) | |$4.12\pm 0.03$| | From RV data |
| |$v \sin i$| (km s|$^{-1}$|) | |$12.0\pm 0.5$| | From ZDI modelling |
| |${R_{\star }}\sin i$| (|${\rm R}_{\odot }$|) | |$0.98\pm 0.05$| | From |$R_{\star }$| and |$v \sin i$| |
| i (|$^\circ$|) | |$26\pm 5$| | From |$R_{\star }$| and |${R_{\star }}\sin i$| |
| |$r_{\rm cor}$| (au) | |$0.035\pm 0.002$| | From |$M_{\star }$| and |$P_{\rm rot}$| |
| |$r_{\rm cor}$| (|$R_{\star }$|) | |$3.4\pm 0.6$| | From |$r_{\rm cor}$| (au) and |$R_{\star }$| |
| |$\log {\dot{M}}$| (|${\rm M}_{\odot }$| yr|$^{-1}$|) | |$-9.0$| to |$-6.2$| | From Pa|${\beta }$| and Br|${\gamma }$| |
| Distance (pc) | |$206.6\pm 2.3$| | Gaia Collaboration (2023) |
| |$\log ({L_{\star }}/{{\rm L}_{\odot }})$| | |$-0.3\pm 0.2$| | |
| |$T_{\rm eff}$| (K) | |$3300\pm 50$| | |
| |$\log g$| (dex) | |$3.30\pm 0.10$| | |
| |$M_{\star }$| (|${\rm M}_{\odot }$|) | |$0.33\pm 0.05$| | Baraffe et al. (2015); Feiden (2016) |
| |$R_{\star }$| (|${\rm R}_{\odot }$|) | |$2.2\pm 0.3$| | Baraffe et al. (2015); Feiden (2016) |
| Age (Myr) | |$\simeq$|0.8 | Baraffe et al. (2015); Feiden (2016) |
| |$P_{\rm rot}$| (d) | 4.12 | Period used to phase data |
| |$P_{\rm rot}$| (d) | |$4.12\pm 0.03$| | From RV data |
| |$v \sin i$| (km s|$^{-1}$|) | |$12.0\pm 0.5$| | From ZDI modelling |
| |${R_{\star }}\sin i$| (|${\rm R}_{\odot }$|) | |$0.98\pm 0.05$| | From |$R_{\star }$| and |$v \sin i$| |
| i (|$^\circ$|) | |$26\pm 5$| | From |$R_{\star }$| and |${R_{\star }}\sin i$| |
| |$r_{\rm cor}$| (au) | |$0.035\pm 0.002$| | From |$M_{\star }$| and |$P_{\rm rot}$| |
| |$r_{\rm cor}$| (|$R_{\star }$|) | |$3.4\pm 0.6$| | From |$r_{\rm cor}$| (au) and |$R_{\star }$| |
| |$\log {\dot{M}}$| (|${\rm M}_{\odot }$| yr|$^{-1}$|) | |$-9.0$| to |$-6.2$| | From Pa|${\beta }$| and Br|${\gamma }$| |
| Distance (pc) | |$206.6\pm 2.3$| | Gaia Collaboration (2023) |
| |$\log ({L_{\star }}/{{\rm L}_{\odot }})$| | |$-0.3\pm 0.2$| | |
| |$T_{\rm eff}$| (K) | |$3300\pm 50$| | |
| |$\log g$| (dex) | |$3.30\pm 0.10$| | |
| |$M_{\star }$| (|${\rm M}_{\odot }$|) | |$0.33\pm 0.05$| | Baraffe et al. (2015); Feiden (2016) |
| |$R_{\star }$| (|${\rm R}_{\odot }$|) | |$2.2\pm 0.3$| | Baraffe et al. (2015); Feiden (2016) |
| Age (Myr) | |$\simeq$|0.8 | Baraffe et al. (2015); Feiden (2016) |
| |$P_{\rm rot}$| (d) | 4.12 | Period used to phase data |
| |$P_{\rm rot}$| (d) | |$4.12\pm 0.03$| | From RV data |
| |$v \sin i$| (km s|$^{-1}$|) | |$12.0\pm 0.5$| | From ZDI modelling |
| |${R_{\star }}\sin i$| (|${\rm R}_{\odot }$|) | |$0.98\pm 0.05$| | From |$R_{\star }$| and |$v \sin i$| |
| i (|$^\circ$|) | |$26\pm 5$| | From |$R_{\star }$| and |${R_{\star }}\sin i$| |
| |$r_{\rm cor}$| (au) | |$0.035\pm 0.002$| | From |$M_{\star }$| and |$P_{\rm rot}$| |
| |$r_{\rm cor}$| (|$R_{\star }$|) | |$3.4\pm 0.6$| | From |$r_{\rm cor}$| (au) and |$R_{\star }$| |
| |$\log {\dot{M}}$| (|${\rm M}_{\odot }$| yr|$^{-1}$|) | |$-9.0$| to |$-6.2$| | From Pa|${\beta }$| and Br|${\gamma }$| |
| Distance (pc) | |$206.6\pm 2.3$| | Gaia Collaboration (2023) |
| |$\log ({L_{\star }}/{{\rm L}_{\odot }})$| | |$-0.3\pm 0.2$| | |
| |$T_{\rm eff}$| (K) | |$3300\pm 50$| | |
| |$\log g$| (dex) | |$3.30\pm 0.10$| | |
| |$M_{\star }$| (|${\rm M}_{\odot }$|) | |$0.33\pm 0.05$| | Baraffe et al. (2015); Feiden (2016) |
| |$R_{\star }$| (|${\rm R}_{\odot }$|) | |$2.2\pm 0.3$| | Baraffe et al. (2015); Feiden (2016) |
| Age (Myr) | |$\simeq$|0.8 | Baraffe et al. (2015); Feiden (2016) |
| |$P_{\rm rot}$| (d) | 4.12 | Period used to phase data |
| |$P_{\rm rot}$| (d) | |$4.12\pm 0.03$| | From RV data |
| |$v \sin i$| (km s|$^{-1}$|) | |$12.0\pm 0.5$| | From ZDI modelling |
| |${R_{\star }}\sin i$| (|${\rm R}_{\odot }$|) | |$0.98\pm 0.05$| | From |$R_{\star }$| and |$v \sin i$| |
| i (|$^\circ$|) | |$26\pm 5$| | From |$R_{\star }$| and |${R_{\star }}\sin i$| |
| |$r_{\rm cor}$| (au) | |$0.035\pm 0.002$| | From |$M_{\star }$| and |$P_{\rm rot}$| |
| |$r_{\rm cor}$| (|$R_{\star }$|) | |$3.4\pm 0.6$| | From |$r_{\rm cor}$| (au) and |$R_{\star }$| |
| |$\log {\dot{M}}$| (|${\rm M}_{\odot }$| yr|$^{-1}$|) | |$-9.0$| to |$-6.2$| | From Pa|${\beta }$| and Br|${\gamma }$| |
V347 Aur was reported to undergo regular accretion outbursts generating photometric pulses with a period of about 155 d, featuring sharp (30 d) rises followed by slower (60 d) subsequent decays, and with brightness fluctuations varying from cycle to cycle by more than an order of magnitude (Dahm & Hillenbrand 2020). V347 Aur is also observed to get bluer during the bursts and redder afterwards (Dahm & Hillenbrand 2020). One obvious explanation for this phenomenon could be that V347 Aur is the most massive star of an eccentric binary where both stars interact during periastron passage generating enhanced accretion, as in, e.g. the close T Tauri binary DQ Tau (Mathieu et al. 1997; Fiorellino et al. 2022; Pouilly et al. 2023, 2024) or the more massive Herbig Ae + T Tauri system HD 104 237 (Dunhill, Cuadra & Dougados 2015; Järvinen et al. 2019). However, no evidence for radial velocity (RV) variations in excess of a few km s|$^{-1}$| were reported, leading Dahm & Hillenbrand (2020) to conclude that V347 Aur is not a spectroscopic binary like DQ Tau or HD 104237. A second option put forward by Dahm & Hillenbrand (2020) on the basis of the large amplitude of the observed photometric variations (by factors up to tens in brightness) is that V347 Aur experiences instabilities in its accretion disc, possibly triggered by a low-mass companion further out in the disc. The reported periodicity of 155 d would imply the companion to be located at an average distance of about 0.4 au from V347 Aur. We show further (see Section 5) that V347 Aur is indeed a spectroscopic binary with a low-mass companion, featuring RV variations of about 2 km s|$^{-1}$| peak-to-peak.
3 SPIROU OBSERVATIONS OF V347 AUR
We observed V347 Aur in four consecutive seasons with the SPIRou nIR spectropolarimeter/high-precision velocimeter (Donati et al. 2020b) at CFHT, within the SPIRou Legacy Survey (SLS) in 2019–2020, 2020–2021, and early 2022, then shortly within the SPICE Large Programme in 2022–2023. SPIRou collects unpolarized and polarized stellar spectra, covering a wavelength interval of 0.95–2.50 μm at a resolving power of 70 000 in a single exposure. For this study, we only recorded circularly polarized (Stokes V) and unpolarized (Stokes I) spectra. As in previous studies, polarization observations consist of sequences of four sub-exposures, with each sub-exposure associated with a different azimuth of the Fresnel rhomb retarders of the SPIRou polarimetric unit in order to remove systematics in polarization spectra (to first order; see e.g. Donati et al. 1997). Each recorded sequence yields one Stokes I and one Stokes V spectrum, along with a null polarization check (called N) used to diagnose potential instrumental or data reduction issues.
A total of 89 polarization sequences were recorded for V347 Aur over four main seasons, 18 in 2019–2020 (October to January), 26 in 2020–2021 (December to January), 22 in 2022 (January), and 23 in 2022–2023 (November to April), with a single sequence collected in most clear nights (except in one night where the sequence was repeated due to weather instabilities). Four spectra were discarded in the first season as a result of an instrument problem and another six spectra were left out in the last season due to very low signal-to-noise ratios (SNRs), finally yielding a total of 79 validated Stokes I, V, and N spectra of V347 Aur. This series includes 14, 26, 22, and 17 such spectra for the four seasons, respectively, spanning intervals of 42, 98, 23, and 160 d, and altogether covering a temporal window of 1258 d. The full log of our observations is provided in Table A1 of Appendix A.
Our SPIRou spectra were all processed with Libre ESpRIT, the nominal reduction pipeline of ESPaDOnS at CFHT, optimized for spectropolarimetry and adapted for SPIRou (Donati et al. 2020b). Least-Squares Deconvolution (LSD; Donati et al. 1997) was then applied to all reduced spectra, using a line mask constructed from the VALD-3 data base (Ryabchikova et al. 2015) for |${T_{\rm eff}}=3500$| K and |${{\rm log}\,\, g}=3.5$| adapted to V347 Aur (see Section 2). Atomic lines deeper than 10 per cent of the continuum level were selected, for a total of |$\simeq$|1500 lines with average wavelength and Landé factor of 1750 nm and 1.2, respectively. The noise levels |$\sigma _V$| in the resulting Stokes V LSD profiles range from 1.9 to 4.5 (median 2.5, in units of |$10^{-4} I_{\rm c}$| where |$I_{\rm c}$| denotes the continuum intensity). We also applied LSD with a mask containing the CO lines of the CO bandhead (at 2.3 μm) only, to obtain veiling estimates in the K band (|$r_K$|), in addition to those for the whole spectrum derived from LSD profiles of atomic lines (|$r_{JH}$|; see Section 7 and Table A1). Phases and rotation cycles were derived assuming a rotation period of |${P_{\rm rot}}=4.12$| d (see Section 4 and Table 1) and counting from an arbitrary starting Barycentric Julian Date (BJD) of 2458688.0 (i.e. prior to our first SPIRou observation).
We also constructed a template spectrum of V347 Aur by computing the median of all 79 SPIRou spectra in the stellar rest frame (with a method similar to that described in Cristofari et al. 2022), a process that allows not only to reduce photon noise and boost SNR, but also to get rid of OH airglow emission lines and of most telluric features (except the strongest ones). We then carried out a spectrum characterization study using the ZeeTurbo code developed for SPIRou observations of M dwarfs (Cristofari et al. 2023a, b) and adapted to the specific case of PMS stars and to V347 Aur in particular. The parameter space is explored through a Monte-Carlo Markov Chain (MCMC) process, yielding posterior distributions and error bars for all parameters. Assuming solar metallicity, we find atmospheric parameters equal to |${T_{\rm eff}}=3340\pm 50$| K and |${{\rm log}\,\, g}=3.30\pm 0.10$|, consistent with those derived by Flores et al. (2019), and average veiling values |$r_{JH}\simeq 0.4$| and |$r_K\simeq 1.3$|, in agreement with our measurements from LSD profiles (see Section 7). Simultaneously with the atmospheric parameters, ZeeTurbo allows us to obtain an estimate of the average small-scale field at the surface of the star, found to be equal to |$1.33\pm 0.07$| kG (see Fig. 1) and consistent with Flores et al. (2019). Given the limited SNR of our data, we carried out this analysis on the template spectrum of V347 Aur rather than on the individual spectra (as in e.g. Donati et al. 2023a). A portion of the observed and modelled spectra is shown as an example in Fig. B1, along with the corresponding posterior distributions of the main parameters in Fig. B2, of Appendix B.
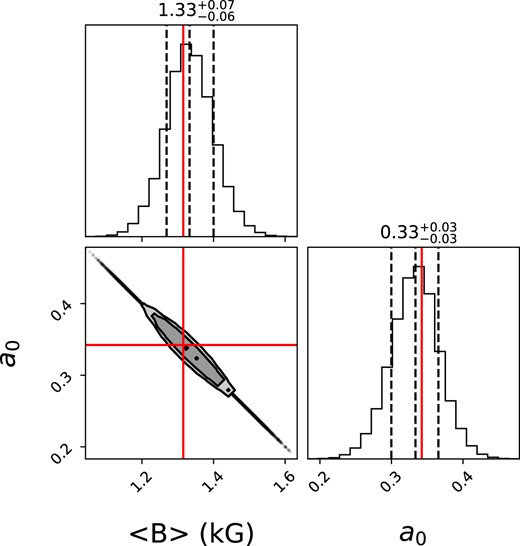
Magnetic parameters of V347 Aur, derived by fitting our median SPIRou spectrum using the atmospheric modelling approach of Cristofari et al. (2023a), which incorporates magnetic fields as well as an MCMC process to determine optimal parameters and their error bars. We find that V347 Aur hosts an average small-scale magnetic field of |$\langle B \rangle =1.33\pm 0.07$| kG, with non-magnetic regions covering a relative area of |$a_0=33\pm 3$| per cent of the visible stellar disc.
4 SPECTROPOLARIMETRY OF V347 AUR
We then examined our Stokes I and V LSD profiles and detected the presence of clear, though weak, Zeeman signatures in the spectral lines of V347 Aur. To quantify our results, we derived the longitudinal field |$B_{\rm \ell }$|, i.e. the line-of-sight projected component of the vector field at the surface of the star averaged over the visible stellar hemisphere, for each pair of Stokes V and I LSD profiles, following Donati et al. (1997). We achieved this by computing the first moment of the Stokes V profile and its error bar, which we normalized with the equivalent width (EW) of the Stokes I LSD profiles estimated through a standard Gaussian fit. In the case of V347 Aur, Stokes V LSD signatures were integrated over a window of |$\pm 24$| km s|$^{-1}$| in the stellar rest frame, an interval adjusted to the width of stellar lines and corresponding to about twice the |$v \sin i$| on both sides of the line centre (the exact integration width having little impact on the result). We find that the longitudinal field of V347 Aur is unambiguously detected, with moderate |$B_{\rm \ell }$| values ranging from –81 to +14 G (median –43 G) and error bars of 12 to 30 G (median 15 G), yielding a reduced chi-square |$\chi ^2_{\rm r}$| (with respect to the |${B_{\rm \ell }}=0$| G line) equal to |${\chi ^2_{\rm r}}=9.7$|. We proceeded in the same way with the polarization check N to verify that the associated pseudo-longitudinal field is consistent with 0 within the error bars and find that |${\chi ^2_{\rm r}}=1.02$|, indicating that no spurious pollution is observed in N and that our analytical error bars are consistent with the observed measurement dispersion within a few per cent. We note in particular that the longitudinal field of V347 Aur is smaller than those of most prototypical classical or weak-line T Tauri stars (e.g. LkCa 4, CI Tau, TW Hya, and GM Aur) or more evolved PMS stars (e.g. AU Mic) whose fields often significantly exceed 100 G in the nIR (e.g. Donati et al. 2023a, 2024a, b; Finociety et al. 2023; Zaire et al. 2024) whereas that of V347 Aur stagnates at about 50 G or less, suggesting that the parent large-scale field is also smaller. This is consistent with our result and that of Flores et al. (2019) on the small-scale field of V347 Tau, also found to be weaker by a factor of |$\simeq$|2 than those of more evolved counterparts.
In a second step, we studied whether temporal variability, including rotational modulation, is detected in our sequence of |$B_{\rm \ell }$| measurements. The rms dispersion of |$B_{\rm \ell }$| values about their weighted average, equal to 23.5 G (|${\chi ^2_{\rm r}}=2.29$|), is inconsistent with our error bars, indicating clear temporal variability. A straightforward periodogram indicates that our |$B_{\rm \ell }$| series is dominated by a periodic signal at a period of about 76 d with a false-alarm probability of 0.02 per cent. Given the main stellar parameters of V347 Aur, in particular |$v \sin i$| and |$R_{\star }$|, yielding |${P_{\rm rot}}\ \lt\ 9.3$| d, this long-period signal cannot be attributed to rotational modulation, and rather reflects an intrinsic periodic variability of the large-scale field, likely akin the well-known solar magnetic cycle but on a much shorter period. To better characterize its properties, we investigated the temporal behaviour of our |$B_{\rm \ell }$| values, arranged in a vector denoted |$\boldsymbol{ \mathit{ y}}$|, using quasi-periodic (QP) Gaussian-Process Regression (GPR), with a covariance function |$c(t,t^{\prime })$| of type
where |$\theta _1$| is the amplitude (in G) of the Gaussian Process (GP), |$\theta _2$| its recurrence period, |$\theta _3$| the evolution time-scale (in d) on which the shape of the |$B_{\rm \ell }$| modulation changes, and |$\theta _4$| a smoothing parameter describing the amount of harmonic complexity needed to describe the data (Rajpaul et al. 2015). We then select the QP GPR fit that features the highest likelihood |$\mathcal {L}$|, defined by
where |$\boldsymbol{ \mathit{ C}}$| is the covariance matrix for our 79 epochs, |$\boldsymbol{\mathit{ \Sigma}}$| the diagonal variance matrix associated with |$\boldsymbol{ \mathit{ y}}$|, and |${\boldsymbol{ \mathit{ S}}}=\theta _5^2 {\boldsymbol{ \mathit{ J}}}$| (|$\boldsymbol{ \mathit{ J}}$| being the identity matrix) the contribution from an additional white noise source that we introduce as a fifth hyperparameter |$\theta _5$| (in case |$B_{\rm \ell }$| is affected by intrinsic variability not included in our analytical error bars). The hyperparameter domain is then explored with an MCMC process, and the marginal logarithmic likelihood |$\log \mathcal {L}_M$| of a given solution is computed using the approach of Chib & Jeliazkov (2001) as in, e.g. Haywood et al. (2014). This is achieved with the same MCMC and GPR modelling tools of our previous studies (e.g. Donati et al. 2023a, b, 2024a, b).
The fit we obtain, associated with |${\chi ^2_{\rm r}}=1.13$| and |$\log \mathcal {L}_M=-347.6$|, yields a much smaller rms (16.5 G) than that about the weighted average of |$B_{\rm \ell }$| values (rms 23.5 G, |${\chi ^2_{\rm r}}=2.29$|), and shows a definite improvement over a fit where only the longest term variation is adjusted (i.e. with |$\theta _2$| fixed to 1500 d, as in Donati et al. 2023b, yielding |${\chi ^2_{\rm r}}=1.69$|, an rms of 20.2 G and |$\log \mathcal {L}_M=-356.6$|). The associated logarithmic Bayes factor |$\log {\rm BF} = \Delta \log \mathcal {L}_M = 9.0$| thus demonstrates that the periodic fluctuation of |$B_{\rm \ell }$| at a period of 76.5 d is definitely real. The periodogram of the residuals now shows a peak at 4.2 d with a false-alarm probability of 0.6 per cent, consistent with what we expect for the rotation period of V347 Aur. To include this second component into our analysis, we added another QP GP to our model, i.e. a new similar QP term to the covariance function of equation (1) defined again by four hyperparameters (called |$\theta _6$| to |$\theta _9$|, and describing, respectively, the amplitude, the recurrence period, the evolution time-scale, and the smoothing parameter of the second GP).
With this dual GP model, we further improve the match to our |$B_{\rm \ell }$| data (see Fig. 2), reaching now |${\chi ^2_{\rm r}}=0.76$| and |$\log \mathcal {L}_M=-343.6$|, i.e.|$\log {\rm BF}=4.0$| compared with the single GP model including the 76.5-d component only. Although short of the usual |$\log {\rm BF}$| threshold (of 5) to firmly validate a detection, we none the less conclude that the 4.2-d component we see in the data, showing up as the only significant peak in the periodogram in the range 2–9 d, is most likely the rotation period of V347 Tau. This preliminary conclusion is confirmed with our RV analysis of V347 Aur (see Section 5). The final values and error bars derived from our GPR fit are listed in Table 2. Note that both evolution time-scales and smoothing parameters, loosely constrained by the |$B_{\rm \ell }$| data, were fixed to their most likely value, with little impact on the final result.
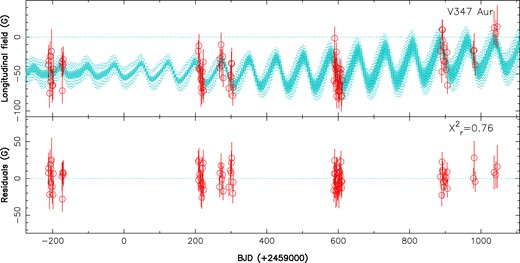
Longitudinal magnetic field |$B_{\rm \ell }$| of V347 Aur (red open circles) as measured with SPIRou (top plot), and QP GPR fit to the data (cyan full line) with corresponding 68-per cent confidence intervals (cyan dotted lines). The residuals are shown in the bottom plot. The rms of the residuals is 13.6 G (|${\chi ^2_{\rm r}}=0.76$|), slightly smaller than our median error bar (15.3 G). The |$\chi ^2_{\rm r}$| with respect to the |${B_{\rm \ell }}=0$| G line is equal to 9.7, indicating a clear magnetic detection. QP fluctuations of |$B_{\rm \ell }$| on a 76.5-d period are also detected, along with a weaker rotational modulation on a 4.2-d period.
Results of our MCMC modelling of the |$B_{\rm \ell }$| curve of V347 Aur with GPR involving two QP GPs, the first one for the 76.5-d |$B_{\rm \ell }$| fluctuation and the second one for the rotational modulation. For each hyperparameter, we list the fitted value, the corresponding error bar, and the assumed prior. The knee of the modified Jeffreys prior is set to |$\sigma _{B}$|, i.e. the median error bar of our |$B_{\rm \ell }$| measurements (i.e. 15.3 G). In the final two rows, we also successively quote the |$\chi ^2_{\rm r}$| and rms of the |$B_{\rm \ell }$| data about the weighted average, once fitted by a single GP (hyperparameters |$\theta _1$| to |$\theta _5$|) and by our dual GP model.
| Parameter . | Name . | Value . | Prior . |
|---|---|---|---|
| Amplitude (G) | |$\theta _1$| | |$22^{+8}_{-6}$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Rec. period (d) | |$\theta _2$| | |$76.5\pm 1.2$| | Gaussian (76.5, 5.0) |
| Evol. time-scale (d) | |$\theta _3$| | 500 | Fixed |
| Smoothing | |$\theta _4$| | 0.75 | Fixed |
| White noise (G) | |$\theta _5$| | |$6\pm 3$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Amplitude (G) | |$\theta _6$| | |$12^{+6}_{-4}$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Rec. period/|$P_{\rm rot}$| (d) | |$\theta _7$| | |$4.19\pm 0.16$| | Gaussian (4.2, 0.5) |
| Evol. time-scale (d) | |$\theta _8$| | 300 | Fixed |
| Smoothing | |$\theta _9$| | 0.75 | Fixed |
| Goodness of fit | |||
| Versus average | Single GP | Dual GP | |
| |$\chi ^2_{\rm r}$| | 2.29 | 1.13 | 0.76 |
| rms (G) | 23.5 | 16.5 | 13.6 |
| Parameter . | Name . | Value . | Prior . |
|---|---|---|---|
| Amplitude (G) | |$\theta _1$| | |$22^{+8}_{-6}$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Rec. period (d) | |$\theta _2$| | |$76.5\pm 1.2$| | Gaussian (76.5, 5.0) |
| Evol. time-scale (d) | |$\theta _3$| | 500 | Fixed |
| Smoothing | |$\theta _4$| | 0.75 | Fixed |
| White noise (G) | |$\theta _5$| | |$6\pm 3$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Amplitude (G) | |$\theta _6$| | |$12^{+6}_{-4}$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Rec. period/|$P_{\rm rot}$| (d) | |$\theta _7$| | |$4.19\pm 0.16$| | Gaussian (4.2, 0.5) |
| Evol. time-scale (d) | |$\theta _8$| | 300 | Fixed |
| Smoothing | |$\theta _9$| | 0.75 | Fixed |
| Goodness of fit | |||
| Versus average | Single GP | Dual GP | |
| |$\chi ^2_{\rm r}$| | 2.29 | 1.13 | 0.76 |
| rms (G) | 23.5 | 16.5 | 13.6 |
Results of our MCMC modelling of the |$B_{\rm \ell }$| curve of V347 Aur with GPR involving two QP GPs, the first one for the 76.5-d |$B_{\rm \ell }$| fluctuation and the second one for the rotational modulation. For each hyperparameter, we list the fitted value, the corresponding error bar, and the assumed prior. The knee of the modified Jeffreys prior is set to |$\sigma _{B}$|, i.e. the median error bar of our |$B_{\rm \ell }$| measurements (i.e. 15.3 G). In the final two rows, we also successively quote the |$\chi ^2_{\rm r}$| and rms of the |$B_{\rm \ell }$| data about the weighted average, once fitted by a single GP (hyperparameters |$\theta _1$| to |$\theta _5$|) and by our dual GP model.
| Parameter . | Name . | Value . | Prior . |
|---|---|---|---|
| Amplitude (G) | |$\theta _1$| | |$22^{+8}_{-6}$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Rec. period (d) | |$\theta _2$| | |$76.5\pm 1.2$| | Gaussian (76.5, 5.0) |
| Evol. time-scale (d) | |$\theta _3$| | 500 | Fixed |
| Smoothing | |$\theta _4$| | 0.75 | Fixed |
| White noise (G) | |$\theta _5$| | |$6\pm 3$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Amplitude (G) | |$\theta _6$| | |$12^{+6}_{-4}$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Rec. period/|$P_{\rm rot}$| (d) | |$\theta _7$| | |$4.19\pm 0.16$| | Gaussian (4.2, 0.5) |
| Evol. time-scale (d) | |$\theta _8$| | 300 | Fixed |
| Smoothing | |$\theta _9$| | 0.75 | Fixed |
| Goodness of fit | |||
| Versus average | Single GP | Dual GP | |
| |$\chi ^2_{\rm r}$| | 2.29 | 1.13 | 0.76 |
| rms (G) | 23.5 | 16.5 | 13.6 |
| Parameter . | Name . | Value . | Prior . |
|---|---|---|---|
| Amplitude (G) | |$\theta _1$| | |$22^{+8}_{-6}$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Rec. period (d) | |$\theta _2$| | |$76.5\pm 1.2$| | Gaussian (76.5, 5.0) |
| Evol. time-scale (d) | |$\theta _3$| | 500 | Fixed |
| Smoothing | |$\theta _4$| | 0.75 | Fixed |
| White noise (G) | |$\theta _5$| | |$6\pm 3$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Amplitude (G) | |$\theta _6$| | |$12^{+6}_{-4}$| | Mod Jeffreys (|$\sigma _{B}$|) |
| Rec. period/|$P_{\rm rot}$| (d) | |$\theta _7$| | |$4.19\pm 0.16$| | Gaussian (4.2, 0.5) |
| Evol. time-scale (d) | |$\theta _8$| | 300 | Fixed |
| Smoothing | |$\theta _9$| | 0.75 | Fixed |
| Goodness of fit | |||
| Versus average | Single GP | Dual GP | |
| |$\chi ^2_{\rm r}$| | 2.29 | 1.13 | 0.76 |
| rms (G) | 23.5 | 16.5 | 13.6 |
We find in particular that both the 76.5-d cyclic fluctuation and the 4.2-d rotational modulation of |$B_{\rm \ell }$| increase with time over the duration of our observations (see Fig. 2). Moreover, our result already suggests that the large-scale field of V347 Aur, in addition to being weaker than that of most prototypical classical T Tauri and older PMS stars, is also more axisymmetric, with longitudinal fields keeping the same sign with rotation phase and exhibiting only marginal rotational modulation (of amplitude about twice smaller than that of the main 76.5-d fluctuation, see Table 2). We finally note that the 76.5-d fluctuation time-scale of |$B_{\rm \ell }$| is consistent with the half recurrence period of the accretion outbursts and photometric pulses reported for V347 Aur (Dahm & Hillenbrand 2020), most likely not a coincidence. We also investigated whether the outburst recurrence period itself was in fact the true period of the medium term fluctuations of |$B_{\rm \ell }$|, but found this hypothesis less probable (with |$\log {\rm BF}=-2.5$|). We come back on this point in Section 8.
5 RV ANALYSIS AND ORBITAL PARAMETERS OF V347 AUR
In the next step, we focussed on our Stokes I LSD profiles of V347 Aur, from which we extracted RVs and corresponding error bars for our 79 data points. We achieved this by describing each individual LSD profile as a simple first-order Taylor expansion constructed from the median of all LSD profiles. This approach is similar to that used in the ‘line-by-line’ technique (Artigau et al. 2022), but applied to our LSD profiles (corrected from veiling; see Section 6) rather than to individual spectral lines. In practice, we start by fitting the median LSD profile with a Gaussian, then adjust each differential LSD profile with respect to the median with a scaled version of the first derivative (with respect to velocity) of the Gaussian fit to the median LSD profile. The scaling factors directly yield the RV shifts of our observations with respect to the median LSD profile, with the corresponding error bars on the RV shifts being computed from the SNRs, the full widths at half maximum, and the EWs of the individual LSD profiles. We find this approach to be slightly more precise and stable than a straightforward Gaussian fit to our LSD profiles, thanks in particular to the cleaner continuum levels one gets by dividing each LSD profile by the median. The derived RVs, ranging from 6.8 to 9.5 km s|$^{-1}$| (median 8.6 km s|$^{-1}$|), and associated error bars (median 0.2 km s|$^{-1}$|) are listed in Table A1. We note in particular that V347 Aur is indeed RV variable, with a peak-to-peak variation exceeding 2 km s|$^{-1}$| (i.e. 10|$\times$| our median RV error bar), thereby confirming the suspicion of Dahm & Hillenbrand (2020) that it is a spectroscopic binary.
We modelled our RV data with a Keplerian function describing the orbital motion of the primary star, along with a (single) QP GP to account for the activity jitter. The orbital motion is very clearly detected, with a semi-amplitude |$K=1.05\pm 0.06$| km s|$^{-1}$| measured at a 17.5|$\sigma$| confidence level and an orbital period |${P_{\rm orb}}=154.6\pm 0.7$| d fully consistent with the estimate of Dahm & Hillenbrand (2020; also 154.6 d with no quoted error bar). Although our phase coverage of the orbit is still incomplete, we can safely claim that the orbital motion is eccentric, with an ellipticity of |$e=0.28\pm 0.12$| and a difference in |$\log {\rm BF}$| reaching 9.4 in favour of the elliptic case compared with the circular one.
The activity jitter is also clearly detected despite its semi-amplitude (0.22 km s|$^{-1}$|; see Table 3) being only slightly larger than our median error bar, the |$\log {\rm BF}$| in favour of the model including a GP reaching now 8.5 compared with that featuring no GP. Besides, this model also yields a more accurate value of |$P_{\rm rot}$| (|${P_{\rm rot}}=4.12\pm 0.03$| d) than that derived from our |$B_{\rm \ell }$| data (see Section 4), and further confirms that both |$B_{\rm \ell }$| and RV exhibit consistent rotational modulation. The results of our analysis are depicted in Fig. 3 whereas the derived parameters are listed in Table 3. We also show in Fig. 4 our RV data and inferred orbital RV curve phase-folded on the derived orbital period of 154.6 d.
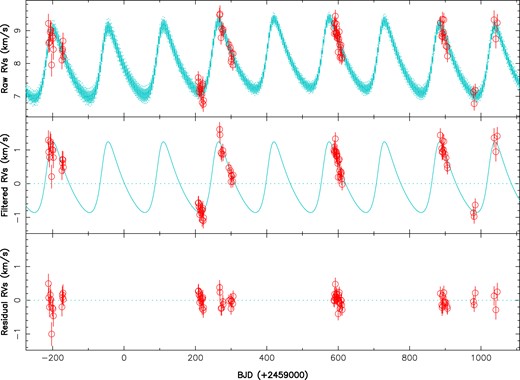
Raw (top plot), activity filtered (middle plot), and residual (bottom plot) RVs of V347 Aur (red open circles). The top plot shows the MCMC fit to the RV data, including a QP GPR modelling of the activity and the orbital motion of the primary star (cyan full line, with cyan dotted lines illustrating the 68-per cent confidence intervals), whereas the middle plot shows the orbital motion only once activity is filtered out. The rms of the RV residuals is 0.19 km s|$^{-1}$|.
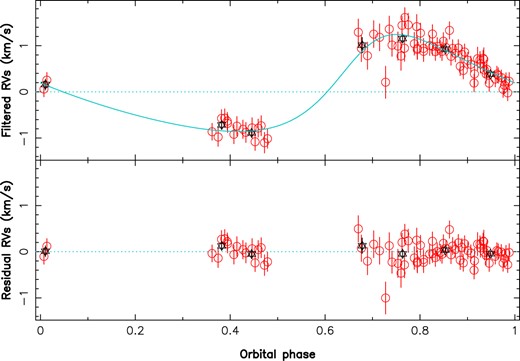
Filtered (top plot) and residual (bottom plot) RVs of V347 Aur phase-folded on the 154.6-d period. The red open circles are the individual RV points with the respective error bars, whereas the black stars are average RVs over 0.1 phase bins. As in Fig. 3, the dispersion of RV residuals is 0.19 km s|$^{-1}$|.
MCMC results of our RV analysis of V347 Aur. We list the recovered GP and orbital parameters with their error bars (with T|$_{\rm c}$| and T|$_{\rm p}$| denoting the times of inferior conjunction and periastron passage, respectively, a the semimajor axis of the orbit, and |$a_{\rm p}$| and |$a_{\rm a}$| the distances between both components at periastron and apoastron, respectively), as well as the corresponding priors whenever relevant. The last two rows give the |$\chi ^2_{\rm r}$| and the rms of the best fit to our RV data.
| Parameter . | Value . | Prior . |
|---|---|---|
| |$\theta _1$| (km s|$^{-1}$|) | |$0.22^{+0.07}_{-0.06}$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| |$\theta _2$| (d) | |$4.12\pm 0.03$| | Gaussian (4.12, 0.2) |
| |$\theta _3$| (d) | 300 | |
| |$\theta _4$| | 0.85 | |
| |$\theta _5$| (km s|$^{-1}$|) | |$0.08\pm 0.06$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| K (km s|$^{-1}$|) | |$1.05\pm 0.06$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| |$P_{\rm orb}$| (d) | |$154.6\pm 0.7$| | Gaussian (155, 5) |
| T|$_{\rm c}$| (2459000+) | |$457.5\pm 3.0$| | Gaussian (458, 10) |
| T|$_{\rm p}$| (2459000+) | |$408.0\pm 4.2$| | From orbital elements |
| |$\sqrt{e}\cos \omega$| | |$0.33\pm 0.08$| | Gaussian (0, 1) |
| |$\sqrt{e}\sin \omega$| | |$-0.42\pm 0.12$| | Gaussian (0, 1) |
| e | |$0.28\pm 0.12$| | From |$\sqrt{e}\cos \omega$| and |$\sqrt{e}\sin \omega$| |
| |$\omega$| (rad) | |$-0.91\pm 0.18$| | From |$\sqrt{e}\cos \omega$| and |$\sqrt{e}\sin \omega$| |
| |$M_b \sin i$| (|${\rm M}_{2\!\!_{\mathbf +} }$|) | |$12.7\pm 0.7$| | From K, |$P_{\rm orb}$| and |$M_{\star }$| |
| |$M_b$| (|${\rm M}_{2\!\!_{\mathbf +} }$|) | |$29.0\pm 1.6$| | From |$M_b \sin i$| and i |
| a (au) | |$0.39\pm 0.02$| | From |$P_{\rm orb}$|, |$M_{\star }$| and e |
| |$a_{\rm p}$| (au) | |$0.28\pm 0.05$| | From a and e |
| |$a_{\rm a}$| (au) | |$0.50\pm 0.05$| | From a and e |
| |$\chi ^2_{\rm r}$| | 0.93 | |
| rms (km s|$^{-1}$|) | 0.19 |
| Parameter . | Value . | Prior . |
|---|---|---|
| |$\theta _1$| (km s|$^{-1}$|) | |$0.22^{+0.07}_{-0.06}$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| |$\theta _2$| (d) | |$4.12\pm 0.03$| | Gaussian (4.12, 0.2) |
| |$\theta _3$| (d) | 300 | |
| |$\theta _4$| | 0.85 | |
| |$\theta _5$| (km s|$^{-1}$|) | |$0.08\pm 0.06$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| K (km s|$^{-1}$|) | |$1.05\pm 0.06$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| |$P_{\rm orb}$| (d) | |$154.6\pm 0.7$| | Gaussian (155, 5) |
| T|$_{\rm c}$| (2459000+) | |$457.5\pm 3.0$| | Gaussian (458, 10) |
| T|$_{\rm p}$| (2459000+) | |$408.0\pm 4.2$| | From orbital elements |
| |$\sqrt{e}\cos \omega$| | |$0.33\pm 0.08$| | Gaussian (0, 1) |
| |$\sqrt{e}\sin \omega$| | |$-0.42\pm 0.12$| | Gaussian (0, 1) |
| e | |$0.28\pm 0.12$| | From |$\sqrt{e}\cos \omega$| and |$\sqrt{e}\sin \omega$| |
| |$\omega$| (rad) | |$-0.91\pm 0.18$| | From |$\sqrt{e}\cos \omega$| and |$\sqrt{e}\sin \omega$| |
| |$M_b \sin i$| (|${\rm M}_{2\!\!_{\mathbf +} }$|) | |$12.7\pm 0.7$| | From K, |$P_{\rm orb}$| and |$M_{\star }$| |
| |$M_b$| (|${\rm M}_{2\!\!_{\mathbf +} }$|) | |$29.0\pm 1.6$| | From |$M_b \sin i$| and i |
| a (au) | |$0.39\pm 0.02$| | From |$P_{\rm orb}$|, |$M_{\star }$| and e |
| |$a_{\rm p}$| (au) | |$0.28\pm 0.05$| | From a and e |
| |$a_{\rm a}$| (au) | |$0.50\pm 0.05$| | From a and e |
| |$\chi ^2_{\rm r}$| | 0.93 | |
| rms (km s|$^{-1}$|) | 0.19 |
MCMC results of our RV analysis of V347 Aur. We list the recovered GP and orbital parameters with their error bars (with T|$_{\rm c}$| and T|$_{\rm p}$| denoting the times of inferior conjunction and periastron passage, respectively, a the semimajor axis of the orbit, and |$a_{\rm p}$| and |$a_{\rm a}$| the distances between both components at periastron and apoastron, respectively), as well as the corresponding priors whenever relevant. The last two rows give the |$\chi ^2_{\rm r}$| and the rms of the best fit to our RV data.
| Parameter . | Value . | Prior . |
|---|---|---|
| |$\theta _1$| (km s|$^{-1}$|) | |$0.22^{+0.07}_{-0.06}$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| |$\theta _2$| (d) | |$4.12\pm 0.03$| | Gaussian (4.12, 0.2) |
| |$\theta _3$| (d) | 300 | |
| |$\theta _4$| | 0.85 | |
| |$\theta _5$| (km s|$^{-1}$|) | |$0.08\pm 0.06$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| K (km s|$^{-1}$|) | |$1.05\pm 0.06$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| |$P_{\rm orb}$| (d) | |$154.6\pm 0.7$| | Gaussian (155, 5) |
| T|$_{\rm c}$| (2459000+) | |$457.5\pm 3.0$| | Gaussian (458, 10) |
| T|$_{\rm p}$| (2459000+) | |$408.0\pm 4.2$| | From orbital elements |
| |$\sqrt{e}\cos \omega$| | |$0.33\pm 0.08$| | Gaussian (0, 1) |
| |$\sqrt{e}\sin \omega$| | |$-0.42\pm 0.12$| | Gaussian (0, 1) |
| e | |$0.28\pm 0.12$| | From |$\sqrt{e}\cos \omega$| and |$\sqrt{e}\sin \omega$| |
| |$\omega$| (rad) | |$-0.91\pm 0.18$| | From |$\sqrt{e}\cos \omega$| and |$\sqrt{e}\sin \omega$| |
| |$M_b \sin i$| (|${\rm M}_{2\!\!_{\mathbf +} }$|) | |$12.7\pm 0.7$| | From K, |$P_{\rm orb}$| and |$M_{\star }$| |
| |$M_b$| (|${\rm M}_{2\!\!_{\mathbf +} }$|) | |$29.0\pm 1.6$| | From |$M_b \sin i$| and i |
| a (au) | |$0.39\pm 0.02$| | From |$P_{\rm orb}$|, |$M_{\star }$| and e |
| |$a_{\rm p}$| (au) | |$0.28\pm 0.05$| | From a and e |
| |$a_{\rm a}$| (au) | |$0.50\pm 0.05$| | From a and e |
| |$\chi ^2_{\rm r}$| | 0.93 | |
| rms (km s|$^{-1}$|) | 0.19 |
| Parameter . | Value . | Prior . |
|---|---|---|
| |$\theta _1$| (km s|$^{-1}$|) | |$0.22^{+0.07}_{-0.06}$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| |$\theta _2$| (d) | |$4.12\pm 0.03$| | Gaussian (4.12, 0.2) |
| |$\theta _3$| (d) | 300 | |
| |$\theta _4$| | 0.85 | |
| |$\theta _5$| (km s|$^{-1}$|) | |$0.08\pm 0.06$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| K (km s|$^{-1}$|) | |$1.05\pm 0.06$| | Mod Jeffreys (|$\sigma _{\rm RV}$|) |
| |$P_{\rm orb}$| (d) | |$154.6\pm 0.7$| | Gaussian (155, 5) |
| T|$_{\rm c}$| (2459000+) | |$457.5\pm 3.0$| | Gaussian (458, 10) |
| T|$_{\rm p}$| (2459000+) | |$408.0\pm 4.2$| | From orbital elements |
| |$\sqrt{e}\cos \omega$| | |$0.33\pm 0.08$| | Gaussian (0, 1) |
| |$\sqrt{e}\sin \omega$| | |$-0.42\pm 0.12$| | Gaussian (0, 1) |
| e | |$0.28\pm 0.12$| | From |$\sqrt{e}\cos \omega$| and |$\sqrt{e}\sin \omega$| |
| |$\omega$| (rad) | |$-0.91\pm 0.18$| | From |$\sqrt{e}\cos \omega$| and |$\sqrt{e}\sin \omega$| |
| |$M_b \sin i$| (|${\rm M}_{2\!\!_{\mathbf +} }$|) | |$12.7\pm 0.7$| | From K, |$P_{\rm orb}$| and |$M_{\star }$| |
| |$M_b$| (|${\rm M}_{2\!\!_{\mathbf +} }$|) | |$29.0\pm 1.6$| | From |$M_b \sin i$| and i |
| a (au) | |$0.39\pm 0.02$| | From |$P_{\rm orb}$|, |$M_{\star }$| and e |
| |$a_{\rm p}$| (au) | |$0.28\pm 0.05$| | From a and e |
| |$a_{\rm a}$| (au) | |$0.50\pm 0.05$| | From a and e |
| |$\chi ^2_{\rm r}$| | 0.93 | |
| rms (km s|$^{-1}$|) | 0.19 |
The inferred minimum mass for the companion is equal to |$M_b \sin i=12.7\pm 0.7$||${\rm M}_{2\!\!_{\mathbf +} }$|, at the limit between the planet and brown dwarf domain. If we further assume that the companion orbits within the equatorial plane of the star (presumably coinciding with the plane of the accretion disc) we end up with a companion mass of |$M_b=29.0\pm 1.6$||${\rm M}_{2\!\!_{\mathbf +}}$| and a mass ratio q of the system equal to |$q=0.009\pm 0.003$|. This makes the companion a bona fide brown dwarf, orbiting V347 Aur with a semimajor axis |$a=0.39\pm 0.02$| au, and with periastron and apoastron distances equal to |$a_{\rm p}=0.28\pm 0.05$| au and |$a_{\rm a}=0.50\pm 0.05$| au, respectively.
6 ZDI OF V347 AUR
We then analysed the Stokes I and V LSD signatures of V347 Aur using ZDI, to investigate the large-scale magnetic topology of V347 Aur and its evolution with time over the duration of our observations. As ZDI usually works with the assumption that the observed variability mostly relates to rotational modulation, and given that the longitudinal field of V347 Aur was found to also fluctuate with a period longer than |$P_{\rm rot}$| (|$76.5\pm 1.2$| d; see Section 4), we chose to decompose our full data set into seven subsets, respectively, including observations from 2019 October–December (14 spectra), 2020 December–2021 January (13 spectra), 2021 February–April (13 spectra), 2022 January (22 spectra), 2022 November (11 spectra), 2023 February (three spectra), and 2023 April (three spectra), each lasting 5–10 rotation cycles (except for the two final ones lasting only 1–2 rotation cycles). Obviously, the last two subsets do not include enough observations to yield fully reliable ZDI images, but we none the less chose to analyse them as such, keeping in mind the limitations associated with the sparse coverage. These separate subsets also correspond to different phases of the orbital cycle of V347 Aur (see Section 5), thereby allowing us to study how the large-scale field evolves on the previously mentioned time-scales.
The ZDI code used here, already applied several times to SPIRou Stokes V data sets of T Tauri stars (e.g. Finociety et al. 2021, 2023; Donati et al. 2024a, b; Zaire et al. 2024), allows one to reconstruct the topology of the large-scale field at the surface of a star from phase-resolved sets of Stokes V LSD profiles. This is achieved with an iterative process that progressively adds information at the surface of the star, starting from a small magnetic seed and exploring the parameter space in order to minimize the discrepancy between observed and synthetic data (e.g. Brown et al. 1991; Donati & Brown 1997; Donati et al. 2006). As this problem is ill posed, regularization is required to ensure a unique solution. ZDI uses the principles of maximum entropy image reconstruction (Skilling & Bryan 1984) to reach a given agreement with the data, usually |${\chi ^2_{\rm r}}\simeq 1$|, with the minimum amount of information in the reconstructed image.
Technically speaking, the surface of the star is modelled as a grid of 5000 cells. We then compute the spectral contributions of each grid cell, using Unno–Rachkovsky’s analytical solution of the polarized radiative transfer equation in a plane-parallel Milne Eddington atmosphere (Landi degl’Innocenti & Landolfi 2004), and assuming a Landé factor, average wavelength, and Doppler width of 1.2, 1750 nm, and 3 km s|$^{-1}$| for the local profile (as in our previous studies). We then sum up the contributions of all grid cells, taking into account the star and cell characteristics and assuming the star rotates as a solid body, to derive the synthetic profiles at the observed phases of the rotation cycle. The magnetic field at the surface of the star is expressed as a spherical harmonic expansion, using the formalism of Donati et al. (2006; see also Finociety & Donati 2022; Lehmann & Donati 2022; Donati et al. 2023a) in which the poloidal and toroidal components of the vector field depend on three sets of complex spherical harmonic coefficients, |$\alpha _{\ell ,m}$| and |$\beta _{\ell ,m}$| for the poloidal component, and |$\gamma _{\ell ,m}$| for the toroidal component, where |$\ell$| and m note the degree and order of the corresponding spherical harmonic term in the expansion. Given the moderate |$v \sin i$| of V347 Aur and the weak detected magnetic signatures (see Section 4), the spherical harmonic expansion is limited to terms up to |$\ell =5$|.
Before applying ZDI, we started by re-centring the Stokes I and V LSD profiles from the orbital motion outlined in Section 5. Moreover, as spectra of V347 Aur are subject to veiling as a result of accretion (see Section 7), we corrected all Stokes I profiles by normalizing them to the same EW, and applied the derived scaling factors to the corresponding Stokes V profiles as well. Since intrinsic variability induced by variable accretion causes the normalized Stokes I profiles to feature random distortions that ZDI is not able to easily reproduce, we chose not to attempt modelling them and only ensured that the median Stokes I profile of each subset is consistent with the median synthetic profile of our model. This modelling yielded in particular an estimate of |$v \sin i$|, found to be equal to |${v \sin i}=12.0\pm 0.5$| km s|$^{-1}$| (in agreement with Flores et al. 2019). We then ran ZDI on each subset of Stokes V profiles to reconstruct the large-scale magnetic topology at each epoch. The corresponding fits to the Stokes V profiles, matched at a level of |${\chi ^2_{\rm r}}\simeq 1$|, are shown in Fig. 5 for our seven subsets, whereas the reconstructed magnetic maps are depicted in Figs 6 and 7.
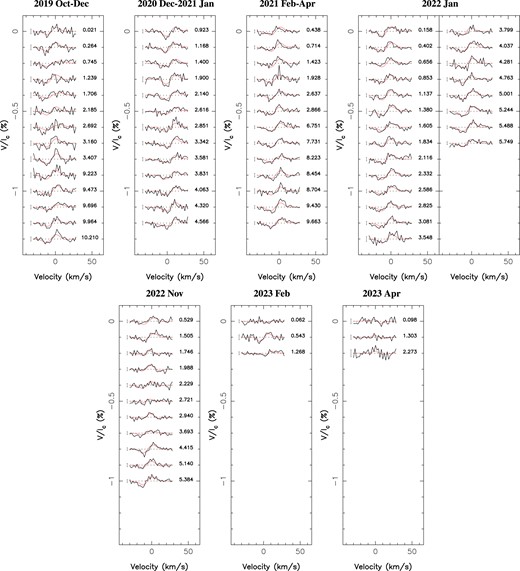
Observed (thick black line) and modelled (thin red line) LSD Stokes V profiles of V347 Aur in the stellar rest frame, for the first four subsets (top row, corresponding to 2019 October–December, 2020 December–2021 January, 2021 February–April, and 2022 January, respectively) and the last three subsets (bottom row, corresponding to 2022 November, 2023 February, and 2023 April, respectively). Observed profiles, obtained by applying LSD to SPIRou spectra (using the atomic line mask outlined in Section 3), were corrected for the orbital motion described in Section 5 and the veiling outlined in Section 7. Note how the Stokes V profiles of each subset are, on average, either blue or redshifted with respect to the line centre, indicating the presence of a strong toroidal field (see text). Rotation cycles (counting from 0, 101, 116, 194, 266, 289, and 303 for subsets #1 to #7, respectively, see Table A1) are indicated to the right of all LSD profiles, while |$\pm 1\sigma$| error bars are added to the left of each profile.
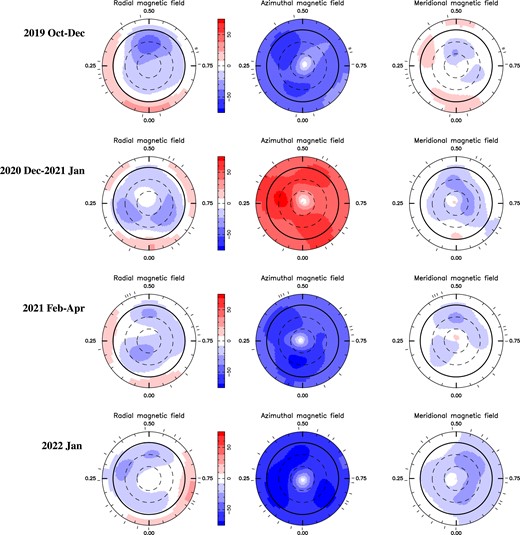
Reconstructed maps of the large-scale field of V347 Aur (left, middle, and right columns for the radial, azimuthal, and meridional components in spherical coordinates, in G), for our first four data subsets (top to bottom rows) derived with ZDI from the Stokes V LSD profiles of Fig. 5. The maps are shown in a flattened polar projection down to latitude |$-30$||$^\circ$|, with the north pole at the centre and the equator depicted as a bold line. Outer ticks indicate phases of observations. Positive radial, azimuthal, and meridional fields, respectively, point outwards, counterclockwise, and polewards.

Same as Fig. 6 for our last three data subsets. Note the limited phase coverage for the last two maps, especially the last one, rendering them much less reliable than the others.
As already pointed out above (see Section 4), we find that the reconstructed large-scale field of V347 Aur is quite weak for such a young active star, with an average strength of only about 50 G (compared with 0.8–1.1 kG for CI Tau and TW Hya; Donati et al. 2024a, b). Another surprise is that the derived large-scale field is mostly toroidal, with the poloidal component gathering only |$\simeq$|20 per cent of the reconstructed magnetic energy (except at the last two epochs, especially the last one, where phase coverage is limited and for which the maps are much less reliable). This dominant toroidal field directly reflects that the average Zeeman signature over each subset is significantly shifted with respect to the line centre (see e.g. Donati et al. 2005; Lehmann & Donati 2022). This is especially obvious in the first five subsets where phase coverage is reasonably even, and for which the shift of the Stokes V signatures with respect to the line centre reaches about |$+$|5 km s|$^{-1}$| (in subset #2) and |$-$|5 km s|$^{-1}$| (in all others; see Fig. 5).
The dipole component of the large-scale field stores 60–85 per cent of the poloidal field energy, with a polar strength of only about 30 G. The poloidal field is mainly axisymmetric for the first four epochs (up to 2022 January), but starts to significantly evolve in 2022 November, i.e. when the modulus of the average longitudinal field progressively weakens (see Fig. 2) and the dipole field gets highly tilted to the rotation axis. The dominant toroidal field is mostly axisymmetric at all times. Moreover, it switches from negative to positive polarity between the first and second subsets (with the mean Zeeman signature shifting from the blue wing to the red wing of the line profile; see Fig. 5) then switches sign again between the second and the third subsets. It may do it one more time between the fifth and sixth subsets, although the sparse phase coverage of the last two epochs (and especially the last one covering less than a fourth of the rotation cycle) makes the latter conclusion far less firm. The derived properties of the large-scale field for each subset are summarized in Table 4.
Properties of the large-scale magnetic field of V347 Aur for our seven data subsets. We list the average reconstructed large-scale field strength |$\langle B_V \rangle$| (column 2), the polar strength of the dipole component |$B_{\rm d}$| (column 3), the tilt of the dipole field to the rotation axis and the phase towards which it is tilted (column 4), and the amount of magnetic energy reconstructed in the poloidal component of the field and in the axisymmetric modes of this component (column 5). Error bars are typically equal to 5–10 per cent for field strengths and percentages, and 5–10|$^\circ$| for field inclinations, for the first five subsets, and at least twice worse for the last two (for which ZDI is less reliable given the sparse phase coverage).
| Data subset . | |$\langle B_V \rangle$| . | |$B_{\rm d}$| . | Tilt/phase . | Poloidal/axisym . |
|---|---|---|---|---|
| . | (G) . | (G) . | (|$^\circ$|) . | (per cent) . |
| 2019 Oct–Dec | 49 | 35 | 27/0.54 | 22/71 |
| 2020 Dec–2021 Jan | 54 | 27 | 7/0.12 | 17/82 |
| 2021 Feb–Apr | 52 | 23 | 13/0.71 | 11/76 |
| 2022 Jan | 62 | 21 | 35/0.31 | 10/81 |
| 2022 Nov | 48 | 31 | 77/0.44 | 20/23 |
| 2023 Feb | 37 | 33 | 65/0.49 | 48/19 |
| 2023 Apr | 21 | 23 | 74/0.01 | 70/8 |
| Data subset . | |$\langle B_V \rangle$| . | |$B_{\rm d}$| . | Tilt/phase . | Poloidal/axisym . |
|---|---|---|---|---|
| . | (G) . | (G) . | (|$^\circ$|) . | (per cent) . |
| 2019 Oct–Dec | 49 | 35 | 27/0.54 | 22/71 |
| 2020 Dec–2021 Jan | 54 | 27 | 7/0.12 | 17/82 |
| 2021 Feb–Apr | 52 | 23 | 13/0.71 | 11/76 |
| 2022 Jan | 62 | 21 | 35/0.31 | 10/81 |
| 2022 Nov | 48 | 31 | 77/0.44 | 20/23 |
| 2023 Feb | 37 | 33 | 65/0.49 | 48/19 |
| 2023 Apr | 21 | 23 | 74/0.01 | 70/8 |
Properties of the large-scale magnetic field of V347 Aur for our seven data subsets. We list the average reconstructed large-scale field strength |$\langle B_V \rangle$| (column 2), the polar strength of the dipole component |$B_{\rm d}$| (column 3), the tilt of the dipole field to the rotation axis and the phase towards which it is tilted (column 4), and the amount of magnetic energy reconstructed in the poloidal component of the field and in the axisymmetric modes of this component (column 5). Error bars are typically equal to 5–10 per cent for field strengths and percentages, and 5–10|$^\circ$| for field inclinations, for the first five subsets, and at least twice worse for the last two (for which ZDI is less reliable given the sparse phase coverage).
| Data subset . | |$\langle B_V \rangle$| . | |$B_{\rm d}$| . | Tilt/phase . | Poloidal/axisym . |
|---|---|---|---|---|
| . | (G) . | (G) . | (|$^\circ$|) . | (per cent) . |
| 2019 Oct–Dec | 49 | 35 | 27/0.54 | 22/71 |
| 2020 Dec–2021 Jan | 54 | 27 | 7/0.12 | 17/82 |
| 2021 Feb–Apr | 52 | 23 | 13/0.71 | 11/76 |
| 2022 Jan | 62 | 21 | 35/0.31 | 10/81 |
| 2022 Nov | 48 | 31 | 77/0.44 | 20/23 |
| 2023 Feb | 37 | 33 | 65/0.49 | 48/19 |
| 2023 Apr | 21 | 23 | 74/0.01 | 70/8 |
| Data subset . | |$\langle B_V \rangle$| . | |$B_{\rm d}$| . | Tilt/phase . | Poloidal/axisym . |
|---|---|---|---|---|
| . | (G) . | (G) . | (|$^\circ$|) . | (per cent) . |
| 2019 Oct–Dec | 49 | 35 | 27/0.54 | 22/71 |
| 2020 Dec–2021 Jan | 54 | 27 | 7/0.12 | 17/82 |
| 2021 Feb–Apr | 52 | 23 | 13/0.71 | 11/76 |
| 2022 Jan | 62 | 21 | 35/0.31 | 10/81 |
| 2022 Nov | 48 | 31 | 77/0.44 | 20/23 |
| 2023 Feb | 37 | 33 | 65/0.49 | 48/19 |
| 2023 Apr | 21 | 23 | 74/0.01 | 70/8 |
We note in particular that the toroidal field apparently switches sign as V347 Aur goes through periastron (between the second and third subsets), and again once it crosses apoastron (between the fifth and sixth subsets, and between the first and second; see Figs 3, 6, and 7). The expected sign switch between our penultimate and last subsets, coinciding again with V347 Aur passing through periastron, does not show up in our reconstructed images, presumably because of the very poor phase coverage of our last subset, and possibly due to the large-scale field evolving on a longer time-scale towards the end of our observations (with a longitudinal field getting closer to zero at this epoch; see Fig. 2).
We also note that, in contrast with the toroidal field apparently switching sign with the orbital period, the poloidal field and its dominant dipole component do not exhibit similar polarity switches, at least not with the same period. The increase in both the dipole tilt and the fractional poloidal field energy stored in non-axisymmetric components that we see towards the end of our observations rather suggests that the poloidal field only switches sign on a time-scale longer than that of our campaign. Similarly, we see no obvious change in the properties of the reconstructed large-scale field that correlates with the 76.5-d fluctuation of |$B_{\rm \ell }$| (see Section 4), apart from the one associated with the toroidal field polarity switches (apparently occurring on a twice longer period). We stress however that the temporal sampling of our seven maps is likely too sparse to precisely document the evolution of the magnetic topology, and in particular of its poloidal component, with the 76.5-d period. We speculate that the 76.5-d fluctuation of |$B_{\rm \ell }$|, mostly sensitive to the poloidal field, actually reflects a forced periodic oscillation of this field component about a non-zero value, likely triggered by the orbital motion, and that a denser monitoring of V347 Aur is required for it to show up more convincingly on ZDI images.
7 VEILING AND EMISSION LINES OF V347 AUR
To complete this analysis, we investigated accretion proxies of V347 Aur, through the veiling of photospheric lines and the profiles of well-known nIR emission lines, i.e. the 1083.3-nm He i triplet, the 1282.16-nm Pa|${\beta }$| line, and the 2166.12-nm Br|${\gamma }$| line.
To measure veiling, we compared LSD profiles of V347 Aur with those of TWA 10, a weak-line T Tauri star of similar temperature (but different |$\log g$|) also monitored with SPIRou. We derived the veiling estimates |$r_{JH}$| from LSD profiles of atomic lines, and |$r_K$| from LSD profiles of the CO bandhead lines (see Section 3). In both cases, veiling estimates were derived by comparing the EWs of each LSD profile of V347 Aur with the corresponding median LSD profile of TWA 10, EWs being measured through standard Gaussian fits. The resulting values of |$r_{JH}$| and |$r_K$| are listed in Table A1 and shown in Fig. C1 in Appendix C. We find that |$r_{JH}$| ranges from 0.0 to 0.92, with a median of 0.26, an average of 0.29, and an rms of 0.17, whereas |$r_K$| ranges from 0.1 to 5.1, with a median of 0.73, an average of 1.00, and an rms of 0.81. We also find that |$r_K$| is well correlated (|$R\simeq 0.8$|) with, and on average 2.9|$\times$| stronger than, |$r_{JH}$|. Our estimates are consistent with those of Sousa et al. (2023), derived from a subset of the same SPIRou spectra (with a different method).
We analysed the temporal variations of |$r_{JH}$| using the same approach as that used for |$B_{\rm \ell }$|, i.e. a QP GPR fit coupled to an MCMC process to derive the optimal hyperparameters describing the time series (see Section 4). The derived model, shown in Fig. 8, exhibits peaks occurring with a period of |$156\pm 6$| d, consistent within error bars with the orbital period of V347 Aur derived from our RV analysis (|${P_{\rm orb}}=154.6\pm 0.7$| d; see Table 3). These peaks (e.g. the one at BJD |$\simeq 2459405$|) coincide with the periastron passage of V347 Aur as derived from our RV analysis (predicting |$T_{\rm p}=2459408.0\pm 4.2$|; see Table 3). We note that the veiling maxima feature unequal strengths (by up to a factor of 2 in our case), qualitatively similar to what was reported for photometric maxima and interpreted as irregular pulsed-accretion events triggered by the orbital motion and occurring close to periastron passage (Dahm & Hillenbrand 2020). Apparently, the two strongest such events in our data set, which at least partly sampled five of these maxima, occurred near the beginning and end of our observations. We also note that |$r_{JH}$| can go down to 0 between two accretion peaks.
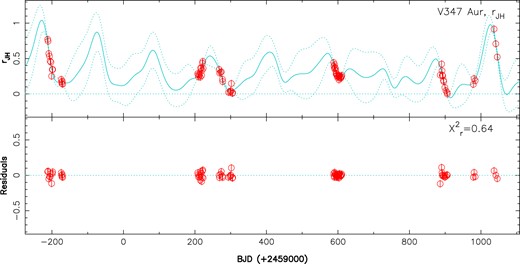
Veiling in |$JH$| bands |$r_{JH}$| of V347 Aur (top plot), as measured from LSD profiles of atomic lines (red open circles), and QP GPR fit to the data (cyan full line) with corresponding 68-per cent confidence intervals (cyan dotted lines). The residuals are shown in the bottom plot.
Both Pa|${\beta }$| and Br|${\gamma }$| are in emission at all times (see upper panels of Fig. 9). Before scaling with veiling, EWs vary by a factor of 4–5|$\times$| throughout our monitoring campaign, scale moderately well with |$r_{JH}$| and |$r_K$| (|$R\simeq 0.5$|) and range from 61 to 249 km s|$^{-1}$| with a median of 130 km s|$^{-1}$| (0.26–1.07 nm, median 0.56 nm) for Pa|${\beta }$| and from 14 to 58 km s|$^{-1}$| with a median of 31 km s|$^{-1}$| (0.10–0.42 nm, median 0.22 nm) for Br|${\gamma }$| (see Table A1). Once scaled up with veiling, EWs reach up to 441 and 254 km s|$^{-1}$| (1.89 and 1.84 nm) for Pa|${\beta }$| and Br|${\gamma }$|, respectively, and their temporal variations, mimicking those of |$r_{JH}$| and |$r_K$|, exhibit irregular peaks every |$157\pm 7$| d (again consistent with |$P_{\rm orb}$|) coinciding with periastron passage. The two-dimensional (2D) periodograms of both lines, shown in the lower panels of Fig. 9, exhibit clear peaks at |$P_{\rm orb}$| and at the first and second harmonics (not shown). The periodograms also indicate that Pa|${\beta }$| and Br|${\gamma }$| vary as a whole with |$P_{\rm orb}$|, with no obvious substructure exhibiting a different pattern than their EWs. In particular, we see no signal at |$P_{\rm rot}$| in either lines that remains consistent over the full duration of our observations, and especially no redshifted absorption events probing disc material accreted along magnetic funnels to high-latitude regions at the surface of the star (as in prototypical classical T Tauri stars).
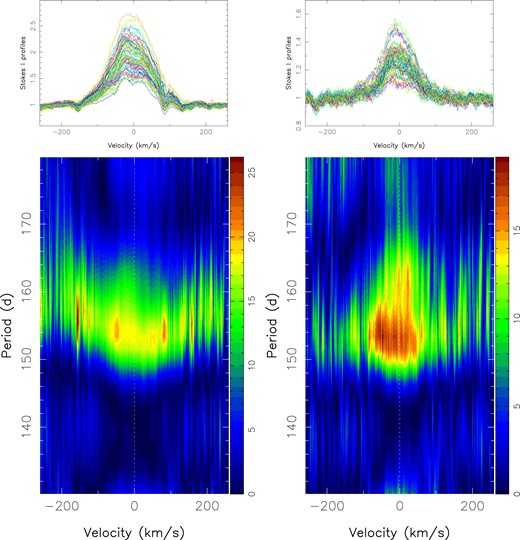
Stacked Stokes I profiles (top row) and 2D periodograms (bottom row) of the 1282.16-nm Pa|${\beta }$| line (left column) and the 2166.12-nm Br|${\gamma }$| line (right column) of V347 Aur, in the stellar rest frame, for our complete data set. The colour scale depicts the logarithmic power of the periodogram.
To derive logarithmic mass accretion rates |${\rm log}\,\, {\dot{M}}$|, we scaled the veiling corrected EWs of Pa|${\beta }$| and Br|${\gamma }$| by the theoretical flux continuum of the appropriate stellar model to obtain line fluxes (in |${\rm L}_{\odot }$|), then used the tabulated relations of Alcalá et al. (2017) to translate these lines fluxes into accretion luminosities, and finally applied the analytical relation of Gullbring et al. (1998) giving mass accretion rates as a function of accretion luminosities and stellar parameters. The log |${\dot{M}}$| values that we obtain range from |$-8.8$| to |$-8.0$| (median |$-8.5$|, in |${\rm M}_{\odot }$| yr|$^{-1}$|) for Pa|${\beta }$| and from |$-9.2$| to |$-7.8$| (median |$-8.7$|) for Br|${\gamma }$|, with both independent estimates agreeing well together. The peak accretion rates we infer are much weaker than those quoted in Dahm & Hillenbrand (2020), reflecting that the accretion outbursts we monitored during our campaign are far less extreme than the mammoth event at BJD |$\simeq 2458435$| described by Dahm & Hillenbrand (2020), with V band photometry rising by up to |$\simeq$|5.5 mag. Archival AAVSO,1 ASAS-SN (Kochanek et al. 2017), and ZTF (Bellm et al. 2019) photometry (see Fig. 10) indeed confirm that this is the case, with V photometry rising by less than |$\simeq$|1.5 magnitudes during our SPIRou observations (which missed the main brightness peak at BJD |$\simeq 2459526$| in this time slot). The brightest event simultaneously monitored with ASAS-SN and SPIRou occurred at the beginning of our time series, and reached a brightness of only 2.4 per cent that of the largest outburst at BJD |$\simeq 2458435$|. Attributing these brightness variations to changes in the accretion luminosity and extrapolating from our log |${\dot{M}}$| measurements would imply a peak log |${\dot{M}}\simeq -6.2$| (in |${\rm M}_{\odot }$| yr|$^{-1}$|) for the strongest accretion events of V347 Aur, an estimate that is consistent with that of Dahm & Hillenbrand (2020). The lowest accretion rates we infer from our data set log (|${\dot{M}}\simeq -9.0$| in |${\rm M}_{\odot }$| yr|$^{-1}$|) correspond to orbital phases away from the periastron and to periods of weak (and sometimes even null) veiling, both suggesting that accretion outside of the pulsed events is quite low and therefore that the central regions of the accretion disc are likely depleted in V347 Aur compared with prototypical single PMS stars. Besides, we find that the periodogram of the archival photometric data over the last 11 yr peaks at 154.7 d, in perfect agreement with our determination of the orbital period of V347 Aur (see Table 3).
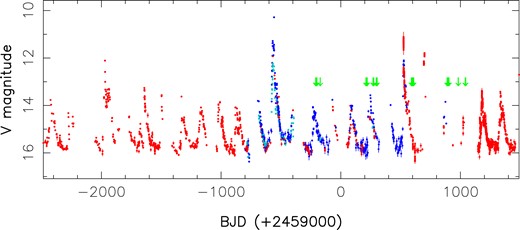
AAVSO, ASAS-SN, and ZTF photometry of V347 Aur over the last 11 yr. Measurements in the V (AAVSO, ASAS-SN), G (ASAS-SN, ZTF), and R (ZTF) bands are depicted as red, blue, and cyan dots (with G and R band data corrected by |$-1.0$| and |$+1.05$| mag, respectively, to match V band data). BJDs of our SPIRou spectra are depicted with green arrows. The periodogram of these photometric data (not shown) peaks at 154.7 d, fully consistent with our estimate of the orbital period (see Table 3).
We finally note that the 1083.3-nm He i triplet shows a P Cygni profile with a blueshifted absorption component extending to |$-300$| km s|$^{-1}$| (and sometimes even |$-400$| km s|$^{-1}$|) that suggests the presence of a strong stellar wind, rather than that of a conical disc wind which would be unable to intersect our line of sight to the star (given the inclination angle i and assuming a disc aligned with the equatorial plane of the star; Kwan, Edwards & Fischer 2007). The He i profile also features a slightly redshifted emission peak varying in strength by over an order of magnitude (see top panel of Fig. 11) and extending up to about 100 km s|$^{-1}$|, probing ongoing accretion. The 2D periodogram, depicted in the bottom panel of Fig. 11 indicates that only the bluest wing (beyond –100 km s|$^{-1}$|) is modulated with the orbital period, as a likely response of the accretion-powered stellar wind to the QP accretion events. Although not the strongest signal in the 2D periodogram, this modulation is none the less clearly detected, reaching powers similar to those associated with the Pa|${\beta }$| and Br|${\gamma }$| emission peaks in their 2D periodograms (see Fig. 9). Surprisingly, the emission component redwards of the line centre is not periodically modulated, even at shorter periods, suggesting longitudinally distributed (rather than localized) accretion, whereas the sharp transition between the absorption and emission components (between –100 and the line centre) is modulated with a longer period of |$\simeq$|173 d for unclear reasons (the weaker feature at 140 d being an alias of the main one). As for Pa|${\beta }$| and Br|${\gamma }$|, we see no evidence of a consistent signal at |$P_{\rm rot}$|, be it in the blueshifted absorption or in the emission components. We finally note that the median He i profile shows a conspicuous Zeeman signature slightly blueshifted with respect to the line centre (see Fig. 12), confirming that some of the emission comes from accretion regions at the stellar surface, and that the axisymmetric component of the magnetic topology in these accretion regions is complex (rather than unipolar, as in e.g. TW Hya; Donati et al. 2024b).

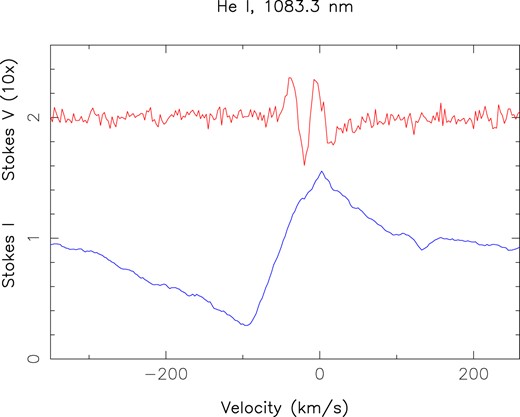
Weighted-average Stokes I (blue) and V (red) LSD profiles of the 1083.3-nm He i line of V347 Aur over our full data set. Zeeman signatures are clearly detected in conjunction with the emission peak. The Stokes V LSD profile is expanded by a factor of 10|$\times$| and shifted upwards by 2.
8 SUMMARY AND DISCUSSION
We carried out a spectropolarimetric and velocimetric monitoring study of the |$\simeq$|0.8-Myr low-mass protostar V347 Aur (|${M_{\star }}=0.33\pm 0.05$||${\rm M}_{\odot }$|; see Section 2) with SPIRou at CFHT in the framework of the SLS and SPICE Large Programmes, and collected 79 validated nIR Stokes I and V spectra of this object over a time frame of 1258 d covering four main seasons (from 2019 October to 2023 April).
We find that V347 Aur is a spectroscopic binary with a brown dwarf companion, orbiting on an eccentric trajectory of period |${P_{\rm orb}}=154.6\pm 0.7$| d and semimajor axis |$a=0.39\pm 0.02$| au, and generating an RV wobble of semi-amplitude |$K=1.05\pm 0.06$| km s|$^{-1}$|. The corresponding minimum mass of the companion is equal to |$M_b \sin i=12.7\pm 0.7$||${\rm M}_{2\!\!_{\mathbf +}}$|, implying a mass of |$M_b=29.0\pm 1.6$||${\rm M}_{2\!\!_{\mathbf +}}$| assuming the companion orbits within the equatorial plane of the star (inclined at |$i=26\pm 5$||$^\circ$| to the line of sight). It classifies V347 Aur b as a bona fide brown dwarf, making it a rare member of the brown dwarf desert of companions around low-mass stars (Marcy & Butler 2000), and in particular around M dwarfs for which there is relatively few close substellar companions (Artigau et al. 2021). The derived eccentricity, equal to |$e=0.28\pm 0.12$|, is reminiscent of that reported for warm Jupiters, which may result from gravitational interactions with accretion discs featuring inner cavities (Debras, Baruteau & Donati 2021). No such inner cavity has yet been reported for V347 Aur, but the low accretion rates measured over most of the orbital motion suggest that there may indeed be one (see below). As previously reported in Dahm & Hillenbrand (2020), we observe enhanced accretion episodes on V347 Aur, which we find are occurring as the companion reaches periastron, likely triggering gravitational instabilities in the disc leading to pulsed accretion on to the primary star. We speculate that this process may be auto-amplifying, with the eccentric motion of the companion progressively inducing a more pronounced cavity, which in turn further increases the eccentricity. This scenario however requires an inner cavity to start with, possibly caused by early planet formation in the inner disc, with the nascent bodies being later destabilized by the migrating brown dwarf companion before being engulfed in the primary star.
We clearly detect the large-scale magnetic field of V347 Aur in the recorded Stokes V LSD profiles, and derive |$B_{\rm \ell }$| values of only a few tens of G, several times weaker than those of prototypical classical or weak-line T Tauri stars (Finociety et al. 2021, 2023; Donati et al. 2024a, b). We also show that |$B_{\rm \ell }$| undergoes temporal fluctuations with a semi-amplitude of about 20 G and a period of |$76.5\pm 1.2$| d, consistent within the error bar with |$P_{\rm orb}$|/2. (The other option that these fluctuations actually occur with a periodicity of |$P_{\rm orb}$| is found to be less likely.) Besides, we detect the rotation period of V347 Aur in both |$B_{\rm \ell }$| and RV data, which we find to be equal to |$4.12\pm 0.03$| d. The corresponding rotational modulation of |$B_{\rm \ell }$| is only about 10 G, i.e. significantly smaller than the average |$B_{\rm \ell }$| value of about –50 G over most of our observations, indicating a large-scale magnetic topology that is mostly axisymmetric about the rotation axis. On a longer time-scale, we also see evolution of the average |$B_{\rm \ell }$|, rising to about –20 G in the last observing season, and suggesting that the overall large-scale field of V347 Aur, and in particular its poloidal component that |$B_{\rm \ell }$| is mostly sensitive to, may switch polarity in the forthcoming seasons.
Applying ZDI to our Stokes V LSD profiles, we find that the large-scale field of V347 Aur is mostly toroidal, with the poloidal component including only about 20 per cent of the reconstructed magnetic energy. This poloidal component, largely axisymmetric for most of our observations, includes a dominant dipole field of about 30 G tilted at about |$20\pm 10$||$^\circ$| to the rotation axis, which evolves into a non-axisymmetric poloidal component with a highly tilted dipole towards the last observing season.
Moreover, we report a polarity switch of the toroidal component, changing from positive polarity before periastron in 2021 January to negative polarity after periastron in 2021 February. We suspect that such polarity switches of the toroidal field happen twice per orbital cycle, once close to periastron and a second time around apoastron, leading to the other observed (negative to positive) polarity switches between 2019 December and 2020 December, and between 2022 November and 2023 February. Surprisingly, the poloidal component keeps the same polarity over the whole orbital cycle, but is likely modulated in amplitude with |$P_{\rm orb}$|/2 (about a non-zero value) given the 76.5-d fluctuation observed for |$B_{\rm \ell }$| (mostly sensitive to the poloidal field). This result comes as the first unambiguous observational evidence that accretion is able to impact magnetic field amplification and dynamo processes in low-mass PMS stars. We speculate that the large-scale field of V347 Aur is (at least partly) induced by what we dub a ‘pulsed dynamo’ mechanism (by analogy with pulsed accretion; Teyssandier & Lai 2020), i.e. indirectly driven by the orbital motion through the enhanced accretion events at periastron passage that act as a forcing mechanism. The accreted material and angular momentum from the disc, regularly injected into the top convective layers of the star, are indeed likely affecting the convective pattern, inducing enhanced radial and latitudinal shearing and thereby boosting the large-scale toroidal field before it relaxes away from periastron (on a convective turnover time). Detailed MHD simulations are obviously required to further investigate these ideas, and to explore in a more quantitative manner how the toroidal and poloidal components of the large-scale dynamo field are expected to respond with time to such a forcing mechanism. Dynamo processes are also likely to operate on a longer time-scale in V347 Aur, with the poloidal component evolving from a mainly axisymmetric to a mainly non-axisymmetric configuration in the last season of our monitoring campaign.
The large-scale field of V347 Aur shares similarities with that of the classical T Tauri star V2247 Oph, of nearly equal mass (0.35 |${\rm M}_{\odot }$|), featuring a complex and dominant toroidal field (Donati et al. 2010). V347 Aur is to date the most extreme such example, with a large-scale field strength weaker than 100 G and a toroidal field which stores about 80 per cent of the magnetic energy during most of our observations. This is consistent with our results and those of Flores et al. (2019) regarding the small-scale field of V347 Aur, also found to be weaker than that of more massive prototypical T Tauri stars (e.g. Johns-Krull 2007; López-Valdivia et al. 2021). Besides, the large-scale field of V347 Aur shares similarities with that of the (more massive) classical T Tauri eccentric close binary DQ Tau (of mass 0.6 |${\rm M}_{\odot }$|; Pouilly et al. 2023, 2024), both featuring a strong toroidal component on the primary star, but exhibiting significant differences as well. Not only is the large-scale field much weaker in V347 Aur, but |$B_{\rm \ell }$| and the reconstructed toroidal field are both modulated with |$P_{\rm orb}$| or its first harmonic in V347 Aur, whereas no such modulation is observed in DQ Tau despite the latter being more eccentric (|$e=0.59$|). We speculate that this comes from |$P_{\rm orb}$| being much longer in V347 Aur and comparable with the convective turnover time in very-low-mass stars (e.g. Wright et al. 2018), thereby leaving time for dynamo processes to react to the varying accretion conditions across the orbit and to reflect them in the large-scale field, whereas dynamo rather averages out the rapidly varying accretion pattern of DQ Tau.
From the veiling in |$JH$| and K bands, we confirm that accretion strengthens near periastron passage in V347 Aur. Given the measured eccentricity (|$e=0.28\pm 0.12$|) and semimajor axis (|$a=0.39\pm 0.02$| au) causing the brown dwarf companion to orbit at distances varying from |$a_{\rm p}=0.28\pm 0.05$| au at periastron to |$a_{\rm a}=0.50\pm 0.05$| au at apoastron, i.e. not as close to the primary star as in DQ Tau or HD 104 237, we speculate following Dahm & Hillenbrand (2020) that enhanced accretion occurs as a result of disc instabilities triggered near periastron passage by the brown dwarf companion. Accretion bursts in V347 Aur are known to induce brightness variations of up to 5.5 mag in V (Dahm & Hillenbrand 2020; see also Fig. 10). From archival AAVSO, ASAS-SN, and ZTF photometry, we find that accretion outbursts monitored during our monitoring campaign are weak ones, with brightness rising by |$\Delta V\ \lt\ 1.5$| mag. We also report that the Pa|${\beta }$| and Br|${\gamma }$| lines, well-known accretion proxies, also show clear emission peaks near periastron passage. From Pa|${\beta }$| and Br|${\gamma }$| emission fluxes corrected from veiling, and using the scaling relations of Alcalá et al. (2017), we infer logarithmic mass accretion rates (in |${\rm M}_{\odot }$| yr|$^{-1}$|) at the time of our observations ranging from about –9.0 away from periastron up to about –7.8 at periastron passage in V347 Aur. Extrapolating to the strongest outburst recorded on V347 Aur, we obtain peak logarithmic mass accretion rates of |$-6.2$| (in |${\rm M}_{\odot }$| yr|$^{-1}$|, consistent with, the results of Dahm & Hillenbrand 2020). The low accretion rates away from periastron also suggest that the inner accretion disc of V347 Aur is significantly depleted with respect to prototypical accretion discs of protostars, and may have acted as a cavity causing the orbital motion of the brown dwarf companion to become eccentric (Debras et al. 2021). We suggest that V347 Aur is a low-mass version of the eccentric binary HD 104 237, where the system is apparently able to clear out a large central cavity in the disc and to give rise to complex accretion streams bridging the disc and the stars, with accretion rates varying by orders of magnitude (Dunhill et al. 2015). This is qualitatively similar to what we see on V347 Aur.
Following Bessolaz et al. (2008), we infer that the weak large-scale magnetic dipole of V347 Aur is not able to disrupt the accretion disc beyond a radius of |${r_{\rm mag}}\simeq 1.3$||$R_{\star }$| (i.e. |${r_{\rm mag}}/{r_{\rm cor}}\simeq 0.4$|), even for a logarithmic accretion rate as low as –9.0, whereas the accretion flow is likely to be barely impacted by the magnetic field in high/extreme accretion episodes. We thus speculate that disc material destabilized by the companion at periastron passage is likely to be more or less free-falling through the field lines towards equatorial regions at the surface of the star, and that accretion will proceed in an unstable fashion at the lowest accretion rates away from periastron, via tongues of disc material penetrating the field (as in Blinova et al. 2016). We note that the 1083.3-nm He i triplet is also modulated at |$P_{\rm orb}$|, but only in its blueshifted absorption component, suggesting that the star is triggering an accretion-powered wind getting stronger during accretion episodes near periastron. On the contrary, the He i emission component is not periodically modulated, neither at |$P_{\rm orb}$| nor at |$P_{\rm rot}$|, as a likely result of accretion taking place in a chaotic way over most stellar longitudes rather than on stable regions at the footpoints of accretion funnels, as in prototypical classical T Tauri stars (e.g. Donati et al. 2024a, b). The complex Zeeman signature detected in the median He i profile is further evidence in this direction.
More observations of V347 Aur with SPIRou such as those reported in this study would be quite worthwhile, gathered this time more evenly across the whole orbital motion and over several orbital cycles featuring accretion outbursts of variable strengths at periastron passages. Besides, high-angular resolution interferometric observations at millimetre (e.g. NOEMA) or infrared (e.g. GRAVITY) wavelengths should come as a great addition to further constraint the disc properties, in particular its inclination and extent, as well as the dynamical mass of the system.Such data would allow us to refine the characterization of this very interesting and rather unique protostar for our understanding of star/planet formation, in particular in binary systems which account for a large fraction of the low-mass star population, and more specifically for unveiling how magnetic fields are able to impact this process. With its unexpectedly weak large-scale field, a likely result of the strong-accretion episodes modifying the convection pattern in the stellar interior and apparently triggering a ‘pulsed-dynamo’ mechanism, V347 Aur is especially interesting in this respect and definitely deserves sustained interest from the young low-mass star community over the forthcoming years.
ACKNOWLEDGEMENTS
We thank an anonymous referee for valuable comments which allowed us to improve the manuscript. This project received funds from the European Research Council (ERC) under the H2020 research & innovation program (grant agreement #740651 NewWorlds), the Agence Nationale pour la Recherche (ANR, project ANR-18-CE31-0019 SPlaSH), and the Investissements d’Avenir program (project ANR-15-IDEX-02). We thank Silvia Alencar and Hsien Shang for comments that helped clarify an earlier version of the manuscript. This work benefited from the SIMBAD CDS data base at URL http://simbad.u-strasbg.fr/simbad, the AAVSO data base at URL https://www.aavso.org, and the ADS system at URL https://ui.adsabs.harvard.edu. Our study is based on data obtained at the CFHT, operated by the CNRC (Canada), INSU/CNRS (France), and the University of Hawaii. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Maunakea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain.
DATA AVAILABILITY
SLS data are publicly available from the Canadian Astronomy Data Center, whereas SPICE data will be available at the same place from mid-2024 to mid-2025.
Footnotes
REFERENCES
APPENDIX A: OBSERVATION LOG
Table A1 gives the full log and associated |$B_{\rm \ell }$| and RV measurements at each observing epoch from our SPIRou spectra.
Observing log of our SPIRou observations of V347 Aur in seasons 2019, 2020, 2021, and 2022. All exposures consist of four sub-exposures of equal length. For each visit, we list the BJD, the UT date, the rotation cycle c and phase |$\phi$| (computed as indicated in Section 3), the total observing time t|$_{\rm exp}$|, the peak SNR in the spectrum (in the H band) per 2.3 km s|$^{-1}$| pixel, the noise level in the LSD Stokes V profile, the estimated |$B_{\rm \ell }$| with error bars, the nightly averaged RVs and corresponding error bars, the veiling in the |$JH$| and in the K bands |$r_{JH}$| and |$r_K$| measured from LSD profiles of atomic lines and CO lines, respectively, and finally the EWs of the Pa|${\beta }$| and Br|${\gamma }$| emission lines with error bars (not scaled up with veiling).
| BJD . | UT date . | c/|$\phi$| . | t|$_{\rm exp}$| . | SNR . | |$\sigma _V$| . | |$B_{\rm \ell }$| . | RV . | |$r_{JH}$|/|$r_K$| . | EW Pa|${\beta }$| . | EW Br|${\gamma }$| . |
|---|---|---|---|---|---|---|---|---|---|---|
| (2459000+) . | . | . | (s) . | (H) . | (|$10^{-4} I_{\rm c}$|) . | (G) . | (km s|$^{-1}$|) . | . | (km s|$^{-1}$|) . | (km s|$^{-1}$|) . |
| |$-$|211.9145299 | 31 Oct 2019 | 0/0.021 | 2407.1 | 245 | 2.43 | |$-$|38 |$\pm$| 21 | 9.22|$\pm$|0.28 | 0.77/1.75 | 249 |$\pm$| 10 | 58 |$\pm$| 3 |
| |$-$|210.9098887 | 1 Nov 2019 | 0/0.265 | 2407.1 | 236 | 2.49 | |$-$|32 |$\pm$| 21 | 8.62 |$\pm$| 0.29 | 0.75/2.54 | 247 |$\pm$| 10 | 57 |$\pm$| 3 |
| |$-$|208.9302687 | 3 Nov 2019 | 0/0.745 | 2407.1 | 230 | 2.54 | |$-$|76 |$\pm$| 20 | 8.65 |$\pm$| 0.29 | 0.57/3.40 | 224 |$\pm$| 10 | 54 |$\pm$| 3 |
| |$-$|206.8956725 | 5 Nov 2019 | 1/0.239 | 2407.1 | 219 | 2.69 | |$-$|26 |$\pm$| 20 | 8.95 |$\pm$| 0.29 | 0.53/2.12 | 218 |$\pm$| 10 | 56 |$\pm$| 3 |
| |$-$|204.9686594 | 7 Nov 2019 | 1/0.707 | 2407.1 | 213 | 2.77 | |$-$|60 |$\pm$| 20 | 9.02 |$\pm$| 0.29 | 0.46/2.28 | 209 |$\pm$| 10 | 51 |$\pm$| 3 |
| |$-$|202.9959549 | 9 Nov 2019 | 2/0.185 | 2407.1 | 149 | 4.21 | |$-$|19 |$\pm$| 30 | 7.96 |$\pm$| 0.35 | 0.45/1.16 | 202 |$\pm$| 10 | 52 |$\pm$| 3 |
| |$-$|200.9071390 | 11 Nov 2019 | 2/0.692 | 2407.1 | 172 | 3.67 | |$-$|66 |$\pm$| 22 | 8.84 |$\pm$| 0.24 | 0.25/0.84 | 151 |$\pm$| 10 | 39 |$\pm$| 3 |
| |$-$|198.9782271 | 13 Nov 2019 | 3/0.161 | 2407.1 | 212 | 2.92 | |$-$|65 |$\pm$| 19 | 8.77 |$\pm$| 0.31 | 0.34/1.29 | 190 |$\pm$| 10 | 50 |$\pm$| 3 |
| |$-$|197.9612905 | 14 Nov 2019 | 3/0.407 | 2407.1 | 190 | 3.16 | |$-$|43 |$\pm$| 21 | 8.43 |$\pm$| 0.31 | 0.34/1.03 | 154 |$\pm$| 10 | 42 |$\pm$| 3 |
| |$-$|174.0001745 | 8 Dec 2019 | 9/0.223 | 2407.1 | 182 | 3.26 | |$-$|34 |$\pm$| 19 | 8.10 |$\pm$| 0.27 | 0.20/0.71 | 134 |$\pm$| 10 | 32 |$\pm$| 3 |
| |$-$|172.9716427 | 9 Dec 2019 | 9/0.473 | 2407.1 | 195 | 3.02 | |$-$|73 |$\pm$| 17 | 8.39 |$\pm$| 0.25 | 0.17/0.69 | 124 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|172.0535410 | 10 Dec 2019 | 9/0.696 | 2312.3 | 214 | 2.71 | |$-$|40 |$\pm$| 15 | 8.44 |$\pm$| 0.20 | 0.15/0.68 | 129 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|170.9462697 | 11 Dec 2019 | 9/0.964 | 2407.1 | 210 | 2.76 | |$-$|36 |$\pm$| 16 | 8.68 |$\pm$| 0.25 | 0.18/0.69 | 123 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|169.9334152 | 12 Dec 2019 | 10/0.210 | 2379.2 | 192 | 3.07 | |$-$|30 |$\pm$| 17 | 8.21 |$\pm$| 0.20 | 0.14/0.65 | 115 |$\pm$| 10 | 28 |$\pm$| 3 |
| 207.9252214 | 24 Dec 2020 | 101/0.924 | 2407.1 | 259 | 2.31 | |$-$|19 |$\pm$| 15 | 7.57 |$\pm$| 0.19 | 0.29/0.81 | 88 |$\pm$| 10 | 22 |$\pm$| 3 |
| 208.9343916 | 25 Dec 2020 | 102/0.169 | 2407.1 | 254 | 2.39 | |$-$|42 |$\pm$| 15 | 7.44 |$\pm$| 0.20 | 0.27/0.75 | 111 |$\pm$| 10 | 25 |$\pm$| 3 |
| 209.8880836 | 26 Dec 2020 | 102/0.400 | 2407.1 | 252 | 2.60 | |$-$|12 |$\pm$| 16 | 7.13 |$\pm$| 0.20 | 0.24/0.55 | 97 |$\pm$| 10 | 23 |$\pm$| 3 |
| 211.9500308 | 28 Dec 2020 | 102/0.900 | 2407.1 | 189 | 3.31 | |$-$|43 |$\pm$| 21 | 7.22 |$\pm$| 0.20 | 0.28/0.35 | 79 |$\pm$| 10 | 18 |$\pm$| 3 |
| 212.9362811 | 29 Dec 2020 | 103/0.140 | 2407.1 | 224 | 2.70 | |$-$|45 |$\pm$| 17 | 7.30 |$\pm$| 0.21 | 0.26/0.32 | 103 |$\pm$| 10 | 29 |$\pm$| 3 |
| 214.8980511 | 31 Dec 2020 | 103/0.616 | 2407.1 | 220 | 2.71 | |$-$|57 |$\pm$| 16 | 7.11 |$\pm$| 0.20 | 0.24/0.33 | 107 |$\pm$| 10 | 27 |$\pm$| 3 |
| 215.8662680 | 1 Jan 2021 | 103/0.851 | 2407.1 | 165 | 3.76 | |$-$|68 |$\pm$| 25 | 7.24 |$\pm$| 0.22 | 0.37/0.55 | 100 |$\pm$| 10 | 26 |$\pm$| 3 |
| 217.8901191 | 3 Jan 2021 | 104/0.342 | 2407.1 | 248 | 2.27 | |$-$|75 |$\pm$| 15 | 7.06 |$\pm$| 0.22 | 0.36/0.43 | 100 |$\pm$| 10 | 25 |$\pm$| 3 |
| 218.8741188 | 4 Jan 2021 | 104/0.581 | 2407.1 | 250 | 2.29 | |$-$|59 |$\pm$| 14 | 6.81 |$\pm$| 0.19 | 0.26/0.40 | 90 |$\pm$| 10 | 20 |$\pm$| 3 |
| 219.9045892 | 5 Jan 2021 | 104/0.831 | 2407.1 | 246 | 2.28 | |$-$|47 |$\pm$| 15 | 7.33 |$\pm$| 0.20 | 0.33/0.59 | 80 |$\pm$| 10 | 18 |$\pm$| 3 |
| 220.8613214 | 6 Jan 2021 | 105/0.063 | 2407.1 | 254 | 2.19 | |$-$|68 |$\pm$| 15 | 7.38 |$\pm$| 0.22 | 0.43/0.77 | 107 |$\pm$| 10 | 26 |$\pm$| 3 |
| 221.9203503 | 7 Jan 2021 | 105/0.320 | 2407.1 | 240 | 2.39 | |$-$|34 |$\pm$| 17 | 6.76 |$\pm$| 0.22 | 0.46/0.73 | 119 |$\pm$| 10 | 30 |$\pm$| 3 |
| 222.9318705 | 8 Jan 2021 | 105/0.566 | 2407.1 | 241 | 2.34 | |$-$|73 |$\pm$| 16 | 6.87 |$\pm$| 0.21 | 0.36/0.76 | 101 |$\pm$| 10 | 23 |$\pm$| 3 |
| 267.7272476 | 22 Feb 2021 | 116/0.439 | 2407.1 | 271 | 2.10 | |$-$|42 |$\pm$| 14 | 9.47 |$\pm$| 0.21 | 0.34/2.38 | 173 |$\pm$| 10 | 39 |$\pm$| 3 |
| 268.8634318 | 23 Feb 2021 | 116/0.714 | 2407.1 | 262 | 2.16 | |$-$|30 |$\pm$| 14 | 9.51 |$\pm$| 0.25 | 0.30/2.45 | 191 |$\pm$| 10 | 42 |$\pm$| 3 |
| 271.7845315 | 26 Feb 2021 | 117/0.423 | 2407.1 | 224 | 2.52 | |$-$|10 |$\pm$| 16 | 8.78 |$\pm$| 0.20 | 0.30/1.42 | 177 |$\pm$| 10 | 41 |$\pm$| 3 |
| 273.8651093 | 28 Feb 2021 | 117/0.928 | 2407.1 | 182 | 3.27 | |$-$|38 |$\pm$| 21 | 9.05 |$\pm$| 0.22 | 0.31/1.43 | 177 |$\pm$| 10 | 40 |$\pm$| 3 |
| 276.7836915 | 3 Mar 2021 | 118/0.637 | 2407.1 | 263 | 2.06 | |$-$|26 |$\pm$| 12 | 8.98 |$\pm$| 0.19 | 0.21/1.22 | 162 |$\pm$| 10 | 36 |$\pm$| 3 |
| 277.7285551 | 4 Mar 2021 | 118/0.866 | 2407.1 | 255 | 2.10 | |$-$|55 |$\pm$| 12 | 9.03 |$\pm$| 0.19 | 0.17/1.09 | 162 |$\pm$| 10 | 37 |$\pm$| 3 |
| 293.7342341 | 20 Mar 2021 | 122/0.751 | 2407.1 | 232 | 2.44 | |$-$|69 |$\pm$| 12 | 8.58 |$\pm$| 0.17 | 0.02/0.36 | 146 |$\pm$| 10 | 39 |$\pm$| 3 |
| 297.7716803 | 24 Mar 2021 | 123/0.731 | 2407.1 | 221 | 2.53 | |$-$|51 |$\pm$| 13 | 8.48 |$\pm$| 0.17 | 0.03/0.33 | 116 |$\pm$| 10 | 29 |$\pm$| 3 |
| 299.7983781 | 26 Mar 2021 | 124/0.223 | 2407.1 | 186 | 3.25 | |$-$|54 |$\pm$| 17 | 8.05 |$\pm$| 0.18 | 0.04/0.29 | 106 |$\pm$| 10 | 28 |$\pm$| 3 |
| 300.7513668 | 27 Mar 2021 | 124/0.454 | 2407.1 | 206 | 3.02 | |$-$|35 |$\pm$| 15 | 8.14 |$\pm$| 0.17 | 0.04/0.37 | 109 |$\pm$| 10 | 27 |$\pm$| 3 |
| 301.7807176 | 28 Mar 2021 | 124/0.704 | 2407.1 | 159 | 3.80 | |$-$|36 |$\pm$| 21 | 8.30 |$\pm$| 0.19 | 0.15/0.86 | 95 |$\pm$| 10 | 25 |$\pm$| 3 |
| 304.7728769 | 31 Mar 2021 | 125/0.430 | 2407.1 | 223 | 2.63 | |$-$|79 |$\pm$| 13 | 7.95 |$\pm$| 0.17 | 0.01/0.44 | 102 |$\pm$| 10 | 22 |$\pm$| 3 |
| 305.7334444 | 1 Apr 2021 | 125/0.663 | 2407.1 | 226 | 2.46 | |$-$|68 |$\pm$| 12 | 8.30 |$\pm$| 0.16 | 0.02/0.37 | 96 |$\pm$| 10 | 24 |$\pm$| 3 |
| 587.9333571 | 8 Jan 2022 | 194/0.159 | 2407.1 | 273 | 2.13 | |$-$|59 |$\pm$| 15 | 9.08 |$\pm$| 0.19 | 0.44/1.63 | 177 |$\pm$| 10 | 41 |$\pm$| 3 |
| 588.9350942 | 9 Jan 2022 | 194/0.402 | 2407.1 | 272 | 2.19 | |$-$|30 |$\pm$| 15 | 8.91 |$\pm$| 0.18 | 0.39/1.89 | 161 |$\pm$| 10 | 39 |$\pm$| 3 |
| 589.9833304 | 10 Jan 2022 | 194/0.656 | 2407.1 | 282 | 2.30 | |$-$|1 |$\pm$| 15 | 9.24 |$\pm$| 0.19 | 0.36/1.66 | 143 |$\pm$| 10 | 35 |$\pm$| 3 |
| 590.7944760 | 11 Jan 2022 | 194/0.853 | 2407.1 | 248 | 2.43 | |$-$|37 |$\pm$| 17 | 9.22 |$\pm$| 0.18 | 0.41/1.48 | 142 |$\pm$| 10 | 37 |$\pm$| 3 |
| 591.9658790 | 12 Jan 2022 | 195/0.137 | 2407.1 | 250 | 2.31 | |$-$|44 |$\pm$| 16 | 9.44 |$\pm$| 0.19 | 0.37/1.18 | 175 |$\pm$| 10 | 46 |$\pm$| 3 |
| 592.9683245 | 13 Jan 2022 | 195/0.381 | 2407.1 | 232 | 3.43 | |$-$|63 |$\pm$| 23 | 8.92 |$\pm$| 0.19 | 0.36/0.94 | 172 |$\pm$| 10 | 43 |$\pm$| 3 |
| 593.8925375 | 14 Jan 2022 | 195/0.605 | 2407.1 | 223 | 3.15 | |$-$|40 |$\pm$| 21 | 8.93 |$\pm$| 0.18 | 0.33/0.93 | 165 |$\pm$| 10 | 42 |$\pm$| 3 |
| 594.8359992 | 15 Jan 2022 | 195/0.834 | 2407.1 | 279 | 2.10 | |$-$|20 |$\pm$| 13 | 9.20 |$\pm$| 0.18 | 0.28/0.92 | 164 |$\pm$| 10 | 39 |$\pm$| 3 |
| 595.9992366 | 16 Jan 2022 | 196/0.116 | 2407.1 | 244 | 2.54 | |$-$|80 |$\pm$| 16 | 8.94 |$\pm$| 0.20 | 0.29/0.92 | 172 |$\pm$| 10 | 43 |$\pm$| 3 |
| 596.8879787 | 17 Jan 2022 | 196/0.332 | 2407.1 | 265 | 2.29 | |$-$|43 |$\pm$| 14 | 8.84 |$\pm$| 0.17 | 0.26/0.72 | 169 |$\pm$| 10 | 43 |$\pm$| 3 |
| 597.9366485 | 18 Jan 2022 | 196/0.587 | 2407.1 | 271 | 2.47 | |$-$|62 |$\pm$| 15 | 8.76 |$\pm$| 0.18 | 0.26/0.76 | 169 |$\pm$| 10 | 39 |$\pm$| 3 |
| 598.9194038 | 19 Jan 2022 | 196/0.825 | 2407.1 | 255 | 2.28 | |$-$|58 |$\pm$| 14 | 8.85 |$\pm$| 0.18 | 0.23/0.67 | 142 |$\pm$| 10 | 36 |$\pm$| 3 |
| 599.9732831 | 20 Jan 2022 | 197/0.081 | 2407.1 | 255 | 2.42 | |$-$|73 |$\pm$| 15 | 8.35 |$\pm$| 0.19 | 0.25/0.83 | 147 |$\pm$| 10 | 38 |$\pm$| 3 |
| 601.8978507 | 22 Jan 2022 | 197/0.548 | 2407.1 | 174 | 3.75 | |$-$|73 |$\pm$| 23 | 8.74 |$\pm$| 0.18 | 0.26/0.48 | 130 |$\pm$| 10 | 35 |$\pm$| 3 |
| 602.9316132 | 23 Jan 2022 | 197/0.799 | 2407.1 | 258 | 2.35 | |$-$|43 |$\pm$| 14 | 8.97 |$\pm$| 0.17 | 0.20/0.50 | 119 |$\pm$| 10 | 29 |$\pm$| 3 |
| 603.9124578 | 24 Jan 2022 | 198/0.037 | 2407.1 | 272 | 2.41 | |$-$|73 |$\pm$| 15 | 8.58 |$\pm$| 0.21 | 0.25/0.67 | 121 |$\pm$| 10 | 29 |$\pm$| 3 |
| 604.9164418 | 25 Jan 2022 | 198/0.281 | 2407.1 | 194 | 3.34 | |$-$|64 |$\pm$| 21 | 8.18 |$\pm$| 0.18 | 0.25/0.57 | 116 |$\pm$| 10 | 30 |$\pm$| 3 |
| 606.9054391 | 27 Jan 2022 | 198/0.763 | 2407.1 | 225 | 2.64 | |$-$|49 |$\pm$| 16 | 8.49 |$\pm$| 0.17 | 0.23/0.54 | 122 |$\pm$| 10 | 36 |$\pm$| 3 |
| 607.8850302 | 28 Jan 2022 | 199/0.001 | 2407.1 | 232 | 2.45 | |$-$|44 |$\pm$| 15 | 8.57 |$\pm$| 0.17 | 0.22/0.40 | 127 |$\pm$| 10 | 30 |$\pm$| 3 |
| 608.8852573 | 29 Jan 2022 | 199/0.244 | 2407.1 | 228 | 3.24 | |$-$|81 |$\pm$| 20 | 8.33 |$\pm$| 0.16 | 0.25/0.46 | 112 |$\pm$| 10 | 27 |$\pm$| 3 |
| 609.8900384 | 30 Jan 2022 | 199/0.488 | 2407.1 | 248 | 2.33 | |$-$|79 |$\pm$| 14 | 8.15 |$\pm$| 0.18 | 0.24/0.58 | 106 |$\pm$| 10 | 26 |$\pm$| 3 |
| 610.9655285 | 31 Jan 2022 | 199/0.749 | 2407.1 | 250 | 2.32 | |$-$|58 |$\pm$| 14 | 8.18 |$\pm$| 0.17 | 0.26/0.66 | 96 |$\pm$| 10 | 24 |$\pm$| 3 |
| 886.1012388 | 2 Nov 2022 | 266/0.529 | 2407.1 | 293 | 1.88 | |$-$|19 |$\pm$| 12 | 9.24 |$\pm$| 0.20 | 0.27/0.92 | 159 |$\pm$| 10 | 39 |$\pm$| 3 |
| 890.1199631 | 6 Nov 2022 | 267/0.505 | 2407.1 | 272 | 2.10 | |$-$|47 |$\pm$| 15 | 8.83 |$\pm$| 0.24 | 0.42/1.31 | 130 |$\pm$| 10 | 30 |$\pm$| 3 |
| 891.1149740 | 7 Nov 2022 | 267/0.746 | 2407.1 | 287 | 2.04 | 10 |$\pm$| 13 | 8.91 |$\pm$| 0.24 | 0.33/1.36 | 148 |$\pm$| 10 | 33 |$\pm$| 3 |
| 892.1127054 | 8 Nov 2022 | 267/0.989 | 2407.1 | 270 | 2.10 | 10 |$\pm$| 13 | 9.35 |$\pm$| 0.22 | 0.26/1.26 | 138 |$\pm$| 10 | 33 |$\pm$| 3 |
| 893.1035281 | 9 Nov 2022 | 268/0.229 | 2407.1 | 239 | 2.29 | |$-$|4 |$\pm$| 14 | 8.81 |$\pm$| 0.22 | 0.26/0.83 | 160 |$\pm$| 10 | 35 |$\pm$| 3 |
| 895.1312799 | 11 Nov 2022 | 268/0.721 | 2407.1 | 223 | 2.58 | |$-$|32 |$\pm$| 15 | 8.94 |$\pm$| 0.22 | 0.19/0.34 | 113 |$\pm$| 10 | 25 |$\pm$| 3 |
| 896.0325625 | 12 Nov 2022 | 268/0.940 | 2407.1 | 269 | 2.03 | |$-$|14 |$\pm$| 12 | 9.33 |$\pm$| 0.20 | 0.18/0.66 | 132 |$\pm$| 10 | 31 |$\pm$| 3 |
| 899.1357048 | 15 Nov 2022 | 269/0.693 | 2407.1 | 257 | 2.22 | |$-$|33 |$\pm$| 12 | 8.79 |$\pm$| 0.20 | 0.09/0.51 | 122 |$\pm$| 10 | 29 |$\pm$| 3 |
| 902.1108546 | 18 Nov 2022 | 270/0.415 | 2407.1 | 254 | 2.27 | |$-$|44 |$\pm$| 12 | 8.53 |$\pm$| 0.19 | 0.05/0.31 | 114 |$\pm$| 10 | 27 |$\pm$| 3 |
| 905.0987525 | 21 Nov 2022 | 271/0.140 | 2407.1 | 211 | 2.65 | |$-$|21 |$\pm$| 13 | 8.51 |$\pm$| 0.20 | 0.02/0.08 | 139 |$\pm$| 10 | 31 |$\pm$| 3 |
| 906.1044391 | 22 Nov 2022 | 271/0.385 | 2407.1 | 230 | 2.41 | |$-$|65 |$\pm$| 12 | 8.23 |$\pm$| 0.18 | 0.00/0.13 | 112 |$\pm$| 10 | 25 |$\pm$| 3 |
| 978.9367863 | 3 Feb 2023 | 289/0.062 | 2407.1 | 227 | 2.44 | |$-$|19 |$\pm$| 14 | 7.14 |$\pm$| 0.18 | 0.14/0.68 | 93 |$\pm$| 10 | 20 |$\pm$| 3 |
| 980.9163238 | 5 Feb 2023 | 289/0.543 | 2407.1 | 176 | 3.82 | |$-$|18 |$\pm$| 23 | 6.77 |$\pm$| 0.20 | 0.22/0.68 | 73 |$\pm$| 10 | 18 |$\pm$| 3 |
| 983.9060551 | 8 Feb 2023 | 290/0.268 | 2407.1 | 238 | 2.36 | |$-$|38 |$\pm$| 14 | 7.19 |$\pm$| 0.19 | 0.19/0.41 | 61 |$\pm$| 10 | 14 |$\pm$| 3 |
| 1036.7643629 | 2 Apr 2023 | 303/0.098 | 2407.1 | 246 | 2.41 | 13 |$\pm$| 23 | 9.33 |$\pm$| 0.28 | 0.92/5.14 | 208 |$\pm$| 10 | 41 |$\pm$| 3 |
| 1041.7274405 | 7 Apr 2023 | 304/0.303 | 2407.1 | 261 | 2.17 | 5 |$\pm$| 18 | 8.74 |$\pm$| 0.28 | 0.71/2.97 | 188 |$\pm$| 10 | 35 |$\pm$| 3 |
| 1045.7255305 | 11 Apr 2023 | 305/0.273 | 2407.1 | 187 | 3.86 | 14 |$\pm$| 29 | 9.24 |$\pm$| 0.26 | 0.52/1.97 | 153 |$\pm$| 10 | 28 |$\pm$| 3 |
| BJD . | UT date . | c/|$\phi$| . | t|$_{\rm exp}$| . | SNR . | |$\sigma _V$| . | |$B_{\rm \ell }$| . | RV . | |$r_{JH}$|/|$r_K$| . | EW Pa|${\beta }$| . | EW Br|${\gamma }$| . |
|---|---|---|---|---|---|---|---|---|---|---|
| (2459000+) . | . | . | (s) . | (H) . | (|$10^{-4} I_{\rm c}$|) . | (G) . | (km s|$^{-1}$|) . | . | (km s|$^{-1}$|) . | (km s|$^{-1}$|) . |
| |$-$|211.9145299 | 31 Oct 2019 | 0/0.021 | 2407.1 | 245 | 2.43 | |$-$|38 |$\pm$| 21 | 9.22|$\pm$|0.28 | 0.77/1.75 | 249 |$\pm$| 10 | 58 |$\pm$| 3 |
| |$-$|210.9098887 | 1 Nov 2019 | 0/0.265 | 2407.1 | 236 | 2.49 | |$-$|32 |$\pm$| 21 | 8.62 |$\pm$| 0.29 | 0.75/2.54 | 247 |$\pm$| 10 | 57 |$\pm$| 3 |
| |$-$|208.9302687 | 3 Nov 2019 | 0/0.745 | 2407.1 | 230 | 2.54 | |$-$|76 |$\pm$| 20 | 8.65 |$\pm$| 0.29 | 0.57/3.40 | 224 |$\pm$| 10 | 54 |$\pm$| 3 |
| |$-$|206.8956725 | 5 Nov 2019 | 1/0.239 | 2407.1 | 219 | 2.69 | |$-$|26 |$\pm$| 20 | 8.95 |$\pm$| 0.29 | 0.53/2.12 | 218 |$\pm$| 10 | 56 |$\pm$| 3 |
| |$-$|204.9686594 | 7 Nov 2019 | 1/0.707 | 2407.1 | 213 | 2.77 | |$-$|60 |$\pm$| 20 | 9.02 |$\pm$| 0.29 | 0.46/2.28 | 209 |$\pm$| 10 | 51 |$\pm$| 3 |
| |$-$|202.9959549 | 9 Nov 2019 | 2/0.185 | 2407.1 | 149 | 4.21 | |$-$|19 |$\pm$| 30 | 7.96 |$\pm$| 0.35 | 0.45/1.16 | 202 |$\pm$| 10 | 52 |$\pm$| 3 |
| |$-$|200.9071390 | 11 Nov 2019 | 2/0.692 | 2407.1 | 172 | 3.67 | |$-$|66 |$\pm$| 22 | 8.84 |$\pm$| 0.24 | 0.25/0.84 | 151 |$\pm$| 10 | 39 |$\pm$| 3 |
| |$-$|198.9782271 | 13 Nov 2019 | 3/0.161 | 2407.1 | 212 | 2.92 | |$-$|65 |$\pm$| 19 | 8.77 |$\pm$| 0.31 | 0.34/1.29 | 190 |$\pm$| 10 | 50 |$\pm$| 3 |
| |$-$|197.9612905 | 14 Nov 2019 | 3/0.407 | 2407.1 | 190 | 3.16 | |$-$|43 |$\pm$| 21 | 8.43 |$\pm$| 0.31 | 0.34/1.03 | 154 |$\pm$| 10 | 42 |$\pm$| 3 |
| |$-$|174.0001745 | 8 Dec 2019 | 9/0.223 | 2407.1 | 182 | 3.26 | |$-$|34 |$\pm$| 19 | 8.10 |$\pm$| 0.27 | 0.20/0.71 | 134 |$\pm$| 10 | 32 |$\pm$| 3 |
| |$-$|172.9716427 | 9 Dec 2019 | 9/0.473 | 2407.1 | 195 | 3.02 | |$-$|73 |$\pm$| 17 | 8.39 |$\pm$| 0.25 | 0.17/0.69 | 124 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|172.0535410 | 10 Dec 2019 | 9/0.696 | 2312.3 | 214 | 2.71 | |$-$|40 |$\pm$| 15 | 8.44 |$\pm$| 0.20 | 0.15/0.68 | 129 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|170.9462697 | 11 Dec 2019 | 9/0.964 | 2407.1 | 210 | 2.76 | |$-$|36 |$\pm$| 16 | 8.68 |$\pm$| 0.25 | 0.18/0.69 | 123 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|169.9334152 | 12 Dec 2019 | 10/0.210 | 2379.2 | 192 | 3.07 | |$-$|30 |$\pm$| 17 | 8.21 |$\pm$| 0.20 | 0.14/0.65 | 115 |$\pm$| 10 | 28 |$\pm$| 3 |
| 207.9252214 | 24 Dec 2020 | 101/0.924 | 2407.1 | 259 | 2.31 | |$-$|19 |$\pm$| 15 | 7.57 |$\pm$| 0.19 | 0.29/0.81 | 88 |$\pm$| 10 | 22 |$\pm$| 3 |
| 208.9343916 | 25 Dec 2020 | 102/0.169 | 2407.1 | 254 | 2.39 | |$-$|42 |$\pm$| 15 | 7.44 |$\pm$| 0.20 | 0.27/0.75 | 111 |$\pm$| 10 | 25 |$\pm$| 3 |
| 209.8880836 | 26 Dec 2020 | 102/0.400 | 2407.1 | 252 | 2.60 | |$-$|12 |$\pm$| 16 | 7.13 |$\pm$| 0.20 | 0.24/0.55 | 97 |$\pm$| 10 | 23 |$\pm$| 3 |
| 211.9500308 | 28 Dec 2020 | 102/0.900 | 2407.1 | 189 | 3.31 | |$-$|43 |$\pm$| 21 | 7.22 |$\pm$| 0.20 | 0.28/0.35 | 79 |$\pm$| 10 | 18 |$\pm$| 3 |
| 212.9362811 | 29 Dec 2020 | 103/0.140 | 2407.1 | 224 | 2.70 | |$-$|45 |$\pm$| 17 | 7.30 |$\pm$| 0.21 | 0.26/0.32 | 103 |$\pm$| 10 | 29 |$\pm$| 3 |
| 214.8980511 | 31 Dec 2020 | 103/0.616 | 2407.1 | 220 | 2.71 | |$-$|57 |$\pm$| 16 | 7.11 |$\pm$| 0.20 | 0.24/0.33 | 107 |$\pm$| 10 | 27 |$\pm$| 3 |
| 215.8662680 | 1 Jan 2021 | 103/0.851 | 2407.1 | 165 | 3.76 | |$-$|68 |$\pm$| 25 | 7.24 |$\pm$| 0.22 | 0.37/0.55 | 100 |$\pm$| 10 | 26 |$\pm$| 3 |
| 217.8901191 | 3 Jan 2021 | 104/0.342 | 2407.1 | 248 | 2.27 | |$-$|75 |$\pm$| 15 | 7.06 |$\pm$| 0.22 | 0.36/0.43 | 100 |$\pm$| 10 | 25 |$\pm$| 3 |
| 218.8741188 | 4 Jan 2021 | 104/0.581 | 2407.1 | 250 | 2.29 | |$-$|59 |$\pm$| 14 | 6.81 |$\pm$| 0.19 | 0.26/0.40 | 90 |$\pm$| 10 | 20 |$\pm$| 3 |
| 219.9045892 | 5 Jan 2021 | 104/0.831 | 2407.1 | 246 | 2.28 | |$-$|47 |$\pm$| 15 | 7.33 |$\pm$| 0.20 | 0.33/0.59 | 80 |$\pm$| 10 | 18 |$\pm$| 3 |
| 220.8613214 | 6 Jan 2021 | 105/0.063 | 2407.1 | 254 | 2.19 | |$-$|68 |$\pm$| 15 | 7.38 |$\pm$| 0.22 | 0.43/0.77 | 107 |$\pm$| 10 | 26 |$\pm$| 3 |
| 221.9203503 | 7 Jan 2021 | 105/0.320 | 2407.1 | 240 | 2.39 | |$-$|34 |$\pm$| 17 | 6.76 |$\pm$| 0.22 | 0.46/0.73 | 119 |$\pm$| 10 | 30 |$\pm$| 3 |
| 222.9318705 | 8 Jan 2021 | 105/0.566 | 2407.1 | 241 | 2.34 | |$-$|73 |$\pm$| 16 | 6.87 |$\pm$| 0.21 | 0.36/0.76 | 101 |$\pm$| 10 | 23 |$\pm$| 3 |
| 267.7272476 | 22 Feb 2021 | 116/0.439 | 2407.1 | 271 | 2.10 | |$-$|42 |$\pm$| 14 | 9.47 |$\pm$| 0.21 | 0.34/2.38 | 173 |$\pm$| 10 | 39 |$\pm$| 3 |
| 268.8634318 | 23 Feb 2021 | 116/0.714 | 2407.1 | 262 | 2.16 | |$-$|30 |$\pm$| 14 | 9.51 |$\pm$| 0.25 | 0.30/2.45 | 191 |$\pm$| 10 | 42 |$\pm$| 3 |
| 271.7845315 | 26 Feb 2021 | 117/0.423 | 2407.1 | 224 | 2.52 | |$-$|10 |$\pm$| 16 | 8.78 |$\pm$| 0.20 | 0.30/1.42 | 177 |$\pm$| 10 | 41 |$\pm$| 3 |
| 273.8651093 | 28 Feb 2021 | 117/0.928 | 2407.1 | 182 | 3.27 | |$-$|38 |$\pm$| 21 | 9.05 |$\pm$| 0.22 | 0.31/1.43 | 177 |$\pm$| 10 | 40 |$\pm$| 3 |
| 276.7836915 | 3 Mar 2021 | 118/0.637 | 2407.1 | 263 | 2.06 | |$-$|26 |$\pm$| 12 | 8.98 |$\pm$| 0.19 | 0.21/1.22 | 162 |$\pm$| 10 | 36 |$\pm$| 3 |
| 277.7285551 | 4 Mar 2021 | 118/0.866 | 2407.1 | 255 | 2.10 | |$-$|55 |$\pm$| 12 | 9.03 |$\pm$| 0.19 | 0.17/1.09 | 162 |$\pm$| 10 | 37 |$\pm$| 3 |
| 293.7342341 | 20 Mar 2021 | 122/0.751 | 2407.1 | 232 | 2.44 | |$-$|69 |$\pm$| 12 | 8.58 |$\pm$| 0.17 | 0.02/0.36 | 146 |$\pm$| 10 | 39 |$\pm$| 3 |
| 297.7716803 | 24 Mar 2021 | 123/0.731 | 2407.1 | 221 | 2.53 | |$-$|51 |$\pm$| 13 | 8.48 |$\pm$| 0.17 | 0.03/0.33 | 116 |$\pm$| 10 | 29 |$\pm$| 3 |
| 299.7983781 | 26 Mar 2021 | 124/0.223 | 2407.1 | 186 | 3.25 | |$-$|54 |$\pm$| 17 | 8.05 |$\pm$| 0.18 | 0.04/0.29 | 106 |$\pm$| 10 | 28 |$\pm$| 3 |
| 300.7513668 | 27 Mar 2021 | 124/0.454 | 2407.1 | 206 | 3.02 | |$-$|35 |$\pm$| 15 | 8.14 |$\pm$| 0.17 | 0.04/0.37 | 109 |$\pm$| 10 | 27 |$\pm$| 3 |
| 301.7807176 | 28 Mar 2021 | 124/0.704 | 2407.1 | 159 | 3.80 | |$-$|36 |$\pm$| 21 | 8.30 |$\pm$| 0.19 | 0.15/0.86 | 95 |$\pm$| 10 | 25 |$\pm$| 3 |
| 304.7728769 | 31 Mar 2021 | 125/0.430 | 2407.1 | 223 | 2.63 | |$-$|79 |$\pm$| 13 | 7.95 |$\pm$| 0.17 | 0.01/0.44 | 102 |$\pm$| 10 | 22 |$\pm$| 3 |
| 305.7334444 | 1 Apr 2021 | 125/0.663 | 2407.1 | 226 | 2.46 | |$-$|68 |$\pm$| 12 | 8.30 |$\pm$| 0.16 | 0.02/0.37 | 96 |$\pm$| 10 | 24 |$\pm$| 3 |
| 587.9333571 | 8 Jan 2022 | 194/0.159 | 2407.1 | 273 | 2.13 | |$-$|59 |$\pm$| 15 | 9.08 |$\pm$| 0.19 | 0.44/1.63 | 177 |$\pm$| 10 | 41 |$\pm$| 3 |
| 588.9350942 | 9 Jan 2022 | 194/0.402 | 2407.1 | 272 | 2.19 | |$-$|30 |$\pm$| 15 | 8.91 |$\pm$| 0.18 | 0.39/1.89 | 161 |$\pm$| 10 | 39 |$\pm$| 3 |
| 589.9833304 | 10 Jan 2022 | 194/0.656 | 2407.1 | 282 | 2.30 | |$-$|1 |$\pm$| 15 | 9.24 |$\pm$| 0.19 | 0.36/1.66 | 143 |$\pm$| 10 | 35 |$\pm$| 3 |
| 590.7944760 | 11 Jan 2022 | 194/0.853 | 2407.1 | 248 | 2.43 | |$-$|37 |$\pm$| 17 | 9.22 |$\pm$| 0.18 | 0.41/1.48 | 142 |$\pm$| 10 | 37 |$\pm$| 3 |
| 591.9658790 | 12 Jan 2022 | 195/0.137 | 2407.1 | 250 | 2.31 | |$-$|44 |$\pm$| 16 | 9.44 |$\pm$| 0.19 | 0.37/1.18 | 175 |$\pm$| 10 | 46 |$\pm$| 3 |
| 592.9683245 | 13 Jan 2022 | 195/0.381 | 2407.1 | 232 | 3.43 | |$-$|63 |$\pm$| 23 | 8.92 |$\pm$| 0.19 | 0.36/0.94 | 172 |$\pm$| 10 | 43 |$\pm$| 3 |
| 593.8925375 | 14 Jan 2022 | 195/0.605 | 2407.1 | 223 | 3.15 | |$-$|40 |$\pm$| 21 | 8.93 |$\pm$| 0.18 | 0.33/0.93 | 165 |$\pm$| 10 | 42 |$\pm$| 3 |
| 594.8359992 | 15 Jan 2022 | 195/0.834 | 2407.1 | 279 | 2.10 | |$-$|20 |$\pm$| 13 | 9.20 |$\pm$| 0.18 | 0.28/0.92 | 164 |$\pm$| 10 | 39 |$\pm$| 3 |
| 595.9992366 | 16 Jan 2022 | 196/0.116 | 2407.1 | 244 | 2.54 | |$-$|80 |$\pm$| 16 | 8.94 |$\pm$| 0.20 | 0.29/0.92 | 172 |$\pm$| 10 | 43 |$\pm$| 3 |
| 596.8879787 | 17 Jan 2022 | 196/0.332 | 2407.1 | 265 | 2.29 | |$-$|43 |$\pm$| 14 | 8.84 |$\pm$| 0.17 | 0.26/0.72 | 169 |$\pm$| 10 | 43 |$\pm$| 3 |
| 597.9366485 | 18 Jan 2022 | 196/0.587 | 2407.1 | 271 | 2.47 | |$-$|62 |$\pm$| 15 | 8.76 |$\pm$| 0.18 | 0.26/0.76 | 169 |$\pm$| 10 | 39 |$\pm$| 3 |
| 598.9194038 | 19 Jan 2022 | 196/0.825 | 2407.1 | 255 | 2.28 | |$-$|58 |$\pm$| 14 | 8.85 |$\pm$| 0.18 | 0.23/0.67 | 142 |$\pm$| 10 | 36 |$\pm$| 3 |
| 599.9732831 | 20 Jan 2022 | 197/0.081 | 2407.1 | 255 | 2.42 | |$-$|73 |$\pm$| 15 | 8.35 |$\pm$| 0.19 | 0.25/0.83 | 147 |$\pm$| 10 | 38 |$\pm$| 3 |
| 601.8978507 | 22 Jan 2022 | 197/0.548 | 2407.1 | 174 | 3.75 | |$-$|73 |$\pm$| 23 | 8.74 |$\pm$| 0.18 | 0.26/0.48 | 130 |$\pm$| 10 | 35 |$\pm$| 3 |
| 602.9316132 | 23 Jan 2022 | 197/0.799 | 2407.1 | 258 | 2.35 | |$-$|43 |$\pm$| 14 | 8.97 |$\pm$| 0.17 | 0.20/0.50 | 119 |$\pm$| 10 | 29 |$\pm$| 3 |
| 603.9124578 | 24 Jan 2022 | 198/0.037 | 2407.1 | 272 | 2.41 | |$-$|73 |$\pm$| 15 | 8.58 |$\pm$| 0.21 | 0.25/0.67 | 121 |$\pm$| 10 | 29 |$\pm$| 3 |
| 604.9164418 | 25 Jan 2022 | 198/0.281 | 2407.1 | 194 | 3.34 | |$-$|64 |$\pm$| 21 | 8.18 |$\pm$| 0.18 | 0.25/0.57 | 116 |$\pm$| 10 | 30 |$\pm$| 3 |
| 606.9054391 | 27 Jan 2022 | 198/0.763 | 2407.1 | 225 | 2.64 | |$-$|49 |$\pm$| 16 | 8.49 |$\pm$| 0.17 | 0.23/0.54 | 122 |$\pm$| 10 | 36 |$\pm$| 3 |
| 607.8850302 | 28 Jan 2022 | 199/0.001 | 2407.1 | 232 | 2.45 | |$-$|44 |$\pm$| 15 | 8.57 |$\pm$| 0.17 | 0.22/0.40 | 127 |$\pm$| 10 | 30 |$\pm$| 3 |
| 608.8852573 | 29 Jan 2022 | 199/0.244 | 2407.1 | 228 | 3.24 | |$-$|81 |$\pm$| 20 | 8.33 |$\pm$| 0.16 | 0.25/0.46 | 112 |$\pm$| 10 | 27 |$\pm$| 3 |
| 609.8900384 | 30 Jan 2022 | 199/0.488 | 2407.1 | 248 | 2.33 | |$-$|79 |$\pm$| 14 | 8.15 |$\pm$| 0.18 | 0.24/0.58 | 106 |$\pm$| 10 | 26 |$\pm$| 3 |
| 610.9655285 | 31 Jan 2022 | 199/0.749 | 2407.1 | 250 | 2.32 | |$-$|58 |$\pm$| 14 | 8.18 |$\pm$| 0.17 | 0.26/0.66 | 96 |$\pm$| 10 | 24 |$\pm$| 3 |
| 886.1012388 | 2 Nov 2022 | 266/0.529 | 2407.1 | 293 | 1.88 | |$-$|19 |$\pm$| 12 | 9.24 |$\pm$| 0.20 | 0.27/0.92 | 159 |$\pm$| 10 | 39 |$\pm$| 3 |
| 890.1199631 | 6 Nov 2022 | 267/0.505 | 2407.1 | 272 | 2.10 | |$-$|47 |$\pm$| 15 | 8.83 |$\pm$| 0.24 | 0.42/1.31 | 130 |$\pm$| 10 | 30 |$\pm$| 3 |
| 891.1149740 | 7 Nov 2022 | 267/0.746 | 2407.1 | 287 | 2.04 | 10 |$\pm$| 13 | 8.91 |$\pm$| 0.24 | 0.33/1.36 | 148 |$\pm$| 10 | 33 |$\pm$| 3 |
| 892.1127054 | 8 Nov 2022 | 267/0.989 | 2407.1 | 270 | 2.10 | 10 |$\pm$| 13 | 9.35 |$\pm$| 0.22 | 0.26/1.26 | 138 |$\pm$| 10 | 33 |$\pm$| 3 |
| 893.1035281 | 9 Nov 2022 | 268/0.229 | 2407.1 | 239 | 2.29 | |$-$|4 |$\pm$| 14 | 8.81 |$\pm$| 0.22 | 0.26/0.83 | 160 |$\pm$| 10 | 35 |$\pm$| 3 |
| 895.1312799 | 11 Nov 2022 | 268/0.721 | 2407.1 | 223 | 2.58 | |$-$|32 |$\pm$| 15 | 8.94 |$\pm$| 0.22 | 0.19/0.34 | 113 |$\pm$| 10 | 25 |$\pm$| 3 |
| 896.0325625 | 12 Nov 2022 | 268/0.940 | 2407.1 | 269 | 2.03 | |$-$|14 |$\pm$| 12 | 9.33 |$\pm$| 0.20 | 0.18/0.66 | 132 |$\pm$| 10 | 31 |$\pm$| 3 |
| 899.1357048 | 15 Nov 2022 | 269/0.693 | 2407.1 | 257 | 2.22 | |$-$|33 |$\pm$| 12 | 8.79 |$\pm$| 0.20 | 0.09/0.51 | 122 |$\pm$| 10 | 29 |$\pm$| 3 |
| 902.1108546 | 18 Nov 2022 | 270/0.415 | 2407.1 | 254 | 2.27 | |$-$|44 |$\pm$| 12 | 8.53 |$\pm$| 0.19 | 0.05/0.31 | 114 |$\pm$| 10 | 27 |$\pm$| 3 |
| 905.0987525 | 21 Nov 2022 | 271/0.140 | 2407.1 | 211 | 2.65 | |$-$|21 |$\pm$| 13 | 8.51 |$\pm$| 0.20 | 0.02/0.08 | 139 |$\pm$| 10 | 31 |$\pm$| 3 |
| 906.1044391 | 22 Nov 2022 | 271/0.385 | 2407.1 | 230 | 2.41 | |$-$|65 |$\pm$| 12 | 8.23 |$\pm$| 0.18 | 0.00/0.13 | 112 |$\pm$| 10 | 25 |$\pm$| 3 |
| 978.9367863 | 3 Feb 2023 | 289/0.062 | 2407.1 | 227 | 2.44 | |$-$|19 |$\pm$| 14 | 7.14 |$\pm$| 0.18 | 0.14/0.68 | 93 |$\pm$| 10 | 20 |$\pm$| 3 |
| 980.9163238 | 5 Feb 2023 | 289/0.543 | 2407.1 | 176 | 3.82 | |$-$|18 |$\pm$| 23 | 6.77 |$\pm$| 0.20 | 0.22/0.68 | 73 |$\pm$| 10 | 18 |$\pm$| 3 |
| 983.9060551 | 8 Feb 2023 | 290/0.268 | 2407.1 | 238 | 2.36 | |$-$|38 |$\pm$| 14 | 7.19 |$\pm$| 0.19 | 0.19/0.41 | 61 |$\pm$| 10 | 14 |$\pm$| 3 |
| 1036.7643629 | 2 Apr 2023 | 303/0.098 | 2407.1 | 246 | 2.41 | 13 |$\pm$| 23 | 9.33 |$\pm$| 0.28 | 0.92/5.14 | 208 |$\pm$| 10 | 41 |$\pm$| 3 |
| 1041.7274405 | 7 Apr 2023 | 304/0.303 | 2407.1 | 261 | 2.17 | 5 |$\pm$| 18 | 8.74 |$\pm$| 0.28 | 0.71/2.97 | 188 |$\pm$| 10 | 35 |$\pm$| 3 |
| 1045.7255305 | 11 Apr 2023 | 305/0.273 | 2407.1 | 187 | 3.86 | 14 |$\pm$| 29 | 9.24 |$\pm$| 0.26 | 0.52/1.97 | 153 |$\pm$| 10 | 28 |$\pm$| 3 |
Observing log of our SPIRou observations of V347 Aur in seasons 2019, 2020, 2021, and 2022. All exposures consist of four sub-exposures of equal length. For each visit, we list the BJD, the UT date, the rotation cycle c and phase |$\phi$| (computed as indicated in Section 3), the total observing time t|$_{\rm exp}$|, the peak SNR in the spectrum (in the H band) per 2.3 km s|$^{-1}$| pixel, the noise level in the LSD Stokes V profile, the estimated |$B_{\rm \ell }$| with error bars, the nightly averaged RVs and corresponding error bars, the veiling in the |$JH$| and in the K bands |$r_{JH}$| and |$r_K$| measured from LSD profiles of atomic lines and CO lines, respectively, and finally the EWs of the Pa|${\beta }$| and Br|${\gamma }$| emission lines with error bars (not scaled up with veiling).
| BJD . | UT date . | c/|$\phi$| . | t|$_{\rm exp}$| . | SNR . | |$\sigma _V$| . | |$B_{\rm \ell }$| . | RV . | |$r_{JH}$|/|$r_K$| . | EW Pa|${\beta }$| . | EW Br|${\gamma }$| . |
|---|---|---|---|---|---|---|---|---|---|---|
| (2459000+) . | . | . | (s) . | (H) . | (|$10^{-4} I_{\rm c}$|) . | (G) . | (km s|$^{-1}$|) . | . | (km s|$^{-1}$|) . | (km s|$^{-1}$|) . |
| |$-$|211.9145299 | 31 Oct 2019 | 0/0.021 | 2407.1 | 245 | 2.43 | |$-$|38 |$\pm$| 21 | 9.22|$\pm$|0.28 | 0.77/1.75 | 249 |$\pm$| 10 | 58 |$\pm$| 3 |
| |$-$|210.9098887 | 1 Nov 2019 | 0/0.265 | 2407.1 | 236 | 2.49 | |$-$|32 |$\pm$| 21 | 8.62 |$\pm$| 0.29 | 0.75/2.54 | 247 |$\pm$| 10 | 57 |$\pm$| 3 |
| |$-$|208.9302687 | 3 Nov 2019 | 0/0.745 | 2407.1 | 230 | 2.54 | |$-$|76 |$\pm$| 20 | 8.65 |$\pm$| 0.29 | 0.57/3.40 | 224 |$\pm$| 10 | 54 |$\pm$| 3 |
| |$-$|206.8956725 | 5 Nov 2019 | 1/0.239 | 2407.1 | 219 | 2.69 | |$-$|26 |$\pm$| 20 | 8.95 |$\pm$| 0.29 | 0.53/2.12 | 218 |$\pm$| 10 | 56 |$\pm$| 3 |
| |$-$|204.9686594 | 7 Nov 2019 | 1/0.707 | 2407.1 | 213 | 2.77 | |$-$|60 |$\pm$| 20 | 9.02 |$\pm$| 0.29 | 0.46/2.28 | 209 |$\pm$| 10 | 51 |$\pm$| 3 |
| |$-$|202.9959549 | 9 Nov 2019 | 2/0.185 | 2407.1 | 149 | 4.21 | |$-$|19 |$\pm$| 30 | 7.96 |$\pm$| 0.35 | 0.45/1.16 | 202 |$\pm$| 10 | 52 |$\pm$| 3 |
| |$-$|200.9071390 | 11 Nov 2019 | 2/0.692 | 2407.1 | 172 | 3.67 | |$-$|66 |$\pm$| 22 | 8.84 |$\pm$| 0.24 | 0.25/0.84 | 151 |$\pm$| 10 | 39 |$\pm$| 3 |
| |$-$|198.9782271 | 13 Nov 2019 | 3/0.161 | 2407.1 | 212 | 2.92 | |$-$|65 |$\pm$| 19 | 8.77 |$\pm$| 0.31 | 0.34/1.29 | 190 |$\pm$| 10 | 50 |$\pm$| 3 |
| |$-$|197.9612905 | 14 Nov 2019 | 3/0.407 | 2407.1 | 190 | 3.16 | |$-$|43 |$\pm$| 21 | 8.43 |$\pm$| 0.31 | 0.34/1.03 | 154 |$\pm$| 10 | 42 |$\pm$| 3 |
| |$-$|174.0001745 | 8 Dec 2019 | 9/0.223 | 2407.1 | 182 | 3.26 | |$-$|34 |$\pm$| 19 | 8.10 |$\pm$| 0.27 | 0.20/0.71 | 134 |$\pm$| 10 | 32 |$\pm$| 3 |
| |$-$|172.9716427 | 9 Dec 2019 | 9/0.473 | 2407.1 | 195 | 3.02 | |$-$|73 |$\pm$| 17 | 8.39 |$\pm$| 0.25 | 0.17/0.69 | 124 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|172.0535410 | 10 Dec 2019 | 9/0.696 | 2312.3 | 214 | 2.71 | |$-$|40 |$\pm$| 15 | 8.44 |$\pm$| 0.20 | 0.15/0.68 | 129 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|170.9462697 | 11 Dec 2019 | 9/0.964 | 2407.1 | 210 | 2.76 | |$-$|36 |$\pm$| 16 | 8.68 |$\pm$| 0.25 | 0.18/0.69 | 123 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|169.9334152 | 12 Dec 2019 | 10/0.210 | 2379.2 | 192 | 3.07 | |$-$|30 |$\pm$| 17 | 8.21 |$\pm$| 0.20 | 0.14/0.65 | 115 |$\pm$| 10 | 28 |$\pm$| 3 |
| 207.9252214 | 24 Dec 2020 | 101/0.924 | 2407.1 | 259 | 2.31 | |$-$|19 |$\pm$| 15 | 7.57 |$\pm$| 0.19 | 0.29/0.81 | 88 |$\pm$| 10 | 22 |$\pm$| 3 |
| 208.9343916 | 25 Dec 2020 | 102/0.169 | 2407.1 | 254 | 2.39 | |$-$|42 |$\pm$| 15 | 7.44 |$\pm$| 0.20 | 0.27/0.75 | 111 |$\pm$| 10 | 25 |$\pm$| 3 |
| 209.8880836 | 26 Dec 2020 | 102/0.400 | 2407.1 | 252 | 2.60 | |$-$|12 |$\pm$| 16 | 7.13 |$\pm$| 0.20 | 0.24/0.55 | 97 |$\pm$| 10 | 23 |$\pm$| 3 |
| 211.9500308 | 28 Dec 2020 | 102/0.900 | 2407.1 | 189 | 3.31 | |$-$|43 |$\pm$| 21 | 7.22 |$\pm$| 0.20 | 0.28/0.35 | 79 |$\pm$| 10 | 18 |$\pm$| 3 |
| 212.9362811 | 29 Dec 2020 | 103/0.140 | 2407.1 | 224 | 2.70 | |$-$|45 |$\pm$| 17 | 7.30 |$\pm$| 0.21 | 0.26/0.32 | 103 |$\pm$| 10 | 29 |$\pm$| 3 |
| 214.8980511 | 31 Dec 2020 | 103/0.616 | 2407.1 | 220 | 2.71 | |$-$|57 |$\pm$| 16 | 7.11 |$\pm$| 0.20 | 0.24/0.33 | 107 |$\pm$| 10 | 27 |$\pm$| 3 |
| 215.8662680 | 1 Jan 2021 | 103/0.851 | 2407.1 | 165 | 3.76 | |$-$|68 |$\pm$| 25 | 7.24 |$\pm$| 0.22 | 0.37/0.55 | 100 |$\pm$| 10 | 26 |$\pm$| 3 |
| 217.8901191 | 3 Jan 2021 | 104/0.342 | 2407.1 | 248 | 2.27 | |$-$|75 |$\pm$| 15 | 7.06 |$\pm$| 0.22 | 0.36/0.43 | 100 |$\pm$| 10 | 25 |$\pm$| 3 |
| 218.8741188 | 4 Jan 2021 | 104/0.581 | 2407.1 | 250 | 2.29 | |$-$|59 |$\pm$| 14 | 6.81 |$\pm$| 0.19 | 0.26/0.40 | 90 |$\pm$| 10 | 20 |$\pm$| 3 |
| 219.9045892 | 5 Jan 2021 | 104/0.831 | 2407.1 | 246 | 2.28 | |$-$|47 |$\pm$| 15 | 7.33 |$\pm$| 0.20 | 0.33/0.59 | 80 |$\pm$| 10 | 18 |$\pm$| 3 |
| 220.8613214 | 6 Jan 2021 | 105/0.063 | 2407.1 | 254 | 2.19 | |$-$|68 |$\pm$| 15 | 7.38 |$\pm$| 0.22 | 0.43/0.77 | 107 |$\pm$| 10 | 26 |$\pm$| 3 |
| 221.9203503 | 7 Jan 2021 | 105/0.320 | 2407.1 | 240 | 2.39 | |$-$|34 |$\pm$| 17 | 6.76 |$\pm$| 0.22 | 0.46/0.73 | 119 |$\pm$| 10 | 30 |$\pm$| 3 |
| 222.9318705 | 8 Jan 2021 | 105/0.566 | 2407.1 | 241 | 2.34 | |$-$|73 |$\pm$| 16 | 6.87 |$\pm$| 0.21 | 0.36/0.76 | 101 |$\pm$| 10 | 23 |$\pm$| 3 |
| 267.7272476 | 22 Feb 2021 | 116/0.439 | 2407.1 | 271 | 2.10 | |$-$|42 |$\pm$| 14 | 9.47 |$\pm$| 0.21 | 0.34/2.38 | 173 |$\pm$| 10 | 39 |$\pm$| 3 |
| 268.8634318 | 23 Feb 2021 | 116/0.714 | 2407.1 | 262 | 2.16 | |$-$|30 |$\pm$| 14 | 9.51 |$\pm$| 0.25 | 0.30/2.45 | 191 |$\pm$| 10 | 42 |$\pm$| 3 |
| 271.7845315 | 26 Feb 2021 | 117/0.423 | 2407.1 | 224 | 2.52 | |$-$|10 |$\pm$| 16 | 8.78 |$\pm$| 0.20 | 0.30/1.42 | 177 |$\pm$| 10 | 41 |$\pm$| 3 |
| 273.8651093 | 28 Feb 2021 | 117/0.928 | 2407.1 | 182 | 3.27 | |$-$|38 |$\pm$| 21 | 9.05 |$\pm$| 0.22 | 0.31/1.43 | 177 |$\pm$| 10 | 40 |$\pm$| 3 |
| 276.7836915 | 3 Mar 2021 | 118/0.637 | 2407.1 | 263 | 2.06 | |$-$|26 |$\pm$| 12 | 8.98 |$\pm$| 0.19 | 0.21/1.22 | 162 |$\pm$| 10 | 36 |$\pm$| 3 |
| 277.7285551 | 4 Mar 2021 | 118/0.866 | 2407.1 | 255 | 2.10 | |$-$|55 |$\pm$| 12 | 9.03 |$\pm$| 0.19 | 0.17/1.09 | 162 |$\pm$| 10 | 37 |$\pm$| 3 |
| 293.7342341 | 20 Mar 2021 | 122/0.751 | 2407.1 | 232 | 2.44 | |$-$|69 |$\pm$| 12 | 8.58 |$\pm$| 0.17 | 0.02/0.36 | 146 |$\pm$| 10 | 39 |$\pm$| 3 |
| 297.7716803 | 24 Mar 2021 | 123/0.731 | 2407.1 | 221 | 2.53 | |$-$|51 |$\pm$| 13 | 8.48 |$\pm$| 0.17 | 0.03/0.33 | 116 |$\pm$| 10 | 29 |$\pm$| 3 |
| 299.7983781 | 26 Mar 2021 | 124/0.223 | 2407.1 | 186 | 3.25 | |$-$|54 |$\pm$| 17 | 8.05 |$\pm$| 0.18 | 0.04/0.29 | 106 |$\pm$| 10 | 28 |$\pm$| 3 |
| 300.7513668 | 27 Mar 2021 | 124/0.454 | 2407.1 | 206 | 3.02 | |$-$|35 |$\pm$| 15 | 8.14 |$\pm$| 0.17 | 0.04/0.37 | 109 |$\pm$| 10 | 27 |$\pm$| 3 |
| 301.7807176 | 28 Mar 2021 | 124/0.704 | 2407.1 | 159 | 3.80 | |$-$|36 |$\pm$| 21 | 8.30 |$\pm$| 0.19 | 0.15/0.86 | 95 |$\pm$| 10 | 25 |$\pm$| 3 |
| 304.7728769 | 31 Mar 2021 | 125/0.430 | 2407.1 | 223 | 2.63 | |$-$|79 |$\pm$| 13 | 7.95 |$\pm$| 0.17 | 0.01/0.44 | 102 |$\pm$| 10 | 22 |$\pm$| 3 |
| 305.7334444 | 1 Apr 2021 | 125/0.663 | 2407.1 | 226 | 2.46 | |$-$|68 |$\pm$| 12 | 8.30 |$\pm$| 0.16 | 0.02/0.37 | 96 |$\pm$| 10 | 24 |$\pm$| 3 |
| 587.9333571 | 8 Jan 2022 | 194/0.159 | 2407.1 | 273 | 2.13 | |$-$|59 |$\pm$| 15 | 9.08 |$\pm$| 0.19 | 0.44/1.63 | 177 |$\pm$| 10 | 41 |$\pm$| 3 |
| 588.9350942 | 9 Jan 2022 | 194/0.402 | 2407.1 | 272 | 2.19 | |$-$|30 |$\pm$| 15 | 8.91 |$\pm$| 0.18 | 0.39/1.89 | 161 |$\pm$| 10 | 39 |$\pm$| 3 |
| 589.9833304 | 10 Jan 2022 | 194/0.656 | 2407.1 | 282 | 2.30 | |$-$|1 |$\pm$| 15 | 9.24 |$\pm$| 0.19 | 0.36/1.66 | 143 |$\pm$| 10 | 35 |$\pm$| 3 |
| 590.7944760 | 11 Jan 2022 | 194/0.853 | 2407.1 | 248 | 2.43 | |$-$|37 |$\pm$| 17 | 9.22 |$\pm$| 0.18 | 0.41/1.48 | 142 |$\pm$| 10 | 37 |$\pm$| 3 |
| 591.9658790 | 12 Jan 2022 | 195/0.137 | 2407.1 | 250 | 2.31 | |$-$|44 |$\pm$| 16 | 9.44 |$\pm$| 0.19 | 0.37/1.18 | 175 |$\pm$| 10 | 46 |$\pm$| 3 |
| 592.9683245 | 13 Jan 2022 | 195/0.381 | 2407.1 | 232 | 3.43 | |$-$|63 |$\pm$| 23 | 8.92 |$\pm$| 0.19 | 0.36/0.94 | 172 |$\pm$| 10 | 43 |$\pm$| 3 |
| 593.8925375 | 14 Jan 2022 | 195/0.605 | 2407.1 | 223 | 3.15 | |$-$|40 |$\pm$| 21 | 8.93 |$\pm$| 0.18 | 0.33/0.93 | 165 |$\pm$| 10 | 42 |$\pm$| 3 |
| 594.8359992 | 15 Jan 2022 | 195/0.834 | 2407.1 | 279 | 2.10 | |$-$|20 |$\pm$| 13 | 9.20 |$\pm$| 0.18 | 0.28/0.92 | 164 |$\pm$| 10 | 39 |$\pm$| 3 |
| 595.9992366 | 16 Jan 2022 | 196/0.116 | 2407.1 | 244 | 2.54 | |$-$|80 |$\pm$| 16 | 8.94 |$\pm$| 0.20 | 0.29/0.92 | 172 |$\pm$| 10 | 43 |$\pm$| 3 |
| 596.8879787 | 17 Jan 2022 | 196/0.332 | 2407.1 | 265 | 2.29 | |$-$|43 |$\pm$| 14 | 8.84 |$\pm$| 0.17 | 0.26/0.72 | 169 |$\pm$| 10 | 43 |$\pm$| 3 |
| 597.9366485 | 18 Jan 2022 | 196/0.587 | 2407.1 | 271 | 2.47 | |$-$|62 |$\pm$| 15 | 8.76 |$\pm$| 0.18 | 0.26/0.76 | 169 |$\pm$| 10 | 39 |$\pm$| 3 |
| 598.9194038 | 19 Jan 2022 | 196/0.825 | 2407.1 | 255 | 2.28 | |$-$|58 |$\pm$| 14 | 8.85 |$\pm$| 0.18 | 0.23/0.67 | 142 |$\pm$| 10 | 36 |$\pm$| 3 |
| 599.9732831 | 20 Jan 2022 | 197/0.081 | 2407.1 | 255 | 2.42 | |$-$|73 |$\pm$| 15 | 8.35 |$\pm$| 0.19 | 0.25/0.83 | 147 |$\pm$| 10 | 38 |$\pm$| 3 |
| 601.8978507 | 22 Jan 2022 | 197/0.548 | 2407.1 | 174 | 3.75 | |$-$|73 |$\pm$| 23 | 8.74 |$\pm$| 0.18 | 0.26/0.48 | 130 |$\pm$| 10 | 35 |$\pm$| 3 |
| 602.9316132 | 23 Jan 2022 | 197/0.799 | 2407.1 | 258 | 2.35 | |$-$|43 |$\pm$| 14 | 8.97 |$\pm$| 0.17 | 0.20/0.50 | 119 |$\pm$| 10 | 29 |$\pm$| 3 |
| 603.9124578 | 24 Jan 2022 | 198/0.037 | 2407.1 | 272 | 2.41 | |$-$|73 |$\pm$| 15 | 8.58 |$\pm$| 0.21 | 0.25/0.67 | 121 |$\pm$| 10 | 29 |$\pm$| 3 |
| 604.9164418 | 25 Jan 2022 | 198/0.281 | 2407.1 | 194 | 3.34 | |$-$|64 |$\pm$| 21 | 8.18 |$\pm$| 0.18 | 0.25/0.57 | 116 |$\pm$| 10 | 30 |$\pm$| 3 |
| 606.9054391 | 27 Jan 2022 | 198/0.763 | 2407.1 | 225 | 2.64 | |$-$|49 |$\pm$| 16 | 8.49 |$\pm$| 0.17 | 0.23/0.54 | 122 |$\pm$| 10 | 36 |$\pm$| 3 |
| 607.8850302 | 28 Jan 2022 | 199/0.001 | 2407.1 | 232 | 2.45 | |$-$|44 |$\pm$| 15 | 8.57 |$\pm$| 0.17 | 0.22/0.40 | 127 |$\pm$| 10 | 30 |$\pm$| 3 |
| 608.8852573 | 29 Jan 2022 | 199/0.244 | 2407.1 | 228 | 3.24 | |$-$|81 |$\pm$| 20 | 8.33 |$\pm$| 0.16 | 0.25/0.46 | 112 |$\pm$| 10 | 27 |$\pm$| 3 |
| 609.8900384 | 30 Jan 2022 | 199/0.488 | 2407.1 | 248 | 2.33 | |$-$|79 |$\pm$| 14 | 8.15 |$\pm$| 0.18 | 0.24/0.58 | 106 |$\pm$| 10 | 26 |$\pm$| 3 |
| 610.9655285 | 31 Jan 2022 | 199/0.749 | 2407.1 | 250 | 2.32 | |$-$|58 |$\pm$| 14 | 8.18 |$\pm$| 0.17 | 0.26/0.66 | 96 |$\pm$| 10 | 24 |$\pm$| 3 |
| 886.1012388 | 2 Nov 2022 | 266/0.529 | 2407.1 | 293 | 1.88 | |$-$|19 |$\pm$| 12 | 9.24 |$\pm$| 0.20 | 0.27/0.92 | 159 |$\pm$| 10 | 39 |$\pm$| 3 |
| 890.1199631 | 6 Nov 2022 | 267/0.505 | 2407.1 | 272 | 2.10 | |$-$|47 |$\pm$| 15 | 8.83 |$\pm$| 0.24 | 0.42/1.31 | 130 |$\pm$| 10 | 30 |$\pm$| 3 |
| 891.1149740 | 7 Nov 2022 | 267/0.746 | 2407.1 | 287 | 2.04 | 10 |$\pm$| 13 | 8.91 |$\pm$| 0.24 | 0.33/1.36 | 148 |$\pm$| 10 | 33 |$\pm$| 3 |
| 892.1127054 | 8 Nov 2022 | 267/0.989 | 2407.1 | 270 | 2.10 | 10 |$\pm$| 13 | 9.35 |$\pm$| 0.22 | 0.26/1.26 | 138 |$\pm$| 10 | 33 |$\pm$| 3 |
| 893.1035281 | 9 Nov 2022 | 268/0.229 | 2407.1 | 239 | 2.29 | |$-$|4 |$\pm$| 14 | 8.81 |$\pm$| 0.22 | 0.26/0.83 | 160 |$\pm$| 10 | 35 |$\pm$| 3 |
| 895.1312799 | 11 Nov 2022 | 268/0.721 | 2407.1 | 223 | 2.58 | |$-$|32 |$\pm$| 15 | 8.94 |$\pm$| 0.22 | 0.19/0.34 | 113 |$\pm$| 10 | 25 |$\pm$| 3 |
| 896.0325625 | 12 Nov 2022 | 268/0.940 | 2407.1 | 269 | 2.03 | |$-$|14 |$\pm$| 12 | 9.33 |$\pm$| 0.20 | 0.18/0.66 | 132 |$\pm$| 10 | 31 |$\pm$| 3 |
| 899.1357048 | 15 Nov 2022 | 269/0.693 | 2407.1 | 257 | 2.22 | |$-$|33 |$\pm$| 12 | 8.79 |$\pm$| 0.20 | 0.09/0.51 | 122 |$\pm$| 10 | 29 |$\pm$| 3 |
| 902.1108546 | 18 Nov 2022 | 270/0.415 | 2407.1 | 254 | 2.27 | |$-$|44 |$\pm$| 12 | 8.53 |$\pm$| 0.19 | 0.05/0.31 | 114 |$\pm$| 10 | 27 |$\pm$| 3 |
| 905.0987525 | 21 Nov 2022 | 271/0.140 | 2407.1 | 211 | 2.65 | |$-$|21 |$\pm$| 13 | 8.51 |$\pm$| 0.20 | 0.02/0.08 | 139 |$\pm$| 10 | 31 |$\pm$| 3 |
| 906.1044391 | 22 Nov 2022 | 271/0.385 | 2407.1 | 230 | 2.41 | |$-$|65 |$\pm$| 12 | 8.23 |$\pm$| 0.18 | 0.00/0.13 | 112 |$\pm$| 10 | 25 |$\pm$| 3 |
| 978.9367863 | 3 Feb 2023 | 289/0.062 | 2407.1 | 227 | 2.44 | |$-$|19 |$\pm$| 14 | 7.14 |$\pm$| 0.18 | 0.14/0.68 | 93 |$\pm$| 10 | 20 |$\pm$| 3 |
| 980.9163238 | 5 Feb 2023 | 289/0.543 | 2407.1 | 176 | 3.82 | |$-$|18 |$\pm$| 23 | 6.77 |$\pm$| 0.20 | 0.22/0.68 | 73 |$\pm$| 10 | 18 |$\pm$| 3 |
| 983.9060551 | 8 Feb 2023 | 290/0.268 | 2407.1 | 238 | 2.36 | |$-$|38 |$\pm$| 14 | 7.19 |$\pm$| 0.19 | 0.19/0.41 | 61 |$\pm$| 10 | 14 |$\pm$| 3 |
| 1036.7643629 | 2 Apr 2023 | 303/0.098 | 2407.1 | 246 | 2.41 | 13 |$\pm$| 23 | 9.33 |$\pm$| 0.28 | 0.92/5.14 | 208 |$\pm$| 10 | 41 |$\pm$| 3 |
| 1041.7274405 | 7 Apr 2023 | 304/0.303 | 2407.1 | 261 | 2.17 | 5 |$\pm$| 18 | 8.74 |$\pm$| 0.28 | 0.71/2.97 | 188 |$\pm$| 10 | 35 |$\pm$| 3 |
| 1045.7255305 | 11 Apr 2023 | 305/0.273 | 2407.1 | 187 | 3.86 | 14 |$\pm$| 29 | 9.24 |$\pm$| 0.26 | 0.52/1.97 | 153 |$\pm$| 10 | 28 |$\pm$| 3 |
| BJD . | UT date . | c/|$\phi$| . | t|$_{\rm exp}$| . | SNR . | |$\sigma _V$| . | |$B_{\rm \ell }$| . | RV . | |$r_{JH}$|/|$r_K$| . | EW Pa|${\beta }$| . | EW Br|${\gamma }$| . |
|---|---|---|---|---|---|---|---|---|---|---|
| (2459000+) . | . | . | (s) . | (H) . | (|$10^{-4} I_{\rm c}$|) . | (G) . | (km s|$^{-1}$|) . | . | (km s|$^{-1}$|) . | (km s|$^{-1}$|) . |
| |$-$|211.9145299 | 31 Oct 2019 | 0/0.021 | 2407.1 | 245 | 2.43 | |$-$|38 |$\pm$| 21 | 9.22|$\pm$|0.28 | 0.77/1.75 | 249 |$\pm$| 10 | 58 |$\pm$| 3 |
| |$-$|210.9098887 | 1 Nov 2019 | 0/0.265 | 2407.1 | 236 | 2.49 | |$-$|32 |$\pm$| 21 | 8.62 |$\pm$| 0.29 | 0.75/2.54 | 247 |$\pm$| 10 | 57 |$\pm$| 3 |
| |$-$|208.9302687 | 3 Nov 2019 | 0/0.745 | 2407.1 | 230 | 2.54 | |$-$|76 |$\pm$| 20 | 8.65 |$\pm$| 0.29 | 0.57/3.40 | 224 |$\pm$| 10 | 54 |$\pm$| 3 |
| |$-$|206.8956725 | 5 Nov 2019 | 1/0.239 | 2407.1 | 219 | 2.69 | |$-$|26 |$\pm$| 20 | 8.95 |$\pm$| 0.29 | 0.53/2.12 | 218 |$\pm$| 10 | 56 |$\pm$| 3 |
| |$-$|204.9686594 | 7 Nov 2019 | 1/0.707 | 2407.1 | 213 | 2.77 | |$-$|60 |$\pm$| 20 | 9.02 |$\pm$| 0.29 | 0.46/2.28 | 209 |$\pm$| 10 | 51 |$\pm$| 3 |
| |$-$|202.9959549 | 9 Nov 2019 | 2/0.185 | 2407.1 | 149 | 4.21 | |$-$|19 |$\pm$| 30 | 7.96 |$\pm$| 0.35 | 0.45/1.16 | 202 |$\pm$| 10 | 52 |$\pm$| 3 |
| |$-$|200.9071390 | 11 Nov 2019 | 2/0.692 | 2407.1 | 172 | 3.67 | |$-$|66 |$\pm$| 22 | 8.84 |$\pm$| 0.24 | 0.25/0.84 | 151 |$\pm$| 10 | 39 |$\pm$| 3 |
| |$-$|198.9782271 | 13 Nov 2019 | 3/0.161 | 2407.1 | 212 | 2.92 | |$-$|65 |$\pm$| 19 | 8.77 |$\pm$| 0.31 | 0.34/1.29 | 190 |$\pm$| 10 | 50 |$\pm$| 3 |
| |$-$|197.9612905 | 14 Nov 2019 | 3/0.407 | 2407.1 | 190 | 3.16 | |$-$|43 |$\pm$| 21 | 8.43 |$\pm$| 0.31 | 0.34/1.03 | 154 |$\pm$| 10 | 42 |$\pm$| 3 |
| |$-$|174.0001745 | 8 Dec 2019 | 9/0.223 | 2407.1 | 182 | 3.26 | |$-$|34 |$\pm$| 19 | 8.10 |$\pm$| 0.27 | 0.20/0.71 | 134 |$\pm$| 10 | 32 |$\pm$| 3 |
| |$-$|172.9716427 | 9 Dec 2019 | 9/0.473 | 2407.1 | 195 | 3.02 | |$-$|73 |$\pm$| 17 | 8.39 |$\pm$| 0.25 | 0.17/0.69 | 124 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|172.0535410 | 10 Dec 2019 | 9/0.696 | 2312.3 | 214 | 2.71 | |$-$|40 |$\pm$| 15 | 8.44 |$\pm$| 0.20 | 0.15/0.68 | 129 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|170.9462697 | 11 Dec 2019 | 9/0.964 | 2407.1 | 210 | 2.76 | |$-$|36 |$\pm$| 16 | 8.68 |$\pm$| 0.25 | 0.18/0.69 | 123 |$\pm$| 10 | 29 |$\pm$| 3 |
| |$-$|169.9334152 | 12 Dec 2019 | 10/0.210 | 2379.2 | 192 | 3.07 | |$-$|30 |$\pm$| 17 | 8.21 |$\pm$| 0.20 | 0.14/0.65 | 115 |$\pm$| 10 | 28 |$\pm$| 3 |
| 207.9252214 | 24 Dec 2020 | 101/0.924 | 2407.1 | 259 | 2.31 | |$-$|19 |$\pm$| 15 | 7.57 |$\pm$| 0.19 | 0.29/0.81 | 88 |$\pm$| 10 | 22 |$\pm$| 3 |
| 208.9343916 | 25 Dec 2020 | 102/0.169 | 2407.1 | 254 | 2.39 | |$-$|42 |$\pm$| 15 | 7.44 |$\pm$| 0.20 | 0.27/0.75 | 111 |$\pm$| 10 | 25 |$\pm$| 3 |
| 209.8880836 | 26 Dec 2020 | 102/0.400 | 2407.1 | 252 | 2.60 | |$-$|12 |$\pm$| 16 | 7.13 |$\pm$| 0.20 | 0.24/0.55 | 97 |$\pm$| 10 | 23 |$\pm$| 3 |
| 211.9500308 | 28 Dec 2020 | 102/0.900 | 2407.1 | 189 | 3.31 | |$-$|43 |$\pm$| 21 | 7.22 |$\pm$| 0.20 | 0.28/0.35 | 79 |$\pm$| 10 | 18 |$\pm$| 3 |
| 212.9362811 | 29 Dec 2020 | 103/0.140 | 2407.1 | 224 | 2.70 | |$-$|45 |$\pm$| 17 | 7.30 |$\pm$| 0.21 | 0.26/0.32 | 103 |$\pm$| 10 | 29 |$\pm$| 3 |
| 214.8980511 | 31 Dec 2020 | 103/0.616 | 2407.1 | 220 | 2.71 | |$-$|57 |$\pm$| 16 | 7.11 |$\pm$| 0.20 | 0.24/0.33 | 107 |$\pm$| 10 | 27 |$\pm$| 3 |
| 215.8662680 | 1 Jan 2021 | 103/0.851 | 2407.1 | 165 | 3.76 | |$-$|68 |$\pm$| 25 | 7.24 |$\pm$| 0.22 | 0.37/0.55 | 100 |$\pm$| 10 | 26 |$\pm$| 3 |
| 217.8901191 | 3 Jan 2021 | 104/0.342 | 2407.1 | 248 | 2.27 | |$-$|75 |$\pm$| 15 | 7.06 |$\pm$| 0.22 | 0.36/0.43 | 100 |$\pm$| 10 | 25 |$\pm$| 3 |
| 218.8741188 | 4 Jan 2021 | 104/0.581 | 2407.1 | 250 | 2.29 | |$-$|59 |$\pm$| 14 | 6.81 |$\pm$| 0.19 | 0.26/0.40 | 90 |$\pm$| 10 | 20 |$\pm$| 3 |
| 219.9045892 | 5 Jan 2021 | 104/0.831 | 2407.1 | 246 | 2.28 | |$-$|47 |$\pm$| 15 | 7.33 |$\pm$| 0.20 | 0.33/0.59 | 80 |$\pm$| 10 | 18 |$\pm$| 3 |
| 220.8613214 | 6 Jan 2021 | 105/0.063 | 2407.1 | 254 | 2.19 | |$-$|68 |$\pm$| 15 | 7.38 |$\pm$| 0.22 | 0.43/0.77 | 107 |$\pm$| 10 | 26 |$\pm$| 3 |
| 221.9203503 | 7 Jan 2021 | 105/0.320 | 2407.1 | 240 | 2.39 | |$-$|34 |$\pm$| 17 | 6.76 |$\pm$| 0.22 | 0.46/0.73 | 119 |$\pm$| 10 | 30 |$\pm$| 3 |
| 222.9318705 | 8 Jan 2021 | 105/0.566 | 2407.1 | 241 | 2.34 | |$-$|73 |$\pm$| 16 | 6.87 |$\pm$| 0.21 | 0.36/0.76 | 101 |$\pm$| 10 | 23 |$\pm$| 3 |
| 267.7272476 | 22 Feb 2021 | 116/0.439 | 2407.1 | 271 | 2.10 | |$-$|42 |$\pm$| 14 | 9.47 |$\pm$| 0.21 | 0.34/2.38 | 173 |$\pm$| 10 | 39 |$\pm$| 3 |
| 268.8634318 | 23 Feb 2021 | 116/0.714 | 2407.1 | 262 | 2.16 | |$-$|30 |$\pm$| 14 | 9.51 |$\pm$| 0.25 | 0.30/2.45 | 191 |$\pm$| 10 | 42 |$\pm$| 3 |
| 271.7845315 | 26 Feb 2021 | 117/0.423 | 2407.1 | 224 | 2.52 | |$-$|10 |$\pm$| 16 | 8.78 |$\pm$| 0.20 | 0.30/1.42 | 177 |$\pm$| 10 | 41 |$\pm$| 3 |
| 273.8651093 | 28 Feb 2021 | 117/0.928 | 2407.1 | 182 | 3.27 | |$-$|38 |$\pm$| 21 | 9.05 |$\pm$| 0.22 | 0.31/1.43 | 177 |$\pm$| 10 | 40 |$\pm$| 3 |
| 276.7836915 | 3 Mar 2021 | 118/0.637 | 2407.1 | 263 | 2.06 | |$-$|26 |$\pm$| 12 | 8.98 |$\pm$| 0.19 | 0.21/1.22 | 162 |$\pm$| 10 | 36 |$\pm$| 3 |
| 277.7285551 | 4 Mar 2021 | 118/0.866 | 2407.1 | 255 | 2.10 | |$-$|55 |$\pm$| 12 | 9.03 |$\pm$| 0.19 | 0.17/1.09 | 162 |$\pm$| 10 | 37 |$\pm$| 3 |
| 293.7342341 | 20 Mar 2021 | 122/0.751 | 2407.1 | 232 | 2.44 | |$-$|69 |$\pm$| 12 | 8.58 |$\pm$| 0.17 | 0.02/0.36 | 146 |$\pm$| 10 | 39 |$\pm$| 3 |
| 297.7716803 | 24 Mar 2021 | 123/0.731 | 2407.1 | 221 | 2.53 | |$-$|51 |$\pm$| 13 | 8.48 |$\pm$| 0.17 | 0.03/0.33 | 116 |$\pm$| 10 | 29 |$\pm$| 3 |
| 299.7983781 | 26 Mar 2021 | 124/0.223 | 2407.1 | 186 | 3.25 | |$-$|54 |$\pm$| 17 | 8.05 |$\pm$| 0.18 | 0.04/0.29 | 106 |$\pm$| 10 | 28 |$\pm$| 3 |
| 300.7513668 | 27 Mar 2021 | 124/0.454 | 2407.1 | 206 | 3.02 | |$-$|35 |$\pm$| 15 | 8.14 |$\pm$| 0.17 | 0.04/0.37 | 109 |$\pm$| 10 | 27 |$\pm$| 3 |
| 301.7807176 | 28 Mar 2021 | 124/0.704 | 2407.1 | 159 | 3.80 | |$-$|36 |$\pm$| 21 | 8.30 |$\pm$| 0.19 | 0.15/0.86 | 95 |$\pm$| 10 | 25 |$\pm$| 3 |
| 304.7728769 | 31 Mar 2021 | 125/0.430 | 2407.1 | 223 | 2.63 | |$-$|79 |$\pm$| 13 | 7.95 |$\pm$| 0.17 | 0.01/0.44 | 102 |$\pm$| 10 | 22 |$\pm$| 3 |
| 305.7334444 | 1 Apr 2021 | 125/0.663 | 2407.1 | 226 | 2.46 | |$-$|68 |$\pm$| 12 | 8.30 |$\pm$| 0.16 | 0.02/0.37 | 96 |$\pm$| 10 | 24 |$\pm$| 3 |
| 587.9333571 | 8 Jan 2022 | 194/0.159 | 2407.1 | 273 | 2.13 | |$-$|59 |$\pm$| 15 | 9.08 |$\pm$| 0.19 | 0.44/1.63 | 177 |$\pm$| 10 | 41 |$\pm$| 3 |
| 588.9350942 | 9 Jan 2022 | 194/0.402 | 2407.1 | 272 | 2.19 | |$-$|30 |$\pm$| 15 | 8.91 |$\pm$| 0.18 | 0.39/1.89 | 161 |$\pm$| 10 | 39 |$\pm$| 3 |
| 589.9833304 | 10 Jan 2022 | 194/0.656 | 2407.1 | 282 | 2.30 | |$-$|1 |$\pm$| 15 | 9.24 |$\pm$| 0.19 | 0.36/1.66 | 143 |$\pm$| 10 | 35 |$\pm$| 3 |
| 590.7944760 | 11 Jan 2022 | 194/0.853 | 2407.1 | 248 | 2.43 | |$-$|37 |$\pm$| 17 | 9.22 |$\pm$| 0.18 | 0.41/1.48 | 142 |$\pm$| 10 | 37 |$\pm$| 3 |
| 591.9658790 | 12 Jan 2022 | 195/0.137 | 2407.1 | 250 | 2.31 | |$-$|44 |$\pm$| 16 | 9.44 |$\pm$| 0.19 | 0.37/1.18 | 175 |$\pm$| 10 | 46 |$\pm$| 3 |
| 592.9683245 | 13 Jan 2022 | 195/0.381 | 2407.1 | 232 | 3.43 | |$-$|63 |$\pm$| 23 | 8.92 |$\pm$| 0.19 | 0.36/0.94 | 172 |$\pm$| 10 | 43 |$\pm$| 3 |
| 593.8925375 | 14 Jan 2022 | 195/0.605 | 2407.1 | 223 | 3.15 | |$-$|40 |$\pm$| 21 | 8.93 |$\pm$| 0.18 | 0.33/0.93 | 165 |$\pm$| 10 | 42 |$\pm$| 3 |
| 594.8359992 | 15 Jan 2022 | 195/0.834 | 2407.1 | 279 | 2.10 | |$-$|20 |$\pm$| 13 | 9.20 |$\pm$| 0.18 | 0.28/0.92 | 164 |$\pm$| 10 | 39 |$\pm$| 3 |
| 595.9992366 | 16 Jan 2022 | 196/0.116 | 2407.1 | 244 | 2.54 | |$-$|80 |$\pm$| 16 | 8.94 |$\pm$| 0.20 | 0.29/0.92 | 172 |$\pm$| 10 | 43 |$\pm$| 3 |
| 596.8879787 | 17 Jan 2022 | 196/0.332 | 2407.1 | 265 | 2.29 | |$-$|43 |$\pm$| 14 | 8.84 |$\pm$| 0.17 | 0.26/0.72 | 169 |$\pm$| 10 | 43 |$\pm$| 3 |
| 597.9366485 | 18 Jan 2022 | 196/0.587 | 2407.1 | 271 | 2.47 | |$-$|62 |$\pm$| 15 | 8.76 |$\pm$| 0.18 | 0.26/0.76 | 169 |$\pm$| 10 | 39 |$\pm$| 3 |
| 598.9194038 | 19 Jan 2022 | 196/0.825 | 2407.1 | 255 | 2.28 | |$-$|58 |$\pm$| 14 | 8.85 |$\pm$| 0.18 | 0.23/0.67 | 142 |$\pm$| 10 | 36 |$\pm$| 3 |
| 599.9732831 | 20 Jan 2022 | 197/0.081 | 2407.1 | 255 | 2.42 | |$-$|73 |$\pm$| 15 | 8.35 |$\pm$| 0.19 | 0.25/0.83 | 147 |$\pm$| 10 | 38 |$\pm$| 3 |
| 601.8978507 | 22 Jan 2022 | 197/0.548 | 2407.1 | 174 | 3.75 | |$-$|73 |$\pm$| 23 | 8.74 |$\pm$| 0.18 | 0.26/0.48 | 130 |$\pm$| 10 | 35 |$\pm$| 3 |
| 602.9316132 | 23 Jan 2022 | 197/0.799 | 2407.1 | 258 | 2.35 | |$-$|43 |$\pm$| 14 | 8.97 |$\pm$| 0.17 | 0.20/0.50 | 119 |$\pm$| 10 | 29 |$\pm$| 3 |
| 603.9124578 | 24 Jan 2022 | 198/0.037 | 2407.1 | 272 | 2.41 | |$-$|73 |$\pm$| 15 | 8.58 |$\pm$| 0.21 | 0.25/0.67 | 121 |$\pm$| 10 | 29 |$\pm$| 3 |
| 604.9164418 | 25 Jan 2022 | 198/0.281 | 2407.1 | 194 | 3.34 | |$-$|64 |$\pm$| 21 | 8.18 |$\pm$| 0.18 | 0.25/0.57 | 116 |$\pm$| 10 | 30 |$\pm$| 3 |
| 606.9054391 | 27 Jan 2022 | 198/0.763 | 2407.1 | 225 | 2.64 | |$-$|49 |$\pm$| 16 | 8.49 |$\pm$| 0.17 | 0.23/0.54 | 122 |$\pm$| 10 | 36 |$\pm$| 3 |
| 607.8850302 | 28 Jan 2022 | 199/0.001 | 2407.1 | 232 | 2.45 | |$-$|44 |$\pm$| 15 | 8.57 |$\pm$| 0.17 | 0.22/0.40 | 127 |$\pm$| 10 | 30 |$\pm$| 3 |
| 608.8852573 | 29 Jan 2022 | 199/0.244 | 2407.1 | 228 | 3.24 | |$-$|81 |$\pm$| 20 | 8.33 |$\pm$| 0.16 | 0.25/0.46 | 112 |$\pm$| 10 | 27 |$\pm$| 3 |
| 609.8900384 | 30 Jan 2022 | 199/0.488 | 2407.1 | 248 | 2.33 | |$-$|79 |$\pm$| 14 | 8.15 |$\pm$| 0.18 | 0.24/0.58 | 106 |$\pm$| 10 | 26 |$\pm$| 3 |
| 610.9655285 | 31 Jan 2022 | 199/0.749 | 2407.1 | 250 | 2.32 | |$-$|58 |$\pm$| 14 | 8.18 |$\pm$| 0.17 | 0.26/0.66 | 96 |$\pm$| 10 | 24 |$\pm$| 3 |
| 886.1012388 | 2 Nov 2022 | 266/0.529 | 2407.1 | 293 | 1.88 | |$-$|19 |$\pm$| 12 | 9.24 |$\pm$| 0.20 | 0.27/0.92 | 159 |$\pm$| 10 | 39 |$\pm$| 3 |
| 890.1199631 | 6 Nov 2022 | 267/0.505 | 2407.1 | 272 | 2.10 | |$-$|47 |$\pm$| 15 | 8.83 |$\pm$| 0.24 | 0.42/1.31 | 130 |$\pm$| 10 | 30 |$\pm$| 3 |
| 891.1149740 | 7 Nov 2022 | 267/0.746 | 2407.1 | 287 | 2.04 | 10 |$\pm$| 13 | 8.91 |$\pm$| 0.24 | 0.33/1.36 | 148 |$\pm$| 10 | 33 |$\pm$| 3 |
| 892.1127054 | 8 Nov 2022 | 267/0.989 | 2407.1 | 270 | 2.10 | 10 |$\pm$| 13 | 9.35 |$\pm$| 0.22 | 0.26/1.26 | 138 |$\pm$| 10 | 33 |$\pm$| 3 |
| 893.1035281 | 9 Nov 2022 | 268/0.229 | 2407.1 | 239 | 2.29 | |$-$|4 |$\pm$| 14 | 8.81 |$\pm$| 0.22 | 0.26/0.83 | 160 |$\pm$| 10 | 35 |$\pm$| 3 |
| 895.1312799 | 11 Nov 2022 | 268/0.721 | 2407.1 | 223 | 2.58 | |$-$|32 |$\pm$| 15 | 8.94 |$\pm$| 0.22 | 0.19/0.34 | 113 |$\pm$| 10 | 25 |$\pm$| 3 |
| 896.0325625 | 12 Nov 2022 | 268/0.940 | 2407.1 | 269 | 2.03 | |$-$|14 |$\pm$| 12 | 9.33 |$\pm$| 0.20 | 0.18/0.66 | 132 |$\pm$| 10 | 31 |$\pm$| 3 |
| 899.1357048 | 15 Nov 2022 | 269/0.693 | 2407.1 | 257 | 2.22 | |$-$|33 |$\pm$| 12 | 8.79 |$\pm$| 0.20 | 0.09/0.51 | 122 |$\pm$| 10 | 29 |$\pm$| 3 |
| 902.1108546 | 18 Nov 2022 | 270/0.415 | 2407.1 | 254 | 2.27 | |$-$|44 |$\pm$| 12 | 8.53 |$\pm$| 0.19 | 0.05/0.31 | 114 |$\pm$| 10 | 27 |$\pm$| 3 |
| 905.0987525 | 21 Nov 2022 | 271/0.140 | 2407.1 | 211 | 2.65 | |$-$|21 |$\pm$| 13 | 8.51 |$\pm$| 0.20 | 0.02/0.08 | 139 |$\pm$| 10 | 31 |$\pm$| 3 |
| 906.1044391 | 22 Nov 2022 | 271/0.385 | 2407.1 | 230 | 2.41 | |$-$|65 |$\pm$| 12 | 8.23 |$\pm$| 0.18 | 0.00/0.13 | 112 |$\pm$| 10 | 25 |$\pm$| 3 |
| 978.9367863 | 3 Feb 2023 | 289/0.062 | 2407.1 | 227 | 2.44 | |$-$|19 |$\pm$| 14 | 7.14 |$\pm$| 0.18 | 0.14/0.68 | 93 |$\pm$| 10 | 20 |$\pm$| 3 |
| 980.9163238 | 5 Feb 2023 | 289/0.543 | 2407.1 | 176 | 3.82 | |$-$|18 |$\pm$| 23 | 6.77 |$\pm$| 0.20 | 0.22/0.68 | 73 |$\pm$| 10 | 18 |$\pm$| 3 |
| 983.9060551 | 8 Feb 2023 | 290/0.268 | 2407.1 | 238 | 2.36 | |$-$|38 |$\pm$| 14 | 7.19 |$\pm$| 0.19 | 0.19/0.41 | 61 |$\pm$| 10 | 14 |$\pm$| 3 |
| 1036.7643629 | 2 Apr 2023 | 303/0.098 | 2407.1 | 246 | 2.41 | 13 |$\pm$| 23 | 9.33 |$\pm$| 0.28 | 0.92/5.14 | 208 |$\pm$| 10 | 41 |$\pm$| 3 |
| 1041.7274405 | 7 Apr 2023 | 304/0.303 | 2407.1 | 261 | 2.17 | 5 |$\pm$| 18 | 8.74 |$\pm$| 0.28 | 0.71/2.97 | 188 |$\pm$| 10 | 35 |$\pm$| 3 |
| 1045.7255305 | 11 Apr 2023 | 305/0.273 | 2407.1 | 187 | 3.86 | 14 |$\pm$| 29 | 9.24 |$\pm$| 0.26 | 0.52/1.97 | 153 |$\pm$| 10 | 28 |$\pm$| 3 |
APPENDIX B: SPECTRAL FIT AND CORNER PLOT
As an example, we show in Fig. B1 a small portion of our template SPIRou spectrum of V347 Aur, along with the best fit achieved with ZeeTurbo (Cristofari et al. 2023a), as described in Section 3, along with the corresponding corner plot (see Fig. B2).
Small portion of our template SPIRou spectrum of V347 Aur in the K band (black circles), along with the optimal fit achieved with ZeeTurbo (red line) using the modelling approach of Cristofari et al. (2023a). The green areas indicate spectral regions considered in the fit.
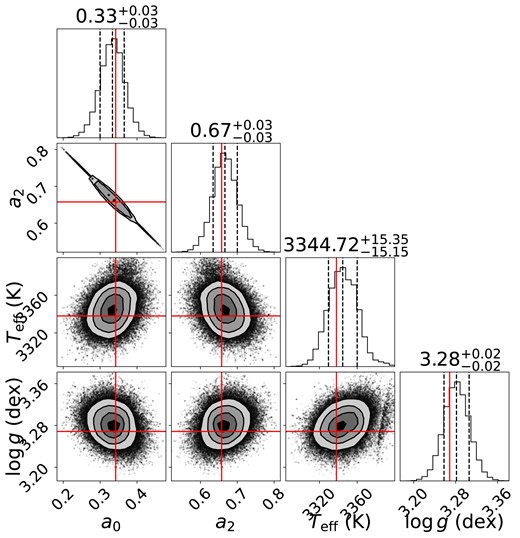
Results of the MCMC fit to the template SPIRou spectrum of V347 Aur with ZeeTurbo. We show here the corner plot and posterior distributions for the main variables, i.e. the two magnetic filling factors |$a_0$| and |$a_2$| corresponding to field strengths of 0 and 2 kG, |$T_{\rm eff}$| and |$\log g$|. To account for additional systematic errors in the fitting process, we adopted conservative error bars for main stellar parameters |$T_{\rm eff}$| and |$\log g$| following Cristofari et al. (2023a) and rounded the derived estimates to |${T_{\rm eff}}=3340\pm 50$| K and |${{\rm log}\,\, g}=3.30\pm 0.10$|.
APPENDIX C: VEILING IN THE JH AND K BANDS
We show in Fig. C1 the measured veiling of V347 Aur in the |$JH$| and in the K bands (|$r_{JH}$| and |$r_K$|, respectively), plotted on the same graph as a function of time.
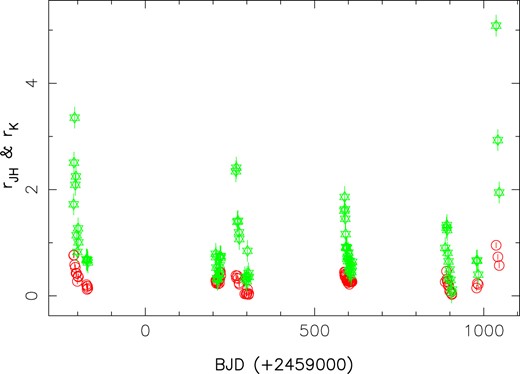
Veiling of V347 Aur as a function of time, in the |$JH$| and in the K bands (|$r_{JH}$| and |$r_{K}$|, red open circles and green stars, respectively, with associated error bars), as measured from LSD profiles of atomic and CO bandhead lines.



