-
PDF
- Split View
-
Views
-
Cite
Cite
Lyubov I Shestakova, Aleksander Serebryanskiy, The role of radiation pressure in lithium deficit for stars in the stage of late accretion: failure of lithium test for young stellar clusters, Monthly Notices of the Royal Astronomical Society, Volume 528, Issue 4, March 2024, Pages 7194–7201, https://doi.org/10.1093/mnras/stae478
Close - Share Icon Share
ABSTRACT
We study the behaviour of lithium atoms in the radiation field of main-sequence (MS) stars. The radiation pressure on atoms in the resonant lines of the |${\rm Li\, {\small I}}$| 6708 Å doublet exceeds the gravity at Teff > 3000 K. The lifetime of |${\rm Li}$| atoms before their ionization is sufficient to achieve the escape velocity. Free |${\rm Li}$| atoms cannot approach the pre-main sequence (PMS) and MS stars if the surrounding gas is sufficiently transparent. Accretion of small bodies (SBs) can partially restore the lithium abundance when SB directly falls on to the star in elongated orbits. In the case of accretion from discs consisting of SB fragments, when the parent bodies move in quasi-circular orbits, the boundary of the SB sublimation region plays a decisive role. Near hot stars, the free |${\rm Li}$| atom is rapidly ionized and participates in accretion on to the star in the form of ions, contributing to an increase in the |${\rm Li}$| abundance. Low-mass stars with low temperatures cannot hold lithium atoms. Near stars with Planck energy distribution in the radiation field, lithium deficiency occurs if 3000 K < Teff < 3400 K. New stars with [Fe/H] = 0.0 may indicate a lithium deficiency at Teff < 5000 K. Failure of the lithium test to estimate the age of a stellar cluster may indicate a significant contribution of accretion in the form of debris discs consisting of SBs.
1 INTRODUCTION
It is believed that the estimation of lithium1 abundance in low-mass stars is an alternative and reliable method to determine the stellar age (Bildsten et al. 1997). Palla & Randich (2005) and Palla et al. (2005,2007) drew attention to the presence of old stars in young stellar clusters in the Orion nebula (ONC). This conclusion was made based on lithium depletion in low-mass stars of spectral class M, with masses of 0.1–0.3 M⊙. Interestingly, ONC does not seem to be an exceptional case, since stars with a low |${\rm Li}$| abundance have been found in other young clusters (Martín 1998; Sacco et al. 2007). This result is surprising given the expected youth of the ONC, the bulk of whose population consists of only 1–2 million years old stars (Hillenbrand 1997). Palla et al. (2007) studied stars of spectral classes from M1 to M4 from the Hillenbrand’s optical catalogue (Hillenbrand 1997). Of the six selected stars, two stars of the spectral class M3 (Teff = 3260 K, M = 0.18|$\, \mathrm{M}_{\odot }$|) and M4 (Teff = 3100 K, M = 0.12|$\, \mathrm{M}_{\odot }$|) showed a strong lithium deficiency with |$A({\rm Li})$| = 1.3 and |$A({\rm Li})$| = 1.8, respectively. For the remaining stars, |$A({\rm Li})$| = 2.4–2.8, which is also less than the interstellar |$A({\rm Li})$| = 3.1–3.3. Palla & Randich (2005) concluded that there are differences in the |${\rm Li}$| content among the low-mass members of very young clusters. Since the lithium abundance depends on age, its variations have been interpreted as significant differences in the age of stars.
In Sacco et al. (2007), of the three stars with a strong lithium deficiency, two have temperatures of Teff = 3750 K and Teff = 3645 K and show an age close to the age determined using isochrones. In a cooler star with Teff = 3345 K, the age determined from the lithium test turned out to be several times (more than three times) older. In Alcalá et al. (2002), it was shown that stars with temperatures of 3400 K and about 3300 K have sharply reduced lithium abundance, and a star with a temperature of 3660 K has a higher abundance, although also slightly lower than that of hotter stars. Sestito, Palla & Randich (2008) carried out the analysis of lithium abundance in PMS stars. In particular, the abundance of |${\rm Li}$| in 22 Taurus–Auriga association stars was measured. An abrupt decrease in the abundance of lithium was found in stars of spectral class M with temperatures from 3700 K and below.
A similar situation is shown in a more recent study (Binks et al. 2021) using Gaia-ESA Survey (GES) data. In particular, GES spectral data were used to determine the lithium depletion boundary (LDB) in the young cluster NGC2232. The age of this cluster is 38 ± 3 Myr obtained by comparing the location of LDB on colour–magnitude diagrams (CMDs) with the predictions of standard models. This age is more than twice that obtained as a result of isochrones approximation for low-mass stars in CMD using the same models.
It should be noted that there are studies in which the age of young clusters obtained in different ways is consistent. For example, in Manzi et al. (2008), when determining LDB in a young open cluster IC4665, it is stated that the LDB provides a reliable and independent tool for determining its age. As a result, it was found that LDB is caused by relatively bright stars still in the contraction phase before they set on main sequence (MS). The mass of stars for this boundary is 0.24 ± 0.04|$\, \mathrm{M}_{\odot }$|. The age determined by the LDB is in good agreement with the age obtained from the approximation by isochrones for both low-mass and high-mass stars. This result is similar to that obtained for a slightly older cluster, NGC2547, in which stars were considered in the contraction phase before the onset of secondary accretion.
Jeffries et al. (2017) showed that non-magnetic models of the evolution of PMS stars cannot give consistent ages obtained from CMD and LDB, which is observed in a cluster of young low-mass stars in the region γ2 Velorum. An age of 7.5 ± 1 Myr was obtained from CMD, which is much less than follows from the strong |${\rm Li}$| depletion observed in the cluster of M dwarfs, and the decrease in the |${\rm Li}$| abundance occurs in much redder colours than predicted. The consent age for γ2 Velorum is 18–21 Myr, both according to CMD and the |${\rm Li}$| abundance, which can be obtained if one assumes that low-mass stars with the same masses and ages have 10 per cent larger sizes.
The discrepancy in determining the age is solved by some combination of magnetic suppression of convection and large cold starspots. Models involving radius inflation suggest that PMS stars similar to stars in the γ2 Velorum cluster, with masses 0.2 < M/M⊙ < 0.7, are at least twice as old and 7 per cent colder than previously assumed, and that their masses are more than 30 per cent larger than follows from conventional non-magnetic models.
Thus, the discrepancy between the results of determining the age of clusters using different methods leads to an increase in the number of models and a change in the time-scales of the evolution of young stellar clusters due to the accelerated depletion of lithium in the red low-mass stars belonging to these clusters.
The piled-up contradictions from observations in determining the age of young star clusters by the lithium test mentioned above prompted us to find alternative mechanisms for lithium loss in the cold, low-mass star population of these clusters. We believe that variations in lithium abundance can be partly explained by differences in accretion mechanisms. For young and cold stars, this mechanism appears as a debris disc orbiting a star in quasi-circular orbits. Thus, it is possible that the lithium test for determining the age of stars may not give accurate age estimates in young clusters where there is a lot of gas, dust, and rocks.
The rest of the paper is organized as follows. Section 2 provides the theoretical background for calculating the radiation pressure in a resonant doublet of lithium atoms and their behaviour in the radiation field of MS stars. Section 3 analyses the behaviour of lithium atoms near MS stars, taking into account the radiation pressure and ionization rate of lithium atoms, and estimates the terminal velocities and lifetime of atoms depending on the temperature of stars and the distance to stars, starting from which lithium leaves the star system. The dependence of the boundary value of Teff on the metallicity, starting from which stars with a lower temperature will be depleted of lithium, is obtained, and different accretion scenarios are analysed: from pure gas to accretion in the form of small bodies (SBs). Section 4 presents the results of the analysis of the effects of various types of accretion on MS stars. We then proceed to discuss the results of our assessments and their impact on a possible change in the view of accretion in the present epoch.
2 THEORY
2.1 Radiation pressure on atoms in the radiation field of stars
In Shestakova (2015), the value of the pressure of solar radiation on atoms and ions after the first stage of ionization was determined. It was concluded that radiation pressure is a plausible mechanism for the acceleration of pickup ions and energetic neutral atoms emitted from an internal source (zodiac dust and sungrazing comets). Such atypical admixtures of atoms and ions formed as a result of a comet’s disintegration or meteor showers near the Sun can accelerate and reach the Earth’s orbit as part of the solar wind.
The force of the radiation pressure, FL, at the centre of the resonance line is defined as
where Bλ is the radiation flux averaged over the disc of the star in a single wavelength interval in the continuum between spectral lines, or the corresponding Planck function; χL is the residual intensity in the centre of the spectral line as a fraction of the flux of the continuum, r is the distance from the centre of the star, Rs is the radius of the star, c is the speed of light, |$\alpha _L = \pi e^2 \lambda ^2 f_L/m_e c^2$| is the absorption coefficient in the spectral line according to Allen (1977), where e and me are the charge and mass of the electron, respectively, and fL is the oscillator strength for radiation in a given spectral line.
The force caused by radiation pressure, Frad, for each atom or ion is determined by the sum of the forces for all resonant lines, L:
The mechanism of acceleration of an atom is provided by the sum of pressures for all resonant lines of a given atom. The greater the strength of oscillator and more powerful the intensity of spectrum of the star at the corresponding wavelength, the stronger the radiation pressure.
Further scenario of the behaviour of an atom or ion depends mainly on its lifetime in the radiation field and the coefficient βL = Frad/Fgrav. If β > 1, the atom of the selected species gains acceleration directed away from the star. Since the forces acting on the atoms of different species are different, their terminal velocities also differ. This circumstance may also cause the spatial separation of elements in the process of their removal from the stellar system and the formation of clouds enriched with different elements.
The equation (1) includes parameters containing atomic data and other constants. These parameters can be combined into a single constant, |$C=\pi e^2/m_e c^2 \cdot \pi /c = 9.2770632\times 10^{-23}$| s, then the equation (1) can be represented as
For each spectral line, the effect of radiation pressure is defined as
where G is the gravitational constant, and Ms is the mass of the star. The total value of β is determined by summing all βL.
Let us simplify the equation (4) using solar parameters. Considering that mL = ALmh, where AL is the atomic weight of the Lth atom, mh is mass in the atomic mass units and G = 6.673 × 10−8 cm3 g−1 s−2, |$\, \mathrm{M}_{\odot }$| = 1.9904 × 1033 g, R⊙ = 696 000 km = 6.96 × 1010 cm, mh = 1.66053 × 10−24 g, we get |$\beta _L = C_0f_L\lambda _L^2B_\lambda \chi _L/A_L$|, where C0 = 2.0376 × 102 s3 kg−1 m−1. To make the dimensions consistent, we take into account that [Bλ] = J s−1 m|$^{-2}\, \rm{\mu m}^{-1}$| sr−1, and [λL] = |$\rm{\mu m}$|. As a result, we obtain an expression for calculating the radiation pressure from the Sun on an atom or ion in a single spectral absorption line L of an element:
To calculate the radiation pressure acting on various elements near any other star, we will rewrite equation (5) using the values of the radius and mass of the star expressed in the corresponding solar values. Then the radiation pressure for the elements is defined as
where Bλ is the Plank function corresponding to the effective temperature of the star.
Shestakova (2015) obtained the values of solar radiation pressure for atoms and ions of several species. For example, the combined effect of radiation pressure on a lithium atom, consisting of the pressures in the spectral lines of the resonant doublet, |$\beta _{{\rm Li},s}$|, turned out to be maximal, |$\beta _{{\rm Li},\odot }$| = 223. Other alkali metals (|${\rm Na}$|, |${\rm K}$| and |${\rm Rb}$|) are also strongly affected by solar radiation pressure (|$\beta _{{\rm Li},\odot }$| > 25). If we consider only lithium atoms, then, knowing the value of |$\beta _{{\rm Li},\odot }$|, we can get |$\beta _{{\rm Li},s}$|:
We calculated the values of |$\beta _{{\rm Li},s}$| for some MS stars, the parameters of which are given in Table 1. Since the accuracy of determining the mass and radius of stars is usually low, we used data from Eker et al. (2018) for comparison, where these parameters are determined directly from observations of binary stars.
| Estimated values using equation (7) . | Close prototype (spectral class) . | Observed values . | ||||
|---|---|---|---|---|---|---|
| Teff (K) . | Rs/R⊙ . | Ms/M⊙ . | . | Teff (K) . | Rs/R⊙ . | Ms/M⊙ . |
| 3000 | 0.12 | 0.10 | Wolf 359 (M6V) | Eker et al. (2018) | ||
| 3200 | 0.21 | 0.20 | Ross128 (M4V) | 3200 | 0.30 | 0.28 |
| 3400 | 0.36 | 0.33 | Laland 21 185 (M2V) | – | – | – |
| 3600 | 0.50 | 0.40 | M1.5V | 3600 | 0.49 | 0.50 |
| 3800 | 0.60 | 0.51 | Lacaille 8760 | – | – | – - |
| 4000 | 0.65 | 0.60 | 61 Cygni B (K7V) | 4000 | 0.62 | 0.61 |
| 4200 | 0.70 | 0.65 | 4200 | 0.67 | 0.69 | |
| 4400 | 0.75 | 0.69 | α Centauri B (K5V) | – | – | – |
| 4600 | 0.77 | 0.73 | 4600 | 0.78 | 0.79 | |
| 4800 | 0.78 | 0.77 | ϵ Eridani (K2V) | – | – | – |
| 5000 | 0.82 | 0.81 | – | – | – | |
| 5200 | 0.85 | 0.84 | σDraconis (K0V) | 5200 | 0.92 | 0.91 |
| 5400 | 0.88 | 0.89 | 61 Ursae Majoris(G8V) | 5400 | 1.00 | 0.95 |
| 5600 | 0.91 | 0.95 | μ Cas (G5V) | – | – | – |
| 5779 | 1.00 | 1.00 | Sun (G2V) | – | – | – |
| 5800 | 1.00 | 1.00 | Sun (G2V) | 6000 | 1.18 | 1.10 |
| 6000 | 1.10 | 1.20 | 6200 | 1.34 | 1.21 | |
| 6400 | 1.20 | 1.35 | Procyon (F5V) | 6400 | 1.48 | 1.30 |
| 6800 | 1.28 | 1.45 | 6800 | 1.88 | 1.56 | |
| 7000 | 1.32 | 1.50 | – | – | – | |
| Estimated values using equation (7) . | Close prototype (spectral class) . | Observed values . | ||||
|---|---|---|---|---|---|---|
| Teff (K) . | Rs/R⊙ . | Ms/M⊙ . | . | Teff (K) . | Rs/R⊙ . | Ms/M⊙ . |
| 3000 | 0.12 | 0.10 | Wolf 359 (M6V) | Eker et al. (2018) | ||
| 3200 | 0.21 | 0.20 | Ross128 (M4V) | 3200 | 0.30 | 0.28 |
| 3400 | 0.36 | 0.33 | Laland 21 185 (M2V) | – | – | – |
| 3600 | 0.50 | 0.40 | M1.5V | 3600 | 0.49 | 0.50 |
| 3800 | 0.60 | 0.51 | Lacaille 8760 | – | – | – - |
| 4000 | 0.65 | 0.60 | 61 Cygni B (K7V) | 4000 | 0.62 | 0.61 |
| 4200 | 0.70 | 0.65 | 4200 | 0.67 | 0.69 | |
| 4400 | 0.75 | 0.69 | α Centauri B (K5V) | – | – | – |
| 4600 | 0.77 | 0.73 | 4600 | 0.78 | 0.79 | |
| 4800 | 0.78 | 0.77 | ϵ Eridani (K2V) | – | – | – |
| 5000 | 0.82 | 0.81 | – | – | – | |
| 5200 | 0.85 | 0.84 | σDraconis (K0V) | 5200 | 0.92 | 0.91 |
| 5400 | 0.88 | 0.89 | 61 Ursae Majoris(G8V) | 5400 | 1.00 | 0.95 |
| 5600 | 0.91 | 0.95 | μ Cas (G5V) | – | – | – |
| 5779 | 1.00 | 1.00 | Sun (G2V) | – | – | – |
| 5800 | 1.00 | 1.00 | Sun (G2V) | 6000 | 1.18 | 1.10 |
| 6000 | 1.10 | 1.20 | 6200 | 1.34 | 1.21 | |
| 6400 | 1.20 | 1.35 | Procyon (F5V) | 6400 | 1.48 | 1.30 |
| 6800 | 1.28 | 1.45 | 6800 | 1.88 | 1.56 | |
| 7000 | 1.32 | 1.50 | – | – | – | |
| Estimated values using equation (7) . | Close prototype (spectral class) . | Observed values . | ||||
|---|---|---|---|---|---|---|
| Teff (K) . | Rs/R⊙ . | Ms/M⊙ . | . | Teff (K) . | Rs/R⊙ . | Ms/M⊙ . |
| 3000 | 0.12 | 0.10 | Wolf 359 (M6V) | Eker et al. (2018) | ||
| 3200 | 0.21 | 0.20 | Ross128 (M4V) | 3200 | 0.30 | 0.28 |
| 3400 | 0.36 | 0.33 | Laland 21 185 (M2V) | – | – | – |
| 3600 | 0.50 | 0.40 | M1.5V | 3600 | 0.49 | 0.50 |
| 3800 | 0.60 | 0.51 | Lacaille 8760 | – | – | – - |
| 4000 | 0.65 | 0.60 | 61 Cygni B (K7V) | 4000 | 0.62 | 0.61 |
| 4200 | 0.70 | 0.65 | 4200 | 0.67 | 0.69 | |
| 4400 | 0.75 | 0.69 | α Centauri B (K5V) | – | – | – |
| 4600 | 0.77 | 0.73 | 4600 | 0.78 | 0.79 | |
| 4800 | 0.78 | 0.77 | ϵ Eridani (K2V) | – | – | – |
| 5000 | 0.82 | 0.81 | – | – | – | |
| 5200 | 0.85 | 0.84 | σDraconis (K0V) | 5200 | 0.92 | 0.91 |
| 5400 | 0.88 | 0.89 | 61 Ursae Majoris(G8V) | 5400 | 1.00 | 0.95 |
| 5600 | 0.91 | 0.95 | μ Cas (G5V) | – | – | – |
| 5779 | 1.00 | 1.00 | Sun (G2V) | – | – | – |
| 5800 | 1.00 | 1.00 | Sun (G2V) | 6000 | 1.18 | 1.10 |
| 6000 | 1.10 | 1.20 | 6200 | 1.34 | 1.21 | |
| 6400 | 1.20 | 1.35 | Procyon (F5V) | 6400 | 1.48 | 1.30 |
| 6800 | 1.28 | 1.45 | 6800 | 1.88 | 1.56 | |
| 7000 | 1.32 | 1.50 | – | – | – | |
| Estimated values using equation (7) . | Close prototype (spectral class) . | Observed values . | ||||
|---|---|---|---|---|---|---|
| Teff (K) . | Rs/R⊙ . | Ms/M⊙ . | . | Teff (K) . | Rs/R⊙ . | Ms/M⊙ . |
| 3000 | 0.12 | 0.10 | Wolf 359 (M6V) | Eker et al. (2018) | ||
| 3200 | 0.21 | 0.20 | Ross128 (M4V) | 3200 | 0.30 | 0.28 |
| 3400 | 0.36 | 0.33 | Laland 21 185 (M2V) | – | – | – |
| 3600 | 0.50 | 0.40 | M1.5V | 3600 | 0.49 | 0.50 |
| 3800 | 0.60 | 0.51 | Lacaille 8760 | – | – | – - |
| 4000 | 0.65 | 0.60 | 61 Cygni B (K7V) | 4000 | 0.62 | 0.61 |
| 4200 | 0.70 | 0.65 | 4200 | 0.67 | 0.69 | |
| 4400 | 0.75 | 0.69 | α Centauri B (K5V) | – | – | – |
| 4600 | 0.77 | 0.73 | 4600 | 0.78 | 0.79 | |
| 4800 | 0.78 | 0.77 | ϵ Eridani (K2V) | – | – | – |
| 5000 | 0.82 | 0.81 | – | – | – | |
| 5200 | 0.85 | 0.84 | σDraconis (K0V) | 5200 | 0.92 | 0.91 |
| 5400 | 0.88 | 0.89 | 61 Ursae Majoris(G8V) | 5400 | 1.00 | 0.95 |
| 5600 | 0.91 | 0.95 | μ Cas (G5V) | – | – | – |
| 5779 | 1.00 | 1.00 | Sun (G2V) | – | – | – |
| 5800 | 1.00 | 1.00 | Sun (G2V) | 6000 | 1.18 | 1.10 |
| 6000 | 1.10 | 1.20 | 6200 | 1.34 | 1.21 | |
| 6400 | 1.20 | 1.35 | Procyon (F5V) | 6400 | 1.48 | 1.30 |
| 6800 | 1.28 | 1.45 | 6800 | 1.88 | 1.56 | |
| 7000 | 1.32 | 1.50 | – | – | – | |
Fig. 1 shows the values of |$\beta _{{\rm Li},s}$| for different models and observational data. Teff, Rs/R⊙ and Ms/M⊙ data for all models are taken from the first three columns of Table 1. In addition to the Planck energy distribution in the spectrum, Phoenix models were used (Husser et al. 2013) with [Fe/H] = −4.0 and [Fe/H] = 0.0, log g = 4.5. The values of Teff for the observational data (Eker et al. 2018) are rounded off to the nearest values used in the models.
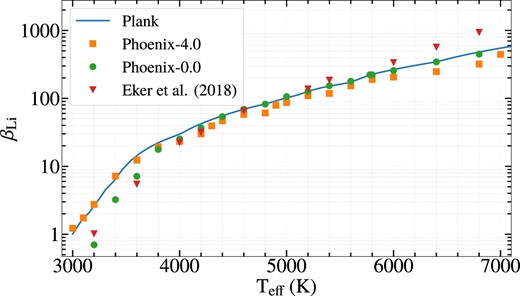
The ratio of radiation pressure to gravitational force, |$\beta _{{\rm Li},s}$| = Frad/Fgrav, depending on Teff for MS stars.
For MS stars of spectral type M6 having mean values Ms = 0.1|$\, \mathrm{M}_{\odot }$|, Rs = 0.12R⊙ and Teff = 3000 K, the parameter |$\beta _{{\rm Li},s}$| = 223 × 0.031 × (0.12)2/0.1 = 0.995 ≈ 1. This means that almost all MS stars with temperatures of Teff > 3000 K efficiently supply lithium to the interstellar medium. It is interesting to note that in cooler stars of spectral type L (Teff = 1300–2500 K), the |${\rm Li\, {\small I}}$| lines are clearly visible. Thus, Martín et al. (1998) reported on the presence of lithium in the substellar object. This result is easy to interpret since, at Teff < 3000 K, the radiation pressure weakens and β < 1. In this case, nothing prevents lithium accretion.
Fig. 1 shows that for all MS stars of spectral types from M to F, that is, for Teff from 3000 to 7000 K, the radiation pressure for standard values of radii and mass exceeds the gravitational force. PMS stars of the TTau type, whose temperature reaches values of ≥2.5 × 106 K in the centre, begin to radiate due to lithium burning, and in conditions of ongoing accretion, the radiation flux influences the surrounding gaseous and dusty nebula. To implement the mechanism of lithium loss from the accreting matter surrounding the star, it is necessary to estimate the lifetime of the lithium atom before its ionization by the radiation of the star. If the atom manages to acquire a velocity equal to the escape velocity, then it will leave the vicinity of the star and join the interstellar medium or settle on objects in the star’s planetary system.
2.2 Behaviour of lithium atoms in the radiation field of MS stars
|${\rm Li\, {\small I}}$| spectral lines are observed only in relatively cool stars with Teff < 8500 K, that is, in stars of spectral types from late A to M. After ionization by the ultraviolet (UV) radiation of the star, the lithium atom becomes an ion that is no longer subject to radiation pressure. To leave the star, the atom must acquire sufficient velocity during its lifetime, which lasts before the ionization. The lifetime of the lithium atom can be estimated from the ratio tlife = 1/N, where N is the total number of photons absorbed by the atom per unit time (photons s−1), which is defined as |$\sum \limits _i n_i\sigma _i$|, where i is the wavelength interval number and σi is the ionization cross-section of the lithium atom in this wavelength interval. In this paper, the values of σi are taken from Sahoo & Ho (2006).
The number of photons in a given wavelength range is ni = E(λ)Δλ/hν, where ν = c/λ, Δλ is the wavelength interval from the ionization threshold in the direction of decreasing λ. Radiation flux at a given distance from the star |$E(\lambda)\Delta \lambda = \pi R_s^2/r^2B(\lambda)\Delta \lambda$|, where r is the distance from the centre of the star. Then:
where |$A=hc/\pi$| = 6.32315 × 10−26 J m. Then the lifetime of the neutral atom before ionization:
To determine the lifetime of lithium atoms before the ionization, data on the energy distribution in the spectrum of stars in the UV region of the spectrum from the ionization threshold at λ2300 Å to the limit of available data up to about λ500 Å are needed. This region of the spectrum is saturated with many absorption lines of various species, and the energy distribution may differ greatly from Planck’s. These differences are stronger the higher the metallicity. To compare the effect of metallicity on lifetime of lithium atoms and related parameters (escape velocity Vesc and corresponding distance resc), we used the Phoenix-4.0 and Phoenix-0.0 models. From the same models, the radiation flux of a star at λ6708 Å corresponding to the resonant transition of a lithium atom was taken to determine the radiation pressure on a lithium atom, as discussed in Section 2.1.
2.2.1 Gaseous accretion
A free atom located at a certain distance r from the star, during its lifetime, can develop a radial velocity directed out of the star equal to
where g = GMs/r2, |$g_0 = G M_s/R_s^2$|. The value of Vterm does not depend on the distance, since the ionizing radiation flux, as well as the gravitational force, is ∼r−2, and the lifetime is ∼r2. The Vterm is equal to Vesc and depends only on the stellar parameters at the surface of star: g0 and Teff. The Vterm for selected MS stars is shown in Fig. 2.

Terminal velocity of lithium atoms for MS stars depending on Teff.
The distribution of energy in the spectrum of a star in the form of a Planck function, B(λ), may be acceptable for the first-generation stars with low metallicity in the early Universe. As can be seen from Fig. 2, models with low metallicity, [Fe/H] = −4.0, show a significant increase in the terminal velocities of lithium atoms in comparison with the Planck energy distribution in the spectrum for stars with Teff < 5000 K. For models with solar metallicity, [Fe/H] = 0.0, such an increase in velocity becomes noticeable for stars with Teff < 7000 K.
For stars with Teff = 3000 K, the parameter β = 1, so the equation (10) is no longer applicable. Under conditions where β = 1, the gravitational force is balanced by the force of radiation pressure, and the atom breaking away from the parent body continues to move further tangentially to the initial orbit. Calculations show that during the lifetime of an atom, it manages to fly away to a distance where its speed exceeds the Vesc, so such stars will also repel lithium atoms. In fact, with free gas accretion, lithium atoms cannot approach both cool and hot stars if the gas in the accreting matter is sufficiently transparent. In cool stars of young stellar clusters that have retained gas, lithium absorption lines with a noticeable Doppler shift can be observed among the interstellar absorption lines. Such observations may provide indirect evidence of the metallicity of a new generation of cluster stars. In hot stars with Teff ≥ 7000 K, the escape velocity is negligible, and the dependence on metallicity is absent.
2.2.2 Accretion in the form of dust, rocks, comets, and other large bodies
For lithium atoms released from SBs during accretion, there is a certain boundary of the region, resc, inside of which the atoms are ionized before they accelerate to the escape velocity Vesc. In this case, they will remain in the vicinity of the star. The boundary of this region can be determined from the equality of the Vesc to the orbital velocity, (GMs/r)1/2. After some manipulations, we get
During accretion in the form of SBs, when free atoms originate at a distance of r < resc, the star can be enriched with lithium since ionized atoms do not experience the influence of radiation pressure and continue to play a role in the accretion process. Accretion in the form of rocks and dust, especially if a disc of fragments forms at the boundary of the sublimation region, leads to the transition of lithium into the phase of gas. In this case, it is important to estimate the lifetime of an atom, tlife, at the distance where the process of sublimation begins (Tdust = 1500 K). Fig. 3 shows the lifetimes of lithium atoms before their ionization according to equation (9) for the initial distance corresponding to the boundary of the sublimation region, r = rsubl. This boundary depends on the temperature of the star and, in the blackbody approximation, is equal to rsubl = (Teff/1500)2Rs/2.

The lifetime of the lithium atom, tlife, before ionization at the boundary of the sublimation region, where Tdust = 1500 K.
The process of acceleration of an atom begins at the moment of its release from the parent body and continues until it is ionized. Fig. 4 shows the resc boundary for stars with different metallicity. Free atoms released from the parent body beyond resc leave the vicinity of the star. Free atoms, located closer than this boundary, have enough time to be ionized, their acceleration ceases, and they will remain in the vicinity of the star, continuing to move towards the star. The behaviour of lithium atoms in the region r > resc may cause interesting consequences: atoms either leave the vicinity of the star and mix with the interstellar medium or settle on external bodies, including planets. In this case, the contradiction between the lithium deficiency in the star and its excess in meteorites and other bodies of the planetary system is easily overcome. For a star with Teff = 3000 K, for which β = 1, the lifetime of the lithium atom is sufficient to escape from any distance, including the surface of the star (Figs 3 and 4).
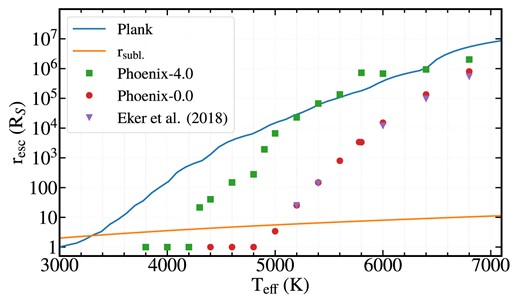
Dependence of the resc on Teff. If lithium atoms are released from the parent body at a distance r > resc, then they leave the MS star under the influence of radiation pressure. At r < resc, the atoms are ionized and their acceleration ceased.
Analysing Figs 2 and 4, we may conclude that the late accretion mentioned in Fu et al. (2015) will not restore the lithium content in the star if the accreting substance consists only of gas. The strong radiation pressure of MS stars with Teff > 3000 K in the case of a transparent gaseous medium will prevent lithium atoms to approach the star. If accretion takes place in the form of a debris disc in which dust and rocks move in quasi-circular orbits near the sublimation region, the process of lithium enrichment of the photosphere of a star is feasible, but only for relatively hot stars. Its efficiency depends on the temperature and metallicity of the star.
As can be seen from Fig. 4, for cool stars of spectral type M with a temperature Teff < 3400 K, with a Planck distribution of energy in the spectrum, compensation for lithium deficiency is impossible. The UV radiation flux of such stars is so low that the lifetime of neutral atoms increases dramatically, and they manage to leave the star even after the parent bodies enter the sublimation region. This temperature boundary shifts towards hotter stars with increasing metallicity. Even for stars with [Fe/H] = −4.0, this boundary corresponds to Teff < 4200 K, and for solar-type stars with [Fe/H] = 0.0, lithium deficiency can begin at Teff < 5000 K.
According to our estimates, the values of Vesc, tlife, and resc for the considered models with two values of metallicity begin to coincide with the Planck flux distribution for stars with temperatures Teff ≥ 5000 K for [Fe/H] = −4.0 and for stars with Teff ≥ 6800 K for [Fe/H] = 0.0.
An exception to the considered scenario may be accretion in the form of SBs moving along elongated orbits close to parabolic. The fragments of such bodies, even after partial evaporation in the region of sublimation and tidal destruction, can directly plunge into the atmosphere of a star. Thus, the ‘late bombardment’ by SBs can partially compensate for the lithium deficiency that occurs in the early stages of the evolution of stars as a result of thermonuclear reactions in their interiors. At the same time, the process of direct SB falling on to the star will not depend on stellar temperature.
3 RESULTS
Analysis of the effect of radiation pressure on lithium atoms during accretion on to stars with [Fe/H] = −4.0 and [Fe/H] = 0.0 allowed us to draw several conclusions that change the understanding of the mechanism of accretion on MS stars at the PMS phase. Lithium atoms in the composition of gas accretion, when it is necessary to take into account the lifetime of lithium before ionization, that is when circumstellar environment becomes transparent in visible light (star birth) including the resonant doublet λ6708 Å, in principle cannot approach a star with a temperature of Teff ≥ 3000 K. Based on the condition β > 1, lithium atoms promptly escaping, remaining in the interstellar medium. Therefore, the so-called late gas accretion mentioned in Fu et al. (2015) and Fu (2017) cannot serve as a source of lithium abundance recovery for MS and PMS stars. The abundance of lithium atoms at the moment of star birth corresponds to the abundance in the interstellar medium. After the star birth, gas accretion will continue with a lithium deficiency and, as the transparency of the medium increases, with a complete absence of lithium in the accreting gas.
Lithium atoms, in the composition of large bodies and SBs, can approach the star up to some distance. In this case, there are at least two regions in the vicinity of the star that one should pay attention to:
a region of free lithium atoms leaving their parent bodies far from the star. For example, as part of a coma from cometary bodies or in the case of collisions, as well as due to sputtering and partial sublimation. The behaviour of such atoms is shown in Fig. 4. It depends on the escape boundary, resc, defined according to equation (11). If the separation of atoms from parent bodies occurs in the region r < resc, then the atoms are ionized, the repulsive effect of radiation pressure ceases, and lithium ions do not leave the vicinity of the star. Due to this process, some compensation for lithium deficiency in the star’s atmosphere may occur.
the sublimation region, where dust and grains melt and a relatively fast transition of solid matter into the gas phase occurs. Such a transition is especially effective for bodies moving in quasi-circular orbits.
If the debris discs in the sublimation region play a significant role in the accretion process, then the following effects may become noticeable, which follow from the results presented in Fig. 4:
For the first generation of metal-depleted stars with a Plank spectral energy distribution, lithium deficiency can be observed at 3000 K < Teff < 3400 K.
For stars with metallicity [Fe/H] = −4.0, this boundary shifts towards hotter stars: Teff < 4200 K.
Stars forming in the modern era with metallicity [Fe/H] = 0.0 may show lithium deficiency at Teff < 5000 K.
These restrictions are valid for accretion in the form of a debris disc. An exception to the considered scenario may be accretion in the form of SBs moving along elongated orbits close to parabolic ones. The fragments of such bodies, even after partial evaporation in the region of sublimation and tidal destruction, can directly plunge into the atmosphere of a star. Thus, as noted above, the ‘late bombardment’ of rocks can partially compensate for the lithium deficiency that occurs in the early stages of stellar evolution. Compensation for lithium deficiency due to late gas accretion is hardly possible.
4 DISCUSSIONS AND CONCLUSION
We analysed the effect of radiation pressure on lithium atoms for stars with Planck energy distribution in the spectrum using Phoenix models with [Fe/H] = −4.0 and [Fe/H] = 0.0. The strongest deviations in lithium abundance in stars from its abundance in the interstellar medium occur after star birth with ongoing gas accretion. In this case, a radiation pressure exceeds the gravitational force for stars with Teff ≥ 3000 K. Replenishing the abundance of lithium through continued gas accretion is not possible if the gas medium becomes transparent. This is a general circumstance that does not depend on the temperature of the star or its metallicity.
The ‘lithium plateau’ or ‘Spit plateau’ (Spite & Spite 1982; Spite, Spite & Bonifacio 2012) of old stars can be explained by the homogeneity of the gas environment at the stage of the formation of these stars. Gas accretion prevailed in the oldest stars, accretion conditions were the same for all stars, and the results were the same, namely the presence of a ‘lithium plateau’. In addition, the ‘lithium plateau’ is detected in stars with Teff ≥ 5000 K, where the effect of accretion in the form of a debris disc populated with SBs is not manifested. After the start of nuclear reactions in the star’s interior, when it began to radiate and the medium became transparent to radiation, accretion continued with a lithium deficiency. The late accretion also did not contribute to lithium enrichment since the radiation from MS stars had a repulsive effect on lithium atoms. Thus, the lithium deficiency formed after its exhaustion as a result of nuclear reactions was not replenished by late accretion.
The dependence of the lithium abundance in the atmospheres of stars of spectral types F-M on the effective temperature Teff and the conclusion that the |${\rm Li}$| content decreases with age, and the faster the lower Teff or MS (Balachandran, Mallik & Lambert 2011), can be explained by the type of accretion. With accretion from the debris disc in the sublimation region, such result is obvious. Note that a similar dependence of |$\log \varepsilon ({\rm Li})$| on Teff is found when studying stars of common cluster since their ages are approximately the same. A similar trend in lithium abundance with a decrease in Teff is observed in the Hyades (Takeda et al. 2013) and the Pleiades (Gondoin 2014) clusters.
According to our results, a steep decrease in lithium abundance reported in PMS stars of spectral type M with Teff ≤ 3700 K in the Taurus–Auriga association (Sestito, Palla & Randich 2008) for stars with Teff ≤ 3660 K (Alcalá et al. 2002), as well as in stars with Teff = 3750 K, Teff = 3645 K, and Teff = 3345 K in the young cluster σOri (Sacco et al. 2007) are more naturally explained by the contribution to the accretion of small bodies from the debris discs. In this case, the contradiction between the age of hot and cold stars is automatically removed.
The question remains open about the evolution stage of the star from which the growth of lithium deficiency begins, that is, from the moment when the accreting matter becomes transparent to the lithium doublet λ6708 Å. The answer to this question can be found, among other things, in an estimate of the mass accumulated in the protostar in the ‘dark epoch’, followed by an assessment of the remainder of the accreted mass by lithium deficiency in the ‘light epoch’, that is, after the star’s birth. The result of this process is the enrichment of the interstellar medium with lithium.
Stars forming in the modern era, in addition to gas accretion, may have accretion in the form of SBs: dust, rocks, or comet-asteroid bodies. In this case, the following scenarios are possible:
SB on parabolic orbits falls on to the star. In this case, there will be no significant lithium deficiency in the forming star clusters, depending on the temperature of the stars, but there is a possibility of rotation acceleration of stars due to the transfer of the momentum of rotation if this process is sufficiently intense. For example, in Bouvier et al. (2016), according to the results of the Gaia-ESA review, it is stated that fast-rotating stars are richer in lithium than slow-rotating ones. It was claimed that the connection between lithium and rotation is established in the PMS stage of the evolution and continues to increase until Zero Age Main Sequence (ZAMS). This leads to the conclusion that the existence of a relation between lithium abundance and rotation in low-mass stars with temperatures Teff = 3800–4400 K and an age of about 5 Myr in the young cluster NGC2264 may indicate a close relationship between the history of accretion, the formation of planets, and the early evolution of angular momentum. The authors point out the possible influence of external matter at the accretion stage, namely the possibility of accretion in the form of a disc or the fall of a planet. Such a relationship between the lithium abundance and the rotation rate at such an early age (5 Myr) is exciting. It can be assumed that when small bodies fall on to a star in elongated orbits close to parabolic, the enrichment of the star with heavy elements will occur directly through the engulfed bodies. Such bodies can contribute to increased angular momentum, which can be significant in low-mass stars. For such elongated orbits, the sublimation of bodies is practically insignificant, and the composition of the falling bodies will correspond to the composition of the interstellar medium. This scenario is possible during the formation of stars in the modern era when the regions of their formation are rich in dust and SBs. The result of this type of accretion will be more noticeable for low-mass stars, which is consistent with the observations (Bouvier et al. 2016). The type of accretion capable of transferring bodies directly into the atmosphere of a star differs significantly from accretion in the form of a debris disc, where bodies move in quasi-circular orbits in the sublimation region and the atoms of these bodies gradually evaporate and pass into the phase of gas. Then, the behaviour of these atoms is determined by the radiation pressure and the ionization rate, and the result, as shown in Figs 2–4, depends on metallicity.
Accretion in the form of debris discs in quasi-circular orbits. In this case, the SB passes into the gas phase at a distance where sublimation is active, that is, at a temperature of ≈1500 K. In this case, cold dwarfs with temperatures of Teff ≤ 3400 K (with Planck energy distribution in the spectrum), or with Teff ≤ 4200 K (at [Fe/H] = −4.0), or with Teff ≤ 5000 K (at [Fe/H] = 0.0) can show a noticeable lithium deficiency since the lifetime of lithium atoms before ionization near cold stars allows these atoms to leave the star under the influence of radiation pressure and enrich the planetary system and interstellar medium with lithium. A significant result in this case may be a failure of the lithium test to determine the age of the cluster. The cold stars of a young star cluster will appear much older than the rest of the stars. But in fact, the difference may not be in age but in the type of accretion.
An intermediate scenario of lithium deficiency can occur in the presence of active ‘bombardment’ of a star by various small bodies on intermediate orbits that gradually lose dust and gas from their surface and become parent bodies for lithium atoms. If the atoms leave their parent bodies inside the region r ≤ resc (Fig. 4), then their lifetime before ionization is not enough to escape. They are ionized and remain within the star system.
Our conclusions do not contradict the explanation of the decrease in the lithium abundance at Teff ≤ 5500 K, discovered back in Spite & Spite (1982), due to deeper convective mixing, which causes accelerated lithium burning in the stellar core, and to a greater extent confirms this observational fact.
The review Norris et al. (2023) investigated the distribution of lithium abundance in metal-poor stars with 5500 K < Teff ≤ 6700 K, −6.0 < [Fe/H] < −1.5 and |$\log g \gtrapprox 3.5$| using data for approximately 200 stars. Norris et al. (2023, fig. 6) show a noticeable tendency to decrease the abundance of lithium towards a decrease in Teff, which is more profound for a group of stars with low metallicity. Although the statistics obtained by Norris et al. (2023) do not cover the lower temperatures, nevertheless, they generally correspond to our conclusions.
Some studies (Israelian et al. 2009; Sousa et al. 2010, 2011) have indicated a strong lithium deficiency in sun-like stars with planets. This problem turned out to be a controversial one. In González Hernández et al. (2011), an average of the same lithium abundance is shown for single stars and stars with planets based on the analysis of 95 solar-like stars in which lithium deficiency was not detected.
The numerous contradictions related to the determination of the age of young stellar clusters show a stronger depletion of lithium in cold and low-mass stars, which is naturally explained within the framework of our concept without resorting to the consideration of complex processes in stars and the necessary increase in the age of entire clusters.
We turn to the conclusion that accretion is more often realized in the form of SBs, where the lithium abundance in low-mass cold stars can serve as a marker in a cluster of young stars. If their high lithium abundance is associated with rapid rotation, then we may consider the fall of SBs in orbits close to parabolic. If there is a clear lithium deficiency, then accretion from the debris discs in quasi-circular orbits prevails. Accretion from the debris discs may depend on metallicity. The higher the metallicity, the higher the temperature limit of stars showing lithium deficiency. With solar metallicity, this boundary is close to Teff ≤ 5000 K. Gas accretion should show lithium deficiency in comparison with the interstellar medium for all stars of the cluster, regardless of the temperature of the stars – the ‘lithium plateau’. This mechanism could significantly influence the emergence of the cosmological problem of lithium deficiency for MS stars.
There are especially many red dwarfs among the multiplanetary stellar systems. Perhaps it is because they initially, while in the accretion phase, contain a lot of matter in the form of SBs. In this regard, it would be interesting to perform the following studies to establish a possible relationship:
a population of fast-rotating stars with no lithium deficiency and the presence of SBs with parabolic orbits;
presence of debris discs in cold lithium-deficient stars with a Teff boundary depending on metallicity.
In conclusion, we note that for the modern era of star formation, the question of revising the ratio of the masses of the gas-and-dust component (in a broad sense, including all SBs) in the regions of star formation has stood out, since deviations from the properties of pure gas accretion are observed in many star clusters. We hope that taking into account this factor, the solution to the problem of the age and evolution of young stellar clusters as a whole will be simplified to some extent. Perhaps taking into account this factor for solar-type stars and stars with planets will lead to new conclusions in the evolution of planetary systems.
ACKNOWLEDGEMENTS
We are thankful to the referee for providing comments and suggestions leading to considerable improvement of our manuscript. This research is funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (grant no. AP19676713 and programme no. BR21881880). The figures were generated using matplotlib (Hunter 2007).
DATA AVAILABILITY
The data underlying the research results described in the article were obtained from sources listed in the reference.
Footnotes
We consider only 7|${\rm Li}$| in this work.



