-
PDF
- Split View
-
Views
-
Cite
Cite
Qian-Cheng Liu, Wen-Juan Zhong, Yang Chen, Pei Wang, Ping Zhou, You-Ling Yue, Di Li, Discovery and timing of pulsar J2016+3711 in supernova remnant CTB 87 with FAST, Monthly Notices of the Royal Astronomical Society, Volume 528, Issue 4, March 2024, Pages 6761–6767, https://doi.org/10.1093/mnras/stae351
Close - Share Icon Share
ABSTRACT
We report on our discovery of the radio pulsar, PSR J2016+3711, in supernova remnant (SNR) CTB 87, with a ∼10.8σ significance of pulses, which confirms the compact nature of the X-ray point source in CTB 87. It is the first pulsar discovered in SNRs using Five-hundred-meter Aperture Spherical radio Telescope (FAST). Its integrated radio pulse profile can be well described by a single component, with a width at 50 per cent of the peak flux density of about 28.1○ and an effective width of about 32.2○. The mean flux density at 1.25 GHz is estimated to be about 15.5 |$\mu$|Jy. Combined with the non-detection of the radio pulse at lower frequencies, the radio spectral index of the pulsar is constrained to be ≲2.3. We also present the timing solution based on 28 follow-up FAST observations. Our results reveal a period of 50.81 ms, period derivative of 7.2 × 10−14 s s−1, and dispersion measure of 428 pc cm−3. The strength of the equatorial surface magnetic dipole magnetic field is inferred to be about 1.9 × 1012 G. Using the ephemeris obtained from the radio observations, we searched Fermi-LAT data for gamma-ray pulsations but detected no pulsed signal. We also searched for radio pulses with FAST towards the X-ray counterpart of the gamma-ray binary HESS J1832−093 proximate to SNR G22.7−00.2 but found no signal.
1 INTRODUCTION
Pulsar wind nebulae (PWNe), one of the most important components of supernova remnants (SNRs), are produced by the relativistic winds of rotation-powered neutron stars as they interact with the surroundings. None the less, only about 1 percent of the known pulsars are found to be directly associated with PWNe and SNRs (e.g. Lyne & Graham-Smith 2012). On the other hand, although the existence of pulsars in PWNe is beyond doubt, about 30 per cent of the known PWNe and PWN candidates have not been confirmed with pulsed emission signals to date (according to Ferrand & Safi-Harb 2012). Finding pulsars in PWNe and SNRs is crucial to studying the pulsar formation and the supernova explosion mechanism, and bridging the gap between the theoretical prediction and the observational results.
SNR CTB 87, appearing located in a superbubble (Liu et al. 2018) and in physical contact with a molecular cloud (e.g. Kothes et al. 2003; Liu et al. 2018), is characterized by the hosted PWN with trailing morphology in X-rays (Matheson et al. 2013). A point-like X-ray source, CXOU J201609.2+371110, has been found in the south-eastern head portion of the trailing structure, which was suggested to be the pulsar candidate (Matheson et al. 2013). Several surveys have covered SNR CTB 87 to search for the radio pulsar. Using the Low Frequency Array (LOFAR), the point-like X-ray source was observed at about 150 MHz with a sensitivity of about 0.4 mJy (Straal & van Leeuwen 2019). Using the Arecibo radio telescope, CTB 87 was fully searched at 430 MHz with a sensitivity of 0.05 mJy (Gorham et al. 1996). Also, it was searched using the 76 m Lovell radio telescope at 606 MHz with sensitivities of 3 mJy (Biggs & Lyne 1996) and 0.16 mJy (Lorimer et al. 1998), respectively. However, no radio pulsation from CTB 87 was ever detected in the previous searches. Proximate to the south-west of SNR G22.7−00.2, an X-ray source (XMMU J183245−0921539) was found consistent with the location of the gamma-ray binary HESS J1832−093 (HESS Collaboration 2015). Recently, near-infrared spectroscopic observations found the companion to be an O6 V star (van Soelen et al. 2024), while the nature of the compact object remains unknown. The X-ray spectrum of XMMU J183245−0921539 is well fitted by a power-law model with a photon index suggesting a pulsar nature (Mori et al. 2017). The steep Australia Telescope Compact Array spectrum of the radio source coincident with the binary is also consistent with the synchrotron radiation from a radio pulsar residing in the binary (Tam et al. 2020).
Although non-detection of radio pulse may be because the beam of the pulsar does not point towards us, it could also result from the instrumental limitations of the surveys. Now, the Five-hundred-meter Aperture Spherical radio Telescope (FAST), with a large effective area, allows us to search for faint pulsars with unprecedented high sensitivity. Actually, a number of faint pulsars have been detected (e.g. Li et al. 2018; Zhang et al. 2019; Cameron et al. 2020; Han et al. 2021) since the first one discovered with FAST (Qian et al. 2019).
We have observed two X-ray point-like sources, CXOU J201609.2+371110 in SNR CTB 87 and XMMU J183245−0921539 proximate to SNR G22.7−00.2, respectively, with FAST. In this paper, we report on our searches for radio pulses towards them and the detection of pulses in CTB 87. We describe the observations and reduction of the data in Section 2. We present our results, the discovery, and timing solution of the pulsar in CTB 87, in Section 3. We discuss the properties of the detected pulsar in Section 4 and summarize this paper in Section 5.
2 OBSERVATION AND DATA REDUCTION
Our radio observations (PI: Y. Chen) were carried out with FAST during 2019 July 15–16 in the ‘risk-sharing’ open session, for a total time of about 1 h for each source. The two target positions are centred at (20h16m09|${_{.}^{\rm s}}$|2, +37○11′10|${_{.}^{\prime\prime}}$|5, J2000) and (18h32m45|${_{.}^{\rm s}}$|0, −9○21′53|${_{.}^{\prime\prime}}$|9, J2000) (denoted as positions PCTB87 and PG22.7 hereafter) for the point-like X-ray sources in SNR CTB 87 and close to SNR G22.7−00.2, respectively (see Fig. 1; Matheson et al. 2013; HESS Collaboration 2015). In the observations, the central beam of the 19-beam 1.05–1.45 GHz receiver (Jiang et al. 2019) was used, with the tracking mode applied. The half-power beamwidth of the telescope is about 3.2 arcmin at 1.25 GHz and the pointing accuracy of the telescope is better than 16 arcsec. The digital back-end provided a bandwidth of 400 MHz with 4096 frequency channels and a time resolution of 49.152 |$\mu$|s. The data were recorded in the search mode of PSRFITS format.
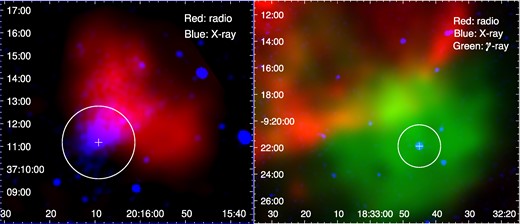
(Left) Dual-wavelength image of SNR CTB 87: NVSS 1.4 GHz radio continuum image in red, and Chandra X-ray (0.5–7 keV) image in blue. The white cross indicates the location of the X-ray point-like source (Matheson et al. 2013). The white circle shows the beam size of FAST at 1.25 GHz towards position PCTB87. (Right) Tri-wavelength image of the south-western part of SNR G22.7−0.02: VGPS 1.4 GHz radio continuum image in red, the XMM–Newton X-ray (0.5–6 keV) image in blue, and the H.E.S.S. gamma-ray (>1 TeV) integral flux image in green. The white cross and circle are similar to those in the left panel, but for position PG22.7. The radio continuum images in both panels and the gamma-ray image in the right panel are re-gridded with a 4 × 4 arcsec resolution.
We used the PulsaR Exploration and Search TOolkit (presto) software (Ransom 2001) to reduce the data. The data were first cleaned from the radio frequency interference (RFI) and then were used to search for periodic signals. The dispersion search ranges of the targets (see Table 1) were limited based on the dispersion measure (DM) predicted by the electron density model (Yao et al. 2017). The data were de-dispersed in steps of 0.1 pc cm−3 below DM = 230 pc cm−3, steps of 0.3 pc cm−3 for 230 pc cm−3 < DM < 446 pc cm−3, steps of 0.5 pc cm−3 for 446 pc cm−3 < DM < 800 pc cm−3 and steps of 1 pc cm−3 above 800 pc cm−3, which were chosen using the ddplan routine in presto. We selected candidates of pulse signals with presto-reported significance above 4σ. The selected candidates were then folded and inspected by eyes to clarify them as either RFI or possible radio pulse. We also searched for single pulses using the single_pulse_search.py routine in presto. Yet no positive candidate of single pulse has been found towards any of the targets.
| Source . | Position . | RA . | Dec. . | Distance d . | Predicted DM . | DMs searched . |
|---|---|---|---|---|---|---|
| . | . | . | . | (kpc) . | (pc cm−3) . | (pc cm−3) . |
| CTB 87 | PCTB87 | 20:16:09.2 | +37:11:10.5 | |$6.1\pm 0.9\,$|a | 197.00|$^{+72}_{-98}$| | 50–500 |
| G22.7−00.2 | PG22.7 | 18:32:45.0 | −9:21:53.9 | |${\sim} 4.5\, $|b | 471.48 | 150–1000 |
| Source . | Position . | RA . | Dec. . | Distance d . | Predicted DM . | DMs searched . |
|---|---|---|---|---|---|---|
| . | . | . | . | (kpc) . | (pc cm−3) . | (pc cm−3) . |
| CTB 87 | PCTB87 | 20:16:09.2 | +37:11:10.5 | |$6.1\pm 0.9\,$|a | 197.00|$^{+72}_{-98}$| | 50–500 |
| G22.7−00.2 | PG22.7 | 18:32:45.0 | −9:21:53.9 | |${\sim} 4.5\, $|b | 471.48 | 150–1000 |
After the radio pulses from the CTB 87 PWN were discovered in the ‘risk-sharing’ observation in 2019 (see Section 3.1 below), 28 follow-up timing observations were then carried out until 2023, with the same receiver and back-end setup as for the discovery observation. A summary of the follow-up observations used in the timing analysis is given in Table 2. The pulse time of arrivals (ToAs) was measured for each observation by cross-correlating the pulse profile against a high-signal-to-noise (S/N) template, which was obtained by fitting a set of Gaussian curves to the best detection. We carried out the subsequent timing analysis of the ToAs with the tempo pulsar timing package (Nice et al. 2015)1 to obtain more accurate measurements of the timing parameters. DM was measured using ToAs from multifrequency sub-bands. As shown in Table 2, the gap between some observations can be 1 month or even much longer, we thus used the dracula script (Freire & Ridolfi 2018)2 to help derive phase-connected timing solution for the pulsar.
| No. . | Date . | MJD . | Tobs . | Detected a . |
|---|---|---|---|---|
| . | (yyyy-mm-dd) . | . | (min) . | Y/N . |
| 1b | 2021 Aug 7 | 59432.8 | 60 | Y |
| 2 | 2021 Aug 27 | 59452.7 | 30 | Y |
| 3 | 2021 Aug 29 | 59455.6 | 30 | Y |
| 4 | 2021 Aug 31 | 59457.5 | 30 | Y |
| 5b | 2021 Sep 2 | 59459.5 | 30 | Y |
| 6 | 2021 Oct 9 | 59496.6 | 30 | Y |
| 7 | 2021 Oct 16 | 59503.5 | 30 | Y |
| 8 | 2021 Oct 23 | 59510.5 | 30 | Y |
| 9 | 2021 Oct 30 | 59517.5 | 30 | Y |
| 10b | 2021 Nov 6 | 59524.4 | 20 | Y |
| 11b | 2022 Aug 8 | 59799.7 | 30 | Y |
| 12 | 2022 Oct 3 | 59855.6 | 30 | Y |
| 13 | 2022 Oct 5 | 59857.6 | 30 | Y |
| 14 | 2022 Oct 7 | 59859.6 | 30 | Y |
| 15 | 2022 Oct 9 | 59861.6 | 30 | N |
| 16 | 2022 Oct 16 | 59868.6 | 30 | N |
| 17 | 2022 Oct 23 | 59875.6 | 30 | Y |
| 18 | 2022 Oct 30 | 59882.5 | 30 | Y |
| 19 | 2022 Nov 6 | 59889.5 | 30 | Y |
| 20 | 2022 Nov 13 | 59896.5 | 30 | Y |
| 21 | 2022 Nov 28 | 59911.4 | 30 | Y |
| 22b | 2022 Dec 13 | 59926.4 | 30 | N |
| 23b | 2022 Dec 28 | 59941.4 | 30 | Y |
| 24 | 2023 Jan 15 | 59959.3 | 30 | Y |
| 25b | 2023 Jan 29 | 59973.3 | 30 | Y |
| 26 | 2023 Aug 19 | 60175.5 | 30 | Y |
| 27b | 2023 Aug 29 | 60184.7 | 30 | N |
| 28 | 2023 Sep 9 | 60196.6 | 30 | Y |
| No. . | Date . | MJD . | Tobs . | Detected a . |
|---|---|---|---|---|
| . | (yyyy-mm-dd) . | . | (min) . | Y/N . |
| 1b | 2021 Aug 7 | 59432.8 | 60 | Y |
| 2 | 2021 Aug 27 | 59452.7 | 30 | Y |
| 3 | 2021 Aug 29 | 59455.6 | 30 | Y |
| 4 | 2021 Aug 31 | 59457.5 | 30 | Y |
| 5b | 2021 Sep 2 | 59459.5 | 30 | Y |
| 6 | 2021 Oct 9 | 59496.6 | 30 | Y |
| 7 | 2021 Oct 16 | 59503.5 | 30 | Y |
| 8 | 2021 Oct 23 | 59510.5 | 30 | Y |
| 9 | 2021 Oct 30 | 59517.5 | 30 | Y |
| 10b | 2021 Nov 6 | 59524.4 | 20 | Y |
| 11b | 2022 Aug 8 | 59799.7 | 30 | Y |
| 12 | 2022 Oct 3 | 59855.6 | 30 | Y |
| 13 | 2022 Oct 5 | 59857.6 | 30 | Y |
| 14 | 2022 Oct 7 | 59859.6 | 30 | Y |
| 15 | 2022 Oct 9 | 59861.6 | 30 | N |
| 16 | 2022 Oct 16 | 59868.6 | 30 | N |
| 17 | 2022 Oct 23 | 59875.6 | 30 | Y |
| 18 | 2022 Oct 30 | 59882.5 | 30 | Y |
| 19 | 2022 Nov 6 | 59889.5 | 30 | Y |
| 20 | 2022 Nov 13 | 59896.5 | 30 | Y |
| 21 | 2022 Nov 28 | 59911.4 | 30 | Y |
| 22b | 2022 Dec 13 | 59926.4 | 30 | N |
| 23b | 2022 Dec 28 | 59941.4 | 30 | Y |
| 24 | 2023 Jan 15 | 59959.3 | 30 | Y |
| 25b | 2023 Jan 29 | 59973.3 | 30 | Y |
| 26 | 2023 Aug 19 | 60175.5 | 30 | Y |
| 27b | 2023 Aug 29 | 60184.7 | 30 | N |
| 28 | 2023 Sep 9 | 60196.6 | 30 | Y |
The signal can be seen in every observation by folding the data with the timing solution.
The positions of the time offsets (‘jumps’).
| No. . | Date . | MJD . | Tobs . | Detected a . |
|---|---|---|---|---|
| . | (yyyy-mm-dd) . | . | (min) . | Y/N . |
| 1b | 2021 Aug 7 | 59432.8 | 60 | Y |
| 2 | 2021 Aug 27 | 59452.7 | 30 | Y |
| 3 | 2021 Aug 29 | 59455.6 | 30 | Y |
| 4 | 2021 Aug 31 | 59457.5 | 30 | Y |
| 5b | 2021 Sep 2 | 59459.5 | 30 | Y |
| 6 | 2021 Oct 9 | 59496.6 | 30 | Y |
| 7 | 2021 Oct 16 | 59503.5 | 30 | Y |
| 8 | 2021 Oct 23 | 59510.5 | 30 | Y |
| 9 | 2021 Oct 30 | 59517.5 | 30 | Y |
| 10b | 2021 Nov 6 | 59524.4 | 20 | Y |
| 11b | 2022 Aug 8 | 59799.7 | 30 | Y |
| 12 | 2022 Oct 3 | 59855.6 | 30 | Y |
| 13 | 2022 Oct 5 | 59857.6 | 30 | Y |
| 14 | 2022 Oct 7 | 59859.6 | 30 | Y |
| 15 | 2022 Oct 9 | 59861.6 | 30 | N |
| 16 | 2022 Oct 16 | 59868.6 | 30 | N |
| 17 | 2022 Oct 23 | 59875.6 | 30 | Y |
| 18 | 2022 Oct 30 | 59882.5 | 30 | Y |
| 19 | 2022 Nov 6 | 59889.5 | 30 | Y |
| 20 | 2022 Nov 13 | 59896.5 | 30 | Y |
| 21 | 2022 Nov 28 | 59911.4 | 30 | Y |
| 22b | 2022 Dec 13 | 59926.4 | 30 | N |
| 23b | 2022 Dec 28 | 59941.4 | 30 | Y |
| 24 | 2023 Jan 15 | 59959.3 | 30 | Y |
| 25b | 2023 Jan 29 | 59973.3 | 30 | Y |
| 26 | 2023 Aug 19 | 60175.5 | 30 | Y |
| 27b | 2023 Aug 29 | 60184.7 | 30 | N |
| 28 | 2023 Sep 9 | 60196.6 | 30 | Y |
| No. . | Date . | MJD . | Tobs . | Detected a . |
|---|---|---|---|---|
| . | (yyyy-mm-dd) . | . | (min) . | Y/N . |
| 1b | 2021 Aug 7 | 59432.8 | 60 | Y |
| 2 | 2021 Aug 27 | 59452.7 | 30 | Y |
| 3 | 2021 Aug 29 | 59455.6 | 30 | Y |
| 4 | 2021 Aug 31 | 59457.5 | 30 | Y |
| 5b | 2021 Sep 2 | 59459.5 | 30 | Y |
| 6 | 2021 Oct 9 | 59496.6 | 30 | Y |
| 7 | 2021 Oct 16 | 59503.5 | 30 | Y |
| 8 | 2021 Oct 23 | 59510.5 | 30 | Y |
| 9 | 2021 Oct 30 | 59517.5 | 30 | Y |
| 10b | 2021 Nov 6 | 59524.4 | 20 | Y |
| 11b | 2022 Aug 8 | 59799.7 | 30 | Y |
| 12 | 2022 Oct 3 | 59855.6 | 30 | Y |
| 13 | 2022 Oct 5 | 59857.6 | 30 | Y |
| 14 | 2022 Oct 7 | 59859.6 | 30 | Y |
| 15 | 2022 Oct 9 | 59861.6 | 30 | N |
| 16 | 2022 Oct 16 | 59868.6 | 30 | N |
| 17 | 2022 Oct 23 | 59875.6 | 30 | Y |
| 18 | 2022 Oct 30 | 59882.5 | 30 | Y |
| 19 | 2022 Nov 6 | 59889.5 | 30 | Y |
| 20 | 2022 Nov 13 | 59896.5 | 30 | Y |
| 21 | 2022 Nov 28 | 59911.4 | 30 | Y |
| 22b | 2022 Dec 13 | 59926.4 | 30 | N |
| 23b | 2022 Dec 28 | 59941.4 | 30 | Y |
| 24 | 2023 Jan 15 | 59959.3 | 30 | Y |
| 25b | 2023 Jan 29 | 59973.3 | 30 | Y |
| 26 | 2023 Aug 19 | 60175.5 | 30 | Y |
| 27b | 2023 Aug 29 | 60184.7 | 30 | N |
| 28 | 2023 Sep 9 | 60196.6 | 30 | Y |
The signal can be seen in every observation by folding the data with the timing solution.
The positions of the time offsets (‘jumps’).
3 RESULTS
3.1 Detection of radio pulses from PSR J2016+3711 and timing
We did not detect radio pulses towards PG22.73 but detected radio pulses towards PCTB87 (Fig. 2), with a significance of ∼10.8σ and a reduced χ2 of 4.3. We will refer to this pulsar as PSR J2016+3711 hereafter. The period (P) of the detected pulses in the 2019 observation is 50.806263(65) ms, and the DM of J2016+3711 is 429.5(5.0) pc cm−3. We note that the period is somewhat similar to that estimated from the X-ray observation of the host PWN (e.g. P ≈ 80 ms in Matheson et al. 2013 or 65 ms in Guest et al. 2020).
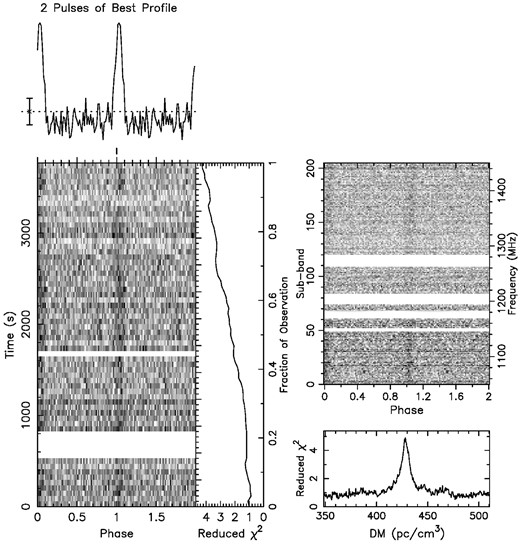
Radio pulses detected towards position PCTB87 in SNR CTB 87. The pulsed signal is present throughout the entire 1 h of the observation within the bandwidth of the data (1.05–1.45 GHz). The DM is 429.5(5.0) pc cm−3 and the period of the radio pulses is 50.806263(65) ms.
Although unlikely, the radio pulses could potentially arise from sideband effect of the single-dish telescope. To clarify if the detected radio pulses are a result of the effect, we searched for published known pulsars in a region centred at position PCTB87 with an angular radius of 5○ using the Australia Telescope National Facility (ATNF) data base (Manchester et al. 2005)4, the Pulsar Arecibo L-band Feed Array Survey Project5, the FAST Galactic Plane Pulsar Snapshot survey (Han et al. 2021; Zhou et al. 2023)6, and the Commensal Radio Astronomy FAST Survey7. With the DM limited in range 429.5 ± 100 pc cm−3, the results are shown in Table 3. There is one pulsar, J2022+3842, which has similar DM and period as those of the radio pulses we detected. We folded our data with the period of J2022+3842, yet no radio pulse was detected. Therefore, the radio pulsation we detected is from the newly discovered pulsar at position PCTB87 in SNR CTB 87, i.e. J2016+3711.
| Pulsar . | RA . | Dec. . | Offset (°) . | DM (pc cm−3) . | Period (ms) . |
|---|---|---|---|---|---|
| J2004+3304g | 20:04:08 | +33:04 | 4.80 | 410.1 | 1193.37 |
| J2004+3429 | 20:04:46.9 | +34:29:17.7 | 3.55 | 351.0 | 240.95 |
| J2005+3411g | 20:05:45 | +34:11 | 3.77 | 489.0 | 651.05 |
| J2005+3547 | 20:05:17.4 | +35:47:25.4 | 2.59 | 401.6 | 615.03 |
| J2005+3552 | 20:05:47.5 | +35:52:24.3 | 2.46 | 455.0 | 307.94 |
| J2010+3230 | 20:10:26.5 | +32:30:07.3 | 4.83 | 371.8 | 1442.45 |
| J2011+3521g | 20:11:04 | +35:20 | 2.12 | 438.1 | 943.23 |
| J2014+3326g | 20:14:24 | +33:26 | 3.77 | 332.7 | 977.28 |
| J2021+3651 | 20:21:05.4 | +36:51:04.8 | 1.04 | 367.5 | 103.74 |
| J2022+3842 | 20:22:21.6 | +38:42:14.8 | 1.95 | 429.1 | 48.58 |
| J2022+3845g | 20:22:11 | +38:45 | 1.76 | 487.5 | 1008.90 |
| J2024+3751g | 20:24:32 | +37:51 | 1.79 | 446.6 | 211.64 |
| J2030+3833g | 20:30:31 | +38:33 | 3.15 | 417.0 | 99999.9a |
| J2030+3929g | 20:30:47 | +39:29 | 3.41 | 491.9 | 1718.42 |
| Pulsar . | RA . | Dec. . | Offset (°) . | DM (pc cm−3) . | Period (ms) . |
|---|---|---|---|---|---|
| J2004+3304g | 20:04:08 | +33:04 | 4.80 | 410.1 | 1193.37 |
| J2004+3429 | 20:04:46.9 | +34:29:17.7 | 3.55 | 351.0 | 240.95 |
| J2005+3411g | 20:05:45 | +34:11 | 3.77 | 489.0 | 651.05 |
| J2005+3547 | 20:05:17.4 | +35:47:25.4 | 2.59 | 401.6 | 615.03 |
| J2005+3552 | 20:05:47.5 | +35:52:24.3 | 2.46 | 455.0 | 307.94 |
| J2010+3230 | 20:10:26.5 | +32:30:07.3 | 4.83 | 371.8 | 1442.45 |
| J2011+3521g | 20:11:04 | +35:20 | 2.12 | 438.1 | 943.23 |
| J2014+3326g | 20:14:24 | +33:26 | 3.77 | 332.7 | 977.28 |
| J2021+3651 | 20:21:05.4 | +36:51:04.8 | 1.04 | 367.5 | 103.74 |
| J2022+3842 | 20:22:21.6 | +38:42:14.8 | 1.95 | 429.1 | 48.58 |
| J2022+3845g | 20:22:11 | +38:45 | 1.76 | 487.5 | 1008.90 |
| J2024+3751g | 20:24:32 | +37:51 | 1.79 | 446.6 | 211.64 |
| J2030+3833g | 20:30:31 | +38:33 | 3.15 | 417.0 | 99999.9a |
| J2030+3929g | 20:30:47 | +39:29 | 3.41 | 491.9 | 1718.42 |
Transient source with just few pulses, no period has been found yet (Zhou et al. 2023).
| Pulsar . | RA . | Dec. . | Offset (°) . | DM (pc cm−3) . | Period (ms) . |
|---|---|---|---|---|---|
| J2004+3304g | 20:04:08 | +33:04 | 4.80 | 410.1 | 1193.37 |
| J2004+3429 | 20:04:46.9 | +34:29:17.7 | 3.55 | 351.0 | 240.95 |
| J2005+3411g | 20:05:45 | +34:11 | 3.77 | 489.0 | 651.05 |
| J2005+3547 | 20:05:17.4 | +35:47:25.4 | 2.59 | 401.6 | 615.03 |
| J2005+3552 | 20:05:47.5 | +35:52:24.3 | 2.46 | 455.0 | 307.94 |
| J2010+3230 | 20:10:26.5 | +32:30:07.3 | 4.83 | 371.8 | 1442.45 |
| J2011+3521g | 20:11:04 | +35:20 | 2.12 | 438.1 | 943.23 |
| J2014+3326g | 20:14:24 | +33:26 | 3.77 | 332.7 | 977.28 |
| J2021+3651 | 20:21:05.4 | +36:51:04.8 | 1.04 | 367.5 | 103.74 |
| J2022+3842 | 20:22:21.6 | +38:42:14.8 | 1.95 | 429.1 | 48.58 |
| J2022+3845g | 20:22:11 | +38:45 | 1.76 | 487.5 | 1008.90 |
| J2024+3751g | 20:24:32 | +37:51 | 1.79 | 446.6 | 211.64 |
| J2030+3833g | 20:30:31 | +38:33 | 3.15 | 417.0 | 99999.9a |
| J2030+3929g | 20:30:47 | +39:29 | 3.41 | 491.9 | 1718.42 |
| Pulsar . | RA . | Dec. . | Offset (°) . | DM (pc cm−3) . | Period (ms) . |
|---|---|---|---|---|---|
| J2004+3304g | 20:04:08 | +33:04 | 4.80 | 410.1 | 1193.37 |
| J2004+3429 | 20:04:46.9 | +34:29:17.7 | 3.55 | 351.0 | 240.95 |
| J2005+3411g | 20:05:45 | +34:11 | 3.77 | 489.0 | 651.05 |
| J2005+3547 | 20:05:17.4 | +35:47:25.4 | 2.59 | 401.6 | 615.03 |
| J2005+3552 | 20:05:47.5 | +35:52:24.3 | 2.46 | 455.0 | 307.94 |
| J2010+3230 | 20:10:26.5 | +32:30:07.3 | 4.83 | 371.8 | 1442.45 |
| J2011+3521g | 20:11:04 | +35:20 | 2.12 | 438.1 | 943.23 |
| J2014+3326g | 20:14:24 | +33:26 | 3.77 | 332.7 | 977.28 |
| J2021+3651 | 20:21:05.4 | +36:51:04.8 | 1.04 | 367.5 | 103.74 |
| J2022+3842 | 20:22:21.6 | +38:42:14.8 | 1.95 | 429.1 | 48.58 |
| J2022+3845g | 20:22:11 | +38:45 | 1.76 | 487.5 | 1008.90 |
| J2024+3751g | 20:24:32 | +37:51 | 1.79 | 446.6 | 211.64 |
| J2030+3833g | 20:30:31 | +38:33 | 3.15 | 417.0 | 99999.9a |
| J2030+3929g | 20:30:47 | +39:29 | 3.41 | 491.9 | 1718.42 |
Transient source with just few pulses, no period has been found yet (Zhou et al. 2023).
In Table 4, we present the timing solution for J2016+3711. We only obtained a timing solution with several time offsets (‘jumps’) left (see Table 2). One possible explanation is the discontinuity in the pulsar’s frequency or its differential, e.g. glitches, which are commonly observed in young pulsars (Lyne & Graham-Smith 2012). The fitted position of J2016+3711 is spatially coincident with the X-ray point source detected by Chandra (Matheson et al. 2013). The post-fit timing residuals with all of the ToAs obtained by the timing solution are shown in Fig. 3.
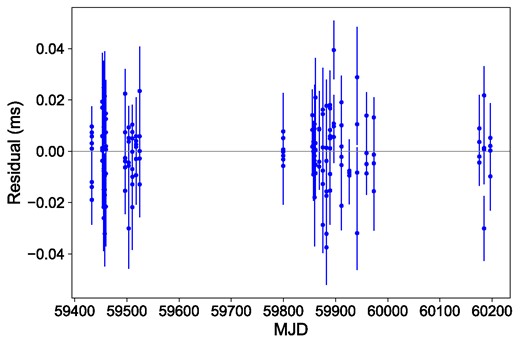
Timing residuals from the best-fitting timing models presented in Table 4 as a function of the observation date for PSR J2016+3711.
| Parameter . | Value . |
|---|---|
| MJD range | 59432–60196 |
| Reference epoch (MJD) | 58 871 |
| RA, α (J2000) | 20:16:09.14(6) |
| Dec., δ (J2000) | +37:11:10.4(1.1) |
| Spin frequency, f (Hz) | 19.68165408(6) |
| First spin frequency derivative, |$\dot{f}\, (10^{-11}\, {\rm Hz\, s}^{-1}$|) | −2.8073(1) |
| Second spin frequency derivative, |$\ddot{f}$| (|$10^{-21}\, {\rm Hz\, s}^{-2}$|) | 2.19(2) |
| DM (pc cm−3) | 428.0(1) |
| Number of ToAs | 156 |
| Residuals rms (|$\mu$|s) | 592.08 |
| Derived parameters | |
| Galactic longitude, l (°) | 74.9437 |
| Galactic latitude b (°) | +1.1142 |
| Spin period, P (ms) | 50.8087377(1) a |
| First spin period derivative |$\dot{P}\, (10^{-14}$| s s−1) | 7.2472(4) |
| Characteristic age, τc (kyr) | 11.1 |
| Surface magnetic field, B (1012 G) | 1.9 |
| Spin-down luminosity, |$\dot{E}$| (1037 erg s−1) | 2.2 |
| Distance, d (kpc) | 13.3 b |
| Parameter . | Value . |
|---|---|
| MJD range | 59432–60196 |
| Reference epoch (MJD) | 58 871 |
| RA, α (J2000) | 20:16:09.14(6) |
| Dec., δ (J2000) | +37:11:10.4(1.1) |
| Spin frequency, f (Hz) | 19.68165408(6) |
| First spin frequency derivative, |$\dot{f}\, (10^{-11}\, {\rm Hz\, s}^{-1}$|) | −2.8073(1) |
| Second spin frequency derivative, |$\ddot{f}$| (|$10^{-21}\, {\rm Hz\, s}^{-2}$|) | 2.19(2) |
| DM (pc cm−3) | 428.0(1) |
| Number of ToAs | 156 |
| Residuals rms (|$\mu$|s) | 592.08 |
| Derived parameters | |
| Galactic longitude, l (°) | 74.9437 |
| Galactic latitude b (°) | +1.1142 |
| Spin period, P (ms) | 50.8087377(1) a |
| First spin period derivative |$\dot{P}\, (10^{-14}$| s s−1) | 7.2472(4) |
| Characteristic age, τc (kyr) | 11.1 |
| Surface magnetic field, B (1012 G) | 1.9 |
| Spin-down luminosity, |$\dot{E}$| (1037 erg s−1) | 2.2 |
| Distance, d (kpc) | 13.3 b |
At the reference epoch (MJD) 58871.
Derived from the electron density model (Yao et al. 2017).
| Parameter . | Value . |
|---|---|
| MJD range | 59432–60196 |
| Reference epoch (MJD) | 58 871 |
| RA, α (J2000) | 20:16:09.14(6) |
| Dec., δ (J2000) | +37:11:10.4(1.1) |
| Spin frequency, f (Hz) | 19.68165408(6) |
| First spin frequency derivative, |$\dot{f}\, (10^{-11}\, {\rm Hz\, s}^{-1}$|) | −2.8073(1) |
| Second spin frequency derivative, |$\ddot{f}$| (|$10^{-21}\, {\rm Hz\, s}^{-2}$|) | 2.19(2) |
| DM (pc cm−3) | 428.0(1) |
| Number of ToAs | 156 |
| Residuals rms (|$\mu$|s) | 592.08 |
| Derived parameters | |
| Galactic longitude, l (°) | 74.9437 |
| Galactic latitude b (°) | +1.1142 |
| Spin period, P (ms) | 50.8087377(1) a |
| First spin period derivative |$\dot{P}\, (10^{-14}$| s s−1) | 7.2472(4) |
| Characteristic age, τc (kyr) | 11.1 |
| Surface magnetic field, B (1012 G) | 1.9 |
| Spin-down luminosity, |$\dot{E}$| (1037 erg s−1) | 2.2 |
| Distance, d (kpc) | 13.3 b |
| Parameter . | Value . |
|---|---|
| MJD range | 59432–60196 |
| Reference epoch (MJD) | 58 871 |
| RA, α (J2000) | 20:16:09.14(6) |
| Dec., δ (J2000) | +37:11:10.4(1.1) |
| Spin frequency, f (Hz) | 19.68165408(6) |
| First spin frequency derivative, |$\dot{f}\, (10^{-11}\, {\rm Hz\, s}^{-1}$|) | −2.8073(1) |
| Second spin frequency derivative, |$\ddot{f}$| (|$10^{-21}\, {\rm Hz\, s}^{-2}$|) | 2.19(2) |
| DM (pc cm−3) | 428.0(1) |
| Number of ToAs | 156 |
| Residuals rms (|$\mu$|s) | 592.08 |
| Derived parameters | |
| Galactic longitude, l (°) | 74.9437 |
| Galactic latitude b (°) | +1.1142 |
| Spin period, P (ms) | 50.8087377(1) a |
| First spin period derivative |$\dot{P}\, (10^{-14}$| s s−1) | 7.2472(4) |
| Characteristic age, τc (kyr) | 11.1 |
| Surface magnetic field, B (1012 G) | 1.9 |
| Spin-down luminosity, |$\dot{E}$| (1037 erg s−1) | 2.2 |
| Distance, d (kpc) | 13.3 b |
At the reference epoch (MJD) 58871.
Derived from the electron density model (Yao et al. 2017).
3.2 The properties of the integrated radio pulse profile
The integrated radio pulse profiles are unique signatures that differ from pulsar to pulsar (e.g. Lyne & Graham-Smith 2012). The integrated radio pulse of the pulsar in CTB 87, J2016+3711, can be well described by a single component with a Gaussian profile (Fig. 4). The width of the profile of a pulsar is usually measured at 10 and 50 per cent of the peak flux density, as denoted by W10 and W50, respectively. Because the significance of the pulses detected here is low, we only estimate the value of W50, which is about 28.1○, with an uncertainty of |$\sigma _{50}=W_{50}/(\sqrt{2}\ln (2)S_{\rm S/N}) =2.7^\circ$|, where SS/N = 10.8 is the signal-to-noise ratio of the radio pulse. The 50 per cent duty cycle of the radio pulse is about (7.8 ± 0.8) per cent.
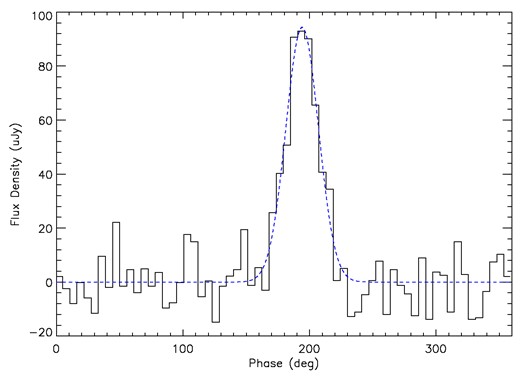
Integrated pulse profile at 1.25 GHz obtained from the FAST observation. The dashed line represents the single component fitted with a Gaussian curve.
Also, we can estimate the effective pulse width Weff, which is defined as the width of a boxcar-like pulse with the same energy and amplitude of the real pulse (e.g. Kramer et al. 1998). The value of Weff is estimated to be 32.2○ ± 1.7○, which is equivalent to 4.5 ± 0.2 ms in units of time.
4 DISCUSSION
4.1 The flux density of PSR J2016+3711
The flux density of the radio pulses at 1.25 GHz can be estimated as (e.g. Dewey et al. 1985)
where β ≈ 1.5 is a factor taking into account the losses and system imperfections, Np = 2 the polarization channels, Δν = 3.4 × 108 Hz the effective bandwidth of the data, tint = 3470 s the on-source integrating time, P the radio pulsation period of the pulsar, Tsys ≈ 25 K (Jiang et al. 2019) the system temperature of the telescope, Tsky ∼ 50 K (Kothes et al. 2020) the averaged background temperature of the sky towards the pulsar at ∼1.25 GHz, and G ≈ 16 K Jy−1 (Jiang et al. 2019) the gain of the telescope. The flux density at 1.25 GHz is estimated to be 15.5 ± 0.7 |$\mu$|Jy, which indicates the faint nature of the pulsar’s radio emission and explains why it has remained undetected in early surveys. Notably, there are only 91 pulsars (|$\lt 3~{{\ \rm per\ cent}}$|) in the ATNF catalogue (v1.71; Manchester et al. 2005) with a flux density less than 16 |$\mu$|Jy at 1.4 GHz, among which over 75 per cent were discovered by FAST (Han et al. 2021).
The flux densities of pulsars are known to have steep spectra (e.g. Sieber 1973), with Fν ∝ ν−α, where Fν is the flux density of the pulsar at frequency ν, and α the spectral index. Here, we crudely constrain the spectral index of PSR J2016+3711, based on the estimated flux density at 1.25 GHz and the non-detection at lower frequencies in early surveys.
The pulsar candidate in SNR CTB 87 had been searched using the LOFAR at about 150 MHz with a sensitivity of about 0.4 mJy (Straal & van Leeuwen 2019), the Arecibo radio telescope at 430 MHz with a sensitivity of 0.05 mJy (Gorham et al. 1996), and the 76 m Lovell radio telescope at 606 MHz with a sensitivity of 3 mJy (Biggs & Lyne 1996) and 0.16 mJy (Lorimer et al. 1998), yet no radio pulse had been detected. The 5σ values of the sensitivities are here used as the upper limits of the flux densities.
Fig. 5 shows the fitting of the flux density of PSR J2016+3711 using |$F_\nu = 15.5 (\nu /1.25\, {\rm GHz})^{-\alpha }\, \mu$|Jy. It is shown that the spectral index of the pulsar should not be larger than ∼2.3. It appears not to contradict the typical spectral indices of radio pulsars, which are in a range of ∼1.4–1.8 (e.g. Lorimer et al. 1995; Toscano et al. 1998; Maron et al. 2000; Bates et al. 2013).
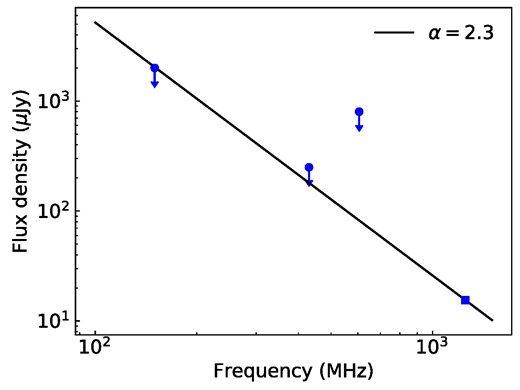
Flux density of PSR J2016+3711 at 150 MHz (Straal & van Leeuwen 2019), 430 MHz (Gorham et al. 1996), 606 MHz (Lorimer et al. 1998), and 1250 MHz. The 5σ values of the flux densities are shown as upper limits at 150, 430, and 606 MHz. The solid line represents the flux density distribution with spectral index α equal to 2.3.
It is noteworthy that the confinement is valid only if the spectral property of the pulsar can be well described by a single power law. Actually, many young pulsars have broken power-law spectra, and some even show a turn-over at low frequencies (e.g. Murphy et al. 2017; Jankowski et al. 2018; Bilous et al. 2020). If there is a similar case for pulsar J2016+3711, the spectral property of it would be more complex than derived above.
4.2 The properties of PSR J2016+3711
The observed period P ≈ 50.81 ms and first period derivative |$\dot{P}\approx 7.25\times 10^{-14}$| s s−1 are crucial to derive some basic physical properties of PSR J2016+3711. The characteristic age of the pulsar can be obtained through |$\tau _{\rm c} = P/[(n-1)\dot{P}] \approx 11.1$| kyr for a dipole radiator with the braking index n = 3. Interestingly, the previous inferences using the empirical relation between the X-ray luminosity of PWNe and the characteristic age of pulsars, ∼9.8 kyr in Matheson et al. (2013) and ∼11.5 kyr in Guest et al. (2020) with a distance 6.1 kpc adopted, are very close to this estimate.
The strength of the equatorial surface dipole magnetic field, can be inferred as (Gaensler & Slane 2006) |$B = 3.2\times 10^{19}I_{45}^{1/2}R_{10}^{-3}(P\dot{P})^{1/2}$||$\approx 1.9\times 10^{12}I_{45}^{1/2}R_{10}^{-3}\tau _{10}^{-1/2}$| G, where I45 is the moment of inertia of the pulsar in units of 1045 g cm−2, and R10 is the radius of the pulsar in units of 10 km. Also, the spin-down luminosity of the pulsar is estimated to be |$\dot{E}=4\pi ^2 I_{45} \dot{P}/P^3 \approx 2.2\times 10^{37}$| erg s−1, which can be used to explore the PWN scenario for the observed TeV gamma-ray emission (Abeysekara et al. 2018).
Using DM = 428.0 pc cm−3 and the electron density model (Yao et al. 2017), the distance to the pulsar is estimated as ∼13.3 kpc, which is about twice the estimate obtained from extinction–distance relation (6.1 ± 0.9 kpc; Kothes et al. 2003). This may be because the line of sight will penetrate the Orion spur, along which many objects (e.g. H ii regions) should contribute significant DMs. Furthermore, we note that the distances to many pulsars estimated from the electron density model could be overestimated for similar reasons (e.g. Yao et al. 2017; Han et al. 2021).
4.3 Searching for a gamma-ray counterpart of the radio pulsation
Pulsars have long been suggested to emit gamma-rays (e.g. Romani & Yadigaroglu 1995). Actually, about 294 pulsars have been detected with pulsed gamma-ray emission to date (Smith et al. 2023).
To search for the possible gamma-ray pulsation, we collected the Fermi-LAT Pass 8 data towards a region that is centred at the pulsar with a radius of 1○, from 2021-08-06 00:00:00 (utc) to 2023-09-09 00:00:00 (utc). The data collected span over 2 yr and cover the same MJD range as the timing analysis. We analysed the data with the standard software fermitools8 version 2.0.8 released on 2021 January 20. We only selected events with zenith angle <90○ to filter out the background gamma-rays from the Earth’s limb. To optimize the S/N ratio, the analysis was restricted to the energy range 500 MeV to 10 GeV. We folded the Fermi-LAT data with the ephemeris (parameter file) obtained from the radio timing results using the tempo2 software (Edwards et al. 2006) and checked the results using H-test. Yet, no clear signature of pulsed profile was found. We also performed the gtpsearch routine of fermi science tools software packages (v10r0p5) to search for pulsation frequencies near the radio pulsation frequency. We adopted the spin frequency, the first and second spin frequency derivatives at 58 871 MJD listed in Table 4 for the search. Still, there was no gamma-ray pulsation found.
None the less, the existence of pulsed gamma-ray emission could not thus be excluded because of the limited statistics and the lack of a precisely determined pulsar ephemeris. More follow-up radio observations spanning over years would be helpful to obtain a more accurate timing solution, which could then be used to fold the gamma-ray data and search for the pulsation.
4.4 Orientation of the emitting regions
The Chandra X-ray observation of the CTB87 PWN displays a jets+torus structure (Matheson et al. 2013). The projected elliptical shape of the torus suggests an inclination angle ∼55○ for the equatorial wind. Similar to that in the G54.1+0.3 PWN, the torus is one-sidedly brightened and can be explained with a Doppler boosting of sub-relativistic downstream flow (Lu et al. 2002). The jets, aligned with the pulsar spin axis, are at an angle ∼55○ with the line of sight.
The radio pulse profile of PSR J2016+3711 is narrow (W50 ≈ 28○, Weff ≈ 32○), without broad wings, which is different from the pulse profile of PSR J1930+1852 in the G54.1+0.3 PWN with broad wings (Camilo et al. 2002). This may indicate that either the pulsar radio beam starting near the magnetic polar cap is intrinsically narrow, or the line of sight sweeps just across a small segment of a broad beam. But, as a reference, the estimates of the beam radius from the relation obtained by Kuz’min, Dagkesamanskaya & Pugachev (1984) ρ = 5○P−1/2 ∼ 22○ or the relation for the case of magnetic inclination angle close to 90○ (Lyne & Manchester 1988) ρ = 6.5○ P−1/3 ∼ 17○ appear not in favour of the broad beam possibility. The detection of the radio pulsation of PSR J2016+3711 implies no small magnetic inclination angle (between the pulsar’s spin, defined by the jets, and the rotating magnetic dipole axis, surrounded by the radio beam that sweeps past the Earth). If the gamma-ray pulsation is indeed undetectable, there could be two possibilities. One could be that the pairs are not accelerated to the gamma-ray emitting energies. The other could be that the direction angles of gamma-ray emission from the outer magnetosphere are offset from the magnetic dipole axis, avoiding the Earth.
5 SUMMARY
We have performed a FAST observation to search for radio-pulsed signals towards two X-ray point-like sources in SNR CTB 87 and proximate to SNR G22.7−0.02, respectively. We discovered radio pulses from the former with a significance of ∼10.8σ, which is thus revealed to be a pulsar and named J2016+3711. This undoubtedly confirms the compact nature of the X-ray point source in SNR CTB 87. This is the first pulsar discovered in SNRs using FAST thanks to its unprecedented sensitivities. The integrated profile of the pulses can be well described by a single component, with a W50 value of about 28.1○. Combining the estimated mean flux density at 1.25 GHz (≈15.5 |$\mu$|Jy) with the non-detection of the radio pulse at lower frequencies, the spectral index of the pulsar is constrained to be ≲2.3. In the 28 follow-up timing observations with FAST, we identified PSR J2016+3711 and measured a period of 50.8087377(1) ms, period derivative of 7.2 × 10−14 s s−1, and DM of 428.0(1) pc cm−3. Additionally, the strength of the equatorial surface magnetic dipole magnetic field, characteristic age, and spin-down luminosity of the pulsar are derived to be about 1.9 × 1012 G, 11.1 kyr, and 2.2 × 1037 erg s−1, respectively. Based on the radio timing results, we also searched for gamma-ray pulsation with the Fermi-LAT data but found no pulsation.
ACKNOWLEDGEMENTS
We are grateful to Zhichen Pan for the help with the timing analysis, and Jian Li for the discussion about the Fermi-LAT gamma-ray data analysis. WJZ thanks Xiao Zhang and Shijie Gao for helpful discussions. YC thanks Jun Fang and Jin-Lin Han for helpful discussions on pulsar physics. QCL acknowledges support from the Program A for Outstanding PhD candidate of Nanjing University. YC acknowledges the support of the National Key R&D Program of China under grant 2017YFA0402600, and the NSFC under grants 12173018 and 12121003. PW acknowledges the support from NSFC under grants 11988101 and U2031117, and the National SKA Program of China no. 2020SKA0120200. PZ acknowledges the support from NSFC under grant 12273010. YLY acknowledges support from CAS ‘Light of West China’ Program. This work made use of data from FAST, a Chinese national mega-science facility built and operated by the National Astronomical Observatories, Chinese Academy of Sciences.
DATA AVAILABILITY
The Fermi-LAT data underlying this work are publicly available, and can be downloaded from https://fermi.gsfc.nasa.gov/ssc/data/access/lat/. Over half of the FAST data we used are already in the public domain and can be accessed in accordance with FAST data policy. The rest of undisclosed data can be obtained by contacting the corresponding author with a reasonable justification.
Footnotes
According to equation (1) below, the upper limit for the flux-density of PG22.7 at 1.25 GHz is roughly estimated to be 5.3 |$\mu$|Jy for SS/N = 5 and |$W_{\rm eff}=0.05P$| assumed.
References
Author notes
Contributed equally



