-
PDF
- Split View
-
Views
-
Cite
Cite
D N DellaGiustina, R -L Ballouz, K J Walsh, A G Marusiak, V J Bray, S H Bailey, Seismology of rubble-pile asteroids in binary systems, Monthly Notices of the Royal Astronomical Society, Volume 528, Issue 4, March 2024, Pages 6568–6580, https://doi.org/10.1093/mnras/stae325
Close - Share Icon Share
ABSTRACT
The mutual gravitational interaction of binary asteroids, which make up approximately 15 per cent of the near-Earth asteroid (NEA) population, provides a continuous tidal force, creating ground motion. We explore the potential of kilometre-sized binary asteroids as targets for seismological studies of their interior structure. We use a numerical model wherein each body is constructed of discrete particles interacting via gravity and contact forces. The system's orbital properties are modelled based on those of typical binary NEAs: a secondary body orbits a primary body at a distance of a few to 10 primary radii, resulting in orbital periods of a few tens of hours. We varied the elastic moduli (stiffness) of the constituent particles and measured a strain of a few micrometres caused by the orbiting satellite. Over eight orbital periods, the acceleration of the strain vector along the primary body's equatorial axis indicates that tidally induced ground motion generated by a binary asteroid system is detectable by modern seismometers, like the instruments deployed on the InSight mission to Mars. Owing to the relatively short orbital period of the satellite – a mean of 25.8 h for known binary NEAs – only a modest mission lifetime would be required for a seismometer to adequately characterize an asteroid's interior through tidally induced deformation. Future deployment of seismometers on binary asteroids will allow for a detailed characterization of the structure of these objects.
1. INTRODUCTION
The internal structure of an asteroid holds important clues to its formation and evolution (Asphaug 2020). Asteroids with different interior structures likely have different histories and formation stories from one another, as well as from those of larger planetary bodies (Richardson et al. 2002; Jutzi et al. 2015; Scheeres et al. 2015; Walsh 2018). An asteroid's interior controls the response of its surface and shape to forces from the space environment, such as impacts (e.g. Chapman 1996; Ballouz et al. 2020; Bottke et al. 2020), tidal effects (e.g. Binzel et al. 2010; Hurford et al. 2016), and solar radiation (Bottke et al. 2006; Walsh, Richardson & Michel 2008). Several studies have sought to constrain internal structures of small bodies through surface geology, gravimetry, spin dynamics, response to cratering, and theoretical studies of their impact histories (Asphaug 1999; Chapman et al. 2002; Prockter et al. 2002; Richardson et al. 2002; Richardson et al. 2005; Buczkowski, Barnouin-Jha & Prockter 2008; Walsh 2018; Richardson, Steckloff & Minton 2020). However, the interior of an asteroid of any size has never been directly characterized.
Here, we build the case for a seismic experiment deployed on the primary asteroid in a binary system to investigate its internal structure. The fundamental goal of a planetary seismic experiment is to determine the seismicity, elastic properties, and internal structure of a body by measuring seismic waves, typically by recording the displacement of an instrument coupled to the ground. We use a numerical study to evaluate the response of a near-Earth asteroid (NEA) to continuous tidal forcing from a secondary asteroid in orbit around it and show that available seismometer technology can adequately measure its interior properties. In Section 2, we review our current understanding of asteroid interiors based on telescopic and spacecraft data, coupled with theoretical insight. This knowledge frames the current open questions regarding asteroid interiors and provides the basis for modelling natural sources of ground motion, which we discuss in Section 3. In Section 3, we demonstrate that binary asteroid systems provide a natural laboratory to probe asteroid interiors through tidally and impact-induced seismic waves, which could be detectable with current seismometer technology. In Section 4, we summarize our findings and provide an outlook for the future study of asteroid interiors.
2. ASTEROIDS SEISMOLOGY: STATE OF FIELD AND STRATEGIC KNOWLEDGE GAPS
2.1 Asteroid interiors
While never directly observed, the internal structures of asteroids have been hypothesized on the basis of telescopic and spacecraft observations (e.g. Scheeres et al. 2015). Generally, asteroids are thought to fall into three broad categories for different combinations of relative porosity and strength (Fig. 1) (Asphaug 1999; Richardson et al. 2002; Britt & Consolmagno 2003): (1) Coherent bodies are high-strength, low-porosity objects made of coherent material; examples include large, differentiated objects, such as the 100-km-scale asteroids Vesta, Ceres, and possibly Lutetia (Weiss et al. 2012), and perhaps monolithic asteroids with diameters <100 m (Pravec, Harris & Michalowski 2002). (2) Fractured interiors occur in low-strength, low-porosity objects that have experienced large stresses, such as a sub-catastrophic impact (Ryan 2000), leading to the formation of large-scale fractures, faults, or joints; for example, bodies with diameters 10–100 km such as Eros, Ida, and Phobos. (3) Rubble piles are low-strength, high-porosity objects that formed from gravitationally reaccumulated material following a catastrophic impact on a parent body (Michel et al. 2001); for instance, >100 m–1 km (‘kilometer-scale’) asteroids such as Itokawa, Ryugu, and Bennu.

Examples of different-sized asteroids visited by spacecraft (top) and hypothesized models of their interior structures (bottom).
NEA sizes are closely related to their response to impact processes. Smaller asteroids more easily break apart, whereas larger objects resist damage from impacts. Furthermore, small (kilometre-scale) NEAs are thought to be formed following the catastrophic disruption of a larger parent body, creating an asteroid family (Zappalà et al. 1995; Michel et al. 2001). As such, these small NEAs are likely the detritus of billions of years of collisions. Observing their interiors is an important test of foundational knowledge of collisional evolution (National Academies of Sciences, Engineering, and Medicine 2023).
Supporting evidence for the rubble-pile nature kilometre-scale and smaller NEAs comes from population-wide size, spin period, and compositional characterization (Pravec et al. 2002; Pravec & Harris 2007), buttressed by physical characterization of meteoritic analogues (Britt & Consolmagno 2003; Pohl & Britt 2020) and close-up spacecraft measurements of asteroid shapes, masses, and bulk densities (Fujiwara et al. 2006; Barnouin et al. 2019; Lauretta et al. 2019a; Scheeres et al. 2019; Sugita et al. 2019; Watanabe et al. 2019). Light-curve observations of the NEA population have shown that objects with diameters ≳200 m do not rotate faster than the spin limit of a cohesion-less gravitational aggregate (∼2.2 h per revolution for a bulk density of ∼3 g cm−3) (Pravec et al. 2002; Richardson et al. 2002). This suggests, but does not demand, that objects with diameters > 200 m and up to ∼10 km are rubble piles (Richardson et al. 2002; Walsh 2018).
However, there are exceptions, with some kilometre-scale NEAs exhibiting supercritical spin periods (i.e. spin periods where centrifugal forces exceed gravity, and the body is expected to disaggregate). Numerical simulations of the rotational disruption of rubble-pile objects have demonstrated that sufficiently strong internal friction (Zhang et al. 2017) or minimal levels of cohesive strength, brought about by close-range contact forces such as Van der Waals between boulders, can allow rubble piles to rotate faster than the spin limit (Sánchez & Scheeres 2014; Zhang et al. 2018). The relative importance of these cohesive forces for NEA evolution depends on the details of the asteroid's interior properties.
Do rubble-pile asteroids have a strong central core surrounded by more weakly adhered material (Walsh, Richardson & Michel 2012; Hirabayashi, Sánchez & Scheeres 2015)? Do sunlight-induced torques such as the YORP (Yarkovsky–O'Keefe–Radzievskii–Paddack) effect cause rotational disruption of NEAs through surface failure (Walsh et al. 2008), internal failure (Hirabayashi et al. 2015), or fission (Jacobson & Scheeres 2011a; Sánchez & Scheeres 2014)? Are rubble-pile interiors layered, as suggested by some geophysical measurements of the near-surface (Arakawa et al. 2020; Tricarico et al. 2021; Walsh et al. 2022)? How much does the YORP effect contribute to generating new NEAs (Scheeres 2018), or do all NEAs originate from the catastrophic disruption of main-belt parent bodies (e.g. Michel et al. 2001)?
Although spacecraft encounters of asteroids are few (14 and counting), they have provided critical geologic context to telescopic observations. Spacecraft imaging of kilometre-scale NEAs and their constituent boulders (Fujiwara et al. 2006; DellaGiustina et al. 2019a; Sugita et al. 2019) support the telescopic inference of their rubble-pile nature, showing that NEAs between ∼0.2 and 10 km in diameter appear to be rubble piles based on their surface characteristics and bulk densities, which suggests large macroporosities when compared to their closest meteoritic analogues (Lauretta et al. 2019a; Watanabe et al. 2019). Rendezvous missions to NEAs have provided the best attempts at asteroid interior characterization, through highly accurate shape modelling combined with spacecraft radio tracking, providing higher order gravity terms and thereby assessing mass distribution (Zuber et al. 2000; Scheeres et al. 2019; Chesley et al. 2020).
NASA's (Origins, Spectral Interpretation, Resource Identification, and Security–Regolith Explorer) OSIRIS-REx mission discovered particles ejecting from rubble-pile asteroid Bennu (Lauretta et al. 2019b); tracking those particles’ trajectories allowed gravity field characterization up to degree and order nine (Chesley et al. 2020; Scheeres et al. 2020; Tricarico et al. 2021). These studies indicated a heterogeneous interior with mass concentrations; however, there was not a unique solution for the mass distribution via inversion of the gravity field terms. It is unclear how mass is distributed, though solutions involving an underdense core are preferred (Scheeres et al. 2020).
An added complexity is that there is evidence that meteorites may not adequately sample the plausible range of asteroid physical properties. Thermal inertia measurements of Bennu's boulder population revealed that they might have larger microporosities than any known carbonaceous chondrite meteorite (Rozitis et al. 2020).
These recent discoveries highlight a gap in our knowledge of NEA interiors that is also a priority for planetary defense. Several mitigation methods have been proposed for the deflection of a potentially hazardous asteroid (PHA), including the kinetic impactor technique. NASA's DART (Double Asteroid Redirection Test) mission demonstrated this technique by impacting the secondary component of the Didymos binary system and measuring the resulting change in linear momentum (Rivkin et al. 2021; Cheng et al. 2023; Daly et al. 2023). However, numerical studies have shown that kinetic impactor efficiency strongly depends on the magnitude and type (micro- versus macro-) of porosity within the target because these properties contribute differently to the outcomes of impact cratering (Jutzi & Michel 2014; Stickle et al. 2017). Therefore, a detailed understanding of asteroid interiors, and the possible diversity among them, is required to characterize the threat to Earth and formulate mitigation strategies.
2.2 Asteroid binaries: natural laboratories for studying interior structure and tidal evolution
Approximately 15 per cent of NEAs are expected to be in a binary configuration (hereafter, ‘binaries’) (Margot et al. 2015), meaning a primary asteroid orbited by a smaller, secondary asteroid. Some theories propose that a large fraction of NEAs participate in an ongoing cycle of satellite formation and loss (Jacobson & Scheeres 2011a), suggesting that the binary configuration is a fundamental process. Small asteroid binaries [primary diameter (d1) ≲ 10 km] have similar physical properties: The secondary bodies are 20–50 per cent the size of the primary (Fig. 2a), in close orbits 2–5 primary radii away (Fig. 2b) (Margot et al. 2015; Walsh & Jacobson 2015) and their orbital periods are typically tens of hours (Fig. 2c). Close-up views of asteroid binary systems (243) Ida, (65803) Didymos, and most recently (152830) Dinkinesh have been returned by the Galileo, DART, and Lucy missions, respectively (Chapman et al. 1995; Daly et al. 2023; Good things come to those who wait 2023).
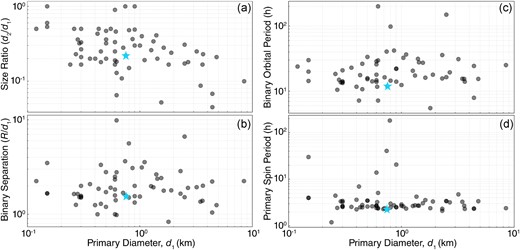
The population of small NEA binary systems, showing their (a) size ratio, (b) binary separation, (c) binary orbital period, and (d) primary spin period as a function of the primary diameter (Johnston 2023). The Didymos system studied here (section 5) is shown as a cyan star in each subpanel, illustrating that its binary properties are typical among the population.
The rotation periods of the primary asteroids in binaries are most commonly about 2 h (Fig. 2d), where cohesion-less bodies suffer failure and/or lose mass (Richardson et al. 2002). This correlation between rapid rotation and the presence of a satellite has led to formation theories involving rotational spin-up by thermal effects (Margot et al. 2015; Walsh & Jacobson 2015). At these rapid spin rates, the equators of the primaries are nearly in Keplerian orbits.
The primary bodies of binaries whose shapes have been measured typically resemble a spinning top, with an equatorial bulge or ridge. However, the shapes of the primaries are not as well observed as their rotation rates, because detailed terrain models require close passes by Earth for radar observation or spacecraft visits. Two recent missions, NASA's OSIRIS-REx and JAXA's Hayabusa2, visited asteroids with equatorial ridges: Bennu and Ryugu, respectively (Barnouin et al. 2019; Lauretta et al. 2019a; Sugita et al. 2019; Watanabe et al. 2019). Neither of these objects has a secondary asteroid orbiting it. This finding, and that of other top-shaped asteroids without secondaries, supports the idea of a cycle of binary formation and destruction, whereby the 15 per cent binary NEA fraction known today represents just the current residents of a steady-state population.
The binary population has proven valuable for measuring asteroid density via Kepler's laws (e.g. Cheng et al. 2023), but these measurements leave questions about the degeneracy between intrinsic material properties (microporosity) and void spaces (macroporosity). Even for one of the best-studied NEAs, Bennu, there is still debate about whether its macroporosity is 12–15 per cent or as large as 50 per cent (Barnouin et al. 2019; Biele et al. 2020; Tricarico et al. 2021). Spacecraft interactions with Bennu and Ryugu indicate an extremely weak and underdense near-surface on both asteroids (Arakawa et al. 2020; Lauretta et al. 2022; Walsh et al. 2022). However, it is unclear whether or how these surface findings may be extended for understanding the interior properties of the bulk asteroid. For example, Daly et al. (2020) show that the morphology of Bennu's largest craters suggest that its interior may be stronger than its near surface.
Measurements of surface displacement (obtained by a seismometer) will constrain the material properties and internal structure of rubble-pile asteroids. These measurements will also elucidate the influence of planetary tidal forces on the spin, orbital, and surface evolution of the Solar System's small-body population. Transient tidal forces by inner planets are hypothesized to affect small bodies through a variety of consequences, including full-body disruption, binary formation, reshaping, mass wasting, and particle shedding (e.g. Bottke, Richardson & Love 1997a, b, 1998; Richardson, Bottke & Love 1998; Walsh 2018; Zhang & Michel 2020). However, very few observations exist to validate these hypotheses. Asteroid seismic measurements could improve our understanding of tidal processes in the Solar System (e.g. Bottke et al. 1997a, b, 1998; Bottke et al. 1999; Noll, Weaver & Feldman 2006) and in debris discs of exoplanetary systems (e.g. Debes et al. 2012; Veras et al. 2014; Zhang & Lin 2020). Tidal evolution in binary systems is complicated by competing mechanisms at play. Direct measurements of the properties of a satellite orbit or orientation changing over time have been hindered, primarily due to short time-scales or challenging observations. Nevertheless, satellites in or near synchronous rotation and nearly circular orbits have been observed, both of which are signatures of tidal dissipation in the system. FG3 is the only binary system with a long enough observational baseline to measure any changes in orbit period; none have been detected (Scheirich et al. 2015), prompting speculation that competition from a thermal effect, Binary-YORP (BYORP), is offsetting tidal expansion of the orbit (Jacobson & Scheeres 2011b). If this ambiguity can be resolved, our understanding of tidally expanding satellite orbits will establish whether the primary is dissipating energy.
3. SEISMIC SIGNALS FROM ASTEROID BINARIES
Are asteroids seismically active worlds? Seismology on asteroids has been studied primarily in the context of impact-induced events (Asphaug & Melosh 1993; Asphaug et al. 1996; Greenberg et al. 1996; Chapman et al. 2002; Richardson et al. 2005; Asphaug 2008; Garcia, Murdoch & Mimoun 2015; Murdoch et al. 2017; Richardson et al. 2020; Nishiyama et al. 2021). NEAs visited by spacecraft exhibit a depletion of craters at small sizes (≲ 50 m) (Bottke et al. 2020). The observed deficiency of small craters demands the existence of either a mechanism that selectively prevents small crater formation, such as boulder armoring (Tatsumi & Sugita 2018; Barnouin et al. 2019; Bierhaus et al. 2022), or a process that preferentially erases them, such as impact-induced seismic shaking (e.g. Richardson et al. 2020). However, the effectiveness of impact-induced seismicity at modifying asteroid surfaces is still a matter of debate (Honda et al. 2021; Nishiyama et al. 2021), as the seismic properties of NEAs, such as regolith seismic wave speed, quality factor, and seismic efficiency, are poorly constrained. A previous study (Murdoch et al. 2017) of the influence of impacts, tidal quakes, and thermal cracking on the seismicity of the binary asteroid Didymos and its secondary Dimorphos – the target of NASA's DART and ESA's Hera missions – assumed a coherent body (Fig. 1, left).
Here we take a different approach by studying seismic signals generated by continuous tidal forcing in a binary system of rubble-pile asteroids (Fig. 1, right) – the most likely interior structure for NEAs, as was recently established for Dimorphos by DART (Daly et al. 2023; Raducan et al. 2023).
3.1 Tidal deformation as a source of ground motion
How consequential are tides for binary asteroid seismology? To estimate the associated ground motion, we first consider the tidal acceleration experienced by the secondary of a two-body system: |${a}_T\ \sim \ ( {2\ G\ {M}_1{r}_2} )/{R}^3$|, where |${M}_1\ $| is the mass of the primary, |${r}_2\ $| is the radius of the secondary, and R is the average distance between the two bodies. We consider |${a}_T\ $|for a binary asteroid, |${a}_{T,\ ast\ }$|, with component masses like the Didymos system (e.g. Richardson et al. 2022) and compare it to |${a}_T$| for the Earth–Moon system, |${a}_{T,\ EM}$|. Although the whole-body tidal deformation observed in our simulations is distinct from that of the deep moonquakes recorded by the Apollo seismometers, it is accepted that tidal forcing by Earth triggered these events deep within the lunar interior (Toksoz, Goins & Cheng 1977; Cheng & Toksoz 1978; Weber, Bills & Johnson 2009; Kawamura et al. 2017). For the Didymos (primary)–Dimorphos (secondary) system, where R ∼ 3 primary radii, we find |${a}_{T,\ ast\ }$|= 3 × 10−6 m s−2. Although the masses of a binary asteroid system are small compared to those of Earth and the Moon, the typical separation of binary asteroids is so small that the tidal accelerations only differ by an order of magnitude from those of the Earth–Moon system (|${a}_{T,\ EM}$| ∼ 2.5 × 10-5 m s−2).
Do these tidal accelerations translate to detectable ground motion on an asteroid? We performed simulations using the N-body collisional code pkdgrav (Richardson et al. 2011; Schwartz, Richardson & Michel 2012; Zhang et al. 2017) that models the asteroids as rubble piles made up of N spherical particles. pkdgrav treats contact forces with a soft-sphere discrete element method (SSDEM) (Schwartz et al. 2012; Zhang et al. 2017), which allows us to accurately model contributions of friction and cohesion in the resolution of collisions between particles (see Section A1 in Supplementary Appendix for further details). Although particles are modelled as spheres, rolling and twisting friction, parametrized through a shape factor, enable the code to capture the bulk behaviour of realistic irregular particle shapes. We use the Didymos system as a case study, recreating the sizes, masses, and binary dynamical properties of the system within pkdgrav (Fig. 3a); however, we do not re-create their shapes and instead model spherical rubble piles.
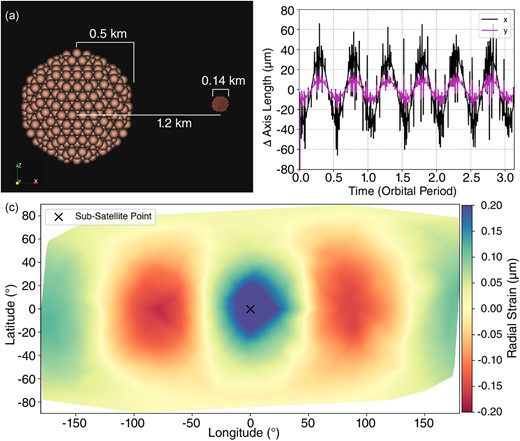
(a) Setup of pkdgrav simulations to measure response of NEA rubble-pile binary components to tidal stresses (x-z plane shown). (b) Simulations provide an estimate of the strain over time on the primary component of the binary (1-km-diameter spherical rubble pile) for given material/interior properties: in this case, Es = 15 MPa. After an initial ‘warm-up’ period (first ∼2.5 h), the simulation stabilizes, and we measure changes in lengths of up to 40 μm along the body axes. The x and y body axes are in the same plane as the orbit. (c) Map of the radial displacement from zero for a snapshot of the simulation with Es = 15 MPa and no spin. The subsatellite point is also shown, overlapping with the point of maximum positive radial strain, 0.2 μm.
For computational feasibility, we adopted N = 1500 for the primary and N = 500 for the secondary, which led to individual particle sizes of 40 and 7 m, respectively. We further assumed a monodisperse particle size distribution within each respective body. The simulations allow us to understand how the mutual gravity and tidal interactions of the two binary components translate to internal strains and stresses.
The friction and restitution coefficients of the pkdgrav particles were set to constant values across all simulations (see Table A1 in the appendix). We varied the spring constants of the particles to explore how the stiffness of the interior leads to changes in the elastic response in the simulations. This, in turn, will allow us to determine if the seismic signals will be diagnostic of the internal properties of the target bodies. We adopted three cases where the individual particles that make up a rubble pile had increasing stiffness, which can be represented by their elastic moduli Es = 15, 153, and 1530 MPa, and longitudinal seismic wave speeds |${v}_{p\ }$|= 70, 230, and 2300 m s−1, respectively. The elastic moduli are estimated by considering the discrete element method (DEM) spring constant, kn, and the radius of the particle, Rp, such that Es = kn/(πRp). Elastic moduli and seismic wave speeds of meteorites are typically on the order of 10 GPa and 2.5 km s−1, respectively (Cotto-Figueroa et al. 2016). Thus, we can consider the stiffest case (Es = 1530 MPa, |${v}_{p\ }$| = 2.3 km s−1) to be a 1:1 representation of a rubble pile with 40-m boulders. For the other two less stiff cases, each particle of the simulated asteroid is a representative volume element of a granular pile (smaller dust, pebble, cobbles, and boulders), which typically have bulk Es ∼ 10 MPa and |${v}_{p\ }\sim $|100 m s−1, respectively (e.g. Goddard 1990; Goldreich & Sari 2009). For the set of simulations that varied material properties, the primary had no spin and assumed 0° inclination and an eccentricity ∼ 0. We also evaluated a more realistic case of a fast-rotating primary with a spin period of P1 = 4 h, with a tidally locked secondary, for Es = 15 MPa. These simulated spin periods are slower than that of the real Didymos system (2.25 h) (Pravec et al. 2006). Additionally, we evaluated the contributions of numerical noise to our analysis by simulating a non-rotating gravitationally settled rubble pile with the same properties as the primary in our binary simulations. By analysing the relative motions of individual particles in this static configuration, we determine that numerical noise in pkdgrav simulations for objects of the size of the simulated rubble piles is < 10−3 μm.
We ran each simulation for approximately eight orbital periods after a brief warm-up period (∼2.5 h) and tracked the interior stresses and strains. Fig. 3(b) shows the strain along the primary's main body axes for the Es = 15 MPa case. After the warm-up, the dynamics reached a steady-state configuration, and the primary experienced continuous strain along its x and y body axes, which lie in the orbital plane (we set the orbital inclination and eccentricity to 0). The simulations capture this continuous flexing of the primary due to the tidal forcing from the secondary. For Es = 15, 153, and 1530 MPa, we found the change in the primary's major axis had an amplitude of 40, 7, and 0.2 μm, respectively.
In Fig. 3(c), we show the radial strain of each particle that composes the surface of the rubble-pile primary at one point in the simulation, where the orbital phase = 0° (for Es = 15 MPa and |${v}_{p{\rm{\ }}}$| = 70 m s−1). We find larger maximum displacements (peak-to-peak amplitude) closer to the equator, which lies on the orbital plane, as expected (e.g. Cheng et al. 2022; Dmitrovskii et al. 2022). The maximum value of the radial strain is 0.28 μm for both no-spin and P1 = 4 h. Fig. 3(c) shows that the tidal bulge coincides with the subsatellite point, lagging behind slightly, as expected for a dissipative body.
We analysed the simulation with a 4-h spin to demonstrate how simulations can be used to study the tidal response of rubble-pile binary systems as a function of their internal structure. Specifically, we show that we can directly measure the values of the tidal Love numbers, h2 and k2, and tidal quality factor, Qtide, of the primary. These factors, along with the rigidity of the primary, μ, control the tidal evolution of binary systems as they describe the internal dissipation of energy in response to the tidal potential. As such, detailed measurements of the orbital evolution of asteroid binary systems can provide constraints on their material properties and internal structure of the constituent bodies (e.g. Jacobson & Scheeres 2011a; Taylor & Margot 2011; Nimmo & Matsuyama 2019; Brož et al. 2022). Here, we compare our simulation results to expectations from theoretical analysis of tidal dissipation in rubble piles.
The maximum radial displacement in the simulation provides a measure of the bulge height, H, which is controlled by the primary's displacement tidal Love number, h2, such that (e.g. Murray & McDermott 1999):
where q is the secondary to primary mass ratio, and r1 is the radius of the primary. Using equation (1) and our measurement of H, we determine that h2 = 2.4 × 10−6 for the primary.
The tidal Love number k2, which controls the gravity response, is typically used to parametrize tidal dissipation in the body, and is defined by the ratio of the rigidity (μ) to self-gravity, such that (MacDonald 1964):
where ρ and g are the primary's bulk density and surface gravity, respectively. For small rubble-pile asteroids, where rigidity dominates over self-gravity, the value of μ can be expressed as (Nimmo & Matsuyama 2019):
where G is the gravitational constant. The value of k2 is of the same order of magnitude as that of the tidal Love number h2, with h2/k2 ∼ 2 for Earth, h2/k2 ∼ 1.6 for a uniform strength-less body (Nimmo & Matsuyama 2019), and h2/k2 = 1.5 when h2 and k2 << 1 (Bernauer et al. 2020). For h2/k2 = 1.5 in our simulated rubble-pile, equation (3) gives μ = 16.9 MPa, which is approximately equal to the value of Es of a simulation particle. Finally, Nimmo & Matsuyama (2019) show that for a rubble-pile asteroid, k2 should scale linearly with the primary radius such that k2 ∼ 10−8r1. This linear relationship arises because of higher yielding in larger asteroids due to greater overburden pressures, which is clear when examining the second term in brackets in equation (2). For a 500-m-radius primary, k2 = 5 × 10−6, which is the same order of magnitude as the h2 measured in our simulations. Overall, we find strong consistency between our simulations and theoretical expectations for tidal dissipation in rubble-pile asteroids if we use material properties for the constituent boulders that are in the softer range of the parameters we explored here. This may be because the real rubble-pile asteroids would be composed of granular material that behaves weakly in bulk. Recent spacecraft exploration of near-Earth asteroids Bennu and Ryugu has shown that their surfaces are much weaker than previous expectations (Arakawa et al. 2020; Walsh et al. 2022).
In addition to tidal Love numbers, we can measure the value of the quality factor of simulated rubble piles by comparing the time lag, Δt, in the satellite position with that of the tidal bulge, such that (e.g. Efroimsky & Lainey 2007):
where ω1 is the spin angular frequency of the primary, and n2 is mean motion of the secondary. The 2|ω1 − n2| denotes the tidal frequency, χ, which is 7.29 h in our P1 = 4 h simulation. The factor of 2 emerges because the secondary causes two elevations on opposites sides of the primary. Fig. 4(a) shows data from the simulation of the normalized radial displacement (cyan) and distance of the secondary (dark blue) from a particle on the primary's equator. We modelled each set of data points with a sinusoid and extracted the frequencies of each signal, which show periods similar to the tidal frequency (Fig. 4b). Finally, by measuring the difference in time between the amplitude of the radial displacement and the coinciding amplitude of the satellite's orbital position (Fig. 4c), we can measure the time lag. As expected for anelastic interiors, the tidal bulge lags behind the satellite position as the primary's interior dissipates energy in response to the disturbance. From our simulation, we measure Δt = 233.7 s, which corresponds to Qtide = 8.97 according to equation (4). This value of Qtide is an order of magnitude smaller than that estimated for monoliths (Goldreich & Sari 2009), and a factor of a few smaller than that determined for the 100-km asteroid Kleopatra through modelling of the tidal lag based on observations of its satellites (Brož et al. 2022). It is also larger than that estimated for Deimos (Qtide ∼ 1) based on modelling of its tidal evolution (Brasser 2020). Furthermore, we can compare our measurement to the theoretical estimate of an effective dissipative factor, Qeff, determined by Nimmo & Matsuyama (2019) for a regolith layer of thickness t:
where N is the number of contacts of individual rubble pile elements, and f = 0.6 is the static friction coefficient. In our simulations, a hexagonally close-packed surface particle would have N = 8. If we consider the regolith layer thickness to be a single particle radius, we find that Qeff = 0.1, nearly two orders of magnitude smaller than our estimate. Thus, we find that our rubble pile is far less dissipative than that expected from the theoretical analysis of Nimmo & Matsuyama (2019). Finally, tidal dissipation in asteroid binaries is typically parametrized through the product of the rigidity and the quality factor, μQtide = 2.26 × 108 Pa in our simulation. This is within an order of the magnitude of the estimate determined by Taylor & Margot (2011) for the Didymos system.
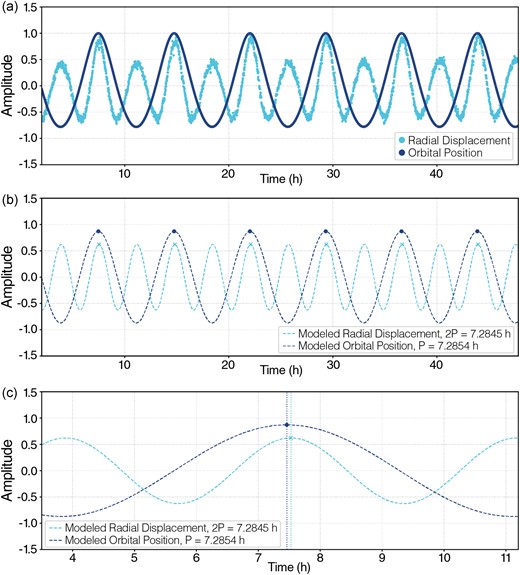
(a) Simulation data for the ES = 15 MPa case showing the normalized radial displacement (cyan) and the normalized distance to the secondary (dark blue) of an equatorial particle on the primary. Normalization factors for the data are their respective maximum values. (b) Sinusoidal fits to the data in (a) show that the frequencies are similar to the tidal period for distance and half the tidal period for radial displacement. (c) The lag in peak positions between the two data sets corresponds to the time lag between the bulge and the secondary position, which is a direct measure of the primary's quality factor at these frequencies.
The difference between our results and the predictions from Nimmo & Matsuyama (2019) may be due to divergent assumptions about the interior structure of the primary. Rather than a monodisperse rubble pile, Nimmo & Matsuyama (2019) assumed that the primary has a coherent interior and is surrounded by a dissipative layer of regolith. It is unclear, of course, which of these models for the interior is more accurate for real NEAs. These findings illustrate how a seismic instrument may be able to reveal details of the interior seismic and physical structure of an asteroid through its response from tidal forcing.
Following DeMartini et al. (2019), we measured the acceleration in the strain along the primary's body axes, tracking the ground motion at those points on the asteroid's surface. We computed an eight-orbit time series at 0.1-s time-steps to determine the power spectral density (PSD) of the acceleration of the strain vector along the body axis that exhibited the largest strain (typically the x or y axis). The PSD reflects the distribution of power of tidal or seismic oscillation with frequency, providing a description of the spectral content of ground motion. We calculated the PSD by means of MATLAB's periodogram function, using the default rectangular window and a discrete Fourier transform length equal to the signal length.
In Fig. 5, we show the resulting PSD for a simulated kilometre-sized rubble pile where Es = 15 MPa and |${v}_{p\ }$| = 70 m s−1. The PSD of the simulated tidal deformation is compared with that of the self-noise from the InSight SEIS Very Broadband (VBB) and Short Period (SP) seismometers (Mimoun et al. 2017; Lognonné et al. 2019), as well as from an SP flight candidate instrument developed by the University of Arizona based on a commercial sensor by Silicon Audio, Inc. (Marusiak et al. 2020; Marusiak et al. 2021). The modelled low-frequency (≲10–4 Hz) signals of whole-body deformation driven by the spin period and tidal cycle are powerful enough that they may be detectable by an SP seismic instrument.
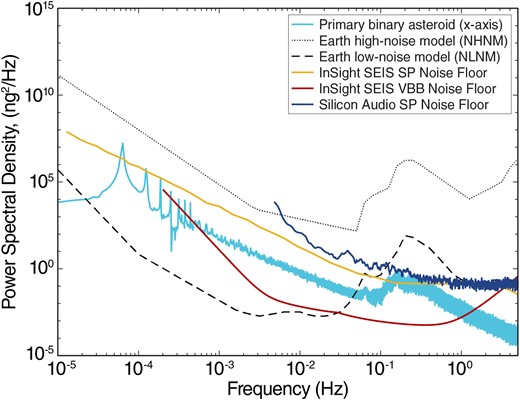
Self-noise of the InSight SEIS VBB (dark red) and SP (gold) seismometers (Mimoun et al. 2017; Lognonné et al. 2019) and the Silicon Audio SP seismometer (dark blue) compared to the predicted ground motion of the major axis of the primary asteroid in the modelled binary system (cyan). The time series used to compute the ground motion (Fig. 6) was from eight orbits. For reference, the New High Noise Model and New Low Noise Model for Earth (Peterson 1993) are shown (black dashed lines).
We also investigated what could be the cause of detectable seismic energy in the rubble-pile system. Is it a purely elastic response due to tidal flexing? Our previous analysis shows that the simulated rubble piles have constituent particles that experience frictional contacts that lead to energy dissipation in the interior. This is directly seen in the time lag of the bulge and a measurable value of the quality factor, which is far smaller than what is expected for elastic monolithic objects. To illustrate this further, we show the surface accelerations at the primary's major, intermediate, and minor axes’ locations in Figs 6(a)–(d), showing successively more detailed views. Fig. 6(a) shows the overall accelerations over the approximately eight orbital periods of the simulations, sampled at a frequency of ∼10 Hz. The regular variations correspond to the tidal frequency of the system, as expected. In conjunction with periodic elastic deformation, we observe stochastic events of variable amplitude and length, with more than a dozen ‘seismic events’ occurring over an hour (Figs 6b–c). We surmise that these acceleration wave packets correspond to anelastic behaviour of the interior particles as they shear against each other, leading to interior jostling. Here, we recall that pkdgrav can model the anelastic interactions between particles through three types of friction forces: static, rolling, and twisting (see Schwartz et al. 2012; Zhang et al. 2017 for details). In combination, these friction forces dampen the energy in the system and allow accurate modelling of tidal dissipation in a rubble-pile asteroid binary. The modelling of normal and tangential restoring and frictional forces also enables accurate representation of shearing forces in the asteroid interiors as the bodies are deformed by tidal forcing. Through these shearing forces, the discrete ‘seismic events’ we observe here, in addition to whole-body flexing, can be captured, because granular material can exhibit slip-stick phenomena. These events are captured in the PSD (Fig. 5) at frequencies ∼0.2 Hz and may be detectable by an SP seismic instrument.
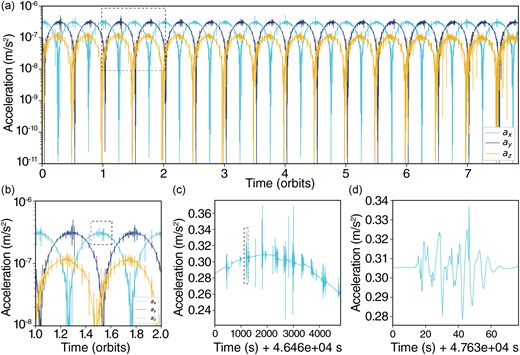
Surface acceleration curves of the primary along its major (ax, cyan), intermediate (ay, dark blue), and minor (az, gold) axes. The view of the data zooms in progressively from (a) to (d): each dashed black box indicates the area shown in the subsequent panel. (a) Surface accelerations over the full eight orbital period simulation. (b) Surface accelerations over one orbital period. (c) Surface accelerations along the major axis over ∼1 h, during which more than a dozen ‘seismic events’ occur. (d) The wave packet of an event, showing its overall profile.
Although not explicitly examined here, continuous tidal forcing will likely generate interior reconfiguration of large blocks, as demonstrated by the transient events observed in our simulations (Fig. 6) and may build stresses that cause cracking within larger coherent boulders; these events are analogous to localized sources generated by faulting (‘quakes’) that are examined in conventional seismological studies.
Previous work by Murdoch et al. (2017) looked at the possibility of tidal quakes in the Didymos system using coherent interiors rather than a rubble-pile structure. In contrast to the elastic tidal deformation examined here, Murdoch et al. (2017) calculated the tidal stresses to identify where a rupture (quake) was most likely to occur on the secondary, Dimorphos. They determined that the displacement amplitudes due to tidal stresses would be on the order of 0.1 nm on Dimorphos. Assuming a rubble-pile interior, we find that the displacement amplitudes would be three to four orders of magnitude greater for the primary, Didymos, based on tidal deformation alone (Fig. 3). This is notable as the tidal acceleration experienced by Didymos is two orders of magnitude less than that of Dimorphos.
3.2 Impacts as a source of ground motion
Murdoch et al. (2017) also showed that impacts by meteoroids at speeds of 6 km s−1 and masses of 1 mg would induce a seismic moment of 4.9 × 103 N m that would generate observable body and surface waves. Using the meteoritic impact frequency for NEAs, Murdoch et al. (2017) concluded that there could be several impacts by meteoroids with masses of 1–10 mg yr−1, but few, if any, for meteoroids with masses >1 g, which would generate seismic moments >1 × 106 N m. Some NEAs, such as Didymos, are main-belt crossers, with aphelia Q that exceed the inner edge of the main asteroid belt (2.1 AU). These NEAs experience a drastically different collisional environment in the main belt than in near-Earth space, with the number of potential impactors increasing by three orders of magnitude (e.g. Bottke et al. 2020). Therefore, detectable impact-induced seismicity on NEAs may occur more frequently than previously thought.
The orbital properties of known NEAs (Giorgini 2020) indicate that ∼75 per cent of those with absolute magnitudes H < 22 (diameters greater than ∼200 m) are main-belt crossers. Of the 75 binary NEAs documented by Johnston (2023), 52 (70 per cent) are main-belt crossers. In Fig. 7, we show a distribution of the time spent in the main belt for these sub-populations of NEAs. Fig. 7 shows, for example, that of the binary NEAs that have Q > 2.1 AU, one-quarter spend ∼55–60 per cent of their orbit in the main belt. Also, the distribution of binary NEAs reflects that of the wider NEA population.
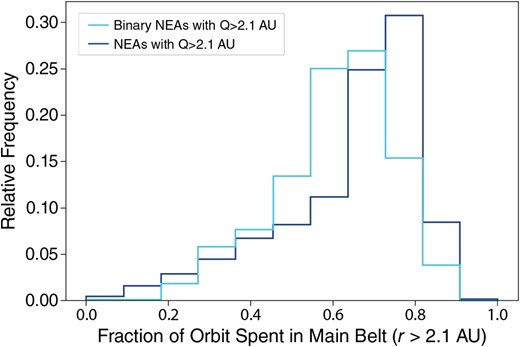
Of the NEAs whose orbits cross into the main asteroid belt, most (∼80 per cent) spend more than half their orbit at heliocentric distances r > 2.1 AU.
We again consider the case of Didymos, which spends approximately 249 d out of its 769-d orbital period in the main asteroid belt. As shown in Richardson et al. (2022), the impact flux on Didymos is dominated by main-belt objects, even though it spends less than half its time in the main belt.
We calculated the frequency of impacts of a given size by combining the impact flux on a Didymos-sized NEA in the main belt (Bottke et al. 2005) and in near-Earth space (Brown et al. 2002) using mean relative impact speeds of 5.2 and 18.5 km s−1, and the relative time spent in each region of 249 and 500 d per orbit, respectively (Section A2 in Supplementary Appendix). This allows us to better constrain the time interval for impacts that would produce a given seismic moment for different parts of Didymos’ orbit (Fig. 8).
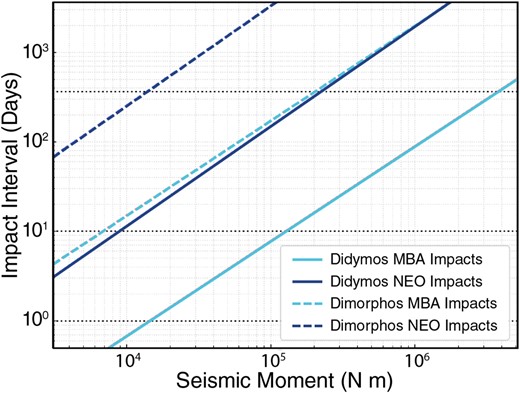
The interval for impacts on Didymos and Dimorphos that induce a given seismic moment, for different locations in their orbit. When the Didymos system is in the main belt (∼32 per cent of its orbital period; red lines) the impact flux increases substantially, leading to shorter intervals between impacts of a given seismic moment compared to near-Earth space (blue lines), despite the decrease in impact speed (∼3 × greater in near-Earth space than in the main belt).
In the main belt, impact-induced seismic moments of 1.4 × 104 N m occur once every 24 h on Didymos and once every ∼20 d on Dimorphos (Fig. 8). As discussed by Murdoch et al. (2017), continuum asteroid interior models show that impact-induced seismic moments of half this magnitude should be detectable on Dimorphos; therefore, impact-induced seismic waves would be readily detected if seismometers were to listen for events during Didymos systems’ main-belt passage. In near-Earth space, a similar impact would occur only once every ∼17 d on Didymos and ∼368 d on Dimorphos (Fig. 8). Impacts of 4.9 × 103 N m should occur once every ∼117 d on Dimorphos in near-Earth space, which is similar to the finding of ‘several per year’ by Murdoch et al. (2017).
As a point of comparison to an active source experiment, 100 g of C4 explosive produces a seismic moment of 1.7 × 106 N m (Walker, Sagebiel & Huebner 2006). An equivalent natural source is expected to occur once every ∼160 d on Didymos during its main-belt passage, well within the total elapsed main-belt time of 249 d. Such impacts will generate additional localized seismic sources that may allow for imaging of the asteroid interior.
Our calculation uses a main-belt impactor population that is extrapolated from observations (Bottke et al. 2005) and, therefore, is not well constrained. Seismic measurements on an asteroid that traverses both populations would help us to fully constrain the main-belt population at these impactor sizes (a few centimetres to decimetres).
4. CONCLUSIONS
The use of tidal forces to probe the interiors of planetary systems, even asteroids, is well understood (see Bernauer et al. 2020 for a review). Direct measurement of the tidal bulge, acceleration, and any phase lags relative to the spin state and orbital period of the binary components will constrain their Love numbers and elastic properties, including the rigidity and bulk and shear moduli (e.g. Lognonné et al. 1996; Caudal 2023).
We show that the natural tidal forcing in a binary system produces continuous and detectable seismic waves that can be used to investigate the interior structure of rubble-pile asteroids. With numerical models, we estimate that a binary asteroid system with rubble-pile structure will have low-frequency tidal surface displacements (≲10–4 Hz) that largely fall between the terrestrial New High Noise Model and New Low Noise Model (Peterson 1993), that is, within measurable range of modern seismometers. Likewise, tidally induced faulting and meteoroid impacts should be detectable by instruments with low self-noise and can provide localized sources that may allow for seismic imaging of the interior. Taken together, our results demonstrate that binaries are attractive targets for exploring kilometre-scale asteroids with seismometers.
Continuous tidal measurements can characterize the primary asteroid's bulk and interior properties on time-scales comparable to the system's orbital period (tens of hours). A seismometer deployed on a binary could return sufficient tidal cycle data over a few Earth days to establish the primary's Love numbers and elastic moduli, while also detecting several localized events induced by tidal cracking. For a main belt crossing binary, a seismometer deployed on the order of 6 Earth months is also likely to detect impacts, providing additional localized and impulsive sources. Better yet, collecting data over a binary's full heliocentric orbit could also constrain impactor rates across the inner solar system and may provide information on how asteroids are affected by the theorized transient tidal forces caused by close passage near the inner planets.
Data returned by the DART mission has provided important clues to the nature of the Didymos and Dimorphos (Daly et al. 2023), and the Hera mission's Juventas CubeSat (Michel et al. 2022) may yield further insight into their interior structure using a monostatic radar. Future results from these investigations will improve the design of asteroid seismometers and help formulate instrument operation in a binary system. Deploying seismometers on other planetary bodies blanketed in low-density regolith has revealed that these surfaces are highly scattering and attenuate seismic waves (Watkins & Kovach 1973). Thermal noise is also a major factor in terrestrial and lunar seismology; on Earth, seismologists build thermally isolating vaults or bury sensors to protect instruments from diurnal temperature swings (Forbriger 2012; Spriggs, Bainbridge & Greig 2014). In the more extreme asteroid thermal environment, instrument burial is likely necessary to achieve an acceptable signal-to-noise ratio by taking advantage of the thermal insulating properties of the regolith while simultaneously reducing scattering attenuation (DellaGiustina et al. 2019b). Fortunately, the sampling operation of OSIRIS-REx on asteroid Bennu demonstrated that the burial of an instrument in a rubble pile may be easier than previously imagined (Walsh et al. 2022).
ACKNOWLEDGEMENTS
This material is based upon work supported by NASA award numbers 80NSSC19K0763 and 80NSSC23K0174 and the University of Arizona Space Institute. We thank Emily C.S. Joseph, Heather Roper, and Catherine Wolner for their assistance in formatting and improving the text and figures presented in this manuscript. We also thank Naomi Murdoch for her careful review which substantially improved this article.
Author contribution statement: DND co-led this study including conceptualization, methodology, software development, validation, formal analysis, investigation, writing (both original draft and review and editing), visualization, supervision, project administration and funding acquisition. RLB co-led this study including conceptualization, methodology, software, validation, formal analysis, investigation, writing (both original draft and review and editing), and visualization. KJW contributed to the methodology, conducted formal analysis, and contributed to the manuscript's writing (both original draft and review and editing). AGM contributed to formal analysis and software development. VJB contributed to the review and editing and methodology. SHB contributed to project administration and funding acquisition, as well as methodology.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
References
, in
SUPPLEMENTARY APPENDIX
A1. Discrete element simulations with pkdgrav
pkdgrav is a combined N-body gravity and discrete element method (DEM) collisional code capable of simulating the complexity of grain–grain and grain–boundary interactions through a soft-sphere discrete element method (SSDEM) (Richardson et al. 2000; Schwartz et al. 2012; Ballouz 2017; Ballouz et al. 2021). In SSDEM, collisions of spherical grains are resolved by allowing them to slightly overlap and then applying multicontact and multifrictional forces, including static, rolling, and twisting friction. Modelling grain friction accurately is a critical component for high-fidelity granular physics simulations. In this manner, the code simulates the complexity in the interaction of irregularly shaped grains by capturing their bulk behaviour correctly (despite modelling spherical particles). New rolling friction and interparticle cohesion models have recently been implemented (e.g. Zhang et al. 2017; Zhang et al. 2018) to enable more accurate modelling of grain shape, angularity, interparticle cohesion, and electrostatic interactions, which may be crucial components for describing grain dynamics in low-gravity environments (Scheeres et al. 2010).
The simulation time-step was 0.01 s and the output step was once every 0.1 s. We did not include interparticle cohesion or vary the size distribution as this work is intended to be a pilot study and not an exhaustive parametric sweep, which we intend to do in future work to fully detail the relationship between rubble pile internal configuration and strength properties, the surface response of tidal deformation, and the seismic signals generated.
The primary body is a hexagonal close-packed monodisperse rubble pile with a mass of 1 × 1012 kg and a bulk density of 2.54 g cm−3. The secondary is a hexagonal close-packed monodisperse rubble pile with a mass of 3.3 × 109 kg and a bulk density of 2.65 g cm−3. The centres of the primary and secondary are separated by 1.2 km and the orbital period is approximately 8.9 h.
Summary of pkdgrav restitution and friction coefficients used in this study. See Zhang et al. (2017) for full details on particle collision modelling in the SSDEM implementation.
| Parameter . | Value . |
|---|---|
| Normal restitution coefficient, εN | 0.55 |
| Tangel restitution coefficient, εT | 0.55 |
| Static friction coefficient, μS | 0.6 |
| Rolling friction coefficient, μR | 1.05 |
| Twisting friction coefficient, μT | 1.3 |
| Shape parameter, β | 0.6 |
| Parameter . | Value . |
|---|---|
| Normal restitution coefficient, εN | 0.55 |
| Tangel restitution coefficient, εT | 0.55 |
| Static friction coefficient, μS | 0.6 |
| Rolling friction coefficient, μR | 1.05 |
| Twisting friction coefficient, μT | 1.3 |
| Shape parameter, β | 0.6 |
Summary of pkdgrav restitution and friction coefficients used in this study. See Zhang et al. (2017) for full details on particle collision modelling in the SSDEM implementation.
| Parameter . | Value . |
|---|---|
| Normal restitution coefficient, εN | 0.55 |
| Tangel restitution coefficient, εT | 0.55 |
| Static friction coefficient, μS | 0.6 |
| Rolling friction coefficient, μR | 1.05 |
| Twisting friction coefficient, μT | 1.3 |
| Shape parameter, β | 0.6 |
| Parameter . | Value . |
|---|---|
| Normal restitution coefficient, εN | 0.55 |
| Tangel restitution coefficient, εT | 0.55 |
| Static friction coefficient, μS | 0.6 |
| Rolling friction coefficient, μR | 1.05 |
| Twisting friction coefficient, μT | 1.3 |
| Shape parameter, β | 0.6 |
A2. The rate of natural impacts on main-belt–crossing near-Earth asteroids
As the majority of NEAs have eccentric orbits that allow them to cross into the inner main belt (heliocentric distance, r > 2.1 AU), we consider two separate impactor population model: an near-Earth Object (NEO) impact flux model, and an Main Belt Asteroid (MBA) impact flux model. While the number of potential impactors in the main asteroid belt is higher than in near-Earth space, the encounter speeds in the main belt are generally lower by a factor of approximately 3.5. For NEO impacts, the impactor flux model of Brown et al. (2002) is used, scaling for target size, and neglecting gravitational focusing. For MBA impacts, the impact flux model of Bottke et al. (2005) is used; however, the MBA population of impactors in the size range of interest (a few centimetres to decametres) is poorly constrained. Indeed, considering main-belt population models that show a depletion in metre-scale impactors (Cibulková, Brož & Benavidez 2014; Zain, de Elía & Di Sisto 2020), the NEO impact flux would dominate over the MBA flux. This is further complicated by the fact that NEA orbits are chaotic. Nevertheless, it is found that the time interval between impacts of a given energy can be constrained by considering the NEO impact flux model of Brown et al. (2002) and the MBA impact flux model of Bottke et al. (2005).
A simplifying assumption is made in the model that encounter speeds in the NEO region and inner main belt occur at 18.5 and 5.2 km s−1, respectively. Encounter speeds by NEAs in the inner main belt may in fact be larger (Michel, Farinella & Froeschlé 1998; Dell'Oro, Marchi & Paolicchi 2011). Therefore, the calculated time intervals for impacts on the Didymos system in near-Earth space are conservative. The seismic moment is calculated using the empirical relationship of Teanby & Wookey (2011), by assuming that the impactors have density of 3 g cm-3 and that the seismic efficiency is 1 × 10–5, like that assumed in calculations presented by Murdoch et al. (2017).
Author notes
These authors made equal contribution to the manuscript



