-
PDF
- Split View
-
Views
-
Cite
Cite
Colin DeGraf, Nianyi Chen, Yueying Ni, Tiziana Di Matteo, Simeon Bird, Michael Tremmel, Rupert Croft, High-redshift supermassive black hole mergers in simulations with dynamical friction modelling, Monthly Notices of the Royal Astronomical Society, Volume 527, Issue 4, February 2024, Pages 11766–11776, https://doi.org/10.1093/mnras/stad3084
Close - Share Icon Share
ABSTRACT
In the near future, projects like Laser Interferometer Space Antenna (LISA) and pulsar timing arrays are expected to detect gravitational waves from mergers between supermassive black holes, and it is crucial to precisely model the underlying merger populations now to maximize what we can learn from this new data. Here, we characterize expected high-redshift (z > 2) black hole mergers using the very large volume Astrid cosmological simulation, which uses a range of seed masses to probe down to low-mass black holes (BHs), and directly incorporates dynamical friction so as to accurately model the dynamical processes that bring black holes to the galaxy centre where binary formation and coalescence will occur. The black hole populations in Astrid include black holes down to |$\sim 10^{4.5} \, \mathrm{M}_\odot$|, and remain broadly consistent with the TNG simulations at scales |$\gt 10^6 \, \mathrm{M}_\odot$| (the seed mass used in TNG). By resolving lower mass black holes, the overall merger rate is ∼5× higher than in TNG. However, incorporating dynamical friction delays mergers compared to a recentring scheme, reducing the high-z merger rate mass-matched mergers by a factor of ∼2×. We also calculate the expected LISA signal-to-noise values, and show that the distribution peaks at high SNR (>100), emphasizing the importance of implementing a seed mass well below LISA’s peak sensitivity (|$\sim 10^6 \, \mathrm{M}_\odot$|) to resolve the majority of LISA’s gravitational wave detections.
1 INTRODUCTION
Supermassive black holes (SMBHs) have been found to exist at the centre of galaxies (Kormendy & Richstone 1995), with a strong correlation to host galaxy properties (Magorrian et al. 1998; Gebhardt et al. 2000; Graham et al. 2001; Ferrarese 2002; Tremaine et al. 2002; Häring & Rix 2004; Gültekin et al. 2009; Kormendy & Ho 2013; McConnell & Ma 2013; Reines & Volonteri 2015; Greene et al. 2016; Schutte, Reines & Greene 2019). These correlations hold true across cosmic time (although with some evidence that the relationships are evolving, e.g. Volonteri & Stark 2011; Venemans et al. 2016; Shao et al. 2017; Decarli et al. 2018), suggesting a coevolutionary growth between black holes and the galaxies that host them. These galaxies (and the dark matter haloes in which they are located) are expected to merge (e.g. Fakhouri, Ma & Boylan-Kolchin 2010; Rodriguez-Gomez et al. 2015). Following a galaxy merger, the central black hole from each progenitor galaxy can migrate towards the Galactic Centre of the newly merged galaxy, where they can form a binary and eventually merge together themselves (e.g. Mayer et al. 2007). Black hole mergers produce strong gravitational wave (GW) signals, and the coalescence of a pair of SMBHs found at the centre of galaxies will produce the strongest GW signals in the Universe.
In the past several years, GWs produced by black hole mergers have been detected using interferometers (e.g. Abbott et al. 2016), but size limitations due to the ground-based nature of these instruments mean that detections to this point have been limited to mergers between stellar mass black holes. Higher mass mergers (i.e. between SMBHs) produce GWs with much longer wavelengths, beyond the sensitivity of ground-based interferometers. However, the upcoming Laser Interferometer Space Antenna (LISA) space mission will focus on lower frequency GWs corresponding to higher mass mergers, with sensitivities peaking at |$\sim 10^4\!-\!10^7 \, \mathrm{M}_\odot$| (Amaro-Seoane et al. 2017). Furthermore, pulsar timing arrays should be capable of detecting even higher mass mergers, reaching black holes above |$10^8 \, \mathrm{M}_\odot$| (e.g. Desvignes et al. 2016; Reardon et al. 2016; Verbiest et al. 2016; Arzoumanian et al. 2018). The GWs detected by these observations should provide a new and powerful mechanism to study SMBHs and their connection with their host galaxies.
SMBH mergers detected through GWs can provide a wide range of constraints on our understanding of black hole–galaxy coevolution, including estimating the rate at which SMBHs merge (e.g. Klein et al. 2016; Salcido et al. 2016; Kelley et al. 2017; Ricarte & Natarajan 2018; Katz et al. 2020; Volonteri et al. 2020), the expected merger/coalescence time-scale (e.g. Volonteri et al. 2020; Banks et al. 2022), how mergers influence the scaling relation between black holes and their host galaxies (e.g. Volonteri & Natarajan 2009; Shankar et al. 2016; Simon & Burke-Spolaor 2016), gas environment and accretion efficiencies (e.g. Kocsis, Yunes & Loeb 2011; Barausse, Cardoso & Pani 2014; Derdzinski et al. 2019), how SMBH seeds initially form (e.g. Sesana, Volonteri & Haardt 2007; Ricarte & Natarajan 2018; DeGraf et al. 2021), and the potential connection with host galaxy morphologies (with multimessenger studies that combine GW and electromagnetic information; e.g. Volonteri et al. 2020; DeGraf et al. 2021). To maximize what we can learn from the initial SMBH merger detections, it is important to understand the underlying merging populations.
Cosmological simulations provide an ideal mechanism to characterize merging populations, as they self-consistently model both black holes and galaxy formation, encompass large volumes that provide robust statistical samples, and span a wide redshift range to investigate evolution over cosmic time. Current simulations (e.g. Dubois et al. 2014; Vogelsberger et al. 2014; Schaye et al. 2015; Feng et al. 2016; Henden et al. 2018; Pillepich et al. 2018b; Davé et al. 2019; Chen et al. 2022b) resolve a wide range of scales, with BHs ranging from |$\sim 10^4\,\mathrm{ to}\,10^{10} \, \mathrm{M}_\odot$|, resolving black hole growth, mergers, and their host galaxy properties. The majority of cosmological simulations, however, tend to only resolve higher mass black holes (of the order of |$10^6 \, \mathrm{M}_\odot$|), which misses the majority of LISA-detectable mergers. Additionally, simulations frequently do not physically model the infall/inspiral of the black holes leading to coalescence, which has the potential to significantly impact merging black hole populations (see e.g. Volonteri et al. 2020; Banks et al. 2022). Here, we study the Astrid simulation (Ni et al. 2022), which includes both low-mass seeds (down to |$10^{4.5} \, \mathrm{M}_\odot$|), thereby resolving mergers at the peak of LISA’s sensitivity; and it directly incorporates dynamical friction to model the orbital dynamics to small scales, providing a more accurate probe of inspiralling black holes, and prevents mergers from occurring during fly-by encounters (Chen et al. 2022a).
This paper is organized as follows: In Section 2, we provide an overview of the Astrid simulation, including black hole and dynamical friction models. In Section 3, we discuss the overall black hole population in Astrid, as well as the expected merging populations. In Section 4, we investigate the GWs emitted by these mergers, and combine with LISA sensitivity to calculate the expected signal-to-noise ratios (SNRs) for the full merger samples (Section 4.1). Finally, we summarize our conclusions in Section 5.
2 METHOD
In this work, we use Astrid (Bird et al. 2022), a cosmological simulation run using a version of the mp-gadget smoothed-particle hydrodynamics (SPH) simulation code, a highly scalable version of the gadget-3 code (Springel et al. 2005). The simulation consists of a (250 h−1 Mpc)3 volume containing 2 × 55003 particles, resolving galactic haloes down to |$10^9 \, \mathrm{M}_\odot$| from z = 99 to z = 2. The cosmological parameters for the simulation are based on measurements from Planck Collaboration VI (2020) (|$\Omega _0 = 0.3089, \Omega _\Lambda = 0.6911, \Omega _b = 0.0486, \sigma _8 = 0.82$|, and h = 0.6774), and has an initial mass resolution of |$M_{\mathrm{ DM}}=6.74 \times 10^6 \ h^{-1} \, \mathrm{M}_\odot\,\mathrm{ and}\,M_{\mathrm{ gas}}=1.27 \times 10^6 \ h^{-1} \, \mathrm{M}_\odot$|, and gravitational softening length of |$\epsilon = 1.5 \ h^{-1} \, \mathrm{kpc}$|.
The Astrid simulation includes detailed models for galaxy formation and evolution, including reionization (Battaglia et al. 2013; Faucher-Giguère 2020) with self-shielding (Rahmati et al. 2013), star formation (Springel & Hernquist 2003) with associated feedback (Okamoto et al. 2010), and metal return (Vogelsberger et al. 2013; Pillepich et al. 2018a). For a more detailed description of the physics modelled in this simulation, see Bird et al. (2022) and Ni et al. (2022).
Of particular import for this analysis is the implementation of black holes in Astrid (Chen et al. 2022a; Ni et al. 2022). Black holes in the Astrid simulation are treated as collisionless sink particles, inserted into haloes above a mass threshold of |$M_{\rm {halo}}=5 \times 10^9 \ h^{-1} \, \mathrm{M}_\odot$| and |$M_* = 2 \times 10^6 \ h^{-1} \, \mathrm{M}_\odot$| that do not already contain a black hole particle. Rather than using a fixed seed mass for black holes, Astrid selects a mass for each newly seeded black hole from a power-law distribution (power-law index = −1) from |$3 \times 10^4\,\mathrm{ to}\,3 \times 10^5 \ h^{-1} \, \mathrm{M}_\odot$|, intended to remain broadly consistent with a variety of SMBH formation pathways and their subsequent growth (e.g. Begelman & Rees 1978; Madau & Rees 2001; Bromm & Loeb 2003; Volonteri, Haardt & Madau 2003; Regan & Haehnelt 2009; Katz, Sijacki & Haehnelt 2015; DeGraf & Sijacki 2020). Once seeded, the black holes grow by merging with other black holes, and via mass accretion following a model based on a Bondi & Hoyle (1944)-like formalism applied to the SPH kernel of the black hole (periods of super-Eddington accretion are permitted, but capped at 2× the Eddington rate). Accreting black holes are assumed to produce a bolometric luminosity proportional to the accretion rate (at 10 per cent efficiency), and 5 per cent of the radiated energy is assumed to couple thermally to the surrounding gas (this feedback energy is deposited isotropically among gas particles within the SPH kernel). Please see Ni et al. (2022) for additional details.
Rather than using a repositioning scheme to simply move all black holes towards nearby potential minima, Astrid implements a dynamical friction model for black holes (Tremmel et al. 2015; Chen et al. 2022b). We assume a Maxwellian distribution for the velocity distribution of the surrounding particles (both stars and dark matter), such that the dynamical friction force can be calculated (see Binney & Tremaine 2008) as
where ρsph and σv are the density and velocity dispersion of the surrounding dark matter and star particles, vBH is the velocity of the black hole relative to the surrounding medium, Λ is the Coulomb logarithm
with bmax = 20 kpc, and |$\mathcal {F}$| is
from integrating the Maxwellian distribution. This dynamical friction implementation produces physically realistic motion for black holes due to small-scale interactions with the nearby matter, and stabilizes the black hole once it reaches the Galactic Centre, which provide more realistic information for the black holes leading up to mergers. For a more detailed discussion of this implementation and the black hole orbital information it produces, see Chen et al. (2022a) and Ni et al. (2022).
3 BLACK HOLE/MERGER POPULATIONS
Before investigating mergers in the Astrid simulation, we first consider the overall populations of black holes over cosmic time. In Fig. 1, we plot the black hole mass function (BHMF) at z = 2, 3, 4, 5, 6, and 7 (solid, dashed, dotted, and dot–dashed, respectively) from the Astrid simulation (red), with a comparison to the TNG300 mass function (blue) at the same redshifts. We find the high end of the mass function (|$M_{\rm {BH}} \gt 3 \times 10^6 \, \mathrm{M}_\odot$|) tends to follow an approximate power law with a slope of ∼−1.05 (for |$M_{\rm {BH}} \gt 10^6 \, \mathrm{M}_\odot$|). The slope is slightly steeper at earlier times, but the primary evolution is the increase in normalization (increasing by more than 2 dex from z = 7 to z = 2; see Table 1 for best-fitting power-law parameters at each redshift). The TNG300 BHMF is broadly consistent with these Astrid results, except that TNG300 produces more high-mass black holes at later times (∼3× more |$\sim 10^8 \ h^{-1} \, \mathrm{M}_\odot$| black holes at z = 4). As such, we can see that massive black holes are able to grow more efficiently in TNG than Astrid at late times (except for the most-massive end), which we can expect to have some impact on the merging populations as well. However, we note that this will only affect the largest black holes at the latest times, and thus will not influence the majority of mergers when comparing the two simulations.
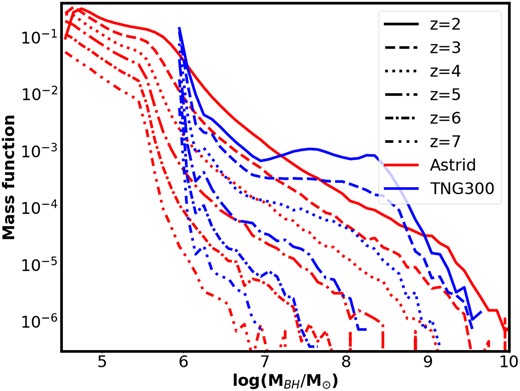
The BHMF for Astrid (red, extending to low masses) and TNG300 (blue), at z = 2–7. For each simulation, the black hole seed model is clearly seen at the lowest masses, but above the seed mass the two simulations broadly agree for z > 4, though TNG300 produces more high-mass black holes at late times.
Best-fitting parameters for BHMF (Fig. 1), fitting |$M_{\rm {BH}} \gt 10^6 \, \mathrm{M}_\odot$| to |$10^a (M/10^7 \, \mathrm{M}_\odot)^b$|, and |$M_{\rm {BH}} \lt 10^{5.5} \, \mathrm{M}_\odot$| (seed-mass range) to |$10^c (M/10^7 \, \mathrm{M}_\odot)^d$|.
| . | High-mass . | Low-mass . | ||
|---|---|---|---|---|
| z . | a . | b . | c . | d . |
| 2 | −2.7 | −1.0 | −1.6 | −0.49 |
| 3 | −3.3 | −1.0 | −2.0 | −0.60 |
| 4 | −3.9 | −1.1 | −2.5 | −0.79 |
| 5 | −4.6 | −1.0 | −2.9 | −0.87 |
| 6 | −5.4 | −1.1 | −3.3 | −0.93 |
| 7 | −6.3 | −1.1 | −3.6 | −0.96 |
| . | High-mass . | Low-mass . | ||
|---|---|---|---|---|
| z . | a . | b . | c . | d . |
| 2 | −2.7 | −1.0 | −1.6 | −0.49 |
| 3 | −3.3 | −1.0 | −2.0 | −0.60 |
| 4 | −3.9 | −1.1 | −2.5 | −0.79 |
| 5 | −4.6 | −1.0 | −2.9 | −0.87 |
| 6 | −5.4 | −1.1 | −3.3 | −0.93 |
| 7 | −6.3 | −1.1 | −3.6 | −0.96 |
Best-fitting parameters for BHMF (Fig. 1), fitting |$M_{\rm {BH}} \gt 10^6 \, \mathrm{M}_\odot$| to |$10^a (M/10^7 \, \mathrm{M}_\odot)^b$|, and |$M_{\rm {BH}} \lt 10^{5.5} \, \mathrm{M}_\odot$| (seed-mass range) to |$10^c (M/10^7 \, \mathrm{M}_\odot)^d$|.
| . | High-mass . | Low-mass . | ||
|---|---|---|---|---|
| z . | a . | b . | c . | d . |
| 2 | −2.7 | −1.0 | −1.6 | −0.49 |
| 3 | −3.3 | −1.0 | −2.0 | −0.60 |
| 4 | −3.9 | −1.1 | −2.5 | −0.79 |
| 5 | −4.6 | −1.0 | −2.9 | −0.87 |
| 6 | −5.4 | −1.1 | −3.3 | −0.93 |
| 7 | −6.3 | −1.1 | −3.6 | −0.96 |
| . | High-mass . | Low-mass . | ||
|---|---|---|---|---|
| z . | a . | b . | c . | d . |
| 2 | −2.7 | −1.0 | −1.6 | −0.49 |
| 3 | −3.3 | −1.0 | −2.0 | −0.60 |
| 4 | −3.9 | −1.1 | −2.5 | −0.79 |
| 5 | −4.6 | −1.0 | −2.9 | −0.87 |
| 6 | −5.4 | −1.1 | −3.3 | −0.93 |
| 7 | −6.3 | −1.1 | −3.6 | −0.96 |
At lower masses, we see that the two simulations diverge significantly, as a result of the seeding model. In the TNG300 simulation, we see a large spike at the lowest mass BH (|$\sim 10^6 \, \mathrm{M}_\odot$|). This peak corresponds to the black hole seed mass used in the TNG simulations, and is a result of recently seeded black holes tending to have very low accretion rates. This is at least partly due to stellar feedback, especially at early times (Weinberger et al. 2017, 2018), but some contribution may also come from the difference in seeding criteria (since TNG uses a mass threshold based only on halo mass, there may be more black holes seeded in gas-poor galaxies where growth is minimal, compared to Astrid that also has a stellar mass cut). Hence a large number of black holes have not grown much beyond their seed masses resulting in the strong spike in the TNG mass function. In contrast, the Astrid BHMF gets slightly steeper at lower masses, but does not have any qualitative shift until |$M_{\rm {BH}} \sim 10^{5.5} \, \mathrm{M}_\odot$|, below which we find a shallower power law. We recall that the seeding model used in Astrid initializes black holes with a starting mass selected from a power-law distribution with slope of −1 (see Section 2), which produces the behaviour we see here. We note that the best-fitting slope for this plateau is slightly shallower than the slope for the seed mass selection (∼−0.9 rather than the −1 used when seeding), and gets gradually shallower with time (from ∼−0.96 at z = 7 to ∼−0.5 at z = 2; see also Table 1). This is due to lower mass seeds gradually growing into the higher mass range for seeding, and hence over time the number of black holes in the high-mass end of the seed range increases. As such the plateau we see in the BHMF is a result of the seed model used combined with a small amount of growth, while for higher mass black holes (e.g. |$\gt 10^6 \, \mathrm{M}_\odot$|) we find a well-behaved BHMF that is consistent with the TNG BHMF.
Overall, we find that Astrid is similar to TNG300 (and comparable simulations), although with two significant differences. First, Astrid spans a larger range of black hole masses, extending to much smaller black holes resulting from the new seed model. Additionally, Astrid has an improved black hole treatment, including dynamical friction, which more accurately models black hole motion and mergers. As such, we expect the merger rates to be more strongly affected, and a potential impact on high-mass black holes (after longer time to grow), hence the discrepancy between Astrid and TNG300 in Fig. 1 increases for late times and high masses.
Next we consider the mergers produced by this black hole population. In Fig. 2, we plot the rate at which GW signals will reach the Earth from SMBH mergers, obtained by integrating the number of mergers in the simulation over redshifts, incorporating the cosmic volume at the given redshift:
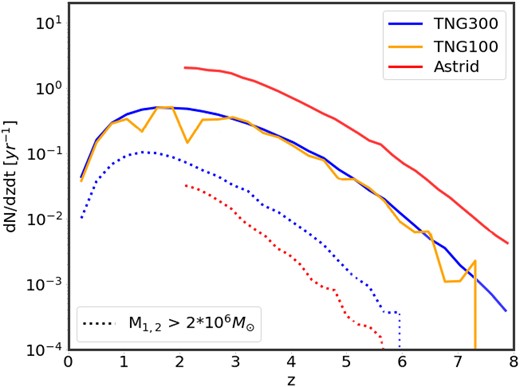
Merger rate signal as a function of redshift in Astrid (red, top curve), TNG300 (blue), and TNG100 (yellow). Since Astrid includes much lower mass black holes than the TNG simulations, the dashed red line shows the Astrid signal rate when limited to only mergers massive enough to be resolved in TNG300. We see that all five simulations have qualitatively similar behaviour, although with different normalization: Astrid has significantly more mergers (due to the lower mass black holes). When considering only mergers between black holes above 2 × MTNG, seed (dotted lines), however, we find a lower merger rate in Astrid.
We see that the TNG simulations (TNG300 – blue; TNG100 – yellow) have broadly comparable behaviour: very rare mergers at high-z, increasing with time to a peak at z ∼ 2, followed by a decrease in expected merger rates. The high-redshift behaviour in Astrid (red) is broadly similar, in that it starts with rare mergers at high-z, and increases with time. However, we find an overall rate significantly higher in Astrid than any of the TNG simulations. Rather than a fundamental difference in mergers, however, this increased rate in Astrid is a result of the seed model initializing lower mass black holes in lower mass galaxies when compared to TNG. As shown in Fig. 1, at high masses the simulations are consistent, but Astrid includes many low-mass BHs below TNG’s seed mass, and hence will include a significant number of mergers that go unresolved in TNG.
To test this, the dashed lines in Fig. 2 show the rates from the Astrid and TNG300 simulations after imposing a cut of 2 × Mseed, TNG (i.e. only mergers with M1 > Mseed, TNG and M2 > Mseed, TNG, where M1 (M2) is the larger (smaller) mass involved in a merger, and Mseed, TNG is the black hole seed mass for the TNG simulations). A cut of M > 2 × Mseed, TNG removes black holes that are not yet seeded by TNG, and also ignores the strong peak in the TNG BH population caused by the seed criteria, and thus we are comparing equivalent black hole populations. Here, we see that the majority of mergers involve low-mass BHs (where at least one BH has MBH < 2 × Mseed, TNG, hence dashed line well below the solid lines), and when limited only to the equivalent merger populations, Astrid actually has a lower merger rate than the TNG simulations by a factor of ∼3.
There are several major differences between the simulations that have the potential to influence the merger rates. One factor is that Astrid seeds black holes into smaller haloes, and the dependence of galaxy merger rates on galaxy mass will influence the rate at which BHs seeded in those galaxies end up merging. However, this will be limited primarily to low-mass galaxies/BHs, and so would not explain the lower rate in Astrid among high-mass mergers. Another factor is the faster growth in TNG, which produces a larger population of high-mass black holes when compared to Astrid (see Fig. 1); at z = 4 TNG has |$\sim 50~{{\ \rm per\ cent}}$| more black holes above 2 × Mseed, TNG. Hence we should expect a higher merger rate in TNG than Astrid, based solely on the population of black holes available to merge. Finally, there is the dynamical friction model: Astrid models black hole motion using a dynamical friction prescription (Chen et al. 2022b) rather than a recentring scheme. As such, when a pair of galaxies merge together, satellite BHs (those found in the smaller of the two merging galaxies) can take longer to reach the galaxy centre where they are then able to merge with the central BH, and the full dynamical friction model allows for fly-by interactions rather than assuming an immediate merger when two black holes are sufficiently close together. Thus we expect black holes in simulations that incorporate dynamical friction to generally merge more slowly than those in simulations that use a recentring scheme. They should therefore have a lower overall merger rate (when controlling for resolved masses), precisely as we see when comparing Astrid to TNG300 (dotted lines in Fig. 2).
To more directly consider merging masses, we plot the mass–redshift distribution of mergers in Fig. 3 for both Astrid (left) and TNG300 (right). Consistent with Figs 1 and 2, we see that the lower seed mass in Astrid provides M1 more than an order of magnitude below what the TNG simulations resolve. Similarly, the lower halo mass threshold for seeding means that Astrid models black hole mergers out to earlier cosmic times, as a result of seeding black holes into smaller galaxies. Above the seed mass scales, however, we see that both Astrid and TNG300 produce remarkably similar distributions, with M1 > Mseed, TNG mergers first occurring at z ∼ 7, and reaching |$M_1 \sim 10^{10} \, \mathrm{M}_\odot$| at z = 2 (although Astrid’s larger volume means there are a few unusually massive mergers at slightly earlier times). This is consistent with Fig. 1, in that black holes well above the seed mass tend to grow at comparable rates in both Astrid and the TNG simulations at high-z, and thus the mass scale involved in the mergers tends to be similar. Combined with Fig. 1, we see that the smaller seeds in Astrid (and the power-law seed mass distribution) are capable of growing high-mass, high-redshift black holes similar to higher seed mass models, as is necessary to explain observations of luminous quasars in the early universe (see e.g. Di Matteo et al. 2012; Aird et al. 2015; Sijacki et al. 2015; Habouzit et al. 2019; Jiang et al. 2022). A complete analysis of typical black hole growth behaviours is beyond the scope of this paper, but will be discussed in an upcoming work.
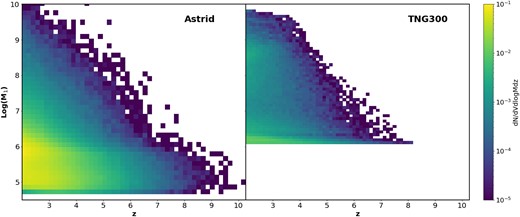
Distribution of primary merger mass (M1) and redshift for Astrid (left) and TNG300 (right; restricted to z > 2 to match Astrid). The different seed models allow Astrid to probe lower masses and higher redshifts, but produce comparable results above Mseed, TNG.
To compare merger rates to black hole populations, in Fig. 4 we plot the BHMF (solid lines), and compare to the merger mass function (dashed line) at z = 2, 3, 4, and 5. We define the merger mass function to be the mass function of M1 (the mass of the more massive BH involved in a merger) for all mergers that take place in the previous 75 Myr. Here, we see that the merger mass function in each simulation is comparable to (although slightly lower than) the corresponding BHMF. In the case of TNG300, we see that above the seed mass both the BHMF and the merger mass function follow a rough power law, and both functions also show a peak at the seed mass (although that spike is smaller in the merger mass function). Similarly, in Astrid we see a rough power law above |$\sim 10^6 \, \mathrm{M}_\odot$|, and a plateau below |$\sim 10^{5.5.} \, \mathrm{M}_\odot$| that corresponds to the power-law seeding model. Similar to TNG, we see that at the seed-mass scale the merger mass function is significantly below the BHMF: although there is a large population of recently seeded black holes, they are less likely to undergo a merger (as they necessarily need time for their host haloes to merge, during which they are able to grow past their seed mass).
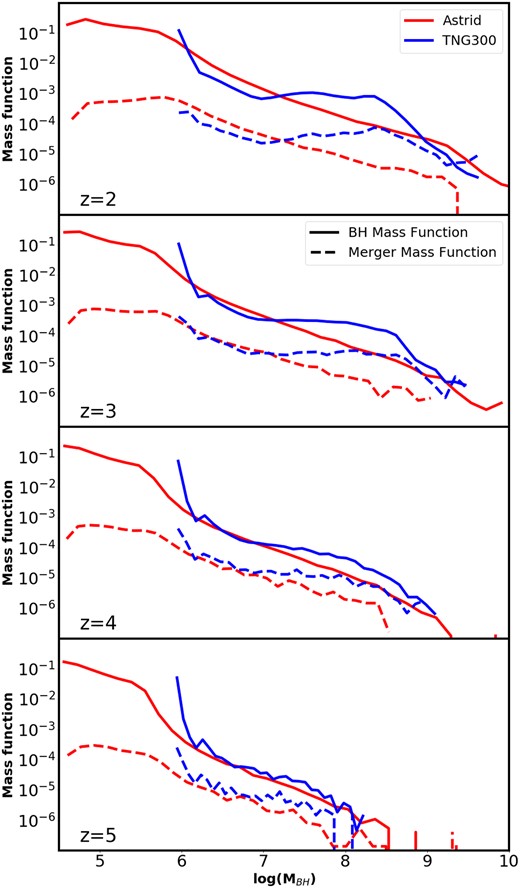
BHMF (solid) for Astrid (red, full mass range) and TNG300 (blue) at z = 2 (top) to z = 5 (bottom), compared to the merger mass function based on the previous 75 Myr (dashed; see text for details). In both simulations, the merger mass functions are similar, although the Astrid merger mass function is smaller relative to the overall BHMF, suggesting a lower merger rate.
Although the ratio between BHMF and merger mass function is qualitatively similar between Astrid and TNG, suggesting a comparable merger rate, when selecting BHs by mass. In Fig. 5, we have divided the merger mass function by the BHMF to obtain a characteristic merger rate as a function of MBH (i.e. the typical number of mergers that a BH with a given mass would undergo in 1 Gyr). As discussed in reference to Fig. 4, we expect the merger rate for BHs near the seed mass to generally be much lower than the merger rate for higher mass black holes: we see this explicitly in Fig. 5, as both Astrid (red) and TNG300 (blue) show a significant dropoff near their respective seed masses. Above the seed masses, however, both simulations show an approximate power law relating merger rate to MBH, such that high-mass black holes have a slightly higher merger rate than lower mass black holes. Furthermore, we see that both Astrid and TNG300 have comparable merger rates; however, we note that this is somewhat coincidental, based on near seed-mass mergers. As seen in Figs 1–4, Astrid contains a large number of low-mass black holes that are unresolved in TNG, but which contribute to the merger rates shown in Fig. 5. We show this explicitly with the dashed line, where we only consider mergers in which M2 > 2 × Mseed, TNG, in which case we have roughly an order of magnitude fewer mergers. None the less, after removing the low-mass (and thus less well-resolved) mergers, we find fairly comparable merger rates except at the highest masses, where Astrid predicts a slightly longer time between mergers.
![The typical merger rate for a BH with a given mass in the Astrid (red, full mass range) and TNG300 (blue) simulations, as well as the merger rates limited to M1, 2 > 2*Mseed, TNG (dotted lines). Both simulations have comparable total merger rates, but the majority of mergers in Astrid involve a low-mass secondary BH; when restricted to the same secondary mass range, Astrid has a merger rate ∼1 dex lower than TNG300. [NOTE: This is not the overall rate of mergers in the simulation/universe; rather it is the rate at which an individual BH of a given mass would be expected to undergo mergers; i.e. lower panel would suggest a z = 5 BH with M$\sim 10^{6.5} \, \mathrm{M}_\odot$ would be expected to undergo about 1 merger per Gyr. That’s true for both TNG and Astrid, but in Astrid that includes mergers with lower mass BHs (below the seed mass of TNG); the dashed line only includes mergers where both BHs are above the seed mass of TNG, so it’s closer to a 1-to-1 comparison.]](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/527/4/10.1093_mnras_stad3084/2/m_stad3084fig5.jpeg?Expires=1750342150&Signature=G4N2ix8hzyRtQcLg41Vbkgqhx4AocRAjKVYAHM0G05omu0f5Dub8QuglmqjAvHDiHxPIcuZAcqPArt3K-fyfBRO1FcTUNa5bkJwvlPWqp0LjeSi~vHyu1mI81EIqcd8jW9r-vf6u-8~uSidBAa9ZxWo-oAx7tx4Z4uCcgq3QsjbWX-X~PeEOJOSByrA7WOil~537T72xYZtlR5~NQIcajTIJYyJEwqedPJO5JZ9M4rciL2jqQbn7TcfH0-UwXTAiwzEECVpT6Lj13lWk60OXPRktc~LzuJ1SVIFo~R-sx4B1gz3kH8kn-tcyknCYywYRs-aqR1nIRDlFILvqF3~n8Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The typical merger rate for a BH with a given mass in the Astrid (red, full mass range) and TNG300 (blue) simulations, as well as the merger rates limited to M1, 2 > 2*Mseed, TNG (dotted lines). Both simulations have comparable total merger rates, but the majority of mergers in Astrid involve a low-mass secondary BH; when restricted to the same secondary mass range, Astrid has a merger rate ∼1 dex lower than TNG300. [NOTE: This is not the overall rate of mergers in the simulation/universe; rather it is the rate at which an individual BH of a given mass would be expected to undergo mergers; i.e. lower panel would suggest a z = 5 BH with M|$\sim 10^{6.5} \, \mathrm{M}_\odot$| would be expected to undergo about 1 merger per Gyr. That’s true for both TNG and Astrid, but in Astrid that includes mergers with lower mass BHs (below the seed mass of TNG); the dashed line only includes mergers where both BHs are above the seed mass of TNG, so it’s closer to a 1-to-1 comparison.]
4 GRAVITATIONAL WAVE SIGNALS
In addition to the underlying black hole merger populations, we consider the GWs emitted by calculating both the frequency and strain of the GW for each merger. We use the characteristic strain, hs, to model the binary signal that accounts for the time the binary spends in each frequency bin (Finn & Thorne 2000). The characteristic strain is given by (e.g. Moore, Cole & Berry 2015)
where |$\tilde{h}(f)$| represents the Fourier transform of a time domain signal. To generate the waveforms, we use the phenomenological waveform PhenomD (Husa et al. 2016; Khan et al. 2016) implemented within the gwsnrcalc python package (Katz & Larson 2019). The input parameters are the binary masses, merging redshift, and the dimensionless spins of the binary. For the SMBH masses, we do not account for mass growth after the numerical merger. However, we note that the SMBH can potentially gain a significant fraction of its mass during the |$\gt 1\, {\rm Gyr}$| of time in the dynamical friction (e.g. Banks et al. 2022) or loss-cone scattering phase. The dimensionless spin a characterizes the alignment of the spin angular momentum with the orbital angular momentum, and the value of a ranges from −1 to 1. However, we do not have any information on the spin of the SMBHs in our simulation. Therefore, following the argument in Katz et al. (2020), we assume a constant dimensionless spin of a1 = a2 = 0.8 for all binaries (e.g. Miller 2007; Reynolds 2013).
In Fig. 6, we plot the range of frequencies and strains for GW signals emitted by mergers in Astrid (panel a), with each frequency-strain bin colour-coded by the mean redshift of the emitting mergers. We see that the majority of GW signals come from the lowest redshift mergers (although note that the lowest redshift here means z ∼ 2, the latest time probed in this analysis), since the merger rate increases with time (at least at high-z; see Fig. 2). We note that high-z does dominate the lowest-strain GW signals, which is not only a direct result the merger being more distant (and hence a weaker signal), but also because high-z mergers tend to involve swallowing a lower M2 BH (which necessarily produces a smaller strain compared to swallowing a higher mass secondary BH). We also see an upper bound on the GW signals, however, we note that is a result of the limited redshift window reached so far by Astrid (as the simulation continues to lower z, the upper right area will continue to be filled in, which we see in panels b and d for TNG300 mergers).
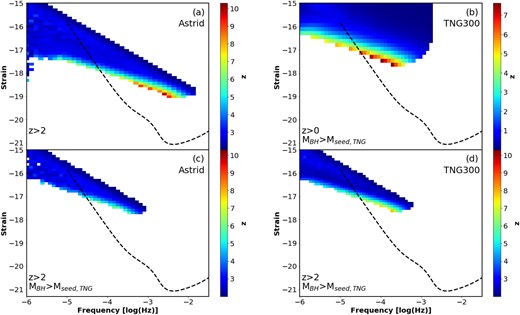
Frequency-strain signals for GWs emitted by BH mergers over cosmic time (binned data) against the LISA sensitivity curve (dashed black line). Each bin is colour-coded by the mean redshift of the source merger that emitted the given GWs. (a) All signals from the Astrid simulation (limited to z > 2). (b) All signals from the TNG300 simulation, which is complete to z = 0 (hence note the different colourscale range), but limited to higher masses. (c) Signals from the Astrid simulation, but limited to the same mass scales as TNG300. (d) Signals from the TNG300 simulation, but limited to the same redshift range (z > 2) as the current state of the Astrid simulation.
In Fig. 6b, we show the frequency-strain signals for the TNG300 mergers, again colour-coded by the merger redshift (although note the range for the colour bar is different, since TNG is complete to z = 0). As in Fig. 6a, we see that most signals come from the lowest redshifts (although here that means near z = 0), and again high-z signals dominate the lowest strains. However, the much larger redshift range makes comparing to these panels problematic; instead, in Fig. 6 d we plot the GW signals from TNG300, but restricted to the same redshift range as Astrid (z > 2). Here, we see a result that is more similar to the Astrid data (Fig. 6a), but that spans a much more limited range of frequency and strain. The z ∼ 2 limit imposes a strict upper limit on the strain, and we see that both Astrid (Fig. 6a) and TNG300 (Fig. 6d) have similar distributions when limited to the same redshift range, with the exception that Astrid extends higher frequencies and lower strain, which we expect since Astrid includes black holes below the resolved mass in TNG300. Overall, we see that the GW signals tend to be dominated by the lowest redshift mergers, with an exception for the highest frequency/lowest strain signals, which tend to be at higher redshifts.
Unlike Fig. 6a, which spans the majority of the LISA frequency range, the frequency-strain distribution for TNG300 (Figs 6 b and d) is limited only to LISA’s low-frequency regime. This is a result of Astrid resolving much lower black hole masses, whose mergers produce higher frequency signals. We see this explicitly in Fig. 6c, which shows the GW signals in Astrid, but limited to the same mass range as TNG300 (i.e. M2 > Mseed, TNG), such that Figs 6 c and d show the results from Astrid and TNG300 for the same mass and redshift ranges. Comparing these panels, we see that Astrid has fewer mergers (at fixed mass/redshift ranges) than TNG300, consistent with Figs 2 and 5 that also show fewer mergers. Since the mass scale is well above the seed mass, this is not a result of the seeding prescriptions. Rather it is a result of the dynamical friction modelling that delays black hole mergers to later times relative to a simpler repositioning scheme. Overall, we see that the largest difference between the two simulations is that Astrid produces more high-frequency and low-strain signals, which correspond to low-mass mergers.
4.1 SNR
Having calculated the GW frequency and strain emitted by merging black holes, we also consider the strength of the GW signal received by LISA. We estimate the SNR by integrating the ratio of the signal to the noise in the frequency domain. The sky, orientation, and polarization averaged SNR are given by
where fstart = f(tstart) and fend = f(tend), with tstart and tend representing the starting and ending time when the signal is observed. Note that here we do not account for the eccentricity of the binaries, and assume circular orbits at the time of merger.
For the current configuration, we assume that the LISA observation lasts for 4 yr. We further assume a most optimistic SNR for all mergers by taking tend = tpeak and tstart = tpeak − 4 yr. Under this assumption, we are always integrating the part of the waveform where the strain is maximized. However, as was discussed in Salcido et al. (2016) and Katz et al. (2020), the actual SNR may be smaller if there is an offset between the LISA observation window and the merger time of the binary.
In Fig. 7, we plot the distribution of SNRs from Astrid (solid red) and TNG300 (solid blue) for z > 2 mergers, normalized by the simulation volume. In both simulations, we find that the SNR peaks at very high values (102–103), with Astrid producing significantly more high-SNR mergers, while TNG300 has a flatter tail extending towards low SNR. Since the majority of mergers tend to occur between low MBH black holes (e.g. see Figs 3 and 4), these differences are expected due to the different seed criteria between the two simulations. For a more direct comparison, the dashed lines show the SNR distribution limited to mergers in which both merging black holes have MBH > 2 × MTNG, seed (i.e. only including BHs more than double the TNG seed mass, to avoid issues related to black hole seeding). Here, we see that the two simulations have a consistent peak at SNR just below 103, although we find that TNG300 has a nearly flat distribution for SNR > 1, whereas Astrid predicts a moderate slope, producing fewer low-SNR mergers. This appears to be due to TNG300 producing more high-mass black holes at z ≤ 4 (see Fig. 4) as a result of more efficient black hole growth. A detailed comparison of black hole growth efficiency between these simulations is beyond the scope of this paper, and is left for a future work. However, we note that the difference only affects the low-SNR end, and will thus have a comparatively minor impact on the LISA detection rate.
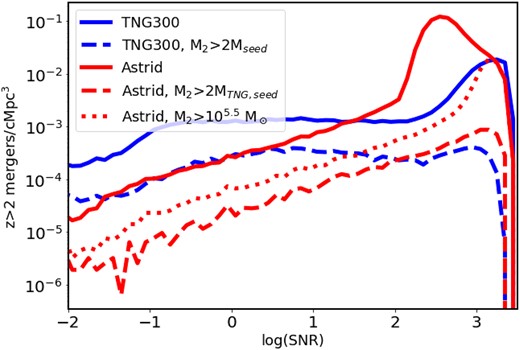
Distribution of SNRs for z > 2 mergers from Astrid and TNG300, normalized by simulation volume (solid lines). Both simulations show qualitatively similar behaviour, with the distribution peaking at high SNR. Because the simulations use different seed masses, we also compare the SNR distribution for mergers in which both merging black holes are above 2× the TNG seed mass (dashed lines), as well as the distribution of Astrid signals for mergers in which both merging black holes are above |$10^{5.5} \ h^{-1} \, \mathrm{M}_\odot$| (the high-end of Astrid’s seed mass range).
On the other hand, the high-SNR end is clearly significantly impacted by the seeding criteria. Although Astrid and TNG agree when limited to merging masses about 2 × MTNG, seed, the majority of mergers are removed when applying such a high-mass cut. One of the major advantages of the Astrid simulation is that the lower seed masses allow us to effectively probe lower mass mergers. We show this with the dotted line in Fig. 7, where we consider any mergers between BHs above the Astrid seed mass distribution (i.e. |$M_{\rm {BH}} \gt 10^{5.5} \ h^{-1} \, \mathrm{M}_\odot$|, hence above the seed-mass dominated regime, as seen in Fig. 1), which provides us with significantly more mergers. We note that including these lower mass black holes produces a peak at the high-SNR end that is missed when imposing a higher mass cut (or higher seed masses). Furthermore, we find roughly triple the number of SNR < 102.5 for |$M_2 \gt 10^{5.5} \ h^{-1} \, \mathrm{M}_\odot$| than for M2 > 2 × Mseed, TNG, emphasizing the importance of low-mass black holes. Furthermore, we note that the slope of the SNR < 102.5 distribution remains roughly the same when using the lower mass cut. Overall, this suggests that the highest-SNR mergers are primarily between two low-mass BHs that are completely missed with a higher mass cut (hence the strong peak which the dashed line completely misses), while the lower SNR mergers frequently involve at least one higher mass black hole, so by including a smaller mass cut we increase the number of mergers at all SNR ranges but without affecting the slope.
We investigate this in more detail in Fig. 8, which shows the mass distribution of merging black holes (M1 versus M2), colour coded by |$\lt \rm {log}(SNR)\gt $| (i.e. the mean logarithmic SNR for mergers in the given mass bin), for z > 2 mergers in Astrid (left) and TNG300 (right). In the mass scales resolved in both simulations, we find comparable SNR results (although we again see more high-mass mergers in TNG as a result of the more efficient growth). As seen in Fig. 7, the larger mass range produced by Astrid’s smaller seed mass results in significantly more mergers, especially for high SNRs. This demonstrates the importance of including lower mass seeds for black holes in cosmological simulations, as it provides a more accurate prediction for overall merger rates and dramatically increases the prediction for the number that should be detectable by LISA. Pushing to even lower seed masses than those probed with Astrid will further increase the number of mergers in the simulation and thus be beneficial for more precise predictions, however, it is not as crucial as having a seed mass below |$10^5 \, \mathrm{M}_\odot$|, which ensures that the simulation includes the mergers that produce GWs with the strongest LISA signals. In particular, the Astrid simulation shows the SNR peaks at |$M_1, M_2 \sim 10^6 \, \mathrm{M}_\odot$|, with the lower masses having weaker (although still strong) signals; they are still well within the detectable range, but are below LISA’s peak sensitivity (see Amaro-Seoane et al. 2017).
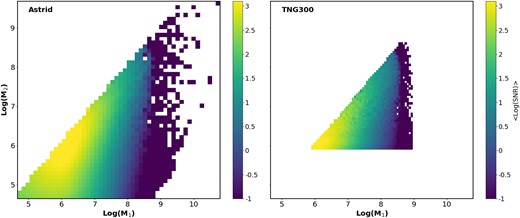
Distribution of merging black hole masses for Astrid (left) and TNG300 (right), colour coded by the mean log(SNR) for the mergers. We find that the strongest SNRs in Astrid are found for |$M_1, M_2 \sim 10^6 \, \mathrm{M}_\odot$|; this is consistent with TNG300, although the higher seed mass in the TNG simulations means that the peak signals roughly correspond to the seed masses of the simulation. In both simulations, we also note that the SNR is more strongly correlated to M1 than M2.
Fig. 8 also shows that SNR depends primarily on the larger mass (M1), while the secondary black hole (M2) has a relatively weak impact on SNR. We show this explicitly in Fig. 9, which plots the correlation between SNR and the merging black hole masses (M1 – left; M2 – right) for Astrid (top) and TNG300 (bottom), colour coded by the number density of mergers. The majority of mergers occur between low mass black holes (as seen, e.g. in Fig. 4), and we again see that the highest SNRs occur when both M1 and M2 are |$\sim 10^6 \, \mathrm{M}_\odot$|. We also see that SNR correlates quite strongly with M1, spanning ∼1 dex at |$M_1 \sim 10^6 \, \mathrm{M}_\odot$| up to ∼2 dex at higher masses. In contrast, a low M2 spans a much higher range of SNRs, corresponding to the wide range of possible M1 (i.e. mass of the swallowing black hole), although most low-M2 mergers still have high SNR (since the majority of mergers will still have a low M1). The relatively weak dependence on M2 means that the growth of the secondary BH does not play a significant role in the expected SNR for a given merger. However, it is none the less very important to include lower mass black holes to probe the full range of mergers that we expect LISA to be able to detect: mergers between |$\sim 10^6 \, \mathrm{M}_\odot$| black holes are both extremely common and produce the strongest GW signals from LISA, so limiting simulations to higher masses will necessarily miss the majority of mergers and their associated GW signals. On the other hand, we note that the LISA SNR peaks at both |$M_1 \sim 10^6 \, \mathrm{M}_\odot$| and |$M_2 \sim 10^6 \, \mathrm{M}_\odot$|. So although incorporating smaller seed masses in simulations will provide more accurate estimates for the overall merger rates (which are dominated by low-mass mergers), below |$\sim 10^5 \, \mathrm{M}_\odot$| will primarily consist of lower SNR signals, and thus would be beneficial, but not vital to include in future simulations.
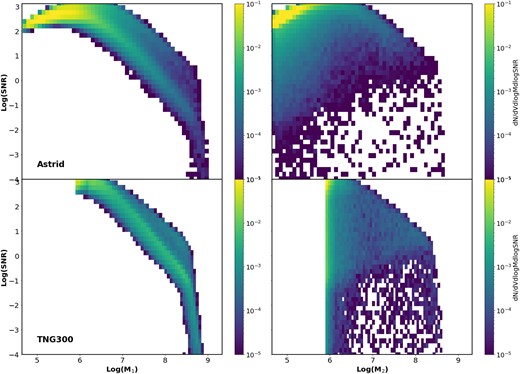
Distribution of SNR versus mass (left: M1; right: M2) for z > 2 mergers in Astrid (top) and TNG300 (bottom), colour-coded by density of mergers in the simulation volume. Consistent with Fig. 8, we see that SNR is much more strongly correlated wtih M1 than M2, and we again find that Astrid and TNG300 are broadly consistent above the TNG seed mass.
5 CONCLUSIONS
In this work, we have investigated the black hole population in the Astrid simulation, which seeds black holes at masses as low as |$10^{4.5} \ h^{-1} \, \mathrm{M}_\odot$|, well below what is frequently used in comparable cosmological simulations. We have particularly focused on the mergers between black holes, looking at the overall merger rates, the merging masses, and the expected GW signals they produce, noting that Astrid directly incorporates a dynamical friction model that produces more realistic merger behaviour. Our main results are as follows:
The Astrid simulation produces a comparable population of high-redshift black holes when compared to prior simulations (esp. TNG300), but with an alternate seed model that extends to much lower mass black holes. Above the masses resolved by both simulations, we see that Astrid and TNG have comparable mass functions (Fig. 1), and also typical merging masses as a function of redshift (Fig. 3).
The overall merger rate is much higher in Astrid than in earlier TNG simulations, primarily due to mergers involving low-mass black holes that are not resolved in simulations with higher seed masses. When considering the same mass scales, Astrid has fewer mergers, likely a result of the added infall time resulting from the dynamical friction model incorporated in Astrid.
The merger rate for a given black hole is mass-dependent, with massive black holes undergoing mergers more frequently than low-mass black holes. A typical black hole can be expected to undergo a merger every ∼1–10 Gyr.
Including low-mass black holes (i.e. lower mass seeding prescriptions) is crucial for modelling LISA detections. High-mass seed models will only probe the low-frequency, high-strain regime within the LISA sensitivity band, while lower seed masses can extend across the full range of potential LISA detections.
In addition to decreasing the overall merger rate, including dynamical friction can be expected to preferentially affect low-frequency, low-strain GW signals, which are primarily generated by low-M2 mergers. This further emphasizes the importance of including accurate models for both seeding and infall dynamics, as both have the potential to not only affect the expected signal rate, but also the frequency-strain distribution of GW signals that LISA will be expected to detect.
The SNR distribution follows a rough power law until the highest signals (SNR > 102), at which point there is a peak caused by |$M_{\rm {BH}} \sim 10^6 \, \mathrm{M}_\odot$| mergers. This peak is poorly resolved in simulations with high seed masses, but is 0.5–1.5 dex above the Astrid seed masses, providing a well resolved sample. Additionally, SNR is strongly correlated with the more massive black hole (M1), and weakly correlated to the less massive black hole (M2; although note that M1 and M2 are correlated to each other).
The LISA SNR has a weak dependence on redshift, at least in the early universe (z > 2). There is evolution in the merging populations of black holes, with later times including higher mass (and correspondingly smaller SNR) mergers. However, low-mass mergers have stronger signals, are more common, and have relatively weak dependence on redshift (at least for z > 2, probed here).
In summary, we have shown that using a wide range of black hole seed masses extending down to |$10^{4.5} \ h^{-1} \, \mathrm{M}_\odot$| produces a high-mass population of black holes comparable to simulations that use higher seed masses, while simultaneously allowing us to investigate smaller black holes, mergers, and the associated GWs they emit. In particular, we are able to provide a detailed investigation into mergers spanning much of the LISA sensitivity range, provide estimates for the expected GW signal detections, and the correlation between these detections and the underlying merger masses and redshifts, in a simulation that directly models dynamical friction to produce more accurate merger behaviour.
ACKNOWLEDGEMENTS
Astrid was run on the Frontera facility at the Texas Advanced Computing Center. TDM acknowledges funding from the NSF AI Institute: Physics of the Future, NSF PHY-2020295, NASA ATP NNX17AK56G, and NASA ATP 80NSSC18K101. TDM acknowledges additional support from NSF ACI-1614853, NSF AST-1616168, NASA ATP 19-ATP19-0084, and NASA ATP 80NSSC20K0519. SPB was supported by NASA ATP 80NSSC22K1897.
DATA AVAILABILITY
The code used for the simulation is available at https://github.com/MP-Gadget/MP-Gadget. Halo catalogues and BH data are available upon reasonable request to the authors.
References
APPENDIX A: FREQUENCY STRAIN COUNTS
Similar to Fig. 6, in Fig. A1 we show the frequency-strain distribution for both the Astrid and TNG300 simulations, but here colour-coded by the number density of mergers. Here, we see that the peak in the frequency-strain distribution occurs at the highest frequencies, and lowest strain, corresponding to low-mass mergers taking place at low redshift, consistent with the merger mass functions in Fig. 4. Here, we again see the importance of including lower mass black hole seeds, as a higher seed mass will cut out the majority of mergers, which also correspond to the peak sensitivity range for LISA (compare Fig. A1 panel a to panel c). By comparing Astrid to TNG, we also note that the higher seed mass results in a higher number of low-frequency GWs, especially at the lowest redshifts.
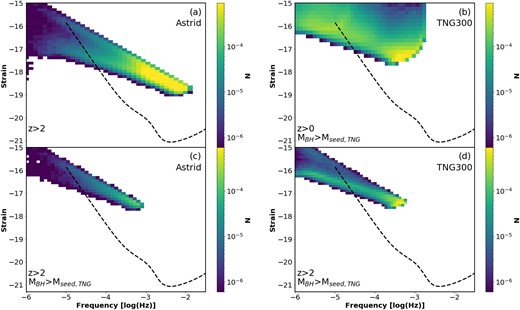
Same as Fig. 6, but colour coded by the number density of mergers, rather than the mean redshift. We see that the merger frequency tends to peak towards higher frequencies (corresponding to lower merger masses), and thus higher LISA SNR. This is strongest when considering lower mass mergers (e.g. when considering mergers down to the Astrid seed mass scale, in the top left panel), or when limited to high redshift (when black holes tend to be smaller).



