Kinetic rate coefficients for electron-driven collisions with CH+: dissociative recombination and rovibronic excitation

ABSTRACT

Cross-sections and rate coefficients for rovibronic excitation of the CH⁺ ion by electron impact and dissociative recombination of CH⁺ with electrons are evaluated using a theoretical approach combining an R-matrix method and molecular quantum defect theory. The method has been developed and tested, comparing the theoretical results with the data from the recent Cryogenic Storage Ring experiment. The obtained cross-sections and rate coefficients evaluated for temperatures from 1 to 10 000 K could be used for plasma modelling in the interpretation of astrophysical observations and also in the technological applications where the molecular hydrocarbon plasma is present.

astrochemistry, molecular processes, plasmas, scattering, ISM: clouds

1 INTRODUCTION

Hydrides and their ions are often used to trace various characteristics of the interstellar medium (ISM). Understanding their formation and destruction mechanisms is therefore necessary for using them as accurate tracers. The CH⁺ ion, discovered in the ISM by Douglas & Herzberg (1941) and Adams (1941), was originally thought to be formed primarily through the reaction

$$\begin{eqnarray} {\rm C^+ + H_2 \longrightarrow CH^+ + H}. \end{eqnarray}$$

(1)

The reaction is endothermic, requiring 0.398 eV (∼4620 K) to proceed (Hierl, Morris & Viggiano 1997), but typical kinetic temperatures of diffuse clouds are roughly between 40 and 130 K (Shull, Danforth & Anderson 2021). Hence, the reaction cannot explain the observed abundance of CH⁺ in diffuse clouds (Godard & Cernicharo 2013). Observations of CH⁺ in diffuse clouds have motivated many theoretical and experimental studies on the structure and reactivity of the ion. The structure of the ion has been well established for several decades, while there is still need for cross-sections for processes involving collisions of CH⁺ with electrons. In particular, the knowledge of cross-sections for excitation of the ion by electron impact is important for the interpretations of astrophysical observations. For example, rotational excitation (RE) of CH⁺ by electron impact was found to be the dominant process producing CH⁺ in the ISM (Godard & Cernicharo 2013).

Besides astronomical applications, cross-sections and rate coefficients for e⁻ + CH⁺ collisions are important for the interpretation and modelling of the hydrocarbon plasma behaviour. Other than RE, mentioned above, one needs the data on vibrational and electronic excitation and dissociative recombination (DR). CH⁺ is also a suitable candidate for benchmark theoretical studies of such processes. On the one hand, this is because there are several experimental measurements (Amitay et al. 1996; Kálosi et al. 2022; Paul et al. 2022) available – of DR in particular. On the other hand, the ion has a relatively complex electronic structure, such that the theoretical methods could be tested on this system and, if successful, be applied to other similar problems.

Our recent theoretical study (Forer et al. 2023) has demonstrated that theory can now accurately describe the DR process in CH⁺. The theoretical approach developed in that study [originated from several previous works (Hamilton & Greene 2002; Kokoouline & Greene 2003; Čurík, Hvizdoš & Greene 2020)] with small modifications can also be used to obtain cross-sections for rotational, vibrational, and even electronic excitation of the CH⁺ ion by electron impact. Because the theoretical method was validated comparing the DR results with the experimental data, it is expected to provide reliable data on the electron-impact excitation processes as well. This study is devoted to the theoretical evaluation of cross-sections and rate coefficients for rovibronic excitation (RVE) of CH⁺ ion by electron impact. The only available experimental result on excitation of CH⁺ is from a recent study in the Cryogenic Storage Ring (CSR) (Kálosi et al. 2022), where the rate coefficient for RE from the ground rovibrational level v = 0, j = 0 of CH⁺ to the first excited v = 0, j = 1 was measured. However, there have been several theoretical studies on RE using the Coulomb-Born approximation (Chu & Dalgarno 1974; Dickinson & Munoz 1977; Lim, Rabadán & Tennyson 1999) and a semiclassical method (Flower 1979). More recently, vibronic excitation (VE) of CH⁺ was studied by Jiang et al. (2019) using a combination of an R-matrix approach (Carr et al. 2012) and molecular quantum defect theory (Seaton 1983; Aymar, Greene & Luc-Koenig 1996).

This study is based on a fully quantum description of e⁻ + CH⁺ collisions and considers rotational and vibrational degrees of freedom of the target ion, as well as its electronic structure, including the three lowest electronic states and the corresponding Rydberg resonances appearing in the CH⁺ + e⁻ collisional spectrum. The article is organized in the following way: Section 2 gives an overview of the present theoretical approach and the differences between its application for DR and RVE; Section 3 presents our DR rate coefficients; Section 4 describes the Coulomb-Born approximation and its application to the present RE calculations; Section 5 is devoted to the discussion of obtained results on RVE; and Section 6 concludes our findings.

2 THEORETICAL APPROACH

The method described in this section combines fixed-nuclei electron-scattering calculations with the R-matrix method, rovibrational frame transformation, and multichannel quantum defect theory (MQDT). Only the main elements of the approach will be presented here. We use the same method to calculate scattering matrices as in our previous study of the DR of CH⁺ (Forer et al. 2023). The theory and computational details have only two main differences: the formula for obtaining the RVE cross-sections (instead of DR cross-sections) and the vibrational Hamiltonian used in the vibrational frame transformation of the electronic S-matrix.

We perform electron-scattering calculations with the R-Matrix method implemented in UKRMol (Tennyson 2010; Carr et al. 2012), accessed via the Quantemol-N interface (Tennyson et al. 2007). The K-matrices for the e⁻ + CH⁺ system are represented in a basis of electronic scattering channels, indexed by n, l, and λ. The quantum numbers l and λ correspond to the magnitude of the orbital angular momentum of the incident electron and its projection on the molecular axis, respectively. The electronic states of the target, CH⁺, are indexed by n. K-matrices are obtained for several values of R, the internuclear distance of CH⁺. We then transform the K-matrices into the S-matrix, via the intermediary matrix of phase shifts, |$\underline{\delta }(R)$|⁠. The matrices are formally related by

$$\begin{eqnarray} \underline{K}(R) = \tan \underline{\delta }(R), \quad \underline{S}(R) = (I+iK)(I-iK)^{-1} = e^{\underline{\delta }(R)}. \end{eqnarray}$$

(2)

The reasons for this transformation are twofold: the S-matrix is a smooth function of R, which is necessary to have a more accurate vibrational integral in the frame transformation, and the S-matrix is used in the formula to compute the cross-sections.

After the electronic S-matrices are obtained for each value of R, we proceed with the vibrational frame transformation. The first difference in this approach with our study of DR (Forer et al. 2023) is that the vibrational Hamiltonian is Hermitian. To study DR, we used a complex absorbing potential to represent absorption by discretizing the continuum. Here, we only need to obtain vibrational wave functions for bound states. The vibrational frame transformation proceeds as

$$\begin{eqnarray} S^\Lambda _{n^{\prime }v^{\prime }l^{\prime }\lambda ^{\prime },nvl\lambda } = \int \mathrm{ d}R\,\, \phi _{n^{\prime }v^{\prime }}(R)\,\, S^\Lambda _{n^{\prime }l^{\prime }\lambda ^{\prime },nl\lambda }\,\, \phi _{nv}(R), \end{eqnarray}$$

(3)

where v indexes a vibrational level. The superscript Λ indicates that the S-matrices are block diagonal with respect to Λ, the projection of the total angular momentum on the molecular axis.

The Hermitian Hamiltonian implies, of course, real eigenvalues. The channel energies in the case of DR are complex, with a non-zero imaginary part for continuum states. Here, all channel energies and vibrational wave functions ϕ_nv(R) are real-valued. The S-matrix on the left-hand side of (3) is the vibronic S-matrix and, unlike in the case of DR, unitarity is defined with the usual spectral norm, i.e. S^JS^J† = I. Following the vibrational frame transformation, we perform the rotational frame transformation on the vibronic S-matrix to obtain the rovibronic S-matrix, i.e.

$$\begin{eqnarray} S^J_{n^{\prime }v^{\prime }j^{\prime }\mu ^{\prime }l^{\prime },nvj{\mu }l} = \sum \limits _\Lambda \sum \limits _{\lambda \lambda ^{\prime }} (-1)^{l^{\prime }+l+\lambda ^{\prime }+\lambda } C^{j^{\prime }\mu ^{\prime }}_{l^{\prime }-\lambda ^{\prime },J\Lambda } S^\Lambda _{n^{\prime }v^{\prime }l^{\prime }\lambda ^{\prime },nvl\lambda } C^{j\mu }_{l-\lambda ,J\Lambda }, \\ \end{eqnarray}$$

(4)

where the total angular momentum of the ion–electron system is |$\overset{\rightharpoonup }{J} = \overset{\rightharpoonup }{j} + \overset{\rightharpoonup }{l}$|⁠, |$\overset{\rightharpoonup }{j}$| is the total angular momentum of the ion, and μ is the projection of j on the molecular axis. The S-matrix, now expressed in a basis of rovibronic channels, block diagonal over J.

For each scattering energy, we then partition S^J into blocks corresponding to the open (o) and closed (c) channels and construct the diagonal matrix |$\underline{\beta }$| for closed channels,

$$\begin{eqnarray} \underline{S}^J = {\begin{pmatrix}\underline{S}_{oo} & \underline{S}_{oc} \\ \underline{S}_{co} & \underline{S}_{cc} \end{pmatrix}}, \quad \beta _{i^{\prime }i}(E_\text{tot}) = \frac{\pi }{\sqrt{2(E_i-E_\text{tot})}} \delta _{i^{\prime }i}, \end{eqnarray}$$

(5)

where E_i is the energy of the ith channel and is real, and E_tot is the total energy of the ion–electron system. We proceed with the closed-channel elimination procedure, borrowed from MQDT, to reduce the S-matrix to only open channels.

$$\begin{eqnarray} \underline{S}^{J,phys} (E_\text{tot}) = \underline{S}_{oo}-\underline{S}_{oc} \left(\underline{S}_{cc}-e^{-2i\underline{\beta }} \right) \underline{S}_{co}. \end{eqnarray}$$

(6)

The physical S-matrix, S^{J, phys}, is then used to calculate the total RVE cross-section from some initial channel |nvjμ〉 to some final channel |n′v′j′μ′〉,

$$\begin{eqnarray} \sigma _{n^{\prime }v^{\prime }j^{\prime }\mu ^{\prime } \leftarrow nvj\mu } (E_{\mathrm{ el}}) = \frac{\pi }{2m_\mathrm{ e}E_{\mathrm{ el}}} \sum \limits _J \frac{2J+1}{2j+1} \sum \limits _{ll^{\prime }} \left|S^{J,phys}_{n^{\prime }v^{\prime }j^{\prime }\mu ^{\prime }l^{\prime },nvj\mu l}\right|^2,\\ \end{eqnarray}$$

(7)

where m_e is the mass of an electron and E_el is the incident electron energy. It is also possible to calculate VE cross-sections, i.e. not including the rotational structure, by simply skipping the rotational frame transformation (4). The closed-channel elimination procedure remains identical, except that the S-matrices are block diagonal over Λ and not J. The total VE cross-section from some initial channel |nv〉 to some final channel |n′v′〉 is then

$$\begin{eqnarray} \sigma _{n^{\prime }v^{\prime } \leftarrow nv} (E_{el}) = \frac{\pi }{2m_eE_{el}} \sum \limits _{ll^{\prime }}\sum \limits _{\lambda \lambda ^{\prime }} \left|S^{\Lambda ,phys}_{n^{\prime }v^{\prime }l^{\prime }\lambda ^{\prime },nvl\lambda }\right|^2. \end{eqnarray}$$

(8)

The cross-sections obtained from (7) and (8) only describe a single scattering event. To better describe conditions in the ISM, kinetic rate coefficients are needed, which rely on the above cross-sections. State-selected kinetic rate coefficients, for DR, RVE, or VE, are obtained following

$$\begin{eqnarray} \alpha _k(T) = \frac{ \int \limits _0^\infty \sigma (E_{el}) \sqrt{2E_{el}/m_e} \sqrt{E_{el}} e^{-E_{el}/kT} \mathrm{ d}E_{el} }{\int \limits _0^\infty \sqrt{E_{el}} e^{-E_{el}/kT} \mathrm{ d}E_{el}}, \end{eqnarray}$$

(9)

where k is the Boltzmann constant and σ is a cross-section. In practice, these integrals are carried out numerically. Additionally, one can average the state-selected rate coefficients obtained from (9) by

$$\begin{eqnarray} \overline{\alpha }_k(T) = \frac{ \sum \limits _{i} \alpha _k^i(T) (2j_i+1) e^{-E_{i}/kT} }{ \sum \limits _{i} (2j_i+1) e^{-E_{i}/kT} }, \end{eqnarray}$$

(10)

where i indexes starting channels where the total angular momentum quantum number of the ion is j_i. The rate coefficient (DR or (R)VE), starting from some channel indexed by i and obtained with (9), is given by |$\alpha _k^i(T)$|⁠. If |$\alpha _k^i(T)$| is a rate coefficient without rotational resolution, j_i can be taken to be zero in (10).

The precision of theoretical cross-sections are only limited by the numerical precision of the calculations. Experimental measurements have much larger uncertainties, so comparisons are often made by convolving theoretical results with experimental parameters. The convolution function differs for every experimental set-up, but Gaussian functions are fairly common:

$$\begin{eqnarray} \overset{\sim }{\sigma }(E) = \frac{ \int \mathrm{ d}E \sigma (E_{el}) e^{-\left(E_{el}-E\right)^2/(2\gamma ^2) } }{ \int \mathrm{ d}E e^{-\left(E_{el}-E\right)^2/(2\gamma ^2)} } \end{eqnarray}$$

(11)

$$\begin{eqnarray} \overset{\sim }{\sigma }(E) = \frac{1}{\gamma \sqrt{2\pi }} \int \mathrm{ d}E \sigma (E_{el}) e^{-\left(E_{el}-E\right)^2/ (2\gamma ^2) }. \end{eqnarray}$$

(12)

The parameter γ is the convolution width (in the same energy units as the electron energy grid). The pre-factor in (12) is the analytic expression of the denominator in (11). Because calculations are performed numerically on pre-determined grids of scattering energies, (12) and (11) may give different results near the endpoints.

3 RATE COEFFICIENTS FOR DISSOCIATIVE RECOMBINATION

Fig. 1 compares state-selected kinetic DR rate coefficients obtained with the present method (Forer et al. 2023). DR and RVE are related in the sense that they are competing processes. During a collision between an ion and an electron, if the initial channel is not the only open channel, both processes may take place. This is why we take the DR probability to be the probability that no RVE occurs. Therefore, DR results exhibiting a certain level of agreement with experimental results would suggest that RVE is described, overall, with similar accuracy. The present method produces much more accurate kinetic DR rate coefficients than the previous theoretical results of Mezei et al. (2019) when compared to recent measurements made at the CSR (Paul et al. 2022) over most displayed temperatures (10–10 000 K). The inset shows the rate coefficient over typical astrophysically relevant temperatures for diffuse clouds, about 40–130 K (Shull, Danforth & Anderson 2021), although temperatures above 1000 K are likely important in the case of CH⁺ (Falgarone & Puget 1995; Myers, McKee & Li 2015).

Figure 1.

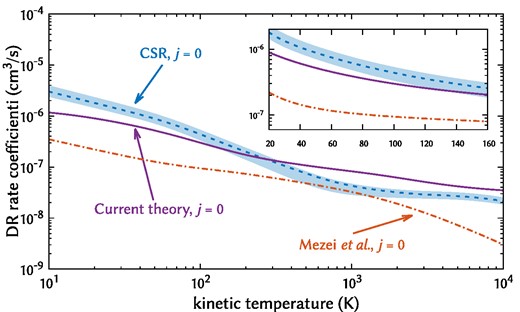
State-selected DR cross-sections from the ground vibronic state of CH⁺. The solid line was obtained with (9) using the theoretical DR cross-sections obtained with the current method (Forer et al. 2023). The dashed line with an error-curve represents recent experimental data (Paul et al. 2022). The dot–dashed line represents previous calculations (Mezei et al. 2019).

Open in new tab Download slide

4 ON THE COULOMB-BORN APPROXIMATION FOR ROTATIONAL AND VIBRATIONAL (DE-)EXCITATION

The dipole moment of CH⁺ – present in the molecular centre-of-mass about which the molecule rotates – couples partial waves of Δl = ±1, which reduces the accuracy of our partial wave basis (l = 0–2) for such a long-range process as RE. We include the effect of higher partial waves in the Coulomb-Born approximation (Boikova & Ob’edkov 1968; Chu & Dalgarno 1974; Gailitis 1976), similar to the method described in the work of Rabadán & Tennyson (1998), by calculating three different cross-sections: cross-sections obtained from our R-matrix method (σ^R-mat, calculated according to 7), total cross-sections obtained in the Coulomb-Born approximation representing the contribution of all partial waves (σ^TCB, 16), and partial cross-sections obtained in the Coulomb-Born approximation representing the contribution of the partial waves included in our basis (σ^PCB, 14). The final rovibrational excitation cross-sections are then a sum of the R-matrix cross-sections and the difference between the total and partial Coulomb-Born cross-sections, i.e.

$$\begin{eqnarray} \sigma ^\text{RVE} = \sigma ^\text{R-mat} + \sigma ^\text{TCB}-\sigma ^\text{PCB}. \end{eqnarray}$$

(13)

Lower partial-wave scattering is typically not well described by the Coulomb-Born approximation because the electron is too close to the molecule for the dipole interaction to be considered a perturbation. This is especially true for s-wave scattering. Therefore, we replace the l = 0–2 partial wave contribution from the Coulomb-Born approximation with those in our R-matrix calculations. The partial Coulomb-Born cross-sections are given by

$$\begin{eqnarray} \sigma ^\text{PCB}_{j^{\prime }v^{\prime }\leftarrow jv} &=& 16 \pi \frac{k^{\prime }}{k} \left|\mathinner {\langle {v^{\prime }|Q_\xi (R)|v}\rangle }\right|^2 \frac{2j^{\prime }+1}{2\xi +1} {{\begin{pmatrix}j&j^{\prime }&\xi \\ 0&0&0 \end{pmatrix}}} ^2 \\ && \times \, \sum \limits _{ll^{\prime }}^{l_\text{max}} (2l+1)(2l^{\prime }+1) {{\begin{pmatrix}l&l^{\prime }&\xi \\ 0&0&0 \end{pmatrix}}}^2\left|M_{ll^{\prime }}^\xi \right|^2, \end{eqnarray}$$

(14)

where l_max = 2 because our R-matrix calculations only include up to l = 2 partial waves. The dipole moment function is given by Q_ξ(R) and the matrix elements |$M^\xi _{ll^{\prime }}$| are given by

$$\begin{eqnarray} M^{\xi }_{ll^{\prime }} = \frac{1}{kk^{\prime }} \int \limits _0^\infty \mathrm{ d}r F_l(\eta ,r) r^{-\xi -1} F_{l^{\prime }}(\eta ^{\prime },r), \end{eqnarray}$$

(15)

where F_l(η, r) is the regular radial Coulomb function, η = −1/k, and η′ = −1/k′.

For an approach that does not treat vibration, the integral |$\mathinner {\langle {v^{\prime }|Q_\xi (R)|v}\rangle }$| in (14) can be replaced with the dipole moment at the equilibrium geometry of the ion. Considering the dipolar coupling (ξ = 1), the partial Coulomb-Born cross-sections (14) converge to the following as l_max → ∞:

$$\begin{eqnarray} \sigma ^\text{TCB}_{j^{\prime }v^{\prime }\leftarrow jv} = \frac{8}{3}\frac{\pi ^3}{k^2} \left|\mathinner {\langle {v^{\prime }|Q_\xi (R)|v}\rangle }\right|^2 (2j^{\prime }+1) {{\begin{pmatrix}j&j^{\prime }&1 0&0&0 \end{pmatrix}}}^2 f(\eta ,\eta ^{\prime }), \\ \end{eqnarray}$$

(16)

where

$$\begin{eqnarray} && f(\eta ,\eta ^{\prime }) = \frac{e^{2\pi \eta }}{(e^{2\pi \eta }-1)(e^{2\pi \eta ^{\prime }}-1)} \chi _0 \frac{d}{d\chi _0} \left|{}_2F_1(-i\eta ,-i\eta ^{\prime };1;\chi _0)\right|^2,\\ && \zeta = \eta ^{\prime }-\eta , \quad \chi _0 = -4 \eta \eta ^{\prime }/\zeta ^2. \end{eqnarray}$$

(17)

The function ₂F₁(a, b; c; z) is the Gaussian hypergeometric function defined as

$$\begin{eqnarray} {}_2F_1(a,b;c;z) = \sum \limits _{n=0}^\infty \frac{(a)_n(b)_n}{(c)_n}, \quad (q)_n = \frac{\Gamma (q+n)}{\Gamma (q)}. \end{eqnarray}$$

(18)

When calculating the partial Coulomb-Born cross-section σ^PCB in (13) and (14), the upper limit in the integral of (15) was not chosen to be infinity, but instead to the value at which the R-matrix amplitudes and, correspondingly, the cross-section σ^R-mat in (13) were computed. We also note that the cross-section σ^PCB is sensitive to the choice of the upper limit in the integral of (15), unless the limit is of the order of ∼1000 bohr or larger. However, the correction σ^PCB in equation (13) is small and the ambiguity in the choice of the upper limit of integral (15) does not significantly influence the cross-section σ^RVE. It should be further noted that we only include the Coulomb-Born correction to Δj = ±1 transitions; our Δj = ±2 transitions are obtained purely from our R-matrix method. For further detail in computing (17), we invite the reader to read the work of Chu & Dalgarno (1974). Additionally, the work of Rabadán & Tennyson (1998) contains minor errors (non-squared Wigner 3-j symbols) in their equations (3) and (4), which are corrected here.

5 RATE COEFFICIENTS FOR ROVIBRONIC (DE-)EXCITATION

Fig. 2 shows the VE rate coefficients obtained by the present method. The corresponding state-selected kinetic rate coefficients agree well with those of Jiang et al. (2019), as shown in Fig. 2. In Fig. 3, we compare the present VE rate coefficients to the same work, starting from the ground vibronic state to the first excited electronic state. The agreement is worse for excitation between electronic states, possibly due to our improved treatment of channels attached to the excited electronic states. Fig. 4 shows the present RE cross-sections convolved with a Gaussian distribution according to (11,12) with widths (γ) of 1 and 5 meV to demonstrate the smoothing out of resonances and to compare their overall magnitude. The Δj = ±1 transition is the largest over all displayed electron energies (<1 eV), as expected for such a strongly dipolar system as CH⁺. Fig. 5 shows the individual cross-sections of (13), which show an increasing correction as a function of the incident electron energy. The σ^RVE and σ^R-mat cross-sections are not convolved, unlike Fig. 4.

Figure 2.

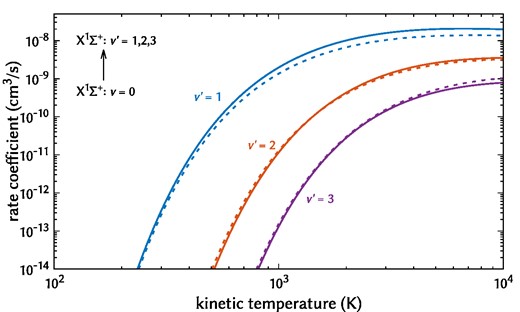
State-selected kinetic VE rate coefficients within the ground electronic state of CH⁺. The solid lines represent rate coefficients from the present calculations, and the dashed lines are taken from a previous calculation (Jiang et al. 2019). The cross-sections are obtained according to (8) and the kinetic rates are obtained according to (9).

Open in new tab Download slide

Figure 3.

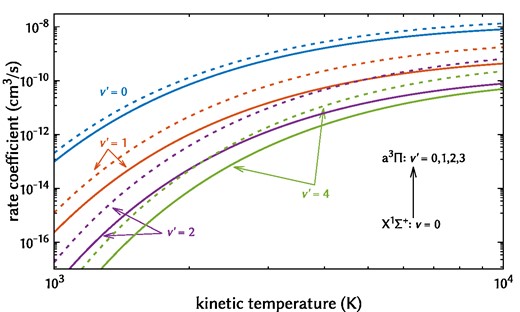
State-selected kinetic VE rate coefficients from the ground electronic state of CH⁺ to the first excited state of CH⁺. The solid lines represent rate coefficients from the present calculations, and the dashed lines are taken from a previous calculation (Jiang et al. 2019). The cross-sections are obtained according to (8) and the kinetic rates are obtained according to (9).

Open in new tab Download slide

Figure 4.

RE cross-sections within the ground vibronic state of CH⁺. The cross-sections are obtained according to (7), and convolved with a Gaussian as per (11) with γ = 1 meV (thin lines) and γ = 5 meV (thick lines).

Open in new tab Download slide

Figure 5.

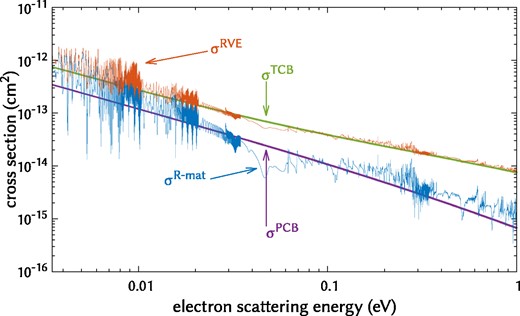
Comparison of cross-sections for RE j = 0 → j′ = 1 obtained using the R-matrix approach with s, p, and d partial waves (σ^R-mat) and the closed-form total Coulomb-Born approximation (σ^TCB). The figure shows also the partial Coulomb-Born cross-section obtained with s, p, and d partial waves (σ^PCB) and the cross-section where the R matrix data are combined with the total Coulomb-Born cross-section accounting for partial wave with l > 2 (σ^RVE).

Open in new tab Download slide

Fig. 6 compares the present RE rate coefficients with those obtained by Hamilton, Faure & Tennyson (2015), who included the Coulomb-Born correction for Δj = ±1, ±2 transitions. We only include this correction for Δj = ±1 transitions, but the agreement between the results is good overall. Hamilton, Faure & Tennyson (2015) also use an R-matrix approach, but use the adiabatic-nuclei-rotation approximation to obtain RE cross-sections and rate coefficients, while we use a frame transformation (4) to describe the rotational structure of the ion. Fig. 7 illustrates the difference between the state-selected RE rates with and without the Coulomb-Born approximation, compared to the experimentally determined RE rate coefficient at the CSR (Kálosi et al. 2022) and again to the results of Hamilton, Faure & Tennyson (2015). Our present results with the Coulomb-Born correction show the best overall agreement with the CSR measurements, although all theoretical rates are within the provided 1σ uncertainty for most of the kinetic temperatures shown (10–140 K).

Figure 6.

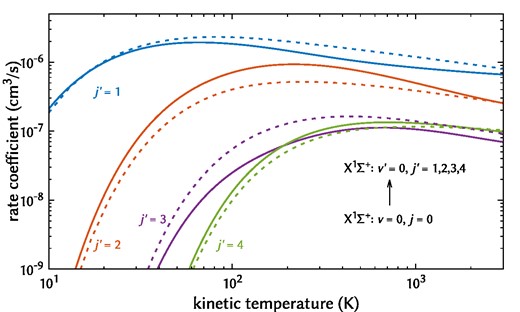
State-selected kinetic RE rate coefficients within the ground vibronic state of CH⁺. The solid lines represent the present theory, and the dashed lines represent the results of Hamilton, Faure & Tennyson (2015).

Open in new tab Download slide

Figure 7.

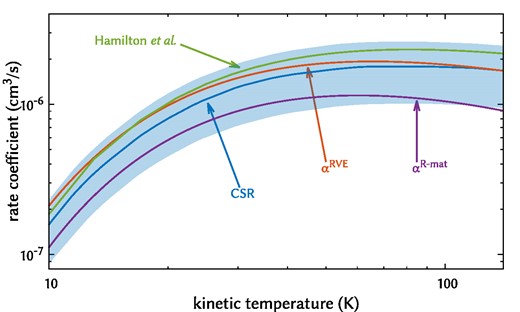
State-selected kinetic RE rate coefficients from j = 0 to j′ = 1 within the ground vibronic state of CH⁺. The measured rates coefficients from the CSR (Kálosi et al. 2022) are compared to the results of Hamilton, Faure & Tennyson (2015) and our kinetic rate coefficients with (α^RVE) and without (α^R-mat) the Coulomb-Born correction.

Open in new tab Download slide

6 CONCLUSIONS

This paper presents kinetic state-selected DR, VE, and RE rate coefficients obtained with our DR method (Forer et al. 2023), which also allows us to calculate RVE cross-sections and rate coefficients with little extra effort. The DR rate coefficients agree well overall with recent experimental measurements made at the CSR (Paul et al. 2022) and better than previous theoretical treatments. Our VE rate coefficients, compared to the work of Jiang et al. (2019), agree well for vibrational excitation within the ground electronic state of CH⁺. However, the results differ by up to an order of magnitude for VE to the first excited state of CH⁺, which we attribute to a more accurate description of channels attached to excited electronic states (Forer et al. 2023).

We also obtain RE rate coefficients within the ground electronic state of CH⁺, which we compare to the work of Hamilton, Faure & Tennyson (2015) which is an R-matrix method that describes RE with the adiabatic-nuclei-rotation approximation and does not treat vibration. They correct their Δj = ±1, ±2 transitions with the Coulomb-Born approximation, while we only do so for Δj = ±1 transitions. Results between our approaches agree well over the presented kinetic temperatures. Compared to j = 0 → j′ = 1 rate coefficients recently measured at the CSR (Kálosi et al. 2022), our theoretical results using the Coulomb-Born correction agree better over all plotted kinetic temperatures than our theoretical results without the Coulomb-Born correction, and slightly better than the recent theoretically determined rate coefficients of Hamilton, Faure & Tennyson (2015) over most kinetic temperatures between 10 and 140 K. However, all theoretically determined rates under 100 K are within the experimental uncertainty.

ACKNOWLEDGEMENTS

We are thankful for the support from the National Science Foundation, Grant Nos. 2110279 (UCF) and 2102187 (Purdue), the Fulbright-University of Bordeaux Doctoral Research Award, and the program ‘Accueil des chercheurs étrangers’ of CentraleSupélec. VK acknowledges the help of Yaroslav Kokoulin with the development of the code for the Coulomb-Born approximation.

DATA AVAILABILITY

State-selected kinetic rate coefficients from the present calculations are included in the supplementary materials.

References

Adams

W. S.

1941

ApJ

Month:	Total Views:
November 2023	21
December 2023	66
January 2024	71
February 2024	28
March 2024	57
April 2024	9
May 2024	23
June 2024	45
July 2024	13
August 2024	23
September 2024	24
October 2024	24
November 2024	8
December 2024	11
January 2025	8
February 2025	14
March 2025	17
April 2025	19
May 2025	8

Article Contents

Kinetic rate coefficients for electron-driven collisions with CH+: dissociative recombination and rovibronic excitation Open Access

ABSTRACT

1 INTRODUCTION

2 THEORETICAL APPROACH

3 RATE COEFFICIENTS FOR DISSOCIATIVE RECOMBINATION

4 ON THE COULOMB-BORN APPROXIMATION FOR ROTATIONAL AND VIBRATIONAL (DE-)EXCITATION

5 RATE COEFFICIENTS FOR ROVIBRONIC (DE-)EXCITATION

6 CONCLUSIONS

ACKNOWLEDGEMENTS

DATA AVAILABILITY

References

Supplementary data

Citations

Views

Altmetric

Email alerts

See also

Companion Article

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Kinetic rate coefficients for electron-driven collisions with CH⁺: dissociative recombination and rovibronic excitation