-
PDF
- Split View
-
Views
-
Cite
Cite
Efrain Gatuzz, T W Gorczyca, M F Hasoglu, E Costantini, Javier A García, Timothy R Kallman, Sulphur X-ray absorption in the local ISM, Monthly Notices of the Royal Astronomical Society, Volume 527, Issue 2, January 2024, Pages 1648–1655, https://doi.org/10.1093/mnras/stad3231
Close - Share Icon Share
ABSTRACT
We present a study S K-edge using high-resolution HETGS Chandra spectra of 36 low-mass X-ray binaries. For each source, we have estimated column densities for S i, S ii, S iii, S xiv, S xv, and S xvi ionic species, which trace the neutral, warm, and hot phases of the Galactic interstellar medium. We also estimated column densities for a sample of interstellar dust analogues. We measured their distribution as a function of Galactic latitude, longitude, and distances to the sources. While the cold-warm column densities tend to decrease with the Galactic latitude, we found no correlation with distances or Galactic longitude. This is the first detailed analysis of the sulphur K-edge absorption due to ISM using high-resolution X-ray spectra.
1 INTRODUCTION
The interstellar medium (ISM) is one of the essential components in Galactic dynamics because it regulates the star life cycles as well as cooling and Galactic star formation rates (Wong & Blitz 2002; Bigiel et al. 2008; Leroy et al. 2008; Lada, Lombardi & Alves 2010; Lilly et al. 2013). Defined as gas and dust between stars, the ISM shows multiple phases characterized by different gas temperatures, which vary from 10 to 106 K (e.g. McKee & Ostriker 1977; Falgarone et al. 2005; Tonnesen & Bryan 2009; Draine 2011; Jenkins & Tripp 2011; Rupke & Veilleux 2013; Zhukovska et al. 2016; Stanimirović & Zweibel 2018).
Such a complex environment can be analysed using the high-resolution X-ray spectroscopy technique. Bright X-ray sources, acting as lamps, are required to carry out such an analysis. The physical properties of the gas between the observer and the source are studied by modelling the absorption features identified in the X-ray spectra. In the last decade, the O, Fe, Ne, Mg, N, and Si K absorption edges associated with the ISM have been analysed by applying this method (Pinto et al. 2010, 2013; Costantini et al. 2012; Gatuzz et al. 2013a, b, 2014, 2015, 2016; Joachimi et al. 2016; Gatuzz & Churazov 2018; Gatuzz et al. 2018a, b; Gatuzz, García & Kallman 2019; Zeegers et al. 2019; Gatuzz et al. 2020a; Psaradaki et al. 2020; Gatuzz, García & Kallman 2021; Rogantini et al. 2021; Yang et al. 2022; Gatuzz et al. 2023).
Sulphur constitutes an excellent diagnostic tool for studying various astrophysical environments, although its chemistry still needs to be fully understood (Laas & Caselli 2019). Sulphur remains in ionized atomic form within primitive ISM environments (Savage & Sembach 1996; Jenkins 2009). Sulphur-bearing molecules probe the physical structure of star-forming regions (Lada, Bally & Stark 1991; Plume et al. 1997). Depletion into dust grains has been proposed due to the drastic reduction of the cosmic sulphur abundance in molecular clouds (Keller et al. 2002; Scappini et al. 2003; Wakelam et al. 2004).
Here, we present an S K-edge absorption region analysis using Chandra observation of low-mass X-ray binaries (LMXBs). Section 2 describes the data sample and spectral fitting procedure. Section 3 describes the atomic data calculation and photoabsorption cross-sections included in the modelling. Section 4 discusses the results obtained from the fits. Finally, we summarize the main results of our analysis in Section 5.
2 X-RAY OBSERVATIONS AND SPECTRAL FITTING
We analyse Chandra spectra of 36 LMXBs along different lines of sight. To build our sample, we have selected those sources for which we have at least 1000 counts in the sulphur edge absorption region (4.5–5.5 Å). To get an unbiased sample, we did not impose any constraints on the significance of the detection for a particular line (e.g. S xvi K α detection). Table 1 shows the specifications of the sources, including Galactic coordinates, hydrogen column densities taken from Willingale et al. (2013), and distances, if available. We note that Willingale et al. (2013) column densities correspond to N(H i + H2) average values along line of sights, covering all material in the galaxy. However, they can be safely used because our analysis covers a small wavelength region (∼1 Å).
| Source . | Galactic . | Distance . | N(H i + H2) . |
|---|---|---|---|
| . | Coordinates . | (kpc) . | . |
| 4U 0614 + 091 | (200.88, −3.36) | |$2.2 _{ -0.7 }^{ +0.8 }$|a | 5.86 |
| 4U 1254 − 690 | (303.48, −6.42) | 13 ± 3b | 3.46 |
| 4U 1630 − 472 | (336.91, 0.25) | 4c | 17.6 |
| 4U 1636 − 53 | (332.92, −4.82) | 6 ± 0.5d | 4.04 |
| 4U 1702 − 429 | (343.89, −1.32) | 6.2 ± 0.9e | 12.3 |
| 4U 1705 − 44 | (343.32, −2.34) | 8.4 ± 1.2e | 8.37 |
| 4U 1728 − 16 | (8.51, 9.04) | 4.4c | 3.31 |
| 4U 1728 − 34 | (354.30, −0.15) | 5.3 ± 0.8e | 13.9 |
| GX 9 + 9 | (8.51, 9.04) | 4.4c | 3.31 |
| H1743 − 322 | (357.26, −1.83) | 10.4 ± 2.9f | 8.31 |
| IGRJ17091 − 3624 | (349.52, 2.21) | − | 7.72 |
| NGC 6624 | (2.79, −7.91) | 7g | 2.33 |
| EXO 1846 − 031 | (29.96, −0.92) | − | 13.9 |
| GRS 1758 − 258 | (4.51, −1.36) | 8.5c | 9.03 |
| GRS 1915 + 105 | (45.37, −0.22) | |$11 _{ -4 }^{ +1 }$|e | 15.1 |
| GS 1826 − 238 | (9.27, −6.09) | 7.5 ± 0.5h | 3.00 |
| GX 13 + 1 | (13.52, 0.11) | 7 ± 1i | 13.6 |
| GX 17 + 2 | (16.43, 1.28) | |$14 _{ -2.1 }^{ +2 }$|e | 10.0 |
| GX 3 + 1 | (2.29, 0.79) | |$5 _{ -0.7 }^{ +0.8 }$|j | 10.7 |
| GX 339 − 4 | (338.94, −4.33) | |$10 _{ -4 }^{ +5 }$|k | 5.18 |
| GX 340 + 0 | (339.59, −0.08) | 11c | 20.0 |
| GX 349 + 2 | (349.10, 2.75) | 9.2c | 6.13 |
| GX 354 + 0 | (354.30, −0.15) | 5.3 ± 0.8e | 13.9 |
| GX 5 − 1 | (5.08, −1.02) | 0.21 ± 0.01l | 10.4 |
| V4641 Sgr | (6.77, −4.79) | − | 3.23 |
| X1543 − 62 | (321.76, −6.34) | 7m | 3.79 |
| X1822 − 371 | (356.85, −11.29) | 2.5 ± 0.5n | 1.40 |
| XTEJ1814 − 338 | (358.75, −7.59) | − | 2.29 |
| 4U 1735 − 44 | (346.05, −6.99) | 9.4 ± 1.4e | 3.96 |
| GX 9 + 1 | (9.08, 1.15) | 4.4 ± 1.3o | 9.89 |
| 4U 1916 − 053 | (31.36, −8.46) | 8.8 ± 1.3e | 3.72 |
| 4U 1957 + 11 | (51.31, −9.33) | − | 2.01 |
| A1744-361 | (354.12, −4.19) | 9p | 4.44 |
| Cir X−1 | (322.12, 0.04) | |$9.2 _{ -1.4 }^{ +1.3 }$| | 16.4 |
| Cyg X−2 | (87.33, −11.32) | |$13.4 _{ -2 }^{ +1.9 }$|e | 3.09 |
| Ser X−1 | (36.12, 4.84) | 11.1 ± 1.6e | 5.42 |
| Source . | Galactic . | Distance . | N(H i + H2) . |
|---|---|---|---|
| . | Coordinates . | (kpc) . | . |
| 4U 0614 + 091 | (200.88, −3.36) | |$2.2 _{ -0.7 }^{ +0.8 }$|a | 5.86 |
| 4U 1254 − 690 | (303.48, −6.42) | 13 ± 3b | 3.46 |
| 4U 1630 − 472 | (336.91, 0.25) | 4c | 17.6 |
| 4U 1636 − 53 | (332.92, −4.82) | 6 ± 0.5d | 4.04 |
| 4U 1702 − 429 | (343.89, −1.32) | 6.2 ± 0.9e | 12.3 |
| 4U 1705 − 44 | (343.32, −2.34) | 8.4 ± 1.2e | 8.37 |
| 4U 1728 − 16 | (8.51, 9.04) | 4.4c | 3.31 |
| 4U 1728 − 34 | (354.30, −0.15) | 5.3 ± 0.8e | 13.9 |
| GX 9 + 9 | (8.51, 9.04) | 4.4c | 3.31 |
| H1743 − 322 | (357.26, −1.83) | 10.4 ± 2.9f | 8.31 |
| IGRJ17091 − 3624 | (349.52, 2.21) | − | 7.72 |
| NGC 6624 | (2.79, −7.91) | 7g | 2.33 |
| EXO 1846 − 031 | (29.96, −0.92) | − | 13.9 |
| GRS 1758 − 258 | (4.51, −1.36) | 8.5c | 9.03 |
| GRS 1915 + 105 | (45.37, −0.22) | |$11 _{ -4 }^{ +1 }$|e | 15.1 |
| GS 1826 − 238 | (9.27, −6.09) | 7.5 ± 0.5h | 3.00 |
| GX 13 + 1 | (13.52, 0.11) | 7 ± 1i | 13.6 |
| GX 17 + 2 | (16.43, 1.28) | |$14 _{ -2.1 }^{ +2 }$|e | 10.0 |
| GX 3 + 1 | (2.29, 0.79) | |$5 _{ -0.7 }^{ +0.8 }$|j | 10.7 |
| GX 339 − 4 | (338.94, −4.33) | |$10 _{ -4 }^{ +5 }$|k | 5.18 |
| GX 340 + 0 | (339.59, −0.08) | 11c | 20.0 |
| GX 349 + 2 | (349.10, 2.75) | 9.2c | 6.13 |
| GX 354 + 0 | (354.30, −0.15) | 5.3 ± 0.8e | 13.9 |
| GX 5 − 1 | (5.08, −1.02) | 0.21 ± 0.01l | 10.4 |
| V4641 Sgr | (6.77, −4.79) | − | 3.23 |
| X1543 − 62 | (321.76, −6.34) | 7m | 3.79 |
| X1822 − 371 | (356.85, −11.29) | 2.5 ± 0.5n | 1.40 |
| XTEJ1814 − 338 | (358.75, −7.59) | − | 2.29 |
| 4U 1735 − 44 | (346.05, −6.99) | 9.4 ± 1.4e | 3.96 |
| GX 9 + 1 | (9.08, 1.15) | 4.4 ± 1.3o | 9.89 |
| 4U 1916 − 053 | (31.36, −8.46) | 8.8 ± 1.3e | 3.72 |
| 4U 1957 + 11 | (51.31, −9.33) | − | 2.01 |
| A1744-361 | (354.12, −4.19) | 9p | 4.44 |
| Cir X−1 | (322.12, 0.04) | |$9.2 _{ -1.4 }^{ +1.3 }$| | 16.4 |
| Cyg X−2 | (87.33, −11.32) | |$13.4 _{ -2 }^{ +1.9 }$|e | 3.09 |
| Ser X−1 | (36.12, 4.84) | 11.1 ± 1.6e | 5.42 |
| Source . | Galactic . | Distance . | N(H i + H2) . |
|---|---|---|---|
| . | Coordinates . | (kpc) . | . |
| 4U 0614 + 091 | (200.88, −3.36) | |$2.2 _{ -0.7 }^{ +0.8 }$|a | 5.86 |
| 4U 1254 − 690 | (303.48, −6.42) | 13 ± 3b | 3.46 |
| 4U 1630 − 472 | (336.91, 0.25) | 4c | 17.6 |
| 4U 1636 − 53 | (332.92, −4.82) | 6 ± 0.5d | 4.04 |
| 4U 1702 − 429 | (343.89, −1.32) | 6.2 ± 0.9e | 12.3 |
| 4U 1705 − 44 | (343.32, −2.34) | 8.4 ± 1.2e | 8.37 |
| 4U 1728 − 16 | (8.51, 9.04) | 4.4c | 3.31 |
| 4U 1728 − 34 | (354.30, −0.15) | 5.3 ± 0.8e | 13.9 |
| GX 9 + 9 | (8.51, 9.04) | 4.4c | 3.31 |
| H1743 − 322 | (357.26, −1.83) | 10.4 ± 2.9f | 8.31 |
| IGRJ17091 − 3624 | (349.52, 2.21) | − | 7.72 |
| NGC 6624 | (2.79, −7.91) | 7g | 2.33 |
| EXO 1846 − 031 | (29.96, −0.92) | − | 13.9 |
| GRS 1758 − 258 | (4.51, −1.36) | 8.5c | 9.03 |
| GRS 1915 + 105 | (45.37, −0.22) | |$11 _{ -4 }^{ +1 }$|e | 15.1 |
| GS 1826 − 238 | (9.27, −6.09) | 7.5 ± 0.5h | 3.00 |
| GX 13 + 1 | (13.52, 0.11) | 7 ± 1i | 13.6 |
| GX 17 + 2 | (16.43, 1.28) | |$14 _{ -2.1 }^{ +2 }$|e | 10.0 |
| GX 3 + 1 | (2.29, 0.79) | |$5 _{ -0.7 }^{ +0.8 }$|j | 10.7 |
| GX 339 − 4 | (338.94, −4.33) | |$10 _{ -4 }^{ +5 }$|k | 5.18 |
| GX 340 + 0 | (339.59, −0.08) | 11c | 20.0 |
| GX 349 + 2 | (349.10, 2.75) | 9.2c | 6.13 |
| GX 354 + 0 | (354.30, −0.15) | 5.3 ± 0.8e | 13.9 |
| GX 5 − 1 | (5.08, −1.02) | 0.21 ± 0.01l | 10.4 |
| V4641 Sgr | (6.77, −4.79) | − | 3.23 |
| X1543 − 62 | (321.76, −6.34) | 7m | 3.79 |
| X1822 − 371 | (356.85, −11.29) | 2.5 ± 0.5n | 1.40 |
| XTEJ1814 − 338 | (358.75, −7.59) | − | 2.29 |
| 4U 1735 − 44 | (346.05, −6.99) | 9.4 ± 1.4e | 3.96 |
| GX 9 + 1 | (9.08, 1.15) | 4.4 ± 1.3o | 9.89 |
| 4U 1916 − 053 | (31.36, −8.46) | 8.8 ± 1.3e | 3.72 |
| 4U 1957 + 11 | (51.31, −9.33) | − | 2.01 |
| A1744-361 | (354.12, −4.19) | 9p | 4.44 |
| Cir X−1 | (322.12, 0.04) | |$9.2 _{ -1.4 }^{ +1.3 }$| | 16.4 |
| Cyg X−2 | (87.33, −11.32) | |$13.4 _{ -2 }^{ +1.9 }$|e | 3.09 |
| Ser X−1 | (36.12, 4.84) | 11.1 ± 1.6e | 5.42 |
| Source . | Galactic . | Distance . | N(H i + H2) . |
|---|---|---|---|
| . | Coordinates . | (kpc) . | . |
| 4U 0614 + 091 | (200.88, −3.36) | |$2.2 _{ -0.7 }^{ +0.8 }$|a | 5.86 |
| 4U 1254 − 690 | (303.48, −6.42) | 13 ± 3b | 3.46 |
| 4U 1630 − 472 | (336.91, 0.25) | 4c | 17.6 |
| 4U 1636 − 53 | (332.92, −4.82) | 6 ± 0.5d | 4.04 |
| 4U 1702 − 429 | (343.89, −1.32) | 6.2 ± 0.9e | 12.3 |
| 4U 1705 − 44 | (343.32, −2.34) | 8.4 ± 1.2e | 8.37 |
| 4U 1728 − 16 | (8.51, 9.04) | 4.4c | 3.31 |
| 4U 1728 − 34 | (354.30, −0.15) | 5.3 ± 0.8e | 13.9 |
| GX 9 + 9 | (8.51, 9.04) | 4.4c | 3.31 |
| H1743 − 322 | (357.26, −1.83) | 10.4 ± 2.9f | 8.31 |
| IGRJ17091 − 3624 | (349.52, 2.21) | − | 7.72 |
| NGC 6624 | (2.79, −7.91) | 7g | 2.33 |
| EXO 1846 − 031 | (29.96, −0.92) | − | 13.9 |
| GRS 1758 − 258 | (4.51, −1.36) | 8.5c | 9.03 |
| GRS 1915 + 105 | (45.37, −0.22) | |$11 _{ -4 }^{ +1 }$|e | 15.1 |
| GS 1826 − 238 | (9.27, −6.09) | 7.5 ± 0.5h | 3.00 |
| GX 13 + 1 | (13.52, 0.11) | 7 ± 1i | 13.6 |
| GX 17 + 2 | (16.43, 1.28) | |$14 _{ -2.1 }^{ +2 }$|e | 10.0 |
| GX 3 + 1 | (2.29, 0.79) | |$5 _{ -0.7 }^{ +0.8 }$|j | 10.7 |
| GX 339 − 4 | (338.94, −4.33) | |$10 _{ -4 }^{ +5 }$|k | 5.18 |
| GX 340 + 0 | (339.59, −0.08) | 11c | 20.0 |
| GX 349 + 2 | (349.10, 2.75) | 9.2c | 6.13 |
| GX 354 + 0 | (354.30, −0.15) | 5.3 ± 0.8e | 13.9 |
| GX 5 − 1 | (5.08, −1.02) | 0.21 ± 0.01l | 10.4 |
| V4641 Sgr | (6.77, −4.79) | − | 3.23 |
| X1543 − 62 | (321.76, −6.34) | 7m | 3.79 |
| X1822 − 371 | (356.85, −11.29) | 2.5 ± 0.5n | 1.40 |
| XTEJ1814 − 338 | (358.75, −7.59) | − | 2.29 |
| 4U 1735 − 44 | (346.05, −6.99) | 9.4 ± 1.4e | 3.96 |
| GX 9 + 1 | (9.08, 1.15) | 4.4 ± 1.3o | 9.89 |
| 4U 1916 − 053 | (31.36, −8.46) | 8.8 ± 1.3e | 3.72 |
| 4U 1957 + 11 | (51.31, −9.33) | − | 2.01 |
| A1744-361 | (354.12, −4.19) | 9p | 4.44 |
| Cir X−1 | (322.12, 0.04) | |$9.2 _{ -1.4 }^{ +1.3 }$| | 16.4 |
| Cyg X−2 | (87.33, −11.32) | |$13.4 _{ -2 }^{ +1.9 }$|e | 3.09 |
| Ser X−1 | (36.12, 4.84) | 11.1 ± 1.6e | 5.42 |
All spectra have been obtained with the high-energy grating (HEG) from the high-energy transmission grating (HETGS) in combination with the Advanced CCD Imaging Spectrometer (ACIS). Observations were reduced using the Chandra Interactive Analysis of Observations (ciao,1 version 4.15.1), including background subtraction and following the standard procedure. All observations were fitted with the xspec package (version 12.11.12) in the 4.5–5.5 Å wavelength region. We modelled the continuum with a powerlaw model. For each source, all observations were fitted simultaneously with γ and the normalization as independent parameters to account for changes in the continuum at different epochs. Finally, we use the χ2 statistics in combination with the Churazov et al. (1996) weighting method.
3 ATOMIC DATA CALCULATION
To fit the S K-edge absorption region, we computed S i-S xiv photoabsorption cross-sections (i.e. Li-like) as follows. From a single-configuration perspective for the inner-shell photoexcitation of the sulphur ground state, the specific processes to be considered are the followings:
This intermediate autoionizing, or resonant, state can decay via two qualitatively different Auger pathways. Firstly, there is participator Auger decay
in which the valence electron np participates in the autoionization process, thus giving a decay rate that scales as 1/n3. On the other hand, secondly spectator Auger decay
proceeds via a stronger, n-independent Auger rate, causing a massive broadening of the entire Rydberg series of resonances below the K-edge. Participator Auger decay is accounted for straightforwardly by explicitly including all final S ii ionic channels in the standard R-matrix implementation (Burke 2011; Berrington, Eissner & Norrington 1995).
A point needs to be made regarding an alternate, and sometimes significant, decay pathway: that of spontaneous core radiative decay. This would occur most strongly, following the above initial photoabsorption, as the alternate 1s2s22p63s23p4np → 1s22s22p63s23p3np + hν decay. However, using the structure and collision code AUTOSTRUCTURE (Badnell 1986, 1997), it has been determined that the fluorescence branching ratio is small, less than 1 per cent, and any minor correction to these Auger Lorentzian widths is eventually washed out once a broader, less-certain X-ray spectral (Gaussian) resolution is considered. Furthermore, even though there exist other R-matrix and/or AUTOSTRUCTURE calculations for the positions and widths of the associated resonances involved, it is not clear how useful a detailed comparison of these would be since there are inherent uncertainties in energy positions due to the variational principle for approximate wavefunctions. And the more important quantity is really the integrated oscillator strength (or cross-section, which tends to give much more accurate Maxwellian (say) rate coefficients as needed in astrophysical plasma modelling.
Present calculations utilize the modified R-matrix method (Berrington, Eissner & Norrington 1995; Burke 2011) to account for the spectator Auger broadening via an optical potential described by Gorczyca & Robicheaux (1999). This enhanced R-matrix method with pseudo-resonance elimination; Gorczyca et al. (1995) has been used in describing experimental synchrotron measurements for argon (Gorczyca & Robicheaux 1999), oxygen (Gorczyca & McLaughlin 2000; Gorczyca et al. 2013), neon (Gorczyca 2000), and carbon (Hasoglu et al. 2010) accurately.
The employed orbital basis consists of physical and pseudo-orbitals to account for relaxation effects following 1s vacancy. For the system with number of electrons in target states N ≥ 10, 1s, 2s, 2p, 3s, 3p, |$\overline{3d}$|, |$\overline{4s}$|, and |$\overline{4p}$| are treated as physical orbitals and pseudo-orbitals, respectively. For the cases N < 10, using only 1s, 2s, and 2p physical orbitals and |$\overline{3s}$|, |$\overline{3p}$|, and |$\overline{3d}$| pseudo-orbitals are found to be sufficient. The physical orbitals are formed by using the Hartree–Fock method, and pseudo-orbitals are optimized by using the multiconfiguration Hartree–Fock method on the configuration lists, including single and double promotions from the 1s-vacancy target state to account for important orbital relaxation effects due to the K-shell vacancy.
To compute Auger widths used for the spectator Auger broadening effects in 1snℓq autoionizing states target states by using the R-matrix method, we rely on Wigner Time Delay Method (Smith 1960), as it was applied in the recent photoabsorption works on C-, Mg-, and Si-isonuclear sequences (Hasoglu et al. 2010; Hasoğlu et al. 2014; Gatuzz et al. 2020c). R-matrix method on e− + 1s2nℓq − 2 scattering problem is employed in the same manner as photoabsorption calculations in terms of basis set and configuration lists. Further details on the significance of spectator Auger broadening effects and application of R-matrix along with the Wigner Time Delay method can be found in the previous works (Gorczyca & Robicheaux 1999; Gorczyca & McLaughlin 2000; Gorczyca 2000; Hasoglu et al. 2010; Gorczyca et al. 2013; Hasoğlu et al. 2014).
3.1 S K-edge photoabsorption cross-sections
We consider the S i, S ii, S iii, and S xiv photoabsorption cross-sections computed as described above in the model. Previously reported K-absorption (1s → np) cross-sections of sulphur ionized species for N < 11 and N ≥ 11 were computed by Witthoeft et al. (2009, 2011), respectively, by utilizing a similar R-matrix approach with inclusion of Auger broadening effects. However, important orbital relaxation effects were neglected due to the fact that the single-electron orbitals were obtained by using a Thomas–Fermi–Dirac statistical model potential. Inclusion of relaxation effects primarily becomes important due to the change in the potential perceived by the outer electrons upon an excitation or ionization of an electron from the K-shell; this change in potential strength becomes more significant for low-charged ions. In particular, S ii is expected to be the most affected by relaxation effects, as evidenced by the K-shell threshold being overestimated by approximately 7 eV (see Fig. 1). Previous calculations for N < 11 by Witthoeft et al. (2009) were performed using the Breit–Pauli R-matrix method that showed significant fine-structure splitting of resonance series (see fig. 1 for S xiv), which are included here. However, such relatively small shifts in energy are essentially washed out of any convolution as needed for plasma modelling.
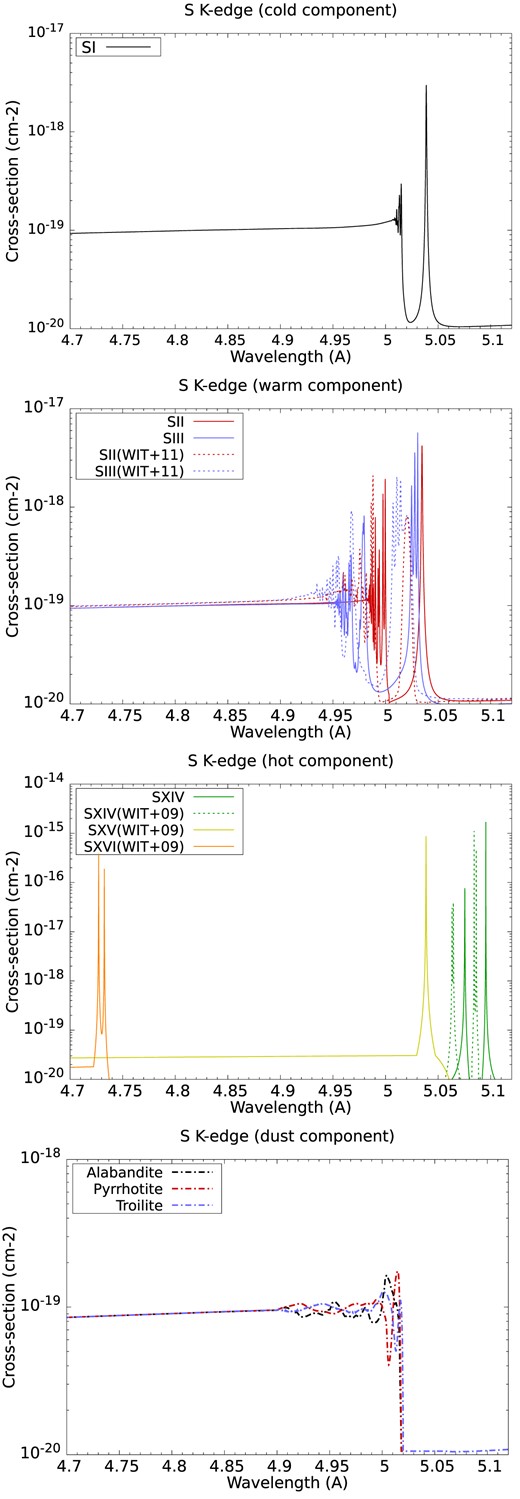
Photoabsorption cross-sections included in the model for S i (top panel), S ii, S iii (second panel), S xiv, S xv, and S xvi (third panel) and three samples of interstellar dust analogues, namely alabandite, pyrrhotite, and troilite (bottom panel). Photoabsorption cross-sections, previously computed by Witthoeft et al. (2009), Witthoeft et al. (2011), are also shown. While the general profiles are quite similar, differences exist in the K-edge positions between the two calculations because orbital relaxation effects are considered in this work for generating a basis tailored to inner-shell ionization.
We have also included extinction cross-sections (i.e. absorption + scattering) for three samples of interstellar dust analogues, namely alabandite, pyrrhotite, and troilite, measured by Costantini et al. (2019). Fig. 1 shows the sulphur photoabsorption cross-sections considered in the model, which takes into account the cold (top panel), warm (second panel), hot (third panel), and dust (bottom panel) phases of the ISM. Photoabsorption cross-sections computed by Witthoeft et al. (2009, 2011) are also included.
We included these cross-sections in a modified version of the ISMabs model (Gatuzz et al. 2015) to model the S K-edge. In this way, the column densities for the ionic species of interest are free parameters in the spectral fitting. For each source, we fixed the H iISMabs column densities to the values provided by Willingale et al. (2013). Given the spectral resolution of the instrument, we note that a detailed benchmarking of the doublet/triplet resonance line positions (see Fig. 1) cannot be performed. For example, for the S iii K α resonance lines, we have a separation of Δλ ∼ 5 mÅ while the nominal HEG resolution is Δλ ∼ 12 mÅ. For example, Fig. 2 shows the best fit obtained for the LMXB GX13 + 1. Black points correspond to the observation in flux units, while the red line corresponds to the best-fitting model. Residuals are included in units of (data − model)/error. The position of the K α absorption lines for the gaseous component is indicated for each ion, following the colour code used in Fig. 1.
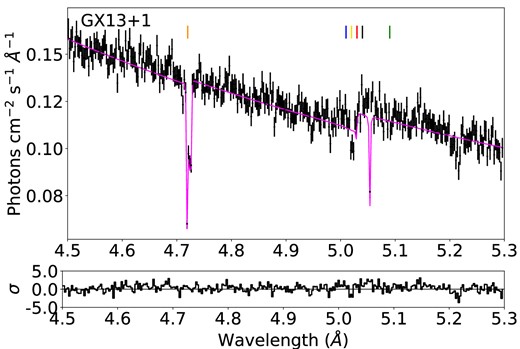
Best-fitting results in the S K-edge photoabsorption region for the LMXB GX13 + 1. The black data points correspond to the observations (in flux units and combined for illustrative purposes), while the solid red line corresponds to the best-fitting model. The position of the K α absorption lines are indicated for each ion, following the colour code used in Fig. 1.
4 RESULTS AND DISCUSSION
Table 2 shows the best-fitting results. We have found good fits to the observed sulphur K-edge spectra for all observations. We noted that for most of the sources, we had obtained upper limits for the relevant parameters, including the dust component. We identified the different phases of the gaseous ISM as cold (S i), warm (S ii + S iii), hot (S xiv + S xv + S xvi), and dust (alabandite + pyrrohtite + troilite). The best-fitting column densities obtained are shown in Fig. 3. We note that the column densities between the different gaseous phases are in the same range, while the dust column densities tend to be much lower than the cold component.
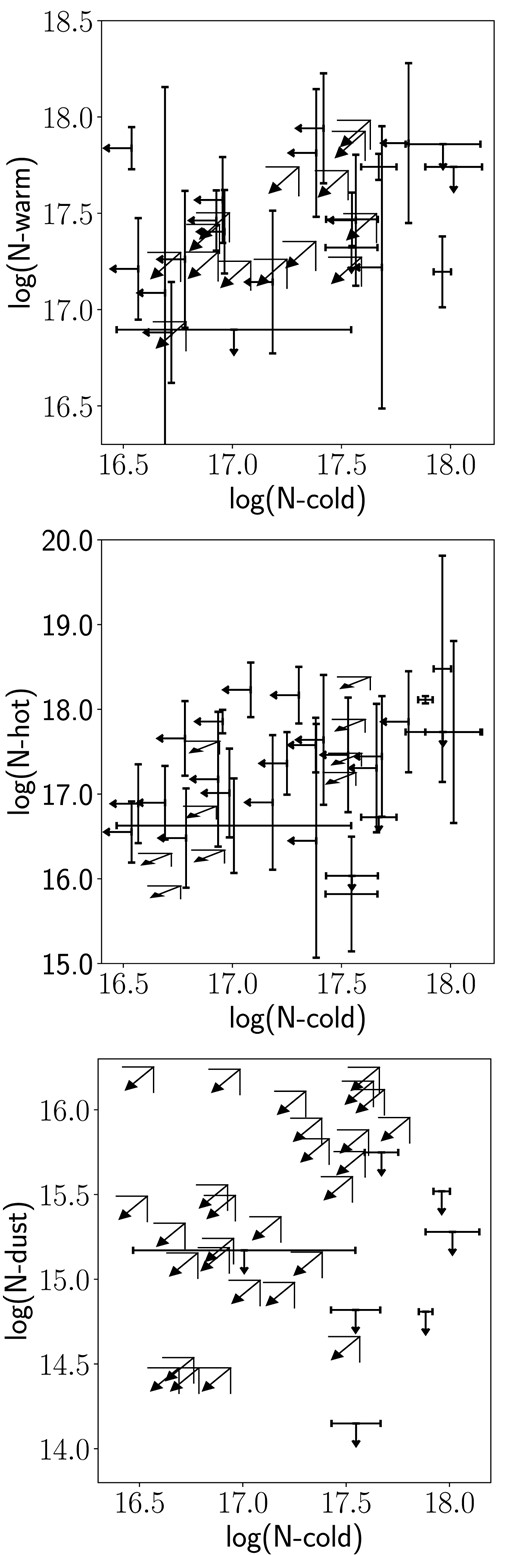
Best-fitting column densities for the cold (S i), warm (S ii + S iii), hot (S xiv + S xv + S xvi), and dust ISM phases.
| Source . | S i . | S ii . | S iii . | S xiv . | S xv . | S xvi . | Alabandite . | Pyrrohtite . | Troilite . | χ2/d.of. . |
|---|---|---|---|---|---|---|---|---|---|---|
| 4U0614 + 091 | <15.3 | <7.3 | 13.9 ± 8.5 | 4.3 ± 0.8 | <2.4 | 3.3 ± 0.5 | <8.1 | <7.5 | <7.8 | 1269.0/1259 |
| 4U1254 − 690 | <40.6 | <61.8 | <22.4 | <33.7 | <12.8 | <29.5 | <26.9 | <23.8 | <25.5 | 355.9/308 |
| 4U1630 − 472 | <3.7 | <3.1 | 16.3 ± 9.0 | <1.1 | <2.9 | 7.3 ± 6.9 | <12.4 | <62.1 | <104.4 | 1315.7/1259 |
| 4U1636 − 53 | <6.1 | <3.5 | <5.2 | <0.7 | <1.3 | 2.8 ± 0.4 | <4.6 | <3.7 | <4.4 | 3130.1/2846 |
| 4U1702 − 429 | 103.4 ± 31.4 | <32.7 | <22.4 | <47.2 | <13.8 | <37.8 | <0.1 | <0.1 | <19.0 | 292.8/308 |
| 4U1705 − 44 | 35.1 ± 10.3 | <17.0 | <4.0 | <0.3 | <0.9 | <0.6 | <2.3 | <2.2 | <2.1 | 1642.1/1576 |
| 4U1728 − 16 | <8.6 | <15.0 | <4.9 | 14.3 ± 2.2 | <4.4 | <2.9 | <0.1 | <15.4 | <0.1 | 322.5/308 |
| 4U1728 − 34 | <26.2 | 84.7 ± 39.9 | <24.3 | <82.1 | <26.5 | <42.5 | <22.6 | <22.9 | <21.9 | 334.7/308 |
| GX9 + 9 | 10.2 ± 8.7 | <5.0 | <2.8 | <4.6 | <0.5 | 3.2 ± 2.1 | <5.2 | <5.0 | <4.6 | 291.9/308 |
| H1743 − 322 | 92.4 ± 35.4 | <60.5 | <11.7 | <25.7 | <25.2 | <3.1 | <0.1 | <0.1 | <0.1 | 2200.6/2527 |
| IGRJ17091 − 3624 | <4.9 | <14.0 | <6.8 | <0.5 | <1.1 | 7.8 ± 6.9 | <4.5 | <5.2 | <4.3 | 2548.9/2527 |
| NGC6624 | <9.7 | <6.4 | <25.4 | <6.2 | <10.3 | <1.0 | <95.1 | <42.9 | <35.4 | 612.3/625 |
| EXO1846 − 031 | <3.5 | 35.8 ± 9.8 | 33.1 ± 7.2 | <0.2 | <0.1 | 3.6 ± 2.9 | <10.8 | <10.8 | <9.3 | 1660.7/1576 |
| GRS1758 − 258 | <64.2 | <70.5 | 73.2 ± 41.1 | <71.3 | <4.6 | <4.7 | <39.2 | <22.5 | <28.2 | 637.8/625 |
| GRS1915 + 105 | 91.7 ± 8.5 | <1.2 | 15.7 ± 6.0 | <0.3 | <0.3 | 30 ± 14.6 | <12.0 | <11.0 | <10.0 | 1809.0/1579 |
| GS1826 − 238 | <8.7 | <9.8 | <17.9 | <32.5 | <1.2 | <8.3 | <9.9 | <9.3 | <8.7 | 329.9/308 |
| GX13 + 1 | 76.7 ± 5.8 | <0.7 | <0.8 | <0.6 | <0.1 | 129.7 ± 12.5 | <2.1 | <2.1 | <2.3 | 3182.2/2844 |
| GX17 + 2 | <36.8 | <30.1 | 24.1 ± 10.8 | <13.8 | <0.7 | <3.4 | <4.6 | <0.1 | <0.1 | 281.8/308 |
| GX3 + 1 | <9.2 | 22.6 ± 7.9 | <7.2 | <1.2 | <0.1 | <0.8 | <10.8 | <10.4 | <10.0 | 3099.2/3161 |
| GX339 − 4 | <8.4 | <4.6 | 29.0 ± 8.3 | <6.5 | <0.4 | <0.3 | <19.4 | <8.1 | <8.6 | 953.5/942 |
| GX340 + 0 | 46.9 ± 8.6 | <3.8 | 55.1 ± 6.8 | <4.8 | <0.3 | <0.2 | <20.0 | <18.1 | <18.0 | 1341.3/1262 |
| GX349 + 2 | <5.3 | <5.9 | 7.6 ± 3.1 | <1.5 | <0.1 | <0.4 | <7.1 | <7.1 | <7.3 | 2069.7/1893 |
| GX354 + 0 | <24.2 | 38.8 ± 24.3 | 26.3 ± 16.7 | <1.7 | 2.2 ± 0.44 | <6.7 | <7.3 | <0.1 | <7.1 | 821.9/942 |
| GX5 − 1 | 35.3 ± 9.2 | 22.9 ± 6.8 | 6.5 ± 3.1 | <0.9 | <0.0 | <0.1 | <0.1 | <1.4 | <0.1 | 2558.3/2527 |
| V4641Sgr | <33.9 | <42.4 | <10.1 | <16.5 | <1.3 | 28.8 ± 3.62 | <20.0 | <0.1 | <20.3 | 565.3/625 |
| X1543 − 62 | <45.8 | <17.9 | <13.6 | <7.1 | 20.2 ± 2.9 | <9.6 | <64.0 | <55.7 | <58.4 | 306.9/308 |
| X1822 − 371 | <12.1 | <10.3 | <7.6 | <16.8 | <11.8 | <0.7 | <0.1 | <9.9 | <0.1 | 533.4/625 |
| XTEJ1814 − 338 | <42.9 | <43.9 | <52.2 | <0.0 | <181.0 | <60.1 | <49.8 | <48.8 | <48.9 | 317.1/308 |
| 4U1735 − 44 | <39.1 | <11.4 | <7.3 | <25.1 | <4.4 | <0.8 | <16.8 | <20.6 | <19.4 | 346.4/308 |
| GX9 + 1 | <48.5 | <35.6 | 16.3 ± 12.3 | 27.8 ± 19.9 | <1.2 | <4.4 | <44.4 | <44.0 | <43.2 | 637.5/625 |
| 4U1916 − 053 | <20.2 | <40.1 | <14.9 | 57.9 ± 33.7 | <4.6 | 88.5 ± 48.2 | <31.8 | <39.9 | <57.0 | 1966.7/1893 |
| 4U1957 + 11 | <17.8 | <8.5 | <9.7 | <1.2 | <0.6 | 23.0 ± 18.0 | <0.1 | <0.1 | <9.6 | 946.3/942 |
| A1744 − 361 | <6.1 | <5.7 | 18.2 ± 11.4 | 43.1 ± 36.8 | <1.3 | <11.2 | <4.9 | <4.6 | <4.8 | 884.7/942 |
| CIRX − 1 | <9.0 | 25.7 ± 10.9 | 11.3 ± 8.7 | <0.7 | <4.1 | 71.1 ± 21.0 | <7.0 | <6.7 | <3.7 | 1366.0/1259 |
| CYGX − 2 | <24.1 | <11.7 | <10.9 | 35.0 ± 22.9 | 1.9 ± 1.3 | <4.3 | <28.7 | <30.2 | <30.3 | 740.0/625 |
| SERX − 1 | <5.8 | <13.3 | <6.5 | <0.2 | <0.5 | <0.1 | <0.1 | <3.4 | <0.1 | 978.7/942 |
| Source . | S i . | S ii . | S iii . | S xiv . | S xv . | S xvi . | Alabandite . | Pyrrohtite . | Troilite . | χ2/d.of. . |
|---|---|---|---|---|---|---|---|---|---|---|
| 4U0614 + 091 | <15.3 | <7.3 | 13.9 ± 8.5 | 4.3 ± 0.8 | <2.4 | 3.3 ± 0.5 | <8.1 | <7.5 | <7.8 | 1269.0/1259 |
| 4U1254 − 690 | <40.6 | <61.8 | <22.4 | <33.7 | <12.8 | <29.5 | <26.9 | <23.8 | <25.5 | 355.9/308 |
| 4U1630 − 472 | <3.7 | <3.1 | 16.3 ± 9.0 | <1.1 | <2.9 | 7.3 ± 6.9 | <12.4 | <62.1 | <104.4 | 1315.7/1259 |
| 4U1636 − 53 | <6.1 | <3.5 | <5.2 | <0.7 | <1.3 | 2.8 ± 0.4 | <4.6 | <3.7 | <4.4 | 3130.1/2846 |
| 4U1702 − 429 | 103.4 ± 31.4 | <32.7 | <22.4 | <47.2 | <13.8 | <37.8 | <0.1 | <0.1 | <19.0 | 292.8/308 |
| 4U1705 − 44 | 35.1 ± 10.3 | <17.0 | <4.0 | <0.3 | <0.9 | <0.6 | <2.3 | <2.2 | <2.1 | 1642.1/1576 |
| 4U1728 − 16 | <8.6 | <15.0 | <4.9 | 14.3 ± 2.2 | <4.4 | <2.9 | <0.1 | <15.4 | <0.1 | 322.5/308 |
| 4U1728 − 34 | <26.2 | 84.7 ± 39.9 | <24.3 | <82.1 | <26.5 | <42.5 | <22.6 | <22.9 | <21.9 | 334.7/308 |
| GX9 + 9 | 10.2 ± 8.7 | <5.0 | <2.8 | <4.6 | <0.5 | 3.2 ± 2.1 | <5.2 | <5.0 | <4.6 | 291.9/308 |
| H1743 − 322 | 92.4 ± 35.4 | <60.5 | <11.7 | <25.7 | <25.2 | <3.1 | <0.1 | <0.1 | <0.1 | 2200.6/2527 |
| IGRJ17091 − 3624 | <4.9 | <14.0 | <6.8 | <0.5 | <1.1 | 7.8 ± 6.9 | <4.5 | <5.2 | <4.3 | 2548.9/2527 |
| NGC6624 | <9.7 | <6.4 | <25.4 | <6.2 | <10.3 | <1.0 | <95.1 | <42.9 | <35.4 | 612.3/625 |
| EXO1846 − 031 | <3.5 | 35.8 ± 9.8 | 33.1 ± 7.2 | <0.2 | <0.1 | 3.6 ± 2.9 | <10.8 | <10.8 | <9.3 | 1660.7/1576 |
| GRS1758 − 258 | <64.2 | <70.5 | 73.2 ± 41.1 | <71.3 | <4.6 | <4.7 | <39.2 | <22.5 | <28.2 | 637.8/625 |
| GRS1915 + 105 | 91.7 ± 8.5 | <1.2 | 15.7 ± 6.0 | <0.3 | <0.3 | 30 ± 14.6 | <12.0 | <11.0 | <10.0 | 1809.0/1579 |
| GS1826 − 238 | <8.7 | <9.8 | <17.9 | <32.5 | <1.2 | <8.3 | <9.9 | <9.3 | <8.7 | 329.9/308 |
| GX13 + 1 | 76.7 ± 5.8 | <0.7 | <0.8 | <0.6 | <0.1 | 129.7 ± 12.5 | <2.1 | <2.1 | <2.3 | 3182.2/2844 |
| GX17 + 2 | <36.8 | <30.1 | 24.1 ± 10.8 | <13.8 | <0.7 | <3.4 | <4.6 | <0.1 | <0.1 | 281.8/308 |
| GX3 + 1 | <9.2 | 22.6 ± 7.9 | <7.2 | <1.2 | <0.1 | <0.8 | <10.8 | <10.4 | <10.0 | 3099.2/3161 |
| GX339 − 4 | <8.4 | <4.6 | 29.0 ± 8.3 | <6.5 | <0.4 | <0.3 | <19.4 | <8.1 | <8.6 | 953.5/942 |
| GX340 + 0 | 46.9 ± 8.6 | <3.8 | 55.1 ± 6.8 | <4.8 | <0.3 | <0.2 | <20.0 | <18.1 | <18.0 | 1341.3/1262 |
| GX349 + 2 | <5.3 | <5.9 | 7.6 ± 3.1 | <1.5 | <0.1 | <0.4 | <7.1 | <7.1 | <7.3 | 2069.7/1893 |
| GX354 + 0 | <24.2 | 38.8 ± 24.3 | 26.3 ± 16.7 | <1.7 | 2.2 ± 0.44 | <6.7 | <7.3 | <0.1 | <7.1 | 821.9/942 |
| GX5 − 1 | 35.3 ± 9.2 | 22.9 ± 6.8 | 6.5 ± 3.1 | <0.9 | <0.0 | <0.1 | <0.1 | <1.4 | <0.1 | 2558.3/2527 |
| V4641Sgr | <33.9 | <42.4 | <10.1 | <16.5 | <1.3 | 28.8 ± 3.62 | <20.0 | <0.1 | <20.3 | 565.3/625 |
| X1543 − 62 | <45.8 | <17.9 | <13.6 | <7.1 | 20.2 ± 2.9 | <9.6 | <64.0 | <55.7 | <58.4 | 306.9/308 |
| X1822 − 371 | <12.1 | <10.3 | <7.6 | <16.8 | <11.8 | <0.7 | <0.1 | <9.9 | <0.1 | 533.4/625 |
| XTEJ1814 − 338 | <42.9 | <43.9 | <52.2 | <0.0 | <181.0 | <60.1 | <49.8 | <48.8 | <48.9 | 317.1/308 |
| 4U1735 − 44 | <39.1 | <11.4 | <7.3 | <25.1 | <4.4 | <0.8 | <16.8 | <20.6 | <19.4 | 346.4/308 |
| GX9 + 1 | <48.5 | <35.6 | 16.3 ± 12.3 | 27.8 ± 19.9 | <1.2 | <4.4 | <44.4 | <44.0 | <43.2 | 637.5/625 |
| 4U1916 − 053 | <20.2 | <40.1 | <14.9 | 57.9 ± 33.7 | <4.6 | 88.5 ± 48.2 | <31.8 | <39.9 | <57.0 | 1966.7/1893 |
| 4U1957 + 11 | <17.8 | <8.5 | <9.7 | <1.2 | <0.6 | 23.0 ± 18.0 | <0.1 | <0.1 | <9.6 | 946.3/942 |
| A1744 − 361 | <6.1 | <5.7 | 18.2 ± 11.4 | 43.1 ± 36.8 | <1.3 | <11.2 | <4.9 | <4.6 | <4.8 | 884.7/942 |
| CIRX − 1 | <9.0 | 25.7 ± 10.9 | 11.3 ± 8.7 | <0.7 | <4.1 | 71.1 ± 21.0 | <7.0 | <6.7 | <3.7 | 1366.0/1259 |
| CYGX − 2 | <24.1 | <11.7 | <10.9 | 35.0 ± 22.9 | 1.9 ± 1.3 | <4.3 | <28.7 | <30.2 | <30.3 | 740.0/625 |
| SERX − 1 | <5.8 | <13.3 | <6.5 | <0.2 | <0.5 | <0.1 | <0.1 | <3.4 | <0.1 | 978.7/942 |
Note. Column densities in units of 1016 cm−2 for the ionic species and 1014 cm−2 for the dust samples.
| Source . | S i . | S ii . | S iii . | S xiv . | S xv . | S xvi . | Alabandite . | Pyrrohtite . | Troilite . | χ2/d.of. . |
|---|---|---|---|---|---|---|---|---|---|---|
| 4U0614 + 091 | <15.3 | <7.3 | 13.9 ± 8.5 | 4.3 ± 0.8 | <2.4 | 3.3 ± 0.5 | <8.1 | <7.5 | <7.8 | 1269.0/1259 |
| 4U1254 − 690 | <40.6 | <61.8 | <22.4 | <33.7 | <12.8 | <29.5 | <26.9 | <23.8 | <25.5 | 355.9/308 |
| 4U1630 − 472 | <3.7 | <3.1 | 16.3 ± 9.0 | <1.1 | <2.9 | 7.3 ± 6.9 | <12.4 | <62.1 | <104.4 | 1315.7/1259 |
| 4U1636 − 53 | <6.1 | <3.5 | <5.2 | <0.7 | <1.3 | 2.8 ± 0.4 | <4.6 | <3.7 | <4.4 | 3130.1/2846 |
| 4U1702 − 429 | 103.4 ± 31.4 | <32.7 | <22.4 | <47.2 | <13.8 | <37.8 | <0.1 | <0.1 | <19.0 | 292.8/308 |
| 4U1705 − 44 | 35.1 ± 10.3 | <17.0 | <4.0 | <0.3 | <0.9 | <0.6 | <2.3 | <2.2 | <2.1 | 1642.1/1576 |
| 4U1728 − 16 | <8.6 | <15.0 | <4.9 | 14.3 ± 2.2 | <4.4 | <2.9 | <0.1 | <15.4 | <0.1 | 322.5/308 |
| 4U1728 − 34 | <26.2 | 84.7 ± 39.9 | <24.3 | <82.1 | <26.5 | <42.5 | <22.6 | <22.9 | <21.9 | 334.7/308 |
| GX9 + 9 | 10.2 ± 8.7 | <5.0 | <2.8 | <4.6 | <0.5 | 3.2 ± 2.1 | <5.2 | <5.0 | <4.6 | 291.9/308 |
| H1743 − 322 | 92.4 ± 35.4 | <60.5 | <11.7 | <25.7 | <25.2 | <3.1 | <0.1 | <0.1 | <0.1 | 2200.6/2527 |
| IGRJ17091 − 3624 | <4.9 | <14.0 | <6.8 | <0.5 | <1.1 | 7.8 ± 6.9 | <4.5 | <5.2 | <4.3 | 2548.9/2527 |
| NGC6624 | <9.7 | <6.4 | <25.4 | <6.2 | <10.3 | <1.0 | <95.1 | <42.9 | <35.4 | 612.3/625 |
| EXO1846 − 031 | <3.5 | 35.8 ± 9.8 | 33.1 ± 7.2 | <0.2 | <0.1 | 3.6 ± 2.9 | <10.8 | <10.8 | <9.3 | 1660.7/1576 |
| GRS1758 − 258 | <64.2 | <70.5 | 73.2 ± 41.1 | <71.3 | <4.6 | <4.7 | <39.2 | <22.5 | <28.2 | 637.8/625 |
| GRS1915 + 105 | 91.7 ± 8.5 | <1.2 | 15.7 ± 6.0 | <0.3 | <0.3 | 30 ± 14.6 | <12.0 | <11.0 | <10.0 | 1809.0/1579 |
| GS1826 − 238 | <8.7 | <9.8 | <17.9 | <32.5 | <1.2 | <8.3 | <9.9 | <9.3 | <8.7 | 329.9/308 |
| GX13 + 1 | 76.7 ± 5.8 | <0.7 | <0.8 | <0.6 | <0.1 | 129.7 ± 12.5 | <2.1 | <2.1 | <2.3 | 3182.2/2844 |
| GX17 + 2 | <36.8 | <30.1 | 24.1 ± 10.8 | <13.8 | <0.7 | <3.4 | <4.6 | <0.1 | <0.1 | 281.8/308 |
| GX3 + 1 | <9.2 | 22.6 ± 7.9 | <7.2 | <1.2 | <0.1 | <0.8 | <10.8 | <10.4 | <10.0 | 3099.2/3161 |
| GX339 − 4 | <8.4 | <4.6 | 29.0 ± 8.3 | <6.5 | <0.4 | <0.3 | <19.4 | <8.1 | <8.6 | 953.5/942 |
| GX340 + 0 | 46.9 ± 8.6 | <3.8 | 55.1 ± 6.8 | <4.8 | <0.3 | <0.2 | <20.0 | <18.1 | <18.0 | 1341.3/1262 |
| GX349 + 2 | <5.3 | <5.9 | 7.6 ± 3.1 | <1.5 | <0.1 | <0.4 | <7.1 | <7.1 | <7.3 | 2069.7/1893 |
| GX354 + 0 | <24.2 | 38.8 ± 24.3 | 26.3 ± 16.7 | <1.7 | 2.2 ± 0.44 | <6.7 | <7.3 | <0.1 | <7.1 | 821.9/942 |
| GX5 − 1 | 35.3 ± 9.2 | 22.9 ± 6.8 | 6.5 ± 3.1 | <0.9 | <0.0 | <0.1 | <0.1 | <1.4 | <0.1 | 2558.3/2527 |
| V4641Sgr | <33.9 | <42.4 | <10.1 | <16.5 | <1.3 | 28.8 ± 3.62 | <20.0 | <0.1 | <20.3 | 565.3/625 |
| X1543 − 62 | <45.8 | <17.9 | <13.6 | <7.1 | 20.2 ± 2.9 | <9.6 | <64.0 | <55.7 | <58.4 | 306.9/308 |
| X1822 − 371 | <12.1 | <10.3 | <7.6 | <16.8 | <11.8 | <0.7 | <0.1 | <9.9 | <0.1 | 533.4/625 |
| XTEJ1814 − 338 | <42.9 | <43.9 | <52.2 | <0.0 | <181.0 | <60.1 | <49.8 | <48.8 | <48.9 | 317.1/308 |
| 4U1735 − 44 | <39.1 | <11.4 | <7.3 | <25.1 | <4.4 | <0.8 | <16.8 | <20.6 | <19.4 | 346.4/308 |
| GX9 + 1 | <48.5 | <35.6 | 16.3 ± 12.3 | 27.8 ± 19.9 | <1.2 | <4.4 | <44.4 | <44.0 | <43.2 | 637.5/625 |
| 4U1916 − 053 | <20.2 | <40.1 | <14.9 | 57.9 ± 33.7 | <4.6 | 88.5 ± 48.2 | <31.8 | <39.9 | <57.0 | 1966.7/1893 |
| 4U1957 + 11 | <17.8 | <8.5 | <9.7 | <1.2 | <0.6 | 23.0 ± 18.0 | <0.1 | <0.1 | <9.6 | 946.3/942 |
| A1744 − 361 | <6.1 | <5.7 | 18.2 ± 11.4 | 43.1 ± 36.8 | <1.3 | <11.2 | <4.9 | <4.6 | <4.8 | 884.7/942 |
| CIRX − 1 | <9.0 | 25.7 ± 10.9 | 11.3 ± 8.7 | <0.7 | <4.1 | 71.1 ± 21.0 | <7.0 | <6.7 | <3.7 | 1366.0/1259 |
| CYGX − 2 | <24.1 | <11.7 | <10.9 | 35.0 ± 22.9 | 1.9 ± 1.3 | <4.3 | <28.7 | <30.2 | <30.3 | 740.0/625 |
| SERX − 1 | <5.8 | <13.3 | <6.5 | <0.2 | <0.5 | <0.1 | <0.1 | <3.4 | <0.1 | 978.7/942 |
| Source . | S i . | S ii . | S iii . | S xiv . | S xv . | S xvi . | Alabandite . | Pyrrohtite . | Troilite . | χ2/d.of. . |
|---|---|---|---|---|---|---|---|---|---|---|
| 4U0614 + 091 | <15.3 | <7.3 | 13.9 ± 8.5 | 4.3 ± 0.8 | <2.4 | 3.3 ± 0.5 | <8.1 | <7.5 | <7.8 | 1269.0/1259 |
| 4U1254 − 690 | <40.6 | <61.8 | <22.4 | <33.7 | <12.8 | <29.5 | <26.9 | <23.8 | <25.5 | 355.9/308 |
| 4U1630 − 472 | <3.7 | <3.1 | 16.3 ± 9.0 | <1.1 | <2.9 | 7.3 ± 6.9 | <12.4 | <62.1 | <104.4 | 1315.7/1259 |
| 4U1636 − 53 | <6.1 | <3.5 | <5.2 | <0.7 | <1.3 | 2.8 ± 0.4 | <4.6 | <3.7 | <4.4 | 3130.1/2846 |
| 4U1702 − 429 | 103.4 ± 31.4 | <32.7 | <22.4 | <47.2 | <13.8 | <37.8 | <0.1 | <0.1 | <19.0 | 292.8/308 |
| 4U1705 − 44 | 35.1 ± 10.3 | <17.0 | <4.0 | <0.3 | <0.9 | <0.6 | <2.3 | <2.2 | <2.1 | 1642.1/1576 |
| 4U1728 − 16 | <8.6 | <15.0 | <4.9 | 14.3 ± 2.2 | <4.4 | <2.9 | <0.1 | <15.4 | <0.1 | 322.5/308 |
| 4U1728 − 34 | <26.2 | 84.7 ± 39.9 | <24.3 | <82.1 | <26.5 | <42.5 | <22.6 | <22.9 | <21.9 | 334.7/308 |
| GX9 + 9 | 10.2 ± 8.7 | <5.0 | <2.8 | <4.6 | <0.5 | 3.2 ± 2.1 | <5.2 | <5.0 | <4.6 | 291.9/308 |
| H1743 − 322 | 92.4 ± 35.4 | <60.5 | <11.7 | <25.7 | <25.2 | <3.1 | <0.1 | <0.1 | <0.1 | 2200.6/2527 |
| IGRJ17091 − 3624 | <4.9 | <14.0 | <6.8 | <0.5 | <1.1 | 7.8 ± 6.9 | <4.5 | <5.2 | <4.3 | 2548.9/2527 |
| NGC6624 | <9.7 | <6.4 | <25.4 | <6.2 | <10.3 | <1.0 | <95.1 | <42.9 | <35.4 | 612.3/625 |
| EXO1846 − 031 | <3.5 | 35.8 ± 9.8 | 33.1 ± 7.2 | <0.2 | <0.1 | 3.6 ± 2.9 | <10.8 | <10.8 | <9.3 | 1660.7/1576 |
| GRS1758 − 258 | <64.2 | <70.5 | 73.2 ± 41.1 | <71.3 | <4.6 | <4.7 | <39.2 | <22.5 | <28.2 | 637.8/625 |
| GRS1915 + 105 | 91.7 ± 8.5 | <1.2 | 15.7 ± 6.0 | <0.3 | <0.3 | 30 ± 14.6 | <12.0 | <11.0 | <10.0 | 1809.0/1579 |
| GS1826 − 238 | <8.7 | <9.8 | <17.9 | <32.5 | <1.2 | <8.3 | <9.9 | <9.3 | <8.7 | 329.9/308 |
| GX13 + 1 | 76.7 ± 5.8 | <0.7 | <0.8 | <0.6 | <0.1 | 129.7 ± 12.5 | <2.1 | <2.1 | <2.3 | 3182.2/2844 |
| GX17 + 2 | <36.8 | <30.1 | 24.1 ± 10.8 | <13.8 | <0.7 | <3.4 | <4.6 | <0.1 | <0.1 | 281.8/308 |
| GX3 + 1 | <9.2 | 22.6 ± 7.9 | <7.2 | <1.2 | <0.1 | <0.8 | <10.8 | <10.4 | <10.0 | 3099.2/3161 |
| GX339 − 4 | <8.4 | <4.6 | 29.0 ± 8.3 | <6.5 | <0.4 | <0.3 | <19.4 | <8.1 | <8.6 | 953.5/942 |
| GX340 + 0 | 46.9 ± 8.6 | <3.8 | 55.1 ± 6.8 | <4.8 | <0.3 | <0.2 | <20.0 | <18.1 | <18.0 | 1341.3/1262 |
| GX349 + 2 | <5.3 | <5.9 | 7.6 ± 3.1 | <1.5 | <0.1 | <0.4 | <7.1 | <7.1 | <7.3 | 2069.7/1893 |
| GX354 + 0 | <24.2 | 38.8 ± 24.3 | 26.3 ± 16.7 | <1.7 | 2.2 ± 0.44 | <6.7 | <7.3 | <0.1 | <7.1 | 821.9/942 |
| GX5 − 1 | 35.3 ± 9.2 | 22.9 ± 6.8 | 6.5 ± 3.1 | <0.9 | <0.0 | <0.1 | <0.1 | <1.4 | <0.1 | 2558.3/2527 |
| V4641Sgr | <33.9 | <42.4 | <10.1 | <16.5 | <1.3 | 28.8 ± 3.62 | <20.0 | <0.1 | <20.3 | 565.3/625 |
| X1543 − 62 | <45.8 | <17.9 | <13.6 | <7.1 | 20.2 ± 2.9 | <9.6 | <64.0 | <55.7 | <58.4 | 306.9/308 |
| X1822 − 371 | <12.1 | <10.3 | <7.6 | <16.8 | <11.8 | <0.7 | <0.1 | <9.9 | <0.1 | 533.4/625 |
| XTEJ1814 − 338 | <42.9 | <43.9 | <52.2 | <0.0 | <181.0 | <60.1 | <49.8 | <48.8 | <48.9 | 317.1/308 |
| 4U1735 − 44 | <39.1 | <11.4 | <7.3 | <25.1 | <4.4 | <0.8 | <16.8 | <20.6 | <19.4 | 346.4/308 |
| GX9 + 1 | <48.5 | <35.6 | 16.3 ± 12.3 | 27.8 ± 19.9 | <1.2 | <4.4 | <44.4 | <44.0 | <43.2 | 637.5/625 |
| 4U1916 − 053 | <20.2 | <40.1 | <14.9 | 57.9 ± 33.7 | <4.6 | 88.5 ± 48.2 | <31.8 | <39.9 | <57.0 | 1966.7/1893 |
| 4U1957 + 11 | <17.8 | <8.5 | <9.7 | <1.2 | <0.6 | 23.0 ± 18.0 | <0.1 | <0.1 | <9.6 | 946.3/942 |
| A1744 − 361 | <6.1 | <5.7 | 18.2 ± 11.4 | 43.1 ± 36.8 | <1.3 | <11.2 | <4.9 | <4.6 | <4.8 | 884.7/942 |
| CIRX − 1 | <9.0 | 25.7 ± 10.9 | 11.3 ± 8.7 | <0.7 | <4.1 | 71.1 ± 21.0 | <7.0 | <6.7 | <3.7 | 1366.0/1259 |
| CYGX − 2 | <24.1 | <11.7 | <10.9 | 35.0 ± 22.9 | 1.9 ± 1.3 | <4.3 | <28.7 | <30.2 | <30.3 | 740.0/625 |
| SERX − 1 | <5.8 | <13.3 | <6.5 | <0.2 | <0.5 | <0.1 | <0.1 | <3.4 | <0.1 | 978.7/942 |
Note. Column densities in units of 1016 cm−2 for the ionic species and 1014 cm−2 for the dust samples.
Fig. 4 shows the column density distribution for each ISM gaseous phase as a function of the Galactic latitude (top panels) and the Galactic longitude (bottom panels). The cold-warm phases tend to decrease with the Galactic latitude (top panels), while the hot phase does not appear to show a clear correlation, although we note that, for many sources, the best-fitting results correspond to upper limits. Gatuzz et al. (2021) found a similar homogeneous distribution for the warm-hot ISM component in their nitrogen K-edge photoabsorption region analysis. It is commonly assumed that the neutral component of the ISM exponentially decreases along the perpendicular direction to the Galactic plane, with larger column densities near the Galactic centre (see e.g. Robin et al. 2003; Kalberla & Kerp 2009). However, the sulphur depletion into dust may lead to departures from such distribution. Fig. 5 shows the column density distribution for each phase as a function of the distance for those sources where available. There is no clear correlation between both parameters.
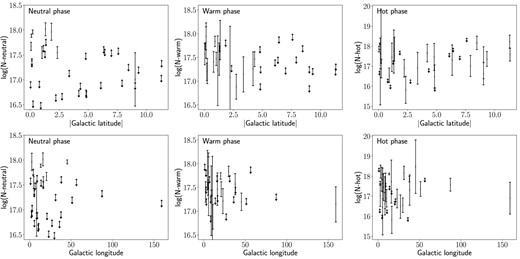
S column densities distribution for each ISM phase as function of Galactic latitude (top panels) and Galactic longitude (bottom panels).
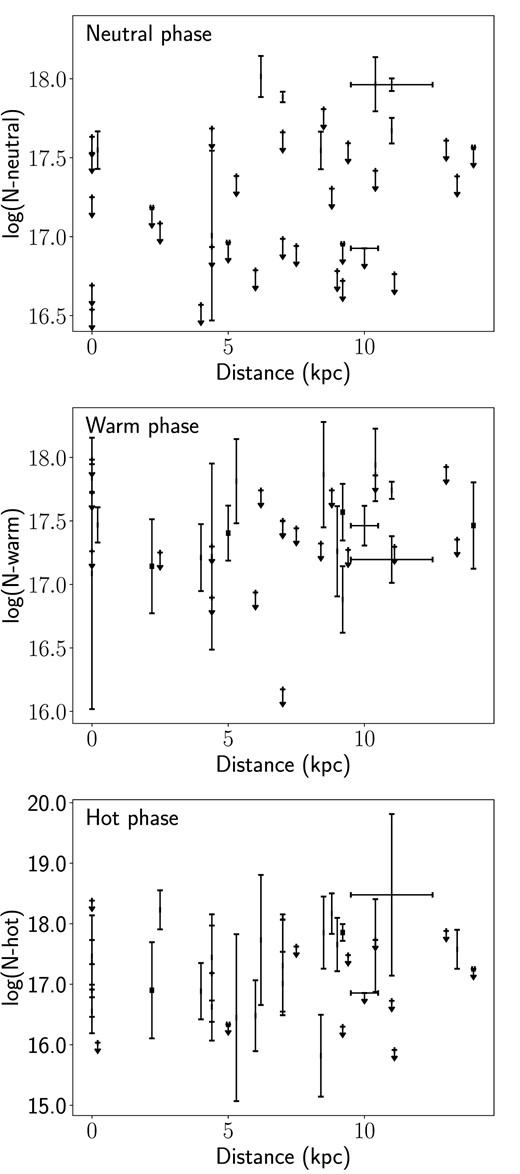
S column densities distribution for each ISM phase as function of the distance.
Previous analysis of the ISM using X-ray absorption have shown that the gaseous state is dominated by the neutral component with mass fractions for the different phases in the Galactic disc of |$\sim ~ 90{{\ \rm per\ cent}}$|, warm |$\sim 8{{\ \rm per\ cent}}$|, and hot |$\sim 2{{\ \rm per\ cent}}$| of the total contribution (e.g. Yao & Wang 2006; Pinto et al. 2013; Gatuzz & Churazov 2018). Given the uncertainties in the obtained column densities, we cannot accurately compute mass fractions for all sources. Moreover, we are not considering ionization equilibrium for the sulphur ionic species because the column densities in the ISMabs model are free parameters. Therefore, the hot phase temperature, as described in previous works, could not be hot enough in order to produce highly ionized S. Furthermore, the hot phase could include a contribution from an ionized static absorber intrinsic to the source (see for example Gatuzz et al. 2020b). A complete thermodynamic analysis of the ISM component is beyond the scope of this work, which focuses on measuring the column densities for the neutral and ionic S species. For the dust component, we have found upper limits for all sources, with a contribution of |$\lt 10{{\ \rm per\ cent}}$| for the cold gas.
4.1 Future prospects
Future X-ray observatories will allow us to resolve the K α resonance lines for the different S ionic species. For the neutral S i component, it is crucial to compute new accurate atomic data, including radiation and Auger damping, in order to model not only the gaseous phase but also to differentiate it with the modulations and spectral features induced by interstellar grains extinction (Costantini et al. 2019). For example, Fig. 6 shows simulations for a Galactic source (i.e. GX13 + 1) obtained with Athena (Nandra et al. 2013) and LEM (Kraft et al. 2022). The plot shows the extraordinary capabilities of the different instruments, where the main resonance absorption lines are easily visible, including the S i K resonance lines. Moreover, by simultaneously measuring K α and K β absorption lines for the same ions, more accurate constraints on the abundances, broadening, and ionization state of the ISM absorber will be obtained. It is important to note that this simulation includes only the gaseous component. While the total dust contribution could also be measured, the distinction between different dust samples is more challenging. A detailed dust simulation for Athena was computed by Costantini et al. (2019).
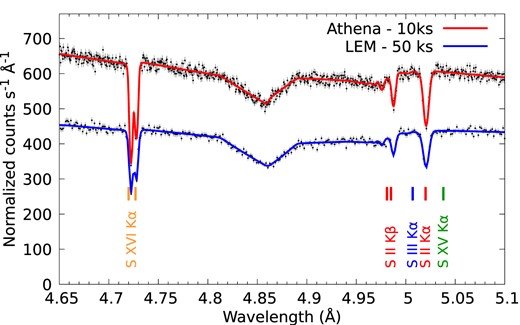
Athena and LEM simulation of the S K-edge photoabsorption region for a Galactic source (e.g. GX13 + 1). The total exposure time is indicated.
5 CONCLUSIONS
We have analyzed the sulphur K-edge X-ray absorption region (4.5–5.5 Å) using Chandra high-resolution spectra of 36 LMXBs. We fitted each source with a simple powerlaw for the continuum and a modified version of the ISMabs model, including extinction cross-sections for three samples of interstellar dust analogues (e.g. alabandite, pyrrhotite, and troilite). We found that the absorption features identified in the spectra are well modeled with the theoretical photoabsorption cross-section, even though individual K α doublets/triplets cannot be resolved. With this model, we have estimated column densities for S i, S ii, S iii, S v, S vi and S vii ionic species as well as upper limits for the dust component, which trace the multiphase ISM. While the cold-warm column densities tend to decrease with the Galactic latitude, we found no correlation with distances or Galactic longitude. Finally, our simulations using response files from future X-ray observatories such as Athena indicate that a detailed benchmarking of the atomic data will be possible with such instruments.
ACKNOWLEDGEMENTS
We thank the anonymous referee for the careful reading of our manuscript and the valuable comments.
DATA AVAILABILITY
Observations analyzed in this article are available in the Chandra Grating-Data Archive and Catalog (TGCat) (http://tgcat.mit.edu/about.php). The ISMabs model is included in the xspec data analysis software (https://heasarc.gsfc.nasa.gov/xanadu/xspec/). This research was carried out on the High Performance Computing resources of the cobra cluster at the Max Planck Computing and Data Facility (MPCDF) in Garching operated by the Max Planck Society (MPG)



