-
PDF
- Split View
-
Views
-
Cite
Cite
P Pirlot Jankowiak, F Lique, P J Dagdigian, Collisional excitation of C2H and C2D by molecular hydrogen, Monthly Notices of the Royal Astronomical Society, Volume 526, Issue 1, November 2023, Pages 885–894, https://doi.org/10.1093/mnras/stad2821
Close - Share Icon Share
ABSTRACT
The determination of physical conditions in interstellar clouds requires reliable estimation of radiative and collisional data for molecules detected in space. In this work, rate coefficients for de-excitation of C2H and C2D induced by collisions with both ortho- and para-H2 are presented. Calculations have been carried out using a recently published four-dimensional C2H–H2 potential energy surface. Fine-structure resolved cross-sections were computed with the time-independent close-coupling approach. We report cross-sections for transitions between the first 41 levels of C2H and corresponding rate coefficients up to 500 K. We also computed cross-sections for transitions between the first 31 levels of C2D and corresponding rate coefficients up to 200 K. Then, hyperfine structure resolved cross-sections and rate coefficients were computed using the recoupling technique. The hyperfine structure resolved rate coefficients for C2H–H2 and C2D–H2 are calculated for the first 38 hyperfine C2H energy levels and first 55 hyperfine C2D energy levels both for temperatures up to 100 K. These collisional data were used in a simple radiative transfer modelling.
1 INTRODUCTION
The ethynyl radical C2H was first detected by Tucker, Kutner & Thaddeus (1974) in the interstellar medium (ISM) through the n = 1 → 0 rotational line. Later, experimental studies (Sastry et al. 1981; Gottlieb, Gottlieb & Thaddeus 1983) reported spectroscopic measurements for the n = 2 → 1 and n = 3 → 2 lines, providing accurate spectroscopic data for the X2Σ+ electronic state of this radical. Since then, C2H has been detected in a wide range of astrophysical environments such as molecular clouds (Wootten et al. 1980; Sakai et al. 2010), star-forming regions (Beuther et al. 2008; Treviño-Morales et al. 2014; Yoshida et al. 2019), pre-stellar cores (Padovani et al. 2009), protoplatenary discs (Dutrey, Guilloteau & Guélin 1996) and photodissociation regions (PDRs; Ziurys et al. 1982; Teyssier et al. 2003; Cuadrado et al. 2015; Nagy et al. 2015) and is one of the most abundant hydrocarbon molecules in the ISM.
Also, the high abundance of C2H in the ISM makes possible the observation of its deuterated isotopologue C2D. Indeed, the first detection of the C2D radical in the ISM was reported by Combes et al. (1985) in the Kleinman–Low nebula through the n = 3 → 2 rotational line. This observation was corroborated by two parallel laboratory studies (Bogey, Demuynck & Destombes 1985; Vrtilek et al. 1985). This isotopologue has been subject to additional detections in molecular clouds (Turner 2001), PDR (Parise et al. 2009), and star-forming regions (Treviño-Morales et al. 2014).
The abundance ratio between hydrogenated and deuterated molecules is usually found to deviate from the cosmological elemental ratio [D/H] ∼2 × 10−5 (Linsky et al. 2006). This abundance ratio can vary by several orders of magnitude from a source to another and also on the molecule, since the abundance of a molecule depends on its formation path and on the physical conditions of the medium. An accurate determination of the abundance of C2H and C2D is of interest to better understand and constrain the deuteration fraction in the ISM. That can give an insight on the evolution of molecular clouds, the abundance of deuterated molecules showing to strongly depend on the age of these objects in chemical models (Treviño-Morales et al. 2014).
The knowledge of the physical conditions of the ISM and especially molecular abundances relies on the interpretation of observational spectra through radiative transfer modelling. Notwithstanding, interstellar environments are subject to low density and energy levels of the detected molecules are out of the local thermodynamic equilibrium (LTE; Roueff & Lique 2013). Then, it is necessary to study excitation mechanisms including both radiative and collisional processes. On one hand, radiative mechanisms are related to Einstein coefficients which depend on the dipole moment of the molecule involved and are determined through spectroscopic analysis. On the other hand, collisional processes are quantified by rate coefficients and can be determined through (quantum) calculations for a given collisional system. It is then of interest to study the excitation of both C2H and C2D with molecular hydrogen which is the main collider in molecular clouds where these two isotopologues are mainly observed.
The first collisional study implying C2H target was done by Spieldiedel et al. (2012), providing fine and hyperfine rate coefficients for transitions induced by He as a substitute of H2. Najar et al. (2014) provided rate coefficients up to 100 K for the C2H-para-H2 collisional system, taking into account only the fine-structure splitting of C2H. To do so, they computed a potential energy surface (PES) based on the rigid rotor approximation, considering para-H2 as a pseudo-atom. This approach excluded the contribution of excited levels of H2(j2 ≥ 1, j2 being the rotational state of H2) in the scattering calculations. This potential has also been used by Dumouchel et al. (2017) to compute hyperfine resolved rate coefficients of C2H and C2D with para-H2 up to 80 K. In a more recent work, Dagdigian (2018a) used the coupled cluster theory to compute a new 4D PES of the C2H–H2 collisional system. This author employed this PES to provide hyperfine rate coefficients of C2H with para-H2 and the first collisional data with ortho-H2 up to 300 K (Dagdigian 2018b). A reasonable agreement was found with the work from Najar et al. (2014) for C2H–para-H2 fine-structure resolved rate coefficients. The differences between these results mostly come from the size of H2 rotational basis in scattering calculations. One can expect that these discrepancies would impact results for the C2D–H2 collisional system as well, and new calculations with the 4D PES can be useful.
As far as we know, there are no data about collisional excitation of C2D with ortho-H2. Such data are necessary for modelling environments where ortho-H2 is significantly populated (Treviño-Morales et al. 2014). The purpose of this paper is to fill this lack of data. We report the first hyperfine resolved rate coefficients for C2D collisions with ortho-H2 and improved C2D–para-H2 collisional data up to 100 K using the 4D PES computed by Dagdigian (2018a). We also recompute hyperfine resolved rate coefficients for the C2H–H2 collisional system up to 100 K.1 We also extend the range of temperature of fine-structure C2H–H2 collisional data up to 500 K. New fine-structure rate coefficients have been computed for the C2D–H2 collisional system up to 200 K. These data are expected to cover the temperature range of environments where C2H and C2D are detected (Treviño-Morales et al. 2014; Nagy et al. 2015).
The paper is organized as follows: Section 2 presents the features of the PES used in scattering calculations and how to make it suitable for molecular dynamics of the C2D–H2 collisional system. State-to-state de-excitation rate coefficients of both C2H and C2D in collision with molecular hydrogen are presented in Section 3 (It should be noted that excitation rate coefficients can be obtained from the de-excitation rate coefficients through detailed balance). As an application of this new data, we perform a simple radiative transfer application in Section 4. A conclusion summarizes this work in Section 5.
2 METHODOLOGY
2.1 Potential energy surface
The PES describing the electronic interaction of the C2H–H2 collisional system has been computed by one of the authors of the present paper (Dagdigian 2018a). This author used the restricted coupled cluster formalism including single, double, and (perturbative) triple excitations [RCCSDT] (Knowles, Hampel & Werner 1993) to perform ab initio calculations using the molpro software (Werner, Knowles & et al. 2020). The aug-cc-pVQZ basis set (Dunning 1989) was used to ensure convergence of the interaction potential around the global minimum. The interaction energy of the bimolecular complex depends on four degrees of freedom: The separation R between the centres of mass of C2H and H2 PES; the angle θ1 between the C2H internuclear axis and the Jacobi vector R; the angle θ2 between the H2 internuclear axis and the Jacobi vector R; and the dihedral angle ϕ between the (C2H,R) plane and H2 axis. Both C2H and H2 are considered as rigid rotors, where their nuclear geometries are taken as their respective equilibrium configurations in the ground vibrational state.
The fit of the PES was represented by an expansion in bispherical harmonics:
The |$A_{l_{1}l_{2}l}(\theta _{1},\theta _{2}, \phi)$| in equation (1) depend on the angular coordinates of the system, defined as:
where the Ylm are spherical harmonics, (....|..) are Clebsch–Gordan coefficients, [x] ≡ (2x + 1). The |$v_{l_{1}l_{2}l}(R)$| are the radial coefficients for a given distance R, and l1, l2, l are chosen such that |l1 − l2| < l < l1 + l2. Equations (1) and (2) are the most suitable form of the PES for time-independent scattering calculations. The global minimum was found for R = 7.82a0 and the θ1 = 180°, θ2 = 90°, ϕ = 0° orientation with an associated well depth De of 133.4 cm−1.
Within the Born–Oppenheimer approximation, it is possible to use the C2H–H2 PES to describe the interaction of the C2D–H2 complex. This can be performed with a transformation of the coordinates through a shift δr of the centre of mass of the targeted molecule (see Fig. 1). The transformation from one isotopologue frame to the other one can be obtained through:
where r(C2H) and r(C2D) are the positions of the centre of mass of C2H and C2D respectively along the internuclear axis (see Fig. 1). The same bond lengths are assumed for C2D than for C2H since the molecule is assumed to be rigid. The transformation of the coordinates θ2 and ϕ was not necessary since the impact on the dynamics is found to be negligible. The centre of mass is shifted by δr = +0.1157a0, toward the deuterium end. This transformation leads to a new expansion of the PES for the C2D–H2 complex. Dagdigian (2018a) obtained a fit for l1 = 12 and l2 = 6, leading to 174 radial coefficients for C2H–H2. For the C2D–H2 collisional system, we expanded the PES with the same number of coefficients as for C2H–H2 using a Gauss–Legendre quadrature with 686 geometries.
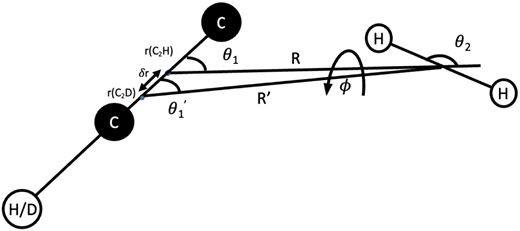
Representation of the C2H–H2 and C2D–H2 geometries. The unprimed and primed quantities refer to C2H and C2D respectively.
It is interesting to check the impact of the isotopic substitution on the contour plots of the PES for given geometries. Fig. 2 shows the angular dependence of the PES of the C2H–H2 and C2D–H2 complexes for two geometries around the global minimum. One can see that for both isotopologues, the most repulsive interaction occurs when θ1 = 180°, corresponding to the orientation of the targeted hydrogen/deuterium toward the collider, and for θ2 = 0° and θ2 = 180°.
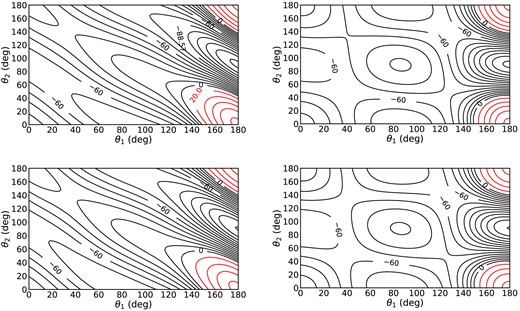
Contour plots of the interaction potential of C2H (upper panels) and C2D (lower panels) for an intermolecular separation R = 7.82a0. The left and right panels have ϕ = 0° (left panels) and 30° (right panels). Contours in red represent a repulsive interaction, contours in black an attractive interaction. The values of the potential are given in cm−1.
The most attractive part of the PES corresponds to a T-shaped structure of the complexes (θ1 = 180°, θ2 = 90°), where the global minimum is reached. These contour plots illustrate the large anisotropy of the PES. Even if the shapes of the interaction energy look very similar in both isotopologue frames, one can see slight differences in the range θ1 = 140–180°, where larger anisotropy is seen for the C2H–H2 complex. Such differences will have impact on the magnitude of the C2H–H2 and C2D–H2 excitation cross-sections as will be seen in Section 3.
2.2 Scattering formalism
Both C2H and C2D are open-shell molecules with a 2Σ+ electronic ground state. The unpaired electron, with spin S1 = 1/2, couples with the rotational angular momentum n1 to yield the total angular momentum j1 of the molecule:
During the collision, j1 and the rotational angular momentum j2 of the projectile will be coupled with the rotation of the target. The total angular momentum J of the complex thus equals
where L is the orbital angular momentum and j12 = j1 + j2 is the vector sum of the molecular angular momenta. This coupling scheme has been used in quantum time-independent calculations with the close coupling method (CC) to determine fine-structure resolved cross-sections in the same way as employed by Dagdigian (2018b).
In addition, both C2H and C2D possess a non-zero nuclear spin due to the H and D nuclei. The coupling of the nuclear spin to the rotation yields a hyperfine splitting of the fine-structure energy levels where
where F1 denotes the total angular momentum of the targeted isotopologue including its nuclear spin, IX is the nuclear spin (X = H or D), IH = 1/2, and ID = 1. When the hyperfine splittings are small, it is possible to consider them as degenerate and carry out hyperfine structure calculations using a recoupling technique (Alexander & Dagdigian 1985). Then, the nuclear spin can be recoupled to the total angular momentum of the complex as J + IX = JT.
This approach consists of using nuclear spin-free T-matrix elements |$T^{J}_{n_{1}j_{1}j_{2}j_{12}L,n_{1}^{\prime }j_{1}^{\prime }j_{2}^{\prime }j_{12}^{\prime }L^{\prime }}$| computed by the CC method to determine hyperfine resolved cross-sections. The T-matrix elements including the nuclear spin can be obtained using the spin-free T-matrix elements (Offer, van Hemert & van Dishoeck 1993):
Here, j2 + L = jR and jR + F1 = JT. The T-matrix elements in equation (6) can be used to compute hyperfine resolved cross-sections:
where k2 is the wave vector of the initial state.
Nuclear spin-free calculations have been carried out for C2D collisions with both ortho- and para-H2 up to 1618.7 cm−1 and 1500 cm−1, respectively, for energy levels up to n1 ≤ 15 (see Appendix A for more details about the used parameters in scattering calculations). These calculations have been performed including a rotational basis of j2 = 0, 2 for para-H2. In the case of ortho-H2 collisions, only a basis j2 = 1 was necessary.
For collisions of C2D with ortho-H2 and para-H2, hyperfine rate coefficients have been computed for 55 energy levels up to n1 = 9 and for temperatures between 5 and 100 K. For the C2H–H2 collisional system, fine-structure calculations were performed up to a total energy of 3500 cm−1 for collisions with para-H2 and 3618.7 cm−1 for collisions with ortho-H2. Energy levels with n1 up to 20 were taken into account in the CC calculations. Fine-structure rate coefficients were then computed up to 500 K. All scattering calculations (both CC and recoupling) were performed with the hibridon scattering code (Alexander et al. 2023). For the highest total energies considered, greater than 1500 cm−1, the convergence of cross-sections with respect to the H2 basis used is moderate, up to a few tens of per cents of mean absolute deviation. Such intensive calculations may be accomplished by using the coupled state approximation. However, this method is not implemented yet in the hibridon code for molecule–molecule collisions. However, this truncated H2 basis moderately impacts the rate coefficients presently computed.
The rate coefficient from an initial level i to a final level f consists in integrating the cross-section in equation (7) over a Maxwell–Boltzmann distribution of the collisional energies Ec:
where μ is the reduced mass of the given collisional system and kB is the Boltzmann’s constant.
3 RATE COEFFICIENTS
3.1 C2H–H2 rate coefficients
Both fine and hyperfine structure resolved rate coefficients calculated in this work for the C2H–H2 collisional system are essentially the same with the same propensity rules as in the calculations by Dagdigian (2018b) and will not be discussed in details here. We just review the main features of these collisional data. It is found that the rate coefficients for collisions involving ortho-H2 are larger than those with para-H2 (see also Fig. 3). For fine-structure transitions induced by para- and ortho-H2, propensity rules (Alexander 1982) are observed for Δn1 = Δj1 transitions (see Fig. 6) with Δn1 = Δj1 = 2 transitions dominating over Δn1 = Δj1 = 1 transitions. These effects have an impact on the behaviour of hyperfine structure transitions, where fine structure conserving transitions displayed larger intensities for Δj1 = ΔF1 transitions than for Δn1 ≠ Δj1 ones.
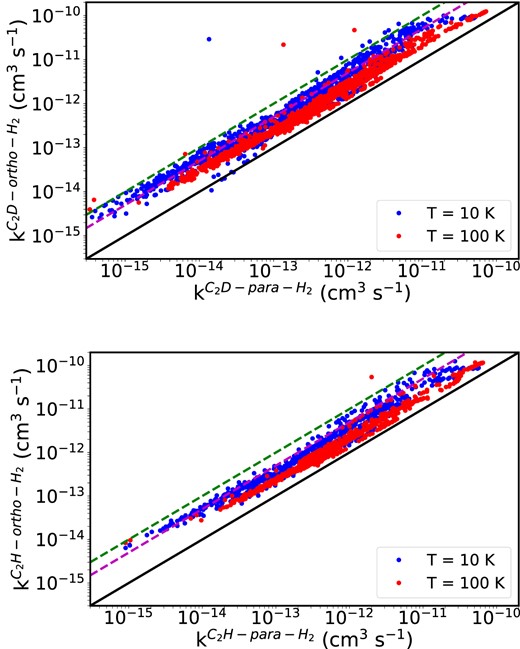
Systematic comparison of hyperfine rate coefficients for C2D–ortho- and para-H2 collisions (upper panel) and for C2H–ortho- and para-H2 collisions (lower panel) at 10 K and 100 K. Magenta and green dashed lines represent deviations within a factor of 5 and 10, respectively.
3.2 C2D–H2 rate coefficients
Fig. 3 shows a comparison between hyperfine resolved C2D–ortho-H2 and C2D–para-H2 rate coefficients at 10 K and 100 K. One can see that all rate coefficients are larger for C2D–ortho-H2 collisions by a factor of 10 at low temperatures. Such deviations come from the PES features, where larger anisotropies are expected for the ortho-H2 collider. These differences are still an order of a factor of 5 at 100 K. This also can be seen in Fig. 4, where ortho-H2 rate coefficients are dominating the corresponding para-H2 quantities. Such effect is well known for neutral collisional systems such as PN–H2 (Desrousseaux et al. 2021) or HC2NC–H2 and HNC3–H2 (Bop et al. 2021).
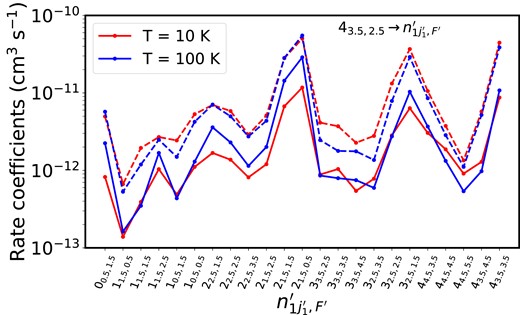
Hyperfine structure resolved transitions for C2D in collision with para-H2 (solid lines) and ortho-H2 (dashed lines) from the 43.5,2.5 energy level toward lower levels.
It is also possible to see a propensity rule in favour of fine structure conserving (Δn1 = Δj1) transitions, which is consistent with results observed in C2H collisions (Dagdigian 2018b). This propensity rules results from the fact that the electron spin is a spectator in the collision. This effect is generally observed for open-shell molecules such as CCS (Godard Palluet & Lique 2023), CN (Kalugina, Kłos & Lique 2013) or SH+ (Dagdigian 2019). A propensity rule for even Δn1 = Δj1 transitions is observed.
More specifically, in the case of the hyperfine structure excitation, a propensity rule (Alexander & Dagdigian 1985) is also observed for Δj1 = ΔF1 transitions. Similar to the propensity rule for fine-structure transitions, this hyperfine propensity rule results from the spectator role that nuclear spin plays in the collision. With the propensity rule for fine-structure transitions, the largest rate coefficients occur for Δn1 = Δj1 = ΔF1 transitions. The weakest transitions occur when Δn1 ≠ Δj1 ≠ ΔF1, sometimes by one order of magnitude compared to the dominant transitions.
It is interesting to compare the C2D–H2 rate coefficients with the previous study of Dumouchel et al. (2017). In their work, the 2D averaged PES computed by Najar et al. (2014) for the C2H–H2 collisional system and transformed to describe the C2D–H2 system was used for scattering calculations. The computed rate coefficients were computed with only j2 = 0 in the H2 rotational basis. Fig. 5 shows a comparison between the two sets of collisional data for two given temperatures. One can see that most of the transitions are contained within a factor of 2 of differences, whereas the largest ones are relatively well reproduced. Such differences can come from several possibilities. First, the inclusion of two more degrees of freedom in the C2H–H2 interaction potential leads to more anisotropies (see Fig. 2) and radial coefficients to take into account in scattering calculations. Second, the inclusion of j2 = 0, 2 rotational basis is often necessary to converge cross-sections computed with the CC approach.
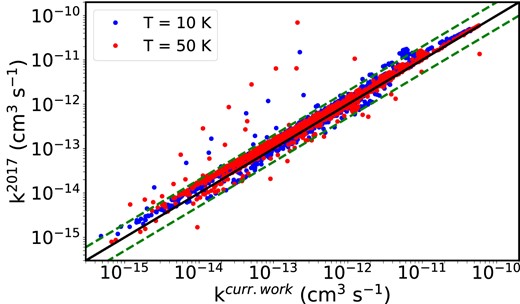
Systematic comparison of C2D–para-H2 hyperfine rate coefficients computed in this work and the previous study by Dumouchel et al. (2017) for transitions at 10 K and 50 K. Green dashed lines represent deviations within a factor of 2.
3.3 C2H–H2 versus C2D–H2 rate coefficients
Fig. 6 presents comparisons of several fine-structure rate coefficients of C2H and C2D in collisions with both ortho- and para-H2. It should be noted that the isotopologues have different numbers of hyperfine transitions because of the differences values of the H and D nuclear spins. The strongest impact of the isotopic substitution can be observed for Δn1 = Δj1 = 1 transitions for both H2 colliders, in a more moderate way for ortho-H2 than para-H2. Such differences mostly come from the shift of the centre of mass of the PES, leading to significant differences in expansion coefficients |$v_{l_{1}l_{2}l}$|. Especially, radial coefficients with odd l1 indexes are larger for the C2H–H2 complex than the C2D–H2 one. This is related to the fact that the centre of mass is closer of the centre of the molecule in the case of C2D and leads to less anisotropy in the PES (see Fig. 1).
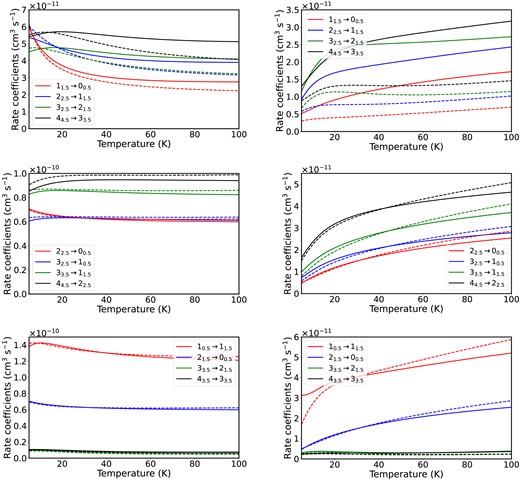
Temperature dependence of fine-structure resolved rate coefficients for C2H (solid lines) and C2D (dashed lines) in collision with ortho-H2 (left panel) and para-H2 (right panel). Comparisons are done for Δn1 = Δj1 = 1 (upper), Δn1 = Δj1 = 2 (middle), and Δn1 ≠ Δj1 (lower) transitions.
For the other cases (Δn1 = Δj1 = 2 and Δn1 ≠ Δj1), the impact of isotopic substitution is moderate and rate coefficients are of the same order of magnitude for both collisional systems. Since the PES expansion coefficients involved in the CC equations for these types of transitions are very similar, these slight differences can mostly come from the spectroscopic structure of the two targets since their rotational constant are quite different, where |$B_{\rm {C_{2}H}}$| = 1.457 cm−1 and |$B_{\rm {C_{2}D}}$| = 1.203 cm−1 (Gottlieb et al. 1983; Vrtilek et al. 1985).
4 EXCITATION OF C2D IN THE ISM
Once hyperfine resolved rate coefficients are computed, it is possible to illustrate the impact of the new set of collisional data on radiative transfer modelling. Such modelling has already be done for the C2H–H2 collisional system (Dagdigian 2018b) and will not be discussed here. The following discussion will focus on the new data of the C2D–H2 collisional system. This was carried out using the radex code (Van der Tak et al. 2007) with the escape probability approximation. Calculations were performed in order to model typical cold environments where C2D is detected, such as TMC-1 (Turner 2001) or L1527 (Yoshida et al. 2019). The kinetic temperature Tkin was set to 10 K, a linewidth of 0.5 km s−1, and a typical column density of 1 × 1013 cm−2. A background temperature Tbg was assumed to be 2.73 K, representing the cosmic microwave background. Einstein coefficients were taken from the Cologne Database for Molecular Spectroscopy (Endres et al. 2016). Another calculation has been done at Tkin = 50 K to model warmer environments such as Monoceros R2 (Treviño-Morales et al. 2014), with a typical linewidth of 1 km s−1.
Fig. 7 shows the dependence of excitation temperatures upon the density of H2 for several hyperfine transitions of the C2D n1 = 1–0 rotational line for kinetic temperature (Tkin) of 10 K and n1 = 2–1 for Tkin = 50 K. The range of excitation temperature varies from Tex = Tbg at very low densities where radiative processes are dominant, to Tex = Tkin at high densities, where the LTE is reached due to the domination of collisional processes.
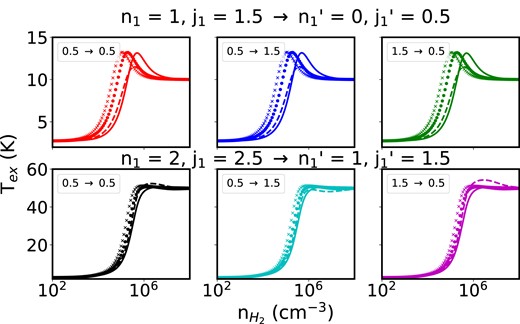
Excitation temperatures as a function of the density of H2 at Tkin = 10 K (upper panels) and 50 K (lower panels) for several hyperfine radiative transitions of C2D. Numbers in legend represent F → F′ quantum numbers. Dashed lines are related to the set of data from Dumouchel et al. (2017), solid lines the set of data of the present work with 100 per cent of para-H2 density, dotted lines with 25 per cent of ortho-H2 and crossed lines with 75 per cent of ortho-H2.
Comparisons were carried out with the set of data for C2D–para-H2 from Dumouchel et al. (2017). Also, the impact of the new ortho-H2 collisions will be assessed with different ortho-to-para-H2 ratio (OPR) taken for the radiative transfer calculations. For Tkin = 10 K, one can see that for 100 per cent of para-H2, excitation temperatures coincide with the kinetic temperature at |$n_{\rm {H}_{2}} \sim 2 \times 10^{7}$| cm−3, showing that a very dense gas is needed to thermalize, whereas modelling obtained using Dumouchel et al. (2017) reaches LTE conditions at |$n_{\rm {H}_{2}} \sim 8 \times 10^{6}$| cm−3. This is not surprising since most of rate coefficients for C2D–para-H2 of Dumouchel et al. (2017) are larger by up to a factor of 2, making collisions more efficient than the set of data provided in this work. However, most of the differences in this modelling are not more than 20 per cent. The increasing of the OPR to 25 per cent and 75 per cent involves the contribution of C2D–ortho-H2 rate coefficients. It has an impact on the critical density because of the differences between ortho- and para-H2 collisions. In addition, excitation temperatures of the presented transitions at Tkin = 50 K are less sensitive to ortho-H2 collisions. For most of the models, LTE is reached around 106 cm−3. That can also be related to the order of magnitude of the rate coefficients, having a strongly different behaviour at 10 K between ortho- and para-H2 collisions than at higher temperatures (see Fig. 3) and be less sensitive to the modelling.
It is interesting to reinterpret C2D observations made on L1527 by Yoshida et al. (2019) and to derive the C2D column density with our new set of rate coefficients. We determined the column density range of C2D by computing integrated intensity of different detected lines that best reproduce these observations (see Table 1), minimizing the following χ2 parameter
where N denotes the number of observed lines, |$F_{\mathrm{ i}}^{\mathrm{ obs}}$| and |$F_{\mathrm{ i}}^{\mathrm{ calc}}$| are the integrated intensities observed and calculated respectively, and σi is the uncertainty of the ith observation. We varied the column density in the range [1012–1014] cm−2 and the H2 density [5 × 105 − 3 × 106] cm−3 for two fixed kinetic temperatures of 10 K and 15 K.
| Frequency . | Transition . | ∫Tmbdv . |
|---|---|---|
| (GHz) . | |$(n_{1},j_{1},F) \rightarrow (n_{1}^{\prime },j_{1}^{\prime },F^{\prime })$| . | (K km s−1) . |
| 72.101715 | (1,1.5,1.5) → (0,0.5,1.5) | 0.147(16)a |
| 72.107700 | (1,1.5,2.5) → (0,0.5,1.5) | 0.395(16) |
| 72.109114 | (1,1.5,0.5) → (0,0.5,0.5) | 0.117(14) |
| 72.112399 | (1,1.5,1.5) → (0,0.5,0.5) | 0.144(15) |
| 72.187704 | (1,0.5,1.5) → (0,0.5,1.5) | 0.165(20) |
| 72.189505 | (1,0.5,0.5) → (0,0.5,1.5) | 0.12(3) |
| 72.198388 | (1,0.5,1.5) → (0,0.5,0.5) | 0.065(16) |
| Frequency . | Transition . | ∫Tmbdv . |
|---|---|---|
| (GHz) . | |$(n_{1},j_{1},F) \rightarrow (n_{1}^{\prime },j_{1}^{\prime },F^{\prime })$| . | (K km s−1) . |
| 72.101715 | (1,1.5,1.5) → (0,0.5,1.5) | 0.147(16)a |
| 72.107700 | (1,1.5,2.5) → (0,0.5,1.5) | 0.395(16) |
| 72.109114 | (1,1.5,0.5) → (0,0.5,0.5) | 0.117(14) |
| 72.112399 | (1,1.5,1.5) → (0,0.5,0.5) | 0.144(15) |
| 72.187704 | (1,0.5,1.5) → (0,0.5,1.5) | 0.165(20) |
| 72.189505 | (1,0.5,0.5) → (0,0.5,1.5) | 0.12(3) |
| 72.198388 | (1,0.5,1.5) → (0,0.5,0.5) | 0.065(16) |
Note. aParenthesis represent the errors of last significant digits.
| Frequency . | Transition . | ∫Tmbdv . |
|---|---|---|
| (GHz) . | |$(n_{1},j_{1},F) \rightarrow (n_{1}^{\prime },j_{1}^{\prime },F^{\prime })$| . | (K km s−1) . |
| 72.101715 | (1,1.5,1.5) → (0,0.5,1.5) | 0.147(16)a |
| 72.107700 | (1,1.5,2.5) → (0,0.5,1.5) | 0.395(16) |
| 72.109114 | (1,1.5,0.5) → (0,0.5,0.5) | 0.117(14) |
| 72.112399 | (1,1.5,1.5) → (0,0.5,0.5) | 0.144(15) |
| 72.187704 | (1,0.5,1.5) → (0,0.5,1.5) | 0.165(20) |
| 72.189505 | (1,0.5,0.5) → (0,0.5,1.5) | 0.12(3) |
| 72.198388 | (1,0.5,1.5) → (0,0.5,0.5) | 0.065(16) |
| Frequency . | Transition . | ∫Tmbdv . |
|---|---|---|
| (GHz) . | |$(n_{1},j_{1},F) \rightarrow (n_{1}^{\prime },j_{1}^{\prime },F^{\prime })$| . | (K km s−1) . |
| 72.101715 | (1,1.5,1.5) → (0,0.5,1.5) | 0.147(16)a |
| 72.107700 | (1,1.5,2.5) → (0,0.5,1.5) | 0.395(16) |
| 72.109114 | (1,1.5,0.5) → (0,0.5,0.5) | 0.117(14) |
| 72.112399 | (1,1.5,1.5) → (0,0.5,0.5) | 0.144(15) |
| 72.187704 | (1,0.5,1.5) → (0,0.5,1.5) | 0.165(20) |
| 72.189505 | (1,0.5,0.5) → (0,0.5,1.5) | 0.12(3) |
| 72.198388 | (1,0.5,1.5) → (0,0.5,0.5) | 0.065(16) |
Note. aParenthesis represent the errors of last significant digits.
Fig. 8 shows the dependence of the χ2 parameter upon the H2 density and the range of derived C2D column densities for the best reproduced observations. One can see that for both kinetic temperatures, this procedure was not able to constrain the H2 density within the proposed grid. For Tkin = 10 K, the column density is determined as N = (3.2 − 4.9) × 1013 cm−2 within a confidence level of 99 per cent, where observations derived a value of N = (4.7 ± 0.3) × 1013 cm−2. For Tkin = 15 K, the column density is found to be N = (3.6 − 5.8) × 1013 cm−2 compared with observations where N = (5.6 ± 1.1) × 1013 cm−2. These calculations agree with the literature within a factor ∼1.5 which is relatively consistent regarding the used methods and uncertainties involved. The column densities derived from observations were carried out in the LTE conditions, finding that lines are optically thin so no corrections need to be applied on brightness temperatures and used a least-squares fitting method. In our calculations, the computed opacities are never greater than 0.1 for all lines and the two kinetic temperatures. However, it should be noted that the density influences excitation temperatures. The considered lines reproduced observations for excitation temperatures varying from ∼11 to 13 K and from ∼16 to 26 K for Tkin = 10 K and Tkin = 15 K respectively. This corresponds to a regime where lines are in a slight suprathermal effect and close to LTE conditions. Since the excitation temperatures do not match with the kinetic temperature, one can see that the derived ranges of column densities tends to decrease the observed values. Our best solutions where the |$\chi ^{2}_{\rm {min}}$| is reached correspond to N = 4.1 × 1013 cm−2, |$n_{\rm {H}_{2}} = 6 \times 10^{5}$| cm−3 and Tex ∼ 24 K for all hyperfine lines for Tkin =15 K. For the case where Tkin =10 K, |$\chi ^{2}_{\rm {min}}$| is reached when N = 3.7 × 1013 cm−2, |$n_{\rm {H}_{2}} = 6.5 \times 10^{5}$| cm−3, and Tex ∼ 13 K for the multiplet. This would mean that the population of these states under LTE conditions are underestimated compared to non-LTE modelling. In our case, we increase the population of the lower levels of these lines by ∼14 per cent and ∼20 per cent at Tkin = 10 K and Tkin = 15 K, respectively.
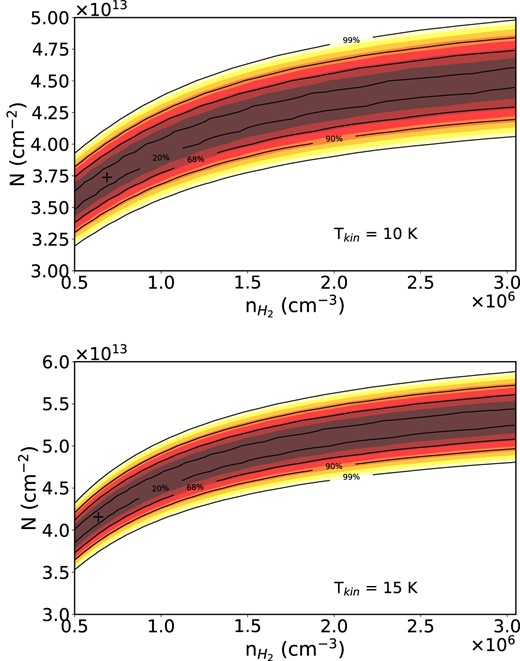
Dependence of the χ2 parameter with the column density and the H2 density for kinetic temperatures at 10 K (upper panel) and 15 K (lower panel). Values are shown for 20 per cent, 68 per cent, 90 per cent, and 99 per cent levels of confidence representing |$\chi ^{2}_{\rm {min}}$| + (0.45, 2.3, 4.61, 9.21; Lampton, Margon & Bowyer 1976; Schöier et al. 2002). The crossed dot represents the minimum of the χ2.
5 CONCLUSION
We computed hyperfine resolved rate coefficients for C2H and C2D in collision with both ortho- and para-H2. These data take into account the first 38 C2H hyperfine levels and the first 55 C2D hyperfine levels up to 100 K. We also extended the range of temperature for fine-structure C2H–H2 collisions up to 500 K for levels up to n1 = 20. We also computed C2D–H2 fine-structure resolved rate coefficients for levels up to n1 = 15 and for temperatures up to 200 K. These data were computed using the 4D PES of Dagdigian (2018a) and the recoupling method (Alexander & Dagdigian 1985; Offer et al. 1993). C2D–ortho-H2 and C2D–para-H2 rate coefficients show very different behaviours, where differences are observed up to a factor of 10. This is a standard observation for neutral systems, showing the importance of taking into account the internal structure of H2 in scattering calculations. We observed more specifically that fine-structure conserving transitions are larger than fine-structure changing ones for C2D collisions and display even larger rate coefficients for the Δn1 = Δj1 = ΔF = 2 propensity rule.
With isotopic substitution C2H and C2D rate coefficients can differ up to factor of 2 for Δn1 = Δj1 = 1 transitions, especially when collisions occur with para-H2. For Δn1 = Δj1 = 2 transitions, both isotopologues with ortho- and para-H2 are the same order of magnitude. Such results reflect the shift of the centre of mass between the two isotopologues in the PES, their energetic structure and the larger anisotropies of the PES for the ortho-H2 collider.
This new set of data has been compared with the previous work done by Dumouchel et al. (2017), where they used a transformed 2D PES for the C2D–H2 system (i.e. neglecting the internal structure of H2). It has been shown that the inclusion of j2 = 0, 2 in the rotational basis for scattering calculations lead differences up to a factor of 2.
We carried out a radiative transfer modelling to illustrate the impact of the new set of C2D–H2 rate coefficients. Differences in excitation temperatures are moderate between the new set of data and the one obtained by Dumouchel et al. (2017) compared to the usual uncertainties involved in astrophysical applications when only para-H2 collisions occur. However, larger differences are observed when collisions with ortho-H2 take place. We computed and reinterpreted the column density of C2D under non-LTE conditions with the literature in the case of the low-mass star-forming region L1527 (Yoshida et al. 2019). The agreement with observations was found to be within a factor ∼1.5, which can be considered good regarding the uncertainties due to, on one hand, the methods used for calculations of the PES and rate coefficients, assumptions made by non-LTE modelling, and on the other hand uncertainties of the measurements and the methods used to compute column densities under the LTE assumption. Especially, LTE modelling are underestimating the population of the lower levels of a given transition compared to calculations done under non-LTE conditions.
These data are expected to be used for the interpretation of astronomical observations in order to determine physical conditions in regions where ortho-H2 is significantly populated.
ACKNOWLEDGEMENTS
We acknowledge financial support from the European Research Council (Consolidator grant COLLEXISM, grant agreement no. 811363). We wish to acknowledge the support from the CEA/GENCI (Grand Equipement National de Calcul Intensif) for awarding us access to the TGCC (Très Grand Centre de Calcul) Joliot Curie/IRENE supercomputer within the A0110413001 project.
DATA AVAILABILITY
Fine and hyperfine structure resolved rate coefficients for C2H–H2 and C2D–H2 will be available on the following databases: EMAA (https://dx.doi.org/10.17178/EMAA), LAMDA (Van der Tak et al. 2020), and BASECOL (Dubernet et al. 2012).
Footnotes
It has been found that the most recent available collisional data (Dagdigian 2018b) was overestimated by a factor ∼1.4. Also, we figured out a bug in the recoupling approach from the scattering software used in this work did not correctly calculate quasi-elastic transitions.
References
APPENDIX: DISCUSSION ON THE SCATTERING CONVERGED PARAMETERS
Fine-structure resolved cross-sections for C2H and C2D in collision with both ortho- and para-H2 were determined through solution of the CC equations. To do so, the rotational basis of the targeted molecule nmax and the total angular momentum Jtot are converged for different total energies Etot at different energy steps ΔE. For all collisional systems, the rotational basis of the H2 collider was chosen to be j2, max = 0, 2 for para-H2 and j2, max = 1 for ortho-H2. The largest parameters are presented in Tables A1–A2. Optimization was done in order to converge cross-sections within 1 per cent of accuracy for each parameter. The propagation of the partial waves was done from Rmin = 4.25a0 to Rmax = 50a0 for C2H collisions, and from Rmin = 4.25a0 to Rmax = 60a0 for C2D collisions. Then, hyperfine calculations were done using the nuclear spin-free S-matrices computed with these parameters.
Values of the converged parameters used for scattering calculations for the C2H–H2 collisional system. The rotational basis nmax of the targeted molecule, total angular momentum Jtot and total energies Etot with energy steps ΔE are presented.
| C2H–ortho-H2 . | C2H–para-H2 . | ||||||
|---|---|---|---|---|---|---|---|
| Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . | Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . |
| 118.8–168.7 | 0.1 | 9 | 18 | 0.1–50 | 0.1 | 10 | 18 |
| 168.8–218.7 | 0.1 | 12 | 24 | 50.1–100 | 0.1 | 12 | 24 |
| 218.9–318.7 | 0.1 | 15 | 30 | 100.1–200 | 0.1 | 15 | 27 |
| 319.7–618.7 | 0.1 | 17 | 42 | 200.2–300 | 0.1 | 19 | 39 |
| 620.7–818.7 | 2 | 20 | 48 | 301–500 | 1 | 19 | 39 |
| 823.7–1118.7 | 5 | 24 | 57 | 505–700 | 5 | 22 | 45 |
| 1128.7–1618.7 | 10 | 27 | 69 | 710–1000 | 10 | 25 | 51 |
| 1718.7–2118.7 | 100 | 27 | 85 | 1050–1500 | 50 | 28 | 60 |
| 2318.7–3118.7 | 200 | 27 | 100 | 1600–2000 | 100 | 28 | 81 |
| 3618.7 | 500 | 27 | 100 | 2200–3000 | 200 | 28 | 100 |
| – | – | – | – | 3500 | 500 | 28 | 100 |
| C2H–ortho-H2 . | C2H–para-H2 . | ||||||
|---|---|---|---|---|---|---|---|
| Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . | Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . |
| 118.8–168.7 | 0.1 | 9 | 18 | 0.1–50 | 0.1 | 10 | 18 |
| 168.8–218.7 | 0.1 | 12 | 24 | 50.1–100 | 0.1 | 12 | 24 |
| 218.9–318.7 | 0.1 | 15 | 30 | 100.1–200 | 0.1 | 15 | 27 |
| 319.7–618.7 | 0.1 | 17 | 42 | 200.2–300 | 0.1 | 19 | 39 |
| 620.7–818.7 | 2 | 20 | 48 | 301–500 | 1 | 19 | 39 |
| 823.7–1118.7 | 5 | 24 | 57 | 505–700 | 5 | 22 | 45 |
| 1128.7–1618.7 | 10 | 27 | 69 | 710–1000 | 10 | 25 | 51 |
| 1718.7–2118.7 | 100 | 27 | 85 | 1050–1500 | 50 | 28 | 60 |
| 2318.7–3118.7 | 200 | 27 | 100 | 1600–2000 | 100 | 28 | 81 |
| 3618.7 | 500 | 27 | 100 | 2200–3000 | 200 | 28 | 100 |
| – | – | – | – | 3500 | 500 | 28 | 100 |
Values of the converged parameters used for scattering calculations for the C2H–H2 collisional system. The rotational basis nmax of the targeted molecule, total angular momentum Jtot and total energies Etot with energy steps ΔE are presented.
| C2H–ortho-H2 . | C2H–para-H2 . | ||||||
|---|---|---|---|---|---|---|---|
| Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . | Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . |
| 118.8–168.7 | 0.1 | 9 | 18 | 0.1–50 | 0.1 | 10 | 18 |
| 168.8–218.7 | 0.1 | 12 | 24 | 50.1–100 | 0.1 | 12 | 24 |
| 218.9–318.7 | 0.1 | 15 | 30 | 100.1–200 | 0.1 | 15 | 27 |
| 319.7–618.7 | 0.1 | 17 | 42 | 200.2–300 | 0.1 | 19 | 39 |
| 620.7–818.7 | 2 | 20 | 48 | 301–500 | 1 | 19 | 39 |
| 823.7–1118.7 | 5 | 24 | 57 | 505–700 | 5 | 22 | 45 |
| 1128.7–1618.7 | 10 | 27 | 69 | 710–1000 | 10 | 25 | 51 |
| 1718.7–2118.7 | 100 | 27 | 85 | 1050–1500 | 50 | 28 | 60 |
| 2318.7–3118.7 | 200 | 27 | 100 | 1600–2000 | 100 | 28 | 81 |
| 3618.7 | 500 | 27 | 100 | 2200–3000 | 200 | 28 | 100 |
| – | – | – | – | 3500 | 500 | 28 | 100 |
| C2H–ortho-H2 . | C2H–para-H2 . | ||||||
|---|---|---|---|---|---|---|---|
| Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . | Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . |
| 118.8–168.7 | 0.1 | 9 | 18 | 0.1–50 | 0.1 | 10 | 18 |
| 168.8–218.7 | 0.1 | 12 | 24 | 50.1–100 | 0.1 | 12 | 24 |
| 218.9–318.7 | 0.1 | 15 | 30 | 100.1–200 | 0.1 | 15 | 27 |
| 319.7–618.7 | 0.1 | 17 | 42 | 200.2–300 | 0.1 | 19 | 39 |
| 620.7–818.7 | 2 | 20 | 48 | 301–500 | 1 | 19 | 39 |
| 823.7–1118.7 | 5 | 24 | 57 | 505–700 | 5 | 22 | 45 |
| 1128.7–1618.7 | 10 | 27 | 69 | 710–1000 | 10 | 25 | 51 |
| 1718.7–2118.7 | 100 | 27 | 85 | 1050–1500 | 50 | 28 | 60 |
| 2318.7–3118.7 | 200 | 27 | 100 | 1600–2000 | 100 | 28 | 81 |
| 3618.7 | 500 | 27 | 100 | 2200–3000 | 200 | 28 | 100 |
| – | – | – | – | 3500 | 500 | 28 | 100 |
Values of the converged parameters used for scattering calculations for the C2D–H2 collisional system. The rotational basis nmax of the targeted molecule, total angular momentum Jtot, and total energies Etot with energy steps ΔE are presented.
| C2D–ortho-H2 . | C2D–para-H2 . | ||||||
|---|---|---|---|---|---|---|---|
| Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . | Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . |
| 118.8–168.7 | 0.1 | 12 | 18 | 0.1–50 | 0.1 | 11 | 18 |
| 168.8–218.7 | 0.1 | 12 | 24 | 50.1–100 | 0.1 | 13 | 24 |
| 218.9–318.7 | 0.1 | 13 | 30 | 100.1–200 | 0.1 | 16 | 30 |
| 318.9–618.7 | 0.2 | 15 | 45 | 200.2–500 | 0.2 | 20 | 42 |
| 619.2–818.7 | 0.5 | 18 | 51 | 500.5–700 | 1 | 23 | 48 |
| 819.7–1118.7 | 1 | 21 | 57 | 705–1000 | 5 | 28 | 54 |
| 1123.7–1618.7 | 5 | 25 | 66 | 1010–1500 | 10 | 34 | 60 |
| C2D–ortho-H2 . | C2D–para-H2 . | ||||||
|---|---|---|---|---|---|---|---|
| Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . | Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . |
| 118.8–168.7 | 0.1 | 12 | 18 | 0.1–50 | 0.1 | 11 | 18 |
| 168.8–218.7 | 0.1 | 12 | 24 | 50.1–100 | 0.1 | 13 | 24 |
| 218.9–318.7 | 0.1 | 13 | 30 | 100.1–200 | 0.1 | 16 | 30 |
| 318.9–618.7 | 0.2 | 15 | 45 | 200.2–500 | 0.2 | 20 | 42 |
| 619.2–818.7 | 0.5 | 18 | 51 | 500.5–700 | 1 | 23 | 48 |
| 819.7–1118.7 | 1 | 21 | 57 | 705–1000 | 5 | 28 | 54 |
| 1123.7–1618.7 | 5 | 25 | 66 | 1010–1500 | 10 | 34 | 60 |
Values of the converged parameters used for scattering calculations for the C2D–H2 collisional system. The rotational basis nmax of the targeted molecule, total angular momentum Jtot, and total energies Etot with energy steps ΔE are presented.
| C2D–ortho-H2 . | C2D–para-H2 . | ||||||
|---|---|---|---|---|---|---|---|
| Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . | Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . |
| 118.8–168.7 | 0.1 | 12 | 18 | 0.1–50 | 0.1 | 11 | 18 |
| 168.8–218.7 | 0.1 | 12 | 24 | 50.1–100 | 0.1 | 13 | 24 |
| 218.9–318.7 | 0.1 | 13 | 30 | 100.1–200 | 0.1 | 16 | 30 |
| 318.9–618.7 | 0.2 | 15 | 45 | 200.2–500 | 0.2 | 20 | 42 |
| 619.2–818.7 | 0.5 | 18 | 51 | 500.5–700 | 1 | 23 | 48 |
| 819.7–1118.7 | 1 | 21 | 57 | 705–1000 | 5 | 28 | 54 |
| 1123.7–1618.7 | 5 | 25 | 66 | 1010–1500 | 10 | 34 | 60 |
| C2D–ortho-H2 . | C2D–para-H2 . | ||||||
|---|---|---|---|---|---|---|---|
| Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . | Etot (cm−1) . | ΔE (cm−1) . | nmax . | Jtot . |
| 118.8–168.7 | 0.1 | 12 | 18 | 0.1–50 | 0.1 | 11 | 18 |
| 168.8–218.7 | 0.1 | 12 | 24 | 50.1–100 | 0.1 | 13 | 24 |
| 218.9–318.7 | 0.1 | 13 | 30 | 100.1–200 | 0.1 | 16 | 30 |
| 318.9–618.7 | 0.2 | 15 | 45 | 200.2–500 | 0.2 | 20 | 42 |
| 619.2–818.7 | 0.5 | 18 | 51 | 500.5–700 | 1 | 23 | 48 |
| 819.7–1118.7 | 1 | 21 | 57 | 705–1000 | 5 | 28 | 54 |
| 1123.7–1618.7 | 5 | 25 | 66 | 1010–1500 | 10 | 34 | 60 |



