-
PDF
- Split View
-
Views
-
Cite
Cite
Marie Gueguen, François Lique, Collisional excitation of N+(3P) in interstellar clouds, Monthly Notices of the Royal Astronomical Society, Volume 522, Issue 4, July 2023, Pages 6251–6257, https://doi.org/10.1093/mnras/stad1436
Close - Share Icon Share
ABSTRACT
The detection of the N+ ion in ionized interstellar regions, as well as its use as a tracer for atomic nitrogen (N) in interstellar media, makes it an interesting ion from the astrophysical point of view. Accurate determination of the N+ abundance in the interstellar clouds requires detailed modelling of its excitation conditions. Hence, collisional excitation induced by the dominant interstellar species has to be studied. In this paper, we study the collisional excitation of N+ by He and H2. We provide new potential energy surfaces describing the interactions between N+ and He and between N+ and H2 considered as a structureless collider. Quantum calculations of the excitation cross-sections for collisions of N+ with He and H2 are provided, as well as the first excitation rate coefficients for N+ induced by these two species. The results are compared to collisional data for the excitation induced by electrons. It is shown that the excitation of N+ by a neutral collider can play a significant role in weakly ionized regions as well as in warm molecular clouds.
1 INTRODUCTION
N and N2, the dominant nitrogen-bearing elements (Maret, Bergin & Lada 2006; Le Gal et al. 2014) in the interstellar medium (ISM) are respectively impossible and difficult to detect spectroscopically through infrared or millimeter-wavelength transitions. This is due to the fact that N and N2 do not have fine-structure levels and dipole moment, respectively. Proxy is thus used to infer their abundance in interstellar clouds (Le Gal et al. 2014). The N+ ion is detected in the warm and ionized ISM (Goldsmith et al. 2015; Langer et al. 2017; Doherty et al. 2020) and could qualify as such a proxy. Indeed, N+ is considered as an important tracer for N in (fully) ionized regions. It can also be used for discriminating between fully and weakly ionized regions. Despite not (yet) detected in cold molecular clouds, N+ is also expected to be important constituent of such region that initiates the nitrogen chemistry and particularly the formation of ubiquitous ammonia (Dislaire et al. 2012).
The spin–orbit interaction in ionized nitrogen N+ splits its ground electronic state into a triplet of fine-structure levels 3Pj with j = 0, 1, 2. The 3P1 and 3P2 levels are at 48.738 cm−1 and 130.8 cm−1 above 3P0 (Shen et al. 2022), respectively. Transitions with Δj = 1 are allowed and thus make the detection of N+ possible.
Collisional data are needed for interpreting N+ observations and estimating physical conditions. Indeed, in environments that do not reach local thermodynamic equilibrium (LTE), the population of N+ levels has to be modelled through the competition between radiative and collisional processes (Roueff & Lique 2013). Collisional data for N+, although known for the excitation induced by electrons (Tayal 2011), are still missing for the excitation induced by heavier species such as He or H2. Without them, astrophysical observations must be interpreted on the basis of the LTE assumption, which does not allow to make the most of the highly resolved molecular spectra that recently developed facilities do offer. Due to the lack of collisional data available for N+ with the main neutral colliders (He, H, and H21), Persson et al. (2014) had to model spectral observations based on scaled C–H rate coefficients. Such approximation may lead to significant errors in the observations, interpretation, and exploitation.
Calculation of these data requires first to compute an interaction potential between N+ and the projectile (H2 or He in the present study). He and H2 are the dominant colliders in cold molecular clouds where N+ is expected to play a significant role in nitrogen chemistry. In warm (ionized) clouds, where N+ has been detected, H is the dominant neutral projectile. Calculations with H projectile are difficult to perform and we estimate that calculations with He and H2 projectiles can serve as template for the modelling of the impact of neutral colliders (Roueff & Lique 2013). Two studies (Soldán & Hutson 2002; Aïssaoui, Knowles & Bouledroua 2020) have provided potential energy curves (henceforth PECs) for N+–He in the last two decades. However, their PECs are based on coupled cluster methods with an incomplete basis. Nowadays, computing facilities should allow to improve the description of the N+–He interaction. At the opposite, the determination of global N+–H2 potential energy surfaces (henceforth PESs) involved in the collisional process as well as in the non-adiabatic and spin–orbit couplings between them is a very challenging task because of the reactive nature of the system. In order to overcome this difficulty, Gómez-Carrasco et al. (2022) have recently provided PESs for the reactant and product channels separately without considering the intermediate region and have simulated the dynamics of the N+ + H2 → NH+ + H reaction using statistical theories.
Full-dimensional quantum time independent close-coupling (CC) calculations are the method of choice to obtain accurate collisional rate coefficients. Such an approach can be easily used for non-reactive collisional systems such as N+–He. However, in the case of reactive systems such as N+–H2 (Gómez-Carrasco et al. 2022), this approach is impractical due to its memory and CPU requirements and approximate treatments have to be considered.
In this paper, we provide new highly accurate PECs for studying the collisional excitation of N+ by He. We also provide PECs averaged over H2 rotations for N+–H2 interaction. This later potential relies on important approximations, as it treats this system as a non-reactive system. Then, we report inelastic cross-sections of the collisional systems from quantum CC calculations, and we derive collisional data for both systems. This paper is organized as follows: in Section 2, we present the new N+–He PECs, as well as the spherically averaged PECs for the N+–H2 interaction. Section 3 presents the inelastic cross-sections and the rate coefficients obtained from our new PECs. Finally, in Section 4, we discuss our results and their astrophysical implications.
2 N+–He AND N+–H2 INTERACTION POTENTIALS
2.1 N+–He potential energy curves
The interaction of a closed-shell rare-gas atom with a 3P-state atom gives rise to two electronic states: a 3Σ state and a doubly degenerate 3Π state. Ab initio calculations were performed for internuclear distances in the range 1.8 < R < 100 a0 for the 3Σ electronic state and 2.5 < R <100 a0 for the 3Π electronic state, using the spin restricted coupled cluster method with single and double excitation and a perturbative treatment of triple excitation [RCCSD(T)] (Knowles, Hampel & Werner 1993, 2000) and the molpro package (Werner et al. 2020).
As is usually the case in standard ab initio calculations, the spin–orbit coupling was neglected, but taken into account in the scattering calculations. Calculations were performed with the augmented correlation consistent [aug-cc-pVXZ (X = T, Q, 5)] basis set and extrapolated to the complete basis set (CBS) using the procedure of Peterson, Woon & Dunning Jr (1994). Standard corrections were applied to account for the basis set superposition error, using Boys & Bernardi (1970)’s procedure.
In order to obtain an analytical representation, suitable for scattering calculations, we have used the following procedure. For short-range (SR) R-distances, we have used the Born–Mayer formula that traditionally describes the ion–atom curves such as:
with α and β being constants parameters (Pauly 1979). Three coefficients (C4, C6, and C8) adjusted from the ab initio energy values at 15, 20, and 25 a0 were used to describe the PES at long-range (LR) R-distances using the following analytical formula:
Table 1 shows the value calculated for the SR and LR parameters.
| Parameters . | 3Σ . | 3Π . |
|---|---|---|
| α | 95.65 | 19.38 |
| β | 4.09 | 2.12 |
| C4 | 0.69 | −0.69 |
| C6 | 7.54 | −3.50 |
| C8 | 78.67 | −6.69 |
| Parameters . | 3Σ . | 3Π . |
|---|---|---|
| α | 95.65 | 19.38 |
| β | 4.09 | 2.12 |
| C4 | 0.69 | −0.69 |
| C6 | 7.54 | −3.50 |
| C8 | 78.67 | −6.69 |
| Parameters . | 3Σ . | 3Π . |
|---|---|---|
| α | 95.65 | 19.38 |
| β | 4.09 | 2.12 |
| C4 | 0.69 | −0.69 |
| C6 | 7.54 | −3.50 |
| C8 | 78.67 | −6.69 |
| Parameters . | 3Σ . | 3Π . |
|---|---|---|
| α | 95.65 | 19.38 |
| β | 4.09 | 2.12 |
| C4 | 0.69 | −0.69 |
| C6 | 7.54 | −3.50 |
| C8 | 78.67 | −6.69 |
C4, C6, and C8 correspond to the leading terms in the LR expansion of the N+–He interaction: dipole–dipole induction coefficient, dispersion, and induction coefficients, respectively, (Côté & Dalgarno 2000; Bouchelaghem & Bouledroua 2014).
Finally, we used a cubic spline for interpolating smoothly our ab initio data points.
Fig. 1 presents the N+–He PECs obtained. The PECs are characterized by a minimum at 2.9 a0 of −2037 cm−1 for the 3Σ state and at 5.0 a0 of –204.05 cm−1 for the 3Π state. The well is thus much deeper for 3Σ than for 3Π, which can easily be explained since the 3Σ state corresponds to approaches of He along the unoccupied p orbital. In that case, He can get much closer to the ion and the well will thus be much deeper. Note that our results, although improving upon former PECs published by Soldán & Hutson (2002) and Aïssaoui et al. (2020) as relying on an extrapolation to the CBS, are in good agreement with them, with a difference of less than 0.2 per cent and 4.5 per cent for the 3Σ and 3Π minima, respectively. Table 2 shows and compares the main characteristics of the PECs obtained by Soldán & Hutson (2002) (SH02), Aïssaoui et al. (2020) (A20), and in this work.
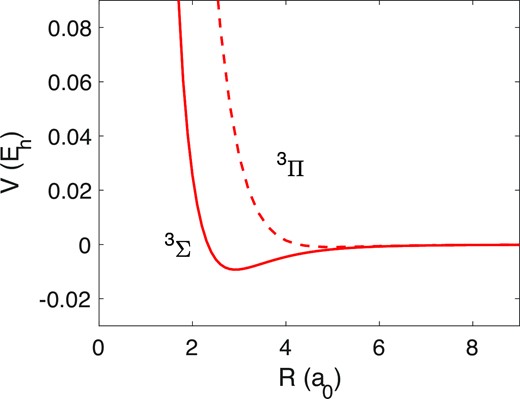
| . | 3Σ . | 3Π . | ||
|---|---|---|---|---|
| . | R (a0) . | V (cm−1) . | R (a0) . | V (cm−1) . |
| SH02 | 2.9 | −2004.85 | 5.0 | −202.49 |
| A20 | 3.0 | −2041.03 | 5.0 | −213.15 |
| This work | 2.9 | −2037.33 | 5.0 | −204.05 |
| . | 3Σ . | 3Π . | ||
|---|---|---|---|---|
| . | R (a0) . | V (cm−1) . | R (a0) . | V (cm−1) . |
| SH02 | 2.9 | −2004.85 | 5.0 | −202.49 |
| A20 | 3.0 | −2041.03 | 5.0 | −213.15 |
| This work | 2.9 | −2037.33 | 5.0 | −204.05 |
| . | 3Σ . | 3Π . | ||
|---|---|---|---|---|
| . | R (a0) . | V (cm−1) . | R (a0) . | V (cm−1) . |
| SH02 | 2.9 | −2004.85 | 5.0 | −202.49 |
| A20 | 3.0 | −2041.03 | 5.0 | −213.15 |
| This work | 2.9 | −2037.33 | 5.0 | −204.05 |
| . | 3Σ . | 3Π . | ||
|---|---|---|---|---|
| . | R (a0) . | V (cm−1) . | R (a0) . | V (cm−1) . |
| SH02 | 2.9 | −2004.85 | 5.0 | −202.49 |
| A20 | 3.0 | −2041.03 | 5.0 | −213.15 |
| This work | 2.9 | −2037.33 | 5.0 | −204.05 |
2.2 N+–H2 spherically averaged potential energy curves
As mentioned in the introduction, obtaining global PESs for the H2N+ system is highly challenging because of the reactive nature of this system, as exemplified by the work done by Gómez-Carrasco et al. (2022). Indeed, these authors only computed a PES for the entrance (N+ + H2) and exit (NH+ + H) channel, neglecting the intermediate (|$\mathrm{NH}_2 ^+$|) region. Here, we used a different strategy and we selected a reduced dimensional approach, where the H2 molecule is described as a structureless sphere. This approach requires to keep the intermolecular distance between the two H atoms fixed, which amounts to treating the complex as non-reactive. Then, we averaged the PECs thus obtained for limited H2 orientations which means that we treat H2 as a pseudo-atom rather than as a molecule.
Hence, as shown in Fig. 2, the N+–H2 PECs are described by the two Jacobi coordinates R, the distance from the centre of mass of H2 molecules to the N+ atom, and θ, the angle between R and the H2 bond axis r. We considered that the H2 molecule only approaches the ion linearly (θ = 0°) or perpendicularly (θ = 90°).

N+–H2 collisional system in Jacobi coordinates. On the left, the linear approach corresponding to θ = 0°. On the right, the perpendicular approach, where θ = 90°.
Ab initio calculations were performed using the RCCSD(T) approach with the augmented correlation consistent triple zeta (aug-cc-pVTZ) basis set. We chose to stay at this level of precision given the level of approximations involved in the spherically averaged approach that we adopted. Calculations were performed in the range 1.3 < R < 100 a0 for all electronic states considered here. Interactions between the ion N+ and H2 along the linear approach give rise to three electronic states: a 3Σ state and two degenerate 3Π states. Regarding the perpendicular approach, the degeneracy disappears and the 3Σ and 3Π state split into 3A2 (for 3Σ), 3B1 and 3B2 (for 3Π) electronic states in the C2v symmetry group, respectively.
Thus, we calculated a total of five PECs, two for the linear approach (3Σ and 3Π) and three for the perpendicular approach (3A2, 3B1, and 3B2). Fig. 3 presents the five PECs obtained.
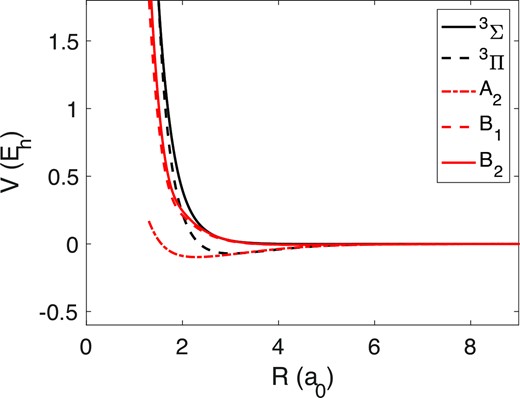
PECs for the five orientations of N+–H2. Black lines correspond to the linear approaches, and the red lines to the perpendicular ones.
N+–H2 spherically averaged PECs (|$V^{i}_{av}(R)$|) are obtained by averaging over the linear and perpendicular approaches using the following formula, with Vi the interaction potential at a given distance R:
Note that we tested three different ways of proceeding to this average to get the N+–H2 PECs for 3Σ and 3Π pseudo-states. First, the average was done over the linear potential and the perpendicular potential using only the 3B1 state and the 3A2 state for the latter; only the 3B2 state and the 3A2 state; and finally an average over the 3B1, 3B2 state, and the 3A2 state. Given that we did not observe significant differences between the final PECs thus obtained, we adopted the averaged curve over 3B1 and 3B2 for the scattering calculations, as displayed in Fig. 4, albeit physically meaningless. Such a weak influence of the use of 3B1 or 3B2 states for the generation of the N+–H2 spherically averaged PECs can be explained by the fact that the two 3B1 or 3B2 states are almost degenerate up to R-distances of 2.4 a0.
Similarly to what has been done for the analytical representation of the N+–He PECs, the extrapolation to SR distances is based on the Born–Mayer formula, with α = 1223.76 and β = 3.05 au for the 3Σ state and α = 9328.61 and β = 8.42 au for 3Π state. The extrapolation for LR distances relies on multipolar expansion (R−n terms) through the C3, C4, and C5 coefficients, whose value is determined from LR ab initio points and correspond, respectively, to 0.0514, −2.7823, and 1.0847 au for the Σ state; and 0.0619, −3.2309, and 3.2563 au for the Π state. Finally, ab initio points were smoothly connected on the basis of a cubic spline interpolation.
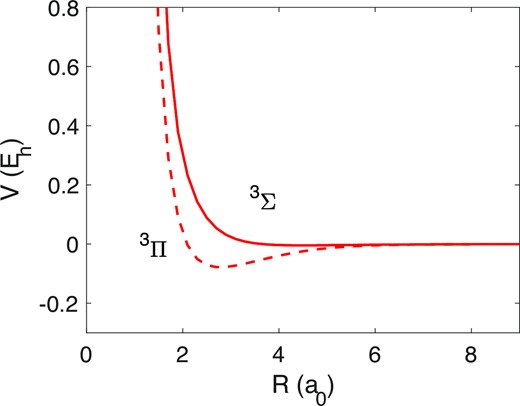
Fig. 4 presents the PECs obtained for the 3Σ and the 3Π states through this spherically averaged approach. Compared to the PECs of N+–He, we observe an inversion of the states’ hierarchy: the potential well is deeper for the 3Π state than for 3Σ one, and the minima are much deeper than for He (see Table 3 for PECs characteristics).
| . | 3Σ . | 3Π . | ||
|---|---|---|---|---|
| . | R (a0) . | V (cm−1) . | R (a0) . | V (cm−1) . |
| This work | 4.5 | −968.32 | 2.7 | −17121.22 |
| . | 3Σ . | 3Π . | ||
|---|---|---|---|---|
| . | R (a0) . | V (cm−1) . | R (a0) . | V (cm−1) . |
| This work | 4.5 | −968.32 | 2.7 | −17121.22 |
| . | 3Σ . | 3Π . | ||
|---|---|---|---|---|
| . | R (a0) . | V (cm−1) . | R (a0) . | V (cm−1) . |
| This work | 4.5 | −968.32 | 2.7 | −17121.22 |
| . | 3Σ . | 3Π . | ||
|---|---|---|---|---|
| . | R (a0) . | V (cm−1) . | R (a0) . | V (cm−1) . |
| This work | 4.5 | −968.32 | 2.7 | −17121.22 |
3 QUANTUM SCATTERING CALCULATIONS
3.1 State-to-state cross-sections
Scattering calculations for N+–He and N+–H2 were performed with the CC approach (Arthurs & Dalgarno 1960), following the method described by Alexander, Orlikowski & Straub (1983); Orlikowski & Alexander (1984) for 3P-atom – structureless projectile collisions and implemented in the hibridon code (Alexander et al. 2021). The spin–orbit couplings dependence on R was neglected. As is usually done, we use the asymptotic experimental spin–orbit splittings of N+(3P), Δj = 1 = 48.738 cm−1, and Δj = 2 = 130.8 cm−1, respectively, to determine spin–orbit corrected PECs. The hybrid log-derivative/airy propagator implemented in the hibridon code has been used, starting from Rmin = 1.5 a0 to Rmid = 25 a0 for the log-derivative method, and from Rmid = 25 a0 to Rmax = 250 a0 for the Airy propagator for N+–He collisions and from Rmin = 1.2 a0 to Rmid = 40 a0 for the log-derivative method, and from Rmid = 40 a0 to Rmax = 200 a0 for the Airy propagator for N+–H2 collisions. All these parameters were adequate to ensure a convergence of cross-sections to better than 1 per cent. These calculations have been performed for total energies up to 10 000 cm−1. For the energy grid, we have used a variable step. For energies smaller than 100 cm−1, the step is 0.2 cm−1. Then, between 100 and 200 cm−1, the step is increased to 0.5 cm−1, between 200 and 400 cm−1 to 2, between 400 and 600 cm−1 to 10. Finally, between 600 and 1000 cm−1, the step is increased to 20 cm−1 and to 100 cm−1 above that limit. The reduced mass of the complexes were μ = 3.11 u for N+–He and μ = 1.76 u for N+–H2. For the former, the maximum total angular momentum considered was J = 20 for energies lower than 300 cm−1, J = 30 for energies between 300 and 1000, J = 50 for energies between 1000 and 2500, and J = 80 for energies greater than 2500 cm−1. For the latter, the maximum total angular momentum considered was J = 30 for energies lower than 300 cm−1, J = 50 for energies between 300 and 1000 and J = 80 for energies superior to 1000 cm−1.
Fig. 5 shows the state-to-state cross-sections for the de-excitation transitions of N+ induced by collisions with He. We can see that the transition from 3P2 to 3P1 dominates the de-excitation process and that the 3P1 to 3P0 transition is weak, which is not surprising as this transition is classically forbidden (Monteiro & Flower 1987). This behaviour has been noticed for others atoms with a 3P electronic ground state in collision with He (Alexander et al. 1983; Monteiro & Flower 1987; Lique et al. 2018).
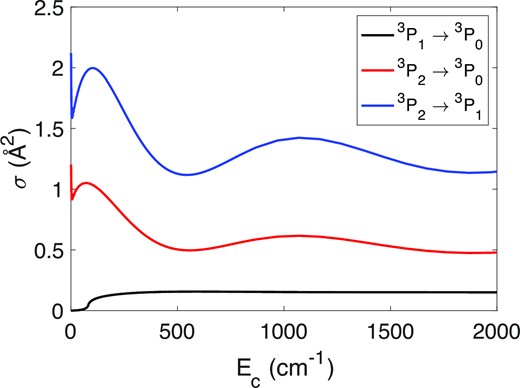
State-to-state cross-sections of N+ with He as a function of energy.
Fig. 6 presents the state-to-state cross-sections of N+ with H2. Cross-sections at low collision energy (Ec) exhibit strong Feshbach and shape resonances due to the attractive potential wells (Costes & Naulin 2016). These resonances disappear when Ec is large compared to the well depth. The transition from 3P2 to 3P1 is the most efficient; and the transition from 3P1 to 3P0 dominates over the 3P2 to 3P0 at low energy, thanks to a coupling through 3P2 that is stronger at low energy, as noted in Alexander et al. (1983).
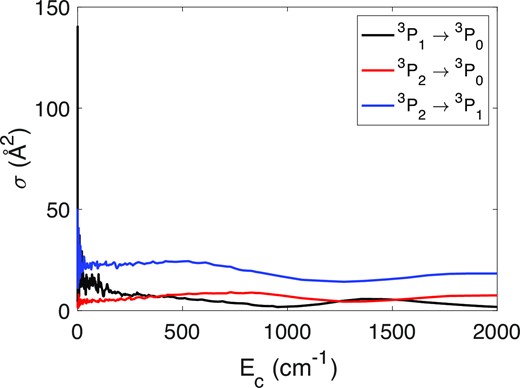
State-to-state cross-sections of N+ with H2 as a function of energy.
3.2 Rate coefficients
From the inelastic cross-sections σ(Ec), one can derive the corresponding rate coefficients at temperature T by an averaging over the collision energy (Ec):
where kB is the Boltzmann constant, and i and j denote the initial and final levels of the target, respectively. Calculations of the cross-sections at total energies up to 10 000 cm−1 allow the determination of rates up to 2000 K without loss of accuracy.
Unsurprisingly, the rate coefficients derived from the N+–He cross-sections reflect the hierarchy of transitions observed for the latter, as shown in Fig. 7. The transition from the 3P2 state to the 3P1 one largely dominates the other transitions and the 3P1 to 3P0 remains negligible. Likewise, in the case of N+–H2, the same behaviour is observed for the transitions’ hierarchy with respect to rate coefficients than for the cross-sections, with the transition from 3P1 to 3P0 dominating over the 3P2 to 3P0 up to ∼500 K.
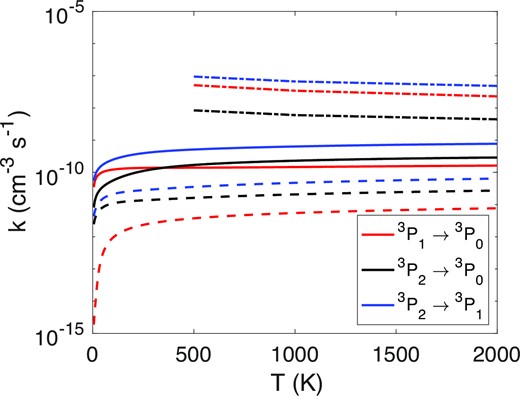
Comparison between collisional rate coefficients for N+–He (dashed lines), for N+–H2 (solid lines), and for N+–e (dash–dotted lines) (Tayal 2011) as a function of temperature.
3.3 Discussion and comparison with electronic excitation rate coefficients
As mentioned in the introduction, H2 is the most abundant partner in interstellar molecular clouds and thus the dominant collisional partner in such media. Despite significant update for many interstellar atoms and molecules (Roueff & Lique 2013; van der Tak et al. 2020), collisional data are still difficult to produce for collisions with H2, especially for reactive molecules and ions. When data for collisions with He are available, it has often been proposed to derive H2-rate coefficients from He-rate coefficients calculated for the same molecule. Such an approach (Schöier et al. 2005; Lique et al. 2008) consists in assuming that the excitation cross-sections are similar for both colliding systems and that the rate coefficients would only differ by a scaling factor, that corresponds to the square root of the ratio between the reduced masses appearing in the conversion of the cross-sections into rate coefficients (equation 4). Hence, the following scaling relationship could be used in our case:
Note that this approximation is only supposed to be used for H2 at low temperatures (e.g. when most H2 is in its ground state), but has already been challenged for many species; for a general criticism of this assumption, see Roueff & Lique (2013).
Here, we discuss the validity of estimating H2-rate coefficients from He ones when it comes to our system, i.e, to determine whether He can be a good template model for understanding and quantifying the collisional excitation of N+ by H2. One caveat that must be addressed in order to answer this question is the following: we do not have state-of-the-art results for H2, but only quantum scattering calculations performed on the basis of interaction potentials containing important approximations. N+–H2 was treated as a non-reactive system given that the intermolecular distance between the two H was fixed, and H2 was treated as a pseudo-atom given that we averaged the PESs over H2 rotations. There is no way to determine how these approximations impact the collisional rate coefficients obtained for N+–H2. We have reasons however to believe that, albeit these approximations, our calculations may provide the right order of magnitude of the fine structure resolved rate coefficients. Thus, we may be allowed to use them at least to interpret the exact results obtained for He and to determine on this basis whether the 1.4 scaling factor assumption is valid for this system.
We see in Figs 5 and 6 that, as expected, given the deeper potential well in the N+–H2 interaction as compared to N+–He one, H2 cross-sections are much larger for the He ones. A difference of one order of magnitude can be observed between the corresponding cross-sections. The order of magnitude of the cross-sections is not the only difference between the two collisional complexes. The behaviour of the state-to-state cross-sections observed for the N+–H2 system is very different from the one observed for N+–He one. Whereas the 3P1 to 3P0 transition induced by He collisions was negligible, for N+–H2 collisions, it is not only much more important proportionally, and it actually dominates over the 3P2 to 3P0 transition thanks to an efficient coupling of the 3P0 and 3P1 states with the 3P2 one. Our results show that He is not a correct model to describe the excitation of N+ induced by H2.
In astrophysical media where N+ is found, electronic collisions are also supposed to play a significant role for the excitation of N+. Thus, it is important to compare the efficiency of electron and neutral collisional partners (He and H2) for the excitation of N+. In Fig. 7, we compare rate coefficients for the de-excitation of N+ induced by electron impact (Tayal 2011) to the de-excitation rate coefficients induced by He and H2 collisions computed in this work. Rate coefficients for the (de-)excitation of N+ by electrons are ∼2–3 orders of magnitude higher than that of the collisional (de-)excitation induced by H2. Such a difference suggests that in astrophysical environments where the electronic fraction is low (ne− ≤ 10−4), collisions with H2 will compete or even dominate the excitation of N+, and indicates that N+–H2 collisional data should be used in order to accurately model N+ excitation in interstellar clouds. At the opposite, in highly ionized media, the electronic excitation will dominate.
4 The excitation of N+ in interstellar media
Calculations of critical densities can help to identify more precisely when such N+ rate coefficients would need to be considered in radiative transfer models. The concept of critical density refers to the ratio between the Einstein coefficients, expressed in s−1 and the collisional de-excitation rate coefficients for a given transition (in cm−3 s−1). Put differently, the ratio of the Einstein coefficients Ai → j to the collisional de-excitation rate coefficients ki → j defines the critical density n* of a given line, i.e. the density at which photon de-excitation and collisional de-excitation are equal.
Above such density, LTE conditions can generally be safely assumed. Critical densities for electrons had already been calculated by Goldsmith et al. (2015), on the basis of Tayal’s collisional rates. Fig. 8 displays the critical densities for He, H2, and electrons for the two allowed radiative transitions as a function of temperature.
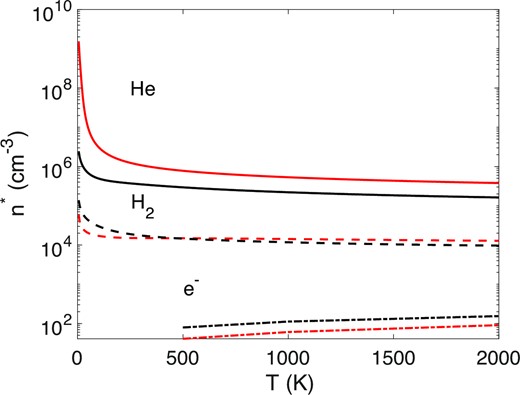
Critical densities for He, H2, and electrons as a function of temperature. Red lines correspond to the 3P1 to 3P0 transition and black lines to the 3P2 to 3P1 transition.
It can be seen that for ionized warm media where N+ has been detected (with densities lower than 102 cm−3), LTE conditions are not met and that rate coefficients are required to model the N+ emissions, although most often ignored to this day.
Then, we decided to test the impact of our rate coefficients on the excitation of N+ in astrophysical media, by performing radiative transfer calculations for physical conditions corresponding to media where N+ is detected. Non-LTE calculations were performed with the radex code (Van der Tak et al. 2007). Both collisional and radiative processes are taken into account. We focus on the calculation of the excitation temperature for N+ transitions, with a background temperature of 2.73 K and a N+ column density of 1014 cm−2. H2 is used as the only representative of neutral colliders.2
Fig. 9 shows the excitation temperature of 3P1 to 3P0 and 3P2 to 3P1 transitions as a function of the density of neutral species, with the electronic density kept fixed at ne− = 10−2 cm−3 and ne− = 1 cm−3, respectively. A kinetic temperature of 2000 K3 was adopted. One observes that at low densities of neutral species, even with a neutral to electron abundance ratio greater than 102, the excitation temperature remains weakly sensitive to the density of neutral species. It is only above a critical threshold of n(H2) ≥ 103–104 cm−3 that the excitation temperature increases and that the media start to thermalize very fast as the density increases, with an excitation temperature equal to the kinetic temperature around n(H2) ≥ 105 cm−3. Below this threshold, collisions are inefficient and do not contribute significantly to the excitation of the N+ ion, regardless of the ratio neutral species to electrons and of the density of electrons. Note that this neutral density value is much higher than the one typically observed in warm ionized clouds, i.e. 0.1 to 100 cm−3. Thus, environments where N+ is detected do not satisfy the LET, and collisional rate coefficients are needed to appropriately model observations.
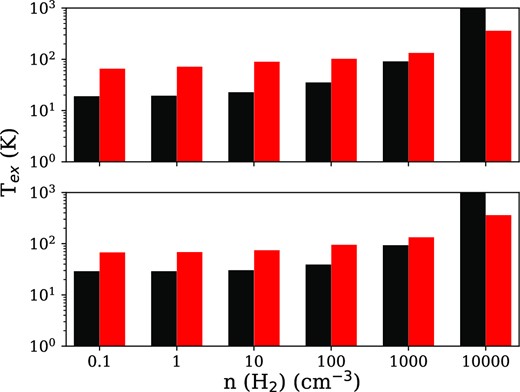
Excitation temperature of the 3P1 to 3P0 (black) and 3P2 to 3P1 (red) transitions as a function of the density of neutral species at 2000 K. The electronic density is kept fixed at |$n_{e^-} = 10^{-1}$| cm−3 (upper panel) and |$n_{e^-} = 1$| cm−3 (bottom panel).
As a second application of our rate coefficients, we decided to verify assumptions made about N+ in modelling the nitrogen chemistry in cold environments such as dark clouds. As emphasized in Dislaire et al. (2012), N+ + H2 → NH+ + H is identified as a key reaction for the formation of nitrogen hydrides in dark clouds (Agúndez & Wakelam 2013; Hily-Blant et al. 2013; Le Gal et al. 2014). Whether the reaction N+ + H2 → NH+ + H is efficient enough to reproduce the observed amount of ammonia in dark clouds has actually been debated since the original claim made by Le Bourlot (1991), a claim later challenged by updated calculations of the rate coefficients for N+ + H2 → NH+ + H (Dislaire et al. 2012), which felt below the critical value that had been inferred to explain the observed abundance of ammonia. However, due to the fact that in such cold environments, N+ cannot be detected, assumptions have to be made about the distribution of its fine structure population. It is thus interesting to check the assumption according to which its population follows an LTE distribution in cold molecular clouds.
In such environments, the exact population of N+ fine structure levels is not known and can influence the reactivity of N+. LTE conditions are usually assumed but not checked because of the lack of collisional data (Gómez-Carrasco et al. 2022). Thus, we decided to perform radiative transfer calculations to determine the population levels of the fine structure levels of N+ as a function of the density of neutral species (n(H2)), where ‘neutral species’ refer to 90 per cent of H2 and 10 per cent of He, at 10, 20, and 50 K, respectively, (see Fig. 10). At 10 K, as could have been anticipated, almost 100 per cent of N+ is in its ground state (not shown here), even at high densities according to the LTE distribution. But the level of population changes as the temperature increases: at 20 K already, one observes 2–5 per cent of N+ in level 3P1 at densities of 104–105 cm−3. At 50 K, 20 per cent to 30 per cent of the whole N+ is in the 3P1 level for a density of neutral species of 104–105 cm−3. Such values are below the LTE conditions that predict ∼10 per cent and ∼40 per cent of N+ is in 3P1 level, respectively. Given that the N+ + H2 → NH+ + H rate coefficients depend on the N+ energy level population, this means that the reaction will not happen as predicted by the model. This could possibly have an important impact on the determination of the age of the clouds when the abundance of NH3 is taken as the main tracer of it.
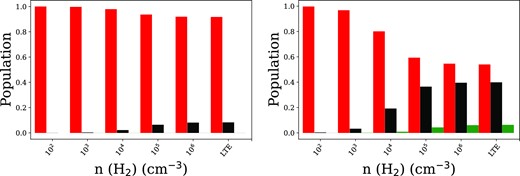
Population level for 3P0, 3P1, and 3P2 states at 20 K (left) and at 50 K (right) as a function of the density of neutral species (H2 and He, respectively, in proportions 90 per cent and 10 per cent). LTE conditions correspond to a density of 1012 cm−3.
5 CONCLUSION
We have calculated new PECs for N+–He at the RCCSD(T) level of theory with an extrapolation to the CBS. The calculations were found to be in good agreement with former theoretical studies. Using these new PECs, we have performed CC calculations in order to determine collisional excitation cross-sections for N+–He and derive collisional rate coefficients.
N+–H2 has also been studied. These data have been computed also using RCCSD(T) approach on the basis of a spherically averaged approach to the PECs for N+–H2, relying on important approximations. The comparison of the N+–H2 rate coefficients with the N+–He one shows that significant differences exist. The differences are of such nature, e.g. differences in the hierarchy of different de-excitation transitions, that even scaled by the square root of the collision reduced mass, the He rate coefficients cannot be reasonable approximation to the N+–H2 rate coefficients.
Then, we considered the astrophysical consequences of our calculations. First, we have shown that media where N+ is typically observed are not at LTE, and that LTE conditions are reached only for densities much higher than the typical conditions of warm ionized clouds. This illustrates the importance of taking into account the collisional rates coefficients. Furthermore, we have tested some important assumptions that are traditionally part of the modelling of nitrogen and ammonia. Our results show that the assumption of LTE distribution of the N+ energy levels at temperatures below 50 K is not verified above 10 K. This could have an important impact on the modelling of ammonia, especially on the determination of the age of the clouds where N+ is detected. Finally, we emphasize that the present study should be completed by the theoretical study of the collisional excitation of N+ by H and H+, the dominant heavy projectiles in warm (ionized) clouds in order to fully interpret and exploit the N+ observations recently performed.
ACKNOWLEDGEMENTS
This project received funding from the European Research Council (ERC) under the European Union Horizon 2020 research and innovation programme (grant agreement no. 811363) and from the European Union Horizon 2020 research and innovation programme under the Marie Slodowska-Curie grant agreement no. 101026214.
DATA AVAILABILITY
The data underlying this article will be made available through the EMAA,4 LAMDA (Schöier et al. 2005; van der Tak et al. 2020), and BASECOL (Dubernet, M.-L. et al. 2013) data bases. The PECs computed in this work are available upon request from the authors.
Footnotes
H2 is usually by far the dominant collider in molecular clouds.
In such media, H is expected to be the dominant neutral collider and our results should be considered with caution despite the fact that the H2 and H rate coefficients are usually of similar magnitude (Schöier et al. 2005).
N+ has been detected in interstellar clouds with a typical temperature of ∼8000 K but we restrict our models at 2000 K in agreement with the temperature range of our new data. We anticipate that because of the weak dependence of the rate coefficients, the results obtained at 2000 K will not vary significantly at 8000 K.



