-
PDF
- Split View
-
Views
-
Cite
Cite
Marcin Wesołowski, Modelling of the processes of dunes formation on the surface of comet 67P/Churyumov–Gerasimenko, Monthly Notices of the Royal Astronomical Society, Volume 521, Issue 1, May 2023, Pages 1570–1577, https://doi.org/10.1093/mnras/stad658
Close - Share Icon Share
ABSTRACT
The paper discusses selected mechanisms that can significantly contribute to the formation of dune structures on the surface of comets. In these considerations, mechanisms related to the dynamics of dust on the surface of the nucleus were taken into account. In the first step, the maximum dimensions of particles that can be entrained into the cometary atmosphere as a result of local sublimation of water ice have been determined. Then, three processes related to the movement of dust on the surface of the comet nucleus were considered, such as dust migration, a landslide that can turn into a local avalanche, and fluidization of unstable dust. The thermodynamic process responsible for initiating these mechanisms is ice sublimation. These mechanisms cause the dust to move by liquefaction of the given layer. Due to the complex and regular structure of a cometary nucleus, moving dust can suddenly stop flowing. For individual mechanisms responsible for the formation of dune structures, the maximum angular width for a given particle, particle mobility coefficient, and static fluidization pressure were determined. It should be noted that in those parts of the comet nucleus that are illuminated by the Sun, these mechanisms can occur almost simultaneously, leading to the formation of dune structures by piling up particles.
1 INTRODUCTION
Observations of comet 67P/Churyumov–Gerasimenko during the Rosetta mission confirmed that the surface structure of the nucleus is non-uniform. In some parts, there are completely smooth areas covered with loose dust material, and in some parts of the nucleus, there are high cliffs or rocky fragments. The main factor that shows the activity of comets is the sublimation of given ice. In the vicinity of the perihelion, sublimation activity is usually controlled by water ice. In further heliocentric distances, more volatile ices such as carbon dioxide and carbon monoxide are responsible for sublimation. Note that, we have at least one exception to this rule, which was the case of comet 103P/Hartley. The sublimation activity of this comet in the perihelion of its orbit (q = 1.06 au) was controlled by the sublimation of carbon dioxide, not water ice (A’Hearn et al. 2011).
Let us emphasize that the sublimation of given ice leads to a loosening of the dust layer. Consequently, its participation is important in the following processes: erosion of surface layers, emission, and migration of particles, as well as the formation of local landslides and fluidization of the dust layer. All these processes were recorded during the Rosetta mission (Thomas et al. 2015a; Steckloff & Melosh 2016; Shou et al. 2017; Wesołowski, Gronkowski & Tralle 2020). In the case of comet 9P/Tempel 1, the changes observed between the two missions Deep Impact and Stardust-NExT showed a retreat of the scarp by more than 50 m (Thomas, A’Hearn & Belton 2013). Local sublimation erosion is believed to be the probable cause of this process. In addition, smooth regions were identified on the same comet, which was formed as a result of the liquefaction of layers of loose dust material (Thomas et al. 2013).
When considering the formation of dune-like structures, we must note that three parameters play a key role. The first is the presence of dust, the second is an obstruction, and the third is ‘wind’. The first parameter is self-explanatory so we leave it without further discussion. The second parameter is the obstacle that stops the largest particles that form the basis for the construction of the dune. This means that the largest particles are in front of the obstacle, while the smallest fall behind the obstacle. The third parameter is ‘wind’, which in the case of comets is caused by the pressure difference between the side of the comet illuminated by the Sun and the shaded side (Jia, Andreotti & Claudin 2017). Let us note that depending on the changing environmental and wind conditions, the mechanisms responsible for the process of dune formation can vary significantly (Delorme et al. 2020). It is the sublimating ice that is responsible for the creation of an extremely rare and transient cometary atmosphere (coma). In addition, it is able to transport particles with dimensions ranging from a few to several centimetres (Kelley et al. 2013; Gronkowski & Wesołowski 2015, 2017; Wesołowski, Gronkowski & Tralle 2019). If the above three parameters occur simultaneously, the formation of a dune is practically certain. If the resulting dune is larger than the obstacle itself, it will become an obstacle itself. The presented analysis shows that structures similar to dunes can appear on all celestial bodies with an atmosphere, even extremely rare, as in the case of comets. In addition to comets and Earth, dunes have also been observed on Mars, Venus, and Titan. An example is one of the largest dune deserts (Olympia Undae) which extends around the northern polar cap of Mars.
This paper aims to provide an analysis of the formation of dune-like structures based on selected dust dynamics mechanisms. The process responsible for initiating these mechanisms is the sublimation of ice. These mechanisms can significantly contribute to the qualitative multiplication of dune structures visible on the surface of comet 67P/Churyumov–Gerasimenko (see Fig. 1).

Evidence of dune-like structures in the surface dust of Comet 67P/Churyumov–Gerasimenko. Such features may be the result of dust transport that initiates ice sublimation. The characteristic crests of the wave are marked with arrows. By analysing the observed dune structures, you can see their two windward and leeward sides, as in the case of dunes on Earth and Mars. The image was taken by the OSIRIS narrow-angle camera on 2014 August 23. Source: ESA/Rosetta/MPS for OSIRIS Team MPS/UPD/LAM/IAA/SSO/INTA/UPM/DASP/IDA.
2 PHYSICAL MODEL
When considering the formation of dunes on the surface of a comet, we must point out that the key aspect is the structure of the nucleus. In the proposed approach, we assume that the cometary nucleus consists of agglomerates and their clusters (Güttler et al. 2019) with an average radius of the order of 1 mm. The agglomerate is a porous dust particle that is characterized by an irregular shape and a complex structure. The basic element of the agglomerate is a monomer that contains ice and dust in its structure and its average radius is about 0.1 × 10−6 m (Bentley et al. 2016; Levasseur-Regourd et al. 2018; Fulle, Blum & Rotundi 2019; Mannel et al. 2019). Moreover, individual monomers inside the agglomerate can create fractal structures (Fulle & Blum 2017). Between the individual monomers, there are voids (pores) through which the sublimating water ice can reach the surface of the agglomerate. However, the process of full sublimation is hampered by the presence of a layer of dust on the surface of the nucleus. This layer is also characterized by a porous structure and consists of refractory materials. According to (Filacchione et al. 2019), the refractory material contains aliphatic and polycyclic aromatic hydrocarbons. In addition, various organic compounds (Goesmann et al. 2015; Altwegg et al. 2017), as well as iron silicates and sulphides, were also confirmed.
2.1 The energy balance
When considering the processes occurring on the surface of comets initiated by ice sublimation, it should be noted that the key parameter is the determination of temperature. Due to the complex and irregular surface of cometary nuclei, uneven heating and cooling should be taken into account in the energy balance (Wesołowski, Gronkowski & Kossacki 2022). Because in our approach, we want to determine the maximum values of individual parameters, we limit ourselves to determining the maximum temperature T, i.e. at the cometary equator. In this case, the energy balance equation is given as:
The left-hand side of the equation (1) describes the solar radiation power, while the right-hand side is the sum of the power radiated by the nucleus and the power used to sublimate the comet ice. All these powers are calculated per unit area of the comet nucleus. In this equation, the following notation is adopted: S⊙ is the solar constant (S⊙ = 1361.1 Wm−2, Gueymard 2018), AN is the albedo, ϵ is the infrared emissivity of the nucleus, σ is the Stefan Boltzmann constant, H(T) is the latent heat of sublimation, and F(T) is the mass flux of subliming vapour, respectively. In order to solve equation (1), we must additionally take into account the relations describing two parameters H(T) and F(T):
In equations (2) and (3), the individual symbols mean: cv is the specific heat of vapour (cv = 1846.1J K−1 kg−1, Marquet 2015), ci is the specific heat of ice (ci(T) = 185 + 7.037 T), α is the sticking coefficient of the gas molecules on to the surface (the value of this coefficient is in the range 0 < α < 1), mg is the mass of a gas molecule and |$\dot{Z}(T)$| is the rate of ice sublimation. In addition to calculate the mass flux F(T), we used the classic Hertz–Knudsen formula to determine the rate of ice sublimation. Then equation (3) is given by the following relationship
where psat(T) is the pressure of the phase equilibrium [psat(T) = 3.56 · 1012exp(−6141.667/T)] and kB is the Boltzmann constant. As a result of solving the above equations, we obtain the temperature on the surface of the cometary nucleus. This temperature determines the local rate of sublimation, which in turn is responsible for the dynamics of ice-dust particles on the surface of the nucleus.
2.2 Emission of particles during quiet sublimation
Considering the emission of a particle from the surface of a comet nucleus, we assume that three forces act on it (Gronkowski and Wesołowski 2015):
- gravity force (Fg) coming from the cometary nucleus:(5)$$\begin{eqnarray*} F_{\mathrm{g}} = m_{\mathrm{gr}}\, g_{\mathrm{c}}, \end{eqnarray*}$$
- centrifugal force (Fc) resulting from the rotation of the nucleus about the axis passing through its centre of mass:(6)$$\begin{eqnarray*} F_{\mathrm{c}} = m_{\mathrm{gr}}\, \omega ^{2}\, x, \end{eqnarray*}$$
- drag force (Fd) resulting from the sublimation of the cometary matter:(7)$$\begin{eqnarray*} F_{\mathrm{d}} = 0.5\, C_{\mathrm{D}}\, \pi \, r_{\mathrm{gr}}^{2}\, v_{\mathrm{g}}\, F(T). \end{eqnarray*}$$
In equations (5)–(7), the following notation is used for individual symbols: mgr is the mass of cometary grains, gc is the gravitational acceleration of the cometary nucleus, ω is the angular velocity with which the nucleus rotates around its own axis (ω = 2πP−1), P is the period of rotation, x is the distance of the particle from the axis of rotation of the nucleus (|${\rm x}={\it R}_{\mathrm{N}}\cdot \mathrm{cos}\, \varphi$|), φ is the cometocentric latitude, RN is the radius of cometary nucleus, CD is the modified free-molecular drag coefficient for spherical body (Crifo et al. 2005), vg is the gas velocity, and rgr is the radius of the particle.
The graphical distribution of these three forces is shown in Fig. 2. Note that, in addition to these three forces additional forces may act on the particle: the force related to electromagnetic solar radiation, the solar tidal force which is related to the orbital motion of the comet, the coriolis force which is a consequence of the comet rotation and motion of particles, and the rocket force. It should be noted that only the first three forces [given by equations (5)–(7) have a dominant effect on the size of particles emitted from the surface, while the influence of the next three forces is negligible (Houpis & Mendis 1981)]. In the case of the rocket force, it plays an important role only for particles that sublimate asymmetrically (Kelley et al. 2013). In our analysis, however we assume that the particles either do not exhibit sublimation activity or sublime isotropically.
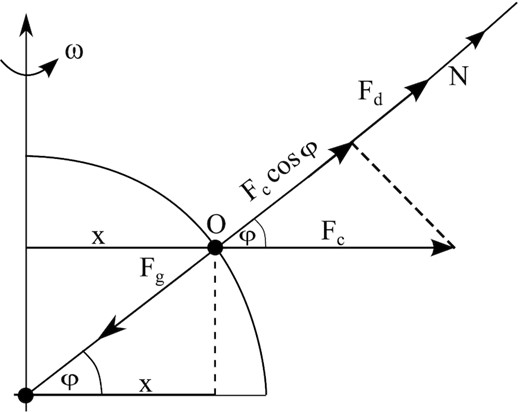
A simplified diagram of the distribution of forces acting on a comet particle located at point O on the surface of the comet nucleus.
Based on Fig. 2, the equation of motion for a comet particle is given as:
where N is the resultant force (N = mgr |$\ddot{\mathrm{r}}$|). Then, using equations (5)–(7), the particle equation of motion is given as:
To determine the maximum radius of a particle rgr that can be ejected from the surface of the nucleus into space, the condition that |$\ddot{\mathrm{r}}\, \le$| 0 must be met. Then, based on equation (9), we can write that
where ϱgr is the particle density and ψi is the porosity of the particles. Notice that the index ‘i’ takes two values i = 1 or i= 2, (if i = 1, we consider aggregates, and if i = 2, we consider agglomerates). For the first type of particles (aggregates), the porosity is ψagg < 10 per cent, while for the second type of particles (agglomerates), the porosity increases even to ψagl > 95 per cent (Güttler et al. 2019). In our calculations, it was assumed that the porosity of the aggregate is ψagg = 5 per cent, and in the case of agglomerates ψagl = 70–80 per cent, which corresponds to the porosity given by Groussin et al. (2019).
2.3 Migration of particles along the surface of the nucleus
When considering the dynamics for medium-sized particles, it should be noted that the local sublimation of water ice is not a sufficient process to emit them into space. Despite this, sublimation contributes to the loosening of the dust layer, initiating the migration of these particles on the surface of the nucleus. Describing the motion of a particle on the surface of a rotating comet nucleus, we take into account the same forces as in the case of particle emission from the surface of the nucleus. In addition, we take into account the friction force Ff and a centrifugal force component that acts as a sliding force Ft. We can define these forces as:
where µ is the coefficient of friction. In order to correctly describe the particle migration process, in the next step, the distribution of forces acting on the cometary particle should be presented (see Fig. 3). The condition for sliding particles towards the cometary equator is given by equation (13):
Then, the migration coefficient is given by the following relationship:
Based on the equation (14), we can determine the maximum angular width that a particle can travel, provided that the following relationship is valid: |$\mu \, \le \, \mathrm{f(\phi)}$|. Knowing the angular width, we can determine the migration time of a particle from areas with higher cometolatitude latitudes ϕ2 to areas with lower cometolatitude latitudes ϕ1 based on the following equation (15):
Here, |$\ddot{\mathrm{r}}$| denotes the particle acceleration, tangent to the surface of the cometary nucleus, and directed towards its equator. Based on equations (4–8, 11–12, and 15), we can write:
Note that, the minus sign next to one of the terms in equation (16) is due to the fact that the particles move in the direction of decreasing latitude f of the comet.
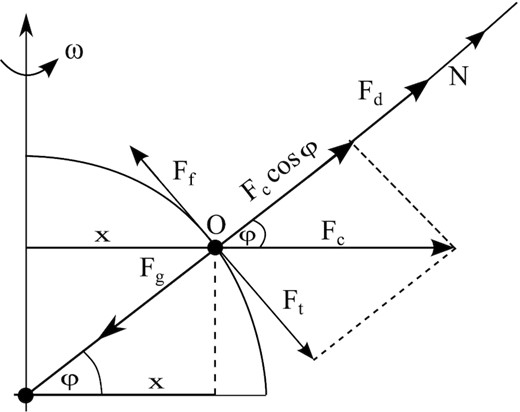
A simplified diagram of the distribution of forces acting on a cometary particle during its migration towards the cometary equator.
2.4 Fluidization of unstable dust
The fluidization phenomenon is similar to liquefaction in which cometary particles change their static state to dynamic. The cause of this process is the sublimation of ice through the porous structure of the layer of dust. This causes the loosening of this layer and at the same time increases the porosity of this layer (Kossacki, Skóra & Czechowski 2020; Kossacki et al. 2022). The gas flowing through this layer reduces the friction between the porous agglomerates constituting the layer. Therefore, an important parameter is to determine the static pressure during fluidization (ps). This dependence can be defined as
where z is the slope height. The other symbols have the same meaning as above. Note that, the gas density is much smaller than the particle density, so equation (17) can be expressed as:
Additionally, the slope height can be expressed as: z = l · sin(β), where β is the slope-to-horizontal angle and l is the slope length. Then, the static fluidization pressure (equation 18) can be expressed as equation (19):
2.5 Local landslides
A landslide of unstable dust material located on the slopes of comets should be treated as a form of gravitational movement (Czechowski & Kossacki 2020). The value of the resting angle for the dust material ranges from 25° to 40° (Groussin et al. 2015; Steckloff and Melosh 2016; Vincent et al. 2016). However, laboratory studies have shown that landslides of dry material (e.g. quartz sand) are possible at a smaller slope angle (Kossacki et al. 2022). The most likely cause of this phenomenon is the sublimation of ice under a layer of dried dust and the instability of the substrate. Another factor that may contribute to the formation of a landslide is the collapse of the cliff. An example is the collapse of the cliff in Aswan, which was recorded by the OSIRIS narrow-band camera and the NavCam navigation camera during the Rosetta mission (Pajola et al. 2016). The consequence of these factors is the initiation of the movement of cometary matter, which transforms into a local landslide and also initiates the formation of a cometary avalanche (Steckloff and Melosh 2016; Wesołowski et al. 2020). Problems related to the dynamics of the movement of cometary matter located on inclined slopes were the subject of many important considerations (Kochan et al. 1990; Britt et al. 2004; Belton & Melosh 2009; Kossacki et al. 2022). Note that, the downward movement of comet material can lead to the formation of sediments or structures similar to dunes.
When considering the formation of a landslide as a form of gravitational motion, we consider the same forces that act on a particle as in the case of the emission of matter from the surface of a comet. In addition, the cohesion force between individual particles was taken into account in the considerations. Then, the mobility coefficient γ is determined by the relationship:
In the equation (20), the symbol Sc is the material coefficient (for the lunar soil Sc = 1, Perko, Nelson & Sadeh 2001). The other symbols have the same meaning as above.
3 THE RESULT OF NUMERICAL SIMULATIONS
The paper discusses selected mechanisms related to the dynamics of dust, which may contribute to the formation of dunes on the surface of comet 67P/Churyumov–Gerasimenko (hereinafter referred to as 67P). The paper discusses selected mechanisms related to the dynamics of dust, which may contribute to the formation of dunes on the surface of comet 67P. In the context of our considerations, it is crucial to adopt the appropriate shape of the nucleus and to determine the heliocentric distance for which numerical simulations were carried out. In our case, it is the perihelion of the orbit of comet 67P (d = 1.2432 au), and its activity is controlled by the sublimation of water ice. Recall that the studies carried out during the Rosetta mission show that the nucleus of comet 67P has a distinct bilobate shape with overall dimensions along the main axes: 4.34 × 2.60 × 2.12 km. The two lobes are connected by a short neck and the larger lobe has a size of about 4.1 × 3.52 × 1.63 km while the smaller lobe has a size of about 2.50 × 2.14 × 1.64 km (Jorda et al. 2016). The cometary nucleus rotates with the period P = 12.4 hr (Preusker et al. 2015). The average density of the nucleus ρN = 537.0 ± 0.7 kgm−3 (Preusker et al. 2017). The average mean radius is RN = 1720 m, and gc is the average acceleration due to gravity on the cometary surface [we assume that gc = 2.25 × 10−4 ms−2 (Vincent et al. 2016)]. The total surface area SN of the 67P nucleus based on the SPG SHAP7 model is 51.7 ± 0.1 km2 (Preusker et al. 2017). On the surface of comet 67P, numerous craters, peaks, cracks, and even landslides are visible. In the structure of such a landslide, we can observe particles of complex shapes and different sizes. Therefore, in further consideration, the particles were divided into three groups depending on their mobility. The first group includes small particles (of the order of micrometres), i.e. those that are emitted into space as a result of the local outbursts (Wesołowski 2021, 2022a; Wesołowski et al. 2022). The second group describes medium-sized particles which due to local sublimation, can migrate (slide) on the surface of the nucleus. The third group is associated with large particles which despite local sublimation, remain immobile. In further consideration, we will refer to the first two groups.
For the first group, i.e. small particles, the maximum particle size that can be lifted into the coma due to local sublimation was determined based on equation (10). In this case, two models of the comet nucleus were considered. The first model is a slow-rotating model, i.e. one for which the rotation period P → ∞, while the second model is a fast-rotating model, i.e. for which we assumed the rotation period P = 12.4 hr. In addition, the calculations took into account that due to local sublimation, aggregates and agglomerates are emitted from the surface of the comet nucleus. Making a direct comparison with the same base density (original density) of the particle, it was found that the dimensions of the agglomerates in relation to the aggregates are 3.17 times larger. However, when comparing the fast-rotating model with the slow-rotating model, it can be stated that the fast-rotating model increases the dimensions of the emitted particles from the nucleus surface by 1.18 times. Moreover, the size of the particle lifted from the surface of the nucleus depends on the velocity of the gas vg and the mass flux of the sublimating vapour F(T). Let us emphasize that according to the equation (3), the measure of the flux F(T) is the local rate of sublimation |$\dot{Z}$|(T) and sticking coefficient of the gas molecules on to the surface α. The calculations show that in the case of aggregates, the dimensions of the lifted particles are of the order of 10−2 m, while in the case of agglomerates, the dimensions are an order of magnitude greater. The results of numerical simulations of the particle radius distribution as a function of the basic density are presented in Fig. 4.
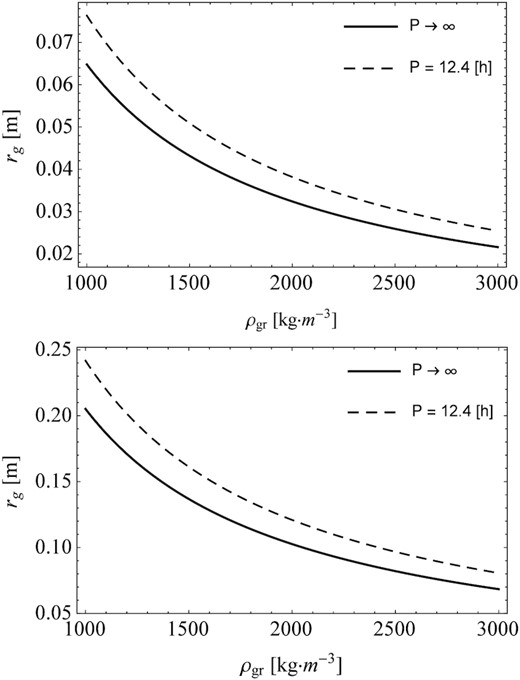
The maximum radius of comet particles, rgr (in metres), that can be lifted into the coma from the surface of the comet nucleus during quiet sublimation as a function of the base density of the particles. The upper panel concerns the emission of aggregates with porosity ψ = 0.05, while the lower panel concerns the emission of agglomerates with porosity ψ = 0.70.
In the case of the second group of medium-sized particles, due to local sublimation, we considered their possible migration, i.e. sliding on the surface of the comet nucleus. Based on equation (14), the distribution of the migration coefficient f(ϕ) as a function of the cometocentric latitude ϕ was determined. This analysis shows that the angular width that a migrating particle can travel depends on its size and also on the coefficient of friction µ. In the context of particle migration over the surface of the nucleus, we can distinguish the following belts:
the polar caps for which the angular width is 90° → ϕ2,
the mid-latitude belt for which the angular width is ϕ2 → ϕ1,
the equatorial belt for which the angular width is ϕ1 → 0°.
In the considered case, the migration of particles takes place in the mid-latitude belt, i.e. from the cometocentric latitude ϕ2 to the cometocentric latitude ϕ1. At the same time, the width of this migration belt depends on the assumed shape of the comet nucleus (Wesołowski et al. 2019). As in the case of particle emission from the surface of the nucleus, both aggregates and agglomerates were taken into account in the case of particle migration. The results of numerical simulations are shown in Figs (5 and 6). In addition, these calculations show that the smaller the particle moves across the surface of the comet, the greater the angular width it travels. The dimensions of these angular paths also determine the maximum cometocentric latitudes at which particle migration can occur. In other words, it is an area where the process of dune formation may begin as a result of the pile up of particles.
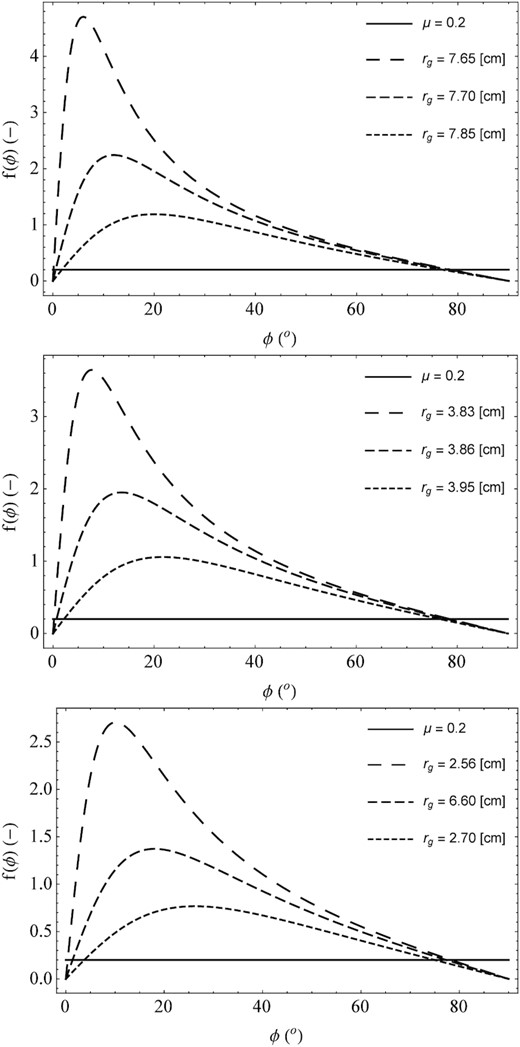
Distribution of the dust particle migration coefficient f(ϕ) as a function of the cometocentric latitude ϕ. In this case, we consider the migration of aggregates along the surface of a rotating comet nucleus. In the top panel, the base particle density is assumed to be ρgr = 1000 kg m−3, in the middle panel the base particle density is ρgr = 2000 kg m−3, and in the bottom panel the base particle density is ρgr = 3000 kg m−3. For this distribution, the average angular latitude is 76.23°, and the migration time is about 6.05 hr.
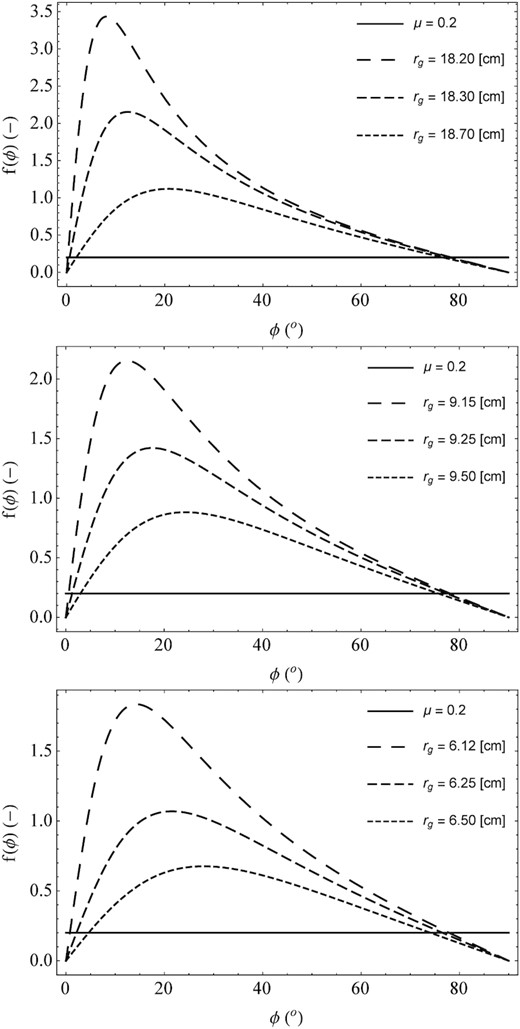
Distribution of the dust particle migration coefficient f(ϕ) as a function of latitude of comet ϕ for agglomerates. Basic particle densities for individual panels are analogous to Fig. 5. In the case of agglomerate migration, the average angular latitude was 75.33° and the migration time is 6.09 hr.
In the context of particle migration, we can deal with the following two situations. First, a migrating particle moving towards the equator due to the higher rate of sublimation can be lifted up into a coma. Secondly, the migrating particle, due to the heterogeneous structure of the surface, can get stuck in any part of it and thus become an obstacle, i.e. one of the main factors guaranteeing the initiation of the dune formation process.
In the next case, fluidization was considered, which is related to the flow of gas through a porous layer of dust. Based on numerical simulations, the results of which are presented in Fig. 7, the static pressure distribution of fluidization as a function of the length of the dust layer was determined. Moreover, the value of this pressure also depends on the degree of porosity of the particles included in the layer under consideration and the angle of its inclination. Based on the obtained results, it was found that in the case of a layer containing porous agglomerates, the static pressure during fluidization is lower than in the case of a layer consisting of aggregates for a fixed value of the base density (ϱgr = 3000 kg m−3). The values of this pressure for a slope length l = 100 m and its slope angle from 25° to 35° are equal to:
for aggregates with porosity ψ = 0.05: 27.10 Pa ≤ ps ≤ 36.78 Pa,
for agglomerates with porosity ψ = 0.70: 8.56 Pa ≤ ps ≤ 11.61 Pa,
for agglomerates with porosity ψ = 0.80: 5.71 Pa ≤ ps ≤ 7.74 Pa.
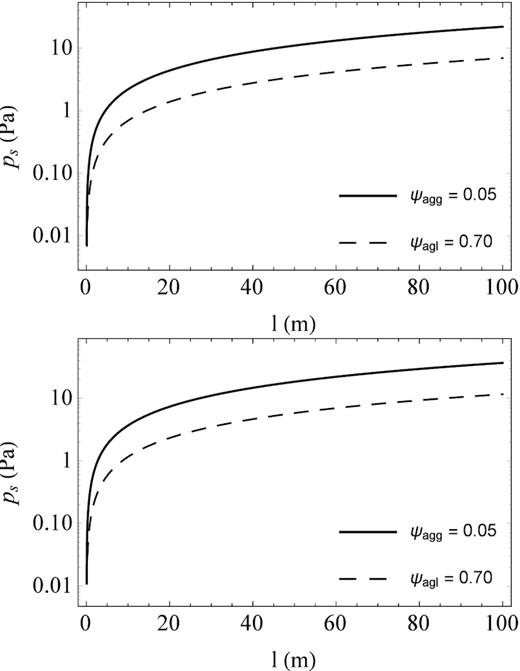
Distribution of fluidization static pressure depending on the length l and the angle of inclination to the horizontal (β). On the top panel, the angle of inclination is β = 25°, and on the bottom panel, the angle of inclination is β = 35°. In these calculations, it was assumed that the base grain density is equal to ϱgr = 3000 kg m−3. The considerations take into account that aggregates and agglomerates are porous, so the actual value of the particle density for which the calculations were made was equal to: ϱagg(ψ = 0.05) = 2850 kg m−3, ϱagl(ψ = 0.70) = 900 kg m−3, and ϱagl(ψ = 0.80) = 600 kg m−3.
The last mechanism that may be responsible for the formation of dunes is the formation of a local landslide. The basic parameter in this case is to determine the mobility coefficient γ for the considered particles. The main factors that influence the value of the mobility coefficient are the velocity of sublimating gas molecules and dust density. Note that in this case, the effect of the porosity of the dust particle is negligible because the contribution of the cohesive force is much greater than the gravitational force coming from the cometary nucleus. The distribution of the mobility coefficient as a function of the particle radius is shown in Fig. 8. As an example, we give the exact values of the mobility coefficient for the radius of the particle rg = 0.001 m depending on the temperature:
γ(T = 180 K) = 7.41 × 10−4,
γ(T = 200 K) = 2.25 × 10−2,
γ(T = 220 K) = 3.67 × 10−1.
Note that, the coefficient of mobility applies to all particles in a given dust layer. This means that for the particles on the top of this layer, the mobility coefficient may be greater than in the case of the particles on the bottom of the layer (Kossacki et al. 2022). This situation is a consequence of the temperature distribution and the thickness of the considered dust layer.
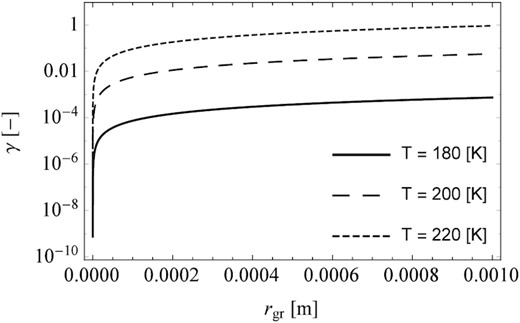
Distribution of the mobility coefficient as a function of a wide range of radii of cometary particles. Calculations were made for three exemplary cometary temperatures.
4 SUMMARY AND CONCLUSIONS
This paper discusses three mechanisms that may be responsible for the formation of dune-like structures. Such structures were recorded by the Rosetta probe apparatus on the surface of comet 67P. The first dunes have been observed spotted in the comet 67P neck region – the narrow zone between the two lobes in regions Ma’at, Nut, Maftet, and Hapi whose forms resemble characteristic dune fields (El-Maarry et al. 2015; La Forgia et al. 2015). Locally, deposits of fine dust particles resemble terrestrial linear dunes, which are formed when the wind blows from more than one direction, although one direction must be dominant (Thomas et al. 2015a; Giacomini et al. 2016).
To explain the formation of dunes on the surface of comet 67P, a mechanism has been proposed that is associated with local outburst activity (Thomas et al. 2015a, b). In the case of comet 67P, many outbursts were recorded during the Rosetta mission, the amplitude of which was less than 1 mag. In the context of a cometary outburst, the key question that still remains unanswered is what mechanism could be responsible for the outburst. When determining the amplitude of the outburst, it should be clearly noted that two parameters play an important role. The first is the fraction of the surface that is active during the outburst and the second is the total scattering cross-section (Wesołowski 2022b). The measure of this cross-section is the rejected mass resulting from the destruction and emission of particles in the phase of quiet sublimation and during the outburst, respectively. Then, the incident sunlight is more effectively scattered, causing the comet to increase in brightness, i.e. its outburst. Note that the scattering of incident sunlight occurs on particles of the order of millimetres or less, which gain enough velocity to overcome the cometary gravity. They then become part of a coma and even a dust tail if their lifetime is long enough. On the other hand, in the case of particles of the order of centimetres or larger, they fall back to the surface of the cometary nucleus. Then, we can talk about the redistribution of particles (Thomas et al. 2015a), and about the change of the original location of the particle as a consequence of sublimation and rotation of the comet nucleus. Then, the ice-dust particle is located in the new cometocentric latitude and may have an impact on increasing the local water ice sublimation rate. The total effect of such grains on the rate of gas production has been investigated by Rubin et al. (2014). Moreover, such a redistribution of cometary particles may be responsible for the formation of dune fields and fluffy plains, among other things.
The formation of dune-like structures involves a thorough understanding of the ice sublimation process. The key challenge is to accurately analyse the sublimation rate of ice, including the admixtures of organic substances detected in cometary nucleus (Kossacki 2021). At this point, it should be clearly noted that each comet is different in terms of the percentage content of individual components in relation to water ice. Moreover, it is necessary to answer the question of whether a given part of the surface of the comet nucleus is characterized by the appropriate topography, which can naturally contribute to the formation of a dune or can initiate the movement of a layer of dried dust. It should be noted that the processes presented in this article are related to dust dynamics and should be considered as an extension of the process presented by Thomas et al. (2015a,b), which may be responsible for the formation of dune structures on the surface of comets.
Acknowledgement
This work has been done due to the support the author received from the Center for Innovation and Transfer of Natural Sciences and Engineering Knowledge, University of Rzeszów, Poland (RPPK.01.03.00-18-001/10-00).
We thank the reviewers for their helpful comments which significantly contributed to the improvement of our paper.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.



