-
PDF
- Split View
-
Views
-
Cite
Cite
Benjamin Metha, Michele Trenti, The internal metallicity distributions of simulated galaxies from EAGLE, Illustris, and IllustrisTNG at z = 1.8–4 as probed by gamma-ray burst hosts, Monthly Notices of the Royal Astronomical Society, Volume 520, Issue 1, March 2023, Pages 879–896, https://doi.org/10.1093/mnras/stad165
Close - Share Icon Share
ABSTRACT
Massive stars are thought to be progenitors of long gamma-ray bursts (GRBs), most likely with a bias favouring low-metallicity progenitors. Because galaxies do not have a constant metallicity throughout, the combination of line-of-sight absorption metallicity inferred from GRB afterglow spectroscopy and of host galaxy global metallicity derived from emission lines diagnostics represents a powerful way to probe both the bias function for GRB progenitors and the chemical inhomogeneities across star-forming regions. In this study, we predict the relationship between Zabs and Zemiss using three different hydrodynamical cosmological simulations: Illustris, EAGLE, and IllustrisTNG. We find that while the qualitative shape of the curve relating emission versus absorption metallicity remains the same, the predicted relationship between these two observables is significantly different between the simulations. Using data for the host galaxy of GRB121024A for which both Zabs and Zemiss have been measured, we find marginal support for the Illustris simulation as producing the most-realistic internal metallicity distributions within star-forming galaxies at cosmic noon. Overall, all simulations predict similar properties for the bulk of the GRB host galaxy population, but each has distinct features in the tail of the Zabs-Zemiss distribution that in principle allow to discriminate between models if a sufficiently large sample of observations are available (i.e. N ≳ 11 on average). Substantial progress is expected in the near future, with upcoming JWST/NIRspec observations of 10 GRB host galaxies for which absorption metallicity from the afterglow spectra exists.
1 INTRODUCTION
Over the past few decades, significant progress has been made in understanding how galaxies form and evolve over time. Thanks to recent advancements in numerical methods and an improved understanding of galaxy-scale physics, several different high-resolution cosmological hydrodynamical simulations of sufficiently large volumes of the Universe exist, all of which reproduce to good accuracy the observed properties of galaxy populations in the local Universe (see e.g. Vogelsberger et al. 2020 for a review). Interestingly, it is often the case that these simulations rely on very different subgrid physical prescriptions, yet agree in the predicted bulk properties of galaxy populations (Naab & Ostriker 2017). An opportunity to discriminate among different subgrid physical prescriptions that give rise to similar global properties of galaxies is thus to investigate predictions of the internal structures of galaxies.
One way in which this can be done is by comparing the internal gas-phase metallicity distributions of simulated galaxies to observations.1 Metallicity (denoted by the symbol Z) is a fundamental property of galaxies. Metals (elements heavier than Helium) are produced in stars (Burbidge et al. 1957) and released into the interstellar media (ISM) of galaxies by supernovae. The total metallicity of a galaxy, therefore, is related to the total amount of stars that a galaxy has formed over its lifetime (e.g. Maiolino & Mannucci 2019).
Observations have shown that galaxies do not have constant metallicities throughout. For star-forming galaxies in the local Universe, the central regions of galaxies generally exhibit more metal enrichment than their outskirts (e.g. Searle 1971; Shaver et al. 1983; Vila-Costas & Edmunds 1992; Berg et al. 2013, 2020; Ho et al. 2015; Belfiore et al. 2017; Sánchez 2020). The average rate at which metallicity changes with the distance from a galaxy’s centre is described as a metallicity gradient, with a positive gradient meaning lower central metallicity.
Negative metallicity gradients are theoretically well understood. Analytical studies have been able to explain the presence of negative radial metallicity gradients in galaxy discs by accounting for the difference in time-scales between gas flows and star formation (Tinsley 1980), assuming either an exponential star formation profile within galaxy discs (e.g Edmunds & Greenhow 1995; Mo, Mao & White 1998), or that galaxies grow over time due to the accretion of gas onto their outskirts, triggering star formation at larger galactic radii as time goes on (the inside-out model of galaxy formation, see e.g. Boissier & Prantzos 1999; Pilkington et al. 2012). Negative metallicity gradients have also been seen in numerical simulations of galaxy formation. As an early example, Churches, Nelson & Edmunds (2001) predicted that negative metallicity gradients establish quickly from the combination of an exponential gas profile (Freeman 1970) with a Schmidt star formation law (Schmidt 1959; Kennicutt 1989). Modern studies have been conducted comparing the metallicity gradients predicted for galaxies in state-of-the-art simulations to observations, finding that these simulations produce fairly realistic gradients for local galaxies (Hemler et al. 2021; Tissera et al. 2022) and allowing connections to be drawn between metallicity gradients and cold gas accretion, stellar feedback, and galaxy mergers (e.g. Porter et al. 2022).
At higher redshifts (z ∼ 2–4), the internal metallicity structure of star-forming galaxies becomes more complicated. Often, the metallicity structure is asymmetric, clumpy, and irregular (e.g. Guo et al. 2012; Johnson et al. 2017; Wang et al. 2020, 2022). When a linear metallicity profile is fit, these galaxies may show flattened gradients (e.g. Kewley, Geller & Barton 2006; Rupke, Kewley & Chien 2010; Wuyts et al. 2016) or inverted positive gradients (e.g. Cresci et al. 2010; Queyrel et al. 2012; Wang et al. 2022), which can be explained through either galaxy–galaxy interactions (e.g. Tissera et al. 2016), stronger feedback in low-mass starbursting systems disrupting gradients (e.g. Ma et al. 2017), or the funnelling of cold gas into the central regions of these galaxies (e.g. Dekel et al. 2009a; Dekel, Sari & Ceverino 2009b; Stott et al. 2014; Ellison et al. 2018). These inverted gradients have also been seen in cosmological simulations at high redshift (e.g Hemler et al. 2021; Tissera et al. 2022). However, the two-dimensional metallicity profiles of these galaxies often show large azimuthal asymmetries, raising the question whether describing such galaxies with a simple metallicity gradient model is appropriate (Curti et al. 2020; Florian et al. 2021). Whether or not the detailed chemical structure of such galaxies can be predicted from any subgrid models of galaxy evolution is yet to be determined. Observations of the internal metallicity structures of these galaxies are challenging due to their large distances, small sizes, intrinsic faintness, and the presence of star-forming clumps with uncharacteristically low/high metallicities (Yuan, Kewley & Rich 2013; Carton et al. 2017). However, it is possible to indirectly compare the internal metallicity structures of real and simulated high-redshift galaxies by assessing the relationship between emission metallicities (Zemiss) determined using well-calibrated diagnostics and emission-line ratios, and absorption metallicities (Zabs) associated with long gamma-ray bursts (GRBs).
Strong emission-line diagnostics are widely used to determine the gas-phase metallicities of galaxies (Kewley, Nicholls & Sutherland 2019; Maiolino & Mannucci 2019). These diagnostics allow ratios of bright emission lines within a galaxy to be converted into metallicity determinations, and may be calibrated either to theoretical models of H ii regions (e.g. Kewley & Dopita 2002; Dopita et al. 2016), or empirical metallicity observations determined directly by measuring the temperatures of interstellar gas (e.g. Pilyugin & Thuan 2005; Pilyugin & Grebel 2016). Regardless of the diagnostic used, such emission-line based metallicity measurements (hereafter Zemiss) will be necessarily biased to the brightest regions of the galaxy, in which young stars have recently been formed.
An alternative way to determine the metallicity of a high-redshift galaxy is by using absorption-based spectroscopy (Zabs hereafter). This method relies on measuring the absorption spectrum of a bright background source, such as a quasar or a GRB, as it passes through the galaxy. Unlike Zemiss, Zabs is not biased to regions of higher star formation, as the absorbing abilities of gas does not depend on its ionization state. However, these absorption methods only measure the metallicity along the line of sight (LOS) between the observer and the source of the emission.
Differences have been found between Zabs and Zemiss in quasar-absorbing systems. Invariably, Zemiss is greater than Zabs (e.g. Chen, Kennicutt & Rauch 2005; Péroux, Kulkarni & York 2014), but this difference can be largely explained by the large distances between quasar lines of sight and the galaxy centre, together with a negative metallicity gradient model (e.g. Christensen et al. 2014; Rahmani et al. 2016; Krogager et al. 2020). For the local dwarf galaxy SBS 1543 + 593, metallicities inferred from the absorption spectrum of a quasar that passes through the galactic disc are consistent with emission-line metallicities inferred from H ii region spectroscopy (Schulte-Ladbeck et al. 2004, 2005). All of this implies that for quasar absorbing systems, Zemiss and Zabs are consistent with each other, implying that there is no large intrinsic bias between Zemiss and Zabs, and any observed difference should come from physical properties of the galaxies observed.
For GRB host systems, we do not expect Zabs and Zemiss to agree. The GRB progenitor is expected to originate in a low-metallicity region of star formation within the galaxy (Woosley 1993; Metha & Trenti 2020). Zemiss and Zabs, then, can be understood to trace the metallicity of two different subsets of the ISM of that galaxy. While Zemiss measures the overall metallicity of star-forming gas, Zabs must originate in a low-metallicity region of star formation, and is therefore biased to prefer low metallicities. For high-redshift galaxies with non-homogeneous metallicity distributions, these two metallicity measures are not expected to be equal. Therefore, by observing the difference between these two measured quantities in a representative sample of GRB hosts at redshift z ∼ 2–4 and by comparing results to theoretical predictions from cosmological simulations, we have the opportunity to constrain subgrid models of metal mixing and enrichment.
We started exploring this idea in Metha, Cameron & Trenti (2021a), where predictions of the relationship between Zabs and Zemiss were constructed using the state-of-the-art cosmological magneto-hydrodynamic simulation The Next Generation Illustris Simulation (IllustrisTNG). Motivated by approved JWST spectroscopic observations of a sample of GRB host galaxies with Zabs already measured from the afterglow, in this paper, we extend our earlier analysis, constructing explicit predictions for the relationship between Zabs and Zemiss for two other large-volume hydrodynamic simulations: the original Illustris simulation (Vogelsberger et al. 2014a) and the Evolution and Assembly of GaLaxies and their Environments (EAGLE) simulation (Schaye et al. 2015). Our aim is to identify which key features of the Zabs versus Zemiss relationship are shared across simulations, and which are unique and thus offer predictions that can be falsified by the upcoming JWST Cycle 1 data.
This paper is organized as follows. In Section 2, the three simulations analysed in our work are discussed, with a focus on the similarities and differences between the subgrid methods relevant for chemical enrichment. We outline our Monte-Carlo methodology for measuring the Zabs–Zemiss relation for these simulations in Section 3, and show the predicted form of this relationship for each simulation in Section 4. In Section 5, we compare the predictions of the simulations, and calculate how many observational data points would be necessary in order to rule out any of the models of galaxy evolution. We discuss our findings in Section 6 and summarize our main results in Section 7.
2 SIMULATIONS
In this section, we introduce the three cosmological simulations that we compare in this work. These are Illustris-1 from the Illustris simulation suite, Ref-L0100N1504 from the EAGLE simulation suite, and TNG100-1 from the IllustrisTNG simulation suite. Moving forward, we will refer to these simulations as Illustris, EAGLE, and TNG, for brevity. All three of these simulations have similar mass resolutions for baryonic particles and cover similar cosmic volumes of ∼(100 cMpc)3, but differ in many other respects. A broad overview of the similarities and differences between these three models is summarized in Table 1.
Overview of the similarities and differences between the subgrid physical prescriptions that are most important in affecting the metallicity distribution of the ISM, for the three simulations compared in this work.
| EAGLE . | Illustris . | IllustrisTNG . |
|---|---|---|
| Ref-L0100N1504 . | Illustris-1 . | TNG100-1 . |
| (100 cMpc)3 | (106.5 cMpc)3 | (110.7 cMpc)3 |
| mbaryon ∼ 1.8 × 106M⊙ | mbaryon ∼ 1.3 × 106M⊙ | mbaryon ∼ 1.4 × 106M⊙ |
| Planck 2013 cosmology | WMAP-9 cosmology | Planck 2015 cosmology |
| TreePM SPHs | AREPO moving mesh code | AREPO moving mesh code |
| Chabrier (2003) IMF | Chabrier (2003) IMF | Chabrier (2003) IMF |
| Stochastic star formation with Z-dependant density threshold | Stochastic star formation with fixed density threshold | Stochastic star formation with fixed density threshold |
| Portinari, Chiosi & Bressan (1998) stellar lifetimes | Portinari et al. (1998) stellar lifetimes | Portinari et al. (1998) stellar lifetimes |
| Stochastic thermal stellar feedback | Kinetic stellar feedback | Improved kinetic stellar feedback |
| Wiersma, Schaye & Smith (2009) cooling | Wiersma et al. (2009) cooling | Wiersma et al. (2009) cooling |
| No self-shielding correction | Self-shielding correction | Self-shielding correction |
| 11 elements tracked | 9 elements tracked | 9 elements + ‘other metals’ tracked |
| Stellar yields of Portinari et al. (1998) and Marigo (2001) | Stellar yields of Portinari et al. (1998) and Karakas (2010) | Combined stellar yield model; see Table 2 of Pillepich et al. (2018a) |
| BH seeds of mass 105M⊙ h−1 | BH seeds of mass 105M⊙ h−1 | BH seeds of mass 8 × 105M⊙ h−1 |
| Bondi–Hoyle accretion, up to Eddington limit | Boosted Bondi–Hoyle accretion, up to Eddington limit | Bondi–Hoyle accretion, up to Eddington limit |
| Stochastic thermal feedback for all AGN | Bubble model of Sijacki et al. (2007) for low accretion rate AGN | Stochastic kinetic feedback for low accretion rate AGN |
| Continuous thermal energy injection for rapidly accreting AGN | Continuous thermal energy injection for rapidly accreting AGN | |
| No magnetism | No magnetism | Includes magnetism |
| EAGLE . | Illustris . | IllustrisTNG . |
|---|---|---|
| Ref-L0100N1504 . | Illustris-1 . | TNG100-1 . |
| (100 cMpc)3 | (106.5 cMpc)3 | (110.7 cMpc)3 |
| mbaryon ∼ 1.8 × 106M⊙ | mbaryon ∼ 1.3 × 106M⊙ | mbaryon ∼ 1.4 × 106M⊙ |
| Planck 2013 cosmology | WMAP-9 cosmology | Planck 2015 cosmology |
| TreePM SPHs | AREPO moving mesh code | AREPO moving mesh code |
| Chabrier (2003) IMF | Chabrier (2003) IMF | Chabrier (2003) IMF |
| Stochastic star formation with Z-dependant density threshold | Stochastic star formation with fixed density threshold | Stochastic star formation with fixed density threshold |
| Portinari, Chiosi & Bressan (1998) stellar lifetimes | Portinari et al. (1998) stellar lifetimes | Portinari et al. (1998) stellar lifetimes |
| Stochastic thermal stellar feedback | Kinetic stellar feedback | Improved kinetic stellar feedback |
| Wiersma, Schaye & Smith (2009) cooling | Wiersma et al. (2009) cooling | Wiersma et al. (2009) cooling |
| No self-shielding correction | Self-shielding correction | Self-shielding correction |
| 11 elements tracked | 9 elements tracked | 9 elements + ‘other metals’ tracked |
| Stellar yields of Portinari et al. (1998) and Marigo (2001) | Stellar yields of Portinari et al. (1998) and Karakas (2010) | Combined stellar yield model; see Table 2 of Pillepich et al. (2018a) |
| BH seeds of mass 105M⊙ h−1 | BH seeds of mass 105M⊙ h−1 | BH seeds of mass 8 × 105M⊙ h−1 |
| Bondi–Hoyle accretion, up to Eddington limit | Boosted Bondi–Hoyle accretion, up to Eddington limit | Bondi–Hoyle accretion, up to Eddington limit |
| Stochastic thermal feedback for all AGN | Bubble model of Sijacki et al. (2007) for low accretion rate AGN | Stochastic kinetic feedback for low accretion rate AGN |
| Continuous thermal energy injection for rapidly accreting AGN | Continuous thermal energy injection for rapidly accreting AGN | |
| No magnetism | No magnetism | Includes magnetism |
Overview of the similarities and differences between the subgrid physical prescriptions that are most important in affecting the metallicity distribution of the ISM, for the three simulations compared in this work.
| EAGLE . | Illustris . | IllustrisTNG . |
|---|---|---|
| Ref-L0100N1504 . | Illustris-1 . | TNG100-1 . |
| (100 cMpc)3 | (106.5 cMpc)3 | (110.7 cMpc)3 |
| mbaryon ∼ 1.8 × 106M⊙ | mbaryon ∼ 1.3 × 106M⊙ | mbaryon ∼ 1.4 × 106M⊙ |
| Planck 2013 cosmology | WMAP-9 cosmology | Planck 2015 cosmology |
| TreePM SPHs | AREPO moving mesh code | AREPO moving mesh code |
| Chabrier (2003) IMF | Chabrier (2003) IMF | Chabrier (2003) IMF |
| Stochastic star formation with Z-dependant density threshold | Stochastic star formation with fixed density threshold | Stochastic star formation with fixed density threshold |
| Portinari, Chiosi & Bressan (1998) stellar lifetimes | Portinari et al. (1998) stellar lifetimes | Portinari et al. (1998) stellar lifetimes |
| Stochastic thermal stellar feedback | Kinetic stellar feedback | Improved kinetic stellar feedback |
| Wiersma, Schaye & Smith (2009) cooling | Wiersma et al. (2009) cooling | Wiersma et al. (2009) cooling |
| No self-shielding correction | Self-shielding correction | Self-shielding correction |
| 11 elements tracked | 9 elements tracked | 9 elements + ‘other metals’ tracked |
| Stellar yields of Portinari et al. (1998) and Marigo (2001) | Stellar yields of Portinari et al. (1998) and Karakas (2010) | Combined stellar yield model; see Table 2 of Pillepich et al. (2018a) |
| BH seeds of mass 105M⊙ h−1 | BH seeds of mass 105M⊙ h−1 | BH seeds of mass 8 × 105M⊙ h−1 |
| Bondi–Hoyle accretion, up to Eddington limit | Boosted Bondi–Hoyle accretion, up to Eddington limit | Bondi–Hoyle accretion, up to Eddington limit |
| Stochastic thermal feedback for all AGN | Bubble model of Sijacki et al. (2007) for low accretion rate AGN | Stochastic kinetic feedback for low accretion rate AGN |
| Continuous thermal energy injection for rapidly accreting AGN | Continuous thermal energy injection for rapidly accreting AGN | |
| No magnetism | No magnetism | Includes magnetism |
| EAGLE . | Illustris . | IllustrisTNG . |
|---|---|---|
| Ref-L0100N1504 . | Illustris-1 . | TNG100-1 . |
| (100 cMpc)3 | (106.5 cMpc)3 | (110.7 cMpc)3 |
| mbaryon ∼ 1.8 × 106M⊙ | mbaryon ∼ 1.3 × 106M⊙ | mbaryon ∼ 1.4 × 106M⊙ |
| Planck 2013 cosmology | WMAP-9 cosmology | Planck 2015 cosmology |
| TreePM SPHs | AREPO moving mesh code | AREPO moving mesh code |
| Chabrier (2003) IMF | Chabrier (2003) IMF | Chabrier (2003) IMF |
| Stochastic star formation with Z-dependant density threshold | Stochastic star formation with fixed density threshold | Stochastic star formation with fixed density threshold |
| Portinari, Chiosi & Bressan (1998) stellar lifetimes | Portinari et al. (1998) stellar lifetimes | Portinari et al. (1998) stellar lifetimes |
| Stochastic thermal stellar feedback | Kinetic stellar feedback | Improved kinetic stellar feedback |
| Wiersma, Schaye & Smith (2009) cooling | Wiersma et al. (2009) cooling | Wiersma et al. (2009) cooling |
| No self-shielding correction | Self-shielding correction | Self-shielding correction |
| 11 elements tracked | 9 elements tracked | 9 elements + ‘other metals’ tracked |
| Stellar yields of Portinari et al. (1998) and Marigo (2001) | Stellar yields of Portinari et al. (1998) and Karakas (2010) | Combined stellar yield model; see Table 2 of Pillepich et al. (2018a) |
| BH seeds of mass 105M⊙ h−1 | BH seeds of mass 105M⊙ h−1 | BH seeds of mass 8 × 105M⊙ h−1 |
| Bondi–Hoyle accretion, up to Eddington limit | Boosted Bondi–Hoyle accretion, up to Eddington limit | Bondi–Hoyle accretion, up to Eddington limit |
| Stochastic thermal feedback for all AGN | Bubble model of Sijacki et al. (2007) for low accretion rate AGN | Stochastic kinetic feedback for low accretion rate AGN |
| Continuous thermal energy injection for rapidly accreting AGN | Continuous thermal energy injection for rapidly accreting AGN | |
| No magnetism | No magnetism | Includes magnetism |
In this section, we will outline the most relevant details on the subgrid physical prescriptions of each model, focusing on the treatments of stellar and active galactic nucleus (AGN) feedback and metal enrichment. We will also explain which observables each simulation has been calibrated to, and whether there are any known tensions with observations. Readers who are already familiar with these three simulation suites or are not interested in the details of the subresolution models may wish to skip this section. Conversely, readers who wish to learn more about the wide variety of cosmological simulations used today are encouraged to read the review by Vogelsberger et al. (2020).
2.1 EAGLE
The EAGLE is a large-scale hydrodynamical simulation suite that contains both dark matter and baryonic particles (Schaye et al. 2015). Using the TreePM smoothed particle hydrodynamics (SPH) code Gadget 3 (Springel 2005), a large number (3.4 trillion in the simulation we are using) of dark-matter particles are allowed to evolve with time under the ΛCDM model of gravity, using the cosmological parameters reported in Planck Collaboration (2014). Unlike other large-scale simulations (e.g. Springel et al. 2005; Ishiyama et al. 2021), EAGLE also simulates baryonic particles, allowing them to flow in the gravitational field created by the dark matter particles. The distribution of these baryonic particles then affect the distribution of dark matter in real-time, producing physically motivated descriptions of galaxies without relying on semi-analytical modelling.
In EAGLE, star formation occurs when gas clouds cool and condense below a metallicity-dependent threshold density (Schaye 2004). The metallicity-dependent cooling rates are taken from Wiersma et al. (2009). As the simulation does not have the resolution to model individual stars, simple stellar populations of mass ∼106M⊙ are formed, with metallicities inherited from the gas cells they are formed from, and masses taken from a Chabrier (2003) initial mass function (IMF). These stellar populations are then evolved following the models of Portinari et al. (1998), releasing mass and metals throughout their lives as the stars they are composed of collapse. The metallicity yields of stars that end their lives as core-collapse supernovae are taken from Portinari et al. (1998) and Marigo (2001).
Historically, feedback from supernovae and AGN has been difficult to model in hydrodynamical simulations. Thermally injected feedback radiates away too efficiently to drive shocks, a challenge termed the ‘overcooling’ problem (e.g. Katz, Weinberg & Hernquist 1996; Springel & Hernquist 2003; Naab & Ostriker 2017). EAGLE solves this problem by increasing the amount of energy injected by core-collapse supernovae such that any cell receiving energy from supernova feedback must undergo a temperature change of at least ΔT = 107.5 K, while simultaneously decreasing the frequency of feedback events so that the total amount of energy injected from supernovae is conserved. The higher temperature of the heated gas particles increases the time taken for thermal energy to be dissipated, allowing stellar feedback to be more efficient at driving galactic winds (Dalla Vecchia & Schaye 2012). This approach, known as stochastic thermal feedback, leads to burstier feedback with more realistic thermal gradients, and it is used to model feedback from both supernovae and AGN.
EAGLE was calibrated to reproduce three key observables at redshift zero: the galaxy stellar mass function (GSMF); the galaxy mass–size relation; and the relationship between the stellar mass of galaxies and the masses of their central supermassive black holes. While it has been found to further reproduce many other galaxy-scale properties of the local Universe, some tensions have been found. For example, Yates, Péroux & Nelson (2021) suggested that simulation Ref-L0100N1504 (the reference run we are using) may retain too many metals in the ISM compared to observations, in turn affecting the mass–metallicity relation (MZR) at redshift zero (Schaye et al. 2015). Also, the specific SFR at redshift zero for low-mass galaxies is lower than observed (see figs 11 and 13 of Schaye et al. 2015), both of which may significantly impact the population of GRB host galaxies found within this simulation. Finally, we note that the number density of large galaxies produced at z ∼ 2 in the EAGLE simulation is substantially lower than the number produced by the Illustris/TNG simulations (Oppenheimer et al. 2020).
2.2 Illustris
Similarly to EAGLE, the Illustris project (Vogelsberger et al. 2014a, b; Genel et al. 2014; Sijacki et al. 2015) also seeks so simulate large-scale structure formation in a ΛCDM Universe (although with a slightly different set of cosmological parameters from WMAP-9; Hinshaw et al. 2013), accounting for baryonic physics using subresolution models in order to create theoretical predictions of galaxy properties on a cosmic scale.
Unlike EAGLE, which uses SPHs, the Illustris simulation suite takes advantage of the moving-mesh code arepo (Springel 2010). By allowing a set of mesh-generating points to flow freely under a velocity field, a 3D Voronoi tessellation is constructed at each time-step. Mass, metals, momentum, and energy are then allowed to flow between these Voronoi cells using a mesh-based solution to the laws of ideal hydrodynamics, which in turn sets the velocities of the mesh-generating points for the next time-step. This mathematical approach combines aspects of SPH with Eulerian mesh-based methods, simultaneously avoiding numerical issues that both other methods possess (Vogelsberger et al. 2013).
Star formation occurs stochastically in gas cells with a density greater than 0.1 cm−3 (unlike EAGLE, this threshold is not metallicity-dependent). Metal-line cooling is computed for each cell based on the cooling rates of Wiersma et al. (2009), but with an additional factor for self-shielding based on the results of Rahmati et al. (2013). Stellar evolution is modelled to follow the evolutionary tracks of Portinari et al. (1998), with metal yields informed by Portinari et al. (1998) and Karakas (2010).
To overcome the overcooling problem, in Illustris, stellar feedback is injected kinetically rather than thermally. Star-forming gas cells stochastically transform a fraction of their mass into ‘wind particles’, which are launched in a bipolar direction out of the galactic plane. The metallicity of these wind particles is set to be 0.4× the metallicity of the gas cell from which they are launched, in order to help match the MZR for low-mass galaxies (Zahid et al. 2012). While they are travelling, these wind particles are not permitted to interact with other particles in the simulation, except gravitationally. The velocity of these wind particles are set to be proportional to the velocity dispersion of the dark matter halo, and their masses are then computed based on the available energy from all core-collapse supernovae. Once the wind particles enters a low-density region (below |$5{{\ \rm per\ cent}}$| of the density required for star formation), they dissolve, depositing all of their mass, metals, momentum, and thermal energy into the closest gas cell.
This prescription neglects delay-times associated with core-collapse supernovae, which are short. Furthermore, the process of decoupling wind particles from the ISM may effect galaxy properties on large scales (Dalla Vecchia & Schaye 2008) and will undoubtedly impact the small-scale metallicity structure of the ISM.
Three forms of AGN feedback are accounted for thermal, mechanical, and electromagnetic, to reflect the multitude of distinct physical processes that contribute to AGN feedback (e.g. Begelman 2014). For black holes with accretion rates below |$5{{\ \rm per\ cent}}$| of the Eddington limit, mechanical energy is injected directly into a spherical bubble at a distance of ≲100 kpc from the AGN, following the phenomenological model of Sijacki et al. (2007). For black holes with larger accretion rates, thermal energy is continuously injected into the environment around the AGN to simulate quasar activity. All accreting black holes are also presumed to produce ionizing radiation that heats up the gas cells surrounding them, as an additional form of feedback.
The Illustris simulation suite was calibrated to reproduce the redshift zero GSMF, the stellar-to-halo mass relation (M* − Mhalo) at z = 0, and the SFR density as a function of cosmic time. Similarly to EAGLE, Illustris has shown broad agreement to a range of galaxy-scale observations at low and intermediate redshifts. However, Nelson et al. (2015) list several tensions between this simulation and observational data. Relevant to our work, the Illustris100-1 simulation has been found to overproduce both large (M* ≳ 1011.5M⊙) and small (M* ≲ 1010M⊙) galaxies. Furthermore, in that study, galaxies of mass M* ≲ 1010.7M⊙ were found to be too spatially extended, and the gas fraction of galaxy groups to be too low.
2.3 IllustrisTNG
To resolve these and other tensions, and to take advantage of newly discovered physical models and improved numerical recipes, IllustrisTNG was constructed as a sequel to the Illustris simulation suite (Marinacci et al. 2018; Naiman et al. 2018; Nelson et al. 2018; Springel et al. 2018; Pillepich et al. 2018b). Both Illustris and IllustrisTNG are run using the arepo moving mesh code, and the TNG100-1 simulation has a comparable volume and resolution to the Illustris-1 simulation.
One major change from Illustris to IllustrisTNG is the incorporation of magnetic fields. The inclusion of this physics significantly increases the accretion rates of black holes and the gas fractions of small haloes (M < 1012M⊙), and significantly suppresses star formation at z ≲ 3, especially in large haloes (Pillepich et al. 2018a).
The TNG simulations use the same overall physical prescriptions for star formation and stellar feedback, but with a few important changes. Stellar yield tables are constructed from a variety of sources (Nomoto et al. 1997; Portinari et al. 1998; Kobayashi et al. 2006; Karakas 2010; Doherty et al. 2014; Fishlock et al. 2014), covering a range of initial masses and metallicities. Stellar winds are still launched from star-forming gas cells, but (1) winds are launched isotropically rather than preferentially out of the galactic plane; (2) a wind velocity floor is imposed to ensure that the mass of wind particles is not too high; (3) winds are faster and are dependent on redshift; (4) winds from low-metallicity gas cells are taken to be more energetic; and (5) 10 per cent of wind energy is injected as thermal energy, rather than kinetic energy, to prevent shocks from driving spurious star formation. Overall, the winds in TNG are faster than those in Illustris and more efficient at preventing star formation in all galaxies, regardless of their redshift or mass.
The low-accretion mode of black hole feedback has also been updated. In TNG, momentum is added in a random direction once a certain energy threshold is reached – similar to the prescription used in the EAGLE subgrid model, but delivering energy kinetically, rather than thermally. Both other methods of black hole feedback, thermal and electromagnetic, remain qualitatively the same as in Illustris.
The TNG simulations are calibrated to reproduce six observables of galaxy populations: (1) the cosmic star formation density as a function of redshift; (2) the GSMF at z = 0; (3) the M*–Mhalo relation at z = 0; (4) the MBH–Mhalo relation at z = 0; (5) the gas fraction of galaxies; and (6) the sizes of galaxies. The stellar feedback models implemented in IllustrisTNG show improved agreements with observations over the Illustris model for all six of these observables. However, Yates et al. (2021) note that the star formation rate (SFR) in TNG peaks at z ∼ 3, in tension with observational determinations of the cosmic star formation history that infer a z ∼ 2 peak location (e.g. see Madau & Dickinson 2014 and Driver et al. 2018). This may lead to an excess of metals being produced at lower redshifts compared to other simulations.
3 METHODS
For each simulation, the predicted difference between Zabs and Zemiss for GRB host galaxies was determined at four redshifts: z = 1.74, z = 2.32, z = 3.0, and z = 4.0. The four snapshots closest to these redshifts were downloaded for each simulation.2
In the three simulations, there exists a known issue with the subfind algorithm occasionally erroneously identifying overdensities in subhaloes as satellite galaxies Pillepich et al. (2018a). To circumvent this problem, we follow the prescription for identifying galaxies described in Metha & Trenti (2020), whereby a galaxy is defined as a collection of star-forming baryonic particles that could not be visually separated by typical observations. In practice, this is done by merging all gas particles identified with subhaloes whose half-star radii overlap in 3D. This definition ensures that galaxies in the simulations match what is observed in large, high-redshift surveys.
Five different cutoff models were explored, with Zmax=0.2, 0.4, 0.6, 0.8, and 1.0Z⊙. We also tested one model with no metallicity bias where the rate of GRB formation was assumed to be directly proportional to the SFR, in order to separate the effects of a metallicity bias from geometric effects. In Metha et al. (2021a), even a model with no metallicity bias was found to be able to impart a significant difference between Zabs and Zemiss.
For each snapshot of each simulation, under each GRB metallicity bias model, 2000 gas cells were selected with random LOS directions from the simulation directly, with the likelihood of each gas cell being selected weighted by its probability to form a GRB progenitor (equation 1). This prescription automatically selects GRB host galaxies from the simulation volumes in a consistent way, allowing one host galaxy to host multiple GRBs with their jets oriented in different directions.3
Unlike Illustris and TNG, the EAGLE simulation is not a mesh-based cosmological hydrodynamic simulation. To make this definition compatible with the SPHs scheme of EAGLE, we instead treat the metallicity and density of the ISM at any point to be equal to the metallicity and density of the closest gas particle. This is mathematically equivalent to constructing a 3D Voronoi tessellation for the EAGLE simulation using the gas particles as mesh-generating points, but is much less computationally intense.
4 RESULTS
4.1 Predictions from TNG
As a reference starting point for our results, in Fig. 1, we show the median values for Zabs at a fixed value of Zemiss (left) and Zemiss at a fixed value of Zabs (right), for the 2000 GRBs simulated at snapshot 30 of the TNG simulation used at a redshift of z = 2.32, investigating the effects of changing the cutoff metallicity for GRB formation in this simulation. Similar plots are also shown in Metha et al. (2021a), but for the convenience of the reader, we represent them here along with our main relevant conclusions of that paper.
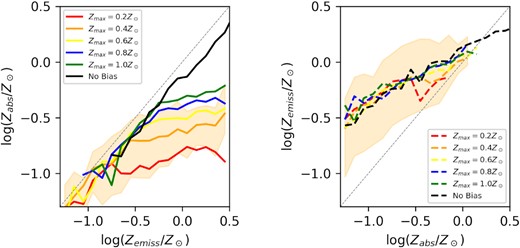
Left: The median value of Zabs for TNG GRB host galaxies with a fixed value of Zemiss. Right: The median value of Zemiss for TNG GRB host galaxies with a fixed value of Zabs. Both of these plots show the distribution at a redshift of z = 2.32. An error region showing the 16th and 84th percentiles for a GRB metallicity bias function with Zmax = 0.4Z⊙ is shown in both panels – error regions are of a similar size for all other models.
From these figures, we see that the shape of the median Zabs–Zemiss relation looks different depending on which axis is treated as the independent variable. For a given value of Zemiss, the median value of Zabs roughly follows Zemiss when Zemiss ≲ Zmax, the maximum metallicity for GRB formation. After this value, the median value of Zabs grows much slower. Such a feature is to be expected from the nature of our model, as in galaxies with a higher average metallicity, the location of GRB formation will be restricted to the lower-metallicity regions, and lines of sight originating from these locations are less likely to travel through high-metallicity regions of star formation.4
When Zabs is fixed, the median value of Zemiss shows little dependence on the threshold metallicity for GRB formation Zmax. Instead, Zemiss evolves linearly with Zabs, with a slope of ∼0.4 (Metha & Trenti 2020). The shape of this trend depends on the internal metallicity structures of the population of star-forming galaxies at this redshift and is different for different simulations (see discussion in Section 5).
In Fig. 2, we show how these relationships change with redshift, using a value of Zmax = 0.4Z⊙ as our fiducial model. We find that the median value of Zabs as a function of Zemiss changes very slowly, with higher redshift galaxies harbouring lower metallicity regions of star-forming gas. This relationship is more clearly observed in the right-hand panel, where the median value of Zemiss for given values of Zabs is found to drop significantly from z = 1.74 to z = 4.0. This feature reflects the cosmic metal enrichment taking place between these two epochs in the TNG simulation. The same trends are seen for all cutoffs explored in this section, implying that the redshift evolution of the Zabs–Zemiss relation is mild for all values of Zmax.
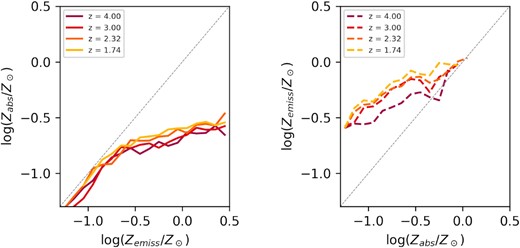
Left: Redshift evolution of the median value of Zabs for TNG galaxies with a fixed value of Zemiss. Right: Redshift evolution of the median value of Zemiss for TNG galaxies with a fixed value of Zabs. All of these plots assume a maximum metallicity for GRB progenitors of Zmax = 0.4Z⊙.
4.2 Predictions from EAGLE
In Fig. 3, we plot an analog of Fig. 1 using data from the EAGLE RefL0100N1504 simulation at a redshift of 2.33.
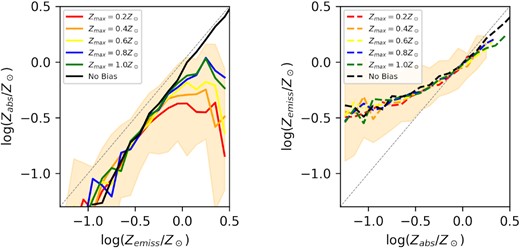
Left: The median value of Zabs for EAGLE galaxies with a fixed value of Zemiss. Right: The median value of Zemiss for EAGLE galaxies with a fixed value of Zabs. Both of these plots show the distribution at a redshift of z = 2.32. An error region showing the 16th and 84th percentiles for a GRB metallicity bias function with Zmax = 0.4Z⊙ is shown in both panels – error regions are of a similar size for all models.
Interestingly, we see that when Zemiss ≲ 0.5Z⊙, the median value of Zabs at fixed Zemiss does not seem to depend on the cutoff metallicity for GRB formation. This feature was seen at all redshifts in the EAGLE snapshots investigated in this work. We can explain this feature by noting that (i) Zabs and Zemiss are expected to be equal when a galaxy is chemically homogeneous and (ii) low-metallicity galaxies tend to have lower masses. Therefore, such low-metallicity galaxies are more likely to be well mixed due to efficient feedback processes being able to operate on the scales of these dwarf galaxies.
This result is consistent with, and extends on, the findings of Tissera et al. (2022), who show that galaxies produced in the EAGLE simulation tend to have metallicity gradients close to zero, with little dependence on stellar mass or redshift. Such a zero metallicity gradient could be consistent with one of two scenarios: either the galaxy is chemically well mixed; or it contains asymmetric metallicity fluctuations that cannot be captured by a simple linear gradient model. Our Zabs–Zemiss relation shows that both of these possibilities occur in the EAGLE simulation: larger galaxies tend to have a non-uniform, non-radial metallicity structure, whereas smaller galaxies tend to be more chemically homogeneous. Tissera et al. (2022) also show that low- and intermediate-mass galaxies in EAGLE have an enhanced star formation efficiency, which would also lead to an increased amount of feedback, giving a physical explanation to the higher degree of homogeneity seen in these smaller galaxies.
When no metallicity bias is imposed, for low-metallicity galaxies, the value of Zabs is substantially lower than the reported value for Zemiss. An investigation of the data revealed that while the bulk of the population follow a trend where Zabs ≈ Zemiss, a small population of galaxies with extremely low values of Zabs (10−5–10−2Z⊙) was also found. These anomalously low galaxies existed at all values of Zemiss but began to dominate the population at low metallicities, where the number of regular galaxies was lower. We discuss this population further in Section 4.2.1.
The trend of the median value of Zemiss at any given Zabs is also seen in TNG. However, the shapes of these relations are very different between the two simulations. While the relationship for TNG was nearly linear, the relationship seen for EAGLE appears to be closer to a quadratic, with a flatter slope for Zabs ≲ 0.3Z⊙ and a steeper slope elsewhere. This indicates that the predictions of the internal structure of the ISM generally differs between simulations that use different physical prescriptions for metal production and transport.
In Fig. 4, we show how these relationships depend on redshift for the model with Zmax = 0.4Z⊙. We see that while the value of Zabs at fixed Zemiss shows very little redshift evolution (left-hand panel), the median value of Zemiss at fixed Zabs is much higher for lower redshift galaxies. This effect is especially significant at low values of Zabs. Such an evolution reflects chemical enrichment in the EAGLE simulation over cosmic time and is consistent with what is observed in the TNG simulation.
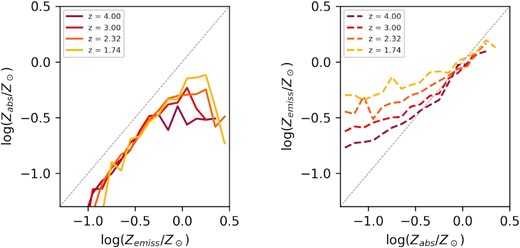
Left: Redshift evolution of the median value of Zabs for EAGLE galaxies with a fixed value of Zemiss. Right: Redshift evolution of the median value of Zemiss for EAGLE galaxies with a fixed value of Zabs. All of these plots assume a maximum metallicity for GRB progenitors of Zmax = 0.4Z⊙.
4.2.1 The population of extremely low-metallicity GRB absorbing systems in EAGLE
In every snapshot of the EAGLE simulation we considered, for every value of Zmax tested, a population of galaxies with log (Zabs/Z⊙) < −2 was identified. This is more than an order of magnitude lower than the median value of Zabs found in each galaxy sample. This population is most common at high redshift where the metallicity of galaxies is lower, and for low values of Zmax, where extremely low values of Zabs are favoured. At z = 4 with a cutoff of Zmax=0.2Z⊙, this low-metallicity sample makes up |$14.8{{\ \rm per\ cent}}$| of GRB hosts seen in the EAGLE simulation. At lower redshifts (z ≤ 2.3), for all values of Zmax tested, this low-metallicity population made up less than |$5.5{{\ \rm per\ cent}}$| of GRB hosts. The median stellar masses of these galaxies are generally low (M* ≈ 1 − 6 × 106⊙, with lower median masses at higher redshifts), representing typically dwarf galaxies with only a few stellar population particles, but exhibiting a wide range, from galaxies with no stars (caught on the cusp of star formation), to large Milky Way size discs with M* ∼ 1011M⊙. Such an extreme low-metallicity subpopulation is not seen in our analysis of either the Illustris or the TNG simulations.
Further analysis of this population reveals that the values of Zabs measured for these galaxies appear to be not inconsistent with the metallicities of the gas particles from which the GRB originated. Such extremely low-metallicity systems are associated instead to extremely low-metallicity star-forming gas particles, with LOS directed away from the more enriched regions of these galaxies, which contribute to a higher Zemiss.
The existence of such systems implies that galaxies in the EAGLE simulation contain pockets of star-forming gas with extremely low metallicities. In turn, this suggests that galactic fountains are inefficient at mixing metals into the outer regions of galaxies at redshifts of z ∼ 1.8–4 in the EAGLE simulation. This may be due to the lack of metal diffusion between SPH particles in the EAGLE simulation, as no metal diffusion between SPH particles was implemented in EAGLE due to the high uncertainties on mixing coefficients (Schaye et al. 2015). This allows extremely low-metallicity regions of gas to persist for longer in EAGLE than they would in Illustris or TNG, where metals are allowed to flow between different Voronoi cells. A second possible cause for these low-metallicity regions could be attributed to lower efficiency of the feedback system implemented in EAGLE for low-mass galaxies, as stochastic thermal feedback is less likely to occur in systems with a low number of star particles.
Whether these systems are artefacts of the numerical choices made when building EAGLE or represent a true population of high-redshift galaxies with inefficient galactic fountains remains to be seen. Presently, only two GRB host galaxies with log (Zabs/Z⊙)<−2 have been reported: the host of GRB050730A at a redshift of z = 3.97 with log (Zabs/Z⊙) = −2.31 ± 0.1 (Wiseman et al. 2017); and the host of GRB140311A at a redshift of z = 4.96 with log (Zabs/Z⊙) = −2.00 ± 0.11 (Bolmer et al. 2019). We describe how measurements of Zemiss and Zabs for the same GRB host galaxy can help confirm or falsify the presence of the poorly mixed GRB host systems predicted by EAGLE in Section 5.2.
4.3 Predictions from Illustris
In Fig. 5, we show an analogous figure to Fig. 1 for the sample of 2000 GRB host galaxies drawn from the Illustris simulation at z = 2.32.
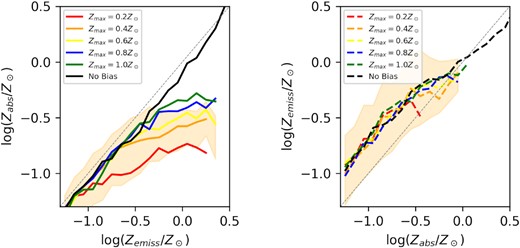
Left: The median value of Zabs for Illustris galaxies with a fixed value of Zemiss. Right: The median value of Zemiss for Illustris galaxies with a fixed value of Zabs. Both of these plots show the distribution at a redshift of z = 2.32. An error region showing the 16th and 84th percentiles for a GRB metallicity bias function with Zmax = 0.4Z⊙ is shown in both panels – error regions are of a similar size for all models.
In the left-hand panel, the median value of Zabs at a fixed value of Zemiss is shown. Unlike EAGLE, this figure shows much greater agreement to the Zabs–Zemiss relation predicted using the TNG simulation, with the predictions for a model with a cutoff of Zmax only agreeing with the metallicity bias-free model when Zemiss≤Zmax.
In the right-hand panel, the median value of Zabs at fixed Zemiss is displayed. Unlike EAGLE, and similarly to TNG, this relationship appears to be linear. However, the slope of this relation appears to be very close to 1. As this holds for all values of Zmax tested, we ascribe this relation to be driven more by the population of galaxies produced by Illustris rather than any details on the model of GRB formation.
In Fig. 6, we show how the Zabs–Zemiss relation depends on redshift for the Illustris simulation, with a fixed value of Zmax = 0.4Z⊙. While the median value of Zabs at a fixed value of Zemiss shows no significant redshift evolution, the median value of Zemiss at fixed Zabs shows a slight increase at lower redshifts, consistent with the results of the other two simulations. This trend can be attributed to the chemical enrichment of the Universe between z = 4.0 and z = 1.74.
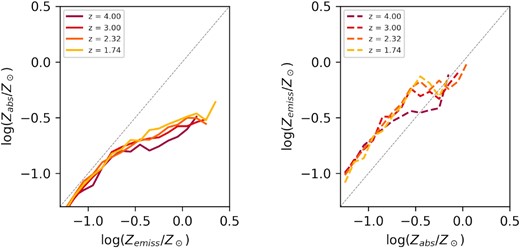
Left: Redshift evolution of the median value of Zabs for Illustris galaxies with a fixed value of Zemiss. Right: Redshift evolution of the median value of Zemiss for Illustris galaxies with a fixed value of Zabs. All of these plots assume a maximum metallicity for GRB progenitors of Zmax = 0.4Z⊙.
5 COMPARISON BETWEEN SIMULATIONS
Several similarities can be seen between the Zabs–Zemiss relations predicted by all of the three cosmological simulations tested in this work. At fixed values of Zemiss, the median value of Zabs follows a particular shape; evolving near linearly until Zemiss ≈ Zmax, and then turning off to a much shallower slope. For all simulations tested, this relation shows little evolution with redshift between z = 1.74 and z = 4.0.
When Zabs is fixed, the median value of Zemiss does not depend on Zmax, the maximum threshold for GRB production. Instead, the shape of this relationship depends on the populations of star-forming galaxies present at each redshift and how chemically homogeneous they are. For this reason, different simulations predict significantly different shapes for this relation. In EAGLE and TNG, this relationship depends substantially on redshift, with higher values of Zemiss at lower redshifts; but for Illustris, it is fairly constant over the redshift range we have examined.
Rather than considering the apparent tensions between different cosmological simulations as a weakness of our model, we see this as an opportunity. If different simulations predict different relationships between Zemiss and Zabs, then a set of observations of GRB host galaxy metallicities using both absorption and emission methods would hold the power to discriminate between different simulations of high-redshift galaxies using a set of data that none of these simulations have been tuned to reproduce. The Zabs–Zemiss relation is set by the overall degree of chemical inhomogeneity within galaxies. It depends not only on the presence of large-scale metallicity trends within these galaxies, but also on the small-scale structure of the gas inside galaxies, which varies on scales of ∼1 kpc (e.g. Metha, Trenti & Chu 2021b; Li et al. 2022; Metha et al. 2022) and is difficult to observe outside of gravitationally lensed targets at redshifts ≳2 (e.g. Treu et al. 2022; Wang et al. 2022). Understanding the relationship between Zemiss and Zabs provides a novel set of data that allows us to observe chemical inhomogeneities in high-redshift galaxies from a new angle, giving new insights into understanding how feedback shapes galaxies at cosmic noon.
In Appendix A, we plot the full 2D distributions of Zabs and Zemiss recovered for all galaxies, comparing each pair of simulations discussed in this work for every redshift and every value of Zmax that we test. We find that regardless of the particular value of Zmax, no two simulations make the same predictions for the Zabs–Zemiss relation at all redshifts. This means that, in principle, a survey that sought to measure Zemiss of GRB host galaxies with known values of Zabs at a variety of redshifts would be able to provide observational evidence for and against different models of galaxy formation and chemical evolution. We discuss this possibility further in Section 5.2.
5.1 What can GRB121024A tell us?
At time of writing, only one GRB host galaxy exists for which both Zemiss and Zabs has been measured – this is the host galaxy of GRB121024A (Arabsalmani et al. 2018). In this section, we investigate what this data point can tell us about the realism of the subresolution metal-enrichment schemes implemented in EAGLE, Illustris, and TNG.
This galaxy has a redshift of z ∼ 2.3, with an absorption-metallicity of log (Zabs/Z⊙) = −0.68 ± 0.07 (Bolmer et al. 2019), an emission-line metallicity of log (Zemiss/Z⊙)|$= -0.33^{+0.12}_{-0.24}$|, and a Vega magnitude of 22.4 ± 0.1 in the K-filter of VLT/HAWK-I (Friis et al. 2015), corresponding to a K-corrected rest-frame U-band AB magnitude of 21.7 ± 0.1, assuming a flat spectral energy distribution (Metha et al. 2021a). To ensure a fair comparison to data, we follow Metha et al. (2021a) and include only simulated galaxies with a similar brightness to this galaxy, defined as those with rest-frame U-band magnitudes that are equal to this galaxy’s, to within 0.75. This magnitude cut is important, as it excludes a substantial number of galaxies with fainter magnitudes that would not be bright enough at this redshift for emission spectroscopy to be performed using current ground-based instruments. Therefore, without imposing a flux cut, the data-model comparison would be biased.
For each simulation, the selection procedure described in Section 3 was re-run after discarding all galaxies with rest-frame U-magnitudes outside of the selection range for each simulation’s snapshot at z = 2.32, in order to produce three magnitude-limited simulated samples of GRB120124A analogs. We note that this cut effectively limits the sample of host galaxies to only the brightest, most massive galaxies in each simulation, which do not generally follow the overall trends seen in the more general galaxy populations shown in the previous sections.
The likelihood of each simulation hosting a bright GRB-host galaxy with similar values of Zabs and Zemiss to the host of GRB121024A was determined using the general method described in section 4.1 of Metha et al. (2021a). Briefly, for each galaxy in the magnitude-limited sample at z = 2.32 of each simulation, the probability of the measured values of Zabs and Zemiss for the host galaxy of GRB121024A being drawn given (i) the uncertainties in the measured values of Zabs and Zemiss for the host of GRB121024A, and (ii) the simulated values of Zabs and Zemiss for each simulated galaxy was computed. Then, this value was multiplied by the probability of each galaxy in the sample hosting a GRB given that one GRB is observed from a bright galaxy at z = 2.32. The distribution for the true value of Zabs for the host of GRB121024A was taken to be a log-normal distribution, as this is the highest entropy distribution for log (Zabs) when only the mean and uncertainty of this value are known (Hogg, Bovy & Lang 2010). For Zemiss, the distribution was taken to be the posterior distribution as computed using NebulaBayes in Metha et al. (2021a).
To thoroughly investigate the dependence of this result on the value of Zmax, a finer grid was used for this investigation, exploring values of Zmax ranging from 0.1 to 1.0Z⊙ in increments of 0.1Z⊙, as well as the model with no cutoff metallicity. We found that the most likely model for the formation of a GRB121024A host-analog galaxy was the Illustris simulation with a metallicity cutoff of Zmax|$=0.2Z_\odot -0.3\, \mathrm{Z}_\odot$|.5 The relative log-likelihood of each other model compared to the most likely model is reported in Table 2. At any fixed value of Zmax, the most likely simulation to host a GRB121024A analog was Illustris. All of the EAGLE models are disfavoured, with log-odds ratios ≥ −1.3, which corresponds to a significant |$\ge 95{{\ \rm per\ cent}}$| preference for Illustris over EAGLE – however, we note that this result is due to a dearth of bright galaxies produced in EAGLE at this redshift with values of Zemiss similar to the host of GRB121024A and not the measured value of Zabs. The most likely Illustris models are also favoured slightly over the most likely TNG model with Zmax|$=0.3\, \mathrm{Z}_\odot$| with a log-odds ratio of ∼−0.3, corresponding to a ∼2: 1 preference for the Zabs–Zemiss relation of Illustris over TNG. This result hints that the feedback procedures in Illustris may lead to more realistic chemical enrichment than in the TNG simulation, but this single data point is far from significant. A larger sample of observed data points would be required in order to make any definite claims about the relative realism of the feedback processes between these two models.
Relative log-likelihoods (base 10) for each simulation/model hosting an analog of GRB121024A.
| Zmax . | TNG . | Illustris . | EAGLE . |
|---|---|---|---|
| 0.1 | −0.703 | −0.559 | −1.337 |
| 0.2 | −0.450 | −0.079 | −1.427 |
| 0.3 | −0.344 | 0 | −1.454 |
| 0.4 | −0.497 | −0.180 | −1.382 |
| 0.5 | −0.574 | −0.337 | −1.584 |
| 0.6 | −0.685 | −0.404 | −1.495 |
| 0.7 | −0.806 | −0.515 | −1.530 |
| 0.8 | −0.711 | −0.518 | −1.546 |
| 0.9 | −0.845 | −0.531 | −1.611 |
| 1.0 | −0.842 | −0.562 | −1.533 |
| No Cutoff | −1.291 | −0.937 | −2.021 |
| Zmax . | TNG . | Illustris . | EAGLE . |
|---|---|---|---|
| 0.1 | −0.703 | −0.559 | −1.337 |
| 0.2 | −0.450 | −0.079 | −1.427 |
| 0.3 | −0.344 | 0 | −1.454 |
| 0.4 | −0.497 | −0.180 | −1.382 |
| 0.5 | −0.574 | −0.337 | −1.584 |
| 0.6 | −0.685 | −0.404 | −1.495 |
| 0.7 | −0.806 | −0.515 | −1.530 |
| 0.8 | −0.711 | −0.518 | −1.546 |
| 0.9 | −0.845 | −0.531 | −1.611 |
| 1.0 | −0.842 | −0.562 | −1.533 |
| No Cutoff | −1.291 | −0.937 | −2.021 |
Relative log-likelihoods (base 10) for each simulation/model hosting an analog of GRB121024A.
| Zmax . | TNG . | Illustris . | EAGLE . |
|---|---|---|---|
| 0.1 | −0.703 | −0.559 | −1.337 |
| 0.2 | −0.450 | −0.079 | −1.427 |
| 0.3 | −0.344 | 0 | −1.454 |
| 0.4 | −0.497 | −0.180 | −1.382 |
| 0.5 | −0.574 | −0.337 | −1.584 |
| 0.6 | −0.685 | −0.404 | −1.495 |
| 0.7 | −0.806 | −0.515 | −1.530 |
| 0.8 | −0.711 | −0.518 | −1.546 |
| 0.9 | −0.845 | −0.531 | −1.611 |
| 1.0 | −0.842 | −0.562 | −1.533 |
| No Cutoff | −1.291 | −0.937 | −2.021 |
| Zmax . | TNG . | Illustris . | EAGLE . |
|---|---|---|---|
| 0.1 | −0.703 | −0.559 | −1.337 |
| 0.2 | −0.450 | −0.079 | −1.427 |
| 0.3 | −0.344 | 0 | −1.454 |
| 0.4 | −0.497 | −0.180 | −1.382 |
| 0.5 | −0.574 | −0.337 | −1.584 |
| 0.6 | −0.685 | −0.404 | −1.495 |
| 0.7 | −0.806 | −0.515 | −1.530 |
| 0.8 | −0.711 | −0.518 | −1.546 |
| 0.9 | −0.845 | −0.531 | −1.611 |
| 1.0 | −0.842 | −0.562 | −1.533 |
| No Cutoff | −1.291 | −0.937 | −2.021 |
To illustrate this point, in Fig. 7, we plot kernel density estimates (KDEs) for the magnitude-limited GRB host galaxy samples from each simulation at z = 2.32, assuming Zmax = 0.3Z⊙, which is one of the most likely models.6 We also plot in magenta the location of the Zabs and Zemiss measurements for the host of GRB121024A, too, so that this data point can be directly compared to the predictions of simulations. This plot shows that, while this data point agrees best with the predictions of the Illustris simulation and disfavours the EAGLE simulation, any of the three simulations tested would be capable of generating this data point, due to the large uncertainties on the measured values of Zabs and Zemiss.
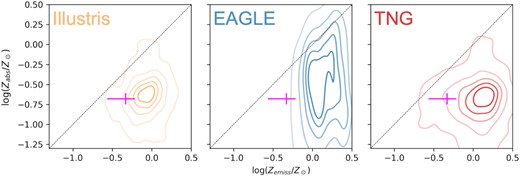
KDE plots showing the expected Zabs–Zemiss relation at z = 2.32 for the magnitude-limited samples of simulated GRB hosts, assuming a value of Zmax = 0.3Z⊙. In magenta, the location of the host galaxy of GRB121024A on the Zabs–Zemiss plane is plotted, with uncertainties. This data point shows the greatest agreement with the sample of bright simulated galaxies in Illustris and disfavours the EAGLE simulation.
5.2 How many observations are needed to get a significant conclusion about the more likely feedback model?
Using our simulated galaxy samples, we now consider the question: how many data points would need to be observed in order to provide a significant log-odds ratio that can be used to rule out certain simulation-driven models of the Zabs–Zemiss relation?
To assess this, the following procedure was undertaken. For each simulation, using each value of Zmax, a GRB host galaxy was chosen based on its rate of GRB formation. Gaussian random noise was added to the logarithm of the values of Zabs and Zemiss for the simulated galaxy to reflect the difficulty in observing these quantities. For Zabs, the observational uncertainty was modelled as being 0.11 dex, which is the median value of the measured uncertainties of absorption-line based metallicity measurements of GRB host galaxies reported in Metha et al. (2021a). For Zemiss, the observational uncertainty was modelled as 0.2 dex, typical of the uncertainties associated with strong emission-line based metallicity measurements at this redshift range (Arabsalmani et al. 2018).7 This data point (with its observational error) was then used to compute log-likelihood ratios for the probability of generating this data point using the simulation that it came from over the probability of generating it from either of the two alternative models (using the same metallicity bias model for GRB progenitors every time).
This procedure was repeated 2.5 × 105 times, using all four downloaded snapshots at different redshifts for this comparison. The relative likelihood of a GRB coming from each redshift was taken using the observed cosmic GRB rate of SHOALS (Perley et al. 2016). No magnitude-dependent selections were used to restrict the samples in this analysis, as this would depend on the capabilities of the survey instrument.
These trials were organized into |$10\, 000$| ‘mock observational’ runs, each observing values of Zabs and Zemiss for 25 GRB hosts at a redshift range of z = 1.74–4.0. The increase in the evidence for the generative model (log-odds ratio) as the number of observations (N) increased was computed for each simulated observing run. We show the median value of this relationship, and the 1σ and 2σ scatter, in Fig. 8 using our most likely model with Zmax = 0.3Z⊙. We find that the EAGLE model of chemical enrichment and mixing generates a predicted Zabs–Zemiss relation that can be easily distinguished from the other two models. In over half of the trials conducted, only N = 8 observations are needed in order to rule out the other models with high significance (a log-odds ratio greater than two). The Illustris simulation is the second easiest to separate, requiring about N = 11 observations to reach this level of significance over |$50{{\ \rm per\ cent}}$| of the time, with TNG requiring N = 17 observations. This result can be explained by comparing the similarity of the subgrid physical prescriptions governing the structure of the ISM within these simulations. As the subgrid prescriptions and numerical methods used in the EAGLE simulation are very different to those used in the Illustris/TNG simulation, only a small number of observational data points are needed to discern the Zabs–Zemiss relation predicted by EAGLE from the other two alternative models. On the other hand, the TNG and Illustris simulations are far more similar. Furthermore, TNG has some feedback modes inspired by EAGLE (discussed in Section 2.3), which may lead to the internal chemical structures of star-forming galaxies in TNG being more similar to EAGLE than those in Illustris, increasing the number of observational data points needed to confidently conclude that the TNG model is the preferred generative model.
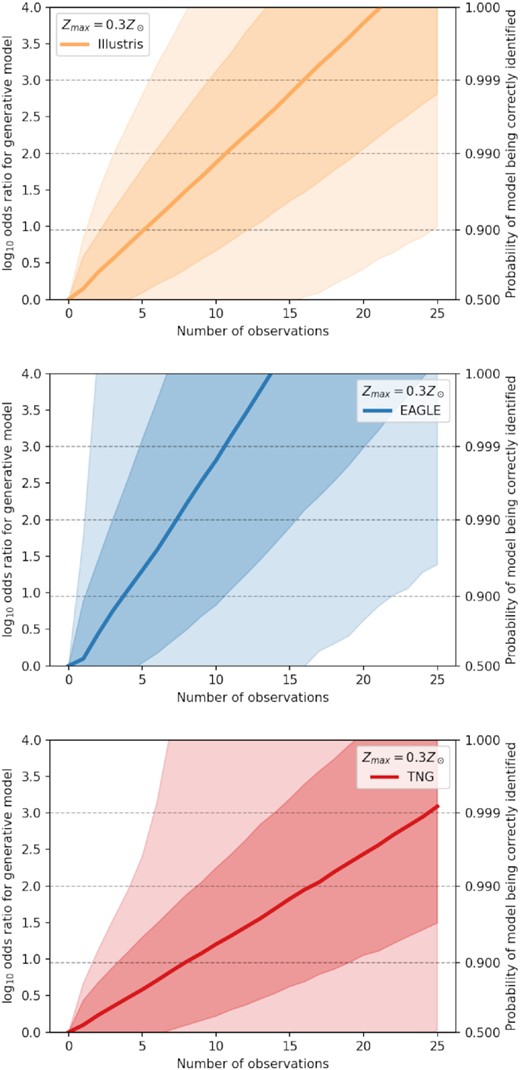
Odds ratio for the generative model as a function of the number of GRB host galaxies with observed values for Zabs and Zemiss. Bold lines represent the median log odds ratio, with the dark- and light-shaded regions representing the |$68{{\ \rm per\ cent}}$| and |$95{{\ \rm per\ cent}}$| symmetric confidence intervals around this median. We find that a small number (N ∼ 8–17) of observations is sufficient for distinguishing the correct model from the alternatives most of the time; however, the variance in the recovered log odds ratios were found to be very high, due to the width of the intrinsic scatter in the simulated Zabs–Zemiss relations and large observational uncertainties.
In all cases, the scatter in the possible values of the log odds ratio for the generative model over the alternatives as a function of the number of observed data points is very large. This is due to the intrinsic scatter within the Zabs–Zemiss relation predicted by all models (see Figs A1–A3). For any generative models, it is possible to select either (i) a GRB host with values of Zabs and Zemiss that cannot be generated from another simulation, which vastly raises the likelihood, or (ii) a GRB host that is far more likely to come from one of the alternative models than the generative model, which lowers the odds ratio for identifying the correct simulation. Together, these two effects produce a very large variance in the log-odds ratio for each model as a function of N, the number of observations. Samples of GRB host galaxies drawn from the tails of the Zabs-Zemiss distribution are necessary to distinguish between the models investigated in this work. This may be achieved in as few as N = 5 observations, or it may take more than N = 25. By examining the 2D distributions of galaxies on the Zabs- Zemiss plane for the three simulations compared in this work (Appendix A), we see that targeting low-redshift galaxies with low values of Zemiss is the best way to distinguish between the different predicted Zabs–Zemiss relations. However, in practice, the number of GRBs with measured values of Zabs for which spectroscopic follow-up is feasible is limited; and the exact number of GRB hosts that are needed to constrain this relation is simply up to chance.
This analysis was repeated for models other than the most likely model with Zmax = 0.3Z⊙. We found that for lower values of Zmax (stricter GRB metallicity bias functions), a smaller number of data points were needed to correctly identify the generative model in all cases. When GRBs were assumed to be unbiased tracers of star formation, a median value of 15–20 observations were required to achieve a log-odds ratio of 1 for the correct generative model. This indicates that using metallicity-biased tracers of star formation, such as GRBs, can play an important role in determining the internal metallicity structure of distant galaxies.
6 DISCUSSION
As discussed in Section 5.1, currently only one GRB host galaxy has had its metallicity measured with both strong emission-line diagnostics and by examining the absorption spectrum of the transient. A significant difference is seen between Zabs and Zemiss (|$0.35^{+ 0.14}_{- 0.25}$| dex; Metha et al. 2021a). Similar differences have also been reported by various teams examining the relationship between Zabs and Zemiss for quasar-absorbing galaxies: Christensen et al. (2014) report a mean offset of 0.44 ± 0.10 dex. However, the physical origin of this offset is very different for quasar- and GRB-absorbing systems.
For quasar-absorbing systems, Christensen et al. (2014) find that the difference between the measured values of Zabs and Zemiss correlates heavily with the distance between the quasar LOS and the galaxy centre. Such a relationship is expected from any theory of galaxy formation that produces negative metallicity gradients (e.g. Boissier & Prantzos 1999). As Zemiss is biased to the brightest regions of star formation and galaxies are generally brightest in their central regions, Zemiss can be taken as a tracer of the metallicity near the centre of a galaxy, while Zabs traces only the metallicity of the gas along the LOS. An offset between Zemiss and Zabs is expected, then, when a quasar LOS passes through the outskirts of a galaxy, due to the different environments that these two processes are probing.
On the other hand, for GRB-absorbing systems, the LOS necessarily originates from a region of recently star-forming gas, as GRBs are associated with core-collapse supernovae that have short delay times (Fruchter et al. 2006; Briel et al. 2022). For this reason, the spatial regions traced by Zabs and Zemiss for GRB host galaxies must overlap, to some extent. Furthermore, at high redshifts, galaxies with a wide variety of metallicity gradients are seen, both in observations (e.g. Cresci et al. 2010; Leethochawalit et al. 2016; Wuyts et al. 2016; Wang et al. 2022) and in simulations (Ma et al. 2017; Hemler et al. 2021; Tissera et al. 2022). Therefore, we must carefully consider how Zabs is expected to differ from Zemiss in galaxies with negative (standard) metallicity gradients, positive (inverted) gradients, and galaxies with no metallicity gradient at all. We discuss each of these cases below.
If a galaxy has a negative metallicity gradient, then Zabs is expected to be lower than Zemiss. Under our model, only low-metallicity regions of a galaxy are able to form GRBs. This means it is more likely for a GRB to form away from the high-metallicity central regions of these galaxies. While it is still possible for the LOS from this GRB to pass through the higher metallicity central regions, it is far more likely for it to go either out of the disc, or pass through the disc away from the central regions, avoiding the high metallicity central regions. On the other hand, Zemiss will be biased to the metallicity of the central region where the SFR is highest, making Zemiss larger than Zabs.
If a galaxy has an inverted/positive metallicity gradient, then Zabs is still expected to be higher than Zemiss, on average, but with a larger scatter compared to the previous case. In fact, in this scenario, GRB formation will be biased to the low-metallicity central regions of a galaxy. This will especially be true if the inverted metallicity gradient comes from a cold gas inflow into a galaxy’s central regions, which would trigger enhanced star formation in the low-metallicity centre (as suggested by e.g. Dekel et al. 2009a; Dekel et al. 2009b; Stott et al. 2014; Ellison et al. 2018). When the GRB LOS is directed out of the disc, Zabs will reflect predominately the low metallicity of the galaxy’s central regions. This will be lower than Zemiss, which will be integrated over a larger area including higher metallicity regions. However, when the LOS of the GRB is aligned such that it passes through the disc, Zabs will return the integrated metallicity along higher metallicity regions. Depending on the orientation of the jet, this may result in a value of Zabs that is comparable to or larger than Zemiss.
For a galaxy with no metallicity gradient, the relationship between Zabs and Zemiss depends on how well metals are mixed throughout the galaxy. For a perfectly homogeneous galaxy, Zemiss and Zabs would be equal. However, recent studies of the two-dimensional metallicity structure of local galaxies have shown that they exhibit significant variations in metallicity (of the order of ∼0.1 dex) on scales of ∼1 kpc (Metha et al. 2021b, 2022; Li et al. 2022). Such small-scale variations in metallicity may allow GRBs to be formed in low-metallicity regions of high-metallicity galaxies, along lines of sight that, when integrated, allow values of Zabs that are still lower than Zemiss.
All of these results suggest that the Zabs–Zemiss relation does not trace whether or not galaxies have negative, positive, or no gradients. Rather, the shape of this relationship depends on the overall degree of chemical inhomogeneity within galaxies at high redshift. As the numerical methods and subresolution physical prescriptions of all these simulations are very different (see Section 2), it would be very challenging to ascribe differences in the Zabs-Zemiss relations predicted between these simulations (which depends on the small-scale chemical structure of the ISM of the simulated galaxies) to any specific features, such as the feedback models used, or the presence or absence of magnetism. All factors described in Section 2 likely play a role, to some extent. A rigorous discussion into what sets the Zabs–Zemiss relation is beyond the purpose of this paper, as our focus is more on observational consequences.
Qualitatively, the form of the Zabs–Zemiss relation is consistent among a selection of three galaxy formation models (Figs 1, 3, and 5). For all simulations, the most likely value of Zmax was fit using the data on the host galaxy of GRB121024A, and was found to be 0.3Z⊙ for Illustris and TNG, and could only be constrained to ≤0.4Z⊙ for EAGLE. The agreement between these different simulations in determining this value tells us that we may be confident in using the Zabs–Zemiss relation to determine Zmax robustly. We note that for the EAGLE simulation only galaxies with Zemiss≳ 0.5Z⊙ show differences between the median value of Zabs at fixed Zemiss for different values of Zmax.
In Metha et al. (2021a), it was shown that using the TNG simulation, the median value of Zemiss at a specific Zabs depends not on the value of Zmax. This result was also found in this work when EAGLE and Illustris were used. However, as was conjectured in Metha et al. (2021a), the dependence of the value of Zemiss at fixed Zabs was found to be very sensitive to the model of galaxy evolution employed.
This means that the Zabs–Zemiss relation can tell us two things: (i) the metallicity bias function for GRB progenitor stars, and (ii) some information about how metals are mixed and redistributed in high-redshift galaxies. This information can be used to compare cosmological simulations along a new axis that has not been calibrated a priori, to provide a novel test that is sensitive to the subresolution models of chemical enrichment and galaxy evolution.
7 SUMMARY AND CONCLUSIONS
In this study, we investigated the impact that chemical inhomogeneities of star-forming galaxies have on the relationship between Zabs, the metallicity measured using absorption-line spectroscopy, and Zemiss, the metallicity measured using gas emission lines, for GRB host galaxies. We analysed three distinct hydrodynamical cosmological simulations: EAGLE, Illustris, and IllustrisTNG, all of which employ different numerical methods and subgrid physical prescriptions to generate realistic populations of galaxies. Using a consistent methodology across all three simulations, GRB host galaxies were identified from snapshots at different redshifts through a Monte Carlo approach that includes a preference for low metallicity hosts (treated as a free parameter). The relationship between Zabs and Zemiss was computed using a range of GRB metallicity bias functions at redshifts 1.74 ≤ z ≤ 4.0. Our main conclusions are as follows:
Different simulations predict different forms of the Zabs–Zemiss relation. This implies that this relationship, which depends on the degree of chemical homogeneity within galaxies, is sensitive to choices of subresolution physics and details of chemical enrichment and mixing used in simulations.
The form of the Zabs–Zemiss relation predicted from the EAGLE simulation is notably different to that predicted from the Illustris and TNG simulations. At all redshifts and for all values of Zmax tested, the values of Zabs and Zemiss are more likely to agree for this simulation. This implies that most high-redshift galaxies in EAGLE are predicted to be more homogeneous than those produced in Illustris or TNG.
On the other hand, the EAGLE simulation also exhibited a small population (|$\sim 5-10{{\ \rm per\ cent}}$|) of galaxies with extremely low values of Zabs (10−5–10−2Z⊙). These galaxies have regions of extremely metal poor gas, indicating that the feedback and metal mixing schemes implemented in EAGLE may be inefficient at redistributing metals into a galaxy’s outer regions. Such a low Zabs GRB host population was not seen in either Illustris or TNG.
A statistical analysis of the Zemiss and Zabs values determined for the host galaxy of GRB121024A was constructed. This single data point favours the TNG and Illustris models with a metallicity cutoff at Zmax ≈ 0.3Z⊙, and specifically prefers Illustris over TNG. The EAGLE simulation was significantly disfavoured, as bright galaxies with low values of Zemiss < 0.5Z⊙ are rare in this simulation.
Using Monte Carlo methods, a mock survey was constructed measuring the Zabs–Zemiss relation across a redshift range of 1.74–4.0 for the three simulations. We found that, assuming a GRB bias function with Zmax = 0.3Z⊙, an observing campaign targeting 8–17 GRB hosts would likely be sufficient to gather a significant amount of evidence for or against the modelled metallicity distributions of these high-redshift simulated galaxies.
An upcoming observational campaign using the JWST will collect Zemiss measurements for 10 GRB host galaxies at 2.0 < z < 4.7 for which Zabs has already been determined (Schady et al. 2021). Data from this population of GRB host galaxies will greatly increase the constraining power of observations on the Zabs–Zemiss relation. In fact, we expect the data set will allow us to achieve a better understanding of both the metallicity bias for GRB progenitors, and the small-scale metallicity structures of high-redshift galaxies. However, based on our analysis, whether or not this sample of N = 10 additional GRB host galaxies will be large enough to discriminate between any of the Zabs–Zemiss relations predicted from different cosmological simulations at a reasonably high confidence level still remains to be seen. In fact, our results shown in Fig. 8 indicate that the sample size may have to be increased to N ≳ 17. Given that the limiting factor for further progress is the availability of GRBs with robust absorption metallicity measurements at high redshift, future facilities for all-sky gamma-ray monitoring and for rapid follow-up at infrared wavelengths, such as the HERMES/SpIRIT constellation (Fiore et al. 2020, Thomas et al. 2022, submitted) and the SkyHopper infrared space telescope (Thomas et al. 2022), have the potential to play a contributing role along with flagships such as JWST to advance our understanding of how chemical elements are distributed in the interstellar and intergalactic medium.
ACKNOWLEDGEMENTS
The authors thank the anonymous referee for providing insightful comments and suggestions that improved the quality of the manuscript. BM acknowledges support from an Australian Government Research Training Program (RTP) Scholarship and a Laby PhD Travelling Scholarship. This research is supported in part by the Austrailian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013.
DATA AVAILABILITY
Data products from the EAGLE simulation suite are available for public download via the Virgo consortium’s website: virgodb.dur.ac.uk. Data products from the Illustris simulation are available from www.illustris-project.org/data/. Data products from the IllustrisTNG simulation are available from www.tng-project.org/data/. Any further data products presented in this work, as well as the python code used to construct them, are available from the corresponding author (BM) upon reasonable request.
Footnotes
Hereafter, we will refer to gas-phase metallicity simply as ‘metallicity’.
For Illustris, the snapshot numbers were 54, 60, 66, and 71, all available at http://www.illustris-project.org/data/. For TNG, snapshots 21, 25, 30, and 36 were downloaded from http://www.tng-project.org/data/. For EAGLE, snapshots 10, 12, 14, and 16 were downloaded from http://virgodb.dur.ac.uk/.
We note that this prescription is subtly different from the methodology used in Metha et al. (2021a), wherein one GRB host gas cell is selected for each galaxy before a sample of GRB host galaxies are selected.
This is true regardless of whether the metallicity gradient of the galaxy is negative (as is seen in galaxies in the local Universe), positive (as is found for high-redshift galaxies in the TNG simulation by Hemler et al. 2021), or flat, as long as the galaxy does not have a uniform metallicity throughout. We discuss this point further in Section 6.
The log-odds ratio between these two models is −0.079, which corresponds to a slight, non-significant (|$\sim 20{{\ \rm per\ cent}}$|) preference for a model with Zmax=0.3Z⊙.
A metallicity cutoff of Zmax≈0.3Z⊙ is also supported by the investigations of Metha & Trenti (2020).
This analysis does not account for any bias in the measured value of Zemiss. Different emission-line ratio based metallicity diagnostics are known to produce metallicities that can vary in their absolute values by up to 0.7 dex (e.g. Kewley & Ellison 2008), so this bias may be significant. For the purposes of this analysis, we assume an observer that is successful at eliminating any bias from their metallicity measurements.
REFERENCES
APPENDIX A: COMPARISON OF Zabs–Zemiss RELATIONS BETWEEN SIMULATIONS
In Figs A1–A3, we compare the predicted Zabs–Zemiss relations between each pair of simulations, showing the full 2D kernel density estimates for each simulation, varying the redshift and the metallicity cutoff for GRB formation.
From these plots, it is clear that the predicted Zabs–Zemiss relation depends greatly on the subgrid prescriptions of the model used. The differences between the predicted simulations becomes more severe at lower values of Zmax, as details of the internal metallicity structure of galaxies have a greater role in setting the morphology of the Zabs–Zemiss relation when a more stringent cutoff is used. Differences seen are also more intense for low redshift. Here, metallicities of galaxies are generally higher, so imposing a low-metallicity cutoff has a greater effect on the Zabs–Zemiss relation. This is good news for prospects of future observations, as Zemiss is easier to measure at lower redshift.
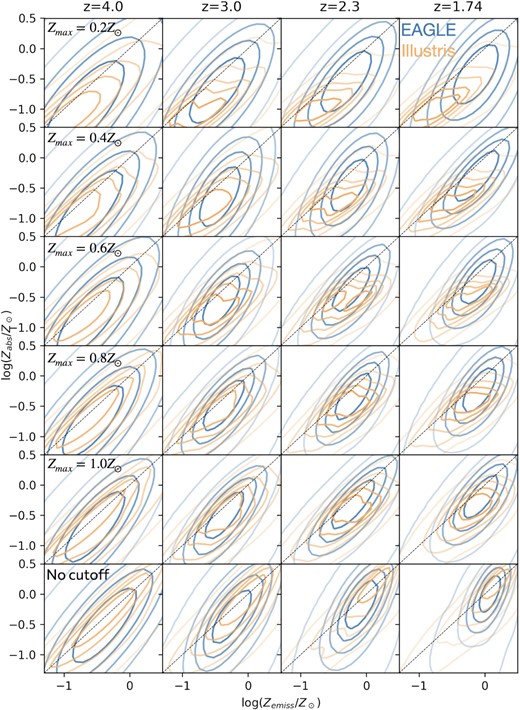
Comparing the predicted Zabs–Zemiss relations between the Illustris and EAGLE simulations, at all redshifts, for all GRB bias models tested.
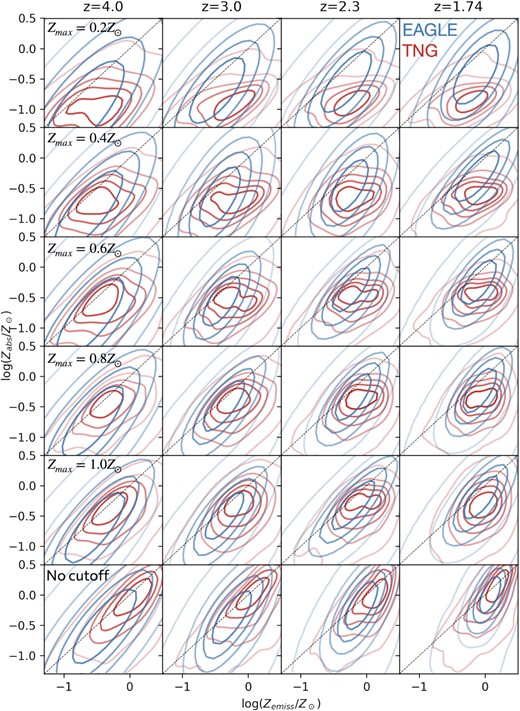
Comparing the predicted Zabs–Zemiss relations between the EAGLE and TNG simulations, at all redshifts, for all GRB bias models tested.
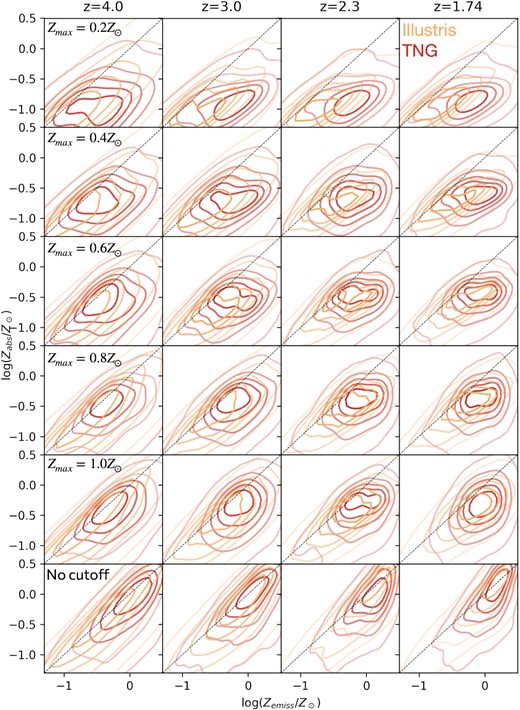
Comparing the predicted Zabs–Zemiss relations between the Illustris and TNG simulations, at all redshifts, for all GRB bias models tested.
These plots also demonstrate how both Zabs and Zemiss evolve with redshift. In all simulations and for all values of Zmax displayed, at lower redshifts, values of both Zabs and Zemiss are higher. This reflects the chemical enrichment of the Universe, which all simulations capture. Note that this result does not contradict our result of Section 4, in which we showed that the median value of Zabs at a fixed value of Zemiss shows very little redshift evolution in any simulation (see left-hand panel of Figs 2, 4, and 6): at higher redshifts, the number of galaxies with high values of Zemiss is lower; but for any fixed value of Zemiss, the median value of Zabs shows very little dependence on redshift.
Even when the predicted distributions peak at the same location on the Zabs–Zemiss plane, different models show large differences in the tails of the simulations, implying that with a large enough collection of observations, a few rare events may be able to distinguish between such models. This implies that a survey aimed at collecting values of Zemiss for GRB host galaxies for which Zabs estimates have already been established at a range of redshifts will be able to constrain models of chemical evolution within galaxies (see Section 5.2 for further details).



