-
PDF
- Split View
-
Views
-
Cite
Cite
Isabel M E Santos-Santos, Julio F Navarro, Alan McConnachie, The Tucana dwarf spheroidal: a distant backsplash galaxy of M31?, Monthly Notices of the Royal Astronomical Society, Volume 520, Issue 1, March 2023, Pages 55–62, https://doi.org/10.1093/mnras/stad085
Close - Share Icon Share
ABSTRACT
We use the APOSTLE Local Group (LG) cosmological hydrosimulations to examine the properties of ‘backsplash’ galaxies, i.e. dwarfs that were within the virial boundaries of the Milky Way (MW) or M31 in the past, but are today outside their virial radius (r200). More than half of all dwarfs between |$1\text{ and }2\, r_{200}$| of each primary are backsplash. More distant backsplash systems, i.e. those reaching distances well beyond |$2\, r_{200}$|, are typically close to apocentre of nearly radial orbits, and, therefore, essentially at rest relative to their primary. We use this result to investigate which LG dwarfs beyond ∼500 kpc of either primary could be a distant backsplash satellite of MW or M31. Tucana dSph, one of the few known quiescent LG field dwarfs, at dM31 ≈ 1350 kpc and dMW ≈ 880 kpc, is a promising candidate. Tucana’s radial velocity is consistent with being at rest relative to M31. Further, Tucana is located close to M33’s orbital plane around M31, and simple orbit integrations indicate that Tucana may have been ejected during an early pericentric passage of M33 ∼11 Gyr ago, a timing that approximately coincides with Tucana’s last episode of star formation. We suggest that Tucana may have been an early-infalling satellite of M31 or M33, providing a compelling explanation for its puzzling lack of gas and ongoing star formation despite its isolated nature. In this scenario, M33 should have completed some orbits around M31, a result that may help to explain the relative dearth of M33 satellite candidates identified so far.
1 INTRODUCTION
In the Lambda cold dark matter (LCDM) cosmological paradigm, galaxies form at the centre of dark matter haloes that grow hierarchically, continuously accreting smaller systems. Of all accreted systems, the most massive ones quickly spiral to the centre and merge with the main halo, but lower mass systems may remain in orbit for a long time and are today identified with satellite galaxies (see e.g. Wang et al. 2011, and references therein).
Satellites are strongly affected by their host, both gravitationally, as tides gradually pull away matter, and hydrodynamically, as the circumgalactic gas of the primary ram pressure strips away the gaseous envelopes of subhaloes, depriving them of star formation fuel and eventually extinguishing their star formation activity (Tolstoy, Hill & Tosi 2009).
This scenario leads naturally to differences between the properties of satellite galaxies compared with dwarf galaxies of similar mass in the field. In particular, it successfully explains the origin of the environmental dependence of dwarf galaxy types in the Local Group (LG): the majority of satellites are quiescent, gas-free dwarf spheroidal systems, whereas field dwarfs are typically gas-rich dwarf irregulars with ongoing star formation (see e.g. Grebel 1998; Weisz et al. 2014).
Given the importance of these environment-driven processes, it is important to establish how far away from a galaxy they may operate. Early work on galaxy clusters led to the realization that environmental effects may extend well beyond the nominal virial boundary of a system (Balogh, Navarro & Morris 2000), conventionally defined as the radius,1r200, where the circular orbit time-scale is comparable to the age of the Universe.
The reasons for the unexpectedly large ‘radius of influence’ of a primary system on its associated subsystems are twofold. One reason is that many subhalo orbits are fairly radial, and may reach outside the virial radius during their first trip to apocentre after accretion (Mamon et al. 2004; Gill, Knebe & Gibson 2005; Knebe et al. 2011). Indeed, most subhaloes first accreted 2–3 Gyr ago into a halo like that of the Milky Way (MW) are expected to be at present outside the virial radius (Barber et al. 2014). These so-called ‘backsplash’ galaxies are especially abundant just outside the virial radius, representing a fraction of that may exceed ∼50 per cent of subhaloes with 1 < d/r200 < 2.5 (Garrison-Kimmel et al. 2014; Simpson et al. 2018; Buck et al. 2019; Applebaum et al. 2021; Bakels, Ludlow & Power 2021).
The second reason is that many subhaloes come as members of virialized groups that are tidally dissociated soon after first infall into the primary halo. As discussed in detail by Sales et al. (2007) and Ludlow et al. (2009), some subhaloes may gain enough energy during the disruption of their group to be expelled much further away, to distances as far as 5 virial radii or beyond (see also Teyssier, Johnston & Kuhlen 2012). Systems on these extreme orbits are typically a small fraction of the low-mass members of the group, whose heavier members typically stay tightly bound to the primary. Identifying these ‘extreme backsplash’ cases therefore requires not only some evidence for dynamical association, but also the existence of a more massive ‘parent’ progenitor to help propel them into highly energetic orbits.
In the cosmological context of the LG, the above discussion suggests the existence of a rare population of low-mass field dwarfs, located far away (out to ∼1.5 Mpc) from the MW and Andromeda (M31), but showing properties consistent with satellites of either of them, such as lack of ongoing star formation. These galaxies are indeed unusual, since most isolated galaxies discovered so far in the LG field and beyond are currently star forming (Geha et al. 2012).
To date, the only known examples of field dSph galaxies within 1.5 Mpc of the LG mid-point are Cetus, Tucana, and And XVIII, currently at ∼755(674), ∼877(1345), and ∼1330(580) kpc from the MW (M31), respectively (Lavery & Mighell 1992; Whiting, Hau & Irwin 1999; McConnachie et al. 2008). All three show little to no gas content and predominantly old stellar populations formed roughly ∼9–10 Gyr ago (Castellani, Marconi & Buonanno 1996; Monelli et al. 2010a,b; Makarova et al. 2017; Savino et al. 2019). Further away, at ∼2 Mpc, the only other examples of quiescent dwarfs known are KKR25 and KKs3 (Karachentsev et al. 2001; Karachentsev, Kniazev & Sharina 2015), plus the recent discoveries of Tucana B (Sand et al. 2022) and COSMOS-dw1 in the COSMOS-CANDELS field beyond the LG (Polzin et al. 2021).
The origin of isolated dwarf galaxies with no recent star formation activity remains poorly understood, but it has been argued that, in the case of Cetus and Tucana, they may have resulted from either a backsplash interaction with the MW (e.g. Sales et al. 2007; Fraternali et al. 2009; Teyssier et al. 2012) or from ram-pressure stripping with the cosmic web (e.g. Benítez-Llambay et al. 2013). More recently, a novel proposal associating them with the effects of the photoionizing background has been put forward by Pereira Wilson et al. (2022).
We use in this paper distant backsplash dwarfs in the APOSTLE cosmological hydrodynamical simulations (Fattahi et al. 2016; Sawala et al. 2016) to characterize the kinematic properties of such systems in the LG. We focus on seemingly isolated galaxies at distances larger than ∼500 kpc from the MW and M31, noting as well that, as reported in earlier work, many dwarfs between |$r_{200}\lt d\lt 2.5\, r_{200}$| (roughly out to ∼500 kpc of the MW or M31) are indeed backsplash galaxies.
This paper is organized as follows: In Section 2, we describe the APOSTLE simulations and the observational data used. Our results on distant backsplash galaxies in APOSTLE are presented in Section 3.1. Section 3.2 shows our analysis of LG dwarfs in light of the simulation results. Finally, in Section 3.3 we focus on the Tucana dSph and provide evidence supporting a hypothetical backsplash origin. Section 4 summarizes our conclusions.
2 METHODS
2.1 Numerical simulations
The APOSTLE simulations are a set of cosmological volumes chosen to include two massive primary haloes with masses, relative distance, relative radial velocity, and surrounding Hubble flow similar to that observed for the MW and M31 pair (Fattahi et al. 2016). In this work, we have used four volumes run at the highest resolution in APOSTLE (labelled ‘L1’ level in previous literature). These runs have initial dark matter and gas particle masses of mDM ∼ 5 × 104 M⊙ and mgas ∼ 1 × 104 M⊙, respectively, and a gravitational softening length of 134 pc at z = 0. The zoom-in region of each APOSTLE volume fully contains a sphere of radius r ∼ 3.5 Mpc from the mid-point of the MW and M31 ‘primary’ haloes.
APOSTLE used the EAGLE galaxy formation code (Crain et al. 2015; Schaye et al. 2015). This model includes subgrid physics prescriptions for star formation in gas exceeding a metallicity-dependent density threshold, radiative cooling of gas, stellar feedback (from stellar winds, radiation pressure, and supernovae), homogeneous X-ray/ultraviolet background radiation, supermassive black hole growth, and AGN feedback (the latter have negligible effects on dwarf galaxies).
APOSTLE assumes a flat ΛCDM cosmological model following WMAP-7 parameters (Komatsu et al. 2011): Ωm = 0.272; ΩΛ = 0.728; Ωbar = 0.0455; |$H_0 = 100\, h$| km s−1 Mpc−1; σ = 0.81; and h = 0.704.
2.1.1 Simulated galaxies
Haloes and subhaloes in APOSTLE have been identified using the friends-of-friends group-finding algorithm (Davis et al. 1985) (with linking length equal to 0.2 times the mean interparticle separation) and the SUBFIND halo finder (Springel, Yoshida & White 2001; Dolag et al. 2009).
Simulated galaxies are haloes where star formation has led to the formation of a luminous component. In APOSTLE, this restricts galaxy formation to field haloes more massive than |$M_{200}\sim 10^9\, \mathrm{M}_\odot$|. Satellite galaxies may exist in subhaloes with lower mass, because of tidal stripping; see for details Fattahi et al. (2018).
We shall define galaxies associated with each APOSTLE primary as those that have been within the virial radius of the primary’s most massive progenitor at some time during its evolution. Associated galaxies include satellites (i.e. galaxies within r200 at z = 0) and backsplash galaxies (i.e. associated galaxies located today outside the virial radius of the primary). Backsplash systems were identified by tracking back in time all galaxies found outside the virial radius of both main primaries at z = 0.2
Each of the main APOSTLE primaries presents halo masses M200 ranging from 0.78 to 2.05 × 1012 M⊙, with primary–secondary mass ratios in the range of ∼0.33–0.96.
2.2 Observational data
In this work, we consider the currently known LG dwarf galaxies within ∼1.5 Mpc of the mid-point between the MW and M31. We use the latest position and velocity data in the McConnachie (2012) compilation of nearby galaxies.3 We refer to dwarf galaxies within 300 kpc of the MW or M31 as ‘satellites’ of that primary; the rest are considered ‘isolated’ or ‘field’ dwarfs.
For M31 and its satellite M33 (i.e. Triangulum), we adopt the positions and velocities derived from the combined Gaia DR2 and Hubble Space Telescope (HST) proper motions by van der Marel et al. (2019).
Galactocentric positions and velocities have been computed assuming a Galactocentric distance for the Sun of R⊙ = 8.29 kpc, a peculiar velocity with respect to the local standard of rest (LSR) of (U⊙, V⊙, W⊙) = (11.1, 12.24, 7.25) km s−1 (Schönrich, Binney & Dehnen 2010), and a circular velocity for the LSR of V0 = 239 km s−1 (McMillan 2011).
We make use of updated Gaia EDR3 systemic proper motions for a set of distant LG dwarf galaxies for which such data have been measured (McConnachie et al. 2021). For dwarfs without proper motion measurements, we convert the heliocentric line-of-sight velocities to the Galactic standard of rest (GSR) as |$\vec{V}_{\rm GSR}= \vec{V}_{\rm hel} + \vec{V}_{\odot ,\rm proj}$|, where |$\vec{V}_{\odot ,\rm proj}$| is the projection of the Sun’s motion (|$\vec{V}_{0}+\vec{V}_{\rm pec}$|) along the Galactocentric radial direction to the dwarf galaxy.
Tables 1 and 2 present the specific data values used for M31, M33, and Tucana, the objects which we will focus on later in the paper (see Section 3.3).4
Observational data used in this work for M31, M33, and Tucana. Columns show right ascension and declination, distance from the Sun, heliocentric line-of-sight velocity, and proper motions. References: McConnachie (2012) and van der Marel et al. (2012, 2019). In red are our predicted proper motions for Tucana if it is a backsplash galaxy of M31, computed by assuming it is at rest with respect to M31 (see Section 3.3).
| Galaxy . | RA (deg) . | Dec. (deg) . | D⊙ (kpc) . | Vhel (km s−1) . | μRA* (mas yr−1) . | μDec. (mas yr−1) . |
|---|---|---|---|---|---|---|
| M31 | 10.684 | 41.269 | 770 ± 40 | −301 ± 1 | 0.049 ± 0.011 | −0.038 ± 0.011 |
| M33 | 23.462 | 30.660 | 794 ± 23 | −180 ± 1 | 0.024 ± 0.007 | 0.003 ± 0.008 |
| Tucana | 340.456 | −64.419 | 887 ± 50 | 194 ± 4.3 | 0.0206 | −0.0754 |
| Galaxy . | RA (deg) . | Dec. (deg) . | D⊙ (kpc) . | Vhel (km s−1) . | μRA* (mas yr−1) . | μDec. (mas yr−1) . |
|---|---|---|---|---|---|---|
| M31 | 10.684 | 41.269 | 770 ± 40 | −301 ± 1 | 0.049 ± 0.011 | −0.038 ± 0.011 |
| M33 | 23.462 | 30.660 | 794 ± 23 | −180 ± 1 | 0.024 ± 0.007 | 0.003 ± 0.008 |
| Tucana | 340.456 | −64.419 | 887 ± 50 | 194 ± 4.3 | 0.0206 | −0.0754 |
Observational data used in this work for M31, M33, and Tucana. Columns show right ascension and declination, distance from the Sun, heliocentric line-of-sight velocity, and proper motions. References: McConnachie (2012) and van der Marel et al. (2012, 2019). In red are our predicted proper motions for Tucana if it is a backsplash galaxy of M31, computed by assuming it is at rest with respect to M31 (see Section 3.3).
| Galaxy . | RA (deg) . | Dec. (deg) . | D⊙ (kpc) . | Vhel (km s−1) . | μRA* (mas yr−1) . | μDec. (mas yr−1) . |
|---|---|---|---|---|---|---|
| M31 | 10.684 | 41.269 | 770 ± 40 | −301 ± 1 | 0.049 ± 0.011 | −0.038 ± 0.011 |
| M33 | 23.462 | 30.660 | 794 ± 23 | −180 ± 1 | 0.024 ± 0.007 | 0.003 ± 0.008 |
| Tucana | 340.456 | −64.419 | 887 ± 50 | 194 ± 4.3 | 0.0206 | −0.0754 |
| Galaxy . | RA (deg) . | Dec. (deg) . | D⊙ (kpc) . | Vhel (km s−1) . | μRA* (mas yr−1) . | μDec. (mas yr−1) . |
|---|---|---|---|---|---|---|
| M31 | 10.684 | 41.269 | 770 ± 40 | −301 ± 1 | 0.049 ± 0.011 | −0.038 ± 0.011 |
| M33 | 23.462 | 30.660 | 794 ± 23 | −180 ± 1 | 0.024 ± 0.007 | 0.003 ± 0.008 |
| Tucana | 340.456 | −64.419 | 887 ± 50 | 194 ± 4.3 | 0.0206 | −0.0754 |
Galactocentric position and velocities for M31, M33, and Tucana derived from data in Table 1.
| Galaxy . | X (kpc) . | Y (kpc) . | Z (kpc) . | Vrad or VGSR (km s−1) . | VX (km s−1) . | VY (km s−1) . | VZ (km s−1) . |
|---|---|---|---|---|---|---|---|
| M31 | −378.95 | 612.66 | −283.12 | −108.91 | 34.99 | −123.82 | −17.02 |
| M33 | −476.09 | 491.06 | −412.86 | −35.17 | 44.34 | 90.95 | 125.10 |
| Tucana | 470.99 | −652.71 | −362.36 | 91.42 | – | – | – |
| Galaxy . | X (kpc) . | Y (kpc) . | Z (kpc) . | Vrad or VGSR (km s−1) . | VX (km s−1) . | VY (km s−1) . | VZ (km s−1) . |
|---|---|---|---|---|---|---|---|
| M31 | −378.95 | 612.66 | −283.12 | −108.91 | 34.99 | −123.82 | −17.02 |
| M33 | −476.09 | 491.06 | −412.86 | −35.17 | 44.34 | 90.95 | 125.10 |
| Tucana | 470.99 | −652.71 | −362.36 | 91.42 | – | – | – |
Galactocentric position and velocities for M31, M33, and Tucana derived from data in Table 1.
| Galaxy . | X (kpc) . | Y (kpc) . | Z (kpc) . | Vrad or VGSR (km s−1) . | VX (km s−1) . | VY (km s−1) . | VZ (km s−1) . |
|---|---|---|---|---|---|---|---|
| M31 | −378.95 | 612.66 | −283.12 | −108.91 | 34.99 | −123.82 | −17.02 |
| M33 | −476.09 | 491.06 | −412.86 | −35.17 | 44.34 | 90.95 | 125.10 |
| Tucana | 470.99 | −652.71 | −362.36 | 91.42 | – | – | – |
| Galaxy . | X (kpc) . | Y (kpc) . | Z (kpc) . | Vrad or VGSR (km s−1) . | VX (km s−1) . | VY (km s−1) . | VZ (km s−1) . |
|---|---|---|---|---|---|---|---|
| M31 | −378.95 | 612.66 | −283.12 | −108.91 | 34.99 | −123.82 | −17.02 |
| M33 | −476.09 | 491.06 | −412.86 | −35.17 | 44.34 | 90.95 | 125.10 |
| Tucana | 470.99 | −652.71 | −362.36 | 91.42 | – | – | – |
3 RESULTS
3.1 Backsplash galaxies in APOSTLE
Fig. 1 shows the radial velocity versus distance from the primary for all galaxies identified in the four APOSTLE high-resolution volumes studied. This figure is centred on each of the eight available primaries and shows a stack of all luminous galaxies in each of the simulated volumes.

Radial velocity versus distance for galaxies in the APOSTLE LG simulations in the reference frame of one of its primaries. Results for all eight primaries are stacked. Associated galaxies are shown in red, being either satellites (i.e. within r200, smaller circles) or backsplash galaxies (i.e. outside r200, larger circles). Field dwarfs not associated with the primary are shown as open grey circles. Satellites of the other primary in the volume are shown as small grey dots. For reference, a vertical grey band indicates the 10–90 percentile range of r200 values for all eight APOSTLE primaries. The ±1σ radial velocity dispersion of associated galaxies as a function of distance is shown with a red shaded area. The radial distance to the second primary in each APOSTLE volume, rP2, is marked with an arrow for reference. An upper auxiliary panel indicates the average fraction of associated galaxies, over all galaxies in the volume, as a function of radial distance from the primary.
‘Associated’ galaxies are shown in red, being either satellites (small circles) or backsplash galaxies (big circles with black edges). A vertical shaded area delimits the 10–90 percentile range of r200 values for the eight primaries, 196–261 kpc, which separates the overall satellite and backsplash populations.
‘Isolated’ dwarfs are shown as grey open circles. Note that because of the binary nature of the LG, some of the isolated galaxies could be backsplash galaxies of the other primary in the same volume. For reference, the radial distance to the other primary, rP2, is marked with an arrow.
We find an average of ∼43 satellites and ∼9 backsplash per primary, down to a limit of one star particle, or roughly |$M_*\sim 10^4\, \mathrm{M}_\odot$|. This is best regarded as a lower limit, as the raw number is very likely affected by numerical limitations. There are actually more associated subhaloes outside than inside the virial radius (Ludlow et al. 2009), but the vast majority of them are low-mass subhaloes without stars in them.
The upper panel in Fig. 1 shows the fraction of associated galaxies over all dwarfs in the simulated LG, as a function of radial distance from the primary. In APOSTLE, more than |$\gt 80{{\ \rm per\ cent}}$| (|$50{{\ \rm per\ cent}}$|) of dwarfs within 300 (400) kpc of a primary are associated with it, emphasizing that the virial radius does not represent a true physical boundary separating objects that have or have not been influenced dynamically by the primary. At 550 kpc, only |$25{{\ \rm per\ cent}}$| of dwarfs are associated; at 700 kpc, fewer than |$10{{\ \rm per\ cent}}$| are. The furthest backsplash case we find is at a distance of ∼1.2 Mpc from its primary, roughly 6 × r200.
How can some backsplash galaxies reach such large distances (∼1 Mpc) from the primary? As explained in Sales et al. (2007) and developed further by Ludlow et al. (2009), low-mass galaxies can be ejected out to large distances during the tidal dissociation of groups of dwarfs during their first infall. The tides induce the formation of two ‘tails’ of subhaloes as the group disrupts: one that loses and another one that gains orbital energy during disruption (see e.g. fig. 4 of Ludlow et al. 2009). The subhaloes carried away in the latter tail can sometimes reach very large distances, and formally even ‘escape’ the primary. Typically, the lowest mass and least bound subhaloes in the group are the ones more susceptible to being propelled to extreme orbits.
As may be expected, distant associated galaxies are close to the apocentre of their orbits, and are thus basically at rest with the primary. This is seen in Fig. 1, which shows that the radial velocities of very distant backsplash systems, which are on nearly radial orbits, decrease systematically with increasing distance, approaching zero for the most distant ones. (The red shaded region in Fig. 1 shows the radial velocity dispersion of associated systems as a function of distance.) On the other hand, at similar distances, the radial velocities of other, unassociated dwarfs in the LG span a wide range of values.
This result suggests that a low relative velocity may in principle be used as a robust criterion to identify candidate ‘extreme backsplash’ galaxies (i.e. those located at d > 2–|$3\, r_{200}$|) associated with a given primary. We use this finding next to identify galaxies in the LG that may have been previously associated with the MW or M31.
3.2 Distant backsplash candidates in the Local Group
Fig. 2 shows the radial distance to the MW versus the radial distance to M31, for observed LG dwarf galaxies within ∼1.5 Mpc from the LG mid-point.
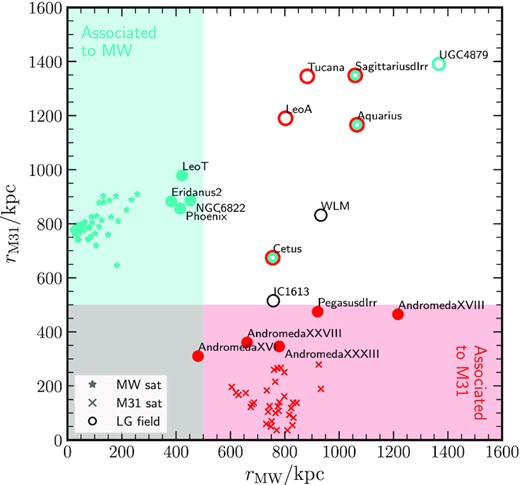
Distances to MW and M31 for LG dwarfs within 1.5 Mpc of its mid-point. MW satellites are shown with star symbols, M31 satellites as ‘x’ symbols, and field dwarfs as circles with labels. Objects within 500 kpc of either primary are coloured (cyan for the MW and red for M31). Some field galaxies outside 500 kpc are coloured as well, according to radial velocity criteria introduced in Fig. 3 that identifies them as backsplash candidates of primary.
The shaded areas in Fig. 2 highlight distances within 500 kpc of the MW (cyan) or M31 (red). Objects within these boundaries are likely associated with that primary, and are coloured accordingly. In each case, this includes the satellites (i.e. those with d < 300 kpc, shown as star symbols for MW satellites or ‘x’ symbols for M31 satellites) and dwarfs with 300 < d/kpc < 500 that, according to APOSTLE, have fairly high probability of being backsplash galaxies, shown as circles. One galaxy, And XVI, overlaps both samples as it is located at rMW = 450 kpc and rM31 = 310 kpc. We assume it is associated with M31, to which it is closer.
Eight dwarf galaxies are at larger distances (i.e. Aquarius, Cetus, IC1613, LeoA, Sagittarius dIrr, Tucana, UGC4879, and WLM), and we will consider them as potential distant backsplash candidates for the rest of our study.
Any galaxy from this subsample that is a backsplash of the MW or of M31 should be essentially at rest relative to its primary. We illustrate this idea in Fig. 3. This figure shows the Galactocentric radial velocity of each of these galaxies (Vrad) versus the Galactocentric radial velocity they would have if they were at rest relative to M31 (Vpred). Note that we only use the radial velocity component in this diagnostic because proper motions for most distant dwarfs are unknown.
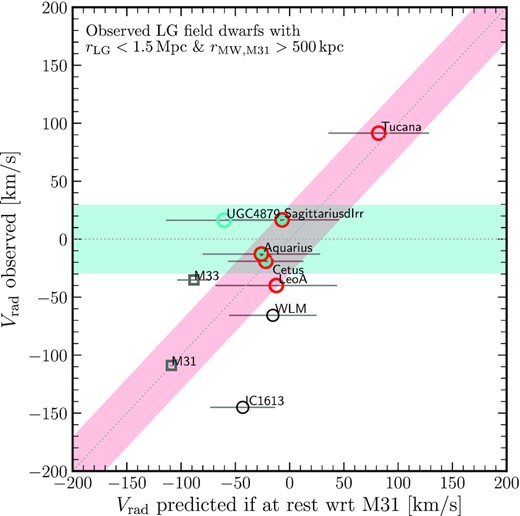
Observed Galactocentric radial velocity versus that predicted if the galaxy was at rest with respect to M31. Only LG field galaxies within 1.5 Mpc from the LG’s mid-point and outside 500 kpc of the MW and M31 are considered. The cyan and red shaded bands mark an area of ±1σ in Vrad, as measured for distant backsplash galaxies from the APOSTLE LG simulations (see Fig. 1). Galaxies within the horizontal cyan band present radial velocities compatible with being backsplash galaxies of the MW. Galaxies within the red diagonal band present radial velocities compatible with being backsplash galaxies of M31. The dotted line marks the 1:1 correspondence. Error bars indicate the minimum and maximum ‘predicted’ Vrad values when considering the uncertainties in M31’s proper motion data. For reference, M33 and M31 are shown as grey squares.
A cyan shaded area indicates a region of ±1σrad around Vrad = 0 km s−1 on the y-axis, where σrad = ±29 km s−1, the radial velocity dispersion of distant (d > 500 kpc) backsplash systems in APOSTLE (see Fig. 1).
Dwarfs in the cyan area are compatible with being backsplash galaxies of the MW and have been coloured in cyan. Alternatively, dwarfs falling in the red shaded area around the 1:1 line – with a width also equal to ±1σrad – have observed radial velocities compatible with being backsplash galaxies of M31 and are coloured in red.
For reference, M31 and M33 (Triangulum) are shown as grey squares. M31 falls exactly on the 1:1 line by construction. Error bars correspond to the minimum and maximum Vpred obtained when considering the uncertainties in M31’s proper motion data.
Six out of eight dwarfs are plausible backsplash candidates according to this criterion. UGC4879, Sagittarius dIrr, Aquarius, and Cetus could have been associated with the MW. The last three, plus possibly Leo A, are also compatible with being backsplash candidates of M31. The Tucana dSph, on the other hand, stands out as a clear M31 distant backsplash candidate, with a Galactocentric radial velocity in very close agreement with that expected for an object at rest relative to M31.
3.3 Cetus and Tucana as distant backsplash candidates
The case of Cetus and Tucana as backsplash candidates is of particular interest given that they are two of the few LG field dSphs. Because of their low gas content, as well as their predominantly old stellar populations, these systems resemble MW or M31 satellites rather than field dwarfs (Fraternali et al. 2009; Monelli et al. 2010a,b), and it is therefore tempting to associate them with backsplash systems.
Are there any other further hints that Tucana or Cetus may actually be distant backsplash systems? Both seem to satisfy the low radial velocity dispersion criterion (see Fig. 3), but so do several other distant LG dwarfs. As discussed in Section 1, further evidence for a backsplash origin may include the identification of a plausible ‘parent’ satellite system whose tidal dissolution may have expelled the dSph. Both the MW and M31 have satellites massive enough to be plausible parents of either Tucana or Cetus, in particular, the Magellanic Clouds in the case of the MW and the Triangulum galaxy (M33) in the case of M31.
For the clouds, there is now robust evidence that they are just past the first pericentric approach of their orbit around the MW (Besla et al. 2012; Kallivayalil et al. 2013). This disfavours them as possible parents of distant backsplash systems, as these objects are ejected after a pericentric passage, and they would require several Gyrs to travel to their current location. A similar reasoning disfavours the Sagittarius dSph as a potential parent, since the latest orbital modelling suggests that Sagittarius first approach to the MW happened only ∼5–6 Gyr ago (Laporte et al. 2018). As we shall see below, reaching the large distances of Cetus and Tucana requires that the ejection must have occurred much earlier than that.
It is in principle possible that a massive progenitor could have merged with the central galaxy soon after pericentre, but there is little evidence that the MW has undergone a substantial merger in the recent past. The lack of an obvious parent system therefore suggests that none of the MW distant backsplash candidates in Fig. 3 (i.e. those in the cyan band) have actually been associated with the MW in the past.
Could some of the distant candidates be associated with the accretion of M33 into M31? Since proper motions and radial velocities are available for both of these systems, it is possible to estimate the 3D relative velocity of the M31–M33 pair using the data compiled in Table 1. The resulting velocity, |$V_{\rm M31 \textrm {--} M33}\sim 258$| km s−1, is not much higher than the rotation speed of M31 (Vmax ∼ 226 km s−1; Carignan et al. 2006) and likely well below the M31 escape velocity at M33’s location. M33 is thus likely to be on a fairly bound orbit and may have completed a few pericentric passages in the past (see e.g. McConnachie et al. 2009; Patel, Besla & Sohn 2017; van der Marel et al. 2019), making it a plausible ‘parent’ for backsplash systems.
We investigate further a possible connection between the distant LG dwarfs and the M31–M33 pair in Fig. 4, where we show, in an Aitoff projection, the position of various LG galaxies in an M31-centric reference frame. We choose the ‘equatorial plane’ of the projection (b = 0°) to coincide with the MW plane and the N–S direction of the polar axis so that MW is in the Northern hemisphere of the projection. The MW–M31 orbital plane is shown by the thick grey curve in Fig. 4; the M33 orbital plane around M31, on the other hand, is shown by the thick red curve.
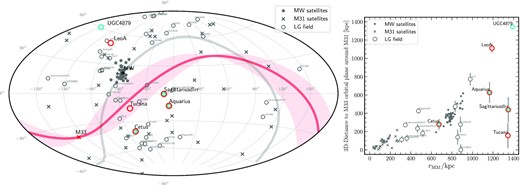
Left: Aitoff sky projection of the LG dwarf galaxies in a reference system centred on M31 and oriented such that latitude b = 0° is aligned with the MW’s disc. MW satellites are shown as star symbols, M31 satellites are shown as ‘x’ symbols, and field dwarfs within 1.4 Mpc of the LG are shown as circles. Dwarfs shown in colour are distant backsplash candidates of the MW (cyan) or M31 (red). A thick grey line marks the MW’s orbital plane, whereas a thick red line marks M33’s orbital plane around M31. A red shade indicates the uncertainty on this orbital plane as inferred from M33’s proper motion errors. Tucana lies very close to M33’s orbital plane. Right: 3D distances from LG dwarfs to the orbital plane of M33 around M31, versus their distances to M31. Error bars show ±1σ uncertainties in the distances to M33’s orbital plane, computed by randomly sampling M33’s proper motion, including errors.
The latter plane is especially significant, since we would expect systems that may have been expelled during the accretion of M33 into M31 to share the same orbital plane of the main progenitor and to remain close to it after ejection (see e.g. Sales et al. 2011; Santos-Santos et al. 2021). This reasoning singles out the Tucana dSph in Fig. 4 as the most promising candidate of them all. Indeed, Tucana is only 6.6° (<150 kpc) away from the M33 orbital plane, which is only about a tenth of its current distance from M31 (see the right-hand panel of Fig. 4).
This could be, of course, just an extraordinary coincidence, but it motivates us to examine further a potential association between Tucana and M33/M31. A powerful extra constraint may be placed by requiring that the ‘flight time’ from M31 to Tucana’s present location is shorter than the Hubble time. We may estimate this by assuming that Tucana is a test particle presently at the apocentre of a nearly radial orbit, and integrating backwards in time to find when it was propelled into such orbit. The estimate requires an assumption for the gravitational potential of M31, for which we adopt a standard NFW halo (Navarro, Frenk & White 1997) with a virial mass |$M_{200}=3\times 10^{12}\, \mathrm{M}_\odot$| (van der Marel et al. 2012; Fardal et al. 2013, about three times more massive than the MW according to most current estimates, Deason, Belokurov & Sanders 2019) and concentration c = 7.8, following Ludlow et al. (2016).5
The orbit of Tucana, under these assumptions, is shown by the solid green curve in Fig. 5. The dashed green curve assumes a different M200 of |$2.8\times 10^{12}\, \mathrm{M}_\odot$|, and is included just to illustrate the sensitivity of this result to variations in M31’s assumed virial mass. For these choices, we see that Tucana could reach its present location if it was ejected from M31 roughly 11 Gyr ago. Remarkably, this roughly coincides with the time when Tucana ceased forming stars, according to detailed modelling of its star formation history by Monelli et al. (2010b).
![Orbits of the Tucana and M33 dwarfs around M31, approximating M31’s potential by an NFW potential with M200 = 2.8(3) × 1012 M⊙ [shown in solid (dashed) linestyles]. We assume that Tucana is at present at the apocentre of a radial orbit around M31. For M33, we employ its actual 3D velocity as derived from current observational data (see Table 2). Black points mark the dwarfs’ distances at z = 0. The grey data point with error bar indicates the observational estimates for star formation cessation in Tucana dSph according to Monelli et al. (2010b). Specifically, the error bar spans the temporal period between the build-up of $50\!-\!90{{\ \rm per\ cent}}$ of the stellar mass, and the point indicates when $70{{\ \rm per\ cent}}$ of the mass was acquired.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/520/1/10.1093_mnras_stad085/1/m_stad085fig5.jpeg?Expires=1750220485&Signature=yQBg1SKjfumRkbyIae6zYa5Ri5RPCipU8TyXD5OsyDTzRWnzq8iVe3xbNuuixQeV2W3XA9w4JewDj1yEJCQ74YX2HQD6xSvROZoc-mQTZqy5jSBq51NLxDeC~6RbHlMDvPToHnfz~Xc8AT8TevW~LU1oNi37FrwjvQshZ6f6MF0npVEq6KT-GXc2LV4aVbj-gNGdXOTr~P0hGrkWfWwzd0oxrXDWlB7noPg9qPvQF2P~2mZ~1czdAR8iF5PlSwGBoMnOhVgS4V6CQ6g2GPtha8mzSOHKVnU6m4kBp-1Qx8Z9CcMtkBMi92JrYZId3RE7ReFSPATlT3Ozp7fEwjOzgg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Orbits of the Tucana and M33 dwarfs around M31, approximating M31’s potential by an NFW potential with M200 = 2.8(3) × 1012 M⊙ [shown in solid (dashed) linestyles]. We assume that Tucana is at present at the apocentre of a radial orbit around M31. For M33, we employ its actual 3D velocity as derived from current observational data (see Table 2). Black points mark the dwarfs’ distances at z = 0. The grey data point with error bar indicates the observational estimates for star formation cessation in Tucana dSph according to Monelli et al. (2010b). Specifically, the error bar spans the temporal period between the build-up of |$50\!-\!90{{\ \rm per\ cent}}$| of the stellar mass, and the point indicates when |$70{{\ \rm per\ cent}}$| of the mass was acquired.
Finally, we may also integrate M33’s orbit backwards assuming it is a test particle within the same M31 potential. The results are shown by the red curves in Fig. 5, and suggest a further coincidence. M33 is today approaching M31 on an orbit with a radial period of roughly ∼5 Gyr. This places M33 near orbital pericentre at about the time when Tucana may have been propelled into its highly energetic orbit.
We note that this timing coincidence depends sensitively on the assumed M31’s mass, and would be much less compelling if M31’s was, for example, two times more (or less) massive than assumed here. Indeed, for a virial mass as low as |${\sim} 10^{12}\, \mathrm{M}_\odot$|, M33’s orbital period would be so long that it could be on its first infall into M31 (e.g. Patel et al. 2017). A virial mass that low, however, would make M31’s halo comparable to that of the MW, which we find rather unlikely given its much larger stellar mass. Note as well that our M33 integration assumes a static, spherical potential with no dynamical friction, so the timing coincidence highlighted above may very well disappear upon more detailed scrutiny. Our main result, however (i.e. that there is enough time within a Hubble time for Tucana to travel to its current radial distance from M31), remains valid.
In summary, we believe that the sum of all these potential coincidences (radial velocity, planar alignment, flight time and star formation cessation, and concurrent pericentric passage) adds up to a credible case for a true physical association between Tucana and M31/M33.
Although it may be difficult to prove such association beyond reasonable doubt, it is important to identify what data may, in the future, be used to validate or falsify this scenario. Tighter constraints on M31’s virial mass, together with improved estimates of M31 and M33’s proper motions, could help, as would estimates of Tucana’s proper motion. Indeed, the backsplash scenario posits that Tucana is essentially at rest relative to M31, which allows us to predict its proper motion: μRA* = 0.0206 mas yr−1 and μDec. = −0.0754 mas yr−1, respectively.
Due to Tucana’s large distance and lack of bright supergiant stars, this measurement is probably beyond the reach of the Gaia satellite, but it might be possible with HST and/or JWST (see McConnachie et al. 2021, and references therein). Confirming that Tucana is indeed at rest relative to M31 would provide strong support for the backsplash origin envisioned here.
3.4 Tucana dSph as a satellite of M33
We briefly discuss here the idea of Tucana as an ejected satellite of M33 in the context of M33’s predicted satellite population. Given M33’s high stellar mass and implied halo mass, hierarchical clustering in LCDM predicts that it should have its own luminous satellites. The satellite mass function (SMF) of dwarf galaxies is still observationally unconstrained. None the less, one can utilize that of the MW – which is well known down to M* ≈ 105 M⊙ – together with the assumption that the SMF is scale free (similarly to the underlying LCDM subhalo mass function; Sales et al. 2013), to quantify M33’s expected satellite population. Considering the ratio of stellar masses between Tucana and M33,6 this exercise yields that M33 may have harboured up to ∼5 satellites with masses larger than that of Tucana.
As most likely the SMF is not scale free and self-similar (see e.g. Santos-Santos et al. 2022), the actual number could in principle be lower. Indeed, the only example of a galaxy of similar mass as M33 with observed satellite candidates is the LMC, for which simulations and current observational data constraints indicate that it may host up to three satellites with |$M_*\gt M_*^{\rm Tuc}$| (see Santos-Santos et al. 2021). Given that the LMC is now at first infall, this number probably represents the total number of original satellites of that mass expected around the LMC, since there has not been enough time for MW tidal effects to disperse their orbits. If, following the scenario we propose here, M33 was accreted by M31 long ago, even fewer satellites of M33 should remain at z = 0 due to tidal stripping after subsequent pericentric passages (see Patel et al. 2018).
Therefore, a natural consequence of our proposed scenario for Tucana as a backsplash of an early-infalling M33 on to M31 is that M33 is likely to have lost its satellite population by now. This prediction agrees with the current observational data where only one satellite candidate is found within ∼100 kpc around M33 (AndXXII; Martin et al. 2009).
4 SUMMARY
We have used the APOSTLE cosmological simulations to characterize the population of galaxies dynamically associated with the two primary galaxies (MW and M31) of the LG. ‘Associated’ systems are defined as those that have been, at some time during their evolution, within the virial radius of one of the primaries. Associated galaxies outside the virial radius at z = 0 are denoted as ‘backsplash’; those inside r200 are defined as ‘satellites’.
The fraction of dwarfs associated with a primary in APOSTLE drops quickly outside its virial radius, from ∼50 per cent at 400 kpc (roughly 2 × r200) to roughly |$10{{\ \rm per\ cent}}$| at 600 kpc. The most distant backsplash galaxy in all four APOSTLE volumes analysed is located at ∼1.2 Mpc, roughly 6× the average virial radius of APOSTLE primaries.
Distant backsplash galaxies originate during the tidal disruption of an accreted ‘parent’ group of dwarfs, when they are propelled into highly energetic orbits. Today, they are found mainly close to apocentre of nearly radial orbits (i.e. essentially at rest) relative to their primaries, with a radial velocity dispersion of only ±29 km s−1 beyond ∼600 kpc.
We use this feature to examine which, if any, of the isolated LG dwarfs could be a distant backsplash of the MW or M31. We focus, in particular, on M31 backsplash candidates linked to the accretion of M33, given the lack of obvious ‘parent’ in the MW. (The Magellanic Clouds are at present on first approach, and therefore could not have caused backsplash systems as distant as the ones we examine here.)
There are at present eight LG dwarfs known outside 500 kpc from the MW and M31 and within ∼1.5 Mpc from the LG mid-point: Aquarius, Cetus, IC1613, LeoA, Sagittarius dIrr, Tucana, UGC4879, and WLM. Several of these have low relative radial velocities relative to M31, but one of them stands out: the Tucana dSph.
Tucana appears to be not only at rest relative to M31 in terms of its radial velocity, but it also lies almost perfectly on the orbital plane of M33 around M31. Further, its flight time to its present location is roughly ∼10 Gyr, which coincides with the time when Tucana ceased forming stars. It also coincides with one of the previous M33 pericentric passages around M31, assuming that M31’s virial mass is |${\sim} 3\times 10^{12}\, \mathrm{M}_\odot$|. Each of these ‘coincidences’ could be dismissed individually, but, taken together, we believe that they make a compelling case for identifying Tucana with a former satellite of either M31 or M33 that was ejected from the M31 system, likely during M33’s first infall.
Further support for this scenario could come from tighter constraints on the kinematics of M31 and M33 or on the virial mass of M31, or from a measurement of Tucana’s proper motion. For this scenario to work, Tucana must be nearly at rest relative to M31, which allows us to predict its proper motion: μRA* = 0.0206 mas yr−1 and μDec. = −0.0754 mas yr−1, respectively. Confirming such prediction would provide strong evidence for the backsplash origin of the Tucana dSph we propose here.
ACKNOWLEDGEMENTS
We thank the referee for useful comments. ISS acknowledges support from the Arthur B. McDonald Canadian Astroparticle Physics Research Institute and from the European Research Council (ERC) through Advanced Investigator grant to C.S. Frenk, DMIDAS (GA 786910). We wish to acknowledge the generous contributions of all those who made possible the Virgo Consortium’s EAGLE/APOSTLE simulation projects. This work used the DiRAC@Durham facility managed by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). The equipment was funded by BEIS capital funding via STFC capital grants ST/K00042X/1, ST/P002293/1, ST/R002371/1, and ST/S002502/1, Durham University, and STFC operations grant ST/R000832/1. DiRAC is part of the National e- Infrastructure. This research made use of astropy (http://www.astropy.org), a community-developed core python package for Astronomy.
DATA AVAILABILITY
The simulation data underlying this article can be shared on reasonable request to the corresponding author. The references for the observational data for LG dwarfs used in this article are listed in Section 2.2.
Footnotes
More precisely, the virial radius is defined as the radius where the mean enclosed density equals 200× the critical density for closure. We shall use the subscript ‘200’ to identify quantities measured at or within the virial boundary.
In this work, we do not distinguish galaxies that are today satellites of one of the primaries, but were associated with the other primary at an earlier time (see e.g. Newton et al. 2021).
see https://www.cadc-ccda.hia-iha.nrc-cnrc.gc.ca/en/community/nearby/, and references therein.
We choose such a set-up for simplicity, as it is enough for our purposes here, but acknowledge that the actual orbits of Tucana and M33 would look differently in detail when including a proper treatment for dynamical friction, the evolution of M31’s potential, and the influence of an evolving cosmic web at early times.



