-
PDF
- Split View
-
Views
-
Cite
Cite
Hai-Nan Lin, Li Tang, Rui Zou, Revised constraints on the photon mass from well-localized fast radio bursts, Monthly Notices of the Royal Astronomical Society, Volume 520, Issue 1, March 2023, Pages 1324–1331, https://doi.org/10.1093/mnras/stad228
Close - Share Icon Share
ABSTRACT
We constrain the photon mass from well-localized fast radio bursts (FRBs) using Bayes inference method. The probability distributions of dispersion measures (DMs) of host galaxy and intergalactic medium are properly taken into account. The photon mass is tightly constrained from 17 well-localized FRBs in the redshift range 0 < z < 0.66. Assuming that there is no redshift evolution of host DM, the 1σ and 2σ upper limits of photon mass are constrained to be mγ < 4.8 × 10−51 kg and mγ < 7.1 × 10−51 kg, respectively. Monte Carlo simulations show that even enlarging the FRB sample to 200 and extending the redshift range to 0 < z < 3 could not significantly improve the constraining ability on photon mass. This is because of the large uncertainty on the DM of intergalactic medium.
1 INTRODUCTION
The invariance of the speed of light, which states that the speed of light in vacuum is a constant with respect to any inertial frame, is one of the two principles of Einstein’s special relativity. A direct inference of this principle is that photon is massless. The non-zero photon mass, no matter how small it is, would imply new physics beyond the special relativity. Therefore, strictly constraining photon mass is of great importance. To this end, several methods, ranging from particle physics to cosmology scales, have been proposed to put tight constraint on photon mass. For instance, experimentally test of Coulomb’s law (Williams, Faller & Hill 1971), investigation of the gravitational deflection of electromagnetic radiation (Lowenthal 1973), measurement of the magnetic field of Jupiter (Davis, Goldhaber & Nieto 1975), testing the Ampere’s law by observing large-scale magnetic fields in galaxies (Ryutov 2010), observation of the spin of supermassive black hole (Pani et al. 2012), measurement of the spin-down rate of pulsars (Yang & Zhang 2017), and so on.
In the cosmological aspect, one possible way to constrain photon mass is to measure the frequency-dependent velocity of electromagnetic waves from astrophysical transients, see e.g. Wei & Wu (2021) for recent review. If photon has non-zero mass, then electromagnetic waves of different frequencies travel with different velocities, hence we can observe relative time delay if non-monochromatic electromagnetic waves propagate from cosmological scale. For example, Lovell, Whipple & Solomon (1964) analysed the time delay between optical and radio emissions from flare stars, and obtained an upper limit on the photon mass of mγ < 1.6 × 10−45 kg. Warner & Nather (1969) analysed the optical emission of different wavelength from the Crab Nebula pulsar, and obtained mγ < 5.2 × 10−44 kg. Schaefer (1999) analysed the time delay between gamma-ray emission and radio afterglow from gamma-ray bursts (GRBs), and obtained mγ < 4.2 × 10−47 kg. Zhang et al. (2016) investigated the radio afterglows and multiband radio peaks from a large sample of GRBs, and obtained the strictest constraint mγ < 1.062 × 10−47 kg from GRB 050416A. Wei & Wu (2018) investigated the dispersion measures of a sample of extragalactic radio pulsars, and put robust limit on photon mass with mγ < 1.51 × 10−48 kg.
Fast radio bursts (FRBs), as milliseconds radio transients happening in the Universe, are ideal astrophysical sources to constrain photon mass. The use of FRBs to constrain photon mass was first proposed by Wu et al. (2016), who obtained a stringent upper limits on photon mass mγ < 5.2 × 10−50 kg by analysing the frequency-dependent time delays of FRB 150418. The result of Wu et al. (2016) is based on the assumption that the time delay is purely caused by the non-zero photon mass. This is of course not reasonable, because a large part, if not all of the time delay is induced by the dispersion of photon by electrons. As is known, the dispersion-induced time delay and the time delay caused by non-zero photon mass have the same frequency dependence (Δt ∝ ν−2), thus these two parts is indistinguishable using a single FRB. Shao & Zhang (2017) pointed out that, although the two parts of time delay have the same frequency dependence, they have remarkably different redshift dependence. Therefore, the degeneracy between them can be broken using a large sample of FRBs at different redshift. Shao & Zhang (2017) developed a Bayesian framework to constrain photon mass from a sample of FRBs with and without redshift measurement, and obtained mγ < 8.7 × 10−51 kg. Later on, Wei & Wu (2020) used the same method to constrain photon mass with nine well-localized FRBs, and obtained mγ < 7.1 × 10−51 kg.
There are still some difficulties in using FRBs to constrain photon mass. The dispersion measure (DM) of an extragalactic FRB consists of several parts (see the next section for details), among which the DM of host galaxy is poorly known. Too many factors may affect the host DM, such as the galaxy type, the mass of host galaxy, the separation of FRB source from Galactic Centre, the inclination angle of host galaxy, etc. Previous work often treated the host DM as a constant parameter (Shao & Zhang 2017), or parametrized it tracing the star formation rate (Wei & Wu 2020). The constant assumption is of course inappropriate, as the host DM may vary significantly from bursts to bursts. On the other hand, Lin, Li & Tang (2022) found no strong evidence for the correlation between host DM and star formation rate. A more proper way to deal with host DM is to consider the probability distribution and marginalize over it (Macquart et al. 2020; Zhang et al. 2020). Another difficulty is that it is hard to calculate the DM of intergalactic medium (DMIGM) due to the matter fluctuation of the Universe. Previous work often calculated DMIGM using the mean matter density, and introduced an uncertainty term to account for the possible deviation from the mean (Shao & Zhang 2017; Wei & Wu 2020). This treatment is based on the underlying assumption that the probability distribution of DMIGM is Gaussian. However, theoretical analysis and numerical simulations show that the actual value of DMIGM may deviate from the mean significantly, and the probability distribution is non-Gaussian, which has a flat tail at large value (Macquart et al. 2020; Zhang et al. 2021b). The probability distribution of DMIGM may affect the constraints on photon mass, which remains to be further investigated.
As more well-localized FRBs are observed recently, in this paper we will use them to constrain the photon mass, by properly taking into account the probability distribution of DMs of host galaxy and IGM. The structure of this paper is arranged as follows: The theoretical method is introduced in Section 2. The observed FRBs and the constraining results on photon mass are presented in Section 3. In Section 4, we use Monte Carlo simulations to forecast the constraining ability on photon mass if more well-localized FRBs at high redshift are observed in the future. Finally, discussion and conclusions are given in Section 5.
2 METHODOLOGY
Comparing equation (3) and equation (8), we see that the two terms DMIGM and DMγ have remarkably different redshift dependence. In Fig. 1, we plot the redshift dependence of He(z) and Hγ(z), as well as their derivatives. He(z) increases with redshift much faster than Hγ(z), since FRBs at higher redshift encounter electrons that are much denser than present day, thus causes the plasma effect to have a strong net increase with redshift. Furthermore, these two terms also differ from the DMhost term, which evolves with redshift as (1 + z)−1. Therefore, the degeneracy between DMIGM, DMγ and DMhost is expected to break down if a large sample of FRBs at different redshift is observed.
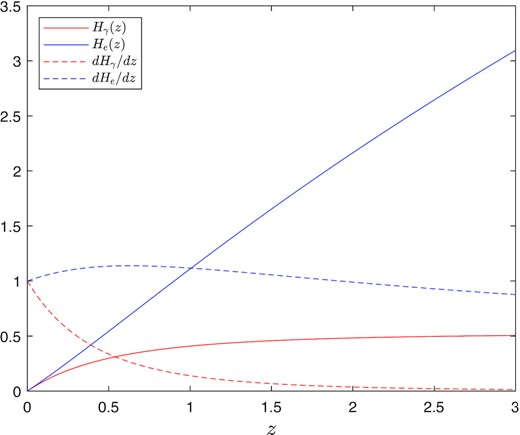
The redshift dependence of He(z), Hγ(z) and their derivatives.
3 DATA AND RESULTS
So far, there are in total 19 extragalactic FRBs that have direct measurement of redshift.1 Among them, we ignore FRB20200120E and FRB20190614D. The former is so close to our Galaxy (D ≈ 3.6 Mpc) that its redshfit is negtive (z = −0.0001)2 (Bhardwaj et al. 2021a; Kirsten et al. 2022), while the latter has no measurement of spectroscopic redshift, but has photometric redshift (zph ≈ 0.6) (Law et al. 2020). All the rest 17 FRBs have well-measured spectroscopic redshift. The main properties of the 17 FRBs are listed in Table 1, which will be used to constrain photon mass.
The main properties of 17 well-localized FRBs. DMMW is calculated using the NE2001 model, and |${\rm DM_{obs}^{\prime }}$| is calculated by subtracting |${\rm DM_{\rm MW}}$| and |${\rm DM_{\rm halo}}$| from the observed |${\rm DM_{\rm obs}}$|, assuming |${\rm DM_{\rm halo}}=50~{\rm pc~cm^{-3}}$|.
| FRBs . | RA . | Dec. . | DMobs . | DMMW . | |${\rm DM_{obs}^{\prime }}$| . | zsp . | Repeat? . | Reference . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (pc cm−3) . | (pc cm−3) . | (pc cm−3) . | . | . | . |
| 20121102A | 82.99 | 33.15 | 557.00 | 157.60 | 349.40 | 0.1927 | Yes | Chatterjee et al. (2017) |
| 20180301A | 93.23 | 4.67 | 536.00 | 136.53 | 349.47 | 0.3305 | Yes | Bhandari et al. (2022) |
| 20180916B | 29.50 | 65.72 | 348.80 | 168.73 | 130.07 | 0.0337 | Yes | Marcote et al. (2020) |
| 20180924B | 326.11 | −40.90 | 362.16 | 41.45 | 270.71 | 0.3214 | No | Bannister et al. (2019) |
| 20181030A | 158.60 | 73.76 | 103.50 | 40.16 | 13.34 | 0.0039 | Yes | Bhardwaj et al. (2021b) |
| 20181112A | 327.35 | −52.97 | 589.00 | 41.98 | 497.02 | 0.4755 | No | Prochaska et al. (2019) |
| 20190102C | 322.42 | −79.48 | 364.55 | 56.22 | 258.33 | 0.2913 | No | Macquart et al. (2020) |
| 20190523A | 207.06 | 72.47 | 760.80 | 36.74 | 674.06 | 0.6600 | No | Ravi et al. (2019) |
| 20190608B | 334.02 | −7.90 | 340.05 | 37.81 | 252.24 | 0.1178 | No | Macquart et al. (2020) |
| 20190611B | 320.74 | −79.40 | 332.63 | 56.60 | 226.03 | 0.3778 | No | Macquart et al. (2020) |
| 20190711A | 329.42 | −80.36 | 592.60 | 55.37 | 487.23 | 0.5217 | Yes | Macquart et al. (2020) |
| 20190714A | 183.98 | −13.02 | 504.13 | 38.00 | 416.13 | 0.2365 | No | Heintz et al. (2020) |
| 20191001A | 323.35 | −54.75 | 507.90 | 44.22 | 413.68 | 0.2340 | No | Heintz et al. (2020) |
| 20191228A | 344.43 | −29.59 | 297.50 | 33.75 | 213.75 | 0.2432 | No | Bhandari et al. (2022) |
| 20200430A | 229.71 | 12.38 | 380.25 | 27.35 | 302.90 | 0.1608 | No | Bhandari et al. (2022) |
| 20200906A | 53.50 | −14.08 | 577.80 | 36.19 | 491.61 | 0.3688 | No | Bhandari et al. (2022) |
| 20201124A | 77.01 | 26.06 | 413.52 | 126.49 | 237.03 | 0.0979 | Yes | Fong et al. (2021) |
| FRBs . | RA . | Dec. . | DMobs . | DMMW . | |${\rm DM_{obs}^{\prime }}$| . | zsp . | Repeat? . | Reference . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (pc cm−3) . | (pc cm−3) . | (pc cm−3) . | . | . | . |
| 20121102A | 82.99 | 33.15 | 557.00 | 157.60 | 349.40 | 0.1927 | Yes | Chatterjee et al. (2017) |
| 20180301A | 93.23 | 4.67 | 536.00 | 136.53 | 349.47 | 0.3305 | Yes | Bhandari et al. (2022) |
| 20180916B | 29.50 | 65.72 | 348.80 | 168.73 | 130.07 | 0.0337 | Yes | Marcote et al. (2020) |
| 20180924B | 326.11 | −40.90 | 362.16 | 41.45 | 270.71 | 0.3214 | No | Bannister et al. (2019) |
| 20181030A | 158.60 | 73.76 | 103.50 | 40.16 | 13.34 | 0.0039 | Yes | Bhardwaj et al. (2021b) |
| 20181112A | 327.35 | −52.97 | 589.00 | 41.98 | 497.02 | 0.4755 | No | Prochaska et al. (2019) |
| 20190102C | 322.42 | −79.48 | 364.55 | 56.22 | 258.33 | 0.2913 | No | Macquart et al. (2020) |
| 20190523A | 207.06 | 72.47 | 760.80 | 36.74 | 674.06 | 0.6600 | No | Ravi et al. (2019) |
| 20190608B | 334.02 | −7.90 | 340.05 | 37.81 | 252.24 | 0.1178 | No | Macquart et al. (2020) |
| 20190611B | 320.74 | −79.40 | 332.63 | 56.60 | 226.03 | 0.3778 | No | Macquart et al. (2020) |
| 20190711A | 329.42 | −80.36 | 592.60 | 55.37 | 487.23 | 0.5217 | Yes | Macquart et al. (2020) |
| 20190714A | 183.98 | −13.02 | 504.13 | 38.00 | 416.13 | 0.2365 | No | Heintz et al. (2020) |
| 20191001A | 323.35 | −54.75 | 507.90 | 44.22 | 413.68 | 0.2340 | No | Heintz et al. (2020) |
| 20191228A | 344.43 | −29.59 | 297.50 | 33.75 | 213.75 | 0.2432 | No | Bhandari et al. (2022) |
| 20200430A | 229.71 | 12.38 | 380.25 | 27.35 | 302.90 | 0.1608 | No | Bhandari et al. (2022) |
| 20200906A | 53.50 | −14.08 | 577.80 | 36.19 | 491.61 | 0.3688 | No | Bhandari et al. (2022) |
| 20201124A | 77.01 | 26.06 | 413.52 | 126.49 | 237.03 | 0.0979 | Yes | Fong et al. (2021) |
The main properties of 17 well-localized FRBs. DMMW is calculated using the NE2001 model, and |${\rm DM_{obs}^{\prime }}$| is calculated by subtracting |${\rm DM_{\rm MW}}$| and |${\rm DM_{\rm halo}}$| from the observed |${\rm DM_{\rm obs}}$|, assuming |${\rm DM_{\rm halo}}=50~{\rm pc~cm^{-3}}$|.
| FRBs . | RA . | Dec. . | DMobs . | DMMW . | |${\rm DM_{obs}^{\prime }}$| . | zsp . | Repeat? . | Reference . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (pc cm−3) . | (pc cm−3) . | (pc cm−3) . | . | . | . |
| 20121102A | 82.99 | 33.15 | 557.00 | 157.60 | 349.40 | 0.1927 | Yes | Chatterjee et al. (2017) |
| 20180301A | 93.23 | 4.67 | 536.00 | 136.53 | 349.47 | 0.3305 | Yes | Bhandari et al. (2022) |
| 20180916B | 29.50 | 65.72 | 348.80 | 168.73 | 130.07 | 0.0337 | Yes | Marcote et al. (2020) |
| 20180924B | 326.11 | −40.90 | 362.16 | 41.45 | 270.71 | 0.3214 | No | Bannister et al. (2019) |
| 20181030A | 158.60 | 73.76 | 103.50 | 40.16 | 13.34 | 0.0039 | Yes | Bhardwaj et al. (2021b) |
| 20181112A | 327.35 | −52.97 | 589.00 | 41.98 | 497.02 | 0.4755 | No | Prochaska et al. (2019) |
| 20190102C | 322.42 | −79.48 | 364.55 | 56.22 | 258.33 | 0.2913 | No | Macquart et al. (2020) |
| 20190523A | 207.06 | 72.47 | 760.80 | 36.74 | 674.06 | 0.6600 | No | Ravi et al. (2019) |
| 20190608B | 334.02 | −7.90 | 340.05 | 37.81 | 252.24 | 0.1178 | No | Macquart et al. (2020) |
| 20190611B | 320.74 | −79.40 | 332.63 | 56.60 | 226.03 | 0.3778 | No | Macquart et al. (2020) |
| 20190711A | 329.42 | −80.36 | 592.60 | 55.37 | 487.23 | 0.5217 | Yes | Macquart et al. (2020) |
| 20190714A | 183.98 | −13.02 | 504.13 | 38.00 | 416.13 | 0.2365 | No | Heintz et al. (2020) |
| 20191001A | 323.35 | −54.75 | 507.90 | 44.22 | 413.68 | 0.2340 | No | Heintz et al. (2020) |
| 20191228A | 344.43 | −29.59 | 297.50 | 33.75 | 213.75 | 0.2432 | No | Bhandari et al. (2022) |
| 20200430A | 229.71 | 12.38 | 380.25 | 27.35 | 302.90 | 0.1608 | No | Bhandari et al. (2022) |
| 20200906A | 53.50 | −14.08 | 577.80 | 36.19 | 491.61 | 0.3688 | No | Bhandari et al. (2022) |
| 20201124A | 77.01 | 26.06 | 413.52 | 126.49 | 237.03 | 0.0979 | Yes | Fong et al. (2021) |
| FRBs . | RA . | Dec. . | DMobs . | DMMW . | |${\rm DM_{obs}^{\prime }}$| . | zsp . | Repeat? . | Reference . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (pc cm−3) . | (pc cm−3) . | (pc cm−3) . | . | . | . |
| 20121102A | 82.99 | 33.15 | 557.00 | 157.60 | 349.40 | 0.1927 | Yes | Chatterjee et al. (2017) |
| 20180301A | 93.23 | 4.67 | 536.00 | 136.53 | 349.47 | 0.3305 | Yes | Bhandari et al. (2022) |
| 20180916B | 29.50 | 65.72 | 348.80 | 168.73 | 130.07 | 0.0337 | Yes | Marcote et al. (2020) |
| 20180924B | 326.11 | −40.90 | 362.16 | 41.45 | 270.71 | 0.3214 | No | Bannister et al. (2019) |
| 20181030A | 158.60 | 73.76 | 103.50 | 40.16 | 13.34 | 0.0039 | Yes | Bhardwaj et al. (2021b) |
| 20181112A | 327.35 | −52.97 | 589.00 | 41.98 | 497.02 | 0.4755 | No | Prochaska et al. (2019) |
| 20190102C | 322.42 | −79.48 | 364.55 | 56.22 | 258.33 | 0.2913 | No | Macquart et al. (2020) |
| 20190523A | 207.06 | 72.47 | 760.80 | 36.74 | 674.06 | 0.6600 | No | Ravi et al. (2019) |
| 20190608B | 334.02 | −7.90 | 340.05 | 37.81 | 252.24 | 0.1178 | No | Macquart et al. (2020) |
| 20190611B | 320.74 | −79.40 | 332.63 | 56.60 | 226.03 | 0.3778 | No | Macquart et al. (2020) |
| 20190711A | 329.42 | −80.36 | 592.60 | 55.37 | 487.23 | 0.5217 | Yes | Macquart et al. (2020) |
| 20190714A | 183.98 | −13.02 | 504.13 | 38.00 | 416.13 | 0.2365 | No | Heintz et al. (2020) |
| 20191001A | 323.35 | −54.75 | 507.90 | 44.22 | 413.68 | 0.2340 | No | Heintz et al. (2020) |
| 20191228A | 344.43 | −29.59 | 297.50 | 33.75 | 213.75 | 0.2432 | No | Bhandari et al. (2022) |
| 20200430A | 229.71 | 12.38 | 380.25 | 27.35 | 302.90 | 0.1608 | No | Bhandari et al. (2022) |
| 20200906A | 53.50 | −14.08 | 577.80 | 36.19 | 491.61 | 0.3688 | No | Bhandari et al. (2022) |
| 20201124A | 77.01 | 26.06 | 413.52 | 126.49 | 237.03 | 0.0979 | Yes | Fong et al. (2021) |
We constrain the free parameters (F, μ0, σhost, ε, mγ) from simultaneously using 17 well-localized FRBs. In practice, we use |$e^{\mu _0}$| instead of μ0 as a free parameter, because the former directly represents the median value of DMhost (at z = 0). The posterior probability density functions of the free parameters are calculated with the Markov chain Monte Carlo method using the publicly available python code emcee (Foreman-Mackey et al. 2013), while the other cosmological parameters are fixed to the Planck 2018 values (Aghanim et al. 2020). Flat priors are adopted for all the free parameters: |$F\in \mathcal {U}(0.01,0.5)$|, |$e^{\mu _0}\in \mathcal {U}(20,200)~{\rm pc~cm^{-3}}$|, |$\sigma _{\rm host}\in \mathcal {U}(0.2,2.0)$|, |$\varepsilon \in \mathcal {U}(-2,2)$|, and |$m_\gamma \in \mathcal {U}(10^{-69},10^{-42})$| kg.3 We report the median values and the 1σ uncertainties of the parameters in Table 2. For the photon mass, the 1σ and 2σ upper limits are reported. The posterior probability density functions and the confidence contours of the parameters are plotted in the left-hand panel of Fig. 2. The parameters F, |$e^{\mu _0}$|, and σhost can be tightly constrained, with |$F=0.36_{-0.11}^{+0.09}$|, |$e^{\mu _0}=90.86_{-31.09}^{+43.81}~ {\rm pc~cm^{-3}}$|, and |$\sigma _{\rm host}=1.13_{-0.24}^{+0.33}$|. However, the parameter ε cannot be tightly constrained, with |$\varepsilon =0.05_{-1.33}^{+1.22}$|. The 1σ (2σ) upper limit of photon mass is constrained to be mγ < 0.67 × 10−50 kg (mγ < 1.01 × 10−50 kg).

The contour plot of the free parameters (|$F, e^{\mu _0}, \sigma _{\rm host}, \varepsilon , m_\gamma$|) constrained from 17 well-localized FRBs. The contours from the inner to outer represent 1σ, 2σ, and 3σ confidence regions, respectively. Left-hand panel: ε is a free parameter; Right-hand panel: ε = 0 fixed.
The parameters |$(F,e^{\mu _0},\sigma _{\rm host},\varepsilon ,m_\gamma)$| constrained from 17 well-localized FRBs. The uncertainties are given at 1σ confidence level. For the photon mass, the 1σ and 2σ upper limits are reported.
| F . | |$e^{\mu _0}/{\rm pc~cm^{-3}}$| . | σhost . | ε . | mγ/10−50 kg . |
|---|---|---|---|---|
| |$0.36_{-0.11}^{+0.09}$| | |$90.86_{-31.09}^{+43.81}$| | |$1.13_{-0.24}^{+0.33}$| | |$0.05_{-1.33}^{+1.22}$| | <0.67 (< 1.01) |
| |$0.36_{-0.11}^{+0.10}$| | |$92.17_{-30.01}^{+36.99}$| | |$1.11_{-0.23}^{+0.33}$| | ε = 0 (fixed) | <0.48 (< 0.71) |
| F . | |$e^{\mu _0}/{\rm pc~cm^{-3}}$| . | σhost . | ε . | mγ/10−50 kg . |
|---|---|---|---|---|
| |$0.36_{-0.11}^{+0.09}$| | |$90.86_{-31.09}^{+43.81}$| | |$1.13_{-0.24}^{+0.33}$| | |$0.05_{-1.33}^{+1.22}$| | <0.67 (< 1.01) |
| |$0.36_{-0.11}^{+0.10}$| | |$92.17_{-30.01}^{+36.99}$| | |$1.11_{-0.23}^{+0.33}$| | ε = 0 (fixed) | <0.48 (< 0.71) |
The parameters |$(F,e^{\mu _0},\sigma _{\rm host},\varepsilon ,m_\gamma)$| constrained from 17 well-localized FRBs. The uncertainties are given at 1σ confidence level. For the photon mass, the 1σ and 2σ upper limits are reported.
| F . | |$e^{\mu _0}/{\rm pc~cm^{-3}}$| . | σhost . | ε . | mγ/10−50 kg . |
|---|---|---|---|---|
| |$0.36_{-0.11}^{+0.09}$| | |$90.86_{-31.09}^{+43.81}$| | |$1.13_{-0.24}^{+0.33}$| | |$0.05_{-1.33}^{+1.22}$| | <0.67 (< 1.01) |
| |$0.36_{-0.11}^{+0.10}$| | |$92.17_{-30.01}^{+36.99}$| | |$1.11_{-0.23}^{+0.33}$| | ε = 0 (fixed) | <0.48 (< 0.71) |
| F . | |$e^{\mu _0}/{\rm pc~cm^{-3}}$| . | σhost . | ε . | mγ/10−50 kg . |
|---|---|---|---|---|
| |$0.36_{-0.11}^{+0.09}$| | |$90.86_{-31.09}^{+43.81}$| | |$1.13_{-0.24}^{+0.33}$| | |$0.05_{-1.33}^{+1.22}$| | <0.67 (< 1.01) |
| |$0.36_{-0.11}^{+0.10}$| | |$92.17_{-30.01}^{+36.99}$| | |$1.11_{-0.23}^{+0.33}$| | ε = 0 (fixed) | <0.48 (< 0.71) |
As we can see, ε is well consistent with zero, implying no strong evidence for the redshift evolution of DMhost. Therefore, we fix ε = 0 and fit the remaining four parameters (|$F,e^{\mu _0},\sigma _{\rm host},m_\gamma$|). The best-fitting results are: |$F=0.36_{-0.11}^{+0.10}$|, |$e^{\mu _0}=92.17_{-30.01}^{+36.99}~{\rm pc~cm^{-3}}$|, |$\sigma _{\rm host}=1.11_{-0.23}^{+0.33}$|, and the 1σ (2σ) upper limit of photon mass is mγ < 0.48 × 10−50 kg (mγ < 0.71 × 10−50 kg). The posterior probability density functions and the confidence contours of the parameters are plotted in the right-hand panel of Fig. 2. As is seen, the four-parameter fit and the five-parameter fit give consistent results, further confirming that there is no obvious redshift evolution of DMhost.
4 MONTE CARLO SIMULATIONS
With the running of new radio telescopes, such as the Canadian Hydrogen Intensity Mapping Experiment (CHIME; Amiri et al. 2018) and the Five-hundred-meter Aperture Spherical Telescope (FAST; Nan et al. 2011), it is expected that more and more FRBs can be discovered in the next years, among which several of them can be well localized. Therefore, it is interesting to investigate the constraining ability on photon mass if more well-localized FRBs are available in the future. To this end, we perform Monte Carlo simulations.
We simulate a mock sample of FRBs, each FRB contains the parameters (|$z,{\rm DM_{obs}^{\prime }}$|). The simulations are performed based on the standard ΛCDM model with the Planck2018 parameters: H0 = 67.4 km s−1 Mpc−1, Ωm = 0.315, |$\Omega _\Lambda =0.685$|, and Ωb = 0.0493 (Aghanim et al. 2020). The other fiducial parameters are F = 0.3, |$e^{\mu _0}=100~{\rm pc~cm^{-3}}$|, σhost = 1, ε = 0, and mγ = 0. As we are interested in the constraint on photon mass, rather than the redshift evolution of DMhost, we just treat eμ as a constant (i.e. fix ε = 0). This is reasonable at present, since there is no evidence for the redshift evolution of eμ in the real FRB data. The procedures of simulation are as follows:
Randomly draw redshift z from the probability distribution in equation (15), with the upper limit zmax = 3.
Calculate the mean value 〈DMIGM(z)〉 according to equation (7).
Randomly draw DMIGM from the probability distribution in equation (9).
Randomly draw DMhost from the probability distribution in equation (10).
Calculate |${\rm DM_{obs}^{\prime }}$| according to equation (6), where DMγ = 0 (zero photon mass).
With the mock FRB sample, we constrain photon mass (together with other parameters F, |$e^{\mu _0}$| and σhost) using the method described in Section 2. In Fig. 3, we shows the contour plots of parameter space in two arbitrary realizations of simulation with different number of FRBs (left-hand panel: N = 100; right-hand panel: N = 200). We see that the best-fitting parameters F, |$e^{\mu _0}$| and σhost can correctly recover the fiducial values within 1σ uncertainty, and the upper limit of photon mass can be tightly constrained. Compared with the real data, the precision of the parameter F is highly improved. However, the precision of the other parameters does not change significantly. We also note that enlarging the FRB sample from 100 to 200 does not significantly improve the constraining ability on photon mass.
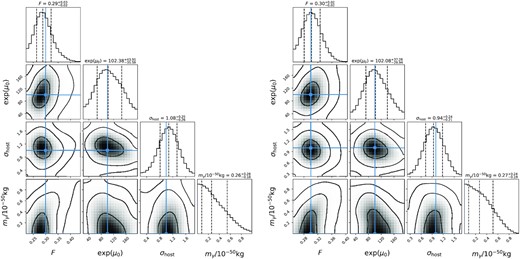
The contour plot of the free parameters (|$F, e^{\mu _0}, \sigma _{\rm host}, m_\gamma$|) constrained from different number of mock FRBs (left-hand panel: N = 100; right-hand panel: N = 200). The vertical dashed lines from left to right in each subfigures represent the 16 per cent, 50 per cent, and 84 per cent quantiles of the distributions, respectively. The solid lines represent the fiducial values. The contours from the inner to outer represent 1σ, 2σ, and 3σ confidence regions, respectively.
Considering the statistical fluctuation, we simulate 1000 times for a fixed number of FRBs. In each simulation, we calculate the median value of the parameters (|$F, e^{\mu _0},\sigma _{\rm host}$|), and the 1σ upper limit of the photon mass (mγ). The distributions of the parameters in 1000 simulations are shown in Fig. 4 (top panels for N = 100 and bottom panels for N = 200). We see that the distribution of each parameter is approximately Gaussian. We calculate the 16 per cent, 50 per cent, and 84 per cent quantiles of each distribution and list the results in Table 3 (also shown in Fig. 4 as the dashed lines). We can see that the fiducial value of each parameter (|$F, e^{\mu _0},\sigma _{\rm host}$|) falls into the 1σ confidence region of the distribution. We note that the distribution of |$e^{\mu _0}$| is well consistent with the fiducial value, but the parameters F and σhost are a little biased. The median value of F is larger than the fiducial value. On the contrary, the median value of σhost is smaller than the fiducial value. This may be caused by the correlation between parameters. Nevertheless, all the parameters are consistent with the fiducial values within 1σ uncertainty. With 100 and 200 FRBs, the photon mass can be constrained at the level of mγ < 0.55 × 10−50 kg and mγ < 0.49 × 10−50 kg, respectively. This further confirms that increasing the number of FRBs cannot significantly tighten the constraint on photon mass, and the possible reasons will be discussed in the next section.
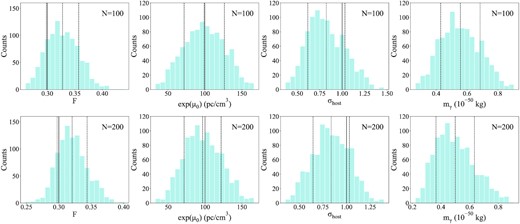
The distributions of the best-fitting parameters in 1000 simulations. The vertical dashed lines from left to right in each subfigures represent the 16 per cent, 50 per cent, and 84 per cent quantiles of the distributions, respectively. The vertical solid lines represent the fiducial values. Top panels: N = 100; bottom panels: N = 200.
The median values and 1σ confidence regions of the parameters (|$F, e^{\mu _0},\sigma _{\rm host},m_\gamma$|) in 1000 simulations. The fiducial parameters used in the simulations are F = 0.3, |$e^{\mu _0}=100~{\rm pc~cm~^{-3}}$|, σhost = 1, and mγ = 0.
| N . | F . | |$e^{\mu _0}/{\rm pc~cm^{-3}}$| . | σhost . | mγ/10−50 kg . |
|---|---|---|---|---|
| 100 | |$0.32_{-0.03}^{+0.03}$| | |$98.90_{-28.62}^{+28.10}$| | |$0.80_{-0.19}^{+0.24}$| | |$0.55_{-0.12}^{+0.15}$| |
| 200 | |$0.32_{-0.03}^{+0.03}$| | |$94.88_{-23.28}^{+28.16}$| | |$0.83_{-0.19}^{+0.20}$| | |$0.49_{-0.12}^{+0.16}$| |
| N . | F . | |$e^{\mu _0}/{\rm pc~cm^{-3}}$| . | σhost . | mγ/10−50 kg . |
|---|---|---|---|---|
| 100 | |$0.32_{-0.03}^{+0.03}$| | |$98.90_{-28.62}^{+28.10}$| | |$0.80_{-0.19}^{+0.24}$| | |$0.55_{-0.12}^{+0.15}$| |
| 200 | |$0.32_{-0.03}^{+0.03}$| | |$94.88_{-23.28}^{+28.16}$| | |$0.83_{-0.19}^{+0.20}$| | |$0.49_{-0.12}^{+0.16}$| |
The median values and 1σ confidence regions of the parameters (|$F, e^{\mu _0},\sigma _{\rm host},m_\gamma$|) in 1000 simulations. The fiducial parameters used in the simulations are F = 0.3, |$e^{\mu _0}=100~{\rm pc~cm~^{-3}}$|, σhost = 1, and mγ = 0.
| N . | F . | |$e^{\mu _0}/{\rm pc~cm^{-3}}$| . | σhost . | mγ/10−50 kg . |
|---|---|---|---|---|
| 100 | |$0.32_{-0.03}^{+0.03}$| | |$98.90_{-28.62}^{+28.10}$| | |$0.80_{-0.19}^{+0.24}$| | |$0.55_{-0.12}^{+0.15}$| |
| 200 | |$0.32_{-0.03}^{+0.03}$| | |$94.88_{-23.28}^{+28.16}$| | |$0.83_{-0.19}^{+0.20}$| | |$0.49_{-0.12}^{+0.16}$| |
| N . | F . | |$e^{\mu _0}/{\rm pc~cm^{-3}}$| . | σhost . | mγ/10−50 kg . |
|---|---|---|---|---|
| 100 | |$0.32_{-0.03}^{+0.03}$| | |$98.90_{-28.62}^{+28.10}$| | |$0.80_{-0.19}^{+0.24}$| | |$0.55_{-0.12}^{+0.15}$| |
| 200 | |$0.32_{-0.03}^{+0.03}$| | |$94.88_{-23.28}^{+28.16}$| | |$0.83_{-0.19}^{+0.20}$| | |$0.49_{-0.12}^{+0.16}$| |
5 DISCUSSION AND CONCLUSIONS
In this paper, we constrained the photon mass from a sample of well-localized FRBs using Bayes inference method. The probability distributions of DMs of IGM and host galaxy were properly taken into account. The degeneracy between time delays induced by DM and non-zero photon mass was broken thanks to the different redshift dependence. The 1σ and 2σ upper limits of photon mass were tightly constrained to be mγ < 4.8 × 10−51 kg and mγ < 7.1 × 10−51 kg, respectively. Moreover, we also investigated the possible redshift evolution of host DM, but no strong evidence was found. Monte Carlo simulations showed that, the constraint on photon mass can be significantly tightened even if we enlarge the FRB sample to 200 and extend the redshift range up to z = 3. One possible reason is that the uncertainty on the DMIGM is large at high redshift.4 This means that the distribution of DMIGM spreads to a wide range at high redshift. Therefore, when marginalizing over the probability distribution of other parameters (including DMIGM), the posterior probability distribution of photon mass can’t be tightened significantly. This can also be see from Figs 2 and 3, as enlarging the FRB sample from 17 (the real data) to 100 or 200 (the mock data) mainly tightens the constraint on F, but the precision of other parameters is not changed significantly. Another reason is that the DMγ term is insensitive to redshift. As is seen from Fig. 1, Hγ(z) is approximately redshift-independent at z > 1, while He(z) evolves with redshift fast at high redshift. This is the reason why extending the redshift range of FRB sample mainly tighten the constraints on F, but not the photon mass.
In fact, FRBs have been already widely used to constrain photon mass. Using a single FRB 150418 at redshift z = 0.492, Wu et al. (2016) obtained the 1σ upper limits on photon mass mγ < 5.2 × 10−50. With the combination of FRB 121102 at redshift z = 0.19273 and 20 FRBs without direct redshift measurement, Shao & Zhang (2017) obtained mγ < 8.7 × 10−51 kg. With a sample of nine well-localized FRBs in the redshift range 0 < z < 0.66, Wei & Wu (2020) obtained mγ < 7.1 × 10−51 kg. In this paper, we constrained photon mass using 17 well-localized FRBs in the redshift range 0 < z < 0.66, and obtained mγ < 4.8 × 10−51 kg. Our constraint on photon mass is a little tighter than that of Wei & Wu (2020), which is due to the enlargement of FRB sample (17 FRBs versus 9 FRBs). However, the photon mass is constrained at the same order of magnitude (∼10−51 kg), which is because the FRB sample used in our paper and that used in Wei & Wu (2020) fall into the same redshift range (0 < z < 0.66).
With the constrained photon mass mγ < 4.8 × 10−51 kg, the effective DM induced by the non-zero photon mass can be estimated according to equation 4. At the maximum redshift z = 0.66, we have DMγ ≲ 8 pc cm−3, and 〈DMIGM〉 ≈ 600 pc cm−3. We see that DMγ is only about one per cent of 〈DMIGM〉. At redshift z = 3, we have DMγ ≲ 12 pc cm−3, which is much smaller than 〈DMIGM〉 ≈ 2500 pc cm−3 at the same redshift. Therefore, the DM induced by the non-zero photon mass is in general negligible.
ACKNOWLEDGEMENTS
This work has been supported by the National Natural Science Fund of China (grant nos. 11873001, 12147102, and 12275034), and the Fundamental Research Funds for the Central Universities of China (grant no. 2022CDJXY-002).
DATA AVAILABILITY
The Host/FRB catalogue is available at the FRB Host Database http://frbhosts.org.
Footnotes
The FRB Host Database, http://frbhosts.org/
The redshift is dominated by peculiar velocity, rather than the Hubble flow.
The lower limit of mγ is determined by the uncertainty principle mγc2T ≳ h, where T ≈ 1010 yr is the age of the Universe. The upper limit of mγ is determined by the requirement that mγc2 ≲ hν, where ν ≈ 1 GHz is the frequency of FRB emission.
Although the relative uncertain σIGM ∝ z−1/2 decreases with the increasing of redshift, the absolute uncertainty (σIGMDMIGM) increases with redshift.



