-
PDF
- Split View
-
Views
-
Cite
Cite
Albert Bruch, TESS light curves of cataclysmic variables – II – Superhumps in old novae and novalike variables, Monthly Notices of the Royal Astronomical Society, Volume 519, Issue 1, February 2023, Pages 352–376, https://doi.org/10.1093/mnras/stac3493
Close - Share Icon Share
ABSTRACT
Superhumps are among the abundant variable phenomena observed in the light curves of cataclysmic variables (CVs). They come in two flavours as positive and negative superhumps, distinguished by periods slightly longer or shorter, respectively, than the orbital periods of these interacting binary systems. Positive superhumps are ubiquitous in superoutbursting short-period dwarf novae of the SU UMa type but are less common in longer period systems with accretion discs in a permanent bright state, such as novalike variables and most old novae. Negative superhumps do not seem to have a preference for a particular type of CV. Here, I take advantage of the long high-cadence light curves provided by TESS for huge number of stars, selecting all old novae and novalike variables with past reported superhumps for which TESSlight curves are available and have not yet been analysed in previous publications in order to study their superhump behaviour. In combination with information taken from the literature, the results enable to compile the most complete census of superhumps in these stars so far. As a corollary, for the eclipsing systems in the present sample of objects, eclipse epochs derived from the TESS light curves and in some cases from archival light curves are listed and used to update orbital ephemeris and to discuss period changes.
1 INTRODUCTION
Variability in cataclysmic variables (CVs) occurs in a multitude of different forms and on a wide range of time-scales. Most of it is associated to mass transfer or aspect variations in these close binary systems composed of a white dwarf primary star and a Roche lobe filling late-type secondary component transferring matter to the primary, which – in the absence of a strong magnetic field of the white dwarf – forms an accretion disc around the compact star before it is accreted on to its surface.
A good characterization of many of the variable phenomena requires extensive observations of the respective stars with a suitable time resolution over as long a time base as possible. In this respect, the long continuous high-cadence light curves provided by the Kepler mission have been extremely beneficial (e.g. Osaki & Kato 2013; Ramsay, Hakala & Wood 2016; Bruch 2022a, to cite only a few examples). However, Kepler observed a few CVs. This changed considerably with the launch of the Transit Exoplanet Survey Satellite (TESS; Ricker et al. 2014), which – although equipped with much smaller telescopes and pointing at a given sector of the sky for less time – provided light curves of many more CVs with a time base and a temporal resolution well suited to address many issues concerning the variability in these stars.
A particular type of consistent modulations in numerous CVs are the so-called superhumps (SHs); i.e. variations with a period a few per cent different from the orbital period of the binary. SHs come in two flavours: positive SHs (pSHs) with periods slightly longer than the orbital period, and negative SHs (nSHs) the periods of which are a bit shorter than the orbit.
pSHs were first observed in dwarf nova type CVs of the SU UMa subclass during superoutburst (Vogt 1974) and have since become the hallmark of this particular outburst stage of SU UMa stars (Kato et al. 2009, and other publications of this series). pSHs are thought to arise when the accretion disc expands such that the revolution period of matter at its outer rim reaches the 3:1 resonance radius with the binary orbit. This condition is most easily attained during large-scale (super-) outbursts in short-period dwarf novae, i.e. SU UMa stars. The tidal interaction of the disc with the secondary star then induces an elliptical deformation in the former (Whitehurst 1988; Whitehurst & King 1991). Whenever the secondary star passes close to the elongated part of the disc tidal, stresses cause an increase of the disc luminosity. This occurs on a period slightly longer than the orbital period because of a prograde precession of the deformed disc.
pSHs are not restricted to SU UMa stars in superoutburst but are also observed in increasing number in non-outbursting CVs, such as novalike variables (NLs) and old novae (which have an accretion disc in a similar state as the NLs). Most of these have periods longer than the SU UMa stars. Since the secondary star mass in CVs increases systematically with the orbital period, their mass ratio q = Mprim/Msec is on average also higher and may reach (or even surpass, see Section 4) the theoretical limit for the condition required to generate SHs. This limit is contested but appears to lie somewhere in the range q = 0.22…0.39 (Whitehurst & King 1991; Pearson 2006; Smak 2020).
While the basic physics of pSHs are thus thought to be reasonably well-understood, this is not the case for nSHs. Phenomenologically, they are explained to arise in a warped accretion disc or a disc inclined with respect to the orbital plane. In such a configuration, depending on the variable aspect between the disc and the stream of infalling matter from the secondary star, the latter penetrates more or less deeply into the gravitational well of the white dwarf before it hits the accretion disc and thus liberates a variable amount of energy, leading to a modulation of the disc luminosity. The inclined disc precesses retrogradely such that the same aspect between the disc and the infalling stream of matter repeats on a period slightly less than the orbital period. While this scenario is widely accepted to explain nSHs, there is no consensus about the mechanism, which causes a warp or an inclination of the accretion disc in the first place (Montgomery 2009; Thomas & Wood 2015). Thus, there are no theoretical constraints for the appearance of nSHs. Observationally, they are found in short-period dwarf novae (Wood et al. 2011; Osaki & Kato 2014) as well as in long period NLs (Kimura, Osaki & Kato 2020).
The periods of both, pSHs and nSHs, are not strictly constant but exhibit small variations depending on details of the distribution of mass within the the accretion disc.
Recently, Bruch (2022b; hereafter referred to as Paper I) investigated the TESS light curves of a sample of NLs and old novae and identified SHs in several systems, which were hitherto not known to be superhumpers. In extension of that study, I investigate here the TESS light curves of all NLs and old novae with SHs, either positive or negative, reported in the literature which have been observed by TESS, and the TESS data of which have not already been the subject of other publications. The data used and methods applied are briefly outlined in Section 2. Thereafter, the individual systems are discussed in Section 3. For some eclipsing CVs, additional eclipse epochs, an update of the orbital period, and an assessment of period variations are also included as a corollary. In Section 4, I present a census of all superhumping NLs and old novae. A summary of results concludes this study in Section 5.
2 DATA AND DATA HANDLING
The details of the data used in this study and their handling are largely the same as in Paper I and were described there. Therefore, I will only give a summary here. SAP data with a time resolution of 2 min were downloaded from the Barbara A. Misulski Archive for Space Telescopes (MAST).1 For one object (KIC 8751494), data from the Kepler mission, retrieved from the same source, are also used. Whenever observations from different TESS sectors were obtained in immediate succession, they were combined into a single light curve. Different light curves of the same object are referred to as LC#1, LC#2, etc. The start and end epochs of the light curves are listed in Table 1.
| Name . | LC . | Start time . | End time . |
|---|---|---|---|
| . | number . | BJD 2450000 + . | |
| PX And | 1 | 8764.69 | 8788.92 |
| UU Aqr | 1 | 9447.70 | 9473.16 |
| KR Aur | 1 | 9474.17 | 9550.63 |
| BZ Cam | 1 | 8816.88 | 8868.83 |
| 2 | 9010.26 | 9035.13 | |
| 3 | 9390.65 | 9418.85 | |
| V592 Cas | 1 | 8764.69 | 8789.68 |
| 2 | 8955.79 | 8982.27 | |
| RR Cha | 1 | 9333.86 | 9389.72 |
| V751 Cyg | 1 | 8711.37 | 5737.41 |
| V1974 Cyg | 1 | 8738.65 | 8763.32 |
| 2 | 9418.99 | 9446.58 | |
| BB Dor | 1 | 8325.29 | 8682.36 |
| 2 | 9036.28 | 9389.72 | |
| BH Lyn | 1 | 8842.51 | 8868.83 |
| 2 | 9579.82 | 9606.94 | |
| BK Lyn | 1 | 8870.44 | 8897.79 |
| AH Men | 1 | 8325.30 | 8353.17 |
| 2 | 8410.90 | 8436.83 | |
| 3 | 8596.78 | 8682.36 | |
| 4 | 9036.28 | 9060.64 | |
| 5 | 9333.86 | 9389.72 | |
| RR Pic | 1 | 8354.11 | 8595.68 |
| 2 | 8624.97 | 8682.36 | |
| 3 | 9036.28 | 9060.64 | |
| 4 | 9088.24 | 9332.58 | |
| 5 | 9361.29 | 9389.72 | |
| AO Psc | 1 | 9447.70 | 9473.16 |
| AY Psc | 1 | 9447.69 | 9498.81 |
| V348 Pup | 1 | 9201.74 | 9254.07 |
| RW Tri | 1 | 8790.66 | 8814.27 |
| UX UMa | 1 | 8711.36 | 8763.32 |
| 2 | 8899.32 | 8954.88 | |
| DW UMa | 1 | 8870.46 | 8897.78 |
| 2 | 9607.94 | 9635.97 | |
| HS 1813 + 6122 | 1 | 8683.35 | 8841.14 |
| 2 | 8870.17 | 9037.40 | |
| 3 | 9419.99 | 9456.58 | |
| 4 | 9579.81 | 9664.31 | |
| RX J2133.7 + 5107 | 1 | 8711.36 | 8763.32 |
| KIC 8751494 | 1 | 8711.37 | 8737.41 |
| 2 | 9390.66 | 9446.58 | |
| KIC 9406652 | 1 | 8683.36 | 8710.21 |
| 2 | 8711.37 | 8737.41 | |
| 3 | 8085.66 | 9446.58 | |
| NSV 1907 | 1 | 9174.23 | 9200,23 |
| Name . | LC . | Start time . | End time . |
|---|---|---|---|
| . | number . | BJD 2450000 + . | |
| PX And | 1 | 8764.69 | 8788.92 |
| UU Aqr | 1 | 9447.70 | 9473.16 |
| KR Aur | 1 | 9474.17 | 9550.63 |
| BZ Cam | 1 | 8816.88 | 8868.83 |
| 2 | 9010.26 | 9035.13 | |
| 3 | 9390.65 | 9418.85 | |
| V592 Cas | 1 | 8764.69 | 8789.68 |
| 2 | 8955.79 | 8982.27 | |
| RR Cha | 1 | 9333.86 | 9389.72 |
| V751 Cyg | 1 | 8711.37 | 5737.41 |
| V1974 Cyg | 1 | 8738.65 | 8763.32 |
| 2 | 9418.99 | 9446.58 | |
| BB Dor | 1 | 8325.29 | 8682.36 |
| 2 | 9036.28 | 9389.72 | |
| BH Lyn | 1 | 8842.51 | 8868.83 |
| 2 | 9579.82 | 9606.94 | |
| BK Lyn | 1 | 8870.44 | 8897.79 |
| AH Men | 1 | 8325.30 | 8353.17 |
| 2 | 8410.90 | 8436.83 | |
| 3 | 8596.78 | 8682.36 | |
| 4 | 9036.28 | 9060.64 | |
| 5 | 9333.86 | 9389.72 | |
| RR Pic | 1 | 8354.11 | 8595.68 |
| 2 | 8624.97 | 8682.36 | |
| 3 | 9036.28 | 9060.64 | |
| 4 | 9088.24 | 9332.58 | |
| 5 | 9361.29 | 9389.72 | |
| AO Psc | 1 | 9447.70 | 9473.16 |
| AY Psc | 1 | 9447.69 | 9498.81 |
| V348 Pup | 1 | 9201.74 | 9254.07 |
| RW Tri | 1 | 8790.66 | 8814.27 |
| UX UMa | 1 | 8711.36 | 8763.32 |
| 2 | 8899.32 | 8954.88 | |
| DW UMa | 1 | 8870.46 | 8897.78 |
| 2 | 9607.94 | 9635.97 | |
| HS 1813 + 6122 | 1 | 8683.35 | 8841.14 |
| 2 | 8870.17 | 9037.40 | |
| 3 | 9419.99 | 9456.58 | |
| 4 | 9579.81 | 9664.31 | |
| RX J2133.7 + 5107 | 1 | 8711.36 | 8763.32 |
| KIC 8751494 | 1 | 8711.37 | 8737.41 |
| 2 | 9390.66 | 9446.58 | |
| KIC 9406652 | 1 | 8683.36 | 8710.21 |
| 2 | 8711.37 | 8737.41 | |
| 3 | 8085.66 | 9446.58 | |
| NSV 1907 | 1 | 9174.23 | 9200,23 |
| Name . | LC . | Start time . | End time . |
|---|---|---|---|
| . | number . | BJD 2450000 + . | |
| PX And | 1 | 8764.69 | 8788.92 |
| UU Aqr | 1 | 9447.70 | 9473.16 |
| KR Aur | 1 | 9474.17 | 9550.63 |
| BZ Cam | 1 | 8816.88 | 8868.83 |
| 2 | 9010.26 | 9035.13 | |
| 3 | 9390.65 | 9418.85 | |
| V592 Cas | 1 | 8764.69 | 8789.68 |
| 2 | 8955.79 | 8982.27 | |
| RR Cha | 1 | 9333.86 | 9389.72 |
| V751 Cyg | 1 | 8711.37 | 5737.41 |
| V1974 Cyg | 1 | 8738.65 | 8763.32 |
| 2 | 9418.99 | 9446.58 | |
| BB Dor | 1 | 8325.29 | 8682.36 |
| 2 | 9036.28 | 9389.72 | |
| BH Lyn | 1 | 8842.51 | 8868.83 |
| 2 | 9579.82 | 9606.94 | |
| BK Lyn | 1 | 8870.44 | 8897.79 |
| AH Men | 1 | 8325.30 | 8353.17 |
| 2 | 8410.90 | 8436.83 | |
| 3 | 8596.78 | 8682.36 | |
| 4 | 9036.28 | 9060.64 | |
| 5 | 9333.86 | 9389.72 | |
| RR Pic | 1 | 8354.11 | 8595.68 |
| 2 | 8624.97 | 8682.36 | |
| 3 | 9036.28 | 9060.64 | |
| 4 | 9088.24 | 9332.58 | |
| 5 | 9361.29 | 9389.72 | |
| AO Psc | 1 | 9447.70 | 9473.16 |
| AY Psc | 1 | 9447.69 | 9498.81 |
| V348 Pup | 1 | 9201.74 | 9254.07 |
| RW Tri | 1 | 8790.66 | 8814.27 |
| UX UMa | 1 | 8711.36 | 8763.32 |
| 2 | 8899.32 | 8954.88 | |
| DW UMa | 1 | 8870.46 | 8897.78 |
| 2 | 9607.94 | 9635.97 | |
| HS 1813 + 6122 | 1 | 8683.35 | 8841.14 |
| 2 | 8870.17 | 9037.40 | |
| 3 | 9419.99 | 9456.58 | |
| 4 | 9579.81 | 9664.31 | |
| RX J2133.7 + 5107 | 1 | 8711.36 | 8763.32 |
| KIC 8751494 | 1 | 8711.37 | 8737.41 |
| 2 | 9390.66 | 9446.58 | |
| KIC 9406652 | 1 | 8683.36 | 8710.21 |
| 2 | 8711.37 | 8737.41 | |
| 3 | 8085.66 | 9446.58 | |
| NSV 1907 | 1 | 9174.23 | 9200,23 |
| Name . | LC . | Start time . | End time . |
|---|---|---|---|
| . | number . | BJD 2450000 + . | |
| PX And | 1 | 8764.69 | 8788.92 |
| UU Aqr | 1 | 9447.70 | 9473.16 |
| KR Aur | 1 | 9474.17 | 9550.63 |
| BZ Cam | 1 | 8816.88 | 8868.83 |
| 2 | 9010.26 | 9035.13 | |
| 3 | 9390.65 | 9418.85 | |
| V592 Cas | 1 | 8764.69 | 8789.68 |
| 2 | 8955.79 | 8982.27 | |
| RR Cha | 1 | 9333.86 | 9389.72 |
| V751 Cyg | 1 | 8711.37 | 5737.41 |
| V1974 Cyg | 1 | 8738.65 | 8763.32 |
| 2 | 9418.99 | 9446.58 | |
| BB Dor | 1 | 8325.29 | 8682.36 |
| 2 | 9036.28 | 9389.72 | |
| BH Lyn | 1 | 8842.51 | 8868.83 |
| 2 | 9579.82 | 9606.94 | |
| BK Lyn | 1 | 8870.44 | 8897.79 |
| AH Men | 1 | 8325.30 | 8353.17 |
| 2 | 8410.90 | 8436.83 | |
| 3 | 8596.78 | 8682.36 | |
| 4 | 9036.28 | 9060.64 | |
| 5 | 9333.86 | 9389.72 | |
| RR Pic | 1 | 8354.11 | 8595.68 |
| 2 | 8624.97 | 8682.36 | |
| 3 | 9036.28 | 9060.64 | |
| 4 | 9088.24 | 9332.58 | |
| 5 | 9361.29 | 9389.72 | |
| AO Psc | 1 | 9447.70 | 9473.16 |
| AY Psc | 1 | 9447.69 | 9498.81 |
| V348 Pup | 1 | 9201.74 | 9254.07 |
| RW Tri | 1 | 8790.66 | 8814.27 |
| UX UMa | 1 | 8711.36 | 8763.32 |
| 2 | 8899.32 | 8954.88 | |
| DW UMa | 1 | 8870.46 | 8897.78 |
| 2 | 9607.94 | 9635.97 | |
| HS 1813 + 6122 | 1 | 8683.35 | 8841.14 |
| 2 | 8870.17 | 9037.40 | |
| 3 | 9419.99 | 9456.58 | |
| 4 | 9579.81 | 9664.31 | |
| RX J2133.7 + 5107 | 1 | 8711.36 | 8763.32 |
| KIC 8751494 | 1 | 8711.37 | 8737.41 |
| 2 | 9390.66 | 9446.58 | |
| KIC 9406652 | 1 | 8683.36 | 8710.21 |
| 2 | 8711.37 | 8737.41 | |
| 3 | 8085.66 | 9446.58 | |
| NSV 1907 | 1 | 9174.23 | 9200,23 |
Frequency analysis of the data were performed with Fourier techniques applying the Lomb–Scargle algorithm (Lomb 1976; Scargle 1982) or following Deeming (1975). Unless variations on longer time-scales were targeted, these were removed by subtraction of a Savitzky & Golay (1964) filtered version of the light curve, using a cut-off time-scale of 2 d and a fourth-order smoothing polynomial for the filter. The frequency errors of power spectrum signals were estimated using the prescription of Schwarzenberg-Czerny (1991), which, due to flickering and window patterns of real variations, may overestimate the true errors.
Comparing TESS light curves with terrestrial data, it should be kept in mind that the TESS passband encompasses a wide range between 6000 and 10 000 Å, centred on the Cousins I-band.
For the deeply eclipsing CVs in the present sample, eclipse epochs were measured to enable an update of the orbital ephemeris and for future reference. Instead of measuring individual eclipse timings, the light curves were folded on the orbital period, choosing the epoch such that the centre of the primary eclipse coincides with phase 0. This was done individually for the data of each TESS sector, yielding more than one eclipse epoch for the light curves combined from several sectors. The corresponding results are listed in Table 2. For four CVs (UU Aqr, V348 Pup, RW Tri, and UX UMa) additional eclipse epochs were measured in light curves downloaded from the American Association of Variable Star Observers (AAVSO) archives (Kafka 2021) and the data bank of the Observatório do Pico dos Dias2 (LNA Data Bank) as the minima of polynomials of suitable degree fitted to the eclipse profiles. They are listed in Appendix A. The transformation from JD to BJD was performed using the online tool of Eastman, Siverd & Gaudi (2010).
| Star . | Light curve . | Epoch (BJD) . | Cycle number1 . |
|---|---|---|---|
| PX And | LC#1 | 2458779.1330 | 65187 |
| UU Aqr | LC#1 | 2459462.1633 | 47111 |
| RR Cha | LC#1 | 2459363.0160 | 0 |
| AH Men | LC#1 | 2458340.0867 | 0 |
| LC#2 | 2458425.0527 | 668 | |
| LC#3 (part 1) | 2458611.0146 | 2130 | |
| LC#3 (part 2) | 2458646.1193 | 2406 | |
| LC#3 (part 3) | 2458671.0497 | 2602 | |
| LC#4 | 2459051.1099 | 5590 | |
| LC#5 (part 1) | 2459348.1110 | 7925 | |
| LC#5 (part 2) | 2459373.0414 | 8121 | |
| BH Lyn | LC#1 | 2458857.1359 | 74911 |
| LC#2 | 2459591.1530 | 79620 | |
| AY Psc | LC#1 (part 1) | 2459462.1062 | 54476 |
| LC#1 (part 2) | 2459488.1850 | 54596 | |
| V348 Pup | LC#1 (part 1) | 2459211.0279 | 104276 |
| LC#1 (part 2) | 2459238.0154 | 104541 | |
| RW Tri | LC#1 | 245880.0263 | 22112 |
| UX UMa | LC#1 (part 1) | 2458726.0252 | 37658 |
| LC#1 (part 2) | 2458746.0858 | 37760 | |
| LC#2 (part 1) | 2458914.0431 | 38614 | |
| LC#2 (part 2) | 2458944.1338 | 38767 | |
| DW UMa | LC#1 | 2458885.0575 | 56178 |
| LC#2 | 2459622.0503 | 61573 | |
| HS 1813-6122 | LC#1 (part 1) | 2458693.0878 | 0 |
| LC#1 (part 2) | 2458723.0351 | 203 | |
| LC#1 (part 3) | 2458753.1285 | 407 | |
| LC#1 (part 4) | 2458773.0430 | 542 | |
| LC#1 (part 5) | 2458803.1372 | 746 | |
| LC#1 (part 6) | 2458833.0826 | 949 | |
| LC#2 (part 1) | 2458880.1437 | 1268 | |
| LC#2 (part 2) | 2458910.0900 | 1471 | |
| LC#2 (part 3) | 2458940.0367 | 1674 | |
| LC#2 (part 4) | 2458970.1298 | 1878 | |
| LC#2 (part 5) | 2459000.0758 | 2081 | |
| LC#2 (part 6) | 2459020.1399 | 2217 | |
| LC#3 | 2459429.0664 | 4989 | |
| LC#4 (part 1) | 2459589.1243 | 6074 | |
| LC#4 (part 3) | 2459649.0186 | 6480 | |
| NSV 1907 | LC#1 | 2459189.1635 | 7710 |
| Star . | Light curve . | Epoch (BJD) . | Cycle number1 . |
|---|---|---|---|
| PX And | LC#1 | 2458779.1330 | 65187 |
| UU Aqr | LC#1 | 2459462.1633 | 47111 |
| RR Cha | LC#1 | 2459363.0160 | 0 |
| AH Men | LC#1 | 2458340.0867 | 0 |
| LC#2 | 2458425.0527 | 668 | |
| LC#3 (part 1) | 2458611.0146 | 2130 | |
| LC#3 (part 2) | 2458646.1193 | 2406 | |
| LC#3 (part 3) | 2458671.0497 | 2602 | |
| LC#4 | 2459051.1099 | 5590 | |
| LC#5 (part 1) | 2459348.1110 | 7925 | |
| LC#5 (part 2) | 2459373.0414 | 8121 | |
| BH Lyn | LC#1 | 2458857.1359 | 74911 |
| LC#2 | 2459591.1530 | 79620 | |
| AY Psc | LC#1 (part 1) | 2459462.1062 | 54476 |
| LC#1 (part 2) | 2459488.1850 | 54596 | |
| V348 Pup | LC#1 (part 1) | 2459211.0279 | 104276 |
| LC#1 (part 2) | 2459238.0154 | 104541 | |
| RW Tri | LC#1 | 245880.0263 | 22112 |
| UX UMa | LC#1 (part 1) | 2458726.0252 | 37658 |
| LC#1 (part 2) | 2458746.0858 | 37760 | |
| LC#2 (part 1) | 2458914.0431 | 38614 | |
| LC#2 (part 2) | 2458944.1338 | 38767 | |
| DW UMa | LC#1 | 2458885.0575 | 56178 |
| LC#2 | 2459622.0503 | 61573 | |
| HS 1813-6122 | LC#1 (part 1) | 2458693.0878 | 0 |
| LC#1 (part 2) | 2458723.0351 | 203 | |
| LC#1 (part 3) | 2458753.1285 | 407 | |
| LC#1 (part 4) | 2458773.0430 | 542 | |
| LC#1 (part 5) | 2458803.1372 | 746 | |
| LC#1 (part 6) | 2458833.0826 | 949 | |
| LC#2 (part 1) | 2458880.1437 | 1268 | |
| LC#2 (part 2) | 2458910.0900 | 1471 | |
| LC#2 (part 3) | 2458940.0367 | 1674 | |
| LC#2 (part 4) | 2458970.1298 | 1878 | |
| LC#2 (part 5) | 2459000.0758 | 2081 | |
| LC#2 (part 6) | 2459020.1399 | 2217 | |
| LC#3 | 2459429.0664 | 4989 | |
| LC#4 (part 1) | 2459589.1243 | 6074 | |
| LC#4 (part 3) | 2459649.0186 | 6480 | |
| NSV 1907 | LC#1 | 2459189.1635 | 7710 |
| Star . | Light curve . | Epoch (BJD) . | Cycle number1 . |
|---|---|---|---|
| PX And | LC#1 | 2458779.1330 | 65187 |
| UU Aqr | LC#1 | 2459462.1633 | 47111 |
| RR Cha | LC#1 | 2459363.0160 | 0 |
| AH Men | LC#1 | 2458340.0867 | 0 |
| LC#2 | 2458425.0527 | 668 | |
| LC#3 (part 1) | 2458611.0146 | 2130 | |
| LC#3 (part 2) | 2458646.1193 | 2406 | |
| LC#3 (part 3) | 2458671.0497 | 2602 | |
| LC#4 | 2459051.1099 | 5590 | |
| LC#5 (part 1) | 2459348.1110 | 7925 | |
| LC#5 (part 2) | 2459373.0414 | 8121 | |
| BH Lyn | LC#1 | 2458857.1359 | 74911 |
| LC#2 | 2459591.1530 | 79620 | |
| AY Psc | LC#1 (part 1) | 2459462.1062 | 54476 |
| LC#1 (part 2) | 2459488.1850 | 54596 | |
| V348 Pup | LC#1 (part 1) | 2459211.0279 | 104276 |
| LC#1 (part 2) | 2459238.0154 | 104541 | |
| RW Tri | LC#1 | 245880.0263 | 22112 |
| UX UMa | LC#1 (part 1) | 2458726.0252 | 37658 |
| LC#1 (part 2) | 2458746.0858 | 37760 | |
| LC#2 (part 1) | 2458914.0431 | 38614 | |
| LC#2 (part 2) | 2458944.1338 | 38767 | |
| DW UMa | LC#1 | 2458885.0575 | 56178 |
| LC#2 | 2459622.0503 | 61573 | |
| HS 1813-6122 | LC#1 (part 1) | 2458693.0878 | 0 |
| LC#1 (part 2) | 2458723.0351 | 203 | |
| LC#1 (part 3) | 2458753.1285 | 407 | |
| LC#1 (part 4) | 2458773.0430 | 542 | |
| LC#1 (part 5) | 2458803.1372 | 746 | |
| LC#1 (part 6) | 2458833.0826 | 949 | |
| LC#2 (part 1) | 2458880.1437 | 1268 | |
| LC#2 (part 2) | 2458910.0900 | 1471 | |
| LC#2 (part 3) | 2458940.0367 | 1674 | |
| LC#2 (part 4) | 2458970.1298 | 1878 | |
| LC#2 (part 5) | 2459000.0758 | 2081 | |
| LC#2 (part 6) | 2459020.1399 | 2217 | |
| LC#3 | 2459429.0664 | 4989 | |
| LC#4 (part 1) | 2459589.1243 | 6074 | |
| LC#4 (part 3) | 2459649.0186 | 6480 | |
| NSV 1907 | LC#1 | 2459189.1635 | 7710 |
| Star . | Light curve . | Epoch (BJD) . | Cycle number1 . |
|---|---|---|---|
| PX And | LC#1 | 2458779.1330 | 65187 |
| UU Aqr | LC#1 | 2459462.1633 | 47111 |
| RR Cha | LC#1 | 2459363.0160 | 0 |
| AH Men | LC#1 | 2458340.0867 | 0 |
| LC#2 | 2458425.0527 | 668 | |
| LC#3 (part 1) | 2458611.0146 | 2130 | |
| LC#3 (part 2) | 2458646.1193 | 2406 | |
| LC#3 (part 3) | 2458671.0497 | 2602 | |
| LC#4 | 2459051.1099 | 5590 | |
| LC#5 (part 1) | 2459348.1110 | 7925 | |
| LC#5 (part 2) | 2459373.0414 | 8121 | |
| BH Lyn | LC#1 | 2458857.1359 | 74911 |
| LC#2 | 2459591.1530 | 79620 | |
| AY Psc | LC#1 (part 1) | 2459462.1062 | 54476 |
| LC#1 (part 2) | 2459488.1850 | 54596 | |
| V348 Pup | LC#1 (part 1) | 2459211.0279 | 104276 |
| LC#1 (part 2) | 2459238.0154 | 104541 | |
| RW Tri | LC#1 | 245880.0263 | 22112 |
| UX UMa | LC#1 (part 1) | 2458726.0252 | 37658 |
| LC#1 (part 2) | 2458746.0858 | 37760 | |
| LC#2 (part 1) | 2458914.0431 | 38614 | |
| LC#2 (part 2) | 2458944.1338 | 38767 | |
| DW UMa | LC#1 | 2458885.0575 | 56178 |
| LC#2 | 2459622.0503 | 61573 | |
| HS 1813-6122 | LC#1 (part 1) | 2458693.0878 | 0 |
| LC#1 (part 2) | 2458723.0351 | 203 | |
| LC#1 (part 3) | 2458753.1285 | 407 | |
| LC#1 (part 4) | 2458773.0430 | 542 | |
| LC#1 (part 5) | 2458803.1372 | 746 | |
| LC#1 (part 6) | 2458833.0826 | 949 | |
| LC#2 (part 1) | 2458880.1437 | 1268 | |
| LC#2 (part 2) | 2458910.0900 | 1471 | |
| LC#2 (part 3) | 2458940.0367 | 1674 | |
| LC#2 (part 4) | 2458970.1298 | 1878 | |
| LC#2 (part 5) | 2459000.0758 | 2081 | |
| LC#2 (part 6) | 2459020.1399 | 2217 | |
| LC#3 | 2459429.0664 | 4989 | |
| LC#4 (part 1) | 2459589.1243 | 6074 | |
| LC#4 (part 3) | 2459649.0186 | 6480 | |
| NSV 1907 | LC#1 | 2459189.1635 | 7710 |
3 RESULTS
3.1 PX And: no superhumps in the TESS light curve
PX And is an eclipsing NL variable. Stanishev et al. (2002) derived the most accurate value for the orbital period: 0.146352739(11) d. The same authors also found a periodic variation at 0.1415 d, which they attribute to an nSH, and another one at 0.207 d, the origin of which remained unexplained. The only significant signals in the power spectrum of the single TESS light curve correspond to the orbital period and its overtones. Fig. 1a shows the frequency range around the orbital signal (which is truncated in order to better visualize any faint signals in its vicinity). No trace of an SH, either positive or negative, or of the 0.207 d period appears. Their frequencies are marked by red arrows in the figure. A representative eclipse epoch derived from the TESS data is listed in Table 2.
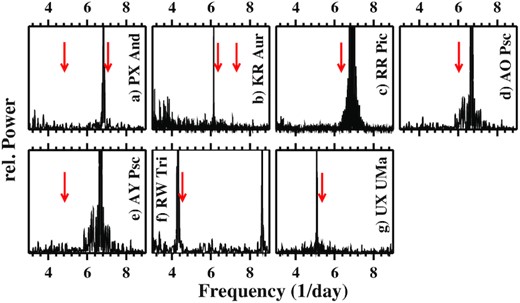
Power spectra in the range around the orbital frequency of six CVs with SHs reported in the past but with no indications for SHs in the TESS light curves. The orbital signals are heavily truncated in order to better visualize any faint signals in their vicinity. The frequencies of previously identified periodic signals are marked with red arrows. Note that the broad base around the orbital frequency (in particular in the RR Pic, AO Psc, and AY Psc power spectra) are not independent signals but the unavoidable sidelobes of the main peak.
3.2 UU Aqr: the superhump vanished
UU Aqr is an eclipsing NL variable. Although known as a variable star for almost a century (Beljawsky 1926), it was identified as a CV only in 1986 by Volkov, Shugarov & Seregina (1986). SHs were observed by Patterson et al. (2005) but were absent in extensive photometry of Bruch (2019a). Lima et al. (2021) make no mention of SHs but claim to see a photometric period of 54.4 min, and of 25.7 min in circular polarization.
TESS observed UU Aqr in a single sector. The power spectrum of the light curve, after masking eclipses and removing variations on time-scale above 2 d, is shown in the upper frame of Fig. 2. In the low (<20 d−1) frequency range the orbital signal and the first two overtones stand out moderately strong above a multitude of peaks with decreasing power towards higher frequencies which can be attributed to non-coherent fluctuations in the brightness of UU Aqr on time-scales of hours. An increase of power between 10 and 11 d−1 may be significant. No outstanding signal is present near 5.711 d−1 (marked by a red arrow in the figure), i.e. the frequency of the SH which is so prominent in the observations of Patterson et al. (2005; see their fig. 3). Thus, the SH was not active during the epoch of the TESS observations.
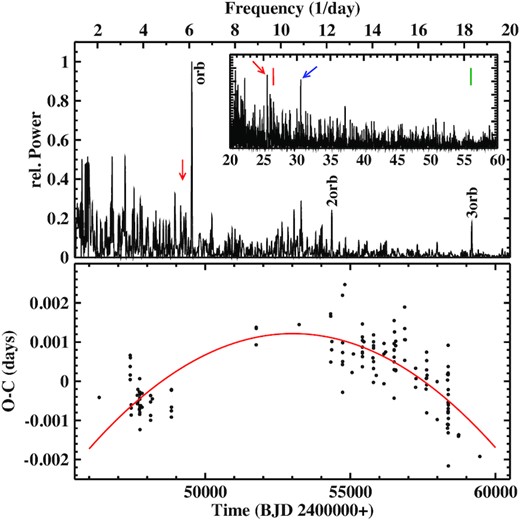
Top: Low frequency part of the power spectrum of the UU Aqr light curve. The insert shows the adjacent higher frequency part at on expanded power scale. The marks drawn into the figure are explained in the text. Bottom: O − C diagram of eclipse timings of UU Aqr with respect to linear ephemeris according to equation (1). The red graph represents the best-fitting second-order polynomial.
At higher frequencies (insert in Fig. 2), the fourth overtone of Forb is the only signal that can be attributed to orbital variations (blue arrow). A stronger signal at 25.55 d−1 (P = 56.36 min; red arrow) is distinct from the third orbital overtone, but is possibly related to the 54.4-min photometric periodicity mentioned by Lima et al. (2021). Although the corresponding frequency (red bar) is somewhat higher, the power spectrum in fig. 7 of Lima et al. (2021) contains numerous alias peaks reaching out until well beyond 56.36 min. I note, however, that the light curves of Bruch (2019a) do not contain an indication for variations in this period range. On the other hand, the power spectrum of those data has a marginally significant peak compatible with the 25.7-min polarimetric period, which Lima et al. (2021) take as an indication for an intermediate polar nature of UU Aqr. But no such signal can be discerned in the TESS data (green bar in Fig. 2).
The orbital period of UU Aqr was last refined by Baptista et al. (1995) almost 30 yr ago. It is based on eclipse epoch measurements over a time base of about 7 yr. I am not aware of any published eclipse timings since then which would enable to enlarge the time base for period determination. A representative eclipse epoch derived from the TESS light curve is listed in Table 2. The AAVSO archives and the LNA Data Bank contain many more time resolved light curves of UU Aqr observed between 2000 and 2019, which can be used to measure additional eclipse timings. After rejecting a couple of eclipses because their timings led to excessive O − C values, I am left with 99 additional eclipse epochs, which are listed in Table A1. These new data extend the time base for period determination by more than a factor of 5.
3.3 KR Aur: the superhumps subsided
KR Aur is a well-known NL variable of the VY Scl subtype. The long-term behaviour has been extensively monitored in the literature (see e.g. Honeycutt & Kafka 2004). For the early history of the system, see Kato, Ishioka & Uemura (2002). The orbital period was measured spectroscopically by Hutchings, Link & Crampton (1983) and Shafter (1983) and more recently photometrically by Rodríguez-Gil et al. (2020) who provide the most accurate value of 0.162771641(49) d. Apart from the frequent low states, which characterize KR Aur as a VY Scl star, the system exhibits variability also on short time-scales, i.e. the usual flickering seen in all CVs, but stronger than in most NLs (Bruch 2021). Significant signals with unstable periods on the time-scale of several hundred seconds have been seen by Singh et al. (1993) and Kato et al. (2002). Biryukov & Borisov (1990) claim the presence of 25 min variations, but these are quite unstable and can at most be classified as quasi-periodic oscillations (QPOs). In contrast, Kozhevnikov (2007) reports the presence in 2004, January and February, of an nSH at a period of 0.15713(2) d. Similar signals were, however, not detected in observations of Kato et al. (2002). In contrast, more recently, in 2021 January, Boeva, Latev & Zamanov (2021) observed an nSH at a period of 0.1367(2) d, significantly shorter than that seen by Kozhevnikov (2007). All these observations were performed in high states.
Some months later, between September and November of the same year, again in a high state, TESS observed KR Aur in three sectors in subsequent time intervals. Apart from multiple signals at frequencies <4 d−1 due to random variations on longer time-scales, only a strong signal at the orbital frequency is outstanding. No indications for SHs can be detected (Fig. 1b). Thus, the variations seen by Boeva et al. (2021) had subsided. The appearance of SHs in KR Aur is consequently not permanent but an intermittent phenomenon. Moreover, the high-frequency part of the power spectrum does not contain power in excess of the usual red flickering noise on the times-scales indicated by Singh et al. (1993), Kato et al. (2002), or Biryukov & Borisov (1990).
3.4 BZ Cam: lots of unstable signals
The long-term photometric behaviour of BZ Cam, classified as an NL variable, is somewhat unusual for its class. For many years, it remained at a seemingly stable magnitude of ∼13 after a low state at ∼14 mag in 1928 (Garnavich & Szkody 1988). Another low state occurred in 1999 (Greiner et al. 2001; Kato & Uemura 2001). This would make BZ Cam a typical VY Scl star. But the AAVSO long-term light curve, starting in late 2000, contains several excursions to a brighter state around 12 mag (apart from a short glitch to the low state level).
Combining spectroscopic and photometric data Patterson, Patino & Thorstensen (1996) derived an orbital period of 0.153693(7) d. They also saw very complicated structures in the power spectra of their light curves with a concentration of multiple signals in the frequency range below ∼20 d−1. They tried to isolate specific signals and to discuss them in terms of positive and nSHs, but admitted that their interpretation is not unique. Kato & Uemura (2001), in contrast, claim the presence of a pSH at 0.15634(1) during the 1999 low state of BZ Cam.
The TESS observations of BZ Cam can be combined into three light curves. Their power spectra (upper frames of Fig. 3) are similar to those shown by Patterson et al. (1996) with a concentration of peaks in the range between 8 and 14 d−1 (periods between 1.7 and 3 h). The orbital frequency is marked by red vertical bars in the figure. Orbital variations clearly manifest themselves in LC#1 and LC#3, but are absent in LC#2. No trace of the SH seen by Kato & Uemura (2001) is present in the power spectra.
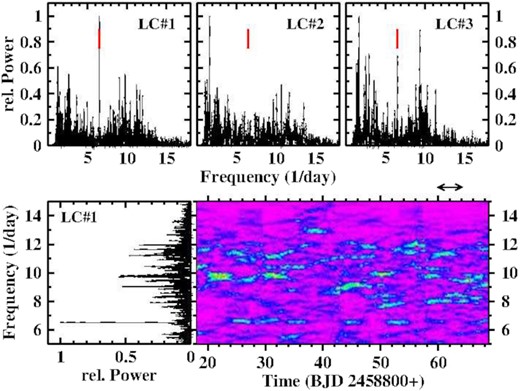
Top: Power spectra of the light curves of BZ Cam. The red vertical lines indicate the orbital frequency. Bottom: Part of the power spectrum of LC#1 in a conventional representation (left) together with a 3D plot of the power (colour coded) as a function of frequency and time (right). The double arrow above the plot indicates the width of the time intervals used to calculate the power spectrum and thus its time resolution.
In order to further investigate the occurrence of multiple apparently quite unstable periods of a few hours, time resolved power spectra were calculated using a sliding window with a widths of 4 d. The results for LC#1 are shown in the lower-right frame of Fig. 3 (those for the other light curves are qualitatively similar). For comparison, the conventional power spectrum of the entire light curve is reproduced in the left-hand frame. The time resolved spectrum is dominated by a profusion of signals that appear at random, vanish after a couple of days, and can change their frequency during their lifetime. This is the typical behaviour of QPOs that are not uncommon in CVs but normally have shorter periods in the range of minutes to some tens of minutes. Their behaviour in BZ Cam is, however, somewhat reminiscent of CP Pup (see Paper I). These QPOs having been seen by Patterson et al. (1996) in 1994–1995 and by TESS between 2019 and 2021 suggest that they are a permanent property of BZ Cam.
Another interesting feature in the time resolved power spectrum is the coming and going of the orbital signal that semiperiodically appears and vanishes on the time-scale of several days.
3.5 V592 Cas: no nSH and drastically changed pSH waveform
V592 Cas was discovered by Greenstein, Sargent & Haug (1970) as LSI 55o-8. The orbital period was measured spectroscopically to be 0.115063(1) d by Taylor et al. (1998). The latter authors also found strong pSHs at a period of 0.12228(1) d. Additionally, in 1997–1998, they saw a weak signal at 0.11193(5) d, which they interpreted as an nSH. This was not detected in the 1993 observing season.
The overall properties of the two available TESS light curves taken about 6 months apart are similar. The upper frame of Fig. 4 shows LC#2. It is characterized by regular but non-periodic variations on the time-scale of a day. This is reflected in the power spectra in the lower left frame of the figure, which contains numerous peaks at frequencies below 4 d−1. A faint peak corresponding to a period of 0.1151(1) d in both power spectra can be identified with the orbital period of V592 Cas. I consider another signal at a slightly lower frequency, corresponding to a period of 0.1225(1) d, very similar to that reported by Taylor et al. (1998), as being caused by a pSH. However, its first overtone is vastly stronger. This is explained by the SH waveform shown in the lower right frame of Fig. 4, which consists of two maxima separated by minima of quite different depth. Except for a reversal of the slightly different heights of the two maxima, the waveform is the same in both light curves. It is drastically different from the simple saw-tooth shape observed by Taylor et al. (1998).
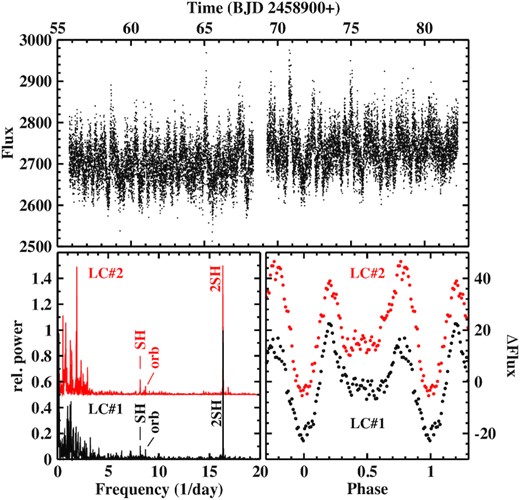
Top: Light-curve LC#2 of V592 Cas. Bottom: Power spectra (left) and SH waveforms (right) derived from light curves LC#1 (black) and LC#2 (red, shifted vertically for clarity).
With one notable exception, apart from overtones and simple arithmetic combinations of the orbital and SH frequencies, the power spectra contain no indications of other significant periodicities. In particular, even after applying the same technique as Taylor et al. (1998), i.e. subtracting the pSH variation from the light curve, the present data reveal no trace of an nSH. The exception is a peak at low frequencies (period: 0.53 d) seen in LC#2, which is about as strong as the dominant first overtone of the SH. It is not present in LC#1. One might therefore suspect it to be due to an accidental alignment of the random low frequency variations of V592 Cas. But this seems not to be the case because it is equally present at very nearly the same frequency in the first and in the second half of the light curve and thus persists at least over its total time base. This periodicity has no obvious relationship to the orbital or the SH period. Its nature remains unclear.
Finally, there is a broad enhancement of power between 65 and 170 d−1 (8.5–22 min), which may explain the 22 min oscillation observed by Kato & Starkey (2002).
3.6 RR Cha: superhumps and a revision of the WD spin period
Few detailed studies of the quiescent phase of Nova Chamaeleontis 1953 (RR Cha) have been published. Most relevant in the present context is the paper of Woudt & Warner (2002) who discovered eclipses in RR Cha, recurring at a period of 0.1401 d. Moreover, they detected pSHs, as well as nSHs, at periods of 0.14442 d and 0.13529 d, respectively. They also identify a signal in the power spectra of their data corresponding to a period of 32.5 min and suspect RR Cha to be an intermediate polar. Further evidence for this is provided by Rodríguez-Gil & Potter (2003) who observed circular polarization in RR Cha, which ‘appears to be modulated on the spin period of the primary and harmonics of the pSH period’.
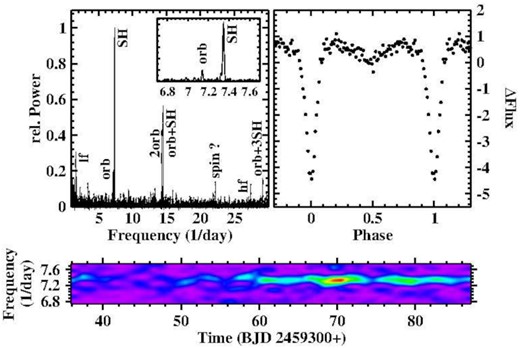
Top Left: Power spectrum of RR Cha. On the scale of the plot, the orbital and SH signals are only marginally resolved. Therefore, the insert shows the corresponding frequency range on an expanded scale. Top Right: Average waveform of the orbital variations of RR Cha. Bottom: Time-resolved power spectrum of the range around the SH frequency.
The power spectrum of RR Cha, after masking the eclipses, is reproduced in the upper-left-hand frame of Fig. 5. It is dominated by a signal at FSH = 7.346(1) d−1 (PSH = 0.13613(2) d), just above the orbital frequency. The period is very close to that of the nSH seen by Woudt & Warner (2002). A time resolved power spectrum reveals a significant evolution of the strength of this signal. It starts rather weakly, gains strength in the third quarter of the light curve, and then looses power again, as can be seen in the time-resolved power spectrum shown in the lower frame of Fig. 5. The TESS light curve does not contain the pSH detected by Woudt & Warner (2002).
Other signals in the power spectrum can be identified as the first overtone of the orbital frequency and arithmetic combinations of the orbital and the SH frequencies. However, a peak at 22.215(3) d−1 cannot be explained in this way. The corresponding period of 64.821(9) min is almost exactly twice the 32.5 min period seen by Woudt & Warner (2002; with no error margin attached to it) and which they interpret as either the white dwarf spin period or its beat with the orbital period. This can hardly be a coincidence. Depending on the detailed conditions in an individual system, the interplay between orbital motion and the white dwarf spin can lead to many different periodic modulations in the light curves (Warner 1986; Norton, Beardmore & Taylor 1996). Signals at twice the spin frequency are, for instance, seen in the intermediate polar AO Psc (see Sects. 3.14). It is therefore conceivable that the period seen by Woudt & Warner (2002) is the first overtone of the spin period (which is not seen in the present TESS data) and that a change in the system configuration leads to a signal at the fundamental period seen now.
Two more apparently significant signals can be detected in the power spectrum, one identified in Fig. 5 as Flf = 1.622(2) d−1 (Plf = 0.6164(7) d) and the other as Fhf = 27.381(3) d−1 (Phf = 0.036522(4) d). Neither |$P_{\rm lf} = 14.8\, {\rm h}$| nor |$P_{\rm hf} = 52.6\, {\rm min}$| has an obvious relationship to other periods in RR Cha. Thus, their origin remains unexplained.
3.7 V751 Cyg: nothing new
Patterson, Thorstensen & Fried (2001) measured a spectroscopic orbital period of 0.1445(1) d for V751 Cyg and found an nSH at 0.13948(7) d. The latter was also seen by Papadaki et al. (2009). The single TESS light curve confirms the continued presence of the SH at a period of 0.13930(2) d with a very nearly sinusoidal waveform. Fig. 6 shows the light curve, the power spectrum and the SH waveform. The orbital frequency is marked by a red arrow in the power spectrum, indicating that an orbital signal is notably absent in the light curve. Instead, a clear signal at 1.87 d, i.e. the beat between orbit and SH, is clearly seen (marked by a red bar in the insert of the lower-left-hand frame of Fig. 6). It also appears in the power spectrum of Patterson et al. (2001) The power spectrum does not contain other coherent signals but an enhancement of power between 60 and 75 d−1 (20–24 min), possibly due to QPOs.
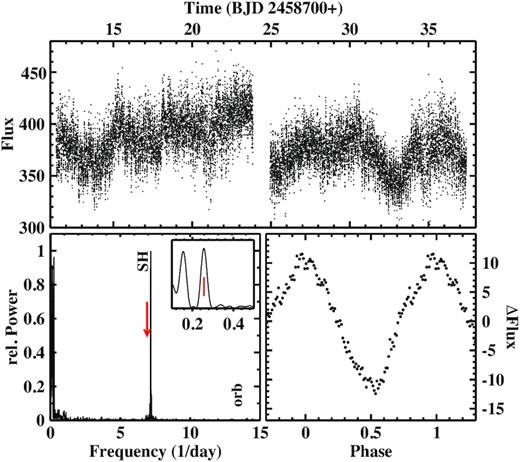
Top: Light curve of V751 Cyg. Bottom left: Power spectrum of V751 Cyg. The red arrow indicates the frequency of the orbital period, which is not detectable in the light curve. The insert shows the low frequency part the power spectrum where the beat frequency between orbital and the SH signals is marked by a red bar. Bottom right: Waveform of the SH modulation.
3.8 V1974 Cyg: superhumps and a 1.3 d variation
V1974 Cyg (Nova Cygni 1992) exhibits two distinct photometric periodicities. The first one, at 0.0812585(5) d (DeYoung & Schmidt 1993; Retter, Leibowitz & Ofek 1997), is considered to be orbital. A second slightly variable period close to 0.0850 d (Semeniuk et al. 1994, 1995; Retter et al. 1997) can be interpreted as a pSH. A third periodicity of 0.08304 d was seen in 1994 by Retter et al. (1997) but did not show up in 1995.
The two available TESS light curves, separated by 2 yr, confirm the presence of the orbital signal at 0.08127(2) d while the SH signal yields slightly different periods of 0.08504(2) and 0.08525(2) d in LC#1 and LC#2 (Fig. 7). Both signals are of comparable strength in the power spectra. Additionally, the power spectrum of LC#2 contains another peak, marked with a question mark in the figure, which is almost as strong as the SH signal. It corresponds to a period of 1.281(7) d. Note that this is not the beat period between the orbital and SH modulations. Its origin remains unclear but is reminiscent of the 0.53 d period seen in LC#2 of V592 Cas (Section 3.5). The 0.083 d period reported by Retter et al. (1997) cannot be detected in the TESS light curves.
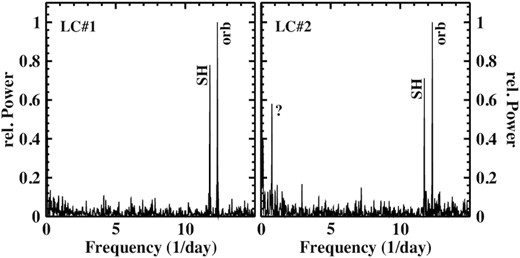
It is noteworthy, however, that in addition to the SH, Semeniuk et al. (1994) found a period of 3.75 d in their data. Although they do not quote error limits, their fig. 7 suggests that this period is compatible with twice the beat between the orbital and the SH periods (1.84 d; see also Semeniuk et al. 1995), similar to what has been seen by Bruch & Cook (2018) in V603 Aql.
3.9 BB Dor: four periods, but not the orbital one
BB Dor (= EC 05287-5847) was identified as a CV by Chen et al. (2001). Their tentative classification as a VY Scl type star was confirmed by Rodríguez-Gil et al. (2012). The latter authors observed long-term variations with a period of 36.43 d as well as a spectroscopic orbital period of 0.154095(30) d. A period of 0.14923(7) d – observed and thought to be orbital by Patterson et al. (2005) – would then be due to an nSH, while a weaker signal at 0.1633 d indicates a pSH. Another still much weaker signal in their power spectrum has a frequency of 12.833 d−1, very nearly the sum of the two SH frequencies.
TESS observed BB Dor in no less than 20 sectors. The star remained in a stable high state all the time. The individual light curves can be combined into two long ones, both with baselines of almost a year (there is a gap of 27 d in the second light curve). LC#1 is shown in the upper frame of Fig. 8. The middle frame contains the light curve of sector 12. Periodic or semiperiodic variations are obvious on three different time-scales: some tens of days, just over 1 day, and a fraction of a day. Predicted times of maxima for the first two of these, based on a formal period measurement (see below) are marked by red dots on top of the light curves in the figure.

Top: Light curve LC#1 of BB Dor. Middle: Light curve of TESS sector 12. The red dots above the light-curves mark predicted times of maxima of variations with a period/quasi-period of 32.15 d (top) and 1.35 d (middle). Bottom left: Power spectrum of LC#1. The insert contains an expanded view of the low frequency range. Bottom right: LC#1 folded on the four independent periods identified in the light curves (after subtracting variations on longer time-scales).
The power spectrum LC#1 is reproduced in the lower-left-hand frame of Fig. 8. That of LC#2 is practically identical. Four independent signals can be identified. The corresponding frequencies F1 - F4 are marked in the figures and listed together with the corresponding periods in Table 3. On a low-power level (not resolved in the figure), several more significant peaks appear, but they all occur at frequencies equal to simple arithmetic combinations of the main signals and are therefore not independent. P1 varies significantly, P2 – P4 only slightly between LC#1 and LC#2. In fact, in the power spectrum of the combined data, the corresponding peaks split up into two. Therefore, values derived from both light curves are listed in the table.
Independent frequencies and their corresponding periods identified in the light curves of BB Dor.
| . | LC . | Frequency (d−1) . | Period (d) . |
|---|---|---|---|
| F1 | LC#1 | 0.0311 (2) | 32.1 (2) |
| LC#2 | 0.0267 (2) | 37.5 (3) | |
| F2 | LC#1 | 0.2225 (2) | 4.495 (3) |
| LC#2 | 0.2231 (1) | 4.483 (3) | |
| F3 | LC#1 | 0.7549 (2) | 1.3247 (3) |
| LC#2 | 0.7533 (2) | 1.3227 (4) | |
| F4 | LC#1 | 6.714 02 (2) | 0.148 9422 (4) |
| LC#2 | 6.714 54 (3) | 0.148 9305 (6) |
| . | LC . | Frequency (d−1) . | Period (d) . |
|---|---|---|---|
| F1 | LC#1 | 0.0311 (2) | 32.1 (2) |
| LC#2 | 0.0267 (2) | 37.5 (3) | |
| F2 | LC#1 | 0.2225 (2) | 4.495 (3) |
| LC#2 | 0.2231 (1) | 4.483 (3) | |
| F3 | LC#1 | 0.7549 (2) | 1.3247 (3) |
| LC#2 | 0.7533 (2) | 1.3227 (4) | |
| F4 | LC#1 | 6.714 02 (2) | 0.148 9422 (4) |
| LC#2 | 6.714 54 (3) | 0.148 9305 (6) |
Independent frequencies and their corresponding periods identified in the light curves of BB Dor.
| . | LC . | Frequency (d−1) . | Period (d) . |
|---|---|---|---|
| F1 | LC#1 | 0.0311 (2) | 32.1 (2) |
| LC#2 | 0.0267 (2) | 37.5 (3) | |
| F2 | LC#1 | 0.2225 (2) | 4.495 (3) |
| LC#2 | 0.2231 (1) | 4.483 (3) | |
| F3 | LC#1 | 0.7549 (2) | 1.3247 (3) |
| LC#2 | 0.7533 (2) | 1.3227 (4) | |
| F4 | LC#1 | 6.714 02 (2) | 0.148 9422 (4) |
| LC#2 | 6.714 54 (3) | 0.148 9305 (6) |
| . | LC . | Frequency (d−1) . | Period (d) . |
|---|---|---|---|
| F1 | LC#1 | 0.0311 (2) | 32.1 (2) |
| LC#2 | 0.0267 (2) | 37.5 (3) | |
| F2 | LC#1 | 0.2225 (2) | 4.495 (3) |
| LC#2 | 0.2231 (1) | 4.483 (3) | |
| F3 | LC#1 | 0.7549 (2) | 1.3247 (3) |
| LC#2 | 0.7533 (2) | 1.3227 (4) | |
| F4 | LC#1 | 6.714 02 (2) | 0.148 9422 (4) |
| LC#2 | 6.714 54 (3) | 0.148 9305 (6) |
The bottom-right-hand frame of Fig. 8, finally, shows LC#1 folded on the four periods, after variations on appropriate longer time-scales have been subtracted in the case of P2 − P4. The waveforms derived from LC#2 are not significantly different.
The slight differences in time between the brightness peaks and the red dots in the upper frame of Fig. 8 and the significantly different periods found in LC#1 and LC#2 indicate that the P1 variations are not strictly periodic. Nevertheless, they can clearly be identified with the quasi-periodic brightenings observed by Rodríguez-Gil et al. (2012). The different periods in the two TESS light curves [embracing the period of Rodríguez-Gil et al. (2012)], separated by a year, indicate that they are not caused by a stable clock in BB Dor. However, their persistence over more than 14 yr tells us that this is not just a transient phenomenon. Rodríguez-Gil et al. (2012) speculate that these variations are due to mass-transfer variation caused by migrating star-spots on the secondary star or stunted outbursts. But it is then not obvious why the brightenings occur with a reasonable well-defined periodicity. The convex shape of the light between maxima suggests a gradual build-up and subsequent decay of the (so far unknown) process responsible for the modulations.
P4 is very close to the main photometric period seen by Patterson et al. (2005) and which is interpreted by Rodríguez-Gil et al. (2012) as due to an nSH. One of the fainter power spectrum peaks mentioned above (better defined in LC#2 than in LC#1) has a frequency of 6.4918 (5) d−1, which, on the one hand, is within the error margin of the spectroscopic orbital period, and, on the other hand, is almost identical to F4 − F2. Thus, P4 can indeed be identified with an nSH period, and P2 is correspondingly the nodal precession period of a warped accretion disc.
What about P3? Could it be the apsidal precession period of an excentric disc? In that case, the expected frequency of a pSH would be F3 + Forb = 7.245 (1) d−1. The closest marginally significant peak in the power spectrum of LC#1 is at 7.2558(6) d−1. The period difference between the orbital and the SH periods would then be three times as large for the positive than for the nSH. While not impossible, this is significantly more than the canonical difference of a factor of two. It may also be questioned why the SH signal is then so much fainter than that due to the apsidal disc motion. An alternative, but equally unsatisfactory hypothesis is an interplay between P1 and P2. Is it a coincidence that in both light curves 3(F1 + F2) = F3 within the formal 1σ error margin? As long as the origin of P1 remains unknown, it is difficult even to speculate about a reason for such an interplay.
The long light curves permit a closer look at the temporal development of the periodic signals. The time resolved power spectrum of LC#2, in the frequency range of the nSH and of F3, constructed using a sliding window with a width of 10 d, is shown in the middle and lower frames, respectively, of Fig. 9, with the light curve shown in the upper frame. The corresponding power spectrum of LC#1 is very similar. The SH signal itself does not vary significantly with time. But it is flanked symmetrically on both sides (stronger at frequencies lower than the SH frequency) by structures modulated with the long period (P1) variations. Their frequency difference with respect to the SH frequency is equal to the frequency of the F3 signal in the lower frame of the figure. F3 is approximate constant during ‘quiescent’ phases, subsides at the onset of the brightenings, and reappears at a lower frequency during their maxima.
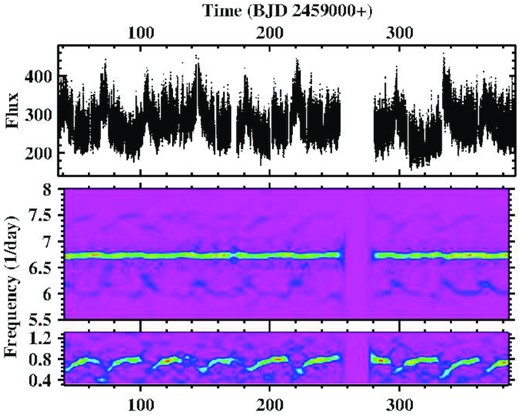
Top: Light curve LC#2 of BB Dor. Middle: Time resolved power spectrum of the light curve in a small range around the nSH frequency. Bottom: The same for a frequency range around F3.
As a final remark on BB Dor, I note that the power spectra of the TESS light curves contain an excess of power between 30 and 100 d−1, encompassing the range in which Chen et al. (2001) observed QPOs.
The complex variability of BB Dra disclosed by the long TESS light curves certainly deserves a more detailed investigation and interpretation. But this is beyond the scope of the present paper and must await a specific study.
3.10 BH Lyn: positive superhumps and QPOs
BH Lyn was discovered as PG 0818 + 513 in the Palomar–Green survey (Green, Schmidt & Liebert 1986). The system is eclipsing and thus makes it easy to determine a reliable orbital period which has been derived many times in the past. The most precise value of 0.155875577(14) d was measured by Stanishev, Kraicheva & Genkov (2006). They also noted the presence of variations at a slightly smaller period of 0.1450(65) d which they interpret as an nSH. A similar variation at 0.1490(011) d was also seen by Patterson (1999). Additionally, Stanishev et al. (2006) observe the presence of a signal close to 32 d−1 in the power spectra of most of their light curves that they attribute to QPOs.
The two available TESS light curves of BH Lyn exhibit irregular variations on time-scales of a few days. Apart from the primary eclipse, the orbital waveform exhibits a clear secondary eclipse. More interesting, however, are the power spectra (after masking the primary eclipses). On the left-hand side of Fig. 10, the power spectrum of LC#1 is reproduced, concentrating on a frequency range of ±2.5 d−1 around the orbital frequency and its first, second, and third overtones. The peak caused by the orbital variations is highlighted in red. On the right-hand side of the figure, the time resolved power spectra in the same frequency range are shown, based on a sliding window with a widths of 4 d (thus structures separated by less than 4 d are not independent). The general appearence of the power spectra of LC#2 is very similar.
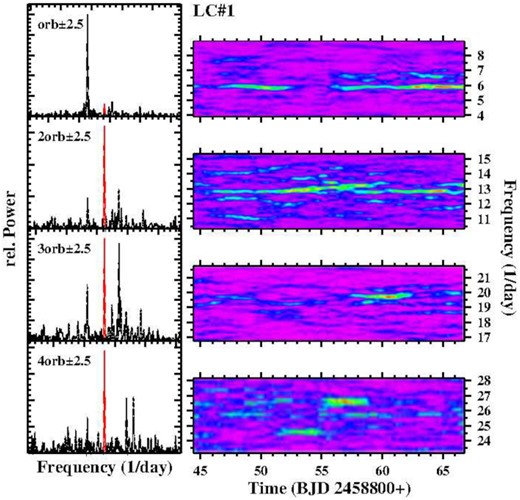
Left: Power spectra of LC#1 of BH Lyn in four narrow frequency ranges of ±2.5 d−1 around the orbital frequency and its first, second, and third overtones (highlighted in red). Right: Time-resolved power spectra of the same frequency range, using a sliding window with a width of 4 d.
While in none of the power spectra a significant peak is detected at a frequency close to that corresponding to the nSHs seen by Patterson (1999) and Stanishev et al. (2006), the dominant signal in the upper frames of the figure has a frequency just below the orbital frequency. The time-resolved power spectrum shows that, albeit exhibiting some modulation in its strength, this signal is persistent over the whole extend of the light curve. It indicates thus the presence of a pSH with a period of 0.17059(5) d in LC#1. A similar persistent pSH is also seen in LC#2, but at a significantly shorter period of 0.16484(4) d. The period excess ϵ = (PSH − Porb)/Porb thus drops from 0.094 in LC#1 to 0.058 in LC#2. While it is known that SH periods can change over time, such a large difference of ϵ at different epochs is unusual.
Apart from the orbital and SH signals, the power spectra contain a multitude of peaks in narrow frequency ranges around the orbital frequency and its overtones. They appear less clearly also at higher overtones than shown in Fig. 10 [note that the QPOs claimed by Stanishev et al. (2006) at 32 d−1 are very close to the forth overtone of the orbital frequency]. No simple relation between them is apparent, meaning that they are independent from each other. The time-resolved power spectra reveal that they can appear for considerable time intervals with varying strength and frequency changes. These are characteristics of QPOs. Their concentration around the orbital frequency and its overtones is noteworthy. While not as extreme, this behaviour is reminiscent of similar properties observed in the old nova CP Pup (see Paper I) and BZ Cam (Section 3.4).
Finally, representative eclipse epochs of BH Lyn are listed in Table 2 for future reference.
3.11 BK Lyn: positive superhump, yes, but no negative one
BK Lyn (= PG 0917 + 342) is an NL variable with some curious peculiarities. At an orbital period of 0.07498(4) d (Ringwald et al. 1996), it is one of the very few (non-magnetic) NL variables below the CV period gap. In a never before seen transition, in 2005, BK Lyn morphed into a ER UMa star (Patterson et al. 2013), i.e. an SU UMa star with many normal outbursts in quick succession and a very short supercycle. However, in 2014, the system returned to the more stable high brightness state of an NL, as is evident from the AAVSO long-term light curve. SHs were first seen in BK Lyn by Howell et al. (1991) but misinterpreted as orbital variations. Skillman & Patterson (1993) then correctly identified a 113.1 min modulation with a slightly varying period as a pSH, which was later confirmed by Misselt & Shafter (1995). In a more extensive photometric study, Patterson et al. (2013), in addition to pSHs, also detected their negative counterparts in some observing seasons. Finally, Yang, Chou & Ngeow (2017) claim the presence of a long-term period of 42.05(1) d in BK Lyn.
The only TESS light curve available (upper frame of Fig. 11) shows a clear modulation on the time-scale of about 1.5 d superposed on a longer period variation. The latter is well-fit by a sine wave with a period of 17.29(3) d (the red line in the figure). But since the light curve covers only just about 1.5 cycles, it is by no means clear that this modulation is, in fact, periodic and persistent. The origin of the more rapid variations becomes immediately clear looking at the power spectrum in the lower-left-hand frame of Fig. 11, which is dominated by a strong signal at FSH = 12.7096(3) d−1 (PSH = 0.078681(2) d). It is evidently due to the pSH observed on previous occasions and now has a slightly longer period. A much fainter signal is present at a higher frequency of Forb = 13.344(2) d−1 (Porb = 0.074942(9) d). Within the error quoted by Ringwald et al. (1996), this period is identical to the spectroscopic orbital period but has a higher precision. Another signal appears at a low frequency of Fb = 0.633(1) d−1 (Pb = 1.579(3) d). Within the error margins, this is the difference between Forb and FSH and thus the period of the apsidal motion of an eccentric disc in the canonical interpretation of pSHs. It explains the shorter time-scale modulations seen in the light curve. At higher frequencies signals at simple arithmetic combinations of Forb and FSH appear, but the data contain no trace of the nSH seen by Patterson et al. (2013).
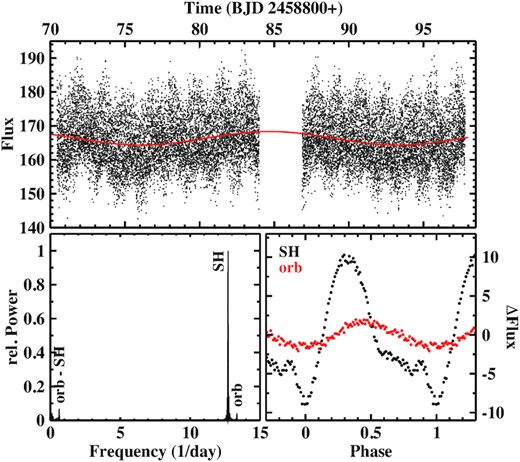
Top: Light curve of BK Lyn. The red graph represents a least-squares sine fit with a period of 17.29 d. Bottom: Power spectrum of BK Lyn (left) and waveforms of the SH and orbital modulations (right).
The waveform of the SH variations (in black, together with the unconspicious quasi-sinusoidal orbital waveform in red) is shown in the lower-right-hand frame of Fig. 11. Over the years, the SH shape varies. In the TESS data, it comprises only the first have of the cycle. The second half is characterized by an only slighly declining level in the phase range 0.55–0.85 before dropping to the minimum at phase 0. In Patterson et al. (2013; their fig. 3), the waveform is clearly double humped, while Skillman & Patterson (1993) observed an almost sinusoidal SH (their fig. 6).
3.12 AH Men: shallow eclipses and a strong negative superhump
Buckley et al. (1993) published the first encompassing photometric study of AH Men (1H05551-819). Apart from QPO-like variations in the range of 600–2400 s, they detected the presence of a quasi-sinusoidal modulation at 0.1392202(9) d. Radial velocities measurements confirm that this variation ‘occurs at, or very near to, the orbital period’. This, however, is at odds with later observations of Patterson (1995) who noted the continuous presence of a signal at 0.1229934 (6)d. While in 1995 AH Men did not exhibit other coherent variations, between 1993 December and 1994 February Patterson saw strong variations at 0.127208 d (which he considers orbital), 0.12300, 0.062517, and 3.7 d, as well as oscillations in the range of 17–22 min. In a later paper, Patterson (1998) mentions an SH period of 0.1385(2) d. Should this [and the period seen by Buckley et al. (1993)] be due to a pSH, while the 0.12300 d period points at an nSH?
The upper frame of Fig. 12 shows one of the five available TESS light curves (LC#5). It is dominated by regular variations, which, as we will see, are due to the beat between the orbital and an nSH period. While this signal shows up in the power spectra of all light curves, it is obvious to the eye only in LC#3 and later. Apart from this periodicity, the power spectrum of LC#5 (lower-left-hand frame of the figure) just as that of all other light curves is dominated by a strong peak close to 8.09 d−1 and some much fainter satellite lines, as shown in the lower-left-hand frame of the figure and on an expanded scale in the left insert. I interpret the strong FSH = 8.09 d−1 signal as being due to an nSH and a smaller peak at Forb = 7.86 d−1 as orbital. Other signals are related to the beat between them. At higher frequencies, another group of signals appears (right insert), the strongest occurring at 2Forb = 15.72361(8). At still higher frequencies, additional peaks are seen, which can all be interpreted as linear combinations of Forb and FSH.
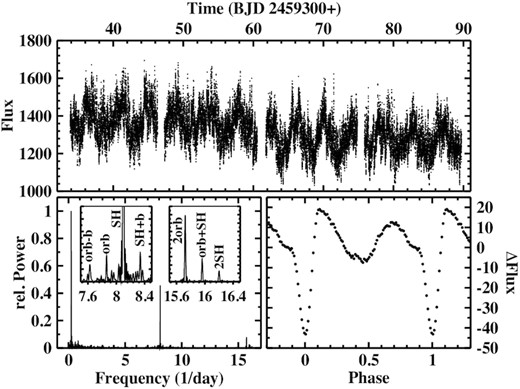
Top: Part of LC#5 of AH Men. Bottom left: Power spectrum of the light curve. The inserts contain small frequency intervals of this power spectrum on an expanded vertical scale. Here, ‘b’ stands for the beat frequency between the orbital and SH signals. Bottom right: Orbital waveform of AH Men (average of all light curves).
Although rather stable, the period of the SH varies slightly. The corresponding values measured in the individual light curves are: 0.12364(3) (LC#1), 0.12383(3) (LC#2), 0.123485(5) (LC#3), 0.12337(2) (LC#4), and 0.123446(6) (LC#5).
3.13 RR Pic: only transient superhumps
RR Pic is a well-studied old nova. The orbital period reveals itself in the form of a clear and persistent hump, first seen by van Houten (1966) and ever since. The most precise value of 0.145025959 d was derived by Fuentes-Morales, Vogt, & Tappert (2018). They also saw pSHs with a period of 0.1577 d in 2007. Schmidtobreick et al. (2008) report another SH instance in 2005 with the same period and which went along with a signal at the beat between the SH and orbital periods.
The numerous sectorial data sets of RR Pic observed by TESS can be combined into five contiguous light curves, two of which encompass about 8 months. The orbital signal is outstanding in the respective power spectra, but no trace of an SH is visible, even after carefully subtracting the average orbital waveform from the data (Fig. 1c). It is, however, remarkable that the waveform is extremely stable [and quite similar to the one shown in fig. 3 of Schmidtobreick et al. (2008)] over the almost 3 yr spanned by the data. Even small details are faithfully repeated in the waveforms derived from the individual light curves.
Schmidtobreick et al. (2008) and Fuentes-Morales et al. (2018) analysed light curves of RR Pic from 11 observing seasons and saw SHs only twice. Adding to this, the TESS data without SHs (over a total time base of ≈3 yr) make it clear that SHs in this system are only rare and transient events.
3.14 AO Psc: no confirmation of superhumps
The optical light curve of the well-known intermediate polar AO Psc is dominated by the orbital period at 0.1495 d and the orbital side band of the white dwarf spin period at 14.31 min (Motch & Pakull 1981; Patterson & Price 1981). SHs in AO Psc, with a period of 0.149627 d, are only mentioned briefly by Patterson (2001) who referred details to a publication in preparation, which, however, never appeared.
The power spectrum of the single TESS light curves contains strong signals at the orbital frequency Forb, the orbital sideband of the white dwarf spin frequency Fspin − Forb, and weaker signals at 2Forb, Fspin, Fspin − 2Forb, 2Fspin, and 2Fspin − 2Forb. But there are no indications of SHs (Fig. 1d).
3.15 AY Psc: no superhumps, but an increasing orbital period
In contrast to the other objects in this study, AY Psc is a dwarf nova. It belongs to the Z Cam stars (Mercado & Honeycutt 2002), i.e. those dwarf novae which occasionally remain in a standstill. The TESS light curve, observed in subsequent time intervals in two sectors and covering 51 d, is rather stable and does not contain the usual alternations between outbursts and quiescent phases with a quasi-period of 18.3 d (Han et al. 2017). It may therefore be concluded that the system was in a standstill during the entire observing period. During such phases, the accretion disc is expected to be in a hot state similar to those of NLs and old novae. Therefore, I include AY Psc in this study.
AY Psc is an eclipsing system as first noticed by Szkody et al. (1989). Orbital ephemeris were provided by Diaz & Steiner (1990) and later refined by Gülsecen, Retter & Esenoǧlu (2009) and Han et al. (2017). Gülsecen et al. (2009) reported the presence of nSHs with a slightly changing period between 0.2057 and 0.2073 d during three observing missions in 2003, 2004, and 2005. The total amplitude of the light variations of AY Psc in each of these missions was about 2.25 mag, which is similar to its average outburst amplitude (Han et al. 2017). Thus, the system was observed during a period of normal dwarf nova activity. Gülsecen et al. (2009) did not investigate a dependence of the SH properties on the phase of the outburst cycle.
The power spectrum of the TESS light curve (after masking the eclipses) does not confirm the presence of SHs Fig 1e). The only significant signals are at the orbital frequency and its overtones. Thus, if nSHs occur during the normal activity cycle of AY Psc, they subsided at least during the prolonged standstill covered by TESS.
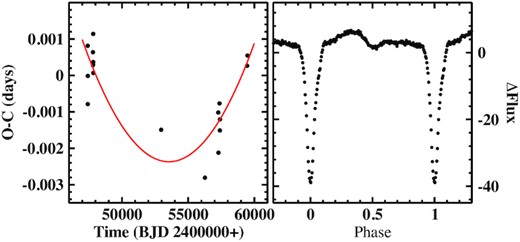
Left: O − C diagram of eclipse timings of AY Psc with respect to linear ephemeris (equation 4). The red graph is a least-squares fit of a second-order polynomial to the data. Right: Orbital waveform of AY Psc during standstill.
The light curve, folded on the orbital period, yields the waveform shown in the right-hand frame of Fig. 13. Apart from the primary eclipse, a secondary eclipse occurs at phase 0.5. It is preceded by a hump. No hump is apparent at the phases before the primary eclipse, in contrast to what is often seen in other eclipsing CVs and is attributed to enhanced emission from a bright-spot. The waveform is thus different from that observed by Gülsecen et al. (2009) in white light (see their fig. 3), but this may at least in part be due to the different passband of TESS.
3.16 V348 Pup: superhumps confirmed
At an orbital period of 0.101838931(14) d (Rolfe, Haswell & Patterson 2000), V348 Pup is an eclipsing NL variable right at the centre of the CV period gap. Photometric variations with a period slightly different from the orbital one made Tuohy et al. (1990) suspect the star to be what would nowadays be considered an asynchronous polar; a notion which could neither be confirmed nor rejected in pointed X-ray observations by Rosen et al. (1994), while Froning, Long & Baptista (2003) found no evidence for a magnetic nature. Instead, Rolfe et al. (2000) reported SHs with a slightly variable period in V348 Pup in 1991, 1993, and 1995, which, however, were not seen when Saito & Baptista (2016) observed the star at a later epoch.
The light curve of V348 Pup, combining data from two TESS sectors, is shown in the upper frame of Fig. 14. The strong out-of-eclipse variations have a period of 1.797(1) d and immediately suggest to be due to the beat between the orbital and an SH period and thus the precession period of an accretion disc. This is confirmed by the power spectrum (lower-left-hand frame of the figure) which, apart from the dominating signal at the beat frequency, contains a peak at the orbital frequency Forb and a strong signal at |$F_{\rm SH} = 9.2626(8)\, {\rm d}^{-1}$| (PSH = 0.107961(9) d). The period of the latter lies within the range of SH periods observed by Rolfe et al. (2000), leaving no doubt that it is due to a pSH. Other signals and a multitude of peaks at frequencies beyond the range shown in the figure can all be expressed as simple arithmetic combinations of Forb and FSH. The waveform of the SH is significantly structured as seen in the lower-right-hand frame of Fig. 14.
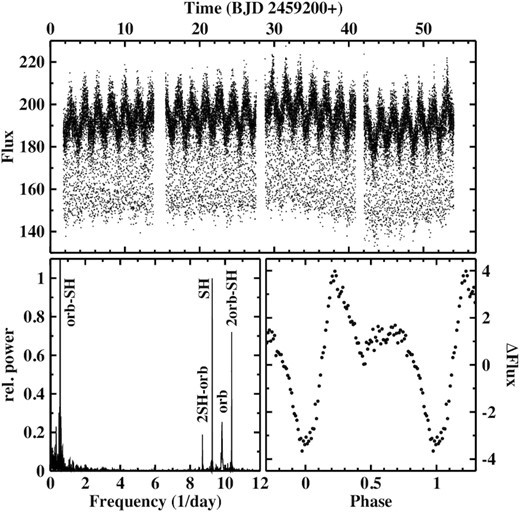
Top: Light curve of V348 Pup. Bottom: Power spectrum (left) and SH waveform (right).
3.17 RW Tri: no superhumps in TESS data
RW Tri is a deeply eclipsing NL variable of the UX UMa type. Low amplitude (≈0.5 mag) oscillations on time-scales of some tens of days have been observed by Honeycutt et al. (1994), Honeycutt (2001), and even more clearly by Bruch (2020). Apart from this, the system is relatively stable as is corroborated by the long-term AAVSO light curve. Smak (2019) reports nSHs with a period of 0.2203 d in his observations obtained in 1984 and possibly in 1957. They were, however, not present in 2015–2016 (Bruch 2020). The more extensive continuous TESS data permit an additional verification of Smak’s claim of SHs in RW Tri.
A single TESS light curve of the system is available (upper frame of Fig. 15). Over its 24 d time base, a gradual rise and subsequent decline in brightness occurs, which is roughly compatible with the oscillations mentioned above. The flux level at the bottom of the eclipses follows these variations. This means that the responsible light source is not eclipsed.
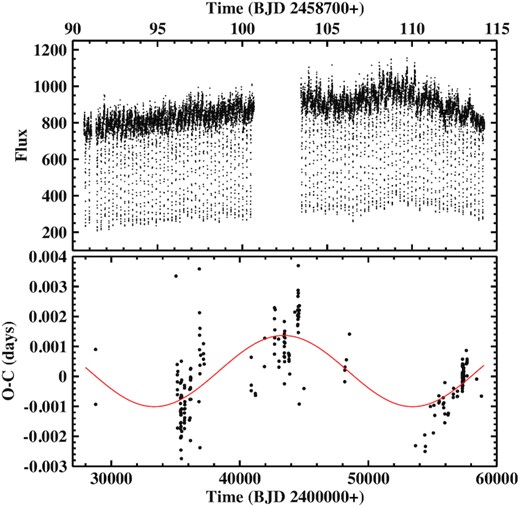
Top: TESS light curve of RW Tri. Bottom: O − C diagram of eclipse timings of RW Tri with respect to linear ephemeris (equation 7). The red graph is a least-squares sine fit.
The power spectrum does not contain significant signals at frequencies other than the orbital frequency and its overtones (Fig. 1f). Thus, at least during the epoch of the TESS observations, no SHs were excited in RW Tri.
3.18 UX UMa: superhumps remain to be isolated events
UX UMa is the prototype of NL variables, in particular of those system, which, in contrast to VY Scl stars, have never been observed to go into a low state. As the prototype of its class and the brightest eclipsing NL variable, UX UMa has been extensively studied in the past (see Neustroev et al. 2011, for a summary of previous observations). The orbital period was last refined by Baptista et al. (1995). In extensive photometric observations during the 2015 observing season, de Miguel et al. (2016) found a modulation with a period of 3.680 d in the light curve of UX UMa, which they interpret as being due to a retrograde precession of the accretion disc. An associated nSH at the beat period of the precession and the orbit is also seen. Bruch (2020) confirmed this behaviour but also noted that it was restricted to that particular season and did not repeat itself in previous or following years.
Is there any trace of the unusual behaviour observed in 2015 to be found in the TESS observations taken in 2019 August–October and 2020 February–April? No, there is not. The power spectra of the two TESS light curves do not contain any significant signal other than the orbital one and its overtones (Fig. 1g). The orbital waveform (left-hand frame of Fig. 16) is characterized – apart from the primary eclipse – by a single hump, interrupted by the secondary eclipse that gives the hump the structure of two separate ‘horns’. The primary eclipse egress exhibits a clear change of gradient, i.e. the typical sign of a retarded egress of a hot-spot. The flux level just after eclipse egress is considerably lower than just before ingress. This waveform is different from that normally observed at shorter wavelengths (see fig. 20 of Bruch 2020). A comparison of the waveforms out of eclipse resulting from LC#1 (black) and LC#2 (red) is shown in the right-hand frame of the figure. Only slight variations occur in the 6 months between the light curves.
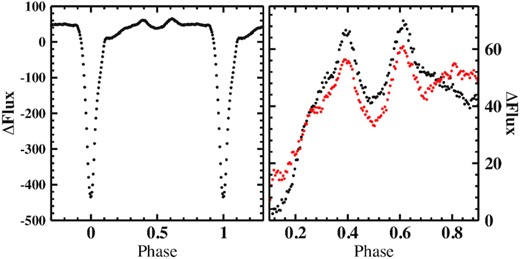
Left: Orbital waveform of UX UMa (average of LC#1 and LC#2). Right: The same on an expanded vertical scale, restricted to out-of-eclipse phases and shown separately for LC#1 (black) and LC#2 (red).
Just as for UU Aqr and RW Tri, the orbital period of UX UMa was last refined almost 30 yr ago (Baptista et al. 1995). Again, I took advantage of light curves observed between 1999 and 2022 found in the AAVSO archives, as well as of some unpublished light curves taken between 1977 and 1992, provided by R.E. Nather and E.L. Robinson (private communication). They yielded no less than 291 useful additional eclipse epochs (Table A4). Representative eclipse epochs derived from the TESS light curves are listed in Table 2.
It turns out that within the 1σ error, the period is identical to the one derived by Baptista et al. (1995).3 Indeed, in spite of the much longer time base, the formal error increased. This is explained by the O − C diagram, reproduced in the left-hand frame of Fig. 17, which reveals an increased non-random scatter of the data points in recent years.
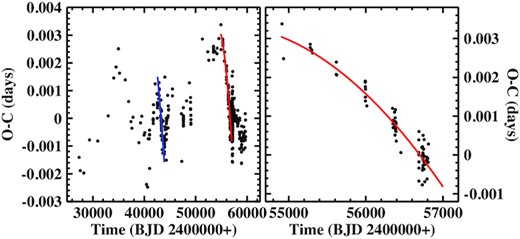
Left: O − C diagram of the eclipses in UX UMa. The blue and red lines mark intervals of particularly strong gradients. Right: Detail of the O − C diagram corresponding to the interval marked by the red line in the left-hand frame, together with the least-squares parabolic fit to the data.
In the early years, a 29 yr cyclic variation of the orbital period of UX UMa was first suspected by Mandel (1965) and further discussed by Nather & Robinson (1974) and Africano & Wilson (1976), but then called into question by Kukarkin (1977) and Quigley & Africano (1978). Regarding the O − C diagram in fig. 5 of Baptista et al. (1995), this hypothesis can clearly be rejected. This is impressively confirmed by the present results (Fig. 17), which extends the time base by about a factor of 2. The O − C diagram indicates non-periodic but systematic variations of the the orbital period on widely varying time-scales. The most rapid O − C (and consequently period) changes are highlighted by blue and red lines in the figure which have very nearly the same gradient. The right-hand frame of Fig. 17 contains an enlarged version of one of these O − C diagram sections. The red line represents a least-squares second-order polynomial fit to the data that yields a period change of |$\dot{P} = -1.97 \times 10^{-10}$|. This corresponds to a time-scale for the period decrease as short as |$P/\dot{P} = 2.73 \times 10^6$| yr.
On secular time-scales, the periods of CV are expected to decrease due to angular momentum loss of the system via magnetic breaking and gravitational radiation. Such variations are monotonic and occur on vastly longer time-scales than observed here. Period variations on time-scales of years and with changing sign are not uncommon in CVs. If they are cyclic, they are often explained by the presence of a third body in the system (a hypothesis more often than not disproved by additional observations). Alternatively, the Applegate mechanism (Applegate 1992) is frequently invoked with mixed success. However, it appears fair to say that so far no generally excepted idea to explain the often erratic period variations has been put forward.
3.19 DW UMa: a positive, yes, but no negative superhump
The eclipsing system DW UMa has been subjected to many photometric studies which revealed the presence of positive and nSHs. The most extensive investigation was performed by Boyd et al. (2017) who also cite references to other relevant papers. The orbital period is 0.1366065324(7) d. SHs were observed with slightly varying periods around 0.133 d (nSH) and 0.145 d (pSH). The beat period between the orbit and the SHs is also clearly seen.
The latter feature is impressively confirmed in the two TESS light curves, the first of which is reproduced in the upper frame of Fig. 18. The power spectra (after masking the eclipses) basically confirm the earlier results with the noticeable exception that no trace of an nSH is present. Without assessing their formal significance, I identified no less than 40 (LC#1) and 35 (LC#2) peaks up to the Nyquist frequency, which appear to stand out above the surrounding ‘continuum’. All except 3 (LC#1) and 5 (LC#2) can be explained as nForb + mFb where Fb = Forb − FSH and n and m are integer values in the range 1 ≤ n ≤ 46 and −4 ≤ m ≤ 2. The pSHs have significantly different periods of 0.14387(2) d (LC#1) and 0.14479(3) d (LC#2) in the two light curves separated by ≈2 yr. The orbital (eclipses masked) and SH waveforms are shown in the lower frames of Fig. 18. Large (orbital) and moderate (SH) differences between LC#1 and LC#2 are evident. For future reference, representative eclipse epochs for the time intervals covered by the light curves are listed in Table 2.
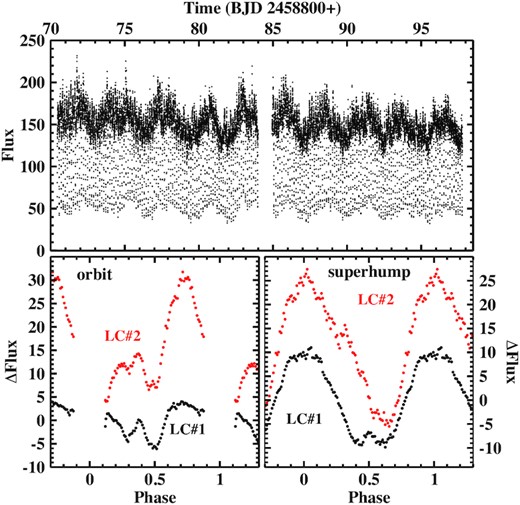
Top: Light curve LC#1 of DW UMa. Bottom: Orbital (left) and SH waveforms (right) derived from light curves LC#1 (black) and LC#2 (red, shifted vertically for clarity).
3.20 HS 1813 + 6122: transient superhumps, transient outbursts, and partial eclipses
Almost all our limited knowledge about the configuration and physics of HS 1813 + 6122 (HS 1813 hereafter) comes from a single publication: Rodríguez-Gil et al. (2007). They performed photometric and spectroscopic observations on various occasions between 2000 and 2004 and derived an orbital period of 3.55 h. Their photometry also contained a modulation at 3.39 h, which they interpreted as an nSH. In contrast to what is seen in the present TESS data (see below), Rodríguez-Gil et al. (2007) apparently did not observe outburst of HS 1813, nor could they identify eclipses. Based on the spectroscopic evidence, they classify the system as an SW Sex type star.
TESS observed HS 1813 in many sectors, permitting to construct two almost half year long light curves (LC#1 and LC#2), separated by just 1 month, and two shorter light curves at later epochs (see Table 2). The flux level differs strongly and systematically from one sector to the next. This cannot be real and must be attributed to difficulties to define the zero-point of flux for the TESS light curves. The discontinuous flux levels thus required to add or subtract constants when stitching together data from different sectors to form a continuous light curve. This introduces considerable uncertainties in the general trend of the resulting curves, but should not affect relative variations within a given sector or high-frequency variations.
The upper and lower right frames of Fig. 19 show LC#1 and LC#2, respectively, binned in intervals of 0.5 d. They contain quite unusual and surprising features. The single sector light curve LC#3 only contains low level variations, while the longer LC#4 is not unlike LC#1. Disregarding the long-term trends which may well be artificial (see above), the light curve is characterized by some brightenings above an otherwise quiescent background (LC#1), and then rapidly morphs into a decidedly dwarf NL light curve (LC#2). Due to the uncertainty of the flux zero-point, it is difficult to determine the amplitude of the outbursts. Assuming that the flux scale of LC#2 is at least approximately correct, the amplitude reached up to ≈0.5 mag and thus remained considerably below normal dwarf nova outburst amplitudes. The rapid change in behaviour between LC#1 and LC#2, which is also manifest in other than the outburst characteristics (see below), is rather unique. I am not aware of another CV which has been observed to behave similarly with the possible exception of the transient ER UMa-type behaviour of BK Lyn (Section 3.11). This certainly deserves a deeper investigation, but is not the topic of this study.
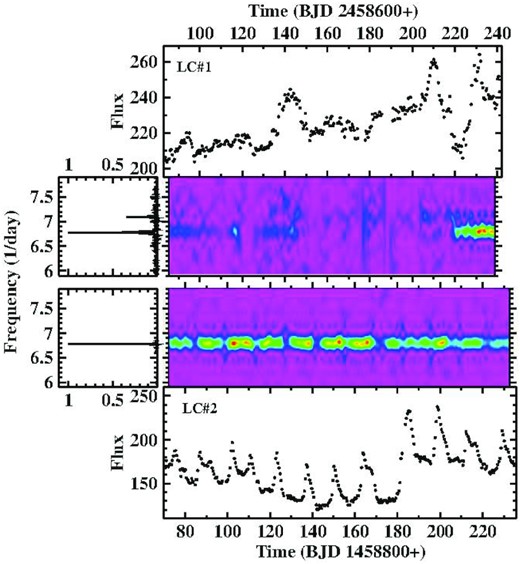
Light curves LC#1 and LC#2 of HS 1813 and their power spectra. The right upper and lower frames show light curves (binned in intervals of 0.5 d) of a very different general aspect, but close in time. The left-hand frames contain the respective power spectra in a small interval around the orbital (dominating signal) and SH frequencies (only present in LC#1). The remaining frames show the time resolved power spectra of the same frequency range and aligned in time with the light curves.
The power spectra of all light curves are dominated by signals at the orbital frequency and overtones. Their strengths, however, vary considerably over time as is evident in the time resolved power spectra in the two middle-right hand frames of Fig. 19 (the frames on the left-hand side contain the conventional power spectra of the entire light curves in the same frequency range). In LC#1, the orbital signal is present during the first weeks, gets fainter thereafter, and then suddenly increases strongly in power at the end of the light curve. Similar fluctuations in strength are also present in LC#3 and LC#4 (not shown). In constrast, in LC#2, i.e. during the episode of dwarf NL outbursts, it remains on a constant high level.
The SH reported by Rodríguez-Gil et al. (2007) is only present in the latter part of LC#1 and at the same frequency of |$F_{\rm SH} = 7.0890(5)\, {\rm d}^{-1}$| (PSH = 0.141063(9) d) observed by them. It cannot be detected in any of the other light curves and must therefore be considered transient.
The orbital waveforms, as derived from LC#1 and LC#2, are shown in Fig. 20, separately for bright (black) and quiescent (red) intervals. While differences between bright and quiescent intervals remain small, significant changes between LC#1 to LC#2 are evident. In both light curves, the waveform is dominated by a broad hump, cut in by a shallow V-shaped (and thus partial) eclipse. In LC#1, the hump is somewhat more structured (possibly doubles) than in LC#2. Moreover, it shifts by 0.3 units to later phases and the minimum broadens in LC#2. This indicates an obvious change in the structure of the dominating light sources in HS 1813. It is close at hand to speculate that this change is somehow related to the onset of the dwarf nova-type brightenings. It is noteworthy, however, that in dwarf novae, the waveform normally changes significantly between quiescence and outbursts while this is not the case here.
Orbital waveform of HS 1813 during epochs of low (LC1#1, left) and high (LC#2, right) outburst activity. Black symbols refer to outburst epochs and red ones to intervals between outbursts.
3.21 RX J2133.7 + 5107: superhumps and an unidentified 325 s modulation
This system was detected in the ROSAT Galactic Plane Survey (Motch et al. 1998) and identified by Bonnet-Bidaud et al. (2006) as long period (Porb = 0.297431(5) d; Thorstensen, Peters & Skinner 2010) intermediate polar with a white dwarf spin period of 570.82 s. They also saw the orbital side band of the spin period in their power spectra. In a multiyear campaign, de Miguel et al. (2017) encountered an nSH with a slightly varying period in all observing seasons between 2010 and 2016.
The TESS light curve confirms these findings. The strongest signal in the power spectrum (left-hand frame of Fig. 21) corresponds to a period of 0.28916(3) d, which is very close to the average nSH period observed by de Miguel et al. (2017). Just as their observations, the TESS data do not contain a signal at the beat between orbital and SH period. But in contrast to the former, the power spectrum of the latter (weakly) reveals orbital variations. The continued presence of the SH in all appropriate observations since 2010 allows classifying it as permanent.
Power spectra of the RX J2133.7 + 5107 light curve, including the SH and orbital signals (left), the white dwarf spin signal and its orbital sideband (middle), and an unidentified high frequency signal (right). The vertical scale is the same in the left-hand and middle frames, but greatly expanded in the right-hand frame.
Not surprisingly, the power spectrum of the TESS light curves also contains a strong signal at the white dwarf spin period (measured to be 570.8914(5) s; middle panel of Fig. 21), the orbital side band and the first overtone (not shown). de Miguel et al. (2017) also mention signals at Fsp − Forb + FSH and Fsp − Forb − FSH. On close inspection, both of these are also weakly present in the TESS light curve. de Miguel et al. (2017) noted that the spin period is decreasing over the years. The TESS data permit to add an additional point, which excellently confirms the linear trend. A least squared fit to all available data yields dP/dt = −3.8 ± 0.2 msec yr−1.
While the above results just confirm previous knowledge, the TESS light curves reveal an additional modulation at a high frequency of F = 265.898(2) d−1 (P = 324.937(3) s; right-hand frame of Fig. 21). It does not have any obvious relation to the other periodicities in the system. Time-resolved power spectra reveal that its is persistent – with some variations in its strength – throughout the entire light curve.
The nature of this modulation remains thus unclear. Its coherence over at least 2 months makes the accretion disc unlikely as the place of origin. I am also not aware of any mechanism inherent in the secondary star that may lead to such short-period variations. It may be permitted to speculate about white dwarf pulsations as their origin. The period is within the range observed in well-established white dwarf pulsators in CVs such as GW Lib (van Zyl et al. 2004; Chote & Sullivan 2016, and others) and V455 And (Araujo-Betancor et al. 2005; Szkody et al. 2013; Bruch 2020). But then, in these stars, more than one pulsation mode is excited, leading to multiple power spectrum signals, differently from what is observed in RX J2133.7+5107. Moreover, they are short-period CVs where the accretion disc is expected to be weak so as not to outshine the white dwarf. At the long period of RX J2133.7 + 5107, the (precessing) accretion disc and the accretion regions close to the magnetic poles of the WD in this intermediate polar will dominate the optical emission and are thus likely to mask any contribution from the white dwarf itself.
3.22 KIC 8751494: strongly contaminated TESS light curves
KIC 8751494 was detected as a NL variable, possibly of the SW Sex subtype, in Kepler data by Williams et al. (2010). They detected variations with a period of 0.1223(7) d. Later, Kato & Maehara (2013), also using Kepler data, found this period to be slightly variable and interpreted it as a pSH, the orbital modulations – much fainter than the SH – having a period of 0.114379(1) d.
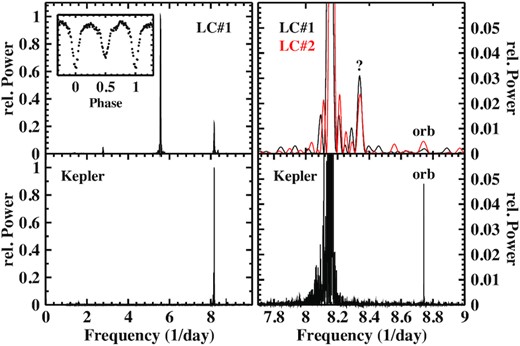
Top left: Power spectrum of LC#1 of KIC 871494. The insert shows the data folded on the period corresponding to half of the frequency of the dominating signal. These variations can be attributed to contamination from the star ATO J291.0335 + 44.9915 located close to KIC 871494. Top right: Parts of the power spectra of LC#1 (black) and LC#2 (red) on an expanded scale. Bottom: The same for the power spectrum of the Kepler data of KIC 871494.
In addition to the contamination from ATO J291.0335 + 44.9915, the TESS power spectra also contain signals coming from KIC 8751494 itself. The SH is clearly present at slightly different frequencies of FSH = 8.152(1) d−1 (PSH = 0.12267(2) d) in LC#1 and FSH = 8.1617(3) d−1 (PSH = 0.12252(5) d) in LC#2. However, the orbital signal prominently seen in the Kepler data (power spectrum in the lower frames of Fig. 22) is only very weakly present (see right-hand frames of the figure). Instead, the power spectra of the TESS data contain a significant peak between the SH and the orbital frequencies, marked with a question mark in the figure. The frequency is identical on the 2σ level in both light curves. The average is F = 8.335(5) d−1 (P = 0.11969(7) d). The nature of this additional periodicity is not immediately obvious and I leave this question open.
3.23 KIC 9406652: alternating positive and negative superhumps
This object was identified as a variable star by Debosscher et al. (2011) in Kepler data. The first detailed investigation, based on low cadence light curves taken during Kepler quarters 1 through 15, was performed by Gies, Guo & Howell (2013) who pointed out its similarity to old novae and NL variables. They found the orbital period [later refined by Kimura et al. (2020) to be 0.25451 d], an nSH with a period of 0.2397 d, and a supraorbital period of 4.131 d, which is the beat between the orbital and SH periods. The light curve is punctuated by semiregular brightenings that made Kimura et al. (2020) classify KIC 9406652 as an IW And-type star, i.e. an unusual type of Z Cam-type dwarf novae. KIC 9406652 may thus not be a genuine NL variable. Considering that the TESS data were apparently taken during such a standstill when the accretion disc – just as in the case of AY Psc (Section 3.15) – is in a similar hot state as those of NLs and old novae I include KIC 9406652 in this study.
TESS observed the star in four sectors. The first and the last two of these, separated in time by about 2 yr (taken in 2019 and 2021, respectively), are consecutive. The data of the latter can be combined into a single light curve. However, those of the former have drastically different flux levels (which may be an artefact considering the known uncertainties concerning the absolute flux scale of TESS light curves) and somewhat distinct properties (see below). Therefore, I prefer not to combine them.
The behaviour of KIC 9406652 is quite different during the two epochs. I first concentrate on the 2019 data [LC#1 and LC#2; Fig. 23: light curves (top), power spectra (middle), and orbital, and SH waveforms (bottom)]. Both light curves exhibit variations on time-scales of several days. The power spectra reveal signals with periods of several hours. In LC#1, the strongest signal corresponds to a period exactly twice that of the second-highest peak and must therefore be interpreted as the first overtone of a modulation with a period of P = 0.2864(1) d. This period is 12.5 per cent longer than the orbital period Porb, which is also manifested in the power spectrum together with its first overtone. It is thus close at hand to identify P = PpSH with the first appearance of a pSH in KIC 9406652. The power spectrum also contains a fainter peak at FpSH + Forb (and still fainter signals at higher overtones of the principal signals), but the beat period 1/FpSH − 1/Forb and thus the apsidal precession period of the implied eccentric accretion disc is notably absent. The waveform of the orbital modulations (black graph in the bottom frame of Fig. 23) is qualitatively explained by ellipsoidal variations of the secondary star, considering the long period of this system and the red TESS passband, where the secondary minimum is partially filled in by reflection of light from the primary component. In contrast to the easily explained orbital waveform, the shape of the SH waveform (red graph) is quite peculiar with two peaks of different extension and decidedly pointed minima and maxima.

Properties of light curves LC#1 (left column) and LC#2 (right column) of KIC 9406652: light curves (top), low frequency part of the power spectra (middle), and orbital (black) and SH (red) waveforms (bottom).
In LC#2, the strength of the fundamental SH mode and its first overtone is inverted. The SH amplitude is enhanced, and the waveform – still double humped but now superposed upon a single larger maximum – has a much more gentle (rounded) shape. The orbital waveform has not changed much with respect to LC#1. At PpSH = 0.28502(5) d, the SH period is slightly but significantly shorter than in LC#1.
In 2021, the light curve of KIC 9406652 was quite different (upper-left-hand frame of Fig. 24). It exhibits a clear periodicity on the time-scale of several days. The corresponding peak in the power spectrum (lower-left-hand frame of the figure) indicates a period of 3.998(9) d, which is close to the beat between the orbital period and the period PnSH = 0.239197 (8) d corresponding to the main signal in the power spectrum. The latter is within the range of nSH periods seen in the Kepler data (Kimura et al. 2020). Thus, the nSH is back and the pSH has gone. On the scale of the figure, the orbital period is only manifested in the power spectrum by its first overtone. This is easily explained by the orbital waveform (upper-right-hand frame of the figure), which is somewhat different than in LC#1 and LC#2, having maxima of different height and a deeper secondary minimum. The SH waveform (lower right) is dominated by a strong maximum with two small humps on top.

Properties of light curve LC#3 of KIC 9406652: light curve (upper left), low frequency part of the power spectrum (lower left), orbital waveform (upper right), and SH light curve (lower right).
3.24 NSV 1907: superhumps confirmed
Discovered as a variable star a long time ago (Hoffmeister 1963), NSV 1907 (= CRTS J051654.1 + 33252) remained largely unstudied until quite recently, when Hümmerich et al. (2017) identified it as a deeply eclipsing NL CV, possibly of the RW Sex subclass. The eclipses permitted them to measured an accurate orbital period of 0.2761069(2) d, i.e. on the longer side of the CV period distribution. A secondary minimum at eclipse phase 0.5 in their white light, V and B light curves attests to a non-negligible contribution of the secondary star at this long period. Hümmerich et al. (2017) also observed a 4.2 d modulation, which they interpret as the nodal precession period of an accretion disc and which they use to predict a period of 0.2591 d for a (negative) SH.
The TESS light observations confirm the presence of the SH as well as the nodal precession period. The light curve is shown in the upper frame of Fig. 25. Apart from the eclipses, it is characterized by a strong increase and subsequent decrease of the brightness of NSV 1907 in its second half. Nevertheless the flux at eclipse minimum remains almost the same, meaning that the light source responsible for these variations is largely eclipsed. The out-of-eclipse flux level exhibits wiggles on the time-scale of a few days, which grow much stronger during the phase of increased brightness in the latter part of the light curve. A power spectrum of the data after removal of the eclipses and the longer-term variations contains a strong peak at a frequency of 0.232(2) d−1. The corresponding period of 4.30(5) d is very close to the period seen by Hümmerich et al. (2017) and thus confirms their results.
Top: Light curve of NSV 1907. Bottom left: Power spectrum of the light curve in a small range around the orbital frequency. Bottom right: Average waveform of the orbital variations of NSV 1907 normalized such that the eclipse minimum has 50 per cent of the average flux of the two maxima.
At higher frequencies the power spectrum is dominated by signals at the orbital frequency and its overtones even after removal of the eclipses from the light curves. The lower left frame of Fig. 25 shows a narrow range around Forb. Apart from the orbital signal, it contains a weaker peak at FSH = 3.860(3) d−1 (PSH = 0.2591(1) d), leaving no doubt that this is the SH signal predicted by Hümmerich et al. (2017) but not seen directly in their data.
Finally, the orbital waveform, normalized in the same way as was done for AC Cnc in Paper I, is shown in the lower right frame of Fig. 25. It impressively confirms the presence of secondary eclipses which, not surprisingly, are better defined in the redder TESS passband than in the earlier observations. Before the secondary eclipse, the hump in the waveform has a significantly smaller amplitude that afterwards also appears to have some peculiar structure. I tested if the hump maxima are modulated on the beat period between orbital and SH variations as has been seen in AC Cnc (Paper I). This is indeed the case, but the effect is much smaller than in AC Cnc.
4 DISCUSSION: A CENSUS OF SUPERHUMPS
An assessment of SHs and their implications for the understanding of the structure, dynamics, and evolution of CVs has been made many times in the past (e.g. Patterson 1998, 2001, Patterson et al. 2005). A huge body of observational information on pSHs in SU UMa type dwarf nova has been collected by Kato et al. (2009) and in subsequent publications of this series. Much of this work deals with dwarf novae and with pSHs, while specific studies of nSHs and SH in non-outbursting CVs are considerably rarer. Among observational papers with some emphasis on SHs in NLs and old novae, I cite Fuentes-Morales et al. (2018). For theoretical studies of nSHs, I refer to Thomas & Wood (2015) and citations therein. Concerning our theoretical understanding of pSHs, I mention the classical papers of Whitehurst (1988), Whitehurst & King (1991), and Hirose, Osaki & Mineshige (1991).
Table 4 contains a census of the properties of positive and nSHs in all novae and NL variables for which I could find reports on such variations in the literature. Apart from the orbital period, it lists the SH period (which is many cases is the average of several slightly different values measured at different epochs) and the period excess defined as ϵ = (PSH − Porb)/Porb. The table also provides information about the SH waveform, the detection or not of the apsidal or nodal precession period in the light curves, and the frequency of occurrence of SHs. I define three categories for the waveform: S indicates an approximately sinusoidal waveform, which includes slight deviations from a pure sine such as a sawtooth shape, DH stands for a double humped waveform, and C is used for more complex shapes. Of course, these distinctions (in particular between DH and C) are sometimes subjective. The presence or absence of variations on the disc precession period is indicated by Y(es) or N(o) only in those cases where information in the literature permits a secure statement. The occurrence of SHs is categorized as permanent (P) whenever it is seen in all available observations (but see below), and as transient (T) when it is seen in some observations but not in others.
Summary of positive and nSH properties observed in NL variables and old novae. All periods are expressed in days.
| Name . | Porb . | nSH . | pSH . | Ref.a . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | PnSH . | |$\epsilon _{\rm nSH}^b$| . | WFc . | Precd . | Occe . | PpSH . | |$\epsilon _{\rm pSH}^b$| . | WFc . | Precd . | Occe . | . |
| CP Pup | 0.06139 | 0.06250 | 0.0181 | S | N | T | 3 | |||||
| BK Lyn | 0.07494 | 0.07280 | −0.0286 | S | N | T | 0.07848 | 0.0472 | S/C | Y | P | 1,4,5,6 |
| V1974 Cyg | 0.08126 | 0.08507 | 0.0469 | S | Y | P | 1,7,8,9 | |||||
| V348 Pup | 0.10184 | 0.10740 | 0.0546 | S/C | Y | T | 1,10 | |||||
| V795 Her | 0.10825 | 0.10474 | −0.0324 | C | N | T | 0.11619 | 0.0733 | S | N | T | 2,11-18 |
| KIC 8751494 | 0.11438 | 0.12249 | 0.0709 | S | N | P | 1,19,20 | |||||
| V592 Cas | 0.11506 | 0.11193 | −0.0272 | S | N | T | 0.12239 | 0.0637 | S/DH | N | P | 1,21 |
| DM Gem | 0.11570 | 0.12423 | 0.0737 | S | N | P? | 2,22 | |||||
| V630 Sgr | 0.11793 | 0.12417 | 0.0529 | ? | Y | T | 23,24 | |||||
| LQ Peg | 0.11850 | 0.12480 | 0.0532 | ? | Y | P | 25,26 | |||||
| V1084 Her | 0.12056 | 0.11696 | −0.0299 | S | Y | ? | 27 | |||||
| V442 Oph | 0.12443 | 0.12090 | −0.0284 | S | Y | P? | 27 | |||||
| V4633 Sgr | 0.12557 | 0.12823 | 0.0212 | S | N | T | 24,28 | |||||
| AH Men | 0.12721 | 0.12355 | −0.0288 | S | Y | T | 0.13886 | 0.0916 | S | N | T | 1,29-31 |
| MV Lyr | 0.13290 | 0.12816 | −0.0357 | S | N | T | 0.13790 | 0.0376 | S | Y | T | 2,32,33 |
| DW UMa | 0.13661 | 0.13264 | −0.0291 | S | Y | T | 0.14478 | 0.0598 | S | Y | P | 1,34 |
| TT Ari | 0.13755 | 0.13296 | −0.0334 | S | Y | P | 0.14927 | 0.0852 | S | N | T | 2,35-50 |
| V603 Aql | 0.13822 | 0.13390 | −0.0313 | S | N | T | 0.14548 | 0.0525 | S | Y | P | 51-58 |
| V378 Peg | 0.13858 | 0.13476 | −0.0276 | S | P | 59,60 | ||||||
| RR Cha | 0.14010 | 0.13621 | −0.0278 | S | P | 0.14442 | 0.0308 | N | T | 1,61 | ||
| AQ Men | 0.14147 | 0.13646 | −0.0354 | S | Y | P | 0.15047 | 0.0636 | C | Y | T | 2,62,63 |
| LS Cam | 0.14238 | 0.13753 | −0.0341 | Y | P | 0.15485 | 0.0876 | N | T | 64 | ||
| V751 Cyg | 0.14458 | 0.13936 | −0.0361 | S | Y | P | 1,65,66 | |||||
| RR Pic | 0.14503 | 0.15770 | 0.0874 | S | N | T | 1,67,68 | |||||
| IM Eri | 0.14563 | 0.13841 | −0.0496 | S | Y | P | 62 | |||||
| PX And | 0.14634 | 0.14150 | −0.0331 | S | Y | T | 1,69 | |||||
| V533 Her | 0.14737 | 0.14289 | −0.0304 | N | T | 0.15706 | 0.0658 | S | Y | T | 2,70 | |
| HS 1813 + 6122 | 0.14752 | 0.14095 | −0.0445 | S | N | T | 1,71 | |||||
| V2574 Oph | 0.14773 | 0.14164 | −0.0412 | S | T | 72 | ||||||
| BB Dor | 0.14923 | 0.14093 | −0.0556 | S | Y | P | 0.16330 | 0.0943 | S | T | 1,73 | |
| AO Psc | 0.14950 | 0.16580 | 0.1090 | T | 1,74 | |||||||
| BZ Cam | 0.15369 | 0.15634 | 0.0172 | DH | T | 1,75 | ||||||
| V704 And | 0.15424 | 0.14772 | −0.0423 | S | Y | T | 2 | |||||
| BH Lyn | 0.15588 | 0.14700 | −0.0570 | T | 0.16772 | 0.0760 | S | Y | T | 2,76,77 | ||
| BG Tri | 0.15844 | 0.15150 | −0.0438 | S | Y | T | 0.17270 | 0.09000 | S | T | 78 | |
| KR Aur | 0.16274 | 0.15713 | −0.0345 | S | T | 1,79 | ||||||
| V1193 Ori | 0.16500 | 0.15883 | −0.0374 | S | N | T | 0.17622 | 0.0680 | DH/C | N | T | 2 |
| UU Aqr | 0.16580 | 0.17510 | 0.0561 | T | 1,73 | |||||||
| UX UMa | 0.19667 | 0.18668 | −0.0508 | S | T | 1,26,80 | ||||||
| AY Psc | 0.21732 | 0.20640 | −0.0502 | S | T | 1,81 | ||||||
| TV Col | 0.22860 | 0.21611 | −0.0546 | S | Y | T | 2,82-85 | |||||
| RW Tri | 0.23188 | 0.22190 | −0.0430 | S | T | 2,26,86 | ||||||
| KIC 9406652 | 0.25451 | 0.22945 | −0.0985 | S | Y | T | 0.29071 | 0.1422 | C | N | T | 1,87,88 |
| NSV 1907 | 0.27611 | 0.25910 | −0.0616 | S | Y | P? | 1,89 | |||||
| RX 2133.7 + 5107 | 0.29743 | 0.28132 | −0.0542 | S | N | P | 1,90 | |||||
| RZ Gru | 0.41750 | 0.52000 | 0.2455 | S | 2 | |||||||
| Name . | Porb . | nSH . | pSH . | Ref.a . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | PnSH . | |$\epsilon _{\rm nSH}^b$| . | WFc . | Precd . | Occe . | PpSH . | |$\epsilon _{\rm pSH}^b$| . | WFc . | Precd . | Occe . | . |
| CP Pup | 0.06139 | 0.06250 | 0.0181 | S | N | T | 3 | |||||
| BK Lyn | 0.07494 | 0.07280 | −0.0286 | S | N | T | 0.07848 | 0.0472 | S/C | Y | P | 1,4,5,6 |
| V1974 Cyg | 0.08126 | 0.08507 | 0.0469 | S | Y | P | 1,7,8,9 | |||||
| V348 Pup | 0.10184 | 0.10740 | 0.0546 | S/C | Y | T | 1,10 | |||||
| V795 Her | 0.10825 | 0.10474 | −0.0324 | C | N | T | 0.11619 | 0.0733 | S | N | T | 2,11-18 |
| KIC 8751494 | 0.11438 | 0.12249 | 0.0709 | S | N | P | 1,19,20 | |||||
| V592 Cas | 0.11506 | 0.11193 | −0.0272 | S | N | T | 0.12239 | 0.0637 | S/DH | N | P | 1,21 |
| DM Gem | 0.11570 | 0.12423 | 0.0737 | S | N | P? | 2,22 | |||||
| V630 Sgr | 0.11793 | 0.12417 | 0.0529 | ? | Y | T | 23,24 | |||||
| LQ Peg | 0.11850 | 0.12480 | 0.0532 | ? | Y | P | 25,26 | |||||
| V1084 Her | 0.12056 | 0.11696 | −0.0299 | S | Y | ? | 27 | |||||
| V442 Oph | 0.12443 | 0.12090 | −0.0284 | S | Y | P? | 27 | |||||
| V4633 Sgr | 0.12557 | 0.12823 | 0.0212 | S | N | T | 24,28 | |||||
| AH Men | 0.12721 | 0.12355 | −0.0288 | S | Y | T | 0.13886 | 0.0916 | S | N | T | 1,29-31 |
| MV Lyr | 0.13290 | 0.12816 | −0.0357 | S | N | T | 0.13790 | 0.0376 | S | Y | T | 2,32,33 |
| DW UMa | 0.13661 | 0.13264 | −0.0291 | S | Y | T | 0.14478 | 0.0598 | S | Y | P | 1,34 |
| TT Ari | 0.13755 | 0.13296 | −0.0334 | S | Y | P | 0.14927 | 0.0852 | S | N | T | 2,35-50 |
| V603 Aql | 0.13822 | 0.13390 | −0.0313 | S | N | T | 0.14548 | 0.0525 | S | Y | P | 51-58 |
| V378 Peg | 0.13858 | 0.13476 | −0.0276 | S | P | 59,60 | ||||||
| RR Cha | 0.14010 | 0.13621 | −0.0278 | S | P | 0.14442 | 0.0308 | N | T | 1,61 | ||
| AQ Men | 0.14147 | 0.13646 | −0.0354 | S | Y | P | 0.15047 | 0.0636 | C | Y | T | 2,62,63 |
| LS Cam | 0.14238 | 0.13753 | −0.0341 | Y | P | 0.15485 | 0.0876 | N | T | 64 | ||
| V751 Cyg | 0.14458 | 0.13936 | −0.0361 | S | Y | P | 1,65,66 | |||||
| RR Pic | 0.14503 | 0.15770 | 0.0874 | S | N | T | 1,67,68 | |||||
| IM Eri | 0.14563 | 0.13841 | −0.0496 | S | Y | P | 62 | |||||
| PX And | 0.14634 | 0.14150 | −0.0331 | S | Y | T | 1,69 | |||||
| V533 Her | 0.14737 | 0.14289 | −0.0304 | N | T | 0.15706 | 0.0658 | S | Y | T | 2,70 | |
| HS 1813 + 6122 | 0.14752 | 0.14095 | −0.0445 | S | N | T | 1,71 | |||||
| V2574 Oph | 0.14773 | 0.14164 | −0.0412 | S | T | 72 | ||||||
| BB Dor | 0.14923 | 0.14093 | −0.0556 | S | Y | P | 0.16330 | 0.0943 | S | T | 1,73 | |
| AO Psc | 0.14950 | 0.16580 | 0.1090 | T | 1,74 | |||||||
| BZ Cam | 0.15369 | 0.15634 | 0.0172 | DH | T | 1,75 | ||||||
| V704 And | 0.15424 | 0.14772 | −0.0423 | S | Y | T | 2 | |||||
| BH Lyn | 0.15588 | 0.14700 | −0.0570 | T | 0.16772 | 0.0760 | S | Y | T | 2,76,77 | ||
| BG Tri | 0.15844 | 0.15150 | −0.0438 | S | Y | T | 0.17270 | 0.09000 | S | T | 78 | |
| KR Aur | 0.16274 | 0.15713 | −0.0345 | S | T | 1,79 | ||||||
| V1193 Ori | 0.16500 | 0.15883 | −0.0374 | S | N | T | 0.17622 | 0.0680 | DH/C | N | T | 2 |
| UU Aqr | 0.16580 | 0.17510 | 0.0561 | T | 1,73 | |||||||
| UX UMa | 0.19667 | 0.18668 | −0.0508 | S | T | 1,26,80 | ||||||
| AY Psc | 0.21732 | 0.20640 | −0.0502 | S | T | 1,81 | ||||||
| TV Col | 0.22860 | 0.21611 | −0.0546 | S | Y | T | 2,82-85 | |||||
| RW Tri | 0.23188 | 0.22190 | −0.0430 | S | T | 2,26,86 | ||||||
| KIC 9406652 | 0.25451 | 0.22945 | −0.0985 | S | Y | T | 0.29071 | 0.1422 | C | N | T | 1,87,88 |
| NSV 1907 | 0.27611 | 0.25910 | −0.0616 | S | Y | P? | 1,89 | |||||
| RX 2133.7 + 5107 | 0.29743 | 0.28132 | −0.0542 | S | N | P | 1,90 | |||||
| RZ Gru | 0.41750 | 0.52000 | 0.2455 | S | 2 | |||||||
aReferences: (1) This work; (2) Paper I; (3) Patterson & Warner (1998); (4) Skillman & Patterson (1993) (5) Misselt & Shafter (1995); (6) Patterson et al. (2013); (7) Semeniuk et al. (1994); (8) Semeniuk et al. (1995); (9) Retter et al. (1997); (10) Rolfe et al. (2000); (11) Mironov, Moshkalev & Shugarov (1983); (12) Baidak et al. (1985); (13) Kałuzny (1989); (14) Rosen et al. (1989); (15) Shafter et al. (1990); (16) Zhang et al. (1991); (17) Papadaki et al (2006); (18) Šimon et al. (2012); (19) Williams et al. (2010); (20) Kato & Maehara (2013); (21) Taylor et al. (1998); (22) Rodríguez-Gil & Torres (2005); (23) Woudt & Warner (2001); (24) Mróz et al. (2015); (25) Rude & Ringwald (2012); (26) Bruch (2020); (27) Patterson et al. (2002); (28) Lipkin & Leibowitz (2008); (29) Buckley et al. (1993) (30) Patterson (1995); (31) Patterson (1998); (32) Borisov (1992); (33) Skillman, Patterson & Thorstensen (1995); (34) Boyd et al. (2017); (35) Andronov et al. (1992); (36) Andronov et al. (1999); (37) Belova et al. (2013); (38) Bruch (2019b); (39) Kim et al. (2009); (40) Kraichva et al. (1999); (41) Rössiger (1988); (42) Semeniuk (1987); (43) Skillman, Harvey & Patterson (1998); (44) Smak & Stȩpień (1975); (45) Sztanjo (1979); (46) Tremko et al. (1992); (47) Udalski (1988); (48) Volpi, Natali & D’Antona (1998); (49) Weingrill et al. (2009); (50) Wu et al. (2002); (51) Bruch (1991); (52) Bruch & Cook (2018); (53) Haefner (1981); (54) Haefner & Metz (1985); (55) Hollander, Kraakman H., van Paradijs (1997); (56) Patterson et al. (1997); (57) Patterson & Richman (1991); (58) Patterson et al. (1993); (59) Kozhevnikov (2012); (60) Ringwald et al. (2012); (61) Woudt & Warner (2002); (62) Armstrong et al. (2013); (63) Iłkiewicz et al. (2021); (64) Rawat et al. (2022); (65) Patterson et al. (2001); (66) Papadaki et al. (2009); (67) Fuentes-Morales et al. (2018); (68) Schmidtobreick et al. (2008); (69) Stanishev et al. (2002); (70) McQuillin et al. (2012); (71) Rodríguez-Gil et al. (2007); (72) Kang et al. (2006); (73) Patterson et al. (2005); (74) Patterson (2001) (75) Kato & Uemura (2001); (76) Stanishev et al. (2006); (77) Patterson (1999); (78) Stefanov et al. (2022); (79) Kozhevnikov (2007); (80) de Miguel et al. (2016); (81) Gülsecen et al. (2009); (82) Augusteijn et al. (1994); (83) Barrett, O’Donoghue & Warner (1988); (84) Hutchings et al. (1981); (85) Motch (1981); (86) Smak (2019); (87) Gies et al. (2013); (88) Kimura et al. (2020); (89) Hümmerich et al. (2017); (90) de Miguel et al. (2017).
bPeriod excess defined as ϵ = (PSH − Porb)/Porb
cWaveform: S = sinusoidal; DH = double humped; C = complex
dPrecession period detected (Yes/No)
eOccurrence of SH: P = permanent; T = transient
Summary of positive and nSH properties observed in NL variables and old novae. All periods are expressed in days.
| Name . | Porb . | nSH . | pSH . | Ref.a . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | PnSH . | |$\epsilon _{\rm nSH}^b$| . | WFc . | Precd . | Occe . | PpSH . | |$\epsilon _{\rm pSH}^b$| . | WFc . | Precd . | Occe . | . |
| CP Pup | 0.06139 | 0.06250 | 0.0181 | S | N | T | 3 | |||||
| BK Lyn | 0.07494 | 0.07280 | −0.0286 | S | N | T | 0.07848 | 0.0472 | S/C | Y | P | 1,4,5,6 |
| V1974 Cyg | 0.08126 | 0.08507 | 0.0469 | S | Y | P | 1,7,8,9 | |||||
| V348 Pup | 0.10184 | 0.10740 | 0.0546 | S/C | Y | T | 1,10 | |||||
| V795 Her | 0.10825 | 0.10474 | −0.0324 | C | N | T | 0.11619 | 0.0733 | S | N | T | 2,11-18 |
| KIC 8751494 | 0.11438 | 0.12249 | 0.0709 | S | N | P | 1,19,20 | |||||
| V592 Cas | 0.11506 | 0.11193 | −0.0272 | S | N | T | 0.12239 | 0.0637 | S/DH | N | P | 1,21 |
| DM Gem | 0.11570 | 0.12423 | 0.0737 | S | N | P? | 2,22 | |||||
| V630 Sgr | 0.11793 | 0.12417 | 0.0529 | ? | Y | T | 23,24 | |||||
| LQ Peg | 0.11850 | 0.12480 | 0.0532 | ? | Y | P | 25,26 | |||||
| V1084 Her | 0.12056 | 0.11696 | −0.0299 | S | Y | ? | 27 | |||||
| V442 Oph | 0.12443 | 0.12090 | −0.0284 | S | Y | P? | 27 | |||||
| V4633 Sgr | 0.12557 | 0.12823 | 0.0212 | S | N | T | 24,28 | |||||
| AH Men | 0.12721 | 0.12355 | −0.0288 | S | Y | T | 0.13886 | 0.0916 | S | N | T | 1,29-31 |
| MV Lyr | 0.13290 | 0.12816 | −0.0357 | S | N | T | 0.13790 | 0.0376 | S | Y | T | 2,32,33 |
| DW UMa | 0.13661 | 0.13264 | −0.0291 | S | Y | T | 0.14478 | 0.0598 | S | Y | P | 1,34 |
| TT Ari | 0.13755 | 0.13296 | −0.0334 | S | Y | P | 0.14927 | 0.0852 | S | N | T | 2,35-50 |
| V603 Aql | 0.13822 | 0.13390 | −0.0313 | S | N | T | 0.14548 | 0.0525 | S | Y | P | 51-58 |
| V378 Peg | 0.13858 | 0.13476 | −0.0276 | S | P | 59,60 | ||||||
| RR Cha | 0.14010 | 0.13621 | −0.0278 | S | P | 0.14442 | 0.0308 | N | T | 1,61 | ||
| AQ Men | 0.14147 | 0.13646 | −0.0354 | S | Y | P | 0.15047 | 0.0636 | C | Y | T | 2,62,63 |
| LS Cam | 0.14238 | 0.13753 | −0.0341 | Y | P | 0.15485 | 0.0876 | N | T | 64 | ||
| V751 Cyg | 0.14458 | 0.13936 | −0.0361 | S | Y | P | 1,65,66 | |||||
| RR Pic | 0.14503 | 0.15770 | 0.0874 | S | N | T | 1,67,68 | |||||
| IM Eri | 0.14563 | 0.13841 | −0.0496 | S | Y | P | 62 | |||||
| PX And | 0.14634 | 0.14150 | −0.0331 | S | Y | T | 1,69 | |||||
| V533 Her | 0.14737 | 0.14289 | −0.0304 | N | T | 0.15706 | 0.0658 | S | Y | T | 2,70 | |
| HS 1813 + 6122 | 0.14752 | 0.14095 | −0.0445 | S | N | T | 1,71 | |||||
| V2574 Oph | 0.14773 | 0.14164 | −0.0412 | S | T | 72 | ||||||
| BB Dor | 0.14923 | 0.14093 | −0.0556 | S | Y | P | 0.16330 | 0.0943 | S | T | 1,73 | |
| AO Psc | 0.14950 | 0.16580 | 0.1090 | T | 1,74 | |||||||
| BZ Cam | 0.15369 | 0.15634 | 0.0172 | DH | T | 1,75 | ||||||
| V704 And | 0.15424 | 0.14772 | −0.0423 | S | Y | T | 2 | |||||
| BH Lyn | 0.15588 | 0.14700 | −0.0570 | T | 0.16772 | 0.0760 | S | Y | T | 2,76,77 | ||
| BG Tri | 0.15844 | 0.15150 | −0.0438 | S | Y | T | 0.17270 | 0.09000 | S | T | 78 | |
| KR Aur | 0.16274 | 0.15713 | −0.0345 | S | T | 1,79 | ||||||
| V1193 Ori | 0.16500 | 0.15883 | −0.0374 | S | N | T | 0.17622 | 0.0680 | DH/C | N | T | 2 |
| UU Aqr | 0.16580 | 0.17510 | 0.0561 | T | 1,73 | |||||||
| UX UMa | 0.19667 | 0.18668 | −0.0508 | S | T | 1,26,80 | ||||||
| AY Psc | 0.21732 | 0.20640 | −0.0502 | S | T | 1,81 | ||||||
| TV Col | 0.22860 | 0.21611 | −0.0546 | S | Y | T | 2,82-85 | |||||
| RW Tri | 0.23188 | 0.22190 | −0.0430 | S | T | 2,26,86 | ||||||
| KIC 9406652 | 0.25451 | 0.22945 | −0.0985 | S | Y | T | 0.29071 | 0.1422 | C | N | T | 1,87,88 |
| NSV 1907 | 0.27611 | 0.25910 | −0.0616 | S | Y | P? | 1,89 | |||||
| RX 2133.7 + 5107 | 0.29743 | 0.28132 | −0.0542 | S | N | P | 1,90 | |||||
| RZ Gru | 0.41750 | 0.52000 | 0.2455 | S | 2 | |||||||
| Name . | Porb . | nSH . | pSH . | Ref.a . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | PnSH . | |$\epsilon _{\rm nSH}^b$| . | WFc . | Precd . | Occe . | PpSH . | |$\epsilon _{\rm pSH}^b$| . | WFc . | Precd . | Occe . | . |
| CP Pup | 0.06139 | 0.06250 | 0.0181 | S | N | T | 3 | |||||
| BK Lyn | 0.07494 | 0.07280 | −0.0286 | S | N | T | 0.07848 | 0.0472 | S/C | Y | P | 1,4,5,6 |
| V1974 Cyg | 0.08126 | 0.08507 | 0.0469 | S | Y | P | 1,7,8,9 | |||||
| V348 Pup | 0.10184 | 0.10740 | 0.0546 | S/C | Y | T | 1,10 | |||||
| V795 Her | 0.10825 | 0.10474 | −0.0324 | C | N | T | 0.11619 | 0.0733 | S | N | T | 2,11-18 |
| KIC 8751494 | 0.11438 | 0.12249 | 0.0709 | S | N | P | 1,19,20 | |||||
| V592 Cas | 0.11506 | 0.11193 | −0.0272 | S | N | T | 0.12239 | 0.0637 | S/DH | N | P | 1,21 |
| DM Gem | 0.11570 | 0.12423 | 0.0737 | S | N | P? | 2,22 | |||||
| V630 Sgr | 0.11793 | 0.12417 | 0.0529 | ? | Y | T | 23,24 | |||||
| LQ Peg | 0.11850 | 0.12480 | 0.0532 | ? | Y | P | 25,26 | |||||
| V1084 Her | 0.12056 | 0.11696 | −0.0299 | S | Y | ? | 27 | |||||
| V442 Oph | 0.12443 | 0.12090 | −0.0284 | S | Y | P? | 27 | |||||
| V4633 Sgr | 0.12557 | 0.12823 | 0.0212 | S | N | T | 24,28 | |||||
| AH Men | 0.12721 | 0.12355 | −0.0288 | S | Y | T | 0.13886 | 0.0916 | S | N | T | 1,29-31 |
| MV Lyr | 0.13290 | 0.12816 | −0.0357 | S | N | T | 0.13790 | 0.0376 | S | Y | T | 2,32,33 |
| DW UMa | 0.13661 | 0.13264 | −0.0291 | S | Y | T | 0.14478 | 0.0598 | S | Y | P | 1,34 |
| TT Ari | 0.13755 | 0.13296 | −0.0334 | S | Y | P | 0.14927 | 0.0852 | S | N | T | 2,35-50 |
| V603 Aql | 0.13822 | 0.13390 | −0.0313 | S | N | T | 0.14548 | 0.0525 | S | Y | P | 51-58 |
| V378 Peg | 0.13858 | 0.13476 | −0.0276 | S | P | 59,60 | ||||||
| RR Cha | 0.14010 | 0.13621 | −0.0278 | S | P | 0.14442 | 0.0308 | N | T | 1,61 | ||
| AQ Men | 0.14147 | 0.13646 | −0.0354 | S | Y | P | 0.15047 | 0.0636 | C | Y | T | 2,62,63 |
| LS Cam | 0.14238 | 0.13753 | −0.0341 | Y | P | 0.15485 | 0.0876 | N | T | 64 | ||
| V751 Cyg | 0.14458 | 0.13936 | −0.0361 | S | Y | P | 1,65,66 | |||||
| RR Pic | 0.14503 | 0.15770 | 0.0874 | S | N | T | 1,67,68 | |||||
| IM Eri | 0.14563 | 0.13841 | −0.0496 | S | Y | P | 62 | |||||
| PX And | 0.14634 | 0.14150 | −0.0331 | S | Y | T | 1,69 | |||||
| V533 Her | 0.14737 | 0.14289 | −0.0304 | N | T | 0.15706 | 0.0658 | S | Y | T | 2,70 | |
| HS 1813 + 6122 | 0.14752 | 0.14095 | −0.0445 | S | N | T | 1,71 | |||||
| V2574 Oph | 0.14773 | 0.14164 | −0.0412 | S | T | 72 | ||||||
| BB Dor | 0.14923 | 0.14093 | −0.0556 | S | Y | P | 0.16330 | 0.0943 | S | T | 1,73 | |
| AO Psc | 0.14950 | 0.16580 | 0.1090 | T | 1,74 | |||||||
| BZ Cam | 0.15369 | 0.15634 | 0.0172 | DH | T | 1,75 | ||||||
| V704 And | 0.15424 | 0.14772 | −0.0423 | S | Y | T | 2 | |||||
| BH Lyn | 0.15588 | 0.14700 | −0.0570 | T | 0.16772 | 0.0760 | S | Y | T | 2,76,77 | ||
| BG Tri | 0.15844 | 0.15150 | −0.0438 | S | Y | T | 0.17270 | 0.09000 | S | T | 78 | |
| KR Aur | 0.16274 | 0.15713 | −0.0345 | S | T | 1,79 | ||||||
| V1193 Ori | 0.16500 | 0.15883 | −0.0374 | S | N | T | 0.17622 | 0.0680 | DH/C | N | T | 2 |
| UU Aqr | 0.16580 | 0.17510 | 0.0561 | T | 1,73 | |||||||
| UX UMa | 0.19667 | 0.18668 | −0.0508 | S | T | 1,26,80 | ||||||
| AY Psc | 0.21732 | 0.20640 | −0.0502 | S | T | 1,81 | ||||||
| TV Col | 0.22860 | 0.21611 | −0.0546 | S | Y | T | 2,82-85 | |||||
| RW Tri | 0.23188 | 0.22190 | −0.0430 | S | T | 2,26,86 | ||||||
| KIC 9406652 | 0.25451 | 0.22945 | −0.0985 | S | Y | T | 0.29071 | 0.1422 | C | N | T | 1,87,88 |
| NSV 1907 | 0.27611 | 0.25910 | −0.0616 | S | Y | P? | 1,89 | |||||
| RX 2133.7 + 5107 | 0.29743 | 0.28132 | −0.0542 | S | N | P | 1,90 | |||||
| RZ Gru | 0.41750 | 0.52000 | 0.2455 | S | 2 | |||||||
aReferences: (1) This work; (2) Paper I; (3) Patterson & Warner (1998); (4) Skillman & Patterson (1993) (5) Misselt & Shafter (1995); (6) Patterson et al. (2013); (7) Semeniuk et al. (1994); (8) Semeniuk et al. (1995); (9) Retter et al. (1997); (10) Rolfe et al. (2000); (11) Mironov, Moshkalev & Shugarov (1983); (12) Baidak et al. (1985); (13) Kałuzny (1989); (14) Rosen et al. (1989); (15) Shafter et al. (1990); (16) Zhang et al. (1991); (17) Papadaki et al (2006); (18) Šimon et al. (2012); (19) Williams et al. (2010); (20) Kato & Maehara (2013); (21) Taylor et al. (1998); (22) Rodríguez-Gil & Torres (2005); (23) Woudt & Warner (2001); (24) Mróz et al. (2015); (25) Rude & Ringwald (2012); (26) Bruch (2020); (27) Patterson et al. (2002); (28) Lipkin & Leibowitz (2008); (29) Buckley et al. (1993) (30) Patterson (1995); (31) Patterson (1998); (32) Borisov (1992); (33) Skillman, Patterson & Thorstensen (1995); (34) Boyd et al. (2017); (35) Andronov et al. (1992); (36) Andronov et al. (1999); (37) Belova et al. (2013); (38) Bruch (2019b); (39) Kim et al. (2009); (40) Kraichva et al. (1999); (41) Rössiger (1988); (42) Semeniuk (1987); (43) Skillman, Harvey & Patterson (1998); (44) Smak & Stȩpień (1975); (45) Sztanjo (1979); (46) Tremko et al. (1992); (47) Udalski (1988); (48) Volpi, Natali & D’Antona (1998); (49) Weingrill et al. (2009); (50) Wu et al. (2002); (51) Bruch (1991); (52) Bruch & Cook (2018); (53) Haefner (1981); (54) Haefner & Metz (1985); (55) Hollander, Kraakman H., van Paradijs (1997); (56) Patterson et al. (1997); (57) Patterson & Richman (1991); (58) Patterson et al. (1993); (59) Kozhevnikov (2012); (60) Ringwald et al. (2012); (61) Woudt & Warner (2002); (62) Armstrong et al. (2013); (63) Iłkiewicz et al. (2021); (64) Rawat et al. (2022); (65) Patterson et al. (2001); (66) Papadaki et al. (2009); (67) Fuentes-Morales et al. (2018); (68) Schmidtobreick et al. (2008); (69) Stanishev et al. (2002); (70) McQuillin et al. (2012); (71) Rodríguez-Gil et al. (2007); (72) Kang et al. (2006); (73) Patterson et al. (2005); (74) Patterson (2001) (75) Kato & Uemura (2001); (76) Stanishev et al. (2006); (77) Patterson (1999); (78) Stefanov et al. (2022); (79) Kozhevnikov (2007); (80) de Miguel et al. (2016); (81) Gülsecen et al. (2009); (82) Augusteijn et al. (1994); (83) Barrett, O’Donoghue & Warner (1988); (84) Hutchings et al. (1981); (85) Motch (1981); (86) Smak (2019); (87) Gies et al. (2013); (88) Kimura et al. (2020); (89) Hümmerich et al. (2017); (90) de Miguel et al. (2017).
bPeriod excess defined as ϵ = (PSH − Porb)/Porb
cWaveform: S = sinusoidal; DH = double humped; C = complex
dPrecession period detected (Yes/No)
eOccurrence of SH: P = permanent; T = transient
Some of the stars listed in the table may have low credentials as superhumpers because of sparse of observations, weak indications for SHs, or alternative explications for the observed variations. They are included in the table anyway for the sake of completeness, but it should be kept in mind that they may not exhibit genuine SHs. In particular, I mention: (1) CP Pup. Patterson & Warner (1998) observed an unstable period, which they interpreted as being due to an SH. As I showed in Paper I, the TESS light curves of CP Pup exhibit a multitude of transient QPO-like variations in the respective period range that cannot be considered to be SHs, and which, in more limited terrestrial observations, may mimick SHs. (2) BZ Cam. This case is similar to CP Pup. Kato & Uemura (2001) claim to have seen SHs, but the multitude of power spectrum peaks in the data of Patterson et al. (1996) and the time resolved power spectrum in Fig. 3 suggest only the occurrence of QPO-like variations. (3) RZ Gru. This star was identified in Paper I as a system with pSHs, but the corresponding power spectrum peak may not be outstanding enough to provide convincing evidence. Moreover, at the long orbital period, RZ Gru is not expected to develop a precessing accretion disc (however, I try to avoid a bias based on theoretical preconceptions). (4) RW Tri. This system is claimed to have exhibited nSHs restricted to the 1984 and possibly 1957 observing seasons (Smak 2019), but not in other years (Bruch 2020). While this alone does not discredit it as a transient SH system, I consider the peaks in Smak’s power spectra, on which he bases his claim, not of sufficient strength to convincingly indicate a consistent periodicity. (5) V4633 Sgr. Fuentes-Morales et al. (2018) list this star as a superhumping old nova, but Lipkin & Leibowitz (2008) interpret the corresponding variations in an asynchronous polar scenario, where the rotation of a magnetic white dwarf got out of synchronization with the orbital period as a consequence of the recent nova outburst of V4633 Sgr in 1998. (6) LQ Peg. It is not clear if the consistent photometric variations in this star are due to the orbital motion or an SH. For a thorough discussion of this issue, see Bruch (2020). (7) AO Psc. As noticed in Section 3.14, AO Psc is only briefly mentioned as a superhumper by Patterson (2001), while the announced publication of details never occurred.
Including the systems with low credentials, Table 4 contains 46 stars. Of these, 30 exhibit positive and 33 nSHs. Thus, statistically among novae and NL variable both species are about equally probable, unless there is an observational bias favouring the detection of one over the other. In nine stars, both kinds of SHs have even been seen simultaneously (V603 Aql, TT Ari, LS Cam, V592 Cas, RR Cha, BB Dor, BK Lyn, AQ Men, and DW UMa).
Stolz & Schoembs (1984) were the first to note a linear relationship between the period excess ϵ and the SH period PSH in SU UMa type dwarf novae; a relationship which – albeit less strictly – is also valid for pSHs in other CVs. It has been refined and discussed many times in subsequent years and sometimes replaced by a relation between Porb and PSH (e.g. Gänsicke, Dillon & Southworth 2009; Fuentes-Morales, Vogt, & Tappert 2018). Both relations are largely equivalent, but if ϵ versus PSH is linear, Porb versus PSH becomes notably non-linear if a wider range of periods is regarded. Therefore, I use here the original notation of the Stolz–Schoembs relation.
For all pSH systems listed in Table 4, ϵ is plotted as a function of PpSH as large dots in the upper frame of Fig. 26. For comparison, the respective data taken from table 9 of Patterson et al. (2005) are drawn as smaller orange dots. The bulk of them refers to short period SU UMa type dwarf novae. Several lessons can be learned from this diagram. As is already obvious from the data of Patterson et al. (2005) and is also mentioned by Fuentes-Morales et al. (2018), the scatter of the points corresponding to nova and NL variables (i.e. almost all points with PpSH > 0.1 d) exhibit a much higher scatter than the dwarf novae below the CV period gap. Thus, the Stolz–Schoembs relation becomes less well defined for these systems. There are some outliers with low ϵ values, two of which (V4633 Sgr and BZ Cam) can be identified with low credential SH systems. These two are ignored subsequently. In contrast, other systems with low credentials – CP Pup (green dot in the figure) and LQ Peg (blue dot) – follow the general trend well. For LQ Peg, this may be an indication that the persistent light-curve variability is indeed due to SHs and not the orbital motion. DM Gem (red dot) was found in Paper I to exhibit two periods. But it could not be decided which of these is due to the orbital motion and SHs. In Fig. 26, DM Gem follows the general trend; a good argument in favour of its interpretation of a positive (instead of negative) SH.
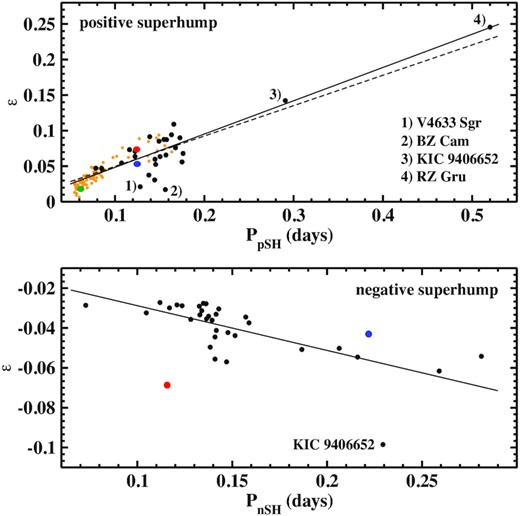
Top: Relation between the period excess and the SH period for pSHs. The large dots represent data taken from Table 4. For comparison, data taken from table 9 of Patterson et al. (2005) are also plotted as smaller orange dots. The solid line is a linear least-squares fit to all data from Table 4, excluding the low credential SH systems V4633 Sgr and BZ Cam. The dashed line is the same, additionally excluding the long-period systems KIC 9406652 and RZ Gru. The red, blue, and green dots represent DM Gem, LQ Peg, and CP Pup, respectively. For further details, see text. Bottom: The same for nSHs. The red and blue dots represent DM Gem under the assumption that it is a negative superhumper, and the low credential system RW Tri, respectively. The solid line is a linear least-squares fit to all points except DM Gem.
Two systems, not previously discussed in the context of the Stolz–Schoembs relation, extend this relation to much longer periods: KIC 9406652 and RZ Gru. While the credentials for SHs in RZ Gru may not be totally convincing (see above), there is no doubt about the strong pSH in KIC 9406652 (see Section 3.23). Excluding these two stars, a linear least-squares fit to the remaining points yields the dashed line in Fig. 26. In spite of their significantly longer periods, the points corresponding to KIC 9406652 and RZ Gru lie only 0.8σ and 1.3σ, respectively, above the extrapolated PpSH–ϵ relation defined by the other systems, where σ is the standard deviation of their scatter around the dashed line. Thus, both of the long-period systems follow well the Stolz–Schoembs relation for nova and NL stars. The solid line is a least-squares fit to all data, yielding |$\epsilon = 0.002(3) + 0.47(2)\, P_{\rm psh}$|.
KIC 9406652 and RZ Gru present a challenge to theoretical explanations of pSHs. As mentioned in the Introduction section, these are thought to be caused by the extra tidal stresses in the outer regions of an asymmetric accretion disc when its elongated part extends towards the secondary star. The disc can become elliptical when the revolution period of particles in its outer part reaches the 3:1 resonance with the orbital period (Whitehurst 1988). This is expected to be possible only in systems with a small mass ratio q = MWD/Msec. Just how small q must be is a matter of debate. Limits cited in the literature range from 0.22 to 0.39 (Whitehurst & King 1991; Pearson 2006; Smak 2020). The mass ratio of RZ Gru is unknown. Assuming the secondary star to have a mass according to the semi-empirical mass–period relation of Knigge, Baraffe & Patterson (2011) and the white dwarf mass to be equal to the average mass of the compact object in CVs (Zorotovic, Schreiber & Gänsicke 2011), the mass ratio is 0.41, which is higher than but still close to the upper limit of the theoretically permitted range. Based on radial-velocity measurements of absorption and emission lines, Gies et al. (2013) derived q = 0.83 ± 0.07 for KIC 9406652, way beyond this range.
As also outlined in the Introduction section, the phenomenological understanding of nSHs as arising in a warped or tilted accretion disc is widely accepted. But their is no consensus on the mechanisms that cause the warp or inclination of the disc. In contrast to pSHs, it is therefore not possible to specify any limits imposed by theory on the occurrence of nSHs and to confront such limits with observations. The ϵ–PnSH relation constructed from Table 4 is shown in the lower frame of Fig. 26. I also insert as a red dot the location of DM Gem under the assumption that it is a negative superhumper. It falls drastically below the general trend. This is thus a further argument in favour to a pSH nature of this system. The low credential system RW Tri (blue dot) follows the general trend reasonably well and may thus in fact exhibit SHs sporadically. This leaves KIC 9406652 as the only true outlier in the diagram with a much more negative period excess than expected at its period. There is, however, no reason to suspect anything to be wrong with its SH period. A linear least-squares fit to the data points (including KIC 9406652 but, of course, not DM Gem) yields |$\epsilon = -0.006(2) - 0.22(1)\, P_{\rm nSH}$| and is shown as a solid line in the figure. I note that the ratio of the inclination of this relation to the corresponding relation for pSHs is −0.48, confirming the conventional wisdom that the period deficit in nSHs systems is about half of that of the period excess in their positive counterparts at a given period.
In most cases where the corresponding information is available, the negative, as well as the pSHs, have a roughly sinusoidal shape, consisting of a single hump extending over all phases. Sometimes, it is distorted into a saw tooth with the steeper side leading or trailing, or the maximum is broader or narrower than the minimum. Often, the waveform changes somewhat from one epoch to another. More interesting are the rarer cases of double humped or complex waveforms, which occur more frequently in pSH than in nSH systems. Extreme examples are observed in AQ Men (Iłkiewicz et al. 2021), V348 Pup (Fig. 14), or KIC 9406652 (Fig. 23). Such waveforms constitute a valuable source of information about the mechanisms leading to SHs and the structure of superhumping accretion discs which has not yet been tapped adequately.
Often SHs are accompanied with variations on the beat period between orbital and SH periods, i.e. at the precession period of the accretion disc. Particularly impressive examples are V348 Pup (Fig. 14) and DW UMa (Fig. 18). But in about a third of all cases variations on the beat period have not been detected. Sometimes this may be explained by absent or only weak variations on the orbital period, but there are counterexamples. The orbital and SH signals are of comparable strength in the power spectrum of the first half of the TESS light curve of V795 Her (Paper I), yet no signal is seen at the beat frequency. In contrast, the orbital is much weaker than the SH signal in BK Lyn, but the light curve prominently exhibits variations on the beat period (Fig. 11). Of especial interest are a few systems where supraorbital periods are not seen on the beat period but on multiples thereof. These are V603 Aql (Bruch & Cook 2018), RZ Gru (Paper I), and possibly V1974 Cyg (Section 3.8).
With a limited number of observations, it is, of course, never possible to be certain that SHs in any CV are really permanent. Here, I classify a system tentatively as a permanent superhumper if observations at different epochs are available and SHs were always found when they have been searched for in data of suitable quality and quantity, and unless they are substituted by other long-term features in the light curve [such as the temporary substitution of negative by pSHs or the temporary transition into a low state in TT Ari; Bruch (2020)]. In this sense, the most convincing permanent SH systems are V603 Aql (pSH) and TT Ari (nSH; see the numerous references cited in Table 4). Classifying a system as a transient superhumper is much more straightforward: it is sufficient if SHs are seen at one or several epochs but not at others. Adopting this criterium, transient SHs are significantly more frequent than permanent ones.
5 SUMMARY
In this paper, I took advantage of the enormous richness of information of the month long (or many times even longer) almost continuous high-cadence light curves provided by the TESS mission to explore the properties and the temporal behaviour (periods, occurrence or absence, waveforms, interplay with orbital periods) of SHs, either negative or positive, in the majority of NL variables and old novae, where such phenomena were observed in the past and for which TESS data are available. The results of this study, in combination with Paper I and information collected from the literature, enabled a more complete census of the SH properties in these systems than was possible hitherto. This compilation of old and new observational attributes should serve to provide boundary conditions for physical models for SHs. In this context, I draw special attention to the sometimes vexing morphological complexity and temporal variability of SH waveforms, which merit more attention than they received so far.
As a corollary, for the eclipsing CVs among the targets of this study, eclipse epochs were derived from the TESS data. In some cases, these were used together with additional eclipse epochs measured in archival terrestrial light curves to update the sometimes decades old orbital ephemeris, and to discuss systematic or erratic period variations.
It is common knowledge that pSHs are abundant – even a defining characteristic – in superoutbursts of short period dwarf novae (SU UMa stars). SHs – both, positive and negative ones – are not observed as routinely in the longer period NLs and old novae, but the fraction of such systems exhibiting SHs is by no means small. The identification of several more such systems in Paper I suggests that many more superhumpers lurk among those systems, which have not yet been systematically investigated for SHs. TESS light curves of a significant number of such NLs and old novae are available. An effort to analyse these is currently underway and will hopefully lead to a third paper of this small series.
ACKNOWLEDGEMENTS
This paper is based on data collected by the TESS and Kepler missions and obtained from the MAST data archive at the Space Telescope Science Institute (STScI). Funding for the missions is provided by the NASA Explorer Program and the NASA Science Mission Directorate for TESS and Kepler, respectively. STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. Supportive data were obtained from the data archives operated by the American Association of Variable Star Observers and the Laboratório Nacional de Astrofísica.
DATA AVAILABILITY
All data used in the present study are publicly available at the Barbara A. Mikulski Archive for Space Telescopes (MAST: https://mast.stsci.edu/portal/Mashub/clients/MAST/Portal.html), the AAVSO website (https://www.aavso.org), and the LNA Data Bank (http://databank.lna.br).
Footnotes
Using only the data available to Baptista et al. (1995), I could reproduce, of course, their period precisely, but the error is 10 times larger.
REFERENCES
APPENDIX A: ADDITIONAL ECLIPSE TIMINGS
UU Aqr eclipse epochs (zero-point for cycle counts as defined by equation 1).
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 51755.7281 | 0 | 55415.8404 | 22375 | 56215.4214 | 27263 | 57249.7401 | 33586 | 58368.6292 | 40426 |
| 51756.5464 | 5 | 55416.6578 | 22380 | 56507.5749 | 29049 | 57262.4991 | 33664 | 58369.4481 | 40431 |
| 51756.7100 | 6 | 55416.8217 | 22381 | 56507.7392 | 29050 | 57609.4530 | 35785 | 58369.6107 | 40432 |
| 53234.6594 | 9041 | 55417.6403 | 22386 | 56508.5574 | 29055 | 57617.4687 | 35834 | 58370.4295 | 40437 |
| 54322.4696 | 15691 | 55417.8032 | 22387 | 56508.7214 | 29056 | 57627.6106 | 35896 | 58370.5924 | 40438 |
| 54323.4510 | 15697 | 55418.6214 | 22392 | 56509.5399 | 29061 | 57627.7741 | 35897 | 58370.7575 | 40439 |
| 54325.4128 | 15709 | 55418.7846 | 22393 | 56509.7027 | 29062 | 57628.5922 | 35902 | 58371.5731 | 40444 |
| 54357.4749 | 15905 | 55469.4949 | 22703 | 56510.6839 | 29068 | 57628.7564 | 35903 | 58371.7378 | 40445 |
| 54365.4905 | 15954 | 55778.4979 | 24592 | 56510.6842 | 29068 | 57629.5739 | 35908 | 58372.5563 | 40450 |
| 54728.4749 | 18173 | 55795.5097 | 24696 | 56523.4439 | 29146 | 57629.7363 | 35909 | 58372.7188 | 40451 |
| 54731.4211 | 18191 | 55799.5995 | 24721 | 56563.5208 | 29391 | 57630.5556 | 35914 | 58373.5371 | 40456 |
| 54734.5267 | 18210 | 55799.7637 | 24722 | 56563.5209 | 29391 | 57630.7185 | 35915 | 58373.7004 | 40457 |
| 54734.6915 | 18211 | 55800.5812 | 24727 | 56563.6837 | 29392 | 57642.4966 | 35987 | 58374.5178 | 40462 |
| 54735.3454 | 18215 | 55800.7451 | 24728 | 56563.6837 | 29392 | 57991.7407 | 38122 | 58377.6263 | 40481 |
| 54736.3271 | 18221 | 55801.5633 | 24733 | 56872.6888 | 31281 | 57995.6656 | 38146 | 58378.4439 | 40486 |
| 54810.2672 | 18673 | 55801.7268 | 24734 | 56872.8515 | 31282 | 58349.6548 | 40310 | 58378.6062 | 40487 |
| 54830.2252 | 18795 | 55893.3309 | 25294 | 56874.6512 | 31293 | 58349.8171 | 40311 | 58726.5426 | 42614 |
| 55059.3979 | 20196 | 56157.6775 | 26910 | 56874.8140 | 31294 | 58350.4714 | 40315 | 58726.7062 | 42615 |
| 55106.3460 | 20483 | 56159.4761 | 26921 | 56893.4627 | 31408 | 58351.6177 | 40322 | 58733.5766 | 42657 |
| 55415.6770 | 22374 | 56160.4586 | 26927 | 57249.5761 | 33585 | 58351.7801 | 40323 |
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 51755.7281 | 0 | 55415.8404 | 22375 | 56215.4214 | 27263 | 57249.7401 | 33586 | 58368.6292 | 40426 |
| 51756.5464 | 5 | 55416.6578 | 22380 | 56507.5749 | 29049 | 57262.4991 | 33664 | 58369.4481 | 40431 |
| 51756.7100 | 6 | 55416.8217 | 22381 | 56507.7392 | 29050 | 57609.4530 | 35785 | 58369.6107 | 40432 |
| 53234.6594 | 9041 | 55417.6403 | 22386 | 56508.5574 | 29055 | 57617.4687 | 35834 | 58370.4295 | 40437 |
| 54322.4696 | 15691 | 55417.8032 | 22387 | 56508.7214 | 29056 | 57627.6106 | 35896 | 58370.5924 | 40438 |
| 54323.4510 | 15697 | 55418.6214 | 22392 | 56509.5399 | 29061 | 57627.7741 | 35897 | 58370.7575 | 40439 |
| 54325.4128 | 15709 | 55418.7846 | 22393 | 56509.7027 | 29062 | 57628.5922 | 35902 | 58371.5731 | 40444 |
| 54357.4749 | 15905 | 55469.4949 | 22703 | 56510.6839 | 29068 | 57628.7564 | 35903 | 58371.7378 | 40445 |
| 54365.4905 | 15954 | 55778.4979 | 24592 | 56510.6842 | 29068 | 57629.5739 | 35908 | 58372.5563 | 40450 |
| 54728.4749 | 18173 | 55795.5097 | 24696 | 56523.4439 | 29146 | 57629.7363 | 35909 | 58372.7188 | 40451 |
| 54731.4211 | 18191 | 55799.5995 | 24721 | 56563.5208 | 29391 | 57630.5556 | 35914 | 58373.5371 | 40456 |
| 54734.5267 | 18210 | 55799.7637 | 24722 | 56563.5209 | 29391 | 57630.7185 | 35915 | 58373.7004 | 40457 |
| 54734.6915 | 18211 | 55800.5812 | 24727 | 56563.6837 | 29392 | 57642.4966 | 35987 | 58374.5178 | 40462 |
| 54735.3454 | 18215 | 55800.7451 | 24728 | 56563.6837 | 29392 | 57991.7407 | 38122 | 58377.6263 | 40481 |
| 54736.3271 | 18221 | 55801.5633 | 24733 | 56872.6888 | 31281 | 57995.6656 | 38146 | 58378.4439 | 40486 |
| 54810.2672 | 18673 | 55801.7268 | 24734 | 56872.8515 | 31282 | 58349.6548 | 40310 | 58378.6062 | 40487 |
| 54830.2252 | 18795 | 55893.3309 | 25294 | 56874.6512 | 31293 | 58349.8171 | 40311 | 58726.5426 | 42614 |
| 55059.3979 | 20196 | 56157.6775 | 26910 | 56874.8140 | 31294 | 58350.4714 | 40315 | 58726.7062 | 42615 |
| 55106.3460 | 20483 | 56159.4761 | 26921 | 56893.4627 | 31408 | 58351.6177 | 40322 | 58733.5766 | 42657 |
| 55415.6770 | 22374 | 56160.4586 | 26927 | 57249.5761 | 33585 | 58351.7801 | 40323 |
UU Aqr eclipse epochs (zero-point for cycle counts as defined by equation 1).
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 51755.7281 | 0 | 55415.8404 | 22375 | 56215.4214 | 27263 | 57249.7401 | 33586 | 58368.6292 | 40426 |
| 51756.5464 | 5 | 55416.6578 | 22380 | 56507.5749 | 29049 | 57262.4991 | 33664 | 58369.4481 | 40431 |
| 51756.7100 | 6 | 55416.8217 | 22381 | 56507.7392 | 29050 | 57609.4530 | 35785 | 58369.6107 | 40432 |
| 53234.6594 | 9041 | 55417.6403 | 22386 | 56508.5574 | 29055 | 57617.4687 | 35834 | 58370.4295 | 40437 |
| 54322.4696 | 15691 | 55417.8032 | 22387 | 56508.7214 | 29056 | 57627.6106 | 35896 | 58370.5924 | 40438 |
| 54323.4510 | 15697 | 55418.6214 | 22392 | 56509.5399 | 29061 | 57627.7741 | 35897 | 58370.7575 | 40439 |
| 54325.4128 | 15709 | 55418.7846 | 22393 | 56509.7027 | 29062 | 57628.5922 | 35902 | 58371.5731 | 40444 |
| 54357.4749 | 15905 | 55469.4949 | 22703 | 56510.6839 | 29068 | 57628.7564 | 35903 | 58371.7378 | 40445 |
| 54365.4905 | 15954 | 55778.4979 | 24592 | 56510.6842 | 29068 | 57629.5739 | 35908 | 58372.5563 | 40450 |
| 54728.4749 | 18173 | 55795.5097 | 24696 | 56523.4439 | 29146 | 57629.7363 | 35909 | 58372.7188 | 40451 |
| 54731.4211 | 18191 | 55799.5995 | 24721 | 56563.5208 | 29391 | 57630.5556 | 35914 | 58373.5371 | 40456 |
| 54734.5267 | 18210 | 55799.7637 | 24722 | 56563.5209 | 29391 | 57630.7185 | 35915 | 58373.7004 | 40457 |
| 54734.6915 | 18211 | 55800.5812 | 24727 | 56563.6837 | 29392 | 57642.4966 | 35987 | 58374.5178 | 40462 |
| 54735.3454 | 18215 | 55800.7451 | 24728 | 56563.6837 | 29392 | 57991.7407 | 38122 | 58377.6263 | 40481 |
| 54736.3271 | 18221 | 55801.5633 | 24733 | 56872.6888 | 31281 | 57995.6656 | 38146 | 58378.4439 | 40486 |
| 54810.2672 | 18673 | 55801.7268 | 24734 | 56872.8515 | 31282 | 58349.6548 | 40310 | 58378.6062 | 40487 |
| 54830.2252 | 18795 | 55893.3309 | 25294 | 56874.6512 | 31293 | 58349.8171 | 40311 | 58726.5426 | 42614 |
| 55059.3979 | 20196 | 56157.6775 | 26910 | 56874.8140 | 31294 | 58350.4714 | 40315 | 58726.7062 | 42615 |
| 55106.3460 | 20483 | 56159.4761 | 26921 | 56893.4627 | 31408 | 58351.6177 | 40322 | 58733.5766 | 42657 |
| 55415.6770 | 22374 | 56160.4586 | 26927 | 57249.5761 | 33585 | 58351.7801 | 40323 |
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 51755.7281 | 0 | 55415.8404 | 22375 | 56215.4214 | 27263 | 57249.7401 | 33586 | 58368.6292 | 40426 |
| 51756.5464 | 5 | 55416.6578 | 22380 | 56507.5749 | 29049 | 57262.4991 | 33664 | 58369.4481 | 40431 |
| 51756.7100 | 6 | 55416.8217 | 22381 | 56507.7392 | 29050 | 57609.4530 | 35785 | 58369.6107 | 40432 |
| 53234.6594 | 9041 | 55417.6403 | 22386 | 56508.5574 | 29055 | 57617.4687 | 35834 | 58370.4295 | 40437 |
| 54322.4696 | 15691 | 55417.8032 | 22387 | 56508.7214 | 29056 | 57627.6106 | 35896 | 58370.5924 | 40438 |
| 54323.4510 | 15697 | 55418.6214 | 22392 | 56509.5399 | 29061 | 57627.7741 | 35897 | 58370.7575 | 40439 |
| 54325.4128 | 15709 | 55418.7846 | 22393 | 56509.7027 | 29062 | 57628.5922 | 35902 | 58371.5731 | 40444 |
| 54357.4749 | 15905 | 55469.4949 | 22703 | 56510.6839 | 29068 | 57628.7564 | 35903 | 58371.7378 | 40445 |
| 54365.4905 | 15954 | 55778.4979 | 24592 | 56510.6842 | 29068 | 57629.5739 | 35908 | 58372.5563 | 40450 |
| 54728.4749 | 18173 | 55795.5097 | 24696 | 56523.4439 | 29146 | 57629.7363 | 35909 | 58372.7188 | 40451 |
| 54731.4211 | 18191 | 55799.5995 | 24721 | 56563.5208 | 29391 | 57630.5556 | 35914 | 58373.5371 | 40456 |
| 54734.5267 | 18210 | 55799.7637 | 24722 | 56563.5209 | 29391 | 57630.7185 | 35915 | 58373.7004 | 40457 |
| 54734.6915 | 18211 | 55800.5812 | 24727 | 56563.6837 | 29392 | 57642.4966 | 35987 | 58374.5178 | 40462 |
| 54735.3454 | 18215 | 55800.7451 | 24728 | 56563.6837 | 29392 | 57991.7407 | 38122 | 58377.6263 | 40481 |
| 54736.3271 | 18221 | 55801.5633 | 24733 | 56872.6888 | 31281 | 57995.6656 | 38146 | 58378.4439 | 40486 |
| 54810.2672 | 18673 | 55801.7268 | 24734 | 56872.8515 | 31282 | 58349.6548 | 40310 | 58378.6062 | 40487 |
| 54830.2252 | 18795 | 55893.3309 | 25294 | 56874.6512 | 31293 | 58349.8171 | 40311 | 58726.5426 | 42614 |
| 55059.3979 | 20196 | 56157.6775 | 26910 | 56874.8140 | 31294 | 58350.4714 | 40315 | 58726.7062 | 42615 |
| 55106.3460 | 20483 | 56159.4761 | 26921 | 56893.4627 | 31408 | 58351.6177 | 40322 | 58733.5766 | 42657 |
| 55415.6770 | 22374 | 56160.4586 | 26927 | 57249.5761 | 33585 | 58351.7801 | 40323 |
V348 Pup eclipse epochs (zero-point for cycle counts as defined by Dai et al. (2010)).
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 56631.6506 | 78948 | 56633.6873 | 78968 | 57008.7600 | 82651 | 57728.7619 | 89721 | 57729.7803 | 89731 |
| 56633.5858 | 78967 | 56633.7889 | 78969 | 57728.6603 | 89720 | 57729.6783 | 89730 |
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 56631.6506 | 78948 | 56633.6873 | 78968 | 57008.7600 | 82651 | 57728.7619 | 89721 | 57729.7803 | 89731 |
| 56633.5858 | 78967 | 56633.7889 | 78969 | 57728.6603 | 89720 | 57729.6783 | 89730 |
V348 Pup eclipse epochs (zero-point for cycle counts as defined by Dai et al. (2010)).
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 56631.6506 | 78948 | 56633.6873 | 78968 | 57008.7600 | 82651 | 57728.7619 | 89721 | 57729.7803 | 89731 |
| 56633.5858 | 78967 | 56633.7889 | 78969 | 57728.6603 | 89720 | 57729.6783 | 89730 |
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 56631.6506 | 78948 | 56633.6873 | 78968 | 57008.7600 | 82651 | 57728.7619 | 89721 | 57729.7803 | 89731 |
| 56633.5858 | 78967 | 56633.7889 | 78969 | 57728.6603 | 89720 | 57729.6783 | 89730 |
RW Tri eclipse epochs (zero-point for cycle counts as defined by equation 7).
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 53672.6223 | 0 | 56228.4405 | 11022 | 57328.2638 | 15765 | 57337.5394 | 15805 | 57409.6550 | 16116 |
| 54392.3882 | 3104 | 56609.4252 | 12665 | 57329.4233 | 15770 | 57338.6984 | 15810 | 57410.5828 | 16120 |
| 54419.5180 | 3221 | 56619.3963 | 12708 | 57329.6556 | 15771 | 57339.3944 | 15813 | 57415.6840 | 16142 |
| 54447.3442 | 3341 | 56636.3240 | 12781 | 57329.8875 | 15772 | 57340.3218 | 15817 | 57416.6113 | 16146 |
| 54835.2862 | 5014 | 56922.4676 | 14015 | 57330.5834 | 15775 | 57342.4087 | 15826 | 57419.3941 | 16158 |
| 55063.4584 | 5998 | 56933.3661 | 14062 | 57330.8145 | 15776 | 57343.3362 | 15830 | 57420.3215 | 16162 |
| 55106.3577 | 6183 | 56935.4533 | 14071 | 57331.2785 | 15778 | 57344.2639 | 15834 | 57421.4813 | 16167 |
| 55172.4441 | 6468 | 57314.3506 | 15705 | 57331.5104 | 15779 | 57345.4232 | 15839 | 57422.4087 | 16171 |
| 55487.3422 | 7826 | 57315.7423 | 15711 | 57332.6698 | 15784 | 57391.7998 | 16039 | 57423.3364 | 16175 |
| 55490.3565 | 7839 | 57317.5974 | 15719 | 57332.9016 | 15785 | 57397.8289 | 16065 | 57424.4957 | 16180 |
| 55533.4868 | 8025 | 57319.6843 | 15728 | 57333.3658 | 15787 | 57399.6844 | 16073 | 57424.7273 | 16181 |
| 55822.4132 | 9271 | 57320.3800 | 15731 | 57334.2930 | 15791 | 57400.3797 | 16076 | 57623.4522 | 17038 |
| 55828.4424 | 9297 | 57321.3071 | 15735 | 57334.5248 | 15792 | 57400.6118 | 16077 | 57642.4662 | 17120 |
| 55867.3985 | 9465 | 57321.5389 | 15736 | 57334.7571 | 15793 | 57401.7710 | 16082 | 57645.4807 | 17133 |
| 55881.3116 | 9525 | 57324.5538 | 15749 | 57335.4523 | 15796 | 57402.6986 | 16086 | 57684.9010 | 17303 |
| 55950.4122 | 9823 | 57326.4088 | 15757 | 57335.9160 | 15798 | 57403.3943 | 16089 | 57685.5961 | 17306 |
| 55953.4270 | 9836 | 57326.6406 | 15758 | 57336.3799 | 15800 | 57403.6260 | 16090 | 57685.8285 | 17307 |
| 55957.3700 | 9853 | 57327.3361 | 15761 | 57336.6115 | 15801 | 57407.5681 | 16107 | 57686.7559 | 17311 |
| 56200.3826 | 10901 | 57327.5684 | 15762 | 57336.8436 | 15802 | 57408.7277 | 16112 | 58431.3325 | 20522 |
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 53672.6223 | 0 | 56228.4405 | 11022 | 57328.2638 | 15765 | 57337.5394 | 15805 | 57409.6550 | 16116 |
| 54392.3882 | 3104 | 56609.4252 | 12665 | 57329.4233 | 15770 | 57338.6984 | 15810 | 57410.5828 | 16120 |
| 54419.5180 | 3221 | 56619.3963 | 12708 | 57329.6556 | 15771 | 57339.3944 | 15813 | 57415.6840 | 16142 |
| 54447.3442 | 3341 | 56636.3240 | 12781 | 57329.8875 | 15772 | 57340.3218 | 15817 | 57416.6113 | 16146 |
| 54835.2862 | 5014 | 56922.4676 | 14015 | 57330.5834 | 15775 | 57342.4087 | 15826 | 57419.3941 | 16158 |
| 55063.4584 | 5998 | 56933.3661 | 14062 | 57330.8145 | 15776 | 57343.3362 | 15830 | 57420.3215 | 16162 |
| 55106.3577 | 6183 | 56935.4533 | 14071 | 57331.2785 | 15778 | 57344.2639 | 15834 | 57421.4813 | 16167 |
| 55172.4441 | 6468 | 57314.3506 | 15705 | 57331.5104 | 15779 | 57345.4232 | 15839 | 57422.4087 | 16171 |
| 55487.3422 | 7826 | 57315.7423 | 15711 | 57332.6698 | 15784 | 57391.7998 | 16039 | 57423.3364 | 16175 |
| 55490.3565 | 7839 | 57317.5974 | 15719 | 57332.9016 | 15785 | 57397.8289 | 16065 | 57424.4957 | 16180 |
| 55533.4868 | 8025 | 57319.6843 | 15728 | 57333.3658 | 15787 | 57399.6844 | 16073 | 57424.7273 | 16181 |
| 55822.4132 | 9271 | 57320.3800 | 15731 | 57334.2930 | 15791 | 57400.3797 | 16076 | 57623.4522 | 17038 |
| 55828.4424 | 9297 | 57321.3071 | 15735 | 57334.5248 | 15792 | 57400.6118 | 16077 | 57642.4662 | 17120 |
| 55867.3985 | 9465 | 57321.5389 | 15736 | 57334.7571 | 15793 | 57401.7710 | 16082 | 57645.4807 | 17133 |
| 55881.3116 | 9525 | 57324.5538 | 15749 | 57335.4523 | 15796 | 57402.6986 | 16086 | 57684.9010 | 17303 |
| 55950.4122 | 9823 | 57326.4088 | 15757 | 57335.9160 | 15798 | 57403.3943 | 16089 | 57685.5961 | 17306 |
| 55953.4270 | 9836 | 57326.6406 | 15758 | 57336.3799 | 15800 | 57403.6260 | 16090 | 57685.8285 | 17307 |
| 55957.3700 | 9853 | 57327.3361 | 15761 | 57336.6115 | 15801 | 57407.5681 | 16107 | 57686.7559 | 17311 |
| 56200.3826 | 10901 | 57327.5684 | 15762 | 57336.8436 | 15802 | 57408.7277 | 16112 | 58431.3325 | 20522 |
RW Tri eclipse epochs (zero-point for cycle counts as defined by equation 7).
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 53672.6223 | 0 | 56228.4405 | 11022 | 57328.2638 | 15765 | 57337.5394 | 15805 | 57409.6550 | 16116 |
| 54392.3882 | 3104 | 56609.4252 | 12665 | 57329.4233 | 15770 | 57338.6984 | 15810 | 57410.5828 | 16120 |
| 54419.5180 | 3221 | 56619.3963 | 12708 | 57329.6556 | 15771 | 57339.3944 | 15813 | 57415.6840 | 16142 |
| 54447.3442 | 3341 | 56636.3240 | 12781 | 57329.8875 | 15772 | 57340.3218 | 15817 | 57416.6113 | 16146 |
| 54835.2862 | 5014 | 56922.4676 | 14015 | 57330.5834 | 15775 | 57342.4087 | 15826 | 57419.3941 | 16158 |
| 55063.4584 | 5998 | 56933.3661 | 14062 | 57330.8145 | 15776 | 57343.3362 | 15830 | 57420.3215 | 16162 |
| 55106.3577 | 6183 | 56935.4533 | 14071 | 57331.2785 | 15778 | 57344.2639 | 15834 | 57421.4813 | 16167 |
| 55172.4441 | 6468 | 57314.3506 | 15705 | 57331.5104 | 15779 | 57345.4232 | 15839 | 57422.4087 | 16171 |
| 55487.3422 | 7826 | 57315.7423 | 15711 | 57332.6698 | 15784 | 57391.7998 | 16039 | 57423.3364 | 16175 |
| 55490.3565 | 7839 | 57317.5974 | 15719 | 57332.9016 | 15785 | 57397.8289 | 16065 | 57424.4957 | 16180 |
| 55533.4868 | 8025 | 57319.6843 | 15728 | 57333.3658 | 15787 | 57399.6844 | 16073 | 57424.7273 | 16181 |
| 55822.4132 | 9271 | 57320.3800 | 15731 | 57334.2930 | 15791 | 57400.3797 | 16076 | 57623.4522 | 17038 |
| 55828.4424 | 9297 | 57321.3071 | 15735 | 57334.5248 | 15792 | 57400.6118 | 16077 | 57642.4662 | 17120 |
| 55867.3985 | 9465 | 57321.5389 | 15736 | 57334.7571 | 15793 | 57401.7710 | 16082 | 57645.4807 | 17133 |
| 55881.3116 | 9525 | 57324.5538 | 15749 | 57335.4523 | 15796 | 57402.6986 | 16086 | 57684.9010 | 17303 |
| 55950.4122 | 9823 | 57326.4088 | 15757 | 57335.9160 | 15798 | 57403.3943 | 16089 | 57685.5961 | 17306 |
| 55953.4270 | 9836 | 57326.6406 | 15758 | 57336.3799 | 15800 | 57403.6260 | 16090 | 57685.8285 | 17307 |
| 55957.3700 | 9853 | 57327.3361 | 15761 | 57336.6115 | 15801 | 57407.5681 | 16107 | 57686.7559 | 17311 |
| 56200.3826 | 10901 | 57327.5684 | 15762 | 57336.8436 | 15802 | 57408.7277 | 16112 | 58431.3325 | 20522 |
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 53672.6223 | 0 | 56228.4405 | 11022 | 57328.2638 | 15765 | 57337.5394 | 15805 | 57409.6550 | 16116 |
| 54392.3882 | 3104 | 56609.4252 | 12665 | 57329.4233 | 15770 | 57338.6984 | 15810 | 57410.5828 | 16120 |
| 54419.5180 | 3221 | 56619.3963 | 12708 | 57329.6556 | 15771 | 57339.3944 | 15813 | 57415.6840 | 16142 |
| 54447.3442 | 3341 | 56636.3240 | 12781 | 57329.8875 | 15772 | 57340.3218 | 15817 | 57416.6113 | 16146 |
| 54835.2862 | 5014 | 56922.4676 | 14015 | 57330.5834 | 15775 | 57342.4087 | 15826 | 57419.3941 | 16158 |
| 55063.4584 | 5998 | 56933.3661 | 14062 | 57330.8145 | 15776 | 57343.3362 | 15830 | 57420.3215 | 16162 |
| 55106.3577 | 6183 | 56935.4533 | 14071 | 57331.2785 | 15778 | 57344.2639 | 15834 | 57421.4813 | 16167 |
| 55172.4441 | 6468 | 57314.3506 | 15705 | 57331.5104 | 15779 | 57345.4232 | 15839 | 57422.4087 | 16171 |
| 55487.3422 | 7826 | 57315.7423 | 15711 | 57332.6698 | 15784 | 57391.7998 | 16039 | 57423.3364 | 16175 |
| 55490.3565 | 7839 | 57317.5974 | 15719 | 57332.9016 | 15785 | 57397.8289 | 16065 | 57424.4957 | 16180 |
| 55533.4868 | 8025 | 57319.6843 | 15728 | 57333.3658 | 15787 | 57399.6844 | 16073 | 57424.7273 | 16181 |
| 55822.4132 | 9271 | 57320.3800 | 15731 | 57334.2930 | 15791 | 57400.3797 | 16076 | 57623.4522 | 17038 |
| 55828.4424 | 9297 | 57321.3071 | 15735 | 57334.5248 | 15792 | 57400.6118 | 16077 | 57642.4662 | 17120 |
| 55867.3985 | 9465 | 57321.5389 | 15736 | 57334.7571 | 15793 | 57401.7710 | 16082 | 57645.4807 | 17133 |
| 55881.3116 | 9525 | 57324.5538 | 15749 | 57335.4523 | 15796 | 57402.6986 | 16086 | 57684.9010 | 17303 |
| 55950.4122 | 9823 | 57326.4088 | 15757 | 57335.9160 | 15798 | 57403.3943 | 16089 | 57685.5961 | 17306 |
| 55953.4270 | 9836 | 57326.6406 | 15758 | 57336.3799 | 15800 | 57403.6260 | 16090 | 57685.8285 | 17307 |
| 55957.3700 | 9853 | 57327.3361 | 15761 | 57336.6115 | 15801 | 57407.5681 | 16107 | 57686.7559 | 17311 |
| 56200.3826 | 10901 | 57327.5684 | 15762 | 57336.8436 | 15802 | 57408.7277 | 16112 | 58431.3325 | 20522 |
UX UMa eclipse epochs (zero-point for cycle counts as defined by equation 8).
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 43311.7185 | −40718 | 56688.7090 | 27299 | 57116.6640 | 29475 | 57143.8064 | 29613 | 57525.7421 | 31555 |
| 43660.8097 | −38943 | 56725.2894 | 27485 | 57117.6483 | 29480 | 57144.0029 | 29614 | 57526.7250 | 31560 |
| 43998.6925 | −37225 | 56725.4859 | 27486 | 57118.4352 | 29484 | 57144.3959 | 29616 | 57529.6749 | 31575 |
| 48779.7710 | −12915 | 56731.3853 | 27516 | 57119.4182 | 29489 | 57144.7893 | 29618 | 57530.6580 | 31580 |
| 51319.7821 | 0 | 56733.3520 | 27526 | 57119.6150 | 29490 | 57145.7726 | 29623 | 57785.9373 | 32878 |
| 52363.5161 | 5307 | 56733.5494 | 27527 | 57119.8115 | 29491 | 57145.9689 | 29624 | 57804.8179 | 32974 |
| 52551.3369 | 6262 | 56734.3363 | 27531 | 57120.4025 | 29494 | 57146.7558 | 29628 | 57809.5381 | 32998 |
| 53466.6455 | 10916 | 56734.5324 | 27532 | 57121.3857 | 29499 | 57147.7394 | 29633 | 57811.8981 | 33010 |
| 53473.9221 | 10953 | 56738.2695 | 27551 | 57121.5827 | 29500 | 57148.5256 | 29637 | 57883.6832 | 33375 |
| 53476.8723 | 10968 | 56738.4663 | 27552 | 57121.7789 | 29501 | 57150.6887 | 29648 | 57888.7966 | 33401 |
| 53477.8555 | 10973 | 56739.2526 | 27556 | 57122.3686 | 29504 | 57150.8855 | 29649 | 57890.7632 | 33411 |
| 53481.7887 | 10993 | 56739.4495 | 27557 | 57122.5651 | 29505 | 57152.4585 | 29657 | 57907.6769 | 33497 |
| 53495.7527 | 11064 | 56741.4160 | 27567 | 57122.7608 | 29506 | 57152.8521 | 29659 | 57939.3410 | 33658 |
| 53760.8655 | 12412 | 56741.6130 | 27568 | 57122.9581 | 29507 | 57153.4429 | 29662 | 58154.8926 | 34754 |
| 54154.4047 | 14413 | 56742.3995 | 27572 | 57123.3518 | 29509 | 57153.8352 | 29664 | 58173.3798 | 34848 |
| 54187.4456 | 14581 | 56742.5968 | 27573 | 57123.7447 | 29511 | 57154.4258 | 29667 | 58173.5762 | 34849 |
| 54512.3469 | 16233 | 56743.3830 | 27577 | 57124.5319 | 29515 | 57154.6222 | 29668 | 58175.3468 | 34858 |
| 54912.7701 | 18269 | 56749.4800 | 27608 | 57124.7287 | 29516 | 57157.5729 | 29683 | 58175.5431 | 34859 |
| 54933.6164 | 18375 | 56751.4463 | 27618 | 57125.3192 | 29519 | 57158.5561 | 29688 | 58179.8698 | 34881 |
| 55279.3648 | 20133 | 56752.4297 | 27623 | 57125.5155 | 29520 | 57160.5220 | 29698 | 58181.8367 | 34891 |
| 55279.7582 | 20135 | 56754.3964 | 27633 | 57126.4985 | 29525 | 57162.4906 | 29708 | 58192.6534 | 34946 |
| 55298.6385 | 20231 | 56754.5929 | 27634 | 57126.6951 | 29526 | 57163.4728 | 29713 | 58212.5173 | 35047 |
| 55309.6520 | 20287 | 56756.3637 | 27643 | 57127.4820 | 29530 | 57164.4564 | 29718 | 58246.7381 | 35221 |
| 55616.4587 | 21847 | 56757.3465 | 27648 | 57127.6771 | 29531 | 57165.4392 | 29723 | 58527.3874 | 36648 |
| 55617.4423 | 21852 | 56757.5433 | 27649 | 57128.6623 | 29536 | 57166.4216 | 29728 | 58527.5843 | 36649 |
| 55621.3754 | 21872 | 56763.4428 | 27679 | 57128.8586 | 29537 | 57166.6203 | 29729 | 58554.7254 | 36787 |
| 55993.2806 | 23763 | 56785.6671 | 27792 | 57129.6454 | 29541 | 57168.3892 | 29738 | 58554.9221 | 36788 |
| 55993.4773 | 23764 | 56789.6006 | 27812 | 57129.8413 | 29542 | 57168.5861 | 29739 | 58559.4450 | 36811 |
| 55994.2636 | 23768 | 56789.7974 | 27813 | 57130.6284 | 29546 | 57169.5706 | 29744 | 58559.6411 | 36812 |
| 55994.4605 | 23769 | 56792.3540 | 27826 | 57131.4158 | 29550 | 57169.7664 | 29745 | 58620.6092 | 37122 |
| 55995.2469 | 23773 | 56794.3202 | 27836 | 57131.8085 | 29552 | 57170.5534 | 29749 | 58627.6898 | 37158 |
| 55995.4438 | 23774 | 56802.7776 | 27879 | 57132.0061 | 29553 | 57170.7493 | 29750 | 58898.8991 | 38537 |
| 56012.7505 | 23862 | 56807.6943 | 27904 | 57132.3987 | 29555 | 57171.5348 | 29754 | 58915.2223 | 38620 |
| 56346.5016 | 25559 | 56811.6282 | 27924 | 57132.5952 | 29556 | 57173.5031 | 29764 | 58915.4194 | 38621 |
| 56351.6146 | 25585 | 57078.7074 | 29282 | 57132.7923 | 29557 | 57177.4367 | 29784 | 58922.4999 | 38657 |
| 56353.3848 | 25594 | 57081.6568 | 29297 | 57132.9895 | 29558 | 57190.4161 | 29850 | 58923.2869 | 38661 |
| 56353.5812 | 25595 | 57081.8539 | 29298 | 57133.3822 | 29560 | 57191.4004 | 29855 | 58923.4825 | 38662 |
| 56372.4621 | 25691 | 57083.8209 | 29308 | 57133.7748 | 29562 | 57192.5799 | 29861 | 58941.5776 | 38754 |
| 56376.3951 | 25711 | 57092.8677 | 29354 | 57133.9721 | 29563 | 57193.5634 | 29866 | 58941.7736 | 38755 |
| 56378.3616 | 25721 | 57098.5713 | 29383 | 57134.3648 | 29565 | 57194.5476 | 29871 | 59283.7852 | 40494 |
| 56381.3120 | 25736 | 57099.3580 | 29387 | 57134.7581 | 29567 | 57198.4803 | 29891 | 59293.8150 | 40545 |
| 56381.5088 | 25737 | 57099.5551 | 29388 | 57135.5457 | 29571 | 57199.4629 | 29896 | 59310.7292 | 40631 |
| 56382.2954 | 25741 | 57099.7514 | 29389 | 57135.7420 | 29572 | 57202.4135 | 29911 | 59317.6125 | 40666 |
| 56383.2791 | 25746 | 57100.3415 | 29392 | 57135.9383 | 29573 | 57207.5266 | 29937 | 59317.8093 | 40667 |
| 56383.4753 | 25747 | 57100.5382 | 29393 | 57136.5285 | 29576 | 57208.5098 | 29942 | 59332.7564 | 40743 |
| 56385.4419 | 25757 | 57102.7016 | 29404 | 57136.7258 | 29577 | 57209.4956 | 29947 | 59352.6205 | 40844 |
| 56386.4253 | 25762 | 57103.2916 | 29407 | 57138.4943 | 29586 | 57222.4738 | 30013 | 59364.6172 | 40905 |
| 56388.3921 | 25772 | 57103.4888 | 29408 | 57139.6757 | 29592 | 57223.4576 | 30018 | 59605.3423 | 42129 |
| 56391.3420 | 25787 | 57104.4708 | 29413 | 57140.4630 | 29596 | 57224.4399 | 30023 | 59605.5396 | 42130 |
| 56391.5389 | 25788 | 57107.4216 | 29428 | 57140.6594 | 29597 | 57226.4081 | 30033 | 59622.4531 | 42216 |
| 56393.3089 | 25797 | 57107.6197 | 29429 | 57140.8548 | 29598 | 57227.3907 | 30038 | 59639.3667 | 42302 |
| 56395.2752 | 25807 | 57108.7979 | 29435 | 57141.4453 | 29601 | 57227.7848 | 30040 | 59639.5644 | 42303 |
| 56454.6696 | 26109 | 57108.9958 | 29436 | 57141.6419 | 29602 | 57467.3300 | 31258 | 59675.7512 | 42487 |
| 56686.3487 | 27287 | 57109.7807 | 29440 | 57141.8388 | 29603 | 57467.5267 | 31259 | 59703.6790 | 42629 |
| 56686.5451 | 27288 | 57110.7647 | 29445 | 57142.4293 | 29606 | 57470.6735 | 31275 | 59703.8751 | 42630 |
| 56687.3310 | 27292 | 57111.7481 | 29450 | 57142.6257 | 29607 | 57471.6567 | 31280 | ||
| 56687.5284 | 27293 | 57111.9446 | 29451 | 57142.8231 | 29608 | 57494.6675 | 31397 | ||
| 56688.3147 | 27297 | 57113.7153 | 29460 | 57143.4127 | 29611 | 57520.6280 | 31529 | ||
| 56688.5115 | 27298 | 57114.8952 | 29466 | 57143.6087 | 29612 | 57520.8249 | 31530 |
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 43311.7185 | −40718 | 56688.7090 | 27299 | 57116.6640 | 29475 | 57143.8064 | 29613 | 57525.7421 | 31555 |
| 43660.8097 | −38943 | 56725.2894 | 27485 | 57117.6483 | 29480 | 57144.0029 | 29614 | 57526.7250 | 31560 |
| 43998.6925 | −37225 | 56725.4859 | 27486 | 57118.4352 | 29484 | 57144.3959 | 29616 | 57529.6749 | 31575 |
| 48779.7710 | −12915 | 56731.3853 | 27516 | 57119.4182 | 29489 | 57144.7893 | 29618 | 57530.6580 | 31580 |
| 51319.7821 | 0 | 56733.3520 | 27526 | 57119.6150 | 29490 | 57145.7726 | 29623 | 57785.9373 | 32878 |
| 52363.5161 | 5307 | 56733.5494 | 27527 | 57119.8115 | 29491 | 57145.9689 | 29624 | 57804.8179 | 32974 |
| 52551.3369 | 6262 | 56734.3363 | 27531 | 57120.4025 | 29494 | 57146.7558 | 29628 | 57809.5381 | 32998 |
| 53466.6455 | 10916 | 56734.5324 | 27532 | 57121.3857 | 29499 | 57147.7394 | 29633 | 57811.8981 | 33010 |
| 53473.9221 | 10953 | 56738.2695 | 27551 | 57121.5827 | 29500 | 57148.5256 | 29637 | 57883.6832 | 33375 |
| 53476.8723 | 10968 | 56738.4663 | 27552 | 57121.7789 | 29501 | 57150.6887 | 29648 | 57888.7966 | 33401 |
| 53477.8555 | 10973 | 56739.2526 | 27556 | 57122.3686 | 29504 | 57150.8855 | 29649 | 57890.7632 | 33411 |
| 53481.7887 | 10993 | 56739.4495 | 27557 | 57122.5651 | 29505 | 57152.4585 | 29657 | 57907.6769 | 33497 |
| 53495.7527 | 11064 | 56741.4160 | 27567 | 57122.7608 | 29506 | 57152.8521 | 29659 | 57939.3410 | 33658 |
| 53760.8655 | 12412 | 56741.6130 | 27568 | 57122.9581 | 29507 | 57153.4429 | 29662 | 58154.8926 | 34754 |
| 54154.4047 | 14413 | 56742.3995 | 27572 | 57123.3518 | 29509 | 57153.8352 | 29664 | 58173.3798 | 34848 |
| 54187.4456 | 14581 | 56742.5968 | 27573 | 57123.7447 | 29511 | 57154.4258 | 29667 | 58173.5762 | 34849 |
| 54512.3469 | 16233 | 56743.3830 | 27577 | 57124.5319 | 29515 | 57154.6222 | 29668 | 58175.3468 | 34858 |
| 54912.7701 | 18269 | 56749.4800 | 27608 | 57124.7287 | 29516 | 57157.5729 | 29683 | 58175.5431 | 34859 |
| 54933.6164 | 18375 | 56751.4463 | 27618 | 57125.3192 | 29519 | 57158.5561 | 29688 | 58179.8698 | 34881 |
| 55279.3648 | 20133 | 56752.4297 | 27623 | 57125.5155 | 29520 | 57160.5220 | 29698 | 58181.8367 | 34891 |
| 55279.7582 | 20135 | 56754.3964 | 27633 | 57126.4985 | 29525 | 57162.4906 | 29708 | 58192.6534 | 34946 |
| 55298.6385 | 20231 | 56754.5929 | 27634 | 57126.6951 | 29526 | 57163.4728 | 29713 | 58212.5173 | 35047 |
| 55309.6520 | 20287 | 56756.3637 | 27643 | 57127.4820 | 29530 | 57164.4564 | 29718 | 58246.7381 | 35221 |
| 55616.4587 | 21847 | 56757.3465 | 27648 | 57127.6771 | 29531 | 57165.4392 | 29723 | 58527.3874 | 36648 |
| 55617.4423 | 21852 | 56757.5433 | 27649 | 57128.6623 | 29536 | 57166.4216 | 29728 | 58527.5843 | 36649 |
| 55621.3754 | 21872 | 56763.4428 | 27679 | 57128.8586 | 29537 | 57166.6203 | 29729 | 58554.7254 | 36787 |
| 55993.2806 | 23763 | 56785.6671 | 27792 | 57129.6454 | 29541 | 57168.3892 | 29738 | 58554.9221 | 36788 |
| 55993.4773 | 23764 | 56789.6006 | 27812 | 57129.8413 | 29542 | 57168.5861 | 29739 | 58559.4450 | 36811 |
| 55994.2636 | 23768 | 56789.7974 | 27813 | 57130.6284 | 29546 | 57169.5706 | 29744 | 58559.6411 | 36812 |
| 55994.4605 | 23769 | 56792.3540 | 27826 | 57131.4158 | 29550 | 57169.7664 | 29745 | 58620.6092 | 37122 |
| 55995.2469 | 23773 | 56794.3202 | 27836 | 57131.8085 | 29552 | 57170.5534 | 29749 | 58627.6898 | 37158 |
| 55995.4438 | 23774 | 56802.7776 | 27879 | 57132.0061 | 29553 | 57170.7493 | 29750 | 58898.8991 | 38537 |
| 56012.7505 | 23862 | 56807.6943 | 27904 | 57132.3987 | 29555 | 57171.5348 | 29754 | 58915.2223 | 38620 |
| 56346.5016 | 25559 | 56811.6282 | 27924 | 57132.5952 | 29556 | 57173.5031 | 29764 | 58915.4194 | 38621 |
| 56351.6146 | 25585 | 57078.7074 | 29282 | 57132.7923 | 29557 | 57177.4367 | 29784 | 58922.4999 | 38657 |
| 56353.3848 | 25594 | 57081.6568 | 29297 | 57132.9895 | 29558 | 57190.4161 | 29850 | 58923.2869 | 38661 |
| 56353.5812 | 25595 | 57081.8539 | 29298 | 57133.3822 | 29560 | 57191.4004 | 29855 | 58923.4825 | 38662 |
| 56372.4621 | 25691 | 57083.8209 | 29308 | 57133.7748 | 29562 | 57192.5799 | 29861 | 58941.5776 | 38754 |
| 56376.3951 | 25711 | 57092.8677 | 29354 | 57133.9721 | 29563 | 57193.5634 | 29866 | 58941.7736 | 38755 |
| 56378.3616 | 25721 | 57098.5713 | 29383 | 57134.3648 | 29565 | 57194.5476 | 29871 | 59283.7852 | 40494 |
| 56381.3120 | 25736 | 57099.3580 | 29387 | 57134.7581 | 29567 | 57198.4803 | 29891 | 59293.8150 | 40545 |
| 56381.5088 | 25737 | 57099.5551 | 29388 | 57135.5457 | 29571 | 57199.4629 | 29896 | 59310.7292 | 40631 |
| 56382.2954 | 25741 | 57099.7514 | 29389 | 57135.7420 | 29572 | 57202.4135 | 29911 | 59317.6125 | 40666 |
| 56383.2791 | 25746 | 57100.3415 | 29392 | 57135.9383 | 29573 | 57207.5266 | 29937 | 59317.8093 | 40667 |
| 56383.4753 | 25747 | 57100.5382 | 29393 | 57136.5285 | 29576 | 57208.5098 | 29942 | 59332.7564 | 40743 |
| 56385.4419 | 25757 | 57102.7016 | 29404 | 57136.7258 | 29577 | 57209.4956 | 29947 | 59352.6205 | 40844 |
| 56386.4253 | 25762 | 57103.2916 | 29407 | 57138.4943 | 29586 | 57222.4738 | 30013 | 59364.6172 | 40905 |
| 56388.3921 | 25772 | 57103.4888 | 29408 | 57139.6757 | 29592 | 57223.4576 | 30018 | 59605.3423 | 42129 |
| 56391.3420 | 25787 | 57104.4708 | 29413 | 57140.4630 | 29596 | 57224.4399 | 30023 | 59605.5396 | 42130 |
| 56391.5389 | 25788 | 57107.4216 | 29428 | 57140.6594 | 29597 | 57226.4081 | 30033 | 59622.4531 | 42216 |
| 56393.3089 | 25797 | 57107.6197 | 29429 | 57140.8548 | 29598 | 57227.3907 | 30038 | 59639.3667 | 42302 |
| 56395.2752 | 25807 | 57108.7979 | 29435 | 57141.4453 | 29601 | 57227.7848 | 30040 | 59639.5644 | 42303 |
| 56454.6696 | 26109 | 57108.9958 | 29436 | 57141.6419 | 29602 | 57467.3300 | 31258 | 59675.7512 | 42487 |
| 56686.3487 | 27287 | 57109.7807 | 29440 | 57141.8388 | 29603 | 57467.5267 | 31259 | 59703.6790 | 42629 |
| 56686.5451 | 27288 | 57110.7647 | 29445 | 57142.4293 | 29606 | 57470.6735 | 31275 | 59703.8751 | 42630 |
| 56687.3310 | 27292 | 57111.7481 | 29450 | 57142.6257 | 29607 | 57471.6567 | 31280 | ||
| 56687.5284 | 27293 | 57111.9446 | 29451 | 57142.8231 | 29608 | 57494.6675 | 31397 | ||
| 56688.3147 | 27297 | 57113.7153 | 29460 | 57143.4127 | 29611 | 57520.6280 | 31529 | ||
| 56688.5115 | 27298 | 57114.8952 | 29466 | 57143.6087 | 29612 | 57520.8249 | 31530 |
UX UMa eclipse epochs (zero-point for cycle counts as defined by equation 8).
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 43311.7185 | −40718 | 56688.7090 | 27299 | 57116.6640 | 29475 | 57143.8064 | 29613 | 57525.7421 | 31555 |
| 43660.8097 | −38943 | 56725.2894 | 27485 | 57117.6483 | 29480 | 57144.0029 | 29614 | 57526.7250 | 31560 |
| 43998.6925 | −37225 | 56725.4859 | 27486 | 57118.4352 | 29484 | 57144.3959 | 29616 | 57529.6749 | 31575 |
| 48779.7710 | −12915 | 56731.3853 | 27516 | 57119.4182 | 29489 | 57144.7893 | 29618 | 57530.6580 | 31580 |
| 51319.7821 | 0 | 56733.3520 | 27526 | 57119.6150 | 29490 | 57145.7726 | 29623 | 57785.9373 | 32878 |
| 52363.5161 | 5307 | 56733.5494 | 27527 | 57119.8115 | 29491 | 57145.9689 | 29624 | 57804.8179 | 32974 |
| 52551.3369 | 6262 | 56734.3363 | 27531 | 57120.4025 | 29494 | 57146.7558 | 29628 | 57809.5381 | 32998 |
| 53466.6455 | 10916 | 56734.5324 | 27532 | 57121.3857 | 29499 | 57147.7394 | 29633 | 57811.8981 | 33010 |
| 53473.9221 | 10953 | 56738.2695 | 27551 | 57121.5827 | 29500 | 57148.5256 | 29637 | 57883.6832 | 33375 |
| 53476.8723 | 10968 | 56738.4663 | 27552 | 57121.7789 | 29501 | 57150.6887 | 29648 | 57888.7966 | 33401 |
| 53477.8555 | 10973 | 56739.2526 | 27556 | 57122.3686 | 29504 | 57150.8855 | 29649 | 57890.7632 | 33411 |
| 53481.7887 | 10993 | 56739.4495 | 27557 | 57122.5651 | 29505 | 57152.4585 | 29657 | 57907.6769 | 33497 |
| 53495.7527 | 11064 | 56741.4160 | 27567 | 57122.7608 | 29506 | 57152.8521 | 29659 | 57939.3410 | 33658 |
| 53760.8655 | 12412 | 56741.6130 | 27568 | 57122.9581 | 29507 | 57153.4429 | 29662 | 58154.8926 | 34754 |
| 54154.4047 | 14413 | 56742.3995 | 27572 | 57123.3518 | 29509 | 57153.8352 | 29664 | 58173.3798 | 34848 |
| 54187.4456 | 14581 | 56742.5968 | 27573 | 57123.7447 | 29511 | 57154.4258 | 29667 | 58173.5762 | 34849 |
| 54512.3469 | 16233 | 56743.3830 | 27577 | 57124.5319 | 29515 | 57154.6222 | 29668 | 58175.3468 | 34858 |
| 54912.7701 | 18269 | 56749.4800 | 27608 | 57124.7287 | 29516 | 57157.5729 | 29683 | 58175.5431 | 34859 |
| 54933.6164 | 18375 | 56751.4463 | 27618 | 57125.3192 | 29519 | 57158.5561 | 29688 | 58179.8698 | 34881 |
| 55279.3648 | 20133 | 56752.4297 | 27623 | 57125.5155 | 29520 | 57160.5220 | 29698 | 58181.8367 | 34891 |
| 55279.7582 | 20135 | 56754.3964 | 27633 | 57126.4985 | 29525 | 57162.4906 | 29708 | 58192.6534 | 34946 |
| 55298.6385 | 20231 | 56754.5929 | 27634 | 57126.6951 | 29526 | 57163.4728 | 29713 | 58212.5173 | 35047 |
| 55309.6520 | 20287 | 56756.3637 | 27643 | 57127.4820 | 29530 | 57164.4564 | 29718 | 58246.7381 | 35221 |
| 55616.4587 | 21847 | 56757.3465 | 27648 | 57127.6771 | 29531 | 57165.4392 | 29723 | 58527.3874 | 36648 |
| 55617.4423 | 21852 | 56757.5433 | 27649 | 57128.6623 | 29536 | 57166.4216 | 29728 | 58527.5843 | 36649 |
| 55621.3754 | 21872 | 56763.4428 | 27679 | 57128.8586 | 29537 | 57166.6203 | 29729 | 58554.7254 | 36787 |
| 55993.2806 | 23763 | 56785.6671 | 27792 | 57129.6454 | 29541 | 57168.3892 | 29738 | 58554.9221 | 36788 |
| 55993.4773 | 23764 | 56789.6006 | 27812 | 57129.8413 | 29542 | 57168.5861 | 29739 | 58559.4450 | 36811 |
| 55994.2636 | 23768 | 56789.7974 | 27813 | 57130.6284 | 29546 | 57169.5706 | 29744 | 58559.6411 | 36812 |
| 55994.4605 | 23769 | 56792.3540 | 27826 | 57131.4158 | 29550 | 57169.7664 | 29745 | 58620.6092 | 37122 |
| 55995.2469 | 23773 | 56794.3202 | 27836 | 57131.8085 | 29552 | 57170.5534 | 29749 | 58627.6898 | 37158 |
| 55995.4438 | 23774 | 56802.7776 | 27879 | 57132.0061 | 29553 | 57170.7493 | 29750 | 58898.8991 | 38537 |
| 56012.7505 | 23862 | 56807.6943 | 27904 | 57132.3987 | 29555 | 57171.5348 | 29754 | 58915.2223 | 38620 |
| 56346.5016 | 25559 | 56811.6282 | 27924 | 57132.5952 | 29556 | 57173.5031 | 29764 | 58915.4194 | 38621 |
| 56351.6146 | 25585 | 57078.7074 | 29282 | 57132.7923 | 29557 | 57177.4367 | 29784 | 58922.4999 | 38657 |
| 56353.3848 | 25594 | 57081.6568 | 29297 | 57132.9895 | 29558 | 57190.4161 | 29850 | 58923.2869 | 38661 |
| 56353.5812 | 25595 | 57081.8539 | 29298 | 57133.3822 | 29560 | 57191.4004 | 29855 | 58923.4825 | 38662 |
| 56372.4621 | 25691 | 57083.8209 | 29308 | 57133.7748 | 29562 | 57192.5799 | 29861 | 58941.5776 | 38754 |
| 56376.3951 | 25711 | 57092.8677 | 29354 | 57133.9721 | 29563 | 57193.5634 | 29866 | 58941.7736 | 38755 |
| 56378.3616 | 25721 | 57098.5713 | 29383 | 57134.3648 | 29565 | 57194.5476 | 29871 | 59283.7852 | 40494 |
| 56381.3120 | 25736 | 57099.3580 | 29387 | 57134.7581 | 29567 | 57198.4803 | 29891 | 59293.8150 | 40545 |
| 56381.5088 | 25737 | 57099.5551 | 29388 | 57135.5457 | 29571 | 57199.4629 | 29896 | 59310.7292 | 40631 |
| 56382.2954 | 25741 | 57099.7514 | 29389 | 57135.7420 | 29572 | 57202.4135 | 29911 | 59317.6125 | 40666 |
| 56383.2791 | 25746 | 57100.3415 | 29392 | 57135.9383 | 29573 | 57207.5266 | 29937 | 59317.8093 | 40667 |
| 56383.4753 | 25747 | 57100.5382 | 29393 | 57136.5285 | 29576 | 57208.5098 | 29942 | 59332.7564 | 40743 |
| 56385.4419 | 25757 | 57102.7016 | 29404 | 57136.7258 | 29577 | 57209.4956 | 29947 | 59352.6205 | 40844 |
| 56386.4253 | 25762 | 57103.2916 | 29407 | 57138.4943 | 29586 | 57222.4738 | 30013 | 59364.6172 | 40905 |
| 56388.3921 | 25772 | 57103.4888 | 29408 | 57139.6757 | 29592 | 57223.4576 | 30018 | 59605.3423 | 42129 |
| 56391.3420 | 25787 | 57104.4708 | 29413 | 57140.4630 | 29596 | 57224.4399 | 30023 | 59605.5396 | 42130 |
| 56391.5389 | 25788 | 57107.4216 | 29428 | 57140.6594 | 29597 | 57226.4081 | 30033 | 59622.4531 | 42216 |
| 56393.3089 | 25797 | 57107.6197 | 29429 | 57140.8548 | 29598 | 57227.3907 | 30038 | 59639.3667 | 42302 |
| 56395.2752 | 25807 | 57108.7979 | 29435 | 57141.4453 | 29601 | 57227.7848 | 30040 | 59639.5644 | 42303 |
| 56454.6696 | 26109 | 57108.9958 | 29436 | 57141.6419 | 29602 | 57467.3300 | 31258 | 59675.7512 | 42487 |
| 56686.3487 | 27287 | 57109.7807 | 29440 | 57141.8388 | 29603 | 57467.5267 | 31259 | 59703.6790 | 42629 |
| 56686.5451 | 27288 | 57110.7647 | 29445 | 57142.4293 | 29606 | 57470.6735 | 31275 | 59703.8751 | 42630 |
| 56687.3310 | 27292 | 57111.7481 | 29450 | 57142.6257 | 29607 | 57471.6567 | 31280 | ||
| 56687.5284 | 27293 | 57111.9446 | 29451 | 57142.8231 | 29608 | 57494.6675 | 31397 | ||
| 56688.3147 | 27297 | 57113.7153 | 29460 | 57143.4127 | 29611 | 57520.6280 | 31529 | ||
| 56688.5115 | 27298 | 57114.8952 | 29466 | 57143.6087 | 29612 | 57520.8249 | 31530 |
| Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . | Epoch (BJD) . | Cycle . |
|---|---|---|---|---|---|---|---|---|---|
| (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . | (2400000 +) . | No. . |
| 43311.7185 | −40718 | 56688.7090 | 27299 | 57116.6640 | 29475 | 57143.8064 | 29613 | 57525.7421 | 31555 |
| 43660.8097 | −38943 | 56725.2894 | 27485 | 57117.6483 | 29480 | 57144.0029 | 29614 | 57526.7250 | 31560 |
| 43998.6925 | −37225 | 56725.4859 | 27486 | 57118.4352 | 29484 | 57144.3959 | 29616 | 57529.6749 | 31575 |
| 48779.7710 | −12915 | 56731.3853 | 27516 | 57119.4182 | 29489 | 57144.7893 | 29618 | 57530.6580 | 31580 |
| 51319.7821 | 0 | 56733.3520 | 27526 | 57119.6150 | 29490 | 57145.7726 | 29623 | 57785.9373 | 32878 |
| 52363.5161 | 5307 | 56733.5494 | 27527 | 57119.8115 | 29491 | 57145.9689 | 29624 | 57804.8179 | 32974 |
| 52551.3369 | 6262 | 56734.3363 | 27531 | 57120.4025 | 29494 | 57146.7558 | 29628 | 57809.5381 | 32998 |
| 53466.6455 | 10916 | 56734.5324 | 27532 | 57121.3857 | 29499 | 57147.7394 | 29633 | 57811.8981 | 33010 |
| 53473.9221 | 10953 | 56738.2695 | 27551 | 57121.5827 | 29500 | 57148.5256 | 29637 | 57883.6832 | 33375 |
| 53476.8723 | 10968 | 56738.4663 | 27552 | 57121.7789 | 29501 | 57150.6887 | 29648 | 57888.7966 | 33401 |
| 53477.8555 | 10973 | 56739.2526 | 27556 | 57122.3686 | 29504 | 57150.8855 | 29649 | 57890.7632 | 33411 |
| 53481.7887 | 10993 | 56739.4495 | 27557 | 57122.5651 | 29505 | 57152.4585 | 29657 | 57907.6769 | 33497 |
| 53495.7527 | 11064 | 56741.4160 | 27567 | 57122.7608 | 29506 | 57152.8521 | 29659 | 57939.3410 | 33658 |
| 53760.8655 | 12412 | 56741.6130 | 27568 | 57122.9581 | 29507 | 57153.4429 | 29662 | 58154.8926 | 34754 |
| 54154.4047 | 14413 | 56742.3995 | 27572 | 57123.3518 | 29509 | 57153.8352 | 29664 | 58173.3798 | 34848 |
| 54187.4456 | 14581 | 56742.5968 | 27573 | 57123.7447 | 29511 | 57154.4258 | 29667 | 58173.5762 | 34849 |
| 54512.3469 | 16233 | 56743.3830 | 27577 | 57124.5319 | 29515 | 57154.6222 | 29668 | 58175.3468 | 34858 |
| 54912.7701 | 18269 | 56749.4800 | 27608 | 57124.7287 | 29516 | 57157.5729 | 29683 | 58175.5431 | 34859 |
| 54933.6164 | 18375 | 56751.4463 | 27618 | 57125.3192 | 29519 | 57158.5561 | 29688 | 58179.8698 | 34881 |
| 55279.3648 | 20133 | 56752.4297 | 27623 | 57125.5155 | 29520 | 57160.5220 | 29698 | 58181.8367 | 34891 |
| 55279.7582 | 20135 | 56754.3964 | 27633 | 57126.4985 | 29525 | 57162.4906 | 29708 | 58192.6534 | 34946 |
| 55298.6385 | 20231 | 56754.5929 | 27634 | 57126.6951 | 29526 | 57163.4728 | 29713 | 58212.5173 | 35047 |
| 55309.6520 | 20287 | 56756.3637 | 27643 | 57127.4820 | 29530 | 57164.4564 | 29718 | 58246.7381 | 35221 |
| 55616.4587 | 21847 | 56757.3465 | 27648 | 57127.6771 | 29531 | 57165.4392 | 29723 | 58527.3874 | 36648 |
| 55617.4423 | 21852 | 56757.5433 | 27649 | 57128.6623 | 29536 | 57166.4216 | 29728 | 58527.5843 | 36649 |
| 55621.3754 | 21872 | 56763.4428 | 27679 | 57128.8586 | 29537 | 57166.6203 | 29729 | 58554.7254 | 36787 |
| 55993.2806 | 23763 | 56785.6671 | 27792 | 57129.6454 | 29541 | 57168.3892 | 29738 | 58554.9221 | 36788 |
| 55993.4773 | 23764 | 56789.6006 | 27812 | 57129.8413 | 29542 | 57168.5861 | 29739 | 58559.4450 | 36811 |
| 55994.2636 | 23768 | 56789.7974 | 27813 | 57130.6284 | 29546 | 57169.5706 | 29744 | 58559.6411 | 36812 |
| 55994.4605 | 23769 | 56792.3540 | 27826 | 57131.4158 | 29550 | 57169.7664 | 29745 | 58620.6092 | 37122 |
| 55995.2469 | 23773 | 56794.3202 | 27836 | 57131.8085 | 29552 | 57170.5534 | 29749 | 58627.6898 | 37158 |
| 55995.4438 | 23774 | 56802.7776 | 27879 | 57132.0061 | 29553 | 57170.7493 | 29750 | 58898.8991 | 38537 |
| 56012.7505 | 23862 | 56807.6943 | 27904 | 57132.3987 | 29555 | 57171.5348 | 29754 | 58915.2223 | 38620 |
| 56346.5016 | 25559 | 56811.6282 | 27924 | 57132.5952 | 29556 | 57173.5031 | 29764 | 58915.4194 | 38621 |
| 56351.6146 | 25585 | 57078.7074 | 29282 | 57132.7923 | 29557 | 57177.4367 | 29784 | 58922.4999 | 38657 |
| 56353.3848 | 25594 | 57081.6568 | 29297 | 57132.9895 | 29558 | 57190.4161 | 29850 | 58923.2869 | 38661 |
| 56353.5812 | 25595 | 57081.8539 | 29298 | 57133.3822 | 29560 | 57191.4004 | 29855 | 58923.4825 | 38662 |
| 56372.4621 | 25691 | 57083.8209 | 29308 | 57133.7748 | 29562 | 57192.5799 | 29861 | 58941.5776 | 38754 |
| 56376.3951 | 25711 | 57092.8677 | 29354 | 57133.9721 | 29563 | 57193.5634 | 29866 | 58941.7736 | 38755 |
| 56378.3616 | 25721 | 57098.5713 | 29383 | 57134.3648 | 29565 | 57194.5476 | 29871 | 59283.7852 | 40494 |
| 56381.3120 | 25736 | 57099.3580 | 29387 | 57134.7581 | 29567 | 57198.4803 | 29891 | 59293.8150 | 40545 |
| 56381.5088 | 25737 | 57099.5551 | 29388 | 57135.5457 | 29571 | 57199.4629 | 29896 | 59310.7292 | 40631 |
| 56382.2954 | 25741 | 57099.7514 | 29389 | 57135.7420 | 29572 | 57202.4135 | 29911 | 59317.6125 | 40666 |
| 56383.2791 | 25746 | 57100.3415 | 29392 | 57135.9383 | 29573 | 57207.5266 | 29937 | 59317.8093 | 40667 |
| 56383.4753 | 25747 | 57100.5382 | 29393 | 57136.5285 | 29576 | 57208.5098 | 29942 | 59332.7564 | 40743 |
| 56385.4419 | 25757 | 57102.7016 | 29404 | 57136.7258 | 29577 | 57209.4956 | 29947 | 59352.6205 | 40844 |
| 56386.4253 | 25762 | 57103.2916 | 29407 | 57138.4943 | 29586 | 57222.4738 | 30013 | 59364.6172 | 40905 |
| 56388.3921 | 25772 | 57103.4888 | 29408 | 57139.6757 | 29592 | 57223.4576 | 30018 | 59605.3423 | 42129 |
| 56391.3420 | 25787 | 57104.4708 | 29413 | 57140.4630 | 29596 | 57224.4399 | 30023 | 59605.5396 | 42130 |
| 56391.5389 | 25788 | 57107.4216 | 29428 | 57140.6594 | 29597 | 57226.4081 | 30033 | 59622.4531 | 42216 |
| 56393.3089 | 25797 | 57107.6197 | 29429 | 57140.8548 | 29598 | 57227.3907 | 30038 | 59639.3667 | 42302 |
| 56395.2752 | 25807 | 57108.7979 | 29435 | 57141.4453 | 29601 | 57227.7848 | 30040 | 59639.5644 | 42303 |
| 56454.6696 | 26109 | 57108.9958 | 29436 | 57141.6419 | 29602 | 57467.3300 | 31258 | 59675.7512 | 42487 |
| 56686.3487 | 27287 | 57109.7807 | 29440 | 57141.8388 | 29603 | 57467.5267 | 31259 | 59703.6790 | 42629 |
| 56686.5451 | 27288 | 57110.7647 | 29445 | 57142.4293 | 29606 | 57470.6735 | 31275 | 59703.8751 | 42630 |
| 56687.3310 | 27292 | 57111.7481 | 29450 | 57142.6257 | 29607 | 57471.6567 | 31280 | ||
| 56687.5284 | 27293 | 57111.9446 | 29451 | 57142.8231 | 29608 | 57494.6675 | 31397 | ||
| 56688.3147 | 27297 | 57113.7153 | 29460 | 57143.4127 | 29611 | 57520.6280 | 31529 | ||
| 56688.5115 | 27298 | 57114.8952 | 29466 | 57143.6087 | 29612 | 57520.8249 | 31530 |



