Planet engulfment signatures in twin stars

ABSTRACT

1 INTRODUCTION

The formation and evolution of planetary systems can alter the primordial elemental abundances of planet host stars. For example, planet engulfment can produce refractory element enhancements within the engulfing star convective region due to ingestion of rocky planetary material (e.g. Oh et al. 2018). However, such refractory enhancements may be weakened by internal mixing processes over time. While gravitational settling alone is not sufficiently rapid to diminish these enhancements (e.g. Pinsonneault, DePoy & Coffee 2001), thermohaline mixing may more effectively deplete overlying refractory material by allowing it to sink below the convective zone via ‘metallic fingers’ that stretch towards the deep stellar interior (e.g. Ulrich 1972; Kippenhahn, Ruschenplatt & Thomas 1980; Vauclair 2004; Théado & Vauclair 2012; Bauer & Bildsten 2019). As a form of double-diffusive mixing driven by heat diffusion, thermohaline mixing acts in the presence of a mean-molecular-weight (μ) gradient, and is theorized to be particularly effective at removing accreted refractory material from the thin convective zones of hot stars due to more rapid cooling at the bottom of the convective envelope.

Vauclair (2004) was the first to consider thermohaline mixing in stellar interiors following accretion of planetary material. They analytically determined that thermohaline instabilities are capable of depleting accreted rocky matter out of convective envelopes on time-scales of ∼1000 yr, leaving only a small μ-gradient at the end of the mixing process. Later work by Garaud (2011) presented numerical and semi-analytical estimations of thermohaline mixing using the coefficient derived by Traxler, Garaud & Stellmach (2011) from empirical fitting of 3D numerical simulation results, and found that the refractory depletion time-scale following engulfment of a 1 M_J planet depends strongly on increasing stellar mass, with enhancements dropping to 10 per cent within 600 Myr for a 1.3 M_⊙ star, 60 Myr for a 1.4 M_⊙ star, etc.

More recently, Théado & Vauclair (2012) modelled engulfment with planet masses ranging from 1 M_⊕ to 1.5 M_J using the Toulouse–Geneva Evolution Code (Richard, Théado & Vauclair 2004; Hui-Bon-Hoa 2008) considering thermohaline mixing and atomic diffusion. They found that the μ-gradient is softened on time-scales of a few to tens of Myr depending on the accretion scenario, and noted that their depletion time-scale is much larger than those of previous studies because they correctly assumed the characteristic mixing length to be the entire mixed region rather than just the ‘metallic finger’ dimensions. Théado & Vauclair (2012) showed how different mixing prescriptions could lead to different results, especially in the case of a small composition gradient (near the minimum for thermohaline instability to operate), as often occurs in models of planet engulfment. This highlights the need for stellar models that include all relevant interior processes for accurately constraining depletion time-scales. Such time-scales are important for investigations of engulfment because they determine how long engulfment signatures remain observable, which is necessary for placing engulfment events within planetary system histories.

Stellar abundance patterns suggestive of planet engulfment have been observed in several systems, indicating that engulfment may be more common than predictions from theory suggest (Galactic occurrence rates of 0.1–1 yr⁻¹; Metzger, Giannios & Spiegel 2012). More specifically, there are several individual binary systems reported in the literature with significant (>0.05 dex¹) refractory differences between the two stars (Ramírez et al. 2011; Mack et al. 2014; Tucci Maia, Meléndez & Ramírez 2014; Teske et al. 2015; Ramírez et al. 2015; Biazzo et al. 2015; Saffe et al. 2016; Teske, Khanal & Ramírez 2016; Adibekyan et al. 2016; Saffe et al. 2017; Maia et al. 2019; Ramírez et al. 2019; Nagar, Spina & Karakas 2020; Galarza et al. 2021; Jofré et al. 2021). Such abundances differences between stellar siblings suggest post-birth chemodynamical processes such as engulfment because bound stellar companions are born from the same natal gas cloud and thus assumed to be chemically homogeneous at birth to within ∼0.05 dex (e.g. De Silva, Freeman & Bland-Hawthorn 2009). Larger binary samples exhibit abundance differences as well. For example, Hawkins et al. (2020) assessed 25 comoving wide binaries and found that 5 systems exhibit Δ[Fe/H] ∼ 0.10 dex.

To determine how planet engulfment signatures are affected by stellar mixing processes, namely thermohaline instabilities, we ran tests with the mesa (Modules for Experiments in Stellar Astrophysics) stellar evolution code (Paxton et al. 2011, 2013, 2015, 2018, 2019). Our mesa stellar models and implementation of non-standard mixing processes such as thermohaline instabilities are outlined in Section 2. The results of our mesa models considering different engulfment conditions are presented in Section 3. We discuss the implications of these results for planet engulfment signatures in Section 4, and provide a summary in Section 5.

2 STELLAR MODELS

We computed our stellar models using the open-source 1D stellar evolution code mesa. These models are non-rotating with masses of 0.5–1.2 M_⊙ and solar metallicities of Z = 0.017. We did not include more massive stars, where gravitational settling and radiative levitation can potentially produce huge changes in surface composition, but are complicated by poorly understood additional mixing processes not included in our models (e.g. Eddington–Sweet circulation and wave mixing).

Our modelling procedure follows that of Sevilla, Behmard & Fuller (2022). In brief, the models were run in three stages, where the first stage evolved the stars up to the zero-age main sequence (ZAMS), the second stage simulated planet engulfment of a 1, 10, or 50 M_⊕ planet via accretion of bulk-Earth composition material, and the third stage evolved the stars up to the end of their main-sequence (MS) lifetimes. We then computed the refractory species mass fraction remaining in their convective zones as a function of stellar age to assess the time-scales over which engulfment signatures remained observable. Throughout these mesa runs, we applied relevant mixing processes, namely convective overshoot, elemental diffusion, radiative levitation, thermohaline instabilities, and additional mixing required to reproduce observations of surface lithium abundances. These processes are discussed in more detail below.

2.1 Input physics

We implemented elemental diffusion via the prescription detailed in Paxton et al. (2015, 2018) that solves the Burgers’ equations in a similar fashion to Thoul, Bahcall & Loeb (1994). In mesa, diffusion is carried out for a set of chemical species organized in ‘classes’, where a single class may contain several isotopes, and a chosen representative isotope is used to solve the diffusion equations and set the diffusion velocities for all species in that class. In our case, we created individual classes for each of the 13 most abundant species included in our bulk-Earth accretion that simulates engulfment, so each species is its own representative isotope.

We also applied radiative levitation according to Hu et al. (2011), implemented in mesa as described in Paxton et al. (2015). The Hu et al. (2011) prescription is based on that of Thoul et al. (1994), with a few modifications. These include an additional force term in the basic diffusion equations that describes the radiative acceleration on a chemical species as a function of its average ion charge. We only applied radiative levitation to our stellar models with masses of 0.7 M_⊙ and above. This is justified because radiative levitation dominates atomic diffusion for stars with temperatures above 6000 K (e.g. Richer et al. 1998; Deal et al. 2020; Campilho, Deal & Bossini 2022), and is not expected to operate efficiently in low-mass stars.

There are other mixing processes at play that we did not explicitly model because their effects are poorly understood, e.g. rotationally induced mixing. To account for this, we included a min_D_mix = 700 command in our mesa inlist. This amount of extra mixing allowed us to reproduce the observed lithium abundances for ∼1 M_⊙ stars from Sestito & Randich (2005). For more details on the comparison with lithium observations, see Sevilla et al. (2022).

2.2 Bulk-Earth accretion

To simulate planet engulfment, we began accreting bulk-Earth composition material once the mesa stellar models reached ZAMS, consisting of the top 13 most abundant elements (McDonough 2003). For a complete analysis of the lithium enrichment evolution, see Sevilla et al. (2022). Because mesa chemical networks are written in terms of isotopic species, we accreted the most abundant isotope of each element included in our bulk-Earth accretion scheme.

mesa does not allow for instantaneous engulfment of a planetary mass body. Instead, planet engulfment was simulated through rapid accretion of bulk-Earth composition material. We chose accretion rates that ensured the total planetary mass was accreted within 10 000 yr for all combinations of 1, 10, and 50 M_⊕ engulfed masses and host stars of 0.5–1.2 M_⊙. An accretion period of 10 000 yr is appropriately short for simulating engulfment events, and should not affect our results because our observed refractory depletion occurs on time-scales of >1 Myr (Fig. 1).

Figure 1.

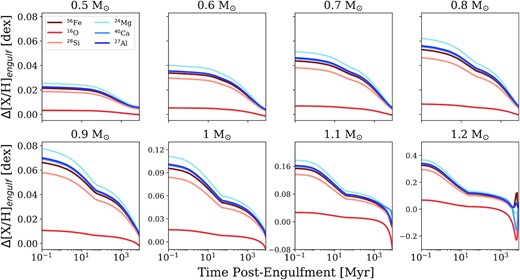
Post-engulfment abundances for the top six most abundant bulk-Earth elements over time for our complete stellar mass model range (0.5–1.2 M_⊙) following near-instantaneous accretion of a 10 M_⊕ bulk-Earth composition planet. The abundances of comparison mesa models with no accretion were subtracted off. Each element is represented by its most abundant isotope because mesa chemical networks are written in terms of isotopic species.

Open in new tabDownload slide

We also tested two alternative accretion prescriptions that mimic late heavy bombardment (LHB) and disc accretion scenarios. LHB-like accretion begins when the star reaches an age of 500 Myr and lasts for 300 Myr (e.g. Bottke & Norman 2017), while disc accretion begins 10 Myr after the star is born and lasts for 3 Myr, the nominal disc lifetime for MS stars (e.g. Hartmann, Herczeg & Calvet 2016). We tested accretion of 1 and 10 M_⊕ of planetary material for both scenarios. After engulfment according to near-instantaneous, LHB, or disc accretion scenarios, we evolved the stellar models to the ends of their MS lifetimes. We utilized the default definition for the end of the MS, which is when the core hydrogen mass fraction drops below 10⁻¹⁰.

3 RESULTS

3.1 Near-instantaneous engulfment

We first examined how refractory enrichment resulting from engulfment changes as a function of engulfed planet mass and stellar type. This was carried out by running mesa models that included accretion of 1, 10, or 50 M_⊕ of planetary material with bulk-Earth compositions, and models with no accretion as comparison points. We took the differential abundances between the engulfment and non-engulfment models as our potential engulfment signatures. These differential measurements mimic the signatures found in observations because refractory enrichments from engulfment are detected with respect to pristine chemically homogeneous stars, e.g. a bound companion or fellow cluster member.

As shown in Fig. 1, for low-mass stars (0.5–0.7 M_⊙), engulfment of a 10 M_⊕ planet does not produce observable enrichment at >0.05 dex levels because the accreted material is heavily diluted within the deep stellar convective envelope. The enrichment is more pronounced for more massive stars with thinner convective envelopes; for solar-like stars (0.8–1.2 M_⊙), engulfing 10 M_⊕ of planetary material initially produces enrichment at levels of ∼0.06–0.33 dex. Because the 0.8–0.9 M_⊙ stars still have comparatively deep envelopes, the initial enrichment is not well above 0.05 dex to begin with, and drops below this after by ∼20 Myr. However, the higher mass stars in this range (1–1.2 M_⊙) maintain enrichment at >0.05 dex for ∼90 Myr⁻² Gyr.

Fig. 1 shows that for models with higher mass (⁠|$M \gtrsim 1 \, \rm{M}_\odot$|⁠), the refractory abundances of a star that engulfed a planet are predicted to eventually decrease below those of a star that did not engulf a planet within 8 Gyr post-engulfment. The strength of this counter-intuitive effect increases with stellar mass. Inspection of our |$1.2 \, \rm{M}_\odot$| models with engulfment reveals that they are typically ∼200 K cooler and ∼1.5 per cent larger in radius than their reference models. Surprisingly, the models with engulfment have thinner surface convection zones, leading to faster gravitational settling of heavy elements and hence lower refractory abundances long after the engulfment event. The exact cause of this structural difference is not clear and should be examined in future work. There is an exception for certain isotopic species that are subject to radiative levitation (e.g, ⁵⁶Fe, ²⁷Al, ²⁸Si), whose abundances increase at ∼5 Gyr in the |$1.2 \, \rm{M}_\odot$| model (Figs 1 and 2).

Figure 2.

Post-engulfment [Fe/H] abundances over time for our complete stellar mass model range (0.5–1.2 M_⊙) following near-instantaneous accretion of a 1, 10, or 50 M_⊕ bulk-Earth composition planet, marked in red, blue, and navy, respectively. The abundances of comparison mesa models with no accretion were subtracted off.

Open in new tabDownload slide

Apart from this case, we found little difference between the chemical species in our models; the relative abundance of each decreases on nearly identical time-scales. For thermohaline mixing, this is expected as it affects all elements equally. In principle, gravitational settling causes heavier elements to sink below the convective zone faster, but the difference is not discernible in our results. Note that the enrichment signature provided by oxygen is much weaker than those of other elements due to the large amount of oxygen already present in the star.

3.2 Dependence on planet mass

We also examined near-instantaneous engulfment events of 1 and 50 M_⊕ of planetary material (Fig. 2). For 1 M_⊕ engulfment, refractory depletion behaviour across different stellar mass regimes is similar to that of 10 M_⊕ engulfment, but the initial enrichment levels are lower. Consequently, stars with masses in the range 0.5–1.1 M_⊙ do not exhibit enrichment above ∼0.05 dex immediately post-engulfment, rendering their engulfment signatures undetectable. The 1.2 M_⊙ model begins with ∼0.05 dex enrichment and sustains this level of enrichment for ∼100 Myr.

For 50 M_⊕ engulfment, the initial enrichment is comparatively high as expected from accretion of more planetary material. Stars in the 0.5–0.7 M_⊙ mass regime begin with enrichment at 0.10–0.19 dex levels, and maintain enrichment above ∼0.05 dex for ∼900 Myr⁻³ Gyr. Solar-like stars (0.8–1.2 M_⊙) begin with enrichment at ∼0.25–1.0 dex, and maintain ∼0.05 dex enrichment on time-scales of ∼4–8 Gyr.

3.3 LHB and disc accretion

The LHB is considered to be the last dramatic dynamical event in the history of the Solar system, when giant planet migration disrupted the orbits of inward-lying planetesimals and perhaps shepherded some into the Sun. We modelled LHB-like events to compare how the resulting engulfment signatures may differ from those of engulfment at ZAMS. To mimic LHB-like accretion, we ran a 1 M_⊙ model undergoing gradual accretion of 1 M_⊕ of bulk-Earth composition planetesimals from a stellar age of 500–800 Myr, thus beginning ∼470 Myr after ZAMS. We found that engulfment signatures from an LHB-like event are almost completely depleted post-engulfment because refractory material is continuously depleted over the longer accretion period. The engulfment signature after LHB-like accretion is complete is shown in Fig. 3.

Figure 3.

Post-engulfment [Fe/H] abundances over time for a 1 M_⊙mesa model that underwent accretion of a 1 M_⊕ planet under different conditions: the standard post-ZAMS near-instantaneous engulfment scenario (gray–dashed), an LHB-like scenario (blue), and a disc accretion-like scenario (navy). The abundances of comparison mesa models with no accretion were subtracted off.

Open in new tabDownload slide

We were also interested in modelling a protoplanetary disc accretion scenario, which by definition occurs while the disc is still present. To mimic these conditions, we began accretion once the star reached an age of 10 Myr, for a duration of 3 Myr as mentioned in Section 2.2. At 10 Myr, the star is still in the pre-MS phase, ∼20 Myr away from reaching ZAMS and almost fully convective. Thus, any accreted material will become heavily diluted within a large volume of the stellar interior. We tested accretion of 1 and 10 M_⊕, and found that the resulting engulfment signatures are slightly stronger than those resulting from LHB scenarios, but weaker compared to those of near-instantaneous engulfment scenarios because the refractory material is comparatively diluted (Fig. 3).

3.4 Late-stage engulfment

Finally, we tested near-instantaneous engulfment occurring at 300 Myr, 1 Gyr, or 3 Gyr post-ZAMS rather than exactly at ZAMS to examine refractory enrichment evolution from late-stage accretion. For these cases, we considered engulfment of a 10 M_⊕ mass by a 1 M_⊙ star. Notably, later engulfment results in systematically larger surface refractory enhancements; for the 3 Gyr model, the enhancement is ∼1.5–2 times that of the ZAMS accretion model at ≳10 Myr post-engulfment times (Fig. 4). This effect is also shown in the trends of different engulfed masses; we tested engulfment of a 1, 10, or 50 M_⊕ bulk-Earth planetary companion by a 1 M_⊙ star at 1 Gyr post-ZAMS (Fig. 5), and found that the 1 Gyr post-ZAMS cases all exhibit slower depletion of surface refractory enhancement compared to ZAMS engulfment (Fig. 2).

Figure 4.

Post-engulfment [Fe/H] abundances over time for a 1 M_⊙mesa model that underwent accretion of a 10 M_⊕ planet at different times: ZAMS (gray–dashed), 300 Myr post-ZAMS (red), 1 Gyr post-ZAMS (blue), and 3 Gyr post-ZAMS (navy). The abundances of comparison mesa models with no accretion were subtracted off.

Open in new tabDownload slide

Figure 5.

Post-engulfment [Fe/H] abundances over time for a 1 M_⊙mesa model that underwent accretion of a 1 (red), 10 (blue), or 50 (navy) M_⊕ planet at 1 Gyr post-ZAMS. The abundances of comparison mesa models with no accretion were subtracted off.

Open in new tabDownload slide

The primary reason for the larger signal in late-stage engulfment is a smaller amount of thermohaline mixing, which results in less depletion after engulfment as shown in Figs 4 and 5. The weakened thermohaline mixing arises due to its interaction with gravitational settling. As stars age, gravitational settling slowly creates a stabilizing μ-gradient as helium settles downwards. This inhibits thermohaline mixing when planetary material is engulfed, thus weakening refractory depletion and leading to longer-lived engulfment signatures. This effect is discussed further in Théado & Vauclair (2012) and Sevilla et al. (2022).

To further illustrate how this manifests in our mesa models, we plotted [Fe/H], [He/H], and the compositional component of the Brunt–Väisälä frequency (⁠|$N^2_{\rm comp}$|⁠) as a function of mass coordinate for the 1 M_⊙ model with 10 M_⊕ engulfment considering both ZAMS and 1 Gyr post-ZAMS engulfment (Fig. 6). The [Fe/H] panels of Fig. 6 showcase that some gravitational settling has already occurred in the 1 Gyr post-ZAMS model compared to the ZAMS model, increasing the value of [Fe/H] at larger depths. Similarly, helium settling creates a stabilizing composition gradient beneath the convection zone, as can be seen by the increasing value of [He/H] and [Fe/H] with depth below the convective zone in the post-engulfment models (though note that nuclear burning also increases [He/H] near the core).

Figure 6.

Plots of [Fe/H], [He/H], and |$N^2_{\rm comp}$| as a function of mass coordinate for a |$1 \, \rm{M}_\odot$|mesa stellar model. Negative |$N^2_{\rm comp}$| values are shown via dashed line (absolute values are used to enable visualization in log scale). The left-hand panel corresponds to the case of a 1 M_⊙ model engulfing 10 M_⊕ of planetary material exactly at ZAMS, while the right-hand panel corresponds to an equivalent case, but with engulfment occurring at 1 Gyr post-ZAMS. We sampled these quantities at five different time points (measured relative to the ZAMS age) from engulfment to an age of ∼2 Gyr, as depicted by different line colors.

Open in new tabDownload slide

We further examined this effect on the μ-gradient by plotting |$N^2_{\rm comp}$|⁠, a measure of stability to convection in a fluid medium. A positive |$N^2_{\rm comp}$| indicates a stable μ-gradient, while a negative value indicates that thermohaline mixing can occur. In both models, the bottom panels of Fig. 6 show that |$N^2_{\rm comp}$| is negative just below the convective zone of the post-engulfment model. However, at larger depths, |$N^2_{\rm comp}$| has lower values for engulfment at ZAMS compared to engulfment at 1 Gyr post-ZAMS, which indicates that the 1 Gyr post-ZAMS μ-gradient is more stable to begin with. Thermohaline mixing cannot penetrate as deeply into the interior in the 1 Gyr post-ZAMS model, which thus experiences less refractory depletion via thermohaline mixing over time.

3.5 Engulfing star metallicity

Figure 7.

Post-engulfment [Fe/H] abundances over time for 1 M_⊙ models following near-instantaneous accretion of a 10 M_⊕ bulk-Earth composition planetary companion at ZAMS. The three 1 M_⊙ models have different metallicities of slightly sub-solar (Z = 0.012, blue), solar (Z = 0.017, red), and slightly super-solar (Z = 0.022, navy). The abundances of comparison mesa models with no accretion were subtracted off. The refractory enhancements drop by a factor of ∼2 after ∼45 Myr. For the sub-solar metallicity model, observable signatures last for ∼3 Gyr.

Open in new tabDownload slide

Notably, the lowest metallicity model with Z = 0.012 exhibits an engulfment signature that remains above the 0.05 dex observable level for ∼3 Gyr. This implies that stars with sub-solar metallicities may exhibit engulfment signatures that are fairly long lived. For context, the Z distribution of ∼300 G dwarfs in the Solar neighbourhood ranges from ∼0.001–0.043, and peaks at ∼0.009 dex (Rocha-Pinto & Maciel 1996). A more recent study of ∼17 000 K and ∼24 000 G dwarfs outside the Solar vicinity at 0.2–2.3 kpc from the Galactic plane derived similar Z distributions, ranging from ∼0.0002–0.03 and peaking at ∼0.01 (Schlesinger et al. 2012). Thus, the distribution of solar-like stars in our neighbourhood leans relatively metal-poor, indicating that observable engulfment signatures may persist on ∼3 Gyr time-scales for many nearby |$\sim \! 1 \, \rm{M}_\odot$| stars.

3.6 Binary observation simulations

As mentioned in Section 3.1, engulfment signatures are detected in observations as patterns in the differential abundances of an engulfing star and a comparison stellar companion. The characteristic pattern indicative of an engulfment event is a trend of increasing differential abundances as a function of the elemental condensation temperature T_c (e.g. Oh et al. 2018). We expect a T_c-dependent abundance pattern following engulfment; elements with higher T_c are more likely to remain in the condensed phase throughout the disc and become locked in solid planetary material. Thus, planet compositions will exhibit higher abundances of species in order of T_c, which will be reflected in the photosphere of a star that has engulfed a planet.

We simulated how engulfment signatures would appear in binary system observations by computing differential abundances for elements that span a range of T_c between two G-type (1 M_⊙) stars, one of which underwent engulfment of a 10 M_⊕ bulk-Earth composition planet at ZAMS. The differential abundances from mesa display the characteristic T_c trend that signifies engulfment (Fig. 8, coloured points). We also constructed an engulfment model similar to that of Oh et al. (2018) for estimating the mass of bulk-Earth composition (McDonough 2003) material engulfed in one star given abundance measurements for a binary pair. This model estimates the apparent engulfed mass, which is the quantity inferred from stellar surface measurements assuming the planetary material is mixed throughout the convective zone, but not deeper.

Figure 8.

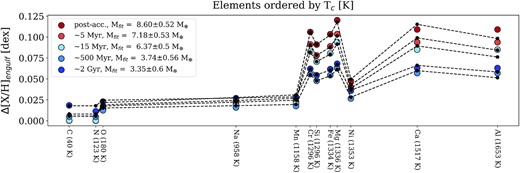
Differential abundances between a 1 M_⊙ model and a 1 M_⊙ model that accreted 10 M_⊕ of bulk-Earth composition material (coloured circles) for several post-engulfment times. The abundances are ranked by T_c of elements for solar-composition gas from Lodders (2003). The modelled abundances are represented by the black dots. The amount of apparent engulfed material at each time is provided in the upper left corner of the plot.

Open in new tabDownload slide

We fit for the apparent amount of engulfed mass according to our model at five different time points that span from immediately post-engulfment to ∼2 Gyr after the engulfment event (Fig. 8, black points connected via dashed line). The fitted mass begins at 8.60 ± 0.52 M_⊕ and falls to 3.35 ± 0.60 M_⊕ over this time period. Our model underestimates the initial engulfed mass because it assumes all accreted material is initially contained in the convective zone, which is not completely accurate; overshoot mixing pulls engulfed material underneath the convective zone to an additional depth of ∼10 per cent the convective zone mass. We note that while the signature appears clear even at the ∼2 Gyr post-engulfment point, abundance measurements from real observations will exhibit scatter due to instrumental effects, observing conditions, etc., making refractory enhancements below the 0.05 dex level at this point nearly undetectable.

4 DISCUSSION

The strength and duration of planet engulfment signatures are affected by the amount of mass engulfed, the properties of the engulfing star, and the conditions of the engulfment event, e.g. when the event occurred within the lifetime of the system. We discuss how these factors influence engulfment signature evolution here.

We considered engulfed masses of 1, 10, and 50 M_⊕. 10 M_⊕ engulfment can be considered nominal as formation of a solid ∼10 M_⊕ core triggers runaway gas accretion according to the core accretion model of planet formation. However some giant planets may possess up to ∼100 M_⊕ worth of refractory material, perhaps due to protoplanet merger events that occurred prior to disc outgassing (Ginzburg & Chiang 2020). We tested planet masses up to 50 M_⊕ to account for occasional engulfment of such ‘heavy metal Jupiters’. Larger amounts of engulfed mass result in higher initial enrichment, but also stronger μ-gradients that enhance thermohaline mixing and subsequent refractory depletion. These effects are illustrated throughout different engulfing star-mass regimes (Fig. 2). For low-mass stars (0.5–0.7 M_⊙), observable enrichment is only achieved for engulfed planetary masses of ≥50 M_⊕, and last for ∼900 Myr⁻³ Gyr. For more massive, solar-like (0.8–1.2 M_⊙) stars with thinner convective envelopes, observable signatures result from 10 M_⊕ engulfment, and last for ∼1 Myr⁻² Gyr. Thus, engulfment signature detection in stars older than 2 Gyr assuming near-instantaneous nominal 10 M_⊕ engulfment near ZAMS will be rare.

The lifetimes of observable engulfment signatures can increase under different accretion scenarios, or with different engulfing star parameters. Late-stage engulfment of a 10 M_⊕ planet by a 1 M_⊙ star at 300 Myr⁻³ Gyr post-ZAMS produces observable enrichment on time-scales of ∼1.5 Gyr. For comparison, engulfment under the same conditions but occurring exactly at ZAMS results in signatures that remain observable for only ∼90 Myr. Lowering the engulfing star metallicity also increases engulfment signature lifetimes; 1 M_⊙ models with sub-solar metallicities (Z = 0.012) sustain >0.05 dex levels of enrichment for ∼3 Gyr following engulfment of a 10 M_⊕ planet. Thus, engulfment signatures in stars older than 1.5 Gyr are more likely to be observed if the star is low metallicity, and/or if engulfment occurred late in the lifetime of the system.

4.1 Comparison to observations

As mentioned in Section 1, there are several reported binaries with >0.05 dex refractory differences. All the potentially engulfing stars in these systems are in the solar-like mass regime, and those with reported ages are older than 1.5–2 Gyr. Late ages are typical for these systems; the strongest engulfment detection reported thus far is HD 240429–30 (Kronos–Krios), which is 4.0–4.28 Gyr old (Oh et al. 2018). Such refractory enrichments are unlikely to stem from ZAMS engulfment because our mesa models do not exhibit observable engulfment signatures on time-scales longer than ∼2 Gyr for solar-like stars under these conditions. Late-stage (300 Myr⁻³ Gyr post-ZAMS) engulfment is also unlikely as signatures will persist on time-scales of only ∼1.5 Gyr for 1 M_⊙ stars. However, four of the reported systems have sub-solar metallicities (ζ² Reticuli, HD 134439–40, HIP 34407–26, and HD 133131) below Z = 0.012, which increase signature time-scales from nominal 10 M_⊕ engulfment to ∼3 Gyr.

The non-engulfing (Krios) and engulfing (Kronos) companions of Kronos–Krios have metallicities of [Fe/H] = 0.01 and 0.20 dex (Z = 0.017 and 0.027), respectively. Thus, potential explanations for the strong signature (15 M_⊕ of estimated engulfed material; Oh et al. 2018) in this system could be some combination of late-stage engulfment, a large (≳50 M_⊕) amount of mass engulfed, and chance observation of Kronos–Krios soon after its engulfment event. An alternative explanation is that the Kronos–Krios abundance differences are primordial rather than due to planet engulfment. This possibility is supported by the large projected separation of the system (11 000 ± 12 au), which we calculated from Gaia DR3 astrometry. These lengths exceed typical turbulence scales in molecular clouds (0.05–0.2 pc; Brunt, Heyer & Mac Low 2009 and references therein), indicating that Kronos–Krios may have formed in distinct areas of chemodynamical space within their birth cloud.

Stellar twin pairs (ΔT_eff < 200 K; Andrews et al. 2019) are best for uncovering engulfment signatures because their abundances are free from differences due to mass-dependent evolution. However, many stellar binaries are composed of stars with different masses and stellar types. We found that higher mass stars (⁠|$M \gtrsim 1 \, \rm{M}_\odot$|⁠) with thinner convective zones exhibit faster refractory depletion following engulfment (Fig. 1). Sevilla et al. (2022) found this can be true even in the absence of engulfment due to gravitational settling. Thus, binary pair stars with different masses that begin chemically homogeneous may have different surface abundances at late times, even without planet engulfment. We thus argue that engulfment signatures are most reliable for twin binaries with nearly equal mass components, and observations targeting planet engulfment should focus on such systems.

Our models indicate that engulfment signatures are longest lived in stars with M ≈ 1.1–1.2 M_⊙ (ZAMS temperatures of T_eff ≈ 6100–6400 K) and are thus more likely to be observed in stars slightly hotter than the Sun. We also predict longer-lived signatures in lower metallicity stars, which are hotter at the same mass. While the primordial metallicity (i.e. the metal content not including the engulfed planetary material) of stars is not easy to determine, we predict that stars with observable engulfment signatures will have lower primordial metallicity on average than non-enriched stars. This prediction could be tested with abundance measurements of non-refractory material (e.g. carbon or nitrogen) to estimate the pre-engulfment metallicity of the star.

4.2 Limitations

There are a few limitations in our mesa implementation that could be addressed in future studies. One issue is how we implemented mixing beyond thermohaline, overshoot, diffusion, and radiative levitation to account for other poorly understood mixing processes that operate within stellar interiors, e.g. turbulence and rotationally induced mixing. We used a constant min_D_mix coefficient to add this extra mixing in order to match observations of lithium depletion in solar-like stars (Sevilla et al. 2022). However, this simple prescription will not reproduce the higher amount of mixing expected below the convective zones of massive stars due to, e.g. meridional circulation. Radiative levitation will also play a more prominent role in hotter and more massive stars. More accurate prescriptions for additional mixing processes would be a good addition to future studies of planet engulfment.

As discussed in Section 2.2, we were unable to implement instantaneous accretion representing planet engulfment because mesa failed to converge. Instead, we implemented engulfment via rapid accretion, resulting in an engulfment duration of slightly shorter than 10 000 yr. While this period is much shorter than time-scales of refractory depletion (>1 Myr), it is still much longer than instantaneous engulfment, which should occur within years. In addition, we did not consider the scenario of rapid engulfment that could plunge an engulfed planet deep within the stellar interior, and lead to its slow disintegration within the star (Jia & Spruit 2018). This could even result in the planet plunging past the convective zone in more massive stars, significantly decreasing the strength and duration of refractory enhancements in the photosphere. These issues should be taken into consideration to more accurately model different engulfment scenarios.

5 SUMMARY

We used mesa models to simulate planet engulfment and mixing of material throughout the star due to convection, thermohaline mixing, diffusion, gravitational settling, and radiative levitation. We examined the evolution of measurable surface abundances under a range of accretion scenarios by varying the engulfed planet mass, the properties of the engulfing star, and the engulfment time and/or duration (pre-MS disc accretion, ZAMS, late heavy bombardment, and late-stage). We found that these conditions greatly affect the strength and duration of resultant planet engulfment signatures.

Near-instantaneous engulfment occurring when the engulfing star reaches ZAMS results in different time-scales for observable engulfment signatures as a function of engulfing star mass. At solar metallicity, the signature is largest and longest-lived for stars with M ≈ 1.1–1.2 M_⊙. We found that following planetary engulfment, thermohaline mixing quickly depletes the engulfment signature, lowering the increased surface abundances by a factor of ∼2 in the first ∼5–45 Myr. Afterwards, gravitational settling further depletes surface abundance enhancements on longer time-scales. Observable signatures last for less than ∼2 Gyr in all our models, apart from our |$1.2 \, \rm{M}_\odot$| model where radiative levitation causes a ∼5 Gyr post-engulfment increase in surface abundances of certain chemical species (e.g. ⁵⁶Fe, ²⁷Al, ²⁸Si). Engulfment scenarios mimicking LHB or pre-MS disc accretion result in shorter observable signature time-scales compared to ZAMS engulfment. In LHB engulfment, refractory material is continuously depleted throughout longer accretion periods, resulting in almost no refractory enrichment post-engulfment. In disc accretion, refractory material is ingested by the star earlier in its lifetime, and is more heavily diluted within its larger convective envelope (relative to the size of a convective envelope of a star at ZAMS). This results in signatures weaker than those of ZAMS scenarios, but slightly stronger than those of LHB scenarios.

Observable engulfment signature lifetimes increase for late-stage engulfment (300 Myr⁻³ Gyr post-ZAMS) scenarios, where the signatures of |$10 \, \rm{M}_\odot$| engulfment can persist for ∼1.5 Gyr in solar-like stars. Observable signatures are also more prominent for low-metallicity stars, lasting for ∼3 Gyr in |$1\, \rm{M}_\odot$| stars with Z = 0.012 and ZAMS accretion. These conditions are thus more likely explanations for engulfment signatures observed in solar-like stars with ages >1.5 Gyr.

The strong dependence of engulfment signature strength and duration on stellar type, along with fewer theoretical uncertainties when modelling equal-mass stars, both underscore that stellar twin binaries are best suited for observational planet engulfment surveys. We conclude that twin binaries with 1.1–1.2 M_⊙ masses are the most promising targets for engulfment detections.

Software:numpy (Harris et al. 2020), matplotlib (Hunter 2007), pandas (McKinney 2010), scipy (Virtanen et al. 2020), astropy (Astropy Collaboration et al. 2013, 2018).

SUPPORTING INFORMATION

Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

ACKNOWLEDGEMENTS

AB acknowledges funding from the National Science Foundation Graduate Research Fellowship under grant no. DGE1745301. This work benefited from involvement in ExoExplorers, which is sponsored by the Exoplanets Program Analysis Group (ExoPAG) and NASA’s Exoplanet Exploration Program Office (ExEP).

DATA AVAILABILITY

The data underlying this article will be uploaded to Zenodo.org at https://zenodo.org/communities/mesa upon acceptance for publication.

Footnotes

REFERENCES