Direct collapse of exceptionally heavy black holes in the merger-driven scenario Free

ABSTRACT

1 INTRODUCTION

After the first radio observations and key theoretical insights of the 1960s (see, e.g. Bolton, Gardner & Mackey 1963; Schmidt 1963; Zel’dovich 1964), recent surveys have found several quasars with estimated masses exceeding 10⁹M_⊙ at redshift z ≳ 7, i.e. only 700 million years after the big bang (see, e.g. Mazzucchelli et al. 2017; Lyke et al. 2020; Wang et al. 2021). These observations are both impressive and unexpected. They call for satisfying theoretical models, able to both explain the existence of such behemoths, as well as the uncountable number of smaller supermassive black holes (SMBHs) that likely exist at high redshift. Or perhaps it would be more reasonable for such extreme outliers to form via completely independent mechanisms from the large majority of SMBHs? We will return to this question in the conclusion of this work.

Barring primordial BHs scenarios (for some recent constraints, see, e.g. Bellomo et al. 2018; Zhou et al. 2022a, b), proposed mechanisms for early SMBH formation can be broadly separated into two categories. In the so-called ‘light seeds’ scenario, BHs can form at z ≳ 15 as the last stage in the evolution of population III stars (see, e.g. Madau & Rees 2001; Abel, Bryan & Norman 2002; Schneider et al. 2002; Hirano et al. 2014). Despite the large stellar masses, population III stellar evolution models consistently predict compact remains of around ≲ 10² M_⊙. Considering the fact that Eddington-limited accretion can typically only double BH masses on a Salpeter time of ∼5 × 10⁷ yr (Eddington 1921; Salpeter 1964), it has become doubtful whether light seed models can satisfyingly explain the enormous masses of high-redshift quasars (see, e.g. Alvarez, Wise & Abel 2008; Smith et al. 2018; Zhu et al. 2020; Sassano et al. 2021). A more promising origin for SMBHs is provided by ‘direct collapse’ models (DCMs). What defines a DCM is the possibility for large amounts of gas to collapse into a ‘heavy seed’, typically with a mass of around ∼10⁴ to ∼10⁵ M_⊙, which provides a significant jump-start for the growth towards higher masses. However, DCMs often require a very specific balance between angular momentum loss and cooling mechanisms in order for gas structures to contract without fragmenting or reaching new equilibrium states. The question of BH growth is also not completely resolved, since several hundred million-year stretches of Eddington-limited accretion are still necessary for a 10⁵ M_⊙ seed to reach observed SMBH masses by z ∼ 7. While possible in principle, such sustained growth rates require rather compliant gas reservoirs and have (arguably) proven difficult to achieve in simulations where accretion is not assumed a priori. Several works have shown that seeds are only able to grow by a few orders of magnitude before further accretion is progressively quenched by stellar feedback, supernovae or even out-flowing winds (see, e.g. Fiacconi & Rossi 2016; Lupi et al. 2016; Regan et al. 2019; Sassano et al. 2022). Due to the many uncertainties in the modelling of high-redshift galaxies, the degree to which some (or all) DCMs might be too idealized is still unclear, and no consensus has yet been reached with regards to which might be the most realistic. We refer the reader to the many insightful reviews on the advantages and disadvantages of different DCMs (see, e.g. Natarajan 2011; Volonteri 2012; Haiman 2013; Mayer & Bonoli 2019; Woods et al. 2019) and we will mention specific ones throughout this work.

In recent years, Mayer et al. have proposed a scenario in which many of the typical problems specific to DCMs might be largely by-passed. This pathway to the formation of SMBHs originates from simulations of major gas-rich galaxy mergers at z ∼ 10 (Mayer et al. 2010; Bonoli, Mayer & Callegari 2014; Mayer et al. 2015) and is therefore referred to as the ‘merger-driven’ DCM. In these simulations, tidal torques and hydrodynamical instabilites caused by the merger induce gas inflow rates in excess of ∼10⁴ M_⊙ yr⁻¹. Enormous quantities of gas are rushed into the centre of the newly merged protogalaxy, where they form a rotationally supported disc-like gas structure. These ‘supermassive discs’ (SMDs) typically contain upwards of 10⁹ M_⊙, localized in a region of only ≲ 1 pc. In contrast to typical protogalactic discs, they are opaque to radiation, stable to fragmentation and contain up to Solar metallicity due to their relatively late formation. The argument in Mayer et al. (2010,2015) (hereafter MI and MII, respectively) is that SMDs represent an optimal environment for the rapid formation of an SMBH, either through an intermediate supermassive star (SMS) phase (see, e.g. Haemmerlé et al. 2020, 2021), or directly via the collapse of a general relativistic (GR)-unstable region. The advantages of the merger-driven scenario are that the formation of SMDs does not require any specific restrictions on thermodynamical conditions of the gas, nor any specific angular momentum loss mechanism other than the ones provided by the hydrodynamics of galaxy mergers. However, the exact process by which an SMD might produce a BH is unspecified, since its formation is likely to occur well below the resolution limit of the aforementioned simulations. The aim of this work is thus set: revisit the peculiar conditions present in SMDs to determine the mass of BHs predicted by the merger-driven scenario.

The paper is structured as follows: In Section 2, we briefly discuss the peculiar initial conditions, time-scales, and physical processes that govern the evolution of SMDs. In Section 3, we use thermodynamical arguments to describe the accretion of the SMD onto a hydrostatic core via a generic angular momentum loss mechanism. We derive a mass–radius–temperature relation for the core and show that it can grow to significant size before approaching the GR instability regime. We provide a simple fitting formula for the mass of the resulting BHs, which have a typical scale of a few 10⁷ M_⊙. In Section 4, we discuss the implications as well as some caveats of our model. We focus on the direct observational consequences of the merger-driven DCM, highlighting possible electromagnetic and gravitational counterparts. Finally, we summarize our findings and present some concluding remarks in Section 5.

2 THE PHYSICS OF SUPERMASSIVE DISCS

2.1 The initial configuration

The formation of SMDs has been discussed extensively in several works (MI; Mayer et al. 2010; MII; Mayer et al. 2015, Bonoli et al. 2014, Mayer & Bonoli 2019). For the purposes of this work, we assume that the final stages of the aforementioned multiscale simulations are representative of the fate of gas in major galaxy mergers at z ∼ 10. In particular, we take the SMDs analysed in MII as a baseline case, but allow for important parameters such as mass, size and temperature to vary slightly from the simulated results, in case the latter are contaminated by numerical artefacts and spurious sub-grid physics.

The initial thermal state of an SMD is determined by the dynamics of its formation. The competition between atomic cooling, shock heating and turbulent dissipation results in a disc which is approximately isothermal at a temperature of T_d ∼ 7 × 10³ K, in which fragmentation is suppressed regardless of the presence of metals. Despite the different physics at play, this final state is comparable to the virial temperatures commonly expected in smaller, metal-free protogalactic discs which are often invoked in DCMs (see e.g. Rees & Ostriker 1977; White & Frenk 1991). At typical temperatures of ≲ 10⁴ K, the total thermal energy of the gas is not sufficient for spherical hydrostatic equilibrium and the inflows settle into a largely rotationally supported disc. In MI and MII, the resulting SMDs display a constant scale height of ∼0.1R_d, likely due to the resolution limit. In this paper, we assume the standard scaling for the disc’s scale height, H ∼ c_s/ω, where ω is the angular velocity and c_s is the isothermal speed of sound for a mixture of gas and radiation.

Any self-gravitating fluid is likely to exhibit some degree of mass concentration, i.e. a density profile of the form ρ ∼ r⁻ⁿ. Pressure-less thin discs with arbitrary density profiles have been famously studied in Mestel (1963), and the allowed rotational configurations range from constant angular velocity (ρ ∼ r⁰ and v_t ∼ r) to constant tangential velocity (ρ ∼ r⁻² and v_t ∼ r⁰). A steep density profile also implies that the inner parts of SMDs are likely entirely opaque. Accordingly, the diffusion time-scale within a given sub-region of the SMD must be larger relative to the whole system. Matter concentration can also induce substantial variations in the balance between radiation pressure and gas pressure, leading to a more complex behaviour of the sound speed and the scale height. Temperature fluctuations can potentially also affect the balance of pressure. Whenever a system is optically thick, however, radiative heat transfer can be approximated via the Rosseland diffusion equation (Rosseland 1936; Mihalas & Mihalas 1984). One consequence of diffusion is to smooth out any sufficiently strong temperature variability, suggesting that the isothermality seen in MI and MII is also a good approximation at scales that are below the resolution limits.

2.2 Mechanisms of angular momentum loss

In order to contract, a rotationally supported disc must dissipate large amounts of rotational energy and angular momentum. Various scenarios for the disposal of angular momentum have been proposed in the context of DCMs. For the purposes of this paper, we broadly separate them in the two categories of secular and dynamical angular momentum loss mechanisms. Secular mechanisms involve the slow transformation of rotational energy into internal energy. The contraction of the disc occurs through a succession of quasi-equilibrium states, over a period of several dynamical time-scales. Examples in the literature include friction against the cosmic radiation background (Umemura, Loeb & Turner 1993) as well as viscous dissipation caused by turbulence (Eisenstein & Loeb 1995; Mineshige & Umemura 1997; Mineshige, Nakayama & Umemura 1997). In many of these scenarios however, cooling and fragmentation occur on much quicker time-scales than what is required for the disc to contract significantly. This adds the requirement of a nearby reservoir of heat which can influence the energy balance of the disc, in particular the ionization fraction of hydrogen (commonly by a source of Lyman-α radiation, see, e.g. Agarwal et al. 2012; Latif et al. 2013; Regan, Johansson & Wise 2014; Agarwal et al. 2016; Habouzit et al. 2016; Johnson & Dijkstra 2017). Dynamical mechanisms involve the rapid transport of angular momentum, inducing a contraction of the disc on time-scales comparable with gravitational free-fall. While these processes can potentially circumvent the issue of fragmentation, they are conditional to specific triggers (such as a nearby supernova explosion, Colgate et al. 2003) or to the onset of global gravitational instabilities (e.g. Koushiappas, Bullock & Dekel 2004; Begelman, Volonteri & Rees 2006; Lodato & Natarajan 2006, 2007; Begelman 2008). A mechanism based on cold, turbulent gas inflows has been proposed recently and could circumvent some of the aforementioned challenges, producing DC BHs with masses of the order ∼10⁴ M_⊙ (Latif et al. 2022).

2.3 GR instability

3 THE FATE OF SUPERMASSIVE DISCS

3.1 Hydrostatic cores in SMDs

The results of equation (19) are visualized in Fig. 2 for several values of the initial temperature of the SMD. The size of the hydrostatic core varies significantly depending on the parameter n, i.e. the degree of matter concentration: SMDs with shallower density profiles (n ≲ 1) form large radiation pressure dominated cores, while more concentrated discs form smaller, gas pressure-dominated cores. The presence of such a core suggests that the inevitable contraction of SMDs caused by angular momentum loss should be thought as an accretion process onto a spherical, pressure-supported central region.

Figure 1.

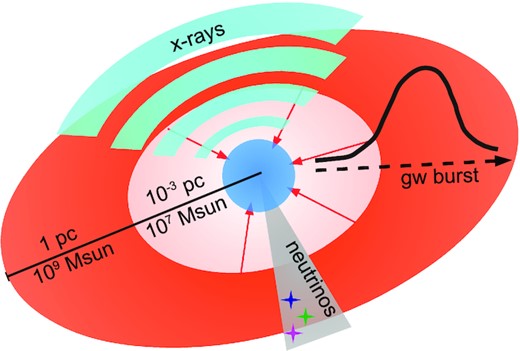
A simple cartoon of the merger-driven DC scenario and its observational signatures. An SMD with a typical size of 1 pc and a typical mass of 10⁹ M_⊙ loses angular momentum by a secular or dynamical mechanism (see Section 2.2). The central regions accrete onto a hydrostatic core, which increases in size, mass, and internal energy. The core reaches the GR instability at a mass of a few 10⁷ M_⊙ (see Section 3.3). It then rapidly collapses into a fully fledged SMBH, producing a burst of X-rays, gravitational waves, and neutrinos along the way (see Section 4.1).

Open in new tabDownload slide

Figure 2.

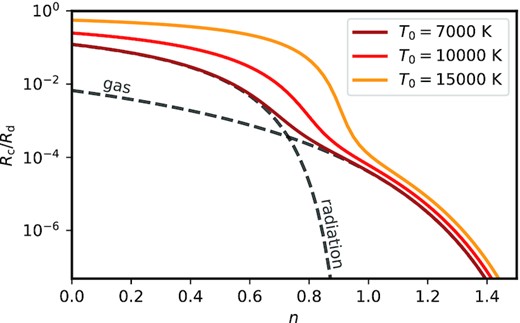
The approximate size of the initial hydrostatic core in an SMD with an initial mass of 10⁹ M_⊙ and a radius of 1 pc. The numerical results are plotted as coloured lines as a function of the mass concentration parameter n(see equation 15). Clearly, visible is the transition betewen gas pressure and radiation pressure-dominated cores for a value of n ∼ 0.8. The grey dashed lines denote the analytical solutions equations (17) and (18) (shown for a temperature of 7000 K).

Open in new tabDownload slide

3.2 Accretion of the disc onto the core

In the case of dynamical mechanisms, which can transport angular momentum without necessarily dissipating its associated energy, we still expect the integral term in equation (19) to appear alongside the adiabatic contributions. The reason for this is slightly subtler and is due to an effect observed in contracting, self-gravitating fluids known as turbulent support (see, e.g. Larson 1981; Murray & Chang 2015; Li 2018; Xu & Lazarian 2020). If a seed of turbulence is present within a fluid element (which is the case in SMDs), any global contraction causes it to heat up, i.e to increase in turbulent mean-root-square velocity (Robertson & Goldreich 2012; Hennebelle 2021). In the case of radial self-gravitating flows, turbulence is thus driven to a steady state in which a significant fraction of the inflows’ kinetic energy is redirected into turbulent eddies, supporting the system against its own gravity. Since the inflow velocity is ultimately sourced by the gravitational potential, the amount energy that is dissipated by turbulent viscosity will necessarily be proportional to the gravitational energy. Essentially, turbulent heating acts to ‘locally virialize’ the internal energy in a contracting fluid, leading to an integral term in equation (19) even in the case of a dynamical angular momentum loss mechanism (with a possible prefactor of the order of unity, which we neglect). The interesting implication of this local virialization is that the energy content of fluid elements is unaffected by the details of the angular momentum loss mechanism, in particular, the time-scale on which it acts (provided it is shorter than a diffusion time-scale, as discussed in Section 2.2). This is a stark contrast between the merger-driven scenario and other DCMs and is partially responsible for the robustness of the predicted BH masses in Section 3.3.

Figure 3.

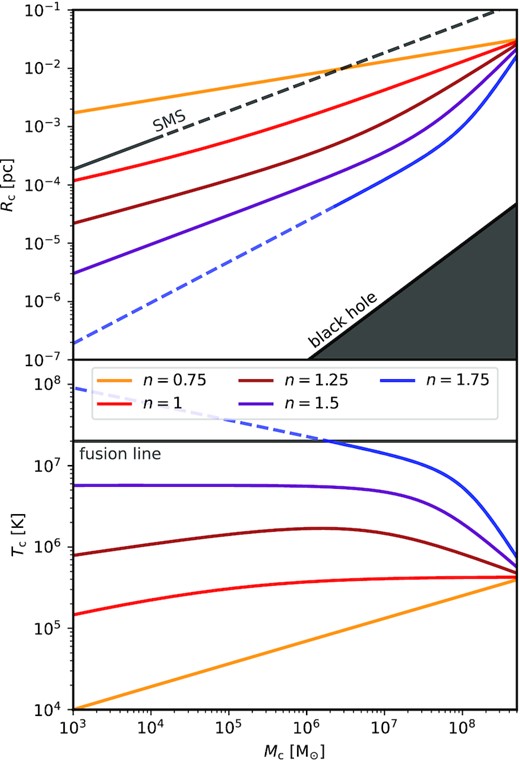
The mass–radius and temperature relations for the core of an SMD with mass 10⁹ M_⊙ and size 1 pc. The coloured lines represent realizations of the disc with different enclosed mass profiles (equation 15). As more shells are accreted, the core increases in size, mass, and internal energy. In the upper panel, the grey line represents the expected mass radius relation for an SMS, extrapolated beyond its known validity range by the dashed line (see, e.g. Hosokawa, Omukai & Yorke 2012). The boundary of the grey triangle denotes the mass–radius relation of a BH. In the lower panel, the grey line denotes the ignition temperature for hydrogen fusion, which is ∼ 2 × 10⁷K.

Open in new tabDownload slide

As discussed previously, the mass–radius relationship for the core relies exclusively on the assumptions of adiabaticity and virialization of rotational energy. It is therefore a generic feature of the evolution of SMDs that does not depend on the details of angular momentum loss. Adiabaticity can be broken in the presence of significant amounts of nuclear fusion, which would provide an additional heating term. For the purposes of this paper, we adopt a temperature limit of ∼2 × 10⁷ K for the ignition of hydrogen within the core (see, e.g. Stahler & Palla 2004), and consider any core whose virial temperature exceeds this limit to be affected by nuclear fusion. As is visible in the lower panel of Fig. 3, only SMDs with high degrees of mass concentration (n ≳ 1.7) produce cores in which nuclear fusion is likely. In this case, the cores would tend to heat up and increase in radius faster than what our relations predict, possibly evolving along SMS tracks (see, e.g. Hosokawa et al. 2012; Haemmerlé 2021). We refer the reader to Section 4.2 for a more thorough discussion.

3.3 Formation of a BH via the GR instability

The results of our computations are visualized in Fig. 4. Typically, the GR-unstable cores collapse from an initial compactness of ∼100, far from the strong gravity regime of GR. The final BH seed masses strongly depend on the value of the parameter n and can range from ∼10⁶ to 10⁸ M_⊙. Within this range is the direct formation of exceptionally heavy seeds, all the way up to fully fledged SMBHs. The model is therefore not only consistent with the largest observed high redshift quasars, but can easily explain their masses, since it only requires the seeds to accrete at Eddington levels for a few Salpeter time-scales rather than dozens. The additional mass can be provided by the rest of the SMD, which must eventually settle into an accretion disc around the newly formed seed, likely powering quasar emission.

Figure 4.

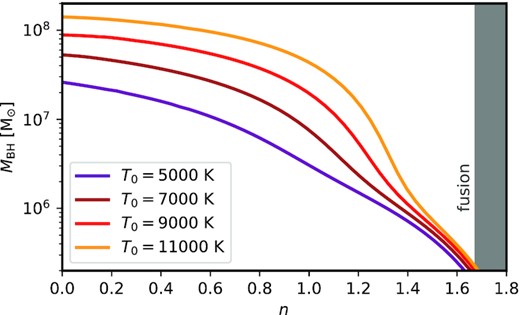
The mass of the final BH seed formed in an SMD with mass 10⁹ M_⊙ and size 1 pc. The coloured lines represent realizations of the disc with different initial temperatures, plotted as a function of the mass profile parameter n (equation 15). More concentrated SMDs produce smaller BH seeds, while shallower discs produce larger ones. The seeds are formed rapidly, at most ∼10⁵ yr after the formation of the SMD at z ∼ 10. These exceptionally heavy DC BHs are not only consistent with, but can easily explain even the largest observed high-redshift quasars.

Open in new tabDownload slide

4 DISCUSSION

4.1 Smoking gun observational signatures

Figure 5.

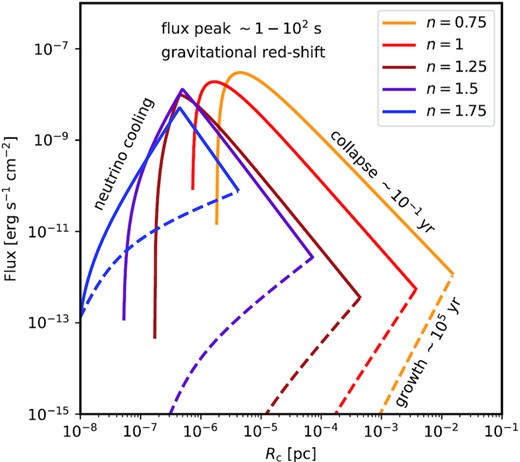
The bolometric flux tracks of SMD cores observed at z = 10, plotted as a function of the core radii for different values of the parameter n. The growth phase (dashed lines) ends once the GR instability is reached and dynamical collapse is triggered. The luminosity increases dramatically during the collapse, until it is suppressed by gravitational redshift or neutrino cooling (solid lines). The resulting X-ray and neutrino transients would constitute a smoking gun signature of the merger-driven DCM. The tracks assume that the radiation from the cores is able to escape the host protogalaxy without being absorbed or scattered.

Open in new tabDownload slide

As can be seen in the figure, the tracks initially follow the growth of the core. During this phase, the flux typically peaks at values of ∼10⁻¹² erg s⁻¹ cm⁻² and is mostly concentrated in the ultraviolet and soft X-ray bands. The duration of this phase depends on the angular momentum loss mechanism, which can range from ∼10² to ∼10⁵ yr. Once the GR instability is triggered, the cores start to contract and the flux rapidly increases by several orders of magnitudes due to the rise in temperature. The signatures of this phase are extremely bright, hard X-ray (and potentially gamma ray) transients that peak at a bolometric flux of ∼10⁻⁸ erg s⁻¹ cm⁻². The duration of this phase depends on the size of the core as it becomes unstable. In general, the peak luminosity is limited to an extremely short period of a few seconds to minutes. During this phase, the core detaches from the rest of the disc due to its rapid collapse, leaving behind a cavity at the centre of the disc. Depending on the configuration and the disc geometry, it possible that radiation may escape from the protogalaxy, as suggested by the cartoon in Fig. 1. The very last stages of the tracks differ qualitatively for SMDs with shallow (n ≲ 1) or steep (n ≳ 1) initial density profiles. For the former, the flux is smoothly reduced by gravitational redshift in the moments before a BH is formed. For the latter, the temperatures are high enough for neutrino cooling to suddenly become efficient. While the electromagnetic luminosity is reduced, neutrino cooling induces a flux of particles with a scale of ∼10⁻⁷ erg s⁻¹ cm⁻². Neutrinos are much more likely to freely exit the protogalaxy, and the collapse of an SMD core could in principle be detectable as a point-source transient by current and future instruments (see, e.g. Abbasi et al. 2011; IceCube Collaboration et al. 2013; Hallmann et al. 2021).

We can roughly estimate the event rate at which the transients discussed above are expected to occur. An estimate of the rate of appropriate major mergers that can produce SMDs is provided in Mayer & Bonoli (2019), ranging between 10⁻⁷ and 10⁻⁵ mergers per Mpc³. Here, we consider an interesting redshift window between z = 7 and 12, where the lower value is given by the furthest observed high-mass quasars while the larger one is an arbitrary boundary above which major mergers are not expected. We can simply multiply the merger rate with the co-moving volume between z = 7 and 12, which amounts to ∼1500 Gpc³ for a flat ΛCDM universe (Wright 2006). We find that the total amount of appropriate mergers amounts to ∼10⁵ to ∼10⁷. Dividing the number by 500 million years, i.e. the elapsed time between z = 7 and 12, we find that we should expect a rate of ∼10⁻² to ∼1 gravitational, neutrino and electromagnetic transients per year, assuming that every suitable major merger inevitably leads to a DC event.⁷ The likelihood for detecting a counterpart is boosted significantly with instruments sensitive enough to observe the growth and the initial collapse phases of the cores due to their longer duration.

We look forward to the feedback of the X-ray, neutrino and gravitational wave astronomy communities to assess whether these signatures are detectable in the foreseeable future, or might even be present in existing wide-field surveys.

4.2 Caveats

The largest caveat of our analysis is the simplistic treatment of the hydrostatic cores, which are likely to settle into structures resembling SMSs. The arguments used in Section 3.2 only allow for an order of magnitude estimate of their properties, e.g. the radius, mass and energy content. A more precise analysis would require full solutions to the equation of hydrostatic equilibrium, which necessarily implies the use of numerical models. In particular, the latter show that the structure of SMSs depend critically on their mass accretion rate. For rates greater than 0.01 M_⊙ yr⁻¹, accretion prevents thermal relaxation on fully convective, polytropic structures. The SMS evolves instead as a ’red supergiant protostar’ (Hosokawa et al. 2012, 2013; Haemmerlé et al. 2018a), whose internal structure consists of a convective core produced by H-burning, a radiative zone containing most of the stellar mass, and a convective envelope that covers a dominant fraction of the photospheric radius. These structures can be approximated by ’hylotropes’ (Begelman 2010), in particular for rates ≳ 10 M_⊙yr⁻¹, at which the contraction is adiabatic (Haemmerlé et al. 2019). The hydrodynamical simulations of Mayer et al. (2010, 2015) show accretion rates up to ∼10⁵ M_⊙ yr⁻¹ down to a fraction of a pc during the assembly of the SMD. Gravitational free-fall can maintain such rates down to the stellar surface only if its mass exceeds ∼10⁵ M_⊙. Milder rates up to ∼1000 M_⊙ yr⁻¹ can be driven if the attractor’s mass exceeds ∼1000 M_⊙ (Haemmerlé et al. 2021), which is comparable to our estimates for the mass of the initial hydrostatic cores in SMDs. A dynamical angular momentum loss mechanism (as discussed in Section 2) could supply accretion rates close to the maximum value allowed by gravitational free-fall. At such rates, masses up to 10⁸−10⁹M_⊙ could be reached before the final collapse, which corresponds to similar estimates as those of Section 3.3.

Another important factor, we neglect to model explicitly is rotation. Because of the prominent role of radiation pressure, SMSs must have surface velocities lesser than |$10{{\%}}$| of the Keplerian velocity (Haemmerlé et al. 2018b; Haemmerlé & Meynet 2019). As a consequence, the centrifugal acceleration represents at maximum a percent of the gravitational acceleration, implying that rotation has a negligible impact on the hydrostatic structure and that deformation remains small. On the other hand, rotation impacts significantly the dynamical stability of the structure (Fowler 1966; Bisnovatyi-Kogan, Zel’dovich & Novikov 1967; Baumgarte & Shapiro 1999; Shibata, Uchida & Sekiguchi 2016; Haemmerlé 2021). The mass at which rapidly accreting SMSs reach the GR instability depends on both the accretion rate of mass and angular momentum. Without any angular momentum, reaching masses ≳ 10⁶ M_⊙ before becoming unstable typically requires accretion rates larger than 1000 M_⊙ yr⁻¹ (Haemmerlé 2020). However, even a small amount of angular momentum postpones this limit by orders of magnitude, and maximally rotating SMSs can remain stable potentially up to ∼10⁹ M_⊙ (Fowler 1966; Haemmerlé 2021). Since the growth of the cores described in Section 3.2 results from the accretion of a rotationally supported disc, it is likely that some amount of angular momentum will be retained even in the final hydrostatic structure. Some combination of high accretion rates and retention of angular momentum is exceedingly likely in SMD cores, strongly supporting that the high final BH masses reported in Fig. 4 are realistic estimates despite the simplifying assumptions.

The final issue that requires further discussion is fragmentation. As shown in MI and MII, the innermost region of SMDs (whithin ∼1 pc) is stabilized by the extreme shear forces, preventing the formation of stars. However, it is possible that significant fragmentation may occur at the outer edges, where the Toomre parameter approaches its critical value. Thus, the consequence of fragmentation would be to enable the formation of a stellar disc with a typical size of a few pc. Understanding the interplay between fragmentation, migration and relaxation processes within the SMD and its stellar counterpart would require significant modelling, and would be best tackled by a purpose built numerical simulation. If the scenario lead to a significant flux of stars towards the central region, it could perhaps enable an extreme version of the stellar bombardment model proposed in Tagawa, Haiman & Kocsis (2020), in which runaway mergers of stars take over the mass and energy balance of the growing SMD core. Both the dynamics of the stellar disc and the evolution and structure of SMD cores under bombardment are extremely interesting and deserve further investigation.

5 SUMMARY AND CONCLUSION

In this work we revisited the merger-driven scenario in order to asses its promise as a DCM. In Section 2, we show that the thermodynamical evolution of SMDs is fundamentally different than more typical protogalactic discs. First, SMDs are optically thick and therefore evolve adiabatically over periods comparable with the diffusion time-scale of ≲ 5 × 10⁵ yr (see equation 3). Fragmentation is therefore naturally suppressed without the requirement of an external source of ionizing radiation. Secondly, SMDs are expected to lose angular momentum on time-scales comparable or shorter than a diffusion time-scale, both in the case of dynamical as well as secular mechanisms (see equation 4 for the case of turbulent viscous dissipation). In combination with the adiabaticity, this implies that our analysis is independent of the choice of an angular momentum loss mechanism. We sumarize the DCM as follows: As an SMD loses rotational support, more and more concentric shells accrete onto to a central spherical hydrostatic core (see Section 3.2). Every shell adds a specific amount of mass and internal energy, which determines the core’s mass–radius and temperature relation (shown in Fig. 3). Eventually, the cores approach the GR instability regime and collapse into a compact object, producing several observational counterparts that can be considered smoking gun signatures of the model. The main findings of our analysis are listed here:

• The mass of BHs produced in the merger-driven scenario has a typical scale of a few 10⁷ M_⊙, ranging from 10⁶ to 10⁸ M_⊙ depending on the initial disc configuration (see Fig. 4). SMDs are therefore optimal locations to produce fully fledged SMBHs by direct collapse. The collapse occurs very rapidly, at most ∼5 × 10⁵ yr after the formation of an SMD at z ∼ 10. A simple-fitting formula for the final BH mass is provided by equation (31) and can be implemented as a sub-grid model in future simulations.

• The collapse of an SMD core produces a characteristic luminosity curve, shown in Fig. (33). It exhibits an extremely bright (∼10⁻⁸ erg s⁻¹ cm⁻²) but short (∼ few second) X-ray transient. In certain cases, the electromagnetic signature might be accompanied by a burst of neutrinos (∼10⁻⁷ erg s⁻¹ cm⁻² in flux) and of gravitational wave radiation (∼10⁻²¹ in amplitude, see equation (38)), potentially detectable by current and future instruments. If identified, these counterparts would represent a smoking gun signature of the merger-driven DCM. Their expected rate is ∼10⁻² to ∼1 per year.

The merger-driven scenario has the advantage of not requiring any specific assumptions on the thermodynamics or on the angular momentum loss mechanisms of protogalactic discs, provided that they are massive enough to behave adiabatically over long time-scales. This is a unique feature, which is at odds with other DCMs. In this paper, we have shown that once an SMD forms, it is inevitable that it will produce a large BH on a very rapid time-scale, without requiring any further additional assumption other than conventional hydrodynamics of ideal gas flow and the large-scale dynamics imposed by the merger. The trade-off is that only relatively rare major mergers of galaxies well exceeding the typical mass of star-forming galaxies at z > 10 can form SMDs, implying that this flavour of DC must be rare by construction (see Bonoli et al. 2014; Mayer & Bonoli 2019, for an estimate of the occurence rate of such systems, and its agreement with the abundance of high-z quasars.).

Returning to the question posed in the introduction, the merger-driven scenario implies the possibility that high red-shift BHs with varying masses might form by different mechanisms. In this scenario, an uncountable number of smaller BH seeds can form early, by any of the several models present throughout the literature, including the other more conventional DC channels. These might then slowly grow by accretion or by repeated mergers to become one of the many BHs, ranging from 10⁵ to 10⁸ M_⊙, that we identify at the centre of galaxies in our local universe. The BH mass function at high redshift could therefore start off rather ‘under-weight’, and remain so up until the sudden appearance of merger-driven DC BHs at z ∼ 10. These would form fast and late, by a completely separate mechanism from the majority. They would instantly surpass their older, tamer counterparts, becoming visible as 10⁹ M_⊙ quasars at z ∼ 7 and possibly explaining the formation of the exceptionally massive quasars such as TON618, Holmberg 15A and many others. Incidentally, these heaviest of SMBHs tend to reside in elliptical early-type galaxies, the likely outcome of the massive mergers required to form SMDs in the first place (see, e.g. Colla et al. 1970; Cattaneo & Bernardi 2003; McConnell & Ma 2013; López-Cruz et al. 2014; Yoon et al. 2019).

In conclusion, it is hard to argue which answer would be more satisfying: a single DCM, in which the most massive outliers are explained as improbable statistical flukes? Or rather the co-existence of several models, which can explain BHs in different mass ranges more naturally? Perhaps the answer must come from astronomical observation. With a new generation of detectors coming, we are certainly hopeful that a careful analysis of the redshift-dependent BH mass function, as well as the constant monitoring of the electromagnetic, neutrino and gravitational wave skies will be sufficient to untangle the question of early BH formation, be it merger-driven or otherwise.

ACKNOWLEDGEMENTS

The authors acknowledge support from the Swiss National Science Foundation under the Grant 200020_192092. We acknowledge Pedro R. Capelo, Andrea Derdzinski, and Mudit Garg for insightful discussions. LH has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 833925, project STAREX). RSK acknowledges financial support from the European Research Council in the ERC Synergy Grant ‘ECOGAL’ (project ID 855130), from the Heidelberg Cluster of Excellence ‘STRUCTURES’ (EXC 2181 - 390900948), from the German Science Foundation (DFG) via the Collaborative Research Center ‘The Milky Way System’ (SFB 881, Funding-ID 138713538, subprojects A1, B1, B2, B8), and from the German Ministry for Economic Affairs and Climate Action in the project ‘MAINN’ (funding ID 50OO2206). We thank the Kavli Institute for Theoretical Physics at UC Santa Barbara for hospitality during the development of this work, in particular, the program BINARY22 supported in part by the National Science Foundation under Grant No. NSF PHY-1748958.

DATA AVAILABILITY

Our python scripts will be shared upon reasonable request.

Footnotes

REFERENCES