-
PDF
- Split View
-
Views
-
Cite
Cite
D R Flower, Electron attachment to interstellar grains, Monthly Notices of the Royal Astronomical Society, Volume 517, Issue 1, November 2022, Pages 175–181, https://doi.org/10.1093/mnras/stac2701
Close - Share Icon Share
ABSTRACT
We have performed quantum mechanical calculations of cross-sections and rate coefficients for electron attachment to small, neutral, and positively charged grains. In addition to the polarization potential and – for charged grains – the Coulomb potential, we considered the influence of the interaction between the charge of the electron and a possible permanent electric dipole on the grain. We found large discrepancies between the predictions of classical and quantal models of electron scattering on neutral grains at low energies (temperatures) in the absence of a permanent dipole moment, but much closer agreement when a dipole moment was present. The presence of the long-range Coulomb potential also leads to better agreement between classical and quantal models.
1 INTRODUCTION
The attachment of electrons to interstellar grains can have a number of consequences. In molecular clouds, the depletion of electrons on to small grains or large molecules, such as polycyclic aromatic hydrocarbons, could change the free electron concentration and hence the rates of chemical reactions involving electrons, notably dissociative recombination with molecular ions. In the presence of a flow transverse to a magnetic field, charged grains can reduce the rate of ambipolar diffusion of the ionized relative to the neutral medium, with consequences for the rate of gravitational collapse or for the structure of shock waves (Draine 1980; Flower & Pineau des Forêts 2003). It is therefore important to determine the rate at which electrons can attach themselves to dust grains.
Draine & Sutin (1987) considered the charging of interstellar grains by charged particles, treating the motion of the charged particles, relative to the grains, by means of classical mechanics. Flower & Middleton (2004) subsequently investigated electron attachment to neutral grains using quantum mechanics and found significant quantal effects for low temperatures (T ≲ 100 K) and for small (a ≲ 3 × 10−6 cm or 0.03 μm) grains. At low collision energies, the de Broglie wavelength of the electron becomes comparable with the dimensions of small grains, and the wave properties of the electron assume significance. This transition – from macroscopic (classical) to microscopic (quantal) physics – is an interesting topic in its own right.
Jordan & Weingartner (2009) used the classical equations of motion to study the scattering and attachment of electrons to grains in the presence of Coulomb and charge–dipole interactions. In the present study, we investigate the effects of a dipole moment on the rate of electron attachment to grains, using quantum mechanics to solve the scattering problem.
In Section 2, we describe the model that we have used and illustrate the influence of the charge–dipole interaction on collisions with both charged and neutral grains. The rate coefficients for electron attachment are presented and discussed in Section 3. Our conclusions are summarized in Section 4.
2 A QUANTUM MECHANICAL MODEL OF ELECTRON–GRAIN COLLISIONS
The creation of trapped electron–hole pairs in a grain can result in a net electric dipole moment whose magnitude is of the order |p| ≈ ea. The dipole moment varies with time, owing to photoelectric emission and collisional charging, principally electron attachment (Jordan & Weingartner 2009). Although interstellar grains are expected to carry a net charge (Weingartner & Draine 2001), it is none the less instructive to consider electron attachment to both charged and neutral grains that possess a dipole moment. In the numerical calculations, we adopted |p| = ea. Furthermore, rather than consider the somewhat artificial case of a perfectly conducting grain, we modify the charge-induced-dipole interaction to the case of a finite dielectric constant, taking ϵ = 3. We have verified that our previous results (Flower & Middleton 2004, table 1), for a perfectly conducting grain (ϵ → ∞), were correctly reproduced.
2.1 Neutral grains
In the corresponding quantum mechanical model, the value of b given by equation (8) provides the upper limit of r in the integration of the differential equations [equation 12 of Flower & Middleton (2004)] that describe a scattering event. These equations are integrated outwards from r = a, where the wavefunction vanishes, to r = b, where the scattering (S-)matrix and the cross-sections are derived. Extending the integration beyond this upper limit has no significant effect in the case of the polarization potential, which is proportional to r−4 at sufficiently long range. However, in the presence of the charge–dipole potential, which is proportional to r−2, integrating beyond r = b would lead to the inclusion of the contributions of scattering events from values of the relative angular momentum (equivalently, impact parameters) that are too large to satisfy the criterion for orbiting.
In Fig. 1, we compare values of the cross-section, as a function of the collision energy, obtained using both the classical model and quantum mechanics. In the latter case are shown the results obtained both with and without the charge–dipole interaction. In the absence of the charge–dipole interaction, the quantal values of the cross-section fall below the predictions of the classical model owing to wave mechanical interference effects, more so for the smaller value of the grain size, a; this is the same result as was found by Flower & Middleton (2004). The significance of the interaction of the electron charge with the dipole moment of the grain is evident in Fig. 1. The long-range attraction of the electron by the dipolar grain enhances the cross-section, increasingly so as the collision energy decreases. As a consequence, the quantal and classical values of the cross-section become similar. In essence, the additional (charge–dipole) interaction enhances the cross-section at low energies to the upper limit that is provided by the classical model, in which wave-mechanical interference is absent.

The reduced momentum transfer (diffusion) cross-section, σ/πa2, where a = 0.01 μm (upper panel) or a = 0.003 μm (lower panel) is the adopted value of the radius of the (neutral) grain, as a function of the collision energy, E/kB (K). Values obtained using a classical model, equation (8) (red curve with filled circles), and quantum mechanics, equation (4), are shown. In the latter case, the results obtained on including (blue curve with filled squares) and excluding (green curve with filled lozenges) the charge–dipole interaction are plotted. Note that the polarizability, a3, and dipole moment, ea, depend on a.
The approach adopted in the present study, and by Flower & Middleton (2004), is to obtain stationary solutions of the Schrödinger equation that satisfy the appropriate scattering boundary conditions. In this (time-independent) approach, the development of the scattering wavefunction as a function of the scattering coordinates, r and θ, is determined by the variations in the contributions to the local wavefunction of the various states included in the rotational basis: see, for example, Flower (2007). Thus, averaging over the angle θ in the course of the collision is implicit in the quantum mechanical calculations.
It is the electron that exhibits wave-mechanical properties at low collision energies, with the grain behaving as a classical particle. In particular, the large mass of even small grains ensures that their moment of inertia is large, and the corresponding rotational constant is small compared with even the lowest collision energy considered here. Nevertheless, in the quantum-mechanical scattering calculations, the grain has to be assigned a rotational basis and rotational energies.4 The rotational basis has to comprise at least the states with rotational quantum numbers J = 0 and J = 1, in order for the angle-dependent charge–dipole interaction, which depends on cos θ, to influence the scattering process. Indeed, including only the lowest state, J = 0, in the basis leads to results that are practically identical to those obtained on neglecting the charge–dipole interaction altogether. On the other hand, extending the rotational basis leads to rapid convergence of the cross-section to values that are very similar to those predicted by the classical model, as is shown in Fig. 2, where the rotational basis is 0 ≤ J ≤ 2, as compared with 0 ≤ J ≤ 15 in Fig. 1. In both Figs 1 and 2 are apparent diffraction effects in the wave-mechanical calculations, as the collision energy falls to values such that the de Broglie wavelength becomes comparable to the dimensions of the grain.

As Fig. 1, but comparing values of the cross-section computed using the classical model (red curve with filled circles) with the results obtained with the quantal model, including only the rotational state J = 0 (green curve with filled lozenges) or the states J = 0, 1, 2 (blue curve with filled squares) in the rotational basis describing the grain.
2.2 Charged grains
We consider the illustrative and important case of a singly, positively charged grain (Z = 1), for which the Coulomb potential is attractive. In Fig. 3 are plotted the values obtained with and without the charge–dipole interaction, together with the classical result, derived from equation (10). It is clear from this figure that the charge–dipole interaction is not significant for a = 0.01 μm, in the presence of the longer-range Coulomb attraction. However, the charge–dipole interaction is significant, at intermediate collision energies, for a = 0.003 μm.

As Fig. 1 but for the case of a singly, positively charged grain (Z = 1).
In the absence of the charge–dipole interaction (equivalently, restricting the rotational basis to J = 0), departures from the classical cross-section, as the collision energy decreases, are expected to be greater for the smaller value of a, as already seen in Figs 1 and 2. However, at very low energies, the Coulomb potential is completely dominant, and the neglect of the charge–dipole interaction has little effect, as is apparent in Fig. 3.
3 RATE COEFFICIENTS FOR ELECTRON ATTACHMENT
In Fig. 4 are plotted the rate coefficients, as functions of the kinetic temperature, for the transfer of momentum to uncharged grains. At the larger value of the grain radius, a = 0.01 μm, the results obtained using the classical model, equation (8), are similar to the predictions of the quantal model, when the charge–dipole interaction is included in the quantum-mechanical calculations of the cross-section. On the other hand, at a = 0.003 μm and in the absence of a permanent dipole moment, the rate coefficient falls increasingly below the classical results as the temperature decreases, the discrepancy attaining a factor of 4 at T = 10 K. Furthermore, for this lower value of a, the classical and quantal models are discrepant when the charge–dipole interaction is present, particularly for temperatures T ≳ 100 K.

Rate coefficients, q (cm3 s−1), for momentum transfer from electrons to uncharged grains of radius a = 0.01 μm (upper panel) or a = 0.003 μm (lower panel), as a function of the kinetic temperature T (K). Values obtained using a classical model, equation (8) (red curve with filled circles), and quantum mechanics, equation (4), are shown. In the latter case, the results obtained on including (blue curve with filled squares) and excluding (green curve with filled lozenges) the charge–dipole interaction are plotted. Note that the polarizability, a3, and dipole moment, ea, depend on a.
The corresponding results for singly charged grains are shown in Fig. 5. At a = 0.01 μm, the classical and quantal cross-sections, with or without the charge–dipole interaction, are essentially in agreement and only the classical values of the rate coefficient, obtained using equation (10), are plotted. At a = 0.003 μm, the values obtained when the charge–dipole interaction is present in the quantal calculations of the cross-section also agree with the classical results. On the other hand, in the absence of a grain dipole, the quantal rate coefficient diverges from the classical result at intermediate temperatures, falling below the classical prediction by a factor of approximately 2.5 at T = 1000 K.

As in Fig. 4 but for a singly, positively charged grain (Z = 1). In the case of a = 0.01 μm (upper panel), only the classical results – derived using equation (10) – are plotted, in view of the close similarity of the classical and quantal cross-sections, with or without the charge–dipole interaction: cf. Fig. 3 (upper panel).
4 CONCLUDING REMARKS
We have considered electron attachment to neutral and positively charged grains both in the presence and absence of a permanent dipole on the grain. It was found that classical and quantal models of the electron–grain collision process are most discrepant for small, neutral grains and low electron collision energies, confirming an earlier study of Flower & Middleton (2004). Introducing the long-range Coulomb attraction that characterizes positively charged grains tends to reduce these discrepancies, which are reduced still further if the grain possesses a permanent dipole moment.
Any evaluation of the grain charge distribution needs also to adopt a value for the sticking coefficient. For the macroscopic grains studied here, the sticking coefficient is likely to take values s ≈ 1, but this is not the case of still smaller grains (cf. Weingartner & Draine 2001), which morph into large molecules. In such cases, the internal structure of the grain should be taken into account when treating the electron–grain collision process, thereby obtaining simultaneously the cross-sections for elastic and inelastic scattering, in addition to that for electron capture.
ACKNOWLEDGEMENTS
I am grateful to Bruce Draine for answering a question relating to his 1987 paper with Brian Sutin and to the referee for a thoughtful report. I have benefitted from the provision of local computing resources.
DATA AVAILABILITY
The data generated by this study are available on request to the author.
Footnotes
Following a suggestion of the referee, some preliminary calculations were performed for a potential which has a well at short range, rather than an infinite barrier. These calculations showed the cross-section to be modified qualitatively at high, rather than low, collision energies.
p = 480 debye when a = 0.01 μm, and p = 144 debye when a = 0.003 μm.
The Langevin (orbiting) model is appropriate to the case of isotropic (angle-independent) interaction potentials that behave, at long range, as V(r) ∝ − 1/rn, where the integer n > 2.
The cross-section is insensitive to the values of the rotational energies, providing that they are much smaller than the lowest collision energy. On the other hand, the electron must lose at least some of its incident kinetic energy in order for attachment to occur, by transfer of energy to the material of the grain itself or, possibly, to the molecules comprising an ice covering its surface; but such considerations take us beyond our immediate objectives.
We note that the alternative, of adopting the Debye shielding distance (Spitzer 1962), is inappropriate here and would lead to unrealistically large values of the cross-section.
This lower limit for E would be reduced by the (attractive) polarization interaction.
REFERENCES
APPENDIX A: MOMENTUM TRANSFER CROSS-SECTION FOR A COULOMB POTENTIAL
APPENDIX B: PARTIAL CROSS-SECTIONS
In Fig. B1, we plot partial momentum transfer cross-sections for an illustrative case of a collision of an electron with a neutral grain. The classical value of the angular momentum at the orbiting radius is |$L = \sqrt{2\mu E} b$|, where μ is the reduced mass, E the incident energy, and b the impact parameter, given by equation (8).
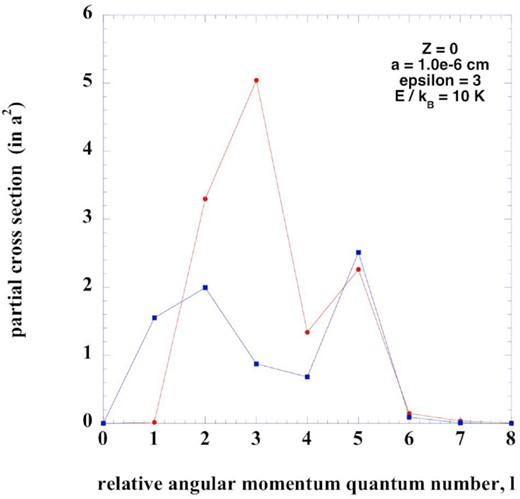
Partial cross-sections, in units of a2, computed for the case of a neutral grain of radius a = 0.01 μm, with (red curve) and without (blue curve) a dipole moment, and for a collision energy E/kB = 10 K, as a function of the relative angular momentum quantum number, l. The corresponding classical value of the angular momentum at the orbiting radius is l = 5.3. Note that, when the dipole is present (red curve), the partial cross-section for l = 1 is small but not zero.
We note that the relative angular momentum vector, l, is perpendicular to the collision plane, and hence its projection in the direction of the dipole moment, p, is zero. Furthermore, the cross-section is independent of the value of the projection of the total angular momentum, l + J, where J is the rotational angular momentum assigned to the grain, on the space-fixed z-axis.



