-
PDF
- Split View
-
Views
-
Cite
Cite
Mallory D Thorp, Sara L Ellison, Hsi-An Pan, Lihwai Lin, David R Patton, Asa F L Bluck, Dan Walters, Jillian M Scudder, The ALMaQUEST Survey X: what powers merger induced star formation?, Monthly Notices of the Royal Astronomical Society, Volume 516, Issue 1, October 2022, Pages 1462–1480, https://doi.org/10.1093/mnras/stac2288
Close - Share Icon Share
ABSTRACT
Galaxy mergers are known to trigger both extended and central star formation. However, what remains to be understood is whether this triggered star formation is facilitated by enhanced star formation efficiencies (SFEs), or an abundance of molecular gas fuel. This work presents spatially resolved measurements of CO emission collected with the Atacama Large Millimetre Array (ALMA) for 20 merging galaxies (either pairs or post-mergers) selected from the Mapping Nearby Galaxies at Apache Point Observatory (MaNGA) survey. Eleven additional merging galaxies are selected from the ALMA MaNGA QUEnching and STar formation (ALMaQUEST) survey, resulting in a set of 31 mergers at various stages of interaction and covering a broad range of star formation rates (SFRs). We investigate galaxy-to-galaxy variations in the resolved Kennicutt–Schmidt relation, (rKS: |$\Sigma _{\textrm {H}_2}$| versus ΣSFR), the resolved molecular gas main sequence (rMGMS: Σ⋆ versus |$\Sigma _{\textrm {H}_2}$|), and the resolved star-forming main sequence (rSFMS: Σ⋆ versus ΣSFR). We quantify offsets from these resolved relations to determine if SFR, molecular gas fraction, or/and SFE is/are enhanced in different regions of an individual galaxy. By comparing offsets in all three parameters, we can discern whether gas fraction or SFE powers an enhanced ΣSFR. We find that merger-induced star formation can be driven by a variety of mechanisms, both within a galaxy and between different mergers, regardless of interaction stage.
1 INTRODUCTION
Evidence has consistently demonstrated that galaxy–galaxy mergers can trigger star formation: from the bluer colour of peculiar galaxies (Larson & Tinsley 1978; Barton Gillespie, Geller & Kenyon 2003; Lambas et al. 2012) and excess H α emission noted in interacting pairs (Kennicutt et al. 1987; Knapen & James 2009), to large single-fibre spectroscopic surveys revealing an excess of star formation as a merger event progresses (Ellison et al. 2008; Woods et al. 2010; Scudder et al. 2012; Patton et al. 2013; Knapen, Cisternas & Querejeta 2015). Hydrodynamical simulations illustrate how induced star formation likely stems from gas losing angular momentum and fuelling centralized star formation, as a result of the non-axisymmetric structures generated by gravitational forces in an interaction (Barnes & Hernquist 1991; Mihos & Hernquist 1996; Iono, Yun & Mihos 2004; Hopkins et al. 2013). The degree to which star formation is enhanced can vary drastically depending on the properties of an interaction, with orbital parameters (Di Matteo et al. 2007; D’Onghia et al. 2010; Moreno et al. 2015), mass ratio between constituents (Cox et al. 2006, 2008), and gas fraction of the interacting disc (Bournaud et al. 2011; Perez, Michel-Dansac & Tissera 2011; Scudder et al. 2015; Fensch et al. 2017) all leading to varied star formation strengths. In simulations, star formation tends to peak when the interacting galaxies are either close to pericentric passage or at the moment of coalescence (Lotz et al. 2008; Scudder et al. 2012; Hani et al. 2020). Such results are supported by observational evidence, which has consistently demonstrated that global star formation rate (SFR) values are the greatest for interactions with equal mass ratios and small projected separations (Nikolic, Cullen & Alexander 2004; Lin et al. 2007; Ellison et al. 2008, 2013; Woods et al. 2010; Scudder et al. 2012; Bickley et al. 2022).
Resolved spectroscopic studies have revealed further complexity of merger-induced star formation on a local scale. Integral Field Spectroscopy (IFS) surveys such as the MaNGA Survey (Bundy et al. 2015), the Calar Alto Legacy Integral Field Area Survey (CALIFA; Sánchez et al. 2012), and the Sydney-Australian Astronomical-Observatory Multi-object Integral field spectrograph Survey (SAMI; Allen et al. 2015) have allowed for the collection of resolved spectroscopic data of large samples of galaxies from which robust statistical results can be attained. Investigations of interacting galaxy pairs in IFS surveys have further corroborated the central enhancement of star formation noted in global studies, but often find a diversity of behaviours in the outskirts of the galaxy where star formation can be unaffected, enhanced, or suppressed (Barrera-Ballesteros et al. 2015; Pan et al. 2019; Steffen et al. 2021). Such variation may be linked to the global galaxy properties, with only the higher mass galaxy in a pair showing enhanced star formation in the outskirts (Steffen et al. 2021). However, evidence also suggests only galaxies at pericentre and coalescence have elevated star formation at large radii (Pan et al. 2019). Significant variations in spatial star formation enhancement are therefore apparent even in a single stage of interaction.
Whereas pairs of galaxies represent the pre-merger regime, post-merger galaxies allow us to study the late stages of the interaction sequence. On average, post-mergers have central star formation enhancements that moderately fall off with radius, but galaxies with similar central star formation enhancements can have enhanced, normal, or suppressed star formation in the outskirts (Thorp et al. 2019). Just as the unique properties of a galaxy and its interaction parameters can lead to a diverse range of global star formation enhancement, there is equal if not greater complexity when star formation is examined on the resolved scale.
A stepping stone towards understanding the variation of star formation seen in merging galaxies is to characterize the gas which fuels star formation on a kpc-scale. The tight correlation between SFR and molecular gas mass (|$\textrm {M}_{\textrm {H}_2}$|) which exists on a global scale (often called the Kennicutt–Schmidt relation for its flagship publications Schmidt 1959 and Kennicutt 1989) exists on a local scale as well, resulting in the resolved Kennicutt–Schmidt (rKS; Bigiel et al. 2008; Leroy et al. 2008; Schruba et al. 2011). A high star formation efficiency (SFE = SFR/|$\textrm {M}_{\textrm {H}_2}$|) can lead to regions notably above the rKS from a local boost in star formation (Leroy et al. 2013; Bolatto et al. 2017; Utomo et al. 2017). Offsets from the rKS are the primary driver of offsets in the resolved star-forming main sequence (rSFMS, the strong correlation between ΣSFR and Σ⋆; Sánchez et al. 2013; Cano-Díaz et al. 2016; González Delgado et al. 2016), demonstrating that although the SFR surface density (ΣSFR) is regulated by molecular gas mass surface density (|$\Sigma _{\textrm {H}_2}$|) as predicted by the rKS, more varied behaviour in star formation stems from changes in SFE (Ellison et al. 2020b).
However, there are other ways star formation can be augmented, such as a high gas surface density to fuel stellar growth (Bigiel et al. 2008;Schruba et al. 2011; Leroy et al. 2013). A surplus of molecular gas manifests as an offset from the correlation between |$\Sigma _{\textrm {H}_2}$| and the stellar mass surface density (Σ⋆), otherwise known as the resolved molecular gas main sequence (rMGMS; Wong et al. 2013; Lin et al. 2019; Ellison et al. 2021a). Environmental effects on the Σ⋆ profile can also boost star formation (Usero et al. 2015; Gallagher et al. 2018; Jiménez-Donaire et al. 2019). Examining how mergers deviate from the rKS and rMGMS will help discern what drives enhancements in star formation on a kpc-scale.
Several attempts have been made to pinpoint the relative importance of the total molecular gas fraction (|$f_{\textrm {H}_2}$|=|$\textrm {M}_{\textrm {H}_2}$|/M⋆) and the SFE to driving enhanced star formation in mergers. Early studies measuring total molecular gas mass with single dish telescopes found conflicting results concerning whether total molecular gas fraction or SFE drives enhanced star formation in mergers (Braine & Combes 1992; Casasola, Bettoni & Galletta 2004; Huchtmeier et al. 2008). More recent studies have leaned towards an enhanced gas fraction driving star formation in both interacting pair (Pan et al. 2018; Violino et al. 2018) and post-merger galaxies (Ellison, Catinella & Cortese 2018). SFEs for merging galaxies are mostly normal, except for very close pairs and equal-mass systems whose violent interactions lead to enhanced SFEs (Pan et al. 2018). What remains unclear is how these global properties drive kpc-scale variations in star formation.
Only recently have observations of resolved molecular gas properties been collected for large samples to complement large optical IFS surveys, allowing for the combined analysis of |$\Sigma _{\textrm {H}_2}$| and ΣSFR. The Extragalactic Database for Galaxy Evolution (EDGE) - CALIFA survey (Bolatto et al. 2017) targeted 126 CALIFA galaxies with the Combined Array for Millimeter-wave Astronomy (CARMA) to investigate depletion time gradients within galaxies (Utomo et al. 2017; Colombo et al. 2018) and the processes which regulate star formation on a kpc-scale (Barrera-Ballesteros et al. 2021). The ALMA-MaNGA QUEnching and STar formation (ALMaQUEST) survey (Lin et al. 2020) observed MaNGA galaxies with ALMA to not only confirm that the key scaling relations between SFR, molecular gas, and stellar mass that exist on a global scale stem from a kpc-scale relationship, but also that the rSFMS is likely the result of the two other relations (Lin et al. 2019; Ellison et al. 2021a; Baker et al. 2022). ALMaQUEST has also revealed that even though the absolute SFR in a galaxy is primarily driven by the amount of molecular gas, the scatter in the resolved SFE is mostly driven by local changes in SFE (Ellison et al. 2020a). Given that variations in star formation in the outskirts of mergers are by definition scatter from the rSFMS, such a result might imply that SFE may drive star formation for individual regions of galaxy, even if globally gas reservoir is the dominant driver. Further investigation of the interplay between star formation and molecular gas has been done on the scale of molecular clouds with the Physics at High Angular resolution in Nearby Galaxies (PHANGS)-ALMA survey (Leroy et al. 2021). With resolution on the order of ∼100 pc, PHANGS-ALMA found greater scatter in all three scaling relations compared to lower resolution studies, revealing significant variation in star formation and molecular gas content even within similar morphological environments (Pessa et al. 2021; Querejeta et al. 2021).
Although EDGE-CALIFA, the largest of surveys of this kind, does have a small number of mergers that may be responsible for changes in SFR and depletion times (Bolatto et al. 2017; Utomo et al. 2017; Chown et al. 2019), none of the surveys with both IFS and molecular gas data have a sufficient number of mergers to make a dedicated study of interaction induced physics. A handful of detailed case-studies of the resolved star formation efficiency of pre-merger galaxies have been completed, revealing significant diversity of depletion time on a resolved scale (Tomičić et al. 2018; Bemis & Wilson 2019). A study dedicated to a diverse sample of merging and post-merger galaxies is required to better understand the most extreme variations in star formation and gas properties.
In this work, we have observed a sample of 31 merging galaxies with a broad range of interaction progressions and SFR, with the specific goal of investigating how merger properties effect the mechanisms which drive star formation. Eleven of these mergers are taken from the main ALMaQUEST sample (Lin et al. 2020), plus we present observations for 20 additional galaxies with new CO(1–0) data obtained from ALMA. Together, we refer to this sample of 31 galaxies as the ALMaQUEST merger sample. In this paper, we aim to distinguish whether SFE or molecular gas fraction drives spatial changes in SFR. In Pan et al. (in preparation), we will further investigate how the resolved star formation and gas properties vary with merger configuration.
In Section 2, we describe our methods for selecting a sample of mergers, as well as the MaNGA and ALMA observations utilized in this investigation. Section 3 presents our main results, comparing individual resolved scaling relations for our merger sample, as well as comparing offsets from all three scaling relations. We summarize the impact of this work in Section 4. Throughout the work, we adopt a cosmology in which H0 = 70 km s–1 Mpc–1, ΩM = 0.3, and ΩΛ = 0.7.
2 DATA
2.1 Merger sample selection
Our sample of merging galaxies is collected from the MaNGA data release 15 (DR15), which was the most recent publicly available release at the time of our observations and for the duration of this project. We visually classify post-merger and interacting galaxies from the ∼4800 galaxies in DR15 using the Sloan Digital Sky Survey (SDSS) Sky Server gri-images (r-band half-light surface brightness limit of 23.0 mag arcsec−2; Strauss et al. 2002). Post-merger galaxies are distinguished by clear morphological disturbances indicating a recent interaction, such as tidal tails or shells, but with no obvious companion. Galaxies in an interacting pair are identified with similar indicators, with the addition of a clear visual connection to a second disturbed galaxy (such as tidal bridges).
Beyond the visually selected sample, we also identify a group of spectroscopic pairs, where a visible connection between a galaxy and a possible companion is unclear, but spatial and redshift information reveal the two galaxies may be interacting. Spectroscopic pairs are selected using the Patton et al. (2016) catalogue, which provides the closest companion for each galaxy in SDSS data release 7 (DR7), with a companion boundary at projected separation rp = 1 Mpc and a maximum difference in velocity between the two of Δv = 1000 km s–1. We assume any MaNGA galaxies with a projected separation less than 2 arcsec from the Patton et al. (2016) galaxy position are the same object. We limit our spectroscopic pairs to those with a mass ratio between 0.1 and 10 (meaning the smaller of the pair is more than 10 |${{\ \rm per\ cent}}$| the mass of the larger), and only include galaxies whose companion is within rp <100 kpc and Δv < 500 km s–1. For simplicity, the rest of this work will not distinguish visually and spectroscopically selected pairs; we will simply refer to ‘pairs’. The combination of the pair and post-merger galaxies yields a total sample of 903 galaxies in DR15 which we hence refer to as the parent merger sample, from which we can select a subsample for ALMA observations.
To select candidate mergers for ALMA observations, we first exclude all mergers with declination greater than 20°, leaving only those with positions that overlap with ALMA’s observational range. From the initial parent merger sample only 143 galaxies meet this criterion. We next select mergers for which our target CO line S/N can be achieved in less than 5 h, to ensure we can observe as many mergers as possible within a competitive proposal (see Section 2.2 for more details). What remains is a sample of six post-mergers and 14 pairs, which are observed as part of an ALMA Cycle 7 program (2019.1.00260.S, P.I.: Hsi-An Pan, details in Section 2.2). We also make use of 11 galaxies from the ALMaQUEST survey that show clear signs of an interaction within our classification scheme: 8 post-mergers and 3 pairs (Lin et al. 2020; Ellison et al. 2020a). The SDSS gri-images of three of the galaxies in the final ALMaQUEST merger sample are included in the left-hand panels of Fig. 1 (continued for all mergers in supplementary material online). The final sample of 14 post-merger and 17 pair galaxies is summarized in Table 1. Included in the table are key global properties from the MaNGA pipe3d Value Added Catalogue (VAC) including total stellar mass (M⋆), total SFR, and redshift (z). We also include the offset from the global star-forming main sequence ΔSFR, where ΔSFR = log SFRgalaxy − log SFRcontrol. SFRcontrol is the median SFR value of galaxies within 2σ of a fit to the star-forming main sequence (controls are also matched within 0.1 dex in M⋆ and 0.005 in z). Merger properties are listed as well, including rp, Δv, and mass ratio. Post-merger galaxies have empty rp, Δv, and mass ratio values since there is no companion with which to compare. Pair galaxies that were visually identified do not have measured Δv and mass ratio values, since there is no spectroscopic information from their companion.
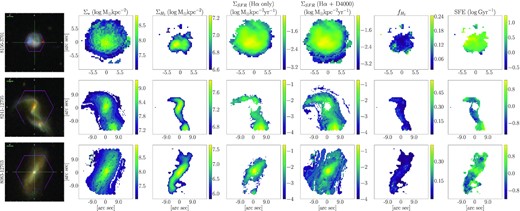
Data product maps for three of the galaxies in the ALMaQUEST merger sample (maps for the remaining 28 galaxies are available online), a post-merger (top), a visual pair (middle), and a spectroscopic pair with the companion out of frame (bottom). From left- to right-hand panel: the SDSS gri-image, inclination corrected stellar mass surface density (from pipe3d), inclination corrected molecular gas surface density (computed from CO luminosity), inclination corrected SFR surface density (computed from H α luminosity), inclination corrected SFR surface density (computed from H α luminosity and sSFR–D4000 relation), molecular gas fraction (|$\Sigma _{\textrm {H}_2}$|/Σ⋆), and SFE (ΣSFR/|$\Sigma _{\textrm {H}_2}$|). Note the significant increase in spaxel count when both H α and D4000 ΣSFR are used. The central gap still present in the combined ΣSFR map for 8241-12705 (second row, fifth column) is the result of D4000 exceeding 1.4 in those pixels. By including D4000–ΣSFR measurements, we optimize the overlap between |$\Sigma _{\textrm {H}_2}$| and ΣSFR for our analysis.
Summary of global properties of post-merger and pair galaxies observed with ALMA, with post-mergers first (no rp values), followed by pairs ordered by rp. Key global properties derived from the MaNGA VAC are included (M⋆, SFR, ΔSFR, z), as well as merger properties such as rp, Δv, and mass ratio (the mass of the galaxy divided by that of its companion). Post-mergers have empty columns for merger properties, which require information about a companion galaxy. Pair galaxies that were visually identified only have rp values, since spectrscopic information is not available for the companion. Also included are spaxel counts for each galaxy that meet our various star-forming and CO S/N cuts, along with the overlap between these regions. Galaxies with less than 10 spaxels of CO + SF(H α + D4000) overlap are excluded for plots of individual galaxies.
| Plate-ifu . | log M⋆ . | log SFR . | Δ SFR . | z . | rp . | Δ v . | Mass . | SF . | SF . | CO S/N > 3 . | CO + SF . | CO + SF . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | . | ratio . | (H α) . | (H α + D4000) . | . | (H α) . | (H α + D4000) . |
| . | (log M⊙) . | (log M⊙ yr–1) . | (dex) . | . | (kpc) . | (km s–1) . | . | # Spaxels . | # Spaxels . | # Spaxels . | # Overlap . | # Overlap . |
| 9195-3702 | 11.14 | 1.10 | 0.62 | 0.064 | – | – | – | 0 | 53 | 204 | 0 | 5 |
| 9194-3702 | 11.06 | 0.97 | 0.52 | 0.075 | – | – | – | 0 | 811 | 379 | 0 | 328 |
| 8083-9101 | 11.14 | 0.59 | 0.11 | 0.038 | – | – | – | 331 | 1163 | 322 | 60 | 186 |
| 8952-12701 | 10.73 | −0.38 | −0.23 | 0.029 | – | – | – | 21 | 37 | 354 | 18 | 28 |
| 8084-3702 | 10.23 | 0.43 | 0.60 | 0.022 | – | – | – | 240 | 1007 | 552 | 150 | 531 |
| 8156-3701 | 10.52 | 0.87 | 0.66 | 0.053 | – | – | – | 778 | 941 | 279 | 279 | 279 |
| 8081-9101 | 10.60 | 0.32 | 0.23 | 0.028 | – | – | – | 321 | 600 | 436 | 255 | 335 |
| 8615-3703 | 10.19 | 0.40 | 0.45 | 0.018 | – | – | – | 324 | 997 | 538 | 276 | 519 |
| 9512-3704 | 10.70 | 0.14 | −0.03 | 0.055 | – | – | – | 168 | 552 | 136 | 33 | 40 |
| 7977-12705 | 10.85 | 0.47 | 0.26 | 0.027 | – | – | – | 981 | 1472 | 538 | 197 | 201 |
| 8623-1902 | 10.17 | −1.00 | −0.84 | 0.025 | – | – | – | 4 | 175 | 257 | 2 | 87 |
| 8616-12702 | 10.76 | −0.24 | −0.40 | 0.031 | – | – | – | 469 | 1113 | 258 | 78 | 104 |
| 9195-3703 | 10.39 | 0.47 | 0.42 | 0.027 | – | – | – | 225 | 833 | 504 | 110 | 460 |
| 8615-1901 | 9.68 | −0.08 | 0.51 | 0.020 | – | – | – | 461 | 588 | 2 | 2 | 2 |
| 8153-12702 | 9.90 | −0.74 | −0.45 | 0.038 | 0.46 | – | – | 333 | 1119 | 0 | 0 | 0 |
| 7975-6104 | 11.01 | 0.61 | 0.17 | 0.079 | 7.04 | – | – | 209 | 588 | 391 | 209 | 320 |
| 8241-12705 | 10.40 | 0.00 | −0.05 | 0.027 | 8.23 | 80.0 | 3.14 | 847 | 1678 | 592 | 381 | 508 |
| 8082-9102 | 10.74 | 0.73 | 0.53 | 0.037 | 12.24 | – | – | 554 | 1197 | 668 | 422 | 591 |
| 7977-9102 | 10.93 | 0.83 | 0.41 | 0.063 | 13.78 | – | – | 524 | 1129 | 380 | 287 | 354 |
| 9195-9101 | 10.74 | 0.39 | 0.16 | 0.057 | 15.36 | – | – | 678 | 1797 | 722 | 455 | 675 |
| 8616-9101 | 11.10 | 0.75 | 0.28 | 0.092 | 19.89 | 276.0 | 4.19 | 112 | 1044 | 363 | 84 | 249 |
| 8078-12703 | 10.81 | 0.14 | −0.02 | 0.028 | 20.20 | 102.0 | – | 1208 | 2597 | 1128 | 444 | 796 |
| 7968-12705 | 11.30 | −1.41 | −1.37 | 0.086 | 20.45 | 13.0 | 0.80 | 0 | 93 | 8 | 0 | 0 |
| 8078-6104 | 10.41 | 0.23 | 0.16 | 0.044 | 26.15 | 109.0 | 0.42 | 197 | 1039 | 433 | 153 | 431 |
| 8085-12701 | 10.43 | 0.59 | 0.61 | 0.030 | 29.51 | – | – | 2293 | 2601 | 458 | 456 | 458 |
| 8085-6101 | 11.07 | −0.73 | −1.09 | 0.052 | 31.48 | – | – | 0 | 0 | 2 | 0 | 0 |
| 8083-12703 | 10.46 | 0.32 | 0.24 | 0.025 | 45.24 | 60.6 | – | 822 | 2201 | 1264 | 641 | 1171 |
| 8082-12704 | 11.42 | 0.77 | 0.05 | 0.132 | 51.28 | – | – | 3 | 1617 | 451 | 3 | 244 |
| 8085-3704 | 10.72 | 0.66 | 0.43 | 0.037 | 58.73 | 37.0 | 0.89 | 319 | 727 | 608 | 299 | 552 |
| 8450-6102 | 10.43 | 0.64 | 0.54 | 0.042 | 75.35 | 102.0 | 1.81 | 1162 | 1550 | 536 | 503 | 536 |
| 8728-3701 | 10.64 | −0.37 | −0.49 | 0.028 | 89.75 | 113.0 | 1.96 | 0 | 31 | 156 | 0 | 0 |
| Plate-ifu . | log M⋆ . | log SFR . | Δ SFR . | z . | rp . | Δ v . | Mass . | SF . | SF . | CO S/N > 3 . | CO + SF . | CO + SF . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | . | ratio . | (H α) . | (H α + D4000) . | . | (H α) . | (H α + D4000) . |
| . | (log M⊙) . | (log M⊙ yr–1) . | (dex) . | . | (kpc) . | (km s–1) . | . | # Spaxels . | # Spaxels . | # Spaxels . | # Overlap . | # Overlap . |
| 9195-3702 | 11.14 | 1.10 | 0.62 | 0.064 | – | – | – | 0 | 53 | 204 | 0 | 5 |
| 9194-3702 | 11.06 | 0.97 | 0.52 | 0.075 | – | – | – | 0 | 811 | 379 | 0 | 328 |
| 8083-9101 | 11.14 | 0.59 | 0.11 | 0.038 | – | – | – | 331 | 1163 | 322 | 60 | 186 |
| 8952-12701 | 10.73 | −0.38 | −0.23 | 0.029 | – | – | – | 21 | 37 | 354 | 18 | 28 |
| 8084-3702 | 10.23 | 0.43 | 0.60 | 0.022 | – | – | – | 240 | 1007 | 552 | 150 | 531 |
| 8156-3701 | 10.52 | 0.87 | 0.66 | 0.053 | – | – | – | 778 | 941 | 279 | 279 | 279 |
| 8081-9101 | 10.60 | 0.32 | 0.23 | 0.028 | – | – | – | 321 | 600 | 436 | 255 | 335 |
| 8615-3703 | 10.19 | 0.40 | 0.45 | 0.018 | – | – | – | 324 | 997 | 538 | 276 | 519 |
| 9512-3704 | 10.70 | 0.14 | −0.03 | 0.055 | – | – | – | 168 | 552 | 136 | 33 | 40 |
| 7977-12705 | 10.85 | 0.47 | 0.26 | 0.027 | – | – | – | 981 | 1472 | 538 | 197 | 201 |
| 8623-1902 | 10.17 | −1.00 | −0.84 | 0.025 | – | – | – | 4 | 175 | 257 | 2 | 87 |
| 8616-12702 | 10.76 | −0.24 | −0.40 | 0.031 | – | – | – | 469 | 1113 | 258 | 78 | 104 |
| 9195-3703 | 10.39 | 0.47 | 0.42 | 0.027 | – | – | – | 225 | 833 | 504 | 110 | 460 |
| 8615-1901 | 9.68 | −0.08 | 0.51 | 0.020 | – | – | – | 461 | 588 | 2 | 2 | 2 |
| 8153-12702 | 9.90 | −0.74 | −0.45 | 0.038 | 0.46 | – | – | 333 | 1119 | 0 | 0 | 0 |
| 7975-6104 | 11.01 | 0.61 | 0.17 | 0.079 | 7.04 | – | – | 209 | 588 | 391 | 209 | 320 |
| 8241-12705 | 10.40 | 0.00 | −0.05 | 0.027 | 8.23 | 80.0 | 3.14 | 847 | 1678 | 592 | 381 | 508 |
| 8082-9102 | 10.74 | 0.73 | 0.53 | 0.037 | 12.24 | – | – | 554 | 1197 | 668 | 422 | 591 |
| 7977-9102 | 10.93 | 0.83 | 0.41 | 0.063 | 13.78 | – | – | 524 | 1129 | 380 | 287 | 354 |
| 9195-9101 | 10.74 | 0.39 | 0.16 | 0.057 | 15.36 | – | – | 678 | 1797 | 722 | 455 | 675 |
| 8616-9101 | 11.10 | 0.75 | 0.28 | 0.092 | 19.89 | 276.0 | 4.19 | 112 | 1044 | 363 | 84 | 249 |
| 8078-12703 | 10.81 | 0.14 | −0.02 | 0.028 | 20.20 | 102.0 | – | 1208 | 2597 | 1128 | 444 | 796 |
| 7968-12705 | 11.30 | −1.41 | −1.37 | 0.086 | 20.45 | 13.0 | 0.80 | 0 | 93 | 8 | 0 | 0 |
| 8078-6104 | 10.41 | 0.23 | 0.16 | 0.044 | 26.15 | 109.0 | 0.42 | 197 | 1039 | 433 | 153 | 431 |
| 8085-12701 | 10.43 | 0.59 | 0.61 | 0.030 | 29.51 | – | – | 2293 | 2601 | 458 | 456 | 458 |
| 8085-6101 | 11.07 | −0.73 | −1.09 | 0.052 | 31.48 | – | – | 0 | 0 | 2 | 0 | 0 |
| 8083-12703 | 10.46 | 0.32 | 0.24 | 0.025 | 45.24 | 60.6 | – | 822 | 2201 | 1264 | 641 | 1171 |
| 8082-12704 | 11.42 | 0.77 | 0.05 | 0.132 | 51.28 | – | – | 3 | 1617 | 451 | 3 | 244 |
| 8085-3704 | 10.72 | 0.66 | 0.43 | 0.037 | 58.73 | 37.0 | 0.89 | 319 | 727 | 608 | 299 | 552 |
| 8450-6102 | 10.43 | 0.64 | 0.54 | 0.042 | 75.35 | 102.0 | 1.81 | 1162 | 1550 | 536 | 503 | 536 |
| 8728-3701 | 10.64 | −0.37 | −0.49 | 0.028 | 89.75 | 113.0 | 1.96 | 0 | 31 | 156 | 0 | 0 |
Summary of global properties of post-merger and pair galaxies observed with ALMA, with post-mergers first (no rp values), followed by pairs ordered by rp. Key global properties derived from the MaNGA VAC are included (M⋆, SFR, ΔSFR, z), as well as merger properties such as rp, Δv, and mass ratio (the mass of the galaxy divided by that of its companion). Post-mergers have empty columns for merger properties, which require information about a companion galaxy. Pair galaxies that were visually identified only have rp values, since spectrscopic information is not available for the companion. Also included are spaxel counts for each galaxy that meet our various star-forming and CO S/N cuts, along with the overlap between these regions. Galaxies with less than 10 spaxels of CO + SF(H α + D4000) overlap are excluded for plots of individual galaxies.
| Plate-ifu . | log M⋆ . | log SFR . | Δ SFR . | z . | rp . | Δ v . | Mass . | SF . | SF . | CO S/N > 3 . | CO + SF . | CO + SF . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | . | ratio . | (H α) . | (H α + D4000) . | . | (H α) . | (H α + D4000) . |
| . | (log M⊙) . | (log M⊙ yr–1) . | (dex) . | . | (kpc) . | (km s–1) . | . | # Spaxels . | # Spaxels . | # Spaxels . | # Overlap . | # Overlap . |
| 9195-3702 | 11.14 | 1.10 | 0.62 | 0.064 | – | – | – | 0 | 53 | 204 | 0 | 5 |
| 9194-3702 | 11.06 | 0.97 | 0.52 | 0.075 | – | – | – | 0 | 811 | 379 | 0 | 328 |
| 8083-9101 | 11.14 | 0.59 | 0.11 | 0.038 | – | – | – | 331 | 1163 | 322 | 60 | 186 |
| 8952-12701 | 10.73 | −0.38 | −0.23 | 0.029 | – | – | – | 21 | 37 | 354 | 18 | 28 |
| 8084-3702 | 10.23 | 0.43 | 0.60 | 0.022 | – | – | – | 240 | 1007 | 552 | 150 | 531 |
| 8156-3701 | 10.52 | 0.87 | 0.66 | 0.053 | – | – | – | 778 | 941 | 279 | 279 | 279 |
| 8081-9101 | 10.60 | 0.32 | 0.23 | 0.028 | – | – | – | 321 | 600 | 436 | 255 | 335 |
| 8615-3703 | 10.19 | 0.40 | 0.45 | 0.018 | – | – | – | 324 | 997 | 538 | 276 | 519 |
| 9512-3704 | 10.70 | 0.14 | −0.03 | 0.055 | – | – | – | 168 | 552 | 136 | 33 | 40 |
| 7977-12705 | 10.85 | 0.47 | 0.26 | 0.027 | – | – | – | 981 | 1472 | 538 | 197 | 201 |
| 8623-1902 | 10.17 | −1.00 | −0.84 | 0.025 | – | – | – | 4 | 175 | 257 | 2 | 87 |
| 8616-12702 | 10.76 | −0.24 | −0.40 | 0.031 | – | – | – | 469 | 1113 | 258 | 78 | 104 |
| 9195-3703 | 10.39 | 0.47 | 0.42 | 0.027 | – | – | – | 225 | 833 | 504 | 110 | 460 |
| 8615-1901 | 9.68 | −0.08 | 0.51 | 0.020 | – | – | – | 461 | 588 | 2 | 2 | 2 |
| 8153-12702 | 9.90 | −0.74 | −0.45 | 0.038 | 0.46 | – | – | 333 | 1119 | 0 | 0 | 0 |
| 7975-6104 | 11.01 | 0.61 | 0.17 | 0.079 | 7.04 | – | – | 209 | 588 | 391 | 209 | 320 |
| 8241-12705 | 10.40 | 0.00 | −0.05 | 0.027 | 8.23 | 80.0 | 3.14 | 847 | 1678 | 592 | 381 | 508 |
| 8082-9102 | 10.74 | 0.73 | 0.53 | 0.037 | 12.24 | – | – | 554 | 1197 | 668 | 422 | 591 |
| 7977-9102 | 10.93 | 0.83 | 0.41 | 0.063 | 13.78 | – | – | 524 | 1129 | 380 | 287 | 354 |
| 9195-9101 | 10.74 | 0.39 | 0.16 | 0.057 | 15.36 | – | – | 678 | 1797 | 722 | 455 | 675 |
| 8616-9101 | 11.10 | 0.75 | 0.28 | 0.092 | 19.89 | 276.0 | 4.19 | 112 | 1044 | 363 | 84 | 249 |
| 8078-12703 | 10.81 | 0.14 | −0.02 | 0.028 | 20.20 | 102.0 | – | 1208 | 2597 | 1128 | 444 | 796 |
| 7968-12705 | 11.30 | −1.41 | −1.37 | 0.086 | 20.45 | 13.0 | 0.80 | 0 | 93 | 8 | 0 | 0 |
| 8078-6104 | 10.41 | 0.23 | 0.16 | 0.044 | 26.15 | 109.0 | 0.42 | 197 | 1039 | 433 | 153 | 431 |
| 8085-12701 | 10.43 | 0.59 | 0.61 | 0.030 | 29.51 | – | – | 2293 | 2601 | 458 | 456 | 458 |
| 8085-6101 | 11.07 | −0.73 | −1.09 | 0.052 | 31.48 | – | – | 0 | 0 | 2 | 0 | 0 |
| 8083-12703 | 10.46 | 0.32 | 0.24 | 0.025 | 45.24 | 60.6 | – | 822 | 2201 | 1264 | 641 | 1171 |
| 8082-12704 | 11.42 | 0.77 | 0.05 | 0.132 | 51.28 | – | – | 3 | 1617 | 451 | 3 | 244 |
| 8085-3704 | 10.72 | 0.66 | 0.43 | 0.037 | 58.73 | 37.0 | 0.89 | 319 | 727 | 608 | 299 | 552 |
| 8450-6102 | 10.43 | 0.64 | 0.54 | 0.042 | 75.35 | 102.0 | 1.81 | 1162 | 1550 | 536 | 503 | 536 |
| 8728-3701 | 10.64 | −0.37 | −0.49 | 0.028 | 89.75 | 113.0 | 1.96 | 0 | 31 | 156 | 0 | 0 |
| Plate-ifu . | log M⋆ . | log SFR . | Δ SFR . | z . | rp . | Δ v . | Mass . | SF . | SF . | CO S/N > 3 . | CO + SF . | CO + SF . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | . | ratio . | (H α) . | (H α + D4000) . | . | (H α) . | (H α + D4000) . |
| . | (log M⊙) . | (log M⊙ yr–1) . | (dex) . | . | (kpc) . | (km s–1) . | . | # Spaxels . | # Spaxels . | # Spaxels . | # Overlap . | # Overlap . |
| 9195-3702 | 11.14 | 1.10 | 0.62 | 0.064 | – | – | – | 0 | 53 | 204 | 0 | 5 |
| 9194-3702 | 11.06 | 0.97 | 0.52 | 0.075 | – | – | – | 0 | 811 | 379 | 0 | 328 |
| 8083-9101 | 11.14 | 0.59 | 0.11 | 0.038 | – | – | – | 331 | 1163 | 322 | 60 | 186 |
| 8952-12701 | 10.73 | −0.38 | −0.23 | 0.029 | – | – | – | 21 | 37 | 354 | 18 | 28 |
| 8084-3702 | 10.23 | 0.43 | 0.60 | 0.022 | – | – | – | 240 | 1007 | 552 | 150 | 531 |
| 8156-3701 | 10.52 | 0.87 | 0.66 | 0.053 | – | – | – | 778 | 941 | 279 | 279 | 279 |
| 8081-9101 | 10.60 | 0.32 | 0.23 | 0.028 | – | – | – | 321 | 600 | 436 | 255 | 335 |
| 8615-3703 | 10.19 | 0.40 | 0.45 | 0.018 | – | – | – | 324 | 997 | 538 | 276 | 519 |
| 9512-3704 | 10.70 | 0.14 | −0.03 | 0.055 | – | – | – | 168 | 552 | 136 | 33 | 40 |
| 7977-12705 | 10.85 | 0.47 | 0.26 | 0.027 | – | – | – | 981 | 1472 | 538 | 197 | 201 |
| 8623-1902 | 10.17 | −1.00 | −0.84 | 0.025 | – | – | – | 4 | 175 | 257 | 2 | 87 |
| 8616-12702 | 10.76 | −0.24 | −0.40 | 0.031 | – | – | – | 469 | 1113 | 258 | 78 | 104 |
| 9195-3703 | 10.39 | 0.47 | 0.42 | 0.027 | – | – | – | 225 | 833 | 504 | 110 | 460 |
| 8615-1901 | 9.68 | −0.08 | 0.51 | 0.020 | – | – | – | 461 | 588 | 2 | 2 | 2 |
| 8153-12702 | 9.90 | −0.74 | −0.45 | 0.038 | 0.46 | – | – | 333 | 1119 | 0 | 0 | 0 |
| 7975-6104 | 11.01 | 0.61 | 0.17 | 0.079 | 7.04 | – | – | 209 | 588 | 391 | 209 | 320 |
| 8241-12705 | 10.40 | 0.00 | −0.05 | 0.027 | 8.23 | 80.0 | 3.14 | 847 | 1678 | 592 | 381 | 508 |
| 8082-9102 | 10.74 | 0.73 | 0.53 | 0.037 | 12.24 | – | – | 554 | 1197 | 668 | 422 | 591 |
| 7977-9102 | 10.93 | 0.83 | 0.41 | 0.063 | 13.78 | – | – | 524 | 1129 | 380 | 287 | 354 |
| 9195-9101 | 10.74 | 0.39 | 0.16 | 0.057 | 15.36 | – | – | 678 | 1797 | 722 | 455 | 675 |
| 8616-9101 | 11.10 | 0.75 | 0.28 | 0.092 | 19.89 | 276.0 | 4.19 | 112 | 1044 | 363 | 84 | 249 |
| 8078-12703 | 10.81 | 0.14 | −0.02 | 0.028 | 20.20 | 102.0 | – | 1208 | 2597 | 1128 | 444 | 796 |
| 7968-12705 | 11.30 | −1.41 | −1.37 | 0.086 | 20.45 | 13.0 | 0.80 | 0 | 93 | 8 | 0 | 0 |
| 8078-6104 | 10.41 | 0.23 | 0.16 | 0.044 | 26.15 | 109.0 | 0.42 | 197 | 1039 | 433 | 153 | 431 |
| 8085-12701 | 10.43 | 0.59 | 0.61 | 0.030 | 29.51 | – | – | 2293 | 2601 | 458 | 456 | 458 |
| 8085-6101 | 11.07 | −0.73 | −1.09 | 0.052 | 31.48 | – | – | 0 | 0 | 2 | 0 | 0 |
| 8083-12703 | 10.46 | 0.32 | 0.24 | 0.025 | 45.24 | 60.6 | – | 822 | 2201 | 1264 | 641 | 1171 |
| 8082-12704 | 11.42 | 0.77 | 0.05 | 0.132 | 51.28 | – | – | 3 | 1617 | 451 | 3 | 244 |
| 8085-3704 | 10.72 | 0.66 | 0.43 | 0.037 | 58.73 | 37.0 | 0.89 | 319 | 727 | 608 | 299 | 552 |
| 8450-6102 | 10.43 | 0.64 | 0.54 | 0.042 | 75.35 | 102.0 | 1.81 | 1162 | 1550 | 536 | 503 | 536 |
| 8728-3701 | 10.64 | −0.37 | −0.49 | 0.028 | 89.75 | 113.0 | 1.96 | 0 | 31 | 156 | 0 | 0 |
The merger sample covers a broad range of M⋆ and SFR. Fig. 2 compares these properties for our post-merger (orange circles) and pair (triangles) galaxies with respect to the rest of MaNGA, shown as grey hexbins. Pairs are colour-coded by the projected separation from their closest companion. Our sample is representative of a typical merger sample, containing galaxies with both greatly elevated and comparatively low SFRs. The inset histogram of Fig. 2 shows the distribution of the offset from the star-forming main sequence ΔSFR of our post-merger (orange) and pair (blue) galaxies with respect to the rest of MaNGA (grey). Although the pair and post-merger samples have on average larger ΔSFR values than non-interacting galaxies, we still cover a broad range of ΔSFR values to reflect the overall variety of behaviours seen in larger galaxy merger studies and to probe any corresponding diversity in the molecular gas properties of those mergers. We note that there may be some selection bias in the sample, given some post-mergers come from the ALMaQUEST starburst sample of Ellison et al. (2020a), and the rest still need to have enough gas for detectable CO as described in the following section.
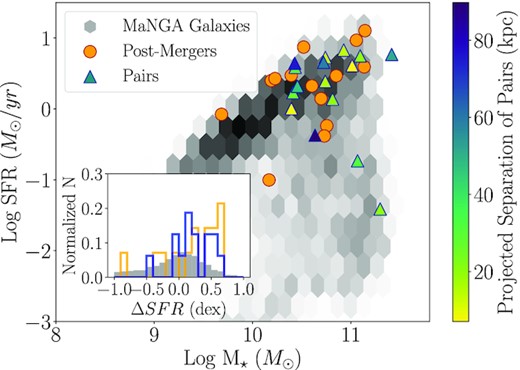
Position of our post-merger (orange circles) and pair (triangles) galaxies on the global star-forming main sequence defined by the rest of the MaNGA survey (grey hexbin). Pair galaxies are colour-coded by the projected separation from their closest companion (in kpc). Galaxies that were excluded due to a lack of viable CO spaxels are excluded from this diagram (see Table 1 and Section 2.2 for details). An inset histogram shows the distribution in ΔSFR for post-mergers (orange) and pair (blue) galaxies with respect to MaNGA (grey). Although our mergers probe more highly star-forming galaxies than a random population, our sample still covers a broad range of ΔSFR values.
2.2 ALMA observations
Observations of CO J = 1 → 0 (CO hereafter), rest frame 115 GHz, were completed for 6 post-merger and 14 pair galaxies as part of Cycle 7 ALMA program 2019.1.00260.S (P.I.: Hsi-An Pan). The remaining 11 mergers were already available from the original ALMaQUEST sample (Lin et al. 2020). Cycle 7 observations were designed to replicate the methodology used in the original ALMaQUEST survey, the details of which can be found in the survey paper by Lin et al. (2020). We provide a brief summary of those techniques below.
Observations were carried out using the Band 3 receiver, taken in the C43-2 configuration to achieve a synthesized beam full width half-maximum (FWHM) of 2.5 arcsec in order to match the effective resolution of the MaNGA survey (Law et al. 2015). The ALMA field of view in our chosen configuration is ∼50 arcsec which is sufficient to cover the MaNGA footprint for all of our galaxies. The spectral set up includes one high resolution spectral window targeting the CO emission (∼10 km s–1), and three low-resolution spectral windows around the target line to detect the continuum (∼90 km s–1). To reach a CO S/N greater than 3 for 50 |${{\ \rm per\ cent}}$| of spaxels with H α S/N > 3, the on-target integration time varied between 0.1 and 3.3 h. The same methodology is used for the main ALMaQUEST sample, ensuring consistent data quality between ALMaQUEST data and that acquired in Cycle 7 (Lin et al. 2017, 2020).
Data were calibrated using the ALMA data reduction software casa (Common Astronomy Software Applications; McMullin et al. 2007) using version 5.4 for all but three galaxies (which were observed in earlier cycles and thus used casa version 4.5), along with the standard ALMA reduction pipeline. In ALMA’s Band 3, the systematic flux uncertainty inherent with calibration is roughly 5–10 |${{\ \rm per\ cent}}$| (Diaz Trigo et al. 2019). Continua were subtracted in the visibility domain for a handful of galaxies both in the original ALMaQUEST and the Cycle 7 galaxies. Once the continuum was subtracted, the task CLEAN was used to clean data down to 1σ and produce spectral line data cubes with a Briggs weighting (robust parameter = 0.5), resulting in a native effective beam size ranging from 1.6−2.8 arcsec depending on the target. The data were then re-imaged with a user-specified spaxel size (0.5 arcsec) and a restoring beamsize (2.5 × 2.5 arcsec2) to match the MaNGA image grid (prior) and spatial resolution (latter). The final cubes have channel widths of 11 km s–1 and σrms ∼0.2–2 mJy beam–1. We applied the casa task IMMOMENTS to these datacubes to determine moment 0 (integrated intensity) maps. IMMOMENTS can also generate moment 1 (intensity-weighted velocity) and moment 2 (intensity-weighted velocity dispersion) maps, but those are not relevant to the analysis of this work and are saved for future projects. Moment 0 maps are constructed by integrating the CO emission from a set velocity range without any clipping in signal. Table 1 lists the number of spaxels in each galaxy where the CO line emission from the Moment 0 map has S/N > 3. Four of the merger galaxies observed as part of Cycle 7 (8615-1901, 8153-12702, 7968-12705, 8085-6101, all four early-type galaxies) have less than 10 spaxels with CO S/N > 3, and are, thus, excluded from any further analysis that looks at individual galaxies (rather than spaxels).
The CO luminosity per spaxel determined from the moment 0 map is converted to molecular gas surface density |$\Sigma _{\textrm {H}_2}$| (M⊙ kpc–2) using a constant conversion factor of αCO = 4.35 [M⊙(K km s−1 pc2)−1] (Bolatto, Wolfire & Leroy 2013). All |$\Sigma _{\textrm {H}_2}$| values are then inclination corrected using the b/a axial ratios from the NASA Sloan Atlas (NSA) catalogue, themselves determined from single Sérsic fits. Three example |$\Sigma _{\textrm {H}_2}$| maps are provided in Fig. 1, with the rest of the |$\Sigma _{\textrm {H}_2}$| maps from the sample available with supplementary material online. There has been extensive research into the viability of a constant conversion factor, and many suggest using a metallicity dependent (Accurso et al. 2017; Sun et al. 2020) or metallicity and line intensity dependent (Narayanan et al. 2012) conversion instead. The requirements needed to determine accurate metallicity measurements would limit our spaxel count significantly, given the sparse overlap between high S/N star-forming spaxels and CO measurements (see Table 1), as we will discuss further in Section 2.3.1. To minimize the loss of spaxels, we choose to use a constant conversion factor. In Appendix A, we characterize the difference in |$\Sigma _{\textrm {H}_2}$| measurements when a metallicity dependent αCO is used (for spaxels where that is possible), and confirm that key results from this work cannot result from inaccuracies of conversion factor.
2.3 MaNGA data products
The work presented here primarily uses MaNGA data products from the pipe3d spectral fitting pipeline, described in detail in Sánchez et al. (2016a,b). Along with global values provided by the pipe3d VAC mentioned previously, we also make extensive use of the pipe3d stellar mass surface density (Σ⋆) and emission line fluxes. We correct all emission line fluxes for dust using a Milky Way dust extinction curve (Cardelli, Clayton & Mathis 1989), assuming an intrinsic H α/H β ratio of 2.85. SFR surface densities (ΣSFR) are determined from the dust corrected H α luminosity using the Kennicutt, Tamblyn & Congdon (1994) relation and assuming a Salpeter intitial mass function (Salpeter 1955). Both Σ⋆ and ΣSFR are inclination corrected using the b/a axial ratios (derived from single Sérsic fits) provided in the NSA catalogue. The same b/a ratio is used to compute an inclination corrected galactocentric radius from the V-band centre of the MaNGA map. We also use the 4000 Å break strength (D4000) provided by pipe3d, as it serves a crucial role in expanding our SFR measurements described in the next section.
2.3.1 Star formation rates - D4000 versus H α
The work presented here requires that both SFRs and molecular gas surface densities are measured in a given spaxel. Ideally, we would use SFRs determined from H α and only consider the ΣSFR values of star-forming spaxels defined by the Kauffmann et al. (2003) designation on a Baldwin, Phillips & Terlevich diagram (BPT; Baldwin, Phillips & Terlevich 1981). Along with a Kauffmann et al. (2003) star-forming cut, we also impose a S/N > 3 cut for the flux of each diagnostic emission line, as well as requiring an H α equivalent width (EW) > 6Å limit to ensure H α flux stems from a young stellar population. Of the 13 046 spaxels with CO detections S/N > 3, only 44.5 per cent pass all of these star-forming criteria. Table 1 provides for each galaxy the total count of spaxels which pass the star-forming criteria cut for H α, which have CO S/N > 3, and which pass both criteria.
To maximize the number of spaxels with both CO and SFR measurements, we elect to approximate ΣSFR for spaxels that are not star-forming (based on our BPT and EW criteria) using the relationship between sSFR and D4000 found for both global (Brinchmann et al. 2004) and local (Spindler et al. 2018; Wang et al. 2019; Bluck et al. 2020) scales. We adopt an empirical approach similar to that in Bluck et al. (2020), who tested the validity of this approximation in the MaNGA pipe3d data products. For bins of D4000, we compute a median sSFR value based on all star-forming spaxels (using our previous criteria). For any spaxel that does not meet our star-forming criteria, either due to low S/N or AGN contamination based on the BPT cut, we assign the median sSFR from the closest D4000 bin, and convert that to ΣSFR by multiplying sSFR and Σ⋆. Fig. 3 displays the complete sSFR-D4000 distribution for star-forming spaxels in MaNGA along with a red line showing the median sSFR value, up to D4000 = 1.45, used to approximate ΣSFR when a spaxel is not star forming.
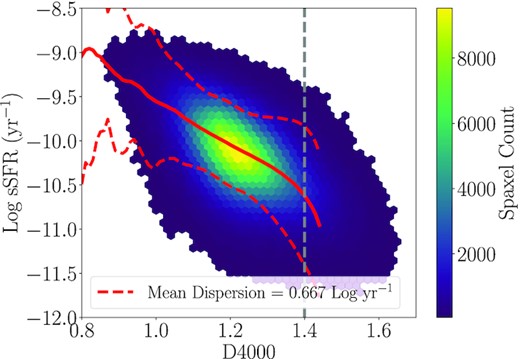
The sSFR–D4000 distribution for all star-forming spaxels in MaNGA (shown as a density hexbin). The median sSFR value in each D4000 bin is shown as red line out to D4000 = 1.45; this value is used to approximate ΣSFR based on D4000 for spaxels which do not meet our star-forming criteria. The standard deviation of sSFR within each bin is shown as a red dashed line. The median sSFR value steeply changes at high D4000, leading to very different sSFR values in relatively close D4000 bins. We therefore only use the D4000–sSFR calibration when D4000 < 1.4 (vertical dashed line).
Spaxels with D4000 > 1.45 are generally quenched and therefore the sSFR–D4000 relation is no longer viable (Bluck et al. 2020). As can be seen from Fig. 3, the D4000–sSFR relation turns steeply downwards at D4000 > 1.4. We therefore only estimate ΣSFR from D4000 when D4000 < 1.4, which represents a slightly stricter cut than that used in Bluck et al. (2020). Table 1 provides the increased spaxel count when both H α- and D4000–ΣSFR values are employed. Of the 13 046 spaxels with CO S/N > 3, now 78.8 per cent of spaxels have measurable ΣSFR, almost doubled from the 44.5 per cent of our previous criteria. 9195-3702 and 8450-6102, despite having a considerable number of spaxels with CO S/N > 3, still have less than 10 spaxels of overlap between good CO and ΣSFR measurements. These two galaxies are, thus, excluded from individual galaxy analysis later in this work, along with the other four galaxies previously mentioned. Thus, we have 25 galaxies which can be studied on an individual basis, and we limit our studies to these 25 for the rest of the work. Multiple tests are performed to check how using D4000 approximated ΣSFR might impact our results, details of which are included in Appendix B. Adopting this method of measuring ΣSFR sacrifices accuracy for completeness in our analysis; to assess how this will impact our results, we repeat key parts of our analysis using only H α−ΣSFR (for galaxies where that is possible). Unless specified otherwise, for the rest of this work ΣSFR and any derived products, use the combined H α + D4000 ΣSFR values for both the merger and isolated sample.
Fig. 1 summarizes the various data products from MaNGA and ALMA used within this work for three galaxies from our sample: a post-merger galaxy (top), an interacting pair (middle), and a spectroscopic pair (bottom). We display maps of H α–ΣSFR, as well as our combined H α + D4000–ΣSFR map. The middle galaxy is a clear case where we are able to recover a significant number of spaxels using the combined ΣSFR values. In particular, a significant fraction of spaxels in the outskirts of the galaxy are recovered to maximize the spatial coverage of our analysis. Though the middle galaxy demonstrates how the combined H α + D4000–ΣSFR method recovers lower ΣSFR values, the method also recovers AGN dominated spaxels. Thus, the main limitation of our analysis becomes the CO signal-to-noise ratio, and the overlap between CO and ΣSFR.
2.3.2 Spaxel offsets from resolved relations
Following Ellison et al. (2020a), we compute offsets from the rKS, rSFMS, and rMGMS to quantify how an individual spaxel may deviate from the average spaxel behaviour. All offsets are computed as the log difference between a spaxel value and the median value of a set of control spaxels that defines the average behaviour, i.e. ΔX = log X − <log Xcontrol > median. For example, we define an offset from the SFMS as ΔΣSFR, with positive ΔΣSFR values corresponding to enhanced star formation compared to the control sample. The sample of control spaxels is collected from all DR15 MaNGA spaxels from non-merging galaxies (as classified in Section 2.1) with b/a > 0.34 (excluding galaxies with inclination greater than 70°) and which are star-forming based on our cuts for the H α–ΣSFR measurements described in Section 2.3.1. All MaNGA ΣSFR values are included, not just ALMaQUEST, such that the requirement for CO detections in ALMaQUEST spaxels does not bias our control spaxel set to higher ΣSFR. Note that we exclude D4000–ΣSFR values from the control sample, given we want to know the difference from the star-forming population that defines the rSFMS. The majority of spaxels on the rSFMS for which we can measure accurate D4000–ΣSFR tend to not meet our star-forming criteria due to low S/N in BPT diagnostic emission lines, rather than being classified as AGN or composite spaxels. Including D4000–ΣSFR in the control would lead to slightly lower ΔΣSFR values as a result of the contribution from low S/N spaxels. We have tested whether the inclusion of D4000–ΣSFR in our control would alter any major conclusions of this work, and find our results remain unchanged. From the set of star-forming controls, we select a subset that is matched within 0.1-dex Σ⋆, 0.1 R/Re (where R is the inclination corrected galactocentric radius, and the effective radius Re is the r-band half-light radius from the NSA catalogue), and 0.1 dex M⋆ of the merger spaxel. The median of this control set defines our ‘regular’ star-forming behaviour. Similar offsets can be determined for the other scaling relations.
An offset from the resolved KS is referred to as ΔSFE; a value above the KS would have a larger SFR given the molecular gas in a spaxel, i.e. an enhancement in the efficiency at which gas is converted to stars. Rather than rely on S/N and BPT cuts to define star-forming spaxels, as was achieved with ΔΣSFR, we instead make use of the ΔΣSFR value to construct the star-forming rKS. The control sample is also limited to galaxies in ALMaQUEST, rather than all of DR15, given |$\Sigma _{\textrm {H}_2}$| is required to compute ΔSFE. Thus, the control sample is selected from non-interacting ALMaQUEST galaxies with b/a > 0.34, with the additional cut of –0.5 < ΔΣSFR< 0.5 to select star-forming spaxels. A subset of the control is found by matching to the merger spaxel within 0.1 dex |$\Sigma _{\textrm {H}_2}$|, 0.1 R/Re, and 0.1 dex M⋆.
Using the same control spaxel sample as for ΔSFE, we determine offsets from the rMGMS, referred to as |$\Delta f_{H_2}$|. The control spaxels are again taken from non-interacting ALMaQUEST galaxies and matched within 0.1 dex |$\Sigma _{\textrm {H}_2}$|, 0.1 R/Re, and 0.1 dex M⋆. Unlike the other two offset metrics, |$\Delta f_{H_2}$| can be computed for any spaxels with CO S/N > 3. Since there is no dependence on whether ΣSFR is measurable, or if measured ΣSFR values overlap with good CO measurements, maps of |$\Delta f_{H_2}$| tend to be more complete than the other two offsets. Maps of offset parameters for the merger sample are available online.
One key difference between Ellison et al. (2020a), who first introduced these offset methods, and the methods used here is we do not match control spaxels by metallicity. Limiting our analysis to spaxels with valid metallicity measurements drastically diminishes our total spaxel count, as described in detail in Section 2.2, limiting the spatial coverage of some galaxies and removing three from viable examination entirely. None the less, we have repeated the analysis described in this section with a metallicity control (similar to that used in Ellison et al. 2020a), and find little change in our key results for those galaxies on which this check can be performed [i.e. those with large CO + SFR(H α) overlap].
3 ANALYSIS
3.1 Resolved scaling relations
The stellar mass surface density (Σ⋆), SFR surface density (ΣSFR), and molecular gas surface density (|$\Sigma _{\textrm {H}_2}$|) are all interconnected in three well established resolved relations: the rKS relation and the rMGMS, which together drive the rSFMS (Lin et al. 2019; Ellison et al. 2021a; Baker et al. 2022). We investigate these three scaling relations both for merger populations and for individual galaxies in our merger sample.
Fig. 4 compares the resolved scaling relations for post-merger (orange) and pair (blue) galaxies with respect to the relatively isolated galaxies in the rest of ALMaQUEST (grey). Histograms of the ΣSFR, |$\Sigma _{\textrm {H}_2}$|, and Σ⋆ are provided for context as well. Note that the grey histogram does not represent the control spaxel population used to compute various offset parameters as described in Section 2.3.2, rather all spaxels where ΣSFR can be measured for ALMaQUEST. Given the selection of the original ALMaQUEST sample, including a sample of starburst galaxies, the non-interacting spaxels may be biased to high ΣSFR. This is likely why the median ΣSFR for non-interacting galaxies (shown as a dashed line in the ΣSFR histogram) is slightly larger than the median ΣSFR of the pair sample. We perform Kolmagorov–Smirnov (KS) tests between all three samples to ascertain whether the pair or post-merger ΣSFR/|$\Sigma _{\textrm {H}_2}$|/Σ⋆values could be drawn randomly from the non-interacting spaxel sample. We find the probability of this hypothesis to be approximately zero for all three properties (PKS ≈ 0). The pair sample has a tail towards lower |$\Sigma _{\textrm {H}_2}$|, which seems to be driven by two individual galaxies with uniquely low Σ⋆ and |$\Sigma _{\textrm {H}_2}$| values (8078-6104 and 8083-12703). The post-merger sample also has a tail towards large ΣSFR, |$\Sigma _{\textrm {H}_2}$|, and Σ⋆ values, which manifests at the upper end of each scaling relation. Along with the clear lack of post-merger spaxels with |$\Sigma _{\textrm {H}_2}$| < 6.5log M⊙ kpc–2, it is clear that our post-merger sample probes regions of heightened SFR and molecular gas properties.
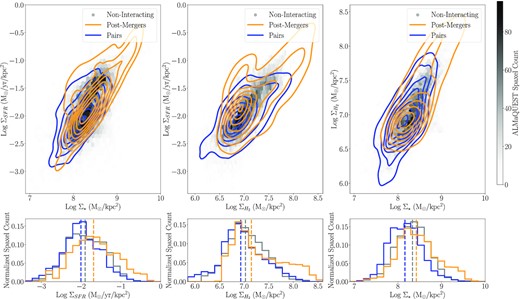
Resolved scaling relations for non-interacting ALMaQUEST galaxies (grey histogram), pairs (blue contours), and post-mergers (orange contours). The rSFMS is shown on the left-hand panel, the rKS is shown in the middle panel, and the rMGMS is show on the right-hand panel. All measurements required a CO S/N > 3, along with the quality criteria to measure ΣSFR with either H α or D4000 methods as described in Section 2.3.1. This results in 22782 isolated spaxels, 7990 pair spaxels, and 4012 post-merger spaxels. Below each histogram distributions of ΣSFR, |$\Sigma _{\textrm {H}_2}$|, and Σ⋆ are included, separated into non-interacting, post-merger, and pair populations. The median value of each distribution is shown as a horizontal dashed line. Note that the non-interacting ALMaQUEST sample is biased towards higher ΣSFR values resulting from the population of starbursts in the original ALMaQUEST sample (see Section 2.3.2 for clarification on how this differs from offset parameter controls). A KS-test reveals that all three populations are distinct from each other in ΣSFR, |$\Sigma _{\textrm {H}_2}$|, and Σ⋆. The pair sample has a small offset to lower ΣSFR, |$\Sigma _{\textrm {H}_2}$|, and Σ⋆, which is driven by two pair galaxies with uniquely low Σ⋆ and |$\Sigma _{\textrm {H}_2}$| values (8078-6104 and 8083-12703). But overall, all three populations cover a similar range of surface densities.
There is significant diversity on a galaxy-per-galaxy basis to consider, as has been seen in other studies (Vulcani et al. 2019; Ellison et al. 2021a; Pessa et al. 2021; Brown et al. in preparation). Fig. 5 shows the rSFMS for each post-merger and pair galaxy. The star-forming spaxels are colour-coded by radius, while the D4000–ΣSFR are a plain yellow if they did not meet our S/N cuts or brown if they are AGN based on the Kauffmann et al. (2003) criteria. The non-interacting ALMaQUEST spaxels are shown as a grey histogram for comparison (including both H α-ΣSFR and D4000–ΣSFR). By examining galaxies as individuals, we see clear divergence from the spaxels in non-interacting galaxies, as well as a diversity of behaviour within post-merger and pair classifications. Many mergers show a large population of spaxels above the star-forming main sequence, as is expected if mergers trigger star formation, such as 8156-3701 (first row, fifth column), 8615-3703 (second row, second column), and 8085-12701 (fifth row, first column). We note that three post-mergers (8084-3702, 8156-3701, 8615-3703) and one pair (8450-6102) were selected from the starburst sample as part of the original ALMaQUEST (ALMA program 2018.1.00541.S, PI: Ellison), which could bias our merger sample towards strongly star-forming galaxies. Yet many spaxels and at times entire mergers are also below the star-forming main sequence, such as 9194-3702 (first row, first column), 7975-6104 (third row, third column), and 8078-12703 (fourth row, fourth column). In particular, both galaxies with concentrations of ‘AGN’ spaxels as defined by the BPT diagram tend to lie below the non-interacting rSFMS [see 9194-3702 (first row, first column) and 9195-3703 (third row, second column)], as has been observed previously with global quantities (Ellison et al. 2016; Leslie et al. 2016; McPartland et al. 2019). This range of enhanced and suppressed SFR drives much of the overall scatter of our sample on the global star-forming main sequence (refer back to Fig. 2).
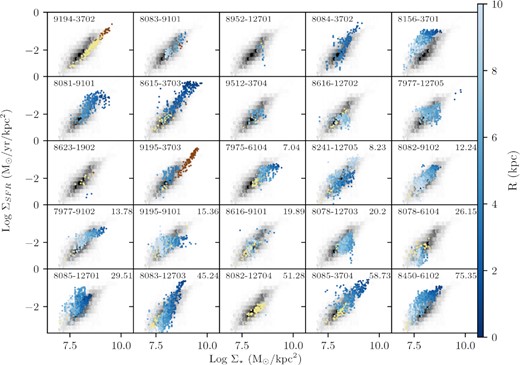
Resolved star-forming main sequence for all merger galaxies, with the MaNGA plate-ifu of the galaxy in the left-hand corner and rp (kpc) in the right-hand corner (left blank for post-mergers). Star-forming spaxels are colour-coded by radius, and spaxels with ΣSFR determined by D4000 are yellow (low H α S/N) or brown (AGN contamination). The non-interacting galaxies in ALMaQUEST are shown as a grey histogram, for reference (including both H α–ΣSFR and D4000–ΣSFR). Note that there is a diversity of star formation behaviour in the merger sample. Some post-mergers and pairs are significantly offset from the rest of ALMaQUEST. Those which exhibit suppressed star formation (such as 8241-12705, 7975-6104, and 8078-6104) can be derived from both H α- and D4000– ΣSFR values, confirming the validity of our combined ΣSFR method.
Mergers present diverse behaviour in the rKS as well, as shown in Fig. 6. Many post-mergers and pairs have overall greater scatter in the rKS than the non-interacting sample [see 8615-3703 (second row, second column), 8085-12701 (fifth row, first column), 8083-12703 (fifth row, second column)], looking ‘puffier’; a similar effect as was seen in Ellison et al. (2021a). The increased scatter could represent smaller regions of enhanced SFE in a merger that, on average, has a low or normal global SFE. Note that although D4000–ΣSFR values tend to be lower on the rKS, many still overlap with H α–ΣSFR spaxels. Spaxels which are classified as ‘AGN’ by a BPT diagram (brown in the figure) tend to exist at larger |$\Sigma _{\textrm {H}_2}$| and ΣSFR values, reflecting their central location in the galaxy and the overall radial dependence of the rKS (smaller radii predominantly fill the upper end of the rKS). However, AGN spaxels at large |$\Sigma _{\textrm {H}_2}$| could also support a scenario where the infall of molecular gas fuels a central AGN. The two largest AGN spaxel populations belonging to post-mergers appears to support such a scenario, though two galaxies alone are not enough to determine if one scenario is more likely than another. Such a query can be further investigated by looking for enhancements in the molecular gas main sequence at high |$\Sigma _{\textrm {H}_2}$| values.
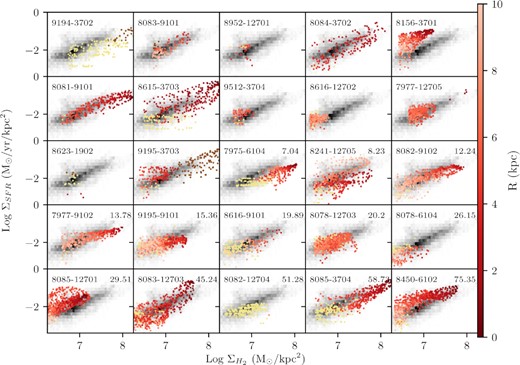
Resolved Kennicutt–Schmidt relation for all merger galaxies, with the MaNGA plate-ifu of the galaxy in the left-hand corner and rp (kpc) in the right-hand corner (left blank for post-mergers). Star-forming spaxels are red and colour-coded by radius, and spaxels with ΣSFR determined by D4000 are yellow (low H α S/N) or brown (AGN contamination). The non-interacting galaxies in ALMaQUEST are shown as a grey histogram, for reference, (including both H α-ΣSFR and D4000–ΣSFR). By examining mergers on an individual basis, we see many mergers that are offset, both above and below, the non-interacting rKS.
Fig. 7 appears to confirm that variations in the rMGMS are the least drastic of the three relations, as was found for non-interacting galaxies by Ellison et al. (2021a). Interestingly, the AGN spaxels (shown in brown) are not offset to below the rMGMS, as would be implied by the comparatively low gas fractions found for AGN spaxels with MaNGA (Sánchez et al. 2018) and EDGE-CALIFA (Ellison et al. 2021b). Rather the AGN spaxels in the merger sample are comparable to star-forming isolated spaxels, or even enhanced in the case of 9194-3702 (first row, first column) and 9195-3703 (third row, second column). What seems to be an inconsistency may stem from the unique nature of the merger stage. Rather than capture central gas depletion triggered by an AGN, as in the isolated galaxies of Ellison et al. (2021b), mergers may have more recently funnelled molecular gas to the galaxy’s centre which has yet to be consumed by the AGN. In the next section, we will investigate what drives a merger galaxy to be offset from the resolved scaling relations by comparing spaxel offsets from scaling relations.
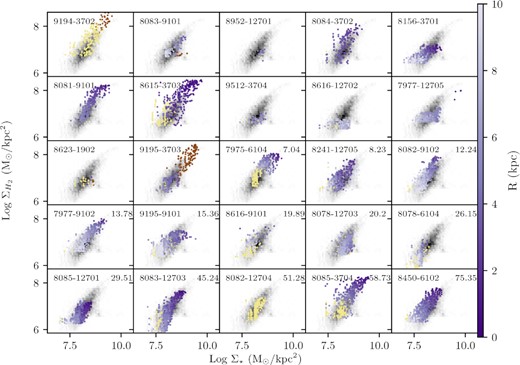
Resolved molecular gas main sequence for all merger galaxies, with the MaNGA plate-ifu of the galaxy in the left-hand corner and rp (kpc) in the right-hand corner (left blank for post-mergers). Star-forming spaxels are colour-coded purple by radius, and spaxels with ΣSFR determined by D4000 are yellow (low H α S/N) or brown (AGN contamination). The non-interacting galaxies in ALMaQUEST are shown as a grey histogram, for reference. Many merging galaxies have tails at the high mass end of the molecular gas main sequence, at times for AGN spaxels as well (supporting a paradigm where mergers fuel AGN).
3.2 Efficiency versus fuel driven enhanced star formation
We can use maps of spaxel offsets from resolved scaling relations (ΔΣSFR, ΔSFE, and |$\Delta f_{H_2}$|, as described in Section 2.3.2), to discern whether changes in SFE or |$f_{\textrm {H}_2}$| drive enhancements in SFR. Fig. 8 shows the offset maps for an example post-merger galaxy, maps for the entire sample are available online, for which we can attempt to discern whether star formation is driven by enhanced SFE or enhanced |$f_{\textrm {H}_2}$|. Star formation in this post-merger is generally enhanced (ΔΣSFR> 0), as is expected given the average spatial enhancement of post-mergers (see Thorp et al. 2019). That enhancement corresponds to a global enhancement in star formation efficiency (positive ΔSFE). Interestingly, this post-merger mostly has a deficit in molecular gas (negative |$\Delta f_{H_2}$|), with some smaller regions of surplus gas. Fig. 8, thus, implies that the boost of star formation in this post-merger in particular is predominantly driven by an enhanced efficiency at which gas is converted to stars, not an enhanced amount of gas to fuel that star formation.
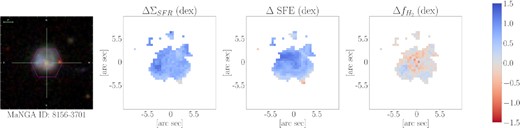
Maps of the offset parameters for an example post-merger galaxy. First column: the SDSS gri-image of the galaxy, for reference. Second column: ΔΣSFR distribution, with blue representing an enhancement in star formation. Third column: ΔSFE distribution, with blue representing enhanced SFE. Fourth column: |$\Delta f_{H_2}$| distribution, with blue representing enhanced gas fraction in a spaxel. The correlation between a uniform enhancement in ΣSFR and SFE, along with the patchy deficits of molecular gas, imply that the star formation in this galaxy is driven by an enhanced efficiency at which gas is converted to stars.
From the offset maps alone, we can infer some interesting behaviour. Many pair galaxies, for example, have large |$\Delta f_{H_2}$| values along spiral arms (see 9195-9101, 7977-9102, and 8241-12705 in supplementary materials). Some pair galaxies have central enhancements in |$\Sigma _{\textrm {H}_2}$| that correspond to a central burst of star formation, such as 9195-3703 and 8078-6104. These two galaxies support a scenario where inflow of molecular gas fuels merger triggered central star formation. Post-merger galaxies 8615-3703 and 8084-3702 have an excess of molecular gas across the galaxy’s surface, rather than a central concentration. Yet that is not a universal scenario; within our sample, 8156-3701 has one of the strongest enhancements in SFR, but has suppressed |$\Sigma _{\textrm {H}_2}$| across the galaxy.
Although the distribution of these offset parameters can reveal interesting results for individual galaxy behaviour, it is difficult to extract general trends for merging and post-merger galaxies from visual examination alone. In particular, it is difficult to parse whether enhanced SFE or enhanced |$\Sigma _{\textrm {H}_2}$| drives any merger-triggered star formation. To discern which mechanism is likely more influential over star formation enhancements, we implement an analysis which includes all three offset parameters in a single diagram as pioneered by Ellison et al. (2020a) using ALMaQUEST and Moreno et al. (2021) using simulations.
Fig. 9 shows the offsets in SFE versus the offsets in molecular gas, for all spaxels with enhanced star formation (ΔΣSFR> 0). We separate the galaxies into three categories: the non-interacting set from ALMaQUEST, pair galaxies, and post-merger galaxies. For these diagrams, we plot the line of equality which is used to distinguish an ‘efficiency driven’ and ‘fuel driven’ regime, i.e. where one offset is greater than the other. If a spaxel lies above this line of equality, then ΔSFE > |$\Delta f_{H_2}$|; if ΔΣSFR> 0, this would imply enhanced efficiency is prompting the enhanced star formation, more so than the gas fraction. All three galaxy populations have a relatively equal percentage of spaxels in the efficiency driven and fuel driven regime, implying that enhanced star formation is equally driven by enhanced fuel and SFE when all spaxels are examined together. There is a slight bias towards efficiency driven star formation for the post-merger spaxels, with 63 per cent of spaxels in the efficiency driven regime. We remind the reader that the original ALMaQUEST sample includes 11 galaxies that were deliberately selected to be starbursts (Ellison et al. 2020a). Three of these starbursts are in our post-merger sample, one is in the pairs sample, and 12 are in our isolated sample. Since Ellison et al. (2020a) showed that starbursts tend to be dominated by high SFEs, the isolated sample in Fig. 9 is not statistically representative of a normal galaxy distribution.
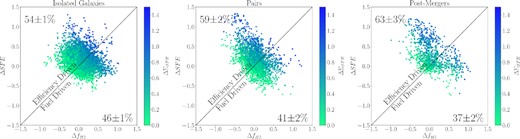
ΔSFE versus |$\Delta f_{H_2}$| for all spaxels that have ΔΣSFR > 0, separated into spaxels which belong to isolated galaxies (left-hand panel), pair galaxies (middle panel), and post-merger galaxies (right-hand). Spaxels are colour-coded by ΔΣSFR. The line of equality is shown to delineate the efficiency driven regime (where ΔSFE > |$\Delta f_{H_2}$|) and the fuel driven regime (where ΔSFE < |$\Delta f_{H_2}$|). The percentage of isolated/pair/post-merger spaxels in each regime is overplotted on the figure, with the uncertainty in the percentage being propogated error of the number of spaxels above/below the line divided by the total number of spaxels. Based on these percentages there is a slight bias towards efficiency driven star formation in post-mergers and pairs (though more so in the former), but other than that the amount of efficiency and fuelled spaxels with enhanced star formation is relatively even.
Fig. 9 might lead us to believe that enhancements in both SFE and |$f_{\textrm {H}_2}$| are equally important for driving SFR enhancements in both post-mergers and pairs. However, in the previous subsection, we found that ensemble spaxel distributions showed considerable diversity when plotted on a galaxy-by-galaxy basis. We now investigate whether the same is true for distributions of offset properties. Fig. 10 replicates the combined offset diagram from Fig. 9, but for a single post-merger galaxy (the same one that is shown in Fig. 8). Ninety six per cent of spaxels with ΔΣSFR> 0 in this galaxy are in the efficiency driven regime, confirming that the star formation in this galaxy is driven by enhanced SFE as is evident from visually inspecting Fig. 8. Fig. 10 highlights that whilst the ensemble of spaxels across all galaxies might have a relatively even split between those whose star formation is enhanced by SFE or gas fraction (Fig. 9), individual galaxies may be strongly driven by one process or the other.
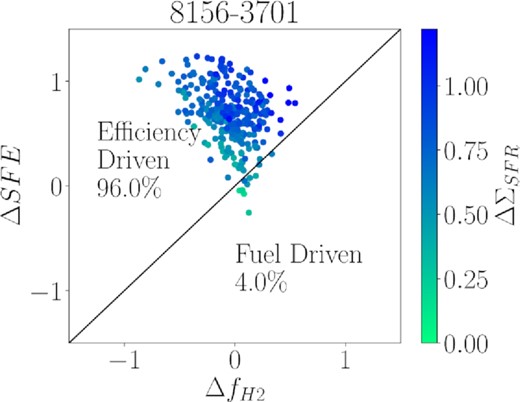
ΔSFE versus |$\Delta f_{H_2}$| for all spaxels with ΔΣSFR> 0 in an example post-merger galaxy (MaNGA plate-ifu = 8156-3701). In this galaxy, almost all spaxels are in the efficiency driven regime, as we might expect from examining the distribution of offset parameters in Fig. 8.
Offset diagrams like that in Fig. 10 are provided for all mergers which have more than 20 spaxels where ΔΣSFR > 0 in Fig. 11, including the percentage of spaxels in the fuel/efficiency driven regimes. There are cases of both post-merger and pair galaxies that are indisputably driven by a single mechanism, such as 9194-3702 (fuel driven) or 8085-12701 (efficiency driven), but for the majority the dominant star formation driver is less clear. In order to classify the dominance of fuel or efficiency in driving star formation enhancements on a galaxy-by-galaxy basis, we quantify the percentage of spaxels in the fuel/efficiency driven regime of our offset diagrams. If more than 60 |${{\ \rm per\ cent}}$| of a galaxy’s ΔΣSFR > 0 spaxels are in the fuel-driven regime (i.e. |$\Delta f_{H_2}$|>ΔSFE), then we classify the galaxy as ‘fuel-driven’. If less than 40 |${{\ \rm per\ cent}}$| of a galaxy’s ΔΣSFR > 0 spaxels are in the fuel-driven regime, then we classify the galaxy as ‘efficiency driven’. If the percentage of spaxels in the fuel-driven regime is between 40 and 60 |${{\ \rm per\ cent}}$|, we can assume that enhanced amounts of gas and enhanced SFE are approximately equally contributing to the enhanced star formation. Note that this method of classification gives equal weight to all spaxels, regardless of the strength of star formation in each spaxel. By doing so, our analysis focuses on what mechanism drives star formation for most regions in a galaxy, not necessarily the mechanism which drives ‘the most’ star formation.

ΔSFE versus |$\Delta f_{H_2}$| for all spaxels with ΔΣSFR > 0 in each post-merger galaxies with more than 20 spaxels with ΔΣSFR> 0, the plate-ifu number of each galaxy is provided in the left-hand corner of every plot. Spaxels are colour-coded by ΔΣSFR. The percentage of spaxels above and below the line of equality are provided as well, which help discern whether the star formation in a galaxy is predominantly driven by enhanced SFE or enhanced |$f_{\textrm {H}_2}$|. We label galaxies which are predominantly efficiency driven (|$\lt 40{{\ \rm per\ cent}}$| below the line) and fuel driven (|$\gt 60{{\ \rm per\ cent}}$| above the line) for reference. For some galaxies, there is clearly a dominant mechanism driving star formation, but many galaxies have contributions from both efficiency and fuel driven SFR enhancements.
The fraction of fuel driven spaxels for every merger is listed in Table 2. We calculate this fraction for both our combined ΣSFR values and for the H α–ΣSFR only, although some mergers do not have enough H α–ΣSFR spaxels to meet our criteria. For galaxies which have enough H α–ΣSFR spaxels to measure the fuel-driven fraction, we find adding D4000–ΣSFR to the analysis does not change the classification of the galaxy as fuel or efficiency driven (except for 8616-9101). Interestingly, those galaxies that we are only able to analyse with the inclusion of D4000–ΣSFR tend to have large fractions of fuel driven spaxels, i.e. the star formation is driven by an excess of fuel. All four recovered galaxies miss our H α-ΣSFR criteria based on low signal-to-noise, implying that the star formation in these galaxies is truly low (and thus a small or negative ΔSFE is to be expected). Further discussion on how D4000–ΣSFR impacts the fraction of fuel driven spaxels is included in Appendix B, where we find the inclusion of D4000–ΣSFR does not drastically change our results. For both ΣSFR measurement methods, there is a relatively similar number of fuel and efficiency driven galaxies, with slightly fewer galaxies driven by neither mechanism. We also consider whether variations in the fraction of fuel driven spaxels could be driven by inaccuracies resulting from using a constant αCO conversion factor. We investigate the error in |$\Sigma _{\textrm {H}_2}$| from using a constant conversion factor, and its impact on the fraction of fuel driven spaxels, in Appendix A, and find our results are robust to variations in αCO.
The fraction of ΔΣSFR > 0 spaxels in the fuel driven regime (i.e. |$\Delta f_{H_2}$| > ΔSFE) for each merger with more than 20 ΔΣSFR > 0 spaxels. The fraction of fuel driven spaxels is computed using the combined H α + D4000 ΣSFR, as well as just the H α SFR (with appropriate cuts). Note some galaxies do not have fractions computed for H α, because they do not have more than 20 spaxels that meet our star-forming cuts. Fractions greater than 0.6, what we consider a fuel driven merger, are coloured blue. Fractions less than 0.4, what we consider an efficiency driven merger, are coloured red. Those between 0.4 and 0.6 are left black, since both mechanisms contribute relatively equally.
| Plate-ifu . | Fraction of . | Fraction of . |
|---|---|---|
| . | fuel driven spaxels . | fuel driven spaxels . |
| . | . | (H α only) . |
| 9195-3702 | – | – |
| 9194-3702 | 0.97 | – |
| 8083-9101 | 0.59 | 0.50 |
| 8952-12701 | – | – |
| 8084-3702 | 0.78 | 0.75 |
| 8156-3701 | 0.04 | 0.04 |
| 8081-9101 | 0.50 | 0.53 |
| 8615-3703 | 0.60 | 0.64 |
| 9512-3704 | – | – |
| 7977-12705 | 0.06 | 0.06 |
| 8623-1902 | 0.52 | – |
| 8616-12702 | – | – |
| 9195-3703 | 0.33 | 0.05 |
| 7975-6104 | 0.97 | 0.97 |
| 8241-12705 | 0.52 | 0.52 |
| 8082-9102 | 0.64 | 0.62 |
| 7977-9102 | 0.69 | 0.68 |
| 9195-9101 | 0.51 | 0.55 |
| 8616-9101 | 0.34 | 0.60 |
| 8078-12703 | 0.10 | 0.14 |
| 8078-6104 | 0.16 | 0.21 |
| 8085-12701 | 0.05 | 0.05 |
| 8083-12703 | 0.38 | 0.39 |
| 8082-12704 | – | – |
| 8085-3704 | 0.60 | 0.67 |
| 8450-6102 | 0.24 | 0.24 |
| Plate-ifu . | Fraction of . | Fraction of . |
|---|---|---|
| . | fuel driven spaxels . | fuel driven spaxels . |
| . | . | (H α only) . |
| 9195-3702 | – | – |
| 9194-3702 | 0.97 | – |
| 8083-9101 | 0.59 | 0.50 |
| 8952-12701 | – | – |
| 8084-3702 | 0.78 | 0.75 |
| 8156-3701 | 0.04 | 0.04 |
| 8081-9101 | 0.50 | 0.53 |
| 8615-3703 | 0.60 | 0.64 |
| 9512-3704 | – | – |
| 7977-12705 | 0.06 | 0.06 |
| 8623-1902 | 0.52 | – |
| 8616-12702 | – | – |
| 9195-3703 | 0.33 | 0.05 |
| 7975-6104 | 0.97 | 0.97 |
| 8241-12705 | 0.52 | 0.52 |
| 8082-9102 | 0.64 | 0.62 |
| 7977-9102 | 0.69 | 0.68 |
| 9195-9101 | 0.51 | 0.55 |
| 8616-9101 | 0.34 | 0.60 |
| 8078-12703 | 0.10 | 0.14 |
| 8078-6104 | 0.16 | 0.21 |
| 8085-12701 | 0.05 | 0.05 |
| 8083-12703 | 0.38 | 0.39 |
| 8082-12704 | – | – |
| 8085-3704 | 0.60 | 0.67 |
| 8450-6102 | 0.24 | 0.24 |
The fraction of ΔΣSFR > 0 spaxels in the fuel driven regime (i.e. |$\Delta f_{H_2}$| > ΔSFE) for each merger with more than 20 ΔΣSFR > 0 spaxels. The fraction of fuel driven spaxels is computed using the combined H α + D4000 ΣSFR, as well as just the H α SFR (with appropriate cuts). Note some galaxies do not have fractions computed for H α, because they do not have more than 20 spaxels that meet our star-forming cuts. Fractions greater than 0.6, what we consider a fuel driven merger, are coloured blue. Fractions less than 0.4, what we consider an efficiency driven merger, are coloured red. Those between 0.4 and 0.6 are left black, since both mechanisms contribute relatively equally.
| Plate-ifu . | Fraction of . | Fraction of . |
|---|---|---|
| . | fuel driven spaxels . | fuel driven spaxels . |
| . | . | (H α only) . |
| 9195-3702 | – | – |
| 9194-3702 | 0.97 | – |
| 8083-9101 | 0.59 | 0.50 |
| 8952-12701 | – | – |
| 8084-3702 | 0.78 | 0.75 |
| 8156-3701 | 0.04 | 0.04 |
| 8081-9101 | 0.50 | 0.53 |
| 8615-3703 | 0.60 | 0.64 |
| 9512-3704 | – | – |
| 7977-12705 | 0.06 | 0.06 |
| 8623-1902 | 0.52 | – |
| 8616-12702 | – | – |
| 9195-3703 | 0.33 | 0.05 |
| 7975-6104 | 0.97 | 0.97 |
| 8241-12705 | 0.52 | 0.52 |
| 8082-9102 | 0.64 | 0.62 |
| 7977-9102 | 0.69 | 0.68 |
| 9195-9101 | 0.51 | 0.55 |
| 8616-9101 | 0.34 | 0.60 |
| 8078-12703 | 0.10 | 0.14 |
| 8078-6104 | 0.16 | 0.21 |
| 8085-12701 | 0.05 | 0.05 |
| 8083-12703 | 0.38 | 0.39 |
| 8082-12704 | – | – |
| 8085-3704 | 0.60 | 0.67 |
| 8450-6102 | 0.24 | 0.24 |
| Plate-ifu . | Fraction of . | Fraction of . |
|---|---|---|
| . | fuel driven spaxels . | fuel driven spaxels . |
| . | . | (H α only) . |
| 9195-3702 | – | – |
| 9194-3702 | 0.97 | – |
| 8083-9101 | 0.59 | 0.50 |
| 8952-12701 | – | – |
| 8084-3702 | 0.78 | 0.75 |
| 8156-3701 | 0.04 | 0.04 |
| 8081-9101 | 0.50 | 0.53 |
| 8615-3703 | 0.60 | 0.64 |
| 9512-3704 | – | – |
| 7977-12705 | 0.06 | 0.06 |
| 8623-1902 | 0.52 | – |
| 8616-12702 | – | – |
| 9195-3703 | 0.33 | 0.05 |
| 7975-6104 | 0.97 | 0.97 |
| 8241-12705 | 0.52 | 0.52 |
| 8082-9102 | 0.64 | 0.62 |
| 7977-9102 | 0.69 | 0.68 |
| 9195-9101 | 0.51 | 0.55 |
| 8616-9101 | 0.34 | 0.60 |
| 8078-12703 | 0.10 | 0.14 |
| 8078-6104 | 0.16 | 0.21 |
| 8085-12701 | 0.05 | 0.05 |
| 8083-12703 | 0.38 | 0.39 |
| 8082-12704 | – | – |
| 8085-3704 | 0.60 | 0.67 |
| 8450-6102 | 0.24 | 0.24 |
Fig. 12 displays the distribution of the fraction of fuel driven spaxels, both for the merger sample as a whole (grey) and the pair (blue) and post-merger (orange) sub-samples. Both the post-merger and pair sample show relatively equal distribution in fuel fraction implying a diversity of star formation drivers throughout the interaction process. There is an intriguing excess of extremely low fuel fractions (below 0.1), compared to the more uniform distribution above a fuel fraction of 0.5, implying that ‘efficiency driven’ mergers have ΔSFE > |$\Delta f_{H_2}$| in most spaxels. However, given only three post-mergers are below a fuel fraction of 0.4, this could be the result of small number statistics.
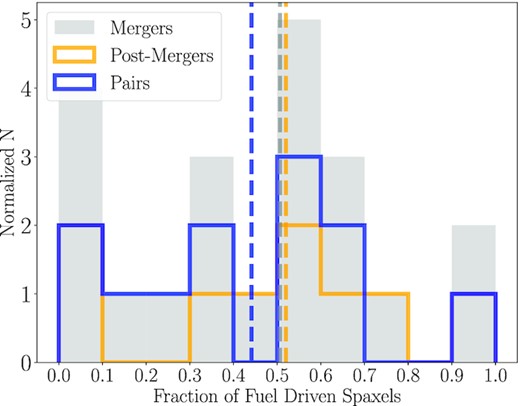
Distributions of the fraction of fuel driven spaxels for the merger sample (grey), along with the pair (blue) and post-merger (orange) sub-samples. The median of each distribution is shown with a vertical dashed line: 0.51 for the entire merger sample, 0.44 for pairs, and 0.52 for post-mergers. The median value of each sub-smaple being so similar, and so close to 0.5, confirms that there are an equal number of fuel and efficiency driven mergers.
Both observations (Ellison et al. 2013; Patton et al. 2013; Knapen et al. 2015) and simulations (Cox et al. 2008; Torrey et al. 2012; Moreno et al. 2019; Patton et al. 2020) have demonstrated that merger induced star formation peaks at coalescence. Despite the diversity demonstrated in Table 2, it is interesting to note that two of the three post-mergers with a global ΔSFR > 0.5 are fuel driven enhancements (9194-3702, 8084-3702). We might wonder, then, if there is some correlation between the fraction of fuel driven spaxels and the interaction stage, with the largest fraction of fuel driven spaxels occurring at coalescence when the star formation is strongest. The higher percentage of efficiency driven galaxies in the pair sample (50 per cent as opposed to 33 per cent in the post-mergers) would agree with a scenario where efficiency driven star formation becomes less important towards coalescence. Such a correlation would fit with the hypothesis that merger-induced star formation stems from non-axisymmetric structures causing a loss of angular momentum for gas, which then funnels into the centre of the galaxy towards the end of an interaction.
Fig. 13 is a visual representation of Table 2, showing the fraction of fuel driven spaxels as a function of projected separation between pairs, with each point colour-coded by global offset from the star-forming main sequence. The post-mergers are shown with a projected separation as arbitrary values below zero, in the grey bar. Fig. 13 reveals no clear correlation with the fraction of fuel driven spaxels and the projected separation (Pearson’s correlation coefficient = −0.355). Thus, there is no evidence from our sample that the merger stage is strongly linked to whether enhanced star formation is driven by elevated fuel or efficiency. It is important to note that projected separation is not a perfect representation of merger stage due to both uncertainty on whether a galaxy has already completed one or more pericentric passages, as well as projection effects. Morphological signs can serve as an additional indicator for interaction stage given galaxies are most disturbed at first passage and right before coalescence (Lotz, Primack & Madau 2004; Lotz et al. 2008; Hambleton et al. 2011). Unfortunately most of our mergers have some degree of visual disturbance, making it difficult to directly link morphology to a distinct interaction stage (outside of pre- and post-coalescence). We attempt to account for this by highlighting pair galaxies which are connected to their companion by a tidal arm on Fig. 13, as a more concrete indicator that first passage has already occurred. Even with this additional category, no trend with merger stage and fraction of fuel driven spaxels arises, further affirming that interaction stage plays a secondary role influencing how star formation is enhanced.
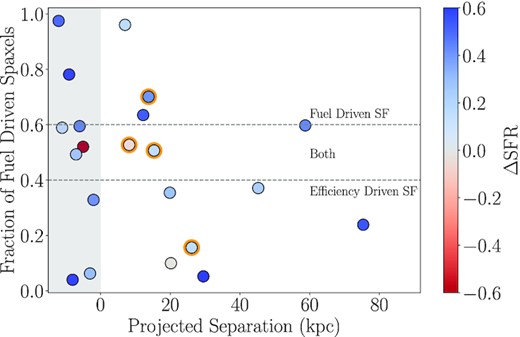
Fraction of fuel driven spaxels as a function of projected separation in kpc, with post-mergers in the grey region (since projected separation cannot be measured without a companion). All points are colour-coded by the galaxy’s global offset from the star-forming main sequence, ΔSFR (bluer points have globally enhanced SFR, red points have globally suppressed SFR, compared with the global SFMS). Note that galaxies with negative ΔSFR can still have regions of enhanced star formation, which we use to compute a fuel fraction. Pairs that have tidal arms connecting the two galaxies are highlighted with orange. Neither projected separation, nor this secondary morphology characteristic, show any trend with the fraction of fuel driven spaxels.
Fig. 13 encapsulates one of the main conclusions of this paper: interacting galaxies show a broad diversity of the relative contributions of fuel and efficiency, with no obvious dependence on the merger stage we adopted. This sample suggests that the properties of the galaxies themselves (e.g. gas fractions, morphologies) as well as the details of the interaction (orbit and mass ratio) play a larger role in how star formation is enhanced. We have checked to see if the fraction of fuel driven spaxels correlates with M⋆, |$\textrm {M}_{\textrm {H}_2}$|, |$f_{\textrm {H}_2}$|, SFR, and ΔSFR, and found only |$\textrm {M}_{\textrm {H}_2}$| and |$f_{\textrm {H}_2}$| have a Pearson’s correlation coefficient greater than 0.6 (note that |$f_{\textrm {H}_2}$| and |$\textrm {M}_{\textrm {H}_2}$| are themselves correlated, with a Pearson’s correlation coefficient of 0.69). However, a correlation between the fraction of spaxels driven by enhanced amounts of molecular gas and large gas fractions is not a particularly noteworthy result. More likely, it is the combined properties of the galaxy and its companion that drive the diversity of star formation properties observed. Recent simulations have found that mass ratio and orbital geometry can both impact how star formation is powered in mergers (Moreno et al. 2021). It is possible that, with a larger sample, more pronounced correlations with merger stage or integrated galaxy property would emerge, but for this sample such trends are not obvious.
3.3 What drives resolved changes in star formation?
We have shown that, for both pair and post-merger galaxies, either enhanced SFE or enhanced |$f_{\textrm {H}_2}$| can drive the subsequent star formation enhancement that results from an interaction. The merger sample is split evenly between galaxies whose star formation driven by SFE, by |$f_{\textrm {H}_2}$|, and those equally driven by both. An underlying issue yet to be addressed is how the mechanism which powers star formation relates to the spatial variations in star formation.
Fig. 14 displays radial profiles of ΔΣSFR for the merger sample separated into distinct categories of efficiency driven, fuel driven, or driven by both based on the fraction of fuel driven spaxels in Table 2 (profiles are additionally colour-coded by the exact fuel fraction computed). By creating radial profiles of offsets in ΣSFR, we can investigate whether the fuel fraction we have computed can help explain the diversity of merger radial profiles seen with previous MaNGA studies (i.e. Pan et al. 2019; Thorp et al. 2019; Steffen et al. 2021). A more detailed analysis of merger radial profiles for different ALMaQUEST data products will be included in Pan et al. (in preparation); what is discussed here is simply to assess how our global fuel fraction might relate to variations in ΣSFR already noted by previous works.
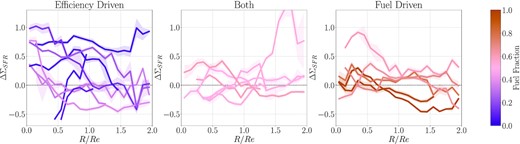
Radial profiles of the median ΔΣSFR in bins of effective radius for post-merger and pair galaxies included in our analyses, separated into groups of ‘Efficiency Driven’, ‘Both’, and ‘Fuel Driven’ based on the fuel fraction value (the second column of Table 2). Each profile is also colour-coded by the fuel fraction. Radial profiles are plotted as a function of the effective radius, with the solid line representing the median in a bin of 0.1 Re, and the faded width of the line representing the error on the mean. Efficiency driven mergers tend to have the strongest and most extended enhancements in star formation. Whereas fuel driven mergers are more likely to have centrally concentrated bursts of star formation, likely due to an inflow of gas.
The efficiency driven and fuel driven radial profiles in Fig. 14 have clearly distinct behaviour. Fuel driven mergers tend to have greater ΔΣSFR at small radii, though that does not always lead to a suppression of star formation in the outskirts. Efficiency driven mergers have both greater peaks in ΔΣSFR (five out of nine surpass 0.5 dex enhancement at one point) and a greater diversity in profile behaviour. Profiles for the efficiency driven mergers can both increase ΔΣSFR with radius, decrease ΔΣSFR with radius, or have consistent ΔΣSFR out to 2Re. Thus, it is likely that a diversity of fuel fraction values could explain some of the diversity of post-merger profiles noted in Thorp et al. (2019). Interestingly, the fuel driven mergers show similar profiles to the starburst ΔΣSFR profiles found in Ellison et al. (2020a), despite non-interacting starbursts being primarily driven by enhanced SFE. It is possible that mergers provide one route to a starburst by funnelling gas to a centralized starburst, and the resulting SFR enhancement profile is indistinguishable from secular starbursts. Efficiency driven mergers, on the other hand, are more likely to have stronger and continuous SFR enhancements that distinguish them from isolated galaxies of a similar ΔSFR. In the case of the latter, the strongest bursts of star formation cannot be driven by enhanced gas reservoirs alone.
There are still issues with applying a single ‘fuel driven’ prescription to what is clearly quite variable on the resolved scale. Simulations of the resolved gas properties of mergers have demonstrated that mergers with overall suppressed star formation can still have appreciable amounts of centralized cold-dense gas (Moreno et al. 2021). We can see this in our handful of fuel-driven mergers that have suppressed star formation beyond 1Re, despite centralized boosts in star formation. It is possible that, though a merger is primarily fuel or efficiency driven, there are regions that deviate from this norm. After all, the mergers which are driven by ‘both’ are lacking any trend in radial profile unlike the other two categories. It is clearly worthwhile to explore how the dominant mechanism might vary within a galaxy.
We attempt to pinpoint spatial variations in the dominant star-forming mechanism by examining the difference between ΔSFE and |$\Delta f_{H_2}$|. The difference between two offset parameters provides a rough approximation of which offset is dominant in an individual spaxel by simply quantifying which is larger. The difference between ΔSFE and |$\Delta f_{H_2}$| is a bit like a fuel fraction for each spaxel, though we note that the number attributed to each has no physical meaning beyond comparing offset values. We can, thus, construct maps of ΔSFE−|$\Delta f_{H_2}$| to demonstrate which mechanism is more important within a certain region of a galaxy. We only consider this for spaxels where ΔΣSFR, ΔSFE, and |$\Delta f_{H_2}$| are positive, to avoid interpreting the contribution of suppressed SFE or |$f_{\textrm {H}_2}$|.
Fig. 15 displays maps of ΔSFE−|$\Delta f_{H_2}$| for three example galaxies, in conjunction with the ΔSFE versus |$\Delta f_{H_2}$| diagram colour-coded by ΔSFE−|$\Delta f_{H_2}$|. Note how the magnitude of ΔSFE−|$\Delta f_{H_2}$| scales with distance from the line of equality, where the contribution from SFE and |$f_{\textrm {H}_2}$| is equal. Regions where ΔSFE is greater are shown in purple, and regions where |$\Delta f_{H_2}$| is greater are shown in brown. We specifically chose three galaxies that are predominantly efficiency or fuel driven, to demonstrate how this clear-cut classification may break down on a spaxel-per-spaxel basis.

First column: gri-image of the merger galaxy. Second column: ΔSFE versus |$\Delta f_{H_2}$| for all spaxels where ΔΣSFR > 0, colour-coded by ΔSFE−|$\Delta f_{H_2}$|. Third column: spatially resolved map of ΔSFE−|$\Delta f_{H_2}$| for pixels where all three offset parameters are positive. The colour bars change slightly for each merger, which have different spans of ΔSFE−|$\Delta f_{H_2}$|, but zero is always white. Note that ΔSFE–|$\Delta f_{H_2}$| scales with distance from the line of equality shown in the second column. Within each galaxy there is distinct variability in the importance of ΔSFE and |$\Delta f_{H_2}$|, particularly between the centre and outskirts of the galaxy.
Fig. 15 demonstrates that, even within a given galaxy, the dominant driver of enhanced star formation can vary spatially. The first row of Fig. 15 shows a post-merger galaxy with a global fuel fraction of 0.33, indicating that SFE is the dominant driver of enhanced star formation. However, a more complicated picture emerges when we look at the spatially resolved map of ΔSFE−|$\Delta f_{H_2}$| in the right-hand column. Although the extended spiral arms are indeed dominated by enhanced SFE, the core is dominated by enhanced gas fractions. Similar results were found for the Antennae merging galaxies, which had central enhancements in dense gas along with lowered SFE (Bemis & Wilson 2019). By examining maps of ΔSFE−|$\Delta f_{H_2}$| for all mergers (included with offset parameter maps available online), we find that most of our merger sample follows a similar trend of |$\Delta f_{H_2}$| dominating the central regions of the galaxy.
To quantify whether |$\Delta f_{H_2}$| is more important in the centre of a merging galaxy, we compute a gradient in ΔSFE−|$\Delta f_{H_2}$| for each merger, subtracting the median ΔSFE−|$\Delta f_{H_2}$| within 1Re from the median where R > 1Re. All but two mergers have a positive gradient (i.e. |$\Delta f_{H_2}$| is more important in the centres than the outskirts), confirming that similar to previous case studies, |$\Delta f_{H_2}$| plays a key role in triggering central bursts of star formation. Positive gradients are found both within efficiency driven and fuel driven mergers, with no correlation to the global fraction of fuel driven spaxels (Pearson’s correlation coefficient = −0.19). Efficiency driven mergers have mostly efficiency driven spaxels (positive values in ΔSFE−|$\Delta f_{H_2}$| maps) with fuel driven central starbursts; but given there are more spaxels at large radii than small, those efficiency driven spaxels dominate the percentage of star-forming regions overall. The two mergers with negative gradients, 8156-3701 and 8081-9101, are not unique in their global galaxy properties, but have distinct ΔΣSFR profiles. 8156-3701 (a post-merger with fuel fraction = 0.04) has ΔΣSFR > 0.5 out to two effective radii, powered by predominantly ΔSFE. In contrast, 8081-9101 (a post-merger fuel fraction = 0.5) has brief suppressions in star formation at the centre and edge of the galaxy, but enhancements ∼0.25 dex for the majority of the galaxy. Though no substantial result can be derived from two galaxies alone, it is interesting that mergers without central fuel enhancements display two of the most chaotic ΔΣSFR profiles. However, on average, our sample confirms that central bursts of star formation in mergers require centralized enhancements in gas fraction.
Clearly the consistency of positive gradients in ΔSFE−|$\Delta f_{H_2}$| does not negate further variations between galaxies, as can be seen in the examples from Fig. 15 alone. The middle row of Fig. 15 shows a post-merger with a negative gradient in ΔSFE−|$\Delta f_{H_2}$|. Though star formation in this merger is clearly driven by enhanced SFE (it has a fuel fraction of 0.04), |$f_{\textrm {H}_2}$| plays a slightly more important role in the outskirts than in the centre (though ΔSFE is always greater). But even galaxies with a positive gradient, as expected, can have local variations from the norm. The last row of Fig. 15 shows a fuel driven post-merger (fuel fraction 0.78) with a positive ΔSFE−|$\Delta f_{H_2}$| gradient. However, regions where ΔSFE−|$\Delta f_{H_2}$| < 0 persist out to large radii as well, following a central extended structure within the galaxy. In this case, fuel-driven star formation is not limited to the centre of the galaxy (though ΔSFE becomes more important at large radii as well). Such variations are similar to those found in studies of isolated galaxies, where the slope and offset of the rSFMS, rKS, and rMGMS can vary significantly depending on the local galaxy environment (particularly for spiral arms, Pessa et al. 2021). In summary, we find that there is not only considerable diversity from galaxy-to-galaxy in terms of the relative importance of fuel and efficiency, but even within a given galaxy, different regions show considerable variation.
4 SUMMARY AND CONCLUSION
We have presented MaNGA + ALMA CO(1–0) observations of 31 merging galaxies from the ALMaQUEST merger sample in order to study whether interaction-induced star formation is driven primarily by enhancements in SFE or gas fraction. The sample includes 14 post-merger galaxies and 17 pairs with projected separations up to 90 kpc. We compare the rSFMS, rKS, and rMGMS of the merger galaxies to relatively isolated galaxies in the ALMaQUEST survey. Although the ensemble of spaxels in the post-mergers, pairs, and isolated galaxies have similar scaling relations (Fig. 4), significant variation can be seen when examining the resolved relations for individual mergers (see Figs 5, 6, and 7).
In order to better understand the spatial variations in each merger, we construct maps of offsets from these resolved relations (ΔΣSFR, ΔSFE, and |$\Delta f_{H_2}$|). By directly comparing ΔSFE and |$\Delta f_{H_2}$| for all spaxels with enhanced star formation, we can identify whether the star formation is driven by an enhanced gas reservoir, or an enhanced efficiency at which gas is converted into stars. We find that when all spaxels in all galaxies are considered together, |$f_{\textrm {H}_2}$| and SFE contribute equally to enhanced star formation (Fig. 9).
However, the approximately equal importance of fuel and efficiency across the entire sample is misleading.. When we examine galaxies on an individual basis, a different picture emerges. Some mergers are clearly dominated by either efficiency or fuel driven star formation, with all points lying in one regime of Fig. 11. About a third of the merger sample is predominantly efficiency driven, a third is fuel driven, and a third is driven equally by both. We investigate whether the dominant star formation mechanism might be correlated with global galaxy properties (SFR, M⋆, |$\textrm {M}_{\textrm {H}_2}$|, |$f_{\textrm {H}_2}$|, ΔSFR), and find only an unsurprising correlation with fuel driven star formation and large gas fractions.
The driving star formation mechanism does not depend on the stage of an interaction either. The percentage of fuel driven post-mergers is somewhat more than the percentage of fuel driven pair galaxies. But fuel fraction does not correlate with other indicators of interaction stage, such as projected separation and tidal connections (Fig. 13). The progression of the interaction does not lead to clear evolution in the fuel fraction, which implies the unique properties of the progenitors are more influential on which mechanisms powers enhancements in star formation.
In Section 3.3, we investigate how the dominant star-forming mechanism leads to variations on a spatial scale. Radial profiles of ΔΣSFR for the merger sample are shown in Fig. 14, separated into three categories based on fuel fraction. We find that ‘fuel driven’ mergers (with fuel fractions > 0.6) have relatively distinct ΔΣSFR profiles compared to ‘efficiency driven’ mergers (fuel fraction < 0.4), which often have stronger and more extended ΔΣSFR enhancements. Thus, a range of fuel fractions in mergers could explain the diversity of star formation offset profiles seen in previous merger studies (Pan et al. 2019; Thorp et al. 2019; Steffen et al. 2021).
The range of ΔΣSFR profiles in these three categories implies more internal variation within a galaxy than a single fuel fraction can capture. Fig. 15 demonstrates this variation in the dominant mechanism within a galaxy by presenting 2D maps of ΔSFE−|$\Delta f_{H_2}$|, indicating which offset parameter is the largest in each spaxel. Even galaxies which are driven predominantly by a single mechanism on a global scale can exhibit internal deviations from the dominant mechanism. For example, both efficiency and fuel driven mergers tend to have |$\Delta f_{H_2}$| > ΔSFE in their centre, confirming that enhanced amounts of molecular gas are crucial to merger-induced central starbursts, even if the rest of the galaxy has efficiency driven star formation.
The work presented here is the first to investigate the resolved molecular gas and star formation properties for a relatively large set of mergers spanning a wide range of sSFRs and stages of interaction, with the explicit goal of understanding how gas and star formation evolve with an interaction. Our work adds to the growing evidence that, despite following overall scaling relationships, galaxies are diverse in their details. Moreover, we have shown that in addition to diversity on a global scale (i.e. some mergers have their star formation driven by fuel, others by efficiency), there is significant internal variation on kpc-scales.
SUPPORTING INFORMATION
ALMaQUEST_DP.pdf
ALMaQUEST_offsets.pdf
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
We acknowledge and respect the Lekwungen peoples on whose traditional territories the University of Victoria stands and where the majority of this work was conducted. We strive to honour the Songhees, Esquimalt, and WSÁNEC peoples who were the first astronomers of this land and whose continued stewardship is crucial to its preservation.
MDT thanks Jorge Moreno, Shoshannah Byrne-Mamahit, Salvatore Quai, Robert Bickley, Scott Wilkinson, and Joanna Woo for discussion throughout the creation of this work, as well as William Baker and Fangting Yuan for key editorial remarks. SLE and DRP gratefully acknowledge NSERC of Canada for Discovery Grants which helped to fund this research. HAP acknowledges support by the Ministry of Science and Technology of Taiwan under grant 110-2112-M-032-020-MY3. SLE, MDT, LL, and HAP also gratefully acknowledge grant MOST 107-2119-M-001-024 and 108-2628-M-001-001-MY3 for travel funding that facilitated both the ALMA data reduction and analysis of ALMaQUEST survey.
This paper makes use of the following ALMA data: ADS/JAO.ALMA#2015.1.01225.S, ADS/JAO.ALMA#2017.1.01093.S, ADS/JAO.ALMA#2018.1.00558.S, ADS/JAO.ALMA#2018.1.00541.S, ADS/JAO.ALMA#2019.1.00260.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Tai- wan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSSIV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU) / University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatory of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional / MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
DATA AVAILABILITY
The MaNGA data cubes used in this work are publicly available at https://www.sdss.org/dr15/. The ALMA data used in this work are publicly available after the standard 1-yr proprietary period via the ALMA archive: http://almascience.nrao.edu/aq/.
REFERENCES
APPENDIX A: METALLICITY DEPENDENT CO CONVERSION FACTOR
Throughout this work, we elect to use a constant αCO rather than a metallicity dependent one. This is highly beneficial to our analysis in that we can include spaxels which do not meet the requirements to measure accurate gas-phase metallicities (requiring high signal-to-noise ratio in multiple emission lines). As a result, our |$\Sigma _{\textrm {H}_2}$| measurements will be imperfect, leading to the possibility that variations ΔSFE and |$\Delta f_{\rm H_2}$| (both of which require |$\Sigma _{\textrm {H}_2}$|) could be the result of inaccuracies in αCO. Depending on the degree of that inaccuracy this could sully our final conclusions concerning the role enhanced efficiency and fuel play in increasing star formation activity.
Though we cannot compute a metallicity dependent αCO (αCO, met from here on) for every spaxel, we can characterize the change in |$\Sigma _{\textrm {H}_2}$| for spaxels where αCO, met is measurable. We compute a αCO, met for all spaxels that are star-forming based on the criteria described in Subsection 2.3.1, for which we can also measure the gas phase metallicity using the O3N2 calibration of Pettini & Pagel (2004). We set αCO, met = 4.35 × Z′ −1.6(M⊙(K km–1s pc2)−1) where Z′ is the metallicity normalized to solar metallicity (|$Z^{\prime }=10^{\textrm {PP04}_{\textrm {O3N2}}-8.69}$|; Sun et al. 2020). We find the median difference between |$\Sigma _{\textrm {H}_2}$| and |$\Sigma _{\textrm {H}_2, \textrm {met}}$| to be −0.068 dex, with a standard deviation of 0.124 dex. If we want to be conservative, we can say that |$\Delta f_{H_2}$| and ΔSFE both have an uncertainty of 2σ on the difference in |$\Sigma _{\textrm {H}_2}$|, or 0.248 dex. Fig. A1 is a replication of Fig. 11, with a grey bar representing 0.248 dex of uncertainty; points within this range could change from fuel to efficiency driven, or vice versa, if one switched from a constant to a metallicity dependent αCO. We can, thus, exclude spaxels within this grey bar from our calculation of the fuel fraction to achieve a value that is independent of variations in αCO. By excluding borderline spaxels, most galaxies tend to be more ‘fuel’ or ‘efficiency’ driven.
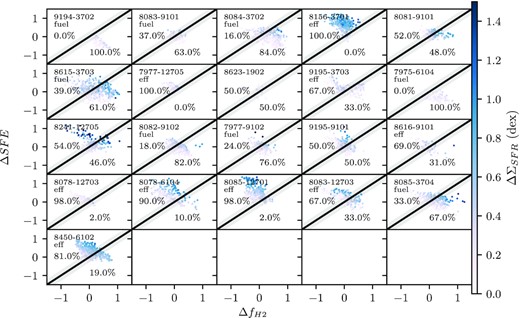
A replication of Fig. 11, but now with a grey line indicating the 0.248 dex error on both offset parameters from using a constant αCO. Pixels within this grey region are not considering when calculating the fraction of fuel driven spaxels. This biases the distribution of fuel fractions to the extreme ends (very high or very low), as spaxels further away from the line become more important in the calculation.
Fig. A2 directly compares the original fuel fraction, using a constant αCO, to this new one which incorporates error from not using αCO, met. Ideally, all points would be along the line of equality, confirming that the fraction of fuel driven spaxels does not change. Instead galaxies which are fuel driven become more fuel driven, rising above the line of equality, and galaxies which are efficiency driven become more efficiency driven. As a result, very few galaxies change whether we would consider them ‘efficiency’ or ‘fuel’ driven. We highlight regions where both the new and old fuel fractions agree on the dominant mechanism: where efficiency dominates (red), fuel fraction dominates (blue), or both equally influence star formation (grey). Only two mergers change which mechanism dominates: both are mergers where efficiency and fuel are equally important with a constant αCO, but then change to fuel driven. This shift is not the result of a significant change in fuel fraction, rather the two mergers were already at the border between categories. As discussed in the main analysis, these categories of ‘efficiency’ and ‘fuel’ driven are less robust than the continuously changing fuel fraction measurement.
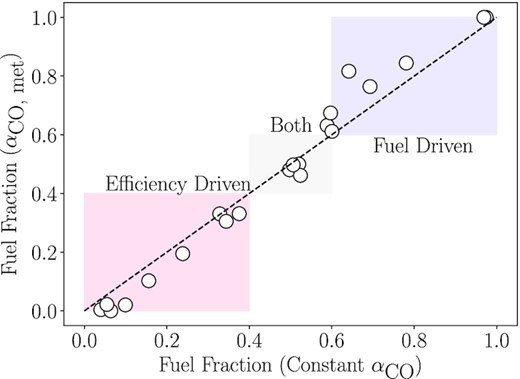
The fuel fraction determined from Fig. A1, considering uncertainties from not using αCO, met, plot against the original fuel fraction determined from Fig. 11. Note that efficiency driven mergers move below the line of equality (black dashed line), and fuel driven mergers move above the line; thus the dominant star-forming mechanism only appears more dominant when uncertainties in αCO are considered. We have highlighted regions that indicate the dominant mechanism has not changed (ideally where all points would lie): where both fractions imply star formation is efficiency driven (red), where both fractions imply star formation is fuel driven (blue), and where both fractions imply star formation is driven by both (grey). Only two mergers change category (from ‘both’ to ‘fuel driven’), though both galaxies were already at the border between these two categories.
In summary, our measured fuel fraction changes little when uncertainties in αCO are considered. Moreover, our results concerning ΔSFE being more important to star formation than |$\Delta f_{H_2}$| (or vice versa) are unlikely to stem from local variations in conversion factor. Rather, they characterize the true relationship between star formation and molecular gas in a merger event.
APPENDIX B: SSFR-D4000
The SFRs presented herein include those that have been calibrated from D4000. Here, we demonstrate that our conclusions are not significantly affected by the inclusion of SFRs computed in this way. Fig. B1 shows the distribution of sSFR versus D4000 for all star forming spaxels in MaNGA, based on our star forming criteria described in Section 2.3.1, with contours representing the density of the distribution of hexbins colour-coded by the median ΔΣSFR value in that bin. The asymptotic nature of the sSFR-D4000 relation as D4000 approaches 1.45 can lead to drastic difference in approximated ΣSFR for spaxels with very similar D4000 values. Therefore, only spaxels with D4000 > 1.4 are used for SFR calculations.
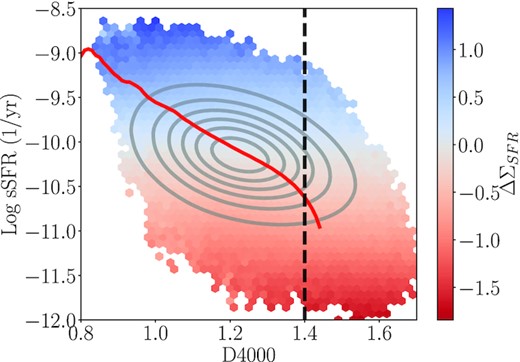
sSFR versus D4000 for all star forming spaxels in MaNGA. Density contours of this distribution are shown in grey, over a hexbin distribution colour-coded by the median ΔΣSFR value in each bin. The median sSFR value in a D4000 bin is shown in red: these points are used to approximate ΣSFR for spaxels that do not meet our star-forming criteria. We exclude spaxels with D4000 > 1.4, given the asymptotic nature of the sSFR-D4000 at high D4000. Note that there is a significant scatter in this relation, which correlates with ΔΣSFR.
There is a non-negligible scatter in the sSFR-D4000 relation which is strongly correlated with ΔΣSFR. This is to be expected; by definition a spaxel with high sSFR given the D4000 index would have a higher ΣSFR given its Σ⋆. The red line is a median sSFR in a bin so it makes sense that scatter significantly above the line would correspond to large, positive ΔΣSFR. Thus by approximating ΣSFR from the median sSFR, we will always underestimate the offset of the star formation from regular behaviour (both enhancements and deficits). That bias works in favour of this analysis, where we are looking for strong offsets in ΣSFR. Thus for D4000–ΣSFR values, any enhancement or suppression in star formation is a lower limit on the true offset; the same can be said for enhancements and deficits in SFE.
When D4000–ΣSFR is used the absolute value of ΔΣSFR and ΔSFE will be underestimated, but |$\Delta f_{H_2}$| (which does not depend on a ΣSFR measurement) will not be changed. The dependence of ΔSFE on ΣSFR is crucial when comparing ΔSFE and |$\Delta f_{H_2}$| to determine which mechanism drives enhanced star formation. When using a D4000–ΣSFR the value of ΔSFE is a lower limit, so ΔSFE > |$\Delta f_{H_2}$| will be consistent even if D4000–ΣSFR is less accurate than H α-ΣSFR. However if ΔSFE < |$\Delta f_{H_2}$|, ΔSFE could be underestimated and the statement might not be true if we could measure a H α-ΣSFR. We therefore have to consider that galaxies with a large fraction of fuel driven spaxels (i.e. ΔSFE < |$\Delta f_{H_2}$|) might have a smaller fraction if we were not dependent on D4000–ΣSFR measurements.
To check how this bias might alter our results, we calculate the fraction of fuel driven spaxels both with our combined H α + D4000 ΣSFR values, as well as those which only have H α-ΣSFR. Four galaxies do not have at least 20 spaxels with viable H α-ΣSFR, so can not be part of the test. Both fractions are included in Table 2 and discussed in the text, though we provide additional comparison here. Fig. B2 directly compares the fuel fraction determined from only H α spaxels to the fuel fraction when both H α and D4000 spaxels are included. Ideally, these two values would be equal and all galaxies would lie on the line of equality, but as expected there is some difference between the two. Difference between the two fuel fractions can be acceptable so long as it does not change which mechanism predominantly drives star formation. To better demonstrate this distinction, we highlight regions where both fractions agree: that star formation is efficiency drive (red), fuel driven (blue), or both (grey). Only one galaxy is outside these acceptable regions: 8616-9101, which is efficiency driven when both H α and D4000 spaxels are included, but fuel driven when only H α spaxels are considered. Galaxy 8616-9101 is an interesting case given we expect spaxels that use D4000–ΣSFR to underestimate ΔSFE and bias towards large fuel fractions, but in this case including D4000 spaxels leads to a smaller fuel fraction. Considering only one galaxy changes dominant mechanism, we are assured that our results are not dependent on the inclusion of D4000–ΣSFR values.
The fuel fraction determined from only H α spaxels compared to the fuel fraction when both H α and D4000 spaxels are included. Ideally all galaxies would lie on the line of equality, implying that the inclusion of D4000 spaxels does not drastically change our results. But realistically there is scatter about the line of equality as more spaxels are included in the analysis. Difference between the two fuel fractions is alright, so long as it does not change which mechanism predominantly drives star formation. We have highlighted regions that ideally the points should lie within: where both fractions imply star formation is efficiency driven (red), where both fractions imply star formation is fuel driven (blue), and where both fractions imply star formation is driven by both (grey). Only one point lies outside these acceptable regions: 8616-9101, which is efficiency driven when both H α and D4000 spaxels are included, but fuel driven when only H α spaxels are considered.



