-
PDF
- Split View
-
Views
-
Cite
Cite
Junehyoung Jeon, Volker Bromm, Steven L Finkelstein, Maximal X-ray feedback in the pre-reionization Universe, Monthly Notices of the Royal Astronomical Society, Volume 515, Issue 4, October 2022, Pages 5568–5575, https://doi.org/10.1093/mnras/stac2182
Close - Share Icon Share
ABSTRACT
X-ray feedback in the pre-reionization Universe provided one of the major energy sources for reionization and the thermal evolution of the early intergalactic medium. However, X-ray sources at high redshift have remained largely inaccessible to observations. One alternative approach to study the overall effects of X-ray feedback in the early Universe is a full cosmological simulation. Towards this goal, in this paper we create an analytic model of X-ray feedback from accretion on to supermassive black holes (SMBHs), to be used as a sub-grid model in future cosmological simulations. Our analytic model provides a relation between the mass of a dark matter halo and the SMBH it hosts, where the efficiency is governed by an energy balance argument between thermal feedback and the confining gravitational potential of the halo. To calibrate the model, we couple the halo-level recipe with the Press–Schechter halo mass function and derive global mass and energy densities. We then compare our model to various observational constraints, such as the resulting soft X-ray and IR cosmic radiation backgrounds, to test our choice of model parameters. We in particular derive model parameters that do not violate any constraints, while providing maximal X-ray feedback prior to reionization. In addition, we consider the contribution of SMBH X-ray sources to reionization and the global 21 cm absorption signal.
1 INTRODUCTION
In the early Universe, sources of X-ray radiation had a significant effect on cosmic history (Mesinger, Ferrara & Spiegel 2013). First, X-ray and UV radiation drove the early stages of reionization (Glover & Brand 2003; Baek et al. 2010). Noticeable differences in the timing and topology of reionization occur depending on the leading radiation source. When UV sources dominate, reionization is thought to occur in bubbles of ionized gas within a neutral background (e.g. Loeb & Barkana 2001; McQuinn et al. 2007). However, when X-ray sources dominate, the ionized regions are distributed more evenly due to the large mean free path of X-rays (Pritchard & Furlanetto 2007; Fragos et al. 2013). Furthermore, the X-ray radiation would have delayed reionization by increasing the Jeans mass through pre-heating, so that the time-scale for halo formation was longer (Jeon et al. 2014; Finkelstein et al. 2019). On the contrary, X-ray radiation could suppress small-scale structure formation, thus in turn reducing recombination losses of ionizing photons, to accelerate reionization (Finlator et al. 2012; Emberson, Thomas & Alvarez 2013). However, there is still considerable uncertainty on what sources dominate reionization. The general view is that UV sources dominate and drive reionization (e.g. Ciardi, Ferrara & White 2003; Robertson et al. 2015; Parsa, Dunlop & McLure 2018; Finkelstein et al. 2019; Naidu et al. 2020), while some studies stress the role of active galactic nuclei (AGNs) in completing reionization (e.g. Madau & Haardt 2015; Volonteri et al. 2016).
The overall impact of X-ray feedback on star formation in the early Universe is complex. On the one hand, sources heat nearby gas and thus hinder star formation (Jeon et al. 2014). However, at larger distances, X-ray feedback may be able to compensate for the negative feedback from the UV photodissociation of molecular hydrogen, the main coolant in primordial star-forming haloes. The partial ionization from X-rays can result in an enhanced abundance of free electrons in predominantly neutral hydrogen gas, in turn catalysing the formation of hydrogen molecules (Glover & Brand 2003). The net effect can be additional cooling in protogalaxies, thus enhancing the early star formation rate (SFR).
Moreover, from the observed AGN X-ray and bolometric luminosities, the black hole (BH) accretion rate can be inferred if a constant radiative efficiency is assumed. Previous work found evidence for a correlation between the BH accretion rate and the SFR for bulge-dominated galaxies (Yang et al. 2019), possibly because the supermassive black holes (SMBHs) co-evolve with the stellar component of host galaxies (e.g. Kormendy & Ho 2013; Davis, Graham & Cameron 2018). This correlation can be used to determine the BH accretion density, to constrain models of BH formation and evolution (Yang et al. 2021). However, the known accretion density inferred from X-ray observations is an order-of-magnitude lower than what is predicted in theoretical simulation results (e.g. Crain et al. 2015; Volonteri et al. 2016; Weinberger et al. 2017). The reason for the discrepancy may be the observational bias due to obscured AGNs at high redshift (Weigel et al. 2015; Vito et al. 2016; Yang et al. 2021). Therefore, the nature of X-ray feedback, its sources and overall strength, needs to be better understood to deduce the progress of reionization, the formation and evolution of protogalaxies, and the implications from observations with frontier facilities, such as the James Webb Space Telescope (JWST).
Although X-ray feedback has been considered in many simulations of the early Universe (e.g. Fragos et al. 2013; Jeon et al. 2014; Ahn et al. 2015; Monsalve et al. 2019), its overall amplitude is highly uncertain, mainly due to the current lack of direct observations (Reines & Comastri 2016). Here, we therefore seek to determine the maximum X-ray feedback allowed by existing cosmological constraints, to be employed as a ‘maximal’ sub-grid model in future cosmological simulations. Direct constraints are the SMBH mass density at lower redshifts and the quasar luminosity function. For the SMBH mass density, we will consider local measurements (e.g. Fukugita & Peebles 2004; Marconi et al. 2004; Graham & Driver 2007), as well as semi-empirical determinations around z ∼ 4 (e.g. Mahmood, Devriendt & Silk 2005; Tucci & Volonteri 2017). While we model sources at z ∼ 5–15, beyond current observational capabilities, we compare extrapolations of our model to existing observations of the quasar luminosity function at z ∼ 5 (e.g. Shen et al. 2020). Furthermore, X-ray sources have a significant impact on reionization, as stated previously, and they also indirectly affect the signal from 21 cm cosmology. Finally, X-ray feedback has to be consistent with cosmic radiation backgrounds, including the soft X-ray background.1 We further consider the cosmic infrared background (CIB) as an indirect constraint, as the CIB is a global repository of reprocessed ionizing radiation at high redshifts, including the ionization resulting from X-ray photons.
Our resulting model of maximal X-ray feedback in the early Universe can be tested and improved with upcoming frontier facilities over a large range of wavelengths. Among them are the Euclid mission to study the CIB (Kashlinsky et al. 2018), the Square Kilometer array to map the cosmological 21 cm line (Ghara et al. 2017), the JWST to observe AGN emission from accretion at high redshifts (Volonteri et al. 2017), and the Athena and Lynx X-ray observatories (Barret et al. 2013; Gaskin et al. 2019) to directly observe high-redshift AGNs and quasar X-ray sources.
This paper is organized as follows. In Section 2, we discuss our modelling of X-ray feedback. We first model the number density and energy output for each X-ray source. In Section 3, we discuss the cosmological constraints considered here: reionization, the quasar luminosity function, the soft X-ray background, the CIB, and the 21 cm line. We conclude by summarizing our results in Section 4.
2 MODELLING X-RAY FEEDBACK
We will model X-ray feedback in the pre-reionization Universe by considering AGN/SMBH and X-ray binaries (Baek et al. 2010; Mirabel et al. 2011; Fragos et al. 2013; Jeon et al. 2014). For SMBH sources, we consider ‘standard’ formation pathways from massive stellar seeds, and will only briefly comment on the alternative direct collapse black hole (DCBH) channel, as the conditions for DCBH seed formation may be rare and difficult to achieve (Bromm & Loeb 2003; Habouzit et al. 2016).
2.1 Number and mass density of sources
2.1.1 AGN/SMBH sources
From Fig. 1, it is evident that the resulting SMBH mass density does not overproduce the approximate value estimated for z = 4–5 (e.g. Mahmood et al. 2005; Tucci & Volonteri 2017), and is clearly less than the local density at z = 0 (e.g. Graham & Driver 2007). This is also a consistency check on our simplifying assumption that every halo hosts an SMBH. Even though this may not be strictly correct for increasingly high redshifts, every halo eventually will host an SMBH at later times. Changing our assumption on the SMBH occupation fraction would thus only affect the high-z parts of Fig. 1, while the lower redshift prediction is quite robust. Furthermore, the choice of lower limit for the halo mass does not make a significant difference at lower redshifts, where typical SMBH host masses are much larger, and where most of our constraints are tested.
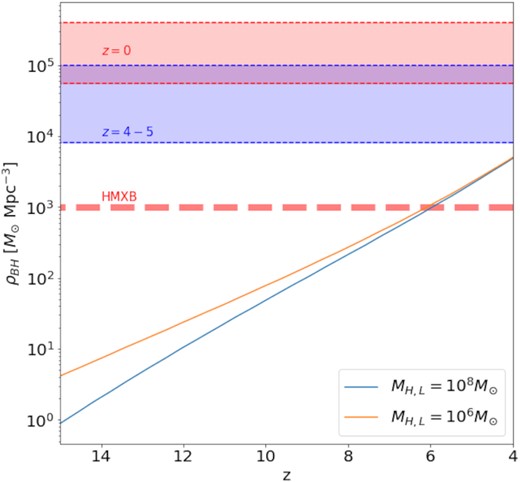
BH mass density versus redshift for two lower limits for the halo mass function. Assuming that every halo produces a BH, the integrated halo mass density is converted to an SMBH mass density using equations (1), (4), and (7). The red region indicates the approximate SMBH mass density at z = 0 (Graham & Driver 2007), and the blue region the modelled SMBH density at z = 4–5 (Mahmood et al. 2005; Tucci & Volonteri 2017). For comparison, we also show the extrapolated BH mass density (red dashed line) from accretion on to HMXBs (Jeon et al. 2014). The HMXB contribution here appears as a constant, because Jeon et al. (2014) considered mainly Pop III binaries at z ≳ 15, and not the complete populations of metal-enriched stars at lower redshifts. Our model is consistent with observations as the mass density does not exceed the model values at z ∼ 4.
Fig. 2 shows the relation between host halo mass and SMBH mass within our model, based on equation (1), and for comparison also the empirical M–σ relation from Evrard et al. (2008) and Kormendy & Ho (2013). Our idealized model is comparable in slope and scale to the observed M–σ relation. To avoid SMBH mass values that are unrealistically low, we have also added seed BH masses to our relation, such that |$M_\rm{BH}(t)=M_\rm{seed}+\dot{M}_\rm{acc}t$|. The seed masses are set as MH × 2 × 10−6, and have lower and upper limits of 102 and 105 M⊙ to not have unrealistic seed BH masses (e.g. Inayoshi, Visbal & Haiman 2020). The effects of the seed BHs are further discussed in Section 2.1.3.
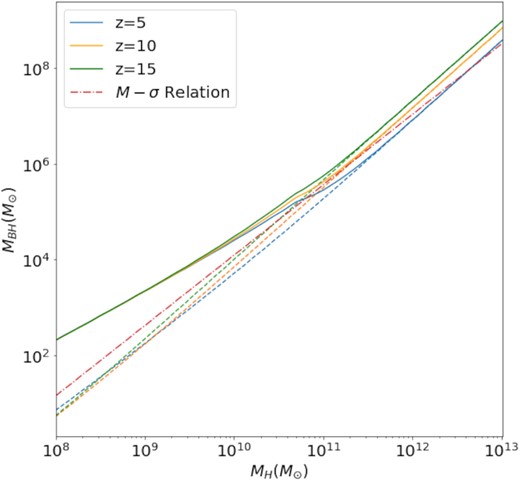
The resulting halo to SMBH mass relation, based on our model (see equation 1), and the empirical M–σ relation at z = 0 for comparison (Evrard et al. 2008; Kormendy & Ho 2013). The dashed lines represent the unmodified equation (1), whereas the solid lines show the augmented model where BH seeds are added to the mass budget. As can be seen, our idealized model matches the slope and overall normalization of the observed relation at z = 0 quite well.
2.1.2 Stellar X-ray binaries
Another important source of X-ray feedback in the early Universe is provided by stellar-remnant X-ray binaries (e.g. Mirabel et al. 2011), in particular high-mass X-ray binaries (HMXBs). A number of studies have focused on the binary statistics of Pop III stars (Stacy & Bromm 2013; Liu, Meynet & Bromm 2021), also extrapolating to the final remnant stage, with considerable uncertainties remaining. As an illustrative example, Jeon et al. (2014) selected around 30 per cent of Pop III binaries in their simulation to form HMXBs, following Power et al. (2009). While Jeon et al. (2014) capture HMXBs from Pop III, their modelling of subsequent, metal-enriched populations is highly incomplete. Comprehensively determining the contribution from HMXBs to the aggregate mass and energy densities considered here would require a separate, dedicated study, which is beyond the scope of this paper. With this caveat in mind, we reproduce their HMXB mass accretion density, as shown in Fig. 1, as a ballpark comparison for our BH model. We do not however explicitly include the HMXB contribution in our modelling, but only consider SMBH emission.
2.1.3 Seed black holes
We now consider the impact of explicitly modelling seed BHs in the resulting global BH mass densities in somewhat greater detail. Specifically including the mass-dependent seed masses used in producing Fig. 2, we show the modified densities in Fig. 3, which is to be compared with Fig. 1, where seed BHs had been ignored. Now, to not violate the density constraints, the lower halo mass limit becomes important. Evidently, for a lower limit of 106 M⊙, the global mass density in SMBH is overproduced, even challenging the z = 0 constraint. The lower limit of 108 M⊙, on the other hand, corresponding to an atomic cooling halo, produces a more realistic mass density. Therefore, the 106 M⊙ (minihalo) mass limit can be considered as the minimum halo mass required to trigger Pop III star formation (e.g. Bromm 2013), whereas the minimum halo mass to host a central SMBH is 108 M⊙, which is of the same order as the suggested minimum mass to host a bona-fide first galaxy (e.g. Bromm & Yoshida 2011).
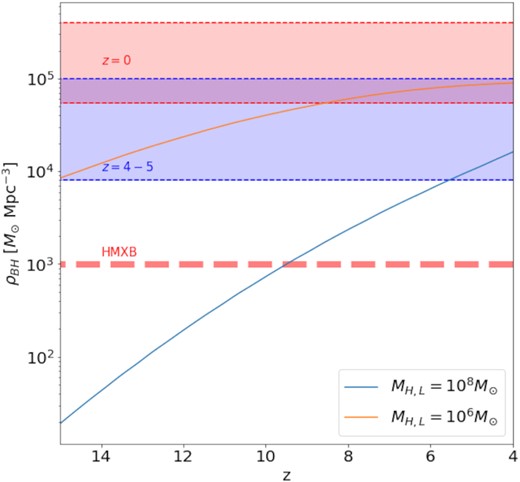
Impact of seed BHs on global mass densities. We consider the same quantities as in Fig. 1, except that here seed BH masses are included. Now, the choice of lower limit on the halo mass is reflected in significant differences in the resulting mass densities. Specifically, a lower limit of 106 M⊙, coupled with a seed BH mass of ∼100 M⊙, overproduces the empirical mass density at z ≃ 4–5, and even challenges the present-day constraint. The larger lower limit for the halo mass, on the other hand, still leads to overall consistent results.
Furthermore, we conclude that DCBH seeds of ∼105 M⊙ need to be rare, at least compared to our optimistic assumption that every halo hosts a central SMBH, to not overproduce the resulting mass density (also see Smith & Bromm 2019, and references therein). If we included a 105 M⊙ DCBH seed BH in every atomic cooling halo, the total BH mass density would be overproduced. More specifically, the fraction of atomic cooling haloes hosting DCBH seeds may be as low as 10−2–10−7 (assuming a comoving number density of atomic cooling haloes of ∼10 Mpc−3 at z = 10), depending on the strength of the Lyman–Werner background at that time (Habouzit et al. 2016). Finally, not all minihaloes near ∼106 M⊙ can host 100 M⊙ seeds, as the global mass density would be overproduced in that case, as shown in Fig. 3. However, the remaining constraints and tests are based on the radiation output (Soltan 1982), and will thus only depend on the mass accreted on to the SMBH, shown in Fig. 1. Therefore, the halo lower mass limit will not greatly affect the other tests applied to our model, and choosing 108 M⊙ as the lower limit is reasonable, as this choice also satisfies the global BH mass density constraint.
2.2 Energy density
3 COSMOLOGICAL CONSTRAINTS
3.1 Reionization
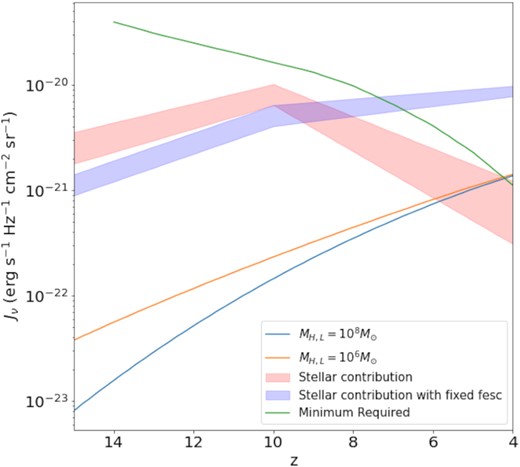
Ionizing radiation intensity versus redshift. We show the UV intensity produced by AGN sources prior to reionization (blue and orange lines), together with the intensity from star-forming galaxies (shaded blue and red zones), based on an extrapolation of observations of non-ionizing UV emission from galaxies at z ≃ 4–10 (Finkelstein et al. 2019). For the AGN UV contribution, we consider lower limits for the halo mass of 106 M⊙ (blue line) and 108 M⊙ (orange line). The stellar contribution is subject to the uncertainty regarding the escape fraction of ionizing photons. The blue shaded region shows the results when a fixed ionizing photon escape fraction of 13 per cent is used for all galaxies, while the red shaded region shows the results when assuming a halo-mass dependence for the escape fraction. We also indicate the critical intensity required to complete reionization from Madau et al. (1999), representing the instantaneous emissivity required to sustain a reionized IGM, which depends on the IGM clumping factor (green line). We assume a clumping factor similar to Finkelstein et al. (2019). The studies referenced above report UV emissivities, which we convert to photon densities by multiplying with the Hubble time.
3.2 X-ray luminosity function
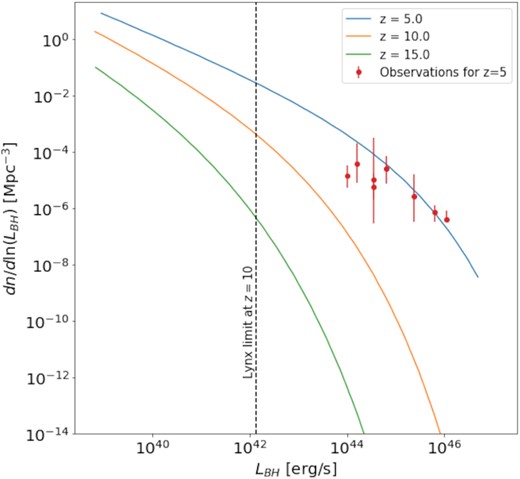
AGN luminosity function at high redshift. We show comoving number densities versus bolometric luminosity, derived from our PS mass functions for select redshifts. The observed luminosity function at z = 5 is reproduced from Shen et al. (2020). We also mark the limiting luminosity that can be reached with the Lynx observatory at z = 10 (Ricarte & Natarajan 2018). As can be seen, our luminosity function at z = 5 is in overall agreement with the observations.
3.3 Soft X-ray background
The soft X-ray background is the lower energy part of the X-ray background (≤2 keV) with contributions mainly from AGNs, but also from galaxies and stellar sources (Cappelluti et al. 2012; McQuinn 2012). While most of the background has been resolved into point and extended sources with Chandra and XMM–Newton (Moretti et al. 2003; Bauer et al. 2004; Lehmer et al. 2012), a sizeable 5–10 per cent of the background remains unresolved. Low-luminosity AGNs most likely make up the bulk of this unresolved fraction, and for consistency, our model cannot overproduce the energy deposited into the X-ray background. For simplicity, we assume that the entire BH mass density, as shown in Fig. 1, has been assembled through radiatively efficient accretion, such that ρacc ∼ ρBH. We thus effectively neglect any contribution to the BH mass budget from seed BHs and mergers. At least the former approximation is well justified, as discussed above. With these idealized assumptions, we plot SMBH mass accretion densities in Fig. 6, and compare to the upper limit for the unresolved soft X-ray background, expressed in the same units (Salvaterra et al. 2012). As can be seen, our model does not exceed this limit even at z = 4, demonstrating overall consistency with the X-ray background observations.
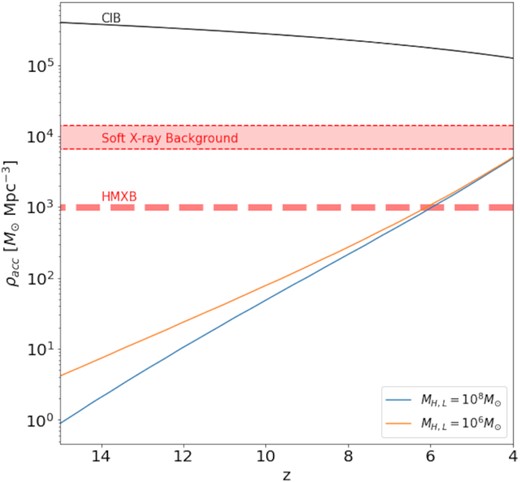
Cosmic radiation backgrounds from SMBH mass accretion. Similar to Fig. 1, we show our model SMBH mass accretion densities, compared to upper limits from cosmological backgrounds. The soft X-ray background limit corresponds to the maximal possible accretion for z ≳ 5, based on the unresolved background from Salvaterra et al. (2012). The CIB limit is the mass accretion required for SMBHs to produce the observed CIB fluctuations at a given redshift, provided in Helgason et al. (2016).
3.4 Cosmic infrared background
X-ray feedback contributes indirectly to the CIB, as well. More specifically, recombining gas that is ionized by X-rays produces Ly α photons. The Ly α radiation, emitted at z ∼ 10, is then redshifted into the infrared by z = 0, thus contributing to the CIB today (Rybicki & Lightman 1986; Santos, Bromm & Kamionkowski 2002). The current limits on the unresolved CIB therefore impose another global constraint on pre-reionization X-ray feedback. To illustrate this additional constraint, Fig 6 also shows the accretion density required for SMBHs to produce the observed CIB fluctuations, given by equation 16 in Helgason et al. (2016). Our model accretion lies far below this value, thus obeying the CIB constraint, but also predicting that SMBHs alone cannot account for the observed level of CIB fluctuations.
3.5 21 cm radiation
In general, X-ray sources indirectly contribute to the cosmological 21 cm signature (e.g. Furlanetto, Oh & Briggs 2006). The X-ray emission heats the surrounding neutral hydrogen gas and produces Ly α photons. The total Ly α radiation, including all available sources, is then able to produce observable 21 cm lines from the Wouthuysen–Field effect (Wouthuysen 1952; Field 1958). Here, neutral hydrogen absorbs Ly α photons and produces a change in spin state during relaxation, thus rendering the 21 cm transition detectable in absorption relative to the CMB (Pritchard & Loeb 2012). In Fig. 7, we compare the Ly α intensity from our model to the critical intensity required to produce the 21 cm line via the Wouthuysen–Field coupling (Ciardi & Madau 2003). For simplicity, we assume that each ionization event results in the emission of a Lyman-α photon, such that Jα ≃ JUV, ν (see equation 12). A detailed modelling of the complex radiative transfer and nebular reprocessing involved is beyond the scope of this paper.3 For comparison with the AGN contribution, we also reproduce the Ly α intensity originating in massive Pop III stars (Schauer et al. 2019). Our model does not reach the minimum intensity until z = 8, while the stellar intensity does at z = 20.
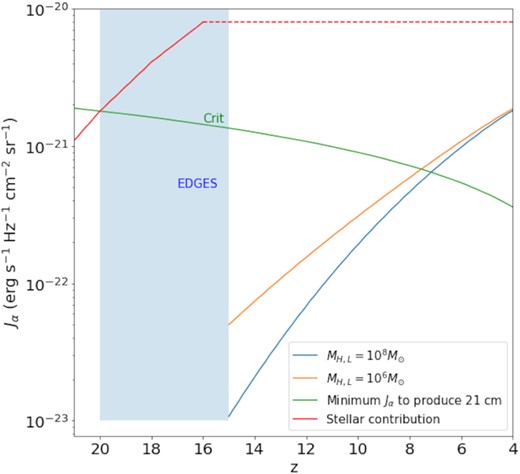
The cosmic Lyman-α intensity versus redshift, from stellar sources (galaxies) and AGN feedback, similar to Fig. 4. We reproduce the minimum Ly α intensity required to imprint a global 21 cm absorption feature, taken from Ciardi & Madau (2003). We also show the stellar contribution, mostly from Pop III, as modelled in Schauer, Liu & Bromm (2019). The EDGES timing constraint from Mirocha & Furlanetto (2019) is indicated with the blue shaded region. The stellar contribution at z = 16 is extrapolated to z = 4 (dashed line), to compare to the AGN contribution modelled here. Our model does not reach the necessary intensity until z ∼ 8, and thus does not produce the 21 cm line too early.
The moment of ‘cosmic dawn’, when Wouthuysen–Field coupling first becomes effective, is currently under vigorous debate. The Experiment to Detect the Global Epoch of Reionization Signature (EDGES) had reported a strong, global absorption feature at 78 MHz, corresponding to a redshift of z ∼ 17 for the line centre (Bowman et al. 2018). We indicate the EDGES constraint in Fig. 7, as well, implying that our modelled AGN intensity does not produce the 21 cm line too early, and is thus consistent with observations. We note that the recent result from the Shaped Antenna Measurement of the Background Radio Spectrum (SARAS) has cast doubt on the original EDGES detection (Singh et al. 2022), but the radio-astronomical debate is far from over.
Besides the Wouthuysen–Field effect, X-ray feedback can affect the 21 cm signal through pre-heating of the diffuse gas. Specifically, HMXBs have been shown to pre-heat the intergalactic medium (IGM) and increase the brightness temperature on large scales (e.g. Jeon et al. 2014). The overall effect is that the heated IGM, outside the regions that are ionized by stellar sources, can produce the 21 cm line at early times, whereas the fully ionized IGM at later times cannot (Baek et al. 2010). However, this effect is difficult to assess with our current model considering the complex physics of the IGM and the clustering of AGN sources. A cosmological simulation will be able to study this heating effect comprehensively.
4 SUMMARY AND CONCLUSIONS
In this paper, we have constructed a model to explore the impact of X-ray feedback from high-redshift AGNs on the Universe before reionization. X-ray feedback can have conflicting effects on reionization and early star formation, so we assess limits on the available X-ray feedback within our model. We follow a semi-analytical approach, starting with the PS halo mass function (Press & Schechter 1974), and imposing a balance between the dark matter halo gravitational potential energy and the feedback energy from a central SMBH, to derive a relationship between the halo and BH mass. We further use the halo–SMBH mass relation to predict SMBH mass densities over cosmic time. We in particular choose our model parameters to produce the maximum amount of X-ray feedback possible. The SMBH occupation fraction is set to unity, so that every halo above a critical mass (106 or 108 M⊙) hosts at least one SMBH for maximal feedback.
We subject our model to a number of tests to see if it violates any observational constraints. Among the tests, we consider the global SMBH mass density, the completion of reionization, the quasar luminosity function, select cosmic radiation backgrounds, and the (redshifted) 21 cm line, imprinted by neutral hydrogen in the early IGM. Regarding the mass density, luminosity function, and the cosmic backgrounds considered, our model does not overproduce the current observational constraints. Regarding reionization and the 21 cm line, our model does not produce the corresponding couplings between radiation fields and hydrogen gas too early, and is thus also consistent with these observations. Our X-ray feedback model, thus tested and constrained, can serve as a sub-grid model in future cosmological simulations of high-z galaxy formation.
In our derivation of the model, only a few free parameters remain including the SMBH occupation fraction and the 3D geometry of |$\rm {H}\scriptstyle \mathrm{II}$| regions in the halo. However, modifying the free parameters may contradict the empirical constraints. Our model predictions are close to the observed upper limits on the luminosity function and the soft X-ray background, as shown in Figs 5 and 6, such that the feedback cannot be much higher. We further argue that our choice for these parameters has physical merit. The chosen ionized fraction of the halo is in line with previous work on AGN opening angles (Sazonov et al. 2015). The occupation fraction is most likely unity at lower redshifts, as every observed galaxy hosts a BH at its centre (Kormendy & Ho 2013). Although deviations from our simple ‘one SMBH per halo’ assumption are likely at high redshifts, imposing this condition on all haloes and cosmic times is adequate for our current semi-analytic model.
We seemingly have little freedom in designing our subgrid model, because the model parameters are tightly constrained by seemingly robust physical arguments. Within the original energy feedback argument, the dimensionless parameter f is effectively set by assuming Eddington-limited accretion, occurring over the Salpeter time-scale. However, some previous studies have argued that in the early Universe, SMBHs went through super-Eddington accretion instead (e.g. Pezzulli, Valiante & Schneider 2016; Regan et al. 2019). We have also assumed a simple, bipolar geometry for the ionized |$\rm {H}\scriptstyle \mathrm{II}$| regions, whereas the true situation is likely much more complex, requiring sophisticated 3D radiative transfer simulations to fully capture reality (Alvarez & Abel 2007; McQuinn et al. 2007). Nevertheless, our idealized model serves to explore the relevant parameter space, thus informing follow-up cosmological simulations.
Our modelling is subject to a number of caveats. Clearly, our treatment of SMBH accretion and the structure of the ionized halo regions is highly idealized. The constraints mostly derive from observations at lower redshifts, so that the high-z modelling is only indirectly tested. For example, the most direct constraints considered here, the SMBH mass density and the quasar luminosity function, are currently observed only at low redshifts (Shen et al. 2020), and even the constraint at z = 4–5 on the BH mass density involves model extrapolations (Mahmood et al. 2005; Tucci & Volonteri 2017). Even the most robust tests therefore exhibit considerable uncertainties, which will be addressed with future observations at higher redshifts.
Overall, our model indicates that X-ray feedback was important in the evolution of the early Universe. While the model X-ray feedback does not significantly contribute to the CIB or the 21 cm line, Fig. 4 indicates that the contribution from AGNs may have been comparable to stellar sources in completing the reionization of the Universe. Furthermore, Fig. 6 implies that high-z AGNs could explain the unresolved soft X-ray background. Thus, excluding X-ray feedback when studying early cosmic evolution will not be realistic. In contrast, previous work such as Cappelluti et al. (2017) concluded that the emission from high-z AGN sources would have to be heavily obscured in Compton-thick envelopes to not violate existing constraints. In this case, the large optical depth would significantly reduce the impact of any AGN feedback. In future work, employing cosmological simulations, we will more thoroughly explore such radiative transfer effects. To improve our modelling of X-ray feedback, direct observations of high-redshift AGN/SMBH sources will be needed. More specifically, distinguishing the feedback from AGNs and stars at high redshifts may be possible with future X-ray observatories, such as Athena and Lynx (Barret et al. 2013; Ricarte & Natarajan 2018; Gaskin et al. 2019), or with observations of the rest-frame UV at different wavebands with JWST (Volonteri et al. 2017).
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
Footnotes
However, a number of additional empirical constraints on the quasar luminosity function at z ∼ 6 exist (e.g. Jiang et al. 2016).
The standard nebula physics of case-B recombination predicts that only 0.68 of all recombinations would result in the emission of a Ly α photon. Such order-unity corrections would not change any of our conclusions.



