-
PDF
- Split View
-
Views
-
Cite
Cite
Enia Xhakaj, Alexie Leauthaud, Johannes Lange, Andrew Hearin, Benedikt Diemer, Neal Dalal, Beyond mass: detecting secondary halo properties with galaxy-galaxy lensing, Monthly Notices of the Royal Astronomical Society, Volume 514, Issue 2, August 2022, Pages 2876–2890, https://doi.org/10.1093/mnras/stac941
Close - Share Icon Share
ABSTRACT
Secondary halo properties beyond mass, such as the mass accretion rate (MAR), concentration, and the half mass scale, are essential in understanding the formation of large-scale structure and dark matter haloes. In this paper, we study the impact of secondary halo properties on the galaxy-galaxy lensing observable, ΔΣ. We build an emulator trained on N-body simulations to model ΔΣ and quantify the impact of different secondary parameters on the ΔΣ profile. We focus on the impact of MAR on ΔΣ. We show that a 3σ detection of variations in MAR at fixed halo mass could be achieved with the Hyper Suprime Cam survey assuming no baryonic effects and a proxy for MAR with scatter <1.5. We show that the full radial profile of ΔΣ depends on secondary properties at fixed halo mass. Consequently, an emulator that can perform full shape fitting yields better than two times improvement upon the constraints on MAR than only using the outer part of the halo. Finally, we highlight that miscentring and MAR impact the radial profile of ΔΣ in a similar fashion, implying that miscentring and MAR need to be modelled jointly for unbiased estimates of both effects. We show that present-day lensing data sets have the statistical capability to place constraints on halo MAR within our assumptions. Our analysis opens up new possibilities for observationally measuring the assembly history of the dark matter haloes that host galaxies and clusters.
1 INTRODUCTION
In the concordance cosmological model, dark matter is the dominant form of matter in the Universe. Small density perturbations in the early Universe, coupled with the effects of gravity, lead to the formation of virialized structures, called dark matter haloes (e.g. Gunn & Gott 1972; Fillmore & Goldreich 1984). The rate at which haloes accrete dark matter can be crucial in understanding the growth of both large-scale structure and galaxies. It has long been known that halo mass accretion rate (MAR) is correlated with the baryon cooling rate (e.g. White & Rees 1978; Fall & Efstathiou 1980; Blumenthal et al. 1986). This, in turn, influences the formation of clusters and luminous galaxies. From a galaxy formation perspective, many recent studies have confirmed that MAR correlates with star formation and is therefore valuable in probing galaxy growth (e.g. Diemer, Kravtsov & More 2013; Wetzel & Nagai 2015; O’Donnell, Behroozi & More 2021).
Furthermore, it has been shown that halo clustering depends on secondary halo properties other than mass, the most notable of which is mass accretion history (MAH; e.g. Wechsler et al. 2001; Gao, Springel & White 2005; Wechsler et al. 2006; Li, Mo & Gao 2008). This effect is commonly referred to as ‘halo assembly bias’. Early work on this topic primarily focused on its manifestation on large scales. Recent work has highlighted an aspect of assembly bias that is especially relevant for the present paper: secondary halo properties beyond mass produce distinct, scale-dependent features upon large-scale structure observables that have the potential to serve as signatures of the particular secondary property (Sunayama et al. 2016; Behroozi, Hearin & Moster 2022). Having an adequate understanding of the spatial distribution of haloes is essential in interpreting how galaxies cluster. Thus, understanding the MAHs of haloes is a key ingredient in accurately modelling the dark matter distribution in the Universe. Finally, MAR can also be used as an independent cosmological probe to constrain σ8 and Ωm. For example, Hurier (2019) showed that certain definitions of MAR can be nearly independent of halo mass. As such, MAR can constrain the σ8-Ωm degeneracy without needing to calibrate a mass–observable relation.
Given the importance of MAR in understanding the fundamentals of structure formation, a natural question is whether it can be measured in observations. Halo outskirts have shown strong prospects in detecting MARs. For instance, Diemer & Kravtsov (2014) model density profiles as comprised of three parts: an Einasto profile (i.e. the one-halo term), a power-law term (i.e. the two-halo term), and a function that models the transition of the one- and two-halo terms by truncating the Einasto profile. The radius at which this truncation happens is defined as rt. Diemer & Kravtsov (2014) show a strong correlation between rt and the splashback radius. Both these quantities are, in turn, determined by MAR. The splashback feature has been previously proposed as a potential observable for detecting MARs (Diemer & Kravtsov 2014; Xhakaj et al. 2020). It is well known that the splashback feature is tightly correlated with MAR (e.g. Adhikari, Dalal & Chamberlain 2014; Diemer & Kravtsov 2014; More, Diemer & Kravtsov 2015). Xhakaj et al. (2020) studied how well this correlation can be detected with present and future surveys. They showed that detecting MAR through the splashback radius would be feasible, assuming ideal observational proxies of both halo mass and MAR. Thus, both rt and the splashback radius can be used as observational probes to detect MAR.
Moreover, it has long been known that halo profiles correlate with concentration. Wechsler et al. (2002) showed that the concentration parameter from the Navarro-Frenk-White profile (NFW; Navarro, Frenk & White 1996) correlates with the halo mass assembly history. Ludlow et al. (2013) further showed that the Einasto profile shape parameters correlate with concentration and halo assembly history. However, both of these studies use concentration as a proxy for MAH. This is because concentration can be conveniently measured as the ratio of the virial to the scale radius of the halo |$(c_{\rm vir} = \frac{R_{\rm vir}}{R_{\rm s}})$|, where Rs is the scale radius and Rvir is the virial radius of the halo. The scale radius Rs is one of two free parameters in the NFW profile. However, concentration is a descriptive parameter that simply tells us about the shape of the present-day halo profile. In this paper, we wish instead to study the impact of physical properties on halo profiles. We therefore study the impact of MAHs on mass profiles directly, without adopting cvir as a proxy.
Galaxy-galaxy lensing is potentially the most direct method for tracing the mass profiles of dark matter haloes in observations. Lensing studies of galaxies or clusters often assume that samples have been selected purely by mass. However, a selection by richness mass may result in an unintentional selection by MAR. For example, Bradshaw et al. (2020) showed that richness selected samples might be biased towards young haloes with larger recent accretion than other haloes of similar mass. As another example, a selection of blue galaxies may result in a selection of haloes with higher present MAR compared to average. Until recently, lensing measurements did not have enough signal to noise for the impact of secondary halo properties to be of great importance. As lensing surveys continue to expand, it is timely to thoroughly investigate the effect of secondary halo properties on the galaxy-galaxy lensing profile.
This paper introduces the idea that the whole galaxy-galaxy lensing profile contains information about secondary halo properties, including MAR. Another goal is to show that full weak lensing profiles have better constraining power on MAR than the information contained in the location of halo outskirts (e.g. Diemer & Kravtsov 2014; Xhakaj et al. 2020). Fig. 5 of Xhakaj et al. (2020; also displayed in Fig. 1) showed that MAR has a strong impact on the shape of ΔΣ. In this paper, we follow up on that analysis by studying how different secondary halo properties affect the shape of the weak lensing profile. Then, we examine whether MAR is detectable with the full area of Hyper Suprime Cam survey (HSC; Aihara et al. 2018). Given that there is no analytical expression for the variation of the galaxy-galaxy lensing profile with MAR, we build a model based on N-body simulations. We use an emulation technique to predict the weak lensing profiles given halo mass and MAR. We study how constraints are affected by observational scatter in proxies of halo mass and MAR. Then, we analyse how cluster-finding systematics such as miscentring can bias detections of MAR. Finally, we compare our method for detecting MAR with the methods introduced in Diemer & Kravtsov (2014) and Xhakaj et al. (2020). We conclude that full shape profile fitting results in better constraints on MAR than the splashback radius alone.

Weak lensing profiles of dark matter haloes binned by halo MAR at fixed mass. The shape of the lensing profile depends on MAR.
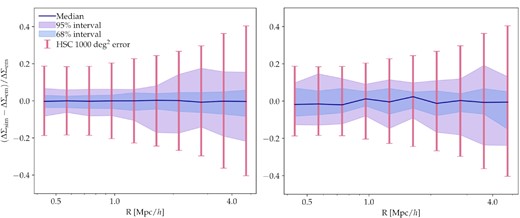
Performance of the 2D (left) and 4D (right) emulators over the respective test samples. Here, we measure the deviation of the ΔΣ profile of the test points (ΔΣsim) from the respective emulated profiles (ΔΣem). Blue and purple contours display the 1σ and 2σ errors of the emulator. The vertical error bars display the predicted HSC 1σ measurement error for the fiducial cluster sample and the full 1000 deg2 area. The error for both emulators is smaller than the observational error. Specifically, it is 10 per cent of the measurement error for the 2D emulator and 20 per cent of the measurement error for the 4D emulator.
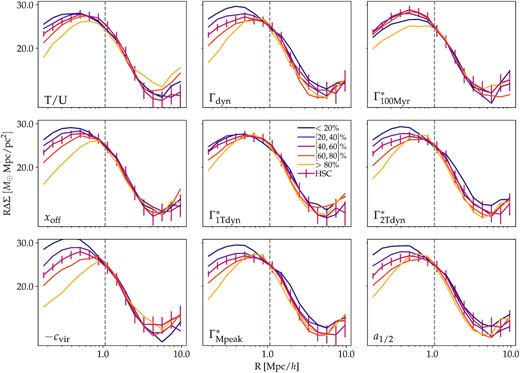
Impact of secondary halo parameters on the shape of the weak lensing profile, ΔΣ. Each panel displays variations in ΔΣ with secondary halo properties at fixed halo mass (M200m = 1014 M⊙ h−1). Halos are binned by the value of the secondary property using percentiles conditioned on mass as described in Section 5.1. For example, in the upper left, orange corresponds to the 20th percentile of haloes with the highest values of T/U, and purple corresponds to the 20th percentile of haloes with the lowest values of T/U. The left column shows instantaneous parameters. The middle and right columns display MAH parameters. Anticipated errors from the 1000 deg2 HSC wide-field surveys are overlaid as a reference on each of the panels. The dashed line displays the mean R200m of the halo sample. Different halo properties lead to different ΔΣ profiles, and these differences are especially pronounced in the one-halo regime.
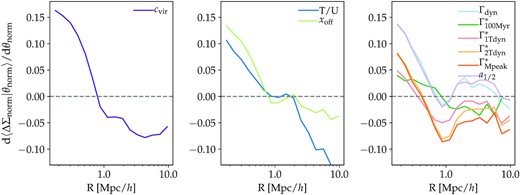
Variance of the normalized ΔΣ profile with respect to a given secondary halo parameter, θ in MDPL2. The y-axis can be thought of as the fractional change in ΔΣ for a 1σ change in the secondary halo parameter. The left-hand panel displays cvir. The middle panel displays other instantaneous halo parameters. The right-hand panel displays MAH parameters. All parameters except T/U show stronger variations in the inner regions than in the outer regions. These variations can reach up |$16 {{\ \rm per\ cent}}$| in the inner regions. The largest variations are on R = 0.2 − 0.4 Mpc h−1 scales. Among instantaneous parameters, cvir displays the largest variations. Among MAR parameters, Γdyn and a1/2 have the strongest impact.
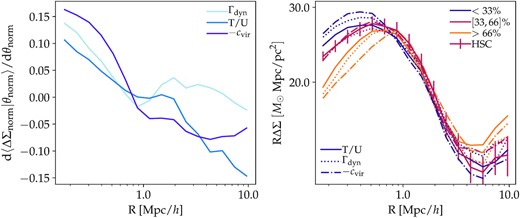
Halo properties that have the strongest impact on the shape of the lensing profile. Left: variance of the normalized ΔΣ profiles with respect to secondary parameters (Fig. 4). Right: illustration of how the ΔΣ profile changes when we bin by each parameter. Of the three parameters plotted here, cvir displays the largest impact in the one-halo regime, followed by Γdyn and then T/U. This is also illustrated in the right-hand panel, in which the ΔΣ profiles show the largest variance when binned by cvir. Each parameter also imparts a distinct radial dependence on the shape of ΔΣ.
This paper is structured as follows. We introduce the numerical simulations and the emulator in Sections 2 and 3. Section 4 describes secondary halo parameters that correlate with the shape of the weak lensing profile. We show results in Section 5 and discuss them in Section 6. Finally, we summarize and conclude in Section 7. We adopt the cosmology of the MultiDark Planck 2 simulation (MDPL2; Prada et al. 2012), namely, a flat, ΛCDM cosmology with |$\Omega _\mathrm{\rm m} = 0.307$|, |$\Omega _\mathrm{\rm b} = 0.0482$|, σ8 = 0.829, h = 0.678, |$n_\mathrm{\rm s}=0.9611$|, corresponding to the best-fitting Planck cosmology (Planck Collaboration XXXI 2014).
2 NUMERICAL SIMULATIONS AND CLUSTER SAMPLE
2.1 Numerical simulation
We study cluster-sized haloes from the publicly available MDPL2 simulation, which follows 38403 particles in a cubic box of size 1 Gpc h−1. Halos are identified using the ROCKSTAR halo finder (Behroozi, Wechsler & Wu 2013a). Merger trees are constructed using Consistent Trees, an algorithm that models the evolution of haloes among different snapshots (Behroozi et al. 2013b). We select host haloes at z = 0.36 and |$M_\mathrm{200m}\in [10^{13.5}, 10^{14.5}]\, h^{-1}{\rm M}_\odot$| where M200m is the halo mass enclosed in an overdensity of 200 times the mean matter density of the Universe. We choose this mass range because of the availability of high-signal-to-noise weak lensing measurements around samples of luminous red galaxies (e.g. Leauthaud et al. 2017; Singh et al. 2019; Lange et al. 2021) and clusters (e.g. Chang et al. 2018). In Section 3.3.2, we build an emulator to model weak lensing profiles over this mass range.
In addition, we remove a small number of haloes with negative Γdyn values, where Γdyn is the MAR computed over one dynamical time as defined in equation (14; see Section 4.2). A negative value of Γdyn can be caused by mergers or fly-bys. After these cuts, haloes have Γdyn values ranging from 0 to 8. Our final set consists of 89 790 haloes. To compute lensing signals, we use a downsampled catalog of 50 million particles (see Section 3.1).
2.2 Fiducial mock cluster sample
We now consider a fiducial sample of clusters drawn from a more narrow mass and MAR range than in the previous section. This baseline cluster sample consists of haloes with |$M_\mathrm{200m}\in [10^{13.8}, 10^{14.1}]\, h^{-1}{\rm M}_\odot$| and Γdyn ∈ [2.5, 3.5] at z = 0.36 (a total of 4932 haloes). We use this sample to predict signals for a fiducial HSC-like cluster sample. The sample that we consider would be drawn from the HSC final survey area, covering 1000 deg2, and 0.3 < z < 0.6. This HSC-like sample would contain 1776 clusters.
We generate lensing error bars for the HSC cluster sample using the same methodology as Singh et al. (2017). These forecast error bars encompass all the terms needed to describe a Gaussian covariance and assume perfect observational tracers for mass and MAR. With a generous redshift cut to separate source galaxies from lens galaxies, shape noise dominates the covariance. The error bars do not account for effects due to HSC-like selection or masks or the non-Gaussian covariance. Furthermore, we do not account for the photometric errors of the source galaxies. For an HSC-like selection, we overestimate the signal to noise by at most 25 per cent making our predictions somewhat optimistic in this regard. For a redshift range of 0.3 < z < 0.6, the final HSC volume is 0.36 Gpc3 h−3, which is smaller than the volume of MDPL2 (1 Gpc3 h−3). Because of this, we neglect sample variance in MDPL2 when generating models.
We build two fiducial mock cluster samples: in the first sample, clusters are perfectly centred. The other set consists of clusters that have been off-centred by some distance Rmis, where Rmis is defined in Section 3.3.1. Section 3.3.1 also describes how we forward-modelled miscentring in simulated haloes. In the following sections, we subdivide this fiducial sample into smaller bins. HSC weak lensing errors for each sub-division are recomputed with the appropriate number of haloes in each bin.
3 METHODS
3.1 Measuring ΔΣ for the fiducial cluster sample
3.2 The dependence of the shape of ΔΣ on secondary halo properties
If equation (3) is computed such that θ represents an array of all secondary halo properties, then |$\frac{\partial \langle \Delta \Sigma | \theta \rangle }{\partial \theta }$| describes the change in the weak lensing profile over the change in a secondary halo property, while the other halo properties are fixed. However, all secondary halo parameters considered here are tightly correlated with each other. Our goal is to analyse the impact of each parameter on the shape of the galaxy-galaxy lensing profile. Thus, we compute the full derivative, |$\frac{\mathrm{d} \langle \Delta \Sigma | \theta \rangle }{\mathrm{d} \theta }$|, instead. We set θ equal to a single halo property rather than an array of properties as in equation (3). |$\frac{\mathrm{d} \langle \Delta \Sigma | \theta \rangle }{\mathrm{d} \theta }$| describes the change in the shape of the weak lensing profile with respect to the change in halo parameters while allowing the rest of the parameters to be free. To avoid capturing correlations of mass and MAR with the shape of the weak lensing profiles, we select haloes from a narrow range around |$M_\mathrm{200m}\, = 10^{14} h^{-1} \mathrm{M}_\odot$|. The results for this analysis are shown in Section 5.1.
3.3 Modelling weak lensing profiles
We aim to build a model that predicts stacked ΔΣ profiles given halo bins in M200m, Γdyn, and halo miscentring. It has long been known that the shape of the lensing signal can be modelled analytically as an NFW profile with varying concentration (Bartelmann 1996; Wright & Brainerd 2000). However, no analytical model captures the dependence of the weak lensing profiles on other secondary halo properties, such as MAR. Thus, we introduce a model for ΔΣ profiles built directly from N-body simulations. Our model takes the form of an emulator trained on MDPL2 haloes. A more advanced version of the emulator also includes the effect of miscentring on the shape of the profile.
The lensing signal has previously been emulated through N-body simulations (i.e. Dark Quest, Nishimichi et al. 2021). Dark Quest uses a cosmological suite to emulate halo lensing profiles. The main purpose of this emulator is to model the 3D halo-matter correlation function on various cosmological parameters. Assuming spherical symmetry, it then computes the ΔΣ profile via an analytic projection integral. Our emulator is complementary to this effort: while we do not calibrate cosmology dependence, we relax the spherical symmetry assumption. Moreover, we include a dependence on MAR and miscentring effects. Modelling cosmological parameters and MAR by emulating the ΔΣ signal directly would avoid the spherical symmetry assumption and provide more accurate cosmology results. This will be interesting to explore in future work.
In the following sections, we describe the method employed to implement and test the emulator. We perform a likelihood analysis to determine whether Γdyn (a MAH parameter defined in Section 4.2) can be detected with HSC. The results for this analysis are shown in Sections 5.2 and 5.4.
3.3.1 Modelling miscentring
Miscentring is a systematic effect in current cluster finding algorithms (e.g. Rozo et al. 2014; Rozo & Rykoff 2014; Rozo et al. 2015). We believe that miscentring might have a similar impact as secondary halo properties on the shape of the lensing profile. In this section, we describe analytic modelling for miscentring. Then, we show how we forward model it in MDPL2 haloes.
3.3.2 Full profile modelling
We train GPs to build two different emulators: one whose only free parameters are Γdyn and M200m (hereafter the 2D model) and one that includes the miscentring parameters as well (the 4D model). Our training and test sets for both emulators consist of stacked ΔΣ profiles built from 600 bins in Γdyn and M200m containing 800 haloes each. In our sample, 80 per cent belong in the training set, while the rest serve as the test sample. The training and testing parameter range is M200m ∈ [1013.5, 1014.5]M⊙ h−1, Γdyn ∈ [0, 8], fmis ∈ [0.7], and Rmis ∈ [0, 1]Mpc h−1. The mean parameter values of each bin are selected through a latin-hypercube sampling of haloes in the M200m-Γdyn-fmis-Rmis parameter space. We compute stacked ΔΣ profiles through Halotools as described in Section 3.1.
While M200m and Γdyn are intrinsic halo parameters, we forward model the effect of fmis and Rmis on ΔΣ as described in the previous section. Training a GP requires choosing the best-fitting hyper-parameter of our training set. We constrain the kernel function with a heteroscedastic regression. Given that each training bin has an unequal scatter in M200m and Γdyn, we compute the sample variance for each bin through jackknife resampling. We include a different scatter in mass and MAR in order to account for the unequal scatter in the bins of the training sample. Because the number of haloes on each bin is constant, the width of the bins in mass and MAR varies throughout the parameter space. For example, bins in low mass-low MAR region are smaller in width than bins in high mass-high MAR region. This is because there are more haloes in the low mass-low MAR region than in the high mass-high MAR region. The heteroscedastic regression takes into account the different bin widths for mass and MAR when fitting the GP. We construct independent GPs for each radial bin of ΔΣ. Hence, a specific radial bin has its own optimized hyperparameters. This technique ignores the correlation between different radial bins in ΔΣ. Although not ideal, this approach is optimal in balancing emulation speed and accuracy. The emulator predicts ΔΣ over 10 radial bins ranging from 0.4 to 41 Mpc h−1.
To test the trained GP, we simulate stacked ΔΣ profiles (ΔΣsim) for all bins in the test sample. Then, we study how well the 2D and 4D emulators recover ΔΣsim. Fig. 2 displays the error in the 2D and 4D models. For the 2D model, the error in the emulator is 10 per cent of the measurement error, while for the 4D model, it is 20 per cent of the measurement error. The modelling error is smaller than the predicted HSC measurement errors for our fiducial cluster sample for both emulators. Thus, the 2D and the 4D emulators are suitable for modelling ΔΣ for this project.
3.4 Full profile fitting
Following previous work, we impose Gaussian priors on fmis and Rmis (Rykoff et al. 2016; Chang et al. 2018). We set the mean of the distribution to our fiducial values for fmis and Rmis, and the width to the respective priors (|$\sigma _{f_\mathrm{mis}} = 0.11$| and |$\sigma _{R_\mathrm{mis}} = 0.1\, \mathrm{Mpc}\,h^{ -1}$| as in Rykoff et al. 2016). Finally, we set flat priors on Γdyn and M200m. We assess convergence by minimizing the autocorrelation time of the MCMC.
4 SECONDARY HALO PARAMETERS
We classify secondary halo properties into two sets: instantaneous tracers and MAH parameters. The first set corresponds to parameters that describe the present state of the halo. The second set contains parameters that describe the past MAH of the halo measured on different time-scales.
4.1 Instantaneous halo parameters
Instantaneous halo parameters include the ratio of the kinetic to the potential energy of the halo (T/U), the offset between the halo centre and its centre of mass (xoff), and halo concentration (cvir). These parameters can be used as proxies to determine the dynamical state of the halo. For example, haloes with low T/U have more potential than kinetic energy than haloes with high T/U. This implies that haloes with lower T/U are more relaxed. A large value for xoff implies that the centre of mass is misaligned with the centre of the halo. This scenario is possible when the halo experiences (or recently experienced) a major merger and is likely to indicate that the system is in a perturbed state. Finally, the concentration of a halo is defined as cvir = Rvir/Rs where Rvir is the virial radius and Rs is the scale radius. It has been shown that halo concentration correlates with the past MAH (Wechsler et al. 2002; Ludlow et al. 2013). In particular, for massive haloes, larger values of cvir at fixed halo mass, on average, correlate with earlier formation times. Thus, we can think of cvir as an instantaneous halo parameter that correlates with the past MAH.
4.2 Mass accretion history parameters
These parameters quantify the MAHs of haloes on different time-scales. In principle, haloes with lower MAR have stopped growing, so they tend to be older and more relaxed. Consistent Trees measures MAR over different time-scales (Behroozi et al. 2013b). The resulting quantities are contained in ROCKSTAR catalogs (Behroozi et al. 2013a). Below we introduce ROCKSTAR definitions. Hereafter, we denote MAR as Γ, with a subscript indicating the time-scale over which it is measured. Parameters found in ROCKSTAR catalogs will be marked with `*′.
|$\Gamma ^{*}_\mathrm{100Myr}$|: MAR averaged over the past 100 Myr
|$\Gamma ^{*}_\mathrm{1dyn}$|: MAR averaged over the past virial dynamical time
|$\Gamma ^{*}_\mathrm{2dyn}$|: MAR averaged over the past two virial dynamical times
|$\Gamma ^{*}_\mathrm{Mpeak}$|: Growth rate of Mpeak (peak mass over all MAH), averaged from z1 to z1 + 0.5 where z1 is the snapshot under consideration.
In addition, we also use the MAH parameter in SPARTA, which is measured over one dynamical time (Diemer 2017).
The last MAH parameter we study is the halo half-mass scale (a1/2) and is defined as the scale factor in which the halo was half as massive as in the present redshift.
5 RESULTS
We first study how the shape of the ΔΣ profile depends on secondary halo properties beyond halo mass. We then analyse if Γdyn is detectable given forecasted HSC lensing errors and varying value of scatter for observational tracers of Γdyn in MDPL2. Finally, we highlight a degeneracy between Γdyn and miscentring parameters.
5.1 Dependence of ΔΣ on secondary halo properties
We start by studying the correlation between the shape of the galaxy-galaxy lensing profile with secondary halo properties. In Section 4, we divided these parameters into two groups: instantaneous tracers (present halo properties that correlate with its dynamical state) and MAH properties (parameters that measure MAR on different time-scales).
We consider a cluster sample selected in the narrow mass range of M200m ∈ [1013.8, 1014.1]h−1M⊙. We bin this halo sample by each of the secondary halo properties discussed in Section 4. To avoid any bias due to halo mass, we apply the binning methodology introduced in Mao, Zentner & Wechsler (2018) and implemented in Halotools. We weigh the value of each of the secondary halo properties by halo mass. These weights are uniformly distributed between 0 and 1. We rank the weights and bin them into percentiles. This method guarantees that all bins have the same mass distribution.
Fig. 3 displays the impact of each secondary halo parameter on the shape of the galaxy-galaxy lensing. Secondary halo properties have a substantial impact on ΔΣ in the one-halo regime. All instantaneous parameters show a strong correlation with the inner regions. From the MAH parameters, Γdyn and a1/2 have the most considerable impact. Furthermore, the dependence of the shape on the secondary halo parameters is significant given the predicted HSC lensing errors corresponding to the final survey area assuming no baryonic effects. This shows that the impact of secondary halo properties on halo profiles may be detectable with current generation lensing surveys. For this paper, we focus only on the inner profiles (R < 10 Mpc h−1). Larger simulations would be required to study large-scale assembly bias adequately, and this aspect is left for future work.
To quantify the relation between the shape of the ΔΣ profiles and secondary halo parameters, we apply the Gaussian cross-correlation statistic introduced in Section 3.2. The result of this analysis is displayed in Fig. 4. Here, we compute the full derivative of ΔΣ over secondary halo parameters, |$\frac{\mathrm{d} \langle \Delta \Sigma | \theta \rangle }{\mathrm{d} \theta }$|. This is the change in the lensing profile when one parameter is changed while allowing the rest to be free, as described in Section 3.2. Profiles and halo properties are normalized with respect to their mean and standard deviation. The y-axis in Fig. 4 represents the variance of the normalized ΔΣ profile for a given 1σ variation of the secondary halo parameter, θ.
Fig. 4 shows that no single parameter impacts the shape of the lensing profile equally on all scales. Instead, all parameters show a stronger correlation with the inner rather than the outer part of the lensing profile. This correlation is the strongest for cvir. This is not surprising since, by definition, cvir modifies the inner shape of the NFW profile. However, we are more interested in the other parameters, which are physical (in contrast to cvir which simply describes the shape of the halo) and are likely to play an important role in determining the properties of galaxies in clusters. Among the instantaneous physical halo parameters, T/U has the largest impact reaching 14 per cent variations at R = 0.2 Mpc h−1. Among MAH physical halo parameters, Γdyn and a1/2 have the largest impact reaching 14 per cent variations at R = 0.2 Mpc h−1.
Fig. 5 compares variations in ΔΣ for the parameters that have the largest impact. The left-hand panel displays the variance of the normalized ΔΣ profiles with respect to each secondary parameter. The right-hand panel illustrates the ΔΣ profiles binned by each parameter. Fig. 5 reveals two important pieces of information. First, one of the physical parameters with the largest impact on ΔΣ is Γdyn. This is important because hydrodynamic simulations indicate that MAR also correlates with the properties of galaxies in clusters, or the state of the hot gas that is often used to detect clusters, either via X-rays or the tSZ effect (Nelson, Lau & Nagai 2014; Shi et al. 2015). Secondly, while each secondary parameter considered here has a roughly similar impact on ΔΣ, they have distinct radial signatures. This raises the exciting possibility of using ΔΣ to understand which of these secondary halo parameters has the strongest correlations with observed cluster properties (e.g. galaxy content or hot gas).
Having shown that secondary halo properties substantially impact the one-halo ΔΣ profile, we now focus our attention more specifically on one secondary halo property. We choose to focus on Γdyn because a) Γdyn is likely to correlate with galaxies and gas in clusters, and b) Γdyn is one of the parameters that has the most substantial impact in Fig. 5. In the following section, we study if variations in ΔΣ and Γdyn at fixed halo mass are detectable with HSC. Whether or not these variations can be disentangled from variations due to other secondary halo parameters is left for future work.
5.2 Can Γdyn be measured with gravitational lensing?
In this section, we study how well we can constrain the relation between Γdyn and the shape of the lensing profile while ignoring miscentring. We first consider the ideal case in which perfect proxies (zero scatter) are available for Γdyn and M200m. We then study the more realistic case in which proxies only yield noisy estimates of Γdyn and M200m.
5.2.1 Ideal observational tracers
We first examine the constraints in the Γdyn-lensing shape relation when considering a perfect proxy for both M200m and Γdyn. Assuming perfectly centred clusters, we proceed with the full profile fitting routine introduced in Section 3.4. We fit stacked ΔΣ profiles of haloes within a narrow mass range of M200m = 1014M⊙ h−1 and different fiducial values of Γdyn = [0.78, 2.24, 3.73, 5.54]. The last Γdyn bin has a larger range due to the small number of haloes in that parameter space region. Finally, we use predicted HSC error bars corresponding to the final survey area to constrain the model.
Fig. 6 shows the posteriors of Γdyn for the different fiducial bins. The posterior distributions of Γdyn have a mean and 1σ spread of |$\Gamma _\mathrm{dyn}= [0.73 ^{+0.49}_{-0.41} , 2.16^{+0.52}_{-0.51} , 4.00^{+0.61}_{-0.59} , 5.46^{+0.72}_{-0.61} ].$| The emulator recovers the fiducial values of Γdyn within 1σ Thus, assuming ideal observational tracers for the two halo properties, our full profile fitting technique successfully constrains the MAR-lensing shape relation.
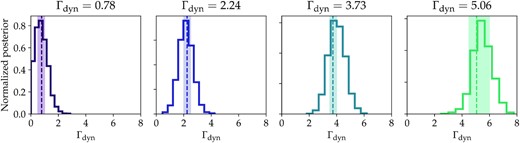
Constraints on Γdyn using full shape fitting, assuming a 1000 deg2 HSC weak lensing survey, and a perfect (zero scatter) observational tracer of Γdyn and assuming no baryonic effects. Shaded regions show the range of the fiducial Γdyn selection. These samples all have the same mass distribution (M200m = 1014M⊙ h−1), but have different mean values of Γdyn (dashed lines). Solid lines show the posteriors for Γdyn using full shape fitting with the emulator. This technique accurately recovers the value of Γdyn for all four samples.
5.2.2 Imperfect observational tracers of halo mass and Γdyn
To detect the impact of MAR on cluster profiles, we would need an observational tracer for MAR. However, no observational tracer is a perfect proxy for either halo mass or MAR. Instead, any tracer will be a noisy estimate of halo mass or MAR, which must be considered. This section aims to study the impact of this scatter on the ΔΣ profile. We focus here on detecting variations in MAR at fixed halo mass (which would be a more difficult correlation to detect than the measurement of the average value of MAR at fixed halo mass). We will explore how high this observational scatter can be before it renders profile differences undetectable.
Next, we consider the scatter in Γdyn at fixed proxy (denoted |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$|). Observational tracers for Γdyn have not yet been developed, and possible scatter values are unknown. For this reason, we instead consider a range of possible values for the scatter in this tracer while ignoring the covariance between richness and the potential Γdyn tracer. To study the impact of scatter on the shape of ΔΣ, we compare ΔΣ at fixed λ for different samples selected by the proxy for MAR while varying |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$|.
Fig. 7 displays the result of this exercise. As the scatter increases, the inner regions of the lensing profiles become more similar. For low values of |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$|, we can differentiate between the shape of the profiles of lower and higher Γdyn bins given predicted HSC error bars. In contrast, the profiles are indistinguishable for high values of |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$|. Therefore, the scatter in Γdyn has a large impact on the shape of the profile and will be an important factor in determining whether or not variations in Γdyn can be detected in ΔΣ at fixed halo mass (richness).
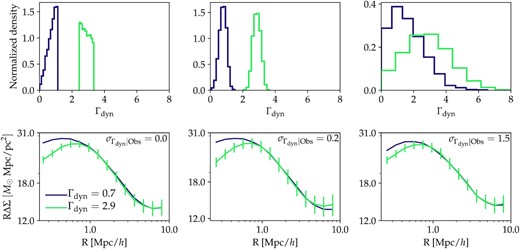
Impact of |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$| on the shape of the ΔΣ profile. Top: true distribution of Γdyn when the 20th and 80th percentiles are selected using a proxy with zero scatter (left), |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$| = 0.2 (middle), and |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$| = 4. (right). Bottom panels: weak lensing profiles corresponding to these selections. Error bars show the forecasted covariance from the full HSC survey scaled by the number density of the haloes in each selection. The ΔΣ signal becomes difficult to distinguish for values of |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$| > 1.5.
Next, we compute the maximum value of |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$| for which we can detect a trend in Γdyn at fixed halo mass when fitting the lensing profiles with the 2D emulator. We start by selecting haloes with λ ∈ [25, 40], where λ is assigned to each halo as described above. Then, we randomly draw haloes from Gaussian distributions with a given mean Γdyn and scatter. We vary the mean Γdyn from 0.3 to 7 and |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$| from 0 to 5. Then, we build ΔΣ profiles for all samples. Predicted HSC lensing error bars are scaled based on the expected number of haloes in each bin. We fit the respective lensing profile with our 2D emulator, whose free parameters are halo mass and MAR. Fig. 8 displays the recovered trends for different values of |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$|.
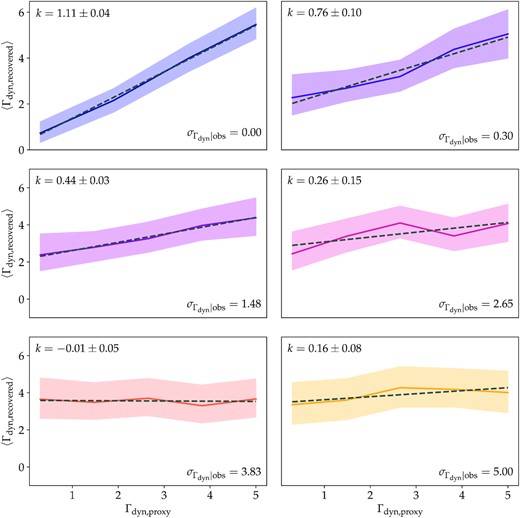
Recovered Γdyn with respect to proxy Γdyn for different values of observational scatter (|$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$|). The best-fitting slopes (k) are displayed on the top left corner of each panel. k = 1 corresponds to the scenario in which we recover the proxy Γdyn. This occurs at |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}=0$| (top-left panel). For high scatter (bottom panels), k = 0. At high scatter, the profiles become indistinguishable (also shown in Fig. 7) and the trend cannot be detected. Assuming the full HSC survey area and neglecting baryonic effects, we can expect to detect variations in lensing profiles due to Γdyn at fixed halo mass at 3σ significance if |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}\lt 1.5$|.
At zero scatter, the correlation between the recovered and proxy Γdyn is linear with a slope of 1. Thus, at zero scatter, the emulator recovers the proxy Γdyn (also displayed in Fig. 6). As the scatter increases, the linear correlation between the recovered and proxy Γdyn flattens. This is because lensing profiles have become more similar with increasing scatter (also shown in Fig. 7). Finally, at high scatter (bottom panel), the slope of the correlation is zero. Regardless of the proxy Γdyn, the recovered Γdyn is constant across all bins. This agrees with Fig. 7, which shows that for high scatter, the ΔΣ profiles for high and low MAR are indistinguishable.
To quantify the maximum |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$| at which we can hope to detect Γdyn, we perform a linear fit of correlation at each value of scatter. We then measure the maximum |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}$| for which the slope is greater than 0 at 3σ significance. This corresponds to |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}= 1.5$|. We conclude that a proxy for MAR with |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}\lt 1.5$| is required to detect MAR in observational data. This analysis accounts for the scatter between halo mass and richness but ignores possible correlations between tracers for MAR and λ. Possible avenues for constructing a tracer for Γdyn are discussed in Section 6.1.1. Furthermore, this analysis does not include the effect that baryons are going to have on the shape of the profile. We discuss this in more detail in Section 6.1.2.
5.3 Full profile fitting versus halo outskirts
This section compares constraints on MAR when using the scaling relation from DK14 with those obtained from full profile fitting. We use a sample of mock clusters with perfect centring and with |$M_\mathrm{200m}\, \in [10^{13.8},10^{14.1}] \mathrm{M}_\odot\,h^{ -1}$| and |$\Gamma _\mathrm{dyn}\, \in [2.5, 3.5]$|. We constrain the free parameters of each model, assuming HSC full survey errors. We adopt a Bayesian approach to fit the lensing profile with both DK14 and our model. Finally, we sample the posterior of rt with an MCMC analysis implemented in emcee. Given that DK14 does not measure Γdyn directly, we compute the posterior of Γdyn with equation (17).
Fig. 9 compares MAR constraints from the rt-Γdyn scaling relation and a full profile modelling technique. It is clear that our method gives tighter constraints on Γdyn than the rt − Γdyn relation. The rt-Γdyn scaling relation constrains MAR with an error of |$\sigma _{\Gamma _\mathrm{dyn}} = 2.4$|. In contrast, full profile fitting yields |$\sigma _{\Gamma _\mathrm{dyn}} = 1.1$|. The full profile fitting method is 2.1 times more constraining than the rt − Γdyn relation. The difference between the two methods relates to the length of their fiducial data vectors. The rt − Γdyn relation only uses information from a narrow radial range whereas full shape fitting uses all radial scales of ΔΣ. As we learned from Figs 3 and 4, secondary halo parameters are most correlated with the inner region of the halo. Given that the DK14 scaling relation focuses only on halo outskirts, while the full shape modelling technique models both the inner regions and halo outskirts, it is not surprising that the full shape modelling technique gives better constraints for MAR.
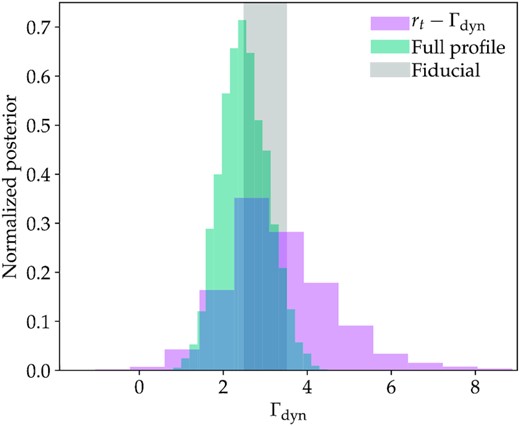
Comparison of constraints on Γdyn using full shape fitting versus the location of halo outskirts via the DK14rt − Γdyn scaling relation. The grey shaded region shows the range of Γdyn values in the sample. The full shape fitting yields an error on Γdyn of |$\sigma _{\Gamma _\mathrm{dyn}}=1.1$|, whereas the location of halo outskirts yields |$\sigma _{\Gamma _\mathrm{dyn}}=2.4$|. This is because the full ΔΣ profile contains more information about Γdyn than the rt − Γdyn scaling relation.
5.4 Impact of miscentring
Miscentring is a systematic effect introduced when the central galaxy of the cluster is misidentified. This translates into an artificial change in the shape of the ΔΣ profile. One can model the effect of cluster miscentring through two free parameters, fmis and Rmis, as described in Section 3.3.1. Fig. 10 displays the impact of these two parameters on the shape of ΔΣ for haloes with mean M200m = 1014 h−1 M⊙ and mean Γdyn = 0.67. The top panel shows how the profile changes as we increase the fraction of miscentred haloes at fixed Rmis = 0.3 h−1 Mpc. The bottom panel shows the impact of the miscentring distance at fixed fmis = 0.3. Both panels indicate that miscentring introduces changes in the inner part of the ΔΣ profile. It is important to notice that fmis causes variations in ΔΣ similar to those caused by variations in Γdyn (see Fig. 3). While the impact of Rmis is qualitatively different from Γdyn, low values of Rmis still affect the shape of the profile on smaller scales. Thus, we expect fmis and Rmis to be degenerated at some level with Γdyn.
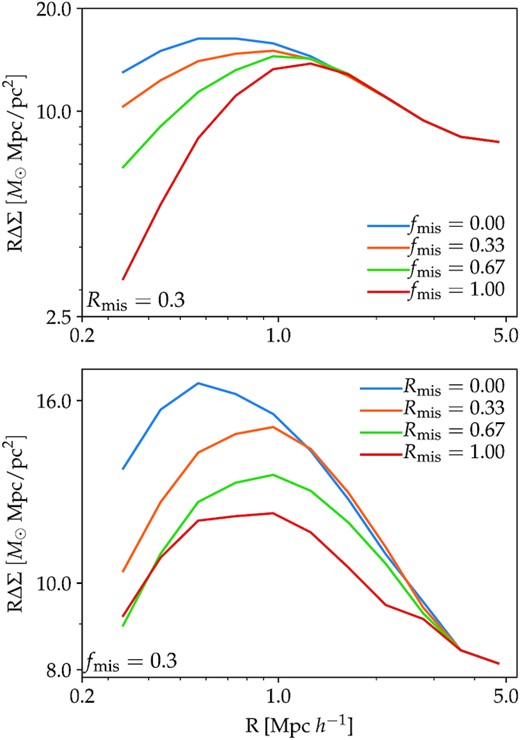
Effect of miscentring on the shape of the ΔΣ profile while varying fmis (top) and Rmis (bottom). Both parameters impact the one-halo regime in a similar fashion as Γdyn (compare with Fig. 3). Therefore, miscentring and MAR are likely to be correlated.
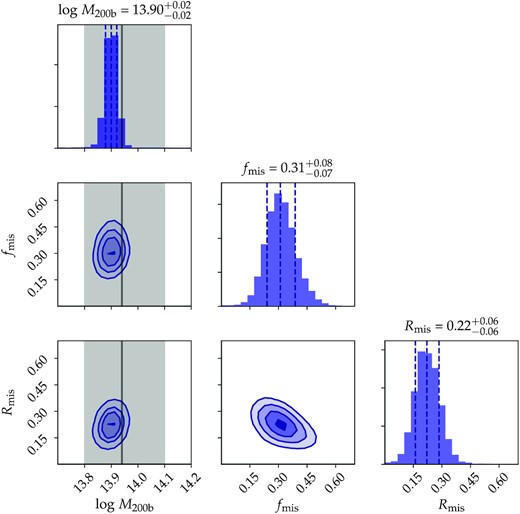
We include fmis and Rmis as two additional parameters in our emulator to quantify this degeneracy. We fit the fiducial data vector of the halo sample that contains miscentred haloes. The fiducial parameters are |$M_\mathrm{200m}\, \in [10^{13.8},10^{14.1}] \mathrm{M}_\odot\,h^{ -1}$|, |$\Gamma _\mathrm{dyn}\, \in [2.5, 3.5]$|, fmis = 0.22, and Rmis = 0.1 h−1 Mpc. The values for the two miscentring parameters are justified by the priors used for modelling miscentring in Rykoff et al. (2016) and Chang et al. (2018). Finally, the parameters are constrained through the predicted HSC error bars. Fig. 11 shows the results of the fit. We recover all four fiducial parameters within 1σ. The marginalized posteriors of Γdyn with fmis and Rmis in Fig. 11 imply that Γdyn is correlated with both miscentring parameters as predicted from Fig. 10. If not modelled properly, this degeneracy can potentially impact our physical understanding of haloes.
![Posteriors of full profile fitting for a set of clusters with mean Γdyn = 3 and miscentred assuming Rmis = 0.1 Mpc h−1 and fmis = 0.22. Grey shaded regions indicate the cuts on M200m and Γdyn that define the fiducial sample (M200m ∈ [13.8, 14.1] and Γdyn ∈ [2.5, 3.5]). Solid grey lines correspond to the mean halo values and the true miscentring values. Dashed lines indicate the 1σ contours of the posterior distribution. Although halo mass and MAR are uncorrelated, there is a strong correlation between Γdyn and the two miscentring parameters. This is because miscentring and Γdyn have a similar impact on the shape of the one-halo term.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/514/2/10.1093_mnras_stac941/1/m_stac941fig11.jpeg?Expires=1750288875&Signature=Nifgp44BIfZsgy-0VSGA1XinnvepDXznqP~7GFpaGRnJDUqSSsNDjl5Vno32itYUmfGQO~htaRM8RBr58m8bl5GaYUbwJ4xObn3KxbeVoXGEBiM5NnJ-t7fKU7enEautbqy2du7cmzZCVvX2w33xrNv2IvVkcFEaTisZ3XEgNN5LrXLqDiDWV64~BTlDWtvfsWEkk68tUrMYrCJdMuykq2~08dMSS4HvMicI1lBruudRqCxLMR4UjIGWpmxlaAc99TGsUSl4if5m7BImzFEJvoQ07FaclsxX488ORjdGWkQVp3Rm46HUrrxF5jjVfVPfW69wlDFMB8rlgy-Ch0zkHQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Posteriors of full profile fitting for a set of clusters with mean Γdyn = 3 and miscentred assuming Rmis = 0.1 Mpc h−1 and fmis = 0.22. Grey shaded regions indicate the cuts on M200m and Γdyn that define the fiducial sample (M200m ∈ [13.8, 14.1] and Γdyn ∈ [2.5, 3.5]). Solid grey lines correspond to the mean halo values and the true miscentring values. Dashed lines indicate the 1σ contours of the posterior distribution. Although halo mass and MAR are uncorrelated, there is a strong correlation between Γdyn and the two miscentring parameters. This is because miscentring and Γdyn have a similar impact on the shape of the one-halo term.
The correlation of miscentring with secondary halo properties is already known. Melchior et al. (2017) studied how miscentring affects cluster mass and concentration measured though lensing. They use lensing measured around red-sequence Matched-filter Probabilistic Percolation clusters (redMaPPer; Rozo et al. 2014; Rozo & Rykoff 2014; Rozo et al. 2015). They apply a miscentring model similar to ours and fit for miscentring using two free parameters: ρ, the well-centred fraction of clusters (analog to fmis, and τ, the centring offset of mis-centred redMaPPer clusters (analog to Rmis). In Fig. 9, they show that both ρ and τ affect concentration. This agrees with our result in Fig. 11, where both miscentring parameters are degenerated with Γdyn.
The fact that miscentring and Γdyn parameters are correlated has two implications. First, neglecting the impact of miscentring could bias attempts to measure Γdyn. Secondly, if cluster samples are selected by halo mass and Γdyn, but the Γdyn selection is ignored, then miscentring parameters could be biased. We now study these two effects.
To study the impact of miscentring on the detection of Γdyn, we fit the same fiducial set of clusters as above (M200m = 1014 M⊙ and Γdyn ∈ [2.5, 3.5]). We apply miscentring to these clusters assuming fmis = 0.3 and Rmis = 0.3Mpc h−1. Finally, we constrain the parameters with error bars corresponding to the final HSC survey area. Here, we aim to study the bias in Γdyn due to miscentring. We fit both fiducial samples of clusters (perfectly centred and miscentred) with the 2D emulator (which does not model miscentring effects). Fig. 12 shows the results of these fits. Both samples have the same distribution of M200m and Γdyn, so they should, in principle, recover the same range of parameters. However, while the emulator recovers the true M200m and Γdyn in the absence of miscentring, it fails to do so for miscentred clusters. Thus, not including miscentring in the model introduces a bias in the detection of Γdyn.
![Impact of ignoring miscentring when fitting for Γdyn. Here, we assume a fiducial halo sample with M200m ∈ [13.8, 14.1] and Γdyn ∈ [2.5, 3.5]. Shaded regions display the M200m and Γdyn cuts that define the sample. Dashed lines are the mean values. Pink contours show posteriors when the sample is perfectly centred. In this case, halo properties are recovered accurately. Blue contours show posteriors when clusters are miscentred with fmis = 0.3 and $R_\mathrm{mis}=0.3\, \mathrm{Mpc}\,h^{ -1}$, but miscentring is ignored when performing the fit. Ignoring miscentring biases the recovery of Γdyn.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/514/2/10.1093_mnras_stac941/1/m_stac941fig12.jpeg?Expires=1750288875&Signature=DVxJfc3M2iMdORYQFvydVx2wfW4nmIw1p-kbh9ww-ECzLMdPNhwBiEjg6Mu3nQMXh1EKrXEHqMoy0tyeXxhMmP2zNmyDpkq~jnJua0T4Xbt0N4itvANZFp8kZnMNwxxw-GM9qib7AmA2uJ9e7HdeRWjhYe6xSxvUvmgrItPQsmLfw3uUSGrIG7U6S7vNdyNR7pcDGs7ok7hgsKu35A~lgOjf0FTjZwGrDbLaT439AGJWvZZCCNWfxeeMYJYczYdtG9JZ~s97I3SqAy3JbvEfcQ5ylsajn9Oq-PfK74JLJA1JVMcw7CJ4rDWYqgl4BZsnUDtrcBYGqL2baPqSYUw3kg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Impact of ignoring miscentring when fitting for Γdyn. Here, we assume a fiducial halo sample with M200m ∈ [13.8, 14.1] and Γdyn ∈ [2.5, 3.5]. Shaded regions display the M200m and Γdyn cuts that define the sample. Dashed lines are the mean values. Pink contours show posteriors when the sample is perfectly centred. In this case, halo properties are recovered accurately. Blue contours show posteriors when clusters are miscentred with fmis = 0.3 and |$R_\mathrm{mis}=0.3\, \mathrm{Mpc}\,h^{ -1}$|, but miscentring is ignored when performing the fit. Ignoring miscentring biases the recovery of Γdyn.
Next, we explore the case when the model includes miscentring but not Γdyn. This time we allow for M200m, fmis, and Rmis to be the only free parameters in the full profile fitting routine. We fit for the same fiducial samples as above and consider only the sample with perfectly centred clusters. We constrain the parameters with the forecasted error bars of the HSC final survey area. Fig. 13 displays the posteriors of the fit. The emulator overestimates the impact of miscentring in the shape of the profile. This can be an issue as miscentring is routinely used in modelling ΔΣ profiles, while MAR is not. For a Γdyn biased selected sample, one could erroneously overrate the impact of miscentring on the profile. Given the results from Figs 12 and 13, it is clear that joint modelling of halo MAR and observational miscentring may be necessary in order to avoid introducing biases when studying weak lensing profiles around clusters. Furthermore, it is likely that miscentring correlates with other cluster properties. To our knowledge, the correlation between miscentring and cluster properties is currently poorly known. In addition, miscentring is a systematic effect in cluster finding algorithms. As such, the way it manifests itself in the data is cluster finder-dependent. In future work, we will study the correlation of MAR and miscentring in hydrodynamic simulations. This will also shed light on the correlation between miscentring and other cluster properties.
Impact of ignoring Γdyn when modelling ΔΣ profiles. The fiducial sample contains only perfectly centred clusters such that fmis = 0 and Rmis = 0 Mpc h−1. Grey shaded regions indicate the fiducial M200m range. Dashed lines indicate the 1σ contours of the posterior distribution. We assume perfect tracers of halo mass and MAR. In fitting the fiducial profile, we allow the emulator only to vary M200m, fmis, and Rmis. Both fmis and Rmis are overestimated (the true values are fmis = 0 and Rmis = 0 Mpc h−1). This bias comes from not accounting for the effect of MAR on the shape of the profile.
6 DISCUSSION
6.1 On the possibility of detecting Γdyn in observational data
6.1.1 Observational proxies for Γdyn
To constrain MAR in observational data, one first needs a low scatter tracer of MAR. Although tracers for halo mass have been well studied, tracers for MAR have yet to be developed. Multiple approaches could be used to identify a suitable tracer. One approach would be to study scaling relations from empirical models such as the Universe Machine (Behroozi et al. 2019), Emerge (Moster, Naab & White 2018), etc. The advantage of this approach is that several empirical models are publicly available, and looking for a low scatter tracer of Γdyn would be a relatively straightforward undertaking. Another approach would be to study the covariance among different halo and cluster properties through hydrodynamic simulations. For example, Farahi, Ho & Trac (2020) use the TNG300 simulation (Springel et al. 2018) to improve the halo mass to cluster property relation. They find that conditioning on the magnitude gap lowers the scatter in the tracer to halo–mass relation. One could, in principle, repeat the same analysis for MAR. Finally, a third approach would be to employ Machine Learning (ML) techniques. ML has been proposed as a new tool to connect galaxy and halo properties. One can use unsupervised learning to detect patterns in the data set without assuming a physical model. For example, Moster et al. (2021) introduce GalaxyNet, a neural network that studies correlations between galaxy and halo properties. By utilizing reinforcement learning, GalaxyNet is instead trained directly on observed data. The algorithm is rewarded or penalized at specific points during learning, based on how well it recovers the observed statistics. As such, it is not informed about the underlying physics. Moster et al. (2021) demonstrate that ML provides reliable and unbiased methods for finding proxies for halo properties in observations. We will explore such techniques in future work.
6.1.2 Impact of baryons
Fig. 4 showed that the shape of ΔΣ varies when secondary halo properties are varied at fixed halo mass. We also showed that the one-halo regime could also be impacted by cluster finding systematics such as miscentring (Fig. 10). This leads to a degeneracy between MAR and miscentring (Section 5.4). Baryonic effects can influence the shape of the profile at scales below a few Mpc. Leauthaud et al. (2017) and Lange et al. (2021) show that baryons impact the one-halo regime (|$R\lt 4\, \mathrm{Mpc}\,h^{ -1}$|) and can modify ΔΣ by up to 20 per cent (see fig. 12 in Leauthaud et al. 2017). Henson et al. (2017) demonstrated that due to the additional mass from baryons, dark matter haloes get contracted (otherwise known as adiabatic contraction, Gnedin et al. 2004). Furthermore, baryons get condensed in the cluster centre. Thus, clusters in hydrodynamic simulations are more concentrated in the central regions. Overall the mass–concentration relation of haloes gets flatter in hydrodynamic simulations.
Furthermore, Shirasaki, Lau & Nagai (2018) showed that baryonic effects affect halo concentrations differently depending on halo formation time. Younger haloes that accrete mass faster will be less affected by baryonic feedback than older haloes. On the other hand, older haloes slowly accrete new material. As such, most of the new material resides in the outskirts, and baryonic feedback dominates in the core regions. Thus, the concentration of older haloes is much more susceptible to baryionic effects.
It is clear from previous work that the effect of MAR and baryonic feedback will both impact the lensing profile shape on scales below a few Mpc. We cannot study this degeneracy with our current model since the emulator is trained in dark matter-only simulations. In future work, we will aim to quantify the covariance of baryonic effects and other secondary halo properties. Furthermore, we will study the if MAR and baryonic effects have distinct radial signatures that allow them to be disentangled.
6.2 Subhalo cross-correlations
While galaxy-galaxy lensing is an excellent tracer of the total mass distribution in haloes, a joint analysis with subhalo cross-correlations could help improve constraints on MAR. The use of subhalo cross-correlations has become more popular for constraining halo properties (e.g. More et al. 2016; Chang et al. 2018; Baxter et al. 2017). While including subhalo cross-correlations is likely to tighten constraints on Γdyn, modelling subhalos adds complexity to the analysis for two reasons. First, subhalos in simulations are prone to numerical artifacts in N-body simulations such as artificial disruption (van den Bosch & Ogiya 2018). Therefore, a robust way to identify them in N-body simulations and ensuring that the relationship between subhalo profiles and Γdyn at fixed halo mass is preserved will be critical. Secondly, the relationship between the galaxy selection function and the subhalo profiles needs to be adequately modeled. It is well known that red and blue galaxies are not identically distributed around the cluster (Dressler 1980; Postman & Geller 1984; Goto et al. 2003). Red, elliptical galaxies, with low star formation rates are concentrated inside the cluster and while blue, star-forming galaxies are concentrated in the infalling regions (i.e. outskirts) of the cluster. Furthermore, blue galaxies show a shallower slope in their two-point correlation profiles than red galaxies (e.g. Norberg et al. 2002; Madgwick et al. 2003; Baxter et al. 2017). Finally, other effects such as tidal stripping of subhalos and mass segregation also need to be considered. Future work will tackle these caveats and explore the possibility of using galaxy cross-correlations as observational probes to detect MAR.
7 SUMMARY AND CONCLUSIONS
In this paper, we use the MDPL2 simulation to study the impact of secondary halo properties on the shape of the ΔΣ lensing profile at fixed halo mass. We also study whether or not it will be possible to detect the relationship between weak lensing shape and Γdyn using the full HSC weak lensing data set under the given assumptions (i.e. low scatter proxy for MAR and exclusion of baryonic effects). To achieve these goals, we build an emulator trained on MDPL2 that models ΔΣ given halo mass, MAR, and miscentring parameters. Our main findings are:
All secondary halo properties considered in this paper impact the shape of ΔΣ on scales below 10 Mpc h−1. The impact of these parameters is significant compared to the predicted errors on ΔΣ assuming a 1000 deg2 HSC survey and clusters drawn from 0.3 < z < 0.6 (Fig. 3). While each secondary parameter has a roughly similar impact on ΔΣ, they have distinct radial signatures (Figs 4 and 5). This raises the exciting possibility of using ΔΣ to understand which of these secondary halo parameters has the strongest correlations with cluster properties such as galaxy content or hot gas.
Among those parameters considered, cvir has the largest impact on ΔΣ. However, this is by definition since cvir characterizes variations in the shape of the NFW profile. Instead, in this paper, we focused more specifically on the impact of physical halo parameters on ΔΣ. This is important because galaxies or hot gas in clusters are likely to correlate with physical secondary halo properties (such as halo accretion rate over one dynamical time, Γdyn). Among physical parameters, T/U, Γdyn, and a1/2 have the largest impact on the shape of ΔΣ with variations reaching up to 14 per cent at R = 0.2Mpc h−1 (Fig. 4).
We then investigate whether or not we can constrain the relation between Γdyn and the shape of the lensing profile with the full 1000 deg2 HSC survey. Assuming that a perfect observational tracer for Γdyn is available, we show that a cluster sample drawn from 0.3 < z < 0.6 could be used to successfully constrain this relation (Fig. 6).
We further consider the impact of scatter between an observational tracer and Γdyn. The scatter on Γdyn impacts the smaller scales of ΔΣ (Fig. 7). We show that a proxy with |$\sigma _{\Gamma _\mathrm{dyn}|\mathrm{obs}}\lt 1.5$| is required to detect Γdyn (Fig. 8) with the full HSC survey.
We compare constraints on Γdyn obtained from full shape fitting with the emulator to those obtained from the DK14rt–Γdyn scaling relation. We find that the full profile fitting routine constrains Γdyn 2.1 times better than the rt–Γdyn scaling relation (Fig. 9).
Finally, we study the interplay between miscentring and MAR. We find that the effect of miscentring on ΔΣ is degenerate with MAR (Fig. 11). This means that miscentring needs to be taken into account for an unbiased detection of Γdyn (Fig. 12). Similarly, to avoid biased estimates of miscentring parameters, the impact of Γdyn should be carefully considered (Fig. 13). This is important because it is likely that common cluster selection techniques (such as richness or X-ray selections) may preferentially select clusters according to Γdyn in addition to mass.
We have shown that present-day lensing data sets have the statistical capability to place constraints on the relation between weak lensing shape and halo accretion rates. This will open new possibilities for studying correlations between galaxy and cluster properties and secondary halo properties such as Γdyn. Observational insights into these correlations may lead to new methods for constraining the growth rate (Hurier 2019) and will help improve semi-analytic and empirical models of galaxy formation. Three main challenges will need to be tackled to carry out this program. First, it will be necessary to identify and characterize a low scatter proxy for Γdyn. Secondly, it will be essential to understand the interplay between observational tracers, Γdyn, and other secondary halo properties impacting ΔΣ in different ways. Third, it will alos be necessary to consider the impact of baryonic effects. With the Roman Space Telescope (Dore et al. 2019), the Vera Rubin Observatory Legacy Survey of Space and Time (LSST, The LSST Dark Energy Science Collaboration 2018), and Euclid (Laureijs et al. 2011) on the horizon, the coming decade will usher in the potential for even stronger constraints on ΔΣ than those considered here. Techniques for measuring and disentangling secondary halo properties are thus becoming paramount, and the methodology introduced here paves the way for a new generation of lensing-based constraints on the mass and assembly history of dark matter haloes.
ACKNOWLEDGEMENTS
EX is grateful to Joe DeRose and Christopher Bradshaw for helpful conversations. This work was wrapped up during the Coronavirus pandemic and would not have been possible without the hard work of all the essential workers who did not have the privilege of working from home. EX is also grateful to her cat for offering emotional support and motivation to advance this project. This research was supported in part by the National Science Foundation under grant no. NSF PHY-1748958. This material is based on work supported by the United States Department of Energy, Office of Science, Office of High Energy Physics under Award Number DE-SC0019301. AL acknowledges support from the David and Lucille Packard Foundation and the Alfred. P Sloan foundation. EX acknowledges the generous support of Mr. and Mrs. Levy via the LEVY fellowship.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.



