Early-type galaxy density profiles from IllustrisTNG – III. Effects on outer kinematic structure

Wang, Yunchong; Mao, Shude; Vogelsberger, Mark; Springel, Volker; Hernquist, Lars; Wechsler, Risa H

doi:10.1093/mnras/stac1375

ABSTRACT

Early-type galaxies (ETGs) possess total density profiles close to isothermal, which can lead to non-Gaussian line-of-sight velocity dispersion (LOSVD) under anisotropic stellar orbits. However, recent observations of local ETGs in the MASSIVE Survey reveal outer kinematic structures at 1.5R_eff (effective radius) that are inconsistent with fixed isothermal density profiles; the authors proposed varying density profiles as an explanation. We aim to verify this conjecture and understand the influence of stellar assembly on these kinematic features through mock ETGs in IllustrisTNG. We create mock Integral-Field-Unit observations to extract projected stellar kinematic features for 207 ETGs with stellar mass |$M_{\ast }\geqslant 10^{11} \, \mathrm{M_{\odot}}$| in TNG100-1. The mock observations reproduce the key outer (1.5R_eff) kinematic structures in the MASSIVE ETGs, including the puzzling positive correlation between velocity dispersion profile outer slope γ_outer and the kurtosis h₄’s gradient. We find that h₄ is uncorrelated with stellar orbital anisotropy beyond R_eff; instead, we find that the variations in γ_outer and outer h₄ (a good proxy for h₄ gradient) are both driven by variations of the density profile at the outskirts across different ETGs. These findings corroborate the proposed conjecture and rule out velocity anisotropy as the origin of non-Gaussian outer kinematic structure in ETGs. We also find that the outer kurtosis and anisotropy correlate with different stellar assembly components, with the former related to minor mergers or flyby interactions while the latter is mainly driven by major mergers, suggesting distinct stellar assembly origins that decorrelates the two quantities.

galaxies: elliptical and lenticular, cD, galaxies: evolution, galaxies: kinematics and dynamics, galaxies: structure, methods: numerical

1 INTRODUCTION

Early-type galaxies (ETGs; Dressler 1980; Djorgovski & Davis 1987) are recognized as the ‘red and dead’ end products of hierarchical galaxy formation (Cole et al. 2000; Springel et al. 2001; De Lucia et al. 2006; De Lucia & Blaizot 2007). Numerical simulations over the past decade have shown that the formation path of early-type galaxies is well represented by a two-phase scenario (Naab et al. 2007; Guo & White 2008; Oser et al. 2010; Johansson, Naab & Ostriker 2012; Moster, Naab & White 2013; Rodriguez-Gomez et al. 2016), comprising an active phase (z ≳ 2) dominated by gas-rich mergers and bursty in situ star formation (Hopkins et al. 2006, 2008a, b, 2009c, d; Wellons et al. 2015), as well as a passive phase (z ≲ 2) dominated by dry mergers and accretion of ex situ formed stars (Nipoti, Treu & Bolton 2009a; Nipoti et al. 2009b; Remus et al. 2013; Wellons et al. 2016), as well as quenching by active galactic nucleus (AGN) feedback (Silk & Rees 1998; King 2003; Wyithe & Loeb 2003; Di Matteo, Springel & Hernquist 2005; Springel, Di Matteo & Hernquist 2005; Fabian 2012; Kormendy & Ho 2013).

An important feature of ETGs found in observations through strong and weak gravitational lensing (Koopmans et al. 2006; Gavazzi et al. 2007; Barnabè et al. 2009, 2011; Koopmans et al. 2009; Auger et al. 2010; Ruff et al. 2011; Sonnenfeld et al. 2013; Li, Shu & Wang 2018b; Lyskova, Churazov & Naab 2018), dynamical modelling (Tortora et al. 2014; Cappellari et al. 2015; Serra et al. 2016; Poci, Cappellari & McDermid 2017; Bellstedt et al. 2018; Li et al. 2019), and X-ray observations of gas dynamics (Humphrey et al. 2006; Humphrey & Buote 2010) is that their total radial matter density profile is well described by a single power-law model |$\rho (r)\propto r^{-\gamma ^{\prime }}$| with small intrinsic scatter around the slope of γ′ = 2. This feature is known as the ‘bulge–halo conspiracy’, as neither stars nor dark matter follow a single power-law model with the slope of γ′ = 2, but their combined profile ‘conspires’ to take the form of a singular isothermal sphere (SIS; an ideal gas sphere under gravitational-hydrostatic equilibrium):

$$\begin{eqnarray} \rho (r) = \frac{\sigma ^2}{2\pi G r^2} \Longleftrightarrow \rho (r)\propto r^{-\gamma ^{\prime }},\gamma ^{\prime }=2 \end{eqnarray}$$

(1)

where σ is the one-dimensional velocity dispersion of stars. In the case of isotropic stellar orbits, σ = σ_r = σ_θ = σ_ϕ where the subscripts denote the (r, θ, ϕ) directions in spherical coordinates. In this case, a constant σ leads to a constant circular velocity v_c with radius:

$$\begin{eqnarray} v_{c}^2(r) = \frac{G M(\lt r)}{r} = \frac{G}{r}\int _{0}^{r} \rho (r^{\prime })4\pi r^{\prime 2} {\rm d}r^{\prime } = 2\sigma ^2 . \end{eqnarray}$$

(2)

Therefore, the ETG total density profile characterized by γ′ = 2 is naturally linked to its kinematic structure characterized by a flat velocity dispersion/circular velocity radial profile under stellar orbit isotropy. Any deviations from a flat velocity dispersion curve (or the underlying circular velocity) will indicate a deviation of the total density profile from an SIS model (γ′ ≠ 2). If the 3D velocity dispersion profile can be approximated by a power law σ(r) ∝ r^α, then γ′ < 2 when α > 0 and γ′ > 2 when α < 0.

However, in the presence of a radial or tangential stellar orbital anisotropy, the projected stellar velocity dispersion can also vary with radius even when γ′ = 2 and v_c remains constant with radius. As the anisotropy cannot be measured directly in observations, neither the 3D velocity dispersion profile (Binney & Mamon 1982) nor the density profile logarithmic slope (Cappellari 2008; Xu et al. 2017) can be determined in an unbiased manner without an assumed velocity anisotropy. This causes a degeneracy in the derived mass profile/velocity dispersion profile and the assumed velocity anisotropy. None the less, if higher order velocity moments are measured, which provides non-Gaussian information (especially the kurtosis h₄, which is the fourth velocity moment) of the LOSVD, this degeneracy can in theory be broken through the opposite behaviour of h₄ under radial and tangential velocity anisotropy (Dejonghe & Merritt 1992; Gerhard 1993; Merritt & Saha 1993; Read & Steger 2017).

Recent results from the MASSIVE Survey (Ma et al. 2014) found that massive local ETGs with stellar mass ≳ 10^11.5M_⊙ that have rising velocity dispersion profiles towards their outskirts tend to have positive h₄ and positive h₄ gradient (Veale et al. 2017, 2018). Ene et al. (2019) also found that most of MASSIVE ETGs have dropping inner velocity dispersion profiles and increasing h₄ towards the Galactic Centre. These trends are in contradiction to the theoretical expectations that under a fixed total density profile, radial velocity anisotropy induces a more positive h₄ accompanied by a decreasing LOSVD towards the outskirts of a galaxy (vice versa towards the centre). To explain this observed tension, Veale et al. (2018) proposed that the presence of circular velocity gradients could be the cause, and galaxy-to-galaxy variations of the total density profile slope (γ′) could be present in ETGs. Therefore, we aim to verify this conjecture using simulated ETGs from the state-of-the-art cosmological hydrodynamic simulation IllustrisTNG (Marinacci et al. 2018; Naiman et al. 2018; Nelson et al. 2018; Pillepich et al. 2018b; Springel et al. 2018), which possesses a well-studied ETG sample with near-isothermal total density profiles that are broadly consistent with their observed counterparts (Wang et al. 2020,Paper I).

If the outer kinematic structures of ETGs are indeed influenced by the variations in their density profiles, we expect to see a correlation of their outer kinematic structures with minor mergers. This is due to the fact that the evolution of the ETG total density profile at z < 0.5 is mainly driven by minor mergers as found in Wang et al. (2019, Paper II) and similarly in earlier works (Johansson et al. 2012; Hilz, Naab & Ostriker 2013; Remus et al. 2013; Sonnenfeld, Nipoti & Treu 2014). Interestingly, Greene et al. (2019) found strong correlations between h₄ and stellar population probes (i.e. metallicity and metallicity gradients) and suggested cumulative minor mergers might have led to the old-aged, radially anisotropic ETGs having positive h₄ at the outskirts. Since galaxy mergers also affect the velocity dispersion profile (Bender, Burstein & Faber 1992; Schauer et al. 2014; Nipoti et al. 2020) and tend to induce radial velocity anisotropy (Romanowsky et al. 2003; Hilz et al. 2012), we will also investigate the role of minor mergers in the co-evolution of ETG outer kinematic structure and their density profile using the merger histories of the simulated ETGs.

This paper is organized as follows. In Section 2, we introduce the simulation and selection criteria through which we select our ETG catalogue, as well as the methods to mimic observations for extracting kinematic structure information out of the ETGs; in Section 3, we present the results for the kinematic properties of our selected ETG sample along with comparisons to observations; in Section 4, we further explore the physical interpretation for the formation of outer kinematic structure in ETGs relating to their total density profiles, stellar assembly histories, and environment; in Section 5, we summarize our main conclusions and provide an outlook for future directions of work. In the following analysis, we assume the Planck-2016 flat-ΛCDM cosmology (Planck Collaboration 2016) parameters used by the IllustrisTNG simulations: h = 0.6774, Ω_m = 0.3089, Ω_b = 0.0486, Ω_Λ = 0.6911, and σ₈ = 0.8159.

2 METHODOLOGY

2.1 IllustrisTNG simulations

Cosmological simulations have tremendously improved our understanding of galaxy formation and cosmology over the past few decades (see Vogelsberger et al. 2020a for a recent review). The Next Generation Illustris Simulations¹ (Marinacci et al. 2018; Naiman et al. 2018; Nelson et al. 2018; Pillepich et al. 2018b; Springel et al. 2018), IllustrisTNG for short, is a recent set of cosmo-magneto hydrodynamic simulations evolved with the state-of-the-art moving mesh hydrodynamics code arepo (Springel 2010). They advance the merits of the Illustris Simulations (Vogelsberger et al. 2013; Torrey et al. 2014), and improve the Illustris models (Genel et al. 2014; Vogelsberger et al. 2014a, b; Nelson et al. 2015; Sijacki et al. 2015) in terms of AGN and stellar feedback physics (Weinberger et al. 2017; Pillepich et al. 2018a).

The full physics IllustrisTNG simulation suite reproduces many key relations in observed galaxies, including the galaxy–colour bimodality in the Sloan Digital Sky Survey (SDSS; Nelson et al. 2018), the fraction of dark matter within galaxies at z = 0 (Lovell et al. 2018), the galaxy mass–metallicity relation (Torrey et al. 2018, 2019) and the intracluster metal distribution (Vogelsberger et al. 2018), the galaxy size–mass relation evolution (Genel et al. 2018), galaxy morphology transition (Tacchella et al. 2019) and stellar orbital fraction (Xu et al. 2019), early-type galaxy total density profiles (Wang et al. 2020), molecular and atomic hydrogen content in low redshift galaxies (Diemer et al. 2019; Stevens et al. 2019), star formation activities and quenched fractions (Donnari et al. 2019), ram-pressure stripping in dense environments (Yun et al. 2019), gas-phase metallicity gradients in star-forming galaxies (Hemler et al. 2020), as well as AGN galaxy occupation and X-ray luminosities (Weinberger et al. 2018; Habouzit et al. 2019; Terrazas et al. 2020). Although some facets of these comparisons still exhibit discrepancies with observations to different levels, the significant improvements over Illustris and the multitude of agreement in galaxy and cluster level properties with observations demonstrates the predictive power of IllustrisTNG (e.g. predictions of JWST observation for high-redshift galaxies Vogelsberger et al. 2020b). Therefore, we use ETGs selected from IllustrisTNG to gain insights on the origin of their outer kinematic structure as seen in the MASSIVE Survey.

The simulation suite of IllustrisTNG comprises three cubic boxes with periodic boundary conditions, i.e. TNG100 (side length |$75\, \mathrm{Mpc}\,h^{-1}$|⁠, same as original Illustris), TNG300 (side length |$205\, \mathrm{Mpc}\,h^{-1}$|⁠), and TNG50 (side length |$35\, \mathrm{Mpc}\,h^{-1}$|⁠), with overall higher resolution in smaller boxes and each box contains several runs with different numerical resolutions. In this paper, we select galaxies from the highest resolution run of the TNG100 box, which is best for our purpose of studying ETGs with stellar mass ≳ 10¹¹M_⊙, since it provides a substantial sample size of ETGs in this mass range with reasonable mass resolution. TNG100 has a baryonic matter mass resolution of |$m_{\mathrm{baryon}} = 1.4\times 10^{6} \, \mathrm{M}_{\mathrm{\odot}}$| and a dark matter mass resolution of |$m_{\mathrm{DM}} = 8.9\times 10^{6} \, \mathrm{M}_{\mathrm{\odot}}$|⁠, each with 1820³ resolution elements. The softening length scale of dark matter and stellar particles is |$\epsilon = 0.74\, \mathrm{kpc}$| [valid for z ≤ 1, scales as (1 + z)⁻¹ϵ at z > 1], whereas the gravitational softening of the gas cells is adaptive and has a minimum length scale of 0.19 comoving kpc. The simulation runs of TNG50, TNG100, and TNG300 boxes are now available for public data access (Nelson et al. 2019).

2.2 Sample selection

Galaxies in IllustrisTNG are identified as gravitationally bound structures (subhaloes) by Subfind (Springel et al. 2001; Dolag et al. 2009) win haloes found using the Friends-of-Friends (FoF) algorithm based on mean particle separation length. The largest subhalo in a halo together with its baryonic component is defined as the central galaxy, and all other subhaloes in the halo are defined as satellite galaxies. We select central galaxies in TNG100 with total stellar masses of M_* ≥ 10¹¹M_⊙ (≳ 7 × 10⁴ resolution elements), which covers the stellar mass range of the MASSIVE ETGs (M_* ≥ 3 × 10¹¹M_⊙, Veale et al. 2018). Merger trees that trace the comprehensive assembly histories of galaxies and dark matter haloes are constructed using the algorithm Sublink (Rodriguez-Gomez et al. 2015).

We follow Papers I and II for galaxy morphology classification, which is based on the optical luminosity reconstruction approach detailed in Xu et al. (2017). The optical light of a galaxy is derived using the Stellar Population Synthesis (SPS) model (Bruzual & Charlot 2003) based on the metallicity and age of its stellar particles that are treated as coeval stellar populations with Chabrier initial mass function (Chabrier 2003). A projection dependent dust attenuation is then applied to the galaxy luminosity and we take the SDSS r-band luminosity after dust processing to calculate azimuthally averaged galaxy luminosity radial profiles for morphological classification. We fit single-component models, i.e. the de Vaucouleurs profile (Sérsic n = 4) and the exponential profile (Sérsic n = 1), as well as a combined two-component model of exponential and de Vaucouleurs profiles to the projected radial luminosity profiles of galaxies. If a galaxy is better fit (lower minimum χ²) by the de Vaucouleurs profile, and demonstrates bulge dominance in the two-component fit (bulge-to-total ratio >0.5) in all three independent projections (along the x, y, and z axes of the simulation box), then it is considered as early type.

To make our ETG classification more robust according to Integral Field Unit (IFU) observations (Li et al. 2018a), we fit a single Sérsic profile to the projected luminosity profiles of the selected ETGs, and keep only those with Sérsic indices satisfying n_x ≥ 2.5, n_y ≥ 2.5, and n_z ≥ 2.5 in all three projections simultaneously (Li et al. 2018a selected ETGs based on n ≥ 2.5). For the MASSIVE ETGs (Ma et al. 2014), they were selected based on morphology (E and S0 types from Paturel et al. 2003) without any specific Sérsic index cut applied, and 77 out of 105 galaxies have n ranging from 2 to 6 cross-referencing the NSA catalogue. Therefore, we consider our generic ETG selection criteria a reasonable choice when comparing to MASSIVE ETGs and we arrive at a sample of 221 well-resolved ETGs after the above-mentioned photometric selections. This will be further reduced to a final sample of 207 ETGs after removing galaxies that have been through recent major mergers (see Section 3.1).

2.3 Mock observations

We summarize the main steps in post-processing simulation particle and catalogue data to retrieve kinematic properties of our mock ETG sample that mimics kinematic properties from the observational IFU spectroscopic surveys. Our pipeline is largely based upon the public code |${\small ILLUSTRIS-TOOLS}$|² (Li et al. 2016) to make mock IFU observations, with edits for our IllustrisTNG ETG sample applied. Fig. 1 shows the work flow of our post-processing pipeline.

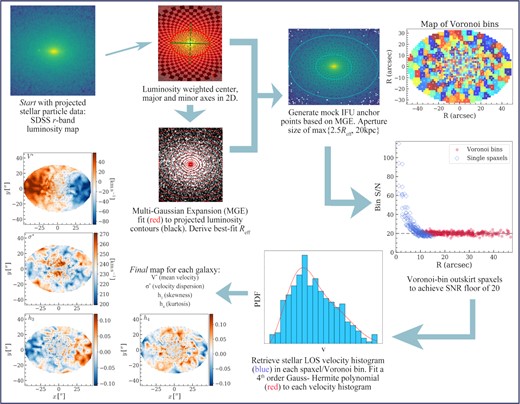
$Schematic flow chart of the main steps for our mock-IFU post-processing pipeline. The input starts from the projected stellar luminosity map from particle data, and the output is the 2D kinematic structure maps for each galaxy, i.e. mock IFU data products. The example galaxy (Subfind ID = 257302) shown has typical elliptical geometry in its luminosity map. The central projected region is well resolved with a large number of high SNR spaxels, and there are increasing fractions of Voronoi bins towards the outskirts. The velocity histogram indicates one of the spaxel/Voronoi bin demonstrating a significant non-Gaussian LOS velocity profile. Comparing the mean velocity and dispersion maps shows that the galaxy is dominated by randomized stellar motion, while its skewness h3 distribution is anticorrelated with the mean velocity distribution, and kurtosis h4 is generally positive for most of the spaxels/Voronoi bins in the map.$

Figure 1.

Schematic flow chart of the main steps for our mock-IFU post-processing pipeline. The input starts from the projected stellar luminosity map from particle data, and the output is the 2D kinematic structure maps for each galaxy, i.e. mock IFU data products. The example galaxy (Subfind ID = 257302) shown has typical elliptical geometry in its luminosity map. The central projected region is well resolved with a large number of high SNR spaxels, and there are increasing fractions of Voronoi bins towards the outskirts. The velocity histogram indicates one of the spaxel/Voronoi bin demonstrating a significant non-Gaussian LOS velocity profile. Comparing the mean velocity and dispersion maps shows that the galaxy is dominated by randomized stellar motion, while its skewness h₃ distribution is anticorrelated with the mean velocity distribution, and kurtosis h₄ is generally positive for most of the spaxels/Voronoi bins in the map.

Open in new tab Download slide

We find the centre of the stellar component of the galaxy by comparing the centre of mass for all stellar particles in the galaxy and its central 20|${{\ \rm per\ cent}}$| of particles (in 3D radial distance). We do this recursively by setting the central 20 |${{\ \rm per\ cent}}$| as the total region considered to be the total region in the next step, and compare its centre of mass to the 20 |${{\ \rm per\ cent}}^2$| particles centre of mass, until the difference between the two centre of masses in a step drops below 0.01 kpc. This centre for the stellar component is within ∼0.05 kpc of the minimum gravitational potential point defined by Subfind for our ETG sample. We assume the mean velocity of the stellar particles to be the mass-weighted average of particle velocities within 15 kpc of the stellar component centre found as above. We calibrate coordinates and velocities of stellar particles with respect to the stellar component centre and mean velocity of their galaxy.

Afterwards, we make 2D projections of the stellar particles in random directions (along the z-axis of the simulation box) to mimic realistic observational conditions (we have also tried random projections in the x and y axes, as well as along the edge-on direction of the galaxy, which all largely preserve the main findings of this paper). We pixelize the SDSS r-band luminosities of the projected stellar particles on to an |$80\, \mathrm{kpc}\times 80\, \mathrm{kpc}$| square aperture centred on the stellar component centre. We set our pixel size to |$0.5\, \mathrm{kpc}\times 0.5\, \mathrm{kpc}$|⁠, imitating the local ETG population of the MASSIVE survey, and we place our fiducial ETGs at z = 0.03 (angular diameter distance 128 Mpc) for our mock observations. The angular resolution of our mock luminosity map is 0.806 arcsec at that redshift, while the MASSIVE galaxies were observed using the Hobby-Eberly Telescope (HET; Hill et al. 2008) at the McDonald Observatory, where its operational seeing has a full width at half-maximum (FWHM) of 1.5 arcsec (σ_PSF = 0.64 arcsec). If we convolve a Gaussian PSF kernel matching the HET seeing, which has a Gaussian scatter than our mock pixel size, the PSF normalization will boost each pixel’s value by itself and does not smear out its flux to other neighbouring pixels. As such, we consider our pixelization has effectively accounted for the seeing with it being marginally coarser than the expected PSF.

Next, we model the projected luminosity map with the Multi-Gaussian-Expansion (MGE) formalism (Emsellem et al. 1994) with the publicly available python package MgeFit³ (Cappellari 2002). The MGE method models the surfaced brightness of a galaxy with a stack of (we choose N = 15) elliptical 2D Gaussians:

$$\begin{eqnarray} \Sigma (x^{\prime }, y^{\prime }) = \sum _{k = 1}^{N}\frac{L_{k}}{2\pi \sigma _{k}^{2}q_{k}^{\prime }}\mathrm{exp}\left[-\frac{1}{2\sigma _{k}^{2}}\left(x^{\prime 2} + \frac{y^{\prime 2}}{q_{k}^{\prime 2}}\right)\right], \end{eqnarray}$$

(3)

where L_k, σ_k, |$q_{k}^{\prime }$| are the normalization, standard deviation, and axial ratio of the kth Gaussian. The primed coordinates x′, y′ are the projected 2D angular coordinates (placing the galaxy at 128 Mpc) in a system where the origin is at the centre of the galaxy and x′ axis being aligned with the galaxy’s major axis (Cappellari 2002). The centre and major (minor) axis of the galaxy’s projected luminosity map are calculated using the top |$10{{\ \rm per\ cent}}$|-brightest pixels (Li et al. 2016), with the centre being determined by luminosity-weighting and the major (minor) axis following the eigenvectors of the 2D inertial tensor (Allgood et al. 2006) spanned by the selected pixels.

The luminosity profile is then sampled in equal angular bins and logarithmic radial bins to perform the MGE fit. The result of this step produces an analytical best-fitting description of the galaxy surface brightness map with 2D Gaussians, and also provides realistic effective radius (half-light radius) of our mock ETGs that mimics observations by integrating the best-fitting surface brightness profiles. A comparison between the MGE-derived effective radius |$R_{\mathrm{eff}}^{\mathrm{MGE}}$| and the effective radius obtained by directly projecting all stellar particles assigned to the galaxy by Subfind (R_eff) is shown in Appendix A, which shows that |$R_{\mathrm{eff}}^{\mathrm{MGE}}$| gives a more realistic description of galaxy sizes removing much of the intracluster light especially in more massive ETGs. This choice of effective radius is also more flexible to capture different distinct components in the ETG luminosity profile compared to simpler half-light-ellipse or single Sérsic fits often adopted in observations (see section 3.2 in Ma et al. 2014). In the rest of this paper, we refer to |$R_{\mathrm{eff}}^{\mathrm{MGE}}$| when we mention the effective radius of our simulated ETGs.

Furthermore, we generate mock IFU maps for our simulated ETGs focused on their central regions satisfying:

$$\begin{eqnarray} r^{\prime } = \sqrt{x^{\prime 2} + \frac{y^{\prime 2}}{q_\mathrm{p}^2}} \lt \left(\frac{R_{\mathrm{max}}}{\sqrt{q_{\mathrm{p}}}}\right), \end{eqnarray}$$

(4)

where |$R_{\mathrm{max}} = \mathrm{max}\lbrace 2.5 R_{\mathrm{eff}}^{\mathrm{MGE}}, 20\, \mathrm{kpc}\rbrace$| is our mock IFU aperture that mimics observations (Veale et al. 2017). This aperture setting guarantees that the kinematic maps we generate sample the outskirts of the galaxies well. After we select these central pixels, we assume that each individual pixel corresponds to an IFU spaxel (single fibre in an IFU bundle). We use the Convex-Hull method to efficiently identify stellar particles that are projected within our IFU aperture, and assign them to their nearest spaxel by querying the KD-Tree constructed for all spaxel anchor points. Following that, we Voronoi-bin the outskirt spaxels to the target signal-to-noise ratio (SNR) of 20 to ensure kinematic information quality, and leave single spaxels in the central region with high SNR unbinned.

Finally, we calculate the line-of-sight (LOS) stellar velocity distribution for each spaxel/Voronoi-bin in the 2D IFU aperture. If a spaxel/Voronoi-bin has N stellar particles projected within it, then we construct the LOS velocity histogram of these particles using |$\left[ \sqrt{N} \right]$| equivelocity bins. We perform a least-squares fit to the stellar LOS velocity histogram in each spaxel/Voronoi-bin with a fourth-order Gauss–Hermite function to extract the mean (⁠|$\bar{v}$|⁠), dispersion (σ), skewness (h₃), and kurtosis (h₄) of the LOS velocity distribution:

$$\begin{eqnarray} f(v) &=& \frac{1}{\sqrt{2\pi \sigma ^{2}}}\, \mathrm{exp}\left(-\frac{x^2}{2}\right) \\ && \times \left[1 + h_{3}\mathrm{H_{3}}\left(x\right) + h_{4}\mathrm{H_{4}}\left(x\right)\right], x = \frac{v - \bar{v}}{\sigma }, \end{eqnarray}$$

(5)

where |$\bar{\nu }$| and σ are the mean velocity and dispersion in the spaxel/Voronoi bin. |$\mathrm{H_{3}}(x)= (2/\sqrt{3})x^{3} - \sqrt{3}x$| and |$\mathrm{H_{4}}(x) = (\sqrt{6}/3)x^{4} - \sqrt{6}x^{2} + \sqrt{6}/4$| are the third and fourth order normalized Gauss–Hermite functions, while their coefficients contain the important kinematic information of the third velocity moment h₃ (skewness) and the fourth velocity moment h₄ (kurotsis). Qualitatively, a positive h₃ indicates asymmetric bias of the velocity distribution towards velocities less than the mean, and vice versa for negative h₃. A positive h₄ indicates symmetric deviation from a normal Gaussian with larger tails and a more centrally peaked velocity distribution, while negative h₄ indicates smaller tails and centrally flat (sometimes double peaked) velocity distribution (van der Marel & Franx 1993). To wrap up, we store the 2D map of the mean, dispersion, skewness, and kurtosis of the line-of-sight (LOS) velocity distribution for each individual ETG, and proceed to obtaining radial profiles of these kinematic properties in the next section.

3 RESULTS OF KINEMATIC FEATURES

3.1 The galaxy sample

In this section, we present the fundamental properties of our selected ETG sample. Fig. 2 shows the stellar mass (M_*), the effective radius derived with the best-fitting MGE model (⁠|$R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠), and the mass-weighted average LOS velocity dispersion (⁠|$\sigma _{\mathrm{eff}}^{\mathrm{MGE}}$|⁠) within |$R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠. The sample is a typical massive (median stellar mass log₁₀(M_*/M_⊙) = 11.18) ETG sample with well-resolved spatial extent (median effective radius of 7 kpc), and dynamically hot with significant velocity dispersion (median velocity dispersion |$162\, \mathrm{km\, s^{-1}}$|⁠). The LOS velocity dispersion within the effective radius positively correlates with stellar mass following the Tully–Fisher relation M_* ∝ σ⁴ (McGaugh et al. 2000; Bell & de Jong 2001; Williams, Bureau & Cappellari 2010). It also correlates with the effective radius, which is observed to roughly follow |$R_{\mathrm{eff}} \propto M_{\ast }^{0.5}$| in the local universe (Cassata et al. 2013; Huertas-Company et al. 2013; Xie et al. 2015), and leads to a scaling with the LOS stellar velocity dispersion in the form of R_eff ∝ σ². We fit these two scaling relations to our IllustrisTNG ETG sample with fixed power-law slopes and free intercepts (shown as dashed lines in Fig. 2). We also plot in Fig. 2 the stellar masses, effective radii, and the average LOS stellar velocity dispersion for MASSIVE galaxies in Veale et al. (2018). The M_*–σ scaling of MASSIVE galaxies is rather consistent with the IllustrisTNG ETGs, although IllustrisTNG approaches the volume limit for massive galaxies (only 18 galaxies with log₁₀(M_*/M_⊙) ≥ 11.6) versus the MASSIVE Survey (89 galaxies with log₁₀(M_*/M_⊙) ≥ 11.6). The effective sizes quoted in the right-hand panel of Fig. 2 are from the 2MASS catalogue which covers essentially all MASSIVE ETGs. However, due to the shallower survey depth of 2MASS, galaxy sizes are underestimated by a factor of ∼2 due to insufficient sensitivity to galaxy outskirts compared to sizes from the NSA catalogue which is based on SDSS DR8 photometry (see section 3.2 in Ma et al. 2014). We also plot a scaling relation that shifts the IllustrisTNG ETG R_eff–σ scaling by half the effective radii in Fig. 2 that coincides well with the MASSIVE ETGs.

Figure 2.

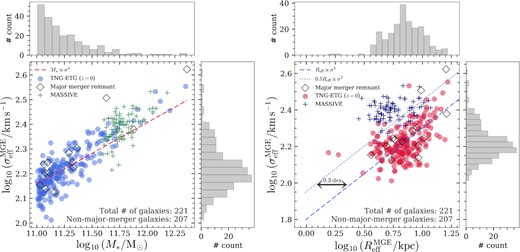
The distribution of stellar mass (left-hand panel) and effective radius (right-hand panel) versus the velocity dispersion measured within the effective radius. The open markers indicate those ETGs that are either undergoing major mergers found via their kinematic maps, or that have been through a recent one (mass ratio >1/3) in the previous snapshot recorded in the merger tree. We remove them in the following analysis and figures following Veale et al. (2018), and only include the filled marker points in our samples below (207 galaxies remaining out of 221). The histograms at the sides in each subplot show the marginalized distributions of these three quantities (histograms include the major merger galaxies). Dashed lines in both panels indicate scaling relations (fixed slope and fitted intercept) for ETGs as expected from observations. ‘Plus’ markers in both panels indicate the MASSIVE sample in Veale et al. (2018). Our simulated ETG sample has only 18 galaxies with log₁₀(M_*/M_⊙) ≥ 11.6) versus 89 in MASSIVE, owing to the volume limit of the simulation. The effective radius for MASSIVE ETGs quoted here are from the 2MASS catalogue (which underestimates galaxy sizes by a factor ∼2 (0.3 dex) compared to the NSA catalogue, but covers the entire MASSIVE sample) as summarized in Ma et al. (2014). We also show a dotted line in the right-hand panel that indicates a scaling relation with half the effect radius of the fitted IllustrisTNG ETG scaling that coincides well with the MASSIVE galaxies.

Open in new tab Download slide

Before diving in to the results, we would like to point out that the selection of galaxy samples in the MASSIVE Survey (Ma et al. 2014; Veale et al. 2018) has deliberately removed galaxies in ongoing mergers or show complex merger remnant structures. We therefore also remove such out-of-equilibrium galaxies from our sample to further make fair comparisons with the observations. First, we remove galaxies at z = 0 that are currently going through major mergers apparent from their kinematic structure (mainly LOS mean velocity) and luminosity maps. Secondly, we also trace every ETG in our sample back one snapshot from z = 0 to z ≈ 0.01 (140 Myr ago) along their main progenitor branch, and remove all galaxies that are remnants of recent major mergers in that snapshot with merger stellar mass ratio μ_* ≥ 1/3. Combining these two removal criteria, our original 221 ETG sample reduces to 207 galaxies, and the removed galaxies are indicated by empty diamonds in Fig. 2. We proceed with our analysis in the following with the final 207 galaxies without significant perturbation.

In Fig. 3, we show the projected profiles of the mean velocity (〈v_LOS〉), the stellar velocity dispersion (σ_LOS), the skewness (h₃), and kurtosis (h₄) of our 207 ETGs sample. We bin the spaxels/Voronoi bins of the projected map radially for each galaxy in 20 equal-number bins, and calculate the flux-weighted (SDSS r-band) value of the four quantities in each bin to represent the value for the average velocity profile in that radial bin. The left column has the projected physical distance R as the x-axis, while the right column has the scaled projected distance in units of |$R_{\mathrm{eff}}^{\mathrm{MGE}}$| as x-axis. We can see that in both radial scalings the mean velocity and the skewness profiles are largely flat, while the LOS velocity dispersion profile takes the form of a variety of shapes, and that the h₄ profiles show a mildly increasing trend towards larger radii.

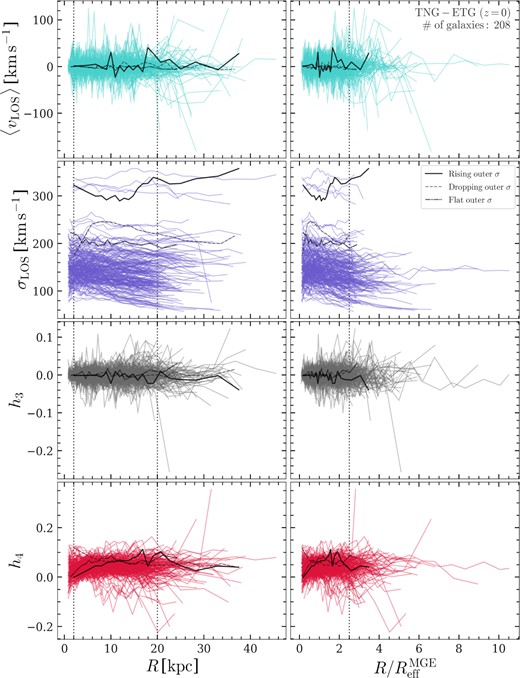
$From top to bottom, the profiles of the line-of-sight mean velocity (〈vLOS〉), velocity dispersion σLOS, skewness (h3), and kurtosis (h4) are shown for each individual galaxy in our ETG sample. Each curve represents one galaxy’s flux-weighted radial profile of the four kinematic quantities. The left row shows the profile with respect to the projected physical distance to the galaxy centre, while the right row shows the results w.r.t. the projected distance in units of the effective radius $R_{\mathrm{eff}}^{\mathrm{MGE}}$ for each individual galaxy. The vertical dotted lines in the left column indicate the location of R = 2 kpc and R = 20 kpc, while the vertical dotted lines in the right column indicate the location of $R = 2.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$. We select three individual galaxies that have rising (solid), flat (dot–dashed), dropping (dashed) outer velocity dispersion profiles at 20 kpc (see Section 3.2 for definitions), and highlight their kinematic profiles in each panel.$

Figure 3.

From top to bottom, the profiles of the line-of-sight mean velocity (〈v_LOS〉), velocity dispersion σ_LOS, skewness (h₃), and kurtosis (h₄) are shown for each individual galaxy in our ETG sample. Each curve represents one galaxy’s flux-weighted radial profile of the four kinematic quantities. The left row shows the profile with respect to the projected physical distance to the galaxy centre, while the right row shows the results w.r.t. the projected distance in units of the effective radius |$R_{\mathrm{eff}}^{\mathrm{MGE}}$| for each individual galaxy. The vertical dotted lines in the left column indicate the location of R = 2 kpc and R = 20 kpc, while the vertical dotted lines in the right column indicate the location of |$R = 2.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠. We select three individual galaxies that have rising (solid), flat (dot–dashed), dropping (dashed) outer velocity dispersion profiles at 20 kpc (see Section 3.2 for definitions), and highlight their kinematic profiles in each panel.

Open in new tab Download slide

3.2 Inner and outer slopes of the velocity dispersion profile

To measure the slopes of the projected velocity dispersion profile and compare with the results of Veale et al. (2018), we follow their modeling by fitting a double-power-law model to the dispersion profile. The dispersion profile model takes the form:

$$\begin{eqnarray} \sigma _{\mathrm{fit}}(R) = \sigma _{0} 2^{\gamma _{1} - \gamma _{2}} \left(\frac{R}{R_{\mathrm{B}}}\right)^{\gamma _{1}} \left(1+\frac{R}{R_{\mathrm{B}}}\right)^{\gamma _{2} - \gamma _{1}}, \end{eqnarray}$$

(6)

where γ₁ and γ₂ are the asymptotic slopes of the profile towards zero and infinity, R_B the break radius is set to 5 kpc following Veale et al. (2018), and σ₀ is the normalization of the dispersion profile. We have verified that the break radius of 5 kpc is a reasonable description of the IllustrisTNG ETGs. We fit each galaxy’s radial velocity dispersion profile in the radial range [|$2\, \mathrm{kpc}$|⁠, R_max] (see equation 4 for R_max) to avoid core softening in the central regions of the ETGs due to the resolution limit of the simulation. With an analytic double-power-law description of the dispersion profiles, we can define the logarithmic slope of the fitted dispersion profile at any radius R as

$$\begin{eqnarray} \gamma (R) = \frac{{\rm d} \mathrm{log}\, \sigma _{\mathrm{fit}}(R)}{{\rm d} \mathrm{log} R} = \gamma _{1} + \left(\gamma _{2} - \gamma _{1}\right) \left(\frac{R}{R_{\mathrm{B}}}\right) \left(1 + \frac{R}{R_{\mathrm{B}}}\right)^{-1}. \end{eqnarray}$$

(7)

Since in the MASSIVE Survey, the inner and outer slopes of the dispersion profile are measured at R = 2 kpc and R = 20 kpc, we follow that definition and obtain the inner (γ_inner) and outer (γ_outer) slopes of the velocity dispersion profile:

$$\begin{eqnarray} \gamma _{\mathrm{inner}} = \gamma (2) = \frac{5}{7} \gamma _{1} + \frac{2}{7} \gamma _{2},\ \gamma _{\mathrm{outer}} = \gamma (20) = \frac{1}{5} \gamma _{1} + \frac{4}{5} \gamma _{2}. \end{eqnarray}$$

(8)

Using the slopes γ₁ and γ₂ obtained from the best double-power-law fit in equation (6), we can derive the γ_inner and γ_outer values for our ETGs accordingly. We also follow uncertainties introduced in the fitting procedure to γ₁ and γ₂, and propagate them appropriately to uncertainties in γ_inner and γ_outer. Galaxies consistent with γ_outer = 0 within the uncertainties are defined having ‘flat’ outer dispersion profiles (0 within upper and lower bounds of γ_outer), galaxies with lower bound of γ_outer > 0 are defined as having ‘rising’ outer dispersion profiles, and galaxies with upper bound γ_outer < 0 are defined as having ‘dropping’ outer dispersion profiles, consistent with Veale et al. (2018).

The distribution of the inner and outer slopes (along with their uncertainties) of the dispersion profiles of our ETG sample are shown in Fig. 4. Galaxies with flat, rising, or dropping outer dispersion profiles are indicated with differently coloured markers, and we also overplot the best-fitting values of the observed MASSIVE ETGs from Veale et al. (2018). From the figure, we see that the γ_outer of the IllustrisTNG ETGs generally agree with the range of outer slopes in the observations. The simulation also has similar levels of uncertainties in the slopes (∼0.1, not shown for the observed values) as the observations. The range of γ_inner < 0 values for our ETGs is also very similar to observations; however, it is noticeable that there are apparently more galaxies having γ_inner > 0 within the uncertainties in our sample, which could be produced by systematic underestimation of the central stellar velocity dispersion. Since we mainly focus on the behaviour of γ_outer in this work, the discrepancy in γ_inner with observations does not affect our findings below. Nevertheless, this systematic underestimation of the central stellar velocity dispersion again points to the fact that IllustrisTNG galaxies are subject to higher central dark matter fractions (Lovell et al. 2018) and halo contraction (Wang et al. 2020), which adds another galaxy property that needs to be anchored by future improvements of the underlying feedback physics model of the simulation.

Figure 4.

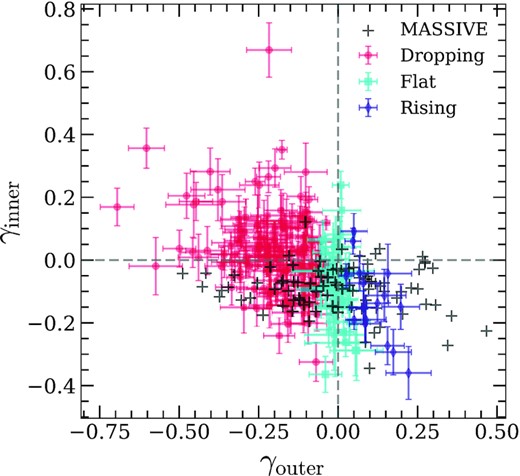
The distribution of the inner and outer slopes of the velocity distribution profile. The point (0, 0) indicates the case for a single-power-law isothermal density profile. The coloured points indicate simulated ETGs with rising (blue), flat (green), and dropping (red) outer velocity dispersion profile slopes (γ_outer). The error bars of the points are the combined fitting errors of the velocity dispersion profile for the inner and outer slopes. Observation values from the MASSIVE Survey (Veale et al. 2018) are shown for comparison with plus sign markers.

Open in new tab Download slide

3.3 Higher order velocity moments h₃ and h₄

In this section, we make direct comparison of the results of h₄ and γ_outer for IllustrisTNG ETGs with fig. 6 in Veale et al. (2018), which is the pivotal comparison for this work. With the h₄ profiles for individual galaxies derived in the previous section, we compute the average kurtosis within the effective radii |$\langle h_4 \rangle _{R_{\mathrm{eff}}^{\mathrm{MGE}}}$| with the SDSS r-band luminosity weighted value of h₄ in all spaxels/Voronoi bins projected within |$R_{\mathrm{eff}}^{\mathrm{MGE}}$| of each galaxy. To derive the gradient of the kurtosis Δh₄(R)/ΔlogR, we adopt the definitions in the observations (Veale et al. 2017, 2018) and define:

$$\begin{eqnarray} \frac{\Delta h_{4}(R)}{\Delta \mathrm{log} R} = \frac{h_{4}\left(1.5R_{\mathrm{eff}}^{\mathrm{MGE}} \right) - h_{4}\left(0.5R_{\mathrm{eff}}^{\mathrm{MGE}} \right)}{\mathrm{log_{10}}\left(1.5R_{\mathrm{eff}}^{\mathrm{MGE}} \right) - \mathrm{log_{10}}\left(0.5R_{\mathrm{eff}}^{\mathrm{MGE}} \right)}, \end{eqnarray}$$

(9)

which is the luminosity-weighted average slope of h₄ within the logarithmic radial range of [|$0.5R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠, |$1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$|]. The spaxels/Voronoi bins included in the calculation of h₄(R) at |$1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$| are taken from a thin annulus ±0.5 kpc that of R. Due to limited amount of spaxels available near the galactic centre, we compute h₄(R) at |$0.5R_{\mathrm{eff}}^{\mathrm{MGE}}$| as the luminosity-weighted average h₄ for all spaxels within |$R\leqslant 0.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠. The results of the mean kurtosis |$\langle h_4 \rangle _{R_{\mathrm{eff}}^{\mathrm{MGE}}}$| and the kurtosis gradient Δh₄(R)/ΔlogR versus the velocity dispersion profile outer slope γ_outer for our ETG sample are shown in Fig. 5. In both panels, observation values from Veale et al. (2018) are overplotted for comparison to the simulation results. In the right-hand panel, we also show the best-linear-fit comparison between the IllustrisTNG and MASSIVE Δh₄(R)/ΔlogR–γ_outer relations.

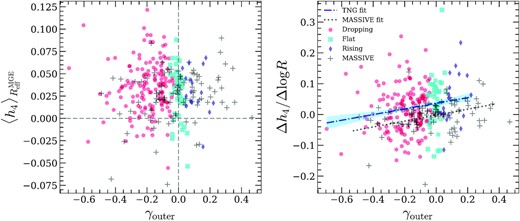
$The average kurtosis (left-hand panel, measured within the effective radius) and kurtosis gradient (right-hand panel, measured within $0.5R_{\mathrm{eff}}^{\mathrm{MGE}} \lt R \lt 1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$) versus the velocity dispersion profile outer slope γouter. The coloured dots indicate the three types of simulated ETGs with different outer slopes of their velocity dispersion profiles, while the open markers are observations from the MASSIVE Survey. The point (0, 0) in the left-hand panel indicates the point where the line-of-sight velocity distribution is a perfect Gaussian and independent of the projected radius. In the right-hand panel, the dotted line indicates the best linear fit for the MASSIVE ETGs (from fig. 6 in Veale et al. 2018, slope b = 0.096 ± 0.037, p = 0.012), and the blue dot–dashed line indicates the best linear fit for the IllustrisTNG ETGs (slope b = 0.092 ± 0.035, p = 0.009, shaded region stands for $68{{\ \rm per\ cent}}$ confidence interval). Clearly, the IllustrisTNG ETGs also show positive correlation between the kurtosis gradient and outer slope of the velocity dispersion profile, but there is larger scatter in the h4 gradient compared to observations. The TNG ETGs extend not as far as their MASSIVE Survey counterparts in the Δh4(R)/ΔlogR–γouter relation due to the less abundant sampling of the galaxy (Fig. 3) and halo (Fig. 9) masses in TNG100.$

Figure 5.

The average kurtosis (left-hand panel, measured within the effective radius) and kurtosis gradient (right-hand panel, measured within |$0.5R_{\mathrm{eff}}^{\mathrm{MGE}} \lt R \lt 1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠) versus the velocity dispersion profile outer slope γ_outer. The coloured dots indicate the three types of simulated ETGs with different outer slopes of their velocity dispersion profiles, while the open markers are observations from the MASSIVE Survey. The point (0, 0) in the left-hand panel indicates the point where the line-of-sight velocity distribution is a perfect Gaussian and independent of the projected radius. In the right-hand panel, the dotted line indicates the best linear fit for the MASSIVE ETGs (from fig. 6 in Veale et al. 2018, slope b = 0.096 ± 0.037, p = 0.012), and the blue dot–dashed line indicates the best linear fit for the IllustrisTNG ETGs (slope b = 0.092 ± 0.035, p = 0.009, shaded region stands for |$68{{\ \rm per\ cent}}$| confidence interval). Clearly, the IllustrisTNG ETGs also show positive correlation between the kurtosis gradient and outer slope of the velocity dispersion profile, but there is larger scatter in the h₄ gradient compared to observations. The TNG ETGs extend not as far as their MASSIVE Survey counterparts in the Δh₄(R)/ΔlogR–γ_outer relation due to the less abundant sampling of the galaxy (Fig. 3) and halo (Fig. 9) masses in TNG100.

Open in new tab Download slide

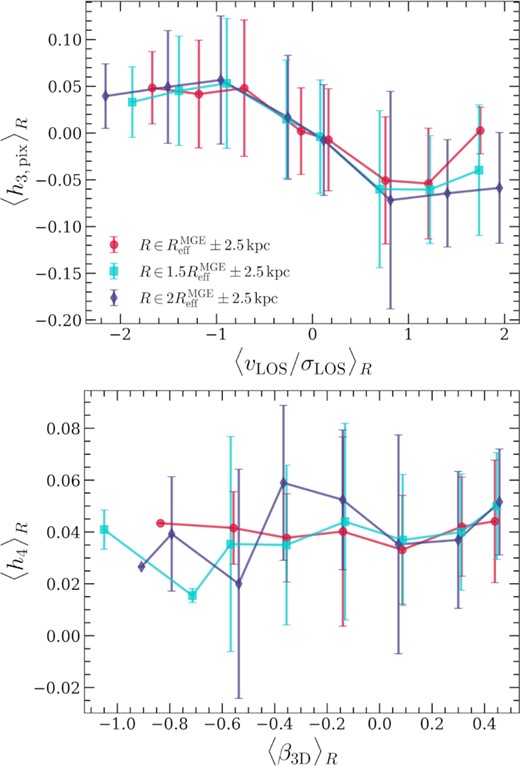
Upper panel: The correlation between the skewness h3 and the rotation to dispersion ratio v/σ at the pixel level measured around three different radii. Lower panel: The correlation between the average kurtosis h4 and the spherical velocity anisotropy parameter β3D measured in 3D apertures of different radii. Solid curves indicate the mean while the shaded regions/error bars represent the 1σ confidence intervals in both panels.

Figure 6.

Upper panel: The correlation between the skewness h₃ and the rotation to dispersion ratio v/σ at the pixel level measured around three different radii. Lower panel: The correlation between the average kurtosis h₄ and the spherical velocity anisotropy parameter β_3D measured in 3D apertures of different radii. Solid curves indicate the mean while the shaded regions/error bars represent the 1σ confidence intervals in both panels.

Open in new tab Download slide

In the left-hand panel of Fig. 5, the IllustrisTNG ETGs’ average kurtosis are consistent with the range of h₄ values from observations. In the right-hand panel of Fig. 5, although the kurtosis gradients of the simulated ETGs have larger scatter than the observed ETGs, it is remarkable that the simulation reproduces the key positive correlation between Δh₄(R)/ΔlogR and γ_outer as in fig. 6 of Veale et al. (2018). The dot–dashed blue line represents the best linear fit to the IllustrisTNG ETGs (slope b = 0.092 ± 0.035, p = 0.009, shaded region stands for 1σ confidence interval), and the dotted black line indicates the best linear fit to the MASSIVE ETGs (slope b = 0.096 ± 0.037, p = 0.012, see fig. 6 in Veale et al. 2018). Thus, both the slope and correlation significance for IllustrisTNG ETGs are statistically consistent with the MASSIVE ETGs, which justifies the use of our mock ETG sample as a benchmark for understanding the origin of Δh₄(R)/ΔlogR–γ_outer correlation in the outer kinematic structure of ETGs.

To further check the consistency of higher order kinematic properties of our simulated ETGs with observations (e.g. fig. 10 in Veale et al. 2017), we show the relation of the skewness h₃ versus the rotation to dispersion ratio 〈v_LOS〉/σ_LOS in the upper panel of Fig. 6. Values of h₃ and v/σ for individual spaxels/Voronoi bins from the different radial apertures (scaled to |$R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠) in different galaxies are stacked together. Unlike h₄ which is the fourth velocity moment and has even parity, the reason why we keep track of the individual spaxel/Voronoi bin level h₃ information is due to its odd parity, otherwise projection in circular apertures would average out any underlying signal. The anticorrelation between h₃ and v/σ seen for the simulated ETGs is consistent with the theoretical expectation that galaxies with substantial rotation (large |v/σ|) will have a large low velocity tail due to the projection effect of distant background and foreground stars along the line of sight, especially when the galaxy is viewed edge-on. The magnitude of |h₃| ∼ 0.1 is prevalent from small (⁠|$\sim 1 R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠) to large (⁠|$\sim 2 R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠) radii, which also shows consistency with observations (Krajnović et al. 2011; Veale et al. 2017). Thus, both h₃ and h₄ measurements of the IllustrisTNG ETG sample from our mock IFU pipeline resembles that of the observed MASSIVE sample, indicating that physical interpretations (Section 4) of these kinematic structures analysed from the simulation can be confidently applied to understanding the formation process of these features in real world ETGs.

3.4 De-correlated outer kurtosis and velocity anisotropy

The core puzzle in Veale et al. (2018) that sparked the current study is the positive correlation between Δh₄(R)/ΔlogR and γ_outer. If an intrinsically flat velocity dispersion profile (assuming no ordered rotation in an ideal ETG, v/σ = 0) is affected by the projection effects of velocity anisotropy at the outskirts, we expect to find radial anisotropy driving positive h₄ and ‘dropping’ γ_outer (vice versa for the tangential case), producing an anticorrelation of Δh₄(R)/ΔlogR and γ_outer (Gerhard et al. 1998). This theoretical expectation is exactly opposite to what was observed in Veale et al. (2018). A crucial assumption of this prediction is that they were evaluated under fixed density profiles (Gerhard 1993), typically comprising a SIS halo potential (fixed γ′ = 2) and a spherical stellar distribution that have a steeper density profile (fixed γ′ = 3 or 4), which naturally leads to Veale et al. (2018) proposing variations in the total density profile as an explanation.

Before presenting the connection between the outer kinematic structure and the density profile, we show in the lower panel of Fig. 6 how the velocity anisotropy (β_3D) correlates with h₄ in our ETGs. The spherical velocity anisotropy is defined as (Binney & Tremaine 2008)

$$\begin{eqnarray} \beta _{\mathrm{3D}} = 1 - \frac{\sigma _{\mathrm{\phi }}^{2} + \sigma _{\mathrm{\theta }}^{2}}{2\sigma _{\mathrm{r}}^{2}}\, , \end{eqnarray}$$

(10)

where σ_ϕ, σ_θ, and σ_r are the velocity dispersion in the azimuthal, polar, and radial directions. As shown in Fig. 6, there is almost no correlation between β_3D and h₄ averaged in across different aperture sizes. Particularly, we find a positive h₄ (median ∼0.04) even for tangential anisotropy (β < 0), and only a slight positive trend consistent across different radii at 〈β_3D〉_R ≳ 0.1. This suggests that positive h₄ towards the galactic outskirts is unlikely driven by systematic radial velocity anisotropy prevalent in ETGs.

In concordance with the conjecture in Veale et al. (2018), we elaborate in Section 4.1 that the positive Δh₄(R)/ΔlogR–γ_outer correlation is in fact driven by the variation of their total density profiles across our ETG sample. The variations in the outer kurtosis and velocity anisotropy also show hints to be driven by different routes of stellar assembly (Section 4.2). The de-correlated behaviour between the outer h₄ and β_3D (⁠|$R \geqslant R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠) shown in Fig. 6 can then be accounted for by the dominant effect from gradients in circular velocity (Gerhard 1993; Baes, Dejonghe & Buyle 2005), where the effect of varying density profiles can overwhelm and randomize the rather weak correlation between h₄ and velocity anisotropy.

4 LINKING KINEMATIC STRUCTURE WITH DENSITY PROFILE, ASSEMBLY HISTORY, AND ENVIRONMENT

As shown in the previous section, the IllustrisTNG ETGs have consistent outer slopes of the velocity dispersion profile (γ_outer) and higher order velocity moments (h₃, h₄) compared to observations. The simulated ETGs also reproduce the observed positive correlation between Δh₄(R)/ΔlogR and γ_outer, and that velocity anisotropy is insufficient to explain the formation of this trend. In this section, we explore the validity of circular velocity gradients as a driving factor of this trend of following the hypothesis in Veale et al. (2018). We also explore the connection of their kinematic structure to their stellar assembly and environment.

4.1 Correlation with density profile

Before proceeding into the details of exploring the density profiles, we make a change in the quantity characterizing the non-Gaussian outer kinematic structure from the kurtosis gradient Δh₄(R)/ΔlogR to the outer kurtosis 〈h₄〉 (measured at |$1.5 R_{\mathrm{eff}}^{\mathrm{MGE}} \pm 2.5\, \mathrm{kpc}$|⁠), which is the luminosity-weighted h₄ for spaxels/Voronoi bins within a 5 kpc annulus around |$1.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠. The motivation for our choice is twofold: on the one hand, since we focus on the correlation with γ_outer, we would prefer to isolate the contribution from outer h₄ alone; on the other hand, this change of variable can also avoid the systematics in the stellar velocity distribution at small radii pertinent to resolution effects (core softening) and feedback physics (dark matter fraction) as discussed in Section 3.2. In the upper left panel of Fig. 7, we show Δh₄(R)/ΔlogR versus the outer h₄ for the IllustrisTNG ETGs. The best linear fit of the correlation has slope b = 0.159 ± 0.022, p = 5.12 × 10⁻¹², and Pearson correlation coefficient r = 0.456, justifying that the outer h₄ is a decent representative of the kurtosis gradient. Following that, we show in the upper right panel of Fig. 7 that a positive correlation (slope b = 0.020 ± 0.012, p = 0.104) also exists between the outer h₄ and the outer velocity dispersion profile slope γ_outer. Combining these two panels, we anchor our following discussion regarding the link to density profiles and assembly history on the outer h₄.

$Upper left: the relation between the h4 gradient and the outer h4 values measure at around $1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$. Upper right: The relation between the outer h4 values and the outer velocity dispersion profile slopes γouter. Lower left: the relation between outer h4 and the mass-weighted density profile slope $\gamma ^{\prime }_{\mathrm{m}}$ (equation 11) measured at $1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$. Lower right: The relation between the velocity dispersion profile outer slope and the density profile slope. In all panels, The different ETGs with rising, flat, and dropping γouter are indicated by the different-coloured scattered dots, following Fig. 4. The blue dot–dashed lines and shaded regions stand for the best linear fit and their [$16{{\ \rm per\ cent}}$, $84{{\ \rm per\ cent}}$] confidence intervals for each of the correlations.$

Figure 7.

Upper left: the relation between the h₄ gradient and the outer h₄ values measure at around |$1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠. Upper right: The relation between the outer h₄ values and the outer velocity dispersion profile slopes γ_outer. Lower left: the relation between outer h₄ and the mass-weighted density profile slope |$\gamma ^{\prime }_{\mathrm{m}}$| (equation 11) measured at |$1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠. Lower right: The relation between the velocity dispersion profile outer slope and the density profile slope. In all panels, The different ETGs with rising, flat, and dropping γ_outer are indicated by the different-coloured scattered dots, following Fig. 4. The blue dot–dashed lines and shaded regions stand for the best linear fit and their [|$16{{\ \rm per\ cent}}$|⁠, |$84{{\ \rm per\ cent}}$|] confidence intervals for each of the correlations.

Open in new tab Download slide

The power-law slope of the total density profile, |$\gamma _{\rm PL}^{\prime }$| (same as γ′ in equation (1), renaming to avoid confusion with the velocity dispersion profiles’ inner and outer slopes) reflects the underlying gradient in circular velocity (interchangeable with velocity dispersion in the isotropic case, equation 2) such that |$\gamma ^{\prime }_{\mathrm{PL}} \gt 2$| corresponds to a ‘dropping’ circular velocity profile, |$\gamma ^{\prime }_{\mathrm{PL}} \lt 2$| a ‘rising’ circular velocity profile, and a flat circular velocity profile in the exact isothermal case (⁠|$\gamma ^{\prime }_{\mathrm{PL}} = 2$|⁠). In Papers I and II, this parameter was obtained by a linear fit to the combined log ρ–log r profile of dark matter, stars, and gas in 100 logarithmic radial bins from 0.4R_eff to 4R_eff, where R_eff is the projected stellar half mass radius. To study the total density profile at the outskirts of these ETGs, we approximate the power-law slope with the ‘mass-weighted’ logarithmic density slope (Dutton & Treu 2014; Wang et al. 2020):

$$\begin{eqnarray} \gamma ^{\prime }_{\mathrm{m}}(R) = \frac{-1}{M(\lt R)}\int _{0}^{R} \gamma ^{\prime }_{\mathrm{PL}}(r) 4\pi r^{2} \rho (r) {\rm d}r = 3 - \frac{4\pi R^{3}\rho (R)}{M(\lt R)}, \end{eqnarray}$$

(11)

where M(< R) is the mass enclosed within a 3D spherical aperture with radius R, and ρ(R) is the average local density at radius R. We evaluate the mass-weighted slope |$\gamma ^{\prime }_{\mathrm{m}}$| at |$1.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$| (local density ρ(R) calculated in a thin shell |$\pm 2{{\ \rm per\ cent}}$| at this radius) to compare with the outer h₄ and γ_outer. The correlations along with the best linear fit results are shown in the bottom panels in Fig. 7.

Intriguingly, both the outer h₄ (bottom left-hand panel) and the velocity dispersion profile outer slope γ_outer (bottom right-hand panel) are anticorrelated with the outer mass-weighted density profile slope at |$1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠. Apparently, there is noticeable scatter in both relations which lead to the scatter seen in the Δh₄(R)/ΔlogR-γ_outer correlation in Fig. 5. Nevertheless, both of these negative correlations are statistically significant, with p = 0.028 for the outer h₄–|$\gamma ^{\prime }_{\mathrm{m}}$| correlation (slope b = −0.031 ± 0.014) and p = 0.027 for the γ_outer–|$\gamma ^{\prime }_{\mathrm{m}}$| correlation (slope b = −0.177 ± 0.079). With the velocity anisotropy ruled out as a plausible explanation as discussed in Section 3.4, these two correlations suggest that it is indeed the systematic variation of the total density profile being shallower than isothermal (⁠|$\gamma ^{\prime }_{\mathrm{m}}\lt 2$|⁠) that leads to ‘rising’ gradients in the velocity dispersion profiles (γ_outer > 0) and produces positive outer h₄ in these ETGs (vice versa for the steeper than isothermal case where |$\gamma ^{\prime }_{\mathrm{m}}\gt 2$|⁠), giving rise to an overall positive correlation between Δh₄(R)/ΔlogR and γ_outer. The physical interpretation behind this correlation is that ongoing or past remnants of minor mergers producing positive outer h₄ while simultaneously driving the total density profile shallower than isothermal (Section 4.2). Moreover, combined with our finding in Paper I that there is no significant correlation between the density profile slope and velocity anisotropy (see fig. 8 in Wang et al. 2020), having the main driving factor of a non-zero h₄ being a deviation from an isothermal density profile allows for randomness between h₄ and β_3D, leading to the de-correlated h₄–β_3D trend as seen in the bottom panel of Fig. 6.

$Left column: The relation between the outer h4 values and stellar assembly contributions. Major (minor) mergers are defined as mergers having stellar mass ratio larger (smaller) than 0.25. Right column: The relation between the outer β3D and stellar assembly contributions. In each column, the upper panel shows the link to the fraction of stellar mass accreted in major mergers, while the lower panel shows the link to the fraction of stellar mass accreted in minor perturbations, i.e. minor mergers and flyby interactions. The key takeaway is that the outer 〈h4〉 correlates with minor perturbations but not major mergers, while the velocity anisotropy 〈β3D〉 correlates more strongly with major mergers. The three types of ETGs with rising, flat, and dropping outer velocity dispersion profiles are shown by the scattered dots. The open markers with solid lines (dashed lines) denote the median ($68{{\ \rm per\ cent}}$ scatter) of the rising, dropping, and flat γouter ETGs combined. The blue dot–dashed lines and shaded regions stand for the best linear fit and their [$16{{\ \rm per\ cent}}$, $84{{\ \rm per\ cent}}$] confidence intervals (see the text in Section 4.2 for best-fitting slopes and p-values).$

Figure 8.

Left column: The relation between the outer h₄ values and stellar assembly contributions. Major (minor) mergers are defined as mergers having stellar mass ratio larger (smaller) than 0.25. Right column: The relation between the outer β_3D and stellar assembly contributions. In each column, the upper panel shows the link to the fraction of stellar mass accreted in major mergers, while the lower panel shows the link to the fraction of stellar mass accreted in minor perturbations, i.e. minor mergers and flyby interactions. The key takeaway is that the outer 〈h₄〉 correlates with minor perturbations but not major mergers, while the velocity anisotropy 〈β_3D〉 correlates more strongly with major mergers. The three types of ETGs with rising, flat, and dropping outer velocity dispersion profiles are shown by the scattered dots. The open markers with solid lines (dashed lines) denote the median (⁠|$68{{\ \rm per\ cent}}$| scatter) of the rising, dropping, and flat γ_outer ETGs combined. The blue dot–dashed lines and shaded regions stand for the best linear fit and their [|$16{{\ \rm per\ cent}}$|⁠, |$84{{\ \rm per\ cent}}$|] confidence intervals (see the text in Section 4.2 for best-fitting slopes and p-values).

Open in new tab Download slide

4.2 Correlation with stellar assembly history

Galaxy mergers play an important role in the non-dissipative (dry) evolution of ETGs at low redshift (Nipoti et al. 2009a, b; Remus et al. 2013; Wellons et al. 2016). In Paper I, we demonstrated that the stellar assembly history of ETGs parametrized by the fraction of in situ formed stars (f_{in situ}) positively correlates with the total density profile power-law slope within 4R_eff (see fig. 10 in Wang et al. 2020). In Paper II, we have shown that gas-poor mergers at low redshift (z ≲ 0.5), both major and minor mergers alike, work in coordination to reduce γ′ of the total density profile and establish the positive f_{in situ}−γ′ correlation (see fig. 7 in Wang et al. 2019). Motivated by these finding and the positive relation of h₄ at |$1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$| and |$\gamma ^{\prime }_{\mathrm{m}}$| as shown above in Fig. 7, we expect to also find a correlation between the outer h₄ and the stellar assembly history of these ETGs.

In Fig. 8, we present the relations between the outer h₄ (left column) and outer β_3D (right column) measured at |$1.5R_{\mathrm{eff}}^{\mathrm{MGE}}$| as a function of the mass fraction of stars in these ETGs accreted either from major mergers (upper row) or minor perturbations combining the contribution from minor mergers and flyby interactions (lower row). Major (minor) mergers are defined as mergers into the main progenitors of our z = 0 ETGs having stellar mass ratios larger (smaller) than 1/4. The solid line and open markers denote the median of the combined sample including the rising, dropping, and flat outer velocity dispersion profile ETGs, while the dashed lines represent the [|$16{{\ \rm per\ cent}}$|⁠, |$84{{\ \rm per\ cent}}$|] range (⁠|$1\, \sigma$|⁠) of the distributions. The outer h₄ shows almost no correlation with the stellar constituent from major mergers (best linear fit slope b = −0.0006 ± 0.0103, p = 0.9545, statistically insignificant). Intriguingly, the outer h₄ demonstrates a positive correlation (best linear fit slope b = 0.0254 ± 0.0128, p = 0.0474, statistically significant) with the stellar assembly contribution from minor perturbations at f_{minor merger⊕flyby} ≲ 0.3. This correlation is shaped by the majority of galaxies in our sample that demonstrates consistent increase in the median as well as the |$1\, \sigma$| region. We also notice that there is a slight decrease in outer h₄ at f_{minor merger⊕flyby} ∼ 0.4, beyond which h₄ remains largely constant. This fluctuation in the outer h₄ at high minor perturbation fractions could be due to the limited sample size at the massive end.

Nevertheless, the outer 3D velocity anisotropy shows positive correlations with stellar assembly through both major mergers and minor perturbations, with both relations having large scatter as well. The main difference regarding these two correlations is that major mergers seem to drive a more significant (∼0.4 versus ∼0.1) and steady (monotonic versus fluctuating) increase in the outer β_3D compared to minor perturbations. This is also evident from the steeper slope of the linear fit between 〈β_3D〉 and f_{major merger} (slope b = 0.702 ± 0.115, p = 5.83 × 10⁻⁹, very significant) versus f_{minor merger⊕flyby} (slope b = 0.196 ± 0.157, p = 0.213, poor statistical significance). Hence, the positive outer h₄ in ETGs tends to be built up by minor mergers and galaxy interactions (at least for the majority of galaxies with f_{minor merger⊕flyby} ≲ 0.4), but the radial anisotropy of stars (β_3D) at the galaxy outskirts is mainly driven by major mergers, resulting in an almost decoupled h₄–β_3D relation as seen in Fig. 6.

Although the four sets of relations shown above all possess scatter, their differences hint that the seemingly decoupled outer h₄ and β_3D (Fig. 6) trends originate from the different impacts of major and minor perturbations during the formation process of ETGs. Major mergers can create cuspy (wet merger) or cored (dry merger) central stellar densities depending on the gas fraction of the merger (Hopkins et al. 2008c, 2009a, b, d; Kormendy et al. 2009; Tacchella et al. 2019), modifying the central density profile. Major mergers can also drastically change the morphology and dynamics of a massive galaxy from being tangentially biased disc galaxies (late-type) to radial-orbit-dominated ETGs (Kormendy et al. 2009; Kormendy & Bender 2012; Rodriguez-Gomez et al. 2017), which explains the positive correlation between β_3D and f_major-merger. Although in isolated galaxy merger simulations, a bump in the velocity dispersion profile can also be created at radii >R_eff via major mergers (Schauer et al. 2014), simultaneous minor mergers could counter-act that effect in a cosmological setting (1 ≤ z ≤ 2, Wang et al. 2019). In addition, minor mergers contribute significantly to the growth of ETGs compared to major mergers (Guo & White 2008), perpetuate the inside–out growth of extensive stellar haloes and modify stellar velocity distributions of ETGs at large radii (Murante et al. 2007; Bernardi 2009; Khochfar et al. 2011; Hilz et al. 2012, 2013; Pulsoni et al. 2021; Dolfi et al. 2021).

By visually inspecting the kinematic maps of h₃ and h₄ for individual galaxies, we find that at the locations where h₃ and h₄ locally peak, it is also a common location to find a coinciding overdensity in the projected luminosity map (see Appendix B for examples). These overdensities reflect the transient infall phases of accreted satellite galaxies on to the host ETGs, before they are tidally disrupted and identified as minor mergers by Sublink. The corresponding LOS velocity profile in the spaxels/Voronoi-bins that cut through these satellites show peaks that are phase from the mean velocity of the galaxy, which leads to large h₃ and h₄ values in those spaxels/Voronoi-bins. Eventually, the cumulative effect of these minor perturbations (which are predominantly dry mergers at low redshift, see fig. 7 of Wang et al. 2019 for simulation evidence and Derkenne et al. 2021 for latest dynamical modeling constraints from VLT-MUSE) not only leads to positive outer h₄ but also drives the outer density profile to be shallower than isothermal (⁠|$\gamma ^{\prime }_{\mathrm{m}}$|⁠), establishing the positive correlation between Δh₄(R)/ΔlogR and γ_outer. Combined with the aforementioned impact of minor mergers on the formation of ETGs, the formation of the non-Gaussian outer kinematic structure in early-type galaxies is a natural consequence of hierarchical structure formation, and it co-evolves with the outer density profile mainly via contributions from minor perturbations. As we will discuss in the following, these trends are also consistent with the results from the probes of galaxy (halo) environment.

4.3 Correlation with environment

Another interesting feature related to the Δh₄(R)/ΔlogR–γ_outer found in Veale et al. (2018) is that there is an increasing fraction of ETGs with ‘rising’ outer velocity dispersion profiles living in denser environments and more massive haloes. Again, the authors speculate that this is also induced by the systematic variation of density profiles instead of velocity anisotropy across different ETGs. Since the environmental measures ν₁₀ and δ_g in Veale et al. (2017, 2018) are based on the galaxy K-band luminosity weighted on the MASSIVE Survey limiting magnitude and completeness, we do not attempt to perform mock observations of our simulated ETGs based on raw SDSS K-band magnitude output by IllustrisTNG. Hence, we focus on comparing the total stellar (M_*) and host dark matter halo masses (M₂₀₀, mass contained in the radius where the mean density is 200 × the universal critical density) of our ETG sample to the trends observed in the MASSIVE Survey. The stellar and halo masses serve as sensible proxies of the ETG environment as all targets in MASSIVE are central galaxies and we follow the same selection for our mock IllustrisTNG ETGs.

In Fig. 9, we show γ_outer, as well as the fraction of ETGs having ‘rising’, ‘flat’, or ‘dropping’ velocity dispersion profile outer slopes, against their stellar (left-hand panel) and halo masses (right-hand panel). The scattered dots are individual galaxies coloured by their outer h₄ values, the solid curve with diamond markers denotes the binned median, and the dashed lines represent the [|$16{{\ \rm per\ cent}}$|⁠, |$84{{\ \rm per\ cent}}$|] interval of the distribution within each mass bin. We see that γ_outer increases with both increasing stellar and halo masses in agreement with the trend of MASSIVE median values (red crosses). We notice that the MASSIVE ETGs (89 galaxies, Veale et al. 2018, also see their figs 7, 8, and 9 which also shows large scatter in γ_outer) have a slightly steeper relation with M_*, possibly due to a more complete sample of heavy galaxies with log₁₀(M_*/M_⊙) ≥ 11.6 compared to the IllustrisTNG ETG sample (18 galaxies). The same trend is reflected in the upper side plots for the fraction of galaxies with different velocity dispersion profile outer slopes. The general trend in both columns indicate that higher fractions of galaxies will have ‘rising’ γ_outer with increasing galaxy and halo mass (the error bars in the upper panels are the Wilson score |$68{{\ \rm per\ cent}}$| confidence intervals, Wilson 1927).

$Left-hand panel: The correlation between the outer velocity dispersion profile slope (γouter) and the total stellar mass (M*) of our simulated ETGs, colour-coded by their outer h4 values measured at around $1.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$. Right-hand panel: The correlation between γouter and the host halo mass (M200) of our simulated ETGs, colour-coded by their outer h4 values measured at around $1.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$. The open markers with solid lines in both panels denote the median, while the dashed lines represent the [$16{{\ \rm per\ cent}}$, $84{{\ \rm per\ cent}}$] of the distribution for γouter in different stellar mass and halo mass bins. The red crossed with dot–dashed lines are median values for the same correlations from Veale et al. (2018). The upper side plots show the fraction of galaxies with rising (blue), flat (grey), and dropping (red) outer dispersion profiles in each stellar/halo mass bin. The error bars in each bin stand for the $68{{\ \rm per\ cent}}$ Wilson score confidence intervals.$

Figure 9.

Left-hand panel: The correlation between the outer velocity dispersion profile slope (γ_outer) and the total stellar mass (M_*) of our simulated ETGs, colour-coded by their outer h₄ values measured at around |$1.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠. Right-hand panel: The correlation between γ_outer and the host halo mass (M₂₀₀) of our simulated ETGs, colour-coded by their outer h₄ values measured at around |$1.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠. The open markers with solid lines in both panels denote the median, while the dashed lines represent the [|$16{{\ \rm per\ cent}}$|⁠, |$84{{\ \rm per\ cent}}$|] of the distribution for γ_outer in different stellar mass and halo mass bins. The red crossed with dot–dashed lines are median values for the same correlations from Veale et al. (2018). The upper side plots show the fraction of galaxies with rising (blue), flat (grey), and dropping (red) outer dispersion profiles in each stellar/halo mass bin. The error bars in each bin stand for the |$68{{\ \rm per\ cent}}$| Wilson score confidence intervals.

Open in new tab Download slide

Recasting on the findings in Paper I (Wang et al. 2020), the power-law slope of the total density profile anticorrelating with the total stellar mass (fig. 4) is driven by the variation in the inner dark matter density profile (fig. 17), and hence anticorrelating with the halo mass (fig. 15). Given that the variation in γ_outer is mainly driven by a negative correlation with the density profile (lower right-hand panel in Fig. 7), the findings in Paper I self-consistently predict the trends seen in Fig. 9, once again confirming the conjecture for the observed phenomena in Veale et al. (2018). The colour index in the figure shows that the outer h₄ also tend to be higher in ETGs with higher stellar and halo mass, consistent with the positive Δh₄(R)/ΔlogR–γ_outer relation.

The physical interpretation for the emergence of the γ_outer–mass correlation also fits in to the multiphase formation path of near-isothermal ETG density profiles in Paper II (Wang et al. 2019): heavier ETGs are quenched earlier by AGN feedback (figs 4 and 8) and enter earlier into the non-dissipative evolution phase dominated by gas-poor mergers at lower redshift z ≲ 2 (fig. 7), where the total density profile progressively evolves shallower, and more massive galaxies living in more massive haloes (denser environments) experience more mergers. Although ETGs go through both major and minor mergers, with previous studies suggesting that major mergers start to dominate the ex situ stellar population at stellar masses log₁₀(M_*/M_⊙) ≳ 11.2 (e.g. fig. 10 in Tacchella et al. 2019), which is also the case for our ETG sample with median f_{major merger} = 0.31 and median f_{minor merger⊕flyby} = 0.12, the stellar mass fraction from both minor and major mergers increase with M_*. Since the outer h₄ is mainly driven by minor perturbations instead of major mergers (Section 4.2, lower left-hand panel in Fig. 8), the mass trend of f_{minor merger⊕flyby} alone dictates the mass trend of γ_outer and outer h₄. This eventually creates the positive correlation between γ_outer and the kurtosis gradient through the mass-dependent variation of the total density profile, indicating that the formation of the outer (non-Gaussian) kinematic structure in ETGs stands as a natural consequence of hierarchical galaxy–halo assembly.

5 CONCLUSIONS AND OUTLOOK

We study the relation between the kinematic structure and density profiles of 207 massive (log₁₀(M_*/M_⊙) ∈ [11.0, 12.4], non-major-merger, Fig. 2) early-type galaxies selected from the IllustrisTNG Simulations (Marinacci et al. 2018; Naiman et al. 2018; Nelson et al. 2018; Pillepich et al. 2018b; Springel et al. 2018). We produce mock IFU spectroscopic observations (Fig. 1) for these ETGs in random projections and compute the second (velocity dispersion σ), third (skewness h₃), and fourth (kurtosis h₄) velocity moments of the projected stellar velocity profiles (Fig. 3). The outer slope (γ_outer) of the LOSVD profiles (Fig. 4) and the key positive correlation between γ_outer and the kurtosis gradient (Δh₄(R)/ΔlogR, Fig. 5) for the simulated ETGs are consistent with that found in the MASSIVE Survey (Ma et al. 2014; Veale et al. 2017, 2018). This realistic mock ETG sample serves as a benchmark for disentangling the correlation between the outer non-Gaussian kinematic features and velocity dispersion profiles in observed ETGs from the MASSIVE Survey (Veale et al. 2018). In particular, we find the following:

The average velocity anisotropy and h₄ show almost no correlation with the 3D velocity anisotropy β_3D at radii |$\geqslant R_{\mathrm{eff}}^{\mathrm{MGE}}$| (Fig. 6, lower panel), indicating that positive outer h₄ values is unlikely to be produced by stellar velocity anisotropy under fixed density profiles (Gerhard 1993).
The outer h₄ measured at |$\sim 1.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$| is a good proxy for the kurtosis gradient and also positively correlates with γ_outer (Fig. 7, upper row). The mass-weighted slope of the total density profile at that radius negatively correlates with both the outer h₄ and γ_outer (Fig. 7, lower row). This justifies the conjecture (Veale et al. 2018) that systematic variations around an exact isothermal profile drive the positive correlation between Δh₄(R)/ΔlogR and γ_outer.
The outer h₄ positively correlates with the mass fraction of stars accreted via minor perturbations (minor mergers and flyby interactions), while the outer velocity anisotropy correlates more significantly with the stellar mass fraction from major mergers (Fig. 8), resulting in a seemingly decoupled h₄–β_3D relation at the ETG outskirts (Fig. 6).
The values of γ_outer, outer h₄, and the fraction of ETGs with ‘rising’ outer velocity dispersion profiles increase with increasing stellar and halo masses. This is mainly driven by the increase in minor merger fractions with increasing ETG stellar mass affecting the outer kinematic structure and density profile simultaneously (Fig. 9).

As an augmentation to the detailed studies of the ETG density profiles in Papers I and II, this work generalizes those findings and links them with the outer kinematic structure in these galaxies. Our finding that the outer h₄ correlates with minor mergers and the density profile, while the outer β_3D correlates with major mergers, also explains the apparent stochasticity between the total density profile and stellar velocity anisotropy of ETGs found in fig. 8 of Paper I. The outer h₄–minor merger correlation is also consistent with our previous finding: in systems where the stellar assembly in ETGs is dominated by minor perturbations at low redshift (z < 0.5), a higher accreted stellar fraction leads to steeper density profile slopes (fig. 10, Paper I). The dependence of γ_outer and outer h₄ with environment is consistent with the previous findings that both stellar and halo masses anticorrelate with the steepness of the total density profile (figs 4, 15, and 17 in Paper I), and fits in smoothly to the low-redshift (z < 0.5) minor-merger-driven evolution phase of the ETG density profiles as discussed in Paper II (figs 4, 7, 8). Combining the effects of stellar assembly on outer h₄, we conclude that the outer kinematic structure of ETGs co-evolves with their total density profiles, which is a natural consequence of hierarchical assembly in cosmological structure formation. The broad agreement of our results with the MASSIVE Survey ETGs also highlights the power of IllustrisTNG to elucidate the underlying correlations in a realistic formation scenario, that could not otherwise be discerned from observations alone.

Apart from the many aspects of our findings that do reproduce and explain the observed ETG kinematic features, we highlight that there are important systematics involving the central stellar velocity dispersion of the IllustrisTNG galaxies. We observe more galaxies with positive γ_inner compared to MASSIVE ETGs (Fig. 4) indicating underestimation of the central stellar velocity dispersion, which is consistent with the tendency of over-predicting central dark matter fraction (producing halo contraction) in IllustrisTNG galaxies (Lovell et al. 2018; Wang et al. 2020). This is also related to the negative h₄–β_3D correlation within |$0.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$| as seen in Fig. 6. These limitations pave a way forward for better understanding the interplay between dark matter and baryons, as well as for future improvements of the simulation subgrid physics model (especially related to AGN feedback), which could be better constrained by refined kinematic features at both large and small galactic radii.

Another interesting feature is that the presence of infalling substructures can significantly boost h₃ and h₄ along the line of sight at the outskirts of ETGs (Appendix B). Although quantifying the impact of mergers and their remnants on the kinematic structure of ETGs is beyond the scope of this work, this finding ties in neatly to our finding of the ETG outer kinematic structure by the fraction of stars acquired through minor perturbations. With ultra-high resolution IFU spectroscopy from MUSE (Bacon et al. 2010) on the Very Large Telescope (VLT) or KCWI (Morrissey et al. 2018) on the Keck Telescope, non-Gaussian kinematic features could potentially provide a novel approach for discovering faint satellites around ETG hosts. Combined with upcoming photometric campaigns such as the Vera C. Rubin Observatory (LSST, Ivezić et al. 2019), the Nancy Grace Roman Space Telescope (WFIRST, Spergel et al. 2015), and Euclid (Amiaux et al. 2012) that advance in survey depth and field of view, we will soon be able to establish a more profound understanding of the co-evolution between the kinematic structure, density profile, and even the build-up of the stellar halo around ETGs in the broad context of hierarchical structure formation.

ACKNOWLEDGEMENTS

We thank Dandan Xu, Ethan O. Nadler, Philip Mansfield, and Shengdong Lu for helpful discussions and support during the preparation of this paper. We thank the anonymous referee for insightful comments that helped to improve the draft. YW acknowledges the past support from the Tsinghua Xuetang Talents Programme and current support from a Stanford-KIPAC Chabolla Fellowship. This work is partly supported by the National Key Basic Research and Development Programme of China (No. 2018YFA0404501 to SM), and by the National Science Foundation of China (grant no. 11821303 and 11761131004 to SM). MV acknowledges support through an MIT RSC award, a Kavli Research Investment Fund, NASA ATP grant NNX17AG29G, and NSF grants AST-1814053 and AST-1814259. VS acknowledges support by the Deutsche Forschungsgemeinschaft through project SP 709/5-1. This research made use of computational resources at the MIT/Harvard computing facilities supported by FAS and MIT MKI; the authors are thankful for the support from the FAS Research Computing team. The flagship simulations of the IllustrisTNG project used in this work have been run on the HazelHen Cray XC40-system at the High Performance Computing Center Stuttgart as part of project GCS-ILLU of the Gauss Centre for Supercomputing (GCS). This research made extensive use of arXiv.org and NASA’s Astrophysics Data System for bibliographic information.

DATA AVAILABILITY

The IllustrisTNG public data can be accessed at https://www.tng-project.org/data/. The data in this article that are not part of the IllustrisTNG data release will be shared upon reasonable request to the corresponding author.

Footnotes

1

www.tng-project.org

2

https://github.com/HongyuLi2016/illustris-tools

3

https://www-astro.physics.ox.ac.uk/~mxc/software/

REFERENCES

Allgood

B.

,

Flores

R. A.

,

Primack

J. R.

,

Kravtsov

A. V.

,

Wechsler

R. H.

,

Faltenbacher

A.

,

Bullock

J. S.

,

2006

,

MNRAS

,

367

,

1781

10.1111/j.1365-2966.2006.10094.x

Crossref

Search ADS

Amiaux

J.

et al. ,

2012

, in

Clampin

M. C.

,

Fazio

G. G.

,

MacEwen

H. A.

,

Oschmann Jacobus

M. J.

, eds,

Proc. SPIE Conf. Ser. Vol. 8442, Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave

.

SPIE

,

Bellingham

, p.

84420Z

Auger

M. W.

,

Treu

T.

,

Bolton

A. S.

,

Gavazzi

R.

,

Koopmans

L. V. E.

,

Marshall

P. J.

,

Moustakas

L. A.

,

Burles

S.

,

2010

,

ApJ

,

724

,

511

10.1088/0004-637X/724/1/511

Crossref

Search ADS

Bacon

R.

et al. ,

2010

, in

McLean

I. S.

,

Ramsay

S. K.

,

Takami

H.

, eds,

Proc. SPIE Conf. Ser. Vol. 7735, Ground-based and Airborne Instrumentation for Astronomy III

.

SPIE

,

Bellingham

, p.

77350

Baes

M.

,

Dejonghe

H.

,

Buyle

P.

,

2005

,

A&A

,

432

,

411

10.1051/0004-6361:20041907

Crossref

Search ADS

Barnabè

M.

,

Czoske

O.

,

Koopmans

L. V. E.

,

Treu

T.

,

Bolton

A. S.

,

Gavazzi

R.

,

2009

,

MNRAS

,

399

,

21

10.1111/j.1365-2966.2009.14941.x

Crossref

Search ADS

Barnabè

M.

,

Czoske

O.

,

Koopmans

L. V. E.

,

Treu

T.

,

Bolton

A. S.

,

2011

,

MNRAS

,

415

,

2215

10.1111/j.1365-2966.2011.18842.x

Crossref

Search ADS

Bell

E. F.

,

de Jong

R. S.

,

2001

,

ApJ

,

550

,

212

10.1086/319728

Crossref

Search ADS

Bellstedt

S.

et al. ,

2018

,

MNRAS

,

476

,

4543

10.1093/mnras/sty456

Crossref

Search ADS

Bender

R.

,

Burstein

D.

,

Faber

S. M.

,

1992

,

ApJ

,

399

,

462

10.1086/171940

Crossref

Search ADS

Bernardi

M.

,

2009

,

MNRAS

,

395

,

1491

10.1111/j.1365-2966.2009.14601.x

Crossref

Search ADS

Binney

J.

,

Mamon

G. A.

,

1982

,

MNRAS

,

200

,

361

10.1093/mnras/200.2.361

Crossref

Search ADS

Binney

J.

,

Tremaine

S.

,

2008

,

Galactic Dynamics

, 2nd edn.

Princeton Univ. Press

,

Princeton

Bruzual

G.

,

Charlot

S.

,

2003

,

MNRAS

,

344

,

1000

10.1046/j.1365-8711.2003.06897.x

Crossref

Search ADS

Cappellari

M.

,

2002

,

MNRAS

,

333

,

400

10.1046/j.1365-8711.2002.05412.x

Crossref

Search ADS

Cappellari

M.

,

2008

,

MNRAS

,

390

,

71

10.1111/j.1365-2966.2008.13754.x

Crossref

Search ADS

Cappellari

M.

et al. ,

2015

,

ApJ

,

804

,

L21

10.1088/2041-8205/804/1/L21

Crossref

Search ADS

Cassata

P.

et al. ,

2013

,

ApJ

,

775

,

106

10.1088/0004-637X/775/2/106

Crossref

Search ADS

Chabrier

G.

,

2003

,

PASP

,

115

,

763

10.1086/376392

Crossref

Search ADS

Cole

S.

,

Lacey

C. G.

,

Baugh

C. M.

,

Frenk

C. S.

,

2000

,

MNRAS

,

319

,

168

10.1046/j.1365-8711.2000.03879.x

Crossref

Search ADS

De Lucia

G.

,

Blaizot

J.

,

2007

,

MNRAS

,

375

,

2

10.1111/j.1365-2966.2006.11287.x

Crossref

Search ADS

De Lucia

G.

,

Springel

V.

,

White

S. D. M.

,

Croton

D.

,

Kauffmann

G.

,

2006

,

MNRAS

,

366

,

499

10.1111/j.1365-2966.2005.09879.x

Crossref

Search ADS

Dejonghe

H.

,

Merritt

D.

,

1992

,

ApJ

,

391

,

531

10.1086/171368

Crossref

Search ADS

Derkenne

C.

,

McDermid

R. M.

,

Poci

A.

,

Remus

R.-S.

,

Jørgensen

I.

,

Emsellem

E.

,

2021

,

MNRAS

,

506

,

3691

10.1093/mnras/stab1996

Crossref

Search ADS

Di Matteo

T.

,

Springel

V.

,

Hernquist

L.

,

2005

,

Nature

,

433

,

604

Diemer

B.

et al. ,

2019

,

MNRAS

,

487

,

1529

10.1093/mnras/stz1323

Crossref

Search ADS

Djorgovski

S.

,

Davis

M.

,

1987

,

ApJ

,

313

,

59

10.1086/164948

Crossref

Search ADS

Dolag

K.

,

Borgani

S.

,

Murante

G.

,

Springel

V.

,

2009

,

MNRAS

,

399

,

497

10.1111/j.1365-2966.2009.15034.x

Crossref

Search ADS

Dolfi

A.

,

Forbes

D. A.

,

Couch

W. J.

,

Bekki

K.

,

Ferré-Mateu

A.

,

Romanowsky

A. J.

,

Brodie

J. P.

,

2021

,

MNRAS

,

504

,

4923

10.1093/mnras/stab1023

Crossref

Search ADS

Donnari

M.

et al. ,

2019

,

MNRAS

,

485

,

4817

10.1093/mnras/stz712

Crossref

Search ADS

Dressler

A.

,

1980

,

ApJ

,

236

,

351

10.1086/157753

Crossref

Search ADS

Dutton

A. A.

,

Treu

T.

,

2014

,

MNRAS

,

438

,

3594

10.1093/mnras/stt2489

Crossref

Search ADS

Emsellem

E.

,

Monnet

G.

,

Bacon

R.

,

Nieto

J. L.

,

1994

,

A&A

,

285

,

739

Ene

I.

,

Ma

C.-P.

,

McConnell

N. J.

,

Walsh

J. L.

,

Kempski

P.

,

Greene

J. E.

,

Thomas

J.

,

Blakeslee

J. P.

,

2019

,

ApJ

,

878

,

57

10.3847/1538-4357/ab1f04

Crossref

Search ADS

Fabian

A. C.

,

2012

,

ARA&A

,

50

,

455

10.1146/annurev-astro-081811-125521

Crossref

Search ADS

Gavazzi

R.

,

Treu

T.

,

Rhodes

J. D.

,

Koopmans

L. V. E.

,

Bolton

A. S.

,

Burles

S.

,

Massey

R. J.

,

Moustakas

L. A.

,

2007

,

ApJ

,

667

,

176

10.1086/519237

Crossref

Search ADS

Genel

S.

et al. ,

2014

,

MNRAS

,

445

,

175

10.1093/mnras/stu1654

Crossref

Search ADS

Genel

S.

et al. ,

2018

,

MNRAS

,

474

,

3976

10.1093/mnras/stx3078

Crossref

Search ADS

Gerhard

O. E.

,

1993

,

MNRAS

,

265

,

213

10.1093/mnras/265.1.213

Crossref

Search ADS

Gerhard

O.

,

Jeske

G.

,

Saglia

R. P.

,

Bender

R.

,

1998

,

MNRAS

,

295

,

197

10.1046/j.1365-8711.1998.29511341.x

Crossref

Search ADS

Greene

J. E.

et al. ,

2019

,

ApJ

,

874

,

66

10.3847/1538-4357/ab01e3

Crossref

Search ADS

Guo

Q.

,

White

S. D. M.

,

2008

,

MNRAS

,

384

,

2

10.1111/j.1365-2966.2007.12619.x

Crossref

Search ADS

Habouzit

M.

et al. ,

2019

,

MNRAS

,

484

,

4413

10.1093/mnras/stz102

Crossref

Search ADS

Hemler

Z. S.

et al. ,

2021

,

MNRAS

,

506

,

3024

10.1093/mnras/stab1803

Crossref

Search ADS

Hill

G. J.

,

MacQueen

P. J.

,

Palunas

P.

,

Barnes

S. I.

,

Shetrone

M. D.

,

2008

, in

McLean

I. S.

,

Casali

M. M.

, eds,

Proc. SPIE Conf. Ser. Vol. 7014, Ground-based and Airborne Instrumentation for Astronomy II

.

SPIE

,

Bellingham

, p.

92

Hilz

M.

,

Naab

T.

,

Ostriker

J. P.

,

Thomas

J.

,

Burkert

A.

,

Jesseit

R.

,

2012

,

MNRAS

,

425

,

3119

10.1111/j.1365-2966.2012.21541.x

Crossref

Search ADS

Hilz

M.

,

Naab

T.

,

Ostriker

J. P.

,

2013

,

MNRAS

,

429

,

2924

10.1093/mnras/sts501

Crossref

Search ADS

Hopkins

P. F.

,

Hernquist

L.

,

Cox

T. J.

,

Robertson

B.

,

Springel

V.

,

2006

,

ApJS

,

163

,

50

10.1086/499493

Crossref

Search ADS

Hopkins

P. F.

,

Hernquist

L.

,

Cox

T. J.

,

Kereš

D.

,

2008a

,

ApJS

,

175

,

356

10.1086/524362

Crossref

Search ADS

Hopkins

P. F.

,

Cox

T. J.

,

Kereš

D.

,

Hernquist

L.

,

2008b

,

ApJS

,

175

,

390

10.1086/524363

Crossref

Search ADS

Hopkins

P. F.

,

Hernquist

L.

,

Cox

T. J.

,

Dutta

S. N.

,

Rothberg

B.

,

2008c

,

ApJ

,

679

,

156

10.1086/587544

Crossref

Search ADS

Hopkins

P. F.

,

Cox

T. J.

,

Dutta

S. N.

,

Hernquist

L.

,

Kormendy

J.

,

Lauer

T. R.

,

2009a

,

ApJS

,

181

,

135

10.1088/0067-0049/181/1/135

Crossref

Search ADS

Hopkins

P. F.

,

Lauer

T. R.

,

Cox

T. J.

,

Hernquist

L.

,

Kormendy

J.

,

2009b

,

ApJS

,

181

,

486

10.1088/0067-0049/181/2/486

Crossref

Search ADS

Hopkins

P. F.

et al. ,

2009c

,

MNRAS

,

397

,

802

10.1111/j.1365-2966.2009.14983.x

Crossref

Search ADS

Hopkins

P. F.

,

Cox

T. J.

,

Younger

J. D.

,

Hernquist

L.

,

2009d

,

ApJ

,

691

,

1168

10.1088/0004-637X/691/2/1168

Crossref

Search ADS

Huertas-Company

M.

et al. ,

2013

,

MNRAS

,

428

,

1715

10.1093/mnras/sts150

Crossref

Search ADS

Humphrey

P. J.

,

Buote

D. A.

,

2010

,

MNRAS

,

403

,

2143

10.1111/j.1365-2966.2010.16257.x

Crossref

Search ADS

Humphrey

P. J.

,

Buote

D. A.

,

Gastaldello

F.

,

Zappacosta

L.

,

Bullock

J. S.

,

Brighenti

F.

,

Mathews

W. G.

,

2006

,

ApJ

,

646

,

899

10.1086/505019

Crossref

Search ADS

Ivezić

Ž.

et al. ,

2019

,

ApJ

,

873

,

111

10.3847/1538-4357/ab042c

Crossref

Search ADS

Johansson

P. H.

,

Naab

T.

,

Ostriker

J. P.

,

2012

,

ApJ

,

754

,

115

10.1088/0004-637X/754/2/115

Crossref

Search ADS

Khochfar

S.

et al. ,

2011

,

MNRAS

,

417

,

845

10.1111/j.1365-2966.2011.19486.x

Crossref

Search ADS

King

A.

,

2003

,

ApJ

,

596

,

L27

10.1086/379143

Crossref

Search ADS

Koopmans

L. V. E.

,

Treu

T.

,

Bolton

A. S.

,

Burles

S.

,

Moustakas

L. A.

,

2006

,

ApJ

,

649

,

599

10.1086/505696

Crossref

Search ADS

Koopmans

L. V. E.

et al. ,

2009

,

ApJ

,

703

,

L51

10.1088/0004-637X/703/1/L51

Crossref

Search ADS

Kormendy

J.

,

Bender

R.

,

2012

,

ApJS

,

198

,

2

10.1088/0067-0049/198/1/2

Crossref

Search ADS

Kormendy

J.

,

Ho

L. C.

,

2013

,

ARA&A

,

51

,

511

10.1146/annurev-astro-082708-101811

Crossref

Search ADS

Kormendy

J.

,

Fisher

D. B.

,

Cornell

M. E.

,

Bender

R.

,

2009

,

ApJS

,

182

,

216

10.1088/0067-0049/182/1/216

Crossref

Search ADS

Krajnović

D.

et al. ,

2011

,

MNRAS

,

414

,

2923

10.1111/j.1365-2966.2011.18560.x

Crossref

Search ADS

Li

H.

,

Li

R.

,

Mao

S.

,

Xu

D.

,

Long

R. J.

,

Emsellem

E.

,

2016

,

MNRAS

,

455

,

3680

10.1093/mnras/stv2565

Crossref

Search ADS

Li

H.

et al. ,

2018a

,

MNRAS

,

476

,

1765

10.1093/mnras/sty334

Crossref

Search ADS

Li

R.

,

Shu

Y.

,

Wang

J.

,

2018b

,

MNRAS

,

480

,

431

10.1093/mnras/sty1813

Crossref

Search ADS

Li

R.

et al. ,

2019

,

MNRAS

,

490

,

2124

10.1093/mnras/stz2565

Crossref

Search ADS

Lovell

M. R.

et al. ,

2018

,

MNRAS

,

481

,

1950

10.1093/mnras/sty2339

Crossref

Search ADS

Lyskova

N.

,

Churazov

E.

,

Naab

T.

,

2018

,

MNRAS

,

475

,

2403

10.1093/mnras/sty018

Crossref

Search ADS

Ma

C.-P.

,

Greene

J. E.

,

McConnell

N.

,

Janish

R.

,

Blakeslee

J. P.

,

Thomas

J.

,

Murphy

J. D.

,

2014

,

ApJ

,

795

,

158

10.1088/0004-637X/795/2/158

Crossref

Search ADS

Marinacci

F.

et al. ,

2018

,

MNRAS

,

480

,

5113

10.1093/mnras/sty2206

Crossref

Search ADS

McGaugh

S. S.

,

Schombert

J. M.

,

Bothun

G. D.

,

de Blok

W. J. G.

,

2000

,

ApJ

,

533

,

L99

10.1086/312628

Crossref

Search ADS

Merritt

D.

,

Saha

P.

,

1993

,

ApJ

,

409

,

75

10.1086/172643

Crossref

Search ADS

Morrissey

P.

et al. ,

2018

,

ApJ

,

864

,

93

10.3847/1538-4357/aad597

Crossref

Search ADS

Moster

B. P.

,

Naab

T.

,

White

S. D. M.

,

2013

,

MNRAS

,

428

,

3121

10.1093/mnras/sts261

Crossref

Search ADS

Murante

G.

,

Giovalli

M.

,

Gerhard

O.

,

Arnaboldi

M.

,

Borgani

S.

,

Dolag

K.

,

2007

,

MNRAS

,

377

,

2

10.1111/j.1365-2966.2007.11568.x

Crossref

Search ADS

Naab

T.

,

Johansson

P. H.

,

Ostriker

J. P.

,

Efstathiou

G.

,

2007

,

ApJ

,

658

,

710

10.1086/510841

Crossref

Search ADS

Naiman

J. P.

et al. ,

2018

,

MNRAS

,

477

,

1206

10.1093/mnras/sty618

Crossref

Search ADS

Nelson

D.

et al. ,

2015

,

Astron. Comput.

,

13

,

12

10.1016/j.ascom.2015.09.003

Crossref

Search ADS

Nelson

D.

et al. ,

2018

,

MNRAS

,

475

,

624

10.1093/mnras/stx3040

Crossref

Search ADS

Nelson

D.

et al. ,

2019

,

Comput. Astrophys. Cosmol.

,

6

,

2

10.1186/s40668-019-0028-x

Crossref

Search ADS

Nipoti

C.

,

Treu

T.

,

Bolton

A. S.

,

2009a

,

ApJ

,

703

,

1531

10.1088/0004-637X/703/2/1531

Crossref

Search ADS

Nipoti

C.

,

Treu

T.

,

Auger

M. W.

,

Bolton

A. S.

,

2009b

,

ApJ

,

706

,

L86

10.1088/0004-637X/706/1/L86

Crossref

Search ADS

Nipoti

C.

,

Cannarozzo

C.

,

Calura

F.

,

Sonnenfeld

A.

,

Treu

T.

,

2020

,

MNRAS

,

499

,

559

10.1093/mnras/staa2812

Crossref

Search ADS

Oser

L.

,

Ostriker

J. P.

,

Naab

T.

,

Johansson

P. H.

,

Burkert

A.

,

2010

,

ApJ

,

725

,

2312

10.1088/0004-637X/725/2/2312

Crossref

Search ADS

Paturel

G.

,

Petit

C.

,

Prugniel

P.

,

Theureau

G.

,

Rousseau

J.

,

Brouty

M.

,

Dubois

P.

,

Cambrésy

L.

,

2003

,

A&A

,

412

,

45

10.1051/0004-6361:20031411

Crossref

Search ADS

Pillepich

A.

et al. ,

2018a

,

MNRAS

,

473

,

4077

10.1093/mnras/stx2656

Crossref

Search ADS

Pillepich

A.

et al. ,

2018b

,

MNRAS

,

475

,

648

10.1093/mnras/stx3112

Crossref

Search ADS

Planck Collaboration

,

2016

,

A&A

,

594

,

A13

10.1051/0004-6361/201525830

Crossref

Search ADS

Poci

A.

,

Cappellari

M.

,

McDermid

R. M.

,

2017

,

MNRAS

,

467

,

1397

10.1093/mnras/stx101

Crossref

Search ADS

Pulsoni

C.

,

Gerhard

O.

,

Arnaboldi

M.

,

Pillepich

A.

,

Rodriguez-Gomez

V.

,

Nelson

D.

,

Hernquist

L.

,

Springel

V.

,

2021

,

A&A

,

647

,

A95

10.1051/0004-6361/202039166

Crossref

Search ADS

Read

J. I.

,

Steger

P.

,

2017

,

MNRAS

,

471

,

4541

10.1093/mnras/stx1798

Crossref

Search ADS

Remus

R.-S.

,

Burkert

A.

,

Dolag

K.

,

Johansson

P. H.

,

Naab

T.

,

Oser

L.

,

Thomas

J.

,

2013

,

ApJ

,

766

,

71

10.1088/0004-637X/766/2/71

Crossref

Search ADS

Rodriguez-Gomez

V.

et al. ,

2015

,

MNRAS

,

449

,

49

10.1093/mnras/stv264

Crossref

Search ADS

Rodriguez-Gomez

V.

et al. ,

2016

,

MNRAS

,

458

,

2371

10.1093/mnras/stw456

Crossref

Search ADS

Rodriguez-Gomez

V.

et al. ,

2017

,

MNRAS

,

467

,

3083

10.1093/mnras/stx305

Crossref

Search ADS

Romanowsky

A. J.

,

Douglas

N. G.

,

Arnaboldi

M.

,

Kuijken

K.

,

Merrifield

M. R.

,

Napolitano

N. R.

,

Capaccioli

M.

,

Freeman

K. C.

,

2003

,

Science

,

301

,

1696

10.1126/science.1087441

Crossref

Search ADS

PubMed

Ruff

A. J.

,

Gavazzi

R.

,

Marshall

P. J.

,

Treu

T.

,

Auger

M. W.

,

Brault

F.

,

2011

,

ApJ

,

727

,

96

10.1088/0004-637X/727/2/96

Crossref

Search ADS

Schauer

A. T. P.

,

Remus

R.-S.

,

Burkert

A.

,

Johansson

P. H.

,

2014

,

ApJ

,

783

,

L32

10.1088/2041-8205/783/2/L32

Crossref

Search ADS

Serra

P.

,

Oosterloo

T.

,

Cappellari

M.

,

den Heijer

M.

,

Józsa

G. I. G.

,

2016

,

MNRAS

,

460

,

1382

10.1093/mnras/stw1010

Crossref

Search ADS

Sijacki

D.

,

Vogelsberger

M.

,

Genel

S.

,

Springel

V.

,

Torrey

P.

,

Snyder

G. F.

,

Nelson

D.

,

Hernquist

L.

,

2015

,

MNRAS

,

452

,

575

10.1093/mnras/stv1340

Crossref

Search ADS

Silk

J.

,

Rees

M. J.

,

1998

,

A&A

,

331

,

L1

Sonnenfeld

A.

,

Treu

T.

,

Gavazzi

R.

,

Suyu

S. H.

,

Marshall

P. J.

,

Auger

M. W.

,

Nipoti

C.

,

2013

,

ApJ

,

777

,

98

10.1088/0004-637X/777/2/98

Crossref

Search ADS

Sonnenfeld

A.

,

Nipoti

C.

,

Treu

T.

,

2014

,

ApJ

,

786

,

89

10.1088/0004-637X/786/2/89

Crossref

Search ADS

Spergel

D.

et al. ,

2015

,

preprint (arXiv:1503.03757)

Springel

V.

,

2010

,

MNRAS

,

401

,

791

10.1111/j.1365-2966.2009.15715.x

Crossref

Search ADS

Springel

V.

,

White

S. D. M.

,

Tormen

G.

,

Kauffmann

G.

,

2001

,

MNRAS

,

328

,

726

10.1046/j.1365-8711.2001.04912.x

Crossref

Search ADS

Springel

V.

,

Di Matteo

T.

,

Hernquist

L.

,

2005

,

MNRAS

,

361

,

776

10.1111/j.1365-2966.2005.09238.x

Crossref

Search ADS

Springel

V.

et al. ,

2018

,

MNRAS

,

475

,

676

10.1093/mnras/stx3304

Crossref

Search ADS

Stevens

A. R. H.

et al. ,

2019

,

MNRAS

,

483

,

5334

10.1093/mnras/sty3451

Crossref

Search ADS

Tacchella

S.

et al. ,

2019

,

MNRAS

,

487

,

5416

10.1093/mnras/stz1657

Crossref

Search ADS

Terrazas

B. A.

et al. ,

2020

,

MNRAS

,

493

,

1888

10.1093/mnras/staa374

Crossref

Search ADS

Torrey

P.

,

Vogelsberger

M.

,

Genel

S.

,

Sijacki

D.

,

Springel

V.

,

Hernquist

L.

,

2014

,

MNRAS

,

438

,

1985

10.1093/mnras/stt2295

Crossref

Search ADS

Torrey

P.

et al. ,

2018

,

MNRAS

,

477

,

L16

10.1093/mnrasl/sly031

Crossref

Search ADS

Torrey

P.

et al. ,

2019

,

MNRAS

,

484

,

5587

10.1093/mnras/stz243

Crossref

Search ADS

Tortora

C.

,

La Barbera

F.

,

Napolitano

N. R.

,

Romanowsky

A. J.

,

Ferreras

I.

,

de Carvalho

R. R.

,

2014

,

MNRAS

,

445

,

115

10.1093/mnras/stu1616

Crossref

Search ADS

van der Marel

R. P.

,

Franx

M.

,

1993

,

ApJ

,

407

,

525

10.1086/172534

Crossref

Search ADS

Veale

M.

et al. ,

2017

,

MNRAS

,

464

,

356

10.1093/mnras/stw2330

Crossref

Search ADS

Veale

M.

,

Ma

C.-P.

,

Greene

J. E.

,

Thomas

J.

,

Blakeslee

J. P.

,

Walsh

J. L.

,

Ito

J.

,

2018

,

MNRAS

,

473

,

5446

10.1093/mnras/stx2717

Crossref

Search ADS

Vogelsberger

M.

,

Genel

S.

,

Sijacki

D.

,

Torrey

P.

,

Springel

V.

,

Hernquist

L.

,

2013

,

MNRAS

,

436

,

3031

10.1093/mnras/stt1789

Crossref

Search ADS

Vogelsberger

M.

et al. ,

2014a

,

MNRAS

,

444

,

1518

10.1093/mnras/stu1536

Crossref

Search ADS

Vogelsberger

M.

et al. ,

2014b

,

Nature

,

509

,

177

10.1038/nature13316

Crossref

Search ADS

Vogelsberger

M.

et al. ,

2018

,

MNRAS

,

474

,

2073

10.1093/mnras/stx2955

Crossref

Search ADS

Vogelsberger

M.

,

Marinacci

F.

,

Torrey

P.

,

Puchwein

E.

,

2020a

,

Nature Rev. Phys.

,

2

,

42

10.1038/s42254-019-0127-2

Crossref

Search ADS

Vogelsberger

M.

et al. ,

2020b

,

MNRAS

,

492

,

5167

10.1093/mnras/staa137

Crossref

Search ADS

Wang

Y.

et al. ,

2019

,

MNRAS

,

490

,

5722

10.1093/mnras/stz2907

(Paper II)

Crossref

Search ADS

Wang

Y.

et al. ,

2020

,

MNRAS

,

491

,

5188

10.1093/mnras/stz3348

(Paper I)

Crossref

Search ADS

Weinberger

R.

et al. ,

2017

,

MNRAS

,

465

,

3291

10.1093/mnras/stw2944

Crossref

Search ADS

Weinberger

R.

et al. ,

2018

,

MNRAS

,

479

,

4056

10.1093/mnras/sty1733

Crossref

Search ADS

Wellons

S.

et al. ,

2015

,

MNRAS

,

449

,

361

10.1093/mnras/stv303

Crossref

Search ADS

Wellons

S.

et al. ,

2016

,

MNRAS

,

456

,

1030

10.1093/mnras/stv2738

Crossref

Search ADS

Williams

M. J.

,

Bureau

M.

,

Cappellari

M.

,

2010

,

MNRAS

,

409

,

1330

10.1111/j.1365-2966.2010.17406.x

Crossref

Search ADS

Wilson

E. B.

,

1927

,

J. Am. Stat. Assoc.

,

22

,

209

https://doi.org/10.1080/01621459.1927.10502953

Crossref

Search ADS

Wyithe

J. S. B.

,

Loeb

A.

,

2003

,

ApJ

,

595

,

614

10.1086/377475

Crossref

Search ADS

Xie

L.

,

Guo

Q.

,

Cooper

A. P.

,

Frenk

C. S.

,

Li

R.

,

Gao

L.

,

2015

,

MNRAS

,

447

,

636

10.1093/mnras/stu2487

Crossref

Search ADS

Xu

D.

,

Springel

V.

,

Sluse

D.

,

Schneider

P.

,

Sonnenfeld

A.

,

Nelson

D.

,

Vogelsberger

M.

,

Hernquist

L.

,

2017

,

MNRAS

,

469

,

1824

10.1093/mnras/stx899

Crossref

Search ADS

Xu

D.

et al. ,

2019

,

MNRAS

,

489

,

842

10.1093/mnras/stz2164

Crossref

Search ADS

Yun

K.

et al. ,

2019

,

MNRAS

,

483

,

1042

10.1093/mnras/sty3156

Crossref

Search ADS

APPENDIX A: THE EFFECTIVE RADIUS

In this section, we show the differences between the projected 2D effective radius (⁠|$R_{\mathrm{eff}}^{\mathrm{2D, proj}}$|⁠) and |$R_{\mathrm{eff}}^{\mathrm{MGE}}$| of galaxies given by the best MGE fit. |$R_{\mathrm{eff}}^{\mathrm{2D, proj}}$| is measured by projecting galaxies in random directions (along the z-axis of the simulation box) and searching for the radius at which the enclosed projected stellar mass is half of the total stellar mass. However, this procedure includes all stellar particles assigned to galaxies by Subfind, and includes large contributions from the intra-cluster light (ICL) component around the massive ETGs that we selected. Another approach is to first model the galaxy’s projected luminosity distribution in its central region (square aperture with 80 kpc side length) using Multi-Gaussian Expansion (Emsellem et al. 1994), and calculate the half-light radius using the set of analytic best-fitting 2D Gaussians which eventually removes most of the ICL. It also has the advantage over simpler effective radius definitions in 2MASS (semimajor axis length of an ellipse enclosing half the total galaxy luminosity) and the NSA catalogue (half light radius from a single Sérsic fit) to flexibly preserve information of the spatial distribution for different components in the galaxy luminosity profile.

The comparison between the effective radii derived using these two methods is shown in Fig. A1. For smaller galaxies (R_eff ≲ 10 kpc), the two definitions yield consistent size measurements, while for larger galaxies the MGE effective radii are significantly smaller than the 2D projected effective radii, which is due to the removal of the ICL. We adopt |$R_{\mathrm{eff}}^{\mathrm{MGE}}$| in our comparison with observational data.

Figure A1.

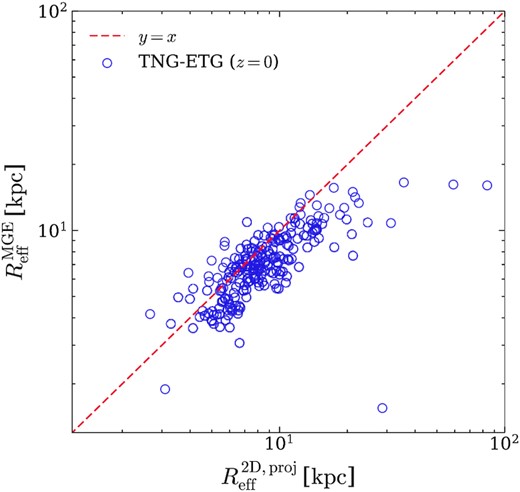
The comparison between the projected 2D effective radius calculated with all stellar particles assigned to the galaxy determined by Subfind, versus the MGE effective radius output by our mock observation pipeline. The MGE effective radii closely follow the 2D projected effective radii for galaxies with small sizes (R_eff ≲ 10 kpc). For the larger galaxies, the MGE effective radii are significantly smaller than the projected effective radii, which results from the MGE approach removing most of the diffuse intracluster light component assigned to the galaxy by Subfind, giving more realistic estimates of the effective radii for larger galaxies.

Open in new tab Download slide

Figure A2.

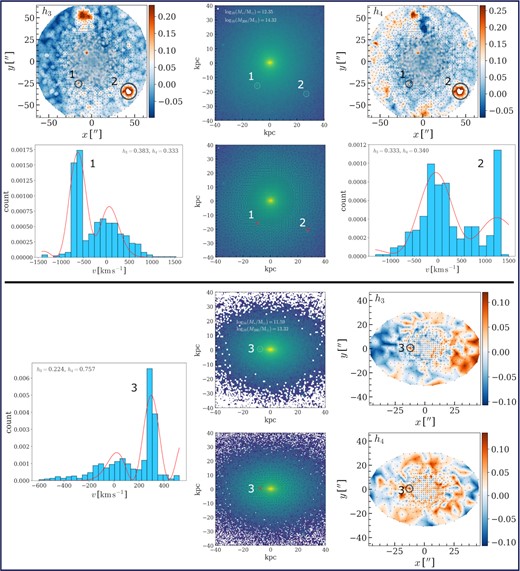
Three examples of spaxels/Voronoi bins cutting through infalling satellite galaxies around two different host galaxies that introduces large h₃ and h₄. Upper panel: Host Subfind ID 69507, with stellar mass 10^12.35M_⊙ and halo mass 10^14.32M_⊙. Lower panel: Host Subfind ID 257302, with stellar mass 10^11.59M_⊙ and halo mass 10^13.32M_⊙. The dashed circles in the luminosity maps indicate the location of these satellites, while the red crosses indicate the location of the spaxels/Voronoi bins covering them. Blue histograms show the LOS stellar velocity distribution in those bins (centred on the mean velocity, v = 0, large peak offsets from the zero-point indicate satellite stars), whereas the red curves indicate the fourth-order Gauss–Hermite function fit. Their corresponding locations in the h₃ and h₄ maps are also marked by black circles.

Open in new tab Download slide

APPENDIX B: EXAMPLES OF MINOR MERGERS IMPACTING THE OUTER KINEMATIC STRUCTURE

In this section, we showcase three examples of ongoing minor mergers introducing large non-Gaussian moments to the outer kinematic structure of ETGs. In Fig. A2, we mark out three infalling satellites (overdensities in the luminosity maps) around two different host ETGs, with spaxels/Voronoi bins cutting through them along the line of sight, and resulting in significant h₃ and h₄ values. Clearly, these three pixels all demonstrate large peak offsets from the mean velocity (centred on v = 0). While h₃ produced in this manner may diminish over time as the satellite orbits around the host due to its odd parity, a positive h₄ can be preserved over time due to its even parity. The cumulative effect of such in many minor mergers (along with flyby interactions that tidally heat galaxies, accelerating stars into the tails of the LOS velocity distribution) can gradually build up a global positive h₄ in the outskirts (⁠|$\gtrsim 1.5 R_{\mathrm{eff}}^{\mathrm{MGE}}$|⁠) of ETGs, leading to the positive correlation of the outer h₄ and stellar mass fraction from minor perturbations (minor mergers plus flyby interactions) as seen in Fig. 7.

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
May 2022	9
June 2022	30
July 2022	7
August 2022	4
September 2022	7
October 2022	6
November 2022	12
December 2022	1
January 2023	4
February 2023	3
March 2023	6
April 2023	6
May 2023	10
June 2023	13
July 2023	11
August 2023	21
September 2023	13
October 2023	15
November 2023	11
December 2023	17
January 2024	18
February 2024	2
March 2024	13
April 2024	19
May 2024	39
June 2024	19
July 2024	34
August 2024	10
September 2024	12
October 2024	15
November 2024	26
December 2024	12
January 2025	4
February 2025	13
March 2025	14
April 2025	22
May 2025	7

Article Contents

Early-type galaxy density profiles from IllustrisTNG – III. Effects on outer kinematic structure

ABSTRACT

1 INTRODUCTION

2 METHODOLOGY

2.1 IllustrisTNG simulations

2.2 Sample selection

2.3 Mock observations

3 RESULTS OF KINEMATIC FEATURES

3.1 The galaxy sample

3.2 Inner and outer slopes of the velocity dispersion profile

3.3 Higher order velocity moments h₃ and h₄

3.4 De-correlated outer kurtosis and velocity anisotropy

4 LINKING KINEMATIC STRUCTURE WITH DENSITY PROFILE, ASSEMBLY HISTORY, AND ENVIRONMENT

4.1 Correlation with density profile

4.2 Correlation with stellar assembly history

4.3 Correlation with environment

5 CONCLUSIONS AND OUTLOOK

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

APPENDIX A: THE EFFECTIVE RADIUS

APPENDIX B: EXAMPLES OF MINOR MERGERS IMPACTING THE OUTER KINEMATIC STRUCTURE

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Early-type galaxy density profiles from IllustrisTNG – III. Effects on outer kinematic structure Free

ABSTRACT

1 INTRODUCTION

2 METHODOLOGY

2.1 IllustrisTNG simulations

2.2 Sample selection

2.3 Mock observations

3 RESULTS OF KINEMATIC FEATURES

3.1 The galaxy sample

3.2 Inner and outer slopes of the velocity dispersion profile

3.3 Higher order velocity moments h3 and h4

3.4 De-correlated outer kurtosis and velocity anisotropy

4 LINKING KINEMATIC STRUCTURE WITH DENSITY PROFILE, ASSEMBLY HISTORY, AND ENVIRONMENT

4.1 Correlation with density profile

4.2 Correlation with stellar assembly history

4.3 Correlation with environment

5 CONCLUSIONS AND OUTLOOK

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

APPENDIX A: THE EFFECTIVE RADIUS

APPENDIX B: EXAMPLES OF MINOR MERGERS IMPACTING THE OUTER KINEMATIC STRUCTURE

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Early-type galaxy density profiles from IllustrisTNG – III. Effects on outer kinematic structure

3.3 Higher order velocity moments h₃ and h₄