-
PDF
- Split View
-
Views
-
Cite
Cite
L Mallick, A C Fabian, J A García, J A Tomsick, M L Parker, T Dauser, D R Wilkins, B De Marco, J F Steiner, R M T Connors, G Mastroserio, A G Markowitz, C Pinto, W N Alston, A M Lohfink, P Gandhi, High-density disc reflection spectroscopy of low-mass active galactic nuclei, Monthly Notices of the Royal Astronomical Society, Volume 513, Issue 3, July 2022, Pages 4361–4379, https://doi.org/10.1093/mnras/stac990
Close - Share Icon Share
ABSTRACT
The standard alpha-disc model predicts an anticorrelation between the density of the inner accretion disc and the black hole mass times square of the accretion rate, as seen in higher mass (MBH > 106 M⊙) active galactic nuclei (AGNs). In this work, we test the predictions of the alpha-disc model and study the properties of the inner accretion flow for the low-mass end (MBH ≈ 105–6 M⊙) of AGNs. We utilize a new high-density disc reflection model where the density parameter varies from ne = 1015 to 1020 cm−3 and apply it to the broad-band X-ray (0.3–10 keV) spectra of the low-mass AGN sample. The sources span a wide range of Eddington fractions and are consistent with being sub-Eddington or near-Eddington. The X-ray spectra reveal a soft X-ray excess below ∼1.5 keV which is well modelled by high-density reflection from an ionized accretion disc of density ne ∼ 1018 cm−3 on average. The results suggest a radiation pressure-dominated disc with an average of 70 per cent fraction of the disc power transferred to the corona, consistent with that observed in higher mass AGNs. We show that the disc density higher than 1015 cm−3 can result from the radiation pressure compression when the disc surface does not hold a strong magnetic pressure gradient. We find tentative evidence for a drop in black hole spin at low-mass regimes.
1 INTRODUCTION
Active galactic nuclei (AGNs) are luminous nuclear sources powered by the accretion of matter from the host galaxy (see e.g. Storchi-Bergmann & Schnorr-Múller 2019) on to a supermassive black hole (SMBH; Lynden-Bell 1969; Rees 1984) of mass ∼105–1010 M⊙ (see Reines, Greene & Geha 2013; Baldassare et al. 2015; The Event Horizon Telescope Collaboration 2019). They are characterized by complex spatial and time-variable emission observed over the entire electromagnetic spectrum, from very high-energy gamma-rays to radio wavebands. The X-ray energy band provides a unique window as the X-ray photons come from the immediate vicinity of the central SMBH and help us probe the extreme gravity just outside the event horizon of the black hole (e.g. Fabian et al. 1989, 2002; Wilkins et al. 2021). We can characterize black holes fundamentally by two parameters: mass and spin, which play a crucial role in understanding the physical nature of the AGN central engine and the cosmological evolution of galaxies which is directly associated with the energy output from the SMBHs (e.g. Fabian 2012; Kormendy & Ho 2013). However, most of our knowledge on the physical processes occurring in the AGN central engine is confined to active galaxies hosting SMBHs of mass greater than 106 M⊙. The low-mass end (MBH ≲ 106 M⊙) of AGNs is a less explored, yet intriguing domain that serves as the missing link to probe whether the accretion process is the same at all mass scales. The least massive AGNs can play a significant role in probing the nature of primordial SMBHs, which are crucial to constrain the cosmological black hole growth models.
X-ray spectroscopy is a powerful tool to probe strong-field accretion in the innermost regions of the AGN central engine. It allows us to determine the physical conditions of the plasma surrounding the central X-ray source. The properties of the inner accretion discs of AGNs are measured through X-ray reflection spectra, which show a soft X-ray excess below ∼2 keV, a broad emission profile due to Fe K lines at ∼6.4–7.1 keV, and Compton hump above 10 keV (e.g. Marinucci et al. 2014; Matt et al. 2014; Zoghbi et al. 2015; García et al. 2019; Xu et al. 2021). The physical modelling of these features provides direct probes for the inner disc atmosphere and black hole spin (e.g. Brenneman & Reynolds 2006; Walton et al. 2013; García et al. 2014; Reynolds 2019, 2021; Bambi et al. 2021), the measurement of which is essential to study the cosmic evolution of spin and the long-term growth of black holes (e.g. Volonteri et al. 2013).
Traditional reflection models assume that the density of the disc atmosphere is constant and fixed at ne = 1015 cm−3 (e.g. Ross & Fabian 1993, 2005; García et al. 2013, 2014). These constant density disc reflection models work well for high-mass (MBH > 107 M⊙) black holes and higher accretion rates. However, the standard Shakura & Sunyaev (1973) (hereafter SS73) disc model predicts that the density of the inner accretion disc is likely to be higher than 1015 cm−3 for lower mass (log MBH ∼ 5–7) SMBHs and stellar-mass BH X-ray binaries (BHXRBs). The theoretical calculations of Svensson & Zdziarski (1994) (hereafter SZ94) reveal that the inner disc density is even higher than that predicted from the SS73 disc model if we consider the fraction of the transferred power from the accretion disc into the corona. García et al. (2016) investigated the effects of the gas density on the X-ray reflection spectra and provided a model (relxillD) where the density is a free parameter varying from ne = 1015 to 1019 cm−3. High-density disc reflection models successfully explain the soft X-ray excess, broad Fe K emission line, and Compton hump in low-mass (MBH ∼ 106–7 M⊙) AGNs (e.g. Jiang et al. 2018; Mallick et al. 2018). Some studies challenge the constant density (ne = 1015 cm−3) disc reflection origin of the soft excess and prefer an additional warm Comptonization component (e.g. Mallick et al. 2017; Petrucci et al. 2018; Porquet et al. 2018). Application of the variable density reflection model to the X-ray spectra of several AGNs (e.g. García et al. 2019; Jiang et al. 2019; Xu et al. 2021) and XRBs (e.g. Tomsick et al. 2018; Jiang et al. 2020) has lately become more prevalent.
In this paper, we apply our recently developed variable density (log [ne/cm-3] = 15–20) reflection model to the broad-band (0.3–10 keV) X-ray spectra of a sample of low-mass (MBH ≈ 105–6 M⊙) AGNs, study their spectral properties and compare them with higher mass AGNs from the literature. Miniutti et al. (2009) and Ludlam et al. (2015) studied some of these sources and detected a soft X-ray excess which was modeled by a black-body component. The detection of soft X-ray reverberation time-lags in some of these low-mass AGNs (Mallick et al. 2021) is the strongest supporting evidence for the reflection origin of the soft X-ray excess.
We organize the paper as follows. In Section 2, we describe the details of the sample and data reduction techniques. In Section 3, we perform the spectral analysis of the low-mass AGN sample using the variable density reflection model. We interpret the results of the spectral modelling and compare the measured accretion properties of the sample with their higher mass counterparts in Section 4. We conclude the results in Section 5. Finally, we outline the future work in Section 6.
2 SAMPLE SELECTION AND DATA REDUCTION
To study the accretion properties of the low-mass AGN end, we obtained a sample of the least massive AGNs from the Greene & Ho (2007) (hereafter GH07) catalogue and one AGN, POX 52, from Barth et al. (2004), with central BH masses of ∼105–6 M⊙. We searched the XMM–Newton (Jansen et al. 2001) archive and found that a total of 29 AGNs from the sample are present in the field of view of the European Photon Imaging Camera (EPIC).
We reduced all the available observations in the Scientific Analysis System (SAS v.18.0.0) with the most recent (as of 2021 February) calibration files. We generated raw event files by processing the EPIC pn and MOS data with the SAS tasks EPPROC and EMPROC, respectively. To filter the raw EPIC pn and MOS events, we employed PATTERN ≤ 4 and PATTERN ≤ 12, respectively, and removed bad pixel events with FLAG==0. We produced flare-filtered clean event files by excluding the proton flare intervals using the method described in Mallick et al. (2021). We confirmed the absence of any pile-up effects using the task EPATPLOT. We extracted the source and background spectra from a circular region centred on the source and nearby source-free zone of radius 20 and 40 arcsec, respectively. The Redistribution Matrix File (RMF) and Ancillary Response File (ARF) for each observation were generated with the SAS tasks RMFGEN and ARFGEN, respectively. We then grouped the spectral data to have a minimum of 10 counts per bin and to oversample by at most a factor of 3 using the SPECGROUP task. We excluded sources that do not have EPIC-pn counts above 4 keV after background subtraction. To obtain a clear view of the central engine, we selected only Seyfert 1 class AGNs. These criteria resulted in a final sample of 13 AGNs. The observation log and source properties are presented in Tables 1 and 2, respectively.
Summary of XMM–Newton observations of the sample used in this work. The source name, right ascension, and declination are given in columns (1), (2), and (3), respectively. The observation ID and start date are shown in columns (4) and (5), respectively. Total net exposure time for EPIC pn+MOS is listed in column (6). The net exposure time is the background filtered, live time of the instrument. Column (7) shows the 0.3–10 keV EPIC pn+MOS background-subtracted net source count rate.
| Source name (Short) . | RA . | Dec. . | Obs. ID . | Start date . | Net total . | Net source count . |
|---|---|---|---|---|---|---|
| . | (Deg) . | (Deg) . | . | (yyyy-mm-dd) . | exp. (ks) . | rate (ct/s) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| SDSS J010712.03+140844.9 [J0107] | 16.800 | 14.146 | 0305920101 | 2005-07-22 | 68.8 | 0.33 |
| SDSS J022849.51–090153.7 [J0228] | 37.206 | −9.032 | 0674810101 | 2012-01-17 | 28.5 | 0.24 |
| SDSS J094057.19+032401.2 [J0940] | 145.238 | 3.400 | 0306050201 | 2005-10-30 | 72.8 | 0.27 |
| SDSS J102348.44+040553.7 [J1023] | 155.952 | 4.098 | 0108670101 | 2000-12-05 | 148.3 | 0.08 |
| 0605540201 | 2009-12-13 | 306.6 | 0.11 | |||
| 0605540301 | 2009-05-08 | 129.1 | 0.08 | |||
| SDSS J114008.71+030711.4 [J1140] | 175.036 | 3.120 | 0305920201 | 2005-12-03 | 111.9 | 0.72 |
| 0724840101 | 2013-12-18 | 110.6 | 0.33 | |||
| 0724840301 | 2014-01-01 | 146.3 | 0.64 | |||
| SDSS J134738.23+474301.9 [J1347] | 206.909 | 47.717 | 0744220701 | 2014-11-22 | 72.1 | 0.59 |
| SDSS J135724.52+652505.8 [J1357] | 209.352 | 65.418 | 0305920601 | 2005-06-23 | 40.3 | 0.48 |
| SDSS J143450.62+033842.5 [J1434] | 218.711 | 3.645 | 0305920401 | 2005-08-18 | 61.5 | 0.13 |
| 0674810501 | 2011-08-16 | 35.4 | 0.13 | |||
| SDSS J154150.85+310037.2 [J1541] | 235.462 | 31.010 | 0744220401 | 2015-01-31 | 30.3 | 0.33 |
| SDSS J155909.62+350147.4 [J1559] | 239.790 | 35.030 | 0744290101 | 2015-03-02 | 204.5 | 2.7 |
| 0744290201 | 2015-02-24 | 236.3 | 2.5 | |||
| SDSS J162636.40+350242.0 [J1626] | 246.652 | 35.045 | 0674811001 | 2012-01-17 | 30.1 | 0.11 |
| SDSS J163159.59+243740.2 [J1631] | 247.998 | 24.628 | 0674810601 | 2011-08-28 | 39.1 | 0.07 |
| POX52 | 180.737 | −20.934 | 0302420101 | 2005-07-08 | 245.4 | 0.07 |
| Source name (Short) . | RA . | Dec. . | Obs. ID . | Start date . | Net total . | Net source count . |
|---|---|---|---|---|---|---|
| . | (Deg) . | (Deg) . | . | (yyyy-mm-dd) . | exp. (ks) . | rate (ct/s) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| SDSS J010712.03+140844.9 [J0107] | 16.800 | 14.146 | 0305920101 | 2005-07-22 | 68.8 | 0.33 |
| SDSS J022849.51–090153.7 [J0228] | 37.206 | −9.032 | 0674810101 | 2012-01-17 | 28.5 | 0.24 |
| SDSS J094057.19+032401.2 [J0940] | 145.238 | 3.400 | 0306050201 | 2005-10-30 | 72.8 | 0.27 |
| SDSS J102348.44+040553.7 [J1023] | 155.952 | 4.098 | 0108670101 | 2000-12-05 | 148.3 | 0.08 |
| 0605540201 | 2009-12-13 | 306.6 | 0.11 | |||
| 0605540301 | 2009-05-08 | 129.1 | 0.08 | |||
| SDSS J114008.71+030711.4 [J1140] | 175.036 | 3.120 | 0305920201 | 2005-12-03 | 111.9 | 0.72 |
| 0724840101 | 2013-12-18 | 110.6 | 0.33 | |||
| 0724840301 | 2014-01-01 | 146.3 | 0.64 | |||
| SDSS J134738.23+474301.9 [J1347] | 206.909 | 47.717 | 0744220701 | 2014-11-22 | 72.1 | 0.59 |
| SDSS J135724.52+652505.8 [J1357] | 209.352 | 65.418 | 0305920601 | 2005-06-23 | 40.3 | 0.48 |
| SDSS J143450.62+033842.5 [J1434] | 218.711 | 3.645 | 0305920401 | 2005-08-18 | 61.5 | 0.13 |
| 0674810501 | 2011-08-16 | 35.4 | 0.13 | |||
| SDSS J154150.85+310037.2 [J1541] | 235.462 | 31.010 | 0744220401 | 2015-01-31 | 30.3 | 0.33 |
| SDSS J155909.62+350147.4 [J1559] | 239.790 | 35.030 | 0744290101 | 2015-03-02 | 204.5 | 2.7 |
| 0744290201 | 2015-02-24 | 236.3 | 2.5 | |||
| SDSS J162636.40+350242.0 [J1626] | 246.652 | 35.045 | 0674811001 | 2012-01-17 | 30.1 | 0.11 |
| SDSS J163159.59+243740.2 [J1631] | 247.998 | 24.628 | 0674810601 | 2011-08-28 | 39.1 | 0.07 |
| POX52 | 180.737 | −20.934 | 0302420101 | 2005-07-08 | 245.4 | 0.07 |
Summary of XMM–Newton observations of the sample used in this work. The source name, right ascension, and declination are given in columns (1), (2), and (3), respectively. The observation ID and start date are shown in columns (4) and (5), respectively. Total net exposure time for EPIC pn+MOS is listed in column (6). The net exposure time is the background filtered, live time of the instrument. Column (7) shows the 0.3–10 keV EPIC pn+MOS background-subtracted net source count rate.
| Source name (Short) . | RA . | Dec. . | Obs. ID . | Start date . | Net total . | Net source count . |
|---|---|---|---|---|---|---|
| . | (Deg) . | (Deg) . | . | (yyyy-mm-dd) . | exp. (ks) . | rate (ct/s) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| SDSS J010712.03+140844.9 [J0107] | 16.800 | 14.146 | 0305920101 | 2005-07-22 | 68.8 | 0.33 |
| SDSS J022849.51–090153.7 [J0228] | 37.206 | −9.032 | 0674810101 | 2012-01-17 | 28.5 | 0.24 |
| SDSS J094057.19+032401.2 [J0940] | 145.238 | 3.400 | 0306050201 | 2005-10-30 | 72.8 | 0.27 |
| SDSS J102348.44+040553.7 [J1023] | 155.952 | 4.098 | 0108670101 | 2000-12-05 | 148.3 | 0.08 |
| 0605540201 | 2009-12-13 | 306.6 | 0.11 | |||
| 0605540301 | 2009-05-08 | 129.1 | 0.08 | |||
| SDSS J114008.71+030711.4 [J1140] | 175.036 | 3.120 | 0305920201 | 2005-12-03 | 111.9 | 0.72 |
| 0724840101 | 2013-12-18 | 110.6 | 0.33 | |||
| 0724840301 | 2014-01-01 | 146.3 | 0.64 | |||
| SDSS J134738.23+474301.9 [J1347] | 206.909 | 47.717 | 0744220701 | 2014-11-22 | 72.1 | 0.59 |
| SDSS J135724.52+652505.8 [J1357] | 209.352 | 65.418 | 0305920601 | 2005-06-23 | 40.3 | 0.48 |
| SDSS J143450.62+033842.5 [J1434] | 218.711 | 3.645 | 0305920401 | 2005-08-18 | 61.5 | 0.13 |
| 0674810501 | 2011-08-16 | 35.4 | 0.13 | |||
| SDSS J154150.85+310037.2 [J1541] | 235.462 | 31.010 | 0744220401 | 2015-01-31 | 30.3 | 0.33 |
| SDSS J155909.62+350147.4 [J1559] | 239.790 | 35.030 | 0744290101 | 2015-03-02 | 204.5 | 2.7 |
| 0744290201 | 2015-02-24 | 236.3 | 2.5 | |||
| SDSS J162636.40+350242.0 [J1626] | 246.652 | 35.045 | 0674811001 | 2012-01-17 | 30.1 | 0.11 |
| SDSS J163159.59+243740.2 [J1631] | 247.998 | 24.628 | 0674810601 | 2011-08-28 | 39.1 | 0.07 |
| POX52 | 180.737 | −20.934 | 0302420101 | 2005-07-08 | 245.4 | 0.07 |
| Source name (Short) . | RA . | Dec. . | Obs. ID . | Start date . | Net total . | Net source count . |
|---|---|---|---|---|---|---|
| . | (Deg) . | (Deg) . | . | (yyyy-mm-dd) . | exp. (ks) . | rate (ct/s) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| SDSS J010712.03+140844.9 [J0107] | 16.800 | 14.146 | 0305920101 | 2005-07-22 | 68.8 | 0.33 |
| SDSS J022849.51–090153.7 [J0228] | 37.206 | −9.032 | 0674810101 | 2012-01-17 | 28.5 | 0.24 |
| SDSS J094057.19+032401.2 [J0940] | 145.238 | 3.400 | 0306050201 | 2005-10-30 | 72.8 | 0.27 |
| SDSS J102348.44+040553.7 [J1023] | 155.952 | 4.098 | 0108670101 | 2000-12-05 | 148.3 | 0.08 |
| 0605540201 | 2009-12-13 | 306.6 | 0.11 | |||
| 0605540301 | 2009-05-08 | 129.1 | 0.08 | |||
| SDSS J114008.71+030711.4 [J1140] | 175.036 | 3.120 | 0305920201 | 2005-12-03 | 111.9 | 0.72 |
| 0724840101 | 2013-12-18 | 110.6 | 0.33 | |||
| 0724840301 | 2014-01-01 | 146.3 | 0.64 | |||
| SDSS J134738.23+474301.9 [J1347] | 206.909 | 47.717 | 0744220701 | 2014-11-22 | 72.1 | 0.59 |
| SDSS J135724.52+652505.8 [J1357] | 209.352 | 65.418 | 0305920601 | 2005-06-23 | 40.3 | 0.48 |
| SDSS J143450.62+033842.5 [J1434] | 218.711 | 3.645 | 0305920401 | 2005-08-18 | 61.5 | 0.13 |
| 0674810501 | 2011-08-16 | 35.4 | 0.13 | |||
| SDSS J154150.85+310037.2 [J1541] | 235.462 | 31.010 | 0744220401 | 2015-01-31 | 30.3 | 0.33 |
| SDSS J155909.62+350147.4 [J1559] | 239.790 | 35.030 | 0744290101 | 2015-03-02 | 204.5 | 2.7 |
| 0744290201 | 2015-02-24 | 236.3 | 2.5 | |||
| SDSS J162636.40+350242.0 [J1626] | 246.652 | 35.045 | 0674811001 | 2012-01-17 | 30.1 | 0.11 |
| SDSS J163159.59+243740.2 [J1631] | 247.998 | 24.628 | 0674810601 | 2011-08-28 | 39.1 | 0.07 |
| POX52 | 180.737 | −20.934 | 0302420101 | 2005-07-08 | 245.4 | 0.07 |
The source name and redshift are given in columns (1) and (2), respectively. Columns (3) and (4) represent the black hole mass and Eddington ratio, respectively, and are obtained from Thornton et al. (2008) for POX52; for all other sources from the GH07 catalogue. The BH mass uncertainty is ∼0.3 dex for the GH07 sample. Columns (5) and (6) show the optical class of each source obtained from NED/SIMBAD and the Galactic hydrogen column density (Willingale et al. 2013), respectively. The maximum disc temperature for Schwarzschild and Kerr black holes are presented in columns (7) and (8), respectively. Column (9) shows the temperature of the soft X-ray excess component when fitted with a disc blackbody model.
| Source . | z . | MBH . | Lbol/LE . | Optical . | NH,Gal . | Tmax (a = 0) . | Tmax (a = 0.998) . | TSE . |
|---|---|---|---|---|---|---|---|---|
| . | . | (105 M⊙) . | . | Type . | (1020 cm−2) . | (eV) . | (eV) . | (eV) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| J0107 | 0.0767 | 16.0|$^{+16.0}_{-8.0}$| | 0.40 | NLSy1 | 3.94 | 29.5 | 58.6 | 186|$^{+16}_{-17}$| |
| J0228 | 0.0722 | 3.2|$^{+3.1}_{-1.6}$| | 0.25 | BLSy1 | 3.88 | 39.3 | 78.1 | 151|$^{+15}_{-17}$| |
| J0940 | 0.0606 | 16.0|$^{+16.0}_{-8.0}$| | 0.40 | NLSy1 | 3.73 | 29.5 | 58.6 | 150|$^{+12}_{-13}$| |
| J1023 | 0.0989 | 5.0|$^{+5.0}_{-2.5}$| | 0.50 | NLSy1 | 2.9 | 41.7 | 82.7 | 156|$^{+20}_{-25}$| |
| J1140 | 0.081 | 12.6|$^{+12.5}_{-6.3}$| | 0.63 | NLSy1 | 2.06 | 35.0 | 69.6 | 170|$^{+4}_{-5}$| |
| J1347 | 0.0643 | 10.0|$^{+10.0}_{-5.0}$| | 0.50 | NLSy1 | 1.9 | 35.0 | 69.6 | 166|$^{+6}_{-6}$| |
| J1357 | 0.106 | 16.0|$^{+16.0}_{-8.0}$| | 0.50 | NLSy1 | 1.45 | 31.2 | 62.0 | 150|$^{+11}_{-10}$| |
| J1434 | 0.0283 | 6.3|$^{+6.3}_{-3.1}$| | 0.10 | Sy1 | 2.76 | 26.3 | 52.2 | 173|$^{+28}_{-30}$| |
| J1541 | 0.0684 | 16.0|$^{+16.0}_{-8.0}$| | 0.25 | BLSy1 | 2.67 | 26.3 | 52.2 | 114|$^{+20}_{-19}$| |
| J1559 | 0.031 | 16.0|$^{+16.0}_{-8.0}$| | 0.63 | NLSy1 | 2.28 | 33.1 | 65.7 | 144|$^{+2}_{-3}$| |
| J1626 | 0.0341 | 5.0|$^{+5.0}_{-2.5}$| | 0.32 | Sy 1.5 | 1.52 | 37.1 | 73.7 | 103|$^{+25}_{-22}$| |
| J1631 | 0.0433 | 6.3|$^{+6.3}_{-3.1}$| | 0.32 | BLSy1 | 4.08 | 35.0 | 69.6 | 128|$^{+31}_{-29}$| |
| POX52 | 0.021 | 3.2|$^{+1.0}_{-1.0}$| | 0.35 | Sy 1.8 | 4.41 | 42.6 | 84.6 | 243|$^{+36}_{-34}$| |
| Source . | z . | MBH . | Lbol/LE . | Optical . | NH,Gal . | Tmax (a = 0) . | Tmax (a = 0.998) . | TSE . |
|---|---|---|---|---|---|---|---|---|
| . | . | (105 M⊙) . | . | Type . | (1020 cm−2) . | (eV) . | (eV) . | (eV) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| J0107 | 0.0767 | 16.0|$^{+16.0}_{-8.0}$| | 0.40 | NLSy1 | 3.94 | 29.5 | 58.6 | 186|$^{+16}_{-17}$| |
| J0228 | 0.0722 | 3.2|$^{+3.1}_{-1.6}$| | 0.25 | BLSy1 | 3.88 | 39.3 | 78.1 | 151|$^{+15}_{-17}$| |
| J0940 | 0.0606 | 16.0|$^{+16.0}_{-8.0}$| | 0.40 | NLSy1 | 3.73 | 29.5 | 58.6 | 150|$^{+12}_{-13}$| |
| J1023 | 0.0989 | 5.0|$^{+5.0}_{-2.5}$| | 0.50 | NLSy1 | 2.9 | 41.7 | 82.7 | 156|$^{+20}_{-25}$| |
| J1140 | 0.081 | 12.6|$^{+12.5}_{-6.3}$| | 0.63 | NLSy1 | 2.06 | 35.0 | 69.6 | 170|$^{+4}_{-5}$| |
| J1347 | 0.0643 | 10.0|$^{+10.0}_{-5.0}$| | 0.50 | NLSy1 | 1.9 | 35.0 | 69.6 | 166|$^{+6}_{-6}$| |
| J1357 | 0.106 | 16.0|$^{+16.0}_{-8.0}$| | 0.50 | NLSy1 | 1.45 | 31.2 | 62.0 | 150|$^{+11}_{-10}$| |
| J1434 | 0.0283 | 6.3|$^{+6.3}_{-3.1}$| | 0.10 | Sy1 | 2.76 | 26.3 | 52.2 | 173|$^{+28}_{-30}$| |
| J1541 | 0.0684 | 16.0|$^{+16.0}_{-8.0}$| | 0.25 | BLSy1 | 2.67 | 26.3 | 52.2 | 114|$^{+20}_{-19}$| |
| J1559 | 0.031 | 16.0|$^{+16.0}_{-8.0}$| | 0.63 | NLSy1 | 2.28 | 33.1 | 65.7 | 144|$^{+2}_{-3}$| |
| J1626 | 0.0341 | 5.0|$^{+5.0}_{-2.5}$| | 0.32 | Sy 1.5 | 1.52 | 37.1 | 73.7 | 103|$^{+25}_{-22}$| |
| J1631 | 0.0433 | 6.3|$^{+6.3}_{-3.1}$| | 0.32 | BLSy1 | 4.08 | 35.0 | 69.6 | 128|$^{+31}_{-29}$| |
| POX52 | 0.021 | 3.2|$^{+1.0}_{-1.0}$| | 0.35 | Sy 1.8 | 4.41 | 42.6 | 84.6 | 243|$^{+36}_{-34}$| |
The source name and redshift are given in columns (1) and (2), respectively. Columns (3) and (4) represent the black hole mass and Eddington ratio, respectively, and are obtained from Thornton et al. (2008) for POX52; for all other sources from the GH07 catalogue. The BH mass uncertainty is ∼0.3 dex for the GH07 sample. Columns (5) and (6) show the optical class of each source obtained from NED/SIMBAD and the Galactic hydrogen column density (Willingale et al. 2013), respectively. The maximum disc temperature for Schwarzschild and Kerr black holes are presented in columns (7) and (8), respectively. Column (9) shows the temperature of the soft X-ray excess component when fitted with a disc blackbody model.
| Source . | z . | MBH . | Lbol/LE . | Optical . | NH,Gal . | Tmax (a = 0) . | Tmax (a = 0.998) . | TSE . |
|---|---|---|---|---|---|---|---|---|
| . | . | (105 M⊙) . | . | Type . | (1020 cm−2) . | (eV) . | (eV) . | (eV) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| J0107 | 0.0767 | 16.0|$^{+16.0}_{-8.0}$| | 0.40 | NLSy1 | 3.94 | 29.5 | 58.6 | 186|$^{+16}_{-17}$| |
| J0228 | 0.0722 | 3.2|$^{+3.1}_{-1.6}$| | 0.25 | BLSy1 | 3.88 | 39.3 | 78.1 | 151|$^{+15}_{-17}$| |
| J0940 | 0.0606 | 16.0|$^{+16.0}_{-8.0}$| | 0.40 | NLSy1 | 3.73 | 29.5 | 58.6 | 150|$^{+12}_{-13}$| |
| J1023 | 0.0989 | 5.0|$^{+5.0}_{-2.5}$| | 0.50 | NLSy1 | 2.9 | 41.7 | 82.7 | 156|$^{+20}_{-25}$| |
| J1140 | 0.081 | 12.6|$^{+12.5}_{-6.3}$| | 0.63 | NLSy1 | 2.06 | 35.0 | 69.6 | 170|$^{+4}_{-5}$| |
| J1347 | 0.0643 | 10.0|$^{+10.0}_{-5.0}$| | 0.50 | NLSy1 | 1.9 | 35.0 | 69.6 | 166|$^{+6}_{-6}$| |
| J1357 | 0.106 | 16.0|$^{+16.0}_{-8.0}$| | 0.50 | NLSy1 | 1.45 | 31.2 | 62.0 | 150|$^{+11}_{-10}$| |
| J1434 | 0.0283 | 6.3|$^{+6.3}_{-3.1}$| | 0.10 | Sy1 | 2.76 | 26.3 | 52.2 | 173|$^{+28}_{-30}$| |
| J1541 | 0.0684 | 16.0|$^{+16.0}_{-8.0}$| | 0.25 | BLSy1 | 2.67 | 26.3 | 52.2 | 114|$^{+20}_{-19}$| |
| J1559 | 0.031 | 16.0|$^{+16.0}_{-8.0}$| | 0.63 | NLSy1 | 2.28 | 33.1 | 65.7 | 144|$^{+2}_{-3}$| |
| J1626 | 0.0341 | 5.0|$^{+5.0}_{-2.5}$| | 0.32 | Sy 1.5 | 1.52 | 37.1 | 73.7 | 103|$^{+25}_{-22}$| |
| J1631 | 0.0433 | 6.3|$^{+6.3}_{-3.1}$| | 0.32 | BLSy1 | 4.08 | 35.0 | 69.6 | 128|$^{+31}_{-29}$| |
| POX52 | 0.021 | 3.2|$^{+1.0}_{-1.0}$| | 0.35 | Sy 1.8 | 4.41 | 42.6 | 84.6 | 243|$^{+36}_{-34}$| |
| Source . | z . | MBH . | Lbol/LE . | Optical . | NH,Gal . | Tmax (a = 0) . | Tmax (a = 0.998) . | TSE . |
|---|---|---|---|---|---|---|---|---|
| . | . | (105 M⊙) . | . | Type . | (1020 cm−2) . | (eV) . | (eV) . | (eV) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| J0107 | 0.0767 | 16.0|$^{+16.0}_{-8.0}$| | 0.40 | NLSy1 | 3.94 | 29.5 | 58.6 | 186|$^{+16}_{-17}$| |
| J0228 | 0.0722 | 3.2|$^{+3.1}_{-1.6}$| | 0.25 | BLSy1 | 3.88 | 39.3 | 78.1 | 151|$^{+15}_{-17}$| |
| J0940 | 0.0606 | 16.0|$^{+16.0}_{-8.0}$| | 0.40 | NLSy1 | 3.73 | 29.5 | 58.6 | 150|$^{+12}_{-13}$| |
| J1023 | 0.0989 | 5.0|$^{+5.0}_{-2.5}$| | 0.50 | NLSy1 | 2.9 | 41.7 | 82.7 | 156|$^{+20}_{-25}$| |
| J1140 | 0.081 | 12.6|$^{+12.5}_{-6.3}$| | 0.63 | NLSy1 | 2.06 | 35.0 | 69.6 | 170|$^{+4}_{-5}$| |
| J1347 | 0.0643 | 10.0|$^{+10.0}_{-5.0}$| | 0.50 | NLSy1 | 1.9 | 35.0 | 69.6 | 166|$^{+6}_{-6}$| |
| J1357 | 0.106 | 16.0|$^{+16.0}_{-8.0}$| | 0.50 | NLSy1 | 1.45 | 31.2 | 62.0 | 150|$^{+11}_{-10}$| |
| J1434 | 0.0283 | 6.3|$^{+6.3}_{-3.1}$| | 0.10 | Sy1 | 2.76 | 26.3 | 52.2 | 173|$^{+28}_{-30}$| |
| J1541 | 0.0684 | 16.0|$^{+16.0}_{-8.0}$| | 0.25 | BLSy1 | 2.67 | 26.3 | 52.2 | 114|$^{+20}_{-19}$| |
| J1559 | 0.031 | 16.0|$^{+16.0}_{-8.0}$| | 0.63 | NLSy1 | 2.28 | 33.1 | 65.7 | 144|$^{+2}_{-3}$| |
| J1626 | 0.0341 | 5.0|$^{+5.0}_{-2.5}$| | 0.32 | Sy 1.5 | 1.52 | 37.1 | 73.7 | 103|$^{+25}_{-22}$| |
| J1631 | 0.0433 | 6.3|$^{+6.3}_{-3.1}$| | 0.32 | BLSy1 | 4.08 | 35.0 | 69.6 | 128|$^{+31}_{-29}$| |
| POX52 | 0.021 | 3.2|$^{+1.0}_{-1.0}$| | 0.35 | Sy 1.8 | 4.41 | 42.6 | 84.6 | 243|$^{+36}_{-34}$| |
3 VARIABLE DENSITY DISC REFLECTION MODELLING
We explore our physically motivated variable density disc reflection model relxillDCp to study the broad-band (0.3–10 keV) X-ray spectra of the sample. The model allows a higher density for the accretion disc varying from ne = 1015 to 1020 cm−3 and includes a Comptonization continuum (nthComp) with a variable coronal temperature as the incident spectrum instead of a simple power law. The high-energy cutoff of the relxillDCp model is parametrized by the electron temperature (kTe) of the hot corona and spans within the range of 1–400 keV. This new version of the model will soon be included in the next official release of RELXILL v.1.5.0.
The spectral fitting was performed in the XSPEC (v.12.11.1) software (Arnaud 1996). We employed C-stat (Cash 1979) to find the best-fitting values of the model parameters and χ2-statistics to test the goodness of fit. All the reported errors are estimated through Markov chain Monte Carlo (MCMC) simulations and correspond to the 90 per cent confidence intervals unless otherwise specified.
First, we fit the hard band (2–10 keV) continuum spectra with the phenomenological power-law (zpowerlw) model modified by the absorption due to the Galactic interstellar medium (ISM). We used the Tuebingen–Boulder ISM absorption model (Tbabs) to account for the Galactic absorption. The model considers the solar ISM abundances of Wilms, Allen & McCray (2000) and the photoionization cross-section table of Verner et al. (1996). We employed the Galactic absorption column density (NH,Gal) calculated by Willingale et al. (2013), which accounts for the column density of both the atomic (NHI) and molecular (NH2) hydrogen. The Galactic hydrogen column density (NH,Gal) for each source, as listed in Table 2, was kept fixed throughout the spectral modelling. The absorbed power-law model describes the hard X-ray emission well for all AGNs except J1559 which showed a narrow Fe Kα emission line at 6.4 keV. The presence of a narrow Fe Kα line cannot be tested in most of the sources due to the low statistics. We modelled the Fe Kα emission profile of J1559 by a narrow Gaussian (zgauss) line with the width fixed at 10 eV. The addition of the narrow Gaussian line improved the test statistics by Δχ2 = 21 for 2 degrees of freedom. The significance of the emission line is ≥99.99 per cent, estimated by the maximum-likelihood ratio (MLR) test. We find that the hard X-ray spectrum of J1559 is well explained by an absorbed power-law model along with a narrow Fe Kα emission line. It is likely that any of these spectra do not have sufficient counts in the 2–10 keV band to significantly detect the broad Fe Kα emission line. A study by de la Calle Pérez et al (2010) demonstrated that at least 1.5 × 105 hard X-ray (2–10 keV) counts are needed for a significant detection of the relativistic Fe Kα line in Type 1 AGNs.
We then model the observed soft X-ray excess using the new variable density relativistic reflection model (relxillDCp), which assumes a sandwich configuration for corona that encircles the surrounding disc. The heating of the inner disc by coronal X-rays leads to quasi-thermal emission in the soft X-rays, which is fully represented by the high-density effects in the model (see García et al. 2016). As the density parameter is increased, the effective temperature of the reprocessed emission at soft energies increases, leading to a quasi-thermal emission component that appears in the soft band. The model adjusts the temperature of the reflector so that flux in equals flux out, and hence it does not require further thermalization of the disc.
The relxillDCp model combines the ionized disc reflection code xillverDCp (García et al. 2013, 2016) with the convolution model relconv (Dauser et al. 2013). The relconv model determines the relativistic effects in the reflection spectrum and assumes a broken power-law emissivity profile for the illumination of the disc by an X-ray corona. The emissivity profile has the following form: |$\epsilon (r)\propto r^{-q_{{\rm in}}}$| for rin ≤ r ≤ rbr, and |$\epsilon (r)\propto r^{-q_{{\rm out}}}$| for |$r_{\rm br}\le r\le r_{{\rm {\rm out}}}$|, where qin and qout represent inner and outer emissivity indices, respectively, rbr is the break radius, rin and rout are the inner and outer disc radii, respectively. The other parameters that characterize the disc reflection model are: black hole spin (a), the inclination angle (θ○) of the disc to the observer, reflection fraction (refl_frac), iron abundance (AFe), ionization state (log ξ), and number density (ne) of electrons in the disc atmosphere. The disc irradiation profile is considered Newtonian over the outer regions of the disc, and hence we fixed the outer emissivity index at 3. We fixed the break radius at 6rg, which is a typical AGN coronal radius (e.g. Wilkins & Fabian 2011; Mallick et al. 2021). We assume the solar abundance of iron and fixed the inner and outer radii of the accretion disc at the innermost stable circular orbit (risco) and 1000rg (rg = GMBH/c2), respectively. We set refl_frac=−1 in the relxillDCp model to solely describe the disc reflection. Since relxillDCp considers the thermal Comptonization model nthComp (Zdziarski, Johnson & Magdziarz 1996; Źycki, Done & Smith 1999) as the irradiating (primary) continuum, we replaced the zpowerlw continuum with nthComp. The slope of the nthComp and relxillDCp components are tied. The seed photon temperature in the nthComp model was set at the maximum possible disc temperature (see column 8 of Table 2) for each source. We fixed the electron temperature of the hot coronal plasma at a typical value of 100 keV. The relative strength of reflection was measured as a ratio of the disc reflected flux to the irradiating primary source flux in the 0.3–10 keV band. We find that the broad-band best-fitting spectral model is Tbabs×(relxillDCp+nthComp) for all the sources in the sample, except for J1559 and POX 52. The source, J1559, showed an absorption feature at ∼0.7 keV, which was modeled by a Gaussian absorption line gabs. The gabs component improves the fit statistic by Δχ2 = 92.9 for 3 free parameters. The expression for the broad-band best-fit model of J1559 is Tbabs×gabs×(zgauss+relxillDCp+nthComp). To model the absorption curvature present in the 1–2 keV band of POX 52, we included an ionized partial covering absorption component (zxipcf; Reeves et al. 2008). The zxipcf model has three free parameters: column density (NH,wa), ionization state (log ξwa) of the absorbing medium and covering fraction (Cf). The inclusion of the ionized absorption component provided an improvement of Δχ2 = 237.5 for three additional free parameters. The maximum-likelihood ratio (MLR) test suggests that the zxipcf model component is ≥99.99 per cent significant. The best-fitting model for POX 52 has the following expression: Tbabs×zxipcf×(relxillDCp+nthComp). We find that the relativistic reflection from an ionized, higher density accretion disc can self-consistently explain the soft X-ray excess emission for the low-mass AGN sample. The best-fitting unfolded spectral models, model components, and data-to-model ratio plots are shown in Fig. 1. We show the broad-band photon count spectra, best-fitting models, and residuals plots in Fig. A2.
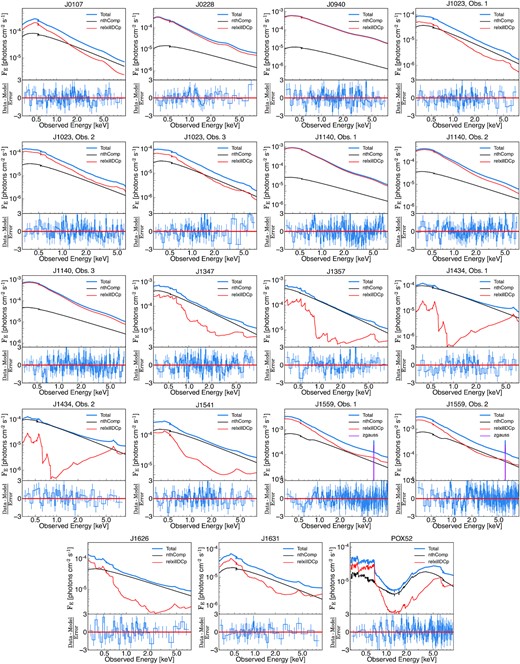
The top panels represent the best-fitting flux-energy spectral model (in blue) along with model components (black: nthComp, red: relxillDCp, purple: zgauss). The total model expressions are Tbabs×gabs×(zgauss+relxillDCp+nthComp), Tbabs×zxipcf×(relxillDCp+nthComp), and Tbabs×(relxillDCp+nthComp), respectively, for J1559, POX 52, and all other AGNs. The bottom panels show the corresponding residual plots.
To check the robustness of the parameter measurements and determine the constraints on each free parameter, we conducted a Markov chain Monte Carlo (MCMC) analysis utilizing the Goodman–Weare algorithm in XSPEC. We run the Markov Chain for 150 000 iterations with 100 walkers. We burned the initial 50 000 events to obtain a steady chain and used 100 000 steady-state samples to determine the parameter distributions and their 90 per cent confidence intervals. We performed Gelman–Rubin’s MCMC convergence test and ensured that the chains have converged with the potential scale reduction factor below 1.2 for each parameter. The contour plots of various parameters infer that the parameter space is not degenerate (see Figs A3, A4, and A5). The best-fitting spectral model parameters, their 90 per cent confidence intervals and fit statistics for the sample are presented in Tables A1 and A2.
The 2–10 keV intrinsic luminosity at the source frame, average bolometric correction factor, and the Eddington ratio as measured from the bolometric corrected 2–10 keV source luminosity are presented in columns (2), (3), and (4), respectively. The innermost stable circular orbit risco in units of rg and radiative efficiency η = rg/2risco are listed in columns (5) and (6), respectively. Columns (7) and (8) represent the dimensionless mass accretion rate |$\dot{m}=\frac{\dot{M}}{\dot{M}_{\rm E}}=\frac{L_{\rm bol}}{\eta L_{\rm E}}$| and Eddington accretion limit |$\dot{m}_{\rm E}=1/\eta$|, respectively.
| Source . | L2–10 keV . | κ . | Lbol/LE . | risco . | η . | |$\dot{m}$| . | |$\dot{m}_{\rm E}$| . |
|---|---|---|---|---|---|---|---|
| . | (1041 erg s−1) . | . | . | (rg) . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| J0107 | |$31.3^{+0.7}_{-0.7}$| | 20|$^{+7}_{-7}$| | 0.28|$^{+0.48}_{-0.19}$| | |$2.5_{-0.6}^{+1.2}$| | |$0.20_{-0.06}^{+0.06}$| | |$1.4_{-1.1}^{+4.2}$| | |$5.0_{-1.1}^{+2.4}$| |
| J0228 | |$18.4^{+0.7}_{-0.7}$| | 18|$^{+6}_{-6}$| | 0.75|$^{+1.24}_{-0.50}$| | |$2.8_{-1.2}^{+0.4}$| | |$0.18_{-0.02}^{+0.14}$| | |$4.2_{-3.4}^{+8.7}$| | |$5.6_{-2.5}^{+0.9}$| |
| J0940 | |$37.7^{+0.8}_{-0.8}$| | 21|$^{+7}_{-7}$| | 0.36|$^{+0.59}_{-0.24}$| | |$1.3_{-0.05}^{+0.3}$| | |$0.38_{-0.07}^{+0.02}$| | |$0.9_{-0.6}^{+2.1}$| | |$2.6_{-0.1}^{+0.6}$| |
| J1023 | |$12.8^{+0.2}_{-0.2}$| | 16|$^{+6}_{-5}$| | 0.29|$^{+0.51}_{-0.19}$| | |$4.1_{-1.9}^{+0.6}$| | |$0.12_{-0.02}^{+0.11}$| | |$2.4_{-2.0}^{+5.1}$| | |$8.3_{-3.9}^{+1.2}$| |
| J1140 | |$38.2^{+0.3}_{-0.3}$| | 21|$^{+7}_{-8}$| | 0.45|$^{+0.76}_{-0.31}$| | |$1.7_{-0.2}^{+0.2}$| | |$0.3_{-0.03}^{+0.03}$| | |$1.5_{-1.1}^{+3.0}$| | |$3.4_{-0.3}^{+0.4}$| |
| J1347 | |$33.0^{+0.5}_{-0.5}$| | 20|$^{+7}_{-7}$| | 0.47|$^{+0.80}_{-0.32}$| | |$3.1_{-1.2}^{+1.8}$| | |$0.16_{-0.06}^{+0.10}$| | |$2.9_{-2.3}^{+9.4}$| | |$6.2_{-2.4}^{+3.6}$| |
| J1357 | |$85.3^{+1.9}_{-1.9}$| | 26|$^{+9}_{-9}$| | 1.0|$^{+1.7}_{-0.7}$| | |$4.8_{-0.6}^{+0.3}$| | |$0.10_{-0.01}^{+0.01}$| | |$9.6_{-6.8}^{+17.9}$| | |$9.6_{-1.2}^{+0.6}$| |
| J1434 | |$3.0^{+0.1}_{-0.1}$| | 13|$^{+5}_{-4}$| | 0.04|$^{+0.08}_{-0.03}$| | |$3.7_{-1.4}^{+1.7}$| | |$0.14_{-0.04}^{+0.08}$| | |$0.3_{-0.2}^{+1.0}$| | |$7.4_{-2.8}^{+3.4}$| |
| J1541 | |$37.5^{+1.2}_{-1.2}$| | 21|$^{+7}_{-8}$| | 0.35|$^{+0.59}_{-0.24}$| | |$2.3_{-0.7}^{+1.2}$| | |$0.22_{-0.08}^{+0.10}$| | |$1.6_{-1.2}^{+4.9}$| | |$4.5_{-1.4}^{+2.3}$| |
| J1559 | |$40.1^{+0.1}_{-0.1}$| | 21|$^{+7}_{-7}$| | 0.38|$^{+0.63}_{-0.25}$| | |$1.24_{-0.0}^{+0.4}$| | |$0.40_{-0.11}^{+0.0}$| | |$0.9_{-0.6}^{+2.5}$| | |$2.5_{-0.0}^{+0.9}$| |
| J1626 | |$3.8^{+0.2}_{-0.2}$| | 14|$^{+4}_{-5}$| | 0.08|$^{+0.12}_{-0.05}$| | |$3.5_{-1.7}^{+0.9}$| | |$0.14_{-0.03}^{+0.13}$| | |$0.5_{-0.4}^{+1.2}$| | |$7.0_{-3.3}^{+1.8}$| |
| J1631 | |$3.1^{+0.2}_{-0.2}$| | 13|$^{+5}_{-4}$| | 0.05|$^{+0.08}_{-0.03}$| | |$3.2_{-0.9}^{+0.8}$| | |$0.16_{-0.03}^{+0.06}$| | |$0.3_{-0.2}^{+0.7}$| | |$6.4_{-1.8}^{+1.6}$| |
| POX52 | |$4.8^{+0.1}_{-0.1}$| | 14|$^{+5}_{-5}$| | 0.15|$^{+0.15}_{-0.08}$| | |$4.0_{-1.8}^{+1.7}$| | |$0.12_{-0.04}^{+0.10}$| | |$1.2_{-0.9}^{+2.1}$| | |$8.0_{-3.6}^{+3.3}$| |
| Source . | L2–10 keV . | κ . | Lbol/LE . | risco . | η . | |$\dot{m}$| . | |$\dot{m}_{\rm E}$| . |
|---|---|---|---|---|---|---|---|
| . | (1041 erg s−1) . | . | . | (rg) . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| J0107 | |$31.3^{+0.7}_{-0.7}$| | 20|$^{+7}_{-7}$| | 0.28|$^{+0.48}_{-0.19}$| | |$2.5_{-0.6}^{+1.2}$| | |$0.20_{-0.06}^{+0.06}$| | |$1.4_{-1.1}^{+4.2}$| | |$5.0_{-1.1}^{+2.4}$| |
| J0228 | |$18.4^{+0.7}_{-0.7}$| | 18|$^{+6}_{-6}$| | 0.75|$^{+1.24}_{-0.50}$| | |$2.8_{-1.2}^{+0.4}$| | |$0.18_{-0.02}^{+0.14}$| | |$4.2_{-3.4}^{+8.7}$| | |$5.6_{-2.5}^{+0.9}$| |
| J0940 | |$37.7^{+0.8}_{-0.8}$| | 21|$^{+7}_{-7}$| | 0.36|$^{+0.59}_{-0.24}$| | |$1.3_{-0.05}^{+0.3}$| | |$0.38_{-0.07}^{+0.02}$| | |$0.9_{-0.6}^{+2.1}$| | |$2.6_{-0.1}^{+0.6}$| |
| J1023 | |$12.8^{+0.2}_{-0.2}$| | 16|$^{+6}_{-5}$| | 0.29|$^{+0.51}_{-0.19}$| | |$4.1_{-1.9}^{+0.6}$| | |$0.12_{-0.02}^{+0.11}$| | |$2.4_{-2.0}^{+5.1}$| | |$8.3_{-3.9}^{+1.2}$| |
| J1140 | |$38.2^{+0.3}_{-0.3}$| | 21|$^{+7}_{-8}$| | 0.45|$^{+0.76}_{-0.31}$| | |$1.7_{-0.2}^{+0.2}$| | |$0.3_{-0.03}^{+0.03}$| | |$1.5_{-1.1}^{+3.0}$| | |$3.4_{-0.3}^{+0.4}$| |
| J1347 | |$33.0^{+0.5}_{-0.5}$| | 20|$^{+7}_{-7}$| | 0.47|$^{+0.80}_{-0.32}$| | |$3.1_{-1.2}^{+1.8}$| | |$0.16_{-0.06}^{+0.10}$| | |$2.9_{-2.3}^{+9.4}$| | |$6.2_{-2.4}^{+3.6}$| |
| J1357 | |$85.3^{+1.9}_{-1.9}$| | 26|$^{+9}_{-9}$| | 1.0|$^{+1.7}_{-0.7}$| | |$4.8_{-0.6}^{+0.3}$| | |$0.10_{-0.01}^{+0.01}$| | |$9.6_{-6.8}^{+17.9}$| | |$9.6_{-1.2}^{+0.6}$| |
| J1434 | |$3.0^{+0.1}_{-0.1}$| | 13|$^{+5}_{-4}$| | 0.04|$^{+0.08}_{-0.03}$| | |$3.7_{-1.4}^{+1.7}$| | |$0.14_{-0.04}^{+0.08}$| | |$0.3_{-0.2}^{+1.0}$| | |$7.4_{-2.8}^{+3.4}$| |
| J1541 | |$37.5^{+1.2}_{-1.2}$| | 21|$^{+7}_{-8}$| | 0.35|$^{+0.59}_{-0.24}$| | |$2.3_{-0.7}^{+1.2}$| | |$0.22_{-0.08}^{+0.10}$| | |$1.6_{-1.2}^{+4.9}$| | |$4.5_{-1.4}^{+2.3}$| |
| J1559 | |$40.1^{+0.1}_{-0.1}$| | 21|$^{+7}_{-7}$| | 0.38|$^{+0.63}_{-0.25}$| | |$1.24_{-0.0}^{+0.4}$| | |$0.40_{-0.11}^{+0.0}$| | |$0.9_{-0.6}^{+2.5}$| | |$2.5_{-0.0}^{+0.9}$| |
| J1626 | |$3.8^{+0.2}_{-0.2}$| | 14|$^{+4}_{-5}$| | 0.08|$^{+0.12}_{-0.05}$| | |$3.5_{-1.7}^{+0.9}$| | |$0.14_{-0.03}^{+0.13}$| | |$0.5_{-0.4}^{+1.2}$| | |$7.0_{-3.3}^{+1.8}$| |
| J1631 | |$3.1^{+0.2}_{-0.2}$| | 13|$^{+5}_{-4}$| | 0.05|$^{+0.08}_{-0.03}$| | |$3.2_{-0.9}^{+0.8}$| | |$0.16_{-0.03}^{+0.06}$| | |$0.3_{-0.2}^{+0.7}$| | |$6.4_{-1.8}^{+1.6}$| |
| POX52 | |$4.8^{+0.1}_{-0.1}$| | 14|$^{+5}_{-5}$| | 0.15|$^{+0.15}_{-0.08}$| | |$4.0_{-1.8}^{+1.7}$| | |$0.12_{-0.04}^{+0.10}$| | |$1.2_{-0.9}^{+2.1}$| | |$8.0_{-3.6}^{+3.3}$| |
The 2–10 keV intrinsic luminosity at the source frame, average bolometric correction factor, and the Eddington ratio as measured from the bolometric corrected 2–10 keV source luminosity are presented in columns (2), (3), and (4), respectively. The innermost stable circular orbit risco in units of rg and radiative efficiency η = rg/2risco are listed in columns (5) and (6), respectively. Columns (7) and (8) represent the dimensionless mass accretion rate |$\dot{m}=\frac{\dot{M}}{\dot{M}_{\rm E}}=\frac{L_{\rm bol}}{\eta L_{\rm E}}$| and Eddington accretion limit |$\dot{m}_{\rm E}=1/\eta$|, respectively.
| Source . | L2–10 keV . | κ . | Lbol/LE . | risco . | η . | |$\dot{m}$| . | |$\dot{m}_{\rm E}$| . |
|---|---|---|---|---|---|---|---|
| . | (1041 erg s−1) . | . | . | (rg) . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| J0107 | |$31.3^{+0.7}_{-0.7}$| | 20|$^{+7}_{-7}$| | 0.28|$^{+0.48}_{-0.19}$| | |$2.5_{-0.6}^{+1.2}$| | |$0.20_{-0.06}^{+0.06}$| | |$1.4_{-1.1}^{+4.2}$| | |$5.0_{-1.1}^{+2.4}$| |
| J0228 | |$18.4^{+0.7}_{-0.7}$| | 18|$^{+6}_{-6}$| | 0.75|$^{+1.24}_{-0.50}$| | |$2.8_{-1.2}^{+0.4}$| | |$0.18_{-0.02}^{+0.14}$| | |$4.2_{-3.4}^{+8.7}$| | |$5.6_{-2.5}^{+0.9}$| |
| J0940 | |$37.7^{+0.8}_{-0.8}$| | 21|$^{+7}_{-7}$| | 0.36|$^{+0.59}_{-0.24}$| | |$1.3_{-0.05}^{+0.3}$| | |$0.38_{-0.07}^{+0.02}$| | |$0.9_{-0.6}^{+2.1}$| | |$2.6_{-0.1}^{+0.6}$| |
| J1023 | |$12.8^{+0.2}_{-0.2}$| | 16|$^{+6}_{-5}$| | 0.29|$^{+0.51}_{-0.19}$| | |$4.1_{-1.9}^{+0.6}$| | |$0.12_{-0.02}^{+0.11}$| | |$2.4_{-2.0}^{+5.1}$| | |$8.3_{-3.9}^{+1.2}$| |
| J1140 | |$38.2^{+0.3}_{-0.3}$| | 21|$^{+7}_{-8}$| | 0.45|$^{+0.76}_{-0.31}$| | |$1.7_{-0.2}^{+0.2}$| | |$0.3_{-0.03}^{+0.03}$| | |$1.5_{-1.1}^{+3.0}$| | |$3.4_{-0.3}^{+0.4}$| |
| J1347 | |$33.0^{+0.5}_{-0.5}$| | 20|$^{+7}_{-7}$| | 0.47|$^{+0.80}_{-0.32}$| | |$3.1_{-1.2}^{+1.8}$| | |$0.16_{-0.06}^{+0.10}$| | |$2.9_{-2.3}^{+9.4}$| | |$6.2_{-2.4}^{+3.6}$| |
| J1357 | |$85.3^{+1.9}_{-1.9}$| | 26|$^{+9}_{-9}$| | 1.0|$^{+1.7}_{-0.7}$| | |$4.8_{-0.6}^{+0.3}$| | |$0.10_{-0.01}^{+0.01}$| | |$9.6_{-6.8}^{+17.9}$| | |$9.6_{-1.2}^{+0.6}$| |
| J1434 | |$3.0^{+0.1}_{-0.1}$| | 13|$^{+5}_{-4}$| | 0.04|$^{+0.08}_{-0.03}$| | |$3.7_{-1.4}^{+1.7}$| | |$0.14_{-0.04}^{+0.08}$| | |$0.3_{-0.2}^{+1.0}$| | |$7.4_{-2.8}^{+3.4}$| |
| J1541 | |$37.5^{+1.2}_{-1.2}$| | 21|$^{+7}_{-8}$| | 0.35|$^{+0.59}_{-0.24}$| | |$2.3_{-0.7}^{+1.2}$| | |$0.22_{-0.08}^{+0.10}$| | |$1.6_{-1.2}^{+4.9}$| | |$4.5_{-1.4}^{+2.3}$| |
| J1559 | |$40.1^{+0.1}_{-0.1}$| | 21|$^{+7}_{-7}$| | 0.38|$^{+0.63}_{-0.25}$| | |$1.24_{-0.0}^{+0.4}$| | |$0.40_{-0.11}^{+0.0}$| | |$0.9_{-0.6}^{+2.5}$| | |$2.5_{-0.0}^{+0.9}$| |
| J1626 | |$3.8^{+0.2}_{-0.2}$| | 14|$^{+4}_{-5}$| | 0.08|$^{+0.12}_{-0.05}$| | |$3.5_{-1.7}^{+0.9}$| | |$0.14_{-0.03}^{+0.13}$| | |$0.5_{-0.4}^{+1.2}$| | |$7.0_{-3.3}^{+1.8}$| |
| J1631 | |$3.1^{+0.2}_{-0.2}$| | 13|$^{+5}_{-4}$| | 0.05|$^{+0.08}_{-0.03}$| | |$3.2_{-0.9}^{+0.8}$| | |$0.16_{-0.03}^{+0.06}$| | |$0.3_{-0.2}^{+0.7}$| | |$6.4_{-1.8}^{+1.6}$| |
| POX52 | |$4.8^{+0.1}_{-0.1}$| | 14|$^{+5}_{-5}$| | 0.15|$^{+0.15}_{-0.08}$| | |$4.0_{-1.8}^{+1.7}$| | |$0.12_{-0.04}^{+0.10}$| | |$1.2_{-0.9}^{+2.1}$| | |$8.0_{-3.6}^{+3.3}$| |
| Source . | L2–10 keV . | κ . | Lbol/LE . | risco . | η . | |$\dot{m}$| . | |$\dot{m}_{\rm E}$| . |
|---|---|---|---|---|---|---|---|
| . | (1041 erg s−1) . | . | . | (rg) . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| J0107 | |$31.3^{+0.7}_{-0.7}$| | 20|$^{+7}_{-7}$| | 0.28|$^{+0.48}_{-0.19}$| | |$2.5_{-0.6}^{+1.2}$| | |$0.20_{-0.06}^{+0.06}$| | |$1.4_{-1.1}^{+4.2}$| | |$5.0_{-1.1}^{+2.4}$| |
| J0228 | |$18.4^{+0.7}_{-0.7}$| | 18|$^{+6}_{-6}$| | 0.75|$^{+1.24}_{-0.50}$| | |$2.8_{-1.2}^{+0.4}$| | |$0.18_{-0.02}^{+0.14}$| | |$4.2_{-3.4}^{+8.7}$| | |$5.6_{-2.5}^{+0.9}$| |
| J0940 | |$37.7^{+0.8}_{-0.8}$| | 21|$^{+7}_{-7}$| | 0.36|$^{+0.59}_{-0.24}$| | |$1.3_{-0.05}^{+0.3}$| | |$0.38_{-0.07}^{+0.02}$| | |$0.9_{-0.6}^{+2.1}$| | |$2.6_{-0.1}^{+0.6}$| |
| J1023 | |$12.8^{+0.2}_{-0.2}$| | 16|$^{+6}_{-5}$| | 0.29|$^{+0.51}_{-0.19}$| | |$4.1_{-1.9}^{+0.6}$| | |$0.12_{-0.02}^{+0.11}$| | |$2.4_{-2.0}^{+5.1}$| | |$8.3_{-3.9}^{+1.2}$| |
| J1140 | |$38.2^{+0.3}_{-0.3}$| | 21|$^{+7}_{-8}$| | 0.45|$^{+0.76}_{-0.31}$| | |$1.7_{-0.2}^{+0.2}$| | |$0.3_{-0.03}^{+0.03}$| | |$1.5_{-1.1}^{+3.0}$| | |$3.4_{-0.3}^{+0.4}$| |
| J1347 | |$33.0^{+0.5}_{-0.5}$| | 20|$^{+7}_{-7}$| | 0.47|$^{+0.80}_{-0.32}$| | |$3.1_{-1.2}^{+1.8}$| | |$0.16_{-0.06}^{+0.10}$| | |$2.9_{-2.3}^{+9.4}$| | |$6.2_{-2.4}^{+3.6}$| |
| J1357 | |$85.3^{+1.9}_{-1.9}$| | 26|$^{+9}_{-9}$| | 1.0|$^{+1.7}_{-0.7}$| | |$4.8_{-0.6}^{+0.3}$| | |$0.10_{-0.01}^{+0.01}$| | |$9.6_{-6.8}^{+17.9}$| | |$9.6_{-1.2}^{+0.6}$| |
| J1434 | |$3.0^{+0.1}_{-0.1}$| | 13|$^{+5}_{-4}$| | 0.04|$^{+0.08}_{-0.03}$| | |$3.7_{-1.4}^{+1.7}$| | |$0.14_{-0.04}^{+0.08}$| | |$0.3_{-0.2}^{+1.0}$| | |$7.4_{-2.8}^{+3.4}$| |
| J1541 | |$37.5^{+1.2}_{-1.2}$| | 21|$^{+7}_{-8}$| | 0.35|$^{+0.59}_{-0.24}$| | |$2.3_{-0.7}^{+1.2}$| | |$0.22_{-0.08}^{+0.10}$| | |$1.6_{-1.2}^{+4.9}$| | |$4.5_{-1.4}^{+2.3}$| |
| J1559 | |$40.1^{+0.1}_{-0.1}$| | 21|$^{+7}_{-7}$| | 0.38|$^{+0.63}_{-0.25}$| | |$1.24_{-0.0}^{+0.4}$| | |$0.40_{-0.11}^{+0.0}$| | |$0.9_{-0.6}^{+2.5}$| | |$2.5_{-0.0}^{+0.9}$| |
| J1626 | |$3.8^{+0.2}_{-0.2}$| | 14|$^{+4}_{-5}$| | 0.08|$^{+0.12}_{-0.05}$| | |$3.5_{-1.7}^{+0.9}$| | |$0.14_{-0.03}^{+0.13}$| | |$0.5_{-0.4}^{+1.2}$| | |$7.0_{-3.3}^{+1.8}$| |
| J1631 | |$3.1^{+0.2}_{-0.2}$| | 13|$^{+5}_{-4}$| | 0.05|$^{+0.08}_{-0.03}$| | |$3.2_{-0.9}^{+0.8}$| | |$0.16_{-0.03}^{+0.06}$| | |$0.3_{-0.2}^{+0.7}$| | |$6.4_{-1.8}^{+1.6}$| |
| POX52 | |$4.8^{+0.1}_{-0.1}$| | 14|$^{+5}_{-5}$| | 0.15|$^{+0.15}_{-0.08}$| | |$4.0_{-1.8}^{+1.7}$| | |$0.12_{-0.04}^{+0.10}$| | |$1.2_{-0.9}^{+2.1}$| | |$8.0_{-3.6}^{+3.3}$| |
Δχ2 denotes the changes in the chi-squared statistic compared to a constant density (1015 cm−3) disc. C.I.-MLR and C.I.-FTEST, respectively, represent the significance of the high-density over a constant density (1015 cm−3) reflection model estimated by the maximum likelihood ratio test and F-test. We did not perform these significance tests for five sources where we obtain only an upper limit on the disc density.
| Source . | Δχ2 . | C.I.-MLR (per cent) . | C.I.-FTEST (per cent) . |
|---|---|---|---|
| J0107 | 8.8 | 99.7 | 99.9 |
| J0228 | 3.0 | 91.8 | 96.1 |
| J0940 | 4.5 | 96.6 | 95.4 |
| J1023 | − | − | − |
| J1140 | 14.0 | 99.98 | 99.98 |
| J1347 | 16.5 | 99.99 | 99.99 |
| J1357 | − | − | − |
| J1434 | − | − | − |
| J1541 | 6.2 | 98.7 | 99.2 |
| J1559 | 23.5 | 99.99 | 99.99 |
| J1626 | − | − | − |
| J1631 | − | − | − |
| POX52 | 8.0 | 99.5 | 99.0 |
| Source . | Δχ2 . | C.I.-MLR (per cent) . | C.I.-FTEST (per cent) . |
|---|---|---|---|
| J0107 | 8.8 | 99.7 | 99.9 |
| J0228 | 3.0 | 91.8 | 96.1 |
| J0940 | 4.5 | 96.6 | 95.4 |
| J1023 | − | − | − |
| J1140 | 14.0 | 99.98 | 99.98 |
| J1347 | 16.5 | 99.99 | 99.99 |
| J1357 | − | − | − |
| J1434 | − | − | − |
| J1541 | 6.2 | 98.7 | 99.2 |
| J1559 | 23.5 | 99.99 | 99.99 |
| J1626 | − | − | − |
| J1631 | − | − | − |
| POX52 | 8.0 | 99.5 | 99.0 |
Δχ2 denotes the changes in the chi-squared statistic compared to a constant density (1015 cm−3) disc. C.I.-MLR and C.I.-FTEST, respectively, represent the significance of the high-density over a constant density (1015 cm−3) reflection model estimated by the maximum likelihood ratio test and F-test. We did not perform these significance tests for five sources where we obtain only an upper limit on the disc density.
| Source . | Δχ2 . | C.I.-MLR (per cent) . | C.I.-FTEST (per cent) . |
|---|---|---|---|
| J0107 | 8.8 | 99.7 | 99.9 |
| J0228 | 3.0 | 91.8 | 96.1 |
| J0940 | 4.5 | 96.6 | 95.4 |
| J1023 | − | − | − |
| J1140 | 14.0 | 99.98 | 99.98 |
| J1347 | 16.5 | 99.99 | 99.99 |
| J1357 | − | − | − |
| J1434 | − | − | − |
| J1541 | 6.2 | 98.7 | 99.2 |
| J1559 | 23.5 | 99.99 | 99.99 |
| J1626 | − | − | − |
| J1631 | − | − | − |
| POX52 | 8.0 | 99.5 | 99.0 |
| Source . | Δχ2 . | C.I.-MLR (per cent) . | C.I.-FTEST (per cent) . |
|---|---|---|---|
| J0107 | 8.8 | 99.7 | 99.9 |
| J0228 | 3.0 | 91.8 | 96.1 |
| J0940 | 4.5 | 96.6 | 95.4 |
| J1023 | − | − | − |
| J1140 | 14.0 | 99.98 | 99.98 |
| J1347 | 16.5 | 99.99 | 99.99 |
| J1357 | − | − | − |
| J1434 | − | − | − |
| J1541 | 6.2 | 98.7 | 99.2 |
| J1559 | 23.5 | 99.99 | 99.99 |
| J1626 | − | − | − |
| J1631 | − | − | − |
| POX52 | 8.0 | 99.5 | 99.0 |
4 RESULTS AND DISCUSSION
4.1 Eddington ratio and limit
We measured the Eddington ratio (Lbol/LE) of the sample through the bolometric correction factor, κ = Lbol/L2–10 keV. The hard X-ray (2–10 keV) absorption corrected luminosity of the sample is found to be in the range of L2–10 keV ≈ 3 × 1041 − 9 × 1042 erg s−1. The average bolometric correction factor and associated uncertainties for each source were obtained from the bolometric correction factor versus 2–10 keV luminosity curve (Hopkins, Richards & Hernquist 2007; Vasudevan & Fabian 2007). The measured Eddington ratio is in the range of Lbol/LE = κL2–10 keV/LE ≈ 0.01–1.0, considering the uncertainties of the BH mass estimates. We then estimated the dimensionless mass accretion rate using the formula |$\dot{m}=\frac{\dot{M}}{\dot{M}_{\rm E}}=\frac{L_{\rm bol}}{\eta L_{\rm E}}$|, where the radiative efficiency η = rg/2risco. The innermost stable circular orbit risco was computed using the equation (2) of Reynolds (2021). The mass accretion rate is below the Eddington accretion limit of |$\dot{m}_{\rm E}=1/\eta$| for the sample except for J1357 which has |$\dot{m}\sim 10.0$| (see Table 3). Therefore, we conclude that the discs of these low-mass AGNs are accumulating matter at sub-Eddington or near-Eddington accretion rates. The measurements are in agreement with the Eddington ratio estimated from the luminosity of the H β line for POX 52 (Thornton et al. 2008) and H α line for the GH07 sample. The hard band absorption-corrected source luminosity, bolometric correction factor, Eddington ratio, innermost stable circular orbit, radiative efficiency, accretion rate and Eddington limit for each AGN are presented in Table 3.
4.2 Disc gas density
We first verified the significance of higher disc densities by fitting all the spectra with a constant disc of density log [ne/cm-3] = 15, which resulted in a steeper photon index, higher disc ionization state, and worsened the statistics. The changes in the χ2-statistics are quoted in Table 4. We excised five sources for which we only obtain an upper limit on the disc density. We then estimated the confidence levels by performing the maximum likelihood ratio (MLR) test and F-test. These tests suggest that a higher density disc is preferred for eight out of 13 AGNs with ≥90 per cent confidence.
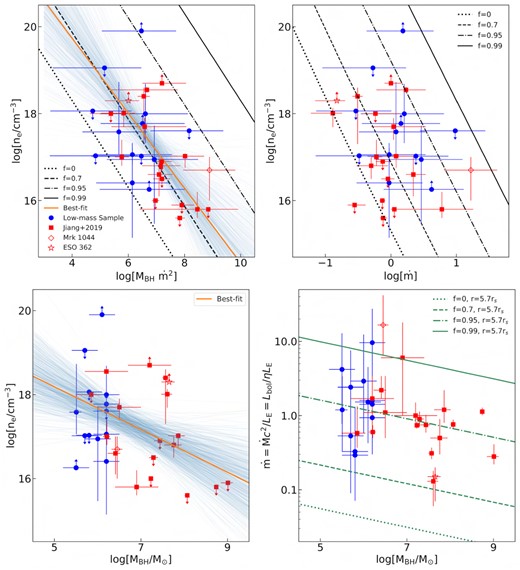
The top left and right-hand panels show the variation of disc density log ne with |$\log (M_{\rm BH}\dot{m}^{2})$| and |$\log \dot{m}$|, respectively, where |$\dot{m}=\frac{\dot{M}c^{2}}{L_{\rm E}}=L_{\rm bol}/\eta L_{\rm E}$| is the dimensionless mass accretion rate. The dotted, dashed, dash–dotted, and solid black lines represent solutions of a radiation pressure-dominated disc at the radius of r = rs for f = 0, 0.7, 0.95, 0.99, respectively, where f is the fraction of the total power released by the disc into the corona. The circle, square, diamond, and star-shaped data points represent density measurements of 13 AGNs from this work, 17 AGNs from Jiang et al. (2019), the Sy 1 AGN Mrk 1044 from Mallick et al. (2018), and Sy 1.5 AGN ESO 362−G18 from Xu et al. (2021), respectively. The bottom left panel depicts the variation of disc density with log MBH. The best-fitting linear model and corresponding 1σ confidence area are presented by the orange solid line and skyblue shaded area, respectively. The bottom right panel shows the variation of dimensionless mass accretion rate with log MBH. The dotted, dashed, dash–dotted, and solid green lines denote the SZ94 solutions at the radius of r = 5.7rs for f = 0, 0.7, 0.95, 0.99, respectively, below which gas thermal pressure dominates the radiation pressure.
We also showed the variation of disc density with the accretion rate for the combined sample in Fig. 2 (top right). We did not find any correlation between the disc density and accretion rate and hence did not fit a linear model to the log ne versus |$\log (\dot{m})$| plane. The SZ94 solutions for various values of f are shown by black lines in the top right panel of Fig. 2.
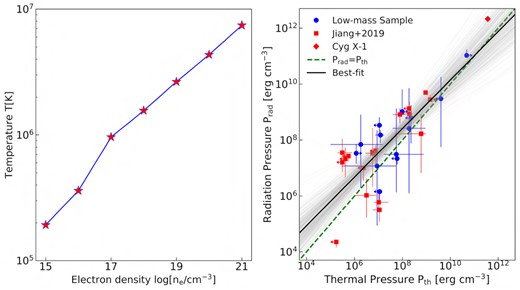
Left: temperature at the illuminated atmosphere of the accretion disc as a function density calculated at the Thomson depth of τ = 1. Right: variation of ionizing radiation pressure with gas thermal pressure for the low-mass AGN sample from this work, 17 Sy 1 galaxies from Jiang et al. (2019) and Cyg X-1 from Tomsick et al. (2018). The best-fitting linear model and corresponding 1σ confidence level for the combined sample are shown by the solid black line and grey shaded area, respectively. The dashed green line shows the Prad = Pth solution. The plot is mostly intended to show agreement and consistency with the reflection model, rather than as a correlation (note that the density contributes to both axes).
4.3 Disc ionization state
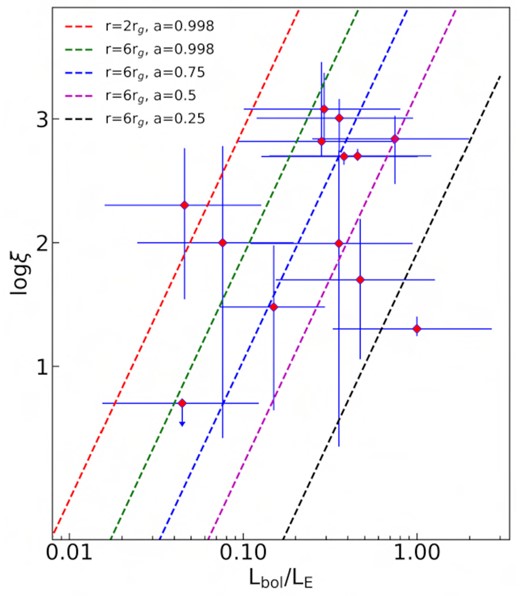
Disc ionization parameter log ξ versus Eddington ratio Lbol/LE for the sample. The dashed red, green, blue, magenta, and black lines show model log ξ as a function of Lbol/LE for (a = 0.998, r = 2rg), (a = 0.998, r = 6rg), (a = 0.75, r = 6rg), (a = 0.5, r = 6rg), and (a = 0.25, r = 6rg), respectively.
4.4 Black hole spin
We measured the black hole spin of the low-mass AGN sample from the modelling of the relativistic reflection continuum. Walton et al. (2013) employed a similar approach to estimate the BH spin of bare AGNs. We find that the black holes at the center of these low-mass AGNs are spinning with an average value of ∼0.75. The BH spin determines the location of the ISCO and hence the inner edge of the accretion disc. Therefore, the spin has a direct impact on the area of the reflector, which affects the reflection strength. Dauser et al. (2014) had shown that it is possible to check for any unphysical solutions of BH spin using the measured strength of reflection in the 20–50 keV band. However, we determine the reflection strength as the ratio between the disc reflected flux and irradiating source flux in the observed 0.3–10 keV band to be consistent with Jiang et al. (2019). In Fig. 5, we show the dependence of the reflection strength Rs on the BH spin for our sample together with the AGN sample from Jiang et al. (2019), where both the black hole spin and reflection strength were calculated using the high-density disc reflection model. We then overplotted the Dauser et al. (2014) model predicted maximum possible reflection strength versus spin curves for four different combinations of disc density and ionization parameters: (log ne = 15, log ξ = 1.5), (log ne = 15, log ξ = 3), (log ne = 19, log ξ = 1.5), and (log ne = 19, log ξ = 3), where the units of ne and ξ are cm−3 and erg cm s−1, respectively. We assume a lamppost configuration for corona to compute the maximum strength of reflection. We find that the low-mass AGN sample rules out the log ne = 15, log ξ = 1.5 combination and prefers higher density or higher ionization for the accretion disc. Additionally, all four theoretical Rs − a curves disfavour unrealistic solutions of low spin and large Rs for both samples and support the reflection origin of their broad-band spectra.
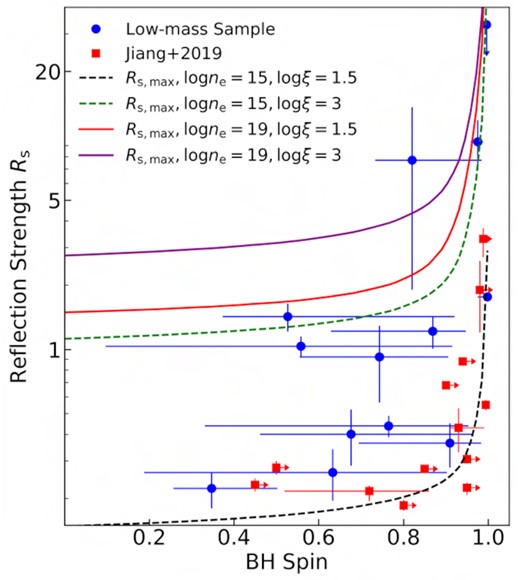
Reflection strength Rs as a function of the BH spin. The circles and squares denote AGNs from our work and Jiang et al. (2019), respectively. For sources with multiple Obs. IDs, we computed the mean value of Rs. The black, green, red, and purple lines show theoretical models of the maximum possible reflection strength versus spin for (log ne = 15, log ξ = 1.5), (log ne = 15, log ξ = 3), (log ne = 19, log ξ = 1.5), and (log ne = 19, log ξ = 3), respectively. The units of ne and ξ are cm−3 and erg cm s−1, respectively.
To study the evolution of BH spin as a function of mass, we constructed the BH spin versus mass plane for our low-mass sample along with 32 AGNs from Reynolds (2021), which is shown in Fig. 6. For the low-mass AGNs, the spin parameter ranges from amin ∼ 0.25 to amax ∼ 0.998, suggesting the presence of slow to rapidly spinning black holes at the centre of these AGNs. We noticed a population of more slowly spinning black holes below MBH ∼ 106 M⊙ and above MBH ∼ 5 × 107 M⊙. To test the significance of the differences between the low (MBH ≤ 106 M⊙), medium (106 M⊙ ≤ MBH ≤ 108 M⊙), and high-mass (108 M⊙ ≤ MBH ≤ 1010 M⊙) black hole spin populations, we performed a Kolmogorov–Smirnov (KS) test between the low-mass and medium-mass bins, and between the medium-mass and high-mass bins. The KS tests suggest that samples were drawn from distinct populations with 99 per cent significance. Therefore, we conclude that the variation of black hole spin as a function of mass is intrinsic and not driven by the randomness of samples. One possible explanation for the low spin is that the black holes at the centre of the low-mass AGNs could result from the collision or merger of intermediate-mass black holes with mass ∼105 M⊙ or lower. The detection of gravitational waves from intermediate-mass black holes with the laser interferometer space antenna (LISA) can confirm the collision/merger as one of the possible formation mechanisms for the low-mass end of supermassive black holes. The objects with high spin have higher radiative efficiency for the same mass accretion rate and can be approximately five times more luminous than those with zero spins and hence tend to dominate flux-limited samples (Vasudevan et al. 2016).
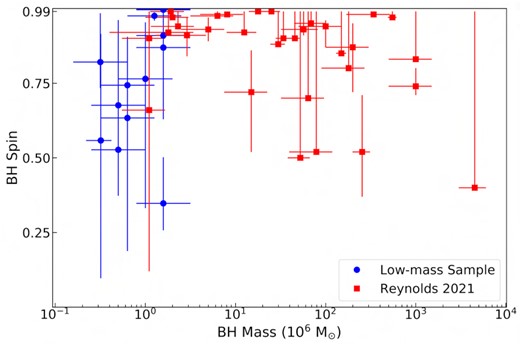
Evolution of black hole spin as a function of mass. The circles and squares represent spin measurements for 13 Seyfert 1 galaxies from this work and 32 AGNs from Reynolds (2021), respectively. The error bars on the spin parameter correspond to the 90 per cent confidence intervals for both samples.
In Mallick et al. (2021), we estimated the height and radius of the X-ray emitting corona through time-lag analysis for six low-mass AGNs, namely J0107, J1023, J1140, J1347, J1434, and J1559, in which we detected reverberation lags with |$\gt 90{{\ \rm per\ cent}}$| confidence. The coronal height was measured as the light-crossing distance between the corona and accretion disc, and it depends on the amplitude of the soft reverberation lag and black hole mass. On the other hand, the coronal radius was determined by the hard viscous propagation time delay, coronal height, and black hole mass. Both the observed soft and hard X-ray lags were dilution-corrected. Additionally, the reverberation lags were corrected for the ‘Shapiro’ delays. Here we investigate the dependence of coronal extents on the black hole spin. Fig. 7 depicts the variation of coronal height and radius with the spin of the central black hole for these six AGNs. The right-hand panel of Fig. 7 has a strikingly similar shape to the half-light radius of a Novikov–Thorne (NT) disc (see fig. 1 of Agol & Krolik 2000). This is the radius within which half of the radiation flux is emitted by the disc. Our results suggest hc ∼ rc, which is relevant for radio-quiet AGNs. Hence, the coronal height can be approximated as hc ≈ 5+28(1 − a) (Fabian et al. 2014). The dashed red line shows model hc as a function of spin for the NT disc. The variation of coronal size with black hole spin indicates that the most compact corona can be found only around the most rapidly spinning black holes for which the ISCO is at a smaller radius. If the corona is formed from magnetic field lines anchored at the disc, we can expect a higher density of field lines at a smaller radius. The results also point out that spin cannot be well measured unless the innermost parts of the disc are well illuminated, which means the coronal extent has to be ≲10rg for rapidly spinning black holes and ≲25rg for moderately rotating black holes. Presumably, an observational selection effect is at play. However, precise measurements of coronal height or radius require detailed physical modeling of X-ray time-lag spectra. Therefore, the observed spin dependence of coronal extents needs to be tested through simultaneous time-lag and flux-energy spectral modelling.
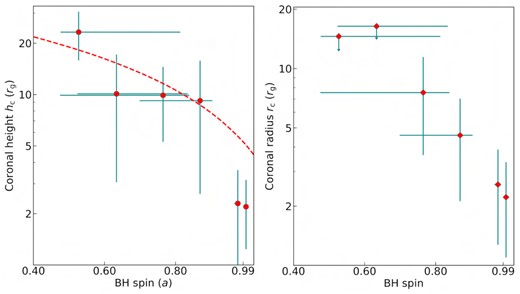
Variation of coronal height (hc) and radius (rc) as a function of black hole spin for six low-mass AGNs where the detection significance of soft reverberation lags exceeded 90 per cent (see table 2 of Mallick et al. 2021). Error bars on both X and Y variables represent 1σ confidence levels. The dashed red line represents the dependence of coronal height on the black hole spin for a Novikov–Thorne disc.
5 CONCLUSIONS
In this paper, we study the broad-band (0.3–10 keV) XMM–Newton spectra of a sample of 13 low-mass (MBH ≈ 105–6 M⊙) AGNs using the new high-density disc reflection model and determine the detailed accretion properties of the low-mass end of SMBHs in the X-ray energy band. We conclude the main results of this work below:
The X-ray spectra of the sample reveal excess emission below ∼1.5 keV. Additionally, we detect a narrow Fe Kα emission line in the NLS1 galaxy J1559 and an ionized, partial covering absorption in the Sy 1.5 galaxy POX 52. The soft X-ray excess emission is well described by the relativistic reflection from an ionized, higher density disc. The modelling of the reflection continuum prefers a density considerably higher than 1015 cm−3 for 8 out of 13 sources in our sample with significance ≥90 per cent. The average value of the disc density as inferred from the reflection modelling is ∼1018 cm−3.
The accretion discs of the low-mass active galaxies are found to be accreting matter at sub-Eddington or near-Eddington rates, and the surface density of the disc atmosphere depends both on the accretion rate and BH mass. We noticed an anticorrelation between log ne and the BH mass times accretion rate squared, |$\log (M_{\rm BH}\dot{m}^{2})$|, which is expected for a radiation pressure-supported disc. The fraction of the total power released from the disc into the corona is estimated to be ∼70 per cent in the inner regions of the radiation pressure-dominated disc. When the disc power transferred to the corona is below 70 per cent, the gas pressure starts dominating the disc.
The variation of the ionizing radiation pressure with thermal pressure suggests a magnetic pressure gradient across the surface of the disc, and the incident radiation pressure is balanced by both thermal and excess magnetic pressure. When the magnetic pressure gradient across the disc surface is weak, the radiation pressure compression (RPC) mechanism compresses the X-ray illuminated disc atmosphere in the vertical direction and consequently increases the disc density.
The illuminated gas in the inner accretion disc is found to be moderate to highly ionized and agrees with the ionization parameter calculated from the disc density and irradiating source flux at the ISCO within 2σ confidence limits. The dependence of the disc ionization state on the Eddington ratio is consistent with the predictions of the radiation pressure-dominated SS73 disc model for a geometrically thick corona. The log ξ–Lbol/LE relation prescribes that if the relativistic reflection originated from within six gravitational radii of the disc, the black hole spin should be in the range of a ∈ [0.25, 0.998].
The nuclei of the low-mass active galaxies harbour mild to fast-spinning black holes, where the measured spin parameter is a ≳ 0.25, and the most compact corona is likely to be located around the most rapidly spinning black holes. The relatively low spin provides a hint that the merger of IMBH pairs is perhaps responsible for the formation of the low-mass end of SMBHs, which can be confirmed with the future gravitational wave detector LISA.
6 FUTURE WORK
Our current high-density relativistic reflection model relxillDCp allows the density parameter to vary within the range log [ne/cm-3] = 15–20 and can provide the physical understanding of the broad-band (0.3–10 keV) AGN spectra. The observations of these low-mass AGNs with NuSTAR in the 3–78 keV band are required to test the validity of the high-density reflection model for the description of the Compton hump, which is usually observed at around 15–30 keV.
We find that the density is pegged at the upper bound of the model for a few sources in our sample, which argues for the existence of an even higher density disc. We, therefore, plan to extend the density parameter of the relxillDCp model up to log [ne/cm-3] = 22 in the future version.
ACKNOWLEDGEMENTS
LM is supported by NASA ADAP grant 80NSSC21K1567. JAG acknowledges support from NASA grant 80NSSC21K1567 and from the Alexander von Humboldt Foundation. JAT acknowledges partial support from NASA ADAP grant 80NSSC19K0586. BDM acknowledges support via Ramón y Cajal Fellowship RYC2018-025950-I. AGM acknowledges partial support from Polish National Science Center (NCN) grant numbers 2016/23/B/ST9/03123 and 2018/31/G/ST9/03224. We thank the anonymous reviewer for a constructive report. We dedicate this paper to doctors and nurses fighting the COVID-19 global pandemic. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the NASA. This research has made use of data, software and/or web tools obtained from the High Energy Astrophysics Science Archive Research Center (HEASARC), a service of the Astrophysics Science Division at NASA/GSFC and of the Smithsonian Astrophysical Observatory’s High Energy Astrophysics Division.
DATA AVAILABILITY
All the data used in this article are publicly available from ESA XMM–Newton Science Archive (XSA; http://nxsa.esac.esa.int/) and NASA High Energy Astrophysics Science Archive Research Center (HEASARC; https://heasarc.gsfc.nasa.gov/).
Footnotes
See column (5) of Table 3 for risco.
We used the Monte Carlo bootstrapping method to determine the mean and corresponding 2σ confidence limits.
REFERENCES
APPENDIX A: ADDITIONAL TABLES AND PLOTS
![The top panel shows the broad-band (0.3–10 keV) EPIC-pn (red), MOS1 (green), and MOS2 (blue) spectral data and hard band (2–10 keV) best-fitting model (Tbabs×[zgauss+zpowerlw] for J1559 and Tbabs×zpowerlw for all other sources) extrapolated down to 0.3 keV. The bottom panels depict the residual plots, which reveal excess emission below around ∼1 keV. For POX 52, we notice an absorption curvature in the range of ∼1–2 keV, which is a sign of partial covering absorption. The spectra are binned up for plotting purposes only.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/513/3/10.1093_mnras_stac990/2/m_stac990figa1.jpeg?Expires=1749425113&Signature=TrETo3fBAieTgsGreYwFg~BWGfnlrimULRuM~dgCPBiY3Eteto9MYmCeqtBENBWp0pxS9CEb8vyZP1F61xGlWJ~ThJan5INsxNlBaNigzpvgNj6sncMzANoSLVo--~kcqUgcg-Iki1y3-ieqX98xBbX8gz0~cdUB4oQCIp~r9h33RJsa7yo5Z7T0oHHtZigXdHA4OnIdweu~ORXHKgayI~O5wOKZ7t9h7XXYwsYK0bNYHzlIBhjbGr3tsdkaD3cSFpmnCdyqnhn09euKZs~k3I2EaDRauMSIpBKwAMlXSHhrlnMVsPCZjfYICeAPRuXMf4xPR-aNIKq3E77QB7ZYwg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The top panel shows the broad-band (0.3–10 keV) EPIC-pn (red), MOS1 (green), and MOS2 (blue) spectral data and hard band (2–10 keV) best-fitting model (Tbabs×[zgauss+zpowerlw] for J1559 and Tbabs×zpowerlw for all other sources) extrapolated down to 0.3 keV. The bottom panels depict the residual plots, which reveal excess emission below around ∼1 keV. For POX 52, we notice an absorption curvature in the range of ∼1–2 keV, which is a sign of partial covering absorption. The spectra are binned up for plotting purposes only.
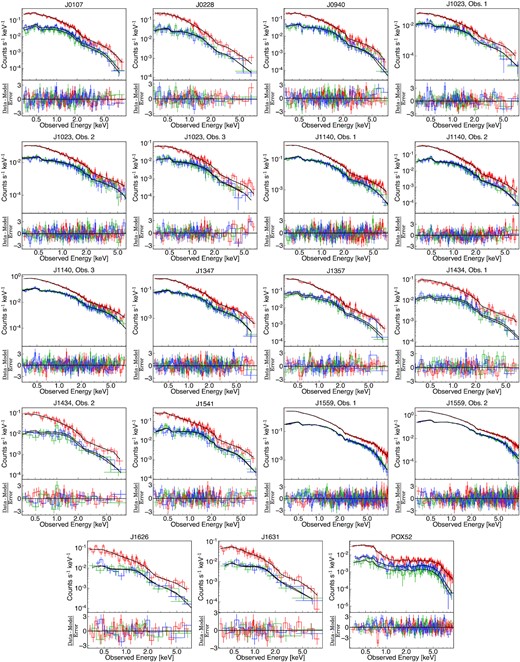
The broad-band (0.3–10 keV) EPIC-pn (red), MOS1 (green), and MOS2 (blue) photon count spectra, the best-fitting high-density disc reflection model, Tbabs×(relxillDCp+nthComp) and the residuals. For J1559 and POX52, the best-fitting spectral models are Tbabs×gabs×(zgauss+relxillDCp+nthComp) and Tbabs×zxipcf×(relxillDCp+nthComp), respectively.
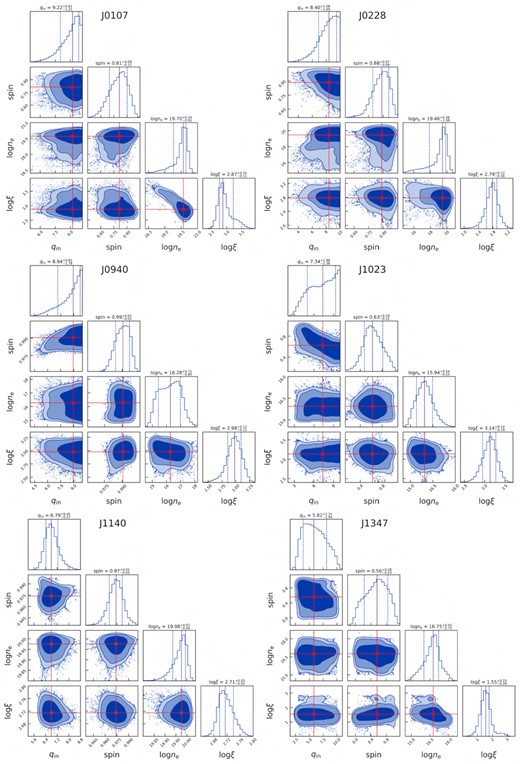
Corner plots of various spectral parameters resulting from the MCMC analysis. The histograms on the diagonal show the probability distributions for each parameter with medians and their 1σ uncertainties (vertical dashed lines). The off-diagonals show contour plots for each pair of parameters, with dark blue, medium blue, and light blue regions representing 68.3, 90, and 95 per cent confidence contours, respectively, and square symbols indicating medians of parameters.
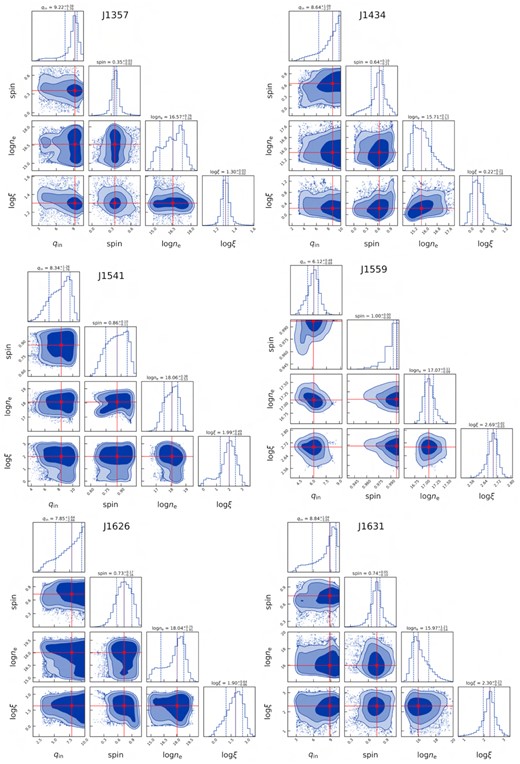
Fig. A3 is continued for J1357, J1434, J1541, J1559, J1626, and J1631.

The best-fitting model parameters of the sample as obtained from the broad-band X-ray spectral fitting of the EPIC-pn+MOS data with the model, Tbabs×(relxillDCp+nthComp). The fixed and tied parameters are denoted by symbols ‘(f)’ and ‘*’, respectively. The 90 per cent confidence intervals of parameters are estimated through Monte Carlo simulations. The columns are (1) source name, (2) observation ID, (3) photon index of the primary continuum, (4) Primary continuum normalization in units of photons cm−2 s−1 keV−1, (5) inner emissivity index, (6) BH spin, (7) disc inclination angle, (8) disc ionization parameter, (9) disc density in logarithmic units, (10) normalization of relxillDCp, (11) reflection strength Rs, and (12) fit statistic.
| Source . | Obs. ID . | . | . | nthComp . | . | . | . | relxillDCp . | . | . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | Γ . | Knth . | qin . | a . | θ○ . | |$\log [\frac{\xi }{\rm erg~cm~s^{-1}}]$| . | |$\log [\frac{n_{\rm e}}{{\rm cm^{-3}}}]$| . | Kref . | Rs . | |$\frac{C-\rm {stat}}{\rm {d.o.f}}$| . |
| . | . | . | [10−5] . | . | . | . | . | . | [10−6] . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| J0107 | 0305920101 | |$2.03_{-0.03}^{+0.17}$| | |$5.3_{-4.6}^{+2.0}$| | ≥7.1 | |$0.87_{-0.24}^{+0.08}$| | |$41_{-25}^{+9}$| | |$2.8_{-0.1}^{+0.6}$| | ≥17.8 | |$0.7_{-0.3}^{+0.5}$| | |$1.2_{-0.2}^{+0.2}$| | |$\frac{193.8}{240}$| |
| J0228 | 0674810101 | |$1.91_{-0.12}^{+0.45}$| | ≤4.3 | ≥5.6 | |$0.82_{-0.09}^{+0.16}$| | ≤45 | |$2.8_{-0.4}^{+0.2}$| | ≥16.3 | |$1.1_{-0.6}^{+0.5}$| | |$7.7_{-5.8}^{+5.9}$| | |$\frac{82.2}{116}$| |
| J0940 | 0306050201 | |$2.06_{-0.07}^{+0.11}$| | ≤14.4 | ≥5.9 | |$0.996_{-0.015}^{+0.001}$| | |$65_{-14}^{+4}$| | |$3.0_{-0.3}^{+0.1}$| | |$16.4_{-1.3}^{+0.9}$| | |$9.5_{-5.2}^{+2.6}$| | ≤33.2 | |$\frac{243.7}{232}$| |
| J1023 | 0108670101 | |$2.28_{-0.06}^{+0.08}$| | |$1.7_{-0.9}^{+0.7}$| | ≥4.0 | |$0.53_{-0.15}^{+0.39}$| | |$27_{-8}^{+13}$| | |$3.1_{-0.2}^{+0.3}$| | ≤17.0 | |$0.3_{-0.1}^{+0.1}$| | |$0.9_{-0.2}^{+0.2}$| | |$\frac{586.4}{645}$| |
| 0605540201 | 2.28* | |$1.5_{-1.4}^{+1.2}$| | − | 0.53* | 27* | 3.1* | − | |$0.6_{-0.2}^{+0.2}$| | |$2.1_{-0.4}^{+0.4}$| | – | |
| 0605540301 | 2.28* | |$1.4_{-1.0}^{+0.8}$| | − | 0.53* | 27* | 3.1* | − | |$0.3_{-0.1}^{+0.1}$| | |$1.3_{-0.4}^{+0.4}$| | – | |
| J1140 | 0305920201 | |$2.04_{-0.03}^{+0.02}$| | |$1.3_{-1.2}^{+0.7}$| | |$6.9_{-0.7}^{+1.3}$| | |$0.975_{-0.016}^{+0.012}$| | |$44_{-9}^{+6}$| | |$2.7_{-0.01}^{+0.06}$| | ≥19.9 | |$2.6_{-0.3}^{+0.4}$| | |$16.0_{-7.0}^{+7.1}$| | |$\frac{1047.5}{1042}$| |
| 0724840101 | 2.04* | |$1.8_{-0.8}^{+0.4}$| | 6.9* | 0.975* | 44* | 2.7* | – | |$1.1_{-0.1}^{+0.2}$| | |$4.7_{-1.0}^{+1.1}$| | – | |
| 0724840301 | 2.04* | |$2.4_{-1.4}^{+0.6}$| | 6.9* | 0.975* | 44* | 2.7* | – | |$2.2_{-0.2}^{+0.4}$| | |$7.4_{-1.5}^{+1.6}$| | – | |
| J1347 | 0744220701 | |$2.33_{-0.07}^{+0.07}$| | |$15.5_{-2.1}^{+2.7}$| | |$5.3_{-2.1}^{+4.0}$| | |$0.77_{-0.43}^{+0.19}$| | |$34_{-13}^{+19}$| | |$1.7_{-0.6}^{+0.5}$| | |$17.0_{-1.5}^{+0.8}$| | |$5.0_{-2.0}^{+1.4}$| | |$0.44_{-0.05}^{+0.05}$| | |$\frac{296.6}{302}$| |
| J1357 | 0305920601 | |$2.31_{-0.07}^{+0.05}$| | |$14.8_{-1.5}^{+1.0}$| | ≥4.7 | |$0.35_{-0.09}^{+0.15}$| | |$34_{-11}^{+15}$| | |$1.3_{-0.1}^{+0.1}$| | ≤17.6 | |$3.6_{-1.6}^{+2.4}$| | |$0.22_{-0.04}^{+0.04}$| | |$\frac{169.8}{178}$| |
| J1434 | 0305920401 | |$2.10_{-0.15}^{+0.20}$| | |$4.9_{-0.4}^{+0.2}$| | ≥4.5 | |$0.63_{-0.45}^{+0.27}$| | |$48_{-26}^{+16}$| | ≤0.7 | ≤17.0 | |$3.4_{-1.8}^{+0.3}$| | |$0.25_{-0.09}^{+0.09}$| | |$\frac{215.7}{224}$| |
| 0674810501 | 2.10* | |$5.1_{-0.5}^{+0.3}$| | − | 0.63* | 48* | − | − | |$4.0_{-2.3}^{+2.2}$| | |$0.28_{-0.11}^{+0.12}$| | – | |
| J1541 | 0744220401 | |$1.94_{-0.12}^{+0.13}$| | |$9.1_{-1.6}^{+1.7}$| | |$8.7_{-3.1}^{+1.2}$| | |$0.91_{-0.21}^{+0.07}$| | |$43_{-11}^{+11}$| | |$2.0_{-1.6}^{+0.8}$| | |$18.0_{-0.7}^{+0.7}$| | |$2.2_{-1.4}^{+1.8}$| | |$0.36_{-0.08}^{+0.09}$| | |$\frac{160.1}{177}$| |
| J1626 | 0674811001 | |$1.75_{-0.13}^{+0.31}$| | |$2.9_{-1.2}^{+0.6}$| | ≥3.7 | |$0.68_{-0.21}^{+0.28}$| | |$27_{-11}^{+14}$| | |$2.0_{-1.6}^{+0.8}$| | ≤19.1 | |$1.0_{-0.6}^{+1.8}$| | |$0.4_{-0.1}^{+0.1}$| | |$\frac{92.5}{73}$| |
| J1631 | 0674810601 | |$1.96_{-0.15}^{+0.13}$| | |$1.5_{-0.2}^{+0.6}$| | ≥3.9 | |$0.74_{-0.19}^{+0.16}$| | |$26_{-8}^{+9}$| | |$2.3_{-0.8}^{+0.5}$| | ≤18.1 | |$1.0_{-0.8}^{+0.3}$| | |$0.9_{-0.4}^{+0.4}$| | |$\frac{38.9}{62}$| |
| Source . | Obs. ID . | . | . | nthComp . | . | . | . | relxillDCp . | . | . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | Γ . | Knth . | qin . | a . | θ○ . | |$\log [\frac{\xi }{\rm erg~cm~s^{-1}}]$| . | |$\log [\frac{n_{\rm e}}{{\rm cm^{-3}}}]$| . | Kref . | Rs . | |$\frac{C-\rm {stat}}{\rm {d.o.f}}$| . |
| . | . | . | [10−5] . | . | . | . | . | . | [10−6] . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| J0107 | 0305920101 | |$2.03_{-0.03}^{+0.17}$| | |$5.3_{-4.6}^{+2.0}$| | ≥7.1 | |$0.87_{-0.24}^{+0.08}$| | |$41_{-25}^{+9}$| | |$2.8_{-0.1}^{+0.6}$| | ≥17.8 | |$0.7_{-0.3}^{+0.5}$| | |$1.2_{-0.2}^{+0.2}$| | |$\frac{193.8}{240}$| |
| J0228 | 0674810101 | |$1.91_{-0.12}^{+0.45}$| | ≤4.3 | ≥5.6 | |$0.82_{-0.09}^{+0.16}$| | ≤45 | |$2.8_{-0.4}^{+0.2}$| | ≥16.3 | |$1.1_{-0.6}^{+0.5}$| | |$7.7_{-5.8}^{+5.9}$| | |$\frac{82.2}{116}$| |
| J0940 | 0306050201 | |$2.06_{-0.07}^{+0.11}$| | ≤14.4 | ≥5.9 | |$0.996_{-0.015}^{+0.001}$| | |$65_{-14}^{+4}$| | |$3.0_{-0.3}^{+0.1}$| | |$16.4_{-1.3}^{+0.9}$| | |$9.5_{-5.2}^{+2.6}$| | ≤33.2 | |$\frac{243.7}{232}$| |
| J1023 | 0108670101 | |$2.28_{-0.06}^{+0.08}$| | |$1.7_{-0.9}^{+0.7}$| | ≥4.0 | |$0.53_{-0.15}^{+0.39}$| | |$27_{-8}^{+13}$| | |$3.1_{-0.2}^{+0.3}$| | ≤17.0 | |$0.3_{-0.1}^{+0.1}$| | |$0.9_{-0.2}^{+0.2}$| | |$\frac{586.4}{645}$| |
| 0605540201 | 2.28* | |$1.5_{-1.4}^{+1.2}$| | − | 0.53* | 27* | 3.1* | − | |$0.6_{-0.2}^{+0.2}$| | |$2.1_{-0.4}^{+0.4}$| | – | |
| 0605540301 | 2.28* | |$1.4_{-1.0}^{+0.8}$| | − | 0.53* | 27* | 3.1* | − | |$0.3_{-0.1}^{+0.1}$| | |$1.3_{-0.4}^{+0.4}$| | – | |
| J1140 | 0305920201 | |$2.04_{-0.03}^{+0.02}$| | |$1.3_{-1.2}^{+0.7}$| | |$6.9_{-0.7}^{+1.3}$| | |$0.975_{-0.016}^{+0.012}$| | |$44_{-9}^{+6}$| | |$2.7_{-0.01}^{+0.06}$| | ≥19.9 | |$2.6_{-0.3}^{+0.4}$| | |$16.0_{-7.0}^{+7.1}$| | |$\frac{1047.5}{1042}$| |
| 0724840101 | 2.04* | |$1.8_{-0.8}^{+0.4}$| | 6.9* | 0.975* | 44* | 2.7* | – | |$1.1_{-0.1}^{+0.2}$| | |$4.7_{-1.0}^{+1.1}$| | – | |
| 0724840301 | 2.04* | |$2.4_{-1.4}^{+0.6}$| | 6.9* | 0.975* | 44* | 2.7* | – | |$2.2_{-0.2}^{+0.4}$| | |$7.4_{-1.5}^{+1.6}$| | – | |
| J1347 | 0744220701 | |$2.33_{-0.07}^{+0.07}$| | |$15.5_{-2.1}^{+2.7}$| | |$5.3_{-2.1}^{+4.0}$| | |$0.77_{-0.43}^{+0.19}$| | |$34_{-13}^{+19}$| | |$1.7_{-0.6}^{+0.5}$| | |$17.0_{-1.5}^{+0.8}$| | |$5.0_{-2.0}^{+1.4}$| | |$0.44_{-0.05}^{+0.05}$| | |$\frac{296.6}{302}$| |
| J1357 | 0305920601 | |$2.31_{-0.07}^{+0.05}$| | |$14.8_{-1.5}^{+1.0}$| | ≥4.7 | |$0.35_{-0.09}^{+0.15}$| | |$34_{-11}^{+15}$| | |$1.3_{-0.1}^{+0.1}$| | ≤17.6 | |$3.6_{-1.6}^{+2.4}$| | |$0.22_{-0.04}^{+0.04}$| | |$\frac{169.8}{178}$| |
| J1434 | 0305920401 | |$2.10_{-0.15}^{+0.20}$| | |$4.9_{-0.4}^{+0.2}$| | ≥4.5 | |$0.63_{-0.45}^{+0.27}$| | |$48_{-26}^{+16}$| | ≤0.7 | ≤17.0 | |$3.4_{-1.8}^{+0.3}$| | |$0.25_{-0.09}^{+0.09}$| | |$\frac{215.7}{224}$| |
| 0674810501 | 2.10* | |$5.1_{-0.5}^{+0.3}$| | − | 0.63* | 48* | − | − | |$4.0_{-2.3}^{+2.2}$| | |$0.28_{-0.11}^{+0.12}$| | – | |
| J1541 | 0744220401 | |$1.94_{-0.12}^{+0.13}$| | |$9.1_{-1.6}^{+1.7}$| | |$8.7_{-3.1}^{+1.2}$| | |$0.91_{-0.21}^{+0.07}$| | |$43_{-11}^{+11}$| | |$2.0_{-1.6}^{+0.8}$| | |$18.0_{-0.7}^{+0.7}$| | |$2.2_{-1.4}^{+1.8}$| | |$0.36_{-0.08}^{+0.09}$| | |$\frac{160.1}{177}$| |
| J1626 | 0674811001 | |$1.75_{-0.13}^{+0.31}$| | |$2.9_{-1.2}^{+0.6}$| | ≥3.7 | |$0.68_{-0.21}^{+0.28}$| | |$27_{-11}^{+14}$| | |$2.0_{-1.6}^{+0.8}$| | ≤19.1 | |$1.0_{-0.6}^{+1.8}$| | |$0.4_{-0.1}^{+0.1}$| | |$\frac{92.5}{73}$| |
| J1631 | 0674810601 | |$1.96_{-0.15}^{+0.13}$| | |$1.5_{-0.2}^{+0.6}$| | ≥3.9 | |$0.74_{-0.19}^{+0.16}$| | |$26_{-8}^{+9}$| | |$2.3_{-0.8}^{+0.5}$| | ≤18.1 | |$1.0_{-0.8}^{+0.3}$| | |$0.9_{-0.4}^{+0.4}$| | |$\frac{38.9}{62}$| |
The best-fitting model parameters of the sample as obtained from the broad-band X-ray spectral fitting of the EPIC-pn+MOS data with the model, Tbabs×(relxillDCp+nthComp). The fixed and tied parameters are denoted by symbols ‘(f)’ and ‘*’, respectively. The 90 per cent confidence intervals of parameters are estimated through Monte Carlo simulations. The columns are (1) source name, (2) observation ID, (3) photon index of the primary continuum, (4) Primary continuum normalization in units of photons cm−2 s−1 keV−1, (5) inner emissivity index, (6) BH spin, (7) disc inclination angle, (8) disc ionization parameter, (9) disc density in logarithmic units, (10) normalization of relxillDCp, (11) reflection strength Rs, and (12) fit statistic.
| Source . | Obs. ID . | . | . | nthComp . | . | . | . | relxillDCp . | . | . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | Γ . | Knth . | qin . | a . | θ○ . | |$\log [\frac{\xi }{\rm erg~cm~s^{-1}}]$| . | |$\log [\frac{n_{\rm e}}{{\rm cm^{-3}}}]$| . | Kref . | Rs . | |$\frac{C-\rm {stat}}{\rm {d.o.f}}$| . |
| . | . | . | [10−5] . | . | . | . | . | . | [10−6] . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| J0107 | 0305920101 | |$2.03_{-0.03}^{+0.17}$| | |$5.3_{-4.6}^{+2.0}$| | ≥7.1 | |$0.87_{-0.24}^{+0.08}$| | |$41_{-25}^{+9}$| | |$2.8_{-0.1}^{+0.6}$| | ≥17.8 | |$0.7_{-0.3}^{+0.5}$| | |$1.2_{-0.2}^{+0.2}$| | |$\frac{193.8}{240}$| |
| J0228 | 0674810101 | |$1.91_{-0.12}^{+0.45}$| | ≤4.3 | ≥5.6 | |$0.82_{-0.09}^{+0.16}$| | ≤45 | |$2.8_{-0.4}^{+0.2}$| | ≥16.3 | |$1.1_{-0.6}^{+0.5}$| | |$7.7_{-5.8}^{+5.9}$| | |$\frac{82.2}{116}$| |
| J0940 | 0306050201 | |$2.06_{-0.07}^{+0.11}$| | ≤14.4 | ≥5.9 | |$0.996_{-0.015}^{+0.001}$| | |$65_{-14}^{+4}$| | |$3.0_{-0.3}^{+0.1}$| | |$16.4_{-1.3}^{+0.9}$| | |$9.5_{-5.2}^{+2.6}$| | ≤33.2 | |$\frac{243.7}{232}$| |
| J1023 | 0108670101 | |$2.28_{-0.06}^{+0.08}$| | |$1.7_{-0.9}^{+0.7}$| | ≥4.0 | |$0.53_{-0.15}^{+0.39}$| | |$27_{-8}^{+13}$| | |$3.1_{-0.2}^{+0.3}$| | ≤17.0 | |$0.3_{-0.1}^{+0.1}$| | |$0.9_{-0.2}^{+0.2}$| | |$\frac{586.4}{645}$| |
| 0605540201 | 2.28* | |$1.5_{-1.4}^{+1.2}$| | − | 0.53* | 27* | 3.1* | − | |$0.6_{-0.2}^{+0.2}$| | |$2.1_{-0.4}^{+0.4}$| | – | |
| 0605540301 | 2.28* | |$1.4_{-1.0}^{+0.8}$| | − | 0.53* | 27* | 3.1* | − | |$0.3_{-0.1}^{+0.1}$| | |$1.3_{-0.4}^{+0.4}$| | – | |
| J1140 | 0305920201 | |$2.04_{-0.03}^{+0.02}$| | |$1.3_{-1.2}^{+0.7}$| | |$6.9_{-0.7}^{+1.3}$| | |$0.975_{-0.016}^{+0.012}$| | |$44_{-9}^{+6}$| | |$2.7_{-0.01}^{+0.06}$| | ≥19.9 | |$2.6_{-0.3}^{+0.4}$| | |$16.0_{-7.0}^{+7.1}$| | |$\frac{1047.5}{1042}$| |
| 0724840101 | 2.04* | |$1.8_{-0.8}^{+0.4}$| | 6.9* | 0.975* | 44* | 2.7* | – | |$1.1_{-0.1}^{+0.2}$| | |$4.7_{-1.0}^{+1.1}$| | – | |
| 0724840301 | 2.04* | |$2.4_{-1.4}^{+0.6}$| | 6.9* | 0.975* | 44* | 2.7* | – | |$2.2_{-0.2}^{+0.4}$| | |$7.4_{-1.5}^{+1.6}$| | – | |
| J1347 | 0744220701 | |$2.33_{-0.07}^{+0.07}$| | |$15.5_{-2.1}^{+2.7}$| | |$5.3_{-2.1}^{+4.0}$| | |$0.77_{-0.43}^{+0.19}$| | |$34_{-13}^{+19}$| | |$1.7_{-0.6}^{+0.5}$| | |$17.0_{-1.5}^{+0.8}$| | |$5.0_{-2.0}^{+1.4}$| | |$0.44_{-0.05}^{+0.05}$| | |$\frac{296.6}{302}$| |
| J1357 | 0305920601 | |$2.31_{-0.07}^{+0.05}$| | |$14.8_{-1.5}^{+1.0}$| | ≥4.7 | |$0.35_{-0.09}^{+0.15}$| | |$34_{-11}^{+15}$| | |$1.3_{-0.1}^{+0.1}$| | ≤17.6 | |$3.6_{-1.6}^{+2.4}$| | |$0.22_{-0.04}^{+0.04}$| | |$\frac{169.8}{178}$| |
| J1434 | 0305920401 | |$2.10_{-0.15}^{+0.20}$| | |$4.9_{-0.4}^{+0.2}$| | ≥4.5 | |$0.63_{-0.45}^{+0.27}$| | |$48_{-26}^{+16}$| | ≤0.7 | ≤17.0 | |$3.4_{-1.8}^{+0.3}$| | |$0.25_{-0.09}^{+0.09}$| | |$\frac{215.7}{224}$| |
| 0674810501 | 2.10* | |$5.1_{-0.5}^{+0.3}$| | − | 0.63* | 48* | − | − | |$4.0_{-2.3}^{+2.2}$| | |$0.28_{-0.11}^{+0.12}$| | – | |
| J1541 | 0744220401 | |$1.94_{-0.12}^{+0.13}$| | |$9.1_{-1.6}^{+1.7}$| | |$8.7_{-3.1}^{+1.2}$| | |$0.91_{-0.21}^{+0.07}$| | |$43_{-11}^{+11}$| | |$2.0_{-1.6}^{+0.8}$| | |$18.0_{-0.7}^{+0.7}$| | |$2.2_{-1.4}^{+1.8}$| | |$0.36_{-0.08}^{+0.09}$| | |$\frac{160.1}{177}$| |
| J1626 | 0674811001 | |$1.75_{-0.13}^{+0.31}$| | |$2.9_{-1.2}^{+0.6}$| | ≥3.7 | |$0.68_{-0.21}^{+0.28}$| | |$27_{-11}^{+14}$| | |$2.0_{-1.6}^{+0.8}$| | ≤19.1 | |$1.0_{-0.6}^{+1.8}$| | |$0.4_{-0.1}^{+0.1}$| | |$\frac{92.5}{73}$| |
| J1631 | 0674810601 | |$1.96_{-0.15}^{+0.13}$| | |$1.5_{-0.2}^{+0.6}$| | ≥3.9 | |$0.74_{-0.19}^{+0.16}$| | |$26_{-8}^{+9}$| | |$2.3_{-0.8}^{+0.5}$| | ≤18.1 | |$1.0_{-0.8}^{+0.3}$| | |$0.9_{-0.4}^{+0.4}$| | |$\frac{38.9}{62}$| |
| Source . | Obs. ID . | . | . | nthComp . | . | . | . | relxillDCp . | . | . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | Γ . | Knth . | qin . | a . | θ○ . | |$\log [\frac{\xi }{\rm erg~cm~s^{-1}}]$| . | |$\log [\frac{n_{\rm e}}{{\rm cm^{-3}}}]$| . | Kref . | Rs . | |$\frac{C-\rm {stat}}{\rm {d.o.f}}$| . |
| . | . | . | [10−5] . | . | . | . | . | . | [10−6] . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| J0107 | 0305920101 | |$2.03_{-0.03}^{+0.17}$| | |$5.3_{-4.6}^{+2.0}$| | ≥7.1 | |$0.87_{-0.24}^{+0.08}$| | |$41_{-25}^{+9}$| | |$2.8_{-0.1}^{+0.6}$| | ≥17.8 | |$0.7_{-0.3}^{+0.5}$| | |$1.2_{-0.2}^{+0.2}$| | |$\frac{193.8}{240}$| |
| J0228 | 0674810101 | |$1.91_{-0.12}^{+0.45}$| | ≤4.3 | ≥5.6 | |$0.82_{-0.09}^{+0.16}$| | ≤45 | |$2.8_{-0.4}^{+0.2}$| | ≥16.3 | |$1.1_{-0.6}^{+0.5}$| | |$7.7_{-5.8}^{+5.9}$| | |$\frac{82.2}{116}$| |
| J0940 | 0306050201 | |$2.06_{-0.07}^{+0.11}$| | ≤14.4 | ≥5.9 | |$0.996_{-0.015}^{+0.001}$| | |$65_{-14}^{+4}$| | |$3.0_{-0.3}^{+0.1}$| | |$16.4_{-1.3}^{+0.9}$| | |$9.5_{-5.2}^{+2.6}$| | ≤33.2 | |$\frac{243.7}{232}$| |
| J1023 | 0108670101 | |$2.28_{-0.06}^{+0.08}$| | |$1.7_{-0.9}^{+0.7}$| | ≥4.0 | |$0.53_{-0.15}^{+0.39}$| | |$27_{-8}^{+13}$| | |$3.1_{-0.2}^{+0.3}$| | ≤17.0 | |$0.3_{-0.1}^{+0.1}$| | |$0.9_{-0.2}^{+0.2}$| | |$\frac{586.4}{645}$| |
| 0605540201 | 2.28* | |$1.5_{-1.4}^{+1.2}$| | − | 0.53* | 27* | 3.1* | − | |$0.6_{-0.2}^{+0.2}$| | |$2.1_{-0.4}^{+0.4}$| | – | |
| 0605540301 | 2.28* | |$1.4_{-1.0}^{+0.8}$| | − | 0.53* | 27* | 3.1* | − | |$0.3_{-0.1}^{+0.1}$| | |$1.3_{-0.4}^{+0.4}$| | – | |
| J1140 | 0305920201 | |$2.04_{-0.03}^{+0.02}$| | |$1.3_{-1.2}^{+0.7}$| | |$6.9_{-0.7}^{+1.3}$| | |$0.975_{-0.016}^{+0.012}$| | |$44_{-9}^{+6}$| | |$2.7_{-0.01}^{+0.06}$| | ≥19.9 | |$2.6_{-0.3}^{+0.4}$| | |$16.0_{-7.0}^{+7.1}$| | |$\frac{1047.5}{1042}$| |
| 0724840101 | 2.04* | |$1.8_{-0.8}^{+0.4}$| | 6.9* | 0.975* | 44* | 2.7* | – | |$1.1_{-0.1}^{+0.2}$| | |$4.7_{-1.0}^{+1.1}$| | – | |
| 0724840301 | 2.04* | |$2.4_{-1.4}^{+0.6}$| | 6.9* | 0.975* | 44* | 2.7* | – | |$2.2_{-0.2}^{+0.4}$| | |$7.4_{-1.5}^{+1.6}$| | – | |
| J1347 | 0744220701 | |$2.33_{-0.07}^{+0.07}$| | |$15.5_{-2.1}^{+2.7}$| | |$5.3_{-2.1}^{+4.0}$| | |$0.77_{-0.43}^{+0.19}$| | |$34_{-13}^{+19}$| | |$1.7_{-0.6}^{+0.5}$| | |$17.0_{-1.5}^{+0.8}$| | |$5.0_{-2.0}^{+1.4}$| | |$0.44_{-0.05}^{+0.05}$| | |$\frac{296.6}{302}$| |
| J1357 | 0305920601 | |$2.31_{-0.07}^{+0.05}$| | |$14.8_{-1.5}^{+1.0}$| | ≥4.7 | |$0.35_{-0.09}^{+0.15}$| | |$34_{-11}^{+15}$| | |$1.3_{-0.1}^{+0.1}$| | ≤17.6 | |$3.6_{-1.6}^{+2.4}$| | |$0.22_{-0.04}^{+0.04}$| | |$\frac{169.8}{178}$| |
| J1434 | 0305920401 | |$2.10_{-0.15}^{+0.20}$| | |$4.9_{-0.4}^{+0.2}$| | ≥4.5 | |$0.63_{-0.45}^{+0.27}$| | |$48_{-26}^{+16}$| | ≤0.7 | ≤17.0 | |$3.4_{-1.8}^{+0.3}$| | |$0.25_{-0.09}^{+0.09}$| | |$\frac{215.7}{224}$| |
| 0674810501 | 2.10* | |$5.1_{-0.5}^{+0.3}$| | − | 0.63* | 48* | − | − | |$4.0_{-2.3}^{+2.2}$| | |$0.28_{-0.11}^{+0.12}$| | – | |
| J1541 | 0744220401 | |$1.94_{-0.12}^{+0.13}$| | |$9.1_{-1.6}^{+1.7}$| | |$8.7_{-3.1}^{+1.2}$| | |$0.91_{-0.21}^{+0.07}$| | |$43_{-11}^{+11}$| | |$2.0_{-1.6}^{+0.8}$| | |$18.0_{-0.7}^{+0.7}$| | |$2.2_{-1.4}^{+1.8}$| | |$0.36_{-0.08}^{+0.09}$| | |$\frac{160.1}{177}$| |
| J1626 | 0674811001 | |$1.75_{-0.13}^{+0.31}$| | |$2.9_{-1.2}^{+0.6}$| | ≥3.7 | |$0.68_{-0.21}^{+0.28}$| | |$27_{-11}^{+14}$| | |$2.0_{-1.6}^{+0.8}$| | ≤19.1 | |$1.0_{-0.6}^{+1.8}$| | |$0.4_{-0.1}^{+0.1}$| | |$\frac{92.5}{73}$| |
| J1631 | 0674810601 | |$1.96_{-0.15}^{+0.13}$| | |$1.5_{-0.2}^{+0.6}$| | ≥3.9 | |$0.74_{-0.19}^{+0.16}$| | |$26_{-8}^{+9}$| | |$2.3_{-0.8}^{+0.5}$| | ≤18.1 | |$1.0_{-0.8}^{+0.3}$| | |$0.9_{-0.4}^{+0.4}$| | |$\frac{38.9}{62}$| |
The best-fitting spectral parameters as derived from the fitting of the EPIC-pn+MOS data with the model, Tbabs×gabs×(zgauss+relxillDCp+nthComp), and Tbabs×zxipcf×(relxillDCp+nthComp), respectively, for J1559 and POX52.
| Model . | Source . | J1559 . | J1559 . | POX52 . | Description . |
|---|---|---|---|---|---|
| Component . | Obs. ID . | 0744290101 . | 0744290201 . | 0302420101 . | . |
| zxipcf | NH, wa [1021 cm−2] | |$7.9^{+0.3}_{-0.7}$| | Column density of the absorber | ||
| ξwa [erg cm s−1] | |$10^{+3}_{-7}$| | Ionization parameter | |||
| Cf[per cent] | |$97.9^{+0.6}_{-0.5}$| | Covering fraction | |||
| gabs | Eabs [keV] | |$0.67^{+0.01}_{-0.02}$| | 0.67* | Line energy [observed frame] | |
| σabs [eV] | |$83.1^{+13.9}_{-12.0}$| | 83.1* | Line width | ||
| τabs [10−2] | |$3.6^{+1.0}_{-0.5}$| | 3.6* | Line depth | ||
| zgauss | Erest [keV] | |$6.43^{+0.04}_{-0.04}$| | 6.43* | Rest-frame line centroid energy | |
| Kga [10−6] | |$1.2^{+0.4}_{-0.4}$| | 1.2* | Line normalization | ||
| nthComp | Γ | |$2.07_{-0.03}^{+0.02}$| | 2.07* | |$2.49_{-0.36}^{+0.19}$| | Photon index |
| Knth[10−4] | |$3.5_{-0.6}^{+0.5}$| | |$3.8_{-0.5}^{+0.4}$| | |$2.6_{-0.3}^{+1.1}$| | Primary continuum normalization | |
| relxillDCp | qin | |$6.1_{-1.3}^{+0.9}$| | 6.1* | |$6.8_{-3.5}^{+2.8}$| | Inner emissivity index |
| a | |$0.998_{-0.023}^{+0.0}$| | 0.998* | |$0.56_{-0.46}^{+0.36}$| | BH spin | |
| θ○ | |$59_{-5}^{+4}$| | 59* | |$28_{-14}^{+13}$| | Disc inclination angle | |
| |$\log [\frac{\xi }{\rm erg~cm~s^{-1}}]$| | |$2.7_{-0.1}^{+0.1}$| | 2.7* | |$1.5_{-0.8}^{+0.5}$| | Disc ionization parameter | |
| log [ne/cm-3] | |$17.1_{-0.2}^{+0.3}$| | 17.1* | |$17.6_{-0.5}^{+1.1}$| | Disc density | |
| Kref[10−5] | |$2.6_{-0.8}^{+0.3}$| | |$2.1_{-0.7}^{+0.3}$| | |$1.1_{-0.6}^{+1.1}$| | Reflection normalization | |
| Rs | |$2.0_{-0.07}^{+0.07}$| | |$1.5_{-0.05}^{+0.05}$| | |$1.0_{-0.1}^{+0.1}$| | Reflection strength | |
| |$\frac{C-\rm {stat}}{\rm {d.o.f}}$| | |$\frac{961}{942}$| | – | |$\frac{331}{295}$| | Fit statistic |
| Model . | Source . | J1559 . | J1559 . | POX52 . | Description . |
|---|---|---|---|---|---|
| Component . | Obs. ID . | 0744290101 . | 0744290201 . | 0302420101 . | . |
| zxipcf | NH, wa [1021 cm−2] | |$7.9^{+0.3}_{-0.7}$| | Column density of the absorber | ||
| ξwa [erg cm s−1] | |$10^{+3}_{-7}$| | Ionization parameter | |||
| Cf[per cent] | |$97.9^{+0.6}_{-0.5}$| | Covering fraction | |||
| gabs | Eabs [keV] | |$0.67^{+0.01}_{-0.02}$| | 0.67* | Line energy [observed frame] | |
| σabs [eV] | |$83.1^{+13.9}_{-12.0}$| | 83.1* | Line width | ||
| τabs [10−2] | |$3.6^{+1.0}_{-0.5}$| | 3.6* | Line depth | ||
| zgauss | Erest [keV] | |$6.43^{+0.04}_{-0.04}$| | 6.43* | Rest-frame line centroid energy | |
| Kga [10−6] | |$1.2^{+0.4}_{-0.4}$| | 1.2* | Line normalization | ||
| nthComp | Γ | |$2.07_{-0.03}^{+0.02}$| | 2.07* | |$2.49_{-0.36}^{+0.19}$| | Photon index |
| Knth[10−4] | |$3.5_{-0.6}^{+0.5}$| | |$3.8_{-0.5}^{+0.4}$| | |$2.6_{-0.3}^{+1.1}$| | Primary continuum normalization | |
| relxillDCp | qin | |$6.1_{-1.3}^{+0.9}$| | 6.1* | |$6.8_{-3.5}^{+2.8}$| | Inner emissivity index |
| a | |$0.998_{-0.023}^{+0.0}$| | 0.998* | |$0.56_{-0.46}^{+0.36}$| | BH spin | |
| θ○ | |$59_{-5}^{+4}$| | 59* | |$28_{-14}^{+13}$| | Disc inclination angle | |
| |$\log [\frac{\xi }{\rm erg~cm~s^{-1}}]$| | |$2.7_{-0.1}^{+0.1}$| | 2.7* | |$1.5_{-0.8}^{+0.5}$| | Disc ionization parameter | |
| log [ne/cm-3] | |$17.1_{-0.2}^{+0.3}$| | 17.1* | |$17.6_{-0.5}^{+1.1}$| | Disc density | |
| Kref[10−5] | |$2.6_{-0.8}^{+0.3}$| | |$2.1_{-0.7}^{+0.3}$| | |$1.1_{-0.6}^{+1.1}$| | Reflection normalization | |
| Rs | |$2.0_{-0.07}^{+0.07}$| | |$1.5_{-0.05}^{+0.05}$| | |$1.0_{-0.1}^{+0.1}$| | Reflection strength | |
| |$\frac{C-\rm {stat}}{\rm {d.o.f}}$| | |$\frac{961}{942}$| | – | |$\frac{331}{295}$| | Fit statistic |
The best-fitting spectral parameters as derived from the fitting of the EPIC-pn+MOS data with the model, Tbabs×gabs×(zgauss+relxillDCp+nthComp), and Tbabs×zxipcf×(relxillDCp+nthComp), respectively, for J1559 and POX52.
| Model . | Source . | J1559 . | J1559 . | POX52 . | Description . |
|---|---|---|---|---|---|
| Component . | Obs. ID . | 0744290101 . | 0744290201 . | 0302420101 . | . |
| zxipcf | NH, wa [1021 cm−2] | |$7.9^{+0.3}_{-0.7}$| | Column density of the absorber | ||
| ξwa [erg cm s−1] | |$10^{+3}_{-7}$| | Ionization parameter | |||
| Cf[per cent] | |$97.9^{+0.6}_{-0.5}$| | Covering fraction | |||
| gabs | Eabs [keV] | |$0.67^{+0.01}_{-0.02}$| | 0.67* | Line energy [observed frame] | |
| σabs [eV] | |$83.1^{+13.9}_{-12.0}$| | 83.1* | Line width | ||
| τabs [10−2] | |$3.6^{+1.0}_{-0.5}$| | 3.6* | Line depth | ||
| zgauss | Erest [keV] | |$6.43^{+0.04}_{-0.04}$| | 6.43* | Rest-frame line centroid energy | |
| Kga [10−6] | |$1.2^{+0.4}_{-0.4}$| | 1.2* | Line normalization | ||
| nthComp | Γ | |$2.07_{-0.03}^{+0.02}$| | 2.07* | |$2.49_{-0.36}^{+0.19}$| | Photon index |
| Knth[10−4] | |$3.5_{-0.6}^{+0.5}$| | |$3.8_{-0.5}^{+0.4}$| | |$2.6_{-0.3}^{+1.1}$| | Primary continuum normalization | |
| relxillDCp | qin | |$6.1_{-1.3}^{+0.9}$| | 6.1* | |$6.8_{-3.5}^{+2.8}$| | Inner emissivity index |
| a | |$0.998_{-0.023}^{+0.0}$| | 0.998* | |$0.56_{-0.46}^{+0.36}$| | BH spin | |
| θ○ | |$59_{-5}^{+4}$| | 59* | |$28_{-14}^{+13}$| | Disc inclination angle | |
| |$\log [\frac{\xi }{\rm erg~cm~s^{-1}}]$| | |$2.7_{-0.1}^{+0.1}$| | 2.7* | |$1.5_{-0.8}^{+0.5}$| | Disc ionization parameter | |
| log [ne/cm-3] | |$17.1_{-0.2}^{+0.3}$| | 17.1* | |$17.6_{-0.5}^{+1.1}$| | Disc density | |
| Kref[10−5] | |$2.6_{-0.8}^{+0.3}$| | |$2.1_{-0.7}^{+0.3}$| | |$1.1_{-0.6}^{+1.1}$| | Reflection normalization | |
| Rs | |$2.0_{-0.07}^{+0.07}$| | |$1.5_{-0.05}^{+0.05}$| | |$1.0_{-0.1}^{+0.1}$| | Reflection strength | |
| |$\frac{C-\rm {stat}}{\rm {d.o.f}}$| | |$\frac{961}{942}$| | – | |$\frac{331}{295}$| | Fit statistic |
| Model . | Source . | J1559 . | J1559 . | POX52 . | Description . |
|---|---|---|---|---|---|
| Component . | Obs. ID . | 0744290101 . | 0744290201 . | 0302420101 . | . |
| zxipcf | NH, wa [1021 cm−2] | |$7.9^{+0.3}_{-0.7}$| | Column density of the absorber | ||
| ξwa [erg cm s−1] | |$10^{+3}_{-7}$| | Ionization parameter | |||
| Cf[per cent] | |$97.9^{+0.6}_{-0.5}$| | Covering fraction | |||
| gabs | Eabs [keV] | |$0.67^{+0.01}_{-0.02}$| | 0.67* | Line energy [observed frame] | |
| σabs [eV] | |$83.1^{+13.9}_{-12.0}$| | 83.1* | Line width | ||
| τabs [10−2] | |$3.6^{+1.0}_{-0.5}$| | 3.6* | Line depth | ||
| zgauss | Erest [keV] | |$6.43^{+0.04}_{-0.04}$| | 6.43* | Rest-frame line centroid energy | |
| Kga [10−6] | |$1.2^{+0.4}_{-0.4}$| | 1.2* | Line normalization | ||
| nthComp | Γ | |$2.07_{-0.03}^{+0.02}$| | 2.07* | |$2.49_{-0.36}^{+0.19}$| | Photon index |
| Knth[10−4] | |$3.5_{-0.6}^{+0.5}$| | |$3.8_{-0.5}^{+0.4}$| | |$2.6_{-0.3}^{+1.1}$| | Primary continuum normalization | |
| relxillDCp | qin | |$6.1_{-1.3}^{+0.9}$| | 6.1* | |$6.8_{-3.5}^{+2.8}$| | Inner emissivity index |
| a | |$0.998_{-0.023}^{+0.0}$| | 0.998* | |$0.56_{-0.46}^{+0.36}$| | BH spin | |
| θ○ | |$59_{-5}^{+4}$| | 59* | |$28_{-14}^{+13}$| | Disc inclination angle | |
| |$\log [\frac{\xi }{\rm erg~cm~s^{-1}}]$| | |$2.7_{-0.1}^{+0.1}$| | 2.7* | |$1.5_{-0.8}^{+0.5}$| | Disc ionization parameter | |
| log [ne/cm-3] | |$17.1_{-0.2}^{+0.3}$| | 17.1* | |$17.6_{-0.5}^{+1.1}$| | Disc density | |
| Kref[10−5] | |$2.6_{-0.8}^{+0.3}$| | |$2.1_{-0.7}^{+0.3}$| | |$1.1_{-0.6}^{+1.1}$| | Reflection normalization | |
| Rs | |$2.0_{-0.07}^{+0.07}$| | |$1.5_{-0.05}^{+0.05}$| | |$1.0_{-0.1}^{+0.1}$| | Reflection strength | |
| |$\frac{C-\rm {stat}}{\rm {d.o.f}}$| | |$\frac{961}{942}$| | – | |$\frac{331}{295}$| | Fit statistic |



