Rotating neutron stars without light cylinders

Lyutikov, Maxim; Sharma, Praveen

doi:10.1093/mnras/stac868

ABSTRACT

We find a class of twisted and differentially rotating neutron star magnetospheres that do not have a light cylinder, generate no wind, and thus do not spin-down. The magnetosphere is composed of embedded differentially rotating flux surfaces, with the angular velocity decreasing as Ω ∝ 1/r (equivalently, becoming smaller at the foot-points closer to the axis of rotation). For each given North–South self-similar twist profile there is a set of self-similar angular velocity profiles (limited from above) with a ‘smooth’, dipolar-like magnetic field structure extending to infinity. For spin parameters larger than some critical value, the light cylinder appears, magnetosphere opens up, and the wind is generated.

pulsars: general

1 INTRODUCTION

Magnetospheres of pulsars are highly magnetized and relativistically rotating (Goldreich & Julian 1969). Though the initial set-up is very simple – rotating magnetized sphere with dipolar magnetic field – the non-linear effects of charges and currents on the open field lines modify the field and make the problem highly non-linear (Beskin, Gurevich & Istomin 1988; Contopoulos, Kazanas & Fendt 1999; Gruzinov 2005; Spitkovsky 2006).

Another complication comes from possible non-dipolar, current-carrying magnetospheric fields in the closed zone (Thompson, Lyutikov & Kulkarni 2002; Lyutikov 2013; Parfrey, Beloborodov & Hui 2013). Current-loaded magnetospheres, e.g. slightly twisted dipole (so that the northern foot-point is at different azimuthal angle ϕ than the southern foot-point) are not the same as vacuum multipoles (though they can be expanded as a sum of). Qualitatively, a given twist of a field line concentrates at the point of lowest guiding field. Hence at the furthest point (along closed field lines) in a (nearly) dipolar magnetosphere. This is especially important for magnetar phenomena (Thompson et al. 2002; Lyutikov 2013; Parfrey et al. 2013).

Yet another complication comes from possible differential rotation of the foot points. This is induced by the electron Hall dynamics in the neutron star crust (Goldreich & Reisenegger 1992; Wood, Hollerbach & Lyutikov 2014; Gourgouliatos et al. 2015). In a ‘Solar flare’ model of magnetar activity Lyutikov (2006, 2015) slow, plastic twisting of footprints leads to kink instabilities, generation of flares and coronal mass ejections.

Overall the system becomes very complicated/non-linear. This puts special emphasis on possible (semi)-analytical solutions, that solve the complicated mathematics problem, and yet can be easily traced to the first principles. In this paper, we discuss a class of (quasi)-analytical solutions of pulsar magnetospheres with a highly unusual properties: rotating and twisted pulsar magnetospheres without light cylinders.

2 SELF-SIMILAR ROTATING AND TWISTED MAGNETOSPHERES

The workhorse of analytical investigation of pulsar magnetospheres is the relativistic generalization of the Grad-Shafranov equation (Shafranov 1966; Grad 1967; Michel 1973; Scharlemann & Wagoner 1973; Beskin 2009) which expresses the force balance in an axially symmetric magnetosphere. The conditions of zero-divergence of the magnetic field, the ideal condition and axial symmetry allow the force balance to be expressed as a single scalar equation for the shape of the magnetic flux function Ψ(r, θ). There is a mathematical problem, though: the source terms (the poloidal current and in the case of differentially rotating magnetosphere the spin) enter as terms that are functions of the solution itself, not as independent quantities. This leads to mathematical complication: the equation to be solved and the solution need to be found self-consistently.

Few analytical roads remain. First, one can prescribe I(Ψ) and solve for Ψ. For example, linear relations I = αΨ lead to simple, linear, and hence highly useful analytical solutions, spheromaks in spherical geometry. Alternatively, Lynden-Bell & Boily (1994) suggested a self-similar approach, where the structure has a power-law scaling with the spherical radius. (They were adopted to cylindrical coordinates by Lyutikov 2020b). Twisted configurations of Lynden-Bell & Boily (1994) are especially useful for astrophysical magnetars (Thompson et al. 2002).

In what follows we generalize the non-linear self-similar solutions of twisted magnetospheres of Lynden-Bell & Boily (1994) to twisted and differentially rotating configurations.

2.1 Self-similar twisted and rotating magnetospheres

For a stationary axially symmetric configuration, Fig. 1, the Grad-Shafranov prescription involves field parametrization

$$\begin{eqnarray} {\bf B}&=&(\nabla \Psi) \times (\nabla \phi) + I(\Psi) (\nabla \phi) \\ {\bf E}&=& -\nabla \Phi (\Psi) \\ \Omega &=& - \Phi ^{\prime }. \end{eqnarray}$$

(1)

The force balance

$$\begin{eqnarray} {\bf E}{\rm \, div\, }{\bf E}+ (\nabla \times {\bf B}) \times {\bf B}=0 \end{eqnarray}$$

(2)

gives then the Grad-Shafranov equation (Shafranov 1966; Grad 1967; Scharlemann & Wagoner 1973; Beskin 2009)

$$\begin{eqnarray} \left(1 - r^2 \sin ^2 \theta \Omega ^2 \right) \Delta \Psi - 2 \frac{ \left(r \partial _r \Psi + \cot \theta \partial _\theta \Psi \right) }{ r^2} + I I^{\prime }- (\nabla \Psi)^2 r^2 \sin ^2 \theta \Omega \Omega ^{\prime } =0, \end{eqnarray}$$

(3)

(factors of 4π omitted). (Ω is not the rate of shearing of foot-points, it’s an angular velocity of rotation of a give flux surface.)

Let’s look for self-similar solutions to (3) in a form of

$$\begin{eqnarray} \Psi &=& r^{-p} F(\theta) \\ I &=& c_1 \Psi ^{\alpha } \\ \Omega &=& C_2 \Psi ^{\beta } \end{eqnarray}$$

(4)

By dimensional analysis

$$\begin{eqnarray} \alpha &=& 1+1/p, \\ \beta &=& 1/p \end{eqnarray}$$

(5)

so that the radial scaling of all the components of the magnetic field is ∝ r^{−2 − p}: The electric part has the same power-law scaling as the magnetic. (We also comment that for p = 0 one recovers Michel’s solution Ψ = 1 − cos θ, but with arbitrary Ω(θ), I = (1/2)sin ²θΩ(θ); Blandford & Znajek 1977; Lyutikov 2011).

The angular part of the Grad-Shafranov equation (3) then obeys

$$\begin{eqnarray} && \left(p(1+p) F +C_1 F^{1+2/p} + \left(1-\mu ^2 \right) F^{\prime \prime } \right) - \\ && 2 C_2 ^2 \frac{ (1+p)^2}{p^3} \left(1-\mu ^2 \right) F^{2/p-1} \left(p^3 F^2 + \left(1-\mu ^2 \right) F^{\prime ,2} + p F \left(\left(1-\mu ^2 \right) F^{\prime \prime } -2 \mu F^{\prime }\right) \right) =0 , \end{eqnarray}$$

(6)

where μ = cos θ and we redefined |$c_1= \sqrt{C_1} /(2 \sqrt{1+1/p})$| to match the notations in Lynden-Bell & Boily (1994). The first part in parenthesis is the Lynden-Bell & Boily (1994) term. The coefficient C₁ describes the twist of each field line: the northern and southern foot prints have different azimuthal coordinates. The last line is the contribution from self-similar rotations of the magnetosphere. Note that the direction rotation, the C₂ term, does not influence the structure, which depends on |$C_2^2$|⁠. (A particular divergent dipolar solution of (6) found by Petrova & Flanchik 2018, in our notations corresponds to p = 1, F = 1 − μ², α = −1, |$C_2 = \pm \sqrt{ C_1/8}$|⁠)

For given F the fields are given by

$$\begin{eqnarray} {\bf B}&=& \left\lbrace {F^{\prime }}, p {F},\frac{1}{2} \sqrt{\frac{C_1 p}{p+1}} { F^{1+1/p} } \right\rbrace r^{-2-p} {\sin \theta } ^{-1}, \\ {\bf E}&=& \left\lbrace F, -\frac{ F^{\prime }}{p},0 \right\rbrace C_2 (1+p) r^{-2-p} F^{1/p} \end{eqnarray}$$

(7)

Solutions to equation (6) are of the eigenvalue problem: there are three conditions:

$$\begin{eqnarray} F^{\prime } (0) &=&0, \,\, \rm{zero\,\,radial\,\,{magnetic\,\,field}\,\, at}\,\,\theta =\pi /2 \\ F(1) &=&0, \,\,\,\, {\rm{zero}}\,\,{B}_\theta \,\, {\rm{at}} \,\, \theta =0 \\ F^{\prime } (1) &=&-2, \,\, \rm{radial\,\,{magnetic\,\,field}\,\,at\,\,the\,\,pole,\,\,normalized\,\,to\,\,the\,\,dipole\,\,field} \end{eqnarray}$$

(8)

The three boundary conditions (8) impose an eigenvalue constraint on the triad of radial index p, twist C₁, and rotation C₂: given the two, the eigenvalue constraint fixes the third. We also note that relations (8), the condition that the flux function is equal to zero is automatically satisfied for θ = π. This condition provides a zero flux of the magnetic field through the surface of any sphere.

For quasi-static solution without rotation, C₂ = 0, the current decays slowly due to resistivity (e.g. section 5.2 of Thompson et al. 2002). That decay is slow. In a fully stationary case the decay is compensated by the EMF. If the small resistivity is neglected, exactly stationary case, there is no EMF.

Corresponding solutions for p(C₁, C₂) are plotted in Figs 2–4. Rotation first strongly modifies highly twisted solutions p → 0, Fig. 2. As the spin parameter C₂ increase, the range of allowed values of C₁ − p decreases. Solutions become more dipolar-like (in terms of radial profile, p ≈ 1).

Figure 1.

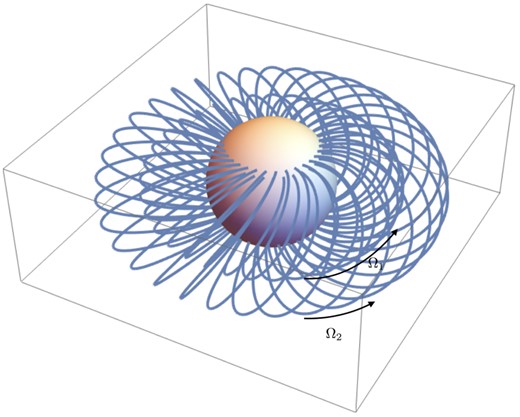
Rotating and twisted magnetosphere without light cylinder. Pictured are magnetic field lines for two flux surfaces. On each flux surface the magnetic field is twisted; in addition flux surfaces are rotating with spin frequency Ω decreasing as a function of maximal radius (equivalently, becoming smaller for smaller polar angles of the foot-points. The magnetosphere is thus composed of onion-like set of nested flux surfaces that rotate each as a solid body, while different surfaces are sheared with respect to each other.

Open in new tab Download slide

$Radial power-law index p as function of the twist parameter C1 for different spins parameters. The dashed line, non-rotating is C2 = 0. Other lines correspond to $C_2= 0.01,\, 0.1, \, 0.2, \, 0.3$ (top to bottom). Note that for cases when there are no self-similar solutions (e.g. for p smaller than some critical value for each C2 ≠ 0) one may still a have no-light cylinder magnetosphere, but its structure is not self-similar.$

Figure 2.

Radial power-law index p as function of the twist parameter C₁ for different spins parameters. The dashed line, non-rotating is C₂ = 0. Other lines correspond to |$C_2= 0.01,\, 0.1, \, 0.2, \, 0.3$| (top to bottom). Note that for cases when there are no self-similar solutions (e.g. for p smaller than some critical value for each C₂ ≠ 0) one may still a have no-light cylinder magnetosphere, but its structure is not self-similar.

Open in new tab Download slide

Radial power-law index p as function of the rotation parameter C2 for untwisted configuration C1 = 0.

Figure 3.

Radial power-law index p as function of the rotation parameter C₂ for untwisted configuration C₁ = 0.

Open in new tab Download slide

Radial power-law index p as function of the spin parameter C2 for different twist parameters. Beyond the plotted values the index p falls down precipitously.

Figure 4.

Radial power-law index p as function of the spin parameter C₂ for different twist parameters. Beyond the plotted values the index p falls down precipitously.

Open in new tab Download slide

Note that in the cases when the eigen-problem cannot be satisfied, there may still be solutions with no light cylinder, but those solutions will be non-self-similar. Eventually, for large enough spin the light cylinder will be formed.

In the case of untwisted magnetospheres, C₁ = 0, the maximal spin parameter is C₂ = 0.34, Fig. 3. We note that finite twists C₁ ≠ 0 allow for larger spins, Fig. 4.

For small twists the electromagnetic velocity is

$$\begin{eqnarray} \frac{{\bf E}\times {\bf B}}{B^2} \approx \left\lbrace -\frac{2 \sqrt{2} \sqrt{C_1} C_2 \sin ^6\theta \cos \theta }{5+3 \cos (2 \theta)},-\frac{\sqrt{2} \sqrt{C_1} C_2 \sin ^7\theta }{5+ 3 \cos (2 \theta)},2 C_2 \sin ^3\theta \right\rbrace . \end{eqnarray}$$

(9)

It is independent of the radius and changes sign at the equator. The Pointing flux ∝ r^{−2(2 + p)} is zero at infinity: the pulsar does not spin-down.

For each solution the angular velocity decreases with radius and increases with polar angle

$$\begin{eqnarray} \Omega = C_2 \left(1+\frac{1}{p} \right) \frac{F(\mu)^{1/p}}{r} = \frac{R_{NS}}{r} {F(\mu)^{1/p}} \Omega _0 , \end{eqnarray}$$

(10)

where typical value at the surface is

$$\begin{eqnarray} \Omega _0 = {C_2 \left(1+\frac{1}{p} \right) } \frac{c}{R_{NS}} \end{eqnarray}$$

(11)

(each flux surface rotates as a solid body.)

Azimuthal velocity is

$$\begin{eqnarray} v_\phi = \Omega r \sin \theta = (R_{NS} \Omega _0)\sin \theta F^{1/p} \end{eqnarray}$$

(12)

The locations of the light cylinder is determined by v_ϕ = c. For the exemplary case of C₂ = 0.1, C₁ = 0.66, p = 0.79 we have Ω₀ = 0.227; the maximal value of Ωrsin θ equals 0.241 ≤ 1. There is no light cylinder.

Generally, rotation leads to further (in addition to twisting) ‘inflation’ of field lines, Fig. 5. (We stress that inflation here occurs due to the rotation of a flux surface as a whole, not due to the shearing of the foot-points of a given field line).

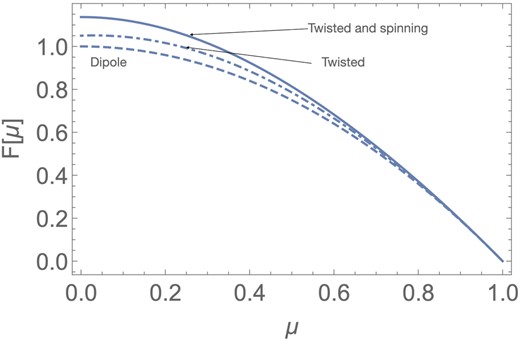
Example that both twist and rotation rotation leads to ‘inflation’ of field lines. The dashed line is for dipole F = 1 − μ2; dot-dashed is for twisted non-rotating case C2 = 0, C1 = 0.66, p = 0.867, solid line is rotating case C2 = 0.1, C1 = 0.66, p = 0.79 (same C1 as non-rotating).

Figure 5.

Example that both twist and rotation rotation leads to ‘inflation’ of field lines. The dashed line is for dipole F = 1 − μ²; dot-dashed is for twisted non-rotating case C₂ = 0, C₁ = 0.66, p = 0.867, solid line is rotating case C₂ = 0.1, C₁ = 0.66, p = 0.79 (same C₁ as non-rotating).

Open in new tab Download slide

The electric potential

$$\begin{eqnarray} \Phi = C_2 r^{-(1+p)} F^{1+1/p} \approx C_2 \frac{\sin ^4 \theta }{r^2} \end{eqnarray}$$

(13)

leads to distributed charge

$$\begin{eqnarray} \rho _e = \Delta \Phi \propto r^{-(3+p)}\approx \frac{ \Omega _0 B_{NS}}{4\pi c } \left(\frac{R_{NS} }{r} \right)^{-(3+p)} \end{eqnarray}$$

(14)

electric field,

$$\begin{eqnarray} {\bf E}= - \nabla \Phi \propto r^{-(2+p)} \end{eqnarray}$$

(15)

Near the neutron star the radial component of the electric field integrated over the surface gives the central charge Q_c

$$\begin{eqnarray} Q_c \approx \frac{ \Omega _0 B_{NS} R_{NS}^3}{c} \end{eqnarray}$$

(16)

Since for r → ∞ E_r → 0 faster than 1/r², the total distributed charge equals the central charge.

3 SIMULATION

3.1 PHAEDRA code

PHAEDRA code (Parfrey, Beloborodov & Hui 2012) is a pseudo-spectral code developed specifically to study highly magnetized plasma regime, force-free electrodynamics, the vanishing-inertia limit of magnetohydrodynamics (Gruzinov 1999; Komissarov 2006)

The code solves Maxwell’s equations

$$\begin{eqnarray} \frac{1}{c} {\partial _t\mathbf {B}}&=&-\nabla \times \mathbf {E} \\ \frac{1}{c} {\partial _t \mathbf {E}}&=&\nabla \times \mathbf {B}-\frac{4 \pi }{c} \mathbf {J} \end{eqnarray}$$

(17)

supplemented by the force-free expression.

$$\begin{eqnarray} \rho \mathbf {E}+\mathbf {J} \times \mathbf {B}=0 \end{eqnarray}$$

(18)

The force free Ohm’s law is then

$$\begin{eqnarray} \frac{4 \pi \mathbf {J_{FF}}}{c}=\frac{B \cdot \nabla \times \mathbf {B}-\mathbf {E} \cdot \nabla \times \mathbf {E}}{B^{2}} \mathbf {B}+\nabla \cdot \mathbf {E} \frac{\mathbf {E} \times \mathbf {B}}{\mathbf {B}^{2}} \end{eqnarray}$$

(19)

Condition |$\mathbf {E}.\mathbf {B} =0$| is satisfied by construction, while |$\mathbf {B}^2 - \mathbf {E}^2 \ge 0$| is assumed (and checked at each step). The code uses a thin frictional absorbing layer next to the outer boundary. The code applies two spectral filters of 8th and 36th order, to maintain stability (Parfrey et al. 2012).

Our results further indicate that the code is very stable and efficient, and has low numerical dissipation. The full numerical grid is defined in axisymmetric spherical coordinates and composed of N_r × N_θ cells along the radial and θ directions, respectively. The simulation zone in our work extends from the stellar surface r_min = R_NS up to r_max = 100R_NS.

The inner boundary is set as the radius of the star (r = R_NS) and the following conditions are strongly enforced at every Runge–Kutta substep.

$$\begin{eqnarray} B_{r}&=&B_{r}(\theta) \\ E_{\theta }&=&-\Omega B_{r} \sin \theta \\ E_{\phi }&=& 0 \end{eqnarray}$$

(20)

3.2 Initialization

Analytical self-similar solutions, Section 2.1, are approximations: the system is generally non-self-similar (there is a special scale – the light cylinder). Thus, we do not expect the numerics to match exactly with analytics, just to follow the general trend. With this in mind, we initialize the simulation setup with analytical approximation for the structure of non-rotating twisted magnetospheres for small/mild twist parameter C₁, and the values of C₂ from the self-similar solution, Fig. 2. For small twists, we can find analytical relation for the structure of non-rotating magnetosphere by expanding near |$p = 1,\, C_{1} = 0$| and the dipolar flux function (Lyutikov 2013):

$$\begin{eqnarray} p &=& 1 - 8 C_{1}/35 \\ { F} &=& \left(1-\mu ^2 \right) \left(1 + {1 \over 140} \left(1- \mu ^2 \right)\left(17 - 5 \mu ^2 \right) C_{1} \right) \\ \mu &=& \cos \theta \end{eqnarray}$$

(21)

In this approximation, the flux magnetic field components and twist angle are given by

$$\begin{eqnarray} \frac{B_r }{B_{NS}} &=& { 2 \mu \over \tilde{r}^{2+p}} \, \left(1+ {3 \left(13 - 18 \mu ^2 +5 \mu ^4 \right) \over 140} C_{1} \right) \\ \frac{B_\theta }{B_{NS}} &=& p { \sqrt{ 1 - \mu ^2} \over \tilde{r}^{2+p}} \, \left(1 + {\left(17 - 22 \mu ^2 + 5 \mu ^4 \right) C_{1} \over 140}\right) \\ \frac{B_\phi }{B_{NS}} &=& { \sqrt{ \frac{ C_{1} p}{1+p} } \frac{ \left(1- \mu ^2 \right)^{3/2} }{ \tilde{r}^{2+p }}} \\ \frac{j_r}{B_{NS}/{4\pi}} &=& 2 \sqrt{2} \mu \left(1-\mu ^2 \right) \tilde{r}^{-3-p } \sqrt{C_{1}} \\ \end{eqnarray}$$

$$\begin{eqnarray} \frac{j_\theta }{B_{NS}/{4\pi } } &=& \sqrt{2} \left(1-\mu ^2 \right)^{3/2} \tilde{r}^{-3-p } \sqrt{C_{1}} \\ \frac{j_\phi }{B_{NS}/{4\pi } } &=& \left(1-\mu ^2 \right)^{5/2} \tilde{r}^{-3-p } C_{1} \\ \Delta \phi &=& \sqrt{2 C_{1}} \mu _{fp} \\ \tilde{r} &=& \frac{r}{R_{NS}} , \end{eqnarray}$$

(22)

where C₁ is a twist parameter, μ_fp is the cosine of the polar angle of the northern foot point, and B_NS is the equatorial magnetic field.

3.3 Results

In order to demonstrate that the simulated magnetic field follows the radial scaling predicted by analytics, we plot a time slice of toroidal magnetic field B_ϕ at |$\theta =\frac{\pi }{2}$| in Fig. 6 and try to fit it to r^{−(2 + p)}. We see that the our radial scaling is in agreement with the analytics.

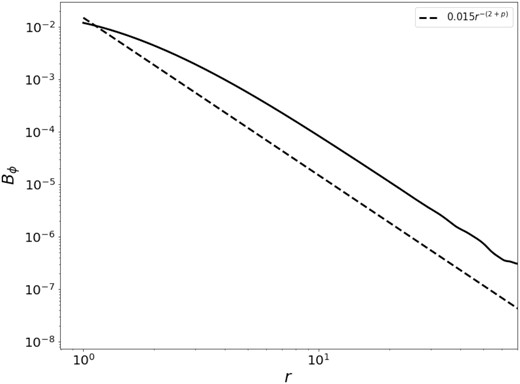
Time slice of toroidal magnetic field Bϕ near the equator for C2 = 0.10, C1 = 0.005, p = 0.9989. The solid line is our simulation results, dashed line is the theoretical expectation r−(2 + p).

Figure 6.

Time slice of toroidal magnetic field B_ϕ near the equator for C₂ = 0.10, C₁ = 0.005, p = 0.9989. The solid line is our simulation results, dashed line is the theoretical expectation r^{−(2 + p)}.

Open in new tab Download slide

In Fig. 7, we plot the scaled azimuthal magnetic field, radial momentum, and the azimuthal velocity for three sets of C₁, C₂. For C₁ = 0.005 ∼ 0 as evident in the top panel, the structure of the rotating magnetosphere clearly matches the analytical result: there are no open field lines, not radial Poynting flux, no energy losses. We see similar structure for the case of C₂ = 0.1, C₁ = 0.66, p = 0.79 (twisted sheared configuration) in bottom panel.

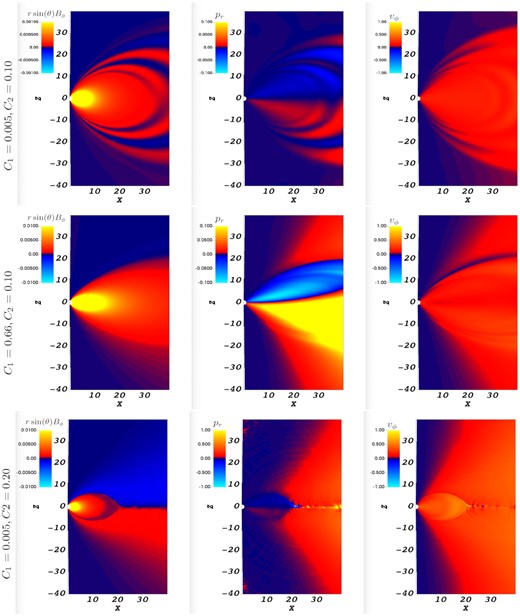
$Zoomed-in time slice of our force-free simulation depicting toroidal magnetic field rsin (θ)Bϕ, radial momentum pr, and toroidal velocity vϕ for the fiducial magnetosphere without light cylinder. In top panel we plot C1 = 0.005, C2 = 0.10, p = 0.9989 case, middle panel is for C1 = 0.66, C2 = 0.10, p = 0.79, bottom panel is for C1 = 0.05, C2 = 0.20, p = 0.9854. The radial momentum is the ${\bf E}\times {\bf B}\propto C_2 \sqrt{C_1}$ drift, equation (7). Since Ω ∝ 1/r, equation (10), azimuthal velocity vϕ remains approximately constant with radius, equation (9), top right-hand panels. We do not observe light cylinder in top two rows. At higher spin parameter C2 = 0.2, C1 = 0.05, p = 0.9854 (lower row) the light cylinder can be clearly identified by the location of the Y-point. The wind is generated (this is especially clearly seen in radial momentum pr, central panel.$

Figure 7.

Zoomed-in time slice of our force-free simulation depicting toroidal magnetic field rsin (θ)B_ϕ, radial momentum p_r, and toroidal velocity v_ϕ for the fiducial magnetosphere without light cylinder. In top panel we plot C₁ = 0.005, C₂ = 0.10, p = 0.9989 case, middle panel is for C₁ = 0.66, C₂ = 0.10, p = 0.79, bottom panel is for C₁ = 0.05, C₂ = 0.20, p = 0.9854. The radial momentum is the |${\bf E}\times {\bf B}\propto C_2 \sqrt{C_1}$| drift, equation (7). Since Ω ∝ 1/r, equation (10), azimuthal velocity v_ϕ remains approximately constant with radius, equation (9), top right-hand panels. We do not observe light cylinder in top two rows. At higher spin parameter C₂ = 0.2, C₁ = 0.05, p = 0.9854 (lower row) the light cylinder can be clearly identified by the location of the Y-point. The wind is generated (this is especially clearly seen in radial momentum p_r, central panel.

Open in new tab Download slide

For small C₂ all twisted configuration do not have a light cylinder (first two panels in Fig. 7 and also bottom row in Fig. 8). When we increase the spin parameter C₂, the picture changed qualitatively, bottom panel in Fig. 7 (Also see middle row in Fig. 8).

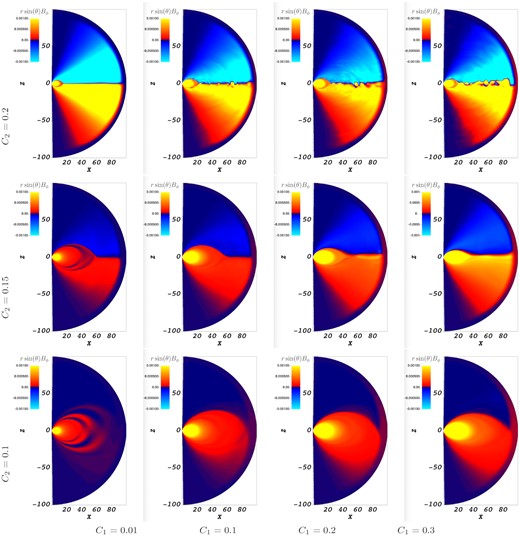
A mosaic of rsin (θ)Bϕ for different twist rotation parameters C1 and C2. C2 = 0.2 (top panel), C2 = 0.15 (middle panel), and C2 = 0.1 (bottom panel). C1 = 0.01, 0.1, 0.2, 0.3 from left to right for both panels at t = 30, measured in light crossing time RNS/c).

Figure 8.

A mosaic of rsin (θ)B_ϕ for different twist rotation parameters C₁ and C₂. C₂ = 0.2 (top panel), C₂ = 0.15 (middle panel), and C₂ = 0.1 (bottom panel). C₁ = 0.01, 0.1, 0.2, 0.3 from left to right for both panels at t = 30, measured in light crossing time R_NS/c).

Open in new tab Download slide

To further verify the observations made in previous paragraphs, we plot scaled toroidal magnetic field for various permutations of C₁, C₂ in Fig. 8.

From the figures, it is clear that the presence of the light cylinder and wind depends strongly on C₂. For slow rotation C₂ = 0.1 (bottom row) there is no light cylinder. The light cylinder appears near C₂ ≥ C_{2, crit} ≈ 0.15. (To guide an eye, formation of the wind requires light cylinder and the corresponding formation of a Y-point. Images with no Y-point imply no wind and no light cylinder.) A more precise critical value of C_{2, crit} could not be determined: at the transition the light cylinder appears at large distances, reaching the absorbing layer next to the outer boundary). For larger C₂ ≥ C_{2, crit} the light cylinder is located closer to the star. We restrict our simulations to C₂ ≤ 0.3. At this moment the light cylinder is located nearly at the star’s surface, but the relaxation time becomes very long (if compared with small C₂ cases).

4 DISCUSSION

We discuss an analytical model of a differentially rotating neutron stars with twisted magnetospheres. We find a new type of solutions without light cylinders. Such configuration could still be a pulsar, a rotating neutron star: it will be more like magnetar producing periodically modulated radio emission driven by magnetic reconnection (Lyutikov 2002, 2020a), not by the rotational energy.

The present model is mostly mathematical. It requires that the twisting motion of the foot-points be comparable to the spin; and the spin shear must be of the particular shape, related to twist. It is a bit surprising that rotating magnetospheres can still be self-similar, since there is a special distance, the light cylinder. Our results indicate that there is a special set of parameters without light cylinder, thus allowing for self-similar solution.

We see the value of the model in that, first, that it provides a clear analytical example of a new types of solutions of the pulsar equation: rotating yet non-spinning down configurations. Secondly, the model might have implication for numerical modelling of twisted, sheared, and rotating magnetospheres of magnetars. Those types of models usually start with stationary neutron star, and then twist, shear, and rotate it. Necessarily, in those simulations the twisting, shearing, and the rotation rate must be similar, as the simulations are limited in their dynamic range: they have to deal with twisting rates similar, just somewhat smaller, to the rotation rate.

ACKNOWLEDGEMENTS

This work had been supported by NASA grants 80NSSC17K0757 and 80NSSC20K0910, NSF grants 1903332 and 1908590. We would like to thank Yiannis Contopoulos, Kyle Parfrey and Alexander Philippov for discussions.

DATA AVAILABILITY

The data underlying this article will be shared on reasonable request to the corresponding author.

REFERENCES

Beskin

V. S.

,

2009

,

MHD Flows in Compact Astrophysical Objects: Accretion, Winds and Jets

.

Springer

,

Berlin

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Beskin

V. S.

,

Gurevich

A. V.

,

Istomin

I. N.

,

1988

,

Ap&SS

,

146

,

205

10.1007/BF00637577

Crossref

Search ADS

Blandford

R. D.

,

Znajek

R. L.

,

1977

,

MNRAS

,

179

,

433

10.1093/mnras/179.3.433

Crossref

Search ADS

Contopoulos

I.

,

Kazanas

D.

,

Fendt

C.

,

1999

,

ApJ

,

511

,

351

10.1086/306652

Crossref

Search ADS

Goldreich

P.

,

Julian

W. H.

,

1969

,

ApJ

,

157

,

869

10.1086/150119

Crossref

Search ADS

Goldreich

P.

,

Reisenegger

A.

,

1992

,

ApJ

,

395

,

250

10.1086/171646

Crossref

Search ADS

Gourgouliatos

K. N.

,

Kondić

T.

,

Lyutikov

M.

,

Hollerbach

R.

,

2015

,

MNRAS

,

453

,

L93

10.1093/mnrasl/slv106

Crossref

Search ADS

Grad

H.

,

1967

,

Phys. Fluids

,

10

,

137

10.1063/1.1761965

Crossref

Search ADS

Gruzinov

A.

,

1999

,

preprint (arXiv:e-print)

Gruzinov

A.

,

2005

,

Phys. Rev. Lett.

,

94

,

021101

Crossref

Search ADS

Komissarov

S. S.

,

2006

,

MNRAS

,

367

,

19

10.1111/j.1365-2966.2005.09932.x

Crossref

Search ADS

Lynden-Bell

D.

,

Boily

C.

,

1994

,

MNRAS

,

267

,

146

10.1093/mnras/267.1.146

Crossref

Search ADS

Lyutikov

M.

,

2002

,

ApJ

,

580

,

L65

10.1086/345493

Crossref

Search ADS

Lyutikov

M.

,

2006

,

MNRAS

,

367

,

1594

10.1111/j.1365-2966.2006.10069.x

Crossref

Search ADS

Lyutikov

M.

,

2011

,

Phys. Rev. D

,

83

,

124035

Lyutikov

M.

,

2013

,

preprint (arXiv:1306.2264)

Lyutikov

M.

,

2015

,

MNRAS

,

447

,

1407

10.1093/mnras/stu2413

Crossref

Search ADS

Lyutikov

M.

,

2020a

,

ApJ

,

922

,

166

10.3847/1538-4357/ac1b32

Lyutikov

M.

,

2020b

,

J. Plasma Phys.

,

86

,

905860210

Crossref

Search ADS

Michel

F. C.

,

1973

,

ApJ

,

180

,

L133

10.1086/181169

Crossref

Search ADS

Parfrey

K.

,

Beloborodov

A. M.

,

Hui

L.

,

2012

,

MNRAS

,

423

,

1416

10.1111/j.1365-2966.2012.20969.x

Crossref

Search ADS

Parfrey

K.

,

Beloborodov

A. M.

,

Hui

L.

,

2013

,

ApJ

,

774

,

92

10.1088/0004-637X/774/2/92

Crossref

Search ADS

Petrova

S. A.

,

Flanchik

A. B.

,

2018

,

Ap&SS

,

363

,

51

10.1007/s10509-018-3269-2

Crossref

Search ADS

Scharlemann

E. T.

,

Wagoner

R. V.

,

1973

,

ApJ

,

182

,

951

10.1086/152195

Crossref

Search ADS

Shafranov

V. D.

,

1966

,

Rev. Plasma Phys.

,

2

,

103

Spitkovsky

A.

,

2006

,

ApJ

,

648

,

L51

10.1086/507518

Crossref

Search ADS

Thompson

C.

,

Lyutikov

M.

,

Kulkarni

S. R.

,

2002

,

ApJ

,

574

,

332

10.1086/340586

Crossref

Search ADS

Wood

T. S.

,

Hollerbach

R.

,

Lyutikov

M.

,

2014

,

Phys. Plasmas

,

21

,

052110

10.1063/1.4879810

Crossref

Search ADS

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
April 2022	2
May 2022	15
June 2022	9
July 2022	9
September 2022	4
October 2022	3
November 2022	2
January 2023	2
February 2023	2
March 2023	4
April 2023	27
May 2023	9
June 2023	9
July 2023	5
August 2023	6
September 2023	12
October 2023	5
November 2023	9
December 2023	6
January 2024	2
February 2024	4
March 2024	14
April 2024	8
May 2024	20
June 2024	6
July 2024	11
August 2024	4
September 2024	7
October 2024	5
November 2024	1
January 2025	4
February 2025	3
March 2025	6
April 2025	8
May 2025	1

Article Contents

Rotating neutron stars without light cylinders

ABSTRACT

1 INTRODUCTION

2 SELF-SIMILAR ROTATING AND TWISTED MAGNETOSPHERES

2.1 Self-similar twisted and rotating magnetospheres

3 SIMULATION

3.1 PHAEDRA code

3.2 Initialization

3.3 Results

4 DISCUSSION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Rotating neutron stars without light cylinders

ABSTRACT

1 INTRODUCTION

2 SELF-SIMILAR ROTATING AND TWISTED MAGNETOSPHERES

2.1 Self-similar twisted and rotating magnetospheres

3 SIMULATION

3.1 PHAEDRA code

3.2 Initialization

3.3 Results

4 DISCUSSION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only