The matter density PDF for modified gravity and dark energy with Large Deviations Theory

Cataneo, Matteo; Uhlemann, Cora; Arnold, Christian; Gough, Alex; Li, Baojiu; Heymans, Catherine

doi:10.1093/mnras/stac904

ABSTRACT

We present an analytical description of the probability distribution function (PDF) of the smoothed 3D matter density field for modified gravity and dark energy. Our approach, based on the principles of Large Deviations Theory, is applicable to general extensions of the standard Lambda cold dark matter (ΛCDM) cosmology. We show that late-time changes to the law of gravity and background expansion can be included through Einstein-de Sitter spherical collapse dynamics combined with linear theory calculations and a calibration measurement of the non-linear variance of the smoothed density field from a simple numerical simulation. In a comparison to N-body simulations for f(R), DGP, and evolving dark energy theories, we find per cent level accuracy around the peak of the distribution for predictions in the mildly non-linear regime. A Fisher forecast of an idealized experiment with a Euclid-like survey volume demonstrates the power of combining measurements of the 3D matter PDF with the 3D matter power spectrum. This combination is shown to halve the uncertainty on parameters for an evolving dark energy model, relative to a power spectrum analysis on its own. The PDF is also found to substantially increase the detection significance for small departures from General Relativity, with improvements of up to six times compared to the power spectrum alone. This analysis is therefore very promising for future studies including non-Gaussian statistics, as it has the potential to alleviate the reliance of these analyses on expensive high-resolution simulations and emulators.

methods: analytical, large-scale structure of Universe, cosmology: theory

1 INTRODUCTION

Over the past two decades an extraordinary and diverse array of experimental evidence has earned the Lambda cold dark matter (ΛCDM) paradigm the status of standard cosmological model (see e.g. Aiola et al. 2020; Hamana et al. 2020; Planck Collaboration VI 2020; Alam et al. 2021; DES Collaboration 2022; Dutcher et al. 2021; Heymans et al. 2021, for recent analyses). However, in recent years mild to severe tensions between early- and late-time probes of the growth of structure and background expansion have put a strain on the ability of ΛCDM to explain our universe (see e.g. Douspis, Salvati & Aghanim 2019; Di Valentino et al. 2021a,b; Perivolaropoulos & Skara 2021, for reviews). Furthermore, Einstein’s general relativity (GR) – the theory of gravity at the foundation of ΛCDM – has been thoroughly tested only on small astrophysical scales and in the strong field regime (Will 2014; Abbott et al. 2017, 2019b), leaving ample room for modifications to the field equations on cosmological scales (Abbott et al. 2019a; Ferreira 2019; Ishak 2019; Pogosian et al. 2021; Raveri et al. 2021; Tröster et al. 2021). Together with the yet unexplained nature of the observed accelerated cosmic expansion (Riess et al. 1998; Perlmutter et al. 1999), these considerations motivate the exploration of alternatives to the cosmological constant (Λ) and standard gravity. In this paper, we focus on extensions of ΛCDM that include modified gravity and (late-time) dark energy, which we will concisely refer to as ‘extended models’.

Two-point statistics are central to many of the leading cosmological analyses of the large-scale structure searching for deviations from ΛCDM (Simpson et al. 2013; Song et al. 2015; Amon et al. 2018; Abbott et al. 2019a; Chudaykin, Dolgikh & Ivanov 2021; Lee et al. 2022; Muir et al. 2021; Tröster et al. 2021; Vazsonyi et al. 2021), and a great deal of effort has gone into accurately modelling the non-linear matter power spectrum in modified gravity and dark energy cosmologies – a theoretical ingredient essential to extract the cosmological information locked in small scales (e.g. Koyama, Taruya & Hiramatsu 2009; Brax & Valageas 2012; Takahashi et al. 2012; Heitmann et al. 2014; Zhao 2014; Casarini et al. 2016; Mead et al. 2016; Cusin, Lewandowski & Vernizzi 2018; Cataneo et al. 2019; Winther et al. 2019; Euclid Collaboration 2021; Ramachandra et al. 2021). However, non-linear gravitational clustering converts the nearly Gaussian initial density field (Planck Collaboration VI 2020) to a late-time density field with significant non-Gaussian features that these standard analyses are unable to access (Bernardeau et al. 2002). Non-Gaussian statistics, such as the bispectrum (Brax & Valageas 2012; Munshi 2017; Yamauchi, Yokoyama & Tashiro 2017; Crisostomi, Lewandowski & Vernizzi 2020; Bose et al. 2020b), higher order weak lensing spectra (Munshi & McEwen 2020), the halo mass function (Lam & Li 2012; Cataneo et al. 2016; Hagstotz et al. 2019; McClintock et al. 2019; Bocquet et al. 2020), the void size function (Perico et al. 2019; Verza et al. 2019; Contarini et al. 2021) and Minkowski functionals (Kratochvil et al. 2012; Fang, Li & Zhao 2017), respond strongly to modified gravity and dark energy through the induced changes in the higher moments of the cosmic density field, and their remarkable complementarity to traditional two-point functions leads to tighter joint constraints on the extra non-standard parameters (Shirasaki et al. 2017; Peel et al. 2018; Sahlén 2019; Liu et al. 2021).

The probability distribution function (hereafter PDF) of the 3D matter density field smoothed on a given scale is one of the simplest non-Gaussian statistics, and accurate predictions allow us to extract additional cosmological information (Uhlemann et al. 2020). Modified gravity and evolving dark energy leave distinctive imprints on the skewness, kurtosis, and higher cumulants of the PDF, which have been observed in N-body simulations (Li, Zhao & Koyama 2012b; Hellwing et al. 2013, 2017; Shin et al. 2017). Thus far, theoretical predictions of the PDF for modified gravity have required either sophisticated and time-consuming approaches for the spherical collapse (Brax & Valageas 2012) or computationally costly simulations (Li et al. 2012b; Hellwing et al. 2013, 2017). Similarly, for the PDF response to dark energy beyond a cosmological constant, so far only ad hoc fitting functions obtained from simulations are available (Shin et al. 2017; Mandal & Nadkarni-Ghosh 2020; Wen, Kemball & Saslaw 2020). In this work, we apply the principles of Large Deviation Theory (LDT) to the cosmic density field to derive a general and analytical prescription for the 3D matter PDF in modified gravity and dark energy cosmologies. We build on the formalism developed in Bernardeau & Reimberg (2016) and Uhlemann et al. (2016), and show that the Einstein-de Sitter (EdS) spherical collapse dynamics together with linear theory calculations can reproduce the 3D matter PDF measured from state-of-the-art simulations to a few per cent accuracy in the mildly non-linear regime. Remarkably, the matter PDF can be accurately predicted requiring only linear information from extended cosmologies, which sources the characteristic differences in the non-linear variance and higher cumulants. Through Fisher forecasts we quantify, for the first time, the ability of the PDF to detect distinct departures from GR and to constrain the dark energy equation of state, especially when combined with the matter power spectrum. Our method implemented in the public code pyLDT¹ delivers fast predictions for the cosmology dependence of the PDF, and it paves the way for the modelling of observable statistics of the large-scale structure in general theories of gravity and dark energy (see Frusciante & Perenon 2020, for a review). Our framework can be applied to predict the weak lensing convergence PDF (Barthelemy et al. 2020; Boyle et al. 2021), galaxy counts-in-cells (Uhlemann et al. 2018a; Repp & Szapudi 2020; Friedrich et al. 2022), and density-split statistics (Friedrich et al. 2018; Gruen et al. 2018).

The paper is structured as follows: Section 2 reviews the LDT framework and provides a simple extension to include the effects of modified gravitational couplings and background expansion on the PDF. Section 3 describes the N-body simulations and PDF measurements used to validate the theoretical predictions. In Section 4, we demonstrate the accuracy of our methodology, as well as the complementarity of the matter PDF and the power spectrum for modified gravity and dark energy parameters using Fisher matrix analyses. We summarize our results and give an outlook on future research in Section 5.

2 THE MATTER DENSITY PDF IN LARGE DEVIATIONS THEORY

2.1 Large deviations theory framework

Large deviations theory (see Touchette 2012, for a basic introduction) provides a means to predict the probability density function (PDF) of non-linear matter densities in spheres (Bernardeau 1994; Valageas 2002; Bernardeau, Pichon & Codis 2014; Bernardeau & Reimberg 2016; Uhlemann et al. 2016). The formalism can be applied on mildly non-linear scales quantified by the value of the non-linear variance |$\sigma _{\rm NL}^2$| at the redshift z and radius R of interest as long as |$\sigma _{\rm NL}^2(R,z)\lt 1$|⁠. For Gaussian initial conditions,² the PDF, |${\cal P}(\delta _{\rm L})$|⁠, of the linear matter density contrast, δ_L, in a sphere of radius r is a Gaussian distribution where the width is fully specified by the linear variance, |$\sigma _{\rm L}^2$| at that scale r and redshift z

$$\begin{eqnarray*} \mathcal {P}_{r,z}^{\rm lin}(\delta _{\rm L}) &= \sqrt{\frac{1}{2\pi \sigma _{\rm L}^2(r,z)}} \exp \left[-\frac{ \delta _{\rm L}^2}{2\sigma ^2_{\rm L}(r,z)}\right]\, . \end{eqnarray*}$$

(1)

The linear variance at scale r is obtained from an integral over the linear power spectrum, P_L, with a spherical top-hat filter in position space

$$\begin{eqnarray*} \sigma ^2_{\rm L}(r,z) = \int \frac{dk}{2\pi ^2} P_{\rm L}(k,z) k^2 W^2_{\rm 3D}(k r)\, , \end{eqnarray*}$$

(2)

where W_3D(k) is the Fourier transform of the 3D spherical top-hat filter.

To describe the impact of non-linear gravitational dynamics on the shape of the initially Gaussian matter PDF, it is informative to look at the exponential decay of the PDF with increasing density contrast. To formalize this argument, one considers the exponential decay of the PDF in equation (1) encoded in the decay-rate function

$$\begin{eqnarray*} \Psi _{r,z}^{\rm lin}(\delta _{\rm L})= \frac{ \delta _{\rm L}^2}{2\sigma ^2_{\rm L}(r,z)}\, . \end{eqnarray*}$$

(3)

In general, the non-linear matter PDF can be written as a path integral over all possible ways to realize a non-linear normalized density ρ = 1 + δ from a given linear density contrast. But since large deviations are exponentially unlikely, there is only one path, namely the least unlikely one, which dominates this complex integral. The dominant contribution is a saddle point of the corresponding functional integral, which is given by the spherical collapse dynamics thanks to the spherical symmetry of the cells and statistical isotropy ensuring average density profiles to be spherical (Bernardeau 1994; Valageas 2002; Ivanov, Kaurov & Sibiryakov 2019). This idea leads to the contraction principle of large deviation statistics (Bernardeau & Reimberg 2016), which states that the decay-rate function of the final sphere density ρ (at scale R and redshift z) can be obtained from the initial one by using the spherical collapse mapping ρ = ρ_SC(δ_L) to obtain the associated most likely linear density contrast δ_L(ρ) and mass conservation for the initial radius r = Rρ^1/3, such that

$$\begin{eqnarray*} \Psi _{R,z}(\rho) = \frac{\sigma ^2_{\rm L}(R,z)}{\sigma _{\rm NL}^2(R,z)} \frac{\delta _{\rm L}^2(\rho)}{2\sigma ^2_{\rm L}(R\rho ^{1/3},z)}\, . \end{eqnarray*}$$

(4)

The prefactor arises from performing calculations with a decay-rate function rescaled with |$\sigma _{\rm L}^2(R,z)$|⁠, which renders it a proper rate function described by large deviation statistics (Bernardeau & Reimberg 2016; Uhlemann et al. 2016) and ensures a well-defined σ → 0 limit, and then restoring the desired final non-linear variance |$\sigma _{\rm NL}^2$|⁠.³

From the decay-rate function in equation (4) one can reconstruct the full PDF. This can be achieved by computing the cumulant generating function via a Legendre transform, which in turn allows to compute the final PDF via an inverse Laplace transform. This integral can be computed numerically (Bernardeau et al. 2014), but an excellent analytical approximation can be obtained from a saddle-point approximation for the log-density μ = ln ρ (Uhlemann et al. 2016). To achieve this, the decay-rate function in equation (4) is rewritten in terms of the logarithmic density μ and its non-linear variance |$\sigma ^2_\mu$|

$$\begin{eqnarray*} \Psi _{R,z}(\mu) = \frac{\sigma ^2_{\rm L}(R,z)}{\sigma _{\rm \mu }^2(R,z)} \frac{\delta _{\rm L}^2(\rho (\mu))}{2\sigma ^2_{\rm L}(R\rho ^{1/3},z)}\, . \end{eqnarray*}$$

(5a)

Then the matter density PDF, |${\cal P}_{R,z}(\rho)$|⁠, is obtained from

$$\begin{eqnarray*} \tilde{{\cal P}}_{R,z}(\tilde{\rho }) = \sqrt{\frac{\Psi ^{\prime \prime }_{R,z}(\tilde{\rho })+\Psi ^{\prime }_{R,z}(\tilde{\rho })/\tilde{\rho }}{2\pi }} \exp \left[-\Psi _{R,z}(\tilde{\rho })\right]\, . \end{eqnarray*}$$

(5b)

The prefactor arises from a combination of the second derivative of the decay-rate function with respect to the logarithmic density and the Jacobian of the non-linear transformation.

Because of the use of the log-transform, one has to ensure the correct mean density |$\langle \rho \rangle =\int d\rho \, \rho \, {\cal P}(\rho)=1$| by specifying the mean of the log-density 〈ln ρ〉. This can be implemented by rescaling the ‘raw’ PDF, |$\tilde{{\cal P}}_{R,z}(\tilde{\rho })$|⁠, from equation (5b) as

$$\begin{eqnarray*} {\cal P}_{R,z}(\rho) &= \tilde{{\cal P}}_{R,z}\left(\rho \cdot \frac{\langle \tilde{\rho }\rangle }{\langle 1\rangle }\right) \cdot \frac{\langle \tilde{\rho }\rangle }{\langle 1\rangle ^2}\, , \end{eqnarray*}$$

(5c)

where |$\langle f(\tilde{\rho }) \rangle =\int d\tilde{\rho }\, f(\tilde{\rho }) \tilde{{\cal P}}(\tilde{\rho })$| for any function |$f(\tilde{\rho })$|⁠, such as f = 1 and |$f=\tilde{\rho }$| here.

Remarkably, for a standard ΛCDM universe, there are only three ingredients that enter this theoretical model for the matter PDF,

the time- and scale-dependence of the linear variance, |$\sigma _{\rm L}^2(r,z)$|⁠,
the mapping from initial to final densities in spheres, ρ_SC(δ_L),
the non-linear variance of the log-density at the sphere radius and redshift of interest, |$\sigma _{\rm NL}^2(R,z) \rightarrow \sigma _{\mu }^2(R,z)$| .

The linear variance and its cosmology dependence can be readily obtained from the linear power spectrum computed from Einstein–Boltzmann codes like CAMB (Lewis, Challinor & Lasenby 2000) or CLASS (Blas, Lesgourgues & Tram 2011).

The spherical collapse mapping entering the matter PDF was shown to be very mildly cosmology-dependent and well-approximated by the redshift-independent EdS result in Uhlemann et al. (2020). This can also be seen in Fig. 1, where the fractional difference between the ΛCDM and the EdS solution remains within 0.25 per cent for all non-linear densities considered. We develop a simple yet accurate EdS-based approximation for spherical collapse within modified gravity in the following section.

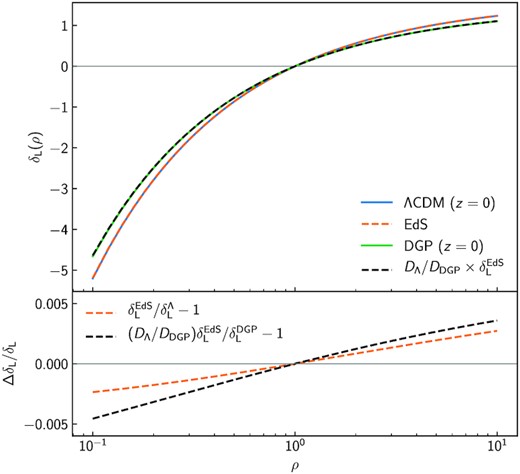
$Mapping between the normalized final density, ρ, and the initial linearly scaled density fluctuation, δL, for a spherical top-hat perturbation. Upper panel: the curves show the density evolution in different background/gravity models. For ΛCDM (blue) and EdS (dashed orange) cosmologies gravity is GR, while for DGP (green) the gravitational constant is modified as in equation (11) with rcH0 = 0.5 (or Ωrc = 0.25). Here, both ΛCDM and DGP are evaluated at z = 0. The dashed black line represents the EdS mapping rescaled by the ratio of the ΛCDM-to-DGP linear growth ratio at z = 0. Lower panel: fractional difference of the EdS mapping from the ΛCDM prediction (dashed orange) and that of the rescaled EdS from the DGP evolution (dashed black). The rescaled $\delta _{\rm L}^{\rm EdS}$ can reproduce the modified gravity phenomenology to better than 0.5 per cent, and it can be seen that most of the difference comes from the discrepancy between the EdS and the ΛCDM predictions.$

Figure 1.

Mapping between the normalized final density, ρ, and the initial linearly scaled density fluctuation, δ_L, for a spherical top-hat perturbation. Upper panel: the curves show the density evolution in different background/gravity models. For ΛCDM (blue) and EdS (dashed orange) cosmologies gravity is GR, while for DGP (green) the gravitational constant is modified as in equation (11) with r_cH₀ = 0.5 (or Ω_rc = 0.25). Here, both ΛCDM and DGP are evaluated at z = 0. The dashed black line represents the EdS mapping rescaled by the ratio of the ΛCDM-to-DGP linear growth ratio at z = 0. Lower panel: fractional difference of the EdS mapping from the ΛCDM prediction (dashed orange) and that of the rescaled EdS from the DGP evolution (dashed black). The rescaled |$\delta _{\rm L}^{\rm EdS}$| can reproduce the modified gravity phenomenology to better than 0.5 per cent, and it can be seen that most of the difference comes from the discrepancy between the EdS and the ΛCDM predictions.

Open in new tab Download slide

The non-linear variance of the log-density at the sphere radius and redshift of interest, |$\sigma _{\mu }^2(R,z)$|⁠, can be considered a free parameter and measured directly from simulations. Once measured from a single (or small set of) simulations at the fiducial cosmology, its changes with cosmology can be predicted using a phenomenological approximation inspired from the lognormal model (see equation 21). Alternatively, the non-linear variance of the log-density could also be chosen to reproduce a predicted non-linear variance of the density, |$\sigma _{\rho }^2(R,z)$|⁠, obtained from matter power spectrum fitting functions such as halofit (Peacock & Smith 2014), hmcode (Mead et al. 2021), or respresso (Nishimichi, Bernardeau & Taruya 2017).

2.2 Large-deviations statistics in modified gravity and dark energy

For scalar–tensor theories within the Horndeski class (Horndeski 1974) the late-time growth of linear matter perturbations on sub-horizon scales in a spatially flat universe is governed by (Gleyzes et al. 2013; Bellini & Sawicki 2014)

$$\begin{eqnarray*} D^{\prime \prime } + \frac{3}{2a}\left[ 1-w_{\rm eff}(a)\Omega _{\mathrm{eff}}(a) \right] D^{\prime } - \frac{3\Omega _{\mathrm{m}}(a)}{2a^2} [ 1+ \epsilon (k,a) ] D = 0 \, , \nonumber \\ \end{eqnarray*}$$

(6)

where D is the linear growth function such that the final linear density fluctuation |$\hat{\delta }_{\rm L}(k,z) = D(k,z)\delta _{\rm ini}$|⁠, primes denote derivatives with respect to the scale factor, a, Ω_eff(a) and w_eff(a) are the energy density and equation of state, respectively, of the effective dark energy fluid driving the background acceleration, and ϵ(k, a) represents the scale- and time-dependent fractional deviation from the gravitational constant. We can recover the well-known result for ΛCDM by setting w_eff = −1 and ϵ = 0. In what follows we shall consider only late-time extensions (‘ext’) to the standard cosmology, that is, D_ext → D_Λ at sufficiently early times such that the initial conditions and the primary CMB anisotropies remain unchanged. Hence, the linear matter power spectrum in any of these extensions can be obtained by rescaling the initial ΛCDM power spectrum as

$$\begin{eqnarray*} P_{\rm L}^{\rm ext}(k,z) = \left[ \frac{D_{\rm ext}(k, z)}{D_\Lambda (z_{\rm i})} \right]^2 P_{\rm L}^{\Lambda }(k,z_{\rm i}) \, , \end{eqnarray*}$$

(7)

where z_i is taken deep in the matter-dominated era. This equation can then be used together with equation (2) to provide the linear variance as a function of smoothing scale and redshift.

The next ingredient required in equation (4) is the function mapping the final density, ρ, to the linearly forward-propagated initial density, δ_L. A spherical top-hat density fluctuation, δ, evolves as (see e.g. Schmidt et al. 2009)

$$\begin{eqnarray*} \ddot{\delta }+ 2 H \dot{\delta }- \frac{4}{3} \frac{\dot{\delta }^{2}}{(1+\delta)} = \frac{3}{2} H^2 \Omega _{\mathrm{m}}(1 + {\cal F}) (1+\delta)\delta \, , \end{eqnarray*}$$

(8)

where dots denote derivatives with respect to cosmic time, H is the Hubble parameter, and for simplicity we have omitted the time dependence from all quantities. Here, |${\cal F}$| is a function describing departures from GR which also incorporates a generic screening mechanism to restore standard gravity in high-density environments (see e.g. Koyama 2018; Lombriser 2018). Note that in the limit of small linear fluctuations |${\cal F} \rightarrow \epsilon$|⁠, and equation (8) reduces to equation (6). In the rest of this work we will neglect any non-linear screening mechanism and, in fact, we will argue that in the mildly non-linear regime (R ≳ 10 |$\mathrm{Mpc}\, h^{-1}$|⁠) any modified gravity and dark energy effect on the spherical collapse/expansion can be accurately captured by the following approximation:

$$\begin{eqnarray*} \delta _{\rm L}^{\rm ext}(\rho ,z) \approx \frac{\sigma _{\rm L}^{\Lambda }(R\rho ^{1/3},z)}{\sigma _{\rm L}^{\rm ext}(R\rho ^{1/3},z)} \delta _{\rm L}^{\rm EdS}(\rho) \, , \end{eqnarray*}$$

(9)

where |$\delta _{\rm L}^{\rm EdS}$| corresponds to the mapping between the final and the initial density fluctuations in an EdS universe, i.e. Ω_m(a) = 1 and |${\cal F} = 0$| in equation (8). For reasons that will be discussed in Section 2.2.1, our definition of |$\delta _{\rm L}^{\rm ext}$| in equation (9) does not match the linear density contrast solution to equation (6), in that we use the ΛCDM linear growth, D_Λ, to extrapolate the initial density fluctuation, δ_ini,ext, to the final redshift rather than the modified growth, D_ext. For scale-independent late-time extensions (i.e. |$\sigma _{\rm L}^{\Lambda }/\sigma _{\rm L}^{\rm ext}=D_\Lambda /D_{\rm ext}$| and |$\sigma _{\rm L}^{\rm ext, ini} \approx \sigma _{\rm L}^{\rm \Lambda , ini}$|⁠), one can alternatively use the modified growth for the extrapolation, i.e. |$\tilde{\delta }_{\rm L}^{\rm ext} \equiv D_{\rm ext}\delta _{\rm ini,ext}$|⁠, and arrive at the following approximation |${\tilde{\delta }_{\rm L}}^{\rm ext}(\rho ,z) \approx \delta _{\rm L}^{\rm EdS}(\rho)$|⁠.⁴ It is easy to show that these two approximations are equivalent and provide the same rate function – we opt for equation (9) simply because it explicitly accounts for scale-dependent modifications as well.

2.2.1 Modified gravity

Since Horndeski gravity encompasses a large number of extensions to GR, here we focus on two well-studied models within this class displaying very different phenomenology: DGP braneworld gravity⁵ (Dvali, Gabadadze & Porrati 2000) and f(R) gravity⁶ (see e.g. De Felice & Tsujikawa 2010, for a review). In particular, we will consider the normal branch of DGP with an additional smooth dark energy component such that the background expansion is identical to ΛCDM (Schmidt 2009), that is,

$$\begin{eqnarray*} \left(\frac{H}{H_0} \right)^2 = \Omega _{\mathrm{m}}a^{-3} + \Omega _{\Lambda }\, , \end{eqnarray*}$$

(10)

with Ω_Λ = 1 − Ω_m, and the subscript ‘0’ denotes present-day values here and throughout. For f(R) gravity we will use the functional form of Hu & Sawicki (2007), which has an expansion history also well described by equation (10) for viable parameter values.

The linear growth of structure in DGP is modified by time-varying changes to the gravitational constant given by

$$\begin{eqnarray*} \epsilon _{\rm DGP}(a) = \frac{1}{3\beta (a)} \, , \end{eqnarray*}$$

(11)

where

$$\begin{eqnarray*} \beta (a) \equiv 1 + 2 r_{\rm c}H \left(1 + \frac{aH^\prime }{3H} \right) \, , \end{eqnarray*}$$

(12)

with r_c being the crossover scale parameter. Deviations from GR in this model can be parametrized in terms of the effective energy density contribution (see e.g. Lombriser et al. 2009)

$$\begin{eqnarray*} \Omega _{\mathrm{rc}}\equiv \frac{1}{4(r_{\rm c}H_0)^2} \, , \end{eqnarray*}$$

(13)

such that for Ω_rc → 0 we recover the standard growth.

In the non-linear regime, the evolution of spherical top-hat overdensities in DGP is correctly described by equation (8). For underdensities, instead, the same function |$\cal F$| incorporating the Vainshtein screening (see e.g. Schmidt, Hu & Lima 2010) produces either unphysical solutions or a strength of the fifth force exceeding the expected linear limit for voids (Falck, Koyama & Zhao 2015). Here, we neglect the Vainshtein screening by linearizing the modification to gravity and show in Section 4 that this approach accounts for most of the difference between EdS and DGP spherical evolution. In practice, to ensure the distribution of the matter density peaks/troughs, ν = δ/σ, defined at the initial time is preserved at later epochs even for scale-dependent modifications (Kopp et al. 2013; Lombriser et al. 2013), and to effectively separate the impact of new physics from changes to the standard cosmological parameters (Brax & Valageas 2012), the mapping |$\delta _{\rm L}^{\rm DGP}(\rho ,z)$| is obtained by setting |${\cal F} = \epsilon _{\rm DGP}$| and by extrapolating the initial density fluctuation, δ_i(ρ), to an arbitrary redshift z < z_i as⁷

$$\begin{eqnarray*} \frac{{\delta _i(\rho ,z)}}{\sigma _{\rm L}^\Lambda (R\rho ^{1/3},z_i)} = \frac{D_\Lambda (z)\delta _i(\rho ,z)}{D_\Lambda (z)\sigma _{\rm L}^\Lambda (R\rho ^{1/3},z_i)} = \frac{\delta _{\rm L}^{\rm DGP}(\rho ,z)}{\sigma _{\rm L}^\Lambda (R\rho ^{1/3},z)} \, . \end{eqnarray*}$$

(14)

Fig. 1 shows that we can further approximate |$\delta _{\rm L}^{\rm DGP}$| to better than 0.5 per cent accuracy with the EdS-based approximation from equation (9), thus removing entirely the necessity for solving the spherical evolution dynamics beyond the EdS cosmology.

In f(R) gravity the new scalar degree of freedom acquires a mass, |$m_{f_R}$|⁠, defining the effective range of the fifth force interaction (i.e. the Compton wavelength λ_C), which for linearized fluctuations reads

$$\begin{eqnarray*} \lambda _{\rm C}(a) \equiv m_{f_R}^{-1} = \sqrt{3 c^2 (n+1) |f_{R0}| \frac{\bar{R}^{n+1}(a=1)}{\bar{R}^{n+2}(a)}} \, , \end{eqnarray*}$$

(15)

where overbars represent background quantities, n and f_R0 are free parameters of the theory, c is the speed of light and the Ricci scalar is given by

$$\begin{eqnarray*} \bar{R}(a) = 12H^2 + 6a HH^\prime \, . \end{eqnarray*}$$

(16)

The dynamics of the linear growth modifications is controlled by

$$\begin{eqnarray*} \epsilon _{f(R)}(k,a) = \frac{(k \lambda _{\rm C}/a)^2}{3 \left[ 1 + (k \lambda _{\rm C}/a)^2 \right]} \, , \end{eqnarray*}$$

(17)

with ϵ_f(R) ≈ 0 for kλ_C/a ≪ 1, and reaches a maximum of ϵ_f(R) ≈ 1/3 for kλ_C/a ≫ 1. GR is restored on all scales for |f_R0| = 0.

The non-linear evolution of top-hat density fluctuations in f(R) gravity is complicated by the violation of mass conservation and shell-crossing (Borisov, Jain & Zhang 2012; Brax & Valageas 2012; Li & Efstathiou 2012; Kopp et al. 2013; Lombriser et al. 2013). Therefore, equation (8) cannot be used to find the exact |$\delta _{\rm L}^{f(R)}(\rho)$| mapping even when neglecting the chameleon screening. However, we can gauge the accuracy of the approximation in equation (9) by looking at how well the reduced cumulants, S_n = 〈δ ⁿ〉 _c/σ^{2(n − 1)}, of the modified gravity PDF can be predicted in the assumption of EdS evolution. The next-to-leading order (NLO) predictions for the first two non-trivial reduced cumulants can be derived as discussed in Uhlemann et al. (2016)

$$\begin{eqnarray*} S_3^{\rm NLO} = S_3^{\rm tree} + \sigma ^2_{\rho } &\left[ \frac{3}{2}S_4^{\rm tree} - 4 S_3^{\rm tree} - 2(S_3^{\rm tree})^2 + 7 \right] \, , \end{eqnarray*}$$

(18a)

$$\begin{eqnarray*} S_4^{\rm NLO} &=& S_4^{\rm tree} + \sigma ^2_{\rho } \left[ 2 S_5^{\rm tree} - \frac{17}{2}S_4^{\rm tree} + 66 S_3^{\rm tree} - 12(S_3^{\rm tree})^2 \right. \nonumber \\ &&\left. - 3 S_4^{\rm tree} S_3^{\rm tree} - 45 \right] \, , \end{eqnarray*}$$

(18b)

where all quantities vary with smoothing scale and redshift, |$\sigma ^2_{\rho }$| is the non-linear variance of the density field, and the standard tree-level (or leading order) expressions can be found in, e.g. Bernardeau et al. (2002). In Fig. 2, we compare these predictions against the reduced cumulants measured from the f(R) and ΛCDM simulations described in Section 3 (see also Hellwing et al. 2013, for similar measurements), with the non-linear variance entering equation (18) also computed from the same simulations (values can be found in Table B1). The striking similarity between the performance in f(R) gravity and that in ΛCDM suggests that the EdS prescription works equally well for the two cosmologies on mildly non-linear scales. The tree level predictions for S_N contain a constant ‘raw value’ along with smoothing corrections from logarithmic derivatives of the linear variance dlog σ_L(R, z)/dlog R. Departures from GR are largely captured by changes to the linear variance entering the tree-level terms. Changes to the raw value of S₃ are negligible compared to this, as was explicitly shown in Bernardeau & Brax (2011) for the Linder γ-model (Linder 2005).

$Reduced cumulants associated with skewness (top) and kurtosis (bottom) of the smoothed matter density PDF at z = 0 (left) and z = 1 (right) for ΛCDM (blue) and f(R) gravity with |fR0| = 10−5 and n = 1 (orange). For each smoothing radius, R = 10, 15, 20 $\mathrm{Mpc}\, h^{-1}$, the coloured bands represent the mean and error on the mean across 8 N-body realizations, and the lines correspond to the theoretical predictions. Solid lines are computed with the tree-level approximation and dashed lines use the next-to-leading order (NLO) correction equation (18), with all vertices derived from the EdS spherical collapse dynamics. The cosmology dependence and modified gravity effects are mostly sourced by the linear variance, while the non-linear variance contributes only to a minor extent.$

Figure 2.

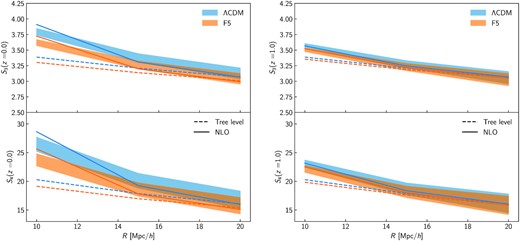
Reduced cumulants associated with skewness (top) and kurtosis (bottom) of the smoothed matter density PDF at z = 0 (left) and z = 1 (right) for ΛCDM (blue) and f(R) gravity with |f_R0| = 10⁻⁵ and n = 1 (orange). For each smoothing radius, R = 10, 15, 20 |$\mathrm{Mpc}\, h^{-1}$|⁠, the coloured bands represent the mean and error on the mean across 8 N-body realizations, and the lines correspond to the theoretical predictions. Solid lines are computed with the tree-level approximation and dashed lines use the next-to-leading order (NLO) correction equation (18), with all vertices derived from the EdS spherical collapse dynamics. The cosmology dependence and modified gravity effects are mostly sourced by the linear variance, while the non-linear variance contributes only to a minor extent.

Open in new tab Download slide

Table 1.

Open in new tab

Baseline ΛCDM cosmological parameters for the three simulation suites used in this work. The first column refers to the extension investigated within that particular suite. Ω_m and Ω_b are, respectively, the present-day background total matter and baryon density in units of the critical density, h = H₀/100 is the dimensionless Hubble constant, A_s and n_s are the amplitude and slope of the primordial power spectrum, and |$\sigma _8^\Lambda$| is the amplitude of mass fluctuations for the baseline ΛCDM cosmology.

	Ω_m	Ω_b	h	n_s	A_s × 10⁹	\|$\sigma _8^\Lambda$\|
DGP	0.3072	0.0481	0.68	0.9645	2.085	0.821
f(R)	0.31315	0.0492	0.6737	0.9652	2.097	0.822
DE	0.26	0.044	0.72	0.96	2.082	0.79

	Ω_m	Ω_b	h	n_s	A_s × 10⁹	\|$\sigma _8^\Lambda$\|
DGP	0.3072	0.0481	0.68	0.9645	2.085	0.821
f(R)	0.31315	0.0492	0.6737	0.9652	2.097	0.822
DE	0.26	0.044	0.72	0.96	2.082	0.79

Table 1.

Open in new tab

Baseline ΛCDM cosmological parameters for the three simulation suites used in this work. The first column refers to the extension investigated within that particular suite. Ω_m and Ω_b are, respectively, the present-day background total matter and baryon density in units of the critical density, h = H₀/100 is the dimensionless Hubble constant, A_s and n_s are the amplitude and slope of the primordial power spectrum, and |$\sigma _8^\Lambda$| is the amplitude of mass fluctuations for the baseline ΛCDM cosmology.

	Ω_m	Ω_b	h	n_s	A_s × 10⁹	\|$\sigma _8^\Lambda$\|
DGP	0.3072	0.0481	0.68	0.9645	2.085	0.821
f(R)	0.31315	0.0492	0.6737	0.9652	2.097	0.822
DE	0.26	0.044	0.72	0.96	2.082	0.79

	Ω_m	Ω_b	h	n_s	A_s × 10⁹	\|$\sigma _8^\Lambda$\|
DGP	0.3072	0.0481	0.68	0.9645	2.085	0.821
f(R)	0.31315	0.0492	0.6737	0.9652	2.097	0.822
DE	0.26	0.044	0.72	0.96	2.082	0.79

Table 2.

Open in new tab

Detection significance for a fiducial f(R) gravity model with |f_R0| = 10⁻⁶, and a fiducial DGP model with Ω_rc = 0.0625. The constraints on f(R) gravity from the PDF are stronger than in DGP owing to the additional skewness produced by the scale-dependent fifth force, which is visible in the |f_R0| derivatives shown in Fig. 11. Moreover, unlike DGP, where the approximate theory PDF matches the ΛCDM prediction at z = 0, in f(R) gravity the PDF differs from that of the standard cosmology at low redshifts, which allows even more non-linear information to be extracted.

	F6 detection	DGPw detection
PDF, 3 scales + prior	5.15σ	1.17σ
P(k), \|$k_{\rm max} = 0.2\ h \,\rm Mpc^{ -1}$\| + prior	2.01σ	2.42σ
PDF + P(k) + prior	13.40σ	5.19σ

	F6 detection	DGPw detection
PDF, 3 scales + prior	5.15σ	1.17σ
P(k), \|$k_{\rm max} = 0.2\ h \,\rm Mpc^{ -1}$\| + prior	2.01σ	2.42σ
PDF + P(k) + prior	13.40σ	5.19σ

Table 2.

Open in new tab

Detection significance for a fiducial f(R) gravity model with |f_R0| = 10⁻⁶, and a fiducial DGP model with Ω_rc = 0.0625. The constraints on f(R) gravity from the PDF are stronger than in DGP owing to the additional skewness produced by the scale-dependent fifth force, which is visible in the |f_R0| derivatives shown in Fig. 11. Moreover, unlike DGP, where the approximate theory PDF matches the ΛCDM prediction at z = 0, in f(R) gravity the PDF differs from that of the standard cosmology at low redshifts, which allows even more non-linear information to be extracted.

	F6 detection	DGPw detection
PDF, 3 scales + prior	5.15σ	1.17σ
P(k), \|$k_{\rm max} = 0.2\ h \,\rm Mpc^{ -1}$\| + prior	2.01σ	2.42σ
PDF + P(k) + prior	13.40σ	5.19σ

	F6 detection	DGPw detection
PDF, 3 scales + prior	5.15σ	1.17σ
P(k), \|$k_{\rm max} = 0.2\ h \,\rm Mpc^{ -1}$\| + prior	2.01σ	2.42σ
PDF + P(k) + prior	13.40σ	5.19σ

Table 3.

Open in new tab

Constraints from mildly non-linear scales on σ₈, w₀, and w_a derived including a prior on {Ω_b, n_s}, as well as dark energy Figure of Merit (FoM) for the matter PDF, power spectrum and their combination.

	\|$\frac{\sigma [\sigma _8]}{\sigma _8^{\rm fid}}$\|	σ[w₀]	σ[w_a]	FoM
PDF, 3 scales + prior	0.18 per cent	0.37	1.25	27
\|$P(k), k_{\rm max}=0.2 \, h\, \mathrm{Mpc}^{-1}$\| + prior	0.45 per ent	0.24	1.03	50
PDF + P(k) + prior	0.17 per cent	0.09	0.40	243

	\|$\frac{\sigma [\sigma _8]}{\sigma _8^{\rm fid}}$\|	σ[w₀]	σ[w_a]	FoM
PDF, 3 scales + prior	0.18 per cent	0.37	1.25	27
\|$P(k), k_{\rm max}=0.2 \, h\, \mathrm{Mpc}^{-1}$\| + prior	0.45 per ent	0.24	1.03	50
PDF + P(k) + prior	0.17 per cent	0.09	0.40	243

Table 3.

Open in new tab

Constraints from mildly non-linear scales on σ₈, w₀, and w_a derived including a prior on {Ω_b, n_s}, as well as dark energy Figure of Merit (FoM) for the matter PDF, power spectrum and their combination.

	\|$\frac{\sigma [\sigma _8]}{\sigma _8^{\rm fid}}$\|	σ[w₀]	σ[w_a]	FoM
PDF, 3 scales + prior	0.18 per cent	0.37	1.25	27
\|$P(k), k_{\rm max}=0.2 \, h\, \mathrm{Mpc}^{-1}$\| + prior	0.45 per ent	0.24	1.03	50
PDF + P(k) + prior	0.17 per cent	0.09	0.40	243

	\|$\frac{\sigma [\sigma _8]}{\sigma _8^{\rm fid}}$\|	σ[w₀]	σ[w_a]	FoM
PDF, 3 scales + prior	0.18 per cent	0.37	1.25	27
\|$P(k), k_{\rm max}=0.2 \, h\, \mathrm{Mpc}^{-1}$\| + prior	0.45 per ent	0.24	1.03	50
PDF + P(k) + prior	0.17 per cent	0.09	0.40	243

In summary, the matter PDF in modified gravity can be predicted using the LDT formalism discussed in Section 2.1 with the following replacements to the decay-rate function in equation (4)

$$\begin{eqnarray*} &\sigma _{\rm L} \longrightarrow \sigma _{\rm L}^{\rm ext} \, , \end{eqnarray*}$$

(19a)

$$\begin{eqnarray*} &\sigma _{\rm NL} \longrightarrow \sigma _{\ln \rho }^{\rm ext} \, , \end{eqnarray*}$$

(19b)

$$\begin{eqnarray*} &\delta _{\rm L}(\rho ,z) \longrightarrow \delta _{\rm L}^{\rm EdS}(\rho) \, , \end{eqnarray*}$$

(19c)

From a practical perspective, by approximating δ_L(ρ, z) with the EdS mapping we can substantially accelerate the calculations of the PDF in exchange for only a minor loss in accuracy – a welcomed feature for applications requiring a large number of evaluations. Note that our approach differs from the method developed in Brax & Valageas (2012), in that they solely focus on modifications to the spherical dynamics by evolving a ‘typical’ density profile whose shape is approximated by the linear power spectrum, while neglecting the effect of the fifth force on the linear variance.

2.2.2 Evolving dark energy

As evident from equation (6), although gravity in smooth dark energy cosmologies is still described by GR (ϵ = 0), the growth of structure can deviate from ΛCDM through changes in the expansion history (w_eff ≠ −1). Here, we will consider equations of state parametrized by (Chevallier & Polarski 2001; Linder 2003)

$$\begin{eqnarray*} w_{\rm eff}(a) = w_0 + w_a(1-a) \, , \end{eqnarray*}$$

(20)

where {w₀, w_a} are phenomenological parameters. In particular, we will refer to models with vanishing w_a as w₀CDM cosmologies, while referring to models with an evolving equation of state as w₀w_aCDM cosmologies.

The non-linear growth of spherical top-hat fluctuations is also affected by the evolving dark energy density via the Hubble parameter in equation (8). However, we follow the approach proposed by Codis et al. (2016) (i.e. keeping the spherical evolution fixed as in EdS) and compute the matter PDF by means of equation (19). We quantify a posteriori the goodness of this choice by comparing our predictions against state-of-the-art cosmological simulations in Section 4.

2.2.3 pyLDT

We have implemented the large-deviation theory predictions described in Section 2.1 together with equations (19) in pyLDT, a modularized and user-friendly python code that takes advantage of the PyJulia interface for computationally intensive tasks. The linear growth for f(R) gravity and DGP is obtained by solving equation (6), while the linear power spectrum for the standard cosmology, as well as for the evolving dark energy models, is computed with camb⁸ (Lewis et al. 2000). Extensions to other modified gravity theories only require either to add a specific function describing changes to the gravitational constant, ϵ(k, a), or to couple the code to dedicated Einstein–Boltzmann solvers such as hi_class (Zumalacárregui et al. 2017; Bellini, Sawicki & Zumalacárregui 2020) and EFTCAMB (Hu et al. 2014).

By default, pyLDT uses an empirical parametrization of the log-density field non-linear variance in terms of the corresponding linear variance given by (Uhlemann et al. 2020)

$$\begin{eqnarray*} \sigma _{\rm NL}^2\rightarrow \sigma _{\ln \rho }^2(R,z) \simeq \frac{\ln \left[1 + \sigma ^2_{\rm L}(R,z)\right]}{\ln \left[1 + \sigma ^2_{\rm L, fid}(R,z)\right]} \sigma _{\ln \rho , \rm fid}^2(R,z) \, . \end{eqnarray*}$$

(21)

This relation allows us to predict the non-linear variance for arbitrary cosmologies given the measured non-linear variance at one fiducial ΛCDM cosmology, |$\sigma ^2_{\rm L}$|⁠, with a typical accuracy of 0.2–1 per cent for the extensions studied in this work. In terms of the matter PDF, for densities |ln ρ − 〈ln ρ〉| < 2σ_ln ρ the lognormal approximation above returns predictions that are within 2 per cent of those based on the non-linear variance measured from the simulations. Unless stated otherwise, direct comparisons to simulations performed in Section 4 are the output of pyLDT with equation (21) replaced by the actual non-linear variance extracted from the simulations. For the Fisher forecasts presented in Section 4.3, instead, we rely on the parametrization in equation (21) to compute the response to changing cosmological parameters and MG scenarios.

3 SIMULATIONS

3.1 f(R) gravity simulations

The simulations in f(R) gravity used for the analysis in this work were carried out with the arepo cosmological simulation code (Springel 2010; Weinberger, Springel & Pakmor 2020) employing the MG extension introduced in Arnold, Leo & Li (2019). The simulation suite consists of eight independent realizations, each run for a baseline ΛCDM cosmology (see Table 1 for the selected parameter values), and for f(R) Hu–Sawicki models with n = 1 and |f_R0| = 10⁻⁵ (F5), 10⁻⁶ (F6). The suite is completed by two pseudo cosmology runs per f(R) model, one for the final output redshift z_f = 0 and the other for z_f = 1. In short, a pseudo cosmology is a ΛCDM cosmology with initial conditions adapted so that its linear matter power spectrum at a later epoch, z_f, matches that of the real beyond-ΛCDM cosmology of interest (Mead 2017; Cataneo et al. 2019),

$$\begin{eqnarray*} P_{\rm L}^{\rm pseudo}(k,z_{\rm f}) = P_{\rm L}^{\rm real}(k,z_{\rm f}) \, . \end{eqnarray*}$$

(22)

Each simulation uses N_p = 1024³ dark matter particles in a L_box = 500 |$\mathrm{Mpc}\, h^{-1}$| side-length box.

The initial conditions (ICs) of the independent realizations were selected such that the large-scale sample, or cosmic, variance in the 3D matter power spectrum is minimal when averaged over the simulations. In order to implement this we created 100 independent initial conditions using 2lptic (Crocce, Pueblas & Scoccimarro 2006) and measured their 3D matter power spectrum. We then considered all possible pairs of these ICs and selected the four ‘best’ pairs according to the following criteria (this follows the procedure outlined in Harnois-Deraps, Giblin & Joachimi 2019 to find ICs with approximately opposite modes on large scale):

each individual power spectrum of a selected pair, as well as their average power spectrum, should deviate as little as possible from the desired linear theory power spectrum for k < k_Ny/2 = πN_p/2L_box;
and the relative difference of each individual power spectrum to the theory spectrum should fluctuate around zero on large scales rather than being positive or negative over large k-ranges to avoid a leakage of power from large to small scales.

To simulate structure formation in f(R) gravity the simulation code has to solve both the standard Newtonian forces and the fifth force. arepo computes the standard gravity forces using a Tree Particle-Mesh algorithm in our simulations. The f(R) gravity forces are computed employing an iterative solver on an adaptively refining mesh which ensures increased resolution in high-density regions (see Arnold et al. 2019, for details).

Due to the very non-linear behaviour of the scalar field in f(R) gravity, tracking its evolution is computationally very expensive. To keep the computational cost of the simulations as small as possible, arepo therefore employs an adaptive timestepping scheme which only updates the MG forces when necessary (Arnold et al. 2019). The standard gravity accelerations are largest (and change most frequently) within large haloes, so that they have to be updated with a very small time-step. However, these very same regions in f(R) gravity are largely screened for |f_R0| ≲ 10⁻⁵. Therefore, the maximum MG acceleration will typically be much smaller than the maximum standard gravity acceleration, allowing a larger MG time-step without compromising the accuracy of the simulations.

3.2 DGP simulations

The DGP simulations used in this work were first presented in Cataneo et al. (2019), and they were carried out using the ecosmog code (Li, Zhao & Koyama 2013; Li et al. 2012a), which is based on the publicly available Newtonian cosmological N-body and hydrodynamical simulation code ramses (Teyssier 2002). This code solves the non-linear equation of motion of the scalar field in the DGP model using adaptively refined meshes, where a cell in the mesh splits into 8 son cells when the effective particle number of simuation particles in it exceeds 8. We have run one realization with box size L_box = 512 Mpc h⁻¹ and particle number N_p = 1024³ for each of the following: a baseline ΛCDM cosmology with cosmological parameters listed in Table 1, two DGP models with Ω_rc = 0.25 (DGPm) and Ω_rc = 0.0625 (DGPw), and the corresponding pseudo cosmologies with final output redshifts z_f = 0 and z_f = 1. These runs adopt a domain grid, i.e. a regular base grid with uniform resolution that covers the entire simulation domain, with 1024³ cells. Although it has been shown that, for many of the usual statistics of matter and dark matter halo fields, very fine simulation meshes are not necessary for the DGP model (Barreira, Bose & Li 2015), in these runs we have not set an upper limit of the highest refinement level, given that they were designed to be used to study novel statistics. At late times, the most refined regions in the simulation domain have a cell size that is 1/2⁶ times the domain grid cell size; this corresponds to an effective force resolution (twice the cell size) of ≃ 15.3 kpc h⁻¹ in those regions.

The ICs of these simulations are again generated using 2lptic, with an initial redshift z_ini = 49. This is lower than the initial redshift used for the f(R) runs described above (z_ini = 127), but the second-order Lagrangian perturbation theory is still a good approximation at z = 49. Since the effect of modified gravity is negligible at z > 49, it is neglected in the ICs.

3.3 Evolving dark energy simulations

For the evolving dark energy cosmologies we used the publicly available matter density PDFs⁹ measured from a suite of single-realization N-body simulations with N_p = 2048³ and L_box = 1024 |$\mathrm{Mpc}\, h^{-1}$| described in Shin et al. (2017). The baseline flat ΛCDM cosmology has the parameters listed in Table 1, and for the w₀w_aCDM cosmologies we have the four pairs {w₀, w_a} = { − 1.5, 0}, { − 0.5, 0}, { − 1, −1}, and { − 1, +1}. The power spectrum normalization at z = 0 is fixed to its baseline value for all dark energy extensions except for {w₀, w_a} = { − 1, +1}, which we found to have a somewhat smaller σ₈.¹⁰

3.4 PDF measurements from the simulations

For our f(R) gravity, DGP and corresponding pseudo and ΛCDM simulations we measured the PDFs of the smoothed matter density field as follows. First, for each snapshot we reconstruct the continuous density field using the Delaunay Tassellation Field Estimator method (Schaap & van de Weygaert 2000) and sample it over a 1024³ mesh, all of which is automatically performed by the public code dtfe¹¹ (Cautun & van de Weygaert 2011). Next, we convolve the sampled density field with spherical top-hat filters of radii R = 10, 15, and 20 |$\mathrm{Mpc}\, h^{-1}$| (an operation we do in Fourier space). Lastly, we construct the PDF by collecting the normalized density values, ρ_R = 1 + δ_R, in 99 logarithmically spaced bins in the range [0.01,100]. In Appendix A, we show that this method produces PDFs in excellent agreement with those obtained by applying the Cloud-in-Cell (CiC) mass assignment scheme. We report variances and means extracted from the simulations for both the density and the log-density fields in Appendix B.

For the DE simulation suite, instead, the smoothed density field was obtained by summing over the mass of all the particles contained in spheres centred at the 2048³ nodes of a regular grid and dividing by the volume of the spheres. In this work, we consider the PDFs measured in spheres of radius R = 10 and 25 |$\mathrm{Mpc}\, h^{-1}$| for the z = 0, 0.5, and 1 snapshots.

4 RESULTS

In the following, we first present our results for the modified gravity and dark energy cosmologies discussed in Section 2.2, and then examine the detection potential of departures from ΛCDM for idealized statistical analyses combining the full shape of the PDF and the matter power spectrum.

4.1 Modified gravity

As discussed in Section 2.2, on mildly non-linear scales the EdS dynamics approximates well the evolution of spherical top-hat density fluctuations even in cosmologies where the law of gravity deviates substantially from GR. Here, by using state-of-the-art simulations we assess how such an approximation impacts the accuracy of the LDT predictions for the matter PDF in two specific modified gravity scenarios, DGPm and F5 (see Section 3 for details). Equivalent results for DGPw and F6 can be found in Appendix C.

Fig. 3 shows how the global shape of the PDF responds to scale-independent (left) or scale-dependent (right) modifications to the linear growth. As expected, when sharing the same initial conditions with ΛCDM both PDFs approach the standard result at high redshifts and exhibit their largest deviations at low redshifts, and do so at a rate specific to the model under consideration. However, there are clear differences that reflect the infinite or finite range of the fifth force. In DGP, structures on all scales are subject to the same modification, and changes to the higher moments of the distribution are mainly driven by increases in the variance. This follows immediately from the expressions for the reduced cumulants in equation (18) – where the tree-level terms are identical for DGP and ΛCDM – and will be explored in more detail below. In f(R) gravity, instead, density fluctuations evolve in different gravity conditions depending on their size. For example, the present-day Compton wavelength in our F5 cosmology is approximately 8 |$\mathrm{Mpc}\, h^{-1}$| (and smaller at earlier times). Therefore, spherical overdensities reaching a final radius R = 10 |$\mathrm{Mpc}\, h^{-1}$| experience very little fifth force for most of their collapse history. In contrast, spherical underdensities have sizes comparable to or smaller than the Compton wavelength (at the same epoch) and thus experience the fifth force in the later stages of their expansion (i.e. z ≲ 2), with the emptiest regions experiencing a full 33 per cent enhancement of the gravitational force. It is this asymmetric behaviour that contributes to the increased skewness of the PDF in f(R) gravity compared to ΛCDM (see also Hellwing et al. 2013), our model equation (19) can capture it thanks to the linear variance term probing different scales, r = Rρ^1/3, depending on the density of the sphere, ρ (see also equation 4).

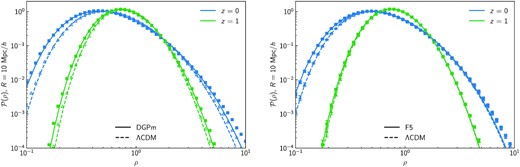
$Matter PDF in spheres of radius R = 10 $\mathrm{Mpc}\, h^{-1}$ at z = 0 (blue) and z = 1 (green) for ΛCDM (dashed) and modified gravity (solid). Left: Data points are the simulation measurements from a single realization (triangles for ΛCDM and squares for DGPm) and lines represent the theory predictions. For DGP the primary effect of the enhanced growth is that of increasing the variance of the distribution, which in turn results in heavier tails, i.e. more under/overdense structures compared to the standard cosmology. Right: data points and corresponding uncertainties are the mean and error on the mean measured from 8 realizations (triangles for ΛCDM and squares for F5). Note that, contrary to the DGP cosmology, the modified growth in f(R) gravity substantially affects the skewness of the distribution, thus leading to an asymmetric enhancement over ΛCDM.$

Figure 3.

Matter PDF in spheres of radius R = 10 |$\mathrm{Mpc}\, h^{-1}$| at z = 0 (blue) and z = 1 (green) for ΛCDM (dashed) and modified gravity (solid). Left: Data points are the simulation measurements from a single realization (triangles for ΛCDM and squares for DGPm) and lines represent the theory predictions. For DGP the primary effect of the enhanced growth is that of increasing the variance of the distribution, which in turn results in heavier tails, i.e. more under/overdense structures compared to the standard cosmology. Right: data points and corresponding uncertainties are the mean and error on the mean measured from 8 realizations (triangles for ΛCDM and squares for F5). Note that, contrary to the DGP cosmology, the modified growth in f(R) gravity substantially affects the skewness of the distribution, thus leading to an asymmetric enhancement over ΛCDM.

Open in new tab Download slide

The central and right-hand panels of Fig. 4 present comparisons of the modified gravity predictions to the simulation measurements for different smoothing radii and redshifts. In all cases, the prescription described by equation (19) provides PDF predictions that are within a few per cent from the simulations, which is consistent with the results for ΛCDM (left-hand panel). Note that the seemingly poorer performance for DGP is likely driven by sample variance, as we only have a single realization for this cosmology. We also note that despite differences in N-body codes (arepo vs gadget-III), mass-assignment schemes (DTFE v CiC), mass resolution (⁠|$m_{\rm p} \approx 10^{10} \, \mathrm{ M}_{\odot }\,h^{ -1}$| vs |$m_{\rm p} \approx 8 \times 10^{10} \, \mathrm{ M}_{\odot }\,h^{ -1}$|⁠), and number of realizations (8 vs 100) the left-most panels of Fig. 4 illustrate that our measured PDFs are very much consistent with those of Uhlemann et al. (2020) (see their fig. 7), irrespective of smoothing radius and redshift.

$Residuals between the measured and predicted matter PDF normalized to the theory predictions for z = 0 (top) and z = 1 (bottom) in ΛCDM (left), f(R) gravity (centre), and DGP (right). When data points and error bars are both present they correspond to the mean and error on the mean across 8 realizations. Different colours indicate the radii of the spheres used for smoothing the density field, 10 $\mathrm{Mpc}\, h^{-1}$ (blue), 15 $\mathrm{Mpc}\, h^{-1}$ (orange), and 20 $\mathrm{Mpc}\, h^{-1}$ (green). The solid and dashed lines mark 1 and 2 per cent accuracy, respectively. Despite significant changes to the growth of structure, the accuracy of the modified gravity predictions based on the EdS spherical dynamics is comparable to that of the standard cosmology.$

Figure 4.

Residuals between the measured and predicted matter PDF normalized to the theory predictions for z = 0 (top) and z = 1 (bottom) in ΛCDM (left), f(R) gravity (centre), and DGP (right). When data points and error bars are both present they correspond to the mean and error on the mean across 8 realizations. Different colours indicate the radii of the spheres used for smoothing the density field, 10 |$\mathrm{Mpc}\, h^{-1}$| (blue), 15 |$\mathrm{Mpc}\, h^{-1}$| (orange), and 20 |$\mathrm{Mpc}\, h^{-1}$| (green). The solid and dashed lines mark 1 and 2 per cent accuracy, respectively. Despite significant changes to the growth of structure, the accuracy of the modified gravity predictions based on the EdS spherical dynamics is comparable to that of the standard cosmology.

Open in new tab Download slide

Fig. 5 shows in detail how the PDFs in the two modified gravity scenarios analysed in this work differ from their ΛCDM counterparts. With a lowering of the peak compensated by heavier tails, DGP modifications (left-hand panel) resemble very closely changes in the power spectrum normalization (cf. fig. 8 in Uhlemann et al. 2020). This can be explained by the near equivalence between the boost of the linear matter power spectrum amplitude induced by the fifth force and an increase in σ₈. More complicated variations to the shape of the PDF in f(R) gravity (right-hand panel) follow from the combination of two effects: suppression of the non-linear variance compared to a DGP cosmology with a similar σ₈, and scale-mixing regulated by the redshift-dependent Compton wavelength. The former is a direct consequence of the chameleon screening mechanism acting on a broad range of scales, even in the mildly non-linear regime (see e.g. Cataneo et al. 2019); while the latter preferentially enhances the formation of density fluctuations with initial comoving size Rρ^1/3 ≲ λ_C(z)(1 + z). At high redshifts and for large smoothing radii, this condition becomes increasingly difficult to satisfy for typical values of the density field (i.e. |ln ρ − 〈ln ρ〉| < 3σ_ln ρ). As the PDF approaches the ΛCDM result, the small residual deviations can be described by simple changes in the variance. The solid lines in both panels of Fig. 5 represent the theory predictions with the log-density variances measured from the simulations, while the dashed lines use the lognormal approximation equation (21) to compute the modified gravity |$\sigma _\mu ^2$| from that of the corresponding ΛCDM cosmology. The LDT prescription, even when ignoring the impact of the fifth force on the evolution of spherical density fluctuations can capture deviations from GR remarkably well. As we shall see below, a detailed comparison to standard cosmologies sharing the same linear theory predictions (the so-called pseudo-cosmologies) can help isolate very small effects that are characteristic of the non-standard interaction.

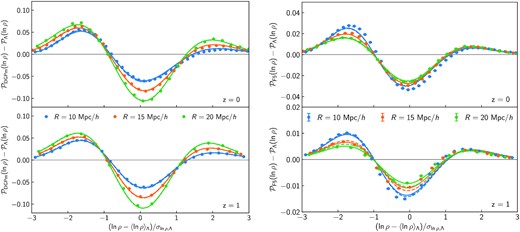
$Simulated (data points) and predicted (lines) differences from ΛCDM of the modified gravity matter PDF at z = 0 (top) and z = 1 (bottom). The density field is averaged in spheres of radius R = 10 $\mathrm{Mpc}\, h^{-1}$ (blue), 15 $\mathrm{Mpc}\, h^{-1}$ (orange), and 20 $\mathrm{Mpc}\, h^{-1}$ (green). Solid lines are obtained from the measured non-linear variance, $\sigma ^2_\mu$, while dashed lines use equation (21) in pyLDT. The close agreement between the two type of predictions supports the use of the lognormal approximation for the non-linear variance. Left: in DGP the shape of these changes is very similar to that induced by variations in σ8 (cf. fig. 8 in Uhlemann et al. 2020). Right: f(R) gravity departures from the standard cosmology are more prominent for underdense regions and become less significant with increasing smoothing radii owing to the finite range of the fifth force.$

Figure 5.

Simulated (data points) and predicted (lines) differences from ΛCDM of the modified gravity matter PDF at z = 0 (top) and z = 1 (bottom). The density field is averaged in spheres of radius R = 10 |$\mathrm{Mpc}\, h^{-1}$| (blue), 15 |$\mathrm{Mpc}\, h^{-1}$| (orange), and 20 |$\mathrm{Mpc}\, h^{-1}$| (green). Solid lines are obtained from the measured non-linear variance, |$\sigma ^2_\mu$|⁠, while dashed lines use equation (21) in pyLDT. The close agreement between the two type of predictions supports the use of the lognormal approximation for the non-linear variance. Left: in DGP the shape of these changes is very similar to that induced by variations in σ₈ (cf. fig. 8 in Uhlemann et al. 2020). Right: f(R) gravity departures from the standard cosmology are more prominent for underdense regions and become less significant with increasing smoothing radii owing to the finite range of the fifth force.

Open in new tab Download slide

4.1.1 Pseudo-cosmologies

Although, by definition, for the pseudo cosmologies we have |$\sigma _{\rm L}^{\rm pseudo}(R,z_{\rm f}) = \sigma _{\rm L}^{\rm real}(R,z_{\rm f})$| (see equation 22), new late-time physics affects the growth of structure beyond the linear regime. Therefore, the non-linear power spectrum of the pseudo-cosmology differs from its real non-ΛCDM counterpart and |$\sigma _{\rm NL}^{\rm pseudo}(R,z_{\rm f}) \ne \sigma _{\rm NL}^{\rm real}(R,z_{\rm f})$|⁠. We can use this to compute the PDFs of the pseudo-MG cosmologies and compare them to the predictions for DGP and f(R) gravity – given the identity in equation (22), any significant difference not captured by a simple change to the non-linear variance will then signal modifications to the spherical dynamics due to the action of the fifth force. We recall that the linear power spectrum determines the scale dependence of the linear variance and hence the density dependence of the exponent of the PDF given by equation (4), while the non-linear power spectrum determines the non-linear variance and hence the width of the PDF. To a lesser extent, the non-linear variance can also alter the scale dependence of the PDF through its impact on the rescaling step in the PDF construction (see equation 5c).

Fig. 6 shows the difference between the real and pseudo-cosmology PDFs for DGPm (left-hand panel) and F5 (right-hand panel). First, let us note that these differences are about an order of magnitude smaller than the departures of modified gravity from ΛCDM shown in Fig. 5. In general, the two PDFs agree to per cent level or better for |ln ρ − 〈ln ρ〉| < 2σ_ln ρ. Thus, for densities not too far into the tails and in the mildly non-linear regime, the pseudo and real cosmology PDFs become indistinguishable for all intents and purposes. This result confirms the findings of Cataneo et al. (2019) and extends them to statistics describing non-Gaussian properties of the density field. Our predictions using the EdS spherical collapse for both the pseudo and the real MG cosmologies (solid lines) can partially explain the observed minute differences as changes in the variance of the distribution, especially at high redshifts. To gauge the contribution of the fifth force to the remaining unexplained difference, we also compute the PDFs for DGPm by including the linearized modification to the gravitational interaction (equation 11) into the dynamics of spherical top-hat density fluctuations (equation 8). These are shown as dashed lines in Fig. 6. Although the modified non-linear evolution can better account for the differences between the real and pseudo-cosmology, residuals associated with the neglected screening mechanism and intrinsic inaccuracies of the LDT formalism persist. To fully disentangle these two contributions one should run linearized modified gravity simulations (akin to Schmidt 2009; Koyama et al. 2009), which is, however, beyond the scope of this work. For the case of f(R) gravity shown in the right-hand panel, a change in the variance (solid line) can only partially explain their observed differences. Modifications to the spherical collapse in f(R) gravity due to non-linear couplings even in the absence of screening (such as modelled by Brax & Valageas 2012) are a potential source of the remaining discrepancy. The shape of the differences hints at an additional skewness with a slightly increased S₃ that cannot be captured by the EdS-based approximation in equation (9). The overall good agreement of the PDF in the real and pseudo-cosmologies together with the successful prediction of their minute qualitative differences validate our PDF modelling assumptions for modified gravity.

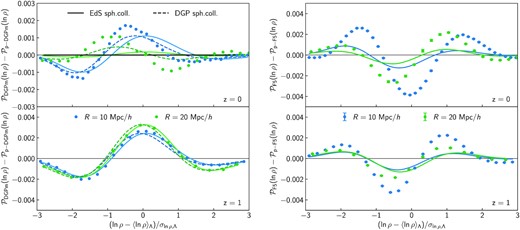
$Simulated (data points) and predicted (lines) differences of the modified gravity matter PDFs from their pseudo-cosmology counterparts at z = 0 (top) and z = 1 (bottom). The density field is averaged in spheres of radius R = 10 $\mathrm{Mpc}\, h^{-1}$ (blue) and 20 $\mathrm{Mpc}\, h^{-1}$ (green). Solid lines are obtained from the measured non-linear variance, $\sigma ^2_\mu$, and the EdS mapping shown in Fig. 1. Note that the amplitude of these differences is about ten times smaller than in Fig. 5, confirming the remarkable similarities between the pseudo and real cosmology on mildly non-linear scales. Left: by replacing the EdS spherical evolution with that produced by the linearized DGP model (dashed lines) we can better predict some of the minute differences sourced by pure modifications to GR which are not captured by simple changes to σ8 in a ΛCDM cosmology. Remaining differences are likely the result of modelling inaccuracies in LDT and unaccounted for Vainshtein screening phenomenology. Right: contrary to DGP, the violation of Birkhoff’s theorem in f(R) gravity precludes any attempt to find a simple solution to the evolution of spherical top-hat density perturbations even in the absence of screening mechanism (Borisov et al. 2012; Brax & Valageas 2012; Kopp et al. 2013). Here we only show the predictions accounting for changes in the non-linear variance and note that both the finite range of the fifth force and chameleon screening slightly modify the spherical collapse dynamics, which in turn leads to small additional variations in the PDF.$

Figure 6.

Simulated (data points) and predicted (lines) differences of the modified gravity matter PDFs from their pseudo-cosmology counterparts at z = 0 (top) and z = 1 (bottom). The density field is averaged in spheres of radius R = 10 |$\mathrm{Mpc}\, h^{-1}$| (blue) and 20 |$\mathrm{Mpc}\, h^{-1}$| (green). Solid lines are obtained from the measured non-linear variance, |$\sigma ^2_\mu$|⁠, and the EdS mapping shown in Fig. 1. Note that the amplitude of these differences is about ten times smaller than in Fig. 5, confirming the remarkable similarities between the pseudo and real cosmology on mildly non-linear scales. Left: by replacing the EdS spherical evolution with that produced by the linearized DGP model (dashed lines) we can better predict some of the minute differences sourced by pure modifications to GR which are not captured by simple changes to σ₈ in a ΛCDM cosmology. Remaining differences are likely the result of modelling inaccuracies in LDT and unaccounted for Vainshtein screening phenomenology. Right: contrary to DGP, the violation of Birkhoff’s theorem in f(R) gravity precludes any attempt to find a simple solution to the evolution of spherical top-hat density perturbations even in the absence of screening mechanism (Borisov et al. 2012; Brax & Valageas 2012; Kopp et al. 2013). Here we only show the predictions accounting for changes in the non-linear variance and note that both the finite range of the fifth force and chameleon screening slightly modify the spherical collapse dynamics, which in turn leads to small additional variations in the PDF.

Open in new tab Download slide

4.2 Evolving dark energy

Analogously to modified gravity, the fractional deviations of the theory predictions from the simulation measurements shown in Fig. 7 confirm that, despite neglecting the impact of dark energy on the spherical collapse, the LDT prescription in equation (19) yields accuracies within a few per cent for densities |ln ρ − 〈ln ρ〉| < 2σ_ln ρ. Although the results presented here are only for density fields averaged in spheres of radius R = 10 |$\mathrm{Mpc}\, h^{-1}$|⁠, we found similar or better performance for larger smoothing radii. Fig. 8 illustrates that in most cases deviations from the cosmological constant can be described very well by simple changes to the non-linear variance (lines). In fact, after fixing the standard cosmological parameters, the w₀w_aCDM and ΛCDM cosmologies share the same shape of the linear matter power spectrum, and when using the EdS approximation for the spherical dynamics the only degree of freedom left in equation (4) is the non-linear variance. However, the small yet visible discrepancies between theory and simulations for the w₀ = −0.5 cosmology suggest that in this extreme scenario the background expansion appreciably alters the spherical evolution and it should be taken into account to accurately predict the measured PDF deviations from ΛCDM at both redshifts.

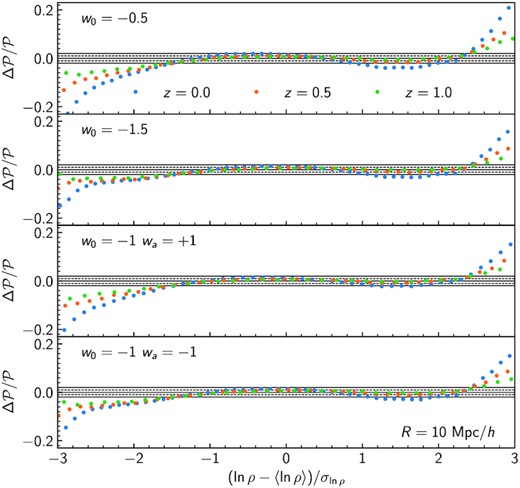
$Residuals between the measured and predicted matter PDF in spheres of radius 10 $\mathrm{Mpc}\, h^{-1}$ normalized to the theory predictions for various evolving dark energy cosmologies (from top to bottom). Different colours correspond to z = 0 (blue), z = 0.5 (orange), and z = 1 (green). The solid and dashed lines mark the 1 and 2 per cent accuracy, respectively. Note that for these simulations only one realization is available, and the estimation of the smoothed density field differs from that used for the modified gravity simulations. Despite these differences the residuals are consistent with those for ΛCDM, f(R) gravity, and DGP in Fig. 4.$

Figure 7.

Residuals between the measured and predicted matter PDF in spheres of radius 10 |$\mathrm{Mpc}\, h^{-1}$| normalized to the theory predictions for various evolving dark energy cosmologies (from top to bottom). Different colours correspond to z = 0 (blue), z = 0.5 (orange), and z = 1 (green). The solid and dashed lines mark the 1 and 2 per cent accuracy, respectively. Note that for these simulations only one realization is available, and the estimation of the smoothed density field differs from that used for the modified gravity simulations. Despite these differences the residuals are consistent with those for ΛCDM, f(R) gravity, and DGP in Fig. 4.

Open in new tab Download slide

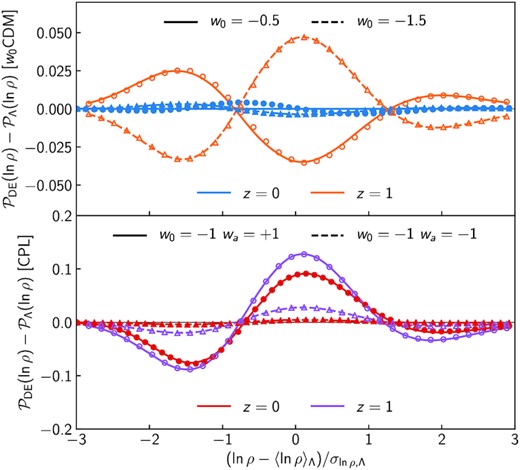
$Measured (data points) and predicted (lines) differences from ΛCDM of the w0CDM (top) and the w0waCDM (bottom) cosmologies at z = 0 and z = 1. The density field is averaged in spheres of radius R = 10 $\mathrm{Mpc}\, h^{-1}$ and the linear power spectra for all cosmologies (except {w0, wa} = {−1, +1}) are normalized such that $\sigma _8^{\rm DE}(z=0) = \sigma _8^{\Lambda }(z=0)$. Predictions are obtained from the measured non-linear variance, $\sigma ^2_\mu$, together with EdS spherical collapse. Except for w0 = −0.5, knowledge of the non-linear variance is enough to accurately describe departures from the standard cosmology.$

Figure 8.

Measured (data points) and predicted (lines) differences from ΛCDM of the w₀CDM (top) and the w₀w_aCDM (bottom) cosmologies at z = 0 and z = 1. The density field is averaged in spheres of radius R = 10 |$\mathrm{Mpc}\, h^{-1}$| and the linear power spectra for all cosmologies (except {w₀, w_a} = {−1, +1}) are normalized such that |$\sigma _8^{\rm DE}(z=0) = \sigma _8^{\Lambda }(z=0)$|⁠. Predictions are obtained from the measured non-linear variance, |$\sigma ^2_\mu$|⁠, together with EdS spherical collapse. Except for w₀ = −0.5, knowledge of the non-linear variance is enough to accurately describe departures from the standard cosmology.

Open in new tab Download slide

4.3 Fisher forecasts

This section presents forecasts for DGP and f(R) gravity and w₀w_aCDM combining the matter PDF and the matter power spectrum on mildly non-linear scales. For the MG models we determine the ability of future experiments to detect relatively small deviations from GR (i.e. F6 and DGPw) at a statistical significance >5σ (see Table 2), while for evolving DE we will be interested in the FoM using ΛCDM as fiducial cosmology (see Table 3).

4.3.1 Fisher formalism

To forecast the errors on a set of cosmological parameters, |$\vec{\theta }$|⁠, we use the Fisher matrix formalism. The Fisher matrix given a (set of) summary statistics in the data vector |$\vec{S}$| is defined as

$$\begin{eqnarray*} F_{ij}= \sum _{\alpha ,\beta }\frac{\partial S_\alpha }{\partial \theta _i}C^{-1}_{\alpha \beta }\frac{\partial S_\beta }{\partial \theta _j}~, \quad \end{eqnarray*}$$

(23)

where S_α is the α-th element of the data vector |$\vec{S}$| and C⁻¹ denotes the matrix-inverse of the covariance matrix C, whose components are

$$\begin{eqnarray*} C_{\alpha \beta } = \left\langle \left(S_\alpha -\bar{S}_\alpha \right)\left(S_\beta - \bar{S}_\beta \right) \right\rangle \, ,\quad \bar{S}_\alpha = \langle S_\alpha \rangle ~. \end{eqnarray*}$$

(24)

The parameter covariance matrix |$\mathbf {C}(\vec{\theta })$| is then obtained as inverse of the Fisher matrix. In the Fisher formalism, marginalization over a subset of parameters is achieved by simply selecting the appropriate sub-elements of the parameter covariance.

We consider three data vectors for our forecasts, corresponding to the three sets of constraints in Figs 9, 10, and 12. These are the PDF alone, the matter power spectrum alone, and a stacked data vector which combines both the PDF and the matter power spectrum. For the PDF data vector, we only use the central region of the PDF around the peak (located in underdense regions), removing the lowest |$3{{\ \rm per\ cent}}$| and highest 10 per cent of densities (as advocated in Uhlemann et al. 2020). We choose this approach in order to limit the impact of small-scale effects (like baryonic feedback, non-linear galaxy bias, shot noise, and redshift-space distortions) that are more severe for rare events and would otherwise degrade the constraining power when moving from the 3D matter PDF to an actual observable like the spectroscopic tracer PDF. For the matter power spectrum data vector, we limit ourselves to mildly non-linear scales up to |$k_{\rm max}=0.2\, h$|Mpc⁻¹ to ensure the accuracy of theoretical derivatives from fitting functions, see Fig. C3. We found the conservative scale cut for the power spectrum to be crucial to facilitate an agreement between parameter constraints and degeneracy directions from predicted and simulated derivatives, especially when considering the full set of cosmological parameters. For all cosmological parameters, we compute partial derivatives from two-point finite differences

$$\begin{eqnarray*} \frac{\partial \vec{S}}{\partial \theta }\simeq \frac{\vec{S}(\theta +d\theta)-\vec{S}(\theta -d\theta)}{2d\theta }\, . \end{eqnarray*}$$

(25)

We rely on partial derivatives determined from theoretical predictions for the matter PDF from pyLDT and the matter power spectrum from ReACT (Bose et al. 2020a) combined with hmcode (Mead et al. 2021), which provides flexibility to compute constraints or the detection significance for extended models at the desired fiducial cosmology. The step sizes have been chosen to ensure convergence of the derivatives, and agree with the step sizes used in the quijote simulation suite for the set of w₀CDM parameters. The theory generated derivatives for w₀CDM parameters are validated with measurements from the Quijote simulations in Appendix C. As discussed in Appendix C, we adopt Gaussian priors for {Ω_b, n_s} to ensure compatibility of the matter power spectrum derivatives between simulations and theoretical predictions. The prior widths correspond to σ[n_s] = 0.0041 (Planck Collaboration VI 2020) and σ[100Ω_bh²] = 0.052 (Cooke et al. 2016; Abbott et al. 2018).

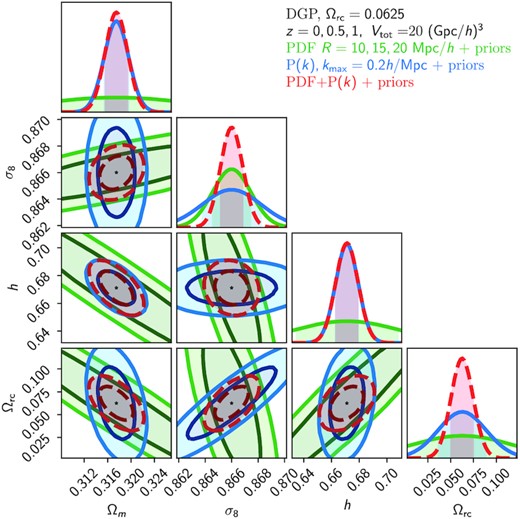
Marginalized Fisher forecast constraints on {Ωm, σ8, h, Ωrc} using external prior information on ns and Ωb (as described in the text) for a DGPw fiducial cosmology. Contours correspond to the matter PDF at 3 scales and 3 redshifts (green), the matter power spectrum up to k = 0.2 h Mpc−1 (blue), and their combination, which includes the covariance between the PDF and power spectrum (red dashed).

Figure 9.

Marginalized Fisher forecast constraints on {Ω_m, σ₈, h, Ω_rc} using external prior information on n_s and Ω_b (as described in the text) for a DGPw fiducial cosmology. Contours correspond to the matter PDF at 3 scales and 3 redshifts (green), the matter power spectrum up to k = 0.2 h Mpc⁻¹ (blue), and their combination, which includes the covariance between the PDF and power spectrum (red dashed).

Open in new tab Download slide

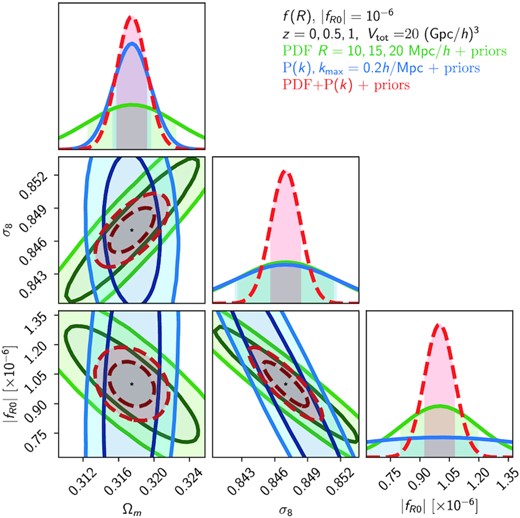
Marginalized Fisher forecast constraints on {Ωm, σ8, |fR0|} using external prior information on ns and Ωb (as described in the text) for an F6 fiducial cosmology. Contours correspond to the matter PDF at 3 scales and 3 redshifts (green), the matter power spectrum up to k = 0.2 h Mpc−1 (blue), and their combination, which includes the covariance between the PDF and the power spectrum (red dashed).

Figure 10.

Marginalized Fisher forecast constraints on {Ω_m, σ₈, |f_R0|} using external prior information on n_s and Ω_b (as described in the text) for an F6 fiducial cosmology. Contours correspond to the matter PDF at 3 scales and 3 redshifts (green), the matter power spectrum up to k = 0.2 h Mpc⁻¹ (blue), and their combination, which includes the covariance between the PDF and the power spectrum (red dashed).

Open in new tab Download slide

Figure 11.

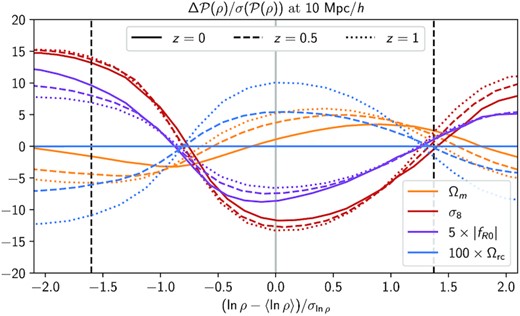
Comparison of PDF differences divided by the error on the PDF as estimated from the quijote simulations. Line style indicates the redshift, while colour indicates parameter being deviated. The vertical lines represent the region used at each redshift to construct the PDF data vector. While the shape of the σ₈ and Ω_rc derivatives are similar, their different redshift dependence allows the degeneracy to be broken when combining redshifts. The f_R0 derivatives, in addition to having different redshift dependence, exhibit a skewness not present in the σ₈ derivatives, allowing significant information to be extracted even at a single redshift, including z = 0. Note that the amplitudes between parameters should not be directly compared, as the f_R0 and Ω_rc lines have been scaled up to be visible on the same scale as σ₈.

Open in new tab Download slide

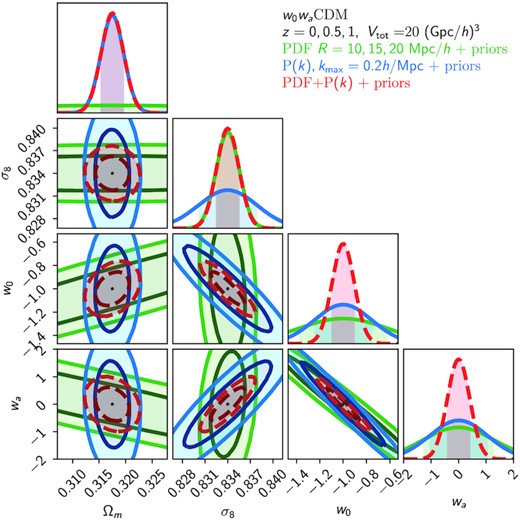
Fisher forecast constraints on {Ωm, σ8, w0, wa} (marginalized over {Ωb, ns} using the external prior described in the text) for the w0CDM model around the fiducial quijote ΛCDM cosmology. Contours correspond to the matter PDF at 3 scales and 3 redshifts (green), the matter power spectrum up to k = 0.2 h Mpc−1 (blue), and their combination which includes the covariance between the PDF and power spectrum (red dashed).

Figure 12.

Fisher forecast constraints on {Ω_m, σ₈, w₀, w_a} (marginalized over {Ω_b, n_s} using the external prior described in the text) for the w₀CDM model around the fiducial quijote ΛCDM cosmology. Contours correspond to the matter PDF at 3 scales and 3 redshifts (green), the matter power spectrum up to k = 0.2 h Mpc⁻¹ (blue), and their combination which includes the covariance between the PDF and power spectrum (red dashed).

Open in new tab Download slide

In this work, we use the covariance matrix obtained from a set of 15 000 simulations of the quijote N-body simulation suite (Villaescusa-Navarro et al. 2020) using the fiducial ΛCDM cosmology (Ω_m = 0.3175, Ω_b = 0.049, H₀ = 68 km s⁻¹ Mpc⁻¹, n_s = 0.96, σ₈ = 0.834). The joint covariance matrix of the mildly non-linear matter PDF and the matter power spectrum is described in Uhlemann et al. (2020), see particularly their fig. 12. We make the approximation that the covariance matrix of the matter PDF and matter power spectrum in the mildly non-linear regime is independent of cosmology and theory of gravity and well-captured by the 15 000 simulations of the quijote simulation suite. To mitigate potential effects of modified gravity on the covariance, we fix the standard cosmological parameters to the values of the fiducial quijote cosmology. In particular, we set A_s = 2.13 × 10⁻⁹ such that σ₈ increases only slightly for the modified gravity cosmologies, that is, by 1.6 per cent for F6 and 3.8 per cent for DGPw. As those are small perturbations from the fiducial ΛCDM cosmology, they will only induce a small error on the true covariances and hence only marginally affect parameter constraints. As this error will affect both the PDF and power spectrum covariance in a similar way, comparisons of their respective constraining power are expected to be robust. For future high precision cosmology, covariance estimation for PDF-based observables from galaxy clustering and weak lensing can rely on tuned lognormal mocks (Gruen et al. 2018; Boyle et al. 2021), potentially complemented with predictions for effects induced by variations in the local mean density (Jamieson & Loverde 2020). To correct for a potential bias depending on the size of the data vector N_S compared to the number of simulations N_sim, we multiply the inverse of the simulated covariance matrix by the Kaufman–Hartlap factor (Kaufman 1967; Hartlap, Simon & Schneider 2006), f_KH = (N_sim − 2 − N_S)/(N_sim − 1). Since in our case the number of simulations for covariance estimation is very large (15 000) compared to the maximal length of the data vector (218 for our three-redshift analysis of the PDF at three scales and the mildly non-linear power spectrum), this factor will be close to one throughout, f_KH ≥ 0.985. We mimic a Euclid-like effective comoving survey volume of |$V \approx 20 \, ({\rm Gpc}\,h^{ -1})^3$| split across three redshift bins of equal width Δz = 0.2 located at z = 0, 0.5, 1 by multiplying the covariance at each redshift with the ratio of the comoving shell volume to the simulation volume |$V_{\rm sim}=1 \, ({\rm Gpc}\,h^{ -1})^3$|⁠.

4.3.2 Modified gravity

We now compare the constraining power of the matter PDF to that of the matter power spectrum (with |$k_{\rm max} = 0.2 \ h \ \rm Mpc^{-1}$|⁠) for DGP and f(R) gravity. In all cases, the forecasts shown are marginalized over all remaining ΛCDM parameters.

Figs 9 and 10 show the Fisher forecasts for DGP and f(R) cosmologies, respectively. Table 2 summarizes the detection significance for particular flavours of these modified gravity models expressed in units of standard deviation from GR. In a universe where the growth of structure is governed by DGP gravity with Ω_rc = 0.0625, a 5σ detection of modified gravity can still be reached by combining the matter PDF with the matter power spectrum. Combining the PDF and power spectrum as complementary probes is beneficial in both MG scenarios. In particular, for DGP the matter PDF is important for constraining σ₈, while the power spectrum is important for obtaining the correct value of Ω_m. This is because while Ω_m has a distinctive signature in the power spectrum (see Fig. C3), the matter PDF is sensitive to the total matter density only through its impact on the skewness and the linear growth factor, D(z). The anticorrelation between the Hubble parameter, h, and Ω_m visible in Fig. 9 can be explained by their similar impact on the skewness of the PDF (see fig. 9 in Uhlemann et al. 2020). Evolving dark energy also presents this feature, although we do not show it in Fig. 12 as it does not create any unexpected degeneracy directions as in the DGP model.

The partial degeneracy in the PDF between σ₈ and the modified gravity parameters, |f_R0| or Ω_rc, seen in Figs 9 and 10 is understood by noticing that the presence of modified gravity changes the width of the matter PDF, as can be seen in Fig. 11. However, the responses of the PDF to the presence of modified gravity or changes in σ₈ have different scale and time dependence, therefore by combining the information from different scales and redshifts we can break this degeneracy. Fig. 11 shows that σ₈ and Ω_rc have opposite effects on the PDF, which would lead to a positive correlation between these parameters. However, in Fig. 9 the σ₈–Ω_rc plane shows an anticorrelation for the PDF, which is indirectly induced by the strong positive correlation between Ω_rc and h. We checked that when h is fixed to its fiducial value, rather than marginalized over, the PDF contours do indeed display a positive correlation between σ₈ and Ω_rc, as indicated by the derivatives in Fig. 11.

In the case of f(R) gravity, the matter PDF is particularly useful, reaching a 5σ detection before combining with the matter power spectrum. This is due to an additional skewness in the |f_R0| derivatives sourced by the scale-dependent fifth force and the fact that the PDF holds information about deviations from ΛCDM even at redshift 0, unlike in DGP. However, Fig. C2 shows that using the non-linear variance predicted by equation (21) is a better approximation in DGP than in f(R) gravity, and we thus expect the forecasted constraints to be more reliable for the DGP model than for f(R) gravity.

4.3.3 Evolving dark energy

In this section, we consider a dark energy fluid with an equation of state described by equation (20). Many of the features of the parameter constraints from the matter PDF and matter power spectrum are similar to the features seen for scale-independent modifications to GR. In particular, the matter PDF is much better at constraining σ₈ than the power spectrum, while the power spectrum more directly measures Ω_m, as can be seen in Fig. 12. A summary of constraints on σ₈, w₀, and w_a, along with the dark energy Figure of Merit (FoM) is shown in Table 3. The FoM is calculated from the inverse of the error ellipse area in the w₀–w_a plane as

$$\begin{eqnarray*} \mathrm{FoM} = \frac{1}{\sqrt{\det (\mathbf {C}(w_0, w_a))}}\, , \end{eqnarray*}$$

(26)

where |$\mathbf {C}(w_0, w_a)$| is the parameter covariance matrix marginalized over all parameters except w₀ and w_a. The combined FoM for the matter PDF and matter power spectrum is a factor of 9 larger than the PDF alone, and 5 times better than the power spectrum when only information from the mildly non-linear regime is included. This combined FoM of 243 sits between the range of the pessimistic and optimistic predictions for combined galaxy clustering and weak lensing from Euclid (see table 13 from Euclid Collaboration 2020). The PDF is sufficient to measure σ₈ to sub-per cent accuracy, with the inclusion of the power spectrum improving this constraint only marginally.

Increasing either w₀ or w_a increases the growth rate and hence the variances at z > 0 (with marginal changes at z = 0 due to fixed σ₈), which amounts to an anticorrelation between w₀ and w_a. Most of the other degeneracy directions in the w₀w_aCDM case can be understood by considerations of linear theory. Changing a single parameter at fixed σ₈ (or similarly when σ₈ is allowed to vary) induces a change in the growth rate. Suitable pairs of parameters can then produce growth rates close to the fiducial cosmology. For example, the positive correlation between w₀ and Ω_m arises from the suppression of the growth rate by increasing Ω_m while keeping σ₈ fixed. While one would expect w₀ and w_a to vary in the same way with Ω_m and σ₈, they in fact vary in opposing directions as shown in Fig. 12. However, when w₀ is fixed to its fiducial value, rather than marginalized over, the contours do indeed flip in sign to the direction expected, suggesting that the tight anticorrelation in the w₀–w_a plane dominates the other degeneracies.

5 SUMMARY AND DISCUSSION

To harness the full statistical power of current and forthcoming galaxy surveys we must push past 2-point correlation functions. Gravitationally driven non-Gaussianities are particularly sensitive to the late-time growth of structure. As a result, the full shape of the matter density PDF responds strongly to departures from GR and the cosmological constant making it a promising probe of new physics. In this work we built on the findings of Uhlemann et al. (2016) with the aim of extending the large-deviation theory formalism for the 3D matter PDF to cosmologies with universally coupled fifth forces and non-standard expansion histories. As for ΛCDM, our analytical predictions are derived from linear theory calculations and spherical collapse dynamics, with the fiducial non-linear variance being a free parameter that can be measured from simulations. However, contrary to previous approaches (cf. Brax & Valageas 2012), we approximate the collapse or expansion of spherical top-hat fluctuations with a EdS evolution, and showed that in the mildly non-linear regime this choice produces PDFs matching the simulations to better than a few per cent around the peak of the distribution. Although in this work we analysed in great detail specific modified gravity and dark energy cosmologies, our method is readily applicable to more general models, as changes to the standard cosmology only enter the PDF through the linear matter power spectrum and the non-linear variance of the smoothed density field. We also implemented the LDT equations in pyLDT, an easy-to-install and user-friendly python package that enables fast calculations of the PDF of the spherically averaged matter density field in ΛCDM, modified gravity and evolving dark energy cosmologies. We employed pyLDT in Fisher analyses of a Euclid-like survey to estimate the additional information brought in by the matter PDF compared to 2-point statistics restricted to mildly non-linear scales. In all cases investigated the constraints on new physics (be it G_eff ≠ G_Newton or w ≠ −1) from the combination of the matter PDF and power spectrum are substantially tighter than those obtained separately by the two statistics – a clear sign of complementarity (see also Uhlemann et al. 2020, for massive neutrino cosmologies). For modified gravity, adding the matter PDF to the power spectrum can double the detection significance for the DGPw model to lift it above 5σ and increase the F6 detection significance sixfold as summarized in Table 2. For dark energy, combining the matter PDF with the power spectrum can also double our constraining power on the clustering amplitude, σ₈, and both of the dark energy equation of state parameters w₀ and w_a as shown in Table 3.

In spite of the idealized experimental set-up focusing on the statistics of the 3D matter field, our results are also encouraging for more realistic scenarios. The formalism described in this paper can be translated to galaxy survey observables accessible from weak lensing (Barthelemy et al. 2020; Boyle et al. 2021; Thiele, Hill & Smith 2020), galaxy clustering (Repp & Szapudi 2020; Friedrich et al. 2022) as well as their combination in density-split statistics (Friedrich et al. 2018; Gruen et al. 2018), which have been shown to be able to simultaneously extract galaxy bias, galaxy stochasticity, and cosmological parameters. In particular, the LDT approach developed for the ΛCDM lensing convergence PDF could be straightforwardly applied to the entire class of scalar–tensor theories with lensing potential |$\Phi _{\rm lens}^{\rm MG} \approx \Phi _{\rm lens}^{\rm GR}$|⁠, which includes f(R) gravity and DGP. The PDF could also be useful for disentangling modified gravity and massive neutrinos (Giocoli, Baldi & Moscardini 2018), but we leave the combination of those two scenarios for future work. Including the PDF of observable fields like cosmic shear or galaxy counts could help break degeneracies between astrophysical (e.g. baryonic feedback, intrinsic alignment, and galaxy bias) and cosmological parameters present in the analyses of two-point statistics (Patton et al. 2017; Hadzhiyska et al. 2021).

ACKNOWLEDGEMENTS

We are grateful to Marius Cautun for his support in setting up dtfe, to Fabian Schmidt for sharing his 1D relaxation code at an early stage of this work, to Alexandre Barreira for giving access to his DGP simulations, to Jihye Shin for sharing the means and variances of the DE simulations, and to Alexander Mead for his support with hmcode. We also thank Yanchuan Cai and Wojciech Hellwing for useful discussions. The figures in this work were created with matplotlib (Hunter 2007) and chaincosumer (Hinton 2016), making use of the numpy (Harris et al. 2020) and scipy (Virtanen et al. 2020) Python libraries. MC and CH acknowledge support from the European Research Council under grant number 647112. CH also acknowledges support from the Max Planck Society and the Alexander von Humboldt Foundation in the framework of the Max Planck-Humboldt Research Award endowed by the Federal Ministry of Education and Research. AG is supported by an EPSRC studentship under Project 2441314 from UK Research & Innovation. CA and BL are supported by the European Research Council (ERC) through a starting Grant (ERC-StG-716532 PUNCA). BL is further supported by the UK Science and Technology Funding Council (STFC) Consolidated Grant No. ST/I00162X/1 and ST/P000541/1. This work used the DiRAC@Durham facility managed by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). The equipment was funded by BEIS capital funding via STFC capital grants ST/K00042X/1, ST/P002293/1, ST/R002371/1, andST/S002502/1, Durham University and STFC operations grant ST/R000832/1. DiRAC is part of the National e-Infrastructure.

DATA AVAILABILITY

Our code to compute the matter PDF predictions is publicly available at https://github.com/mcataneo/pyLDT-cosmo. The f(R) gravity simulation data used in this paper may be available upon request to the corresponding author. The matter PDF measured from the Quijote simulations are publicly available at https://quijote-simulations.readthedocs.io/en/latest/. The matter PDF measurements for the dark energy cosmologies are publicly available at https://astro.kias.re.kr/jhshin/.

Footnotes

1

https://github.com/mcataneo/pyLDT-cosmo

2

For extensions that include primordial non-Gaussianity see Uhlemann et al. (2018b) and Friedrich et al. (2020).

3

Physically speaking, this procedure amounts to asserting that the reduced cumulants (discussed later), encoded in the large deviation statistics rate function and predicted from spherical collapse in the limit σ² → 0, can reliably be extrapolated to small, non-zero variances (as demonstrated with simulated data in Uhlemann et al. 2016). The |$\sigma _{\rm NL}^2$| factor in the denominator then plays the role of converting the reduced cumulants back to the cumulants using the correct non-linear variance, which controls the width of the PDF.

4

At first glance this result seems at odds with the notion that dark energy and modified gravity affect the growth of structure. However, here we are fixing the final non-linear density, ρ, such that enhancements (suppressions) of the linear growth require lower (higher) initial density contrasts, δ_ini, to match that particular ρ. In other words, adjustments to the initial conditions compensate for the linear growth modifications to a very good approximation.

5

Technically speaking, DGP is a higher dimensional theory of gravity that falls outside the Horndeski theory landscape. However, the scales relevant for structure formation are well within the regime in which DGP can be treated as a 4D scalar–tensor theory (Nicolis & Rattazzi 2004; Park, Zurek & Watson 2010).

6

Here, R denotes the Ricci scalar and it must not be confused with the smoothing radius defined above. In what follows we shall keep the same notation for both quantities as their meaning should be clear from context.

7

Note that the linearly extrapolated top-hat density fluctuation, δ_L, so defined (see also equation 9) is just an effective quantity, and in ΛCDM extensions will in general differ from the linear theory |$\hat{\delta }_{\rm L}$| defined below equation (6).

8

Note that the common approximation for the linear growth |$D(z)\propto H(a)\int _0^a {\rm d} a^{\prime } (a^{\prime } H(a^{\prime }))^{-3}$| [quoted in equation (6) of Codis et al. (2016) and (A1) of Uhlemann et al. (2020)] is not accurate enough to estimate the response of the PDF to changing w beyond a cosmological constant.

9

https://astro.kias.re.kr/jhshin/

10

Because the linear theory normalization cancels out in equation (4), knowledge of σ₈ is irrelevant for the LDT predictions when measurements of the variance of the simulated density field are available. In fact, the non-linear variance carries information on σ₈ so that, ultimately, its impact on the theory PDF is properly accounted for.

11

https://github.com/MariusCautun/DTFE

REFERENCES

Abbott

B. P.

et al. ,

2017

,

ApJ

,

848

,

L13

10.3847/2041-8213/aa920c

Crossref

Search ADS

Abbott

T. M. C.

et al. ,

2018

,

MNRAS

,

480

,

3879

10.1093/mnras/sty1939

Crossref

Search ADS

Abbott

T. M. C.

et al. ,

2019a

,

Phys. Rev. D

,

99

,

123505

10.1103/PhysRevD.99.123505

Crossref

Search ADS

Abbott

B. P.

et al. ,

2019b

,

Phys. Rev. Lett.

,

123

,

011102

10.1103/PhysRevLett.123.011102

Crossref

Search ADS

Aiola

S.

et al. ,

2020

,

J. Cosmol. Astropart. Phys.

,

2020

,

047

10.1088/1475-7516/2020/12/047

Crossref

Search ADS

Alam

S.

et al. ,

2021

,

Phys. Rev. D

,

103

,

083533

10.1103/PhysRevD.103.083533

Crossref

Search ADS

Amon

A.

et al. ,

2018

,

MNRAS

,

479

,

3422

10.1093/mnras/sty1624

Crossref

Search ADS

Arnold

C.

,

Leo

M.

,

Li

B.

,

2019

,

Nat. Astron.

,

3

,

945

10.1038/s41550-019-0823-y

Crossref

Search ADS

Barreira

A.

,

Bose

S.

,

Li

B.

,

2015

,

J. Cosmol. Astropart. Phys.

,

12

,

059

10.1088/1475-7516/2015/12/059

Crossref

Search ADS

Barthelemy

A.

,

Codis

S.

,

Uhlemann

C.

,

Bernardeau

F.

,

Gavazzi

R.

,

2020

,

MNRAS

,

492

,

3420

10.1093/mnras/staa053

Crossref

Search ADS

Bellini

E.

,

Sawicki

I.

,

2014

,

J. Cosmol. Astropart. Phys.

,

2014

,

050

10.1088/1475-7516/2014/07/050

Crossref

Search ADS

Bellini

E.

,

Sawicki

I.

,

Zumalacárregui

M.

,

2020

,

J. Cosmol. Astropart. Phys.

,

2020

,

008

10.1088/1475-7516/2020/02/008

Crossref

Search ADS

Bernardeau

F.

,

1994

,

ApJ

,

427

,

51

10.1086/174121

Crossref

Search ADS

Bernardeau

F.

,

Brax

P.

,

2011

,

J. Cosmol. Astropart. Phys.

,

2011

,

019

10.1088/1475-7516/2011/06/019

Crossref

Search ADS

Bernardeau

F.

,

Reimberg

P.

,

2016

,

Phys. Rev. D

,

94

,

063520

10.1103/PhysRevD.94.063520

Crossref

Search ADS

Bernardeau

F.

,

Colombi

S.

,

Gaztañaga

E.

,

Scoccimarro

R.

,

2002

,

Phys. Rep.

,

367

,

1

10.1016/S0370-1573(02)00135-7

Crossref

Search ADS

Bernardeau

F.

,

Pichon

C.

,

Codis

S.

,

2014

,

Phys. Rev. D

,

90

,

103519

10.1103/PhysRevD.90.103519

Crossref

Search ADS

Blas

D.

,

Lesgourgues

J.

,

Tram

T.

,

2011

,

J. Cosmol. Astropart. Phys.

,

2011

,

34

10.1088/1475-7516/2011/07/034

Crossref

Search ADS

Bocquet

S.

,

Heitmann

K.

,

Habib

S.

,

Lawrence

E.

,

Uram

T.

,

Frontiere

N.

,

Pope

A.

,

Finkel

H.

,

2020

,

ApJ

,

901

,

5

10.3847/1538-4357/abac5c

Crossref

Search ADS

Borisov

A.

,

Jain

B.

,

Zhang

P.

,

2012

,

Phys. Rev. D

,

85

,

063518

10.1103/PhysRevD.85.063518

Crossref

Search ADS

Bose

B.

,

Cataneo

M.

,

Tröster

T.

,

Xia

Q.

,

Heymans

C.

,

Lombriser

L.

,

2020a

,

MNRAS

,

498

,

4650

10.1093/mnras/staa2696

Crossref

Search ADS

Bose

B.

,

Byun

J.

,

Lacasa

F.

,

Moradinezhad Dizgah

A.

,

Lombriser

L.

,

2020b

,

J. Cosmol. Astropart. Phys.

,

2020

,

025

10.1088/1475-7516/2020/02/025

Crossref

Search ADS

Boyle

A.

,

Uhlemann

C.

,

Friedrich

O.

,

Barthelemy

A.

,

Codis

S.

,

Bernardeau

F.

,

Giocoli

C.

,

Baldi

M.

,

2021

,

MNRAS

,

505

,

2886

10.1093/mnras/stab1381

Brax

P.

,

Valageas

P.

,

2012

,

Phys. Rev. D

,

86

,

063512

10.1103/PhysRevD.86.063512

Crossref

Search ADS

Casarini

L.

,

Bonometto

S. A.

,

Tessarotto

E.

,

Corasaniti

P.-S.

,

2016

,

J. Cosmol. Astropart. Phys.

,

2016

,

008

10.1088/1475-7516/2016/08/008

Crossref

Search ADS

Cataneo

M.

,

Rapetti

D.

,

Lombriser

L.

,

Li

B.

,

2016

,

J. Cosmol. Astropart. Phys.

,

2016

,

024

10.1088/1475-7516/2016/12/024

Crossref

Search ADS

Cataneo

M.

,

Lombriser

L.

,

Heymans

C.

,

Mead

A. J.

,

Barreira

A.

,

Bose

S.

,

Li

B.

,

2019

,

MNRAS

,

488

,

2121

10.1093/mnras/stz1836

Crossref

Search ADS

Cautun

M. C.

,

van de Weygaert

R.

,

2011

,

preprint (arXiv:1105.0370)

Chevallier

M.

,

Polarski

D.

,

2001

,

Int. J. Mod. Phys. D

,

10

,

213

10.1142/S0218271801000822

Crossref

Search ADS

Chudaykin

A.

,

Dolgikh

K.

,

Ivanov

M. M.

,

2021

,

Phys. Rev. D

,

103

,

023507

10.1103/PhysRevD.103.023507

Crossref

Search ADS

Codis

S.

,

Pichon

C.

,

Bernardeau

F.

,

Uhlemann

C.

,

Prunet

S.

,

2016

,

MNRAS

,

460

,

1549

10.1093/mnras/stw1084

Crossref

Search ADS

Contarini

S.

,

Marulli

F.

,

Moscardini

L.

,

Veropalumbo

A.

,

Giocoli

C.

,

Baldi

M.

,

2021

,

MNRAS

,

504

,

5021

10.1093/mnras/stab1112

Crossref

Search ADS

Cooke

R. J.

,

Pettini

M.

,

Nollett

K. M.

,

Jorgenson

R.

,

2016

,

ApJ

,

830

,

148

10.3847/0004-637X/830/2/148

Crossref

Search ADS

Crisostomi

M.

,

Lewandowski

M.

,

Vernizzi

F.

,

2020

,

Phys. Rev. D

,

101

,

123501

10.1103/PhysRevD.101.123501

Crossref

Search ADS

Crocce

M.

,

Pueblas

S.

,

Scoccimarro

R.

,

2006

,

MNRAS

,

373

,

369

10.1111/j.1365-2966.2006.11040.x

Crossref

Search ADS

Cusin

G.

,

Lewandowski

M.

,

Vernizzi

F.

,

2018

,

J. Cosmol. Astropart. Phys.

,

2018

,

005

10.1088/1475-7516/2018/04/005

Crossref

Search ADS

De Felice

A.

,

Tsujikawa

S.

,

2010

,

Living Rev. Relat.

,

13

,

3

10.12942/lrr-2010-3

Crossref

Search ADS

DES Collaboration

,

2022

,

Phys. Rev. D

,

105

,

023520

10.1103/PhysRevD.105.023520

Di Valentino

E.

et al. ,

2021a

,

Class. Quantum Gravity

,

38

,

153001

10.1088/1361-6382/ac086d

Crossref

Search ADS

Di Valentino

E.

et al. ,

2021b

,

Astropart. Phys.

,

131

,

102604

10.1016/j.astropartphys.2021.102604

Crossref

Search ADS

Douspis

M.

,

Salvati

L.

,

Aghanim

N.

,

2019

,

preprint (arXiv:1901.05289)

Dutcher

D.

et al. ,

2021

,

Phys. Rev. D

,

104

,

022003

10.1103/PhysRevD.104.022003

Crossref

Search ADS

Dvali

G.

,

Gabadadze

G.

,

Porrati

M.

,

2000

,

Phys. Lett. B

,

485

,

208

10.1016/S0370-2693(00)00669-9

Crossref

Search ADS

Euclid Collaboration

,

2020

,

A&A

,

642

,

A191

10.1051/0004-6361/202038071

Crossref

Search ADS

Euclid Collaboration

,

2021

,

MNRAS

,

505

,

2840

10.1093/mnras/stab1366

Crossref

Search ADS

Falck

B.

,

Koyama

K.

,

Zhao

G.-B.

,

2015

,

J. Cosmol. Astropart. Phys.

,

2015

,

049

10.1088/1475-7516/2015/07/049

Crossref

Search ADS

Fang

W.

,

Li

B.

,

Zhao

G.-B.

,

2017

,

Phys. Rev. Lett.

,

118

,

181301

10.1103/PhysRevLett.118.181301

Crossref

Search ADS

Ferreira

P. G.

,

2019

,

ARA&A

,

57

,

335

10.1146/annurev-astro-091918-104423

Crossref

Search ADS

Friedrich

O.

et al. ,

2018

,

Phys. Rev. D

,

98

,

23508

10.1103/physrevd.98.023508

Crossref

Search ADS

Friedrich

O.

,

Uhlemann

C.

,

Villaescusa-Navarro

F.

,

Baldauf

T.

,

Manera

M.

,

Nishimichi

T.

,

2020

,

MNRAS

,

498

,

464

10.1093/mnras/staa2160

Crossref

Search ADS

Friedrich

O.

,

Halder

A.

,

Boyle

A.

,

Uhlemann

C.

,

Britt

D.

,

Codis

S.

,

Gruen

D.

,

Hahn

C.

,

2022

,

MNRAS

,

510

,

5069

10.1093/mnras/stab3703

Frusciante

N.

,

Perenon

L.

,

2020

,

Phys. Rep.

,

857

,

1

10.1016/j.physrep.2020.02.004

Crossref

Search ADS

Giocoli

C.

,

Baldi

M.

,

Moscardini

L.

,

2018

,

MNRAS

,

481

,

2813

10.1093/mnras/sty2465

Crossref

Search ADS

Gleyzes

J.

,

Langlois

D.

,

Piazza

F.

,

Vernizzi

F.

,

2013

,

J. Cosmol. Astropart. Phys.

,

2013

,

025

10.1088/1475-7516/2013/08/025

Crossref

Search ADS

Gruen

D.

et al. ,

2018

,

Phys. Rev. D

,

98

,

023507

10.1103/PhysRevD.98.023507

Crossref

Search ADS

Hadzhiyska

B.

,

Liu

S.

,

Somerville

R. S.

,

Gabrielpillai

A.

,

Bose

S.

,

Eisenstein

D.

,

Hernquist

L.

,

2021

,

MNRAS

,

508

,

698

10.1093/mnras/stab2564

Hagstotz

S.

,

Costanzi

M.

,

Baldi

M.

,

Weller

J.

,

2019

,

MNRAS

,

486

,

3927

10.1093/mnras/stz1051

Crossref

Search ADS

Hamana

T.

et al. ,

2020

,

PASJ

,

72

,

16

10.1093/pasj/psz138

Crossref

Search ADS

Harnois-Deraps

J.

,

Giblin

B.

,

Joachimi

B.

,

2019

,

A&A

,

631

,

A160

10.1051/0004-6361/201935912

Crossref

Search ADS

Harris

C. R.

et al. ,

2020

,

Nature

,

585

,

357

10.1038/s41586-020-2649-2

Crossref

Search ADS

Hartlap

J.

,

Simon

P.

,

Schneider

P.

,

2006

,

A&A

,

464

,

399

10.1051/0004-6361:20066170

Crossref

Search ADS

Heitmann

K.

,

Lawrence

E.

,

Kwan

J.

,

Habib

S.

,

Higdon

D.

,

2014

,

ApJ

,

780

,

111

10.1088/0004-637X/780/1/111

Crossref

Search ADS

Hellwing

W. A.

,

Li

B.

,

Frenk

C. S.

,

Cole

S.

,

2013

,

MNRAS

,

435

,

2806

10.1093/mnras/stt1430

Crossref

Search ADS

Hellwing

W. A.

,

Koyama

K.

,

Bose

B.

,

Zhao

G.-B.

,

2017

,

Phys. Rev. D

,

96

,

023515

10.1103/PhysRevD.96.023515

Crossref

Search ADS

Heymans

C.

et al. ,

2021

,

A&A

,

646

,

A140

10.1051/0004-6361/202039063

Crossref

Search ADS

Hinton

S. R.

,

2016

,

J. Open Source Softw.

,

1

,

00045

10.21105/joss.00045

Crossref

Search ADS

Horndeski

G. W.

,

1974

,

Int. J. Theor. Phys.

,

10

,

363

10.1007/BF01807638

Crossref

Search ADS

Hu

W.

,

Sawicki

I.

,

2007

,

Phys. Rev. D

,

76

,

064004

10.1103/PhysRevD.76.064004

Crossref

Search ADS

Hu

B.

,

Raveri

M.

,

Frusciante

N.

,

Silvestri

A.

,

2014

,

Phys. Rev. D

,

89

,

103530

10.1103/PhysRevD.89.103530

Crossref

Search ADS

Hunter

J. D.

,

2007

,

Comput. Sci. Eng.

,

9

,

90

10.1109/MCSE.2007.55

Crossref

Search ADS

Ishak

M.

,

2019

,

Living Rev. Relat.

,

22

,

1

10.1007/s41114-018-0017-4

Crossref

Search ADS

Ivanov

M. M.

,

Kaurov

A. A.

,

Sibiryakov

S.

,

2019

,

J. Cosmol. Astropart. Phys.

,

2019

,

009

10.1088/1475-7516/2019/03/009

Crossref

Search ADS

Jamieson

D.

,

Loverde

M.

,

2020

,

Phys. Rev. D

,

102

,

123546

10.1103/physrevd.102.123546

Crossref

Search ADS

Kaufman

G. M.

,

1967

,

Report No. 6710, Center for Operations Research and Econometrics

,

Catholic University of Louvain

,

Heverlee, Belgium

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Kopp

M.

,

Appleby

S. A.

,

Achitouv

I.

,

Weller

J.

,

2013

,

Phys. Rev. D

,

88

,

084015

10.1103/PhysRevD.88.084015

Crossref

Search ADS

Koyama

K.

,

2018

,

Int. J. Mod. Phys. D

,

27

,

1848001

10.1142/S0218271818480012

Crossref

Search ADS

Koyama

K.

,

Taruya

A.

,

Hiramatsu

T.

,

2009

,

Phys. Rev. D

,

79

,

123512

10.1103/PhysRevD.79.123512

Crossref

Search ADS

Kratochvil

J. M.

,

Lim

E. A.

,

Wang

S.

,

Haiman

Z.

,

May

M.

,

Huffenberger

K.

,

2012

,

Phys. Rev. D

,

85

,

103513

10.1103/PhysRevD.85.103513

Crossref

Search ADS

Lam

T. Y.

,

Li

B.

,

2012

,

MNRAS

,

426

,

3260

10.1111/j.1365-2966.2012.21746.x

Crossref

Search ADS

Lee

S.

et al. ,

2022

,

MNRAS

,

509

,

4982

10.1093/mnras/stab3129

Lewis

A.

,

Challinor

A.

,

Lasenby

A.

,

2000

,

ApJ

,

538

,

473

10.1086/309179

Crossref

Search ADS

Li

B.

,

Efstathiou

G.

,

2012

,

MNRAS

,

421

,

1431

10.1111/j.1365-2966.2011.20404.x

Crossref

Search ADS

Li

B.

,

Zhao

G.-B.

,

Teyssier

R.

,

Koyama

K.

,

2012a

,

J. Cosmol. Astropart. Phys.

,

01

,

051

10.1088/1475-7516/2012/01/051

Crossref

Search ADS

Li

B.

,

Zhao

G.-B.

,

Koyama

K.

,

2012b

,

MNRAS

,

421

,

3481

10.1111/j.1365-2966.2012.20573.x

Crossref

Search ADS

Li

B.

,

Zhao

G.-B.

,

Koyama

K.

,

2013

,

J. Cosmol. Astropart. Phys.

,

05

,

023

10.1088/1475-7516/2013/05/023

Crossref

Search ADS

Linder

E. V.

,

2003

,

Phys. Rev. Lett.

,

90

,

091301

10.1103/PhysRevLett.90.091301

Crossref

Search ADS

Linder

E. V.

,

2005

,

Phys. Rev. D

,

72

,

043529

10.1103/PhysRevD.72.043529

Crossref

Search ADS

Liu

R.

,

Valogiannis

G.

,

Battaglia

N.

,

Bean

R.

,

2021

,

Phys. Rev. D

,

104

,

103519

10.1103/PhysRevD.104.103519

Lombriser

L.

,

2018

,

Int. J. Mod. Phys. D

,

27

,

1848002

10.1142/S0218271818480024

Crossref

Search ADS

Lombriser

L.

,

Hu

W.

,

Fang

W.

,

Seljak

U.

,

2009

,

Phys. Rev. D

,

80

,

063536

10.1103/PhysRevD.80.063536

Crossref

Search ADS

Lombriser

L.

,

Li

B.

,

Koyama

K.

,

Zhao

G.-B.

,

2013

,

Phys. Rev. D

,

87

,

123511

10.1103/PhysRevD.87.123511

Crossref

Search ADS

Mandal

A.

,

Nadkarni-Ghosh

S.

,

2020

,

MNRAS

,

498

,

355

10.1093/mnras/staa2073

Crossref

Search ADS

McClintock

T.

et al. ,

2019

,

ApJ

,

872

,

53

10.3847/1538-4357/aaf568

Crossref

Search ADS

Mead

A. J.

,

2017

,

MNRAS

,

464

,

1282

10.1093/mnras/stw2312

Crossref

Search ADS

Mead

A. J.

,

Heymans

C.

,

Lombriser

L.

,

Peacock

J. A.

,

Steele

O. I.

,

Winther

H. A.

,

2016

,

MNRAS

,

459

,

1468

10.1093/mnras/stw681

Crossref

Search ADS

Mead

A. J.

,

Brieden

S.

,

Tröster

T.

,

Heymans

C.

,

2021

,

MNRAS

,

502

,

1401

10.1093/mnras/stab082

Crossref

Search ADS

Muir

J.

et al. ,

2021

,

Phys. Rev. D

,

103

,

023528

10.1103/PhysRevD.103.023528

Crossref

Search ADS

Munshi

D.

,

2017

,

J. Cosmol. Astropart. Phys.

,

2017

,

049

10.1088/1475-7516/2017/01/049

Crossref

Search ADS

Munshi

D.

,

McEwen

J. D.

,

2020

,

MNRAS

,

498

,

5299

10.1093/mnras/staa2706

Crossref

Search ADS

Nicolis

A.

,

Rattazzi

R.

,

2004

,

J. High Energy Phys.

,

2004

,

059

10.1088/1126-6708/2004/06/059

Crossref

Search ADS

Nishimichi

T.

,

Bernardeau

F.

,

Taruya

A.

,

2017

,

Phys. Rev. D

,

96

,

123515

10.1103/PhysRevD.96.123515

Crossref

Search ADS

Park

M.

,

Zurek

K. M.

,

Watson

S.

,

2010

,

Phys. Rev. D

,

81

,

124008

10.1103/PhysRevD.81.124008

Crossref

Search ADS

Patton

K.

,

Blazek

J.

,

Honscheid

K.

,

Huff

E.

,

Melchior

P.

,

Ross

A. J.

,

Suchyta

E.

,

2017

,

MNRAS

,

472

,

439

10.1093/mnras/stx1626

Crossref

Search ADS

Peacock

J. A.

,

Smith

R. E.

,

2014

,

Astrophysics Source Code Library, record

.

ascl:1402.032

Peel

A.

,

Pettorino

V.

,

Giocoli

C.

,

Starck

J.-L.

,

Baldi

M.

,

2018

,

A&A

,

619

,

A38

10.1051/0004-6361/201833481

Crossref

Search ADS

Perico

E. L. D.

,

Voivodic

R.

,

Lima

M.

,

Mota

D. F.

,

2019

,

A&A

,

632

,

A52

10.1051/0004-6361/201935949

Perivolaropoulos

L.

,

Skara

F.

,

2021

,

preprint (arXiv:2105.05208)

Perlmutter

S.

et al. ,

1999

,

ApJ

,

517

,

565

10.1086/307221

Crossref

Search ADS

Planck Collaboration VI

,

2020

,

A&A

,

641

,

A6

10.1051/0004-6361/201833910

Crossref

Search ADS

Pogosian

L.

,

Raveri

M.

,

Koyama

K.

,

Martinelli

M.

,

Silvestri

A.

,

Zhao

G.-B.

,

2021

,

preprint (arXiv:2107.12992)

Ramachandra

N.

,

Valogiannis

G.

,

Ishak

M.

,

Heitmann

K.

,

LSST Dark Energy Science Collaboration

,

2021

,

Phys. Rev. D

,

103

,

123525

10.1103/PhysRevD.103.123525

Crossref

Search ADS

Raveri

M.

et al. ,

2021

,

preprint (arXiv:2107.12990)

Repp

A.

,

Szapudi

I.

,

2020

,

MNRAS

,

498

,

L125

10.1093/mnrasl/slaa139

Crossref

Search ADS

Riess

A. G.

et al. ,

1998

,

AJ

,

116

,

1009

10.1086/300499

Crossref

Search ADS

Sahlén

M.

,

2019

,

Phys. Rev. D

,

99

,

063525

10.1103/PhysRevD.99.063525

Crossref

Search ADS

Schaap

W. E.

,

van de Weygaert

R.

,

2000

,

A&A

,

363

,

L29

Schmidt

F.

,

2009

,

Phys. Rev. D

,

80

,

123003

10.1103/PhysRevD.80.123003

Crossref

Search ADS

Schmidt

F.

,

Lima

M.

,

Oyaizu

H.

,

Hu

W.

,

2009

,

Phys. Rev. D

,

79

,

083518

10.1103/PhysRevD.79.083518

Crossref

Search ADS

Schmidt

F.

,

Hu

W.

,

Lima

M.

,

2010

,

Phys. Rev. D

,

81

,

063005

10.1103/PhysRevD.81.063005

Crossref

Search ADS

Shin

J.

,

Kim

J.

,

Pichon

C.

,

Jeong

D.

,

Park

C.

,

2017

,

ApJ

,

843

,

73

10.3847/1538-4357/aa74b9

Crossref

Search ADS

Shirasaki

M.

,

Nishimichi

T.

,

Li

B.

,

Higuchi

Y.

,

2017

,

MNRAS

,

466

,

2402

10.1093/mnras/stw3254

Crossref

Search ADS

Simpson

F.

et al. ,

2013

,

MNRAS

,

429

,

2249

10.1093/mnras/sts493

Crossref

Search ADS

Song

Y.-S.

et al. ,

2015

,

Phys. Rev. D

,

92

,

043522

10.1103/PhysRevD.92.043522

Crossref

Search ADS

Springel

V.

,

2010

,

MNRAS

,

401

,

791

10.1111/j.1365-2966.2009.15715.x

Crossref

Search ADS

Takahashi

R.

,

Sato

M.

,

Nishimichi

T.

,

Taruya

A.

,

Oguri

M.

,

2012

,

ApJ

,

761

,

152

10.1088/0004-637X/761/2/152

Crossref

Search ADS

Teyssier

R.

,

2002

,

A&A

,

385

,

337

10.1051/0004-6361:20011817

Crossref

Search ADS

Thiele

L.

,

Hill

J. C.

,

Smith

K. M.

,

2020

,

Phys. Rev. D

,

102

,

123545

10.1103/physrevd.102.123545

Crossref

Search ADS

Touchette

H.

,

Prellberg

T.

,

Just

W.

,

2012

,

J. Phys. Astron.

,

45

,

395002

Tröster

T.

et al. ,

2021

,

A&A

,

649

,

A88

10.1051/0004-6361/202039805

Crossref

Search ADS

Uhlemann

C.

,

Codis

S.

,

Pichon

C.

,

Bernardeau

F.

,

Reimberg

P.

,

2016

,

MNRAS

,

460

,

1529

10.1093/mnras/stw1074

Crossref

Search ADS

Uhlemann

C.

et al. ,

2018a

,

MNRAS

,

473

,

5098

10.1093/mnras/stx2616

Crossref

Search ADS

Uhlemann

C.

,

Pajer

E.

,

Pichon

C.

,

Nishimichi

T.

,

Codis

S.

,

Bernardeau

F.

,

2018b

,

MNRAS

,

474

,

2853

10.1093/mnras/stx2623

Crossref

Search ADS

Uhlemann

C.

,

Friedrich

O.

,

Villaescusa-Navarro

F.

,

Banerjee

A.

,

Codis

S.

,

2020

,

MNRAS

,

495

,

4006

10.1093/mnras/staa1155

Crossref

Search ADS

Valageas

P.

,

2002

,

A&A

,

382

,

412

10.1051/0004-6361:20011663

Crossref

Search ADS

Vazsonyi

L.

,

Taylor

P. L.

,

Valogiannis

G.

,

Ramachandra

N. S.

,

Ferté

A.

,

Rhodes

J.

,

2021

, ,

Phys. Rev. D

,

104

,

83527

10.1103/PhysRevD.104.083527

Verza

G.

,

Pisani

A.

,

Carbone

C.

,

Hamaus

N.

,

Guzzo

L.

,

2019

,

J. Cosmol. Astropart. Phys.

,

2019

,

040

10.1088/1475-7516/2019/12/040

Crossref

Search ADS

Villaescusa-Navarro

F.

et al. ,

2020

,

ApJS

,

250

,

2

10.3847/1538-4365/ab9d82

Crossref

Search ADS

Virtanen

P.

et al. ,

2020

,

Nat. Methods

,

17

,

261

10.1038/s41592-019-0686-2

Crossref

Search ADS

Weinberger

R.

,

Springel

V.

,

Pakmor

R.

,

2020

,

ApJS

,

248

,

32

10.3847/1538-4365/ab908c

Crossref

Search ADS

Wen

D.

,

Kemball

A. J.

,

Saslaw

W. C.

,

2020

,

ApJ

,

890

,

160

10.3847/1538-4357/ab6d6f

Crossref

Search ADS

Will

C. M.

,

2014

,

Living Rev. Relat.

,

17

,

4

10.12942/lrr-2014-4

Crossref

Search ADS

Winther

H. A.

,

Casas

S.

,

Baldi

M.

,

Koyama

K.

,

Li

B.

,

Lombriser

L.

,

Zhao

G.-B.

,

2019

,

Phys. Rev. D

,

100

,

123540

10.1103/PhysRevD.100.123540

Crossref

Search ADS

Yamauchi

D.

,

Yokoyama

S.

,

Tashiro

H.

,

2017

,

Phys. Rev. D

,

96

,

123516

10.1103/PhysRevD.96.123516

Crossref

Search ADS

Zhao

G.-B.

,

2014

,

ApJS

,

211

,

23

10.1088/0067-0049/211/2/23

Crossref

Search ADS

Zumalacárregui

M.

,

Bellini

E.

,

Sawicki

I.

,

Lesgourgues

J.

,

Ferreira

P. G.

,

2017

,

J. Cosmol. Astropart. Phys.

,

2017

,

019

10.1088/1475-7516/2017/08/019

Crossref

Search ADS

APPENDIX A: THE IMPACT OF MASS-ASSIGNMENT SCHEMES ON THE PDF

The various methods designed to interpolate the simulated density field on a grid may lead to differences between the measured PDFs large enough to potentially bias the predictive accuracy of a particular theoretical framework. In Fig. A1, we compare two such popular methods–the CiC algorithm and the Delaunay tassellation field estimator – using as summary statistic the PDF extracted from a single snapshot after applying top-hat filters with three different smoothing radii. Reassuringly, the distributions agree to better than 1 per cent for all densities but the rarest underdensities, thus validating the performance of LDT discussed in Section 4 and previously presented in Uhlemann et al. (2020).

Figure A1.

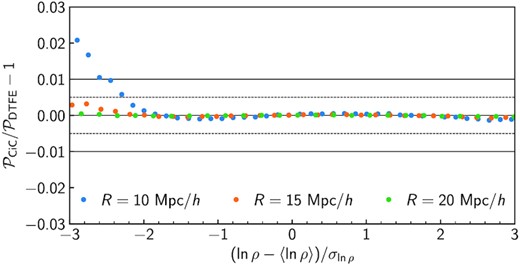
Relative deviation between the matter PDF constructed from the CiC mass-assignment scheme and that based on the Delaunay tassellation (DTFE). Data points represent measurements from a single z = 0 snapshot of a ΛCDM simulation. The agreement between the two mass-assignment schemes is excellent over the entire range of densities relevant for this work.

Open in new tab Download slide

APPENDIX B: MEANS AND VARIANCES OF THE SIMULATED NON-LINEAR DENSITY FIELD

Table B1 lists variances and means extracted from the simulations for various smoothing radii and redshifts, which we used to produce the ΛCDM and modified gravity results presented in Section 4. The corresponding quantities for the dark energy cosmologies can be requested to the authors of Shin et al. (2017).

Table B1.

Open in new tab

Measured variances and means of the smoothed density and log-density field for the standard cosmology, f(R) gravity with |f_R0| = 10⁻⁵ and DGP gravity with Ω_rc = 0.25. All values for ΛCDM and F5 are the average over eight realizations.

	ΛCDM			F5			DGPm
	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉
R = 10 Mpc h⁻¹
z = 0	0.567	0.392	−0.205	0.612	0.428	−0.223	0.716	0.465	−0.246
z = 1	0.195	0.167	−0.0836	0.199	0.171	−0.0857	0.223	0.188	−0.0953
R = 15 Mpc h⁻¹
z = 0	0.276	0.233	−0.118	0.291	0.248	−0.126	0.345	0.282	−0.144
z = 1	0.0993	0.093	−0.0468	0.101	0.0945	−0.0475	0.114	0.106	−0.0532
R = 20 Mpc h⁻¹
z = 0	0.163	0.149	−0.0745	0.17	0.157	−0.078	0.204	0.184	−0.0922
z = 1	0.0598	0.0579	−0.0285	0.0603	0.0586	−0.0288	0.0684	0.0661	−0.033

	ΛCDM			F5			DGPm
	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉
R = 10 Mpc h⁻¹
z = 0	0.567	0.392	−0.205	0.612	0.428	−0.223	0.716	0.465	−0.246
z = 1	0.195	0.167	−0.0836	0.199	0.171	−0.0857	0.223	0.188	−0.0953
R = 15 Mpc h⁻¹
z = 0	0.276	0.233	−0.118	0.291	0.248	−0.126	0.345	0.282	−0.144
z = 1	0.0993	0.093	−0.0468	0.101	0.0945	−0.0475	0.114	0.106	−0.0532
R = 20 Mpc h⁻¹
z = 0	0.163	0.149	−0.0745	0.17	0.157	−0.078	0.204	0.184	−0.0922
z = 1	0.0598	0.0579	−0.0285	0.0603	0.0586	−0.0288	0.0684	0.0661	−0.033

Table B1.

Open in new tab

Measured variances and means of the smoothed density and log-density field for the standard cosmology, f(R) gravity with |f_R0| = 10⁻⁵ and DGP gravity with Ω_rc = 0.25. All values for ΛCDM and F5 are the average over eight realizations.

	ΛCDM			F5			DGPm
	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉
R = 10 Mpc h⁻¹
z = 0	0.567	0.392	−0.205	0.612	0.428	−0.223	0.716	0.465	−0.246
z = 1	0.195	0.167	−0.0836	0.199	0.171	−0.0857	0.223	0.188	−0.0953
R = 15 Mpc h⁻¹
z = 0	0.276	0.233	−0.118	0.291	0.248	−0.126	0.345	0.282	−0.144
z = 1	0.0993	0.093	−0.0468	0.101	0.0945	−0.0475	0.114	0.106	−0.0532
R = 20 Mpc h⁻¹
z = 0	0.163	0.149	−0.0745	0.17	0.157	−0.078	0.204	0.184	−0.0922
z = 1	0.0598	0.0579	−0.0285	0.0603	0.0586	−0.0288	0.0684	0.0661	−0.033

	ΛCDM			F5			DGPm
	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉	\|$\sigma _\rho ^2$\|	\|$\sigma _\mu ^2$\|	〈μ〉
R = 10 Mpc h⁻¹
z = 0	0.567	0.392	−0.205	0.612	0.428	−0.223	0.716	0.465	−0.246
z = 1	0.195	0.167	−0.0836	0.199	0.171	−0.0857	0.223	0.188	−0.0953
R = 15 Mpc h⁻¹
z = 0	0.276	0.233	−0.118	0.291	0.248	−0.126	0.345	0.282	−0.144
z = 1	0.0993	0.093	−0.0468	0.101	0.0945	−0.0475	0.114	0.106	−0.0532
R = 20 Mpc h⁻¹
z = 0	0.163	0.149	−0.0745	0.17	0.157	−0.078	0.204	0.184	−0.0922
z = 1	0.0598	0.0579	−0.0285	0.0603	0.0586	−0.0288	0.0684	0.0661	−0.033

APPENDIX C: VALIDATION OF LDT PREDICTIONS FOR SMALL DEVIATIONS FROM ΛCDM FIDUCIAL

C1 Modified gravity

Our theoretical prediction for the matter PDF have been validated with numerical simulations in the main text for the two modified gravity models F5 and DGPm (see Fig. 5). Figs C1 and C2 illustrate the accuracy of the theoretical predictions for F6 and DGPw in the form of residuals from the simulations and departures from ΛCDM, as well as the impact of using the lognormal approximation (equation 21) in pyLDT.

C2 Dark energy

Our theoretical prediction for the matter PDF have been validated with numerical simulations in the main text for large changes in the parametrized dark energy equation of state (see Fig. 8). A similar comparison for all ΛCDM parameters has been provided in Uhlemann et al. (2020), see figs 8 and 9 therein. Here, we provide complementary results for the full set of w₀CDM parameters available from the Quijote simulations (Villaescusa-Navarro et al. 2020).

To further validate our joint matter PDF and matter power spectrum constraints, we compare theoretical power spectrum derivatives from hmcode to measured derivatives from the Quijote simulations in Fig. C3. When limiting ourselves to mildly non-linear scales |$k\lt k_{\rm max}=0.2 \ h\, \mathrm{Mpc}^{-1}$| we find good agreement between the two. We notice slight discrepancies for some parameters that turn out to be unimportant when constraining just a few parameters, but hampering agreement between theory and simulation matter power spectrum in a Fisher forecast simultaneously varying all w₀CDM parameters. To mitigate this minor issue for the power spectrum, we decided to include an external prior on {Ω_b, n_s}, as described in the main text.

Using this prior, we successfully validated the constraints obtained using our theoretical derivatives against simulations by performing a Fisher forecast with all six w₀CDM parameters for which derivatives are available from the Quijote simulation suite. In Fig. C4, we demonstrate that we obtain virtually identical results for both the degeneracy directions and the individual parameter constraints when marginalized over all other parameters.

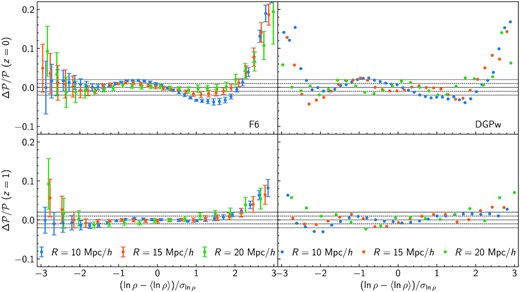
$Residuals between the measured and predicted matter PDF normalized to the theory predictions for z = 0 (top) and z = 1 (bottom) in f(R) gravity with |fR0| = 10−6 (left) and DGP with Ωrc = 0.0625 (right). Different colours indicate the radii of the spheres used for smoothing the density field, 10 (blue), 15 (orange), and 20 $\mathrm{Mpc}\, h^{-1}$ (green). The solid and dashed lines mark the 1 and 2 per cent accuracy, respectively.$

Figure C1.

Residuals between the measured and predicted matter PDF normalized to the theory predictions for z = 0 (top) and z = 1 (bottom) in f(R) gravity with |f_R0| = 10⁻⁶ (left) and DGP with Ω_rc = 0.0625 (right). Different colours indicate the radii of the spheres used for smoothing the density field, 10 (blue), 15 (orange), and 20 |$\mathrm{Mpc}\, h^{-1}$| (green). The solid and dashed lines mark the 1 and 2 per cent accuracy, respectively.

Open in new tab Download slide

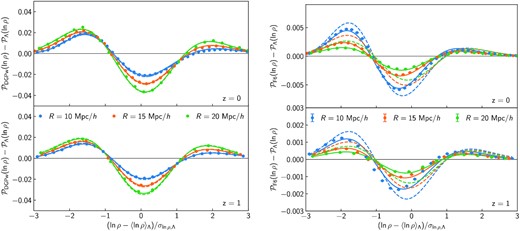
$Measured (data points) and predicted (lines) responses of the matter PDF to modified gravity at z = 0 (top) and z = 1 (bottom). The density field is averaged in spheres of radius R = 10 (blue), 15 (orange), and 20 $\mathrm{Mpc}\, h^{-1}$ (green). Solid lines are obtained from the measured non-linear variance, $\sigma ^2_\mu$, while dashed lines from its approximation equation (21) used in pyLDT. Left: differences from ΛCDM for DGP gravity with Ωrc = 0.0625. Right: same as left-hand panel for f(R) gravity with |fR0| = 10−6.$

Figure C2.

Measured (data points) and predicted (lines) responses of the matter PDF to modified gravity at z = 0 (top) and z = 1 (bottom). The density field is averaged in spheres of radius R = 10 (blue), 15 (orange), and 20 |$\mathrm{Mpc}\, h^{-1}$| (green). Solid lines are obtained from the measured non-linear variance, |$\sigma ^2_\mu$|⁠, while dashed lines from its approximation equation (21) used in pyLDT. Left: differences from ΛCDM for DGP gravity with Ω_rc = 0.0625. Right: same as left-hand panel for f(R) gravity with |f_R0| = 10⁻⁶.

Open in new tab Download slide

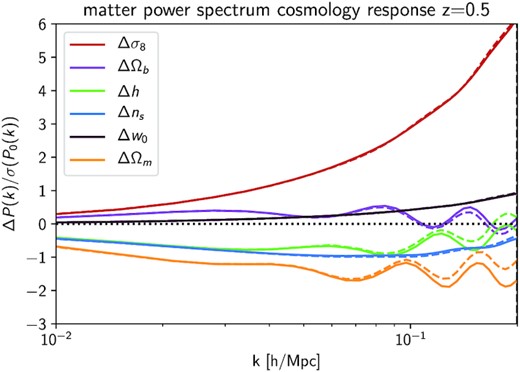
$Validation of matter power spectrum derivatives up to kmax = 0.2 $h\, \mathrm{Mpc}^{-1}$ at z = 0.5 as obtained from hmcode (dashed lines) compared to measurements in the Quijote simulation suite (solid lines) for the full set of 6 cosmological parameters for w0CDM. We show the results as a signal-to-noise like ratio of the differences in the matter power spectrum, ΔP(k), and the expected error on the fiducial power spectrum from the diagonal of the covariance matrix, σ(P0(k)).$

Figure C3.

Validation of matter power spectrum derivatives up to k_max = 0.2 |$h\, \mathrm{Mpc}^{-1}$| at z = 0.5 as obtained from hmcode (dashed lines) compared to measurements in the Quijote simulation suite (solid lines) for the full set of 6 cosmological parameters for w₀CDM. We show the results as a signal-to-noise like ratio of the differences in the matter power spectrum, ΔP(k), and the expected error on the fiducial power spectrum from the diagonal of the covariance matrix, σ(P₀(k)).

Open in new tab Download slide

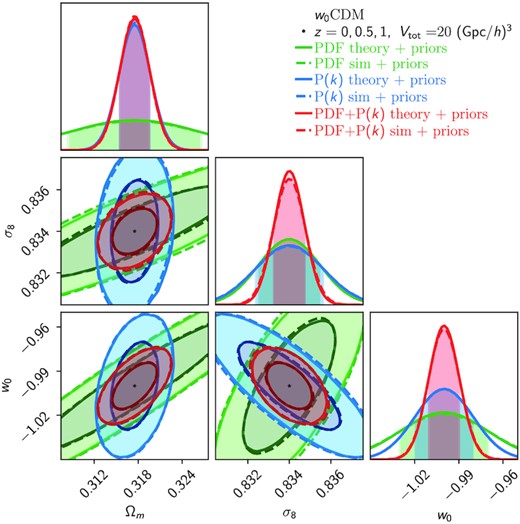
Marginalized constraints on Ωm, σ8, and w0 from a w0CDM Fisher forecast obtained from using the theory derivatives for the matter PDF and power spectrum (solid lines) or the simulated derivatives from the Quijote simulation suite (dashed lines), both when including a prior on {Ωb, ns}. This validates the robustness of our theoretical predictions used for the forecasts in the main text.

Figure C4.

Marginalized constraints on Ω_m, σ₈, and w₀ from a w₀CDM Fisher forecast obtained from using the theory derivatives for the matter PDF and power spectrum (solid lines) or the simulated derivatives from the Quijote simulation suite (dashed lines), both when including a prior on {Ω_b, n_s}. This validates the robustness of our theoretical predictions used for the forecasts in the main text.

Open in new tab Download slide

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
April 2022	1
May 2022	35
June 2022	15
July 2022	9
September 2022	9
October 2022	23
November 2022	1
December 2022	1
January 2023	7
February 2023	2
March 2023	20
April 2023	14
May 2023	2
June 2023	4
August 2023	3
September 2023	4
October 2023	4
November 2023	7
December 2023	1
January 2024	15
February 2024	10
March 2024	20
April 2024	15
May 2024	16
June 2024	16
July 2024	18
August 2024	14
September 2024	23
October 2024	44
November 2024	14
December 2024	7
January 2025	8
February 2025	15
March 2025	32
April 2025	15
May 2025	1

Article Contents

The matter density PDF for modified gravity and dark energy with Large Deviations Theory

ABSTRACT

1 INTRODUCTION

2 THE MATTER DENSITY PDF IN LARGE DEVIATIONS THEORY

2.1 Large deviations theory framework

2.2 Large-deviations statistics in modified gravity and dark energy

2.2.1 Modified gravity

2.2.2 Evolving dark energy

2.2.3 pyLDT

3 SIMULATIONS

3.1 f(R) gravity simulations

3.2 DGP simulations

3.3 Evolving dark energy simulations

3.4 PDF measurements from the simulations

4 RESULTS

4.1 Modified gravity

4.1.1 Pseudo-cosmologies

4.2 Evolving dark energy

4.3 Fisher forecasts

4.3.1 Fisher formalism

4.3.2 Modified gravity

4.3.3 Evolving dark energy

5 SUMMARY AND DISCUSSION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

APPENDIX A: THE IMPACT OF MASS-ASSIGNMENT SCHEMES ON THE PDF

APPENDIX B: MEANS AND VARIANCES OF THE SIMULATED NON-LINEAR DENSITY FIELD

APPENDIX C: VALIDATION OF LDT PREDICTIONS FOR SMALL DEVIATIONS FROM ΛCDM FIDUCIAL

C1 Modified gravity

C2 Dark energy

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only