-
PDF
- Split View
-
Views
-
Cite
Cite
M V Legnardi, A P Milone, L Armillotta, A F Marino, G Cordoni, A Renzini, E Vesperini, F D’Antona, M McKenzie, D Yong, E Dondoglio, E P Lagioia, M Carlos, M Tailo, S Jang, A Mohandasan, Constraining the original composition of the gas forming first-generation stars in globular clusters, Monthly Notices of the Royal Astronomical Society, Volume 513, Issue 1, June 2022, Pages 735–751, https://doi.org/10.1093/mnras/stac734
Close - Share Icon Share
ABSTRACT
Disentangling distinct stellar populations along the red-giant branches (RGBs) of globular clusters (GCs) is possible by using the pseudo-two-colour diagram dubbed chromosome map (ChM). One of the most intriguing findings is that the so-called first-generation (1G) stars, characterized by the same chemical composition of their natal cloud, exhibit extended sequences in the ChM. Unresolved binaries and internal variations in helium or metallicity have been suggested to explain this phenomenon. Here, we derive high-precision Hubble Space Telescope photometry of the GCs NGC 6362 and NGC 6838 and build their ChMs. We find that both 1G RGB and main-sequence (MS) stars exhibit wider ChM sequences than those of second-generation (2G). The evidence of this feature even among unevolved 1G MS stars indicates that chemical inhomogeneities are imprinted in the original gas. We introduce a pseudo-two-magnitude diagram to distinguish between helium and metallicity, and demonstrate that star-to-star metallicity variations are responsible for the extended 1G sequence. Conversely, binaries provide a minor contribution to the phenomenon. We estimate that the metallicity variations within 1G stars of 55 GCs range from less than [Fe/H]∼0.05 to ∼0.30 and mildly correlate with cluster mass. We exploit these findings to constrain the formation scenarios of multiple populations showing that they are qualitatively consistent with the occurrence of multiple generations. In contrast, the fact that 2G stars have more homogeneous iron content than the 1G challenges the scenarios based on accretion of material processed in massive 1G stars on to existing protostars.
1 INTRODUCTION
Globular clusters (GCs) are thought to form out of high-density regions within supergiant molecular clouds that trace back to earliest epochs (e.g. Harris & Pudritz 1994). While these objects are of fundamental importance for a range of astrophysical studies, the origin of such compact and massive agglomerates of stars is still strongly debated. Conversely, it is now a well-established fact that GCs host multiple stellar populations with different chemical composition. A considerable number of works has provided strong evidence that these stellar systems harbour at least two main populations of stars, commonly dubbed first- (1G) and second-generation (2G). The latter includes stars that, being enhanced in He, N, and Na and depleted in C and O, exhibit abundance patterns distinctive of GC stars. On the contrary, 1G stars are characterized by an ‘original’ chemical composition that retains memories of their natal cloud chemistry (e.g. Kraft 1994; Carretta et al. 2009a; Marino et al. 2019a). In light of this feature and since Galactic GCs are among the most ancient objects of the Galaxy, studying 1G stars provides the unique opportunity to trace the original chemical composition of the clouds where GCs formed in the early Universe.
A powerful tool to infer the relative chemical composition of GC stars is the ‘Chromosome Map’ (ChM; Milone et al. 2015), a pseudo-two-colour diagram, constructed with appropriate photometric bands of the Hubble Space Telescope (HST), which is particularly sensitive to the chemistry of the distinct stellar populations thus maximizing the separation between them. On the ChM reference frame, |$\Delta _{\rm {\it C}\, F275W, F336W, F438W}$| versus ΔF275W,F814W,1 the 2G sequence is elongated towards large |$\Delta _{\rm {\it C}\, F275W, F336W, F438W}$| and low ΔF275W,F814W values, whereas 1G stars lay in proximity of the origin. As pointed out by Milone et al. (2017), the ΔF275W,F814W colour and |$\Delta _{\rm {\it C}\, F275W, F336W, F438W}$| pseudo-colour distributions of both 1G and 2G stars are wider than photometric errors (including errors associated with differential reddening corrections), thus demonstrating that neither of the two components is consistent with simple stellar populations. This phenomenon can be naturally explained for the 2G component using the dependence of ΔF275W,F814W and |$\Delta _{\rm {\it C}\, F275W, F336W, F438W}$| pseudo-colours on light-element abundances. As illustrated in details by Milone et al. (2018, see section 4), indeed, the 2G colour spread can be reproduced by a combination of variations in the N and He abundances, as expected for 2G stars characterized by a chemical composition produced by various degrees of CNO processing. The extension of the 1G sequence, instead, has revealed to be a more puzzling result.
Given that the position of stars along the ChM x-axis of monometallic GCs is predominantly affected by their helium abundance, Milone et al. (2018) tentatively attributed the 1G colour spread to a pure helium variation without any appreciable enrichment in other light elements, like N. Inhomogeneities in the helium content of the gas forming 1G stars may arise in regions of the Universe where the baryon-to-photon ratio was considerably enhanced, possibly by many orders of magnitude (e.g. Arbey, Auffinger & Silk 2020). Conversely, according to basic stellar nucleosynthesis, reproducing significant helium enhancements (even of the order of δY1G ∼ 0.1) not accompanied by appreciable nitrogen variations, is extremely difficult and all the scenarios considered by Milone et al. (2018, see their discussion in section 8) are unable to reproduce observations. In addition, the analysis of M 3 horizontal-branch (HB) stars by Tailo et al. (2019a) demonstrates that pure helium variations among 1G stars lead to inconsistent properties of HB stars thus making this scenario even more implausible.
An alternative hypothesis was suggested first by D’Antona et al. (2016) based on theoretical arguments and then by spectroscopy of 1G stars by Marino et al. (2019a, b). According to these authors, variations in iron abundances could mimic the effect on the 1G ChM colour distribution caused by a spread in helium. Marino et al. (2019b) analysed the chemical abundances of 18 red-giant branch (RGB) stars belonging to the 1G of NGC 3201 finding a spread in the overall metallicity of the order of ∼0.1 dex. The fact that GC stars are not chemically homogeneous is additionally supported by the pioneering work by Yong et al. (2013), based on high-precision differential abundances of 1G and 2G stars in the GC NGC 6752. Iron variations in the gas forming 1G stars might have been inherited from the interstellar medium (ISM) out of which proto-cluster molecular clouds formed. In turn, chemical inhomogeneities in the ISM might result from incomplete mixing of supernova ejecta with the ISM (e.g. Krumholz & Ting 2018; Wirth et al. 2021; Bailin & von Klar 2022). Alternatively, iron variations might be the product of stellar feedback inside the cloud itself (e.g. McKenzie & Bekki 2021).
Among the investigated targets, Marino and collaborators identified three binary candidates as the stars with the lowest ΔF275W,F814W values, thus suggesting that binarity could be responsible for the elongation of the 1G component. The authors explored deeply this possibility demonstrating that a large number of binaries is required to account for the observed 1G colour spread. This finding allows to conclude that binaries provide only a minor contribution to the elongation of the 1G sequence (see also Kamann et al. 2020; Martins et al. 2020).
More recently, extended sequences of 1G stars have been also detected along the red HB of 12 Galactic GCs (Dondoglio et al. 2021), thus demonstrating that this phenomenon is not a peculiarity of RGB stars. The spectro-photometric analysis by Dondoglio and collaborators have shown that the extended red-HB sequences are consistent with either star-to-star iron variations or with an internal helium spread, in close analogy with what has been observed along the RGB ChM.
With the aim of shedding new light on this intriguing phenomenon, in this work we combine multiband HST photometry and synthetic spectra analysis techniques to investigate for the first time chemical variations among unevolved main-sequence (MS) stars of the Galactic GCs NGC 6362 and NGC 6838. We choose to analyse these two clusters because the ChM of their RGB stars display an elongated colour sequence that is not consistent with observational errors alone (see figs 3 and 4 of Milone et al. 2017). Moreover, they display a quite simple multiple population pattern with only two distinct groups of 1G and 2G stars that reveal to be well separated at all evolutionary stages, both in ChMs and other appropriate photometric diagrams. For a general overview of the two GCs, we listed their main parameters in Table 1.
Main parameters of NGC 6362 and NGC 6838. Metallicities are derived from high-resolution spectroscopy by Massari et al. (2017) and Carretta et al. (2009b). The values of distance modulus, age, and reddening are taken from Dotter et al. (2010), whereas absolute visual magnitudes and cluster masses are provided by the 2010 version of the Harris (1996) catalogue and Baumgardt & Hilker (2018), respectively.
| Cluster ID . | [Fe/H] . | (m−M)V . | Age . | E(B−V) . | MV . | Mass . |
|---|---|---|---|---|---|---|
| . | . | (mag) . | (Gyr) . | (mag) . | (mag) . | (M⊙) . |
| NGC 6362 | −1.07 ± 0.01 | 14.55 | 12.5 ± 0.50 | 0.07 | −6.95 | 1.47 ± 0.04 × 105 |
| NGC 6838 | −0.82 ± 0.02 | 13.40 | 12.5 ± 0.75 | 0.22 | −5.61 | 4.91 ± 0.47 × 104 |
| Cluster ID . | [Fe/H] . | (m−M)V . | Age . | E(B−V) . | MV . | Mass . |
|---|---|---|---|---|---|---|
| . | . | (mag) . | (Gyr) . | (mag) . | (mag) . | (M⊙) . |
| NGC 6362 | −1.07 ± 0.01 | 14.55 | 12.5 ± 0.50 | 0.07 | −6.95 | 1.47 ± 0.04 × 105 |
| NGC 6838 | −0.82 ± 0.02 | 13.40 | 12.5 ± 0.75 | 0.22 | −5.61 | 4.91 ± 0.47 × 104 |
Main parameters of NGC 6362 and NGC 6838. Metallicities are derived from high-resolution spectroscopy by Massari et al. (2017) and Carretta et al. (2009b). The values of distance modulus, age, and reddening are taken from Dotter et al. (2010), whereas absolute visual magnitudes and cluster masses are provided by the 2010 version of the Harris (1996) catalogue and Baumgardt & Hilker (2018), respectively.
| Cluster ID . | [Fe/H] . | (m−M)V . | Age . | E(B−V) . | MV . | Mass . |
|---|---|---|---|---|---|---|
| . | . | (mag) . | (Gyr) . | (mag) . | (mag) . | (M⊙) . |
| NGC 6362 | −1.07 ± 0.01 | 14.55 | 12.5 ± 0.50 | 0.07 | −6.95 | 1.47 ± 0.04 × 105 |
| NGC 6838 | −0.82 ± 0.02 | 13.40 | 12.5 ± 0.75 | 0.22 | −5.61 | 4.91 ± 0.47 × 104 |
| Cluster ID . | [Fe/H] . | (m−M)V . | Age . | E(B−V) . | MV . | Mass . |
|---|---|---|---|---|---|---|
| . | . | (mag) . | (Gyr) . | (mag) . | (mag) . | (M⊙) . |
| NGC 6362 | −1.07 ± 0.01 | 14.55 | 12.5 ± 0.50 | 0.07 | −6.95 | 1.47 ± 0.04 × 105 |
| NGC 6838 | −0.82 ± 0.02 | 13.40 | 12.5 ± 0.75 | 0.22 | −5.61 | 4.91 ± 0.47 × 104 |
The paper is organized as follows. Section 2 presents the photometric data set for NGC 6362 and NGC 6838 and the procedure employed to reduce it. In Section 3, we investigate multiple stellar populations and derive the ChM of MS stars for both clusters. A detailed analysis of the 1G colour spread observed on the ChM is developed in Sections 4 and 5 by using MS and sub-giant branch (SGB) stars, respectively. In Section 6, we extend our considerations to a sample of 55 Galactic GCs calculating the internal iron variations within the 1G and searching for correlations between this quantity and the main host GC parameters. Finally, in Section 7, we summarize the main results of this work and discuss physical reasons that could explain the presence of iron inhomogeneities among 1G stars. We also speculate about possible implications on the formation scenarios of 2G stars within GCs.
2 DATA AND DATA REDUCTION
In this work, the astro-photometric catalogues of the Galactic GCs NGC 6362 and NGC 6838 were obtained starting from the archive images taken with the Wide Field Camera of the Advanced Camera for Surveys (WFC/ACS) and the Ultraviolet and Visual Channel of the Wide Field Camera 3 (UVIS/WFC3) onboard HST. Specifically, to investigate the 1G colour spread in NGC 6838 we used exposures collected through 5 filters, namely F275W, F336W, F438W, F606W, and F814W. A similar data set has been exploited for NGC 6362 with the only exception that also images in the F625W and F658N filters of WFC/ACS were available. The main properties of the complete set of exposures used in this work are summarized in Table 2.
Summary information about the archive images of NGC 6362 and NGC 6838 used in this work.
| DATE . | N × EXPTIME . | INSTRUMENT . | FILTER . | PROGRAM . | PI . |
|---|---|---|---|---|---|
| NGC 6362 | |||||
| 2014 March 30 | 2 × 720 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2014 July 1 | 2 × 829 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2010 August 13 | |$368\rm \, s+4\times 450$| s | UVIS/WFC3 | F336W | 12008 | A. Kong |
| 2014 March 29 | 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 March 30 | 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 July 1 | 2 × 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 March 29 | 68 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2014 July 1 | 67 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2006 May 30 | |$10 \rm \, s+4\times 130$| s | WFC/ACS | F606W | 10775 | A. Sarajedini |
| 2011 March 30 | |$140\rm \, s+145\rm \, s$| | WFC/ACS | F625W | 12008 | A. Kong |
| 2011 March 30 | |$750 \rm \, s+766 \rm \, s$| | WFC/ACS | F658N | 12008 | A. Kong |
| 2006 May 30 | |$10 \rm \, s+4\times 150$| s | WFC/ACS | F814W | 10775 | A. Sarajedini |
| NGC 6838 | |||||
| 2013 October 23 | 2 × 792 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2014 May 03 | 2 × 750 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2013 October 23 | 2 × 303 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 May 3 | 2 × 303 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2013 October 23 | 65 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2014 May 3 | 65 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2006 May 12 | |$4\rm \, s+4\times 75$| s | WFC/ACS | F606W | 10775 | A. Sarajedini |
| 2013 August 20 | |$5\times 500\rm \, s+3\times 466\rm \, s+2\times 459\rm \, s$| | WFC/ACS | F606W | 12932 | F. Ferraro |
| 2006 May 12 | |$4\rm \, s+4\times 80$| s | WFC/ACS | F814W | 10775 | A. Sarajedini |
| 2013 August 20 | |$440\rm \, s+3\times 357\rm \, s+5\times 337\rm \, s$| | WFC/ACS | F814W | 12932 | F. Ferraro |
| 2020 December 12 | |$35\rm \, s+4\times 337\rm \, s$| | WFC/ACS | F814W | 16298 | M. Libralato |
| DATE . | N × EXPTIME . | INSTRUMENT . | FILTER . | PROGRAM . | PI . |
|---|---|---|---|---|---|
| NGC 6362 | |||||
| 2014 March 30 | 2 × 720 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2014 July 1 | 2 × 829 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2010 August 13 | |$368\rm \, s+4\times 450$| s | UVIS/WFC3 | F336W | 12008 | A. Kong |
| 2014 March 29 | 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 March 30 | 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 July 1 | 2 × 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 March 29 | 68 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2014 July 1 | 67 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2006 May 30 | |$10 \rm \, s+4\times 130$| s | WFC/ACS | F606W | 10775 | A. Sarajedini |
| 2011 March 30 | |$140\rm \, s+145\rm \, s$| | WFC/ACS | F625W | 12008 | A. Kong |
| 2011 March 30 | |$750 \rm \, s+766 \rm \, s$| | WFC/ACS | F658N | 12008 | A. Kong |
| 2006 May 30 | |$10 \rm \, s+4\times 150$| s | WFC/ACS | F814W | 10775 | A. Sarajedini |
| NGC 6838 | |||||
| 2013 October 23 | 2 × 792 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2014 May 03 | 2 × 750 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2013 October 23 | 2 × 303 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 May 3 | 2 × 303 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2013 October 23 | 65 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2014 May 3 | 65 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2006 May 12 | |$4\rm \, s+4\times 75$| s | WFC/ACS | F606W | 10775 | A. Sarajedini |
| 2013 August 20 | |$5\times 500\rm \, s+3\times 466\rm \, s+2\times 459\rm \, s$| | WFC/ACS | F606W | 12932 | F. Ferraro |
| 2006 May 12 | |$4\rm \, s+4\times 80$| s | WFC/ACS | F814W | 10775 | A. Sarajedini |
| 2013 August 20 | |$440\rm \, s+3\times 357\rm \, s+5\times 337\rm \, s$| | WFC/ACS | F814W | 12932 | F. Ferraro |
| 2020 December 12 | |$35\rm \, s+4\times 337\rm \, s$| | WFC/ACS | F814W | 16298 | M. Libralato |
Summary information about the archive images of NGC 6362 and NGC 6838 used in this work.
| DATE . | N × EXPTIME . | INSTRUMENT . | FILTER . | PROGRAM . | PI . |
|---|---|---|---|---|---|
| NGC 6362 | |||||
| 2014 March 30 | 2 × 720 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2014 July 1 | 2 × 829 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2010 August 13 | |$368\rm \, s+4\times 450$| s | UVIS/WFC3 | F336W | 12008 | A. Kong |
| 2014 March 29 | 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 March 30 | 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 July 1 | 2 × 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 March 29 | 68 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2014 July 1 | 67 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2006 May 30 | |$10 \rm \, s+4\times 130$| s | WFC/ACS | F606W | 10775 | A. Sarajedini |
| 2011 March 30 | |$140\rm \, s+145\rm \, s$| | WFC/ACS | F625W | 12008 | A. Kong |
| 2011 March 30 | |$750 \rm \, s+766 \rm \, s$| | WFC/ACS | F658N | 12008 | A. Kong |
| 2006 May 30 | |$10 \rm \, s+4\times 150$| s | WFC/ACS | F814W | 10775 | A. Sarajedini |
| NGC 6838 | |||||
| 2013 October 23 | 2 × 792 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2014 May 03 | 2 × 750 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2013 October 23 | 2 × 303 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 May 3 | 2 × 303 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2013 October 23 | 65 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2014 May 3 | 65 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2006 May 12 | |$4\rm \, s+4\times 75$| s | WFC/ACS | F606W | 10775 | A. Sarajedini |
| 2013 August 20 | |$5\times 500\rm \, s+3\times 466\rm \, s+2\times 459\rm \, s$| | WFC/ACS | F606W | 12932 | F. Ferraro |
| 2006 May 12 | |$4\rm \, s+4\times 80$| s | WFC/ACS | F814W | 10775 | A. Sarajedini |
| 2013 August 20 | |$440\rm \, s+3\times 357\rm \, s+5\times 337\rm \, s$| | WFC/ACS | F814W | 12932 | F. Ferraro |
| 2020 December 12 | |$35\rm \, s+4\times 337\rm \, s$| | WFC/ACS | F814W | 16298 | M. Libralato |
| DATE . | N × EXPTIME . | INSTRUMENT . | FILTER . | PROGRAM . | PI . |
|---|---|---|---|---|---|
| NGC 6362 | |||||
| 2014 March 30 | 2 × 720 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2014 July 1 | 2 × 829 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2010 August 13 | |$368\rm \, s+4\times 450$| s | UVIS/WFC3 | F336W | 12008 | A. Kong |
| 2014 March 29 | 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 March 30 | 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 July 1 | 2 × 323 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 March 29 | 68 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2014 July 1 | 67 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2006 May 30 | |$10 \rm \, s+4\times 130$| s | WFC/ACS | F606W | 10775 | A. Sarajedini |
| 2011 March 30 | |$140\rm \, s+145\rm \, s$| | WFC/ACS | F625W | 12008 | A. Kong |
| 2011 March 30 | |$750 \rm \, s+766 \rm \, s$| | WFC/ACS | F658N | 12008 | A. Kong |
| 2006 May 30 | |$10 \rm \, s+4\times 150$| s | WFC/ACS | F814W | 10775 | A. Sarajedini |
| NGC 6838 | |||||
| 2013 October 23 | 2 × 792 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2014 May 03 | 2 × 750 s | UVIS/WFC3 | F275W | 13297 | G. Piotto |
| 2013 October 23 | 2 × 303 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2014 May 3 | 2 × 303 s | UVIS/WFC3 | F336W | 13297 | G. Piotto |
| 2013 October 23 | 65 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2014 May 3 | 65 s | UVIS/WFC3 | F438W | 13297 | G. Piotto |
| 2006 May 12 | |$4\rm \, s+4\times 75$| s | WFC/ACS | F606W | 10775 | A. Sarajedini |
| 2013 August 20 | |$5\times 500\rm \, s+3\times 466\rm \, s+2\times 459\rm \, s$| | WFC/ACS | F606W | 12932 | F. Ferraro |
| 2006 May 12 | |$4\rm \, s+4\times 80$| s | WFC/ACS | F814W | 10775 | A. Sarajedini |
| 2013 August 20 | |$440\rm \, s+3\times 357\rm \, s+5\times 337\rm \, s$| | WFC/ACS | F814W | 12932 | F. Ferraro |
| 2020 December 12 | |$35\rm \, s+4\times 337\rm \, s$| | WFC/ACS | F814W | 16298 | M. Libralato |
Accurate measurements of stellar position and magnitudes have been derived by using the computer program KS2 developed by Jay Anderson as an evolution of kitchen_sync (Anderson et al. 2008). Briefly, KS2 performs different iterations to find and measure stars: it first identifies only the brightest stars and then, after subtracting them, it looks for progressively fainter stars that satisfy a set of different criteria based on the distance, on the peak position or on the quality fit parameter. This program offers the possibility to measure stars with distinct methods optimized to provide the best possible photometry according to their luminosities (see e.g. Sabbi et al. 2016; Bellini et al. 2017; Nardiello et al. 2018, for a detailed description of how KS2 works). Specifically, the positions and magnitudes of relatively bright sources, having enough flux to be detected in single images, are measured by fitting the appropriate PSF model in each exposure independently and then averaged together to derive the best estimates. Since faint stars do not produce a significant peak in all the exposures this approach is not suited to measure them making necessary to combine the information from all the images to derive their positions and magnitudes.
KS2 also provides various diagnostics to test whether the photometric and astrometric measurements are reliable or not. Following the procedure described in Milone et al. (2009) and Bedin et al. (2009), we exploited these parameters to select a sample of relatively isolated stars well fitted by the PSF.
The next step was to calibrate photometry into the Vega system. To do that we exploited the procedure by Nardiello et al. (2018) using the updated zero points retrieved from the Space Telescope Science Institute webpage.2 Finally, magnitudes have been corrected for the effects of differential reddening following the recipe introduced by Milone et al. (2012a, see their section 3 for details on the procedure).
2.1 Artificial stars
To estimate the photometric uncertainties associated with our measurements and generate simulated diagrams we performed artificial-star (AS) tests extending the procedure introduced by Anderson et al. (2008) to NGC 6362 and NGC 6838.
Briefly, we first generated a list of coordinates and magnitudes of 99 999 stars with a spatial distribution along the field of view resembling the one of cluster stars. The magnitudes of ASs were derived starting from a set of fiducial lines obtained from the observed colour–magnitude diagrams (CMDs).
We reduced ASs by using once again KS2. In particular, the program derives for ASs the same parameters used to evaluate the astrometric and photometric quality of real stars. To select a sample of relatively isolated ASs well fitted by the PSF we applied the same stringent criteria obtained from the reduction of real stars.
3 MULTIPLE POPULATIONS IN NGC 6362 AND NGC 6838
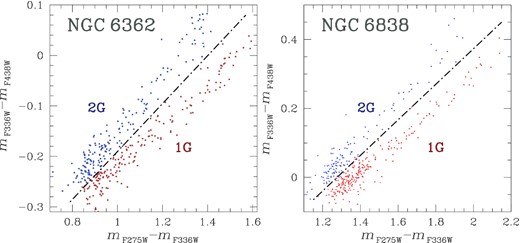
A visual inspection at the mF814W versus CF275W,F336W,F438W diagrams of NGC 6362 and NGC 6838 illustrated in panels (a1–b1) of Fig. 1, respectively, immediately reveals that both clusters exhibit two distinct sequences that run almost parallel from the bottom of the MS to the upper part of the RGB. These sequences correspond to stellar populations with different abundances in light elements. Indeed, the CF275W,F336W,F438W pseudo-colour, encompassing the absorption features of the OH, NH, CH, and CN molecules, allows us to separate stellar populations with different content of C, N, and O.
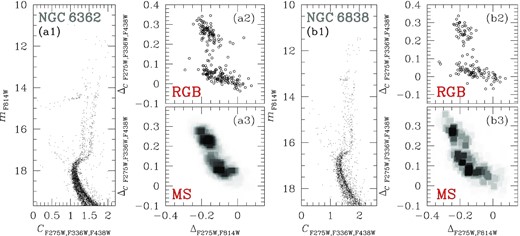
Panels (a1) and (b1) show the mF814W versus CF275W,F336W,F438W CMDs for NGC 6362 and NGC 6838, respectively. This diagram has been exploited in combination with the mF814W versus mF275W − mF814W CMD to derive the ΔF275W,F814W and the |$\Delta _{\rm {\it C}\, F275W,F336W,F438W}$| pseudo-colours used to build the ChMs of MS and RGB stars. The ChMs of RGB stars are shown in panels (a2–b2), whereas the Hess diagrams of the MS ChMs are plotted in panels (a3–b3).
To better investigate stellar populations, we show in panels (a2–b2) of Fig. 1 the ChMs of RGB stars for NGC 6362 and NGC 6838, respectively (Milone et al. 2017). Similarly, panels (a3–b3) of Fig. 1 reproduce the Hess diagram of the ChM for MS stars. These diagrams were derived adapting the method by Milone et al. (2015, 2017) to MS stars. In the case of NGC 6362, for example, we first selected stars with 18.75 ≤ mF814W ≤ 19.75 in the mF814W versus CF275W,F336W,F438W and mF814W versus mF275W − mF814W CMDs and divided this sample of MS stars into magnitude bins of size 0.2 mag. For each bin, we calculated the 4th and the 96th percentile of the mF275W − mF814W colour and CF275W,F336W,F438W pseudo-colour distribution. We then interpolated these values with the mean mF814W magnitudes to infer the blue and red boundaries of the selected MS stars. Finally, to obtain the |$\Delta _{\rm {\it C}\, F275W, F336W, F438W}$| and ΔF275W,F814W pseudo-colours, we ‘verticalized’ the two diagrams as in Milone et al. (2017). We derived the ChM of NGC 6838 in the same way but by using MS stars with 17.75 ≤ mF814W ≤ 18.75.
As illustrated in panels (a3) and (b3) of Fig. 1, the distribution of MS stars in the |$\Delta _{\rm {\it C}\, F275W, F336W, F438W}$| versus ΔF275W,F814W plane is bimodal, in close analogy with what is observed for the RGB, indicating the presence of multiple populations among the MS.
4 THE EXTENDED FIRST-GENERATIONS OF NGC 6362 AND NGC 6838
To further investigate multiple populations of NGC 6362 and NGC 6838, we reproduce the ChMs of RGB stars and the ΔF275W,F814W kernel-density distributions of 1G, 2G, and observational errors in the upper panels of Fig. 2. Stars near the origin of the ChM reference frame may reflect the chemical composition of their natal cloud and correspond to the 1G, whereas the 2G component, which is He- and N-enhanced and C- and O-depleted, defines the sequence elongated towards large |$\Delta _{\rm {\it C}\, F275W, F336W, F438W}$| and low ΔF275W,F814W values (e.g. Milone et al. 2020a; Jang et al. 2021). Hence, the aqua dash–dotted lines, drawn by hand, separate 1G and 2G stars that we coloured red and blue, respectively. Both 1G and 2G stars of each cluster span wider ΔF275W,F814W intervals than what is expected from observational errors alone, indicated by orange dots in Fig. 2.
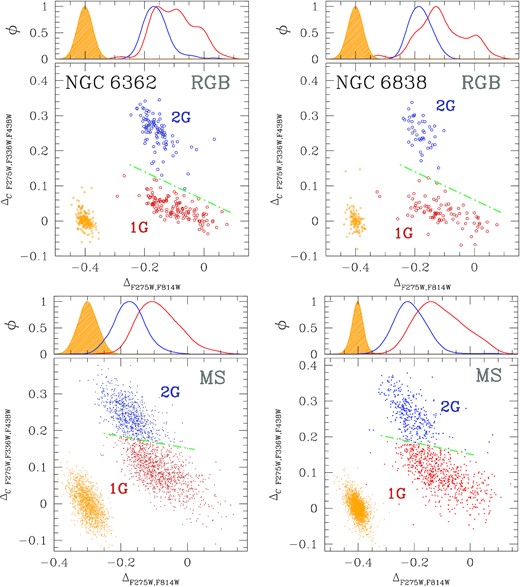
ChM of RGB (upper panels) and MS (lower panels) stars in NGC 6362 (left) and NGC 6838 (right). 1G and 2G stars are coloured red and blue, respectively, while the error distribution is represented by orange points on the bottom-left corner. The kernel-density distributions of 1G, 2G stars, and observational errors are plotted on the top panel of each figure.
Moreover, 1G and 2G stars exhibit different patterns in the ChM. The kernel-density distributions of ΔF275W,F814W reveal that 2G stars in both clusters have nearly symmetric patterns and are centred around ΔF275W,F814W ∼ −0.18 mag. Conversely, the kernel-density distributions of 1G stars present more-complex behaviours with hints of multiple peaks. In both clusters, for example, the frequencies of 1G stars suddenly increase from ΔF275W,F814W ∼ −0.20 to −0.15 mag, where they approach their maximum values, and gently decline towards ΔF275W,F814W ∼ 0.0 mag. Some hints of secondary peak(s) are visible towards ΔF275W,F814W ∼ −0.1–0.0. Clearly, in both clusters 1G stars display more extended ChM sequences than the 2G.
In the following, we investigate whether the extended 1G sequences are peculiarities of the RGB or are also present among unevolved MS stars. To do this, we exploit multiband HST photometry to analyse the colour distributions of 1G stars along the MSs of NGC 6362 and NGC 6838. In the next subsection, we demonstrate that MS 1G stars of both GCs exhibit intrinsic colour extensions (Section 4.1). We then continue our analysis of the 1G colour spread exploring the physical phenomenon responsible for it. Specifically, in Section 4.2, we consider the role of binaries in shaping the 1G ChM sequence, whereas in Section 4.3 we constrain the chemical composition of the 1G by considering MS stars. Finally, in Section 4.4, we use the ΔF275W,F814W pseudo-colour broadening to derive the metallicity distribution of 1G stars.
4.1 Chemical inhomogeneities among 1G MS stars
Lower panels of Fig. 2 reproduce the ChMs for MS stars in NGC 6362 and NGC 6838 together with the ΔF275W,F814W kernel-density distributions of 1G, 2G, and observational errors. Though the 1G–2G separation in MS ChMs is not as sharp as in the RGB, due to higher photometric errors tending to fill the gap, we were still able to identify two distinct sequences on the MS ChM of both clusters, corresponding to the 1G and 2G component. The aqua dash–dotted line, drawn by hand to separate the two main stellar populations, defines the samples of bona-fide 1G and 2G stars, marked with red and blue colours, respectively.
Consistently with what is observed on the RGB ChMs, the 1G MS stars of NGC 6362 and NGC 6838 display a well-elongated distribution along the ΔF275W,F814W direction. Conversely, the 2G sequence exhibits a narrower ΔF275W,F814W spread on the MS ChM of both clusters, as highlighted by the corresponding kernel-density distribution. To investigate whether the F275W−F814W colour distribution of 1G stars is entirely due to observational errors or it is intrinsically broad, we exploited three distinct approaches.
The first evidence that 1G MS stars are not consistent with a simple stellar population is provided by the fact that the observed ΔF275W,F814W spread of NGC 6362 (|$\sigma ^{\rm obs, 1G}_{\rm F275W,F814W}$| = 0.062 ± 0.003 mag) and NGC 6838 (|$\sigma ^{\rm obs, 1G}_{\rm F275W,F814W}$| = 0.086 ± 0.003 mag) are significantly wider than the colour broadening inferred from the simulated ChM of a simple population (|$\sigma ^{\rm sim}_{\rm F275W,F814W}$| = 0.026 mag and 0.022 mag, respectively, orange points in the bottom-left corner of lower panels in Fig. 2). To account for the inclination of the 1G sequence in the ChM, we rotated the ChM as in Milone et al. (2017, see their fig. 2) in such a way that the abscissa of the new reference frame is parallel to the 1G sequence. We repeated the comparison between the observed pseudo-colour distribution and the AS tests as described above but in the rotated reference frame. We found that the observed pseudo-colour spreads are much wider than the broadening associated with observational errors, thus confirming the conclusion of an intrinsic colour spread in 1G stars.
As highlighted by the comparison of the ΔF275W,F814W kernel distributions of 1G and 2G stars, the 1G exhibits wider colour broadening than the 2G in both clusters (|$\sigma ^{\rm obs, 2G}_{\rm F275W,F814W}$| = 0.038 ± 0.003 and 0.049 ± 0.003 for NGC 6362 and NGC 6838, respectively). Since similar observational uncertainties affect the two stellar populations, this fact proves that the 1G is intrinsically broad.
To emphasize that the colour spread of 1G MS stars observed on the ChM is intrinsic, we extended to NGC 6362 and NGC 6838 the procedure used by Anderson et al. (2009) to prove that the MS of the GC 47 Tucanae is composed of multiple populations. Their method is based on the idea that, if the MS broadening is due to observational errors alone, a star that is red (or blue) in a given photometric diagram has the same probability of being either red or blue in other diagrams built from a different data set. On the contrary, separated colour distributions are the signature of an intrinsic colour spread.
The procedure is illustrated in Fig. 3 for NGC 6362. We identified by eye in panel (a) four groups of 1G stars with different ΔF275W,F814W values, namely 1GI–IV, with the criteria that each group comprises about one-fourth of 1G stars. The same stars are plotted in the other panels of Fig. 3. Specifically, panel (b) of Fig. 3 shows the mF606W versus ΔF336W, F606W diagram, which is derived from a distinct data set than that shown in panel (a). Clearly, the four stellar groups, identified in panel (a), have, on average, different ΔF336W, F606W pseudo-colours, thus confirming that the colour spread is intrinsic. The fact that the average colours of the four stellar groups remain well separated is further illustrated in panels (c) and (d), where we show the ΔF275W,F814W and ΔF336W, F606W histogram distributions, respectively. Finally, the correlation of the ΔF336W,F606W and ΔF275W,F814W pseudo-colours is provided in panel (e) of Fig. 3. The distribution of 1G stars in the ΔF336W,F606W versus ΔF275W,F814W plane reinforces the conclusion that the 1G colour spread is intrinsic.
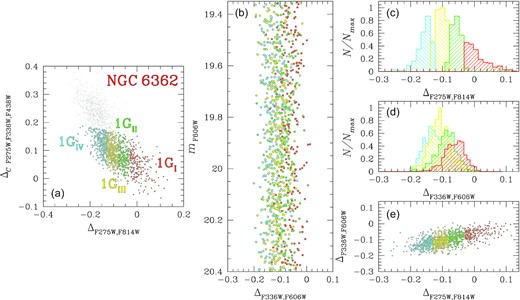
Panel (a): ChM of MS stars in NGC 6362 where we have highlighted in orange, green, yellow, and cyan the samples of 1GI–IV stars, respectively. Panel (b): mF606W versus ΔF336W,F606W diagram where we have plotted only 1G stars identified on the ChM. Panels (c) and (d): Normalized histograms of the ΔF275W,F814W and ΔF336W, F606W distributions for each sample of 1G stars identified on the ChM. Panel (e): Correlation between the ΔF336W, F606W and ΔF275W,F814W pseudo-colours.
The discovery of extended 1G sequence among unevolved MS stars rules out the possibility that chemical inhomogeneities are the result of stellar evolution and suggests that 1G stars of GCs may be records of the chemical inhomogeneities in the original cloud where they formed at high redshift. Moreover, the fact that the 2G sequence displays a narrower colour spread than the 1G on the ChM demonstrates that these inhomogeneities have been partially erased before the formation of 2G stars.
4.2 The role of binaries in shaping the 1G colour extension
As illustrated in Fig. 2, the ΔF275W,F814W distributions of 1G stars along the RGB and the MS follow similar patterns. In particular, the distributions of both MS and RGB stars are not symmetric with respect to the peak, with a gentle decline towards ΔF275W,F814W ∼ 0.0. This feature would provide crucial constraints on the effect of binaries in shaping the ChM. Indeed, binary systems composed of two MS stars would populate the reddest part of the MS thus contributing to the red tail of the ChM. On the contrary, pairs of RGB stars exhibit bluer colours than single RGB stars and are responsible for the blue tail in the ChM (Marino et al. 2019b).
The fact that the ΔF275W,F814W distributions of both MS and RGB exhibit a tail towards redder colour demonstrates that unresolved binaries provide a minor contribution to the extension of the 1G sequence in the ChM. This finding is consistent with previous conclusion based on radial velocities of 1G stars (Marino et al. 2019b; Kamann et al. 2020) and supported by studies on the comparison of the observed 1G of NGC 6752 with appropriate isochrones (Martins et al. 2020).
4.3 Insights from multiband photometry of MS stars
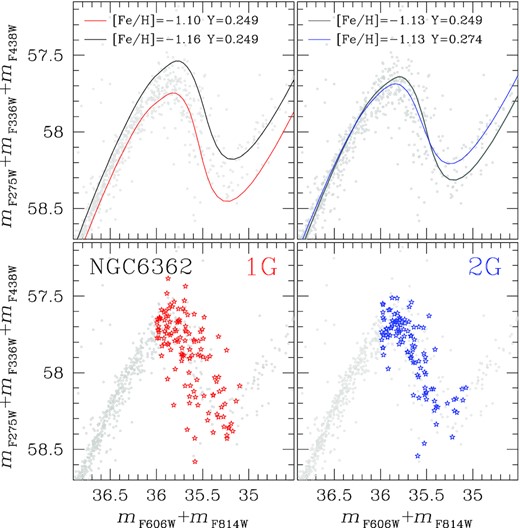
To shed light on the physical phenomenon that is responsible for the colour extension of the 1G sequence on the ChM, we applied to 1G stars of NGC 6362 and NGC 6838 the procedure by Milone et al. (2012b,2018). This method, shown in Fig. 4 for NGC 6362, consists in comparing the observed colour widths of 1G stars with the predictions from appropriate isochrones that account for variations in light elements, helium, and iron.

This figure illustrates the procedure used to derive the colour differences between the two sub-groups of 1GA and 1GB stars for NGC 6362. The upper-left panel reproduces the ChM of MS stars with the orange and cyan points that identify 1GA and 1GB stars, respectively. The lower panels show the mF814W versus mX − mF814W CMDs where X = F275W, F336W, F438W, and F606W (the same has been done for F625W and F658N filters) in which the fiducial lines obtained for 1GA and 1GB are plotted in orange and cyan. In each panel, the horizontal dotted line corresponds to the reference F814W magnitude at which we calculate the colour separation, Δ(mX − mF814W). The upper-right panel shows the Δ(mX − mF814W) calculated at |$m^{\rm ref}_{\rm F814W}=19.5$| against the central wavelength of the X filter. The colours inferred from the best-fitting synthetic spectra are overplotted with blue triangles and red starred symbols (see text for details).
We first identified two groups of 1G stars along the direction of the 1G colour spread on the ChM, namely 1GA and 1GB, with the criteria that each sample comprises about half of 1G members. 1GA and 1GB stars are respectively marked with orange and cyan dots in the upper-left panel of Fig. 4. We then selected these two groups of 1G stars in the mF814W versus mX − mF814W CMDs, where X = F275W, F336W, F438W, F606W, F625W, and F658N and derived the corresponding fiducial line. To do this, we divided the MS into a series of mF814W bins of size δm defined over a grid of points separated by fixed intervals of magnitude (|$\rm \delta m/4$|). For each bin the median mF814W magnitude and mX − mF814W colour have been calculated and then smoothed by means of boxcar averaging, where each point has been replaced by the average of the three adjacent points. The fiducial lines for 1GA and 1GB stars were derived by linearly interpolating the resulting points and are plotted with orange and cyan lines, respectively, in the lower panels of Fig. 4.
Subsequently, we defined a list of N reference points along the MS regularly spaced in mF814W by 0.25. For each point, i, we calculated the Δ(mX − mF814W) colour difference between the fiducial of 1GA and 1GB stars. The Δ(mX − mF814W) values derived for |$m_{\rm F814W, \it {i}}=19.5$| (dotted horizontal line in bottom panels of Fig. 4) in NGC 6362 are represented as filled circles in the upper-right panel of Fig. 4. Clearly, the colour separation between 1GA and 1GB stars changes with the width of the colour baseline reaching its maximum value for X = F275W.
The Δ(mX − mF814W) values measured for each filter were then compared with the colours inferred from a grid of synthetic spectra with appropriate chemical compositions. To derive them, as a preliminary step, we estimated gravity and effective temperature corresponding to each point, i, by using the isochrones from the Dartmouth data base (Dotter et al. 2008) and adopting the same age, reddening, distance modulus, metallicity, and [α/Fe] listed in Dotter et al. (2010) for NGC 6362 and NGC 6838, respectively. For each reference point i, we then used the codes ATLAS12 and SYNTHE (Castelli 2005; Kurucz 2005; Sbordone, Bonifacio & Castelli 2007) to compute a reference synthetic spectrum and a grid of comparison spectra with different chemical compositions.
To calculate the reference one, we used the values of effective temperature, gravity, and metallicity (Z) derived previously from the best-fitting isochrone, together with helium, |$\rm Y=0.245+1.5\times Z$|, solar abundances of C and N, and |$\rm [O/Fe]=0.40$|. Comparison spectra, instead, were derived by using the same chemical composition as the reference one but changing the abundances of He, C, N, O, and Fe. Specifically, in close analogy with Milone et al. (2018), we simulated a grid of spectra enhanced in [N/Fe] up to 1.5 dex in steps of 0.1 dex, with [O/Fe] ranging from −0.2 to 0.4 in steps of 0.1 dex, [C/Fe] from −0.4 to 0.0 in steps of −0.1. Helium has been changed up to 0.33 and [Fe/H] by ±0.2 dex.
The atmospheric parameters, gravity, and effective temperature, of the reference spectra have been derived from the Dartmouth isochrones (Dotter et al. 2008), accordingly with their metallicity and helium content. The colour differences Δ(mX − mF814W)synth between the comparison and reference spectrum have been determined from the integration of each spectrum over the transmission curves of the seven HST filters used in this work for NGC 6362. We applied the same procedure to NGC 6838 with the only exception that for this cluster magnitudes in F625W and F658N filters were missing.
Results from the analysis of NGC 6362 1G stars with |$m_{\rm F814W, \it {i}}=19.5$| are illustrated in the upper-right panel of Fig. 4, where we compare the observed colour differences between 1GA and 1GB stars with those inferred from the best-fitting synthetic spectra. We found that colours derived from spectra with different light-element abundances provide poor fit to the observations. We conclude that 1G stars of NGC 6362 share the same abundances of C, N, and O within our uncertainty of ∼0.1 dex. As a consequence, for a fixed luminosity, they exhibit internal variations in their effective temperature. This fact indicates that the colour broadening of the 1G component is due either to helium (|$\rm \Delta Y=0.024$|) or iron (|$\rm \Delta [Fe/H]=0.06$| dex) variations. Indeed, the colour differences inferred from spectra of 1GB and 1GA stars that differ either in [Fe/H] and or in Y alone provides a good match with the observed colour differences (upper-right panel of Fig. 4). Similar results have been found for NGC 6838, where the 1G is consistent with the presence of two groups of stars with either metallicity variations of |$\rm \Delta [Fe/H]=0.05$| dex or helium differences of |$\rm \Delta Y=0.020$|.3
Our results, based on multiband photometry of 1G MS stars, together with similar findings, based on spectroscopy of 1G RGB stars (e.g. Marino et al. 2019a, b; Kamann et al. 2020), indicate that 1G stars have constant light-element abundances.
4.4 The metallicity distribution of 1G stars
In this subsection, we derive the [Fe/H] distribution of 1G stars in NGC 6362 and NGC 6838, by assuming that the ΔF275W,F814W pseudo-colour broadening of the 1G is entirely due to metallicity variations. To do this, we adapted to the ChMs of RGB and MS stars, the method by Stauffer (1980) and Cignoni et al. (2010) by comparing the observed ΔF275W,F814W distribution of 1G stars and the corresponding distributions of grids of simulated ChMs, where all stars have nearly pristine helium content (Y = 0.249) and the same light-element abundances. In a nutshell, we simulated the ChMs of N stellar populations with different metallicities in the interval between [Fe/H]0 − 0.5 and [Fe/H]0 + 0.5 dex, where [Fe/H]0 is the iron abundance corresponding to ΔF275W,F814W = 0. We assumed [Fe/H]0 = −1.1 for NGC 6362 and [Fe/H]0 = −0.8 for NGC 6838, as inferred from high-resolution spectroscopy (Carretta et al. 2009b; Massari et al. 2017). We adopted for each stellar population a Gaussian [Fe/H] distribution with a tiny iron dispersion (σ = 0.01 dex) and assumed that two adjacent populations differ in their average iron abundance by 0.01 dex.
Results are illustrated in Fig. 5, where we show the histogram distributions of the relative iron abundances of 1G stars, δ[Fe/H], and show that we get comparable [Fe/H] distributions from RGB and MS stars that span similar intervals of 0.1 dex for NGC 6362 and NGC 6838.
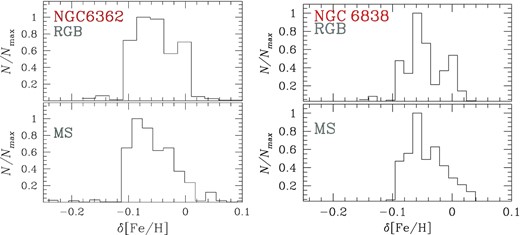
Histograms of the iron distribution of 1G stars in NGC 6362 (left) and NGC 6838 (right) inferred from MS stars (bottom) and RGB stars (top).
5 INSIGHTS FROM THE SUB-GIANT BRANCH
To disentangle the effect of helium and metallicity variations on the colour extension of the 1G component, we introduce here a new approach based on SGB stars.
We first identified the sample of SGB cluster members in the mF814W versus mF438W − mF814W CMD and plotted these stars in the mF336W − mF438W versus mF275W − mF336W two-colour diagram of Fig. 6. In this plane, SGB stars of both NGC 6362 and NGC 6838 exhibit a bimodal colour distribution allowing us to identify the 1G and 2G components as the groups of stars on the right and on the left of the dash–dotted line, respectively.
mF336W − mF438W versus mF275W − mF336W two-colour diagram for SGB stars of NGC 6362 (left) and NGC 6838 (right). The black dash–dotted line separates 1G and 2G stars, coloured in red and blue, respectively.
We focused on SGB stars because, in appropriate photometric diagrams, differences in helium and metallicity lead to different SGB morphologies, thus breaking the degeneracy observed in other evolutionary phases. As an example, the upper panels of Fig. 7 compare the photometry of NGC 6362 stars with four alpha-enhanced isochrones ([α/Fe] = 0.4) from the Dartmouth data base (Dotter et al. 2008) in the mF275W + mF336W + mF438W versus mF606W + mF814W plane. Specifically, the upper-left panel of Fig. 7 compares two isochrones with nearly pristine helium abundance (Y = 0.249) and different iron abundances ([Fe/H] = −1.10 and [Fe/H] = −1.16), whereas both isochrones plotted on the upper-right panel share the same metallicity [Fe/H] = −1.13 but different helium mass fractions, Y = 0.249 and Y = 0.274. The iron and helium differences match the values inferred from the colour broadening of MS 1G stars. We adopted for all isochrones an age of 12.5 Gyr, distance modulus, (m − M)0=13.34 mag, and reddening E(B − V) = 0.07 mag, to match the observations of NGC 6362. The SGBs of the two isochrones with different metallicities define parallel sequences, whereas the isochrones with different helium abundances exhibit smaller magnitude separations and cross to each other near the RGB base. Clearly, the isochrone behaviour justifies the choice of the adopted pseudo-magnitude–magnitude plane. Indeed, it maximizes the separation between isochrones with different iron content and allows us to disentangle the effect of helium and metallicity.
Pseudo-two-magnitude diagrams for NGC 6362 cluster members (grey dots) zoomed around the SGB. Upper panels compare isochrones from Dartmouth data base (Dotter et al. 2008) with different helium content and metallicities. Lower panels mark 1G and 2G SGB stars selected in Fig. 6 with red and blue colours, respectively.
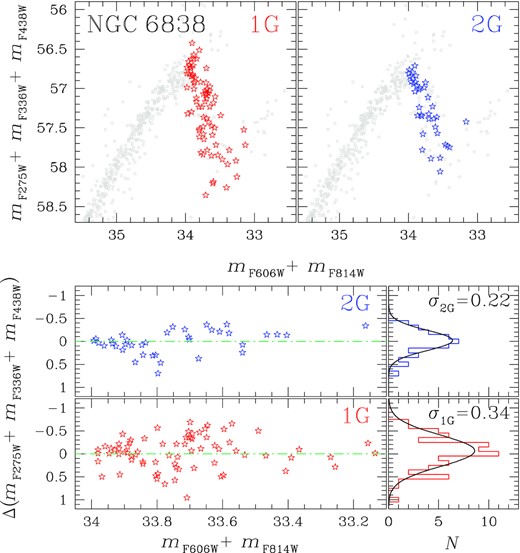
Lower panels of Fig. 7 mark with red and blue starred symbols the two groups of 1G and 2G stars selected in Fig. 6, respectively. To quantify the magnitude broadening of SGB stars, we adopted the procedure illustrated in Fig. 8 for NGC 6362.
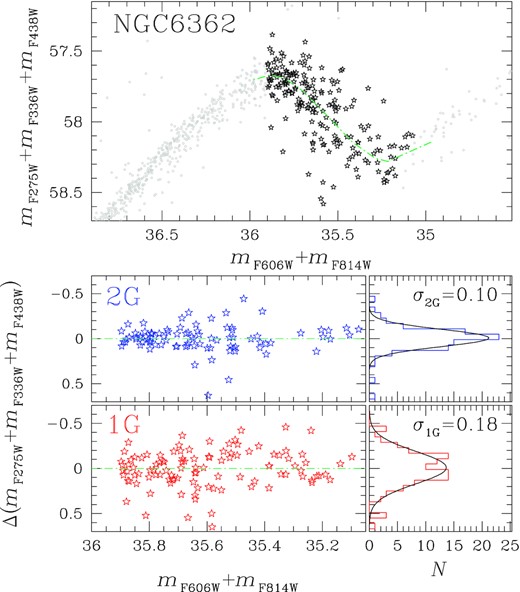
Upper panel: Reproduction of the mF275W + mF336W + mF438W versus mF606W + mF814W diagram of NGC 6362 introduced in Fig. 7. Black starred symbols mark the studied 1G and 2G SGB stars. The aqua dash–dotted line is the fiducial line of the SGB. Lower panels: Normalized Δ(mF275W + mF336W + mF438W) versus mF606W + mF814W diagram for 1G (bottom) and 2G stars (top). The corresponding Δ(mF275W + mF336W + mF438W) histogram distributions are plotted on the right together with the best-fitting least-squares Gaussian functions.
Briefly, we first derived the fiducial line of the SGB stars in the mF275W + mF336W + mF438W versus mF606W + mF814W diagram plotted in the upper panel of Fig. 8. To do this, we defined 0.15-mag wide intervals of mF606W + mF814W and calculated the median values of mF606W + mF814W and mF275W + mF336W + mF438W in each bin. The fiducial is obtained by linearly interpolating these median points, and is represented with the aqua dash–dotted line. Finally, we calculated the mF275W + mF336W + mF438W residuals of SGB stars, by subtracting to the mF275W + mF336W + mF438W pseudo-magnitude of each star the corresponding value of the fiducial at the same mF606W + mF814W value. The Δ(mF275W + mF336W + mF438W) values of 1G and 2G stars are plotted in the bottom-left panels of Fig. 8 as a function of mF606W + mF814W. The corresponding histogram distributions are shown in the bottom-right panels together with the best-fitting least-squares Gaussian functions. Clearly, 1G SGB stars exhibit a wider pseudo-magnitude broadening than the 2G, as indicated by the standard deviation of the best-fitting Gaussian functions of 0.18 and 0.10 mag, respectively.
To investigate whether the magnitude broadening of 1G SGB stars is due to internal metallicity or helium variations,5 we compared observations with simulated pseudo-two-magnitude diagrams, as illustrated in Fig. 9 for NGC 6362. We first used ASs to generate the synthetic mF275W + mF336W + mF438W versus mF606W + mF814W diagram for stellar populations with Y = 0.249 and the metallicity distribution inferred in Section 4.4 (upper-left panel of Fig. 9). We adopted the isochrones from Dotter et al. (2008) and the values of distance, reddening, and age introduced before for NGC 6362. This diagram is used to derive the mF275W + mF336W + mF438W residuals of SGB stars that we plotted against mF606W + mF814W in the middle-left panel of Fig. 9 and used to derive the Δ(mF275W + mF336W + mF438W) histogram distribution, shown in the bottom-left panel of Fig. 9. We found that the Δ(mF275W + mF336W + mF438W) distribution of simulated SGB stars is reproduced by a Gaussian function with dispersion |$\sigma ^{\rm \delta Fe}_{\rm sim}=0.16$|, which is comparable with the corresponding broadening of 1G SGB stars (σ1G = 0.18). Similarly, we simulated the diagram shown in the upper-right panel of Fig. 9 adopting constant [Fe/H] = −1.13 and the helium distribution derived with the procedure described in Section 4.4 but by assuming that the broadening of 1G stars is entirely due to helium variations. In this case, we obtained a much smaller value for the Δ(mF275W + mF336W + mF438W) dispersion of |$\sigma ^{\rm \delta He}_{\rm sim}=0.06$|, which is not consistent with the observations of 1G stars.
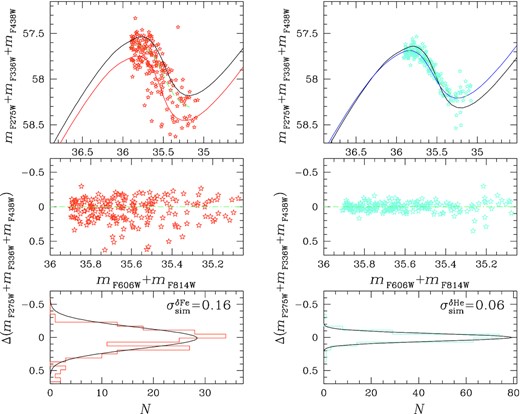
Upper panels: Simulated pseudo-two-magnitude diagrams for SGB stars of composite stellar populations with the iron distribution (left-hand panel) and helium distribution (right-hand panel) inferred from 1G MS stars of NGC 6362. The aqua dashed lines are the SGB fiducials. Middle panels: Δ(mF275W + mF336W + mF438W) against mF606W + mF814W. Lower panels: Histogram distributions of Δ(mF275W + mF336W + mF438W) for SGB stars. The best-fitting least-squares Gaussian functions are represented with black lines and the corresponding σ are quoted in each panel.
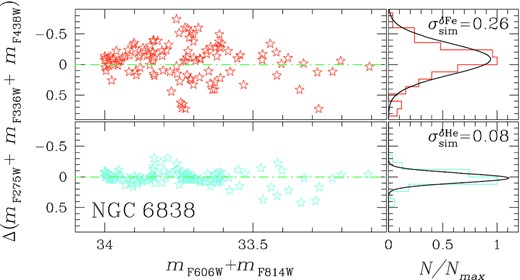
We carried out the same analysis for NGC 6838 SGB stars and summarized the results in Fig. 10. The upper-panels represent the mF275W + mF336W + mF438W versus mF606W + mF814W diagram where we marked 1G and 2G stars with red and blue starred symbols, respectively. The Δ(mF275W + mF336W + mF438W) values of 1G and 2G stars are plotted as a function of mF606W + mF814W in the bottom-left panels while the corresponding histogram distributions are shown in the bottom-right ones together with the best-fitting least-squares Gaussian functions. In close analogy with NGC 6362, 1G SGB stars of NGC 6838 are characterized by a wider pseudo-magnitude broadening (σ1G = 0.34) than the 2G (σ2G = 0.22). Moreover, we generated a synthetic mF275W + mF336W + mF438W versus mF606W + mF814W diagram by using the metallicity distribution derived from MS stars of NGC 6838 in Section 4.4. This diagram has been then exploited to infer the mF275W + mF336W + mF438W residuals of SGB stars and the correspondent histogram distribution, illustrated in the upper-left and -right panel of Fig. 11, respectively. In this case, the Δ(mF275W + mF336W + mF438W) distribution is reproduced by a Gaussian function with dispersion |$\sigma ^{\rm \delta Fe}_{\rm sim}=0.26$|, which is comparable with the corresponding broadening of 1G SGB stars. Conversely, exploiting the helium distribution to generate the synthetic mF275W + mF336W + mF438W versus mF606W + mF814W diagram, the best-fitting Gaussian function has a smaller dispersion (|$\sigma ^{\rm \delta He}_{sim}=0.08$|) which is not consistent with observations of 1G stars, as illustrated in bottom panels of Fig. 11.
Upper panels: Pseudo-two-magnitude diagrams for NGC 6838 cluster members (grey dots) zoomed around the SGB. 1G (left) and 2G (right) SGB stars selected in Fig. 6 are marked with red and blue starred symbols, respectively. Lower panels: Normalized Δ(mF275W + mF336W + mF438W) versus mF606W + mF814W diagram for 1G (bottom) and 2G stars (top). The corresponding Δ(mF275W + mF336W + mF438W) histogram distributions are plotted on the right together with the best-fitting least-squares Gaussian functions.
The results obtained from the analysis of SGB stars of NGC 6362 and NGC 6838 allow us to disentangle the effect of helium and metallicity and conclude that star-to-star metallicity variations are primarily responsible for the extended 1G sequence in the ChM.
6 METALLICITY VARIATIONS IN GALACTIC GLOBULAR CLUSTERS
In the previous section, we have demonstrated that the colour extension of 1G stars observed on the ChMs of NGC 6362 and NGC 6838 is the signature of intrinsic metallicity variations. By extending this conclusion to all GCs, in the following we use the colours of 1G RGB stars to infer the maximum iron abundance spread within the 1G of 55 Galactic GCs. Moreover, we investigate the relations between the iron spread and the main parameters of the host GC.
To quantify the |$\rm \Delta _{F275W, F814W}$| extension of 1G stars observed on the ChM, Milone et al. (2017) have estimated the intrinsic colour width of 1G RGB stars belonging to 55 Galactic GCs (|$W^{\rm 1G}_{\rm F275W,F814W}$|). By assuming that iron variations are the only responsible for the 1G colour spread, we exploited the colour–metallicity relations by Dotter et al. (2008) to transform the values of |$W^{\rm 1G}_{\rm F275W,F814W}$| into internal [Fe/H] variation (|$\rm \delta [Fe/H]_{\rm 1G}$|).
Results are listed in Table 3. As illustrated in the left-hand panel of Fig. 12, where we show the |$\rm \delta [Fe/H]_{\rm 1G}$| histogram distribution, the internal iron variation within the 1G component changes dramatically from one cluster to another ranging from ∼0.00 to ∼0.30, with an average value of |$\rm \delta [Fe/H]_{\rm 1G} \sim 0.12$|.
![Histogram distribution of $\rm \delta [Fe/H]_{\rm 1G}$ (left) for 55 Galactic GCs. The relations between $\rm \delta [Fe/H]_{\rm 1G}$ and cluster mass, 1G mass, and [Fe/H] are plotted in the other three panels. The Spearman’s rank correlation coefficient and the associated p-value are quoted in the upper-left corners.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/513/1/10.1093_mnras_stac734/2/m_stac734fig12.jpeg?Expires=1750469238&Signature=ZeshWijzOohAMaL~LmDILCpv1h0uFeQ1~IFOjll~RSBL~GDVC1oiPVR3Yf7VkqJ4eMkDJCuMvwLopXzf-l63WUEjaH5bCpoxxm2~p02A1qRKorQNWg9yZYe3lJnRHmfAncCy40xA8z8b2dH3wv~gj5suLEudK9-pkpLKmompQo06Cnrq7VjgdJhOjCU91VlrLsBSSdn76QM8AcEH7f47UAiygoocmnOnYgfes9zjJpfl66heR6BWyYGdnOxjkwz9C5NdRfzoqpccSPqRLorXLVfT6YVdW32gcywD5HtoCEZT-dOZjaVWh0VjFXg59nPOPiJazDHf-ANSkqLqm0UYQQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Histogram distribution of |$\rm \delta [Fe/H]_{\rm 1G}$| (left) for 55 Galactic GCs. The relations between |$\rm \delta [Fe/H]_{\rm 1G}$| and cluster mass, 1G mass, and [Fe/H] are plotted in the other three panels. The Spearman’s rank correlation coefficient and the associated p-value are quoted in the upper-left corners.
Internal iron variations among 1G stars (|$\rm \delta [Fe/H]_{\rm 1G}$|) for the 55 Galactic GCs studied in this work.
| Cluster ID . | |$\rm \delta [Fe/H]_{\rm 1G}$| . | Cluster ID . | |$\rm \delta [Fe/H]_{\rm 1G}$| . |
|---|---|---|---|
| NGC 0104 | 0.087 ± 0.009 | NGC 6304 | 0.125 ± 0.028 |
| NGC 0288 | 0.066 ± 0.007 | NGC 6341 | 0.156 ± 0.022 |
| NGC 0362 | 0.075 ± 0.010 | NGC 6352 | 0.064 ± 0.018 |
| NGC 1261 | 0.129 ± 0.022 | NGC 6362 | 0.051 ± 0.020 |
| NGC 1851 | 0.063 ± 0.007 | NGC 6366 | 0.017 ± 0.030 |
| NGC 2298 | 0.234 ± 0.046 | NGC 6397 | 0.130 ± 0.019 |
| NGC 2808 | 0.110 ± 0.010 | NGC 6441 | 0.074 ± 0.007 |
| NGC 3201 | 0.142 ± 0.038 | NGC 6496 | 0.080 ± 0.011 |
| NGC 4590 | 0.123 ± 0.015 | NGC 6535 | 0.128 ± 0.022 |
| NGC 4833 | 0.238 ± 0.023 | NGC 6541 | 0.125 ± 0.014 |
| NGC 5024 | 0.307 ± 0.029 | NGC 6584 | 0.121 ± 0.028 |
| NGC 5053 | 0.096 ± 0.024 | NGC 6624 | 0.112 ± 0.016 |
| NGC 5139 | 0.148 ± 0.011 | NGC 6637 | 0.061 ± 0.009 |
| NGC 5272 | 0.252 ± 0.015 | NGC 6652 | 0.087 ± 0.011 |
| NGC 5286 | 0.172 ± 0.012 | NGC 6656 | 0.195 ± 0.038 |
| NGC 5466 | 0.091 ± 0.055 | NGC 6681 | 0.056 ± 0.012 |
| NGC 5897 | 0.129 ± 0.030 | NGC 6717 | 0.019 ± 0.010 |
| NGC 5904 | 0.135 ± 0.027 | NGC 6723 | 0.111 ± 0.011 |
| NGC 5927 | 0.215 ± 0.023 | NGC 6752 | 0.106 ± 0.017 |
| NGC 5986 | 0.074 ± 0.006 | NGC 6779 | 0.192 ± 0.083 |
| NGC 6093 | 0.107 ± 0.010 | NGC 6809 | 0.115 ± 0.011 |
| NGC 6101 | 0.079 ± 0.016 | NGC 6838 | 0.067 ± 0.010 |
| NGC 6121 | 0.039 ± 0.031 | NGC 6934 | 0.123 ± 0.028 |
| NGC 6144 | 0.161 ± 0.031 | NGC 6981 | 0.151 ± 0.028 |
| NGC 6171 | 0.066 ± 0.011 | NGC 7078 | 0.204 ± 0.014 |
| NGC 6205 | 0.113 ± 0.024 | NGC 7089 | 0.156 ± 0.023 |
| NGC 6218 | 0.060 ± 0.015 | NGC 7099 | 0.000 ± 0.020 |
| NGC 6254 | 0.173 ± 0.022 |
| Cluster ID . | |$\rm \delta [Fe/H]_{\rm 1G}$| . | Cluster ID . | |$\rm \delta [Fe/H]_{\rm 1G}$| . |
|---|---|---|---|
| NGC 0104 | 0.087 ± 0.009 | NGC 6304 | 0.125 ± 0.028 |
| NGC 0288 | 0.066 ± 0.007 | NGC 6341 | 0.156 ± 0.022 |
| NGC 0362 | 0.075 ± 0.010 | NGC 6352 | 0.064 ± 0.018 |
| NGC 1261 | 0.129 ± 0.022 | NGC 6362 | 0.051 ± 0.020 |
| NGC 1851 | 0.063 ± 0.007 | NGC 6366 | 0.017 ± 0.030 |
| NGC 2298 | 0.234 ± 0.046 | NGC 6397 | 0.130 ± 0.019 |
| NGC 2808 | 0.110 ± 0.010 | NGC 6441 | 0.074 ± 0.007 |
| NGC 3201 | 0.142 ± 0.038 | NGC 6496 | 0.080 ± 0.011 |
| NGC 4590 | 0.123 ± 0.015 | NGC 6535 | 0.128 ± 0.022 |
| NGC 4833 | 0.238 ± 0.023 | NGC 6541 | 0.125 ± 0.014 |
| NGC 5024 | 0.307 ± 0.029 | NGC 6584 | 0.121 ± 0.028 |
| NGC 5053 | 0.096 ± 0.024 | NGC 6624 | 0.112 ± 0.016 |
| NGC 5139 | 0.148 ± 0.011 | NGC 6637 | 0.061 ± 0.009 |
| NGC 5272 | 0.252 ± 0.015 | NGC 6652 | 0.087 ± 0.011 |
| NGC 5286 | 0.172 ± 0.012 | NGC 6656 | 0.195 ± 0.038 |
| NGC 5466 | 0.091 ± 0.055 | NGC 6681 | 0.056 ± 0.012 |
| NGC 5897 | 0.129 ± 0.030 | NGC 6717 | 0.019 ± 0.010 |
| NGC 5904 | 0.135 ± 0.027 | NGC 6723 | 0.111 ± 0.011 |
| NGC 5927 | 0.215 ± 0.023 | NGC 6752 | 0.106 ± 0.017 |
| NGC 5986 | 0.074 ± 0.006 | NGC 6779 | 0.192 ± 0.083 |
| NGC 6093 | 0.107 ± 0.010 | NGC 6809 | 0.115 ± 0.011 |
| NGC 6101 | 0.079 ± 0.016 | NGC 6838 | 0.067 ± 0.010 |
| NGC 6121 | 0.039 ± 0.031 | NGC 6934 | 0.123 ± 0.028 |
| NGC 6144 | 0.161 ± 0.031 | NGC 6981 | 0.151 ± 0.028 |
| NGC 6171 | 0.066 ± 0.011 | NGC 7078 | 0.204 ± 0.014 |
| NGC 6205 | 0.113 ± 0.024 | NGC 7089 | 0.156 ± 0.023 |
| NGC 6218 | 0.060 ± 0.015 | NGC 7099 | 0.000 ± 0.020 |
| NGC 6254 | 0.173 ± 0.022 |
Internal iron variations among 1G stars (|$\rm \delta [Fe/H]_{\rm 1G}$|) for the 55 Galactic GCs studied in this work.
| Cluster ID . | |$\rm \delta [Fe/H]_{\rm 1G}$| . | Cluster ID . | |$\rm \delta [Fe/H]_{\rm 1G}$| . |
|---|---|---|---|
| NGC 0104 | 0.087 ± 0.009 | NGC 6304 | 0.125 ± 0.028 |
| NGC 0288 | 0.066 ± 0.007 | NGC 6341 | 0.156 ± 0.022 |
| NGC 0362 | 0.075 ± 0.010 | NGC 6352 | 0.064 ± 0.018 |
| NGC 1261 | 0.129 ± 0.022 | NGC 6362 | 0.051 ± 0.020 |
| NGC 1851 | 0.063 ± 0.007 | NGC 6366 | 0.017 ± 0.030 |
| NGC 2298 | 0.234 ± 0.046 | NGC 6397 | 0.130 ± 0.019 |
| NGC 2808 | 0.110 ± 0.010 | NGC 6441 | 0.074 ± 0.007 |
| NGC 3201 | 0.142 ± 0.038 | NGC 6496 | 0.080 ± 0.011 |
| NGC 4590 | 0.123 ± 0.015 | NGC 6535 | 0.128 ± 0.022 |
| NGC 4833 | 0.238 ± 0.023 | NGC 6541 | 0.125 ± 0.014 |
| NGC 5024 | 0.307 ± 0.029 | NGC 6584 | 0.121 ± 0.028 |
| NGC 5053 | 0.096 ± 0.024 | NGC 6624 | 0.112 ± 0.016 |
| NGC 5139 | 0.148 ± 0.011 | NGC 6637 | 0.061 ± 0.009 |
| NGC 5272 | 0.252 ± 0.015 | NGC 6652 | 0.087 ± 0.011 |
| NGC 5286 | 0.172 ± 0.012 | NGC 6656 | 0.195 ± 0.038 |
| NGC 5466 | 0.091 ± 0.055 | NGC 6681 | 0.056 ± 0.012 |
| NGC 5897 | 0.129 ± 0.030 | NGC 6717 | 0.019 ± 0.010 |
| NGC 5904 | 0.135 ± 0.027 | NGC 6723 | 0.111 ± 0.011 |
| NGC 5927 | 0.215 ± 0.023 | NGC 6752 | 0.106 ± 0.017 |
| NGC 5986 | 0.074 ± 0.006 | NGC 6779 | 0.192 ± 0.083 |
| NGC 6093 | 0.107 ± 0.010 | NGC 6809 | 0.115 ± 0.011 |
| NGC 6101 | 0.079 ± 0.016 | NGC 6838 | 0.067 ± 0.010 |
| NGC 6121 | 0.039 ± 0.031 | NGC 6934 | 0.123 ± 0.028 |
| NGC 6144 | 0.161 ± 0.031 | NGC 6981 | 0.151 ± 0.028 |
| NGC 6171 | 0.066 ± 0.011 | NGC 7078 | 0.204 ± 0.014 |
| NGC 6205 | 0.113 ± 0.024 | NGC 7089 | 0.156 ± 0.023 |
| NGC 6218 | 0.060 ± 0.015 | NGC 7099 | 0.000 ± 0.020 |
| NGC 6254 | 0.173 ± 0.022 |
| Cluster ID . | |$\rm \delta [Fe/H]_{\rm 1G}$| . | Cluster ID . | |$\rm \delta [Fe/H]_{\rm 1G}$| . |
|---|---|---|---|
| NGC 0104 | 0.087 ± 0.009 | NGC 6304 | 0.125 ± 0.028 |
| NGC 0288 | 0.066 ± 0.007 | NGC 6341 | 0.156 ± 0.022 |
| NGC 0362 | 0.075 ± 0.010 | NGC 6352 | 0.064 ± 0.018 |
| NGC 1261 | 0.129 ± 0.022 | NGC 6362 | 0.051 ± 0.020 |
| NGC 1851 | 0.063 ± 0.007 | NGC 6366 | 0.017 ± 0.030 |
| NGC 2298 | 0.234 ± 0.046 | NGC 6397 | 0.130 ± 0.019 |
| NGC 2808 | 0.110 ± 0.010 | NGC 6441 | 0.074 ± 0.007 |
| NGC 3201 | 0.142 ± 0.038 | NGC 6496 | 0.080 ± 0.011 |
| NGC 4590 | 0.123 ± 0.015 | NGC 6535 | 0.128 ± 0.022 |
| NGC 4833 | 0.238 ± 0.023 | NGC 6541 | 0.125 ± 0.014 |
| NGC 5024 | 0.307 ± 0.029 | NGC 6584 | 0.121 ± 0.028 |
| NGC 5053 | 0.096 ± 0.024 | NGC 6624 | 0.112 ± 0.016 |
| NGC 5139 | 0.148 ± 0.011 | NGC 6637 | 0.061 ± 0.009 |
| NGC 5272 | 0.252 ± 0.015 | NGC 6652 | 0.087 ± 0.011 |
| NGC 5286 | 0.172 ± 0.012 | NGC 6656 | 0.195 ± 0.038 |
| NGC 5466 | 0.091 ± 0.055 | NGC 6681 | 0.056 ± 0.012 |
| NGC 5897 | 0.129 ± 0.030 | NGC 6717 | 0.019 ± 0.010 |
| NGC 5904 | 0.135 ± 0.027 | NGC 6723 | 0.111 ± 0.011 |
| NGC 5927 | 0.215 ± 0.023 | NGC 6752 | 0.106 ± 0.017 |
| NGC 5986 | 0.074 ± 0.006 | NGC 6779 | 0.192 ± 0.083 |
| NGC 6093 | 0.107 ± 0.010 | NGC 6809 | 0.115 ± 0.011 |
| NGC 6101 | 0.079 ± 0.016 | NGC 6838 | 0.067 ± 0.010 |
| NGC 6121 | 0.039 ± 0.031 | NGC 6934 | 0.123 ± 0.028 |
| NGC 6144 | 0.161 ± 0.031 | NGC 6981 | 0.151 ± 0.028 |
| NGC 6171 | 0.066 ± 0.011 | NGC 7078 | 0.204 ± 0.014 |
| NGC 6205 | 0.113 ± 0.024 | NGC 7089 | 0.156 ± 0.023 |
| NGC 6218 | 0.060 ± 0.015 | NGC 7099 | 0.000 ± 0.020 |
| NGC 6254 | 0.173 ± 0.022 |
6.1 Relations with the host GC parameters
In the following, we investigate the relations between the internal iron variations among 1G stars (|$\rm \delta [Fe/H]_{\rm 1G}$|) and the main parameters of the host GC.
Overall, our analysis includes 20 global GC parameters. Iron abundance ([Fe/H]), absolute visual magnitude (MV), ellipticity (ϵ), central concentration (c), central stellar density (ρ0), and central surface brightness (μV) have been taken from the 2010 version of the Harris catalogue (Harris 1996). Present-day (|$\rm M$|) and initial (|$\rm M_{\rm in}$|) mass of the host cluster, central escape velocity (|$\rm v_{\rm esc}$|), central velocity dispersion (σv), core density (ρc), and core relaxation time at half mass (|$\rm \tau _{hm}$|) have been derived by Baumgardt & Hilker (2018). To compute the 1G mass (M1G), we exploited the fraction of 1G stars measured in previous papers by Milone et al. (2017, 2020a) and Dondoglio et al. (2021). Finally, GC ages have been derived by Marín-Franch et al. (2009, MF09), Dotter et al. (2010, D10), VandenBerg et al. (2013, V13), and Tailo et al. (2020, T20), while the fractions of binary stars in GCs have been calculated by Milone et al. (2012a) within the cluster core (|$f^{\rm C}_{\rm bin}$|), in the region between the core and the half-mass radius (|$f^{\rm C-HM}_{\rm bin}$|), and beyond the half-mass radius (|$f^{\rm oHM}_{\rm bin}$|).
For each pair of analysed quantities, we estimated the statistical correlation between the two by calculating the Spearman’s rank coefficient (RS) and the corresponding p-value. The results of the correlations between |$\rm \delta [Fe/H]_{\rm 1G}$| and the cluster parameters are listed in Table 4, where for each couple of variables we provide RS, the corresponding p-value, and the number of degrees of freedom.
Relation between the internal iron variations among 1G stars (|$\rm \delta [Fe/H]_{\rm 1G}$|), obtained in this work, and 20 GC parameters. For each parameter, the Spearman’s rank correlation coefficient is reported together with the associated p-value, indicative of the significance of the relation, and the number of degrees of freedom.
| Parameter . | |$\rm \delta [Fe/H]_{\rm 1G}$| . | Parameter . | |$\rm \delta [Fe/H]_{\rm 1G}$| . |
|---|---|---|---|
| Age (MF09) | −0.16, 0.247, 52 | |$f_{\rm bin}^{\rm C}$| | 0.44,0.008,33 |
| Age (D10) | 0.23,0.098,53 | |$f_{\rm bin}^{\rm C-HM}$| | 0.25,0.094,44 |
| Age (V13) | 0.15,0.286,48 | |$f_{\rm bin}^{\rm oHM}$| | 0.05,0.742,39 |
| Age (T20) | 0.11,0.476,44 | c | 0.06,0.656,53 |
| |$\rm [Fe/H]$| | −0.43, <0.001, 53 | |$\log (\rm \tau _{hm})$| | 0.31,0.020,53 |
| |$\log (\rm M/M_{\odot })$| | 0.35,0.008,53 | μV | 0.02,0.884,53 |
| |$\log (\rm M_{in}/M_{\odot })$| | 0.17,0.213,53 | log (ρc) | −0.08, 0.547, 53 |
| |$\log (\rm M_{1G}/M_{\odot })$| | 0.39,0.004,50 | σv | 0.19,0.174,53 |
| |$\rm M_{V}$| | −0.36, 0.007, 53 | |$\rm v_{\rm esc}$| | 0.19,0.175,53 |
| ϵ | 0.23,0.091,51 | ρ0 | 0.06,0.658,53 |
| Parameter . | |$\rm \delta [Fe/H]_{\rm 1G}$| . | Parameter . | |$\rm \delta [Fe/H]_{\rm 1G}$| . |
|---|---|---|---|
| Age (MF09) | −0.16, 0.247, 52 | |$f_{\rm bin}^{\rm C}$| | 0.44,0.008,33 |
| Age (D10) | 0.23,0.098,53 | |$f_{\rm bin}^{\rm C-HM}$| | 0.25,0.094,44 |
| Age (V13) | 0.15,0.286,48 | |$f_{\rm bin}^{\rm oHM}$| | 0.05,0.742,39 |
| Age (T20) | 0.11,0.476,44 | c | 0.06,0.656,53 |
| |$\rm [Fe/H]$| | −0.43, <0.001, 53 | |$\log (\rm \tau _{hm})$| | 0.31,0.020,53 |
| |$\log (\rm M/M_{\odot })$| | 0.35,0.008,53 | μV | 0.02,0.884,53 |
| |$\log (\rm M_{in}/M_{\odot })$| | 0.17,0.213,53 | log (ρc) | −0.08, 0.547, 53 |
| |$\log (\rm M_{1G}/M_{\odot })$| | 0.39,0.004,50 | σv | 0.19,0.174,53 |
| |$\rm M_{V}$| | −0.36, 0.007, 53 | |$\rm v_{\rm esc}$| | 0.19,0.175,53 |
| ϵ | 0.23,0.091,51 | ρ0 | 0.06,0.658,53 |
Relation between the internal iron variations among 1G stars (|$\rm \delta [Fe/H]_{\rm 1G}$|), obtained in this work, and 20 GC parameters. For each parameter, the Spearman’s rank correlation coefficient is reported together with the associated p-value, indicative of the significance of the relation, and the number of degrees of freedom.
| Parameter . | |$\rm \delta [Fe/H]_{\rm 1G}$| . | Parameter . | |$\rm \delta [Fe/H]_{\rm 1G}$| . |
|---|---|---|---|
| Age (MF09) | −0.16, 0.247, 52 | |$f_{\rm bin}^{\rm C}$| | 0.44,0.008,33 |
| Age (D10) | 0.23,0.098,53 | |$f_{\rm bin}^{\rm C-HM}$| | 0.25,0.094,44 |
| Age (V13) | 0.15,0.286,48 | |$f_{\rm bin}^{\rm oHM}$| | 0.05,0.742,39 |
| Age (T20) | 0.11,0.476,44 | c | 0.06,0.656,53 |
| |$\rm [Fe/H]$| | −0.43, <0.001, 53 | |$\log (\rm \tau _{hm})$| | 0.31,0.020,53 |
| |$\log (\rm M/M_{\odot })$| | 0.35,0.008,53 | μV | 0.02,0.884,53 |
| |$\log (\rm M_{in}/M_{\odot })$| | 0.17,0.213,53 | log (ρc) | −0.08, 0.547, 53 |
| |$\log (\rm M_{1G}/M_{\odot })$| | 0.39,0.004,50 | σv | 0.19,0.174,53 |
| |$\rm M_{V}$| | −0.36, 0.007, 53 | |$\rm v_{\rm esc}$| | 0.19,0.175,53 |
| ϵ | 0.23,0.091,51 | ρ0 | 0.06,0.658,53 |
| Parameter . | |$\rm \delta [Fe/H]_{\rm 1G}$| . | Parameter . | |$\rm \delta [Fe/H]_{\rm 1G}$| . |
|---|---|---|---|
| Age (MF09) | −0.16, 0.247, 52 | |$f_{\rm bin}^{\rm C}$| | 0.44,0.008,33 |
| Age (D10) | 0.23,0.098,53 | |$f_{\rm bin}^{\rm C-HM}$| | 0.25,0.094,44 |
| Age (V13) | 0.15,0.286,48 | |$f_{\rm bin}^{\rm oHM}$| | 0.05,0.742,39 |
| Age (T20) | 0.11,0.476,44 | c | 0.06,0.656,53 |
| |$\rm [Fe/H]$| | −0.43, <0.001, 53 | |$\log (\rm \tau _{hm})$| | 0.31,0.020,53 |
| |$\log (\rm M/M_{\odot })$| | 0.35,0.008,53 | μV | 0.02,0.884,53 |
| |$\log (\rm M_{in}/M_{\odot })$| | 0.17,0.213,53 | log (ρc) | −0.08, 0.547, 53 |
| |$\log (\rm M_{1G}/M_{\odot })$| | 0.39,0.004,50 | σv | 0.19,0.174,53 |
| |$\rm M_{V}$| | −0.36, 0.007, 53 | |$\rm v_{\rm esc}$| | 0.19,0.175,53 |
| ϵ | 0.23,0.091,51 | ρ0 | 0.06,0.658,53 |
As shown in Fig. 12, we find mild correlations between |$\rm \delta [Fe/H]_{\rm 1G}$| and cluster mass and 1G mass (RS = 0.35, and 0.39, respectively), with massive GCs having on average larger 1G metallicity spreads. Moreover, the internal iron variation of 1G stars decreases with cluster metallicity (RS = −0.43).
6.1.1 M3- and M13-like clusters
To study further the relations between |$\rm \delta [Fe/H]_{\rm 1G}$| and the host cluster parameters, we divided GCs in two categories of M 3-like and M 13-like GCs (Milone et al. 2014; Tailo et al. 2020). This selection is based on the HB morphology and on the parameter L1, defined as the colour difference between the RGB and the reddest part of the HB (Milone et al. 2014). Specifically, as in Tailo et al. (2020), we defined M 3-like GCs with |$\rm L_{1}\le 0.35$| and M 13-like GCs with |$\rm L_{1}\gt 0.35$|. M 3-like GCs mostly include GCs having red HBs while M 13-like GCs present the blue HB only.6
Intriguingly, the 1G iron variations of the two groups of GCs exhibit different behaviours. As illustrated in the left-hand panels of Fig. 13, there is no correlation between the |$\rm \delta [Fe/H]_{\rm 1G}$| iron variation of M 13-like GCs and cluster mass (Rs = 0.09), whereas M 3-like GCs show a significant correlation with cluster mass (Rs = 0.60). Moreover, M 13-like GCs display smaller iron variations than M 3-like GCs with similar metallicity. To support this statement, we had least-squares fitted the |$\rm \delta [Fe/H]_{\rm 1G}$| versus [Fe/H] relation for M 3- and M 13-like clusters, respectively, with a straight-line, as shown in the right-hand panel of Fig. 13. To do that we considered only the common range of metallicity between the two groups of clusters, namely −2.2 <[Fe/H]<−1.2, omitting GCs with [Fe/H]≤−2.2 that deviate from the common trend. The best-fitting straight lines are given by |$\rm \delta [Fe/H]_{\rm 1G}=(-0.139\pm 0.056)\times [Fe/H]+(-0.058\pm 0.093)$| (M 3-like GCs, red line) and |$\rm \delta [Fe/H]_{\rm 1G}=(-0.138\pm 0.046)\times [Fe/H]+(-0.120\pm 0.079)$| (M 13-like GCs, blue line), respectively, thus corroborating the evidence that M 13-like GCs exhibit smaller internal iron variations than M 3-like GCs with similar metallicity. This fact is further confirmed by the most metal-poor clusters that we excluded from the fit. Indeed, the only M 13-like object in this sample is characterized by the lowest |$\rm \delta [Fe/H]_{\rm 1G}$| iron variation.
![Left-hand panels: Internal iron variation of 1G stars, $\rm \delta [Fe/H]_{\rm 1G}$, against the logarithm of cluster mass for M 13-like (top) and M 3-like GCs (bottom). Right-hand panel: $\rm \delta [Fe/H]_{\rm 1G}$ against [Fe/H]. Blue dots correspond to M 13-like GCs while red ones to M 3-like GCs. The best-fitting least-squares straight lines derived for M 13- and M 3-like clusters with −2.2 <[Fe/H]<−1.2 are coloured blue and red, respectively. The Spearman’s rank correlation coefficient is reported for each couple of quantities.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/513/1/10.1093_mnras_stac734/2/m_stac734fig13.jpeg?Expires=1750469238&Signature=F~0L5MrkBNxt66yRGDr2nCtJJHvK0lFQuMM9s56VfDbyp7gHy-kQw4EzTvvtewP4UFrZBCNb5qo2kAQZVTHAjKbuEj-B-rBr1vsMD8u-~vcMYaQyIbEfJVy6bGHwxI8IWALujTaNxTDbkc27LrubtKkarqnKCztaSvpkVEgMMBu~9PpmvvpCBaQQ4LeUvT9wt8Ji2JI0Q6bNUY~3debRkk6UQCDf54YqNgNxkJI8CLAC5a8pSvVi7t8DFUvXaFJBLRB9QR67IgqrjvFgjY-RtsjP~5PcVYjPqnF0YTzxBBxgGveUpNaDiAl4EQ2Fph8tM3oyVBemlmLfb213VcIteg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Left-hand panels: Internal iron variation of 1G stars, |$\rm \delta [Fe/H]_{\rm 1G}$|, against the logarithm of cluster mass for M 13-like (top) and M 3-like GCs (bottom). Right-hand panel: |$\rm \delta [Fe/H]_{\rm 1G}$| against [Fe/H]. Blue dots correspond to M 13-like GCs while red ones to M 3-like GCs. The best-fitting least-squares straight lines derived for M 13- and M 3-like clusters with −2.2 <[Fe/H]<−1.2 are coloured blue and red, respectively. The Spearman’s rank correlation coefficient is reported for each couple of quantities.
7 SUMMARY AND DISCUSSION
We have exploited HST multiband images to present a photometric investigation of stellar populations within the Galactic GCs NGC 6362 and NGC 6838. The main purpose is to shed light on the physical reasons that are responsible for the extended 1G sequence in their ChMs. Results can be summarized as follows:
We derived the ChM of MS stars of both GCs, where 1G and 2G stars define distinct sequences. We found that the 1G sequence has an intrinsic F275W−F814W colour broadening in close analogy with what is observed for the RGB ChM. The evidence of extended 1G sequences among unevolved MS stars demonstrates that the colour extension is not due to stellar evolution. Alternatively, this phenomenon could be the signature of chemical inhomogeneities in the proto-cluster cloud.
We introduced the pseudo-two-magnitude diagram mF275W + mF336W + mF438W versus mF606W + mF814W, where the SGBs of isochrones with different metallicities and helium abundances display different behaviours. The distribution of 1G SGB stars in these diagrams is consistent with internal variations in [Fe/H] but not with helium variations. The evidence that 1G SGB stars exhibit star-to-star iron variations, implies that the colour extension of 1G sequences in the ChMs of 1G RGB and MS stars is due to metallicity variations up to δ[Fe/H]1G = 0.1 dex.
Moreover, we compared the distributions of 1G and 2G stars along the ChM. Results have the potential to constrain the formation scenarios of multiple populations in GCs.
We found that the F275W−F814W colour extension of 2G MS stars of both NGC 6362 and NGC 6838 is significantly narrower than that of the 1G, but wider than the colour broadening expected by observational errors. Specifically, subtracting in quadrature the effect of observational errors, the F275W−F814W spread of 2G stars is two times smaller than the corresponding 1G colour spread. This fact demonstrates that the gaseous environment where 2G stars formed had more homogeneous iron content compared to the environment where 1G stars formed.
We exploited the 1G F275W−F814W colour extension of the RGB from Milone et al. (2017) to estimate [Fe/H] variations within 1G stars of 55 GCs in the hypothesis that metallicity spread is the only responsible for the RGB broadening. The internal iron variation ranges from less than [Fe/H]∼0.05 to ∼0.30 and mildly correlates with cluster mass and metallicity.
Noticeably, the 2G sequences of NGC 6362 and NGC 6838 ChMs join the 1Gs on their metal-poor sides. In the hypothesis that the ΔF275W,F814W pseudo-colour of 2G stars at the bottom of the 2G sequence is indicative of their iron abundance, these 2G stars would share the same metallicity as the metal-poor 1G stars. However, this is not a universal property of GCs. A visual inspection at the ChMs of Galactic GCs shows that the relative position between 1G and 2G sequences significantly changes from one cluster to another (see figs 3–7 from Milone et al. 2017). While many clusters (e.g. NGC 2808 and NGC 6981) behave like NGC 6362 and NGC 6838, the 2G sequences of other clusters like NGC 104 and NGC 5272 are distributed on the metal-intermediate and, possibly, the metal-rich side of the 1G sequence.
1G stars of M 13-like GCs, namely GCs with the blue HB only, present smaller iron variations than M 3-like GCs with the same metallicity and no correlation with cluster mass. On the contrary, M 3-like clusters exhibit significant correlation with cluster mass (Rs = 0.60).
The presence of metallicity variations among 1G stars might be due to the presence of metallicity variations within the ISM from which proto-cluster molecular clouds were born. Analytical models show that the metallicity scatter among the stars must however be lower than the scatter initially present in the gas (e.g. Murray & Lin 1990; Bland-Hawthorn, Krumholz & Freeman 2010). Turbulent diffusion within a proto-cluster cloud should smooth out chemical inhomogeneities at the scale of the cloud in roughly a crossing time – defined as the ratio between the cloud radius and the cloud velocity dispersion – and smaller scale inhomogeneities even more quickly. Star formation in a molecular cloud also appears to begin in no more than a crossing time after its formation (see Krumholz, McKee & Bland-Hawthorn 2019, and references therein). This suggests that chemical inhomogeneities initially present in the gas should be reduced at the onset of star formation (see also Feng & Krumholz 2014; Armillotta, Krumholz & Fujimoto 2018). In this picture, the presence of more or less metallicity variation in a given 1G population might be explained either by the presence of more or less metallicity variation in the original gas, or by different diffusion efficiencies during the cloud collapse. For example, we note that the cloud crossing time increases in low-density extended clouds, while decreases in high-density turbulent clouds.
Another possible explanation for the presence of metallicity variations among 1G stars is that the process of star formation within the cloud was still at play when the first supernovae exploded. In this picture, the cloud was nearly homogeneous at the onset of the star formation. Inhomogeneities arose at later times as supernovae polluted the surrounding star-forming gas. This possibility is explored in a recent work by McKenzie & Bekki (2021). Through simulations of a gas-rich dwarf galaxy, the authors find that self-enrichment of star-forming clouds from short-lived massive stars may increase the metallicity dispersion within the resulting populations of 1G stars (see also Bailin 2018). In their fiducial model, McKenzie & Bekki (2021) measure [Fe/H] abundance variations of the order of 0.1 dex, a value consistent with the average spread found in this paper. In comparison, He abundance spreads are found to be of the order of 0.001 dex, in agreement with the result that He alone is insufficient in elongating the 1G population in the ChM. However, as pointed out by McKenzie & Bekki (2021), the degree of self-enrichment is strongly sensitive to the star formation and feedback prescriptions adopted in the simulation. For example, the sole thermal feedback from supernovae implemented in their simulations is not effective in removing gas from the cloud, allowing star formation to proceed for a long time. This results in enhanced self-enrichment within the cluster. Besides, by means of analytical arguments, Bland-Hawthorn et al. (2010) argue that the time over which star formation takes place is larger than the time required for the first supernovae to explode only in very massive clouds (M > 107 M⊙ under the typical conditions of high-redshift environments, where GCs were born). High-resolution simulations able to capture the details of star formation and feedback are clearly required to shed light on this scenario.
Another interesting outcome of this work is that, both in NGC 6362 and NGC 6838, the metallicity spread among 2G stars is generally lower than the metallicity spread among 1G stars. This result would provide a challenge for scenarios of multiple population formation based on accretion of material processed in massive stars on to protostars. Gieles et al. (2018) suggest that supermassive stars (SMSs) with masses bigger than ∼103 M⊙ are responsible for the distinctive chemical composition of 2G stars in GCs (see also Denissenkov & Hartwick 2014). In this scenario, protostars accrete the hot-hydrogen burning material processed in SMSs and expelled through strong SMS winds. The processed material, diluted with original gas, is responsible for the observed chemical composition of 2G stars. Similarly, in the scenario proposed by Bastian et al. (2013), pre-MS stars are polluted with processed material released by interacting massive binaries and fast-rotating stars. The released gas is first accreted into the circumstellar discs and then on to the pre-MS stars, thus addressing the origin of the HeCNONa abundance anomalies of 2G stars (see Renzini et al. 2015, for critical discussion on the formation scenarios). More recently, Wang et al. (2020) investigated the role of mergers of binary star components for the formation of multiple stellar populations and suggested that 2G stars form from the gas polluted by mergers-driven ejection winds.
In these scenarios, 1G and 2G stars are expected to share the same iron abundance. In particular, an iron spread among 1G stars should result in nearly identical iron variations among the 2G. This fact is in contrast with what is observed in both NGC 6362 and NGC 6838, where the 2G exhibits small, if any, internal iron variations when compared with the 1G.
Alternative scenarios suggest that GCs experienced multiple star-formation episodes. 1G stars are supposed to form first. Their formation stops when feedback from massive stars clears any remaining gas from the cluster. At a later time, 2G stars form in the innermost and densest cluster region from original gas (i.e. gas that shares the same abundances as the 1G stars) reaccreted from the ISM and diluted with the material processed by more-massive 1G stars (e.g. Ventura et al. 2001; D’Antona & Caloi 2004; Decressin et al. 2007; D’Ercole et al. 2008, 2010; De Mink et al. 2009; Denissenkov & Hartwick 2014; D’Antona et al. 2016; Calura et al. 2019). Even though the level of iron inhomogeneities present in the ISM gas is expected to be the same, the lower metallicity spread observed among 2G stars can be explained by a different dynamical state of the proto-cluster environment. We know that the time required to smooth out initial chemical inhomogeneities in the gas is smaller in denser environments characterized by a higher gas velocity dispersion (see above). Hence, the chemical homogeneity of 2G stars is consistent with the idea that they formed in highly dense environments, as predicted by multigeneration scenarios.
In this context, the evidence that 1G stars of M 3- and M 13-like GCs exhibit different internal iron variations may indicate different properties of the formation environment. Specifically, the smaller iron variation of M 13-like GCs is consistent with a scenario where these clusters formed in high-density environments as suggested by Tailo et al. (2019a,b, 2020, 2021) based on the larger amount of RGB mass-loss of 1G stars in these clusters.
ACKNOWLEDGEMENTS
We thank the anonymous referee for the useful suggestions. This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research innovation programme (Grant Agreement ERC-StG 2016, No 716082 ‘GALFOR’, PI: Milone, http://progetti.dfa.unipd.it/GALFOR). APM, MT, and GC acknowledge support from Ministero dell'Istruzione, dell'Università e della Ricerca (MIUR) through the FARE project R164RM93XW SEMPLICE (PI: Milone). APM, ED, and MC acknowledge support from MIUR under the Progetti di Rilevante Interesse Nazionale (PRIN) program 2017Z2HSMF (PI: Bedin).
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
Footnotes
https://acszeropoints.stsci.edu and https://www.stsci.edu/hst/instrumentation/wfc3/data-analysis/photometric-calibration for ACS/WFC and UVIS/WFC3, respectively.
To demonstrate that the conclusions on internal chemical variations do not depend on colours that involve the F814W filter, we repeated the analysis based on mX − mF606W (or mF606W − mX) colours. We verified that we obtain identical results on the internal variations in iron and helium deriving colours based on the F606W filter instead of the F814W one.
An effect of changing the helium mass fraction (Y), is that for a fixed metal mass fraction (Z), a change in Y modifies the hydrogen mass fraction, thus affecting the metal-to-hydrogen ratio Z/X (see Yong et al. 2013, for details). As a consequence, increasing Y would result in rising [Fe/H]. However, it is unlikely that metallicity variations of NGC 6362 and NGC 6838 are induced by helium variations. Indeed, helium enhanced stars should be located at low values of ΔF275W,F814W (e.g. Marino et al. 2019a; Milone et al. 2020b), whereas metal-rich stars populate the ChM region with large ΔF275W,F814W values.
Another distinctive feature of M 13-like clusters is that their 1G stars suffer higher RGB mass-loss than 1G stars of M 3-like GCs and stars in simple-population GCs (Tailo et al. 2020, 2021). For this reason, the authors suggested that 1G stars of M 13-like GCs form in high-density environments. As an alternative interpretation of the results from Tailo and collaborators, we can speculate that M 13-like GCs have entirely lost their 1G stars as first suggested by D’Antona & Caloi (2008). In this scenario, the stars that we name 1G are 2G stars that formed in a dense environment in the cluster centre.



