-
PDF
- Split View
-
Views
-
Cite
Cite
M E Shultz, S P Owocki, A ud-Doula, A Biswas, D Bohlender, P Chandra, B Das, A David-Uraz, V Khalack, O Kochukhov, J D Landstreet, P Leto, D Monin, C Neiner, Th Rivinius, G A Wade, MOBSTER – VI. The crucial influence of rotation on the radio magnetospheres of hot stars, Monthly Notices of the Royal Astronomical Society, Volume 513, Issue 1, June 2022, Pages 1429–1448, https://doi.org/10.1093/mnras/stac136
Close - Share Icon Share
ABSTRACT
Numerous magnetic hot stars exhibit gyrosynchrotron radio emission. The source electrons were previously thought to be accelerated to relativistic velocities in the current sheet formed in the middle magnetosphere by the wind opening magnetic field lines. However, a lack of dependence of radio luminosity on the wind power, and a strong dependence on rotation, has recently challenged this paradigm. We have collected all radio measurements of magnetic early-type stars available in the literature. When constraints on the magnetic field and/or the rotational period are not available, we have determined these using previously unpublished spectropolarimetric and photometric data. The result is the largest sample of magnetic stars with radio observations that has yet been analysed: 131 stars with rotational and magnetic constraints, of which 50 are radio-bright. We confirm an obvious dependence of gyrosynchrotron radiation on rotation, and furthermore find that accounting for rotation neatly separates stars with and without detected radio emission. There is a close correlation between H α emission strength and radio luminosity. These factors suggest that radio emission may be explained by the same mechanism responsible for H α emission from centrifugal magnetospheres, i.e. centrifugal breakout (CBO), however, while the H α-emitting magnetosphere probes the cool plasma before breakout, radio emission is a consequence of electrons accelerated in centrifugally driven magnetic reconnection.
1 INTRODUCTION
Approximately 10 per cent of OBA stars possess magnetic fields (Sikora et al. 2019a; Grunhut et al. 2017), with properties that are remarkably consistent across the Hertzsprung–Russell diagram (HRD): they are strong (102–104 G; Shultz et al. 2019d); topologically simple (i.e. with only a few exceptions, approximately dipolar; Kochukhov, Shultz & Neiner 2019); and, in all cases for which sufficient data are available for evaluation, stable over at least thousands of rotational cycles (i.e. at least decades; Shultz et al. 2018b). Unlike stars with convective envelopes, for which surface magnetic field strength increases with rotation (Vidotto et al. 2014; Folsom et al. 2016, 2018), there is no such correlation with rotation for the magnetic fields of stars with radiative envelopes (Shultz et al. 2019d; Sikora et al. 2019b). Instead, hot star magnetic fields decline in strength with age in a fashion consistent with conservation of magnetic flux in an expanding atmosphere (for intermediate mass stars; Sikora et al. 2019b) or gradual decay of magnetic flux (for stars above about 5 M⊙; Landstreet et al. 2007; Fossati et al. 2016; Shultz et al. 2019d). These properties, together with the absence of a sustainable dynamo mechanism in radiative zones, have led to the interpretation of hot star magnetic fields as ‘fossils’ left over from a previous epoch, a scenario supported by magnetohydrodynamic (MHD) calculations and simulations that have demonstrated the stability of fossil magnetic fields over evolutionary time-scales, as well as the ability of processes such as binary mergers to generate fossil fields (Braithwaite & Spruit 2004; Braithwaite 2009; Duez, Braithwaite & Mathis 2010; Schneider et al. 2019).
Strong magnetic fields stabilize the atmospheres of hot stars, enabling various chemical elements to accumulate in long-lived surface patches via radiative diffusion (e.g. Michaud, Charland & Megessier 1981; Alecian 2015; Alecian & Stift 2019). This leads directly to modulation of the light curve on rotational time-scales (e.g. Krtička et al. 2009, 2012, 2015), making it straightforward to infer precise rotation periods from photometric time series (e.g. Renson & Catalano 2001). A key goal of the MOBSTER collaboration (Magnetic OB(A) Stars with TESS: probing their Evolutionary and Rotational properties; David-Uraz et al. 2019) is to leverage space photometry from the TESS mission in order to dramatically expand the number of known rotational periods for magnetic chemically peculiar (mCP) stars (e.g. Sikora et al. 2019c), as a means of investigating the evolutionary and magnetospheric characteristics of this population.
The radiation-driven winds of hot stars serve as ion sources which feed their magnetospheres (Landstreet & Borra 1978; Babel & Montmerle 1997; ud-Doula & Owocki 2002). Hot star magnetospheres have a number of observable consequences. They were first detected by Landstreet & Borra (1978) via eclipsing of σ Ori E by the dense plasma clouds of its magnetosphere. Ultraviolet observations demonstrated that the wind-sensitive resonance lines of magnetic hot stars exhibit clear rotational modulation indicating departures from spherical symmetry (e.g. Henrichs et al. 2013). Optical and near-infrared H emission is also formed in the dense plasma of the magnetosphere (Petit et al. 2013; Oksala et al. 2015b). Magnetically confined wind-shocks lead to X-ray emission (Nazé et al. 2014; ud-Doula et al. 2014). Finally, a large fraction of magnetic hot stars show gyrosynchrotron radiation at high frequencies (e.g. Drake et al. 1987) and occasionally auroral radio emission at low frequencies (e.g. Trigilio et al. 2000; Das, Chandra & Wade 2018).
With the exception of radio diagnostics, magnetospheric emission is believed to be formed within the inner magnetosphere, i.e. the magnetically dominated region within the Alfvén surface, in which the wind kinetic energy density is less than the magnetic energy density. By contrast, radio diagnostics are believed to be a consequence of activity in the middle magnetosphere, a region beyond the Alfvén radius in which magnetically enforced corotation of the plasma with the star breaks down, while the ram pressure of the winds opens the magnetic field lines, the combination of which leads to the formation of a current sheet (CS). Inside the CS, electrons are accelerated to relativistic velocities, some of which then return to the star, along magnetic fields lines, leading to gyrosynchrotron emission (Trigilio et al. 2004) and, for those that are caught in auroral circuits, electron-cyclotron maser emission (ECME; Trigilio et al. 2011; Leto et al. 2016; Das, Mondal & Chandra 2020).
Rotation has emerged as a key parameter governing the structure of the inner magnetosphere. In the absence of rotation, inner magnetosphere plasma exists in dynamical equilibrium: flowing up along magnetic field lines, colliding at the magnetic equator, and then being pulled back to the star by gravity (ud-Doula & Owocki 2002). These dynamical magnetospheres are generally detectable in H α only for stars with high mass-loss rates (i.e. O-type stars; Petit et al. 2013). Due to corotation of the inner magnetosphere plasma, around rapid rotators centrifugal forces can prevent gravitational infall (ud-Doula, Owocki & Townsend 2008). This leads to the formation of a centrifugal magnetosphere (CM) between the Kepler corotation radius (the equilibrium distance between the gravitational and centrifugal forces) and the Alfvén radius. Within the CM, plasma can accumulate to high enough densities for H α emission to be detectable even around stars with low mass-loss rates (i.e. B-type stars; Petit et al. 2013; Shultz et al. 2019d). Rotational influence furthermore distorts the plasma distribution, such that (for a tilted dipole) it departs from a torus in the magnetic equator to two distinct clouds located at the intersections of the rotational and magnetic equatorial planes, as described by the Rigidly Rotating Magnetosphere (RRM; Townsend & Owocki 2005) model. In addition to the prototypical CM host star σ Ori E (e.g. Landstreet & Borra 1978; Oksala et al. 2015a), the variable H α profiles of a large number of CM host stars has been examined in detail and found to be phenomenologically consistent with the RRM model (e.g. Leone et al. 2010; Bohlender & Monin 2011; Grunhut et al. 2012; Rivinius et al. 2013; Sikora et al. 2015, 2016; Shultz et al. 2021a), with significant differences so far apparent only in the case of tidally locked binaries (Shultz et al. 2018a).
The current understanding of radio magnetospheres assumes that the inner magnetosphere plasma makes no contribution to the CS (Trigilio et al. 2004). Within this framework, the only importance of the inner magnetosphere is absorption and diffraction of radio emission due to the denser plasma in this region, and the primary role of rotation is signal modulation due to the changing projection of a tilted dipole on the sky, and a reduced density in the inner magnetosphere due to centrifugal stress on the magnetic field. However, Shultz et al. (2020) and Owocki et al. (2020) have recently demonstrated that the H α emission properties of magnetic early B-type stars can only be explained if mass-balancing in the CM is accomplished by centrifugal breakout (CBO), rather than steady-state leakage mechanisms operating via a combination of diffusion and drift across magnetic field lines (Owocki & Cranmer 2018). This process, analogous to magnetotail reconnection in planetary magnetospheres, occurs when mass-loading by the wind drives the plasma density beyond the ability of the magnetic field to contain it, at which point the plasma is ejected outwards in a centrifugally driven reconnection process (ud-Doula, Townsend & Owocki 2006; ud-Doula et al. 2008). In contrast to previous expectations that this should result in large-scale reorganization of the inner magnetosphere due to emptying of the plasma (e.g. Townsend et al. 2013), observations instead suggest that CBO events happen more or less continuously over small spatial scales, with the CM maintained at a constant state of near-breakout density (Shultz et al. 2020).
Since plasma ejected by CBO must flow away from the star and, therefore, should pass through the middle magnetosphere, it is reasonable to ask whether there might be some connection between gyrosynchrotron emission and rotation. Linsky, Drake & Bastian (1992) searched for just such a connection but were unable to find anything statistically significant. Since then the number of stars with precisely determined rotation periods has dramatically increased. A connection between rotation and gyrosynchrotron emission was suggested by Kurapati et al. (2017), who did not detect radio emission from slow rotators; however, their small sample size prevented firm conclusions. Leto et al. (2021) have recently demonstrated a close connection between rotation and radio luminosity, suggesting that the wind-driven CS model advanced by Trigilio et al. (2004) be abandoned in favour of a radiation belt model in which radio emission originates from a magnetic shell unrelated to the middle magnetospheric regions, where the magnetic field lines are opened by the wind ram pressure. However, Das & Chandra (2021) have recently reported the detection of correlated flux enhancements emanating via the electron cyclotron maser mechanism (ECM) from auroral circuits above both magnetic poles of CU Vir, which they interpreted as a possible result of CBO events in the inner magnetosphere injecting electrons into both magnetic hemispheres, suggesting that gyrosynchrotron emission may also be connected to CBO.
In the current work, we collect together all magnetic stars for which radio observations, magnetic data, and rotational periods have been obtained, both for radio-bright and radio-dim stars (i.e. stars from which radio emission respectively is and is not detected), in order to investigate the influence of rotation in gyrosynchrotron emission from hot star magnetospheres. Literature data are supplemented with unpublished magnetometry, photometry, and radio observations in order to provide the most comprehensive sample of radio emission from magnetic early-type stars that has been analysed to date. In Section 2, the sample and observations are described, together with the determination of atmospheric, fundamental, rotational, and magnetic parameters. The parameter space distributions of radio-bright and -dim stars are examined in Section 3, together with comparison to H α emission, and analysis of correlations between radio luminosities and various parameters. The implications of these results are discussed in Section 4, and the conclusions are summarized in Section 5. Stellar parameters are tabulated in Appendix A. The online appendices B, C, and D, respectively, provide the observation log of newly presented radio measurements, notes on individual stars for which new magnetic and rotational analyses are presented together with newly published magnetic data, and the tabulated radio flux density measurements for the individual stars.
2 SAMPLE
The sample started with all chemically peculiar or magnetic OBA stars, which have been observed in at least one radio band. For Ap/Bp stars, we assume them to be magnetic even if magnetic data are not available, as chemical peculiarity of this type is invariably associated with strong surface magnetic fields. For magnetic OB stars (i.e. stars of spectral type B0 and hotter, in which strong winds inhibit the formation of surface chemical abundance spots), only those stars known to be magnetic via spectropolarimetric measurement of the Zeeman effect are included, as chemical peculiarity is not an indicator of magnetism at the top of the main sequence since stellar winds strip surface material faster than chemical abundance anomalies can accumulate. The sources consulted for radio data are summarized in Table 1. In addition to literature measurements, we also include new radio measurements of 19 stars (see below). Note that there is a considerable overlap in targets between the various surveys; across all papers, 192 unique targets were observed.
| Source . | Number of stars . | Wavelength (cm) . |
|---|---|---|
| Drake et al. (1987) | 33 | 6 |
| Linsky et al. (1992) | 42 | 2, 3.6, 6, 20 |
| Leone, Trigilio & Umana (1994) | 40 | 6 |
| Leone, Umana & Trigilio (1996) | 7 | 1.3, 2, 6, 20 |
| Leone et al. (2004) | 11 | 0.3 |
| Drake, Wade & Linsky (2006) | 19 | 6 |
| Chandra et al. (2015) | 9 | 20, 50 |
| Kounkel et al. (2017) | 2 | 6 |
| Kurapati et al. (2017) | 19 | 1, 3, 13 |
| Leto et al. (2017) | 1 | 1, 2, 3 |
| Leto et al. (2018) | 1 | 1, 2, 3, 20 |
| Das et al. (2019b) | 1 | 50 |
| Leto et al. (2020a) | 1 | 1, 2, 3, 6 |
| Leto et al. (2020b) | 1 | 2, 3, 6, 13, 20 |
| Pritchard et al. (2021) | 5 | 20 |
| Leto et al. (2021) | 1 | 3 |
| Das & Chandra (2021) | 1 | 50 |
| Das et al. (2021) | 4 | 50 |
| Drake (private communication) | 46 | 6 |
| This work | 19 | 20, 50 |
| Source . | Number of stars . | Wavelength (cm) . |
|---|---|---|
| Drake et al. (1987) | 33 | 6 |
| Linsky et al. (1992) | 42 | 2, 3.6, 6, 20 |
| Leone, Trigilio & Umana (1994) | 40 | 6 |
| Leone, Umana & Trigilio (1996) | 7 | 1.3, 2, 6, 20 |
| Leone et al. (2004) | 11 | 0.3 |
| Drake, Wade & Linsky (2006) | 19 | 6 |
| Chandra et al. (2015) | 9 | 20, 50 |
| Kounkel et al. (2017) | 2 | 6 |
| Kurapati et al. (2017) | 19 | 1, 3, 13 |
| Leto et al. (2017) | 1 | 1, 2, 3 |
| Leto et al. (2018) | 1 | 1, 2, 3, 20 |
| Das et al. (2019b) | 1 | 50 |
| Leto et al. (2020a) | 1 | 1, 2, 3, 6 |
| Leto et al. (2020b) | 1 | 2, 3, 6, 13, 20 |
| Pritchard et al. (2021) | 5 | 20 |
| Leto et al. (2021) | 1 | 3 |
| Das & Chandra (2021) | 1 | 50 |
| Das et al. (2021) | 4 | 50 |
| Drake (private communication) | 46 | 6 |
| This work | 19 | 20, 50 |
| Source . | Number of stars . | Wavelength (cm) . |
|---|---|---|
| Drake et al. (1987) | 33 | 6 |
| Linsky et al. (1992) | 42 | 2, 3.6, 6, 20 |
| Leone, Trigilio & Umana (1994) | 40 | 6 |
| Leone, Umana & Trigilio (1996) | 7 | 1.3, 2, 6, 20 |
| Leone et al. (2004) | 11 | 0.3 |
| Drake, Wade & Linsky (2006) | 19 | 6 |
| Chandra et al. (2015) | 9 | 20, 50 |
| Kounkel et al. (2017) | 2 | 6 |
| Kurapati et al. (2017) | 19 | 1, 3, 13 |
| Leto et al. (2017) | 1 | 1, 2, 3 |
| Leto et al. (2018) | 1 | 1, 2, 3, 20 |
| Das et al. (2019b) | 1 | 50 |
| Leto et al. (2020a) | 1 | 1, 2, 3, 6 |
| Leto et al. (2020b) | 1 | 2, 3, 6, 13, 20 |
| Pritchard et al. (2021) | 5 | 20 |
| Leto et al. (2021) | 1 | 3 |
| Das & Chandra (2021) | 1 | 50 |
| Das et al. (2021) | 4 | 50 |
| Drake (private communication) | 46 | 6 |
| This work | 19 | 20, 50 |
| Source . | Number of stars . | Wavelength (cm) . |
|---|---|---|
| Drake et al. (1987) | 33 | 6 |
| Linsky et al. (1992) | 42 | 2, 3.6, 6, 20 |
| Leone, Trigilio & Umana (1994) | 40 | 6 |
| Leone, Umana & Trigilio (1996) | 7 | 1.3, 2, 6, 20 |
| Leone et al. (2004) | 11 | 0.3 |
| Drake, Wade & Linsky (2006) | 19 | 6 |
| Chandra et al. (2015) | 9 | 20, 50 |
| Kounkel et al. (2017) | 2 | 6 |
| Kurapati et al. (2017) | 19 | 1, 3, 13 |
| Leto et al. (2017) | 1 | 1, 2, 3 |
| Leto et al. (2018) | 1 | 1, 2, 3, 20 |
| Das et al. (2019b) | 1 | 50 |
| Leto et al. (2020a) | 1 | 1, 2, 3, 6 |
| Leto et al. (2020b) | 1 | 2, 3, 6, 13, 20 |
| Pritchard et al. (2021) | 5 | 20 |
| Leto et al. (2021) | 1 | 3 |
| Das & Chandra (2021) | 1 | 50 |
| Das et al. (2021) | 4 | 50 |
| Drake (private communication) | 46 | 6 |
| This work | 19 | 20, 50 |
Since some of the stars observed in the early surveys belong to non-magnetic classes (e.g. classical Be stars, HgMn stars), these stars (33 in total) were removed from the sample. After cross-referencing the catalogues and removing non-magnetic stars, 156 stars have at least one radio frequency observation, 50 of which are detected. These stars are listed in Table A1, with the observed fluxes given online in table D1. Where more than one observation is available at a given wavelength, the radio luminosity corresponds to the maximum observed flux density.
2.1 Stellar parameters
We searched the literature for determinations of atmospheric parameters effective temperature Teff and bolometric luminosity log Lbol, and projected rotational velocities vsin i. These are given together with references in Table A1. When stellar parameters could not be found in existing compilations or single studies, they were determined photometrically. As a first step, the catalogue was cross-referenced with SIMBAD,1 in order to obtain spectral types and Johnson photometry. Distances were obtained from the Gaia early Data Release 3 Catalogue (Gaia Collaboration 2021); in the few cases where these were not available, Hipparcos parallaxes (van Leeuwen 2007) generally were. Distances were calculated by inverting Gaussian parallax distributions, with the resulting asymmetric error bars propagated through to determinations of bolometric luminosity; however, in most cases the relative parallax errors are small enough (the median relative error is about 2 per cent) that the difference between positive and negative distance uncertainties is negligible. If Strömgren photometry is available (using the catalogues provided by Hauck & Mermilliod 1998; Paunzen 2015), effective temperatures were determined with the idl program uvbybeta2 (which uses the calibration determined by Napiwotzki, Schoenberner & Wenske 1993). If Strömgren photometry is not available, Johnson photometry was used to obtain Teff. All available de-reddened colours were compared to the empirical calibration provided by Worthey & Lee (2011). Reddening was found using the Stilism 3D tomographic dust map (Lallement et al. 2014; Capitanio et al. 2017; Lallement et al. 2018) based on the positions and Gaia distances of the individual stars. While Stilism typically extends only out to around 1 kpc, the overwhelming majority of the sample stars are well within this distance; the few stars beyond this distance have stellar parameters available in the literature. Extinctions were determined with the usual reddening law (AV = 3.1E(B − V)). For mCP stars, the bolometric correction BC determined by Netopil et al. (2008) for mCP stars was used to determine Lbol. Since the Netopil et al. (2008) BC is only calibrated up to 19 kK, for mCP stars hotter than this limit, a larger uncertainty was adopted following Shultz et al. (2019b). For chemically normal stars, the Nieva (2013) BC was used.
We then searched the literature for determinations of rotational periods Prot and magnetic oblique rotator model (ORM) parameters. In the simplest case of a tilted dipole (appropriate to first order for the vast majority of stars with fossil fields), an ORM consists of an inclination i of the rotational axis from the line of sight, an obliquity angle β of the magnetic axis from the rotational axis, and a polar surface strength Bd of the magnetic dipole at the stellar surface. In the simplest case of a tilted dipole, appropriate to the vast majority of stars (e.g. Kochukhov et al. 2019), the rotation of the star will lead to a sinusoidal variation in the longitudinal, or line of sight, magnetic field 〈Bz〉 averaged over the stellar disc. If Prot is known, the 〈Bz〉 curve can then be used to obtain the ORM parameters (Preston 1967), however there is a degeneracy between the angular parameters i and β. Breaking this degeneracy requires knowledge of vsin i and the stellar radius R*.
Where ORM parameters were not already available, we searched for longitudinal magnetic field measurements 〈Bz〉 with which to determine them. ORM parameters were determined simultaneously with fundamental, rotational, and magnetospheric parameters using the Monte Carlo Hertzsprung–Russell diagram (MCHRD) sampler described by Shultz et al. (2019d). The MCHRD sampler combines all available measurements with evolutionary models in order to infer self-consistent fundamental, ORM, wind, and magnetospheric parameters, automatically accounting for correlated error bars. In this case we utilized the rotating or non-rotating Geneva evolutionary models calculated by Ekström et al. (2012), as appropriate for a given stellar rotational period (non-rotating models were used if Prot > 10 d). In some cases, ORM parameters have been revised to those obtained from the MCHRD sampler, in order to ensure methodological consistency across the full sample; it is these values which are reported in Table A1.
2.2 Radio observations
2.2.1 VLA
We report previously unpublished 6 cm observations of 46 stars acquired at the Very Large Array (VLA). The data were acquired in 1992 and 1994 in the context of the survey presented by Drake et al. (1987, 2006) and Linsky et al. (1992), and were reduced and analysed following the procedures described in those works. They were provided by Drake (private communication). All 46 observations are non-detections. One of the stars in this sample, HD 118022, was reanalysed by Leto et al. (2021) and found to be a detection.
2.2.2 uGMRT
We report new 20 and 50 cm radio observations of 19 magnetic hot stars, including four new detections (HD 11503, HD 64740, HD 189775, and HD 200775). These data were acquired with the upgraded Giant Metrewave Radio Telescope (uGMRT), located at Pune, India. The uGMRT is a radio interferometer consisting of 30 antennae, and operates over the frequency range of 120–1450 MHz divided into four bands. Our observation frequency corresponds to bands 4 (550–900 MHz) and 5 (1050–1450 MHz). For each observation, we observed a set of calibrators in order to calibrate the absolute flux density scale and the bandpass (flux calibrator), and the time-dependent antenna gains (phase calibrator). The details of these observations, including the calibrators used, are provided online in table B1. The data were analysed using the Common Astronomy Software Applications (casa; McMullin et al. 2007) following the procedure described in Das et al. (2019b, a).
Nine stars were observed in the context of the GMRT legacy survey. 10 stars, indicated in table D1, were acquired in the context of an ongoing uGMRT survey aiming to detect and characterize auroral radio pulses emitted via the ECM (Das et al. 2018, 2019a, b, 2021; Das & Chandra 2021). These pulses occur at or near 〈Bz〉 nulls (i.e. at phases corresponding to the magnetic equator bisecting the stellar disc) since they are emitted tangent to the auroral circuits above the magnetic poles (e.g. Trigilio et al. , 2011; Leto et al. 2016; Das et al. 2020). For this reason, observations were acquired close to magnetic nulls, and care is required to ensure that the adopted flux density reflects basal gyrosynchrotron emission rather than the much stronger ECM pulse. For five additional stars for which phase coverage was insufficient to cover the basal flux density level, uGMRT data were not included. It should be noted that, since gyrosynchrotron emission is rotationally modulated and, unlike ECM pulses, is at a minimum rather than a maximum at magnetic nulls (e.g. Leto et al. 2017, 2018), there is the possibility that these data systematically underestimate the peak 50 cm flux densities of these targets. However, in most cases when observations at other wavelengths are available, the measurements are comparable, consistent with expectations that the radio spectrum is approximately flat and that rotational modulation of the flux density is generally only a factor of a few (e.g. Trigilio et al. 2004; Leto et al. 2012, 2017, 2018, 2020a).
2.3 Spectropolarimetric and photometric observations
When neither ORM parameters nor published 〈Bz〉 measurements were available, or when rotation periods were unknown, we utilized both public and private archives of spectropolarimetric and space photometric data with which to constrain magnetic and rotational properties. These were then used in conjunction with stellar parameters and the MCHRD sampler to infer ORM models as described above. The data used for this analysis are described in detail in appendix C. In total, we provide new magnetic data for 30 stars, of which magnetic fields were detected in 16, and utilized magnetic and/or photometric data to evaluate rotational periods for 59 stars, of which we refined the published periods of 14 stars and determined new periods for 16 stars. In some cases (HD 36629, HD 37041, HD 49606, and HD 89822), these analyses also led to the rejection of published rotational periods and magnetic data as spurious results arising from noisy data; these stars were removed from the sample.
2.3.1 Dominion Astrophysical Observatory spectropolarimetry
The dimaPol spectropolarimeter is a medium-resolution (λ/Δλ ∼ 10 000) instrument covering the 25 nm region centred on the laboratory wavelength of the H β line. It is mounted on the 1.8 m Dominion Astrophysical Observatory (DAO) Plaskett Telescope. The instrument and reduction pipeline are described in detail by Monin et al. (2012). Magnetic measurements are obtained primarily using the wings of H β and are therefore fairly insensitive to either vsin i or surface chemical abundance patches (e.g. Borra & Landstreet 1977).
Unpublished DAO measurements are available for 20 stars in the sample, although in some cases no magnetic field can be detected at the available precision (generally hundreds of G). Of the 12 stars for which a magnetic field can certainly be detected and good constraints do not already exist, 217 individual measurements are available, with a median of 18 measurements per star. These data are analysed in detail in appendix C, and the measurements are available as supplementary material through Vizier.
2.3.2 ESPaDOnS and Narval spectropolarimetry
Échelle SPectropolarimetric Device for the Observations of Stars (ESPaDOnS) and Narval are identical high-resolution (λ/Δλ) spectropolarimeters, respectively, mounted at the 3.6 m Canada-France-Hawaii Telescope (CFHT) and the 2 m Bernard Lyot Telescope (TBL). They cover a wavelength range of approximately 370–1050 nm across 40 overlapping spectral orders. Each observation consists of four differently polarized subexposures, yielding four unpolarized (Stokes I) spectra, one circularly polarized (Stokes V) spectrum, and two diagnostic null (N) spectra with which to check for normal instrument operation and determination of noise. The characteristics of the instruments and data reduction were described in detail by Wade et al. (2016).
We queried the PolarBase database of Narval and ESPaDOnS spectropolarimetry for unpublished spectropolarimetric measurements (Petit et al. 2014). These were found for 20 stars (overlapping with the DAO data set). Magnetic fields were detected via the multiline least-squares deconvolution (Donati et al. 1997; Kochukhov, Makaganiuk & Piskunov 2010) method in six stars. The magnetic analysis of these measurements is described in appendix C.
2.3.3 Space photometry
The surface abundance spots of mCP stars lead to photometric variability that can be used to infer their rotational periods. We searched public archives (the Hipparcos archive and MAST, the Mikulsi Archive for Space Telscopes) for the light curves from the High precision parallax collecting satellite (Hipparcos), Kepler, and Transiting Exoplanet Survey Satellite (TESS) space telescopes. These light curves are provided in appendix C. Period analysis was performed using the Lomb-Scargle program period04 (Lenz & Breger 2005). This was accomplished by identifying the lowest-frequency term in a harmonic series, fixing higher harmonics to whole number multiples of the rotational harmonic, and then optimizing the phases and amplitudes of the terms to minimize residuals, as is standard practice for the strictly periodic rotational variability of mCP stars (e.g. David-Uraz et al. 2019; Sikora et al. 2019c).
Hipparcos was an astrometric space telescope, whose mission lasted from 1989 to 1993. While the primary aim was to obtain high-precision trigonometric parallaxes, it also obtained time series photometry for a large number of stars (Perryman et al. 1997; van Leeuwen 2007), which is available for 12 stars without published rotation periods.
The NASA Kepler satellite was a μmag-precision space photometer with a 110 square degree field of view operating in the 400 to 850 nm bandpass, intended for high-cadence, long-duration observations with the goal of detecting transiting exoplanets (Borucki et al. 2010). The K2 mission was an extension of the original Kepler mission, following the failure of two of the satellite’s reaction wheels; by utilizing pressure from the solar wind, the satellite could be stabilized on a given field of view for about 3 months, enabling it to observe fields along the ecliptic (Howell et al. 2014). A K2 light curve is available for 1 star.
TESS uses four cameras with a total field of view of 24° × 96°, with a bandpass covering 600–1050 nm (Ricker et al. 2015). The initial 2-yr TESS mission began in 2018, during which it completed coverage of almost the entire sky. During each year, 13 sectors were observed for 27 d each, with a nominal precision of 60 ppm h−1 (although this varies between fields and targets). High-priority targets are observed with a 2-min cadence, and the processed light curves made available on the MAST archive immediately following reduction. 2-min cadence TESS data are available for nine stars. In other cases, we used the 30-min cadence data extracted from Full Frame Images, obtained from MAST when available or, for nine stars for which this was not the case, extracted ourselves. In total, we utilized TESS data for 46 stars.
2.4 Final sample
In the end, magnetic data are available for 142 stars, rotational periods for 138 stars, and both for 131 stars, of which 50 have detected radio emission (note that these numbers do not include the magnetic O-type stars, which are dropped from the analysis for reasons explained below in Section 3.1.). Dipolar magnetic field strengths and rotation periods are given together with references in Table A1, along with all quantities necessary to calculate the various parameters examined in the subsequent analysis. In the cases in which ORM parameters were determined here using published 〈Bz〉 measurements, the references to the measurements are also included.
Radio luminosities were determined using parallax distances. When multiple radio measurements are available, the highest flux density measurement was chosen as a representative of the radio luminosity of the star. When they have been measured, the spectral indices of radio emission from magnetic hot stars are approximately flat between 1 and 100 GHz (as has been shown by Leto et al. 2021, for the largest sample to date of stars with a sufficient number of multifrequency observations to perform this analysis), and the difference between measurements at different frequencies for a given star in the present sample is in general small. It is therefore likely that radio luminosities can be estimated with reasonable accuracy from single observations at a single frequency (which are all that are available for much of the sample). Following this, radio luminosity was determined by integrating a trapezoidal function between between 600 MHz (50 cm) and 100 GHz (0.3 cm), with values of unity between 1.5 GHz (20 cm) and 30 GHz (1 cm), and zero at the extrema. This was then scaled by the peak specific intensity measured across all observations (when more than one observation is available). Integrating with values at unity at all wavelengths, or only integrating between 1.5 and 30 GHz, were also tried; however, the trapezoidal approximation gives the closest agreement with radio luminosities acquired for stars with observations at four or more wavelengths. In the end, 0.3 cm measurements were discarded as likely outliers due to significant discrepancies between these and observations at other wavelengths for the same stars; only two stars are detected at 0.3 cm, and in both cases the stars were also detected at other wavelengths, therefore this does not affect the detection statistics. While this is a less-than-perfect approximation of the actual spectral energy distributions (SEDs) of the sample stars, in the absence of multiwavelength measurements constraining the variation of SEDs across stellar parameters it is not yet possible to adopt a more sophisticated approach. Furthermore, rotational modulation of the signal and the reliance on snapshot observations makes it likely that the maximum flux density is underestimated for much of the sample, for which this trapezoidal function approach may partially compensate given that it may overestimate the radio luminosity by failing to account for departures from perfectly flat spectral indices. As a check on this approximation, Fig. 1 shows the radio luminosity approximated from the maximum flux density, versus the radio luminosity measured via integration of measured flux densities across the same frequency range, for those stars with observations sampling at least four frequencies. While there are outliers by up to about 1 dex, there is generally a good correlation between the two quantities, suggesting this approach is a reasonable approximation of the actual radio luminosities of the sample.
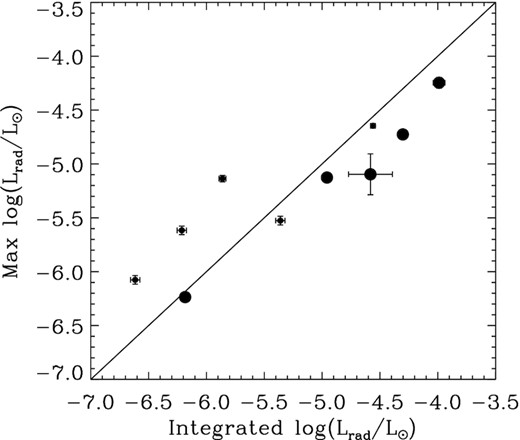
Radio luminosities inferred from the maximum flux density versus radio luminosities obtained by integrating flux density across the full frequency range, for those stars with observations sampling at least four frequencies. Symbol size is proportional to number of observations (either four, small, or five, large).
As can be seen in Fig. 2, radio luminosity varies over about four orders of magnitude. While radio emission is rotationally modulated, the amplitude of this modulation is a factor of a few (e.g. Trigilio et al. 2004; Leto et al. 2012, 2017, 2018), i.e. much smaller than the differences between individual stars in the sample. That radio observations sampling the entire phase curve are in general unavailable, and that the true peak luminosity is therefore unknown, is unimportant at the level of the full population.
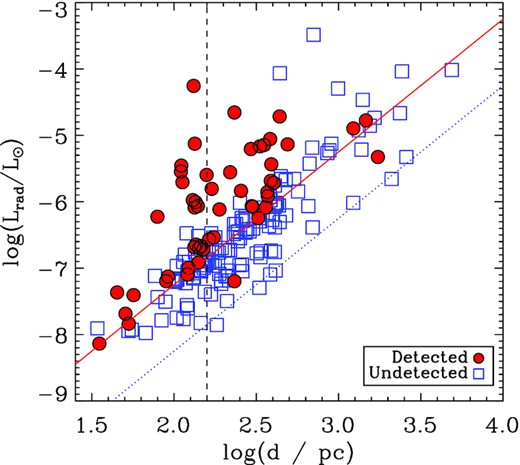
Radio luminosity as a function of a distance. Solid and dotted lines indicate distance-dependent detection limits as defined by the lower bounds of detected and non-detected stars, respectively. The vertical dashed line indicates the distance beyond which the observed lower detection limit begins to rise with increasing distance. Non-detections are upper limits.
Another consideration that is apparent from Fig. 2 is that the detection limit is a function of distance. However, below a distance of log (d/pc) = 2.2, the lower detection limit is fairly constant, with radio non-detections being comparable in luminosity to the weakest radio detections. Beyond this distance, it is more likely that radio-dim stars would have been detected if they were closer; below it, this scenario is less likely. This nearby sub-sample is therefore in a sense more complete than the full sample, and can be used to test conclusions derived from the full sample of stars.
3 PARAMETER STUDY
We begin our analysis by examining the distributions of radio-bright and radio-dim stars in atmospheric, magnetic, rotational, and magnetospheric parameter space, examining the effectiveness of each parameter in separating the two populations, as well as the strength of the correlation between radio luminosity and a given parameter.
3.1 Hertzsprung–Russell diagram
The top left panel of Fig. 3 shows all magnetic stars with radio observations on the HRD, where we have shown the non-rotating evolutionary models calculated with the solar metallicity Geneva evolutionary code by Ekström et al. (2012). Most radio-bright stars are between about 3 and 9 M⊙, and are generally close to the Zero-Age Main Sequence (ZAMS). They are relatively evenly distributed within this mass range, with no obvious tendency to cluster at high luminosities, consistent with the finding from Leto et al. (2021) that gyrosynchrotron emission is more or less independent of the wind power. There are two stars which are very obviously not near the ZAMS, highlighted in Fig. 3. These are HD 200775, which is a magnetic Herbig Be star (Alecian et al. 2008a), and HD 171247, which is examined in further detail below.
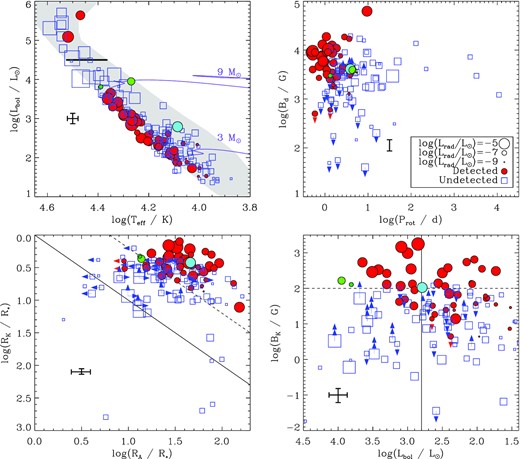
Parameter space distribution of the sample. Filled red circles indicate radio-bright stars, open blue squares radio-dim stars, and symbol size is proportional to radio luminosity (or its upper limit). Mean uncertainties are indicated by error bars. Filled dark green, light blue, and light green circles highlight HD 64740, HD 171247, and HD 200775, respectively (discussed in the text). Top Left: HRD showing all magnetic stars with radio observations. The grey shaded region indicates the main sequence. The thick line indicates the empirical bolometric luminosity cutoff applied to the subsequent analysis. Top right: the sample on the log Bd − log Prot plane. Bottom left: the sample on the rotation-magnetic wind confinement diagram. The solid line indicates RA = RK: points below have dynamical magnetospheres only, points above possess CM. The dashed line shows log RA/RK = 0.8, the approximate minimum threshold for H α emission. Bottom right: the log BK − log Lbol plane. The minimum value of log BK extends to about −6; none of the stars not shown are detected in radio. The dashed line indicates the approximate BK threshold for H α emission, while the solid line indicates the lower luminosity limit for H α.
As discussd by Chandra et al. (2015), the strong winds of O-type stars lead to radio photospheres that are, in general, much larger than their Alfvén radii, and swallow any gyrosynchrotron emission that might be produced. Thermal radio emission from O-type stars can be produced by their winds (e.g. Bieging, Abbott & Churchwell 1989; Lamers & Leitherer 1993), and while this can, in principle, be rotationally modulated due to symmetry-breaking in the presence of a magnetic field (Daley-Yates, Stevens & ud-Doula 2019), this is unrelated to the gyrosynchrotron emission of interest here. Furthermore, non-thermal synchrotron emission can be produced in the colliding wind shocks of close binaries (e.g. Pittard et al. 2006; Blomme et al. 2010). Only two O-type stars are detected in the sample (Kurapati et al. 2017), these being ζ Ori A3 (which has a thermal radio spectrum) and Plaskett’s Star (a spectroscopic colliding wind binary; Linder et al. 2008). O-type stars were therefore excluded from the sample, as indicated by the horizontal thick bar in Fig. 3. This removed 11 stars from the sample.
3.2 Rotation and magnetic field strength
The top right panel of Fig. 3 shows the sample on the log Bd − log Prot plane. The period axis is truncated for clarity, omitting three stars with periods on the order of several years, none of which are detected in the radio. Notably, all radio-bright stars are both strongly magnetic (as expected) and rapidly rotating (Prot ≲ 5 d, with Babcock’s Star, HD 215441, the only exception – a ‘slow’ rotator with a period of about 10 d). There is some indication in Fig. 3 that the stronger the magnetic field, the slower the rotation can be while still producing detectable radio emission.
Comparing radio-dim and radio-bright stars, their rotational and magnetic properties are clearly different. The mean rotational period and surface magnetic dipole strengths of the radio emitters are |$\log {(P_{\rm rot / {\rm d})} = 0.14^{+0.23}_{-0.14}}$| and |$\log {(B_{\rm d} / {\rm G})} = 3.70^{+0.23}_{-0.25}$|, while the corresponding means for the radio-dim stars are |$\log {(P_{\rm rot / {\rm d})} = 0.81^{+0.87}_{-0.22}}$| and |$\log {(B_{\rm d} / {\rm G})} = 3.31^{+0.24}_{-0.49}$|, where the error bars correspond to standard deviations above and below the mean value. Notably, radio emission is not detected in any star with log Prot > 1, regardless of magnetic field strength.
3.3 The rotation-magnetic wind confinement diagram
If RK > RA the inner magnetosphere is purely dynamical, meaning that rotation plays no role; no stars in this regime show radio emission. When RK < RA the inner magnetosphere forms a centrifugal component. The dashed line indicates log (RA/RK) = 0.8, the approximate threshold for H α emission (Petit et al. 2013; Shultz et al. 2019d). Essentially all of the radio-bright stars are above this threshold, once again indicating that rotation plays a crucial role. It is also noteworthy that radio and H α emission occur in the same part of the rotation-magnetic confinement diagram. Furthermore, while there are relatively few stars in the DM-only regime with radio observations, there are numerous stars in the small-CM regime (0 < log (RA/RK) < 0.8), almost all of which are undetected in the radio (with the two detected stars having limiting values of Bd). Since it seems to be necessary for a star to have a large CM for it to display gyrosynchrotron emission, it also seems unlikely that additional observations will detect DM stars with non-thermal radio (although this should naturally be verified in the future).
3.4 Magnetic field at the Kepler radius
Shultz et al. (2020) showed that H α emission is regulated directly by the strength of the magnetic field at the Kepler radius in the magnetic equatorial plane, which for a dipole is |$B_{\rm K} = B_{\rm eq}~/ R_{\rm K}^3$|, for RK in units of stellar radii. H α emission appears only in stars with BK ∼ 100 G. As demonstrated by Owocki et al. (2020), this is the magnetic field strength necessary for the plasma density at RK to reach an H α optical depth of unity, under the assumption that mass balancing is governed by CBO.
The bottom right panel of Fig. 3 shows the sample on the log BK − log Lbol plane (compare to the right-hand panel of Fig. 3 in Shultz et al. 2020). The dashed line indicates the H α emission threshold; essentially all stars above this threshold are radio-bright. The vertical line indicates the low-luminosity cutoff for H α emission; notably, radio emission extends to lower luminosities, including essentially the entire B-type spectral sequence. Gyrosynchrotron emission is also seen at lower values of BK than those at which H α can be detected, down to about 10 G.
3.5 Evolution of radio luminosity
As is apparent from the HRD in Fig. 3, the majority of radio-bright stars are found close to the ZAMS. Fig. 4 shows radio luminosity as a function of fractional main sequence age τMS, and demonstrates that radio luminosity drops precipitously by about 2 dex beyond a fractional main-sequence age of τMS ∼ 0.2. The stars with the weakest radio emission are furthermore found in the second half of the main sequence. This is just as would be expected if radio emission is tied to rotation, since magnetic braking rapidly removes angular momentum (ud-Doula, Owocki & Townsend 2009; Keszthelyi et al. 2019, 2020). A similar phenomenon has been seen in the H α magnetospheres of early B-type stars: emission is found only in young stars (Shultz et al. 2019d), and drops in strength steeply with age (Shultz et al. 2020).
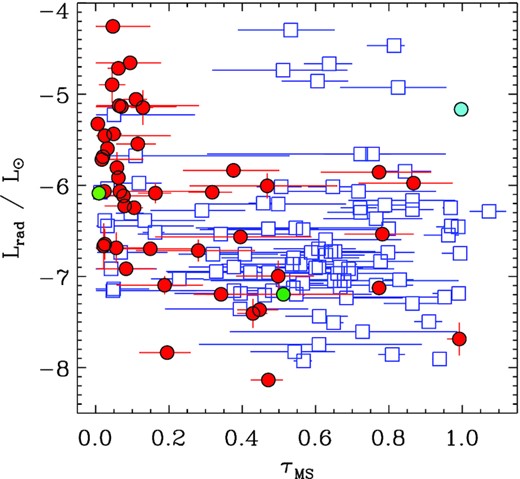
Radio luminosity as a function of fractional main sequence age τMS. HD 64740, HD 171247, and HD 200775 are highlighted as in Fig. 3.
The one exception to this trend is HD 171247, highlighted in Figs 3 and 4 with a filled light blue circle. This is a somewhat curious object as its radio luminosity is relatively high (log Lrad = −5.16 ± 0.02) despite being a relatively slow rotator (Prot = 3.9 d) with a surface magnetic field of average strength (Bd ∼ 4.1 kG). Furthermore, in contrast to the general case in which radio-bright stars are found close to the ZAMS, HD 171247 is apparently a fairly evolved object very near to the terminal age main sequence. As described in appendix C, there is a considerable uncertainty regarding HD 171247’s rotational period, as strikingly different values (about 1 d versus 4 d) are found from 〈Bz〉 and photometry.
It is possible that HD 171247 is affected by some other factor. For example, an undetected binary companion might lead to an overestimated bolometric luminosity or, in the case of an interacting system, enhance its radio luminosity; however, there is nothing particularly strange about the measurements from the well-studied binary systems HD 36485 or HD 37017 (Leone et al. 2010; Bolton et al. 1998), and there is furthermore no indication of asymmetry or radial velocity variability in the available DAO spectra. The star does, however, has a substellar companion of approximately 46 Jupiter masses at a separation of about 2 AU, detected via Gaia astrometry (Kervella et al. 2019); if the companion is also magnetic, it may be an additional source of radio emission. Alternatively, its reported radio flux density measurement might have been obtained at a rotational phase corresponding to an auroral radio emission pulse, which can result in substantial enhancements over the basal flux (while its 6 cm observations are not in the usual wavelength regime for this phenomenon, which is predominantly seen at longer wavelengths, ECM was detected at this wavelength by Das & Chandra 2021, in the case of HD 124224). Given HD 171247’s anomalous position on the HRD, and the uncertainty in its rotational period, this object was removed from the subsequent analysis as likely suffering from one or more systematic errors.
3.6 Wind absorption
To determine to what degree the remaining sample might still be affected by wind absorption, following Chandra et al. (2015) we calculated the ratio between the radius of free–free emission Rff and RA, where Rff gives the extent of the radio photosphere at a given frequency. If Rff > RA, it is likely that gyrosynchrotron emission will be absorbed by the wind, and any radio emission detected from the source will arise from free–free emission in the wind. Fig. 5 shows Rff/RA as a function of Teff. Since Rff is a strong function of wavelength, this analysis was done for observations at specific wavelengths rather than integrated values. As can be seen in Fig. 5, for all but one radio-bright star Rff ≪ RA. The sole exception is HD 64740, which is the hottest and most luminous of the radio-bright stars remaining in the sample after removing the O-type stars, and the only radio-bright B-type star with a mass above 9 M⊙. This star is highlighted in Fig. 3 by a small green circle. HD 64740 has a relatively low radio luminosity, log Lrad/L⊙ = −7.16 ± 0.06, and was subsequently found to be under-luminous in comparison to stars with similar rotational, magnetic, and stellar parameters. Following Kurapati et al. (2017)’s equation. 1, the minimum mass-loss rate that could explain the star’s radio luminosity via free–free emission is ∼2 × 10−7 M⊙ yr−1, which is about 100 times higher than the star’s CAK mass-loss rate, indicating that the detected radio emission cannot be due to free–free emission from the wind. While HD 64740’s radio emission is therefore almost certainly gyrosynchrotron, it seems probable that the sole 50 cm observation of this star is strongly attenuated by self-absorption in the wind, and it was therefore removed from the subsequent analysis.
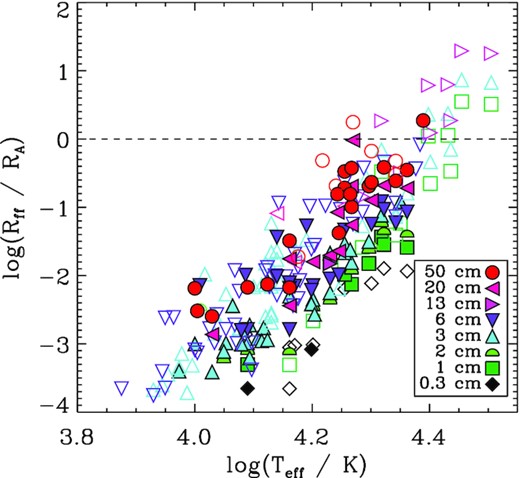
Ratio between the radius of the free–free emission photosphere Rff and the Alfvén radius RA as a function of Teff. Symbol colour and type indicates wavelength; filled symbols correspond to radio-bright stars. Above the dashed line, the radio photosphere is larger than RA for the given frequency. Only one radio-bright star, HD 64740, is above the dashed line.
3.7 Comparison to H α emission
The co-occurrence of radio-bright and H α-bright stars in the same part of the rotation-magnetic confinement diagram (see Fig. 3) is suggestive of a relationship between the two forms of magnetospheric emission. Fig. 6 demonstrates that the two forms of emission do in fact correlate. H α emission equivalent widths (EWs) were taken from the measurements of Shultz et al. (2020), with the addition of measurements of HD 156424 (Shultz et al. 2021b), ALS 9522 (Shultz et al. 2021a), and HD 147932 (Shultz et al., in preparation). For stars in which both gyrosynchrotron emission and H α emission are detected, Pearson’s correlation coefficient is r = 0.88.
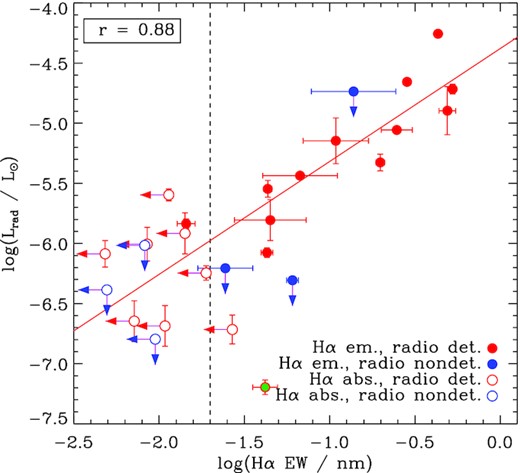
Radio luminosity as a function of H α emission EW. The solid diagonal line shows a fit to the measurements of stars detected in both H α and radio. The vertical dashed line indicates the approximate noise floor identified by Shultz et al. (2020). Red and blue points are stars detected and not detected in the radio; filled and open symbols are stars with H α in emission and absorption, respectively. HD 64740 is highlighted with dark green.
The only outlier to the trend is HD 64740 (highlighted in Fig. 6), for which its radio luminosity is under-luminous compared to its H α emission EW. This is consistent with its gyrosynchrotron emission being partially absorbed by its large free–free radio photosphere, as described is Section 3.6. HD 64740 was therefore not included in the fit in Fig. 6.
Stars without H α emission (open symbols) are of course all at or below the noise level (dashed line) inferred from the median EW error bar. Furthermore, the radio luminosities of these stars are systematically lower than those of stars with H α emission, consistent with magnetic confinement in their CMs being too weak to contain plasma that is optically thick in H α. Only two stars have H α emission but are not detected in radio; in these cases, the upper limits on their radio luminosities lie very close to the regression line.
3.8 Regression analysis
In order to identify the primary parameters affecting radio emission in a relatively hypothesis-independent fashion, we compared radio luminosities to a variety of stellar, magnetic, and rotational parameters, using one-, two-, and three-variable regressions (regressions with four variables yielded no statistical improvement). The results of these tests are summarized in Table 2. The best regressions are shown in Fig. 7.
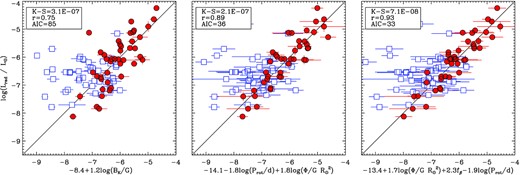
Best results for (left – right) single-, double-, and triple-variable regressions of various parameters versus radio luminosity. Red circles show radio-bright stars; open squares are upper limits for radio-dim stars. Legends give the K-S probability for separating radio-bright and -dim stars into different populations; Pearson’s r; and the Akaike Information Criterion (AIC).
Regression parameters for maximum radio luminosity. From left to right, the columns give: the tested variable; the two-sample K-S test probability that the variable separates radio-bright and -dim stars into separate populations; Pearson’s correlation coefficient r; the reduced χ2 of the regression; the AIC for the regression; and the slope of the regression.
| Variable . | K-S . | r . | χ2/ν . | AIC . | Slope . |
|---|---|---|---|---|---|
| One-Variable Regressions | |||||
| log (Lbol/L⊙) | 0.87 | 0.64 | 5.1 | 103 | 1.0 ± 0.2 |
| log (Teff/K) | 0.53 | 0.78 | 4.1 | 84 | 6.6 ± 0.8 |
| log (R*/R⊙) | 0.06 | 0.18 | 6.3 | 124 | 1.3 ± 1.1 |
| log (M*/M⊙) | 0.66 | 0.70 | 4.2 | 88 | 4.0 ± 0.6 |
| log (Prot/d) | 10−7 | −0.50 | 6.4 | 126 | −1.5 ± 0.4 |
| log (Bd/G) | 10−2 | 0.60 | 3.5 | 75 | 1.6 ± 0.3 |
| |$\log {(\dot{M} / {\rm M_\odot ~yr^{-1}})}$| | 0.83 | 0.50 | 5.2 | 105 | 0.5 ± 0.1 |
| log (RA/R*) | 0.08 | −0.17 | 6.2 | 121 | −0.7 ± 0.6 |
| log (RK/R*) | 10−5 | −0.45 | 6.1 | 120 | −2.1 ± 0.6 |
| log (RA/RK) | 0.35 | −0.28 | 6.0 | 120 | −0.7 ± 0.4 |
| log (BK/G) | 10−7 | 0.75 | 4.1 | 86 | 1.2 ± 0.2 |
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 0.19 | 0.67 | 4.0 | 84 | 1.6 ± 0.3 |
| log fβ | 0.29 | 0.33 | 7.1 | 137 | 2.9 ± 1.3 |
| Best Two-Variable Regression | |||||
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 10−7 | 0.89 | 1.2 | 36 | 1.8 ± 0.2 |
| log (Prot/d) | −1.8 ± 0.2 | ||||
| Best Three-Variable Regression | |||||
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 10−8 | 0.93 | 0.8 | 33 | 1.7 ± 0.2 |
| log (Prot/d) | −1.9 ± 0.2 | ||||
| fβ | 2.3 ± 0.5 | ||||
| Variable . | K-S . | r . | χ2/ν . | AIC . | Slope . |
|---|---|---|---|---|---|
| One-Variable Regressions | |||||
| log (Lbol/L⊙) | 0.87 | 0.64 | 5.1 | 103 | 1.0 ± 0.2 |
| log (Teff/K) | 0.53 | 0.78 | 4.1 | 84 | 6.6 ± 0.8 |
| log (R*/R⊙) | 0.06 | 0.18 | 6.3 | 124 | 1.3 ± 1.1 |
| log (M*/M⊙) | 0.66 | 0.70 | 4.2 | 88 | 4.0 ± 0.6 |
| log (Prot/d) | 10−7 | −0.50 | 6.4 | 126 | −1.5 ± 0.4 |
| log (Bd/G) | 10−2 | 0.60 | 3.5 | 75 | 1.6 ± 0.3 |
| |$\log {(\dot{M} / {\rm M_\odot ~yr^{-1}})}$| | 0.83 | 0.50 | 5.2 | 105 | 0.5 ± 0.1 |
| log (RA/R*) | 0.08 | −0.17 | 6.2 | 121 | −0.7 ± 0.6 |
| log (RK/R*) | 10−5 | −0.45 | 6.1 | 120 | −2.1 ± 0.6 |
| log (RA/RK) | 0.35 | −0.28 | 6.0 | 120 | −0.7 ± 0.4 |
| log (BK/G) | 10−7 | 0.75 | 4.1 | 86 | 1.2 ± 0.2 |
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 0.19 | 0.67 | 4.0 | 84 | 1.6 ± 0.3 |
| log fβ | 0.29 | 0.33 | 7.1 | 137 | 2.9 ± 1.3 |
| Best Two-Variable Regression | |||||
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 10−7 | 0.89 | 1.2 | 36 | 1.8 ± 0.2 |
| log (Prot/d) | −1.8 ± 0.2 | ||||
| Best Three-Variable Regression | |||||
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 10−8 | 0.93 | 0.8 | 33 | 1.7 ± 0.2 |
| log (Prot/d) | −1.9 ± 0.2 | ||||
| fβ | 2.3 ± 0.5 | ||||
Regression parameters for maximum radio luminosity. From left to right, the columns give: the tested variable; the two-sample K-S test probability that the variable separates radio-bright and -dim stars into separate populations; Pearson’s correlation coefficient r; the reduced χ2 of the regression; the AIC for the regression; and the slope of the regression.
| Variable . | K-S . | r . | χ2/ν . | AIC . | Slope . |
|---|---|---|---|---|---|
| One-Variable Regressions | |||||
| log (Lbol/L⊙) | 0.87 | 0.64 | 5.1 | 103 | 1.0 ± 0.2 |
| log (Teff/K) | 0.53 | 0.78 | 4.1 | 84 | 6.6 ± 0.8 |
| log (R*/R⊙) | 0.06 | 0.18 | 6.3 | 124 | 1.3 ± 1.1 |
| log (M*/M⊙) | 0.66 | 0.70 | 4.2 | 88 | 4.0 ± 0.6 |
| log (Prot/d) | 10−7 | −0.50 | 6.4 | 126 | −1.5 ± 0.4 |
| log (Bd/G) | 10−2 | 0.60 | 3.5 | 75 | 1.6 ± 0.3 |
| |$\log {(\dot{M} / {\rm M_\odot ~yr^{-1}})}$| | 0.83 | 0.50 | 5.2 | 105 | 0.5 ± 0.1 |
| log (RA/R*) | 0.08 | −0.17 | 6.2 | 121 | −0.7 ± 0.6 |
| log (RK/R*) | 10−5 | −0.45 | 6.1 | 120 | −2.1 ± 0.6 |
| log (RA/RK) | 0.35 | −0.28 | 6.0 | 120 | −0.7 ± 0.4 |
| log (BK/G) | 10−7 | 0.75 | 4.1 | 86 | 1.2 ± 0.2 |
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 0.19 | 0.67 | 4.0 | 84 | 1.6 ± 0.3 |
| log fβ | 0.29 | 0.33 | 7.1 | 137 | 2.9 ± 1.3 |
| Best Two-Variable Regression | |||||
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 10−7 | 0.89 | 1.2 | 36 | 1.8 ± 0.2 |
| log (Prot/d) | −1.8 ± 0.2 | ||||
| Best Three-Variable Regression | |||||
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 10−8 | 0.93 | 0.8 | 33 | 1.7 ± 0.2 |
| log (Prot/d) | −1.9 ± 0.2 | ||||
| fβ | 2.3 ± 0.5 | ||||
| Variable . | K-S . | r . | χ2/ν . | AIC . | Slope . |
|---|---|---|---|---|---|
| One-Variable Regressions | |||||
| log (Lbol/L⊙) | 0.87 | 0.64 | 5.1 | 103 | 1.0 ± 0.2 |
| log (Teff/K) | 0.53 | 0.78 | 4.1 | 84 | 6.6 ± 0.8 |
| log (R*/R⊙) | 0.06 | 0.18 | 6.3 | 124 | 1.3 ± 1.1 |
| log (M*/M⊙) | 0.66 | 0.70 | 4.2 | 88 | 4.0 ± 0.6 |
| log (Prot/d) | 10−7 | −0.50 | 6.4 | 126 | −1.5 ± 0.4 |
| log (Bd/G) | 10−2 | 0.60 | 3.5 | 75 | 1.6 ± 0.3 |
| |$\log {(\dot{M} / {\rm M_\odot ~yr^{-1}})}$| | 0.83 | 0.50 | 5.2 | 105 | 0.5 ± 0.1 |
| log (RA/R*) | 0.08 | −0.17 | 6.2 | 121 | −0.7 ± 0.6 |
| log (RK/R*) | 10−5 | −0.45 | 6.1 | 120 | −2.1 ± 0.6 |
| log (RA/RK) | 0.35 | −0.28 | 6.0 | 120 | −0.7 ± 0.4 |
| log (BK/G) | 10−7 | 0.75 | 4.1 | 86 | 1.2 ± 0.2 |
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 0.19 | 0.67 | 4.0 | 84 | 1.6 ± 0.3 |
| log fβ | 0.29 | 0.33 | 7.1 | 137 | 2.9 ± 1.3 |
| Best Two-Variable Regression | |||||
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 10−7 | 0.89 | 1.2 | 36 | 1.8 ± 0.2 |
| log (Prot/d) | −1.8 ± 0.2 | ||||
| Best Three-Variable Regression | |||||
| |$\log {(\Phi / {\rm G~R_\odot ^2})}$| | 10−8 | 0.93 | 0.8 | 33 | 1.7 ± 0.2 |
| log (Prot/d) | −1.9 ± 0.2 | ||||
| fβ | 2.3 ± 0.5 | ||||
The particular quantities chosen for regression analysis are: Lbol; Teff; the stellar radius R*; the stellar mass M*; the rotation period Prot; the surface magnetic dipole strength Bd; the mass-loss rate |$\dot{M}$|; the Alfvén radius RA; the Kepler radius RK; the dimensionless size of the CM log (RA/RK); the strength of the equatorial magnetic field at the Kepler radius BK; the unsigned magnetic flux |$\Phi = B_{\rm d}R_*^2$|; and as a test of the dependence on the geometry of the magnetic field, fβ = (1 + cos β)/2, where β is the obliquity angle of the magnetic axis from the rotational axis. The inclusion of the geometric parameter fβ is motivated by the RRM model, since at higher β the amount of plasma retained in the CM is reduced (Townsend & Owocki 2005).
Each parameter was tested in several ways. First, the two-sample Kolmogorov–Smirnov test was used to compare the distributions of stars with and without detected radio emission, in order to determine if the parameter or combinination of parameters effectively separates the two populations. Secondly, for the radio-bright stars, Pearson’s correlation coefficient r was calculated for each parameter or set of parameters, where r values close to ±1 indicate a strong correlation, and values close to 0 no correlation. Thirdly, the reduced χ2/ν (where ν is the number of degrees of freedom) was calculated, in order to estimate the quality of the fit of the linear regression to the data. Finally, the AIC was calculated, which provides a relative estimator of the quality of a given model based upon the fit and the number of variables (a lower value indicating a superior fit despite additional model parameters). Since adding additional parameters to a regression will naturally improve the fit to the data, χ2/ν and AIC help to determine whether the improvement is a meaningfully better fit, or simply a consequence of the additional degrees of freedom. In calculating χ2/ν and the AIC, we used the uncertainties in the radio luminosities, rather than also including the uncertainties in the tested parameters, since the latter are widely variable between parameters (e.g. on the order of 10 per cent or higher in Bd, as compared to around 0.0001 per cent in Prot), and including these uncertainties results in the goodness-of-fit tests simply reflecting the parameter uncertainties, making meaningful comparison difficult.
For one-variable regressions, stellar parameters (Teff, log Lbol, R*, M*, |$\dot{M}$|) have large K-S probabilities, indicating that they do not separate the radio-bright and -dim populations. However, r is relatively high for Teff, log Lbol, and M*, indicating that stellar parameters play some role. By contrast, parameters associated with the magnetic field or rotation achieve K-S probabilities close to 0, indicating that they do a good job of distinguishing between radio-bright and -dim stars, with parameters involving rotation (Prot, RK, BK) achieving the smallest K-S probabilities. Interestingly, the correlation coefficients associated with Bd and Prot are lower than those achieved for some stellar parameters. Of the magnetic and rotational parameters, the highest r is achieved for BK, while Bd gives the smallest AIC.
The one-variable results indicate that radio emission is primarily an effect of magnetic field strength and rotation, however they also point to at least some role for stellar parameters. With the addition of a second variable, the best r = 0.89 and AIC = 36 is provided by |$L_{\rm rad} \propto \Phi ^{1.8 \pm 0.2}P_{\rm rot}^{-1.8 \pm 0.2}$|, which also yields a very small K-S probability. Adding a third variable yields the best r = 0.93 for |$L_{\rm rad} \propto \Phi ^{1.7 \pm 0.2}P_{\rm rot}^{-1.9 \pm 0.2}f_\beta ^{2.3 \pm 0.5}$|, with a smaller AIC from the best two-variable result. Both the two- and three-variable regressions yield χ2/nu close to 1, indicating a good fit. While the three-variable result is slightly less than 1, suggesting a possible over-fit to the data, the lower AIC indicates that the improvement in the fit achieved by adding a third variable is real.
The overall results favour a strong dependence of radio luminosity on surface magnetic field strength, rotational period, and the size of the star, with a possible residual dependence on the magnetic geometry. The overall basic best-fit regression seems to go as |$L_{\rm rad} \propto (\Phi /P_{\rm rot})^2 = (B_{\rm d}R_*^2/P_{\rm rot})^2$|. This confirms the basic result found by Leto et al. (2021).
As demonstrated by Fig. 2, beyond a distance of log (d/pc) = 2.2 the lower limit on Lrad is a strong function of distance. If the above analysis is repeated only using those stars closer than this distance, the basic results are qualitatively unchanged. The best single-variable regression (K-S =0.01, r = 0.85, AIC =42) is given by |$L_{\rm rad} \propto B_{\rm K}^{1.4 \pm 0.2}$|. Two variables yield a best fit (K-S =0.02, r = 0.93, AIC =28) for |$L_{\rm rad} \propto B_{\rm K}^{1.1 \pm 0.1}T_{\rm eff}^{4.2 \pm 0.9}$|. Adding a third variable provides the overall best model (K-S =0.02, r = 0.97, AIC =21) for |$L_{\rm rad} \propto \Phi ^{1.7 \pm 0.2}P_{\rm rot}^{-2.4 \pm 0.2}f_\beta ^{2.6 \pm 0.6}$|. Once again, the results favour a dependence of radio luminosity on magnetic field strength, and an inverse dependence on rotation period. The best one- and three-variable regressions are identical to those obtained with the full data set.
In order to test the robustness against individual outliers, the analysis was repeated removing individual stars. Results were qualitatively unchanged in all cases. Results were also qualitatively unchanged if HD 171247 and HD 64740 were reintroduced to the analysis (see Section 3), although r was reduced and the AIC increased (further suggesting them to be outliers).
3.9 Summary
Radio gyrosynchrotron emission is found in the same parameter space in which H α emission from CM is seen – i.e. in young, strongly magnetic, and rapidly rotating stars (Shultz et al. 2019d). Indeed, radio-bright stars occupy essentially the same part of the rotation-magnetic wind confinement diagram as that occupied by H α-bright stars. Radio luminosity drops rapidly with age, declining by about 2 orders of magnitude over the first 10 per cent of a star’s main sequence lifetime. This is consistent with the abrupt spin-down that is an expected and observed consequence of hot star magnetic fields (Shultz et al. 2019d; Keszthelyi et al. 2020), and is similar to the precipitious decline in H α emission strength observed in magnetic early B-type stars (Shultz et al. 2020). Among those stars with both radio and H α emission, there is a strong correlation between the two. Finally, 91 per cent of the variance in radio luminosity is explained by the total unsigned magnetic flux and the rotational period, with a residual dependence on the obliquity angle of the magnetic field explaining a further 3 per cent of the variance.
4 DISCUSSION
4.1 Comparison to previous results
Linsky et al. (1992) found an empirical relationship of |$L_{\rm rad} \propto \dot{M}^{0.38}B_{\rm rms}^{1.06}P_{\rm rot}^{-0.32}$|, where Brms is the root-mean square 〈Bz〉 (as Bd was not available for most of the stars). The improvement of this relationship over a two-parameter scaling relationship involving only |$\dot{M}$| and Brms was only marginal. The much stronger dependence on magnetic field strength and rotation period is due to our much larger sample, as well as the fact that magnetic field strengths and rotational periods have now been derived for a much larger number of stars.
Leto et al. (2021) found an essentially identical scaling relationship to that found here, i.e. a dependence of radio luminosity on the ratio Φ/Prot. Our results therefore confirm those of Leto et al., albeit with a significantly larger sample. Further, since our sample includes stars that are not detected in radio, we have been able to demonstrate that this magneto-rotational empirical scaling relationship efficiently separates stars with radio emission from those in which such emission has not yet been detected. The principle difference between our results, and those given by Leto et al., is the weak dependence on β, a factor which they did not consider.
Scaling relationships for the luminosity of auroral radio emission were also explored by Das et al. (2021) in their analysis of the largest sample to date of ‘main sequence radio pulse emitters’ (MRPs), i.e. early-type stars exhibiting pulsed ECME. Das et al. found most of the variance of their sample to be explained by the relationship LECME ∝ B0, max/(Teff − 16.5 kK)2, i.e. a linear dependence on the maximum surface magnetic field strength, and a dependence on the inverse square of the difference between the effective temperature and a reference value of 16.5 kK. They interpreted this as indicating that for stars with Teff below 16.5 kK, the increasingly weak winds lead to less populated magnetospheres and therefore weaker emission, while above this temperature the increasing circumstellar density acts to attenuate the beamed emission via self-absorption. While no strong Teff dependence was found in the present work, it is notable that HD 64740 is under-luminous compared to expectations, which seems to be a consequence of self-absorption. Notably, Das et al. found that ECME luminosity is independent of rotation; however, since all but one of their stars were rapid rotators (periods between 0.7 and 2 d), the small variance in Prot may have hidden any such dependence. Given the similarity between the ECME luminosity scaling relationship found by Das et al. (2021), and the initial gyrosynchrotron scaling relationship found by Linsky et al. (1992) – both exhibiting linear dependence on the magnetic field strength, with the remaining dependence explained by the strength of the wind – it will be instructive to revisit the relationship when a larger sample spanning a wider range of rotational properties is available.
4.2 Interpretation of the results
Until now the prevailing paradigm explaining gyrosynchrotron emission from hot stars has been the wind-powered CS model described by Trigilio et al. (2004). This model is illustrated in the left half of Fig. 8. In this interpretation, a CS forms in the ‘middle magnetosphere’ just beyond the Alfvén surface, where the wind’s ram pressure opens the magnetic field lines, forming helmet streamers in which the opposite polarities of the magnetic field reconnect in the magnetic equatorial plane. Electrons injected into the CS by the wind are accelerated to relativistic velocities, following which they return to the star, along the magnetic field lines, emitting gyrosynchrotron radiation as they go. This model is now challenged on two fronts. First, it makes absolutely no reference to the rotational properties of the star, since the power source is provided directly by the wind; yet, as shown by Leto et al. (2021), and as verified here, rotation is absolutely crucial. Secondly, and more fundamentally, Leto et al. (2021) demonstrated via detailed modelling that the wind does not actually contain enough power to explain the observed radio luminosities. For the coolest stars examined by Leto et al., the difference between the required mass-loss rates and those predicted by the theoretical prescription given by Krtička (2014) are up to four orders of magnitude. The higher Vink et al. (2001) or CAK mass-loss rates do not qualitatively change this picture.
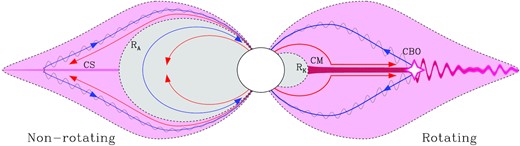
Schematic of the proposed interpretation. Pink-shaded regions indicate magnetic field lines contributing plasma to the electron acceleration region; grey-shaded regions indicate magnetospheric regions isolated from the locus of electron acceleration. In the non-rotating case (meaning that rotation is dynamically unimportant), plasma in the inner magnetosphere is in dynamical equilibrium, with upflow (red arrows) and downflow (blue arrows) occurring at the same rate. Beyond the Alfvén radius RA, corotation ceases, and ram pressure from the wind stretches magnetic field lines, leading to the formation of a CS, which accelerates electrons to relativistic velocities. The electrons return to the star, along magnetic field lines, leading to the emission of gyrosynchrotron radiation. The inner magnetosphere is entirely isolated from the CS, as all plasma flow is internal. By contrast, in the rotating case, centrifugal support of plasma above the Kepler corotation radius RK leads to the formation of a CM, in which plasma accumulates to high density (below RK the magnetosphere remains dynamical, as in the non-rotating case). When gas pressure overloads the ability of the magnetic field to confine the plasma, plasma is ejected outwards by a CBO event. Magnetic reconnection during CBO leads to flaring, which accelerates electrons to high energies (indicated by the starburst), thereby providing the source electrons to populate the radio magnetosphere. Note also that the fraction of the wind plasma captured by the CM is much higher than that captured by the CS in the non-rotating case.
The close correlation with H α emission EWs is suggestive of a resolution. Shultz et al. (2020) and Owocki et al. (2020) demonstrated via a combined empirical and theoretical analysis that H α emission from CMs is fully explained by a CBO process in which the plasma density in the CM is set by the ability of the magnetic field to confine the plasma. The lack of secular variation, demonstrated by both Shultz et al. (2020) and Townsend et al. (2013), indicates that the magnetosphere must be constantly maintained at the breakout density. This means that the large-scale emptying and reorganization of the CM observed in the 2D MHD simulations conducted by ud-Doula et al. (2008) does not, in practice, happen in three dimensions; instead, breakout events must be small in azimuthal extent and effectively continuous.
The dependence of radio on rotation, and the close correlation with H α, suggest that CBO may also be the explanation for radio emission. There are two, not necessarily mutually exclusive, mechanisms by which this might take place, both illustrated in the right half of Fig. 8.
First, CBO involves an outward ejection of material, necessarily establishing a flow of plasma from the inner to the middle magnetosphere. In the absence of a CM, no such flow takes place, and the middle and inner magnetospheres should be effectively isolated from one another. This means that the total fraction of the wind captured by that part of the magnetosphere capable of contributing to gyrosynchrotron is greatly increased by the presence of a CM.
Secondly, and perhaps most importantly, CBO is by its very nature a magnetic reconnection process. This means that each CBO event should be accompanied by an explosive release of energy, in which electrons will naturally be accelerated to high energies. In this case, the electron acceleration region is no longer the CS, but directly within the CM.
Notably, following from their detection of a ‘giant pulse’ from the MRP CU Vir, apparently originating simultaneously from both magnetic hemispheres, Das & Chandra (2021) speculated that CBO in the inner magnetosphere might have led to an enhanced injection of electrons into the auroral current systems around both magnetic poles. If so, CBO might also play a role in auroral radio emission.
The dependence of radio luminosity on the tilt angle β of the magnetic field is consistent with the CBO hypothesis. In the RRM model, the amount of plasma trapped in the CM is a function of β. When β = 0 (i.e. a magnetic axis aligned with the rotational axis), the CM is an azimuthally symmetric torus in the common magnetic and rotational equatorial planes, with the inner edge coinciding with RK. Since plasma is most strongly confined at the intersections of the two planes, as β increases the disc becomes increasingly warped, ultimately separating into two clouds concentrated at the intersections. The β dependence found here is consistent with the radio luminosity of aligned rotators being intrinsically stronger, and dropping by a factor of about 4 as β increases to 90°. This is exactly as would be expected if the plasma trapped in the CM is the ultimate source population for the high-energy electrons in the radio magnetosphere.
Leto et al. (2021) noted that the scaling relationship has the physical dimension of an electromotive force. However, dimensional analysis of the correlation with Prot, Bd, and R* is suggestive of an alternative interpretation. B2 is the magnetic energy density, while |$R_*^3$| suggests the volume of the star; combined, this yields the magnetic energy of the system. The relationship |$B_{\rm d}^2R_*^3/P_{\rm rot}$| then directly yields a luminosity: the magnetic energy of the star being tapped on a rotational time-scale. Indeed, if Bd, R*, and Prot are allowed to vary independently, the best-fitting relationship is |$L_{\rm rad} \propto B_{\rm d}^{2.0 \pm 0.2}P_{\rm rot}^{-1.8 \pm 0.2}R_*^{3.4 \pm 0.6}$|, i.e. a somewhat weaker R* dependence is favoured than in the case of the magnetic flux. The dependence on the inverse square of the rotation period introduces an extra dimension of time, which must somehow be accounted for, as must the possible additional R* term. It is suggestive, however, that the scaling relationship contains within it the natural units of luminosity. In Paper II by Owocki et al., we show that this scaling relationship is a natural consequence of CBO, and demonstrate the origin of the extra dependence on Prot.
4.3 Indirect magnetometry
The magneto-rotational scaling law discovered by Leto et al. (2021), confirmed in the present work, and explained in the companion paper by Owocki et al. as a consequence of CBO reconnection shows the potential, as pointed out by Leto et al., to be utilized as a reliable form of ‘indirect magnetometry’, enabling measurement of stellar magnetic fields in objects beyond the reach of contemporary spectropolarimeters. Three stars in the present sample are radio-bright and have known rotational periods, but do not have detected magnetic fields. While these stars could not be used to constrain the scaling law, they can serve as test cases for the predictive ability of the scaling law. Table 3 summarizes their key parameters.
| Parameter . | HD 143699 . | HD 146001 . | HD 77653 . |
|---|---|---|---|
| Prot/d | 0.894 | 0.586a | 1.488b |
| R*/R⊙ | 3.0 ± 0.3 | 2.5 ± 0.3 | 2.6 ± 0.1 |
| M*/M⊙ | 5.3 ± 0.3 | 4.3 ± 0.2 | 3.4 ± 0.1 |
| log (Lrad/L⊙) | −7.08 ± 0.17c | −6.69 ± 0.17c | −5.71 ± 0.08d |
| Bd/G (obs.) | <600 | <500 | – |
| Bd/G (pred.) | 300 | 430 | 2900 |
| Parameter . | HD 143699 . | HD 146001 . | HD 77653 . |
|---|---|---|---|
| Prot/d | 0.894 | 0.586a | 1.488b |
| R*/R⊙ | 3.0 ± 0.3 | 2.5 ± 0.3 | 2.6 ± 0.1 |
| M*/M⊙ | 5.3 ± 0.3 | 4.3 ± 0.2 | 3.4 ± 0.1 |
| log (Lrad/L⊙) | −7.08 ± 0.17c | −6.69 ± 0.17c | −5.71 ± 0.08d |
| Bd/G (obs.) | <600 | <500 | – |
| Bd/G (pred.) | 300 | 430 | 2900 |
| Parameter . | HD 143699 . | HD 146001 . | HD 77653 . |
|---|---|---|---|
| Prot/d | 0.894 | 0.586a | 1.488b |
| R*/R⊙ | 3.0 ± 0.3 | 2.5 ± 0.3 | 2.6 ± 0.1 |
| M*/M⊙ | 5.3 ± 0.3 | 4.3 ± 0.2 | 3.4 ± 0.1 |
| log (Lrad/L⊙) | −7.08 ± 0.17c | −6.69 ± 0.17c | −5.71 ± 0.08d |
| Bd/G (obs.) | <600 | <500 | – |
| Bd/G (pred.) | 300 | 430 | 2900 |
| Parameter . | HD 143699 . | HD 146001 . | HD 77653 . |
|---|---|---|---|
| Prot/d | 0.894 | 0.586a | 1.488b |
| R*/R⊙ | 3.0 ± 0.3 | 2.5 ± 0.3 | 2.6 ± 0.1 |
| M*/M⊙ | 5.3 ± 0.3 | 4.3 ± 0.2 | 3.4 ± 0.1 |
| log (Lrad/L⊙) | −7.08 ± 0.17c | −6.69 ± 0.17c | −5.71 ± 0.08d |
| Bd/G (obs.) | <600 | <500 | – |
| Bd/G (pred.) | 300 | 430 | 2900 |
For HD 143699 and HD 146001, the ‘observed’ values of Bd correspond to the 1σ upper limits derived via modelling their 〈Bz〉 error bars (both around 70 G; see appendix C) using the MCHRD sampler, where in both cases high-resolution spectropolarimetry was used. The predicted Bd was found via solving the scaling relationship from Paper II in this series by Owocki et al. for Bd, using an efficiency factor of ϵ = 10−8 (i.e. ignoring the correction for β, which is unknowable). For the two stars with available 〈Bz〉 measurements, the predicted Bd – a few hundred G in both cases – is in both cases just below the upper limits. For HD 77653, for which spectropolarimetry is not available, the scaling relationship predicts Bd ∼ 3 kG, which should be easily detectable. Follow-up magnetometry of these stars will provide a useful test of this scaling relationship.
4.4 Radio emission from stars with ultra-weak magnetic fields
The nearby A7 V star Altair was recently discovered by White et al. (2021) to emit non-thermal radio at cm wavelengths, with a brightness temperature around 104 K and a luminosity of around log Lrad/L⊙ ∼ −10.5. White et al. (2021) interpreted this as chromospheric emission, possibly related to the equatorial convection zone formed due to the star’s extremely rapid rotation. Robrade & Schmitt (2009) furthermore detected X-ray emission from Altair, which they interpreted as magnetic activity.
Altair was observed with Narval as a part of the BRIght Target Explorer (BRITE; Weiss et al. 2014) spectropolarimetric survey (BRITEpol; Neiner et al. 2017). No magnetic field was detected, with an uncertainty in 〈Bz〉 of about 10 G, implying that a surface magnetic dipole of around 100 G could well have gone undetected. Using the fundamental parameters (equatorial radius Req = 2.008 ± 0.006 R⊙, M* = 1.86 ± 0.03 M⊙) and rotation period Prot = 0.323 d determined via careful interferometric modelling performed by Bouchaud et al. (2020) yields a critical rotation parameter W = 0.75 and a Kepler corotation radius RK = 1.2 R*. The star’s CAK mass-loss rate is |$\dot{M} = 10^{-13}~{\rm M_\odot ~yr^{-1}}$|; assuming a terminal velocity of 3000 km s−1, RK will be inside the Alfvén surface so long as Bd > 0.1 G, well within the upper limits on Altair’s surface magnetic field and consistent with the range of ultra-weak fields detected in other main sequence A-type stars (Petit et al. 2010; Blazère et al. 2020).
To see if the star’s non-thermal radio emission might be consistent with a magnetospheric origin given the limits on the surface magnetic field, we follow the same method as above in Section 4.3. for Bd. We again assumed the efficiency ϵ ∼ 10−8. This yields a predicted surface magnetic field of Bd ∼ 10 G. Altair’s radio emission may therefore be consistent with a magnetospheric origin, although actually detecting such a weak field (which would require uncertainties on the order of 1 G) is a challenging prospect given the star’s broad spectral lines.
Unlike Altair, magnetic fields have actually been detected in Vega and Sirius (Petit et al. 2010, 2011), with both stars having sub-gauss 〈Bz〉. Radio observations at mm and sub-mm wavelengths of both stars are consistent with thermal emission (Hughes et al. 2012; White et al. 2019). Sirius is a slow rotator and therefore unlikely to produce gyrosynchrotron emission. Taking Vega’s stellar parameters (Yoon et al. 2010) and 0.732 d rotation period (Petit et al. 2010) yields RK = 1.5 R⊙. With the CAK mass-loss rate |$\dot{M} = 10^{-11.9}~{\rm M_\odot ~yr^{-1}}$| and the same assumption of a 3000 km s−1 wind terminal velocity, the minimum surface dipole strength capable of confining the wind out to RK is 2.3 G, 4× higher than the dipolar component of about 0.5 G recovered via Zeeman Doppler Imaging (Petit et al. 2010). The expected radio luminosity from the breakout scaling is then log Lrad/L⊙ = −12, translating at 1 cm to 0.15 μJy at Vega’s 7.67 pc distance: certainly undetectable, since this is much less than the expected 1 cm photospheric flux of about 0.5 mJy. Radio observations of other stars with ultra-weak fields do not seem to be available, although at least in the case of Alhena the relatively long ∼9 d period and ∼30 G surface field makes it unlikely the star would produce detectable emission (Blazère, Neiner & Petit 2016a; Blazère et al. 2020), while in the cases of β UMa and θ Leo (Blazère et al. 2016b) the rotational periods are not known, making their radio luminosities impossible to estimate.
5 CONCLUSIONS
By combining both published and unpublished radio observations, published rotational and magnetic data, and new determinations of magnetic models and rotational periods via space photometry and previously unpublished high- and low-resolution spectropolarimetry, we have conducted the largest analysis of the gyrosynchrotron emission properties of magnetic early-type stars undertaken to date.
We find that radio-bright stars occur in the same part of the rotation-magnetic confinement diagram as stars with H α emission originating from CM: that is to say, gyrosynchrotron emission requires rapid rotation, as well as a strong magnetic field. This confirms the central result of Leto et al. (2021). Radio-bright stars are additionally generally young, with a steep drop in radio luminosity with age consistent with magnetospheric braking rapidly removing the angular momentum necessary to power the radio magnetosphere, similar to the drop observed by Shultz et al. (2020) for H α emission. Furthermore, there is a close correlation between the H α emission EW and radio luminosity, which is strongly suggestive of a unifying mechanism.
Multivariable regression analysis of radio luminosity yields a relation of the form |$L_{\rm rad} \propto B^2R_*^4/P_{\rm rot}^2 = (\Phi /P_{\rm rot})^2$|, further confirming the results of Leto et al. (2021), although we add the refinement of an additional dependence on the geometry of the magnetic dipole such that radio luminosity declines with increasing tilt angle β.
We propose that the close correlation between H α and radio emission strengths, and their cohabitation in parameter space, imply a unifying mechanism for the two phenomena, i.e. CBO, which has already been shown to explain H α emission properties. Paper II by Owocki et al. provides a preliminary theoretical exploration of this concept.
The empirical relationship found by Leto et al. (2021) and confirmed here suggests that radio observations may have utility as a form of indirect magnetometry. If the distance, stellar radius, and rotational period are known, a single radio observation may be sufficient to infer the global surface magnetic field strength of the star. In the era of Gaia and TESS, in which distances and rotational periods can be determined for a much larger number of stars than can be easily observed with optical spectropolarimetry, this may prove to be an important means of dramatically increasing the number of stars for which the surface magnetic field strength is known.
There is a pressing need for more radio observations of magnetic early-type stars to be acquired. SEDs have been measured for only a small number of magnetic hot stars, and it is not known how these vary with fundamental, magnetic, or rotational parameters. Rotational phase coverage is likewise available in only a small number of cases; the geometrical dependence found here for the radio luminosity suggests that comparable effects might be seen in phase curves, which may be important in reconstructing plasma distributions out of the magnetic-equatorial plane probed by visible data. More sensitive observations might seek to discover if gyrosynchrotron emission disappears entirely in stars without CM, or if slowly rotating stars in fact emit ultra-weak radio driven by the classical middle magnetosphere CS mechanism. Indeed, while gyrosynchroton emission has not yet been detected from slow rotators, there are very few stars in the dynamical magnetosphere regime with radio data. Finally, as pointed out by Leto et al. (2021), the close correlation between radio luminosity and magnetic field strength suggests that radio data might become an important form of indirect magnetometry for stars that are too dim for their surface magnetic fields to be measured using Zeeman effect spectropolarimetry, but for which rotational periods are known via e.g. TESS space photometry.
SUPPORTING INFORMATION
suppl_data
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
The authors thank Dr. Stephen Drake for providing his unpublished radio measurements, which they hope have been put to good use. This work is based on observations obtained at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council of Canada, the Institut National des Sciences de l’Univers (INSU) of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii, and at the Observatoire du Pic du Midi (France), operated by the INSU; and based on observations obtained at the Dominion Astrophysical Observatory, National Research Council Herzberg Astronomy and Astrophysics Research Centre, National Research Council of Canada. This paper includes data collected by the TESS mission, which are publicly available from the Mikulski Archive for Space Telescopes (MAST). Funding for the TESS mission is provided by NASA's Science Mission directorate. We thank the staff of the GMRT that made the uGMRT observations possible. The GMRT is run by the National Centre for Radio Astrophysics of the Tata Institute of Fundamental Research. This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. MES acknowledges the financial support provided by the Annie Jump Cannon Fellowship, supported by the University of Delaware and endowed by the Mount Cuba Astronomical Observatory. AuD acknowledges support by NASA through Chandra Award 26 number TM1-22001B issued by the Chandra X-ray Observatory 27 Center, which is operated by the Smithsonian Astrophysical Observatory for and behalf of NASA under contract NAS8-03060. VK acknowledges support by Natural Sciences and Engineering Research Council of Canada (NSERC). AB, BD, and PC acknowledge support of the Department of Atomic Energy, Government of India, under project no. 12-R&D-TFR-5.02-0700. GAW acknowledges Discovery Grant support from NSERC. JDL acknowledges support from NSERC, funding reference number 6377–2016. OK acknowledges support by the Swedish Research Council and the Swedish National Space Board. The material is based upon work supported by NASA under award number 80GSFC21M0002.
DATA AVAILABILITY STATEMENT
Reduced ESPaDOnS spectra are available at the CFHT archive maintained by the CADC,5 where they can be found via standard stellar designations. ESPaDOnS and Narval data can also be obtained at the PolarBase archive.6Kepler-2 and TESS data are available at the MAST archive.7Hipparcos data are available through SIMBAD and Vizier.8 DAO and uGMRT observations are available from the authors at request.
Footnotes
This system is actually a spectroscopic binary, in which the Aa component is magnetic (Hummel et al. 2013; Blazère et al. 2015). However, given the long 7.3 yr orbit, the Aa and Ab components are not interacting, and the radio emission is dominated by the effectively single wind of the Aa component.
While essentially all of these stars are chemically peculiar, detailed mean surface abundances are not generally available.
REFERENCES
APPENDIX A: SAMPLE SUMMARY TABLE
Stellar parameters, rotational periods, dipolar magnetic field strengths, and radio luminosities for the sample. Stars with superscripts are listed in appendix B if they have new radio (f)lux density observations, and are discussed in appendix C if new (m)agnetic data or (r)otational periods are available. Appendices B and C are available online as supplementary material. Superscipt numbers in square brackets in other columns correspond to the reference key at the end of the table.
| Star . | |$\log {\frac{L_{\rm bol}}{L_\odot }}$| . | |$\frac{T_{\rm eff}}{{\rm kK}}$| . | |$\frac{M_*}{{\rm M_\odot }}$| . | |$\frac{v\sin {i}}{{\rm km~s^{-1}}}$| . | |$\frac{P_{\rm rot}}{{\rm d}}$| . | |$\frac{\beta }{{\rm deg}}$| . | |$\frac{B_{\rm d}}{{\rm kG}}$| . | |$\log {\frac{L_{\rm rad}}{{\rm L_\odot }}}$| . |
|---|---|---|---|---|---|---|---|---|
| ALS8988r | 4.05 ± 0.27 | 27.3 ± 1.4[127] | 10.6 ± 0.6 | 23[40] | – | – | >1.5[40] | <-4.40[85] |
| ALS9522 | 3.65 ± 0.12 | 22.4 ± 1.1[118] | 6.0 ± 0.1 | 105[118] | 1.091[118] | 78|$^{+ 2}_{- 3}$| | 11|$^{+3}_{-1}\, {^{[118]}}$| | -5.29 ± 0.04[85] |
| CPD-271791 | 3.69 ± 0.09 | 23.8 ± 1.6[127] | 8.8 ± 0.4 | 37[89] | 2.641[89] | – | >3.9[89] | <-4.71[6] |
| HD3360f | 3.82 ± 0.06 | 20.8 ± 0.2[104] | 8.6 ± 0.1 | 19[93] | 5.370[25] | 82|$^{+ 1}_{- 1}$| | 0.15|$^{+0.03}_{-0.03}\, {^{[107]}}$| | <-7.79[85, 127] |
| HD5737 | 3.33 ± 0.16 | 13.9 ± 0.4[41] | 5.0 ± 0.4 | 17[106] | 21.7[23] | 73|$^{+ 6}_{- 7}$| | 1.8|$^{+0.2}_{-0.3}\, {^{[4,10,18,127]}}$| | <-6.44[6] |
| HD11503f | 1.52 ± 0.03 | 10.1 ± 0.2[102] | 2.35 ± 0.03 | 54[102] | 1.610[103] | 84|$^{+ 4}_{-37}$| | 2.3|$^{+3.7}_{-0.7}\, {} ^{[103]}$| | -7.85 ± 0.04[14, 127] |
| HD12447 | 1.73 ± 0.06 | 10.0 ± 0.2[102] | 2.49 ± 0.05 | 70[102] | 1.491[103] | 87|$^{+ 1}_{- 9}$| | 1.7|$^{+0.5}_{-0.4}\, {}^{[103,127]}$| | -7.40 ± 0.04[34] |
| HD12767 | 2.43 ± 0.15 | 13.0 ± 0.3[41] | 4.0 ± 0.1 | 40[30] | 1.892[23] | 89|$^{+ 0}_{- 3}$| | 2.0|$^{+0.5}_{-0.6}\, {} ^{[9,113,127]}$| | <-6.88[125] |
| HD19832 | 2.08 ± 0.16 | 12.4 ± 0.4[41] | 3.3 ± 0.1 | 160[96] | 0.728[111] | 89|$^{+ 0}_{- 3}$| | 2.7|$^{+0.6}_{-0.3}\, {} ^{[111]}$| | -6.70 ± 0.04[34] |
| HD21699mr | 2.78 ± 0.04 | 16.0 ± 0.1[41] | 4.7 ± 0.2 | 35[106] | 2.492[23, 127] | 78|$^{+ 2}_{- 2}$| | 2.8|$^{+0.5}_{-0.1}\, {} ^{[5,127]}$| | <-6.49[6] |
| HD22470 | 2.43 ± 0.13 | 13.8 ± 0.3[41] | 3.8 ± 0.2 | 62[30] | 1.929[111] | 87|$^{+ 1}_{- 2}$| | 7.5|$^{+1.2}_{-0.5}\, {} ^{[111]}$| | <-6.87[6] |
| HD22920mr | 2.64 ± 0.12 | 13.6 ± 0.2[67] | 4.2 ± 0.1 | 34[30] | 3.947[20, 127] | 28|$^{+ 6}_{- 7}$| | 1.6|$^{+1.1}_{-0.0}\, {} ^{[4,127]}$| | <-6.77[125] |
| HD25267 | 2.32 ± 0.03 | 12.6 ± 0.2[116] | 3.5 ± 0.2 | 20[102] | 3.823[116] | 17|$^{+ 7}_{- 8}$| | 1.0|$^{+0.1}_{-0.1}\, {} ^{[116]}$| | <-7.25[125] |
| HD27309 | 1.88 ± 0.02 | 11.2 ± 0.3[102] | 2.81 ± 0.04 | 56[102] | 1.569[103] | 3|$^{+ 5}_{- 3}$| | 1.9|$^{+2.6}_{-0.6}\, {} ^{[103]}$| | -7.20 ± 0.04[34] |
| HD28843mr | 2.51 ± 0.07 | 14.8 ± 0.2[41] | 4.20 ± 0.06 | 91[127] | 1.374[23, 127] | 87|$^{+ 1}_{- 5}$| | 0.93|$^{+0.30}_{-0.24}\, {} ^{[4,127]}$| | <-6.85[6] |
| HD32633 | 1.94 ± 0.12 | 12.5 ± 0.5[87] | 3.50 ± 0.09 | 25[96] | 6.430[19] | 76|$^{+ 3}_{- 3}$| | 17|$^{+1}_{-2}\, {} ^{[58,73]}$| | <-6.74[14] |
| HD34452 | 2.45 ± 0.27 | 13.8 ± 0.8[41] | 4.2 ± 0.1 | 53[96] | 2.469[23] | 35|$^{+13}_{-16}$| | 3.6|$^{+1.1}_{-1.4}\, {} ^{[3,15,127]}$| | -6.69 ± 0.04[6, 14] |
| HD35298 | 2.40 ± 0.14 | 15.8 ± 0.8[104] | 4.3 ± 0.2 | 60[93] | 1.855[93] | 77|$^{+ 2}_{- 2}$| | 11|$^{+1}_{-1}\, {} ^{[107]}$| | -5.35 ± 0.04[14, 29, 34] |
| HD35456 | 2.88 ± 0.29 | 13.5 ± 1.4[127] | 4.1 ± 0.5 | 22[77] | 4.951[77] | 15|$^{+ 9}_{-11}$| | 2.2|$^{+0.2}_{-0.3}\, {} ^{[77,127]}$| | <-6.19[125] |
| HD35502f | 2.95 ± 0.12 | 18.4 ± 0.6[104] | 5.8 ± 0.2 | 78[93] | 0.854[78] | 70|$^{+ 1}_{- 1}$| | 7.3|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | -5.05 ± 0.04[34, 127] |
| HD35575r | 3.11 ± 0.09 | 16.7 ± 1.3[127] | 5.8 ± 0.3 | 150[99] | 0.984[127] | – | <1.3[99, 127] | <-7.09[16] |
| HD36313r | 2.04 ± 0.19 | 13.0 ± 0.5[114] | 3.4 ± 0.2 | 160[114] | 0.589[114, 127] | 88|$^{+ 1}_{- 5}$| | 9.0|$^{+1.8}_{-1.3}\, {} ^{[114,127]}$| | -6.10 ± 0.04[34] |
| HD36429mr | 2.42 ± 0.02 | 13.8 ± 0.1[127] | 3.87 ± 0.03 | 77[127] | 15.6[127] | – | <0.20[26, 127] | <-6.13[125] |
| HD36485 | 3.10 ± 0.20 | 20.0 ± 2.0[104] | 6.3 ± 0.2 | 33[93] | 1.478[48] | 3|$^{+ 1}_{- 1}$| | 8.9|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | -5.43 ± 0.04[6, 14, 29, 72] |
| HD36526f | 2.30 ± 0.24 | 15.0 ± 2.0[104] | 4.3 ± 0.2 | 59[93] | 1.542[93] | 56|$^{+ 1}_{- 2}$| | 11|$^{+0}_{-0}\, {} ^{[107]}$| | <-6.29[14, 127] |
| HD36540mr | 2.73 ± 0.15 | 14.9 ± 0.7[87] | 4.54 ± 0.09 | 80[83] | 2.173[127] | 9|$^{+26}_{- 8}$| | 1.4|$^{+3.2}_{-0.1}\, {} ^{[83,127]}$| | <-5.99[125] |
| HD36668mr | 2.40 ± 0.19 | 13.5 ± 0.2[114] | 3.81 ± 0.05 | 60[114] | 2.119[114, 127] | 80|$^{+ 5}_{- 6}$| | 4.5|$^{+2.3}_{-2.7}\, {} ^{[114,127]}$| | <-6.05[125] |
| HD36916mr | 2.10 ± 0.20 | 14.7 ± 0.2[83] | 4.2 ± 0.1 | 78[83] | 1.565[83, 127] | 30|$^{+ 8}_{-10}$| | 3.4|$^{+3.3}_{-0.2}\, {} ^{[4,66,83,91,111,127]}$| | <-6.92[14, 16] |
| HD37017 | 3.42 ± 0.25 | 21.0 ± 2.0[104] | 8.4 ± 0.5 | 134[93] | 0.901[93] | 56|$^{+ 2}_{- 3}$| | 6.2|$^{+0.9}_{-0.9}\, {} ^{[107]}$| | -5.11 ± 0.04[6, 14, 17, 29, 72, 82, 124] |
| HD37058 | 2.90 ± 0.11 | 18.6 ± 0.6[104] | 5.8 ± 0.2 | 11[93] | 14.6[93] | 55|$^{+11}_{-13}$| | 2.5|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-5.95[14] |
| HD37061f | 3.30 ± 0.30 | 22.0 ± 1.0[104] | 7.7 ± 0.4 | 100[93] | 1.095[101] | 59|$^{+ 4}_{- 4}$| | 9.2|$^{+1.0}_{-1.0}\, {} ^{[107]}$| | -5.68 ± 0.04[82, 127] |
| HD37140mr | 2.12 ± 0.09 | 13.5 ± 0.2[114] | 3.46 ± 0.05 | 25[127] | 2.761[114, 127] | 80|$^{+ 3}_{- 4}$| | 3.9|$^{+0.7}_{-0.4}\, {} ^{[114,127]}$| | <-6.08[125] |
| HD37151 | 2.08 ± 0.08 | 13.5 ± 0.9[127] | 3.4 ± 0.2 | – | – | 87|$^{+ 1}_{-12}$| | 1.4|$^{+1.2}_{-1.4}\, {} ^{[115,127]}$| | <-6.39[125] |
| HD37210mr | 2.51 ± 0.05 | 13.5 ± 0.6[127] | 3.92 ± 0.09 | 20[115] | 11.0[20, 127] | 78|$^{+ 7}_{- 8}$| | 1.8|$^{+0.9}_{-0.1}\, {} ^{[66,115,127]}$| | <-5.71[125] |
| HD37479 | 3.51 ± 0.21 | 23.0 ± 2.0[104] | 7.9 ± 0.2 | 145[93] | 1.191[47] | 37|$^{+ 7}_{-10}$| | 10|$^{+11}_{-0}\, {} ^{[71]}$| | -4.73 ± 0.04[6, 14, 17, 29, 72] |
| HD37642mr | 2.42 ± 0.10 | 16.0 ± 0.5[115] | 4.3 ± 0.1 | 85[115] | 1.079[115, 127] | 74|$^{+ 3}_{- 3}$| | 18|$^{+1}_{-0}\, {} ^{[115,127]}$| | -5.69 ± 0.04[34] |
| HD37752 | 2.63 ± 0.14 | 15.0 ± 0.7[41] | 4.5 ± 0.2 | 35[30] | 1.305[87] | – | <2.4[26] | <-7.08[16] |
| HD37776f | 3.30 ± 0.15 | 22.0 ± 1.0[104] | 8.3 ± 0.3 | 101[93] | 1.539[81] | 47|$^{+ 8}_{-10}$| | 6.1|$^{+0.7}_{-0.7}\, {} ^{[54,107]}$| | <-6.35[6, 127] |
| HD37808mr | 2.28 ± 0.10 | 14.5 ± 0.2[115] | 3.90 ± 0.08 | 30[96] | 1.099[109, 115, 127] | 45|$^{+20}_{-24}$| | 3.2|$^{+1.0}_{-0.3}\, {} ^{[115,127]}$| | -6.16 ± 0.04[16, 29] |
| HD40312 | 2.33 ± 0.01 | 10.2 ± 0.1[102] | 3.11 ± 0.06 | 55[96] | 3.619[103] | 68|$^{+13}_{-15}$| | 1.3|$^{+0.4}_{-0.2}\, {} ^{[97]}$| | -7.78 ± 0.04[14] |
| HD41269mr | 2.30 ± 0.08 | 12.9 ± 0.9[127] | 3.5 ± 0.2 | 85[30] | 1.048[127] | 0|$^{+16}_{- 0}$| | 1.3|$^{+0.5}_{-0.3}\, {} ^{[127]}$| | <-7.20[16] |
| HD43819 | 2.15 ± 0.20 | 10.9 ± 0.4[38] | 3.1 ± 0.2 | 10[38] | 15.0[38] | 47|$^{+16}_{-19}$| | 2.6|$^{+75.7}_{-0.1}\, {} ^{[38]}$| | <-6.79[16] |
| HD45583 | 2.07 ± 0.12 | 13.3 ± 0.3[42] | 3.35 ± 0.09 | 70[96] | 1.177[111] | 69|$^{+ 2}_{- 2}$| | 9.1|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.24 ± 0.04[34, 124] |
| HD46328 | 4.49 ± 0.11 | 27.0 ± 1.0[104] | 14.4 ± 0.8 | 8[93] | 30.0 (yr)[88, 95, 120] | 89|$^{+ 0}_{- 9}$| | 1.2|$^{+0.6}_{-0.1}\, {} ^{[107]}$| | <-7.03[85] |
| HD47777 | 3.42 ± 0.15 | 22.0 ± 1.0[104] | 7.9 ± 0.4 | 60[93] | 2.640[61] | 82|$^{+ 5}_{- 5}$| | 3.3|$^{+0.7}_{-0.7}\, {} ^{[107]}$| | <-6.40[85] |
| HD49333 | 2.73 ± 0.04 | 15.8 ± 0.1[41] | 4.8 ± 0.3 | 65[30] | 2.180[23] | 85|$^{+ 3}_{-12}$| | 3.6|$^{+1.0}_{-1.2}\, {} ^{[15,127]}$| | <-6.49[14] |
| HD49606mr | 2.59 ± 0.06 | 13.5 ± 0.1[41] | 4.08 ± 0.06 | 19[96] | 8.546[123] | – | <0.040[127] | <-6.25[125] |
| HD51418mr | 1.80 ± 0.04 | 9.5 ± 0.8[100] | 2.48 ± 0.09 | 28[84] | 5.431[113, 127] | 89|$^{+ 0}_{- 0}$| | 3.5|$^{+1.0}_{-0.4}\, {} ^{[84,127]}$| | <-6.65[125] |
| HD55522f | 3.00 ± 0.18 | 17.4 ± 0.4[104] | 5.9 ± 0.2 | 70[93] | 2.729[93] | 89|$^{+ 0}_{- 1}$| | 3.1|$^{+0.4}_{-0.4}\, {} ^{[107]}$| | <-6.16[127] |
| HD58260 | 3.22 ± 0.26 | 19.3 ± 1.3[104] | 6.2 ± 0.5 | 3[93] | – | 0|$^{+ 5}_{- 0}$| | 6.5|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | <-6.69[6, 85] |
| HD60344r | 3.58 ± 0.09 | 21.0 ± 0.3[41] | 7.9 ± 0.2 | 55[106] | – | – | >1.2[89, 127] | <-4.76[6] |
| HD61556f | 3.12 ± 0.24 | 18.5 ± 0.8[70] | 6.1 ± 0.3 | 58[70] | 1.909[70] | 58|$^{+ 6}_{- 7}$| | 2.8|$^{+0.3}_{-0.3}\, {} ^{[107]}$| | -5.93 ± 0.04[117, 127] |
| HD64740f | 3.81 ± 0.15 | 24.5 ± 1.0[104] | 10.1 ± 0.5 | 135[93] | 1.330[93] | 71|$^{+ 5}_{- 5}$| | 3.0|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | -7.19 ± 0.04[127] |
| HD65339 | 1.45 ± 0.02 | 8.5 ± 0.1[102] | 2.09 ± 0.02 | 13[96] | 8.027[103] | 89|$^{+ 0}_{- 1}$| | 15|$^{+2}_{-1}\, {} ^{[28]}$| | <-7.50[6, 14] |
| HD66665 | 4.69 ± 0.23 | 28.5 ± 1.0[104] | 15.9 ± 1.1 | 8[93] | 24.5[93] | 75|$^{+ 3}_{- 3}$| | 0.56|$^{+0.10}_{-0.10}\, {} ^{[107]}$| | <-4.96[85] |
| HD66765f | 3.44 ± 0.24 | 20.0 ± 2.0[63] | 7.2 ± 0.6 | 58[93] | 1.608[93] | 73|$^{+ 5}_{- 5}$| | 2.8|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-6.23[127] |
| HD79158 | 2.61 ± 0.06 | 13.3 ± 0.1[41] | 4.3 ± 0.1 | 49[96] | 3.835[92] | 87|$^{+ 1}_{- 4}$| | 3.1|$^{+0.4}_{-0.4}\, {} ^{[92]}$| | -6.55 ± 0.04[6, 34] |
| HD90044 | 1.66 ± 0.10 | 10.0 ± 0.2[87] | 2.8 ± 0.3 | 23[102] | 4.379[23] | 89|$^{+ 0}_{- 0}$| | 4.4|$^{+1.2}_{-1.5}\, {} ^{[15,22,127]}$| | <-7.71[16] |
| HD105382 | 3.04 ± 0.16 | 18.0 ± 0.5[24] | 5.8 ± 0.2 | 74[93] | 1.295[24] | 51|$^{+ 7}_{- 8}$| | 2.6|$^{+0.1}_{-0.1}\, {} ^{[107]}$| | -6.07 ± 0.04[117] |
| HD112413 | 1.97 ± 0.02 | 11.3 ± 0.2[102] | 2.93 ± 0.03 | 15[96] | 5.469[103] | 88|$^{+ 1}_{- 8}$| | 3.5|$^{+0.8}_{-0.2}\, {} ^{[64,65]}$| | -8.13 ± 0.04[6, 34] |
| HD118022 | 1.53 ± 0.04 | 9.4 ± 0.1[102] | 2.26 ± 0.02 | 12[102] | 3.722[103] | 65|$^{+15}_{-17}$| | 3.2|$^{+8.0}_{-0.2}\, {} ^{[103]}$| | -7.41 ± 0.04[121] |
| HD122532 | 2.37 ± 0.12 | 11.9 ± 0.5[87] | 2.99 ± 0.04 | – | 3.681[12] | 89|$^{+ 0}_{- 3}$| | 3.0|$^{+0.7}_{-0.9}\, {} ^{[7,13,15,113,127]}$| | <-7.00[14] |
| HD124224 | 1.93 ± 0.01 | 12.3 ± 0.2[102] | 3.02 ± 0.01 | 169[102] | 0.521[81] | 87|$^{+ 2}_{-11}$| | 4.0|$^{+0.3}_{-0.2}\, {} ^{[62]}$| | -6.24 ± 0.04[16, 18, 29, 34, 117, 122] |
| HD125248 | 1.39 ± 0.23 | 9.7 ± 0.3[41] | 2.42 ± 0.07 | 11[96] | 9.300[39] | 89|$^{+ 0}_{- 3}$| | 9.0|$^{+1.1}_{-1.3}\, {} ^{[75]}$| | <-7.17[125] |
| HD125823 | 3.16 ± 0.20 | 19.0 ± 2.0[104] | 5.9 ± 0.2 | 16[93] | 8.817[93] | 75|$^{+ 4}_{- 6}$| | 1.8|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | <-6.54[6] |
| HD126515 | 1.36 ± 0.16 | 8.9 ± 0.2[127] | 2.65 ± 0.07 | 16[127] | 129.9[21] | 84|$^{+ 4}_{-13}$| | 13|$^{+1}_{-0}\, {} ^{[21]}$| | <-7.13[14] |
| HD131120mr | 3.15 ± 0.09 | 19.4 ± 1.5[127] | 6.3 ± 0.3 | 57[30] | 1.569[55, 127] | – | <0.17[66] | <-6.97[14] |
| HD133029mr | 1.98 ± 0.08 | 11.8 ± 0.9[41] | 2.8 ± 0.1 | 27[30] | 2.888[44, 127] | 12|$^{+ 4}_{- 4}$| | 9.0|$^{+5.0}_{-0.3}\, {} ^{[3,127]}$| | <-6.89[14] |
| HD133652 | 2.02 ± 0.10 | 12.8 ± 0.5[87] | 3.27 ± 0.09 | 48[96] | 2.304[23] | 65|$^{+ 8}_{-11}$| | 7.6|$^{+0.8}_{-1.0}\, {} ^{[15,127]}$| | -7.16 ± 0.04[34] |
| HD133880 | 1.73 ± 0.06 | 10.7 ± 0.1[41] | 3.08 ± 0.08 | 103[96] | 0.877[80] | 83|$^{+ 1}_{- 1}$| | 12|$^{+0}_{-1}\, {} ^{[80]}$| | -5.44 ± 0.04[72, 34] |
| HD135679mr | 2.46 ± 0.19 | 15.1 ± 2.8[127] | 2.86 ± 0.06 | 1[84] | 5.321[127] | 14|$^{+ 6}_{- 8}$| | 4.4|$^{+9.3}_{-0.2}\, {} ^{[84,91,127]}$| | <-7.04[16] |
| HD137193mr | 1.91 ± 0.13 | 10.6 ± 0.7[87] | 3.5 ± 0.2 | – | 4.867[127] | 0|$^{+25}_{- 0}$| | 3.5|$^{+16.1}_{-0.5}\, {} ^{[8,127]}$| | <-6.51[14] |
| HD137909 | 1.46 ± 0.01 | 7.5 ± 0.1[102] | 1.98 ± 0.03 | 3[96] | 18.5[103] | 89|$^{+ 0}_{- 2}$| | 5.2|$^{+7.1}_{-1.0}\, {} ^{[103,127]}$| | <-7.90[6] |
| HD138764 | 2.62 ± 0.17 | 15.7 ± 2.7[127] | 4.3 ± 0.4 | 19[30] | 1.259[87] | – | <0.049[46] | <-7.63[16] |
| HD142184 | 2.85 ± 0.13 | 18.5 ± 0.5[104] | 5.7 ± 0.1 | 288[93] | 0.508[56] | 8|$^{+ 3}_{- 3}$| | 9.0|$^{+2.0}_{-2.0}\, {} ^{[107]}$| | -4.25 ± 0.04[94, 117] |
| HD142301 | 2.56 ± 0.07 | 15.9 ± 0.2[41] | 4.46 ± 0.05 | 78[30] | 1.459[111] | 47|$^{+ 9}_{-11}$| | 12|$^{+9}_{-0}\, {} ^{[111]}$| | -5.62 ± 0.04[14, 16, 17, 29] |
| HD142884mr | 2.17 ± 0.12 | 14.3 ± 0.5[87] | 3.7 ± 0.1 | 127[30] | 0.803[109] | – | <0.75[4, 127] | <-6.84[14] |
| HD142990 | 2.93 ± 0.13 | 18.0 ± 0.5[104] | 5.6 ± 0.2 | 122[93] | 0.979[105] | 83|$^{+ 2}_{- 3}$| | 4.7|$^{+0.4}_{-0.4}\, {} ^{[107]}$| | -5.77 ± 0.04[14, 16, 17, 29, 98] |
| HD143473 | 1.87 ± 0.10 | 12.4 ± 1.0[87] | 2.25 ± 0.08 | 25[30] | 2.843[25] | 18|$^{+ 5}_{- 6}$| | 18|$^{+2}_{-2}\, {} ^{[13,15,127]}$| | -6.56 ± 0.04[34] |
| HD143699mr | 2.65 ± 0.12 | 15.5 ± 0.4[41] | 4.6 ± 0.2 | 115[127] | 0.894[127] | – | <0.60[4, 37, 127] | -7.21 ± 0.04[14, 125] |
| HD144334 | 2.34 ± 0.12 | 14.8 ± 0.4[41] | 4.0 ± 0.1 | 82[30] | 1.495[111] | 55|$^{+ 7}_{- 8}$| | 3.6|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.79 ± 0.04[14, 16, 29] |
| HD145102 | 2.02 ± 0.12 | 10.8 ± 0.5[87] | 3.0 ± 0.1 | 84[30] | 1.418[57] | – | <0.98[8] | <-6.90[125] |
| HD145482r | 3.59 ± 0.17 | 24.2 ± 4.3[127] | 8.1 ± 0.8 | 166[30] | 5.804[127] | – | <0.38[8] | <-6.94[14] |
| HD145501C | 2.46 ± 0.15 | 14.5 ± 0.5[87] | 4.0 ± 0.2 | 70[30] | 1.026[111] | 89|$^{+ 0}_{- 2}$| | 5.8|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.08 ± 0.04[14, 16, 124] |
| HD146001mr | 2.38 ± 0.14 | 13.8 ± 0.3[41] | 3.61 ± 0.06 | 90[30] | 0.586[57] | – | <0.50[4, 127] | -6.87 ± 0.04[14] |
| HD147010 | 1.65 ± 0.08 | 12.5 ± 0.6[87] | 2.45 ± 0.09 | 15[96] | 3.921[60] | 10|$^{+ 4}_{- 5}$| | 19|$^{+0}_{-0}\, {} ^{[18,113,127]}$| | <-7.10[14] |
| HD147890 | 2.43 ± 0.12 | 11.3 ± 0.5[87] | 3.7 ± 0.2 | 65[30] | 4.336[57] | – | <0.90[8] | <-6.24[125] |
| HD147932 | 2.50 ± 0.20 | 17.0 ± 1.0[111] | 4.8 ± 0.3 | 140[52] | 0.864[90] | 0|$^{+ 6}_{- 0}$| | 7.6|$^{+9.6}_{-0.5}\, {} ^{[111,126]}$| | -5.14 ± 0.04[112] |
| HD147933 | 3.30 ± 0.17 | 20.8 ± 0.5[110] | 7.3 ± 0.2 | 200[110] | 0.747[110] | 75|$^{+ 9}_{-11}$| | 4.7|$^{+0.5}_{-0.4}\, {} ^{[110,126]}$| | -5.55 ± 0.04[110] |
| HD148112 | 1.85 ± 0.02 | 9.2 ± 0.1[102] | 2.52 ± 0.01 | 44[38] | 3.044[103] | 0|$^{+ 9}_{- 0}$| | 0.76|$^{+0.41}_{-0.11}\, {} ^{[103,127]}$| | <-7.19[6] |
| HD148199 | 1.88 ± 0.12 | 11.7 ± 0.7[87] | 2.5 ± 0.1 | 15[30] | 7.726[25] | 63|$^{+ 9}_{-12}$| | 5.0|$^{+0.6}_{-0.7}\, {} ^{[8,15,127]}$| | <-6.54[14] |
| HD149438 | 4.47 ± 0.13 | 32.0 ± 1.0[104] | 17.5 ± 0.9 | 7[93] | 41.0[35] | 75|$^{+ 7}_{- 8}$| | 0.31|$^{+0.10}_{-0.01}\, {} ^{[77]}$| | <-7.83[85] |
| HD149822mr | 1.85 ± 0.18 | 10.8 ± 0.3[41] | 2.7 ± 0.2 | 60[30] | 1.966[127] | 87|$^{+ 2}_{- 3}$| | 4.0|$^{+2.1}_{-1.1}\, {} ^{[15,36,66,127]}$| | <-7.36[16] |
| HD151346 | 2.44 ± 0.17 | 13.7 ± 1.1[87] | 3.8 ± 0.2 | 46[30] | 2.180[87] | – | <1.7[4] | <-6.66[14] |
| HD152107 | 1.47 ± 0.01 | 8.8 ± 0.1[102] | 2.15 ± 0.01 | 21[102] | 3.857[103] | 19|$^{+ 4}_{- 5}$| | 4.2|$^{+0.5}_{-0.2}\, {} ^{[103,127]}$| | <-8.01[6, 14] |
| HD156424 | 3.00 ± 0.40 | 18.0 ± 3.0[119] | 4.6 ± 0.3 | 7[93] | 0.524[119] | 39|$^{+18}_{-21}$| | 8.0|$^{+12.0}_{-2.0}\, {} ^{[119]}$| | -4.91 ± 0.04[85] |
| HD163472 | 3.81 ± 0.10 | 25.2 ± 1.1[104] | 10.3 ± 0.5 | 62[93] | 3.639[27] | 46|$^{+13}_{-14}$| | 1.1|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-6.83[85] |
| HD164429mr | 1.85 ± 0.04 | 12.0 ± 0.5[127] | 2.99 ± 0.06 | 90[30] | 1.082[127] | 88|$^{+ 1}_{-12}$| | 3.0|$^{+0.7}_{-0.3}\, {} ^{[15,127]}$| | -6.91 ± 0.04[16, 34] |
| HD165474 | 2.06 ± 0.26 | 13.2 ± 3.4[127] | 1.82 ± 0.08 | 18[30] | 9.0 (yr)[79] | 89|$^{+ 0}_{- 0}$| | 3.0|$^{+4.9}_{-1.8}\, {} ^{[79,127]}$| | <-6.96[125] |
| HD168785r | 3.48 ± 0.08 | 23.0 ± 1.2[127] | 8.1 ± 0.4 | 14[106] | – | – | >4.0[89] | <-5.25[125] |
| HD168856mr | 2.10 ± 0.09 | 11.9 ± 1.2[127] | 3.0 ± 0.1 | 73[76] | 2.428[109] | 55|$^{+15}_{-16}$| | 3.5|$^{+3.7}_{-0.6}\, {} ^{[76,84,35,127]}$| | <-6.77[125] |
| HD170000 | 2.36 ± 0.01 | 11.6 ± 0.0[102] | 3.47 ± 0.02 | 83[102] | 1.716[103] | 70|$^{+10}_{-12}$| | 1.8|$^{+0.0}_{-0.1}\, {} ^{[103]}$| | -7.11 ± 0.04[34] |
| HD170973mr | 2.32 ± 0.13 | 10.8 ± 0.2[41] | 3.39 ± 0.06 | 4[96] | 18.1[127] | 83|$^{+ 2}_{- 3}$| | 4.8|$^{+11.2}_{-0.5}\, {} ^{[15,13,127]}$| | <-6.56[125] |
| HD171247mr | 2.79 ± 0.16 | 12.2 ± 0.3[41] | 4.0 ± 0.2 | 68[96] | 3.910[127] | 85|$^{+ 3}_{-34}$| | 4.1|$^{+3.1}_{-0.4}\, {} ^{[127]}$| | -5.16 ± 0.04[16, 29] |
| HD175132r | 2.78 ± 0.04 | 13.2 ± 0.5[127] | 4.0 ± 0.2 | 40[30] | 8.030[127] | – | >3.5[26] | <-6.69[16, 125] |
| HD175362f | 2.64 ± 0.12 | 17.6 ± 0.4[104] | 5.3 ± 0.2 | 34[93] | 3.674[93] | 68|$^{+ 5}_{- 6}$| | 17|$^{+0}_{-0}\, {} ^{[107]}$| | -6.72 ± 0.04[14, 16, 17, 127] |
| HD175744mr | 2.65 ± 0.09 | 12.6 ± 0.2[41] | 4.00 ± 0.08 | 50[30] | 2.799[127] | – | <0.50[31, 108, 127] | <-7.25[16, 125] |
| HD176582 | 2.90 ± 0.15 | 17.0 ± 1.0[104] | 5.6 ± 0.2 | 103[93] | 1.582[53] | 89|$^{+ 0}_{- 1}$| | 5.4|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | -6.07 ± 0.04[34] |
| HD177003 | 3.05 ± 0.10 | 17.7 ± 0.7[87] | 5.7 ± 0.2 | 12[30] | 1.800[87] | – | <0.81[26] | <-7.19[16] |
| HD177410m | 2.30 ± 0.15 | 14.5 ± 0.5[32] | 3.6 ± 0.1 | 100[32] | 1.123[45] | – | <1.7[15, 68, 127] | <-7.23[16] |
| HD179527 | 2.63 ± 0.16 | 10.4 ± 0.3[38] | 3.39 ± 0.05 | 33[38] | 7.098[38] | 88|$^{+ 1}_{-12}$| | 0.52|$^{+0.71}_{-0.11}\, {} ^{[38]}$| | <-6.54[125] |
| HD182180f | 3.09 ± 0.18 | 19.8 ± 1.4[104] | 6.5 ± 0.2 | 306[93] | 0.521[50, 49] | 81|$^{+ 3}_{- 4}$| | 9.5|$^{+0.6}_{-0.6}\, {} ^{[107]}$| | -4.65 ± 0.04[86, 127] |
| HD183056 | 2.69 ± 0.11 | 11.7 ± 0.4[38] | 4.0 ± 0.2 | 35[96] | 2.992[38] | 82|$^{+ 3}_{- 4}$| | 1.6|$^{+2.4}_{-0.4}\, {} ^{[38]}$| | <-7.14[16] |
| HD183339r | 2.70 ± 0.05 | 14.0 ± 0.6[127] | 4.3 ± 0.1 | 41[30] | 4.204[127] | – | >4.5[26] | <-6.39[125] |
| HD184927f | 3.59 ± 0.16 | 22.0 ± 1.0[104] | 8.4 ± 0.5 | 8[93] | 9.531[69] | 67|$^{+ 3}_{- 4}$| | 8.8|$^{+1.4}_{-0.5}\, {} ^{[69]}$| | <-6.06[16, 125, 127] |
| HD184961mr | 2.35 ± 0.08 | 11.8 ± 1.0[127] | 3.47 ± 0.09 | 34[30] | 6.335[127] | 4|$^{+ 3}_{- 4}$| | 4.3|$^{+9.0}_{-0.4}\, {} ^{[127]}$| | <-6.36[125] |
| HD186205 | 3.84 ± 0.25 | 19.6 ± 0.8[104] | 8.3 ± 0.6 | 6[93] | 37.2[93] | 7|$^{+ 3}_{- 4}$| | 3.0|$^{+1.0}_{-0.5}\, {} ^{[107]}$| | <-4.82[125] |
| HD187474 | 1.76 ± 0.03 | 9.9 ± 0.1[102] | 2.52 ± 0.02 | 0[96] | 6.4 (yr)[103] | 89|$^{+ 0}_{- 3}$| | 7.2|$^{+2.1}_{-0.2}\, {} ^{[103]}$| | <-7.29[125] |
| HD188041mr | 1.40 ± 0.01 | 8.5 ± 0.1[102] | 2.07 ± 0.04 | 4[96] | 224.0[103] | 0|$^{+25}_{- 0}$| | 4.1|$^{+16.6}_{-0.4}\, {} ^{[103,127]}$| | <-7.46[125] |
| HD189775f | 2.91 ± 0.11 | 17.5 ± 0.6[104] | 5.6 ± 0.2 | 58[93] | 2.607[93] | 43|$^{+11}_{-12}$| | 4.3|$^{+0.7}_{-0.7}\, {} ^{[107]}$| | -5.83 ± 0.04[127] |
| HD192678 | 1.65 ± 0.27 | 9.0 ± 0.1[41] | 2.5 ± 0.2 | 6[127] | 12.9[21] | 25|$^{+11}_{-12}$| | 5.5|$^{+4.4}_{-0.1}\, {} ^{[21,127]}$| | <-6.79[125] |
| HD196178mr | 2.15 ± 0.10 | 13.1 ± 0.5[87] | 4.2 ± 0.2 | 50[32] | 1.101[127] | 41|$^{+ 7}_{- 9}$| | 3.9|$^{+0.4}_{-0.2}\, {} ^{[3,127]}$| | -5.99 ± 0.04[34] |
| HD196502 | 2.01 ± 0.39 | 8.9 ± 0.4[41] | 2.55 ± 0.05 | 9[96] | 20.3[25] | 88|$^{+ 1}_{-12}$| | 1.7|$^{+0.3}_{-0.3}\, {} ^{[1,2,11,113,127]}$| | <-6.54[6] |
| HD200775f | 3.95 ± 0.30 | 18.6 ± 2.0[43] | 9.0 ± 0.8 | 26[43] | 4.381[43] | 89|$^{+ 0}_{- 6}$| | 3.9|$^{+1.7}_{-0.7}\, {} ^{[45,127]}$| | -6.11 ± 0.04[127] |
| HD202671 | 2.70 ± 0.07 | 13.2 ± 0.1[41] | 4.0 ± 0.2 | 20[96] | 1.992[87] | – | <0.056[51] | <-7.04[125] |
| HD205021f | 4.26 ± 0.11 | 25.0 ± 1.0[104] | 11.9 ± 1.1 | 34[93] | 12.0[59] | 86|$^{+ 2}_{- 4}$| | 0.26|$^{+0.03}_{-0.03}\, {} ^{[107]}$| | <-7.42[85, 127] |
| HD208057f | 3.01 ± 0.11 | 16.5 ± 1.2[104] | 5.3 ± 0.3 | 105[93] | 1.368[93] | 89|$^{+ 0}_{- 0}$| | 0.60|$^{+0.20}_{-0.20}\, {} ^{[107]}$| | <-7.30[127] |
| HD215441 | 2.31 ± 0.09 | 14.5 ± 0.4[41] | 3.9 ± 0.1 | 5[96] | 9.490[21] | 37|$^{+ 7}_{- 7}$| | 62|$^{+6}_{-3}\, {} ^{[21]}$| | -5.13 ± 0.04[6, 14, 17, 29, 72] |
| HD224801 | 2.19 ± 0.10 | 11.9 ± 0.5[87] | 3.2 ± 0.1 | 27[30] | 3.740[20] | – | >4.6[1] | <-6.61[125] |
| HD260858r | 3.52 ± 0.27 | 18.0 ± 1.0[41] | 6.7 ± 0.4 | 47[106] | – | – | >1.8[91] | <-4.86[6] |
| HD335238 | 1.62 ± 0.23 | 9.4 ± 0.5[87] | 2.25 ± 0.04 | – | 48.7[79] | 85|$^{+ 4}_{-44}$| | 5.9|$^{+2.0}_{-2.5}\, {} ^{[79,108,127]}$| | <-6.18[125] |
| Star . | |$\log {\frac{L_{\rm bol}}{L_\odot }}$| . | |$\frac{T_{\rm eff}}{{\rm kK}}$| . | |$\frac{M_*}{{\rm M_\odot }}$| . | |$\frac{v\sin {i}}{{\rm km~s^{-1}}}$| . | |$\frac{P_{\rm rot}}{{\rm d}}$| . | |$\frac{\beta }{{\rm deg}}$| . | |$\frac{B_{\rm d}}{{\rm kG}}$| . | |$\log {\frac{L_{\rm rad}}{{\rm L_\odot }}}$| . |
|---|---|---|---|---|---|---|---|---|
| ALS8988r | 4.05 ± 0.27 | 27.3 ± 1.4[127] | 10.6 ± 0.6 | 23[40] | – | – | >1.5[40] | <-4.40[85] |
| ALS9522 | 3.65 ± 0.12 | 22.4 ± 1.1[118] | 6.0 ± 0.1 | 105[118] | 1.091[118] | 78|$^{+ 2}_{- 3}$| | 11|$^{+3}_{-1}\, {^{[118]}}$| | -5.29 ± 0.04[85] |
| CPD-271791 | 3.69 ± 0.09 | 23.8 ± 1.6[127] | 8.8 ± 0.4 | 37[89] | 2.641[89] | – | >3.9[89] | <-4.71[6] |
| HD3360f | 3.82 ± 0.06 | 20.8 ± 0.2[104] | 8.6 ± 0.1 | 19[93] | 5.370[25] | 82|$^{+ 1}_{- 1}$| | 0.15|$^{+0.03}_{-0.03}\, {^{[107]}}$| | <-7.79[85, 127] |
| HD5737 | 3.33 ± 0.16 | 13.9 ± 0.4[41] | 5.0 ± 0.4 | 17[106] | 21.7[23] | 73|$^{+ 6}_{- 7}$| | 1.8|$^{+0.2}_{-0.3}\, {^{[4,10,18,127]}}$| | <-6.44[6] |
| HD11503f | 1.52 ± 0.03 | 10.1 ± 0.2[102] | 2.35 ± 0.03 | 54[102] | 1.610[103] | 84|$^{+ 4}_{-37}$| | 2.3|$^{+3.7}_{-0.7}\, {} ^{[103]}$| | -7.85 ± 0.04[14, 127] |
| HD12447 | 1.73 ± 0.06 | 10.0 ± 0.2[102] | 2.49 ± 0.05 | 70[102] | 1.491[103] | 87|$^{+ 1}_{- 9}$| | 1.7|$^{+0.5}_{-0.4}\, {}^{[103,127]}$| | -7.40 ± 0.04[34] |
| HD12767 | 2.43 ± 0.15 | 13.0 ± 0.3[41] | 4.0 ± 0.1 | 40[30] | 1.892[23] | 89|$^{+ 0}_{- 3}$| | 2.0|$^{+0.5}_{-0.6}\, {} ^{[9,113,127]}$| | <-6.88[125] |
| HD19832 | 2.08 ± 0.16 | 12.4 ± 0.4[41] | 3.3 ± 0.1 | 160[96] | 0.728[111] | 89|$^{+ 0}_{- 3}$| | 2.7|$^{+0.6}_{-0.3}\, {} ^{[111]}$| | -6.70 ± 0.04[34] |
| HD21699mr | 2.78 ± 0.04 | 16.0 ± 0.1[41] | 4.7 ± 0.2 | 35[106] | 2.492[23, 127] | 78|$^{+ 2}_{- 2}$| | 2.8|$^{+0.5}_{-0.1}\, {} ^{[5,127]}$| | <-6.49[6] |
| HD22470 | 2.43 ± 0.13 | 13.8 ± 0.3[41] | 3.8 ± 0.2 | 62[30] | 1.929[111] | 87|$^{+ 1}_{- 2}$| | 7.5|$^{+1.2}_{-0.5}\, {} ^{[111]}$| | <-6.87[6] |
| HD22920mr | 2.64 ± 0.12 | 13.6 ± 0.2[67] | 4.2 ± 0.1 | 34[30] | 3.947[20, 127] | 28|$^{+ 6}_{- 7}$| | 1.6|$^{+1.1}_{-0.0}\, {} ^{[4,127]}$| | <-6.77[125] |
| HD25267 | 2.32 ± 0.03 | 12.6 ± 0.2[116] | 3.5 ± 0.2 | 20[102] | 3.823[116] | 17|$^{+ 7}_{- 8}$| | 1.0|$^{+0.1}_{-0.1}\, {} ^{[116]}$| | <-7.25[125] |
| HD27309 | 1.88 ± 0.02 | 11.2 ± 0.3[102] | 2.81 ± 0.04 | 56[102] | 1.569[103] | 3|$^{+ 5}_{- 3}$| | 1.9|$^{+2.6}_{-0.6}\, {} ^{[103]}$| | -7.20 ± 0.04[34] |
| HD28843mr | 2.51 ± 0.07 | 14.8 ± 0.2[41] | 4.20 ± 0.06 | 91[127] | 1.374[23, 127] | 87|$^{+ 1}_{- 5}$| | 0.93|$^{+0.30}_{-0.24}\, {} ^{[4,127]}$| | <-6.85[6] |
| HD32633 | 1.94 ± 0.12 | 12.5 ± 0.5[87] | 3.50 ± 0.09 | 25[96] | 6.430[19] | 76|$^{+ 3}_{- 3}$| | 17|$^{+1}_{-2}\, {} ^{[58,73]}$| | <-6.74[14] |
| HD34452 | 2.45 ± 0.27 | 13.8 ± 0.8[41] | 4.2 ± 0.1 | 53[96] | 2.469[23] | 35|$^{+13}_{-16}$| | 3.6|$^{+1.1}_{-1.4}\, {} ^{[3,15,127]}$| | -6.69 ± 0.04[6, 14] |
| HD35298 | 2.40 ± 0.14 | 15.8 ± 0.8[104] | 4.3 ± 0.2 | 60[93] | 1.855[93] | 77|$^{+ 2}_{- 2}$| | 11|$^{+1}_{-1}\, {} ^{[107]}$| | -5.35 ± 0.04[14, 29, 34] |
| HD35456 | 2.88 ± 0.29 | 13.5 ± 1.4[127] | 4.1 ± 0.5 | 22[77] | 4.951[77] | 15|$^{+ 9}_{-11}$| | 2.2|$^{+0.2}_{-0.3}\, {} ^{[77,127]}$| | <-6.19[125] |
| HD35502f | 2.95 ± 0.12 | 18.4 ± 0.6[104] | 5.8 ± 0.2 | 78[93] | 0.854[78] | 70|$^{+ 1}_{- 1}$| | 7.3|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | -5.05 ± 0.04[34, 127] |
| HD35575r | 3.11 ± 0.09 | 16.7 ± 1.3[127] | 5.8 ± 0.3 | 150[99] | 0.984[127] | – | <1.3[99, 127] | <-7.09[16] |
| HD36313r | 2.04 ± 0.19 | 13.0 ± 0.5[114] | 3.4 ± 0.2 | 160[114] | 0.589[114, 127] | 88|$^{+ 1}_{- 5}$| | 9.0|$^{+1.8}_{-1.3}\, {} ^{[114,127]}$| | -6.10 ± 0.04[34] |
| HD36429mr | 2.42 ± 0.02 | 13.8 ± 0.1[127] | 3.87 ± 0.03 | 77[127] | 15.6[127] | – | <0.20[26, 127] | <-6.13[125] |
| HD36485 | 3.10 ± 0.20 | 20.0 ± 2.0[104] | 6.3 ± 0.2 | 33[93] | 1.478[48] | 3|$^{+ 1}_{- 1}$| | 8.9|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | -5.43 ± 0.04[6, 14, 29, 72] |
| HD36526f | 2.30 ± 0.24 | 15.0 ± 2.0[104] | 4.3 ± 0.2 | 59[93] | 1.542[93] | 56|$^{+ 1}_{- 2}$| | 11|$^{+0}_{-0}\, {} ^{[107]}$| | <-6.29[14, 127] |
| HD36540mr | 2.73 ± 0.15 | 14.9 ± 0.7[87] | 4.54 ± 0.09 | 80[83] | 2.173[127] | 9|$^{+26}_{- 8}$| | 1.4|$^{+3.2}_{-0.1}\, {} ^{[83,127]}$| | <-5.99[125] |
| HD36668mr | 2.40 ± 0.19 | 13.5 ± 0.2[114] | 3.81 ± 0.05 | 60[114] | 2.119[114, 127] | 80|$^{+ 5}_{- 6}$| | 4.5|$^{+2.3}_{-2.7}\, {} ^{[114,127]}$| | <-6.05[125] |
| HD36916mr | 2.10 ± 0.20 | 14.7 ± 0.2[83] | 4.2 ± 0.1 | 78[83] | 1.565[83, 127] | 30|$^{+ 8}_{-10}$| | 3.4|$^{+3.3}_{-0.2}\, {} ^{[4,66,83,91,111,127]}$| | <-6.92[14, 16] |
| HD37017 | 3.42 ± 0.25 | 21.0 ± 2.0[104] | 8.4 ± 0.5 | 134[93] | 0.901[93] | 56|$^{+ 2}_{- 3}$| | 6.2|$^{+0.9}_{-0.9}\, {} ^{[107]}$| | -5.11 ± 0.04[6, 14, 17, 29, 72, 82, 124] |
| HD37058 | 2.90 ± 0.11 | 18.6 ± 0.6[104] | 5.8 ± 0.2 | 11[93] | 14.6[93] | 55|$^{+11}_{-13}$| | 2.5|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-5.95[14] |
| HD37061f | 3.30 ± 0.30 | 22.0 ± 1.0[104] | 7.7 ± 0.4 | 100[93] | 1.095[101] | 59|$^{+ 4}_{- 4}$| | 9.2|$^{+1.0}_{-1.0}\, {} ^{[107]}$| | -5.68 ± 0.04[82, 127] |
| HD37140mr | 2.12 ± 0.09 | 13.5 ± 0.2[114] | 3.46 ± 0.05 | 25[127] | 2.761[114, 127] | 80|$^{+ 3}_{- 4}$| | 3.9|$^{+0.7}_{-0.4}\, {} ^{[114,127]}$| | <-6.08[125] |
| HD37151 | 2.08 ± 0.08 | 13.5 ± 0.9[127] | 3.4 ± 0.2 | – | – | 87|$^{+ 1}_{-12}$| | 1.4|$^{+1.2}_{-1.4}\, {} ^{[115,127]}$| | <-6.39[125] |
| HD37210mr | 2.51 ± 0.05 | 13.5 ± 0.6[127] | 3.92 ± 0.09 | 20[115] | 11.0[20, 127] | 78|$^{+ 7}_{- 8}$| | 1.8|$^{+0.9}_{-0.1}\, {} ^{[66,115,127]}$| | <-5.71[125] |
| HD37479 | 3.51 ± 0.21 | 23.0 ± 2.0[104] | 7.9 ± 0.2 | 145[93] | 1.191[47] | 37|$^{+ 7}_{-10}$| | 10|$^{+11}_{-0}\, {} ^{[71]}$| | -4.73 ± 0.04[6, 14, 17, 29, 72] |
| HD37642mr | 2.42 ± 0.10 | 16.0 ± 0.5[115] | 4.3 ± 0.1 | 85[115] | 1.079[115, 127] | 74|$^{+ 3}_{- 3}$| | 18|$^{+1}_{-0}\, {} ^{[115,127]}$| | -5.69 ± 0.04[34] |
| HD37752 | 2.63 ± 0.14 | 15.0 ± 0.7[41] | 4.5 ± 0.2 | 35[30] | 1.305[87] | – | <2.4[26] | <-7.08[16] |
| HD37776f | 3.30 ± 0.15 | 22.0 ± 1.0[104] | 8.3 ± 0.3 | 101[93] | 1.539[81] | 47|$^{+ 8}_{-10}$| | 6.1|$^{+0.7}_{-0.7}\, {} ^{[54,107]}$| | <-6.35[6, 127] |
| HD37808mr | 2.28 ± 0.10 | 14.5 ± 0.2[115] | 3.90 ± 0.08 | 30[96] | 1.099[109, 115, 127] | 45|$^{+20}_{-24}$| | 3.2|$^{+1.0}_{-0.3}\, {} ^{[115,127]}$| | -6.16 ± 0.04[16, 29] |
| HD40312 | 2.33 ± 0.01 | 10.2 ± 0.1[102] | 3.11 ± 0.06 | 55[96] | 3.619[103] | 68|$^{+13}_{-15}$| | 1.3|$^{+0.4}_{-0.2}\, {} ^{[97]}$| | -7.78 ± 0.04[14] |
| HD41269mr | 2.30 ± 0.08 | 12.9 ± 0.9[127] | 3.5 ± 0.2 | 85[30] | 1.048[127] | 0|$^{+16}_{- 0}$| | 1.3|$^{+0.5}_{-0.3}\, {} ^{[127]}$| | <-7.20[16] |
| HD43819 | 2.15 ± 0.20 | 10.9 ± 0.4[38] | 3.1 ± 0.2 | 10[38] | 15.0[38] | 47|$^{+16}_{-19}$| | 2.6|$^{+75.7}_{-0.1}\, {} ^{[38]}$| | <-6.79[16] |
| HD45583 | 2.07 ± 0.12 | 13.3 ± 0.3[42] | 3.35 ± 0.09 | 70[96] | 1.177[111] | 69|$^{+ 2}_{- 2}$| | 9.1|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.24 ± 0.04[34, 124] |
| HD46328 | 4.49 ± 0.11 | 27.0 ± 1.0[104] | 14.4 ± 0.8 | 8[93] | 30.0 (yr)[88, 95, 120] | 89|$^{+ 0}_{- 9}$| | 1.2|$^{+0.6}_{-0.1}\, {} ^{[107]}$| | <-7.03[85] |
| HD47777 | 3.42 ± 0.15 | 22.0 ± 1.0[104] | 7.9 ± 0.4 | 60[93] | 2.640[61] | 82|$^{+ 5}_{- 5}$| | 3.3|$^{+0.7}_{-0.7}\, {} ^{[107]}$| | <-6.40[85] |
| HD49333 | 2.73 ± 0.04 | 15.8 ± 0.1[41] | 4.8 ± 0.3 | 65[30] | 2.180[23] | 85|$^{+ 3}_{-12}$| | 3.6|$^{+1.0}_{-1.2}\, {} ^{[15,127]}$| | <-6.49[14] |
| HD49606mr | 2.59 ± 0.06 | 13.5 ± 0.1[41] | 4.08 ± 0.06 | 19[96] | 8.546[123] | – | <0.040[127] | <-6.25[125] |
| HD51418mr | 1.80 ± 0.04 | 9.5 ± 0.8[100] | 2.48 ± 0.09 | 28[84] | 5.431[113, 127] | 89|$^{+ 0}_{- 0}$| | 3.5|$^{+1.0}_{-0.4}\, {} ^{[84,127]}$| | <-6.65[125] |
| HD55522f | 3.00 ± 0.18 | 17.4 ± 0.4[104] | 5.9 ± 0.2 | 70[93] | 2.729[93] | 89|$^{+ 0}_{- 1}$| | 3.1|$^{+0.4}_{-0.4}\, {} ^{[107]}$| | <-6.16[127] |
| HD58260 | 3.22 ± 0.26 | 19.3 ± 1.3[104] | 6.2 ± 0.5 | 3[93] | – | 0|$^{+ 5}_{- 0}$| | 6.5|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | <-6.69[6, 85] |
| HD60344r | 3.58 ± 0.09 | 21.0 ± 0.3[41] | 7.9 ± 0.2 | 55[106] | – | – | >1.2[89, 127] | <-4.76[6] |
| HD61556f | 3.12 ± 0.24 | 18.5 ± 0.8[70] | 6.1 ± 0.3 | 58[70] | 1.909[70] | 58|$^{+ 6}_{- 7}$| | 2.8|$^{+0.3}_{-0.3}\, {} ^{[107]}$| | -5.93 ± 0.04[117, 127] |
| HD64740f | 3.81 ± 0.15 | 24.5 ± 1.0[104] | 10.1 ± 0.5 | 135[93] | 1.330[93] | 71|$^{+ 5}_{- 5}$| | 3.0|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | -7.19 ± 0.04[127] |
| HD65339 | 1.45 ± 0.02 | 8.5 ± 0.1[102] | 2.09 ± 0.02 | 13[96] | 8.027[103] | 89|$^{+ 0}_{- 1}$| | 15|$^{+2}_{-1}\, {} ^{[28]}$| | <-7.50[6, 14] |
| HD66665 | 4.69 ± 0.23 | 28.5 ± 1.0[104] | 15.9 ± 1.1 | 8[93] | 24.5[93] | 75|$^{+ 3}_{- 3}$| | 0.56|$^{+0.10}_{-0.10}\, {} ^{[107]}$| | <-4.96[85] |
| HD66765f | 3.44 ± 0.24 | 20.0 ± 2.0[63] | 7.2 ± 0.6 | 58[93] | 1.608[93] | 73|$^{+ 5}_{- 5}$| | 2.8|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-6.23[127] |
| HD79158 | 2.61 ± 0.06 | 13.3 ± 0.1[41] | 4.3 ± 0.1 | 49[96] | 3.835[92] | 87|$^{+ 1}_{- 4}$| | 3.1|$^{+0.4}_{-0.4}\, {} ^{[92]}$| | -6.55 ± 0.04[6, 34] |
| HD90044 | 1.66 ± 0.10 | 10.0 ± 0.2[87] | 2.8 ± 0.3 | 23[102] | 4.379[23] | 89|$^{+ 0}_{- 0}$| | 4.4|$^{+1.2}_{-1.5}\, {} ^{[15,22,127]}$| | <-7.71[16] |
| HD105382 | 3.04 ± 0.16 | 18.0 ± 0.5[24] | 5.8 ± 0.2 | 74[93] | 1.295[24] | 51|$^{+ 7}_{- 8}$| | 2.6|$^{+0.1}_{-0.1}\, {} ^{[107]}$| | -6.07 ± 0.04[117] |
| HD112413 | 1.97 ± 0.02 | 11.3 ± 0.2[102] | 2.93 ± 0.03 | 15[96] | 5.469[103] | 88|$^{+ 1}_{- 8}$| | 3.5|$^{+0.8}_{-0.2}\, {} ^{[64,65]}$| | -8.13 ± 0.04[6, 34] |
| HD118022 | 1.53 ± 0.04 | 9.4 ± 0.1[102] | 2.26 ± 0.02 | 12[102] | 3.722[103] | 65|$^{+15}_{-17}$| | 3.2|$^{+8.0}_{-0.2}\, {} ^{[103]}$| | -7.41 ± 0.04[121] |
| HD122532 | 2.37 ± 0.12 | 11.9 ± 0.5[87] | 2.99 ± 0.04 | – | 3.681[12] | 89|$^{+ 0}_{- 3}$| | 3.0|$^{+0.7}_{-0.9}\, {} ^{[7,13,15,113,127]}$| | <-7.00[14] |
| HD124224 | 1.93 ± 0.01 | 12.3 ± 0.2[102] | 3.02 ± 0.01 | 169[102] | 0.521[81] | 87|$^{+ 2}_{-11}$| | 4.0|$^{+0.3}_{-0.2}\, {} ^{[62]}$| | -6.24 ± 0.04[16, 18, 29, 34, 117, 122] |
| HD125248 | 1.39 ± 0.23 | 9.7 ± 0.3[41] | 2.42 ± 0.07 | 11[96] | 9.300[39] | 89|$^{+ 0}_{- 3}$| | 9.0|$^{+1.1}_{-1.3}\, {} ^{[75]}$| | <-7.17[125] |
| HD125823 | 3.16 ± 0.20 | 19.0 ± 2.0[104] | 5.9 ± 0.2 | 16[93] | 8.817[93] | 75|$^{+ 4}_{- 6}$| | 1.8|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | <-6.54[6] |
| HD126515 | 1.36 ± 0.16 | 8.9 ± 0.2[127] | 2.65 ± 0.07 | 16[127] | 129.9[21] | 84|$^{+ 4}_{-13}$| | 13|$^{+1}_{-0}\, {} ^{[21]}$| | <-7.13[14] |
| HD131120mr | 3.15 ± 0.09 | 19.4 ± 1.5[127] | 6.3 ± 0.3 | 57[30] | 1.569[55, 127] | – | <0.17[66] | <-6.97[14] |
| HD133029mr | 1.98 ± 0.08 | 11.8 ± 0.9[41] | 2.8 ± 0.1 | 27[30] | 2.888[44, 127] | 12|$^{+ 4}_{- 4}$| | 9.0|$^{+5.0}_{-0.3}\, {} ^{[3,127]}$| | <-6.89[14] |
| HD133652 | 2.02 ± 0.10 | 12.8 ± 0.5[87] | 3.27 ± 0.09 | 48[96] | 2.304[23] | 65|$^{+ 8}_{-11}$| | 7.6|$^{+0.8}_{-1.0}\, {} ^{[15,127]}$| | -7.16 ± 0.04[34] |
| HD133880 | 1.73 ± 0.06 | 10.7 ± 0.1[41] | 3.08 ± 0.08 | 103[96] | 0.877[80] | 83|$^{+ 1}_{- 1}$| | 12|$^{+0}_{-1}\, {} ^{[80]}$| | -5.44 ± 0.04[72, 34] |
| HD135679mr | 2.46 ± 0.19 | 15.1 ± 2.8[127] | 2.86 ± 0.06 | 1[84] | 5.321[127] | 14|$^{+ 6}_{- 8}$| | 4.4|$^{+9.3}_{-0.2}\, {} ^{[84,91,127]}$| | <-7.04[16] |
| HD137193mr | 1.91 ± 0.13 | 10.6 ± 0.7[87] | 3.5 ± 0.2 | – | 4.867[127] | 0|$^{+25}_{- 0}$| | 3.5|$^{+16.1}_{-0.5}\, {} ^{[8,127]}$| | <-6.51[14] |
| HD137909 | 1.46 ± 0.01 | 7.5 ± 0.1[102] | 1.98 ± 0.03 | 3[96] | 18.5[103] | 89|$^{+ 0}_{- 2}$| | 5.2|$^{+7.1}_{-1.0}\, {} ^{[103,127]}$| | <-7.90[6] |
| HD138764 | 2.62 ± 0.17 | 15.7 ± 2.7[127] | 4.3 ± 0.4 | 19[30] | 1.259[87] | – | <0.049[46] | <-7.63[16] |
| HD142184 | 2.85 ± 0.13 | 18.5 ± 0.5[104] | 5.7 ± 0.1 | 288[93] | 0.508[56] | 8|$^{+ 3}_{- 3}$| | 9.0|$^{+2.0}_{-2.0}\, {} ^{[107]}$| | -4.25 ± 0.04[94, 117] |
| HD142301 | 2.56 ± 0.07 | 15.9 ± 0.2[41] | 4.46 ± 0.05 | 78[30] | 1.459[111] | 47|$^{+ 9}_{-11}$| | 12|$^{+9}_{-0}\, {} ^{[111]}$| | -5.62 ± 0.04[14, 16, 17, 29] |
| HD142884mr | 2.17 ± 0.12 | 14.3 ± 0.5[87] | 3.7 ± 0.1 | 127[30] | 0.803[109] | – | <0.75[4, 127] | <-6.84[14] |
| HD142990 | 2.93 ± 0.13 | 18.0 ± 0.5[104] | 5.6 ± 0.2 | 122[93] | 0.979[105] | 83|$^{+ 2}_{- 3}$| | 4.7|$^{+0.4}_{-0.4}\, {} ^{[107]}$| | -5.77 ± 0.04[14, 16, 17, 29, 98] |
| HD143473 | 1.87 ± 0.10 | 12.4 ± 1.0[87] | 2.25 ± 0.08 | 25[30] | 2.843[25] | 18|$^{+ 5}_{- 6}$| | 18|$^{+2}_{-2}\, {} ^{[13,15,127]}$| | -6.56 ± 0.04[34] |
| HD143699mr | 2.65 ± 0.12 | 15.5 ± 0.4[41] | 4.6 ± 0.2 | 115[127] | 0.894[127] | – | <0.60[4, 37, 127] | -7.21 ± 0.04[14, 125] |
| HD144334 | 2.34 ± 0.12 | 14.8 ± 0.4[41] | 4.0 ± 0.1 | 82[30] | 1.495[111] | 55|$^{+ 7}_{- 8}$| | 3.6|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.79 ± 0.04[14, 16, 29] |
| HD145102 | 2.02 ± 0.12 | 10.8 ± 0.5[87] | 3.0 ± 0.1 | 84[30] | 1.418[57] | – | <0.98[8] | <-6.90[125] |
| HD145482r | 3.59 ± 0.17 | 24.2 ± 4.3[127] | 8.1 ± 0.8 | 166[30] | 5.804[127] | – | <0.38[8] | <-6.94[14] |
| HD145501C | 2.46 ± 0.15 | 14.5 ± 0.5[87] | 4.0 ± 0.2 | 70[30] | 1.026[111] | 89|$^{+ 0}_{- 2}$| | 5.8|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.08 ± 0.04[14, 16, 124] |
| HD146001mr | 2.38 ± 0.14 | 13.8 ± 0.3[41] | 3.61 ± 0.06 | 90[30] | 0.586[57] | – | <0.50[4, 127] | -6.87 ± 0.04[14] |
| HD147010 | 1.65 ± 0.08 | 12.5 ± 0.6[87] | 2.45 ± 0.09 | 15[96] | 3.921[60] | 10|$^{+ 4}_{- 5}$| | 19|$^{+0}_{-0}\, {} ^{[18,113,127]}$| | <-7.10[14] |
| HD147890 | 2.43 ± 0.12 | 11.3 ± 0.5[87] | 3.7 ± 0.2 | 65[30] | 4.336[57] | – | <0.90[8] | <-6.24[125] |
| HD147932 | 2.50 ± 0.20 | 17.0 ± 1.0[111] | 4.8 ± 0.3 | 140[52] | 0.864[90] | 0|$^{+ 6}_{- 0}$| | 7.6|$^{+9.6}_{-0.5}\, {} ^{[111,126]}$| | -5.14 ± 0.04[112] |
| HD147933 | 3.30 ± 0.17 | 20.8 ± 0.5[110] | 7.3 ± 0.2 | 200[110] | 0.747[110] | 75|$^{+ 9}_{-11}$| | 4.7|$^{+0.5}_{-0.4}\, {} ^{[110,126]}$| | -5.55 ± 0.04[110] |
| HD148112 | 1.85 ± 0.02 | 9.2 ± 0.1[102] | 2.52 ± 0.01 | 44[38] | 3.044[103] | 0|$^{+ 9}_{- 0}$| | 0.76|$^{+0.41}_{-0.11}\, {} ^{[103,127]}$| | <-7.19[6] |
| HD148199 | 1.88 ± 0.12 | 11.7 ± 0.7[87] | 2.5 ± 0.1 | 15[30] | 7.726[25] | 63|$^{+ 9}_{-12}$| | 5.0|$^{+0.6}_{-0.7}\, {} ^{[8,15,127]}$| | <-6.54[14] |
| HD149438 | 4.47 ± 0.13 | 32.0 ± 1.0[104] | 17.5 ± 0.9 | 7[93] | 41.0[35] | 75|$^{+ 7}_{- 8}$| | 0.31|$^{+0.10}_{-0.01}\, {} ^{[77]}$| | <-7.83[85] |
| HD149822mr | 1.85 ± 0.18 | 10.8 ± 0.3[41] | 2.7 ± 0.2 | 60[30] | 1.966[127] | 87|$^{+ 2}_{- 3}$| | 4.0|$^{+2.1}_{-1.1}\, {} ^{[15,36,66,127]}$| | <-7.36[16] |
| HD151346 | 2.44 ± 0.17 | 13.7 ± 1.1[87] | 3.8 ± 0.2 | 46[30] | 2.180[87] | – | <1.7[4] | <-6.66[14] |
| HD152107 | 1.47 ± 0.01 | 8.8 ± 0.1[102] | 2.15 ± 0.01 | 21[102] | 3.857[103] | 19|$^{+ 4}_{- 5}$| | 4.2|$^{+0.5}_{-0.2}\, {} ^{[103,127]}$| | <-8.01[6, 14] |
| HD156424 | 3.00 ± 0.40 | 18.0 ± 3.0[119] | 4.6 ± 0.3 | 7[93] | 0.524[119] | 39|$^{+18}_{-21}$| | 8.0|$^{+12.0}_{-2.0}\, {} ^{[119]}$| | -4.91 ± 0.04[85] |
| HD163472 | 3.81 ± 0.10 | 25.2 ± 1.1[104] | 10.3 ± 0.5 | 62[93] | 3.639[27] | 46|$^{+13}_{-14}$| | 1.1|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-6.83[85] |
| HD164429mr | 1.85 ± 0.04 | 12.0 ± 0.5[127] | 2.99 ± 0.06 | 90[30] | 1.082[127] | 88|$^{+ 1}_{-12}$| | 3.0|$^{+0.7}_{-0.3}\, {} ^{[15,127]}$| | -6.91 ± 0.04[16, 34] |
| HD165474 | 2.06 ± 0.26 | 13.2 ± 3.4[127] | 1.82 ± 0.08 | 18[30] | 9.0 (yr)[79] | 89|$^{+ 0}_{- 0}$| | 3.0|$^{+4.9}_{-1.8}\, {} ^{[79,127]}$| | <-6.96[125] |
| HD168785r | 3.48 ± 0.08 | 23.0 ± 1.2[127] | 8.1 ± 0.4 | 14[106] | – | – | >4.0[89] | <-5.25[125] |
| HD168856mr | 2.10 ± 0.09 | 11.9 ± 1.2[127] | 3.0 ± 0.1 | 73[76] | 2.428[109] | 55|$^{+15}_{-16}$| | 3.5|$^{+3.7}_{-0.6}\, {} ^{[76,84,35,127]}$| | <-6.77[125] |
| HD170000 | 2.36 ± 0.01 | 11.6 ± 0.0[102] | 3.47 ± 0.02 | 83[102] | 1.716[103] | 70|$^{+10}_{-12}$| | 1.8|$^{+0.0}_{-0.1}\, {} ^{[103]}$| | -7.11 ± 0.04[34] |
| HD170973mr | 2.32 ± 0.13 | 10.8 ± 0.2[41] | 3.39 ± 0.06 | 4[96] | 18.1[127] | 83|$^{+ 2}_{- 3}$| | 4.8|$^{+11.2}_{-0.5}\, {} ^{[15,13,127]}$| | <-6.56[125] |
| HD171247mr | 2.79 ± 0.16 | 12.2 ± 0.3[41] | 4.0 ± 0.2 | 68[96] | 3.910[127] | 85|$^{+ 3}_{-34}$| | 4.1|$^{+3.1}_{-0.4}\, {} ^{[127]}$| | -5.16 ± 0.04[16, 29] |
| HD175132r | 2.78 ± 0.04 | 13.2 ± 0.5[127] | 4.0 ± 0.2 | 40[30] | 8.030[127] | – | >3.5[26] | <-6.69[16, 125] |
| HD175362f | 2.64 ± 0.12 | 17.6 ± 0.4[104] | 5.3 ± 0.2 | 34[93] | 3.674[93] | 68|$^{+ 5}_{- 6}$| | 17|$^{+0}_{-0}\, {} ^{[107]}$| | -6.72 ± 0.04[14, 16, 17, 127] |
| HD175744mr | 2.65 ± 0.09 | 12.6 ± 0.2[41] | 4.00 ± 0.08 | 50[30] | 2.799[127] | – | <0.50[31, 108, 127] | <-7.25[16, 125] |
| HD176582 | 2.90 ± 0.15 | 17.0 ± 1.0[104] | 5.6 ± 0.2 | 103[93] | 1.582[53] | 89|$^{+ 0}_{- 1}$| | 5.4|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | -6.07 ± 0.04[34] |
| HD177003 | 3.05 ± 0.10 | 17.7 ± 0.7[87] | 5.7 ± 0.2 | 12[30] | 1.800[87] | – | <0.81[26] | <-7.19[16] |
| HD177410m | 2.30 ± 0.15 | 14.5 ± 0.5[32] | 3.6 ± 0.1 | 100[32] | 1.123[45] | – | <1.7[15, 68, 127] | <-7.23[16] |
| HD179527 | 2.63 ± 0.16 | 10.4 ± 0.3[38] | 3.39 ± 0.05 | 33[38] | 7.098[38] | 88|$^{+ 1}_{-12}$| | 0.52|$^{+0.71}_{-0.11}\, {} ^{[38]}$| | <-6.54[125] |
| HD182180f | 3.09 ± 0.18 | 19.8 ± 1.4[104] | 6.5 ± 0.2 | 306[93] | 0.521[50, 49] | 81|$^{+ 3}_{- 4}$| | 9.5|$^{+0.6}_{-0.6}\, {} ^{[107]}$| | -4.65 ± 0.04[86, 127] |
| HD183056 | 2.69 ± 0.11 | 11.7 ± 0.4[38] | 4.0 ± 0.2 | 35[96] | 2.992[38] | 82|$^{+ 3}_{- 4}$| | 1.6|$^{+2.4}_{-0.4}\, {} ^{[38]}$| | <-7.14[16] |
| HD183339r | 2.70 ± 0.05 | 14.0 ± 0.6[127] | 4.3 ± 0.1 | 41[30] | 4.204[127] | – | >4.5[26] | <-6.39[125] |
| HD184927f | 3.59 ± 0.16 | 22.0 ± 1.0[104] | 8.4 ± 0.5 | 8[93] | 9.531[69] | 67|$^{+ 3}_{- 4}$| | 8.8|$^{+1.4}_{-0.5}\, {} ^{[69]}$| | <-6.06[16, 125, 127] |
| HD184961mr | 2.35 ± 0.08 | 11.8 ± 1.0[127] | 3.47 ± 0.09 | 34[30] | 6.335[127] | 4|$^{+ 3}_{- 4}$| | 4.3|$^{+9.0}_{-0.4}\, {} ^{[127]}$| | <-6.36[125] |
| HD186205 | 3.84 ± 0.25 | 19.6 ± 0.8[104] | 8.3 ± 0.6 | 6[93] | 37.2[93] | 7|$^{+ 3}_{- 4}$| | 3.0|$^{+1.0}_{-0.5}\, {} ^{[107]}$| | <-4.82[125] |
| HD187474 | 1.76 ± 0.03 | 9.9 ± 0.1[102] | 2.52 ± 0.02 | 0[96] | 6.4 (yr)[103] | 89|$^{+ 0}_{- 3}$| | 7.2|$^{+2.1}_{-0.2}\, {} ^{[103]}$| | <-7.29[125] |
| HD188041mr | 1.40 ± 0.01 | 8.5 ± 0.1[102] | 2.07 ± 0.04 | 4[96] | 224.0[103] | 0|$^{+25}_{- 0}$| | 4.1|$^{+16.6}_{-0.4}\, {} ^{[103,127]}$| | <-7.46[125] |
| HD189775f | 2.91 ± 0.11 | 17.5 ± 0.6[104] | 5.6 ± 0.2 | 58[93] | 2.607[93] | 43|$^{+11}_{-12}$| | 4.3|$^{+0.7}_{-0.7}\, {} ^{[107]}$| | -5.83 ± 0.04[127] |
| HD192678 | 1.65 ± 0.27 | 9.0 ± 0.1[41] | 2.5 ± 0.2 | 6[127] | 12.9[21] | 25|$^{+11}_{-12}$| | 5.5|$^{+4.4}_{-0.1}\, {} ^{[21,127]}$| | <-6.79[125] |
| HD196178mr | 2.15 ± 0.10 | 13.1 ± 0.5[87] | 4.2 ± 0.2 | 50[32] | 1.101[127] | 41|$^{+ 7}_{- 9}$| | 3.9|$^{+0.4}_{-0.2}\, {} ^{[3,127]}$| | -5.99 ± 0.04[34] |
| HD196502 | 2.01 ± 0.39 | 8.9 ± 0.4[41] | 2.55 ± 0.05 | 9[96] | 20.3[25] | 88|$^{+ 1}_{-12}$| | 1.7|$^{+0.3}_{-0.3}\, {} ^{[1,2,11,113,127]}$| | <-6.54[6] |
| HD200775f | 3.95 ± 0.30 | 18.6 ± 2.0[43] | 9.0 ± 0.8 | 26[43] | 4.381[43] | 89|$^{+ 0}_{- 6}$| | 3.9|$^{+1.7}_{-0.7}\, {} ^{[45,127]}$| | -6.11 ± 0.04[127] |
| HD202671 | 2.70 ± 0.07 | 13.2 ± 0.1[41] | 4.0 ± 0.2 | 20[96] | 1.992[87] | – | <0.056[51] | <-7.04[125] |
| HD205021f | 4.26 ± 0.11 | 25.0 ± 1.0[104] | 11.9 ± 1.1 | 34[93] | 12.0[59] | 86|$^{+ 2}_{- 4}$| | 0.26|$^{+0.03}_{-0.03}\, {} ^{[107]}$| | <-7.42[85, 127] |
| HD208057f | 3.01 ± 0.11 | 16.5 ± 1.2[104] | 5.3 ± 0.3 | 105[93] | 1.368[93] | 89|$^{+ 0}_{- 0}$| | 0.60|$^{+0.20}_{-0.20}\, {} ^{[107]}$| | <-7.30[127] |
| HD215441 | 2.31 ± 0.09 | 14.5 ± 0.4[41] | 3.9 ± 0.1 | 5[96] | 9.490[21] | 37|$^{+ 7}_{- 7}$| | 62|$^{+6}_{-3}\, {} ^{[21]}$| | -5.13 ± 0.04[6, 14, 17, 29, 72] |
| HD224801 | 2.19 ± 0.10 | 11.9 ± 0.5[87] | 3.2 ± 0.1 | 27[30] | 3.740[20] | – | >4.6[1] | <-6.61[125] |
| HD260858r | 3.52 ± 0.27 | 18.0 ± 1.0[41] | 6.7 ± 0.4 | 47[106] | – | – | >1.8[91] | <-4.86[6] |
| HD335238 | 1.62 ± 0.23 | 9.4 ± 0.5[87] | 2.25 ± 0.04 | – | 48.7[79] | 85|$^{+ 4}_{-44}$| | 5.9|$^{+2.0}_{-2.5}\, {} ^{[79,108,127]}$| | <-6.18[125] |
Reference key:
1, Babcock (1958); 2, Wolff & Bonsack (1972); 3, Borra & Landstreet (1980); 4, Borra, Landstreet & Thompson (1983); 5, Brown, Shore & Sonneborn (1985); 6, Drake et al. (1987); 7, Bohlender et al. (1987); 8, Thompson, Brown & Landstreet (1987); 9, Ruediger & Scholz (1988); 10, Shore & Brown (1990); 11, Weiss, Malanushenko & Shakhovskoi (1990); 12, Lanz & Mathys (1991); 13, Mathys (1991); 14, Linsky et al. (1992); 15, Bohlender, Landstreet & Thompson (1993); 16, Leone et al. (1994); 17, Leone et al. (1996); 18, Mathys & Hubrig (1997); 19, Adelman (1997); 20, Catalano & Renson (1998); 21, Landstreet & Mathys (2000); 22, Leone & Catanzaro (2001); 23, Renson & Catalano (2001); 24, Briquet, Aerts & De Cat (2001); 25, Neiner et al. (2003a); 26, Bychkov, Bychkova & Madej (2003); 27, Neiner et al. (2003b); 28, Kochukhov et al. (2004); 29, Leone et al. (2004); 30, Głȩbocki & Gnaciński (2005); 31, Kochukhov & Bagnulo (2006); 32, Lehmann et al. (2006); 33, Hubrig et al. (2006); 34, Drake et al. (2006); 35, Donati et al. (2006); 36, Kudryavtsev et al. (2006); 37, Landstreet et al. (2007); 38, Aurière et al. (2007); 39, Hubrig, North & Schöller (2007); 40, Alecian et al. (2008b); 41, Netopil et al. (2008); 42, Semenko et al. (2008); 43, Alecian et al. (2008a); 44, Adelman (2008); 45, Krtička et al. (2009); 46, Silvester et al. (2009); 47, Townsend et al. (2010); 48, Leone et al. (2010); 49, Rivinius et al. (2010); 50, Oksala et al. (2010); 51, Makaganiuk et al. (2011); 52, Alecian et al. (2011); 53, Bohlender & Monin (2011); 54, Kochukhov et al. (2011); 55, Dubath et al. (2011); 56, Grunhut et al. (2012); 57, Wraight et al. (2012); 58, Silvester et al. (2012); 59, Henrichs et al. (2013); 60, Bailey & Landstreet (2013); 61, Fossati et al. (2014); 62, Kochukhov et al. (2014); 63, Alecian et al. (2014); 64, Silvester, Kochukhov & Wade (2014a); 65, Silvester, Kochukhov & Wade (2014b); 66, Bagnulo et al. (2015a); 67, Khalack & LeBlanc (2015); 68, Romanyuk, Semenko & Kudryavtsev (2015); 69, Yakunin et al. (2015); 70, Shultz et al. (2015); 71, Oksala et al. (2015a); 72, Chandra et al. (2015); 73, Silvester, Kochukhov & Wade (2015); 74, Kochukhov & Wade (2016); 75, Rusomarov et al. (2016); 76, Romanyuk et al. (2016b); 77, Romanyuk et al. (2016a); 78, Sikora et al. (2016); 79, Mathys (2017); 80, Kochukhov et al. (2017); 81, Mikulášek et al. (2017); 82, Kounkel et al. (2017); 83, Romanyuk et al. (2017a); 84, Romanyuk et al. (2017b); 85, Kurapati et al. (2017); 86, Leto et al. (2017); 87, Netopil et al. (2017); 88, Shultz et al. (2017); 89, Järvinen et al. (2018); 90, Rebull et al. (2018); 91, Romanyuk et al. (2018); 92, Oksala et al. (2018); 93, Shultz et al. (2018b); 94, Leto et al. (2018); 95, Shultz et al. (2018c); 96, Ghazaryan, Alecian & Hakobyan (2018); 97, Kochukhov et al. (2019); 98, Das et al. (2019b); 99, Romanyuk et al. (2019); 100, Moiseeva et al. (2019); 101, Shultz et al. (2019a); 102, Sikora et al. (2019a); 103, Sikora et al. (2019b); 104, Shultz et al. (2019b); 105, Shultz et al. (2019c); 106, Ghazaryan, Alecian & Hakobyan (2019); 107, Shultz et al. (2019d); 108, Romanyuk et al. (2020); 109, Bernhard, Hümmerich & Paunzen (2020); 110, Leto et al. (2020a); 111, Shultz et al. (2020); 112, Leto et al. (2020b); 113, Bychkov, Bychkova & Madej (2021); 114, Romanyuk et al. (2021a); 115, Romanyuk et al. (2021b); 116, Woodcock et al. (2021); 117, Pritchard et al. (2021); 118, Shultz et al. (2021a); 119, Shultz et al. (2021b); 120, Erba et al. (2021); 121, Leto et al. (2021); 122, Das & Chandra (2021); 123, Kochukhov et al. (2021); 124, Das et al. (2021); 125, Drake (private communication); 126, Shultz et al. (in preparation); 127, This Work
Stellar parameters, rotational periods, dipolar magnetic field strengths, and radio luminosities for the sample. Stars with superscripts are listed in appendix B if they have new radio (f)lux density observations, and are discussed in appendix C if new (m)agnetic data or (r)otational periods are available. Appendices B and C are available online as supplementary material. Superscipt numbers in square brackets in other columns correspond to the reference key at the end of the table.
| Star . | |$\log {\frac{L_{\rm bol}}{L_\odot }}$| . | |$\frac{T_{\rm eff}}{{\rm kK}}$| . | |$\frac{M_*}{{\rm M_\odot }}$| . | |$\frac{v\sin {i}}{{\rm km~s^{-1}}}$| . | |$\frac{P_{\rm rot}}{{\rm d}}$| . | |$\frac{\beta }{{\rm deg}}$| . | |$\frac{B_{\rm d}}{{\rm kG}}$| . | |$\log {\frac{L_{\rm rad}}{{\rm L_\odot }}}$| . |
|---|---|---|---|---|---|---|---|---|
| ALS8988r | 4.05 ± 0.27 | 27.3 ± 1.4[127] | 10.6 ± 0.6 | 23[40] | – | – | >1.5[40] | <-4.40[85] |
| ALS9522 | 3.65 ± 0.12 | 22.4 ± 1.1[118] | 6.0 ± 0.1 | 105[118] | 1.091[118] | 78|$^{+ 2}_{- 3}$| | 11|$^{+3}_{-1}\, {^{[118]}}$| | -5.29 ± 0.04[85] |
| CPD-271791 | 3.69 ± 0.09 | 23.8 ± 1.6[127] | 8.8 ± 0.4 | 37[89] | 2.641[89] | – | >3.9[89] | <-4.71[6] |
| HD3360f | 3.82 ± 0.06 | 20.8 ± 0.2[104] | 8.6 ± 0.1 | 19[93] | 5.370[25] | 82|$^{+ 1}_{- 1}$| | 0.15|$^{+0.03}_{-0.03}\, {^{[107]}}$| | <-7.79[85, 127] |
| HD5737 | 3.33 ± 0.16 | 13.9 ± 0.4[41] | 5.0 ± 0.4 | 17[106] | 21.7[23] | 73|$^{+ 6}_{- 7}$| | 1.8|$^{+0.2}_{-0.3}\, {^{[4,10,18,127]}}$| | <-6.44[6] |
| HD11503f | 1.52 ± 0.03 | 10.1 ± 0.2[102] | 2.35 ± 0.03 | 54[102] | 1.610[103] | 84|$^{+ 4}_{-37}$| | 2.3|$^{+3.7}_{-0.7}\, {} ^{[103]}$| | -7.85 ± 0.04[14, 127] |
| HD12447 | 1.73 ± 0.06 | 10.0 ± 0.2[102] | 2.49 ± 0.05 | 70[102] | 1.491[103] | 87|$^{+ 1}_{- 9}$| | 1.7|$^{+0.5}_{-0.4}\, {}^{[103,127]}$| | -7.40 ± 0.04[34] |
| HD12767 | 2.43 ± 0.15 | 13.0 ± 0.3[41] | 4.0 ± 0.1 | 40[30] | 1.892[23] | 89|$^{+ 0}_{- 3}$| | 2.0|$^{+0.5}_{-0.6}\, {} ^{[9,113,127]}$| | <-6.88[125] |
| HD19832 | 2.08 ± 0.16 | 12.4 ± 0.4[41] | 3.3 ± 0.1 | 160[96] | 0.728[111] | 89|$^{+ 0}_{- 3}$| | 2.7|$^{+0.6}_{-0.3}\, {} ^{[111]}$| | -6.70 ± 0.04[34] |
| HD21699mr | 2.78 ± 0.04 | 16.0 ± 0.1[41] | 4.7 ± 0.2 | 35[106] | 2.492[23, 127] | 78|$^{+ 2}_{- 2}$| | 2.8|$^{+0.5}_{-0.1}\, {} ^{[5,127]}$| | <-6.49[6] |
| HD22470 | 2.43 ± 0.13 | 13.8 ± 0.3[41] | 3.8 ± 0.2 | 62[30] | 1.929[111] | 87|$^{+ 1}_{- 2}$| | 7.5|$^{+1.2}_{-0.5}\, {} ^{[111]}$| | <-6.87[6] |
| HD22920mr | 2.64 ± 0.12 | 13.6 ± 0.2[67] | 4.2 ± 0.1 | 34[30] | 3.947[20, 127] | 28|$^{+ 6}_{- 7}$| | 1.6|$^{+1.1}_{-0.0}\, {} ^{[4,127]}$| | <-6.77[125] |
| HD25267 | 2.32 ± 0.03 | 12.6 ± 0.2[116] | 3.5 ± 0.2 | 20[102] | 3.823[116] | 17|$^{+ 7}_{- 8}$| | 1.0|$^{+0.1}_{-0.1}\, {} ^{[116]}$| | <-7.25[125] |
| HD27309 | 1.88 ± 0.02 | 11.2 ± 0.3[102] | 2.81 ± 0.04 | 56[102] | 1.569[103] | 3|$^{+ 5}_{- 3}$| | 1.9|$^{+2.6}_{-0.6}\, {} ^{[103]}$| | -7.20 ± 0.04[34] |
| HD28843mr | 2.51 ± 0.07 | 14.8 ± 0.2[41] | 4.20 ± 0.06 | 91[127] | 1.374[23, 127] | 87|$^{+ 1}_{- 5}$| | 0.93|$^{+0.30}_{-0.24}\, {} ^{[4,127]}$| | <-6.85[6] |
| HD32633 | 1.94 ± 0.12 | 12.5 ± 0.5[87] | 3.50 ± 0.09 | 25[96] | 6.430[19] | 76|$^{+ 3}_{- 3}$| | 17|$^{+1}_{-2}\, {} ^{[58,73]}$| | <-6.74[14] |
| HD34452 | 2.45 ± 0.27 | 13.8 ± 0.8[41] | 4.2 ± 0.1 | 53[96] | 2.469[23] | 35|$^{+13}_{-16}$| | 3.6|$^{+1.1}_{-1.4}\, {} ^{[3,15,127]}$| | -6.69 ± 0.04[6, 14] |
| HD35298 | 2.40 ± 0.14 | 15.8 ± 0.8[104] | 4.3 ± 0.2 | 60[93] | 1.855[93] | 77|$^{+ 2}_{- 2}$| | 11|$^{+1}_{-1}\, {} ^{[107]}$| | -5.35 ± 0.04[14, 29, 34] |
| HD35456 | 2.88 ± 0.29 | 13.5 ± 1.4[127] | 4.1 ± 0.5 | 22[77] | 4.951[77] | 15|$^{+ 9}_{-11}$| | 2.2|$^{+0.2}_{-0.3}\, {} ^{[77,127]}$| | <-6.19[125] |
| HD35502f | 2.95 ± 0.12 | 18.4 ± 0.6[104] | 5.8 ± 0.2 | 78[93] | 0.854[78] | 70|$^{+ 1}_{- 1}$| | 7.3|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | -5.05 ± 0.04[34, 127] |
| HD35575r | 3.11 ± 0.09 | 16.7 ± 1.3[127] | 5.8 ± 0.3 | 150[99] | 0.984[127] | – | <1.3[99, 127] | <-7.09[16] |
| HD36313r | 2.04 ± 0.19 | 13.0 ± 0.5[114] | 3.4 ± 0.2 | 160[114] | 0.589[114, 127] | 88|$^{+ 1}_{- 5}$| | 9.0|$^{+1.8}_{-1.3}\, {} ^{[114,127]}$| | -6.10 ± 0.04[34] |
| HD36429mr | 2.42 ± 0.02 | 13.8 ± 0.1[127] | 3.87 ± 0.03 | 77[127] | 15.6[127] | – | <0.20[26, 127] | <-6.13[125] |
| HD36485 | 3.10 ± 0.20 | 20.0 ± 2.0[104] | 6.3 ± 0.2 | 33[93] | 1.478[48] | 3|$^{+ 1}_{- 1}$| | 8.9|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | -5.43 ± 0.04[6, 14, 29, 72] |
| HD36526f | 2.30 ± 0.24 | 15.0 ± 2.0[104] | 4.3 ± 0.2 | 59[93] | 1.542[93] | 56|$^{+ 1}_{- 2}$| | 11|$^{+0}_{-0}\, {} ^{[107]}$| | <-6.29[14, 127] |
| HD36540mr | 2.73 ± 0.15 | 14.9 ± 0.7[87] | 4.54 ± 0.09 | 80[83] | 2.173[127] | 9|$^{+26}_{- 8}$| | 1.4|$^{+3.2}_{-0.1}\, {} ^{[83,127]}$| | <-5.99[125] |
| HD36668mr | 2.40 ± 0.19 | 13.5 ± 0.2[114] | 3.81 ± 0.05 | 60[114] | 2.119[114, 127] | 80|$^{+ 5}_{- 6}$| | 4.5|$^{+2.3}_{-2.7}\, {} ^{[114,127]}$| | <-6.05[125] |
| HD36916mr | 2.10 ± 0.20 | 14.7 ± 0.2[83] | 4.2 ± 0.1 | 78[83] | 1.565[83, 127] | 30|$^{+ 8}_{-10}$| | 3.4|$^{+3.3}_{-0.2}\, {} ^{[4,66,83,91,111,127]}$| | <-6.92[14, 16] |
| HD37017 | 3.42 ± 0.25 | 21.0 ± 2.0[104] | 8.4 ± 0.5 | 134[93] | 0.901[93] | 56|$^{+ 2}_{- 3}$| | 6.2|$^{+0.9}_{-0.9}\, {} ^{[107]}$| | -5.11 ± 0.04[6, 14, 17, 29, 72, 82, 124] |
| HD37058 | 2.90 ± 0.11 | 18.6 ± 0.6[104] | 5.8 ± 0.2 | 11[93] | 14.6[93] | 55|$^{+11}_{-13}$| | 2.5|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-5.95[14] |
| HD37061f | 3.30 ± 0.30 | 22.0 ± 1.0[104] | 7.7 ± 0.4 | 100[93] | 1.095[101] | 59|$^{+ 4}_{- 4}$| | 9.2|$^{+1.0}_{-1.0}\, {} ^{[107]}$| | -5.68 ± 0.04[82, 127] |
| HD37140mr | 2.12 ± 0.09 | 13.5 ± 0.2[114] | 3.46 ± 0.05 | 25[127] | 2.761[114, 127] | 80|$^{+ 3}_{- 4}$| | 3.9|$^{+0.7}_{-0.4}\, {} ^{[114,127]}$| | <-6.08[125] |
| HD37151 | 2.08 ± 0.08 | 13.5 ± 0.9[127] | 3.4 ± 0.2 | – | – | 87|$^{+ 1}_{-12}$| | 1.4|$^{+1.2}_{-1.4}\, {} ^{[115,127]}$| | <-6.39[125] |
| HD37210mr | 2.51 ± 0.05 | 13.5 ± 0.6[127] | 3.92 ± 0.09 | 20[115] | 11.0[20, 127] | 78|$^{+ 7}_{- 8}$| | 1.8|$^{+0.9}_{-0.1}\, {} ^{[66,115,127]}$| | <-5.71[125] |
| HD37479 | 3.51 ± 0.21 | 23.0 ± 2.0[104] | 7.9 ± 0.2 | 145[93] | 1.191[47] | 37|$^{+ 7}_{-10}$| | 10|$^{+11}_{-0}\, {} ^{[71]}$| | -4.73 ± 0.04[6, 14, 17, 29, 72] |
| HD37642mr | 2.42 ± 0.10 | 16.0 ± 0.5[115] | 4.3 ± 0.1 | 85[115] | 1.079[115, 127] | 74|$^{+ 3}_{- 3}$| | 18|$^{+1}_{-0}\, {} ^{[115,127]}$| | -5.69 ± 0.04[34] |
| HD37752 | 2.63 ± 0.14 | 15.0 ± 0.7[41] | 4.5 ± 0.2 | 35[30] | 1.305[87] | – | <2.4[26] | <-7.08[16] |
| HD37776f | 3.30 ± 0.15 | 22.0 ± 1.0[104] | 8.3 ± 0.3 | 101[93] | 1.539[81] | 47|$^{+ 8}_{-10}$| | 6.1|$^{+0.7}_{-0.7}\, {} ^{[54,107]}$| | <-6.35[6, 127] |
| HD37808mr | 2.28 ± 0.10 | 14.5 ± 0.2[115] | 3.90 ± 0.08 | 30[96] | 1.099[109, 115, 127] | 45|$^{+20}_{-24}$| | 3.2|$^{+1.0}_{-0.3}\, {} ^{[115,127]}$| | -6.16 ± 0.04[16, 29] |
| HD40312 | 2.33 ± 0.01 | 10.2 ± 0.1[102] | 3.11 ± 0.06 | 55[96] | 3.619[103] | 68|$^{+13}_{-15}$| | 1.3|$^{+0.4}_{-0.2}\, {} ^{[97]}$| | -7.78 ± 0.04[14] |
| HD41269mr | 2.30 ± 0.08 | 12.9 ± 0.9[127] | 3.5 ± 0.2 | 85[30] | 1.048[127] | 0|$^{+16}_{- 0}$| | 1.3|$^{+0.5}_{-0.3}\, {} ^{[127]}$| | <-7.20[16] |
| HD43819 | 2.15 ± 0.20 | 10.9 ± 0.4[38] | 3.1 ± 0.2 | 10[38] | 15.0[38] | 47|$^{+16}_{-19}$| | 2.6|$^{+75.7}_{-0.1}\, {} ^{[38]}$| | <-6.79[16] |
| HD45583 | 2.07 ± 0.12 | 13.3 ± 0.3[42] | 3.35 ± 0.09 | 70[96] | 1.177[111] | 69|$^{+ 2}_{- 2}$| | 9.1|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.24 ± 0.04[34, 124] |
| HD46328 | 4.49 ± 0.11 | 27.0 ± 1.0[104] | 14.4 ± 0.8 | 8[93] | 30.0 (yr)[88, 95, 120] | 89|$^{+ 0}_{- 9}$| | 1.2|$^{+0.6}_{-0.1}\, {} ^{[107]}$| | <-7.03[85] |
| HD47777 | 3.42 ± 0.15 | 22.0 ± 1.0[104] | 7.9 ± 0.4 | 60[93] | 2.640[61] | 82|$^{+ 5}_{- 5}$| | 3.3|$^{+0.7}_{-0.7}\, {} ^{[107]}$| | <-6.40[85] |
| HD49333 | 2.73 ± 0.04 | 15.8 ± 0.1[41] | 4.8 ± 0.3 | 65[30] | 2.180[23] | 85|$^{+ 3}_{-12}$| | 3.6|$^{+1.0}_{-1.2}\, {} ^{[15,127]}$| | <-6.49[14] |
| HD49606mr | 2.59 ± 0.06 | 13.5 ± 0.1[41] | 4.08 ± 0.06 | 19[96] | 8.546[123] | – | <0.040[127] | <-6.25[125] |
| HD51418mr | 1.80 ± 0.04 | 9.5 ± 0.8[100] | 2.48 ± 0.09 | 28[84] | 5.431[113, 127] | 89|$^{+ 0}_{- 0}$| | 3.5|$^{+1.0}_{-0.4}\, {} ^{[84,127]}$| | <-6.65[125] |
| HD55522f | 3.00 ± 0.18 | 17.4 ± 0.4[104] | 5.9 ± 0.2 | 70[93] | 2.729[93] | 89|$^{+ 0}_{- 1}$| | 3.1|$^{+0.4}_{-0.4}\, {} ^{[107]}$| | <-6.16[127] |
| HD58260 | 3.22 ± 0.26 | 19.3 ± 1.3[104] | 6.2 ± 0.5 | 3[93] | – | 0|$^{+ 5}_{- 0}$| | 6.5|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | <-6.69[6, 85] |
| HD60344r | 3.58 ± 0.09 | 21.0 ± 0.3[41] | 7.9 ± 0.2 | 55[106] | – | – | >1.2[89, 127] | <-4.76[6] |
| HD61556f | 3.12 ± 0.24 | 18.5 ± 0.8[70] | 6.1 ± 0.3 | 58[70] | 1.909[70] | 58|$^{+ 6}_{- 7}$| | 2.8|$^{+0.3}_{-0.3}\, {} ^{[107]}$| | -5.93 ± 0.04[117, 127] |
| HD64740f | 3.81 ± 0.15 | 24.5 ± 1.0[104] | 10.1 ± 0.5 | 135[93] | 1.330[93] | 71|$^{+ 5}_{- 5}$| | 3.0|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | -7.19 ± 0.04[127] |
| HD65339 | 1.45 ± 0.02 | 8.5 ± 0.1[102] | 2.09 ± 0.02 | 13[96] | 8.027[103] | 89|$^{+ 0}_{- 1}$| | 15|$^{+2}_{-1}\, {} ^{[28]}$| | <-7.50[6, 14] |
| HD66665 | 4.69 ± 0.23 | 28.5 ± 1.0[104] | 15.9 ± 1.1 | 8[93] | 24.5[93] | 75|$^{+ 3}_{- 3}$| | 0.56|$^{+0.10}_{-0.10}\, {} ^{[107]}$| | <-4.96[85] |
| HD66765f | 3.44 ± 0.24 | 20.0 ± 2.0[63] | 7.2 ± 0.6 | 58[93] | 1.608[93] | 73|$^{+ 5}_{- 5}$| | 2.8|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-6.23[127] |
| HD79158 | 2.61 ± 0.06 | 13.3 ± 0.1[41] | 4.3 ± 0.1 | 49[96] | 3.835[92] | 87|$^{+ 1}_{- 4}$| | 3.1|$^{+0.4}_{-0.4}\, {} ^{[92]}$| | -6.55 ± 0.04[6, 34] |
| HD90044 | 1.66 ± 0.10 | 10.0 ± 0.2[87] | 2.8 ± 0.3 | 23[102] | 4.379[23] | 89|$^{+ 0}_{- 0}$| | 4.4|$^{+1.2}_{-1.5}\, {} ^{[15,22,127]}$| | <-7.71[16] |
| HD105382 | 3.04 ± 0.16 | 18.0 ± 0.5[24] | 5.8 ± 0.2 | 74[93] | 1.295[24] | 51|$^{+ 7}_{- 8}$| | 2.6|$^{+0.1}_{-0.1}\, {} ^{[107]}$| | -6.07 ± 0.04[117] |
| HD112413 | 1.97 ± 0.02 | 11.3 ± 0.2[102] | 2.93 ± 0.03 | 15[96] | 5.469[103] | 88|$^{+ 1}_{- 8}$| | 3.5|$^{+0.8}_{-0.2}\, {} ^{[64,65]}$| | -8.13 ± 0.04[6, 34] |
| HD118022 | 1.53 ± 0.04 | 9.4 ± 0.1[102] | 2.26 ± 0.02 | 12[102] | 3.722[103] | 65|$^{+15}_{-17}$| | 3.2|$^{+8.0}_{-0.2}\, {} ^{[103]}$| | -7.41 ± 0.04[121] |
| HD122532 | 2.37 ± 0.12 | 11.9 ± 0.5[87] | 2.99 ± 0.04 | – | 3.681[12] | 89|$^{+ 0}_{- 3}$| | 3.0|$^{+0.7}_{-0.9}\, {} ^{[7,13,15,113,127]}$| | <-7.00[14] |
| HD124224 | 1.93 ± 0.01 | 12.3 ± 0.2[102] | 3.02 ± 0.01 | 169[102] | 0.521[81] | 87|$^{+ 2}_{-11}$| | 4.0|$^{+0.3}_{-0.2}\, {} ^{[62]}$| | -6.24 ± 0.04[16, 18, 29, 34, 117, 122] |
| HD125248 | 1.39 ± 0.23 | 9.7 ± 0.3[41] | 2.42 ± 0.07 | 11[96] | 9.300[39] | 89|$^{+ 0}_{- 3}$| | 9.0|$^{+1.1}_{-1.3}\, {} ^{[75]}$| | <-7.17[125] |
| HD125823 | 3.16 ± 0.20 | 19.0 ± 2.0[104] | 5.9 ± 0.2 | 16[93] | 8.817[93] | 75|$^{+ 4}_{- 6}$| | 1.8|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | <-6.54[6] |
| HD126515 | 1.36 ± 0.16 | 8.9 ± 0.2[127] | 2.65 ± 0.07 | 16[127] | 129.9[21] | 84|$^{+ 4}_{-13}$| | 13|$^{+1}_{-0}\, {} ^{[21]}$| | <-7.13[14] |
| HD131120mr | 3.15 ± 0.09 | 19.4 ± 1.5[127] | 6.3 ± 0.3 | 57[30] | 1.569[55, 127] | – | <0.17[66] | <-6.97[14] |
| HD133029mr | 1.98 ± 0.08 | 11.8 ± 0.9[41] | 2.8 ± 0.1 | 27[30] | 2.888[44, 127] | 12|$^{+ 4}_{- 4}$| | 9.0|$^{+5.0}_{-0.3}\, {} ^{[3,127]}$| | <-6.89[14] |
| HD133652 | 2.02 ± 0.10 | 12.8 ± 0.5[87] | 3.27 ± 0.09 | 48[96] | 2.304[23] | 65|$^{+ 8}_{-11}$| | 7.6|$^{+0.8}_{-1.0}\, {} ^{[15,127]}$| | -7.16 ± 0.04[34] |
| HD133880 | 1.73 ± 0.06 | 10.7 ± 0.1[41] | 3.08 ± 0.08 | 103[96] | 0.877[80] | 83|$^{+ 1}_{- 1}$| | 12|$^{+0}_{-1}\, {} ^{[80]}$| | -5.44 ± 0.04[72, 34] |
| HD135679mr | 2.46 ± 0.19 | 15.1 ± 2.8[127] | 2.86 ± 0.06 | 1[84] | 5.321[127] | 14|$^{+ 6}_{- 8}$| | 4.4|$^{+9.3}_{-0.2}\, {} ^{[84,91,127]}$| | <-7.04[16] |
| HD137193mr | 1.91 ± 0.13 | 10.6 ± 0.7[87] | 3.5 ± 0.2 | – | 4.867[127] | 0|$^{+25}_{- 0}$| | 3.5|$^{+16.1}_{-0.5}\, {} ^{[8,127]}$| | <-6.51[14] |
| HD137909 | 1.46 ± 0.01 | 7.5 ± 0.1[102] | 1.98 ± 0.03 | 3[96] | 18.5[103] | 89|$^{+ 0}_{- 2}$| | 5.2|$^{+7.1}_{-1.0}\, {} ^{[103,127]}$| | <-7.90[6] |
| HD138764 | 2.62 ± 0.17 | 15.7 ± 2.7[127] | 4.3 ± 0.4 | 19[30] | 1.259[87] | – | <0.049[46] | <-7.63[16] |
| HD142184 | 2.85 ± 0.13 | 18.5 ± 0.5[104] | 5.7 ± 0.1 | 288[93] | 0.508[56] | 8|$^{+ 3}_{- 3}$| | 9.0|$^{+2.0}_{-2.0}\, {} ^{[107]}$| | -4.25 ± 0.04[94, 117] |
| HD142301 | 2.56 ± 0.07 | 15.9 ± 0.2[41] | 4.46 ± 0.05 | 78[30] | 1.459[111] | 47|$^{+ 9}_{-11}$| | 12|$^{+9}_{-0}\, {} ^{[111]}$| | -5.62 ± 0.04[14, 16, 17, 29] |
| HD142884mr | 2.17 ± 0.12 | 14.3 ± 0.5[87] | 3.7 ± 0.1 | 127[30] | 0.803[109] | – | <0.75[4, 127] | <-6.84[14] |
| HD142990 | 2.93 ± 0.13 | 18.0 ± 0.5[104] | 5.6 ± 0.2 | 122[93] | 0.979[105] | 83|$^{+ 2}_{- 3}$| | 4.7|$^{+0.4}_{-0.4}\, {} ^{[107]}$| | -5.77 ± 0.04[14, 16, 17, 29, 98] |
| HD143473 | 1.87 ± 0.10 | 12.4 ± 1.0[87] | 2.25 ± 0.08 | 25[30] | 2.843[25] | 18|$^{+ 5}_{- 6}$| | 18|$^{+2}_{-2}\, {} ^{[13,15,127]}$| | -6.56 ± 0.04[34] |
| HD143699mr | 2.65 ± 0.12 | 15.5 ± 0.4[41] | 4.6 ± 0.2 | 115[127] | 0.894[127] | – | <0.60[4, 37, 127] | -7.21 ± 0.04[14, 125] |
| HD144334 | 2.34 ± 0.12 | 14.8 ± 0.4[41] | 4.0 ± 0.1 | 82[30] | 1.495[111] | 55|$^{+ 7}_{- 8}$| | 3.6|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.79 ± 0.04[14, 16, 29] |
| HD145102 | 2.02 ± 0.12 | 10.8 ± 0.5[87] | 3.0 ± 0.1 | 84[30] | 1.418[57] | – | <0.98[8] | <-6.90[125] |
| HD145482r | 3.59 ± 0.17 | 24.2 ± 4.3[127] | 8.1 ± 0.8 | 166[30] | 5.804[127] | – | <0.38[8] | <-6.94[14] |
| HD145501C | 2.46 ± 0.15 | 14.5 ± 0.5[87] | 4.0 ± 0.2 | 70[30] | 1.026[111] | 89|$^{+ 0}_{- 2}$| | 5.8|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.08 ± 0.04[14, 16, 124] |
| HD146001mr | 2.38 ± 0.14 | 13.8 ± 0.3[41] | 3.61 ± 0.06 | 90[30] | 0.586[57] | – | <0.50[4, 127] | -6.87 ± 0.04[14] |
| HD147010 | 1.65 ± 0.08 | 12.5 ± 0.6[87] | 2.45 ± 0.09 | 15[96] | 3.921[60] | 10|$^{+ 4}_{- 5}$| | 19|$^{+0}_{-0}\, {} ^{[18,113,127]}$| | <-7.10[14] |
| HD147890 | 2.43 ± 0.12 | 11.3 ± 0.5[87] | 3.7 ± 0.2 | 65[30] | 4.336[57] | – | <0.90[8] | <-6.24[125] |
| HD147932 | 2.50 ± 0.20 | 17.0 ± 1.0[111] | 4.8 ± 0.3 | 140[52] | 0.864[90] | 0|$^{+ 6}_{- 0}$| | 7.6|$^{+9.6}_{-0.5}\, {} ^{[111,126]}$| | -5.14 ± 0.04[112] |
| HD147933 | 3.30 ± 0.17 | 20.8 ± 0.5[110] | 7.3 ± 0.2 | 200[110] | 0.747[110] | 75|$^{+ 9}_{-11}$| | 4.7|$^{+0.5}_{-0.4}\, {} ^{[110,126]}$| | -5.55 ± 0.04[110] |
| HD148112 | 1.85 ± 0.02 | 9.2 ± 0.1[102] | 2.52 ± 0.01 | 44[38] | 3.044[103] | 0|$^{+ 9}_{- 0}$| | 0.76|$^{+0.41}_{-0.11}\, {} ^{[103,127]}$| | <-7.19[6] |
| HD148199 | 1.88 ± 0.12 | 11.7 ± 0.7[87] | 2.5 ± 0.1 | 15[30] | 7.726[25] | 63|$^{+ 9}_{-12}$| | 5.0|$^{+0.6}_{-0.7}\, {} ^{[8,15,127]}$| | <-6.54[14] |
| HD149438 | 4.47 ± 0.13 | 32.0 ± 1.0[104] | 17.5 ± 0.9 | 7[93] | 41.0[35] | 75|$^{+ 7}_{- 8}$| | 0.31|$^{+0.10}_{-0.01}\, {} ^{[77]}$| | <-7.83[85] |
| HD149822mr | 1.85 ± 0.18 | 10.8 ± 0.3[41] | 2.7 ± 0.2 | 60[30] | 1.966[127] | 87|$^{+ 2}_{- 3}$| | 4.0|$^{+2.1}_{-1.1}\, {} ^{[15,36,66,127]}$| | <-7.36[16] |
| HD151346 | 2.44 ± 0.17 | 13.7 ± 1.1[87] | 3.8 ± 0.2 | 46[30] | 2.180[87] | – | <1.7[4] | <-6.66[14] |
| HD152107 | 1.47 ± 0.01 | 8.8 ± 0.1[102] | 2.15 ± 0.01 | 21[102] | 3.857[103] | 19|$^{+ 4}_{- 5}$| | 4.2|$^{+0.5}_{-0.2}\, {} ^{[103,127]}$| | <-8.01[6, 14] |
| HD156424 | 3.00 ± 0.40 | 18.0 ± 3.0[119] | 4.6 ± 0.3 | 7[93] | 0.524[119] | 39|$^{+18}_{-21}$| | 8.0|$^{+12.0}_{-2.0}\, {} ^{[119]}$| | -4.91 ± 0.04[85] |
| HD163472 | 3.81 ± 0.10 | 25.2 ± 1.1[104] | 10.3 ± 0.5 | 62[93] | 3.639[27] | 46|$^{+13}_{-14}$| | 1.1|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-6.83[85] |
| HD164429mr | 1.85 ± 0.04 | 12.0 ± 0.5[127] | 2.99 ± 0.06 | 90[30] | 1.082[127] | 88|$^{+ 1}_{-12}$| | 3.0|$^{+0.7}_{-0.3}\, {} ^{[15,127]}$| | -6.91 ± 0.04[16, 34] |
| HD165474 | 2.06 ± 0.26 | 13.2 ± 3.4[127] | 1.82 ± 0.08 | 18[30] | 9.0 (yr)[79] | 89|$^{+ 0}_{- 0}$| | 3.0|$^{+4.9}_{-1.8}\, {} ^{[79,127]}$| | <-6.96[125] |
| HD168785r | 3.48 ± 0.08 | 23.0 ± 1.2[127] | 8.1 ± 0.4 | 14[106] | – | – | >4.0[89] | <-5.25[125] |
| HD168856mr | 2.10 ± 0.09 | 11.9 ± 1.2[127] | 3.0 ± 0.1 | 73[76] | 2.428[109] | 55|$^{+15}_{-16}$| | 3.5|$^{+3.7}_{-0.6}\, {} ^{[76,84,35,127]}$| | <-6.77[125] |
| HD170000 | 2.36 ± 0.01 | 11.6 ± 0.0[102] | 3.47 ± 0.02 | 83[102] | 1.716[103] | 70|$^{+10}_{-12}$| | 1.8|$^{+0.0}_{-0.1}\, {} ^{[103]}$| | -7.11 ± 0.04[34] |
| HD170973mr | 2.32 ± 0.13 | 10.8 ± 0.2[41] | 3.39 ± 0.06 | 4[96] | 18.1[127] | 83|$^{+ 2}_{- 3}$| | 4.8|$^{+11.2}_{-0.5}\, {} ^{[15,13,127]}$| | <-6.56[125] |
| HD171247mr | 2.79 ± 0.16 | 12.2 ± 0.3[41] | 4.0 ± 0.2 | 68[96] | 3.910[127] | 85|$^{+ 3}_{-34}$| | 4.1|$^{+3.1}_{-0.4}\, {} ^{[127]}$| | -5.16 ± 0.04[16, 29] |
| HD175132r | 2.78 ± 0.04 | 13.2 ± 0.5[127] | 4.0 ± 0.2 | 40[30] | 8.030[127] | – | >3.5[26] | <-6.69[16, 125] |
| HD175362f | 2.64 ± 0.12 | 17.6 ± 0.4[104] | 5.3 ± 0.2 | 34[93] | 3.674[93] | 68|$^{+ 5}_{- 6}$| | 17|$^{+0}_{-0}\, {} ^{[107]}$| | -6.72 ± 0.04[14, 16, 17, 127] |
| HD175744mr | 2.65 ± 0.09 | 12.6 ± 0.2[41] | 4.00 ± 0.08 | 50[30] | 2.799[127] | – | <0.50[31, 108, 127] | <-7.25[16, 125] |
| HD176582 | 2.90 ± 0.15 | 17.0 ± 1.0[104] | 5.6 ± 0.2 | 103[93] | 1.582[53] | 89|$^{+ 0}_{- 1}$| | 5.4|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | -6.07 ± 0.04[34] |
| HD177003 | 3.05 ± 0.10 | 17.7 ± 0.7[87] | 5.7 ± 0.2 | 12[30] | 1.800[87] | – | <0.81[26] | <-7.19[16] |
| HD177410m | 2.30 ± 0.15 | 14.5 ± 0.5[32] | 3.6 ± 0.1 | 100[32] | 1.123[45] | – | <1.7[15, 68, 127] | <-7.23[16] |
| HD179527 | 2.63 ± 0.16 | 10.4 ± 0.3[38] | 3.39 ± 0.05 | 33[38] | 7.098[38] | 88|$^{+ 1}_{-12}$| | 0.52|$^{+0.71}_{-0.11}\, {} ^{[38]}$| | <-6.54[125] |
| HD182180f | 3.09 ± 0.18 | 19.8 ± 1.4[104] | 6.5 ± 0.2 | 306[93] | 0.521[50, 49] | 81|$^{+ 3}_{- 4}$| | 9.5|$^{+0.6}_{-0.6}\, {} ^{[107]}$| | -4.65 ± 0.04[86, 127] |
| HD183056 | 2.69 ± 0.11 | 11.7 ± 0.4[38] | 4.0 ± 0.2 | 35[96] | 2.992[38] | 82|$^{+ 3}_{- 4}$| | 1.6|$^{+2.4}_{-0.4}\, {} ^{[38]}$| | <-7.14[16] |
| HD183339r | 2.70 ± 0.05 | 14.0 ± 0.6[127] | 4.3 ± 0.1 | 41[30] | 4.204[127] | – | >4.5[26] | <-6.39[125] |
| HD184927f | 3.59 ± 0.16 | 22.0 ± 1.0[104] | 8.4 ± 0.5 | 8[93] | 9.531[69] | 67|$^{+ 3}_{- 4}$| | 8.8|$^{+1.4}_{-0.5}\, {} ^{[69]}$| | <-6.06[16, 125, 127] |
| HD184961mr | 2.35 ± 0.08 | 11.8 ± 1.0[127] | 3.47 ± 0.09 | 34[30] | 6.335[127] | 4|$^{+ 3}_{- 4}$| | 4.3|$^{+9.0}_{-0.4}\, {} ^{[127]}$| | <-6.36[125] |
| HD186205 | 3.84 ± 0.25 | 19.6 ± 0.8[104] | 8.3 ± 0.6 | 6[93] | 37.2[93] | 7|$^{+ 3}_{- 4}$| | 3.0|$^{+1.0}_{-0.5}\, {} ^{[107]}$| | <-4.82[125] |
| HD187474 | 1.76 ± 0.03 | 9.9 ± 0.1[102] | 2.52 ± 0.02 | 0[96] | 6.4 (yr)[103] | 89|$^{+ 0}_{- 3}$| | 7.2|$^{+2.1}_{-0.2}\, {} ^{[103]}$| | <-7.29[125] |
| HD188041mr | 1.40 ± 0.01 | 8.5 ± 0.1[102] | 2.07 ± 0.04 | 4[96] | 224.0[103] | 0|$^{+25}_{- 0}$| | 4.1|$^{+16.6}_{-0.4}\, {} ^{[103,127]}$| | <-7.46[125] |
| HD189775f | 2.91 ± 0.11 | 17.5 ± 0.6[104] | 5.6 ± 0.2 | 58[93] | 2.607[93] | 43|$^{+11}_{-12}$| | 4.3|$^{+0.7}_{-0.7}\, {} ^{[107]}$| | -5.83 ± 0.04[127] |
| HD192678 | 1.65 ± 0.27 | 9.0 ± 0.1[41] | 2.5 ± 0.2 | 6[127] | 12.9[21] | 25|$^{+11}_{-12}$| | 5.5|$^{+4.4}_{-0.1}\, {} ^{[21,127]}$| | <-6.79[125] |
| HD196178mr | 2.15 ± 0.10 | 13.1 ± 0.5[87] | 4.2 ± 0.2 | 50[32] | 1.101[127] | 41|$^{+ 7}_{- 9}$| | 3.9|$^{+0.4}_{-0.2}\, {} ^{[3,127]}$| | -5.99 ± 0.04[34] |
| HD196502 | 2.01 ± 0.39 | 8.9 ± 0.4[41] | 2.55 ± 0.05 | 9[96] | 20.3[25] | 88|$^{+ 1}_{-12}$| | 1.7|$^{+0.3}_{-0.3}\, {} ^{[1,2,11,113,127]}$| | <-6.54[6] |
| HD200775f | 3.95 ± 0.30 | 18.6 ± 2.0[43] | 9.0 ± 0.8 | 26[43] | 4.381[43] | 89|$^{+ 0}_{- 6}$| | 3.9|$^{+1.7}_{-0.7}\, {} ^{[45,127]}$| | -6.11 ± 0.04[127] |
| HD202671 | 2.70 ± 0.07 | 13.2 ± 0.1[41] | 4.0 ± 0.2 | 20[96] | 1.992[87] | – | <0.056[51] | <-7.04[125] |
| HD205021f | 4.26 ± 0.11 | 25.0 ± 1.0[104] | 11.9 ± 1.1 | 34[93] | 12.0[59] | 86|$^{+ 2}_{- 4}$| | 0.26|$^{+0.03}_{-0.03}\, {} ^{[107]}$| | <-7.42[85, 127] |
| HD208057f | 3.01 ± 0.11 | 16.5 ± 1.2[104] | 5.3 ± 0.3 | 105[93] | 1.368[93] | 89|$^{+ 0}_{- 0}$| | 0.60|$^{+0.20}_{-0.20}\, {} ^{[107]}$| | <-7.30[127] |
| HD215441 | 2.31 ± 0.09 | 14.5 ± 0.4[41] | 3.9 ± 0.1 | 5[96] | 9.490[21] | 37|$^{+ 7}_{- 7}$| | 62|$^{+6}_{-3}\, {} ^{[21]}$| | -5.13 ± 0.04[6, 14, 17, 29, 72] |
| HD224801 | 2.19 ± 0.10 | 11.9 ± 0.5[87] | 3.2 ± 0.1 | 27[30] | 3.740[20] | – | >4.6[1] | <-6.61[125] |
| HD260858r | 3.52 ± 0.27 | 18.0 ± 1.0[41] | 6.7 ± 0.4 | 47[106] | – | – | >1.8[91] | <-4.86[6] |
| HD335238 | 1.62 ± 0.23 | 9.4 ± 0.5[87] | 2.25 ± 0.04 | – | 48.7[79] | 85|$^{+ 4}_{-44}$| | 5.9|$^{+2.0}_{-2.5}\, {} ^{[79,108,127]}$| | <-6.18[125] |
| Star . | |$\log {\frac{L_{\rm bol}}{L_\odot }}$| . | |$\frac{T_{\rm eff}}{{\rm kK}}$| . | |$\frac{M_*}{{\rm M_\odot }}$| . | |$\frac{v\sin {i}}{{\rm km~s^{-1}}}$| . | |$\frac{P_{\rm rot}}{{\rm d}}$| . | |$\frac{\beta }{{\rm deg}}$| . | |$\frac{B_{\rm d}}{{\rm kG}}$| . | |$\log {\frac{L_{\rm rad}}{{\rm L_\odot }}}$| . |
|---|---|---|---|---|---|---|---|---|
| ALS8988r | 4.05 ± 0.27 | 27.3 ± 1.4[127] | 10.6 ± 0.6 | 23[40] | – | – | >1.5[40] | <-4.40[85] |
| ALS9522 | 3.65 ± 0.12 | 22.4 ± 1.1[118] | 6.0 ± 0.1 | 105[118] | 1.091[118] | 78|$^{+ 2}_{- 3}$| | 11|$^{+3}_{-1}\, {^{[118]}}$| | -5.29 ± 0.04[85] |
| CPD-271791 | 3.69 ± 0.09 | 23.8 ± 1.6[127] | 8.8 ± 0.4 | 37[89] | 2.641[89] | – | >3.9[89] | <-4.71[6] |
| HD3360f | 3.82 ± 0.06 | 20.8 ± 0.2[104] | 8.6 ± 0.1 | 19[93] | 5.370[25] | 82|$^{+ 1}_{- 1}$| | 0.15|$^{+0.03}_{-0.03}\, {^{[107]}}$| | <-7.79[85, 127] |
| HD5737 | 3.33 ± 0.16 | 13.9 ± 0.4[41] | 5.0 ± 0.4 | 17[106] | 21.7[23] | 73|$^{+ 6}_{- 7}$| | 1.8|$^{+0.2}_{-0.3}\, {^{[4,10,18,127]}}$| | <-6.44[6] |
| HD11503f | 1.52 ± 0.03 | 10.1 ± 0.2[102] | 2.35 ± 0.03 | 54[102] | 1.610[103] | 84|$^{+ 4}_{-37}$| | 2.3|$^{+3.7}_{-0.7}\, {} ^{[103]}$| | -7.85 ± 0.04[14, 127] |
| HD12447 | 1.73 ± 0.06 | 10.0 ± 0.2[102] | 2.49 ± 0.05 | 70[102] | 1.491[103] | 87|$^{+ 1}_{- 9}$| | 1.7|$^{+0.5}_{-0.4}\, {}^{[103,127]}$| | -7.40 ± 0.04[34] |
| HD12767 | 2.43 ± 0.15 | 13.0 ± 0.3[41] | 4.0 ± 0.1 | 40[30] | 1.892[23] | 89|$^{+ 0}_{- 3}$| | 2.0|$^{+0.5}_{-0.6}\, {} ^{[9,113,127]}$| | <-6.88[125] |
| HD19832 | 2.08 ± 0.16 | 12.4 ± 0.4[41] | 3.3 ± 0.1 | 160[96] | 0.728[111] | 89|$^{+ 0}_{- 3}$| | 2.7|$^{+0.6}_{-0.3}\, {} ^{[111]}$| | -6.70 ± 0.04[34] |
| HD21699mr | 2.78 ± 0.04 | 16.0 ± 0.1[41] | 4.7 ± 0.2 | 35[106] | 2.492[23, 127] | 78|$^{+ 2}_{- 2}$| | 2.8|$^{+0.5}_{-0.1}\, {} ^{[5,127]}$| | <-6.49[6] |
| HD22470 | 2.43 ± 0.13 | 13.8 ± 0.3[41] | 3.8 ± 0.2 | 62[30] | 1.929[111] | 87|$^{+ 1}_{- 2}$| | 7.5|$^{+1.2}_{-0.5}\, {} ^{[111]}$| | <-6.87[6] |
| HD22920mr | 2.64 ± 0.12 | 13.6 ± 0.2[67] | 4.2 ± 0.1 | 34[30] | 3.947[20, 127] | 28|$^{+ 6}_{- 7}$| | 1.6|$^{+1.1}_{-0.0}\, {} ^{[4,127]}$| | <-6.77[125] |
| HD25267 | 2.32 ± 0.03 | 12.6 ± 0.2[116] | 3.5 ± 0.2 | 20[102] | 3.823[116] | 17|$^{+ 7}_{- 8}$| | 1.0|$^{+0.1}_{-0.1}\, {} ^{[116]}$| | <-7.25[125] |
| HD27309 | 1.88 ± 0.02 | 11.2 ± 0.3[102] | 2.81 ± 0.04 | 56[102] | 1.569[103] | 3|$^{+ 5}_{- 3}$| | 1.9|$^{+2.6}_{-0.6}\, {} ^{[103]}$| | -7.20 ± 0.04[34] |
| HD28843mr | 2.51 ± 0.07 | 14.8 ± 0.2[41] | 4.20 ± 0.06 | 91[127] | 1.374[23, 127] | 87|$^{+ 1}_{- 5}$| | 0.93|$^{+0.30}_{-0.24}\, {} ^{[4,127]}$| | <-6.85[6] |
| HD32633 | 1.94 ± 0.12 | 12.5 ± 0.5[87] | 3.50 ± 0.09 | 25[96] | 6.430[19] | 76|$^{+ 3}_{- 3}$| | 17|$^{+1}_{-2}\, {} ^{[58,73]}$| | <-6.74[14] |
| HD34452 | 2.45 ± 0.27 | 13.8 ± 0.8[41] | 4.2 ± 0.1 | 53[96] | 2.469[23] | 35|$^{+13}_{-16}$| | 3.6|$^{+1.1}_{-1.4}\, {} ^{[3,15,127]}$| | -6.69 ± 0.04[6, 14] |
| HD35298 | 2.40 ± 0.14 | 15.8 ± 0.8[104] | 4.3 ± 0.2 | 60[93] | 1.855[93] | 77|$^{+ 2}_{- 2}$| | 11|$^{+1}_{-1}\, {} ^{[107]}$| | -5.35 ± 0.04[14, 29, 34] |
| HD35456 | 2.88 ± 0.29 | 13.5 ± 1.4[127] | 4.1 ± 0.5 | 22[77] | 4.951[77] | 15|$^{+ 9}_{-11}$| | 2.2|$^{+0.2}_{-0.3}\, {} ^{[77,127]}$| | <-6.19[125] |
| HD35502f | 2.95 ± 0.12 | 18.4 ± 0.6[104] | 5.8 ± 0.2 | 78[93] | 0.854[78] | 70|$^{+ 1}_{- 1}$| | 7.3|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | -5.05 ± 0.04[34, 127] |
| HD35575r | 3.11 ± 0.09 | 16.7 ± 1.3[127] | 5.8 ± 0.3 | 150[99] | 0.984[127] | – | <1.3[99, 127] | <-7.09[16] |
| HD36313r | 2.04 ± 0.19 | 13.0 ± 0.5[114] | 3.4 ± 0.2 | 160[114] | 0.589[114, 127] | 88|$^{+ 1}_{- 5}$| | 9.0|$^{+1.8}_{-1.3}\, {} ^{[114,127]}$| | -6.10 ± 0.04[34] |
| HD36429mr | 2.42 ± 0.02 | 13.8 ± 0.1[127] | 3.87 ± 0.03 | 77[127] | 15.6[127] | – | <0.20[26, 127] | <-6.13[125] |
| HD36485 | 3.10 ± 0.20 | 20.0 ± 2.0[104] | 6.3 ± 0.2 | 33[93] | 1.478[48] | 3|$^{+ 1}_{- 1}$| | 8.9|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | -5.43 ± 0.04[6, 14, 29, 72] |
| HD36526f | 2.30 ± 0.24 | 15.0 ± 2.0[104] | 4.3 ± 0.2 | 59[93] | 1.542[93] | 56|$^{+ 1}_{- 2}$| | 11|$^{+0}_{-0}\, {} ^{[107]}$| | <-6.29[14, 127] |
| HD36540mr | 2.73 ± 0.15 | 14.9 ± 0.7[87] | 4.54 ± 0.09 | 80[83] | 2.173[127] | 9|$^{+26}_{- 8}$| | 1.4|$^{+3.2}_{-0.1}\, {} ^{[83,127]}$| | <-5.99[125] |
| HD36668mr | 2.40 ± 0.19 | 13.5 ± 0.2[114] | 3.81 ± 0.05 | 60[114] | 2.119[114, 127] | 80|$^{+ 5}_{- 6}$| | 4.5|$^{+2.3}_{-2.7}\, {} ^{[114,127]}$| | <-6.05[125] |
| HD36916mr | 2.10 ± 0.20 | 14.7 ± 0.2[83] | 4.2 ± 0.1 | 78[83] | 1.565[83, 127] | 30|$^{+ 8}_{-10}$| | 3.4|$^{+3.3}_{-0.2}\, {} ^{[4,66,83,91,111,127]}$| | <-6.92[14, 16] |
| HD37017 | 3.42 ± 0.25 | 21.0 ± 2.0[104] | 8.4 ± 0.5 | 134[93] | 0.901[93] | 56|$^{+ 2}_{- 3}$| | 6.2|$^{+0.9}_{-0.9}\, {} ^{[107]}$| | -5.11 ± 0.04[6, 14, 17, 29, 72, 82, 124] |
| HD37058 | 2.90 ± 0.11 | 18.6 ± 0.6[104] | 5.8 ± 0.2 | 11[93] | 14.6[93] | 55|$^{+11}_{-13}$| | 2.5|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-5.95[14] |
| HD37061f | 3.30 ± 0.30 | 22.0 ± 1.0[104] | 7.7 ± 0.4 | 100[93] | 1.095[101] | 59|$^{+ 4}_{- 4}$| | 9.2|$^{+1.0}_{-1.0}\, {} ^{[107]}$| | -5.68 ± 0.04[82, 127] |
| HD37140mr | 2.12 ± 0.09 | 13.5 ± 0.2[114] | 3.46 ± 0.05 | 25[127] | 2.761[114, 127] | 80|$^{+ 3}_{- 4}$| | 3.9|$^{+0.7}_{-0.4}\, {} ^{[114,127]}$| | <-6.08[125] |
| HD37151 | 2.08 ± 0.08 | 13.5 ± 0.9[127] | 3.4 ± 0.2 | – | – | 87|$^{+ 1}_{-12}$| | 1.4|$^{+1.2}_{-1.4}\, {} ^{[115,127]}$| | <-6.39[125] |
| HD37210mr | 2.51 ± 0.05 | 13.5 ± 0.6[127] | 3.92 ± 0.09 | 20[115] | 11.0[20, 127] | 78|$^{+ 7}_{- 8}$| | 1.8|$^{+0.9}_{-0.1}\, {} ^{[66,115,127]}$| | <-5.71[125] |
| HD37479 | 3.51 ± 0.21 | 23.0 ± 2.0[104] | 7.9 ± 0.2 | 145[93] | 1.191[47] | 37|$^{+ 7}_{-10}$| | 10|$^{+11}_{-0}\, {} ^{[71]}$| | -4.73 ± 0.04[6, 14, 17, 29, 72] |
| HD37642mr | 2.42 ± 0.10 | 16.0 ± 0.5[115] | 4.3 ± 0.1 | 85[115] | 1.079[115, 127] | 74|$^{+ 3}_{- 3}$| | 18|$^{+1}_{-0}\, {} ^{[115,127]}$| | -5.69 ± 0.04[34] |
| HD37752 | 2.63 ± 0.14 | 15.0 ± 0.7[41] | 4.5 ± 0.2 | 35[30] | 1.305[87] | – | <2.4[26] | <-7.08[16] |
| HD37776f | 3.30 ± 0.15 | 22.0 ± 1.0[104] | 8.3 ± 0.3 | 101[93] | 1.539[81] | 47|$^{+ 8}_{-10}$| | 6.1|$^{+0.7}_{-0.7}\, {} ^{[54,107]}$| | <-6.35[6, 127] |
| HD37808mr | 2.28 ± 0.10 | 14.5 ± 0.2[115] | 3.90 ± 0.08 | 30[96] | 1.099[109, 115, 127] | 45|$^{+20}_{-24}$| | 3.2|$^{+1.0}_{-0.3}\, {} ^{[115,127]}$| | -6.16 ± 0.04[16, 29] |
| HD40312 | 2.33 ± 0.01 | 10.2 ± 0.1[102] | 3.11 ± 0.06 | 55[96] | 3.619[103] | 68|$^{+13}_{-15}$| | 1.3|$^{+0.4}_{-0.2}\, {} ^{[97]}$| | -7.78 ± 0.04[14] |
| HD41269mr | 2.30 ± 0.08 | 12.9 ± 0.9[127] | 3.5 ± 0.2 | 85[30] | 1.048[127] | 0|$^{+16}_{- 0}$| | 1.3|$^{+0.5}_{-0.3}\, {} ^{[127]}$| | <-7.20[16] |
| HD43819 | 2.15 ± 0.20 | 10.9 ± 0.4[38] | 3.1 ± 0.2 | 10[38] | 15.0[38] | 47|$^{+16}_{-19}$| | 2.6|$^{+75.7}_{-0.1}\, {} ^{[38]}$| | <-6.79[16] |
| HD45583 | 2.07 ± 0.12 | 13.3 ± 0.3[42] | 3.35 ± 0.09 | 70[96] | 1.177[111] | 69|$^{+ 2}_{- 2}$| | 9.1|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.24 ± 0.04[34, 124] |
| HD46328 | 4.49 ± 0.11 | 27.0 ± 1.0[104] | 14.4 ± 0.8 | 8[93] | 30.0 (yr)[88, 95, 120] | 89|$^{+ 0}_{- 9}$| | 1.2|$^{+0.6}_{-0.1}\, {} ^{[107]}$| | <-7.03[85] |
| HD47777 | 3.42 ± 0.15 | 22.0 ± 1.0[104] | 7.9 ± 0.4 | 60[93] | 2.640[61] | 82|$^{+ 5}_{- 5}$| | 3.3|$^{+0.7}_{-0.7}\, {} ^{[107]}$| | <-6.40[85] |
| HD49333 | 2.73 ± 0.04 | 15.8 ± 0.1[41] | 4.8 ± 0.3 | 65[30] | 2.180[23] | 85|$^{+ 3}_{-12}$| | 3.6|$^{+1.0}_{-1.2}\, {} ^{[15,127]}$| | <-6.49[14] |
| HD49606mr | 2.59 ± 0.06 | 13.5 ± 0.1[41] | 4.08 ± 0.06 | 19[96] | 8.546[123] | – | <0.040[127] | <-6.25[125] |
| HD51418mr | 1.80 ± 0.04 | 9.5 ± 0.8[100] | 2.48 ± 0.09 | 28[84] | 5.431[113, 127] | 89|$^{+ 0}_{- 0}$| | 3.5|$^{+1.0}_{-0.4}\, {} ^{[84,127]}$| | <-6.65[125] |
| HD55522f | 3.00 ± 0.18 | 17.4 ± 0.4[104] | 5.9 ± 0.2 | 70[93] | 2.729[93] | 89|$^{+ 0}_{- 1}$| | 3.1|$^{+0.4}_{-0.4}\, {} ^{[107]}$| | <-6.16[127] |
| HD58260 | 3.22 ± 0.26 | 19.3 ± 1.3[104] | 6.2 ± 0.5 | 3[93] | – | 0|$^{+ 5}_{- 0}$| | 6.5|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | <-6.69[6, 85] |
| HD60344r | 3.58 ± 0.09 | 21.0 ± 0.3[41] | 7.9 ± 0.2 | 55[106] | – | – | >1.2[89, 127] | <-4.76[6] |
| HD61556f | 3.12 ± 0.24 | 18.5 ± 0.8[70] | 6.1 ± 0.3 | 58[70] | 1.909[70] | 58|$^{+ 6}_{- 7}$| | 2.8|$^{+0.3}_{-0.3}\, {} ^{[107]}$| | -5.93 ± 0.04[117, 127] |
| HD64740f | 3.81 ± 0.15 | 24.5 ± 1.0[104] | 10.1 ± 0.5 | 135[93] | 1.330[93] | 71|$^{+ 5}_{- 5}$| | 3.0|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | -7.19 ± 0.04[127] |
| HD65339 | 1.45 ± 0.02 | 8.5 ± 0.1[102] | 2.09 ± 0.02 | 13[96] | 8.027[103] | 89|$^{+ 0}_{- 1}$| | 15|$^{+2}_{-1}\, {} ^{[28]}$| | <-7.50[6, 14] |
| HD66665 | 4.69 ± 0.23 | 28.5 ± 1.0[104] | 15.9 ± 1.1 | 8[93] | 24.5[93] | 75|$^{+ 3}_{- 3}$| | 0.56|$^{+0.10}_{-0.10}\, {} ^{[107]}$| | <-4.96[85] |
| HD66765f | 3.44 ± 0.24 | 20.0 ± 2.0[63] | 7.2 ± 0.6 | 58[93] | 1.608[93] | 73|$^{+ 5}_{- 5}$| | 2.8|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-6.23[127] |
| HD79158 | 2.61 ± 0.06 | 13.3 ± 0.1[41] | 4.3 ± 0.1 | 49[96] | 3.835[92] | 87|$^{+ 1}_{- 4}$| | 3.1|$^{+0.4}_{-0.4}\, {} ^{[92]}$| | -6.55 ± 0.04[6, 34] |
| HD90044 | 1.66 ± 0.10 | 10.0 ± 0.2[87] | 2.8 ± 0.3 | 23[102] | 4.379[23] | 89|$^{+ 0}_{- 0}$| | 4.4|$^{+1.2}_{-1.5}\, {} ^{[15,22,127]}$| | <-7.71[16] |
| HD105382 | 3.04 ± 0.16 | 18.0 ± 0.5[24] | 5.8 ± 0.2 | 74[93] | 1.295[24] | 51|$^{+ 7}_{- 8}$| | 2.6|$^{+0.1}_{-0.1}\, {} ^{[107]}$| | -6.07 ± 0.04[117] |
| HD112413 | 1.97 ± 0.02 | 11.3 ± 0.2[102] | 2.93 ± 0.03 | 15[96] | 5.469[103] | 88|$^{+ 1}_{- 8}$| | 3.5|$^{+0.8}_{-0.2}\, {} ^{[64,65]}$| | -8.13 ± 0.04[6, 34] |
| HD118022 | 1.53 ± 0.04 | 9.4 ± 0.1[102] | 2.26 ± 0.02 | 12[102] | 3.722[103] | 65|$^{+15}_{-17}$| | 3.2|$^{+8.0}_{-0.2}\, {} ^{[103]}$| | -7.41 ± 0.04[121] |
| HD122532 | 2.37 ± 0.12 | 11.9 ± 0.5[87] | 2.99 ± 0.04 | – | 3.681[12] | 89|$^{+ 0}_{- 3}$| | 3.0|$^{+0.7}_{-0.9}\, {} ^{[7,13,15,113,127]}$| | <-7.00[14] |
| HD124224 | 1.93 ± 0.01 | 12.3 ± 0.2[102] | 3.02 ± 0.01 | 169[102] | 0.521[81] | 87|$^{+ 2}_{-11}$| | 4.0|$^{+0.3}_{-0.2}\, {} ^{[62]}$| | -6.24 ± 0.04[16, 18, 29, 34, 117, 122] |
| HD125248 | 1.39 ± 0.23 | 9.7 ± 0.3[41] | 2.42 ± 0.07 | 11[96] | 9.300[39] | 89|$^{+ 0}_{- 3}$| | 9.0|$^{+1.1}_{-1.3}\, {} ^{[75]}$| | <-7.17[125] |
| HD125823 | 3.16 ± 0.20 | 19.0 ± 2.0[104] | 5.9 ± 0.2 | 16[93] | 8.817[93] | 75|$^{+ 4}_{- 6}$| | 1.8|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | <-6.54[6] |
| HD126515 | 1.36 ± 0.16 | 8.9 ± 0.2[127] | 2.65 ± 0.07 | 16[127] | 129.9[21] | 84|$^{+ 4}_{-13}$| | 13|$^{+1}_{-0}\, {} ^{[21]}$| | <-7.13[14] |
| HD131120mr | 3.15 ± 0.09 | 19.4 ± 1.5[127] | 6.3 ± 0.3 | 57[30] | 1.569[55, 127] | – | <0.17[66] | <-6.97[14] |
| HD133029mr | 1.98 ± 0.08 | 11.8 ± 0.9[41] | 2.8 ± 0.1 | 27[30] | 2.888[44, 127] | 12|$^{+ 4}_{- 4}$| | 9.0|$^{+5.0}_{-0.3}\, {} ^{[3,127]}$| | <-6.89[14] |
| HD133652 | 2.02 ± 0.10 | 12.8 ± 0.5[87] | 3.27 ± 0.09 | 48[96] | 2.304[23] | 65|$^{+ 8}_{-11}$| | 7.6|$^{+0.8}_{-1.0}\, {} ^{[15,127]}$| | -7.16 ± 0.04[34] |
| HD133880 | 1.73 ± 0.06 | 10.7 ± 0.1[41] | 3.08 ± 0.08 | 103[96] | 0.877[80] | 83|$^{+ 1}_{- 1}$| | 12|$^{+0}_{-1}\, {} ^{[80]}$| | -5.44 ± 0.04[72, 34] |
| HD135679mr | 2.46 ± 0.19 | 15.1 ± 2.8[127] | 2.86 ± 0.06 | 1[84] | 5.321[127] | 14|$^{+ 6}_{- 8}$| | 4.4|$^{+9.3}_{-0.2}\, {} ^{[84,91,127]}$| | <-7.04[16] |
| HD137193mr | 1.91 ± 0.13 | 10.6 ± 0.7[87] | 3.5 ± 0.2 | – | 4.867[127] | 0|$^{+25}_{- 0}$| | 3.5|$^{+16.1}_{-0.5}\, {} ^{[8,127]}$| | <-6.51[14] |
| HD137909 | 1.46 ± 0.01 | 7.5 ± 0.1[102] | 1.98 ± 0.03 | 3[96] | 18.5[103] | 89|$^{+ 0}_{- 2}$| | 5.2|$^{+7.1}_{-1.0}\, {} ^{[103,127]}$| | <-7.90[6] |
| HD138764 | 2.62 ± 0.17 | 15.7 ± 2.7[127] | 4.3 ± 0.4 | 19[30] | 1.259[87] | – | <0.049[46] | <-7.63[16] |
| HD142184 | 2.85 ± 0.13 | 18.5 ± 0.5[104] | 5.7 ± 0.1 | 288[93] | 0.508[56] | 8|$^{+ 3}_{- 3}$| | 9.0|$^{+2.0}_{-2.0}\, {} ^{[107]}$| | -4.25 ± 0.04[94, 117] |
| HD142301 | 2.56 ± 0.07 | 15.9 ± 0.2[41] | 4.46 ± 0.05 | 78[30] | 1.459[111] | 47|$^{+ 9}_{-11}$| | 12|$^{+9}_{-0}\, {} ^{[111]}$| | -5.62 ± 0.04[14, 16, 17, 29] |
| HD142884mr | 2.17 ± 0.12 | 14.3 ± 0.5[87] | 3.7 ± 0.1 | 127[30] | 0.803[109] | – | <0.75[4, 127] | <-6.84[14] |
| HD142990 | 2.93 ± 0.13 | 18.0 ± 0.5[104] | 5.6 ± 0.2 | 122[93] | 0.979[105] | 83|$^{+ 2}_{- 3}$| | 4.7|$^{+0.4}_{-0.4}\, {} ^{[107]}$| | -5.77 ± 0.04[14, 16, 17, 29, 98] |
| HD143473 | 1.87 ± 0.10 | 12.4 ± 1.0[87] | 2.25 ± 0.08 | 25[30] | 2.843[25] | 18|$^{+ 5}_{- 6}$| | 18|$^{+2}_{-2}\, {} ^{[13,15,127]}$| | -6.56 ± 0.04[34] |
| HD143699mr | 2.65 ± 0.12 | 15.5 ± 0.4[41] | 4.6 ± 0.2 | 115[127] | 0.894[127] | – | <0.60[4, 37, 127] | -7.21 ± 0.04[14, 125] |
| HD144334 | 2.34 ± 0.12 | 14.8 ± 0.4[41] | 4.0 ± 0.1 | 82[30] | 1.495[111] | 55|$^{+ 7}_{- 8}$| | 3.6|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.79 ± 0.04[14, 16, 29] |
| HD145102 | 2.02 ± 0.12 | 10.8 ± 0.5[87] | 3.0 ± 0.1 | 84[30] | 1.418[57] | – | <0.98[8] | <-6.90[125] |
| HD145482r | 3.59 ± 0.17 | 24.2 ± 4.3[127] | 8.1 ± 0.8 | 166[30] | 5.804[127] | – | <0.38[8] | <-6.94[14] |
| HD145501C | 2.46 ± 0.15 | 14.5 ± 0.5[87] | 4.0 ± 0.2 | 70[30] | 1.026[111] | 89|$^{+ 0}_{- 2}$| | 5.8|$^{+0.3}_{-0.3}\, {} ^{[111]}$| | -6.08 ± 0.04[14, 16, 124] |
| HD146001mr | 2.38 ± 0.14 | 13.8 ± 0.3[41] | 3.61 ± 0.06 | 90[30] | 0.586[57] | – | <0.50[4, 127] | -6.87 ± 0.04[14] |
| HD147010 | 1.65 ± 0.08 | 12.5 ± 0.6[87] | 2.45 ± 0.09 | 15[96] | 3.921[60] | 10|$^{+ 4}_{- 5}$| | 19|$^{+0}_{-0}\, {} ^{[18,113,127]}$| | <-7.10[14] |
| HD147890 | 2.43 ± 0.12 | 11.3 ± 0.5[87] | 3.7 ± 0.2 | 65[30] | 4.336[57] | – | <0.90[8] | <-6.24[125] |
| HD147932 | 2.50 ± 0.20 | 17.0 ± 1.0[111] | 4.8 ± 0.3 | 140[52] | 0.864[90] | 0|$^{+ 6}_{- 0}$| | 7.6|$^{+9.6}_{-0.5}\, {} ^{[111,126]}$| | -5.14 ± 0.04[112] |
| HD147933 | 3.30 ± 0.17 | 20.8 ± 0.5[110] | 7.3 ± 0.2 | 200[110] | 0.747[110] | 75|$^{+ 9}_{-11}$| | 4.7|$^{+0.5}_{-0.4}\, {} ^{[110,126]}$| | -5.55 ± 0.04[110] |
| HD148112 | 1.85 ± 0.02 | 9.2 ± 0.1[102] | 2.52 ± 0.01 | 44[38] | 3.044[103] | 0|$^{+ 9}_{- 0}$| | 0.76|$^{+0.41}_{-0.11}\, {} ^{[103,127]}$| | <-7.19[6] |
| HD148199 | 1.88 ± 0.12 | 11.7 ± 0.7[87] | 2.5 ± 0.1 | 15[30] | 7.726[25] | 63|$^{+ 9}_{-12}$| | 5.0|$^{+0.6}_{-0.7}\, {} ^{[8,15,127]}$| | <-6.54[14] |
| HD149438 | 4.47 ± 0.13 | 32.0 ± 1.0[104] | 17.5 ± 0.9 | 7[93] | 41.0[35] | 75|$^{+ 7}_{- 8}$| | 0.31|$^{+0.10}_{-0.01}\, {} ^{[77]}$| | <-7.83[85] |
| HD149822mr | 1.85 ± 0.18 | 10.8 ± 0.3[41] | 2.7 ± 0.2 | 60[30] | 1.966[127] | 87|$^{+ 2}_{- 3}$| | 4.0|$^{+2.1}_{-1.1}\, {} ^{[15,36,66,127]}$| | <-7.36[16] |
| HD151346 | 2.44 ± 0.17 | 13.7 ± 1.1[87] | 3.8 ± 0.2 | 46[30] | 2.180[87] | – | <1.7[4] | <-6.66[14] |
| HD152107 | 1.47 ± 0.01 | 8.8 ± 0.1[102] | 2.15 ± 0.01 | 21[102] | 3.857[103] | 19|$^{+ 4}_{- 5}$| | 4.2|$^{+0.5}_{-0.2}\, {} ^{[103,127]}$| | <-8.01[6, 14] |
| HD156424 | 3.00 ± 0.40 | 18.0 ± 3.0[119] | 4.6 ± 0.3 | 7[93] | 0.524[119] | 39|$^{+18}_{-21}$| | 8.0|$^{+12.0}_{-2.0}\, {} ^{[119]}$| | -4.91 ± 0.04[85] |
| HD163472 | 3.81 ± 0.10 | 25.2 ± 1.1[104] | 10.3 ± 0.5 | 62[93] | 3.639[27] | 46|$^{+13}_{-14}$| | 1.1|$^{+0.5}_{-0.5}\, {} ^{[107]}$| | <-6.83[85] |
| HD164429mr | 1.85 ± 0.04 | 12.0 ± 0.5[127] | 2.99 ± 0.06 | 90[30] | 1.082[127] | 88|$^{+ 1}_{-12}$| | 3.0|$^{+0.7}_{-0.3}\, {} ^{[15,127]}$| | -6.91 ± 0.04[16, 34] |
| HD165474 | 2.06 ± 0.26 | 13.2 ± 3.4[127] | 1.82 ± 0.08 | 18[30] | 9.0 (yr)[79] | 89|$^{+ 0}_{- 0}$| | 3.0|$^{+4.9}_{-1.8}\, {} ^{[79,127]}$| | <-6.96[125] |
| HD168785r | 3.48 ± 0.08 | 23.0 ± 1.2[127] | 8.1 ± 0.4 | 14[106] | – | – | >4.0[89] | <-5.25[125] |
| HD168856mr | 2.10 ± 0.09 | 11.9 ± 1.2[127] | 3.0 ± 0.1 | 73[76] | 2.428[109] | 55|$^{+15}_{-16}$| | 3.5|$^{+3.7}_{-0.6}\, {} ^{[76,84,35,127]}$| | <-6.77[125] |
| HD170000 | 2.36 ± 0.01 | 11.6 ± 0.0[102] | 3.47 ± 0.02 | 83[102] | 1.716[103] | 70|$^{+10}_{-12}$| | 1.8|$^{+0.0}_{-0.1}\, {} ^{[103]}$| | -7.11 ± 0.04[34] |
| HD170973mr | 2.32 ± 0.13 | 10.8 ± 0.2[41] | 3.39 ± 0.06 | 4[96] | 18.1[127] | 83|$^{+ 2}_{- 3}$| | 4.8|$^{+11.2}_{-0.5}\, {} ^{[15,13,127]}$| | <-6.56[125] |
| HD171247mr | 2.79 ± 0.16 | 12.2 ± 0.3[41] | 4.0 ± 0.2 | 68[96] | 3.910[127] | 85|$^{+ 3}_{-34}$| | 4.1|$^{+3.1}_{-0.4}\, {} ^{[127]}$| | -5.16 ± 0.04[16, 29] |
| HD175132r | 2.78 ± 0.04 | 13.2 ± 0.5[127] | 4.0 ± 0.2 | 40[30] | 8.030[127] | – | >3.5[26] | <-6.69[16, 125] |
| HD175362f | 2.64 ± 0.12 | 17.6 ± 0.4[104] | 5.3 ± 0.2 | 34[93] | 3.674[93] | 68|$^{+ 5}_{- 6}$| | 17|$^{+0}_{-0}\, {} ^{[107]}$| | -6.72 ± 0.04[14, 16, 17, 127] |
| HD175744mr | 2.65 ± 0.09 | 12.6 ± 0.2[41] | 4.00 ± 0.08 | 50[30] | 2.799[127] | – | <0.50[31, 108, 127] | <-7.25[16, 125] |
| HD176582 | 2.90 ± 0.15 | 17.0 ± 1.0[104] | 5.6 ± 0.2 | 103[93] | 1.582[53] | 89|$^{+ 0}_{- 1}$| | 5.4|$^{+0.2}_{-0.2}\, {} ^{[107]}$| | -6.07 ± 0.04[34] |
| HD177003 | 3.05 ± 0.10 | 17.7 ± 0.7[87] | 5.7 ± 0.2 | 12[30] | 1.800[87] | – | <0.81[26] | <-7.19[16] |
| HD177410m | 2.30 ± 0.15 | 14.5 ± 0.5[32] | 3.6 ± 0.1 | 100[32] | 1.123[45] | – | <1.7[15, 68, 127] | <-7.23[16] |
| HD179527 | 2.63 ± 0.16 | 10.4 ± 0.3[38] | 3.39 ± 0.05 | 33[38] | 7.098[38] | 88|$^{+ 1}_{-12}$| | 0.52|$^{+0.71}_{-0.11}\, {} ^{[38]}$| | <-6.54[125] |
| HD182180f | 3.09 ± 0.18 | 19.8 ± 1.4[104] | 6.5 ± 0.2 | 306[93] | 0.521[50, 49] | 81|$^{+ 3}_{- 4}$| | 9.5|$^{+0.6}_{-0.6}\, {} ^{[107]}$| | -4.65 ± 0.04[86, 127] |
| HD183056 | 2.69 ± 0.11 | 11.7 ± 0.4[38] | 4.0 ± 0.2 | 35[96] | 2.992[38] | 82|$^{+ 3}_{- 4}$| | 1.6|$^{+2.4}_{-0.4}\, {} ^{[38]}$| | <-7.14[16] |
| HD183339r | 2.70 ± 0.05 | 14.0 ± 0.6[127] | 4.3 ± 0.1 | 41[30] | 4.204[127] | – | >4.5[26] | <-6.39[125] |
| HD184927f | 3.59 ± 0.16 | 22.0 ± 1.0[104] | 8.4 ± 0.5 | 8[93] | 9.531[69] | 67|$^{+ 3}_{- 4}$| | 8.8|$^{+1.4}_{-0.5}\, {} ^{[69]}$| | <-6.06[16, 125, 127] |
| HD184961mr | 2.35 ± 0.08 | 11.8 ± 1.0[127] | 3.47 ± 0.09 | 34[30] | 6.335[127] | 4|$^{+ 3}_{- 4}$| | 4.3|$^{+9.0}_{-0.4}\, {} ^{[127]}$| | <-6.36[125] |
| HD186205 | 3.84 ± 0.25 | 19.6 ± 0.8[104] | 8.3 ± 0.6 | 6[93] | 37.2[93] | 7|$^{+ 3}_{- 4}$| | 3.0|$^{+1.0}_{-0.5}\, {} ^{[107]}$| | <-4.82[125] |
| HD187474 | 1.76 ± 0.03 | 9.9 ± 0.1[102] | 2.52 ± 0.02 | 0[96] | 6.4 (yr)[103] | 89|$^{+ 0}_{- 3}$| | 7.2|$^{+2.1}_{-0.2}\, {} ^{[103]}$| | <-7.29[125] |
| HD188041mr | 1.40 ± 0.01 | 8.5 ± 0.1[102] | 2.07 ± 0.04 | 4[96] | 224.0[103] | 0|$^{+25}_{- 0}$| | 4.1|$^{+16.6}_{-0.4}\, {} ^{[103,127]}$| | <-7.46[125] |
| HD189775f | 2.91 ± 0.11 | 17.5 ± 0.6[104] | 5.6 ± 0.2 | 58[93] | 2.607[93] | 43|$^{+11}_{-12}$| | 4.3|$^{+0.7}_{-0.7}\, {} ^{[107]}$| | -5.83 ± 0.04[127] |
| HD192678 | 1.65 ± 0.27 | 9.0 ± 0.1[41] | 2.5 ± 0.2 | 6[127] | 12.9[21] | 25|$^{+11}_{-12}$| | 5.5|$^{+4.4}_{-0.1}\, {} ^{[21,127]}$| | <-6.79[125] |
| HD196178mr | 2.15 ± 0.10 | 13.1 ± 0.5[87] | 4.2 ± 0.2 | 50[32] | 1.101[127] | 41|$^{+ 7}_{- 9}$| | 3.9|$^{+0.4}_{-0.2}\, {} ^{[3,127]}$| | -5.99 ± 0.04[34] |
| HD196502 | 2.01 ± 0.39 | 8.9 ± 0.4[41] | 2.55 ± 0.05 | 9[96] | 20.3[25] | 88|$^{+ 1}_{-12}$| | 1.7|$^{+0.3}_{-0.3}\, {} ^{[1,2,11,113,127]}$| | <-6.54[6] |
| HD200775f | 3.95 ± 0.30 | 18.6 ± 2.0[43] | 9.0 ± 0.8 | 26[43] | 4.381[43] | 89|$^{+ 0}_{- 6}$| | 3.9|$^{+1.7}_{-0.7}\, {} ^{[45,127]}$| | -6.11 ± 0.04[127] |
| HD202671 | 2.70 ± 0.07 | 13.2 ± 0.1[41] | 4.0 ± 0.2 | 20[96] | 1.992[87] | – | <0.056[51] | <-7.04[125] |
| HD205021f | 4.26 ± 0.11 | 25.0 ± 1.0[104] | 11.9 ± 1.1 | 34[93] | 12.0[59] | 86|$^{+ 2}_{- 4}$| | 0.26|$^{+0.03}_{-0.03}\, {} ^{[107]}$| | <-7.42[85, 127] |
| HD208057f | 3.01 ± 0.11 | 16.5 ± 1.2[104] | 5.3 ± 0.3 | 105[93] | 1.368[93] | 89|$^{+ 0}_{- 0}$| | 0.60|$^{+0.20}_{-0.20}\, {} ^{[107]}$| | <-7.30[127] |
| HD215441 | 2.31 ± 0.09 | 14.5 ± 0.4[41] | 3.9 ± 0.1 | 5[96] | 9.490[21] | 37|$^{+ 7}_{- 7}$| | 62|$^{+6}_{-3}\, {} ^{[21]}$| | -5.13 ± 0.04[6, 14, 17, 29, 72] |
| HD224801 | 2.19 ± 0.10 | 11.9 ± 0.5[87] | 3.2 ± 0.1 | 27[30] | 3.740[20] | – | >4.6[1] | <-6.61[125] |
| HD260858r | 3.52 ± 0.27 | 18.0 ± 1.0[41] | 6.7 ± 0.4 | 47[106] | – | – | >1.8[91] | <-4.86[6] |
| HD335238 | 1.62 ± 0.23 | 9.4 ± 0.5[87] | 2.25 ± 0.04 | – | 48.7[79] | 85|$^{+ 4}_{-44}$| | 5.9|$^{+2.0}_{-2.5}\, {} ^{[79,108,127]}$| | <-6.18[125] |
Reference key:
1, Babcock (1958); 2, Wolff & Bonsack (1972); 3, Borra & Landstreet (1980); 4, Borra, Landstreet & Thompson (1983); 5, Brown, Shore & Sonneborn (1985); 6, Drake et al. (1987); 7, Bohlender et al. (1987); 8, Thompson, Brown & Landstreet (1987); 9, Ruediger & Scholz (1988); 10, Shore & Brown (1990); 11, Weiss, Malanushenko & Shakhovskoi (1990); 12, Lanz & Mathys (1991); 13, Mathys (1991); 14, Linsky et al. (1992); 15, Bohlender, Landstreet & Thompson (1993); 16, Leone et al. (1994); 17, Leone et al. (1996); 18, Mathys & Hubrig (1997); 19, Adelman (1997); 20, Catalano & Renson (1998); 21, Landstreet & Mathys (2000); 22, Leone & Catanzaro (2001); 23, Renson & Catalano (2001); 24, Briquet, Aerts & De Cat (2001); 25, Neiner et al. (2003a); 26, Bychkov, Bychkova & Madej (2003); 27, Neiner et al. (2003b); 28, Kochukhov et al. (2004); 29, Leone et al. (2004); 30, Głȩbocki & Gnaciński (2005); 31, Kochukhov & Bagnulo (2006); 32, Lehmann et al. (2006); 33, Hubrig et al. (2006); 34, Drake et al. (2006); 35, Donati et al. (2006); 36, Kudryavtsev et al. (2006); 37, Landstreet et al. (2007); 38, Aurière et al. (2007); 39, Hubrig, North & Schöller (2007); 40, Alecian et al. (2008b); 41, Netopil et al. (2008); 42, Semenko et al. (2008); 43, Alecian et al. (2008a); 44, Adelman (2008); 45, Krtička et al. (2009); 46, Silvester et al. (2009); 47, Townsend et al. (2010); 48, Leone et al. (2010); 49, Rivinius et al. (2010); 50, Oksala et al. (2010); 51, Makaganiuk et al. (2011); 52, Alecian et al. (2011); 53, Bohlender & Monin (2011); 54, Kochukhov et al. (2011); 55, Dubath et al. (2011); 56, Grunhut et al. (2012); 57, Wraight et al. (2012); 58, Silvester et al. (2012); 59, Henrichs et al. (2013); 60, Bailey & Landstreet (2013); 61, Fossati et al. (2014); 62, Kochukhov et al. (2014); 63, Alecian et al. (2014); 64, Silvester, Kochukhov & Wade (2014a); 65, Silvester, Kochukhov & Wade (2014b); 66, Bagnulo et al. (2015a); 67, Khalack & LeBlanc (2015); 68, Romanyuk, Semenko & Kudryavtsev (2015); 69, Yakunin et al. (2015); 70, Shultz et al. (2015); 71, Oksala et al. (2015a); 72, Chandra et al. (2015); 73, Silvester, Kochukhov & Wade (2015); 74, Kochukhov & Wade (2016); 75, Rusomarov et al. (2016); 76, Romanyuk et al. (2016b); 77, Romanyuk et al. (2016a); 78, Sikora et al. (2016); 79, Mathys (2017); 80, Kochukhov et al. (2017); 81, Mikulášek et al. (2017); 82, Kounkel et al. (2017); 83, Romanyuk et al. (2017a); 84, Romanyuk et al. (2017b); 85, Kurapati et al. (2017); 86, Leto et al. (2017); 87, Netopil et al. (2017); 88, Shultz et al. (2017); 89, Järvinen et al. (2018); 90, Rebull et al. (2018); 91, Romanyuk et al. (2018); 92, Oksala et al. (2018); 93, Shultz et al. (2018b); 94, Leto et al. (2018); 95, Shultz et al. (2018c); 96, Ghazaryan, Alecian & Hakobyan (2018); 97, Kochukhov et al. (2019); 98, Das et al. (2019b); 99, Romanyuk et al. (2019); 100, Moiseeva et al. (2019); 101, Shultz et al. (2019a); 102, Sikora et al. (2019a); 103, Sikora et al. (2019b); 104, Shultz et al. (2019b); 105, Shultz et al. (2019c); 106, Ghazaryan, Alecian & Hakobyan (2019); 107, Shultz et al. (2019d); 108, Romanyuk et al. (2020); 109, Bernhard, Hümmerich & Paunzen (2020); 110, Leto et al. (2020a); 111, Shultz et al. (2020); 112, Leto et al. (2020b); 113, Bychkov, Bychkova & Madej (2021); 114, Romanyuk et al. (2021a); 115, Romanyuk et al. (2021b); 116, Woodcock et al. (2021); 117, Pritchard et al. (2021); 118, Shultz et al. (2021a); 119, Shultz et al. (2021b); 120, Erba et al. (2021); 121, Leto et al. (2021); 122, Das & Chandra (2021); 123, Kochukhov et al. (2021); 124, Das et al. (2021); 125, Drake (private communication); 126, Shultz et al. (in preparation); 127, This Work



