-
PDF
- Split View
-
Views
-
Cite
Cite
A J Goodwin, S van Velzen, J C A Miller-Jones, A Mummery, M F Bietenholz, A Wederfoort, E Hammerstein, C Bonnerot, J Hoffmann, L Yan, AT2019azh: an unusually long-lived, radio-bright thermal tidal disruption event, Monthly Notices of the Royal Astronomical Society, Volume 511, Issue 4, April 2022, Pages 5328–5345, https://doi.org/10.1093/mnras/stac333
Close - Share Icon Share
ABSTRACT
Tidal disruption events (TDEs) occur when a star is destroyed by a supermassive black hole at the centre of a galaxy, temporarily increasing the accretion rate on to the black hole and producing a bright flare across the electromagnetic spectrum. Radio observations of TDEs trace outflows and jets that may be produced. Radio detections of the outflows from TDEs are uncommon, with only about one-third of TDEs discovered to date having published radio detections. Here, we present over 2 yr of comprehensive, multiradio frequency monitoring observations of the TDE AT2019azh taken with the Very Large Array and MeerKAT radio telescopes from approximately 10 d pre-optical peak to 810 d post-optical peak. AT2019azh shows unusual radio emission for a thermal TDE, as it brightened very slowly over 2 yr, and showed fluctuations in the synchrotron energy index of the optically thin synchrotron emission from 450 d post-disruption. Based on the radio properties, we deduce that the outflow in this event is likely non-relativistic and could be explained by a spherical outflow arising from self-stream intersections or a mildly collimated outflow from accretion on to the supermassive black hole. This data set provides a significant contribution to the observational data base of outflows from TDEs, including the earliest radio detection of a non-relativistic TDE to date, relative to the optical discovery.
1 INTRODUCTION
The central mass in a galaxy influences the dynamics and spatial distributions of stars in the inner regions. In some rare cases, a supermassive black hole (SMBH) can capture and destroy a star if it passes within the radius at which the tidal shear forces on the star from the black hole exceed the star’s self-gravity (Rees 1988). Such tidal disruption events (TDEs) produce bright flares across the electromagnetic spectrum that are usually visible for time-scales of 1–2 yr, with approximately half of the debris remaining in orbits bound to the black hole, and other parts flung out on hyperbolic orbits with large velocities (e.g. Lacy, Townes & Hollenbach 1982; Rees 1988; Evans & Kochanek 1989; Lodato, King & Pringle 2009). The bound stellar debris may circularize and form an accretion disc (e.g. Shiokawa et al. 2015; Bonnerot et al. 2016; Hayasaki, Stone & Loeb 2016; Liptai et al. 2019; Bonnerot & Lu 2020; Mummery & Balbus 2020), producing X-ray emission from the accretion stream as the material falls back towards the black hole and optical emission possibly from the reprocessing of the X-rays in the disc (e.g. Cannizzo, Lee & Goodman 1990; Strubbe & Quataert 2009; Metzger & Stone 2016; Roth et al. 2016; Auchettl, Guillochon & Ramirez-Ruiz 2017; van Velzen et al. 2020; Gezari 2021). The disc circularization time, and thus the time taken for disc formation and accretion on to the SMBH to begin, is a subject of debate (Bonnerot & Stone 2021). Some models predict varying circularization time-scales depending on the physical properties of the star, SMBH, and system (e.g. Hayasaki et al. 2016; Liptai et al. 2019; Lu & Bonnerot 2020; Bonnerot & Stone 2021). X-ray observations of TDEs that trace accretion on to the SMBH have shown variable behaviour, with some TDEs showing bright X-ray emission early on (e.g. Miller et al. 2015) and others showing delayed X-ray flares (e.g. Hinkle et al. 2021). In some cases, radio emission is also observed from outflowing material.
Radio observations of TDEs trace the outflows produced by the debris from the destroyed star that may be ejected from the black hole (see Alexander et al. 2020, for a review), enabling detailed insight into the launching of outflows from SMBHs, the circumnuclear density, and how such outflows might provide feedback and influence the evolution of the host galaxy. The radio properties of the TDEs observed to date are diverse, with some exhibiting high-luminosity emission (νLν > 1040 erg s−1) that is well described by a relativistic jet [e.g. Swift J164449.3+573451 (Sw J1644+57); Bloom et al. 2011; Burrows et al. 2011; Levan et al. 2011; Zauderer et al. 2011; Cendes et al. 2021a] and others exhibiting lower luminosity emission (νLν < 1040 erg s−1) that could be described by synchrotron emission from a non-relativistic spherical or mildly collimated outflow (e.g. ASASSN-14li; Alexander et al. 2016; van Velzen et al. 2016). The time relative to the optical/X-ray flare at which the radio emission is observed could provide insight into the mechanism launching the outflow, the star that was destroyed, and the nature of its orbit around the black hole. Recently, it has been suggested that delayed radio emission may be common in TDEs (Horesh et al. 2021b), based on late-time radio flares observed for the thermal TDEs ASASSN-15oi and iPTF16fnl. However, radio observations of TDEs at early times are uncommon, and the apparent lack of detected early-time radio emission could naturally result from a lack of early-time observations, as we demonstrate through early-time radio observations of the thermal TDE AT2019azh in this work.
Due to the diverse properties of the TDEs that have been observed in the radio to date, there is no consistent explanation for the type of outflows that may be produced in any single event. In some rare cases, as in Sw J1644+57, a relativistic jet is produced with energy of ∼1051 erg (Burrows et al. 2011; Zauderer et al. 2011; Cenko et al. 2012; Pasham et al. 2015; Brown et al. 2017). These arise in TDEs that present a non-thermal X-ray spectrum, and the radio emission can be well described by a relativistic jet model in which synchrotron emission is produced as the jet shocks the circumnuclear medium (CNM) and slows, producing emission similar to a gamma-ray burst (e.g. Metzger, Giannios & Mimica 2012; Kumar et al. 2013). In other cases, where the TDEs exhibit a thermal X-ray spectrum (as, for example, in ASASSN-14li and AT2019dsg), a less energetic (E ∼ 1046−1050 erg), non-relativistic outflow is produced.
There are a few possible scenarios for producing the observed properties of these non-relativistic outflows, some of which are difficult to rule out with the current set of observations. The prevalent models include a disc wind model in which the outflow is produced early on by accretion on to the SMBH, and emits synchrotron radiation as it moves through the interstellar medium around the black hole (e.g. Alexander et al. 2016). Alternatively, in a similar scenario, a mildly collimated, non-relativistic jet could be produced by the accretion on to the SMBH (e.g. van Velzen et al. 2016). In this case, the jet, emitting radio emission by an internal emission mechanism, could switch on at later times and a constant injection of energy could be observed, with the energy increasing with time (e.g. Falcke & Biermann 1995). Another possibility is a collision-induced outflow (CIO), in which the debris from the destroyed star undergoes stream–stream collisions as it circularizes into an accretion disc, with a significant amount of gas becoming unbound and ejected in an approximately spherical outflow (Lu & Bonnerot 2020). Finally, the radio emission could also be produced by the unbound tidal debris stream, which would be ejected from the system with escape velocities of ∼104 km s−1 in a concentrated cone close to the orbital plane (Krolik et al. 2016).
Recently, there has been an increase in the number of TDEs with radio detections (e.g. Alexander et al. 2016, 2017; van Velzen et al. 2016; Cendes et al. 2021b; Horesh, Cenko & Arcavi 2021a), with the next few years expected to bring a large number of new radio observations of these unique events due to targeted radio campaigns to follow up optical and X-ray detected events. These new observations will be crucial in characterizing the mechanism behind the radio-emitting outflows that can be produced, and identifying whether there is a single mechanism behind all radio outflows or whether the type of outflow differs between individual systems.
In this work, we present over 2 yr of radio monitoring observations of the thermal TDE AT2019azh. AT2019azh was first discovered on 2019 February 22 by the All-Sky Automated Survey for Supernovae (ASASSN; Brimacombe et al. 2019) and named ASASSN-19dj. It was detected by the Zwicky Transient Facility (ZTF) on 2019 February 12 and denoted as ZTFaaazdba (van Velzen et al. 2019). The source was coincident with the nucleus of the E + A galaxy KUG 0810+227, with a redshift of z = 0.022 (luminosity distance of 96 Mpc). Spectra obtained by the Nordic Optical Telescope Unbiased Transient Survey on 2019 February 22 (Heikkila et al. 2019), ePESSTO on 2019 February 25 (Barbarino et al. 2019), and the Spectral Energy Distribution Machine mounted on the Palomar 60-inch telescope on 2019 February 24 and March 10 (van Velzen et al. 2019) all revealed a blue, featureless spectrum with narrow emission and Balmer absorption features associated with the host galaxy. The event was also detected in X-ray and ultraviolet (UV) with the Neil Gehrels Swift Observatory and was found to have a high X-ray blackbody temperature (kT) of 0.06 eV assuming a thermal spectrum (van Velzen et al. 2019). The combination of optical spectral properties, high blackbody temperature, location at centre of host galaxy, and lack of spectroscopic active galactic nucleus (AGN) or supernova features led van Velzen et al. (2019) to classify the source as a TDE. The first reported radio detection of the event was by Perez-Torres et al. (2019) with the electronic Multi-Element Remotely Linked Interferometer Network (e-MERLIN) at 5 GHz on 2019 May 21 and 2019 June 11. In this work, we present an earlier radio detection on 2019 March 9.
Hinkle et al. (2021) analysed the optical, UV, and X-ray observations of AT2019azh from 30 d before to ∼300 d after the optical peak. During the first 200 d, there was very low level X-ray emission with a harder spectral index and strong optical/UV emission that evolved as expected for a thermal TDE. The X-rays brightened by a factor of 30–100 approximately 250 d after discovery, and the X-ray spectrum became softer. The optical/UV flare was observed to begin on MJD 58528 (2019 February 14) and peaked on approximately MJD 58560 (2019 March 18; Hinkle et al. 2021). From a power-law fit of the optical rise observed by ASASSN, Hinkle et al. (2021) inferred that the time of first light for the event was MJD 58522 (2019 February 8).
Liu et al. (2022) found X-ray flaring episodes during the early times, which were temporally uncorrelated with the optical/UV emission. They deduced that the optical and X-ray data could be explained by a two-process scenario in which the early emission in UV/optical is explained by emission from debris stream–stream collisions as the bound debris is becoming circularized, and the low-level early X-ray emission is due to a low-mass accretion disc forming during this time. Liu et al. (2022) explain the late X-ray brightening as due to the major body of the disc forming after circularization of the bound stellar debris. However, Hinkle et al. (2021) concluded that the late-time X-ray brightening was a consequence of an increase in the area of the X-ray-emitting region via the blackbody radius, while the short-term X-ray variability was due to changes in the X-ray temperature. In this scenario, the late-time X-ray brightening is not due to delayed accretion disc formation, but rather an expansion of the X-ray-emitting region. However, Mummery (2021b) recently showed that the X-ray blackbody radius is not a good measure of length-scales in a TDE system, implying that the change in blackbody radius may not be caused by a change in the disc radius. The nature of AT2019azh is thus a subject of debate, with evidence both for and against a delayed accretion scenario to explain the multiwavelength emission from the event.
In this work, we present 13 epochs of radio observations of AT2019azh taken with the Very Large Array (VLA) and MeerKAT beginning 2019 March 9 (before the optical peak) and spanning until 2021 June 5. These radio observations enable further insight into the nature of the TDE, including the disc formation and launching of the outflow. The paper is outlined as follows: In Section 2, we describe the radio observations and data processing. In Section 3, we present the radio spectral observations and synchrotron emission fits. In Section 4, we describe the modelling of the radio emission to predict physical properties of the outflow. In Section 5, we present a more detailed accretion-disc model of the multiwavelength observations. In Section 6, we discuss the implications of these results and the possible nature of the outflow in AT2019azh, and relate the outflow properties to those of other TDEs. Finally, in Section 7 we provide a summary of our results and concluding remarks.
2 OBSERVATIONS
2.1 VLA observations
We obtained radio observations of AT2019azh with the NRAO’s Karl G. Janksy VLA spanning from 2019 March 9 to 2021 February 26 across 300 MHz to 24 GHz (P to K bands; program IDs 19A-395 and 20A-392). In our first observation, on 2019 March 9, we observed the optical position of the source (RA, Dec.) 08:13:16.945, +22:38:54.03 and detected faint radio emission at 10 GHz with a flux density of |$150\pm 12\, \mathrm{\mu Jy}$|. The position of this radio emission was (RA, Dec.) 8:13:16.95, +22.38.54.02 with a positional accuracy of 1 arcsec, coincident with the optical position. We subsequently triggered follow-up observations over a broader frequency range, and continued to monitor the source evolution over the following 2.5 yr, taking 13 epochs of observations in total. The observations are summarized in Table 1 (flux densities and frequencies are available in the online machine-readable format of the table).
| Epoch . | Date (UTC) . | δt (d) . | Array . | Configuration . | Frequency bands . |
|---|---|---|---|---|---|
| 1 | 2019-03-09 1:10 | 29 | VLA | B | X |
| 2 | 2019-04-14 2:34 | 65 | VLA | B | K, X, C |
| 3 | 2019-05-12 20:39 | 94 | VLA | B | Ku, X, C |
| 4 | 2019-05-20 23:51 | 102 | VLA | B | C, S,L |
| 5 | 2019-06-19 23:40 | 132 | VLA | B | X, C, S, L |
| 6 | 2019-08-09 19:06 | 183 | VLA | A | X, C, S, L |
| 7 | 2019-10-19 15:04 | 254 | VLA | A | X, S, L |
| 7 | 2019-11-25 1:02 | – | MeerKAT | – | L |
| 8 | 2019-11-30 12:32 | 296 | VLA | D | X, C, S |
| 8 | 2020-01-29 21:50 | – | MeerKAT | – | L |
| 9 | 2020-01-24 9:27 | 350 | VLA | D | X, S |
| 9 | 2020-05-05 15:08 | – | MeerKAT | – | L |
| 10 | 2020-05-11 22:19 | 459 | VLA | C | X, C, S |
| 10 | 2020-11-14 4:40 | – | MeerKAT | – | L |
| 11 | 2020-12-05 08:02 | 666 | VLA | bnA->A | X, C, S, L, P |
| 12 | 2021-02-26 07:03 | 749 | VLA | A | X, C, S, L, P |
| 13 | 2021-05-06 20:02 | 849 | VLA | D->C | X, C, S, L |
| Epoch . | Date (UTC) . | δt (d) . | Array . | Configuration . | Frequency bands . |
|---|---|---|---|---|---|
| 1 | 2019-03-09 1:10 | 29 | VLA | B | X |
| 2 | 2019-04-14 2:34 | 65 | VLA | B | K, X, C |
| 3 | 2019-05-12 20:39 | 94 | VLA | B | Ku, X, C |
| 4 | 2019-05-20 23:51 | 102 | VLA | B | C, S,L |
| 5 | 2019-06-19 23:40 | 132 | VLA | B | X, C, S, L |
| 6 | 2019-08-09 19:06 | 183 | VLA | A | X, C, S, L |
| 7 | 2019-10-19 15:04 | 254 | VLA | A | X, S, L |
| 7 | 2019-11-25 1:02 | – | MeerKAT | – | L |
| 8 | 2019-11-30 12:32 | 296 | VLA | D | X, C, S |
| 8 | 2020-01-29 21:50 | – | MeerKAT | – | L |
| 9 | 2020-01-24 9:27 | 350 | VLA | D | X, S |
| 9 | 2020-05-05 15:08 | – | MeerKAT | – | L |
| 10 | 2020-05-11 22:19 | 459 | VLA | C | X, C, S |
| 10 | 2020-11-14 4:40 | – | MeerKAT | – | L |
| 11 | 2020-12-05 08:02 | 666 | VLA | bnA->A | X, C, S, L, P |
| 12 | 2021-02-26 07:03 | 749 | VLA | A | X, C, S, L, P |
| 13 | 2021-05-06 20:02 | 849 | VLA | D->C | X, C, S, L |
Notes. δt is measured with reference to the estimated outflow launch date, t0 = MJD 58522. For the frequency bands: P= 0.23–0.47 GHz, L = 1–2 GHz, S = 2–4 GHz, C= 4–8 GHz, X = 8–12 GHz, Ku = 12–18 GHz, and K = 18–26.5 GHz. A complete version of this table including flux density measurements is available in a machine-readable format with the online version of this article.
| Epoch . | Date (UTC) . | δt (d) . | Array . | Configuration . | Frequency bands . |
|---|---|---|---|---|---|
| 1 | 2019-03-09 1:10 | 29 | VLA | B | X |
| 2 | 2019-04-14 2:34 | 65 | VLA | B | K, X, C |
| 3 | 2019-05-12 20:39 | 94 | VLA | B | Ku, X, C |
| 4 | 2019-05-20 23:51 | 102 | VLA | B | C, S,L |
| 5 | 2019-06-19 23:40 | 132 | VLA | B | X, C, S, L |
| 6 | 2019-08-09 19:06 | 183 | VLA | A | X, C, S, L |
| 7 | 2019-10-19 15:04 | 254 | VLA | A | X, S, L |
| 7 | 2019-11-25 1:02 | – | MeerKAT | – | L |
| 8 | 2019-11-30 12:32 | 296 | VLA | D | X, C, S |
| 8 | 2020-01-29 21:50 | – | MeerKAT | – | L |
| 9 | 2020-01-24 9:27 | 350 | VLA | D | X, S |
| 9 | 2020-05-05 15:08 | – | MeerKAT | – | L |
| 10 | 2020-05-11 22:19 | 459 | VLA | C | X, C, S |
| 10 | 2020-11-14 4:40 | – | MeerKAT | – | L |
| 11 | 2020-12-05 08:02 | 666 | VLA | bnA->A | X, C, S, L, P |
| 12 | 2021-02-26 07:03 | 749 | VLA | A | X, C, S, L, P |
| 13 | 2021-05-06 20:02 | 849 | VLA | D->C | X, C, S, L |
| Epoch . | Date (UTC) . | δt (d) . | Array . | Configuration . | Frequency bands . |
|---|---|---|---|---|---|
| 1 | 2019-03-09 1:10 | 29 | VLA | B | X |
| 2 | 2019-04-14 2:34 | 65 | VLA | B | K, X, C |
| 3 | 2019-05-12 20:39 | 94 | VLA | B | Ku, X, C |
| 4 | 2019-05-20 23:51 | 102 | VLA | B | C, S,L |
| 5 | 2019-06-19 23:40 | 132 | VLA | B | X, C, S, L |
| 6 | 2019-08-09 19:06 | 183 | VLA | A | X, C, S, L |
| 7 | 2019-10-19 15:04 | 254 | VLA | A | X, S, L |
| 7 | 2019-11-25 1:02 | – | MeerKAT | – | L |
| 8 | 2019-11-30 12:32 | 296 | VLA | D | X, C, S |
| 8 | 2020-01-29 21:50 | – | MeerKAT | – | L |
| 9 | 2020-01-24 9:27 | 350 | VLA | D | X, S |
| 9 | 2020-05-05 15:08 | – | MeerKAT | – | L |
| 10 | 2020-05-11 22:19 | 459 | VLA | C | X, C, S |
| 10 | 2020-11-14 4:40 | – | MeerKAT | – | L |
| 11 | 2020-12-05 08:02 | 666 | VLA | bnA->A | X, C, S, L, P |
| 12 | 2021-02-26 07:03 | 749 | VLA | A | X, C, S, L, P |
| 13 | 2021-05-06 20:02 | 849 | VLA | D->C | X, C, S, L |
Notes. δt is measured with reference to the estimated outflow launch date, t0 = MJD 58522. For the frequency bands: P= 0.23–0.47 GHz, L = 1–2 GHz, S = 2–4 GHz, C= 4–8 GHz, X = 8–12 GHz, Ku = 12–18 GHz, and K = 18–26.5 GHz. A complete version of this table including flux density measurements is available in a machine-readable format with the online version of this article.
All data were reduced in the Common Astronomy Software Application package (casa 5.6; McMullin et al. 2007) using standard procedures. Where possible, we calibrated the data using the VLA calibration pipeline available in casa. In all observations, 3C 147 was used as the flux density calibrator. For phase calibration, we used ICRF J082324.7+222303 for 12–26 GHz (K and Ku bands); ICRF J083216.0+183212 for 4–12 GHz (X and C bands); ICRF J084205.0+183540 for 1–4 GHz (S and L bands); and PKS J0801+1414 for 0.23–0.47 GHz (P band). The P-band data were reduced manually using standard procedures in casa, including phase and amplitude self-calibration. Images of the target field of view were created using the casa tasks CLEAN or TCLEAN (for epochs post 2019 April) for all bands except the P band, where we used the WSCLEAN (w-stacking CLEAN) imager (Offringa et al. 2014; Offringa & Smirnov 2017). The source flux density was measured in the image plane, by fitting an elliptical Gaussian fixed to the size of the synthesized beam using the casa task IMFIT. The errors associated with the measured flux densities include a statistical uncertainty and a systematic one due to the uncertainty in the flux-density bootstrapping, estimated at 5 per cent. Where enough bandwidth was available, we split the L-, C-, and S-band data into four sub-bands when imaging, and the X-band data into two sub-bands. The source was detected at a 4σ confidence level in the P-band observations, so we did not split these data into sub-bands.
2.2 MeerKAT observations
We also observed AT2019azh with MeerKAT on four occasions between 2019 November 29 and 2020 November 14. We used the 4K (4096-channel) wide-band continuum mode and observed with a bandwidth of 856 MHz around a central frequency of 1.28 GHz. Each observation was about 2 h long in total, except for that on 2020 November 14, which was only 1 h long.
The data were reduced using the OxKAT scripts (Heywood 2020). We used PKS J0408−6544 (QSO B0408−65) to set the flux density scale and calibrate the bandpass and ICRF J084205.0+183540 as a secondary calibrator. The final images were made using the WSCLEAN imager (Offringa et al. 2014; Offringa & Smirnov 2017), and resolved into eight layers in frequency. WSCLEAN deconvolves the eight frequency layers together by fitting a polynomial in frequency to the brightness in the eight frequency layers. Our flux densities include both the statistical uncertainty and a systematic one due to the uncertainty in the flux-density bootstrapping, estimated at 5 per cent.
To ensure no systematic offset between epochs and instruments, in Appendix A we present an analysis of flux density measurements of three background sources for nine epochs of the VLA data and four epochs of the MeerKAT data. We found no significant systematic offset between the two instruments, and found that flux densities between VLA epochs were consistent to within |${\sim} 10{{\ \rm per\ cent}}$|. The flux scale obtained through calibration of the VLA data is consistent across epochs to within a few per cent, indicating that the flux density fluctuations we infer between epochs are larger than those expected through calibration differences alone. However, there is no systematic frequency dependence for these inter-epoch flux density variations, and these differences between epochs could be due to intrinsic variability of the background sources, which are expected to be variable at some level.
2.3 Multiwavelength observations
We obtained forced point spread function fitting photometry of AT2019azh from the public ZTF MSIP data through the ZTF forced-photometry service (Masci et al. 2019). We filtered the resulting optical light curves for observations impacted by bad pixels, and required thresholds for the signal-to-noise of the observations, seeing, the sigma per pixel in the input science image, and several parameters relating to the photometric and astrometric calibrators.
The majority of the Swift UVOT observations were published in van Velzen et al. (2021). Here, we include new observations taken after the publication of that work. We used the uvotsource package to analyse the Swift UVOT photometry and the resulting UV data have been host galaxy subtracted. We also include NICER and XMM–Newton observations reported in Hinkle et al. (2021).
3 RADIO LIGHT CURVE AND SPECTRA
The 2.25, 5, and 9 GHz VLA light curves for AT2019azh are plotted in Fig. 1, as well as a comparison of the 5 GHz light curve with other thermal TDE light curves. The radio emission from AT2019azh rose relatively slowly at all radio wavelengths until approximately 625 d post-optical discovery, at which time the higher frequency (>4 GHz) emission started to decrease while the 2 GHz emission remained relatively constant. Such a slow rise in the radio relative to the optical peak, which occurred around the time of our first radio detection, places AT2019azh in the slow-rising thermal TDE population (Fig. 1). In contrast, some thermal TDEs have been observed to begin fading in the radio soon after the optical peak (e.g. Alexander et al. 2016; Horesh et al. 2021a).
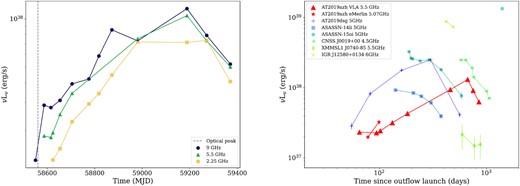
Left: The luminosity of AT2019azh inferred from VLA observations at 9 (purple circles), 5.5 (green triangles), and 2.25 (yellow squares) GHz. Right: The luminosity of AT2019azh at 5.5 GHz inferred from VLA monitoring (purple triangles) and e-MERLIN observations reported in Perez-Torres et al. (2019) (purple stars). For comparison, the ≈5 GHz luminosity of six other radio-detected thermal TDEs is shown. TDE data are from Alexander et al. (2016), van Velzen et al. (2016) (ASSASN-14li), Cendes et al. (2021b), Stein et al. (2021) (AT2019dsg), Horesh et al. (2021a) (ASASSN-15oi), Anderson et al. (2020) (CNSS J0019+00), Alexander et al. (2017) (XMSSL J0740−85), and Irwin et al. (2015) (IGR J12580+0134). All luminosities are plotted with reference to the approximate inferred outflow launch date or the inferred optical first light if no estimate of the launch date is available. Error bars are plotted but obscured by the markers.
The 5 GHz luminosity of AT2019azh increases approximately linearly with time, similar to that of the relativistic event Sw J1644+57. However, Sw J1644+57 rose to a peak within ∼100 d (Eftekhari et al. 2018), whereas AT2019azh took over ∼600 d. We note that AT2019azh was detected in the radio significantly earlier relative to the optical peak than the other thermal TDEs, and a similar slow rise cannot be ruled out for ASSASN-14li, CNSS J0019+00, or XMMSL1 J0740−85. The rise observed for AT2019azh is significantly different than those of ASASSN-15oi, which had early radio non-detections (Horesh et al. 2021a), and AT2019dsg, which rose to a peak over <350 d with L ∝ t2.5 (Stein et al. 2021).
The luminosity of AT2019azh is now sharply decreasing, similar to the fading rates of AT2019dsg, ASASSN-14li, CNSS J0019+00, and ASASSN-15oi (Fig. 1).
3.1 Spectral fitting
We fit the spectra for all epochs using a python implementation of Markov chain Monte Carlo (MCMC), emcee (Foreman-Mackey et al. 2013). We use a Gaussian likelihood function where the variance is underestimated by some fractional amount f. We assume flat prior distributions for all parameters, and allow p to fall in the range 2.5–4.0. While it is a common practice to fix p between epochs (e.g. Alexander et al. 2016; Cendes et al. 2021b), there is evidence in the observations that the spectral slope is not constant for this event (see Fig. 2), so we do not fix p in our modelling. To constrain the host flux density and spectral index (equation 2), we first ran an MCMC fit for epoch 11 (2020 December 12) only, where the synchrotron spectrum is very well constrained by the observations, ensuring that F0 < 0.41 mJy and −2 < α0 < 2. We found the best solution for F0 = 0.175 mJy and α0 = −0.84. Next, we fit the total flux density using the determined host contribution as a function of frequency for the energy index, p, the flux normalization, Fν,ext, the minimum frequency, νm, and the self-absorption frequency, νa, for all epochs using equation (3). For the first three epochs, the peak frequencies and flux densities are not well constrained due to the lack of low-frequency radio coverage. The MCMC spectral fitting results for the synchrotron self-absorption break and peak flux density for these epochs are dependent on the choice of prior. Thus, for these epochs we provide upper and lower limits, respectively, for νa and Fpeak.
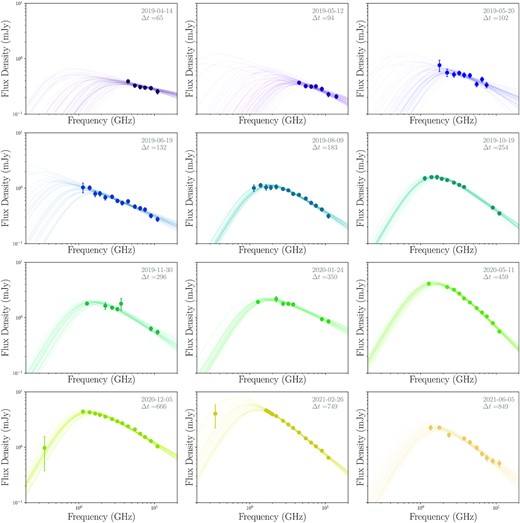
MCMC spectral fits (solid lines) of 12 epochs of radio observations (scatter points) of AT2019azh using the combined VLA and MeerKAT data. 50 random samples from the MCMC chains are plotted after discarding the first 1000 steps for burn-in. Note that the peak flux density and frequency of the first four epochs are not well constrained due to the lack of low-frequency coverage.
The spectral fits for each epoch are plotted in Fig. 2, and the best-fitting peak flux densities and frequencies from the spectral fits are reported in Table 2 and plotted in Fig. 3. For the epochs where the peak of the synchrotron spectrum is well constrained, we find that the peak frequency, νpeak, remained relatively constant at νpeak = 1.1 ± 0.3 GHz, with a slight downwards trend over the 800 d spanned by our observations, while the peak flux density, Fpeak, increased approximately linearly with time and only showed signs of decreasing in the final epoch, 820 d post-disruption. The index of the electron energy distribution, p, remains roughly constant at p ≈ 2.7 ± 0.2, similar to that of other thermal events (e.g. Alexander et al. 2016; Cendes et al. 2021b; Horesh et al. 2021a; Stein et al. 2021) excepting three epochs at 254, 459, and 749 d post-disruption at which the energy index shows a significant steepening to p ≈ 3, 3.7, and 3.3, respectively. We note that the slight spectral steepening at 255 d is likely not real based on an analysis of the flux density of background sources in the field for the different epochs presented in Appendix A and that the significance of the change in p is 3σ and 2σ, respectively, for the other two epochs. We found no evidence in the background source measurements for inconsistent calibration with frequency for the two other epochs where we observed a steepening, although there are small systematic flux density offsets between most epochs (see Appendix A), which we account for with the added systematic uncertainty of |$5{{\ \rm per\ cent}}$| to the flux densities. We thus conclude that the steepenings we observed are real for 2020 May (epoch 10) and 2021 February (epoch 12), and are not artefacts of inconsistent calibration over the frequency ranges for those epochs. We note that the 10 per cent flux density offset between epochs on the background sources suggests a possible systematic uncertainty of 10 per cent in the flux density calibration. Such a systematic uncertainty would affect our peak flux density values; however, the uncertainty of the peak flux density is dominated by the peak not being well constrained in many of the epochs due to the paucity of the data at low frequencies.
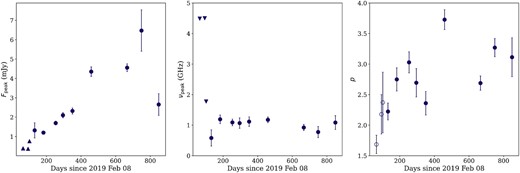
Spectral fit properties of the radio emission inferred using equation (3) and shown in Fig. 2. Upper and lower limits (triangles) are given for the epochs where the peak flux and frequency are not well constrained by the radio observations and all error bars represent the 1σ confidence intervals from the MCMC fitting. Open circles indicate epochs where the peak flux density and frequency were not well constrained. The peak flux density increases approximately linearly with time, excepting the final epoch, which showed a significant drop in peak flux density. The peak frequency is approximately constant for all well-constrained epochs, with a slight downwards trend after the radio light-curve peak (t > 600 d). The energy index, p, shows significant fluctuations after 400 d.
Predicted outflow properties of AT2019azh based on MCMC fitting of the observed radio spectrum and a synchrotron equipartition analysis.
| . | Epoch . | δt (d) . | νpeak (GHz) . | Fpeak (mJy) . | p . | log10 R (cm) . | log10 E (erg) . | β . | log10 B (G) . | log10 ne (cm−3) . |
|---|---|---|---|---|---|---|---|---|---|---|
| 2a | 65 | <4.5 | >0.39 | 1.7 ± 0.2 | <16.9 | <47.9 | <0.39 | <−0.56 | <3.14 | |
| 3a | 94 | <4.5 | >0.37 | 2.2 ± 0.3 | <16.9 | <48.3 | <0.28 | <−0.22 | <3.89 | |
| 4a | 102 | <1.8 | >0.76 | 2.4 ± 0.5 | <17.0 | <48.9 | <0.34 | <−0.36 | <3.78 | |
| 5 | 132 | 0.6 ± 0.3 | 1.3 ± 0.4 | 2.2 ± 0.1 | 17.1 ± 0.2 | 48.9 ± 0.3 | 0.27 ± 0.13 | −1.8 ± 1.3 | 1.8 ± 1.5 | |
| Spherical | 6 | 183 | 1.2 ± 0.1 | 1.20 ± 0.05 | 2.7 ± 0.2 | 16.80 ± 0.05 | 49.0 ± 0.1 | 0.12 ± 0.01 | −1.3 ± 0.3 | 2.9 ± 0.4 |
| fA = 1 | 7 | 254 | 1.1 ± 0.1 | 1.7 ± 0.1 | 3.0 ± 0.2 | 16.93 ± 0.05 | 49.5 ± 0.05 | 0.12 ± 0.01 | −1.3 ± 0.3 | 3.0 ± 0.4 |
| fV = 4/3 | 8 | 296 | 1.1 ± 0.2 | 2.1 ± 0.1 | 2.7 ± 0.2 | 16.96 ± 0.07 | 49.34 ± 0.08 | 0.11 ± 0.02 | −1.4 ± 0.5 | 2.7 ± 0.6 |
| Γ = 1 | 9 | 350 | 1.1 ± 0.2 | 2.3 ± 0.2 | 2.4 ± 0.2 | 16.93 ± 0.06 | 49.06 ± 0.07 | 0.09 ± 0.01 | −1.5 ± 0.4 | 2.5 ± 0.5 |
| 10 | 459 | 1.2 ± 0.1 | 4.4 ± 0.3 | 3.7 ± 0.2 | 17.14 ± 0.04 | 50.51 ± 0.05 | 0.11 ± 0.01 | −1.1 ± 0.2 | 3.5 ± 0.4 | |
| 11 | 666 | 0.9 ± 0.1 | 4.6 ± 0.2 | 2.7 ± 0.1 | 17.18 ± 0.05 | 49.80 ± 0.05 | 0.08 ± 0.01 | −1.5 ± 0.3 | 2.5 ± 0.4 | |
| 12 | 749 | 0.8 ± 0.2 | 6.5 ± 1.1 | 3.3 ± 0.1 | 17.4 ± 0.1 | 50.6 ± 0.1 | 0.11 ± 0.03 | −1.4 ± 0.7 | 2.8 ± 1.0 | |
| 13 | 849 | 1.1 ± 0.2 | 2.7 ± 0.6 | 3.1 ± 0.3 | 17.0 ± 0.1 | 49.8 ± 0.1 | 0.05 ± 0.01 | −1.3 ± 0.6 | 3.0 ± 0.9 | |
| 2a | 65 | <4.5 | >0.39 | 1.7 ± 0.2 | <17.2 | <48.3 | <0.75 | <−0.87 | <2.5 | |
| 3a | 94 | <4.5 | >0.37 | 2.2 ± 0.3 | <17.2 | <48.8 | <0.57 | <−0.51 | <3.3 | |
| 4a | 102 | <1.8 | >0.76 | 2.4 ± 0.5 | <17.4 | <49.4 | <0.67 | <−0.64 | <3.2 | |
| 5a | 132 | 0.6 ± 0.3 | 1.3 ± 0.4 | 2.2 ± 0.1 | 17.5 ± 0.2 | 49.4 ± 0.3 | 0.46 ± 0.22 | −2.1 ± 1.3 | 1.2 ± 1.5 | |
| Conical | 6 | 183 | 1.2 ± 0.1 | 1.20 ± 0.05 | 2.7 ± 0.2 | 17.17 ± 0.05 | 49.6 ± 0.1 | 0.24 ± 0.03 | −1.6 ± 0.3 | 2.4 ± 0.4 |
| fA = 0.13 | 7 | 254 | 1.1 ± 0.1 | 1.7 ± 0.1 | 3.0 ± 0.2 | 17.31 ± 0.05 | 50.0 ± 0.1 | 0.24 ± 0.03 | −1.5 ± 0.3 | 2.5 ± 0.4 |
| fV = 1.15 | 8 | 296 | 1.1 ± 0.2 | 2.1 ± 0.1 | 2.7 ± 0.2 | 17.33 ± 0.07 | 49.84 ± 0.08 | 0.22 ± 0.04 | −1.7 ± 0.5 | 2.2 ± 0.6 |
| Γ = 1 | 9 | 350 | 1.1 ± 0.2 | 2.3 ± 0.2 | 2.4 ± 0.2 | 17.30 ± 0.06 | 49.54 ± 0.07 | 0.18 ± 0.03 | −1.8 ± 0.4 | 1.9 ± 0.5 |
| 10 | 459 | 1.2 ± 0.1 | 4.4 ± 0.3 | 3.7 ± 0.2 | 17.52 ± 0.04 | 51.09 ± 0.05 | 0.22 ± 0.02 | −1.3 ± 0.2 | 3.0 ± 0.4 | |
| 11 | 666 | 0.9 ± 0.1 | 4.6 ± 0.2 | 2.7 ± 0.1 | 17.55 ± 0.05 | 50.3 ± 0.1 | 0.17 ± 0.02 | −1.8 ± 0.3 | 2.0 ± 0.4 | |
| 12 | 749 | 0.8 ± 0.2 | 6.5 ± 1.1 | 3.3 ± 0.1 | 17.7 ± 0.1 | 51.1 ± 0.1 | 0.23 ± 0.06 | −1.7 ± 0.7 | 2.3 ± 1.0 | |
| 13 | 849 | 1.1 ± 0.2 | 2.7 ± 0.6 | 3.1 ± 0.3 | 17.4 ± 0.1 | 50.3 ± 0.1 | 0.11 ± 0.02 | −1.5 ± 0.6 | 2.5 ± 0.9 |
| . | Epoch . | δt (d) . | νpeak (GHz) . | Fpeak (mJy) . | p . | log10 R (cm) . | log10 E (erg) . | β . | log10 B (G) . | log10 ne (cm−3) . |
|---|---|---|---|---|---|---|---|---|---|---|
| 2a | 65 | <4.5 | >0.39 | 1.7 ± 0.2 | <16.9 | <47.9 | <0.39 | <−0.56 | <3.14 | |
| 3a | 94 | <4.5 | >0.37 | 2.2 ± 0.3 | <16.9 | <48.3 | <0.28 | <−0.22 | <3.89 | |
| 4a | 102 | <1.8 | >0.76 | 2.4 ± 0.5 | <17.0 | <48.9 | <0.34 | <−0.36 | <3.78 | |
| 5 | 132 | 0.6 ± 0.3 | 1.3 ± 0.4 | 2.2 ± 0.1 | 17.1 ± 0.2 | 48.9 ± 0.3 | 0.27 ± 0.13 | −1.8 ± 1.3 | 1.8 ± 1.5 | |
| Spherical | 6 | 183 | 1.2 ± 0.1 | 1.20 ± 0.05 | 2.7 ± 0.2 | 16.80 ± 0.05 | 49.0 ± 0.1 | 0.12 ± 0.01 | −1.3 ± 0.3 | 2.9 ± 0.4 |
| fA = 1 | 7 | 254 | 1.1 ± 0.1 | 1.7 ± 0.1 | 3.0 ± 0.2 | 16.93 ± 0.05 | 49.5 ± 0.05 | 0.12 ± 0.01 | −1.3 ± 0.3 | 3.0 ± 0.4 |
| fV = 4/3 | 8 | 296 | 1.1 ± 0.2 | 2.1 ± 0.1 | 2.7 ± 0.2 | 16.96 ± 0.07 | 49.34 ± 0.08 | 0.11 ± 0.02 | −1.4 ± 0.5 | 2.7 ± 0.6 |
| Γ = 1 | 9 | 350 | 1.1 ± 0.2 | 2.3 ± 0.2 | 2.4 ± 0.2 | 16.93 ± 0.06 | 49.06 ± 0.07 | 0.09 ± 0.01 | −1.5 ± 0.4 | 2.5 ± 0.5 |
| 10 | 459 | 1.2 ± 0.1 | 4.4 ± 0.3 | 3.7 ± 0.2 | 17.14 ± 0.04 | 50.51 ± 0.05 | 0.11 ± 0.01 | −1.1 ± 0.2 | 3.5 ± 0.4 | |
| 11 | 666 | 0.9 ± 0.1 | 4.6 ± 0.2 | 2.7 ± 0.1 | 17.18 ± 0.05 | 49.80 ± 0.05 | 0.08 ± 0.01 | −1.5 ± 0.3 | 2.5 ± 0.4 | |
| 12 | 749 | 0.8 ± 0.2 | 6.5 ± 1.1 | 3.3 ± 0.1 | 17.4 ± 0.1 | 50.6 ± 0.1 | 0.11 ± 0.03 | −1.4 ± 0.7 | 2.8 ± 1.0 | |
| 13 | 849 | 1.1 ± 0.2 | 2.7 ± 0.6 | 3.1 ± 0.3 | 17.0 ± 0.1 | 49.8 ± 0.1 | 0.05 ± 0.01 | −1.3 ± 0.6 | 3.0 ± 0.9 | |
| 2a | 65 | <4.5 | >0.39 | 1.7 ± 0.2 | <17.2 | <48.3 | <0.75 | <−0.87 | <2.5 | |
| 3a | 94 | <4.5 | >0.37 | 2.2 ± 0.3 | <17.2 | <48.8 | <0.57 | <−0.51 | <3.3 | |
| 4a | 102 | <1.8 | >0.76 | 2.4 ± 0.5 | <17.4 | <49.4 | <0.67 | <−0.64 | <3.2 | |
| 5a | 132 | 0.6 ± 0.3 | 1.3 ± 0.4 | 2.2 ± 0.1 | 17.5 ± 0.2 | 49.4 ± 0.3 | 0.46 ± 0.22 | −2.1 ± 1.3 | 1.2 ± 1.5 | |
| Conical | 6 | 183 | 1.2 ± 0.1 | 1.20 ± 0.05 | 2.7 ± 0.2 | 17.17 ± 0.05 | 49.6 ± 0.1 | 0.24 ± 0.03 | −1.6 ± 0.3 | 2.4 ± 0.4 |
| fA = 0.13 | 7 | 254 | 1.1 ± 0.1 | 1.7 ± 0.1 | 3.0 ± 0.2 | 17.31 ± 0.05 | 50.0 ± 0.1 | 0.24 ± 0.03 | −1.5 ± 0.3 | 2.5 ± 0.4 |
| fV = 1.15 | 8 | 296 | 1.1 ± 0.2 | 2.1 ± 0.1 | 2.7 ± 0.2 | 17.33 ± 0.07 | 49.84 ± 0.08 | 0.22 ± 0.04 | −1.7 ± 0.5 | 2.2 ± 0.6 |
| Γ = 1 | 9 | 350 | 1.1 ± 0.2 | 2.3 ± 0.2 | 2.4 ± 0.2 | 17.30 ± 0.06 | 49.54 ± 0.07 | 0.18 ± 0.03 | −1.8 ± 0.4 | 1.9 ± 0.5 |
| 10 | 459 | 1.2 ± 0.1 | 4.4 ± 0.3 | 3.7 ± 0.2 | 17.52 ± 0.04 | 51.09 ± 0.05 | 0.22 ± 0.02 | −1.3 ± 0.2 | 3.0 ± 0.4 | |
| 11 | 666 | 0.9 ± 0.1 | 4.6 ± 0.2 | 2.7 ± 0.1 | 17.55 ± 0.05 | 50.3 ± 0.1 | 0.17 ± 0.02 | −1.8 ± 0.3 | 2.0 ± 0.4 | |
| 12 | 749 | 0.8 ± 0.2 | 6.5 ± 1.1 | 3.3 ± 0.1 | 17.7 ± 0.1 | 51.1 ± 0.1 | 0.23 ± 0.06 | −1.7 ± 0.7 | 2.3 ± 1.0 | |
| 13 | 849 | 1.1 ± 0.2 | 2.7 ± 0.6 | 3.1 ± 0.3 | 17.4 ± 0.1 | 50.3 ± 0.1 | 0.11 ± 0.02 | −1.5 ± 0.6 | 2.5 ± 0.9 |
Note. All times are reported with reference to t0, MJD 58522.
The peak of the synchrotron spectrum is not well constrained by the radio observations.
Predicted outflow properties of AT2019azh based on MCMC fitting of the observed radio spectrum and a synchrotron equipartition analysis.
| . | Epoch . | δt (d) . | νpeak (GHz) . | Fpeak (mJy) . | p . | log10 R (cm) . | log10 E (erg) . | β . | log10 B (G) . | log10 ne (cm−3) . |
|---|---|---|---|---|---|---|---|---|---|---|
| 2a | 65 | <4.5 | >0.39 | 1.7 ± 0.2 | <16.9 | <47.9 | <0.39 | <−0.56 | <3.14 | |
| 3a | 94 | <4.5 | >0.37 | 2.2 ± 0.3 | <16.9 | <48.3 | <0.28 | <−0.22 | <3.89 | |
| 4a | 102 | <1.8 | >0.76 | 2.4 ± 0.5 | <17.0 | <48.9 | <0.34 | <−0.36 | <3.78 | |
| 5 | 132 | 0.6 ± 0.3 | 1.3 ± 0.4 | 2.2 ± 0.1 | 17.1 ± 0.2 | 48.9 ± 0.3 | 0.27 ± 0.13 | −1.8 ± 1.3 | 1.8 ± 1.5 | |
| Spherical | 6 | 183 | 1.2 ± 0.1 | 1.20 ± 0.05 | 2.7 ± 0.2 | 16.80 ± 0.05 | 49.0 ± 0.1 | 0.12 ± 0.01 | −1.3 ± 0.3 | 2.9 ± 0.4 |
| fA = 1 | 7 | 254 | 1.1 ± 0.1 | 1.7 ± 0.1 | 3.0 ± 0.2 | 16.93 ± 0.05 | 49.5 ± 0.05 | 0.12 ± 0.01 | −1.3 ± 0.3 | 3.0 ± 0.4 |
| fV = 4/3 | 8 | 296 | 1.1 ± 0.2 | 2.1 ± 0.1 | 2.7 ± 0.2 | 16.96 ± 0.07 | 49.34 ± 0.08 | 0.11 ± 0.02 | −1.4 ± 0.5 | 2.7 ± 0.6 |
| Γ = 1 | 9 | 350 | 1.1 ± 0.2 | 2.3 ± 0.2 | 2.4 ± 0.2 | 16.93 ± 0.06 | 49.06 ± 0.07 | 0.09 ± 0.01 | −1.5 ± 0.4 | 2.5 ± 0.5 |
| 10 | 459 | 1.2 ± 0.1 | 4.4 ± 0.3 | 3.7 ± 0.2 | 17.14 ± 0.04 | 50.51 ± 0.05 | 0.11 ± 0.01 | −1.1 ± 0.2 | 3.5 ± 0.4 | |
| 11 | 666 | 0.9 ± 0.1 | 4.6 ± 0.2 | 2.7 ± 0.1 | 17.18 ± 0.05 | 49.80 ± 0.05 | 0.08 ± 0.01 | −1.5 ± 0.3 | 2.5 ± 0.4 | |
| 12 | 749 | 0.8 ± 0.2 | 6.5 ± 1.1 | 3.3 ± 0.1 | 17.4 ± 0.1 | 50.6 ± 0.1 | 0.11 ± 0.03 | −1.4 ± 0.7 | 2.8 ± 1.0 | |
| 13 | 849 | 1.1 ± 0.2 | 2.7 ± 0.6 | 3.1 ± 0.3 | 17.0 ± 0.1 | 49.8 ± 0.1 | 0.05 ± 0.01 | −1.3 ± 0.6 | 3.0 ± 0.9 | |
| 2a | 65 | <4.5 | >0.39 | 1.7 ± 0.2 | <17.2 | <48.3 | <0.75 | <−0.87 | <2.5 | |
| 3a | 94 | <4.5 | >0.37 | 2.2 ± 0.3 | <17.2 | <48.8 | <0.57 | <−0.51 | <3.3 | |
| 4a | 102 | <1.8 | >0.76 | 2.4 ± 0.5 | <17.4 | <49.4 | <0.67 | <−0.64 | <3.2 | |
| 5a | 132 | 0.6 ± 0.3 | 1.3 ± 0.4 | 2.2 ± 0.1 | 17.5 ± 0.2 | 49.4 ± 0.3 | 0.46 ± 0.22 | −2.1 ± 1.3 | 1.2 ± 1.5 | |
| Conical | 6 | 183 | 1.2 ± 0.1 | 1.20 ± 0.05 | 2.7 ± 0.2 | 17.17 ± 0.05 | 49.6 ± 0.1 | 0.24 ± 0.03 | −1.6 ± 0.3 | 2.4 ± 0.4 |
| fA = 0.13 | 7 | 254 | 1.1 ± 0.1 | 1.7 ± 0.1 | 3.0 ± 0.2 | 17.31 ± 0.05 | 50.0 ± 0.1 | 0.24 ± 0.03 | −1.5 ± 0.3 | 2.5 ± 0.4 |
| fV = 1.15 | 8 | 296 | 1.1 ± 0.2 | 2.1 ± 0.1 | 2.7 ± 0.2 | 17.33 ± 0.07 | 49.84 ± 0.08 | 0.22 ± 0.04 | −1.7 ± 0.5 | 2.2 ± 0.6 |
| Γ = 1 | 9 | 350 | 1.1 ± 0.2 | 2.3 ± 0.2 | 2.4 ± 0.2 | 17.30 ± 0.06 | 49.54 ± 0.07 | 0.18 ± 0.03 | −1.8 ± 0.4 | 1.9 ± 0.5 |
| 10 | 459 | 1.2 ± 0.1 | 4.4 ± 0.3 | 3.7 ± 0.2 | 17.52 ± 0.04 | 51.09 ± 0.05 | 0.22 ± 0.02 | −1.3 ± 0.2 | 3.0 ± 0.4 | |
| 11 | 666 | 0.9 ± 0.1 | 4.6 ± 0.2 | 2.7 ± 0.1 | 17.55 ± 0.05 | 50.3 ± 0.1 | 0.17 ± 0.02 | −1.8 ± 0.3 | 2.0 ± 0.4 | |
| 12 | 749 | 0.8 ± 0.2 | 6.5 ± 1.1 | 3.3 ± 0.1 | 17.7 ± 0.1 | 51.1 ± 0.1 | 0.23 ± 0.06 | −1.7 ± 0.7 | 2.3 ± 1.0 | |
| 13 | 849 | 1.1 ± 0.2 | 2.7 ± 0.6 | 3.1 ± 0.3 | 17.4 ± 0.1 | 50.3 ± 0.1 | 0.11 ± 0.02 | −1.5 ± 0.6 | 2.5 ± 0.9 |
| . | Epoch . | δt (d) . | νpeak (GHz) . | Fpeak (mJy) . | p . | log10 R (cm) . | log10 E (erg) . | β . | log10 B (G) . | log10 ne (cm−3) . |
|---|---|---|---|---|---|---|---|---|---|---|
| 2a | 65 | <4.5 | >0.39 | 1.7 ± 0.2 | <16.9 | <47.9 | <0.39 | <−0.56 | <3.14 | |
| 3a | 94 | <4.5 | >0.37 | 2.2 ± 0.3 | <16.9 | <48.3 | <0.28 | <−0.22 | <3.89 | |
| 4a | 102 | <1.8 | >0.76 | 2.4 ± 0.5 | <17.0 | <48.9 | <0.34 | <−0.36 | <3.78 | |
| 5 | 132 | 0.6 ± 0.3 | 1.3 ± 0.4 | 2.2 ± 0.1 | 17.1 ± 0.2 | 48.9 ± 0.3 | 0.27 ± 0.13 | −1.8 ± 1.3 | 1.8 ± 1.5 | |
| Spherical | 6 | 183 | 1.2 ± 0.1 | 1.20 ± 0.05 | 2.7 ± 0.2 | 16.80 ± 0.05 | 49.0 ± 0.1 | 0.12 ± 0.01 | −1.3 ± 0.3 | 2.9 ± 0.4 |
| fA = 1 | 7 | 254 | 1.1 ± 0.1 | 1.7 ± 0.1 | 3.0 ± 0.2 | 16.93 ± 0.05 | 49.5 ± 0.05 | 0.12 ± 0.01 | −1.3 ± 0.3 | 3.0 ± 0.4 |
| fV = 4/3 | 8 | 296 | 1.1 ± 0.2 | 2.1 ± 0.1 | 2.7 ± 0.2 | 16.96 ± 0.07 | 49.34 ± 0.08 | 0.11 ± 0.02 | −1.4 ± 0.5 | 2.7 ± 0.6 |
| Γ = 1 | 9 | 350 | 1.1 ± 0.2 | 2.3 ± 0.2 | 2.4 ± 0.2 | 16.93 ± 0.06 | 49.06 ± 0.07 | 0.09 ± 0.01 | −1.5 ± 0.4 | 2.5 ± 0.5 |
| 10 | 459 | 1.2 ± 0.1 | 4.4 ± 0.3 | 3.7 ± 0.2 | 17.14 ± 0.04 | 50.51 ± 0.05 | 0.11 ± 0.01 | −1.1 ± 0.2 | 3.5 ± 0.4 | |
| 11 | 666 | 0.9 ± 0.1 | 4.6 ± 0.2 | 2.7 ± 0.1 | 17.18 ± 0.05 | 49.80 ± 0.05 | 0.08 ± 0.01 | −1.5 ± 0.3 | 2.5 ± 0.4 | |
| 12 | 749 | 0.8 ± 0.2 | 6.5 ± 1.1 | 3.3 ± 0.1 | 17.4 ± 0.1 | 50.6 ± 0.1 | 0.11 ± 0.03 | −1.4 ± 0.7 | 2.8 ± 1.0 | |
| 13 | 849 | 1.1 ± 0.2 | 2.7 ± 0.6 | 3.1 ± 0.3 | 17.0 ± 0.1 | 49.8 ± 0.1 | 0.05 ± 0.01 | −1.3 ± 0.6 | 3.0 ± 0.9 | |
| 2a | 65 | <4.5 | >0.39 | 1.7 ± 0.2 | <17.2 | <48.3 | <0.75 | <−0.87 | <2.5 | |
| 3a | 94 | <4.5 | >0.37 | 2.2 ± 0.3 | <17.2 | <48.8 | <0.57 | <−0.51 | <3.3 | |
| 4a | 102 | <1.8 | >0.76 | 2.4 ± 0.5 | <17.4 | <49.4 | <0.67 | <−0.64 | <3.2 | |
| 5a | 132 | 0.6 ± 0.3 | 1.3 ± 0.4 | 2.2 ± 0.1 | 17.5 ± 0.2 | 49.4 ± 0.3 | 0.46 ± 0.22 | −2.1 ± 1.3 | 1.2 ± 1.5 | |
| Conical | 6 | 183 | 1.2 ± 0.1 | 1.20 ± 0.05 | 2.7 ± 0.2 | 17.17 ± 0.05 | 49.6 ± 0.1 | 0.24 ± 0.03 | −1.6 ± 0.3 | 2.4 ± 0.4 |
| fA = 0.13 | 7 | 254 | 1.1 ± 0.1 | 1.7 ± 0.1 | 3.0 ± 0.2 | 17.31 ± 0.05 | 50.0 ± 0.1 | 0.24 ± 0.03 | −1.5 ± 0.3 | 2.5 ± 0.4 |
| fV = 1.15 | 8 | 296 | 1.1 ± 0.2 | 2.1 ± 0.1 | 2.7 ± 0.2 | 17.33 ± 0.07 | 49.84 ± 0.08 | 0.22 ± 0.04 | −1.7 ± 0.5 | 2.2 ± 0.6 |
| Γ = 1 | 9 | 350 | 1.1 ± 0.2 | 2.3 ± 0.2 | 2.4 ± 0.2 | 17.30 ± 0.06 | 49.54 ± 0.07 | 0.18 ± 0.03 | −1.8 ± 0.4 | 1.9 ± 0.5 |
| 10 | 459 | 1.2 ± 0.1 | 4.4 ± 0.3 | 3.7 ± 0.2 | 17.52 ± 0.04 | 51.09 ± 0.05 | 0.22 ± 0.02 | −1.3 ± 0.2 | 3.0 ± 0.4 | |
| 11 | 666 | 0.9 ± 0.1 | 4.6 ± 0.2 | 2.7 ± 0.1 | 17.55 ± 0.05 | 50.3 ± 0.1 | 0.17 ± 0.02 | −1.8 ± 0.3 | 2.0 ± 0.4 | |
| 12 | 749 | 0.8 ± 0.2 | 6.5 ± 1.1 | 3.3 ± 0.1 | 17.7 ± 0.1 | 51.1 ± 0.1 | 0.23 ± 0.06 | −1.7 ± 0.7 | 2.3 ± 1.0 | |
| 13 | 849 | 1.1 ± 0.2 | 2.7 ± 0.6 | 3.1 ± 0.3 | 17.4 ± 0.1 | 50.3 ± 0.1 | 0.11 ± 0.02 | −1.5 ± 0.6 | 2.5 ± 0.9 |
Note. All times are reported with reference to t0, MJD 58522.
The peak of the synchrotron spectrum is not well constrained by the radio observations.
4 MODELLING OF THE RADIO EMISSION
We model the radio emission from the outflow using the standard synchrotron emission model outlined in Barniol Duran, Nakar & Piran (2013), in which the ambient electrons are accelerated into a power-law distribution by the blastwave from the outflow, N(γ) ∝ γ−p, where γ is the electron Lorentz factor (γ ≥ γm, where γm is the minimum Lorentz factor) and p is the synchrotron energy index. We assume equipartition between the electron and magnetic field energy densities in order to derive the equipartition energy and radius. Although the emitting region may not be in equipartition, we can derive estimates of the physical system parameters by parametrizing the deviation from equipartition and accounting for its effect. This approach allows us to estimate key physical quantities such as the ambient electron density, magnetic field strength, mass of the emitting region, and velocity of the ejecta. We assume that the fraction of the total energy in the magnetic field is 0.1|${{\ \rm per\ cent}}$|, ϵB = 10−3, based on observations of other TDEs and supernovae (e.g. Horesh et al. 2013; Eftekhari et al. 2018). We assume that 10|${{\ \rm per\ cent}}$| of the total energy is carried by the electrons, ϵe = 0.1, given that electrons are typically accelerated much less efficiently than protons in astrophysical accelerators (e.g. Morlino & Caprioli 2012). We find no evidence of a relativistic outflow (see Section 6.2), and assume that the outflow is non-relativistic (i.e. the bulk Lorentz factor, Γ = 1), and that the peak of the radio spectrum is associated with the synchrotron self-absorption frequency (i.e. νa = νp). We model two different geometries, one where the emitting region is approximately spherical (with geometric factors1 fA = 1 and fV = 4/3) and one where the emitting region is conical (with geometric factors fA = 0.13 and fV = 1.15), corresponding to a mildly collimated outflow with a half-opening angle of 30 deg.
The physical outflow properties as predicted by these equations are listed in Table 2 and plotted in Fig. 4. All uncertainties reported correspond to the 1σ uncertainty obtained through propagating the uncertainty of νpeak, Fpeak, and p obtained through the MCMC modelling of the observed spectra.
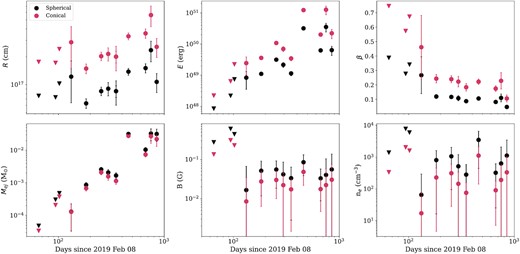
Physical properties of the outflow produced in the TDE AT2019azh inferred from an equipartition analysis of the peak radio flux and frequency assuming a spherical, non-relativistic outflow (black) and a conical, non-relativistic outflow (red). Upper limits (triangles) are given for the epochs where the peak flux and frequency are not well constrained by the radio observations. The energy and radius increase approximately linearly with time until the final epoch. The velocity and magnetic field remain approximately constant over the ∼800 d spanned by our observations.
The derived radius of the outflow increases with time, following the relation R ∝ t0.65 (reduced χ2 = 1.79) or R ∝ t (reduced χ2 = 2.67). We thus deduce that the outflow is roughly undergoing free expansion, with the velocity remaining approximately constant at β ≈ 0.2 ± 0.1 (conical) or β ≈ 0.1 ± 0.06 (spherical) until the final epoch in which the velocity shows a slight decrease. We note that the power-law fit to R, indicating a decelerating outflow, is statistically preferred to the constant velocity case. However, given the underlying assumptions of the radius calculation, that the synchrotron peak flux density and frequency were not resolved by the observations for the first few epochs, and that outflows from other thermal TDEs have all been observed to undergo approximately free expansion at early times (e.g. Alexander et al. 2016; Cendes et al. 2021b), in the sections that follow we operate under the assumption that the outflow was freely expanding with approximately constant velocity until at least the radio light-curve peak (t ≈ 650 d).
The derived energy of the outflow increases approximately linearly with time for all observations, but also seems to show statistically significant non-uniform fluctuations with time. The magnetic field shows a slight decrease with time and the inferred mass in the emitting region of the outflow also increases with time (based on the energy prediction).
A simple linear fit (assuming constant velocity) to the predicted radius gives an outflow launch date of MJD 58435 ± 10 (2018 November 13, conical) or MJD 58432 ± 10 (2018 November 10, spherical), approximately 120 d before the first radio detection on MJD 58551 (2019 March 9). The optical/UV flare was observed to begin on MJD 58528 (2019 February 14), ∼90 d after the estimated outflow launch date, and peaked on approximately MJD 58560 (2019 March 18; Liu et al. 2022; Hinkle et al. 2021). From a power-law fit of the optical rise observed by ASASSN, Hinkle et al. (2021) inferred that the time of first light for the event was MJD 58522 (2019 February 8), indicating the radio outflow was likely launched later than MJD 58433 with an initial velocity higher than 0.1c. Thus, in this work we assume an outflow launch date of MJD 58522, coincident with the optical time of first light.
4.1 Expected future evolution of the outflow in the Sedov–Taylor decay phase
The predicted evolution with time of the outflow’s velocity (Fig. 4) is consistent with either an outflow expanding with constant velocity until the last three epochs (post-radio peak) or a gradually decelerating outflow. In the case that the outflow had approximately constant velocity of ≈0.1c until the last three epochs, we suggest that this could be indicative of an outflow that was ‘coasting’ until the peak radio flux was reached (t ≈ 650 d), and is now decelerating as the flux decays. However, the data could be equally well explained by a model in which the outflow consistently decelerates over the course of the observations. Under the assumption that the outflow did exhibit a coasting phase, the outflow sweeps up material from the CNM, increasing the energy released in the emitting region as the outflow impacts the CNM (e.g. Generozov et al. 2017). The onset of deceleration could indicate that the outflow is entering the Sedov–Taylor phase of its evolution, at which time the outflow has reached peak energy/flux emission in the free expansion phase by sweeping up mass from the CNM, and begins to decelerate with constant energy as the blastwave approaches spherical symmetry (e.g. Sironi & Giannios 2013). In Fig. 4, there is some evidence of deceleration of the outflow in the last three epochs of observations from 660 d post-disruption, corresponding to the epochs post-radio luminosity peak, with the deceleration most evident in the final epoch. We note, however, that an alternate velocity evolution consisting of a power-law evolution in radius and velocity with time fits the radius measurements equally well.
Under the assumption that the outflow velocity only began decelerating after the light curve peaked, the Sedov–Taylor phase enables predictions about the rate of decay of the emission for observing frequencies much above the self-absorption frequency and much below the cooling frequency for a stratified CNM density profile and the synchrotron spectrum power-law index p (Sironi & Giannios 2013). In Fig. 5, we show the Sedov–Taylor solution for different CNM density stratifications with p = 3 (suitable for the final epoch of observations) for the 5.5 GHz light curve of AT2019azh. The predicted flux evolution is calculated assuming late-time radio emission in the Sedov–Taylor phase, in which a spherical shock runs into a stratified medium with density profile n ∝ r−k and the electrons in the shock are accelerated into a synchrotron power-law distribution (Sironi & Giannios 2013). The best-fitting solution is for a steep CNM density gradient, with k = 2.5, similar to the density gradients observed for ASASSN-14li and AT2019dsg (Fig. 7). The current decay rate of the radio emission at 5.5 GHz is well fitted by the Sedov–Taylor approximation for a CNM density n ∝ r−2.5 and p = 3.
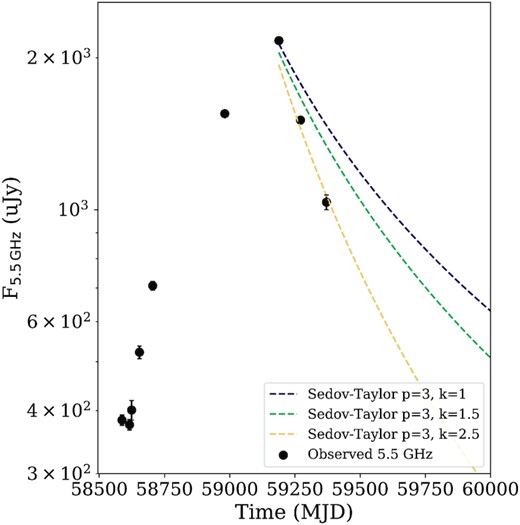
The observed 5.5 GHz light curve of AT2019azh (black) and the predicted decay rates for a Sedov–Taylor solution with different CNM density stratifications (n ∝ r−k) for p = 3 (dashed lines). The current decay rate at 5.5 GHz indicates that a steeper CNM density stratification is preferred, with k ≈ 2.5.
5 MULTIWAVELENGTH MODELLING: ACCRETION DISC EVOLUTION
Given the simplifications applied in the modelling (the black hole spin is fixed to zero and the observer inclination angle is fixed to θobs = 30°), the best-fitting parameter values and their associated uncertainties should be treated with some caution, although Mummery & Balbus (2020) found only a moderate change (factor of ∼1.5) in best-fitting black hole mass over a wide range of black hole spins.
Finally, we determine the best-fitting system parameters by simultaneously minimizing the sum of the squared differences between the model and the different UV and X-ray light curves of AT2019azh. As in previous works, we anticipate large formal values of the reduced χ2. These large values result as a consequence of short time-scale fluctuations present in the well-sampled TDE light curves, and are to be expected in any theoretical model using a smooth functional form for the time dependence of the turbulent stress tensor. Our standard approach implicitly averages over rapid turbulent variations. Short time-scale fluctuations are likely to be highly correlated so that accurately assessing the statistical significance of the fit is not straightforward. We have therefore used χ2 minimization as a sensible guide towards finding a best fit.
The observed and modelled optical, UV, and X-ray light curves for AT2019azh are plotted in Fig. 6 for two scenarios: early accretion and delayed accretion. The observed optical and UV data are well fitted by both the early and delayed accretion models, with little difference between the two. The observed X-ray light curve is significantly better fitted by the delayed accretion model at early times, while the late-time X-ray light curve is well fitted by either model. We note that in the case of significant X-ray obscuration at early times the early accretion model may also be viable.
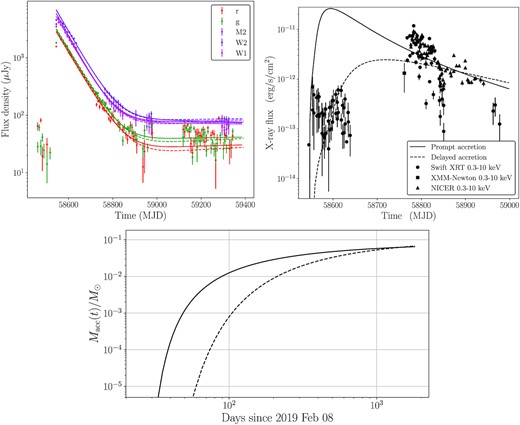
The observed values, shown as points with error bars, and the modelled values, shown by solid or dashed lines of the optical/UV (top left) or X-ray (top right) properties of the disc and modelled accreted mass (mass past the ISCO radius, bottom) in the TDE AT2019azh. The ZTF r- and g-band observations are shown in red and green, respectively, and the Swift UVM2 filter and 2–10 keV X-ray observations are shown in magenta and black, respectively. We model two scenarios: a delayed disc formation (dashed lines) and an early disc formation (solid lines). The optical and UV observations are well fitted by either model, while the X-ray observations are better fitted by the delayed accretion scenario, unless in the case of significant X-ray obscuration at early times. The X-ray observations are from Hinkle et al. (2021) and only the 0.3–10 keV data from each telescope were used in the fitting.
5.1 Different disc evolution scenarios
The X-ray evolution of AT2019azh is, as discussed in the ‘Introduction’ section, somewhat atypical for a TDE. Thus, we present two models for the light-curve evolution of AT2019azh: ‘early’ and ‘delayed’ accretion. There are two ways in which the peak X-ray luminosity of a TDE may be delayed. The X-ray luminosity of a TDE is primarily a function of the hottest temperature in the TDE disc (Mummery & Balbus 2020), as the TDE peak X-ray luminosity is only reached once the TDE inner disc density reaches its maximum. As typical TDE feeding radii are tens to hundreds of gravitational radii, a large viscous time-scale (which delays the build-up of the inner disc density by increasing the length of time it takes for the disc material to propagate inwards) can suppress early TDE X-ray emission. Alternatively, if there is substantial obscuration of the inner regions of the accretion disc at early times, which then clears at larger times, this may also lead to a late-time rise in X-ray luminosity. We model both scenarios in this section. In the delayed accretion model, we fit to the entire X-ray light curve, finding as expected a large viscous time-scale tvisc = 220 ± 20 d. The accreted mass, |$M_{\rm acc} = 0.1 \pm 0.02\, {\rm M}_\odot$|, is consistent with a star of stellar mass |$M_\star \simeq 0.2\, {\rm M}_\odot$| (i.e. no missing energy problem, as in Mummery 2021b). The best-fitting black hole mass |$M_{\rm BH} = 3.2^{+0.15}_{-0.1} \times 10^6\, {\rm M}_\odot$| is consistent with the galaxy scaling measurement |$M_{\rm BH} \lt 4 \times 10^6\, {\rm M}_\odot$| (van Velzen et al. 2016). The peak Eddington ratio of this model is lpeak = 0.22 (Lpeak = 8.5 × 1043 erg s−1), and the total radiated energy was Erad ≃ 8 × 1051 erg. In the early accretion model, which requires substantial early-time obscuration, we find a viscous time-scale tvisc = 65 ± 10 d. The accreted mass, |$M_{\rm acc} = 0.07 \pm 0.01\, {\rm M}_\odot$|, and best-fitting black hole mass |$M_{\rm BH} = 2.1^{+0.15}_{-0.1} \times 10^6\, {\rm M}_\odot$| are again consistent with their expected values. The peak Eddington ratio of this model is lpeak = 0.75 (Lpeak = 2.1 × 1044 erg s−1), and the total radiated energy was Erad ≃ 5 × 1051 erg. The difference between the two accretion evolution scenarios can be seen in Fig. 6, which shows the accreted mass as a function of time (plotted in the same units as Fig. 4).
6 DISCUSSION
Our findings reveal a likely non-relativistic outflow with constant (or gradually decreasing) velocity and continuous kinetic energy increase during the radio rise (up to 666 d), and constant energy post-radio peak (from 666 to 849 d). We infer that the outflow ranges from radii of ∼3 × 1016 to 2 × 1017 cm with energies of ∼3 × 1047to 1 × 1051 erg. These energy and radii correspond to a magnetic field of ∼0.05 G and an ambient electron density of ∼50–3000 cm−3. The observed energy and radius increased with time until the peak radio luminosity was reached.
The optical and X-ray observations, particularly the late-time X-ray rise, have been explained with either a delayed-accretion disc formation scenario (Liu et al. 2022) or due to an increase in the X-ray-emitting region (Hinkle et al. 2021). We modelled two disc emission scenarios in Section 5, and found that the observed UV/optical behaviour of the event was well fitted by either model (Fig. 6). The X-ray emission is better fitted by a delayed accretion scenario except in the case of significant X-ray obscuration at early times.
6.1 The unusual late-time steepening of the synchrotron spectrum
We observed statistically significant fluctuations (at a 3σ level) in the synchrotron energy index, p, of the optically thin part of the synchrotron spectrum from ∼450 d post-disruption. We found that the energy index steepened to p = 3.7 ± 0.2 at t = 460 d, reducing back to p ≈ 2.6 at t = 660 d, steepening again to p = 3.3 ± 0.1 at t = 750 d, and finally reducing back to p ≈ 3 in the final epoch at t = 850 d post-disruption. The mean value of p for the epochs without spectral steepenings is 2.7 ± 0.2 (1σ error, excluding the first four epochs where the spectra were not well constrained), indicating the spectral steepening at t = 460 d is significant to 3σ, and the steepening at t = 750 d is significant to 2σ. After detailed investigation (see Appendix A), we found that these fluctuations are not due to calibration issues with the data or inconsistent flux density scaling between epochs as there is no such systematic difference in three background sources that we examined in the field of view for each epoch (excepting the first minor steepening at 200 d, which we conclude is not statistically significant; see Appendix A).
Fluctuations in the energy index have not been observed in the radio emission from thermal TDEs to date, and are difficult to explain in the current (single-zone) synchrotron emission model. Usually, the steepening of a synchrotron spectrum can be attributed to adiabatic cooling of the electrons, and would indicate the detection of a cooling break in the spectrum (Granot & Sari 2002). However, the adiabatic cooling time-scales are too long to explain the fluctuations on time-scales of ∼months that we observed in this event, and we find no evidence of the presence of a cooling break in any of the spectra (see Appendix B).
We propose that the energy index fluctuations could be due to a spherical or collimated outflow encountering an inhomogeneous CNM or fluctuations in the energy injection rate of a collimated jet-like outflow. In the spherical outflow scenario, different populations of electrons from different regions of the outflow might encounter inhomogeneous clumps of the CNM, changing the emitting properties of different populations of electrons, each with their own synchrotron spectrum. Smaller populations will fade quickly, contributing less to the total radio emission and allowing the flux to fall at higher frequencies. The synchrotron spectra we observe at each epoch are the sum of the emission from these different populations of electrons. If the fluctuations in p are due to the changes in the shock acceleration efficiency, we expect more fluctuations in the radio light curve at 9 GHz than at 5 GHz, as indeed is seen in Fig. 1.
6.2 The outflow mechanism
With the addition of the radio observations to the multiwavelength data, we are able to obtain a more robust picture of the event and how the different types of emissions may have been produced. The empirical properties of the outflow in AT2019azh obtained partly from the radio observations are key to modelling and understanding the mechanism that produced the outflow. What is crucial to understanding the event is that the radio outflow was first observed early, around the time of disruption, and well before the X-ray emission brightened, in contrast to the suggestion that delayed radio emission is common in TDEs (Horesh et al. 2021b). Furthermore, the energy index fluctuations observed in the radio emission place strong constraints on the geometry of the outflow; a spherical homogeneous outflow cannot produce the observed fluctuations. Below, we discuss different scenarios that could explain the observed properties of the outflow in AT2019azh.
6.2.1 Accretion-driven wind outflow
Accretion on to an SMBH can produce winds and outflows that would be observable in the radio as they travel through the CNM at velocities of |${\sim} 0.01\!-\!0.1\, c$| (e.g. Strubbe & Quataert 2009; Tchekhovskoy et al. 2014; Mohan et al. 2022). A popular model to explain non-relativistic outflows from TDEs is a spherical wind driven by accretion on to the SMBH (e.g. Alexander et al. 2016; Cendes et al. 2021b). In this scenario, the radio outflow should appear at approximately the time that high accretion luminosities are observed at X-ray wavelengths, provided there is no obscuration of the X-ray emission. A wind outflow would have approximately spherical geometry (e.g. Mohan et al. 2022), and produce radio emission from a forward shock from the non-relativistic outflow expanding into the CNM driven by the gas accretion on to the SMBH.
The early radio emission for AT2019azh is difficult to explain as an accretion wind-induced outflow in the delayed accretion scenario, due to the lack of bright X-ray emission indicative of significant accretion (requiring FX ∼ 1011 erg s−1 cm−2) and the lack of any X-ray/optical correlation, unless there was strong obscuration of the X-ray emission. In Section 5, we found that the optical, UV, and X-ray observations are well fitted by either delayed accretion or early accretion with significant X-ray obscuration (Fig. 6). In the delayed accretion scenario, the radio outflow could not be produced by an accretion-driven wind due to the lack of significant amounts of material reaching the black hole to be ejected into the outflow at early times, when the first radio emission was observed.
6.2.2 Sub-relativistic jet
In the scenario of a mildly relativistic or sub-relativistic jet, a collimated outflow is produced by accretion on to the SMBH and the radio emission could be produced by either a forward shock that the jet drives into the surrounding medium or internally through shocks inside the jet (e.g. van Velzen et al. 2016), both of which would produce synchrotron emission. A sub-relativistic or mildly relativistic jet was proposed initially for ASASSN-14li (van Velzen et al. 2016) and AT2019dsg (Stein et al. 2021). The main argument against a jet-like outflow relies on the geometric factors and the level of collimation required to obtain a self-consistent solution for the outflow properties.
We deduce that a relativistic jet explanation for the radio properties of AT2019azh is not supported by the data. Similar to the argument against a relativistic jet provided in Alexander et al. (2016), if we introduce an additional parameter, the bulk Lorentz factor (Γ) to the synchrotron equipartition model outlined in Section 4 (Barniol Duran et al. 2013), in order to obtain a self-consistent result where Γ ≳ 2 (i.e. a relativistic outflow), requires fA ≲ 0.01, i.e. a jet with an opening angle of |${\lesssim} 0.1\deg$|. Such a small opening angle is not possible for SMBH outflows (e.g. Jorstad et al. 2005) and rules out the possibility of a relativistic jet for the outflow from AT2019azh.
The late-time evolution of a sub-relativistic jet and a mildly relativistic spherical outflow appears very similar at radio frequencies (Nakar & Piran 2011); however, early on an initially on-axis relativistic jet that decelerates to non-relativistic velocities would appear much more energetic (with energies comparable to Sw J1644+57 ∼1052 erg). The luminosity we observed for AT2019azh (L ∼ 1038 erg s−1) disfavours the possibility of an initially relativistic on-axis jet for the early radio emission. With observations of this event spanning the peak of the radio light curve, we can also deduce that the outflow is likely non-relativistic due to the observed behaviour of the light curve as the outflow transitioned from freely expanding to decelerating. The Doppler factors are no longer important when the outflow begins decelerating (e.g. Sironi & Giannios 2013), so the radius constraint obtained is the true radius of the outflow. If the radio emission was produced by an off-axis relativistic jet, at the time of deceleration it would be emitting isotropically and we would expect to see a flux increase, which is not observed in the radio light curve. Under the assumption that the outflow transitioned into the sub-relativistic Sedov–Taylor decay phase after the peak of the radio light curve (Fig. 5), the inferred radius at the time of transition yields an average speed of the outflow that is significantly less than the speed of light. This would further confirm the sub-relativistic nature of this event, in contrast to the assumed relativistic event Arp 299-B AT1, which was found to initially move at relativistic speeds for the first ∼760 d (Mattila et al. 2018). Alternatively, in the scenario in which the outflow was constantly decelerating over the course of the radio observations, we cannot rule out initially relativistic speeds of the outflow prior to the first radio detection.
A sub-relativistic jet, with Γ ≈ 1, would not require such extreme collimation of the emission. A sub-relativistic jet may present similarly to our conical geometry model (Table 2 and Fig. 4). Such a jet would have slightly larger radii, higher velocity, increased energy, and require a lower CNM density to self-consistently explain the observed properties of the emission, than would a spherical outflow. A collimated outflow may also explain the energy index fluctuations in the case of an inhomogeneous CNM. As a sub-relativistic jet travels through the CNM, it would sweep up material, slowing down and causing the jet to spread laterally (e.g. van Velzen et al. 2016). In this scenario, the emission from the jet is more isotropic due to the Doppler factor close to unity, and a narrow viewing angle is not necessary in order to observe the radio-emitting region. A sub-relativistic jet driven by accretion may have continued energy injection until the central engine switches off (e.g. Mohan et al. 2022), which could explain the continuous energy increase observed for AT2019azh (Fig. 4). Furthermore, the material ejected from close to the black hole could easily reach velocities and energies as high as we predict for AT2019azh due to energy conservation and the angular momentum available at the inner orbits of the SMBH. However, through our disc modelling (Section 5), we infer that the accretion rate never exceeds 0.2 times the Eddington rate in the delayed accretion scenario and 0.7 in the early accretion scenario. For the observed radio emission to be explained by an accretion-driven outflow, it would require inefficient accretion on to the SMBH, which has not been confirmed in observations of SMBHs. Thus, we deduce that a mildly collimated sub-relativistic jet may explain the observed properties of the outflow in AT2019azh, under the condition that the accretion disc formation was not delayed and there was significant X-ray obscuration at early times.
6.2.3 Collision-induced outflow
Lu & Bonnerot (2020) modelled the self-intersection of tidal debris streams during a TDE and deduced that during stream–stream collisions of the tidal debris, a significant amount of gas will become unbound and ejected as a CIO. This kind of outflow would have kinetic energies between 1050 and 1052 erg and velocities between 0.01 and 0.1c, similar to the properties we infer for the outflow of AT2019azh (Fig. 4).
Due to the lack of evidence at early times of significant accretion that could produce an outflow from inefficient accretion on to the SMBH (unless in the case of significant X-ray obscuration), the CIO model is quite promising to explain the radio emission from AT2019azh. A CIO will be launched when the streams intersect, an event that precedes the start of accretion on to the black hole, which could well explain the early radio detection. Liu et al. (2022) proposed that a CIO model could explain the UV/optical and X-ray emission from AT2019azh at early times as the debris is becoming circularized; our radio detection pre-optical peak supports this theory.
In the case of a CIO, the outflow would be produced by a prompt injection of energy during the circularization, and the outflow emission would evolve over time as the spherical ejecta is slowly shocked by the CNM and sweeps up material. In order to reach velocities as high as |$0.1 c$|, the pericentre of the destroyed star would need to be within 10–15 Rg of the SMBH (depending on the black hole spin); otherwise, the CIO would not be strong enough to reach the observed velocities and energies of AT2019azh. A CIO outflow is well described by a ‘coasting’, free expansion and a Sedov–Taylor decay phase once the peak luminosity is reached (Lu & Bonnerot 2020), in contrast to a jet-like outflow that could begin with an expansion phase during which the outflow is powered by the jet engine, and then a Sedov–Taylor decay phase when the jet switches off. The deceleration radius and transition from the free expansion to Sedov–Taylor phase correspond to the time at which the light curve peaks, and are characterized by |$E_{\rm {k}}=(1/2)N(r_{\rm {dec}}m_{\rm {p}}v_0^2$|) (e.g. Lu & Bonnerot 2020); i.e. the deceleration is caused by the outflow interacting with the CNM.
6.2.4 Unbound debris stream
When a star is destroyed by an SMBH, approximately half of the stellar debris will be captured by the gravitational well of the black hole to be accreted, while the remaining half of the star is unbound, and may be ejected from the system with high escape velocities (v > 104 km s−1; Rees 1988). This unbound debris will interact with the CNM, emitting synchrotron radiation in the bow shock that forms along the leading edge of the debris stream (e.g. Krolik et al. 2016). The earliest emitting region will correspond to the fastest unbound debris, expanding at velocities of |${\sim} 0.05 c$| (Krolik et al. 2016). Over time, the bulk of the unbound debris will decelerate and eventually become visible, adding to the emitting region of the outflow. The unbound material would be confined to a very small solid angle (Kochanek 1994; Guillochon, Manukian & Ramirez-Ruiz 2014; Coughlin et al. 2016), which is often used as a justification to rule out radio-emitting outflows being produced by the unbound debris stream (e.g. Alexander et al. 2016, for ASASSN-14li).
The predicted mass in the outflow for the radio-emitting region of AT2019azh is significantly less than expected for the entire unbound debris [Fig. 4, assuming that an |${\sim} 1\, \mathrm{ M}_{\odot }$| star was destroyed and approximately half of the stellar debris is ejected in the unbound debris stream (e.g. Rees 1988)]. However, only the debris with the fastest escape velocities would be visible early on, corresponding to a very small fraction of the unbound debris. If the outflow in AT2019azh were produced by the unbound debris, we may expect to see the radio evolving at later times as the slower debris catches up. However, in the unbound debris model, the outflow should continue to expand at a constant velocity without slowing down until the ejecta has swept up a mass comparable to its own (Krolik et al. 2016). In Fig. 4, we find weak evidence of fluctuations in the velocity of the outflow and some downwards trend between t = 250 and 850 d. The velocity of the outflow we infer even in the spherical geometry model (≳0.1c) is higher than expected in models of the unbound debris (|${\approx} 0.05 c$|) and the inferred energy of the outflow (≳1048 erg) is also greater than expected for the unbound debris stream (∼1047 erg; e.g. Krolik et al. 2016). An unbound debris stream outflow would require slightly higher collimation of the emission than we consider in the conical model (fA ≈ 0.2) in Section 4, which would only increase the predicted energy and velocities.
We thus conclude that the multiwavelength emission of the outflow from AT2019azh could be explained self-consistently by either a CIO or, less likely, an accretion-driven wind or sub-relativistic jet. The equipartition analysis in Section 4 provides a robust estimate of the size of the emitting region, and thus its velocity, but it does not enable strong discrimination between the energy source of the emission and thus the driving source of the outflow. The early radio emission combined with the low X-ray emission and lack of early optical/X-ray correlation points towards the radio outflow not being produced through accretion on to the SMBH, unless there was significant X-ray obscuration. Our disc modelling of the multiwavelength observations in Section 5 indicates that the optical/UV and X-ray emission is well fitted by either an early accretion scenario or a delayed accretion scenario with X-ray obscuration. The observed fluctuations of energy and p could be explained by an inhomogeneous CNM, in which different populations of electrons in the outflow are emitting and being observed at different times.
A more energetic outflow is possible in a disc-driven outflow than a CIO as the ejected material can be ejected with larger energy, translating to a faster, more energetic outflow, but both scenarios could reach the energies and velocities we deduce for the outflow in AT2019azh. Further, detailed modelling of the multiwavelength properties of this event, building on the detailed optical and X-ray analysis presented in Hinkle et al. (2021), is necessary to truly gain a deep understanding of how to reconcile the X-ray, optical, and radio observations in a self-consistent way.
6.3 AT2019azh in the context of other TDEs
On comparison of the outflow properties of AT2019azh with other TDEs with spectrally resolved radio observations, we find that AT2019azh fits well into the population of thermal TDEs (Fig. 7). There is only one other thermal TDE (AT2019dsg) with multifrequency radio coverage at early times (t < 100 d post-distribution). AT2019dsg showed an order of magnitude increase in energy early on, in contrast to the slow rise in radio that we observed for AT2019azh (Fig. 1).
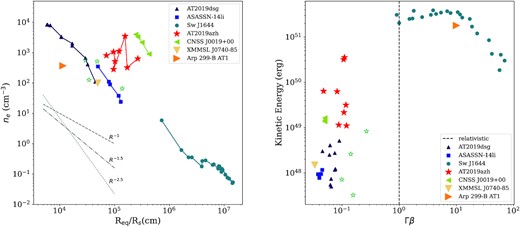
Left: The scaled radius and ambient density inferred from the radio emission of known TDEs. Right: The energy and velocity inferred from the radio emission of the known radio TDEs. AT2019azh is shown in red stars. TDE data and assumed SMBH masses are from Cendes et al. (2021b), Stein et al. (2021) (AT2019dsg, MBH = 5 × 106 M⊙), Alexander et al. (2016) (ASASSN-14li, MBH = 1 × 106 M⊙), Eftekhari et al. (2018) (Sw J1644+57, MBH = 1 × 106 M⊙), Anderson et al. (2020) (CNSS J0019+00, MBH = 1 × 106 M⊙), Mattila et al. (2018) (Arp 299-B AT1, MBH = 2 × 107 M⊙), and Alexander et al. (2017) (XMMSL1 J0740−85, MBH = 3.5 × 106 M⊙). For AT2019azh, we assume MBH = 3 × 106 M⊙. Rs is the Schwarzschild radius of the black hole and Req is the predicted equipartition radius of the outflow.
We find that the ambient density is approximately proportional to R−2.5 for most TDEs, while AT2019azh shows significant variation and could be described by n ∝ R−1 to R−2.5 (Fig. 7). Fig. 7 indicates that for higher ambient densities the radio emission is brighter and peaks earlier (Lu & Bonnerot 2020), as indeed is the case for the light curve of AT2019dsg compared to AT2019azh (Fig. 1).
Inhomogeneity of the CNM density for AT2019azh compared to that of other TDEs could possibly explain the fluctuations in energy index we observed that were not seen in the other early-time TDE observations; however, other studies of thermal TDE radio spectra do not comprehensively assess the possibility of variations in p. In Fig. 7, there is some evidence that the ambient density around AT2019azh is more inhomogeneous than the other thermal TDEs based on the inferred spectral properties. The kinetic energy and velocity we infer for AT2019azh are somewhat larger than those for other thermal events, but do not reach the energies (or velocities) observed for relativistic events. Interestingly, the predicted radii of the outflow for AT2019azh, as well as other thermal TDEs, of 1016–1017 cm match the expected radius of an outflow that produces the spectroscopically observed H α line lag with respect to the continuum (e.g. Charalampopoulos et al. 2021).
The late-time X-ray brightening of AT2019azh resembles the behaviour observed in the TDEs ASASSN-15oi and OGLE16aaa (Kajava et al. 2020; Horesh et al. 2021a). However, in the case of ASASSN-15oi, there was no radio emission detected early on, in stark contrast to the pre-optical peak radio detection of AT2019azh. Thus, the argument for delayed accretion, while likely for ASASSN-15oi, is difficult to justify for AT2019azh if the outflow was accretion disc driven.
The thermal TDE ASASSN-15oi also exhibited a change in energy index of the optically thin part of the synchrotron spectrum at late times (Horesh et al. 2021a). ASASSN-15oi exhibited some lower level radio activity, which faded with time, ∼100 d post-disruption, and a drastic increase in radio flux at ∼600 d post-disruption (Horesh et al. 2021a). Interestingly, the energy index of the optically thin synchrotron emission became much flatter in the late-time flare compared to the earlier emission. The early emission exhibited a standard energy index (p) of 2–3, whereas for the later flare it was much flatter at p = 0.2 (Horesh et al. 2021a). Horesh et al. (2021a) deduce that the standard spherical outflow model from a super-Eddington wind cannot explain both the delayed onset of radio emission and late-time flare from this event, which later would require an outflow to be launched at late times, and possibly into an inhomogeneous CNM. They also propose that the emission could be explained by a transition in accretion state on to the SMBH at late times. However, for AT2019azh we observed the opposite behaviour in p: a steepening of the energy index at later times, followed by fluctuations over the next months.
The late-time radio emission of AT2019azh behaves similarly to that of the TDE AT2019dsg (Stein et al. 2021), which is explained by Cendes et al. (2021b) to likely be driven by a spherical outflow from a super-Eddington wind. However, the outflow properties Cendes et al. (2021b) determined for AT2019dsg could equally well be explained by the CIO model (e.g. Matsumoto, Piran & Krolik 2022). Stein et al. (2021) and Mohan et al. (2022) suggest that the initially increasing energy and flux density observed from AT2019dsg (as in AT2019azh) are produced by a constant energy injection at the source of the outflow, which later switches off and causes the radio emission to fade. At this point, the outflow naturally decelerates due to the shutting off of the central engine, rather than due to interactions with the CNM. This could be the case for AT2019azh in the sub-relativistic jet outflow scenario; however, the increasing energy can also be explained by the outflow sweeping up CNM material at a constant velocity (Sironi & Giannios 2013).
7 SUMMARY
We followed the radio evolution of the TDE AT2019azh for 850 d post-disruption. The radio emission rose slowly to a peak over 650 d, and is now decaying following the expected decay rate for the Sedov–Taylor solution. We modelled the radio emission as a spherical (or conical), non-relativistic outflow and infer energies of 3.5 × 1047 to 2.7 × 1050 erg (9 × 1047 to 1 × 1051 erg), radii of 2 × 1016 to 2 × 1017 cm (5 × 1016 to 5 × 1017 cm), and a circumnuclear density of 70–1100 cm−3 (15–1000 cm−3), for a velocity of |${\approx} 0.1 c$|. We detected radio emission approximately 10 d before the optical peak, which is the first radio detection of a thermal TDE at such early times, and well before the X-ray emission indicated any signs of significant accretion. This early-time radio detection is in contrast to the suggestion that late-time radio flares or delayed radio emission is common in TDEs (Horesh et al. 2021b). Such an early radio detection could rule out the accretion-driven wind outflow model at early times, but through detailed disc modelling we found that both a scenario with delayed accretion and one with early accretion but significant X-ray obscuration could explain the optical, UV, and X-ray properties of the event.
Interestingly, we observed the electron energy index determined from the optically thin part of the synchrotron emission to fluctuate between p ≈ 2.6 and p = 3–3.5 from 400 d post-disruption on time-scales of months. We deduce that these fluctuations could be due to either inhomogeneous emitting regions in a spherical or conical outflow or fluctuations in the energy injection rate of a conical outflow. We rule out the possibility of a relativistic jet producing the outflow in this event since it would require an opening angle of the jet that is smaller than expected for a jet from an SMBH. We found that the mean speed of the outflow to t = 183 d was ∼0.1c, thus ruling out a long-lived relativistic outflow. We also found a possible increase in deceleration, suggesting a transition to a Sedov-like evolution after t ∼ 600 d.
We deduce that the unbound debris stream is unlikely to explain the radio properties of this event due to the high energy inferred through an equipartition analysis of the synchrotron emission. We propose that the outflow could have originated from an accretion-driven wind or sub-relativistic jet, or a collision induced outflow from stream–stream intersections of the tidal debris. Further detailed modelling of the multiwavelength properties of this event is required to differentiate between outflow models and explain some of the unique properties observed. Future observations of the radio decay of AT2019azh will enable more robust constraints on the CNM density and further insight into the nature of the outflow.
SOFTWARE
This research made use of matplotlib, a community-developed python package (Hunter 2007), NASA’s Astrophysics Data System Bibliographic Services, the Common Astronomy Software Application package casa (McMullin et al. 2007), the w-stacking CLEAN imager (Offringa et al. 2014), and the python packages cmasher (van der Velden 2020) and emcee (Foreman-Mackey et al. 2013).
SUPPORTING INFORMATION
AT2019azh_radio_observations.dat
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
The authors thank K. Alexander for helpful discussions, W. Lu for providing helpful comments on an earlier version of this manuscript, and N. Blagorodnova, S. Kulkarni, A. de Witt, B. Cenko, S. Gezari, R. Fender, P. Woudt, and M. Bottcher for their contributions, as well as the anonymous referee for helpful comments. This work was supported by the Australian government through the Australian Research Council’s Discovery Projects funding scheme (DP200102471). The ZTF forced-photometry service was funded under the Heising-Simons Foundation grant |$\#$|12540303 (PI: Graham). The MeerKAT telescope is operated by the South African Radio Astronomy Observatory, which is a facility of the National Research Foundation, an agency of the Department of Science and Innovation. This work was carried out in part using facilities and data processing pipelines developed at the Inter-University Institute for Data Intensive Astronomy (IDIA). IDIA is a partnership of the Universities of Cape Town, of the Western Cape and of Pretoria. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement number 836751.
DATA AVAILABILITY
The spectral fitting and equipartition modelling software written for the purpose of this work is publicly available on Github at https://github.com/adellej/tde_spectra_fit. The observations presented in Table 1 will be published online in a machine-readable format.
Footnotes
The geometric factors, defined in Barniol Duran et al. (2013), are given by fA = A/(πR2/Γ2) and fv = V/(πR3/Γ4), for an outflow with area A, volume V, and distance from the origin of the outflow R.
REFERENCES
APPENDIX A: CONSISTENCY OF RADIO OBSERVATIONS ACROSS EPOCHS
Due to the use of both the MeerKAT and VLA telescopes, and different configurations at the latter, we performed a consistency check of the data to ensure there were no instrumental or systematic offsets between epochs and between the VLA and MeerKAT L-band observations. We measured the flux densities of three background sources in the field of view for nine of the VLA epochs and four of the MeerKAT epochs. We applied a primary beam correction to the images before extracting the flux densities. The flux densities for these three sources in all bands are shown in Fig. A1, demonstrating that there is no significant systematic offset between the two instruments.
Flux density measurements of three background sources for eight epochs of observations including VLA and MeerKAT data. The data indicate that no systematic offset is present between epochs or between instruments, but that fluctuations of the order of |${\sim} 10{{\ \rm per\ cent}}$| are present between epochs of VLA observations.
In Fig. A1, there is evidence of fluctuations between VLA epochs of the order of |${\sim} 10{{\ \rm per\ cent}}$|. We examined the flux density scale obtained during calibrations of the secondary calibrator for the VLA observations. We found fluctuations of only a few per cent between epochs, consistent with the expected flux-density calibration errors. Thus, the fluctuations between epochs are larger than expected due to flux calibration alone, and may be attributed to intrinsic fluctuations in the sources we examined, primary beam corrections, resolution changes from different configurations, or other calibration inconsistencies.
In the spectral observations of AT2019azh, we identify steepenings of the synchrotron energy index. Here, we rule out the possibility of these being artificial steepenings due to inconsistencies in the data calibration between epochs. In Fig. A1, there is no evidence of inconsistent calibration with frequency for single epochs, except the 2019 October epoch. If the steepenings were artificial, we would expect to see the epochs where the steepenings were observed to show a trend of being lower at the higher frequencies and higher at the lower frequencies than the epochs in which no steepenings were observed. The only epoch where evidence of this frequency trend is present is the 2019 October epoch, and thus we deduce that the slight steepening observed in this epoch (from p ≈ 2.7 to 3) is likely not real and merely an artefact of the data calibration. For the other epochs, 2020 May and 2021 Feb, there is no evidence in Fig. A1 of any such trend with frequency, and we deduce that the spectral steepenings we observed are real.
The flux density offsets between epochs present in Fig. A1 would only affect the peak flux densities that we infer from the spectra, and not the spectral slope, since the offsets are not frequency dependent within epochs. Since the peak flux density is often not well constrained in our observations, the uncertainty in the peak flux density is dominated by the spectral fit uncertainty, and the fluctuations of order |${\sim} 10{{\ \rm per\ cent}}$| between epochs are outweighed.
APPENDIX B: SYNCHROTRON EMISSION FITS INCLUDING A COOLING BREAK
Here, we define one model being significantly better than other if the preferred model has an AIC or BIC score of at least 2 units lower. A score of 0–2 means minimal confidence, a score of 2–6 means positive confidence, and a score >6 indicates strong confidence that the model is preferred.
We carried out the same MCMC fitting as described in Section 2 but with the inclusion of the cooling break term in the model for epochs t > 321 d. When the additional cooling break was included in the fits, we found that the uncertainties on the peak frequency, peak flux, and p increased, and the cooling break was identified to be around 4 GHz. In Table B1, we show the calculated AIC and BIC for the original model (model 1) and the model including a cooling break (model 2) for the epoch fit.
AIC and BIC values for the observed flux spectra for each epoch fit with the original model (model 1) and the model including a cooling break (model 2).
| δt (d) . | 296 . | 350 . | 459 . | 666 . | 749 . | 849 . |
|---|---|---|---|---|---|---|
| AIC1 | 87.5 | 84.0 | 133.9 | 170.8 | 128.0 | 107.0 |
| AIC2 | 89.9 | 85.9 | 135.7 | 169.2 | 132.9 | 110.9 |
| BIC1 | 87.8 | 84.4 | 135.8 | 173.6 | 130.2 | 108.2 |
| BIC2 | 90.2 | 86.3 | 138.1 | 172.7 | 135.7 | 112.4 |
| δt (d) . | 296 . | 350 . | 459 . | 666 . | 749 . | 849 . |
|---|---|---|---|---|---|---|
| AIC1 | 87.5 | 84.0 | 133.9 | 170.8 | 128.0 | 107.0 |
| AIC2 | 89.9 | 85.9 | 135.7 | 169.2 | 132.9 | 110.9 |
| BIC1 | 87.8 | 84.4 | 135.8 | 173.6 | 130.2 | 108.2 |
| BIC2 | 90.2 | 86.3 | 138.1 | 172.7 | 135.7 | 112.4 |
AIC and BIC values for the observed flux spectra for each epoch fit with the original model (model 1) and the model including a cooling break (model 2).
| δt (d) . | 296 . | 350 . | 459 . | 666 . | 749 . | 849 . |
|---|---|---|---|---|---|---|
| AIC1 | 87.5 | 84.0 | 133.9 | 170.8 | 128.0 | 107.0 |
| AIC2 | 89.9 | 85.9 | 135.7 | 169.2 | 132.9 | 110.9 |
| BIC1 | 87.8 | 84.4 | 135.8 | 173.6 | 130.2 | 108.2 |
| BIC2 | 90.2 | 86.3 | 138.1 | 172.7 | 135.7 | 112.4 |
| δt (d) . | 296 . | 350 . | 459 . | 666 . | 749 . | 849 . |
|---|---|---|---|---|---|---|
| AIC1 | 87.5 | 84.0 | 133.9 | 170.8 | 128.0 | 107.0 |
| AIC2 | 89.9 | 85.9 | 135.7 | 169.2 | 132.9 | 110.9 |
| BIC1 | 87.8 | 84.4 | 135.8 | 173.6 | 130.2 | 108.2 |
| BIC2 | 90.2 | 86.3 | 138.1 | 172.7 | 135.7 | 112.4 |
In Table B1, it is clear that the AIC and BIC for model 1 are always lower than for model 2, with the model without a cooling break clearly preferred for the epoch at 850 d, and marginally preferred for the other epochs. In this analysis, we do not conclusively detect the presence of a cooling break.



