-
PDF
- Split View
-
Views
-
Cite
Cite
Devina Mohan, Anna M M Scaife, Fiona Porter, Mike Walmsley, Micah Bowles, Quantifying uncertainty in deep learning approaches to radio galaxy classification, Monthly Notices of the Royal Astronomical Society, Volume 511, Issue 3, April 2022, Pages 3722–3740, https://doi.org/10.1093/mnras/stac223
Close - Share Icon Share
ABSTRACT
In this work we use variational inference to quantify the degree of uncertainty in deep learning model predictions of radio galaxy classification. We show that the level of model posterior variance for individual test samples is correlated with human uncertainty when labelling radio galaxies. We explore the model performance and uncertainty calibration for different weight priors and suggest that a sparse prior produces more well-calibrated uncertainty estimates. Using the posterior distributions for individual weights, we demonstrate that we can prune 30 per cent of the fully connected layer weights without significant loss of performance by removing the weights with the lowest signal-to-noise ratio. A larger degree of pruning can be achieved using a Fisher information based ranking, but both pruning methods affect the uncertainty calibration for Fanaroff–Riley type I and type II radio galaxies differently. Like other work in this field, we experience a cold posterior effect, whereby the posterior must be down-weighted to achieve good predictive performance. We examine whether adapting the cost function to accommodate model misspecification can compensate for this effect, but find that it does not make a significant difference. We also examine the effect of principled data augmentation and find that this improves upon the baseline but also does not compensate for the observed effect. We interpret this as the cold posterior effect being due to the overly effective curation of our training sample leading to likelihood misspecification, and raise this as a potential issue for Bayesian deep learning approaches to radio galaxy classification in future.
1 INTRODUCTION
A new generation of radio astronomy facilities around the world such as the Low-Frequency Array (LOFAR; van Haarlem et al. 2013), the Murchison Widefield Array (MWA; Beardsley et al. 2019), the MeerKAT telescope (Jarvis et al. 2016), and the Australian SKA Pathfinder (ASKAP) telescope (Johnston et al. 2008) are generating large volumes of data. In order to extract scientific impact from these facilities on reasonable timescales, a natural solution has been to automate the data processing as far as possible and this has lead to the increased adoption of machine learning methodologies.
In particular for new sky surveys, automated classification algorithms are being developed to replace the by eye approaches that were possible historically. In radio astronomy specifically, studies looking at morphological classification using convolutional neural networks (CNNs) and deep learning have become increasingly common, especially with respect to the classification of radio galaxies.
The Fanaroff–Riley (FR) classification of radio galaxies was introduced over four decades ago (Fanaroff & Riley 1974), and has been widely adopted and applied to many catalogues since then. The morphological divide seen in this classification scheme has historically been explained primarily as a consequence of differing jet dynamics. Fanaroff–Riley type I (FR I) radio galaxies have jets that are disrupted at shorter distances from the central super-massive black hole host and are therefore centrally brightened, whilst Fanaroff–Riley type II (FR II) radio galaxies have jets that remain relativistic to large distances, resulting in bright termination shocks. These observed structural differences may be due to the intrinsic power in the jets, but will also be influenced by local environmental densities (Bicknell 1995; Kaiser & Best 2007).
Intrinsic and environmental effects are difficult to disentangle using radio luminosity alone as systematic differences in particle content, environmental effects, and radiative losses make radio luminosity an unreliable proxy for jet power (Croston, Ineson & Hardcastle 2018). Hence the use of morphology is important for gaining a better physical understanding of the FR dichotomy, and of the full morphological diversity of the population, which in turn is useful for inferring the environmental impact on radio galaxy populations (Mingo et al. 2019). It is hoped that the new generation of radio surveys, with improved resolution, sensitivity, and dynamic range, will play a key part in finally answering this question.
From a deep learning perspective, the ground work for morphological classification in this field was done by Aniyan & Thorat (2017), who used CNNs to classify FR I, FR II, and bent-tail sources. This was followed by other works involving the use of deep learning in source classification (e.g. Banfield et al. 2015; Lukic et al. 2018; Wu et al. 2018). More recently, Bowles et al. (2021) showed that an attention-gated CNNs could perform classification of radio galaxies with equivalent performance to other applications in the literature, but using ∼50 per cent fewer learnable parameters, Scaife & Porter (2021) showed that using group-equivariant convolutional layers that preserved the rotational and reflectional isometries of the Euclidean group resulted in improved overall model performance and stability of model confidence for radio galaxies at different orientations, and Bastien et al. (2021) generated synthetic populations of radio galaxies using structured variational inference.
Applying deep learning to radio astronomy comes with unique challenges. Unlike terrestrial labelled data sets such as MNIST, which contains ∼70 000 images, and ImageNet, which contains 14 million images, there is a dearth of labelled data in radio astronomy. The largest labelled data sets for Fanaroff–Riley classification contain of order 103 labelled images.1 For deep learning applications, this creates the need to augment data sets. However, this augmentation can lead to any biases associated with these small data sets being propagated into the larger augmented data sets used to train deep learning models and hence into any analysis that uses the outputs of those models.
Another challenge is that of artefacts, misclassifed objects, and ambiguity arising from how the morphologies in these data sets are defined. Underestimation and miscalibration of uncertainties associated with model outcomes for data samples that are peripheral to the main data mass are well documented in the machine learning literature (see e.g. Guo et al. 2017b), and it has been demonstrated that out-of-distribution data points will be misclassified with arbitrarily high precision by standard neural networks (Hein, Andriushchenko & Bitterwolf 2018).
To provide uncertainties on model outputs, probabilistic methods such as Bayesian (and approximately Bayesian) neural networks are required (MacKay 1992a,b). When properly calibrated, the uncertainty estimates from these approaches can serve as a diagnostic tool to mitigate the effect of increasingly distant data points and out-of-distribution examples. However, with the exception of Scaife & Porter (2021), to date there has been little work done on understanding the degree of confidence with which CNN models predict the class of individual radio galaxies. In modern radio astronomy, where astrophysical analysis is driven by population analyses, quantifying the confidence with which each object is assigned to a particular classification is crucial for understanding the propagation of uncertainties within that analysis.
In this work we use variational inference (VI) to implement a fully Bayesian CNN and quantify the degree of uncertainty in deep learning predictions of radio galaxy classifications. This differs from the approach of Scaife & Porter (2021) who used dropout as a Bayesian approximation to estimate model confidence (Gal & Ghahramani 2016). They studied one specific aspect of the model performance (variation with sample orientation), and as such it is not directly comparable to this work. We compare the variance of our posterior predictions to qualifications present in our test data that indicate the level of human confidence in assigning a classification label and show that model uncertainty is correlated with human uncertainty. We also investigate a number of the challenges that face the systematic use of Bayesian deep learning from the perspective of radio astronomy.
The structure of the paper is as follows: in Section 2 we introduce the variational inference method and its application to neural networks; in Section 3 we describe how different measures of uncertainty can be recovered from the learned variational posteriors using this approach; and in Section 4 we describe the data set being used in this work. In Section 5 we introduce the convolutional neural network that forms the primary model for this work, as well as how it is trained; in Section 6 we describe the results of that training in terms of model performance and uncertainty quantification in the context of the specific radio galaxy classification problem being addressed, as well as the wider machine learning literature; in Section 7 we discuss the cold posterior effect and hypotheses for mitigating it; and in Section 8 we draw our conclusions.
2 VARIATIONAL INFERENCE FOR DEEP LEARNING
The notion of ‘noisy weights’ that can adapt during training was first proposed by Hinton & van Camp (1993) to reduce the amount of information in network weights and prevent overfitting in neural networks. Graves (2011) developed a stochastic variational inference (SVI) method by applying stochastic gradient descent to VI using biased estimates of gradients. SVI allows VI to scale to large data sets by taking advantage of mini-batching and Graves (2011) considered various choices of standard prior and posterior distributions such as the Delta function, Gaussian, and Laplace distributions. Blundell et al. (2015) built on this work and proposed the Bayes by backprop (BBB) algorithm, which combines stochastic VI with the reparameterization trick (Kingma, Salimans & Welling 2015) to overcome the problems encountered while using backpropagation with SVI. Using this algorithm, one can calculate unbiased estimates of the gradients and use any tractable probability distribution to represent uncertainties in the weights.
To set up the problem of Bayesian inference, we consider a set of observations, |$\mathbf {x}$|, and a set of hypotheses, |$\mathbf {z}$|. For instance, for a neural network |$\mathbf {z}$| are the parameters of the model.
2.1 The variational inference cost function
In variational inference, a parameterized probability distribution, q(z), is defined as a variational approximation to the true posterior, p(z|x). The family of probability distributions, |$\mathbb {D}$|, defines the complexity of the solution that can be modelled. For instance, a family of Gaussians parameterized by mean, μ, and variance, σ2, may be defined. The goal of VI is to find the selection of parameters that most closely approximates the exact posterior.
The name ELBO stems from the fact that the log evidence is bounded by this function such that: |$\log p(x) \ge \rm {ELBO}$|. Consequently, variational inference reduces Bayesian inference to an optimization problem that can then be solved by standard deep learning optimization algorithms such as SGD and Adam.
2.2 VI for neural networks
The cost function shown in equation (11) is composed of two components: the first term is a complexity cost that depends on the prior over the weights, P(w), and the second is a likelihood cost that depends on the data and describes how well the model fits to the data. The cost function also has a minimum description length interpretation according to which the best model is the one that minimizes the cost of describing the model and the misfit between the model and the data to a receiver (Hinton & van Camp 1993; Graves 2011).
The cost, |$\mathcal {F}$|, is an expectation of the function, f(w, θ), with respect to the variational posterior, q(w|θ). In order to optimize the cost function, we need to calculate its gradient with respect to the variational parameters, θ. To make |$\mathcal {F}(D,\theta)$| differentiable, one must first employ the reparameterization trick (Kingma & Welling 2013; Kingma et al. 2015) to calculate samples from the variational posterior, q(w|θ), that are differentiable and then use Monte Carlo (MC) estimates of the gradients to approximate the cost function.
2.2.1 Mini-batching
To take advantage of mini-batch optimization for BBB, a weighted complexity cost is used (Graves 2011). This is because the likelihood cost is calculated for each mini-batch to update the weights when the model sees new data, whereas the complexity cost, which involves calculating the prior and posterior over the weights of the entire network, should be calculated only once per epoch because it is independent of data.
Several published results have reported a cold posterior effect which involves further down-weighting of the complexity cost (e.g. Wenzel et al. 2020). This effect is discussed in more detail in Sections 5.3 and 7.
2.3 Variational posteriors
The reparameterization trick allows us to use a variety of family densities for the variational distribution. Kingma & Welling (2013) give some examples of q(w|θ) for which the reparameterization trick can be applied. These include any tractable family of densities such as the exponential, logistic, cauchy distributions; and any location-scale family such as Gaussian, Laplace, or Uniform densities can be used with the function: t(.) = location + scale · ϵ.
Following Blundell et al. (2015), we can then calculate the gradient of the cost function with respect to the variational parameters θ = (μ, ρ) using the standard optimization algorithms that are used with neural networks.
2.4 Priors
In this work we also consider a Laplace prior which is parameterized by a location parameter, μ, and a scale parameter, b, and a Laplace Mixture Model (LMM) prior with two mixture components weighted by π, similar in form to the definition of the GMM prior.
Some regularization techniques used with point-estimate neural networks have theoretical justifications using Bayesian inference. For instance, it can be shown that Maximum a posteriori estimation of neural networks with some priors is equivalent to regularization (Jospin et al. 2020). For example, using a Gaussian prior over the weights is equivalent to weight decay regularization, whereas using a Laplace prior induces L1 regularization. Gal & Ghahramani (2016) showed that dropout can also be considered an approximation to variational inference, where the variational family is a Bernoulli distribution.
2.5 Bayesian convolutional neural networks
The BBB algorithm can be extended for convolutional neural networks by sampling the weights from a variational distribution defined over the shared weights of the convolutional kernels. This is followed by fully connected layers that have weights with a variational distribution defined over them. For simplicity, our implementation differs from that proposed by Shridhar, Laumann & Liwicki (2019), in which work the activations of each convolutional layer were sampled instead of the weights in order to accelerate convergence.
2.6 Posterior predictive distribution
From equation (24), we see how the posterior predictive distribution is an average of all possible variational parameters weighted by their posterior probability.
The posterior predictive distribution can be estimated using MC samples as follows:
Sample variational parameters from the variational posterior distribution conditioned on data D: w(i) ∼ q(w|D).
Sample prediction D*(i) from q(D*|w(i)).
- Repeat steps (i) and (ii) to construct an approximation to q(D*|D) using N samples such that:(25)$$\begin{eqnarray*} q(D^{*}|D) & = & \mathbb {E}_{q(w|D)} q(D^{*}|w) \end{eqnarray*}$$(26)$$\begin{eqnarray*} & = & \mathbb {E}_{w^{(i)} \sim q(w|D)} q\left(D^{*}|w^{(i)}\right) \end{eqnarray*}$$(27)$$\begin{eqnarray*} & \approx & \frac{1}{N}\sum _{i=1}^N q\left(D^{*}|w^{(i)}\right). \end{eqnarray*}$$
Thus BBB can be used to construct an approximate posterior predictive distribution, which can further be used to estimate uncertainties.
3 UNCERTAINTY QUANTIFICATION
The sources of uncertainty in the predictions of neural network models can broadly be divided into two categories: epistemic and aleatoric (Gal 2016; Abdar et al. 2021). Epistemic uncertainty quantifies how uncertain the model is in its predictions and this can be reduced with more data. Aleatoric uncertainty on the other hand represents the uncertainty inherent in the data and cannot be reduced. Uncertainty inherent in the input data along with model uncertainty is propagated to the output, which gives us predictive uncertainty (Abdar et al. 2021). BBB allows us to capture model uncertainty by defining distributions over model parameters.
3.1 Predictive entropy
We use the natural logarithm for all the equations described in this section and the values are reported in nats, which is the natural unit of information. The entropy thus attains a maximum value of ∼0.693 nats, when the predictive entropy is maximum and a minimum value close to zero.
3.2 Mutual information
3.3 Average entropy
It can be seen from equations (32) and (33) that the predictive uncertainty in equation (30) is a sum of epistemic uncertainty and aleatoric uncertainty.
3.4 Overlap index
In addition to the uncertainty metrics described above, we also define two overlap indices: ηsoft, to quantify how much the distributions of predicted Softmax values for the two classes overlap; and ηlogits, to quantify how much the distributions of logits for the two classes overlap.3 A higher degree of overlap indicates a higher level of predictive uncertainty. The overlap parameters have contributions from both epistemic and aleatoric uncertainties.
where Mz defines the step size of z such that |$\lbrace z_i\rbrace _{i=1}^{M_z}$| ranges from zero to one in Mz steps.
3.5 Uncertainty calibration
Bayesian neural networks allow us to obtain uncertainty estimates on model predictions, but these estimates have often been shown to be poorly calibrated due to the use of approximate inference methods and model misspecification (Foong et al. 2020; Krishnan & Tickoo 2020). A model is considered to be well calibrated if the degree of uncertainty is correlated with the accuracy, i.e. low uncertainty predictions are more likely to be classified correctly and high uncertainty predictions are more likely to be misclassified. Therefore, when comparing different models one must also take the calibration of uncertainty metrics into account, in addition to the overall accuracy of a model.
4 DATA
Radio galaxies are a sub-class of active galactic nuclei (AGN). These galaxies are characterized by large-scale jets and lobes that can extend up to mega-parsec distances from the central black hole and are observed in the radio spectrum. Fanaroff & Riley (1974) proposed a classification of such extended radio sources based on the ratio of the distance between the highest surface brightness regions on either side of the galaxy to the total extent of the radio source, RFR. Based on a threshold ratio of 0.5, the galaxies were classified into two classes as follows: if RFR < 0.5, the source was classified into Class I (FR I; edge-darkened), and if RFR > 0.5 it was classified into Class II (FR II; edge-brightened). Over the years, several other morphologies such as bent-tail (Rudnick & Owen 1976; O’Dea & Owen 1985), hybrid (Gopal-Krishna & Wiita 2000), and double-double (Schoenmakers et al. 2000) sources have also been observed and there is still a continuing debate about the exact interplay between extrinsic effects, such as the interaction between the jet and the environment, and intrinsic effects, such as differences in central engines and accretion modes, that give rise to the different morphologies. In this work we use only the binary FR I/FR II classification.
We have used the MiraBest data set which consists of 1256 images of radio galaxies pre-processed to be used specifically for deep learning tasks (e.g. Bowles et al. 2021; Scaife & Porter 2021). The data set was constructed using the sample selection and classification described in Miraghaei & Best (2017), who made use of the parent galaxy sample from Best & Heckman (2012). Optical data from data release 7 of Sloan Digital Sky Survey (SDSS DR7; Abazajian et al. 2009) was cross-matched with NRAO VLA Sky Survey (NVSS; Condon et al. 1998) and Faint Images of the Radio Sky at Twenty-Centimeters (FIRST; Becker, White & Helfand 1995) radio surveys. Parent galaxies were selected such that their radio counterparts had an AGN host rather than emission dominated by star formation. To enable classification of sources based on morphology, sources with multiple components in either of the radio catalogues were considered.
The morphological classification was done by visual inspection at three levels: (i) The sources were first classified as FR I/FR II based on the original classification scheme of Fanaroff & Riley (1974). Additionally, 35 Hybrid sources were identified as sources having FR I-like morphology on one side and FR II-like on the other. Of the 1329 extended sources inspected, 40 were determined to be unclassifiable. (ii) Each source was then flagged as ‘Confident’ or ‘Uncertain’ to represent the degree of belief in the human classification. (iii) Some of the sources which did not fit exactly into the standard FR I/FR II dichotomy were given additional tags to identify their sub-type. These sub-types include 53 Wide Angle Tail (WAT), nine Head Tail (HT), and five Double-Double (DD) sources. To represent these three levels of classification, each source was given a three-digit identifier as shown in Table 1.
| Digit 1 . | Digit 2 . | Digit 3 . |
|---|---|---|
| 1: FR I | 0: Confident | 0: Standard |
| 2: FR II | 1: Uncertain | 1: Double Double |
| 3: Hybrid | 2: Wide Angle Tail | |
| 4: Unclassifiable | 3: Diffuse | |
| 4: Head Tail |
| Digit 1 . | Digit 2 . | Digit 3 . |
|---|---|---|
| 1: FR I | 0: Confident | 0: Standard |
| 2: FR II | 1: Uncertain | 1: Double Double |
| 3: Hybrid | 2: Wide Angle Tail | |
| 4: Unclassifiable | 3: Diffuse | |
| 4: Head Tail |
| Digit 1 . | Digit 2 . | Digit 3 . |
|---|---|---|
| 1: FR I | 0: Confident | 0: Standard |
| 2: FR II | 1: Uncertain | 1: Double Double |
| 3: Hybrid | 2: Wide Angle Tail | |
| 4: Unclassifiable | 3: Diffuse | |
| 4: Head Tail |
| Digit 1 . | Digit 2 . | Digit 3 . |
|---|---|---|
| 1: FR I | 0: Confident | 0: Standard |
| 2: FR II | 1: Uncertain | 1: Double Double |
| 3: Hybrid | 2: Wide Angle Tail | |
| 4: Unclassifiable | 3: Diffuse | |
| 4: Head Tail |
To construct the machine learning data set, several pre-processing steps were applied to the data following the approach described in Aniyan & Thorat (2017) and Tang, Scaife & Leahy (2019):
In order to minimize the background noise in the images, all pixels below the |$3\sigma$| level of the background noise were set to 0. This threshold was chosen because among the classifiers trained by Aniyan & Thorat (2017) on images with |$2\sigma$|, 3σ, and 5σ cut-offs, 3σ performed most well.
The images were clipped to 150 × 150 pixels, centred on the source.
- The images were normalized as follows:(43)$$\begin{eqnarray*} {\rm Output} = 255 ~ ~ \frac{ {\rm Input} - {\rm Input_{min}}}{{\rm Input_{max}} - {\rm Input_{min}}} ~ , \end{eqnarray*}$$
where Input refers to the input image, Inputmin and Inputmax are the minimum and maximum pixel values in the input image, and Output is the image after normalization.
To ensure the integrity of the machine learning data set, the following 73 objects out of the 1329 extended sources identified in the catalogue were not included: (i) 40 unclassifiable objects; (ii) 28 objects with extent greater than the chosen image size of 150 × 150 pixels; (iii) four objects which were found in overlapping regions of the FIRST survey; (iv) one object in category 103 (FR I Confident Diffuse). Since this was the only instance of this category, it would not have been possible for the test set to be representative of the training set. The composition of the final data set is shown in Table 2. We do not include the sub-types in this table as we have not considered their classification.
| Class . | Confidence . | No. . |
|---|---|---|
| FR I | Confident | 397 |
| Uncertain | 194 | |
| FR II | Confident | 436 |
| Uncertain | 195 | |
| Hybrid | Confident | 19 |
| Uncertain | 15 |
| Class . | Confidence . | No. . |
|---|---|---|
| FR I | Confident | 397 |
| Uncertain | 194 | |
| FR II | Confident | 436 |
| Uncertain | 195 | |
| Hybrid | Confident | 19 |
| Uncertain | 15 |
| Class . | Confidence . | No. . |
|---|---|---|
| FR I | Confident | 397 |
| Uncertain | 194 | |
| FR II | Confident | 436 |
| Uncertain | 195 | |
| Hybrid | Confident | 19 |
| Uncertain | 15 |
| Class . | Confidence . | No. . |
|---|---|---|
| FR I | Confident | 397 |
| Uncertain | 194 | |
| FR II | Confident | 436 |
| Uncertain | 195 | |
| Hybrid | Confident | 19 |
| Uncertain | 15 |
In this work, we use the MiraBest Confident subset to train the BBB models. Examples of FR I and FR II galaxies from the MiraBest Confident data set are shown in Fig. 1.
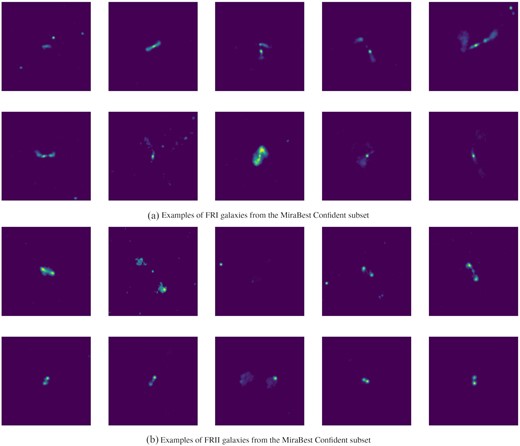
Examples of (a) FR I and (b) FR II galaxies from the MiraBest Confident subset.
Additionally, we use 49 samples from the MiraBest Uncertain subset and 30 samples from the MiraBest Hybrid class to test the trained model’s ability to correctly represent different measures of uncertainty, since these samples can be considered as being drawn from the same data generating distribution as the MiraBest Confident samples, but have a differing degree of belief in their classification. We note that there may be components of both epistemic and aleatoric uncertainty in the Uncertain and Hybrid samples, and this is discussed further in Section 6.
We note that all the previous work published using this data set uses some form of data augmentation. In this work we do not use any data augmentation, although the effect of data augmentation is discussed further in Section 7.2. The reasons for this are two-fold: firstly, that unprincipled data augmentation has been suggested to negatively affect the performance of Bayesian deep learning models (Nabarro et al. 2021); and second, that a noted advantage of Bayesian models is their ability to obtain good performance using only small data sets (e.g. Xiong, Barash & Frey 2011; Jospin et al. 2020; Semenova et al. 2020).
5 MODEL
5.1 Architecture
The architecture used to classify the MiraBest data set using BBB is shown in Table 3. We use a LeNet-5-style architecture (LeCun et al. 1998) with two additional convolutional layers. We found it essential to add two convolutional layers to the LeNet-5 architecture in order to obtain good model performance. Adding additional fully connected and convolutional layers beyond this resulted in no further improvement. The number of channels in the additional convolutional layers were also optimized. We used a kernel support size of 5 to be consistent with previous CNN-style architectures used with the MiraBest data set (e.g. Scaife & Porter 2021). ReLU activation functions are used for each layer with the exception of the output layer and max-pooling is used to down-sample the feature data after each convolutional layer.
CNN architecture. Stride = 1 is used for all the convolutional and max pooling layers.
| Operation . | Kernel . | Channels . | Padding . |
|---|---|---|---|
| Convolution | 5 × 5 | 6 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 16 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 26 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 32 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Fully connected | 120 | ||
| ReLU | |||
| Fully connected | 84 | ||
| ReLU | |||
| Fully connected | 2 | ||
| Log Softmax |
| Operation . | Kernel . | Channels . | Padding . |
|---|---|---|---|
| Convolution | 5 × 5 | 6 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 16 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 26 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 32 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Fully connected | 120 | ||
| ReLU | |||
| Fully connected | 84 | ||
| ReLU | |||
| Fully connected | 2 | ||
| Log Softmax |
CNN architecture. Stride = 1 is used for all the convolutional and max pooling layers.
| Operation . | Kernel . | Channels . | Padding . |
|---|---|---|---|
| Convolution | 5 × 5 | 6 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 16 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 26 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 32 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Fully connected | 120 | ||
| ReLU | |||
| Fully connected | 84 | ||
| ReLU | |||
| Fully connected | 2 | ||
| Log Softmax |
| Operation . | Kernel . | Channels . | Padding . |
|---|---|---|---|
| Convolution | 5 × 5 | 6 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 16 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 26 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Convolution | 5 × 5 | 32 | 1 |
| ReLU | |||
| Max pooling | 2 × 2 | ||
| Fully connected | 120 | ||
| ReLU | |||
| Fully connected | 84 | ||
| ReLU | |||
| Fully connected | 2 | ||
| Log Softmax |
The functional form of our priors is as defined in Section 2.4 and the hyper-parameters of the priors were tuned using the validation data set. We build models with four different priors: (i) a simple Gaussian prior with σ = 0.1, (ii) a GMM prior with {π, σ1, σ2} = {0.75, 1, 9.10−4}, (iii) a Laplace prior with b = 1, and (iv) a LMM prior with {π, b1, b2} = {0.75, 1, 10−3}.
We use a Gaussian distribution as our variational approximation to the posterior over both the weights and biases in our network. Models using the BBB method are known to be highly sensitive to the initialization of this posterior and in this work we initialize the posterior means, μ, from a uniform distribution, |$\mathcal {U}(-0.1,0.1)$|, and the posterior variance parametrization, ρ, from |$\mathcal {U}(-5,-4)$|.
5.2 Training
The MiraBest data set has a predefined training: test split. We further divide the training data into a ratio of 80:20 to create training and validation sets. The final split contains 584 training samples, 145 validation samples, and 104 test samples.
All the models are trained for 500 epochs, with mini-batches of size 50. We train the models using the Adam optimizer with a learning rate of ℓ = 5 × 10−5 for all the priors. A learning rate scheduler is implemented which reduces the learning rate by 95 per cent if the validation likelihood cost does not improve for four consecutive epochs.
After a model has been trained, the test error is calculated as the percentage of incorrectly classified galaxies by comparing the output of the model to the labels in the test set.
5.3 Cold posterior effect
We found it necessary to temper our posterior in order to get a good performance from the Bayesian neural network, without which the accuracy remains around |$55{{\ \rm per\ cent}}$|. We tempered the posterior for a range of temperature values, T, between [10−5, 1) and chose the largest value of T for which the validation accuracy was improved significantly. Thus, for all experiments described in the following sections we use T = 10−2 in equation (44).
Several hypotheses have been proposed to explain the cold posterior effect including model or prior misspecification (Wenzel et al. 2020), and data augmentation or data set curation leading to likelihood misspecification (Aitchison 2021). These are discussed in detail and investigated further in Section 7.
5.4 Weight pruning
Variational inference based neural networks have several advantages over non-Bayesian neural networks; however, for a typical variational posterior such as the Gaussian distribution, the number of parameters in the network double compared to a non-Bayesian model with the same architecture because both the mean and standard deviation values need to be learned. This increases the computational and memory overhead at test time and during deployment. Thus, there is a need to develop network pruning approaches which can be used to remove the parameters that contain least or no useful information. Several authors have also considered pruning to improve the generalization performance of the network (LeCun, Denker & Solla 1989). Many of the pruning methods that have been developed can also be applied to non-Bayesian neural networks, but in this section we discuss a signal-to-noise ratio (SNR) based pruning criterion which can be applied naturally to a model trained with Gaussian variational densities (Graves 2011; Blundell et al. 2015).
We adapt SNR-based pruning for a convolutional Bayesian neural network by considering only the fully connected layer weights of the model for pruning, instead of all the weights of the network. This is because the convolutional layer weights are shared weights and removing even a small fraction may result in disastrous consequences for model performance. However, the fully connected layers make up |$\sim 85{{\ \rm per\ cent}}$| of the total weights of our network, so pruning methods are still worth considering for convolutional BBB models. Pruning only the fully connected layers is also consistent with pruning methods developed for standard CNN models (e.g. Gong et al. 2014; Soulié, Gripon & Robert 2016; Tu et al. 2016).
For the model trained on the MiraBest data set with a Laplace prior, we find that up to 30 per cent of the fully connected layer weights can be pruned without a significant change in performance. This is discussed further in Section 6.4.
6 RESULTS
6.1 Classification and calibration
The results of our classification experiments are shown in Table 4. The mean and standard deviation values of the test error are calculated by taking 100 samples from the posterior predictive distribution for each test data point in the MiraBest Confident data set.
Classification error and percentage cUCE on MiraBest Confident test set using BBB-CNN. The percentage cUCE is shown separately for predictive uncertainty as measured by predictive entropy (PE), epistemic uncertainty as measured by mutual information (MI), and aleatoric uncertainty as measured by average entropy (AE) as calculated on the MiraBest Confident test set. For a fuller explanation of these metrics, please see Section 3.
| . | . | cUCE per cent . | ||
|---|---|---|---|---|
| Prior . | Test error . | PE . | MI . | AE . |
| Gaussian prior | |$14.48 \pm 3.40\ \mathrm{ per \, cent}$| | 30.49 | 21.90 | 25.48 |
| GMM prior | |$12.89 \pm 2.23\ \mathrm{ per \, cent}$| | 19.92 | 18.86 | 16.86 |
| Laplace prior | |$11.62 \pm 2.38\ \mathrm{ per \, cent}$| | 9.69 | 16.37 | 10.84 |
| LMM prior | |$17.29 \pm 2.71\ \mathrm{ per \, cent}$| | 21.02 | 26.05 | 17.69 |
| . | . | cUCE per cent . | ||
|---|---|---|---|---|
| Prior . | Test error . | PE . | MI . | AE . |
| Gaussian prior | |$14.48 \pm 3.40\ \mathrm{ per \, cent}$| | 30.49 | 21.90 | 25.48 |
| GMM prior | |$12.89 \pm 2.23\ \mathrm{ per \, cent}$| | 19.92 | 18.86 | 16.86 |
| Laplace prior | |$11.62 \pm 2.38\ \mathrm{ per \, cent}$| | 9.69 | 16.37 | 10.84 |
| LMM prior | |$17.29 \pm 2.71\ \mathrm{ per \, cent}$| | 21.02 | 26.05 | 17.69 |
Classification error and percentage cUCE on MiraBest Confident test set using BBB-CNN. The percentage cUCE is shown separately for predictive uncertainty as measured by predictive entropy (PE), epistemic uncertainty as measured by mutual information (MI), and aleatoric uncertainty as measured by average entropy (AE) as calculated on the MiraBest Confident test set. For a fuller explanation of these metrics, please see Section 3.
| . | . | cUCE per cent . | ||
|---|---|---|---|---|
| Prior . | Test error . | PE . | MI . | AE . |
| Gaussian prior | |$14.48 \pm 3.40\ \mathrm{ per \, cent}$| | 30.49 | 21.90 | 25.48 |
| GMM prior | |$12.89 \pm 2.23\ \mathrm{ per \, cent}$| | 19.92 | 18.86 | 16.86 |
| Laplace prior | |$11.62 \pm 2.38\ \mathrm{ per \, cent}$| | 9.69 | 16.37 | 10.84 |
| LMM prior | |$17.29 \pm 2.71\ \mathrm{ per \, cent}$| | 21.02 | 26.05 | 17.69 |
| . | . | cUCE per cent . | ||
|---|---|---|---|---|
| Prior . | Test error . | PE . | MI . | AE . |
| Gaussian prior | |$14.48 \pm 3.40\ \mathrm{ per \, cent}$| | 30.49 | 21.90 | 25.48 |
| GMM prior | |$12.89 \pm 2.23\ \mathrm{ per \, cent}$| | 19.92 | 18.86 | 16.86 |
| Laplace prior | |$11.62 \pm 2.38\ \mathrm{ per \, cent}$| | 9.69 | 16.37 | 10.84 |
| LMM prior | |$17.29 \pm 2.71\ \mathrm{ per \, cent}$| | 21.02 | 26.05 | 17.69 |
Using the model trained with a Laplace prior, we recover a test error of |$11.62 \pm 2.38 {{\ \rm per\ cent}}$|. We also recover a comparable test error of |$12.89 \pm 2.23 {{\ \rm per\ cent}}$| using a GMM prior. The standard deviation values represent the spread in the overall test error and indicate the model’s confidence in its predictions on the test set. Bowles et al. (2021) who augment the MiraBest Confident samples by a factor of 72 report a test error of |$8{{\ \rm per\ cent}}$|, whereas Scaife & Porter (2021) who use random rotations of the same data set as a function of epoch to augment the data, report a test error of |$5.95 \pm 1.37 {{\ \rm per\ cent}}$| with a LeNet-5 style CNN with MC dropout, and |$3.43\pm 1.29 {{\ \rm per\ cent}}$| using a D16 group-equivariant CNN with MC dropout. We again emphasize that the test error values we report are without any data augmentation. If we include data augmentation using random rotations from 0 to 360 degrees this improves the BBB test error using the Laplace prior to |$7.41 \pm 2.22{{\ \rm per\ cent}}$|, but at the cost of increased uncertainty calibration error. We note that the wider effect of using augmentation with Bayesian models is a subject of debate in the literature and this is discussed further in Section 7.2.
Whilst differences in performance are often used to choose a preferred model, it is also the case that more accurate point-wise models are overconfident in their predictions. This problem of overconfidence in standard NNs is well documented in the literature (see e.g. Nguyen, Yosinski & Clune 2015). In particular this effect has been shown to lead to miscalibrated uncertainty in predictions, especially for data samples that are less similar to canonical examples of a class (Guo et al. 2017b; Hein et al. 2018).
Table 4 shows the percentage cUCE values of the uncertainty metrics calculated for the MiraBest Confident test set (see Section 3.5). Among the four priors tested in this work, we find that the Laplace prior gives the most well-calibrated uncertainty metrics, followed by the GMM prior. Given the uncertainties on each test error due to the small size of our test set, we cannot draw any strong conclusions about which prior should be preferred. However, after analysing the uncertainty calibration error for each prior, we suggest that the Laplace prior produces the most well-calibrated uncertainties. We also find that the cold posterior effect is less pronounced in the case of the Laplace prior model (see Fig. 2). Similarly to the model accuracy, these results indicate that learning benefits most from a sparser prior and consequently in the following analysis we report results for the Laplace prior.
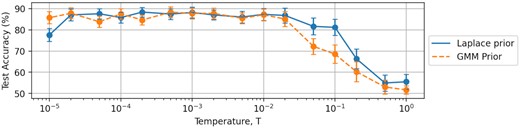
The ‘cold posterior’ effect for the MiraBest classification problem (see Section 7 for details). Data are shown for the BBB models with no data augmentation and the original ELBO cost function trained with a Laplace prior (solid blue line), and trained with a GMM prior (orange dashed line).
6.2 Uncertainty quantification
We first look at some illustrative examples of galaxies from the MiraBest Confident test set to build intuition about the uncertainty metrics used. For each test sample we make N = 200 forward passes through the trained model. This results in a distribution of model outputs following the learned predictive posterior, which allow us to estimate the different uncertainty measures described in Section 3.
We show some examples of galaxies that have been correctly classified with high confidence in Fig. 3. These galaxies correspond to typical FR I/FR II classifications. The corresponding uncertainty metrics are shown in Table 5. The predictive entropy and mutual information for all the galaxies shown are very low (<0.01 nats). The overlap indices ηsoft and ηlogits are ≪10−5, which indicates that there is virtually no overlap, as can be seen in the distributions of Softmax probabilities in Fig. 3.
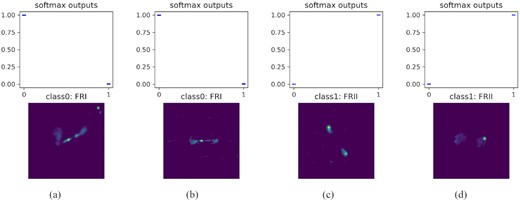
Examples of galaxies correctly classified with high predictive confidence. Top: Softmax values for 200 forward passes through the trained model. Bottom: Input data images.
Predictive entropy (PE), mutual information (MI), and overlap indices for Softmax (ηsoft) and logit-space (ηlogits) for galaxies correctly classified with high confidence shown in Fig. 3.
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 3a | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3b | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3c | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3d | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 3a | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3b | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3c | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3d | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
Predictive entropy (PE), mutual information (MI), and overlap indices for Softmax (ηsoft) and logit-space (ηlogits) for galaxies correctly classified with high confidence shown in Fig. 3.
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 3a | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3b | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3c | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3d | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 3a | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3b | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3c | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
| 3d | <0.01 | <0.01 | ≪10−5 | ≪10−5 |
We then consider galaxies for which the predictive uncertainty is high, as shown in Fig. 4. These galaxies have the highest predictive entropy among the test samples of the MiraBest Confident data set and large values of overlap indices in both the Softmax and logit space. These samples also have high mutual information, which indicates that the model’s confidence in its classification is very low. The values of uncertainty metrics corresponding to these galaxies are shown in Table 6.
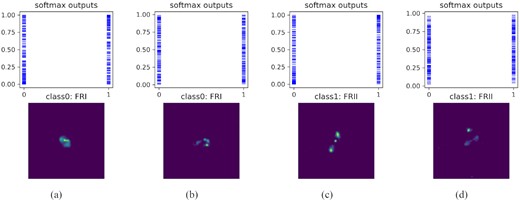
Examples of galaxies classified with low predictive confidence. Top: Softmax values for 200 forward passes through the trained model. Bottom: Input data images.
Predictive entropy (PE), mutual information (MI), and overlap indices for Softmax (ηsoft) and logit-space (ηlogits) for galaxies classified with low confidence shown in Fig. 4.
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 4a | 0.68 | 0.25 | 0.72 | 0.10 |
| 4b | 0.69 | 0.20 | 0.90 | 0.08 |
| 4c | 0.67 | 0.27 | 0.70 | 0.08 |
| 4d | 0.69 | 0.14 | 0.88 | 0.12 |
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 4a | 0.68 | 0.25 | 0.72 | 0.10 |
| 4b | 0.69 | 0.20 | 0.90 | 0.08 |
| 4c | 0.67 | 0.27 | 0.70 | 0.08 |
| 4d | 0.69 | 0.14 | 0.88 | 0.12 |
Predictive entropy (PE), mutual information (MI), and overlap indices for Softmax (ηsoft) and logit-space (ηlogits) for galaxies classified with low confidence shown in Fig. 4.
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 4a | 0.68 | 0.25 | 0.72 | 0.10 |
| 4b | 0.69 | 0.20 | 0.90 | 0.08 |
| 4c | 0.67 | 0.27 | 0.70 | 0.08 |
| 4d | 0.69 | 0.14 | 0.88 | 0.12 |
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 4a | 0.68 | 0.25 | 0.72 | 0.10 |
| 4b | 0.69 | 0.20 | 0.90 | 0.08 |
| 4c | 0.67 | 0.27 | 0.70 | 0.08 |
| 4d | 0.69 | 0.14 | 0.88 | 0.12 |
Finally in Fig. 5, we show one example where the model has incorrectly classified a galaxy with high confidence. The galaxy has been labelled an FR II and the model incorrectly classifies it as an FR I. The predictive entropy, mutual information, and overlap indices are very low, as shown in Table 7, which means that the model’s confidence in its prediction is very high for this galaxy. We can see that the galaxy deviates from the typical FR II classification because it has additional bright components and its label is somewhat ambiguous. Thus, the bias introduced by the ambiguity in the definition of FR I/FR II and the ambiguity in the labels gives rise to uncertainty metrics that can potentially be misleading.
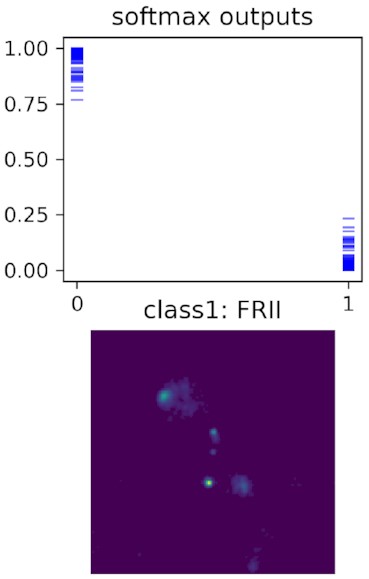
A galaxy that has been incorrectly classified with high predictive confidence. Top: Softmax values for 200 forward passes through the trained model. Bottom: Input data image.
Predictive entropy (PE), mutual information (MI), and overlap indices for Softmax (ηsoft) and logit-space (ηlogits) for a galaxy incorrectly classified with high confidence shown in Fig. 5.
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 5 | 0.10 | 0.02 | <0.01 | <0.01 |
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 5 | 0.10 | 0.02 | <0.01 | <0.01 |
Predictive entropy (PE), mutual information (MI), and overlap indices for Softmax (ηsoft) and logit-space (ηlogits) for a galaxy incorrectly classified with high confidence shown in Fig. 5.
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 5 | 0.10 | 0.02 | <0.01 | <0.01 |
| Galaxy . | PE . | MI . | |$\boldsymbol{\eta _{\rm soft}}$| . | |$\boldsymbol{\eta _{\rm logits}}$| . |
|---|---|---|---|---|
| 5 | 0.10 | 0.02 | <0.01 | <0.01 |
In this section we saw how high or low values of predictive entropy, mutual information, and overlap indices indicate the model’s confidence in making predictions about individual galaxies; in the next section we analyse the distributions of uncertainty metrics for all the galaxies in the data set.
6.3 Analysis of uncertainty estimates
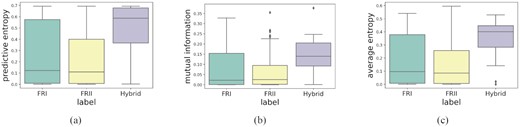
We test the trained model’s ability to capture different measures of uncertainty by calculating uncertainty metrics for (i) the MiraBest Uncertain test samples (49 objects), and (ii) the MiraBest Hybrid samples (30 objects), using the model trained on the MiraBest Confident samples. As before this is done by making N = 200 forward passes through the model for each test input. Overall distributions for each uncertainty metric as a function of the three different test sets are shown in Fig. 6.

Distributions of uncertainty metrics for MiraBest Confident (MBFR_Conf), Uncertain (MBFR_Uncert), and Hybrid (MBHybrid) data sets. (a) Predictive uncertainty as measured using predictive entropy; (b) Epistemic uncertainty as measured using mutual information; and (c) Aleatoric uncertainty as measured using average entropy. For a fuller explanation of these metrics, please see Section 3.
The MiraBest Uncertain samples are considered to be drawn from the same distribution as the MiraBest Confident samples, and from a machine learning perspective would therefore be denoted as in-distribution. The MiraBest Hybrid samples are a more complex case: in principle they are a separate class that was not considered when training the model and therefore might be denoted as being out-of-distribution by some measures; however, given that they are still a sub-population of the over-all radio galaxy population, and moreover that they are defined as amalgams of the two classes used to train the model, they could also be considered to be in-distribution. Consequently, in this work we treat the MiraBest Hybrid test sample as being in-distribution.
6.3.1 Analysis of uncertainty estimates on MiraBest Uncertain
Fig. 6 shows that the MiraBest Uncertain test set has on average higher measures of uncertainty across all estimators than the MiraBest Confident test set. In Fig. 7(a) we can see that this is also reflected in the median values of the predictive entropy distribution being higher for both FR I and FR II classes in the MiraBest Uncertain test set compared to the Confident test set, and that the interquartile range is also larger. This indicates that a larger number of galaxies are being classified with higher predictive entropy. The predictive entropy distribution has a higher median value for FR II objects for both MiraBest Confident and Uncertain samples. However, the distributions are wider for FR I objects.

Class-wise distributions of uncertainty metrics for MiraBest Confident and MiraBest Uncertain data sets. (a) Predictive uncertainty as measured using predictive entropy; (b) Epistemic uncertainty as measured using mutual information; and (c) Aleatoric uncertainty as measured using average entropy. For a fuller explanation of these metrics, please see Section 3.
The distribution of mutual information is shown in Fig. 6(b). The mutual information is also higher for samples from the MiraBest Uncertain test set. This indicates a higher epistemic uncertainty in classifying these samples, which is consistent with how the data sets are defined. We also find that FR IIs have a wider distribution of epistemic uncertainty than FR Is for MiraBest Uncertain samples (see Fig. 7b).
Using the average entropy of a test sample as a measure of aleatoric uncertainty, we see in Fig. 6(c) that the Uncertain samples have higher median value and a larger interquartile range than the Confident samples. From Fig. 7(c) we note that that for both FR I and FR II type galaxies, the interquartile range has shifted to a higher value and the median average entropy is also higher.
From Fig. 8, we can also see that FR II samples have lower uncertainty than FR I samples when combined across the Confident and Uncertain test sets, which could be because the training set contains ∼7 per cent more FR IIs than FR Is.
Morphology-wise distributions of uncertainty metrics for the MiraBest data set. (a) Predictive uncertainty as measured using predictive entropy; (b) Epistemic uncertainty as measured using mutual information; and (c) Aleatoric uncertainty as measured using average entropy. For a fuller explanation of these metrics, please see Section 3.
Thus in general we find that BBB can correctly represent model uncertainty in radio galaxy classification, and that this uncertainty is correlated with how human classifiers defined the MiraBest Confident and Uncertain qualifications.
6.3.2 Analysis of uncertainty estimates on MiraBest Hybrid
In Fig. 6 we can see that the interquartile range of the distributions of uncertainty metrics for the MiraBest Hybrid samples are well separated from the distributions for the MiraBest Confident samples.
The median predictive entropy of the Hybrid samples is higher than the MiraBest Confident samples by 0.5 nats, as shown in Fig. 6(a). This indicates that there is a high degree of predictive uncertainty associated with the hybrid samples, which is expected as the training set does not contain any hybrid samples. This behaviour is also echoed as a function of overall morphology (see Fig. 8). It can be seen that the MiraBest Hybrid samples have substantially higher median uncertainties than either the FR I or FR II objects (combined across the MiraBest Confident and MiraBest Uncertain samples).
In Fig. 6(b) we see that the median value for the distribution of mutual information for the Hybrid test set is higher than the upper quartile of the MiraBest Confident test set. This high degree of epistemic uncertainty could be because the model did not see any Hybrid samples during training. We also note that among the sub-classes of the Hybrid data set, the confidently labelled samples have higher epistemic uncertainty than the uncertainly labelled samples, as shown in Fig. 9(b). We suggest that this may be because the uncertain samples are more similar to the FR I/FR II galaxies than the model has seen during training, i.e. their classification as a Hybrid was considered uncertain by a human classifier because the morphology was biased towards one of the standard FR I or FR II classifications. In which case their epistemic uncertainty might be expected to be lower since the model was trained to predict those morphologies.
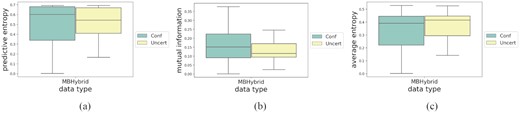
Class-wise distributions of uncertainty metrics for MiraBest Hybrid data set. (a) Predictive uncertainty as measured using predictive entropy; (b) Epistemic uncertainty as measured using mutual information; and (c) Aleatoric uncertainty as measured using average entropy. For a fuller explanation of these metrics, please see Section 3.
The distribution of the average entropy (aleatoric uncertainty) has a higher median value and the interquartile range has shifted to higher values of average entropy compared to the Confident and Uncertain test sets (see Fig. 6c). While it can be seen that Hybrid samples have higher aleatoric uncertainty on average, in Fig. 9(c) we can also see how the aleatoric uncertainty is distributed among the classes in the hybrid samples. The confidently labelled Hybrid samples span almost the entire range of the entropy function between (0, 0.693] nats. The uncertainty labelled samples also have a high degree of aleatoric uncertainty.
Thus we find that the Hybrid test set has an even higher degree of uncertainty than the Uncertain test set.
6.4 Alternative pruning approaches
In Section 5.4 we found that 30 per cent of the weights in the fully connected layers of our trained model could be pruned without a loss of performance using an SNR-based pruning approach. In this section, we discuss an alternative pruning approach based on Fisher information. We compare the performance of our BBB model trained on radio galaxies for different pruning methods and analyse the effect of pruning on uncertainty estimates.
A number of alternative methods for model pruning have been described in the literature. Hessian based methods have been proposed to rank model parameters by their importance, but in practice the calculation of a full Hessian for typical deep learning models is in general prohibitively expensive in terms of computation. Consequently, one of the most popular methods is to simply rank parameters by their magnitude, where magnitude refers to the absolute value of the weights. The SNR approach, where parameters with low magnitudes or high variances are removed (Section 5.4), may be considered a natural extension of this method. Tu et al. (2016) showed that for deterministic neural networks it is possible to improve on a simple magnitude-based pruning by using the Fisher information matrix (FIM) for a particular parameter of the network, θ. Here we implement the method of Tu et al. (2016) and compare it to the SNR-based pruning method.
These two approaches are based on fundamentally different methodologies: while SNR pruning takes into account ‘noisy’ weights that are either too small in magnitude or have large posterior variances, the Fisher-information based method removes parameters based on their contribution to the gradients. If a parameter has smaller FIM values, this indicates that the gradients of the parameter did not change much during training, i.e. that the parameter contained less information and was less relevant to producing the optimized model. Thus one method may be preferred to the other in specific applications.
The results of our pruning experiments are shown in Fig. 10. As also observed by Tu et al. (2016), pruning the weights based on Fisher information alone does not allow for a large number of parameters to be pruned effectively because many values in the FIM diagonal are close to zero. We find this to be true for our model as well, and that only 10 per cent of the fully connected layers can be pruned using Fisher information alone without incurring a significant penalty in performance.
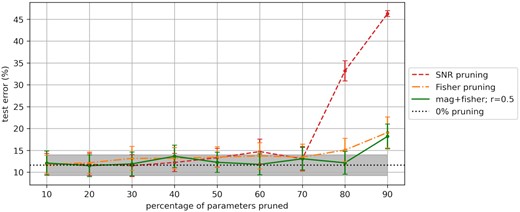
Comparison of model performance for different pruning methods based on: SNR, Fisher information, and a combination of magnitude and Fisher information. The grey shaded portion indicates the standard deviation of test error for the unpruned model.
To remedy this, Tu et al. (2016) suggest combining Fisher pruning with magnitude-based pruning. Following their approach, we define a parameter, r, to determine the proportion of weights that are pruned by either of these methods. To prune P parameters from the network, we perform the following steps in order: (i) remove the P(1 − r) weights with the lowest magnitude; (ii) remove the |$P \, r$| parameters with the lowest FIM values. The parameter r is between (0,1) and is tuned like a hyper-parameter. We get an optimal pruning performance with r = 0.5. We find that up to 60 per cent of the fully connected layer weights can be pruned using this method without a significant change in performance, which is double the volume of weights pruned by the SNR-based method discussed in Section 5.4. We refer to this method as Fisher pruning in the following sections for conciseness.
6.4.1 Analysis of uncertainty estimates for different pruning methods
The effect of pruning on uncertainty quantification for the MiraBest Confident test set is shown in Fig. 11. We plot uncertainty metrics for the two pruning methods discussed in this work: (i) based on SNR, with 30 per cent pruning, and (ii) Fisher pruning which is based on magnitude combined with Fisher information, with 60 per cent pruning, and compare them to the metrics obtained for the unpruned model. We complement this with an analysis of the change in uncertainty calibration error for the two pruning methods considered in this work.
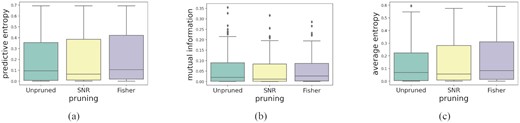
Distributions of uncertainty metrics for different pruning methods for the MiraBest Confident data set. (a) Predictive uncertainty as measured using predictive entropy; (b) Epistemic uncertainty as measured using mutual information; and (c) Aleatoric uncertainty as measured using average entropy. For a fuller explanation of these metrics, please see Section 3.
From Fig. 11 a we note that predictive entropy increases with pruning. The interquartile range increases for both pruning methods. This increase is mainly due to an increase in predictive entropy for FR I galaxies in case of SNR pruning and for FR II galaxies in case of Fisher pruning (see Fig. 12a). The median predictive entropy and interquartile range increase for FR IIs with Fisher pruning.
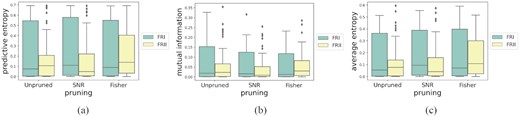
Class-wise distributions of uncertainty metrics for different pruning methods for the MiraBest Confident data set. (a) Predictive uncertainty as measured using predictive entropy; (b) Epistemic uncertainty as measured using mutual information; and (c) Aleatoric uncertainty as measured using average entropy. For a fuller explanation of these metrics, please see Section 3.
We also find that the cUCE of predictive entropy increases with pruning, and that this increase is larger in the case of SNR pruning (see Table 8). SNR pruning has more of an adverse effect on the classification of FR I samples than FR II samples, whereas the effect of Fisher pruning is similar for both classes.
Percentage cUCE on MiraBest Confident test set for our BBB-CNN model trained with a Laplace prior, pruned to its threshold limit for SNR and Fisher pruning. The percentage cUCE is shown separately for the predictive entropy (PE), mutual information (MI), and average entropy (AE) as calculated on the MiraBest Confident test set.
| . | . | per cent cUCE . | ||
|---|---|---|---|---|
| Prior . | Pruning . | PE . | MI . | AE . |
| Laplace | Unpruned | 9.69 | 16.37 | 10.84 |
| SNR | 14.35 | 16.82 | 13.93 | |
| Fisher | 13.43 | 15.29 | 11.25 | |
| . | . | per cent cUCE . | ||
|---|---|---|---|---|
| Prior . | Pruning . | PE . | MI . | AE . |
| Laplace | Unpruned | 9.69 | 16.37 | 10.84 |
| SNR | 14.35 | 16.82 | 13.93 | |
| Fisher | 13.43 | 15.29 | 11.25 | |
Percentage cUCE on MiraBest Confident test set for our BBB-CNN model trained with a Laplace prior, pruned to its threshold limit for SNR and Fisher pruning. The percentage cUCE is shown separately for the predictive entropy (PE), mutual information (MI), and average entropy (AE) as calculated on the MiraBest Confident test set.
| . | . | per cent cUCE . | ||
|---|---|---|---|---|
| Prior . | Pruning . | PE . | MI . | AE . |
| Laplace | Unpruned | 9.69 | 16.37 | 10.84 |
| SNR | 14.35 | 16.82 | 13.93 | |
| Fisher | 13.43 | 15.29 | 11.25 | |
| . | . | per cent cUCE . | ||
|---|---|---|---|---|
| Prior . | Pruning . | PE . | MI . | AE . |
| Laplace | Unpruned | 9.69 | 16.37 | 10.84 |
| SNR | 14.35 | 16.82 | 13.93 | |
| Fisher | 13.43 | 15.29 | 11.25 | |
Pruning does not seem to have a large effect on the distributions of mutual information, which narrow by a small amount for both pruning methods (see Fig. 11b). The cUCE does not increase significantly with SNR pruning and reduces with Fisher pruning (see Table 8).
Looking at the class-wise distributions of mutual information in Fig. 12(b), we can see that both pruning methods narrow the distribution of mutual information for FR I galaxies. However, SNR pruning increases the uncertainty calibration error for FR Is and decreases UCE for FR IIs. Fisher pruning on the other hand decreases UCE for FR Is and increases UCE for FR IIs. Therefore, SNR and Fisher pruning both seem to be adversely affecting the uncertainty calibration for one of the two classes.
The average entropy increases with both pruning methods and the distribution becomes more broad in the case of Fisher pruning (see Fig. 11c). However, we also find that Fisher pruning does not significantly change cUCE and that there is more increase in cUCE with SNR pruning (see Table 8).
Fig. 12(c) shows that average entropy increases with pruning for FR I galaxies for both pruning methods and there is a greater increase in average entropy with Fisher pruning for FR II galaxies. We find that SNR pruning increases UCE for both FR I and FR II galaxies, but the increase is more significant for FR I galaxies. Fisher pruning reduces UCE for FR Is and increases UCE for FR IIs.
Whilst we have described the differing effect of alternative pruning methods on a class-wise basis, we note that pruning itself cannot be applied selectively by class since it depends on the model parameters. However, based on the fundamental differences in the results from SNR and Fisher pruning, we suggest that FR I galaxies are less influential on the gradients of the learnable parameters during training compared to FR IIs and that the learned model weights are less noisy for FR IIs compared to FR Is.
Hüllermeier & Waegeman (2021) argue that epistemic and aleatoric uncertainty are mutable quantities as a function of model specification (see also Kiureghian & Ditlevsen 2009); specifically, that the uncertainty contributed by each is affected by model complexity and class separability. For example, embedding a data set into a higher dimensional feature space may result in greater separability of the target classes leading to lower aleatoric uncertainty, but the additional complexity from the higher dimensionality results in a model with higher epistemic uncertainty. In SNR-based pruning, we are reducing the dimensionality of the feature space, but at the same time we are also removing noisy weights (and hence noisy features) that may adversely affect class separability, and so it is expected that measures of both epistemic and aleatoric uncertainty will be changed as a function of pruning degree.
7 COLD POSTERIOR EFFECT
In Section 5.3 we found that we can improve the generalization performance of our BBB model significantly by cooling the posterior with a temperature T ≪ 1, deviating from the true Bayes posterior. This cold posterior effect is shown in detail in Fig. 13 for our model trained on radio galaxies with the Laplace prior. In Section 5.3 we modified our cost function to down-weight the posterior in equation (44) using a temperature term, T, with all subsequent experiments performed using T = 10−2. In Fig. 13 we show the effect of varying T over a wide range of values.
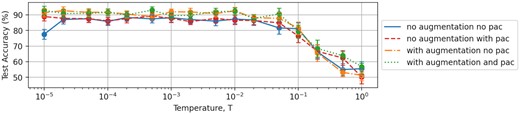
The ‘cold posterior’ effect for the MiraBest classification problem (see Section 7 for details). Data are shown for the BBB model trained with a Laplace prior with no data augmentation and the original ELBO cost function (solid blue line), the BBB model with no data augmentation and the Masegosa posterior cost function (red dashed line), the BBB model with data augmentation and the original ELBO function (orange dot–dashed line), and the BBB model with data augmentation and the Masegosa posterior cost function (green dotted line).
These results suggest that some component of the Bayesian framework in the context of this application is misspecified and it becomes difficult to justify using a Bayesian approach to these models whilst artificially reducing the effect of the components that make the learning Bayesian in the first place.
Finding an explanation for the cold posterior effect is an active area of research and several hypotheses have been proposed to explain this effect (Wenzel et al. 2020): use of uninformative priors, such as the standard Gaussian, which may lead to prior misspecification (Fortuin 2021); model misspecification; data augmentation or data set curation issues which lead to likelihood misspecification (Aitchison 2021; Nabarro et al. 2021). Here we consider two approaches for investigating the effect of these misspecifications.
7.1 Model misspecification
We examine whether the cold posterior effect in our results is due to model misspecification by optimizing the model with a modified cost function, following the work of Masegosa (2019). The cost function is modified on the basis of Probably Approximately Correct (PAC)-Bayesian theory. PAC theory has its roots in Statistical Learning Theory and was first described in Valiant (1984) as a method for evaluating learnability, i.e. how well a machine learns hypotheses given a set of examples. Although PAC started out as a frequentist framework, it was soon combined with Bayesian principles. It has now evolved into a formalized mathematical theory used to give statistical guarantees on the performance of machine learning algorithms by placing bounds on their generalization performance.
McAllester (1999) presented PAC-Bayesian inequalities which combine PAC-learning with Bayesian principles and provide guarantees on the performance of generalized Bayesian algorithms. These algorithms are referred to as generalized because the PAC-Bayes framework has similar components to the Bayesian framework: a prior, π, defined over a set of hypotheses, θ ∈ Θ, and a posterior, ρ, which is updated using Bayes-rule style updates using samples from a data generating distribution, ν(x). But these bounds hold true for all choices of priors, whereas there is no guarantee on performance in Bayesian inference if the data set is not generated from the prior distribution i.e. if the prior assumptions are incorrect. The bounds also hold true for all choices of posteriors, so in principle we can have model-free learning. However, traditionally most of the PAC-Bayes bounds are only applicable to bounded loss functions and this has made it difficult to apply them to the unbounded loss functions that are typically used to train neural networks. Fortunately more recent works have introduced PAC Bayes bounds for unbounded losses as well (e.g. Alquier, Ridgway & Chopin 2016; Germain et al. 2016; Shalaeva et al. 2020). We refer the reader to Guedj (2019) for an overview of the PAC-Bayesian framework.
Since variational inference is an approximation to the Bayesian marginal likelihood, we can use PAC-Bayesian bounds to optimize VI-based Bayesian NNs. By applying these bounds to train Bayesian neural networks, one deviates from the variational inference as defined in the Bayesian paradigm and moves towards a more generalized variational inference algorithm. Training a model with the modified cost function minimizes an upper bound on the test loss and provides a more optimal learning strategy compared to optimizing the Bayesian posterior or its approximations such as the ELBO function. To do this, the cost function is modified such that it minimizes a second-order PAC-Bayesian bound on the cross entropy loss (CE), rather than the standard ELBO. Following the literature, we refer to this new objective function as a ‘Masegosa posterior’.
7.1.1 Masegosa posteriors
The results of this modification for a range of temperatures is shown in Fig. 13, where it can be seen that the Masegosa posterior PAC bound (red dashed line) improves the cold posterior effect over the original BBB model (solid blue line) slightly, but does not fully compensate for the overall behaviour.
7.2 Likelihood misspecification
Aitchison (2021) suggested that rather than prior or model misspecification, the cold posterior effect might be caused by over-curation of training data sets leading to likelihood misspecification, where the training data was not statistically representative of the underlying data distribution. They showed that for highly curated data sets, such as CIFAR-10, the cold posterior effect could be mitigated by adding label noise to the training data. Other works in this area have suggested that unprincipled data augmentation could be a contributing factor to the cold posterior effect (e.g. Izmailov et al. 2021; Nabarro et al. 2021).
The MiraBest data set used in this work is likely to be similarly subject to some over-curation in the same sense as CIFAR-10 as it was compiled using an average or consensus labelling scheme from multiple human classifiers. For CIFAR-10, Aitchison (2021) introduced label noise by augmenting the original data set using all individual classifications from 50 human classifiers in their work, which were provided by the CIFAR-10H data set (Peterson et al. 2019). Here we do not have access to the individual classifications for the MiraBest data set, but we are able to augment our data set in a more standard manner using rotations.
We find that the cold posterior effect observed in our work reduces slightly with data augmentation (see Fig. 13). We suggest that this is because we have augmented the MiraBest data set using principled methods that correspond to an informed prior for how radio galaxies are oriented, as radio galaxy class is assumed to be equivariant to orientation and chirality (see e.g. Ntwaetsile & Geach 2021; Scaife & Porter 2021). Fig. 13 shows the cold posterior effect for the radio galaxy classification problem addressed in this work both with (orange dot–dashed line) and without (blue solid line) data augmentation. It can be seen that there is an improvement in performance at temperatures below T = 0.01 causing the test accuracy to reach a plateau at higher temperatures than for unaugmented data. Data augmentation also improves performance at temperatures above T = 0.01; however, we also find that the uncertainty calibration error increases for the model trained with augmented data for T = 0.01.
Fig. 13 also shows that combining a Masegosa posterior with data augmentation provides the most significant improvement to the cold posterior effect (green dotted line); however, it does not rectify it completely. Since the Masegosa posterior is a more complete test of model misspecification than the data augmentation used here is of likelihood misspecification, we suggest that a key element for exploring the problem of likelihood misspecification in future may be the availability of radio astronomy training sets that do not only present average or consensus target labels, but instead include all individual labels from human classifiers.
8 CONCLUSIONS
In this work we have presented the first application of a variational inference based approach to deep learning classification of radio galaxies, using a binary FR I/FR II classification. Using a Bayesian Convolutional Neural Network based on the Bayes by Backprop (BBB) algorithm, we have shown that posterior uncertainties on the predictions of the model can be estimated by making a variational approximation to the posterior probability distribution over the model parameters.
We have considered the use of four different prior distributions over the parameters of our model. We find that a model trained with a Laplace prior performs better than one using a Gaussian prior in terms of mean test error by |$\sim 3{{\ \rm per\ cent}}$|, and better than a GMM prior by |$\sim 1{{\ \rm per\ cent}}$|; a model trained with a LMM prior performs worse than those using Gaussian priors and the Laplace prior. We also find that the calibration of the posterior uncertainties for a model trained using a Laplace prior is better than for models trained using the other priors considered in this work. This suggests that learning in this case may benefit from sparser weights. However, given the uncertainties on these values we cannot yet draw statistically significant conclusions for prior selection. We also note that this work uses relatively simple priors and that future extensions will look more closely at prior specification and whether more informative priors can help learning.
We note that we obtain a larger error value than that obtained by other neural network based models trained on the MiraBest Confident data set, but emphasize that other works have used data augmentation to increase the size of the data set, whereas we have only used the original samples. This allowed us to study the use of VI-based neural networks on small data sets as well. If we include data augmentation we obtain a comparable performance to previously published results; however, this comes at the cost of increased uncertainty calibration error. Thus there is a trade-off between standard models, which are somewhat more accurate, and BBB, which is reasonably accurate while giving more reliable posteriors and therefore potentially more scientifically useful.
Our analysis of different measures of uncertainty for our deep learning model indicates that model uncertainty is correlated with the degree of belief of the human classifiers who originally assigned the labels in the MiraBest data set. We find that our BBB model trained on confidently labelled radio galaxies is able to reliably estimate its confidence in predictions when presented with radio galaxies that have been classified with a lower degree of confidence. Notably, all measures of uncertainty are higher for the samples qualified as Uncertain. The model also made predictions with higher uncertainty for a sample of Hybrid radio galaxies, which was expected as these samples were not present in the training data, but contained FR I/FR II like components nevertheless. Looking more closely at the class-wise distributions of uncertainties, we found that FR II type objects are associated with a lower degree of uncertainty than FR Is. Among the classes of the Hybrid samples, we found that the uncertainty was higher for the confidently labelled samples compared to the uncertainly labelled Hybrid samples. We suggest that this may be because objects with uncertain labels are more similar to the FR I/FR II samples the model was trained on, which is why the human classifiers were uncertain in their classification as a Hybrid.
We have explored different weight pruning approaches with the motivation of reducing the storage and computation cost of these models at deployment. We find that using a SNR based method using posterior means and variances allows the fully connected layers of the model to be pruned by up to 30 per cent, but a method that combines Fisher information with weight magnitudes allows an even higher proportion of weights to be pruned, by up to 60 per cent, without compromising the model performance. The effect of removing some of these weights can also be seen in the uncertainty metrics. We found that both the uncertainty and the uncertainty calibration error increase with model pruning. However, both pruning methods seem to affect FR I/FR II samples differently. Future work in this area could make a comparison of these methods with augmented data to verify whether one method should be preferred over the other. Another possible extension could be re-training a pruned model to test whether pruning improves the generalization performance of a network.
Finally, we consider the cold posterior effect and its implications for the use of Bayesian deep learning with radio galaxy data in future. We find that the cold posterior effect is worse when using a GMM prior than for a Laplace prior, and we consider the hypothesis that further model misspecification may be causing the observed cold posterior effect. We test this hypothesis by retraining our model with a modified cost function that provides a loose PAC-Bayes bound over the cross-entropy loss. We find that although the modified cost function improves model performance slightly, it does not compensate for the cold posterior effect completely.
We also consider the possibility of likelihood misspecification and test whether a principled data augmentation could improve the cold posterior effect. Similarly, we find that a small improvement is observed, but not a sufficiently large change to remove the effect entirely. Based on these results, we suggest that over-curation of the training data set may be responsible for the majority of the cold posterior effect in radio galaxy classification and recommend that future labelling schemes for radio astronomy data retain full details of labelling from all human classifiers in order to test and potentially mitigate this effect more fully.
In this work we have considered a binary classification of morphology, but a diverse and complex population of galaxies exist in the radio universe. Understanding how populations of radio galaxies are distributed gives us insight into the effect of extrinsic and intrinsic factors that may have led to the morphologies, which in turn help shape our understanding of radio-loud AGN, their excitation and accretion modes, how they evolve, and their relationship with their host galaxies and environments. Deep learning will play an important role in extracting scientific value from the next-generation of radio facilities and understanding how neural network models propagate uncertainties will be crucial for deploying these models scientifically.
ACKNOWLEDGEMENTS
We thank the anonymous referee for their useful comments that improved this work. AMS, MW, and MB gratefully acknowledge support from Alan Turing Institute AI Fellowship EP/V030302/1. FP gratefully acknowledges support from UK Science & Technology Facilities Council (STFC) and IBM through the iCASE studentship ST/P006795/1. MB gratefully acknowledges support from STFC.
DATA AVAILABILITY
Code for this work is available at https://github.com/devinamhn/RadioGalaxies-BBB. This work makes use of the MiraBest machine learning data set, which is publically available under a Creative Commons 4.0 license at https://doi.org/10.5281/zenodo.4288837.
Footnotes
We note that the Radio Galaxy Zoo catalogue (Banfield et al. 2015) contains of order 104 objects, but these are not labelled by morphological type.
Here we refer only to the weights, w, of the network for simplicity, but the equations are applicable to the biases as well.
Logits are the unnormalized outputs of the network, i.e. the outputs of the final layer before the Softmax function is applied.



