Non-linear density–velocity dynamics in f(R) gravity from spherical collapse

Nadkarni-Ghosh, Sharvari; Chowdhury, Sandip

doi:10.1093/mnras/stac133

ABSTRACT

We investigate the joint density–velocity evolution in f(R) gravity using smooth, compensated spherical top-hats as a proxy for the non-linear regime. Using the Hu-Sawicki model as a working example, we solve the coupled continuity, Euler, and Einstein equations using an iterative hybrid Lagrangian–Eulerian scheme. The novel aspect of this scheme is that the metric potentials are solved for analytically in the Eulerian frame. The evolution is assumed to follow GR at very early epochs and switches to f(R) at a pre-determined epoch. Choosing the ‘switching epoch’ too early is computationally expensive because of high frequency oscillations; choosing it too late potentially destroys consistency with ΛCDM. To make an informed choice, we perform an eigenvalue analysis of the background model which gives a ballpark estimate of the magnitude of oscillations. There are two length scales in the problem: the comoving Compton wavelength of the associated scalar field and the width of the top-hat. The evolution is determined by their ratio. When the ratio is large, the evolution is scale-independent and the density–velocity divergence relation (DVDR) is unique. When the ratio is small, the evolution is very close to GR, except for the formation of a spike near the top-hat edge, a feature which has been noted in earlier literature. We are able to qualitatively explain this feature in terms of the analytic solution for the metric potentials, in the absence of the chameleon mechanism. In the intermediate regime, the evolution is profile-dependent and no unique DVDR exists.

dark energy, large-scale structure of Universe, cosmology: theory

1 INTRODUCTION

Observations of type IA supernovae have established that our Universe is undergoing a phase of accelerated expansion. The best explanation so far, is that this acceleration is due to an additional constant energy density component – called the cosmological constant (Λ). On galactic scales, observations of galaxy rotation curves have established the need for a non-baryonic matter component. In the standard ΛCDM model, our Universe today is made up of about 68 per cent of Λ, 28 per cent of dark matter, and 4 per cent baryonic or visible matter (Planck Collaboration VI 2020). While this model agrees remarkably well with a host of other observational constraints, there are still some glaring issues. The physical origin of Λ and dark matter are still unknown. On the observational side, recent measurements indicate that CMB estimates of the Hubble constant (H₀) and the amplitude of fluctuations (σ₈) are in disagreement with other probes of the same quantities (for e.g. Macaulay, Wehus & Eriksen 2013; Di Valentino et al. 2021). Thus, the need arises to explore models beyond ΛCDM. There are two broad avenues that have been considered. One path continues to assume that the observed acceleration is due to an additional ‘dark energy’ component and a plethora of phenomenological models have been explored. The other path assumes that there is no additional energy density, but instead postulates that Einstein’s General Relativity (GR) is incorrect and needs modification (see reviews by De Felice & Tsujikawa 2010; Sotiriou & Faraoni 2010; Clifton et al. 2012; Joyce et al. 2015; Joyce, Lombriser & Schmidt 2016; Nojiri, Odintsov & Oikonomou 2017 for various aspects of this subject). Current and future cosmological surveys aim to constrain modified gravity (MG hereafter) models through a host of observables. The number counts of clusters, their density and velocity profiles, the splashback radius and weak lensing maps are some of the important cluster-scale probes that will help constrain model parameters. Similarly, redshift-space distortions that give estimates of galaxy peculiar velocities also provide complementary constraints (see the recent review by Baker et al. 2021).

In standard GR, the perturbations on sub-horizon scales, in the single stream limit, obey the coupled continuity, Euler and Poisson equations for the fractional overdensity δ, the peculiar velocity v, and the peculiar gravitational potential Ψ. In standard GR, in the linear regime, the density and peculiar velocity are related through the continuity equation as

$$\begin{eqnarray*} \Theta = - f(\Omega _m) \delta , \end{eqnarray*}$$

(1)

where Θ = H⁻¹∇_r · v is the scaled divergence of the peculiar velocity w.r.t. the physical coordinate r. f = dln δ/dln a is defined to be the linear growth rate and is usually expressed as |$f(\Omega _m) = \Omega _m^\gamma$|⁠, where γ is called the growth index and is sensitive to the cosmological model. Indeed, one of the main aims of surveys like DESI¹ (e.g. Alam et al. 2021), SDSS² (e.g. Alam et al. 2017), and Euclid³ (e.g. Amendola et al. 2018) is to test the above relation and constrain f. This relation has also been used extensively to constrain the growth rate from local flow measurements (Nusser, Branchini & Davis 2012; Nusser 2017; Lilow & Nusser 2021) or for measuring the velocity of the Local Group (e.g. Nusser, Davis & Branchini 2014). However, this relation breaks down on non-linear scales and this deviation can contribute to the error budget in the determination of f (Nusser et al. 2012). Velocities provide a bias-independent measure of the underlying density field and hence the non-linear velocity–gravity relation has been of interest since the early 1990s. Analytic estimates were given based on perturbation theory both in Eulerian and Lagrangian frames (for e.g. Bertschinger & Dekel 1989; Nusser et al. 1991; Bernardeau 1992; Gramann 1993b, a; Chodorowski 1997; Chodorowski & Lokas 1997; Susperregi & Buchert 1997; Chodorowski et al. 1998; Kitaura et al. 2012) and were validated and extended by numerical simulations (for e.g. Mancinelli et al. 1993; Mancinelli & Yahil 1995; Bernardeau & van de Weygaert 1996; Bernardeau et al. 1999; Zaroubi, Hoffman & Dekel 1999; Kudlicki et al. 2000; Ciecielg et al. 2003; Scoccimarro 2004; Colombi, Chodorowski & Teyssier 2007; Hahn, Angulo & Abel 2015). Fitting forms for ΛCDM were provided based on spherical collapse (Bilicki & Chodorowski 2008) and extended to other dark energy models and triaxial collapse (Nadkarni-Ghosh 2013; Nadkarni-Ghosh & Singhal 2016; Mandal & Nadkarni-Ghosh 2020).

All of the above-mentioned investigations of the density–velocity divergence relation (DVDR), also sometimes called the velocity–gravity relation have assumed standard GR. One of the important features of standard GR is that the ‘Newtonian’ gravitational potential Ψ, which dictates particle dynamics and appears in the Euler equation is the same as the potential Φ that governs the spatial curvature and is related to the density through the Poisson equation. This equality is violated in most MG models and an extra equation is necessary to evolve the two potentials simultaneously. This changes the fundamental structure of the evolution equations and the interplay between the continuity and Euler equations which couples the density and velocity is different for MG as compared to GR (see figs 1 of Uzan 2007 and Song & Doré 2009 for nice schematics).

In this paper, we aim to understand the joint density–velocity dynamics using the spherical collapse model as a proxy for the non-linear regime. In the linear regime, the DVDR arises from imposing the ‘slaving condition’. It implies that the velocity field is proportional to the acceleration field and is such that there are no perturbations at the big bang epoch. In first order Eulerian perturbation theory, this is equivalent to ignoring the decaying mode in the linear solution for δ (Peebles 1980) and in Lagrangian perturbation theory, it is embedded in the Zeldovich approximation (Zel’Dovich 1970; Buchert 1992). In Nadkarni-Ghosh (2013), it was shown that it is possible to extend this same idea to the non-linear regime to obtain the non-linear DVDR. In a spherically symmetric system, the condition of no perturbations at the big bang, sets a specific relation between the non-linear δ and Θ at any epoch. This relation traces out a special curve in the 2D δ − Θ phase space, which was termed as the ‘Zeldovich curve’ and it was shown that this curve is an invariant set of the dynamical system given by the joint continuity and Euler equations, restricted to spherical symmetry. This means that the curve depends only on the cosmological parameters that govern evolution and not on initial conditions. Perturbations starting anywhere in phase space asymptote to the Zeldovich curve as they evolve. Nadkarni-Ghosh (2013) also showed that this invariance can be potentially exploited to break parameter degeneracy between parameters that govern initial conditions such as σ₈ or n_s and those that govern evolution such as Ω_m or the equation of state w. In this paper, we evolve smoothed, compensated spherical top-hat overdensities and examine the resulting density and velocity profiles using a similar phase space description. Is there a unique relation between the density and velocity divergence akin to GR that is invariant of the initial conditions? For simplicity, we focus on the f(R) model and in particular consider the form given by Hu & Sawicki (2007).

Spherical collapse (SC) in the context of MG has been considered by various authors. Schäfer & Koyama (2008) used the Birkoff’s theorem to write equations of motions for the outer radius of a top-hat for a phenomenological model that interpolated between ΛCDM and the DGP model. They argued that although Birkoff’s theorem is known to be violated in most modified gravity models (Dai, Maor & Starkman 2008), the error associated with this approximation was small. Schmidt, Hu & Lima (2010) coupled SC with the halo model to compute the halo mass function, halo bias, and the non-linear matter power spectrum for the DGP theory. Chakrabarti & Banerjee (2016) investigated collapse in f(R) theories with a perfect fluid to understand the nature of the singularity. In standard GR, SC is most commonly used to compute the critical overdensity for collapse δ_c, an important ingredient of excursion set based approaches such as the Press–Schecter formalism and its extensions (Press & Schechter 1974; Sheth, Mo & Tormen 2001; Paranjape, Sheth & Desjacques 2013). The same is true in MG models. Herrera, Waga & Jorás (2017) computed δ_c for f(R), whereas Li and collaborators gave excursion estimates of the mass function in Galileon and chameleon models and also investigated the effect of the environment & Lam (Li & Efstathiou 2012; Li & Lam 2012; Barreira et al. 2013). Martino, Stabenau & Sheth (2009) computed cluster counts in MG for a Yukawa-like potential. Very recently, SC has also been combined with Large Deviations Theory to make analytic predictions of the matter density probability distribution function (Cataneo et al. 2021). Many of the above investigations model SC in modified gravity similar to that in standard GR, but with a modified effective Newton’s constant.

The treatment of spherical collapse in this paper is akin to that of Borisov, Jain & Zhang (2012) and Kopp et al. (2013) who solve the coupled continuity, Euler, Poisson, and scalar field equations iteratively for an f(R) model. Borisov et al. (2012) solve it in the Lagrangian frame by computing the acceleration of spherical shells at each step, whereas, Kopp et al. (2013) solve the system directly in the Eulerian frame as a coupled non-linear PDE using realistic profiles obtained from peaks theory (Bardeen et al. 1986). However, our treatment differs from these papers in some important aspects. First, we assume that the Compton wavelength is purely time-dependent and does not depend on the density of the perturbation. With this approximation, we cannot model the chameleon screening mechanism wherein the Compton wavelength changes with the density of the perturbation (Khoury & Weltman 2004). However, we illustrate the effect of screening by considering different scales for the width of the top-hat and demonstrate the scale-dependent nature of non-linear evolution. Secondly, we assume that the perturbations obey GR at early epochs and switch to the f(R) evolution at a relatively late time denoted as a_switch. This is necessary because the f(R) model exhibits high frequency oscillations at early epochs (Hu & Sawicki 2007; Song, Hu & Sawicki 2007) making the equations numerically stiff and computationally expensive. However, starting the evolution too late, destroys consistency with the background ΛCDM evolution. Thus, the switching epoch, needs to be chosen judiciously. In this paper, we perform an eigenvalue analysis of the background equations to estimate the magnitude of oscillations and make an informed choice of a_switch. Such an analysis has not been presented in the literature thus far. Finally, we do not solve the equations for the scalar field, but instead, recast the new degree of freedom in terms of the variable χ which is proportional to the difference of the two perturbation potentials Φ and Ψ. We present a closed form analytic solution for χ in spherical symmetry. We solve the system using a hybrid Lagrangian–Eulerian iterative scheme, wherein, the spatial equations for the two potentials are solved analytically in the Eulerian frame and the continuity and Euler equation are solved in the Lagrangian frame by recasting them as second-order evolution equations for the radii of a series of concentric shells.

The rest of the paper is organized as follows. In Section 2 we define the Hu-Sawicki system and perform the eigenvalue analysis of the same. Section 3 lays down the set of equations and initial conditions governing the non-linear evolution. Section 4 outlines the iterative method of solution and gives analytic expressions for the potential χ. In order to illustrate screening, we plot the static solutions to the potentials as a function of the radial coordinate for different choices of the perturbation scale. Section 5 evolves the compensated top-hat profile in the linear regime and Section 6 extends the evolution to the non-linear regime. The late time density and velocity fields are analysed by plotting them on the density–velocity divergence phase space and fitting formulae are provided in certain limits. We summarize in Section 7. The appendix Section A gives the details of the initial top-hat setup and Section B gives the details of the error tests performed to validate the numerical code.

2 BACKGROUND COSMOLOGY IN THE HU-SAWICKI MODEL

2.1 Equations of motion

We consider a f(R) model of modified gravity for which the action has the form

$$\begin{eqnarray*} S = \frac{1}{2 \kappa ^2} \int d^4x \sqrt{-g} \lbrace R + f(R)\rbrace + S_m, \end{eqnarray*}$$

(2)

where κ² = 8πG and S_m is a minimally coupled matter action. The field equations obtained by varying the action with respect to the metric g_μν are

$$\begin{eqnarray*} (1+f_R) R_{\mu \nu } - \frac{1}{2} g_{\mu \nu } (R + f) + (g_{\mu \nu } \Box - \nabla _\mu \nabla _\nu)f_R = \kappa ^2 T_{\mu \nu }, \end{eqnarray*}$$

(3)

where T_μν is the stress–energy tensor, R_μν and R are the metric-dependent Ricci tensor and scalar and f_R = df/dR. For the spatially flat FRW background metric given by ds² = −dt² + a(t)²(dx² + dy² + dz²),

$$\begin{eqnarray*} R = 12 H^2 + 6 H H^{\prime }, \end{eqnarray*}$$

(4)

where H is the Hubble parameter and prime denotes derivative w.r.t. ln a. Assuming that dark matter is well described by a perfect fluid with zero pressure, the stress–energy tensor is

$$\begin{eqnarray*} T_{\mu \nu } = \rho U_\mu U_\nu , \end{eqnarray*}$$

(5)

where U^μ is the rest-frame four-velocity, ρ is the energy density. The Friedman equation for f(R) models is then given by

$$\begin{eqnarray*} H^2 - f_R (H H^{\prime } + H^2) + \frac{1}{6} f + H^2 f_{RR} R^{\prime } = \frac{\kappa ^2 {\bar{\rho }}}{3}. \end{eqnarray*}$$

(6)

In standard GR, the Friedmann equation is a second order equation for the scale factor a. In f(R) gravity, replacing R using equation (4) recasts the Friedmann equation as a fourth order equation in time for the two unknown functions f and a. There are two approaches to solve equation (6). One can assume a particular functional form for f(R) and equation (6) reduces to a second order equation for the scale factor akin to standard GR. Examples include the Starobinsky and Hu-Sawicki models (Starobinsky 1980; Hu & Sawicki 2007). Alternatively, one can adopt the ‘designer approach’ wherein one demands that the background evolution be identical to the ΛCDM evolution and solves the resulting equations for f as a function of time (Song et al. 2007; Pogosian & Silvestri 2008). In this paper, we consider the former approach and in particular the Hu-Sawicki model as a specific example for which f(R) is given by

$$\begin{eqnarray*} f(R) = -m^2 \frac{c_1(R/m^2)^n}{c_2(R/m^2)^n + 1}. \end{eqnarray*}$$

(7)

|$m^2 = H_0^2 \Omega _{m,0}$| denotes the mass scale, where H₀ and Ω_{m, 0} are the Hubble constant and matter density parameters today. There are three parameters in this model: c₁, c₂ and n. Requiring that at high redshifts (large R) the f(R) model should reduce to standard GR gives,

$$\begin{eqnarray*} \frac{c_1}{c_2} \approx 6 \frac{\Omega _{\Lambda ,0}}{\Omega _{m,0}}. \end{eqnarray*}$$

(8)

The parameters n and |$c_1/c_2^2$| are related to the value of the derivative f_R0 through

$$\begin{eqnarray*} f_{R0} \approx -n \frac{c_1}{c_2^2} \left(\frac{12}{\Omega _{m,0}} -9\right)^{-n-1}. \end{eqnarray*}$$

(9)

Thus, choosing n and f_R0 completely specifies the model. Throughout this paper, we choose n = 1. Any theory of modified gravity needs to satisfy certain viability conditions (Pogosian & Silvestri 2008). They are: f_RR > 0 to ensure a stable high-curvature regime, 1 + f_R > 0 to have a positive effective Newton’s constant, f_R < 0 and must asymptote to zero for large R so as to ensure GR at early epochs and finally, f_R0 should be small enough to satisfy Solar system and galactic constraints. The last condition imposes the bound: |f_R0| ≲ 10⁻⁶ (Hu & Sawicki 2007).

We use the value f_R0 = −10⁻⁶ for most of this paper. However, in Section 2.2 and Section 2.3 we use f_R0 = −0.01 because the new aspects of the analysis are best illustrated with a larger f_R0. For the ΛCDM model,

$$\begin{eqnarray*} H_{\Lambda CDM}^2(a) = H_0^2\left(\frac{\Omega _{m,0}}{a^3} + \Omega _{\Lambda ,0} \right) \end{eqnarray*}$$

(10)

and

$$\begin{eqnarray*} R_{\Lambda CDM}(a) = 3H_0^2 \left(\frac{\Omega _{m,0}}{a^3} + 4 \Omega _{\Lambda ,0}\right). \end{eqnarray*}$$

(11)

2.2 Consistency with ΛCDM

The explicit time dependence of f(a) can be obtained by substituting equation (11) in equation (7). With this substitution, equations (4) and (6) become a two dimensional coupled system for the variables R and H. An important, but not obvious, assumption in f(R) models is that the solutions for R and H obtained from solving equations (4) and (6) are ‘consistent’ with the ΛCDM values, namely, the evolution given by equations (10) and (11). We explicitly perform this ‘consistency check’ to validate this assumption. Following Hu & Sawicki (2007), we define the variables

$$\begin{eqnarray*} y_H = \frac{H^2}{m^2} - a^{-3} \quad {\rm and} \quad y_R = \frac{R}{m^2} - 3 a^{-3}. \end{eqnarray*}$$

(12)

These variables have the advantage that their values are constant for the ΛCDM model given by y_{H, ΛCDM} = Ω_{Λ, 0}/Ω_{m, 0} and y_{R, ΛCDM} = 12Ω_{Λ, 0}/Ω_{m, 0}. In terms of these variables, equations (4) and (6) become

$$\begin{eqnarray*} y_H^{\prime }= \frac{1}{3} y_R - 4 y_H, \end{eqnarray*}$$

(13)

$$\begin{eqnarray*} y_R^{\prime }&=& \frac{9}{a^3} -\frac{1}{{\tilde{f}}_{{\tilde{R}}{\tilde{R}}}(y_H + a^{-3})} \nonumber\\ &&\times \,\,\left[ y_H - {\tilde{f}}_{\tilde{R}} \left(\frac{y_R}{6} -y_H -\frac{1}{2 a^3}\right) +\frac{\tilde{f}}{6}\right], \end{eqnarray*}$$

(14)

where

$$\begin{eqnarray*} {\tilde{f}} = \frac{f}{m^2} \quad {\rm and} \quad {\tilde{R}} = \frac{R}{m^2}. \end{eqnarray*}$$

(15)

The choice of the initial epoch is arbitrary and GR is assumed to be valid at that time. The effective equation of state⁴ in terms of these variables is

$$\begin{eqnarray*} 1+ w_{\rm eff}(z) = -\frac{1}{3} \frac{y_H^{\prime }}{y_H}. \end{eqnarray*}$$

(16)

Consistency with ΛCDM demands that w_eff be close to −1. We find that w_eff is oscillatory and in particular the deviation from the ΛCDM value depends sensitively on the starting epoch a_init. Fig. 1 shows w_eff for two values of f_R0 and three values of a_init: 0.2, 0.1, and 0.05 corresponding to z = 4 (blue), 9 (red), and 19 (black), respectively. In order to compare with Hu & Sawicki (2007), we choose Ω_{m, 0} = 0.24 and Ω_{Λ, 0} = 0.76 for this analysis but the discussion is not sensitive to this choice. From the left-hand panel, it is clear that the deviation from ΛCDM at lower redshifts is less when the system has a higher starting redshift. However, the oscillation frequency is higher at higher redshifts. Computationally, this means that the equations are more ‘stiff’ requiring a higher number of steps when starting at a higher redshift. This behaviour poses a challenge: starting evolution too early is computationally expensive whereas starting too late implies greater deviation from the ΛCDM equation of state. This challenge is somewhat mitigated when smaller values of |f_R0| are considered (right-hand panel). The equations remain computationally stiff at high redshifts, however, the oscillation amplitude is significantly reduced implying an evolution very close to ΛCDM. For a_init = 0.2, the deviation of the equation of state, from its ΛCDM value, in the dark energy dominated era can be more than 5 per cent when f_R0 = −0.01 and is less than 0.05 per cent when f_R0 = −10⁻⁶. Thus, for parameter values of this model that satisfy Solar system constraints, the oscillatory behaviour can be circumvented by starting the evolution later. In order to understand this behaviour better and make an informed choice about the starting redshift, we examine the above system by analysing the eigenvalues which give insights into the nature of oscillations.

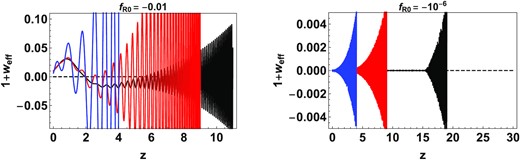
The deviation of the effective equation of state from its ΛCDM value as defined in equation (16) for fR0 = −0.01 (left-hand panel) and fR0 = −10−6 (right-hand panel) plotted for three different starting epochs: zinit = 4 (blue), 9 (red), and 19 (black). The solutions are oscillatory. The amplitude of deviation is high at earlier epochs and decreases as the evolution proceeds. Thus, consistency with ΛCDM at low redshifts i.e. in the ‘dark energy era’ is better if the evolution is started earlier. However, the oscillation frequency is higher when the evolution is started earlier making the system numerically ‘stiff’. The right-hand panel shows that this deviation is significantly smaller for smaller values of |fR0|, however the oscillation frequency is higher (see Fig. 2).

Figure 1.

The deviation of the effective equation of state from its ΛCDM value as defined in equation (16) for f_R0 = −0.01 (left-hand panel) and f_R0 = −10⁻⁶ (right-hand panel) plotted for three different starting epochs: z_init = 4 (blue), 9 (red), and 19 (black). The solutions are oscillatory. The amplitude of deviation is high at earlier epochs and decreases as the evolution proceeds. Thus, consistency with ΛCDM at low redshifts i.e. in the ‘dark energy era’ is better if the evolution is started earlier. However, the oscillation frequency is higher when the evolution is started earlier making the system numerically ‘stiff’. The right-hand panel shows that this deviation is significantly smaller for smaller values of |f_R0|, however the oscillation frequency is higher (see Fig. 2).

Open in new tab Download slide

2.3 Eigenvalue analysis of the Hu-Sawicki background cosmology

We recast the system given by equations (13) and (14) in a more general form as

$$\begin{eqnarray*} \left\lbrace y^{\prime }_H, y^{\prime }_R\right\rbrace = \lbrace {\mathcal {A}}_1(y_H, y_R), {\mathcal {A}}_2(y_H, y_R)\rbrace , \end{eqnarray*}$$

(17)

where |${\mathcal {A}}_1$| and |${\mathcal {A}}_2$| correspond to the right-hand side of equations (13) and (14). If |${\mathcal {A}}_1$| and |${\mathcal {A}}_2$| were linear combinations of y_H and y_R with constant (in time) coefficients, then the system would be a linear, autonomous system. For such a system the eigenvalues of the operator matrix determine the nature of the solution. Real, negative eigenvalues indicate a stable solution, real positive eigenvalues indicate an unstable solution that grows with time and complex eigenvalues indicate oscillatory solutions. The rate of change of amplitude and frequency of the oscillations are determined by the real and complex part of the eigenvalues, respectively. For a non-linear autonomous system, the eigenvalues of the linearized operator give information about the local behaviour of the solution. This interpretation of eigenvalues breaks down when the system is non-autonomous i.e. when the coefficients of the dependent variables are time varying (Slotine & Weiping 1991; Strogatz 1994). The system given by equations (13) and (14) and is both non-linear and non-autonomous. Thus, while the eigenvalues of the linearized system cannot give information about the global behaviour, they can still give qualitative information about the instantaneous solution. In particular they can indicate the presence or absence of oscillations and provide an estimate of the instantaneous oscillation frequency. The linearized differential operator is given by

$$\begin{eqnarray*} {\mathcal {A}}_{\rm lin} =\begin{pmatrix}\frac{\partial {\mathcal {A}}_1}{\partial y_H} &\frac{\partial {\mathcal {A}}_1}{\partial y_R}\\ \\ \frac{\partial {\mathcal {A}}_2}{\partial y_H} &\frac{\partial {\mathcal {A}}_2}{\partial y_R} \end{pmatrix} , \end{eqnarray*}$$

(18)

where

$$\begin{eqnarray*} \frac{\partial {\mathcal {A}}_1}{\partial y_H} = -4, \quad \frac{\partial {\mathcal {A}}_1}{\partial y_R}= \frac{1}{3}, \end{eqnarray*}$$

(19)

$$\begin{eqnarray*} &&{\frac{\partial {\mathcal {A}}_2}{\partial y_H} = -\frac{1 + {\tilde{f}}_{\tilde{R}}}{{\tilde{f}}_{{\tilde{R}}{\tilde{R}}} \left(a^{-3}+ y_H \right)} + \frac{\frac{{\tilde{f}}}{6} + y_H - {\tilde{f}} _ {\tilde{R}} \left(-\frac{1}{2 a^3} - y_H + \frac{y_R}{6} \right)}{{\tilde{f}} _ {{\tilde{R}} {\tilde{R}}}\left(a^{-3}+ y_H \right)^2}} \nonumber\\ &&{{\rm and} \quad \frac{\partial {\mathcal {A}}_2}{\partial y_R} = \frac{{\tilde{f}}_{\tilde{R}}}{6 {\tilde{f}}_{{\tilde{R}}{\tilde{R}}} \left(a^{-3}+y_H\right)}.} \end{eqnarray*}$$

(20)

|${\mathcal {A}}_{\rm lin}$| can be evaluated at any time by using the values of |${\tilde{f}}, {\tilde{f}}_{\tilde{R}}, {\tilde{f}}_{{\tilde{R}} {\tilde{R}}}, y_H$|⁠, and y_R at that time. The values of y_H and y_R can be read off from the numerical solution to equations (13) and (14). We found that using the GR values for y_H and y_R did not give significantly different answers to the eigenvalues.

Fig. 2 shows the eigenvalues of |${\mathcal {A}}_{\rm lin}$|⁠. The black solid line and red dashed lines correspond to f_R0 = −0.01 and f_R0 = −10⁻⁶, respectively. The eigenvalues are complex. The left-hand panel shows the real part of the eigenvalue, which is negative, indicating that the amplitude of the oscillations decreases as evolution proceeds. The right-hand panel shows the imaginary part which indicates the instantaneous frequency of oscillations. The figure shows two distinct regimes. At very high redshifts, the oscillation frequency is large and decreases as a power law in a: |$|\rm {Im}[\nu ]| \sim a^\alpha$|⁠. The best-fitting value was found to be α ∼ −3. At low redshifts, the instantaneous frequency is almost a constant. The epoch where these two asymptotes cross is marked as the transition epoch a_trans ∼ 0.34 corresponding to a redshift of around z ∼ 2. For a smaller value of |f_R0|, the magnitude of the imaginary part is higher implying higher frequency oscillations at the same redshift. However, we find that the transition epoch is independent of |f_R0| and also independent of the value of Ω_{m, 0} for flat models. For a_init < <a_trans, the high frequency oscillations make the system ‘numerically stiff’ and evolving the system is computationally expensive.

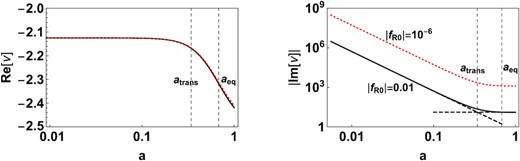
$Instantaneous eigenvalues of the linearized matrix ${\mathcal {A}}$ given by equation (18). The red dashed line indicates fR0 = −10−6 and the black solid line indicates fR0 = −0.01; both models have n = 1. The eigenvalues are complex implying oscillations. The real part (left-hand panel) is negative implying that the oscillation amplitude decreases as a increases. The imaginary part, which determines the oscillation frequency is large at early epochs and decreases as a power law in a and levels off as a approaches 1. atrans denotes the epoch where the two asymptotes cross. At the same redshift, the instantaneous oscillation frequency is larger for smaller values of |fR0| but the transition value is independent of fR0. The initial amplitude is lower for smaller values of |fR0| (not shown here), but the rate of decrease is independent of |fR0| as indicated by the real part.$

Figure 2.

Instantaneous eigenvalues of the linearized matrix |${\mathcal {A}}$| given by equation (18). The red dashed line indicates f_R0 = −10⁻⁶ and the black solid line indicates f_R0 = −0.01; both models have n = 1. The eigenvalues are complex implying oscillations. The real part (left-hand panel) is negative implying that the oscillation amplitude decreases as a increases. The imaginary part, which determines the oscillation frequency is large at early epochs and decreases as a power law in a and levels off as a approaches 1. a_trans denotes the epoch where the two asymptotes cross. At the same redshift, the instantaneous oscillation frequency is larger for smaller values of |f_R0| but the transition value is independent of f_R0. The initial amplitude is lower for smaller values of |f_R0| (not shown here), but the rate of decrease is independent of |f_R0| as indicated by the real part.

Open in new tab Download slide

The perturbed system described in the next section also exhibits oscillations akin to the background. In this paper, we have expressed the perturbation equations in terms of two temporal evolution equations for the density and velocity and two spatial equations for the metric potentials. This form of the equations is not amenable to the eigenvalue analysis discussed above. However, in order to overcome the issue of numerical stiffness we adopt the following strategy. We evolve the perturbations in standard GR starting from an early epoch a_init = 0.001 to a late epoch a_switch, after which the evolution ‘switches’ over to f(R) gravity. Following the insight gained from the eigenanalysis of the background we choose a_switch to be in the vicinity of a_trans. In particular, we choose a_switch = 0.1. It is possible to choose a_switch in a more quantitative manner by setting tolerances for deviation of equation of state or numerical stiffness, but we do not follow such a strategy here. We are interested in the qualitative differences in non-linear growth between the GR and f(R) models. Furthermore, the DVDR, if such a unique relation exists, should depend only on the evolution equations and not on the choice of a_switch. Thus, it suffices to consider only a single choice for a_switch and we do not investigate the dependence of non-linear growth on this parameter. Clearly, choosing a_switch earlier (later) will increase (decrease) the effect of the modification.

High frequency oscillations in the Hu-Sawicki model have been referred to in the original paper (Hu & Sawicki 2007) as well as in follow up studies (Elizalde et al. 2012). They have also been encountered in the context of evolution of designer models (Song et al. 2007) as well as in linear perturbations (see e.g. Pogosian & Silvestri 2008; Lima & Liddle 2013; Silvestri, Pogosian & Buniy 2013). The issue of ΛCDM consistency has been explicitly addressed in the literature (e.g. Appleby & Battye 2007; Starobinsky 2007; Ceron-Hurtado, He & Li 2016; Chakraborty, MacDevette & Dunsby 2021). Some of these studies have been in the context of finding stable f(R) models. We note that stability in the Hu-Sawicki model is guaranteed by the choice of parameters. The system is oscillatory but stable since the amplitude of oscillations decays as evolution proceeds. To the best of our knowledge, an understanding of the oscillatory behaviour based eigenvalue analysis of this system has not been presented so far in the literature.

2.4 Compton wavelength

In the Einstein frame, the f(R) action can be recast as a standard Einstein–Hilbert action with non-minimally coupled scalar field corresponding to the additional degree of freedom represented by f_R (Magnano & Sokołowski 1994; Chiba 2003; Sotiriou & Faraoni 2010). The mass of this field is

$$\begin{eqnarray*} m^2_{f_R} = \frac{m^2}{3} \left(\frac{1 + {\tilde{f}}_{\tilde{R}}}{\tilde{f}_{{\tilde{R}}{\tilde{R}}}} - {\tilde{R}} \right). \end{eqnarray*}$$

(21)

The associated physical Compton wavelength λ_C⁵ is given by

$$\begin{eqnarray*} \lambda _C = \frac{2 \pi }{m_{f_R}} \approx \frac{2 \pi \sqrt{3 {\tilde{f}_{{\tilde{R}}{\tilde{R}}}}}}{ m} . \end{eqnarray*}$$

(22)

We have used the fact that |${\tilde{f}}_{{\tilde{R}}{\tilde{R}}} \lt \lt 1$| and |${\tilde{f}}_{{\tilde{R}}{\tilde{R}}}^{-1} \gt \gt {\tilde{R}}$| throughout the evolution. The comoving Compton wavelength x_C and the reduced comoving Compton wavelength |${\bar{x}}_C$| are defined as

$$\begin{eqnarray*} x_C = \frac{\lambda _C}{a} \quad {\rm and} \quad {\bar{x}}_C = \frac{x_C}{ 2\pi } \approx \frac{ \sqrt{3 {\tilde{f}_{{\tilde{R}}{\tilde{R}}}}}}{ a m}, \end{eqnarray*}$$

(23)

where |$m^2 = H_0^2 \Omega _{m0}$|⁠. This wavelength defines the ‘range’ of the ‘fifth-force’ corresponding to the additional degree of freedom represented by the scalar field. The effects of modified gravity manifest only on scales less than this range. The f(R) model obeys Solar system constraints through the ‘Chameleon screening’ mechanism, wherein the Compton wavelength decreases in high density regions reducing the range of the force (Khoury & Weltman 2004).

Fig. 3 shows the relevant scales and epochs on a plot in the k − a plane. a_eq corresponds to the epoch when the dark energy density is equal to the matter density in the background evolution. a_trans denotes the epoch when frequency of oscillations in the Hu-Sawicki background starts to level off. Starting evolution for a < <a_trans is computationally expensive where as a > >a_trans implies significant deviations from the ΛCDM background, particularly for larger values of |f_R0|. a_trans provides a estimate of the optimal epoch to start evolution. At early epochs, the cosmologically relevant scales (∼1h⁻¹Mpc) are well above the Compton wavelength and one cannot expect to see departures from GR on those scales. Coincidentally, for f_R0 values which are allowed by Solar system and galactic constraints the Compton wavelength becomes greater than ∼1h⁻¹Mpc at around a ∼ a_trans.

Figure 3.

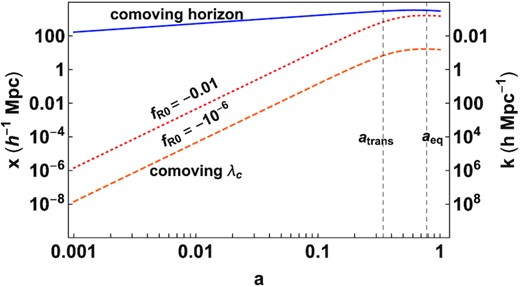
Important scales in the model marked on a k − a plane (left-hand panel). The red dotted and orange dashed lines denote the comoving Compton wavelength x_C of the scalaron field implied by the Hu-Sawicki model for f_R0 = −0.01 and f_R0 = −10⁻⁶, respectively. At any epoch, the effects of modified gravity begin to manifest when x ≲ x_C. The blue solid line indicates the scale when the given mode crosses the horizon. a_eq denotes the epoch of dark energy–matter equality and a_trans is the epoch when the frequency of oscillations in the Hu-Sawicki background start to level off to a constant.

Open in new tab Download slide

3 EQUATIONS FOR NON-LINEAR PERTURBATIONS

3.1 Equations

Assuming only scalar perturbations of the background, the metric in conformal Newtonian gauge is (Ma & Bertschinger 1995)

$$\begin{eqnarray*} \mathrm{ d}s^2 = -a^2(1+2\Psi) \mathrm{ d}\tau ^2 + a^2(1-2 \Phi) \left(\mathrm{ d}x_1^2 + \mathrm{ d}x_2^2 +\mathrm{ d}x_3^2\right). \end{eqnarray*}$$

(24)

Ψ corresponds to the gravitational potential in the Newtonian limit which determines how particles move and Φ denotes the ‘curvature’ fluctuation which is seeded by the matter density. x = (x₁, x₂, x₃) is the comoving coordinate and dτ = dt/a is the conformal time. The Universe is assumed to consist only of cold dark matter modelled to be a pressure-less fluid with no anisotropic stresses. Let δ denote the fractional density and v_i the coordinate velocity, which is equivalent to the peculiar velocity adx_i/dt. We employ the Quasi Static Approximation (QSA) which comprises of two independent assumptions: (1) the time derivatives of the potentials are small compared to the spatial derivatives and (2) the length scales are much smaller than the horizon scale, which is the usual ‘sub-horizon’ approximation. In standard ΛCDM, these two assumptions are identical. The potentials vary on a time-scale of 1/H and both assumptions correspond to ck > >aH, where c is the speed of light. However, in modified theories, the potentials can vary on a time-scale much smaller than the Hubble time. In particular, the potentials can be oscillatory, similar to the behaviour seen in the background. Suppose Ψ ∼ e^iωln aΨ₀, where ω is the frequency of oscillation in the variable ln a, then the first assumption reads ck > >aωH, which need not be satisfied even if the scales are sub-horizon since ω can be large. Thus, the two conditions need to be assumed separately. For the Hu-Sawicki model, with the parameters that satisfy Solar system constraints, these oscillations are undetectable, justifying this assumption (Hojjati et al. 2012; Silvestri et al. 2013). In this limit, the Einstein equations are (Oyaizu 2008; Schmidt et al. 2009; Borisov et al. 2012)

$$\begin{eqnarray*} \nabla _x^2 \delta f_R = \frac{a^2 \delta R}{3c^2} - \frac{H^2 a^2 \Omega _m \delta }{c^2} \end{eqnarray*}$$

(25)

$$\begin{eqnarray*} \nabla _x^2 \Psi = 2 H^2 a^2 \Omega _m \delta - \frac{a^2 \delta R}{6}, \end{eqnarray*}$$

(26)

where δf_R and δR are perturbations to f_R and the Ricci scalar R, respectively. Note that δR is an implicit non-linear function of δf(R). However, assuming that the change in R is small, Taylor expanding around the background gives

$$\begin{eqnarray*} \delta f_R \approx f_{RR} \delta R, \end{eqnarray*}$$

(27)

where f_RR is evaluated at the background R given by equation (11). In the limit of |f_R| < <1 and |f/R| < <1, the difference between the two potentials Φ and Ψ is related to δf_R through (Hu & Sawicki 2007)

$$\begin{eqnarray*} \Phi - \Psi = c^2 \delta f_R. \end{eqnarray*}$$

(28)

This relation also follows from the anisotropy part of the Einstein equations in the QSA. It is further convenient to define the variables (Pogosian & Silvestri 2008)

$$\begin{eqnarray*} \chi = \Phi - \Psi \end{eqnarray*}$$

(29)

$$\begin{eqnarray*} \Phi _+ & = & \frac{\Phi + \Psi }{2}. \end{eqnarray*}$$

(30)

Substituting equations (27), (28), (29), and (30) in equations (25) and (26) and combining with the conservation equations, which stay unchanged in f(R), gives the system

$$\begin{eqnarray*} \frac{\partial \delta }{\partial t} + \left(\frac{{\bf v}}{a} \cdot \nabla _x\right) \delta = -\frac{(1+\delta)}{a} (\nabla _x \cdot {\bf v}) \end{eqnarray*}$$

(31)

$$\begin{eqnarray*} \frac{\partial {\bf v}}{\partial t} + \left(\frac{{\bf v}}{a} \cdot \nabla _x\right) {\bf v} + H {\bf v}& =& -\frac{1}{a} \nabla _x \Psi \end{eqnarray*}$$

(32)

$$\begin{eqnarray*} \nabla _x^2 \Phi _+& =&\frac{3}{2} H^2 a^2 \Omega _m \delta \end{eqnarray*}$$

(33)

$$\begin{eqnarray*} \nabla _x^2 \chi - \frac{ a^2}{3 c^2 f_{RR}} \chi =- H^2 a^2 \Omega _m \delta . \end{eqnarray*}$$

(34)

Note that |$\Psi = \left(\Phi _+ - \frac{\chi }{2}\right)$|⁠. We have retained Ψ in the right-hand side of equation (32) to illustrate that the form of equations (31) and (32) is unchanged from the standard GR case. Ω_m refers to the time-dependent matter density parameter, which is related to its value today as

$$\begin{eqnarray*} \Omega _m(a) = \frac{H_0^2 \Omega _{m,0} a_0^3}{H^2 a^3}. \end{eqnarray*}$$

(35)

This is a coupled system of equations for the variables δ, v, Φ₊, and χ which are functions of space as well as time. These have to be solved given the initial profiles for δ and v and boundary conditions for Φ₊ and χ. Assuming no sources at infinity (homogeneous on large enough scales) and no forces at the origin (solution is not singular at x = 0), gives the boundary conditions for equations (33) and (34)

$$\begin{eqnarray*} \Phi _+(x\rightarrow \infty) &=& 0, \quad \chi (x\rightarrow \infty) =0, \nonumber\\ \left.\frac{\partial \Phi _+}{\partial x}\right|_{x=0} &=& 0 \quad {\rm and} \quad \left.\frac{\partial \chi }{\partial x}\right|_{x=0} =0. \end{eqnarray*}$$

(36)

In what follows, we set Ω_{m, 0} = 0.32 and Ω_{Λ, 0} = 0.68 in accordance with Planck Collaboration VI (2020)⁶ and we use the terms ‘standard GR’ and ΛCDM interchangeably when we refer to this model. The density and velocity profiles are known as a function of the radial coordinate at some initial time a_init. Throughout this work, we consider compensated top-hats as initial conditions. The details of the set-up are given in Appendix A. The perturbation is characterized by a single scale, namely, the width of the top-hat x_top. We note that the coefficient of χ in equation (34) can be re-written as |${\bar{x}}_C^{-2}$| using equation (23) and equation (34) becomes

$$\begin{eqnarray*} \nabla _x^2 \chi - \frac{1}{{\bar{x}_C}^2} \chi =- H^2 a^2 \Omega _m \delta . \end{eqnarray*}$$

(37)

The solution to χ depends on the ratio⁷

$$\begin{eqnarray*} Q =\frac{{\bar{x}}_C}{x_{\rm top}}. \end{eqnarray*}$$

(38)

When Q > >1, equation (37) reduces to ∇²χ ≈ −H²a²Ω_mδ and χ is proportional to Φ₊. In this limit, the gravitational potential Ψ is enhanced by a factor of 4/3 as compared to its value in standard GR (denoted by Ψ_GR) i.e. Ψ = 4/3Ψ_GR. When Q < <1, the solution for χ is given by |$\chi = {\bar{x}}_C^2 H^2 a^2 \Omega _m \delta$|⁠. The dimension-less value of the extra field |$\chi /(H^2 x_{\rm top}^2)$| is suppressed by a factor of Q² and the evolution is close to GR. Q < <1 has been referred to as the ‘Compton condition’ in Hu & Sawicki (2007).

In this work, we assume that |${\bar{x}_C}$| depends only on the value of f_RR in the background and does not change with the perturbation. As a result, we do not capture the ‘chameleon screening mechanism’ wherein the Compton wavelength is small in high density regions; this is responsible for satisfying Solar system constraints (Khoury & Weltman 2004; Hu & Sawicki 2007). Nevertheless, we are able to illustrate ‘screening’ by considering perturbations of differing length scales x_top for a fixed f_R0. We consider three values of x_top = 0.002, 2, and 200 h⁻¹Mpc, which for f_R0 = −10⁻⁶ gives Q = 1217, 1.21, 0.012 at a = 1, respectively. We refer to Q > >1 and Q < <1 as the ‘strong’ and ‘weak’ field regimes, respectively. The evolution of Q for these three scales is shown in Fig. 4. Note that, for x_top ∼ 0.002h⁻¹Mpc, Q > 1 and for x_top ∼ 200h⁻¹Mpc, Q < 1 from a = 0.1 to today and they can be considered as being ‘strong’ and ‘weak’ perturbations over the entire domain of evolution. In what follows, we will refer to the three perturbations with their value of Q today and ignore the temporal evolution of Q.

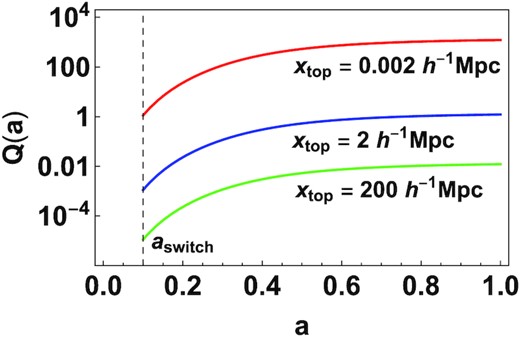
$The parameter $Q = {\bar{x}}_{C}/(x_{\rm top})$ plotted as a function of a for the three values of top-hat widths considered in this paper. The dotted line denotes aswitch, which is the epoch at which evolution is assumed to switch from GR to f(R). In the text, we characterize these three fluctuations by their value of Q today and ignore the time dependence.$

Figure 4.

The parameter |$Q = {\bar{x}}_{C}/(x_{\rm top})$| plotted as a function of a for the three values of top-hat widths considered in this paper. The dotted line denotes a_switch, which is the epoch at which evolution is assumed to switch from GR to f(R). In the text, we characterize these three fluctuations by their value of Q today and ignore the time dependence.

Open in new tab Download slide

4 METHOD OF SOLUTION

4.1 Outline

To proceed we further restrict ourselves to a spherically symmetric perturbation which is modelled as a series of concentric shells. Equations (31) and (32) involve time-derivative operators for the variables δ and v, whereas equations (33) and (34) contain purely spatial derivatives. The gravitational potential depends on the instantaneous density making equations (31) to (34) an integro-differential equation. To solve this system we employ an iterative scheme as follows. The system is evolved from the initial epoch, a_init, to the intermediate epoch, a_switch, in a single step using the equations of GR. The time domain from a_switch to a_final is divided into N_t intervals. The density and velocity profiles are known at the beginning of each interval. We first solve the spatial differential equations (33) and (34) in Eulerian space (fixed radial coordinates) to compute the gravitational potential corresponding to the density at the start of the step. Assuming that this potential is constant over the small time interval, we propagate the system using equations (31) and (32) to obtain the density and velocity at the start of the next step. This temporal evolution is carried out in Lagrangian coordinates. The advantage of using Lagrangian coordinates is that the Lagrangian time derivative is the total time derivative

$$\begin{eqnarray*} \frac{\rm d}{\mathrm{ d}t} = \frac{\partial }{\partial t} + \frac{1}{a}({\bf v} \cdot \nabla _x). \end{eqnarray*}$$

(39)

This converts the non-linear coupled p.d.e. given by equations (31) and (32) to a second-order ordinary differential equation. We perform error tests to check that this iterative hybrid Lagrangian–Eulerian scheme is convergent.

4.2 Lagrangian coordinates

Let origin be the centre of the sphere. Define the Lagrangian coordinate of a shell to be its initial comoving coordinate, denoted by q (we henceforth drop the vectors since the dynamics is only radial). The (Eulerian) comoving coordinate at any later epoch is

$$\begin{eqnarray*} x\equiv x (q,a) = A(q, a) q, \end{eqnarray*}$$

(40)

where A(q, a) can be thought of as a ‘scale factor’ of the shell at q. The q dependence of the scale factor arises because, in general, the density is radially dependent. By definition, for all shells A(q, a_init) = 1. The peculiar velocity at any later time t is

$$\begin{eqnarray*} v(q,a) = a {\dot{A}}(q,a) q = a H(a) A^{\prime }(q, a) q, \end{eqnarray*}$$

(41)

where ‘dot’ denotes the total derivative w.r.t. time t and ‘prime’ denotes derivatives w.r.t. ln a. If δ(q, a_init) is the density at the initial epoch, mass conservation for each shell implies that the density at any later epoch is

$$\begin{eqnarray*} 1+\delta (q, a) = \left(1+ \delta (q,a_{\rm init})\right) \frac{q^2 \mathrm{ d}q}{x^2\mathrm{ d}x} = \frac{(1+ \delta _{\rm init})}{A^3 \left|1+ \frac{q}{A} \frac{\mathrm{ d}A}{\mathrm{ d}q}\right|}. \end{eqnarray*}$$

(42)

Using the definitions in equations (40) and (41) and changing the derivatives to Lagrangian coordinates, it can be easily checked that the density given by the above expression satisfies the continuity equation given by equation (31). The spherically averaged density is defined as

$$\begin{eqnarray*} \Delta (x) = \frac{3}{x^3} \int _0^x \delta (x,a) x^2 \mathrm{ d}x. \end{eqnarray*}$$

(43)

It satisfies the condition

$$\begin{eqnarray*} 1 + \Delta (q,a) = \frac{(1 +\Delta _{\rm init}) A^3_{\rm init}}{A^3}. \end{eqnarray*}$$

(44)

4.3 Equations in the hybrid Eulerian–Lagrangian scheme

Substituting equation (39) and equation (41) in equation (32), imposing spherical symmetry in equations (33) and (34), changing the time variable to ln a and defining |${\tilde{\Phi }} = \Phi /H^2, {\tilde{\chi }} = \chi /H^2$| and |${\tilde{\Psi }} = \Psi /H^2$| recasts the system as

$$\begin{eqnarray*} A^{\prime \prime } + \left(2 - \frac{3}{2} \Omega _m(a) \right) A^{\prime } = -\frac{1}{a^2 q} \nabla _q {\tilde{\Psi }}(q,a) \end{eqnarray*}$$

(45)

$$\begin{eqnarray*} \frac{\partial ^2 {\tilde{\Phi }_+}}{\partial x^2} + \frac{2}{x} \frac{\partial {\tilde{\Phi }}_+}{\partial x} = \frac{3}{2} a^2 \Omega _m(a) \delta (x,a). \end{eqnarray*}$$

(46)

$$\begin{eqnarray*} \frac{\partial ^2 {\tilde{\chi }}}{\partial x^2} + \frac{2}{x} \frac{\partial {\tilde{\chi }}}{\partial x} - \frac{1}{{\bar{x}}_C^2} {\tilde{\chi }} = - a^2 \Omega _m(a) \delta (x,a), \end{eqnarray*}$$

(47)

where the ‘prime’ denotes derivative with respect to ln a. The boundary conditions for each step become

$$\begin{eqnarray*} {\tilde{\Phi }_+}(x\rightarrow \infty) &=& 0, \quad {\tilde{\chi }}(x\rightarrow \infty) =0, \nonumber\\ \left.\frac{\partial {\tilde{\Phi }_+}}{\partial x}\right|_{x=0} &=& 0, \quad {\rm and} \quad \left.\frac{\partial {\tilde{\chi }}}{\partial x}\right|_{x=0} =0. \end{eqnarray*}$$

(48)

From equation (41) and the definition of the Lagrangian coordinate, initial conditions for A are:

$$\begin{eqnarray*} A(q,a_{\rm init}) = 1\quad {\rm and} \quad A^{\prime }(q, a_{\rm init}) = \frac{v_{\rm init}(q, a_{\rm init})}{a_{\rm init}H(a_{\rm init}) q}. \end{eqnarray*}$$

(49)

In the GR regime, |${\tilde{\Phi }_+} = {\tilde{\Psi }}$|⁠. Using the solution to Poisson’s equation in terms of Δ, and the equations reduce to a second-order ODE for A:

$$\begin{eqnarray*} A^{\prime \prime } + \left(2 - \frac{3}{2} \Omega _m(a) \right) A^{\prime } = -\frac{\Omega _m(a) A}{2} \left(\frac{1+ \Delta _{\rm init}}{A^3} -1\right), \end{eqnarray*}$$

(50)

where Δ_init ≡ Δ(q, a_init) is the average density defined in equation (43), evaluated at the initial epoch.

4.4 Initial conditions

We evolve the system assuming GR from a_init = 0.001 to the switching epoch a_switch = 0.1. The initial profile for δ(x, a = 0.001) is a smooth compensated top-hat. Its amplitude is chosen small enough so that the profile does not collapse in either f(R) or GR but large enough to become non-linear. The details of the profiles used in various sections of the paper are given in Appendix A. The velocity profile at a = 0.001 is always set by assuming the Zeldovich condition (Zel’Dovich 1970; Brenier et al. 2003). For a radially varying profile, this gives

$$\begin{eqnarray*} v(x, a_{a\rm init}) = -\frac{f(\Omega _m) H a \Delta (x, a_{\rm init}) x}{3}, \end{eqnarray*}$$

(51)

where Δ(x, a) is defined in equation (43) and |$f(\Omega _m)\sim \Omega _m^{0.55}$| is the linear growth factor in the GR regime. For a_init = 0.001, Ω_m ≈ 1. In Lagrangian coordinates, at the initial time, by definition, x = q and the initial density and velocity are Δ(x, a_init) = Δ(q, a_init) and v(x, a_init) = v(q, a_init). Using equations (40) and (41) gives the initial conditions

$$\begin{eqnarray*} A(q, a_{\rm init}) = 1 \quad {\rm for} \,\, {\rm all} \,\,\,\, q \quad {\rm and} \quad A^{\prime }(q,a_{\rm init}) = - \frac{\Delta (q, a_{\rm init})}{3}. \nonumber\\ \end{eqnarray*}$$

(52)

4.5 Algorithm

Notation: Let a_init and a_final denote the initial and final epochs of interest and a_switch denote the epoch where the evolution switches from GR to f(R). The time between a_switch, to a_final is divided into N_t intervals equi-spaced in ln a. Let a₀ = a_init, a₁ = a_switch, |$a_{N_t} = a_{\rm final}$| and a₂, a₃… denote intermediate epochs. At any epoch a_n, the data at the start of the time interval is defined on a 1-d grid with N_s points uniformly spaced in ln x space. These correspond to radial shells. x_i(a_n), i = 1, 2, …N_s denotes the Eulerian position of the i-th shell at the start of the n-th step. At a_n, the Lagrangian coordinate of the shell i-th shell is defined as q_n, i = x_i(a_n). The density and velocity are known at the time a_n on the uniform grid and are given by δ_i(q_n, a_n) and v_i(q_n, a_n). Here we drop the subscript ‘i’ on q_n but it is understood that q_n is different for each ‘i’.

At the end of the step, i.e. at a_{n + 1}, the Eulerian position, density, and velocity of the i-th shell are denoted as x_i(q_n, a_{n + 1}), δ_i(q_n, a_{n + 1}) and v_i(q_n, a_{n + 1}). However, the Eulerian positions x_i(q_n, a_{n + 1}), i = 1, 2, …N_s are not equi-spaced. At a_{n + 1}, a new grid is defined in Eulerian space which is equi-spaced in ln x over the range x_min to x_max, where x_min and x_max correspond to the Eulerian location of the innermost and outermost shell at a_{n + 1}. This uniform grid is denoted as |$x_{i^{\prime }}(a_{n+1}), i^{\prime } = 1, 2 \dots N_s$|⁠. The i′ indicates that the shell locations are re-defined after each step. Thus, |$x_i(q_n, a_{n+1}) \ne x_{i^{\prime }}(a_{n+1})$|⁠. The number of shells are the same at each step since no shells have collapsed or crossed. The Lagrangian coordinate at a_{n + 1} is given as |$q_{n+1,i^{\prime }} = x_{i^{\prime }}(a_{n+1})$|⁠. The density and peculiar velocity are obtained by interpolating δ_i(q_n, a_{n + 1}) and v_i(q_n, a_{n + 1}) on to the uniform grid. They are denoted as |$\delta _{i^{\prime }}(q_{n+1}, a_{n+1})$| and |$v_{i^{\prime }}(q_{n+1}, a_{n+1})$|⁠, respectively. Step 1. GR evolution:

Evolve the system from a₀ = a_init to a₁ = a_switch using equation (50) and initial conditions equation (52).
Construct the Eulerian position, density, and velocity at a₁ using equations (41) and (42). This gives x_i(q₀, a₁), δ_i(q₀, a₁), and v_i(q₀, a₁) for each shell i, i = 1…N_s.
Re-initialize the system by defining a uniform grid in ln x space, define the new Lagrangian coordinate q₁, and interpolate the density and peculiar velocity to get |$\delta _{i^{\prime }}(q_1, a_1)$| and |$v_{i^{\prime }}(q_1, a_1)$|⁠.

Step 2. f(R) evolution:

At a₁, and at any a_n thereafter, first solve the spatial equations, equations (46) and (47), setting a = a_n and x = q_n. The solutions for Φ₊ and χ can be obtained analytically and are given in the next section. These expressions are evaluated numerically using the values of δ_i(q_n, a_n) known at the start of the step a = a_n.
Using the solutions for Φ₊ and χ compute the r.h.s of equation (45) i.e. ∇_qΨ(q, a) = ∇_qΨ(q, a_n) at each shell i. We assume that throughout the interval a_n to a_{n + 1}, ∇_qΨ_i(q_n, a) = ∇_qΨ_i(q_n, a_n) i.e. the force is constant.
Compute the temporal evolution between a_n and a_{n + 1} using equation (45). There are N_s such equations, one for each shell. Let A_i denote the scale factor of the i-th shell. The initial conditions are
$$\begin{eqnarray*} A_i(q_n,a_n) = 1 \,\,\,\,\,\, {\rm and} \,\,\,\,\,\,A_i^{\prime }(q_n,a_n) = \frac{v(q_n, a_n)}{a_nH(a_n) q_n} \end{eqnarray*}$$
(53)
Construct the density and velocity at a_{n + 1} using equations (41) and (42). This gives x_i(q_n, a_{n + 1}) and δ_i(q_n, a_{n + 1}) and v_i(q_n, a_{n + 1}) for the i-th shell. Compute the end-points x_min and x_max at a_{n + 1} to be the Eulerian positions of the innermost and outermost shells.
Re-initialize: define a new uniform grid over the range x_min and x_max denoted by |$x_{i^{\prime }}(a_{n+1}), i = 1, 2 \dots N_s$|⁠. Define the new Lagrangian coordinate |$q_{n+1} = x_{i^{\prime }}(a_{n+1})$| and interpolate the data given by δ_i(q_n, a_{n + 1}) and v_i(q_n, a_{n + 1}) on to this uniform grid to get the initial data for the next step |$\delta _{i^{\prime }}(q_{n+1}, a_{n+1})$| and |$v_{i^{\prime }}(q_{n+1}, a_{n+1})$| at equi-spaced shell positions.
Go to step 2(i) until a_{n + 1} = a_final.

4.6 Analytic solutions for the potentials

The solutions to equations (46) and (47) subject to the boundary conditions equation (48) are

$$\begin{eqnarray*} {\tilde{\Phi }_+} (x) = -\frac{\mathcal {P}_1}{3} \int _x^{\infty } y \Delta (y) \mathrm{ d}y, \end{eqnarray*}$$

(54)

$$\begin{eqnarray*} {\tilde{\chi }}(x) = \frac{\mathcal {P}_3 }{\sqrt{\mathcal {P}_2}}\frac{1}{x} \left[ \exp \left(-\sqrt{\mathcal {P}_2}x\right) I_1(x) + \sinh \left(\sqrt{\mathcal {P}_2}x\right) I_2(x) \right], \nonumber \\ \end{eqnarray*}$$

(55)

where

$$\begin{eqnarray*} I_1(x) = \int _0^x \left\lbrace \sinh \left(\sqrt{\mathcal {P}_2}y\right) \delta (y) y \right\rbrace \mathrm{ d}y, \end{eqnarray*}$$

(56)

$$\begin{eqnarray*} I_2(x) = \int _x^\infty \left\lbrace \exp \left(-\sqrt{\mathcal {P}_2}y\right)\delta (y) y \right\rbrace \mathrm{ d}y. \end{eqnarray*}$$

(57)

y is a dummy variable in the integrals and Δ represents the spherically averaged fractional density contrast defined in equation (43). |${\mathcal {P}_1}$|⁠, |${\mathcal {P}_2}$|⁠, and |${\mathcal {P}_3}$| are purely time-dependent functions defined as

$$\begin{eqnarray*} {\mathcal {P}}_1(a) = \frac{3 \Omega _m(a) a^2}{2}, \quad {\mathcal {P}_2}(a) = \frac{1}{{\bar{x}}_C^2} \quad {\rm and} \quad {\mathcal {P}_3}(a) = a^2 \Omega _m(a).\nonumber\\ \end{eqnarray*}$$

(58)

The ‘force’ that moves the shells is related to the derivatives of the potentials:

$$\begin{eqnarray*} \nabla _x {\tilde{\Phi }_+} = \frac{\mathcal {P}_1}{3}x \Delta (x), \end{eqnarray*}$$

(59)

$$\begin{eqnarray*} \nabla _x {\tilde{\chi }} &=& - \frac{{\tilde{\chi }} }{x}+ \frac{{\mathcal {P}_3}}{x} \left[-\exp \left(-\sqrt{\mathcal {P}_2}x\right) I_1(x) \right.\nonumber\\ &&+\left. \cosh \left(\sqrt{\mathcal {P}_2}x\right) I_2(x) \right]. \end{eqnarray*}$$

(60)

Fig. 5 shows the solution for the dimension-less χ (second panel), ∇χ (third panel), and the potentials Φ and Ψ (fourth panel) as a function of x for the density profile δ corresponding to a smooth compensated top-hat (top-panel). The solution for χ is evaluated at a = 1 for f_R0 = −10⁻⁶. The |${\bar{x}}_C$| for this f_R0 at a = 1 is 2.43 h⁻¹Mpc. To illustrate how χ changes with the choice of scale we pick three values for the width of the top-hat denoted by x_top = 0.002, 2, and 200 h⁻¹Mpc. This corresponds to Q = 1217, 1.21, 0.012, respectively. Changing the choice of scale is also equivalent to changing the value of f_R0. The effect of the fifth force depends on ∇χ. It is clear from the third panel, that when Q < <1, the extra force ∇χ is non-zero only at the edge of the top-hat. In such a system, the evolved density develops a ‘spike’ at the top-hat boundary (see Section 6.4). This phenomenon has been reported in the literature before (Borisov et al. 2012; Kopp et al. 2013; Lombriser 2016), but in the context of the chameleon mechanism. Here, we provide a mathematical explanation of this feature based on the analytic solution, but in the absence of chameleon screening. A more detailed discussion can be found in Section 6.4. The lowest panel shows the two potentials Φ and Ψ. When Q > >1, the two potentials clearly differ, when Q < <1, the effect of the ‘extra force’ is effectively ‘screened’ and the two potentials almost coincide as is expected in standard GR. The difference in the two potentials is related to χ, which is suppressed by a factor of Q² in this regime.

Figure 5.

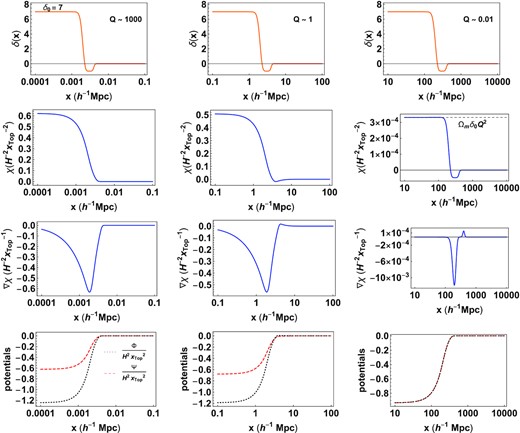
The spatial solutions for dimension-less χ, ∇χ, Φ and Ψ at a = 1 corresponding to a smoothed top-hat source δ(x) (top-panel). In the strong field limit Q > >1, the effect of the modification is the strongest corresponding to the largest difference between Φ and Ψ. In the weak field limit, Q < <1, the solution for χ is proportional to δ and the ‘extra force’ which is proportional to ∇χ is largest at the edge of the top-hat. The amplitude of this additional force is small compared to the potentials and they are effectively equal as is expected in standard GR.

Open in new tab Download slide

Equation (46) implies that the potential Φ₊ has the same equation as the Newtonian potential in standard GR. We denote Φ₊ = Ψ_GR. In the strong field limit, χ ≈ −2/3Φ₊ which gives Ψ ≈ 4/3Ψ_GR, whereas in the weak field limit Ψ ≈ Ψ_GR. Fig. 6 shows the ratio Ψ/Ψ_GR, evaluated at the innermost shell, as a function of the parameter Q of the profile. The strong and weak field asymptotic values are clearly in agreement with expectations. Since, the three values of Q above were not sufficient to characterize this plot, the static potentials were evaluated for additional profiles with different values of Q. The details can be found in Appendix A.

Figure 6.

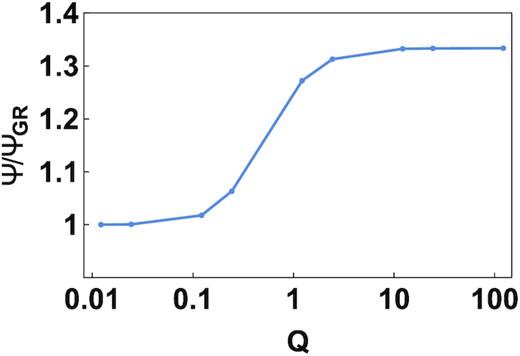
The ratio Ψ/Ψ_GR evaluated at the innermost shell for profiles with different values of Q. In f(R), the ‘Newtonian potential’ Ψ i.e. the potential Ψ, that appears in Euler’s equation is enhanced. In the strong field limit, Q > >1, the ratio Ψ/Ψ_GR ∼ 4/3. In the weak field limit, Q < <1, the ratio asymptotes to unity.

Open in new tab Download slide

5 LINEAR EVOLUTION

In GR, a top-hat remains a top-hat until shells cross. This follows as a consequence of the inverse-square law of Newtonian gravity. The evolution of each shell depends only on the mass enclosed inside the shell. The position dependence of the equations is implicit for a radially varying density profile. This is not the case for f(R) models. The force ∇_xΨ in the Euler equation (45) has a more complicated dependence on x and this introduces a location-dependent evolution for each shell even for a top-hat density distribution. In linear theory, this manifests itself as a scale-dependent linear growth factor. However, as seen above, on scales much smaller than the Compton wavelength, Ψ ≈ 4/3Ψ_GR and the evolution is scale-independent. On these scales, the linear growth equation for δ which in standard GR is

$$\begin{eqnarray*} {\rm Std. GR:} \quad \quad\quad \delta ^{\prime \prime } + \left(2 + \frac{H^{\prime }}{H}\right) \delta ^{\prime } - \frac{3}{2} \Omega _m(a) \delta =0 \end{eqnarray*}$$

(61)

gets changed in modified gravity (MG) models to

$$\begin{eqnarray*} {\rm MG(Q\gt \gt 1):} \quad \delta _{\rm MG}^{\prime \prime } + \left(2 + \frac{H^{\prime }}{H}\right) \delta _{\rm MG}^{\prime } - 2 \Omega _m(a) \delta _{\rm MG}=0. \end{eqnarray*}$$

(62)

The solution to this system can be written as

$$\begin{eqnarray*} \delta _{\rm GR}(a) &=& \delta (a_{\rm init}) \frac{D_{\rm GR}(a)}{D_{\rm GR}(a_{\rm init})} = \delta (a_{\rm init}) {\tilde{D}}_{\rm GR}(a) \nonumber\\ \quad{\rm and} \quad \delta _{\rm MG}(a) &=&\delta (a_{\rm init}) \frac{D_{\rm MG}(a)}{D_{\rm MG}(a_{\rm init})} = \delta _{\rm MG}(a_{\rm init}) {\tilde{D}}_{\rm MG}(a), \end{eqnarray*}$$

(63)

where D_GR(a) corresponds to the growth factor given by the growing mode solution and we define the scaled growth factor |${\tilde{D}}(a)$| through the second equality. An analytic expression for D(a) can be obtained for dark energy models (Dodelson 2003). To compute D_MG for the f(R) model, we solve equations (61) and (62) with δ(a_init) = 0.001 from a_init = 0.1 to a_final = 1 with Zeldovich initial conditions (δ′(a_init) = δ(a_init)). The ratio δ_MG(a)/δ(a_init) gives |${\tilde{D}}_{\rm MG}(a)$|⁠.

To confirm the expectations in the linear regime, we evolve a compensated top-hat density from a_init = 0.1 up to two final epochs a_final = 0.2 and a_final = 0.4 and for two values of Q: Q ∼ 1217 and Q ∼ 1.21. The Q < <1 is not expected to show significant deviation from GR. Since the evolution is over a small time interval, it suffices to use a small number of steps: N_t = 40. The initial velocity is set by assuming Zeldovich initial conditions. The initial and final densities are plotted in Fig. 7. The dashed orange corresponds to the initial profile and the black line is the theoretically expected, linearly evolved profile in GR, the red-dotted line is the numerically evolved profile using the non-linear code for the Hu-Sawicki model with f_R0 = −10⁻⁶ and the cyan line is its theoretical expectation given by multiplying the profile with the scaled linear growth factor defined in equation (63). For the Q > >1, the cyan and the red-dotted lines coincide at both a = 0.2 and a = 0.4. Their deviation from the corresponding GR value is larger for larger final epochs. This serves as a code check of the non-linear code in the linear regime. For Q ∼ 1, the red-dotted lines and the cyan lines do not coincide because equation (62) is no longer valid. The red-dotted lines are now closer to the GR values because the strength of the modification reduces as Q decreases. It is important to note that the linear growth given by equation (62) is in real space. In Fourier space, it is possible to write a linear growth equation for each mode δ_k which is valid for all scales, but is scale-dependent (see for e.g. Bean et al. 2007; Pogosian & Silvestri 2008). Most current and upcoming large-scale structure surveys aim to constrain modified gravity parameter by measuring the linear growth rate of perturbations. Most of these analyses are scale-independent i.e. they only look for a deviation from the growth rate in GR (for e.g. Alam et al. 2021). Although, a systematic scale-dependent measurement of the growth rate is ideal, scale-independent measurements can be used to place upper limits on the Compton wavelength of the scalaron field.

Figure 7.

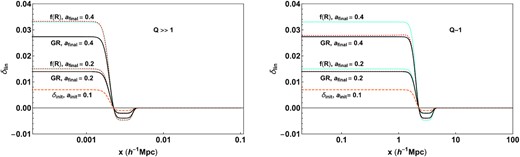
Evolution in the linear regime. The left-hand panel shows the initial density profile (orange, dashed), the expected final density in GR (black, solid), the theoretically expected (cyan), and the numerically (red, dotted) evolved final density in the f(R) model at two final epochs. The cyan and red dotted curves coincide implying the correct linear evolution for Q > >1 given by the scale-independent equation (62). The right-hand panel shows the same data for a profile with Q ∼ 1. The cyan and red-dotted curves deviate since the scale-independent linear growth equation is no longer valid. The deviation from GR is higher in the strong field regime (Q > >1) as compared to the intermediate field regime (Q ∼ 1) as expected.

Open in new tab Download slide

6 NON-LINEAR REGIME

6.1 Non-linear density and velocity

We evolve the compensated top-hat profile from a_init = 0.001 to a_final = 1 using the algorithm outlined in Section 4.5 with a_switch = 0.1. We consider three values of the top-hat scale |$x_{\rm top} = 0.002, 2, 200\, h^{-1}{\rm Mpc}$| and two values of the smoothing parameter σ = 0.0025 (red, dotted, profile I) and σ = 0.1 (blue, dotted, profile II), for each scale. The details of the initial profile are given in Appendix A. Fig. 8 shows the relevant quantities. The top-most panel shows the initial density profile which is the same for both models. The density and its spherical average are defined in equations (42) and (43). The infall velocity and the relative Hubble velocity are defined as

$$\begin{eqnarray*} v_{\rm infall} = - v(q,a) \end{eqnarray*}$$

(64)

$$\begin{eqnarray*} \delta _v = \frac{1}{H} \frac{\dot{r}}{r} - 1 = \frac{v(q,a)}{a H(a) x(q,a)} = \frac{A^{\prime }}{A}. \end{eqnarray*}$$

(65)

The black curves denote the evolution using standard GR from a = 0.001 to a = 1 and the dotted curves denote the evolution using the f(R) model.

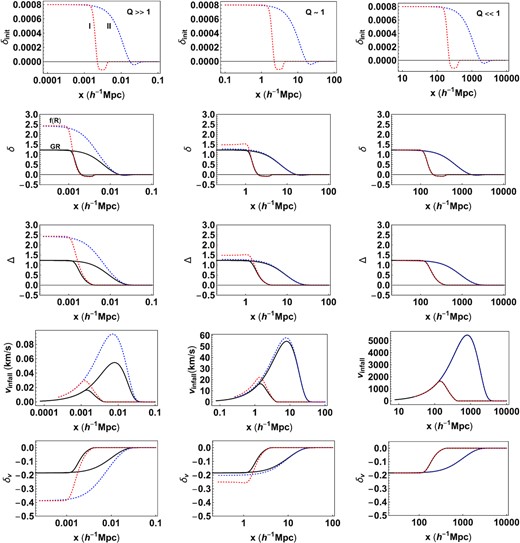
$Initial δ at a = 0.001 and the non-linearly evolved δ, Δ, infall velocity and relative Hubble velocity (δv) at a = 1 for three values of the top-hat scale $x_{\rm top} = 0.002, 2, 200\, h^{-1}{\rm Mpc}$ corresponding to Q > >1, Q ∼ 1, and Q < <1, respectively. The red and blue dotted curves correspond to σ = 0.0025 (profile I) and σ = 0.1 (profile II) evolved with the Hu-Sawicki model with fR0 = −10−6. The solid curves denote the evolution using standard GR from a = 0.001 to a = 1 for the same. The evolution in GR is scale independent. Thus, the final profiles are the same for all values of Q. For the f(R) model, when Q > >1, the evolution equations are structurally similar to GR with an enhanced potential. So the evolved profiles I and II coincide in the interior similar to the GR case, but with an increased final density. When Q < <1, the scale is outside the Compton scale making the system seemingly indistinguishable from GR. When Q ∼ 1, the evolution is scale-dependent and hence profile dependent.$

Figure 8.

Initial δ at a = 0.001 and the non-linearly evolved δ, Δ, infall velocity and relative Hubble velocity (δ_v) at a = 1 for three values of the top-hat scale |$x_{\rm top} = 0.002, 2, 200\, h^{-1}{\rm Mpc}$| corresponding to Q > >1, Q ∼ 1, and Q < <1, respectively. The red and blue dotted curves correspond to σ = 0.0025 (profile I) and σ = 0.1 (profile II) evolved with the Hu-Sawicki model with f_R0 = −10⁻⁶. The solid curves denote the evolution using standard GR from a = 0.001 to a = 1 for the same. The evolution in GR is scale independent. Thus, the final profiles are the same for all values of Q. For the f(R) model, when Q > >1, the evolution equations are structurally similar to GR with an enhanced potential. So the evolved profiles I and II coincide in the interior similar to the GR case, but with an increased final density. When Q < <1, the scale is outside the Compton scale making the system seemingly indistinguishable from GR. When Q ∼ 1, the evolution is scale-dependent and hence profile dependent.

Open in new tab Download slide

In the ΛCDM model, the radial evolution of a shell depends only on the initial average density at the shell location and is independent of the size of the shell (see equation 50). Consequently, in the GR case, the final density profiles for the two σ values, coincide in the interior of the top-hat since the initial density in the interior is same for both profiles. Because of the scale-independent evolution, the final density profiles in GR are the same for all values of Q. The magnitude of the velocity depends on the scale but the dimension-less quantity δ_v defined in equation (65) is also independent of Q.

In the f(R) model, the evolution is, in general, scale-dependent. The evolution of the extra potential χ depends sensitively on the parameter Q. In the strong field regime when Q > >1, the structure of the equations is similar to that of GR. The final densities in the interior of the top-hat are independent of σ as is the case in GR, but because the potential is enhanced by a factor of 4/3, the final density of the top-hat is higher as compared to GR. In the intermediate regime, when Q ∼ 1, the evolution is profile dependent. An un-smooth top-hat is described uniquely by a single scale x_top; smoothing broadens the top-hat edge increasing the effective width of the top-hat and decreasing the effective Q. Thus, the profile I (smaller σ) shows a greater density enhancement than profile II (larger σ). In the weak field regime, when Q < <1, the extra force is suppressed and the evolution is close to GR. There is expected to be some density enhancement at the edge of the top-hat as was discussed in Section 4.6 but it is too small to be seen on the scale of the plot. This effect is demonstrated in Section 6.

6.2 Phase space evolution

In standard gravity, the fractional overdensity and the divergence of the peculiar velocity are related through the coupled continuity and Euler equations. The temporal evolution of this system requires two initial conditions: the initial density and initial velocity field. However, it is physically reasonable to assume that there are ‘no perturbations at the big bang’ and this condition relates the initial density and velocity uniquely. At first order, in Eulerian perturbation theory, this condition is implemented by ignoring the decaying mode in the linear solution for δ and in Lagrangian perturbation theory it is embedded in the ‘Zeldovich approximation’. This is usually referred to as the slaving condition since the velocity field is ‘slaved’ to the acceleration field (Brenier et al. 2003). Thus, the linear DVDR relation is

$$\begin{eqnarray*} \Theta = - f \delta , \end{eqnarray*}$$

(66)

where, Θ = ∇_r · v/H is the scaled velocity divergence. The linear growth rate, f, is primarily dependent on the matter density Ω_m and is usually expressed as |$f \equiv \Omega _m^\gamma$|⁠, where γ, sometimes called the growth index, is a sensitive probe of cosmology.⁸ For a pure matter universe γ = 0.6 (Peebles 1980), for a ΛCDM model γ = 0.55 (Linder 2005), and for the DGP model of gravity, γ = 0.68 (Dvali, Gabadadze & Porrati 2000; Linder & Cahn 2007).

In Nadkarni-Ghosh (2013), N13, hereafter, this relation was extended to the non-linear regime using the spherical top-hat by imposing the condition ‘no perturbations at the big bang’ in the full solution. At any epoch, given an initial δ, it is possible to compute the corresponding Θ that satisfies the condition using the exact evolution equation for the outer edge of the top-hat. This unique relationship traces out a curve in the 2D δ − δ_v phase space which was called the ‘Zeldovich curve’ because it encapsulates the spirit of the Zeldovich approximation. It is not obvious that this is the desired late time non-linear DVDR. In order to check this, N13, examined the dynamics of perturbations using the coupled continuity and Euler equations, which for a top-hat in standard GR reduce to

$$\begin{eqnarray*} \delta ^{\prime } = -(1+ \delta) \Theta \end{eqnarray*}$$

(67)

$$\begin{eqnarray*} \Theta ^{\prime } = -\frac{3}{2} \Omega _m(a) \delta - \Theta \left(2 + \frac{H^{\prime }}{H}\right) -\frac{\Theta ^2}{3}. \end{eqnarray*}$$

(68)

By evolving many initial δ − Θ pairs using the above equations, it was shown that the ‘Zeldovich curve’ is indeed an invariant of the dynamical system described by equations (67) and (68). This means that perturbations that start anywhere in phase space, not necessarily on the curve, eventually converge to it. Those that start on the curve, stay on the curve. Thus, the curve traced out by the ‘no-perturbations at the big bang’ condition indeed is the late time, non-linear DVDR.

Finding such invariants of the dynamical system can be potentially useful in breaking parameter degeneracies as was illustrated in N13. This is because invariant sets depend only on cosmological parameters that appear as coefficients in the dynamical equations and are insensitive to the parameters that describe initial conditions, such as, the amplitude σ₈ or spectral index n_s. One of the primary aims of this paper is to understand if such invariants exist for the f(R) system. Because of the complexity of the equations, it is not practically feasible to implement the algorithm used in N13 to select the δ − Θ pairs that satisfy the ‘slaving condition’. Instead, we evolve the compensated top-hat profiles which start with Zeldovich initial conditions, compute the resulting density–velocity divergence pairs along the evolved curves and examine where they lie in phase space. Is the resulting curve in phase space universal? Or does it depend on the details of the initial profile?

Since the density profile is radially varying, it is easier to use the spherically averaged Δ and the relative Hubble velocity defined in equation (65).⁹ In standard GR, using relations equations (44), (50), and (65) the dynamical equations for the Δ − δ_v system read:

$$\begin{eqnarray*} \Delta ^{\prime } = -3(1+ \Delta) \delta _v \end{eqnarray*}$$

(69)

$$\begin{eqnarray*} \delta _v^{\prime } = -\frac{1}{2} \Omega _m(a) \Delta - \delta _v\left(2 + \frac{H^{\prime }}{H}\right) - \delta _v^2. \end{eqnarray*}$$

(70)

The form of the coupled system given by equations (67)–(68) or equations (69)–(70) hinges on the fact that the potential in Euler’s equation is related to the density through the Poisson’s equation. For f(R) theories, in general, this closure is not possible because of the extra degree of freedom encapsulated in χ. However, in the limit Q > >1, Ψ = 4/3Ψ_GR, and the system can be written as

$$\begin{eqnarray*} \delta _{\rm MG}^{\prime } = -(1+ \delta _{\rm MG}) \Theta _{\rm MG}, \end{eqnarray*}$$

(71)

$$\begin{eqnarray*} \Theta _{\rm MG}^{\prime } = -2 \Omega _m(a) \delta _{\rm MG} - \Theta _{\rm MG}\left(2 + \frac{H^{\prime }}{H}\right) -\frac{\Theta _{\rm MG}^2}{3}, \end{eqnarray*}$$

(72)

or alternately

$$\begin{eqnarray*} \Delta _{\rm MG}^{\prime } = -3(1+ \Delta _{\rm MG}) \delta _{v,\rm MG}, \end{eqnarray*}$$

(73)

$$\begin{eqnarray*} \delta _{v,\rm MG}^{\prime } = -\frac{2}{3} \Omega _m(a) \Delta _{\rm MG} - \delta _{v,\rm MG}\left(2 + \frac{H^{\prime }}{H}\right) - \delta _{v,\rm MG}^2. \end{eqnarray*}$$

(74)

Fig. 9 shows the Δ − δ_v pairs plotted in the 2D phase space for the profiles plotted in Fig. 8. These pairs are directly calculated from the evolved profiles at a = 1 plotted in Fig. 8 for all three values of Q. The red (blue) lines correspond to profiles I and II with σ = 0.0025 and 0.1, respectively. Note that, when Q > >1, although cases I and II have different profiles for Δ and δ_v, the pairs, when plotted in phase space, trace out the same curve. Thus, this curve is an invariant of the dynamics described by equations (73) and (74). Similarly, in the weak field limit, when Q < <1, the Δ − δ_v pairs trace out the same curve for profiles I and II. In this case, this curve coincides with the GR limit and is an invariant of the dynamics given by equations (69) and (70). In the intermediate regime, when Q ∼ 1, the Δ − δ_v curve is different for profiles I and II. This is related to the fact that the dynamics in this regime cannot be described by a closed form dynamical system of the kind discussed above.

$The spherically averaged density Δ and fractional Hubble parameter δv plotted on the Δ − δv phase space for profiles I (red, dotted) and II (blue, dot-dashed). In standard GR, the ‘slaving condition’ imposes a specific relation between the non-linear density and velocity which traces out a special curve in the phase space. This curve is an invariant of the dynamical system described by equations (69) and (70). In the f(R) model, in the strong field regime (Q > >1), the evolution is scale-independent and the dynamics can be described by equations (73) and (74) akin to standard GR and the non-linear relation between Δ and δv is profile independent. In the weak field limit (Q < <1), the curves coincide with the GR (ΛCDM) case. However, in the intermediate regime (Q ∼ 1), the Newtonian force is scale dependent and in the Δ − δv plane, the dynamics is profile dependent.$

Figure 9.

The spherically averaged density Δ and fractional Hubble parameter δ_v plotted on the Δ − δ_v phase space for profiles I (red, dotted) and II (blue, dot-dashed). In standard GR, the ‘slaving condition’ imposes a specific relation between the non-linear density and velocity which traces out a special curve in the phase space. This curve is an invariant of the dynamical system described by equations (69) and (70). In the f(R) model, in the strong field regime (Q > >1), the evolution is scale-independent and the dynamics can be described by equations (73) and (74) akin to standard GR and the non-linear relation between Δ and δ_v is profile independent. In the weak field limit (Q < <1), the curves coincide with the GR (ΛCDM) case. However, in the intermediate regime (Q ∼ 1), the Newtonian force is scale dependent and in the Δ − δ_v plane, the dynamics is profile dependent.

Open in new tab Download slide

There are various parameters that have been used in the literature to characterize the departure of modified gravity models from GR (see for example Silvestri et al. 2013; Lombriser 2016) and it is useful to correlate the departure of the DVDR relation from GR with such parameters. We define the parameter (in real space)

$$\begin{eqnarray*} \eta = \frac{\Psi }{\Phi }. \end{eqnarray*}$$

(75)

This is distinguished from |$\eta _k = \frac{\Phi _k}{\Psi _k}$| defined by Pogosian & Silvestri (2008) which is ratio of the Fourier components of Φ and Ψ. η_k varies smoothly from 0.5 to 1 while traversing the limit from modified gravity to GR. We found that the real space η was constant along the radial direction for the entire range of the perturbation rising sharply to ∞ after the compensated region where Ψ ∼ Φ ∼ 0, since it is ill-defined on that domain. In comparing the deviations, we consider only the domain of the perturbation where η < 1. In Fig. 10, we plot the deviation of the curves in phase space defined as follows. At a given radial point x, the pair {Δ, δ_v, fR} is well-defined from the numerical density and velocity profiles evolved in the f(R) theory and plotted in Fig. 8. The pair {Δ, δ_v, GR} corresponds to the expected value of δ_v if the evolution assumed standard GR. The latter was computed by evolving the same initial profile in standard GR and interpolating the resulting Δ − δ_v curve; it can also be computed using the fit given in N13. The deviation between the two curves is given by

$$\begin{eqnarray*} {\rm deviation}(x) = |\delta _{v,GR}(\Delta (x)) - \delta _{v,fR}(\Delta (x))|. \end{eqnarray*}$$

(76)

The red and blue lines correspond to profiles I and II, respectively. It is clear that there is a direct correspondence between η and the deviation in phase space. Note that η and the deviation both remain approximately constant throughout the radius of the perturbation, although the density, velocity, and potentials are radially varying. As expected, η closer to unity implies as smaller deviation.

Figure 10.

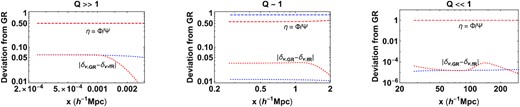
Deviation of the DVDR relation in modified gravity from that in GR at a = 1 corresponding to the curves in Fig. 9. The response of the velocity field to the matter is different in GR and modified gravity. The difference is directly correlated to the difference between the two potentials Ψ (which governs dynamics) and Φ (which governs the curvature). It is interesting to note that while Φ and Ψ vary along the radial direction (see Fig. 5), their ratio is a constant and directly correlated with deviation of the DVDR curve from its GR counterpart in phase space.

Open in new tab Download slide

6.3 Fitting form for the DVDR in the strong field regime

The non-linear density velocity divergence relation has been extensively investigated in the past using perturbation theory both in the Eulerian (Bernardeau 1992; Chodorowski 1997; Chodorowski & Lokas 1997) and Lagrangian frames (Susperregi & Buchert 1997) as well as numerical simulations (Bernardeau & van de Weygaert 1996; Chodorowski et al. 1998; Zaroubi et al. 1999; Kudlicki et al. 2000; Ciecielg et al. 2003; Kitaura et al. 2012). The formula given by Bernardeau (1992) (B92 hereafter) in standard GR reads

$$\begin{eqnarray*} \Theta = \frac{3\Omega _m^{0.6}}{2} \left\lbrace 1-(1+\delta)^{2/3}\right\rbrace \end{eqnarray*}$$

(77)

and is valid in the regime −1 ≤ δ ≤ 2. Bilicki & Chodorowski (2008), BC08 hereafter, gave a fitting form valid for a larger range of δ but is based on the exact analytic solution of the spherical collapse and hence was derived for pure matter cosmologies. N13 gave a formula based on the B92 and BC08, but with the growth index modified to account for a general dark energy component with a constant equation of state w. Mandal & Nadkarni-Ghosh (2020) checked that this formula also holds for early dark energy scenarios where w may vary with time.

In this paper we find a fitting form for DVDR in the strong field regime of f(R) where the dynamics is scale independent. We evaluated the Δ − δ_v pairs for final density and velocity profiles in the range from 0.5 ≤ a ≤ 1 using a function of the form |$\delta _v = A(\Omega _m) [1-(1+\Delta)^{B(\Omega _m})]$|⁠, where A and B were coefficients which depend on the instantaneous Ω_m. B was found to be independent of Ω_m, whereas A varies as a power law. The form

$$\begin{eqnarray*} \delta _v = 0.64 \times \Omega _m^{0.54} [1-(1+\Delta)^{0.61}] \end{eqnarray*}$$

(78)

gave a good fit over the range 0 ≤ Δ ≤ 2 and 0.5 ≤ a ≤ 1. In terms of δ and Θ this relation reads

$$\begin{eqnarray*} \Theta = 1.92 \times \Omega _m^{0.54} [1-(1+\delta)^{0.61}]. \end{eqnarray*}$$

(79)

The r.m.s. relative error between the fit and the data was about 17 per cent over the entire range of Δ and a. In this regime, we do not expect the non-linear DVDR to depend on the exact choice of a_switch. We did not attempt to fit the void region since the top-hats considered here are overdense giving a positive Δ.

Fig. 11 shows the fitting form for the DVDR relation for the ΛCDM case (black) and the f(R) model (red) in the strong field regime as a function of redshift. The red points represent the numerically evolved (Δ, δ_v) points corresponding to the selected epoch. The blue arrows show the streamlines of the flow given by equations (73) and (74). They show the instantaneous direction of the vector defined by |$(\Delta ^{\prime }, \delta _v^{\prime })$|⁠. The system defined by equations (73) and (74) is a non-autonomous system since the coefficients of Δ and δ_v in the r.h.s. are time-dependent. Hence, the streamlines are not constant at all epochs and neither is the DVDR curve. This can be contrasted with the case of a pure Ω_m = 1 flat universe, where the dynamical system for Δ − δ_v is an autonomous system and the DVDR relation is time-independent (see N13 for a detailed discussion).

Figure 11.

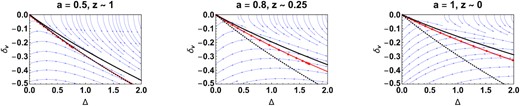
The DVDR in the strong field limit (Q > >1). The red line is the fitting form given in equation (78) and the red dots show the Δ − δ_v pairs computed from the radial profile at the selected epoch. The solid black line shows the DVDR for the reference ΛCDM model considered here and the black dotted line shows the DVDR for the flat EdS model with Ω_m = 1. The dynamical system of equations governing Δ and δ_v is non-autonomous in the case of ΛCDM and f(R) and hence the curves are time-dependent. On the other hand, the EdS curve is the same for all epochs.

Open in new tab Download slide

The DVDR relation based on spherical collapse is one-to-one. However, for realistic density and velocity fields, there is a scatter around a mean relation. Numerical simulations in the case of ΛCDM have shown that the mean relation is close to that given by the spherical collapse model (Bernardeau et al. 1999; Kudlicki et al. 2000; Bilicki & Chodorowski 2008). This scatter is usually attributed to the non-local nature of gravity. The scatter can be related to the shear component of the velocity field as was shown by Chodorowski (1997) using perturbation theory and using triaxial collapse by Nadkarni-Ghosh & Singhal (2016). It remains to be checked whether the mean relation from the joint density–velocity PDF obtained from simulations agrees with the estimate based on spherical collapse given in this paper.

6.4 Density enhancement in non-linear evolution

In this paper, we do not undertake a systematic study of the highly non-linear regime, in particular the process of collapse. However, we illustrate, qualitatively, the difference between highly non-linear evolution in the strong and weak limits. We consider two profiles: both with σ = 0.0025, but with different x_top. One case corresponds to x_top = 0.002h⁻¹Mpc and the other with x_top = 200h⁻¹Mpc. Q > >1 for the former and Q < <1 for the latter over the entire range of evolution from a = 0.1 to a = 1. In each case, the initial amplitude was chosen so that the final evolved density in the f(R) model has δ ∼ 100. This implies that in the strong field limit, the initial amplitude of the perturbation is less than that for the weak field limit. The details are in Appendix A. The resulting non-linear Δ is shown in the top-panel of Fig. 12 and the difference between the f(R) and GR profiles is shown in the bottom panel. For Q > >1, the amplification is large since the effective force is 4/3 times stronger. For Q < <1, the evolved profiles for f(R) and GR apparently coincide. However, the lower panel shows that the f(R) model has a higher density at the edge of the top-hat. This can be explained in terms of the solution for χ as was discussed in Section 4.6. χ is proportional to δ in this regime and the force which is proportional to the gradient is non-zero only at the edge of the top-hat.

Figure 12.

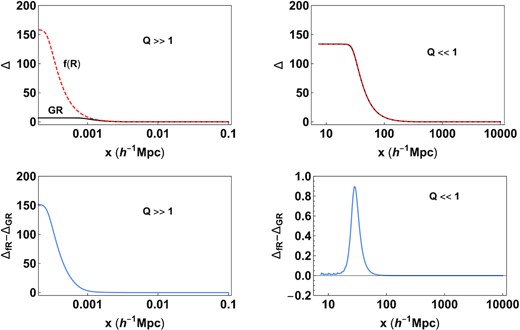
Demonstration of non-linear growth in strong versus weak regimes. In the upper panel, the red dashed denotes f(R) and black solid is the GR value for Δ at a = 1. In the strong regime Q > >1, the profile is amplified as compared to GR, whereas for the weak field regime, where Q < <1, the two profiles coincide by eye. The lower panel profile develops a cusp at the edge of the top-hat. This is related to the solution for χ which is proportional to the density in the weak field limit. Since the force is proportional to the ∇χ, this manifests itself as a cusp at the edge of the top-hat.

Open in new tab Download slide

The density enhancement at the edge has been reported earlier (Borisov et al. 2012; Kopp et al. 2013; Lombriser 2016) but in the presence of the chameleon screening. The appearance of a ‘spike’ at the edge of the top-hat is akin to the presence of a ‘thin-shell’ in the chameleon mechanism, although in this paper we have not explicitly modelled the chameleon screening. Hence, it is worth understanding the relation between these two features. Following the seminal paper on ‘chameleon cosmology’ (Khoury & Weltman 2004), we consider a scalar field ϕ, evolving according to

$$\begin{eqnarray*} \nabla _r^2 \phi = V_{eff}(\phi)_{,\phi }, \end{eqnarray*}$$

(80)

where |$V_{\rm eff} =V(\phi) + \rho e^{\sqrt{8 \pi G} \beta \phi }$| and β is a coupling constant of the order of unity. This equation is solved for an overdense sphere of density ρ embedded in a background of density ρ_∞ < ρ, with boundary conditions ϕ(r → ∞) = ϕ_∞, where ϕ_∞ is the value of the field that minimizes the effective potential at ∞ and dϕ/dr(r → 0) = 0. The ‘chameleon solution’ refers to a special solution of this equation where the effective potential is at its minimum almost everywhere inside the sphere, except for a thin shell at the surface of the sphere. This solution corresponds to |$\nabla _r^2 \phi \approx V_{\rm eff, \phi } \approx 0$| and the ‘extra fifth force’, which is given by ∇ϕ is zero inside the sphere except near the surface. When ρ is large, as is the case inside the sphere, the second derivative of the effective potential at the minimum is larger i.e. the potential is steeper. The mass of the scalar field for this solution is large and correspondingly, the Compton wavelength is small inside the sphere. Outside the sphere, the density is low, the effective potential is shallower, the Compton wavelength is large, and the fifth force is not screened.

In the f(R) model, the scalar field corresponds to χ = δf_R. The Q < <1 solution corresponds to |$\nabla _x^2 \chi \approx 0$|⁠, which gives |$\chi = {\bar{x}}_c^2 H^2 \Omega _m a^2 \delta$|⁠. Since the ‘fifth force’ depends on ∇_xχ, it is zero everywhere except at the edge of the top-hat, where the derivative of the density is non-zero. However, we do not refer to this as ‘chameleon screening’ since the Compton wavelength is constant both inside and outside the top-hat and is independent of δ. This can also be seen by defining an ‘effective potential’ |$V_{\rm eff}(\chi) = \frac{\chi ^2}{2{\bar{x}}_C^2} + H^2 \Omega _m a^2 \delta \chi$|⁠, recasting the equation for χ as |$\nabla _x^2 \chi = V_{\rm eff}(\chi)_{,\chi }$| and noting that the second derivative, V_{eff, χχ}, which is inversely related to the Compton wavelength, is independent of δ. In this paper, we have used the first order of the Taylor expansion |$\delta f_R \sim f_{RR} \delta R + \mathcal {O}(R)$| in obtaining a linear equation for χ. Ideally, as has been argued by Hu-Sawicki, this linearization is not valid when δR is large (high curvature limit). Alternately, it is clear that when the Compton wavelength is small i.e. f_RR is small, higher order corrections to this expansion may become important making the equation for χ non-linear. Higher order terms can be modelled by allowing the Compton wavelength to depend on χ. Thus, the chameleon solution is essentially a solution of the non-linear equation for χ.

Physically, the density spike at the edge is related to the enhanced force on the shells near the edge. For a constant density top-hat, all shells up to the edge experience the same acceleration and the top-hat maintains its shape until the innermost shell collapses first. On the other hand, in f(R) gravity, even though at the initial time, all shells start with the same acceleration, as evolution proceeds, the shells near the edge accelerate faster than they would in GR. The inner shells accelerate at the same rate as GR since the fifth force is screened inside. Mass starts to accumulate at the edge giving rise to an enhanced density, until, eventually, the faster moving shells cross the inner slower shells giving rise to a caustic at the edge. This was observed in Borisov et al. (2012). It is important to note that this density enhancement is pronounced for a top-hat due to the presence of a steep gradient. The ratio of the additional force to the GR force is

$$\begin{eqnarray*} \frac{\nabla _x \chi }{\nabla _x \Phi _{\rm GR}} \sim {\bar{x}}_C \frac{\mathrm{ d} \ln \delta }{\mathrm{ d}x}. \end{eqnarray*}$$

(81)

Enhancement will be prominent only when the density changes over a scale much smaller than the Compton wavelength of the scalar field. For a smooth radial density, enhancement will be minimal in the weak field regime. Thus, the edge effect is observed when the scale of the density perturbation is larger than the Compton wavelength, but the scale of the density gradients are larger than the Compton wavelength. In the strong field regime, when Q > >1, the Compton wavelength is large compared to the scale of the perturbation. There are no edge effects since the ‘fifth force’ and the associated density enhancement is uniform; the final density is higher as compared to GR. When Q ∼ 1, there is a slight edge effect (see middle panel of ∇χ in Fig. 5), but is suppressed compared to the Q < <1 case because the Compton wavelength is larger. Understanding this behaviour for the full non-linear equation is left for future work.

7 SUMMARY AND DISCUSSION

In this work, we have investigated the non-linear evolution of cosmological perturbations in f(R) models using the compensated spherical top-hat as a proxy for the non-linear regime. Our algorithm is an iterative hybrid Lagrangian–Eulerian scheme; the continuity equation and Euler equation are solved in Lagrangian coordinates and the equations for the metric potentials are purely spatial and are solved analytically in Eulerian space. Specifically, we chose the Hu & Sawicki (2007) model for simplicity, with majority of the results obtained by setting f_R0 = −10⁻⁶ and n = 1. The evolution equations depend upon the ratio of |$Q = {\bar{x}_C}/{x_{\rm top}}$|⁠, where |${\bar{x}_C}$| is the reduced comoving Compton wavelength of the model given by equation (23). The Compton wavelength is assumed to depend only on the background cosmology; thus we do not model the chameleon screening mechanism (Khoury & Weltman 2004). However, we demonstrate the role played by the Compton wavelength by changing the scale of the top-hat (x_top). We consider three values of x_top = 0.002, 2, and 200 h⁻¹Mpc, corresponding to Q = 1217, 1.21, and 0.012 at a = 1. There are several new features of this work.

Analysis of oscillations in the background evolution
It is well known that the f(R) model exhibits high frequency oscillations at high redshifts, both in the background and perturbation evolution making the system numerically stiff. To overcome this, it is favourable to assume GR at early epochs and ‘switch’ to f(R) evolution at a late epoch denoted by a_switch. By performing an eigenvalue analysis of the linearized background equations, we were able to assess the nature of oscillations and make an informed choice of a_switch. Such an eigenanalysis has been performed for the Boltzmann hierarchy in order to gain insights for optimizing solvers (Nadkarni-Ghosh & Refregier 2017) and a similar analysis can also be performed for the linear perturbation system of f(R) or other models of modified gravity. In particular, it could help us in putting the Quasi-Static-Approximation on firmer grounds (Hojjati et al. 2012; Sawicki & Bellini 2015; Pace et al. 2021).
Analytic solutions for the metric potentials and density-enhancement
Growth of perturbations in standard GR is governed by the joint continuity, Euler and Poisson equations. In f(R) models, there is an extra equation corresponding to the ‘extra’ degree of freedom, usually encapsulated by the variable f_R. In the limit |f_R| < <1 and |f/R| < <1, the perturbations in f_R can be expressed as the difference of the two potentials Φ − Ψ, where Φ and Ψ are the metric perturbations corresponding to the ‘curvature’ potential and ‘Newtonian’ potential, respectively. We derive an analytic solution for χ = Φ − Ψ in real space in spherical symmetry valid for all values of Q. In the strong field limit, when the scale of the perturbation is much less than its Compton wavelength (Q > >1), χ obeys the Poisson equation and Ψ is 4/3 times its value in standard GR. In the weak field limit, when the scale of the perturbation is much greater than its Compton wavelength (Q < <1), χ ∝ δ. This means that the force, which is proportional to the gradient of χ is non-zero only at the edge of the top-hat. This results in a density enhancement at the top-hat edge, a phenomenon that has been previously reported in the literature (Borisov et al. 2012; Kopp et al. 2013) in the context of ‘chameleon screening’. Here we demonstrate the same effect in the absence of a chameleon mechanism. If the Compton wavelength is allowed to change within the perturbation, then the resulting equation for χ is non-linear, possibly enhancing this effect. A more quantitative exploration is left for future investigations. Nevertheless, the analytic solutions presented here can also serve as a ‘test case’ to check other numerical schemes, similar in spirit to the use of spherical collapse as a ‘control case’ for numerical simulations (see Joyce & Labini 2012).
Phase space analysis of evolution of perturbations and the density–velocity divergence DVDR relation in the strong field limit
We evolve the compensated top-hats and examine the evolution of the perturbations in the 2D density–velocity divergence phase space. For the radially varying profiles, it is easier to compute the Δ − δ_v pairs instead of the δ − Θ pairs, where Δ is the spherically averaged density and δ_v is the fractional Hubble velocity of the shell. In the strong field limit, where the evolution of perturbations is scale-invariant, it is possible to define a unique DVDR relation and we give a fitting form for the same. In the intermediate field limit, Q ∼ 1, the evolution of perturbations is profile dependent and an invariant relation between δ and Θ does not exist. In the weak field limit, the dynamics is approximately that of GR.

There are several caveats in this work. The spherical collapse is a simplistic model: the system does not take into account any effect of the environment or rotations and ignores mode–mode coupling. The first step forward is to consider triaxial collapse. Triaxial collapse, which is an important ingredient in mock catalogue generators like PINOCCHIO (Monaco 2016; Rizzo et al. 2017; Moretti et al. 2020; Song et al. 2021) has not been studied in great detail in the context of modified gravity, albeit, with the exception of some recent efforts (Burrage, Copeland & Stevenson 2015; Burrage et al. 2018; Ruan, Zhang & Hu 2020). To capture the effects of mode coupling in the analytic framework, it is necessary to consider perturbation theory, either in the Eulerian or Lagrangian frame and related schemes (see e.g. Aviles & Cervantes-Cota 2017; Baojiu 2018; Aviles, Cervantes-Cota & Mota 2019; Valogiannis, Bean & Aviles 2020; Aviles et al. 2021). The hybrid Eulerian–Lagrangian scheme outlined here does not rely on spherical geometry. Equations (31)–(34) are general and the hybrid scheme can also be incorporated with a multistep Lagrangian perturbation theory (Nadkarni-Ghosh & Chernoff 2011, 2013), which guarantees convergence in ΛCDM models up until shell-crossing. However, convergence and shell-crossing related issues in modified gravity scenarios remain to be investigated (see for example Rampf & Frisch 2017; Rampf & Hahn 2020 for a discussion of these matters in standard GR). A code, called SELCIE, based on Finite Element Methods to solve the chameleon equations of motion in arbitrary mass distributions has recently been developed by Briddon et al. (2021). However, it is currently not set up to perform temporal evolution of the matter distribution in the presence of chameleon screening. It may be possible to couple iterative methods used in this paper with such tools. In addition, for the f(R) model considered here, the relevant scales for which the system is in the strong field limit, are not cosmological scales, but correspond to smaller bodies governed by additional astrophysical processes which have also been ignored in this treatment.

The f(R) model, in the metric formalism can be considered as a special case of Brans–Dickie theories, which in turn belongs to the more general class of Horndeski theories (De Felice & Tsujikawa 2010; Kobayashi 2019). More recently, the effective field theory of dark energy has become a popular formalism which is aimed at capturing a wide class of modified theory models (see review by Frusciante & Perenon 2020). Other kinds of f(R) modifications have also been introduced in the context of understanding galaxy rotation curves (for e.g. Dey, Bhattacharya & Sarkar 2013, 2015) or in the context of unified models of dark energy and inflation (for e.g. Nojiri & Odintsov 2007; Cognola et al. 2008; Nojiri & Odintsov 2011). Spherically symmetric solutions play an important role in understanding the collapse processes in such systems (Astashenok et al. 2019; Chowdhury et al. 2020; Jaryal & Chatterjee 2021). Furthermore, many future tests of modified gravity will involve measurements on a very wide range of astrophysical and cosmological scales depending upon the magnitude of modification to the ‘curvature’ and ‘potential’ fields (Baker, Psaltis & Skordis 2015). Many of these systems are often modelled by spherical symmetry. We hope that some of the techniques presented in this work may be extended to gain insights into these generalized models of modified gravity in such systems.

ACKNOWLEDGEMENTS

SN would like to acknowledge the Department of Science and Technology, Govt. of India, for the grant no. WOS-A/PM-21/2018. SC would like to acknowledge the Council of Scientific and Industrial Research (CSIR) for the grant no. 09/092(0930)/2015-EMR-I. Both authors would like to thank Tapobrata Sarkar for useful discussions through the course of this project and for detailed comments on the manuscript. SN would like to thank Alessandra Silvestri for pointing out some useful references.

DATA AVAILABILITY

Data generated by the numerical runs available on request from the corresponding author.

Footnotes

1

https://www.desi.lbl.gov/

2

https://www.sdss.org

3

http://sci.esa.int/euclid/.

4

w_eff is defined through the relation |$H^2 = H_0^2\left(\frac{\Omega _{m,0}}{a^3} + \Omega _{de,0} \exp \left[{-\int _{a}^1 \left\lbrace 1+ w_{\rm eff}(u)\right\rbrace \frac{\mathrm{ d}u}{u}}\right]\right)$|⁠, u being a dummy variable.

5

Putting in the dimensions this gives |$\lambda _C =\frac{c \sqrt{3 {\tilde{f}_{{\tilde{R}}{\tilde{R}}}}}}{H_0 \sqrt{\Omega _{m,0}}}$|⁠.

6

https://www.cosmos.esa.int/web/planck

7

The Q defined here is different but related to the Q defined in Fourier space in Pogosian & Silvestri (2008).

8

γ defined here differs from the post-Newtonian parameter sometimes used in literature (Bertschinger & Zukin 2008; Joyce et al. 2016).

9

N13, used the variables δ − δ_v to describe the phase-space. For constant density perturbations considered in that paper, the two are equivalent Θ = 3δ_v.

REFERENCES

Alam

S.

et al. ,

2017

,

MNRAS

,

470

,

2617

10.1093/mnras/stx721

Crossref

Search ADS

Alam

S.

et al. ,

2021

,

J. Cosmol. Astropart. Phys.

,

11

,

050

Amendola

L.

et al. ,

2018

,

Living Rev. Relat.

,

21

,

2

10.1007/s41114-017-0010-3

Crossref

Search ADS

Appleby

S.

,

Battye

R.

,

2007

,

Phys. Lett. B

,

654

,

7

10.1016/j.physletb.2007.08.037

Crossref

Search ADS

Astashenok

A. V.

,

Mosani

K.

,

Odintsov

S. D.

,

Samanta

G. C.

,

2019

,

Int. J. Geom. Methods Mod. Phys.

,

16

,

1950035

10.1142/S021988781950035X

Crossref

Search ADS

Aviles

A.

,

Cervantes-Cota

J. L.

,

2017

,

Phys. Rev. D

,

96

,

123526

Crossref

Search ADS

Aviles

A.

,

Cervantes-Cota

J. L.

,

Mota

D. F.

,

2019

,

A&A

,

622

,

A62

10.1051/0004-6361/201834383

Crossref

Search ADS

Aviles

A.

,

Valogiannis

G.

,

Rodriguez-Meza

M. A.

,

Cervantes-Cota

J. L.

,

Li

B.

,

Bean

R.

,

2021

,

J. Cosmol. Astropart. Phys.

,

2021

,

039

Crossref

Search ADS

Baker

T.

et al. ,

2021

,

Rev. Mod. Phys.

,

93

,

015003

10.1103/RevModPhys.93.015003

Crossref

Search ADS

Baker

T.

,

Psaltis

D.

,

Skordis

C.

,

2015

,

ApJ

,

802

,

63

10.1088/0004-637X/802/1/63

Crossref

Search ADS

Baojiu

L.

,

2018

,

Int. J. Mod. Phys.

,

27

,

1848007

Bardeen

J. M.

,

Bond

J. R.

,

Kaiser

N.

,

Szalay

A. S.

,

1986

,

ApJ

,

304

,

15

10.1086/164143

Crossref

Search ADS

Barreira

A.

,

Li

B.

,

Baugh

C. M.

,

Pascoli

S.

,

2013

,

J. Cosmol. Astropart. Phys.

,

11

,

056

10.1088/1475-7516/2013/11/056

Crossref

Search ADS

Bean

R.

,

Bernat

D.

,

Pogosian

L.

,

Silvestri

A.

,

Trodden

M.

,

2007

,

Phys. Rev. D

,

75

,

064020

10.1103/PhysRevD.75.064020

Crossref

Search ADS

Bernardeau

F.

,

1992

,

ApJ

,

390

,

L61

10.1086/186372

Crossref

Search ADS

Bernardeau

F.

,

van de Weygaert

R.

,

1996

,

MNRAS

,

279

,

693

10.1093/mnras/279.2.693

Crossref

Search ADS

Bernardeau

F.

,

Chodorowski

M. J.

,

Łokas

E. L.

,

Stompor

R.

,

Kudlicki

A.

,

1999

,

MNRAS

,

309

,

543

10.1046/j.1365-8711.1999.02856.x

Crossref

Search ADS

Bertschinger

E.

,

Dekel

A.

,

1989

,

ApJ

,

336

,

L5

10.1086/185348

Crossref

Search ADS

Bertschinger

E.

,

Zukin

P.

,

2008

,

Phys. Rev. D

,

78

,

024015

10.1103/PhysRevD.78.024015

Crossref

Search ADS

Bilicki

M.

,

Chodorowski

M. J.

,

2008

,

MNRAS

,

391

,

1796

10.1111/j.1365-2966.2008.13988.x

Crossref

Search ADS

Borisov

A.

,

Jain

B.

,

Zhang

P.

,

2012

,

Phys. Rev. D

,

85

,

63518

10.1103/PhysRevD.85.063518

Crossref

Search ADS

Brenier

Y.

,

Frisch

U.

,

Hénon

M.

,

Loeper

G.

,

Matarrese

S.

,

Mohayaee

R.

,

Sobolevskiĭ

A.

,

2003

,

MNRAS

,

346

,

501

10.1046/j.1365-2966.2003.07106.x

Crossref

Search ADS

Briddon

C.

,

Burrage

C.

,

Moss

A.

,

Tamosiunas

A.

,

2021

,

J. Cosmol. Astropart. Phys.

,

2021

,

043

Crossref

Search ADS

Buchert

T.

,

1992

,

MNRAS

,

254

,

729

10.1093/mnras/254.4.729

Crossref

Search ADS

Burrage

C.

,

Copeland

E. J.

,

Stevenson

J. A.

,

2015

,

Phys. Rev. D

,

91

,

65030

Crossref

Search ADS

Burrage

C.

,

Copeland

E. J.

,

Moss

A.

,

Stevenson

J. A.

,

2018

,

J. Cosmol. Astropart. Phys.

,

2018

,

056

Crossref

Search ADS

Cataneo

M.

,

Uhlemann

C.

,

Arnold

C.

,

Gough

A.

,

Li

B.

,

Heymans

C.

,

2021

,

preprint (arXiv:2109.02636)

Ceron-Hurtado

J. J.

,

He

J.-. hua .

,

Li

B.

,

2016

,

Phys. Rev. D

,

94

,

064052

10.1103/PhysRevD.94.064052

Crossref

Search ADS

Chakrabarti

S.

,

Banerjee

N.

,

2016

,

Gen. Relativ. Gravit.

,

48

,

57

10.1007/s10714-016-2045-2

Crossref

Search ADS

Chakraborty

S.

,

MacDevette

K.

,

Dunsby

P.

,

2021

,

Phys. Rev. D

,

103

,

124040

Crossref

Search ADS

Chiba

T.

,

2003

,

Phys. Lett. B

,

575

,

1

10.1016/j.physletb.2003.09.033

Crossref

Search ADS

Chodorowski

M. J.

,

1997

,

MNRAS

,

292

,

695

10.1093/mnras/292.3.695

Crossref

Search ADS

Chodorowski

M. J.

,

Lokas

E. L.

,

1997

,

MNRAS

,

287

,

591

10.1093/mnras/287.3.591

Crossref

Search ADS

Chodorowski

M. J.

,

Lokas

E. L.

,

Pollo

A.

,

Nusser

A.

,

1998

,

MNRAS

,

300

,

1027

10.1046/j.1365-8711.1998.01959.x

Crossref

Search ADS

Chowdhury

S.

,

Pal

K.

,

Pal

K.

,

Sarkar

T.

,

2020

,

Eur. Phys. J. C

,

80

,

902

10.1140/epjc/s10052-020-08459-w

Crossref

Search ADS

Ciecielg

P.

,

Chodorowski

M. J.

,

Kiraga

M.

,

Strauss

M. A.

,

Kudlicki

A.

,

Bouchet

F. R.

,

2003

,

MNRAS

,

339

,

641

10.1046/j.1365-8711.2003.06202.x

Crossref

Search ADS

Clifton

T.

,

Ferreira

P. G.

,

Padilla

A.

,

Skordis

C.

,

2012

,

Phys. Rep.

,

513

,

1

10.1016/j.physrep.2012.01.001

Crossref

Search ADS

Cognola

G.

,

Elizalde

E.

,

Nojiri

S.

,

Odintsov

S. D.

,

Sebastiani

L.

,

Zerbini

S.

,

2008

,

Phys. Rev. D

,

77

,

46009

Crossref

Search ADS

Colombi

S.

,

Chodorowski

M. J.

,

Teyssier

R.

,

2007

,

MNRAS

,

375

,

348

10.1111/j.1365-2966.2006.11330.x

Crossref

Search ADS

Dai

D.-C.

,

Maor

I.

,

Starkman

G.

,

2008

,

Phys. Rev. D

,

77

,

64016

10.1103/PhysRevD.77.064016

Crossref

Search ADS

De Felice

A.

,

Tsujikawa

S.

,

2010

,

Living Rev. Relat.

,

13

,

3

10.12942/lrr-2010-3

Crossref

Search ADS

Dey

D.

,

Bhattacharya

K.

,

Sarkar

T.

,

2013

,

Phys. Rev. D

,

87

,

103505

Crossref

Search ADS

Dey

D.

,

Bhattacharya

K.

,

Sarkar

T.

,

2015

,

Gen. Relativ. Gravit.

,

47

,

103

Crossref

Search ADS

Di Valentino

E.

et al. ,

2021

,

Class. Quantum Gravity

,

38

,

153001

10.1088/1361-6382/ac086d

Crossref

Search ADS

Dodelson

S.

,

2003

,

Modern Cosmology

.

Academic Press

,

Cambridge

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Dvali

G.

,

Gabadadze

G.

,

Porrati

M.

,

2000

,

Phys. Lett. B

,

485

,

208

10.1016/S0370-2693(00)00669-9

Crossref

Search ADS

Elizalde

E.

,

Odintsov

S. D.

,

Sebastiani

L.

,

Zerbini

S.

,

2012

,

Eur. Phys. J. C

,

72

,

1843

10.1140/epjc/s10052-011-1843-7

Crossref

Search ADS

Frusciante

N.

,

Perenon

L.

,

2020

,

Phys. Rep.

,

857

,

1

10.1016/j.physrep.2020.02.004

Crossref

Search ADS

Gramann

M.

,

1993a

,

ApJ

,

405

,

449

10.1086/172377

Crossref

Search ADS

Gramann

M.

,

1993b

,

ApJ

,

405

,

L47

10.1086/186762

Crossref

Search ADS

Hahn

O.

,

Angulo

R. E.

,

Abel

T.

,

2015

,

MNRAS

,

454

,

3920

10.1093/mnras/stv2179

Crossref

Search ADS

Herrera

D.

,

Waga

I.

,

Jorás

S. E.

,

2017

,

Phys. Rev. D

,

95

,

64029

Crossref

Search ADS

Hojjati

A.

,

Pogosian

L.

,

Silvestri

A.

,

Talbot

S.

,

2012

,

Phys. Rev. D

,

86

,

123503

Crossref

Search ADS

Hu

W.

,

Sawicki

I.

,

2007

,

Phys. Rev. D

,

76

,

104043

10.1103/PhysRevD.76.104043

Crossref

Search ADS

Jaryal

S. C.

,

Chatterjee

A.

,

2021

,

Eur. Phys. J. C

,

81

,

273

Crossref

Search ADS

Joyce

M.

,

Labini

F. S.

,

2012

,

MNRAS

,

429

,

1088

10.1093/mnras/sts390

Crossref

Search ADS

Joyce

A.

,

Jain

B.

,

Khoury

J.

,

Trodden

M.

,

2015

,

Phys. Rep.

,

568

,

1

10.1016/j.physrep.2014.12.002

Crossref

Search ADS

Joyce

A.

,

Lombriser

L.

,

Schmidt

F.

,

2016

,

Annu. Rev. Nucl. Part. Sci.

,

66

,

95

10.1146/annurev-nucl-102115-044553

Crossref

Search ADS

Khoury

J.

,

Weltman

A.

,

2004

,

Phys. Rev. D

,

69

,

044026

10.1103/PhysRevD.69.044026

Crossref

Search ADS

Kitaura

F.-S.

,

Angulo

R. E.

,

Hoffman

Y.

,

Gottlöber

S.

,

2012

,

MNRAS

,

425

,

2422

10.1111/j.1365-2966.2012.21589.x

Crossref

Search ADS

Kobayashi

T.

,

2019

,

Rep. Prog. Phys.

,

82

,

086901

10.1088/1361-6633/ab2429

Crossref

Search ADS

PubMed

Kopp

M.

,

Appleby

S. A.

,

Achitouv

I.

,

Weller

J.

,

2013

,

Phys. Rev. D

,

88

,

084015

10.1103/PhysRevD.88.084015

Crossref

Search ADS

Kudlicki

A.

,

Chodorowski

M.

,

Plewa

T.

,

Różyczka

M.

,

2000

,

MNRAS

,

316

,

464

10.1046/j.1365-8711.2000.03463.x

Crossref

Search ADS

Li

B.

,

Efstathiou

G.

,

2012

,

MNRAS

,

421

,

1431

10.1111/j.1365-2966.2011.20404.x

Crossref

Search ADS

Li

B.

,

Lam

T. Y.

,

2012

,

MNRAS

,

425

,

730

10.1111/j.1365-2966.2012.21592.x

Crossref

Search ADS

Lilje

P. B.

,

Lahav

O.

,

1991

,

ApJ

,

374

,

29

10.1086/170094

Crossref

Search ADS

Lilow

R.

,

Nusser

A.

,

2021

,

MNRAS

,

507

,

1557

Crossref

Search ADS

Lima

N. A.

,

Liddle

A. R.

,

2013

,

Phys. Rev. D

,

88

,

043521

10.1103/PhysRevD.88.043521

Crossref

Search ADS

Linder

E. V.

,

2005

,

Phys. Rev. D

,

72

,

43529

10.1103/PhysRevD.72.043529

Crossref

Search ADS

Linder

E. V.

,

Cahn

R. N.

,

2007

,

Astropart. Phys.

,

28

,

481

10.1016/j.astropartphys.2007.09.003

Crossref

Search ADS

Lombriser

L.

,

2016

,

J. Cosmol. Astropart. Phys.

,

11

,

039

10.1088/1475-7516/2016/11/039

Crossref

Search ADS

Macaulay

E.

,

Wehus

I. K.

,

Eriksen

H. K.

,

2013

,

Phys. Rev. Lett.

,

111

,

161301

Crossref

Search ADS

PubMed

Magnano

G.

,

Sokołowski

L. M.

,

1994

,

Phys. Rev. D

,

50

,

5039

10.1103/PhysRevD.50.5039

Crossref

Search ADS

Ma

C.-P.

,

Bertschinger

E.

,

1995

,

ApJ

,

455

,

7

10.1086/176550

Crossref

Search ADS

Mancinelli

P. J.

,

Yahil

A.

,

1995

,

ApJ

,

452

,

75

10.1086/176280

Crossref

Search ADS

Mancinelli

P. J.

,

Yahil

A.

,

Canon

G.

,

Dekel

A.

,

1993

, in

Bouchet

F. R.

,

Lachièze-Rey

M.

, eds,

osmic Velocity Fields, Proceedings of the 9th IAP Astrophysics Meeting, Institut d'Astrophysique, Paris

. p.

215

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Mandal

A.

,

Nadkarni-Ghosh

S.

,

2020

,

MNRAS

,

498

,

355

10.1093/mnras/staa2073

Crossref

Search ADS

Martino

M. C.

,

Stabenau

H. F.

,

Sheth

R. K.

,

2009

,

Phys. Rev. D

,

79

,

084013

10.1103/PhysRevD.79.084013

Crossref

Search ADS

Monaco

P.

,

2016

,

Galaxies

,

4

,

53

10.3390/galaxies4040053

Crossref

Search ADS

Moretti

C.

,

Mozzon

S.

,

Monaco

P.

,

Munari

E.

,

Baldi

M.

,

2020

,

MNRAS

,

493

,

1153

10.1093/mnras/staa312

Crossref

Search ADS

Nadkarni-Ghosh

S.

,

2013

,

MNRAS

,

428

,

1166

10.1093/mnras/sts099

Crossref

Search ADS

Nadkarni-Ghosh

S.

,

Chernoff

D. F.

,

2011

,

MNRAS

,

410

,

1454

10.1111/j.1365-2966.2010.17529.x

Crossref

Search ADS

Nadkarni-Ghosh

S.

,

Chernoff

D. F.

,

2013

,

MNRAS

,

431

,

799

10.1093/mnras/stt217

Crossref

Search ADS

Nadkarni-Ghosh

S.

,

Refregier

A.

,

2017

,

MNRAS

,

471

,

2391

10.1093/mnras/stx1662

Crossref

Search ADS

Nadkarni-Ghosh

S.

,

Singhal

A.

,

2016

,

MNRAS

,

457

,

2773

10.1093/mnras/stw075

Crossref

Search ADS

Nojiri

S.

,

Odintsov

S. D.

,

2007

,

Phys. Lett. B

,

657

,

238

10.1016/j.physletb.2007.10.027

Crossref

Search ADS

Nojiri

S.

,

Odintsov

S. D.

,

2011

,

Phys. Rep.

,

505

,

59

10.1016/j.physrep.2011.04.001

Crossref

Search ADS

Nojiri

S.

,

Odintsov

S. D.

,

Oikonomou

V. K.

,

2017

,

Phys. Rep.

,

692

,

1

10.1016/j.physrep.2017.06.001

Crossref

Search ADS

Nusser

A.

,

2017

,

MNRAS

,

470

,

445

10.1093/mnras/stx1225

Crossref

Search ADS

Nusser

A.

,

Dekel

A.

,

Bertschinger

E.

,

Blumenthal

G. R.

,

1991

,

ApJ

,

379

,

6

10.1086/170480

Crossref

Search ADS

Nusser

A.

,

Branchini

E.

,

Davis

M.

,

2012

,

ApJ

,

744

,

193

10.1088/0004-637X/744/2/193

Crossref

Search ADS

Nusser

A.

,

Davis

M.

,

Branchini

E.

,

2014

,

ApJ

,

788

,

157

10.1088/0004-637X/788/2/157

Crossref

Search ADS

Oyaizu

H.

,

2008

,

Phys. Rev. D

,

78

,

123523

10.1103/PhysRevD.78.123523

Crossref

Search ADS

Pace

F.

,

Battye

R. A.

,

Bellini

E.

,

Lombriser

L.

,

Vernizzi

F.

,

Bolliet

B.

,

2021

,

J. Cosmol. Astropart. Phys.

,

2021

,

017

Crossref

Search ADS

Paranjape

A.

,

Sheth

R. K.

,

Desjacques

V.

,

2013

,

MNRAS

,

431

,

1503

10.1093/mnras/stt267

Crossref

Search ADS

Peebles

P.

,

1980

,

The Large-Scale Structure of the Universe

.

Princeton Univ. Press

,

Princeton

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Planck Collaboration VI

2020

,

A&A

,

641

,

A6

Crossref

Search ADS

Pogosian

L.

,

Silvestri

A.

,

2008

,

Phys. Rev. D

,

77

,

023503

10.1103/PhysRevD.77.023503

Crossref

Search ADS

Press

W. H.

,

Schechter

P.

,

1974

,

ApJ

,

187

,

425

10.1086/152650

Crossref

Search ADS

Rampf

C.

,

Frisch

U.

,

2017

,

MNRAS

,

471

,

671

10.1093/mnras/stx1613

Crossref

Search ADS

Rampf

C.

,

Hahn

O.

,

2020

,

MNRAS

,

501

,

L71

10.1093/mnrasl/slaa198

Crossref

Search ADS

Rizzo

L. A.

,

Villaescusa-Navarro

F.

,

Monaco

P.

,

Munari

E.

,

Borgani

S.

,

Castorina

E.

,

Sefusatti

E.

,

2017

,

J. Cosmol. Astropart. Phys.

,

2017

,

008

Crossref

Search ADS

Ruan

C.-Z.

,

Zhang

T.-J.

,

Hu

B.

,

2020

,

MNRAS

,

492

,

4235

10.1093/mnras/staa006

Crossref

Search ADS

Sawicki

I.

,

Bellini

E.

,

2015

,

Phys. Rev. D

,

92

,

084061

10.1103/PhysRevD.92.084061

Crossref

Search ADS

Schäfer

B. M.

,

Koyama

K.

,

2008

,

MNRAS

,

385

,

411

10.1111/j.1365-2966.2008.12841.x

Crossref

Search ADS

Schmidt

F.

,

Lima

M.

,

Oyaizu

H.

,

Hu

W.

,

2009

,

Phys. Rev. D

,

79

,

83518

10.1103/PhysRevD.79.083518

Crossref

Search ADS

Schmidt

F.

,

Hu

W.

,

Lima

M.

,

2010

,

Phys. Rev. D

,

81

,

63005

Crossref

Search ADS

Scoccimarro

R.

,

2004

,

Phys. Rev. D

,

70

,

83007

10.1103/PhysRevD.70.083007

Crossref

Search ADS

Sheth

R. K.

,

Mo

H. J.

,

Tormen

G.

,

2001

,

MNRAS

,

323

,

1

10.1046/j.1365-8711.2001.04006.x

Crossref

Search ADS

Silvestri

A.

,

Pogosian

L.

,

Buniy

R. V.

,

2013

,

Phys. Rev. D

,

87

,

104015

10.1103/PhysRevD.87.104015

Crossref

Search ADS

Slotine

J. E.

,

Weiping

L.

,

1991

,

Applied Non-Linear Control

.

Prentice-Hall Inc

,

Englewood Cliffs, NJ

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Song

Y.

,

Moretti

C.

,

Monaco

P.

,

Hu

B.

,

2021

,

preprint (arXiv:2111.02240)

Song

Y.-S.

,

Doré

O.

,

2009

,

J. Cosmol. Astropart. Phys.

,

2009

,

025

Crossref

Search ADS

Song

Y.-S.

,

Hu

W.

,

Sawicki

I.

,

2007

,

Phys. Rev. D

,

75

,

044004

10.1103/PhysRevD.75.044004

Crossref

Search ADS

Sotiriou

T. P.

,

Faraoni

V.

,

2010

,

Rev. Mod. Phys.

,

82

,

451

10.1103/RevModPhys.82.451

Crossref

Search ADS

Starobinsky

A. A.

,

1980

,

Phys. Lett. B

,

91

,

99

10.1016/0370-2693(80)90670-X

Crossref

Search ADS

Starobinsky

A. A.

,

2007

,

Sov. J. Exp. Theoret. Phys. Lett.

,

86

,

157

10.1134/S0021364007150027

Crossref

Search ADS

Strogatz

S. H.

,

1994

,

Non-Linear Dynamics and Chaos

.

Perseus Publishing

,

Cambridge, MA

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Susperregi

M.

,

Buchert

T.

,

1997

,

A&A

,

323

,

295

Uzan

J.-P.

,

2007

,

Gen. Relativ. Gravit.

,

39

,

307

,

Crossref

Search ADS

Valogiannis

G.

,

Bean

R.

,

Aviles

A.

,

2020

,

J. Cosmol. Astropart. Phys.

,

2020

,

055

Crossref

Search ADS

Wolfram Research

I.

,

2018

,

Mathematica, version 11.3.0 edn.

Wolfram Research, Inc

,

Champaign, IL

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Zaroubi

S.

,

Hoffman

Y.

,

Dekel

A.

,

1999

,

ApJ

,

520

,

413

10.1086/307473

Crossref

Search ADS

Zel’Dovich

Y. B.

,

1970

,

A&A

,

5

,

84

APPENDIX A: INITIAL PROFILES

The compensated top-hat is a 1D function represented as

$$\begin{eqnarray*} \delta _{\rm top}(x) = A\quad \quad \quad 0\lt x \le x_{\rm top} \end{eqnarray*}$$

(A1)

$$\begin{eqnarray*} = -1 \quad x_{\rm top} \lt x \le x_u \end{eqnarray*}$$

(A2)

$$\begin{eqnarray*} = 0 \quad {\rm otherwise,} \end{eqnarray*}$$

(A3)

where A is the amplitude of the top-hat. x_top and x_u are the boundaries of the overdense region and the underdense compensating region and are related to through conservation of mass as

$$\begin{eqnarray*} (1+A) x_{\rm top}^3 = x_u^3. \end{eqnarray*}$$

(A4)

A smooth top-hat is obtained by the following function

$$\begin{eqnarray*} \delta _{\rm smooth}(x) &=& \frac{1}{\sqrt{2 \pi \sigma ^2 x^2}}\bigg\lbrace \int _0^{x_{\rm top}} A \left(e^{-\frac{(x-y)}{2 \sigma ^2}} - e^{-\frac{(x+y)}{2 \sigma ^2}}\right) y \mathrm{ d}y \nonumber\\&&+ \int _{x_{\rm top}}^{x_u} (-1) \left(e^{-\frac{(x-y)}{2 \sigma ^2}} - e^{-\frac{(x+y)}{2 \sigma ^2}}\right) y \mathrm{ d}y \bigg\rbrace , \end{eqnarray*}$$

(A5)

where σ is the smoothing parameter. In this paper we have used two different profiles with σ = 0.1 and σ = 0.0025. In the numerical implementation, L_min and L_max denote the minimum and maximum values of the grid points along the x-direction. The value of A and x_top are chosen according to the calculation performed. N_t gives the number of time steps used to divide the time interval from the initial epoch a_switch to the final epoch a_final. N_s denotes the number of spatial grid points, equi-spaced in ln x along the radial direction. Tables A1 and A2 give the list of parameters used in different sections of the paper.

Table A1.

Open in new tab

Table denoting the parameters of the two profiles used. The profiles 1e-1j are used only in Fig. 6.

Profile name	σ	x_top	Q (for f_R0 = −10⁻⁶)	L_min (h⁻¹Mpc)	L_max (h⁻¹Mpc)
1a	0.0025	0.002	1217	0.0001	0.1
1b	0.0025	2	1.21	0.1	100
1c	0.0025	200	0.012	10	10 000
1d	0.0025	0. 02	121	0.001	1
1e	0.0025	0.1	24.34	0.005	5
1f	0.0025	0.2	12.1	0.01	10
1g	0.0025	1	2.43	0.05	50
1h	0.0025	10	0.24	0.5	500
1i	0.0025	20	0.12	1	1000
1j	0.0025	100	0.024	5	5000
2a	0.1	0.002	1217	0.0001	0.1
2b	0.1	2	1.21	0.1	100
2c	0.1	200	0.012	10	10 000
2d	0.1	0.02	121	0.001	1

Profile name	σ	x_top	Q (for f_R0 = −10⁻⁶)	L_min (h⁻¹Mpc)	L_max (h⁻¹Mpc)
1a	0.0025	0.002	1217	0.0001	0.1
1b	0.0025	2	1.21	0.1	100
1c	0.0025	200	0.012	10	10 000
1d	0.0025	0. 02	121	0.001	1
1e	0.0025	0.1	24.34	0.005	5
1f	0.0025	0.2	12.1	0.01	10
1g	0.0025	1	2.43	0.05	50
1h	0.0025	10	0.24	0.5	500
1i	0.0025	20	0.12	1	1000
1j	0.0025	100	0.024	5	5000
2a	0.1	0.002	1217	0.0001	0.1
2b	0.1	2	1.21	0.1	100
2c	0.1	200	0.012	10	10 000
2d	0.1	0.02	121	0.001	1

Table A1.

Open in new tab

Table denoting the parameters of the two profiles used. The profiles 1e-1j are used only in Fig. 6.

Profile name	σ	x_top	Q (for f_R0 = −10⁻⁶)	L_min (h⁻¹Mpc)	L_max (h⁻¹Mpc)
1a	0.0025	0.002	1217	0.0001	0.1
1b	0.0025	2	1.21	0.1	100
1c	0.0025	200	0.012	10	10 000
1d	0.0025	0. 02	121	0.001	1
1e	0.0025	0.1	24.34	0.005	5
1f	0.0025	0.2	12.1	0.01	10
1g	0.0025	1	2.43	0.05	50
1h	0.0025	10	0.24	0.5	500
1i	0.0025	20	0.12	1	1000
1j	0.0025	100	0.024	5	5000
2a	0.1	0.002	1217	0.0001	0.1
2b	0.1	2	1.21	0.1	100
2c	0.1	200	0.012	10	10 000
2d	0.1	0.02	121	0.001	1

Profile name	σ	x_top	Q (for f_R0 = −10⁻⁶)	L_min (h⁻¹Mpc)	L_max (h⁻¹Mpc)
1a	0.0025	0.002	1217	0.0001	0.1
1b	0.0025	2	1.21	0.1	100
1c	0.0025	200	0.012	10	10 000
1d	0.0025	0. 02	121	0.001	1
1e	0.0025	0.1	24.34	0.005	5
1f	0.0025	0.2	12.1	0.01	10
1g	0.0025	1	2.43	0.05	50
1h	0.0025	10	0.24	0.5	500
1i	0.0025	20	0.12	1	1000
1j	0.0025	100	0.024	5	5000
2a	0.1	0.002	1217	0.0001	0.1
2b	0.1	2	1.21	0.1	100
2c	0.1	200	0.012	10	10 000
2d	0.1	0.02	121	0.001	1

Table A2.

Open in new tab

Table characterizing the initial data used in various figures in the text. Figs 5 and 6 correspond to static solutions and there are no parameters for the temporal evolution.

Figure	Profile used	A	N_s	N_t	a_switch	a_final
Fig. 5	1a,b,c	7	3000	–	–	–
Fig. 6	1b-1j	7	3000	–	–	–
Fig. 7	1a and 1b	0.0007	500	40	0.1	0.2, 0.4
Figs 8, 9, 10	1a,b,c and 2a,b,c	0.0008	1600	320	0.1	1
Fig. 11	1a	0.0008	1600	320	0.1	1
Fig. 12	1a and 1c	0.0015 (for 1c) 0.002 (for 1d)	1600	320	0.1	1
Fig. B1	1d	0.0008	5 × N_t	20 to 640	0.1	1

Figure	Profile used	A	N_s	N_t	a_switch	a_final
Fig. 5	1a,b,c	7	3000	–	–	–
Fig. 6	1b-1j	7	3000	–	–	–
Fig. 7	1a and 1b	0.0007	500	40	0.1	0.2, 0.4
Figs 8, 9, 10	1a,b,c and 2a,b,c	0.0008	1600	320	0.1	1
Fig. 11	1a	0.0008	1600	320	0.1	1
Fig. 12	1a and 1c	0.0015 (for 1c) 0.002 (for 1d)	1600	320	0.1	1
Fig. B1	1d	0.0008	5 × N_t	20 to 640	0.1	1

Table A2.

Open in new tab

Table characterizing the initial data used in various figures in the text. Figs 5 and 6 correspond to static solutions and there are no parameters for the temporal evolution.

Figure	Profile used	A	N_s	N_t	a_switch	a_final
Fig. 5	1a,b,c	7	3000	–	–	–
Fig. 6	1b-1j	7	3000	–	–	–
Fig. 7	1a and 1b	0.0007	500	40	0.1	0.2, 0.4
Figs 8, 9, 10	1a,b,c and 2a,b,c	0.0008	1600	320	0.1	1
Fig. 11	1a	0.0008	1600	320	0.1	1
Fig. 12	1a and 1c	0.0015 (for 1c) 0.002 (for 1d)	1600	320	0.1	1
Fig. B1	1d	0.0008	5 × N_t	20 to 640	0.1	1

Figure	Profile used	A	N_s	N_t	a_switch	a_final
Fig. 5	1a,b,c	7	3000	–	–	–
Fig. 6	1b-1j	7	3000	–	–	–
Fig. 7	1a and 1b	0.0007	500	40	0.1	0.2, 0.4
Figs 8, 9, 10	1a,b,c and 2a,b,c	0.0008	1600	320	0.1	1
Fig. 11	1a	0.0008	1600	320	0.1	1
Fig. 12	1a and 1c	0.0015 (for 1c) 0.002 (for 1d)	1600	320	0.1	1
Fig. B1	1d	0.0008	5 × N_t	20 to 640	0.1	1

We found that it was numerically more stable to use compensated top-hats because the potentials Φ and Ψ analytically vanish after a finite extent. For a pure top-hat or a more realistic profile such as the one based on peaks theory (Bardeen et al. 1986; Lilje & Lahav 1991) and used in Nadkarni-Ghosh (2013) or Kopp et al. (2013) is not as stable because the fields are non-zero at any finite radius (which is inevitable in the discretization).

APPENDIX B: CONVERGENCE TESTS

The algorithm outlined in Section 4.5 was used to evolve an initial profile from a = 0.001 to a = 1 with the transition from f(R) to GR at a_switch = 0.1. The evolution from a = 0.1 to a = 1 was carried out using successive runs with N_t = 20, 40, 80, 160, 320, and 640 steps. For each run, the spatial domain was divided into N_s steps equi-spaced in the ln x direction. In order to achieve convergence, the spatial domain needs to be refined along with the refinement in the temporal domain. We choose N_s = 5 × N_t. All solutions to the second order ordinary differential equations (O.D.E.s), we computed using the inbuilt function NDSolve in the software package mathematica (Wolfram Research 2018).

In the GR case, the exact answer can be computed in a single step. As a code test, we computed approximate answers for the GR case using the same algorithm but assuming Φ = Ψ and compared to the exact answer as well as compared successive approximations to give the Cauchy error. For the f(R) evolution we compared only successive approximations. We define the errors as follows

$$\begin{eqnarray*} {\mathcal {E}}(N) = \sqrt{\frac{1}{N} \sum _{i=1}^{N_s} |f_N(x_i) - f_{\rm exact}(x_i)|^2} \end{eqnarray*}$$

(B1)

$$\begin{eqnarray*} {\mathcal {E}}_{\rm Cauchy}(N) = \sqrt{\frac{1}{N} \sum _{i=1}^{N_s} |f_N(x_i) - f_{2N}(x_i)|^2}, \end{eqnarray*}$$

(B2)

where f denotes the function to be compared. The first error cannot be computed in the f(R) case for lack of knowledge of the exact solution. The spatial domain has a different grid spacing in each approximation. Thus to compare, we need to interpolate the approximation which has the finer grid and compute it at the domain points corresponding to the coarser grid. Fig. B1 plots the errors for both GR and f(R) in the evolved average density Δ for the profile 1d with the parameters as shown in Table A2. We found the trends to be the same for the variables δ and v for profile 1e and the same trends for all three variables for profile 2d.

Figure B1.

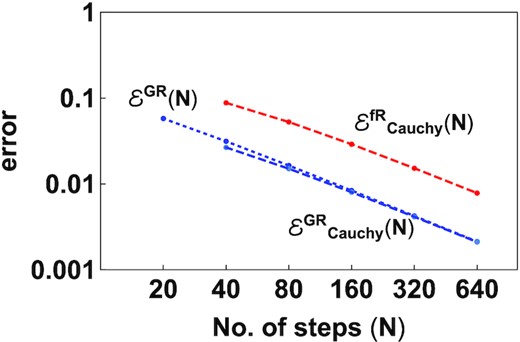
Convergence test of the algorithm. Comparison of successive approximations for evolution from a = 0.1 to a = 1 for profile 1a for the variable Δ. The algorithm was applied to a ΛCDM model with Φ = Ψ and an f(R) model with f_R0 = −10⁻⁶.

Open in new tab Download slide

APPENDIX C: DERIVATION OF THE ANALYTICAL SOLUTION

The equation for Φ₊ is the usual Poisson equation with the solution given by

$$\begin{eqnarray*} \Phi _+(x) = C_1 + \int _{k_1}^x \left\lbrace \frac{C_2}{z^2}+ \frac{1}{z^2} \int _{k_2}^z {\mathcal {P}}_1(a) \delta (y) y^2 \mathrm{ d}y \right\rbrace \mathrm{ d}z, \end{eqnarray*}$$

(C1)

where y and z are dummy variables for the integrals and

$$\begin{eqnarray*} {\mathcal {P}}_1(a) = \frac{3 \Omega _m(a) a^2}{2}. \end{eqnarray*}$$

(C2)

k₁ and k₂ are arbitrary constants which are related to the boundary points along the x axis. Imposing the boundary condition at x = ∞, gives

$$\begin{eqnarray*} C_1= - \int _{k_1}^\infty \left\lbrace \frac{C_2}{z^2}+ \frac{1}{z^2} \int _{k_2}^z {\mathcal {P}}_1(a) \delta (y) y^2 \mathrm{ d}y \right\rbrace \mathrm{ d}z, \end{eqnarray*}$$

(C3)

The derivative

$$\begin{eqnarray*} \left.\nabla _x {\tilde{\Phi }_+}\right|_{x=0} &=& \frac{C_2}{x^2} + \frac{1}{x^2} \int _{k_2}^y {\mathcal {P}}_1(a) \delta (y) y^2\mathrm{ d}y =0 \Rightarrow C_2 \nonumber\\ &=& \int _0^{k_2}{ \mathcal {P}}(a) \delta (y). y^2 \mathrm{ d}y \end{eqnarray*}$$

(C4)

Thus, |${\tilde{\Phi }_+}$| and its derivative (force) are

$$\begin{eqnarray*} {\tilde{\Phi }_+} (x) = {\mathcal {P}}_1(a) \int _\infty ^x \frac{1}{z^2} \int _0^z \delta (y) y^2 \mathrm{ d}y = \frac{{\mathcal {P}}_1(a)}{3} \int _\infty ^x z \Delta (z) \mathrm{ d}z \end{eqnarray*}$$

(C5)

$$\begin{eqnarray*} \nabla _x {\tilde{\Phi }_+} = {\mathcal {P}}_1(a) \frac{1}{x^2} \int _0^x \delta (y) y^2 \mathrm{ d}y = \frac{{\mathcal {P}}_1(a)}{3} x \Delta (x), \end{eqnarray*}$$

(C6)

where the spherically averaged fractional density contrast Δ is defined as:

$$\begin{eqnarray*} \Delta (x) = \frac{3}{x^3} \int _0^x \delta (y) y^2 \mathrm{ d}y. \end{eqnarray*}$$

(C7)

The general solution of equation (47) for |${\tilde{\chi }}$|

$$\begin{eqnarray*} {\tilde{\chi }}(x) &=& C_1 \frac{e^{-\sqrt{{\mathcal {P}}_2} x}}{x} + \frac{C_2}{2 \sqrt{{\mathcal {P}}_2}} \frac{e^{\sqrt{{\mathcal {P}}_2}x}}{x}+ \frac{{{\mathcal {P}}_3}}{2\sqrt{{\mathcal {P}}_2}} \frac{e^{-\sqrt{{\mathcal {P}}_2}x}}{ x}\nonumber\\ && \times \int _{k_1}^x e^{\sqrt{{\mathcal {P}}_2}y} y\delta (y) \mathrm{ d}y - \frac{{{\mathcal {P}}_3}}{2\sqrt{{\mathcal {P}}_2}} \frac{e^{\sqrt{{\mathcal {P}}_2}x}}{x} \int _{k_2}^x e^{-\sqrt{{\mathcal {P}}_2}y} y\delta (y) \mathrm{ d}y, \nonumber\\ \end{eqnarray*}$$

(C8)

where

$$\begin{eqnarray*} {{\mathcal {P}}_2} = \frac{1}{{\bar{x}}_C^2} \quad {\rm and} \quad {{\mathcal {P}}_3} = a^2 \Omega _m(a). \end{eqnarray*}$$

(C9)

At x = ∞, the first and third terms vanish since δ(x) has a finite extent. Thus, imposing the boundary condition at x = ∞ gives

$$\begin{eqnarray*} C_2 = {{\mathcal {P}}_3}\int _{k_2}^\infty e^{-\sqrt{{\mathcal {P}}_2}y} y\delta (y) \mathrm{ d}y. \end{eqnarray*}$$

(C10)

This gives

$$\begin{eqnarray*} {\tilde{\chi }}(x) &=& C_1 \frac{e^{-\sqrt{{\mathcal {P}}_2}x}}{x} + \frac{{\mathcal {P}}_3}{2 \sqrt{{\mathcal {P}}_2}x}\nonumber\\ && \times \left[ e^{\sqrt{{\mathcal {P}}_2}x} L_2(k_2,\infty) +e^{-\sqrt{{\mathcal {P}}_2}x} L_1(k_1,x) - e^{\sqrt{{\mathcal {P}}_2}x} L_2(k_2,x) \right]\nonumber\\ , \end{eqnarray*}$$

(C11)

where

$$\begin{eqnarray*} L_1(k_1,x) = \int _{k1}^x e^{\sqrt{{\mathcal {P}}_2}y} y\delta (y) \mathrm{ d}y \end{eqnarray*}$$

(C12)

$$\begin{eqnarray*} L_2(k_2,x) = \int _{k_2}^x e^{-\sqrt{{\mathcal {P}}_2}y} y\delta (y) \mathrm{ d}y \end{eqnarray*}$$

(C13)

Taking the derivative

$$\begin{eqnarray*} \frac{\mathrm{ d }{\tilde{\chi }}}{\mathrm{ d}x} &=& -\frac{C_1 e^{-\sqrt{{\mathcal {P}}_2}x}}{x^2} (1 + \sqrt{{\mathcal {P}}_2} x)\\ &&+\,\, \frac{{\mathcal {P}}_3}{2 \sqrt{{\mathcal {P}}_2}x^2 }\bigg[ L_2(k_2, \infty) \left(\sqrt{\mathcal {P}}_2 x -1\right) e^{\sqrt{\mathcal {P}}_2 x} \nonumber\\ && -\,\, L_1(k,x) (1 + \sqrt{\mathcal {P}}_2 x) e^{-\sqrt{\mathcal {P}}_2 x}\nonumber\\ && -\,\, L_2(k,x) \left(\sqrt{\mathcal {P}}_2 x -1\right) e^{\sqrt{\mathcal {P}}_2 x}\bigg] \end{eqnarray*}$$

(C14),(C15)

Setting |$\left.\frac{\mathrm{ d} {\tilde{\chi }}}{\mathrm{ d}x}\right|_{x \approx 0} = 0$| gives

$$\begin{eqnarray*} C_1 = - \frac{{\mathcal {P}}_3}{2 \sqrt{{\mathcal {P}}_2}} \left[L_1(k_1,0) - L_2(k_2,0) + L_2(k_2, \infty) \right] \end{eqnarray*}$$

(C16)

Substituting for C₁ and C₂, writing

$$\begin{eqnarray*} &&{-L_2(k_2,0) + L_2(k_2, \infty) = \int _0^\infty e^{-\sqrt{{\mathcal {P}}_2}y} y\delta (y) \mathrm{ d}y }\nonumber\\ &&{\quad= \int _0^x e^{-\sqrt{{\mathcal {P}}_2}y} y\delta (y) \mathrm{ d}y + \int _x^\infty e^{-\sqrt{{\mathcal {P}}_2}y} y\delta (y) \mathrm{ d}y } \end{eqnarray*}$$

(C17)

and rearranging the terms gives

$$\begin{eqnarray*} {\tilde{\chi }}(x) = \frac{\mathcal {P}_3 }{\sqrt{\mathcal {P}_2}}\frac{1}{x} \left[ \exp \left(-\sqrt{\mathcal {P}_2}x\right) I_1(x) + \sinh \left(\sqrt{\mathcal {P}_2}x\right) I_2(x) \right],\nonumber\\ \end{eqnarray*}$$

(C18)

$$\begin{eqnarray*} \nabla _x {\tilde{\chi }} &=& - \frac{{\tilde{\chi }} }{x}+ \frac{{\mathcal {P}_3}}{x} \left[-\exp \left(-\sqrt{\mathcal {P}_2}x\right) I_1(x)\right.\nonumber\\ &&+\left. \cosh \left(\sqrt{\mathcal {P}_2}x\right) I_2(x) \right], \end{eqnarray*}$$

(C19)

where

$$\begin{eqnarray*} I_1(x) = \int _0^x \left\lbrace \sinh \left(\sqrt{\mathcal {P}_2}y\right) \delta (y) y \right\rbrace \mathrm{ d}y, \end{eqnarray*}$$

(C20)

$$\begin{eqnarray*} I_2(x) = \int _x^\infty \left\lbrace \exp \left(-\sqrt{\mathcal {P}_2}y\right)\delta (y) y \right\rbrace \mathrm{ d}y. \end{eqnarray*}$$

(C21)

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
January 2022	2
February 2022	12
March 2022	11
April 2022	5
May 2022	9
June 2022	3
July 2022	9
August 2022	4
September 2022	5
October 2022	3
December 2022	1
February 2023	5
March 2023	2
April 2023	2
May 2023	3
June 2023	1
August 2023	2
October 2023	1
December 2023	1
January 2024	21
February 2024	9
March 2024	2
April 2024	3
May 2024	14
June 2024	15
July 2024	19
August 2024	5
September 2024	12
October 2024	11
December 2024	2
January 2025	5
February 2025	1
March 2025	11
April 2025	2
May 2025	8

Article Contents

Non-linear density–velocity dynamics in f(R) gravity from spherical collapse Free

ABSTRACT

1 INTRODUCTION

2 BACKGROUND COSMOLOGY IN THE HU-SAWICKI MODEL

2.1 Equations of motion

2.2 Consistency with ΛCDM

2.3 Eigenvalue analysis of the Hu-Sawicki background cosmology

2.4 Compton wavelength

3 EQUATIONS FOR NON-LINEAR PERTURBATIONS

3.1 Equations

4 METHOD OF SOLUTION

4.1 Outline

4.2 Lagrangian coordinates

4.3 Equations in the hybrid Eulerian–Lagrangian scheme

4.4 Initial conditions

4.5 Algorithm

4.6 Analytic solutions for the potentials

5 LINEAR EVOLUTION

6 NON-LINEAR REGIME

6.1 Non-linear density and velocity

6.2 Phase space evolution

6.3 Fitting form for the DVDR in the strong field regime

6.4 Density enhancement in non-linear evolution

7 SUMMARY AND DISCUSSION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

APPENDIX A: INITIAL PROFILES

APPENDIX B: CONVERGENCE TESTS

APPENDIX C: DERIVATION OF THE ANALYTICAL SOLUTION

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Non-linear density–velocity dynamics in f(R) gravity from spherical collapse