-
PDF
- Split View
-
Views
-
Cite
Cite
F Tarsitano, C Bruderer, K Schawinski, W G Hartley, Image feature extraction and galaxy classification: a novel and efficient approach with automated machine learning, Monthly Notices of the Royal Astronomical Society, Volume 511, Issue 3, April 2022, Pages 3330–3338, https://doi.org/10.1093/mnras/stac233
Close - Share Icon Share
ABSTRACT
In this work, we explore the possibility of applying machine learning methods designed for 1D problems to the task of galaxy image classification. The algorithms used for image classification typically rely on multiple costly steps, such as the point spread function deconvolution and the training and application of complex Convolutional Neural Networks of thousands or even millions of parameters. In our approach, we extract features from the galaxy images by analysing the elliptical isophotes in their light distribution and collect the information in a sequence. The sequences obtained with this method present definite features allowing a direct distinction between galaxy types. Then, we train and classify the sequences with machine learning algorithms, designed through the platform Modulos AutoML. As a demonstration of this method, we use the second public release of the Dark Energy Survey (DES DR2). We show that we are able to successfully distinguish between early-type and late-type galaxies, for images with signal-to-noise ratio greater than 300. This yields an accuracy of |$86{{\ \rm per\ cent}}$| for the early-type galaxies and |$93{{\ \rm per\ cent}}$| for the late-type galaxies, which is on par with most contemporary automated image classification approaches. The data dimensionality reduction of our novel method implies a significant lowering in computational cost of classification. In the perspective of future data sets obtained with e.g. Euclid and the Vera Rubin Observatory, this work represents a path towards using a well-tested and widely used platform from industry in efficiently tackling galaxy classification problems at the peta-byte scale.
1 INTRODUCTION
Galaxy morphology plays an important role in our studies and understanding of galaxy evolution. Structural components such as bulges, discs, spiral arms, and bars formed during galaxies’ aggregated formation histories (Combes & Sanders 1981; de Jong 1996; Elmegreen et al. 1996). As such, morphology is related to other properties that depend on formation and assembly history, such as colour, stellar-mass and recent star formation rate (SFR; Baldry et al. 2004; Noeske et al. 2007; Cano-Díaz et al. 2019). By looking at the relation between mass and SFR (Schiminovich et al. 2007; Goncalves et al. 2012; Peterken et al. 2021), astronomers have been able to distinguish between three different populations. Most star-forming galaxies belong to the main sequence, and present morphological features typical of spiral or irregular galaxies. Objects in this population are also called late-type galaxies (LTG). We can identify another population with much lower SFR and different shapes, mostly elliptical or bulge-dominated morphologies: we refer to these as early-type galaxies (ETG). The transition between ETG and the main sequence is smoothed by an intermediate and less heavily populated region, called the green valley (Salim 2014; Schawinski et al. 2014).
Historically, galaxies were classified as early or late type by visual inspection, with a modern example of classification in this way provided by Nair & Abraham (2010). Recent citizen science projects like Galaxy Zoo (Lintott et al. 2008; Simmons et al. 2017; Lingard et al. 2020) use the same approach, while benefiting from a huge network of volunteers who are asked to classify galaxies.
Quantitative methods for classifying structural properties include modeling galaxy light profiles with 2D analytical functions, and fitting them to galaxy images. The most commonly used model is the Sérsic profile (Sérsic 1963), a parametric function with parameters describing structural properties such as size, magnitude, ellipticity, inclination, and the rate at which light intensity falls off with radius (Sérsic index). The latter quantifies the concentration of light and it is often used to distinguish between ETG and LTG due to its very tight correlation with visual morphology classes. In fitting galaxy images, the Sérsic model must be convolved with the point spread function (PSF), in order to account for the seeing and any instrumental distortions of the image. This method is proven to be robust when the multidimensional fitting delivers non-degenerate solutions but can be costly for large surveys of galaxies.
Alternative non-parametric approaches can be used to analyse the light distribution and quantify the galaxy concentration and level of asymmetry and to search for clumpy regions (Conselice, Bershady & Jangren 2000). In this case, the PSF is not taken into account and the selection criteria for ETG and LTG classes need to be adapted for the apparent size of the object in question and characteristics of the survey. Several large catalogues of galaxy morphologies exist, based on parametric fitting (Simard et al. 2011), a non-parametric approach (Cano-Díaz et al. 2019) or both (Tarsitano et al. 2018).
Beyond the traditional methods previously mentioned, machine learning (ML) algorithms present an attractive way forward in classifying galaxy images. Early work in the field (e.g. Banerji et al. 2010) used outputs from source detection and measurement software as features in an artificial neural network and visual classifications from Galaxy Zoo (Lintott et al. 2010) for the target quantity. The input features represent one possible choice of feature extraction, or image data compression, which was already sufficient to perform well: |$\sim 85{{\ \rm per\ cent}}$| accuracy using adaptive light moment input features, albeit on a bright, well-resolved sample. Further successful examples of automated galaxy classification with ML algorithms are presented in Walmsley et al. (2020, 2022), where data sets from Galaxy Zoo were used combining human and machine intelligence. Furthermore, Vavilova et al. (2021) explore the performance of five supervised ML techniques (logistic regression, k-nearest neighbours, naive Bayes, Random Forest, and Support Vector Machine) applied to the task of galaxy classification using the SDSS DR9 data set (Ahn et al. 2012). Their findings indicate the Random Forest, together with the Support Vector Machine, as the most accurate algorithm. As we will discuss in the next sections, similarly in our analysis, we are able to optimize the classification between ETG and LTG by adopting either Random Forest or XGBoost (Extreme Gradient Boosting), which are both Decision-Tree-based algorithms. XGBoost and Random Forest have been at the centre of a broader range of application in this field, as showed in Calderon & Berlind (2019) where they successfully use these algorithms to predict galaxies dark matter halo masses.
The rapid development of Convolutional Neural Networks (CNN) in industry has become a great benefit for astronomy as the technique has been adapted and translated to astrophysical problems, including galaxy classification. In particular, supervised CNN have been used with Galaxy Zoo (Dieleman, Willett & Dambre 2015), on candels images (Grogin et al. 2011; Koekemoer et al. 2011) to provide galaxy visual classifications (Huertas-Company et al. 2015; Tuccillo et al. 2018), to find specific structural features such as bars (Abraham et al. 2018) and to classify galaxies according to their bulge+disc composition (Ghosh et al. 2020). CNNs build up complex features from elementary filters, often in the form of small (a few pixels per side), high-contrast images. As such they are extremely adept at identifying objects with clearly defined outlines or strong characteristic shapes within them. In the case of galaxy classification, particularly moderately high-redshift galaxies in ground-based imaging, the outskirts of galaxies blend gently into the background, and strong features such as clumps and spiral arms are blurred by the PSF. Nevertheless, just as expert humans are able to differentiate between different galaxy types from relatively fuzzy images with a reasonable degree of accuracy, so too are CNN, with the near-term prospect that they will be able to outperform human observers. Further notable recent examples of the application of CNNs to the task of galaxy classification include Cheng et al. (2020), where a sample of ∼2800 galaxies from the first year of the Dark Energy Survey (DES) data with visual classification from the Galaxy Zoo 1 was used for the ground-truth classes, and Cheng et al. (2021), presenting one of the largest galaxy morphological classification catalogues to date, using the DES Year 3 data. Similarly, Vega-Ferrero et al. (2021) applied a CNN to the first public DES release (DES DR1; Abbott et al. 2018), working on public DES images as we do in this work. Rather than aim for completeness, they sought to identify the galaxies which their network could classify with high confidence. Their performance metric is therefore not directly comparable with our work. Nevertheless, the |$87{{\ \rm per\ cent}}$| of confident classifications (ETG versus LTG) down to mr < 21.5 is highly encouraging, especially if these confident classifications can be shown to be correct by ground-truth measurements in the future.
Despite the increasing adoption and successes of CNNs for galaxy classification it’s worth noting that any method will have weaknesses as well as strengths. These may be intrinsic to the method, or perhaps arise due to choices in application (e.g. the size of the image cut-out that the analysis is performed on). A familiar example of a limitation in morphological measurement is the differentiation between the faint outer wings of a galaxy’s light distribution and the level of the sky background; another may be the maximum radius to use when applying a CNN or other ML approach and how this choice effectively weights different components of a galaxy (its bulge and disc). Mitigating the impact of these weaknesses is possible, but will not generally remove them entirely.
Through combining different approaches with different weaknesses and different analysis choices, however, it is likely that we can achieve a more robust and potentially a more information rich classification, similar to how Sersic profile fits and non-parametric measurements can be combined to provide greater understanding of a galaxy’s structure and morphology (Tarsitano et al. 2018). Moreover, with the exponential rise in the amount of data from modern and future surveys such as the Vera Rubin Observatory and Euclid, we need to be able to automatically identify cases where a classification may be incorrect or suspect. One possible way of achieving that is to find cases where two rather different, but highly performing, approaches disagree. A further requirement of those approaches is that they are also computationally feasible, and avoid costly steps such as the PSF deconvolution or repeated fitting of a large number of parameters.
In this work, we present our search for an alternative classification method to satisfy these requirements. It performs feature extraction via an isophotal analysis of the galaxy light distribution, stores the information in a more manageable data format and then performs classification, lowering the total computational costs with respect to Sérsic profile fitting and some other ML approaches. As described in the following sections, this workflow does not need to account for the PSF, and reduces galaxy images into 1D sequences that can be conveniently processed with relatively simple ML algorithms. In our work, we show that our method, applied to the second public data release, DR2, (Morganson et al. 2018; Abbott et al. 2021) of the DES, leads to highly promising results: we obtain |$93{{\ \rm per\ cent}}$| correct classifications for LTG and |$86{{\ \rm per\ cent}}$| for ETG, at magnitudes mi < 20. Finally, we describe the potential future avenues for our method in identifying higher-context features such as bars, mergers and clumps.
This paper is structured as follows. Section 2 contains more details about the data set. Our method and details on how we perform the isophotal analysis of galaxy images, extract features from their light distribution and collect those into sequences, is described in Section 3. The sequences are then processed through a neural network designed and run in the framework of Modulos AutoML.1 More details are given in Section 4. We present the results in Section 5 and discuss further developments in Section 6.
2 DATA
In this work, we use public images from the DES DR2 release (Flaugher et al. 2015a; Morganson et al. 2018; Abbott et al. 2021), available through the public DES Data Management.2 In this section, we provide an overview of the survey, describe the structure of the data set and define the selection function for our sample.
2.1 The Dark Energy Survey
The DES is a project aiming to map hundreds of millions of galaxies to measure the effects of dark energy on the expansion history of the Universe and the growth of cosmic structure. The collected data are analysed through different methods: gravitational lensing, galaxy clustering, and Baryonic Acoustic Oscillations. DES used the Dark Energy Camera (DECam) to detect more than 300 million galaxies between the years 2013 and 2019 (Flaugher et al. 2015b). Although conceived for cosmological research, the vast data set assembled by DES represents a powerful survey for the fields of galaxy evolution, stellar populations, and Solar System Science too (Abbott et al. 2016). Moreover, in 2017 DECam provided the optical counterpart of the gravitational wave event GW170817 studied in detail in Palmese et al. (2017). The camera has a 2.2○ diameter field of view and a pixel scale of 0.263 arcsec (Flaugher 2005). It is mounted on the Victor M. Blanco 4-m Telescope at the Cerro Tololo Inter-American Observatory (CTIO) located in the Chilean Andes.
2.2 The data set
The DES survey area is covered by images in five photometric bands, g,r,i,z,Y. The single exposure images have integration time of 90 s in the g,r,i,z and 45 s in the Y band. Data are later processed through the DESDM (DES Data Management) pipeline, which first applies calibrations and coadds the images, then detects and catalogues all the objects in those images (Drlica-Wagner et al.2018; Morganson et al. 2018). In the image co-addition, the pipeline combines overlapping single-epoch images in one filter and remaps them to artificial tiles on the sky as described in Sevilla et al. (2011), Desai et al. (2012), and Mohr et al. (2012). Object detection is made using a specific software, called SE xtractor (Bertin 2011), which extracts structures from the background and distinguishes between point-like (stars) and galaxies. Then, it performs a photometric analysis, where each object is enumerated and assigned to a set of specific properties, collected in a catalogue. For this analysis, properties of the light distribution are measured, namely the object brightness, quantified in MAG_AUTO, and its size, called FLUX_RADIUS, which includes half of the galaxy light. We use these measures to identify and optimize the sample analysed in this work.
2.3 Sample selection
We consider 100 tiles from DR2 public release and apply cuts to the SE xtractor catalogues (see below) to select a final sample of 6525 galaxies (corresponding to an area of ∼54.3 square degrees in the DES survey footprint). We choose objects which are neither truncated nor corrupted or blended to other objects by setting |$\tt {FLAGS}=0,2$|. Additionally, we choose bright objects by applying a cut in magnitude. In Tarsitano et al. (2018), we observe that robust fits are obtained for objects up to a magnitude of 21.5 in the i-band. In order to work with optimal isophotal fitting, in this analysis we make a more conservative cut, setting in the same filter |$\tt {MAG\_AUTO} \le 20$|. For the same reason, we also adopt the cut in signal-to-noise S/N > 300. In Tarsitano et al. (2018), we also flagged those galaxies with size smaller than or comparable to the PSF, because in those cases the PSF significantly affects the way the concentration of light is modelled, leading to degeneracies in the estimation of the size and Sérsic index. Therefore, our selection function excludes the galaxies with size smaller than 4 px in the i-band. We also check that the selected objects have physically meaningful measurements, avoiding galaxies with negative or null radii. In processing the data (see Section 3), we will make use of the Kron radius, which is the radius within which approximately |$90{{\ \rm per\ cent}}$| of the galaxy light is included. According to the definition in SE xtractor, we consider as Kron radius the product between the KRON_RADIUS and the semimajor axis of the galaxy A_IMAGE. Finally, we exclude from our sample the point-like objects by applying a cut to the MODEST parameter (Drlica-Wagner et al. 2018). The sample selection is summarized in Table 1. Additional information about the MODEST star/galaxy classifier and the SE xtractor catalogues can be found here: https://des.ncsa.illinois.edu/releases/y1a1/gold.
Summary of the cuts applied to SE xtractor catalogues for the sample selection.
| SELECTION TYPE . | SELECTION CUT . |
|---|---|
| Image flags | FLAGS = 0, 2 |
| Magnitude | MAG_AUTO_i < 20 |
| Size (I) | FLUX_RADIUS_i > 0 |
| Size (II) | KRON_RADIUS > 0 |
| Size | FLUX_RADIUS_i > 4 px |
| S-G | MODEST > 0.005 |
| S/N | FLUX_AUTO/FLUXERR_AUTO > 300 |
| SELECTION TYPE . | SELECTION CUT . |
|---|---|
| Image flags | FLAGS = 0, 2 |
| Magnitude | MAG_AUTO_i < 20 |
| Size (I) | FLUX_RADIUS_i > 0 |
| Size (II) | KRON_RADIUS > 0 |
| Size | FLUX_RADIUS_i > 4 px |
| S-G | MODEST > 0.005 |
| S/N | FLUX_AUTO/FLUXERR_AUTO > 300 |
Summary of the cuts applied to SE xtractor catalogues for the sample selection.
| SELECTION TYPE . | SELECTION CUT . |
|---|---|
| Image flags | FLAGS = 0, 2 |
| Magnitude | MAG_AUTO_i < 20 |
| Size (I) | FLUX_RADIUS_i > 0 |
| Size (II) | KRON_RADIUS > 0 |
| Size | FLUX_RADIUS_i > 4 px |
| S-G | MODEST > 0.005 |
| S/N | FLUX_AUTO/FLUXERR_AUTO > 300 |
| SELECTION TYPE . | SELECTION CUT . |
|---|---|
| Image flags | FLAGS = 0, 2 |
| Magnitude | MAG_AUTO_i < 20 |
| Size (I) | FLUX_RADIUS_i > 0 |
| Size (II) | KRON_RADIUS > 0 |
| Size | FLUX_RADIUS_i > 4 px |
| S-G | MODEST > 0.005 |
| S/N | FLUX_AUTO/FLUXERR_AUTO > 300 |
3 METHOD
In this section, we describe our process to transform galaxy images into 1D feature vectors for classification using ML. As already mentioned in the introductory sections, this method involves few and fast steps, which is an advantage compared to classification methods that involve several labourious manipulations. More precisely, we refer to two main steps:
production of postage stamp images;
extraction of profiles.
We describe the steps below, highlighting the main differences with existing methods.
3.1 Production of stamps
For each of our selected galaxies (see Section 2.3), we cut square postage-stamp images from the relevant DES tiles, with dimensions equal to four times the Kron radius. This size is chosen to ensure that the image includes the galaxy light distribution entirely and sufficient non-object pixels to be able to determine the background level. For this operation, we use the publicly available CANVAS algorithm3 (Cut ANd VAlidate Stamps), presented and optimized in Tarsitano et al. (2018).
3.1.1 Background and PSF
In standard analyses such as parametric fitting, the background needs to occupy at least |$60{{\ \rm per\ cent}}$| of the area of the stamp, in order to obtain a correct fit. The fitting algorithm, in fact, needs to distinguish the light signal from the sky, which becomes challenging towards the outskirts and faint wings of a galaxy. Therefore, a clear separation is only possible if the background occupies a larger area of the stamp than the galaxy (Peng et al. 2010). A typical workflow for parametric fitting includes also PSF estimation and deconvolution, in order to account for the instrumental response and atmospheric effects. In our work, we extract information solely from the area inside the Kron ellipse of the galaxy. Hence, our approach is robust to minor defects or mis-estimations of the background or the image stamp size, and we need not be concerned with multiplying the size of our input images to ensure sufficient background coverage. Concerning the PSF deconvolution, which is, as mentioned above, is crucial to perform a good parametric fit, we do not need to account for it since we extract information from the galaxy image through isophotal analysis. More details about the extraction of profiles are given in Section 3.2.
3.1.2 Neighbouring objects
A potential source of errors for the galaxy classification is the presence of neighbouring objects. If not taken into account, both standard fitting algorithms and CNNs are prone to imprecise estimations or classification of the galaxy light profile. We consider two cases:
the neighbour falls outside the Kron ellipse of the galaxy;
the neighbour is placed inside the Kron ellipse of the galaxy (partially or fully).
The first scenario is negligible for our analysis, since we only consider the pixels inside of the Kron ellipse. However, we cannot ignore the second case. Our aim is to minimize the number of manipulations applied to the images, so we do not apply any algorithm to identify such cases. Moreover, we would need to distinguish cases that are due to chance alignments from more interesting but possibly similar-appearing cases due to, e.g. galaxy–galaxy mergers or star-forming clumps. This latter task is an avenue of future research for our method, but as contaminants do not change the overall trend of the sequences we obtain for elliptical and spiral galaxies, we do not apply corrections for them in this work.
3.2 Extraction of profiles
The extraction of profiles relies on the elliptical isophote analysis of the galaxy in question. Isophotes are curves connecting locations with the same brightness. We use the algorithm of Elliptical Isophote Analysis available in the Photutils Astropy package (Bradley et al. 2020). The algorithm searches for elliptical isophotes iteratively, as described in detail in Jedrzejewski (1987), up to a user-defined limit, expressed in terms of a maximum value for the semimajor axis of the ellipse. We set this limit to 0.7 times the Kron radius in order to exclude the faint wings of a galaxy light distribution from the analysis. Specifically in our fitting routine we observed that such wings result in a noisy tail in the 1D sequences and do not add information useful for distinguishing between different classes of galaxies. Once we measure the isophotes, we proceed by radially and concentrically collecting the intensity of pixels falling on the curves, one ellipse at a time. The points collected in this order form our sequence, which we convert to logarithmic scale and normalize such that the brightest pixel has value unity. We can visualize this procedure in Fig. 1, where the isophotes and their radial intensities collected in the series are matched by colour.
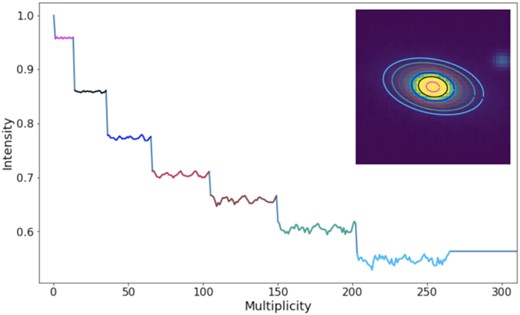
Example of a series extracted from galaxy images and used for classification. The galaxy (an early-type in this case) is processed through an isophote analysis, then the logarithm of the radial intensities of pixels lying on each detected ellipse is read and stored in a series, where the multiplicity axis in the main panel is a counter for the pixel values read. The intensity is from the inner to the outer ellipse. Isophotes and their collected intensities are matched by colour.
The series show a clear and expected pattern of decreasing intensity along the x-axis as the isophotes are read from the centre towards the outskirts of the galaxy. This pattern varies between early and late-type galaxies, as can be seen in Fig. 2. For early-type, mostly elliptical galaxies (upper panel), the trend resembles a step-function, showing regular patterns with decreasing intensity: each step represents an isophote. For LTG, we observe a different trend: in addition to a slower fall off in intensity due to their lower Sérsic index, the presence of spiral arms or clumps adds irregular spikes to the ideal step function. An example is shown in the lower panel of the figure, where we consider a barred-spiral galaxy.
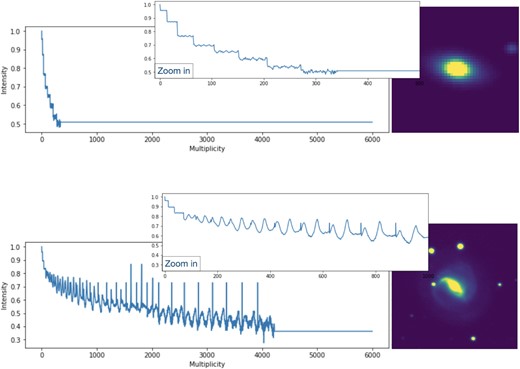
Example of classification between early-type (upper panel) and late-type (lower panel) galaxy, according to their time-series-like profile.
4 AI FRAMEWORK AND MODULOS
We run a Modulos AI workflow on a data set randomly split between a test (2175 galaxies) and training+validation sample (4350 galaxies), with all objects visually inspected according to their corresponding 1D sequences and images. As previously mentioned in Section 3, we show in Fig. 2 examples of sequences for ETG (upper panel) and LTG (lower panel). In this section, we describe the properties of the workflow in more detail. We use the Modulos4AutoML platform (version 0.3.5) to search for suitable models. The platform is designed to perform automated model selection and training for ML tasks, and works in the following way:
Workflow configuration (ML task): the user selects the data set to be processed, and sets an objective for which it is optimized.
Schema matching: the platform detects the schema of the desired input and output. It then proposes the feature extraction methods and ML models applicable to the data set and target objective.
Optimization: using a Bayesian optimizer (Srinivas et al. 2009), the platform tries out various combinations of feature extractors, models and their parameters. At each search step, the platform selects a feature engineering method and a model, chooses its architecture and hyperparameters, and trains it. After completing training, the platform uses a validation set to score this particular choice.
End point: There is no clearly defined end point at which the ‘best model’ has been found. However, after a while, the scores for the models begin to converge. As a default, the platform stops if there are no score improvements within 200 steps.
Download: Any trained model can be downloaded and used. We choose the best-performing model.
The key advantages of a platform such as AutoML are that the search for models and configuration is principled and not biased by human intervention. It is also significantly more efficient than optimization searches performed ‘by hand’. During this project, the vast majority of the time was spent on the preparation and the analysis of the data set, with only a few hours required for the automated classification. In our case, we found a suitable solution within 4.30 h of compute time (14 min 19 s to train the specific solution). To make prediction on the test sample, the algorithm takes 0.01 s per image. For completeness, we report the speed needed to extract the series from the images: it takes between 0.6 and 2.5 s per image, depending from the internal structure of the galaxy. Time increases if the algorithm has to detect complex structural features typical of spiral and irregular galaxies. A faster extraction occurs for galaxies with simple substructure. The whole analysis has been made on a laptop, but it can be re-scaled on multiple cores using parallel computing for larger samples.
5 RESULTS AND DISCUSSION
The automated ML framework returns as best solution an XGBoost model with a PCA decomposition as feature engineering method. XGBoost is a decision-tree based ML algorithm using a gradient boosting framework (Friedman 2001). This model reaches an F1 macro score (see equation 1) of |$90 {{\ \rm per\ cent}}$| on training data and |$89 {{\ \rm per\ cent}}$| on test data, which suggests it is not prone to over or underfitting. Our best model is publicly available at https://github.com/Federica24/Cosmo and can be applied to any DES data processed as described in the previous sections.
5.1 Information extraction
In order to understand why a combination of an XGBoost model and a PCA feature engineering method is found to be performing best, we review the key information accessed during classification by our model and compare it to the structure of our data. In Fig. 3, we show the collection of sequences classified as ETG (in blue) and LTG (in green). Additionally, we have highlighted 10 arbitrary sequences from each class to illustrate the individual profiles. The human eye is able to distinguish between the two classes by looking at the slopes of the sequences (greater for ETG) and comparing the abundance of spike-like features, which correspond to spiral arms of LTG, and to the smoothness of the sequences representing ETG. If spikes occur in the latter, they are more sparse and might refer to the presence of a neighbour (see Section 3 for reference). The information contained in the slopes and features is enhanced by the PCA analysis, which encodes it into a set of components. Each component brings a unique contribution to the automatic classification, giving the features different weight. By computing the Gini feature importance of the collection of decision trees, we can then understand which features contribute the most in predicting a class for a new data point in our model. We show the three most important nodes picked up by the Gini feature importance with black, vertical lines on Fig. 3. These nodes are the ones with the largest discriminatory power for the collection of decision trees, which perform classifications by sequentially dividing up the sequences. We find that the most important node for our best model (numbered 139) is 15 times more important than the others. This may be because it provides the highest signal-to-noise estimate of the light intensity fall-off. The next few most important nodes provide supporting information to effectively distinguish objects’ effective radii. This sequential split becomes especially important to distinguish sequences in the smooth transition region where a few sequences from different classes show similar slopes. This sequential splitting as a qualitative measure of the slopes is physically meaningful: in fact, as commented already in Section 3.2, we expect LTG sequences to fall off slower than ETG, due to their lower Sérsic index. As mentioned in Section 2.3 the PSF can change the rate of fall off from one isophote to the next, leading to a global rescaling of first steps of each sequence. This effect can be particularly significant for galaxies with size smaller than the PSF, but we did not include those in our sample.
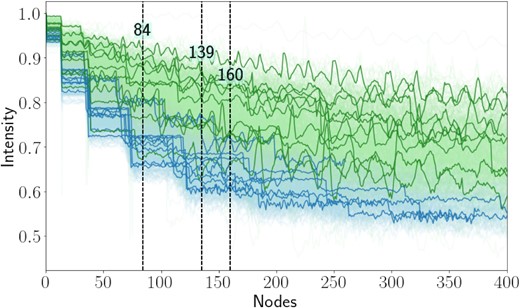
Plot of the sequences corresponding to ETG (in blue) and LTG (in green). Additionally, 10 arbitrary ETG and LTG are drawn. The black, vertical lines indicate the nodes with the largest Gini feature importance.
The scores of all trained solutions provided by the AutoML platform are summarized in Fig. 4. Looking at these offers insights into which combinations of ML models and feature engineering methods are optimal for our task. The models shown are both decision trees-based and are either XGBoost (solid lines) or Random Forest models (dashed lines) and are colour-coded by the feature engineering method. We observe that the PCA decomposition performs the best and is more important to the success of the overall model than the choice of XGBoost versus random forest. PCA rotates the feature space in order to successfully emphasize the slopes of the profiles. On the lower end, we find the Random and the t-test feature selection methods: since they only select a subset of nodes (either random selection or by applying the Student’s t-test), they seem to be less likely to pick up the most important information to distinguish the profiles and their slopes.
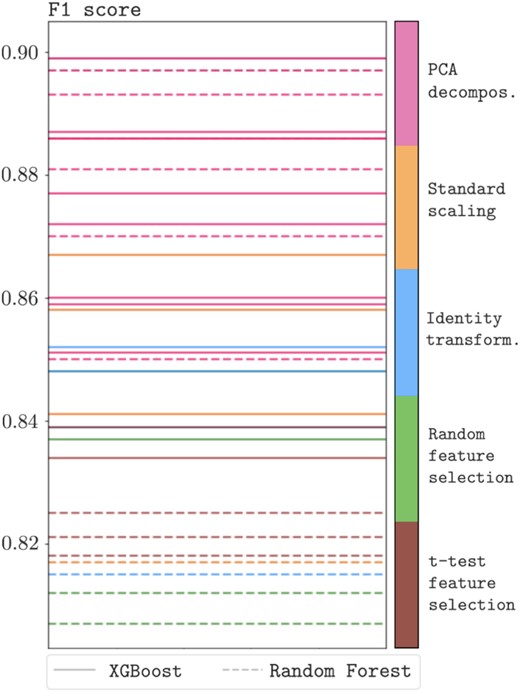
Summary of the results provided by the Modulos AutoML platform. The solutions are Decision Tree models, either XGBoost (solid lines) or Random Forest (dashed lines), which are able to sequentially capture and combine information from the sequences in the data set. The lines are colour-coded by the feature engineering method. PCA decomposition is associated with the solutions maximizing the F1 score (in the y-axis), given their ability in rotating the feature space so to emphasize the most important nodes in the sequences.
Finally, we use the aforementioned best model to make predictions on our test sample. We quantify the distance between the predictions and the true values by computing the confusion matrix (Fig. 5), normalized over the number of predictions, for which we used the Python sklearn library. The main diagonal shows the amount of objects correctly classified, while the off-diagonal elements quantify incorrect classifications. The majority of misclassified galaxies have low S/N ratios and tend to have small sizes and ellipticity, as shown in Fig. 6.

Confusion matrix representing the accuracy achieved in classifying galaxy profiles. The x-axis shows the true values, while the y-axis are the predicted categories. The main diagonal shows the correct classifications. The model seems quite robust in classifying the ETG of the sample.
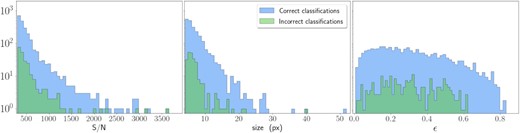
Properties of the classified sample in terms of signal-to-noise ratio (left-hand panel), size (central panel), and ellipticity (right-hand panel), distinguishing between objects with and without successful classification. This diagnostic plot alone cannot trace all the misclassifications. A clearer test is shown in Fig. 7.
5.2 Model failures and future perspective
Although there is by no means a simple cut we can perform to identify wrongly classified cases, inspecting examples of the isophotal fittings of both successful and unsuccessful classifications, we notice that objects with bad isophotal fitting tend to be misclassified more often. This is compatible with the outcome shown in the confusion matrix, where it yields more incorrect classifications for ETG: a poor isophotal fit introduces perturbations into a 1D-sequence which would show a regular pattern typical of such galaxies. A few examples of galaxies with poor isophotal measurements are shown in Fig. 7. Due to the small apparent size or low image resolution, the fitting does not model the light distribution well, resulting in an incorrect fit of the wings. As can be seen in the middle and right-hand panels, this manifests as a sudden change in the angular orientation of some isophotes with respect to the central regions of the galaxy. This issue can be corrected by applying sigma clipping to the recovered set of isophotes, identifying those that have parameters that are discrepant with the majority of fitted isophotes. However, the appropriate level of clipping varies from object to object and, at present, is not straight forward to determine in an automated way. As our aim is to describe a fully automated method that can be run efficiently on large survey data, we thus quote our results without this fix. We will return to the issue of misaligned isophotes in future work, where we develop a routine to perform flexible isophotal fitting automatically, combining the structural information on the isophotes (e.g. position angle, ellipticity) with new feature engineering solutions, and apply our method to more contextual outputs, such as the presence of clumps or spiral arms.

Examples of isophotal fitting for misclassified galaxies. If compared to Fig. 2, here we notice that the fitting fails at modelling galaxy wings and introduces rotations in the isophotal ellipses.
6 CONCLUSIONS
In this work, we describe a novel approach to galaxy morphological classification. It consists of first analysing the main features of the 2D light distribution in a galaxy image with isophotal fitting. This then allows to unravel it to a 1D sequence. The advantage of such an approach is the low complexity of 1D data, which makes both data storage and processing easier and faster compared to classification methods directly analysing images (e.g. parametric fitting). The selection, calibration, and training of classification models is then performed using the Modulos AutoML platform, which allows users to intuitively build and run their workflows and automatizes the search and training of ML solutions. Using this platform also leads to a significant reduction of time spent on building ML algorithms. This allowed us to quickly test hypotheses and focus on the scientific analysis. We found ensembles of decision trees (XGBoost and Random Forest models) with a PCA decomposition as a feature engineering method, which transform the feature space to make the profiles more discrepant, to perform well. The resulting best-performing model (XGBoost) is physically meaningful as it picks up on the differing slopes of the light profiles of galaxies: LTG profiles are expected to fall off slower due to their lower Sérsic index. We make the best ML solution we have found freely available at https://github.com/Federica24/Cosmo. It can be used to predict the galaxy type of other galaxies in the DES DR2 data set. We obtain an overall F1 score of |$90{{\ \rm per\ cent}}$| and |$89{{\ \rm per\ cent}}$| on training and test data, respectively, which proves that the dimensionality reduction of the data, even though it implies information loss, still contains enough information to successfully classify galaxies. In the future, we will expand upon our promising results by developing a more robust isophotal measurement approach to focus on performance at low S/N, and target higher context features, such as bars, spiral arms, and clumps.
SUPPORTING INFORMATION
Supplementary data are available at MNRAS online.
https://github.com/Federica24/Cosmo
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
This research made use of Photutils, an Astropy package for detection and photometry of astronomical sources (Bradley et al. 2020). The authors thanks Modulos for the usage of their platform to perform image training and classification.
This project used public archival data from the Dark Energy Survey (DES). Funding for the DES Projects has been provided by the U.S. Department of Energy, the U.S. National Science Foundation, the Ministry of Science and Education of Spain, the Science and Technology Facilities Council of the United Kingdom, the Higher Education Funding Council for England, the National Center for Supercomputing Applications at the University of Illinois at Urbana-Champaign, the Kavli Institute of Cosmological Physics at the University of Chicago, the Center for Cosmology and Astro-Particle Physics at the Ohio State University, the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, Financiadora de Estudos e Projetos, Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro, Conselho Nacional de Desenvolvimento Científico e Tecnológico and the Ministério da Ciência, Tecnologia e Inovação, the Deutsche Forschungsgemeinschaft, and the collaborating institutions in the Dark Energy Survey. The collaborating institutions are Argonne National Laboratory, the University of California at Santa Cruz, the University of Cambridge, Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas-Madrid, the University of Chicago, University College London, the DES-Brazil Consortium, the University of Edinburgh, the Eidgenössische Technische Hochschule (ETH) Zürich, Fermi National Accelerator Laboratory, the University of Illinois at Urbana-Champaign, the Institut de Ciències de l’Espai (IEEC/CSIC), the Institut de Física d’Altes Energies, Lawrence Berkeley National Laboratory, the Ludwig-Maximilians Universität München and the associated Excellence Cluster Universe, the University of Michigan, the National Optical Astronomy Observatory, the University of Nottingham, The Ohio State University, the OzDES Membership Consortium, the University of Pennsylvania, the University of Portsmouth, SLAC National Accelerator Laboratory, Stanford University, the University of Sussex, and Texas A&M University. Based in part on observations at Cerro Tololo Inter-American Observatory, National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation.
DATA AVAILABILITY
The best automated classification model presented in this paper and discussed in Section 5 is publicly available at https://github.com/Federica24/Cosmo and can be used to classify any DES data from the public release DR2 processed with isophotal fitting, as described in this work.



