-
PDF
- Split View
-
Views
-
Cite
Cite
Qiang Hou, Xing Wei, Why hot Jupiters can be large but not too large, Monthly Notices of the Royal Astronomical Society, Volume 511, Issue 3, April 2022, Pages 3133–3137, https://doi.org/10.1093/mnras/stac169
Close - Share Icon Share
ABSTRACT
Tidal heating is often used to interpret ‘radius anomaly’ of hot Jupiters (i.e. radii of a large fraction of hot Jupiters are in excess of 1.2 Jupiter radius which cannot be interpreted by the standard theory of planetary evolution). In this paper, we find that tidal heating induces another phenomenon ‘runaway inflation’ (i.e. planet inflation becomes unstable and out of control when tidal heating rate is above its critical value). With sufficiently strong tidal heating, luminosity initially increases with inflation, but across its peak it decreases with inflation such that heating is stronger than cooling and runaway inflation occurs. In this mechanism, the opacity near radiative-convective boundary (RCB) scales approximately as temperature to the fourth power and heat cannot efficiently radiate away from planet interior, which induces runaway inflation (similar to a tight lid on a boiling pot). Based on this mechanism, we find that radii of hot Jupiters cannot exceed 2.2RJ, which is in good agreement with the observations. We also give an upper limit for orbital eccentricity of hot Jupiters. Moreover, by comparison to the observations we infer that tidal heating locates near RCB.
1 INTRODUCTION
More than 4000 extrasolar planets (i.e. exoplanets) have been detected as shown in Fig. 1a. The red rectangle shows ‘hot Jupiters’ with their mass and radius comparable to those of Jupiter but on a close orbit with period ≲10 d. A large fraction of hot Jupiters possess radii in excess of 1.2RJ (RJ being Jupiter radius), which cannot be interpreted by the standard theory of planetary evolution (Stevenson & Salpeter 1977; Fortney, Marley & Barnes 2007), no matter whether the initial entropy is high or low (Marley et al. 2007). This is a long-standing problem called ‘radius anomaly’, and some interpretations have been proposed, e.g. Bodenheimer, Lin & Mardling (2001), Gu, Lin & Bodenheimer (2003), Gu, Bodenheimer & Lin (2004), Laine, Lin & Dong (2008), Batygin & Stevenson (2010), Youdin & Mitchell (2010), Guillochon, Ramirez-Ruiz & Lin (2011), Spiegel & Burrows (2013), Komacek & Youdin (2017). In these interpretations, the physical mechanisms involve tidal heating, Ohmic heating, inward transfer of irradiation, and high opacity. The former three mechanisms attribute to the energy sources and the latter one to the suppression of radiative cooling.
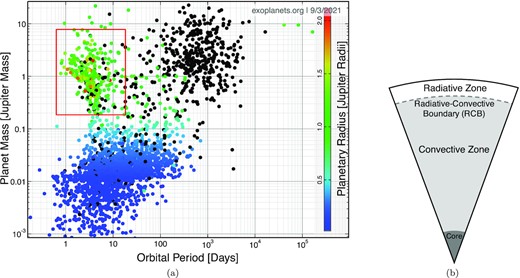
(a) Confirmed exoplanets (http://exoplanets.org/), in the red rectangle are ‘hot Jupiters’, and black points denote planets without known radii. (b) The sketch of planet interior.
However, up to now, exoplanets with radius >2.2RJ have not been detected except perhaps PDS 70 b (Wang et al. 2020), a newly born planet in a protoplanetary disc (the error bars in (Wang et al. 2020) do not rule out <2.2RJ). In this paper, we will study why hot Jupiters can be large but not too large. We find that the reason is the runaway inflation due to tidal heating combined with high opacity near radiative-convective boundary (RCB). That is, when tidal heating rate is above its critical value, luminosity will decrease with inflation such that inflation becomes unstable and out of control. This runaway inflation mechanism has never been reported in the previous studies of planet inflation. In Section 2, we show the mathematical equations for planetary evolution and the numerical method to solve them. In Section 3, we choose a set of typical parameters to show runaway inflation and give the physical interpretation. In Section 4, we investigate the influence of parameters on runaway inflation. In Section 5, we compare our theoretical predictions to the observations. In Section 6, we give a brief summary.
2 METHODS
The sketch of planet interior is shown in Fig. 1b. The mass of thin radiative zone is less than |$1{{\ \rm per\ cent}}$| of the total mass. The convective zone is thick and considered to be adiabatic because heat transfer is very fast and efficient via convection. The interface between radiative and convective zones is called RCB. A rocky core lies near the center as core accretion model describes (Safronov 1972; Mizuno, Nakazawa & Hayashi 1978; Mizuno 1980; Pollack et al. 1996).
We use mesa code (Paxton et al. 2011, 2013, 2015, 2018, 2019) to solve equations (1) along with the equation of state from Saumon, Chabrier & van Horn (1995) and the tabulated opacity from Freedman, Marley & Lodders (2008). The element abundances are hydrogen X = 0.74, helium Y = 0.24, and metal Z = 0.02. The initial age 3 Myr is set, and the initial radius ≈1.9RJ is used (Pollack et al. 1996). For the inner boundary, a coreless planet, and a planet with a rocky core of density ρcore = 5 g/cm3 will be both considered. For the outer boundary, we impose equilibrium temperature Teq ≈ 1500 K, corresponding to a planet with period ≈3 d around a solar-type star.
3 RUNAWAY INFLATION
We choose typical parameters, namely Mp = MJ, Mcore = 10M⊕, Teq = 1500 K, and m0 = 0.99Mp (i.e. tidal heating near RCB), to test the total energy rate εinj. Fig. 2a shows the radius evolution. With low εinj (red and green curves) planet does not inflate too much because injected energy is balanced by luminosity radiated away. However, with high εinj (blue and black curves) planet smoothly inflates to 2.13RJ and then rapidly inflates beyond Hill radius (M⊙/MJ)1/3RJ ≈ 10RJ to be destroyed by its host star. This unstable inflation out of control is called runaway inflation due to energy imbalance (i.e. tidal heating is stronger than radiative cooling). Higher εinj corresponds to earlier runaway inflation (comparison between blue and black curves). Fig. 2b shows luminosity-radius relation. With low εinj (red and green curves) luminosity initially increases with inflation until it balances with injected energy, such that inflation stops at ≈2RJ. However, with high εinj (blue and black curves) luminosity continues to increase to a peak called runaway point. At runaway point, the corresponding luminosity is called critical rate of injected energy εcri = 3.67 × 1028 erg/s and the corresponding radius is called runaway radius Rrun = 2.13RJ. Across runaway point, luminosity decreases with inflation and energy imbalance takes place, i.e. energy injected into planet cannot efficiently radiate away from planet interior. Consequently, inflation becomes unstable and runaway inflation occurs.
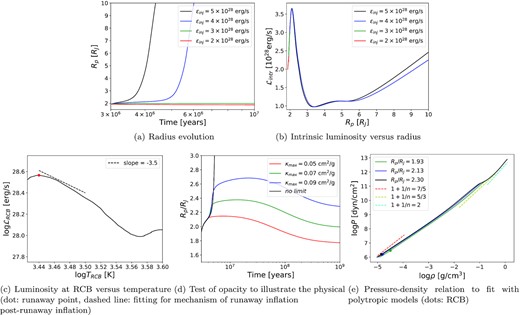
Runaway inflation. Subfigures (a) and (b) show the phenomenon of runaway inflation, and subfigures (c), (d), and (e) illustrate the physical mechanism of runaway inflation.
To understand the physics of runaway inflation, we need to make clear how luminosity changes at runaway point. Before runaway inflation occurs, luminosity increases smoothly with inflation and temperature also increases. When temperature near RCB reaches ≈3000 K, luminosity near RCB turns to be heavily suppressed. We now simply analyse luminosity–temperature relation near RCB. In equations (1), ∇rad is continuous across RCB and equal to ∇ad which is independent of temperature, such that we readily find |$\mathcal {L}_{RCB}\propto T^4/(P\kappa)$|. With the help of polytrope model P ∝ ρ1 + 1/n where n is polytropic index, we obtain P ∝ Tn + 1 for ideal gas. We assume that opacity obeys the power law κ ∝ Tα. Thus, we are led to |$\mathcal {L}_{RCB}\propto T^{3-n-\alpha }$|. Inserting n = 2.5 of diatomic molecular hydrogen and α ≈ 4 due to the contribution from some molecules at temperature ≈3000 K near RCB (Freedman et al. 2008), we find |$\mathcal {L}_{RCB}\propto T^{-3.5}$|. Fig. 2c shows luminosity–temperature relation at RCB (red dot denotes runaway point) and it verifies our power law |$\mathcal {L}_{RCB}\propto T^{-3.5}$| when runaway inflation occurs. That is, a small increase in temperature near RCB will induce a strong suppression on luminosity, such that heat cannot efficiently radiate away and planet will inflate out of control, namely runaway inflation. This process is similar to a tight lid on a boiling pot. Runaway inflation is essentially caused by the suppression of radiation near RCB (i.e. κ ∝ T4).
To validate our interpretation, we carry out numerical tests by setting the upper limit for opacity. Fig. 2d shows radius evolution with εinj = 4 × 1028 erg/s but with different opacity limits. Without opacity limit, εinj = 4 × 1028 erg/s leads to runaway inflation, but with opacity limits runaway inflation disappears. Moreover, a lower limit corresponds to a stronger suppression on runaway inflation. Clearly, this numerical test indicates that runaway inflation is indeed caused by high opacity.
In the physical interpretation, we use polytropic index n = 2.5 near RCB to derive the power law for luminosity–temperature relation. Although equation of state is complicated in planet interior, we may apply the simple polytropic model P ∝ ρ1 + 1/n. Fig. 2e shows pressuredensity relation at three snapshots during evolution, i.e. before, at, and after runaway point. Near RCB (dots) 1 + 1/n = 7/5 (n = 2.5) seems a good fit. In the interior (ρ ≳ 0.1 g/cm3) degeneracy 1 + 1/n = 5/3 (n = 1.5) or partial degeneracy 1 + 1/n = 2 (n = 1) seems a good fit.
4 INVESTIGATION ON PARAMETERS
In this section, we investigate how the parameters influence runaway inflation. These parameters are planet mass Mp, core mass Mcore, energy distribution m0, and equilibrium temperature Teq.
Firstly we investigate planet mass Mp. Fig. 3a shows critical rate of injected energy εcri required for runaway inflation versus planet mass. The polyfit index is about 1, which is physically reasonable because |$\mathcal {L}_{intr}\propto M_p$|. Since |$\dot{E}_{tide}\le \varepsilon _{cri}\propto M_p$|, by (4) and (5), we find that the upper limit for eccentricity is e ≈ 0.17(Mp/MJ)1/2. Fig. 3b shows that runaway radius Rrun is smaller for higher mass. This result gives an upper limit for hot Jupiter radius to be 2.2RJ.
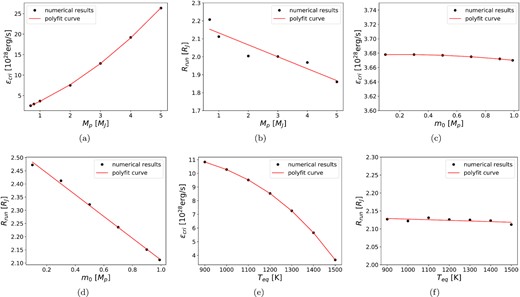
Investigation on parameters: (a) and (b) for planet mass, (c) and (d) for energy distribution, (e) and (f) for equilibrium temperature.
Next, we investigate core mass Mcore from 0 (i.e. coreless planet) until 50 Earth mass. We find that both εcri and Rrun for runaway inflation are independent of core mass. In our calculations, planet core is a rigid boundary but not directly involved in the physical process in the interior. It has been found that Jupiter may have a dilute core (Wahl et al. 2017). A dilute core of exoplanet might influence runaway inflation, but we do not investigate this problem in this paper.
We now investigate energy distribution m0. Fig. 3c shows that εcri is almost independent of energy distribution m0, because it is the total injected energy that matters but not the energy distribution. Fig. 3d shows that a deeper heat source leads to a larger Rrun (uniform distribution yields the same result as m0 = 0.1Mp). This is because of temperature at RCB. With the different energy distributions the temperature at RCB is always about 3000 K (the accurate numerical value is 2750 K) because εcri = 3.67 × 1028 erg/s keeps constant. Thus, a deeper heat source leads to more delayed heat transfer because gas is more condensed in the deeper interior, which accordingly leads to a larger Rrun. This result gives an upper limit for hot Jupiter radius to be 2.5RJ with very central energy source or uniform energy distribution. However, according to the observations, energy source near RCB is more plausible (see next section) and we believe the upper limit to be 2.2RJ.
To end this section, we investigate equilibrium temperature Teq due to irradiation from host star. Irradiation takes place at planet surface close to RCB, so that higher Teq corresponds to lower luminosity near RCB which more easily induces runaway inflation. Fig. 3e shows that εcri indeed decreases with increasing Teq. Fig. 3f shows that Rrun is almost independent of Teq.
5 COMPARISON TO THE OBSERVATIONS
Fig. 4 shows radius–mass relation of confirmed gaseous giant planets (black dots). The red line is a fitted boundary for radius–mass relation. Clearly, higher mass corresponds to smaller radius. The planet with Mp ≈ 3MJ and Rp ≈ 2.7RJ far away from the boundary line is a newly born planet PDS 70 b at age ≈5 Myr when the protoplanetary disk has not been completely dispelled (Wang et al. 2020), and the mechanism for its large radius must be not tidal heating since its orbital semi-major axis ≈20 AU. On this figure, the red dots denote our calculated runaway radius with injected energy near RCB (m0 = 0.99Mp), the green dots in the deep interior (m0 = 0.3Mp), and the blue dots with uniform distribution (green and blues dots for Mp ≥ 3MJ are overlapped with red dots). The boundary line gives an upper limit for planet radius 2.2RJ which is consistent with our calculations. Moreover, the fact that the red dots fit very well with the observational boundary line indicates that tidal heating is very likely to locate near RCB but neither in the deep interior nor with uniform distribution.
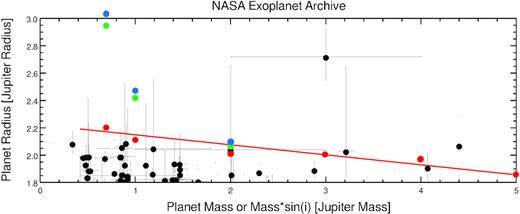
The black dots denote the confirmed exoplanets with error bars (https://exoplanetarchive.ipac.caltech.edu/), the red dots denote our calculated Rrun with m0 = 0.99Mp, the green dots with m0 = 0.3Mp, and the blue dots with uniform distribution. Green and blues dots for Mp ≥ 3MJ are overlapped with red dots.
6 SUMMARY AND DISCUSSIONS
We numerically study planetary evolution with tidal heating and find the runaway inflation induced by high opacity near RCB. We then give the upper limit for hot Jupiter radius to be 2.2RJ (i.e. hot Jupiters can be large but not too large), and for eccentricity to be 0.17(Mp/MJ)1/2. Compared to the observations, we infer that tidal heating locates near RCB.
Equations (4) and (5) show that the tidal heating rate strongly depends on orbital parameters, and vice versa, the planet orbital dynamics certainly depends on the tidal heating since the latter alters planet radius and internal structure which in turn influences the orbital dynamics. In our study, we did not consider this coupling, and it is worth studying in the future. Moreover, when runaway inflation occurs hot Jupiter loses its mass through atmosphere evaporation or accretion by host star, and how mass loss couples with orbital dynamics will be also a problem worth studying. In addition to tidal heating, as we have mentioned in Section 1, Ohmic heating or inward transfer of irradiation can also induce radius inflation. Although this paper focuses on tidal heating, the mechanism of runaway inflation can be also applied to other heating sources. For example, when the electrically conducting atmosphere becomes thick, Ohmic heating may be more significant than tidal heating for inflation, and the observational constraints were studied with Bayesian analysis by Thorngren & Fortney (2018). In the situation that the heating is relevant to irradiation, the runaway inflation will be facilitated as planet radius increases, as studied again by Thorngren & Fortney (2018). These other sources are worth studying in the future.
ACKNOWLEDGEMENTS
This project was initially illuminated by Douglas NC Lin, and Xianfei Zhang helps us on mesa. XW is financially supported by National Natural Science Foundation of China (grant no. 11872246 and 12041301) and Beijing Natural Science Foundation (grant no. 1202015).
DATA AVAILABILITY
The data underlying this article are available in the article.



