-
PDF
- Split View
-
Views
-
Cite
Cite
Davide Bevacqua, Michele Cappellari, Silvia Pellegrini, SDSS-IV MaNGA: integral-field kinematics and stellar population of a sample of galaxies with counter-rotating stellar discs selected from about 4000 galaxies, Monthly Notices of the Royal Astronomical Society, Volume 511, Issue 1, March 2022, Pages 139–157, https://doi.org/10.1093/mnras/stab3732
Close - Share Icon Share
ABSTRACT
We present the integral-field kinematics and stellar population properties of 64 galaxies (61 are Early-Type galaxies; ETGs) with Counter-Rotating stellar Disks (CRD) selected from about 4000 galaxies in the MaNGA survey, based on evidence of counter-rotation or two velocity dispersion peaks in the kinematic maps. For 17 CRDs, the counter-rotating components can also be separated spectroscopically. The frequency of CRDs in MaNGA is <5 per cent for ellipticals, <3 per cent for lenticulars, and <1 per cent for spirals (at 95 per cent confidence level), consistent with previous estimates. We produced age and metallicity maps, and compared the stellar population properties to those of the general ETGs population. We found that CRDs have similar trends in age and metallicity to ETGs, but are less metallic at low masses, and show flatter age and steeper metallicity gradients, on average. A comparison of the velocity fields of the ionized gas and the stars reveals that in 33 cases the gas corotates with either the inner (15 cases) or outer (18 cases) stellar disc, and in nine cases it is misaligned. In most cases the gas corotates with the younger disc. Evidence of multimodality in the stellar population is found in 31 galaxies, while the 14 youngest and least massive galaxies show ongoing star formation; 14 galaxies, instead, exhibit unimodality, and are the oldest and most massive. As a general result, our work indicates that CRDs form primarily via gas accretion in retrograde rotation with respect to a pre-existing stellar disc.
1 INTRODUCTION
Counter-rotation in galaxies is a phenomenon that occurs between two stellar structures (e.g. two discs, the bulge and the disc, a bar and the disc, etc.), as well as between the gaseous and the stellar discs or two gaseous discs (see Corsini 2014 for a review). In this paper, we focus on galaxies hosting two large-scale cospatial counter-rotating stellar discs. Studying this class of objects is interesting because they represent the tip of the iceberg of a (possibly large) class of galaxies in which some of the stars are formed by a separate mechanism from the rest. The detectability of the counter-rotating disc depends on the data quality as well as the characteristics of the two discs. This implies that a larger hidden population than observable must exist. Moreover, if counter-rotating discs are observed, a similar fraction of co-rotating ones must also exist which cannot be detected with the methods discussed in this paper.
The first galaxy with evidence of two counter-rotating stellar discs is the well-studied S0 galaxy NGC 4550 (Rix et al. 1992; Rubin, Graham & Kenney 1992). The presence of two counter-rotating stellar discs in this galaxy was later confirmed with integral-field spectroscopy (Coccato et al. 2013; Johnston et al. 2013) and detailed dynamical modeling (Cappellari et al. 2007). Over the last three decades, many other counter-rotators have been found (Krajnović et al. 2011), but the overall census is still relatively small, and only few of them have been studied in detail [e.g. NGC 3593 (Bertola et al. 1996; Coccato et al. 2013) and NGC 5719 (Vergani et al. 2007; Coccato et al. 2011)]. The first reason for the rarity of these objects is that it may be intrinsically difficult to build up such kinematic structures. A second reason is due to observational limits, both technical and of intrinsic nature (Kuijken, Fisher & Merrifield 1996; Pizzella et al. 2004; Katkov, Sil’chenko & Afanasiev 2013; Rubino et al. 2021); for example, the detection of the counter-rotation depends on the instrumental resolution, as well as on the inclination of the galaxy. Recent large galaxy surveys like Mapping Nearby Galaxies at APO (MaNGA; Bundy et al. 2015; Blanton et al. 2017) and Sydney-AAO Multi-object Integral field spectrograph (SAMI; Croom et al. 2012, Allen et al. 2015) are very promising to determine the incidence of the counter-rotating structures, as well as their origin and intrinsic nature.
The most puzzling question regarding galaxies with counter-rotating stellar discs is their formation history. In fact, they present a variety of observed properties for the two discs, like their stellar population properties, their masses and extensions, and their thickness. Many different formation scenarios have been proposed so far. The peculiar kinematics could be a consequence of internal processes, e.g. the dissolution of a bar (Evans & Collett 1994) or resonance capturing (Tremaine & Yu 2000); however, the significant age difference measured in some cases for the two discs is a strong observational evidence against such scenarios. Recent simulations (Fiteni et al. 2021) also show that internally driven mechanisms are unable to produce counter-rotating discs.
Instead, the origin of counter-rotation may more likely reside in a retrograde accretion of gas from an external source. Simulations have shown that a disc galaxy can form a counter-rotating stellar disc by acquiring a sufficient amount of gas in a retrograde orbit from either a close companion (Thakar & Ryden 1996, 1998), cosmological filaments (Algorry et al. 2014; Taylor, Federrath & Kobayashi 2018; Khoperskov et al. 2021) or a minor merger with a gas-rich dwarf galaxy (Thakar et al. 1997; Di Matteo et al. 2008); in all these cases, the secondary disc is younger and corotating with the gaseous disc. Although they end up with the same kinematical structure, the formation of the counter-rotating component from these three different gas sources corresponds to different predicted properties for the secondary disc, as their extensions and chemical mixtures. Currently, observations (Vergani et al. 2007; Coccato et al. 2013, 2015; Katkov et al. 2013, 2016; Pizzella et al. 2014, 2018) do not favour any of these scenarios in particular.
Another scenario proposed the formation of the counter-rotating disc in a major merger. Even though most major mergers are highly disruptive events, since they enormously heat the progenitor systems and result in a final morphology far from disc-like, Puerari & Pfenniger (2001) showed that, with a fine tuning of the initial conditions, a merger between two equally massive disc galaxies with opposite rotation can reproduce the kinematics of the observed counter-rotators. Simulations by Crocker et al. (2009), for example, reproduced the observed properties of NGC 4550 as a result of a major merger (also supported by observations of Johnston et al. 2013). More recently, Martel & Richard (2020) showed that a major merger between two gas-rich disc galaxies can produce counter-rotating stellar discs even though the progenitors rotate in the same direction.
To properly understand the nature of these objects, and validate or reject formation scenarios, a large sample of galaxies with counter-rotating stellar discs is needed. In this paper, we make use of the statistical power of the MaNGA survey, which has observed ∼10 000 galaxies, to build a large sample of counter-rotators. In Section 2 we describe our method to classify galaxies with counter-rotating stellar discs by inspecting their kinematic maps obtained with MaNGA. After building the sample, in Section 3 we present the procedures to extract the stellar kinematic maps, and look for spectroscopical evidences of the two counter-rotating stellar components; furthermore, we study the alignment or misalignment of the gaseous disc with respect to the stellar ones, by comparing the kinematic position angles. In Section 4, we study the stellar population properties of the sample. In particular, we present the procedure to extract the age and metallicity maps, and how we estimated the ‘global’ stellar population properties, and gradients; then, we compare the age maps with the gaseous and stellar velocity maps to qualitatively determine whether the gas corotates with the younger or the older stellar disc; finally, we perform regularized fits, looking for the presence of single or multiple stellar populations. In Section 5 we present the results, and discuss them in Section 6; in Section 7 we summarize our work.
2 DATA AND SAMPLE SELECTION
2.1 Starting sample from the MaNGA survey
The Integral-Field Spectroscopy (IFS) data used in this study are taken from the Data Release 16 (DR16; Ahumada et al. 2020) of the MaNGA survey. DR16 includes IFS data for 4597 unique galaxies observed in the redshift range 0.01 < z < 0.15, selected to have a flat number density distribution with respect to the i-band absolute magnitude, taken as a proxy for the stellar mass (Wake et al. 2017). Light is fed to the two BOSS spectrographs (Smee et al. 2013), in a spectral range of 360 to 1030 nm, with a median instrumental resolution of ∼ 72 km s−1, corresponding to a spectral resolution ∼ 2000 (Law et al. 2016). The physical properties of these 4597 galaxies (e.g. morphological classification, mass, ellipticity etc.) used in this paper were kindly provided by Mark Graham; an electronic table with these properties is included as supplementary material in the published version of this paper, and we refer the reader to Graham et al. (2019) for a detailed description of how the properties have been measured.
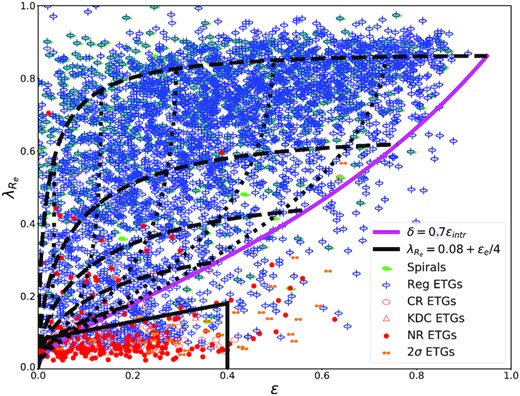
Sample of about 4000 galaxies from the DR16 on the (|$\lambda _{R_e}, \varepsilon$|) diagram. The magenta line, introduced in Cappellari et al. (2007), describes the approximate empirical boundary δ = 0.7ϵintr for the maximum anisotropy, at given ϵ, of edge-on fast rotator galaxies. The black dashed/dotted lines show how the magenta line transforms with inclination. In general, fast rotator galaxies lie within the envelope produced by the inclination tracks, while ‘2σ-galaxies’ (i.e. galaxies with counter-rotating stellar discs) are typically below the magenta line, because counter-rotation lowers the overall measured velocity (and thus |$\lambda _{R_e}$|). The black straight line is the approximate separation between slow rotators (inside) and fast rotators or 2σ-galaxies (outside) proposed by C16. The plotted values were determined by Graham et al. (2019), who also provided the kinematic classification indicated by the symbols.
2.2 Selection criteria
To build a sample of galaxies with counter-rotating stellar discs, we first performed a visual inspection of the kinematic maps, provided by the MaNGA Data Analysis Pipeline (DAP; Westfall et al. 2019), looking for evidences of counter-rotation in the mean stellar velocity (V*) maps, and the presence of the two characteristic peaks in the stellar velocity dispersion (σ*) maps. The ATLAS3D survey (Cappellari et al. 2011) introduced the class of ‘2σ-galaxies’ (Krajnović et al. 2011) to describe the evidence of counter-rotation that produces two symmetric maxima of velocity dispersion along the galaxy major axis (Rubin et al. 1992; Bertola et al. 1996). However, given the modest spatial resolution of MaNGA, we do not expect the two kinematic features to be always detectable in the DAP maps; further, the appearance of one feature does not necessarily imply the other one. In fact, on one hand, if the two counter-rotating discs are indistinguishable (e.g. because of projection effect, for inclined galaxies close to face-on), the counter-rotation pattern does not appear in the velocity field, even when the two peaks in the dispersion map are present. On the other hand, sometimes, while the counter-rotation in the velocity map is clear, the dispersion map may show, for instance, a single central peak due to a prominent bulge. For these reasons, we include in our sample galaxies that show at least one of the two features; further, we do not demand two well-separated σ* peaks, and also include galaxies with a single peak elongated over the major axis. We then introduce the name ‘Counter-Rotating stellar Disks’ (CRD) to designate galaxies that show evidences of counter-rotation or/and the two σ* peaks; with this definition, 2σ-galaxies constitute a subset of CRDs. Two examples of a galaxy showing counter-rotation and lacking the two σ* peaks, and a galaxy with no counter-rotation but with the two σ* peaks, are shown in Fig. 2.
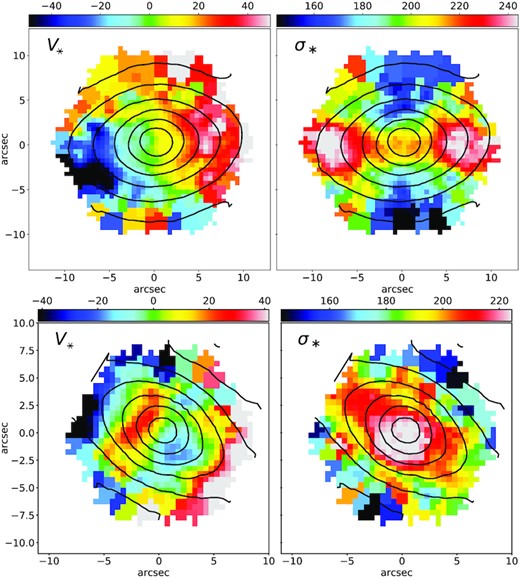
Voronoi-binned velocity, V*, and velocity dispersion, σ*, maps, as produced by the MaNGA DAP, of a galaxy (MaNGA ID 1-248869) exhibiting the characteristic two peaks in σ* but no counter-rotation (upper panels), and of a galaxy (MaNGA ID 1-166613) exhibiting counter-rotation, but a single central peak in σ* (lower panels).
This basic visual selection can however lead to misclassification, for some galaxies that are not truly counter-rotators can exhibit kinematic maps resembling those of CRDs. Fortunately, some peculiarities help us discard ‘fake CRDs’. Therefore, we always inspected also the SDSS image, and, for a proper classification, we made the following selection checks:
Presence of external objects. In general, galaxies in the SDSS image often show neighbouring objects; in some cases, these influence significantly the fitted kinematics. For example, in the first row of Fig. 3, the velocity map appears to exhibit an inversion of the rotation in the northern region. However, the SDSS image, as well as the flux contours, clearly reveal the presence of many external objects; we concluded that the observed kinematic maps are influenced by these objects, which was also supported by the highest velocity dispersion values measured in those same bins where the velocity appears inverted. Therefore, we excluded galaxies with clear evidence of an external influence in the kinematic maps.
Barred galaxies: The presence of a bar can influence the kinematics in such a way that the dispersion map appears elongated over the extension of the bar, as in the second row of Fig. 3. From the SDSS image, we can though spot the presence of a bar, as well as from the characteristic almond-shaped flux contours (Bureau & Athanassoula 2005) in the kinematic maps, as in the fifth contour from the center outwards; visually, almond-shaped contours differ from discy contours because of the sharpening near the major axis. In another case (third row of Fig. 3), we can see the peaks in the velocity dispersion map, but no almond-shaped contours or evidences of bars in the SDSS image; however, in the velocity map the zero-velocity bins (in green) form an S-shape pattern, which arises when a bar is present (e.g. fig. 9 of Cappellari & Copin 2003); thus we excluded such galaxies from our sample.
KDC: Galaxies with a kinematic decoupled core (KDC) may have kinematic maps resembling those of a CRD (e.g. Krajnović et al. 2015). The clearest evidence to identify a KDC is the presence of a kinematic or a photometric twist (e.g. Cappellari 2016, hereafter C16). The former is recognizable from a change of the rotation axis in the velocity map, as well as from asymmetric σ* peaks, and from misalignment of the rotation or the σ* peaks with respect to the photometric major axis; the latter, instead, corresponds to a twist of the flux contours. Another peculiarity of KDC is that the kinematic features are confined in the very inner regions, while those of CRDs typically arise at ≳ Re.
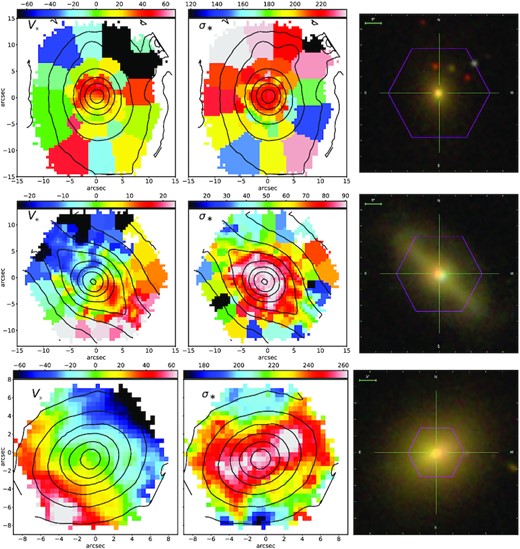
Velocity map, velocity dispersion map, and SDSS image of three galaxies (top to down MaNGA IDs: 1-166739, 1-135524, 1-593972) with kinematic features resembling those of CRD while not truly being so. Colourbars are in km s−1. The same values are assigned to all spaxels of a Voronoi bin. Black lines are the flux contours. First row: In the velocity map an inversion of rotation is seen in the northern region, but from the SDSS image it is evident that kinematic maps are defaced by the presence of external objects. Second and third rows: The dispersion maps present two elongated peaks; the presence of a bar is revealed by the almond-shaped contours in the kinematic maps, and by the SDSS image, in the second row, and by the S-shaped zero-velocity (green) region in the velocity map, in the third row.
Of course, even with accurate checks, no classification is perfect and some misclassified cases can remain. In particular, it is not always easy to distinguish a KDC from a true CRD, because their kinematic maps can be very similar. Aiming at building a large sample, we include borderline cases. For example, our sample includes few galaxies showing both counter-rotation and the two σ* peaks, even though they are confined in the very inner region of the galaxy.
The final sample counts 64 best CRD candidates, which is the largest to date for this kinematic class; the list is given in Table 1 together with the main properties of CRDs used here. The sample is mostly composed of ETGs, of which 38 are ellipticals (E) and 23 are lenticulars (S0); additionally, the sample includes a spiral galaxy (S) and two galaxies with uncertain morphologies. In Fig. 4 we plot CRDs on the (|$\lambda _{R_e},\varepsilon$|) diagram. It is clear that the large majority of the CRDs lie below the magenta line. This can be explained as follows: normal fast rotators, without significant counter-rotation, tend to have a velocity ellipsoid close to oblate (see fig. 11 of C16). They are expected to lie above the magenta line due to the lack of physical axisymmetric equilibrium solutions at high anisotropy when the velocity ellipsoid is close to oblate (Wang, Cappellari & Peng 2021). However, the presence of the counter-rotation lowers the global observed velocity (and thus |$\lambda _{R_e}$|). This tends to bring the CRDs below the magenta line. Finally, it is interesting to notice that the sample includes eight galaxies that appear to be formed just recently, that we labelled as ‘CRD in formation’, based on the bluish colours or irregular shapes in the SDSS image, and disturbed kinematics.
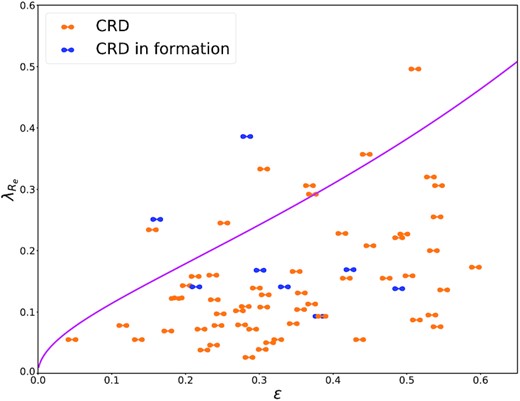
Final sample of CRDs plotted on the (|$\lambda _{R_e},\varepsilon$|) diagram. The magenta line is the same of Fig. 1. Galaxies labelled as ‘CRD in formation’ have a bluish or irregular shape in the SDSS image and disturbed kinematics.
| MaNGA ID . | Morphology . | log10(M*/M⊙) . | Re [kpc] . | ΔPA [°] . | log10Age [yr] . | [M/H] [dex] . | ∇Age . | ∇ [M/H] . | Modality . |
|---|---|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| 12-84617‡ | E | 9.49 | 1.46 | 22.5 (▲) | 9.25 | −1.05 | +0.03 | −0.04 | sf |
| 1-113520 | E | 10.03 | 1.07 | 135.0 (★) | 9.88 | −0.15 | +0.24 | −0.22 | multi |
| 1-115097† | S0 | 10.54 | 2.72 | 11.0 (▲) | 9.92 | −0.16 | +0.10 | −0.35 | multi |
| 1-38347 | E | 11.11 | 2.30 | − | 10.06 | −0.01 | +0.02 | −0.19 | multi |
| 1-339061† | E | 10.67 | 3.41 | 29.0 (•) | 9.79 | −0.09 | −0.18 | −0.53 | multi |
| 1-44047† | E | 10.55 | 1.67 | 17.0 (•) | 10.04 | −0.15 | −0.05 | +0.01 | multi |
| 1-44483† | S0 | 10.49 | 2.33 | 8.0 (•) | 9.95 | −0.08 | +0.17 | −0.36 | multi |
| 1-556514 | E | 11.36 | 4.06 | − | 10.04 | −0.01 | +0.01 | −0.23 | uni |
| 1-37494 | E | 10.62 | 2.07 | 10.0 (•) | 10.06 | −0.33 | −0.01 | −0.07 | − |
| 1-37155 | E | 11.32 | 4.46 | 24.0 (•) | 9.75 | +0.07 | +0.29 | −0.52 | multi |
| 1-38543† | E | 10.73 | 1.76 | 0.5 (▲) | 9.80 | +0.09 | −0.04 | −0.14 | multi |
| 1-47248† | E | 11.56 | 6.06 | − | 10.03 | +0.08 | +0.21 | −0.24 | uni |
| 1-137890 | S0 | 10.39 | 1.67 | 0.5 (▲) | 9.31 | −0.19 | +0.08 | −0.31 | sf |
| 1-255220 | S0 | 10.23 | 1.20 | 30.0 (★) | 9.88 | −0.26 | +0.02 | −0.13 | multi |
| 1-282035‡ | S0 | 10.13 | 1.72 | 120.0 (★) | 8.61 | −0.52 | +0.70 | −0.89 | sf |
| 1-251783 | E | 10.55 | 1.37 | − | 9.75 | −0.06 | +0.02 | −0.16 | multi |
| 1-419257† | S0 | 10.65 | 2.61 | 1.0 (▲) | 9.67 | +0.00 | −0.20 | −0.31 | sf |
| 1-418023 | E | 10.36 | 0.99 | 41.0 (★) | 9.97 | −0.74 | −0.17 | +0.24 | − |
| 1-167555 | E | 9.90 | 2.24 | 85.5 (★) | 9.95 | −0.53 | +0.36 | −0.33 | multi |
| 1-274440 | S0 | 10.0 | 1.20 | 17.5 (▲) | 9.22 | −0.46 | +0.00 | +0.06 | sf |
| 1-274545‡ | U | 10.16 | 2.12 | 4.0 (▲) | 9.27 | −0.59 | −0.08 | −0.05 | sf |
| 1-275185 | E | 11.51 | 6.41 | − | 10.04 | +0.05 | −0.01 | −0.18 | uni |
| 1-167044 | E | 11.58 | 5.83 | − | 10.07 | +0.13 | +0.10 | −0.25 | uni |
| 1-166613 | E | 11.53 | 4.57 | − | 9.86 | +0.13 | +0.06 | −0.27 | multi |
| 1-246175 | S0 | 10.35 | 2.81 | 8.5 (•) | 9.85 | −0.58 | −0.16 | +0.11 | multi |
| 1-210728 | E | 10.77 | 3.08 | − | 10.04 | −0.17 | −0.06 | −0.23 | multi |
| 1-248869† | E | 11.24 | 3.31 | 26.5 (•) | 10.02 | +0.12 | +0.03 | −0.24 | uni |
| 1-136248† | S0 | 10.84 | 4.04 | 1.0 (•) | 9.93 | −0.03 | −0.10 | −0.33 | multi |
| 1-179561 | E | 10.48 | 1.53 | 1.5 (▲) | 9.39 | −0.56 | +0.18 | −0.19 | sf |
| 1-635590† | E | 11.64 | 4.94 | − | 10.07 | +0.14 | +0.04 | −0.37 | uni |
| 1-113698‡ | S0 | 9.38 | 1.10 | 10.5 (▲) | 9.20 | −0.81 | −0.10 | +0.12 | multi |
| 1-44722 | E | 9.88 | 4.68 | − | 10.05 | −0.47 | −0.12 | −0.35 | − |
| 1-45016 | E | 11.67 | 6.27 | − | 10.04 | +0.04 | +0.06 | −0.14 | uni |
| 1-163594 | E | 11.53 | 2.89 | 108.5 (★) | 9.88 | +0.07 | +0.10 | −0.33 | multi |
| 1-248410 | S0 | 9.94 | 1.31 | 2.5 (•) | 9.61 | −0.50 | +0.17 | −0.12 | sf |
| 1-235983 | E | 10.04 | 0.75 | 95.5 (★) | 10.01 | −0.14 | +0.04 | −0.18 | multi |
| 1-236144 | S | 10.92 | 5.77 | 19.0 (•) | 9.92 | −0.35 | −0.01 | −0.30 | multi |
| 1-174947† | S0 | 11.0 | 5.64 | 2.0 (•) | 10.05 | −0.06 | −0.02 | −0.55 | − |
| 1-278079 | E | 11.96 | 7.53 | − | 9.98 | +0.16 | +0.06 | −0.09 | uni |
| 1-188530 | E | 11.0 | 3.69 | 164.0 (▲) | 10.19 | −0.34 | −0.04 | −0.07 | uni |
| 1-149172‡ | S0 | 9.49 | 1.12 | 38.0 (★) | 9.26 | −0.70 | −0.12 | +0.02 | sf |
| 1-94773 | E | 10.56 | 1.6 | − | 9.72 | −0.22 | +0.02 | −0.01 | multi |
| 1-94690† | S0 | 10.56 | 2.63 | 6.0 (▲) | 9.84 | −0.28 | −0.03 | −0.20 | multi |
| 1-323766 | E | 10.16 | 1.04 | 0.5 (▲) | 9.82 | −0.32 | +0.16 | −0.24 | multi |
| 1-323764‡ | S0 | 9.94 | 2.18 | 7.5 (•) | 9.42 | −0.52 | −0.36 | −0.41 | sf |
| 1-135244† | E | 11.19 | 2.53 | − | 9.99 | +0.06 | −0.04 | −0.19 | multi |
| 1-549076† | U | 11.4 | 5.21 | − | 10.01 | +0.09 | −0.05 | −0.12 | uni |
| 1-314719 | E | 11.91 | 15.51 | − | 9.96 | +0.12 | +0.13 | −0.46 | uni |
| 1-299176 | E | 11.66 | 6.79 | − | 9.99 | +0.14 | −0.01 | −0.26 | uni |
| 1-298940 | E | 10.63 | 2.74 | − | 9.94 | −0.24 | −0.11 | −0.18 | multi |
| 1-593328† | E | 11.71 | 6.99 | 0.0 (▲) | 10.02 | +0.11 | −0.14 | −0.27 | uni |
| 1-322291 | S0 | 10.2 | 2.56 | − | 9.76 | −0.22 | +0.07 | −0.37 | multi |
| 1-633000 | S0 | 10.27 | 1.62 | 31.5 (★) | 9.37 | −0.47 | +0.18 | +0.20 | sf |
| 1-251198 | S0 | 10.64 | 2.47 | 17.0 (▲) | 9.87 | −0.35 | +0.11 | +0.02 | multi |
| 1-266244‡ | S0 | 9.63 | 1.18 | − | 9.31 | −0.80 | −0.13 | +0.07 | sf |
| 1-234115 | E | 10.53 | 2.13 | 3.5 (▲) | 10.07 | −0.25 | −0.03 | −0.26 | − |
| 1-457547 | S0 | 10.24 | 1.56 | 13.0 (•) | 9.66 | −0.31 | −0.14 | −0.24 | sf |
| 1-188177† | E | 10.59 | 3.17 | 22.5 (•) | 9.89 | −0.26 | −0.15 | −0.48 | multi |
| 1-269227† | E | 10.76 | 1.54 | − | 10.04 | +0.07 | +0.02 | −0.13 | uni |
| 1-318513 | S0 | 10.24 | 1.39 | 3.0(•) | 9.75 | −0.60 | +0.02 | −0.05 | multi |
| 1-42660‡ | S0 | 10.75 | 2.84 | 6.0 (•) | 9.68 | −0.33 | −0.31 | −0.49 | multi |
| 1-121871 | S0 | 10.41 | 2.72 | 10.5 (•) | 9.61 | −0.29 | +0.02 | −0.22 | sf |
| 1-297822 | E | 10.9 | 2.18 | − | 9.67 | −0.12 | +0.04 | −0.12 | multi |
| 1-386322 | E | 10.22 | 1.56 | 4.0 (•) | 9.87 | −0.20 | +0.06 | −0.24 | multi |
| MaNGA ID . | Morphology . | log10(M*/M⊙) . | Re [kpc] . | ΔPA [°] . | log10Age [yr] . | [M/H] [dex] . | ∇Age . | ∇ [M/H] . | Modality . |
|---|---|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| 12-84617‡ | E | 9.49 | 1.46 | 22.5 (▲) | 9.25 | −1.05 | +0.03 | −0.04 | sf |
| 1-113520 | E | 10.03 | 1.07 | 135.0 (★) | 9.88 | −0.15 | +0.24 | −0.22 | multi |
| 1-115097† | S0 | 10.54 | 2.72 | 11.0 (▲) | 9.92 | −0.16 | +0.10 | −0.35 | multi |
| 1-38347 | E | 11.11 | 2.30 | − | 10.06 | −0.01 | +0.02 | −0.19 | multi |
| 1-339061† | E | 10.67 | 3.41 | 29.0 (•) | 9.79 | −0.09 | −0.18 | −0.53 | multi |
| 1-44047† | E | 10.55 | 1.67 | 17.0 (•) | 10.04 | −0.15 | −0.05 | +0.01 | multi |
| 1-44483† | S0 | 10.49 | 2.33 | 8.0 (•) | 9.95 | −0.08 | +0.17 | −0.36 | multi |
| 1-556514 | E | 11.36 | 4.06 | − | 10.04 | −0.01 | +0.01 | −0.23 | uni |
| 1-37494 | E | 10.62 | 2.07 | 10.0 (•) | 10.06 | −0.33 | −0.01 | −0.07 | − |
| 1-37155 | E | 11.32 | 4.46 | 24.0 (•) | 9.75 | +0.07 | +0.29 | −0.52 | multi |
| 1-38543† | E | 10.73 | 1.76 | 0.5 (▲) | 9.80 | +0.09 | −0.04 | −0.14 | multi |
| 1-47248† | E | 11.56 | 6.06 | − | 10.03 | +0.08 | +0.21 | −0.24 | uni |
| 1-137890 | S0 | 10.39 | 1.67 | 0.5 (▲) | 9.31 | −0.19 | +0.08 | −0.31 | sf |
| 1-255220 | S0 | 10.23 | 1.20 | 30.0 (★) | 9.88 | −0.26 | +0.02 | −0.13 | multi |
| 1-282035‡ | S0 | 10.13 | 1.72 | 120.0 (★) | 8.61 | −0.52 | +0.70 | −0.89 | sf |
| 1-251783 | E | 10.55 | 1.37 | − | 9.75 | −0.06 | +0.02 | −0.16 | multi |
| 1-419257† | S0 | 10.65 | 2.61 | 1.0 (▲) | 9.67 | +0.00 | −0.20 | −0.31 | sf |
| 1-418023 | E | 10.36 | 0.99 | 41.0 (★) | 9.97 | −0.74 | −0.17 | +0.24 | − |
| 1-167555 | E | 9.90 | 2.24 | 85.5 (★) | 9.95 | −0.53 | +0.36 | −0.33 | multi |
| 1-274440 | S0 | 10.0 | 1.20 | 17.5 (▲) | 9.22 | −0.46 | +0.00 | +0.06 | sf |
| 1-274545‡ | U | 10.16 | 2.12 | 4.0 (▲) | 9.27 | −0.59 | −0.08 | −0.05 | sf |
| 1-275185 | E | 11.51 | 6.41 | − | 10.04 | +0.05 | −0.01 | −0.18 | uni |
| 1-167044 | E | 11.58 | 5.83 | − | 10.07 | +0.13 | +0.10 | −0.25 | uni |
| 1-166613 | E | 11.53 | 4.57 | − | 9.86 | +0.13 | +0.06 | −0.27 | multi |
| 1-246175 | S0 | 10.35 | 2.81 | 8.5 (•) | 9.85 | −0.58 | −0.16 | +0.11 | multi |
| 1-210728 | E | 10.77 | 3.08 | − | 10.04 | −0.17 | −0.06 | −0.23 | multi |
| 1-248869† | E | 11.24 | 3.31 | 26.5 (•) | 10.02 | +0.12 | +0.03 | −0.24 | uni |
| 1-136248† | S0 | 10.84 | 4.04 | 1.0 (•) | 9.93 | −0.03 | −0.10 | −0.33 | multi |
| 1-179561 | E | 10.48 | 1.53 | 1.5 (▲) | 9.39 | −0.56 | +0.18 | −0.19 | sf |
| 1-635590† | E | 11.64 | 4.94 | − | 10.07 | +0.14 | +0.04 | −0.37 | uni |
| 1-113698‡ | S0 | 9.38 | 1.10 | 10.5 (▲) | 9.20 | −0.81 | −0.10 | +0.12 | multi |
| 1-44722 | E | 9.88 | 4.68 | − | 10.05 | −0.47 | −0.12 | −0.35 | − |
| 1-45016 | E | 11.67 | 6.27 | − | 10.04 | +0.04 | +0.06 | −0.14 | uni |
| 1-163594 | E | 11.53 | 2.89 | 108.5 (★) | 9.88 | +0.07 | +0.10 | −0.33 | multi |
| 1-248410 | S0 | 9.94 | 1.31 | 2.5 (•) | 9.61 | −0.50 | +0.17 | −0.12 | sf |
| 1-235983 | E | 10.04 | 0.75 | 95.5 (★) | 10.01 | −0.14 | +0.04 | −0.18 | multi |
| 1-236144 | S | 10.92 | 5.77 | 19.0 (•) | 9.92 | −0.35 | −0.01 | −0.30 | multi |
| 1-174947† | S0 | 11.0 | 5.64 | 2.0 (•) | 10.05 | −0.06 | −0.02 | −0.55 | − |
| 1-278079 | E | 11.96 | 7.53 | − | 9.98 | +0.16 | +0.06 | −0.09 | uni |
| 1-188530 | E | 11.0 | 3.69 | 164.0 (▲) | 10.19 | −0.34 | −0.04 | −0.07 | uni |
| 1-149172‡ | S0 | 9.49 | 1.12 | 38.0 (★) | 9.26 | −0.70 | −0.12 | +0.02 | sf |
| 1-94773 | E | 10.56 | 1.6 | − | 9.72 | −0.22 | +0.02 | −0.01 | multi |
| 1-94690† | S0 | 10.56 | 2.63 | 6.0 (▲) | 9.84 | −0.28 | −0.03 | −0.20 | multi |
| 1-323766 | E | 10.16 | 1.04 | 0.5 (▲) | 9.82 | −0.32 | +0.16 | −0.24 | multi |
| 1-323764‡ | S0 | 9.94 | 2.18 | 7.5 (•) | 9.42 | −0.52 | −0.36 | −0.41 | sf |
| 1-135244† | E | 11.19 | 2.53 | − | 9.99 | +0.06 | −0.04 | −0.19 | multi |
| 1-549076† | U | 11.4 | 5.21 | − | 10.01 | +0.09 | −0.05 | −0.12 | uni |
| 1-314719 | E | 11.91 | 15.51 | − | 9.96 | +0.12 | +0.13 | −0.46 | uni |
| 1-299176 | E | 11.66 | 6.79 | − | 9.99 | +0.14 | −0.01 | −0.26 | uni |
| 1-298940 | E | 10.63 | 2.74 | − | 9.94 | −0.24 | −0.11 | −0.18 | multi |
| 1-593328† | E | 11.71 | 6.99 | 0.0 (▲) | 10.02 | +0.11 | −0.14 | −0.27 | uni |
| 1-322291 | S0 | 10.2 | 2.56 | − | 9.76 | −0.22 | +0.07 | −0.37 | multi |
| 1-633000 | S0 | 10.27 | 1.62 | 31.5 (★) | 9.37 | −0.47 | +0.18 | +0.20 | sf |
| 1-251198 | S0 | 10.64 | 2.47 | 17.0 (▲) | 9.87 | −0.35 | +0.11 | +0.02 | multi |
| 1-266244‡ | S0 | 9.63 | 1.18 | − | 9.31 | −0.80 | −0.13 | +0.07 | sf |
| 1-234115 | E | 10.53 | 2.13 | 3.5 (▲) | 10.07 | −0.25 | −0.03 | −0.26 | − |
| 1-457547 | S0 | 10.24 | 1.56 | 13.0 (•) | 9.66 | −0.31 | −0.14 | −0.24 | sf |
| 1-188177† | E | 10.59 | 3.17 | 22.5 (•) | 9.89 | −0.26 | −0.15 | −0.48 | multi |
| 1-269227† | E | 10.76 | 1.54 | − | 10.04 | +0.07 | +0.02 | −0.13 | uni |
| 1-318513 | S0 | 10.24 | 1.39 | 3.0(•) | 9.75 | −0.60 | +0.02 | −0.05 | multi |
| 1-42660‡ | S0 | 10.75 | 2.84 | 6.0 (•) | 9.68 | −0.33 | −0.31 | −0.49 | multi |
| 1-121871 | S0 | 10.41 | 2.72 | 10.5 (•) | 9.61 | −0.29 | +0.02 | −0.22 | sf |
| 1-297822 | E | 10.9 | 2.18 | − | 9.67 | −0.12 | +0.04 | −0.12 | multi |
| 1-386322 | E | 10.22 | 1.56 | 4.0 (•) | 9.87 | −0.20 | +0.06 | −0.24 | multi |
Columns: (1) The MaNGA ID of the galaxy. The symbol ‡ marks galaxies labelled as ‘CRD in formation’ in Section 2.2, while † marks galaxies exhibiting two minima in the χ2 map. (2) Galaxy morphology: ‘E’ for Elliptical, ‘S’ for Spiral, ‘S0’ for Lenticular, ‘U’ for unclassified morphology. (3) Stellar mass taken from Graham et al. 2019. (4) Elliptical Petrosian 50 per cent light radius in SDSS r-band. (5) Difference of the kinematic position angles between the stellar and the gas velocity fields. Symbols in brackets indicate the corotation of the gaseous disk with the inner (▲) and outer (•) stellar disk, and misalignment (★); cyan and red symbols indicate the corotation with the younger and older stellar disk, respectively. Associated error: 7°. (6) and (7) Luminosity weighted mean age and metallicity within 1 Re. Typical errors: 0.04 dex and 0.05 dex, respectively. (8) and (9) Age and metallicity gradients. (10) Modality of the weights maps from regularized fits: ‘uni’ for unimodal, ‘multi’ for multimodal, ‘sf’ for star-forming.
| MaNGA ID . | Morphology . | log10(M*/M⊙) . | Re [kpc] . | ΔPA [°] . | log10Age [yr] . | [M/H] [dex] . | ∇Age . | ∇ [M/H] . | Modality . |
|---|---|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| 12-84617‡ | E | 9.49 | 1.46 | 22.5 (▲) | 9.25 | −1.05 | +0.03 | −0.04 | sf |
| 1-113520 | E | 10.03 | 1.07 | 135.0 (★) | 9.88 | −0.15 | +0.24 | −0.22 | multi |
| 1-115097† | S0 | 10.54 | 2.72 | 11.0 (▲) | 9.92 | −0.16 | +0.10 | −0.35 | multi |
| 1-38347 | E | 11.11 | 2.30 | − | 10.06 | −0.01 | +0.02 | −0.19 | multi |
| 1-339061† | E | 10.67 | 3.41 | 29.0 (•) | 9.79 | −0.09 | −0.18 | −0.53 | multi |
| 1-44047† | E | 10.55 | 1.67 | 17.0 (•) | 10.04 | −0.15 | −0.05 | +0.01 | multi |
| 1-44483† | S0 | 10.49 | 2.33 | 8.0 (•) | 9.95 | −0.08 | +0.17 | −0.36 | multi |
| 1-556514 | E | 11.36 | 4.06 | − | 10.04 | −0.01 | +0.01 | −0.23 | uni |
| 1-37494 | E | 10.62 | 2.07 | 10.0 (•) | 10.06 | −0.33 | −0.01 | −0.07 | − |
| 1-37155 | E | 11.32 | 4.46 | 24.0 (•) | 9.75 | +0.07 | +0.29 | −0.52 | multi |
| 1-38543† | E | 10.73 | 1.76 | 0.5 (▲) | 9.80 | +0.09 | −0.04 | −0.14 | multi |
| 1-47248† | E | 11.56 | 6.06 | − | 10.03 | +0.08 | +0.21 | −0.24 | uni |
| 1-137890 | S0 | 10.39 | 1.67 | 0.5 (▲) | 9.31 | −0.19 | +0.08 | −0.31 | sf |
| 1-255220 | S0 | 10.23 | 1.20 | 30.0 (★) | 9.88 | −0.26 | +0.02 | −0.13 | multi |
| 1-282035‡ | S0 | 10.13 | 1.72 | 120.0 (★) | 8.61 | −0.52 | +0.70 | −0.89 | sf |
| 1-251783 | E | 10.55 | 1.37 | − | 9.75 | −0.06 | +0.02 | −0.16 | multi |
| 1-419257† | S0 | 10.65 | 2.61 | 1.0 (▲) | 9.67 | +0.00 | −0.20 | −0.31 | sf |
| 1-418023 | E | 10.36 | 0.99 | 41.0 (★) | 9.97 | −0.74 | −0.17 | +0.24 | − |
| 1-167555 | E | 9.90 | 2.24 | 85.5 (★) | 9.95 | −0.53 | +0.36 | −0.33 | multi |
| 1-274440 | S0 | 10.0 | 1.20 | 17.5 (▲) | 9.22 | −0.46 | +0.00 | +0.06 | sf |
| 1-274545‡ | U | 10.16 | 2.12 | 4.0 (▲) | 9.27 | −0.59 | −0.08 | −0.05 | sf |
| 1-275185 | E | 11.51 | 6.41 | − | 10.04 | +0.05 | −0.01 | −0.18 | uni |
| 1-167044 | E | 11.58 | 5.83 | − | 10.07 | +0.13 | +0.10 | −0.25 | uni |
| 1-166613 | E | 11.53 | 4.57 | − | 9.86 | +0.13 | +0.06 | −0.27 | multi |
| 1-246175 | S0 | 10.35 | 2.81 | 8.5 (•) | 9.85 | −0.58 | −0.16 | +0.11 | multi |
| 1-210728 | E | 10.77 | 3.08 | − | 10.04 | −0.17 | −0.06 | −0.23 | multi |
| 1-248869† | E | 11.24 | 3.31 | 26.5 (•) | 10.02 | +0.12 | +0.03 | −0.24 | uni |
| 1-136248† | S0 | 10.84 | 4.04 | 1.0 (•) | 9.93 | −0.03 | −0.10 | −0.33 | multi |
| 1-179561 | E | 10.48 | 1.53 | 1.5 (▲) | 9.39 | −0.56 | +0.18 | −0.19 | sf |
| 1-635590† | E | 11.64 | 4.94 | − | 10.07 | +0.14 | +0.04 | −0.37 | uni |
| 1-113698‡ | S0 | 9.38 | 1.10 | 10.5 (▲) | 9.20 | −0.81 | −0.10 | +0.12 | multi |
| 1-44722 | E | 9.88 | 4.68 | − | 10.05 | −0.47 | −0.12 | −0.35 | − |
| 1-45016 | E | 11.67 | 6.27 | − | 10.04 | +0.04 | +0.06 | −0.14 | uni |
| 1-163594 | E | 11.53 | 2.89 | 108.5 (★) | 9.88 | +0.07 | +0.10 | −0.33 | multi |
| 1-248410 | S0 | 9.94 | 1.31 | 2.5 (•) | 9.61 | −0.50 | +0.17 | −0.12 | sf |
| 1-235983 | E | 10.04 | 0.75 | 95.5 (★) | 10.01 | −0.14 | +0.04 | −0.18 | multi |
| 1-236144 | S | 10.92 | 5.77 | 19.0 (•) | 9.92 | −0.35 | −0.01 | −0.30 | multi |
| 1-174947† | S0 | 11.0 | 5.64 | 2.0 (•) | 10.05 | −0.06 | −0.02 | −0.55 | − |
| 1-278079 | E | 11.96 | 7.53 | − | 9.98 | +0.16 | +0.06 | −0.09 | uni |
| 1-188530 | E | 11.0 | 3.69 | 164.0 (▲) | 10.19 | −0.34 | −0.04 | −0.07 | uni |
| 1-149172‡ | S0 | 9.49 | 1.12 | 38.0 (★) | 9.26 | −0.70 | −0.12 | +0.02 | sf |
| 1-94773 | E | 10.56 | 1.6 | − | 9.72 | −0.22 | +0.02 | −0.01 | multi |
| 1-94690† | S0 | 10.56 | 2.63 | 6.0 (▲) | 9.84 | −0.28 | −0.03 | −0.20 | multi |
| 1-323766 | E | 10.16 | 1.04 | 0.5 (▲) | 9.82 | −0.32 | +0.16 | −0.24 | multi |
| 1-323764‡ | S0 | 9.94 | 2.18 | 7.5 (•) | 9.42 | −0.52 | −0.36 | −0.41 | sf |
| 1-135244† | E | 11.19 | 2.53 | − | 9.99 | +0.06 | −0.04 | −0.19 | multi |
| 1-549076† | U | 11.4 | 5.21 | − | 10.01 | +0.09 | −0.05 | −0.12 | uni |
| 1-314719 | E | 11.91 | 15.51 | − | 9.96 | +0.12 | +0.13 | −0.46 | uni |
| 1-299176 | E | 11.66 | 6.79 | − | 9.99 | +0.14 | −0.01 | −0.26 | uni |
| 1-298940 | E | 10.63 | 2.74 | − | 9.94 | −0.24 | −0.11 | −0.18 | multi |
| 1-593328† | E | 11.71 | 6.99 | 0.0 (▲) | 10.02 | +0.11 | −0.14 | −0.27 | uni |
| 1-322291 | S0 | 10.2 | 2.56 | − | 9.76 | −0.22 | +0.07 | −0.37 | multi |
| 1-633000 | S0 | 10.27 | 1.62 | 31.5 (★) | 9.37 | −0.47 | +0.18 | +0.20 | sf |
| 1-251198 | S0 | 10.64 | 2.47 | 17.0 (▲) | 9.87 | −0.35 | +0.11 | +0.02 | multi |
| 1-266244‡ | S0 | 9.63 | 1.18 | − | 9.31 | −0.80 | −0.13 | +0.07 | sf |
| 1-234115 | E | 10.53 | 2.13 | 3.5 (▲) | 10.07 | −0.25 | −0.03 | −0.26 | − |
| 1-457547 | S0 | 10.24 | 1.56 | 13.0 (•) | 9.66 | −0.31 | −0.14 | −0.24 | sf |
| 1-188177† | E | 10.59 | 3.17 | 22.5 (•) | 9.89 | −0.26 | −0.15 | −0.48 | multi |
| 1-269227† | E | 10.76 | 1.54 | − | 10.04 | +0.07 | +0.02 | −0.13 | uni |
| 1-318513 | S0 | 10.24 | 1.39 | 3.0(•) | 9.75 | −0.60 | +0.02 | −0.05 | multi |
| 1-42660‡ | S0 | 10.75 | 2.84 | 6.0 (•) | 9.68 | −0.33 | −0.31 | −0.49 | multi |
| 1-121871 | S0 | 10.41 | 2.72 | 10.5 (•) | 9.61 | −0.29 | +0.02 | −0.22 | sf |
| 1-297822 | E | 10.9 | 2.18 | − | 9.67 | −0.12 | +0.04 | −0.12 | multi |
| 1-386322 | E | 10.22 | 1.56 | 4.0 (•) | 9.87 | −0.20 | +0.06 | −0.24 | multi |
| MaNGA ID . | Morphology . | log10(M*/M⊙) . | Re [kpc] . | ΔPA [°] . | log10Age [yr] . | [M/H] [dex] . | ∇Age . | ∇ [M/H] . | Modality . |
|---|---|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| 12-84617‡ | E | 9.49 | 1.46 | 22.5 (▲) | 9.25 | −1.05 | +0.03 | −0.04 | sf |
| 1-113520 | E | 10.03 | 1.07 | 135.0 (★) | 9.88 | −0.15 | +0.24 | −0.22 | multi |
| 1-115097† | S0 | 10.54 | 2.72 | 11.0 (▲) | 9.92 | −0.16 | +0.10 | −0.35 | multi |
| 1-38347 | E | 11.11 | 2.30 | − | 10.06 | −0.01 | +0.02 | −0.19 | multi |
| 1-339061† | E | 10.67 | 3.41 | 29.0 (•) | 9.79 | −0.09 | −0.18 | −0.53 | multi |
| 1-44047† | E | 10.55 | 1.67 | 17.0 (•) | 10.04 | −0.15 | −0.05 | +0.01 | multi |
| 1-44483† | S0 | 10.49 | 2.33 | 8.0 (•) | 9.95 | −0.08 | +0.17 | −0.36 | multi |
| 1-556514 | E | 11.36 | 4.06 | − | 10.04 | −0.01 | +0.01 | −0.23 | uni |
| 1-37494 | E | 10.62 | 2.07 | 10.0 (•) | 10.06 | −0.33 | −0.01 | −0.07 | − |
| 1-37155 | E | 11.32 | 4.46 | 24.0 (•) | 9.75 | +0.07 | +0.29 | −0.52 | multi |
| 1-38543† | E | 10.73 | 1.76 | 0.5 (▲) | 9.80 | +0.09 | −0.04 | −0.14 | multi |
| 1-47248† | E | 11.56 | 6.06 | − | 10.03 | +0.08 | +0.21 | −0.24 | uni |
| 1-137890 | S0 | 10.39 | 1.67 | 0.5 (▲) | 9.31 | −0.19 | +0.08 | −0.31 | sf |
| 1-255220 | S0 | 10.23 | 1.20 | 30.0 (★) | 9.88 | −0.26 | +0.02 | −0.13 | multi |
| 1-282035‡ | S0 | 10.13 | 1.72 | 120.0 (★) | 8.61 | −0.52 | +0.70 | −0.89 | sf |
| 1-251783 | E | 10.55 | 1.37 | − | 9.75 | −0.06 | +0.02 | −0.16 | multi |
| 1-419257† | S0 | 10.65 | 2.61 | 1.0 (▲) | 9.67 | +0.00 | −0.20 | −0.31 | sf |
| 1-418023 | E | 10.36 | 0.99 | 41.0 (★) | 9.97 | −0.74 | −0.17 | +0.24 | − |
| 1-167555 | E | 9.90 | 2.24 | 85.5 (★) | 9.95 | −0.53 | +0.36 | −0.33 | multi |
| 1-274440 | S0 | 10.0 | 1.20 | 17.5 (▲) | 9.22 | −0.46 | +0.00 | +0.06 | sf |
| 1-274545‡ | U | 10.16 | 2.12 | 4.0 (▲) | 9.27 | −0.59 | −0.08 | −0.05 | sf |
| 1-275185 | E | 11.51 | 6.41 | − | 10.04 | +0.05 | −0.01 | −0.18 | uni |
| 1-167044 | E | 11.58 | 5.83 | − | 10.07 | +0.13 | +0.10 | −0.25 | uni |
| 1-166613 | E | 11.53 | 4.57 | − | 9.86 | +0.13 | +0.06 | −0.27 | multi |
| 1-246175 | S0 | 10.35 | 2.81 | 8.5 (•) | 9.85 | −0.58 | −0.16 | +0.11 | multi |
| 1-210728 | E | 10.77 | 3.08 | − | 10.04 | −0.17 | −0.06 | −0.23 | multi |
| 1-248869† | E | 11.24 | 3.31 | 26.5 (•) | 10.02 | +0.12 | +0.03 | −0.24 | uni |
| 1-136248† | S0 | 10.84 | 4.04 | 1.0 (•) | 9.93 | −0.03 | −0.10 | −0.33 | multi |
| 1-179561 | E | 10.48 | 1.53 | 1.5 (▲) | 9.39 | −0.56 | +0.18 | −0.19 | sf |
| 1-635590† | E | 11.64 | 4.94 | − | 10.07 | +0.14 | +0.04 | −0.37 | uni |
| 1-113698‡ | S0 | 9.38 | 1.10 | 10.5 (▲) | 9.20 | −0.81 | −0.10 | +0.12 | multi |
| 1-44722 | E | 9.88 | 4.68 | − | 10.05 | −0.47 | −0.12 | −0.35 | − |
| 1-45016 | E | 11.67 | 6.27 | − | 10.04 | +0.04 | +0.06 | −0.14 | uni |
| 1-163594 | E | 11.53 | 2.89 | 108.5 (★) | 9.88 | +0.07 | +0.10 | −0.33 | multi |
| 1-248410 | S0 | 9.94 | 1.31 | 2.5 (•) | 9.61 | −0.50 | +0.17 | −0.12 | sf |
| 1-235983 | E | 10.04 | 0.75 | 95.5 (★) | 10.01 | −0.14 | +0.04 | −0.18 | multi |
| 1-236144 | S | 10.92 | 5.77 | 19.0 (•) | 9.92 | −0.35 | −0.01 | −0.30 | multi |
| 1-174947† | S0 | 11.0 | 5.64 | 2.0 (•) | 10.05 | −0.06 | −0.02 | −0.55 | − |
| 1-278079 | E | 11.96 | 7.53 | − | 9.98 | +0.16 | +0.06 | −0.09 | uni |
| 1-188530 | E | 11.0 | 3.69 | 164.0 (▲) | 10.19 | −0.34 | −0.04 | −0.07 | uni |
| 1-149172‡ | S0 | 9.49 | 1.12 | 38.0 (★) | 9.26 | −0.70 | −0.12 | +0.02 | sf |
| 1-94773 | E | 10.56 | 1.6 | − | 9.72 | −0.22 | +0.02 | −0.01 | multi |
| 1-94690† | S0 | 10.56 | 2.63 | 6.0 (▲) | 9.84 | −0.28 | −0.03 | −0.20 | multi |
| 1-323766 | E | 10.16 | 1.04 | 0.5 (▲) | 9.82 | −0.32 | +0.16 | −0.24 | multi |
| 1-323764‡ | S0 | 9.94 | 2.18 | 7.5 (•) | 9.42 | −0.52 | −0.36 | −0.41 | sf |
| 1-135244† | E | 11.19 | 2.53 | − | 9.99 | +0.06 | −0.04 | −0.19 | multi |
| 1-549076† | U | 11.4 | 5.21 | − | 10.01 | +0.09 | −0.05 | −0.12 | uni |
| 1-314719 | E | 11.91 | 15.51 | − | 9.96 | +0.12 | +0.13 | −0.46 | uni |
| 1-299176 | E | 11.66 | 6.79 | − | 9.99 | +0.14 | −0.01 | −0.26 | uni |
| 1-298940 | E | 10.63 | 2.74 | − | 9.94 | −0.24 | −0.11 | −0.18 | multi |
| 1-593328† | E | 11.71 | 6.99 | 0.0 (▲) | 10.02 | +0.11 | −0.14 | −0.27 | uni |
| 1-322291 | S0 | 10.2 | 2.56 | − | 9.76 | −0.22 | +0.07 | −0.37 | multi |
| 1-633000 | S0 | 10.27 | 1.62 | 31.5 (★) | 9.37 | −0.47 | +0.18 | +0.20 | sf |
| 1-251198 | S0 | 10.64 | 2.47 | 17.0 (▲) | 9.87 | −0.35 | +0.11 | +0.02 | multi |
| 1-266244‡ | S0 | 9.63 | 1.18 | − | 9.31 | −0.80 | −0.13 | +0.07 | sf |
| 1-234115 | E | 10.53 | 2.13 | 3.5 (▲) | 10.07 | −0.25 | −0.03 | −0.26 | − |
| 1-457547 | S0 | 10.24 | 1.56 | 13.0 (•) | 9.66 | −0.31 | −0.14 | −0.24 | sf |
| 1-188177† | E | 10.59 | 3.17 | 22.5 (•) | 9.89 | −0.26 | −0.15 | −0.48 | multi |
| 1-269227† | E | 10.76 | 1.54 | − | 10.04 | +0.07 | +0.02 | −0.13 | uni |
| 1-318513 | S0 | 10.24 | 1.39 | 3.0(•) | 9.75 | −0.60 | +0.02 | −0.05 | multi |
| 1-42660‡ | S0 | 10.75 | 2.84 | 6.0 (•) | 9.68 | −0.33 | −0.31 | −0.49 | multi |
| 1-121871 | S0 | 10.41 | 2.72 | 10.5 (•) | 9.61 | −0.29 | +0.02 | −0.22 | sf |
| 1-297822 | E | 10.9 | 2.18 | − | 9.67 | −0.12 | +0.04 | −0.12 | multi |
| 1-386322 | E | 10.22 | 1.56 | 4.0 (•) | 9.87 | −0.20 | +0.06 | −0.24 | multi |
Columns: (1) The MaNGA ID of the galaxy. The symbol ‡ marks galaxies labelled as ‘CRD in formation’ in Section 2.2, while † marks galaxies exhibiting two minima in the χ2 map. (2) Galaxy morphology: ‘E’ for Elliptical, ‘S’ for Spiral, ‘S0’ for Lenticular, ‘U’ for unclassified morphology. (3) Stellar mass taken from Graham et al. 2019. (4) Elliptical Petrosian 50 per cent light radius in SDSS r-band. (5) Difference of the kinematic position angles between the stellar and the gas velocity fields. Symbols in brackets indicate the corotation of the gaseous disk with the inner (▲) and outer (•) stellar disk, and misalignment (★); cyan and red symbols indicate the corotation with the younger and older stellar disk, respectively. Associated error: 7°. (6) and (7) Luminosity weighted mean age and metallicity within 1 Re. Typical errors: 0.04 dex and 0.05 dex, respectively. (8) and (9) Age and metallicity gradients. (10) Modality of the weights maps from regularized fits: ‘uni’ for unimodal, ‘multi’ for multimodal, ‘sf’ for star-forming.
2.3 Detectability of CRDs: method and limitations
To study the detectability of CRDs in the MaNGA survey, we build dynamical models using the Jeans Anisotropic Modelling method and software jam1 (Cappellari 2008; Cappellari 2020); in particular, we used the cylindrically aligned version jamcyl. Briefly, jamcyl models are solutions for the steady-state axisymmetric Jeans equations under the assumption of constant mass-to-light ratio and cylindrically-aligned velocity ellipsoid: β = 1 − (σz/σR)2 and γ = 1 − (σϕ/σR)2.
Although fast rotators are well described by oblate velocity ellipsoid (σϕ ≈ σR ≳ σz) (e.g. section 3.4.3 of C16) CRDs present strong tangential anisotropy due to the counter-rotation; however, their kinematics is well reproduced when modeling the two discs separately, as two fast rotators counter-rotating in the same total gravitational potential, and then sum their contributions (fig. 12 of C16).
We now give the physical properties we used to build our CRD models and discuss these choices and their limitations afterward. We use the same Sérsic index, n = 1, for both discs, resulting in exponential profiles with scale lengths R+ ≡ Re, +/b1, and R− ≡ Re, −/b1, where b1 = 1.678; for the bulge we adopt the median Sersic index measured for bulges by Krajnović et al. (2013), n = 1.7 (then, b1.7 = 3.135). We fix the ratio R+/Re, bulge = 3.1, which is the median value measured for fast rotators by Krajnović et al. (2013), and corresponding to R+ = 2.5 kpc and Re, bulge = 0.8 kpc; Bluck et al. (2014) showed that the great majority of fast rotators in the local Universe have a bulge-to-total mass ratio lower than 0.2, so we fix Mbulge/M+ = 0.25 (thus assuming that the total mass is the sum of the bulge and the disc masses). We fix the intrinsic axial ratios q+ = q− = 0.25 for the two discs, and qb = 0.6 for the bulge, which are the peak values of the distributions of axial ratios for fast and slow rotators, respectively, in the ATLAS3D survey (Weijmans et al. 2014). We also include a central black hole of 108M⊙. We then impose that the gravitational potential is due to the combination of the MGEs describing the three stellar components (a dark matter halo is not included), and corresponding to a total mass equal to the median stellar mass of our CRDs, namely log10(M/M⊙) = 10.575. Finally, we adopt a distance of 154.8 Mpc, corresponding to the angular size distance at the median redshift of MaNGA, z = 0.0376. To take into account the spatial resolution, we convolve the jam models with the full width at half maximum, FWHM = 2.5 arcsec characteristics of the MaNGA data; we also use the spatial sampling and the corresponding signal-to-noise (S/N) of a real CRD (MaNGA ID: 1-94773),3 as produced by the DAP, and a spatial coverage of 1.5Re; further, we use the formal error of the kinematic spectral fitting (see Section 3.2) on each spatial bin as the noise for the final velocity and velocity dispersion model maps.
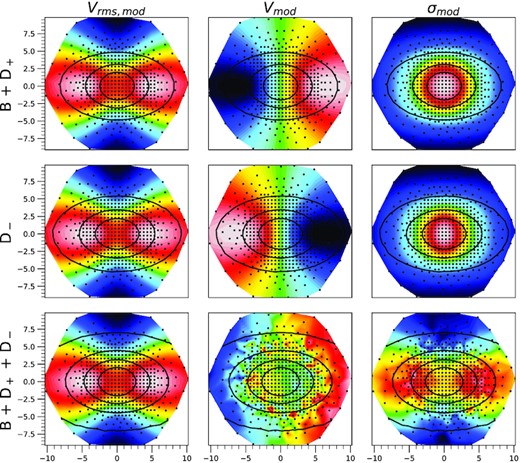
Root mean square velocity (Vrms, mod), velocity (Vmod), and velocity dispersion (σmod) models of the bulge combined with the disc corotating with it (B + D+) (first row), of the counter-rotating disc (D−) (second row), and of the luminosity weighted sums of the two components (third row). The small dots indicate the location of the centroids of each Voronoi bin. These models are produced using M−/M+ = 1, R−/R+ = 3/4 and i = 60°. The maps of Vmod and σmod in the bottom row include a realistic noise level, like that we used for our assessment of the CRDs detectability.
Figs 6–8 show how the final Vmod and σmod maps change at different couples of M−/M+, R−/R+andi, while keeping the third parameter fixed. In these figures we show models produced using values different from those in (i), (ii), and (iii) above, and without any noise, for illustrative purposes of how the maps change with parameters. We visually classified the CRDs of all the models, as we did for the real observations, and we found that of 420 models, 341 show at least one of the two characteristic CRD features; thus, we estimate a detectability of 81 per cent. As one would expect, the great majority of models with undetected CRD features are those with the lowest mass ratio, scale length ratio, and inclination.
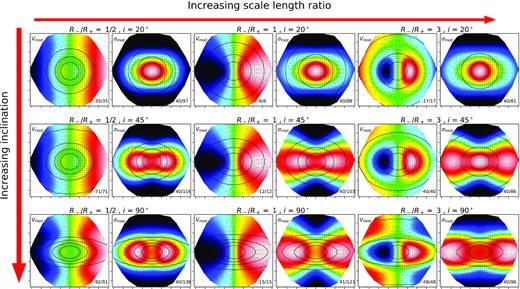
Models with varying R−/R+ and i at fixed M−/M+ = 3/4; in particular, these models are made with R−/R+ = 1/2, 1, 3 and i = 20°, 45°, 90°. The first, third, and fifth columns are Vmod maps, while second, fourth, and sixth columns are σmod maps. Colourmaps vary from blue (lower values) to red (highest values), with green being the zero-velocity; the min/max values (in km s−1) are showed in the bottom right corner of each panel.
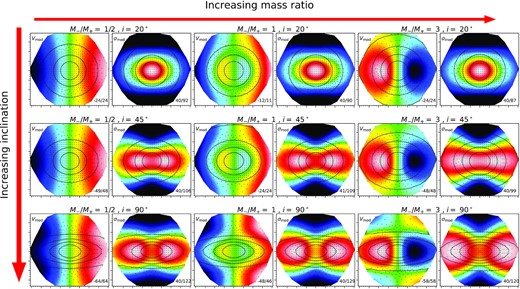
Models with varying M−/M+ and i at fixed R−/R+ = 3/4; in particular, these models are made with M−/M+ = 1/2, 1, 3 and i = 20°, 45°, 90°. The first, third, and fifth columns are the Vmod maps, while the second, fourth, and sixth columns are the σmod maps. Colourmaps vary from blue (lower values) to red (highest values), with green being the zero-velocity; the min/max values (in km s−1) are showed in the bottom right corner of each panel.
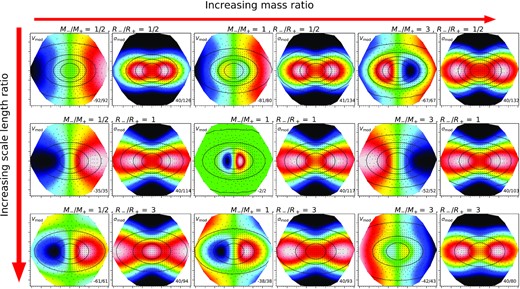
Models with varying M−/M+ and R−/R+ at fixed i = 60°; in particular, these models are made with M−/M+ = 1/2, 1, 3 and R−/R+ = 1/2, 1, 3. The first, third, and fifth columns are the Vmod maps, while the second, fourth, and sixth columns are the σmod maps. Colourmaps vary from blue (lower values) to red (highest values), with green being the zero-velocity; the min/max values (in km s−1) are showed in the bottom right corner of each panel.
Due to the low statistic of CRDs in the literature and to the variety of observed properties for the two discs (e.g. mass fraction, luminosity fraction, extension, thickness, etc.), the choice of the structural parameters to be used in models is not straightforward. Here, we discuss some major concerns:
The bulge in the CRDs studied so far has always been found to be negligible [e.g. NGC 3593, NGC 4550 (Coccato et al. 2013) and IC 719 (Katkov et al. 2013)]. None the less, we tested how the presence of the bulge influences the observed kinematics by changing its fixed parameters and found that it mainly influences the central regions of the velocity dispersion map, resulting in a central peak which is more (less) prominent when increasing (decreasing) its mass, but almost independent of its scale length; further, increasing the Sérsic index produces slightly better maps. The central velocity dispersion peak produced by the bulge prevails in the map only when the mass ratio of the two discs is low (particularly, when M−/M+ ≤ 0.4), and when the viewing angle is low (i < 40°). The counter-rotation feature in the velocity map, instead, is not particularly affected by the presence of the bulge; for this reason, it does not affect importantly the general estimate of the detection rate of CRDs.
The spatial resolution of MaNGA depends on the radial coverage, on the mass, and on the redshift of the galaxy considered. While we adopted parameters characteristic of MaNGA galaxies, a low mass CRD observed at high redshift with a 2.5Re coverage could be missed by our classification. However, among the ∼4000 galaxies we examined only 156 galaxies have a radial coverage reaching 2.5Re; of these, 88 have mass lower than log10(M/M⊙) = 10.575, and 67 of these are at redshift higher than 0.0376. Therefore, given the intrinsic rarity of CRDs among galaxies (a few per cent), we believe that only a few cases could have been missed because of our choices on spatial resolution.
The values of M−/M+ and R−/R+ considered are somehow arbitrary and some cases could be unrealistic: for example, models calculated at highest mass ratio with lowest scale length ratio, e.g. M−/M+ = 1.4 and R−/R+ = 0.5, imply that a galaxy formed a very massive (more than the pre-existing) counter-rotating disc within a small region, which seems unlikely. Such extreme cases may affect our statistics, but only of few per cent; indeed, all the other cases seem reasonable, since we generally expect that CRDs host a variety of mass and scale length ratios.
Other minor concerns (about, e.g. the R+ and Re, bulge values, the mass of the central black hole, and the exclusion of a dark matter halo) could be considered, but they are marginal issues since they do not particularly affect the detectability. In any case, a detailed modeling of CRDs is beyond the scope of this paper. We also point out that the statistics of CRDs we discuss in Section 5.1 are broadly consistent with previous studies, even assuming a detection rate much lower than the 81 per cent estimated by this analysis.
3 STELLAR AND GAS KINEMATICS
3.1 Templates library, resolution matching, and binning criterion
To extract the stellar kinematics of galaxies, a library of stellar templates of different spectral classes is generally fitted to the observed spectra. Libraries with a larger number of templates require larger computation time: for example, for ppxf the execution time is typically ∼O(Ntpl) for Ntpl templates. Thus, we selected a subsample of spectra, representative of the whole library, following the method and software used in Westfall et al. (2019; hereafter, W19) for the DAP: starting from the MILES stellar template library (Sánchez-Blázquez et al. 2006; Falcón-Barroso et al. 2011), which counts 985 stellar spectra, we applied a hierarchical-clustering algorithm4 to produce a desired subsample of ∼50 representative spectra. In brief, the reduced library is obtained by fitting each template with every other one in the MILES library, and, for each couple of templates, measuring the ‘distance’, in terms of residuals of the fit between the two spectra, calculated using equation (1) of W19; finally, spectra with distances lower than a fixed value dmax5 are clustered together.
With maximum distance of dmax = 0.065, we obtained 55 clusters. We then normalized each MILES spectrum to a mean of unity, and averaged all spectra in each cluster, in order to have a single representative spectrum per cluster; these averaged spectra are the templates for the actual kinematic fits. We finally removed from our library three spectra with prominent emission lines, resulting in a final set of 52 templates. W19 showed that using a subsample instead of the whole library leads to marginal biases in the extracted kinematics, while speeding up the computation time very significantly. Like W19, we refer to our distilled library as ‘MILES-HC’.
In general, when measuring the stellar kinematics, one wants the templates’ spectral resolution to match that of the observed spectra. The implications of ignoring the requirement of resolution matching, when fitting MaNGA spectra with the MILES library, are discussed in detail in section 7.4.3 of W19. They found that using spectra with higher spectral resolution than MaNGA data (the median instrumental resolution for MaNGA is ∼16 per cent larger than that of the MILES library) is actually convenient, particularly when the intrinsic stellar velocity dispersion is lower than the resolution of MaNGA. For this reason, we perform the fit of the mean velocity and the velocity dispersion by keeping both template and galaxies spectra at their native resolution.
W19 showed that for MaNGA data an average value of S/N ≥ 10 (in g-band) per log-rebinned spectral pixel of 69 km s−1 (see Section 3.2) is sufficient for reliable measurements of the first two moments of the LOSVD, and they used this value for the DAP. However, when fitting two kinematic components, it is fundamental to have sufficiently high S/N spectra to make the two components spectroscopically more distinguishable. On the other hand, binning data at very high S/N results in a significant loss of spatial resolution, and, in particular, CRDs can lose their peculiar kinematic features. To compromise between the request of a relatively high S/N, in order to better distinguish the two components, and the need for a relatively low S/N, in order to preserve enough spatial resolution, we chose to bin galaxies either with (S/N)min = 25 or (S/N)min = 15, depending on the resulting number of spatial bins: in practice, after excluding all spaxels with S/N ≤ 1, we first bin all galaxies to (S/N)min = 25; if the resulting number of bins is < 100, we rebin to (S/N)min = 15. The binning procedure has been performed using the Voronoi binning method and software6, described in Cappellari & Copin (2003).
Another difference with W19 is that we do not take the covariance between spaxels into account for the production of the maps to avoid too large Voronoi bins at large galactocentric radii at the expense of a slightly lower S/N.
3.2 Single component fits
For the extraction of the stellar kinematics, we fitted the datacubes provided by the MaNGA Data Reduction Pipeline (DRP) (Law et al. 2016), using the penalized pixel fitting method and software7 (ppxf) of Cappellari (2017); in particular, we only fitted the first two moments of the LOSVD. Before the fit starts, we set some parameters. First, as the spectra provided by the DRP are logarithmically rebinned in wavelength, we logarithmically rebinned the template spectra. Secondly, we set a constant velocity scale (which in ppxf corresponds to the wavelength sampling in pixel space) Vscale = cΔln λ ≈ 69 km s−1, where c is the speed of light, as the wavelength sampling of the MaNGA spectra is constant, and defined exactly as Δln (λ) = ln (10) × 10−4, chosen to have a step of 10−4 in log10(λ). To measure the kinematics with respect to the galaxy rest-frame, we de-redshift the observed spectra. We restrict the fitting spectral range, which is smaller for MILES than for MaNGA, to ∼3700−7400 Å. Finally, we masked regions of gas emission.
The kinematics solutions were obtained by performing two fits, both including degree-eight additive Legendre polynomials, which change the strength of spectral lines, to correct the continuum. We first considered as input spectrum the sum of the spectra of all spatial bins, normalized to their median value, and fitted it with all the 52 stellar templates of MILES-HC, setting the input noise to be constant with wavelength. From this first fit, we made a robust estimation of the standard deviation σstd of the residuals, and masked all regions of the spectrum deviating > 3σstd. We then performed a second fit, this time on every spatial bin of the galaxy. As template we only used the best-fit spectrum of the first fit, constructed as the weighted sum of the template spectra of MILES-HC; as the input constant noise we use σstd. Thus, we derived the two kinematic solutions for each spatial bin. The resulting rest-frame stellar velocity (V*) and (corrected) velocity dispersion (σ*) maps obtained for the whole sample are presented in an electronic appendix attached to this article.
3.3 Two-component fits and χ2 maps
To find the intrinsic velocity and velocity dispersion of the two stellar discs separately, one has to fit two kinematic components. However, even when the presence of two counter-rotating discs is obvious from the kinematic maps, the spectroscopical distinction of the two kinematic components is not possible if the velocity difference of the two stellar components is ΔV < σinst, as this implies that the two Gaussians are spectrally unresolved. Similarly, if the velocity dispersions of the two stellar discs are intrinsically large, the LOSVD of the two components will be hardly resolvable; furthermore, the recovery of the two components becomes more difficult when the S/N is low.
The recovery of the two kinematic components presents an additional complication when performing fits with a program designed to find a local minimum, like ppxf, because it requires a precise estimate of the input starting velocities of the two components. In fact, the best-fitting solutions are defined as the ones that minimize the χ2; since ppxf uses a local minimization algorithm, the global minimum will be missed if the input starting velocities are not accurate. To overcome this problem, we looked for the global minimum by creating a grid of χ2 values, obtained by fitting each of the two components with a set of input velocities; for each couple of velocities for the two components, we calculated the reduced χ2 (namely the χ2/DOF, where DOF are the degrees of freedom), and plotted it on a map. This method has already been used in Mitzkus, Cappellari & Walcher (2017) and in Tabor et al. (2017). In the electronic appendix (B) to this paper we give details on the method we used to produce χ2 maps, and the tests we made to improve it. Here, we only state that when the two counter-rotating discs are spectroscopically distinguishable, the χ2 map will have two distinct minima, like those shown in the left-hand panel of Fig. 9; on the contrary, when the two discs are not distinguishable the global minimum χ2 will be a cross, as in the right-hand panel of Fig. 9.
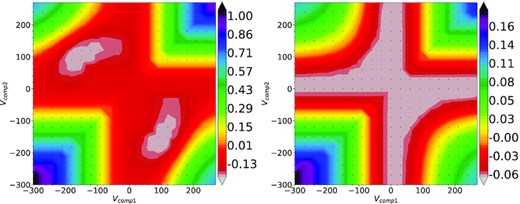
χ2 maps of galaxies with MaNGA IDs 1-38543 (left) and 1-167555 (right). The x- and y-axes are the fitted velocities. The black dots are the couples of velocities at which the local minimum χ2 is estimated. The colourbars are the log10(χ2/DOF). Left-hand panel: The global minimum χ2 is found in two distinct regions (in white) of the map; this indicates that the two counter-rotating discs are spectroscopically distinguishable. Right-hand panel: The global minimum χ2 is found in a single, cross-shaped (white) region; in this case, the two discs are not spectroscopically distinguishable. See the electronic Appendix B for details.
3.4 Gas and stars position angles, and kinematic misalignment
To compare gas and stellar rotation, we calculate the global kinematic position angle (PA) of the major axis, measured from north to east, of the velocity maps using the fit_kinematic_pa routine8, described in appendix C of Krajnović et al. (2006). The stellar kinematics are extracted as described in Section 3.2; for the ionized gas, instead, we simply use the kinematics of the H α emission as extracted by the DAP (W19; Belfiore et al. 2019). We excluded from the sample galaxies whose gas or stellar kinematics do not show a clear rotation pattern, or have many pixels with non-detection, making hard a reliable estimate of the PA, resulting in a sample of 42 CRDs.
When fitting the stellar PA, fit_kinematic_pa does not distinguish between the sense of rotation of the two counter-rotating discs; however, since they share the same rotation axis, we can define the misalignment between gas and stars using the stellar rotation axis as reference, without worrying about the sense of rotation. Furthermore, since the routine returns a PA between 0° and 180°, and does not discriminate between the redshifted and blueshifted sides, we considered misaligned those galaxies with 30° ≤ ΔPA ≤ 150°, namely those whose stellar and gas rotation axes have at least a 30° misalignment, regardless of their direction of rotation. The choice of 30° is arbitrary, and we choose it to allow for a comparison with previous studies (e.g. Davis et al. 2011; Bryant et al. (2019)).
Errors calculated by the routine are the 3σ confidence limit of the fit, and include the error on the χ2. However, the latter, even when the output PA is evidently good, often yields large errors that are not statistically meaningful. This is because the routine compares the observational data to a symmetrized model, and even little deviations from symmetry can yield large errors. This happens commonly when fitting the gas PA, since it often presents asymmetries or clumps. Even larger are the errors on the stellar PA, because of the inversion of the velocity field due to the counter-rotation. For these reasons, we do not provide errors calculated by the routine, and we assume a fixed representative uncertainty of 5° for all fitted PAs, that is the maximum error estimated by Duckworth et al. (2019), and in agreement with the median uncertainty of 5.2° for the ATLAS3D sample quoted by Krajnović et al. (2011). The values of ΔPA are given in Table 1.
For those galaxies who have their gas and stellar PA aligned, we determine whether the gas corotates with the ‘inner’ disc, namely the one whose kinematics prevail in the central regions of the galaxy, or the ‘outer’ disc, i.e. the one prevailing outwards, when the rotation is inverted. To establish which of the two discs the gas corotates with, we checked the kinematic maps and visually determined it. We show examples of alignment with the inner disc, alignment with the outer disc, and misalignment in Fig. 10. For those CRDs lacking the counter-rotation feature in the velocity map, we assume that the only disc that appears is the outer one; for example, if the gas counter-rotates with the only disc that is detected, we assume it is corotating with the inner disc.
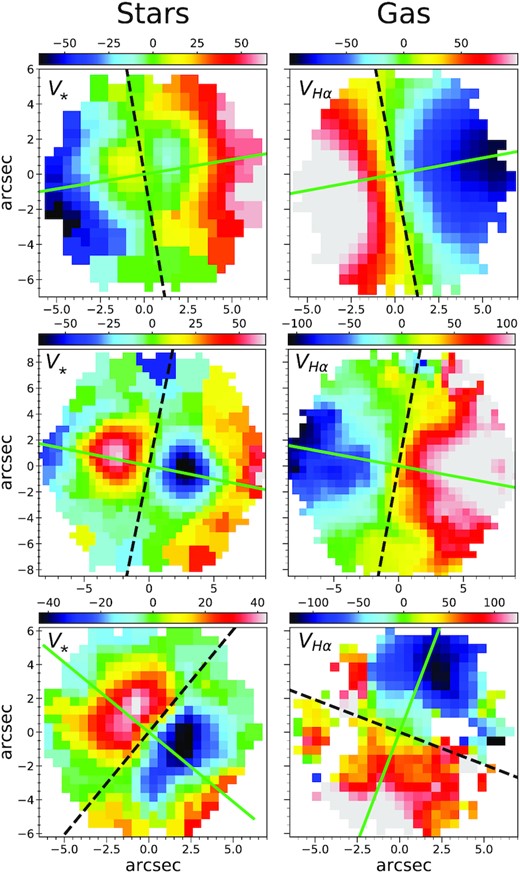
Three representative examples of stars (left columns) and gas (right columns) velocity fields of galaxies with the gaseous disc corotating with the inner disc (upper panels, MaNGA ID: 1-179561), with the outer disc (middle panels, MaNGA ID: 1-136248) and misaligned (lower panels, MaNGA ID: 1-163594). The straight lines in green are the major axis PAs, and the black dashed lines mark the rotation axes (calculated as PA+90°). Colourbars are the velocity ranges in km s−1.
4 STELLAR POPULATION FITTING
4.1 Stellar population maps
Since the strength of the spectral lines is rather sensible to the S/N, we tested if any substantial variation occurs in the fitting of the stellar population properties by increasing the target (S/N)min of the spatial bins. We found that those galaxies binned with (S/N)min = 25 do not show any noticable change when binned up to (S/N)min = 75, while those with (S/N)min = 15 can be different in the external regions, but the overall maps do not change significantly. Therefore, we kept the same spatial binning adopted for the kinematics (Section 3.1), in order to allow for a direct comparison between maps, and limited further considerations on the stellar population properties to the central regions, where the S/N is higher.
To extract the stellar population properties, we simultaneously fitted the stellar and the gas kinematics with ppxf. To fit the stellar component, we use the MIUSCAT SSP models (Vazdekis et al. 2010), based on the Padova isochrones (Girardi et al. 2000), with a Salpeter initial mass function, and we restricted to the safe range of parameters described in Vazdekis et al. (2012). The final library consists of 150 SSP models of 25 different ages, ranging between 0.06 and 15.84 Gyr at logarithmic steps, and six different metallicities [M/H] =−1.71, −1.31, −0.71, −0.4, 0.0, +0.22 dex. The templates for the gas emission lines are Gaussians; in particular, we fit the lines of the Balmer series H α, H β, H γ, and H δ, for which we fixed the flux ratios, the [S ii] doublet at λ = 6717, 6731 Å, [O iii] at λ = 5007 Å, and [N ii] at λ = 6583 Å. Before performing the fits, we de-redshifted the galaxy spectrum to the rest-frame, normalized the SSP templates to their median value, and logarithmically rebinned them; further, we applied a mask for the night sky emission lines of the [O i] at λ = 5578, 6301 Å and Na i at λ = 5890, 5896 Å, for these lines can be important in the MaNGA spectra. When fitting the stellar population, we are interested in the true strength of the spectral lines, and therefore we do not fit any additive polynomial; on the other hand, we use degree-eight multiplicative Legendre polynomials.
4.2 Gas-stars corotation and age maps
For those galaxies with the gas and stellar rotation aligned, we investigated whether the gaseous disc corotates with the younger or the older disc by comparing the velocity maps, both of H α and stars, with the age maps. Age maps are often noisy at large radii, and since the outer disc typically arises at radii larger than Re, in general it is not straightforward to determine which disc is the older and which the younger. Further, the age difference from the inner to the outer regions could be due to a genuine variation of the stellar population, rather than a difference in age of the two discs.
To take into account these considerations, we assigned a distinct age to the disc the gas is corotating with only when the following three conditions are met: (1) the change in the stellar population coincides with the inversion of the stellar rotation; (2) the age difference of neighbouring spaxels in the region of inversion is significant; (3) most spatial bins associated with the inner or the outer disc have the same age within ∼ 0.1 dex. For example, Fig. 11 shows how most bins within the region of inversion have log10Age≳ 10, while outside it most bins have log10Age ≲ 9.75; we can also see the abrupt change in age of neighbouring bins up to ∼0.6 dex in the region of the stellar rotation inversion. Here, the gas clearly corotates with the outer stellar disc, which is also the younger one.
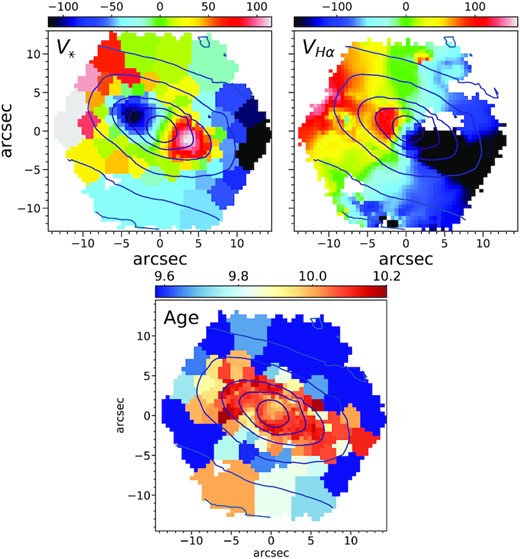
Stellar and gas velocity maps (upper panels) compared to the logarithmic age map (lower panel) of a CRD (MaNGA ID: 1-174947). Velocities are in km s−1. Age values are calculated using equation (8). In this example, we can see an abrupt change in age, coinciding with the inversion of the stellar rotation. The stellar rotation is inverted halfway from the third to the fourth isophote, starting from the center.The outer disc, which is corotating with the ionized gas, is also the younger one.
4.3 Regularized fits and multiple populations
To investigate the presence of multiple stellar populations in the same spatial region, we performed regularized fits in every spatial bin. Regularization is a technique to overcome the ill-posed problem of the recovery of the stellar population properties (e.g. section 3.5 of Cappellari 2017), and it can be considered as a method to smooth the weights of the solution of the SSP models during the fit.
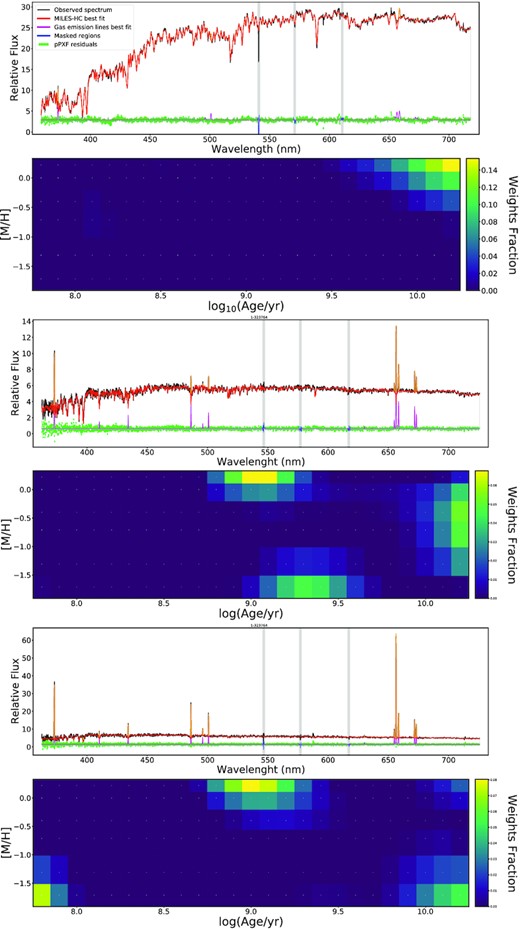
Examples of three stellar population regularized fits with ppxf and relative weights fraction maps of the fitted SSPs. Upper panels: Spectral fits of a central spatial bin of a galaxy (MaNGA ID: 1-248869) showing only one peak in the weights map; the same peak appears in all the other spatial bins considered, thus this galaxy is classified as ‘unimodal’. Middle and lower panels: Spectral fits of two different spatial bins of a galaxy (MaNGA ID: 1-323764) showing multiple peaks in the weights maps. In this case, the peaks change at different spatial bins, and this galaxy is thus classified as ‘star-forming’. Instead, galaxies showing the same multiple peaks at different spatial bins are classified as ‘multimodal’.
Since spatial bins with low S/N provide untrustworthy weights map, we say that a galaxy exhibits unimodality or multimodality by considering only those weights maps whose spatial bins have S/N ≥25. Additionally, we require the weights maps of a galaxy to be similar for all the spatial bins considered; this means that, for instance, to classify as unimodal the galaxy in the upper panels of Fig. 12, we require that all the spatial bins considered exhibit a blob in the upper-right corner of the weights map, and not a single blob that varies in age and metallicity at different bins. Many galaxies exhibiting multimodality also exhibit different weights maps at different (often neighbouring) spatial bins, like, for instance, the second and third maps of Fig. 12. We attribute this behaviour to ongoing star formation. For this reason, we further distinguish multimodal galaxies between those who exhibit the same multimodality in all the considered spatial bins, and those who instead vary significantly at different bins, and label the latter as ‘star-forming’.
5 RESULTS
In the following, we discuss the results of our study. Table 1 lists the main properties of our sample of galaxies hosting CRDs, including those derived here. The morphology and values of M* are taken from Graham et al. (2019). Re is taken from the DRP. The ΔPA values are calculated as described in Section 3.4. The global ages, metallicities, and relative gradients are calculated as described in Section 4. The modality column refers to the distinction in the weights fraction maps of regularized fits, described in Section 4.3. In Fig. 13 we show the SDSS image, along with the extracted maps of an illustrative galaxy. The same maps for all the other CRDs are shown in the electronic appendix A to this paper.
![Columns: (1) SDSS image with MaNGA ID overwritten; (2) and (3) Stellar velocity and velocity dispersion maps (in km s−1); (4) H α velocity map (in km s−1); (5) age map (log10(Age/yr)); (6) metallicity [M/H] map (in dex). Ticks are in arcsec. The same maps for all the other CRDs are shown in the electronic appendix A.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/511/1/10.1093_mnras_stab3732/1/m_stab3732fig13.jpeg?Expires=1750401148&Signature=nlN4PuWejBsSGbqqvvh3LXMVXIeSPnvzZEfNnxMRC081CxLa~zFFLFMoCjGxSgIj~R4rtkQcAja0lGtpInREPy3sTnz6jbfyiQ2aZRv6pYZf5RhKmzI~0Zhn1lQzmFyXu2ZTLLkVtl74U3VfMFL1e1gPPL4Yi4DBiJgZ~zRR0SwYQUowGNa-Gi4TJ22J18RKYIDoAnKrPU-xp3v2hY0OUB2zb~S5SBF6kc~Mj0qZr-~Anqlk1CSPhIzV1bz-~ju-ut9I-sJbpNsZZXXbtJ628VqMaLAcgm3naAIie-Guvl2tfc4Gnt~8MCDG1adRXIHzDU1hcVEITJMfpcIxbQxDaQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Columns: (1) SDSS image with MaNGA ID overwritten; (2) and (3) Stellar velocity and velocity dispersion maps (in km s−1); (4) H α velocity map (in km s−1); (5) age map (log10(Age/yr)); (6) metallicity [M/H] map (in dex). Ticks are in arcsec. The same maps for all the other CRDs are shown in the electronic appendix A.
5.1 Statistics of CRDs
In Section 2.2 we described how we identified 64 counter-rotators from the MaNGA sample, by requiring the appearance, in the kinematic maps, of one or both of two characteristic features: the counter-rotation and the two peaks in σ*. As mentioned in the Introduction, our capability of identifying CRDs is limited by both instrumental and intrinsic issues. To estimate the limits of detectability, we built dynamical models of a representative CRD in MaNGA and checked whether the two discs can be distinguished, by taking into account the instrumental properties of the survey, and by varying the main structural properties of the two discs affecting the kinematic maps, namely their mass ratio and their scale-length radius ratio, and the galaxy inclination. Then, we examined the maps resulting from models and selected CRD based on the criteria used in Section 2.2. The method and limitations of our modeling approach are presented and discussed in Section 2.3. From this analysis, we estimate a CRD detectability of 81 per cent in the MaNGA survey.
In our sample of 64 CRDs, 61 are ETGs, of which 38 are ellipticals and 23 lenticulars. The sample of the DR16 we considered includes 3129 ETGs, of which 1343 are ellipticals and 1786 are lenticulars. Taking into account our detectability estimate, this means that CRDs constitute |$(2.3\pm 0.3){{\ \rm per\ cent}}$| of ETGs (and |$\lt 3{{\ \rm per\ cent}}$| at |$95{{\ \rm per\ cent}}$| confidence11); in particular, |$3{{\ \rm per\ cent}}$| of ellipticals (|$\lt 5{{\ \rm per\ cent}}$| at |$95{{\ \rm per\ cent}}$| confidence11) and |$1{{\ \rm per\ cent}}$| of lenticulars (|$\lt 3{{\ \rm per\ cent}}$| at |$95{{\ \rm per\ cent}}$| confidence11) host a counter-rotating stellar disc (though, since ellipticals could be misclassified lenticulars such estimates should be considered carefully). The fraction of S0s is consistent with the early estimate of an upper limit of |$10{{\ \rm per\ cent}}$| at |$95{{\ \rm per\ cent}}$| confidence from long-slit spectroscopy (Kuijken et al. 1996). It is also consistent with the estimate of (1.5 ± 0.8) per cent (1σ confidence) from integral-field data by Krajnović et al. (2011). Further, among the ∼4000 galaxies considered, we examined the kinematic maps of 787 spirals, and found only one CRD, resulting in a fraction of |$\lt 1{{\ \rm per\ cent}}$| at |$95{{\ \rm per\ cent}}$| confidence11, consistent with the |$\lt 8{{\ \rm per\ cent}}$| estimated by Pizzella et al. (2004).
5.2 Spectroscopic evidence of counter-rotation
To have a spectroscopic confirmation that these galaxies are made of two kinematic stellar components, we have performed two-components fits, and presented the method of χ2 maps. We found that 17 galaxies exhibit distinct minima in the χ2 maps, meaning that the two counter-rotating components are spectroscopically distinguishable. We show the χ2 maps of these galaxies in Fig. 14.
χ2 maps of CRDs exhibiting two distinct minima, namely those where the two kinematic components are spectroscopically distinguishable. These maps were obtained by fitting a single representative spectrum per galaxy, chosen at one of the two σ* peaks, where the separation between the components is the largest (see the electronic appendix B for details). MaNGA-IDs are plotted above each panels. Colourbars values are the log10(χ2/DOF). In each panel, the x- and y-axes are the fitted Vcomp1 and Vcomp2, ranging within ±300 km s−1 at Vstep = 30 km s−1.
Generally speaking, the recovery of the two components with MaNGA data has been possible for galaxies with high S/N, and with clearer CRDs’ kinematic features, while for those galaxies with lower S/N and less clear kinematic maps the recovery of the two kinematic components is ineffective. However, we point out that four of the spectroscopically separable galaxies do not exhibit a clear counter-rotation (but they have very clear σ* peaks); conversely, many galaxies with evident counter-rotation or the two σ* peaks have not been found to be spectroscopically distinguishable. This is because the recovery of the two kinematic components also depends on the intrinsic stellar kinematics of the two discs, and on their contribution to the total flux.
The spectroscopical confirmation of the counter-rotating components for a larger number of CRDs requires data with higher S/N and better spatial resolution.
5.3 Stellar and gaseous discs
In Fig. 15 we show the results on the comparison between the velocity fields of stars and gas by plotting the 42 CRDs for which velocity maps are available for both (Section 3.4) on the mass-size diagram, introduced in Cappellari et al. (2013b). We found that in most of the cases (33 on 42), the gas velocity field is aligned with one of the stellar discs, and, in particular, in 15 cases the gas is corotating with the inner disc, and in 18 cases with the outer one. Therefore, there is no preferable corotation with the inner or the outer disc.
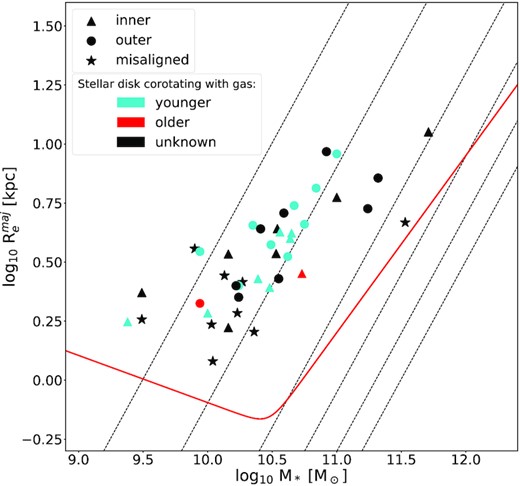
Alignment of the ionised gas with respect to the stellar rotation on the mass-size plane of CRDs. Here, M* is the stellar mass, and R|$_e^{maj} = 1.61 \times \mbox{R}_e$| is the effective radius of the major axis, defined in Cappellari et al. (2013a). The dashed black lines are lines of constant velocity dispersion at (left to right) 50, 100, 200, 300, 400, 500 km s−1. The red straight line is the zone of exclusion, defined in Cappellari et al. (2013a). The labels ‘inner’ and ‘outer’ refer, respectively, to the corotation of the gas with the stellar disc prevailing the inner or outer regions of the velocity field. Misaligned galaxies are those with 30° ≤ Δ PA ≤150°. Red and cyan symbols are for galaxies that have the gas velocity field corotating with either the younger or the older stellar disc, respectively, while unknown cases are black.
Of these 33 galaxies with stars and gas aligned, 18 also have age maps that distinctly change from the inner to the outer stellar disc. In 16 cases the gas corotates with the younger disc, while in two cases it corotates with the older disc. The comparison between stellar and gas velocity fields with age maps suggests that the distinction into inner and outer disc is just a matter of spatial distribution, and it is not helpful in determining which disc is the primary (pre-existing) and which the secondary (acquired).
For nine CRDs, namely 21 per cent of the 42 CRDs with velocity maps for stars and gas, the gas rotation is misaligned with respect to both stellar discs. From the SDSS images, four of these galaxies have neighbouring objects or surrounding blobs, which could be hints of recent gas accretion, and two also have evidences of ongoing star formation; on the other hand, the remaining galaxies appear isolated and undisturbed. In Fig. 15, we can see that misaligned galaxies typically have masses less than the break mass Mb = 3 × 1010 M⊙ (see fig. 23 of C16), with the exception of one galaxy. In the latter case, the misalignment could be related to the central black hole activity (Starkenburg et al. 2019; Duckworth, Tojeiro & Kraljic 2020); in fact, the H α velocity field has a large stellar velocity dispersion in the center, suggesting the presence of an AGN (Law et al. 2021).
5.4 Global stellar population properties
Except for three galaxies, our sample of CRDs is made of ETGs; to compare our results with the literature, we considered the results of Li et al. (2018; (hereafter, Li+18) on ∼900 ETGs from the MaNGA sample. The definition of the global properties, as well as the procedure to calculate gradients, are the same. The only significant difference with Li+18 is that they fitted stellar population properties using a reddening curve instead of multiplicative polynomials. The results by Li+18 are a useful benchmark as they were independently tested in detail by Liu (2020, their fig. 5) who found an excellent agreement.
The sample of Li+18 includes 39 of our CRDs; to evaluate how consistent our results on stellar population are with respect to Li+18, we compared the properties of the galaxies in common by fitting the relation y = a + b(x − x0), where x0 is the median value. As shown in Fig. 16, ages and metallicities show a good correlation; however, the difference in ages is systematic, with our ages being typically ∼0.15 dex older than those calculated by Li+18. We attribute this difference to the difference in the fitting procedure mentioned above. Given the good correlation between the two samples, we assume the typical errors for the age and metallicity values of all CRDs to be |$\Delta /\sqrt{2}$|, where Δ is the observed scatter in the linear fit; then we consider 0.04 and 0.05 dex as the typical errors for age and metallicity, respectively.
Comparison of global age and metallicity for 39 CRDs in common with the sample of Li+18. The blue dots are the values used to fit the linear relation y = a + b(x − x0), with x0 being the mean value, while green dots are outliers excluded by the routine during the fit. The black dashed and dotted lines are the 1σ and 2.6σ confidences, respectively. The red straight line is the y = x line. The best-fitting coefficients are texted on the plots; εy and Δ are the intrinsic and observed scatters, respectively.
On the other hand, gradients do not correlate very well (the correlation coefficients for age and metallicity gradients are r = 0.42 and r = 0.39, respectively, with associated correlation probabilities p = 0.01 and p = 0.02). We ascribe the lack of correlation of gradients to the fact that they are intrinsically difficult to determine, and the method used by us and Li+18 to estimate them is sensitive to small differences in the fitting procedure of the stellar population properties of single bins, as well as the fit of the profiles.
In Fig. 17 we show the stellar population properties of CRDs on the mass-size diagram, and compare them to ETGs from Li+18. It is evident that CRDs follow the same trend in age and metallicity as ETGs. Even though CRDs appear systematically older than ETGs, the age difference is of the same order of that in Fig. 16; therefore we attribute this difference to the difference in the fitting procedures, and conclude that CRDs and ETGs are consistent with having similar ages. From the comparison of the metallicities, instead, it seems that, while having similar metallicities at high masses, CRDs are significantly less metallic at low masses. We verified that this difference is true, and not due to a bad LOESS smoothing (e.g. due to the presence of few outliers with very low metallicities). However, the dispersion of metallicity values for ETGs at low σe (i.e. low masses) is large (see fig. 5 of Li+18), and such that their trend may be consistent with that of CRDs; additionally, the statistics of low mass CRDs is low, and a larger number may result in a trend similar to that of ETGs. We then conclude that, from this study, CRDs appear to be less metallic than ETGs at the lower stellar masses; however, a more thorough statistical analysis is necessary to confirm or disprove this statement.
![LOESS-smoothed log10Age (left columns) and metallicity [M/H] (right columns) of CRDs (upper panels) and ETGs from Li+18 (lower panels). Lines are the same of Fig. 15. Note: Masses of CRDs are calculated from the photometry, using equation (2) of Cappellari (2013); instead, masses in Li+18 are calculated from dynamical models.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/511/1/10.1093_mnras_stab3732/1/m_stab3732fig17.jpeg?Expires=1750401148&Signature=aFiXf0kH-U0OCDtjO5g9UxBaX1Bnqkr-AXkZaGqhy4QGAa6cnrzG8CdPtvvfvSzqXTlU7UEvPMaADjyRh3dpslrHIFAujeqXjMHkQ3BHBch8Yv9aI4cSVJ-4rylxBUUpvg-dCU~hR1qhtrxou7AslsZYLOVJgdFOR4kYU5fwgLDxT27etvkHnoBRRrlRHyDvABNawWciPKj1rO3Wkx0oJxGV5DJr5EHySVDaA23vBajn7wITNR2Z5wQXUAfBk7pvHA0Iv0EWkDMG-KhJZIjD2r~EcMGiTwNijv6CUZue4EGBiOys9pesq6H3V0wea38923aWEYlUsIN2KLc3nSwCNQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
LOESS-smoothed log10Age (left columns) and metallicity [M/H] (right columns) of CRDs (upper panels) and ETGs from Li+18 (lower panels). Lines are the same of Fig. 15. Note: Masses of CRDs are calculated from the photometry, using equation (2) of Cappellari (2013); instead, masses in Li+18 are calculated from dynamical models.
In Fig. 18 we compare gradients of CRDs and ETGs. Metallicity gradients of CRDs, albeit slightly steeper on average, are similar to those of ETGs, and also cover the same range of values; similarly, age gradients of CRDs are typically flatter, but cover a comparable range of values to ETGs.
It should be pointed out that the definition we gave of the global stellar population properties, as well as the relative gradients, refer to the spatial region within the effective radius, namely the typical region where the spectrum is dominated by the inner disc. This implies that results on the stellar population properties can be biased towards the major contributor of the inner regions; in fact, as discussed in Section 4.2, many age maps show an abrupt change of the stellar age from one disc to the other. We verified that results on stellar population properties, especially on age gradients, can be significantly different when extended to larger radii; however, since the external spatial bins generally have low S/N, and fits can be unreliable, we are not confident in presenting such results, and only point out that a more accurate analysis of the stellar population properties of CRDs requires good quality observations out to the most external regions, or the spectroscopic disentangling of the two discs.
5.5 Unimodal, multimodal, and star-forming CRDs
By performing regularized fits, we distinguished galaxies into unimodal, multimodal and star-forming, based on the analysis of the weights map of the stellar population fits. We found 14 CRDs exhibiting unimodality, 31 CRDs exhibiting multimodality, and 14 star-forming CRDs, plus five uncertain cases. In Fig. 19 we show them in a mass versus age diagram.
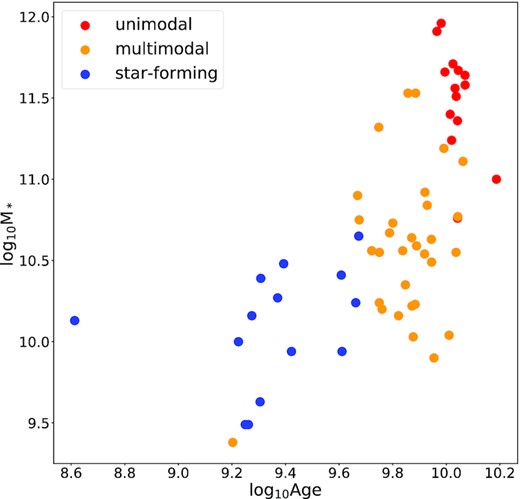
CRDs on the mass versus age diagram. The distinction into unimodal, multimodal, and star-forming is based on the weights maps of regularized fits (Section 4.3) and was possible for 49 CRDs. Unimodal and multimodal galaxies are those exhibiting the same single or multiple blobs all over the galaxy, while those labelled as star-forming have multimodal maps that change at different spatial regions of the galaxy.
From the diagram, we can see a clear distinction between the three classes. All unimodal galaxies are old and massive. Although most of them are confined within the region of slow rotators (Emsellem et al. 2011) on the (|$\lambda _{R_e}, \varepsilon$|) diagram, the fact that most of these galaxies exhibit both counter-rotation and the two σ* peaks at large radii, and that three of them have been spectroscopically found to be counter-rotating, persuade us that they are not misclassified CRDs. On the contrary, star-forming galaxies are the youngest and have low masses (<Mb, for most of them); interestingly, six of the eight ‘CRDs in formation’ (Section 2.2) are included in this class (the other two are multimodal), which further support that these CRDs have formed just recently. Finally, multimodal galaxies have intermediate ages, while spanning a large range of masses.
6 DISCUSSION
In light of the results of this work, we discuss now the applicability of the formation scenarios for CRDs mentioned in the Introduction.
The general statistics of CRDs among MaNGA galaxies is relatively low, in agreement with other galaxy surveys or samples with different targeting criteria, like ATLAS3D (where CRDs constitute the |$4{{\ \rm per\ cent}}$| of the sample). This generally low statistics of CRDs presumably reflects the intrinsic difficulty of building up a massive and extended counter-rotating stellar disc, rather than a low detection rate due to instrumental limits (even though a significant fraction of CRDs is probably missing because of it). Our results, in agreement with previous studies, suggest that the statistics of CRDs decrease from early to late morphological types of the Hubble sequence. This can be interpreted as evidence that the gas accretion scenario is, in general, the most common route to produce a CRD; in fact, to form a counter-rotating disc from an external gas supply, any pre-existing gas in the progenitor galaxy must be swept away before the counter-rotating disc forms. Therefore, it is easier for a CRD to form in a gas-poor galaxy than in a gas-rich one; this would also explain why no late spirals have ever been observed hosting a CRD since they typically have a larger fraction of gas than early spirals and ETGs.
The formation of a counter-rotating stellar disc by accretion of external gas in a retrograde orbit always implies that the secondary disc is also the younger one, and that it corotates with the gaseous disc (e.g. Coccato et al. 2013). The fact that in most of the CRDs with the gaseous and stellar discs aligned and distinct ages for the stellar discs (18 cases) the gas corotates with the younger disc (16 cases) supports this formation scenario against the others. Additionally, 14 of these 16 cases have multimodal or star-forming weights maps (the other two cases are unknown), implying the coexistence of multiple stellar populations with different ages and metallicities in the same spatial regions, and all over the galaxy.
The same scenario of an origin of the counter-rotating disc by retrograde gas accretion may be likely also for those galaxies with misalignment between gas and stars, since this is an evidence of recent gas accretion (note, however, that the misalignment could be due to an accretion event subsequent and unrelated to the formation of the counter-rotating disc). The fraction of misaligned CRDs (|$\sim 21{{\ \rm per\ cent}}$|) is lower than that of misaligned fast rotators (|$\sim 36{{\ \rm per\ cent}}$| in ATLAS3D; Davis et al. 2011), suggesting that CRDs are more likely to have the gas and stars aligned; in fact, if the counter-rotating stellar disc forms via gas accretion, we expect the gaseous disc to be aligned with it. Misalignment as a sign of recent accretion, and linked with the early stages of the formation of the counter-rotating disc, would be the case for three of the nine misaligned CRDs in our sample with ongoing star formation, as resulting from the weights map, from the SDSS images, and from the disturbed stellar kinematics. Further, if a CRD formed via episodic accretion of gas, misalignment could be due to a recent episode of accretion. For the other cases, misalignment is probably unrelated to the formation of the CRD. To further investigate the relation between misalignment and the origin of CRDs, it would be useful to know the dynamical settling time of the gas, to be compared with the duration of gas accretion; the latter could be difficult to determine, though, since it depends on many circumstances, as the source of external gas (Thakar et al. 1997), the accretion modalities (Thakar & Ryden 1996), and the angular momentum of the gas (Bryant et al. 2019). Note that cosmological simulations of a massive ETG in a realistic environment show that the evolution of misaligned discs can be complex, with the misalignment persisting several (∼ 2 to 5) Gyr (van de Voort et al. 2015; Davis & Bureau 2016).
For the two cases where the gas corotates with the older disc, the CRD formation via gas accretion is unlikely; the difference in age between the two discs also discards the formation by internal instabilities. One can advocate a scenario in which a disc galaxy in a prograde orbit merges with a gas-poor galaxy with a younger stellar population that rotates in a retrograde orbit; the latter would then settle into a counter-rotating stellar disc, while the gas, originally associated with the primary disc, keeps corotating with it.
As evident from Fig. 19, all CRDs exhibiting unimodality are also the oldest and most massive. At such old ages, it is not straightforward to determine whether the two discs actually have the same stellar population, or it is rather the technical difficulty of separating the spectra of two very old populations with similar metallicities that makes them appear as one. Therefore, we cannot rely on this analysis to discuss which scenario is most favourable. However, a detailed study on these CRDs would be of great interest; in fact, if these galaxies truly have a single, old stellar population, the two discs must have formed from the same chemical mixture and in the same event of star formation that gave origin to the galaxy, thus supporting the formation scenario by internal processes, so far disproved by observations.
Finally, even the CRD formation in a major merger event seems viable, since it is consistent with the properties observed for some CRDs. For example, a recent merger could explain the highly disturbed kinematics and morphology shown by a number of CRDs; and even the old massive unimodal CRDs could be the result of a major merger that took place a long time ago, in which the stellar discs of the progenitors had the same ages and metallicities (though this is unlikely to apply to all the 14 unimodal CRDs).
To further investigate the formation scenarios of CRDs, a spectral decomposition of the two stellar discs is needed. This analysis would provide additional information on the kinematics, as the velocity dispersions of the two discs, and on the stellar population properties, as the metallicity, the age, and the metallicity gradient separately for the two discs.
If many (or all) of the proposed scenarios are statistically relevant, the major role in the formation of a CRD is played by its environment. For example, merger and interaction may be a more likely origin for CRDs in relatively dense environments, where gas stripping and galaxy motions make gas accretion difficult. In low-density environments and in the field, instead, galaxies can acquire undisturbed a large amount of gas from, e.g. cosmological filaments; for a CRD in such an environment, then, formation via gas accretion seems more probable. In conclusion, a study of CRDs in relation with their environment is of great importance to determine the relevance and the statistics of the many proposed formation scenarios.
Overall, this work supports the idea that galaxies with counter-rotating stellar discs form primarily via a retrograde accretion of gas, although other formation channels cannot be excluded in a number of cases.
7 SUMMARY AND CONCLUSIONS
We used data from the DR16 of the MaNGA survey to construct a sample of galaxies with counter-rotating stellar discs. After excluding problematic cases (Section 2.2), we visually inspected the kinematic maps of about 4000 galaxies, and selected those that exhibit at least one of the two kinematic features characterizing counter-rotators (counter-rotation or two peaks in σ*); we designated these galaxies with the acronym ‘CRD’. We studied the stellar and gas kinematics, and the stellar population properties of these CRDs. We summarize our results as follows:
The sample consists of 64 CRDs, 61 of which are ETGs (38 E and 23 S0), one is a spiral and two have uncertain morphology. CRDs constitute, at 95 per cent confidence, <3 per cent of ETGs (in particular, <5 per cent of E and <3 per cent of S0), and <1 per cent of spirals, in agreement with previous estimates.
From two-components kinematic fits, we obtained spectroscopic confirmation that 17 CRDs comprise two counter-rotating stellar components.
We calculated the difference in the PAs of the gas and the stellar velocity fields of 42 CRDs, and found that in 33 cases the gas is aligned with one of the two stellar discs, without preference for the disc prevailing in the inner or in the outer region. By comparing with the age maps, we were able to qualitatively determine that in 16 cases the gas corotates with the younger disc, and in two cases with the older one. In nine cases, the gaseous disc is misaligned, and in eight of these cases, the stellar mass is lower than the break mass Mb.
The analysis of the stellar population properties indicates that CRDs have similar trend in ages and metallicities as ETGs, but CRDs appear less metallic at low masses. CRDs also have similar age and metallicity gradients, while being, on average, typically flatter the former and steeper the latter.
We distinguished CRDs based on the number of different stellar populations present in the weights maps of the regularized fit of various spatial bins. We found that CRDs exhibiting unimodality (14) are the oldest and most massive. CRDs with a multimodal and variable weights map, that we labelled as star-forming (14), are the youngest and least massive. Finally, CRDs with the same multimodal weights maps all over the galaxy (31) have intermediate ages, and span a wide range of masses.
Based on these results on the first relatively large sample of CRDs, we conclude that the unique kinematic class of galaxies with counter-rotating stellar discs form primarily via external counter-rotating gas accretion. However, Nature is rarely captured by a simple scenario, and also in the case of CRDs other mechanisms are as well possible in specific cases. Older and more massive unimodal CRDs may have formed via internally driven mechanisms; their formation via major merger, albeit unlikely, can not be a priori ruled out.
To further investigate the CRDs in our sample, observations with higher resolution and S/N are needed. Additionally, the spectral decomposition of the two discs for each galaxy would provide cogent evidences to constrain the proposed formation scenarios. Finally, a study of the environment of CRDs would help understand how it correlates with the observed CRD properties, and then its possible role in the different formation scenarios.
SUPPORTING INFORMATION
Figure A1 SDSS and maps of all the sample of 64 CRDs.
Figure B1 Two examples of χ2 maps.
Figure B2 χ2 maps for the galaxy with MaNGA ID: 1-38543.
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
We want to thank the anonymous referee for the constructive comments and suggestions that helped improving this paper.
DATA AVAILABILITY
The data cubes of the DR16 are publicly available, as well as the kinematic maps produced by the DAP, and can be found at https://www.sdss.org/dr16/manga/. The softwares used in this paper are all public. The kinematic and stellar population maps of the whole sample of CRDs are provided in an electronic appendix; values used to produce maps are not provided. Values tabulated in Table 1 are available also in electronic format. Data used for Fig. 1 are available as supplementary electronic material.
Footnotes
Available from https://pypi.org/project/jampy/
Available from https://pypi.org/project/mgefit/
This CRD was selected because its mass and redshift are similar to the values chosen for our model.
Available from https://github.com/micappe/speclus
This corresponds to the parameter threshold in the scipy function cluster.hierarchy.fcluster, with criterion = ‘distance’, used to perform the clustering of the spectra.
Available from https://pypi.org/project/vorbin/
Available from https://pypi.org/project/ppxf/
Available from https://pypi.org/project/pafit/
Available from https://pypi.org/project/loess/.
Available from https://pypi.org/project/ltsfit/
Applying Poisson distribution statistics.




