Role of the radiative stage for cosmic ray acceleration in SNRs

Zirakashvili, V N; Ptuskin, V S

doi:10.1093/mnras/stab3691

ABSTRACT

We consider diffusive shock acceleration in supernova remnants throughout their evolution including a radiative stage. It is found that a more efficient acceleration and fast exit of particles at the radiative stage results in the hardening of the source cosmic ray proton and electron spectra at energies ∼100–500 GeV. The effect is stronger for cosmic ray electrons.

acceleration of particles, shock waves, ISM: supernova remnants

1 INTRODUCTION

Supernova remnants (SNRs) are considered now as a principle source of Galactic cosmic rays (CRs). It is believed that the diffusive shock acceleration (DSA) mechanism (Axford, Leer & Skadron 1977; Krymsky 1977; Bell 1978; Blandford & Ostriker 1978) operates in the vicinity of shocks in SNRs. During the last decades, the modern X-ray and gamma-ray observations supplied the evidence of the presence of multi-TeV energetic particles in these astrophysical objects (see e.g. Lemoine-Goumard 2014 for a review).

Usually, the existing DSA models are applied for young SNRs where the most energetic CRs are accelerated. However, lower energy particles are produced in older SNRs either. The investigation of CR acceleration in SNRs throughout all evolutionary stages is important for the calculation of overall CR spectra produced by SNRs.

In this paper, we describe the modifications of our non-linear DSA model (Zirakashvili & Ptuskin 2012) designed for investigation of DSA over the entire life of SNRs. The preliminary results on the application of this modified model to gamma-ray bright SNRs W28, W44, and IC443 were reported in Zirakashvili (2018) and Zirakashvili & Ptuskin (2016a, 2018a). The main new features are the gas ionization by the radiation of the remnant, radiative cooling of the gas, and damping of magnetohydrodynamic (MHD) waves on neutral atoms at the late stages of SNR evolution. We also performed the modelling of acceleration and production of broad-band electromagnetic emission in the young SNR Tycho and middle-aged SNR W44 to adjust the parameters of the model.

The paper is organized as follows. In Section 2, we describe our model. CR acceleration in IIP type SNRs evolving in the dense medium and modelling of non-thermal emission of SNR W44 is presented in Section 3. The modelling of Ia Type SNRs evolving in a more rarefied medium and the modelling of SNR Tycho are described in Section 4. The discussion of results and conclusions are given in Sections 5 and 6.

2 NON-LINEAR DIFFUSIVE SHOCK ACCELERATION MODEL

Details of our basic model of non-linear DSA can be found in Zirakashvili & Ptuskin (2012). The model contains coupled spherically symmetric hydrodynamic equations and the transport equations for energetic protons, ions, and electrons. The forward and reverse shocks are included in the consideration.

Damping of MHD waves due to the presence of neutral atoms is important for SNRs expanding in not fully ionized gas. To take this effect into account we add the equation that describes the transport and generation of MHD waves (see equation 5 below).

The hydrodynamical equations for the gas density ρ(r, t), gas velocity u(r, t), gas pressure P_g(r, t), wave pressure P_w(r, t), pressure of the regular magnetic field P_m(r, t), and the equation for isotropic part of the CR proton momentum distribution N(r, t, p) in the spherically symmetrical case are given by

$$\begin{eqnarray*} \frac{\partial \rho }{\partial t}=-\frac{1}{r^2}\frac{\partial }{\partial r}r^2u\rho \end{eqnarray*}$$

(1)

$$\begin{eqnarray*} \frac{\partial u}{\partial t}=-u\frac{\partial u}{\partial r}-\frac{1}{\rho } \left(\frac{\partial P_g}{\partial r}+\frac{\partial P_c}{\partial r} +\frac{\partial P_w}{\partial r}+\frac{\partial P_m}{\partial r}\right) \end{eqnarray*}$$

(2)

$$\begin{eqnarray*} &&{\frac{1}{\gamma _g-1}\left(\frac{\partial P_g}{\partial t}+u\frac{\partial P_g}{\partial r} +\frac{\gamma _gP_g}{r^2}\frac{\partial r^2u}{\partial r}\right)}\nonumber\\ &&{\quad =-\Lambda (T_e)n^2+H_{c}+2\Gamma _n\frac{P_w}{\gamma _w-1}-\xi _AV_{Ar}(1-h_w)\frac{\partial P_c}{\partial r} } \end{eqnarray*}$$

(3)

$$\begin{eqnarray*} \frac{\partial P_m}{\partial t}+u\frac{\partial P_m}{\partial r} +\frac{\gamma _mP_m}{r^2}\frac{\partial r^2u}{\partial r}=0 \end{eqnarray*}$$

(4)

$$\begin{eqnarray*} &&{\frac{\partial P_w}{\partial t}+(u+\xi _AV_{Ar})\frac{\partial P_w}{\partial r} +\frac{P_w}{r^2}\frac{\partial r^2(\gamma _wu+\xi _AV_{Ar})}{\partial r}}\nonumber\\ &&{\quad =-h_w(\gamma _w-1)\xi _AV_{Ar}\frac{\partial P_c}{\partial r}-2\Gamma _nP_w } \end{eqnarray*}$$

(5)

$$\begin{eqnarray*} \frac{\partial N}{\partial t}&=&\frac{1}{r^2}\frac{\partial }{\partial r}r^2D(p,r,t) \frac{\partial N}{\partial r} -w\frac{\partial N}{\partial r}+\frac{\partial N}{\partial p} \frac{p}{3r^2}\frac{\partial r^2w}{\partial r}\nonumber\\ &&+\frac{1}{p^2}\frac{\partial }{\partial p}p^2b(p)N+\frac{\eta _fX_i\delta (p-p_{f})}{4\pi p^2_{f}m}\rho (R_f+0,t)\nonumber\\ &&\times \,\,(\dot{R}_f-u(R_f+0,t))\delta (r-R_f(t))+\frac{\eta _b\delta (p-p_{b})}{4\pi p^2_{b}m}\nonumber\\ &&\times \,\,\rho (R_b-0,t)(u(R_b-0,t)-\dot{R}_b)\delta (r-R_b(t)) . \end{eqnarray*}$$

(6)

Here, P_c = 4π∫dpp³vN/3 is the CR pressure, w(r, t) is the advection velocity of CRs, T_e, γ_g, and n are the gas temperature, adiabatic index, and number density, respectively, γ_w is the wave adiabatic index, D(r, t, p) is the CR diffusion coefficient. The radiative cooling of gas is described by the cooling function Λ(T_e). The function b(p) describes the energy losses of particles. In particular, the Coulomb losses of sub-GeV ions and the radiative cooling are important in old SNRs. The energy of sub GeV ions goes to the gas heating described by the term H_c in equation (3).

CR diffusion is determined by the scattering on magnetic inhomogeneities. The CR streaming instability increases the level of MHD turbulence in the shock vicinity (Bell 1978) and even significantly amplifies the absolute value of the magnetic field in young SNRs (Bell 2004; Zirakashvili & Ptuskin 2008a). It decreases the diffusion coefficient and increases the maximum energy of accelerated particles. The results of continuing theoretical study of this effect can be found in review papers (Bell 2014; Caprioli 2014).

CR particles are scattered by moving waves and it is why the CR advection velocity w may differ from the gas velocity u by the value of the radial component of the Alfvén velocity |$V_{Ar}=V_A/\sqrt{3}$| calculated in the isotropic random magnetic field: w = u + ξ_AV_Ar. The factor ξ_A describes the possible deviation of the CR drift velocity from the gas velocity. We use values ξ_A = 1 and ξ_A = −1 upstream of the forward and reverse shocks, respectively, where Alfvén waves are generated by the CR streaming instability and propagate in the corresponding directions.

The situation is less clear in the downstream region of the shocks. Usually, the Alfvén drift is not considered here. However, it is known that Alfvén transport in the downstream region suggested at phenomenological level (Zirakashvili & Ptuskin 2008b) results in steeper spectra of accelerated particles. This also allow avoiding a CR overproduction in evolutionary models of SNRs (Ptuskin et al. 2010).

Recently, the Alfvén transport in the downstream region was indeed observed in hybrid modelling of collisionless shocks (Haggerty & Caprioli 2020). It looks like some non-linear magnetic structures are generated in the shock transition and move with Alfvén speed in the downstream region. The origin of these non-linear waves is unclear. They can be large-scale transverse Alfvén-like waves propagating in the isotropic tangle magnetic field with phase speed |$V_A/\sqrt{3}$| (Moffatt 1986). Or they somehow can be related to sonic waves generated at the shock front.

Below we take the Alfvénic transport in the downstream region into account. We use values ξ_A = −1 and ξ_A = 1 just downstream of forward and reverse shocks, respectively. The Alvénic transport takes place in the narrow region of thickness 0.1 of the distance between the shock and the contact discontinuity.

The pressure of generated waves P_w determines the scattering and diffusion of energetic particles with charge q, momentum p, and speed v

$$\begin{eqnarray*} D=D_B\frac{P_m+P_w}{P_w}, \ D_B=\frac{cpv}{3qB}, \ B=\sqrt{8\pi (P_m+P_w)} , \end{eqnarray*}$$

(7)

where B is the total magnetic field strength, while P_m is the pressure of the regular field. At high wave amplitudes, the diffusion coefficient coincides with the Bohm diffusion coefficient D_B.

The parameter h_w in equations (3, 5) describes the fraction of the wave energy produced by the streaming instability. We use the following dependence h_w(P_w/P_m)

$$\begin{eqnarray*} h_w=1, \ \frac{P_w}{P_m}\lt 10; \ h_w=0.7, \ \frac{P_w}{P_m}\gt 10. \end{eqnarray*}$$

(8)

At high amplitudes, the waves are damped and the fraction 1 − h_w of energy goes into the gas heating upstream of the shocks (McKenzie & Völk 1982) that is described by the last term in equation (3). The heating and wave generation limits the total compression ratio of CR modified shocks. The value of h_w regulates the magnetic amplification in the upstream region of the shock. Since the amplified field is transported into the downstream region, h_w also determines the efficiency of the Alfvénic transport in this region and regulates the spectral slope of accelerated particles. Its value h_w = 0.7 was adjusted to reproduce broad-band modelling of Tycho SNR (see Section 4 below).

The low seed level of the interstellar turbulence |$P_w=10^{-6}B_0^2/8\pi$| is prescribed at the simulation boundary at r = 2R_f. Since the flux of escaped highest energy particles amplifies waves exponentially in time the results depend only logarithmically on the seed level.

In the shock transition region, the wave pressure is increased by a factor of |$\sigma ^{\gamma _w}$|⁠, where σ is the shock compression ratio. Its impact on the shock dynamics is taken into account via the Hugoniot conditions.

Below, we use the adiabatic index of Alfvén waves γ_w = 3/2. For this value of the adiabatic index, the wave pressure P_w = (δB)²/8π equals the wave magnetic energy density. The pressure of the regular field P_m plays a dynamical role at the radiative phase when the field is strongly compressed in the downstream region and produces a significant anisotropic force in the radial direction. To take this into account we use the adiabatic index γ_m = 2 for the regular magnetic field.

The rate of the neutral damping Γ_n = 0.5ν_in is determined by the frequency of ion neutral collisions ν_in in the limit of the high wave frequencies ω > >ν_in. The frequency of ion-neutral collisions is determined by charge-exchange process and is given by (Drury, Duffy & Kirk 1996)

$$\begin{eqnarray*} \nu _{in}=8.9\times 10^{-9} n_n \left(\frac{T}{10^4\ \mathrm{K}}\right) ^{0.4}\ \mathrm{s}^{-1}. \end{eqnarray*}$$

(9)

Here, the number density n_n = X_nn_H of neutral hydrogen atoms is determined by the neutral fraction X_n. A useful review of DSA in partially ionized plasma can be found in Bykov et al. (2013).

The neutral fraction of hydrogen ions X_n is determined by equation

$$\begin{eqnarray*} \frac{\partial X_n}{\partial t}=-u\frac{\partial X_n}{\partial r} +\alpha _{\mathrm{rec}}n_HX^2_i-X_n(q_{\mathrm{th}}+q_{\mathrm{ph}}), \end{eqnarray*}$$

(10)

where X_i = 1 − X_n is the fraction of ionized Hydrogen, α_rec is the recombination rate and q_th and q_ph are thermal ionization and photoionization rates, respectively. The photoionization rate is given by

$$\begin{eqnarray*} q_{\mathrm{ph}}(r)= 2\pi \int ^\pi _0\sin (\theta)d\theta \sigma _{\mathrm{ph}}I(r,\theta) . \end{eqnarray*}$$

(11)

Here, θ is the angle between the photon wavevector and radial direction and σ_ph is the photoionization cross-section of Hydrogen. The intensity of ionizing photons I(r, θ) is determined from the equation of radiative transport

$$\begin{eqnarray*} \cos (\theta)\frac{\partial I}{\partial r} -\frac{\sin (\theta)}{r}\frac{\partial I}{\partial \theta } = \frac{\Lambda _i(T_e) n^2}{4\pi I_H}-\sigma _{\mathrm{ph}}I \end{eqnarray*}$$

(12)

and I_H = 13.6 eV is the ionization potential of Hydrogen. The first term on the right-hand side is the emissivity of ionizing photons that was determined by the partial cooling function Λ_i(T) in the radiation range 300–910 angstrom of Landini & Fossi (1990).

Two last terms in equation (6) correspond to the injection of thermal protons with momenta p = p_f, p = p_b and mass m at the forward and reverse shocks located at r = R_f(t) and r = R_b(t), respectively. The dimensionless parameters η_f and η_b determine the efficiency of injection.

The injection efficiency is taken to be independent of time η_f = 0.001, and the particle injection momentum is |$p_{f}=2m(\dot{R}_f-u(R_f+0,t))$|⁠. Protons of mass m are injected at the forward shock and ions of mass M and mass to charge ratio A/Z = 2 and injection efficiency η_b = 0.001 are injected at the reverse shock.

For high Mach number shocks, this injection efficiency and Alfvén transport in the downstream region limit the pressure of accelerated particles and the magnetic energy density at the level |$10\!-\!20\ {{\ \rm per\ cent}}$| and |$1.5\ {{\ \rm per\ cent}}$| of the ram pressure of the shock, respectively. These numbers are comparable with ones observable in the hybrid modelling of collisionless shocks (Caprioli, Haggerty & Blasi 2020).

We neglect the pressure of energetic electrons and treat them as test particles. The evolution of the electron distribution is described by the equation analogous to equation (6) with function b(p) describing Coulomb, synchrotron, and inverse Compton (IC) losses and additional terms describing the production of secondary leptons by energetic protons and nuclei. The electron injection efficiency η_e at the forward shock was taken in the form

$$\begin{eqnarray*} \eta _e=7\times 10^{-8}\left(\frac{V_f}{c}\right) ^{-0.6}, \end{eqnarray*}$$

(13)

where the numeric parameters were adjusted to reproduce the intensity of radio-emission in SNRs W44 and Tycho. This dependence of η_e on the shock velocity V_f results in a higher electron to proton ratio in older SNRs in comparison with the one in the young SNRs.

3 MODELLING OF DIFFUSIVE SHOCK ACCELERATION IN SNR OF IIP SUPERNOVA

A significant part of core-collapse supernova explosion occurs in molecular gas. The stars with initial masses below 12 M_⊙ have no power stellar winds and therefore do not produce a strong modification of their circumstellar medium. The molecular cloud has been totally destroyed by stellar winds and supernova explosions of more massive stars at the instant of explosion. As a result, the star explodes in the inter-clump medium with the density 5–25 cm⁻³ (Chevalier 1999). Many such SNRs are observed in gamma rays now.

Table 1.

Open in new tab

Physical parameters of SNRs modelled.

Type	SNR	d	R_f	E_SN	M_ej	k_SN	B₀	n_H	X_i0	R_i	T	V_f	B_f
		kpc	pc	10⁵¹ erg	M_⊙		\|$\mu$\|G	cm⁻³		pc	kyr	km s⁻¹	\|$\mu$\|G
IIP	W44	2.8	12.35	1.8	10	9	5	7.0	0.01	4	23	160	51
Ia	Tycho	3.5	4.1	1.2	1.4	7	3	0.2	0.5	8	0.44	5300	210

Type	SNR	d	R_f	E_SN	M_ej	k_SN	B₀	n_H	X_i0	R_i	T	V_f	B_f
		kpc	pc	10⁵¹ erg	M_⊙		\|$\mu$\|G	cm⁻³		pc	kyr	km s⁻¹	\|$\mu$\|G
IIP	W44	2.8	12.35	1.8	10	9	5	7.0	0.01	4	23	160	51
Ia	Tycho	3.5	4.1	1.2	1.4	7	3	0.2	0.5	8	0.44	5300	210

Table 1.

Open in new tab

Physical parameters of SNRs modelled.

Type	SNR	d	R_f	E_SN	M_ej	k_SN	B₀	n_H	X_i0	R_i	T	V_f	B_f
		kpc	pc	10⁵¹ erg	M_⊙		\|$\mu$\|G	cm⁻³		pc	kyr	km s⁻¹	\|$\mu$\|G
IIP	W44	2.8	12.35	1.8	10	9	5	7.0	0.01	4	23	160	51
Ia	Tycho	3.5	4.1	1.2	1.4	7	3	0.2	0.5	8	0.44	5300	210

Type	SNR	d	R_f	E_SN	M_ej	k_SN	B₀	n_H	X_i0	R_i	T	V_f	B_f
		kpc	pc	10⁵¹ erg	M_⊙		\|$\mu$\|G	cm⁻³		pc	kyr	km s⁻¹	\|$\mu$\|G
IIP	W44	2.8	12.35	1.8	10	9	5	7.0	0.01	4	23	160	51
Ia	Tycho	3.5	4.1	1.2	1.4	7	3	0.2	0.5	8	0.44	5300	210

It is believed that the circumstellar medium is almost fully ionized by ultraviolet radiation from the remnant interior at the radiative stage (Chevalier 1999). The same is true for young SNRs because the gas is ionized by the radiation from the shock breakout and in the hot shock precursor produced by accelerated particles. Extended red supergiant progenitors of IIP Type supernovae emit ∼10⁴⁸ erg of radiation during the shock breakout. This amount of energy is sufficient for the ionization of several dozens of solar masses of the circumstellar gas (Chevalier 2005). If so the shock propagates in the preionized medium at the free expansion phase and at the beginning of the Sedov stage. The amount of the breakout radiation is significantly smaller for compact progenitors of Ib/c and Ia type supernovae. However, Wolf–Rayet progenitors itself ionize ∼10³M_⊙ of surrounding gas before the explosion. Some level of the preionization is also expected for Ia Type supernovae because of the ionizing radiation of the accreting white dwarf. In this regard, the assumption of the full ionization is justified for almost all stages of the SNR evolution. The only probable exception is the end of the Sedov stage when the shock might propagate in the neutral medium. In this picture, the number density of neutrals n_n is determined by the ionization history and by the recombination in ionized or preionized plasma.

Bright in GeV gamma-rays middle-aged SNR W44 at distance d = 2.8 kpc from the Earth is at the radiative phase now and shows signs of interaction with molecular gas (Reach, Rho & Jarrett 2005). It contains H i shell expanding with speed 135–150 km s⁻¹ (Koo et al. 1995; Park et al. 2003).

The parameters of our supernova modelling are given in Table 1. The explosion parameters were adjusted to reproduce broad-band observations of SNR W44. The explosion energy E_SN and ambient number density n_H were adjusted to reproduce the expansion speed of H i shell and the observable gamma-ray flux.

The numbers in the three last columns of Table 1 that are the age T, shock speed V_f, and magnetic field strength B_f just downstream of the shock were obtained in the modelling.

We use the parameter of ejecta velocity distribution k_SN = 9 (this parameter describes the power-law density profile |$\rho _{ej}\propto r^{-k_{SN}}$| of the outer part of the ejecta that freely expands after supernova explosion).

The ionized fraction of Hydrogen X_i at the initial instant of time was taken in the form

$$\begin{eqnarray*} X_i=(1-X_{i0})\exp \left(-\left(\frac{r}{R_i}\right) ^2 \right) +X_{i0} , \end{eqnarray*}$$

(14)

where the ionization fraction at infinity X_i0 and the radius of the ionization zone R_i are given in Table 1. It was assumed that about 40 solar masses of Hydrogen is ionized during the supernova explosion.

Figs (1)–(4) illustrate the results of our numerical calculations.

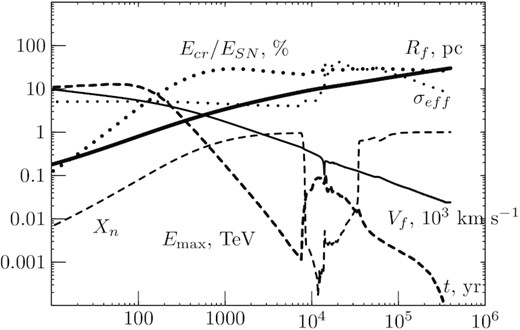
$Dependence on time of the forward shock radius Rf (thick solid line), the shock speed Vf (thin solid line), the shock effective compression ratio σeff (thin dotted line), the maximum energy of particles accelerated at forward shock Emax (dashed line), the fraction of explosion energy transformed into CRs Ecr/ESN (thick dotted line) and neutral fraction Xn (thin dashed line) calculated for SNR of IIP supernovae.$

Figure 1.

Dependence on time of the forward shock radius R_f (thick solid line), the shock speed V_f (thin solid line), the shock effective compression ratio σ_eff (thin dotted line), the maximum energy of particles accelerated at forward shock E_max (dashed line), the fraction of explosion energy transformed into CRs E_cr/E_SN (thick dotted line) and neutral fraction X_n (thin dashed line) calculated for SNR of IIP supernovae.

Open in new tab Download slide

The temporal evolution of the remnant and particle acceleration is illustrated in Fig. 1. The maximum energy of particles E_max at the forward shock was estimated as the energy where the function p⁵N(p) has a maximal value. The shock speed is almost constant at the initial free expansion stage. After 100 yr the Sedov stage begins. Maximum energy of particles is close to 20 TeV at this time. Later the maximum energy drops sharply because of the shock velocity decrease and because of the neutral damping of MHD waves. The neutral fraction X_n increases because of the recombination and later when the shock enters into a neutral medium. Strictly speaking the adequate description of DSA at this stage requires a kinetic treatment for the transport of neutral atoms near the shock (see Morlino et al. 2013). We leave the detailed description of the acceleration at this stage to the future. It seems that this stage does not produce a strong impact on results because the injection rate is proportional to the ionized fraction X_i and therefore the production rate of CRs at this phase is not high.

The ionizing radiation from the shock interior again ionizes the medium after 8 kyr. At this instant of time, the boundary of the ionization zone overtakes the forward shock. The acceleration efficiency increases because of higher injection rate.

Several thousand years after this the radiative stage begins when the cooling behind the shock results in the gas compression in this region and in the formation of a dense shell at the age T = 14 kyr. While the compression ratio of the shock is close to the standard value ∼4 the gas density continues to increase further downstream. To illustrate this we show in Fig. 1 the effective compression ratio σ_eff that is the ratio of the maximum gas density behind the shock to the ambient gas density. This ratio increases up to the value of 40 that is limited by the presence of CRs and regular magnetic fields. This gas compression results in a more efficient acceleration and in an enhanced flux of runaway highest energy particles. This, in turn, produces some temporary constant level of the maximum energy. In addition, the gas cooling behind the shock is accompanied by its recombination. The neutral gas of the shell absorbs the ionizing radiation from the hot remnant interior. This stops ionization in the far upstream region and gas ionized earlier begins to recombine. Particles accelerated earlier leave the neutral shell because of the damping of MHD waves. At 35 kyr, the shock reaches the boundary of the ionized region and enters the neutral medium. At later times the acceleration at the forward shock does not occur.

It should be noted that we use a simplified approach for the description of the radiative cooling and photoionization with the equilibrium cooling functions Λ(T_e) and Λ_i(T_e). In reality, radiative cooling and photoionization depend on the ionization state of ions in plasma that is not in thermal equilibrium. However, we checked by performing a test run without CRs that the reionization, the dense shell formation, and exit of the shock to the neutral medium occur at the same age as in the SNR modelling with a full application of the atomic physics (Sarkar, Gnat & Sternberg 2021).

Radial dependences of physical quantities in SNR W44 at present (T = 23 kyr) are shown in Fig. 2. The gas temperature drops sharply downstream of the forward shock due to the radiative cooling and a thin neutral dense shell is formed behind the forward shock. We obtain the shell mass of the neutral Hydrogen 640 M_⊙ that is somewhat higher than the measured value of 390 M_⊙ (Park et al. 2003). The central part of the remnant is filled by the hot rarefied gas with a temperature of 10⁶–10⁷K.

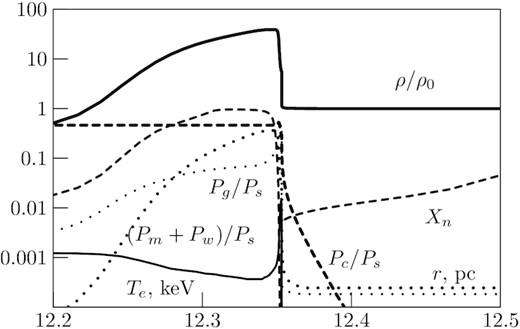
$Radial dependences of the gas density (thick solid line), the gas temperature Te (thin solid line), CR pressure (thick dashed line), neutral fraction Xn (dashed line), the magnetic energy density B2/8π = Pm + Pw (dotted line), and the gas pressure Pg (thin dotted line) at T = 23 kyr in the vicinity of the forward shock in SNR W44. The pressures are normalized to the ram pressure of the shock $P_s=\rho _0V^2_f$.$

Figure 2.

Radial dependences of the gas density (thick solid line), the gas temperature T_e (thin solid line), CR pressure (thick dashed line), neutral fraction X_n (dashed line), the magnetic energy density B²/8π = P_m + P_w (dotted line), and the gas pressure P_g (thin dotted line) at T = 23 kyr in the vicinity of the forward shock in SNR W44. The pressures are normalized to the ram pressure of the shock |$P_s=\rho _0V^2_f$|⁠.

Open in new tab Download slide

Results of multiband modelling of SNR W44 are shown in Fig. 3. Thermal emission has two components. One is produced by the hot gas in the remnant interior while the lower energy component is produced by the dense gas that cooled and recombined behind the shock front. This gas produces a significant amount of the thermal radio emission that dominates the synchrotron radio emission at high frequencies.

Figure 3.

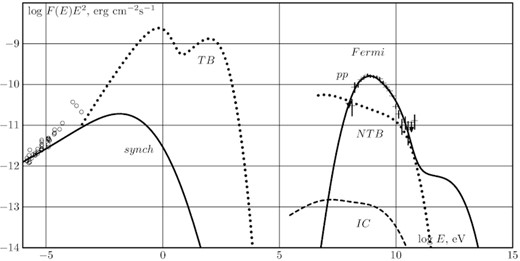
The results of modelling of electromagnetic radiation of W44. The following radiation processes are taken into account: synchrotron radiation of accelerated electrons (solid curve on the left), IC emission (dashed line), gamma-ray emission from pion decay (solid line on the right), thermal bremsstrahlung (dotted line on the left), non-thermal bremsstrahlung (dotted line on the right). Experimental data in gamma-rays by the Fermi LAT (Ackermann et al. 2013) (data with error bars) and in radio bands (Castelletti et al. 2007; Arnaud et al. 2016) (circles) are also shown.

Open in new tab Download slide

The spectra of particles N_int produced during 400 kyr after supernova explosion are shown in Fig. 4. They are calculated via the integration throughout the simulation domain and via the integration on time of the outward diffusive flux at the simulation boundary at r = 2R_f. About |$26{{\ \rm per\ cent}}$| of the kinetic energy of the explosion is transferred to CRs. Almost all this energy is gone with escaped particles. Note that almost all protons and electrons accelerated at the forward shock have left the remnant. This is because the neutral damping of MHD waves, which confine CRs, was taken into account in the downstream region. In this regard, the proton and electron spectra shown in Fig. 4 are the source spectra of galactic CRs. This is not so for the ion spectrum. A significant part of ions accelerated at the reverse shock are still confined in the central part of the remnant, where the gas is fully ionized. The exit of particles from the ionized regions of SNR is regulated by another kind of damping of MHD waves that is not considered here.

Figure 4.

Spectra of protons (thick lines) and electrons (thin lines) produced at the forward shock, and nuclei (normal lines) produced at the reverse shock in SNR of Type IIP during 400 kyr after explosion. The spatially integrated spectra of particles (dotted lines), the spectra of particles escaped from the remnant (dashed lines), and the sum (solid lines) are shown.

Open in new tab Download slide

As was mentioned before the acceleration efficiency increases just before and after the transition to the radiative stage. The corresponding CR spectra of protons and electrons show a spectral hardening at several hundreds GeV. The effect is stronger for electrons because their injection rate increases with time according to equation (13).

4 MODELLING OF DSA IN SNR OF TYPE IA SUPERNOVA

The parameters of supernova modelling are given in Table 1. The explosion parameters were adjusted to reproduce multiwave observations of young SNR Tycho. The distance to this SNR is very uncertain. So we fix the explosion energy to a value E_SN = 1.2 × 10⁵¹ erg of the 1D delayed detonation model of the Tycho supernova explosion (Badenes et al. 2006). Then the distance and the ambient number density n_H were adjusted to reproduce the age of SNR and its angular diameter of 8 arcmin. The parameter h_w = 0.7 in equations (3),(5), and (8) was adjusted to reproduce the observable gamma-ray spectrum.

It was assumed that about 5 solar masses of Hydrogen is ionized before and during the supernova explosion.

Figs (5)–(8) illustrate the results of our numerical calculations.

The remnant evolves in a low-density medium. That is why the transition to the radiative stage occurs at 100 kyr. The regular magnetic field produces a stronger limitation of σ_eff ∼ 10 at this stage.

Spectra of accelerated in Tycho SNR protons, ions, and electrons at present are shown in Fig. 6. They are rather soft due to the Alfvénic transport in the downstream region. This also provides a good agreement with radio, X-ray, and gamma-ray data (see Fig. 7).

The spectra of particles N_int produced during 4 Myr after supernova explosion are shown in Fig. 8. They are calculated via the integration throughout the simulation domain and via the integration on time of the outward diffusive flux at the simulation boundary at r = 2R_f. About |$19{{\ \rm per\ cent}}$| of the kinetic energy of the explosion is transferred to CRs. Almost all this energy is gone with escaped particles. The maximum energy of escaped particles is 50 TeV for this SNR. Similar to the case of IIP type SNR almost all accelerated protons and electrons left the remnant and their spectra can be considered as source spectra of galactic CRs.

The energy of the hardening is lower for Ia Type SNRs. Note that transition to the radiative stage occurs when the shock radius is 40 pc. Probably in many cases, the shock will collide with a denser medium before the transition. Then the situation will be similar to the one considered in the previous section.

5 DISCUSSION

The transition to the radiative stage begins when the radiative losses are comparable with adiabatic losses in the downstream region (see the corresponding terms in equation 3). Assuming a linear profile of the gas velocity we get

$$\begin{eqnarray*} \Lambda (T_e)n_H^2\sigma ^2\sim \frac{(\sigma -1)\gamma _g\xi _g\rho V_f^3}{(\gamma _g-1)\sigma R}. \end{eqnarray*}$$

(15)

Here, |$\xi _g=P_g/\rho V_f^2$| is the ratio of the gas pressure just downstream of the shock P_g to the shock ram pressure |$\rho V_f^2$|⁠, σ is the shock compression ratio. Using the relation

$$\begin{eqnarray*} \rho V_f^2R_f^3=0.2E_{SN} \end{eqnarray*}$$

(16)

at the Sedov stage and numeric values σ = 4, γ_g = 5/3, and ξ_g = 0.75 we can obtain the shock speed V_rad at the time of transition

$$\begin{eqnarray*} V_{\mathrm{rad}}=250\ \mathrm{km\ s}^{-1}n_H^{2/11} \left(\frac{E _{SN}}{10^{51}\,\mathrm{erg}}\right) ^{1/11} \left(\frac{\Lambda }{10^{-22}\,\mathrm{erg\ cm}^{3}\,\mathrm{s}^{-1}}\right) ^{3/11} \nonumber\\ \end{eqnarray*}$$

(17)

In the absence of damping the maximum energy E_max of accelerated particles can be found from the condition that the magnetic field amplified by the CR streaming instability has enough time to grow from the initial value of B_b, that is Γ_crT = ln (B/B_b) ∼ 10 during the age T.

In young SNRs, the streaming instability is non-resonant while in older remnants it is resonant. In spite of the different nature the rates of the resonant and non-resonant instabilities are given by similar expressions. For the estimate we use the non-resonant instability rate Γ_cr (Bell 2004)

$$\begin{eqnarray*} \Gamma _{cr}= \frac{J_{\mathrm{el}}B}{2c\rho v_A}, \end{eqnarray*}$$

(18)

where J_el is the electric current of the highest energy CRs escaping into the upstream region. This results in expression (Zirakashvili & Ptuskin 2008a)

$$\begin{eqnarray*} E_{\max }&=&\frac{\eta _{\mathrm{esc}}qBV_f^3T}{4cv_A\ln (B/B_b) }= 2\ \mathrm{TeV}\left(\frac{\eta _{\mathrm{esc}}}{0.05}\right) \left(\frac{V_f}{10^3\mathrm{km\ s}^{-1}}\right) ^2\nonumber\\ &&\times \,\, m_{\mathrm{exp}}n_H^{0.5}R_{\mathrm{pc}}. \end{eqnarray*}$$

(19)

Here, η_esc is the ratio of the energy flux of highest energy particles to the shock energy flux |$\rho V_f^3/2$| and m_exp = V_fT/R_f is the expansion parameter of the shock. At the beginning of the Sedov stage |$V_f^2=2E_{SN}/M_{ej}, \ R_f=(3{M_{ej}}/(4\pi m\times 1.4n_H))^{1/3}$|⁠, and

$$\begin{eqnarray*} E_{\max }&=& 2\left(\frac{3}{4\pi \times 1.4}\right) ^{1/3} \frac{m_{\mathrm{exp}}\eta _{\mathrm{esc}}qBE_{SN}}{4m^{1/3}n_H^{1/3}M^{2/3}_{ej}cv_A\ln (B/B_b) }\nonumber\\ &=&400\ \mathrm{TeV}\left(\frac{\eta _{\mathrm{esc}}}{0.05}\right) \left(\frac{E_{SN}}{10^{51}\ \mathrm{erg}}\right) \left(\frac{M_{ej}}{\mathrm{ M}_{\odot }}\right) ^{-2/3} m_{\mathrm{exp}}n_H^{1/6}. \end{eqnarray*}$$

(20)

The value η_esc = 0.05 corresponds to the effectively accelerating shock with E⁻² spectrum of particles and CR pressure of the order of |$50{{\ \rm per\ cent}}$| of the shock ram pressure. The Alfvénic transport downstream results in steeper spectra, lower CR pressure (see Fig. 6), and lower η_esc ∼ 0.01. Then for parameters of IIP and Ia Type supernovae (see Table 1) and m_exp = 0.5 we get the maximum energies of 20 and 30 TeV at the beginning of the Sedov stage in qualitative agreement with Figs 1 and 5.

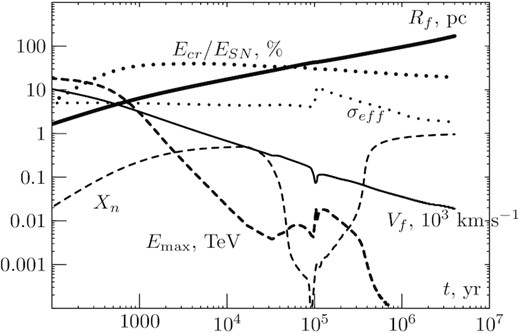
$Dependence on time of the forward shock radius Rf (thick solid line), the shock speed Vf (thin solid line), the effective shock compression ratio σeff (thin dotted line), the maximum energy of particles accelerated at forward shock Emax (dashed line), the fraction of explosion energy transformed into CRs Ecr/ESN (thick dotted line) and neutral fraction Xn (thin dashed line) calculated for SNR of Ia supernovae.$

Figure 5.

Dependence on time of the forward shock radius R_f (thick solid line), the shock speed V_f (thin solid line), the effective shock compression ratio σ_eff (thin dotted line), the maximum energy of particles accelerated at forward shock E_max (dashed line), the fraction of explosion energy transformed into CRs E_cr/E_SN (thick dotted line) and neutral fraction X_n (thin dashed line) calculated for SNR of Ia supernovae.

Open in new tab Download slide

Figure 6.

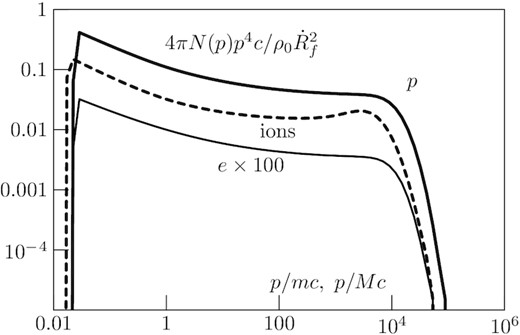
The spectra of particles in Tycho SNR. Proton and electron spectra at the forward shock and spectrum of ions accelerated at the reverse shock are shown.

Open in new tab Download slide

Figure 7.

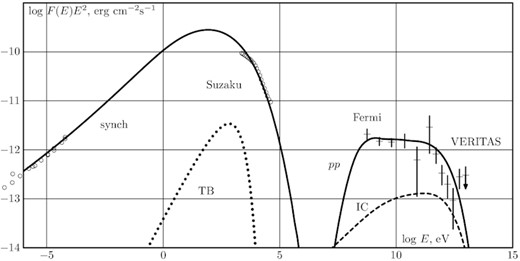
The results of modelling of electromagnetic radiation of Tycho SNR. The following radiation processes are taken into account: synchrotron radiation of accelerated electrons (solid curve on the left), IC emission (dashed line), gamma-ray emission from pion decay (solid line on the right), thermal bremsstrahlung (dotted line on the left). Experimental data in gamma-rays by the Fermi LAT and VERITAS (Archambault et al. 2017); (data with error bars), radio (Klein et al. 1979), and analytical approximation of continuum X-rays by Suzaku (Tamagawa et al. 2009) (circles) are also shown.

Open in new tab Download slide

Figure 8.

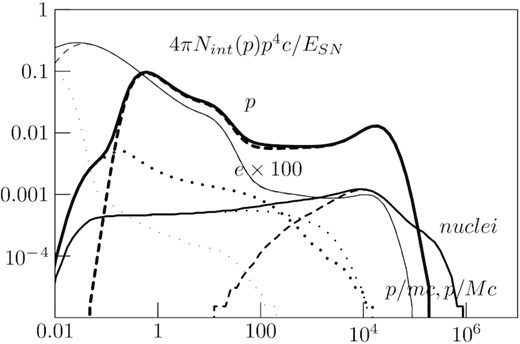
Spectra of protons (thick lines) and electrons (thin lines) produced at the forward shock, and nuclei (normal lines) produced at the reverse shock in SNR of Type Ia during 4 Myr after explosion. The spatially integrated spectra of particles (dotted lines), the spectra of particles escaped from the remnant (dashed lines), and the sum (solid lines) are shown.

Open in new tab Download slide

So the maximum energies determined by CR streaming instability are not higher than 100 TeV in SNRs considered. Higher energies can be reached for SNRs shocks propagating in rarefied bubbles created by Type Ib/c supernova progenitors where the medium is prepared for the efficient DSA (Zirakashvili & Ptuskin 2018b, 2021) or in dense progenitor winds of IIn Type SNRs (Zirakashvili & Ptuskin 2016b).

The maximum energy at the instant of transition to the radiative stage E_rad can be found from equations (16), (17), and (19)

$$\begin{eqnarray*} E_{\mathrm{rad}}&=&200\ \mathrm{GeV}\left(\frac{\eta _{\mathrm{esc}}}{0.01}\right) n_H^{9/22} \left(\frac{E _{SN}}{10^{51}\,\mathrm{erg}}\right) ^{5/11}\nonumber\\ &&\times \left(\frac{\Lambda }{10^{-22}\,\mathrm{erg\ cm}^{3}\,\mathrm{s}^{-1}}\right) ^{4/11} , \end{eqnarray*}$$

(21)

where the value m_exp = 0.4 was used. This gives the energy of hardening 100 and 600 GeV for Ia and IIP Type SNRs.

It is expected that the effect will be similar for light CR nuclei. However, details of the ionization, e.g. a high ionization potential of the Helium can result in some peculiarities of the hardening.

We expect that the effect of the hardening can be different for heavy nuclei. The matter is that the nuclei injected into DSA are single or double charged. The further ionization occurs via collisions with thermal particles (a so-called stripping) and a photoionization. The photoionization is possible when accelerated particles reach high Lorentz factors and interact with optical, infrared, and microwave background photons (Morlino 2011). For example, it takes ∼10⁵ yr for a full ionization of Iron nuclei with a Lorentz factor 100 accelerated in SNR evolving in the dense gas with a number density of 10 cm⁻³ (see fig. 1 of Morlino 2011). This time is higher than the age of the transition to the radiative stage ∼10⁴ yr. Actually, the heavy nuclei have the time for the ionization up to the charge state ∼10. They will be stripped further after the end of the acceleration and during a propagation in the Galaxy. Therefore, it is expected that heavy nuclei have lower observable rigidities of the hardening.

It is important to note that high-energy measurements of protons and nuclei energy spectra in the CR experiment AMS confirm the earlier experimental results of ATIC-2, CREAM, and PAMELA measurements on the presence of spectral hardening at magnetic rigidity at about 200 GV (see e.g. review of Serpico 2018, and references therein). Some peculiarities for the hardening of Iron nuclei were also reported (Schroer, Evoli & Blasi 2021).

The nature of this hardening is not clear yet. In principle, it may reflect the source spectra or the peculiarity of the energy dependence of CR leakage time from the Galaxy.

In our modelling, the hardening at energies 100–500 GeV in the source proton and electron spectra is related with a higher acceleration efficiency after the full reonization of the medium just before the beginning of the radiative stage and with the strong gas compression behind the shock at the radiation stage. Probably this spectral feature is also presented in the energy dependence of the CR leakage time because of the self-confinement of CRs (see a review of Blasi 2019, and references therein). In self-confinement models, CRs generate MHD waves via CR streaming instability. These waves in turn scatter CR particles and regulate their diffusion and confinement in the Galaxy. The streaming instability is produced mainly by protons and α-particles. So the hardening in their source spectra will result in a change of the energy dependence of the interstellar diffusion coefficient.

6 CONCLUSION

Our results and conclusions are the following:

We performed the modelling of particle acceleration in SNRs up to the late stages of the remnant evolution when almost all particles accelerated at the forward shock have left the remnant.
We show that transition to the radiative phase of SNRs is accompanied by a higher acceleration efficiency of CRs. It leads to the hardening of the CR proton and electron source spectrum at energies of several hundreds GeV. This energy is simply the maximum energy of accelerated particles at the time of the transition. CR particles at lower energies are mainly accelerated and escaped the remnant at the radiative stage.
The effect is stronger for CR electrons because of the higher electron injection rate in old SNRs.
We expect that the effect is different for heavy nuclei because of the partial ionization.

ACKNOWLEDGEMENTS

The work was partially supported by the Russian Foundation for Basic Research grant 19-02-00043. The work was also partly performed at the Unique scientific installation ‘Astrophysical Complex of Moscow State University - Irkutsk State University’ (agreement 13.UNU.21.0007). We also thank the referee Luke Drury for valuable comments.

DATA AVAILABILITY

All results in this paper were obtained using available published data.

REFERENCES

Ackermann

M.

et al. ,

2013

,

Science

,

339

,

807

10.1126/science.1231160

Crossref

Search ADS

PubMed

Archambault

S.

et al. ,

2017

,

ApJ

,

836

,

23

10.3847/1538-4357/836/1/23

Crossref

Search ADS

Arnaud

M.

et al. ,

2016

,

A&A

,

586

,

134

Axford

W. I.

,

Leer

E.

,

Skadron

G.

,

1977

,

Proceedings of 15th International Cosmic Ray Conference, Plovdiv, Bulgaria, Bulgarska akademiia na naukite

,

11

,

132

Badenes

C.

,

Borkowski

K. J.

,

Hughes

J. P.

,

Hwang

U.

,

Bravo

E.

,

2006

,

ApJ

,

645

,

1373

10.1086/504399

Crossref

Search ADS

Bell

A. R.

,

1978

,

MNRAS

,

182

,

147

10.1093/mnras/182.2.147

Crossref

Search ADS

Bell

A. R.

,

2004

,

MNRAS

,

353

,

550

10.1111/j.1365-2966.2004.08097.x

Crossref

Search ADS

Bell

A. R.

,

2014

,

Astropart. Phys.

,

43

,

56

10.1016/j.astropartphys.2012.05.022

Crossref

Search ADS

Blandford

R. D.

,

Ostriker

J. P.

,

1978

,

ApJ

,

221

,

L29

10.1086/182658

Crossref

Search ADS

Blasi

P.

,

2019

,

Galaxies

,

7

,

64

10.3390/galaxies7020064

Crossref

Search ADS

Bykov

A. M.

,

Malkov

M. A.

,

Raymond

J. C.

,

Krassilchtchikov

A. M.

,

Vladimirov

A. E.

,

2013

,

Space Sci. Rev.

,

178

,

599

10.1007/s11214-013-9984-7

Crossref

Search ADS

Caprioli

D.

,

2014

,

Nucl. Phys. B

,

256

,

48

10.1016/j.nuclphysbps.2014.10.005

Crossref

Search ADS

Caprioli

D.

,

Haggerty

C. C.

,

Blasi

P.

,

2020

,

ApJ

,

905

,

2

10.3847/1538-4357/abbe05

Crossref

Search ADS

Castelletti

G.

,

Dubner

G.

,

Brogan

C.

,

Kassim

N. E.

,

2007

,

A&A

,

471

,

537

10.1051/0004-6361:20077062

Crossref

Search ADS

Chevalier

R.

,

1999

,

ApJ

,

511

,

798

10.1086/306710

Crossref

Search ADS

Chevalier

R.

,

2005

,

ApJ

,

619

,

839

10.1086/426584

Crossref

Search ADS

Drury

L.O’C.

,

Duffy

P.

,

Kirk

J. G.

,

1996

,

A&A

,

309

,

1002

Haggerty

C. C.

,

Caprioli

D.

,

2020

,

ApJ

,

905

,

1

10.3847/1538-4357/abbe06

Crossref

Search ADS

Klein

U.

,

Emerson

D. T.

,

Haslam

C. G. T.

,

Salter

C. J.

,

1979

,

A&A

,

76

,

120

Koo

B.-C.

,

Heils

C.

,

1995

,

ApJ

,

442

,

679

10.1086/175473

Crossref

Search ADS

Krymsky

G. F.

,

1977

,

Sov. Phys.-Dokl.

,

22

,

327

Landini

M.

,

Monsegniori Fossi

B. C.

,

1990

,

A&AS

,

82

,

229

Lemoine-Goumard

M.

,

2014

,

Proceedings of the International Astronomical Union

,

287

,

1743

10.1017/S1743921313009605

McKenzie

J. F.

,

Völk

H. J.

,

1982

,

A&A

,

116

,

191

Moffatt

H. K.

,

1986

,

J. Fluid Mech.

,

166

,

359

10.1017/S0022112086000198

Crossref

Search ADS

Morlino

G.

,

2011

,

MNRAS

,

412

,

2333

10.1111/j.1365-2966.2010.18054.x

Crossref

Search ADS

Morlino

G.

,

Blasi

P.

,

Bandiera

R.

,

Amato

E.

,

Caprioli

D.

,

2013

,

ApJ

,

768

,

148

10.1088/0004-637X/768/2/148

Crossref

Search ADS

Park

G.

et al. ,

2013

,

ApJ

,

777

,

14

10.1088/0004-637X/777/1/14

Crossref

Search ADS

Ptuskin

V. S.

,

Zirakashvili

V. N.

,

Seo

E. S.

,

2010

,

ApJ

,

718

,

31

10.1088/0004-637X/718/1/31

Crossref

Search ADS

Reach

W. T.

,

Rho

J.

,

Jarrett

T. H.

,

2005

,

ApJ

,

618

,

297

10.1086/425855

Crossref

Search ADS

Sarkar

K. C.

,

Gnat

O.

,

Sternberg

A.

,

2021

,

MNRAS

,

504

,

583

10.1093/mnras/stab582

Crossref

Search ADS

Schroer

B.

,

Evoli

C.

,

Blasi

P.

,

2021

,

Phys. Rev. D

,

103

,

123010

10.1103/PhysRevD.103.123010

Crossref

Search ADS

Serpico

P. D.

,

2018

,

J. Astrophys. Astron.

,

39

,

41

10.1007/s12036-018-9532-7

Crossref

Search ADS

Tamagawa

T.

et al. ,

2009

,

PASJ

,

61

,

S167

10.1093/pasj/61.sp1.S167

Crossref

Search ADS

Zirakashvili

V. N.

,

2018

,

Int. J. Mod. Phys. D

,

27

,

1844023

–

1081-8

.

10.1142/S0218271818440236

Crossref

Search ADS

Zirakashvili

V. N.

,

Ptuskin

V. S.

,

2008a

,

ApJ

,

678

,

939

10.1086/529580

Crossref

Search ADS

Zirakashvili

V. N.

,

Ptuskin

V. S.

,

2008b

,

preprint (arXiv:0807.2754.2008)

Zirakashvili

V. N.

,

Ptuskin

V. S.

,

2012

,

Astropart. Phys.

,

39

,

12

10.1016/j.astropartphys.2011.09.003

Crossref

Search ADS

Zirakashvili

V. N.

,

Ptuskin

V. S.

,

2016a

,

Astropart. Phys.

,

78

,

28

10.1016/j.astropartphys.2016.02.004

Crossref

Search ADS

Zirakashvili

V. N.

,

Ptuskin

V. S.

,

2016b

,

preprint (arXiv:1701.00844)

Zirakashvili

V. N.

,

Ptuskin

V. S.

,

2018a

,

Astron. Lett.

,

44

,

769

10.1134/S1063773718120071

Crossref

Search ADS

Zirakashvili

V. N.

,

Ptuskin

V. S.

,

2018b

,

Astropart. Phys.

,

98

,

21

10.1016/j.astropartphys.2018.01.005

Crossref

Search ADS

Zirakashvili

V. N.

,

Ptuskin

V. S.

,

2021

,

Bull. Russ. Acad. Sci.

,

85

,

366

10.3103/S1062873821040407

Crossref

Search ADS

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
December 2021	2
January 2022	19
February 2022	9
March 2022	1
April 2022	2
May 2022	9
June 2022	6
July 2022	6
August 2022	2
September 2022	7
October 2022	4
March 2023	3
April 2023	2
August 2023	2
October 2023	1
December 2023	2
January 2024	1
February 2024	4
March 2024	7
April 2024	7
May 2024	11
June 2024	10
July 2024	5
August 2024	4
September 2024	4
October 2024	7
November 2024	3
January 2025	3
February 2025	6
March 2025	6
April 2025	1
May 2025	3

Article Contents

Role of the radiative stage for cosmic ray acceleration in SNRs

ABSTRACT

1 INTRODUCTION

2 NON-LINEAR DIFFUSIVE SHOCK ACCELERATION MODEL

3 MODELLING OF DIFFUSIVE SHOCK ACCELERATION IN SNR OF IIP SUPERNOVA

4 MODELLING OF DSA IN SNR OF TYPE IA SUPERNOVA

5 DISCUSSION

6 CONCLUSION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Role of the radiative stage for cosmic ray acceleration in SNRs

ABSTRACT

1 INTRODUCTION

2 NON-LINEAR DIFFUSIVE SHOCK ACCELERATION MODEL

3 MODELLING OF DIFFUSIVE SHOCK ACCELERATION IN SNR OF IIP SUPERNOVA

4 MODELLING OF DSA IN SNR OF TYPE IA SUPERNOVA

5 DISCUSSION

6 CONCLUSION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only