-
PDF
- Split View
-
Views
-
Cite
Cite
T Vieu, S Gabici, V Tatischeff, Non-linear particle reacceleration by multiple shocks, Monthly Notices of the Royal Astronomical Society, Volume 510, Issue 2, February 2022, Pages 2529–2537, https://doi.org/10.1093/mnras/stab3564
Close - Share Icon Share
ABSTRACT
When the pressure of particles accelerated at shock waves is no longer negligible compared to the kinetic pressure of the gas, the linear theory of diffusive shock acceleration breaks down. This is expected in particular when the shock sweeps up pre-existing cosmic rays, or when multiple shocks reaccelerate successively the same particles. To describe these systems, one has to account for the non-linear backreaction of the particles on the magnetohydrodynamic flow. Using an up-to-date semi-analytical model of particle reacceleration at non-linear shocks, we show that the presence of pre-existing energetic particles strongly affects the shock profile, in such a way that the reacceleration of non-thermal particles or the acceleration of particles from the thermal bath becomes less efficient. We further describe the evolution of the distribution of particles after several shocks and study the properties of the asymptotic solution. We detail the case of identical shocks as well as more realistic scenarios, including the heating of the medium or superbubble environments. When the particles are efficiently confined in the acceleration region, it is generally found that the spectrum converges toward a concave solution after a few tens of shocks, with a spectral index around 3.5 at the highest energy. The post-shock cosmic ray pressure reaches an asymptotic value of about 4–5 per cent of the ram pressure of one shock. Most of the shock pressure is transferred to escaping particles.
1 INTRODUCTION
The main sources of cosmic rays (CRs) in our Galaxy are believed to be supernova remnant (SNR) shocks. Particle acceleration at shocks has been investigated for decades under the framework of diffusive shock acceleration (DSA, Axford, Leer & Skadron 1977; Krymskii 1977; Bell 1978a; Blandford & Ostriker 1978). A standard simplifying assumption made in DSA computations is that the accelerated CRs are not energetic enough to influence the fluid dynamics. This gives rise to the theory of linear DSA, which has the remarkable property of predicting a universal power law in momentum for the distribution function of CR accelerated at strong shocks [f(p) ∝ p−4].
The linear theory is, however, expected to break down in most astrophysical environments. The CR luminosity of the Galaxy indeed suggests that a fraction of about 10 per cent of the energy provided by supernovae (SNe) is converted into CRs (Strong et al. 2010). This requires high injection efficiencies at the shock, such that the CR pressure cannot be neglected anymore. Besides, CRs are in equipartition with the gas pressure in the interstellar medium: Not only the shock accelerates fresh CRs, it also sweeps up pre-existing non-thermal particles (hereafter called seeds). When SNRs expand in low density media, they span a large volume, such that the total energy of the seeds may become of the order of 1051 erg, that is, the energy of the SN explosion. In these cases, an accurate DSA computation requires considering non-linear effects.
Since the pioneer works of Eichler (1979), Blandford (1980), and Drury & Voelk (1981), there have been numerous attempts to model non-linear particle acceleration at shocks, including Monte Carlo simulations (Ellison & Eichler 1984), two-fluid models (e.g. Malkov & Voelk 1996), semi-analytical solutions (Blasi 2002; Caprioli et al. 2009), numerical resolutions (e.g. Kang & Ryu 2011), and hydrodynamic simulations (e.g. Caprioli & Spitkovsky 2014). It is now understood that the backreaction of the accelerated particles creates a precursor in the gas upstream of the shock. The compression factor at the subshock decreases while the total compression factor increases, in such a way that the CR spectrum tends to develop a concave shape instead of the universal power law predicted by the linear theory.
All the aforementioned works assumed that no seeds pre-exist in the medium before the acceleration process, i.e. the shock is isolated. Multiple shock acceleration is, however, expected to take place in several physical environments, including, e.g. accretion discs (Spruit 1988; Achterberg 1990), stellar winds (White 1985), and superbubbles (SBs, Bykov 2001; Parizot et al. 2004). Multiple shock acceleration can take place in the latter through successive SN explosions (Ferrand & Marcowith 2010) or in strong supersonic turbulence characterized by an ensemble of stochastic shocks (Bykov 2001). As such, it is a crucial aspect in modelling SB sources, which are likely to be efficient CR accelerators, as suggested by a number of recent observations and arguments (e.g. Bykov et al. 2020; Cao et al. 2021; Tatischeff et al. 2021). Multiple shock acceleration in SBs could be the key ingredient to produce PeV protons (Bykov, Ptuskin & Toptygin 1995; Klepach, Ptuskin & Zirakashvili 2000).
Repeated shock acceleration is also expected to happen in clusters of galaxies. These cosmological structures are formed through the recurrent merger of smaller structures. Every time a merger occurs, a weak shock forms in the intracluster medium, and CRs can be accelerated/reaccelerated (see e.g. Gabici & Blasi 2003; Kang 2021).
Finally, multiple shock acceleration is likely to take place in both active galactic nuclei and gamma-ray bursts jets. In particular, in the internal shock scenario (Piran 2004), shocks are expected to be mildly relativistic. Therefore, the non-relativistic framework discussed in the following could serve as a starting point to build models describing such systems.
Within the framework of linear DSA, it was already shown by Bell (1978b) that multiple shock acceleration efficiently produces hard spectra. Including adiabatic decompression, Melrose & Pope (1993) demonstrated that the spectrum tends towards the asymptotic solution f(p) ∝ p−3. Particle acceleration in a system of two colliding shock waves can also produce a hardening of the particle spectrum at high energies (Vieu, Gabici & Tatischeff 2020). Non-linear effects were tackled in Blasi (2004), where it was shown that the flow profile could be indeed strongly affected by the seeds. Kang & Ryu (2011) also studied such effects in the context of weak cosmological shock waves. As for the reacceleration of particles by an ensemble of non-linear shocks, it has been very scarcely analysed in previous works. Considering the closely related situation of CR acceleration by an ensemble of coexisting shocks, Bykov (2001) included the backreaction of the CRs on to the shocks within a stochastic approach. Although this is a self-consistent way to account for the non-linearities and maintain the energy balance between the shocks and the particles, it does not account for the local changes in the shock profiles due to the CR pressure. The problem of the acceleration by successive non-linear shocks was later briefly investigated numerically by Ferrand, Downes & Marcowith (2008), and more recently by Caprioli, Zhang & Spitkovsky (2018), who showed that the seeds are in particular expected to enhance streaming instabilities.
In this paper, we aim at computing the spectrum of reaccelerated seeds as well as the acceleration by successive shocks of particles from the thermal bath, in the non-linear regime. In Section 2, we describe an up-to-date version of the semi-analytical model of Blasi (2004), including more recent developments describing injection, streaming instability, and Alfvénic drift. In Section 3, we discuss the reacceleration of pre-existing seeds. Particle acceleration by an ensemble of shocks is tackled in Section 4. We conclude in Section 5.
2 NON-LINEAR DIFFUSIVE SHOCK REACCELERATION
2.1 Kinetic equation
Energetic particles are confined at shocks due to repeated scattering of magnetohydrodynamic (e.g. Alfven) waves, that keep the particle distribution function very close to isotropy. Upstream of the shock, a small anisotropy appears [f(x, p) is not spatially uniform] and this triggers the resonant CR streaming instability, resulting in the growth of Alfven waves (Bell 1978a). Only Alfven waves propagating in the direction of the stream of particles grow, i.e. those moving towards the negative x direction. This implies that upstream of the shock the fluid velocity u that appears in equation (1) should be substituted by the velocity of the scattering centres, u − vA where vA is the Alfven speed. At equilibrium, the particle distribution function downstream of the shock is spatially uniform, and therefore streaming instability does not operate there. Moreover, if the magnetic turbulence is isotropized after the passage through the shock, the effective Alfven speed vanishes and scattering centres move away from the shock at the fluid speed u2. In the presence of strong field amplification, the substitution u → u − vA may impact significantly on to the spectrum of accelerated particles, as first noticed in Zirakashvili & Ptuskin (2008) and Caprioli (2012).1
Following here the phenomenological approach presented in Blasi, Gabici & Vannoni (2005), we constrain the injection term in equation (1) in such a way to guarantee the continuity between the momentum distribution of thermal particles downstream of the shock (the Maxwell–Boltzmann distribution) and that of accelerated ones. This approach, admittedly oversimplified, is broadly consistent with results coming from sophisticated numerical simulations of shocks (Caprioli & Spitkovsky 2014). Moreover, in the following, we will assume that seed particles with momentum smaller than p0 are thermalized once they cross the shock. This allows to set the following boundary condition in momentum:
At this point, before describing the procedure used to solve equation (2), it is mandatory to discuss how the shock transition is modified in the presence of a non-negligible pressure carried by CR particles.
2.2 Fluid equations
2.3 Method of solution
Now that two initial values have been obtained for the functions f and ζ, together with the properties of the subshock, equations (16) and (15) can be solved together numerically as follows. Equation (16) gives ζ′(p) and ζ(p + dp) as function of f1(p) and ζ(p). Equation (15) gives f1(p + dp) as function of f1(p), ζ(p), and ζ′(p). We can, therefore, reconstruct the full solutions f1 and ζ for a given guess value of U1. The physical value of U1 is the one for which ζ(pmax) = 1, as the flow profile should not be modified at large distances from the shock. The determination of the maximum momentum pmax is not straightforward as it requires in particular to account for the time dependency of the acceleration process. The maximum momentum pmax is left as a free parameter in this work, together with the Mach number of the shock M0 and the injection parameter ξ.
2.4 Adiabatic decompression
The particles bound to the fluid are compressed by a factor Rtot after the passage of a shock. When successive reaccelerations occur, the decompression of the particles must be computed in between each shock, otherwise one could obtain arbitrarily hard spectra at low energy. An accurate computation of this decompression makes use of Liouville’s theorem: |$f_{\rm decompressed}(p) = f_{1}(R_{\rm tot}^{1/3} p)$| (Melrose & Pope 1993). As pointed out by Ferrand et al. (2008), in doing numerical resolutions the steps of the momentum grid in logarithmic scale should be chosen as exact fractions of the momentum shift log (Rtot)/3. In non-linear shocks, this requirement cannot be fulfilled since the total compression factor is unknown a priori. This introduces numerical errors in the decompressed spectrum. With the momentum resolution used to obtain our results, the relative error between the expected pressure and that obtained numerically is equal to 5 per cent in the worst cases. The overall shape of the CR spectrum is therefore expected to stay accurate. However, when dealing with multiple successive shocks, it is crucial to correct the post-shock pressure, otherwise the errors will accumulate. We, therefore, slightly rescale the decompressed spectrum in order to ensure that an adiabatic change takes place, imposing that |$P_{\mathrm{c},{\rm decompressed}} = R_{\rm tot}^{-\gamma _\mathrm{c}} P_{\mathrm{c},1}$|, where γc is the CR adiabatic index and Pc, 1 the CR pressure at the shock. The renormalization factor is equal to 0.95 in the worst cases.
In the following, the decompressed distribution of CRs remaining after the passage of a shock will be referred to as the ‘post-shock’ distribution.
2.5 Escape flux
3 REACCELERATION OF PRE-EXISTING CRS
In this section, we investigate the effect of the non-linearities on the reacceleration of pre-existing seeds. We set the shock Mach number M0 = 20 (u0 = 3320 km s−1), the density far upstream n0 = 0.01 cm−3, the temperature T0 = 106 K, the adiabatic index of the gas γ = 5/3, the injection parameter ξ = 3, and the maximum momentum pmax = 1 PeV. The spectrum of the seeds is assumed to be a power law of index α.
Fig. 1 shows the spectra resulting from the acceleration of seeds with spectral indices 3 (hard), 4 (flat) and 5 (steep). In the absence of seeds, the spectrum is moderately concave, with a change of slope around 10 GeV. For seed spectra steeper than p−4, the energy of the seeds is initially located around the injection momentum and there is not much difference between the reacceleration of these seeds and the acceleration of particles from the thermal bath, as can be seen in the left-hand panel of Fig. 1. In contrast, if the spectral index of the seeds is ‘flat’ (α = 4), the plasma flow is much more modified compared to the case where seeds are not present. As the compression factor of the subshock decreases, the injection of particles from the thermal pool becomes inefficient. On the other hand, high-energy seeds feel the total compression factor and can thus be efficiently reaccelerated, which hardens the spectra at high energies. This results in hard spectra over almost all energy bands, as can be seen in the middle panel of Fig. 1. Finally, if the spectrum of the seeds is harder than p−4, the reacceleration becomes inefficient at high energies such that the high-energy end of the spectrum is close to that of the seeds. On the other hand, the freshly injected particles are not efficiently accelerated at the subshock, which leads to extremely steep spectra at low energies. This results in very concave spectra, which are basically the superposition of an injection with the pre-existing spectrum, as seen in the right-hand panel of Fig. 1.
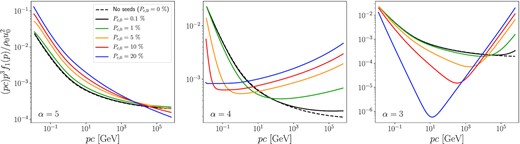
Spectra after reacceleration and decompression of seeds with spectral index α = 5 (left), α = 4 (middle), and α = 3 (right). Each curve corresponds to a different value of the relative CR pressure at upstream infinity.
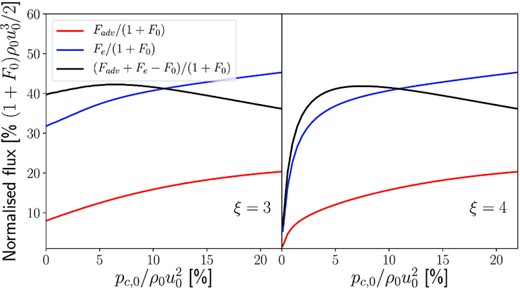
Flux advected downstream Fadv, escape flux upstream Fe, net flux gain Fadv + Fe − F0, all normalized to the upstream incoming flux (ram hydrodynamical flux |$\rho u_0^3/2$| plus flux of pre-existing particles F0), as function of the pressure of the seeds at upstream infinity, for an injection parameter ξ = 3 (left-hand panel) and ξ = 4 (right-hand panel).
4 PARTICLE ACCELERATION BY SUCCESSIVE NON-LINEAR SHOCKS
4.1 Identical shocks
We now aim at investigating the acceleration of particles by multiple shocks. First, we assume that all shocks are identical. This is a simplistic modelling as we expect for instance the medium to be heated by each shock if they all span the same volume, or the density to decrease if the volume expands. The idealistic solution is nevertheless interesting as a benchmark to understand more realistic scenarios, which we shall investigate in the next subsections.
Fig. 3 shows the evolution of the CR spectrum for M0 = 20, T0 = 106 K (u0 = 3320 km s−1), n0 = 0.01 cm−3, ξ = 3, and pmax = 1 PeV. There are no pre-existing particles before the first shock, and particles are injected from the thermal pool at each shock. The bottom-right panel displays the effective flow velocity felt by particles of momentum p. In Bohm’s diffusion regime, the diffusion length is proportional to p such that xp, the distance probed by particles of momentum p ahead of the shock, can be identified with the physical distance up to a rescaling (|$x_{p_{\rm max}}$| being interpreted as the position of a free escape boundary). The curves in the bottom-right panel can therefore be readily identified with the velocity profiles of the scattering centres. One sees how the energetic particles slow down the flow upstream of the shock, leading to the formation of a precursor. The effective compression ratio of the subshock decreases rapidly after the first few shocks and stabilizes around 2.5, which results in a steepening at low energies: The spectral index can be as high as 5. On the other hand, the total compression ratio increases after each shock before it stabilizes around 4.6, which leads to a hardening of the high-energy bands. Asymptotically, the spectrum is harder than p−4 beyond 100 GeV and the spectral index reaches 3.6 at 1 PeV. This demonstrates a striking discrepancy compared with the linear evolution displayed for comparison on the top-right panel of Fig. 3. As shown by e.g. Melrose & Pope (1993), the linear treatment indeed leads to a spectral hardening until the asymptotic p−3 distribution is reached.
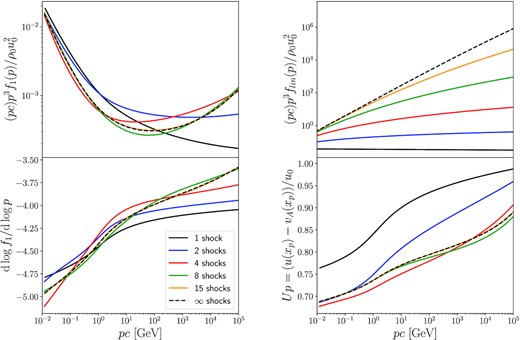
CR spectrum after multiple reaccelerations (top-left panel) and corresponding spectral indices (bottom-left panel) compared with linear diffusive shock reacceleration (top-right panel). The bottom-right panel displays the velocity felt by the particles as defined by equation (3).
Fig. 4 shows the asymptotic solution (typically reached after about 10 reaccelerations) for various sets of parameters. It is striking that the high-energy part of the spectrum above 100 GeV displays a somewhat universal shape, that is, a slight concavity, with a spectral index decreasing from about 3.9 to 3.5. As far as the injection parameter is concerned, it only affects the lower part of the spectrum, which is steeper for high injection efficiencies (small ξ). Furthermore, the asymptotic solution is nearly independent of the Mach number and, up to a rescaling, of the maximum momentum as well.

Asymptotic solution after multiple shock reaccelerations for various sets of parameters. Left-hand panel: M0 = 20, pmax = 106 GeV, and varying ξ. Middle panel: ξ = 3, pmax = 106 GeV, and varying M0. Right-hand panel: M0 = 20, ξ = 3, and varying pmax.
The evolution of the pressure of the post-shock CRs (in between the passage of two shocks, after adiabatic decompression) as function of the number of shocks which have already swept-up the medium is plotted in Fig. 5 for various sets of parameters. The comparison between the linear and non-linear computation displayed on the top-left panel demonstrates the need for a non-linear treatment of the problem in order to avoid energy violation. Noteworthy, with the adopted parameters, the CR pressure calculated in the linear case exceeds 100 per cent after four shocks, even though we chose a very small injection efficiency (ξ = 4). The three other panels show that the evolution of the pressure does not depend much on the parameters and can be divided into three phases. At the first three shocks, the pressure increases, until it overshoots its asymptotic value. Then it decreases and stabilizes after about 10 shocks. The reason behind the decrease of the downstream pressure is that, as discussed above, the acceleration efficiency decreases when the seed pressure is too large. Eventually a balance is set between the downstream advection and the upstream escape. The asymptotic fluxes are such that about 50 per cent of the shock kinetic flux goes into CRs, with about 10 per cent advected downstream and 40 per cent escaping upstream. This means that the reacceleration process saturates when the system approaches an equipartition of kinetic and thermal energy. This is the very reason behind the nearly universal character of the asymptotic solution. Only the injection of fresh particles modulates the low-energy bands of the spectrum and the value of the CR pressure at saturation, which slightly increases as the injection efficiency increases (top-right panel of Fig. 5). This variation is nevertheless very moderate. Only for very low injection fractions (e.g. 10−12), the pressure of post-shock CRs is found to saturate below 1 per cent. This is because in this case the asymptotic test-particle solution f(p) ∝ p−3 is reached before non-linear effects regulate the energy balance. In particular, the energy of the particles always remains negligible compared to that of the shock and equipartition cannot be reached. However, such small efficiencies are not realistic, and therefore we conclude that non-linear effects are unavoidable when dealing with multiple shocks. In this case, for standard values of the injection parameter (ξ ∼ 2–4) the pressure of the CRs remaining in the (decompressed) medium is always about |$3{-}5{{\ \rm per\,cent}}$| of the shock ram pressure.
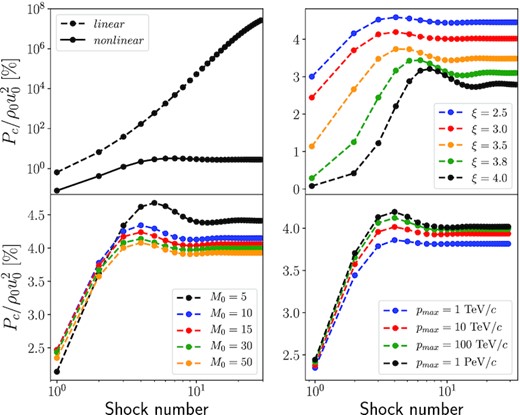
Evolution of the CR pressure after reacceleration by successive shocks. Top-left panel: Comparison between linear and non-linear computations, for |$\mathcal {M}_0=20$|, ξ = 4, and pmax = 1 PeV. Top-right panel: |$\mathcal {M}_0=20$|, pmax = 1 PeV, and varying ξ. Bottom-left panel: ξ = 3, pmax = 1 PeV, and varying M0. Bottom-right panel: |$\mathcal {M}_0=20$|, ξ = 3, and varying pmax.
4.2 Heating
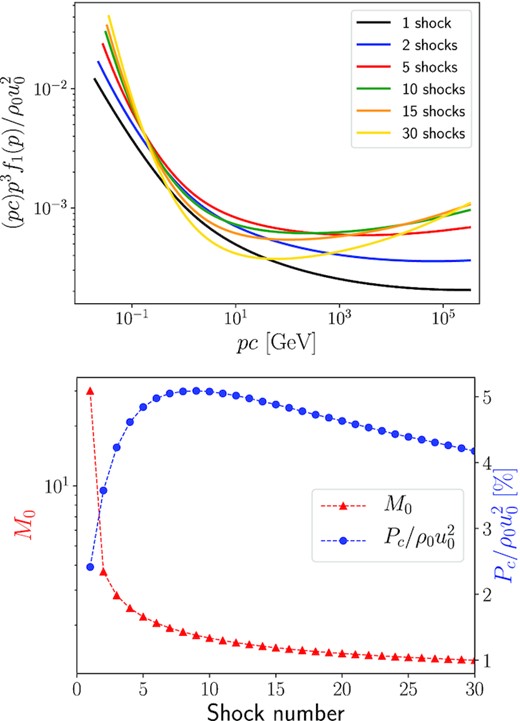
Evolution of the downstream CR spectrum (top panel), the shock Mach number (bottom panel, in red), and the post-shock CR pressure (bottom panel, in blue) when the heating of the medium in between successive shocks is taken into account.
After a few shocks, the Mach number decreases rapidly and the reacceleration becomes inefficient. The spectra are steeper than in the situation where all shocks are identical. Although an asymptotic solution is also expected to be reached in this case, it takes much longer time for the system to converge.
4.3 Towards CR production in SBs
A promising environment where multiple shock acceleration is expected to take place is the interior of a SB. Indeed, confined CRs may be successively reaccelerated by SN shocks inside SBs (Ferrand & Marcowith 2010). Interestingly, the adiabatic expansion of the SB compensates the heating of the medium due to the successive shocks, such that the interior temperature stays nearly constant in time (Parizot et al. 2004). On the other hand, the density is constantly decreasing with time: n(t) ∝ t−22/35. We computed again the reacceleration of CRs by successive shocks taking into account this density drop with a constant temperature.
Fig. 7 shows the evolution of the CR spectrum in an environment where the density decreases as ni ∝ i−22/35, where i is the number of shocks which have swept-up the medium (we assume that the shocks accelerate the particles at regular intervals), and ni is the density far upstream of the ith shock. What is shown is the spectrum just before the (i + 1)th reacceleration (including the decompression of the medium), compared with the post-shock spectrum in the case where the ambient density is constant. The bottom panel of Fig. 7 displays the evolution of the post-shock pressure normalized to the ram pressure of the first shock. Because CRs suffer enhanced adiabatic losses in between shocks, the pressure does not increase as rapidly as in the case of constant density and does not overshoot the asymptotic value. Nevertheless, the asymptotic pressure is identical to that computed in the ideal case of constant density, which is around 4 per cent of the ram pressure of the first shock. Neither are the particle spectra displaying substantial modifications.
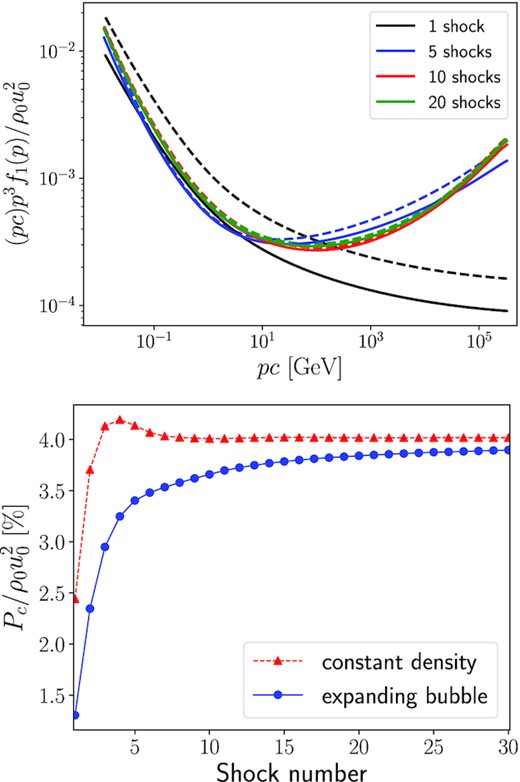
Top panel: Evolution of the CR spectrum during multiple shock acceleration in an expanding medium (solid lines) compared to the spectra computed in the case where all shocks are identical (dashed lines). Bottom panel: Evolution of the CR pressure in an expanding medium. The parameters are n0 = 0.01 cm−3, M0 = 20, and ξ = 3.
Fig. 8 shows the resulting CR spectra and pressure evolution. The ‘benchmark’ asymptotic solution described in Section 4.1 is retrieved up to the momentum such that τesc(p) < Δt. Beyond this momentum, the particles escape and are not reaccelerated. With a small escape parameter τ, the CR production may be intermittent at all energy bands. As shown by the yellow curves in Fig. 8, in this case there are nearly no particles remaining in between the shocks and the CR pressure right before a SN explosion is close to zero. The particles are not reaccelerated and the SB is just a collection of isolated SNe.
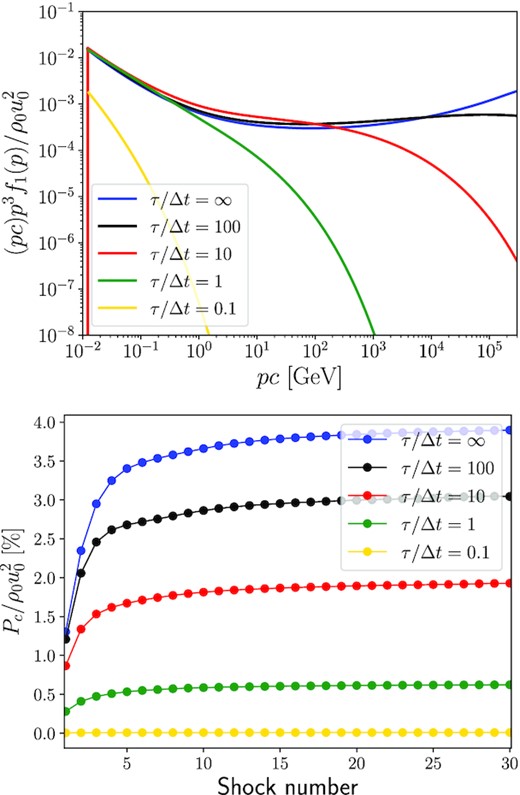
Asymptotic CR spectrum (top panel) and evolution of the pressure (bottom panel) during multiple shock accelerations in an expanding medium where the particles can escape in between the passage of two shocks. The parameters are n0 = 0.01 cm−3, M0 = 20, and ξ = 3. Each curve corresponds to a different ratio of the particle escape time to the time interval between two SN explosions.
On the other hand, the concave asymptotic solution can be retrieved provided the escape parameter is sufficiently large (black curve). This may occur if e.g. the interval between two SNe is Δt ∼ 100 kyr and the escape time is τ ∼ 10 Myr. These are not unrealistic values for clusters hosting hundreds of massive stars in possibly very turbulent environments such as the Galactic centre. We will soon publish a detailed model of particle acceleration in SBs (Vieu et al. 2021), building on the work detailed in this paper.
5 CONCLUSIONS
We tackled the problem of the non-linear reacceleration of particles by a succession of strong shocks, using a semi-analytical computation accounting for the streaming instability as well as the Alfvénic drift effect. We have shown that the linear framework provides a very inaccurate estimate of the solution. The presence of seeds can indeed strongly modify the shock structure and balance the shock pressure such that particle reacceleration becomes less efficient at either low or high energies, depending on the seed spectrum. This can lead to spectra either steep (for steep distributions of seeds), hard (for flat distributions of seeds), or displaying a sharp transition from a steep to a hard component (for hard distributions of seeds).
We then considered the acceleration of particles by multiple identical shocks, in the case where no particles exist before the first shock. The spectrum converges towards an asymptotic solution, typically reached after 20 shocks. Remarkably, the asymptotic spectrum is nearly universal above 10 GeV. In particular, it does not depend on the injection efficiency and shock Mach number. The injection efficiency shapes the low-energy bands, which are steeper for higher efficiencies. The asymptotic solution is eventually characterized by a spectral index which increases from around 5 at the injection momentum to about 3.5 at the maximum energy. This is again very different from the linear solution, f(p) ∝ p−3.
The post-shock CR pressure increases after a few shocks, then quickly stabilizes around an asymptotic value. The latter is about 4–5 per cent of the ram pressure of one shock. Interestingly, this value weakly depends on the injection efficiency. Even for very small efficiencies, a reacceleration by a few shocks is sufficient for the CR pressure to reach a few per cent of the shock energy.
We eventually generalized the analysis to the case of non-identical successive shocks. In a constant volume, the medium is heated between each shock, which leads to a rapid decrease of the shock Mach numbers: The reacceleration of the particles becomes inefficient. On the other hand, assuming an environment undergoing an adiabatic expansion, such as a galactic SB, we found results similar to the case of identical shocks. The particle spectrum converges towards the same asymptotic distribution, with a concave shape and universal spectral index around 3.5 at the maximum energy. Eventually, we allowed the particles to escape the accelerator in between the passage of two shocks, demonstrating that the asymptotic solution would form only in the case where particles are very efficiently confined. This computation will be a building block of a self-consistent model of particle acceleration in SBs (Vieu et al. 2021).
ACKNOWLEDGEMENTS
TV acknowledges Alexandre Marcowith and Etienne Parizot for helpful discussions and suggestions. SG and VT acknowledge support from Agence Nationale de la Recherche (grant ANR-17-CE31-0014).
DATA AVAILABILITY
No new data were generated or analysed in support of this research.
Footnotes
In fact, non-vanishing values of the Alfven speed might also be present downstream, due to the inertia of waves excited upstream and compressed by the shock (Caprioli, Haggerty & Blasi 2020). Such an effect, not considered here, would further increase the impact that the drift of scattering centres has on the spectrum of CRs accelerated at the shock.



