-
PDF
- Split View
-
Views
-
Cite
Cite
Takeru Murase, Toshihiro Handa, Yushi Hirata, Toshihiro Omodaka, Makoto Nakano, Kazuyoshi Sunada, Yoshito Shimajiri, Junya Nishi, Kagoshima galactic object survey with the Nobeyama 45-metre telescope by mapping in ammonia lines (KAGONMA): star formation feedback on dense molecular gas in the W33 complex, Monthly Notices of the Royal Astronomical Society, Volume 510, Issue 1, February 2022, Pages 1106–1117, https://doi.org/10.1093/mnras/stab3472
Close - Share Icon Share
ABSTRACT
We present the results of NH3 (1,1), (2,2), and (3,3) and H2O maser simultaneous mapping observations toward the high-mass star-forming region W33 with the Nobeyama 45-m radio telescope. W33 has six dust clumps, one of which, W33 Main, is associated with a compact H ii region. To investigate star-forming activity feedback on its surroundings, the spatial distribution of the physical parameters was established. The distribution of the rotational temperature shows a systematic change from west to east in our observed region. The high-temperature region obtained in the region near W33 Main is consistent with interaction between the compact H ii region and the peripheral molecular gas. The size of the interaction area is estimated to be approximately 1.25 pc. NH3 absorption features are detected toward the centre of the H ii region. Interestingly, the absorption features were detected only in the NH3 (1,1) and (2,2) transitions, with no absorption feature seen in the (3,3) transition. These complex profiles in NH3 are difficult to explain by a simple model and may suggest that the gas distribution around the H ii region is highly complicated.
1 INTRODUCTION
High-mass stars (>8 M⊙) affect the surrounding environment through expansion of H ii regions, powerful outflows, strong stellar winds, and large amounts of radiation. Consequently, they ultimately play a key role in the evolution of the host galaxy (Kennicutt 2005). In addition, the feedback from high-mass stars influences subsequent star formation. For example, feedback from high-mass stars causes strong shocks in the surrounding molecular gas, which compresses the gas and triggers star formation (e.g. Urquhart et al. 2007; Shimajiri et al. 2008; Thompson et al. 2012; Deharveng et al. 2015; Duronea et al. 2017; Paron, Granada & Areal 2021). In other cases, feedback heats the surrounding molecular gas and suppresses the fragmentation of cores or filaments. This is thought to be a contributing factor in the formation of high-mass stars (e.g. Bate 2009; Hennebelle & Chabrier 2011; Deharveng et al. 2012; Bate & Keto 2015; Hennebelle et al. 2020). In this study, we focus on the effects of the formation processes of high-mass stars on the molecular cloud environment.
Several recent observations as part of the James Clerk Maxwell Telescope (JCMT) Gould Belt survey (Ward-Thompson et al. 2007) have quantified the effect of radiative feedback from OB stars on molecular clouds. Using the dust colour temperature derived from the flux ratios of 450- and 850-μm continuum emission, they found that the dust temperature around OB stars can rise to 40 K, with effects on scales of several parsec (Rumble et al. 2021). They reported that heating of the dust may raise the Jeans mass and enhance the stability of the cores of filaments against gravitational collapse (Hatchell et al. 2013; Rumble et al. 2015, 2016, 2021). In addition to dust data, the gas temperature map using molecular lines (e.g. CO, NH3, N2H+, etc.) can be obtained. Large surveys of nearby star-forming regions in NH3 revealed that the average gas temperature in molecular clouds with inactive star formation is around 15 K, while active star-forming cores have temperatures above 20 K (e.g. Urquhart et al. 2015; Friesen et al. 2017; Hogge et al. 2018; Billington et al. 2019; Keown et al. 2019; Tursun et al. 2020). In the range of hydrogen number densities |$n\mathrm{(H_2)} \gtrsim 10^{4}$| cm−3, the dust and gas temperatures are expected to be well coupled due to frequent collision of dust grains and gas (e.g. Goldsmith 2001; Seifried et al. 2017).
Most stars are recognized to form in cluster mode (Lada & Lada 2003; Krumholz, McKee & Bland-Hawthorn 2019). The heating of molecular gas by radiation feedback from high-mass stars in the cluster may impact the types of stars formed (e.g. Bate 2009; Rumble et al. 2015). In order to study the impact of radiative feedback, it is important to investigate the effects and scales of star-forming regions of various evolutionary stages on the surrounding environment.
There are several techniques to measure the temperature of the interstellar medium (ISM). The dust temperature Tdust can be estimated by fitting a single-temperature greybody model to the observed spectral energy distribution (SED) of the dust continuum thermal emission (Hildebrand 1983). However, there are uncertainties in the assumptions of the dust emissivity coefficient κ and and dust emissivity index β, which affect the accuracy of the derived dust temperature. CO emission lines are commonly used for molecular gas observations. In particular, the gas excitation temperature can easily be obtained from the brightness temperature of 12CO (J = 1–0) by assuming the optically thick and the filling factor in the observed beam is unity. However, it should be noted that the physical parameters in the centre of high-density cores may not reflect this, due to optical thickness and freezing-out on to dust grains (e.g. Willacy, Langer & Velusamy 1998; Tafalla et al. 2002; Christie et al. 2012; Feng et al. 2020).
NH3 has long been recognized as a good thermometer for the ISM (Ho & Townes 1983) and its line observations have the advantage of enabling us to derive physical parameters such as column density and optical depth from the splitting of the inversion transition into hyperfine structure lines, with only reasonable assumptions that the main transitions of the molecule are emitted under similar excitation conditions. The rotational temperature can also be estimated from the relationship between the intensity ratio of two different inversion transition lines and the optical depth. In addition, the inversion transitions in the lowest metastable rotational energy levels are easily excited in the typical temperatures of molecular clouds. Moreover, NH3 molecules are abundant in the gas phase in cold and high-density environments (e.g. Bergin & Langer 1997; Tafalla et al. 2002).
Previous observational studies in NH3 lines have predominantly been single-beam pointings toward infrared dark clouds (IRDCs), young stellar objects (YSOs), and the centres of H ii regions (e.g. Wilson, Batrla & Pauls 1982; Rosolowsky et al. 2008; Dunham et al. 2010; Urquhart et al. 2011; Wienen et al. 2018), and mappings at scales of a few parsec (e.g. Keto, Ho & Haschick 1987; Mangum, Wootten & Mundy 1992; Toujima et al. 2011; Chibueze et al. 2013; Urquhart et al. 2015; Nakano et al. 2017; Billington et al. 2019; Burns et al. 2019). These studies have related the physical conditions of active star-forming cores to the surrounding environment. Recently, large surveys with the Green Bank Telescope (GBT) have been conducted to study the relationship between the kinematics of dense gas and star formation in entire molecular clouds. These observations cover giant molecular clouds (K-band Focal Plane Array (KFPA) Examinations of Young STellar Object Natal Environments (KEYSTONE): Keown et al. 2019), the Gould Belt star-forming regions (the Green Bank Ammonia Survey (GAS): Friesen et al. 2017) and the Galactic plane (the Radio Ammonia Mid-Plane Survey (RAMPS), covering 10° ≤ l ≤ 40°, ∣b∣ ≤ 0°.5: Hogge et al. 2018). These large surveys were made with the on-the-fly (OTF) mapping mode. However, these unbiased surveys are rather shallow, since NH3 line observations require a large amount of time to detect weaker emission. Therefore, we conducted a high-sensitivity NH3 imaging survey targeting dense molecular cores and the regions around them.
For our survey, we identified dense molecular cores based on the C18O (J = 1–0) imaging data obtained as part of the FOREST (FOur-beam REceiver System on the 45m Telescope) Unbiased Galactic plane Imaging survey with the Nobeyama 45-m telescope (FUGIN: Umemoto et al. 2017). By using the clumpfind algorithm (Williams, de Geus & Blitz 1994), we catalogued 72 molecular cores/clumps in part of the first and third quadrants of the Galactic plane (i.e. 10° ≤ l ≤ 50° and 198° ≤ l ≤ 236°, ∣b∣ ≤ 1°). This catalogue includes IRDCs, high-mass star-forming regions, and H ii regions. We have already finished the mapping observations towards seven cores or clumps, which are listed in Table 1. This work is the first report of the KAGONMA survey project, which is an acronym of Kagoshima Galactic Object survey with Nobeyama 45-metre telescope by Mapping in Ammonia lines. We present the results for the W33 high-mass star-forming region, which is identified as KAGONMA 64.
| KAGONMA . | l . | b . | vLSR(C18O)a . | Associated object . |
|---|---|---|---|---|
| name . | [degrees] . | [degrees] . | [km s−1] . | . |
| KAG1 | 44.312 | 0.039 | + 56.9 | G044.3103 + 00.0416* |
| KAG35 | 14.613 | −0.565 | + 18.5 | G14.628−0.572 |
| KAG39 | 14.565 | −0.603 | + 18.7 | G14.555−0.606 |
| KAG45 | 14.454 | −0.102 | + 40.4 | G014.481−00.109* |
| KAG64 | 12.798 | −0.202 | + 35.6 | W33 Main* |
| KAG71 | 224.274 | −0.833 | + 18.0 | CMa OB1 |
| KAG72 | 201.446 | 0.638 | + 6.5 | G201.44 + 00.65 |
| KAGONMA . | l . | b . | vLSR(C18O)a . | Associated object . |
|---|---|---|---|---|
| name . | [degrees] . | [degrees] . | [km s−1] . | . |
| KAG1 | 44.312 | 0.039 | + 56.9 | G044.3103 + 00.0416* |
| KAG35 | 14.613 | −0.565 | + 18.5 | G14.628−0.572 |
| KAG39 | 14.565 | −0.603 | + 18.7 | G14.555−0.606 |
| KAG45 | 14.454 | −0.102 | + 40.4 | G014.481−00.109* |
| KAG64 | 12.798 | −0.202 | + 35.6 | W33 Main* |
| KAG71 | 224.274 | −0.833 | + 18.0 | CMa OB1 |
| KAG72 | 201.446 | 0.638 | + 6.5 | G201.44 + 00.65 |
Notes.a Umemoto et al. (2017).
*H ii region.
| KAGONMA . | l . | b . | vLSR(C18O)a . | Associated object . |
|---|---|---|---|---|
| name . | [degrees] . | [degrees] . | [km s−1] . | . |
| KAG1 | 44.312 | 0.039 | + 56.9 | G044.3103 + 00.0416* |
| KAG35 | 14.613 | −0.565 | + 18.5 | G14.628−0.572 |
| KAG39 | 14.565 | −0.603 | + 18.7 | G14.555−0.606 |
| KAG45 | 14.454 | −0.102 | + 40.4 | G014.481−00.109* |
| KAG64 | 12.798 | −0.202 | + 35.6 | W33 Main* |
| KAG71 | 224.274 | −0.833 | + 18.0 | CMa OB1 |
| KAG72 | 201.446 | 0.638 | + 6.5 | G201.44 + 00.65 |
| KAGONMA . | l . | b . | vLSR(C18O)a . | Associated object . |
|---|---|---|---|---|
| name . | [degrees] . | [degrees] . | [km s−1] . | . |
| KAG1 | 44.312 | 0.039 | + 56.9 | G044.3103 + 00.0416* |
| KAG35 | 14.613 | −0.565 | + 18.5 | G14.628−0.572 |
| KAG39 | 14.565 | −0.603 | + 18.7 | G14.555−0.606 |
| KAG45 | 14.454 | −0.102 | + 40.4 | G014.481−00.109* |
| KAG64 | 12.798 | −0.202 | + 35.6 | W33 Main* |
| KAG71 | 224.274 | −0.833 | + 18.0 | CMa OB1 |
| KAG72 | 201.446 | 0.638 | + 6.5 | G201.44 + 00.65 |
Notes.a Umemoto et al. (2017).
*H ii region.
Fig. 1 shows the Spitzer -GLIMPSE 8.0-|$\rm{\mu m}$| (Benjamin et al. 2003) image of the W33 region. W33 has six dust clumps defined in the Atacama Pathfinder Experiment (APEX) Telescope Large Area Survey of the GALaxy (ATLASGAL) 870-|$\rm{\mu m}$| survey (Schuller et al. 2009; Contreras et al. 2013; Urquhart et al. 2014), which are W33 Main, W33 A, W33 B, W33 Main 1, W33 A1, and W33 B1 (see Fig. 1). Immer et al. (2014) reported that these six dust clumps are at various stages (high-mass protostellar object, hot core, compact H ii region) in the star-forming process, based on their spectral energy distributions (SEDs) from centimetre to far-infrared. In Table 2, the evolutionary stage of each dust clump is listed in order of earliest to latest. W33 Main harbours a compact H ii region found by radio continuum observations (Ho & Townes 1983), indicating massive star formation. Water and methanol maser emission has been detected in W33 A, W33 Main, and W33 B (i.e. Haschick, Menten & Baan 1990; Menten 1991; Immer et al. 2013), and OH maser sources have been detected in W33 A and W33 B (i.e. Caswell 1998; Colom et al. 2015).
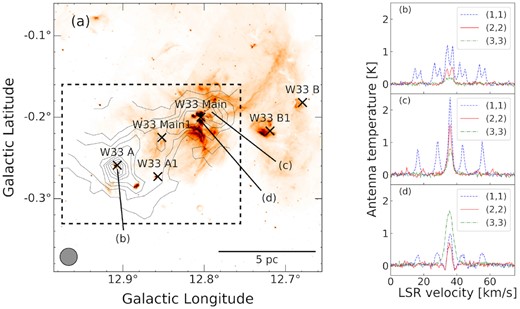
(a): The NH3(1,1) integrated intensity map of the W33 complex in contours over the Spitzer-GLIMPSE 8.0-|$\mu$|m image. The lowest contour and contour steps are 0.8 K km s−1 and 1.2 K km s−1 (30σ), respectively. The cross marks indicate the dust clumps reported by the ATLASGAL 870-|$\mu$|m survey (e.g. Contreras et al. 2013; Urquhart et al. 2014). The dashed rectangle shows our observing area. The NRO 45-m beamsize (FWHM) is indicated by the grey circle shown in the lower left corner in panel (a). The (b)–(d) labels indicate the positions for the profiles shown in panels (b)–(d).
| Source . | l . | b . | Tex(C18O)a . | Evolution stageb . |
|---|---|---|---|---|
| . | [degrees] . | [degrees] . | [K] . | . |
| W33 A1 | 12.857 | −0.273 | 18 | High-mass protostellar object |
| W33 B1 | 12.719 | −0.217 | 23 | High-mass protostellar object |
| W33 Main1 | 12.852 | −0.225 | 19 | High-mass protostellar object |
| W33 A | 12.907 | −0.259 | 18 | Hot core |
| W33 B | 12.679 | −0.182 | 17 | Hot core |
| W33 Main | 12.804 | −0.200 | 34 | Compact H ii region |
| Source . | l . | b . | Tex(C18O)a . | Evolution stageb . |
|---|---|---|---|---|
| . | [degrees] . | [degrees] . | [K] . | . |
| W33 A1 | 12.857 | −0.273 | 18 | High-mass protostellar object |
| W33 B1 | 12.719 | −0.217 | 23 | High-mass protostellar object |
| W33 Main1 | 12.852 | −0.225 | 19 | High-mass protostellar object |
| W33 A | 12.907 | −0.259 | 18 | Hot core |
| W33 B | 12.679 | −0.182 | 17 | Hot core |
| W33 Main | 12.804 | −0.200 | 34 | Compact H ii region |
| Source . | l . | b . | Tex(C18O)a . | Evolution stageb . |
|---|---|---|---|---|
| . | [degrees] . | [degrees] . | [K] . | . |
| W33 A1 | 12.857 | −0.273 | 18 | High-mass protostellar object |
| W33 B1 | 12.719 | −0.217 | 23 | High-mass protostellar object |
| W33 Main1 | 12.852 | −0.225 | 19 | High-mass protostellar object |
| W33 A | 12.907 | −0.259 | 18 | Hot core |
| W33 B | 12.679 | −0.182 | 17 | Hot core |
| W33 Main | 12.804 | −0.200 | 34 | Compact H ii region |
| Source . | l . | b . | Tex(C18O)a . | Evolution stageb . |
|---|---|---|---|---|
| . | [degrees] . | [degrees] . | [K] . | . |
| W33 A1 | 12.857 | −0.273 | 18 | High-mass protostellar object |
| W33 B1 | 12.719 | −0.217 | 23 | High-mass protostellar object |
| W33 Main1 | 12.852 | −0.225 | 19 | High-mass protostellar object |
| W33 A | 12.907 | −0.259 | 18 | Hot core |
| W33 B | 12.679 | −0.182 | 17 | Hot core |
| W33 Main | 12.804 | −0.200 | 34 | Compact H ii region |
The distance to the W33 complex, based on annual parallax, was established as 2.4 kpc using VLBI water maser observations (Immer et al. 2013). W33 is located in the Scutum spiral arm of the Milky Way. Some CO line observations covering the entire W33 region were conducted (e.g. Stier et al. 1984; Sridharan et al. 2002; Kohno et al. 2018; Liu et al. 2021). Kohno et al. (2018) reported that W33 A, W33 Main, and W33 B1 are at a radial velocity of ∼ 35 km s−1 and W33 B has a velocity of ∼ 58 km s−1, while Immer et al. (2013) reported that these clumps exist within a single molecular cloud because these clumps have the same parallactic distance.
This work is organized as follows: in Section 2 we describe the set-up of our observations and data reduction. In Section 3 we present the results and estimated physical parameters of the observed area. We evaluate the influence of star-formation feedback based on the rotational temperature distribution of NH3 lines in Section 4. In Section 5, we summarize our results and our conclusions.
2 OBSERVATIONS
2.1 NH3 and H2O maser observations
We made mapping observations covering a 12 × 12 arcmin2 area including W33 A and W33 Main with the Nobeyama 45-m radio telescope from 2016 December–2019 April. We observed the NH3 (J,K) = (1,1), (2,2), (3,3), and H2O maser lines simultaneously. From 2019 February, we observed NH3 (3,3), (4,4), (5,5), and (6,6) lines at positions where the (3,3) emission line was detected (> 20σ). The (3,3) emission line was observed again for relative calibration. We used the H22 receiver, which is a cooled HEMT (High Electron Mobility Transistor) receiver, and the Spectral Analysis Machine for the 45-m telescope (SAM45: Kuno et al. 2011), which is a digital spectrometer, to observe both polarizations for each line simultaneously. The bandwidth and spectral resolution were 62.5 MHz and 15.26 kHz, respectively. At the frequency of NH3, these correspond to a velocity coverage and resolution of 400 km s−1 and 0.19 km s−1, respectively. The telescope beam size was 75 arcsec at 23 GHz, which corresponds to 0.87 pc at 2.4 kpc. The pointing accuracy was checked every hour using a known H2O maser source, M16A at (α, δ)J2000 = (18h15m19s.4, −13°46′30″.0), and was better than 5 arcsec. The map centre was (l, b) = (12.°820, − 0.°194). The OFF reference position was taken at (l, b) = (13.°481, +0.°314), where neither C18O (J = 1–0), NH3, nor the H2O maser was detected.
We observed 280 positions using a 37.5-arcsec grid in equatorial coordinates using the position switch method. For efficient observation, three ON positions were set for each OFF position and integrations were repeated for 20 seconds at each position. To obtain uniform map noise, the scans were integrated until the root-mean-square (rms) noise level for each polarization of each observed line was reached to below 0.075 K. The typical system noise temperature, Tsys, was between 100 and 300 K. The antenna temperature, |$T_\mathrm{a}^{*}$|, was calibrated by the chopper wheel method (Kutner & Ulich 1981). We summarize the parameters for the NH3 and H2O maser line observations in Table 3.
| Transition . | Frequencya . | |$E_\mathrm{u}/k_\mathrm{B}\, ^a$| . |
|---|---|---|
| . | [GHz] . | [K] . |
| H2O 612–512 (maser) | 22.235080 | – |
| NH3 (1,1) | 23.694495 | 23.3 |
| NH3 (2,2) | 23.722633 | 64.4 |
| NH3 (3,3) | 23.870129 | 123.5 |
| NH3 (4,4) | 24.139416 | 200.5 |
| NH3 (5,5) | 24.532988 | 295.6 |
| NH3 (6,6) | 25.056025 | 408.1 |
| Transition . | Frequencya . | |$E_\mathrm{u}/k_\mathrm{B}\, ^a$| . |
|---|---|---|
| . | [GHz] . | [K] . |
| H2O 612–512 (maser) | 22.235080 | – |
| NH3 (1,1) | 23.694495 | 23.3 |
| NH3 (2,2) | 23.722633 | 64.4 |
| NH3 (3,3) | 23.870129 | 123.5 |
| NH3 (4,4) | 24.139416 | 200.5 |
| NH3 (5,5) | 24.532988 | 295.6 |
| NH3 (6,6) | 25.056025 | 408.1 |
Note.aFrom the JPL Submillimetre, Millimetre, and Microwave Spectral Line catalogue (Pickett et al. 1998). Eu is the energy of the upper level above the ground.
| Transition . | Frequencya . | |$E_\mathrm{u}/k_\mathrm{B}\, ^a$| . |
|---|---|---|
| . | [GHz] . | [K] . |
| H2O 612–512 (maser) | 22.235080 | – |
| NH3 (1,1) | 23.694495 | 23.3 |
| NH3 (2,2) | 23.722633 | 64.4 |
| NH3 (3,3) | 23.870129 | 123.5 |
| NH3 (4,4) | 24.139416 | 200.5 |
| NH3 (5,5) | 24.532988 | 295.6 |
| NH3 (6,6) | 25.056025 | 408.1 |
| Transition . | Frequencya . | |$E_\mathrm{u}/k_\mathrm{B}\, ^a$| . |
|---|---|---|
| . | [GHz] . | [K] . |
| H2O 612–512 (maser) | 22.235080 | – |
| NH3 (1,1) | 23.694495 | 23.3 |
| NH3 (2,2) | 23.722633 | 64.4 |
| NH3 (3,3) | 23.870129 | 123.5 |
| NH3 (4,4) | 24.139416 | 200.5 |
| NH3 (5,5) | 24.532988 | 295.6 |
| NH3 (6,6) | 25.056025 | 408.1 |
Note.aFrom the JPL Submillimetre, Millimetre, and Microwave Spectral Line catalogue (Pickett et al. 1998). Eu is the energy of the upper level above the ground.
2.2 Data reduction
For data reduction, we use the Java newstar software package developed by the Nobeyama Radio Observatory (NRO). Baseline subtraction was conducted individually for all spectra using a line function established using emission-free channels. By combining dual circular polarizations, the rms noise level was typically 0.04 K at each position. A conversion factor of 2.6 Jy K−1 was used to convert the antenna temperature to flux density.
In this work, the intensities are presented as antenna temperature in K. The NH3 lines have five hyperfine components, consisting of one main line and four satellite lines. In our observations, these satellite lines were detected only in the (1,1) transition. The number of map positions in which ≥3σ detections were achieved in (1,1), (2,2) and (3,3) lines were 260, 231, and 172, respectively. No emission from transitions higher than (3,3) was detected.
The NH3 profiles obtained in our observations can be categorized into three types (Figs 1b–d). Fig. 1(b) shows double-peak profiles detected around W33 A. The double-peak profiles were detected at 46 positions (the enclosure in Fig. 2a). The single-peak profiles shown in Fig. 1(c) are typical NH3 profiles. The intensities of these two types of profile become weaker with higher excitation, while (3,3) was detected more strongly than low-excitation lines of the centre of W33 Main, where a compact H ii region is located (Fig. 1d). In this region, we found absorption features at 33 and 39 km s−1 in (1,1) and (2,2) lines (see Section 4.3 for details).
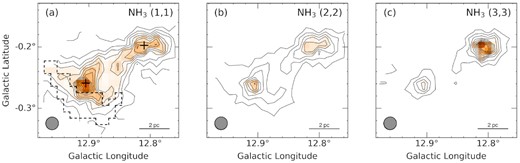
Integrated intensity map of NH3: (a) (1,1), (b) (2,2), and (c) (3,3). The NRO45 beam size is indicated by the grey circle shown in the lower left corner of each panel. The lowest contour and contour steps are 20σ (0.8 K km s−1) in |$T_\mathrm{ a}^{*}$|, respectively. Plus marks indicate the positions of H2O maser emission. The black dashed enclosure shows the region where double-peak profiles were detected.
3 RESULTS
3.1 Spatial distribution of NH3 emission
Fig. 2 shows the integrated intensity maps of the (1,1), (2,2), and (3,3) lines in our observed region. The velocity range of each map is between 32.0 and 40.0 km s−1. NH3(1,1) emission is extended over a region of 12 × 12 arcmin2, or 10 × 10 pc at 2.4 kpc. Two NH3 clumps were detected at W33 Main (l, b) = (12.°804, − 0.°200) and W33 A (l, b) = (12.°907, − 0.°259).
Although maps of both the NH3 (1,1) and (2,2) lines show two peaks in W33 Main with a separation of about 2 arcmin, the (3,3) map shows a single peak between them. After checking the profiles of the (1,1) and (2,2) lines there, we found hints of an absorption signature. Therefore, the actual column density structure of W33 Main has only a single clump with an apparent gap inside caused by the absorption of emission at the midway point. We will discuss the absorption feature further in Section 4.3.
3.2 Linewidth correlations
Fig. 3 shows the correlation plots of linewidths in the NH3 (1,1), (2,2), and (3,3) emission lines. In Fig. 3, we only used the observed positions where single-peak profiles were obtained (except for the enclosed positions in Fig. 2a). In our observations, the range of linewidths for each NH3 line was 2–6 km s−1, which is broader than the expected thermal linewidth for temperatures in W33 (approximately 0.2 km s−1 at a gas temperature of ∼ 20 K). These broader linewidths may be due to internal gas kinematic motions such as turbulence, outflows, and stellar winds. While the linewidths of (1,1) and (2,2) emission show strong correlations, (3,3) emission tends to have systematically broader linewidths than the lower excitation transitions (see also fig. 11 in Urquhart et al. 2011). As shown in Table 3, the NH3 (3,3) lines require approximately five times higher excitation energies than (1,1) lines. Therefore, the emission regions of higher transitions of NH3 lines are considered warmer and with more turbulent gas than (1,1) lines. These results are similar to single-beam observations toward the centres of massive young stellar objects (MYSOs) and H ii regions (Urquhart et al. 2011; Wienen et al. 2018). Our results therefore show that such linewidth correlations in NH3 can also be seen on larger scales than the core scale.
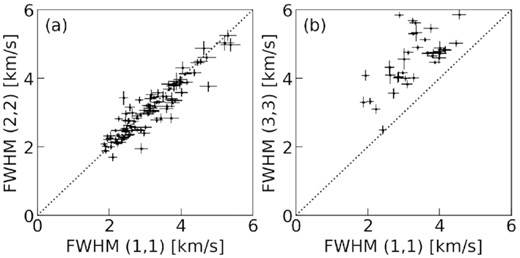
Scatter plots of FWHM linewidth of NH3 (1,1), (2,2), and (3,3) emission. The solid lines indicate the line of equality.
3.3 Deriving physical properties from NH3 lines
Using NH3 line profiles, we can derive several physical properties at each observed position, such as optical depth, rotational temperature, and column density.
Currently, there are two major methods for deriving the optical depth and rotational temperature (see Wang et al. 2020, for details). They are known as the intensity ratio and hyperfine fitting methods. The first method is derived from the intensity ratio between two different excitation lines, assuming a Boltzmann distribution (e.g. Ho & Townes 1983; Mangum et al. 1992). The other method is generating a model spectrum from the radiative transfer function and searching for parameters that match the observed profiles (e.g. Rosolowsky et al. 2008; Urquhart et al. 2015). The common point in these methods is that the physical conditions along the velocity axis are assumed to be uniform. In general, however, molecular lines have a velocity structure and the shape of profiles is asymmetric. Therefore, we used a method to derive physical parameters for each velocity channel based on the intensity ratio method (see Appendix A1 for more details).
3.4 Molecular gas properties
In this subsection, we will report the spatial distribution of the derived physical parameters in W33 (Fig. 4), which were solved in each velocity channel. The physical parameters at each position were derived when the signal-to-noise ratios (S/N) of all peaks of NH3 (1,1) hyperfine components and the (2,2) main line are above 3σ. The optical depth and rotational temperature errors were estimated to be ± 0.10 and ± 0.4 K, respectively (see Appendix A2).
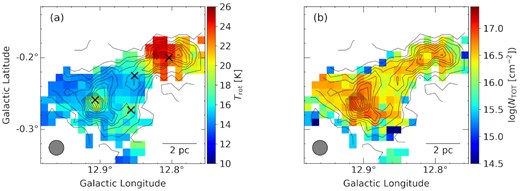
Spatial distributions of the physical parameters described in Section 3.3. The plotted values are representative along the velocity axis. (a) The rotational temperature; (b) the total column density of NH3 gas. Contours indicate the NH3(1,1) integrated intensity map, which is the same as in Fig. 2(a). The NRO45 beam size is indicated by the grey circle shown in the lower left corner of each panel. Cross marks are the same as inside the dashed rectangle in Fig. 1(a).
The derived optical depth ranges from 1 to 2, and its mean value over all observed positions was 1.24 ± 0.10. The optical depth distribution was not significantly different at each position.
Maps of the rotational temperature and total column density are shown in Fig. 4. The range of rotational temperature was between 12 and 25 K (Fig. 4a). We found a clear difference between galactic east and west parts, corresponding to W33 A and W33 Main, respectively. All pixels in W33 A were colder than 18 K, and most pixels in W33 Main were warmer than 20 K. In our NH3 observations, the temperature change was a particularly noticeable characteristic. We will discuss the relationship between the molecular gas temperature and star formation feedback in Section 4.2.
The value of total column density ranges between 2 × 1015 and 8 × 1016 cm−2, as shown in Fig. 4(b). The peak total column densities of W33 Main and W33 A were (5.1 ± 0.1) × 1016 cm−2 and (7.5 ± 0.1) × 1016 cm−2, respectively. In contrast to the difference in the rotational temperature, there was no significant difference in the total column density between W33 Main and W 33 A. A weak dip in the measured column density at the centre of W33 main is apparently due to the compact H ii region.
3.5 H2O maser detection
In our observations, H2O maser emission was detected in W33 A on 2017 May 21 at 26.3 Jy at (l, b) = (12.°905, −0.°257) and W33 Main on 2016 May 7 at 10.7 Jy at (l, b) = (12.°811, −0.°194). These masers are positionally consistent with those reported in the parallax observations of Immer et al. (2013). H2O maser emission is believed to be a signature of star formation in its early evolutionary stages (e.g. Sunada et al. 2007; Urquhart et al. 2011). Therefore, the detection indicates that both W33 A and W33 Main host star-forming activity.
4 DISCUSSION
4.1 Velocity components in W33 complex
Kohno et al. (2018) and Dewangan, Baug & Ojha (2020) reported three velocity components at 35, 45, and 55 km s−1 in the W33 region from FUGIN CO survey data.1 The 35 km s−1 and 55 km s−1 velocity components exhibit similar spatial distributions (see fig. 5 in Kohno et al. 2018). On the other hand, the 45 km s−1 velocity component shows weak emission extended over the wider W33 complex, and its spatial distribution is not exclusively associated with the W33 complex. Kohno et al. (2018) concluded that the 45 km s−1 velocity component is unrelated to star formation activity in the W33 complex. Fig. 6 shows the longitude–velocity diagram using our data and FUGIN 12CO (J = 1–0) data2 integrated over Galactic latitudes between −0.°35 and −0.°12, where contours indicate the NH3 (1,1) main line. The dominant emission in CO and NH3 is detected at 35 km s−1 and gas at this velocity is considered to be a molecular cloud related to the star formation activity in W33.
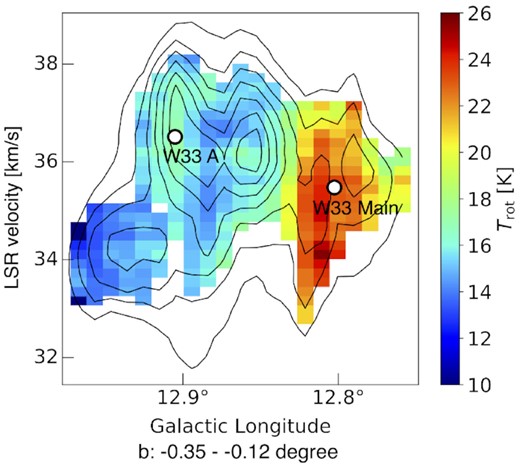
The longitude–velocity diagram of the rotational temperature. White circles, lowest contour level, and contour interval are same as in Fig. 6.
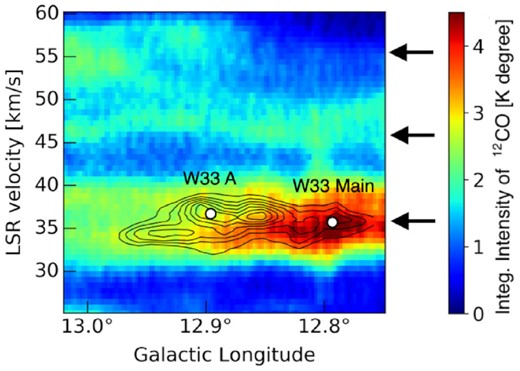
Longitude–velocity diagram of the 12CO (J = 1–0) emission using FUGIN data (colour image) and the NH3(1,1) main line emission (contour). The white circles indicate the peak velocities of W33 A and W33 Main in the C18O(J = 1–0) emission line (Umemoto et al. 2017; Kohno et al. 2018). The arrows show the three velocity components at 35, 45, and 55 km s−1. The lowest contour level and contour intervals are 0.06 K degree and 0.03 K degree, respectively.
Fig. 5 shows the longitude–velocity diagram of the our NH3(1,1) data and rotational temperature. In the remainder of this work, we focus on the 35 km s−1 velocity component. Fig. 5 shows that there are three velocity subcomponents centred on 35 km s−1. In particular, we find that NH3 splits into two velocity components at W33 A (an easternmost component at 34.5 km s−1, and the main component of W33 A at 36.0 km s−1). These components with different velocities give rise to the double-peak profiles at positions shown in Fig. 2(a) and have different properties, as shown below. From Fig. 1(b), the intensity of the satellite lines differs between the two velocity components, although the peak intensities of the NH3(1,1) main line components are approximately the same. It suggests that the optical depths are different in these components, since the intensity ratio of the main and satellite lines depends on optical depth. The mean optical depth of each velocity component was 1.39 (34.5 km s−1) and 1.50 (36.0 km s−1), respectively. We also investigated temperature differences between these two components. The emission at 34.5 km s−1 is colder than 16 K, while the 36.0 km s−1 component is at about 18 K. However, within each velocity component, the temperature is almost uniform (Fig. 6), suggesting there is no direct interaction between these components. In addition, there was no change in the temperature in the region between these two velocity components. We obtained no evidence of interaction, such as collisions between these components, in our observations. On the other hand, the NH3 emission associated with W33 Main at vLSR = 35 km s−1 is warmer than 20 K and will be discussed further below.
4.2 Star formation feedback traced by gas temperature
In Section 3.4, we show that the temperature changes more significantly in the W33 complex than the other physical parameters. In this section, we use the temperature distribution to discuss the influence range of star formation activity.
The rotational temperature in W33 Main is higher than in the other subcomponents (Figs 4a and 5). This suggests that embedded compact H ii regions are having an impact on the physical conditions of the surrounding molecular gas. This feature of temperature distribution is also seen in some IRDCs, MYSOs, and H ii regions (Urquhart et al. 2015; Billington et al. 2019). Previous studies measuring molecular gas temperature have reported that quiescent regions exhibit temperatures of 10–15 K, while active star-forming regions associated with massive young stellar objects and H ii regions show temperatures higher than 20 K (e.g. Urquhart et al. 2015; Friesen et al. 2017; Hogge et al. 2018; Billington et al. 2019; Keown et al. 2019). In this study, observation points that measured temperatures higher than 20 K are defined as the region under the influence of star-formation feedback.
Using Fig. 4(a), we estimated the size of the area influenced. The projected area showing more than 20 K was estimated from the sum of the grid points (each of 37.5 × 37.5 arcsec2 = 0.19 pc2), resulting in a total size of 4.92 pc2. Its equi-areal radius was 1.25 pc. The apparent size of the compact H ii region is 12.6 × 4.6 arcsec2 based on the 5-GHz continuum map obtained by White, Becker & Helfand (2005) with the Very Large Array (VLA), which corresponds to 0.15 pc × 0.05 pc at 2.4 kpc. The heated area is several times larger than the compact H ii region.
In a previous study by our group, we investigated the size of a molecular gas cloud affected by the H ii region at the edge of the Monkey Head Nebula (MHN: Chibueze et al. 2013). They reported no apparent impact of the extended H ii region of the MHN. However, the molecular gas around the compact H ii region S252A has higher temperatures and the size of the heating area was 0.9 pc. We expect that there may be a relationship between the size of the heating area and the properties of the heating source, although the continuum size of S252A is unknown. In order to make more certain statements about any possible relationship, observations of more regions are required.
No temperature increase was obtained in W33 A, where strong NH3 emission was detected. In several previous studies, a large-scale outflow was reported in the centre of W33 A (Galván-Madrid et al. 2010; Kohno et al. 2018). Using 12CO(J=3–2) and (J = 1–0) data, Kohno et al. (2018) investigated the intensity ratio, R3–2/1–0, for the three velocity components at 35, 45, and 55 km s−1. A high R3–2/1–0 was found in W33 A and W33 Main. These results are understood to be due to outflows from protostellar objects and heating by massive stars (Kohno et al. 2018). However, in our results, the temperature distribution estimated by NH3 showed no evidence of heating the molecular cloud around W33 A. We consider that gas heating by outflows is not effective, or else the size of the gas heated by outflows in W33 A is significantly smaller than our beam size (75 arcsec). High-resolution observations may be required to investigate the impact of such stellar feedback in more detail.
4.3 Comparison of emission and absorption components
We tried to reproduce the profile shown in Fig. 1(d) using a combination of emission and absorption using a multi-component Gaussian profile with positive and negative peaks for each of the five hyperfine lines in (1,1) and the main line in (2,2). Then we took the peak intensity, linewidth, and central velocity of each hyperfine line as free parameters. Fig. 7 shows our result for the (1,1)–(3,3) lines. In this result, the peak velocities of both components are consistent within the error.
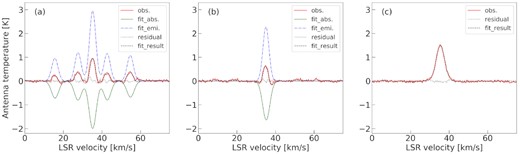
The profile in Fig. 1(d) is reproduced by a multi-component Gaussian. Fit results for (a) the NH3(1,1) profile, (b) the (2,2) profile, and (c) the (3,3) profile. The blue dash–dotted lines, green lines, red lines, and black dashed lines indicate the observed profile, absorption component, emission component, and fitting result profile, respectively. The dotted lines show the residual profile in the same colour. Since no absorption feature was found in the (3,3) profile, we apply only an emission component.
High angular resolution observations toward W33 Main with the GBT, the Max Planck Institute for Radio Astronomy (MPIfR) 100-m radio telescope, and VLA also detected the absorption feature (Wilson et al. 1982; Keto & Ho 1989; Urquhart et al. 2011). NH3 gas in front of a bright continuum source is seen as an absorption feature (e.g. Keto et al. 1987; Henkel et al. 2008). The GBT profile shows the absorption feature more clearly (see fig. A8 of Urquhart et al. 2011). This suggests that the size of the continuum sources is smaller than the beam size of the NRO 45-m. Interferometric observations of the radio continuum also support our interpretation (e.g. Haschick & Ho 1983; Immer et al. 2014). However, in the (3,3) line, observations with either NRO 45-m, MPIfR, or GBT showed no absorption feature. We will discuss this further in the next subsection.
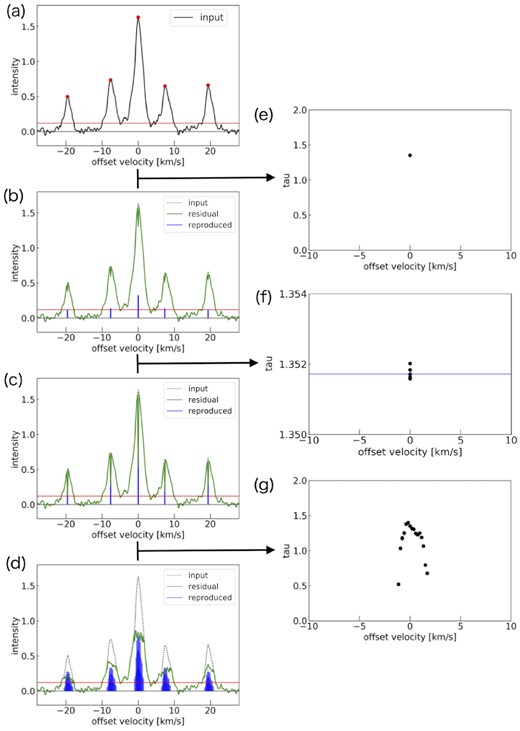
The workflow of our method, based on an observation position at (l, b) = (12.801, −0.196). Panels (a)–(d) and (e)–(g) show the profiles and the estimated optical depth in each step, respectively. The red line in panels (a)–(d) indicates the 3σ level. See the main text for further detail.
The decomposed line profiles show an interesting property in Fig. 7. Previous studies of NH3 lines have reported the combination of absorption and emission lines with different peak velocities, such as P Cygni or inverse P Cygni profiles, in all observed transitions (e.g. Wilson, Bieging & Downes 1978; Urquhart et al. 2011). In W33 Main, the peak velocities of the emission and absorption exhibited consistent velocities within the errors (see the NH3 (1,1) and (2,2) spectra in Fig. 7). We also compared the linewidths of both components (Fig. 8). The absorption components in (1,1) and (2,2) lines show the same linewidth as the emission in the (3,3) line, suggesting they originate in the same gas cloud. In many molecular cores, the higher transitions of NH3 emission lines are thought to be emitted from more compact regions and also show broader linewidths (Urquhart et al. 2011, see also Section 3.2 of this work). Our results may indicate that the absorption component traces more turbulent gas close to the continuum sources.
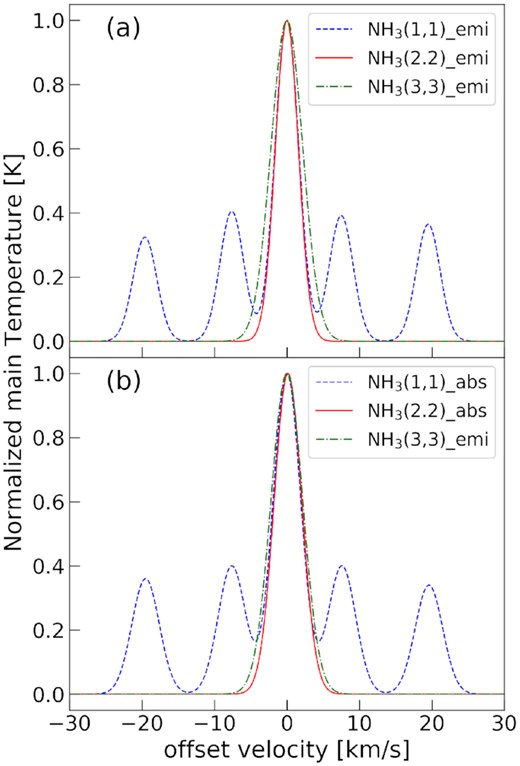
Comparison of the emission and absorption components obtained by Gaussian fitting. The horizontal axis indicates the offset velocity from the central velocity of each transition main line. The vertical axis shows the relative intensity normalized by each main line peak. (a) NH3 (1,1)–(3,3) emission profiles; (b) comparison between the negative-intensity profiles of the absorption components of (1,1) and (2,2) and the positive-intensity profile of (3,3).
Because an absorption feature delineates the physical properties of gas in front of a continuum source, it can be used to separate the physical properties along the line of sight and within an observed beam. The estimated optical depth and rotational temperature are τ = 0.89 ± 0.10 and Trot = 20.9 ± 0.4 K in the emission component, τ = 0.91 ± 0.10 and Trot = 21.1 ± 0.4 K in the absorption component. The physical parameters of the two components are the same within the error. This suggests that the physical conditions of the NH3 gas surrounding the continuum sources are the same. Therefore, the H ii region located in the centre of W33 Main may still be embedded in dense molecular gas with the same motion as the surrounding environment.
4.4 Absence of absorption in NH3 (3,3)
An absorption feature must be located in front of a continuum background and be affected by its brightness. As mentioned in Section 4.3, the continuum source size is smaller than the beam size of the NRO 45-m. Previous studies have reported objects that show P Cygni and inverse P Cygni profiles in all inversion transitions in NH3 (e.g. Wilson et al. 1978; Burns et al. 2019). In models assuming a spherically symmetric molecular gas cloud with the continuum source at its centre, these features can reveal the expansion or contraction of gas in front of the continuum source. The emission and absorption features of NH3 (1,1) and (2,2) lines obtained in our observations are detected with the same line-of-sight velocity. However, for the (3,3) transition, only the emission component was detected, without any hint of absorption. We tried to explain all transition profiles in our observations consistently, but failed under the spherically symmetric model after considering the following three possibilities.
An absorption feature requires a bright continuum background. Therefore, we estimated the brightness temperature of the H ii region in W33 Main using an electron temperature and emission measure of 7800 K and 1.5 × 106 pc cm−6 from observations at 15.375 GHz with the National Radio Astronomy Observatory (NRAO) 140-foot telescope (Schraml & Mezger 1969). The expected brightness temperature of the continuum emission at our observed frequency, Tcont, is calculated to be about 6 K, which is sufficient to produce an absorption feature. Since absorption features are detected in both (1,1) and (2,2) lines, and since NH3 inversion transitions are detected in a narrow frequency range, the continuum brightness temperature is almost the same for all observed NH3 lines. The value of Tcont at the frequency of NH3 (3,3) is therefore also strong enough to produce an absorption feature.
The spatial distribution of the NH3 gas observed in the (3,3) line may differ from that of other lines. If no NH3 gas for producing absorption is located in front of the continuum source, we would not observe any absorption feature, which contradicts the detection of absorption features at NH3 (1,1) and (2,2). It is unlikely that the distributions of the same molecular species are vastly different at different excitation levels. Wilson et al. (1982) observed the centre of W33 Main with the MPIfR 100-m radio telescope in the NH3 (1,1), (2,2), (3,3), and (4,4) lines. They detected absorption features only in para-NH3 lines (see fig. 1 of Wilson et al. 1982). They also failed to explain the absence of absorption in the (3,3) line under an LTE assumption in all four levels, even when considering two molecular clouds with different temperatures.
NH3 maser emission is another possibility. The NH3 (3,3) maser has been detected in star-forming regions (e.g. W51: Zhang & Ho 1995; G030.7206−00.0826: Urquhart et al. 2011; G23.33−0.30: Walsh et al. 2011, Hogge et al. 2019), and has been reported to have a narrow linewidth. Wilson et al. (1982) proposed a similar model: only (3,3) in a state of population inversion. However, this requires coincidental masking of the absorption component by maser emission over the full velocity width, because the (3,3) emission line has a linewidth the same as or broader than the thermal excitation line of NH3 (1,1) and (2,2) lines, as shown in Fig. 8. Therefore, this possibility is not realistic.
High angular resolution and high-sensitivity multi-transition NH3 observations are required to investigate an explanatory model in more detail. This should be possible with the Square Kilometre Array (SKA) and next-generation Very Large Array (ngVLA).
5 CONCLUSIONS
We performed mapping observations toward the W33 high-mass star-forming region in NH3 (1,1), (2,2), (3,3), and H2O maser transitions using the Nobeyama 45-m radio telescope. Our observations detected only a single velocity component around 35 km s−1. NH3 (1,1) and (2,2) lines are extended over the observed region. From these observations, the distribution of the physical parameters of the dense molecular gas was obtained. Consequently, the molecular gas surrounding the H ii region located at W33 Main was found to exhibit a higher temperature (> 20 K) than the rest of the observed area. The size of the influence area is estimated at approximately 1.25 pc. The heating source of the molecular gas is considered to be the compact H ii region in W33 Main. Strong NH3 emission was also detected in W33 A; however, no temperature increase in its molecular gas was obtained.
Molecular gas in front of the compact H ii region in W33 Main was detected as an absorption feature. Gaussian fitting of the emission and absorption components reveals that the peak velocities of both components are almost the same. This suggests that the continuum source located in the centre of W33 Main may still be embedded in the dense molecular gas. Curiously, the absorption feature was detected only in the NH3 (1,1) and (2,2) transitions but not in the (3,3) transition. We tried to explain these NH3 profiles using spherically symmetric models but concluded that no simple model could explain the observed profiles in all three transitions towards W33 Main. It is possible that the spatial distributions of the NH3 (3,3) emitting region and the continuum sources may be different.
ACKNOWLEDGEMENTS
We thank the Nobeyama Radio Observatory staff members (NRO) for their assistance and observation support. We also thank the students of Kagoshima University for their support during the observations. The 45-m radio telescope is operated by the Nobeyama Radio Observatory, a branch of the National Astronomical Observatory of Japan. This publication makes use of data from FUGIN, FOREST Unbiased Galactic plane Imaging survey with the Nobeyama 45-m telescope, a legacy project in the Nobeyama 45-m radio telescope. This study used astropy, a Python package for Astronomy (Astropy Collaboration et al. 2013, 2018), aplpy, a Python open-source package for plotting (Robitaille 2019), matplotlib, a Python package for visualization (Hunter 2007), numpy, a Python package for scientific computing (Harris et al. 2020), and Overleaf, a collaborative tool.
Part of this work was carried out under the common use observation programme at Nobeyama Radio Observatory (NRO).
DATA AVAILABILITY
The NH3 data underlying this article will be shared on reasonable request to the corresponding author.
Footnotes
REFERENCES
APPENDIX A: TECHNICAL DESCRIPTION USED TO ESTIMATE THE PHYSICAL PARAMETERS
A1 The ‘CLEAN’ procedure for an NH3 profile
In many investigations using NH3, the integrated or peak intensity of lines is used to derive the gas physical parameters. However, for objects with velocity structure this procedure may not be ideal, because of the non-linearity of the equations in derivation. Therefore, we should estimate the physical parameters in each velocity component first.
In this subsection, we describe our method used in this work to derive the physical parameters based on the CLEAN algorithm. The CLEAN algorithm was devised by Högbom (1974) and is the most used iterative method to improve radio interferometer images. In general, CLEAN is used in a two-dimensional map with a fixed dirty beam over the whole imaging field. In our method, we assumed that the detected intensities of each channel are a Dirac delta function for each velocity component. However, the NH3 inversion transition line exhibits a hyperfine structure and the observed five-line intensities depend on the optical depth. We employ the hyperfine structure pattern with an optical depth as the dirty beam for each delta-function component.
Our method is composed of the following six steps (Fig. A1).
Find the peak intensity and velocity of the main line from the input profile (Fig. A1a). The frequency and corresponding velocity offsets between the NH3(1,1) main line and the other four satellite lines are fixed as shown in Table A1. This can give the five hyperfine line intensities (indicated as red points in Fig. A1a). From this dataset, the four intensity ratios between the main line and satellite lines are obtained.
Estimate the optical depth using each intensity ratio following equation (1). To get the optical depth for a single velocity component, we take the median of the estimated four optical depths (black dots in Fig. A1e).
Using the estimated optical depth and the main line intensity after step (ii), reproduce the intensity of each satellite line.
Subtract the scaled reproduced main and satellite lines from the original profile. We call the scaling factor of the reproduction the gain factor G < 1 (indicated as blue bars in Fig. A1b). This gain factor corresponds to the loop gain in the CLEAN algorithm. In this work, we adopted a gain factor of 0.2.
Steps (ii)–(iv) are iterated until one of the five hyperfine intensities falls below a 3σ noise level (Fig. A1c). In one velocity channel, it is typically iterated 3–5 times. The resultant profile is used as the input profile in step (i) (the blue horizontal line in Fig. A8f shows the median value of the optical depth for a channel).
Steps (i)–(v) are iterated n times for the subtracted profile. We recommend limiting the velocity range to the main line and searching for the peak intensity (which corresponds to cleanbox in CLEAN). These steps (i)–(v) continue until the peak intensity of the residual main line is below a 3σ noise level (Fig. A1d).
| Transition . | F1 = 0 → 1 . | F1 = 2 → 1 . | F1 = 1 → 1 . | F1 = 1 → 2 . | F1 = 1 → 0 . |
|---|---|---|---|---|---|
| . | . | . | 2 → 2 . | . | . |
| Offset [MHz] | 0.92 | 0.61 | 0 | −0.61 | -0.92 |
| Offset [km s−1] | −19.48 | −7.46 | 0 | 7.59 | 19.61 |
| Transition . | F1 = 0 → 1 . | F1 = 2 → 1 . | F1 = 1 → 1 . | F1 = 1 → 2 . | F1 = 1 → 0 . |
|---|---|---|---|---|---|
| . | . | . | 2 → 2 . | . | . |
| Offset [MHz] | 0.92 | 0.61 | 0 | −0.61 | -0.92 |
| Offset [km s−1] | −19.48 | −7.46 | 0 | 7.59 | 19.61 |
| Transition . | F1 = 0 → 1 . | F1 = 2 → 1 . | F1 = 1 → 1 . | F1 = 1 → 2 . | F1 = 1 → 0 . |
|---|---|---|---|---|---|
| . | . | . | 2 → 2 . | . | . |
| Offset [MHz] | 0.92 | 0.61 | 0 | −0.61 | -0.92 |
| Offset [km s−1] | −19.48 | −7.46 | 0 | 7.59 | 19.61 |
| Transition . | F1 = 0 → 1 . | F1 = 2 → 1 . | F1 = 1 → 1 . | F1 = 1 → 2 . | F1 = 1 → 0 . |
|---|---|---|---|---|---|
| . | . | . | 2 → 2 . | . | . |
| Offset [MHz] | 0.92 | 0.61 | 0 | −0.61 | -0.92 |
| Offset [km s−1] | −19.48 | −7.46 | 0 | 7.59 | 19.61 |
Figs A1(d) and (g) show the final resulting profile and optical depth of each velocity channel. Using the optical depths and the intensity ratio of NH3 (1,1) and (2,2) for each velocity channel, the rotational temperature can be estimated.
A2 Error estimation by the Monte Carlo method
Evaluating the error of observed parameter estimation is important. Although the error is straightforward when calculating the value from direct measurement, an indirect parameter derived through non-linear equations is complicated. Instead of non-linear error propagation analysis, we used a Monte Carlo method in this work. For the sample data of NH3 (1,1), we adopt a noise-free Gaussian profile assuming a constant optical depth in the line-of-sight direction. Here, we used an optical depth value of 1.24 (the average value across the W33 complex). The peak intensity of the (1,1) main line was 1.0 (Fig. A2a). For the (2,2) data, we used a Gaussian profile with half the intensity of the (1,1) emission. Using equation (2), the value of the rotational temperature was derived to be 17.83 K adopting τ = 1.24 and R(2, 2)/(1, 1) = 0.5. The linewidths of (1,1) and (2,2) profiles were assumed to be the same. We added Gaussian noise (σnoise ≃ 0.04) to these profiles and sampled 105 times.
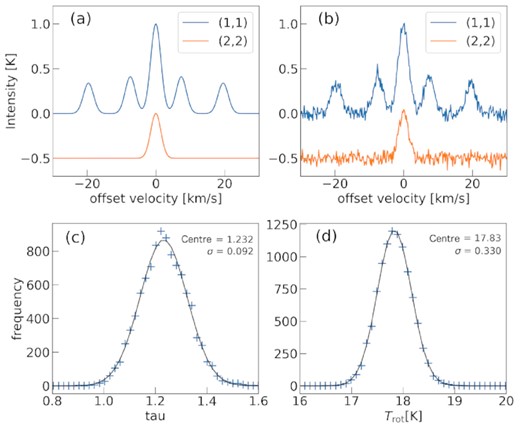
The result of error estimation with our method. (a) Model profiles of NH3 (1,1) (blue) and (2,2) (orange); (b) profiles with Gaussian noise (rms 0.04 K) added to the model profile shown in (a); (c) and (d) frequency distributions of the optical depth and rotational temperature, respectively. The black line shows the best-fitting log–normal function.
Figs A2(c) and (d) show histograms of the distributions of the sampled optical depth and rotational temperature, respectively. These distributions are close to Gaussian (black lines in Figs A2c and d). The standard deviations of the resultant optical depth and rotational temperature for the samples were 0.092 and 0.330 K, respectively. In this work, we determined the errors of these physical parameters as ± 0.10 and ± 0.4 K, respectively.



