Using action space clustering to constrain the recent accretion history of Milky Way-like galaxies Free

ABSTRACT

1 INTRODUCTION

In the currently favoured cosmological paradigm galaxies form hierarchically through the accretion and merger of numerous satellite subhaloes. N-body simulations of galaxy formation make strong predictions about the number of dark matter subhaloes and their mass functions and the mass assembly rates of haloes. Using cosmological simulations, it has been shown that mass functions of subaloes (at different redshifts) is a strong discriminator between cold dark matter (CDM) and alternative forms of dark matter (e.g. Warm Dark Matter, Self-interacting Dark Matter). In particular, the number of subhaloes in present-day Milky Way (MW) mass haloes in the mass range |$10^{6}\!-\!10^{10}{\rm \, M_\odot }$| is sensitive to the nature of dark matter (for recent reviews, see Bullock & Boylan-Kolchin 2017; Zavala & Frenk 2019). In addition, in ΛCDM the merger rate of dark matter haloes per unit mass ratio (relative to the host halo at the time of accretion), per redshift interval has a nearly universal functional form (Fakhouri & Ma 2008).

Several novel methods are being used to detect dark (or nearly dark) subhaloes in the MW’s halo: modelling gaps in thin stellar streams that may have resulted from impact with a dark subhalo (e.g. Erkal et al. 2016; Price-Whelan & Bonaca 2018; Bonaca et al. 2019), perturbations to the Galactic disc by dark matter subhaloes, which might produce bending modes or wiggles or corrugations in the density of the disc (Feldmann & Spolyar 2015) that may already have been detected in the solar vicinity (Widrow et al. 2012) and on slightly larger scales (Antoja et al. 2018). Dark matter subhaloes of masses |$\gtrsim 3\times 10^9{\rm \, M_\odot }$| tend to be massive enough to retain their baryons and form stars (e.g. Lazar et al. 2020). Many of these subhaloes are currently detectable as satellites (dwarf spheroidal galaxies and ultra-faint dwarf galaxies) in the Local Group (LG). In addition, satellites that were accreted throughout the MW’s history have been tidally disrupted by the Galactic potential and now form much of the stellar halo of the MW. If it is possible to observationally dissect the stellar halo of the MW to reliably identify the stellar debris of such satellites, one could use the kinematics and chemical abundance signatures in the debris to determine properties (e.g. masses) of the progenitors. We would also be able to use this information to determine the accretion history of our Galaxy and possibly quantify the mass function of accreted satellites.

Early work (e.g. Johnston, Hernquist & Bolte 1996; Tremaine 1999; Helmi & de Zeeuw 2000; Harding et al. 2001) showed that merger remnants remain coherent in phase space (or integrals-of-motion space) long after they have become so phase mixed that they are impossible to detect via their spatial distributions. Most early works have focused on finding coherent structures in energy, angular-momentum, or velocity space. Since stars in a galaxy are collisionless, the space of orbital actions, integrals-of-motion that are conserved even under adiabatic changes to the underlying gravitational potential, are particularly promising (for a detailed introduction, see Binney & Tremaine 2008). Since accreted substructures are much less massive than the host halo, they occupy a much smaller volume in the action space defined by the gravitational potential of the host halo, implying that stars from the same progenitor could still be clustered in the action space at z = 0, making it possible to detect these mergers events.

The advent of Gaia (Perryman et al. 2001; Gómez et al. 2010; Fabricius et al. 2016; Lindegren et al. 2016, 2018; Evans et al. 2018) is making it possible to obtain 6D phase space information for hundreds of thousands to tens of millions of haloes stars. Numerous efforts are underway to automatically identify substructures in the phase space. With the SDSS-Gaia DR1 catalogue of ∼80 000 main-sequence turn-off halo stars in 7D phase space (3D position+3D velocity+metallicity), Belokurov et al. (2018) showed that metal-rich halo stars were on significantly more radial orbits than metal poor stars. They inferred that this highly anisotropic velocity distribution was consistent with a single, head-on accretion event by a satellite with mass above |$10^{10} {\rm \, M_\odot }$|⁠. This satellite was named the ‘Gaia Sausage’ at that time. It was soon after re-discovered in Gaia-DR2 data based on chemistry, dynamics, and stellar population analysis, and was named ‘Gaia Enceladus’ (Helmi et al. 2018). Now, this satellite is referred to as ‘Gaia Enceladus Sausage’ (GES).

Myeong et al. (2018b) analysed the same SDSS-Gaia catalogue in action space ({J_r, J_z, J_ϕ}) to show that the metal-rich stars were more extended towards high radial action J_r and more concentrated around the J_ϕ = 0, showing different patterns from metal-poor stars, in agreement with Belokurov et al. (2018). Myeong et al. (2018a) developed an algorithm to find overdensities in action space, and used the metallicity as a secondary check. They identified 21 substructures in the SDSS-Gaia catalogue, and argued that five of them are associated with the accretion of the progenitor of ω Centauri, inferring the minimum mass of the ω Centauri progenitor to be |$5 \times 10^8 {\rm \, M_\odot }$|⁠. Borsato, Martell & Simpson (2020) applied the clustering algorithm DBSCAN to search for streams in integrals of motion space. Roederer, Hattori & Valluri (2018) applied several clustering algorithms to energy+actions space coordinates for 35 nearby r-process-enhanced field halo stars (obtained using Gaia proper motions, radial velocities, and parallaxes) and were able to identify eight separate clusters with statistically distinct¹ iron abundances, supporting the view that the 35 stars were likely to have been accreted in eight distinct satellites (clusters) in the action space. Yuan et al. (2020) searched for dynamical substructures in the LAMOST DR3 catalogue of very metal-poor stars cross-matched with Gaia DR2 by applying the self-organizing map algorithm StarGO. They identified 57 dynamically tagged groups, many of which belonged to previously identified accretion events. Limberg et al. (2021) applied the clustering algorithm HBSCAN to 4D energy-action data of around 1500 very metal poor stars based on spectroscopic data from the HK and Hamburg/ESO surveys, and found 38 dynamically tagged groups, with many of them corresponding to previously known substructures and 10 of them being new. Gudin et al. (2021) used HBSCAN on 4D energy-action data of 446 r-process-enhanced stars in the halo and the disc of the MW, and found 30 chemo-dynamically tagged groups (CDTGs), with stars from the same CDTG showing statistically significant similarities in their metallicities, indicating that stars from the same CDTG have experienced common chemical evolution histories in their parent substructures prior to entering the MW halo. Necib et al. (2020a, b) used clustering algorithms to identify clusters in phase space (primarily position–velocity space) and have found debris of several previously known and newly discovered satellites, including evidence for the accretion of a prograde satellite close to the disc plane that they named ‘Nyx’. Recently, Zucker et al. (2021) have used chemical abundances and stellar parameters data from the GaLAH and APOGEE surveys to argue that the ‘Nyx’ stream is more consistent with a high-velocity component of the thick disc origin, rather than a dwarf galaxy origin.

Hamiltonian dynamics tells us that accretion events should remain coherent in the action space for a very long time, as long as the potential changes slowly enough. However, it is as yet uncertain how long one can expect structures to remain coherent in an MW-like galaxy that grows hierarchically. The discovery of fairly massive past mergers like the ‘Gaia Sausage’ and the ‘Sequoia’ (Myeong et al. 2019) galaxy, the ongoing mergers like the Sagittarius stream (Lynden-Bell & Lynden-Bell 1995) and future mergers like the LMC (Besla et al. 2007, 2010) raises questions about how ‘adiabatic’ the evolution of the MW has been and therefore how well one might distinguish other individual merger events. Is there a boundary in infall time such that satellites that fell in before this time have experienced so much phase mixing, that we can no longer find them through cluster analysis in the action space? The average density of satellite within its tidal radius relative to the mean density of the host within the satellite’s orbit roughly determines its rate of tidal disruption. However, the mass of the satellite also determines the initial dispersion of its stars in action space and hence its expected degree of clustering. Therefore, is there an optimal range of mass for satellites that can be detected via cluster analysis in phase space? The reliability of cluster analysis algorithms in finding substructures is also poorly understood: while numerous clusters are often identified by such algorithms, it is unclear how many of them correspond to discrete building blocks (individual satellites), how many are comprised of multiple satellites, how many are subcomponents of individual satellites and how many are spurious. The primary goal of this paper is to find a metric (or metrics) computed from cluster analysis that quantifies the correspondence between groups identified by cluster analysis and real galactic building blocks in the hierarchical galaxy formation framework when we complete and error free data. In a future paper, we will consider how observational error and partial data on individual satellites affect the recovery process.

The cosmological hydrodynamic zoom-in simulations of MW-mass galaxies from the Feedback In Realistic Environments (FIRE) project² (Hopkins et al. 2018) provide a great testbed for addressing these questions. We focus on three MW-mass galaxies from the Latte suite of FIRE-2 simulations that have different merger histories, ranging from one with a very quiescent recent history to one with a very active recent history. In Section 2, we describe how the simulation snapshots were analysed to identify the accreted stars in the three haloes at z = 0. In Section 3.1, we provide a brief introduction to the calculation of actions {J_r, J_z, J_ϕ} in cylindrical coordinates using publicly available agama code (Vasiliev 2018). In Section 3.2, we describe the density-based hierarchical cluster analysis algorithm Enlink (Sharma & Johnston 2009) that we use to perform the cluster analysis in 3D action space. In Section 4.1, we study the overlap between the real stellar building blocks (disrupted satellites) of the three MW-mass galaxies and the groups found by Enlink. We define several metrics that we use to evaluate the accuracy of recovery of substructure with Enlink. We also use a binary classification tree to statistically determine boundaries in infall time (T_infall), total progenitor mass (M_tot), and stellar mass at z = 0 (M_stellar) for well-recovered and poorly recovered satellites. The stellar halo of the host galaxy contains both accreted stars and  in situ  stars. The  in situ  stars are formed in the host galaxy and are in the stellar halo of the host galaxy at z = 0. In Section 4.2, we include varying fractions of  in situ  star particles into our analysis and study the robustness of our results against contamination from these stars. Finally, in Section 5, we discuss how the boundaries (in T_infall M_tot and M_stellar) separating well-recovered and poorly recovered satellites depend on the dynamical history of the host MW-like galaxies. We then summarize our results and conclude.

2 SIMULATION DATA

Our analysis uses cosmological baryonic zoom-in simulations of MW-mass galaxies from the FIRE project (Hopkins et al. 2018). These simulations are run with gizmo (Hopkins 2015) that uses an optimized TREE+PM gravity solver and a Lagrangian mesh-free, finite-mass method for accurate hydrodynamics. Star formation and stellar feedback are also implemented. All haloes were simulated in ΛCDM cosmology at particle mass resolution of |$\sim \! 7100 {\rm \, M_\odot }$| and spatial resolution of 1–4 pc for star/gas particles, and a particle mass resolution of |$\sim \! 35\,000 {\rm \, M_\odot }$| and spatial resolution of 40 pc for dark matter particles. The complete sample currently consists of eight MW-mass galaxies and three LG-like pairs. Wetzel et al. (2016) and Garrison-Kimmel et al. (2019) show that when baryonic physics is included, the properties of dwarf galaxies in the FIRE-2 simulations agree well with observations of LG satellites down to the resolution limit (just below classical dwarf mass of |$\sim \! 10^6 {\rm \, M_\odot }$| in stellar mass). Of particular importance for this work, the simulations produce satellites with mass–size and mass–velocity dispersion relations consistent with observations of the MW and M31 (Garrison-Kimmel et al. 2019) distributed similarly with respect to their massive hosts (Samuel et al. 2020, 2021). This implies that we expect the sizes and relative positions of the accreted structures in action space to resemble those in the MW.

To assign the accreted star particles to particular progenitor galaxies, the dark matter particles in each snapshot of the simulations are first processed with Rockstar to produce halo catalogues, which then are connected in time to form a merger tree (Behroozi, Wechsler & Wu 2013a; Behroozi et al. 2013b). Rockstar computes the maximum circular velocity v_max and the virial radius for each halo and subhalo identified in the dark matter distribution. A star particle is considered part of a halo or subhalo if it is within the virial radius and its velocity with respect to the centre of that halo or subhalo is less than 2v_max(Wetzel & Garrison-Kimmel 2020a, b). Within the host halo, this selection does a good job in picking out star particles gravitationally bound to a subhalo rather than the host halo.

One of the challenges with identifying substructure in the stellar halo is that there are indications from cosmological hydrodynamical simulations that some fraction of the stars in the halo of an MW-like galaxy were not accreted from satellites but were born  in situ  in the host galaxy, both at very early times before the disc was well established (e.g. Santistevan et al. 2020) and in smaller proportions at later times, in gas propelled into the halo by star-forming winds (e.g. Yu et al. 2020). These stars then remain in the stellar haloes of these MW-like galaxies at z = 0, a generic prediction of multiple simulations using independent codes and differing star formation and feedback prescriptions (Zolotov et al. 2009, 2012; Cooper et al. 2010; Font et al. 2011; Tissera et al. 2013; Pillepich, Madau & Mayer 2015; Monachesi et al. 2019). However, these various cosmological simulations predict a wide range of values for the fraction of halo stars that were formed  in situ, which probably varies with assembly history and likely also depends on the feedback prescriptions adopted by different codes. While some simulations predict that up to 80 per cent of the stellar halo was formed  in situ, observations of the MW stellar halo (Bell et al. 2008; Naidu et al. 2020) find that almost all of it shows significant substructure, implying that a significant portion of the MW stellar halo was accreted (although  in situ  stars formed in outflows may also be clustered; Yu et al. 2020). Analysis of data from the cross-match between several stellar surveys like Gaia, RAVE, and APOGEE shows that a fraction of halo stars in the solar neighbourhood (within a few kpc from the Sun) are formed  in situ  in the MW galaxy (Bonaca et al. 2017; Haywood et al. 2018; Helmi et al. 2018; Di Matteo et al. 2019; Gallart et al. 2019; Belokurov et al. 2020).

Recently, Ostdiek et al. (2020) showed that they were able to train and validate a deep learning neural network algorithm on 5D mock Gaia kinematical data (Sanderson et al. 2020) from the same simulations we use here (Wetzel et al. 2016; Hopkins et al. 2018) to separate  in situ  halo stars from accreted stars. They then applied this method to 72 million stars in the Gaia DR2 catalogue with parallax measurement errors of less than 10 per cent and were able to identify over 650 000 stars as accreted. They then used a cluster finding algorithm to identify clusters in phase space and their comparisons with other data sets allowed them to validate both robustness of their neural network algorithm for separating  in situ  stars, and identify several new structures (Necib et al. 2020a, b). Based on the success of such algorithms to separate accreted and  in situ   stars, we assume in this paper that such separation is possible, and we use information derived from the analysis of simulation snapshots to identify accreted satellites in the simulations.

We focus on three MW-mass galaxies: m12i, m12f, and m12m. For each galaxy there are 600 snapshots from z = 99 to z = 0, with a time difference between snapshots of approximately 25 Myr at late times. This relatively high ‘framerate’ allows us to track the time-evolution of accreted structures in much of the host galaxy with ∼10–100 snapshots per dynamical time. Since it takes several dynamical times for a self-bound satellite to be tidally disrupted and turn into a stream, we select luminous haloes that are self-bound between 2.7 to 6.5 Gyr ago and that are within the virial radius of the host galaxy at present day. These time-scales correspond to redshift z ≈ 0.25–0.75. During this time window, these luminous haloes can either be inside (bound) or outside (unbound) the virial radius of the host galaxy. We follow each substructure throughout its evolution to recover most of the star particles that once belonged to the satellite. These star particles are then tracked forward to z = 0. The stellar mass of each substructure at z = 0 is summed up to get M_stellar. From z = 0, star particles belonging to a particular substructure are also traced back in time until the substructure is no longer bound to the host halo. This time is defined as the infall time T_infall of the substructure, and all the mass belonging to this substructure at T_infall is summed up to get the total mass of the satellite (stars, gas, and dark matter) M_tot. Extending the sampling time window to a time beyond 6.5 Gyr ago might help detect satellites that are tidally disrupted very early on. However, these additional satellites are less likely to be clustered in action space because the evolution of the host galaxy potentials are non-adiabatic until ∼5 Gyr ago, which is the end of the bursty phase of star formation in these simulations (Yu et al. 2020). The satellites disrupted prior to this epoch will be studied in Horta et al. (in preparation). Moreover, for z ≳ 2–4, there is no clear ‘host’ galaxy in terms of mass (Santistevan et al. 2020), and the disc of what eventually becomes the most massive galaxy is not usually formed yet at that point (Garrison-Kimmel et al. 2018), so the question of what is accreted on to what is not well defined.

Starting with the star particles assigned to each accreted structure, we make three selections on both real space and velocity space to identify disrupted satellites, both phase-coherent (streams) and phase-mixed satellites. In the first selection, we choose satellites with stellar mass between |$M_\star \approx 10^6{\rm \, M_\odot }$| and |$10^9 {\rm \, M_\odot }$| at z = 0. In the second selection, we use the fact that the ‘size’ of disrupted substructures in physical space is larger than that of satellite galaxies that are still self-gravitating at z = 0. In practice, we define the ‘size’ of a substructure as the maximum value of the pairwise distance between two star particles in a substructure at z = 0. To take advantage of this fact and rule out the self-gravitating satellite galaxies in the z = 0 snapshots, we require the ‘size’ of each substructure we tracked to be greater than 120 kpc, as 120 kpc is much larger than the characteristic size of self-gravitating dwarf galaxies, as well as dwarf galaxies that are only slightly tidally deformed but without prominent tails (see fig. 2 from Panithanpaisal et al. 2021).

The remaining accreted structures are classified by eye into two categories, coherent streams and phase-mixed debris, by viewing their configuration in position and velocity space. Panithanpaisal et al. (2021) show that this by-eye classification corresponds to a selection in the space of stellar mass and local velocity dispersion, where ‘local’ velocity dispersion is defined for each particle using nearest neighbours in phase space rather than position (at fixed stellar mass, phase-mixed satellites have higher local velocity dispersion compared to coherent streams). Although this classification is mildly resolution-dependent, the overall results when this classification is applied to the full sample of streams from all 13 analysed systems in Panithanpaisal et al. (2021) demonstrate the mass- and time-dependence expected from theory for the relative abundance of phase-mixed versus coherent debris, implying that resolution effects do not dominate our classification of coherent streams and phase-mixed structures that are accreted.

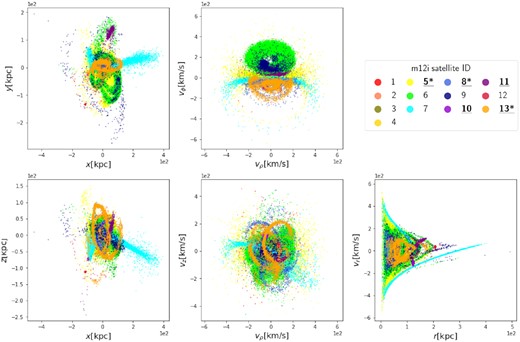
In this work, we are interested in the action space clustering of tidally disrupted systems. Self-bound dwarf galaxies at z = 0 are already spatially clustered. Therefore, in this manuscript, the terms ‘satellites’ and ‘accreted satellites’ refer to disrupted satellites, including both present-day coherent streams and phase-mixed debris. Fig. 1 shows the tidally disrupted satellites in galaxy m12f in position space (left column), velocity space (middle column, velocities are shown in cylindrical coordinates) and r versus v_r phase space (right column), where ρ is the radial coordinate, ϕ is the angular coordinate, and z is the height in cylindrical coordinate system. Star particles from different satellites are coloured differently. For similar plots of the satellites in the other two galaxies, see Appendix  A

Figure 1.

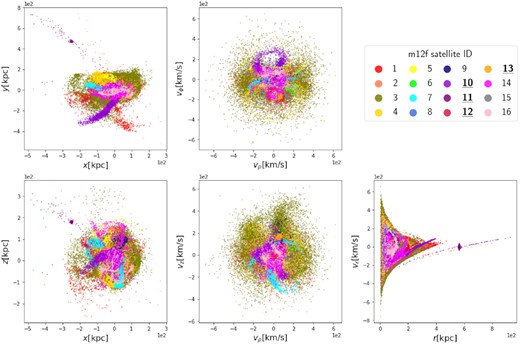
Tidally disrupted satellites in galaxy m12f are plotted in position space (left column), velocity space (middle column), and r versus v_r phase space (right column). Star particles are coloured differently according to different satellites they are assigned to by the tracking process. The well-recovered satellites are indicated with bold and underlined IDs in the legend. The well-recovered satellites outside T_infall < 7.1 Gyr ago and |$M_{\rm tot} \gt 4.0\times 10^8 {\rm \, M_\odot }$| (⁠|$M_{\rm stellar} \gt 1.2\times 10^6 {\rm \, M_\odot }$|⁠) are marked by bold and underlined IDs with a star (*) in the legend. We will explain the terms well-recovered, T_infall, M_tot, and M_stellar in Section 4.1.

Open in new tabDownload slide

3 METHODS

The orbits in a galactic potential are largely quasi-periodic and regular. Therefore, the orbits of most satellites and individual stars in the halo of a galaxy can be described by an elegant set of variables – the action-angle variables. Orbital actions are particularly powerful for understanding the evolution of a galaxy since they are conserved under adiabatic evolution of the potential. Section 3.1 gives a brief introduction to action-angle variables. We then use a publicly available dynamical modeling toolbox agama (Vasiliev 2018), to numerically compute actions (under the assumption of axisymmetry) for the accreted star particles in the three MW-like galaxies in FIRE-2 described in Section 2.

The initial actions of all the stars in a satellite as it orbits a larger galaxy have a small spread compared to the range of possible actions in the Galactic potential. Because actions are adiabatically invariant by construction, star particles from the same progenitor are expected to remain clustered in the action space at z = 0 if the gravitational potential of the host halo has changed only adiabatically (i.e. slowly enough) following their infall. Therefore, the accreted satellites found in Section 2 should be recoverable through cluster analysis in the action space. In Section 3.2, we feed the cluster analysis algorithm Enlink with the 3D orbital actions of accreted star particles, and find several groups. To measure how well the groups found by Enlink recover the satellites tracked in Section 2, we define various metrics in Section 3.3.

3.1 Action evaluation with agama

In order to compute actions from the positions and velocities of star particles at z = 0 one needs an estimate of the gravitational potential. In the case of the real MW, this is derived using a multitude of observational tracers that provide the masses of the various stellar components (the bulge, thin and thick disc, and stellar halo) and kinematics of disc stars and halo objects to derive the mass and density profile of the dark matter halo.

In this paper, we study three simulated disc galaxies from the FIRE-2 simulations with different accretion histories. We use the masses and positions of all the particles (dark matter, gas, stars) within 600 kpc from the centre of galaxy to compute the gravitational potential of each galaxy at z = 0. This is done using agama (Vasiliev 2018) that approximates the gravitational potential via an axisymmetric multipole expansion on a hybrid cylindrical-polar grid (to compute the potential of the flattened stellar disc) and spherical polar grid (to compute the potential of the dark matter halo). The potential generated by dark matter and hot gas in the dark matter halo is represented by an expansion in spherical harmonics with l_max = 4; the potential from stars and cold gas in the disc is expanded in azimuthal-harmonics up to m_max = 4. The star, gas, and dark matter particles within 600 kpc of the galactic centre are used to calculate the potential (for a detailed introduction to how these expansions work, see Vasiliev 2018).

In this work, we have assumed that all space coordinates for dark matter particles, gas particles and star particles are assumed known and without error when computing the potential. The main deviation from the potential used for computing the actions and the true gravitational potential comes from the spherical harmonic expansion. When computing the actions we further assume that the phase space coordinates for all accreted star particles are known perfectly (i.e. no errors are added).

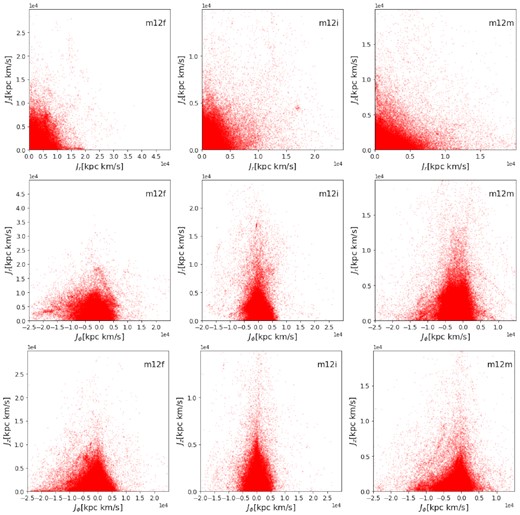
Fig. 2 shows three projections of the actions {J_r, J_ϕ, J_z} for accreted star particles for each of the three MW-like galaxies m12f, m12i, and m12m in FIRE-2 simulation. The colour coding in Fig. 2 corresponds to the individual satellites that are identified by analysing the snapshots from simulation data as described in Section 2 and is shown by the legend in the bottom row.

Figure 2.

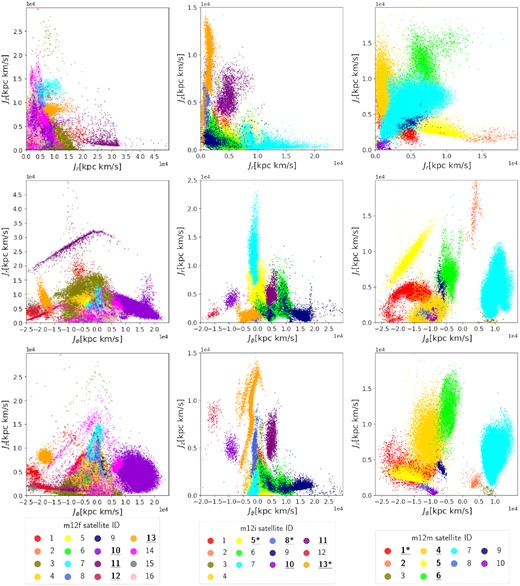
2D projections of actions {J_r, J_z, J_ϕ} for accreted star particles from 3 MW-like galaxies in FIRE-2 simulations. The three columns correspond to the three galaxies in FIRE-2 simulations: m12f, m12i, and m12m, from left to right. Each accreted satellite identified from analysing snapshots from the simulation is indicated by a different colour. The meaning of bold and underlined IDs, and IDs with stars (*) is the same as that in Fig. 1.

Open in new tabDownload slide

3.2 Finding clusters with Enlink

We apply algorithm Enlink (Sharma & Johnston 2009), a density-based hierarchical group finding algorithm capable of identifying structures of any shape and density in multidimensional data sets, to the action space variables {J_r, J_z, J_ϕ} for the three galaxies from FIRE-2. Enlink  is especially useful for astrophysical data as it can effectively detect groups that are not globular. Here, we summarize the basic principles behind Enlink. For more details, see Sharma & Johnston (2009).

• Build a locally adaptive Mahalanobis (LAM) metric|$\Sigma ^{-1}(\mathbf {x})$|. The distance squared between two data points |$\mathbf {x_i}$| and |$\mathbf {x_j}$| is defined as:

  $$\begin{eqnarray*} s^2(\mathbf {x_i},\mathbf {x_j})=|\Sigma (\mathbf {x_i},\mathbf {x_j})|^{\frac{1}{d}} (\mathbf {x_i}-\mathbf {x_j})^{\intercal } \Sigma ^{-1}(\mathbf {x_i},\mathbf {x_j}) (\mathbf {x_i}-\mathbf {x_j}) , \end{eqnarray*}$$

  (2)

  where d is the dimension of data, |$\Sigma ^{-1}(\mathbf {x_i},\mathbf {x_j}) = 0.5(\Sigma ^{-1}(\mathbf {x_i})+\Sigma ^{-1}(\mathbf {x_j}))$|⁠. To build this LAM metric |$\Sigma ^{-1}(\mathbf {x})$|⁠, first divide the whole data set into regions with each region containing (d + 1) data points, and the particles in each region are distributed as uniformly as possible. Then calculate the local covariance matrix |$\Sigma (\mathbf {x})$| of the data points in each region and smooth it so that this local matrix changes continuously and smoothly from region to region.
• Calculate a local density D(x) for each data point. For each data point, find k nearest neighbours to it based on distance squared defined in equation (2). The size of neighbourhood k has a pre-defined default value in Enlink : k = 10. We have tried k = 5–20, and the results are robust against the variation of k in this range. Calculate density as:

  $$\begin{eqnarray*} D(\mathbf {x_j}) = \sum ^k_{i=1}\frac{m_i}{h^d |\Sigma (\mathbf {x_j})|^{\frac{1}{2}}} W(\sqrt{(\mathbf {x_i}-\mathbf {x_j})^{\intercal } \Sigma ^{-1}(\mathbf {x_j}) (\mathbf {x_i}-\mathbf {x_j})}/h) , \end{eqnarray*}$$

  (3)

  where h is the smoothing length corresponding to a given k, d is the dimensionality of data space, W is a kernel function to normalize the integral of density, and m_i is the mass of each particle.
• Identify clusters based on density and preserve significant groups. We start building groups at local density peaks, and these groups grow by absorbing nearby points. Once two groups try to absorb a common particle, a saddle point is reached and the smaller group is absorbed into the bigger one as a subgroup (the subgroup is not canceled and still treated as a separate group). After all the (sub)groups are identified, the significance S of each group is calculated:

  $$\begin{eqnarray*} S = \frac{\ln (D_{\mathrm{max}})-\ln (D_{\mathrm{min}})}{\sigma _{\ln (D)}} , \end{eqnarray*}$$

  (4)

  where D_max and D_min are maximum and minimum densities in that group. σ_ln (D) is the standard deviation of log of densities in one group. Significance measures how inhomogeneous a group is, and should not be confused with statistical significance. We define the size of a satellite as the number of star particles it contains. We denote the minimum size of satellites we tracked by N_S. The minimum number of particles in a group, N_min, is chosen to be of the same order of magnitude as N_S. Then any group with number of particles lower than N_min would have its significance set to 0. For two intersecting groups, we compare their values of significance to a pre-determined threshold S_Th. If both groups have S > S_Th, then keep both of them. Otherwise, the one with lower S is eliminated and its particles are absorbed into the group with higher S.

As can be seen from the description above, four parameters determine the result of cluster finding: size of neighbourhood k, threshold significance S_Th, mass of each particle m_i, and minimum size of group N_min. In this work, we neglect the mass of star particles, so all the m_i is set to 1. Three other parameters have their default values pre-defined in the Enlink program. During our runs, k and S_Th are varied slightly around their default values and N_min is chosen to be in the same order of magnitude as the minimum size of satellites, so that the number of groups that the algorithm yields is close to the number of accreted satellites in a galaxy.

Groups that were identified by Enlink with k = 10, N_min= 300, and S_Th at its default value for the three galaxies from the FIRE-2 simulations are shown in Fig. 3. The minimum number of star particles in each of the satellites in the three galaxies is around 150 (corresponding to a minimum stellar mass of around |$6.0\times 10^5 {\rm \, M_\odot }$|⁠), so a reasonable value for N_min would seem to be 150. With N_min = 150, many small random groups emerge in all three galaxies. With N_min= 300 the identification of large and clear satellites is not affected in m12f and m12m, but in m12i, a satellite with size 184 (located in action space at around J_ϕ = −12 000 kpc × km s⁻¹, J_z = 8000 kpc × km s⁻¹, J_r = 2000 kpc × km s⁻¹) cannot be identified. However, when N_min = 150, large coherent satellites are divided into several groups, which makes it harder to identify the large coherent satellites. Therefore, we keep N_min = 300, which corresponds to a minimum stellar mass of around |$1.2\times 10^6 {\rm \, M_\odot }$| for groups found by Enlink .

Figure 3.

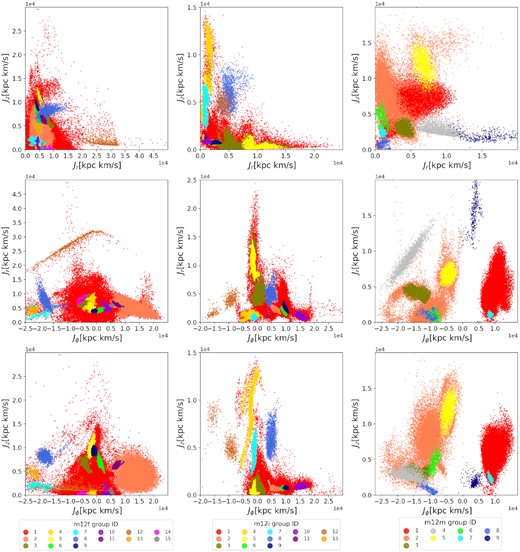
Same as Fig. 2, but with substructures identified by Enlink to see how well Enlink can reproduce the actual satellites in the simulations as shown in Fig. 2. Particles from different groups identified by Enlink are indicated by different colours. Results plotted here are obtained from Enlink runs with size of neighbourhood k = 10, minimum group size N_min = 300 and significance threshold S_Th at its default value.

Open in new tabDownload slide

In applications to observational data, since the sizes of data sets are expected to be much larger and the number of accreted satellites is completely unknown, these four parameters should be determined carefully. It is also likely that one satellite could be split into multiple groups by cluster analysis (Yuan et al. 2020). Adding additional information, such as metallicity or abundances of specific elements (e.g. Ca, N, Fe, Eu; Sanderson et al. 2017; Roederer et al. 2018) can help to confirm the identification of a satellite or identify subcomponents of a single satellite, but this is beyond the scope of this paper. In this paper, we are testing how well cluster analysis in the action space alone can perform under optimum conditions: perfect knowledge of all six phase space coordinates, accurate representation of the galactic potential, and prior insights into the optimum values of parameters like N_min. We also assume that these perfect data are available throughout the halo (out to the radius of the furthest particles) and that all members of a given satellite are detected and in the data set. While these assumptions are not observationally justified, these assumptions allow us to assess how the hierarchical merger history of the galaxy affects our ability to recover accreted satellites. In a future paper, we will repeat this exercise imposing observational errors and selection functions for Gaia and upcoming surveys with the Rubin Observatory and the Roman Space Telescope. These simplifying assumptions enable us to assess how well cluster analysis can perform in the best-case scenario.

3.3 Metrics to assess identification of satellites by clusters

In order to quantify the ability of Enlink to identify accreted satellites in action space, we define three matrices: R_ij, P_ij, and M_ij; and four quantities based on these matrices: recovery, purity, merit, and contrast. We refer to the clusters identified by Enlink as ‘groups’. The number of star particles contained in a group is called the size of the group. In order to quantify the degree to which a group identified by Enlink matches one of the original accreted satellites we also define the ‘best recovery group’ (similarly for purity, merit) and best fit group. Based on recovery, purity, merit and best fit group, we select out the ‘well-recovered satellites’.

• Three matrices R_ij, P_ij, M_ij: The ij component of these three matrices describes the similarity between satellite j and group i:

  $$\begin{eqnarray*} R_{ij} &=&\frac{\mathrm{number~of~particles~shared~by~satellite}~\mathit {j}~\mathrm{and~group}~\mathit {i}}{\mathrm{number~of~particles~in~satellite}~\mathit {j}}, \\ P_{ij} &=&\frac{\mathrm{number~of~particles~shared~by~satellite}~\mathit {j}~\mathrm{and~group}~\mathit {i}}{\mathrm{number~of~particles~in~group}~\mathit {i}}, \\ M_{ij} &=& R_{ij}\times P_{ij}. \end{eqnarray*}$$
• Recovery, purity, merit: For satellite k, the maximum values of R_ik, P_ik, and M_ik are called the recovery (r_k), purity (p_k), and merit (m_k) of this satellite:

  $$\begin{eqnarray*} r_{k} &=& \mathrm{max}_i \lbrace R_{ik}\rbrace , {\rm for\, i\, in\, range\, of\, group\, indices}\\ p_{k} &=& \mathrm{max}_i\lbrace P_{ik}\rbrace , {\rm for\, i\, in\, range\, of\, group\, indices}\\ m_{k} &=& \mathrm{max}_i\lbrace M_{ik}\rbrace , {\rm for\, i\, in\, range\, of\, group\, indices}. \end{eqnarray*}$$

• Best recovery, purity, merit group and best fit group: For satellite k, the group which yields r_k is called the ‘best recovery group’, and likewise p_k and m_k define the ‘best purity group’ and ‘best merit group’ of satellite k, respectively. If a group is both the ‘best recovery group’ and the ‘best purity group’ of satellite k, then it is defined as the ‘best fit group’ of satellite k.

• Contrast: To compare the size of satellite k and its best fit group, we define contrast (c_k) as:

  $$\begin{eqnarray*} c_{k} = \frac{r_k-p_k}{\sqrt{r_k p_k}} , \end{eqnarray*}$$

  (5)

  where r_k and p_k are recovery and purity of satellite k. Note contrast is only defined for a satellite with a best fit group. When c_k is positive, satellite k is smaller than its best fit group (the group contains contaminants – i.e. stars that were not originally part of the satellite), and when c_k is negative, satellite k is larger than its best fit group (not all of the members of the satellite have been identified as group members).

• Well-recovered satellite: If the recovery, purity, and merit of a satellite are all greater than 0.5 and this satellite has a best fit group, then this satellite is called well-recovered or is said to have a high identifiability score. A satellite that is not well-recovered is called poorly recovered.

4 RESULTS

We do a cluster analysis with Enlink on actions {J_r, J_z, J_ϕ} of accreted star particles from three MW-like galaxies in FIRE-2 simulations. In Section 4.1, we calculate the values of recovery, purity, merit, and contrast for each satellite in three galaxies to evaluate how well these satellites are recovered by Enlink. We study the distribution of well-recovered satellites on the M_tot-T_infall plane and M_stellar-T_infall plane, and find the boundaries in M_tot M_stellar and T_infall values that separate well-recovered and poorly recovered satellites by the classification tree method. We also investigate the relation between significance of a group and the identification power of this group (that is, whether this group corresponds to a well-recovered satellite or not). In Section 4.2, we include certain percentages of  in situ  stars into the input data set for cluster analysis. We pick out the well-recovered satellites that are identified when  in situ   star particles are absent. Calculate the values of merit of these satellites under different  in situ  star contamination ratios and demonstrate the robustness of the identification of these satellites under the contamination of  in situ  star particles.

4.1 Cluster analysis on accreted star particles

We apply Enlink to the actions {J_r, J_z, J_ϕ} for accreted star particles from the MW-like galaxies m12f, m12i, and m12m in FIRE-2 simulations. In a manner similar to Fig. 2, three projections of the actions for accreted star particles {J_r, J_ϕ, J_z} are shown in Fig. 3, but now the colour coding corresponds to the individual groups that are identified by Enlink. The legend in the bottom row now indicates the colour coding for the individual groups identified. A comparison with Fig. 2 shows visually that while in m12i and m12m the number of groups identified is one larger than the number of satellites., in m12f only 15 groups (of 16 satellites) are identified. Overall, however, there is an excellent correspondence between the groups identified by Enlink and the original satellites seen in Fig. 2.

Fig. 4 shows the values of recovery, purity, merit, and contrast of 39 satellites in the three simulated galaxies m12f, m12i, and m12m, on an M_tot versus T_infall plot. Each symbol corresponds to one accreted satellite and symbols are colour coded by the value of their recovery (panel a), purity (panel b), merit (panel c), and contrast (panel d), with red coloured points indicating better results. In panels a, b, and c, satellites are also shape coded by whether their best recovery group match their best purity group (triangle) or not (circle) [in other words, whether the satellite has a best fit group (triangle) or not (circle)]. White numbers indicate the group ID (as shown in Fig. 3) signifying best recovery (panel a), best purity (panel b), best merit (panel c), or best fit (panel d) for each satellite. A white letter associated with each data point indicates which galaxy this satellite is from: ‘f’ for ‘m12f’, ‘i’ for ‘m12i’, and ‘m’ for ‘m12m’. Among the 39 satellites, 14 of them are ‘well-recovered’ (their values of recovery, purity, and merit are larger than 0.5 and they have best fit groups), while 25 of them are poorly recovered. With T_infall and |$\log _{10}(M_{\rm tot}/{\rm \, M_\odot })$| as inputs, we grow a classification tree to predict whether a satellite is well recovered or not. (For a brief introduction to classification tree method, see Appendix  C.) The boundaries that the classification tree finds out are: T_infall = 7.1 Gyr ago and M_tot = |$10^{8.6} {\rm \, M_\odot }$|⁠, which are shown as vertical and horizontal blue dashed lines in Fig. 4. 91 per cent (10/11) of the satellites in the region bounded by M_tot|$\gt 4.0\times 10^8 {\rm \, M_\odot }$| and T_infall<7.1 Gyr ago are ‘well-recovered’ satellites. Of the satellites outside this region, 86 per cent of the sample (24/28) are poorly recovered. Three satellites in galaxy m12i (marked by 3i, 4i, and 7i on the plot) fell into the host galaxy far more than 7.1 Gyr ago (T_infall = 9.08–10.33 Gyr ago), but are still well recovered. This can be attributed to the unique dynamic history of galaxy m12i. See Section 5 for more discussion. Group 1 in each galaxy is the ‘best’ group of many satellites, because Group 1 is the largest group and contains star particles from many ‘poorly recovered’ satellites. Group 1 in each of the galaxies can be considered as the ‘background’ group. Panel (d) plots the contrast of satellites, shape coded by whether the contrast is positive (diamond) or negative (square). Only the satellites with a best fit group are plotted in panel (d). Note that a positive contrast means that a satellite is smaller than its best fit group, and a negative contrast means the opposite. Most of the values of contrast are close to 0, with a few extremely large values (above 20). These extremely large values belong to satellites with Group 1 as best fit group, indicating that Group 1 is much larger than these satellites, consistent with the fact that Group 1 contains star particles from many satellites and is the background group. The values of contrast of ‘well-recovered’ satellites are close to 0, meaning the number of particles in these satellites is similar to that in their best groups.

Figure 4.

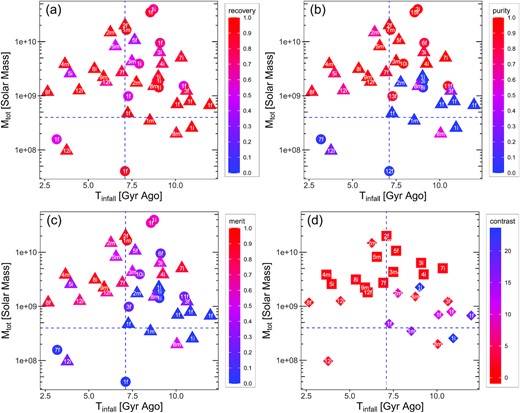
39 satellites in three MW-like galaxies from the FIRE-2 simulations plotted on the M_tot versus T_infall plane. Data points are colour coded by the recovery (panel a), purity (panel b), merit (panel c), or contrast (panel d), with red points indicating better results in all panels. The white number on each symbol indicates the group ID (as shown in Fig. 3) of the ‘best recovery’ (panel a), ‘best purity’ (panel b), ‘best merit’ (panel c), and ‘best fit’ (panel d) group corresponding to each satellite. The white letters associated with each data point indicate which galaxy each satellite is from: ‘f’ for ‘m12f’, ‘i’ for ‘m12i’, and ‘m’ for ‘m12m’. Group 1 in all three galaxies is the ‘best’ group of many satellites because it is the largest group, as shown in Fig. 3, and is generally considered as the ‘background’. A satellite is marked as a triangle if it has a ‘best fit group’ and as a circle otherwise. Satellites are from the analysis of simulation data in Section 2, and groups are identified by Enlink. In panel (d), only satellites with best fit groups are plotted, and shapes indicate whether the contrast is positive (diamond) or negative (square). Among the 39 satellites, 14 of them are well recovered and 25 of them are poorly recovered. The vertical and horizontal dashed lines mark M_tot|$=4.0\times 10^8 {\rm \, M_\odot }$| and T_infall= 7.1 Gyr ago, which are the boundaries identified by the classification tree method. 91 per cent (10/11) of the satellites with M_tot greater than |$4.0\times 10^8 {\rm \, M_\odot }$| and fell into the halo less than 7.1 Gyr ago are well recovered by Enlink.

Open in new tabDownload slide

Similar to Fig. 4, in Fig. 5 we plot the values of recovery, purity, merit, and contrast of 39 satellites in the three simulated galaxies m12f, m12i, and m12m, on the M_stellar versus T_infall plane. The colour code, shape code, and the meaning of the white numbers/letters are the same as those in Fig. 4. The boundaries separating well-recovered and poorly recovered satellites found by the classification tree method in the M_stellar versus T_infall plane are: |$M_{\rm stellar}=1.2\times 10^6 {\rm \, M_\odot }$| and T_infall = 7.1 Gyr ago, marked by the horizontal and vertical blue dashed lines in the four panels. The T_infall boundaries found in M_tot versus T_infall and M_stellar versus T_infall planes agree with each other. 91 per cent (10/11) of the satellites with M_stellar greater than |$1.2\times 10^6 {\rm \, M_\odot }$| and fell into the halo less than 7.1 Gyr ago are well recovered by Enlink.

Figure 5.

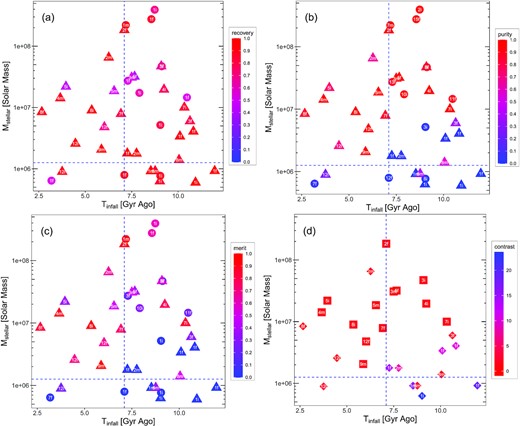
Same as Fig. 4, but the y-axes of these plots are labelling M_stellar. The vertical and horizontal dashed lines mark |$M_{\rm stellar}=1.2\times 10^6 {\rm \, M_\odot }$| and T_infall= 7.1 Gyr ago, which are the boundaries separating well-recovered and poorly recovered satellites identified by the classification tree method. 91 per cent (10/11) of the satellites with M_stellar greater than |$1.2\times 10^6 {\rm \, M_\odot }$| and fell into the halo less than 7.1 Gyr ago are well recovered by Enlink.

Open in new tabDownload slide

For more plots showing values of recovery, purity, merit, and contrast against infall time, total mass, and stellar mass, see Appendix  B. To see where the well-recovered satellites are located in position space, velocity space, and action space, we mark the well-recovered satellites with bold and underlined IDs in the legends of Figs 1, 2, A1, and A2. The well-recovered satellites outside the M_tot|$\gt 4.0\times 10^8 {\rm \, M_\odot }$|⁠, |$M_{\rm stellar} \gt 1.2\times 10^6 {\rm \, M_\odot }$| and T_infall< 7.1 Gyr ago ranges are marked by bold and underlined IDs with a star (*) in those legends.

In Section 3.2, we find that 150 star particles are corresponding to |$M_{\rm stellar}\approx 6\times 10^5{\rm \, M_\odot }$|⁠, so setting N_min = 300 is equivalent to setting the lower bound of M_stellar to be around |$1.2\times 10^6{\rm \, M_\odot }$| for groups found by Enlink. Any group with less stellar mass than |$1.2\times 10^6{\rm \, M_\odot }$| (number of particles smaller than N_min = 300) will not be found by Enlink under our choice of N_min. This lower bound in M_stellar agrees with the |$M_{\rm stellar}=1.2\times 10^6 {\rm \, M_\odot }$| boundary for well-recovered satellites. This agreement raises a caveat that the boundary on M_stellar (probably also on M_tot) might be an artefact due to a particular choice of N_min.

To appreciate how well the boundaries M_tot= |$4.0\times 10^8 {\rm \, M_\odot }$|⁠, |$M_{\rm stellar}=1.2\times 10^6 {\rm \, M_\odot }$|⁠, and T_infall = 7.1 Gyr ago work in separating out well-recovered satellites, we show three kernel density plots of 39 satellites from three galaxies in M_tot(left), M_stellar (middle), and T_infall(right) in Fig. 6. In all three panels, the dotted density curve represents well-recovered satellites, while the solid curve represents poorly recovered satellites. The two curves are normalized separately. The vertical dashed lines in three panels show the boundaries in Figs 4 and 5: M_tot= |$4.0\times 10^8 {\rm \, M_\odot }$|⁠, |$M_{\rm stellar}=1.2\times 10^6 {\rm \, M_\odot }$|⁠, and T_infall = 7.1 Gyr ago. In the left-hand panel, the dotted curve peaks at a higher M_tot than the solid curve, indicating that well-recovered satellites tend to be more massive. However, the peaks of both curves are greater than |$4.0\times 10^8 {\rm \, M_\odot }$|⁠, indicating that the boundary in M_tot alone cannot distinguish between well-recovered and poorly recovered satellites. In the middle panel, the solid curve peaks at a lower value than the dotted curve, indicating that well-recovered satellites tend to have more stellar mass than poorly recovered ones. The peak of the solid curve is close to the |$M_{\rm stellar}=1.2\times 10^6 {\rm \, M_\odot }$| boundary, indicating that M_stellar alone cannot distinguish well-recovered satellites and poorly recovered satellites either. In the right-hand panel, the peaks of dotted and solid density curves are on the two sides of the T_infall boundary, justifying the boundary T_infall= 7.1 Gyr ago.

Figure 6.

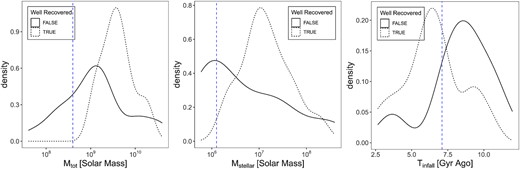
Kernel density plots of 39 satellites from three galaxies in M_tot(left), M_stellar (middle), and T_infall (right). The three blue vertical dashed lines label the boundaries in Figs 4 and 5: M_tot|$=4.0\times 10^8 {\rm \, M_\odot }$| (left), |$M_{\rm stellar}=1.2\times 10^6 {\rm \, M_\odot }$| (middle), and T_infall = 7.1 Gyr ago (right). In all three panels, the dotted density curve labels the well-recovered satellites, while the solid curve labels the poorly recovered satellites. In the left-hand panel, both the dotted and solid density curves peak above M_tot|$=4.0\times 10^8 {\rm \, M_\odot }$|⁠, with the dotted curve peaking at a higher M_tot, indicating that well-recovered satellites tend to be more massive. In the middle panel, the dotted curve peaks at a higher M_stellar, indicating that well-recovered satellites tend to be have more stellar mass. In the right-hand panel, the peaks of dotted and solid curves are on the two sides of T_infall = 7.1 Gyr ago.

Open in new tabDownload slide

We have seen that massive satellites fell into MW-like galaxies relatively recently can be reliably recovered by cluster analysis in action space with Enlink. In future applications to observational data it will be necessary to use a statistical metric provided by Enlink to determine which groups are most likely to correspond to real satellites. The variable significance, assigned by Enlink to each group and calculated by equation (4), is a good indicator of whether a group corresponds to a real satellite or not. In Fig. 7, we plot the values of significance of 34 non-background groups and 3 background groups. The size of a data point is proportional to the number of particles in the group, while the shape shows which galaxy this group is from, and the colour indicates whether the group is a background group (salmon), identifies a satellite well (green) or does not identify a single satellite (blue). A kernel density plot is attached on the side of the scatter plot. The green curve showing the distribution of significance peaks at a higher significance than the blue curve. The black dashed line shows the valley between the green and blue peaks. This valley, located at significance = 11.4 or the 66th percentile of the values of significance of the non-background population, is the cut-off in significance for groups corresponding to well-recovered satellites. Note the cut-off in significance here should not be confused with S_Th in Section 3.2. Among 12 non-background groups with significance above the cut-off, 11 of them are corresponding to ‘well-recovered’ satellites. This result implies that with the results of Enlink cluster analysis in action space alone (i.e. no other information on satellites, and ignoring the largest group identified by Enlink assuming it to be ‘background’), groups with higher significance than 66 per cent of groups found by Enlink are very likely to be corresponding to true satellites.

Figure 7.

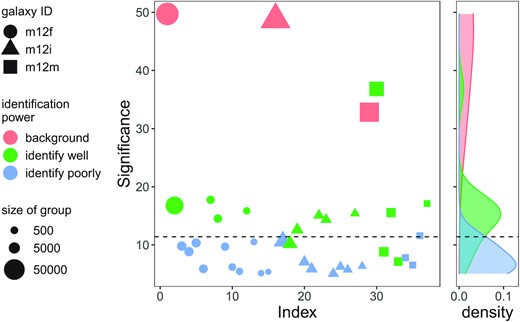
The values of significance of 37 (34 non-background+3 background) groups identified by Enlink in three MW-like galaxies (as shown in Fig. 3) are plotted. ‘Index’ is a number between 1 and 37 to label each group. The size of a data point is proportional to the number of particles in the group. Groups from galaxies m12f, m12i, and m12m are marked by circles, triangles, and squares, respectively. The colour of a data point indicates whether the groups is a background group (salmon), corresponds to a well-recovered satellite (green) or does not identify any satellite (blue). A kernel density plot is attached on the right-hand side of the scatter plot. The black dashed line labelling the valley between green and blue curve peaks shows the cut-off in significance for groups corresponding to well-recovered satellites. The cut-off value in significance for groups corresponding to well-recovered satellites is 11.4, the 66th percentile of the significance of non-background groups.

Open in new tabDownload slide

4.2 The effect of in situ stars

Besides accreted stars, cosmological hydrodynamical simulations predict that  in situ  stars may also contribute to a significant part of the halo star population in a galactic halo. As mentioned earlier, the fraction of  in situ  halo stars is highly uncertain, but estimates in the MW (Bell et al. 2008; Naidu et al. 2020) suggest that it could be as small as 5 per cent overall, while studies of resolved halo stellar populations in external galaxies find that the properties of these halo stars are consistent with being purely accreted (Harmsen et al. 2017) (beyond 30 kpc from the galactic centre). Recent work (Naidu et al. 2020) shows that in the MW halo, the relative fraction of  in situ  stars drops below 0.5 when |$|Z_\mathrm{gal}|\gt 5\, \mathrm{kpc}$|⁠, where |Z_gal| is the distance from the disc plane. We also note that over 95 per cent of the accreted star particles in disrupted satellites in the three MW-like galaxies have |$|Z_{\mathrm{gal}}|\gt 5\, \mathrm{kpc}$|⁠. We contaminate the data sets of accreted star particles with  in situ  star particles drawn from each of the three individual galaxies. The  in situ  star particles in the three simulated galaxies are selected by applying the following three filters: (i) the distance between the birth place of a star particle and centre of host galaxy was required to be smaller than 30 kpc, (ii) the current distance of the star particle from the centre of galaxy is smaller than 300 kpc, and (iii) the star particle’s current |$|Z_{\mathrm{gal}}|\gt 5\, \mathrm{kpc}$|⁠. Since our goal in this paper is to understand how well action space clustering works with complete, error-free data we do not impose additional spatial cuts. This selection yields around 5 × 10⁵  in situ  star particles in each of the three FIRE-2 galaxies, while only 1 × 10⁵ star particles in each galaxy are from disrupted accreted satellites. We show the distribution of  in situ  star particles in {J_r, J_z, J_ϕ} action space in Fig. 8 for each of the three galaxies. The fractions of  in situ  star particles in the simulated stellar haloes (beyond r ∼ 30 kpc and Z_gal > 5 kpc) are much higher than is observed in the MW (Bell et al. 2008; Naidu et al. 2020). Therefore, to study the effects of  in situ  stars on the robustness of satellite identification by cluster analysis in the action space, we build numerous mock data sets with  in situ  contamination ratios equaling 0.1, 0.2, 0.3, 0.4, and 0.5 (where contamination ratio of 0.5 implies that 50 per cent of the halo star sample consists of  in situ  stars) in three MW-like galaxies by randomly sampling the  in situ  star particles in the three galaxies from the FIRE-2 simulations with |$|Z_{\mathrm{gal}}|\gt 5\, \mathrm{kpc}$|⁠. We then calculate the actions {J_r, J_z, J_ϕ} and do cluster analysis with Enlink in the action space on these ‘contaminated’ data sets. We pick out the well-recovered satellites in Section 4.1 and study their values of merit at different contamination ratios. To reduce the effect of the randomness in sampling the  in situ  star particles, for every contamination ratio in each galaxy, we repeat the selection of the  in situ  ‘contaminant’ population 100 times, randomly picking the same fraction of  in situ  stars each time. We then generate the value of merit for each well-recovered satellite from each data set. Each well-recovered satellite at a contamination ratio then has 100 values of merit. We calculate the average and standard deviation of those 100 values. If the previously well-recovered satellite doesn’t have a best fit group in one data set (i.e. the best recovery group doesn’t match with the best purity group), then the merit of that satellite in that run is set to 0.

Figure 8.

In situ star particles in each simulated galaxy analysed in this research are plotted in {J_r, J_z, J_ϕ} action space. Each column is corresponding to one galaxy.

Open in new tabDownload slide

Fig. 9 illustrates the change of values of merit of well-recovered satellites in three MW-like galaxies (as shown in Section 4.1) as the contamination ratio increases from 0 to 0.5. Each data point and error bar in the figure shows the average and standard deviation of results of 100 runs, respectively. Lines of different colours correspond to different well-recovered satellites. 78 per cent (11/14) of the satellites are robust against the contamination from  in situ  star particles, as their values of merit are above 0.5 at all contamination ratios. Other satellites become unidentifiable by Enlink (merit <0.5) as the contamination ratio increases. The standard deviation of the merit of these satellites is also higher than their more robust companions, showing that they are more vulnerable under the random draw of the  in situ  star particles.

Figure 9.

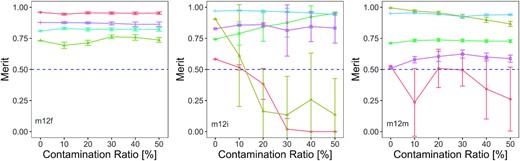
Values of merit of well-recovered satellites in three galaxies (m12f, m12i, m12m from left to right) at different  in situ  contamination ratios. Each differently coloured line corresponds to one well-recovered satellite in each galaxy (the well-recovered satellites in three galaxies are summarized in Fig. 4). The values of merit come from the average of 100 runs and the error bars show the standard deviations. A blue dashed line in 3 panels shows merit= 0.5, the threshold of ‘well-recovered’ objects. 78 per cent (11/14) of the well-recovered satellites have values of merit greater than 0.5 at all contamination ratios, being robust against the contamination from  in situ  star particles. As the contamination ratio increases, the values of merit of some satellites drop below 0.5. These ‘vulnerable’ satellites have higher standard deviations in merit than other robust satellites, showing that they are more affected by the randomness of picking  in situ  star particles. The robustness of well-recovered satellites indicates that Enlink can recover most of the well-recovered satellites when  in situ   star particles are in the data set.

Open in new tabDownload slide

5 DISCUSSION AND CONCLUSIONS

Inspired by the principle of conservation of orbital actions, we use cluster analysis in action space to find accreted satellites with accreted star particles in three MW-like galaxies in the FIRE-2 cosmological hydrodynamical simulations. We summarize the main findings of our work below:

• Classification tree method finds the boundaries separating well-recovered and poorly recovered satellites to be T_infall= 7.1 Gyr ago and M_tot =|$4.0\times 10^8 {\rm \, M_\odot }$|(or|$M_{\rm stellar}=1.2\times 10^6 {\rm \, M_\odot }$|) (see Figs 4 and 5). We note however, that the boundary in M_stellar coincides with the minimum mass of groups that Enlink is set-up to identify, determined by N_min. This coincidence implies that the mass boundary could be an artefact of the choice of N_min.

  The three galaxies have slightly different infall time and mass boundaries for reliable detection. For example, galaxy m12i has three well-recovered satellites that fell into the hosting halo more than 7.1 Gyr ago. This difference could be due to the distinct dynamical/evolutionary histories of the galaxies. Fig. 10 shows the offset angle, Δθ, between the angular momentum vector of the disc at a given look-back time and the present time (z = 0) as a function of look-back time for each of the three galaxies analysed in this paper. The disc stars at each look-back time are defined as star particles that are within 30 kpc and also have formation distance within 30 kpc from the centre of the host galaxy. The graph shows that the direction of the angular momentum vector often changes suddenly and through large angles (presumably due to merger events) for look-back time >8 Gyr ago. Santistevan et al. (2021) show that many of the changes in this Δθ correlate with major gas-rich mergers. In particular, galaxies m12f and m12m experienced numerous chaotic changes in Δθ until 8 Gyr ago, after which Δθ changed much more slowly and steadily. The slow change in Δθ implies the gravitational potentials of these two galaxies have changed adiabatically over the last 8 Gyr, and therefore orbital actions of particles should be reasonably well conserved. The conservation of orbital actions implies that satellites accreted less than 8 Gyr ago should be found clustered in action space at z = 0. This ‘8 Gyr ago’ time limit for finding satellites clustered in action space is in agreement with the time boundary for good recovery that we found in Section 4. Δθ of galaxy m12i changes more smoothly compared with the other two galaxies, so it is expected that satellites accreted a long-time ago would remain clustered in action space. This is in agreement with the fact that three satellites in this galaxy with T_infall >9 Gyr ago are still well recovered by Enlink. In our MW galaxy, Gaia Enceladus, which has T_infall ≈ 10 Gyr ago and progenitor stellar mass |$6\times 10^8 {\rm \, M_\odot }$| (Helmi et al. 2018), can still be recovered in phase space. The recovery of this massive substructure that fell into the MW a long-time ago indicates that the MW might evolve smoothly from relatively early on, like m12i in the FIRE-2 simulations.

• The value of significanceof a group shows a high correlation with the identification power of this group (see Fig. 7). Of the groups with high significance (>11.4, 66th percentile of the significance of non-background groups in three galaxies), most (92 per cent, 11/12) correspond to the well-recovered satellites. This implies that if cluster analysis in action space is applied to observational data, this significance assigned by Enlink can help us determine which groups are most likely to correspond to true accreted satellites.

• Most of the well-recovered satellites are robust against contamination of  in situ  star particles (see Fig. 9). 78 per cent (11/14) of the well-recovered satellites in Section 4.1 stay well-recovered (with merit >0.5) at five different contamination ratios (0.1, 0.2, 0.3, 0.4, and 0.5), where contamination ratio is the percentage of  in situ   star particles in the data set of one galaxy. The satellites that fail to be identified by Enlink in the presence of contamination have higher standard deviations in merit, indicating that they are more sensitive to the randomness in picking  in situ  stars. This robustness against contamination from  in situ  star particles indicates that it will be possible to apply cluster analysis in action space to observation data, even if there is significant contamination from  in situ  stars. This is reassuring since the expected fraction of  in situ  stars in the MW (5 per cent) is at the low end of the contamination fractions we have experimented with.

Figure 10.

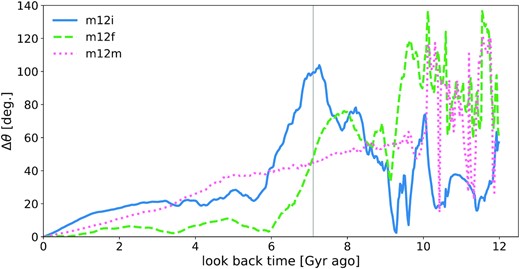
The dynamical histories of the three MW-like simulated galaxies in FIRE-2. The angle Δθ of the normal vector of the galaxy disc relative to its present-day direction is plotted versus look-back time. If Δθ changes rapidly, then the evolution of the galaxy is chaotic; if Δθ changes slowly, then the galaxy evolves smoothly. The disc orientations of galaxies m12f and m12m changed rapidly at the beginning and evolved more smoothly after 8 Gyr ago. Galaxy m12i evolved more smoothly than the other two galaxies before 8 Gyr ago, allowing massive satellites that fell into m12i up to 10.3 Gyr ago to remain clustered in action space at z = 0. A vertical line shows the time boundary for well-recovered satellites-7.1 Gyr ago.

Open in new tabDownload slide

In this work, we have demonstrated, using simulation data, that it is possible to find accreted satellites using cluster analysis in action space. We have deliberately focused on a fairly idealized set of circumstances: (a) we assumed that phase space coordinates of all star particles were known with no error; (b) we assumed nearly perfect knowledge of the gravitational potential arising from stars, dark matter, and gas (although we approximated the potentials as axisymmetric even though they are triaxial); (c) we had perfect knowledge of the merger history of the galaxies and therefore the true masses and infall times of the satellites. In future applications of this method to observational data, the following improvements should be explored.

• As with all cosmological-hydrodynamical simulations, despite being until very recently the highest resolution such simulations ever conducted of MW-mass haloes (Applebaum et al. 2021), resolution limits our results to accreted structures at the stellar mass of classical dwarf galaxies and higher, since each star particle in the FIRE-2 simulations is 7100 |${\rm \, M_\odot }$|⁠. The total number of accreted star particles used in our analysis is also orders of magnitude smaller than the number of accreted stars with 6D phase space coordinates [from Gaia and future large ground-based surveys such as 4MOST (de Jong et al. 2012), WEAVE (Dalton et al. 2014), DESI (DESI Collaboration 2016a, b)], which are expected to yield six phase space coordinates for 3–4 million stars. The performance of our clustering technique when scaled up by 3–4 orders of magnitude in particle number has yet to be tested. On the other hand, if we restrict ourselves to, e.g. RR Lyrae variables, then the conversion rate between the real data set and the simulation data set is about one star per star particle, and the analysis in this work can be more easily done. In addition, real data have observational errors and for this study we have assumed that all phase space coordinates are known perfectly. Additional studies with more realistic mock data sets like the ananke data set (Sanderson et al. 2020) are needed to assess how well Enlink performs under realistic conditions. Currently, the precise 6D kinematics data are available only for stars within tens of kpc from the Solar system, but the amount and precision of data for distant stars will increase significantly in the future. We are preparing another paper discussing the effects of errors from current and future observations, e.g. Gaia DR5, the Rubin observatory’s Legacy Survey of and Space and Time, and Roman Space Telescope’s High Latitude survey, on the cluster analysis in action space results.

• It is necessary to find an objective way to determine N_min, the parameter used by Enlink to determine a ‘reasonable’ size for a cluster (Section 3.2). In this study, N_min was selected by trial and error in order to ensure that the number of groups that Enlink produced was close to the number of satellites that were known to have been accreted (as described in Section 2). An objective way to determine N_min and the other parameters that are used in the Enlink cluster analysis algorithm, is needed to evaluate the quality of clusters found. We found that the conventional silhouette plots (Rousseeuw 1987) are not useful here, since many satellites are irregularly shaped in the action space and could be incorrectly classified by silhouette values. The choice of parameters for cluster analysis has been largely ignored in previous papers, and should be investigated in future.

• Stellar metallicities and the abundance of individual elements in a star are also well conserved quantities that contain a substantial amount of information about the host satellite in which the star was born. However, the stars in a satellite can have a range of [Fe/H] and α-element abundance ratios as well as gradients in the abundances of other elements. Sanderson et al. (2017) show that including the abundance of certain elements (e.g. N, Ca) can improve the recovery of the Galactic mass model built through cluster analysis. Incorporating metallicities of stars as features into cluster analysis might improve the performance of current results from cluster analysis in action space.

• The inclusion of metallicities of stars can also help to determine the masses of individual satellites (through the mass-metallicity relationship) and hence action-space clustering can be used to determine the number of accreted satellites per unit mass N(M), a parameter that is a sensitive probe of the model of dark matter.

• We have assumed in this work that the overall gravitational potential of each galaxy is axisymmetric rather than triaxial. This restriction was driven by the fact that the most efficient action finders available (e.g. agama) are restricted to oblate axisymmetric potentials. Triaxial action finders (Sanders & Binney 2015a, b) exist but are currently not fast enough to be useful for analysis of large data sets. Development of fast triaxial action finders would be extremely helpful.

ACKNOWLEDGEMENTS

MV, YW, and KF acknowledge support from an MICDE Catalyst grant at University of Michigan. MV acknowledges useful discussions with the ‘Stellar Halos group’ of Department of Astronomy, UM and is supported by National Aeronautics and Space Administration-ATP awards NNX15AK79G and 80NSSC20K0509. KF is grateful for support as Jeff and Gail Kodosky Chair of Physics at the University of Texas, Austin. KF acknowledges support from the |$\rm {Vetenskapsr\mathring{a}de}$|t (Swedish Research Council) through contract No. 638-2013-8993 and the Oskar Klein Centre for Cosmoparticle Physics. KF and YW further acknowledge support from Department of Energy grant DE- SC007859 and the LCTP at the University of Michigan. NP and RES acknowledge support from National Aeronautics and Space Administration-ATP award 80NSSC20K0513. RES acknowledges support from the Research Corporation for Science Advancement through the Scialog program on Time Domain Astrophysics, and from HST grant AR-15809 from STScI. AW receives support from National Aeronautics and Space Administration through ATP grants 80NSSC18K1097 and 80NSSC20K0513; HST grants GO-14734,AR-15057, AR-15809, and GO-15902 from Space Science Telescope Institute; a Scialog Award from the Heising-Simons Foundation; and a Hellman Fellowship.

The authors thank the Flatiron Institute Scientific Computing Core for providing computing resources that made this research possible, and especially for their hard work facilitating remote access during the pandemic. Some analysis for this paper was carried out on the Flatiron Institute’s computing cluster rusty, which is supported by the Simons Foundation.

Simulations used in this work were run using XSEDE supported by National Science Foundation grantACI-1548562, Blue Waters via allocation PRAC NSF.1713353 supported by the National Science Foundation, and NASA HEC Program through the NAS Division at Ames Research Center.

DATA AVAILABILITY

Some of the data underlying this paper are publicly available at https://flathub.flatironinstitute.org/sapfire. Other parts of the data will be shared upon reasonable requests to the corresponding author.

Footnotes

REFERENCES

APPENDIX A: SATELLITE DISTRIBUTIONS IN POSITION AND PHASE SPACE

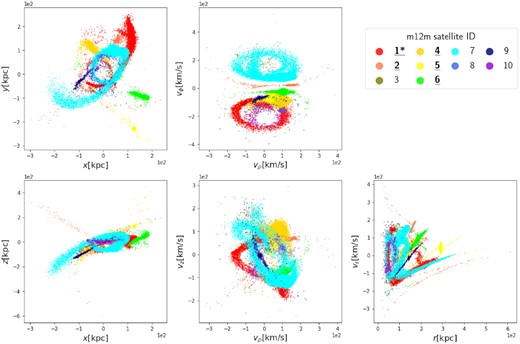
The disrupted satellites in galaxies m12i and m12m in position space (left column), velocity space (middle column), and r versus v_r phase space (right column) are shown in Figs A1 and A2, respectively.

Figure A1.

Same as Fig. 1, but with satellites from galaxy m12i.

Open in new tabDownload slide

Figure A2.

Same as Fig. 1, but with satellites from galaxy m12m.

Open in new tabDownload slide

APPENDIX B: RECOVERY, PURITY, MERIT, AND CONTRAST AS FUNCTIONS OF INFALL TIME, TOTAL MASS, AND STELLAR MASS

The values of recovery, purity, merit, and contrast of 39 disrupted satellites in three MW-like galaxies from the FIRE-2 simulations are plotted against infall time (first row), total mass (second row), and stellar mass (third row) in Fig. B1. Well-recovered satellites are marked as triangles and poorly recovered satellites are marked as circles. Blue dashed lines show the boundaries obtained in Section 4.1: T_infall= 7.1 Gyr ago, M_tot= |$4.0\times 10^8 {\rm \, M_\odot }$|⁠, and |$M_{\rm stellar} = 1.2\times 10^6 {\rm \, M_\odot }$|⁠.

Figure B1.

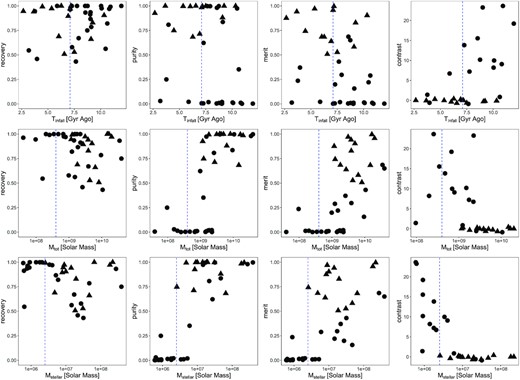
The values of recovery, purity, merit, and contrast of 39 disrupted satellites in three MW-like galaxies from the FIRE-2 simulations are plotted as functions of infall time (first row), total mass (second row), and stellar mass (third row). Well-recovered satellites are marked as triangles and poorly recovered satellites are marked as circles. Blue dashed lines show the boundaries obtained in Section 4.1: T_infall= 7.1 Gyr ago, M_tot= |$4.0\times 10^8 {\rm \, M_\odot }$| and |$M_{\rm stellar} = 1.2\times 10^6 {\rm \, M_\odot }$|⁠. In contrast plots, only satellites with best fit groups are plotted.

Open in new tabDownload slide

APPENDIX C: CLASSIFICATION TREE METHOD

Figure C1.

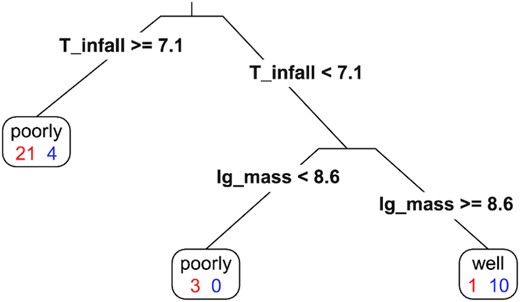
A classification tree used in Section 4.1 to derive the boundaries between well-recovered and poorly recovered satellites. ‘T_infall’ indicates T_infall in Gyr ago, ‘lg_mass’ represents |$\log _{10}(M_{\rm tot}/{\rm \, M_\odot })$|⁠. A ‘well’ or ‘poorly’ in each leaf node indicates the prediction of the label of data points in this node by majority vote, with ‘well’ corresponding to well recovered and ‘poorly’ corresponding to poorly recovered. The red and blue numbers in each leaf node indicate the numbers of poorly recovered and well-recovered satellites in this leaf node, respectively. The tree with |$\log _{10}(M_{\rm stellar}/{\rm \, M_\odot })$| and T_infall in Gyr ago as input is similar, except that the split in |$\log _{10}(M_{\rm stellar}/{\rm \, M_\odot })$| is located at 6.1.

Open in new tabDownload slide