-
PDF
- Split View
-
Views
-
Cite
Cite
Soumak Maitra, Raghunathan Srianand, Prakash Gaikwad, Nishikanta Khandai, Redshift space three-point correlation function of IGM at z < 0.48, Monthly Notices of the Royal Astronomical Society, Volume 509, Issue 3, January 2022, Pages 4585–4607, https://doi.org/10.1093/mnras/stab3308
Close - Share Icon Share
ABSTRACT
Ly α forest decomposed into Voigt profile components allows us to study clustering properties of the intergalactic-medium and its dependence on various physical quantities. Here, we report the first detections of probability excess of low-z (i.e z < 0.48) Ly α absorber triplets over redshift-space scale of r∥ ≤ 8 pMpc (Mpc in physical units) with maximum amplitude of |$8.76^{+1.96}_{-1.65}$| at a longitudinal separation of 1–2 pMpc. We measure non-zero three-point correlation (|$\zeta = 4.76^{+1.98}_{-1.67}$|) only at this scale with reduced three-point correlation Q = |$0.95^{+0.39}_{-0.38}$|. The measured ζ shows an increasing trend with increasing minimum H i column density (NH i) threshold while Q does not show any NH i dependence. About 88 per cent of the triplets contributing to ζ (at z ≤ 0.2) have nearby galaxies (whose distribution is known to be complete for ∼0.1L* at z < 0.1 and for ∼L* at z ∼ 0.25 within 20 arcsec to the quasar sightlines) within velocity separation of 500 km s−1 and median impact parameter of 405 pkpc. The measured impact parameters are consistent with majority of the identified triplets not originating from individual galaxies but tracing the underlying galaxy distribution. Frequency of occurrence of Broad-Ly α absorbers (b > 40 km s−1) in triplets (∼85 per cent) is factor ∼3 higher than that found among the full sample (∼32 per cent). Using four different cosmological simulations, we quantify the effect of peculiar velocities and feedback and show that most of the observed trends are broadly reproduced. However, ζ at small scales (r∥ < 1 pMpc) and its b-dependence found in simulations are inconsistent with observations. This could either be related to the failure of these simulations to reproduce the observed b and NH i distributions for NH i > 1014 cm−2 self-consistently or to the wide spread of signal-to-noise ratio in the observed data.
1 INTRODUCTION
The Ly α absorption seen in the spectra of high-z quasars are frequently used to probe the physics of the intergalactic medium (IGM) and parameters of the background cosmology (see Rauch 1998; Meiksin 2009). While a vast majority of research using ground-based observations have been focusing on higher redshifts Ly α forest (i.e z > 1.8) owing to the atmospheric cut-off, observations using Hubble Space Telescope (HST) allow us to probe Ly α forest at low-z (i.e. z < 1.3) (see e.g. Bahcall et al. 1991, 1993, 1996; Penton, Shull & Stocke 2000; Danforth et al. 2016; Tilton et al. 2016).
At high redshifts, it is believed that most of the baryons are located in the photoionized low-density IGM that traces the underlying dark matter distribution for scales above the pressure smoothing scales (see e.g. Bi & Davidsen 1997). At low-z, the Ly α absorption with a given neutral hydrogen column density, NH i, originates from higher overdensities (i.e Δ ∼ 35 for NH i = 1014 cm−2 at z = 0) compared to that (i.e Δ ∼ 10 for NH i = 1014 cm−2 at z = 2.0) at high-z (Davé et al. 2010; Smith et al. 2011; Gaikwad et al. 2017a). Frequent presence of broad Ly α absorbers (BLAs are defined as systems with Doppler parameter b1 ≥ 40 km s−1, see Richter et al. 2006; Lehner et al. 2007) and ionization modelling of high-ionization absorbers (like Ne viii and O vi, see Savage et al. 2005; Tripp et al. 2008; Hussain et al. 2017) suggests that collisional ionization (e.g. due to structure formation shocks) may also be important for some of the low-z Ly α absorbers.
In principle, it is possible to associate the Ly α absorbers with individual galaxies (or distribution of galaxies) at low-z. Such studies have revealed that the low-z Ly α forest absorption originates from different locations such as cool-dense circumgalactic medium (CGM; Werk et al. 2014), dense hot intracluster medium (ICM; see Muzahid et al. 2017; Burchett et al. 2018) in addition to the filaments and voids defined by the distribution of galaxies (Stocke et al. 1995; Penton, Stocke & Shull 2002; Tejos et al. 2014). It is also found that NH i, b-parameter, and metallicity of the gas depend on their location. Thus, it is an usual procedure to study the properties of the low-z IGM as a function of NH i, b-parameter, and metal abundance.
At low-z it is possible to correlate the spatial distribution and other properties of Ly α forest with the cosmic web (i.e filaments, voids, and clusters in the galaxy distribution) defined by galaxies. Penton et al. (2002), by correlating the Ly α absorbers at 0.003 ≤ z ≤ 0.069 with the galaxy distribution, arrived at the following conclusions. Apart from a few very strong Ly α absorbers (i.e with NH i≥ 1015 cm−2) the strong Ly α absorbers (i.e with NH i = 1013.2−1015.5 cm−2) are found to be aligned with the large-scale distribution of galaxies. A small fraction (i.e 22 ± 8 per cent) of Ly α absorbers are found to be distributed in cosmic voids (see also Stocke et al. 1995). In general these void absorbers are found to have low NH i (i.e NH i ≤ 1013.2 cm−2).
Wakker et al. (2015) studied Ly α absorption towards 24 quasar sightlines that are close to two large local filaments. They find a strong correlation between Ly α equivalent width (as well as b-parameter) and filament impact parameter. All the Ly α absorption with NH i ≥ 1013 cm−2 are found to have the filament impact parameter less than 2.1 pMpc. Interestingly, the four BLAs detected in their sample are all found to be located within 400 pkpc to the filament axis and all the absorbers showing multiple velocity components are located within 1 Mpc to the filament axis. While the trends found in this study are very interesting, these are based on small number of sightlines (and systems) and it is important to expand such an analysis to large number of sightlines. Recently, Bouma, Richter & Wendt (2021) investigated spectra of 302 extragalctic background sources, with 91 of them passing close to local galaxy filaments. They found relative excess of Ly α absorbers as well as a stronger Ly α clustering close to the filament axis with stronger Ly α absorbers appearing closer to the galaxies or the filament axis.
Tejos et al. (2016) have studied absorption towards filaments connecting cluster pairs at z < 0.5 towards the quasar J141038.39+230447. They found tentative excesses of H i (broad as well as narrow) and O vi absorption lines within rest-frame velocities of ≤1000 km s−1 from the cluster-pairs redshifts. They suggested that while O vi absorption may be associated with individual galaxies, narrow and broad H i absorption are intergalactic in origin. They also found the relative excess of BLAs to be larger than that of narrow Ly α absorbers and used this to argue that BLAs may be originating from collisionally ionized gas in the filaments.
The clustering properties of the Ly α absorbers can be used to probe the matter distribution in the Universe. Majority of such studies in the literature focus mainly on high redshifts (z > 1.8). Usually, these clustering studies are carried out in the redshift space using longitudinal (line of sight) correlation or conversely 1D flux power spectrum in the fourier space (McDonald et al. 2000, 2006; Croft et al. 2002; Seljak, Slosar & McDonald 2006). The 1D Ly α forest flux power spectrum has been used to constrain the background cosmology (McDonald et al. 2005; Palanque-Delabrouille et al. 2013), mass of warm dark matter particles (Narayanan et al. 2000; Viel et al. 2013), neutrino mass (Palanque-Delabrouille et al. 2015a,b; Yèche et al. 2017; Palanque-Delabrouille et al. 2020), ionization state (Gaikwad et al. 2017a; Khaire et al. 2019), and the thermal history of the IGM (Walther et al. 2019; Gaikwad et al. 2019, 2020a, b). Clustering studies of Ly α forest can also be carried out in the transverse direction using closely spaced projected quasar pairs or gravitationally lensed quasars (Rauch & Haehnelt 1995; Smette et al. 1995; Petitjean et al. 1998; Aracil et al. 2002; Coppolani et al. 2006; D’Odorico et al. 2006; Hennawi et al. 2010; Rollinde et al. 2013). It is found that correlation in the transverse direction is more sensitive to the 3D matter distribution in comparison to longitudinal direction which is dominated by thermal broadening effects (Peeples et al. 2010a,b).
The next order beyond the two-point correlation statistics (or power spectrum in fourier space) is the three-point correlation statistics (or bispectrum in fourier space). Higher order statistics are useful in studying the non-Gaussianity in clustering imparted by the non-linear gravitational evolution as well as any primordial non-gaussianity in the density fields (Peebles 1980). They can act as an independent tool complementing the two-point statistics in constraining cosmological parameters and remove degeneracies between different cosmological parameters like bias and σ8 (Fry 1994; Bernardeau et al. 2002; Verde et al. 2002). While considerable work has been done studying three-point clustering statistics using galaxies (see e.g. McBride et al. 2011b; Guo et al. 2016), it remains largely unexplored in the case of clustering in Ly α forest.
While the Ly α forest is a good probe of underlying dark matter distribution the exact connection between Ly α optical depth or NH i to the dark matter density is not straightforward. In particular ionization and thermal inhomogeneities can have strong influence on this relation (see Tie et al. 2019; Maitra et al. 2020). All this make probing two- and three-point correlation function of the Ly α forest an important exercise. While all the theoretical explorations using simulations till date focus on transverse correlations, observationally it is possible to study only few triplets sightlines at high-z (e.g Cappetta et al. 2010; Maitra et al. 2019). However, enough spectra are available in the literature to probe the longitudinal (i.e redshift space) three-point correlation function (e.g. Viel et al. 2004) at low and high-z. As discussed above, unlike high-z, the low-z Ly α absorbers can originate from varied environments like ICM, CGM, and IGM. This makes it interesting to probe clustering at different scales. Low-z also provides additional advantage that we will be able to relate the observed Ly α clustering properties with the underlying galaxy distribution and various feedback processes. This forms the main motivation of this work.
While line of sight two-point correlation of Ly α forest at low-z is studied in the past (e.g. Ulmer 1996; Impey, Petry & Flint 1999; Penton et al. 2002; Danforth et al. 2016) higher order clustering is not explored. Here, we measure the redshift space (or longitudinal) 3-point (ζ) and reduced 3-point correlation (Q) function of the IGM at z ≤ 0.48. For this purpose, we use the Voigt profile fitted Ly α absorption components of IGM towards 82 UV-bright QSOs (zem < 0.85) observed using Hubble Space Telescope-Cosmic Origins Spectrograph (HST-COS) presented in Danforth et al. (2016). We report, for the first time, the detection of longitudinal three-point correlation of low-z Ly α absorbers (z < 0.48) at scales ≤2 pMpc (Mpc in proper units). We study the dependence of ζ on NH i, b-parameter and the presence of different metal ion species. We also study the relationship between regions showing triplet absorption and galaxy distribution for z ≤ 0.2.
In the past, simulations have been used to study two-point correlation function of low-z Ly α absorbers (e.g. Pierleoni, Branchini & Viel 2008). Here, we present the analysis of simulated IGM data at z ∼ 0.1 using four available cosmological hydrodynamical simulations. We use these simulations to (i) check whether the observed dependence of clustering on NH i and b-parameters are readily reproduced; (ii) quantify the effect of peculiar velocities on the line-of-sight clustering and (iii) probe the effect of feedback on the line-of-sight clustering. We show the peculiar velocities tend to enhance the two- and three-point correlation signals (by about 40–60 per cent) over the distance scale probed in this study. Presence of wind and AGN feedback (as implemented in the simulations used here) are shown to produce minor effect in the measured two- and three-point correlation functions. As these simulations have problems in reproducing the b-distributions and high NH i end of the column density distribution function, we do not make any serious attempt to exactly match our observations with simulations.
This paper is organized as follows. In Section 2, we provide the details of data used in our study. Section 3 summarizes the results of two-, three-, and reduced three-point correlation of low-z Ly α absorbers measured from observations. Here, we also present the dependence of clustering on NH i, b, z, and the presence of different metal ion species like C iv, O vi, and Si iii. In Section 4, we investigate the connection between Ly α clustering and galaxy distribution. In Section 5, we present our analysis based on a set of z ∼ 0.1 hydrodynamical simulations with and without feedback. We discuss our main results in Section 6. In this work, we use the flat ΛCDM universe with the following cosmological parameter (|$\Omega _\Lambda$|, Ωm, Ωb, h, ns, σ8, Y) ≡ (0.69, 0.31, 0.0486, 0.674, 0.96, 0.83, 0.24) based on (Planck Collaboration XVI 2014). Cosmological parameters used in our simulations are slightly different and are summarized in Section 5. H i column densities are given in the units of cm−2 throughout this paper.
2 DATA SAMPLE
We use the publicly available data sample2 of low-redshift Ly α spectra towards 82 UV-bright QSOs (zem < 0.85) observed using HST-COS by Danforth et al. (2016). The sample covers Ly α forest at z ≤ 0.48 and the spectra were obtained at a resolution of ∼17 km s−1. In Danforth et al. (2016), the spectra were continuum fitted and 5138 absorption line features arising from the intervening IGM were identified. The redshift, column density, Doppler parameter b, equivalent width and the significance level of detection corresponding to each of these absorption features were tabulated. We use publicly available parameters of the Voigt profile components obtained by Danforth et al. (2016) for the clustering study in this work. The redshift distribution of the Ly α absorbers used in this work is given in the top panel of Fig. 1.
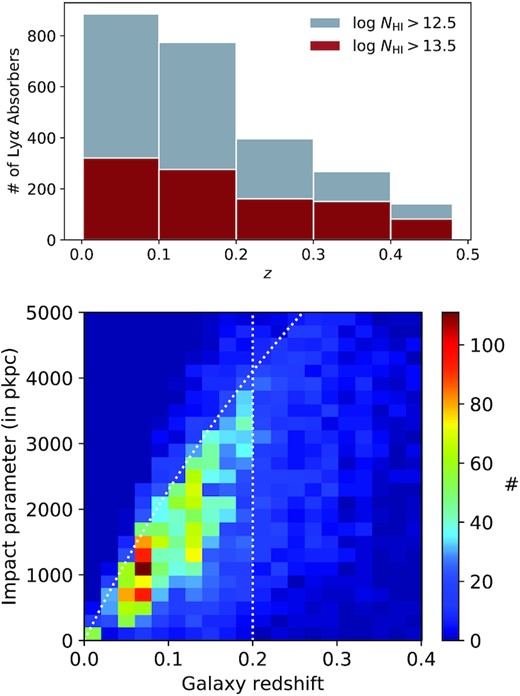
Top: Redshift distribution of number of Ly α absorbers in our sample. We present this for two NH i thresholds. Bottom: 2D histogram plot of redshift versus impact parameter of the galaxy sample along the quasar sightlines used in this study. See Section 2 for discussions related to the completeness of this sample. The vertical dashed line denotes the maximum galaxy redshift used for our study. The dashed curve shows the projected length-scale as a function of redshift for an angular scale of 20 arcmin.
For this work, we consider Ly α absorption lines having z ≤ 0.48, avoiding the proximity regions bluewards to the quasar redshift within 1500 km s−1 (corresponding to a proper distance of 20.65 pMpc at z ∼ 0.1) and within 500 km s−1 redward of z = 0 (similar to Danforth et al. 2016). The velocity range 1500 < Δv < 5000 km s−1 bluewards of the quasar redshift may also be affected by high-velocity outflows from the quasar. So, systems having strong absorption in high ion species but weak H i, strongly non-Gaussian absorption profiles or doublet ratio close to 1:1 indicating possible partial coverage of the source are removed (see section 2.4.2 Danforth et al. 2016). Six quasars in this sample have originally been targeted to study the CGM near z ≤ 0.02 galaxies (Stocke et al. 2013).3 In order to remove any bias, we set a lower redshift limit for these sightlines to 300 km s−1 redwards of the redshift of the target galaxy. The redshift path-length coverage of the Ly α forest after removing these biased regions is about 19.9.
We use a deep and wide galaxy redshift survey along 47 of HST-COS sightlines presented by Keeney et al. (2018) to probe the connection between Ly α clustering and galaxy distributions. We supplemented these data with the galaxies detected within 20 arcmin to the quasar sightline from SDSS and Prochaska et al. (2011). Apart from few cases the galaxy distribution from Keeney et al. (2018) is known to be complete for ∼0.1L* at z < 0.1 and L* at z ≃ 0.25. The data from Prochaska et al. (2011) also reach similar depth but over half the angular scale (i.e up to 10 arcmin from the quasar sightline). 34 sightlines in Danforth et al. (2016) have galaxy information in Keeney et al. (2018). For the limiting magnitude of g ∼ 20 mag, the median ‘overall completeness’ is found to be 97.1, 92.3, 87.5, and 87 per cent within angular scales of 5, 10, 15, and 20 arcmin, respectively. Five of these sightlines were also covered by Prochaska et al. (2011). We also use the galaxy distribution around 7 other sightlines from Prochaska et al. (2011). As reported in their table 1, for r < 19.5 they reach 89 and 90 per cent completeness within angular scales of 5 and 10 arcmin, respectively. In total we have 6174 galaxies close to these 41 sightlines. The redshift and impact parameter distributions of these galaxies are also shown in Fig. 1. Vertical dotted line marks z = 0.2. We also show the impact parameter corresponding to 20 arcmin. We use these data to find the properties of the nearest galaxies to the isolated absorbers and the absorbers showing strong two- and three-point redshift space (or velocity) correlation at z ≤ 0.2. At z ∼ 0.1 an angular scale of 20 arcmin corresponds to a projected length-scale of ∼2.3 pMpc.
3 ABSORBER-BASED STATISTICS
Maitra et al. (2019) and Maitra et al. (2020) presented two- and three-point correlation studies of Ly α forest using Voigt profile components as a suitable probe of the clustering properties of the IGM at z > 2. These Voigt profile components can also be used to explore the connection between galaxies and intergalactic gas (see Rudie et al. 2012, for example). Throughout this paper, we will refer to these individual Voigt profile components as ‘absorbers’. We will use the term absorption ‘system’ to refer to the whole absorption profile. The Ly α absorber based approach allows us to study the two- and three-point correlations as a function of NH i, b and presence of metal ions. In this section, we study the clustering properties of low-z IGM by measuring longitudinal (i.e redshift space) three-point correlation of the Ly α absorbers. For doing so, we first estimate the NH i distribution of the Ly α absorbers for the full sample and various sub-samples. This is an important first step to generate a set of mock sightlines having random distribution of Ly α absorbers that are used as a comparison to estimate the longitudinal three-point correlation. We also measure the longitudinal two-point correlation in order to estimate the reduced three-point correlation, Q.
3.1 Neutral hydrogen column density distribution
In HST-COS spectra, the signal-to-noise ratio (SNR) varies substantially across the observed wavelength range for a given sightline. So, the detectibility of any absorption feature has a wavelength (or z) dependence. We need the intrinsic distribution of Ly α absorbers having different column densities (NH i) to construct the random distribution of the absorbers after appropriately taking into account the z-dependence of detectibility along each sightline.
The redshift path-length calculated in this way takes care of incompleteness coming from regions having the observed SNR lower than what is required for detecting an absorption line in a certain NH i bin.4 We find that 25, 50, and 75 per cent of the observed redshift path-length is sensitive enough to detect absorbers having log NH i (in cm−2) = 12.68, 12.84, and 13.00, respectively. The corresponding values obtained by Danforth et al. (2016) are log NH i (in cm−2) = 12.77, 12.93, and 13.09. The minor differences come from the fact that while Danforth et al. (2016) considers all the NH i measurements (including systems identified based on Ly β absorption for which Ly α is not covered), we consider only systems where Ly α absorption is covered in the HST-COS spectra. Also we avoid regions around 6 known galaxies that were searched for CGM absorption (see Section. 2 for details).
In the top panel of Fig. 2, we plot f(NH i, z) in different logNH i bins for four different redshift intervals (z = 0.00–0.10, 0.10–0.20, 0.20–0.30, and 0.30–0.48). The error in the distribution is larger of the two error estimates: one-sided Poissonian uncertainty in the number of absorbers corresponding to ±1σ or the bootstrapping error computed over all the sightlines in a redshift bin. In the error, we also account for the uncertainty in dz sourcing from the variation of completeness limit for a finite NH i bin width. We then fit f(NH i, z) according to equation (1). The fitted parameter values are |$\rm C_0=31\pm 2$|, β = −0.65 ± 0.03, and γ = 0.7 ± 0.3. The C0 and γ values are similar to |$f(N_{\rm H\,{\small I}})=(167)N_{13}^{-0.65\pm 0.02}\approx (37)N_{14}^{-0.65\pm 0.02}$| reported in Shull et al. (2015), |$f(N_{\rm H\,{\small I}})=(23\pm 1)N_{14}^{-0.67\pm 0.01}$| reported in Danforth & Shull (2008) and |$f(N_{\rm H\,{\small I}})=(25\pm 1)N_{14}^{-0.65\pm 0.02}$| reported in Danforth et al. (2016) considering no redshift evolution in NH i distribution. As seen in Fig. 2, f(NH i, z) depends strongly on the NH i of the absorber while having a weak dependence on z in the redshift range probed. For a sanity check, we compare this distribution with the one obtained in Danforth et al. (2016) in the middle panel of Fig. 2 and find them to be similar within measurement uncertainties. One caveat which needs to be mentioned is that while Danforth et al. (2016) calculate the NH i distribution for the entire sample, we only do so for the Ly α absorbers used in this study. Our computed errors match well with those of Danforth et al. (2016) for log NH i≥ 13.0. At the lowest NH i, the differences seen could come from uncertainty in dz being different due to different samples used.
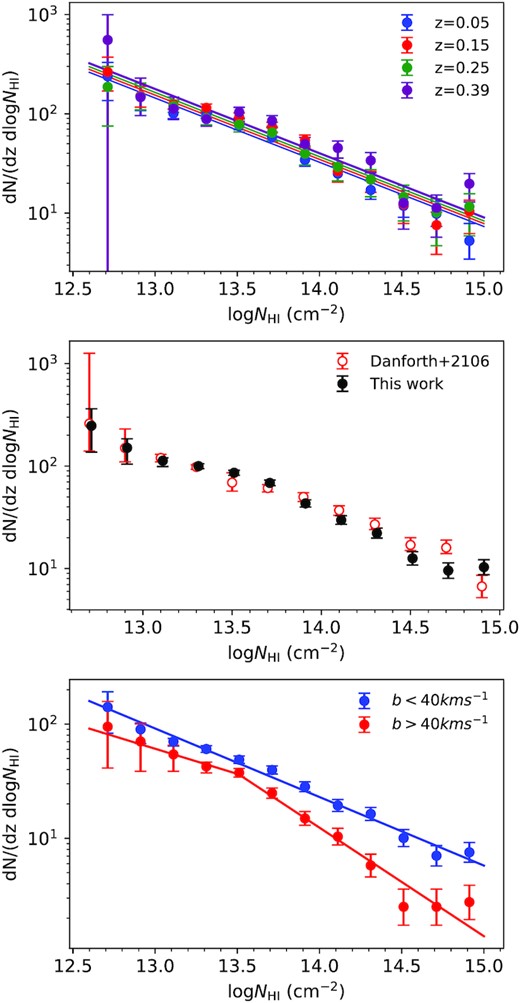
Top panel: NH i distribution of Ly α absorbers for four different redshift intervals (z = 0.05 ± 0.05, 0.15 ± 0.05, 0.25 ± 0.05, and 0.39 ± 0.09). This plot confirms a weak redshift evolution of f(NH i, z). Middle panel: comparison of the NH i distribution obtained by us for the entire sample with that of Danforth et al. (2016). Bottom panel: The NH i distribution for the low-b (b < 40 km s−1) and the high-b (b > 40 km s−1) sub-samples. In the case of high-b sub-sample the distribution is well fitted by a double power law. The double power-law fit to high-b and single power-law fit to the low-b samples are also shown.
In the bottom panel of Fig. 2, we plot NH i distribution in two different bins based on b-values (high-b sample with b > 40 km s−1 and low-b sample with b < 40 km s−1) considering systems in the full sample. The cut-off b-value of 40 km s−1 was chosen to delineate the possible BLAs from rest of the Ly α absorbers as defined in Lehner et al. (2007). About 31.9 per cent of the total Ly α absorbers in our sample have b > 40 km s−1. In both cases, we recalculated the redshift path-length considering the median b-values of the sub-samples. It is evident that both distributions have similar slope at low H i column density end (i.e. |$N_{\rm H\,{\small I}}\, \lt 10^{14}$| cm−2). However, we do notice a fall in the number of high-b systems at high NH i end. We fit the individual distribution using the form given in equation (1) ignoring the redshift evolution. The best-fitting values of C0 and β for low-b and high-b sub-samples are C0 = 23.0 ± 1.5, β = −0.60 ± 0.02 and C0 = 9.5 ± 1.0, β = −0.83 ± 0.04 respectively. In case of the high-b sub-sample, we also fit the distribution with a double power law about NH i = 1013.5 cm−2 and obtain C0 = 22.1 ± 2.4, β = −0.44 ± 0.07 for NH i < 1013.5 cm−2 and C0 = 12.4 ± 1.3, β = −0.95 ± 0.08 for NH i > 1013.5 cm−2. We use these fitted distribution (i.e a single power-law fit in general and double power law in the case of high-b sub-sample) to generate the random distribution of absorbers for the correlation measurements of the sample under consideration.
3.2 Longitudinal two-point correlation function
We compute the two-point correlation logarithmically spaced r∥ bins of [0.5–1, 1–2, 2–4, 4–8, 8–16, 16–32, and 32–64] pMpc. We have taken this binning scheme specifically for the calculation of reduced three-point correlation function (see equation 6). We compute three-point correlation for collinear triplet configurations, which we explain in the next subsection. For such configurations, the third arm of the triplet will be double the length of the other two arms. So, we take the r∥ bins such that the mean of the next bin value is exactly double that of the previous bin value. This makes calculation of the cyclic combination of two-point correlations, |$\overline{\xi (r_1)}\times \overline{\xi (r_2)}+\overline{\xi (r_2)}\times \overline{\xi (r_3)}+\overline{\xi (r_1)}\times \overline{\xi (r_3)}$| (see equation 6), necessary for calculating the reduced three-point correlation at each bin easier.
In panel (a) of Fig. 3, we plot the average two-point correlation of absorbers with NH i > 1012.5 cm−2 for our full sample as a function of r∥. The error in the longitudinal two-point correlation is larger of the two errorbars: one-sided Poissonian uncertainty corresponding to ±1σ or the bootstrapping error for all the data–data pairs. The uncertainty in the pairs for the large number of random absorbers taken is assumed to be relatively negligible. For a sanity check of our method, we compare our measurements with those of Danforth et al. (2016). The two-point correlation profile matches well within the errorbars (see panel a in Fig. 3). Our two-point correlation measurements are given in Table 1.
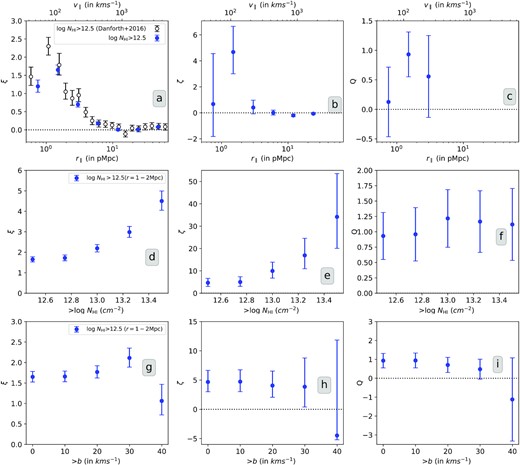
Absorber-based longitudinal two-, three-, and reduced three-point (Q) correlation (left to right) of Ly α absorbers as a function of longitudinal scale (top panels), NH i thresholds (middle panels) and b thresholds (bottom panels). We consider r∥ = 1–2 pMpc scale to probe the NH i and b dependence. The errors correspond to larger of the two errorbars: one-sided poissonian uncertainty corresponding to ±1σ or the bootstrapping error about the mean value. In panel (a), we compare our measurements with those of Danforth et al. (2016) for consistency check. Our measurements of two-point and three-point correlation as a function of longitudinal scale is provided in Table 1.
Observed values of longitudinal two-point (ξ), triplet probability excess (|$\rm PE_3$|), and three-point (ζ) correlations.
| r . | ξ . | |$\rm PE_3$| . | ζ . | ||||
|---|---|---|---|---|---|---|---|
| (in pMpc) . | (in km s−1) . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . |
| 0.5–1 | 36.3–72.6 | |$1.20^{+0.18}_{-0.16}$| | |$3.65^{+0.68}_{-0.60}$| | |$4.77^{+3.87}_{-2.47}$| | |$-1.00^{+32.11}_{-0.00}$| | |$0.72^{+3.89}_{-2.49}$| | |$-12.81^{+32.14}_{-1.28}$| |
| 1–2 | 72.6–145.3 | |$1.65^{+0.13}_{-0.13}$| | |$4.50^{+0.49}_{-0.45}$| | |$8.76^{+1.96}_{-1.65}$| | |$44.33^{+19.34}_{-14.09}$| | |$4.76^{+1.98}_{-1.67}$| | |$34.18^{+19.36}_{-14.12}$| |
| 2–4 | 145.3–290.6 | |$0.70^{+0.07}_{-0.07}$| | |$1.14^{+0.22}_{-0.20}$| | |$1.98^{+0.54}_{-0.46}$| | |$7.76^{+4.32}_{-3.03}$| | |$0.41^{+0.56}_{-0.48}$| | |$4.88^{+4.34}_{-3.06}$| |
| 4–8 | 290.6–581.1 | |$0.18^{+0.04}_{-0.04}$| | |$0.59^{+0.13}_{-0.12}$| | |$0.37^{+0.18}_{-0.16}$| | |$2.66^{+1.32}_{-1.00}$| | |$0.01^{+0.20}_{-0.18}$| | |$1.31^{+1.35}_{-1.04}$| |
| 8–16 | 581.1–1162.2 | |$0.00^{+0.01}_{-0.01}$| | |$0.17^{+0.08}_{-0.08}$| | |$-0.17^{+0.10}_{-0.09}$| | |$1.13^{+0.46}_{-0.39}$| | |$-0.18^{+0.11}_{-0.10}$| | |$0.78^{+0.49}_{-0.42}$| |
| 16–32 | 1162.2–2324.4 | |$0.01^{+0.01}_{-0.01}$| | |$0.01^{+0.05}_{-0.05}$| | |$0.02^{+0.02}_{-0.01}$| | |$0.01^{+0.15}_{-0.13}$| | |$-0.07^{+0.04}_{-0.03}$| | |$0.05^{+0.19}_{-0.17}$| |
| 32–64 | 2324.4–4648.8 | |$0.07^{+0.03}_{-0.03}$| | |$-0.06^{+0.04}_{-0.04}$| | – | – | – | – |
| r . | ξ . | |$\rm PE_3$| . | ζ . | ||||
|---|---|---|---|---|---|---|---|
| (in pMpc) . | (in km s−1) . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . |
| 0.5–1 | 36.3–72.6 | |$1.20^{+0.18}_{-0.16}$| | |$3.65^{+0.68}_{-0.60}$| | |$4.77^{+3.87}_{-2.47}$| | |$-1.00^{+32.11}_{-0.00}$| | |$0.72^{+3.89}_{-2.49}$| | |$-12.81^{+32.14}_{-1.28}$| |
| 1–2 | 72.6–145.3 | |$1.65^{+0.13}_{-0.13}$| | |$4.50^{+0.49}_{-0.45}$| | |$8.76^{+1.96}_{-1.65}$| | |$44.33^{+19.34}_{-14.09}$| | |$4.76^{+1.98}_{-1.67}$| | |$34.18^{+19.36}_{-14.12}$| |
| 2–4 | 145.3–290.6 | |$0.70^{+0.07}_{-0.07}$| | |$1.14^{+0.22}_{-0.20}$| | |$1.98^{+0.54}_{-0.46}$| | |$7.76^{+4.32}_{-3.03}$| | |$0.41^{+0.56}_{-0.48}$| | |$4.88^{+4.34}_{-3.06}$| |
| 4–8 | 290.6–581.1 | |$0.18^{+0.04}_{-0.04}$| | |$0.59^{+0.13}_{-0.12}$| | |$0.37^{+0.18}_{-0.16}$| | |$2.66^{+1.32}_{-1.00}$| | |$0.01^{+0.20}_{-0.18}$| | |$1.31^{+1.35}_{-1.04}$| |
| 8–16 | 581.1–1162.2 | |$0.00^{+0.01}_{-0.01}$| | |$0.17^{+0.08}_{-0.08}$| | |$-0.17^{+0.10}_{-0.09}$| | |$1.13^{+0.46}_{-0.39}$| | |$-0.18^{+0.11}_{-0.10}$| | |$0.78^{+0.49}_{-0.42}$| |
| 16–32 | 1162.2–2324.4 | |$0.01^{+0.01}_{-0.01}$| | |$0.01^{+0.05}_{-0.05}$| | |$0.02^{+0.02}_{-0.01}$| | |$0.01^{+0.15}_{-0.13}$| | |$-0.07^{+0.04}_{-0.03}$| | |$0.05^{+0.19}_{-0.17}$| |
| 32–64 | 2324.4–4648.8 | |$0.07^{+0.03}_{-0.03}$| | |$-0.06^{+0.04}_{-0.04}$| | – | – | – | – |
Observed values of longitudinal two-point (ξ), triplet probability excess (|$\rm PE_3$|), and three-point (ζ) correlations.
| r . | ξ . | |$\rm PE_3$| . | ζ . | ||||
|---|---|---|---|---|---|---|---|
| (in pMpc) . | (in km s−1) . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . |
| 0.5–1 | 36.3–72.6 | |$1.20^{+0.18}_{-0.16}$| | |$3.65^{+0.68}_{-0.60}$| | |$4.77^{+3.87}_{-2.47}$| | |$-1.00^{+32.11}_{-0.00}$| | |$0.72^{+3.89}_{-2.49}$| | |$-12.81^{+32.14}_{-1.28}$| |
| 1–2 | 72.6–145.3 | |$1.65^{+0.13}_{-0.13}$| | |$4.50^{+0.49}_{-0.45}$| | |$8.76^{+1.96}_{-1.65}$| | |$44.33^{+19.34}_{-14.09}$| | |$4.76^{+1.98}_{-1.67}$| | |$34.18^{+19.36}_{-14.12}$| |
| 2–4 | 145.3–290.6 | |$0.70^{+0.07}_{-0.07}$| | |$1.14^{+0.22}_{-0.20}$| | |$1.98^{+0.54}_{-0.46}$| | |$7.76^{+4.32}_{-3.03}$| | |$0.41^{+0.56}_{-0.48}$| | |$4.88^{+4.34}_{-3.06}$| |
| 4–8 | 290.6–581.1 | |$0.18^{+0.04}_{-0.04}$| | |$0.59^{+0.13}_{-0.12}$| | |$0.37^{+0.18}_{-0.16}$| | |$2.66^{+1.32}_{-1.00}$| | |$0.01^{+0.20}_{-0.18}$| | |$1.31^{+1.35}_{-1.04}$| |
| 8–16 | 581.1–1162.2 | |$0.00^{+0.01}_{-0.01}$| | |$0.17^{+0.08}_{-0.08}$| | |$-0.17^{+0.10}_{-0.09}$| | |$1.13^{+0.46}_{-0.39}$| | |$-0.18^{+0.11}_{-0.10}$| | |$0.78^{+0.49}_{-0.42}$| |
| 16–32 | 1162.2–2324.4 | |$0.01^{+0.01}_{-0.01}$| | |$0.01^{+0.05}_{-0.05}$| | |$0.02^{+0.02}_{-0.01}$| | |$0.01^{+0.15}_{-0.13}$| | |$-0.07^{+0.04}_{-0.03}$| | |$0.05^{+0.19}_{-0.17}$| |
| 32–64 | 2324.4–4648.8 | |$0.07^{+0.03}_{-0.03}$| | |$-0.06^{+0.04}_{-0.04}$| | – | – | – | – |
| r . | ξ . | |$\rm PE_3$| . | ζ . | ||||
|---|---|---|---|---|---|---|---|
| (in pMpc) . | (in km s−1) . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . | NH i > 1012.5 cm−2 . | NH i > 1013.5 cm−2 . |
| 0.5–1 | 36.3–72.6 | |$1.20^{+0.18}_{-0.16}$| | |$3.65^{+0.68}_{-0.60}$| | |$4.77^{+3.87}_{-2.47}$| | |$-1.00^{+32.11}_{-0.00}$| | |$0.72^{+3.89}_{-2.49}$| | |$-12.81^{+32.14}_{-1.28}$| |
| 1–2 | 72.6–145.3 | |$1.65^{+0.13}_{-0.13}$| | |$4.50^{+0.49}_{-0.45}$| | |$8.76^{+1.96}_{-1.65}$| | |$44.33^{+19.34}_{-14.09}$| | |$4.76^{+1.98}_{-1.67}$| | |$34.18^{+19.36}_{-14.12}$| |
| 2–4 | 145.3–290.6 | |$0.70^{+0.07}_{-0.07}$| | |$1.14^{+0.22}_{-0.20}$| | |$1.98^{+0.54}_{-0.46}$| | |$7.76^{+4.32}_{-3.03}$| | |$0.41^{+0.56}_{-0.48}$| | |$4.88^{+4.34}_{-3.06}$| |
| 4–8 | 290.6–581.1 | |$0.18^{+0.04}_{-0.04}$| | |$0.59^{+0.13}_{-0.12}$| | |$0.37^{+0.18}_{-0.16}$| | |$2.66^{+1.32}_{-1.00}$| | |$0.01^{+0.20}_{-0.18}$| | |$1.31^{+1.35}_{-1.04}$| |
| 8–16 | 581.1–1162.2 | |$0.00^{+0.01}_{-0.01}$| | |$0.17^{+0.08}_{-0.08}$| | |$-0.17^{+0.10}_{-0.09}$| | |$1.13^{+0.46}_{-0.39}$| | |$-0.18^{+0.11}_{-0.10}$| | |$0.78^{+0.49}_{-0.42}$| |
| 16–32 | 1162.2–2324.4 | |$0.01^{+0.01}_{-0.01}$| | |$0.01^{+0.05}_{-0.05}$| | |$0.02^{+0.02}_{-0.01}$| | |$0.01^{+0.15}_{-0.13}$| | |$-0.07^{+0.04}_{-0.03}$| | |$0.05^{+0.19}_{-0.17}$| |
| 32–64 | 2324.4–4648.8 | |$0.07^{+0.03}_{-0.03}$| | |$-0.06^{+0.04}_{-0.04}$| | – | – | – | – |
There are three scales of interest for longitudinal two-point correlation. At smaller scales (r∥ < 1.0 pMpc), we observe a suppression in the two-point correlation. This region of suppression for Ly α absorbers is affected by thermal broadening along with instrumental resolution which sets a lower limit on scale for identification of multiple Ly α absorption lines during Voigt profile decomposition. We also expect pressure broadening and small-scale clustering (and turbulence) of the baryonic gas to play a part in absorber suppression at smaller scales. At intermediate scales (1.0 pMpc ≤ r∥ ≤ 6 pMpc), longitudinal two-point correlation falls steadily and becomes consistent with zero beyond 10 pMpc.
Next we explore the NH i dependence of ξ in panel (d) of Fig. 3. Here we mainly focus on the r∥ bin of 1–2 pMpc. Consistent with the past studies, the amplitude of the two-point correlation steadily increases with increasing NH i threshold (see e.g. Penton et al. 2002; Danforth et al. 2016). As mentioned in the introduction, there is a strong correlation between NH i and overdensity. Therefore, NH i dependence of clustering reflects the stronger clustering of more overdense regions (see Maitra et al. 2020; Maitra, Srianand & Gaikwad 2021, for discussions on this related to high-z IGM). It is known that stronger Ly α absorbers (i.e with NH i > 1014 cm−2) at low-z are clustered strongly with the galaxies while the weaker absorbers are distributed more randomly or associated with galaxy voids or IGM (Penton et al. 2002; Tejos et al. 2014). Therefore, increase in two-point correlation with NH i threshold, could imply a stronger spatial clustering of Ly α absorbers associated with environments of galaxies.
3.3 Longitudinal three-point correlation function
The probability excess of finding a triplet of Ly α absorbers in the observed data in comparison to a random distribution of absorbers can be used to estimate the longitudinal three-point correlation function. However, the two-point correlations associated with the three arms of the triplet need to be subtracted from this probability excess to get the true three-point correlation function (see equation 5). We consider a triplet to be three collinear points along a sightline having separations r∥, 1 between the first and second points and r∥, 2 between the second and third points. In this work, we mainly consider the equal length configuration r∥, 1 = r∥, 2 = r∥ (within the assumed bin-intervals). Our spatial separation measurements between the absorbers using the redshift difference is influenced by peculiar velocities. We address the effect of peculiar velocities on our measurements using simulated spectra in Section 5.
We measure positive three-point correlation (and probability excess) at scales below 4 pMpc (i.e line of sight velocity scales <300 km s−1). At the scale of 1–2 pMpc, we have the strongest detection in three-point correlation (probability excess of |$8.8^{+2.0}_{-1.7}$| and the corresponding three-point correlation of |$\zeta = 4.8^{+2.0}_{-1.7}$| at ∼2.6σ significance level). The amplitude of the three-point correlation in this r∥ bin is higher than the corresponding two-point correlation. Similar to two-point correlation, we see the effects of suppression at scales below 1 pMpc. In panel (e) of Fig. 3, we plot ζ for different NH i thresholds for the scale 1–2 pMpc. While a trend of increasing ζ with NH i is evident, the measurement errors are large at high NH i end due to small number of high NH i absorbers involved. Our measurement of the probability excess and three-point correlation function as a function of longitudinal scale is provided in Table 1.
Till now we have considered the case of equal length configuration (i.e r∥, 1 = r∥, 2 = r∥). In Fig. 4, we show the distribution of probability excess and three-point correlation for the case of r∥, 1 ≠ r∥, 2 for NH i > 1012.5 cm−2. Among the off-diagonal elements the bins with r∥, 1 = 0.5−1.0 pMpc and r∥, 2 = 1.0−2.0 pMpc and with r∥, 1 = 1.0–2.0 pMpc and r∥, 2 = 2.0–4.0 pMpc show a probability excess of ∼2 at more than 2.5σ level. However, none of these bins have significant non-zero three point correlation. Guo et al. (2016) have presented three point correlation function of galaxies for different configurations for 1:2 arm length ratio. Their result for θ ≃ 0 (i.e squeezed configuration) will correspond to our equal arm configuration. It is evident from their measurements that ζ of Ly α forest is at least an order of magnitude smaller than what has been seen for galaxies for the same scales. In terms of velocity scale, the length over which one sees significant three point correlation function (i.e ≃1–2 pMpc or 146 km s−1 in the velocity scale at the median redshift i.e z ∼ 0.15 of our sample) is consistent with the velocity dispersion of gas clouds in high-mass galactic haloes. Conversely, this can also correspond to the large-scale structures in real space. So it is important to explore how much contribution to the observed three point correlation comes from CGM (see Section 4).
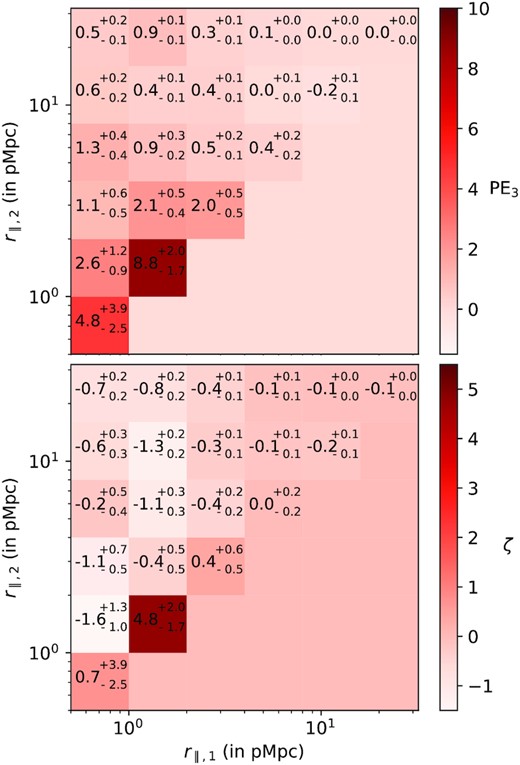
2D-plot of absorber-based longitudinal probability excess of Ly α triplets (top) and three-point correlation (bottom) as a function of scales r∥, 1 and r∥, 2 for absorbers having NH i > 1012.5 cm−2. The measured values with errors are provided in each bin.
3.4 Dependence of clustering on b-parameter
We have seen that Ly α clustering depends on NH i and is stronger for higher NH i absorbers. Here, we explore the dependence of Ly α clustering on b-parameter. Purely based on the existence of |$N_{\rm H\,{\small I}}\, \mathrm{ versus}\, b$| correlations we expect the absorbers with high b-values to cluster more strongly. Additionally, this exercise is motivated by the finding of Wakker et al. (2015), that the BLAs tend to have low impact parameter (i.e ρ ≤ 400 pkpc) with respect to the filament axis compare to the narrow Ly α absorbers that are found up to ρ ∼ 3 pMpc. Tejos et al. (2016) have also found the number of BLA absorption associated with the filaments are ∼6 times in excess of random expectations. These absorbers may trace the warm ionized gas in the intercluster filaments.
Fig. 5 shows the scatter plot for the |$N_{\rm H\,{\small I}}\, \mathrm{ versus}\, b$| distribution in our sample. In our sample, 31.9 per cent of the Ly α components have b ≥ 40 km s−1. It is also evident from this figure that the distribution of NH i seems different for high-b and low-b sub-samples. High-b sub-sample seems to have less number of high NH i (as also seen in Fig. 2). This is similar to the finding of Lehner et al. (2007) based on smaller number of sightlines. While one expects bias against detecting low NH i high-b absorbers when the SNR is low, lack of high-b high NH i absorption can be either physical or systematic bias introduced by the multiple component Voigt profile fits that tend to fit saturated lines with more narrow components.
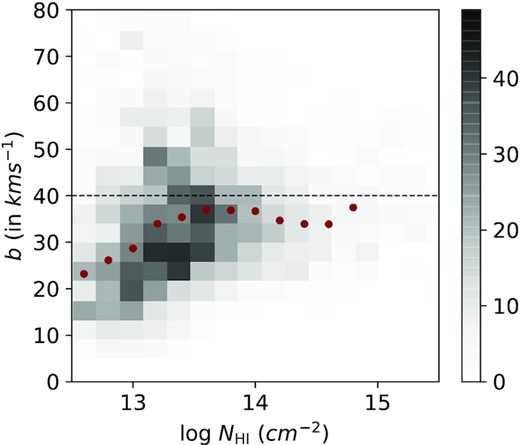
2D histogram of NH i versus b distribution. The horizontal dashed line at b = 40 km s−1 demarcates the high-b and low-b sub-samples. Dots provide the median b value in each NH i bin. A correlation is seen between NH i and b for small values of NH i and no trend is seen at high NH i.
In panel (g) of Fig. 3, we plot the two-point correlation function measured at r∥ = 1–2 pMpc (equal arm configuration) as a function of different b-parameter thresholds. For generating the random distributions, as discussed in section 3.1, we compute the intrinsic NH i distribution separately using appropriate median b values for each sub-sample. Initially, we see a nearly constant two-point correlation with increase in b-parameter values. However, when we consider high-b systems (i.e b > 40 km s−1) we notice that the two-point correlation function decreases. From panel (h) of Fig. 3, we find that the three-point correlation function also shows similar trend with a decline in the amplitude for b > 40 km s−1 case (with large errorbar). The same trend is also shown by Q that we plot in the panel (i) of Fig. 3. We do not find any triplets with all the components having b > 40 km s−1 in r∥ = 1–2 pMpc bin which results in a large negative mean three-point correlation. This could be real or artefact of some bias in the Voigt profile decomposition, in particular at small scales. For example, presence of a broad absorber can conceal other broad components from being detected within the scales considered here (in particular when the SNR is not high), thereby lowering the two-point and three-point correlations.
To see whether this is a scale dependent result, in Fig. 6 we plot the longitudinal two- and three-point correlations as a function of scale separately for high-b and low-b sub-samples for NH i > 1012.5 cm−2. The random distribution of absorbers for each of these cases is drawn separately using the NH i distributions shown in the bottom panel in Fig. 2. As can be seen from Fig. 6, at r∥ < 2 pMpc, the two-point correlation between the low-b absorber (while consistent with the full sample) is stronger than that of high-b absorbers. Over the same scale the high-b absorbers show largely negative three-point correlation. This confirms the lack of triplets with large-b values at small scales consistent with what is shown in Fig. 3. However for the scales of 2–4 pMpc, we see a stronger two-point correlation for the high-b sub-sample. In the case of three-point correlation function, contribution comes from a single triplet of high-b absorbers (b = 42.4, 144.3, and 51.2 km s−1) seen along a single sight line (PKS 0405-123) at the redshift of 0.0251. For all other high r∥ bins, the low-b and high-b sub-samples have two-point and three-point correlation consistent with each other, albeit with low values. The trend seen for the two-point correlation is consistent with the suppression effects being severe in the case of high-b absorbers for r∥ < 2 pMpc and high-b absorbers having higher ξ at 2–4 pMpc. In the case of three-point correlation function, due to large errors we do not find any difference between high-b absorbers and full sample for r∥ > 4 pMpc.
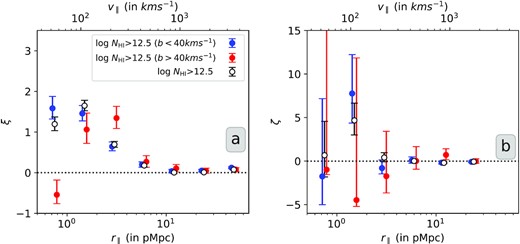
Two- (panel a) and three-point (panel b) correlations of Ly α absorbers as a function of longitudinal scale for full sample, high-b (b > 40 km s−1) and low-b (b < 40 km s−1) sub-samples. The errors represent larger of the two errorbars: one-sided poissonian uncertainty corresponding to ±1σ or the bootstrapping error about the mean value. The results for the low-b sample roughly follow the that of the whole sample. In the case of high-b sub-sample, we do not find any triplets for r∥ < 4 pMpc, this coupled with the low random probability to find high-b triplets at these scale leads to large errors in ζ.
3.5 Effect of presence of metal ions on correlation
One important question which arises is that whether the correlations we detect originate from the IGM or are dominated by a small population of absorbers originating from CGM of intervening galaxies. Danforth et al. (2016) have shown that the metal bearing Ly α systems (based on the presence of O vi) show stronger two-point correlation than the non-metal bearing systems (see their fig. 18). Based on this they concluded that most of the radial velocity clustering of the Ly α systems can be attributed to metal bearing systems originating from the CGM of intervening galaxies. Here, we ask a slightly different question. We would like to know whether the presence of different metal ion species influence the observed clustering properties of Ly α absorbers.
We base our study on C iv, O vi, and Si iii metal line transitions. Considering the wavelength range covered by the HST-COS medium resolution spectrum, redshift ranges over which Ly α, O vi, and Si iii associated with the Ly α can be detectable are z < 0.16, 0.1 < z < 0.48, and z < 0.48, respectively. So, for checking the dependence of Ly α clustering on the presence of C iv, O vi, and Si iii we consider redshift ranges of z < 0.16, 0.1 < z < 0.48, and z < 0.48, respectively. We consider a metal line transition having redshift within the median b-parameter (∼34 km s−1) of the redshift of Ly α absorbers to be associated with it. We only consider components with metal ion line absorption having rest equivalent width above 30 mÅ (as done by, Danforth et al. 2016).
Firstly, we consider Ly α absorbers having NH i > 1012.5 cm−2. For z < 0.16, 5.7 per cent of such Ly α absorbers show detectable C iv absorption. For 0.1 < z < 0.48, 19.8 per cent of the Ly α absorbers show detectable O vi absorption. For z < 0.48, 5.9 per cent of the Ly α absorbers are associated with Si iii absorption. When we consider Ly α absorbers having NH i > 1013.5 cm−2, these percentages increase to 16.8 per cent for C iv, 33.0 per cent for O vi, and 16.1 per cent for Si iii. For calculating these fractions, we have considered all reported detections without applying any column density cut-off based on detection sensitivity.
In top two rows of Fig. 7, we plot the two-point correlation of ‘all Ly α’ absorbers and those ‘without associated metal ion species’ absorption for the three identified metal ion species and two NH i cut-offs. Note the ‘all Ly α’ sample in each of these cases is different owing to different redshift ranges probed (redshift ranges are provided on top of each column in Fig. 7). In the case of absorbers ‘without metal ion species’ we just remove only the Voigt profile components that have associated metal absorption. As only a small fraction of Ly α absorbers will be removed based on the presence of each given metal ion species, we naively expect their influence to be minimal. However, we still draw appropriate random distributions of absorbers for each case separately while calculating ξ and ζ. For NH i > 1012.5 cm−2, the ξ measured for systems without C iv, O vi, and Si iii are consistent with their respective ‘all Ly α’ samples. This seem to be the case for NH i > 1013.5 cm−2 absorbers also. From figs 16 and 18 of Danforth et al. (2016) one can see that their ξ measurements of Ly α absorbers with and without metal systems are not very different from each other. Therefore, it appears that two-point correlation function we measure for the Ly α absorption and its column density dependence may not originate mainly from the Ly α absorbers associated with the metal ions considered here.
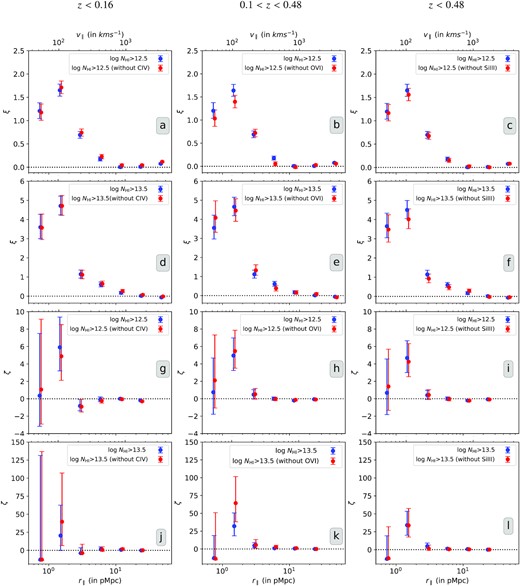
The top two rows show two-point correlation of Ly α absorbers with (blue) or without (red) associated metal lines such as C iv (left-hand panels), O vi (middle panels), and Si iii (right-hand panels) as a function of longitudinal scale for NH i > 1012.5 cm−2 (top row) and NH i > 1013.5 cm−2 (second most top row). The bottom two panels show longitudinal three-point correlation in the same fashion. The errors represent larger of the two errorbars: one-sided Poissonian uncertainty corresponding to ±1σ or the bootstrapping error around the mean value.
In bottom two panels of Fig. 7, we plot the three-point correlations for two NH i cut-offs. The ζ does not show any significant difference between the full sample and the corresponding sample for Ly α without C iv, O vi, or Si iii absorption. The three-point correlation measured for the Ly α absorbers does not source primarily from components associated with these metal ions.
3.6 Redshift evolution
Next, we investigate the redshift evolution of the two- and three-point correlation by considering two redshift bins: z < 0.2 and 0.2 < z < 0.48 for NH i > 1012.5 cm−2. The choice of z = 0.2 as a threshold between these two bins is simply taken as the approximate midpoint of the redshift range of our sample. The left and middle panels in Fig. 8 show the ξ and ζ, respectively, as a function of distance scale for the two sub-samples. It is clear from these two panels that the measured values of ξ and ζ for the low-z and high-z sub-samples are consistent with each other within measurement uncertainties. We do not also find any difference in the Q profile for the two sub-samples (see right-hand panel in Fig. 8). Thus over the redshift range considered here we do not find any evolution in the amplitude of the two- and three-point correlation function.
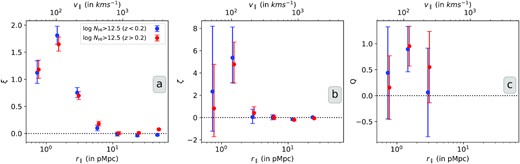
Two-, three- and reduced three-point correlation (left to right) of Ly α absorbers as a function of longitudinal scale for two different z-intervals. The errors represent larger of the two errorbars: one-sided Poissonian uncertainty corresponding to ±1σ or the bootstrapping error about the mean value.
4 CONNECTION TO GALAXIES
In this section, we study the connection between the Ly α absorbers that are isolated, pairs or triplets that contribute to the observed two- and three-point correlations with nearby galaxies in the sample discussed in Section 2. We have not considered the galaxies around 3C 57 for our analysis due to poor completeness of the galaxy sample (see discussions in Keeney et al. 2018). We identify all the Ly α triplets with equal arm (for r∥, 1 ≤ 4 pMpc) and 1:2 configuration (for r∥, 1 ≤ 2 pMpc) at z < 0.2 that are present along 41 sightlines having galaxy information. Triplets with such configurations are chosen because |$\rm PE_3$| is detected significantly for them (see Fig. 4).
Details of the triplets and the associated galaxies are provided in Table 2. First four columns in this table give QSO name, absorption redshift of the central component of the triplet, column densities of individual components in the triplet system and the b-parameters of the components. Fifth column of this table gives the line of sight velocity separation for up to 3 nearest catalogued galaxies with respect to the absorption redshift (redshift of the central absorber). We define nearest galaxies by their transverse distance from the sightlines. We consider only those galaxies that are within ±500 km s−1. This velocity is chosen to account for the typical velocity dispersion in galaxies (i.e ≤350 kms−1) and that of the Ly α triplets (i.e ∼300 km s−1). Impact parameters of these galaxies (the distance between the absorber and the galaxy measured using the angular separation between the QSO sightline and the galaxy at the redshift of the galaxy) are provided in the last column. In eight cases we find nearest galaxies having velocities in the range 500–2500 km s−1(red colour entrees in Table 2). We do not detect any nearby galaxy within 2500 km s−1 for 2 triplets. We discuss these specific cases in detail below.
| QSO sightlinesa . | z (Ly α triplet) . | log NH i of . | b-parameter of . | v∥ (Nearest Galaxy-Ly α triplet)b . | Impact parameter of Galaxy . |
|---|---|---|---|---|---|
| . | . | triplet system . | triplet systems (in km s−1) . | (in km s−1) . | from sightlines2 (in pKpc) . |
| Equal arm length configurations: r∥ = 0.5–1 pMpc | |||||
| PG1116 + 215B, M | 0.1656 | 12.63, 13.39, 13.06 | 15.8, 30.7, 44.9 | +98.3, −197.7, +312.0 | 156.0, 317.0, 531.4 |
| PG1222 + 216B | 0.1446 | 13.41, 13.32, 13.3 | 34.2, 18.6, 47.2 | −956.9, −907.1, −941.2 | 1189.0, 1305.3, 1316.8 |
| PKS2155-304B | 0.1057 | 13.98, 13.33, 13.28 | 47.1, 21.6, 43.2 | −265.1, +36.1, −34.5, +33.4 | 924.0, 952.0, 1025.0, 1094.0 |
| Equal arm length configurations: r∥ = 1–2 pMpc | |||||
| H1821 + 643B | 0.1217 | 14.21, 13.43, 13.14 | 38.1, 53.0, 38.1 | −15.8, + 273.1, −328.7 | 156.3, 1160.5, 1550.4 |
| H1821 + 643B, M | 0.1701 | 13.86, 13.68, 13.36 | 35.3, 58.0, 28.4 | +127.7, + 209.7, −369.7 | 415.4, 1122.2, 1118.7 |
| H1821 + 643 | 0.1895 | 12.6, 12.72, 12.55 | 28.1, 26.1, 16.1 | −140.0, −155.1, −84.5 | 1019.8, 1054.5, 1084.3 |
| PG0953 + 414M | 0.1423 | 12.73, 13.56, 13.48 | 15.3, 26.5, 30.9 | +237.7, +78.0, +51.2 | 405.0, 452.1, 506.7 |
| PG0953 + 414B, M | 0.1426 | 13.56, 13.48, 13.2 | 26.5, 30.9, 52.7 | + 155.4, −4.2, −31.0 | 405.0, 452.1, 506.7 |
| PG1048 + 342B, M | 0.0061 | 14.8, 13.79, 13.99 | 42.7, 33.1, 86.9 | −6.0, −167.0 | 60.2, 149.2 |
| PG1048 + 342B, M | 0.0057 | 14.07, 14.8, 13.79 | 30.4, 42.7, 33.1 | + 84.1, −77.0 | 60.2, 149.2 |
| PG1116 + 215B | 0.1658 | 12.63, 13.06, 14.28 | 15.8, 44.9, 32.7 | +37.8, −258.1, +251.4 | 156.0, 317.0, 531.4 |
| PKS0405-123B | 0.0247 | 12.82, 12.56, 13.18 | 42.4, 13.4, 144.3 | +1174.6, +1423.5, +1420.5 | 673.0, 799.0, 1105.0 |
| PKS0405−123B | 0.1527 | 13.44, 12.54, 13.79 | 25.8, 13.5, 47.8 | 132.0, 223.0, −445.8 | 181.0, 2148.0, 3857.0 |
| Q1230 + 0115B, M | 0.0948 | 12.99, 13.31, 14.33 | 69.7, 30.2, 46.3 | +46.8, −16.1, +16.7 | 113.4, 792.3, 917.2 |
| RXJ0439.6--5311B | 0.1772 | 13.53, 13.6, 13.87 | 100.0, 19.7, 29.9 | −65.8, −183.0, +127.9 | 467.2, 562.5, 1848.2 |
| TON1187B | 0.0354 | 13.38, 13.98, 13.59 | 18.9, 28.2, 56.4 | +1398.9, +1149.7, +1346.8 | 278.1, 276.3, 284.1 |
| Equal arm length configurations: r∥ = 2–4 pMpc | |||||
| H1821 + 643B | 0.1899 | 12.6, 12.55, 12.73 | 28.1, 16.1, 41.6 | −235.5, −250.6, −180.0 | 1019.8,1054.5,1084.3 |
| H1821 + 643B | 0.1901 | 12.55, 12.61, 12.73 | 16.1, 22.4, 41.6 | +481.7,−287.1,−302.2 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1901 | 12.6, 12.61, 12.73 | 28.1, 22.4, 41.6 | +481.7,−287.1,−302.2 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.55, 12.73, 12.57 | 16.1, 41.6, 15.9 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.55, 12.73, 12.67 | 16.1, 41.6, 31.5, | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.61, 12.73, 12.67 | 22.4, 41.6, 31.5 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.61, 12.73, 12.57 | 22.4, 41.6, 15.9 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| PG0953 + 414B | 0.1914 | 12.91, 13.34, 13.27 | 25.2, 40.5, 55.3 | 0.0, −136.0 | 1232.6, 3692.8 |
| PG1116 + 215B, M | 0.1662 | 12.63, 14.28, 13.69 | 15.8, 32.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1116 + 215B, M | 0.1662 | 12.63, 13.39, 13.69 | 15.8, 30.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1216 + 069B | 0.1801 | 13.25, 13.52, 13.48 | 64.8, 53.3, 30.4 | +140.8, −67.6, 214.5 | 588.6, 415.4, 632.0 |
| PG1216 + 069B | 0.1801 | 13.25, 13.52, 12.77 | 64.8, 53.3, 12.4 | +140.8, −67.6, 214.5 | 588.6, 415.4, 632.0 |
| PKS0405−123B | 0.0251 | 12.82, 13.18, 13.11 | 42.4, 144.3, 51.2 | +1051.2, +1300.0, +1297.0 | 673.0, 799.0, 1105.0 |
| PKS0405−123B | 0.1330 | 13.67, 13.22, 13.13 | 27.6, 24.2, 45.0 | +227.7, +235.7, +156.2 | 467.0, 501.0, 714.0 |
| PKS0405−123B | 0.1522 | 12.97, 13.44, 13.79 | 21.8, 25.8, 47.8 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123B | 0.1522 | 12.78, 13.44, 13.79 | 21.2, 25.8, 47.8 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0558−504B | 0.0280 | 14.08, 13.13, 13.61 | 32.2, 47.3, 55.1 | – | – |
| Q1230 + 0115B, M | 0.0057 | 13.68, 15.25, 13.25 | 24.4, 37.3, 42.8 | +505.6, +595.1 | 155.1, 168.0 |
| r1 = r∥, r2 = 2r∥ configurations: r∥ = 0.5–1 pMpc | |||||
| 3C 263B, M | 0.0633 | 13.92, 14.86, 15.24 | 27.5, 52.5, 41.0 | −15.5, −131.2, −119.9 | 62.4, 571.5, 577.9 |
| H1821 + 643B, M | 0.1215 | 14.21, 13.49, 13.43 | 38.1, 35.6, 53.0 | +40.9, +329.8, −272.0 | 156.3, 1160.5, 1550.4 |
| H1821 + 643B, M | 0.1217 | 13.49, 13.43, 13.14 | 35.6, 53.0, 38.1 | −15.8, +273.1, −328.7 | 156.3, 1160.5, 1550.4 |
| H1821 + 643 | 0.1899 | 12.72, 12.55, 12.61 | 26.1, 16.1, 22.4 | −235.5, −250.6, −180.0 | 1019.8,1054.5,1084.3 |
| PG0953 + 414B | 0.0160 | 13.11, 13.48, 12.92 | 39.8, 54.2, 8.9 | +102.8, −92.4 | 159.2, 454.5 |
| PG0953 + 414B | 0.0161 | 13.48, 12.92, 13.52 | 54.2, 8.9, 24.8 | +64.4, −130.4 | 159.2, 454.5 |
| PG1116 + 215B, M | 0.1658 | 13.39, 13.06, 14.28 | 30.7, 44.9, 32.7 | +37.8, −258.1, +251.4 | 156.0, 317.0, 531.4 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 13.52 | 64.8, 33.6, 53.3 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PHL1811B, M | 0.1205 | 13.01, 14.17, 13.8 | 77.4, 52.1, 19.6 | −91.3, +425.4 | 1222.3, 1840.0 |
| PKS0405−123B, M | 0.1666 | 12.6, 13.54, 15.01 | 21.8, 29.3, 50.7 | +116.2, −184.6, −364.7 | 115.0, 2472.0, 3177.0 |
| PKS2155−304 | 0.0170 | 13.43, 13.53, 13.3 | 22.9, 24.5, 39.9 | −25.4 | 113.0 |
| PKS2155−304B | 0.0542 | 13.85, 13.61, 12.75 | 34.9, 52.5, 23.7 | −37.8 | 544.0 |
| TONS210B | 0.0858 | 13.05, 13.07, 12.91 | 73.0, 19.8, 19.5 | – | – |
| r1 = r∥, r2 = 2r∥ configurations: r∥ = 1 − 2 pMpc | |||||
| 3C 263B, M | 0.1137 | 14.06, 13.27, 13.87 | 46.4, 56.8, 22.1 | +13.7, +8.4, +258.9 | 351.0, 689.4, 708.9 |
| 3C 273B | 0.0671 | 14.08, 12.6, 12.62 | 37.0, 73.6, 25.0 | +2168.5 | 661.0 |
| H1821 + 643M | 0.1215 | 14.21, 13.49, 13.14 | 38.1, 35.6, 38.1 | +40.9, +329.8, −272.0 | 156.3, 1160.5, 1550.4 |
| H1821 + 643 | 0.1895 | 12.6, 12.72, 12.61 | 28.1, 26.1, 22.4 | −140.0, −155.1, −84.5 | 1019.8, 1054.5, 1084.3 |
| H1821 + 643B | 0.1899 | 12.72, 12.55, 12.73 | 26.1, 16.1, 41.6 | −235.5, −250.6, −180.0 | 1019.8, 1054.5, 1084.3 |
| H1821 + 643B | 0.1914 | 12.73, 12.57, 12.67 | 41.6, 15.9, 31.5 | +149.8, +200.2, +159.9 | 833.4, 1301.0, 1847.2 |
| HE0153−4520M | 0.1489 | 13.34, 13.25, 12.98 | 35.6, 29.3, 26.0 | −133.4, +229.5, −62.9 | 1079.3, 1085.2, 1477.9 |
| HE0153−4520B, M | 0.1706 | 12.66, 13.71, 14.33 | 32.9, 100.0, 39.6 | −435.7, −64.1, −12.8 | 911.3, 2145.1, 2384.1 |
| PG0953 + 414B | 0.0160 | 13.11, 13.48, 13.52 | 39.8, 54.2, 24.8 | +102.8, −92.4 | 159.2, 454.5 |
| PG0953 + 414 | 0.0161 | 13.11, 12.92, 13.52 | 39.8, 8.9, 24.8 | + 64.4, −130.8 | 159.2, 454.5 |
| PG0953 + 414B, M | 0.1423 | 12.73, 13.56, 13.2 | 15.3, 26.5, 52.7 | +237.7, +78.0, +51.2 | 405.0, 452.1, 506.7 |
| PG0953 + 414B | 0.1426 | 12.73, 13.48, 13.2 | 15.3, 30.9, 52.7 | + 155.4, −4.2, −31.0 | 405.0, 452.1, 506.7 |
| PG1048 + 342B, M | 0.0057 | 14.07, 14.8, 13.99 | 30.4, 42.7, 86.9 | + 84.1, −77.0 | 60.2, 149.2 |
| PG1048 + 342B | 0.0061 | 14.07, 13.79, 13.99 | 30.4, 33.1, 86.9 | −6.0, −167.0 | 60.2, 149.2 |
| PG1116 + 215B, M | 0.1662 | 13.06, 14.28, 13.69 | 44.9, 32.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1216 + 069B, M | 0.1239 | 14.65, 14.6, 14.54 | 24.5, 28.4, 44.6 | +56.1, −64.1, +184.2 | 88.0, 91.6, 389.0 |
| PG1216 + 069M | 0.1239 | 14.65, 14.6, 14.1 | 24.5, 28.4, 23.3 | +56.1, −64.1, +184.2 | 88.0, 91.6, 389.0 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 13.48 | 64.8, 33.6, 30.4 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 12.77 | 64.8, 33.6, 12.4 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PG1307 + 085B, M | 0.1413 | 12.91, 13.92, 13.28 | 49.7, 34.0, 28.5 | −245.5, −421.6 | 1318.0, 1408.0 |
| PG1307 + 085B, M | 0.1413 | 12.91, 13.92, 14.02 | 49.7, 34.0, 40.2 | −245.5, −421.6 | 1318.0, 1408.0 |
| PG1424 + 240B, M | 0.1471 | 14.66, 14.74, 13.51 | 49.9, 38.3, 55.5 | −121.6, +380.5, −464.2 | 493.2, 968.5, 1378.9 |
| PKS0405−123B | 0.0251 | 12.56, 13.18, 13.11 | 13.4, 144.3, 51.2 | +1174.6, +1423.5, +1420.5 | 673.0, 799.0, 1105.0 |
| PKS0405−123 | 0.1522 | 12.97, 13.44, 12.54 | 21.8, 25.8, 13.5 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123 | 0.1522 | 12.78, 13.44, 12.54 | 21.2, 25.8, 13.5 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123B, M | 0.1829 | 14.61, 13.98, 12.7 | 43.7, 33.8, 36.7 | −255.94, −149.4, −169.7 | 3854.0, 4017.0, 5395.0 |
| PKS1302−102B, M | 0.1925 | 14.47, 13.95, 13.64 | 34.0, 39.5, 54.8 | −194.0, −22.9, +120.5 | 209.0, 434.0, 464.0 |
| PKS1302−102M | 0.1925 | 14.47, 13.95, 13.6 | 34.0, 39.5, 23.2 | −194.0, −22.9, +120.5 | 209.0, 434.0, 464.0 |
| Q1230 + 0115 | 0.0485 | 12.75, 13.49, 13.16 | 35.9, 29.9, 20.8 | −95.3, −15.2, −158.2 | 912.3, 1104.2, 1148.3 |
| Q1230 + 0115B | 0.0554 | 12.56, 12.65, 12.92 | 20.7, 38.5, 56.7 | +1559.4, +1673.1, +880.1 | 353.0, 517.0, 533.0 |
| SBS1108 + 560B, M | 0.1385 | 13.27, 15.25, 14.31 | 42.6, 23.9, 25.2 | −89.3, −225.0, −429.3 | 336.3, 453.0, 465.2 |
| SBS1122 + 594B | 0.1375 | 13.34, 13.14, 13.63 | 77.6, 14.9, 100.0 | −453.6, −97.6, −390.3 | 1299.2, 1488.3, 1759.1 |
| SBS1122 + 594B | 0.1381 | 13.14, 13.63, 13.84 | 14.9, 100.0, 150.0 | −264.6, −53.8 | 1488.3, 2189.5 |
| SBS1122 + 594 | 0.1578 | 13.4, 13.91, 13.27 | 33.4, 18.9, 21.3 | −28.5, −261.7, −303.2 | 556.8, 633.4, 687.4 |
| QSO sightlinesa . | z (Ly α triplet) . | log NH i of . | b-parameter of . | v∥ (Nearest Galaxy-Ly α triplet)b . | Impact parameter of Galaxy . |
|---|---|---|---|---|---|
| . | . | triplet system . | triplet systems (in km s−1) . | (in km s−1) . | from sightlines2 (in pKpc) . |
| Equal arm length configurations: r∥ = 0.5–1 pMpc | |||||
| PG1116 + 215B, M | 0.1656 | 12.63, 13.39, 13.06 | 15.8, 30.7, 44.9 | +98.3, −197.7, +312.0 | 156.0, 317.0, 531.4 |
| PG1222 + 216B | 0.1446 | 13.41, 13.32, 13.3 | 34.2, 18.6, 47.2 | −956.9, −907.1, −941.2 | 1189.0, 1305.3, 1316.8 |
| PKS2155-304B | 0.1057 | 13.98, 13.33, 13.28 | 47.1, 21.6, 43.2 | −265.1, +36.1, −34.5, +33.4 | 924.0, 952.0, 1025.0, 1094.0 |
| Equal arm length configurations: r∥ = 1–2 pMpc | |||||
| H1821 + 643B | 0.1217 | 14.21, 13.43, 13.14 | 38.1, 53.0, 38.1 | −15.8, + 273.1, −328.7 | 156.3, 1160.5, 1550.4 |
| H1821 + 643B, M | 0.1701 | 13.86, 13.68, 13.36 | 35.3, 58.0, 28.4 | +127.7, + 209.7, −369.7 | 415.4, 1122.2, 1118.7 |
| H1821 + 643 | 0.1895 | 12.6, 12.72, 12.55 | 28.1, 26.1, 16.1 | −140.0, −155.1, −84.5 | 1019.8, 1054.5, 1084.3 |
| PG0953 + 414M | 0.1423 | 12.73, 13.56, 13.48 | 15.3, 26.5, 30.9 | +237.7, +78.0, +51.2 | 405.0, 452.1, 506.7 |
| PG0953 + 414B, M | 0.1426 | 13.56, 13.48, 13.2 | 26.5, 30.9, 52.7 | + 155.4, −4.2, −31.0 | 405.0, 452.1, 506.7 |
| PG1048 + 342B, M | 0.0061 | 14.8, 13.79, 13.99 | 42.7, 33.1, 86.9 | −6.0, −167.0 | 60.2, 149.2 |
| PG1048 + 342B, M | 0.0057 | 14.07, 14.8, 13.79 | 30.4, 42.7, 33.1 | + 84.1, −77.0 | 60.2, 149.2 |
| PG1116 + 215B | 0.1658 | 12.63, 13.06, 14.28 | 15.8, 44.9, 32.7 | +37.8, −258.1, +251.4 | 156.0, 317.0, 531.4 |
| PKS0405-123B | 0.0247 | 12.82, 12.56, 13.18 | 42.4, 13.4, 144.3 | +1174.6, +1423.5, +1420.5 | 673.0, 799.0, 1105.0 |
| PKS0405−123B | 0.1527 | 13.44, 12.54, 13.79 | 25.8, 13.5, 47.8 | 132.0, 223.0, −445.8 | 181.0, 2148.0, 3857.0 |
| Q1230 + 0115B, M | 0.0948 | 12.99, 13.31, 14.33 | 69.7, 30.2, 46.3 | +46.8, −16.1, +16.7 | 113.4, 792.3, 917.2 |
| RXJ0439.6--5311B | 0.1772 | 13.53, 13.6, 13.87 | 100.0, 19.7, 29.9 | −65.8, −183.0, +127.9 | 467.2, 562.5, 1848.2 |
| TON1187B | 0.0354 | 13.38, 13.98, 13.59 | 18.9, 28.2, 56.4 | +1398.9, +1149.7, +1346.8 | 278.1, 276.3, 284.1 |
| Equal arm length configurations: r∥ = 2–4 pMpc | |||||
| H1821 + 643B | 0.1899 | 12.6, 12.55, 12.73 | 28.1, 16.1, 41.6 | −235.5, −250.6, −180.0 | 1019.8,1054.5,1084.3 |
| H1821 + 643B | 0.1901 | 12.55, 12.61, 12.73 | 16.1, 22.4, 41.6 | +481.7,−287.1,−302.2 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1901 | 12.6, 12.61, 12.73 | 28.1, 22.4, 41.6 | +481.7,−287.1,−302.2 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.55, 12.73, 12.57 | 16.1, 41.6, 15.9 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.55, 12.73, 12.67 | 16.1, 41.6, 31.5, | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.61, 12.73, 12.67 | 22.4, 41.6, 31.5 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.61, 12.73, 12.57 | 22.4, 41.6, 15.9 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| PG0953 + 414B | 0.1914 | 12.91, 13.34, 13.27 | 25.2, 40.5, 55.3 | 0.0, −136.0 | 1232.6, 3692.8 |
| PG1116 + 215B, M | 0.1662 | 12.63, 14.28, 13.69 | 15.8, 32.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1116 + 215B, M | 0.1662 | 12.63, 13.39, 13.69 | 15.8, 30.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1216 + 069B | 0.1801 | 13.25, 13.52, 13.48 | 64.8, 53.3, 30.4 | +140.8, −67.6, 214.5 | 588.6, 415.4, 632.0 |
| PG1216 + 069B | 0.1801 | 13.25, 13.52, 12.77 | 64.8, 53.3, 12.4 | +140.8, −67.6, 214.5 | 588.6, 415.4, 632.0 |
| PKS0405−123B | 0.0251 | 12.82, 13.18, 13.11 | 42.4, 144.3, 51.2 | +1051.2, +1300.0, +1297.0 | 673.0, 799.0, 1105.0 |
| PKS0405−123B | 0.1330 | 13.67, 13.22, 13.13 | 27.6, 24.2, 45.0 | +227.7, +235.7, +156.2 | 467.0, 501.0, 714.0 |
| PKS0405−123B | 0.1522 | 12.97, 13.44, 13.79 | 21.8, 25.8, 47.8 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123B | 0.1522 | 12.78, 13.44, 13.79 | 21.2, 25.8, 47.8 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0558−504B | 0.0280 | 14.08, 13.13, 13.61 | 32.2, 47.3, 55.1 | – | – |
| Q1230 + 0115B, M | 0.0057 | 13.68, 15.25, 13.25 | 24.4, 37.3, 42.8 | +505.6, +595.1 | 155.1, 168.0 |
| r1 = r∥, r2 = 2r∥ configurations: r∥ = 0.5–1 pMpc | |||||
| 3C 263B, M | 0.0633 | 13.92, 14.86, 15.24 | 27.5, 52.5, 41.0 | −15.5, −131.2, −119.9 | 62.4, 571.5, 577.9 |
| H1821 + 643B, M | 0.1215 | 14.21, 13.49, 13.43 | 38.1, 35.6, 53.0 | +40.9, +329.8, −272.0 | 156.3, 1160.5, 1550.4 |
| H1821 + 643B, M | 0.1217 | 13.49, 13.43, 13.14 | 35.6, 53.0, 38.1 | −15.8, +273.1, −328.7 | 156.3, 1160.5, 1550.4 |
| H1821 + 643 | 0.1899 | 12.72, 12.55, 12.61 | 26.1, 16.1, 22.4 | −235.5, −250.6, −180.0 | 1019.8,1054.5,1084.3 |
| PG0953 + 414B | 0.0160 | 13.11, 13.48, 12.92 | 39.8, 54.2, 8.9 | +102.8, −92.4 | 159.2, 454.5 |
| PG0953 + 414B | 0.0161 | 13.48, 12.92, 13.52 | 54.2, 8.9, 24.8 | +64.4, −130.4 | 159.2, 454.5 |
| PG1116 + 215B, M | 0.1658 | 13.39, 13.06, 14.28 | 30.7, 44.9, 32.7 | +37.8, −258.1, +251.4 | 156.0, 317.0, 531.4 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 13.52 | 64.8, 33.6, 53.3 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PHL1811B, M | 0.1205 | 13.01, 14.17, 13.8 | 77.4, 52.1, 19.6 | −91.3, +425.4 | 1222.3, 1840.0 |
| PKS0405−123B, M | 0.1666 | 12.6, 13.54, 15.01 | 21.8, 29.3, 50.7 | +116.2, −184.6, −364.7 | 115.0, 2472.0, 3177.0 |
| PKS2155−304 | 0.0170 | 13.43, 13.53, 13.3 | 22.9, 24.5, 39.9 | −25.4 | 113.0 |
| PKS2155−304B | 0.0542 | 13.85, 13.61, 12.75 | 34.9, 52.5, 23.7 | −37.8 | 544.0 |
| TONS210B | 0.0858 | 13.05, 13.07, 12.91 | 73.0, 19.8, 19.5 | – | – |
| r1 = r∥, r2 = 2r∥ configurations: r∥ = 1 − 2 pMpc | |||||
| 3C 263B, M | 0.1137 | 14.06, 13.27, 13.87 | 46.4, 56.8, 22.1 | +13.7, +8.4, +258.9 | 351.0, 689.4, 708.9 |
| 3C 273B | 0.0671 | 14.08, 12.6, 12.62 | 37.0, 73.6, 25.0 | +2168.5 | 661.0 |
| H1821 + 643M | 0.1215 | 14.21, 13.49, 13.14 | 38.1, 35.6, 38.1 | +40.9, +329.8, −272.0 | 156.3, 1160.5, 1550.4 |
| H1821 + 643 | 0.1895 | 12.6, 12.72, 12.61 | 28.1, 26.1, 22.4 | −140.0, −155.1, −84.5 | 1019.8, 1054.5, 1084.3 |
| H1821 + 643B | 0.1899 | 12.72, 12.55, 12.73 | 26.1, 16.1, 41.6 | −235.5, −250.6, −180.0 | 1019.8, 1054.5, 1084.3 |
| H1821 + 643B | 0.1914 | 12.73, 12.57, 12.67 | 41.6, 15.9, 31.5 | +149.8, +200.2, +159.9 | 833.4, 1301.0, 1847.2 |
| HE0153−4520M | 0.1489 | 13.34, 13.25, 12.98 | 35.6, 29.3, 26.0 | −133.4, +229.5, −62.9 | 1079.3, 1085.2, 1477.9 |
| HE0153−4520B, M | 0.1706 | 12.66, 13.71, 14.33 | 32.9, 100.0, 39.6 | −435.7, −64.1, −12.8 | 911.3, 2145.1, 2384.1 |
| PG0953 + 414B | 0.0160 | 13.11, 13.48, 13.52 | 39.8, 54.2, 24.8 | +102.8, −92.4 | 159.2, 454.5 |
| PG0953 + 414 | 0.0161 | 13.11, 12.92, 13.52 | 39.8, 8.9, 24.8 | + 64.4, −130.8 | 159.2, 454.5 |
| PG0953 + 414B, M | 0.1423 | 12.73, 13.56, 13.2 | 15.3, 26.5, 52.7 | +237.7, +78.0, +51.2 | 405.0, 452.1, 506.7 |
| PG0953 + 414B | 0.1426 | 12.73, 13.48, 13.2 | 15.3, 30.9, 52.7 | + 155.4, −4.2, −31.0 | 405.0, 452.1, 506.7 |
| PG1048 + 342B, M | 0.0057 | 14.07, 14.8, 13.99 | 30.4, 42.7, 86.9 | + 84.1, −77.0 | 60.2, 149.2 |
| PG1048 + 342B | 0.0061 | 14.07, 13.79, 13.99 | 30.4, 33.1, 86.9 | −6.0, −167.0 | 60.2, 149.2 |
| PG1116 + 215B, M | 0.1662 | 13.06, 14.28, 13.69 | 44.9, 32.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1216 + 069B, M | 0.1239 | 14.65, 14.6, 14.54 | 24.5, 28.4, 44.6 | +56.1, −64.1, +184.2 | 88.0, 91.6, 389.0 |
| PG1216 + 069M | 0.1239 | 14.65, 14.6, 14.1 | 24.5, 28.4, 23.3 | +56.1, −64.1, +184.2 | 88.0, 91.6, 389.0 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 13.48 | 64.8, 33.6, 30.4 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 12.77 | 64.8, 33.6, 12.4 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PG1307 + 085B, M | 0.1413 | 12.91, 13.92, 13.28 | 49.7, 34.0, 28.5 | −245.5, −421.6 | 1318.0, 1408.0 |
| PG1307 + 085B, M | 0.1413 | 12.91, 13.92, 14.02 | 49.7, 34.0, 40.2 | −245.5, −421.6 | 1318.0, 1408.0 |
| PG1424 + 240B, M | 0.1471 | 14.66, 14.74, 13.51 | 49.9, 38.3, 55.5 | −121.6, +380.5, −464.2 | 493.2, 968.5, 1378.9 |
| PKS0405−123B | 0.0251 | 12.56, 13.18, 13.11 | 13.4, 144.3, 51.2 | +1174.6, +1423.5, +1420.5 | 673.0, 799.0, 1105.0 |
| PKS0405−123 | 0.1522 | 12.97, 13.44, 12.54 | 21.8, 25.8, 13.5 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123 | 0.1522 | 12.78, 13.44, 12.54 | 21.2, 25.8, 13.5 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123B, M | 0.1829 | 14.61, 13.98, 12.7 | 43.7, 33.8, 36.7 | −255.94, −149.4, −169.7 | 3854.0, 4017.0, 5395.0 |
| PKS1302−102B, M | 0.1925 | 14.47, 13.95, 13.64 | 34.0, 39.5, 54.8 | −194.0, −22.9, +120.5 | 209.0, 434.0, 464.0 |
| PKS1302−102M | 0.1925 | 14.47, 13.95, 13.6 | 34.0, 39.5, 23.2 | −194.0, −22.9, +120.5 | 209.0, 434.0, 464.0 |
| Q1230 + 0115 | 0.0485 | 12.75, 13.49, 13.16 | 35.9, 29.9, 20.8 | −95.3, −15.2, −158.2 | 912.3, 1104.2, 1148.3 |
| Q1230 + 0115B | 0.0554 | 12.56, 12.65, 12.92 | 20.7, 38.5, 56.7 | +1559.4, +1673.1, +880.1 | 353.0, 517.0, 533.0 |
| SBS1108 + 560B, M | 0.1385 | 13.27, 15.25, 14.31 | 42.6, 23.9, 25.2 | −89.3, −225.0, −429.3 | 336.3, 453.0, 465.2 |
| SBS1122 + 594B | 0.1375 | 13.34, 13.14, 13.63 | 77.6, 14.9, 100.0 | −453.6, −97.6, −390.3 | 1299.2, 1488.3, 1759.1 |
| SBS1122 + 594B | 0.1381 | 13.14, 13.63, 13.84 | 14.9, 100.0, 150.0 | −264.6, −53.8 | 1488.3, 2189.5 |
| SBS1122 + 594 | 0.1578 | 13.4, 13.91, 13.27 | 33.4, 18.9, 21.3 | −28.5, −261.7, −303.2 | 556.8, 633.4, 687.4 |
Superscript B and M denotes presence of BLA and any metal ion species, respectively, in at least one of the absorber in the triplet system. The triplets are organized according to the r bin they belong to.
The v∥ and impact parameters of the nearest galaxies which have velocity separations larger than 500 km s−1 from the Ly α triplets have been highlighted in red.
| QSO sightlinesa . | z (Ly α triplet) . | log NH i of . | b-parameter of . | v∥ (Nearest Galaxy-Ly α triplet)b . | Impact parameter of Galaxy . |
|---|---|---|---|---|---|
| . | . | triplet system . | triplet systems (in km s−1) . | (in km s−1) . | from sightlines2 (in pKpc) . |
| Equal arm length configurations: r∥ = 0.5–1 pMpc | |||||
| PG1116 + 215B, M | 0.1656 | 12.63, 13.39, 13.06 | 15.8, 30.7, 44.9 | +98.3, −197.7, +312.0 | 156.0, 317.0, 531.4 |
| PG1222 + 216B | 0.1446 | 13.41, 13.32, 13.3 | 34.2, 18.6, 47.2 | −956.9, −907.1, −941.2 | 1189.0, 1305.3, 1316.8 |
| PKS2155-304B | 0.1057 | 13.98, 13.33, 13.28 | 47.1, 21.6, 43.2 | −265.1, +36.1, −34.5, +33.4 | 924.0, 952.0, 1025.0, 1094.0 |
| Equal arm length configurations: r∥ = 1–2 pMpc | |||||
| H1821 + 643B | 0.1217 | 14.21, 13.43, 13.14 | 38.1, 53.0, 38.1 | −15.8, + 273.1, −328.7 | 156.3, 1160.5, 1550.4 |
| H1821 + 643B, M | 0.1701 | 13.86, 13.68, 13.36 | 35.3, 58.0, 28.4 | +127.7, + 209.7, −369.7 | 415.4, 1122.2, 1118.7 |
| H1821 + 643 | 0.1895 | 12.6, 12.72, 12.55 | 28.1, 26.1, 16.1 | −140.0, −155.1, −84.5 | 1019.8, 1054.5, 1084.3 |
| PG0953 + 414M | 0.1423 | 12.73, 13.56, 13.48 | 15.3, 26.5, 30.9 | +237.7, +78.0, +51.2 | 405.0, 452.1, 506.7 |
| PG0953 + 414B, M | 0.1426 | 13.56, 13.48, 13.2 | 26.5, 30.9, 52.7 | + 155.4, −4.2, −31.0 | 405.0, 452.1, 506.7 |
| PG1048 + 342B, M | 0.0061 | 14.8, 13.79, 13.99 | 42.7, 33.1, 86.9 | −6.0, −167.0 | 60.2, 149.2 |
| PG1048 + 342B, M | 0.0057 | 14.07, 14.8, 13.79 | 30.4, 42.7, 33.1 | + 84.1, −77.0 | 60.2, 149.2 |
| PG1116 + 215B | 0.1658 | 12.63, 13.06, 14.28 | 15.8, 44.9, 32.7 | +37.8, −258.1, +251.4 | 156.0, 317.0, 531.4 |
| PKS0405-123B | 0.0247 | 12.82, 12.56, 13.18 | 42.4, 13.4, 144.3 | +1174.6, +1423.5, +1420.5 | 673.0, 799.0, 1105.0 |
| PKS0405−123B | 0.1527 | 13.44, 12.54, 13.79 | 25.8, 13.5, 47.8 | 132.0, 223.0, −445.8 | 181.0, 2148.0, 3857.0 |
| Q1230 + 0115B, M | 0.0948 | 12.99, 13.31, 14.33 | 69.7, 30.2, 46.3 | +46.8, −16.1, +16.7 | 113.4, 792.3, 917.2 |
| RXJ0439.6--5311B | 0.1772 | 13.53, 13.6, 13.87 | 100.0, 19.7, 29.9 | −65.8, −183.0, +127.9 | 467.2, 562.5, 1848.2 |
| TON1187B | 0.0354 | 13.38, 13.98, 13.59 | 18.9, 28.2, 56.4 | +1398.9, +1149.7, +1346.8 | 278.1, 276.3, 284.1 |
| Equal arm length configurations: r∥ = 2–4 pMpc | |||||
| H1821 + 643B | 0.1899 | 12.6, 12.55, 12.73 | 28.1, 16.1, 41.6 | −235.5, −250.6, −180.0 | 1019.8,1054.5,1084.3 |
| H1821 + 643B | 0.1901 | 12.55, 12.61, 12.73 | 16.1, 22.4, 41.6 | +481.7,−287.1,−302.2 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1901 | 12.6, 12.61, 12.73 | 28.1, 22.4, 41.6 | +481.7,−287.1,−302.2 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.55, 12.73, 12.57 | 16.1, 41.6, 15.9 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.55, 12.73, 12.67 | 16.1, 41.6, 31.5, | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.61, 12.73, 12.67 | 22.4, 41.6, 31.5 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.61, 12.73, 12.57 | 22.4, 41.6, 15.9 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| PG0953 + 414B | 0.1914 | 12.91, 13.34, 13.27 | 25.2, 40.5, 55.3 | 0.0, −136.0 | 1232.6, 3692.8 |
| PG1116 + 215B, M | 0.1662 | 12.63, 14.28, 13.69 | 15.8, 32.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1116 + 215B, M | 0.1662 | 12.63, 13.39, 13.69 | 15.8, 30.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1216 + 069B | 0.1801 | 13.25, 13.52, 13.48 | 64.8, 53.3, 30.4 | +140.8, −67.6, 214.5 | 588.6, 415.4, 632.0 |
| PG1216 + 069B | 0.1801 | 13.25, 13.52, 12.77 | 64.8, 53.3, 12.4 | +140.8, −67.6, 214.5 | 588.6, 415.4, 632.0 |
| PKS0405−123B | 0.0251 | 12.82, 13.18, 13.11 | 42.4, 144.3, 51.2 | +1051.2, +1300.0, +1297.0 | 673.0, 799.0, 1105.0 |
| PKS0405−123B | 0.1330 | 13.67, 13.22, 13.13 | 27.6, 24.2, 45.0 | +227.7, +235.7, +156.2 | 467.0, 501.0, 714.0 |
| PKS0405−123B | 0.1522 | 12.97, 13.44, 13.79 | 21.8, 25.8, 47.8 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123B | 0.1522 | 12.78, 13.44, 13.79 | 21.2, 25.8, 47.8 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0558−504B | 0.0280 | 14.08, 13.13, 13.61 | 32.2, 47.3, 55.1 | – | – |
| Q1230 + 0115B, M | 0.0057 | 13.68, 15.25, 13.25 | 24.4, 37.3, 42.8 | +505.6, +595.1 | 155.1, 168.0 |
| r1 = r∥, r2 = 2r∥ configurations: r∥ = 0.5–1 pMpc | |||||
| 3C 263B, M | 0.0633 | 13.92, 14.86, 15.24 | 27.5, 52.5, 41.0 | −15.5, −131.2, −119.9 | 62.4, 571.5, 577.9 |
| H1821 + 643B, M | 0.1215 | 14.21, 13.49, 13.43 | 38.1, 35.6, 53.0 | +40.9, +329.8, −272.0 | 156.3, 1160.5, 1550.4 |
| H1821 + 643B, M | 0.1217 | 13.49, 13.43, 13.14 | 35.6, 53.0, 38.1 | −15.8, +273.1, −328.7 | 156.3, 1160.5, 1550.4 |
| H1821 + 643 | 0.1899 | 12.72, 12.55, 12.61 | 26.1, 16.1, 22.4 | −235.5, −250.6, −180.0 | 1019.8,1054.5,1084.3 |
| PG0953 + 414B | 0.0160 | 13.11, 13.48, 12.92 | 39.8, 54.2, 8.9 | +102.8, −92.4 | 159.2, 454.5 |
| PG0953 + 414B | 0.0161 | 13.48, 12.92, 13.52 | 54.2, 8.9, 24.8 | +64.4, −130.4 | 159.2, 454.5 |
| PG1116 + 215B, M | 0.1658 | 13.39, 13.06, 14.28 | 30.7, 44.9, 32.7 | +37.8, −258.1, +251.4 | 156.0, 317.0, 531.4 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 13.52 | 64.8, 33.6, 53.3 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PHL1811B, M | 0.1205 | 13.01, 14.17, 13.8 | 77.4, 52.1, 19.6 | −91.3, +425.4 | 1222.3, 1840.0 |
| PKS0405−123B, M | 0.1666 | 12.6, 13.54, 15.01 | 21.8, 29.3, 50.7 | +116.2, −184.6, −364.7 | 115.0, 2472.0, 3177.0 |
| PKS2155−304 | 0.0170 | 13.43, 13.53, 13.3 | 22.9, 24.5, 39.9 | −25.4 | 113.0 |
| PKS2155−304B | 0.0542 | 13.85, 13.61, 12.75 | 34.9, 52.5, 23.7 | −37.8 | 544.0 |
| TONS210B | 0.0858 | 13.05, 13.07, 12.91 | 73.0, 19.8, 19.5 | – | – |
| r1 = r∥, r2 = 2r∥ configurations: r∥ = 1 − 2 pMpc | |||||
| 3C 263B, M | 0.1137 | 14.06, 13.27, 13.87 | 46.4, 56.8, 22.1 | +13.7, +8.4, +258.9 | 351.0, 689.4, 708.9 |
| 3C 273B | 0.0671 | 14.08, 12.6, 12.62 | 37.0, 73.6, 25.0 | +2168.5 | 661.0 |
| H1821 + 643M | 0.1215 | 14.21, 13.49, 13.14 | 38.1, 35.6, 38.1 | +40.9, +329.8, −272.0 | 156.3, 1160.5, 1550.4 |
| H1821 + 643 | 0.1895 | 12.6, 12.72, 12.61 | 28.1, 26.1, 22.4 | −140.0, −155.1, −84.5 | 1019.8, 1054.5, 1084.3 |
| H1821 + 643B | 0.1899 | 12.72, 12.55, 12.73 | 26.1, 16.1, 41.6 | −235.5, −250.6, −180.0 | 1019.8, 1054.5, 1084.3 |
| H1821 + 643B | 0.1914 | 12.73, 12.57, 12.67 | 41.6, 15.9, 31.5 | +149.8, +200.2, +159.9 | 833.4, 1301.0, 1847.2 |
| HE0153−4520M | 0.1489 | 13.34, 13.25, 12.98 | 35.6, 29.3, 26.0 | −133.4, +229.5, −62.9 | 1079.3, 1085.2, 1477.9 |
| HE0153−4520B, M | 0.1706 | 12.66, 13.71, 14.33 | 32.9, 100.0, 39.6 | −435.7, −64.1, −12.8 | 911.3, 2145.1, 2384.1 |
| PG0953 + 414B | 0.0160 | 13.11, 13.48, 13.52 | 39.8, 54.2, 24.8 | +102.8, −92.4 | 159.2, 454.5 |
| PG0953 + 414 | 0.0161 | 13.11, 12.92, 13.52 | 39.8, 8.9, 24.8 | + 64.4, −130.8 | 159.2, 454.5 |
| PG0953 + 414B, M | 0.1423 | 12.73, 13.56, 13.2 | 15.3, 26.5, 52.7 | +237.7, +78.0, +51.2 | 405.0, 452.1, 506.7 |
| PG0953 + 414B | 0.1426 | 12.73, 13.48, 13.2 | 15.3, 30.9, 52.7 | + 155.4, −4.2, −31.0 | 405.0, 452.1, 506.7 |
| PG1048 + 342B, M | 0.0057 | 14.07, 14.8, 13.99 | 30.4, 42.7, 86.9 | + 84.1, −77.0 | 60.2, 149.2 |
| PG1048 + 342B | 0.0061 | 14.07, 13.79, 13.99 | 30.4, 33.1, 86.9 | −6.0, −167.0 | 60.2, 149.2 |
| PG1116 + 215B, M | 0.1662 | 13.06, 14.28, 13.69 | 44.9, 32.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1216 + 069B, M | 0.1239 | 14.65, 14.6, 14.54 | 24.5, 28.4, 44.6 | +56.1, −64.1, +184.2 | 88.0, 91.6, 389.0 |
| PG1216 + 069M | 0.1239 | 14.65, 14.6, 14.1 | 24.5, 28.4, 23.3 | +56.1, −64.1, +184.2 | 88.0, 91.6, 389.0 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 13.48 | 64.8, 33.6, 30.4 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 12.77 | 64.8, 33.6, 12.4 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PG1307 + 085B, M | 0.1413 | 12.91, 13.92, 13.28 | 49.7, 34.0, 28.5 | −245.5, −421.6 | 1318.0, 1408.0 |
| PG1307 + 085B, M | 0.1413 | 12.91, 13.92, 14.02 | 49.7, 34.0, 40.2 | −245.5, −421.6 | 1318.0, 1408.0 |
| PG1424 + 240B, M | 0.1471 | 14.66, 14.74, 13.51 | 49.9, 38.3, 55.5 | −121.6, +380.5, −464.2 | 493.2, 968.5, 1378.9 |
| PKS0405−123B | 0.0251 | 12.56, 13.18, 13.11 | 13.4, 144.3, 51.2 | +1174.6, +1423.5, +1420.5 | 673.0, 799.0, 1105.0 |
| PKS0405−123 | 0.1522 | 12.97, 13.44, 12.54 | 21.8, 25.8, 13.5 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123 | 0.1522 | 12.78, 13.44, 12.54 | 21.2, 25.8, 13.5 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123B, M | 0.1829 | 14.61, 13.98, 12.7 | 43.7, 33.8, 36.7 | −255.94, −149.4, −169.7 | 3854.0, 4017.0, 5395.0 |
| PKS1302−102B, M | 0.1925 | 14.47, 13.95, 13.64 | 34.0, 39.5, 54.8 | −194.0, −22.9, +120.5 | 209.0, 434.0, 464.0 |
| PKS1302−102M | 0.1925 | 14.47, 13.95, 13.6 | 34.0, 39.5, 23.2 | −194.0, −22.9, +120.5 | 209.0, 434.0, 464.0 |
| Q1230 + 0115 | 0.0485 | 12.75, 13.49, 13.16 | 35.9, 29.9, 20.8 | −95.3, −15.2, −158.2 | 912.3, 1104.2, 1148.3 |
| Q1230 + 0115B | 0.0554 | 12.56, 12.65, 12.92 | 20.7, 38.5, 56.7 | +1559.4, +1673.1, +880.1 | 353.0, 517.0, 533.0 |
| SBS1108 + 560B, M | 0.1385 | 13.27, 15.25, 14.31 | 42.6, 23.9, 25.2 | −89.3, −225.0, −429.3 | 336.3, 453.0, 465.2 |
| SBS1122 + 594B | 0.1375 | 13.34, 13.14, 13.63 | 77.6, 14.9, 100.0 | −453.6, −97.6, −390.3 | 1299.2, 1488.3, 1759.1 |
| SBS1122 + 594B | 0.1381 | 13.14, 13.63, 13.84 | 14.9, 100.0, 150.0 | −264.6, −53.8 | 1488.3, 2189.5 |
| SBS1122 + 594 | 0.1578 | 13.4, 13.91, 13.27 | 33.4, 18.9, 21.3 | −28.5, −261.7, −303.2 | 556.8, 633.4, 687.4 |
| QSO sightlinesa . | z (Ly α triplet) . | log NH i of . | b-parameter of . | v∥ (Nearest Galaxy-Ly α triplet)b . | Impact parameter of Galaxy . |
|---|---|---|---|---|---|
| . | . | triplet system . | triplet systems (in km s−1) . | (in km s−1) . | from sightlines2 (in pKpc) . |
| Equal arm length configurations: r∥ = 0.5–1 pMpc | |||||
| PG1116 + 215B, M | 0.1656 | 12.63, 13.39, 13.06 | 15.8, 30.7, 44.9 | +98.3, −197.7, +312.0 | 156.0, 317.0, 531.4 |
| PG1222 + 216B | 0.1446 | 13.41, 13.32, 13.3 | 34.2, 18.6, 47.2 | −956.9, −907.1, −941.2 | 1189.0, 1305.3, 1316.8 |
| PKS2155-304B | 0.1057 | 13.98, 13.33, 13.28 | 47.1, 21.6, 43.2 | −265.1, +36.1, −34.5, +33.4 | 924.0, 952.0, 1025.0, 1094.0 |
| Equal arm length configurations: r∥ = 1–2 pMpc | |||||
| H1821 + 643B | 0.1217 | 14.21, 13.43, 13.14 | 38.1, 53.0, 38.1 | −15.8, + 273.1, −328.7 | 156.3, 1160.5, 1550.4 |
| H1821 + 643B, M | 0.1701 | 13.86, 13.68, 13.36 | 35.3, 58.0, 28.4 | +127.7, + 209.7, −369.7 | 415.4, 1122.2, 1118.7 |
| H1821 + 643 | 0.1895 | 12.6, 12.72, 12.55 | 28.1, 26.1, 16.1 | −140.0, −155.1, −84.5 | 1019.8, 1054.5, 1084.3 |
| PG0953 + 414M | 0.1423 | 12.73, 13.56, 13.48 | 15.3, 26.5, 30.9 | +237.7, +78.0, +51.2 | 405.0, 452.1, 506.7 |
| PG0953 + 414B, M | 0.1426 | 13.56, 13.48, 13.2 | 26.5, 30.9, 52.7 | + 155.4, −4.2, −31.0 | 405.0, 452.1, 506.7 |
| PG1048 + 342B, M | 0.0061 | 14.8, 13.79, 13.99 | 42.7, 33.1, 86.9 | −6.0, −167.0 | 60.2, 149.2 |
| PG1048 + 342B, M | 0.0057 | 14.07, 14.8, 13.79 | 30.4, 42.7, 33.1 | + 84.1, −77.0 | 60.2, 149.2 |
| PG1116 + 215B | 0.1658 | 12.63, 13.06, 14.28 | 15.8, 44.9, 32.7 | +37.8, −258.1, +251.4 | 156.0, 317.0, 531.4 |
| PKS0405-123B | 0.0247 | 12.82, 12.56, 13.18 | 42.4, 13.4, 144.3 | +1174.6, +1423.5, +1420.5 | 673.0, 799.0, 1105.0 |
| PKS0405−123B | 0.1527 | 13.44, 12.54, 13.79 | 25.8, 13.5, 47.8 | 132.0, 223.0, −445.8 | 181.0, 2148.0, 3857.0 |
| Q1230 + 0115B, M | 0.0948 | 12.99, 13.31, 14.33 | 69.7, 30.2, 46.3 | +46.8, −16.1, +16.7 | 113.4, 792.3, 917.2 |
| RXJ0439.6--5311B | 0.1772 | 13.53, 13.6, 13.87 | 100.0, 19.7, 29.9 | −65.8, −183.0, +127.9 | 467.2, 562.5, 1848.2 |
| TON1187B | 0.0354 | 13.38, 13.98, 13.59 | 18.9, 28.2, 56.4 | +1398.9, +1149.7, +1346.8 | 278.1, 276.3, 284.1 |
| Equal arm length configurations: r∥ = 2–4 pMpc | |||||
| H1821 + 643B | 0.1899 | 12.6, 12.55, 12.73 | 28.1, 16.1, 41.6 | −235.5, −250.6, −180.0 | 1019.8,1054.5,1084.3 |
| H1821 + 643B | 0.1901 | 12.55, 12.61, 12.73 | 16.1, 22.4, 41.6 | +481.7,−287.1,−302.2 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1901 | 12.6, 12.61, 12.73 | 28.1, 22.4, 41.6 | +481.7,−287.1,−302.2 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.55, 12.73, 12.57 | 16.1, 41.6, 15.9 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.55, 12.73, 12.67 | 16.1, 41.6, 31.5, | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.61, 12.73, 12.67 | 22.4, 41.6, 31.5 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| H1821 + 643B | 0.1908 | 12.61, 12.73, 12.57 | 22.4, 41.6, 15.9 | +305.1, −463.3, −478.4 | 833.4,1019.8,1054.5 |
| PG0953 + 414B | 0.1914 | 12.91, 13.34, 13.27 | 25.2, 40.5, 55.3 | 0.0, −136.0 | 1232.6, 3692.8 |
| PG1116 + 215B, M | 0.1662 | 12.63, 14.28, 13.69 | 15.8, 32.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1116 + 215B, M | 0.1662 | 12.63, 13.39, 13.69 | 15.8, 30.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1216 + 069B | 0.1801 | 13.25, 13.52, 13.48 | 64.8, 53.3, 30.4 | +140.8, −67.6, 214.5 | 588.6, 415.4, 632.0 |
| PG1216 + 069B | 0.1801 | 13.25, 13.52, 12.77 | 64.8, 53.3, 12.4 | +140.8, −67.6, 214.5 | 588.6, 415.4, 632.0 |
| PKS0405−123B | 0.0251 | 12.82, 13.18, 13.11 | 42.4, 144.3, 51.2 | +1051.2, +1300.0, +1297.0 | 673.0, 799.0, 1105.0 |
| PKS0405−123B | 0.1330 | 13.67, 13.22, 13.13 | 27.6, 24.2, 45.0 | +227.7, +235.7, +156.2 | 467.0, 501.0, 714.0 |
| PKS0405−123B | 0.1522 | 12.97, 13.44, 13.79 | 21.8, 25.8, 47.8 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123B | 0.1522 | 12.78, 13.44, 13.79 | 21.2, 25.8, 47.8 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0558−504B | 0.0280 | 14.08, 13.13, 13.61 | 32.2, 47.3, 55.1 | – | – |
| Q1230 + 0115B, M | 0.0057 | 13.68, 15.25, 13.25 | 24.4, 37.3, 42.8 | +505.6, +595.1 | 155.1, 168.0 |
| r1 = r∥, r2 = 2r∥ configurations: r∥ = 0.5–1 pMpc | |||||
| 3C 263B, M | 0.0633 | 13.92, 14.86, 15.24 | 27.5, 52.5, 41.0 | −15.5, −131.2, −119.9 | 62.4, 571.5, 577.9 |
| H1821 + 643B, M | 0.1215 | 14.21, 13.49, 13.43 | 38.1, 35.6, 53.0 | +40.9, +329.8, −272.0 | 156.3, 1160.5, 1550.4 |
| H1821 + 643B, M | 0.1217 | 13.49, 13.43, 13.14 | 35.6, 53.0, 38.1 | −15.8, +273.1, −328.7 | 156.3, 1160.5, 1550.4 |
| H1821 + 643 | 0.1899 | 12.72, 12.55, 12.61 | 26.1, 16.1, 22.4 | −235.5, −250.6, −180.0 | 1019.8,1054.5,1084.3 |
| PG0953 + 414B | 0.0160 | 13.11, 13.48, 12.92 | 39.8, 54.2, 8.9 | +102.8, −92.4 | 159.2, 454.5 |
| PG0953 + 414B | 0.0161 | 13.48, 12.92, 13.52 | 54.2, 8.9, 24.8 | +64.4, −130.4 | 159.2, 454.5 |
| PG1116 + 215B, M | 0.1658 | 13.39, 13.06, 14.28 | 30.7, 44.9, 32.7 | +37.8, −258.1, +251.4 | 156.0, 317.0, 531.4 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 13.52 | 64.8, 33.6, 53.3 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PHL1811B, M | 0.1205 | 13.01, 14.17, 13.8 | 77.4, 52.1, 19.6 | −91.3, +425.4 | 1222.3, 1840.0 |
| PKS0405−123B, M | 0.1666 | 12.6, 13.54, 15.01 | 21.8, 29.3, 50.7 | +116.2, −184.6, −364.7 | 115.0, 2472.0, 3177.0 |
| PKS2155−304 | 0.0170 | 13.43, 13.53, 13.3 | 22.9, 24.5, 39.9 | −25.4 | 113.0 |
| PKS2155−304B | 0.0542 | 13.85, 13.61, 12.75 | 34.9, 52.5, 23.7 | −37.8 | 544.0 |
| TONS210B | 0.0858 | 13.05, 13.07, 12.91 | 73.0, 19.8, 19.5 | – | – |
| r1 = r∥, r2 = 2r∥ configurations: r∥ = 1 − 2 pMpc | |||||
| 3C 263B, M | 0.1137 | 14.06, 13.27, 13.87 | 46.4, 56.8, 22.1 | +13.7, +8.4, +258.9 | 351.0, 689.4, 708.9 |
| 3C 273B | 0.0671 | 14.08, 12.6, 12.62 | 37.0, 73.6, 25.0 | +2168.5 | 661.0 |
| H1821 + 643M | 0.1215 | 14.21, 13.49, 13.14 | 38.1, 35.6, 38.1 | +40.9, +329.8, −272.0 | 156.3, 1160.5, 1550.4 |
| H1821 + 643 | 0.1895 | 12.6, 12.72, 12.61 | 28.1, 26.1, 22.4 | −140.0, −155.1, −84.5 | 1019.8, 1054.5, 1084.3 |
| H1821 + 643B | 0.1899 | 12.72, 12.55, 12.73 | 26.1, 16.1, 41.6 | −235.5, −250.6, −180.0 | 1019.8, 1054.5, 1084.3 |
| H1821 + 643B | 0.1914 | 12.73, 12.57, 12.67 | 41.6, 15.9, 31.5 | +149.8, +200.2, +159.9 | 833.4, 1301.0, 1847.2 |
| HE0153−4520M | 0.1489 | 13.34, 13.25, 12.98 | 35.6, 29.3, 26.0 | −133.4, +229.5, −62.9 | 1079.3, 1085.2, 1477.9 |
| HE0153−4520B, M | 0.1706 | 12.66, 13.71, 14.33 | 32.9, 100.0, 39.6 | −435.7, −64.1, −12.8 | 911.3, 2145.1, 2384.1 |
| PG0953 + 414B | 0.0160 | 13.11, 13.48, 13.52 | 39.8, 54.2, 24.8 | +102.8, −92.4 | 159.2, 454.5 |
| PG0953 + 414 | 0.0161 | 13.11, 12.92, 13.52 | 39.8, 8.9, 24.8 | + 64.4, −130.8 | 159.2, 454.5 |
| PG0953 + 414B, M | 0.1423 | 12.73, 13.56, 13.2 | 15.3, 26.5, 52.7 | +237.7, +78.0, +51.2 | 405.0, 452.1, 506.7 |
| PG0953 + 414B | 0.1426 | 12.73, 13.48, 13.2 | 15.3, 30.9, 52.7 | + 155.4, −4.2, −31.0 | 405.0, 452.1, 506.7 |
| PG1048 + 342B, M | 0.0057 | 14.07, 14.8, 13.99 | 30.4, 42.7, 86.9 | + 84.1, −77.0 | 60.2, 149.2 |
| PG1048 + 342B | 0.0061 | 14.07, 13.79, 13.99 | 30.4, 33.1, 86.9 | −6.0, −167.0 | 60.2, 149.2 |
| PG1116 + 215B, M | 0.1662 | 13.06, 14.28, 13.69 | 44.9, 32.7, 45.4 | −53.5, −349.4, +160.0 | 156.0, 317.0, 531.4 |
| PG1216 + 069B, M | 0.1239 | 14.65, 14.6, 14.54 | 24.5, 28.4, 44.6 | +56.1, −64.1, +184.2 | 88.0, 91.6, 389.0 |
| PG1216 + 069M | 0.1239 | 14.65, 14.6, 14.1 | 24.5, 28.4, 23.3 | +56.1, −64.1, +184.2 | 88.0, 91.6, 389.0 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 13.48 | 64.8, 33.6, 30.4 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PG1216 + 069B | 0.1799 | 13.25, 13.98, 12.77 | 64.8, 33.6, 12.4 | −7.4, +201.1, +274.9 | 415.4, 588.6, 632.0 |
| PG1307 + 085B, M | 0.1413 | 12.91, 13.92, 13.28 | 49.7, 34.0, 28.5 | −245.5, −421.6 | 1318.0, 1408.0 |
| PG1307 + 085B, M | 0.1413 | 12.91, 13.92, 14.02 | 49.7, 34.0, 40.2 | −245.5, −421.6 | 1318.0, 1408.0 |
| PG1424 + 240B, M | 0.1471 | 14.66, 14.74, 13.51 | 49.9, 38.3, 55.5 | −121.6, +380.5, −464.2 | 493.2, 968.5, 1378.9 |
| PKS0405−123B | 0.0251 | 12.56, 13.18, 13.11 | 13.4, 144.3, 51.2 | +1174.6, +1423.5, +1420.5 | 673.0, 799.0, 1105.0 |
| PKS0405−123 | 0.1522 | 12.97, 13.44, 12.54 | 21.8, 25.8, 13.5 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123 | 0.1522 | 12.78, 13.44, 12.54 | 21.2, 25.8, 13.5 | +267.7, +358.8, −310.4 | 181.0, 2148.0, 3857.0 |
| PKS0405−123B, M | 0.1829 | 14.61, 13.98, 12.7 | 43.7, 33.8, 36.7 | −255.94, −149.4, −169.7 | 3854.0, 4017.0, 5395.0 |
| PKS1302−102B, M | 0.1925 | 14.47, 13.95, 13.64 | 34.0, 39.5, 54.8 | −194.0, −22.9, +120.5 | 209.0, 434.0, 464.0 |
| PKS1302−102M | 0.1925 | 14.47, 13.95, 13.6 | 34.0, 39.5, 23.2 | −194.0, −22.9, +120.5 | 209.0, 434.0, 464.0 |
| Q1230 + 0115 | 0.0485 | 12.75, 13.49, 13.16 | 35.9, 29.9, 20.8 | −95.3, −15.2, −158.2 | 912.3, 1104.2, 1148.3 |
| Q1230 + 0115B | 0.0554 | 12.56, 12.65, 12.92 | 20.7, 38.5, 56.7 | +1559.4, +1673.1, +880.1 | 353.0, 517.0, 533.0 |
| SBS1108 + 560B, M | 0.1385 | 13.27, 15.25, 14.31 | 42.6, 23.9, 25.2 | −89.3, −225.0, −429.3 | 336.3, 453.0, 465.2 |
| SBS1122 + 594B | 0.1375 | 13.34, 13.14, 13.63 | 77.6, 14.9, 100.0 | −453.6, −97.6, −390.3 | 1299.2, 1488.3, 1759.1 |
| SBS1122 + 594B | 0.1381 | 13.14, 13.63, 13.84 | 14.9, 100.0, 150.0 | −264.6, −53.8 | 1488.3, 2189.5 |
| SBS1122 + 594 | 0.1578 | 13.4, 13.91, 13.27 | 33.4, 18.9, 21.3 | −28.5, −261.7, −303.2 | 556.8, 633.4, 687.4 |
Superscript B and M denotes presence of BLA and any metal ion species, respectively, in at least one of the absorber in the triplet system. The triplets are organized according to the r bin they belong to.
The v∥ and impact parameters of the nearest galaxies which have velocity separations larger than 500 km s−1 from the Ly α triplets have been highlighted in red.
4.1 Configuration with equal arm length
There are three triplets in the r∥ = 0.5–1.0 pMpc bin and two of them show associated galaxies. The impact parameter of these galaxies are 156 and 924 pkpc. In the third case the nearest catalogued galaxy has a velocity difference of ∼957 km s−1 (and an impact parameter of ∼1.2 pMpc) with respect to the absorption redshift. All the three triplets have at least one component having b > 40 km s−1. Only one of these absorbers show detectable metals at z = 0.1656 with the nearest cataloged galaxy at an impact parameter of 156 pkpc. Note that none of these systems satisfy the NH i threshold of 1013.5 cm−2.
In the case of r∥ = 1.0–2.0 pMpc bin (where we detect ζ with best significance level), there are 13 triplets contributing to the three-point correlation. Eleven of them have at least one component having b > 40 km s−1and only six show detectable metal absorption with impact parameters to the nearest catalogued galaxies in the range 60–467 pkpc (see column 6 of Table 2). There are two cases where the same absorber contributes twice to our triplet counts (i.e multiple component systems with two combinations consistent with our triplet definition). Therefore, there are 11 independent systems contributing to the triplet count. One of these systems also contribute to r∥ = 0.5–1.0 pMpc. We find nine of these eleven independent systems identified here have nearby galaxies with velocity separations within ±500 km s−1. The impact parameter of the nearby catalogued galaxies varies from 60 pkpc to 1 pMpc with a median impact parameter of 181 pkpc. We notice that systems contributing multiple times to the three-point function tend to have low (i.e <500 pkpc) impact parameters. In the remaining two cases we do identify nearby galaxies but with large velocity separations (i.e between 1000 and 1500 km s−1). Interestingly only two systems (three independent triplets) in this list satisfy NH i ≥ 1013.5 cm−2. In both cases galaxies are found with velocity separations less than 200 km s−1and impact parameter of the nearest galaxy ≤500 pkpc.
In the case of r∥ = 2.0–4.0 pMpc bin there are 18 triplets (from nine independent systems) contributing to the measured ζ. In all these cases at least one of the components has b > 40 km s−1 and only three of them show detectable metal lines. For six of these independent systems we find galaxies with velocity separations within ±500 km s−1. In one case we identify galaxies having velocity separation just above the cut-off. In these six systems the measured impact parameters of the nearest galaxy are in the range 0.156–1.102 pMpc with a median value of 833.4 pkpc. In one case we identify the nearest galaxy to have velocity separations of 1050 km s−1and impact parameter of 673 pkpc. In one case we do not have any galaxies nearest to the absorbers. In the case of z = 0.0280 triplet towards PKS 0558-504 the galaxy observations are complete up to 0.1L*. However, the maximum impact parameter probed is ∼400 pkpc. Considering several of the associated galaxies for this configuration are at impact parameter >400 pkpc (see Table 2), we need to search for galaxies at slightly higher impact parameters before confirming this triplet as a void absorber. Interestingly, none of the triplets satisfy the NH i threshold of 1013.5 cm−2 in this r∥ bin. As discussed before, in only one triplet (i.e z = 0.0251 towards PKS 0405-123), we find all the three components having b > 40 km s−1 the nearest catalogued galaxies have velocity separations in excess of 1000 km s−1and impact parameters in the range 673–1105 pkpc.
4.2 Configuration with arm length ratio 1:2
In the r∥, 1 = 0.5–1 pMpc bin we identify thirteen triplets (and eleven independent systems). Eleven of these triplets show at least one of the components having b > 40 km s−1and only six of them show detectable metal absorption. We could identify at least one nearby galaxy in ten out of eleven independent systems. In these systems the nearest impact parameter ranges from 62 pkpc to 1.2 pMpc with a median value of 158 pkpc. For one triplet (i.e z = 0.085 86 towards TON S210) we do not detect any associated galaxy within 2500 km s−1. Prochaska et al. (2011) quote a completeness of 86 and 90 per cent within ∼0.5 and ∼1 pMpc for finding galaxies (with r < 19.5) to the quasar sightline at the redshift of the triplet. Therefore galaxy observations are deep enough to detect 0.1L* galaxy within an impact parameter of 1 pMpc. Most of the galaxies detected in other cases for this configuration are well within this impact parameter. Therefore, lack of galaxy identification could mean this triplet being a void absorber. Only one system satisfies the NH i threshold of 1013.5 cm−2 and this happen to be the system with the lowest impact parameter in this r∥, 1 bin.
For the r∥, 1 = 1–2 pMpc bin we identify 34 triplets (from 25 independent systems). Out of this, 24 triplets have at least one component with b > 40 km s−1 and only 16 triplets show detectable metal lines. We find thirty-one triplets having at least one nearby galaxy with velocity separation <500 km s−1. For these triplets, the nearest impact parameter range from 60 pkpc to 3.8 pMpc with a median value of 410 pkpc. For three triplets, we find nearest galaxies with large velocity separations (1100–2200 km s−1) with the nearest impact parameters in the range of 350–660 pkpc. Only 7 triplets satisfy NH i threshold of 1013.5 cm−2 and all of these have nearby galaxies within a velocity separation of 200 km s−1 and with impact parameters ranging from 60 pkpc to 500 pkpc.
In summary, for five configurations considered here we identify at least one associated galaxy within a velocity separation of 500 km s−1 for ∼88 per cent of the triplets. The measured impact parameters of the nearest galaxies range from 62–3800 pkpc with a median value of 405 pkpc. Therefore, a good fraction of triplets originate from impact parameters that are inconsistent with them being associated with a single galaxy. The occurrence of b > 40 km s−1 absorbers are more frequent among the triplets (∼85 per cent, as opposed to the 31.9 per cent for isolated absorbers). However, in only one case we see all the three components having b > 40 km s−1. In only 21 cases (∼25 per cent) we have two components having b > 40 km s−1. Only 40 per cent of all the triplets have associated metal line absorption. Most of the triplets are originating form low NH i systems with only ∼14 per cent of the identified triplets having all components with NH i ≥ 1013.5 cm−2.
4.3 Impact parameter distribution
Here we ask the question, is the impact parameter distribution for the triplets different from those of doublets and isolated absorption lines. For this we calculate the cumulative distribution function (CDF) of the impact parameters of respective sightlines from galaxies in three ways: first we consider the impact parameter of the nearest galaxy, second the average impact parameter of the two nearest galaxies (nearest in transverse direction) and third, the average impact parameters of the three nearest galaxies. If we do not find the minimum required number of galaxies, then we do not consider those cases. As above, we consider only galaxies which are within ±500 km s−1 of Ly α pairs (and r∥ within 0.5–1, 1–2, and 2–4 pMpc) that do not belong to a triplet system. Similarly, we also identify galaxies which are within ±500 km s−1 of isolated individual Ly α absorbers (singlet), which do not belong to either a triplet or a pair.
In Fig. 9, we plot the CDF of impact parameters of these galaxies associated with triplet, pair and singlet Ly α systems. The left, middle, and right columns denote impact parameters considered for the nearest galaxy, average of two nearest galaxies and average of three nearest galaxies, respectively. Top panels are for NH i > 1012.5 cm−2 case and the bottom panels are for NH i > 1013.5 cm−2.
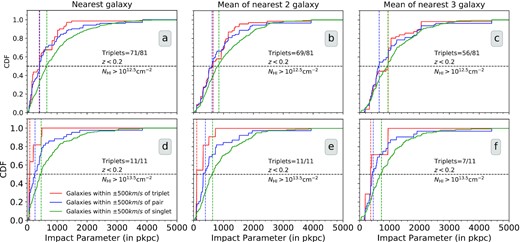
Cumulative distribution function (CDF) of impact parameter of galaxies associated with isolated or ‘singlet’, ‘pair’ (excluding the ones that are part of the triplets) and ‘triplet’ Ly α absorbers. Left, middle, and right columns show results of impact parameter for the nearest, average of two nearest, and three nearest galaxies, respectively. Number of the identified triplets have associated galaxy (or galaxies) is also provided in each panel. Results for log NH i > 12.5 and 13.5 are given in the top and bottom rows, respectively. The vertical dashed lines give the median value of impact parameter for each sub-sample.
As discussed before for the NH i > 1012.5 cm−2 case, the median impact parameter with the nearest galaxies for the triplets in our sample is 405.0 pkpc and the largest separation found is 3.8 pMpc. In the case of doublets (respectively singlets) the median impact parameter is 415.4 pkpc (respectively 645.1 pkpc) and the largest separation found is 3.8 pMpc (respectively 5.4 Mpc). From panels (b) and (c) of Fig. 9, we notice that 69 (i.e 85 per cent triplets) and 56 (i.e 69 per cent triplets) out of 81 triplets have at least two and three nearby galaxies with velocity separation <500 km s−1. The median separations of two nearest galaxies are 658.4, 608.9, and 796.2 pkpc for triplets, doublets, and singlets, respectively. While there is clear distinction in the median impact parameter for the single and multiple (i.e doublets plus triplets) Ly α absorbers, we do not find any significant difference between the median impact parameter of doublets and triplets. The median separation for three nearest galaxies are 953.5, 651.9, and 931.5 pkpc for triplets, doublets, and singlets, respectively. Even though the median separation may seem similar between triplets and singlets, the KS test results below suggest the two distributions are statistically different.
We perform KS-test to compare different CDFs and results are summarized in Table 3. Here D is the maximum absolute difference between the two distributions for the same x-values (i.e impact parameter in this case) and Prob(D) is the evidence against a null hypothesis that the samples are drawn from the same distribution. This table confirms that there is no statistically significant difference between the distribution of impact parameters for triplets and doublets. While the impact parameter distribution of singlet is significantly different from that of triplets.
| Case . | log NH i . | Triplet versus doublet . | Triplet versus singlet . | Doublet versus singlet . | |||
|---|---|---|---|---|---|---|---|
| . | threshold . | D . | Prob(D) . | D . | Prob(D) . | D . | Prob(D) . |
| Nearest neighbour | 12.5 | 0.11 | 0.69 | 0.27 | 0.0001 | 0.23 | 0.0002 |
| 2 neighbours | 12.5 | 0.10 | 0.77 | 0.23 | 0.002 | 0.18 | 0.013 |
| 3 neighbours | 12.5 | 0.12 | 0.74 | 0.23 | 0.01 | 0.16 | 0.05 |
| Nearest neighbour | 13.5 | 0.36 | 0.15 | 0.56 | 0.001 | 0.23 | 0.04 |
| 2 neighbours | 13.5 | 0.40 | 0.09 | 0.58 | 0.001 | 0.25 | 0.03 |
| 3 neighbours | 13.5 | 0.27 | 0.71 | 0.46 | 0.08 | 0.23 | 0.09 |
| Case . | log NH i . | Triplet versus doublet . | Triplet versus singlet . | Doublet versus singlet . | |||
|---|---|---|---|---|---|---|---|
| . | threshold . | D . | Prob(D) . | D . | Prob(D) . | D . | Prob(D) . |
| Nearest neighbour | 12.5 | 0.11 | 0.69 | 0.27 | 0.0001 | 0.23 | 0.0002 |
| 2 neighbours | 12.5 | 0.10 | 0.77 | 0.23 | 0.002 | 0.18 | 0.013 |
| 3 neighbours | 12.5 | 0.12 | 0.74 | 0.23 | 0.01 | 0.16 | 0.05 |
| Nearest neighbour | 13.5 | 0.36 | 0.15 | 0.56 | 0.001 | 0.23 | 0.04 |
| 2 neighbours | 13.5 | 0.40 | 0.09 | 0.58 | 0.001 | 0.25 | 0.03 |
| 3 neighbours | 13.5 | 0.27 | 0.71 | 0.46 | 0.08 | 0.23 | 0.09 |
| Case . | log NH i . | Triplet versus doublet . | Triplet versus singlet . | Doublet versus singlet . | |||
|---|---|---|---|---|---|---|---|
| . | threshold . | D . | Prob(D) . | D . | Prob(D) . | D . | Prob(D) . |
| Nearest neighbour | 12.5 | 0.11 | 0.69 | 0.27 | 0.0001 | 0.23 | 0.0002 |
| 2 neighbours | 12.5 | 0.10 | 0.77 | 0.23 | 0.002 | 0.18 | 0.013 |
| 3 neighbours | 12.5 | 0.12 | 0.74 | 0.23 | 0.01 | 0.16 | 0.05 |
| Nearest neighbour | 13.5 | 0.36 | 0.15 | 0.56 | 0.001 | 0.23 | 0.04 |
| 2 neighbours | 13.5 | 0.40 | 0.09 | 0.58 | 0.001 | 0.25 | 0.03 |
| 3 neighbours | 13.5 | 0.27 | 0.71 | 0.46 | 0.08 | 0.23 | 0.09 |
| Case . | log NH i . | Triplet versus doublet . | Triplet versus singlet . | Doublet versus singlet . | |||
|---|---|---|---|---|---|---|---|
| . | threshold . | D . | Prob(D) . | D . | Prob(D) . | D . | Prob(D) . |
| Nearest neighbour | 12.5 | 0.11 | 0.69 | 0.27 | 0.0001 | 0.23 | 0.0002 |
| 2 neighbours | 12.5 | 0.10 | 0.77 | 0.23 | 0.002 | 0.18 | 0.013 |
| 3 neighbours | 12.5 | 0.12 | 0.74 | 0.23 | 0.01 | 0.16 | 0.05 |
| Nearest neighbour | 13.5 | 0.36 | 0.15 | 0.56 | 0.001 | 0.23 | 0.04 |
| 2 neighbours | 13.5 | 0.40 | 0.09 | 0.58 | 0.001 | 0.25 | 0.03 |
| 3 neighbours | 13.5 | 0.27 | 0.71 | 0.46 | 0.08 | 0.23 | 0.09 |
Next we consider NH i|$\gt \, 10^{13.5}$| cm−2 case, we identify 11 triplets and all of them have nearby galaxies within line-of-sight velocity separation <500 km s−1. All 11 triplets show b > 40 km s−1 components and nine of them show detectable metals. The median separations of these nearby galaxies are 88, 256, and 459 pkpc for the triplets, doublets, and singlets, respectively. In this case it is possible that some of the correlated absorption may originate from the haloes of individual galaxies. Impact parameters measured are systematically smaller than the corresponding values for NH i|$\gt \, 10^{12.5}$| cm−2. We also confirm this with KS-test. The D and Prob(D) values are 0.54 and 0.004, respectively.
As Keeney et al. (2018) also provide stellar mass and luminosities of individual galaxies we also searched for any differences in the luminosities and stellar masses of nearest galaxies (as stated before, within a velocity separation of 500 km s−1) associated with triplets compared to doublets and singlets. We do not find any strong trend. This may once again suggest that most of the Ly α absorbers studied here are not physically linked to individual galaxies. The results presented are consistent with the findings in previous studies that most Ly α absorbers originate from the filamentary structures with BLAs and multiple absorbers having low impact parameters to the filament axis compared to the low NH i isolated absorbers (see Davé et al. 2001, 2010; Penton et al. 2002; Wakker et al. 2015; Tejos et al. 2016). The volume probed and the completeness level reached in terms of luminosity for the galaxy will not allow us to perform an investigation similar to Wakker et al. (2015). However, it will be possible to explore for some of the very low-z triplets using SDSS data base. We leave that exercise to a future work.
5 SIMULATIONS
In this section, we study the clustering of Ly α absorbers using four hydrodynamical simulations for z = 0.1. Main motivations for this exercise are: (i) to measure the two- and three-point correlation functions for different scales; (ii) to quantify the effect of redshift space distortions in the measurement of line of sight correlation functions, (iii) to see whether the observed trends of ζ, ξ and Q with NH i and b are naturally realized in the simulations as well, and (iv) to see the effect of feedback (Wind and AGNs) on the correlation functions. However, we do not make any attempt to fine tune the simulation parameters and/or various sub-grid physics used to reproduce the observations.
The MassiveBlack-II (MBII) hydrodynamic simulation (Khandai et al. 2015) was run in a 100 h−1 cMpc (Mpc in comoving units) cubic periodic box with 2 × 17923 particles using p-gadget which is a hybrid version of gadget-3 upgraded to run on Petaflop-scale supercomputers. This simulation uses the UV background of Haardt & Madau (1996), incorporates feedback associated with star formation and black hole accretion and used cosmological parameters (Ωm = 0.275, ΩΛ = 0.725, Ωb = 0.046, h = 0.702, σ8 = 0.816, andnS = 0.96) from WMAP7 (Komatsu et al. 2011).
We also use three hydrodynamical simulation boxes from publicly available Sherwood Simulation suite5 (Bolton et al. 2017) to explore the effect of wind and AGN feedback. All of them are performed in a 80 h−1 cMpc cubic box with 2 × 5123 particle using P-Gadget-3 (Springel 2005). The model ‘80-512’ is run with quick_lyalpha (as described in Viel et al. 2005) command without any stellar or wind feedback. The second simulation ‘80-512-ps13’ implements the star formation and energy driven wind model of Puchwein & Springel (2013), but without AGN feedback. The third simulation ‘80-512-ps13 + agn’ implements the AGN feedback in addition to the star formation and energy driven wind models. All three simulations have the same initial seed density field, utilize Haardt & Madau (2012) UV background and use the same set of cosmological parameters from Planck Collaboration XVI (2014), where Ωm = 0.308, ΩΛ = 0.692, Ωb = 0.0482, h = 0.678, σ8 = 0.829, and nS = 0.961. Nasir et al. (2017) provide a detailed comparison of predictions of these three models with observations.
Recent studies (see Kollmeier et al. 2014; Khaire & Srianand 2015; Shull et al. 2015; Gaikwad et al. 2017a, b) have shown that the H i ionization rate (ΓH i) at z ∼ 0.1 is higher than those predicted by Haardt & Madau (2012). Therefore, for calculating the H i density fields from the simulations, we use the ΓH i at z ∼ 0.1 from Khaire & Srianand (2019) uniformly for all the four simulations. We do not adjust ΓH i to match the mean flux with observations. We generate 8000 sightlines through the MBII simulation box and 4000 sightlines through each of the Sherwood simulation box using standard procedure described in our earlier papers (Gaikwad et al. 2017b, 2020a; Maitra et al. 2020). We find the mean transmitted flux of 0.973, 0.979, 0.977, and 0.978 for MBII, 80-512, 80-512-PS13, and 80-512-PS13 + AGN simulations, respectively. These are close to what is observed, i.e, 0.961 for the full sample and 0.967 for the Ly α absorption at z < 0.2. We convolve the spectrum with a Gaussian profile with FWHM = 17 km s−1(instead of using HST line spread function), add a Gaussian noise corresponding to SNR = 50 per pixel and use spectral sampling (i.e ∼5 km s−1 per pixel) similar to the HST-COS spectra. The usage of Gaussian LSF is justified as observationally what we have is the deconvolved b-distribution. We use high SNR spectra to get an insight into the intrinsic clustering of the simulated Ly α absorbers. Simulated spectra are fitted with multiple Voigt profile components using viper (see Gaikwad et al. 2017b, for details). As in the observations, we consider only components that satisfy rigorous significant level in excess of 4 for our analysis.
5.1 Distributions of b-parameter and NH i
To begin with, we explore how well the simulations reproduce the observed NH i and b distributions. In panel (a) of Fig. 10, we compare the cumulative distribution function of the b-parameter of Ly α absorbers found in MBII simulation with the observed distribution. We find that the simulation produces lower b-values (median b of ∼25.0 km s−1) in comparison to the observations (median b of ∼34.4 km s−1). Nasir et al. (2017) have found Sherwood simulations also to produce low-b values. The median b-values are 24.4, 24.7, and 26.1 km s−1 for models 80-512, 80-512-ps13, and 80-512-ps13 + agn, respectively, for absorbers with NH i > 1012.5 cm−2.
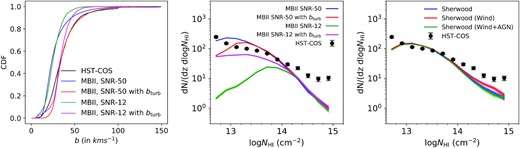
Left-hand panel: Cumulative distribution function for b-parameter for MBII simulations (for two SNR) are compared with the observed distribution. Simulations tend to produce low-b values compared to the observed distribution. Addition of bturb reduces this difference. Our high SNR model produces over all CDF closer to the observed distribution. Middle panel: NH i distribution predicted by MBII simulations are compared with the observed distribution. The high SNR simulation predicts a larger number of low NH i absorbers in comparison to observations. The number goes down with the addition of bturb in the low NH i end. The low SNR simulations produce significantly lesser low NH i absorbers due to incompleteness. On the high NH i ends, the simulations produce significantly lesser absorbers than the observations. Right-hand panel: NH i distribution predicted by Sherwood simulations. Like MBII simulations, absorbers with NH i > 1014 cm−2 are under-predicted. However, the low NH i end matches relatively better than MBII simulations.
This issue of hydrodynamical simulations at low-z is discussed in the literature (Gaikwad et al. 2017b; Nasir et al. 2017; Viel et al. 2017). The solution can come from additional heating sources not considered in these simulations and/or from the inclusion of sub-grid micro-turbulence missing in the simulations (as explored in Oppenheimer & Davé 2009; Gaikwad et al. 2017b). We consider the second case by introducing additional line broadening by adding a non-thermal microturbulence bturb component to the Doppler parameter b in quadrature (|$b^2=b^2_{\rm thermal}+b^2_{\rm turb}$|, see Gaikwad et al. 2017b). This microturbulence term is added to the temperature field along the simulated sightlines before calculating the transmitted flux. We perform Voigt profile decomposition and obtain NH i and b-parameters using viper. As can be seen in panel (a) of Fig. 10, by adding a constant non-thermal turbulence term (bturb ∼ 20 km s−1), we match the median of the observed b-distribution.
In panel (b) of Fig. 10, we compare the NH i distribution we obtained from MBII simulation with the observations. As the observed distribution is corrected for incompleteness, it should reflect the intrinsic distribution. This also justifies the usage of simulated spectra with higher SNR. It is evident from the figure that the simulations slightly over predict the weak NH i absorbers (1013 cm−2 < NH i < 1014 cm−2). However, they tend to produce significantly lesser number of high NH i systems (i.e NH i > 1014 cm−2). While a small increase in |$\Gamma _{\rm{H\,{\small I}}}$| can provide a better matching in the low NH i end, the difference in the high NH i end will be increased. It is also clear from the figure that inclusion of bturb significantly affects the distribution at the low NH i end. In particular, the under prediction of low NH i absorbers can be attributed to the additional line broadening making some weak absorption lines to go below the significant level of detection (i.e for a given SNR and NH i, lines with higher b-values are difficult to detect). However, as expected the additional broadening has not affected the NH i distribution at higher column densities (in this case above 1013.3 cm−2). Similarly, the simulated spectra at lower SNR under predicts the low NH i systems (i.e NH i < 1014.3 cm−2). Addition of bturb moves the NH i values, where the simulated data is complete, to a higher value even in this case. Alternatively, addition of bturb will push some low NH i systems below our detection limit.
In Fig. 11 we plot median b for different NH i-bins (similar to Fig. 5). As expected the MBII simulations with SNR = 50 have lower median b-values compared to observations for all the NH i bins. Addition of turbulence broadening improves the matching. When we consider the lower SNR simulations the difference between the observed and predicted median b-values for a given NH i is larger than that seen for high SNR case. Also simple addition of bturb did not help even when we match the overall median b values with observations (see Fig. 10). This is because at low SNR detection of broad absorption at low NH i is difficult. Also the median b values at high NH i in this is higher as Voigt profile fitting will require less number of components to achieve statistically significant fit.
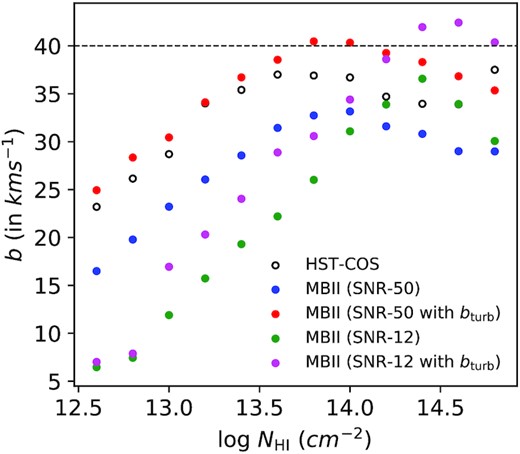
Median b-parameter in different NH i bins obtained from our simulations are compared with observations. The horizontal dotted line at b = 40 km s−1 demarcates the high-b and low-b sub-samples.
The NH i distribution in the case of three Sherwood simulations are shown in panel (c) of Fig. 10. Despite using slightly different |$\Gamma _{\rm{H\,{\small I}}}$| and different Voigt profile fitting routines our results match well with that of Nasir et al. (2017). While inclusion of wind feedback marginally increase the number of high NH i components addition of AGN feedback nullifies this effect. Lack of high NH i systems in the simulated spectra is again a well-known result (see also, Shull et al. 2015; Gurvich, Burkhart & Bird 2017; Nasir et al. 2017; Viel et al. 2017). In summary, we find that there are some inherent short coming in simulations considered here (probably coming from some missing sub-grid physics) in reproducing the observed NH i and b-distribution self-consistently. Keeping this in mind we shall proceed with the clustering analysis.
5.2 Ly α clustering
In the left-hand, middle, and right-hand panels of Fig. 12, we plot two-point, three-point and reduced three-point correlations, respectively, as a function of r∥. Results from MBII simulations (with and without bturb) and Sherwood simulations are presented in the top and bottom rows, respectively. The errors in the correlations are larger of the two errorbars: one-sided poissonian uncertainty corresponding to ±1σ or the bootstrapping error for the data–data pairs computed over 8000 sightlines in case of the MBII simulation and 4000 sightlines for each of the Sherwood simulations. In both cases, unlike in observations, there is no suppression of two- or three-point correlation in the first bin (i.e r∥ < 1 pMpc). In the case of MBII simulations, the predicted two- and three-point functions roughly follow the observations for r∥ > 1 pMpc. In the r∥ = 1–2 pMpc bin, the two- and three-point correlation are found to be |$1.65^{+0.13}_{-0.13}$| and |$4.76^{+1.98}_{-1.67}$|, respectively. In case of simulations, they are found to be |$1.88^{+0.02}_{-0.02}$| and |$3.83^{+0.19}_{-0.18}$|, respectively. When we include bturb, the predicted correlations are higher for r∥ < 4 pMpc. As noted in Fig. 10, in these models there is a reduction in the number of low NH i absorbers. Thus we may be probing clustering among the relatively high NH i absorbers even when we use the same NH i cut-off when we include bturb. This exercise, clearly illustrates that simple addition of a constant bturb in quadrature to thermal b will not provide correct solution to the missing sub-grid physics.
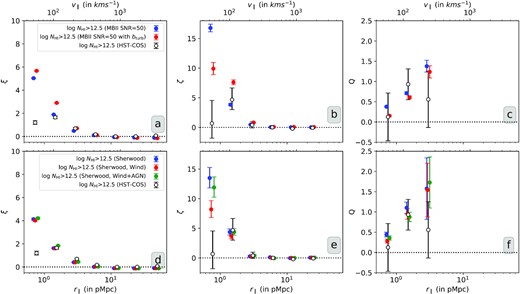
Top panels: Results from MBII simulations. Longitudinal two-point (left), three-point (middle), and reduced three-point (right) correlations of Ly α absorbers as a function of longitudinal scale in simulations for NH i > 1012.5 cm−2. Results for simulated spectra with two different SNR and including bturb in the case of SNR = 50 are presented together with the observations. Bottom panels: Results from all the three simulations in the Sherwood suite studied here.
In the case of Sherwood simulations, the predicted two-point and three-point correlations are also roughly consistent with the observations as well as with the MBII simulation. In the r∥ = 1–2 pMpc bin, the two- and three-point correlation are found to be |$1.84^{+0.04}_{-0.04}$| and |$4.38^{+0.57}_{-0.53}$|, respectively, for the Wind + AGN case. In the case of two-point correlations, the difference between the predictions of the three Sherwood simulations is small (within ∼13 per cent). In the case of three-point correlation the dispersion between the three models is slightly higher (within ∼17 per cent) but still consistent within errors. Therefore, it appears that various feedback process included in the Sherwood simulations produce little difference to the predicted ξ and ζ at various scales.
In summary, the simulations considered here roughly reproduce the observed profile of ξ and ζ at scales greater than 1 pMpc. This could just be the mere reflection of the large-scale Ly α distribution being consistent with matter distribution in the ΛCDM models. The difference between the two simulations can come from slightly different cosmological parameters used (see initial paragraphs of Section 5 for details). However, the models fail to reproduce the large suppression we notice for r∥ < 1 pMpc in the observations. The suppression in the first bin could originate from: (i) difference in the SNR between simulations and observations; (ii) differences in density field at small scales like presence of excess smoothing in the observed data (as suggested by b-distribution) and (iii) differences in the line-fitting routine used. Note the simulated spectra have higher SNR and typically individual components have lower b-values. This helps in the component decomposition of the blended profile and this could provide higher measured correlations at the lowest velocity bin. We confirm that the difference is not due to our automatic Voigt profile routine viper (which we use for fitting simulated spectra) as fits to the observational data using viper (Gaikwad et al. 2017b) produce consistent results to what ones get from the line list of Danforth et al. (2016) (which we have used for calculating observed correlations). Our analysis of simulated data with SNR = 12 did not show large suppression in correlation function at r < 1 pMpc. Using simulated spectra obtained using COS-LSF, we confirm that the differences found can not be attributed to the Gaussian LSF used in the above analysis. Therefore, it is possible that the simulations do not capture the density distribution at small scales (i.e missing sub-grid physics). This could also be the reason for the simulated b distribution being different from the observed one as seen in Fig. 10.
5.2.1 Reduced three-point correlation function (Q)
Maitra et al. (2020), in their z ∼ 2 simulations, have found that the reduced three-point correlation function is less sensitive to the astrophysical parameters compared to ξ or ζ. In panels (c) and (f) of Fig. 12, we plot the Q values predicted in simulations as a function of r∥. In the observations, we do not see any evidence for the scale dependent Q due to large measurement errors. However, it is evident that the simulated Q values increase with increasing scale in the case of MBII simulation. Similar trend is also seen for Sherwood simulations, but with large errorbars. In the case of MBII, Q values tend to be lower in the model with bturb (i.e. Q = |$0.61^{+0.04}_{-0.04}$|) than that without bturb (i.e Q = |$0.71^{+0.04}_{-0.04}$|) at r∥ = 1–2 pMpc bin.
We also notice Q values measured in MBII are slightly lower than what is found in the case of Sherwood simulations (Q for Sherwood simulation having Wind + AGN feedback is |$0.88^{+0.12}_{-0.12}$| at r∥ = 1–2 pMpc bin). However, thanks to large errors, Q values predicted by different simulations are consistent with observed values (|$0.95^{+0.39}_{-0.38}$|) at r∥ = 1–2 pMpc bin. We need to keep in mind that MBII and Sherwood simulations use slightly different cosmologies. However, the differences are not appreciable (i.e Ωm and h differ by ∼10 per cent and σ8 is consistent within 2 per cent). We notice that Q also depends on the feedback process included in the simulations (see panel f in Fig. 12). The 80-512 Sherwood simulation produces slightly large Q values compared to those that include feedback effects. Differences of ∼40 and ∼23 per cent are seen between the three Sherwood simulations at r∥ = 0.5–1 and 1–2 h−1 cmpc bins. However, these differences are not very significant within the given errorbars and are smaller than the difference in Q we see between different scales in simulations.
5.2.2 Effect of peculiar velocities
In this section, using MBII simulations, we study the effects of the line of sight peculiar velocities on the measured correlation functions. For this case, we switch off all the peculiar velocities (considering only the cosmological expansion and thermal broadening effects) while generating the mock spectra. We then fit Voigt profiles to these spectra to identify individual components for our clustering analysis. In the top panels of Fig. 13, we present the ratio of measurements without and with the inclusion of line of sight velocity fields for MBII simulations.
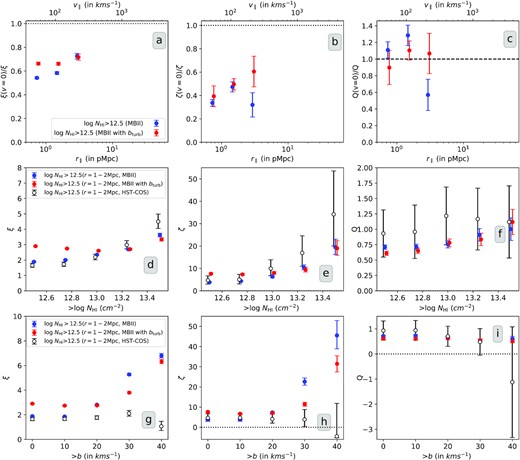
Dependence of redshift space distortions (top panels), NH i thresholds (middle panels) and b thresholds (bottom panels) on the longitudinal two-point (left), three-point (middle) and reduced three-point (right) correlations of Ly α absorbers in MBII simulations. In the top row we show the results as a function of r∥ for two NH i thresholds. In the bottom two rows we show the results for r∥ = 1–2 pMpc, with and without including bturb.
The presence of line of sight velocity field is found increase both ξ and ζ for length-scales of our interest. At the scale of 1.0–2.0 pMpc, two-point and three-point correlations are amplified by a factor of ∼1.7 and 2.1, respectively, by the line-of-sight velocity field. This could imply the Ly α absorbers are part of converging flows. On the other hand, presence of line of sight velocity field makes Q weaker at smaller scales (r∥ < 2 pMpc). At the scale of 1.0–2.0 pMpc, redshift space distortion reduced the intrinsic Q value by a factor of ∼0.3 (though with large errorbars). We confirm similar trends in Sherwood simulations also (not shown here). Due to large errors we did not probe the effect of peculiar velocity on Q at large scales (i.e r > 4 pMpc).
The discussions presented here suggest that the actual matter clustering is smaller (∼60 and 50 per cent in the case of two- and three-point correlations, respectively) than what we measure without accounting for the peculiar velocities. The actual Q values are slightly larger at smaller scales. This trend is similar to what is found in the higher order clustering of galaxies. As shown in fig. 4 of McBride et al. (2011a), the projected measurements of Q are found to be slightly larger than the redshift space measurements at smaller scales. At larger scales, they roughly follow each other. Marín et al. (2008) report similar trends based on the real space versus z-space distribution of galaxies from cosmological simulations.
5.2.3 Dependence on NH i
Next we study the NH i dependence of simulated correlation statistics. In panels (d) and (f) in Fig. 13, we plot two-point(ξ), three-point (ζ), and reduced three-point (Q) correlation functions measured at r∥ = 1–2 pMpc as a function of NH i thresholds. In panels (d) and (e), we find that the two- and three-point correlations steadily increases with increasing NH i threshold. While the trend seen is similar to that seen in observations, we see the increase in ξ and ζ with NH i threshold is slightly slower as compared to what is seen in the case of observations. This could be related to the lack of high NH i absorbers in simulations compared to observed distribution.
The measured ξ and ζ values for low NH i threshold are higher when we include bturb. However, the results are consistent for higher NH i thresholds for models with and without bturb included. As discussed before, inclusion of bturb reduces the number of low NH i systems detected, which cluster weakly. Therefore, for low NH i thresholds we get enhancement in ξ and ζ. However, NH i distribution is not affected at high NH i thresholds by bturb (see Fig. 10). Therefore, ξ and ζ values are similar at high NH i thresholds. This implies that fixing the shortcomings of the simulation (i.e sub-grid physics) using a constant bturb term is not the correct solution.
The dependence of Q on NH i threshold is shown in panel (f) of Fig. 13. The Q remains nearly constant and consistent value with observations. As expected the inclusion of bturb reduces the Q values in the low NH i range.
5.2.4 Dependence on b-parameter
In observations, we found the two- and three-point correlation function is independent of b-threshold for low threshold values (see Fig. 3). We did find the suppression when we consider systems with b > 40 km s−1 (i.e high-b absorbers). When we consider high- and low-b sub-samples (see Fig. 6) three-point correlation was not detected in the case of high-b sub-sample. In panels (g)–(i) in Fig. 13, we plot two-point, three-point, and reduced three-point correlation functions at a scale of 1–2 pMpc as a function of b thresholds. We show the results from MBII simulations with and without addition of bturb. It is evident from this figure that unlike observations both two- and three-point correlation functions show monotonic increasing with increasing b-threshold even for the high-b absorbers. We also notice that Q has very weak dependence on b threshold.
When we include bturb, as expected, the ξ and ζ are independent of limiting b when it is less than 20 km s−1. However, it shows monotonous increase with increasing b-threshold above 20 km s−1. In particular, the detection of positive ζ for b > 40 km s−1 which is not the case in the observations is intriguing. We believe the difference is dominated by two possible effects (i) higher SNR used in our simulations and (ii) the differences in the b-distribution between simulations and observations noted before. That is, a given b-threshold will pick typically high NH i systems in the simulations compared to observation (see Fig. 11).
To investigate this further in Fig. 14, we plot the radial dependence of two- and three-point correlation functions for low- and high-b sub-samples from our simulations (similar to Fig. 6 for observations). For r > 1 pMpc, two and three-point correlation function of high-b systems are found to be larger than those of low-b systems. We notice that when we consider SNR = 12 simulations, as in observations we do not detect positive three-point correlations for r < 4 pMpc. However these models have much larger two-point correlation at r = 1–2 pMpc bin. Therefore we conclude that while low SNR in the observations have a role to play in suppressing the three-point correlation in the case of high-b absorbers this alone can not explain the increase in ξ and ζ we find in the simulations as a function of b-threshold.
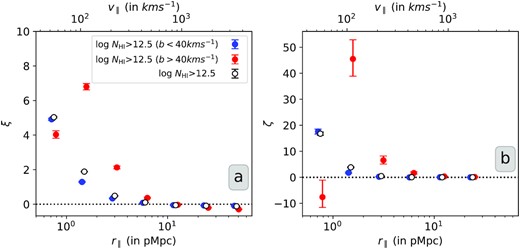
Two-point (panel a) and three-point (panel b) correlations of Ly α absorbers in MBII simulation for full sample, high-b (b > 40 km s−1) and low-b (b < 40 km s−1) sub-samples. Unlike in the case of observations (see Fig. 6) high-b absorbers show stronger two- and three-point correlations at large scales.
6 MAIN RESULTS AND DISCUSSIONS
We report the detection of longitudinal (redshift space) three-point correlation function (ζ at 1–2 pMpc scale) of z ≤ 0.48 Ly α absorbers using HST-COS spectra of 82 QSOs compiled by Danforth et al. (2016). We study the dependence of ζ on NH i, b-parameter, z and presence of metal ions. We also correlate the Ly α absorbers at z < 0.2 contributing to the three-point correlation function with the galaxy distribution for 41 of these sightlines (from Prochaska et al. 2011; Keeney et al. 2018). We compute Ly α clustering using four different simulation boxes at z ∼ 0.1 and compare them with observations. Here, we discuss the main results of our study.
6.1.1 Clustering properties of low-z IGM
Danforth et al. (2016) hasve shown that the low-z Ly α absorbers cluster among themselves up to a scale of ∼10 pMpc with a positive two-point correlation. Using the same data, we report for the first time the detection of a non-zero probability excess in Ly α triplets (|$\rm PE_3$|) up to 8 pMpc, with the strongest detection (|$\rm PE_3=8.8^{+2.0}_{-1.7}$| for absorbers having NH i≥ 1012.5 cm−2) coming from the r∥ = 1–2 pMpc bin with equal arm configuration at a significance level of ∼5σ. In the case of 1:2 arm ratio configuration, we find |$\rm PE_3 = 2.1^{+0.5}_{-0.4}$| (4σ level) for r∥, 1 = 1–2 pMpc and r∥, 2 = 2–4 pMpc. Using the triplet probability excess we obtain positive longitudinal three-point correlation (ζ) at scales below 4 pMpc. The strongest detection is at the scale of 1–2 pMpc with equal arm configuration (|$\zeta =4.8^{+2.0}_{-1.7}$|) for NH i ≥ 1012.5 cm−2). These are the first reported measurements of three-point correlation function from the Ly α forest observations and using Voigt profile decomposed components. We do not detect any three-point correlation for 1:2 arm ratio configurations. The measured amplitudes of Ly α three-point correlation is at least an order of magnitude weaker than that measured for galaxies (ζ ∼ 200 for Mr < −19 galaxies at r ∼ 1 pMpc and θ = 0 for r1: r2 = 1: 2 configuration; see Guo et al. 2016). Using our measured ξ and ζ we obtain the reduced three-point correlation function Q (|$0.95^{+0.39}_{-0.38}$|) for r∥ = 1–2 pMpc bin and equal arm configuration. This is similar to the Q values measured in the case of low-z galaxies (see fig. 4 of McBride et al. 2011a, for θ = 0 for r1: r2 = 1: 2 configurations).
Both two- and three-point correlations are suppressed for r∥ < 1.0 pMpc (or r∥ < 72km s−1 at z ∼ 0.1). This suppression is related to the efficiency at which Voigt profile decomposition can be performed at these scales. This depends on the matter distribution at small scales, instrumental resolution, line blending, SNR of the spectra used (see Danforth et al. 2016). Measuring ζ and ξ in the transverse direction using closely spaced quasar sightlines will be important to have further insights into this issue.
For r∥ > 1 pMpc, both two- and three-point correlations show a decreasing trend with increasing scale. However, we do not notice any scale dependence of Q for r∥ > 1 pMpc range in the observations, thanks to large measurement errors. In the case of galaxies Q values are measured over much larger scales (i.e 3–20 pMpc) and found to be scale independent when peculiar velocity effects are taken care of (McBride et al. 2011b).
6.1.2 Dependence of NH i
As we discussed in the introduction, it is known that the NH i of an absorption feature is related to the underlying baryonic (and dark matter) overdensities. At low-z, it is also known that high NH i systems (NH i > 1014 cm−2) strongly cluster around galaxies while the weaker absorbers are distributed more randomly or associated with low density IGM or galaxy voids (Penton et al. 2002; Tejos et al. 2014). The stronger NH i absorbers are known to have larger two-point correlation compared to low NH i absorbers (see e.g. Penton et al. 2002; Danforth et al. 2016). We find that like two-point correlation the three-point correlation function of the Ly α absorbers also shows an increasing tendency with increasing NH i thresholds for a given scale probed. Compared to |$\zeta =4.8^{+2.0}_{-1.7}$| for NH i > 1012.5 cm−2 absorbers, we obtain |$\zeta =34.2^{+19.4}_{-14.1}$| for NH i > 1013.5 cm−2 absorbers. On the other hand, the reduced three-point correlation Q is relatively independent of the NH i thresholds.
6.1.3 Dependence on b-parameter
While the low-b Ly α absorbers (b < 40 km s−1) probe the cool photoionized gas, some fraction of the high-b Ly α absorbers (b > 40 km s−1) could arise from the highly ionized warm hot intergalactic gas or WHIM (Richter et al. 2006; Tepper-García et al. 2012). Atleast 20 per cent of the total baryonic content of the Universe is located in highly ionized WHIM and the cool photoionized gas comprises of about 30 per cent of the baryons (Lehner et al. 2007). A b-dependent clustering study essentially allows us to probe matter distribution as one transitions from one gaseous phase to another. We find the two-point correlation (probed over 1–2 pMpc) to remain nearly constant for low-b thresholds but shows a decreasing trend when we consider absorbers with b > 40 km s−1. This trend is also seen in the case of three-point correlation albeit with a much sharper decrease. When we consider high- and low-b sub-samples based on b-parameter the measured radial profiles of two- and three-point correlations are found to be very different. While low-b sub-sample shows positive three-point correlation for r∥ < 4 pMpc no correlation is detected for high-b sub-sample over the same scale. The lack of three-point correlation among high-b systems could be related to biases involved in detecting three such absorbers in smaller velocity separations using automatic Voigt profile fits. Therefore, to draw any useful physical conclusions it will be important to confirm this result with high SNR data. Just to quantify this, we considered the number of high-b triplets seen in 8000 sightlines (i.e dz ∼ 290 which is ∼15 times the redshift path of the observed sample used here) of simulated data for two SNR values (i.e 12 and 50). In the case of SNR of 50, we identify 4 and 88 high-b triplets in the first two r bins (i.e 0.5–1.0 and 1.0–2.0 pMpc). However, for SNR of 12, we do not find any triplet. This clearly demonstrates that, while having a larger path-length is always useful for detecting the signal at a higher significant level, better SNR is crucial for the identification of the high-b triplets.
6.1.4 Metal ion components and clustering:
Danforth et al. (2016) have shown that metal bearing Ly α absorbers cluster strongly compared to those without detectable metals. Therefore, we investigated whether the three-point correlation we see comes mainly from these metal ion bearing Ly α components. For this we identified Ly α absorption with associated C iv, O vi, and Si iii absorption (with rest equivalent width more than 30 mÅ). We studied the Ly α clustering excluding components with these metal ion detection. This exercise confirmed that our clustering measurements are not dominated by the Ly α absorbers showing associated C iv, O vi, or Si iii absorption. As metal ion components are sparse it is not possible to probe the three-point correlation between these components using the present data.
6.1.5 Connection to Galaxy distribution
Since the distance scale probed in our study corresponds to velocity ranges consistent with what one expects in galaxy haloes it is also important to see the contribution of CGM absorption to the measured clustering. We use the catalogue of z < 0.2 galaxies around the 41 quasars available in the literature (Prochaska et al. 2011; Keeney et al. 2018) to study the relationship between Ly α triplets and galaxy distribution. We find majority of Ly α triplet systems at z < 0.2 to have nearby galaxies. For the chosen triplet configurations (r1 = r2 = 0.5–1 pMpc, 1–2 pMpc, 2–4 pMpc and r1 = 0.5–1 pMpc, r2 = 1–2 pMpc), we find that 88 per cent of the triplets have at least one nearby galaxy within a velocity separation of 500 km s−1. The impact parameters of these galaxies range from 62 to 3854 pkpc (median of 405 pkpc). Therefore, a good fraction of triplets originate from impact parameters that are inconsistent with them being associated to a single galaxy. We also find that the impact parameters of galaxies associated with isolated Ly α absorption is statistically larger than that of the doublets and triplets. This suggests that multiple component Ly α absorbers are more closely related to galaxies than the isolated absorbers. All these are consistent with the clustered Ly α regions being closer to the galaxy distributions. We also find that b > 40 km s−1 BLA absorbers occur more frequently for triplet systems (∼85 per cent) in comparison to individual absorbers (∼31.9 per cent). As we mentioned before, Wakker et al. (2015) found that the Ly α absorption with NH i≥1013 cm−2 have the filament impact parameter less than 2.1 pMpc and all BLAs are found to be located within 400 pkpc to the filament axis and all the absorbers showing multiple velocity components are located within 1 pMpc to the filament axis. Tejos et al. (2016) have also found the BLAs have high detection rate close to the filament connecting cluster pairs in the redshift range 0.1 < z < 0.5. Thus our results are consistent with clustered regions originating from filament like structures. Establishing such a connection will allow us to interpret the redshift evolution of ζ in terms of evolution on large scale structures. However, we need more sensitive galaxy observations over a wider projected scale compared to what has been used in this study.
6.1.6 Clustering in the simulated data
The four different hydrodynamical simulations considered here roughly reproduce the scale dependence of ξ and ζ for r∥ > 1 pMpc (within 2σ level). This could just be the reflection of matter distribution at large scale being consistent with ΛCDM predictions. At the smallest scale, the simulations (with SNR ∼ 50) do not show decrease in clustering amplitude as seen in the data. The simulations also show a similar dependence of ξ, ζ, and Q on NH i as the observations. However, the slope of increase of ζ and ξ with NH i is found to be lower in simulations. We also note that different feedback processes have little effect on the observed clustering. Unlike observations, simulations show a monotonic increase in ζ and ξ with b-parameter. This differences could be linked to the fact that none of the simulations correctly reproduce the observed distribution of b-parameter and NH i distribution at high NH i range. While low SNR of the observed data may explain lack of three-point correlation among high-b systems, this alone can not explain the b-dependent trend found in observations.
We find that the line of sight peculiar velocities tend to amplify the observed ξ and ζ by a factor of ∼1.7 and 2.1, respectively, compared to the real space clustering. The effect on Q value is smaller. The Q values are seemingly suppressed by ∼30 per cent within r∥ = 2pMpc with large errorbars. This is similar to the findings in McBride et al. (2011a) for clustering of SDSS galaxies, wherein the projected measurements of Q are found to be slightly larger than the redshift space measurements at smaller scales. Similar results are also reported based on galaxy distribution in real space versus redshift space from cosmological simulations in Marín et al. (2008).
6.1.7 Future directions
It is important to accurately measure the three-point correlation and Q preferable over larger scales. This will allow us to measure the linear and non-linear bias parameter for the Ly α forest. With the existing archival data it is possible to improve our measurement by more than 50 per cent. The scale dependence of Q (shown by simulations) is interesting. As we discussed in the introduction, low-z Ly α may originate from CGM, ICM, IGM, or from the interface region between them. If different populations trace different scales that can lead to a scale dependent Q values. Non-linear clustering studies also predict scale dependent Q values. Accurate measurement of Q over different scales is therefore very important.
In the simulation front, it is important to have large simulations with appropriate sub-grid physics to first match the observed NH i and b-distributions before trying to match the observed clustering properties of the Ly α absorbers. It is also important to calibrate the simulations to correctly produce the properties of metal line absorbers to be able to probe the influence of feedback on the clustering properties of low-z absorbers. Such a constrained simulation will allow us to establish a connection between large-scale structure and the Ly α absorbers.
ACKNOWLEDGEMENTS
We acknowledge the use of High performance computing facilities PERSEUS and PEGASUS at IUCAA. We thank Tiziana Di Matteo and Rupert Croft for the MBII simulation, J. Bolton for the Sherwood simulations and Kandaswamy Subramanian, Tirthankar Roy Choudhury and Aseem Pranjape for discussions. We are also grateful to the anonymous referee for his/her valuable comments and inputs regarding the manuscript. Support by ERC Advanced Grant 320596 ‘The Emergence of Structure During the Epoch of reionization’ is gratefully acknowledged. PG acknowledges the support of the UK Science and Technology Facilities Council (STFC). NK acknowledges the support of the Ramanujan Fellowship of DST, India and the IUCAA associateship programme. The Sherwood simulations were performed using the Curie supercomputer at the Tre Grand Centre de Calcul (TGCC), and the DiRAC Data Analytic system at the University of Cambridge, operated by the University of Cambridge High Performance Computing Service on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). This was funded by BIS National E-infrastructure capital grant (ST/K001590/1), STFC capital grants ST/H008861/1 and ST/H00887X/1, and STFC DiRAC Operations grant ST/K00333X/1. DiRAC is part of the National E-Infrastructure. The MBII simulation was run on the Cray XT5 supercomputer– Kraken – at the National Institute for Computational Sciences, supported by the National Science Foundation (NSF) PetaApps program, OCI-0749212.
DATA AVAILABILITY
HST-COS data products of Danforth et al. (2016) used in this study can be accessed from https://archive.stsci.edu/prepds/igm/.
Footnotes
For a pure thermal broadenning, this corresponds to a gas temperature of mb2/2k ≥ 105K, where k is Boltzmann constant and m is the proton mass.
1ES1028 + 511 (czgal = 649 and 934 km s−1); 1SAXJ1032.3 + 5051 (czgal = 649 km s−1); HE0435−5304 (czgal = 1673 km s−1); PG0832 + 251 (czgal = 5226 km s−1); RXJ0439.6−5311 (czgal = 1673 km s−1) and SBS1108 + 560 (czgal = 696 km s−1)
Note that we use the median b values and not the full distribution of b for these calculations.



