-
PDF
- Split View
-
Views
-
Cite
Cite
G Zacharegkas, C Chang, J Prat, S Pandey, I Ferrero, J Blazek, B Jain, M Crocce, J DeRose, A Palmese, S Seitz, E Sheldon, W G Hartley, R H Wechsler, S Dodelson, P Fosalba, E Krause, Y Park, C Sánchez, A Alarcon, A Amon, K Bechtol, M R Becker, G M Bernstein, A Campos, A Carnero Rosell, M Carrasco Kind, R Cawthon, R Chen, A Choi, J Cordero, C Davis, H T Diehl, C Doux, A Drlica-Wagner, K Eckert, J Elvin-Poole, S Everett, A Ferté, M Gatti, G Giannini, D Gruen, R A Gruendl, I Harrison, K Herner, E M Huff, M Jarvis, N Kuropatkin, P-F Leget, N MacCrann, J McCullough, J Myles, A Navarro-Alsina, A Porredon, M Raveri, R P Rollins, A Roodman, A J Ross, E S Rykoff, L F Secco, I Sevilla-Noarbe, T Shin, M A Troxel, I Tutusaus, T N Varga, B Yanny, B Yin, Y Zhang, J Zuntz, T M C Abbott, M Aguena, S Allam, F Andrade-Oliveira, J Annis, D Bacon, E Bertin, D Brooks, D L Burke, J Carretero, F J Castander, M Costanzi, L N da Costa, M E S Pereira, S Desai, J P Dietrich, P Doel, A E Evrard, B Flaugher, J Frieman, J García-Bellido, E Gaztanaga, J Gschwend, G Gutierrez, S R Hinton, D L Hollowood, K Honscheid, B Hoyle, D J James, K Kuehn, M Lima, M A G Maia, J L Marshall, P Melchior, F Menanteau, R Miquel, J Muir, R L C Ogando, F Paz-Chinchón, A Pieres, E Sanchez, S Serrano, M Smith, E Suchyta, G Tarle, D Thomas, C To, R D Wilkinson, (DES Collaboration), Dark Energy Survey Year 3 results: galaxy–halo connection from galaxy–galaxy lensing, Monthly Notices of the Royal Astronomical Society, Volume 509, Issue 3, January 2022, Pages 3119–3147, https://doi.org/10.1093/mnras/stab3155
Close - Share Icon Share
ABSTRACT
Galaxy–galaxy lensing is a powerful probe of the connection between galaxies and their host dark matter haloes, which is important both for galaxy evolution and cosmology. We extend the measurement and modelling of the galaxy–galaxy lensing signal in the recent Dark Energy Survey Year 3 cosmology analysis to the highly non-linear scales (∼100 kpc). This extension enables us to study the galaxy–halo connection via a Halo Occupation Distribution (HOD) framework for the two lens samples used in the cosmology analysis: a luminous red galaxy sample (redmagic) and a magnitude-limited galaxy sample (maglim). We find that redmagic (maglim) galaxies typically live in dark matter haloes of mass log10(Mh/M⊙) ≈ 13.7 which is roughly constant over redshift (13.3−13.5 depending on redshift). We constrain these masses to |${\sim}15{{\ \rm per\ cent}}$|, approximately 1.5 times improvement over the previous work. We also constrain the linear galaxy bias more than five times better than what is inferred by the cosmological scales only. We find the satellite fraction for redmagic (maglim) to be ∼0.1−0.2 (0.1−0.3) with no clear trend in redshift. Our constraints on these halo properties are broadly consistent with other available estimates from previous work, large-scale constraints, and simulations. The framework built in this paper will be used for future HOD studies with other galaxy samples and extensions for cosmological analyses.
1 INTRODUCTION
Understanding the connection between galaxies and dark matter, i.e. how the galaxy properties relate to the properties of their dark matter halo hosts, is essential in forming a comprehensive interpretation of the observed Universe. Cosmological analyses of large-scale structure (LSS) in modern galaxy surveys have reached a point where ignoring the details of this connection (McDonald & Roy 2009; Baldauf et al. 2012), can lead to significant biases in the inferred cosmological constraints (Krause et al. 2017). To avoid this problem, typically we remove data points on the smallest scales until the remaining data is in the linear to quasi-linear regime, and a simple prescription of the galaxy–halo connection (e.g. linear galaxy bias) is sufficient (such as Abbott et al. 2018a). Alternatively, one can invoke more complicated galaxy bias models on small scales (such as Heymans et al. 2021) and marginalize over the model parameters. For either approach, a data-driven model of the galaxy–halo connection on scales below a few Mpc could allow us to significantly improve the cosmological constraints achievable by a given data set. It should be stressed, however, that galaxy bias has inherently non-linear characteristics (as discussed, for example, in Dvornik et al. 2018), and should therefore be treated accordingly. Thus, accurate galaxy–halo connection models provide a wealth of crucial information when modelling galaxy bias. On the other hand, understanding the connection between different galaxy samples and their host haloes also has implications for galaxy evolution (see Wechsler & Tinker 2018, for a review of studies for galaxy–halo connection).
A powerful probe of the galaxy–halo connection is galaxy–galaxy lensing. Galaxy–galaxy lensing refers to the measurement of the cross-correlation between the positions of foreground galaxies and shapes of background galaxies. Due to gravitational lensing, the images of background galaxies appear distorted due to the deflection of light as it passes by foreground galaxies and the dark matter haloes they are in. As a result, this measurement effectively maps the average mass profile of the dark matter haloes hosting the foreground galaxy sample. This is one of the most direct ways to connect the observable properties of a galaxy (brightness, colour, size) to its surrounding invisible dark matter distribution (Tyson et al. 1984; Hoekstra, Yee & Gladders 2004; Mandelbaum et al. 2005; Seljak et al. 2005). A common approach to modelling this measurement is to invoke the Halo Model (Seljak 2000; Cooray & Sheth 2002) and the Halo Occupation Distribution (HOD) framework (Zheng, Coil & Zehavi 2007; Zehavi et al. 2011). In this framework, we consider dark matter haloes to be distinct entities with a large luminous central galaxy in their centres and smaller, less luminous satellite galaxies distributed within the halo, which are also surrounded by their own sub-haloes. The particular way that central and satellite galaxies occupy the dark matter halo is parametrized by a small number of HOD parameters, while all the dark matter haloes contribute separately to the total galaxy–galaxy lensing signal according to the Halo Model. In this paper, we will invoke this HOD framework to model a new set of galaxy–galaxy lensing measurements using the Dark Energy Survey (DES) Year 3 (Y3) data set.
Several previous studies have used galaxy–galaxy lensing to constrain the galaxy–halo connections for particular samples of galaxies. Mandelbaum et al. (2006a) performed an analysis with the MAIN spectroscopic sample from the Sloan Digital Sky Survey (SDSS) DR4, characterizing the HOD parameters for galaxies split in stellar mass, luminosity, morphology, colours, and environment. The study was followed up by Zu & Mandelbaum (2015) using SDSS DR7 with a more sophisticated HOD model. The fact that all lens galaxies used in these studies have measured spectra allowed for good determination of the stellar mass and other galaxy properties. More recently, rapid development of large galaxy imaging surveys provide much more powerful weak lensing data sets to perform similar analyses. Gillis et al. (2013), Velander et al. (2013), and Hudson et al. (2014) used measurements from the Canada–France–Hawaii Telescope Lensing Survey (CFHTLenS; Heymans et al. 2012; Erben et al. 2013), while Sifón et al. (2015), Viola et al. (2015), and van Uitert et al. (2016) used data from the Kilo Degree Survey (KiDS; de Jong et al. 2013; Kuijken et al. 2015) to study the galaxy–halo connection for a range of different galaxy samples. Noticeably, these studies extend to higher redshifts as well as lower mass (including Ultra-Diffused Galaxies at low redshift). Furthermore, Bilicki et al. (2021) used photometry from KiDS, exploiting some overlap with Galaxy And Mass Assembly (GAMA; Driver et al. 2011) spectroscopy, to derive accurate galaxy–galaxy lensing measurements, split in red and blue bright galaxies, to constrain the stellar-to-halo mass relation by fitting the data with a halo model. All together, these studies provide us with pieces of information to constrain models of galaxy formation. In parallel, Clampitt et al. (2017) derived constraints on the halo mass of a luminous red galaxies sample, the red-sequence Matched-filter Galaxy Catalog (redmagic) galaxies (Rykoff et al. 2014), using DES Science Verification (SV) data. The redmagic sample is particularly interesting as it is used heavily in many cosmological studies of LSS due to its excellent photometric redshift precision. For that reason, redmagic is one of the two samples we study in this work. From the studies above, it becomes evident that the basic HOD framework is capable of successfully describing the halo occupation statistics for a wide variety of galaxy samples, as long as it is modified accordingly to account for the specific features of the data set at hand.
The Clampitt et al. (2017) study was later combined with galaxy clustering to constrain cosmological models in Kwan et al. (2016), illustrating how understanding the small-scale galaxy–halo connection (and effectively marginalizing over them) could improve the cosmological constraints. Similar studies include Mandelbaum et al. (2013), Cacciato et al. (2013), Park et al. (2016), Krause & Eifler (2017), and Singh et al. (2020). In particular, Park et al. (2016) demonstrated that to obtain robust constraints from combining large and small scale information, it is necessary to consistently model the full range of scales, and to have good priors on the HOD parameters due to degeneracies between HOD and cosmological parameters. When including the small-scale modelling from HOD in a cosmology analysis using galaxy clustering and weak lensing, Krause & Eifler (2017) showed that the statistical constraints on the dark energy equation of state w improves by up to a factor of three compared to standard analyses using only large-scale information. We leave for future work the exploration of gain in cosmological constraints including our HOD modelling in the DES Y3 cosmology analysis.
Many studies (e.g. Leauthaud et al. 2017; Lange et al. 2019; Singh et al. 2019; Wibking et al. 2019; Yuan, Eisenstein & Leauthaud 2020; Lange et al. 2021) have shown that fitting galaxy clustering measurements with small-scale galaxy–halo connection models, at fixed cosmology, provides precise predictions of the lensing amplitude which is higher than the measured signal. This is the so-called ‘lensing is low’ problem, which becomes especially evident when small scales are considered in the analysis. Figuring out whether this discrepancy can be explained by new physics, cosmology, or by reconsidering our galaxy formation models is an open question. A better understanding of the galaxy–halo connection can play a crucial role in solving this mystery. For example, Zu (2020) found that the ‘lensing is low’ tension can be resolved on small scales; however, the satellite fraction has to be very high, which is not in agreement with observations (e.g. Guo et al. 2014; Reid et al. 2014; Saito et al. 2016)
In this paper, we make use of data from Y3 of DES to study the galaxy–halo connection of two galaxy samples: redmagic and an alternative magnitude-limited galaxy sample defined in Porredon et al. (2021). These two samples are used in the DES Y3 cosmological analysis combining galaxy clustering, galaxy–galaxy lensing, and cosmic shear (commonly referred to as the 3 × 2pt analysis as it combines three two-point functions; DES Collaboration et al. 2021). We measure the galaxy–galaxy lensing signal to well within the one-halo regime, demonstrating the extremely high signal-to-noise ratio coming from the powerful, high-quality data set. We model the measurements by combining the Halo Model and the HOD framework, fixing the background cosmology to be consistent with the DES Y3 cosmology analysis. This work presents one of the most powerful data sets for studying the galaxy–halo connection in a photometric survey and includes two main advances compared to previous work of similar nature: First, we include a number of model components that were previously mostly ignored in studies of the galaxy–halo connection via galaxy–galaxy lensing. Secondly, we borrow heavily from the tools used in cosmological analyses and carry out a set of rigorous tests for systematic effects in the data and modelling, making our results very robust. Both of these advances were driven by the supreme data quality – as the statistical uncertainties shrink, previously subdominant systematic effects in both the measurements and the modelling become important.
With our analysis, we place constraints on the HOD parameters, and derive the average halo mass, galaxy bias and satellite fraction of these samples. Our analysis provides complementary information from the small-scales to the large-scale cosmological analysis in Prat et al. (2021) and informs future cosmology analyses using these two galaxy samples. As shown in Berlind & Weinberg (2002), Zheng et al. (2002), and Abazajian et al. (2005), combining HOD with cosmological parameter inference can greatly improve the cosmological constraints. Our results can also be incorporated into future simulations that include similar galaxy samples.
The structure of the paper is as follows. In Section 2, we describe the baseline formalism for the HOD and Halo Model framework used in this paper. In Section 3, we detail the different components that contribute to the galaxy–galaxy lensing signal that we model. In Section 4, we describe the data products used in this paper. In Section 5, we describe the measurement pipeline, covariance estimation, and the series of diagnostics tests performed on the data. In Section 6, we describe the model fitting procedure and the model parameters that we vary. We also describe how we determine the goodness-of-fit and quote our final constraints. In Section 7, we show the final results of our analysis. We conclude in Section 8 and discuss some of the implications of our results.
2 TWO THEORETICAL PILLARS
In this section, we describe the two fundamental elements in our modelling framework: the HOD model and the halo model. As we discuss later, the combination of the two allows us to predict the observed galaxy–galaxy lensing signal to very small scales given a certain galaxy–halo connection.
2.1 Halo occupation distribution
The halo occupation distribution (HOD) formalism describes the occupation of dark matter haloes by galaxies. There are two types of galaxies that can occupy the halo: central and satellite galaxies. A central galaxy is the large, luminous galaxy which resides at the centre of the halo. The HOD model does not allow for more than one central galaxy to exist inside the halo. On the other hand, the HOD allows for many satellite galaxies to exist in a halo. The higher the mass of the halo the more satellites are expected to exist around the central. Satellite galaxies are smaller and less luminous than the central. They orbit around the centre of the halo and give rise to the non-central part of the galaxy–galaxy lensing signal, as we discuss in more detail later. In what follows, we define the HOD of a galaxy sample which has a minimum luminosity threshold, similarly to Clampitt et al. (2017).
The central galaxy is assumed to be exactly at the centre of the halo, i.e. our model does not account for effects that might come from mis-centering of the central galaxy in its dark matter halo. The number of centrals in our HOD framework is given by a lognormal mass–luminosity distribution (Zehavi et al. 2004; Zheng et al. 2005; Zehavi et al. 2011) and its expectation value is denoted by 〈Nc(Mh)〉. The scatter in the halo mass–galaxy luminosity relation is parametrized by σlog M. The mass scale at which the median galaxy luminosity corresponds to the threshold luminosity will be denoted as Mmin . A third parameter is the fraction of occupied haloes, fcen, which is introduced specifically for redmagic and accounts for the number of central galaxies that did not make it into our sample due to how the galaxies are selected. In more detail, due to the selection process of the redmagic algorithm, for haloes of a fixed mass, not all the central galaxies associated with those haloes will be selected into the lens sample. More specifically, the redmagic selection depends on the photometric-redshift errors, which could result in excluding some galaxies even though they are above the mass limit for observation.1 For most galaxy samples that are selected via properties intrinsic to the sample (luminosity, stellar mass, etc.), however, fcen = 1 is a natural choice.
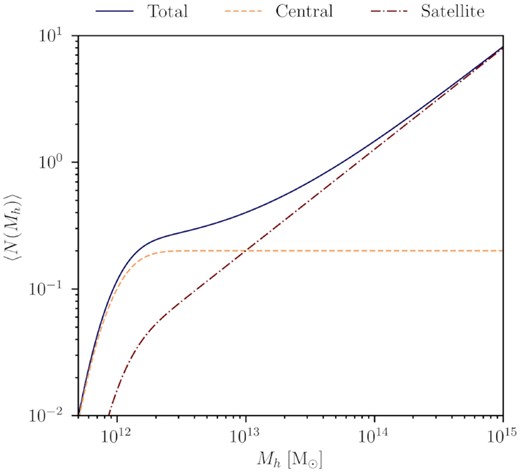
The HOD prediction for the expectation number of central (dashed), satellite (dash–dotted), and the total (solid) number of galaxies as a function of the mass of the dark matter halo inside of which they reside. The HOD parameters used to produce this plot are: Mmin = 1012 M⊙, M1 = 1013 M⊙, fcen = 0.2, α = 0.8, σlog M = 0.25.
2.2 Halo model
In the framework of the current cosmological model, the LSS in the Universe follows a hierarchy based on which smaller structures interact and merge to give rise to structure of larger scale. The abundance of dark matter haloes is described by the halo mass function (HMF) which is denoted by dn/dM and is a function of the halo mass Mh at redshift z. In this work, we utilize analytic fitting functions to model the HMF following Tinker et al. (2008).
For computing the distribution of the dark matter within a hal,o we assume a NFW density profile (Navarro, Frenk & White 1996) with characteristic density ρs and scale radius rs. To calculate the concentration parameter of the dark matter distribution, cdm(Mh, z), we follow Bhattacharya et al. (2013).
In order to calculate the linear matter power spectrum, |$P_{\rm m}^{\rm lin}(k,z)$|, we make use of accurate fitting functions from Eisenstein & Hu (1998) (hereinafter EH98). These fitting functions are accurate to |${\sim}5 {{\ \rm per\ cent}}$| and we use them instead of other numerical codes that calculate the power spectrum, such as camb (Lewis, Challinor & Lasenby 2000), to make our numerical code more efficient. We have performed the necessary numerical tests to show that this modelling choice does not affect the final results. The linear power spectrum, however, poorly describes the power at the small, non-linear scales. In our modelling, we correct for this by using the non-linear matter power spectrum, |$P_{\rm m}^{\rm nl}(k,z)$|, by adopting the halofit approximation based on Takahashi et al. (2012) to modify the EH98 linear spectrum. To account for massive neutrinos in the power spectrum, we have modified the base Takahashi et al. (2012) prediction using the corrections from Bird, Viel & Haehnelt (2012). Note that our method is different from the implementation in camb where the Bird et al. (2012) corrections use, as base, the Takahashi et al. (2012) model. For further discussion on the different halofit versions, see also Appendix B in Mead et al. (2021). We also note that more accurate non-linear corrections exist, for example hmcode,2 but they are not necessary given the required accuracy in our analysis.
3 MODELLING THE OBSERVABLE
Building on Section 2, we now describe our model for the galaxy–galaxy lensing signal. We first describe the individual terms in the matter-cross-galaxy power spectrum Pgm(k, z) (Section 3.1), then we project the 3D Pgm(k, z) into the 2D lensing power spectrum Cgm(ℓ) and finally into the observable, the tangential shear γt(θ) (Section 3.2). In Sections 3.3–3.6, we describe additional astrophysical components that are considered in our model. In Appendix A, we perform a series of tests on our model with simulations and external codes to check for the validity of our code.
Throughout this paper, we fix the cosmological parameters to the σ8 and Ωm values from the DES Y3 analysis and use Planck 2018 (Planck Collaboration VI 2020) for remaining parameters. The cosmological analyses on the two lens samples in DES Y3 give consistent results (DES Collaboration et al. 2021), albeit slightly different, with Ωm and σ8 being the best constrained parameters. For this reason, we choose to only use the DES Y3 results for these two cosmological parameters and use the values as constrained for each lens galaxy sample separately. For redmagic, we use Ωm = 0.341 and σ8 = 0.735, while for maglim, we use Ωm = 0.339 and σ8 = 0.733. For the remaining cosmological parameters, we set Ωb = 0.0486, H0 = 67.37, ns = 0.9649, Ωνh2 = 0.0006, where h is the Hubble constant in units of 100 km s–1Mpc–1. Since we consider the λ-cold dark matter (ΛCDM) cosmological model, we set w = −1 for the dark energy equation of state parameter. In addition, all the halo masses use the definition of M200c, based on the mass enclosed by radius R200c so that the mean density of a halo is 200 times the critical density at the redshift of the halo. We note that the choice of cosmological parameters mostly affects the inferred large-scale galaxy bias, as we show in Section 7.3.1.
In the DES Y3 3 × 2pt cosmological analysis (DES Collaboration et al. 2021) using the redmagic lens sample, it was found that the best-fitting galaxy clustering amplitude, bw, is systematically higher than that of galaxy–galaxy lensing, namely |$b_{\gamma _t}$|. To account for this, a de-correlation parameter Xlens was introduced, that is defined as the ratio of the two biases, |$X_{\rm lens} \equiv b_{\gamma _t}/b_w$|. This parameter varies from 0 to 1 and allows for the two biases to vary independently, thus enabling the model to achieve simultaneously good fits to both γt and w. Nevertheless, the impact of Xlens on the main 3 × 2pt cosmological constraints, especially on S8 ≡ σ8(Ωm/0.3)1/2, were negligible. The exact origin of this inconsistency in redmagic, caused by some measurable unknown systematic effect, is still an open question. Given that we do not know if this systematic is affecting the galaxy clustering or galaxy–galaxy lensing signal, or both to some degree, in our galaxy–galaxy lensing analysis, we choose to use the fiducial cosmological results from the 3 × 2pt analysis and assume Xlens = 1 throughout. However, we briefly discuss the impact on our derived halo properties from changing to the 3 × 2pt best-fitting value of roughly Xlens ≈ 0.877 when we present our results in Section 7.2. We do note, however, that this is the most pessimistic case where the systematic is completely found in γt. Given that γt is a cross-correlation, while e.g. w is an auto-correlation of the lenses, it is likely that clustering is the most affected by the systematic and not galaxy–galaxy lensing. In our case, this means that the shift in constraints we quote later would not be as dramatic in reality.
3.1 Correlations between galaxy positions and the dark matter distribution
The galaxy-cross-matter power spectrum, Pgm(k, z), is composed two terms. The one-halo term, |$P_{\rm gm}^{\rm 1h}(k,z)$|, quantifies correlations between dark matter and galaxies inside the halo. The two-halo term, |$P_{\rm gm}^{\rm 2h}(k,z)$|, quantifies correlations between the halo and neighbouring haloes. Each of these terms receives a contribution from central and satellite galaxies. Below, we summarize the formalism for these four terms separately. The modelling we follow below is similar to what is being commonly used in the literature; for example, see Seljak (2000), Mandelbaum et al. (2005), and Park et al. (2015).
To introduce the two-halo terms, we define the following quantities: the average linear galaxy bias and the average satellite fraction of our sample.
In the two-halo central galaxy-dark matter cross power spectrum of equation (10), in order to avoid double-counting of haloes sometimes the halo exclusion (HE) technique is used. Based on the HE principle (see e.g. Tinker et al. 2005), given a halo of mass Mh1, we only consider nearby haloes of mass Mh2 that satisfy the relation R200c(Mh1) + R200c(Mh2) ≤ r12, where R200c(Mh) is the radius of a halo of mass Mh, and r12 represents the distance between the centres of the two haloes. However, accounting for HE this way is computationally expensive. For this reason, many effective descriptions have been suggested in the literature to bypass this restriction. After performing tests using a simplified HE model in Appendix C, we find that in our case, HE has little to no impact on our model, and we thus decide to neglect it in our fiducial framework.
3.2 Modelling the tangential shear γt
3.3 Tidal stripping of the satellites
3.4 Point-mass contribution
In practice, the amplitude parameter would be allowed to vary as a free parameter or be set to the average stellar mass inside the redshift bin of interest. When let to vary, it accounts for any imperfect modelling of the galaxy-matter cross-correlation on scales smaller than the smallest measured scale used in the model fit. This is similar to the point-mass term derived in MacCrann et al. (2020a) and used in Krause et al. (2021).
3.5 Lens magnification
We now consider the effects of weak lensing magnification on the estimation of our observable. In addition to the distortion (shear) of galaxy shapes, weak lensing also changes the observed flux and number density of galaxies – this effect is referred to as magnification. Following Prat et al. (2021), here we only consider the magnification in flux for the lens galaxies, as that is the dominant effect for galaxy–galaxy lensing.
3.6 Intrinsic alignment
Galaxies are not randomly oriented even in the absence of lensing. On large scales, galaxies can be stretched in a preferable direction by the tidal field of the LSS. On small scales, other effects such as the radial orbit of a galaxy in a cluster can affect their orientation. This phenomenon, where the shape of the galaxies is correlated with the density field, is known as intrinsic alignment (IA); for a review, see Troxel & Ishak (2015).
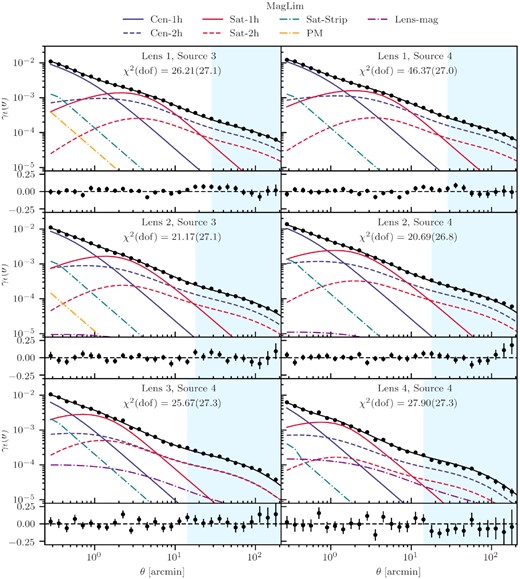
A simple extension of NLA in our HOD framework will be to use our HOD-based Pgm instead of |$b_{g}P_{\rm m}^{\rm nl}$| in equation (24). However, the IA modelling near the one-halo term is likely more complex and would warrant more detailed studies such as those carried out in Blazek, Vlah & Seljak (2015). In this paper, we avoid the complex modelling by choosing redshift bin pairs that are sufficiently separated so that they have significantly low IA contribution (see Section 5.1) and we, thus, choose not to include this component in our fiducial model. However, in Section 7.3.4, we test the full model that includes this IA contribution and show that the results are consistent with our fiducial which does not include IA. We show an example of what all the γt components look like in Fig. 2.
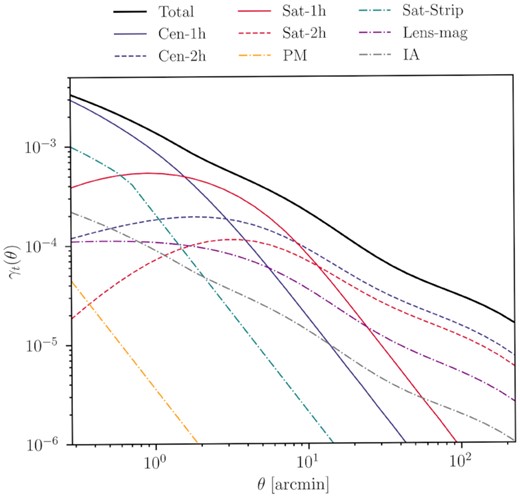
This plots illustrates the theory prediction for the shear (solid black) and how the various components contribute to it. The one- and two-halo components from the central and satellite galaxies are labelled ‘Cen-1h’, ‘Cen-2h’, ‘Sat-1h’, and ‘Sat-2h’, respectively. We also show the contribution from IA, lens magnification (‘Lens-mag’), satellite strip (‘Sat-Strip’), and point mass (‘PM’). The HOD parameters used are the same as in Fig. 1; the stellar mass we used is |$M_\star = 2 \times 10^{10} \,\, {\rm \mathrm{M}_\odot }$|; for IA, we used the amplitude and power-law parameters AIA = 0.1 and ηIA = −0.5, respectively; for the lens magnification coefficient, we set the value to αlmag = 1.3.
Although we have ignored IA in this paper, given that it is negligible for our purposes, we emphasize that its contribution to lensing can be of high importance to future cosmological studies, as it can produce biases in the inference of the cosmological parameters (e.g. Samuroff, Mandelbaum & Di Matteo 2019). In addition, if not properly accounted for, IA can affect the inference of the lens halo properties in lensing analyses. In this case, a halo-model description of IA would be necessary to capture its sample dependence. Fortuna et al. (2021) described a halo model for IA on small and large scales from central and satellite galaxies which is capable of incorporating the galaxy sample characteristics. We leave the further investigation of IA and its modelling for future work.
4 DATA
For this work, we make use of data from the Dark Energy Survey (DES; Flaugher 2005). DES is a photometric survey, with a footprint of about 5000 deg2 of the southern sky, that has imaged hundreds of millions of galaxies. It employs the 570-megapixel Dark Energy Camera (DECam; Flaugher et al. 2015) on the Cerro Tololo Inter-American Observatory (CTIO) 4-m Blanco telescope in Chile. We use data from the first three years (Y3) of DES observations. The basic DES Y3 data products are described in Abbott et al. (2018b) and Sevilla-Noarbe et al. (2020). Below, we briefly describe the source and galaxy samples used in this work. By construction, all the samples are the same as that used in Prat et al. (2021) and in the DES Y3 3 × 2pt cosmological analysis (DES Collaboration et al. 2021).
4.1 Lens galaxies – redmagic
For our first lens sample, we use redmagic galaxies. These are red luminous galaxies which provide the advantage of having small photometric redshift errors. The algorithm used to extract this sample of luminous red galaxies is based on how well they fit a red sequence template, calibrated using the red-sequence Matched-filter Probabilistic Percolation cluster-finding algorithm (redmapper; Rykoff et al. 2014, 2016).
To maintain sufficient separation between lenses and sources, we only use the lower four redshift bins used in Prat et al. (2021). The first three bins at z = {[0.15, 0.35], [0.35, 0.5], [0.5, 0.65]} consist of the so-called ‘high-density sample’. This is a sub-sample which corresponds to luminosity threshold of Lmin = 0.5L⋆, where L⋆ is the characteristic luminosity of the luminosity function and comoving number density of approximately |$\bar{n} \sim 10^{-3} \,\, (h/{\rm Mpc})^3$|. The fourth redshift bin of z = [0.65, 0.8] is characterized by Lmin = L⋆ and |$\bar{n} \sim 4 \times 10^{-4} \,\, (h/{\rm Mpc})^3$|, and is referred to as the ‘high-luminosity sample’. The redshift distributions for all these bins are shown in Fig. 3. As we will discuss in Section 6, we use the number density values as an additional data point in our fits, which helps constrain the fcen HOD parameter. The data we used to derive the mean of |$\bar{n}_g^i$| and its variance in each lens bin i is the same as what is used in Pandey et al. (2021), and the specific values we used are the following: |$\bar{n}_g^i \approx \lbrace 9.8 \pm 0.6, 9.6 \pm 0.3, 9.6 \pm 0.2, 3.8 \pm 0.02 \rbrace \times 10^{-4} \,\, (h/{\rm Mpc})^3$|, respectively for i = 1, 2, 3, 4. We note here that we have also fit our data without the addition of |$\bar{n}_g^i$| and our main conclusions hold, except that fcen becomes unconstrained.
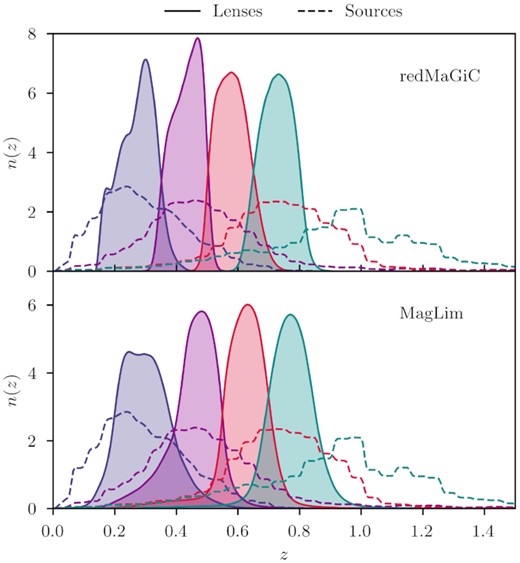
Redshift distribution of the lenses (solid filled) and of the source (dashed) galaxies, for redmagic (upper) and maglim (lower).
4.2 Lens galaxies – maglim
The second sample we use for lens galaxies is maglim, which is defined with a redshift-dependent magnitude cut in i-band. This results in a sample with ∼four times more galaxies compared to redmagic and is divided into six bins in redshift with |${\sim}30{{\ \rm per\ cent}}$| wider redshift distributions, also compared to the redmagic sample. In this sample, galaxies are selected with a magnitude cut that evolves linearly with the photometric redshift estimate: i < azphot + b. The optimization of this selection, using the DNF photometric redshift estimates (De Vicente, Sánchez & Sevilla-Noarbe 2016), yields a = 4.0 and b = 18. This optimization was performed taking into account the trade-off between number density and photometric redshift accuracy, propagating this to its impact in terms of cosmological constraints obtained from galaxy clustering and galaxy–galaxy lensing in Porredon et al. (2021). Effectively this selects brighter galaxies at low redshift while including fainter galaxies as redshift increases. Additionally, we apply a lower cut to remove the most luminous objects, i > 17.5. Single-object fitting (SOF) magnitudes [a variant of multi-object fitting (MOF) described in Drlica-Wagner et al. 2018] from the Y3 Gold Catalog were used for sample selection and as input to the photometric redshift codes. See also Porredon et al. (2021) for more details on this sample. The redshift distributions of the maglim sample are shown in Fig. 3.
4.3 Source galaxies
We use the DES Y3 shear catalogue presented in Gatti et al. (2020). The galaxy shapes are estimated using the metacalibration (Huff & Mandelbaum 2017; Sheldon & Huff 2017) algorithm. The shear catalogue has been thoroughly tested in Gatti et al. (2020), and tests specifically tailored for tangential shear have been presented in Prat et al. (2021). In this paper, we perform additional tests on this shear catalogue for tangential shear measurement on small scales (Section 5.3).
Following Prat et al. (2021), we bin the source galaxies into four redshift bins, where details of the redshift binning and calibration is described in Myles et al. (2020). The redshift distributions for the source samples are shown in Fig. 3.
5 MEASUREMENTS
Our γt measurements are carried out using the fast tree code treecorr3 (Jarvis, Bernstein & Jain 2004). We use the same measurement pipeline as that used in Prat et al. (2021), where details of the estimator, including the implementation of random-subtraction and metacalibration are described therein. The main difference is we extend to smaller scales and add 10 additional logarithmic bins from 0.25 to 2.5 arcmin. The full data vector in our analysis contains 30 logarithmic bins from 0.25 to 250 arcmin.
Figs 4 and 5 show the final measurements using the redmagic and maglim samples as lenses, respectively. The six panels represent the six lens-source redshift bin pairs. The total signal-to-noise ratio for the six redshift bins [Lens, Source] = {[1, 3], [1, 4], [2, 3], [2, 4], [3, 4], [4, 4]} are ∼{65.5, 59.9, 58.2, 65.5, 55.2, 36.6} for redmagic and ∼{104.4, 100.9, 76.6, 99.2, 60.5, 45.5} for maglim numbers. For comparison, the signal-to-noise ratio for the same bin pairs, only accounting for the scales used in the cosmological analysis in Prat et al. (2021) are ∼{25.1, 26.8, 18.7, 22.1, 18.5, 12.3} for the redmagic sample, and ∼{41.2, 35.9, 29.4, 30.4, 21.1, 15.7} for the maglim galaxies. The additional small-scale information from this work increases the signal-to-noise ratio by a factor of 2–3. This again demonstrates that if modelled properly, there is significant statistical power in this data to be harnessed.
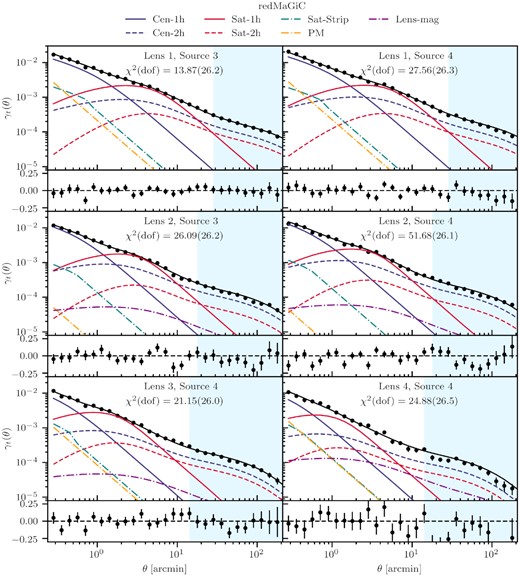
The best-fitting model (solid black) to redmagic for each lens-source redshift bin combination and the residuals with respect to the data (points) attached below each panel. The various components of the model are also shown: central one-halo (solid blue) and two-halo (dashed blue), satellite one-halo (solid red) and two-halo (dashed red), satellite strip (dash–dotted orange), PM (dash–dotted cyan), and lens magnification (dash–dotted green). The blue shaded area marks the scales used in cosmological analyses, while the rest corresponds to the additional small-scale points used in this work. In each panel, we also show the total χ2 of the fit, after applying the Hartlap correction to the inverse covariance matrix, and the number of degrees of freedom.
5.1 Boost factors
While computing the lensing signal, we need to take into account that, since galaxies follow a distribution in redshift namely nℓ(zℓ) and ns(zs) for lenses and sources, respectively, their spatial distributions may overlap. This is something that is naturally accounted for in equation (17) as the lensing efficiency is set to zero when the source is in front of the lens. However, by using fixed nℓ(zℓ) and ns(zs) in equation (16), we implicitly assume there is no spatial variation in the lens and source redshift distribution across the footprint. In reality, galaxies are clustered, and the number of sources around a lens can be larger than what we would expect from a uniform distribution. This is usually quantified by the boost factor (Sheldon et al. 2004), B(θ), estimator which is the excess in the number of sources around a lens with respect to randoms. The difference in our γt measurements with and without boost factors are shown in Figs B1 and B2 (for the full figures, with all lens-source bin combinations, see Prat et al. 2021). As can be seen from the plots, the contribution from this effect can be large at small scales, especially when the bins are more overlapped in redshift. In our analysis, we take the boost factors into account by correcting for it before carrying out the model fit. That is, the measurements shown in Figs 4 and 5 have already been corrected for the boost factor. In addition, since large boost factors will also signal potential failures in parts of our modelling (specifically IA and magnification), we choose to work only with bins that have small boost factors, for which we set a maximum threshold of |${\sim}20{{\ \rm per\ cent}}$| deviation from unity, that result in lens and source redshift bin combinations that are largely separated in redshift. We carry out our analysis with six lens-source pairs for both lens samples: [Lens 1, Source 3], [Lens 1, Source 4], [Lens 2, Source 3], [Lens 2, Source 4], [Lens 3, Source 4], [Lens 4, Source 4].
5.2 Covariance matrix
We use NJK = 150 JK patches for this work defined via the kmeans4 algorithm. NJK is chosen so that the individual JK regions are at least as large as the maximum angular scale we need for our measurements. See Prat et al. (2021) for a comparison between the JK diagonal errors and the halo-model covariance errors, which are in good agreement.
We finally discuss our choice of a JK covariance matrix in this work. The fiducial covariance used in the 3 × 2pt analysis in DES Y3 is derived from an analytic halo-model formulation presented in Friedrich et al. (2020). Since our halo model implementation is different from that work (e.g. the modelling of the one- to two-halo regime and the HOD parametrization), we cannot use the same framework. Furthermore, since our goal is to model very small scales, where the HOD is needed to model the galaxy bias, using as input to the covariance calculation the HOD would lead to a circular process. Therefore, we opt to use the JK covariance which is not relying on halo-model assumptions.
5.3 Systematics diagnostic tests
Similar to Prat et al. (2021), we carry out a series of data-level tests to check for any systematic contamination in the data products. As this work extends from Prat et al. (2021) in terms of the scales used for the analysis, we extend the following tests to the 0.25–2.5 arcmin scales. The tests we performed are the following
Cross component: The tangential shear, γt, is one of the two components when we decompose a spin-2 shear field. The other component is γ×, which is defined by the projection of the field on to a coordinate system which is rotated by 45° relative to the tangential frame. For isotropically oriented lenses, the average of γ× due to gravitational lensing alone should be zero. It is, thus, a useful test to measure this component in the data and make sure that it is consistent with zero for all angular scales. To be able to decide whether this is the case, we report the total χ2 calculated for γ× when compared with the null signal.
Responses: In this work, to measure the shear, we make use of the metacalibration algorithm (Sheldon & Huff 2017; Zuntz et al. 2018). Based on this, a small known shear is applied to the images and then the galaxy ellipticities |$\mathbf {e}$| are re-measure on the sheared images to calculate the response of the estimator to shear. This can be done on every galaxy, and the average response over all galaxies is |$\langle \mathbf {R}_\gamma \rangle$|. Then, the average shear is |$\langle \gamma _t \rangle = \langle \mathbf {R}_\gamma \rangle ^{-1} \langle \mathbf {e} \rangle$|. Moreover, the metacalibration framework allows us to also correct for selection responses, |$\langle \mathbf {R}_S \rangle$|, produced due to selection effects (e.g. by applying redshift cuts). The final response would then be the sum of the two effects, |$\langle \mathbf {R} \rangle = \langle \mathbf {R}_\gamma \rangle + \langle \mathbf {R}_S \rangle$|. In practice, this procedure can be performed in an exact, scale-dependent way or be approximated by an average scale-independent response, 〈Rγ〉. In this test, we show that this approximation is sufficiently good by comparing the measured shear derived from both of these methods.
LSS weights: Photometric surveys are subject to galaxy density variations throughout the survey footprint due to time-dependent observing conditions. This variation in the density of the lenses must be accounted for by applying the LSS-weights, which removes this dependence on observing conditions, such as exposure time and air-mass. In galaxy–galaxy lensing, since it is a cross-correlation probe, the impact of observing conditions is small compared to e.g. galaxy clustering. Therefore, in this test, we compare the shear measurements with and without the application of the LSS-weighting scheme and report the difference between the two.
We show in Appendix B the results of these tests, where we do not find significant signs of systematic effects in our data vector.
6 MODEL FITTING
In this section, we discuss how we have performed the fitting of the HOD model introduced in Section 2 to our data. We have five HOD parameters (Mmin , σlog M, fcen, M1, α), two parameters that correspond to the additional contributions to lensing from point-mass (M⋆) and the different satellite spatial distribution compared to that of the dark matter (a = csat/cdm), and three parameters to account for systematic uncertainties (|$\Delta z_\ell ^i$|, |$\Delta z_s^i$|, mi). For the maglim sample, we have additional parameters (|$\Sigma _\ell ^i$|) that correspond to the stretching factors of the lens redshift distributions, which are further discussed in Porredon et al. (2021).
Our priors on these parameters are shown in Table 1. We will discuss in Section 7 the effects of these priors and whether they are appropriate in fitting all redshift bins. The choice of priors on the HOD parameters was based on previous works on red galaxies (Brown et al. 2008; White et al. 2011; Rykoff et al. 2014, 2016), and is similar to the priors in Clampitt et al. (2017) but modified to better suit our HOD parametrization. As for the Δzi and mi parameters, our Gaussian priors on them are the same as in Myles et al. (2020) and in MacCrann et al. (2020b). The priors we apply on M⋆ and a = csat/cgm are derived from our tests in Section 7.3.3.
Priors on model and uncertainty parameters. If the prior is flat, we present its range, while for Gaussian priors, we list the mean and variance.
| Parameter . | Prior (redmagic) . | Prior (maglim) . |
|---|---|---|
| log (Mmin /M⊙) | |$\mathcal {U}[11, 13]$| | |$\mathcal {U}[11, 12.5]$| |
| log (M1/M⊙) | |$\mathcal {U}[12, 14.5]$| | |$\mathcal {U}[11.5, 14]$| |
| σlog M | |$\mathcal {U}[0.01, 0.5]$| | |$\mathcal {U}[0.01, 0.5]$| |
| fcen | |$\mathcal {U}[0.0, 0.3]$| | – |
| α | |$\mathcal {U}[0.8, 3]$| | |$\mathcal {U}[0.1, 2.5]$| |
| log (M⋆/M⊙) | |$\mathcal {U}[9, 12]$| | |$\mathcal {U}[9, 12]$| |
| a = csat/cdm | |$\mathcal {U}[0.1, 1.1]$| | |$\mathcal {U}[0.1, 1.1]$| |
| |$\Delta z_\ell ^1$| | |$\mathcal {N}(0.006, 0.004)$| | |$\mathcal {N}(-0.009, 0.007)$| |
| |$\Delta z_\ell ^2$| | |$\mathcal {N}(0.001, 0.003)$| | |$\mathcal {N}(-0.035, 0.011)$| |
| |$\Delta z_\ell ^3$| | |$\mathcal {N}(0.004, 0.003)$| | |$\mathcal {N}(-0.005, 0.006)$| |
| |$\Delta z_\ell ^4$| | |$\mathcal {N}(-0.002, 0.005)$| | |$\mathcal {N}(-0.007, 0.006)$| |
| |$\Delta z_s^3$| | |$\mathcal {N}(0.0, 0.006)$| | |$\mathcal {N}(0.0, 0.006)$| |
| |$\Delta z_s^4$| | |$\mathcal {N}(0.0, 0.013)$| | |$\mathcal {N}(0.0, 0.013)$| |
| m3 | |$\mathcal {N}(-0.0255, 0.0085)$| | |$\mathcal {N}(-0.0255, 0.0085)$| |
| m4 | |$\mathcal {N}(-0.0322, 0.0118)$| | |$\mathcal {N}(-0.0322, 0.0118)$| |
| |$\Sigma _\ell ^1$| | – | |$\mathcal {N}(0.975, 0.062)$| |
| |$\Sigma _\ell ^2$| | – | |$\mathcal {N}(1.306, 0.093)$| |
| |$\Sigma _\ell ^3$| | – | |$\mathcal {N}(0.870, 0.054)$| |
| |$\Sigma _\ell ^4$| | – | |$\mathcal {N}(0.918, 0.051)$| |
| αsat | |$\mathcal {U}[0,0.2]$| | – |
| Parameter . | Prior (redmagic) . | Prior (maglim) . |
|---|---|---|
| log (Mmin /M⊙) | |$\mathcal {U}[11, 13]$| | |$\mathcal {U}[11, 12.5]$| |
| log (M1/M⊙) | |$\mathcal {U}[12, 14.5]$| | |$\mathcal {U}[11.5, 14]$| |
| σlog M | |$\mathcal {U}[0.01, 0.5]$| | |$\mathcal {U}[0.01, 0.5]$| |
| fcen | |$\mathcal {U}[0.0, 0.3]$| | – |
| α | |$\mathcal {U}[0.8, 3]$| | |$\mathcal {U}[0.1, 2.5]$| |
| log (M⋆/M⊙) | |$\mathcal {U}[9, 12]$| | |$\mathcal {U}[9, 12]$| |
| a = csat/cdm | |$\mathcal {U}[0.1, 1.1]$| | |$\mathcal {U}[0.1, 1.1]$| |
| |$\Delta z_\ell ^1$| | |$\mathcal {N}(0.006, 0.004)$| | |$\mathcal {N}(-0.009, 0.007)$| |
| |$\Delta z_\ell ^2$| | |$\mathcal {N}(0.001, 0.003)$| | |$\mathcal {N}(-0.035, 0.011)$| |
| |$\Delta z_\ell ^3$| | |$\mathcal {N}(0.004, 0.003)$| | |$\mathcal {N}(-0.005, 0.006)$| |
| |$\Delta z_\ell ^4$| | |$\mathcal {N}(-0.002, 0.005)$| | |$\mathcal {N}(-0.007, 0.006)$| |
| |$\Delta z_s^3$| | |$\mathcal {N}(0.0, 0.006)$| | |$\mathcal {N}(0.0, 0.006)$| |
| |$\Delta z_s^4$| | |$\mathcal {N}(0.0, 0.013)$| | |$\mathcal {N}(0.0, 0.013)$| |
| m3 | |$\mathcal {N}(-0.0255, 0.0085)$| | |$\mathcal {N}(-0.0255, 0.0085)$| |
| m4 | |$\mathcal {N}(-0.0322, 0.0118)$| | |$\mathcal {N}(-0.0322, 0.0118)$| |
| |$\Sigma _\ell ^1$| | – | |$\mathcal {N}(0.975, 0.062)$| |
| |$\Sigma _\ell ^2$| | – | |$\mathcal {N}(1.306, 0.093)$| |
| |$\Sigma _\ell ^3$| | – | |$\mathcal {N}(0.870, 0.054)$| |
| |$\Sigma _\ell ^4$| | – | |$\mathcal {N}(0.918, 0.051)$| |
| αsat | |$\mathcal {U}[0,0.2]$| | – |
Priors on model and uncertainty parameters. If the prior is flat, we present its range, while for Gaussian priors, we list the mean and variance.
| Parameter . | Prior (redmagic) . | Prior (maglim) . |
|---|---|---|
| log (Mmin /M⊙) | |$\mathcal {U}[11, 13]$| | |$\mathcal {U}[11, 12.5]$| |
| log (M1/M⊙) | |$\mathcal {U}[12, 14.5]$| | |$\mathcal {U}[11.5, 14]$| |
| σlog M | |$\mathcal {U}[0.01, 0.5]$| | |$\mathcal {U}[0.01, 0.5]$| |
| fcen | |$\mathcal {U}[0.0, 0.3]$| | – |
| α | |$\mathcal {U}[0.8, 3]$| | |$\mathcal {U}[0.1, 2.5]$| |
| log (M⋆/M⊙) | |$\mathcal {U}[9, 12]$| | |$\mathcal {U}[9, 12]$| |
| a = csat/cdm | |$\mathcal {U}[0.1, 1.1]$| | |$\mathcal {U}[0.1, 1.1]$| |
| |$\Delta z_\ell ^1$| | |$\mathcal {N}(0.006, 0.004)$| | |$\mathcal {N}(-0.009, 0.007)$| |
| |$\Delta z_\ell ^2$| | |$\mathcal {N}(0.001, 0.003)$| | |$\mathcal {N}(-0.035, 0.011)$| |
| |$\Delta z_\ell ^3$| | |$\mathcal {N}(0.004, 0.003)$| | |$\mathcal {N}(-0.005, 0.006)$| |
| |$\Delta z_\ell ^4$| | |$\mathcal {N}(-0.002, 0.005)$| | |$\mathcal {N}(-0.007, 0.006)$| |
| |$\Delta z_s^3$| | |$\mathcal {N}(0.0, 0.006)$| | |$\mathcal {N}(0.0, 0.006)$| |
| |$\Delta z_s^4$| | |$\mathcal {N}(0.0, 0.013)$| | |$\mathcal {N}(0.0, 0.013)$| |
| m3 | |$\mathcal {N}(-0.0255, 0.0085)$| | |$\mathcal {N}(-0.0255, 0.0085)$| |
| m4 | |$\mathcal {N}(-0.0322, 0.0118)$| | |$\mathcal {N}(-0.0322, 0.0118)$| |
| |$\Sigma _\ell ^1$| | – | |$\mathcal {N}(0.975, 0.062)$| |
| |$\Sigma _\ell ^2$| | – | |$\mathcal {N}(1.306, 0.093)$| |
| |$\Sigma _\ell ^3$| | – | |$\mathcal {N}(0.870, 0.054)$| |
| |$\Sigma _\ell ^4$| | – | |$\mathcal {N}(0.918, 0.051)$| |
| αsat | |$\mathcal {U}[0,0.2]$| | – |
| Parameter . | Prior (redmagic) . | Prior (maglim) . |
|---|---|---|
| log (Mmin /M⊙) | |$\mathcal {U}[11, 13]$| | |$\mathcal {U}[11, 12.5]$| |
| log (M1/M⊙) | |$\mathcal {U}[12, 14.5]$| | |$\mathcal {U}[11.5, 14]$| |
| σlog M | |$\mathcal {U}[0.01, 0.5]$| | |$\mathcal {U}[0.01, 0.5]$| |
| fcen | |$\mathcal {U}[0.0, 0.3]$| | – |
| α | |$\mathcal {U}[0.8, 3]$| | |$\mathcal {U}[0.1, 2.5]$| |
| log (M⋆/M⊙) | |$\mathcal {U}[9, 12]$| | |$\mathcal {U}[9, 12]$| |
| a = csat/cdm | |$\mathcal {U}[0.1, 1.1]$| | |$\mathcal {U}[0.1, 1.1]$| |
| |$\Delta z_\ell ^1$| | |$\mathcal {N}(0.006, 0.004)$| | |$\mathcal {N}(-0.009, 0.007)$| |
| |$\Delta z_\ell ^2$| | |$\mathcal {N}(0.001, 0.003)$| | |$\mathcal {N}(-0.035, 0.011)$| |
| |$\Delta z_\ell ^3$| | |$\mathcal {N}(0.004, 0.003)$| | |$\mathcal {N}(-0.005, 0.006)$| |
| |$\Delta z_\ell ^4$| | |$\mathcal {N}(-0.002, 0.005)$| | |$\mathcal {N}(-0.007, 0.006)$| |
| |$\Delta z_s^3$| | |$\mathcal {N}(0.0, 0.006)$| | |$\mathcal {N}(0.0, 0.006)$| |
| |$\Delta z_s^4$| | |$\mathcal {N}(0.0, 0.013)$| | |$\mathcal {N}(0.0, 0.013)$| |
| m3 | |$\mathcal {N}(-0.0255, 0.0085)$| | |$\mathcal {N}(-0.0255, 0.0085)$| |
| m4 | |$\mathcal {N}(-0.0322, 0.0118)$| | |$\mathcal {N}(-0.0322, 0.0118)$| |
| |$\Sigma _\ell ^1$| | – | |$\mathcal {N}(0.975, 0.062)$| |
| |$\Sigma _\ell ^2$| | – | |$\mathcal {N}(1.306, 0.093)$| |
| |$\Sigma _\ell ^3$| | – | |$\mathcal {N}(0.870, 0.054)$| |
| |$\Sigma _\ell ^4$| | – | |$\mathcal {N}(0.918, 0.051)$| |
| αsat | |$\mathcal {U}[0,0.2]$| | – |
Our full data vector for the redmagic sample consists of the γt measurements to which we append the additional data point |$\bar{n}_g^i$|, the average number density of galaxies in each lens redshift bin i, as mentioned in Section 4.1. As we discuss in Section 7.1, the addition of this information helps control some of the model parameter constraints. To account for this in the covariance, we formed the full covariance matrix of our data vector by appending to |$\mathcal {C}_{ij}$| the variance of |$\bar{n}_g^i$| on the diagonal, with zero off-diagonal entries. Our usage of |$\bar{n}_g^i$| effectively serves as a prior in our fits. We note here that we do not add |$\bar{n}_g^i$| in the data vector of maglim, as we discuss in Section 7.1.
Finally, for reasons we will discuss in more detail in Section 7.1, we apply a prior on the satellite fraction specifically in the highest-redshift bin we fit, namely [Lens 4, Source 4], for the redmagic sample. In summary, this prior is based on the observation that most of the galaxies in that redshift range are expected to be central and thus we choose to use the flat prior range [0,0.2] for αsat. Note that a similar approach is adopted in van Uitert et al. (2011) (see Appendix C therein) and Velander et al. (2013) for high-redshift red galaxies.
7 RESULTS
In this section, we present the results from our analysis.6 Before unblinding, we performed several validation tests of our pipeline using simulations and simulated data vectors. After the tests were successfully passed, and after unblinding of the data, we applied our full methodology to the unblind measurements to derive our main results. We first present in Section 7.1 the model fits to the data and the parameter constraints. We then show in Section 7.2 several derived quantities from our model fits: the average halo mass, galaxy bias, and satellite fraction for our samples. We compare these quantities with literature as well as estimations using only the large, cosmological scales. Finally in Section 7.3, we perform a series of tests to demonstrate the robustness of our results to various analysis choices.
7.1 Model fits
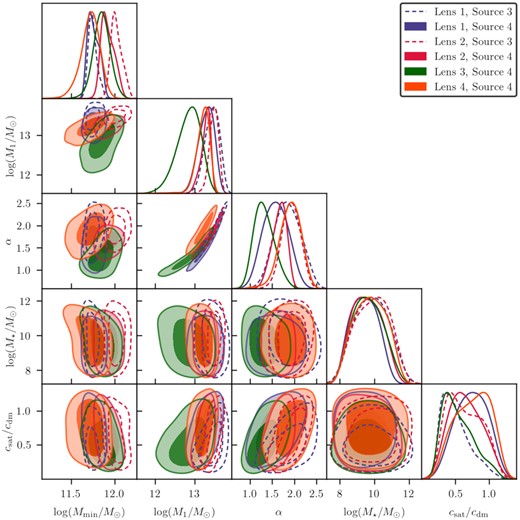
Best-fitting models for all the lens-source redshift bin combinations for the redmagic and maglim lens samples are shown in Figs 4 and 5, respectively, with the χ2 of the fits and the corresponding number of dof listed on the plots. We show the decomposition of the different components that contribute to the final model as described in Section 3. The parameter constraints are shown in Figs 6 and 7, respectively. These plots only show the parameters that are constrained by the data. The best-fitting parameters are listed in Tables D1 and D2.
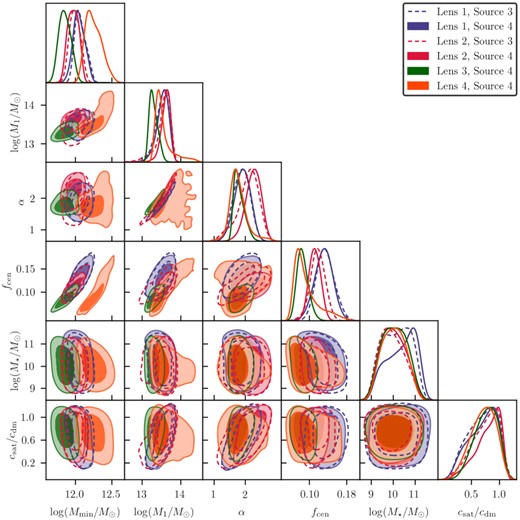
Parameter constraints for redmagic using the fiducial cosmology. Combinations with the same lens bin but different source bins are presented with the same colours (solid versus dashed).
Statistical analysis summary of the chains for Y3 unblind redmagic data (30 data points) using the fiducial cosmology; the average halo masses shown here use the 200ρm-based definition. The error bars correspond to the 1σ posteriors.
| redmagic . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Redshift bin . | log (Mmin /M⊙) . | log (M1/M⊙) . | σlog M . | α . | fcen . | log (M⋆/M⊙) . | csat/cdm . | log (Mh/M⊙) . | |$\bar{b}_{\rm gal}$| . | αsat . |
| Lens 1 | |$11.97^{+0.08}_{-0.07}$| | |$13.51^{+0.16}_{-0.17}$| | |$0.26^{+0.15}_{-0.15}$| | |$1.88^{+0.26}_{-0.27}$| | |$0.12^{+0.02}_{-0.02}$| | |$11.18^{+0.74}_{-0.75}$| | |$1.09^{+0.28}_{-0.29}$| | |$13.66^{+0.06}_{-0.06}$| | |$1.73^{+0.03}_{-0.03}$| | |$0.16^{+0.05}_{-0.05}$| |
| Source 3 | ||||||||||
| Lens 1 | |$12.13^{+0.09}_{-0.08}$| | |$13.64^{+0.16}_{-0.15}$| | |$0.50^{+0.15}_{-0.16}$| | |$2.06^{+0.26}_{-0.25}$| | |$0.13^{+0.02}_{-0.02}$| | |$11.09^{+0.70}_{-0.79}$| | |$0.99^{+0.27}_{-0.29}$| | |$13.67^{+0.06}_{-0.05}$| | |$1.71^{+0.03}_{-0.04}$| | |$0.13^{+0.04}_{-0.04}$| |
| Source 4 | ||||||||||
| Lens 2 | |$12.03^{+0.08}_{-0.08}$| | |$13.79^{+0.17}_{-0.16}$| | |$0.34^{+0.14}_{-0.16}$| | |$2.61^{+0.34}_{-0.33}$| | |$0.13^{+0.02}_{-0.02}$| | |$9.77^{+0.63}_{-0.61}$| | |$1.08^{+0.25}_{-0.26}$| | |$13.59^{+0.07}_{-0.07}$| | |$1.83^{+0.03}_{-0.03}$| | |$0.08^{+0.03}_{-0.04}$| |
| Source 3 | ||||||||||
| Lens 2 | |$12.08^{+0.08}_{-0.08}$| | |$13.73^{+0.12}_{-0.11}$| | |$0.49^{+0.14}_{-0.16}$| | |$2.48^{+0.25}_{-0.25}$| | |$0.13^{+0.01}_{-0.01}$| | |$9.48^{+0.64}_{-0.62}$| | |$1.08^{+0.22}_{-0.23}$| | |$13.59^{+0.05}_{-0.05}$| | |$1.81^{+0.03}_{-0.03}$| | |$0.09^{+0.02}_{-0.02}$| |
| Source 4 | ||||||||||
| Lens 3 | |$11.86^{+0.09}_{-0.08}$| | |$13.18^{+0.12}_{-0.11}$| | |$0.42^{+0.14}_{-0.15}$| | |$1.65^{+0.18}_{-0.17}$| | |$0.08^{+0.01}_{-0.01}$| | |$10.92^{+0.62}_{-0.62}$| | |$0.65^{+0.22}_{-0.21}$| | |$13.36^{+0.04}_{-0.04}$| | |$1.86^{+0.03}_{-0.03}$| | |$0.18^{+0.03}_{-0.03}$| |
| Source 4 | ||||||||||
| Lens 4 | |$12.16^{+0.12}_{-0.11}$| | |$13.26^{+0.19}_{-0.19}$| | |$0.46^{+0.12}_{-0.13}$| | |$1.59^{+0.24}_{-0.24}$| | |$0.06^{+0.03}_{-0.02}$| | |$11.01^{+0.58}_{-0.59}$| | |$0.71^{+0.24}_{-0.23}$| | |$13.27^{+0.09}_{-0.07}$| | |$2.12^{+0.06}_{-0.06}$| | |$0.19^{+0.06}_{-0.06}$| |
| Source 4 | ||||||||||
| redmagic . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Redshift bin . | log (Mmin /M⊙) . | log (M1/M⊙) . | σlog M . | α . | fcen . | log (M⋆/M⊙) . | csat/cdm . | log (Mh/M⊙) . | |$\bar{b}_{\rm gal}$| . | αsat . |
| Lens 1 | |$11.97^{+0.08}_{-0.07}$| | |$13.51^{+0.16}_{-0.17}$| | |$0.26^{+0.15}_{-0.15}$| | |$1.88^{+0.26}_{-0.27}$| | |$0.12^{+0.02}_{-0.02}$| | |$11.18^{+0.74}_{-0.75}$| | |$1.09^{+0.28}_{-0.29}$| | |$13.66^{+0.06}_{-0.06}$| | |$1.73^{+0.03}_{-0.03}$| | |$0.16^{+0.05}_{-0.05}$| |
| Source 3 | ||||||||||
| Lens 1 | |$12.13^{+0.09}_{-0.08}$| | |$13.64^{+0.16}_{-0.15}$| | |$0.50^{+0.15}_{-0.16}$| | |$2.06^{+0.26}_{-0.25}$| | |$0.13^{+0.02}_{-0.02}$| | |$11.09^{+0.70}_{-0.79}$| | |$0.99^{+0.27}_{-0.29}$| | |$13.67^{+0.06}_{-0.05}$| | |$1.71^{+0.03}_{-0.04}$| | |$0.13^{+0.04}_{-0.04}$| |
| Source 4 | ||||||||||
| Lens 2 | |$12.03^{+0.08}_{-0.08}$| | |$13.79^{+0.17}_{-0.16}$| | |$0.34^{+0.14}_{-0.16}$| | |$2.61^{+0.34}_{-0.33}$| | |$0.13^{+0.02}_{-0.02}$| | |$9.77^{+0.63}_{-0.61}$| | |$1.08^{+0.25}_{-0.26}$| | |$13.59^{+0.07}_{-0.07}$| | |$1.83^{+0.03}_{-0.03}$| | |$0.08^{+0.03}_{-0.04}$| |
| Source 3 | ||||||||||
| Lens 2 | |$12.08^{+0.08}_{-0.08}$| | |$13.73^{+0.12}_{-0.11}$| | |$0.49^{+0.14}_{-0.16}$| | |$2.48^{+0.25}_{-0.25}$| | |$0.13^{+0.01}_{-0.01}$| | |$9.48^{+0.64}_{-0.62}$| | |$1.08^{+0.22}_{-0.23}$| | |$13.59^{+0.05}_{-0.05}$| | |$1.81^{+0.03}_{-0.03}$| | |$0.09^{+0.02}_{-0.02}$| |
| Source 4 | ||||||||||
| Lens 3 | |$11.86^{+0.09}_{-0.08}$| | |$13.18^{+0.12}_{-0.11}$| | |$0.42^{+0.14}_{-0.15}$| | |$1.65^{+0.18}_{-0.17}$| | |$0.08^{+0.01}_{-0.01}$| | |$10.92^{+0.62}_{-0.62}$| | |$0.65^{+0.22}_{-0.21}$| | |$13.36^{+0.04}_{-0.04}$| | |$1.86^{+0.03}_{-0.03}$| | |$0.18^{+0.03}_{-0.03}$| |
| Source 4 | ||||||||||
| Lens 4 | |$12.16^{+0.12}_{-0.11}$| | |$13.26^{+0.19}_{-0.19}$| | |$0.46^{+0.12}_{-0.13}$| | |$1.59^{+0.24}_{-0.24}$| | |$0.06^{+0.03}_{-0.02}$| | |$11.01^{+0.58}_{-0.59}$| | |$0.71^{+0.24}_{-0.23}$| | |$13.27^{+0.09}_{-0.07}$| | |$2.12^{+0.06}_{-0.06}$| | |$0.19^{+0.06}_{-0.06}$| |
| Source 4 | ||||||||||
Statistical analysis summary of the chains for Y3 unblind redmagic data (30 data points) using the fiducial cosmology; the average halo masses shown here use the 200ρm-based definition. The error bars correspond to the 1σ posteriors.
| redmagic . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Redshift bin . | log (Mmin /M⊙) . | log (M1/M⊙) . | σlog M . | α . | fcen . | log (M⋆/M⊙) . | csat/cdm . | log (Mh/M⊙) . | |$\bar{b}_{\rm gal}$| . | αsat . |
| Lens 1 | |$11.97^{+0.08}_{-0.07}$| | |$13.51^{+0.16}_{-0.17}$| | |$0.26^{+0.15}_{-0.15}$| | |$1.88^{+0.26}_{-0.27}$| | |$0.12^{+0.02}_{-0.02}$| | |$11.18^{+0.74}_{-0.75}$| | |$1.09^{+0.28}_{-0.29}$| | |$13.66^{+0.06}_{-0.06}$| | |$1.73^{+0.03}_{-0.03}$| | |$0.16^{+0.05}_{-0.05}$| |
| Source 3 | ||||||||||
| Lens 1 | |$12.13^{+0.09}_{-0.08}$| | |$13.64^{+0.16}_{-0.15}$| | |$0.50^{+0.15}_{-0.16}$| | |$2.06^{+0.26}_{-0.25}$| | |$0.13^{+0.02}_{-0.02}$| | |$11.09^{+0.70}_{-0.79}$| | |$0.99^{+0.27}_{-0.29}$| | |$13.67^{+0.06}_{-0.05}$| | |$1.71^{+0.03}_{-0.04}$| | |$0.13^{+0.04}_{-0.04}$| |
| Source 4 | ||||||||||
| Lens 2 | |$12.03^{+0.08}_{-0.08}$| | |$13.79^{+0.17}_{-0.16}$| | |$0.34^{+0.14}_{-0.16}$| | |$2.61^{+0.34}_{-0.33}$| | |$0.13^{+0.02}_{-0.02}$| | |$9.77^{+0.63}_{-0.61}$| | |$1.08^{+0.25}_{-0.26}$| | |$13.59^{+0.07}_{-0.07}$| | |$1.83^{+0.03}_{-0.03}$| | |$0.08^{+0.03}_{-0.04}$| |
| Source 3 | ||||||||||
| Lens 2 | |$12.08^{+0.08}_{-0.08}$| | |$13.73^{+0.12}_{-0.11}$| | |$0.49^{+0.14}_{-0.16}$| | |$2.48^{+0.25}_{-0.25}$| | |$0.13^{+0.01}_{-0.01}$| | |$9.48^{+0.64}_{-0.62}$| | |$1.08^{+0.22}_{-0.23}$| | |$13.59^{+0.05}_{-0.05}$| | |$1.81^{+0.03}_{-0.03}$| | |$0.09^{+0.02}_{-0.02}$| |
| Source 4 | ||||||||||
| Lens 3 | |$11.86^{+0.09}_{-0.08}$| | |$13.18^{+0.12}_{-0.11}$| | |$0.42^{+0.14}_{-0.15}$| | |$1.65^{+0.18}_{-0.17}$| | |$0.08^{+0.01}_{-0.01}$| | |$10.92^{+0.62}_{-0.62}$| | |$0.65^{+0.22}_{-0.21}$| | |$13.36^{+0.04}_{-0.04}$| | |$1.86^{+0.03}_{-0.03}$| | |$0.18^{+0.03}_{-0.03}$| |
| Source 4 | ||||||||||
| Lens 4 | |$12.16^{+0.12}_{-0.11}$| | |$13.26^{+0.19}_{-0.19}$| | |$0.46^{+0.12}_{-0.13}$| | |$1.59^{+0.24}_{-0.24}$| | |$0.06^{+0.03}_{-0.02}$| | |$11.01^{+0.58}_{-0.59}$| | |$0.71^{+0.24}_{-0.23}$| | |$13.27^{+0.09}_{-0.07}$| | |$2.12^{+0.06}_{-0.06}$| | |$0.19^{+0.06}_{-0.06}$| |
| Source 4 | ||||||||||
| redmagic . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Redshift bin . | log (Mmin /M⊙) . | log (M1/M⊙) . | σlog M . | α . | fcen . | log (M⋆/M⊙) . | csat/cdm . | log (Mh/M⊙) . | |$\bar{b}_{\rm gal}$| . | αsat . |
| Lens 1 | |$11.97^{+0.08}_{-0.07}$| | |$13.51^{+0.16}_{-0.17}$| | |$0.26^{+0.15}_{-0.15}$| | |$1.88^{+0.26}_{-0.27}$| | |$0.12^{+0.02}_{-0.02}$| | |$11.18^{+0.74}_{-0.75}$| | |$1.09^{+0.28}_{-0.29}$| | |$13.66^{+0.06}_{-0.06}$| | |$1.73^{+0.03}_{-0.03}$| | |$0.16^{+0.05}_{-0.05}$| |
| Source 3 | ||||||||||
| Lens 1 | |$12.13^{+0.09}_{-0.08}$| | |$13.64^{+0.16}_{-0.15}$| | |$0.50^{+0.15}_{-0.16}$| | |$2.06^{+0.26}_{-0.25}$| | |$0.13^{+0.02}_{-0.02}$| | |$11.09^{+0.70}_{-0.79}$| | |$0.99^{+0.27}_{-0.29}$| | |$13.67^{+0.06}_{-0.05}$| | |$1.71^{+0.03}_{-0.04}$| | |$0.13^{+0.04}_{-0.04}$| |
| Source 4 | ||||||||||
| Lens 2 | |$12.03^{+0.08}_{-0.08}$| | |$13.79^{+0.17}_{-0.16}$| | |$0.34^{+0.14}_{-0.16}$| | |$2.61^{+0.34}_{-0.33}$| | |$0.13^{+0.02}_{-0.02}$| | |$9.77^{+0.63}_{-0.61}$| | |$1.08^{+0.25}_{-0.26}$| | |$13.59^{+0.07}_{-0.07}$| | |$1.83^{+0.03}_{-0.03}$| | |$0.08^{+0.03}_{-0.04}$| |
| Source 3 | ||||||||||
| Lens 2 | |$12.08^{+0.08}_{-0.08}$| | |$13.73^{+0.12}_{-0.11}$| | |$0.49^{+0.14}_{-0.16}$| | |$2.48^{+0.25}_{-0.25}$| | |$0.13^{+0.01}_{-0.01}$| | |$9.48^{+0.64}_{-0.62}$| | |$1.08^{+0.22}_{-0.23}$| | |$13.59^{+0.05}_{-0.05}$| | |$1.81^{+0.03}_{-0.03}$| | |$0.09^{+0.02}_{-0.02}$| |
| Source 4 | ||||||||||
| Lens 3 | |$11.86^{+0.09}_{-0.08}$| | |$13.18^{+0.12}_{-0.11}$| | |$0.42^{+0.14}_{-0.15}$| | |$1.65^{+0.18}_{-0.17}$| | |$0.08^{+0.01}_{-0.01}$| | |$10.92^{+0.62}_{-0.62}$| | |$0.65^{+0.22}_{-0.21}$| | |$13.36^{+0.04}_{-0.04}$| | |$1.86^{+0.03}_{-0.03}$| | |$0.18^{+0.03}_{-0.03}$| |
| Source 4 | ||||||||||
| Lens 4 | |$12.16^{+0.12}_{-0.11}$| | |$13.26^{+0.19}_{-0.19}$| | |$0.46^{+0.12}_{-0.13}$| | |$1.59^{+0.24}_{-0.24}$| | |$0.06^{+0.03}_{-0.02}$| | |$11.01^{+0.58}_{-0.59}$| | |$0.71^{+0.24}_{-0.23}$| | |$13.27^{+0.09}_{-0.07}$| | |$2.12^{+0.06}_{-0.06}$| | |$0.19^{+0.06}_{-0.06}$| |
| Source 4 | ||||||||||
| maglim . | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Redshift bin . | log (Mmin /M⊙) . | log (M1/M⊙) . | σlog M . | α . | log (M⋆/M⊙) . | csat/cdm . | log (Mh/M⊙) . | |$\bar{b}_{\rm gal}$| . | αsat . |
| Lens 1 | |$11.74^{+0.05}_{-0.05}$| | |$13.32^{+0.19}_{-0.20}$| | |$0.27^{+0.12}_{-0.12}$| | |$1.66^{+0.31}_{-0.30}$| | |$11.26^{+1.09}_{-1.10}$| | |$0.41^{+0.23}_{-0.22}$| | |$13.44^{+0.07}_{-0.07}$| | |$1.57^{+0.03}_{-0.03}$| | |$0.14^{+0.04}_{-0.04}$| |
| Source 3 | |||||||||
| Lens 1 | |$11.76^{+0.08}_{-0.07}$| | |$13.41^{+0.20}_{-0.21}$| | |$0.29^{+0.15}_{-0.15}$| | |$1.74^{+0.30}_{-0.31}$| | |$9.38^{+0.86}_{-0.89}$| | |$0.76^{+0.27}_{-0.27}$| | |$13.43^{+0.09}_{-0.10}$| | |$1.54^{+0.03}_{-0.03}$| | |$0.12^{+0.06}_{-0.05}$| |
| Source 4 | |||||||||
| Lens 2 | |$11.96^{+0.07}_{-0.06}$| | |$13.44^{+0.12}_{-0.11}$| | |$0.26^{+0.14}_{-0.14}$| | |$1.82^{+0.22}_{-0.21}$| | |$10.83^{+1.08}_{-1.12}$| | |$0.63^{+0.30}_{-0.28}$| | |$13.46^{+0.04}_{-0.04}$| | |$1.84^{+0.04}_{-0.04}$| | |$0.14^{+0.03}_{-0.03}$| |
| Source 3 | |||||||||
| Lens 2 | |$11.91^{+0.08}_{-0.07}$| | |$13.42^{+0.12}_{-0.13}$| | |$0.30^{+0.15}_{-0.15}$| | |$1.85^{+0.17}_{-0.18}$| | |$8.50^{+0.94}_{-0.94}$| | |$1.07^{+0.28}_{-0.26}$| | |$13.45^{+0.04}_{-0.04}$| | |$1.82^{+0.05}_{-0.04}$| | |$0.13^{+0.05}_{-0.04}$| |
| Source 4 | |||||||||
| Lens 3 | |$11.88^{+0.09}_{-0.09}$| | |$12.84^{+0.31}_{-0.30}$| | |$0.21^{+0.14}_{-0.14}$| | |$1.24^{+0.24}_{-0.23}$| | |$8.59^{+0.96}_{-0.96}$| | |$0.21^{+0.25}_{-0.24}$| | |$13.27^{+0.06}_{-0.05}$| | |$1.99^{+0.04}_{-0.04}$| | |$0.37^{+0.13}_{-0.13}$| |
| Source 4 | |||||||||
| Lens 4 | |$11.82^{+0.10}_{-0.10}$| | |$13.44^{+0.17}_{-0.15}$| | |$0.31^{+0.14}_{-0.15}$| | |$2.29^{+0.24}_{-0.24}$| | |$8.53^{+1.06}_{-1.04}$| | |$1.19^{+0.29}_{-0.31}$| | |$13.31^{+0.05}_{-0.05}$| | |$2.01^{+0.04}_{-0.05}$| | |$0.09^{+0.03}_{-0.04}$| |
| Source 4 | |||||||||
| maglim . | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Redshift bin . | log (Mmin /M⊙) . | log (M1/M⊙) . | σlog M . | α . | log (M⋆/M⊙) . | csat/cdm . | log (Mh/M⊙) . | |$\bar{b}_{\rm gal}$| . | αsat . |
| Lens 1 | |$11.74^{+0.05}_{-0.05}$| | |$13.32^{+0.19}_{-0.20}$| | |$0.27^{+0.12}_{-0.12}$| | |$1.66^{+0.31}_{-0.30}$| | |$11.26^{+1.09}_{-1.10}$| | |$0.41^{+0.23}_{-0.22}$| | |$13.44^{+0.07}_{-0.07}$| | |$1.57^{+0.03}_{-0.03}$| | |$0.14^{+0.04}_{-0.04}$| |
| Source 3 | |||||||||
| Lens 1 | |$11.76^{+0.08}_{-0.07}$| | |$13.41^{+0.20}_{-0.21}$| | |$0.29^{+0.15}_{-0.15}$| | |$1.74^{+0.30}_{-0.31}$| | |$9.38^{+0.86}_{-0.89}$| | |$0.76^{+0.27}_{-0.27}$| | |$13.43^{+0.09}_{-0.10}$| | |$1.54^{+0.03}_{-0.03}$| | |$0.12^{+0.06}_{-0.05}$| |
| Source 4 | |||||||||
| Lens 2 | |$11.96^{+0.07}_{-0.06}$| | |$13.44^{+0.12}_{-0.11}$| | |$0.26^{+0.14}_{-0.14}$| | |$1.82^{+0.22}_{-0.21}$| | |$10.83^{+1.08}_{-1.12}$| | |$0.63^{+0.30}_{-0.28}$| | |$13.46^{+0.04}_{-0.04}$| | |$1.84^{+0.04}_{-0.04}$| | |$0.14^{+0.03}_{-0.03}$| |
| Source 3 | |||||||||
| Lens 2 | |$11.91^{+0.08}_{-0.07}$| | |$13.42^{+0.12}_{-0.13}$| | |$0.30^{+0.15}_{-0.15}$| | |$1.85^{+0.17}_{-0.18}$| | |$8.50^{+0.94}_{-0.94}$| | |$1.07^{+0.28}_{-0.26}$| | |$13.45^{+0.04}_{-0.04}$| | |$1.82^{+0.05}_{-0.04}$| | |$0.13^{+0.05}_{-0.04}$| |
| Source 4 | |||||||||
| Lens 3 | |$11.88^{+0.09}_{-0.09}$| | |$12.84^{+0.31}_{-0.30}$| | |$0.21^{+0.14}_{-0.14}$| | |$1.24^{+0.24}_{-0.23}$| | |$8.59^{+0.96}_{-0.96}$| | |$0.21^{+0.25}_{-0.24}$| | |$13.27^{+0.06}_{-0.05}$| | |$1.99^{+0.04}_{-0.04}$| | |$0.37^{+0.13}_{-0.13}$| |
| Source 4 | |||||||||
| Lens 4 | |$11.82^{+0.10}_{-0.10}$| | |$13.44^{+0.17}_{-0.15}$| | |$0.31^{+0.14}_{-0.15}$| | |$2.29^{+0.24}_{-0.24}$| | |$8.53^{+1.06}_{-1.04}$| | |$1.19^{+0.29}_{-0.31}$| | |$13.31^{+0.05}_{-0.05}$| | |$2.01^{+0.04}_{-0.05}$| | |$0.09^{+0.03}_{-0.04}$| |
| Source 4 | |||||||||
| maglim . | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Redshift bin . | log (Mmin /M⊙) . | log (M1/M⊙) . | σlog M . | α . | log (M⋆/M⊙) . | csat/cdm . | log (Mh/M⊙) . | |$\bar{b}_{\rm gal}$| . | αsat . |
| Lens 1 | |$11.74^{+0.05}_{-0.05}$| | |$13.32^{+0.19}_{-0.20}$| | |$0.27^{+0.12}_{-0.12}$| | |$1.66^{+0.31}_{-0.30}$| | |$11.26^{+1.09}_{-1.10}$| | |$0.41^{+0.23}_{-0.22}$| | |$13.44^{+0.07}_{-0.07}$| | |$1.57^{+0.03}_{-0.03}$| | |$0.14^{+0.04}_{-0.04}$| |
| Source 3 | |||||||||
| Lens 1 | |$11.76^{+0.08}_{-0.07}$| | |$13.41^{+0.20}_{-0.21}$| | |$0.29^{+0.15}_{-0.15}$| | |$1.74^{+0.30}_{-0.31}$| | |$9.38^{+0.86}_{-0.89}$| | |$0.76^{+0.27}_{-0.27}$| | |$13.43^{+0.09}_{-0.10}$| | |$1.54^{+0.03}_{-0.03}$| | |$0.12^{+0.06}_{-0.05}$| |
| Source 4 | |||||||||
| Lens 2 | |$11.96^{+0.07}_{-0.06}$| | |$13.44^{+0.12}_{-0.11}$| | |$0.26^{+0.14}_{-0.14}$| | |$1.82^{+0.22}_{-0.21}$| | |$10.83^{+1.08}_{-1.12}$| | |$0.63^{+0.30}_{-0.28}$| | |$13.46^{+0.04}_{-0.04}$| | |$1.84^{+0.04}_{-0.04}$| | |$0.14^{+0.03}_{-0.03}$| |
| Source 3 | |||||||||
| Lens 2 | |$11.91^{+0.08}_{-0.07}$| | |$13.42^{+0.12}_{-0.13}$| | |$0.30^{+0.15}_{-0.15}$| | |$1.85^{+0.17}_{-0.18}$| | |$8.50^{+0.94}_{-0.94}$| | |$1.07^{+0.28}_{-0.26}$| | |$13.45^{+0.04}_{-0.04}$| | |$1.82^{+0.05}_{-0.04}$| | |$0.13^{+0.05}_{-0.04}$| |
| Source 4 | |||||||||
| Lens 3 | |$11.88^{+0.09}_{-0.09}$| | |$12.84^{+0.31}_{-0.30}$| | |$0.21^{+0.14}_{-0.14}$| | |$1.24^{+0.24}_{-0.23}$| | |$8.59^{+0.96}_{-0.96}$| | |$0.21^{+0.25}_{-0.24}$| | |$13.27^{+0.06}_{-0.05}$| | |$1.99^{+0.04}_{-0.04}$| | |$0.37^{+0.13}_{-0.13}$| |
| Source 4 | |||||||||
| Lens 4 | |$11.82^{+0.10}_{-0.10}$| | |$13.44^{+0.17}_{-0.15}$| | |$0.31^{+0.14}_{-0.15}$| | |$2.29^{+0.24}_{-0.24}$| | |$8.53^{+1.06}_{-1.04}$| | |$1.19^{+0.29}_{-0.31}$| | |$13.31^{+0.05}_{-0.05}$| | |$2.01^{+0.04}_{-0.05}$| | |$0.09^{+0.03}_{-0.04}$| |
| Source 4 | |||||||||
| maglim . | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Redshift bin . | log (Mmin /M⊙) . | log (M1/M⊙) . | σlog M . | α . | log (M⋆/M⊙) . | csat/cdm . | log (Mh/M⊙) . | |$\bar{b}_{\rm gal}$| . | αsat . |
| Lens 1 | |$11.74^{+0.05}_{-0.05}$| | |$13.32^{+0.19}_{-0.20}$| | |$0.27^{+0.12}_{-0.12}$| | |$1.66^{+0.31}_{-0.30}$| | |$11.26^{+1.09}_{-1.10}$| | |$0.41^{+0.23}_{-0.22}$| | |$13.44^{+0.07}_{-0.07}$| | |$1.57^{+0.03}_{-0.03}$| | |$0.14^{+0.04}_{-0.04}$| |
| Source 3 | |||||||||
| Lens 1 | |$11.76^{+0.08}_{-0.07}$| | |$13.41^{+0.20}_{-0.21}$| | |$0.29^{+0.15}_{-0.15}$| | |$1.74^{+0.30}_{-0.31}$| | |$9.38^{+0.86}_{-0.89}$| | |$0.76^{+0.27}_{-0.27}$| | |$13.43^{+0.09}_{-0.10}$| | |$1.54^{+0.03}_{-0.03}$| | |$0.12^{+0.06}_{-0.05}$| |
| Source 4 | |||||||||
| Lens 2 | |$11.96^{+0.07}_{-0.06}$| | |$13.44^{+0.12}_{-0.11}$| | |$0.26^{+0.14}_{-0.14}$| | |$1.82^{+0.22}_{-0.21}$| | |$10.83^{+1.08}_{-1.12}$| | |$0.63^{+0.30}_{-0.28}$| | |$13.46^{+0.04}_{-0.04}$| | |$1.84^{+0.04}_{-0.04}$| | |$0.14^{+0.03}_{-0.03}$| |
| Source 3 | |||||||||
| Lens 2 | |$11.91^{+0.08}_{-0.07}$| | |$13.42^{+0.12}_{-0.13}$| | |$0.30^{+0.15}_{-0.15}$| | |$1.85^{+0.17}_{-0.18}$| | |$8.50^{+0.94}_{-0.94}$| | |$1.07^{+0.28}_{-0.26}$| | |$13.45^{+0.04}_{-0.04}$| | |$1.82^{+0.05}_{-0.04}$| | |$0.13^{+0.05}_{-0.04}$| |
| Source 4 | |||||||||
| Lens 3 | |$11.88^{+0.09}_{-0.09}$| | |$12.84^{+0.31}_{-0.30}$| | |$0.21^{+0.14}_{-0.14}$| | |$1.24^{+0.24}_{-0.23}$| | |$8.59^{+0.96}_{-0.96}$| | |$0.21^{+0.25}_{-0.24}$| | |$13.27^{+0.06}_{-0.05}$| | |$1.99^{+0.04}_{-0.04}$| | |$0.37^{+0.13}_{-0.13}$| |
| Source 4 | |||||||||
| Lens 4 | |$11.82^{+0.10}_{-0.10}$| | |$13.44^{+0.17}_{-0.15}$| | |$0.31^{+0.14}_{-0.15}$| | |$2.29^{+0.24}_{-0.24}$| | |$8.53^{+1.06}_{-1.04}$| | |$1.19^{+0.29}_{-0.31}$| | |$13.31^{+0.05}_{-0.05}$| | |$2.01^{+0.04}_{-0.05}$| | |$0.09^{+0.03}_{-0.04}$| |
| Source 4 | |||||||||
From Figs 4 and 5, we observe that our model generally describes the data well between the measured scales of 0.25–250 arcmin. The χ2 per dof is close to 1 for most bins, with the largest value ∼2 for redmagic bin [Lens 2, Source 4] and maglim bin [Lens 1, Source 4], and the smallest value ∼0.5 for redmagic bin [Lens 2, Source 3]. We do not consider this very problematic given that there is no apparent trends in the model residuals and that these data sets are much more constraining compared to previous work. Nevertheless, the slightly high χ2 values could motivate additional modelling improvements beyond this work. We also note that not all the components in our model are contributing significantly to the fit. For a detailed discussion on how different components contribute to the model, see Section 7.3.4.
From Figs 6 and 7, we observe that the mass parameters Mmin and M1 are well-constrained, with Mmin for the fourth redmagic bin being higher than the first three as a result of the luminosity threshold being higher in that redshift bin. The satellite power-law index parameter α is also constrained mainly by the inclusion of small scales (see discussion in Section 7.3.2). The tight degeneracy between M1 and α is expected to be based on equation (2), since a higher normalization M1 requires a larger α to keep αsat the same and vice versa. The point-mass parameter, M⋆, is not constrained, which means that it is not needed to improve the χ2 of the fits. This implies that our current model for the mass distribution below the scales we measure (∼0.25 arcmin) is not significantly different from what the data prefers.
As a side note, we have found that the inclusion of |$\bar{n}_g^i$| values in the redmagic data vector (see Section 6) constrains the fcen parameter to low values, which indicates that the model prefers a significant number of centrals not being included in our redmagic lens sample by the selection algorithm. Without this additional information, fcen is not constrained.7 On the other hand, for maglim since fcen = 1, we do not see this effect and there is no need to incorporate |$\bar{n}_g^i$| into the data vector of that sample.
7.2 Halo properties
Figs 8 and 9 show the average halo mass (top panel), the average linear galaxy bias (middle panel), and the satellite fraction (bottom panel) for the redmagic and maglim lens samples in the four redshift bins. The points represent the best-fitting maximum posterior and the error bars represent the |$68{{\ \rm per\ cent}}$| confidence intervals from the MCMC chain. To derive these constraints, we calculate equations (31), (7), and (9) at each step of our chains to build the distributions of these three quantities and then estimate the reported constraints.
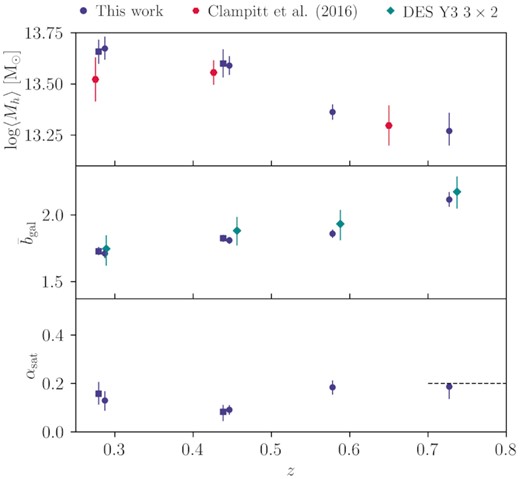
Redshift evolution of redmagic properties. Bin combinations with the same lenses but different sources are shown in different markers (square for source bin 3 and circle for source bin 4) and a small offset of 0.005 between the two has been applied in the horizontal axis to make the plot easier to read. As we discuss in Section 3, these results assume the de-correlation parameter Xlens = 1. Top panel: The average halo mass, compared with results from Clampitt et al. (2017) (red pentagon). Middle panel: The average galaxy bias, compared to constraints from DES Collaboration et al. (2021) (cyan diamond). Bottom panel: the average satellite fraction; the dashed horizontal line shows the prior on αsat applied to the last redshift bin.
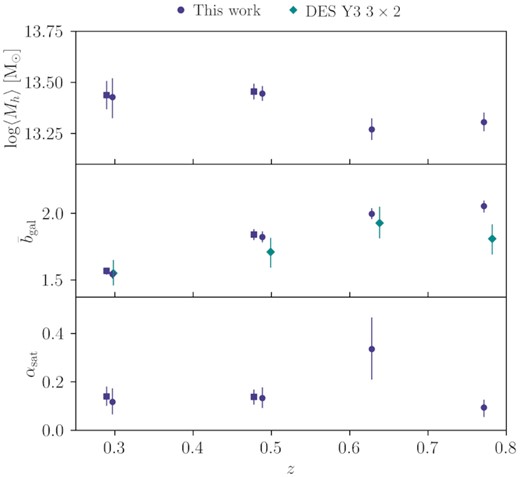
We first focus on redmagic. For the average halo mass, we compare our results with that derived in the DES Science Verification (SV) data in Clampitt et al. (2017). The SV sample is broadly similar to the first three lens bins in terms of the luminosity selection and number density. Note, however, that there are some differences in the lens samples between SV and our three lower redshift bins. In particular, the photometry pipeline and the redmagic code have both been updated since SV, and the redshift bins are not identical. With these differences in mind, our results appear broadly consistent with Clampitt et al. (2017) in the HOD-inferred halo mass, with roughly ∼2 times tighter error bars on average. We point out, however, that due to adding more free parameters to our model compared to Clampitt et al. (2017), our error bars should not be directly compared. Rather, we should take into account that our error bars would be roughly an additional factor of ∼1.5 tighter, had we considered the simplified model in Clampitt et al. (2017), as illustrated in Fig. E2.
The halo mass in the first three redshift bins appears to decrease with redshift. A big part of this is the pseudo-evolution of halo mass due to the mass definition we use. This effect is also mentioned in Clampitt et al. (2017) and is studied in Diemer, More & Kravtsov (2013). In short, since we use the critical (or mean in our plots and tables) density of the Universe at every redshift to define the halo mass, we observe a pseudo-evolution of our mass constraints over redshift as the reference density evolves. According to Diemer et al. (2013), from z ∼ 0.2 to ∼ 0.6 the pseudo-evolution of the 200ρm mass, namely M200m, corresponds to Δlog (M200m/M⊙) ∼ 0.11 for a halo of 200ρm mass ∼1013.8 M⊙ at z = 0. This can account for most of the difference between the first two bins and the third one. Therefore, we do not find significant change in mass beyond this pseudo-evolution. For the last redshift bin, in addition to the pseudo-evolution in mass, we note that the sample is more luminous (see Section 4.1) compared to the first three bins and thus we are looking at more massive haloes, which acts opposite to the trend from the pseudo-evolution. We point out here that the overall trend we observe in redshift for the mass is consistent with that seen in simulations (see Appendix A2). As a further test, we note that we have roughly calculated the ratio of halo mass to stellar mass for the redmagic sample and found it to be a few times 102. This result is reasonable for ∼3 × 1013 M⊙-mass galaxies, based on stellar-to-halo mass relation constraints (for a review, see Wechsler & Tinker 2018).
For the average galaxy bias, we first compare our results with constraints from large-scale cosmology for the same sample presented in DES Collaboration et al. (2021). The large-scale constraints come from combining galaxy–galaxy lensing and two other two-point functions (galaxy density–galaxy density correlation and shear–shear correlation) to form the so-called 3 × 2pt probes, so they are not expected to agree trivially. We find that the DES Y3 3 × 2pt constraints on galaxy bias is quite consistent with our HOD-inferred galaxy bias. The main additional information that our HOD analysis adds to the picture here is the small-scale information, which is consistent with the large-scale information in galaxy–galaxy lensing only (see cyan points in Fig. 8) – as we will show later in Section 7.3.2, most of the constraining power comes from the one-halo regime and our galaxy bias constraints does not change whether or not we include the large cosmological scales. The small-scale constraints are tighter than the large-scale only constraints by a factor of roughly 5. In particular, we note that the main improvement is not coming from the increased signal-to-noise ratio. Rather, it is the wealth of information in the one-halo regime that improves the constraints. The higher galaxy bias measured for the last redshift bin, compared to the first three bins, is mainly a result of the different selection criteria. We remind the reader here that the galaxies which form the last bin are selected using a higher luminosity threshold, as discussed in Section 4.1.
For the satellite fraction, we find that our redmagic sample prefers a low (∼0.2) satellite fraction in all redshift bins we consider. We note that this trend and the values appear quite different from that observed in the MICE simulations (see Appendix A2). They are, however, in good agreement with the high-resolution Buzzard simulations (discussed also in Appendix A2) which show an average satellite fraction of redmagic which is ∼0.2 in all three bins. When looking at a red galaxy sample that is likely to share characteristics with redmagic, Velander et al. (2013) constrained the satellite fraction to be small and decreasing with redshift to ∼0.2 or less, which broadly confirms that our constraints on the redmagic satellite fraction appear reasonable.
As we have discussed in Section 3, throughout our analysis, we assume the de-correlation parameter Xlens = 1. If we were to use the best-fitting value of Xlens ≈ 0.877 from the 3 × 2pt analysis with free Xlens, our constraints would change. Specifically, given that the galaxy–galaxy lensing signal’s amplitude, being multiplied by Xlens, would decrease, our bias constraints would increase by |${\sim}10{{\ \rm per\ cent}}$|. This would also increase the average lens halo mass by the same factor, and our satellite fractions would increase too as a result. Given our little understanding of what is causing the inconsistency between clustering and galaxy–galaxy lensing in redmagic, we choose to keep Xlens fixed to 1 and have these results being our fiducial. Further investigating this issue is out of the scope of this paper.
Next, we turn our attention to the maglim sample. By construction, the maglim sample is designed to be close to a luminosity-selected sample, while maximizing the cosmological constraints when using it as lenses in galaxy clustering and galaxy–galaxy lensing. Compared to redmagic, this sample does not include additional selection on colour or photometric redshift. On the other hand, since it is not exactly a luminosity selection, the physical interpretation of the redshift trends of this sample is not straightforward. There is also no previous literature for comparison.
As shown in Fig. 9, we find the average halo mass of the maglim sample to be on average lower than that of redmagic, with the lower two redshift bins appear more massive than the higher redshift bins by |${\sim}30{{\ \rm per\ cent}}$|. Contrary to intuition, the uncertainties on the halo masses are larger compared to redmagic even though the error bars on the measurements are ∼4 times smaller. This is because the priors in the nuisance parameters for maglim is larger than that of redmagic – this trend has also been seen in DES Collaboration et al. (2021). The galaxy bias appears quite similar to that of redmagic, with the first and last bins somewhat lower. Compared to the 3x2pt constraints we find overall good agreement with our results, with the last bin having a slightly higher bias in our HOD fits. Finally, we find the satellite fraction for the maglim sample to be ∼0.1−0.2 for all bins, except for the third one which is significantly higher at ∼0.35 and not as well-constrained.
Overall, we also observe that for bin combinations that share the same lens bin, the derived halo properties are consistent when using different source bins. This is assuring and a useful check that our model is indeed capturing properties of the lens samples instead of fitting systematic effects.
7.3 Robustness tests
In this section, we study the robustness of our results to a number of analysis choices: cosmology, scale cuts, parameter priors, and the addition of higher order model components. In particular, we are interested in how the average lens halo mass 〈Mh〉, average galaxy bias |$\bar{b}_{\rm gal}$|, and average satellite fraction αsat change under the different analysis choices. We show all the tests in this section for redmagic only, but we expect similar results with the maglim sample.
7.3.1 Robustness to cosmology
In this paper, we present our main results assuming a specific fixed cosmology, namely our fiducial cosmological values introduced in Section 3. We study here the sensitivity to this assumption. The top panel of Fig. 10 shows how our results change when two alternative assumptions for cosmology: (1) best-fitting ΛCDM parameters from Planck 2018 (Planck Collaboration VI 2020) and (2) freeing σ8.
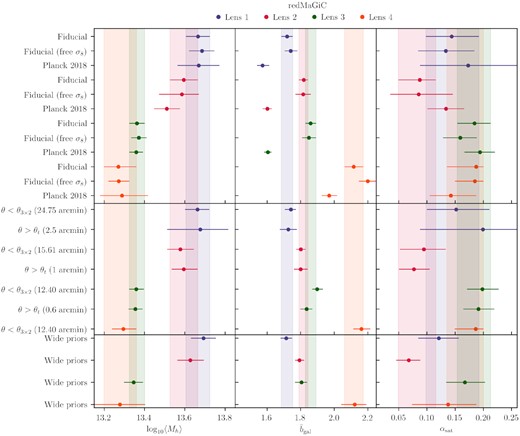
Testing the robustness of the halo properties for different cosmologies (upper panels), to applying angular scale cuts (middle panels), and to changing the prior range on our parameters (lower panels) on the redmagic sample. The vertical bands correspond to the fiducial constraints and we added them for an easier comparison with the rest of our results. Note that, to reduce the size of this figure, we have combined bins with the same lenses and different sources by presenting the mean of the best-fitting values and, to be conservative, the maximum of the error bars.
The average mass of redmagic galaxies and the fraction of satellite galaxies are robust to changing the cosmological parameters to Planck 2018. Given that these quantities are best constrained by the small-scale information (the points below the one-halo to two-halo transition), this implies that varying the cosmology, to a small degree with respect to our fiducial one, leaves the one-halo central model prediction almost unchanged. We remind the reader here that our fiducial cosmology is similar to Planck with the difference that σ8 we use is slightly lower and our Ωm is slightly higher compared to Planck. The average galaxy bias, on the other hand, is degenerate with σ8 on the large scales. This means that changing to the Planck 2018 cosmology directly changes the inferred galaxy bias as seen in Fig. 10 – using the Planck 2018 cosmology with a higher σ8 value results in lower values for the galaxy bias.
Next, we allow for σ8 to freely vary within the prior range [0.4,1.2], fixing all other cosmological parameters to our fiducial cosmology. Fig. 11 presents our results for the σ8 and galaxy bias constraints from this test for the redmagic galaxy sample. In addition, we have compared the average halo mass, galaxy bias, and satellite fraction from these chains in Fig. 10 to the fiducial results. As we can see, our constraints on σ8 from the first three lens bins recover the fiducial value of σ8 quite well. The last bin prefers a lower value of σ8, and a slightly higher galaxy bias – these are still consistent within 1σ though. Overall, the constraints on all these quantities remain consistent with our fiducial ones. We can, therefore, conclude that freeing the matter power spectrum’s amplitude does not alter our constraints in a meaningful way.
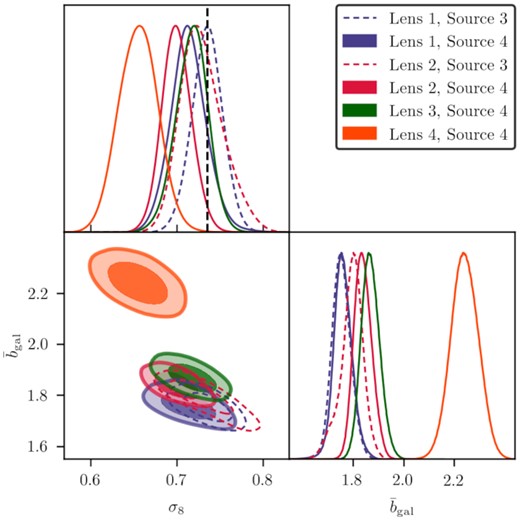
Robustness to freeing σ8 for redmagic galaxies. We present the joint constraints on σ8 and the derived average galaxy bias for all redshift bins we consider. The vertical dashed line shows the fixed value of σ8 used in our fiducial cosmology.
7.3.2 Angular scale cuts
Next, we study how removing data points on different scales from the fits affects our results. For these tests, we first cut out small scales by setting the minimum θ to the threshold values θt = {2.5, 1, 0.6, −} arcmin for each lens redshift bin, after which we find the data is not constraining enough and this leads to non-physical constraints and projection effects.8 This happens because using only the θ > θt scales in our fits, the total central component of γt, namely |$\gamma _t^{\rm cen}$|, becomes identical to |$\gamma _t^{\rm sat}$|, the total satellite term. These two are then identical to the total shear and therefore the fit cannot distinguish between the two. This means the satellite fraction cannot be determined accurately and the other two halo properties suffer too as a result.
To determine the maximum scale cut we can use in each redshift bin without being dominated by projection effects, we perform the following analysis using simulated data vectors.
The simulated data vectors are produced with our model using parameters that correspond to the best-fitting maximum posterior values from our fiducial runs on the redmagic data, as they are presented in Section 7.1. We first fit all angular scales and confirmed our pipeline can recover the input. Next, we remove data points from the smallest scales and repeat the fitting and analysis. We then compared both the constraints on the model parameters and the inferred halo properties from all these runs with different scale cuts. From this comparison, we were able to identify the scale cut with the maximum θmin which was still able to give us results consistent with the full-scale simulated-data runs. At high redshift, the threshold θ was found to be lower since the same angular scale corresponds to higher physical scale. This is especially evident in the last redshift bin where we cannot remove any of the scales since they are all needed to constrain the HOD parameters, and it even requires the additional prior on the satellite fraction, as discussed in Section 6, in order to keep αsat under control.
We also test the case where we remove scales used in the cosmological analysis, derived in Krause et al. (2021), which we refer to as cosmological scales and we denote by θ3 × 2. Since small scales are expected to provide most of the constraining power, we put that to test by comparing our constraints from fitting only the small scales, excluding the cosmology scales.
The middle panels of Fig. 10 present our results for the derived halo properties from applying the above angular scale cuts on redmagic data. For comparison, in the same plots, we have included the vertical bands that correspond to the fiducial chains which use the full range of angular scales. As we can see, using the scale cuts discussed above, all our results stay consistent with our fiducial constraints. In addition to this, we can see that the small scales-only fits are also consistent with all other points. Furthermore, these fits, despite using fewer points, can constrain all halo properties almost as well as the full-scale runs, showcasing the rich information contained in the small scales.
7.3.3 Effect of the priors
In our main analysis, we have performed various tests on how and whether the priors on our model parameters can have an impact on our results. Here, we demonstrate that our parameter priors are not too restrictive and informing the constrained parameters. For our tests in this section, we test the sensitivity of our results when we use roughly two times wider priors than that used in the fiducial analysis for all model parameters, keeping the prior centre the same.
The bottom row of panels of Fig. 10 shows the inferred halo property constraints with the widened priors compared to the fiducial, for the redmagic sample. We see that the derived parameters appear consistent. We note here, however, that during our tests, we found that small shifts in the best-fitting points can occur if the prior range changes or if it is kept the same but the sampler starts at a different position in parameter space. These effects are not significant, though, in our runs and thus our results stay robust, as discussed above.
7.3.4 Model complexity
In Section 3, we described the details of the various model components. In this section, we explain the process we have used to decide whether or not a component has been included in our fiducial model based on how each of them affects the fits and the inferred halo properties.
Our fiducial framework starts with the basic HOD modelling where γt is composed of the following four terms: the one-halo central and satellite contributions |$\gamma _t^{\rm c1h}$| and |$\gamma _t^{\rm s1h}$|, respectively, and their two-halo counterparts |$\gamma _t^{\rm c2h}$| and |$\gamma _t^{\rm s2h}$|. We will refer to the combination of these four components as the HOD-only model. As a first step we like to see if HOD-only can describe our data well. For the six bin combinations, we find that the HOD-only model achieves reduced χ2 of {0.585, 1.144, 1.019, 2.101, 0.879, 1.119}. These fits are already good, but there is room for improvement on bin [Lens 2, Source 4] which has noticeably the worst χ2. Our fiducial model improves the reduced χ2 over the HOD-only model by {0.055, 0.094, 0.023, 0.030, 0.066, 0.181} for redmagic.
The procedure we use to determine our fiducial framework is discussed in detail in Appendix E and goes as follows: Using the HOD-only model as a baseline, we systematically include additional components and test whether the fits to the data improve, by calculating and comparing the reduced χ2 of the corresponding data fits. In addition to a change in the reduced χ2, we also check in each case if the inferred halo properties change significantly as a result of adding a contribution to γt. This step is intended to check if omitting a term would introduce a bias in our constraints. Finally, we consider whether it makes physical sense to include a component. If a component is physically well-motivated, we may decide to keep it even if it does not significantly improve the fit. On the other hand, if a contribution is not well motivated and its modelling is uncertain, we may decide to discard it even if it makes a difference in the goodness-of-fit.
From Appendix E, we decide to include the following additional modelling components to γt from the HOD-only model: (1) Point-mass contribution; (2) Tidal stripping of the satellites; (3) A concentration parameter for the satellites which is different from that of the dark matter’s distribution; (4) Magnification of the lenses. This is the fiducial model which we used to derive the main results in Section 7.
As a further note, the particular choice of the HOD model itself is another aspect of the full model that can be much more complex than, or different from, what we used in this work as described in Section 2.1. To that end, we experimented with various treatments of the galaxy–halo connection and did not find that adding additional parameters to it or modifying its parametrization made a significant difference to our results. Specifically, we have tested the following modifications to our fiducial HOD. We modified the satellite HOD, 〈Ns(Mh)〉 of equation (2), by multiplying it by an exponential cutoff exp (Mh/Mcut), with mass cutoff Mcut, following, for example, Leauthaud et al. (2011) and Zu & Mandelbaum (2015) where the authors expanded the standard HOD to include the stellar mass function in a robust framework to study the galaxy–halo connection. Another similar variance of the HOD model we tested was to modify the satellite terms by replacing (Mh/M1)α by [(Mh − M0)/M1]α, as in Guo et al. (2016) for instance where the HOD was compared to subhalo matching in order to determine which describes better the clustering statistics in SDSS DR7, where we introduce the additional mass cutoff parameter M0, setting 〈Ns(Mh)〉 to zero if Mh/M0 < 1. We, furthermore, tested altering the satellite term by not multiplying 〈Ns(Mh)〉 by fcen, considering this parameter only through 〈Ns(Mh)〉, as in Clampitt et al. (2017). Finally, we modified our model by decoupling the satellites from the central galaxies, setting 〈Ns(Mh)〉 = (Mh/M1)α, thus not multiplying the satellite term by the number of central galaxies. These variants of the HOD framework we tested did not significantly alter our results.
We also compare our HOD modelling choices to previous literature. For instance, Clampitt et al. (2017), which performed an HOD study on redmagic galaxies from the DES SV data, used a basic HOD model that was sufficient to fit their data, given that their statistical uncertainties were much larger compared to this work and the range of scales used was narrower. In another study, Velander et al. (2013) used 154 deg2 of CFHTLenS lensing data, splitting galaxies into blue and red, and considered a more complex model where they included the effects from baryons as a point-mass source and satellite stripping, similarly to our work, although they did not use the full five-parameter HOD model we employ here but rather one similar to Mandelbaum et al. (2005) that fixes the satellite power-law index. Therefore, compared to both Velander et al. (2013) and Clampitt et al. (2017), we have used a more complex model which, although increased our error bars on the parameter constrains, was required to capture the features of our more constraining data. In addition to that, we have taken into account systematic uncertainties by introducing the Δzi and mi parameters (discussed in Section 6) which further increased our error bars.
8 SUMMARY AND DISCUSSION
In this work, we have carried out a detailed analysis on modelling the small-scale galaxy–galaxy lensing measurements for the two lens samples redmagic and maglim using an HOD framework. Our lens samples were divided into four tomographic bins each spanning a redshift range about 0.2–0.9. In this work, we have extended the measurements in Prat et al. (2021) to smaller scales, totalling 30 logarithmic bins in angular scales from 0.25 to 250 arcmin (physical scales from ∼70 kpc in the lowest redshift bin to ∼110 Mpc in the highest redshift bin). Our main findings are as follows:
These measurements increase the signal-to-noise ratio of our measurements by a factor of 2–3 compared to the signal-to-noise ratio from scales used by cosmology analyses.
We constrain the average halo mass of our redmagic (maglim) sample to ∼1013.6 M⊙ (1013.4 M⊙) in the lowest redshift bin and ∼1013.3 M⊙ (1013.3 M⊙) at the highest redshift bin. The uncertainty on these mass constraints are about |${\sim}15{{\ \rm per\ cent}}$|. The redmagic constraints are consistent with previous work in Clampitt et al. (2017). The halo masses of maglim are overall lower compared to redmagic, especially at lower redshift.
We constrain the average linear galaxy bias for the redmagic (maglim) sample to be ∼1.7 (1.5) at low redshift and ∼2.1 (2) at high redshift. Our results are consistent with those inferred only from the large scales from DES Collaboration et al. (2021), but with about five times smaller uncertainties due to the small-scale information.
We constrain the satellite fraction for the redmagic (maglim) sample to be 0.1−0.2 (0.1−0.3) with no clear redshift trend. Our redmagic results appear to be in agreement with other studies which measured the satellite fraction of red galaxies, e.g. in Velander et al. (2013). Our results for maglim, which consists of a more wide variety of galaxies than redmagic, also appear reasonable and in agreement with studies like Mandelbaum et al. (2006b), Coupon et al. (2012), and Velander et al. (2013). In these studies, the authors concluded that the fraction of satellite galaxies is reducing with increasing halo mass and that αsat is roughly what our constraints point to.
Motivated by the increased signal-to-noise ratio, we consider additional model complexity on top of the basic HOD framework: a point-mass component, stripping of the satellites of their outer dark matter, magnification of the lenses, and modifying the spatial distribution of the satellite galaxies by varying its concentration parameter with respect to the distribution of dark matter in the lens haloes. Using this model, we were able to obtain good fits to the measurements over all angular scales and for all redshift bins we considered. We note that two out of twelve bin combinations show a best-fitting χ2 per dof ∼ 2, which could motivate additional modelling developments for the future, or indicate some residual systematic effect that is not well-understood.
To further test our analysis, we have performed various tests where we vary parts of our modelling and fitting procedure to make sure that our results remain robust under small changes around the fiducial framework. We tested the sensitivity of our results to the assumption of cosmology, the angular scales used in the model fit, and the width of our priors – we find that our results are robust to these changes.
There are a number of limitations in our analyses that we point out here for the readers to appropriately interpret our findings. First, in Appendix A2, we showed a series of tests that we performed using available simulations. However, the resolution of these simulations were insufficient for us to conclusively validate our model and methodology on scales deep in the one-halo regime. That is, it is plausible that our fiducial model, although well-fitted to the data, is not the true description of the galaxy–halo connection. Higher resolution simulations exist (Illustris TNG; Nelson et al. 2019), but the simulation volume is much smaller and to exactly match our sample, we would require running the redmapper algorithm on the simulations. We point these out both as caveats for interpreting our results and as inspirations for future studies. The second element that would benefit from future advances is the modelling of the covariance matrix. An analytic covariance model on this large range of scales is possible to calculate, but there are differences in the halo-model assumptions and HOD parametrization between the existing covariance modelling (Friedrich et al. 2020) and our assumptions. Furthermore, we would need to find a sophisticated way of treating the HOD in the analytic covariance calculations, given that the HOD is what we are constraining in our analysis and we, thus, should avoid the resulting circularity. As a result, we have adopted a data-based JK covariance, which has its own issues of being noisy and often overestimated (Friedrich et al. 2016). This is an area of active research and it would be interesting for future studies to re-analyse this data using a more advanced covariance model. Finally, as we mention in Section 3.6, in our analysis an accurate and tested model for IA is missing in the one-halo regime. Therefore, although we found that our simple IA model to contribute insignificantly in our analysis (see relevant discussion in Section 7.3.4), it is plausible that a more accurate IA model could have a larger effect on the full model fit. This again can serve as a starting point for exploration of better IA models in the one-halo regime, now that our data is becoming sufficiently constraining.
In this work, we established a framework to systematically explore a number of modelling choices in the galaxy–galaxy lensing signal from deep in the one-halo regime to the cosmological two-halo regime. Many of these effects were ignored in earlier work as the statistical uncertainties were large relative to these effect. In the final DES Y6 data set, we expect 1.5–2 times more source galaxies and a reach to higher redshift for the lens sample, which will allow us to further test the different model components. What we learn will feed into future analyses with the Rubin Observatory’s Legacy Survey of Space and Time, the Nancy Roman Space Telescope, and the ESA’s Euclid mission. We expect these future data sets to be qualitatively different in terms of data quantity and quality, and a combination of modelling techniques (HOD models like what we studied here, hydrodynamical simulations and emulator approaches) will be needed to understand how galaxies and dark matter haloes are connected at the very small scales.
ACKNOWLEDGEMENTS
CC is supported by the Henry Luce Foundation. JP is supported by DOE grant DE-SC0021429.
Funding for the DES Projects has been provided by the U.S. Department of Energy, the U.S. National Science Foundation, the Ministry of Science and Education of Spain, the Science and Technology Facilities Council of the United Kingdom, the Higher Education Funding Council for England, the National Center for Supercomputing Applications at the University of Illinois at Urbana-Champaign, the Kavli Institute of Cosmological Physics at the University of Chicago, the Center for Cosmology and Astro-Particle Physics at the Ohio State University, the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, Financiadora de Estudos e Projetos, Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro, Conselho Nacional de Desenvolvimento Científico e Tecnológico and the Ministério da Ciência, Tecnologia e Inovação, the Deutsche Forschungsgemeinschaft, and the Collaborating Institutions in the Dark Energy Survey.
The Collaborating Institutions are Argonne National Laboratory, the University of California at Santa Cruz, the University of Cambridge, Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas-Madrid, the University of Chicago, University College London, the DES-Brazil Consortium, the University of Edinburgh, the Eidgenössische Technische Hochschule (ETH) Zürich, Fermi National Accelerator Laboratory, the University of Illinois at Urbana-Champaign, the Institut de Ciències de l’Espai (IEEC/CSIC), the Institut de Física d’Altes Energies, Lawrence Berkeley National Laboratory, the Ludwig-Maximilians Universität München and the associated Excellence Cluster Universe, the University of Michigan, NFS’s NOIRLab, the University of Nottingham, The Ohio State University, the University of Pennsylvania, the University of Portsmouth, SLAC National Accelerator Laboratory, Stanford University, the University of Sussex, Texas A&M University, and the OzDES Membership Consortium.
Based in part on observations at Cerro Tololo Inter-American Observatory at NSF’s NOIRLab (NOIRLab Prop. ID 2012B-0001; PI: J. Frieman), which is managed by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation.
The DES data management system is supported by the National Science Foundation under grant numbers AST-1138766 and AST-1536171. The DES participants from Spanish institutions are partially supported by MICINN under grants ESP2017-89838, PGC2018-094773,PGC2018-102021, SEV-2016-0588, SEV-2016-0597, and MDM-2015-0509, some of which include ERDF funds from the European Union. IFAE is partially funded by the CERCA programme of the Generalitat de Catalunya. Research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Program (FP7/2007-2013) including ERC grant agreements 240672, 291329, and 306478. We acknowledge support from the Brazilian Instituto Nacional de Ciência e Tecnologia (INCT) do e-Universo (CNPq grant 465376/2014-2).
This manuscript has been authored by Fermi Research Alliance, LLC under Contract No. DE-AC02-07CH11359 with the U.S. Department of Energy, Office of Science, Office of High Energy Physics.
DATA AVAILABILITY
The data underlying this article are available on the Dark Energy Survey website at https://www.darkenergysurvey.org/the-des-project/data-access/.
Footnotes
Our model is slightly different from Clampitt et al. (2017) in that fcen is multiplied to both the centrals and the satellites. This choice results in better matching to the MICE simulations (see Appendix A2) and therefore facilitates our testing. Since fcen and M1 are fully degenerate, this difference does not alter the physical form of the model, although we have adjusted the prior ranges on M1 to account for that.
In what follows, we discuss our results after unblinding the data (see Muir et al. 2020 for details on the data blinding procedure).
To understand this, we need to look at equations (7) and (9) which define the average galaxy bias and satellite fraction, respectively. Since in our HOD parametrization both the expectation number for centrals and satellites (equations 1 and 2) are proportional to fcen, and since |$\bar{n}_g \propto f_{\rm cen}$| as well, fcen cancels out in |$\bar{b}_g$| and αsat. It is therefore only through |$\bar{n}_g$| that we can constrain fcen.
Projection effect here means that when we project a multidimensional parameter space to the one-dimensional posterior distributions sometimes the constraints could appear biased.
REFERENCES
APPENDIX A: MODEL VALIDATION
In this appendix, we present tests validating our modelling code using both external code and numerical simulations.
Comparison with DES cosmology pipeline
As part of validating our code, we have done thorough comparisons with cosmosis (Zuntz et al. 2015). cosmosis is the official code basis for DES cosmological analyses. As a result, it is important to establish consistency with cosmosis on the regimes used for cosmology analysis, effectively the two-halo regime. We compare the galaxy-cross-matter power spectrum Pgm, the projected lensing power spectrum Cgm, and the tangential shear γt. For this purpose, we used constant galaxy bias values within a redshift bin to match the predictions from cosmosis at large scales, θ ≳ 30 arcmin. In Fig. A1, we present the residuals between what our code produces and cosmosis. For our comparisons, we have used the same n(z) distributions and cosmological parameters in both cosmosis and our code. The parameter and bias values we used for this comparison are listed in the caption of Fig. A1. We note here that the cosmology, bias, and redshift distributions we used are not the same as what is used or derived from the main analysis of this work.
![cosmosis code comparison residuals for Cgm(ℓ) and γt(θ) for 6 bins of interest. The bias values per each of the four lens bins [1,2,3,4] are $\bar{b}_g = [1.2, 1.6, 1.7, 1.7]$, respectively. For the first panel, we have used the mean redshift of each lens redshift bin to calculate and compare the galaxy-matter cross power spectra. The other two panels show the projected power spectrum and tangential shear comparison for the average over the redshift distributions. These comparisons are done using the following parameters for a flat ΛCMD cosmology: Ωm = 0.25, Ωb = 0.044, σ8 = 0.8, n5 = 0.95, H0 = 70 km s–1Mpc–1 and Ων = 0. Furthermore, note that the redshift distributions, n(z), are not the same as what we used throughout this paper, but both our and the cosmosis results used the same n(z) for lenses and sources.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/509/3/10.1093_mnras_stab3155/1/m_stab3155figa1.jpeg?Expires=1750293645&Signature=Y9weMeSrLJfa~NE9xp4mcJiyhPDviAqGJPlDrkYp0DIvpEcghWhx6k~JuKoTVi4zD9CIeSszTLSl4CXQr6gBSOmt7MDSsVvUepAw4aWTQUB7UhxtBTyKlheBt5mwHdXx8kb0nPivacgeH6jhcGzOm8SYnQ6iZk-j7ycFp8o7gUaef9oq8foSSl-yzvWNNqnHXSz3~x63djWCtYmCZku3LAtS7fAPCQ5Lwmc6q8fDLXceAfq8hzf6aBknMeAWsJOQhgLx3Ebc3V7H1fA6C~UQ5pD9t~O405tf4KIwcCAIVjcqNcJvxb9VPbeX7teSQH2Gp9gN4BuKSUXJdP3QEtluMw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
cosmosis code comparison residuals for Cgm(ℓ) and γt(θ) for 6 bins of interest. The bias values per each of the four lens bins [1,2,3,4] are |$\bar{b}_g = [1.2, 1.6, 1.7, 1.7]$|, respectively. For the first panel, we have used the mean redshift of each lens redshift bin to calculate and compare the galaxy-matter cross power spectra. The other two panels show the projected power spectrum and tangential shear comparison for the average over the redshift distributions. These comparisons are done using the following parameters for a flat ΛCMD cosmology: Ωm = 0.25, Ωb = 0.044, σ8 = 0.8, n5 = 0.95, H0 = 70 km s–1Mpc–1 and Ων = 0. Furthermore, note that the redshift distributions, n(z), are not the same as what we used throughout this paper, but both our and the cosmosis results used the same n(z) for lenses and sources.
The first panel of Fig. A1 validates that our implementation of the Eisenstein & Hu (1998) fitting functions for the linear matter power spectrum and our usage of halofit to calculate the non-linear spectrum is in good agreement with the results from cosmosis which uses camb for the linear spectrum prediction and halofit to apply non-linear corrections to it. Going from Pgm to Cgm in the second panel, we are also testing whether our treatment of the redshift distributions in our averaging procedure works as expected. Finally, to translate Cgm into γt and thus go from the second to the third panel, we are confirming that our code is in agreement with cosmosis when transforming to real space. Note also that cosmosis is using the full-sky formalism to calculate the tangential shear, while we opt for the Hankel transform, i.e. flat-sky approximation, approach to gain in speed. However, for the angular scales we are interested in, we have tested both approaches to confirm that the flat-sky approximation is sufficient, which is what the last panel of Fig. A1 essentially demonstrates.
The upper and middle panels of Fig. A1 show that our galaxy-dark matter cross power spectrum and, as a result, the projected lensing power spectrum, respectively, appear to be systematically lower than the cosmosis output. We trace that to a difference in the matter power spectrum from the two codes, as we are utilizing the Eisenstein–Hu fitting functions to calculate the dark matter transfer function whereas cosmosis is calling camb to evolve the primordial spectrum. Moreover, the presence of baryonic acoustic oscillations complicate the spectrum and the residuals appear worse around the scales that correspond to these wiggles. In addition to that, the calculation of Cgm involves the multiplication of Pgm by geometrical factors (equation 14). cosmosis is using a constant value in each redshift bin for |$\Sigma _{\rm c}^{-1}$|, while we are calculating that quantity as a function of redshift within a given bin, which leads to more differences in the resulting lensing power spectra when averaging over the n(z) distributions. Overall, we find a non-significant |${\sim}2{{\ \rm per\ cent}}$| deviation in Cgm and we also find a good overall agreement to within |${\sim}2{{\ \rm per\ cent}}$| for the tangential shear outputs. In order to quantify the impact on our derived halo properties from using the EH98 functions instead of camb, we have produced a simulated data vector using camb which we then fitted with our fiducial model. From this test, we found that the galaxy bias is recovered to |${\sim}1{{\ \rm per\ cent}}$| accuracy, while the halo mass and satellite fraction is unchanged. To take this into account, we have incorporated this uncertainty into our error bars on the galaxy bias from our main analysis.
Validation against simulations
Although a full end-to-end simulation test is not possible due to the limitations of existing simulations (resolution in mass, spatial resolution in ray-tracing, galaxy selection, etc.), we can validate different components of our analysis pipeline with simulations to ensure robustness of our results.
First, we test whether our fiducial HOD model (equations 1 and 2) is sufficiently flexible to describe the underlying HOD of the lens galaxy sample. We note that this is not trivial especially for redmagic given the particular selection used in the algorithm (see Section 4.1). We check this by measuring the HOD from a set of high-resolution Buzzard mock galaxy catalogue (DeRose et al. 2019), and fit the HOD with our fiducial model. A redmagic sample is constructed from the mocks using the same algorithm as applied to data, and should capture qualitatively the characteristics of the redmagic sample. Fig. A2 shows the measurement from the mocks together with our fit using equations (1) and (2). We find that our model describes qualitatively the redmagic HOD well. The inferred satellite fraction from the fits to the Buzzard HOD is ∼0.2.
![Fits to the HOD measured from Buzzard high-resolution. Each panel corresponds to a different redshift bin. We fit the HOD directly using our model for central (magenta squares) and satellite (orange triangles) galaxies, as well as the total number of galaxies (blue points). The three panels, from top to bottom, correspond, respectively, to the following redshift bins: z ∈ [0.0, 0.32], [0.32,0.84], [0.84,2.35].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/509/3/10.1093_mnras_stab3155/1/m_stab3155figa2.jpeg?Expires=1750293645&Signature=TcL8kFsS7q~LSZbqQu1C1glVv1MHRdNtnQTA34JjMkuzEBvDQHBoX9cq6DsusI2nCX8-W6zPz4An3qqPywdmBiR9aw1OyQX1neqoCLOd0TbsncPb6mq5RiAx-rht4XG~F0HPj4V3fdvTk4cQSHHa-cUVm3M-6Fc9KnK839MbaCDTyT~9AAdyFCW~Uvzf41QvxkTOYg9WXlYgDwyRJvYJkbH9ZEOlNp8MVjB0f5J-zSCyTZzGdavplVSmJzVcPk608CmIIR-u2B3Ol80FMv0MZX45RaSRmgzeQ6l1OhlB-47CAjdrKBijB3XyTIy-Fm7ZogOFgaq9dzO1edyQtleCvA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Fits to the HOD measured from Buzzard high-resolution. Each panel corresponds to a different redshift bin. We fit the HOD directly using our model for central (magenta squares) and satellite (orange triangles) galaxies, as well as the total number of galaxies (blue points). The three panels, from top to bottom, correspond, respectively, to the following redshift bins: z ∈ [0.0, 0.32], [0.32,0.84], [0.84,2.35].
Next, we perform a series of tests with the mice simulations (Carretero et al. 2015; Crocce et al. 2015; Fosalba et al. 2015). The galaxies in the mice simulations are populated according to a given HOD. This makes a similar a priori test as what was described above for Buzzard slightly circular. We can, however, perform a number of other tests. First, for given HOD of galaxy samples, we check if our derived halo mass, galaxy bias, satellite fraction, and galaxy number density agrees with what is measured directly from the simulations. Fig. A3 shows these comparisons. As we can see, our calculations are in good agreement with the mice measurements, although they differ slightly. The trends followed by the points as a function of redshift, however, are always in very good agreement.
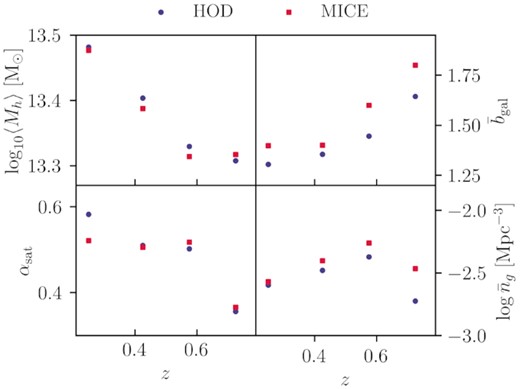
Comparison between average halo mass, galaxy bias, satellite fraction, and galaxy number density from our model prediction (blue points) and the corresponding measured quantities from MICE (orange squares) for the first four lens redshift bins. The HOD parameter vector (log10Mmin , log10M1, α, fcen, σlog M) used in the calculations are, for all four redshift bins, respectively, (12.38,12.61,0.73,0.18,0.5), (12.15,12.74,0.84,0.16,0.22), (12.16,12,72,0.85,0.17,0.27), (12.51,13.3,0.82,0.2,0.26).
Secondly, for given HOD parameters and redshift distributions, we can compare our model prediction for γt with the measurements from the mock galaxy catalogue. This is shown in Fig. A4 for six lens-source redshift bin combinations, as indicated in each panel. The large-scale measurements are generally in good agreement compared to the model prediction, especially for the higher lens redshifts. The small scales in each panel, however, are always in tension. Specifically, the measured γt is consistently lower than the model. Part of the explanation for this is the mass resolution in mice which limits what we can measure, thus leading to lower signal. This could also explain why the large-scale agreement is worse at the lowest redshift bin (Lens 1), since the same angular scale corresponds to smaller objects at low redshifts compared to higher redshifts. However, we do not expect this to be a big limitation in our case, given the big masses of redmagic galaxies. More importantly, the dominant factor of the small-scale disagreement is that, in mice, the galaxy positions do not correlate exactly with the underlying dark matter distribution. Instead, galaxies and dark matter trace each other on the mean, which could lead to small one-halo power spectrum, and thus |$\gamma _t^{\rm 1h}$| measurements. We have checked that the scales where we see the largest disagreement correspond to the one-halo regime in each redshift bin.
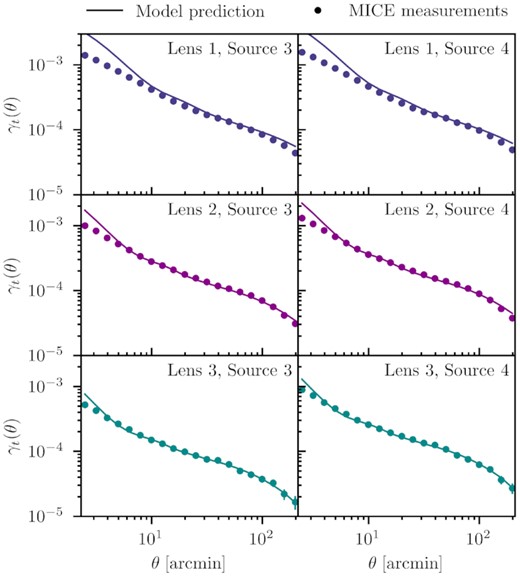
Comparison of the measured γt as a function of θ in MICE simulations (points) and our model prediction (lines) for the lens-source redshift bins indicated in each panel. The HOD parameters used for each model line are the input to the simulations and are listed in the panels of Fig. A3.
APPENDIX B: RESULTS FROM SYSTEMATICS DIAGNOSTICS TESTS
In this appendix, we present the results from the diagnostic tests we describe in Section 5.3, following the methodology from Prat et al. (2021). Figs B1 and B2 show a summary of all these tests for redmagic and maglim, respectively, which include: the cross component, LSS weights, and the responses. We also include the boost factor on this plot as discussed in Section 5.1. In the figures, we also list the χ2 between each curve, and the null hypothesis, using the covariance matrix of our γt measurements. We discuss below our findings for each test.
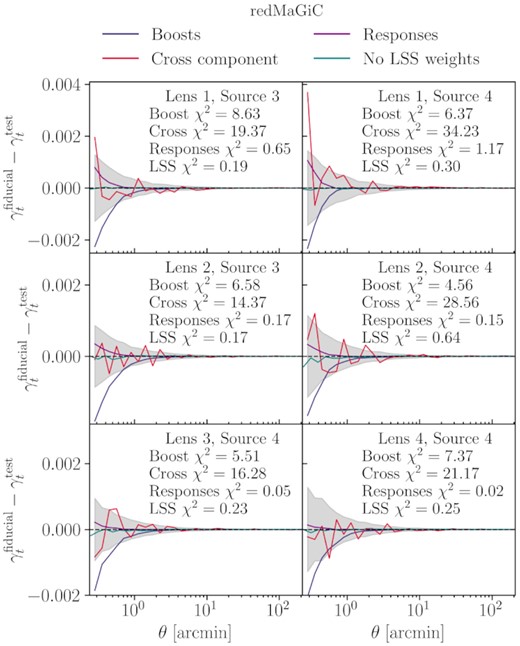
Systematics tests, as discussed in Section 5.3, for the redmagic sample. Boosts: comparison of γt with and without applying the boost factor correction; Cross component: the cross-component of shear; Responses: effect from using the scale-dependent responses compared to applying the average responses in each angular bin; No LSS weights: effect from not applying the LSS weights to correct for observing conditions; Gray area: the error bars on the shear measurement. In each panel, we also list the χ2 between each test and the null, using the covariance of our γt measurements. The number of points for each of the lines is 30.
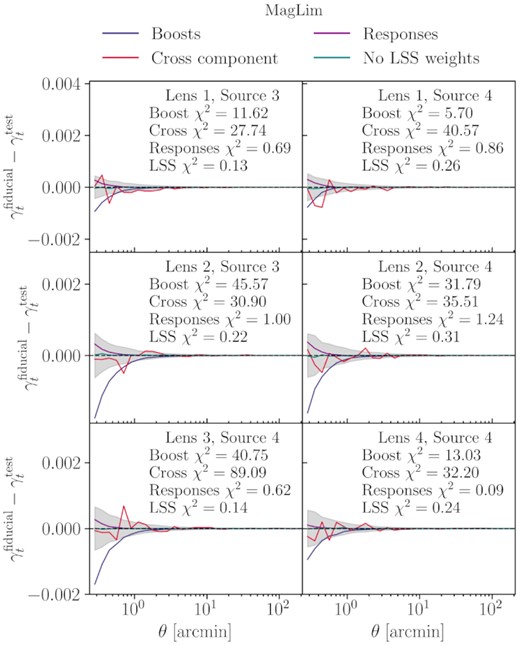
Cross component
The measurements of γ× at large scales are consistent with zero. At smaller scales, below a few arcmin, γ× fluctuates around zero, roughly within the error bars. The most noticeable exception is bin [Lens 1, Source 4] for which the smallest-scale measurements for the cross component get close approaches ∼0.004. Considering that at small scales the level of noise increases, we do not find the behaviour of γ× worrisome. Furthermore, the reduced χ2, even for bin [Lens 1, Source 4], is close to 1, which indicates the absence of significant problems.
Responses
Based on our results, when we compare our fiducial measurements which use a scale-averaged response per bin versus the same measurements when the exact scale-dependent responses are utilized, we find no strong evidence for disagreement between the two methods. In all the bins that we use in this work, this difference is subdominant to the statistical uncertainties, and the reduced χ2 values always very small. We therefore conclude that our analysis based on the scale-averaged responses is good enough for our purposes.
LSS weights correcting for observing conditions
Comparing the measured shear with and without applying the LSS weights leads to no significant differences, as also indicated by the very small reduced χ2 of each panel. This is shown by the fact that the difference between the two is always close to zero and smaller than our error bars. Thus, we find no problems with this test.
APPENDIX C: HALO EXCLUSION
In this appendix, we discuss the effect of incorporating Halo Exclusion (HE) into our modelling. Based on HE, haloes that overlap with each other are excluded from the two-halo components of the galaxy–galaxy lensing model prediction, in order to avoid double counting. There are many different prescriptions for HE in the literature, some of which can be very computationally expensive. Some authors (e.g. Zheng 2004; Tinker et al. 2005; Yoo et al. 2006) adopt the approach of choosing the appropriate upper limits to the halo masses when integrating over the mass function in equations (10) and (11). The maximum masses, namely Mh1 and Mh2, in these models, under the spherical-halo assumption, satisfy the requirement that the distance between the centres of the haloes, r12, is at least equal to the sum of their radii, R200c(Mh1) + R200c(Mh2) ≤ r12. Since this prescription is usually very computationally intensive, simplified versions of HE have been suggested (e.g. Magliocchetti & Porciani 2003; Cacciato et al. 2009) which capture the effects of HE while making the computations more efficient.
We follow a simplified approach in this appendix based on the following prescription. For a given redshift bin of our lens sample and a set of HOD parameters, we estimate the average lens halo mass, 〈Mh〉, based on equation (31) and the radius 〈Rh〉 ≡ R200c(〈Mh〉) it corresponds to. We then set the correlation function of the central two-halo component, |$\xi _{\rm gm}^{\rm c2h}(r)$|, to −1 for r < 〈Rh〉. Since the HE effect is stronger in the central two-halo term (Cacciato et al. 2009), compared to the satellite two-halo component |$\xi _{\rm gm}^{s2h}$|, we did not apply HE on |$\xi _{\rm gm}^{\rm s2h}$|. Fig. C1 shows the fractional differences between the fiducial constraints on the average lens halo mass, galaxy bias, and satellite fraction, and the constraints from fits that take HE, as described above, into account. We find that our results do not change significantly between the two cases. We also did not find a significant difference in the χ2 of our fits. We therefore do not include HE in our fiducial model.
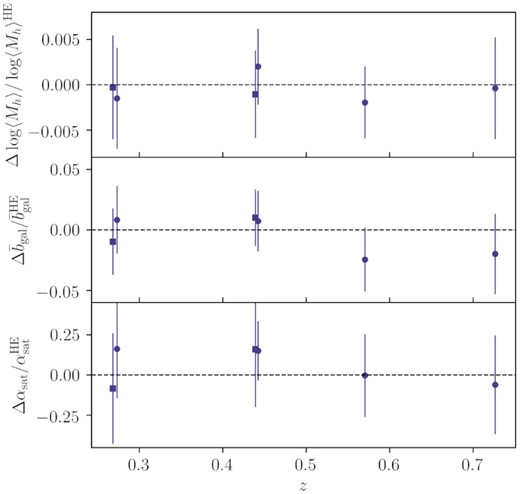
Effect on our average lens halo mass, galaxy bias, and satellite fraction constraints when HE is considered in our fits. This plot presents the fractional differences between the constraints from our fiducial fits and runs where we take into account HE, denoted by the ‘HE’ superscript.
APPENDIX D: CONSTRAINTS FOR ALL MODEL PARAMETERS
In Tables D1 and D2, we summarize the best-fitting parameters and derived quantities for the redmagic and maglim samples, respectively. We report the best-fitting model parameters and the constraints on the average halo mass, linear galaxy bias, and satellite fraction. The error bars show the 1σ posteriors.
APPENDIX E: MODEL COMPLEXITY
In Section 7.3.4, we discuss how adding complexity to our model changes our results. In this appendix, we provide details on our tests that led us to deciding what our fiducial framework is in this paper.
In Fig. E1, we show for all redmagic redshift bins, the fractional differences between the best-fitting γt using the HOD-only model, and the HOD-only model plus one additional contribution at a time. This plot shows how adding various terms to γt changes the best-fitting model as a function of θ, providing more information than the difference in χ2. Fig. E2 shows the constraints on the average halo mass, galaxy bias, and satellite fraction corresponding to these fits, with the vertical bands representing the constraints from our fiducial runs and each point shows the constraints from adding an additional contribution to the model. In the same plot, we also report in parenthesis the difference in goodness-of-fit as the difference in the reduced χ2 between each tested model and the HOD-only fits.
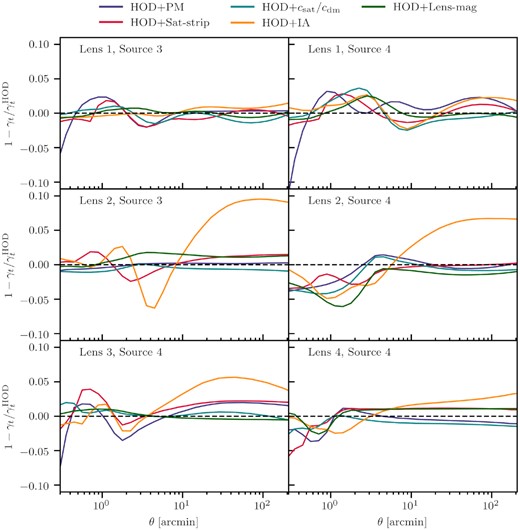
Comparing the basic HOD-only best-fitting γt model prediction for all redmagic lens-source redshift bins to the best-fitting γt after considering additional model complexity.
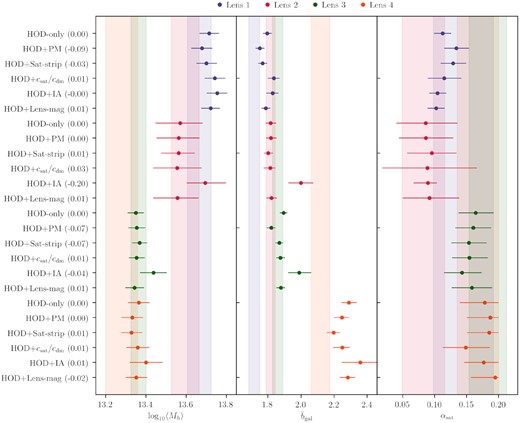
Testing the robustness of the halo properties to adding complexity to our model. We begin from our basic HOD-only model and we add one additional component to it at a time. In parenthesis, we report the difference in the reduced χ2 between the best-fitting HOD-only and the tested model fit. The vertical bands correspond to our constraints from the fiducial model and are added here for a direct comparison with our tests. Note that, to reduce the size of this figure, we have combined bins with the same lenses and different sources by presenting the mean of the best-fitting values and, to be conservative, the maximum of the error bars.
Although adding complexity to the basic HOD-only model is informative, we point out that interactions between additional terms, when more than one of them are considered, can have a much different net effect. Due to the large number of combinations we could explore, it was not feasible to do this full analysis, but we also note that we did not have strong indications that specific combinations of model components lead to radically different results in our fits or halo property constraints. To test for that, as a complement to our tests in Fig. E2, we have performed a test where we start from the full model which includes all additional contributions from Section 3, removing one component at a time and re-fitting the data. Fig. E3 presents our findings from this test.
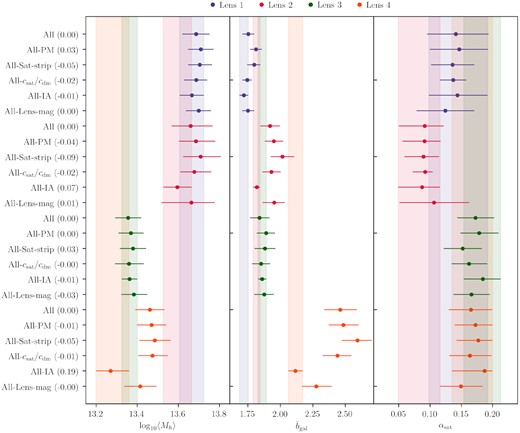
Testing the robustness of the halo properties to adding complexity to our model. We begin from our basic HOD-only model and we add one additional component to it at a time. In parenthesis, we report the difference in the reduced χ2 between the best fit from the runs with all components included and each tested model. The vertical bands correspond to our constraints from the fiducial model and are added here for a direct comparison with our tests. Note that, to reduce the size of this figure, we have combined bins with the same lenses and different sources by presenting the mean of the best-fitting values and, to be conservative, the maximum of the error bars.
Below, we discuss the effect of each contribution to the model fits separately when we simply add it to the basis of only HOD or remove it from the full model with all γt terms.
Point mass (PM)
We find that the PM component mostly affects the small scales in the first lens bin, with the largest effect being |${\sim}10{{\ \rm per\ cent}}$| at the smallest angular scales. This is due to the fact that the smallest angular bins of that redshift bin correspond to the smallest physical scales we consider in this work. We have included PM in our fiducial model as a conservative approach to account for modelling uncertainties at scales below what we measure.
Satellite strip
The effect from striping of satellite galaxies to γt can make a quite significant change on the constraints in some redshift bins, especially in the last one. This component also introduces a nice physical picture to our modelling – it captures the tidal interactions between the central galaxy and the substructure in the lens haloes. We have included this term in our fiducial model.
Satellite galaxy concentration parameter
Allowing for the concentration parameter for the spatial distribution of the satellite galaxies to vary mostly affects the bias constraints. This is because a = csat/cdm modifies the shape of the satellite terms in the one-halo regime making the model more flexible and able to better fit small and large scales at the same time, which forces the large-scale bias to change and adjust accordingly. Furthermore, as discussed in Section 3.1, there is good motivation to allow the concentration of the satellite-galaxy distribution to be different from that of the dark matter’s distribution. We have included this term in our fiducial model.
Lens magnification
The effect of lens magnification becomes stronger at higher redshift bins. Especially in the [Lens 4, Source 4] bin it can have a large impact on the final constraints, even on the halo mass, which is overall the most robust to changes in the model. Furthermore, magnification of lenses is well-motivated and its modelling is straightforward. Our magnification model only depends on fixed coefficients, as discussed in Section 3.5 and therefore does not introduce free parameters. We have included this term in our fiducial model.
Intrinsic alignment
Despite the uncertainty in the IA model in the one-halo term (see discussion in Section 3.6), we test here this term’s contribution to our fits. We find that the change in the best-fitting model can be heavily impacted as a function of angular scale by this component. The constraints can also be significantly affected by IA. In particular, Lens Bin 2 is mostly affected by the addition of IA to our basis HOD model, and the largest effect is noticed on large scales. This is caused by a combination how much overlap in the n(z) distributions of the lenses and sources there is and how much of the one-halo component we can observe in Lens Bin 2. Since a significant number of points in that bin’s measurements belong to the one-halo regime, if the HOD-only model cannot describe both small and large scales well at the same time, the added model flexibility from the inclusion of IA essentially accounts for that and improves the model fit. However, after adding other needed model complexity, besides IA, this effect is ameliorated and IA becomes negligible for the specific lens-source bin combinations we consider in this work. Therefore, and given that we do not trust that our modelling of IA is accurate at small scales, we decide to not take this term into account as part of our fiducial framework.
As a general note, we find that the constraints in the fourth bin are mostly affected by additional contributions to γt, while overall the bias constraints are the most sensitive to changes in our model. We note that our fiducial framework is effectively the ‘All-IA’ model.



