The impact of stellar clustering on the observed multiplicity of super-earth systems: outside–in cascade of orbital misalignments initiated by stellar flybys

Rodet, Laetitia; Lai, Dong

doi:10.1093/mnras/stab3046

ABSTRACT

A recent study suggests that the observed multiplicity of super-Earth (SE) systems is correlated with stellar overdensities: field stars in high phase-space density environments have an excess of single-planet systems compared to stars in low-density fields. This correlation is puzzling as stellar clustering is expected to influence mostly the outer part of planetary systems. Here, we examine the possibility that stellar flybys indirectly excite the mutual inclinations of initially coplanar SEs, breaking their co-transiting geometry. We propose that flybys excite the inclinations of exterior substellar companions, which then propagate the perturbation to the inner SEs. Using analytical calculations of the secular coupling between SEs and companions, together with numerical simulations of stellar encounters, we estimate the expected number of ‘effective’ flybys per planetary system that lead to the destruction of the SE co-transiting geometry. Our analytical results can be rescaled easily for various SE and companion properties (masses and semimajor axes) and stellar cluster parameters (density, velocity dispersion, and lifetime). We show that for a given SE system, there exists an optimal companion architecture that leads to the maximum number of effective flybys; this results from the trade-off between the flyby cross-section and the companion’s impact on the inner system. Subject to uncertainties in the cluster parameters, we conclude that this mechanism is inefficient if the SE system has a single exterior companion, but may play an important role in ‘SE + two companions’ systems that were born in dense stellar clusters. Whether this effect causes the observed correlation between planet multiplicity and stellar overdensities remains to be confirmed.

celestial mechanics, planet–star interactions, planetary systems

1 INTRODUCTION

Planets with masses/radii between Earth and Neptune, commonly called super-Earths (SEs) or mini-Neptunes, can be found around 30 per cent of solar-type stars (e.g. Lissauer et al. 2011; Fabrycky et al. 2014; Winn & Fabrycky 2015; Zhu et al. 2018). A large sample of them were discovered by the Kepler mission, with orbital periods below 300 d. SE systems contain an average of three planets (Zhu et al. 2018), generally ‘dynamically cold’, with eccentricities e ∼ 0.02 and mutual inclinations ΔI ∼ 2^○ (e.g. Winn & Fabrycky 2015). However, there is an observed excess of single transiting planets that could be sign of a dynamically hot sub-population of misaligned planets (so-called Kepler dichotomy, Lissauer et al. 2011; Johansen et al. 2012; Read, Wyatt & Triaud 2017), and indicating that the mutual inclinations in a multiplanet system decrease with the number of planets (Zhu et al. 2018; He, Ford & Ragozzine 2019; Millholland et al. 2021).

Recent work by Longmore, Chevance & Kruijssen (2021) has revealed an intriguing correlation between stellar phase-space density and the architecture of planetary systems, in particular the multiplicity. This work followed a similar analysis by Winter et al. (2020), which uncovered a correlation between stellar phase-space density and the occurrence of hot Jupiters. Using Gaia DR2 data (Gaia Collaboration et al. 2018), Longmore et al. (2021) computed the local stellar phase-space density of planet-hosting stars and their neighbours (within 40 pc) to determine whether the exoplanet host was in a relatively low or high phase-space density zone compared to its neighbours. They hypothesized that stars in current stellar overdensities were previously part of dense stellar clusters, from which only local residual overdensities remain. They showed that Kepler systems in local stellar phase-space overdensities have a significantly larger single-to-multiple ratio compared to those in the low phase-space density environment. The origin of this correlation is puzzling, as stellar clustering is expected to affect mostly the outer part of planetary systems in very dense environments (Laughlin & Adams 1998; Malmberg, Davies & Heggie 2011; Parker & Quanz 2012; Cai et al. 2017; Li, Mustill & Davies 2020a). Recent works have also suggested that the correlation is weaker when using a smaller unbiased stellar sample (Adibekyan et al. 2021), and that the current stellar overdensities could be associated with stellar age or to galactic-scale ripples as opposed to dense birth clusters (Mustill, Lambrechts & Davies 2021; Kruijssen et al. 2021). Alternatively, new studies have suggested that stellar flybys can excite the eccentricities and inclinations of outer planets/companions, which then trigger the formation of hot Jupiters from cold Jupiters via high-eccentricity migration (Wang et al. 2020; Rodet, Su & Lai 2021). For this flyby scenario to be effective, certain requirements (derived analytically in Rodet et al. 2021) on the companion property (mass and semimajor axis) and the cluster property (such as stellar density and age) must be satisfied. In this paper, we will examine a similar ‘outside–in’ effect of stellar flybys on the SE systems. Earlier, Zakamska & Tremaine (2004) examined the excitation and inward propagation of eccentricity disturbances in planetary systems. Our work focuses on inclination disturbances, as they are most relevant in determining the co-transit geometry of multiplanet systems.

In recent years, long-period giant planets have been observed in an increasing number of SE systems. Statistical analysis combining radial velocity and transit observations suggests that, depending on the metallicities of their host stars, 30–60 per cent of inner SE systems have cold Jupiter companions (Zhu & Wu 2018; Bryan et al. 2019). The dynamical perturbations from external companions can excite the eccentricities and mutual inclinations of SEs, thereby influencing the observability (co-transiting geometry) and stability of the inner system (Boué & Fabrycky 2014; Carrera, Davies & Johansen 2016; Lai & Pu 2017; Huang, Petrovich & Deibert 2017; Mustill, Davies & Johansen 2017; Hansen 2017; Becker & Adams 2017; Read et al. 2017; Pu & Lai 2018; Denham et al. 2019; Pu & Lai 2020; Rodet & Lai 2021). This requires the giant planets to be dynamically hot, which can be achieved by planet-planet scattering. Alternatively, in dense stellar environments, the eccentricities and inclinations of giant planets can be increased by stellar flybys.

In this paper, we examine the possibility that SEs systems become misaligned following a stellar encounter (‘flyby-induced misalignment cascade’ scenario), using a combination of analytical calculations (for the secular planet interactions) and numerical simulations (for stellar flybys). In Section 2, we outline the proposed scenario and its key ingredients. In Section 3, we examine the inclination requirement for an outer companion to break the co-transiting geometry of two inner initially coplanar SEs. In Section 4, we evaluate the extent to which a stellar encounter can raise the inclination of an outer companion. In Section 5, we derive the expected number of ‘effective’ flybys (i.e. those that succeed in breaking the co-transiting geometry of SEs) per system as a function of the properties of the planetary system (SEs+companion) and its stellar cluster environment. Finally, in Section 6, we extend our calculation to SE systems with two outer companions. In Section 7, we examine the effect of different flyby masses. In Section 8, we summarize our main results, recalling the key figures and equations of the paper.

2 SCENARIO: FLYBY-INDUCED MISALIGNMENT CASCADE

The observed excess of single-transiting SEs or mini-Neptunes could be sign of a dynamically hot sub-population of inner (≲0.5 au) planets with appreciable mutual inclinations. The recently-evidenced correlation between single-transiting systems and stellar overdensities suggests that stellar environments could play a significant role in this misalignment. However, close-in SEs are largely protected from perturbations induced by the stellar environment thanks to their proximity to the host star.

According to recent statistical estimates, 30–60 per cent of inner SE systems have cold Jupiter companions (≳1 au, mass ≳0.3 M_J; see Zhu & Wu 2018; Bryan et al. 2020). Such companions widen the effective cross-section of the planetary system, and thus its vulnerability to the dynamical perturbations from the stellar environment. The architecture of the inner SEs can be indirectly impacted by stellar flybys through the eccentricity/inclination excitations of the outer companions.

In this paper, we consider a system of two SEs with masses m₁, m₂ and semimajor axes a₁ < a₂ ≲ 0.5 au, on circular coplanar orbits around a host star (mass M = M₁ ∼ 1 M_⊙, radius R₁ ∼ 1 R_⊙). An outer companion (mass m_p ≪ M) is located at a_p on an initially circular coplanar orbit (see Fig. 1). In Section 6, we will consider the case of two exterior companions surrounding SEs.

Figure 1.

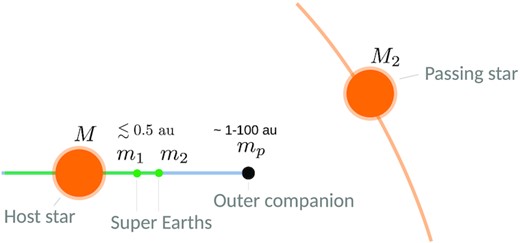
Schematic of the flyby-induced misalignment cascade scenario. An initially coplanar system comprising two inner planets (SEs) and an outer companion encounters a passing star. The stellar flyby changes the orbital inclination of m_p, which then induces misalignment between the orbits of m₁ and m₂.

Open in new tab Download slide

The system may experience close encounters with other stars, if the stellar density is large enough. This is typically the case in the beginning of the planetary system’s life, when it is embedded in its dense birth cluster. Most of these clusters are loosely bound or unbound, so that they tend to be disrupted over tens of millions of years (the current phase-space overdensities would be the remnants of these clusters). However, in the early phase of the cluster, close encounters may be frequent enough to influence the planetary architecture.

We denote by e_p and I_p the eccentricity and inclination of the companion m_p after an encounter with a passing star M₂. The inclined companion then induces mutual inclination within the SEs through secular interactions. In order for the SEs to break their co-transiting geometry, their relative inclination ΔI must be greater than a critical value

$$\begin{eqnarray*} \Delta I_{\rm crit} \simeq \frac{R_1}{a_2} \simeq 0.5^\circ \left(\frac{a_2}{0.5~\mathrm{au}}\right)^{-1} \left(\frac{R_1}{1~\mathrm{R_{\odot }}}\right). \end{eqnarray*}$$

(1)

In the following sections, we will derive the minimum required inclination of the companion I_p,crit to break the SEs co-transiting geometry, and the corresponding likelihood that a stellar encounter would generate such an inclination.

3 SECULAR DYNAMICS OF PLANET MISALIGNMENT

When the outer companion planet to the SEs in an initially coplanar system suddenly becomes misaligned by I_p, the mutual inclination ΔI between the SEs will oscillate around a forced value (Lai & Pu 2017; Rodet & Lai 2021). In the following, we derive the minimum misalignment I_p,crit required for the forced inclination to be greater than the critical value ΔI_crit (see equation 1). In theory however, due to the oscillation of ΔI, the co-transiting geometry of the SEs will be broken only part of the time even if the forced inclination is greater than ΔI_crit.

The forced mutual inclination ΔI of the SEs depends on I_p, m_p, and a_p, as well as on mutual coupling between the inner planets. Denote ω_ik the characteristic nodal precession frequency of planet i induced by the gravitational torque from planet k. The frequencies of mutual interactions in the inner two planets are

$$\begin{eqnarray*} \omega _{12} = \frac{\omega _{21} L_2}{L_1} = \frac{1}{4} n_1 \frac{m_2}{M} \left(\frac{a_1}{a_2}\right)^2 \, b_{\frac{3}{2}}^{(1)}\left(\frac{a_1}{a_2}\right), \end{eqnarray*}$$

(2)

while the precession frequencies of the SEs induced by the companion are

$$\begin{eqnarray*} \omega _{1{\rm p}} \equiv \frac{1}{4} n_1 \frac{m_{\rm p}}{M} \left(\frac{a_1}{a_{\rm p}}\right)^2\, b_{\frac{3}{2}}^{(1)}\left(\frac{a_1}{a_{\rm p}}\right), \end{eqnarray*}$$

(3)

$$\begin{eqnarray*} \omega _{2{\rm {\rm p}}}\equiv \frac{1}{4} n_2 \frac{m_{\rm p}}{M} \left(\frac{a_2}{a_{\rm p}}\right)^2 \, b_{\frac{3}{2}}^{(1)}\left(\frac{a_2}{a_{\rm p}}\right), \end{eqnarray*}$$

(4)

[see equation (7.11) in Murray & Dermott (2000)]. Here, |$n_i = \sqrt{GM/a_i^3}$| and |$L_i = m_i \sqrt{GMa_i}$| are the mean motion and the orbital angular momentum of planet i, and |$b_s^{(j)}(\alpha)$| is the Laplace coefficient:

$$\begin{eqnarray*} b_s^{(j)}(\alpha) = \frac{1}{\pi }\int _{0}^{2\pi } \frac{\cos (jx)\mathrm{d}x}{(1-2\alpha \cos x +\alpha ^2)^s}, \end{eqnarray*}$$

(5)

with |$b_{\frac{3}{2}}^{(1)}(\alpha) \simeq 3\alpha (1+15\alpha ^2/8+175\alpha ^4/64 + ...)$| for α ≪ 1. When the two SEs are away from any mean-motion resonances (see Rodet & Lai 2021), the forced misalignment ΔI between them induced by the inclined companion m_p depends on the coupling parameter ε_12,p (Lai & Pu 2017), given by

$$\begin{eqnarray*} \varepsilon _{\rm 12,p} = \frac{\omega _{2p}-\omega _{1p}}{\omega _{12}+\omega _{21}} \equiv {\varepsilon }_{12} \frac{\tilde{m}_{\rm p}}{\tilde{a}_{\rm p}^3}, \end{eqnarray*}$$

(6)

where we have defined |$\tilde{m}_{\rm p} \equiv m_{\rm p}/(1~\mathrm{M_{J}})$| and |$\tilde{a}_{\rm p} = a_{\rm p} / (1~\mathrm{au})$|⁠. When a₁, a₂ ≪ a_p and m_p ≪ M, ε₁₂ is independent of a_p and m_p:

$$\begin{eqnarray*} \varepsilon _{12} \simeq \frac{1~\mathrm{M_J}}{m_2} \left(\frac{a_2}{1~\mathrm{au}}\right)^3 \hat{\varepsilon }_{12} , \end{eqnarray*}$$

(7)

where

$$\begin{eqnarray*} \hat{\varepsilon }_{12} = \frac{3 a_1/a_2}{b_{{3}/{2}}^{(1)}\left({a_1}/{a_2}\right)} \frac{\left({a_2}/{a_1}\right)^\frac{3}{2}-1}{1 +{L_1}/{L_2}} . \end{eqnarray*}$$

(8)

The accuracy of equation (7) is better than 10 per cent for a_p > 5a₂. Note that |$\hat{\varepsilon }_{12}$| does not depend on the semimajor axis and mass scales of the SE system, and depends only on a₂/a₁ and m₁/m₂. The variation of |$\hat{\varepsilon }_{12}$| with a₂/a₁ is shown in Fig. 2 for different values of m₂/m₁.

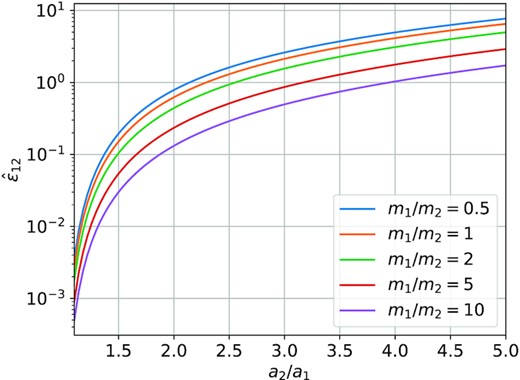
$The rescaled coupling parameter $\hat{\varepsilon }_{12}$ as a function of the semimajor axial ratio a2/a1 of the SE system, for different mass ratios m1/m2 (see equation 8). Systems with higher $\hat{\varepsilon }_{12}$ are more easily perturbed by the outer companion.$

Figure 2.

The rescaled coupling parameter |$\hat{\varepsilon }_{12}$| as a function of the semimajor axial ratio a₂/a₁ of the SE system, for different mass ratios m₁/m₂ (see equation 8). Systems with higher |$\hat{\varepsilon }_{12}$| are more easily perturbed by the outer companion.

Open in new tab Download slide

We can now write down the forced misalignment ΔI of the two SEs as a function of the companion’s inclination I_p and the coupling parameter ε_12,p. We identify two regimes: strong coupling, where ε_12,p ≲ 1, and weak coupling, where ε_12,p ≳ 1. In the strong coupling regime, the companion’s influence is weaker than the coupling between the SEs, and the forced inclination is proportional to ε_12,p:

$$\begin{eqnarray*} \Delta I \simeq \frac{1}{2} \sin (2I_{\rm p}) \varepsilon _{\rm 12, p},\quad (\text{for }\varepsilon _{\rm 12,p} \lesssim 1). \end{eqnarray*}$$

(9)

On the other hand, in the weak coupling regime, the coupling between the SEs is negligible and the forced inclination reaches

$$\begin{eqnarray*} \Delta I \simeq I_{\rm p},\quad (\text{for }\varepsilon _{\rm 12,p} \gtrsim 1). \end{eqnarray*}$$

(10)

In the intermediate regime, ΔI transitions smoothly from equation (9) to equation (10). There is an exception: when m₁ ≪ m₂, the misalignment between the SEs can become very high (larger than I_p) as ε_12,p approaches 1 (Lai & Pu 2017). In this paper, we ignore this resonant case and assume m₁ ≳ m₂, so that equations (9)–(10) provide adequate description for the forced misalignment.

Using equations (6)–(10), we can derive I_p,crit (that gives ΔI = ΔI_crit) as a function of the rescaled semimajor axis of the companion |$\tilde{a}_{\rm p}/\tilde{m}_{\rm p}^{1/3}$| for a given ε₁₂. In the weak coupling regime,

$$\begin{eqnarray*} \varepsilon _{\rm 12, p} \gtrsim 1 \iff \tilde{a}_{\rm p}/\tilde{m}_{\rm p}^{1/3} \lesssim \varepsilon _{12}^{1/3}, \end{eqnarray*}$$

(11)

we have

$$\begin{eqnarray*} I_{\rm p, crit} \simeq \Delta I_{\rm crit}, \end{eqnarray*}$$

(12)

i.e. when the outer companion is close to the inner SE system, the required inclination only needs to be as low as ΔI_crit. In the strong coupling regime,

$$\begin{eqnarray*} \varepsilon _{\rm 12, p} \lesssim 1 \iff \tilde{a}_{\rm p}/\tilde{m}_{\rm p}^{1/3} \gtrsim \varepsilon _{12}^{1/3}, \end{eqnarray*}$$

(13)

we have

$$\begin{eqnarray*} I_{\rm p, crit} &\simeq & \frac{1}{2}\arcsin \left(\frac{2\Delta I_{\rm crit}}{\varepsilon _{\rm 12, p}}\right)\nonumber \\ &=& \frac{1}{2}\arcsin \left(\frac{2\Delta I_{\rm crit} \tilde{a}_{\rm p}^3}{\varepsilon _{12} \tilde{m}_{\rm p}}\right), \end{eqnarray*}$$

(14)

i.e. when the outer companion is far from the SEs, the required inclination increases with a_p. The argument of the arcsin cannot be more than 1; it follows that for given ε₁₂ and |$\tilde{m}_{\rm p}$|⁠, there is a maximum possible |$\tilde{a}_{\rm p}$| for the companion, above which it cannot possibly induce a misalignment ΔI_crit, regardless of the value of I_p. This maximum is set by ΔI_crit = ε_12,p/2, giving

$$\begin{eqnarray*} \tilde{a}_{\rm p, max} &=& \left(\frac{\varepsilon _{\rm 12} \tilde{m}_{\rm p}}{2\Delta I_\mathrm{crit}}\right)^\frac{1}{3}\nonumber \\ &\simeq & 3.9~\varepsilon _{12}^\frac{1}{3} \tilde{m}_{\rm p}^\frac{1}{3} \left(\frac{\Delta I_\mathrm{crit}}{0.5^\circ }\right)^{-\frac{1}{3}}. \end{eqnarray*}$$

(15)

Fig. 3 shows the critical I_p required to produce ΔI_crit = 0.5^○ as a function of |$\tilde{a}_{\rm p}/\tilde{m}_{\rm p}^{1/3}$|⁠, for different SE systems (characterized by different values of ε₁₂). In the next section, we will derive the likelihood for a flyby to excite the companion’s inclination from 0 to I_p > I_p,crit.

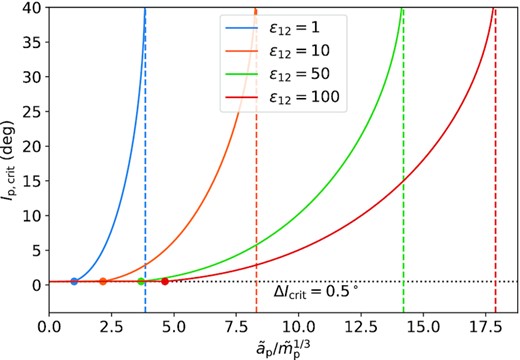
$Minimum companion’s inclination Ip,crit required to produce a forced misalignment ΔIcrit = 0.5○ between two SEs (equations 12 and 14), as a function of the scaled companion semimajor axis, $\tilde{a}_{\rm p}/\tilde{m}_{\rm p}^{1/3} = a_{\rm p}/(1~\mathrm{au}) ~ (m_{\rm p}/\mathrm{M_{J}})^{-1/3}$, for different inner SEs systems, characterized by different values of ε12 (see equation 7). The horizontal dashed line indicates ΔIcrit = 0.5○, the filled circles indicate the change of regimes (between ε12,p > 1 and ε12,p < 1), while the vertical dashed lines indicate the maximum $\tilde{a}_{\rm p}/\tilde{m}_{\rm p}^{1/3}$, beyond which it is impossible to generate ΔIcrit = 0.5○ regardless of the Ip value (see equation 15).$

Figure 3.

Minimum companion’s inclination I_p,crit required to produce a forced misalignment ΔI_crit = 0.5^○ between two SEs (equations 12 and 14), as a function of the scaled companion semimajor axis, |$\tilde{a}_{\rm p}/\tilde{m}_{\rm p}^{1/3} = a_{\rm p}/(1~\mathrm{au}) ~ (m_{\rm p}/\mathrm{M_{J}})^{-1/3}$|⁠, for different inner SEs systems, characterized by different values of ε₁₂ (see equation 7). The horizontal dashed line indicates ΔI_crit = 0.5^○, the filled circles indicate the change of regimes (between ε_12,p > 1 and ε_12,p < 1), while the vertical dashed lines indicate the maximum |$\tilde{a}_{\rm p}/\tilde{m}_{\rm p}^{1/3}$|⁠, beyond which it is impossible to generate ΔI_crit = 0.5^○ regardless of the I_p value (see equation 15).

Open in new tab Download slide

4 EFFECT OF FLYBY ON THE OUTER PLANET

In this section, we calculate the expected effect of a stellar flyby on the orbit of the outer planet/companion, and estimate the likelihood that the companion can attain I_p > I_p,crit. To this end, we perform a suite of N-body simulations to determine the distribution of the post-flyby inclination I_p and eccentricity e_p. Following a similar approach to Rodet et al. (2021), we suppose that the companion (with m_p ≪ M₂, the mass of the flyby star) is on an initially circular orbit, and we ignore the inner planets (their proximity to the host star effectively shields them from stellar encounter). We integrate a nearly parabolic (e = 1.1) encounter between two equal-mass stars using IAS15 from the Rebound package. The integration time is chosen so that the distance between M₁ and M₂ is equal to 100a_p at the beginning and end of each simulation, and the time-step is adaptive. We sample uniformly the dimensionless distance at closest approach |$\tilde{q} \equiv q/a_{\rm p}$| (where q is the periastron of the encounter) from 0.05 to 10, the cosine of the inclination cos i, and the argument of periastron ω of the flyby, and the initial phase λ_p of the planet m_p. For each |$\tilde{q}$|⁠, we carry out 30 × 20 × 20 (in cos i, ω, λ_p) = 12 000 simulations, and obtain the final orbital elements of the planet. The effect of the flyby on I_p is mainly determined by the flyby inclination i, so we interpolate our data using the 30 tested inclinations to produce a denser grid of results (see Fig. A1) and avoid under-sampling effects in computing the I_p distribution (see below).

4.1 Effect on the inclination

For a given |$\tilde{q}$|⁠, we derive p(e_p < 1), the probability that the planet remains bound, and p(I_p > I_p,min), the probability that the planet remains bound and has a final inclination larger than some specified I_p,min. These probabilities are shown in Fig. 4 as a function of |$\tilde{q}$|⁠, for different values of I_p,min. For |$\tilde{q}\gtrsim 3$|⁠, p(I_p > I_p,min) can be derived analytically using the secular approach. This derivation is detailed in the Appendix, as well as the comparison with the N-body results.

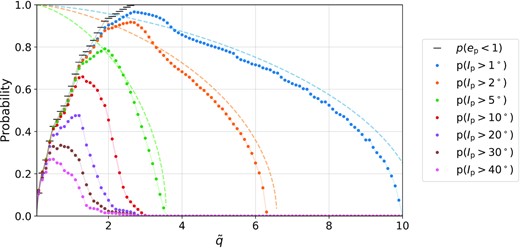
$The probability p(Ip > Ip,min) for a flyby to raise the inclination of the outer planet to Ip > Ip,min (while keeping the planet bound), as a function of the dimensionless distance at closest approach $\tilde{q} = q/a_{\rm p}$. Each point is computed from 30 × 20 × 20 N-body simulations that sample the flyby geometry. The dashed lines are the analytical results in the secular approximation, assuming a parabolic encounter (see the Appendix for derivation and comparison). The difference between the approximation and the simulations is due in part to the N-body set-up, where the eccentricity of the flyby is 1.1 rather than 1. The short bars give p(ep > 1), the probability that the planet remains bound after the flyby.$

Figure 4.

The probability p(I_p > I_p,min) for a flyby to raise the inclination of the outer planet to I_p > I_p,min (while keeping the planet bound), as a function of the dimensionless distance at closest approach |$\tilde{q} = q/a_{\rm p}$|⁠. Each point is computed from 30 × 20 × 20 N-body simulations that sample the flyby geometry. The dashed lines are the analytical results in the secular approximation, assuming a parabolic encounter (see the Appendix for derivation and comparison). The difference between the approximation and the simulations is due in part to the N-body set-up, where the eccentricity of the flyby is 1.1 rather than 1. The short bars give p(e_p > 1), the probability that the planet remains bound after the flyby.

Open in new tab Download slide

Using our result for p(I_p > I_p,min), we can derive the number of flybys that successfully raise the inclination of the outer planet (at a_p) above a certain I_p,min. This number can be written as a product of a scaling factor and a geometric function (Rodet et al. 2021):

$$\begin{eqnarray*} \mathcal {N}(I_{\rm p} \gt I_{\rm p, min}, a_{\rm p}) = \mathcal {N}_\mathrm{close}(a_{\rm p}) \times f(I_{\rm p, min}), \end{eqnarray*}$$

(16)

where |$\mathcal {N}_\mathrm{close}(a_{\rm p})$| is the number of flyby with q < a_p. Assuming that gravitational focusing is dominant in the close encounter and that the velocities of stars in the cluster follow the Maxwell–Boltzmann distribution, we have (Rodet et al. 2021)

$$\begin{eqnarray*} \mathcal {N}_\mathrm{close}(a_{\rm p}) &=& \frac{2 \sqrt{2\pi } a_{\rm p} G M_\mathrm{tot} n_\star }{\sigma _\star }t_\mathrm{cluster}\nonumber \\ &=& 0.2 \left(\frac{t_\mathrm{cluster}}{20~\mathrm{Myr}}\right) \left(\frac{a_\mathrm{p}}{50~\mathrm{au}}\right) \left(\frac{M_\mathrm{tot}}{2~\mathrm{M_{\odot }}}\right)\nonumber \\ &&\times \, \left(\frac{n_\star }{10^3~\mathrm{pc}^{-3}}\right) \left(\frac{\sigma _\star }{1~\mathrm{km\, s^{-1}}}\right)^{-1}, \end{eqnarray*}$$

(17)

where M_tot = M₁ + M₂, n_⋆ is the local stellar density of the cluster, σ_⋆ is its velocity dispersion, and t_cluster is its lifetime. In equation (16), f(I_p,min) measures the overall fraction (for all |$\tilde{q}$| values) of close flybys that raise the inclination of the outer planet by I_p > I_p,min:

$$\begin{eqnarray*} f(I_{\rm p, min}) = \int _{0}^{+\infty } p(I_{\rm p}\gt I_{\rm p, min}) {\rm d}\tilde{q}. \end{eqnarray*}$$

(18)

Note that f(I_p,min) can be more than 1, if the requirement I_p > I_p,min is fulfilled for a non-negligible proportion of flybys with q larger than a_p. Fig. 5 shows f(I_p,min), obtained using the numerical results presented in Fig. 4. The function can be approximated by a power-law fit,

$$\begin{eqnarray*} f(I_{\rm p, min}) \simeq \frac{7}{(I_{\rm p, min}/\mathrm{deg})^{0.79}}. \end{eqnarray*}$$

(19)

We emphasize that the function f(I_p,min) is universal, in the sense that it describes the effect of a general parabolic encounter between two equal-mass stars, and can be applied to all m_p and a_p values (assuming m_p ≪ M). In Section 5, we will apply equations (16) and (19) to ‘SEs + companion’ systems to estimate the likelihood that stellar flybys can destroy the co-transiting geometry of SEs.

Figure 5.

Integrated probability f(I_p,min) (equation 18) for stellar flybys to raise the inclination of the outer planet from 0 to I_p > I_p,min. The blue dots are computed numerically from Fig. 4, and the orange line is a simple power-law fit given by equation (19).

Open in new tab Download slide

4.2 Effect on the eccentricity

Stellar flybys not only change the inclination of the outer planet but also excite the planet’s eccentricity. Fig. 6 shows the joint distribution of I_p and e_p after stellar flybys. The inclination increases are correlated to eccentricity excitations, so that the post-flyby orbit of the planet is not circular. However, its eccentricity will very likely stay low (e_p ≲ 0.5) if the inclination gain is small (I_p ≲ 5^○). In this case, the inclination dynamics presented in Section 3 is largely unchanged compared to the circular orbit case. When we consider higher I_p, then the eccentricity can become larger. In that case, the stability of the system is not guaranteed, so the inclination dynamics for circular orbit may not hold. In the following section, we will show that the occurrence rate of our flyby-induced misalignment scenario depends mostly on the statistics for small I_p, so that we can safely ignore the eccentricity’s effect on the inclination dynamics. In particular, we can neglect the cases where the flyby induces strong scatterings between planets.

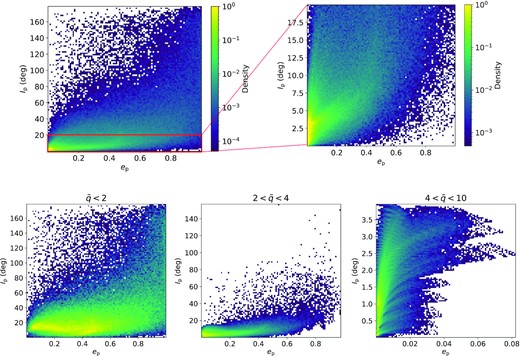
$Correlation between the eccentricity ep and inclination Ip of the outer planet after stellar flybys. The plots are generated from N-body simulations with different flyby geometries and distance at closest approaches, and the colour scales logarithmically with the local density of simulations. The plots only show simulations where the planet remains bound. The upper panels gather all flyby distances at closest approach $\tilde{q}$ (with the right-hand panel showing a zoom-in on the low inclination part of the left-hand panel), the lower panels distinguish three different ranges of $\tilde{q}$. The stripes-like structure in the lower right-hand panel is not physical, and is due to the discrete inclination sampling.$

Figure 6.

Correlation between the eccentricity e_p and inclination I_p of the outer planet after stellar flybys. The plots are generated from N-body simulations with different flyby geometries and distance at closest approaches, and the colour scales logarithmically with the local density of simulations. The plots only show simulations where the planet remains bound. The upper panels gather all flyby distances at closest approach |$\tilde{q}$| (with the right-hand panel showing a zoom-in on the low inclination part of the left-hand panel), the lower panels distinguish three different ranges of |$\tilde{q}$|⁠. The stripes-like structure in the lower right-hand panel is not physical, and is due to the discrete inclination sampling.

Open in new tab Download slide

5 OCCURRENCE RATE OF SUPER-EARTH MISALIGNMENT INDUCED BY STELLAR FLYBYS: SINGLE OUTER PLANET

We now compute the expected number of stellar flybys that generate a misalignment of ΔI > ΔI_crit between the SEs as a function of the outer planet’s semimajor axis a_p and mass m_p for given SE and cluster properties. In Section 3, we derived the required I_p,crit(a_p) (see equations 12 and 14) to induce a misalignment ΔI_crit given an outer planet at a_p. From equation (16), the number of flybys that produce ΔI > ΔI_crit is then

$$\begin{eqnarray*} \mathcal {N}(\Delta I \gt \Delta I_{\rm crit}, a_{\rm p}) &=& \mathcal {N}(I_{\rm p} \gt I_{\rm p, crit}(a_{\rm p}), a_{\rm p})\nonumber \\ &=& \mathcal {N}_\mathrm{close}(a_{\rm p}) \times f\left(I_{\rm p, min} = I_{\rm p, crit}(a_{\rm p})\right). \end{eqnarray*}$$

(20)

We previously identified two regimes for I_p,crit(a_p) (equations 12 and 14), depending of the coupling parameter ε_12,p. These regimes impact how |$\mathcal {N}$| scales with the semimajor axis a_p. In the weak coupling regime, ε_12,p ≳ 1 or |$\tilde{a}_{\rm p} \lesssim (\varepsilon _{12} \tilde{m}_{\rm p})^{1/3}$|⁠, we have I_p,crit(a_p) = ΔI_crit and thus

$$\begin{eqnarray*} \mathcal {N}(\Delta I \gt \Delta I_{\rm crit}, a_{\rm p}) &=& \mathcal {N}_\mathrm{close}(a_{\rm p}) \times f(I_{\rm p, min} =\Delta I_{\rm crit})\nonumber \\ &\propto & t_\mathrm{cluster} n_\star \sigma _\star ^{-1} M_\mathrm{tot}a_{\rm p}\left(\Delta I_{\rm crit}\right)^{-0.79}. \end{eqnarray*}$$

(21)

In the strong coupling regime, ε_12,p ≲ 1 or |$\tilde{a}_{\rm p} \gtrsim (\varepsilon _{12} \tilde{m}_{\rm p})^{1/3}$|⁠, I_p,crit(a_p) is given by equation (14), and assuming I_p,crit(a_p) ≪ 1 we have

$$\begin{eqnarray*} \mathcal {N}(\Delta I \gt \Delta I_{\rm crit}, a_{\rm p}) \propto t_\mathrm{cluster} n_\star \sigma _\star ^{-1} M_\mathrm{tot} a_{\rm p}^{-1.37} \left(\frac{\varepsilon _{12} m_{\rm p} }{\Delta I_{\rm crit}}\right)^{0.79}. \end{eqnarray*}$$

(22)

Figs 7 and 8 show |$\mathcal {N}(\Delta I \gt 0.5^\circ , a_{\rm p})$| as a function of the semimajor axis of the outer planet a_p, for different values of m_p and ε₁₂ [which characterizes the coupling of the inner SE system, see equation (7)]. The two regimes (linear and decreasing power-law dependence of a_p) are clearly visible on the plots. Moreover, there is a maximum a_p,max above which no I_p can induce the required ΔI_crit (see equation 15), and thus |$\mathcal {N}(\Delta I\gt \Delta I_{\rm crit}, a_{\rm p}) = 0$| for a_p > a_p,max.

$Number of stellar flybys that generate ΔI > ΔIcrit = 0.5○ in the SE system as a function of ap of the outer planet companion, for different values of mp [solid lines; see equations (20)–(22)]. Each curve terminates at ap,max, given by equation (15). The peak of each curve is located at $(a_{\rm p, peak}, \mathcal {N}_{\rm max})$. The inner SE system is characterized by ε12 = 10 (equation 7), and the cluster parameters are fixed to the fiducial values of equation (17): tcluster = 20 Myr, σ⋆ = 1 km.s−1, n⋆ = 103 pc−3, and $M_\mathrm{tot} = 2 \, {\rm M}_\odot$.The light dashed lines give $\mathcal {N}(I_{\rm p} \gt I_{\rm p, min}, a_{\rm p})$ for different values of Ip,min (see equation 16).$

Figure 7.

Number of stellar flybys that generate ΔI > ΔI_crit = 0.5^○ in the SE system as a function of a_p of the outer planet companion, for different values of m_p [solid lines; see equations (20)–(22)]. Each curve terminates at a_p,max, given by equation (15). The peak of each curve is located at |$(a_{\rm p, peak}, \mathcal {N}_{\rm max})$|⁠. The inner SE system is characterized by ε₁₂ = 10 (equation 7), and the cluster parameters are fixed to the fiducial values of equation (17): t_cluster = 20 Myr, σ_⋆ = 1 km.s⁻¹, n_⋆ = 10³ pc⁻³, and |$M_\mathrm{tot} = 2 \, {\rm M}_\odot$|⁠.The light dashed lines give |$\mathcal {N}(I_{\rm p} \gt I_{\rm p, min}, a_{\rm p})$| for different values of I_p,min (see equation 16).

Open in new tab Download slide

Same as Fig. 7, except for a fixed mp = 1 MJ and different coupling parameter ε12 (see equation 7) for the inner SE system.

Figure 8.

Same as Fig. 7, except for a fixed m_p = 1 M_J and different coupling parameter ε₁₂ (see equation 7) for the inner SE system.

Open in new tab Download slide

The maximum of each curve in Figs 7 and 8, |$\mathcal {N}_{\rm max}$|⁠, is reached at ε_12,p ≃ 1, or |$\tilde{a}_{\rm p} \simeq (\varepsilon _{12} \tilde{m}_{\rm p})^{1/3}$|⁠. It requires a companion inclination I_p no more than ΔI_crit, justifying our assumption to neglect the eccentricity effect (see Section 4, Fig. 6). They are given by

$$\begin{eqnarray*} a_{\rm p, peak} \simeq 2.2~\mathrm{au} \left(\frac{\varepsilon _{12}}{10}\right)^\frac{1}{3} \left(\frac{m_{\rm p}}{1~\mathrm{M_{J}}}\right)^\frac{1}{3}, \end{eqnarray*}$$

(23)

$$\begin{eqnarray*} \mathcal {N}_{\rm max} &\simeq & 0.1 \left(\frac{\Delta I_{\rm crit}}{0.5^\circ }\right)^{-0.79} \left(\frac{{\varepsilon }_{12}}{10}\right)^\frac{1}{3} \left(\frac{m_{\rm p}}{1~\mathrm{M_{J}}}\right)^\frac{1}{3} \left(\frac{t_\mathrm{cluster}}{20~\mathrm{Myr}}\right)\nonumber \\ &&\times \, \left(\frac{M_\mathrm{tot}}{2~\mathrm{M_{\odot }}}\right) \left(\frac{n_\star }{10^3~\mathrm{pc}^{-3}}\right) \left(\frac{\sigma _\star }{1~\mathrm{km.s^{-1}}}\right)^{-1} \end{eqnarray*}$$

(24)

We recall that ε₁₂ varies with |$a_2^3/m_2$| for fixed a₂/a₁ and m₂/m₁ (see equation 7), so that both |$\mathcal {N}_{\rm max}$| and a_p,peak are proportional to a₂, i.e. to the scale of the inner SE system. Fig. 9 displays |$\mathcal {N}_{\rm max}$| and a_p,peak as a function of ε₁₂ for different m_p. Note that since both |$\mathcal {N}_{\rm max}$| and a_p,peak scale with (ε₁₂m_p)^1/3 in the same way, they can be plotted with the same curves with different vertical scales. From equation (7) and Fig. 2, we see that for typical SE systems, |$\varepsilon _{12} = 2.5 (a_2/0.2~\mathrm{au})^3 (m_2/10~\mathrm{M_{\rm{\oplus }}})^{-1} \hat{\varepsilon }_{12}$| and |$\hat{\varepsilon }_{12} \sim 1$| (for a₂/a₁ ∼ 2). Equation (24) and Fig. 9 then indicate |$\mathcal {N} \lesssim 0.1$| (subject to uncertainties related to various SE and cluster parameters), suggesting that the co-transiting geometry of most SE systems is not affected by stellar flybys. In the next section, we will consider how this result changes when SE systems have two external companions.

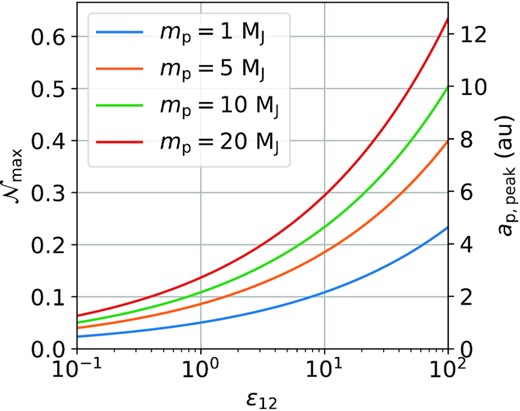
$The maximum possible number of flybys $\mathcal {N}_{\rm max}$ that can produce ΔI > 0.5○ in the SE system and corresponding ap,peak as a function of ε12, for different mp (see equations 23–24). The $\mathcal {N}_{\rm max}$ value uses the cluster parameters tcluster = 20 Myr, σ⋆ = 1 km s−1, and n⋆ = 103 pc−3. $\mathcal {N}_{\rm max}$ scales with $m_{\rm p}^{1/3}$, but can be easily rescaled for different parameters (see equation 17) and different mp (since $\mathcal {N}_\mathrm{max} \propto m_{\rm p}^{1/3}$).$

Figure 9.

The maximum possible number of flybys |$\mathcal {N}_{\rm max}$| that can produce ΔI > 0.5^○ in the SE system and corresponding a_p,peak as a function of ε₁₂, for different m_p (see equations 23–24). The |$\mathcal {N}_{\rm max}$| value uses the cluster parameters t_cluster = 20 Myr, σ_⋆ = 1 km s⁻¹, and n_⋆ = 10³ pc⁻³. |$\mathcal {N}_{\rm max}$| scales with |$m_{\rm p}^{1/3}$|⁠, but can be easily rescaled for different parameters (see equation 17) and different m_p (since |$\mathcal {N}_\mathrm{max} \propto m_{\rm p}^{1/3}$|⁠).

Open in new tab Download slide

6 SUPER-EARTH SYSTEMS WITH TWO EXTERIOR COMPANIONS

In the previous section, we have seen that flyby-induced misalignment of SEs by way of a single outer companion/planet is somewhat inefficient (see equation 24). In this section, we add a second companion m_b in a circular orbit (semimajor axis a_b) around the host star (see Fig. 10). This second companion can be farther away, thus increasing the effect cross-section for flybys. The flyby-induced misalignment I_b on this second companion will misalign the first companion by I_p, which will then increase the mutual inclination ΔI between the SEs.

Figure 10.

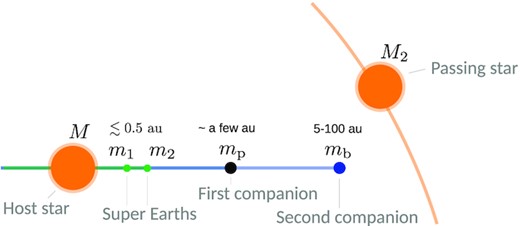
Schematic of the flyby-induced misalignment cascade scenario considered in Section 6: an initially coplanar system comprising two inner planets (SEs) and two outer companions encounters a passing star.

Open in new tab Download slide

Similarly to Section 5, we focus on the cases where the architecture of the system pre-flyby is coplanar. For companions at large separations (≳50 au, Tokovinin 2017), this is not the most likely configuration. If a wide companion form with a primordial inclination, then flybys are not needed to misalign the inner system. In such systems, the stellar environment is expected to play a less important role than the initial conditions in the inner system dynamics. Here, we are interested in systems that are significantly impacted by the stellar environment, so we focus on initially coplanar companions.

Equations (9)–(10) giving the forced mutual inclination ΔI of the SEs as a function of the misalignment I_p of the first companion are still valid. However, I_p is not a direct product of the flyby anymore: it is induced by the misalignment of the second companion m_b. The relationship between I_p and I_b is controlled by a new coupling parameter |$\varepsilon _{\rm \bar{12}p,b}$|⁠, which characterizes the forcing strength of the second companion on the inner (SEs+m_p) system compared to the mutual coupling between the SEs and m_p. To evaluate this parameter, we note that when the two SEs are strongly coupled, we can treat them as a single body (denoted by |$\bar{12}$|⁠), and their orbital axis |$\boldsymbol {L_{\bar{12}}}=\boldsymbol {L_1}+\boldsymbol {L_2}$| precesses around |$\boldsymbol {L_{\rm p}}$| with the characteristic frequency

$$\begin{eqnarray*} \omega _{\rm \bar{12}p} = \frac{L_1\omega _{1p} + L_2\omega _{2p}}{L_1+L_2}, \end{eqnarray*}$$

(25)

where ω_1p and ω_2p are given by equations (3)–(4). For a₁, a₂ ≪ a_p, we can define the effective semimajor axis of |$\bar{12}$| via [see equations (3)–(4) with |$b_{3/2}^{(1)}(\alpha) \simeq 3\alpha$|]

$$\begin{eqnarray*} \omega _{\rm \bar{12}p} \simeq \frac{3}{4} n_{12} \frac{m_{\rm p}}{M} \left(\frac{a_{\bar{12}}}{a_{\rm p}}\right)^3 = \frac{3}{4} \sqrt{\frac{GM}{a_{\bar{12}}^3}} \frac{m_{\rm p}}{M} \left(\frac{a_{\bar{12}}}{a_{\rm p}}\right)^3, \end{eqnarray*}$$

(26)

which gives

$$\begin{eqnarray*} a_{\bar{12}} = \left(\frac{m_1 a_1^2 + m_2 a_2^2}{m_1\sqrt{a_1} + m_2\sqrt{a_2}}\right)^\frac{2}{3}. \end{eqnarray*}$$

(27)

Similarly, the characteristic precession rate of |$\boldsymbol {L_{\bar{12}}}$| around |$\boldsymbol {L_{\rm b}}$| is given by

$$\begin{eqnarray*} \omega _{\rm \bar{12}b} = \frac{L_1\omega _{1b} + L_2\omega _{2b}}{L_1+L_2} = \frac{3}{4} n_{12} \frac{m_{\rm b}}{M} \left(\frac{a_{\bar{12}}}{a_{\rm b}}\right)^3. \end{eqnarray*}$$

(28)

Thus, analogous to equation (6), we can define the coupling parameter

$$\begin{eqnarray*} \varepsilon _{\rm \bar{12}p,b} = \frac{\omega _{\rm pb}-\omega _{\rm \bar{12}b}}{\omega _{\rm \bar{12}p}+\omega _{\rm p \bar{12}}} \simeq \frac{\omega _{\rm pb}}{\omega _{\rm \bar{12}p}} = \frac{m_{\rm b}}{m_{\rm p}} \left(\frac{a_{\rm p}}{a_{\rm b}}\right)^3 \left(\frac{a_{\rm p}}{a_{\bar{12}}}\right)^\frac{3}{2}, \end{eqnarray*}$$

(29)

where in the second equality we have used |$\omega _{\rm p \bar{12}} = (L_{\bar{12}}/L_{\rm p}) \omega _{\rm \bar{12}p} \ll \omega _{\rm \bar{12}p}$| and |$\omega _{\rm \bar{12}b}\ll \omega _{\rm pb}$| – these are valid for |$a_{\bar{12}} \lt a_{\rm p} \ll a_{\rm b}$| and m₁, m₂ ≪ m_p, m_b. When |$\varepsilon _{\rm \bar{12}p,b} \ll 1$|⁠, then the second companion’s influence is weaker than the coupling between the first companion (m_p) and the SEs, and the forced inclination between m_p and the SE system is

$$\begin{eqnarray*} I_{\rm p} \simeq \frac{1}{2} \sin (2I_{\rm b}) \varepsilon _{\rm \bar{12}p,b}. \end{eqnarray*}$$

(30)

On the other hand, when |$\varepsilon _{\rm \bar{12}p,b} \gg 1$|⁠, the coupling between m_p and the SEs is negligible and the forced inclination becomes

$$\begin{eqnarray*} I_{\rm p} \simeq I_{\rm b} . \end{eqnarray*}$$

(31)

The finite I_p will then lead to misalignment ΔI between the two SEs (see Section 3). The critical I_{b, crit} to induce a misalignment ΔI_crit between the SEs depends on the two coupling parameters, ε_12,p and |$\varepsilon _{\rm \bar{12}p,b}$|⁠. This leads to four regimes (Fig. 11):

ε_12,p ≳ 1 and |$\varepsilon _{\rm \bar{12}p, b} \gtrsim 1$|
The first companion m_p has a strong influence on the SEs, and the second companion m_b has a strong influence on the inner ‘SEs+m_p’ system. The misalignment I_b of m_b generated by a flyby is then directly transmitted to m_p and the SEs (i.e. ΔI ≃ I_p ≃ I_b).
ε_12,p ≲ 1 and |$\varepsilon _{\rm \bar{12}p, b} \gtrsim 1$|
The first companion has a weak influence on the SEs, but the second companion has a strong influence on the inner system. The misalignment of m_b is directly transmitted to m_p (i.e. I_p ≃ I_b), but the mutual inclination ΔI of the SEs is reduced from I_p (see equation 9).
ε_12,p ≳ 1 and |$\varepsilon _{\rm \bar{12}p, b} \lesssim 1$|
The first companion has a strong influence on the SEs, but the second companion has a weak influence on the inner system. The misalignment I_p of m_p is then reduced from I_b, while it is directly transmitted to the SEs (i.e. ΔI ≃ I_p).
ε_12,p ≲ 1 and |$\varepsilon _{\rm \bar{12}p, b} \lesssim 1$|
The first companion has a weak influence on the SEs, and the second companion also has a weak influence on the inner system. The misalignment of m_p is then reduced from I_b, and the mutual inclination of the SEs is also reduced from I_p.

$Schematic of the four different regimes characterized by the coupling parameters ε12,p (see equation 6) and $\varepsilon _{\rm \bar{12}p, b}$ (see equation 29). When ε12,p ≳ 1 (≲1), the first companion mp has a stronger (weaker) influence on the SEs (m1 and m2) compared to the mutual coupling between m1 and m2; when $\varepsilon _{\rm \bar{12}p, b} \gtrsim 1$ (≲1), the second companion mb has a stronger (weaker) influence on the inner ‘SEs+mp’ system compared to the mutual coupling between the SEs and mp. In this schematic, a companion is strong if its distance to the inner bodies is similar to the distance between the inner bodies or if it is much more massive.$

Figure 11.

Schematic of the four different regimes characterized by the coupling parameters ε_12,p (see equation 6) and |$\varepsilon _{\rm \bar{12}p, b}$| (see equation 29). When ε_12,p ≳ 1 (≲1), the first companion m_p has a stronger (weaker) influence on the SEs (m₁ and m₂) compared to the mutual coupling between m₁ and m₂; when |$\varepsilon _{\rm \bar{12}p, b} \gtrsim 1$| (≲1), the second companion m_b has a stronger (weaker) influence on the inner ‘SEs+m_p’ system compared to the mutual coupling between the SEs and m_p. In this schematic, a companion is strong if its distance to the inner bodies is similar to the distance between the inner bodies or if it is much more massive.

Open in new tab Download slide

The expression of I_{b, crit} in each regime is

$$\begin{eqnarray*} I_{\rm b, crit} \simeq \left\lbrace \begin{array}{l{@}{\quad}l} \Delta I_{\rm crit} & \text{Regime 1} \\ \frac{1}{2}\arcsin \left(\frac{2\Delta I_{\rm crit}}{\varepsilon _{\rm 12, p}}\right)& \text{Regime 2}\\ \frac{1}{2}\arcsin \left(\frac{2\Delta I_{\rm crit}}{\varepsilon _{\rm \bar{12}p,b}}\right)& \text{Regime 3}\\ \frac{1}{2}\arcsin \left(\frac{1}{\varepsilon _{\rm \bar{12}p, b}}\arcsin \left(\frac{2\Delta I_{\rm crit}}{\varepsilon _{\rm 12, p}}\right)\right)& \text{Regime 4} \end{array} \right. \nonumber\\ \end{eqnarray*}$$

(32)

The maximum possible value for the semimajor axis of the first companion derived in equation (15) still holds, i.e.

$$\begin{eqnarray*} \tilde{a}_{\rm p, max} = \left(\frac{\varepsilon _{\rm 12} \tilde{m}_{\rm p}}{2\Delta I_\mathrm{crit}}\right)^\frac{1}{3}. \end{eqnarray*}$$

(33)

In addition, there is a maximum value of a_b beyond which ΔI > ΔI_crit can never be produced; this a_b,max is set by |$I_{\rm p^, crit} = \varepsilon _{\rm \bar{12}p,b}/2$|⁠, with I_p,crit given by equations (12) and (14), depending on whether ε_12,p ≳ 1 or ε_12,p ≲ 1. Thus we have

$$\begin{eqnarray*} a_{\rm b, max} = \left\lbrace \begin{array}{c{@}{\quad}c}a_{\rm p} \left(\frac{a_{\rm p}}{a_{\bar{12}}}\right)^\frac{1}{2} \left(\frac{m_{\rm b}}{m_{\rm p}} \frac{1}{2\Delta I_\mathrm{crit}} \right)^\frac{1}{3} & \text{if }\varepsilon _{\rm 12, p} \gtrsim 1 \\ a_{\rm p} \left(\frac{a_{\rm p}}{a_{\bar{12}}}\right)^\frac{1}{2} \left(\frac{m_{\rm b}}{m_{\rm p}} \frac{\varepsilon _{\rm 12, p}}{2\Delta I_\mathrm{crit}} \right)^\frac{1}{3} & \text{if }\varepsilon _{\rm 12, p} \lesssim 1 \end{array}. \right. \end{eqnarray*}$$

(34)

Using equation (16) (but applied to the outermost companion m_b), we find that the number of flybys that can produce ΔI > ΔI_crit is

$$\begin{eqnarray*} \mathcal {N}(\Delta I \gt \Delta I_{\rm crit}, a_{\rm b}) &=& \mathcal {N}(I_{\rm b} \gt I_{\rm b, crit}(a_{\rm b}), a_{\rm b}) \nonumber \\ &=& \mathcal {N}_\mathrm{close}(a_{\rm b}) \times f(I_{\rm b, min} = I_{\rm b, crit}(a_{\rm b})). \end{eqnarray*}$$

(35)

Figs 12 and 13 show |$\mathcal {N}(\Delta I \gt \Delta I_{\rm crit}, a_{\rm b})$| as a function of a_b, for given m_b, m_p, a_p, and SE properties ε₁₂ and |$a_{\bar{12}}$|⁠, for the cases of ε_12,p ≳ 1 and ε_12,p ≲ 1, respectively. For a given a_p, the maximum number of flybys |$\mathcal {N}_{\rm max}(a_{\rm p})$| occurs when |$\varepsilon _{\rm \bar{12}p, b} \sim 1$|⁠. The corresponding a_b,peak and |$\mathcal {N}_{\rm max}(a_{\rm p})$| are

$$\begin{eqnarray*} a_{\rm b, peak} = a_{\rm p} \left(\frac{a_{\rm p}}{a_{\bar{12}}}\right)^\frac{1}{2} \left(\frac{m_{\rm b}}{m_{\rm p}} \right)^\frac{1}{3} \end{eqnarray*}$$

(36)

$$\begin{eqnarray*} \mathcal {N}_\mathrm{max} = \mathcal {N}_\mathrm{close}(a_{\rm b, peak}) \times f(I_{\rm p, crit}) \propto a_{\rm b, peak}. \end{eqnarray*}$$

(37)

Fig. 14 displays |$\mathcal {N}_{\rm max}(a_{\rm p})$| and the corresponding a_b,peak as a function of a_p, for two different ε₁₂ (recall that ε₁₂ characterizes the architecture of the inner SE system; see Fig. 2). Note that |$\mathcal {N}_{\rm max}(a_{\rm p})$| has a peak value, reached when a_p = a_p,peak, corresponding to the transition between regimes where ε_12,p ≲ 1 and ε_12,p ≳ 1. In other words, for each SE system, there is an optimal companion architecture (a_p,peak, a_b,peak) that maximizes the number of effective flybys |$\mathcal {N}_{\rm max} = \mathcal {N}_{\rm max, peak}$|⁠, which occurs when both ε_12,p and |$\varepsilon _{\rm \bar{12}p, b}$| are approximately equal to 1. Requiring both coupling ratios to be 1, a_p,peak is given by equation (23),

$$\begin{eqnarray*} a_{\rm p, peak} = (\varepsilon _{12} \tilde{m}_{\rm p})^{1/3}~\mathrm{au}, \end{eqnarray*}$$

(38)

and a_b,peak is given by equation (36) with a_p = a_p,peak:

$$\begin{eqnarray*} a_{\rm b, peak}= \left(\frac{\varepsilon _{12}}{\tilde{a}_{\bar{12}}}\right)^\frac{1}{2} \left(\tilde{m}_{\rm p} \tilde{m}_{\rm b}^2\right)^\frac{1}{6} ~\mathrm{au}, \end{eqnarray*}$$

(39)

where |$\tilde{a}_{\bar{12}} \equiv a_{\bar{12}}/(1~\mathrm{au})$| and |$\tilde{m}_{\rm b} \equiv m_{\rm b}/(1~\mathrm{M_J})$|⁠. For a typical system with Earth-mass planets, a cold Jupiter and an outer brown dwarf, we have

$$\begin{eqnarray*} a_{\rm b, peak} \simeq 16~\mathrm{au} \left(\frac{\varepsilon _{12}}{10}\right)^\frac{1}{2} \left(\frac{m_{\rm p}}{1~\mathrm{M_{J}}}\right)^\frac{1}{6} \left(\frac{m_{\rm b}}{50~\mathrm{M_{J}}}\right)^\frac{1}{3} \left(\frac{a_{\bar{12}}}{0.5~\mathrm{au}}\right)^{-\frac{1}{2}} . \end{eqnarray*}$$

(40)

The corresponding |$\mathcal {N}_{\rm max, peak}$| is

$$\begin{eqnarray*} \mathcal {N}_{\rm max, peak} &=& \mathcal {N}_\mathrm{close}(a_{\rm b, peak}) \times f(\Delta I_\mathrm{crit})\nonumber \\ &\simeq &0.8 \left(\frac{\Delta I_{\rm crit}}{0.5^\circ }\right)^{-0.79} \left(\frac{{\varepsilon }_{12}}{10}\right)^\frac{1}{2} \left(\frac{m_{\rm p}}{1~\mathrm{M_{J}}}\right)^\frac{1}{6} \nonumber \\ &&\times \, \left(\frac{m_{\rm b}}{50~\mathrm{M_{J}}}\right)^\frac{1}{3} \left(\frac{a_{\bar{12}}}{0.5~\mathrm{au}}\right)^{-\frac{1}{2}} \left(\frac{t_\mathrm{cluster}}{20~\mathrm{Myr}}\right) \nonumber \\ &&\times \left(\frac{M_\mathrm{tot}}{2~\mathrm{M_{\odot }}}\right) \left(\frac{n_\star }{10^3~\mathrm{pc}^{-3}}\right) \left(\frac{\sigma _\star }{1~\mathrm{km\, s^{-1}}}\right)^{-1} . \end{eqnarray*}$$

(41)

This maximal ‘peak’ number of flybys is shown in Fig. 15, along with the optimal semimajor axes of the two companions. The result depends on the SE systems through now two parameters, ε₁₂ and |$a_{\bar{12}}$|⁠. Using equation (8), we can rewrite equation (37) to understand the dependence on |$\mathcal {N}_{\rm max, peak}$| on various parameters:

$$\begin{eqnarray*} \mathcal {N}_{\rm max, peak} &\simeq & 0.8 \left(\frac{\Delta I_{\rm crit}}{0.5^\circ }\right)^{-0.79} \left(\frac{\hat{\varepsilon }_{12}}{0.3}\right)^\frac{1}{2} \left(\frac{m_2}{10~\mathrm{M_{\rm{\oplus }}}}\right)^{-\frac{1}{2}}\nonumber \\ &&\times \left(\frac{a_2}{1~\mathrm{au}}\right)^\frac{3}{2} \left(\frac{a_{\bar{12}}}{0.5~\mathrm{au}}\right)^{-\frac{1}{2}} \left(\frac{m_{\rm p}}{1~\mathrm{M_{J}}}\right)^\frac{1}{6} \left(\frac{m_{\rm b}}{50~\mathrm{M_{J}}}\right)^\frac{1}{3} \nonumber \\ &&\times \! \left(\frac{t_\mathrm{cluster}}{20~\mathrm{Myr}}\right) \left(\frac{M_\mathrm{tot}}{2~\mathrm{M_{\odot }}}\right) \left(\frac{n_\star }{10^3~\mathrm{pc}^{-3}}\right) \left(\frac{\sigma _\star }{1~\mathrm{km\, s^{-1}}}\right)^{-1}. \nonumber\\ \end{eqnarray*}$$

(42)

Thus, the maximal ‘peak’ number of effective flybys scales linearly with the SEs semimajor axes. Comparing Figs 9 and 15, we see that adding a second companion strongly increases the number of flybys able to break the co-transiting geometry of the inner SEs. Of course, this increase may be tempered by the lower probability of having a suitable two-companion system instead of an one-companion system.

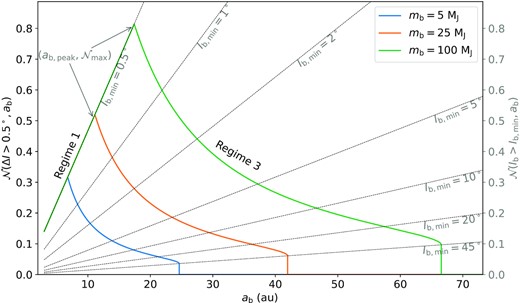
$Number of stellar flybys that generate ΔI ≳ ΔIcrit = 0.5○ in the SE system as a function of ab of the outermost companion, for different values of mb (solid lines; see equation 35). Each curve terminates at ab,max, given by equation (34). The inner SE system is characterized by ε12 = 10 (equation 7), $a_{\bar{12}} = 0.5$ au, and the inner companion’s parameters are fixed to ap = 2 au and mp = 1 MJ, so that ε12,p ≳ 1. This situation corresponds to regimes 1 (for small ab) and 3 (for high ab). The cluster parameters are fixed to the fiducial values of equation (17): tcluster = 20 Myr, σ⋆ = 1 km s−1, and n⋆ = 103 pc−3. The light dashed lines give $\mathcal {N}(I_{\rm b} \gt I_{\rm b, min}, a_{\rm b})$ for different values of Ib,min (see equation 16, applied to the outermost companion). See Figs 7 and 8 for the cases of SEs with a single companion.$

Figure 12.

Number of stellar flybys that generate ΔI ≳ ΔI_crit = 0.5^○ in the SE system as a function of a_b of the outermost companion, for different values of m_b (solid lines; see equation 35). Each curve terminates at a_b,max, given by equation (34). The inner SE system is characterized by ε₁₂ = 10 (equation 7), |$a_{\bar{12}} = 0.5$| au, and the inner companion’s parameters are fixed to a_p = 2 au and m_p = 1 M_J, so that ε_12,p ≳ 1. This situation corresponds to regimes 1 (for small a_b) and 3 (for high a_b). The cluster parameters are fixed to the fiducial values of equation (17): t_cluster = 20 Myr, σ_⋆ = 1 km s⁻¹, and n_⋆ = 10³ pc⁻³. The light dashed lines give |$\mathcal {N}(I_{\rm b} \gt I_{\rm b, min}, a_{\rm b})$| for different values of I_b,min (see equation 16, applied to the outermost companion). See Figs 7 and 8 for the cases of SEs with a single companion.

Open in new tab Download slide

Figure 13.

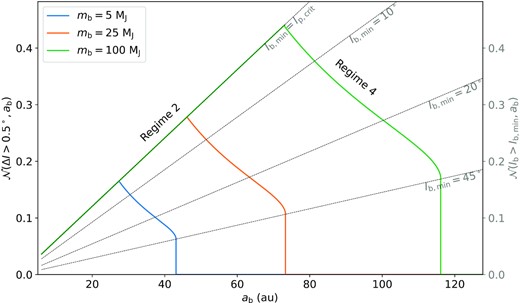
Same as Fig. 12, except for a_p = 5 au, corresponding to ε_12,p = 0.07 (see equation 7). For this value of the coupling parameter, the first companion m_p should have a minimum I_p,crit ∼ 7^○ > ΔI_crit (see equation 14) to generate a misalignment ΔI > ΔI_crit within the inner SE system. This case corresponds to regimes 2 (for small a_b) and 4 (for high a_b).

Open in new tab Download slide

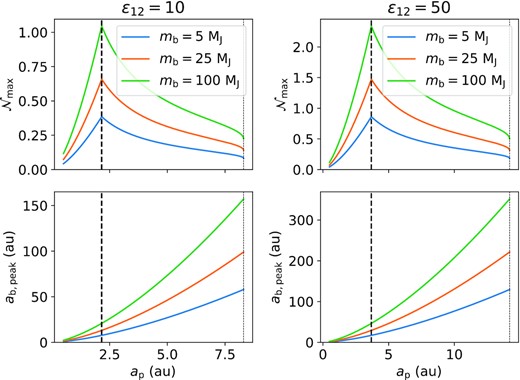
$Maximum number of flybys $\mathcal {N}_{\rm max}$ that gives ΔI ≳ ΔIcrit = 0.5○ (top) and optimal ab,peak (bottom) as a function of ap (equation 37), for different values of mb. Note that ab,peak is chosen so as to maximize the number of flybys, i.e. such that $\varepsilon _{\rm \bar{12}p,b} = 1$ (equation 36). The optimal ap is indicated with a dashed vertical line: it corresponds to ε12,p = 1 and does not depend on mb. The maximum ap at around 8 au (left) or 15 au (right) is similarly independent of mb (equation 15). The SEs system is fixed, with ε12 = 10 (left) and ε12 = 50 (right), $a_{\bar{12}} = 0.5$ au, and the mass of the first companion is fixed to mp = 1 MJ. The cluster parameters are tcluster = 20 Myr, σ⋆ = 1 km s−1 , and n⋆ = 103 pc−3. Note that $\mathcal {N}_{\rm max}$ scales with $a_{\bar{12}}^{-1/2}$ and $m_{\rm p}^{-1/3}$, and is proportional to tcluster, $\sigma _\star ^{-1}$, and n⋆.$

Figure 14.

Maximum number of flybys |$\mathcal {N}_{\rm max}$| that gives ΔI ≳ ΔI_crit = 0.5^○ (top) and optimal a_b,peak (bottom) as a function of a_p (equation 37), for different values of m_b. Note that a_b,peak is chosen so as to maximize the number of flybys, i.e. such that |$\varepsilon _{\rm \bar{12}p,b} = 1$| (equation 36). The optimal a_p is indicated with a dashed vertical line: it corresponds to ε_12,p = 1 and does not depend on m_b. The maximum a_p at around 8 au (left) or 15 au (right) is similarly independent of m_b (equation 15). The SEs system is fixed, with ε₁₂ = 10 (left) and ε₁₂ = 50 (right), |$a_{\bar{12}} = 0.5$| au, and the mass of the first companion is fixed to m_p = 1 M_J. The cluster parameters are t_cluster = 20 Myr, σ_⋆ = 1 km s⁻¹ , and n_⋆ = 10³ pc⁻³. Note that |$\mathcal {N}_{\rm max}$| scales with |$a_{\bar{12}}^{-1/2}$| and |$m_{\rm p}^{-1/3}$|⁠, and is proportional to t_cluster, |$\sigma _\star ^{-1}$|⁠, and n_⋆.

Open in new tab Download slide

$Maximal ‘peak’ number of flybys $\mathcal {N}_{\rm max,peak}$ that gives ΔI ≳ ΔIcrit = 0.5○ (top) and corresponding ab,peak (bottom) as a function of ε12 (equations 41–42), for different values of mb. The optimal ap and ab values, ap,peak and ab,peak, are set by ε12p = 1 and $\varepsilon _{\rm \bar{12}p,b} = 1$ (equations 38–39), so as to maximize the number of flybys. The optimal ap,peak is indicated with a dashed black line on the bottom plot – it does not depend on mb. The SEs location is set to $a_{\bar{12}} = 0.5$ au, and the mass of the first companion is fixed to mp = 1 MJ. The cluster properties are tcluster = 20 Myr, σ⋆ = 1 km s−1, and n⋆ = 103 pc−3, but note that $\mathcal {N}_{\rm max, peak}$ scales with $a_{\bar{12}}^{-1/2}$ and $m_{\rm p}^{1/6}$, and is proportional to tcluster, $\sigma _\star ^{-1}$, and n⋆.$

Figure 15.

Maximal ‘peak’ number of flybys |$\mathcal {N}_{\rm max,peak}$| that gives ΔI ≳ ΔI_crit = 0.5^○ (top) and corresponding a_b,peak (bottom) as a function of ε₁₂ (equations 41–42), for different values of m_b. The optimal a_p and a_b values, a_p,peak and a_b,peak, are set by ε_12p = 1 and |$\varepsilon _{\rm \bar{12}p,b} = 1$| (equations 38–39), so as to maximize the number of flybys. The optimal a_p,peak is indicated with a dashed black line on the bottom plot – it does not depend on m_b. The SEs location is set to |$a_{\bar{12}} = 0.5$| au, and the mass of the first companion is fixed to m_p = 1 M_J. The cluster properties are t_cluster = 20 Myr, σ_⋆ = 1 km s⁻¹, and n_⋆ = 10³ pc⁻³, but note that |$\mathcal {N}_{\rm max, peak}$| scales with |$a_{\bar{12}}^{-1/2}$| and |$m_{\rm p}^{1/6}$|⁠, and is proportional to t_cluster, |$\sigma _\star ^{-1}$|⁠, and n_⋆.

Open in new tab Download slide

7 DEPENDENCE ON THE MASS OF THE STELLAR PERTURBER

Our calculations in the previous sections assume that the stellar perturber has the same mass as the host star of our planetary system (M₁ = M₂). In reality, most of the stars in the Galaxy are less massive than |$1\, {\rm M}_\odot$|⁠, and the impact of a flyby depends on the mass of the perturber M₂. On the other hand, for a fixed stellar mass density, if the mass is mostly distributed between lighter stars, we expect n_⋆ to be higher.

Instead of rerunning all previous simulations with different M₂, we can use the M₁ = M₂ result to estimate the effect of a perturber with different mass. Inspired from the secular result (see the Appendix), all other quantities being the same, the orbital elements of the planet after a flyby with mass ratio M₂/M₁ can be derived from the M₂/M₁ = 1 results by

$$\begin{eqnarray*} I_{\rm p} (M_2/M_1) = \frac{M_2/M_1}{\sqrt{1+M_2/M_1}} I_{\rm p} (M_2/M_1 = 1) \end{eqnarray*}$$

(43)

$$\begin{eqnarray*} e_{\rm p} (M_2/M_1) = \frac{M_2/M_1}{\sqrt{1+M_2/M_1}} e_{\rm p} (M_2/M_1 = 1). \end{eqnarray*}$$

(44)

This scaling arises because the effect of the perturbation is proportional to the mass of the perturber, divided by the timescale of the encounter, the latter being proportional to the square root of the total mass M_tot. We use these estimates to plot Figs 16 and 17. The integrated probability f(I_p,min) is decreased for smaller M₂, roughly by a factor of |$\sqrt{M_2/M_1}$|⁠. Thus, for a fixed stellar number density n_⋆ in the cluster, the effect of flybys will be decreased by a factor of order a few when we allow for a realistic range of stellar masses, compared to our results presented in previous sections. On the other hand, if the stellar mass is entirely distributed within M₂ = M₁/k stars, then n_⋆ is k times higher for the same total mass density. In that case the maximum number of effective encounters |$\mathcal {N}_{\rm max} \propto f(I_{\rm p, min}) n_\star$| is actually proportional to |$\sqrt{M_1/M_2}$| (e.g. equations 24, 37, 41) and will increase for small-mass stars. Thus, we expect that for a given mass density in the cluster, when we consider clusters with a spectrum of stellar masses, the effect of flybys will be increased by a factor of order a few compared to our results presented in previous sections.

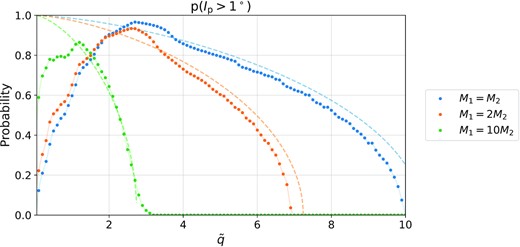
$Similar than Fig. 4, for Ip,min = 1○ and different M2 (equation 43). For the same distance at closest approach, the effect of the flyby decreases with decreasing perturber mass M2. For small $\tilde{q}$, a decreased mass leads to less configurations becoming unbound, which ultimately increases the probability to have a bound system with small inclination.$

Figure 16.

Similar than Fig. 4, for I_p,min = 1^○ and different M₂ (equation 43). For the same distance at closest approach, the effect of the flyby decreases with decreasing perturber mass M₂. For small |$\tilde{q}$|⁠, a decreased mass leads to less configurations becoming unbound, which ultimately increases the probability to have a bound system with small inclination.

Open in new tab Download slide

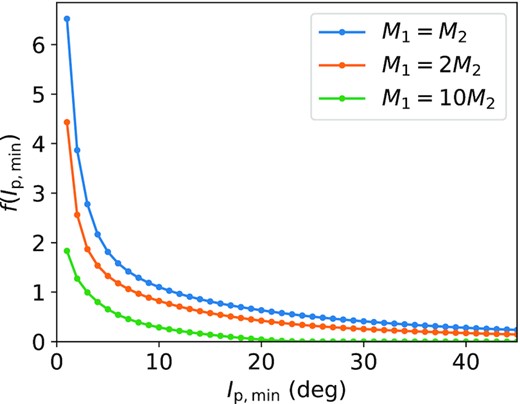
Same as Fig. 5, for different M2 (equation 43).

Figure 17.

Same as Fig. 5, for different M₂ (equation 43).

Open in new tab Download slide

8 SUMMARY AND DISCUSSION

8.1 Summary

In this paper, we have studied a new mechanism for dynamical excitations of Super-Earths (SE) systems following a close stellar encounter. We are motivated by the recently claimed correlation between the multiplicity observed in Kepler transiting systems and stellar overdensities (Longmore et al. 2021). The proposed mechanism consists of stellar flybys exciting the inclinations of one or two exterior companion giant planets (or brown dwarfs), which would then induce misalignment in an initially coplanar SE system. Even a modest misalignment (ΔI ≳ 0.5^○) could break the co-transiting geometry of the SEs, resulting in an apparent excess of single-transiting systems. We study two cases: in one, the SE system has a cold Jupiter companion at a few au; in the other, the SE system has two companions, a cold Jupiter and a wider planetary or substellar companion. Our results can be rescaled easily with the SE system or companion properties.

To evaluate the probability for a system to experience such an ‘effective’ flyby (that can generate ΔI ≳ 0.5^○ for the SEs), we combine analytical calculation (on stellar encounters and the secular coupling between the SEs and companions) with N-body simulations (to evaluate the effects of representative close encounters). Given the large parameter space and related uncertainties, we have attempted to present our results in an analytical or semi-analytical way, so that they can be rescaled easily for different SE and companion properties and stellar cluster parameters.

When the SE system only has one planetary companion, we show that the mechanism is relatively ineffective. If the outer planet is close to the SEs, then stellar flybys will have a small chance of changing its orbital inclination. On the other hand, if the outer planet is farther away, then it will have little impact on the SE dynamics, and on their transiting geometry in particular. This trade-off is shown in Figs 7 and 8. For given density, velocity dispersion, and lifetime of the stellar cluster, we can evaluate the expected number of stellar flybys that will disrupt the co-transiting geometry of the SEs as a function of the SE system (characterized by the coupling parameter ε₁₂, equation 7) and the companion properties (semimajor axis and mass). Fixing all parameters but the companion semimajor axis (a_p), the number of ‘effective’ flybys peaks for an optimal a_p which, for typical Kepler SEs, corresponds to a few astronomical units for m_p ∼ 1 M_J (see equation 23). The corresponding maximum number of effective flybys and its dependencies in all related parameters is displayed in equation (24). With only one companion, this flyby-induced misalignment scenario is unlikely to produce statistically significant effect of the SE multiplicity; even when assuming a high cluster density, less than 1 in 10 suitable systems (with an exterior giant planet) will experience the required stellar flyby.

When the SE system has two companions, the effective cross-section for stellar flybys increases. The misalignment induced on the outermost (second) companion m_b by the flyby can be transmitted to the inner (first) companion m_p, which would them be able to break the co-transiting geometry of the SEs. A relatively close (small a_b) second companion would have a strong influence on the inner system (SEs and m_p) (characterized by the parameter |$\varepsilon _{\rm \bar{12}p, b}$|⁠, equation 29), and transmit its misalignment I_b fully to the first companion (i.e. I_b ∼ I_p for |$\varepsilon _{\rm \bar{12}p, b} \gtrsim 1$|⁠). On the other hand, a far-out second companion has a better chance of experiencing close stellar flybys, but could have a smaller effect on the inner system. The trade-off is shown in Figs 12 and 13 for two different locations of the first companion, close to the SEs or farther away. Fixing the properties of the SEs, the number of effective flybys peaks for an optimal combination of a_p and a_b which, for typical Kepler ‘SE+cold Jupiter systems’, corresponds to a few AU and tens of AU, respectively, for substellar second companions. The corresponding number of flybys and its dependencies on various parameters is displayed in equation (41). The optimal architecture (semimajor axes of the two companions as a function of their masses and the SE parameters) is described in equations (38) and (39) (see Figs 14 and 15). Our calculations show that the number of effective flybys (that can generate ΔI > 0.5^○ for the SEs) increases significantly when a second companion is added, suggesting that most initially coplanar SE systems with two companions in stellar overdensities will experience a flyby that will misalign their orbits, and thus break the co-transiting geometry.

8.2 Discussion

In this paper, we have adopted some simplifications in deriving the analytical estimates of the effect of flybys on SE systems with exterior companions. One of the simplifications that we made was to ignore the encounters with binary stars. Tight binaries with separation a_binary ≪ a_p are expected to behave similarly to a single stellar perturber. On the other hand, only one component will play a role in encounters with large-separation binaries (a_binary ≫ a_p). For intermediate cases, more exploration is needed (see e.g. Li, Mustill & Davies 2020b).

Our calculations show that SE systems with only one outer companion are unlikely to be much impacted by the stellar flybys, while systems with two companions are likely to be impacted (depending on various parameters). However, SE systems with two companions may be rarer than their one-companion counterparts. Ultimately, further information on the correlation between inner SE systems and exterior planets/substellar companions will be needed to determine the relative prevalence of the mechanisms studied in this paper. Moreover, a deeper knowledge on the properties of stellar birth clusters (lifetime and density in particular) and their relation to the observed overdensities characterized in Winter et al. (2020) and Longmore et al. (2021) is needed to draw firm conclusions on the role of the flyby-induced misalignment scenario in multiplanet systems.

ACKNOWLEDGEMENTS

We thank the referee, A. Mustill, for useful comments that have improved this paper. This work has been supported in part by the NSF grant AST-17152 and NASA grant 80NSSC19K0444. We made use of the python libraries numpy (Harris et al. 2020), scipy (Virtanen et al. 2020), and pyqt-fit, and the figures were made with matplotlib (Hunter 2007).

DATA AVAILABILITY

The output of the N-body flyby simulations (Section 4) can be found on https://github.com/LaRodet/FlybySimulations.git. All the figures can be directly reproduced from this data set and from the equations.

REFERENCES

Adibekyan

V.

et al. ,

2021

,

A&A

,

649

,

A111

10.1051/0004-6361/202040201

Crossref

Search ADS

Becker

J. C.

,

Adams

F. C.

,

2017

,

MNRAS

,

468

,

549

10.1093/mnras/stx461

Crossref

Search ADS

Boué

G.

,

Fabrycky

D. C.

,

2014

,

ApJ

,

789

,

111

10.1088/0004-637X/789/2/111

Crossref

Search ADS

Bryan

M. L.

et al. ,

2020

,

AJ

,

159

,

181

10.3847/1538-3881/ab76c6

Crossref

Search ADS

Bryan

M. L.

,

Knutson

H. A.

,

Lee

E. J.

,

Fulton

B. J.

,

Batygin

K.

,

Ngo

H.

,

Meshkat

T.

,

2019

,

AJ

,

157

,

52

10.3847/1538-3881/aaf57f

Crossref

Search ADS

Cai

M. X.

,

Kouwenhoven

M. B. N.

,

Zwart

S. F. P.

,

Spurzem

R.

,

2017

,

MNRAS

,

470

,

4337

10.1093/mnras/stx1464

Crossref

Search ADS

Carrera

D.

,

Davies

M. B.

,

Johansen

A.

,

2016

,

MNRAS

,

463

,

3226

10.1093/mnras/stw2218

Crossref

Search ADS

Denham

P.

,

Naoz

S.

,

Hoang

B.-M.

,

Stephan

A. P.

,

Farr

W. M.

,

2019

,

MNRAS

,

482

,

4146

10.1093/mnras/sty2830

Crossref

Search ADS

Fabrycky

D. C.

et al. ,

2014

,

ApJ

,

790

,

146

10.1088/0004-637X/790/2/146

Crossref

Search ADS

Gaia Collaboration

et al. .,

2018

,

A&A

,

616

,

A1

10.1051/0004-6361/201833051

Crossref

Search ADS

Hansen

B. M. S.

,

2017

,

MNRAS

,

467

,

1531

10.1093/mnras/stx182

Crossref

Search ADS

Harris

C. R.

et al. ,

2020

,

Nature

,

585

,

357

10.1038/s41586-020-2649-2

Crossref

Search ADS

PubMed

He

M. Y.

,

Ford

E. B.

,

Ragozzine

D.

,

2019

,

MNRAS

,

490

,

4575

10.1093/mnras/stz2869

Crossref

Search ADS

Huang

C. X.

,

Petrovich

C.

,

Deibert

E.

,

2017

,

AJ

,

153

,

210

10.3847/1538-3881/aa67fb

Crossref

Search ADS

Hunter

J. D.

,

2007

,

Comput. Sci. Eng.

,

9

,

90

10.1109/MCSE.2007.55

Crossref

Search ADS

Johansen

A.

,

Davies

M. B.

,

Church

R. P.

,

Holmelin

V.

,

2012

,

ApJ

,

758

,

39

10.1088/0004-637X/758/1/39

Crossref

Search ADS

Kruijssen

J. M. D.

,

Longmore

S. N.

,

Chevance

M.

,

Laporte

C. F. P.

,

Motylinski

M.

,

Keller

B. W.

,

Henshaw

J. D.

,

2021

,

preprint (arXiv:2109.06182 [astro-ph])

Lai

D.

,

Pu

B.

,

2017

,

AJ

,

153

,

42

10.3847/1538-3881/153/1/42

Crossref

Search ADS

Laughlin

G.

,

Adams

F. C.

,

1998

,

ApJ

,

508

,

L171

10.1086/311736

Crossref

Search ADS

Li

D.

,

Mustill

A. J.

,

Davies

M. B.

,

2020a

,

MNRAS

,

496

,

1149

10.1093/mnras/staa1622

Crossref

Search ADS

Li

D.

,

Mustill

A. J.

,

Davies

M. B.

,

2020b

,

MNRAS

,

499

,

1212

10.1093/mnras/staa2945

Crossref

Search ADS

Lissauer

J. J.

et al. ,

2011

,

ApJS

,

197

,

8

10.1088/0067-0049/197/1/8

Crossref

Search ADS

Liu

B.

,

Lai

D.

,

2018

,

ApJ

,

863

,

68

10.3847/1538-4357/aad09f

Crossref

Search ADS

Longmore

S. N.

,

Chevance

M.

,

Kruijssen

J. M. D.

,

2021

,

ApJ

,

911

,

L16

10.3847/2041-8213/abeb22

Crossref

Search ADS

Malmberg

D.

,

Davies

M. B.

,

Heggie

D. C.

,

2011

,

MNRAS

,

411

,

859

10.1111/j.1365-2966.2010.17730.x

Crossref

Search ADS

Millholland

S. C.

,

He

M. Y.

,

Ford

E. B.

,

Ragozzine

D.

,

Fabrycky

D.

,

Winn

J. N.

,

2021

,

AJ

,

162

,

166

Murray

C. D.

,

Dermott

S. F.

,

2000

,

Solar System Dynamics

.

Cambridge Univ. Press

,

Cambridge

Mustill

A. J.

,

Davies

M. B.

,

Johansen

A.

,

2017

,

MNRAS

,

468

,

3000

10.1093/mnras/stx693

Crossref

Search ADS

Mustill

A. J.

,

Lambrechts

M.

,

Davies

M. B.

,

2021

,

preprint (arXiv e-prints)

Parker

R. J.

,

Quanz

S. P.

,

2012

,

MNRAS

,

419

,

2448

10.1111/j.1365-2966.2011.19911.x

Crossref

Search ADS

Pu

B.

,

Lai

D.

,

2018

,

MNRAS

,

478

,

197

10.1093/mnras/sty1098

Crossref

Search ADS

Pu

B.

,

Lai

D.

,

2021

,

MNRAS

,

508

,

597

Read

M. J.

,

Wyatt

M. C.

,

Triaud

A. H. M. J.

,

2017

,

MNRAS

,

469

,

171

10.1093/mnras/stx798

Crossref

Search ADS

Rodet

L.

,

Lai

D.

,

2021

,

MNRAS

,

502

,

3746

10.1093/mnras/stab094

Crossref

Search ADS

Rodet

L.

,

Su

Y.

,

Lai

D.

,

2021

,

ApJ

,

913

,

104

10.3847/1538-4357/abf8a7

Crossref

Search ADS

Tokovinin

A.

,

2017

,

ApJ

,

844

,

103

10.3847/1538-4357/aa7746

Crossref

Search ADS

Virtanen

P.

et al. ,

2020

,

Nature Methods

,

17

,

261

10.1038/s41592-019-0686-2

Crossref

Search ADS

PubMed

Wang

Y.-H.

,

Leigh

N. W. C.

,

Perna

R.

,

Shara

M. M.

,

2020

,

ApJ

,

905

,

136

10.3847/1538-4357/abc619

Crossref

Search ADS

Winn

J. N.

,

Fabrycky

D. C.

,

2015

,

ARA&A

,

53

,

409

10.1146/annurev-astro-082214-122246

Crossref

Search ADS

Winter

A. J.

,

Kruijssen

J. M. D.

,

Longmore

S. N.

,

Chevance

M.

,

2020

,

Nature

,

586

,

528

10.1038/s41586-020-2800-0

Crossref

Search ADS

PubMed

Zakamska

N. L.

,

Tremaine

S.

,

2004

,

AJ

,

128

,

869

10.1086/422023

Crossref

Search ADS

Zhu

W.

,

Wu

Y.

,

2018

,

AJ

,

156

,

92

10.3847/1538-3881/aad22a

Crossref

Search ADS

Zhu

W.

,

Petrovich

C.

,

Wu

Y.

,

Dong

S.

,

Xie

J.

,

2018

,

ApJ

,

860

,

101

10.3847/1538-4357/aac6d5

Crossref

Search ADS

APPENDIX: SECULAR PERTURBATION ON THE INCLINATION BY A PARABOLIC FLYBY

The probability p(I_p > I_p,min) for a planet m_p to gain an inclination I_p > I_p,min after a parabolic flyby can be computed in the secular framework, for |$\tilde{q} \equiv q/a_{\rm p} \gtrsim 3$|⁠. Let us first compute the evolution of the unit angular momentum vector |$\boldsymbol {\hat{L}_{\rm p}}$| of an initially circular planet orbit (with semimajor axis a_p and mean-motion n_p). Using the secular approach, averaging over the planet’s orbit, we get [equation (28) in Liu & Lai (2018)]:

$$\begin{eqnarray*} \frac{{\rm d}{\hat{L}_{\rm p}}}{{\rm d}{t}} = -\frac{3 n_{\rm p} M_2 a_{\rm p}^3}{2M_1 R^3} \left(\boldsymbol {\hat{L}_{\rm p}}\cdot \hat{\boldsymbol {R}}\right)\left(\boldsymbol {\hat{L}_{\rm p}}\times \hat{\boldsymbol {R}}\right), \end{eqnarray*}$$

(A1)

where |$\boldsymbol {R}$| represents the instantaneous position of M₂ relative to M₁, and |$\hat{\boldsymbol {R}} = \boldsymbol {R}/R$|⁠. We choose the xy plane as the plane of the parabolic stellar encounter, with the x-axis pointing towards the periastron. We assume that |$\boldsymbol {\hat{L}_{\rm p}}$| remains close to its initial value throughout the flyby. Integrating |$\frac{{\rm d}{\hat{L}_{\rm p}}}{{\rm d}{t}}$| along the parabolic trajectory of the flyby, we find that the change in |$\boldsymbol {\hat{L}_{\rm p}}$| is given by

$$\begin{eqnarray*} \boldsymbol {\delta \hat{L}_{\rm p}} = \frac{3 \pi M_2}{8 \sqrt{2 M_1(M_1+M_2)}} \left(\frac{a_{\rm p}}{q}\right)^\frac{3}{2} \sin (2 i) \begin{pmatrix}\cos \Omega \\ \sin \Omega \\ 0 \end{pmatrix} , \end{eqnarray*}$$

(A2)

where i and Ω are, respectively, the inclination and longitude of the node of the initial orbit of the planet. Thus, the change in the planet’s inclination is

$$\begin{eqnarray*} I_{\rm p} \simeq |\boldsymbol {\delta \hat{L}_{\rm p}}| &=& \frac{3\pi }{8} \frac{M_2}{\sqrt{2 M_1 (M_1 + M_2)}} \left(\frac{a_{\rm p}}{q}\right)^{\frac{3}{2}} \sin (2i)\nonumber \\ &\equiv & I_{\max }(\tilde{q}) \sin (2i). \end{eqnarray*}$$

(A3)

This expression is compared to the N-body results in Fig. A1 for |$\tilde{q} = 6$|⁠. The dependence on i is correctly predicted, but the amplitude is slightly overestimated (by about |$10{{\ \rm per\ cent}}$|⁠). This is due in part to the N-body set-up, where the eccentricity of the flyby is 1.1 rather than 1. This slight overestimate of the amplitude can lead to a larger discrepancy of the probability to generate I_p > I_p,min, if this inclination threshold is close to |$I_{\rm max}(\tilde{q})$|⁠. In fact, we can easily compute the theoretical probability assuming the flyby has a uniform distribution in cos i:

$$\begin{eqnarray*} p\left(I_{\rm p} \gt I_{\rm p, min}\right) &=& \frac{1}{2}\int _{I_{\rm p} \gt I_{\rm p, min}} \sin (i) di\nonumber \\ &=& \int _{i \gt \frac{1}{2}\arcsin (\frac{I_{\rm p, min}}{I_{\rm max}(\tilde{q})})}^{i \lt \frac{\pi }{2} - \frac{1}{2}\arcsin (\frac{I_{\rm p, min}}{I_{\rm max}(\tilde{q})})} \sin (i) di\nonumber \\ &=& \cos \left[\frac{1}{2}\arcsin \left(\frac{I_{\rm p, min}}{I_{\rm max}(\tilde{q})}\right)\right] \nonumber\\ &&-\, \sin \left[\frac{1}{2}\arcsin \left(\frac{I_{\rm p, min}}{I_{\rm max}(\tilde{q})}\right)\right]. \end{eqnarray*}$$

(A4)

This probability is indicated by the dashed lines in Fig. 4.

Figure A1.

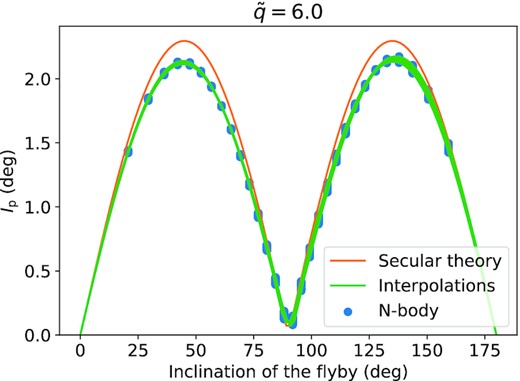
Inclination of the planet after the flyby, from the secular theory (orange, equation A4) and N-body simulations (clustered blue dots). Each of the 30 simulated inclinations groups 20 × 20 simulations, with various ω and λ_p. The green lines are the interpolation of I_p over the inclination of the flyby for each couple (ω, λ_p). These results and interpolations are used to produce Fig. 4.

Open in new tab Download slide

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
November 2021	14
December 2021	13
January 2022	18
February 2022	4
March 2022	3
April 2022	2
May 2022	4
June 2022	4
July 2022	4
August 2022	4
September 2022	2
October 2022	3
November 2022	4
December 2022	8
January 2023	8
February 2023	8
March 2023	8
April 2023	11
May 2023	6
June 2023	6
July 2023	7
August 2023	13
September 2023	1
October 2023	9
November 2023	11
December 2023	14
January 2024	10
February 2024	9
March 2024	13
April 2024	8
May 2024	13
June 2024	24
July 2024	16
August 2024	2
September 2024	6
October 2024	9
November 2024	4
December 2024	4
January 2025	5
February 2025	22
March 2025	17
April 2025	1
May 2025	3

Article Contents

The impact of stellar clustering on the observed multiplicity of super-earth systems: outside–in cascade of orbital misalignments initiated by stellar flybys

ABSTRACT

1 INTRODUCTION

2 SCENARIO: FLYBY-INDUCED MISALIGNMENT CASCADE

3 SECULAR DYNAMICS OF PLANET MISALIGNMENT

4 EFFECT OF FLYBY ON THE OUTER PLANET

4.1 Effect on the inclination

4.2 Effect on the eccentricity

5 OCCURRENCE RATE OF SUPER-EARTH MISALIGNMENT INDUCED BY STELLAR FLYBYS: SINGLE OUTER PLANET

6 SUPER-EARTH SYSTEMS WITH TWO EXTERIOR COMPANIONS

7 DEPENDENCE ON THE MASS OF THE STELLAR PERTURBER

8 SUMMARY AND DISCUSSION

8.1 Summary

8.2 Discussion

ACKNOWLEDGEMENTS

DATA AVAILABILITY

REFERENCES

APPENDIX: SECULAR PERTURBATION ON THE INCLINATION BY A PARABOLIC FLYBY

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

The impact of stellar clustering on the observed multiplicity of super-earth systems: outside–in cascade of orbital misalignments initiated by stellar flybys Free

ABSTRACT

1 INTRODUCTION

2 SCENARIO: FLYBY-INDUCED MISALIGNMENT CASCADE

3 SECULAR DYNAMICS OF PLANET MISALIGNMENT

4 EFFECT OF FLYBY ON THE OUTER PLANET

4.1 Effect on the inclination

4.2 Effect on the eccentricity

5 OCCURRENCE RATE OF SUPER-EARTH MISALIGNMENT INDUCED BY STELLAR FLYBYS: SINGLE OUTER PLANET

6 SUPER-EARTH SYSTEMS WITH TWO EXTERIOR COMPANIONS

7 DEPENDENCE ON THE MASS OF THE STELLAR PERTURBER

8 SUMMARY AND DISCUSSION

8.1 Summary

8.2 Discussion

ACKNOWLEDGEMENTS

DATA AVAILABILITY

REFERENCES

APPENDIX: SECULAR PERTURBATION ON THE INCLINATION BY A PARABOLIC FLYBY

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

The impact of stellar clustering on the observed multiplicity of super-earth systems: outside–in cascade of orbital misalignments initiated by stellar flybys