-
PDF
- Split View
-
Views
-
Cite
Cite
Narjes Shahamat, Shaharam Abbassi, Tong Liu, GRB variabilities and following gravitational waves induced by gravitational instability in NDAFs, Monthly Notices of the Royal Astronomical Society, Volume 508, Issue 4, December 2021, Pages 6068–6076, https://doi.org/10.1093/mnras/stab2989
Close - Share Icon Share
ABSTRACT
The present work proposes a new formalism for the inner regions of a neutrino-dominated accretion flows (NDAFs) by considering the self-gravity, where the neutrino opacity is high enough to make neutrinos trapped becoming a dominant factor in the transportation of energy and angular momentum over the magneto rotational instability. We investigate the possibility of gravitational instability and fragmentation to model the highly variable structure of the prompt emission in gamma-ray bursts (GRBs). The results lead us to introduce the gravitational instability, in these inner regions, as a source of a new viscosity that is of the same functional form as that of the β-prescription of viscosity. Such a consideration brings about fragmentation in the unstable inner disc. In addition, we find the consequent clumpy structure of this area capable to account for the temporal variability of GRB’s light curve, especially for the lower choices of the parameter β, ∼10−5. Finally, we predict the formation of gravitational waves through the migration of fragments before being tidally disrupted. These waves appear to be detectable via a range of current and future detectors from LIGO to Cosmic Explorer.
1 INTRODUCTION
Gamma-ray burst (GRB) is an immediate release of energy, |$\sim 10^{51}\!-\!10^{54} ~\rm erg$|, which lasts from less than |$2~\rm s$|, for short-duration GRBs (SGRBs), up to hundreds of seconds in case of long-duration GRBs (LGRBs; for reviews, see Piran 2004; Kumar & Zhang 2015). The latter’s origin is mainly attributed to the core collapse of massive stars (e.g. Woosley 1993), while the former is thought to emanate from the coalescence of neutron star (NS) binary or NS-black hole (BH) mergers (e.g. Eichler & Cheng 1989; Narayan, Paczynski & Piran 1992). All these scenarios can lead to a hyperaccreting stellar-mass BH with a high mass accretion rate of about |$0.001\!-\!10~\mathrm{M}_{\odot } ~\rm s^{-1}$|, which is hot and dense enough to be cooled via neutrino emission. This hyperaccretion disc is called neutrino-dominated accretion flow (NDAF; see e.g. Liu, Gu & Zhang 2017, for a review), which is considered to be one of the plausible candidates for GRB central engines. Never the less, some may ascribe the LGRB origin, regarding its long-time activity, to the BH lifetime spin (e.g. van Putten & Ostriker 2001; Shahmoradi & Nemiroff 2015). In particular, van Putten & Ostriker (2001) proposed that LGRBs emanate from the rapidly spinning BHs with the suspended accretion due to the large-scale magnetic torques, while SGRBs can be attributed to the hyperaccretion slowly spinning BHs.
Concerning the remarkable temporal variability of the GRB’s light curve, several scenarios have been proposed. This variability has primarily led to the development of the internal shock model, in which the Lorentz factor of the jet varies with time, and consequently the generated luminosity becomes highly variable (e.g. Piran, Shemi & Narayan 1993; Katz 1994). Another approach introduced the dissipation process related to the turbulence or magnetic reconnection in the jet, as a responsible for these rapid fluctuations in prompt emissions (e.g. Narayan & Kumar 2009). From a similar point of view, there are those who argue that the temporal variability may have something to do with the turbulent behaviour in the emission mechanism of GRBs (e.g. Beloborodov, Stern & Svensson 1988, 2000; van Putten, Guidorzi & Frontera 2014; Amati et al. 2018). On the other hand, some authors proposed that this temporal variation could be a clue as to the instabilities occurred in the hyperaccretion disc (as the GRB’s central engine). For instance, based on the detailed treatment of the chemical equilibrium in the gas species, Janiuk et al. (2007) argued that the NDAF can be viscously and thermally unstable at an extremely high accretion rate. Moreover, Lei et al. (2009) proposed that the NDAF could be viscously unstable at a more moderate accretion rate when certain magnetic mechanism, such as the magnetic coupling between the plumping region and the disc, is considered. Regarding the possibility of the viscous instability, Kawanaka & Kohri (2012) found that the thermal equilibrium solutions for the convective hyperaccretion disc, in case of very low accretion rates, would also have a viscously unstable branch. This might lead to the sporadical mass accretion on to the BH resulting in a highly variable light curve. For the rather higher accretion rates (|$\sim 0.003\!-\!0.01 ~ \mathrm{M}_{\odot }~\rm s^{-1}$|), however, Kawanaka, Mineshige & Piran (2013) found a new branch in the thermal equilibrium curves, in which an accretion flow is viscously unstable (but thermally stable) because of efficient neutrino cooling. At even larger accretion rates (|$\gtrsim 0.1 ~ \mathrm{M}_{\odot }~\rm s^{-1}$|), Masada et al. (2007a) introduced a new mechanism that might cause instabilities in hyperaccretion disc resulting in the oscillations observed in the GRB’s light curve. The idea is mainly based on the fact that NDAFs become optically thick to neutrinos in the inner disc. More precisely, Di Matteo, Perna & Narayan (2002) showed that the neutrino opaque region exists inside a radius ∼6–40Rg for |$\dot{M}$| in the range of |$0.1\!-\!10~\mathrm{M}_{\odot }~\rm s^{-1}$|, where Rg = 2GMBH/c2 is the Schwarzchild radius. They argue that for |$\dot{M}\gtrsim 1 ~\mathrm{M}_{\odot }~\rm s^{-1}$|, neutrinos are sufficiently trapped so that flow is advection dominated in this realm. Being inspired by this idea, Masada et al. (2007a) investigated this region to probe for the effectiveness of the magnetorotational instability (MRI) and found that the energy and momentum transport by neutrinos (i.e. neutrino viscosity) could suppress the growth of the MRI significantly, when the magnetic field strength |$B \lesssim 10^{14}~\rm G$| is considered. Having said that, MRI can drive active magnetohydrodynamic turbulence in the outer neutrino-transparent region regardless of the field strength. This gives birth to an accumulation of the baryon matter into the inner dead zone, where the MRI grows inactively and the accretion of matter is suppressed. When the dead zone achieves a large amount of mass and becomes gravitationally unstable, the intense mass accretion on to the BH is triggered through the gravitational torque, episodically. This process can account for the short-term variability in the prompt emission of GRBs.
Concerning the gravitational instability, another approach to treat this variability in both prompt emission and late time flaring activity can be introduced as the clumpy structure of GRB’s central engine. Recently, Coughlin et al. (2020) presented a model to deal with the variable structure of SGRB’s spectrum. Their study reveals that the tails generated from compact object mergers can be gravitationally unstable, leading to the creation of small-scale fragments under their own self-gravity, and consequently, to the variability in fallback rate. This can account for the temporal behaviour of the GRB’s light curve in prompt emission as well as the late time flaring activity (a late-time variability in the GRB’s light curve that occurs |$100\!-\!1000~\rm s$| after the prompt emission), depending on how rapidly the instability occures. Additionally, a similar clumpy structure in the outer hyperaccretion disc has been proposed to be responsible for the late time flaring activity of the central engine (e.g. Perna, Armitage & Zhang 2006; Dall’Osso, Perna & Tanaka 2017; Shahamat & Abbassi 2020).
On the other hand, the impacts of self-gravity have been investigated in the highly dense structure of NDAFs. The feature that might affect this outer disc’s clumpy configuration (e.g. Liu et al. 2014; Shahamat & Abbassi 2017). Similarly, one might think of a clumpy structure in the inner regions of a self-gravitating NDAF to model the oscillations of the prompt emissions’ light curve. However, this is not a possible scenario for the inner disc when the common formalism of the NDAF is applied (as studied by Liu et al. 2014; Shahamat & Abbassi 2017). Having said that, considering the trapped neutrinos in the inner regions of NDAFs (that are assumed to be optically thick to neutrinos (Di Matteo et al. 2002) as a dominant factor in the energy and momentum transport over MRI (Masada et al. 2007a; Masada, Sano & Shibata 2007b), can reduce the accretion rate effectively. This might increase the density of matter inside the NDAF as pointed out by Masada et al. (2007a). Therefore, a self-gravitating formalism for this neutrino opaque region might provide us with an enhanced possibility for the gravitational instability, and probably, fragmentation in this inner zone.
In the hope of developing a possible scenario, we aim to model the temporal variability of the prompt emission via a self-gravitating prescription of NDAF in which neutrino viscosity acts efficiently through the inner regions instead of MRI, and consequently no α-viscosity is considered. In other words, the advection is taken to be the dominant cooling mechanism. Probing the gravitational instability and the possibility of fragmentation in this inner region will provide us with a vision of how successful this formalism can model the temporal variability of GRB’s light curve. However, as can be seen in the following sections, the presence of self-gravity only results in the instability and no fragmentation occurs through this approach, since the disc is cooling down slowly (the local cooling time is larger than the dynamical time-scale of the disc). In this situation, one can consider the gravitational instability as an alternative that facilitates the energy and angular momentum transport, which means another source of viscosity can be implemented (see e.g. Lodato & Rice 2005; Armitage 2011; Lin & Kratter 2016). We will demonstrate that such an additional viscosity term can guarantee the fragmentation in this area as it improves the cooling rate.
This paper is organized as follows. In Section 2, our formalism for the inner regions of a self-gravitating NDAF, regarding the neutrino viscosity as a dominant factor in energy and momentum transportation, is presented. The possibility of gravitational instability and fragmentation is probed in Section 2.1. To make fragmentation plausible, in Section 3, we provide a new prescription of viscosity, i.e. Beta-Neutrino viscosity (a simple combination of β-viscosity term and its neutrino counterpart), identifying the gravitational instability as a source of turbulence inside the neutrino opaque region. A comparison with observational evidences is presented in Section 3.1. Moreover, to make some predictions we study the possibility for gravitational waves (GWs) in Section 4, in the case that fragments migrate prior to tidal disruption. Finally, Section 5 sums up this work, in addition to highlighting our main results and providing some discussions.
2 PHYSICAL MODEL IN NEUTRINO VISCOSITY PRESCRIPTION
2.1 Gravitational instability and fragmentation
The top panel in Fig. 1 represents the contours of Toomre parameter in cases considering with and without self-gravity (the purple and green contours, respectively), depicted in |$\dot{M}\!-\!R$| plane. The results for non-self-gravitating case is achieved through ignoring the first term in equation (6). It should be mentioned that we considered MBH to be 3 M⊙. As it is obvious that, in the self-gravitating case, the upward trend of the Toomre parameter differs from its downward behaviour in the case without self-gravity. In General, one can say the differential rotation works against self-gravity and has a stabilizing impact on the disc. When the self-gravity is taken into account, it affects the outer disc more effectively than the inner disc as a result of the decline in differential rotation. Thus, we think that in the outer radii the interplay between neutrino viscosity and self-gravity can lower the density rather than having an increasing impact. To elaborate more, once the self-gravity compresses these outer radii, the enhancement in the neutrino optical depth can increase the neutrino viscosity. Therefore, we are of the opinion that such an interplay can finally result in a decrease in the surface density as we go further through the disc, which is due to the inverse relation between density and neutrino viscosity (ν ∝ ρ−2). This can be interpreted as an upward trend of the Toomre parameter in the presence of self-gravity (Q ∝ Σ−1).
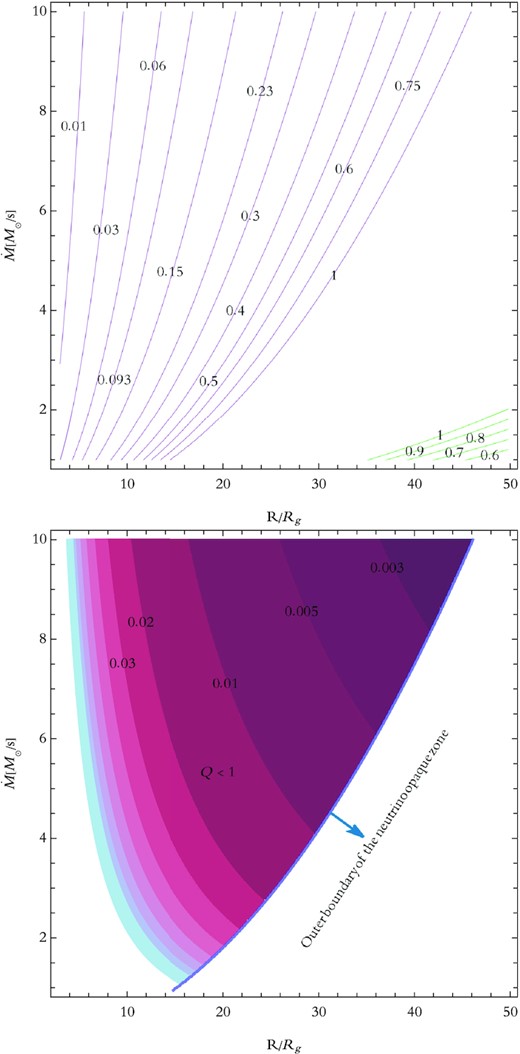
Top panel: gravitationally unstable regions inside the NDAF with and without self-gravity (the purple and green contours of Q parameter, respectively), considering neutrino viscosity. Bottom panel: contours of Toomre parameter (coloured area in purple and blue) with the outer boundary of the neutrino opaque region is depicted by a thick blue line. These contours are related to the Beta-Neutrino viscosity case of a self-gravitating NDAF.
However, it is important to notice the radius inside which our formalism, with high neutrino opacity, is valid. Di Matteo et al. (2002) found that the optically thick region extends out to 4–5Rg at |$\dot{M}=0.1~\mathrm{M}_{\odot }~\rm s^{-1}$|, up to 30–40Rg at |$\dot{M}=10~\mathrm{M}_{\odot }~\rm s^{-1}$|. Regarding such estimates, we consider the neutrino opaque area for the NDAF to be the same as the gravitationally unstable region (the area with purple contours in the top panel of Fig. 1. A probably rough estimation that does not bring about a remarkable impact on our final results other than providing different numbers of data to produce a suitable fit that will appear in Section 3.1.
As can be inferred from the green contours in this panel, there seem not to be any gravitational instability in the inner neutrino opaque regions when the self-gravity is ignored. This result reflects the fact that self-gravity matters in the inner disc using our scenario, unlike what is commonly expected from NDAF structure in which the outer disc is mainly affected by self-gravity (see e.g. Liu et al. 2017; Shahamat & Abbassi 2017).
Considering the top panel in Fig. 2, which represents the contours of tcool/tcrit in the |$\dot{M}\!-\!R$| plane, one can see this criterion is not satisfied, and fragmentation is not possible in the neutrino opaque realm of a self-gravitating NDAF. However, it is argued that in such cases the disc may settle into a quasi-steady state of self-gravitating turbulence, in which an outward transport of angular momentum via gravitational torques is expected (Lynden-Bell & Kalnajs 1972; Lodato & Rice 2004, 2005; Armitage 2011; Lin & Kratter 2016). Being inspired by this idea, we are going to assume the gravitational instability as a source of turbulence, and consequently viscosity, in this unstable region of the disc. On the other hand, to introduce a functional form for this new term of viscosity we consider Duschl & Britsch (2006) approach and take it to be of the same form of the β parameterizations (i.e. ν = βRvϕ). This type of hydrodynamically driven turbulence (β-viscosity) has been proposed by Duschl, Strittmatter & Biermann (1998) and Richard & Zahn (1999), independently, and applied by Duschl, Strittmatter & Biermann (2000) to both self-gravitating and non-self-gravitating discs. They showed that this kind of viscosity yield the standard α-disc prescription in the case of shock dissipation limited, non-self-gravitating discs (for more details, see also Duschl & Britsch 2006). Henceforth, the viscosity in this neutrino opaque region is considered as a combination of neutrino kinematic viscosity and β turbulent vicosity.
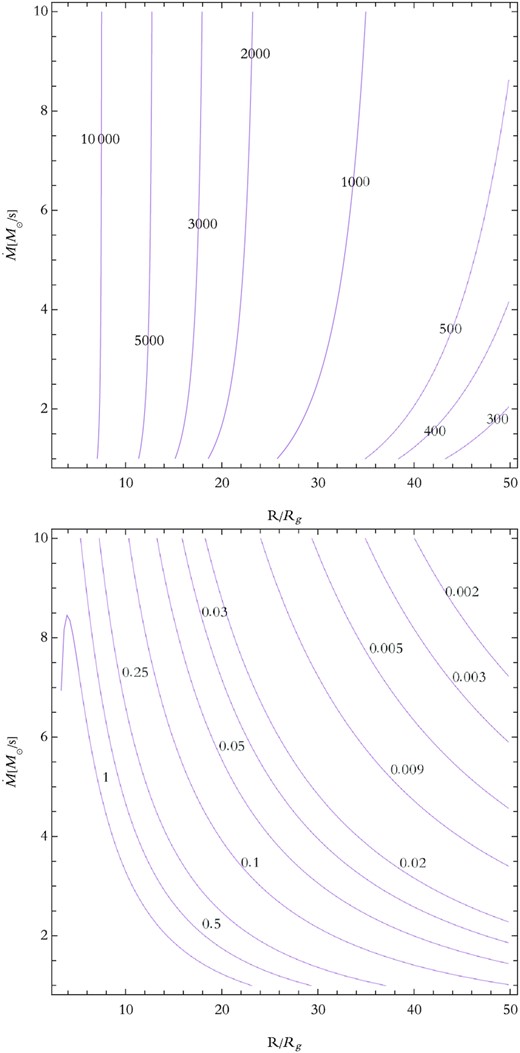
Top panel: contours of tcool/tcrit in |$\dot{M}\!-\!R$| plane in case of ν-viscosity prescription. Bottom panel: contours of tcool/tcrit for the case with β-viscosity. Concerning the criterion introduced in equation (10), the fragmentation seems possible in this scenario.
3 β-NEUTRINO VISCOSITY PRESCRIPTION
We found that fragmentation is possible in this unstable realm, for the cases with |$\dot{M}\geqslant 1.3~\mathrm{M}_{\odot }~\rm s^{-1}$|, regarding |$M_{\rm BH}=3~\rm \mathrm{M}_{\odot }$| and β = 2.5 × 10−5 (see the plot in the bottom panel of Fig. 2 for more precise evaluation).
3.1 Fragment accretion and observable evaluation
Considering the fragment as a uniform spherical mass distribution, one may estimate |$f_{\rm T}={GM_{\rm BH}}/{R^{2}}({l_{\rm f}}/{R})$|, |$f_{\rm SG}={3GM_{\rm f}}/{5l_{\rm f}^{2}}$|, and |$f_{\nu }={l_{\rm f}\nu \Sigma R}/{M_{\rm f}}\mid {\mathrm{d}\Omega }/{\mathrm{d}R}\mid$|, in which Mf and lf are considered to be the fragment’s mass and size. The latter is assumed as the local Jeans length, i.e. |$l_{\rm f}=\lambda _{\rm J}=c_{\rm s}\sqrt{{\pi }/{G\rho }}$|. We also take the Jeans mass to approximate the mass of the fragment, namely |$M_{\rm f}\approx M_{\rm J}=({4}/{3})\pi \rho ({\lambda _{\rm J}}/{2})^{3}$| with ρ ≈ Σ/2H.
Through making use of the condition (13), one can obtain the radius at which the accretion of each fragment is triggered (Racc). Having such a radius in hand, the viscous time during which a fragment is considered to be accreted, is achievable via equation (11).
![Top panel: The 3D panel illustrates the fragment mass Mf [M⊙] versus $\dot{M}~[\mathrm{M}_{\odot }~\rm s^{-1}]$, and radius Rf at which the fragment is considered to be formed (this is actually an arbitrary value of R/Rg), shown as a pink surface. The colourful contours are associated with the delay time td, with their time values given in the plot legend. Bottom panel: This plot demonstrates the contours of Racc in the $\dot{M}\!-\!R$ plane.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2989/1/m_stab2989fig3.jpeg?Expires=1750017230&Signature=dD459bvZrm2zUKswFplQzjoDcxdax5PDN7x0bmUAud6Ycp0Ytr8AqXDSbJhhg9btoc~3Nqim7fIO8baUX2NMQk74Rmu0EanobVoznLd7-uWeSfp3qnX940-n28SuNLtsnKUkifjag4caQY4kfrneB51TDMj9~3aSva47oTfpTJ3jVHKDCLSU2i5~phMs4-u8cu9gpgT83191h-XsYBG7SsV23q0oi6Nx2u5s6B~2pGt~NcWWXc6UO05rVEG84vm2Q4v9JHptH0rL37Uspk3n5Gy-6Rb5urJbVW1HVHf~jjSK70GIZH8HoLt4zpEql0UhTNRXHMsu2vVlygZCgR8JVA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Top panel: The 3D panel illustrates the fragment mass Mf [M⊙] versus |$\dot{M}~[\mathrm{M}_{\odot }~\rm s^{-1}]$|, and radius Rf at which the fragment is considered to be formed (this is actually an arbitrary value of R/Rg), shown as a pink surface. The colourful contours are associated with the delay time td, with their time values given in the plot legend. Bottom panel: This plot demonstrates the contours of Racc in the |$\dot{M}\!-\!R$| plane.
As mentioned previously, Fig. 3 includes representations of the fragments’ features. The pink surface in the top panel depicts the fragments’ mass behaviour versus mass accretion rate and radius (we denoted the location of each fragment as Rf that is actually an arbitrary value of the dimensionless radius R/Rg). The colourful 3D contours are associated with different td (s) with their time values given in the plot’s legend. The plot in the bottom, on the other hand, demonstrates the contours of Racc in the |$\dot{M}\!-\!R$| plane. One can see the larger the accretion rate (|$\dot{M}$|) becomes the smaller the fragment’s mass (Mf), and the accretion radius (Racc) get, while the delay time (td) increases. The decline in Mf can be accounted for by the growth in density ρ, taking our results for Σ and H into consideration, as |$\dot{M}$| rises. Although it is not possible to find a clear relation between |$\dot{M}$| and ρ, it appears from outcomes that an increase in |$\dot{M}$| leads to a larger growth in density comparing their relative variations, i.e. |${\delta \rho }/{\rho }\gt {\delta \dot{M}}/{\dot{M}}$|. The thing that results in a larger increase in the self-gravity force with respect to the shear force. This, consequently, causes the fragment to migrate inwards a larger distance, through a longer time td, prior to accretion. Moreover, at a given accretion rate, fragments with smaller masses are created further in the disc. In other words, there is an inverse relation between Rf and Mf. It gets quite obvious when one infers Mf is proportional to |${1}/{\sqrt{M_{\rm disc}(R_{\rm f})}}$|, considering the previously introduced relations for Mf and lf.
To provide an intuition about the validity of our model, we draw an analogy with empirical outcomes. There seem to be an anticorrelation between gamma-ray luminosity and the minimum variability time-scale (regarded as a characteristic time-scale tc), namely |$t_{\rm c}\propto L_{\gamma }^{-1.0\pm 0.1}$| (Sonbas et al. 2015). The latter is assumed to be the minimum time-scale that separates white noise from red noise in a power density spectrum. There might be some alternatives to account for this anticorrelation in the literature; e.g. van Putten et al. (2015) argue that the interactions between rotating BHs with the surrounding matter can increase inversely proportional to duty cycle in advection of the magnetic flux. In our explanation of such a behaviour, however, we approximate this characteristic time-scale (tc) to be the same as the viscous time of a fragment’s accretion, tν, and probe for its inverse correlation with the luminosity provided by each fragment’s accretion.
We presented an illustration of the characteristic time behaviour in terms of gamma-ray luminosity, in the top panel of Fig. 4. MBH and β are assumed to be 3 M⊙ and 2.5 × 10−5, with different mass accretion rates, ranging within |$1.5\!-\!10~\mathrm{M}_{\odot }~\rm s^{-1}$|, are considered. It should be mentioned that we restricted ourselves to the area of the disc where our formalism is approximately valid (see Section 2). Additionally, since it is of a remarkable uncertainty that fragment will be created throughout this region, we considered a variety of possible fragments that probably form at different radii. Regarding the best-fitting line (dot–dashed curve), a power-law correlation between these two quantities can be confirmed, with a power index of about −0.85. This is interestingly close to its phenomenological value, i.e. ∼−1.
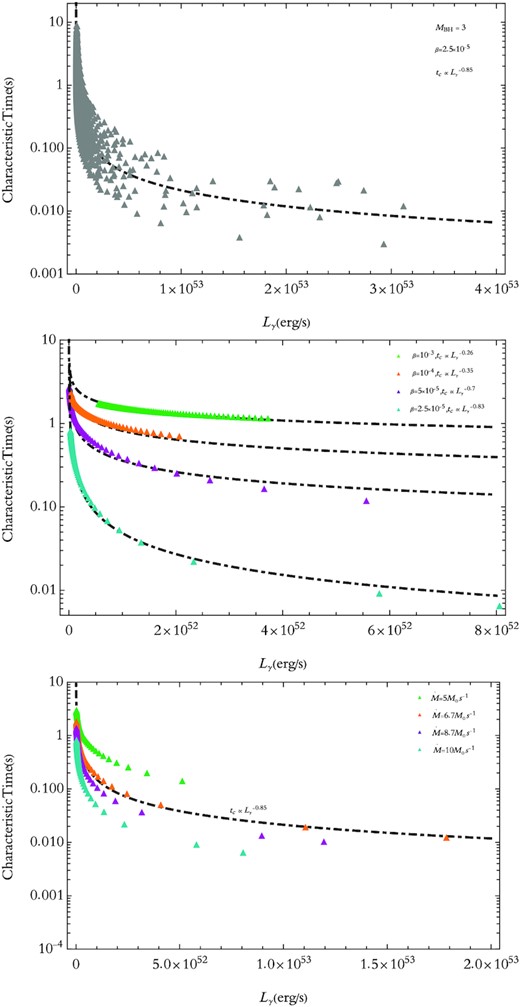
Top panel: the characteristic time behaviour in terms of gamma-ray luminosity for a set of given parameters written inside the plot. Different mass accretion rates, ranging from |$1.5 \ {\rm to} \ 10~\mathrm{M}_{\odot }~\rm s^{-1}$|, are considered as well. Additionally, a variety of possible fragments that might form at different radii are taken into consideration. The black dot–dashed curve is the best-fitting line to our data. Middle panel: different fits for various quantities of β parameter and |$\dot{M}=10~\mathrm{M}_{\odot }~\rm s^{-1}$|, are illustrated. Evidentally, as β decreases, the fit to our data match better with the phenomenological findings. Bottom panel: tc versus Lγ, with a set of various mass accretion rates, i.e. |$\dot{M}=5,6.7,8.7,$| and |$10~\mathrm{M}_{\odot }~\rm s^{-1}$| (with the curves in green, orange, purple, and cyan, respectively), and β = 2.5 × 10−5 are taken into account.
However, to find how our choices of β parameter might affect the outcomes, we plotted different fits taking various quantities of this parameter into account, and considering |$\dot{M}=10~\mathrm{M}_{\odot }~\rm s^{-1}$| (the middle plot in Fig. 4). Obviously, the smaller the β parameter gets, the better our results satisfy the observations, so that it looks quite well matched to the empirical results when β ∼ 10−5, the quantity that is very close to the value estimated by Duschl & Britsch (2006), for a self-gravitating unstable disc.
A similar analogy is provided for different mass accretion rates in the plot at the bottom of Fig. 4. |$\dot{M}$| is assumed to be 5, 6.7, 8.7, and |$10~ \mathrm{M}_{\odot }~\rm s^{-1}$| with the curves in green, orange, purple, and cyan, respectively, and β = 2.5 × 10−5. Evidently, a growth in accretion rate gives birth to a decline in the characteristic time-scale, which indicates a shorter temporal variability in the spectrum, that might be an expected consequence of the increase in |$\dot{M}$|.
Note that in the above analysis we assumed each fragment accretes due to β-viscosity. However, such an assumption might not be a good estimate since it appears through fragmentation that there can be a transition from the so-called gravito-turbulent behaviour (the turbulence due to gravitational instability) in the disc, which means this state might not be sustained after fragmentation (Lin & Kratter 2016). Therefore, regarding this uncertainty, we consider other possible scenarios of the viscosity prescriptions that might be present during the fragment’s accretion. We think that after fragmentation the density of material in the disc has been reduced because of fragmentation, so that the initial high neutrino opacity might not be reliable anymore (remember τtot ∝ ρ). Hence, the MRI-turbulent accretion process seems to be a probable alternative. In this case, if the viscose time-scale is shorter than the fallback time of the fragment to the pericentre radius (comparable to the tidal radius that has been denoted by Racc and archived by equation 13), one can approximate the accretion rate by the fallback rate (for more details on this issue see e.g. Cannizzo, Lee & Goodman 1990; Mockler, Guillochon & Ramirez-Ruiz 2019), so that the fallback time can be considered as tc. Otherwise, the accretion time, tν, would be another possible estimate for tc. Considering α ∼ 0.3 (King, Pringle & Livio 2007; Martin et al. 2019), we found the former as the case in our formalism. Therefore, we assume the fall back time |$t_{\rm fb} \simeq 2\pi R_{\rm acc}^{3} {1}/({l_{\rm f}^{3/2}\sqrt{GM_{\rm BH}}})$| (Falanga et al. 2015; Coughlin et al. 2020), as the characteristic time-scale of our interest. Such a consideration will change the power index of the best-fitting line, in the Lγ − tc panel, to ∼−0.73 with tc reaches an order of |$\sim 0.005\!-\!0.05~\rm s$|. Lower choices for α result in the longer minimum variability time-scales, without making any significant change in the power index, which means a good agreement with observations.
Another issue that sounds worth noting is the probable mechanisms can result in the gamma-ray emission through the jet activity. As we claimed, the variability in the accretion rate can provide us with an inhomogeneous jet structure comprises the shells of different Lorentz factors. Regarding the variability time-scale, which is mostly very short especially for the MRI-driven viscosity scenario (note that in the β − ν viscosity case, Fig. 4, the longer accretion times, corresponding to the outer fragments, might be due to an overestimation in the size of the neutrino trapped region), the jitter radiation (Medvedev, Pothapragada & Reynolds (Medvedev 2000; Medvedev, Pothapragada & Reynolds 2009) or the turbulent model (Narayan & Kumar 2009) can account for the mechanisms to produce the resultant spectrum. However, for the longer variability time-scales that are attributed to the lower fragments’ accretion rates (consider the lower clump’s mass with a longer accretion time), it appears the large-scale magnetic fields within the jet play a dominant role in the emission mechanism via synchrotron radiation or Compton scattering.
4 Fragments’ migration and GWs
In Fig. 5, we provided the outcomes for the characteristic strain in terms of frequency in which we assumed a source distance of |$100~\rm Mpc$|. The curves in cyan are associated with different mass accretion rates, range from |$1.5 \ {\rm to} \ 10~\mathrm{M}_{\odot }~\rm s^{-1}$|, the BH mass 3 M⊙, and β = 2.5 × 10−5. To provide a clear vision of hc trend versus frequency, we distinguished two curves with |$\dot{M}=2$| and |$5.5~\mathrm{M}_{\odot }~\rm s^{-1}$|, through colouring in black. For one thing, the higher mass accretion rates lead to the lower characteristic strain amplitudes in a wider range of frequency. The former reflects the fact that, for higher |$\dot{M}$|, although the number of cycles within a bandwidth increases due to the longer distance of inwards migration, the lower mass of the fragment at higher accretion rates gives birth to such a decline in hc. For another, at a given accretion rate, as we go inward through the disc it appears the increasing fragment’s mass plays a dominate role over the decreasing migration time of the fragments, and, consequently, the declining ncyc, in order to produce GWs with higher characteristic strain.
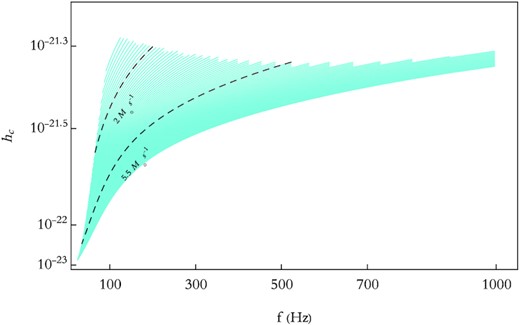
The characteristic strain in terms of frequency for a source distance of |$100~\rm Mpc$|. The curves in cyan are associated with different mass accretion rates, range from |$1.5 \ {\rm to} \ 10~\rm \mathrm{M}_{\odot }s^{-1}$|, the BH mass 3 M⊙ and β = 2.5 × 10−5. We distinguished two curves with |$\dot{M}=2$| and |$5.5~\mathrm{M}_{\odot }~\rm s^{-1}$|, through black colour.
More importantly, such GWs with 10−23 ≲ hc ≲ 5 × 10−22 and |$25\lesssim f\lesssim 1000~\rm Hz$|, are probably detectable via various GW detectors from LIGO (for the lower mass accretion rates) to Einstein Telescope (ET) and Cosmic Explorer (CE) (for the outer disc’s fragments with higher |$\dot{M}$|). This detectability has been illustrated in Fig. 6, in which the sensitivity lines (the noise amplitudes hn) of different detectors have been depicted through solid coloured curves. The area in pink demonstrates our model estimate of hc for a source at a distance of |$\geqslant 100~\rm Mpc$|, considering MBH = 3 M⊙ and β = 2.5 × 10−5. To compare with the other sources, we also demonstrated the realm of GW characteristic strains produced by compact binary inspirals that is represented in purple. This plot has been provided through the website http://rhcole.com/apps/GWplotter, in which similar figures can be generated (Moore, Cole & Berry 2014).
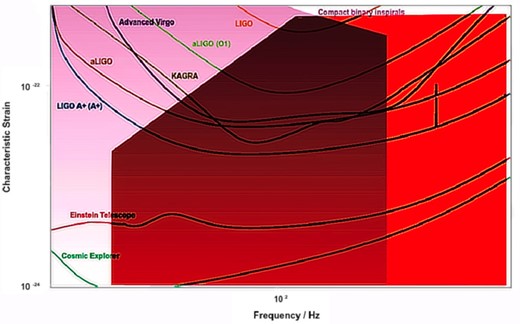
The noise amplitudes hn for different detectors are depicted through coloured curves. The area in pink demonstrates our model estimate of strain amplitude hc for a source at a distance |$\geqslant 100~\rm Mpc$|, concerning MBH = 3 M⊙ and β = 2.5 × 10−5. For the sake of comparison with promising cases of astrophysical objects, data for compact binary inspirals are represented in bright purple.
5 CONCLUSIONS AND DISCUSSION
The main idea of this work emanates from different approach adopted by Masada et al. (2007a) towards the neutrino function in the inner regions of NDAF, where neutrino opacity appears to be high enough to make neutrinos captured (Di Matteo et al. 2002). Such trapped neutrinos are considered as the main responsible for the energy and momentum transport (Masada et al. 2007a). The implementation of this idea in a self-gravitating NDAF, as what we conducted through this study, can account for the rapid fluctuations in GRBs’ prompt emission, if the inner regions become gravitationally unstable and fragmentation gets probable. This is not a possible scenario, however, in case of a self-gravitating NDAF in which (magnetic) α-viscosity is taken into consideration (based on Liu et al. 2014; Shahamat & Abbassi 2017, for instance, only the outer disc is unstable when it comes to self-gravity in the presence of α-viscosity). Our results indicate that such a formalism leads to the gravitational instability in the inner neutrino opaque regions, while the fragmentation does not occur. Hence, being inspired by the idea proposed by Duschl & Britsch (2006), we considered this instability as a source of turbulence and viscosity. To elaborate more, Duschl & Britsch (2006) found that the functional form of this gravitationally driven viscosity is the same as that of the β parametrizations, although they are based on different physical considerations. Through adding such a term to viscosity, we found it possible for the inner disc to undergo fragmentation. We studied the fragments’ features to see if this clumpy structure gives birth to the temporal variability of the prompt emissions. The comparison of outcomes with observational findings showed that this scenario is successful, especially in the case of lower values for β parameter (∼10−5). This is in a good agreement with what has been estimated by Duschl & Britsch (2006) for a self-gravitating unstable disc, on the other hand. Although, we emphasize that the uncertainties in adopting an assured strategy to trace the evolution of the clumps, need more precise studies through simulations to be treated. More interestingly, our simple model could predict the creation of GWs as a result of the fragments’ migration prior to their accretion. The frequency band, |$25\lesssim f\lesssim 1000~\rm Hz$|, and the amplitude of the waves, with 10−23 ≲ hc ≲ 5 × 10−22, made it detectable for a range of current and future detectors from LIGO to CE.
There are some points worth discussing here. For one thing, in case of LGRBs, the initial higher accretion rates, i.e. |$\dot{M}\gtrsim 1~\mathrm{M}_{\odot }~\rm s^{-1}$|, which appear to play a crucial role in our scenario to cause the fragmentation, are probable for the cases of the higher progenitor mass (≳ 40–60 M⊙; see e.g. Wei, Liu & Song 2019). For the lower progenitor mass that is of a smaller initial mass accretion rate, however, the gravitational instability might result in a spiral wave structure that can be another source of variability in the accretion rate of materials towards the BH, as discussed by Masada et al. (2007a). In case of SGRBs, on the other hand, one should note that the more massive fragments are not probable to be formed in the disc of a mass around ∼0.2–0.5 M⊙ (see e.g. Song et al. 2015). Moreover, regarding the accretion time of each clump (see Fig. 4), the outer fragments for the lower mass accretion rates (|$\lesssim 5~\mathrm{M}_{\odot }~\rm s^{-1}$|) should also be ignored due to the accretion time longer than |$~2~\rm s$| (the common time-scale of the SGRB’s prompt emission). Although, these considerations do not affect the final results remarkably.
For another, there are some assumptions we made in order to simplify our model, such as considering the gas pressure as the only effective factor in the total pressure. Granted such a consideration might be a rather good one, as pointed out by Di Matteo et al. (2002), the effectiveness of the radiation pressure factor is probably worth investigating in such an advection-dominated environment with trapped photons.
To shed light on the disc’s cooling, we should add the consideration of the advection cooling, as the only process that cools down the disc, can be modified through taking the photodisintegration mechanism into account, as well. Other cooling processes, i.e. neutrino-antineutrino annihilation and radiation cooling, are not actually important in the inner disc due to the high neutrino opacity and the optically thick nature of this region. However, photodisintegration can affect the energy transpose of the system. As Piro & Pfahl (2007) pointed out, this mechanism can be effective in cooling the outermost region of collapsar discs. The thing that can facilitate the fragmentation of the disc, in the case of being gravitationally unstable, via lowering the local cooling time-scale. In our study, we ignore this mechanism and considered the advection cooling process as the only one, for the sake of simplification. We think that taking the effects of photodisintegration into account can increase the fragmentation possibility, so that the main idea of the model will not be affected, although the estimates we made for the minimum variability time-scale and the strain amplitude may be varied due to a change in the fragments’ features.
Finally, we found that the lower the β parameter is the better the outcomes are confirmed by observations. However, bearing in mind β is assumed to be proportional to the inverse Reynolds number (Duschl et al. 2000), this means a large Reynolds number is required to achieve better results. On the other hand, Masada et al. (2007a) pointed out the MRI can be effectively suppressed by the neutrino viscosity in case of small Reynolds numbers (Re ≲ 1). This reflects the fact that for a self-gravitating NDAF such an assumption might not work well, and it should be investigated if the MRI can be suppressed by neutrino viscosity anymore. The thing that makes it of a probably great significance to consider the α-prescription of viscosity as well.
ACKNOWLEDGEMENTS
This work was supported by the National Natural Science Foundation of China under grants 11822304 and 12173031. We hereby acknowledge Sci-HPC Center of Ferowsi University of Mashhad where some part of this research was performed there.
DATA AVAILABILITY
No new data were generated or analysed in support of this research.



