-
PDF
- Split View
-
Views
-
Cite
Cite
Martyna Chruślińska, Gijs Nelemans, Lumen Boco, Andrea Lapi, The impact of the FMR and starburst galaxies on the (low metallicity) cosmic star formation history, Monthly Notices of the Royal Astronomical Society, Volume 508, Issue 4, December 2021, Pages 4994–5027, https://doi.org/10.1093/mnras/stab2690
Close - Share Icon Share
ABSTRACT
The question how much star formation is occurring at low metallicity throughout the cosmic history appears crucial for the discussion of the origin of various energetic transients, and possibly double black hole mergers. We revisit the observation-based distribution of birth metallicities of stars (fSFR(Z,z)), focusing on several factors that strongly affect its low metallicity part: (i) the method used to describe the metallicity distribution of galaxies (redshift-dependent mass metallicity relation – MZR, or redshift-invariant fundamental metallicity relation – FMR), (ii) the contribution of starburst galaxies and (iii) the slope of the MZR. We empirically construct the FMR based on the low-redshift scaling relations, which allows us to capture the systematic differences in the relation caused by the choice of metallicity and star formation rate (SFR) determination techniques and discuss the related fSFR(Z,z) uncertainty. We indicate factors that dominate the fSFR(Z,z) uncertainty in different metallicity and redshift regimes. The low metallicity part of the distribution is poorly constrained even at low redshifts (even a factor of ∼200 difference between the model variations) The non-evolving FMR implies a much shallower metallicity evolution than the extrapolated MZR, however, its effect on the low metallicity part of the fSFR(Z,z) is counterbalanced by the contribution of starbursts (assuming that they follow the FMR). A non-negligible fraction of starbursts in our model may be necessary to satisfy the recent high-redshift SFR density constraints.
1 INTRODUCTION
The observed populations of stars, their remnants and related transients consist of objects formed at different times and with different metallicities. To model those populations and to correctly interpret observations, it is necessary to know the metallicity dependent star formation history (SFH) of the observed galaxy, galaxies in the probed volume, or even of the entire Universe. Knowledge of the latter – which is the subject of interest of this study – becomes increasingly important in the era of gravitational wave (GW) astrophysics. That is because the time between the formation of the progenitor stars and merger of stellar black holes or neutron stars observed in GW can be comparable to the age of the Universe (e.g. Belczynski et al. 2016). Moreover, the efficiency of formation of merging binaries may show a strong metallicity dependence. In particular, it has been suggested that double black hole mergers may form much more efficiently in low metallicity environments (≲0.1 solar metallicity; e.g. Giacobbo, Mapelli & Spera 2018; Klencki et al. 2018). This makes the modelled properties of the population of such systems particularly sensitive to the assumed distribution of the cosmic star formation rate density (SFRD) at different metallicities and redshifts, fSFR(Z,z) (e.g. Chruslinska, Nelemans & Belczynski 2019; Neijssel et al. 2019; Broekgaarden et al. 2021) and requires knowledge of fSFR(Z,z) even beyond the peak of the cosmic SFH. To confront the model predictions with observations and draw correct conclusions from such a comparison, it is necessary to take into account the fSFR(Z,z) uncertainty, which may be substantial – especially at high redshifts (Chruslinska & Nelemans 2019; Chruślińska et al. 2020; Boco et al. 2021). Given the many uncertain pieces of information that need to be combined to estimate fSFR(Z,z), an (observation-based) determination of this distribution presents a challenge in itself. In this study, we take a closer look at two of those pieces: the empirical correlation between the star formation rate and metallicity of star-forming galaxies (the so-called fundamental metallicity relation, e.g. Ellison et al. 2008; Mannucci et al. 2010) and the contribution of starburst galaxies. We build on the observation-based fSFR(Z,z) model from Chruslinska & Nelemans (2019) (briefly introduced in Section 2) and expand the discussion presented in Boco et al. (2021), aiming to evaluate the uncertainty (or – find realistic, observationally allowed extremes) of the metallicity dependent cosmic SFH in view of those factors. Where appropriate we adopt a standard flat cosmology with ΩM = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1, assume a (universal) Kroupa (2001) initial mass function (IMF) and solar metallicity of 12 + log10(O/H)⊙ = ZO/H⊙ = 8.83 and Z⊙ = 0.017 (Grevesse & Sauval 1998).
2 AN OBSERVATION BASED fSFR(Z, z) DETERMINATION
We construct fSFR(Z,z) building on the framework detailed in Chruslinska & Nelemans (2019). In essence, their method is based on a combination of three key ingredients: the distribution of galaxy stellar masses (galaxy stellar mass function – GSMF), and the distributions describing the star formation rates (SFR) and metallicities of galaxies at fixed stellar mass M*. All distributions are redshift dependent. The GSMF is used to obtain the number density of galaxies of different masses. The contribution of galaxies of different masses to the total SFRD can then be obtained by weighing the number density of galaxies in a given mass range by their SFR. Finally, fSFR(Z,z) is obtained by assigning a metallicity to each M*.
The SFR and metallicity distributions are modelled as lognormal distributions centred on the empirical star formation–mass relation (SFMR) and the mass – (gas-phase) metallicity relation (MZR), respectively, with dispersions σSFMR and σMZR (representing the intrinsic scatter around the two relations). Note that the observational gas-phase metallicity estimates probe the oxygen abundance (ZO/H = 12 + log10(O/H)1), and that is the metallicity measure used in our study. Additional scatter in ZO/H is introduced to model the spread in the metallicity at which the stars are forming within the galaxies. To determine all the necessary ingredients, the authors assemble a compilation of observational results describing the MZR, SFMR and GSMF, combined over a wide range of redshifts (z) and M*. Several variations of the base relations (SFMR, MZR, GSMF) are explored in order to discuss the impact of the uncertain absolute metallicity scale (steming from the differences between the estimates obtained with different metallicity determination methods), the shape of the high-mass end of the SFMR and the redshift evolution of the low-mass end of the GSMF (see Section 2 in Chruslinska & Nelemans 2019 and references therein).
In this study, we explore an alternative method to obtain the redshift-dependent metallicity distribution of star-forming galaxies, based on the fundamental metallicity relation. We then modify the SFR distribution to better account for the contribution of star-forming galaxies that are strong outliers to the general SFMR (starbursts). Our motivation for those modifications and the details of our approach are laid out in Sections 3 and 4, respectively.
3 THE FUNDAMENTAL METALLICITY RELATION
The fundamental metallicity relation (FMR) is a three parameter dependence linking M*, SFR, and gas-phase metallicity of star-forming galaxies (Ellison et al. 2008; Mannucci et al. 2010). The relation implies the mass–metallicity correlation, as observed in the MZR, but it also introduces an anticorrelation between metallicty and SFR, such that galaxies of the same stellar mass showing higher than average SFR also have lower metallicities (i.e. the galaxy’s offset from the average mass–metallicity relation – MZR – is anticorrelated with its offset from the average SFR–mass relation).
The existence of such SFR–metallicity anticorrelation has been reported in numerous observational studies (e.g. Lara-López et al. 2010; Mannucci, Salvaterra & Campisi 2011; Yates, Kauffmann & Guo 2012; Andrews & Martini 2013; Bothwell et al. 2013; Salim et al. 2014; Zahid et al. 2014b; Yabe et al. 2015; Hunt et al. 2016; Sanders et al. 2018; Cresci, Mannucci & Curti 2019; Curti et al. 2020; Sanders et al. 2021) and established up to redshift z ∼ 3.5.
Such correlation is also expected from theoretical models of galaxy evolution and is thought to reflect the changes in the SFR-fuelling gas fraction present within the galaxy (e.g. Ellison et al. 2008; Davé, Finlator & Oppenheimer 2011; Yates et al. 2012; De Lucia et al. 2020). Lower SFR for a given M* then implies that the galaxy has already used up most of its cold gas reservoir (fuelling its SFR in the past), and therefore (in the absence of strong outflows) its interstellar medium is more metal rich than that of the galaxy of the same mass that is still highly star forming. At low SFR there are also fewer supernovae that can remove (especially at low M*) metal-rich gas from the galaxy. In turn, inflowing metal-poor material lowers the metallicity and provides additional fuel for the SFR, increasing the latter. As long as the time-scales on which the SFR and metallicity evolve are of the same order, the anticorrelation between the galaxy offsets from the MZR and SFMR is expected to hold (e.g. Torrey et al. 2018). Those time-scales are similar for the feedback/SFH implementations used in the large-scale cosmological simulations such as EAGLE and Illustris-TNG, which warrants the existence of the FMR up to high redshifts in the simulations (Lagos et al. 2016; De Rossi et al. 2017; Torrey et al. 2018). However, Torrey et al. (2018) point out that the strength of the correlation – especially for low-mass galaxies at high redshift – may be reduced if models with particularly strong and/or bursty feedback are used. Lagos et al. (2016) find that the shape of the FMR in the EAGLE simulations depends on the adopted model of star formation. Therefore, observational confirmation of the existence or breakdown of the FMR at high redshifts will help to discriminate between the different feedback and star formation prescriptions.
Observationally, the FMR is found to show little to no evolution with redshift up to z ∼ 3 within the uncertainty of the current data and range of galaxy properties probed (see Cresci et al. 2019 and Sanders et al. 2021 for recent discussion). Since both the mass and SFR distributions of star-forming galaxies change over time, the apparent lack of FMR evolution implies that galaxies at different redshifts probe different parts of the locally established relation. At fixed M*, a decrease in the average galaxy metallicity as a function of redshift is still expected, as the typical SFR is higher at earlier cosmic times.
At z ≳ 2, the rate of decrease in metallicity implied by a non-evolving FMR is much weaker than that reported by various studies discussing the redshift evolution of the MZR (e.g. Maiolino et al. 2008; Mannucci et al. 2009). Similarly to the FMR, the MZR (and its evolution with redshift) is virtually unconstrained at redshifts z ≳ 3.5 (Maiolino & Mannucci 2019). This uncertainty in the rate of metallicity evolution is one of the key factors affecting the fSFR(Z,z). In particular, different high redshift extrapolations of empirical relations used in the literature lead to drastically different conclusions about the birth metallicities of stars forming beyond the peak of the cosmic SFH (e.g. Chruslinska et al. 2019; Chruslinska & Nelemans 2019; Boco et al. 2021).
Recent observational studies find support for rapid early metal enrichment in high-redshift galaxies, pointing towards a weak MZR evolution that is more in line with the apparently invariant FMR (see section 3 in Boco et al. 2021 and references therein for a recent discussion). Such weaker metallicity evolution is also in agreement with the results of cosmological simulations and semi analytical models of galaxy evolution (e.g. Yates et al. 2012; Torrey et al. 2019). Furthermore, Sanders et al. (2021) show that when the differences in the properties of the ionized gas within H ii regions (responsible for the emission lines used to estimate the metallicity; in particular lower iron to oxygen ratio for the same O/H found in high-redshift galaxies) of galaxies at different redshifts are taken into account, the inferred MZR evolution is milder (i.e. metallicities of high-redshift galaxies are biased low if those differences are neglected). In fact, the MZR evolution found by Sanders et al. (2021) is consistent with the non- or weakly evolving FMR within the redshift and mass range probed in their study. The existence of an FMR also means that if the galaxy sample is biased towards high SFRs, the inferred average metallicity is underestimated. Such biases can be expected in high redshift and low stellar mass galaxy samples, affecting the MZR shape (the low mass end slope) and the rate of evolution with redshift (a decrease in the normalization).
In light of the above discussion, we conclude that the assumptions about the metallicity evolution made in Chruslinska & Nelemans (2019), which rely on the MZR obtained by Mannucci et al. (2009) and extrapolate its redshift evolution based on their two highest redshift bins, are likely to overestimate the rate of metallicity decrease at z ≳ 2 and require revision: either assuming a weaker MZR evolution, or using the FMR to assign metallicity to galaxies. The use of the FMR instead of an MZR in fSFR(Z,z) determination appears advantageous for two reasons: (i) the redshift invariance of the FMR allows to circumvent the problem of the uncertain MZR evolution with redshift - the metallicity distribution at each z is then defined by the local FMR and the SFMR and GSMF (whose z dependence is generally better constrained than that of the MZR). We stress that with the current data there is no guarantee that at z ≳ 3 the FRM remains (close to) redshift invariant. By assuming a non-evolving FMR throughout the entire cosmic history we explore another extreme assumption (with respect to Chruslinska & Nelemans 2019) about the rate of metallicity evolution at high redshift. (ii) if all star-forming galaxies follow the FMR (at present, there is no clear evidence to the contrary), it can be used to describe metallicity of galaxies belonging to populations for which there are little examples of metallicity determinations (e.g. strong outliers of the star-forming main-sequence that are not described by the MZR, such as starburst galaxies, see Section 4).
However, the major problem with this approach is that there is no agreement on the exact form of this three parameter mass–SFR-metallicity dependence. The fSFR(Z,z) derived with the FMR will necessarily strongly depend on the choice of this relation, just as it strongly depends on the choice of MZR and its extrapolated evolution. While the discussion of the systematic effects on the fSFR(Z,z) introduced by the choice of a particular form of the MZR is relatively straightforward (Chruslinska & Nelemans 2019) and to a large extent boils down to the discussion of differences caused by the use of different metallicity determination methods (which are well documented in the literature, e.g. Kewley & Ellison 2008, Maiolino & Mannucci 2019), an analogous discussion for the FMR is not. The observationally inferred FMR is known to non-trivially depend on the metallicity determination method, the SFR determination method and the galaxy sample selection criteria (e.g. Yates et al. 2012; Hunt et al. 2016; Kashino et al. 2016; Telford et al. 2016; Cresci et al. 2019). We note that it is not clear how the FMR depends on each of those factors. Therefore, one needs to be cautious when using different literature results concerning the properties of galaxy populations (e.g. the SFMR) in combination with a particular FMR estimate – if those results are based on different techniques, this would represent an internally inconsistent approach.
Instead of using a particular example from the literature, in our analysis we resort to a phenomenological description of the FMR. We aim to capture the robust observational/theoretical features of the mass–SFR-metallicity dependence and describe the variations in the shape of this dependence caused by different choices of the local MZR and SFMR (that reflect the differences in the metallicity and SFR determination methods used in the literature). This allows us to ensure the consistency of the method and discuss the realistic extremes of the fSFR(Z,z).
3.1 Constructing the FMR from z ∼ 0 scaling relations
To construct our model FMR, we describe its 2D projection on the ZO/H–log10(M*) plane. This projection is the most commonly shown in observational studies. We refer to it as ZO/H(SFR, M*) (see Fig. 1 for the illustration).
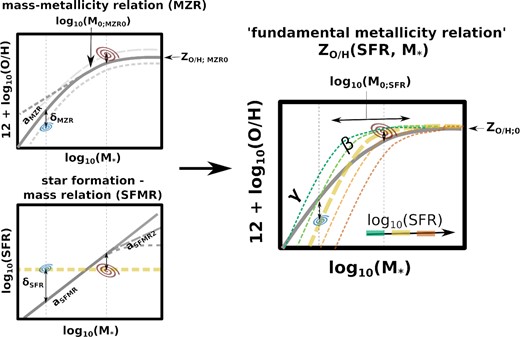
Sketch illustrating the local MZR (top left), SFMR (bottom left), and the three parameter mass–metallicity-SFR dependence ZO/H(SFR, M*) (right), indicating the key parameters of those relations and the observed anticorrelation between the galaxy’s offsets from the MZR (δMZR) and SFMR (δSFMR). We consider different assumptions about the MZR and SFMR relations (i.e. normalization |$\rm \mathit{ Z}_{O/H; MZR0}$| and slope aMZR of the MZR, high-mass end of the SFMR aSFMR2) to cover the range of possibilities present in the literature, as indicated with the thick grey lines in the left-hand panels. In Section 3.1, we relate the parameters of the ZO/H(SFR, M*) to the parameters of the local 2D relations.
3.1.1 The asymptotic metallicity
A clear feature present among the observational ZO/H(SFR, M*) determinations is the high mass flattening. We note that some authors report a reversal of the (anticorrelation at high M* rather than a simple flattening, e.g. Yates et al. 2012; Kashino et al. 2016). Telford et al. (2016) point out that certain sample selection criteria (e.g. applying signal-to-noise ratio cuts on oxygen lines used to estimate the metallicity) may lead to biases against the massive, low SFR galaxies and therefore affect the inferred low SFR and high mass part of the FMR. They argue for such biases as the cause of the reversal of the correlation at high masses as seen in Kashino et al. (2016). The effects of dust (and the applied dust SFR corrections) may also induce biases against massive, metal-rich galaxies (Telford et al. 2016).
Change in the relation at high masses is also supported theoretically, and could be attributed to the increased importance of AGN feedback that can rapidly influence the SFR while the metallicity continues to evolve much more gradually (e.g. De Rossi et al. 2017; Torrey et al. 2018). We therefore assume that the high mass flattening is a robust feature of the ZO/H(SFR, M*) and include it within our model. Observationally, the value of the asymptotic metallicity ZO/H; 0 at which the relation flattens appears to be roughly independent of the SFR and coincide with that of asymptotic metallicity of the average z ∼ 0 MZR (ZO/H; MZR0). As such, it is affected by the choice of the metallicity determination method, which leads to systematic offsets in the normalization of the MZR (compare examples shown in Telford et al. 2016 and in fig. 2 in Cresci et al. 2019). We fix ZO/H; 0 = ZO/H; MZR0, where ZO/H; MZR0 is defined by the choice of the z ∼ 0 MZR.
![Dependence of the parameters γ [ZO/H(SFR, M*) slope at M* << M0; SFR, see equation (1)] and α [slope of the log10(M0; SFR) dependence on log10(SFR), see equation (6)] on the slopes of the z ∼ 0 MZR and SFMR and the parameter ∇FMR0. Hatched areas in the top panels span between the values obtained for aMZR ∼ 0.3 (orange lines/areas) and 0.6 (blue lines/ares) and indicate the variation caused by the different MZR slopes considered in this study. Grey areas in the top panels and in the bottom right panel span between aSFMR = 0.7−1 to illustrate the variation caused by the change in the SFMR slope. The hatched green area in the bottom left panel shows the variation caused by varying ∇FMR0 in the range 0.17–0.3, assuming aSFMR = 0.83 (our default low/intermediate mass slope of the SFMR). The dashed green line falling within that range indicates our fiducial choice of ∇FMR0 = 0.27. Orange (blue) ranges in the bottom right panel show the range of α obtained with aMZR ∼ 0.3 (aMZR ∼ 0.6) and ∇FMR0 in the range 0.17–0.3 for each aSFMR. The orange square shows α and aMZR as found by Curti et al. (2020). The brown diamond shows α/γ calculated with aMZR, aSFMR, and ∇FMR0 from Sanders et al. (2021) (note that it overlaps with the estimate from Curti et al. 2020 in the bottom left panel).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2690/1/m_stab2690fig2.jpeg?Expires=1750313337&Signature=oYv-ISxpmtWvbZRv6iTogxcBtGrxZmEqNmRJcB2BB7WtRNq8QzqeNGbtujA4utU5tQi8Sstci2XDlsMzHr9VQPlDUDnks2lC5X9cjBa6sthGpraOQtm2tavcF9M4gpxQanJKq8WIdh73X0mrNO4JSXsij9igaHWzgWk0AT~wXUiGgJujd4Fq758YDu5~VraGGsyIV3RPB9uZOQbW6zdNvGJIj-21YdEVFp57E2QVVKrFAWEoIWCePpvvUlbvfauW1IcCTB8Cxqg~tg8hC8qYi6E1hcy3hytueAo2yU7ZXQ4huvBtWltuB6YWXTHd~juoex-H0joCeJGdk5aZpfRTnQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Dependence of the parameters γ [ZO/H(SFR, M*) slope at M* << M0; SFR, see equation (1)] and α [slope of the log10(M0; SFR) dependence on log10(SFR), see equation (6)] on the slopes of the z ∼ 0 MZR and SFMR and the parameter ∇FMR0. Hatched areas in the top panels span between the values obtained for aMZR ∼ 0.3 (orange lines/areas) and 0.6 (blue lines/ares) and indicate the variation caused by the different MZR slopes considered in this study. Grey areas in the top panels and in the bottom right panel span between aSFMR = 0.7−1 to illustrate the variation caused by the change in the SFMR slope. The hatched green area in the bottom left panel shows the variation caused by varying ∇FMR0 in the range 0.17–0.3, assuming aSFMR = 0.83 (our default low/intermediate mass slope of the SFMR). The dashed green line falling within that range indicates our fiducial choice of ∇FMR0 = 0.27. Orange (blue) ranges in the bottom right panel show the range of α obtained with aMZR ∼ 0.3 (aMZR ∼ 0.6) and ∇FMR0 in the range 0.17–0.3 for each aSFMR. The orange square shows α and aMZR as found by Curti et al. (2020). The brown diamond shows α/γ calculated with aMZR, aSFMR, and ∇FMR0 from Sanders et al. (2021) (note that it overlaps with the estimate from Curti et al. 2020 in the bottom left panel).
3.1.2 The slope at low masses and high SFR
3.1.3 Turnover mass as a function of SFR
Observational studies suggest that |$M_{0;\rm SFR}$| increases with SFR [i.e. for higher SFR, ZO/H(SFR, M*) flattens at higher masses]. The steepness of this dependence governs the spacing between the ZO/H(M*,SFR) curves obtained for different SFR (see Fig. 1). Examples shown in Telford et al. (2016) and in fig. 2 of Cresci et al. (2019) suggest that both the metallicity and SFR determination methods have impact on the distance between the different SFR lines (and so on M0;SFR). Curti et al. (2020) find that a linear dependence (log10(M0;SFR) ∝ log10(SFR)) can well describe the trend seen for their z ∼ 0 galaxy sample.
3.1.4 The value of β
β describes the bending of the ZO/H(SFR, M*) relation. The higher the value of β, the sharper the transition from the linear to flat regime and the smaller the range of log10(M*) over which the transition happens (see Fig. A1 for illustration). β could in principle depend on the SFR. Curti et al. (2020) let β as a free parameter when fitting their ZO/H(SFR, M*) relation for different SFR bins. While their best-fitting relations give different β values in different SFR bins, the authors note that there is no clear dependence on SFR. Ultimately, they quote a single value of β ∼ 2 to describe the FMR.
In principle, we can numerically solve for β using the condition that galaxies with zero offset from the z ∼ 0 SFMR lie on the z ∼ 0 MZR. This condition allows us to properly recover the z ∼ 0 MZR when sampling the galaxy properties from the z ∼ 0 GSMF and SFMR and assigning their metallicities with ZO/H(SFR, M*). This condition is only applicable in the SFR range that is covered by the z ∼ 0 SFMR (≳10−3 M⊙ yr−1 and ≲102 M⊙ yr−1). Numerous solutions are allowed – especially at low SFR ≲ 10−1 M⊙ yr−1, where the intersection with the z ∼ 0 MZR is reached at log(M*) <log(|$M_{0;\rm SFR}$|) i.e. where ZO/H(SFR, M*) is virtually insensitive to the choice of β. We use the numerical solutions as a guide and adopt a simplified β dependence on log10(SFR), verifying that ZO/H(SFR, M*) for galaxies at z ∼ 0 SFMR leads to ZO/H that agree with the corresponding values from the z ∼ 0 MZR to within 0.01 dex (note that this is smaller than the typically found residual scatter about the ZO/H(SFR, M*) of ∼0.05 dex). Where necessary, we extrapolate the obtained dependence to lower and higher SFR values than probed by z ∼ 0 SFMR. The resulting dependence is shown in Fig. A2 in Appendix A.
3.1.5 The strength of the SFR–metallicity correlation
Observationally, ∇FMR appears to be a function of M* and SFR. Such dependence is evident in the analysis presented by Salim et al. (2014) (see Table 1 therein, where κ corresponds to our ∇FMR), where the authors compare the strength of the correlation for galaxies split in different mass and SFR bins. This is one of the key observed characteristics of the FMR that we aim to reproduce within our description.
The fact that ZO/H; 0 appears to be roughly independent of the SFR means that the observed ZO/H(SFR, M*) flattening does not simply reflect the presence of the high mass flattening of the MZR (and potentially SFMR), but also indicates a weakening/disappearance of the SFR–ZO/H correlation in the high M* regime (i.e. small/zero ∇FMR). Note that, by construction (fixing the value of ZO/H; 0), we recover such high M* weakening of the correlation in our method. A similar behaviour is also seen in the ZO/H – log10(SFR) projection of the FMR, where at fixed log10(M*) the flattening appears at relatively low SFR values (compared to the SFMR). In other words, the correlation between the SFR and metallicity is found to weaken/disappear at low SFR/low specific SFRs (sSFR = SFR/M* ≲ 10−10–10−10.5 yr−1). When projected on to the ZO/H–log10(M*) plane, this means that the correlation is weaker ‘above’ than ’below’ the average z ∼ 0 MZR. That is also the case within our description: for the same absolute value of δSFMR, ∇FMR is smaller above than below the z ∼ 0 MZR due to the SFR-dependent location of the flattening and – in certain model variations – the β dependence on SFR.
While observational studies seem to agree on the existence of those high M* and low SFR/low sSFR weaker correlation regimes, there is no agreement on the precise region of the FMR [in terms of the ZO/H, log10(M*), and log10(SFR) values] in which they appear. Within our description we can qualitatively reproduce those trends. The transition between the strong correlation regime and the part of the FMR where the correlation weakens happens at different log10(M*) and sSFR depending on the parameters of the z ∼ 0 MZR and SFMR. We stress that we only assume that ∇FMR is fixed (i.e. ∇FMR = ∇FMR0, independent of M* and SFR) in the low mass and high SFR part of the FMR – as guided by the observed characteristics of ZO/H(SFR, M*) (but see Appendix C, where we further relax this assumption and introduce an SFR-dependent ∇FMR in this region of the FMR). We do not explicitly assume any value or dependence for ∇FMR in the remaining part of the relation.
∇FMR0 is the only parameter used in our description of the ZO/H(SFR, M*) that is not defined by the choice of the local MZR and SFMR, as a potential dependence of this parameter on the metalicity/SFR derivation method is unclear and only few determinations of ∇FMR are given in the literature. Using the H α based SFR and metallicity derivation method of Mannucci et al. (2010) and Salim et al. (2014) find ∇FMR ∼0.3 in the strong correlation regime. Applying a infrared based SFR derivation method, they find somewhat lower values of ∇FMR ∼0.2. In their study focusing on z ∼ 2.3, Sanders et al. (2018) use several example metallicity calibrations (both strong line-based/theoretical and ’direct’/empirical) and find ∇FMR ∼0.11–0.27, hinting at potential dependence on the choice of metallicity indicator and calibration. However, as argued by Sanders et al. (2021), different metallicity calibrations (or redshift-dependent adjustments to z ∼ 0 based calibrations) may be needed to correctly derive metallicities of star-forming galaxies at different redshifts. This is taken into account in Sanders et al. (2021), where different empirical metallicity calibrations are used at z ∼ 0 and at higher redshifts. They find best-fitting ∇FMR = 0.27 at z ∼ 0 and somewhat shallower dependence at z ∼ 2.3 (∇FMR ∼ 0.19), although consistent within the uncertainty with z ∼ 0 determination (see their Fig. 10).
Torrey et al. (2018) show the strength of the SFR–metallicity correlation split in several log10(M*) and redshift bins as found in the IllustrisTNG simulations (see Table 1 therein). They report values in the range ∇FMR ∼0.25 – 0.34 (except for the lowest log10(M*) ∼9 and highest mass bin log10(M*) >10.5 at z ∼ 0, where noticeably weaker ∇FMR is found: 0.19 and 0.1, respectively), with no clear mass or redshift dependence.
We use ∇FMR0 = 0.27 as recently found by Sanders et al. (2021) as our fiducial choice. Given the uncertainty of this parameter, we consider values between 0.17 and 0.3 dex to discuss the sensitivity of our results to this choice.5
3.1.6 Calculating metallicities of galaxies at different z with ZO/H(SFR, M*)
ZO/H(SFR, M*) constructed as described in this section is fully determined by the choice of ∇FMR0 and the parameters of the z ∼ 0 MZR and SFMR. We introduce the variations of those local relations that we explore in this study in Section 3.4. We further assume that ZO/H(SFR, M*) does not evolve with redshift–metallicity evolution with redshift is then a result of an evolving GSMF and SFMR. We sample galaxy masses from the redshift-dependent GSMF and their SFR from the distribution centred around the redshift-dependent SFMR, as discussed in Section 2. We then use ZO/H(SFR, M*) to assign the metallicity. Furthermore, observational studies indicate the residual scatter around the FMR σFMR ∼ 0.05 dex. To account for that, we add a normally distributed scatter σFMR = 0.05 dex to metallicities assigned with our ZO/H(SFR, M*).
3.2 Differences with respect to Chruslinska & Nelemans (2019)
Even though the metallicity distribution of galaxies used in Chruslinska & Nelemans (2019) relies on the redshift-dependent MZR, the authors include the simplified form of the mass–metallicity-SFR dependence within their framework, assuming that the galaxy offsets from the average MZR and SFMR are fully anticorrelated, i.e. setting the coefficient from equation (2) to |$\nabla _{\mathrm{ FMR}}=\frac{\sigma _{\rm MZR}}{\sigma _{\rm SFMR}}\approx 0.33$|, where σMZR = 0.1 and σSFMR = 0.3 dex describe the scatter around the average MZR and SFMR, respectively. The same ∇FMR is used independent of M*, SFR, or redshift. In the strong correlation regime discussed in Section 3.1.5 (at low/intermediate M* and high SFR) and at z ∼ 0 their description of the mass–metallicity-SFR dependence is effectively the same as implemented in this study (except for the lower value of ∇FMR used in this work). However, the strength of the observed SFR–metallicity correlation appears to weaken at high M* and low SFR/sSFR. This behaviour is not captured with the simple description given by equation (2) with fixed ∇FMR. Another important difference is that, in this study the ZO/H(M*,SFR) (once defined with z ∼ 0 relations) is assumed to be redshift invariant. Chruslinska & Nelemans (2019) use equation (2) to calculate offsets relative to SFMR and MZR as found at any given redshift. This means that, due to strong MZR evolution at z ≳ 2, their ZO/H(M*,SFR) is redshift dependent.
3.3 FMR example: comparison with Sanders et al. (2021)
In this section, we present an example ZO/H(SFR, M*) obtained with our phenomenological model, where we keep all the input assumptions as similar as possible to Sanders et al. (2021). We choose this study, as the authors provide estimates of all the ingredients that are necessary to construct our ZO/H(SFR, M*) (the z ∼ 0 MZR, SFMR, and ∇FMR0),6 which allows for a direct comparison with their results. The resulting ZO/H(SFR, M*) is shown in Fig. 3. In the bottom panels we include two other common 2D projection of the FMR: the ZO/H–log10(SFR) plane (bottom left panel) and the ZO/H–log10(sSFR) plane (bottom middle panel). The thick grey line in the main panel of Fig. 3 shows the z ∼ 0 MZR as given in Sanders et al. (2021). The coloured points around that line represent the z ∼ 0 population of star-forming galaxies from our model.7 The black line indicates a fit to the maximum density region occupied by the z ∼ 0 galaxy sample described above, to ensue that the z ∼ 0 MZR is reproduced. The right bottom panel shows the ZO/H residuals around the MZR obtained that way for several example log10(M*), which shows that the typically indicated intrinsic width of the relation σMZR ∼ 0.1 dex is reasonably reproduced (note that this quantity is not an input in our model). The thick solid coloured lines in the main panel show ZO/H(SFR, M*) for various fixed log10(SFR) values. The faint coloured solid lines in the background were obtained with the best-fitting FMR given by Sanders et al. (2021) (see equation 10 therein), plotted roughly in the range of M* and SFR probed by their galaxy sample. We also plot their z ∼ 2.3 (squares) and z ∼3.3 (circles) data points (obtained for stacked spectra of the observed galaxies, see Table 1 therein). The inner (outer) colours in all symbols correspond to upper (lower) bound on the log10(SFR) within the uncertainties provided by the authors for each of the stacks. The long dashed and dotted grey lines indicate the projected z ∼ 2.3 and z ∼ 3.3 MZR, calculated in the same way as the black line, but using the z ∼ 2.3 and z ∼ 3.3 SFMR from Sanders et al. (2021), respectively, and our GSMF estimated at the corresponding redshifts. The overall agreement is remarkable.
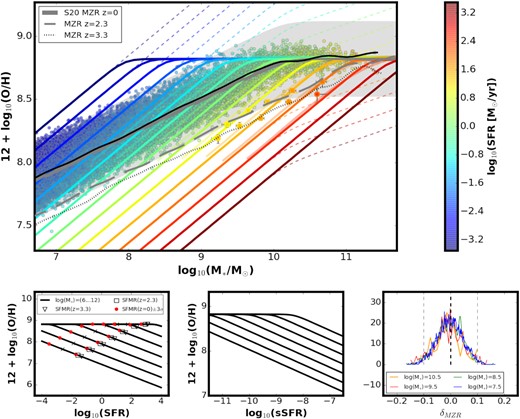
Example ZO/H(SFR, M*) obtained with our method (coloured lines – different log10(SFR) values) and using the z ∼ 0 MZR, SFMR, and ∇FMR0 from Sanders et al. (2021) (S20). Coloured points are sampled from the GSMF and SFMR at z ∼ 0. Black line is plotted to show that z ∼ 0 MZR (shown as thick solid grey line and shaded area – 3 σMZR region) is well reproduced with our ZO/H(SFR, M*) and z ∼ 0 GSMF and SFMR. The grey dashed lines show fits to the maximum density of galaxies sampled from GSMF and SFMR at z = 2.3 and 3.3 to indicate the projected MZR evolution. Data points are z ∼ 2.3 and 3.3 stacks from S20. Faint lines show FMR fitted by S20. Coloured dashed lines show ZO/H(SFR, M*) as would be obtained with equation (2) and ∇FMR0 = 0.27 used at all masses and SFRs. Projections on to ZO/H–log10(SFR) and ZO/H–log10(sSFR) planes are shown in the bottom panels for several log10(M*) values (black lines – log10(M*) from 6 to 12). In the bottom left panel, we indicate the SFR corresponding to SFMR value for a given M* at z = 0 (cross), 2.3 (square), and 3.3 (triangle). Red dots indicate the SFR of a galaxy ±3σSFMR away from the SFMR at z ∼ 0. The rightmost bottom panel shows the offsets of z ∼ 0 model galaxies from the z ∼ 0 MZR, plotted for several mass bins.
We also show ZO/H(SFR, M*) for various fixed log10(SFR) values as would have been obtained with the approach used in Chruslinska & Nelemans (2019) i.e. using equation (2) with ∇FMR = ∇FMR0 = 0.27 fixed (i.e. the same at all SFRs and masses, see coloured dashed lines in the main panel of Fig. 3). It can be seen that the ZO/H(SFR, M*) constructed that way is identical with our model at low/intermediate M* and high SFRs (the strong correlation regime), and starts to deviate at high M* and low SFR (above the z ∼ 0 MZR), where ∇FMR < ∇FMR0. This demonstrates that the mass and SFR dependence of the SFR–metallicity correlation discussed in Section 3.1.5 is present in our description.
3.4 Model variations
In this study we consider several variations of the base z ∼ 0 MZR and SFMR relations, representing extreme choices of the shapes of the two relations and the MZR normalization ZO/H; MZR0 reported in the literature. We also consider two variations of the GSMF: either with fixed low mass end slope (αGSMF = −1.45), or with αGSMF steepening with redshift (see Section 3.1 in Chruslinska & Nelemans 2019 for the details). This allows us to explore the extremes of the fSFR(Z,z) distribution. We briefly introduce each of the MZR and SFMR variations used to construct our ZO/H(SFR,M*) below.
3.4.1 MZR variations
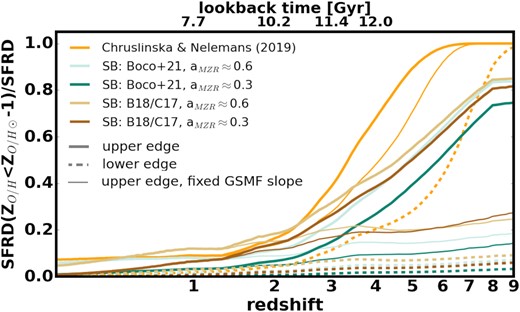
Fraction of the total SFRD that occurs below ZO/H⊙-1 as a function of redshift/lookback time, plotted for the model variations shown in Fig. 12. Different colours correspond to different assumptions about aMZR and starburst galaxies (see legend). Thick solid (dashed) lines mark the upper (lower) edges of the corresponding ranges for each of the model variations. Thin solid lines show the location of the upper edge obtained under the assumption of a non-evolving low-mass end of the GSMF.
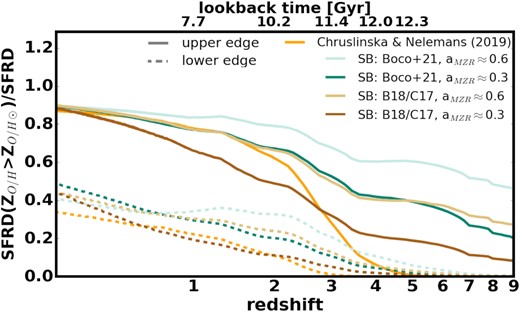
Fraction of the total SFRD that occurs above ZO/H⊙ as a function of redshift/lookback time, plotted for the model variations shown in Fig. 13. Different colours correspond to different assumptions about aMZR and starburst galaxies (see legend). Thick solid (dashed) lines mark the upper (lower) edges of the corresponding ranges for each of the model variations.
Parameters of the different versions of the z ∼ 0 MZR and SFMR used in this study. The first column gives the name used to reference the variation throughout this study.
| . | MZR z ∼ 0 . | |||
|---|---|---|---|---|
| . | aMZR . | log|$_{10}\left(\rm \mathit{ M}_{0;MZR0} \right)$| . | ZO/H; MZR0 . | βMZR . |
| PP04 | 0.6 | 9.19 | 8.81 | 0.6 |
| S20 | 0.28 | 10.16 | 8.82 | 3.43 |
| KK04a | 0.57 | 9.03 | 9.12 | 0.57 |
| KK04b | 0.3 | 9.9 | 9.12 | 0.74 |
| SFRM z ∼ 0 | ||||
| aSFMR | log|$_{10}\left(\rm \mathit{ M}_{0;SFMR0} \right)$| | aSFMR2 | bSFMR | |
| No flattening | 0.83 | – | 0.83 | −8.241 |
| Sharp flatteninga | 0.83 | 9.89 | s0 = −0.033 | |
| Moderate/S20 | 0.83 | 9.73 | 0.72 | −8.241 |
| Moderate/S14 | 0.83 | 9.73 | 0.49 | −8.241 |
| . | MZR z ∼ 0 . | |||
|---|---|---|---|---|
| . | aMZR . | log|$_{10}\left(\rm \mathit{ M}_{0;MZR0} \right)$| . | ZO/H; MZR0 . | βMZR . |
| PP04 | 0.6 | 9.19 | 8.81 | 0.6 |
| S20 | 0.28 | 10.16 | 8.82 | 3.43 |
| KK04a | 0.57 | 9.03 | 9.12 | 0.57 |
| KK04b | 0.3 | 9.9 | 9.12 | 0.74 |
| SFRM z ∼ 0 | ||||
| aSFMR | log|$_{10}\left(\rm \mathit{ M}_{0;SFMR0} \right)$| | aSFMR2 | bSFMR | |
| No flattening | 0.83 | – | 0.83 | −8.241 |
| Sharp flatteninga | 0.83 | 9.89 | s0 = −0.033 | |
| Moderate/S20 | 0.83 | 9.73 | 0.72 | −8.241 |
| Moderate/S14 | 0.83 | 9.73 | 0.49 | −8.241 |
Different SFMR parametrization (see footnote 9).
Parameters of the different versions of the z ∼ 0 MZR and SFMR used in this study. The first column gives the name used to reference the variation throughout this study.
| . | MZR z ∼ 0 . | |||
|---|---|---|---|---|
| . | aMZR . | log|$_{10}\left(\rm \mathit{ M}_{0;MZR0} \right)$| . | ZO/H; MZR0 . | βMZR . |
| PP04 | 0.6 | 9.19 | 8.81 | 0.6 |
| S20 | 0.28 | 10.16 | 8.82 | 3.43 |
| KK04a | 0.57 | 9.03 | 9.12 | 0.57 |
| KK04b | 0.3 | 9.9 | 9.12 | 0.74 |
| SFRM z ∼ 0 | ||||
| aSFMR | log|$_{10}\left(\rm \mathit{ M}_{0;SFMR0} \right)$| | aSFMR2 | bSFMR | |
| No flattening | 0.83 | – | 0.83 | −8.241 |
| Sharp flatteninga | 0.83 | 9.89 | s0 = −0.033 | |
| Moderate/S20 | 0.83 | 9.73 | 0.72 | −8.241 |
| Moderate/S14 | 0.83 | 9.73 | 0.49 | −8.241 |
| . | MZR z ∼ 0 . | |||
|---|---|---|---|---|
| . | aMZR . | log|$_{10}\left(\rm \mathit{ M}_{0;MZR0} \right)$| . | ZO/H; MZR0 . | βMZR . |
| PP04 | 0.6 | 9.19 | 8.81 | 0.6 |
| S20 | 0.28 | 10.16 | 8.82 | 3.43 |
| KK04a | 0.57 | 9.03 | 9.12 | 0.57 |
| KK04b | 0.3 | 9.9 | 9.12 | 0.74 |
| SFRM z ∼ 0 | ||||
| aSFMR | log|$_{10}\left(\rm \mathit{ M}_{0;SFMR0} \right)$| | aSFMR2 | bSFMR | |
| No flattening | 0.83 | – | 0.83 | −8.241 |
| Sharp flatteninga | 0.83 | 9.89 | s0 = −0.033 | |
| Moderate/S20 | 0.83 | 9.73 | 0.72 | −8.241 |
| Moderate/S14 | 0.83 | 9.73 | 0.49 | −8.241 |
Different SFMR parametrization (see footnote 9).
3.4.2 SFMR variations
To describe the z ∼ 0 SFMR we follow Chruslinska & Nelemans (2019) and assume the low/intermediate mass slope aSFMR and normalization bSFMR based on Boogaard et al. (2018). As discussed in Chruslinska & Nelemans (2019), the shape of the high-mass end is debated: while many authors report a varying degree of flattening above a certain mass (e.g. Schreiber et al. 2015; Tomczak et al. 2016; Bisigello et al. 2018), others see no evidence for the change of slope (e.g. Renzini & Peng 2015; Pearson et al. 2018). We consider the same extreme variations as described in Chruslinska & Nelemans (2019): ’no flattening’ – a linear relation between log10(SFR) and log10(M*) with a single slope at all masses and ‘sharp flattening’ – with aSFMR ∼ 0 at high masses [using the parametrization from Tomczak et al. (2016)]9. We focus on those two extremes to discuss our results, but use additional ‘moderate’ variations in some of the figures introducing our FMR model. Those assume that the slope of the SFMR changes from aSFMR to aSFMR2 < aSFMR at log10(M*) = log|$_{10}\left(\rm \mathit{ M}_{0;SFMR0} \right)$|. Variation moderate/S20 assumes a high-mass slope as in the z ∼ 0 SFMR shown in Sanders et al. (2021), while moderate/S14 follows the prescription of Speagle et al. (2014). The relevant parameters for all the SFMR variations are given in the bottom rows of Table 1. The SFMR evolution with redshift is described as in Chruslinska & Nelemans (2019).
3.4.3 The FMR for the considered model variations
In this section, we summarize the key differences between ZO/H(SFR, M*) obtained for the different variations of the z ∼ 0 MZR, SFMR, and ∇FMR0 considered in this study. It can be seen from equation (6) that the impact of the SFMR parameters on the SFR-dependent turnover mass |$\rm log_{10}( \mathit{ M}_{0;SFR})$| (and on α) is reduced by the multiplication by ∇FMR ≲ 0.3. Considering a range of aSFMR ∼ 0.7–1 spanned by different determinations of the low-mass slope of the SFMR present in the literature (see e.g. fig. 10 in Boogaard et al. 2018) instead of using a fixed value aSFMR = 0.83 would only affect α by ≲0.08. This is illustrated by the grey bands in the top panels in Fig. 2. At the same time, for the range of aMZR considered in this study α varies between ∼0.2 and 0.55 (compare the orange and blue lines in Fig. 2, where smaller values correspond to steeper MZR slopes). Variation in ∇FMR between 0.17 and 0.3 affects α by ∼0.15 (see green lines and bottom left panel in Fig. 2). The choice of MZR has a decisive role in setting the ZO/H(SFR, M*). ∇FMR0 also visibly affects the relation, while SFMR has a relatively mild impact on its shape within our framework. ZO/H(SFR, M*) obtained for the different variations of the z ∼ 0 MZR considered in this study and for our fiducial ∇FMR0 = 0.27 is shown in Fig. 4. The shift in normalization between the PP04/S20 and KK04a/b variations (compare top and bottom panels) as well as the difference in the spacing between the different log10(SFR) lines depending on aMZR (compare right-hand and left-hand panels) are evident. The analogous figures showing the impact of different SFMR (Fig. A3) and ∇FMR0 (Fig. A4) choices are shown in Appendix A. The additional ZO/H(SFR, M*) variation with an SFR-dependent ∇FMR is discussed in Appendix C and illustrated in Fig. C1. The choice of the SFMR variation (its high-mass end) has the strongest effect on the β parameter (see Fig. A2 in the Appendix A, which shows the β – log10(SFR) relation for different choices of the local scaling relations). In practice, cases with an SFMR with no flattening/only mild change of slope are well described with a single value of β. The dependence on SFR becomes apparent in cases with SFMR showing a significant deviation from a single power law. The obtained values of β are generally smaller for steeper MZR. β is only weakly affected by the choice of ∇FMR0 (shifting towards smaller values with decreasing ∇FMR0). We note that using the z ∼ 0 MZR from Curti et al. (2020), we can recover their best fit β ∼ 2 (when we assume single power-law SFMR). Before showing the results, we first discuss the treatment of starburst galaxies in our models.
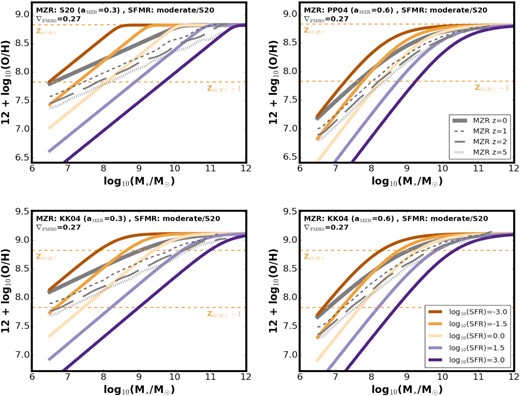
ZO/H(SFR, M*) obtained as described in Section 3.1 – different colours show ZO/H(SFR, M*) at fixed log10(SFR) (increasing from left to right, see legend). Different panels correspond to different choices of the z ∼ 0 MZR (indicated by the thick grey line). All panels assume SFMR with a moderate flattening (z ∼ 0 SFMR with aSFMR = 0.72 at high masses and aSFMR = 0.83 at low masses) and ∇FMR0 = 0.27. Grey dashed lines indicate the projected MZR evolution as obtained by performing fits to maximum density of galaxies in 12 + log10(O/H)–log10(M*) plane, where the galaxies were sampled from GSMF (assuming αGSMF = αfix) and SFMR at several higher redshifts and their ZO/H was assigned using the ZO/H(SFR, M*) shown in each of the panels. Horizontal orange lines indicate solar and 10 per cent solar metallicity, assuming ZO/H⊙ = 8.83 (Grevesse & Sauval 1998).
4 STARBURST GALAXIES
A common approach to describe the SFR distribution of galaxies is to use a Gaussian distribution centred around the redshift-dependent SFMR.10 In reality, the SFR of star-forming galaxies at fixed stellar mass seems to follow a bimodal, double-Gaussian shape. The secondary peak of this distribution is attributed to starburst (SB) galaxies – strong SFMR outliers that feature SFR a few times higher11 than those of the regular star-forming galaxies of the same mass and redshift. Several authors estimate the fraction of starburst galaxies (fSB; the ratio between the number of galaxies associated with the starburst component of the SFR distribution and the total number of star-forming galaxies in the considered mass and redshift range) and report values fSB ∼ 2–3 per cent (e.g. Rodighiero et al. 2011; Béthermin et al. 2012; Sargent et al. 2012; Ilbert et al. 2015; Schreiber et al. 2015). Despite the relatively low fSB values, the starburst’s contribution to the total cosmic SFRD could still amount to |$\sim 10{{\ \rm per\ cent}}$| at z ∼ 2 due to their high SFR. Boco et al. (2021) use the double Gaussian distribution of galaxy SFRs from Sargent et al. (2012) and suggest that accounting for the starburst component can improve the consistency between the cosmic SFRD at z≳ 2 determined with the use of galaxy stellar mass functions paired with SFMR (as used in Chruslinska & Nelemans 2019) and that estimated with the use of SFR functions (which better account for the SFR of dusty galaxies at high redshifts; as used in Boco et al. 2019).
Crucially, the above mentioned fSB determinations are based on galaxy samples limited to relatively massive objects (log10(M*/M⊙) > 10) and z ≲ 2. Studies of Caputi et al. (2017) and Bisigello et al. (2018) extend the analysis of the distribution of star-forming galaxies in the log10(SFR)–log10(M*) plane to much lower masses and higher redshifts. While their results are consistent with the previous determinations at high log10(M*), they show that fSB is a strong function of stellar mass (increasing towards lower log10(M*)) and z (increasing with redshift). Moreover, they indicate that starburst galaxies follow a distinct sequence in the log10(SFR)–log10(M*) plane that is located ∼1 dex above the SFMR. This offset of the starburst sequence relative to SFMR is considerably higher than previously reported (e.g. Béthermin et al. 2012; Sargent et al. 2012). This suggests that the contribution of starburst galaxies to the total SFRD budget can be much higher than previously estimated. If starburst galaxies follow the general FMR (as suggested by the results of Hunt et al. 2012; to our knowledge, there is no evidence to the contrary), they would contribute to the star formation at relatively low metallicities compared to galaxies on the SFMR. Therefore, they affect the low metallicity tail of the fSFR(Z,z) – crucial for the discussion of the origin of transients as long gamma-ray bursts and double black hole mergers. We aim to discuss the possible impact of starbursts on the fSFR(Z,z) in view of the results reported in Caputi et al. (2017) and Bisigello et al. (2018). In the following Section 4.1, we describe the method used to include the contribution of starburst galaxies within our framework.
4.1 Method and considered variations
To account for the contribution of starburst galaxies in our calculations, we follow the procedure outlined below:
At each redshift, we sample log10(M*) of star-forming galaxies from the galaxy stellar mass function as described in Chruslinska & Nelemans (2019).
We use fSB to describe the fractions of starburst galaxies and regular star-forming galaxies at each log10(M*) and z. Our choice is outlined further in this section.
The SFR of regular galaxies is given by the SFMR from Chruslinska & Nelemans (2019). The SFR of starburst galaxies at each log10(M*) follows a normal distribution with scatter σSB. The peak of the distribution can be related to the galaxy’s log10(M*) with a linear relation: |$\rm log_{10}(SFR_{SB}) = a_{SB} log_{10}( \mathit{ M}_{*}) + b_{SB}$|, to which we refer as the starburst sequence We set the value of bSB by defining the offset of the starburst sequence from the SFMR, i.e. bSB = bSFMR + ΔSB − SFMR. The assumed parameters are given further in this section.
To describe the metallicity at which the starburst galaxies produce stars, we assume that they follow the same FMR as regular star-forming galaxies (described in Section 3.1).
We consider two sets of parameters describing the properties of starbursts. First, we follow the same implementation as used in the recent study by Boco et al. (2021), which is based on the works of Sargent et al. (2012) and Béthermin et al. (2012). This implementation assumes a constant fSB = 0.03 (independent of mass and redshift), a starburst sequence with scatter σSB = 0.24, located ΔSB − SFMR = 0.59 dex above the SFMR and parallel to the SFMR (specifically, we assume the starburst sequence slope of aSB = 0.83, corresponding to the low-mass slope of the SFMR from Chruslinska & Nelemans 2019,12). In light of the results of Caputi et al. (2017) and Bisigello et al. (2018) this implementation severely underestimates both fSB and the SFR of galaxies on the starburst sequence. Therefore, it likely provides the absolute lower limit on the contribution of starbursts. Secondly, we follow the results of Caputi et al. (2017) and Bisigello et al. (2018) to model the mass and redshift dependence of fSB and the properties of the starburst sequence. We provide the details of this implementation in Sections 4.1.1 and 4.1.2 and refer to it as the B18/C17 implementation in the reminder of this paper.
4.1.1 The fraction of starbursts
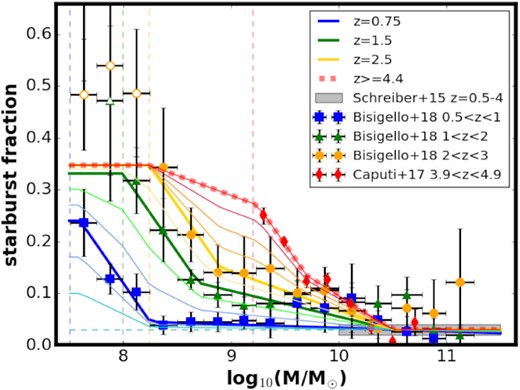
Fraction of starbursts as a function of galaxy stellar mass. Thick lines show the assumed dependence at z ∼ 0.75, 1.5, and 2.5 based on the data from Bisigello et al. (2018) and at z ∼ 4.4 based on Caputi et al. (2017). Thin lines show the interpolation between those redshifts and extrapolation to z = 0 (thin horizontal dashed line), plotted with 0.25 step in redshift at z < 1.5 and with 0.5 step in redshift above. Vertical dashed lines mark log10(Mfix) (see Table 2) for different redshift bins. Open symbols mark estimates where the galaxy sample from Bisigello et al. (2018) is below 90 per cent mass completeness.
All stellar masses in equation (8) are in solar units M⊙. The adopted coefficients are given in Table 2. We assume that the above relation holds strictly in the middle of each redshift bin and interpolate between them to describe fSB at 0.5 < z < 4.4. At z > 4.4 we use the relation from z= 4.4. That way we obtain a conservative estimate of the starburst contribution at higher redshifts. We extrapolate the constructed dependence to lower redshifts, setting a constant starburst fraction of 3 per cent at all masses at z = 0. At z = 0.75, 1.5, and 2.5, log10(Mfix) is the lower edge of the lowest mass bin where the galaxy sample from Bisigello et al. (2018) is within 90 per cent stellar-mass completeness. We make a conservative assumption and use a fixed fSB value below that mass (i.e. |$f_{\mathrm{ SB}\mathrm{ }} =\rm a_{1} log_{10}( \mathit{ M}_{\rm fix}) + b_{1}$|). At z = 4.4, log10(Mfix) = 9.25 corresponds to the lowest mass for which the fraction of starbursts has been estimated in Caputi et al. (2017). At this redshift, fSB is fixed at the same mass as at z = 2.5 (i.e. log10(M*) = 8.24) and we assume a linear relation to describe the dependence between log10(M*) = 8.24 and log10(M*) = 9.25. This exception is necessary to avoid a decrease in the fraction of starbursts at log10(M*) < 9.25 at z > 2.5, which would break the trend seen in the data (see Fig. 5). At log10(M*) > 10.5 there is a lot of scatter in the data and the trend is inconclusive. In this mass range we use a fixed value fSB = 0.03 at all redshifts, as found in earlier studies that focused on the most massive galaxies (e.g. Rodighiero et al. 2011; Schreiber et al. 2015). The steeper, lower mass part of fSB–log10(M*) dependence is well described with the same slope across all four redshift bins. Therefore, for simplicity we assume a1 = −0.3. The slope of the relation in the higher mass part (a2) and the mass log10(M0; SB) separating the high and low mass parts of the relation increase with redshift.
Coefficients used in equation (8), describing fSB as a function of log10(M*) at redshift zbin. The remaining coefficient a1 = −0.3 at all zbin.
| zbin . | b1 . | a2 . | b2 . | log(M0; SB/ M⊙) . | log(Mfix/M⊙) . |
|---|---|---|---|---|---|
| 0.75 | 2.52 | −0.0067 | 0.1 | 8.25 | 7.6 |
| 1.5 | 2.73 | −0.05 | 0.555 | 8.7 | 7.99 |
| 2.5 | 2.82 | −0.075 | 0.817 | 8.9 | 8.24 |
| 4.4 | 3.045 | −0.131 | 1.408 | 9.7 | 9.25 |
| zbin . | b1 . | a2 . | b2 . | log(M0; SB/ M⊙) . | log(Mfix/M⊙) . |
|---|---|---|---|---|---|
| 0.75 | 2.52 | −0.0067 | 0.1 | 8.25 | 7.6 |
| 1.5 | 2.73 | −0.05 | 0.555 | 8.7 | 7.99 |
| 2.5 | 2.82 | −0.075 | 0.817 | 8.9 | 8.24 |
| 4.4 | 3.045 | −0.131 | 1.408 | 9.7 | 9.25 |
Coefficients used in equation (8), describing fSB as a function of log10(M*) at redshift zbin. The remaining coefficient a1 = −0.3 at all zbin.
| zbin . | b1 . | a2 . | b2 . | log(M0; SB/ M⊙) . | log(Mfix/M⊙) . |
|---|---|---|---|---|---|
| 0.75 | 2.52 | −0.0067 | 0.1 | 8.25 | 7.6 |
| 1.5 | 2.73 | −0.05 | 0.555 | 8.7 | 7.99 |
| 2.5 | 2.82 | −0.075 | 0.817 | 8.9 | 8.24 |
| 4.4 | 3.045 | −0.131 | 1.408 | 9.7 | 9.25 |
| zbin . | b1 . | a2 . | b2 . | log(M0; SB/ M⊙) . | log(Mfix/M⊙) . |
|---|---|---|---|---|---|
| 0.75 | 2.52 | −0.0067 | 0.1 | 8.25 | 7.6 |
| 1.5 | 2.73 | −0.05 | 0.555 | 8.7 | 7.99 |
| 2.5 | 2.82 | −0.075 | 0.817 | 8.9 | 8.24 |
| 4.4 | 3.045 | −0.131 | 1.408 | 9.7 | 9.25 |
4.1.2 The starburst sequence
We guide our description of the SFR distribution of starburst galaxies with the results shown in figs 3 and 7 from Caputi et al. (2017) and figs 6 and 7 from Bisigello et al. (2018). The resulting starburst sequence is shown in Fig. 6. The width of the starburst sequence in Caputi et al. (2017) and in Bisigello et al. (2018) is smaller that that of the SFMR, although the values are not given. Guided by the results shown in the figures, we assume σSB = 0.2 dex. Both Caputi et al. (2017) and Bisigello et al. (2018) find a starburst sequence that is steeper than the SFMR. There is no clear evidence for aSB evolution with redshift. For simplicity, we assume aSB = 0.94 (average between the best-fitting values in three redshift bins from Bisigello et al. and high redshift estimate from Caputi et al.). To set the offset of the starburst sequence from the SFMR ΔSB − SFMR we focus on the results for the intermediate masses log10(M10/M⊙) ∼ 9-9.5 (where the sample is complete and the SFMR is not affected strongly by the potential flattening at the high-mass end). We find that ΔSB − SFMR in both Bisigello et al. (2018) and Caputi et al. (2017) is about 1 dex and we assume this value in our calculations. Note that the SFMR shown in Caputi et al. (2017) is likely an upper limit on the SFMR location at z ∼ 4.4, which suggests that at those high redshifts the offset might be even larger.
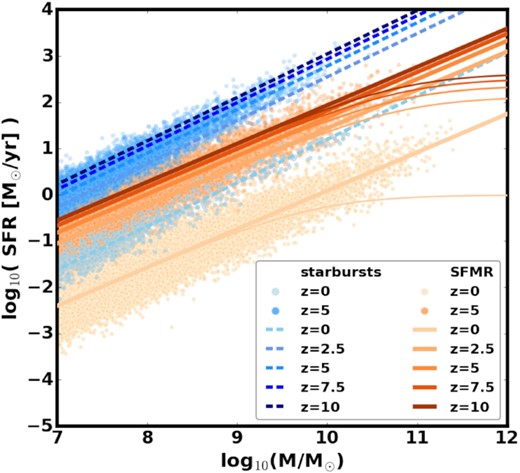
Starburst sequence (SB – dashed lines) compared with the SFMR for extreme assumptions about the high-mass slope of the SFMR: no flattening (thick solid lines) and sharp flattening (thin solid lines). Colours correspond to different redshifts. Points sampled from the GSMF and assigned to the SFMR or starburst sequence using starburst fraction shown in Fig. 5 are plotted for z = 0 and z = 5 to illustrate the increasing fraction of star-forming galaxies that populate the starburst sequence at higher redshifts and lower stellar masses. The properties of starbursts are based on the results from Caputi et al. (2017) and Bisigello et al. (2018).
5 RESULTS: THE DISTRIBUTION OF THE COSMIC SFRD OVER METALLICITIES AND REDSHIFT
In this section, we discuss the distributions of the cosmic SFRD over metallicities and redshift (fSFR(Z,z)) obtained for different variations of our observation-based model (including different choices of the local MZR, SFMR, GSMF, ∇FMR0, and prescriptions to account for starburst galaxies). Ultimately, we aim to explore the extreme fSFR(Z,z) cases in terms of the amount of SFRD occurring at low (below 10 per cent solar metallicity; ZO/H ≤ ZO/H⊙−1) and high (above solar ZO/H ≥ ZO/H⊙) metallicity. In the remainder of this paper we distinguish between two sets of models based on the choice of the local scaling relations (MZR and SFMR): the ‘low metallicity’ fSFR(Z,z) cases – obtained with z ∼ 0 MZR with low normalization (PP04 or S20) and SFMR with sharp flattening at high masses, and the ‘high metallicity’ fSFR(Z,z) cases – obtained with z ∼ 0 MZR with high normalization (KK04a or KK04b) and SFMR with no flattening. Other combinations of the local MZR and SFMR lead to more moderate metallicity distributions.
We note that in order to describe the fSFR(Z,z) at high redshifts and low metallicities (as shown in this Section and needed, for instance, in applications to gravitational wave astrophysics) one needs to extrapolate the FMR well beyond the regions where it is constrained by current observations (in particular to z ≳ 3 and M* ≲ 108 M⊙). The importance of the assumed z ≳ 3 extrapolation is discussed in Section 5.1, where we compare the fSFR(Z,z) obtained with the non-evolving FMR and with the redshift-dependent MZR based approach used in Chruslinska & Nelemans (2019). Metallicity of M* ≲ 108 M⊙ galaxies assigned with our FMR is primarily sensitive to the MZR slope and normalization and the strength of the SFR–metallicity anticorrelation at low masses/SFRs. Those factors are discussed in Section 5.1.1 and further in Appendix C. In Section 5.2, we discuss the fSFR(Z,z) under different assumptions about the contribution of starburst galaxies.
5.1 fSFR(Z,z) with redshift-invariant FMR
The comparison between the fSFR(Z,z) constructed with the use of redshift-invariant ZO/H(SFR,M*) and the corresponding distributions from Chruslinska & Nelemans (2019) are shown in Fig. 7. We compare the variations with z ∼ 0 MZR and SFMR choices as in the high (left) and low (right) metallicity extremes from Chruslinska & Nelemans (2019) (see Section 4.2 and Fig. 8 therein). In this section, we do not explicitly include starburst galaxies, so that all assumptions that are not related to the metallicity distribution of galaxies are the same as in Chruslinska & Nelemans (2019).
![Distribution of the star formation rate density (SFRD) at different metallicities and redshift (z) in this paper (background colours, brown contours; assuming non-evolving FMR and ∇FMR0 = 0.27) compared to Chruslinska & Nelemans (2019) (white contours, assuming redshift-dependent MZR). Colour indicates the amount of SFRD happening in different redshift and metallicity bins, contours indicate constant SFRD and are plotted for 0.01, 0.05, and 0.1 [M⊙/Mpc3yr] (with the highest value corresponding to the most inward contour). Left – model variation with KK04a z ∼ 0 MZR and SFMR with no flattening at high masses compared with the high metallicity extreme from Chruslinska & Nelemans (2019). Right – model variation with PP04 z ∼ 0 MZR and SFMR with sharp flattening at high masses compared with the low metallicity extreme from Chruslinska & Nelemans (2019). All models assume GSMF with non-evolving low-mass end. Orange horizontal dashed lines indicate solar, 10 per cent solar and 1 per cent solar metallicity (assuming Grevesse & Sauval 1998 solar metallicity scale). The right metallicity axis was obtained from ZO/H assuming solar abundance ratios. Note that beyond z ≳ 3 the distribution relies on extrapolation of the MZR/FMR evolution with redshift – in this respect, the plotted contours contrast somewhat extreme assumptions.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2690/1/m_stab2690fig7.jpeg?Expires=1750313337&Signature=YINVpo4xai3JcHBUBzlCqwMp2kgnZfj-Qzz1kiQVQrcn2x9t3WNMYWrz8EZOHYrE1EECkfN7VOmcEV4O6Wf033qo5av-WVAJj3sVHvaROojWzSNS4h1DmPU~FnG4Ki8mMvSHw5P1yAqMp5L6Y3USAhpogesz2DWL8mFYBF2gHVX9nJFodyjrPoub4Gi~ZKoK-dU7klQ~VKr~oNFDnQ0GAQkx4CvFGBFgIaKSlHdFNfMqwxkbDKp5i4qJuvPBctMEble~eYkdbaVW8tH7fvfkOcpvgPI~2q61zSSupnKv~wEnaqQV94jw6QjG0BrYE4knSoi8vrXuW44l4hnY0QF8Qw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Distribution of the star formation rate density (SFRD) at different metallicities and redshift (z) in this paper (background colours, brown contours; assuming non-evolving FMR and ∇FMR0 = 0.27) compared to Chruslinska & Nelemans (2019) (white contours, assuming redshift-dependent MZR). Colour indicates the amount of SFRD happening in different redshift and metallicity bins, contours indicate constant SFRD and are plotted for 0.01, 0.05, and 0.1 [M⊙/Mpc3yr] (with the highest value corresponding to the most inward contour). Left – model variation with KK04a z ∼ 0 MZR and SFMR with no flattening at high masses compared with the high metallicity extreme from Chruslinska & Nelemans (2019). Right – model variation with PP04 z ∼ 0 MZR and SFMR with sharp flattening at high masses compared with the low metallicity extreme from Chruslinska & Nelemans (2019). All models assume GSMF with non-evolving low-mass end. Orange horizontal dashed lines indicate solar, 10 per cent solar and 1 per cent solar metallicity (assuming Grevesse & Sauval 1998 solar metallicity scale). The right metallicity axis was obtained from ZO/H assuming solar abundance ratios. Note that beyond z ≳ 3 the distribution relies on extrapolation of the MZR/FMR evolution with redshift – in this respect, the plotted contours contrast somewhat extreme assumptions.
![Example illustrating the effect of different assumptions about the low mass end slope of the GSMF (αGSMF) on the fSFR(Z,z). Top panel: brown constant SFRD contours and background colours – variation with αGSMF steepening with redshift (i.e. predicting increasing number density of low-mass galaxies), white contours – fixed αGSMF = −1.45. Contours are plotted for 0.01, 0.05, and 0.1 [M⊙/Mpc3yr]. Both model variations assume ∇FMR0 = 0.27 and the same SFMR and z ∼ 0 MZR (indicated in the figure). fSFR(Z,z) significantly deviate at z ≳ 3: a redshift-dependent αGSMF leads to most of the SFRD happening at low metallicity and to a higher total SFRD(z). Bottom panel: ratio of the total SFRD at each redshift as obtained in the two variations.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2690/1/m_stab2690fig8.jpeg?Expires=1750313337&Signature=wCRDOwU469exIY-ScmW4L5CM4SKOUUsvn6U7hB5yFfc1UExwCaWOkv4Iu2nG7sjxfEPdswFkcek3B7C2lrXAdCZinA~2F9gWBG9AvUm3toY-buJseUHj~AX9bqPkrXu2qDe~SzHEOM2oLo69qE3ll~KVbrVnMAovU6CgP8L~8cTTGfj2HJdyex4i4qUMFkLmctSLU0hCJV8ZCHC3-bCViiUhVxLpT2uAYqytJQDJSGAO5K3ZTQUDpEAOHZYkWkiierKytxmyCQocB2pE0mcx9KwFO4njyXfp4zLQGHcpvamv0b9gWbtAqSrY2wgPtZ72nHoYn9aqPP0l9AEWPqDLWg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Example illustrating the effect of different assumptions about the low mass end slope of the GSMF (αGSMF) on the fSFR(Z,z). Top panel: brown constant SFRD contours and background colours – variation with αGSMF steepening with redshift (i.e. predicting increasing number density of low-mass galaxies), white contours – fixed αGSMF = −1.45. Contours are plotted for 0.01, 0.05, and 0.1 [M⊙/Mpc3yr]. Both model variations assume ∇FMR0 = 0.27 and the same SFMR and z ∼ 0 MZR (indicated in the figure). fSFR(Z,z) significantly deviate at z ≳ 3: a redshift-dependent αGSMF leads to most of the SFRD happening at low metallicity and to a higher total SFRD(z). Bottom panel: ratio of the total SFRD at each redshift as obtained in the two variations.
Fig. 7 shows that the metallicity distributions start to deviate around z ≳ 1.5 (compare brown and white contours), where the redshift-dependent MZR predicts a steeper decrease in metallicity than what results from the non-evolving FMR. The difference becomes striking at z ≳ 3, but we stress that neither the MZR nor the FMR is currently constrained in this redshift regime. In particular, there is no guarantee that the FMR holds or continues to show weak/no redshift evolution beyond that redshift. On the other hand, as discussed in Section 3, the extrapolated MZR evolution as assumed by Chruslinska & Nelemans (2019) is likely to overestimate the rate of decrease in metallicity. Therefore, in Fig. 7 we contrast two seemingly extreme assumptions. Until better observational constraints are available, this comparison can serve to illustrate (likely a conservative) range of uncertainty of the high redshift part of fSFR(Z,z) resulting from the extrapolated evolution of the galaxy metallicity distribution with redshift. The extrapolated MZR evolution leads to a z ∼ 10 peak metallicity that is almost 2 dex lower than what results from the non-evolving FMR assumption. The latter leads to SFRD concentrated at higher metallicities (irrespective of the model variation), but the extended low metallicity tail is still present at all redshifts. We note that the difference between the fSFR(Z,z) obtained with a redshift dependent MZR and with the non-evolving FMR was recently discussed in Boco et al. (2021) – qualitatively our results are the same as discussed therein. However, rather than discussing a example fSFR(Z,z) obtained with a particular FMR or MZR taken from the literature, here we model the FMR consistently with the choice of the local SFMR and MZR and can explore the uncertainties of the final result. All variations shown in Fig. 7 assume a GSMF with non-evolving low-mass slope. As discussed in Chruslinska & Nelemans (2019) (see Section 4.1 therein), this assumption has relatively little effect on fSFR(Z,z) at z ≲ 3, but strongly affects the result at higher redshifts (both its low metallicity tail and the total SFRD). This is illustrated in Fig. 8 – the effect of the steepening low-mass end of the GSMF on fSFR(Z,z) is analogous for other model variations.
5.1.1 The effect of the z ∼ 0 MZR slope and ∇FMR0
The effect of the choice of the z ∼ 0 MZR slope (aMZR) and ∇FMR0 on fSFR(Z,z) is shown in Fig. 9. Similarly to Fig. 7, the left-hand and right-hand panels show high and low metallicity model variations, respectively. Top (bottom) panels show variations with aMZR ∼0.3 (aMZR ∼0.6). Different contours illustrate the impact of ∇FMR0.
![Distribution of the star formation rate density (SFRD) at different metallicities and redshift (z) for different assumptions about the z ∼ 0 MZR slope (top panels: variations with aMZR ∼ 0.3, bottom panels: aMZR ∼ 0.6) and ∇FMR0 (compare different contours; background colours are plotted for variations with ∇FMR0 = 0.27). Left-hand (right) panels show model variations with z ∼ 0 MZR and SFMR that maximize the SFRD at high (low) metallicity. Constant SFRD contours are plotted for 0.005, 0.01, 0.05, and 0.1 [M⊙/Mpc3 yr] (the highest value corresponds to the innermost contour). All model variations assume a GSMF with non-evolving low-mass end. Variations with flatter z ∼ 0 MZR lead to a more compact metallicity distribution, but their peak decreases with redshift faster than in variations with a steeper z ∼ 0 MZR.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2690/1/m_stab2690fig9.jpeg?Expires=1750313337&Signature=WEjjFcEX8qhO7RBgTPOH2htM9ReLUhOl80rAAxYDym1J8sLM8G6Gl9OkGSeut5BpEzTOuXozAfaoRB5aee3UEHTm3Mh8~J00IkcERDVGDBYuiNsWymRe3cQaS4b8E1vRVjH01x4t5PF75xG5XA0kuxEOj3oBL1nItCkfGQaZZaeO2KeAsCmcAh0fpeDuOddoQQsnkfw6Ui-PWJ6ILQsGfu43Ox4kE9BYcQGV2LQ5ktQFMhfrPIXnAFHFSOAgtAGmHP~-WG5~7q2W9lvKoBzNnQ93ywCuclD30jTIZWvRaPps2kgCKqgHYyoIFNCdZvcRgBgfdNsmq85pI94MhPIuJw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Distribution of the star formation rate density (SFRD) at different metallicities and redshift (z) for different assumptions about the z ∼ 0 MZR slope (top panels: variations with aMZR ∼ 0.3, bottom panels: aMZR ∼ 0.6) and ∇FMR0 (compare different contours; background colours are plotted for variations with ∇FMR0 = 0.27). Left-hand (right) panels show model variations with z ∼ 0 MZR and SFMR that maximize the SFRD at high (low) metallicity. Constant SFRD contours are plotted for 0.005, 0.01, 0.05, and 0.1 [M⊙/Mpc3 yr] (the highest value corresponds to the innermost contour). All model variations assume a GSMF with non-evolving low-mass end. Variations with flatter z ∼ 0 MZR lead to a more compact metallicity distribution, but their peak decreases with redshift faster than in variations with a steeper z ∼ 0 MZR.
As can be expected, fSFR(Z,z) for variations with steeper z ∼ 0 MZR (higher aMZR values) have a more extended low metallicity tail at each redshift. However, variations with lower aMZR values feature a much steeper metallicity evolution at z ≲ 4. At higher redshifts the metallicity peak of fSFR(Z,z) decreases at a similar rate for the variations with the same ∇FMR0 and same total SFRD (i.e. the same SFMR and GSMF assumptions), irrespective of aMZR.13 This can be understood by looking at the comparison of ZO/H(SFR,M*) obtained for different z ∼ 0 MZR, shown in Fig. 4. In this plane, galaxies with the same log10(M*) at higher redshifts shift to higher log10(SFR) lines. The rate of this shifting is dictated by the redshift-dependent SFMR. The offset in ZO/H between the different log10(SFR) curves at fixed log10(M*) is bigger for variations with lower aMZR (compare left-hand and right-hand panels in Fig. 4) and similarly for higher ∇FMR0 (see Fig. A4 in the Appendix A). This translates into steeper decrease of the fSFR(Z,z) metallicity peak with redshift in the variations with lower aMZR and higher ∇FMR0. At sufficiently high redshifts (where almost all galaxies occupy the high SFR, linear regime of ZO/H(SFR,M*)) the spacing in ZO/H for different log10(SFR) curves is set by the choice of ∇FMR0. Lower ∇FMR0 result in weaker metallicity evolution (compare white and brown contours in Fig. 9). Therefore, for fixed ∇FMR0 and the same assumptions about the SFMR, the rate of metallicity evolution at z ≳ 4 and fixed log10(M*) is essentially the same. However, the full fSFR(Z,z) distribution is also affected by the GSMF. If the low-mass end of the GSMF is allowed to steepen with redshift, the contribution of the low mass (and so – low metallicity) galaxies to the total SFRD at high redshifts is considerably higher than if the low-mass end of the GSFM is fixed (see example shown in Fig. 8). The FMR is not constrained for low-mass, low-SFR galaxies. Results discussed above assume that those galaxies are well described by the same relation as the galaxies with higher M* and SFR, and that the strength of the SFR–metallicity correlation does not change in this part of the parameter space (i.e. ∇FMR = ∇FMR0). In Appendix C, we additionally discuss the variation with an SFR-dependent ∇FMR in which the SFR–metallicity correlation is assumed to disappear (i.e. the FMR breaks down) at SFR corresponding to z ∼ 0 SFMR galaxies with M* ≲ 108 M⊙. Overall, this assumption has minor impact on the estimated fSFR(Z,z) distribution (see Fig. C2).
5.2 fSFR(Z,z): the impact of starbursts
The comparison of fSFR(Z,z) obtained with and without including starbursts is shown Fig. 10. Top and middle panels show the same z ∼ 0 MZR and SFMR variations as in Fig. 9. Different contours correspond to different starburst implementations (introduced in Section 4.1). The effect of including starbursts in our calculations is two-fold: first, a fraction fSB of star-forming galaxies is now assigned a higher SFR than what would result from the SFMR. This means that the total SFRD at each redshift is higher than in the model that does not explicitly account for starbursts (see bottom panel in Fig. 10). Secondly, assuming that starbursts follow the FMR, they contribute to star formation happening at relatively low (for their mass and redshift) metallicity. Therefore, including starbursts shift the peak of the fSFR(Z,z) to lower metallicities and broadens the low metallicity part of the distribution.
![Distribution of the SFRD at different metallicities and redshift (z) for different assumptions about starburst galaxies: no starbursts (background colours, brown contours), starburst sequence, and fSB model based on the results of Bisigello et al. (2018) and Caputi et al. (2017) (B18/C17, white contours) and as in Boco et al. (2021) (black dashed contours). Top and middle panels correspond to different z ∼ 0 MZR and SFMR variations (same as in Fig. 9). Contours indicate constant SFRD and are plotted for 0.01, 0.05, and 0.1 [M⊙/Mpc3yr] (with the highest value corresponding to the innermost contour). Note that different assumptions about starburst galaxies lead to different total SFRD at each redshift – bottom panels show the ratio of the SFRD integrated over metallicities at each z in the model with starbursts (brown – B18/C17 implementation, black – Boco et al 2021 implementation) to the corresponding model without starbursts (the choice of MZR does not affect the total SFRD). All models assume GSMF with non-evolving low-mass end and ∇FMR0 = 0.27.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2690/1/m_stab2690fig10.jpeg?Expires=1750313337&Signature=h4-xdEU8OuBgh3fqFHKIKRvlxgEE~F4U9SPAOdd29RpdttduogpPLld6ACP--mGxfoK8eraEmHQeZXuBVGFYqrbN7PAiS~00j~G~VqY3KcC~10VjcxrSP81XEzcK2Fq5G7-3gfQeXki4EKydteb8MPoIMjAEocdyhcyloGAZvkq5GB0UvOzX0iidCWOgB8q5n3AI0e6pLHXqQpLoa2PVT1xrAof5PGSvdpc2gp886Tj7yFJbhjsl2FVHGEQyS992~EBGneoR8a1JD1gBiMKTLU0Fxsgv9eYPhmA8vTUX9PRrxlh0aH2hBYEJN5VO4CiV~zfQNV0pePPrbYozZoP5bQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Distribution of the SFRD at different metallicities and redshift (z) for different assumptions about starburst galaxies: no starbursts (background colours, brown contours), starburst sequence, and fSB model based on the results of Bisigello et al. (2018) and Caputi et al. (2017) (B18/C17, white contours) and as in Boco et al. (2021) (black dashed contours). Top and middle panels correspond to different z ∼ 0 MZR and SFMR variations (same as in Fig. 9). Contours indicate constant SFRD and are plotted for 0.01, 0.05, and 0.1 [M⊙/Mpc3yr] (with the highest value corresponding to the innermost contour). Note that different assumptions about starburst galaxies lead to different total SFRD at each redshift – bottom panels show the ratio of the SFRD integrated over metallicities at each z in the model with starbursts (brown – B18/C17 implementation, black – Boco et al 2021 implementation) to the corresponding model without starbursts (the choice of MZR does not affect the total SFRD). All models assume GSMF with non-evolving low-mass end and ∇FMR0 = 0.27.
Both effects are clearly seen when the variations including the B18/C17 starburst implementation (white contours in Fig. 10) are compared with the corresponding variations that do not include starbursts (brown contours). The lower edges of white contours extend to lower metallicities with respect to no starburst case at all redshifts, while the upper, high metallicity edges remain the same. This difference increases with redshift due to increasing fSB. The total SFRD is about 2.5 times higher at z ≳ 4 in the case with starbursts (brown line, bottom panel in Fig. 10). Note that we fix fSB beyond z = 4.4 – the highest redshift bin covered by the data in Caputi et al. (2017). If the trend seen at lower redshift continues, the difference at high redshifts would be even higher. If instead we follow the starburst implementation as used in the recent study by Boco et al. (2021) (black dashed contours), the difference with respect to cases without starbursts is negligible. This is expected, given the low fixed fSB = 3 per cent and the fact that in this prescription the starburst sequence is within the 2σSFMR scatter of the SFMR. The difference is slightly more pronounced if SFMR with a sharp flattening at high masses is used (right-hand panels in Fig. 10), as in those cases there is a larger difference in SFR between massive galaxies on the SFMR and on the starburst sequence. The inclusion of starbursts as in Boco et al. (2021) also barely affects the total SFRD (see black dashed line in the bottom panel in Fig. 10).
6 METALLICITY-DEPENDENT COSMIC SFH
In this section we discuss the cosmic SFH – SFRD integrated over all metallicities as a function of redshift/cosmic time, as well as the high and low metallicity cuts of the cosmic SFH (i.e. SFRD occurring above and below certain metallicity thresholds) obtained for different model variations. Note that this is essentially a different way to present our results, which provides less detailed information than the full fSFR(Z,z) distributions shown in Section 5. It allows us to zoom into the interesting parts of the distribution and demonstrate the uncertainty of its various parts more clearly. However, we stress that the discussed cuts of the cosmic SFH are sensitive to the considered low/high metallicity thresholds. In some cases, factors that have minor impact on the overall fSFR(Z,z) distribution may lead to considerable uncertainty in the SFH cut for a particular choice of metallicity threshold. The 10 per cent solar/solar ZO/H thresholds used here were chosen to zoom into the low/high metallicity tails of the distribution. In general, the relevant thresholds may vary depending on the considered problem. When showing the cosmic SFH and its various metallicity cuts, in each case we indicate the range of possible outcomes spanned by the model variations with extreme assumptions about the considered factors. We indicate which of the considered factors drive the uncertainty of the fSFR(Z,z) in different regimes (i.e. low/high metallicity, low/high redshift). As discussed in Section 5, the difference between the fSFR(Z,z) obtained for variations with starburst implementation as in Boco et al. (2021) (i.e. with fixed, small fraction of starbursts) and the corresponding variations with no starbursts are negligible. Therefore, in this section we only discuss the former.
6.1 Cosmic SFH
The cosmic SFH obtained for different model variations considered in this study is shown in Fig. 11. Coloured ranges distinguish different assumptions about the starburst galaxies. They span between the extreme cases resulting from different assumptions about the high-mass end of the SFMR and the low-mass end of the GSMF. Note that the assumptions about the metallicity (z ∼ 0 MZR, redshift evolution of MZR/non-evolving FMR, ∇FMR) have no impact on the (total) cosmic SFH, but affect its different metallicity cuts. For the convenience of use and discussion, we approximate the results shown in Fig. 11 with a broken power law: SFRD = A (1 + z)κ, fitting A and κ in several redshift ranges for the upper and lower edge of each variation. The resulting coefficients are given in Table 3. Coefficients obtained when only variations with non-evolving low-mass end of the GSMF are considered are provided in Table B1 in the Appendix B. Considering variations with fixed assumptions about the starburst galaxies, we note the following:
The uncertainty in the cosmic SFH at z < 2 is dominated by the assumptions about high-mass end of the SFMR: the lower edges of all ranges correspond to variations with SFMR with sharp flattening at high masses (as in low metallicity variations), while the upper edges correspond to variations with SFMR with no flattening (as in high metallicity variations). Assumptions about the GSMF have secondary role in this redshift range.
The evolution of the low-mass end of the GSMF dominates the uncertainty at higher redshifts: the lower (upper) edges of all ranges correspond to variations with non-evolving (steepening) low-mass end of the GSMF. At the same time, the importance of the high-mass end of the SFMR is reduced due to decreasing number density of the most massive galaxies (see e.g. fig. 3 in Chruslinska & Nelemans 2019).
The upper edges of all ranges feature an upturn in the SFRD evolution at z ≳ 4, before the sharp decrease at z > 7. This is due to strongly increasing number density of low-mass galaxies in the variations in which the low-mass end of the GSMF steepens with redshift. We note that such upturn only appears when the SFMR and GSMF are extrapolated to log10(M*) < 8 (see discussion in Chruslinska & Nelemans 2019).
All variations show a sharp decrease in the SFRD at z ∼ 7. This is due to the rapid evolution of the GSMF normalization between z ∼ 7 and 8, seen when observational GSMF estimates from different redshifts are combined (see fig. 3 in Chruslinska & Nelemans 2019).
Star formation rate density as a function of lookback time/redshift. The plotted ranges span between the estimates obtained for different variations of model assumptions about the SFMR and GSMF. The ranges in different colours correspond to different assumptions about the starburst galaxies (turquoise: as in Boco et al. (2021), brown: based on Caputi et al. (2017) – C17 and Bisigello et al. (2018) – B18). The orange region shows the corresponding range from Chruslinska & Nelemans (2019) (with no starburst contribution). The thick solid orange and brown lines show how the upper edge of the corresponding range would look like under the assumption of a non-evolving low-mass end of the GSMF (the effect on the turquoise range follows closely the one that can be seen for Chruslinska & Nelemans 2019, the lower edge is not affected by this assumption). The dashed grey line shows the estimate from Madau & Dickinson (2014) for reference. We overplot the z ≲ 2 infrared-based estimates complied by Casey et al. (2018) and the recent observational high redshift SFRD estimates by Loiacono et al. (2021), Khusanova et al. (2021), and Gruppioni et al. (2020) that account for the contribution of heavily dust obscured galaxies. Note that the latter two provide a lower limit. See text for the discussion of the comparison with observations. Where necessary, we correct for the difference in SFR due to varying IMF assumptions.
Coefficients of the power-law fits to the cosmic SFH (lower and upper edges of the ranges shown in Fig. 11) obtained for different variations of our observation-based model. Within each redshift range indicated in the first column total SFRD can be approximated with the dependence: SFRD = A · (1 + z)κ[M⊙ yr−1]. Note that the cosmic SFH in ‘no SB’ variation is identical with the cosmic SFH from Chruslinska & Nelemans (2019).
| Cosmic SFH – lower edge . | ||||||
|---|---|---|---|---|---|---|
| Variation: . | No SB . | SB: Boco + 21 . | SB: B18/C17 . | |||
| z range . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 1 | 2.6546 | 0.0076 | 2.6093 | 0.0091 | 2.7828 | 0.0123 |
| 1 < z ≤ 1.8 | 2.4050 | 0.0091 | 2.3416 | 0.0109 | 2.7119 | 0.0129 |
| 1.8 < z ≤ 3 | −1.0535 | 0.3195 | −1.1284 | 0.3891 | −0.7558 | 0.4585 |
| 3 < z ≤ 7 | −2.2771 | 1.7427 | −2.2909 | 1.9499 | −1.9628 | 2.4435 |
| 7 < z ≤ 8.8 | −12.5425 | 3.249 × 109 | −12.5526 | 3.607· 109 | −12.4895 | 7.845 × 109 |
| 8.8 < z ≤ 10. | 0 | 0.0012 | 0 | 0.0013 | 0 | 0.0033 |
| Cosmic SFH – upper edge | ||||||
| Variation | no SB | SB: Boco + 21 | SB: B18/C17 | |||
| z range | κ | A | κ | A | κ | A |
| 0 < z ≤ 1 | 2.2214 | 0.0194 | 2.2222 | 0.0209 | 2.3850 | 0.0248 |
| 1 < z ≤ 1.8 | 1.8708 | 0.0247 | 1.8708 | 0.0266 | 2.2515 | 0.0272 |
| 1.8 < z ≤ 4 | −1.2436 | 0.6097 | −1.2445 | 0.6585 | −0.5342 | 0.4793 |
| 4 < z ≤ 7 | 0.6591 | 0.0285 | 0.6585 | 0.0307 | 0.7477 | 0.0609 |
| 7 < z ≤ 8.8 | −9.3760 | 3.29 × 107 | −9.3864 | 3.624 × 107 | −9.4740 | 1.037 × 108 |
| 8.8 < z ≤ 10. | 0 | 0.0168 | 0 | 0.018 | 0 | 0.0421 |
| Cosmic SFH – lower edge . | ||||||
|---|---|---|---|---|---|---|
| Variation: . | No SB . | SB: Boco + 21 . | SB: B18/C17 . | |||
| z range . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 1 | 2.6546 | 0.0076 | 2.6093 | 0.0091 | 2.7828 | 0.0123 |
| 1 < z ≤ 1.8 | 2.4050 | 0.0091 | 2.3416 | 0.0109 | 2.7119 | 0.0129 |
| 1.8 < z ≤ 3 | −1.0535 | 0.3195 | −1.1284 | 0.3891 | −0.7558 | 0.4585 |
| 3 < z ≤ 7 | −2.2771 | 1.7427 | −2.2909 | 1.9499 | −1.9628 | 2.4435 |
| 7 < z ≤ 8.8 | −12.5425 | 3.249 × 109 | −12.5526 | 3.607· 109 | −12.4895 | 7.845 × 109 |
| 8.8 < z ≤ 10. | 0 | 0.0012 | 0 | 0.0013 | 0 | 0.0033 |
| Cosmic SFH – upper edge | ||||||
| Variation | no SB | SB: Boco + 21 | SB: B18/C17 | |||
| z range | κ | A | κ | A | κ | A |
| 0 < z ≤ 1 | 2.2214 | 0.0194 | 2.2222 | 0.0209 | 2.3850 | 0.0248 |
| 1 < z ≤ 1.8 | 1.8708 | 0.0247 | 1.8708 | 0.0266 | 2.2515 | 0.0272 |
| 1.8 < z ≤ 4 | −1.2436 | 0.6097 | −1.2445 | 0.6585 | −0.5342 | 0.4793 |
| 4 < z ≤ 7 | 0.6591 | 0.0285 | 0.6585 | 0.0307 | 0.7477 | 0.0609 |
| 7 < z ≤ 8.8 | −9.3760 | 3.29 × 107 | −9.3864 | 3.624 × 107 | −9.4740 | 1.037 × 108 |
| 8.8 < z ≤ 10. | 0 | 0.0168 | 0 | 0.018 | 0 | 0.0421 |
Coefficients of the power-law fits to the cosmic SFH (lower and upper edges of the ranges shown in Fig. 11) obtained for different variations of our observation-based model. Within each redshift range indicated in the first column total SFRD can be approximated with the dependence: SFRD = A · (1 + z)κ[M⊙ yr−1]. Note that the cosmic SFH in ‘no SB’ variation is identical with the cosmic SFH from Chruslinska & Nelemans (2019).
| Cosmic SFH – lower edge . | ||||||
|---|---|---|---|---|---|---|
| Variation: . | No SB . | SB: Boco + 21 . | SB: B18/C17 . | |||
| z range . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 1 | 2.6546 | 0.0076 | 2.6093 | 0.0091 | 2.7828 | 0.0123 |
| 1 < z ≤ 1.8 | 2.4050 | 0.0091 | 2.3416 | 0.0109 | 2.7119 | 0.0129 |
| 1.8 < z ≤ 3 | −1.0535 | 0.3195 | −1.1284 | 0.3891 | −0.7558 | 0.4585 |
| 3 < z ≤ 7 | −2.2771 | 1.7427 | −2.2909 | 1.9499 | −1.9628 | 2.4435 |
| 7 < z ≤ 8.8 | −12.5425 | 3.249 × 109 | −12.5526 | 3.607· 109 | −12.4895 | 7.845 × 109 |
| 8.8 < z ≤ 10. | 0 | 0.0012 | 0 | 0.0013 | 0 | 0.0033 |
| Cosmic SFH – upper edge | ||||||
| Variation | no SB | SB: Boco + 21 | SB: B18/C17 | |||
| z range | κ | A | κ | A | κ | A |
| 0 < z ≤ 1 | 2.2214 | 0.0194 | 2.2222 | 0.0209 | 2.3850 | 0.0248 |
| 1 < z ≤ 1.8 | 1.8708 | 0.0247 | 1.8708 | 0.0266 | 2.2515 | 0.0272 |
| 1.8 < z ≤ 4 | −1.2436 | 0.6097 | −1.2445 | 0.6585 | −0.5342 | 0.4793 |
| 4 < z ≤ 7 | 0.6591 | 0.0285 | 0.6585 | 0.0307 | 0.7477 | 0.0609 |
| 7 < z ≤ 8.8 | −9.3760 | 3.29 × 107 | −9.3864 | 3.624 × 107 | −9.4740 | 1.037 × 108 |
| 8.8 < z ≤ 10. | 0 | 0.0168 | 0 | 0.018 | 0 | 0.0421 |
| Cosmic SFH – lower edge . | ||||||
|---|---|---|---|---|---|---|
| Variation: . | No SB . | SB: Boco + 21 . | SB: B18/C17 . | |||
| z range . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 1 | 2.6546 | 0.0076 | 2.6093 | 0.0091 | 2.7828 | 0.0123 |
| 1 < z ≤ 1.8 | 2.4050 | 0.0091 | 2.3416 | 0.0109 | 2.7119 | 0.0129 |
| 1.8 < z ≤ 3 | −1.0535 | 0.3195 | −1.1284 | 0.3891 | −0.7558 | 0.4585 |
| 3 < z ≤ 7 | −2.2771 | 1.7427 | −2.2909 | 1.9499 | −1.9628 | 2.4435 |
| 7 < z ≤ 8.8 | −12.5425 | 3.249 × 109 | −12.5526 | 3.607· 109 | −12.4895 | 7.845 × 109 |
| 8.8 < z ≤ 10. | 0 | 0.0012 | 0 | 0.0013 | 0 | 0.0033 |
| Cosmic SFH – upper edge | ||||||
| Variation | no SB | SB: Boco + 21 | SB: B18/C17 | |||
| z range | κ | A | κ | A | κ | A |
| 0 < z ≤ 1 | 2.2214 | 0.0194 | 2.2222 | 0.0209 | 2.3850 | 0.0248 |
| 1 < z ≤ 1.8 | 1.8708 | 0.0247 | 1.8708 | 0.0266 | 2.2515 | 0.0272 |
| 1.8 < z ≤ 4 | −1.2436 | 0.6097 | −1.2445 | 0.6585 | −0.5342 | 0.4793 |
| 4 < z ≤ 7 | 0.6591 | 0.0285 | 0.6585 | 0.0307 | 0.7477 | 0.0609 |
| 7 < z ≤ 8.8 | −9.3760 | 3.29 × 107 | −9.3864 | 3.624 × 107 | −9.4740 | 1.037 × 108 |
| 8.8 < z ≤ 10. | 0 | 0.0168 | 0 | 0.018 | 0 | 0.0421 |
The first three effects are best seen by comparing the thick solid lines in Fig. 11 (corresponding to variations with SFMR with no flattening and GSMF with non-evolving low-mass end) with the upper edges of the relevant ranges. Comparing the variations including starbursts (turquoise/brown ranges) with those from Chruslinska & Nelemans (2019) (that do no explicitly account for their contribution; orange range), one can see that:
The SFRD is increased in the variations including starbursts; starbursts implementation used in Boco et al. (2021) (turquoise) leads to negligible difference, while the B18/C17 implementation (brown) leads to a factor of ∼2.5 increase at high redshifts (see Section 5.2).
Variations including starbursts span a narrower range in cosmic SFH (the lower edge is lifted with respect to no starbursts case). This is due to the fact that assigning high SFR (compared to SFMR values) to a fraction of galaxies (starbursts) effectively reduces the difference between the SFRD in model variations with no/sharp SFMR flattening. The effect is stronger at high redshifts for the B18/C17 prescription, as fSB increases with redshift.
the increasing fraction of starbursts in the B18/C17 variations leads to a broader peak of the cosmic SFH and a shallower SFRD decrease at high redshifts.
In Fig. 11, we contrast the total SFRD that results from various realizations of our observation-based model with several observational determinations of this quantity. At z < 2, there is about a factor of 2 (2.5) offset between the SFRD obtained with model variations that assume SFMR with no flattening at high masses (and C17/B18 starburst implementation) and the commonly used, best-fitting estimate from Madau & Dickinson (2014) (grey-dashed line). However, we note that this offset is within the scatter and uncertainty of the z ≲ 2 observational estimates – in particular, infrared based SFRD determinations suggest higher SFRD than the estimate obtained by Madau & Dickinson (2014), more in agreement with our SFRD determination based on the GSMF, SFMR, and starburst sequence (see also fig. 1 in Casey et al. 2018 – the infrared-based data complied by those authors are also included in Fig. 11; and fig. 2 and discussion in Boco et al. 2021). At higher redshifts (2 < z < 7), our model variations (even those not including starbursts) in general show shallower SFRD decrease than the estimate provided by Madau & Dickinson (2014) (SFRD ∝ (1 + z)−2.9). This is striking for the upper edges of our estimates (see also Table 3). Shallower SFRD evolution than estimated by Madau & Dickinson (2014) is in line with the most recent high redshift observational estimates (e.g. Gruppioni et al. 2020; Khusanova et al. 2021; Loiacono et al. 2021, although the uncertainties in those measurements are still substantial), indicating that a significant fraction of the SFRD at z ≳ 2 still occurs in dust obscured galaxies (and hence was missed by the earlier – mostly UV light-based surveys). Those estimates14 are also included in Fig. 11. However, the comparison of our results with those estimates is not straightforward for two main reasons: (a) observations may be incomplete: the estimate provided by Khusanova et al. (2021) is based on a UV selected sample and may not fully account for extremely dusty galaxies, while the estimate provided by Gruppioni et al. (2020) does not account for the contribution of UV sources (b) the faint (low mass) end of the galaxy population is not directly probed by observations. All estimates shown in Fig. 11 include (different) extrapolations to account for their contribution to the total SFRD. In our models we extrapolate all of the empirical relations down to log10(M*/M⊙) = 6 – as discussed above, the result of this extrapolation at high z is very sensitive to the GSMF slope. Extrapolations used in the high redshift observational estimates give less weight to low-mass galaxies than our models with steepening low-mass end of the GSMF. The estimate by Khusanova et al. (2021) includes extrapolations down to M*/luminosity limit comparable to the extrapolation limit used in our study, but is averaged over the results obtained with different GSMF/UV luminosity functions (with different low mass end slopes) from the literature. Gruppioni et al. (2020) extrapolate the infrared luminosity function down to low luminosities. However, such galaxies are expected to be relatively unobscured and the faint-end slope of the infrared luminosity function is much flatter than that of the UV luminosity function (and the GSMF used in our study) at high redshifts – in that sense, this estimate underestimates the contribution of low-mass galaxies to the total SFRD. Therefore, the observational estimates are likely lower limits when compared to our models. We note that all model variations with fixed low mass end of the GSMF and no/small fraction of starbursts fall below the recent z ∼ 3 limit from Gruppioni et al. (2020). Given the fact that this determination underestimates the contribution of low-mass galaxies to the total SFRD with respect to our models, this offset may hint at the need for higher contribution of massive galaxies than included in those model variations (e.g. higher fraction of starburst galaxies or higher overall normalization of the SFMR at those redshifts). We also note that the z ∼ 4.5 estimate by Khusanova et al. (2021) falls above our estimates obtained with fixed low mass end of the GSMF and no/small fraction of starbursts, but it is unclear how to properly compare this averaged estimate with our results. All model variations are consistent with the limits obtained by Gruppioni et al. (2020) and Loiacono et al. (2021) (although the latter is not particularly constraining due to large uncertainty that overlaps with all of the considered model variations) at similar redshifts.
6.2 A low metallicity cut of the cosmic SFH
6.2.1 Note on the low metallicity threshold
When referring to low metallicity, throughout this paper we use a limit of <10 per cent solar oxygen abundance (with ZO/H⊙ following Grevesse & Sauval 1998) and the numbers quoted later in this section necessarily depend on this choice. This threshold is chosen arbitrarily and serves for illustrative purposes. In general, the relevant definition of low metallicity varies depending on the discussed problem and application. For instance, the abrupt drop commonly seen in the metallicity dependence of the formation efficiency of black hole – black hole mergers formed in the course of isolated binary evolution appears at metallicities 10–50 per cent solar (depending on the considered model of binary/stellar evolution, e.g. Chruslinska et al. 2019; Broekgaarden et al. 2021). In that sense, depending on the model, the interesting low metallicity threshold could be as high as 50 per cent solar metallicity. Furthermore, from the point of view of evolution of massive stars and the related transients, the most relevant metallicity tracer is iron rather than oxygen (which serves as a metallicity proxy in this study; the oxygen abundance is the most easily obtained from emission line measurements and so it is the most commonly used metallicity proxy in studies of interstellar medium of galaxies). That is primarily due to high sensitivity of the radiation-driven mass-loss rates of hot, massive stars to the abundance of this element (e.g. Vink, de Koter & Lamers 2001; Vink & de Koter 2005; Gräfener & Hamann 2008; Sanders et al. 2021). In general, interstellar medium (ISM) of galaxies is enriched in oxygen and iron on different time-scales due to the fact that different sources dominate the production of those elements (core-collapse supernovae with ≲10 Myr delay with respect to star formation for oxygen and SNIa supernovae with ∼0.1–1 Gyr delay for iron; e.g. Wheeler, Sneden & Truran 1989). This means that especially young, highly star-forming galaxies (i.e. typical at high redshifts) are expected to show overabundance of oxygen relative to iron with respect to solar ratios. Recent studies indeed find evidence for supersolar O/Fe≳2 (O/Fe)|⊙ in the ISM of z ∼ 2 star-forming galaxies (e.g. Steidel et al. 2016; Topping et al. 2020; Cullen et al. 2021). Consequently, oxygen (or, more generally, α-element)-enhanced abundance ratios are also found in local stars that formed at earlier cosmic epochs (e.g. Bensby, Feltzing & Lundström 2004; Tolstoy, Hill & Tosi 2009). There is no universal way to translate metallicity measure based on oxygen abundance to iron abundance, in particular the typical oxygen to iron ratio in the ISM (and the interesting low metallicity threshold – if oxygen is used as a proxy) can be expected to vary with redshift and possibly galaxy characteristics. A more thorough discussion of this issue is beyond the scope of this work and is left to future studies.
6.2.2 Results
SFRD that occurs at ZO/H < ZO/H⊙-1 as a function of redshift/time for different variations of our model is shown in Fig. 12. Note that the assumptions about the high-mass end of the SFMR have no impact on the low metallicity tail of fSFR(Z,z) and the low metallicity SFH. Similarly as for the cosmic SFH, we provide the power-law fits to the upper and lower edges of the ranges shown in Fig. 12 fitted in several z ranges. Those are listed in Tables B3 and B2 in the Appendix B. The following features are common to all model variations:
At z ≲ 2, the SFRD occurring at low metallicity increases faster than the total SFRD. The exact slope depends on the variation. In this redshift range the width of the ranges is set by the assumptions about the z ∼ 0 MZR: lower/upper edges of all ranges correspond to variations with high/low MZR normalization (as in the high/low metallicity variations). At those redshifts, assumptions about the low-mass end of the GSMF have negligible impact on the amount of star formation happening at low metallicity.
Beyond the peak of the cosmic SFH assumptions about the low-mass end of the GSMF set the width of the ranges and the behaviour of the upper edges. The lower/upper edges correspond to variations with high/low MZR normalization and non-evolving/steepening GSMF low mass end.
If αGSMF is fixed, the low metallicity cut of the SFH shows a broad peak between z = 2–4 (depending on the variation) and a relatively mild evolution up to z ∼ 7.
If αGSMF evolves with redshift, the increasing abundance of low-mass galaxies (forming stars at low metallicity) causes a continuous increase in the low metallicity cut of the SFH up to z ∼ 7.5–8.
All variations show a sharp decrease in the low metallicity SFRD at z ≳ 8, reflecting the sharp drop in the total SFRD at those redshifts.
![Star formation rate density at low metallicity [i.e. below 10 per cent solar, assuming solar oxygen abundance ZO/H⊙ = 8.83 Grevesse & Sauval (1998)] as a function of lookback time/redshift. The plotted ranges show estimates obtained for different variations of assumptions about the starburst (SB) galaxies (blue/turquoise: as in Boco et al. (2021), brown/beige: based on Caputi et al. (2017) – C17 and Bisigello et al. (2018) – B18) and low-mass slope of the redshift z ∼ 0 MZR (aMZR). The orange region shows the range of the low metallicity SFHs obtained by Chruslinska & Nelemans (2019). Thick solid lines in different colours indicate the location of the upper edge of the corresponding ranges obtained with the assumption of non-evolving low-mass end of the GSMF, demonstrating the importance of this assumption beyond the peak of the cosmic SFH. All variations from this study assume ∇FMR0 = 0.27.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2690/1/m_stab2690fig12.jpeg?Expires=1750313337&Signature=3Bonn3N1FrnjkbyL9ihk76VMebERzp35~0JRLMjZjZC~P~EGEK3fqsk7rRRcC6NT9-DbXTG2OlFXmB2vs8dMRzCKnl1pV7Ydhgl~De1uwdfkwARavoofN~20RI9Y-xw3Ai1RMiLCs4Cs9I4STx07c~xRpomjvgoTR8f17wC2H5eTUyyN7N57gZRTjM~I3CcIPWL-693eu2y3bEIfz7QXy9GaPd-dvEqxga1727xioWqQtGclH4-hvfckM8NtH7VyLuc5ByPirvzTV82KKB1lPQR83VJTr89uGaH~Vw-ywDAbX7L7KfQEu3oTwBVYkiu3TQZZ65X9IrJDabU8Zp4maQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Star formation rate density at low metallicity [i.e. below 10 per cent solar, assuming solar oxygen abundance ZO/H⊙ = 8.83 Grevesse & Sauval (1998)] as a function of lookback time/redshift. The plotted ranges show estimates obtained for different variations of assumptions about the starburst (SB) galaxies (blue/turquoise: as in Boco et al. (2021), brown/beige: based on Caputi et al. (2017) – C17 and Bisigello et al. (2018) – B18) and low-mass slope of the redshift z ∼ 0 MZR (aMZR). The orange region shows the range of the low metallicity SFHs obtained by Chruslinska & Nelemans (2019). Thick solid lines in different colours indicate the location of the upper edge of the corresponding ranges obtained with the assumption of non-evolving low-mass end of the GSMF, demonstrating the importance of this assumption beyond the peak of the cosmic SFH. All variations from this study assume ∇FMR0 = 0.27.
The impact of the assumed z ∼ 0 MZR slope can be seen by comparing pale blue and turquoise or beige and brown ranges in Fig. 12. At low redshifts, variations with steeper MZR slope lead to ∼10 times higher SFRD at low metallicity. This is due to the presence of a more extended low metallicity tail of the fSFR(Z,z) (see Section 5.1.1). Lower aMZR lead to more compact fSFR(Z,z) – in those cases, for the high metallicity variations even the low-mass galaxies contribute to SFRD at ZO/H above the considered threshold of 10 per cent solar metallicity. This difference is reduced at higher redshifts due to steeper metallicity evolution of variations with lower aMZR values – the slope of the low metallicity SFH redshift dependence at z ≲ 2 depends on the z ∼ 0aMZR. The slope of the dependence is also affected by the contribution of starbursts (compare pale blue and beige or turquoise and brown ranges). As expected, if the fraction of starbursts increases with redshift (B18/C17 implementation), the low metallicity cut of the SFH increases faster towards high redshifts. At z ≲0.2 (within the last ∼2 Gyr) there is little difference in the amount of SFRD occurring at low metallicity between the variations with no/low fraction of starbursts and the B18/C17 implementation. The contribution of starbursts only becomes evident at higher redshifts. At the peak of the cosmic SFH variations with the B18/C17 starbursts implementation lead to ≳3 times higher SFRD at ZO/H < ZO/H⊙−1 than the corresponding variations with no/low fraction of starbursts As discussed above, at z ≳ 2 the slope of the redshift dependence of the low metallicity SFRD and the location of the peak of this dependence is dominated by the assumptions about αGSMF. Observational tracers of star formation happening at low metallicity available at high redshifts (e.g. the volumetric rate of long gamma-ray bursts or, potentially, that of black hole – black hole mergers as a function of redshift) could help to discriminate between the different variations of our models. In particular, it could provide information about the contribution of low-mass galaxies to the total SFRD at high redshifts (thereby constraining jointly the low mass SFMR and – to constrain with regular galaxy surveys.
Considering all model variations discussed in this section, the overall spread between the estimates of the SFRD happening below ZO/H < ZO/H⊙−1 ranges between ∼1.6 dex around the peak of the cosmic SFH and ∼3 dex at z > 8. At z ∼ 0 there is ∼2.3 dex variation between the different estimates. The uncertainty is dominated by the assumptions about aMZR. At the peak of the cosmic SFH the spread is somewhat reduced due to steeper metallicity evolution in variations with lower aMZR. At z ∼ 8 the spread increases to ∼2.5 dex if the low-mass end of the GSMF is allowed to steepen with redshift, and remains close to ∼1.6 dex if only variations with fixed αGSMF are considered. Note that the overall spread between the low metallicity SFH estimates discussed in this study is significantly larger than ∼0.5–1.2 dex found in Chruslinska & Nelemans (2019) for the same low metallicity threshold. In their study, effectively only the variations due to the uncertain MZR normalization and the redshift evolution of the low mass end of the GSMF (which are also included in our analysis) were explored. This difference highlights the importance of the additional factors discussed in this study for the low metallicity cut of the cosmic SFH. Note that the spread in the low metallicity SFH estimates as discussed above is not only due to differences in the metallicity distribution of the SFRD at different redshifts found for the considered model variations, but also due to their different total SFRD. The latter differences are effectively eliminated in Fig. B1 in Appendix B, where we additionally show the fraction of the total SFRD that happens at ZO/H < ZO/H⊙−1 as a function of redshift for the discussed model variations.
Finally, we note that the low metallicity part of the SFH is very sensitive to the adopted log10(M*) limit down to which all the empirical relations are extrapolated. This is especially important at z ≲ 1, where the low metallicity star formation is limited to low mass galaxies, and at z ≳ 4, due to the potential steepening of the low-mass end of the GSMF. With the current data there is no guarantee that those relations can be safely extrapolated to galaxy masses below log10(M*/M⊙) ≲8. However, given their abundance, completely neglecting the contribution of those galaxies is not a satisfactory solution either. In variations favoring high metallicity (i.e. with high MZR normalization, shallow MZR slope, no/low contribution of starburst galaxies) ignoring the contribution of galaxies with log10(M*/M⊙) < 8 would lead to negligible amount of SFRD happening below 10 per cent solar metallicity even beyond the peak of the cosmic SFH. If the SFR–metallicity correlation significantly weakens/disappears at low specific SFR (see additional model variation discussed in Appendix C and Fig. C4), this may also significantly reduce the estimated amount of SFRD happening below 10 per cent solar metallicity in variations with relatively flat MZR. In those cases, the low/intermediate redshift star formation can only take place below 10 per cent solar metallicity in low mass galaxies that are MZR outliers (see e.g. left bottom panel in Fig. 4 and in Fig. C1), and so the result strongly depends on the adopted FMR extrapolation. Until better constraints on the properties of the low-mass end the star-forming galaxy population are available, those extrapolations are important source of uncertainty for both the total cosmic SFH, as well as for its low metallicity cut.
6.3 A high metallicity cut of the cosmic SFH
The high metallicity cut of the cosmic SFH – i.e. SFRD that occurs at ZO/H > ZO/H⊙ as a function of redshift/time for different variations of our model is shown in Fig. 13. This quantity is relatively well constrained in our models when compared to the low metallicity cut of the SFH discussed in the previous section: the overall spread between the estimates obtained with different model variations from this study ranges from ∼0.8 dex at z ∼ 0 to ∼1.8 dex at z ≳7. The biggest difference appears between the estimate from Chruslinska & Nelemans (2019) (orange range) and all the variations from this study, which lead to considerably higher SFRD occurring at high metallicity beyond the peak of the cosmic SFH. As discussed in Section 5.1, this is due to the fact that the non-evolving FMR assumption leads to much slower metallicity evolution when compared to that implied by the extrapolated redshift dependent MZR. The general features that can be seen for all ranges shown in Fig. 13 can be summarized as follows:
The high metallicity cut of the SFH shows a gradual increase towards the peak of the SFH (z ∼ 2) and a sharp decrease at high redshifts. This reflects the evolution of the total SFRD. However, the increase towards the peak is shallower and the later decrease is sharper – both due to the overall shifting of the SFRD towards lower metallicities at earler epochs.
The width of the ranges is set by the assumptions about the SFMR and z ∼ 0 MZR: upper edges of all ranges correspond to high metallicity variations, lower edges of all ranges correspond to low metallicity variations. Assumptions about the low mass end of the GSMF have negligible effect on the high metallicity cut of the cosmic SFH.
Comparing the ranges obtained for different assumptions about the MZR slope (brown and beige or pale blue and turquoise), one can see that the results start to deviate at z ≳ 1, where variations with steeper MZR lead to higher SFRD at high metallicity. This is due to slower evolution of the metallicity distribution at z ≲ 4 for those variations, as discussed in Section 5.1.1. Assumptions about starbursts have little effect on the ZO/H > ZO/H⊙ metallicity cut of the cosmic SFH (compare light blue/turquoise and beige/brown ranges). This is due to the fact that (given the FMR), those galaxies only contribute to star formation at relatively low metallicities. The fraction of the total SFRD that happens at ZO/H > ZO/H⊙ as a function of redshift for the discussed model variations is shown in Fig. B2 in Appendix B.
![Star formation rate density at high metallicity [above solar, assuming ZO/H⊙ = 8.83 Grevesse & Sauval (1998)] as a function of lookback time/redshift. The plotted ranges show estimates obtained for different variations of assumptions about the starburst galaxies [blue/turquoise: as in Boco et al. (2021), brown/beige: based on Caputi et al. (2017) – C17 and Bisigello et al. (2018) – B18] and low-mass slope of the redshift z ∼ 0 MZR (aMZR). The ranges span between the low and high metallicity extremes as defined in the text and assume ∇FMR0 = 0.27. The orange region shows the corresponding range from Chruslinska & Nelemans (2019). Note that starburst galaxies contribute to SFRD at relatively low metallicity and have little impact on the high metallicity cut of the SFRD.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2690/1/m_stab2690fig13.jpeg?Expires=1750313337&Signature=cPbWjuBMMVqIC0dT7pUD36NQVlxgy3OCGvW4F705NbZiJ98wFi9otQ0seUeBNPlQd2dMFuOey2j6URpymNYR68FUcesUQcCdP6KYxYHJGy2LtxgwSNPnA~OGWmahLO9q-74Fnn2NFU8f7zUnXJda~uTU5dE7lrWG3nEvYsOxnIijp1CG4njnFSaBXCDYWoVRXaX9u4hgsUlcuZ05J-l0mMO7K99cZ0ovF2YMlAysdIK4O0uZZlNTdwhPdEXdUTYD5UMBwzLpBNX9uvowYnYbLHKxdhQmzk9qqdw4UoCCroEOXk4Hsjnj-z7nHGZ7PNRx7oEbUg4L1KYYsqaOipGheA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Star formation rate density at high metallicity [above solar, assuming ZO/H⊙ = 8.83 Grevesse & Sauval (1998)] as a function of lookback time/redshift. The plotted ranges show estimates obtained for different variations of assumptions about the starburst galaxies [blue/turquoise: as in Boco et al. (2021), brown/beige: based on Caputi et al. (2017) – C17 and Bisigello et al. (2018) – B18] and low-mass slope of the redshift z ∼ 0 MZR (aMZR). The ranges span between the low and high metallicity extremes as defined in the text and assume ∇FMR0 = 0.27. The orange region shows the corresponding range from Chruslinska & Nelemans (2019). Note that starburst galaxies contribute to SFRD at relatively low metallicity and have little impact on the high metallicity cut of the SFRD.
6.4 The impact of ∇FMR0 on the low/high metallicity cut of the cosmic SFH
As discussed in Section 3.1.5, the range of extreme reasonable assumptions about ∇FMR0 and the potential dependence of this parameter for instance, on the metallicity derivation technique, cannot be easily identified with the currently available observational results. We therefore discuss the sensitivity of our result to the choice of this factor. The impact of ∇FMR0 on the high and low metallicity cut of the cosmic SFH for the example model variations is shown in Figs 14 and 15, respectively. In essence, higher (lower) ∇FMR0 increase (decrease) the amount of SFRD that happens at low metallicity (and vice versa for the SFRD at high metallicity). Lower ∇FMR0 means that the difference between the metallicities of highly star-forming galaxies and their quiescent counterparts of the same mass is reduced. As a consequence, if the anticorrelation between the SFR and metallicity is much weaker than with our fiducial assumptions, the impact of starbursts on the low metallicity cut of the SFH is substancially reduced. This can be seen in Fig. 15, where the lower and upper edges of the range obtained with B18/C17 starburst implementation and ∇FMR0 = 0.17 (dashed lines) roughly match the range obtained for the corresponding model variations assuming low fraction of starbursts (turquoise range). This also means that the impact of the choice of ∇FMR0 on the variations with lower fraction of starbursts and/or starburst sequence with smaller offset from the SFMR than in B18/C17 implementation, is smaller than in the examples shown in Figs 15 and 14. As discussed in Section 5.1.1, ∇FMR0 also affects the rate of the overall decrease in metallicity – and so the slope of the different metallicity cuts of the cosmic SFH as a function of redshift. However, while many different factors affect the slope of the low metallicity cut of the SFH below the peak of the cosmic SFH (see Section 6.2), at high redshifts assumptions about the low mass end of the GSMF clearly dominate the uncertainty in the slope regardless of ∇FMR0.
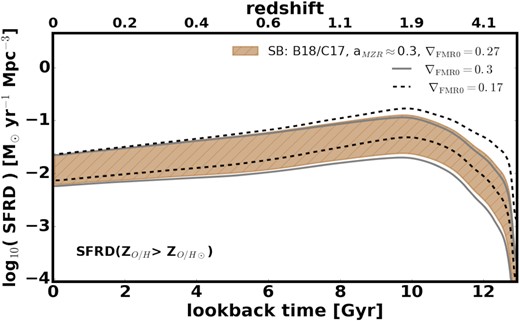
Example illustrating the effect of ∇FMR0 on the high metallicity cut of the cosmic SFH. The plotted range shows estimate obtained with B18/C17 starbursts implementation and aMZR ∼ 0.3, assuming ∇FMR0 = 0.27 (same as in Fig. 13). Grey solid (black dashed) lines mark the location of the upper and lower edges of that range obtained with ∇FMR0 = 0.3 (∇FMR0 = 0.17).
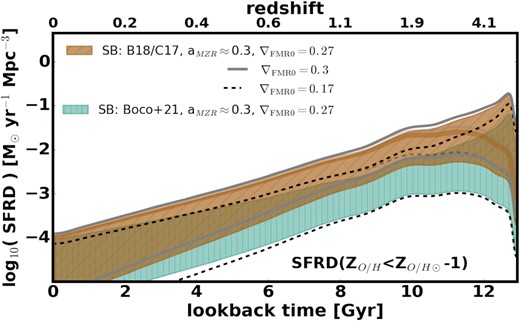
Example illustrating the effect of ∇FMR0 on the low metallicity cut of the cosmic SFH. The brown range shows estimate obtained with B18/C17 starbursts implementation and aMZR ∼ 0.3, assuming ∇FMR0 = 0.27 (same as in Fig. 12). Grey solid (black dashed) lines mark the location of the upper and lower edges of that range obtained with ∇FMR0 = 0.3 (∇FMR0 = 0.17). Faint lines in the corresponding colours show the evolution of the upper edge under the assumption of non-evolving low-mass end of the GSMF. For comparison, we also show the range obtained with Boco et al. (2021) starbursts implementation, aMZR ∼ 0.3 and ∇FMR0 = 0.27 (turquoise, same as in Fig. 12). If the SFR–metallicity correlation is much weaker than implied by our fiducial ∇FMR0 = 0.27, the impact of starbursts on the low metallicity cut of the SFH is substantially reduced.
7 CONCLUSIONS
In this study we expand the framework introduced in Chruslinska & Nelemans (2019) to construct the observation-based distribution of the cosmic SFRD at different metallicities and redshifts. We evaluate its uncertainty in light of additional factors that were not discussed in the original study: the redshift-invariant mass–metallicity-SFR relation (FMR), starburst galaxies and the slope of the local mass–metallicity relation. We show that all of those factors have a strong impact on the low metallicity cut of the cosmic SFH – crucial in the discussion of the origin of various energetic transients. Similarly to Chruslinska & Nelemans (2019), we consider different MZR and SFMR variations to cover the range of possibilities discussed in the literature and explore the realistic extremes of the fSFR(Z,z). The diversity of observational derivations of the MZR and SFMR stems from differences in the applied metallicity and SFR determination techniques – those differences in the methods also affect the FMR determinations. To ensue the consistency of our method, we develop a phenomenological model to construct the FMR based on the local MZR and SFMR. We introduce a parameter ∇FMR0 to characterize the strength of the SFR–metallicity correlation in the high SFR part of the FMR. That is the only parameter which is not constrained by the choice of z ∼ 0 MZR and SFMR within our description and we discuss the sensitivity of our results to this factor. Our description captures all characteristic features of the observationally inferred relation. It reproduces the known systematic differences between the FMR derived with various metallicity and SFR determination techniques and predicts dependence of the properties of the FMR on the parameters of the z ∼ 0 MZR and SFMR that can be verified with future observational studies. Furthermore, we use the results of Caputi et al. (2017) and Bisigello et al. (2018) to describe the properties of starburst galaxies and include their contribution in our fSFR(Z,z) models. We contrast the fSFR(Z,z) derived that way with the fSFR(Z,z) obtained with the description of starbursts as recently used in Boco et al. (2021) (based on Sargent et al. (2012) and Béthermin et al. (2012), which predict a much smaller contribution of strabursts to the total cosmic SFRD budget). In addition to full fSFR(Z,z) distributions obtained for different variations of our model, we discuss the resulting cosmic SFH and its low and high metallicity cuts. Our main conclusions are the following:
As recently discussed in Boco et al. (2021), a redshift-invariant FMR can lead to drastically different conclusions about the metallicity at which the star formation occurs at z ≳ 3 than the redshift-dependent MZR extrapolated to high redshifts (as used in Chruslinska & Nelemans (2019)). However, while the high metallicity cut of the SFH at z .5 is strongly affected by this assumption (Fig. 13), the low metallicity SFH estimate from Chruslinska & Nelemans (2019) falls within the range covered by the variations explored in this study (Fig. 12). In that case, the much shallower metallicity evolution implied by the non-evolving FMR is counterbalanced by the low metallicity contribution of starbursts (assuming that they follow the same FMR as regular star forming galaxies).
The low metallicity tail of the fSFR(Z,z)fSFR(Z,z) is the most sensitive to variations in the model assumptions. We find a factor of ∼200 (∼40) difference in the amount of SFRD occurring below 10 per cent solar metallicity at z ∼ 0 (z ∼ 2) between the extreme model variations considered in this study.
At low redshifts, the uncertainty of the low metallicity SFH is dominated by the assumptions about the slope and normalization of the local MZR, while both MZR and starbursts strongly affect this quantity at z > 1. However, the importance of starbursts for the low metallicity cut of the SFH is highly sensitive to the assumed strength of the SFR–metallicity correlation (∇FMR0).
Beyond the peak of the cosmic SFH, the shape of the low metallicity cut of the SFH (peak location, slope) is set by the assumptions about the low-mass end of the GSMF. Those assumptions also dominate the redshift dependence of the total SFRD at z ≳ 3. Given this sensitivity, we propose that a tracer of the SFR happening at low metallicity available at high redshifts (e.g. volumetric rate of long gamma-ray bursts, or potentially – stellar black hole mergers) could provide constraints on the contribution of low mass galaxies – difficult to constrain otherwise – to the SFRD at those redshifts.
The uncertainty in the total SFRD in our models at z ≲ 1 is dominated by the uncertain shape of the high mass end of the SFMR. Assumptions about the contribution of starbursts dominate the uncertainty of the cosmic SFH at 1 < z ≲ 3. Model variations with SFMR with sharp flattening at high masses, non-evolving low mass slope of the GSMF and no/small fraction of starbursts may underpredict the total SFRD at z ∼3. Model variations which account for the contribution of starbursts with B18/C17 based prescription lead to ∼2.5 times higher SFRD at z ≳4 and shallower redshift evolution of the total SFRD at z ≳2, more in line with the recent SFRD determinations at high redshifts.
ACKNOWLEDGEMENTS
We thank Karina Caputi and Jarle Brinchmann for helpful discussions. We thank the anonymous referee for their thoughtful comments that helped to improve this paper. MC and GN acknowledge support from the Netherlands Organisation for Scientific Research (NWO). AL and LB are supported by PRIN MIUR 2017 prot. 20173ML3WW, ‘Opening the ALMA window on the cosmic evolution of gas, stars and supermassive black holes’, and by the EU H2020-MSCA-ITN-2019 Project 860744 ‘BiD4BESt: Big Data applications for black hole Evolution STudies.’
DATA AVAILABILITY
The results of our calculations (allowing to reproduce all of the results shown in the paper) for all model variations discussed in this study are publicly available under this url: https://ftp.science.ru.nl/astro/mchruslinska.
Footnotes
In contrast to the total metal mass fraction Z or iron abundance commonly used in the simulations/theoretical studies. ZO/H is often used as a proxy for the total Z, but note that this requires assuming a particular (typically solar-like) abundance pattern.
This is similar to e.g. Salim et al. (2014) and Sanders et al. (2018, 2021). Note that many observational studies use the term ’strength of the SFR–metallicity correlation’ when referring to the spread between the ZO/H(M*,SFR) curves at different fixed SFR (which is effectively done by comparing the fitted values of the ’α parameter’ introduced by Mannucci et al. 2010). See also footnote 4.
Within our framework the value of the slope of this dependence is also the value of the α parameter that minimizes the scatter in the 2D projection of the FMR that is conventionally used to discuss the strength of the three parameter dependence: ZO/H − μα where μα = log(M*) − α log(SFR), as originally proposed by Mannucci et al. (2010). Although, as can be seen in equation (6), α is not a good measure of the strength of the correlation between the SFR and metallicity, as it depends strongly on the shape of the two relations, in particular on the slope of the low-mass end of the MZR. What really describes the strength of the correlation is ∇FMR.
Lower values of ∇FMR were also reported, but we find that ∇FMR0 ≲ 0.17 underpredict the redshift evolution of the MZR at z ≲ 1.5 (where the impact of biases discussed in Section 3 is not so severe, and so its evolution is reasonably constrained). Much lower ∇FMR0 also makes it difficult to reproduce the width of the z ∼ 0 MZR of σMZR ∼ 0.1 dex (unless the scatter around the FMR is in reality higher than the typically reported σFMR ∼ 0.05 dex).
Note that while the MZR is often shown in observational studies discussing the FMR, the SFMR that describes the galaxy sample used in that study is typically not and ∇FMR is rarely estimated. This makes it difficult to directly compare our results with other FMR estimates given in the literature.
M* are sampled from our z ∼ 0 GSMF, SFR are sampled from SFMR from Sanders et al. (2021) with Gaussian scatter σSFMR and the metallicity is assigned using our ZO/H(SFR, M*) with scatter σFMR.
Parametrized as follows: |$\rm log_{10}(SFR)=s_{0} - log_{10} \big(1 + \big(\frac{ \mathit{ M}_*}{ \mathit{ M}_{0;SFMR0} }\big)^{-a_{SFMR}}\big)$|.
Note that various criteria are used in the literature to distinguish starbursts and regular star-forming galaxies. Most commonly the criteria are based on the SFR and require that the starburst SFR is at least a factor of a few (factors between 3 and 10 are used in the literature) higher than that of an average galaxy of the same mass and at the same redshift (e.g. Orlitova 2020).
For instance, for the ∇FMR0 = 0.27 cases shown in Fig. 9, the peak metallicity decreases by ∼0.55 dex (∼0.4 dex) between z = 0 and z = 4 in the model with S20 (KK04b) z ∼ 0 MZR. This decrease is only ∼0.1 dex (∼0.15 dex) for the models with steeper PP04 (KK04a) z ∼ 0 MZR. Between z= 4 and z = 10, the peak metallicity decreases by ∼0.1 dex (∼0.18 dex) for the cases with SFMR with no (sharp) flattening (irrespective of the aMZR).
We plot the total SFRD estimate from Khusanova et al. (2021) in which the IR contribution was obtained with GSMF rather than UV luminosity function used in the calculations, as that is closer to our approach.
REFERENCES
APPENDIX A: FMR VARIATIONS – ADDITIONAL FIGURES
In this section, we show additional figures illustrating the sensitivity of ZO/H(SFR,M*) to the parameter β (Fig. A1) and the ZO/H(SFR,M*) dependence on various choices of the parameters of our observation-based model. Fig. A2 shows the values of β as a function of log10(SFR) obtained as described in Section 3.1.4 for different choices of the z ∼ 0 MZR, ∇FMR0, and SFMR used in this study. Figs A3 and A4 show the comparison between the ZO/H(SFR,M*) obtained for different SFMR and ∇FMR0 choices, respectively.
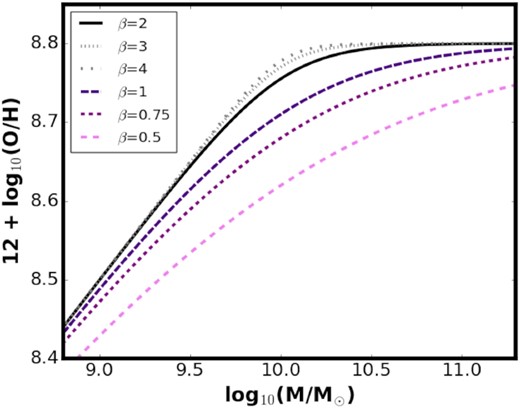
Dependence on β parameter in equation (1), illustrated using the best fit MZR z∼ 0 parameters from Curti et al. (2020) and various choices of β. If β can be constrained to values β ≳1, the ZO/H uncertainty induced by the choice of this parameter is relatively small and affects a relatively small range of galaxy masses. However, if β ≲1, small variation in this parameter can add a appreciable uncertainty to ZO/H.
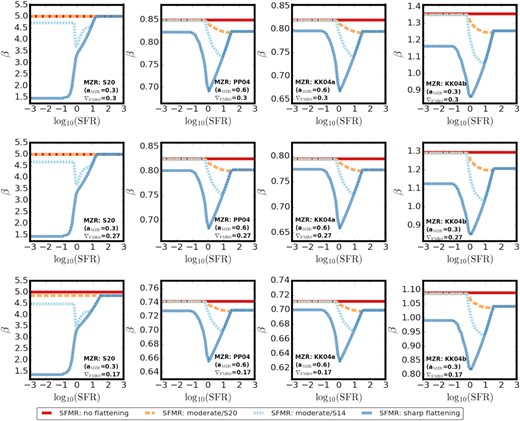
Parameter β as a function of log10(SFR) (see equation 1), depending on the choice of z ∼ 0 MZR (different columns), ∇FMR0 (different rows), and the shape of the high-mass end of the z ∼ 0 SFMR (different lines). Single value of β provides a good description if the SFMR does not significantly depart from a single power law. See Section 3.4 for the description of different model variations.
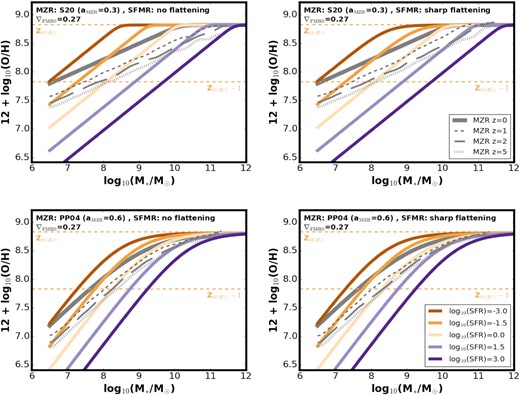
Same as Fig. 4, but for different choices of the z ∼ 0 SFMR and MZR. Left-hand (right-hand) panels assume SFMR with no (sharp) flattening at the high-mass end. Top (bottom) panels assume S20 (PP04) z ∼ 0 MZR. All panels assume ∇FMR0 = 0.27.
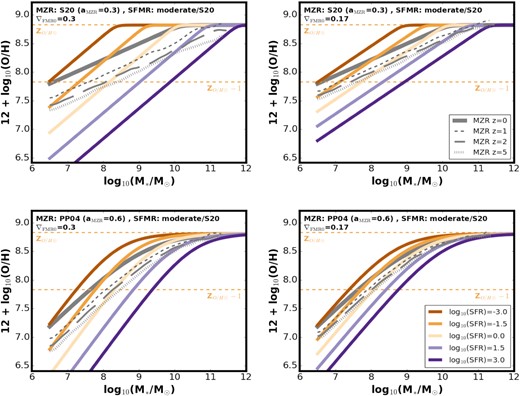
Same as Fig. 4, but for different choices of ∇FMR0. Top (bottom) panels assume S20 (PP04) z ∼ 0 MZR. All panels assume SFMR with a moderate flattening at high masses (aSFMR = 0.72 at the high-mass end).
APPENDIX B: COSMIC SFH – ADDITIONAL MATERIALS
Table B1 provides the coefficients of the broken power-law fits to the total cosmic SFH for the variations with non-evolving low-mass end of the GSMF. Table B2 (B3) provides the corresponding coefficients obtained for the low metallicity cut of the cosmic SFH, fitted for the variations with redshift-dependent (non evolving) low-mass end of the GSMF. Fig. B1 (B2) shows the fraction of the total SFRD that happens below 10 per cent solar metallicity, i.e ZO/H < ZO/H⊙−1 (above solar metallicity, i.e. Z > ZO/H) as a function of redshift/lookback time, obtained for the different variations of our model discussed in Section 6.2 (6.3). Note that those variations in general lead to different total SFRD at different redshift, which also affects the spread between the estimates of the low (high) metallicity part of the cosmic SFH shown in Fig. 12 (13). Fig. B1 allows to directly compare the differences in the low (high) metallicity tail of the fSFR(Z,z) distribution.
Same as Table 3, but considering only variations with non-evolving low-mass end of the GSMF.
| Cosmic SFH – lower edge (αGSMF fixed) . | ||||||
|---|---|---|---|---|---|---|
| Variation: . | No SB . | SB: Boco + 21 . | SB: B18/C17 . | |||
| z range . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 1.0 | 2.6307 | 0.00779 | 2.5875 | 0.00924 | 2.7706 | 0.0125 |
| 1.0 < z ≤ 1.8 | 2.3888 | 0.00922 | 2.3265 | 0.0111 | 2.6969 | 0.0131 |
| 1.8 < z ≤ 3.0 | −1.0535 | 0.319 | −1.1284 | 0.388 | −0.7558 | 0.458 |
| 3.0 < z ≤ 7.0 | −2.2771 | 1.74 | −2.2909 | 1.95 | −1.9628 | 2.44 |
| 7.0 < z ≤ 8.8 | −12.5425 | 3.24· 109 | −12.5526 | 3.6· 109 | −12.4895 | 7.85· 109 |
| 8.8 < z ≤ 10 | 0 | 0.0012 | 0 | 0.0013 | 0 | 0.00327 |
| Cosmic SFH – upper edge (αGSMF fixed) | ||||||
| Variation: | No SB | SB: Boco + 21 | SB: B18/C17 | |||
| z range | κ | A | κ | A | κ | A |
| 0 < z ≤ 1.0 | 2.2211 | 0.0194 | 2.2208 | 0.0209 | 2.3822 | 0.0248 |
| 1.0 < z ≤ 1.8 | 1.8466 | 0.0251 | 1.8463 | 0.027 | 2.2105 | 0.028 |
| 1.8 < z ≤ 4.0 | −1.7884 | 1.06 | −1.7847 | 1.14 | −1.2278 | 0.964 |
| 4.0 < z ≤ 7.0 | −2.6385 | 4.16 | −2.6376 | 4.49 | −2.4769 | 7.2 |
| 7.0 < z ≤ 8.8 | −12.6417 | 4.5· 109 | −12.6485 | 4.93· 109 | −12.5280 | 8.6· 109 |
| 8.8 < z ≤ 10 | 0 | 0.00133 | 0 | 0.00143 | 0 | 0.00328 |
| Cosmic SFH – lower edge (αGSMF fixed) . | ||||||
|---|---|---|---|---|---|---|
| Variation: . | No SB . | SB: Boco + 21 . | SB: B18/C17 . | |||
| z range . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 1.0 | 2.6307 | 0.00779 | 2.5875 | 0.00924 | 2.7706 | 0.0125 |
| 1.0 < z ≤ 1.8 | 2.3888 | 0.00922 | 2.3265 | 0.0111 | 2.6969 | 0.0131 |
| 1.8 < z ≤ 3.0 | −1.0535 | 0.319 | −1.1284 | 0.388 | −0.7558 | 0.458 |
| 3.0 < z ≤ 7.0 | −2.2771 | 1.74 | −2.2909 | 1.95 | −1.9628 | 2.44 |
| 7.0 < z ≤ 8.8 | −12.5425 | 3.24· 109 | −12.5526 | 3.6· 109 | −12.4895 | 7.85· 109 |
| 8.8 < z ≤ 10 | 0 | 0.0012 | 0 | 0.0013 | 0 | 0.00327 |
| Cosmic SFH – upper edge (αGSMF fixed) | ||||||
| Variation: | No SB | SB: Boco + 21 | SB: B18/C17 | |||
| z range | κ | A | κ | A | κ | A |
| 0 < z ≤ 1.0 | 2.2211 | 0.0194 | 2.2208 | 0.0209 | 2.3822 | 0.0248 |
| 1.0 < z ≤ 1.8 | 1.8466 | 0.0251 | 1.8463 | 0.027 | 2.2105 | 0.028 |
| 1.8 < z ≤ 4.0 | −1.7884 | 1.06 | −1.7847 | 1.14 | −1.2278 | 0.964 |
| 4.0 < z ≤ 7.0 | −2.6385 | 4.16 | −2.6376 | 4.49 | −2.4769 | 7.2 |
| 7.0 < z ≤ 8.8 | −12.6417 | 4.5· 109 | −12.6485 | 4.93· 109 | −12.5280 | 8.6· 109 |
| 8.8 < z ≤ 10 | 0 | 0.00133 | 0 | 0.00143 | 0 | 0.00328 |
Same as Table 3, but considering only variations with non-evolving low-mass end of the GSMF.
| Cosmic SFH – lower edge (αGSMF fixed) . | ||||||
|---|---|---|---|---|---|---|
| Variation: . | No SB . | SB: Boco + 21 . | SB: B18/C17 . | |||
| z range . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 1.0 | 2.6307 | 0.00779 | 2.5875 | 0.00924 | 2.7706 | 0.0125 |
| 1.0 < z ≤ 1.8 | 2.3888 | 0.00922 | 2.3265 | 0.0111 | 2.6969 | 0.0131 |
| 1.8 < z ≤ 3.0 | −1.0535 | 0.319 | −1.1284 | 0.388 | −0.7558 | 0.458 |
| 3.0 < z ≤ 7.0 | −2.2771 | 1.74 | −2.2909 | 1.95 | −1.9628 | 2.44 |
| 7.0 < z ≤ 8.8 | −12.5425 | 3.24· 109 | −12.5526 | 3.6· 109 | −12.4895 | 7.85· 109 |
| 8.8 < z ≤ 10 | 0 | 0.0012 | 0 | 0.0013 | 0 | 0.00327 |
| Cosmic SFH – upper edge (αGSMF fixed) | ||||||
| Variation: | No SB | SB: Boco + 21 | SB: B18/C17 | |||
| z range | κ | A | κ | A | κ | A |
| 0 < z ≤ 1.0 | 2.2211 | 0.0194 | 2.2208 | 0.0209 | 2.3822 | 0.0248 |
| 1.0 < z ≤ 1.8 | 1.8466 | 0.0251 | 1.8463 | 0.027 | 2.2105 | 0.028 |
| 1.8 < z ≤ 4.0 | −1.7884 | 1.06 | −1.7847 | 1.14 | −1.2278 | 0.964 |
| 4.0 < z ≤ 7.0 | −2.6385 | 4.16 | −2.6376 | 4.49 | −2.4769 | 7.2 |
| 7.0 < z ≤ 8.8 | −12.6417 | 4.5· 109 | −12.6485 | 4.93· 109 | −12.5280 | 8.6· 109 |
| 8.8 < z ≤ 10 | 0 | 0.00133 | 0 | 0.00143 | 0 | 0.00328 |
| Cosmic SFH – lower edge (αGSMF fixed) . | ||||||
|---|---|---|---|---|---|---|
| Variation: . | No SB . | SB: Boco + 21 . | SB: B18/C17 . | |||
| z range . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 1.0 | 2.6307 | 0.00779 | 2.5875 | 0.00924 | 2.7706 | 0.0125 |
| 1.0 < z ≤ 1.8 | 2.3888 | 0.00922 | 2.3265 | 0.0111 | 2.6969 | 0.0131 |
| 1.8 < z ≤ 3.0 | −1.0535 | 0.319 | −1.1284 | 0.388 | −0.7558 | 0.458 |
| 3.0 < z ≤ 7.0 | −2.2771 | 1.74 | −2.2909 | 1.95 | −1.9628 | 2.44 |
| 7.0 < z ≤ 8.8 | −12.5425 | 3.24· 109 | −12.5526 | 3.6· 109 | −12.4895 | 7.85· 109 |
| 8.8 < z ≤ 10 | 0 | 0.0012 | 0 | 0.0013 | 0 | 0.00327 |
| Cosmic SFH – upper edge (αGSMF fixed) | ||||||
| Variation: | No SB | SB: Boco + 21 | SB: B18/C17 | |||
| z range | κ | A | κ | A | κ | A |
| 0 < z ≤ 1.0 | 2.2211 | 0.0194 | 2.2208 | 0.0209 | 2.3822 | 0.0248 |
| 1.0 < z ≤ 1.8 | 1.8466 | 0.0251 | 1.8463 | 0.027 | 2.2105 | 0.028 |
| 1.8 < z ≤ 4.0 | −1.7884 | 1.06 | −1.7847 | 1.14 | −1.2278 | 0.964 |
| 4.0 < z ≤ 7.0 | −2.6385 | 4.16 | −2.6376 | 4.49 | −2.4769 | 7.2 |
| 7.0 < z ≤ 8.8 | −12.6417 | 4.5· 109 | −12.6485 | 4.93· 109 | −12.5280 | 8.6· 109 |
| 8.8 < z ≤ 10 | 0 | 0.00133 | 0 | 0.00143 | 0 | 0.00328 |
Coefficients of the power-law fits to the low metallicity cut of the cosmic SFH (lower and upper edges of the ranges shown in Fig. 12) obtained for different variations of our observation-based model. Within each redshift range indicated in the first column total SFRD can be approximated with the dependence: SFRD = A · (1 + z)κ[M⊙ yr−1].
| Low metallicity SFH – lower edge . | ||||||||
|---|---|---|---|---|---|---|---|---|
| Variation: . | SB: Boco + 21, aMZR ∼ 0.3 . | SB: Boco + 21, aMZR ∼ 0.6 . | SB: B18/C17, aMZR ∼ 0.3 . | SB: B18/C17, aMZR ∼ 0.6 . | ||||
| z range . | κ . | A . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 0.5 | 6.4712 | 2.912 × 10−6 | 3.8153 | 1 × 10−4 | 8.3323 | 4.519 × 10−6 | 4.8660 | 1 × 10−4 |
| 0.5 < z ≤ 1 | 6.1722 | 3.287 × 10−6 | 3.9229 | 1.036 × 10−4 | 6.8234 | 8.331 × 10−6 | 4.7246 | 1.5941 × 10−4 |
| 1 < z ≤ 1.8 | 4.7030 | 9.101 × 10−6 | 2.9237 | 2.071 × 10−4 | 4.8817 | 3.2 × 10−5 | 3.4034 | 3.9821 × 10−4 |
| 1.8 < z ≤ 7 | −0.6499 | 2.253 × 10−3 | −1.0032 | 0.01181 | −0.6698 | 9.719 × 10−3 | −0.9736 | 0.3608 |
| 7 < z ≤ 8.8 | −11.888 | 3.172 × 107 | −12.176 | 1.455 × 108 | −11.931 | 1.437 × 108 | −12.1147 | 4.1571 × 108 |
| 8.8 < z ≤ 10 | 0 | 5.225 × 10−5 | 0 | 1.239 × 10−4 | 0 | 2.144 × 10−4 | 0 | 4.0771 × 10−4 |
| Low metallicity SFH – upper edge | ||||||||
| Variation: | SB: Boco + 21, aMZR ∼ 0.3 | SB: Boco + 21, aMZR ∼ 0.6 | SB: B18/C17, aMZR ∼ 0.3 | SB: B18/C17, aMZR ∼ 0.6 | ||||
| z range | κ | A | κ | A | κ | A | κ | A |
| 0 < z ≤ 0.5 | 4.4163 | 9.410 × 10−5 | 2.9836 | 6 × 10−4 | 5.9088 | 1.149 × 10−4 | 4.0787 | 6 × 10−4 |
| 0.5 < z ≤ 1 | 4.2247 | 1.017 × 10−4 | 3.0826 | 5.389 × 10−4 | 5.3151 | 1.462 × 10−4 | 4.1063 | 6.262 × 10−4 |
| 1 < z ≤ 1.5 | 3.9141 | 1.261 × 10−4 | 2.7905 | 6.599 × 10−4 | 4.8008 | 2.088 × 10−4 | 3.7273 | 8.143 × 10−4 |
| 1.5 < z ≤ 7 | 2.4934 | 4.636 × 10−4 | 2.0535 | 1.296 × 10−3 | 2.0328 | 2.638 × 10−3 | 1.8127 | 4.707 × 10−3 |
| 7 < z ≤ 8.8 | −8.5779 | 4.619 × 106 | -8.7763 | 7.816 × 106 | −8.896 | 1.954 × 107 | −8.9519 | 2.478 × 107 |
| 8.8 < z ≤ 10 | 0 | 0.01452 | 0 | 0.01562 | 0 | 0.02972 | 0 | 0.03317 |
| Low metallicity SFH – lower edge . | ||||||||
|---|---|---|---|---|---|---|---|---|
| Variation: . | SB: Boco + 21, aMZR ∼ 0.3 . | SB: Boco + 21, aMZR ∼ 0.6 . | SB: B18/C17, aMZR ∼ 0.3 . | SB: B18/C17, aMZR ∼ 0.6 . | ||||
| z range . | κ . | A . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 0.5 | 6.4712 | 2.912 × 10−6 | 3.8153 | 1 × 10−4 | 8.3323 | 4.519 × 10−6 | 4.8660 | 1 × 10−4 |
| 0.5 < z ≤ 1 | 6.1722 | 3.287 × 10−6 | 3.9229 | 1.036 × 10−4 | 6.8234 | 8.331 × 10−6 | 4.7246 | 1.5941 × 10−4 |
| 1 < z ≤ 1.8 | 4.7030 | 9.101 × 10−6 | 2.9237 | 2.071 × 10−4 | 4.8817 | 3.2 × 10−5 | 3.4034 | 3.9821 × 10−4 |
| 1.8 < z ≤ 7 | −0.6499 | 2.253 × 10−3 | −1.0032 | 0.01181 | −0.6698 | 9.719 × 10−3 | −0.9736 | 0.3608 |
| 7 < z ≤ 8.8 | −11.888 | 3.172 × 107 | −12.176 | 1.455 × 108 | −11.931 | 1.437 × 108 | −12.1147 | 4.1571 × 108 |
| 8.8 < z ≤ 10 | 0 | 5.225 × 10−5 | 0 | 1.239 × 10−4 | 0 | 2.144 × 10−4 | 0 | 4.0771 × 10−4 |
| Low metallicity SFH – upper edge | ||||||||
| Variation: | SB: Boco + 21, aMZR ∼ 0.3 | SB: Boco + 21, aMZR ∼ 0.6 | SB: B18/C17, aMZR ∼ 0.3 | SB: B18/C17, aMZR ∼ 0.6 | ||||
| z range | κ | A | κ | A | κ | A | κ | A |
| 0 < z ≤ 0.5 | 4.4163 | 9.410 × 10−5 | 2.9836 | 6 × 10−4 | 5.9088 | 1.149 × 10−4 | 4.0787 | 6 × 10−4 |
| 0.5 < z ≤ 1 | 4.2247 | 1.017 × 10−4 | 3.0826 | 5.389 × 10−4 | 5.3151 | 1.462 × 10−4 | 4.1063 | 6.262 × 10−4 |
| 1 < z ≤ 1.5 | 3.9141 | 1.261 × 10−4 | 2.7905 | 6.599 × 10−4 | 4.8008 | 2.088 × 10−4 | 3.7273 | 8.143 × 10−4 |
| 1.5 < z ≤ 7 | 2.4934 | 4.636 × 10−4 | 2.0535 | 1.296 × 10−3 | 2.0328 | 2.638 × 10−3 | 1.8127 | 4.707 × 10−3 |
| 7 < z ≤ 8.8 | −8.5779 | 4.619 × 106 | -8.7763 | 7.816 × 106 | −8.896 | 1.954 × 107 | −8.9519 | 2.478 × 107 |
| 8.8 < z ≤ 10 | 0 | 0.01452 | 0 | 0.01562 | 0 | 0.02972 | 0 | 0.03317 |
Coefficients of the power-law fits to the low metallicity cut of the cosmic SFH (lower and upper edges of the ranges shown in Fig. 12) obtained for different variations of our observation-based model. Within each redshift range indicated in the first column total SFRD can be approximated with the dependence: SFRD = A · (1 + z)κ[M⊙ yr−1].
| Low metallicity SFH – lower edge . | ||||||||
|---|---|---|---|---|---|---|---|---|
| Variation: . | SB: Boco + 21, aMZR ∼ 0.3 . | SB: Boco + 21, aMZR ∼ 0.6 . | SB: B18/C17, aMZR ∼ 0.3 . | SB: B18/C17, aMZR ∼ 0.6 . | ||||
| z range . | κ . | A . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 0.5 | 6.4712 | 2.912 × 10−6 | 3.8153 | 1 × 10−4 | 8.3323 | 4.519 × 10−6 | 4.8660 | 1 × 10−4 |
| 0.5 < z ≤ 1 | 6.1722 | 3.287 × 10−6 | 3.9229 | 1.036 × 10−4 | 6.8234 | 8.331 × 10−6 | 4.7246 | 1.5941 × 10−4 |
| 1 < z ≤ 1.8 | 4.7030 | 9.101 × 10−6 | 2.9237 | 2.071 × 10−4 | 4.8817 | 3.2 × 10−5 | 3.4034 | 3.9821 × 10−4 |
| 1.8 < z ≤ 7 | −0.6499 | 2.253 × 10−3 | −1.0032 | 0.01181 | −0.6698 | 9.719 × 10−3 | −0.9736 | 0.3608 |
| 7 < z ≤ 8.8 | −11.888 | 3.172 × 107 | −12.176 | 1.455 × 108 | −11.931 | 1.437 × 108 | −12.1147 | 4.1571 × 108 |
| 8.8 < z ≤ 10 | 0 | 5.225 × 10−5 | 0 | 1.239 × 10−4 | 0 | 2.144 × 10−4 | 0 | 4.0771 × 10−4 |
| Low metallicity SFH – upper edge | ||||||||
| Variation: | SB: Boco + 21, aMZR ∼ 0.3 | SB: Boco + 21, aMZR ∼ 0.6 | SB: B18/C17, aMZR ∼ 0.3 | SB: B18/C17, aMZR ∼ 0.6 | ||||
| z range | κ | A | κ | A | κ | A | κ | A |
| 0 < z ≤ 0.5 | 4.4163 | 9.410 × 10−5 | 2.9836 | 6 × 10−4 | 5.9088 | 1.149 × 10−4 | 4.0787 | 6 × 10−4 |
| 0.5 < z ≤ 1 | 4.2247 | 1.017 × 10−4 | 3.0826 | 5.389 × 10−4 | 5.3151 | 1.462 × 10−4 | 4.1063 | 6.262 × 10−4 |
| 1 < z ≤ 1.5 | 3.9141 | 1.261 × 10−4 | 2.7905 | 6.599 × 10−4 | 4.8008 | 2.088 × 10−4 | 3.7273 | 8.143 × 10−4 |
| 1.5 < z ≤ 7 | 2.4934 | 4.636 × 10−4 | 2.0535 | 1.296 × 10−3 | 2.0328 | 2.638 × 10−3 | 1.8127 | 4.707 × 10−3 |
| 7 < z ≤ 8.8 | −8.5779 | 4.619 × 106 | -8.7763 | 7.816 × 106 | −8.896 | 1.954 × 107 | −8.9519 | 2.478 × 107 |
| 8.8 < z ≤ 10 | 0 | 0.01452 | 0 | 0.01562 | 0 | 0.02972 | 0 | 0.03317 |
| Low metallicity SFH – lower edge . | ||||||||
|---|---|---|---|---|---|---|---|---|
| Variation: . | SB: Boco + 21, aMZR ∼ 0.3 . | SB: Boco + 21, aMZR ∼ 0.6 . | SB: B18/C17, aMZR ∼ 0.3 . | SB: B18/C17, aMZR ∼ 0.6 . | ||||
| z range . | κ . | A . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 0.5 | 6.4712 | 2.912 × 10−6 | 3.8153 | 1 × 10−4 | 8.3323 | 4.519 × 10−6 | 4.8660 | 1 × 10−4 |
| 0.5 < z ≤ 1 | 6.1722 | 3.287 × 10−6 | 3.9229 | 1.036 × 10−4 | 6.8234 | 8.331 × 10−6 | 4.7246 | 1.5941 × 10−4 |
| 1 < z ≤ 1.8 | 4.7030 | 9.101 × 10−6 | 2.9237 | 2.071 × 10−4 | 4.8817 | 3.2 × 10−5 | 3.4034 | 3.9821 × 10−4 |
| 1.8 < z ≤ 7 | −0.6499 | 2.253 × 10−3 | −1.0032 | 0.01181 | −0.6698 | 9.719 × 10−3 | −0.9736 | 0.3608 |
| 7 < z ≤ 8.8 | −11.888 | 3.172 × 107 | −12.176 | 1.455 × 108 | −11.931 | 1.437 × 108 | −12.1147 | 4.1571 × 108 |
| 8.8 < z ≤ 10 | 0 | 5.225 × 10−5 | 0 | 1.239 × 10−4 | 0 | 2.144 × 10−4 | 0 | 4.0771 × 10−4 |
| Low metallicity SFH – upper edge | ||||||||
| Variation: | SB: Boco + 21, aMZR ∼ 0.3 | SB: Boco + 21, aMZR ∼ 0.6 | SB: B18/C17, aMZR ∼ 0.3 | SB: B18/C17, aMZR ∼ 0.6 | ||||
| z range | κ | A | κ | A | κ | A | κ | A |
| 0 < z ≤ 0.5 | 4.4163 | 9.410 × 10−5 | 2.9836 | 6 × 10−4 | 5.9088 | 1.149 × 10−4 | 4.0787 | 6 × 10−4 |
| 0.5 < z ≤ 1 | 4.2247 | 1.017 × 10−4 | 3.0826 | 5.389 × 10−4 | 5.3151 | 1.462 × 10−4 | 4.1063 | 6.262 × 10−4 |
| 1 < z ≤ 1.5 | 3.9141 | 1.261 × 10−4 | 2.7905 | 6.599 × 10−4 | 4.8008 | 2.088 × 10−4 | 3.7273 | 8.143 × 10−4 |
| 1.5 < z ≤ 7 | 2.4934 | 4.636 × 10−4 | 2.0535 | 1.296 × 10−3 | 2.0328 | 2.638 × 10−3 | 1.8127 | 4.707 × 10−3 |
| 7 < z ≤ 8.8 | −8.5779 | 4.619 × 106 | -8.7763 | 7.816 × 106 | −8.896 | 1.954 × 107 | −8.9519 | 2.478 × 107 |
| 8.8 < z ≤ 10 | 0 | 0.01452 | 0 | 0.01562 | 0 | 0.02972 | 0 | 0.03317 |
Coefficients of the power-law fits to the low metallicity cut of the cosmic SFH (lower and upper edges of the ranges as in Fig. 12) obtained for different variations of our observation-based model under the assumption of a non-evolving low-mass end of the GSMF. Within each redshift range indicated in the first column total SFRD can be approximated with the dependence: SFRD = A · (1 + z)κ[M⊙ yr−1].
| Low metallicity SFH – lower edge . | ||||||||
|---|---|---|---|---|---|---|---|---|
| ×ariation: . | SB: Boco + 21, aMZR ∼ 0.3 . | SB: Boco + 21, aMZR ∼ 0.6 . | SB: B18/C17, aMZR ∼ 0.3 . | SB: B18/C17, aMZR ∼ 0.6 . | ||||
| z range . | κ . | A . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 0.5 | 6.0172 | 4.393 × 10−6 | 3.3024 | 1.667 × 10−4 | 7.9464 | 6.561 × 10−6 | 4.3940 | 2.085 × 10−4 |
| 0.5 < z ≤ 1 | 5.5287 | 5.355 × 10−6 | 3.3306 | 1.635 × 10−4 | 6.1805 | 1.343 × 10−5 | 4.2022 | 2.381 × 10−4 |
| 1 < z ≤ 1.7 | 4.7328 | 9.297 × 10−6 | 2.8406 | 2.297 × 10−4 | 5.0089 | 3.024 × 10−5 | 3.4101 | 4.123 × 10−4 |
| 1.7 < z ≤ 3.5 | 0.4510 | 6.537 × 10−4 | -0.0495 | 0.004053 | 0.4466 | 0.002809 | 0.0103 | 0.01207 |
| 3.5 < z ≤ 7 | −1.8116 | 0.01965 | -2.2411 | 0.1095 | -1.8350 | 0.08689 | -2.2043 | 0.3376 |
| 7 < z ≤ 8.8 | -11.8876 | 2.471 × 107 | -12.177 | 1.028 × 108 | -11.9308 | 1.139 × 108 | -12.115 | 3.009 × 108 |
| 8.8 < z ≤ 10 | 0 | 4.069 × 10−5 | 0 | 8.754 × 10−5 | 0 | 1.699 × 10−4 | 0 | 2.951 × 10−4 |
| low metallicity SFH - upper edge | ||||||||
| Variation: | SB: Boco + 21, aMZR ∼ 0.3 | SB: Boco + 21, aMZR ∼0.6 | SB: B18/C17, aMZR ∼0.3 | SB: B18/C17, aMZR ∼0.6 | ||||
| z range | κ | A | κ | A | κ | A | κ | A |
| 0 < z ≤ 0.5 | 4.4163 | 9.410 × 10−5 | 2.9836 | 5.772 × 10−4 | 5.9088 | 1.149 × 10−4 | 4.0787 | 6.383 × 10−4 |
| 0.5 < z ≤ 1 | 4.2247 | 1.017 × 10−4 | 3.0826 | 5.389 × 10−4 | 5.3151 | 1.462 × 10−4 | 4.1063 | 6.262 × 10−4 |
| 1 < z ≤ 1.7 | 3.6167 | 1.55 × 10−4 | 2.6761 | 7.143 × 10−4 | 4.4986 | 2.575 × 10−4 | 3.5242 | 9.374 × 10−4 |
| 1.7 < z ≤ 3.5 | 0.1790 | 0.004712 | -0.1177 | 0.01146 | 0.4267 | 0.0147 | 0.0785 | 0.02873 |
| 3.5 < z ≤ 7 | −2.0303 | 0.1307 | -2.3001 | 0.3052 | -1.9322 | 0.5106 | -2.2568 | 0.9633 |
| 7 < z ≤ 8.8 | -12.0388 | 1.429 × 108 | -12.1984 | 2.653 × 108 | -12.0147 | 6.509 × 108 | -12.1707 | 8.648 × 108 |
| 8.8 < z ≤ 10 | 0 | 1.666 × 10−4 | 0 | 2.149 × 10−4 | 0 | 8.02 × 10−4 | 0 | 7.464 × 10−4 |
| Low metallicity SFH – lower edge . | ||||||||
|---|---|---|---|---|---|---|---|---|
| ×ariation: . | SB: Boco + 21, aMZR ∼ 0.3 . | SB: Boco + 21, aMZR ∼ 0.6 . | SB: B18/C17, aMZR ∼ 0.3 . | SB: B18/C17, aMZR ∼ 0.6 . | ||||
| z range . | κ . | A . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 0.5 | 6.0172 | 4.393 × 10−6 | 3.3024 | 1.667 × 10−4 | 7.9464 | 6.561 × 10−6 | 4.3940 | 2.085 × 10−4 |
| 0.5 < z ≤ 1 | 5.5287 | 5.355 × 10−6 | 3.3306 | 1.635 × 10−4 | 6.1805 | 1.343 × 10−5 | 4.2022 | 2.381 × 10−4 |
| 1 < z ≤ 1.7 | 4.7328 | 9.297 × 10−6 | 2.8406 | 2.297 × 10−4 | 5.0089 | 3.024 × 10−5 | 3.4101 | 4.123 × 10−4 |
| 1.7 < z ≤ 3.5 | 0.4510 | 6.537 × 10−4 | -0.0495 | 0.004053 | 0.4466 | 0.002809 | 0.0103 | 0.01207 |
| 3.5 < z ≤ 7 | −1.8116 | 0.01965 | -2.2411 | 0.1095 | -1.8350 | 0.08689 | -2.2043 | 0.3376 |
| 7 < z ≤ 8.8 | -11.8876 | 2.471 × 107 | -12.177 | 1.028 × 108 | -11.9308 | 1.139 × 108 | -12.115 | 3.009 × 108 |
| 8.8 < z ≤ 10 | 0 | 4.069 × 10−5 | 0 | 8.754 × 10−5 | 0 | 1.699 × 10−4 | 0 | 2.951 × 10−4 |
| low metallicity SFH - upper edge | ||||||||
| Variation: | SB: Boco + 21, aMZR ∼ 0.3 | SB: Boco + 21, aMZR ∼0.6 | SB: B18/C17, aMZR ∼0.3 | SB: B18/C17, aMZR ∼0.6 | ||||
| z range | κ | A | κ | A | κ | A | κ | A |
| 0 < z ≤ 0.5 | 4.4163 | 9.410 × 10−5 | 2.9836 | 5.772 × 10−4 | 5.9088 | 1.149 × 10−4 | 4.0787 | 6.383 × 10−4 |
| 0.5 < z ≤ 1 | 4.2247 | 1.017 × 10−4 | 3.0826 | 5.389 × 10−4 | 5.3151 | 1.462 × 10−4 | 4.1063 | 6.262 × 10−4 |
| 1 < z ≤ 1.7 | 3.6167 | 1.55 × 10−4 | 2.6761 | 7.143 × 10−4 | 4.4986 | 2.575 × 10−4 | 3.5242 | 9.374 × 10−4 |
| 1.7 < z ≤ 3.5 | 0.1790 | 0.004712 | -0.1177 | 0.01146 | 0.4267 | 0.0147 | 0.0785 | 0.02873 |
| 3.5 < z ≤ 7 | −2.0303 | 0.1307 | -2.3001 | 0.3052 | -1.9322 | 0.5106 | -2.2568 | 0.9633 |
| 7 < z ≤ 8.8 | -12.0388 | 1.429 × 108 | -12.1984 | 2.653 × 108 | -12.0147 | 6.509 × 108 | -12.1707 | 8.648 × 108 |
| 8.8 < z ≤ 10 | 0 | 1.666 × 10−4 | 0 | 2.149 × 10−4 | 0 | 8.02 × 10−4 | 0 | 7.464 × 10−4 |
Coefficients of the power-law fits to the low metallicity cut of the cosmic SFH (lower and upper edges of the ranges as in Fig. 12) obtained for different variations of our observation-based model under the assumption of a non-evolving low-mass end of the GSMF. Within each redshift range indicated in the first column total SFRD can be approximated with the dependence: SFRD = A · (1 + z)κ[M⊙ yr−1].
| Low metallicity SFH – lower edge . | ||||||||
|---|---|---|---|---|---|---|---|---|
| ×ariation: . | SB: Boco + 21, aMZR ∼ 0.3 . | SB: Boco + 21, aMZR ∼ 0.6 . | SB: B18/C17, aMZR ∼ 0.3 . | SB: B18/C17, aMZR ∼ 0.6 . | ||||
| z range . | κ . | A . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 0.5 | 6.0172 | 4.393 × 10−6 | 3.3024 | 1.667 × 10−4 | 7.9464 | 6.561 × 10−6 | 4.3940 | 2.085 × 10−4 |
| 0.5 < z ≤ 1 | 5.5287 | 5.355 × 10−6 | 3.3306 | 1.635 × 10−4 | 6.1805 | 1.343 × 10−5 | 4.2022 | 2.381 × 10−4 |
| 1 < z ≤ 1.7 | 4.7328 | 9.297 × 10−6 | 2.8406 | 2.297 × 10−4 | 5.0089 | 3.024 × 10−5 | 3.4101 | 4.123 × 10−4 |
| 1.7 < z ≤ 3.5 | 0.4510 | 6.537 × 10−4 | -0.0495 | 0.004053 | 0.4466 | 0.002809 | 0.0103 | 0.01207 |
| 3.5 < z ≤ 7 | −1.8116 | 0.01965 | -2.2411 | 0.1095 | -1.8350 | 0.08689 | -2.2043 | 0.3376 |
| 7 < z ≤ 8.8 | -11.8876 | 2.471 × 107 | -12.177 | 1.028 × 108 | -11.9308 | 1.139 × 108 | -12.115 | 3.009 × 108 |
| 8.8 < z ≤ 10 | 0 | 4.069 × 10−5 | 0 | 8.754 × 10−5 | 0 | 1.699 × 10−4 | 0 | 2.951 × 10−4 |
| low metallicity SFH - upper edge | ||||||||
| Variation: | SB: Boco + 21, aMZR ∼ 0.3 | SB: Boco + 21, aMZR ∼0.6 | SB: B18/C17, aMZR ∼0.3 | SB: B18/C17, aMZR ∼0.6 | ||||
| z range | κ | A | κ | A | κ | A | κ | A |
| 0 < z ≤ 0.5 | 4.4163 | 9.410 × 10−5 | 2.9836 | 5.772 × 10−4 | 5.9088 | 1.149 × 10−4 | 4.0787 | 6.383 × 10−4 |
| 0.5 < z ≤ 1 | 4.2247 | 1.017 × 10−4 | 3.0826 | 5.389 × 10−4 | 5.3151 | 1.462 × 10−4 | 4.1063 | 6.262 × 10−4 |
| 1 < z ≤ 1.7 | 3.6167 | 1.55 × 10−4 | 2.6761 | 7.143 × 10−4 | 4.4986 | 2.575 × 10−4 | 3.5242 | 9.374 × 10−4 |
| 1.7 < z ≤ 3.5 | 0.1790 | 0.004712 | -0.1177 | 0.01146 | 0.4267 | 0.0147 | 0.0785 | 0.02873 |
| 3.5 < z ≤ 7 | −2.0303 | 0.1307 | -2.3001 | 0.3052 | -1.9322 | 0.5106 | -2.2568 | 0.9633 |
| 7 < z ≤ 8.8 | -12.0388 | 1.429 × 108 | -12.1984 | 2.653 × 108 | -12.0147 | 6.509 × 108 | -12.1707 | 8.648 × 108 |
| 8.8 < z ≤ 10 | 0 | 1.666 × 10−4 | 0 | 2.149 × 10−4 | 0 | 8.02 × 10−4 | 0 | 7.464 × 10−4 |
| Low metallicity SFH – lower edge . | ||||||||
|---|---|---|---|---|---|---|---|---|
| ×ariation: . | SB: Boco + 21, aMZR ∼ 0.3 . | SB: Boco + 21, aMZR ∼ 0.6 . | SB: B18/C17, aMZR ∼ 0.3 . | SB: B18/C17, aMZR ∼ 0.6 . | ||||
| z range . | κ . | A . | κ . | A . | κ . | A . | κ . | A . |
| 0 < z ≤ 0.5 | 6.0172 | 4.393 × 10−6 | 3.3024 | 1.667 × 10−4 | 7.9464 | 6.561 × 10−6 | 4.3940 | 2.085 × 10−4 |
| 0.5 < z ≤ 1 | 5.5287 | 5.355 × 10−6 | 3.3306 | 1.635 × 10−4 | 6.1805 | 1.343 × 10−5 | 4.2022 | 2.381 × 10−4 |
| 1 < z ≤ 1.7 | 4.7328 | 9.297 × 10−6 | 2.8406 | 2.297 × 10−4 | 5.0089 | 3.024 × 10−5 | 3.4101 | 4.123 × 10−4 |
| 1.7 < z ≤ 3.5 | 0.4510 | 6.537 × 10−4 | -0.0495 | 0.004053 | 0.4466 | 0.002809 | 0.0103 | 0.01207 |
| 3.5 < z ≤ 7 | −1.8116 | 0.01965 | -2.2411 | 0.1095 | -1.8350 | 0.08689 | -2.2043 | 0.3376 |
| 7 < z ≤ 8.8 | -11.8876 | 2.471 × 107 | -12.177 | 1.028 × 108 | -11.9308 | 1.139 × 108 | -12.115 | 3.009 × 108 |
| 8.8 < z ≤ 10 | 0 | 4.069 × 10−5 | 0 | 8.754 × 10−5 | 0 | 1.699 × 10−4 | 0 | 2.951 × 10−4 |
| low metallicity SFH - upper edge | ||||||||
| Variation: | SB: Boco + 21, aMZR ∼ 0.3 | SB: Boco + 21, aMZR ∼0.6 | SB: B18/C17, aMZR ∼0.3 | SB: B18/C17, aMZR ∼0.6 | ||||
| z range | κ | A | κ | A | κ | A | κ | A |
| 0 < z ≤ 0.5 | 4.4163 | 9.410 × 10−5 | 2.9836 | 5.772 × 10−4 | 5.9088 | 1.149 × 10−4 | 4.0787 | 6.383 × 10−4 |
| 0.5 < z ≤ 1 | 4.2247 | 1.017 × 10−4 | 3.0826 | 5.389 × 10−4 | 5.3151 | 1.462 × 10−4 | 4.1063 | 6.262 × 10−4 |
| 1 < z ≤ 1.7 | 3.6167 | 1.55 × 10−4 | 2.6761 | 7.143 × 10−4 | 4.4986 | 2.575 × 10−4 | 3.5242 | 9.374 × 10−4 |
| 1.7 < z ≤ 3.5 | 0.1790 | 0.004712 | -0.1177 | 0.01146 | 0.4267 | 0.0147 | 0.0785 | 0.02873 |
| 3.5 < z ≤ 7 | −2.0303 | 0.1307 | -2.3001 | 0.3052 | -1.9322 | 0.5106 | -2.2568 | 0.9633 |
| 7 < z ≤ 8.8 | -12.0388 | 1.429 × 108 | -12.1984 | 2.653 × 108 | -12.0147 | 6.509 × 108 | -12.1707 | 8.648 × 108 |
| 8.8 < z ≤ 10 | 0 | 1.666 × 10−4 | 0 | 2.149 × 10−4 | 0 | 8.02 × 10−4 | 0 | 7.464 × 10−4 |
APPENDIX C: ZO/H(SFR, M*) IMPLEMENTATION WITH SFR-DEPENDENT ∇FMR (AND γ)
As discussed in Section 3.1, ZO/H(SFR, M*) at fixed SFR and M* < M0; SFR appear as lines roughly parallel to each other (see e.g. Mannucci et al. 2010; Telford et al. 2016; Cresci et al. 2019) and we assume that the ZO/H(SFR, M*) slope γ is independent of SFR/M*. However, in their recent study Curti et al. (2020) fit the slopes of ZO/H(SFR, M*) in individual log10(SFR) bins and indicate a possible dependence of γ on SFR. They find that γ decreases with decreasing SFR, reaching the value close to that of ∼0 MZR slope at low SFR (see Fig. 9 therein). When ZO/H(SFR, M*) is extrapolated down to low (specific) SFR values, such dependence leads to considerably higher metallicity of galaxies with the lowest masses (M* ≲ 108 M⊙), and therefore can affect the low metallicity tail of the fSFR(Z,z) distribution obtained with our model. We explore additional variation of our model to illustrate the effect of such a dependence on our results. Within our description we can model a similar dependence of γ on SFR to that found by Curti et al. (2020) by implementing a SFR-dependent ∇FMR (and therefore of γ, see equation 5) and requiring that the strength of the correlation weakens towards low SFRs, eventually disappearing at a certain low SFR (where γ approaches the slope of the z ∼ 0 MZR). As discussed in Section 3.1.5, there is some observational evidence for the weakening of the SFR–metallicity correlation below a certain specific SFR threshold (|$\rm \lesssim 10^{-10}/yr$|, but it should be noted that this behaviour is difficult to constrain at low M* ≲ 108.5 M⊙). For simplicity, we assume that there is a linear dependence of ∇FMR on log10(SFR), such that at log10(SFR)≥log10 (SFR∇0) ∇FMR = ∇FMR0 and at log10(SFR) ≤ log10(SFRno corr.) ∇FMR = 0. We set log10(SFRno corr.) = −2, which roughly corresponds to the SFR of M* ∼ 108 M⊙ galaxies according to our z ∼ 0 SFMR. We note that below that mass and SFR the observational FMR is not constrained,15 and by assuming that for those galaxies the correlation disappears we obtain a conservative estimate of the low metallicity contribution of low-mass galaxies. Results of our calculations are also sensitive to the value of the SFR threshold above which γ is fixed: the higher the value of log10 (SFR∇0), the lower the amount of the SFRD happening at low metallicity. The choice of this value is unclear and for the illustrative purposes we show our results using two example thresholds: log10 (SFR∇0) = 0 and log10 (SFR∇0) = 1. The resulting ZO/H(SFR, M*) is illustrated in Fig. C1 using the latter threshold and for the different z ∼ 0 MZR choices considered in our study. The overall fSFR(Z,z) distribution is only mildly affected by the explored variations with SFR-dependent ∇FMR (see Fig. C2, the effect is analogous for the variations with the starburst implementation following Boco et al.). The redshift evolution of the peak metallicity is indistinguishable from that estimated with a fixed ∇FMR = ∇FMR0 case and the only visible difference is in the extent of the low metallicity tail of the distribution (the fixed ∇FMR case leads to more extended low metallicity tail). With the low metallicity threshold of 10 per cent solar metallicity (oxygen abundance) used in our study, the difference in the amount of the total SFRD happening at low metallicity estimated in the model variations with fixed and SFR-dependent ∇FMR is amplified in the cases with flat z ∼ 0 MZR (aMZR ∼ 0.3) and high MZR normalization (compare lower edge of the dark brown range and the lower thick dark brown lines in Fig. C4 – note that the strength of this effect is very sensitive to the exact choice of the low metallicity threshold). In those cases, the result is particularly sensitive to the assumed low mass/SFR FMR extrapolation, as at low redshifts only galaxies that are MZR outliers have metallicities falling below ZO/H < ZO/H⊙−1 (see top left panel in Fig. C1). If there is no correlation between the SFR and metallicity at low SFRs, this leads to a negligible amount of SFRD happening below 10 per cent solar metallicity at low to intermediate redshifts.
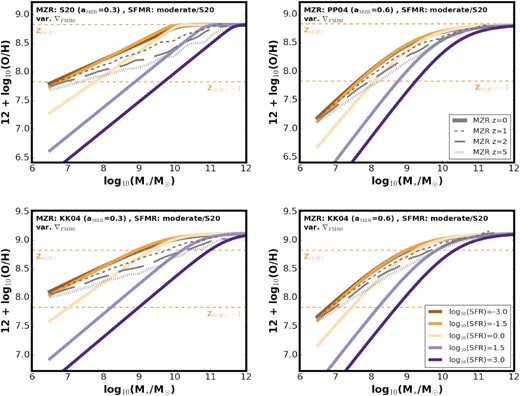
Same as Fig. 4, but assuming a SFR-dependent ∇FMR (leading to SFR-dependent γ). Top (bottom) panels assume S20 (PP04) z ∼ 0 MZR. All panels assume SFMR with a moderate flattening at high masses (aSFMR = 0.72 at the high-mass end), log10 (SFR∇0) = 1, and ∇FMR0 = 0.27.
![Distribution of the cosmic SFRD at different metallicities and redshift for different ZO/H(SFR, M*) implementations, shown for B18/C17 starbursts implementation [effect is analogous for the starburst implementation following Boco et al. (2021)]. Brown contours and background colours correspond to ZO/H(SFR, M*) with a fixed ∇FMR0 = 0.27. Solid white (dashed black) contours correspond to ZO/H(SFR, M*) modelled with ∇FMR varying between log10 (SFR) = −2 and log10 (SFR) = 1 (log10 (SFR) = 0) as described in Section C. Different panels correspond to different z ∼ 0 MZR and SFMR variations (same as in Fig. 9). Contours indicate constant SFRD and are plotted for 0.01, 0.05, and 0.1 [M⊙/Mpc3 yr] (with the highest value corresponding to the innermost contour). The alternative ZO/H(SFR, M*) implementation has a relatively small effect on the overall distribution, but leads to a less extended low metallicity tail.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2690/1/m_stab2690figc2.jpeg?Expires=1750313337&Signature=kB~yb0f9pRYEkeCCw6Ssf95~zhhqO-7u1lSWJZZ6xMudoZFonfZmzMqEjIoqpJ2eN5okXri2yfhvZIz5BQgRBoGuAoOheEGwlAYUzIl8ZFnNANl-~G7ZTc-3HlfLIYR5zHJZfRsbQUbTqpI~jheP0slL2UVUjJ7LuCo4CLawwsyeIvIPBhousIX32OEu0Ul~YNAM~SfQp2gAhVANc~TynxuLP5qNRyFTTmCACdDyd-oYjlApmz4QXKTHPavf2p4XHFkIaDTyZ18QmAmEgdT3DNUrKZCBvEDp6f~cVxI-c8b~sHZZZKfaPw3VdHznFagW-kL8mdvcDd7b0h4Be5wYqw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Distribution of the cosmic SFRD at different metallicities and redshift for different ZO/H(SFR, M*) implementations, shown for B18/C17 starbursts implementation [effect is analogous for the starburst implementation following Boco et al. (2021)]. Brown contours and background colours correspond to ZO/H(SFR, M*) with a fixed ∇FMR0 = 0.27. Solid white (dashed black) contours correspond to ZO/H(SFR, M*) modelled with ∇FMR varying between log10 (SFR) = −2 and log10 (SFR) = 1 (log10 (SFR) = 0) as described in Section C. Different panels correspond to different z ∼ 0 MZR and SFMR variations (same as in Fig. 9). Contours indicate constant SFRD and are plotted for 0.01, 0.05, and 0.1 [M⊙/Mpc3 yr] (with the highest value corresponding to the innermost contour). The alternative ZO/H(SFR, M*) implementation has a relatively small effect on the overall distribution, but leads to a less extended low metallicity tail.
![SFRD happening below 10 per cent solar metallicity (ZO/H < ZO/H⊙−1) as a function of lookback time/redshift estimated with different ZO/H(SFR, M*) implementations, shown for B18/C17 starbursts implementation [effect is analogous for the starburst implementation following Boco et al. (2021)]. The light and dark brown coloured ranges are the same as in Fig. 12 and correspond to a fixed ∇FMR0 = 0.27 and aMZR ≈ 0.3 and aMZR ≈ 0.6, respectively. Dotted grey/brown lines indicate upper and lower edges of the corresponding ranges obtained with ∇FMR0 = 0.17. Solid (log10 (SFR∇0) = 0) and dashed (log10 (SFR∇0) = 1) lines indicate the upper and lower edges of those ranges obtained with an SFR-dependent ∇FMR (leading to SFR-dependent γ, see Section C).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2690/1/m_stab2690figc3.jpeg?Expires=1750313337&Signature=SpdAkA2ouaVaS6HCFYNRlcAww6Zm6qfu5UT~vRDpAWOZZMtxO5Zgu9dqnKLIUOvWCRumWQm6vSN8KtrX2EOXjQHygjCE2Rd4O02~3pLvcmcXhXZaEresOzSaboeN5j8znrOF8cpStHiG1P7VDL4zpz~3BYn50Sh1q9~bjWwlxeXhQusEM6JsC00JPolZt3ZGtRibZIWw4Rp0oOGlw39cMrS7eDDgIHf3KpLakujoS1ZH1IcEC8Gcw4O~WeATg-3WxEWaP28zeRHNbgCfNwEubBdhLSibTCp90scGiohkeKDzxxh48kAtKYobFrm~DbNGj9rWEzMo6EEoc8nPlh9~kA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
SFRD happening below 10 per cent solar metallicity (ZO/H < ZO/H⊙−1) as a function of lookback time/redshift estimated with different ZO/H(SFR, M*) implementations, shown for B18/C17 starbursts implementation [effect is analogous for the starburst implementation following Boco et al. (2021)]. The light and dark brown coloured ranges are the same as in Fig. 12 and correspond to a fixed ∇FMR0 = 0.27 and aMZR ≈ 0.3 and aMZR ≈ 0.6, respectively. Dotted grey/brown lines indicate upper and lower edges of the corresponding ranges obtained with ∇FMR0 = 0.17. Solid (log10 (SFR∇0) = 0) and dashed (log10 (SFR∇0) = 1) lines indicate the upper and lower edges of those ranges obtained with an SFR-dependent ∇FMR (leading to SFR-dependent γ, see Section C).
![Fraction of the total SFRD happening below 10 per cent solar metallicity (ZO/H < ZO/H⊙−1) as a function of lookback time/redshift estimated with different ZO/H(SFR, M*) implementations, shown for B18/C17 starbursts implementation [effect is analogous for the starburst implementation following Boco et al. (2021)]. Top panel shows the estimates obtained for the low metallicity variations (i.e. corresponding to upper edges in Fig. C4), bottom panel shows the estimates obtained for the high metallicity variations. The green (purple) ranges span between the estimates obtained with ZO/H(SFR, M*) with a fixed ∇FMR0 = 0.3 and 0.17 and aMZR ≈ 0.3 (aMZR ≈ 0.6). Different lines indicate the corresponding estimate obtained with ZO/H(SFR, M*) with a SFR-dependent ∇FMR, varying between log10 (SFR) = −2 and log10(SFR) = 0 or 1 (see legend and Section C).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/508/4/10.1093_mnras_stab2690/1/m_stab2690figc4.jpeg?Expires=1750313337&Signature=CNSb7CiwGH24jNmxrV-GOGK~9Ir4fCzYH8RVk9jROeIgHk8HXRmax3~Wu3g5crsdHLj3hFyfmz2sUlEvT3FC3SWDfPutZa0oJNLrXCf9~XWRTV~vMStzagaJYYir-CPml2KuiCS20N56bS6nEkgDLpQdhVEaaY6cCqJtt6rzJ88Xs1BEn96WFr~p94gvDhdhsIqEY009tThRGaKaGKGIsUBh9MZ~YKgA9nisIfG0lR7lrjn0eBmG3rXBkg224MSxtjIRwTkPKmumKhpdQAJLtEvHK3YCCNS5UeeALPqOkpE7izV3TgDxNF6rAgRPfKJNSvD3tjlt-1veP6K211UjXQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Fraction of the total SFRD happening below 10 per cent solar metallicity (ZO/H < ZO/H⊙−1) as a function of lookback time/redshift estimated with different ZO/H(SFR, M*) implementations, shown for B18/C17 starbursts implementation [effect is analogous for the starburst implementation following Boco et al. (2021)]. Top panel shows the estimates obtained for the low metallicity variations (i.e. corresponding to upper edges in Fig. C4), bottom panel shows the estimates obtained for the high metallicity variations. The green (purple) ranges span between the estimates obtained with ZO/H(SFR, M*) with a fixed ∇FMR0 = 0.3 and 0.17 and aMZR ≈ 0.3 (aMZR ≈ 0.6). Different lines indicate the corresponding estimate obtained with ZO/H(SFR, M*) with a SFR-dependent ∇FMR, varying between log10 (SFR) = −2 and log10(SFR) = 0 or 1 (see legend and Section C).



