-
PDF
- Split View
-
Views
-
Cite
Cite
Wei-Hua Wang, Heng Xu, Wei-Yang Wang, Shuang Du, Quan Cheng, Xiao-Ping Zheng, Ren-Xin Xu, Constraining mechanism associated with fast radio burst and glitch from SGR J1935, Monthly Notices of the Royal Astronomical Society, Volume 507, Issue 2, October 2021, Pages 2208–2219, https://doi.org/10.1093/mnras/stab2213
Close - Share Icon Share
ABSTRACT
The discovery of fast radio burst (FRB) 200428 from galactic SGR J1935+2154 makes it possible to measure rotational changes accompanied by FRBs and to test several FRB models which may be simultaneously associated with glitches. Inspired by this idea, we present order of magnitude calculations to the scenarios proposed. FRB models such as global starquakes, crust fractures, and collisions between pulsars and asteroids/comets are discussed. For each mechanism, the maximum glitch sizes are constrained by the isotropic energy release during the X-ray burst and/or the SGR J1935+2154-like radio burst rate. Brief calculations show that, the maximum glitch sizes for different mechanisms differ by order(s) of magnitude. If glitches are detected to be coincident with FRBs from galactic magnetars in the future, glitch behaviours (such as glitch size, rise time-scale, the recovery coefficient, and spin-down rate offset) are promising to serve as criterions to distinguish glitch mechanisms and in turn to constrain FRB models.
1 INTRODUCTION
Fast radio bursts (FRBs) are millisecond-time-scale pulses observed in radio band originated from sources at extragalactic distances (Lorimer et al. 2007; Thornton et al. 2013; Spitler et al. 2016), except the recently reported FRB 200428 from the direction of the galactic soft gamma-ray repeater (SGR) J1935+2154 (Bochenek et al. 2020; CHIME/FRB Collaboration 2020; Lin et al. 2020). The known population of FRBs comes from 118 independent sources,1 and can be divided into one-off bursts (Lorimer et al. 2007; Thornton et al. 2013) and repeating bursts (Spitler et al. 2016; Chawla et al. 2020; CHIME/FRB Collaboration 2020), it is still unclear whether all FRBs will eventually repeat. No other high-energy counterpart associated with FRBs has been detected except the peculiar double-peaked X-ray burst coincident with FRB 200428. The physics behind these mysterious violent radio bursts is still under heated debate, dozens of models regarding different generators have been proposed [see Katz (2018), Petroff et al. (2019), and Zhang (2020) for a recent review, and references therein], most of which involve neutron stars (NSs) or even magnetars considering the time-scale and energy requirements. The recent discovery of spatial and temporal association between FRB 200428 and galactic SGR J1935+2154 strongly support its magnetar origin for at least part of the FRBs (CHIME/FRB Collaboration 2020). The analysis of magnetoionic environments of FRBs even support magnetars behind all FRBs (repeating and non-repeating) as a plausible possibility, except for the source of FRB 121102 which requires extreme conditions under the magnetar model (Wang et al. 2020).
The galactic origin and association with the peculiar X-ray burst makes FRB 200428 from SGR J1935+2154 a promising target to study the physical mechanism behind. Emission properties of the peculiar non-thermal X-ray counterpart of galactic FRB 200428 are presented here. On 2020 April 28, a short, doubled-peaked radio burst, FRB 200428, was reported by CHIME/FRB and STARE independently (Bochenek et al. 2020; CHIME/FRB Collaboration 2020). Simultaneously, a non-thermal X-ray burst was observed with INTEGRAL (Mereghetti et al. 2020), AGILE (Tavani et al. 2021), Konus-Wind (KW; Ridnaia et al. 2021), and Insight-HXMT (Li et al. 2021). According to Ridnaia et al. the burst total energy fluence (in the |$20{-}250~\rm keV$|) during a total duration of |$0.464~\rm s$| is |$(9.7\pm 1.1)\times 10^{-7}~\rm erg\, cm^{-2}$| (Ridnaia et al. 2021) therefore the isotropic burst energy release in X-rays is |$E_{\rm iso-X}\simeq 1.148\times 10^{40}D_{10}^{2}~\rm erg$|. |$D_{10}=D/(10~\rm {kpc})$|, D is the distance to SGR J1935+2154. The SGR J1935+2154-like radio burst rate is estimated to be |$(0.007{-}0.04)~\rm {yr^{-1}}$| magnetar−1 (CHIME/FRB Collaboration 2020).
The galactic origin of FRB 200428 has inspired us that, it is possible to detect the temporal association between FRB and magnetar’s rotational change (glitch or anti-glitch) in the future through multifrequency observations (X-ray and radio). Different glitch triggering mechanisms result in glitches differ by orders of magnitude. If a glitch is confirmed to be in association with an FRB, the glitch size may in turn serve as a constraint on mechanisms of FRBs. Therefore, in this paper, we focus on the subclass of glitch-related FRB models, discussing the glitch size reachable with the constraints from the X-ray burst associated with FRB 200428 and/or the burst rate.
Previously, possible association between glitch and FRBs has been discussed. Wang et al. studied the energy and waiting time distributions of repeater FRB 121102, the similarities to earthquake manifestations may suggest their origins from pulsar starquakes (Wang et al. 2018). Dado and Dar argued that glitch-associated mini contractions within slow rotators may result in highly relativistic dipolar e+e− bunches lunched from the polar caps which then emit FRBs (Dado & Dar 2020). Besides, Suvorov and Kokkotas found that, magnetic deformation may dominate over spin-down strain in the crust of magnetars, reconfiguration of the strong and highly multipolar crustal magnetic fields generates zones of magnetic stress, which is potentially strong enough to facilitate frequent crust cracks and result in local crustquakes (Suvorov & Kokkotas 2019). Apart from starquake, interactions between pulsars and small celestial bodies such as asteroids/comets or asteroid belts may also result in FRBs and glitches (or antiglitches) simultaneously (Geng & Huang 2015; Dai et al. 2016; Dai 2020).
Calculations hereafter are based on rotational parameters of SGR J1935+2154. It has measured spin period and period derivative of |$P=3.24~\rm {s}$| and |$\dot{P}=1.43(1)\times 10^{-11}~\rm {s~s^{-1}}$|, a spin-inferred dipolar magnetic field strength of |$B_{\mathrm{ d}}\sim 2.2\times 10^{14}~\rm {G}$| and a spin-down luminosity of |$L_{\rm sd}\sim 1.7\times 10^{34}~\rm {erg\, s}^{-1}$| (Israel et al. 2016). No persistent radio emission was reported at present (Fong & Berger 2014). Uncertainties in the last quoted digit are given in parentheses. Göğüş et al. argued a local surface magnetic field strength of |$9.6\times 10^{14}~\rm {G}$| through X-ray spectral modelling of the persistent emission (Göğüş et al. 2020). The characteristic age of SGR J1935+2154 is |$\tau _{\rm c}\sim 3.6~\rm {kyr}$|. However, sky location has placed it coincident with supernova remnant (SNR) G57.2+0.8 (Galensler 2014), whose estimated distance ranges from |$1.5\!-\!12.5~\rm {kpc}$| (Kothes et al. 2018; Mereghetti et al. 2020; Zhou et al. 2020; Bailes et al. 2021). Recently, kinetic age of SNR G57.2+0.8 hosting SGR J1935+2154 is estimated to be |$\tau _{\rm k}\ge 2\times 10^{4}~\rm {yr}$| (Zhou et al. 2020).
Surface temperature (Ts) of SGR J1935+2154 is crucial, because it reflects the crustal temperature to some extent, which determines whether superfluidity could exist in the crust of this magnetar. Its spectrum contains a blackbody component with temperature of about |$500~\rm {eV}$| plus a power-law component (Israel et al. 2016). SGR J1935+2154 entered its active episode on 2020 April 27, temperature of the thermal component of the persistent X-ray emission decreases from |$1.6~\rm keV$| at the onset of the outburst to |${\sim}0.5~\rm keV$| in a couple of days. However, it is unknown whether the temperature of |${\sim}0.5~\rm keV$| represents the global temperature of the star or that of a hotspot on the surface (Younes et al. 2020; Yang & Zhang 2021). The possible existence of neutron superfluidity in the crust of SGR J1935+2154 is further discussed in Section 4.
In this article, based on the hypothesis that it is possible to measure the rotational changes associated with FRBs from galactic magnetars, we explore the glitch size achievable for various mechanisms that possibly result in glitches and FRBs simultaneously. Since FRB 200428 from SGR J1935+2154 is the only galactic FRB till now, it is also the only FRB found to be associated with high-energy counterpart, we calculate the glitch size based on rotational parameters of SGR J1935+2154, energy release and burst rate of FRB 200428 throughout this paper. Note that this proposal is general and can be applied to any other FRBs from galactic magnetars in the future. Rotational parameters of SGR J1935+2154 and some emission properties of FRB 200428 are summarized in Table 1. The specific glitch mechanisms include spin-down and magnetic strained starquake of NSs, spin-down strained starquake of solid quark stars (also named strangeon stars) (Xu 2003), interactions between pulsars and small celestial bodies such as asteroids/comets (or asteroid belts) and subsequent vortex unpinning.
| Parameter . | Value . | Refs.a . |
|---|---|---|
| ν | |$0.308~\rm {Hz}$| | (1) |
| |$\dot{\nu }$| | |$-1.356\times 10^{-12}~\rm {Hz\, s}^{-1}$| | (1) |
| Bd | |$2.2\times 10^{14}~\rm {G}$| | (1) |
| Lsd | |$1.7\times 10^{34}~\rm {erg\, s}^{-1}$| | (1) |
| τc | |$3.6~\rm {kyr}$| | (1) |
| τk | |${\gt}20~\rm {kyr}$| | (6) |
| D (Distance) | |$(1.5{-}12.5)~\rm {kpc}$| | (2),(3),(4),(5) |
| Burst rate | |$(0.007{-}0.04)~\rm {yr^{-1}}$| magnetar−1 | (7) |
| Ts | ? | (1),(8) |
| Estimated Eiso-X | |${\sim}10^{40}~\rm {erg}$| | (9) |
| Parameter . | Value . | Refs.a . |
|---|---|---|
| ν | |$0.308~\rm {Hz}$| | (1) |
| |$\dot{\nu }$| | |$-1.356\times 10^{-12}~\rm {Hz\, s}^{-1}$| | (1) |
| Bd | |$2.2\times 10^{14}~\rm {G}$| | (1) |
| Lsd | |$1.7\times 10^{34}~\rm {erg\, s}^{-1}$| | (1) |
| τc | |$3.6~\rm {kyr}$| | (1) |
| τk | |${\gt}20~\rm {kyr}$| | (6) |
| D (Distance) | |$(1.5{-}12.5)~\rm {kpc}$| | (2),(3),(4),(5) |
| Burst rate | |$(0.007{-}0.04)~\rm {yr^{-1}}$| magnetar−1 | (7) |
| Ts | ? | (1),(8) |
| Estimated Eiso-X | |${\sim}10^{40}~\rm {erg}$| | (9) |
| Parameter . | Value . | Refs.a . |
|---|---|---|
| ν | |$0.308~\rm {Hz}$| | (1) |
| |$\dot{\nu }$| | |$-1.356\times 10^{-12}~\rm {Hz\, s}^{-1}$| | (1) |
| Bd | |$2.2\times 10^{14}~\rm {G}$| | (1) |
| Lsd | |$1.7\times 10^{34}~\rm {erg\, s}^{-1}$| | (1) |
| τc | |$3.6~\rm {kyr}$| | (1) |
| τk | |${\gt}20~\rm {kyr}$| | (6) |
| D (Distance) | |$(1.5{-}12.5)~\rm {kpc}$| | (2),(3),(4),(5) |
| Burst rate | |$(0.007{-}0.04)~\rm {yr^{-1}}$| magnetar−1 | (7) |
| Ts | ? | (1),(8) |
| Estimated Eiso-X | |${\sim}10^{40}~\rm {erg}$| | (9) |
| Parameter . | Value . | Refs.a . |
|---|---|---|
| ν | |$0.308~\rm {Hz}$| | (1) |
| |$\dot{\nu }$| | |$-1.356\times 10^{-12}~\rm {Hz\, s}^{-1}$| | (1) |
| Bd | |$2.2\times 10^{14}~\rm {G}$| | (1) |
| Lsd | |$1.7\times 10^{34}~\rm {erg\, s}^{-1}$| | (1) |
| τc | |$3.6~\rm {kyr}$| | (1) |
| τk | |${\gt}20~\rm {kyr}$| | (6) |
| D (Distance) | |$(1.5{-}12.5)~\rm {kpc}$| | (2),(3),(4),(5) |
| Burst rate | |$(0.007{-}0.04)~\rm {yr^{-1}}$| magnetar−1 | (7) |
| Ts | ? | (1),(8) |
| Estimated Eiso-X | |${\sim}10^{40}~\rm {erg}$| | (9) |
| Parameter . | Value . | Refs.b . |
|---|---|---|
| ν | |$0.085~\rm {Hz}$| | (1) |
| |$\dot{\nu }$| | |$-2.95\times 10^{-13}~\rm {Hz\, s}^{-1}$| | (1) |
| Bd | |$7\times 10^{14}~\rm {G}$| | (1) |
| Lsd | |${\sim}10^{33}~\rm {erg\, s}^{-1}$| | (2) |
| τc | |$4.7~\rm {kyr}$| | (2) |
| τk | |$(0.75{\small --}2.1)~\rm {kyr}$| | (2) |
| Ts | |${\sim}3\times 10^{6}~\rm {K}$| | (3) |
| Parameter . | Value . | Refs.b . |
|---|---|---|
| ν | |$0.085~\rm {Hz}$| | (1) |
| |$\dot{\nu }$| | |$-2.95\times 10^{-13}~\rm {Hz\, s}^{-1}$| | (1) |
| Bd | |$7\times 10^{14}~\rm {G}$| | (1) |
| Lsd | |${\sim}10^{33}~\rm {erg\, s}^{-1}$| | (2) |
| τc | |$4.7~\rm {kyr}$| | (2) |
| τk | |$(0.75{\small --}2.1)~\rm {kyr}$| | (2) |
| Ts | |${\sim}3\times 10^{6}~\rm {K}$| | (3) |
| Parameter . | Value . | Refs.b . |
|---|---|---|
| ν | |$0.085~\rm {Hz}$| | (1) |
| |$\dot{\nu }$| | |$-2.95\times 10^{-13}~\rm {Hz\, s}^{-1}$| | (1) |
| Bd | |$7\times 10^{14}~\rm {G}$| | (1) |
| Lsd | |${\sim}10^{33}~\rm {erg\, s}^{-1}$| | (2) |
| τc | |$4.7~\rm {kyr}$| | (2) |
| τk | |$(0.75{\small --}2.1)~\rm {kyr}$| | (2) |
| Ts | |${\sim}3\times 10^{6}~\rm {K}$| | (3) |
| Parameter . | Value . | Refs.b . |
|---|---|---|
| ν | |$0.085~\rm {Hz}$| | (1) |
| |$\dot{\nu }$| | |$-2.95\times 10^{-13}~\rm {Hz\, s}^{-1}$| | (1) |
| Bd | |$7\times 10^{14}~\rm {G}$| | (1) |
| Lsd | |${\sim}10^{33}~\rm {erg\, s}^{-1}$| | (2) |
| τc | |$4.7~\rm {kyr}$| | (2) |
| τk | |$(0.75{\small --}2.1)~\rm {kyr}$| | (2) |
| Ts | |${\sim}3\times 10^{6}~\rm {K}$| | (3) |
This article is organized as follows. The glitch sizes contributed by pure starquakes (global and local starquakes) are calculated in Section 2, the glitch sizes contributed by angular momentum transfer during collisions are calculated in Section 3, glitch sizes amplified by vortex unpinning are estimated in Section 4. Conclusions and discussions are present in Section 5.
2 THE STARQUAKE SCENARIO
The brief picture of starquakes is presented below. NSs are born to be hot and own an initial oblateness before solidification. After their solidification due to cooling, gravity, and the loss of centrifugal force during spin-down tend to make the star spherical, but the elasticity of the solid crust resists this change and tends to make them oblate. In this case, NSs with solid crusts are always more oblate than the rotating incompressible fluid stars with the same mass M and radius R. Stress develops during the resistance before it exceeds the critical stress that the crust can support. Once the stress is relaxed suddenly, a glitch occurs and elastic energy will be released. Apart from the deformation supported by rotation, effect of magnetic stress is more important in magnetar. The magnetically strained local starquakes in magnetars will be further discussed in Sections 2.3 and 4.2.
Crustquake model of NSs has been developed recently (Giliberti et al. 2019, 2020; Rencoret, Aguilera-Gómez & Reisenegger 2021), which got challenged compared with observations. Previously, Baym and Pines found that, crustquakes of NSs encountered difficulty in explaining the frequent and large glitches (Δν/ν ∼ 10−6) in the Vela pulsar, unless the Vela pulsar is a lightest NS and glitch of size ∼10−6 is an extremely unusual event (Baym & Pines 1971). Besides, recent calculations show that, the rigidity parameter b is much smaller than the estimate in Baym & Pines (1971). For example, Cutler et al. found that b ∼ 2 × 10−7 for a more realistic NS structure with a thin solid crust afloat on an incompressible liquid core (Cutler, Ushomirsky & Link 2003), which is a factor of ∼40 smaller than that found by Baym & Pines using a self-gravitating, completely solid, incompressible sphere of constant density and shear modulus (Baym & Pines 1971). Zdunik et al. further studied the dependence of parameters of A and B (and thus b) on stellar mass and equation of state (EOS). A was found to be severely underestimated, while B was found to be around |${\sim}1.4\times 10^{46}~\rm {erg}$| by employing DH EOS for an NS with mass M = 1.4 M⊙ (Zdunik, Bejger & Haensel 2008), much smaller than the value |$B\sim 10^{47}~\rm {erg}$| employed by Baym & Pines (1971). It should be noted that, according to fig. 15 in their work, for the DH EOS, varying the stellar mass from 1.0 to 2.0 M⊙ brings decrease in parameter B by only a factor of about 1, so B is not as sensitive to stellar mass as A. Moreover, Giliberti et al. concluded that, the strain developed between two successive large glitches in the Vela pulsar is impossible to trigger a starquake, unless the sequence of starquakes in a neutron star is an history-dependent process (Giliberti et al. 2020). Recently, Rencoert et al. showed that, even the subclass of small glitches cannot be accounted for by the starquake model of neutron stars from the view of glitch activity (Rencoret et al. 2021). Apart from all these, in the vortex model (Alpar 1977), whether the crustal moment of inertia of an NS is enough or not is still under debate (Yuan et al. 2010) especially when the non-dissipative entrainment effect is taken into account (Andersson et al. 2012; Chamel 2013; Li et al. 2016; Wlazłowski et al. 2016; Watanabe & Pethick 2017).
In this section, we explore the glitch size achievable for starquakes of NSs and strangeon stars (SSs). Note that, though deformation supported by rotation is negligible compared with magnetic deformation in magnetars, the spin-down strained starquakes will still be considered and calculated, for comparison with starquakes in strangeon stars. In the following, NS represents a neutron-rich pulsar unless specifically illustrated.
2.1 Spin down strained starquakes in NSs
Note that, starquake may trigger vortex unpinning which will enlarge the glitch size (Epstein & Link 2000; Layek & Yadav 2020). However, as the strain energy is much less than Eiso-X, there is no need to discuss thermal effect of starquake in NSs.
We conclude that, just as expected, starquake of NSs will only result in pretty tiny glitches with sizes of 1.4 × 10−21–7.1 × 10−15, which is far from detectable. Besides, for the long-term stress-accumulation-type glitches, the elastic energy released during starquake is far from sufficient to explain the energy release during the X-ray burst if the release of magnetic energy in the magnetosphere or that in the crust is not taken into account. If a glitch is found to be associated with FRB 200428, the spin-down strained starquake scenario of NSs will be disfavoured, magnetic energy should be included to explain the high-energy counterpart under the framework of starquake of NSs.
2.2 Spin down strained type I and type II glitches in strangeon stars (SSs)
Strangeon star is a kind of solid quark star with no free magnetic energy in the magnetosphere or in the crust therefore starquakes in SSs are gravitationally and elastically powered (Xu 2003).
We discuss type I glitches in SSs first. Both type I glitches in SSs and the starquake process in NSs result from stress accumulation during secular spin-down phase, the differences lie in two aspects, the volume of the solid crustal component and the shear modulus. Compared with NSs, SSs are totally solid, besides, a statistical research on glitch activity of SSs indicates B ≃ A, which means that the average shear modulus could be as high as |$3\times 10^{34}~\rm {erg\, cm^{-3}}$| (Wang et al. 2021) for an SS with mass M = 1.4 M⊙ and radius |$R=10~\rm {km}$|. These two aspects make it possible for SSs to produce large glitches. Note that, the strangeon star is totally solid and assumed to be incompressible, just like that in Baym & Pines (1971). Therefore, parameter A in equation (2) will be used for strangeon stars, according to equation (2), |$A_{53}=0.621M_{1.4}^{2}R_{10}^{-1}$| in this case.
The waiting time Δtq can be estimated in similar ways with the starquake scenario in NSs. From the mean glitching rate versus the spin-down rate relation, |$\Delta t_{q}\simeq 11~\rm {yr}$|, which is the same with that in NSs. From the view of stress accumulation, the relieved stress during glitches will be |$\Delta \sigma \simeq 3\times 10^{20-26}~\rm {erg\, cm^{-3}}$| if |$\mu \simeq 3\times 10^{34}~\rm {erg\, cm^{-3}}$|. The increase of relieved stress during glitches has no impact on the estimated waiting time since |$\dot{\sigma }\propto \mu$|. Therefore, |$\Delta t_{q}\simeq (0.0035{\small --}17500)~\rm {yr}$| in this case, the same with that presented in equation (17).
Type II glitches in SSs arise from accretion or loss of centrifugal force. Similar with the mini contraction picture in NSs, huge amount of gravitational energy will be released. Therefore, the energy release during the X-ray burst gives constraint on the size of the type II glitch. The glitch size has been presented in equation (23).
To sum up, it is possible for SSs to generate detectable type I glitches of size 10−6 if the recovery coefficient is Q ∼ 10−4. A waiting time of about |$11~\rm {yr}$| will also fulfill the burst rate estimate. Note that, it is possible that local mini contractions are accompanied by type I glitches. If this happens, the tension between energy requirement and supply could be eased for the case of |$\Delta t_{q}\simeq 11~\rm {yr}$|. On the other hand, if Q is similar with those observed in other magnetars and high magnetic field pulsars, i.e. Q ∼ 0.1–1, a waiting time of more than |$2000~\rm {yr}$| will be needed to produce glitches of size 10−6, but such a long waiting time is inconsistent with the burst rate. We stress that, the recovery coefficient is crucial in distinguishing glitch mechanisms of NSs and SSs if glitches are detected to be accompanied by FRBs.
2.3 Magnetically strained local starquakes in magnetars
In the standard magnetar model, magnetars are young, isolated neutron stars powered by magnetic energy, with crustal magnetic fields which are both strong (|$B\gt 10^{14}{\small --}10^{15}~\rm {G}$|) and multipolar (Thompson & Duncan 1995, 1996; Thompson, Lyutikov & Kulkarni 2002), the ellipticity could be as high as 10−4, depending on the equation of state and magnetic field configurations (Haskell et al. 2008). Within the magnetic decay time-scales of ∼105−107 yr (Pons, Miralles & Geppert 2009; Viganò et al. 2013; Gao et al. 2016, 2019) through mechanisms such as Hall drift and Ohmic dissipation, magnetic stress develops in the crust due to internal magnetic field strength evolution and magnetic field reconfiguration (Ruderman, Zhu & Chen 1998). Once the magnetic stresses exceed the critical threshold that the crust can sustain (the strain reaches the critical strain angle, θcr), the crust cracks locally (named crust fractures) (Chugunov & Horowitz 2010; Baiko & Chugunov 2018). This process has been supposed to account for burst properties of FRBs (Suvorov & Kokkotas 2019) and will also result in glitches (Ruderman 1991; Ruderman et al. 1998; Lander et al. 2015).
If FRBs originate from crust fracture processes in young magneatrs, glitches may be accompanied by the crust fractures. We present order of magnitude estimation of size of the glitch that may be associated with FRB 200428 in this subsection. According to Lander et al. (2015), crust fractures tend to occur in the outer equatorial region first. Size of the glitch induced by crust fracture contains two parts, the pure starquake resulting from moment of inertia decrease, and glitch size amplified by sudden unpinning of vortex lines accompanied by crustal movement, among which the latter dominates (Akbal & Alpar 2018). We estimate glitch size contributed by moment of inertia decrease here and left the corresponding vortex unpinning to be discussed in Section 4.2.
3 ORBITAL ANGULAR MOMENTUM TRANSFER SCENARIO
Collisions between NSs and small celestial bodies such as asteroids or comets are also promising to produce FRBs and induce glitches simultaneously. Asteroids/comets are small celestial bodies with typical mass of |$10^{18}~\rm {g}$| (Cordes & Shannon 2008). Previous literature has suggested the possibility of collision between NSs and asteroids/comets (Colgate & Petschek 1981; Mitrofanov & Sagdeev 1990; Katz, Toole & Unruh 1994). Huang et al. argued that, collisions between NSs and asteroids/comets could reasonably explain the main FRBs features such as their durations and radio luminosities (Geng & Huang 2015). Besides, asteroids/comets will bring orbital angular momentum on to NSs, resulting in sudden glitches or antiglitches (Huang & Geng 2014).
4 VORTEX UNPINNING SCENARIO
Vortex unpinning is another efficient way to transfer angular momentum and result in glitches (Baym, Pethick & Pines 1969; Anderson & Itoh 1975). In this section, we discuss glitch size contributed by vortex unpinning induced by starquakes, collisions between NSs and asteroids/comets, and crust fractures.
Since we are talking about vortex unpinning, one critical point should be discussed first, are there superfluid neutrons in the crust of young magnetars? Nobody knows the exact answer, but it can be responded from three aspects. First, a recent statistical work found a constant ratio |$\dot{\nu }_{\rm g}/|\dot{\nu }|=0.010\pm 0.001$| for all rotation powered pulsars, high magnetic field pulsars and magnetars, reflecting their similar fractional moment of inertia (FMoI) of crustal superfluid neutrons (Link, Epstein & Lattimer 1999; Fuentes et al. 2017). |$\dot{\nu }_{\rm g}$| is the average glitch activity, defined in equation (1) in Fuentes et al. (2017). Secondly, magneto-thermal evolution simulations suggest that, although magnetars exhibit high surface temperature and thermal luminosity, there exists a sharp decrease in temperature in the density range |$10^{11}{\small --}10^{13}~\rm {g\, cm^{-3}}$| (Kaminker et al. 2009), making it possible for at least part of the crust to be superfluid. Thirdly, the anomalous X-ray pulsar (AXP), 1E 1841−045, a glitcher with a surface temperature of about |$T_{\rm {s}}\sim 3\times 10^{6}~\rm {K}$| (Viganò et al. 2013), shares many similarities with SGR J1935+2154 from the aspects of high surface temperature, characteristic age, and spin-inferred dipolar magnetic field (see Table 2 in this paper). Inferred FMoI for 1E 1841−045 is 1.2 ± 0.2 percentage, which is a little bit smaller than other mature pulsars with larger characteristic ages and lower surface temperature [see table 1 in Ho et al. (2015) for comparison]. From all these considerations, it is reasonable to speculate that superfluid neutrons do exist in the crust of SGR J1935+2154, just like that in 1E 1841−045.
In the following calculations, we assume SGR J1935+2154 has a FMoI of crustal superfluid of ∼1.2 percentage, comparable with that in 1E 1841−045. Surface temperature of SGR J1935+2154 is unknown, but it is very possible that SGR J1935+2154 is a Crab-like pulsar with high surface temperature given the magnetic energy release in the crust. By Crab-like (Vela-like), we mean pulsars with surface temperature and characteristic ages similar to those of the Crab pulsar (Vela pulsar).
According to Alpar et al. (1984), pinning arises due to the interaction between vortex and nucleus, it is energetically favourable if the cost per particle to form its core is reduced, in other words, the total energy of the vortex–nuclei system is lowered. The energy cost to pin for a vortex line is Δ2/Ef (Alpar et al. 1984), where Δ is the energy gap of superfluid neutrons, Ef is the Fermi energy of neutrons. The pinning energy is |$E_{\rm p}=\frac{3}{8}\gamma (\frac{\Delta ^{2}}{E_{\rm f}}n_{\rm f})V_{\rm vn}$|, where γ is close to unity, |$n_{\rm f}=\frac{k_{\rm F}^{3}}{3\pi ^{2}}$| is number density of bulk neutrons, kF is the Fermi momentum of superfluid neutrons, |$V_{\rm vn}=\frac{4}{3}\pi \xi ^{3}$| is the overlap volume between vortex and the pinned nucleus, |$\xi \simeq 10~\rm {fm}$| is the radius of coherence length of bulk neutrons. Essentially, vortex unpins when the angular velocity difference between the crust (and that coupled to it) and the superfluid component exceeds the critical lag (Alpar et al. 1984).
The glitch size may be amplified by vortex unpinning. As stated above, the starquake process is accompanied by strain energy release, the collision process will deposit gravitational energy as thermal and kinetic energies, both of which may induce vortex unpinning. Besides, crust fracture itself may act as a glitch triggering mechanism (Ruderman 1991; Ruderman et al. 1998). We discuss the thermal effect of starquakes and collisions between NSs and asteroids/comets in Section 4.1, vortex unpinning induced by crust fracture is discussed in Section 4.2, neutron scattering induced by collisions is discussed in Section 4.3. The corresponding glitch sizes are estimated respectively.
4.1 Thermally driven glitches
Link et al. studied the thermal and dynamical responses of an NS to a sudden internal heating in the inner crust for Crab-like, Vela-like, and older pulsars (Link & Epstein 1996). The local temperature increase affects the coupling between superfluid neutrons and the outer crust, resulting in the spin-up phenomenon. The relation between energy deposition and glitch size is presented in fig. 15 in their work. They found that energy deposition of |${\sim}10^{40}~\rm {erg}$| produces delayed spin-ups (also named slow rise glitches) with size just above timing noise level for three kinds of pulsars, while energy deposition of |${\sim}2.1\times 10^{42}~\rm {erg}$| in the crust of hot Crab-like pulsars [surface temperature of the Crab pulsar is about |$1.6\times 10^{6}~\rm {K}$| (Alpar, Nandkumar & Pines 1985)] produces glitches of size Δν/ν ∼ 7 × 10−8 in a time-scale of one day (Link & Epstein 1996). Energy deposition of |${\sim}10^{42}~\rm {erg}$| in the crust of Vela-like pulsars produces glitches of size Δν/ν ∼ 10−6 within a time-scale of minutes. Comparisons between the energy deposited by NS starquakes, collisions between NSs and asteroids/comets and the energy used by Link et al. may shed light upon the corresponding glitch sizes in our cases.
For the NS starquake case, according to equation (20), the elastic energy release is |$\Delta E\simeq (6.6\times 10^{26}{\small --}7.2\times 10^{32})~\rm {erg}\ll 10^{40}~\rm {erg}$|. This amount of energy generates glitches well below timing noise level no matter SGR J1935+2154 is Crab-like, Vela-like or even older. For the collision case, mass of the asteroid/comet is constrained to be |$(10^{18}{\small --}6.2\times 10^{21})~\rm {g}$| in Section 3, which corresponds to the maximum energy deposition of |$\Delta E_{\rm grav}\simeq (9\times 10^{38}{\small --}5.6\times 10^{42})~\rm {erg}$| on the surface of the NS. This energy comes from the gravitational energy of the asteroid/comet, and was converted into thermal and kinetic energy. We discuss effect of the thermal energy in this subsection and left that of kinetic energy to be discussed in Section 4.3.
The thermal energy of collisions is unlikely to be important in the case of SGR J1935+2154. This is because, crustal temperature is higher than the surface temperature, most of the thermal energy deposited by collisions tends to be radiated through thermal emission rather than be transferred inward into the crusts. Besides, even if part of thermal energy is transferred into the crust, time-scale of this process is comparable to thermal relaxation time-scale of the crust, which is at least tens of days (Deibel et al. 2015). Therefore, this process will induce slow rise glitch rather than sudden glitch, which is hard to be detected for magnatars (outbursts appear frequently). Moreover, thermal energy deposited will be no larger than the gravitational energy, which is about |$(9\times 10^{38}{\small --}5.6\times 10^{42})~\rm {erg}$| as stated above. Given the heat conduction timescale and efficiency, size of this slow rise glitch may not be larger than 7 × 10−8 if SGR J1935+2154 is Crab-like or <10−6 if it is Vela-like, as presented by Link & Epstein (1996). As spin frequency of SGR J1935+2154 is low compared with the Crab and Vela pulsars (the Crab and Vela pulsars have spin frequency |$\nu =29.612$| and |$\nu =11.198~\rm {Hz}$| separately), the glitch sizes may be amplified at most by the frequency ratios, which are ∼96 and ∼36, respectively, according to equation (21) in Link & Epstein (1996). The corresponding glitch size is <6.7 × 10−6 for a Crab-like pulsar or <3.6 × 10−5 for a Vela-like pulsar. If mass of the asteroid/comet is reduced to |${\sim}10^{20}~\rm {g}$| (Dai 2020), the maximum energy deposition reduces to |$\Delta E_{\rm dep}\sim 9\times 10^{40}~\rm {erg}$| therefore the corresponding maximum glitch size for SGR J1935+2154 reduces to <10−7 (Crab-like) or <10−6 (Vela-like) according to fig. 15 in Link & Epstein (1996).
Note that, the above results are only order of magnitude estimations, simulations are needed to comprehensively estimate size of the thermally driven glitch, parameters such as surface and crustal temperature of SGR J1935+2154 are therefore urgently needed.
4.2 Vortex unpinning induced by crust fractures
As stated in Section 2.3, crust fracture may amplify glitch size through vortex unpinning. The glitch size depends on the number of vortices attached to the broken crustal plate, vortices unpinned through crustal movement can induce vortex avalanche by perturbing nearby vortices which are close to unpin if the pulsar is Vela-like rather than Crab-like (Alpar et al. 1993). However, the surface area and the fracture geometry of the broken region depend on the topological structure of the magnetic field (Franco et al. 2000; Lander et al. 2015), which is hard to be known except simulation. For order of magnitude estimation, we assume the broken plate is cubic and calculate the number of vortices that can be unpinned. Note that, this method has been used in Akbal & Alpar (2018), they have shown that the number of vortices only differs by a factor of several compared with a prism broken plate. An illustration of the crust fracture is shown in Fig. 1.
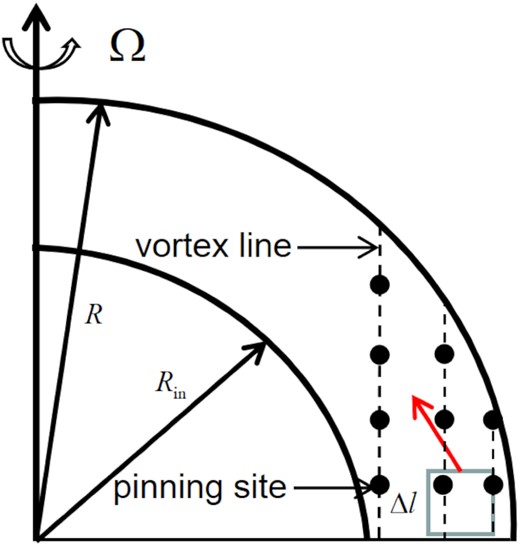
An illustration of the crust fracture. We take the geometry of the broken region to be a cubic plate with length Δl. Rin is the radius of the core of the star, thickness of the crust is R − Rin. The red arrow represents motion direction of the cubic plate.
The glitch size can be further amplified considering the avalanche. The crustal structural difference between Crab-like pulsars and Vela-like pulsars lies in that, the network of vortex unpinning region is sufficiently connected in Vela-like mature pulsars while not in Crab-like young pulsars. Therefore, if the kinetic age of SGR J1935+2154 is reliable, SGR J1935+2154 tends to be Vela-like, larger glitches (Δν/ν > 1.8 × 10−7) can be produced as avalanches.
4.3 Glitches induced by neutron-vortex scattering
Different from the influence of thermal energy (by affecting the coupling between superfluid neutrons and the outer crust), Layek and Yadav proposed that, the strain energy released during starquake may excite unbound superfluid neutrons, inelastic scattering of these excited free neutrons with the vortex core neutrons nearby may overcome the pinning energy barrier and result in glitches of size 10−8–10−7 for Crab-like pulsars and 10−9–10−8 for Vela-like pulsars within a time-scale of |$(0.2\!-\!2)~\rm {s}$|, the glitch size depends on the strain energy released (Layek & Yadav 2020).
The detailed picture proposed by Layek & Yadav (2020) is that, the NS breaks in the inner crust in the equatorial plane. The strain energy (|$\Delta E_{\rm strain}\sim 10^{40}~\rm {erg}$|, or equally, |$\Delta E_{\rm strain}\sim 6.24\times 10^{45}~\rm {MeV}$|) is assumed to be isotropically distributed from the quake site, this energy makes free neutrons excited in a cubical region (similar with the cubic plate as shown in fig. 1). Scattering of these excited neutrons with the surrounding pinned vortices may further unpin a large amount of vortices and induce glitches. Actually, neutrons could be thermally excited, the fractional excited neutrons in the superfluid state is |$e^{-\frac{\Delta }{k_{B}T}}$|, where kB is the Boltzmann constant, T is the temperature. Fraction of excited neutrons is generally small. In Layek & Yadav (2020), neutrons are excited by absorption of elastic energy in the inner crust rather than thermally excited, ratio between excited neutrons to superfluid neutrons is set to be the constant Δ/Ef ≃ 0.07 for both Crab-like and Vela-like pulsars.
Actually, this kind of neutron excitation exists in thermal non-equilibrium state. If neutrons can be excited by the sudden release of strain energy, they may also be excited by other sudden energy release processes, such as the kinetic energy release during collisions. Both the strain and kinetic energy release represent the thermal non-equilibrium state. Besides, the kinetic energy is released around the collision site, similar with the strain energy released around the crustquake site. Therefore, it is reasonable to assume that, the kinetic energy released during collisions may also excite unbound superfluid neutrons and induce vortex unpinning. In this case, calculation in Layek & Yadav (2020) applies here. The upper limit of the kinetic energy is |$\Delta E_{\rm k}\simeq (9\times 10^{38}{\small --}5.6\times 10^{42})~\rm {erg}$| for the mass range of |$(10^{18}{\small --}6.2\times 10^{21})~\rm {g}$|. For order of magnitude analysis, we use the same parameters with Layek & Yadav (2020) as it is very possible that SGR J1935+2154 is a Crab-like high-temperature pulsar. Therefore, |$\Delta =0.06~\rm {MeV}$|, |$E_{\rm f}=0.83~\rm {MeV}$|, Fermi momentum of superfluid neutron in the outer part of the inner crust is |$k_{\rm F}\simeq 0.20~\rm {fm^{-1}}$| (Chamel & Haensel 2008; Pastore, Baroni & Losa 2011; Sinha & Sedrakian 2015). Uncertainties of parameters will be briefly discussed at the end of this subsection.
We discuss influence of parameter uncertainties here. As we can see from equation (52), the total energy release during collisions are much larger than the total pinning energy, number of excited neutrons is also extremely larger than the total number of vortices in the crust of SGR J1935+2154. Therefore, the actual values of Δ, Ef, and kF are of little importance. Choices of these parameters have little influence on our results. What matters is the volume the excited neutrons occupied. If there exists many quake sites in the equatorial plane and the strain energy is distributed isotropically around these quake sites, more vortices may be unpinned. For our collision scenario, it is promising to induce a glitch of size larger than 10−6, depending on the surface area that asteroids/comets collide with the NS or the area that energy will be deposited when collisions happen.
5 CONCLUSIONS AND DISCUSSIONS
Inspired by the idea that FRBs from galactic magnetars may be associated with glitches, we explore the glitch size reachable for several physical processes which could result in FRBs and glitches simultaneously. These physical processes include global starquakes in neutron stars and strangeon stars, crust fractures in magnetars, and collisions between NSs and asteroids/comets. Our calculations are based on rotational parameters of SGR J1935+2154, as FRB 200428 from SGR J1935+2154 is the only galactic FRB detected till now. The glitch size is constrained through the energy release during the X-ray burst and/or the SGR J1935+2154-like radio burst rate. Summary of the glitch sizes for various physical processes and mechanisms are presented in Table 3.
| Physical process . | Mechanism . | Δν/νa . |
|---|---|---|
| Global starquake in NSs | (1) Spin-down strained starquake | ∼1.4 × 10−21–7.1 × 10−15 |
| (2) Mini contraction | ∼7.4 × 10−14 | |
| (3) Vortex unpinning | Neglectable | |
| Global starquake in SSs | (1) Type I glitch | ∼(1–2.3) × 10−9(0.1/Q) |
| (2) Type II glitch | ∼7.4 × 10−14 | |
| Crust fracture in magnetars | (1) Pure local starquake | ∼4.5 × 10−14–4.5 × 10−13 |
| (2) Vortex unpinning induced by crustal movementb | ∼4 × 10−8–1.8 × 10−7 | |
| Collisions between NSs and asteroids/comets (|$m\sim 10^{18}{\small --}6.2\times 10^{21}~\rm {g}$|) | (1) Angular momentum transfer | <5.6 × 10−8 |
| (2) Thermal drivenc | <6.7 × 10−6–3.6 × 10−5 | |
| (3) Neutron-vortex scattering | |${\sim}(0.008{\small --}1.2)\times 10^{-6}(\Delta t_{q}/11~\rm {yr})$| | |
| Collisions between NSs and asteroids/comets (|$m\sim 10^{20}~\rm {g}$|) | (1) Angular momentum transfer | ∼0.9 × 10−9 |
| (2) Thermal driven | <10−7–10−6 | |
| (3) Neutron-vortex scattering | |${\sim}5.6\times 10^{-8}(\Delta t_{q}/11~\rm {yr})$| |
| Physical process . | Mechanism . | Δν/νa . |
|---|---|---|
| Global starquake in NSs | (1) Spin-down strained starquake | ∼1.4 × 10−21–7.1 × 10−15 |
| (2) Mini contraction | ∼7.4 × 10−14 | |
| (3) Vortex unpinning | Neglectable | |
| Global starquake in SSs | (1) Type I glitch | ∼(1–2.3) × 10−9(0.1/Q) |
| (2) Type II glitch | ∼7.4 × 10−14 | |
| Crust fracture in magnetars | (1) Pure local starquake | ∼4.5 × 10−14–4.5 × 10−13 |
| (2) Vortex unpinning induced by crustal movementb | ∼4 × 10−8–1.8 × 10−7 | |
| Collisions between NSs and asteroids/comets (|$m\sim 10^{18}{\small --}6.2\times 10^{21}~\rm {g}$|) | (1) Angular momentum transfer | <5.6 × 10−8 |
| (2) Thermal drivenc | <6.7 × 10−6–3.6 × 10−5 | |
| (3) Neutron-vortex scattering | |${\sim}(0.008{\small --}1.2)\times 10^{-6}(\Delta t_{q}/11~\rm {yr})$| | |
| Collisions between NSs and asteroids/comets (|$m\sim 10^{20}~\rm {g}$|) | (1) Angular momentum transfer | ∼0.9 × 10−9 |
| (2) Thermal driven | <10−7–10−6 | |
| (3) Neutron-vortex scattering | |${\sim}5.6\times 10^{-8}(\Delta t_{q}/11~\rm {yr})$| |
Notes. aThese values are calculated assuming the pulsar has a mass M = 1.4 M⊙ and radius |$R=10~\rm {km}$|.
The upper and lower limits correspond to the critical strain angle of θcr ≃ 0.01 and θcr ≃ 0.1, respectively.
The upper and lower limits correspond to assumptions that SGR J1935+2154 is a Vela-like and a Crab-like pulsar, respectively.
| Physical process . | Mechanism . | Δν/νa . |
|---|---|---|
| Global starquake in NSs | (1) Spin-down strained starquake | ∼1.4 × 10−21–7.1 × 10−15 |
| (2) Mini contraction | ∼7.4 × 10−14 | |
| (3) Vortex unpinning | Neglectable | |
| Global starquake in SSs | (1) Type I glitch | ∼(1–2.3) × 10−9(0.1/Q) |
| (2) Type II glitch | ∼7.4 × 10−14 | |
| Crust fracture in magnetars | (1) Pure local starquake | ∼4.5 × 10−14–4.5 × 10−13 |
| (2) Vortex unpinning induced by crustal movementb | ∼4 × 10−8–1.8 × 10−7 | |
| Collisions between NSs and asteroids/comets (|$m\sim 10^{18}{\small --}6.2\times 10^{21}~\rm {g}$|) | (1) Angular momentum transfer | <5.6 × 10−8 |
| (2) Thermal drivenc | <6.7 × 10−6–3.6 × 10−5 | |
| (3) Neutron-vortex scattering | |${\sim}(0.008{\small --}1.2)\times 10^{-6}(\Delta t_{q}/11~\rm {yr})$| | |
| Collisions between NSs and asteroids/comets (|$m\sim 10^{20}~\rm {g}$|) | (1) Angular momentum transfer | ∼0.9 × 10−9 |
| (2) Thermal driven | <10−7–10−6 | |
| (3) Neutron-vortex scattering | |${\sim}5.6\times 10^{-8}(\Delta t_{q}/11~\rm {yr})$| |
| Physical process . | Mechanism . | Δν/νa . |
|---|---|---|
| Global starquake in NSs | (1) Spin-down strained starquake | ∼1.4 × 10−21–7.1 × 10−15 |
| (2) Mini contraction | ∼7.4 × 10−14 | |
| (3) Vortex unpinning | Neglectable | |
| Global starquake in SSs | (1) Type I glitch | ∼(1–2.3) × 10−9(0.1/Q) |
| (2) Type II glitch | ∼7.4 × 10−14 | |
| Crust fracture in magnetars | (1) Pure local starquake | ∼4.5 × 10−14–4.5 × 10−13 |
| (2) Vortex unpinning induced by crustal movementb | ∼4 × 10−8–1.8 × 10−7 | |
| Collisions between NSs and asteroids/comets (|$m\sim 10^{18}{\small --}6.2\times 10^{21}~\rm {g}$|) | (1) Angular momentum transfer | <5.6 × 10−8 |
| (2) Thermal drivenc | <6.7 × 10−6–3.6 × 10−5 | |
| (3) Neutron-vortex scattering | |${\sim}(0.008{\small --}1.2)\times 10^{-6}(\Delta t_{q}/11~\rm {yr})$| | |
| Collisions between NSs and asteroids/comets (|$m\sim 10^{20}~\rm {g}$|) | (1) Angular momentum transfer | ∼0.9 × 10−9 |
| (2) Thermal driven | <10−7–10−6 | |
| (3) Neutron-vortex scattering | |${\sim}5.6\times 10^{-8}(\Delta t_{q}/11~\rm {yr})$| |
Notes. aThese values are calculated assuming the pulsar has a mass M = 1.4 M⊙ and radius |$R=10~\rm {km}$|.
The upper and lower limits correspond to the critical strain angle of θcr ≃ 0.01 and θcr ≃ 0.1, respectively.
The upper and lower limits correspond to assumptions that SGR J1935+2154 is a Vela-like and a Crab-like pulsar, respectively.
We find that, for the global starquake scenario, glitch size of spin-down strained starquake for SGR J1935+2154 as a normal NS is too small to be detected, besides, the elastic energy release can not fulfill the burst energy requirement, nor will this energy induce vortex unpinning efficiently. Glitch size of spin-down strained starquake for SGR J1935+2154 as a strangeon star could be large, the energy requirement could also be simultaneously fulfilled. However, recovery coefficient of the glitch should be low enough, for example, if a large glitch (Δν/ν ∼ 10−6) is expected, the recovery coefficient should be as low as Q ∼ 10−4. If Q ∼ 1, similar with those observed in other magnetars and high magnetic field pulsars, the strangeon star model will be challenged.
For the local starquake (or crust fracture) scenario, the glitch size contributed by crustal movement and moment of inertia decrease lies in the range 4.5 × 10−14–4.5 × 10−13, the upper limit corresponds to the critical strain angle θcr ≃ 0.01. The glitch can be amplified through vortex unpinning induced by crustal movement. Assuming the geometry of the breaking region to be a cubic broken plate in the equatorial region, the glitch size can be amplified to 4.5 × 10−8–1.8 × 10−7, the upper limit corresponds to θcr ≃ 0.01 again. The glitch size may be further amplified if SGR J1935+2154 is a Vela-like mature pulsar and avalanche occurs. From this point of view, it is important to know the exact age of SGR J1935+2154 and to assess whether it is a Crab-like or Vela-like pulsar.
For the orbital angular momentum transfer scenario, the glitch size is proportional to the mass of the asteroid/comet. Mass of the asteroid/comet has been constrained to be |$(10^{18}{\small --}6.2\times 10^{21})~\rm {g}$| by the burst energy Eiso-X. In the most optimistic case, size of the sudden glitch/antiglitch will not be larger than 5.6 × 10−8. If mass of the asteroid is |${\sim}10^{20}~\rm {g}$| as proposed by Dai (Dai 2020), the corresponding maximum glitch/antiglitch size will be ∼0.9 × 10−9. However, the collision between an NS and the asteroid/comet may deposit energy in the inner crust, resulting in vortex unpinning through heat deposition and/or neutron-vortex scattering. For the heat deposition case, the asteroid maximum mass of |$6.2\times 10^{21}~\rm {g}$| corresponds to a glitch size of <6.7 × 10−6 (a slow rise glitch) for a Crab-like pulsar or <3.6 × 10−5 for a Vela-like pulsar, while a asteroid mass of |${\sim}10^{20}~\rm {g}$| (Dai 2020) corresponds to the maximum glitch size of <10−7 (a slow rise glitch for a Crab-like pulsar) or <10−6 (Vela-like) according to fig. 15 in Link & Epstein (1996). For the neutron-vortex scattering case, the corresponding glitch size is 8 × 10−9–1.2 × 10−6. The upper limit corresponds to a maximum asteroid/comet mass of |$6.2\times 10^{21}~\rm {g}$|. If the mass of the asteroid is |${\sim}10^{20}~\rm {erg}$|, the number of unpinned vortices decreases to ∼4.7 × 10−2Nv according to equations (37) and (49), meanwhile, the maximum glitch size decreases to |$5.6\times 10^{-8}(\Delta t_{q}/11~\rm {yr})$|. Therefore, our preliminary result shows that, the total effects of angular momentum transfer and vortex unpinning through heat deposition and neutron-vortex scattering, are unlikely to result in a large glitch with size up to 10−6 for a asteroid mass of |${\sim}10^{20}~\rm {g}$|. However, the collision may affect the magnetic field configuration and induce redistribution of magnetic stresses in the crust of magnetars, in this case, the geometry of the collision site should be taken into account. We leave this possibility to be discussed in future works.
It should be pointed out that, the glitch sizes contributed by vortex unpinning through different triggering mechanisms have no dependency on the recovery coefficient Q, which makes it different from the strangeon star model.
To sum up, global starquakes in strangeon stars and local starquakes (or crust fractures) in magnetars are both promising to produce large glitches with sizes up to 10−6 in association with FRB 200428; however, the former has dependency on the recovery coefficient Q, and Q should be as low as 10−4. While crust fractures in magnetars have no dependency on Q. This difference may also serve as a criterion to distinguish strangeon star model from neutron star model if a large glitch is found to be coincident with FRBs from galactic magnetars. The magnetar-asteroid impact model is unlikely to produce glitches with amplitudes up to 10−6 if the asteroid mass is |${\sim}10^{20}~\rm {g}$|. Therefore, we conclude that, it is possible to constrain FRB models through glitch behaviours (glitch size, rise time-scale, the recovery coefficient Q, and spin-down rate offset) if glitches are accompanied by FRBs from galactic magnetars in the future.
We stress that, this work represents a very initial work, the accurate surface temperature and crustal temperature profile are needed to model the heat deposition process comprehensively. Evolutionary age of SGR J1935+2154 should also be known to evaluate the possibility of avalanche in this pulsar. Apart from these, the possible involvement of core superfluid in magnetars is not considered here. The catastrophic unpinning of neutron superfluid vortex lines in the inner crust triggered by large starquake deserves careful consideration in future works (Epstein & Link 2000). Besides, this work focus mainly on the FRB-glitch association, if it turns out to be an antiglitch, much more deserves to be done.
If a glitch is detected to be in association with FRB 200428, is it reasonable to constrain FRB models with glitch behaviours? As we konw, large radiative changes are usually accompanied by timing anomalies, but only 20–30 per cent timing anomalies are accompanied by radiative changes in magnetars (Dib & Kaspi 2014; Kaspi & Beloborodov 2017), reflecting no direct connections between glitches/antiglitches and outbursts. Besides, though FRB 200428 appeared after SGR J1935+2154 went into outburst, it is unlikely that this FRB is directly correlated with the outburst or burst itself. This can be illustrated from two aspects. First, the non-thermal X-ray burst makes it different from normal short bursts from magnetars, which prefer thermal origins (Israel et al. 2008; Lin et al. 2012). Secondly, no pulsed radio emission was detected to be coincident with SGR bursts, suggesting the rare FRB-SGR burst associations (Lin et al. 2020). Therefore, we believe that it is reasonable to constrain FRB models with glitch behaviours. A much tighter constraint will be given if the glitch-FRB association is confirmed from quiescent galactic magnatars with persistent radio emission.
ACKNOWLEDGEMENTS
We appreciate the referee for the valuable comments and suggestions, which have helped to improve this manuscript. We are grateful to Yong Gao from KIAA for the useful discussions. This work is supported by the National Key R&D Program of China (Grant No. 2017YFA0402602), the National Natural Science Foundation of China (Grant Nos. 2020SKA0120300, 12003009, 12033001 and 11773011), the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDB23010200), the CAS ‘Light of West China’ Program (Grant No. 2019-XBQNXZ-B-016) and Innovation Fund of Key Laboratory of Quark and Leption Physics (Grant No. QLPL2020P01).
DATA AVAILABILITY
The data underlying this article are available in this article, no new data needed to be generated or analysed.
Footnotes
Please turn to the paper Petroff et al. (2016) and the url (http://www.frbcat.org) for more details.



